Функциональное описание реальных процессов
Почему не бывает животных, какой угодно величины? Почему, например, нет слонов в три раза большего роста, чем существуют, но тех же пропорций? Наш ответ таков: стань слон в три раза больше, вес его тогда увеличился бы в двадцать семь раз, как куб размера, а площадь сечения костей и, следовательно, их прочность — только в девять раз, как квадрат размера. Прочности костей уже не хватило бы, чтобы выдержать непомерно увеличившийся вес. Такой слон был бы раздавлен собственной тяжестью.
В основу рассуждения положены две строгие математические зависимости. Первая устанавливает соответствие между размерами подобных тел и их объемами: объем изменяется, как куб размера. Вторая связывает размеры подобных фигур и их площади: площадь изменяется, как квадрат размера. Этим выразительным примером мы хотим начать разговор о числовых функциях числового аргумента, которые можно использовать для описания реальных процессов.
Чудо английского часового мастера Джон Гаррисон.
Перенесемся на три века вспять. Парусник в открытом море. Как определить долготу места, в котором он находится? Очень просто, если на корабле есть часы, поставленные в порту отправления. Нужно измерить местное время по солнцу и сравнить с показаниями часов. Расхождение пропорционально разнице по долготе между тем пунктом, где находится корабль, и тем, в котором были поставлены часы.
Точный закон этой пропорциональности позволяет вывести простое соотношение: тремстам шестидесяти градусам земной окружности соответствуют двадцать четыре часа, за которые Земля совершает полный оборот вокруг своей оси. Поэтому если часы отстают по сравнению с местным временем на шесть часов, корабль находится на 90° восточнее того места, где были поставлены часы. Спешат на четыре часа — на 60° западнее. Разумеется, для подобного определения долготы нужны очень точные часы.
А как можно требовать точности от маятниковых часов, которыми снабжен парусник? Их ход зависит от длины маятника, а она то и дело меняется: теплый день сменяется прохладной ночью, и во время плавания парусник приближается то к голубым полярным льдам, то к пальмам тропиков. Тепло удлиняет маятник, холод укорачивает. Такова неумолимая реальность.
И все-таки нашелся способ избежать неизбежного зла. Чудо совершил в 1726 году английский часовой мастер Джон Гаррисон. Это удалось ему потому, что он знал функциональную зависимость длины металлического стержня от температуры, до которой стержень нагрет.
Эту функцию описывает прямая линия. Такая зависимость называется линейной. Суть ее в том, что одинаковым приращениям аргумента всегда соответствует одно и то же приращение функции. Иначе говоря, функция изменяется равномерно при равномерном росте аргумента.
В нашем примере равномерному нарастанию температуры соответствует равномерное удлинение стержня. Полное его удлинение пропорционально начальной длине. Но что особенно важно — стержни из разных металлов удлиняются по-разному от одного и того же прироста температуры. Скажем, цинк расширяется примерно в три раза сильнее, чем сталь, этим и воспользовался Гаррисон: он собрал маятник из цинковых и стальных стержней. Общая длина стальных стержней в три раза превышала длину цинковых. Расширяясь при нагревании и сокращаясь при охлаждении, стержни взаимно компенсировали изменения своей длины, и груз маятника оставался на одном и том же расстоянии от точки подвеса.
Ключ к небольшой математической проблеме
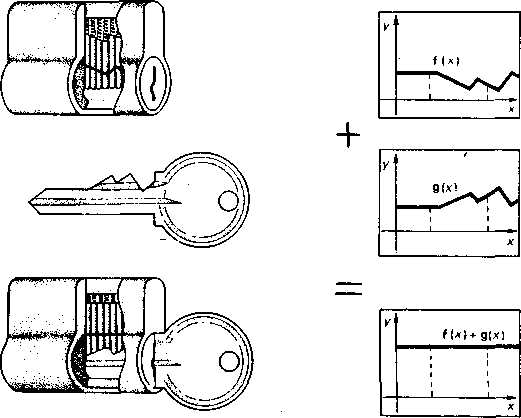
Отметим, что не всякую функциональную зависимость удается выразить краткой формулой, мы не случайно в качестве примера предоставляем вам, ключ от дверного замка: сейчас он в буквальном смысле слова послужит ключом к небольшой математической проблеме, к которой нас подводит беседа о функциях. Знаете ли вы, как таким ключом открывается дверной замок? Что происходит внутри этого слесарно-механического устройства, когда вы вставляете ключ в замочную скважину и делаете положенное число оборотов?

Чтобы замок открылся, нужно провернуть барабан, в котором сделана скважина. Но этому препятствуют штифты, стоящие тесным строем внутри скважины, скользящие вверх-вниз. Каждый из штифтов нужно поднять на такую высоту, чтобы их верхние торцы оказались вровень с поверхностью барабана. Если они выступят за нее, то войдут в прорезь обоймы, расположенную точно над заочной скважиной; если не достигнут поверхности барабана, то из прорези обоймы находящиеся там штифты вдвинутся в замочную скважину. И в том и в другом случае вращение барабана будет застопорено.
Штифты в замочной скважине поднимает ключ, вдвигаемый в нее. При этом высота каждого штифта, будучи сложена с высотой профиля ключа в соответствующей точке, должна дать в сумме диаметр барабана. Только тогда он провернется.
Ну а причем здесь функция? Да притом, что, с точки зрения математика, вся эта механика есть не что иное, как операция сложения двух функций. Одна из них — это профиль ключа. Другая — линия, очерчивающая верхние торцы штифтов, когда замок заперт.
Операция сложения функций состоит в том, что в каждой точке из общей области их определения к значению одной функции прибавляется значение другой. Тем самым определяется, какое значение в данной точке имеет функция, называемая суммой двух исходных. Секрет дверного замка в том, что в результате сложения двух функций, выраженных профилем ключа и строем штифтов, получается функция-константа, постоянное значение которой равно диаметру барабана
Золотое правило механики
Вся богатейшая семья механизмов, окружающих современного человека, начиналась когда-то с семи простых машин. Древние знали рычаг, блок, клин, ворот, винт, наклонную плоскость и зубчатые колеса. Эти нехитрые по теперешним представлениям устройства умножали силу человека. Но, во сколько раз выиграешь в силе — во столько же раз проиграешь в расстоянии. Так гласит золотое правило механики, заключающее в себе теорию семи простых машин.
График, приведенный на этой странице, есть наглядное выражение знаменитого правила. По горизонтальной оси отложена сила, с которой, например, нужно давить на плечо рычага, чтобы поднять заданный груз на заданную высоту. По вертикальной оси — расстояние, которое пройдет при этом точка приложения силы. Линия, выражающая такую функциональную зависимость, называется гиперболой.
Закон обратной пропорциональности глядит на нас и со шкалы радиоприемника. Вы крутите ручку настройки, и стрелка движется вдоль шкалы, на которой два ряда чисел — метры и мегагерцы, длина волн и их частота. Длина волн растет, частота падает. Но присмотритесь: при любом сдвиге стрелки во сколько раз увеличилась длина волны, во столько же раз упала частота.
График гиперболы можно увидеть на лабораторном столе физика, демонстрирующего явления капиллярности. В штативе несколько тонких стеклянных трубочек, расположенных в порядке возрастания диаметров. Известно, что в тонком канале смачивающая жидкость поднимается тем выше, чем меньше его диаметр. Поэтому в самом узком канале жидкость поднялась выше всего, в другом канале, диаметр которого в два раза больше, — в два раза ниже, в третьем, что толще первого в три раза,— в три раза ниже и так далее.
А теперь опустим в эту же жидкость клин, образованный двумя стеклянными пластинками, сомкнутыми по вертикальному ребру. В узкую щель между стеклами жидкость устремится, как в капилляр. Высота ее подъема определится шириной зазора. А он увеличивается равномерно по мере удаления от острия клина. Поэтому свободная поверхность жидкости четко вырисовывает гиперболу — график обратной пропорциональности.
Информационный бум
Сейчас много говорят об информационном буме. Поток информации захлестывает: утверждают, что ее количество удваивается каждые десять лет. Изобразим этот процесс наглядно, в виде графика некоторой функции.
Примем объем информации в некоторый год за единицу. Поскольку эта величина послужит нам началом дальнейших построений, отложим ее над началом координат, в которых будет строиться график, по вертикальной оси. Отрезок, вдвое больший, восставим над единичной отметкой горизонтальной оси, считая, что эта отметка соответствует первому десятку лет.
Еще вдвое больший отрезок восставим над точкой «два», соответствующей второму десятку, еще вдвое больший — над точкой «три». Декада за декадой— избранные нами значения аргумента выстроятся по горизонтальной оси в порядке равномерного нарастания, по закону арифметической прогрессии: один, два, три, четыре... Значения функции отложатся над ними, возрастая каждый раз вдвое,— по закону геометрической прогрессии: два, четыре, восемь, шестнадцать...
А что если посмотреть, как нарастал поток информации до того года, который принят за начальный? Столь же равномерно, откладывая единицу за единицей, пройдемся по оси абсцисс влево от начала координат и над отложенными значениями аргумента, будем наносить на график значения функции уже в порядке убывания — вдвое с каждым шагом.
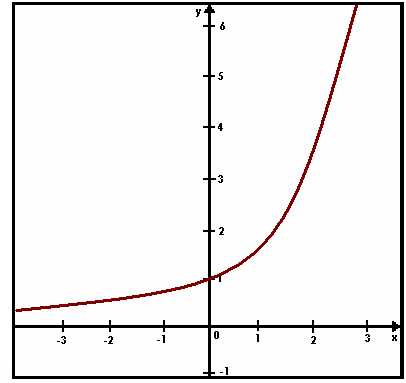
Теперь соединим все нанесенные точки непрерывной гладкой линией — ведь количество информации нарастает от десятилетия к десятилетию плавно, а не скачками. Перед нами график так называемой показательной функции.
Звездный график
Сколько звезд на небе? Одним из первых, кто попытался точно ответить на этот вопрос, был древнегреческий астроном Гиппарх. При его жизни в созвездии Скорпиона вспыхнула новая звезда. Гиппарх был потрясен: звезды смертны, они, как люди, рождаются и умирают. И чтобы будущие исследователи могли следить за возникновением и угасанием звезд, Гиппарх составил свой звездный каталог. Он насчитал около тысячи звезд и разбил их по видимому блеску на шесть групп. Самые яркие Гиппарх назвал звездами первой величины, заметно менее яркие — второй, еще столь же менее яркие — третьей и так далее в порядке равномерного убывания видимого блеска — до звезд, едва видимых невооруженным глазом, которым была присвоена шестая величина.
Когда ученые получили в свое распоряжение чувствительные приборы для световых измерений, стало возможным точно определять блеск звезд. Стало возможным сравнить, насколько соответствует данным таких измерений традиционное распределение звезд по видимому блеску, произведенное на глаз.Оценки того и другого рода сведем на одном графике. От каждой из шести групп, на которые звезды распределил Гиппарх, возьмем по одному типичному представителю. По вертикальной оси будем откладывать блеск звезды в единицах Гиппарха, то есть ее звездную величину, по горизонтальной — показания приборов. За масштабную единицу горизонтальной оси примем блеск звезды «б Тельца», стоящей посредине в ряду представителей звездного солнца.Отметки на горизонтальной оси располагаются неравномерно. Объективные (прибор) и субъективные (глаз) характеристики блеска не пропорциональны друг другу.
С каждым шагом по шкале звездных величин прибор регистрирует возрастание блеска не на одну и ту же величину, как могло бы показаться, а примерно в два с половиной раза. Образно говоря, глаз сравнивает источники света по блеску, задаваясь вопросом «во сколько раз?», а не вопросом «на сколько?». Мы отмечаем не абсолютный, а относительный прирост блеска. И когда нам кажется, что он возрастает или убывает равномерно, в действительности мы шагаем по его шкале все более размашистыми шагами, покрывая при этом поистине гигантский диапазон: в миллион миллионов раз различаются по блеску источники света, самый слабый и самый мощный, воспринимаемые человеческим глазом.
Именно в силу описанной физиологической особенности звезды, ярко горящие на ночном небе, не видны днем, тонут в ослепительном блеске солнца, рассеянном по небосводу. И там и здесь сияние звезд дает одну и ту же добавку к свету фона. Однако в первом случае (ночью) эта добавка велика по сравнению с мерцанием неба, во втором же (днем) составляет весьма незначительную долю от солнечного блеска (менее чем миллиардную даже для самых ярких звезд). Оттого же и голос солиста, когда его пение подхватывает хор, тонет в многоголосом звучании.Суть функциональной зависимости, описанной нами на примере зрения и слуха, в том, что возрастанию аргумента в одно и то же число раз всегда соответствует оно и то же приращение функции. Когда аргумент меняется по закону геометрической прогрессии, функция меняется по закону арифметической прогрессии.
Как же называется функция, с которой мы познакомились по звездному небу? Ординаты выделенных точек графика являются логарифмами абсцисс, взятых по основанию 2,5 . Такую функцию называют логарифмической.
Математические портреты пословиц
Современная математика знает множество функций, и у каждой свой неповторимый облик, как неповторим облик каждого из миллиардов людей, живущих на Земле. Однако при всей непохожести одного человека на другого у каждого есть руки и голова, уши и рот. Точно так же облик каждой функции можно представить сложенным из набора характерных деталей. В них проявляются основные свойства функций.
Функции — это математические портреты устойчивых закономерностей, познаваемых человеком. Чтобы проиллюстрировать характерные свойства функций, нам показалось естественным обратиться к пословицам. Ведь пословицы — это тоже отражение устойчивых закономерностей, выверенное многовековым опытом народа.
«Выше меры конь не скачет» Если представить траекторию скачущего коня как график некоторой функции, то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой «мерой». Это будет знакомый график функции синуса.
«Пересев хуже недосева» Урожай лишь до некоторой поры растет вместе с плотностью посева, дальше он снижается, потому что при чрезмерной густоте ростки начинают глушить друг друга. Эта закономерность станет особенно наглядной, если изобразить ее графиком, где урожай представлен как функция плотности посева. Урожай максимален, когда поле засеяно в меру. Максимум— это наибольшее значение функции по сравнению с ее значениями во всех соседних точках. Это как бы вершина горы, с которой все дороги ведут только вниз, куда ни шагни.
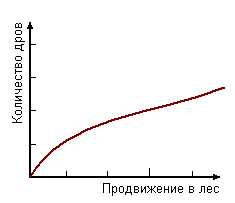
«Чем дальше в лес, тем больше дров» Можно изобразить графиком, как нарастает количество дров по мере продвижения в глубь леса – от опушки, где все давным-давно собрано, до чащоб, куда не ступала нога заготовителя. График представляет количество дров как функцию пути. Согласно пословице эта функция неизменно возрастает. Такое свойство функции называется монотонным возрастанием.
«Каши маслом не испортишь» Качество каши можно рассматривать как функцию количества масла в ней. Согласно пословице эта функция не уменьшается с добавкой масла. Она, возможно, увеличивается, но может оставаться и на прежнем уровне. Подобного рода функция называется монотонно неубывающей.

«Не круто начинай, круто кончай» и «Горяч на почине, да скоро остыл»
Обе функции, зависящие от времени, возрастающие. Но, как видно, расти можно по-разному. Наклон одной кривой постоянно увеличивается. Рост функции усиливается с ростом аргумента. Такое свойство функции называется вогнутостью.
Наклон другой кривой неизменно уменьшается. Рост функции слабеет с ростом аргумента. Такое свойство функции называется выпуклостью.
Нетрудно найти иллюстрации этим понятиям и среди элементарных функций. Показательная функция – вогнутая. Логарифм, корень квадратный – выпуклые. Выпуклую параболу выписывает и снаряд, выпущенный из пушки под углом к горизонту. Вогнутой функцией является гипербола, построенная для положительных значений аргумента. Другая ветвь гиперболы выпуклая.
Математические категории, о которых шла речь, естественным образом делятся на две группы. Одни описывают поведение функции в окрестности некоторых характерных точек (максимум, минимум, перегиб). Другие описывают поведение функции в некоторых промежутках (выпуклость, вогнутость, убывание, возрастание).
Теория реальных газов
Физикам важно знать, как ведут себя газы при различных температурах и давлениях. Поведение газа определяется взаимодействием между его молекулами. Предположим для простоты, как это часто делается в физике, что молекулы — это маленькие упругие шарики. Рассмотрим две такие молекулы, и будем изучать, какому закону подчиняется сила их взаимодействия.
Известно, что на больших расстояниях молекулы взаимно притягиваются, причем с ростом расстояния сила притяжения убывает, стремясь к нулю. При сближении молекул она, напротив, возрастает. Когда шарики сближаются до соприкосновения, в игру вступает еще одна, противоположно направленная сила — сила упругого отталкивания. Она тем больше, чем сильнее прижаты шарики друг к другу, чем меньше расстояние между их центрами. Гипотетически можно представить центры молекул сближающимися на сколь угодно малое расстояние, отчего сила их взаимного отталкивания возросла бы неограниченно.
Над дальним концом положительной полуоси абсцисс проведем прилегающий к ней вогнутый штришок. Своей близостью к горизонтальной оси он покажет, что с удалением молекул друг от друга сила их взаимодействия убывает до нуля, а вогнутой формой — что при сближении молекул сила их взаимного притяжения возрастает все круче. В точке с абсциссой, равной удвоенному радиусу молекулы, на условной высоте отметим точку перегиба; в этой точке силы упругого отталкивания, вступив в игру, заставляют кривую графика сменить свое прежнее, все более крутое возрастание на возрастание все более замедляющееся.
В точке с абсциссой, еще меньшей, на чуть большей высоте проведем дужку выпуклостью кверху. Она означает, что сила взаимодействия достигла максимума: с дальнейшим уменьшением аргумента силы упругого отталкивания преобладают над силами притяжения, кривая устремляется вниз. Выпуклый отвесный штрих проведем у нижнего конца оси ординат, чуть правее от него. Эта деталь показывает, что сила отталкивания между молекулами неограниченно возрастает, когда их центры неограниченно сближаются.
Поскольку сила взаимодействия между молекулами определена для любого расстояния между их центрами, график должен быть непрерывной линией. Соединим намеченные штрихи гладкой кривой. Такую картину часто можно увидеть в книгах по физике, правда, в перевернутом виде; у физиков сложилась традиция трактовать силы притяжения как отрицательные величины, силы отталкивания – как положительные.
Взаимно обратные функции
Перенесемся в поликлинику. Врач велит пациенту измерить температуру. В стеклянной трубочке, которую пациент сует под мышку, заключен столбик ртути. Он удлиняется от тепла человеческого тела. Вспоминается часовая мастерская Гаррисона и опыты, в которых мастер определял длину металлических стержней как функцию их температуры. Здесь врач проделывает нечто обратное: по длине жидкого ртутного «стерженька» он определяет температуру пациента. Он строит обратную функцию по отношению к той, которую изучал Гаррисона.
Разумеется, к вопросу можно подойти с другой стороны и назвать прямой функцию, с которой имеет дело врач, и обратной ту, значение которой прославило Гаррисона. А если быть справедливым до конца, то обе функции нужно назвать взаимно обратными. Противопоставлять их имеет не больше смысла, чем решать, кто из двух близнецов старше. Правда, порой одна из двух взаимно обратных функций более употребительна, более привычна, ее символ примелькался больше, и подобная неравноценность играет свою роль при распределении званий «прямая» и «обратная». Арксинус, арктангенс называют обратными тригонометрическими функциями, молчаливо отдавая звание «прямых» синусу и тангенсу.
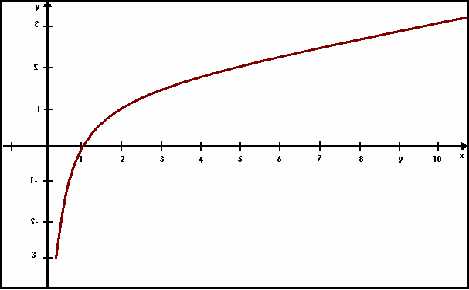
Космодром. Ракета, летящая в космическом пространстве, наращивает скорость по закону логарифма: именно эта функция позволяет по массе израсходованного топлива указать скорость ракеты. Скорость — функция, масса топлива — аргумент. Но часто возникает обратная задача, когда исходным пунктом расчета является скорость ракеты. Чтобы вывести спутник на орбиту, ракета должна развить первую космическую скорость. Какое количество топлива потребуется ракете, чтобы достичь назначенной скорости? Масса топлива в этом вопросе уже мыслится как функция, скорость — как аргумент. Задачу решает функция, обратная к логарифмической функции, — показательная.
Функция логарифмическая и функция показательная. Сведем их на одном графике. Бросается в глаза: они расположены симметрично относительно биссектрисы угла, стороны которого - оси координат. Это не удивительно — ведь переход от прямой функции к обратной заключается в переименовании: функция становится аргументом, аргумент — функцией. Заметим, что функция, обратная линейной, - это опять-таки линейная функция. Квадратный корень и парабола тоже являются взаимно обратными функциями, и графики их тоже симметричны относительно той же биссектрисы.
Какие свойства функции гарантируют то, что обратная к ней окажется однозначной? Эти свойства – непрерывность и монотонность. Линейная и показательная функции, парабола и корень квадратный – каждая из них непрерывна в любой точке своей области существования. Неразрывна всюду, как говорят в таких случаях. Прекрасные примеры всюду непрерывных функций дают процессы движения. Причина в том, что пространство и время непрерывны.
infourok.ru
- Download Link: http://ucenabne.slimkor.ru/?opn&keyword=%D0%A0%D0%B5%D1%84%D0%B5%D1%80%D0%B0%D1%82+%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%D1%8B+%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%BE%D0%BD%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D1%85+%D0%B7%D0%B0%D0%B2%D0%B8%D1%81%D0%B8%D0%BC%D0%BE%D1%81%D1%82%D0%B5%D0%B9+%D0%B2+%D1%80%D0%B5%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D1%85+%D0%BF%D1%80%D0%BE%D1%86%D0%B5%D1%81%D1%81%D0%B0%D1%85+%D0%B8+%D1%8F%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F%D1%85
Скачать тут: http://ucenabne.smallheart.ru/?opn&keyword=%D0%A0%D0%B5%D1%84%D0%B5%D1%80%D0%B0%D1%82+%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%D1%8B+%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%BE%D0%BD%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D1%85+%D0%B7%D0%B0%D0%B2%D0%B8%D1%81%D0%B8%D0%BC%D0%BE%D1%81%D1%82%D0%B5%D0%B9+%D0%B2+%D1%80%D0%B5%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D1%85+%D0%BF%D1%80%D0%BE%D1%86%D0%B5%D1%81%D1%81%D0%B0%D1%85+%D0%B8+%D1%8F%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F%D1%85
-
-
-
-
-
-
-
-
-
-
-
-
Реферат примеры функциональных зависимостей в реальных процессах и явлениях
Дальнейшее развитие математической науки в XIX в. Эта особенность выявляется при построении графика, причем целесообразно рассмотреть два графика: один — в крупном масштабе на промежутке. Освоение индивидуально заданной функции происходит в сопоставлении черт, специфических для неё, с общим представлением о функции. Ток возникает в рамке, которая равномерно вращается в однородном магнитном поле. История математики в школе. Такие функциональные зависимости, например, возраст деревьев, развитие амебы, развитие папоротника изучает наука биология. Понятие функциональной зависимости в данных Кортежи отношений могут представлять экземпляры сущности предметной области или фиксировать их взаимосвязь. С изобретением чувствительных приборов стало возможным точно определить блеск звезд.
Он может быть полезен при реинжиниринге существующей базы данных. Если в течение 5 минут не придет письмо, возможно, допущена ошибка в адресе. Материал этой темы используется при изучении многих классов функций: тригонометрических, показательной, логарифмической и др.
Определение многозначной зависимости: Пусть Х и Y атрибуты некоторого отношения. Скачать бесплатно и без регистрации. Если построить график зависимости объёма информации от времени, то получим некоторую кривую, которая в математике называется экспонентой и является графиком показательной функции рис. Вначале вспомним некоторые понятия: Простой атрибут — это атрибут, значения которого неделимы. Длина сторон прямоугольника и его периметр площадь. Это график магнитного потока. Так как рамка вращается равномерно, то угол ее поворота может служить мерой времени. Изучение психолого-педагогической литературы, постановка проблемы, формулировка цели, предмета, объекта, задач исследования, постановка гипотезы.
Реферат примеры функциональных зависимостей в реальных процессах и явлениях
В связи с таким взглядом Любопытно, что параболоид вращения образует поверхность жидкости в цилиндрическом сосуде, если его вращать относительно своей оси. Цель урока: помочь студентам осознать социальную, практическую и личностную значимость учебного материала, связанного с использованием функциональных зависимостей в реальных процессах и явлениях.
Для подготовки к сознательному усвоению формулируемого в теме достаточного признака возрастания убывания функции до его введения полезно рассмотреть учащимся геометрические иллюстрации, на которых показаны графики функций, имеющих разный характер изменения, а также касательные в точках, принадлежащих к промежуткам возрастания и промежуткам убывания функций. Получившуюся картину зарисовать на плоскости. Однако выработанное на этом пути общее понятие оказывается в дальнейшем связанным главным образом с числовыми функциями одного числового аргумента, т.
www.openstreetmap.org
1 Г(О)Б ПОУ «Задонский политехнический техникум» Научно-исследовательская работа Функциональная зависимость реальных процессов Выполнили: Чернухин Иван Алексеевич, Копенкин Павел Владимирович, студенты группы Тэ-1 Г(О)Б ПОУ «Задонский политехнический техникум» Руководитель: Сторожук Валентина Николаевна, преподаватель математики Г(О)Б ПОУ «Задонский политехнический техникум» Адрес: Липецкая область, г. Задонск, ул. Труда, д уч.г.
2 ОГЛАВЛЕНИЕ Введение Глава 1. Теоретические основы введения понятия функции Из истории возникновения функции Понятие функции и графика функции Глава 2. Практическая часть Исследование функциональной зависимости в повседневной жизни Иллюстрация функциональной зависимости в работе электрика Заключение...22 Список литературы...23 Приложение 1. Виды функций и их свойства. 1
3 Введение Успех человека в современном обществе зависит от того, насколько он компетентен в основах наук, в том числе математике. В математике все явления и зависимости описываются с помощью функций. Функция одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. Разработкой понятия функции занимались великие ученые: Франсуа Виет, Рене Декарт, Ферма, Ньютон, Лейбниц, Бернулли, Эйлер, Даламбер, Фурье и другие ученые. Среди российских ученых можно назвать: Эйлера. Чебышева, Соболева, Лобачевского, Лебедева и других. Функциональная зависимость встречается в жизни «на каждом шагу», поэтому данная тема актуальна как для каждого человека, так и для всего города, а в целом - для всего человечества. Проходят годы, и мы меняемся. Мы также зависим от своей наследственности, от книг, которые мы читаем, от температуры окружающей нас среды и от многих других факторов. И поэтому тему своего исследования мы сформулировали так: «Функциональная зависимость реальных процессов». Мы любим находить различные закономерности в окружающем мире, любим изучать числа, строить графики. Поэтому мы решили подробнее узнать, как можно связать различные моменты жизни с функциями и графиками. Цель нашего исследования: показать примеры нестандартного взгляда на функциональную зависимость в окружающей нас жизни. Для этого мы поставили перед собой следующие задачи: 1. изучить материал по данной теме; 2. познакомиться с историей возникновения понятия функции; 3. ввести понятие функции и графика функции; 4. продемонстрировать различные функциональные зависимости вокруг нас и в работе электрика; 5. оформить презентацию. 2
4 Предмет исследования: совокупность математических методов и моделей. Объект исследования: функции. Методы исследования: изучение и использование научно-публицистических и учебных изданий, обобщение, анализ, синтез, моделирование. Гипотеза: реально происходящие события в жизни человека можно представить в виде графика зависимостей. Материал, связанный с построением графиков функций, изучается недостаточно полно с точки зрения требований предъявленных на экзаменах. Поэтому задачи на построение графиков не редко вызывают затруднение у учащихся и студентов. Основываясь на этом факте, эта тема является необходимой для подробного рассмотрения. Теоретическая значимость нашей исследовательской работы заключается в том, что результаты исследования могут быть использованы для студентов техникумов при изучении темы «Функция». Практическая значимость работы заключается в том, что результаты исследования могут быть использованы студентами техникумов для повышения образовательного уровня при изучении применения функции в практической деятельности электрика. Мы считаем, что данная работа может помочь заинтересовать студентов, дать возможность «заглянуть внутрь» такого сложного математического понятия как «функция». 3
5 Глава I. Теоретическая часть Из истории возникновения функции. Большинство математических понятий прошли долгий путь развития. Сложный путь прошло понятие функции. Оно уходит корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Они еще не умели считать, но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода; чем сильнее натянута тетива лука, тем дальше полетит стрела; чем дольше горит костер, тем теплее будет в пещере. С развитием скотоводства, земледелия, ремесел и обмена увеличивалось количество известных людям зависимостей между величинами. Идея зависимости некоторых величин восходит к древнегреческой науке. Но греки рассматривали лишь вопросы, имеющие геометрическую природу, и не ставили вопроса об общем изучении различных зависимостей. Графическое изображение зависимостей широко использовали Г.Галилей ( ), П.Ферма ( ) и Р.Декарт ( ), который ввел понятие «переменной величины». По определению Декарта: «Функцией переменной величины называется количество, образованное каким угодно способом из этой переменной величины и постоянных». Развитие механики и техники потребовало введения общего понятия функции, что было сделано немецким философом и математиком Г.Лейбницем. Следующий шаг в развитии понятия функции сделал ученик Бернулли, член Петербургской Академии наук Леонард Эйлер ( ). В Дифференциальном исчислении, вышедшем в свет в 1755 г, Л. Эйлер дает общее определение функции: 4
6 Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых. Это наименование, - продолжает далее Эйлер, - имеет чрезвычайно широкий характер; оно охватывает все способы, какими одно количество определяется с помощью других. В общем виде понятие обобщенной функции было введено французом Лораном Шварцем. В 1834 г. в работе Об исчезании тригонометрических строк Н. И. Лобачевский, развивая вышеупомянутое эйлеровское определение функции в 1755г., писал: Общее понятие требует, чтобы функцией от х называть число, которое дается для каждого х и вместе с х постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подает средство испытывать все числа и выбирать одно из них; или, наконец, зависимость может существовать и оставаться неизвестной... Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа, одни с другими в связи, принимать как бы данными вместе. Еще до Лобачевского аналогичная точка зрения на понятие функции была высказана чешским математиком Б. Больцано. В 1837 г. немецкий математик П. Лежен-Дирихле так сформулировал общее определение понятия функции: у есть функция переменной х (на отрезке a ( х ( b), если каждому значению х (на этом отрезке) соответствует совершенно определенное значение у, причем безразлично, каким образом установлено это соответствие - аналитической формулой, графиком, таблицей либо даже просто словами. В 1936 году, 28-летний советский математик и механик С. Л. Соболев первым рассмотрел частный случай обобщенной функции. 5
7 Вывод: Следует отметить, что начиная с XVII в. одним из важнейших математических понятий является понятие функции. Оно сыграло и поныне играет большую роль в познании реального мира. Прослеживая исторический путь развития понятия функции невольно приходишь к мысли о том, что эволюция еще далеко не закончена и, вероятно, никогда не закончится, как никогда не закончится и эволюция математики в целом. Новые открытия и запросы естествознания и других наук приведут к новым расширениям понятия функции и других математических понятий. Математика незавершенная наука, она развивалась на протяжении тысячелетий, развивается в нашу эпоху и будет развиваться в дальнейшем. 6
8 1.2. Определение функции и графика функции. Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира. Функция это не только математическое понятие, но и: функция работа, производимая органом, организмом; роль, значение чего-либо; функция в математике закон зависимости одной величины от другой; функция возможность, опция, умение программы или прибора. функция обязанность, круг деятельности; функция персонажа в литературном произведении; функция вид подпрограммы в информатике социальная функция. Определение. Числовой функцией с областью определения D называется соответствие, при котором каждому числу x из множества D сопоставляется по некоторому правилу единственное число y, зависящее от x. Принято называть x независимой переменной или аргументом, а у зависимой переменной или значением функции. Записывают указанное соотношение между x и у в общем виде так: у = f (x) или у = F (x) и т. п. График функции y = f (х) - это множество всех точек плоскости, координаты (х, у) которых удовлетворяют соотношению y = f(x). Существует несколько способов задания функций: аналитический, словесный, графический, табличный. Аналитический способ. Наиболее распространен аналитический способ задания функции, при 7
9 котором функция задается формулой, устанавливающей, какие вычислительные операции надо произвести над х, чтобы найти у. Пример: у = к х; V = s h ; s = a b Словесный способ (пословицы, поговорки) Чем дальше в лес, тем больше дров. Кашу маслом не испортишь. Меньше слов, больше дела. Любишь кататься, люби и саночки возить. Графический способ. Распространен и графический способ задания функции. Графиком функции у=f(x), где х из множества Е, называется множество точек плоскости с прямоугольными координатами (х,у), где х из Е, у=f(x). Графический способ состоит в проведении линии (графика), у которой абсциссы изображают значения аргумента, а ординаты соответствующие значения функции. Этот способ позволяет наглядно представить функциональную зависимость. Пример: п у т ь км время t,с Табличный способ. При табличном способе задания функция задается в виде таблицы, в которой для каждого значения аргумента указывается соответствующее ему значение функции. Табличный способ общеизвестен (таблица квадратов и таблица кубов натуральных чисел и т. д.). Этот способ сразу даѐт числовое значение функции. В этом его преимущество перед другими 8
10 способами. Пример. Таблица квадратов чисел от 1 до 10: Виды функций (приложение 1): 1) линейная: y = ax + b; 2) квадратичная: y = ax 2 + bx + c; 3) обратная пропорциональность: y = k x ; n 4) корень n- степени: y = x; 5) модуль: y = x ; 6) тригонометрические: y = sinx, y = cosx, y = tgx, y = ctgx; 7) показательная: y = a x ; 8) логарифмическая: y = log a x; 9) обратные тригонометрические функции: y = arcsinx, y = arccosx, y = arctgx, y = arcctgx. Современные энциклопедии, толковые словари рассматривают функцию в 5 значениях: 1. Явление, зависящее от другого и изменяющееся по мере изменения этого другого явления. 2. Переменная величина, меняющаяся в зависимости от изменения другой величины. 3. Работа, производимая органом, организмом. 4. Обязанность, круг деятельности лица, подлежащая исполнению работа. 5. Значение, назначение, роль. Функция как понятие имеет одно родовое значение, но в разных областях деятельности проявляет себя по-разному, оставаясь однозначной сущностью. Понятие функции играет важную роль, являясь базовым понятием в изучении алгебры и начал анализа. 9
11 Вывод: Функция - одно из основных математических и общенаучных понятий, выражающее зависимость одних переменных величин от других. Оно сыграло и поныне играет большую роль в познании реального мира. Понятие функции играет важную роль, являясь базовым понятием в изучении алгебры и начал анализа. 10
12 Глава 2. Практическая часть Исследование функциональной зависимости в повседневной жизни. В повседневной жизни мы постоянно сталкиваемся с функциональными зависимостями. Мы нашли множество примеров функций, изобразили с помощью графиков. которые Задача 1. При температуре 0 о С рельс имеет длину l 0 = 12,5 м. при возрастании температуры происходит тепловое расширение рельса и его длина, выраженная в метрах, меняется по закону l(t о ) = l 0 (1 + t о ),где = 1, коэффициент теплового расширения в градусах Цельсия в минус первой степени, t о температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм. Ответ выразить в градусах Цельсия. Решение. Выразим из заданной формулы t: t = l l 0 αl 0. Заметим, l l 0 = Δl = 6мм = м, тогда t = Ответ: = 100 = 40 C Пример 1. С мороза в комнату внесли банку со льдом и стали наблюдать за изменением температуры вещества в банке: лед постепенно таял, когда он растаял весь, температура воды стала повышаться, пока не сравнялась с температурой в комнате. На рисунке 1 изображен график зависимости температуры от времени. Рис. 1 11
13 Пример 2. Рассмотрим деление праздничного торта между гостями. Отчего зависит количество порций? от числа гостей. А от чего зависит вес порции? тоже от числа гостей. В первом случае, чем больше гостей, тем на большее количество порций мы должны разделить торт (рис. 2). Здесь наглядно можно представить прямую пропорциональную зависимость. Рис. 2 Во втором случае, чем больше гостей, тем меньше вес порции. Здесь мы видим обратную пропорциональную зависимость (рис. 3). Рис. 3 Пример 3. Мы живѐм в век информационных технологий. Ежедневно мы получаем массу информации из различных источников: телевидения, радио, газет, журналов, и, конечно, из Интернета. Известно, что объѐм информации каждые пять лет увеличивается в два раза. Рис. 4 12
14 Если построить график зависимости объѐма информации от времени, то получим некоторую кривую, которая в математике называется экспонентой и является графиком показательной функции (рис. 4). Пример 4. На голове человека растут волосы, которые регулярно стригут. График полученной зависимости (при условии, что стрижку делают регулярно) похож на функцию дробной части числа, смещѐнную на a единиц вверх: y = x + a (рис. 5). Пример 5. За время обучения в школе каждый год переходим в следующий класс. Такая зависимость сходна с функцией целой части числа y = {x} на ограниченном промежутке (рис. 6). Рис. 5 Рис. 6 Пример 6. Изменение температурного режима в нашей климатической зоне подчиняется законам тригонометрических функций (рис. 7) Рис. 7 Пример 7. Садово-огородные процессы тоже можно представить в виде функции и построить график. К примеру, яблоко росло, зрело, потом его высушили (рис. 8). Получили некоторую кусочную функцию. 13
15 Рис. 8 Функции это математические портреты устойчивых закономерностей, познаваемых человеком. Чтобы проиллюстрировать характерные свойства функций обратимся к пословицам и поговоркам. Ведь пословицы это тоже отражение устойчивых закономерностей, выверенное многовековым опытом народа. Графиком можно проиллюстрировать смысл любой пословицы. «Чем дальше в лес, тем больше дров» Рис. 9 График представит количество дров как функцию пути. Вот, например, пословица «Каково жизнь проживешь, такую славу наживешь» на графике будет выглядеть следующим образом (рис.10): Рис
16 Из графика следует, что если на протяжении своей жизни будешь совершать отрицательные дела, поступки, то и слава о тебе будет отрицательная, и наоборот. Или такая пословица «Пересев хуже недосева» на графике будет выглядеть так (рис. 11): Рис. 11 Из графика видно, что если семян мало, то и урожай будет мал, если семян слишком много, то им расти будет плохо, и семена потеряешь, и урожая не соберешь, нужно посадить оптимальное количество семян и урожай будет высоким. Вывод: В повседневной жизни мы постоянно сталкиваемся с функциональными зависимостями. Я нашел множество примеров функций, которые изобразили с помощью графиков. 15
17 2.2. Иллюстрация функциональной зависимости в работе электрика. Задача 1. Электробезопасность (действие электрического тока на организм человека) Действие силы тока на организм человека (в ма) Величина силы тока Различные величины тока частотой 50 Гц действуют следующим образом: 1-2) 5 10 ма боль в мышцах, судорожные их сокращения, руки с трудом можно оторвать от электродов; 2-3) ма боли, руки невозможно оторвать от электродов; 3-4) ма боль в руках и груди, дыхание затруднено, возможен паралич дыхания и потеря сознания; 4-5) ма при длительном действии возможна клиническая смерть; 5-6) 100 ма и более при длительности более 3с возможна клиническая смерть. Задача исследование 2. Исследовать: а) Зависимость силы тока от напряжения. Сила тока, 0,5 1 1,5 ампер Напряжение, вольт 16
18 с и л а 2 1,5 1 т о к а 0, Значения Y напряжение Результаты опытов показывают, что напряжение и сила тока зависят друг от друга, причем эта зависимость прямо пропорциональная, т.е. при увеличении напряжения увеличивается сила тока. б ) Зависимость силы тока от сопротивления проводника при одном и том же напряжении. Я провел опыт с тремя различными проводниками при напряжении в 2 вольта и получил следующие результаты: опыта Сопротивление проводника, Ом Сила тока в цепи, А ,5 с и л а т о к а 2,5 2 1,5 1 0, Столбец1 сопротивление Опыт показывает, что сопротивление и сила тока тоже зависимые величины, чем больше сопротивление проводника, тем меньше сила тока. 17
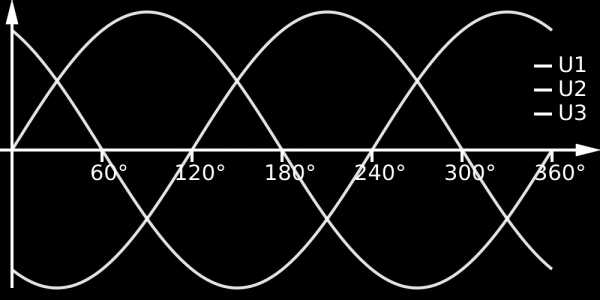
19 Зависимость силы тока, напряжения, сопротивления человек учитывает в своей повседневной жизни, например: линии электропередач изготавливают из металлов с маленьким сопротивлением (медь, алюминий). Задача 3. Невозможно представить жизнь современного человека без переменного электрического тока, так как все приборы: бытовые, электронагревательные, телевизоры, компьютеры и т.д., работают от сети переменного тока. Напряжение в наших розетках изменяется по следующему закону: u= U max cos(wt), где U max = 308 B, w=314. Построить график функции. Задача 4. Начертить развернутую диаграмму трехфазного тока. Развернутая диаграмма трехфазного тока. 18
20 Задача 5. Представить функциональную зависимость формы сигнала электрического тока. Формы сигнала электрического тока: 1. постоянной в виде прямой линии на временно м графике; 2. переменной синусоидальной гармоникой, хорошо описываемой основными тригонометрическими соотношениями; 3. меандром, грубо напоминающим синусоиду, но с резкими, ярко выраженными углами, которые в отдельных случаях могут быть хорошо сглажены; 4. пульсирующей, когда направление остается одним и тем же без изменения, а амплитуда колеблется периодически от нулевого до максимального значения по вполне определенному закону. Задача 6. На данном графике мы видим сравнительную характеристику мощности бытовых приборов. Какие из бытовых приборов имеют наибольшую мощность? 19
21 Мощность бытовых приборов (Вт) Задача 7. Насколько выгодно светодиодное освещение по сравнению с обычными лампами накаливания с экономической точки зрения? Уличное светодиодное освещение очень выгодно с экономической точки зрения. Лишь небольшого количества электроэнергии (например, 100 ватт) достаточно для освещения достаточно большой площади. Для сравнения: световой поток светодиодной лампы, потребляющей 100 ватт, составляет около Люмен, это как от 6 обычных ламп накаливания, то есть экономия более 80%. 20
22 Задача 8. Составить сравнительную характеристику светодиодных ламп, люминесцентных и ламп накаливания. Характеристики Светодиодная лампа Люминесцентная лампа Лампа накаливания Потребляемая мощность 5 W 15W 40 W Эффективность светоотдачи 90 Lm/W 30 Lm/W 10,5 Lm/W Световой поток 450 Lm Lm Рабочая температура 70 C 60 C 180 C Срок службы До часов До часов До часов Экологичность да Содержит ртуть да 21
23 I. Заключение В ходе работы мы проанализировали и изучили литературу по истории развития функции, исследовали на примерах функциональную зависимость в окружающей нас жизни. Краткий обзор развития понятия функции приводит к мысли о том, что эволюция ещѐ далеко не закончена и, вероятно, никогда не закончится, как никогда не закончится и эволюция математики в целом. Новые открытия и запросы естествознания и других наук приведут к новым расширениям понятия функции и других математических понятий. Функция - одно из основных математических и общенаучных понятий, выражающее зависимость одних переменных величин от других. Оно сыграло и поныне играет большую роль в познании реального мира. Понятие функции играет важную роль, являясь базовым понятием в изучении алгебры и начал анализа. Особенностью нашей работы является подбор примеров функциональных зависимостей из повседневной жизни. Мы поняли, что таких примеров можно привести бесконечно много. В результате работы мы достигли понимания важности изучения математики и получили возможность показать однокурсникам красоту и значимость математики. Выполняя работу, мы приобрели не только необходимые знания, умения и навыки, но и определѐнный личностный опыт. Теоретическая значимость нашей исследовательской работы заключается в том, что результаты исследования могут быть использованы для студентов техникумов при изучении темы «Функция». Практическая значимость моей работы заключается в том, что результаты исследования могут быть использованы студентами техникумов для повышения образовательного уровня при изучении применения функции в практической деятельности электрика. 22
24 Литература 1. Виленкин Н. Я. Функции в природе и технике: Книга для внеклассного чтения 2 е изд., испр. М.: Просвещение, Нагибин Ф.Ф. Математическая шкатулка.- М., Просвещение, Ульяновская Н. Н. О, функция, как ты Важна // Математика Энциклопедический словарь юного математика. Составитель Савин А.П.- М., Просвещение, Энциклопедический словарь юного математика. - М.: Педагогика Рыбников К.А. Возникновение и развитие математической науки, Москва, Просвещение, 1987 г. 7. Колягин Ю. М. «Алгебра 10,11 классы»-3-е изд.- М. : Издательство Просвещение, Глейзер Г.И. История математики в школе: 9-10 класс - М.: Просвещение Интернет-ресурсы:http://linear function.ru
25 Виды функций. Приложение 1 Рассмотрим основные существующие виды функций и их свойства. 24
26 25
27 26
28 1. Квадратичная функция. 27
29 28
30 29
31 30
32 31
33 32
34 33
35 34
36 35
37 36
38 37
39 38
40 39
docplayer.ru
План урока.
Группа: 13 «Э».
Учебник: Н.В. Богомолов «Математика».
Тема урока: Примеры функциональных зависимостей в реальных процессах и явлениях.
Цель урока: помочь студентам осознать социальную, практическую и личностную значимость учебного материала, связанного с использованием функциональных зависимостей в реальных процессах и явлениях.
Задачи урока:
закрепить знания и умения по исследованию функций и построению графиков;
учить применять знания, умения по теме «Исследование функции» в реальных процессах и явлениях;
развивать практические навыки по построению графиков функции с использованием компьютера;
воспитывать чувство ответственности при работе в малых группах.
Формы работы и взаимодействия студентов: фронтальная, индивидуальная, индивидуальная интерактивная, парная интерактивная, групповая интерактивная.
Тип урока: урок комплексного применения знаний и умений.
Оборудование: интерактивная доска, компьютеры, мультимедийный проектор, экран, слайды презентации, раздаточный материал - карточки с тестовыми заданиями, карточки по рефлексии, карточки с задачами, заготовки с координатными осями для изображения пословиц, карточки для ответов по тестам.
Деятельностьпреподавателя
Деятельность студентов
Формируемые УУД
Средства определения результата
1
Организационный этап
Приветствует студентов, проверяет готовность группы, проводит рефлексию настроения на начало урока( изобразите свое настроение на начало урока). Задает вопросы по представленным на слайдах изображениях, и подводит к формулировке темы урока. Корректирует ответы студентов, уточняет тему и задачи урока. Объявляет критерии оценок за работу на уроке.
Приветствуют преподавателя, изображают свое настроение на начало урока. Отвечают на поставленные вопросы. Пытаются озвучить тему урока и цели. Подписывают конверты- копилки, куда будут складывать баллы за работу на уроке.
Регулятивные: постановка учебной задачи, планирование, прогнозирование.
Выборочный фронтальный опрос
2
Проверка домашнего задания, воспроизведение и коррекция опорных знаний.
Проводит фронтальный опрос по графику на интерактивной доске.
Что такое функция?
Какова область определения функции?
Назовите множество значений функции.
Имеет ли функция нули?
Имеет ли данная функция точки экстремума?
Назовите промежутки монотонности функции.
Какой является функция: четной или нечетной?
Можно ли ее назвать периодической?
Проводит тестовую проверку знаний по вариантам с последующей самопроверкой по ключу.
Отвечают на вопросы преподавателя.
Выполняют тестовую работу и проверяют её. Набирают себе баллы.
Регулятивные: контроль, коррекция, оценка; личностные: интерес к учебному материалу, способность к самооценке; коммуникативные: умение отвечать на вопросы; познавательные: контролирует и оценивает процесс и результаты деятельности;
Фронтальный опрос.
Тестовая работа.
3
Воспроизведение знаний и умений, проверка их качества.
1.Защита проектов.
Студенты, объединённые в группы, должны были представить собранную информацию по категориям « Демографическая ситуация в Пензенской области на примере п.Сосновоборска и с.Индерки в 2013г.», « Среднемесячная температура воздуха в Пензенской области за 2013г», « Атмосферное давление Пензенской области за октябрь 2013г», «Курс доллара за 9 месяцев текущего года» в виде графиков функций. Анализируются графики функций.
2. Работа с пословицами. Организует посредством групповой работы поиск решения поставленной задачи (Чтобы проиллюстрировать характерные свойства функции, можно обратиться к пословицам. Ведь пословицы – это отражение устойчивых закономерностей, выверенных многовековым опытом. Изобразите пословицу в виде графика – как вы его понимаете, а затем обоснуйте своё решение. На доске заранее начерчены системы координат для экспериментов. Чья группа справится быстрее?
Чем дальше в лес, тем больше дров.
Выше меры конь не скачет.
Тише едешь - дальше будешь.
Пересев хуже недосева).
Анализируют и высказывают решения своих проектных работ.
Совместно в группе пытаются графически изобразить пословицы и доказать свое решение.
Регулятивные: постановка учебной задачи, планирование, прогнозирование, контроль, коррекция, саморегуляция;
познавательные: структурирует знания, строит речевое высказывание в устной форме, выбирает эффективный способ решения проблемной ситуации, совместно с учителем создаёт алгоритм деятельности;
коммуникативные: умеет слушать и вступать в диалог, участвует в коллективном обсуждении проблемы, формулирует собственное мнение и позицию, приходит к общему решению в совместной деятельности;
личностные: интерес к новому учебному материалу и способам деятельности.
Воспроизведение знаний и применение их.
4
Постановка и решение практических задач.
Решение задачи по дисциплине «Защита и охрана лесов» с использованием компьютера. Преподаватель совместно со студентами выполняют решение задачи.
Контроль самостоятельной работы по решению задачи, связанной со специальностью экономика по компьютеру и коррекция знаний.
Выполняют решение задачи в программе Excel с помощью преподавателя.
Решают задачи экономического характера самостоятельно за компьютером и посылают решение на рабочий стол преподавателя.
Регулятивные: планирование, прогнозирование, контроль, коррекция, оценка;
личностные: интерес к учебному материалу, способность к самооценке, понимание причин успеха; коммуникативные: умение слушать и задавать вопросы, контролирует действия партнера, использует речевые средства для различных коммуникативных задач;
познавательные: выбирает эффективные способы решения задач, контролирует и оценивает процесс и результаты деятельности.
Выполнение по образцу.
Анализ деятельности студентов.
6
6
Рефлексия урока. Д/з
Творческое домашнее задание: отыскать функции, описывающие реальные физические процессы, которые вы встречали на уроках физики. Исследуйте эти функции. У кого есть возможность, выдайте график на компьютере. Выставляет оценки. Организует соотнесение результата деятельности с учебной задачей. Проводит рефлексию настроения( изобразите свое настроение в конце урока и сравните его в начале и в конце урока).
Записывают домашнее задание. Подсчитывают баллы, набранные на уроке, и выставляют себе оценке по критериям. Дорисовывают свое настроение на конец урока и сравнивают с тем, что было в начале урока. По кругу дополняют одно из предложений:
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал…
я приобрел…
я научился…
у меня получилось
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
Личностные: имеет адекватную самооценку;
коммуникативные: строит понятные для партнеров речевые высказывания, допускает возможность существования у людей различных точек зрения.
Анализ высказываний студентов, оценочная шкала.
infourok.ru
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Выпуклость функции. Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях.
Сложная функция (композиция функций). Взаимно обратные функции. Область определения и область значений обратной функции. График обратной функции. Нахождение функции, обратной данной.
Зависимость одной переменной от другой называется функциональной зависимостью. Зависимость переменной от переменной называется функцией, если каждому значению соответствует единственное значение .
Обозначение: .
Переменную называют независимой переменной или аргументом, а переменную – зависимой. Говорят, что является функцией от . Значение , соответствующее заданному значению , называют значением функции.
Все значения, которые принимает , образуют область определения функции; все значения, которые принимает , образуют множество значений функции.
Обозначения:
– область определения функции;
– область значений функции;
– значение функции в точке .
– значения аргумента. – значения функции. Если функция задана формулой, то считают, что область определения состоит из всех значений переменной, при которых эта формула имеет смысл.
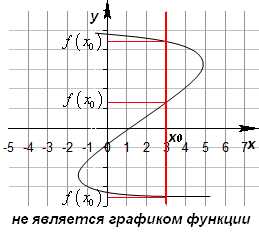
Графиком функции называется множество всех точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. Если некоторому значению соответствуют несколько значений (а не одно) , то такое соответствие не является функцией. Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая параллельная оси , пересекалась с графиком не более чем в одной точке.
Способы задания функции
1) Функция может быть задана аналитически в виде формулы. Например,
2) Функция может быть задана таблицей из множества пар .
3) Функция может быть задана графически. Пары значений изображаются на координатной плоскости.
Определение: Функция называется четной, если для любого из области определения . График произвольной четной функции приведен на рисунке ниже.
Определение. Функция называется нечетной, если для любого из области определения .
График произвольной четной функции приведен на рисунке ниже.
Следует отметить, что помимо четных и нечетных функций, встречаются так же функции ни четные, ни нечетные.
infopedia.su