Контрольные работы по математике "Тригонометрия". Тригонометрия контрольная работа
Проверочные работы по теме "Тригонометрия"
Проверочные работы по теме «Тригонометрия».
Тема: Основные понятия тригонометрии.
Работа по проверке усвоения теоретических знаний.
Перечень объектов контроля и оценки:
Знание определения тригонометрических функций, их четности и периодичности, знание основных тригонометрических формул и умение их доказывать; знание формул приведения и умение их применять.
Вариант 1.
Дать определение синуса и котангенса.
Расставить в координатных четвертях знаки синуса и котангенса.
Какова четность синуса и котангенса.
Чему равны периоды синуса и котангенса.
Доказать основное тригонометрическое тождество.
Упростить по формулам приведения: 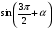 .
.
Упростить по формулам приведения: 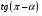 .
.
Вариант 2.
Дать определение косинуса и тангенса.
Расставить в координатных четвертях знаки косинуса и тангенса.
Какова четность косинуса и тангенса.
Чему равны периоды косинуса и тангенса.
Записать шесть основных тригонометрических формул и доказать одну из них.
Упростить по формулам приведения: 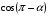 .
.
Упростить по формулам приведения: 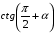 .
.
Время на выполнение: 20 мин.
Критерий оценки:
Оценка «5» ставится за все правильно выполненные задания, «4» - за 6 заданий, оценка «3» - за 5 - 4 правильно выполненных задания.
Расчетное задание.
Перечень объектов контроля и оценки:
Умение упрощать выражения и доказывать тождества, используя тригонометрические формулы, по данному значению одной из тригонометрических функций находить значения трех остальных.
Вариант 1.
Найти значения 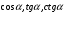 , если
, если 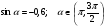
Упростить выражение:
а) 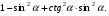 б)
б) 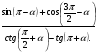
3. Вычислить: 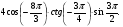
4. Доказать тождество: 
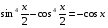 .
.
Вариант 2.

Найти значения 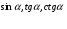 , если
, если 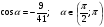
Упростить выражение:
а) 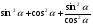 б)
б) 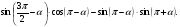
3. Вычислить: 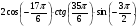
4. Доказать тождество: 
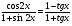 .
.
Вариант 3.
1. Найти значения 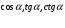 , если
, если 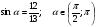
2. Упростить выражение:
а) 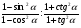 б)
б) 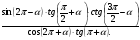
3. Вычислить: 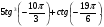
4. Доказать тождество: 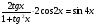 .
.
Вариант 4.
Найти значения 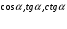 , если
, если 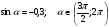
2 Упростить выражение:
а) 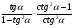
 б)
б) 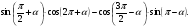
3. Вычислить: 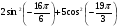
4. Доказать тождество: 
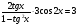 .
.
Время на выполнение: 45 мин.
Критерий оценки:
За каждое верно выполненное задание – один балл.
Ответы:
Вариант1.
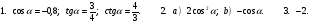
Вариант 2.
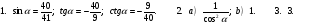
Вариант 3.
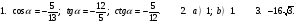
Вариант 4.
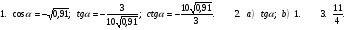
Тема : Тригонометрические уравнения.
Расчетное задание.
Перечень объектов контроля и оценки:
Умение решать простейшие тригонометрические уравнения, уравнения, приводимые к квадратным и однородные. Умение упрощать тригонометрические выражения.
Вариант 1.
№1. Решить уравнения:
1. 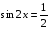 ; 2.
; 2. 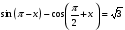 ; 3.
; 3. 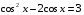 ;
;
4. 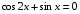 ; 5.
; 5. 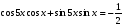
№2. Вычислить: 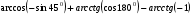 .
.
Вариант 2.
№1. Решить уравнения:
1. 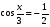 ; 2.
; 2. 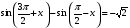 ; 3.
; 3. 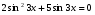 ;
;
4. 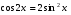 ; 5.
; 5. 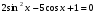 .
.
№2. Вычислить: 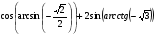 .
.
Вариант 3.
№1. Решить уравнения:
1. 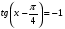 ; 2.
; 2. 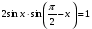 ; 3.
; 3. 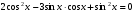 ;
;
4. 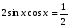 ; 5.
; 5. 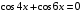
№2. Вычислить: 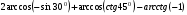 .
.
Вариант 4.
№1. Решить уравнения:
1. 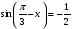 ; 2.
; 2. 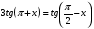 ; 3.
; 3. 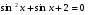 ;
;
4. 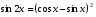 ; 5.
; 5. 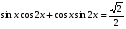 .
.
№2. Вычислить: 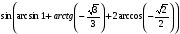 .
.
Время на выполнение: 45 мин.
Критерий оценки:
Оценка «5» ставится за все верно выполненные задания, «4» - за 5 верно выполненных задания, «3» - за 3 - 4 задания.
Ответы.
Вариант 1.
№1.
. 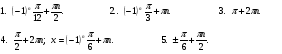
№2. 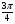 .
.
Вариант 2.
№1.
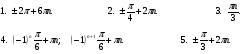
№2. 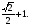
Вариант 3.
№1.
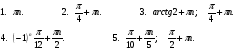
№2. 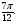
Вариант 4.
№1.
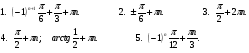
№2. 0,5.
infourok.ru
Примерная контрольная работа по теме «тригонометрия»
Примерная контрольная работа по теме:
«Тригонометрия»
1. Определите знак выражения:
а) sin 2650
б) cos (-750)
в) tg 
Решение:
а) sin 2650 (-), т.к. III четверть
б) cos (-750) (+) т.к. IV четверть
в) tg  = tg 1500 (-) т.к. II четверть
= tg 1500 (-) т.к. II четверть
2. Найдите sina, если cosa =- ,
,  П
П
Решение:
sin2a+ cos2a=1(основное тригонометрическое тождество)
sin2a=1- cos2a
sina= ,
,  aП (II четверть)
aП (II четверть)
sina = =
=
 =
= =
=
Ответ: 
3. Докажите тождество:
а) 1+ ctg2a +
 =
=
Решение:
1+ ctg2a +
 =
= (используем формулу: 1+ ctg2a=
(используем формулу: 1+ ctg2a= )
)
 +
+ =
=
 =
= (используем формулу: sin2a+ cos2a=1)
(используем формулу: sin2a+ cos2a=1)
 =
=
 =
=
Левая часть равенства =Правой части
Ответ: тождество верное
б) 2sin4a –2cos4a +4cos2a = 2
Решение:
2sin4a –2cos4a +4cos2a = 2
2(sin4a –cos4a) +4cos2a = 2
2(sin2a –cos2a) (sin2a +cos2a) +4cos2a = 2 (используем формулу: sin2a+ cos2a=1)
2(sin2a –cos2a) +4cos2a = 2
2sin2a –2cos2a +4cos2a = 2
2sin2a +2cos2a = 2
2(sin2a +cos2a) = 2
2=2
Левая часть равенства =Правой части
Ответ: тождество верное
4. Вычислите:
Sin450+sin150
Sin1050
Решение:
sin450+sin150 =
sin1050
Ответ:1
5. Упростите:
a) cos2  - sin2
- sin2
Решение:
cos2  - sin2
- sin2 =cos2
=cos2 =cos
=cos =
=
б) cos cos
cos + sin
+ sin sin
sin
Решение:
cos cos
cos + sin
+ sin sin
sin = cos(
= cos( -
- )=cos
)=cos =cos
=cos  =0
=0
gigabaza.ru
Контрольные работы по математике "Тригонометрия"
Контрольная работа № 1 (алгебра 10 класс)
I вариант
1. Вычислите: а)  б) cos 1050 в) tg 750
б) cos 1050 в) tg 750
2. Упростите:
а) 
3. Вычислите:
a)sin 2α , если sin α =
б) 4+27 cos 2α, если cosα = 
4. Вычислите:
А) cos2 , если cosα = 0,4 б)
, если cosα = 0,4 б) ctg α = 1
ctg α = 1 
5. Найдите значение выражения: 
6. Представьте в виде произведения сумму:
а) 
б)
II вариант
1. Вычислите: а) tg 750 б) cos 1050 в) 
2. Упростите:
а) 
3. Вычислите:
a)sin 2α , если tg α =
б) 1+9 cos 2α, если cosα =
cos 2α, если cosα =  и 2700
и 2700
4. Вычислите:
А) sin2 б)
б) ctg α = 1
ctg α = 1 
5. Найдите значение выражения:  , если tg 2α = 4
, если tg 2α = 4
6. Представьте в виде произведения сумму:
а) 
б)
Контрольная работа № 2 (алгебра 10 класс)
I вариант
1. Исследуйте функцию и постройте её график
у = 5 – 2х
2. Найдите область значения функции у = g (х) в заданных точках:
а) g (х) =  , при х = -2; 4; 5
, при х = -2; 4; 5
б) g (х) = при х1 =
при х1 =  , х2= 0; х3= 4
, х2= 0; х3= 4
3. Определите четность или нечетность функции:
a)
б)
в)
4. Найдите наименьший положительный период функции: y = f (x)
a) f (x) =
б) f (x) = tg (2x - 4)
в) f (x) =sin
5. Найдите обратную функцию к заданной функции и постройте их графики.
а) у = 3х -7
6. Представьте в виде произведения сумму:
а) 
б)
II вариант
1. Исследуйте функцию и постройте её график
у =
2. Найдите область значения функции у = g (х) в заданных точках:
а) g (х) = , при х = -0,6; 0; 3
б) g (х) = при х = - 5 х= 0; х=
3. Определите четность или нечетность функции:
a)
б)
в)
4. Найдите наименьший положительный период функции: y = f (x)
a) f (x) =
б) f (x) = сtg
в) f (x) =соs22х – sin22x
5. Найдите обратную функцию к заданной функции и постройте их графики.
а) у = 6- 2х
6. Найдите значение выражения: 
videouroki.net
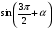 .
.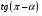 .
.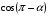 .
.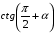 .
.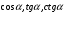 , если
, если 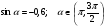
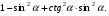 б)
б) 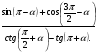
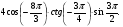

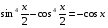 .
.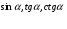 , если
, если 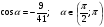
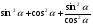 б)
б) 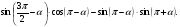
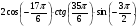
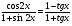 .
. 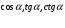 , если
, если 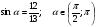
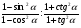 б)
б) 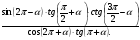
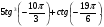
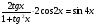 .
.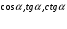 , если
, если 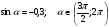
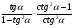
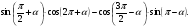
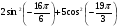
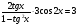 .
.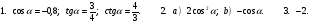
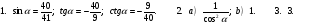
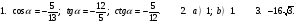
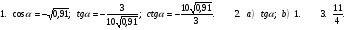
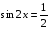 ; 2.
; 2. 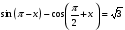 ; 3.
; 3. 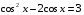 ;
;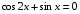 ; 5.
; 5. 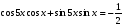
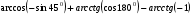 .
.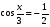 ; 2.
; 2. 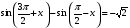 ; 3.
; 3. 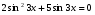 ;
;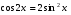 ; 5.
; 5. 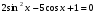 .
.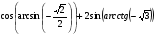 .
.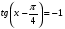 ; 2.
; 2. 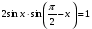 ; 3.
; 3. 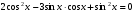 ;
;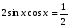 ; 5.
; 5. 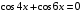
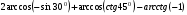 .
.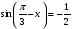 ; 2.
; 2. 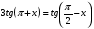 ; 3.
; 3. 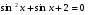 ;
;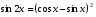 ; 5.
; 5. 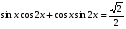 .
.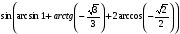 .
.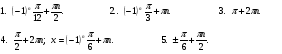
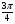 .
.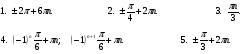
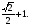
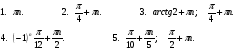
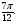
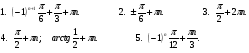

 ,
,  П
П ,
,  =
=
 =
= =
=


 )
) =
= =
=
 - sin2
- sin2
 =
=
 cos
cos + sin
+ sin sin
sin =cos
=cos  =0
=0 б) cos 1050 в) tg 750
б) cos 1050 в) tg 750


 , если cosα = 0,4 б)
, если cosα = 0,4 б) ctg α = 1
ctg α = 1 





 cos 2α, если cosα =
cos 2α, если cosα = 
 б)
б) , если tg 2α = 4
, если tg 2α = 4 , при х = -2; 4; 5
, при х = -2; 4; 5 при х1 =
при х1 =  , х2= 0; х3= 4
, х2= 0; х3= 4








