Контрольная работа по теме "Производная" 11 класс. Производная контрольная работа
Контрольная работа по теме "Производная" 11 класс
В а р и а н т 1. «Производная» К-2
Найти производную функции ( 1 – 3 ):
-
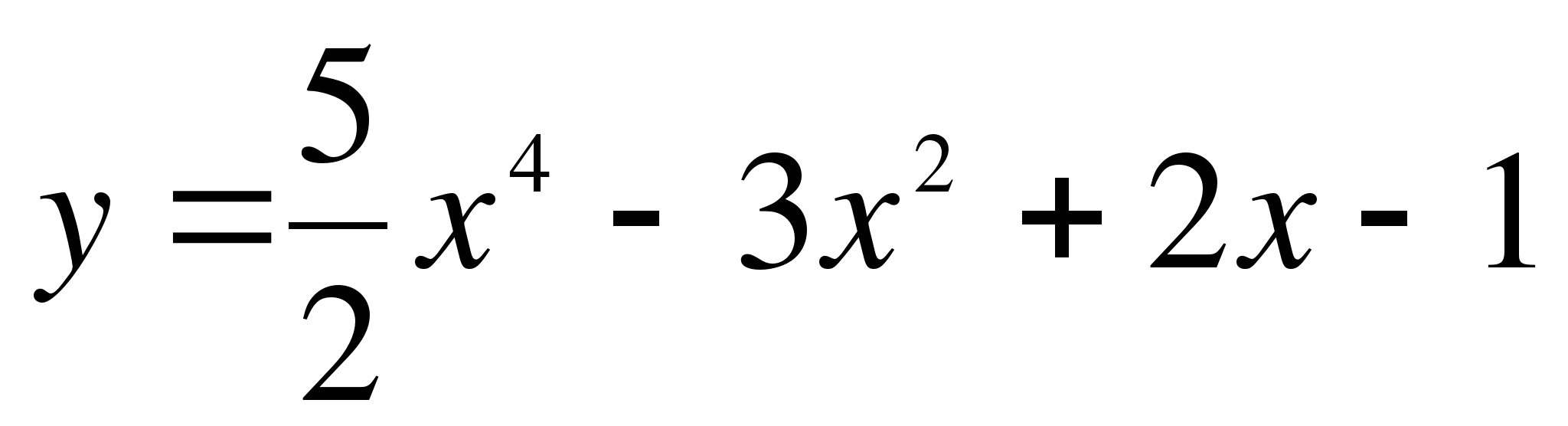
-
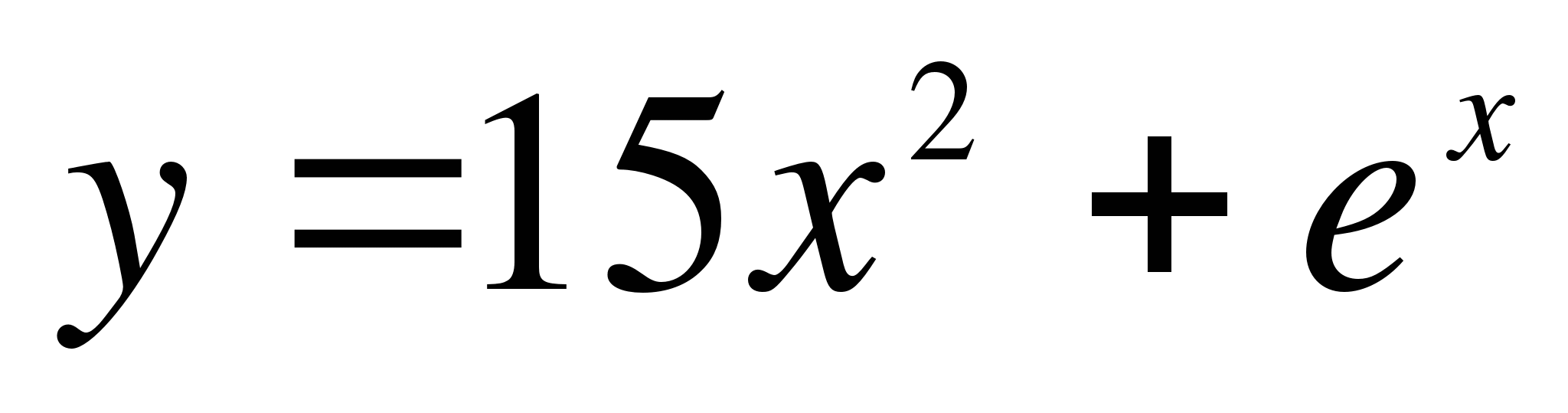
-
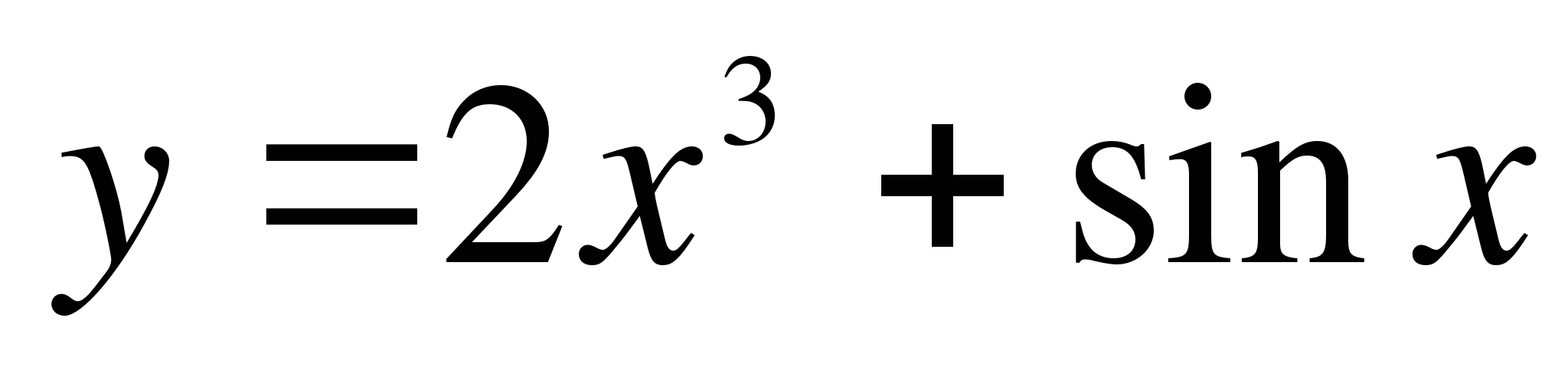
-
Точка движется прямолинейно по закону 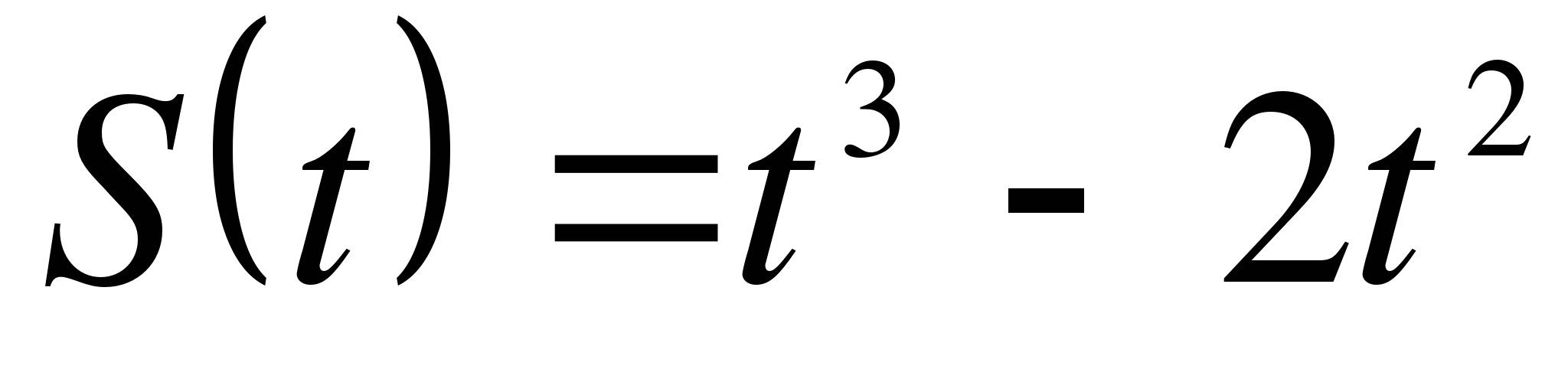 . Какой формулой задается скорость движения этой точки в момент времени t.
. Какой формулой задается скорость движения этой точки в момент времени t.
-
Угловой коэффициент касательной, проведенной к графику функции 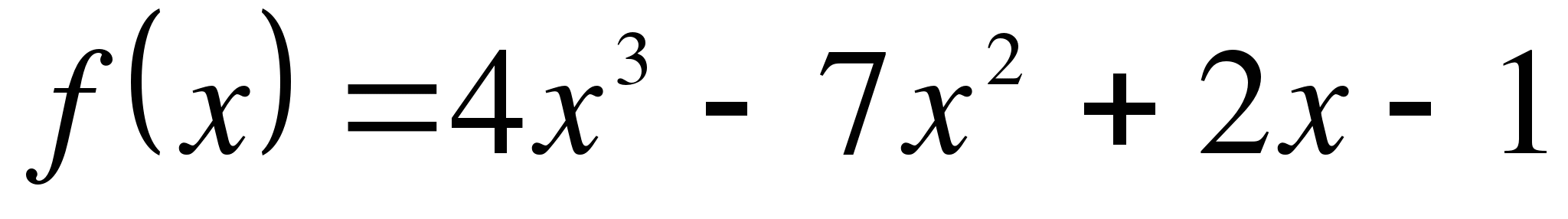 в точке с положительной абсциссой
в точке с положительной абсциссой 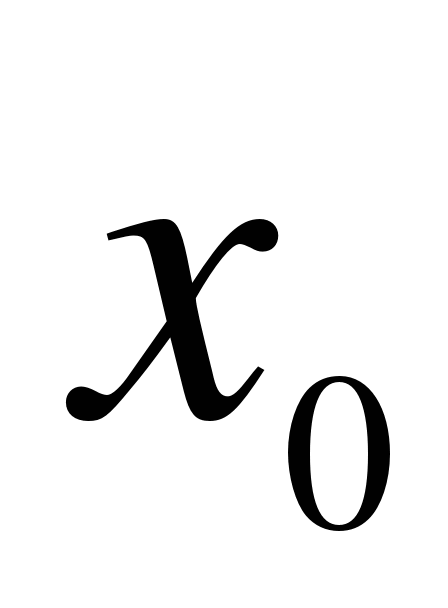 , равен 2. Найдите
, равен 2. Найдите 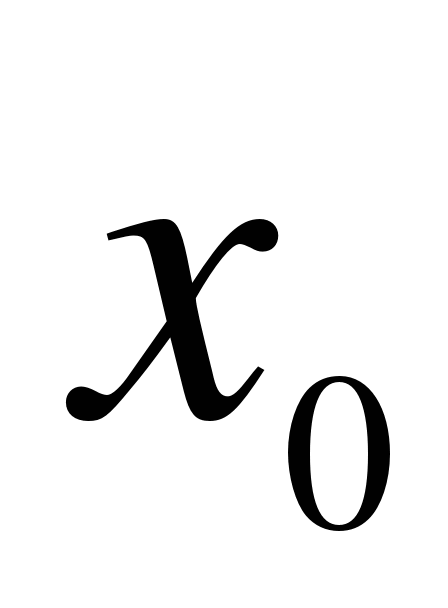 .
.
-
Найдите угловой коэффициент касательной, проведенной к графику функции 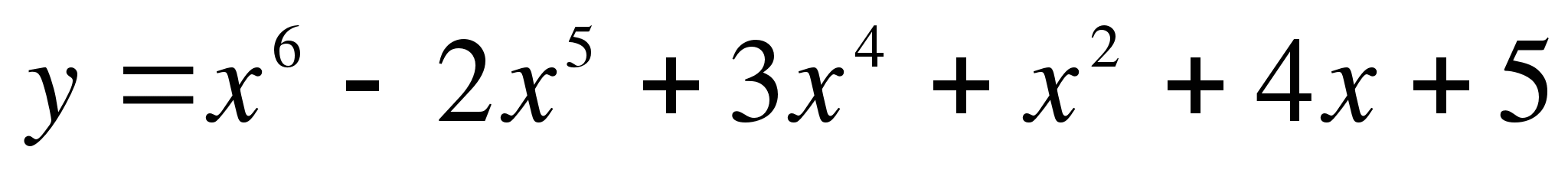 в точке
в точке 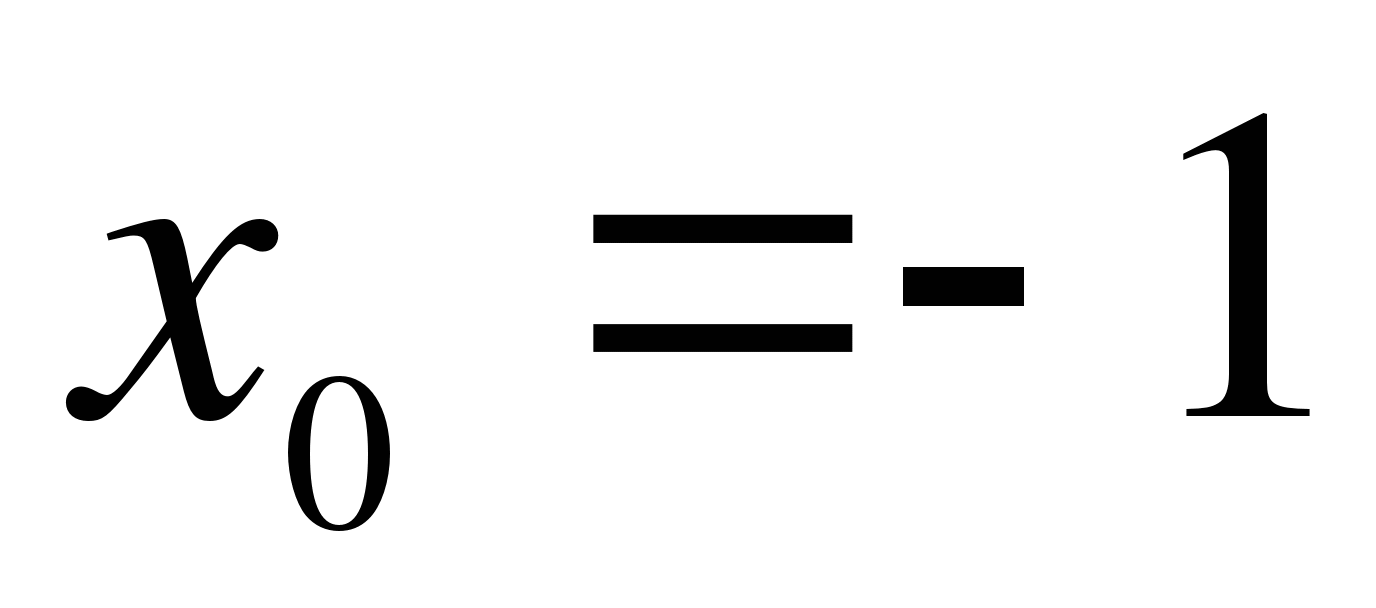 .
.
-
Найдите сумму тангенсов углов наклона касательных к параболе 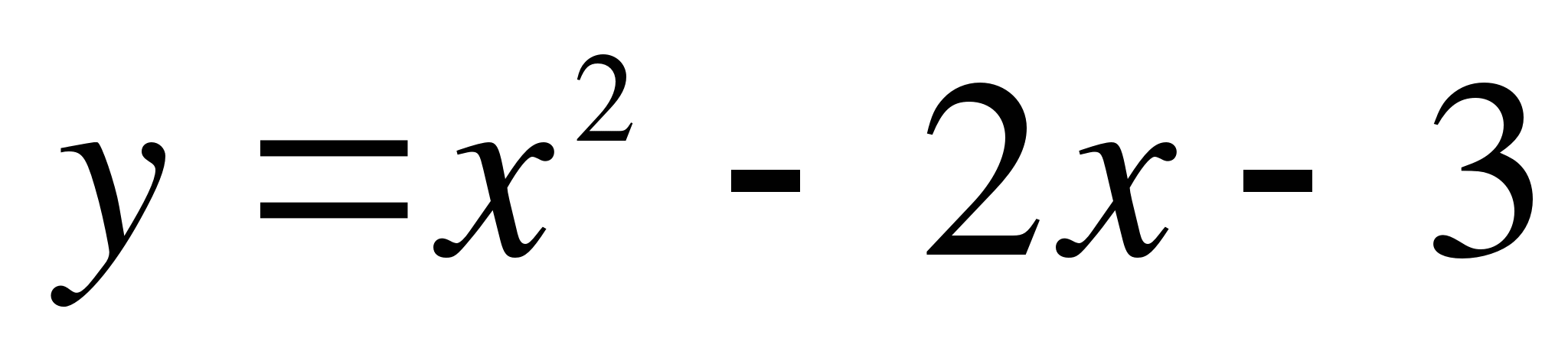 в точках пересечения параболы с осью абсцисс.
в точках пересечения параболы с осью абсцисс.
-
На графике функции 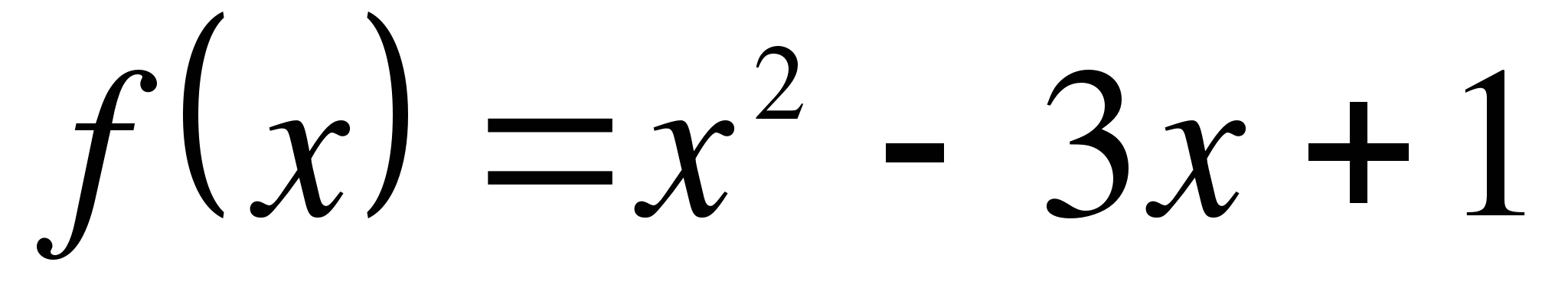 взята точка А, наклонена к оси абсцисс под углом, тангенс которого равен 7,2. Найдите абсциссу точки А.
взята точка А, наклонена к оси абсцисс под углом, тангенс которого равен 7,2. Найдите абсциссу точки А.
Найдите производные функций ( 9 – 11):
-
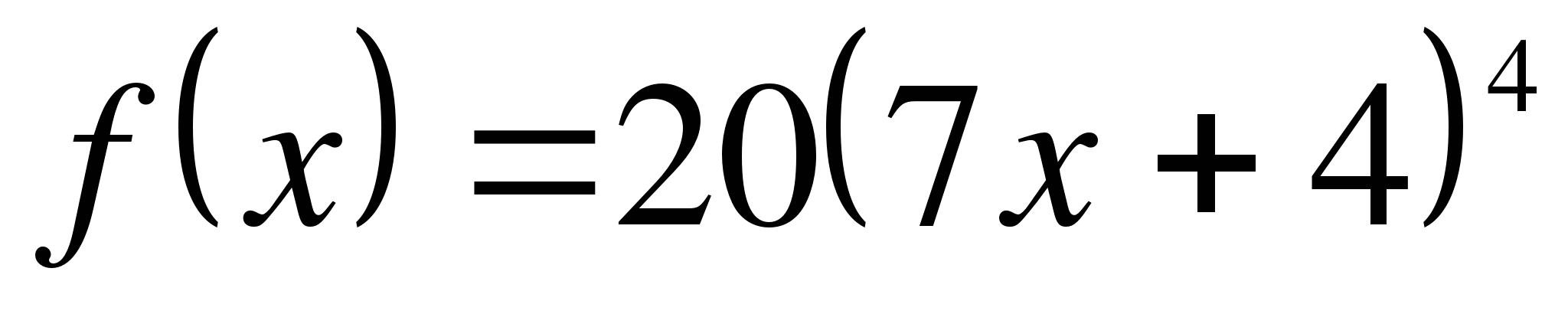
-
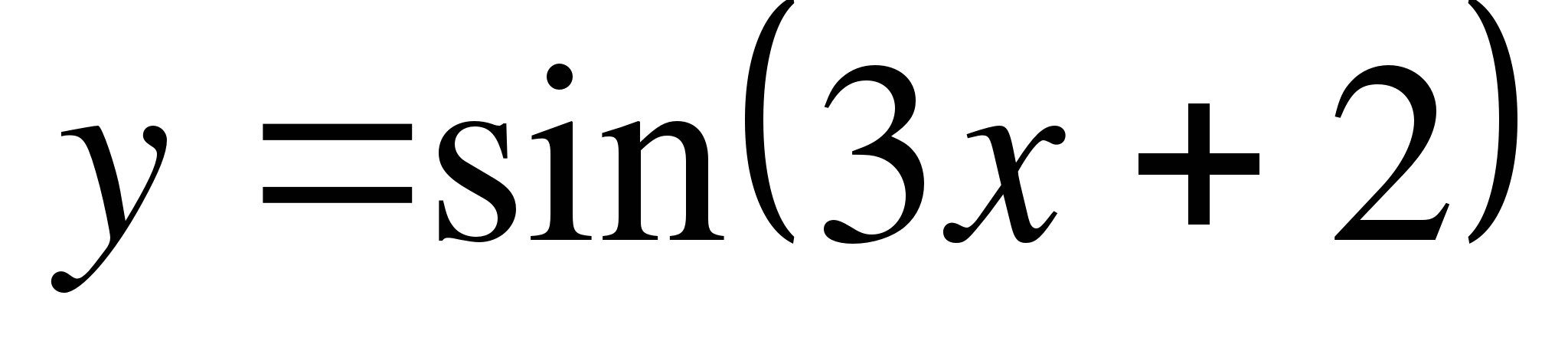
-

-
Найдите значение производной функции 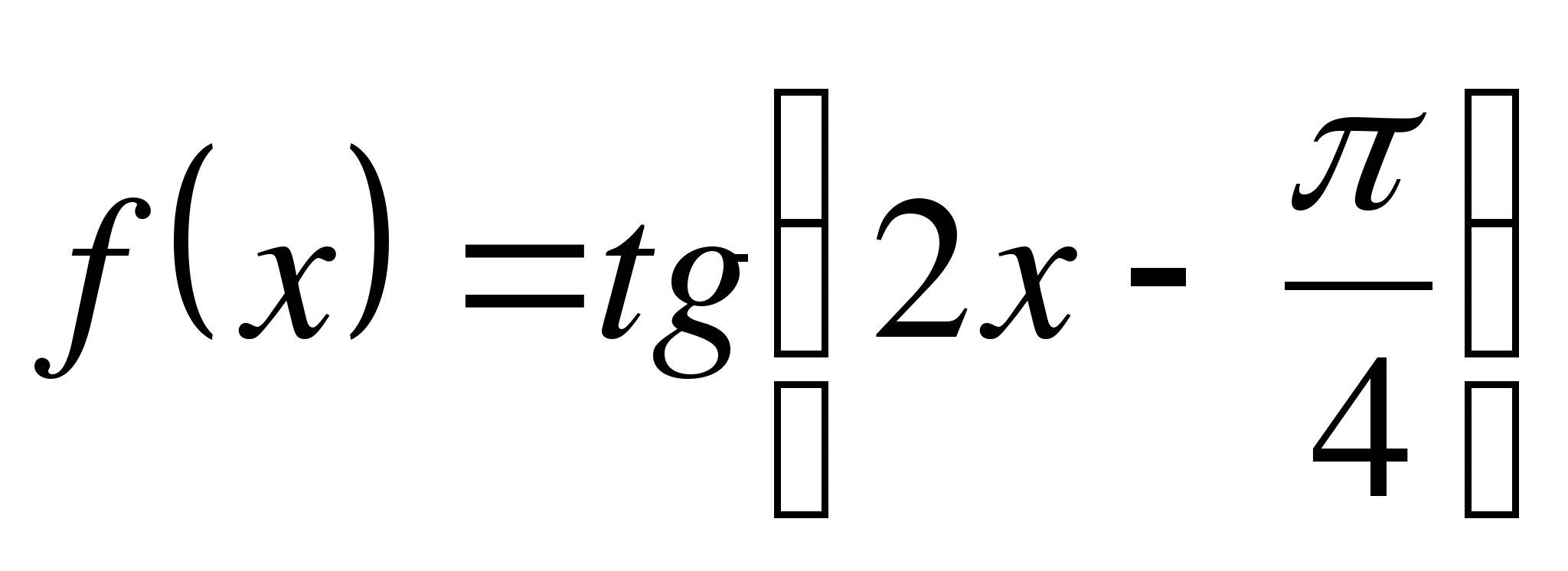 в точке
в точке 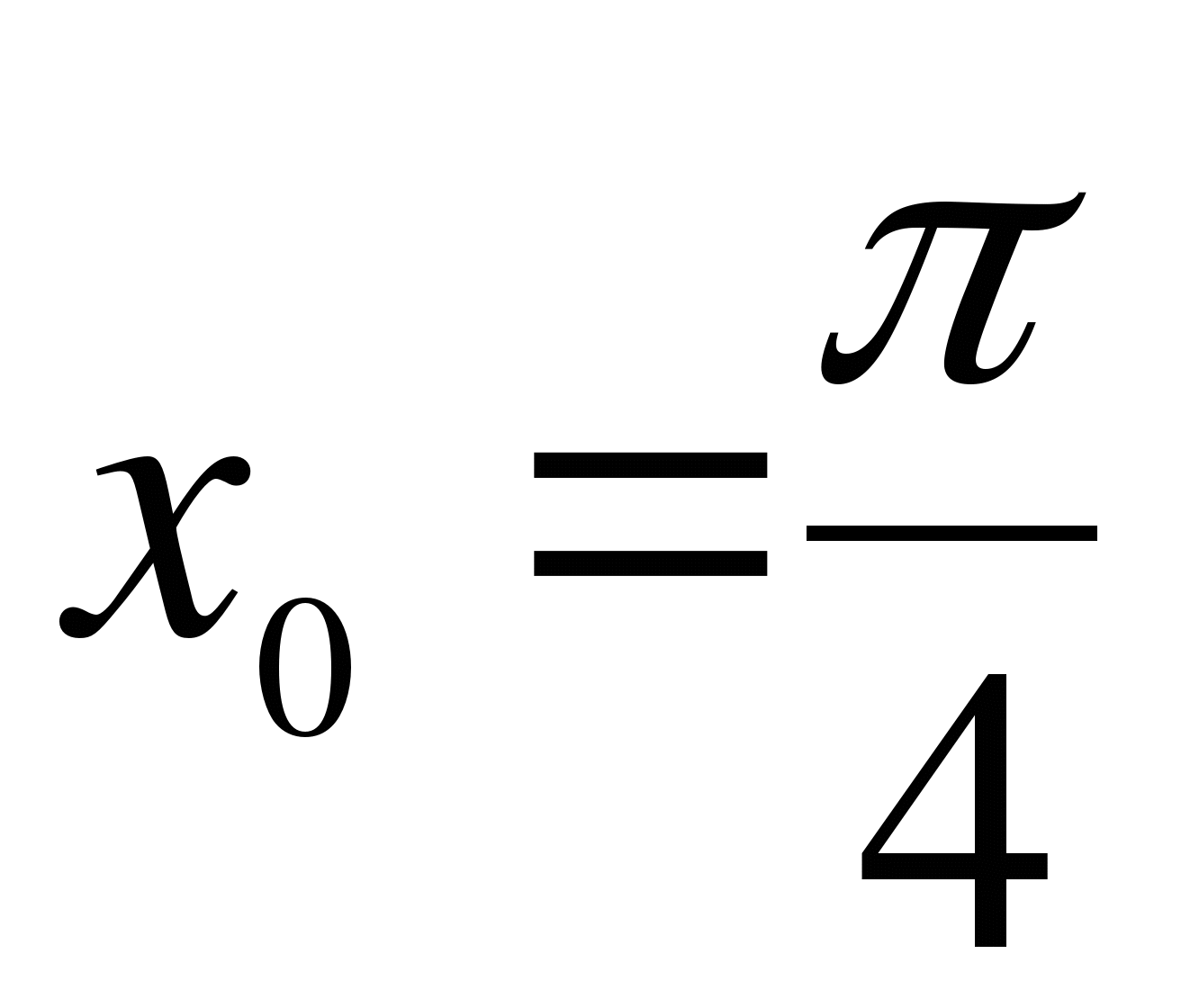 .
.
В а р и а н т 2. «Производная» К-2
Найти производную функции ( 1 – 3 ):
-
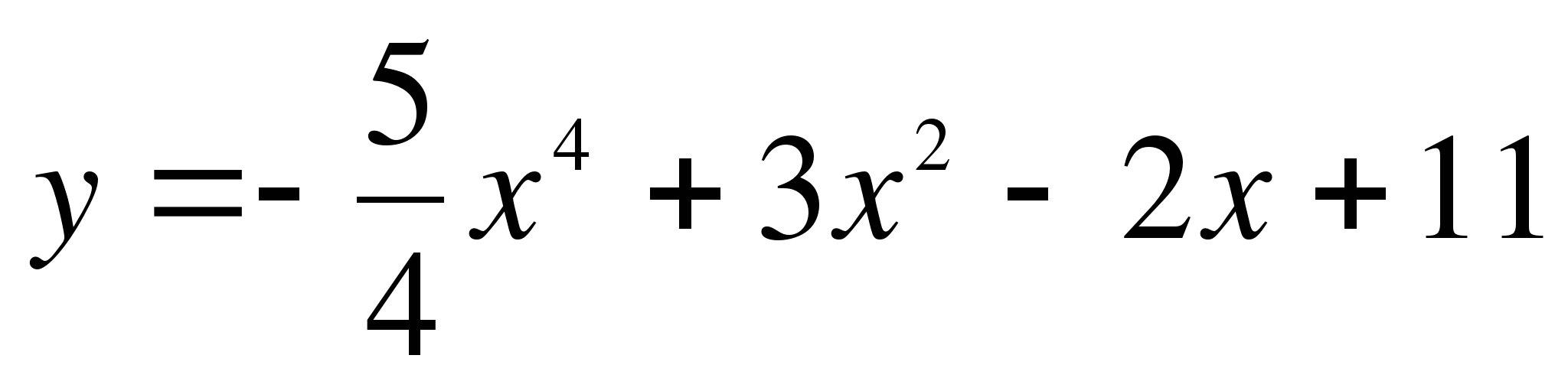
-
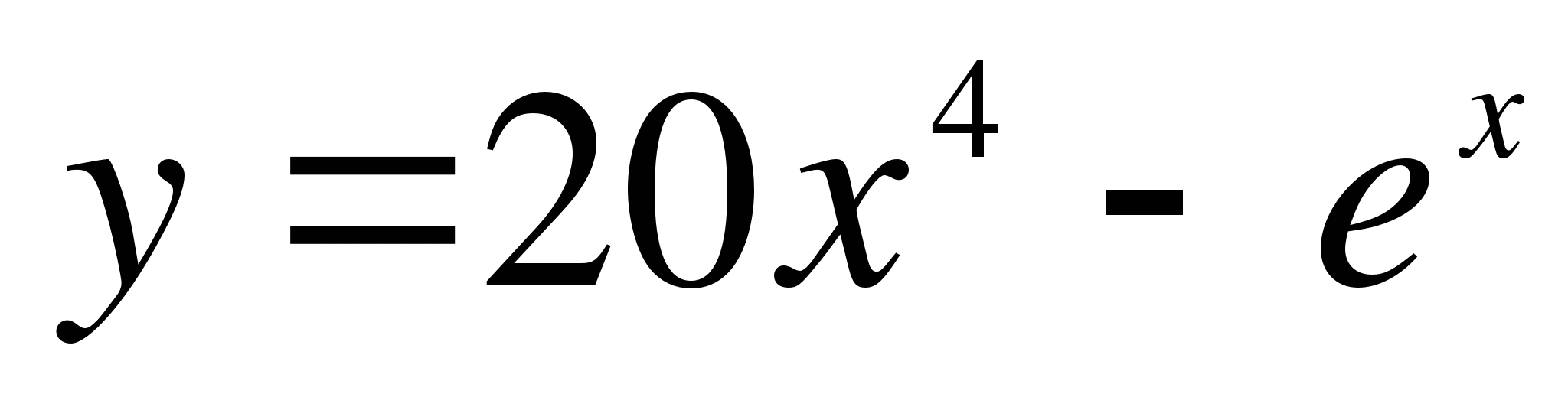
-
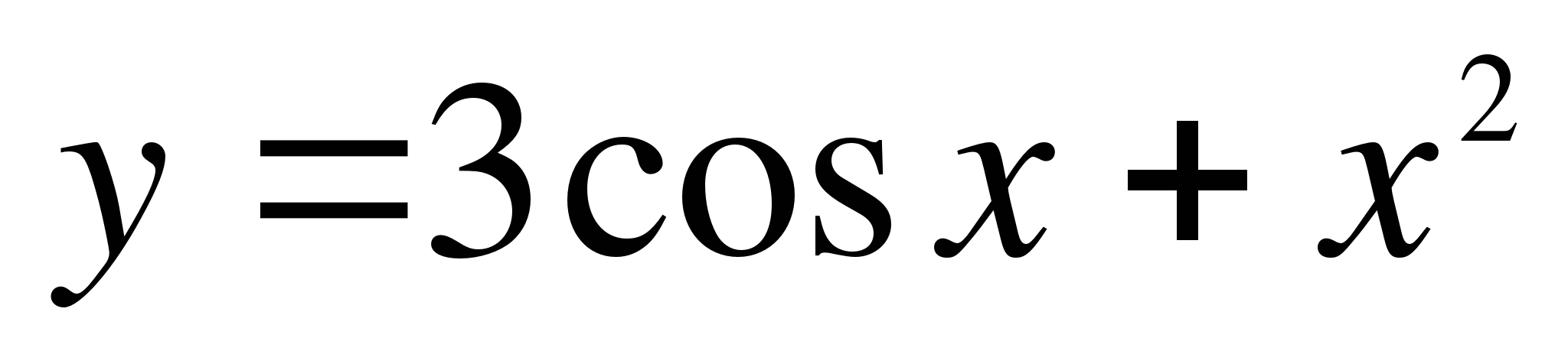
-
Тело движется по прямой так, что его скорость v (м/с) изменяется по закону 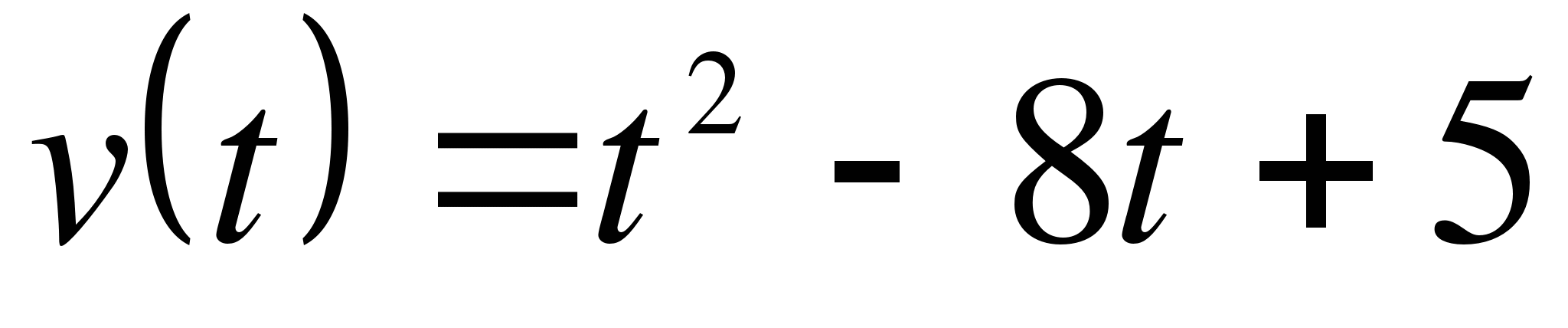 . Какую скорость приобретает тело в момент, когда его ускорение равно 12м/с2.
. Какую скорость приобретает тело в момент, когда его ускорение равно 12м/с2.
-
Найдите тангенс угла наклона касательной, проведенной к графику функции 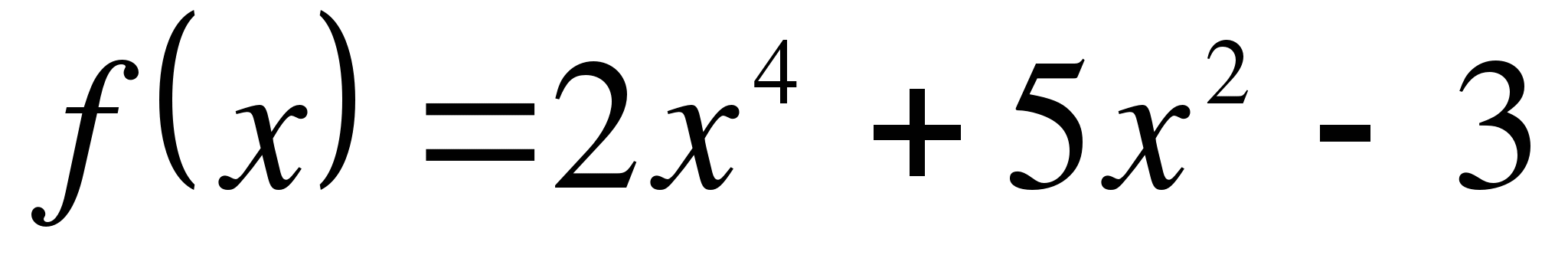 в точке с абсциссой
в точке с абсциссой 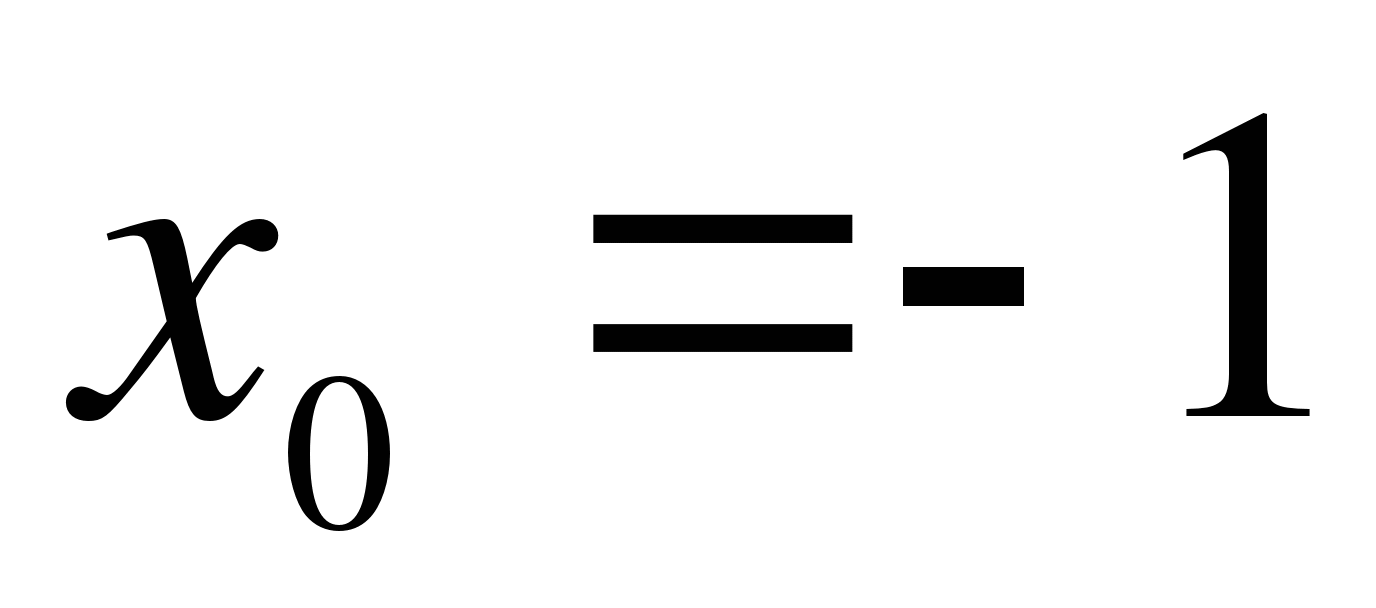 .
.
-
Найдите угловой коэффициент касательной, проведенной к параболе 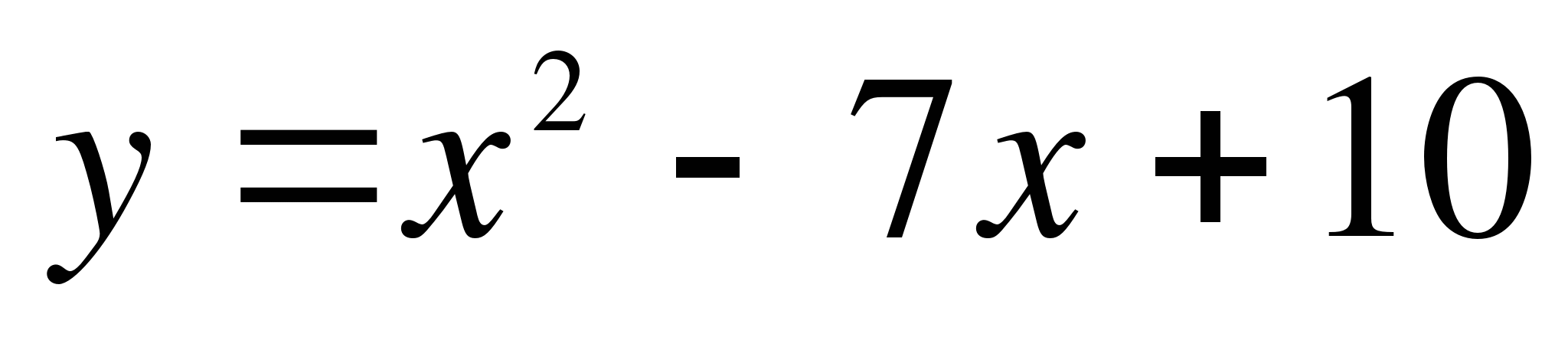 в точке с абсциссой
в точке с абсциссой 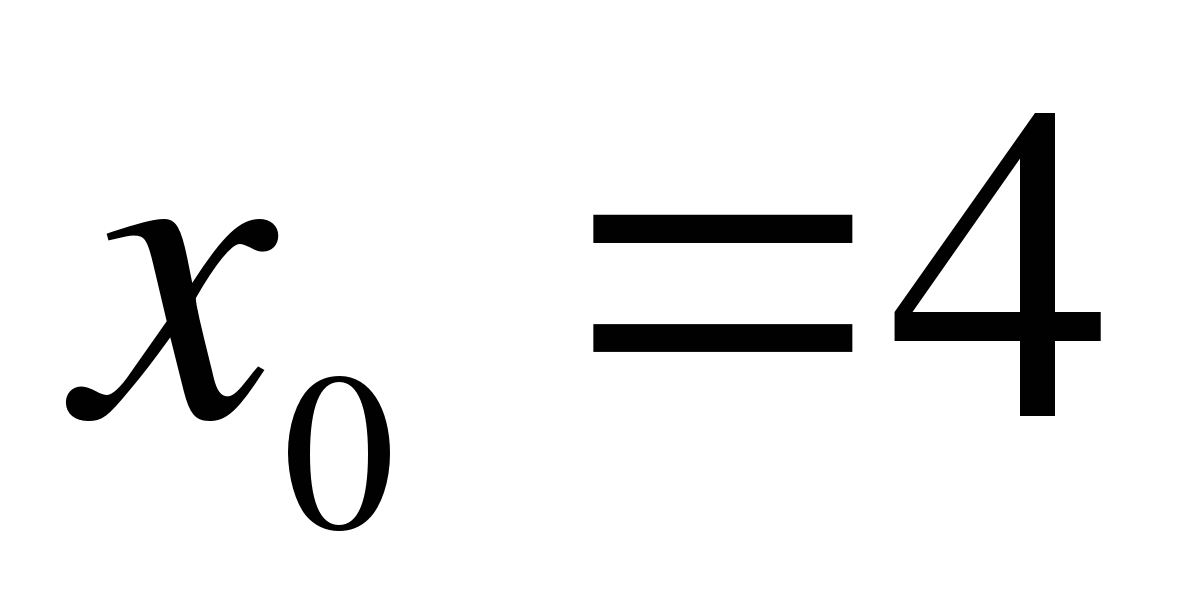 .
.
-
Найдите угол ( в градусах), образованный осью Ох и касательной к графику функции 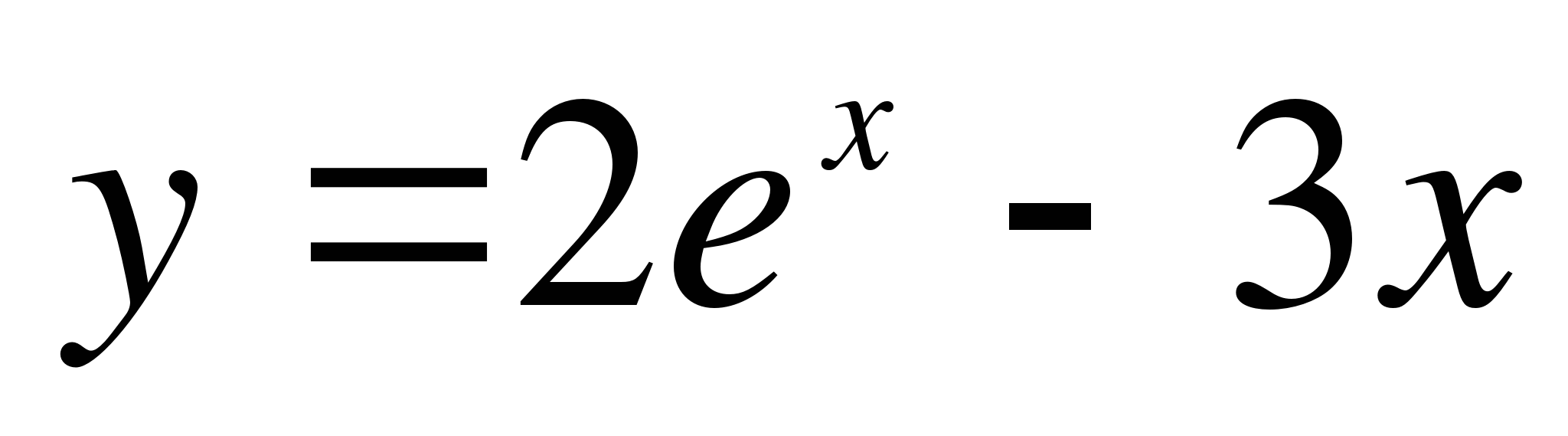 в точке
в точке 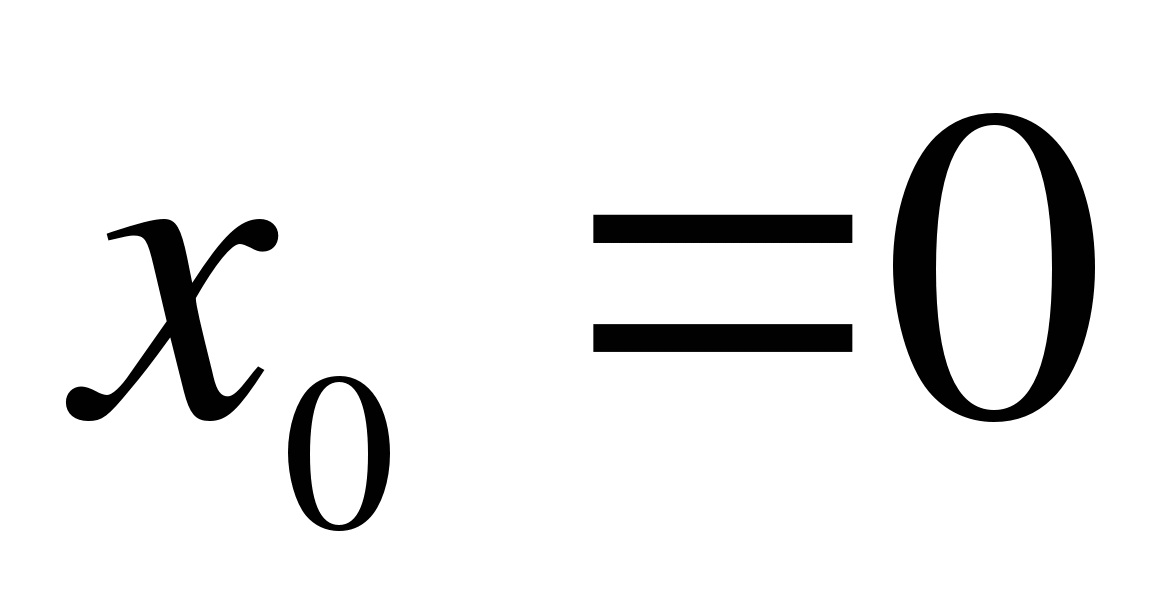
-
Тело удаляется от поверхности Земли по закону 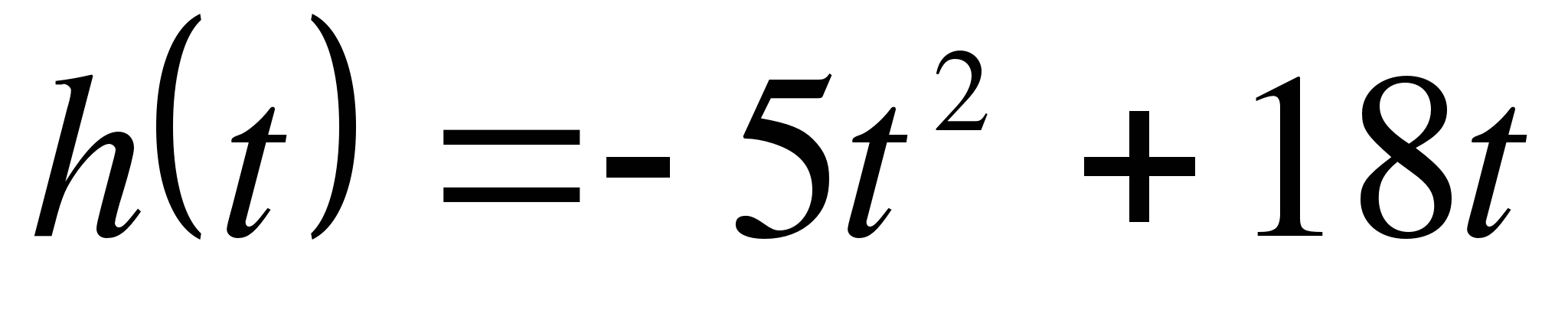 (t – время, h – расстояние от поверхности Земли до тела). В какой момент времени скорость будет равна 3?
(t – время, h – расстояние от поверхности Земли до тела). В какой момент времени скорость будет равна 3?
Найдите производные функций ( 9 – 11):
-
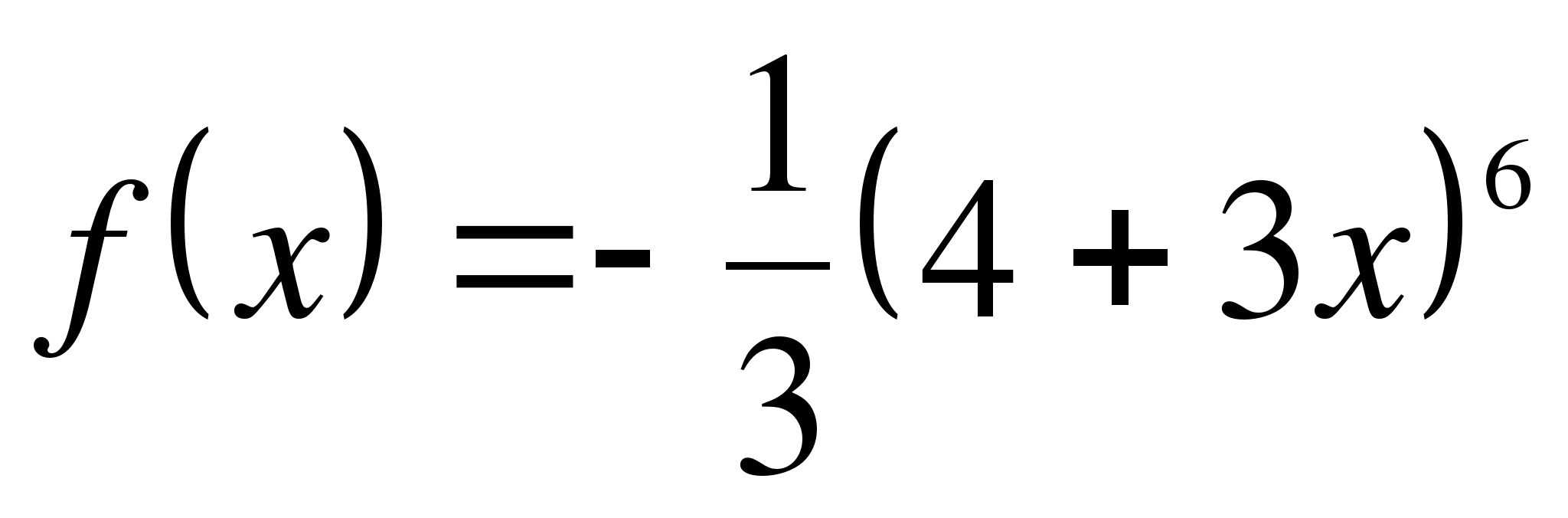
-
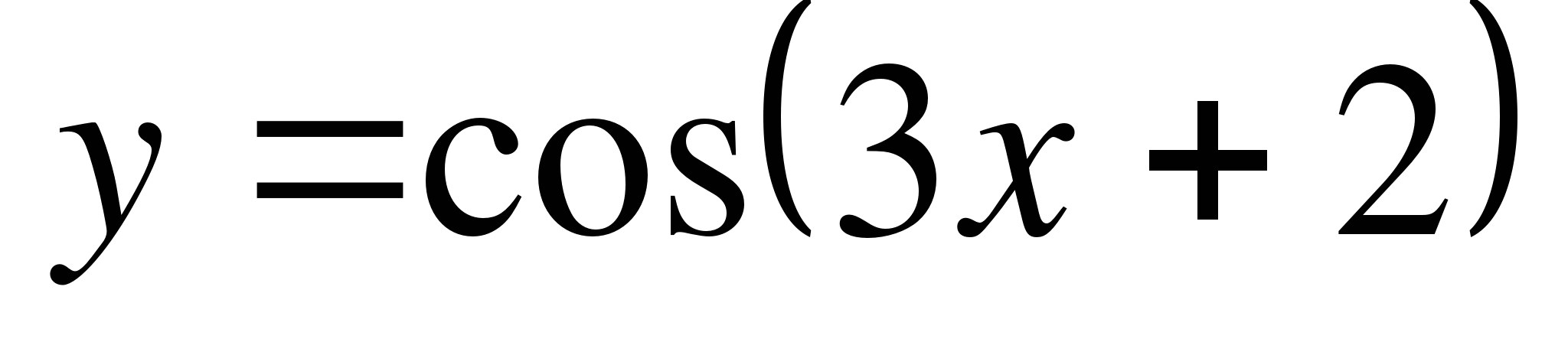
-
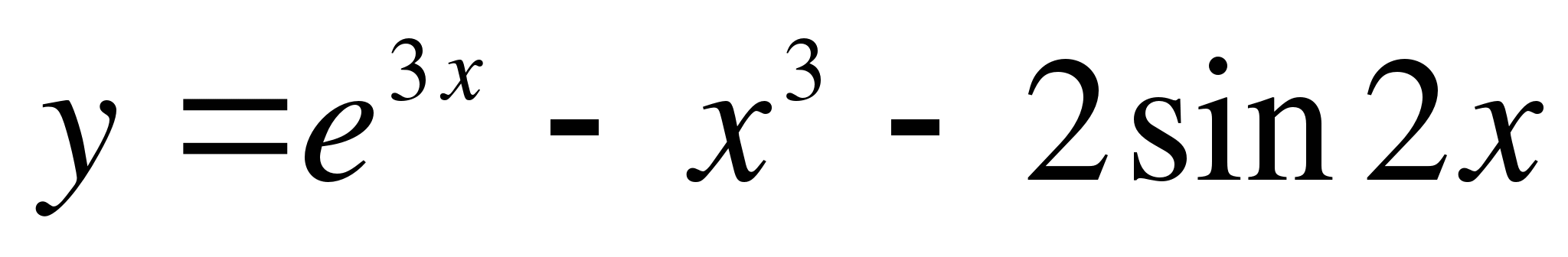
-
Найдите значение производной функции 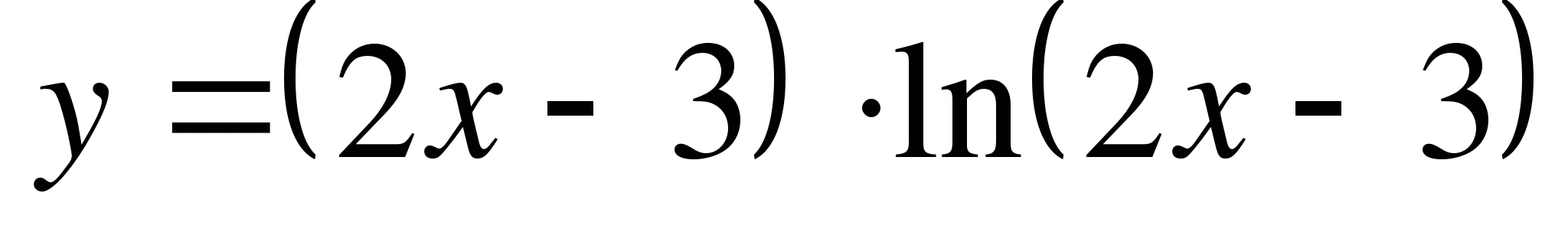 в точке
в точке 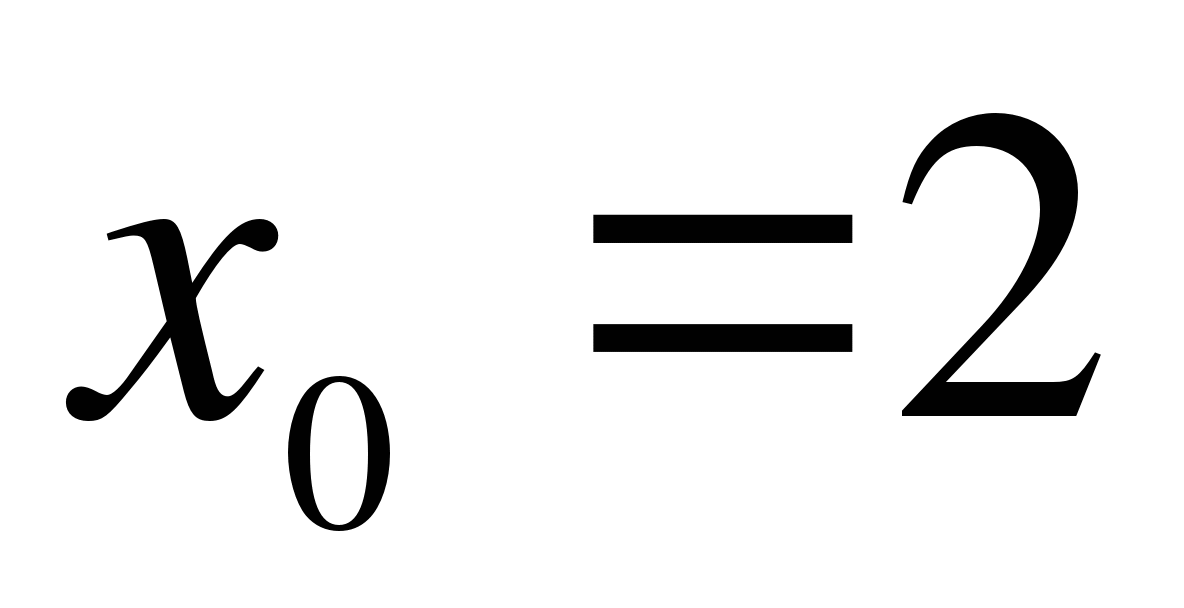 .
.
В а р и а н т 3. «Производная» К-2
Найти производную функции ( 1 – 3 ):
-
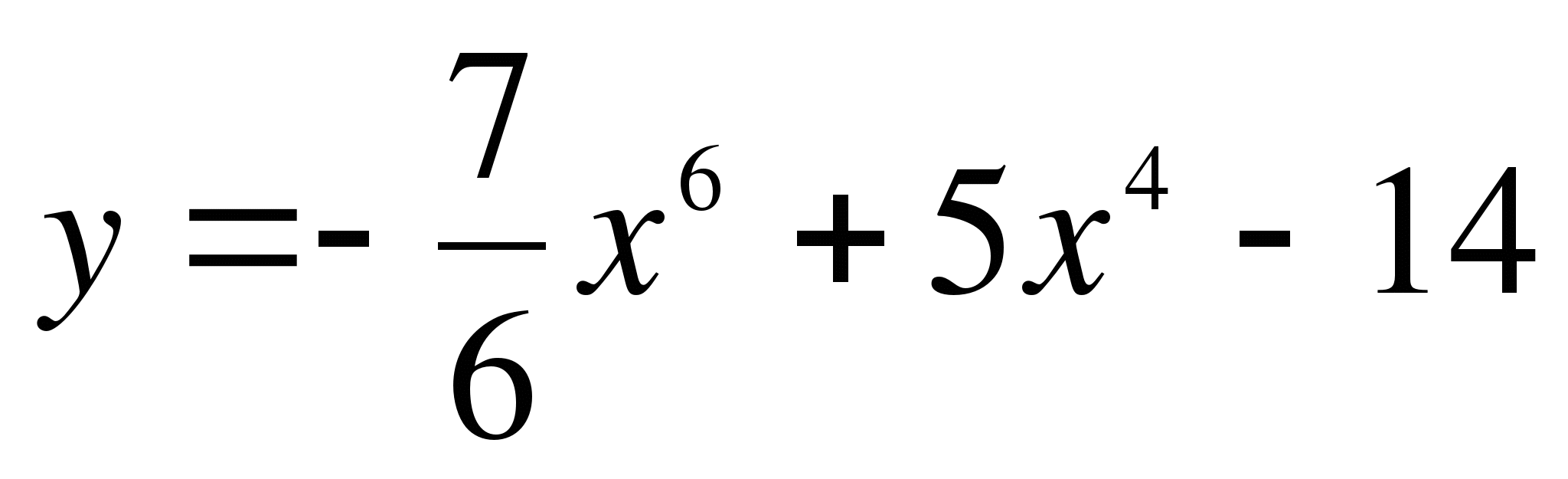
-
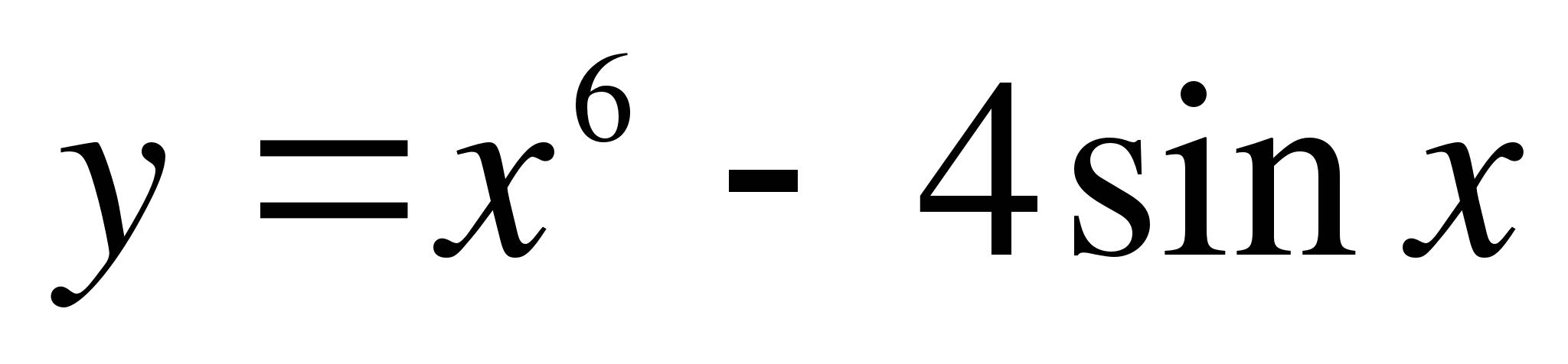
-
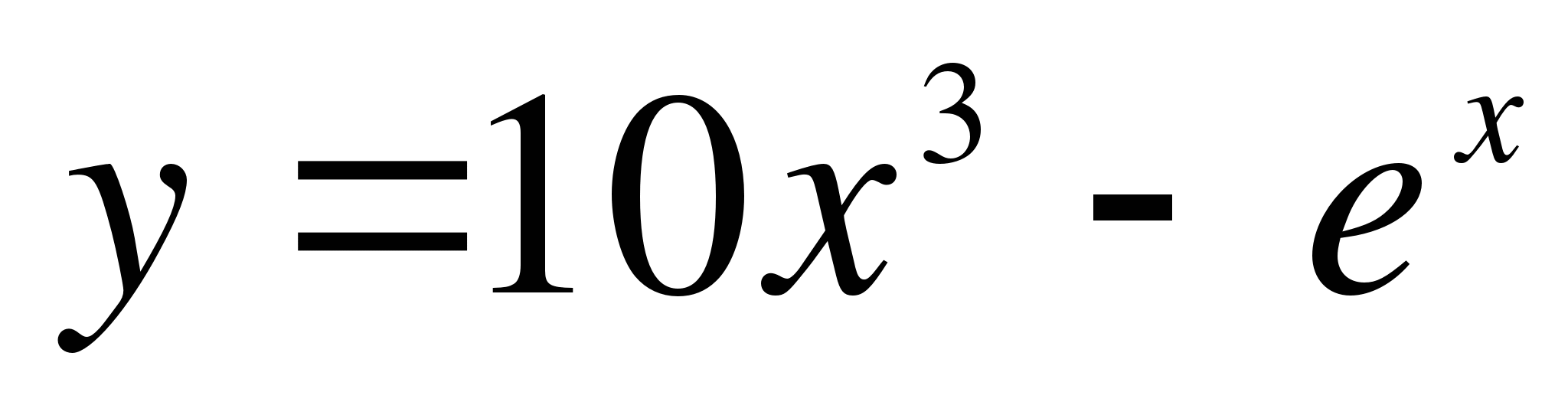
-
При движении тела по прямой от начальной точки М путь 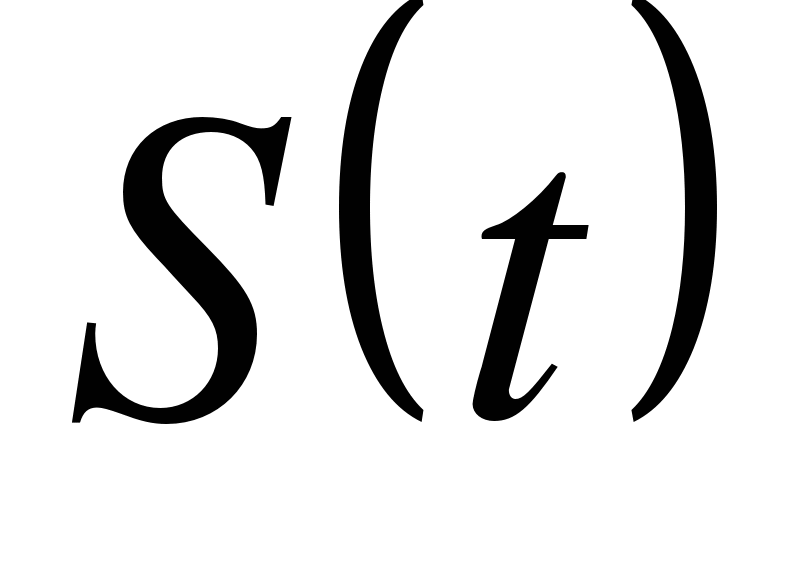 ( в метрах ) изменяется по закону
( в метрах ) изменяется по закону 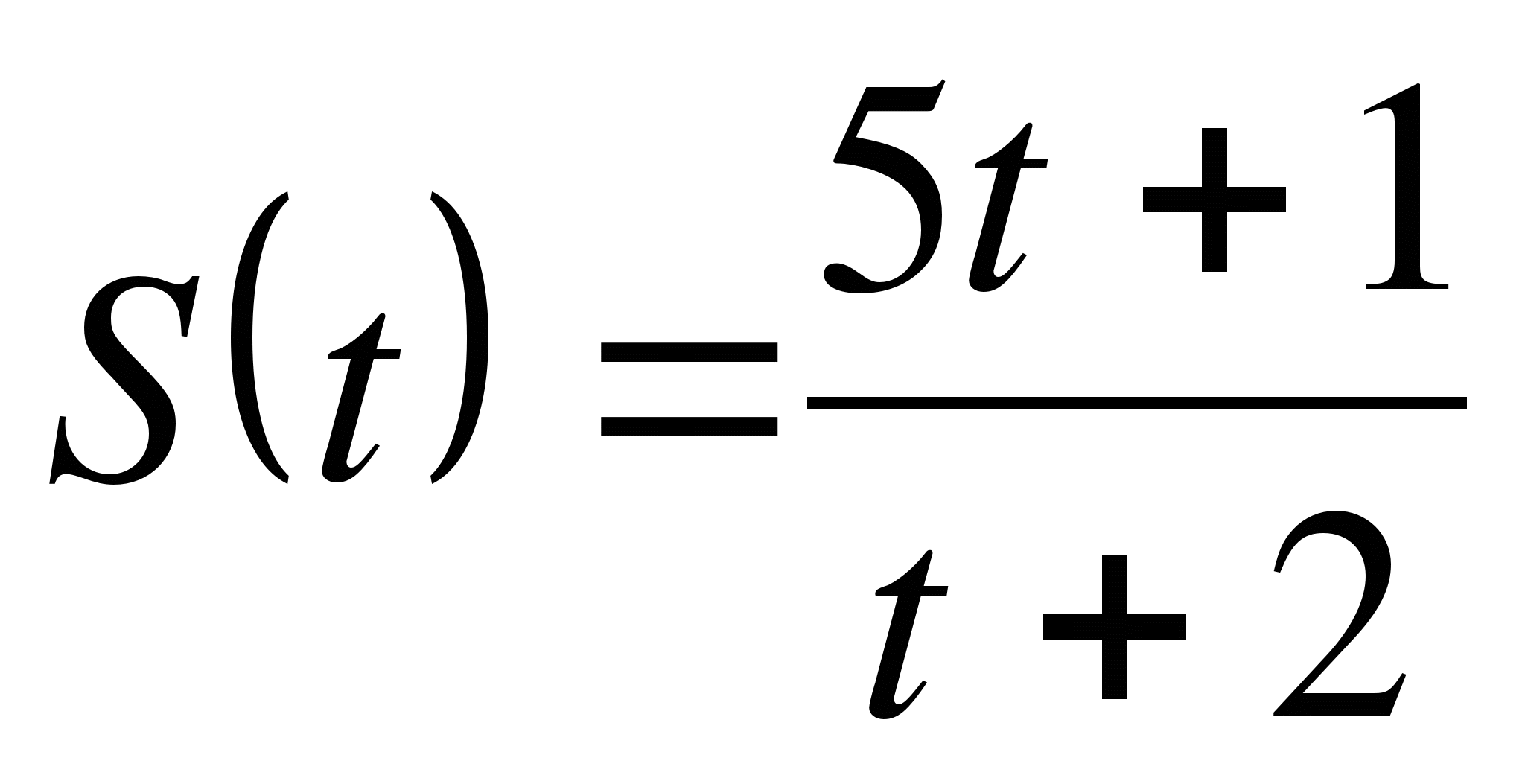 ( t – время в секундах ). Найдите скорость в момент
( t – время в секундах ). Найдите скорость в момент 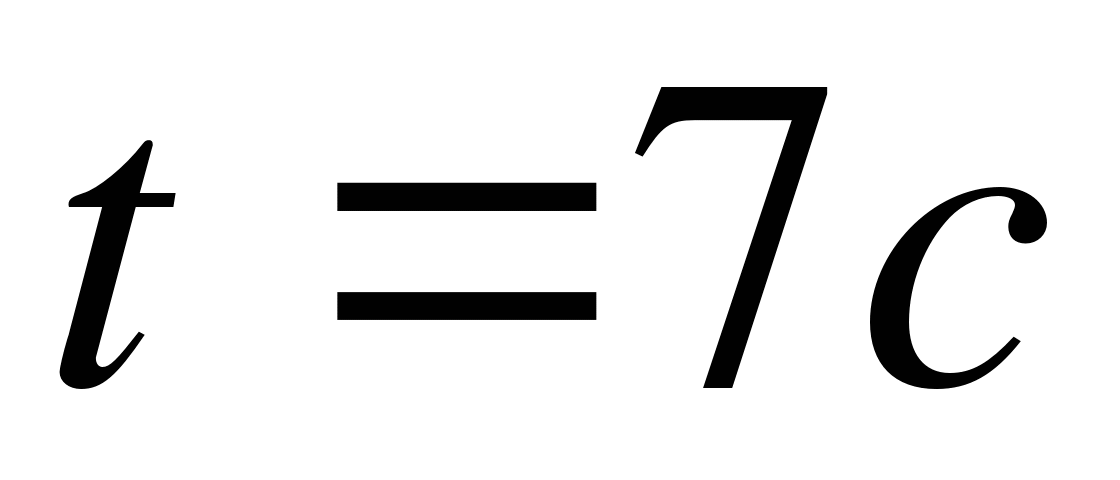 .
.
-
Найдите угловой коэффициент касательной, проведенной к графику функции 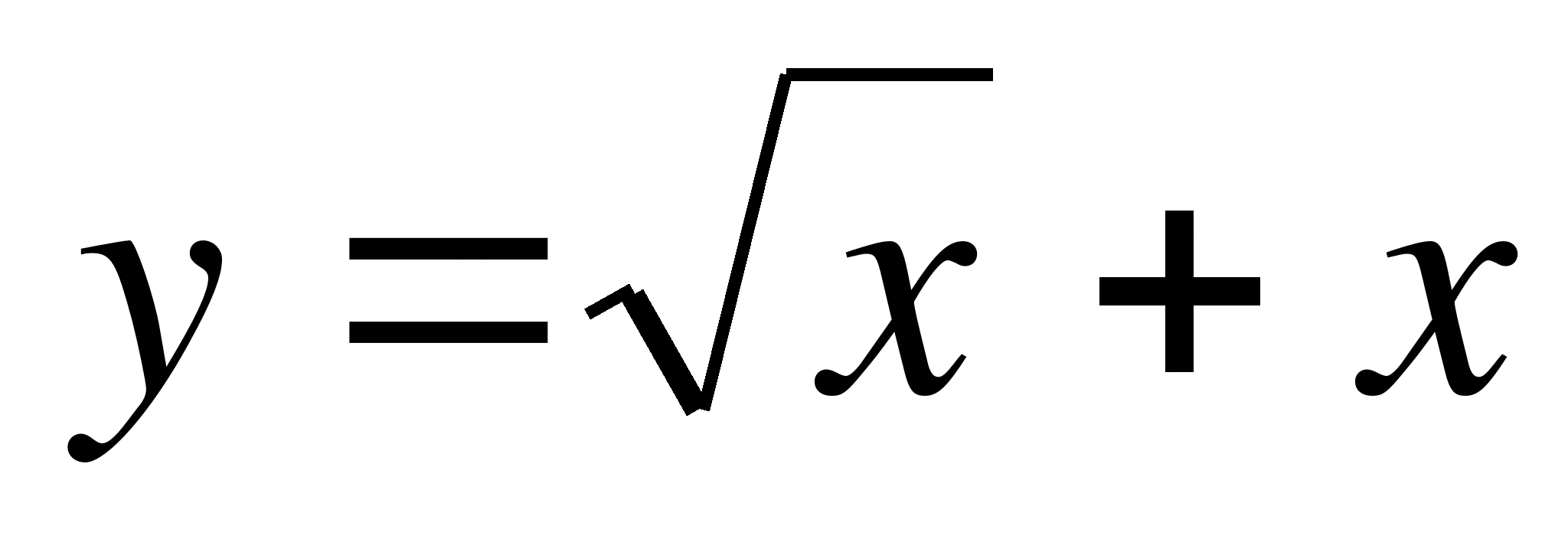 в точке
в точке 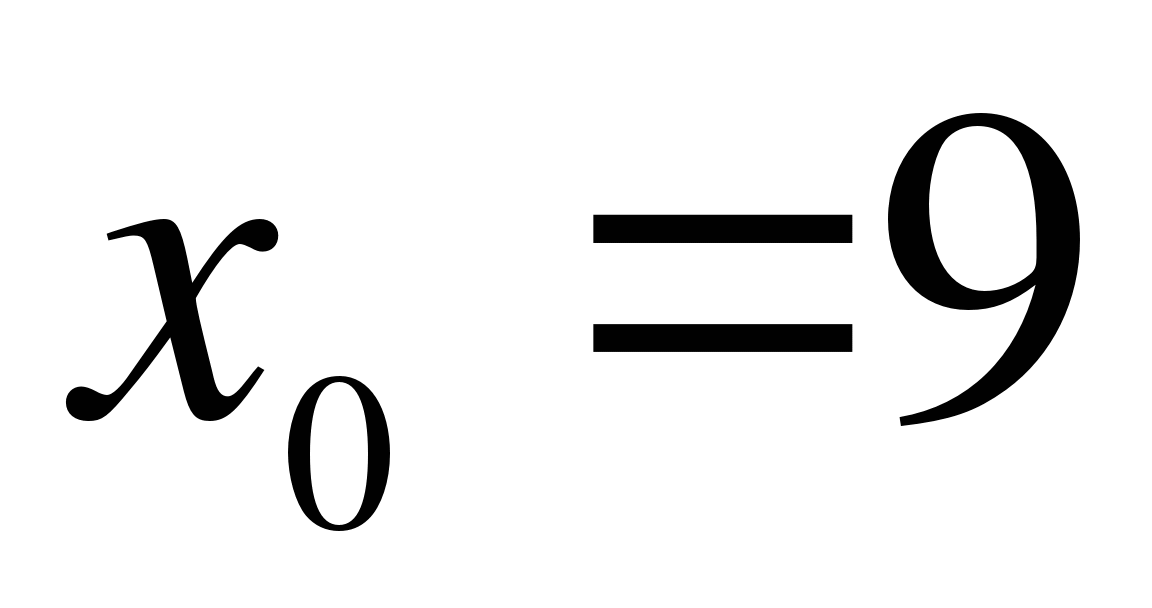 .
.
-
Найдите угловой коэффициент касательной, проведенной к графику функции 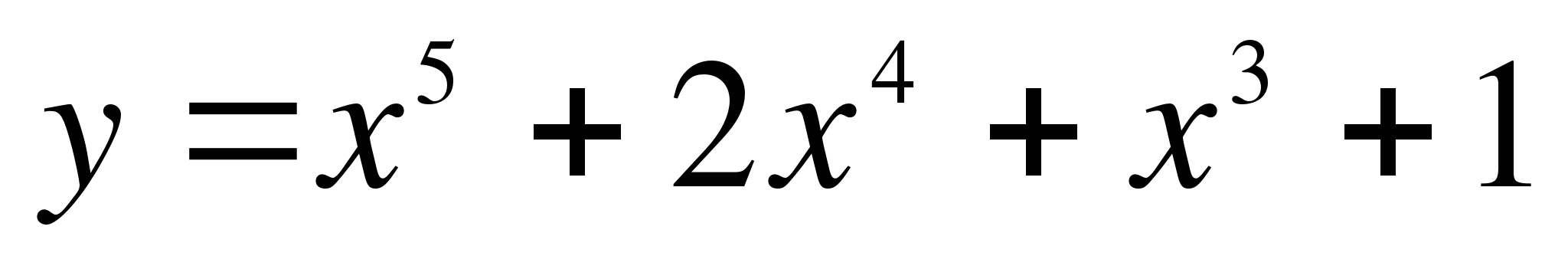 в точке
в точке 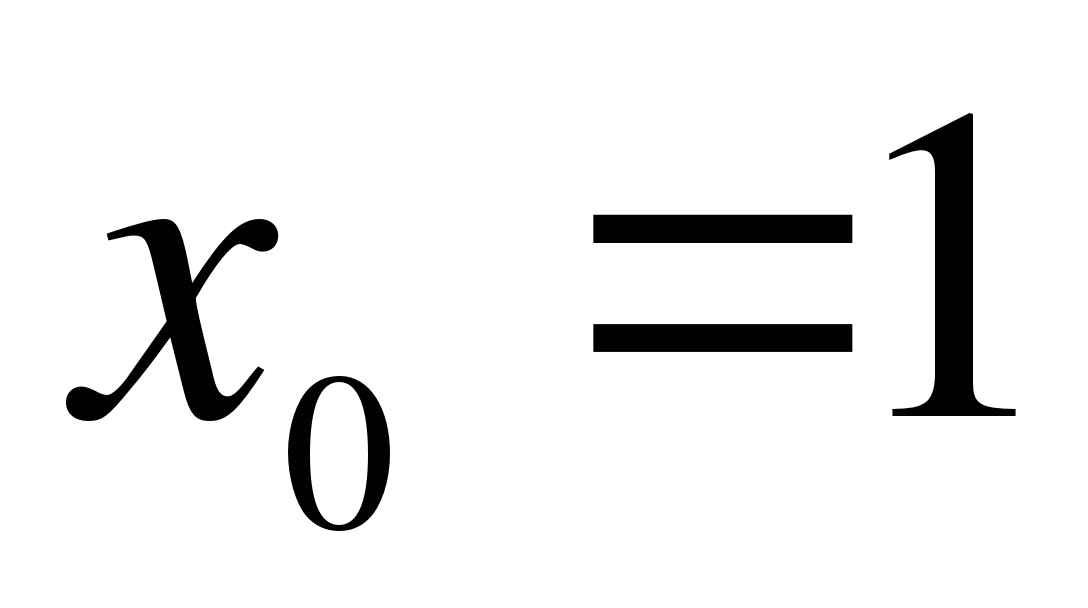 .
.
-
Найдите сумму тангенсов углов наклона касательных к параболе 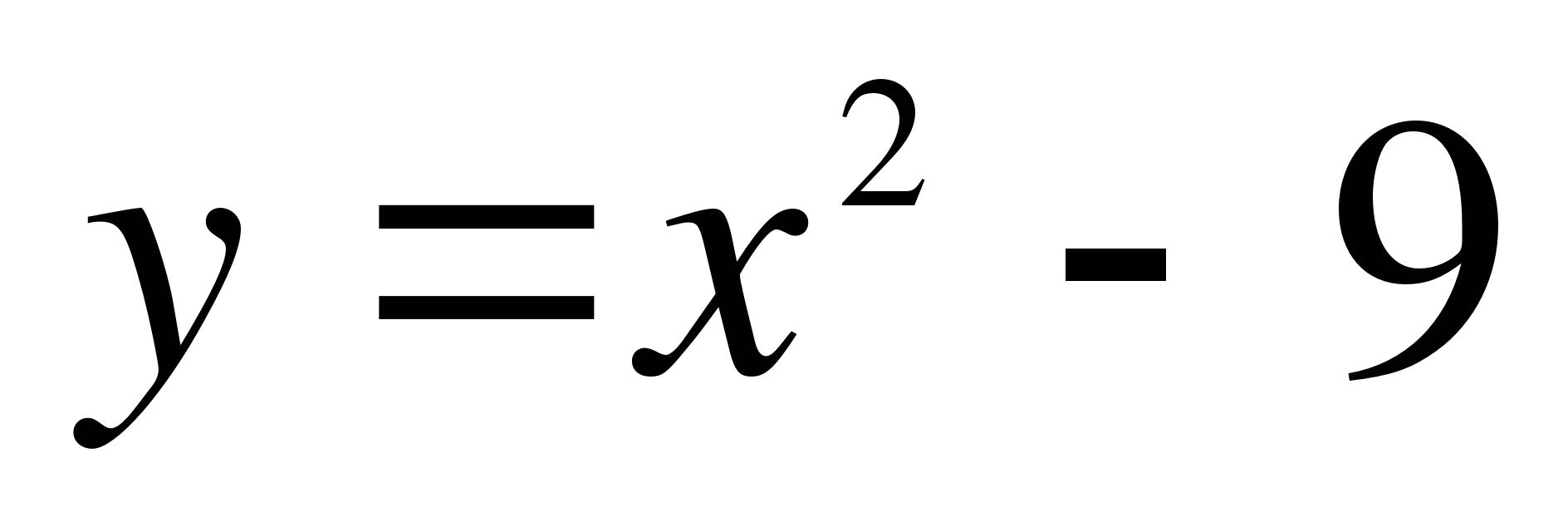 в точках пересечения параболы с осью абсцисс.
в точках пересечения параболы с осью абсцисс.
-
Найдите абсциссу точки графика функции 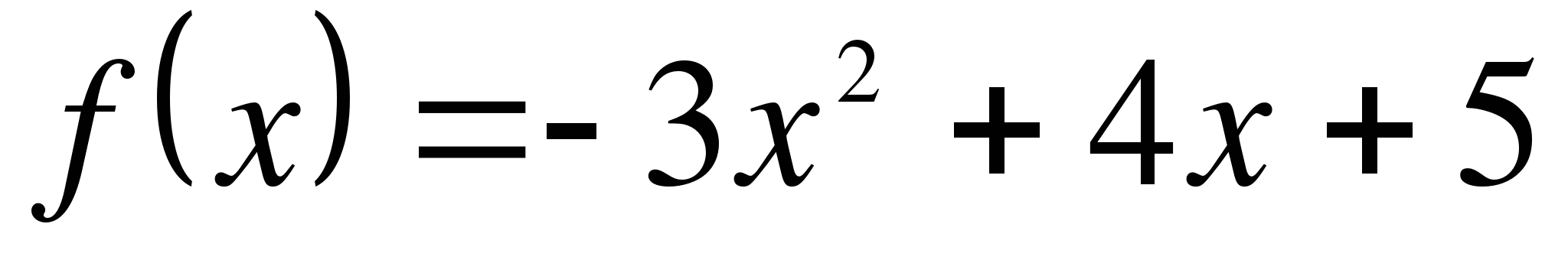 в которой угловой коэффициент касательной равен -8,6.
в которой угловой коэффициент касательной равен -8,6.
Найдите производные функций ( 9 – 11):
-

-
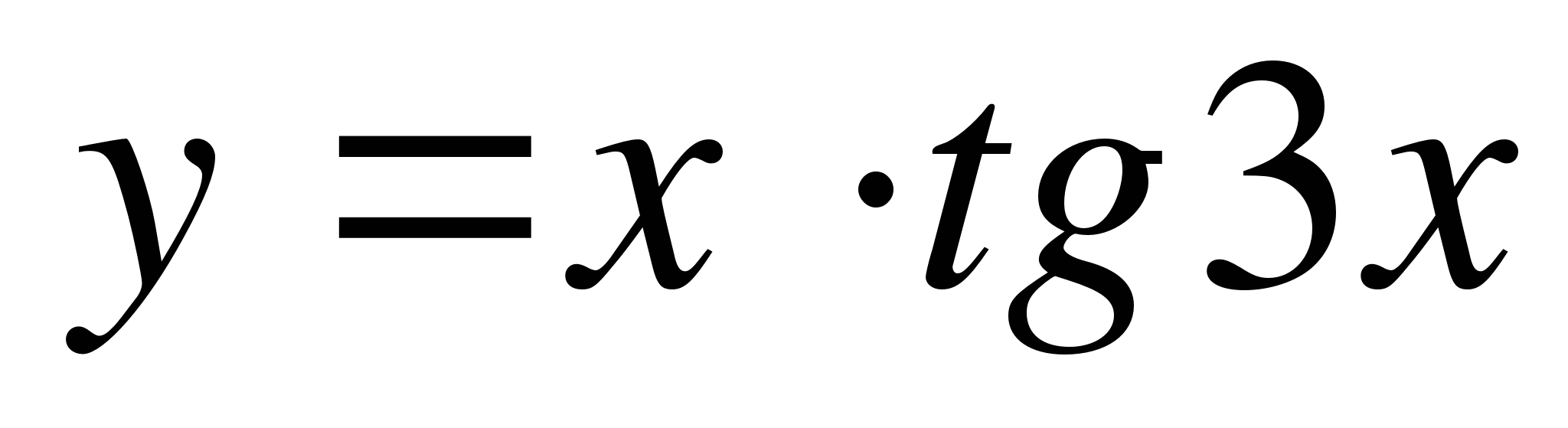
-
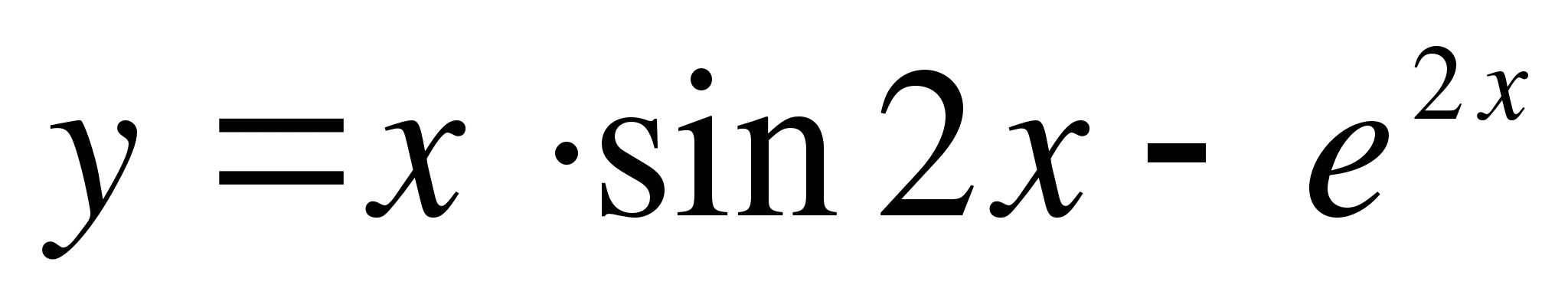
-
Найдите значение производной функции 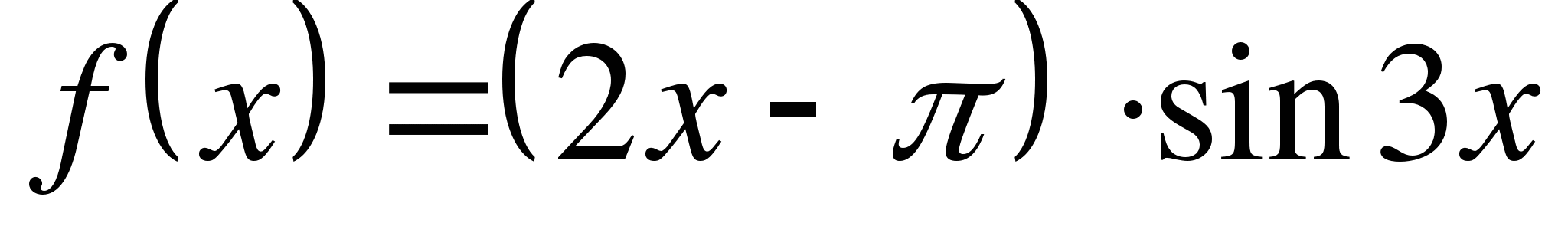 в точке
в точке 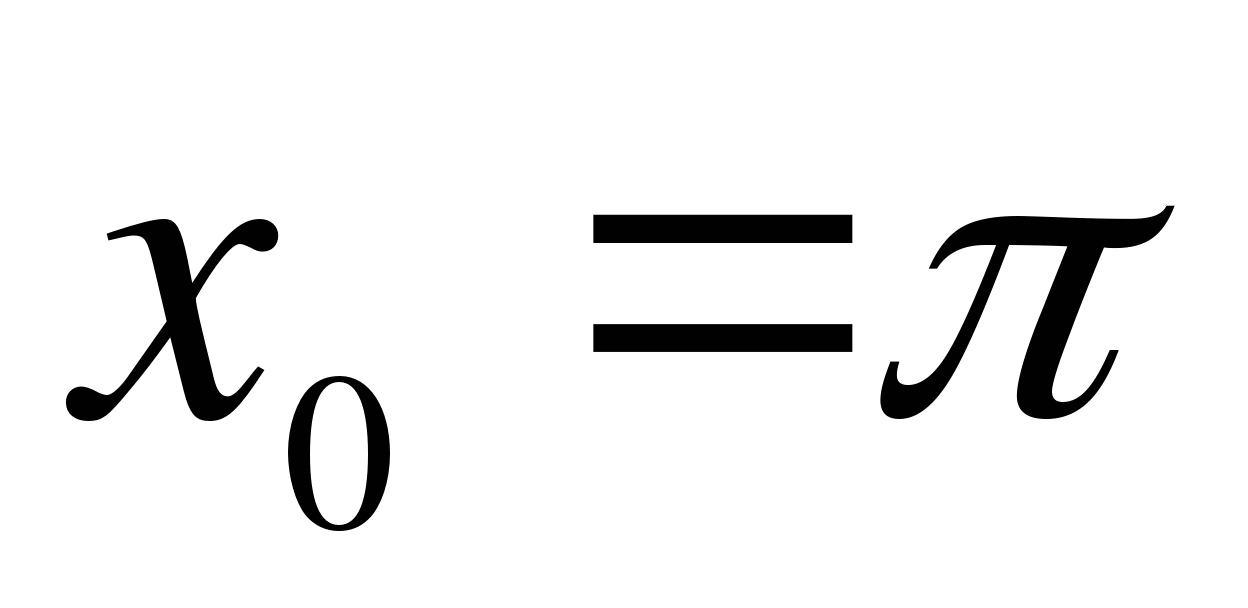 .
.
В а р и а н т 4. «Производная» К-2
Найти производную функции ( 1 – 3 ):
-
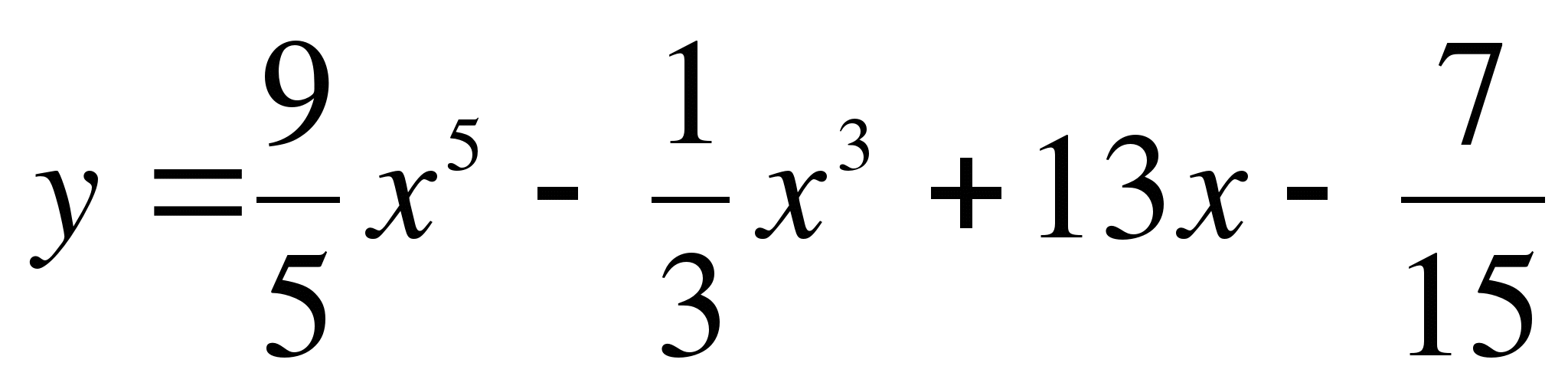
-
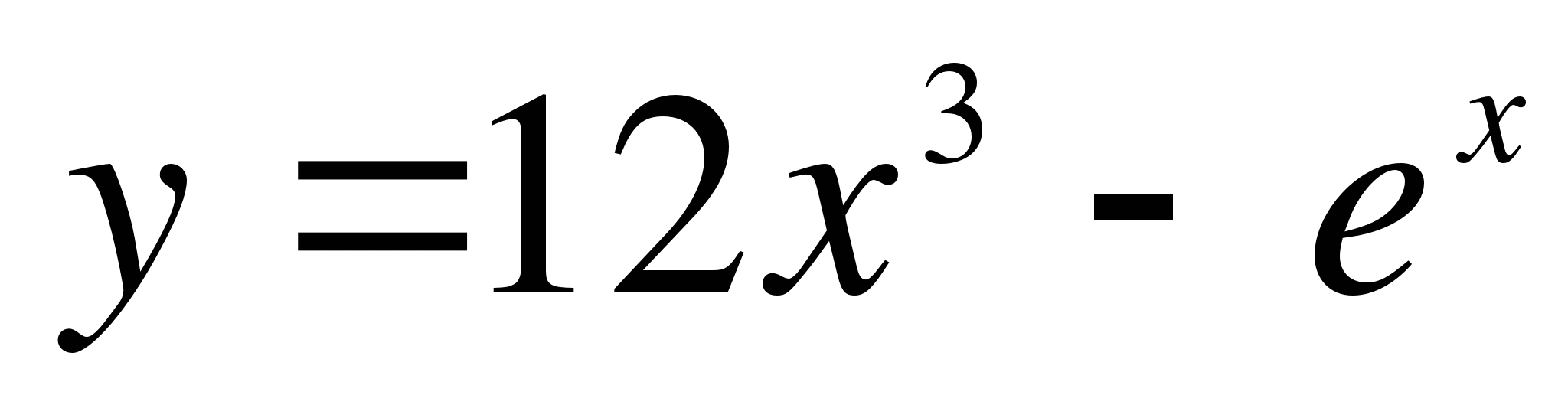
-
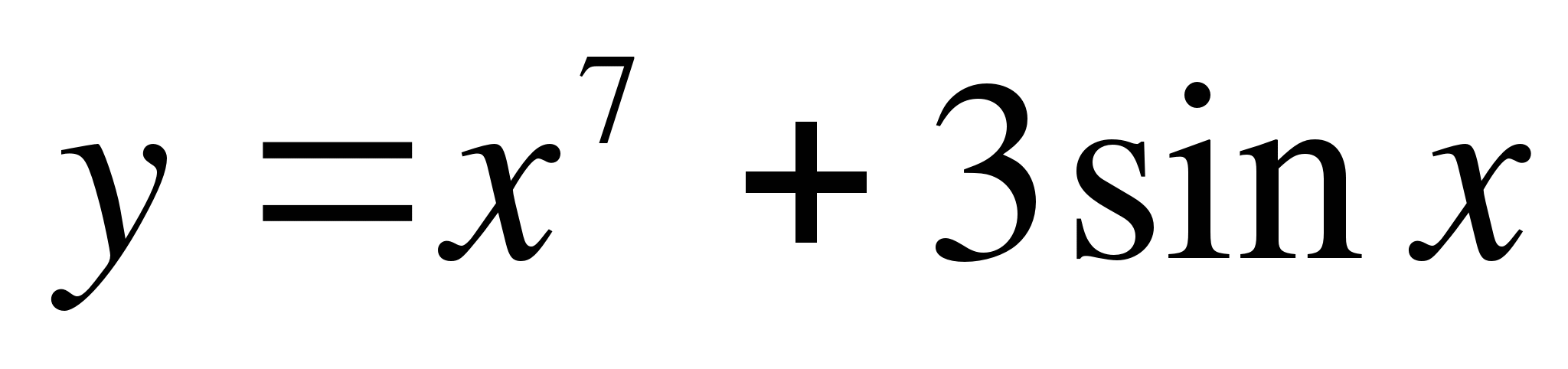
-
Тело движется по прямой так, что его скорость v (м/с) изменяется по закону 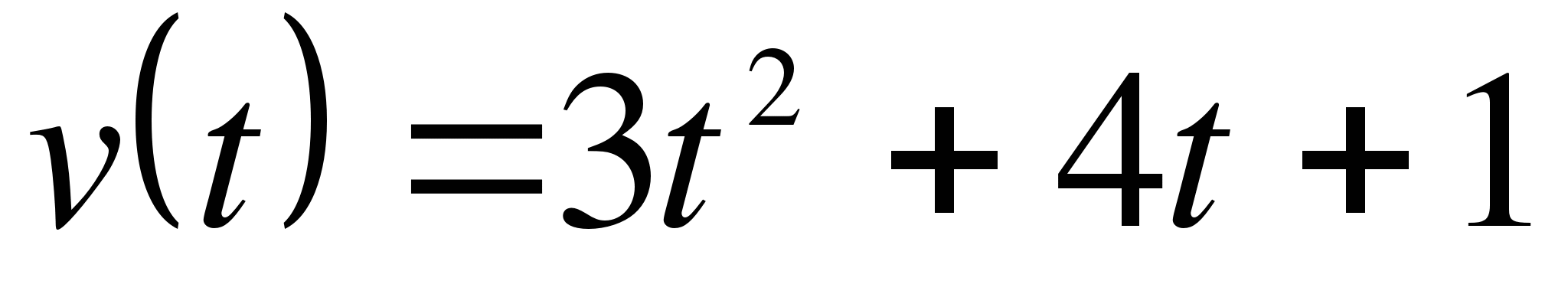 . Какую скорость приобретает тело в момент, когда его его ускорение станет равным 10 м/с2.
. Какую скорость приобретает тело в момент, когда его его ускорение станет равным 10 м/с2.
-
Найдите абсциссу точки, в которой касательная к графику функции наклонена к оси Ох под углом α, если 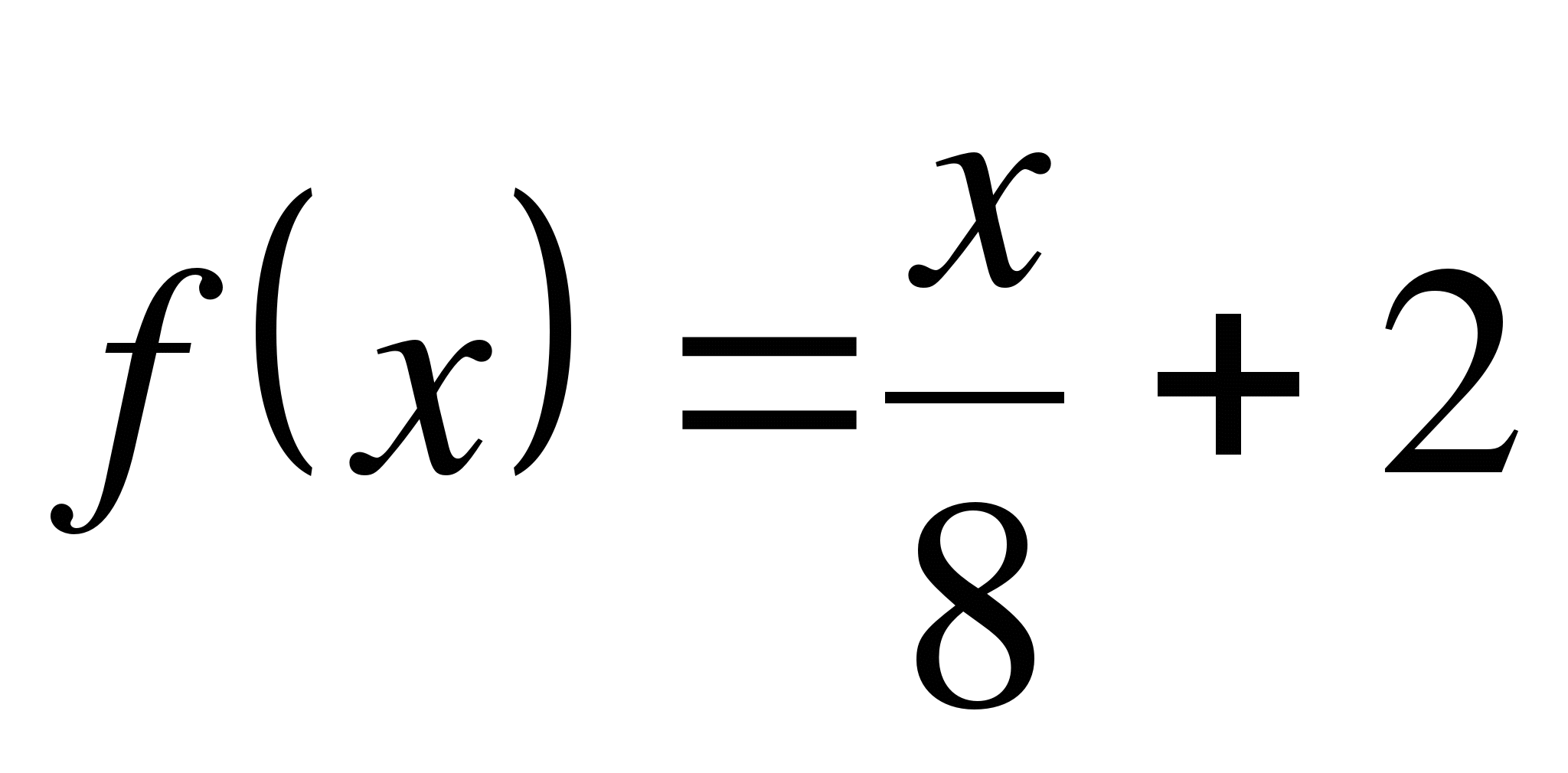 ;
; 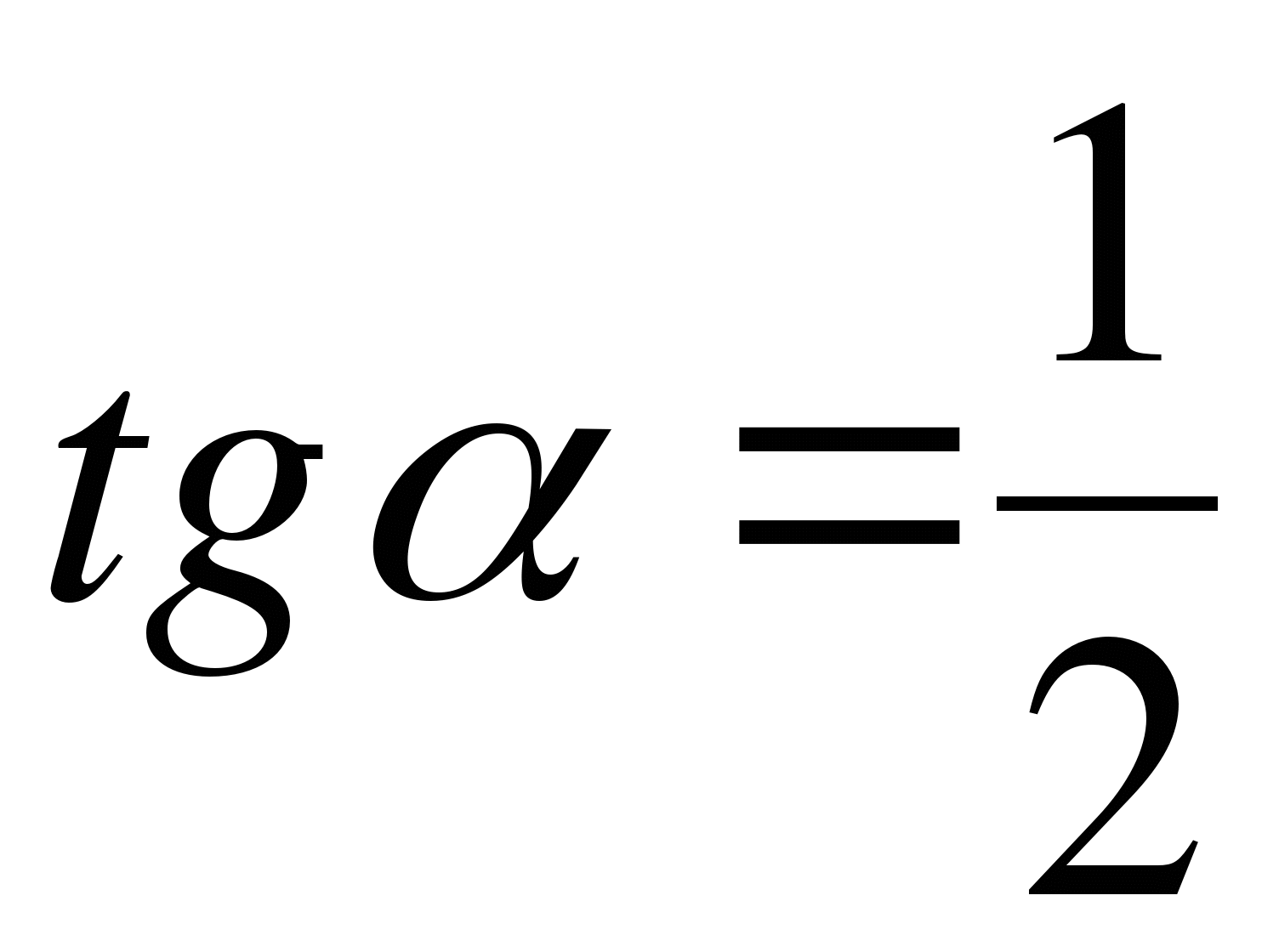 .
.
-
Найдите угловой коэффициент касательной, проведенной к графику функции 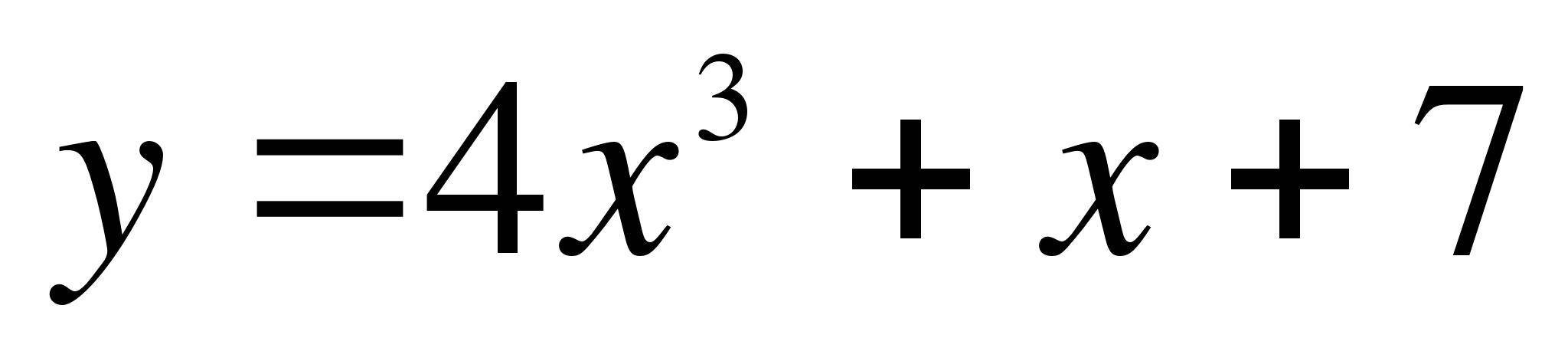 в точке
в точке 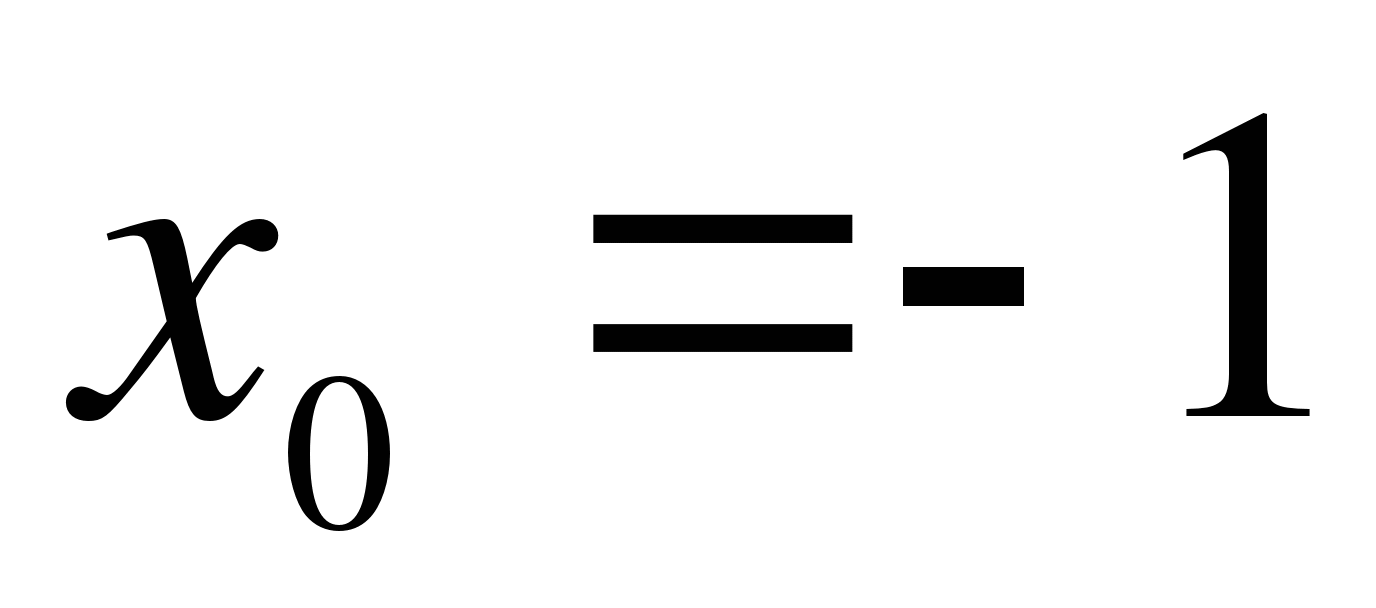 .
.
-
Найдите сумму угловых коэффициентов касательных к параболе 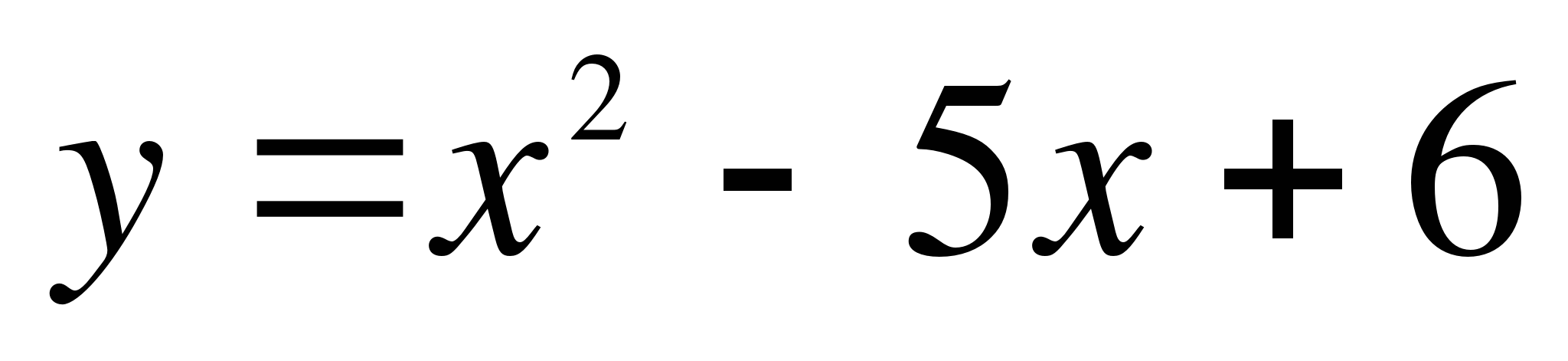 в точках пересечения параболы с осью абсцисс.
в точках пересечения параболы с осью абсцисс.
-
Материальная точка движется прямолинейно по закону 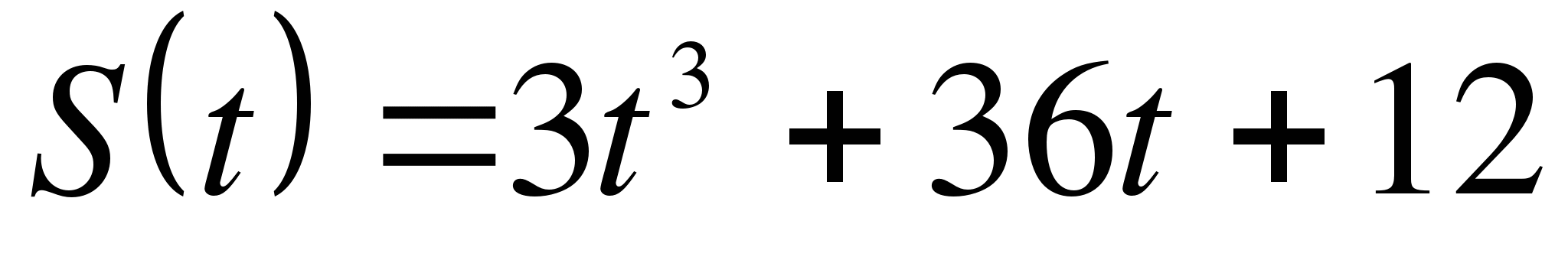 . В какой момент времени скорость точки будет равна 45?
. В какой момент времени скорость точки будет равна 45?
Найдите производные функций ( 9 – 11):
-
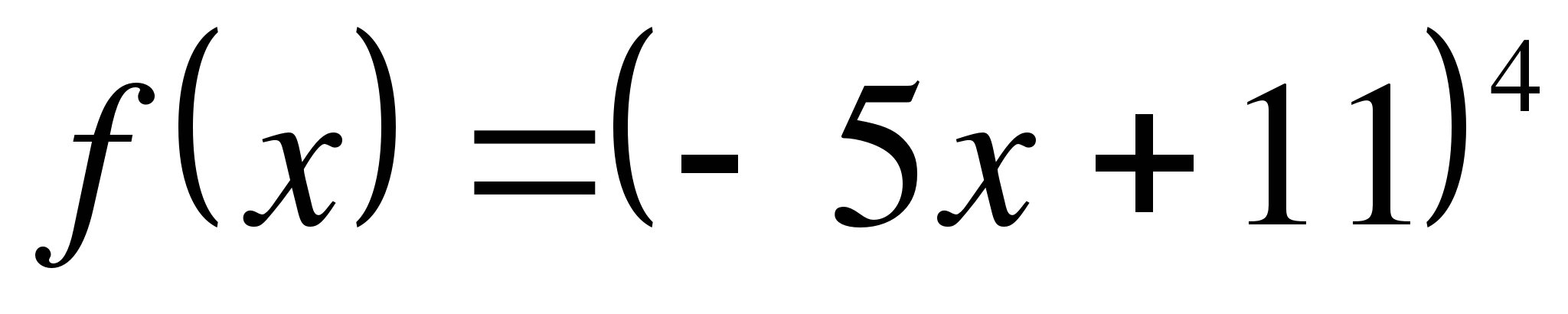
-
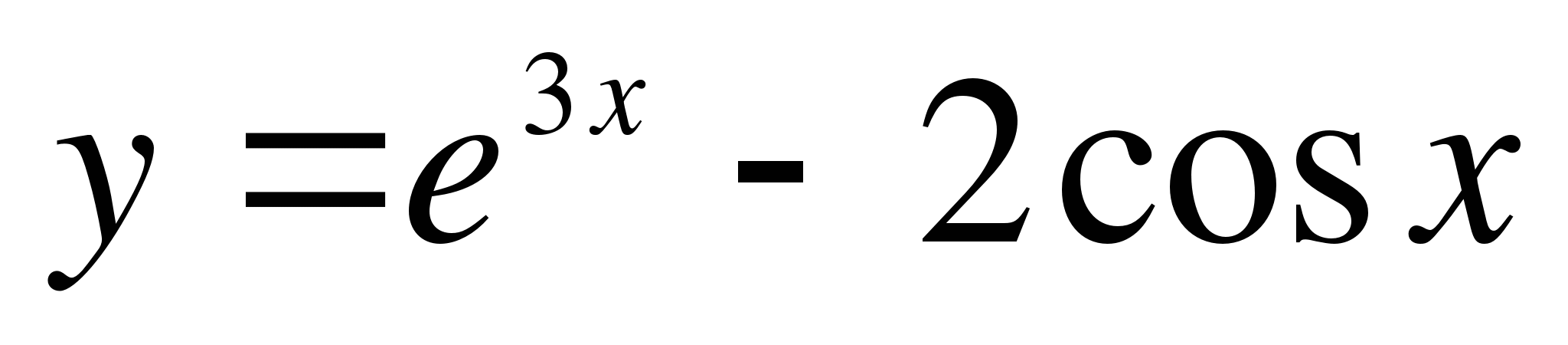
-
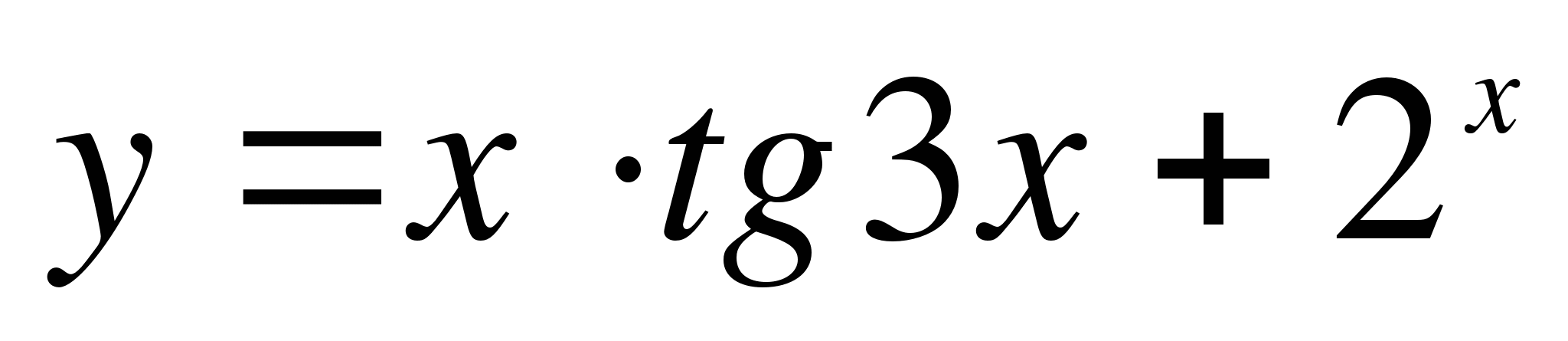
-
Найдите значение производной функции 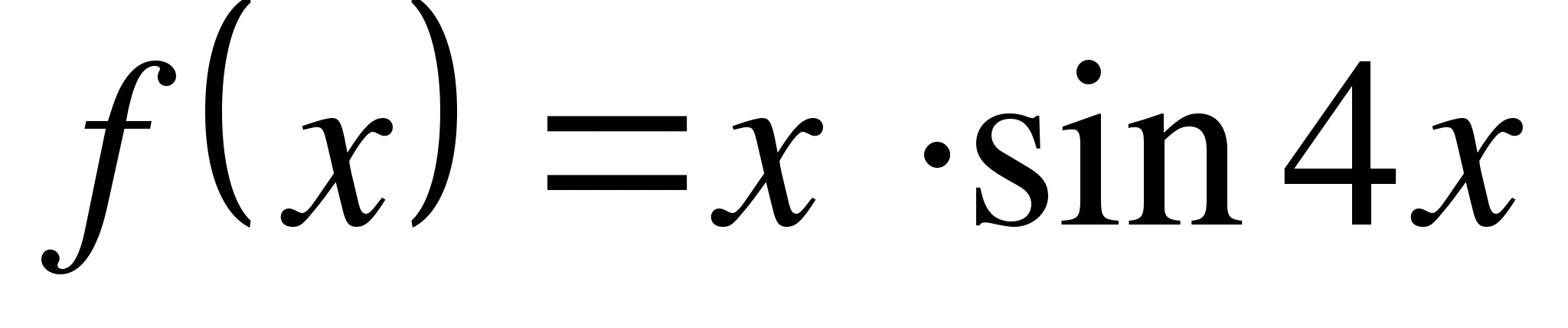 в точке
в точке 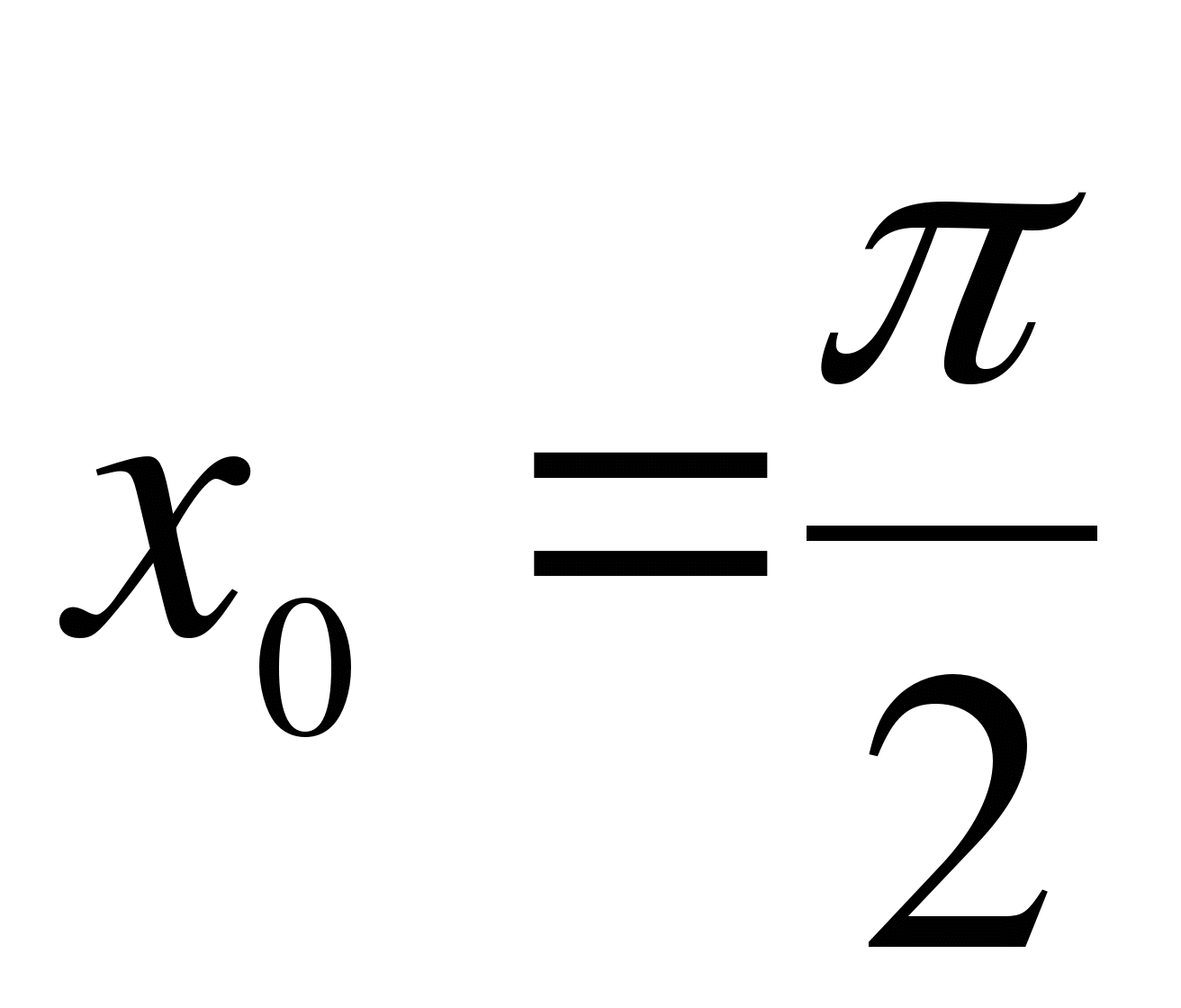 .
.
Демонстрационный в а р и а н т . «Производная» К-2
Найти производную функции ( 1 – 3 ):
-
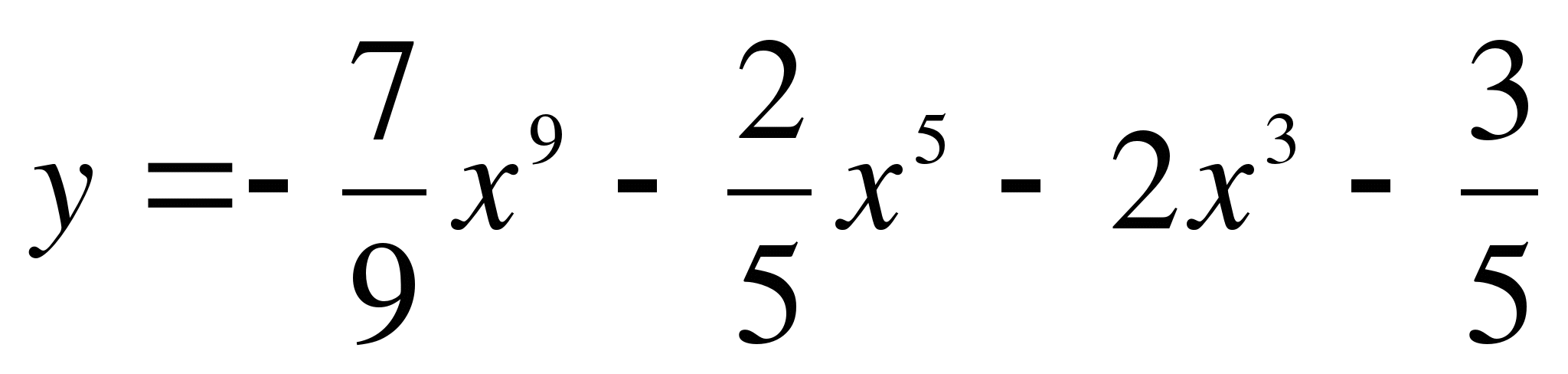
-
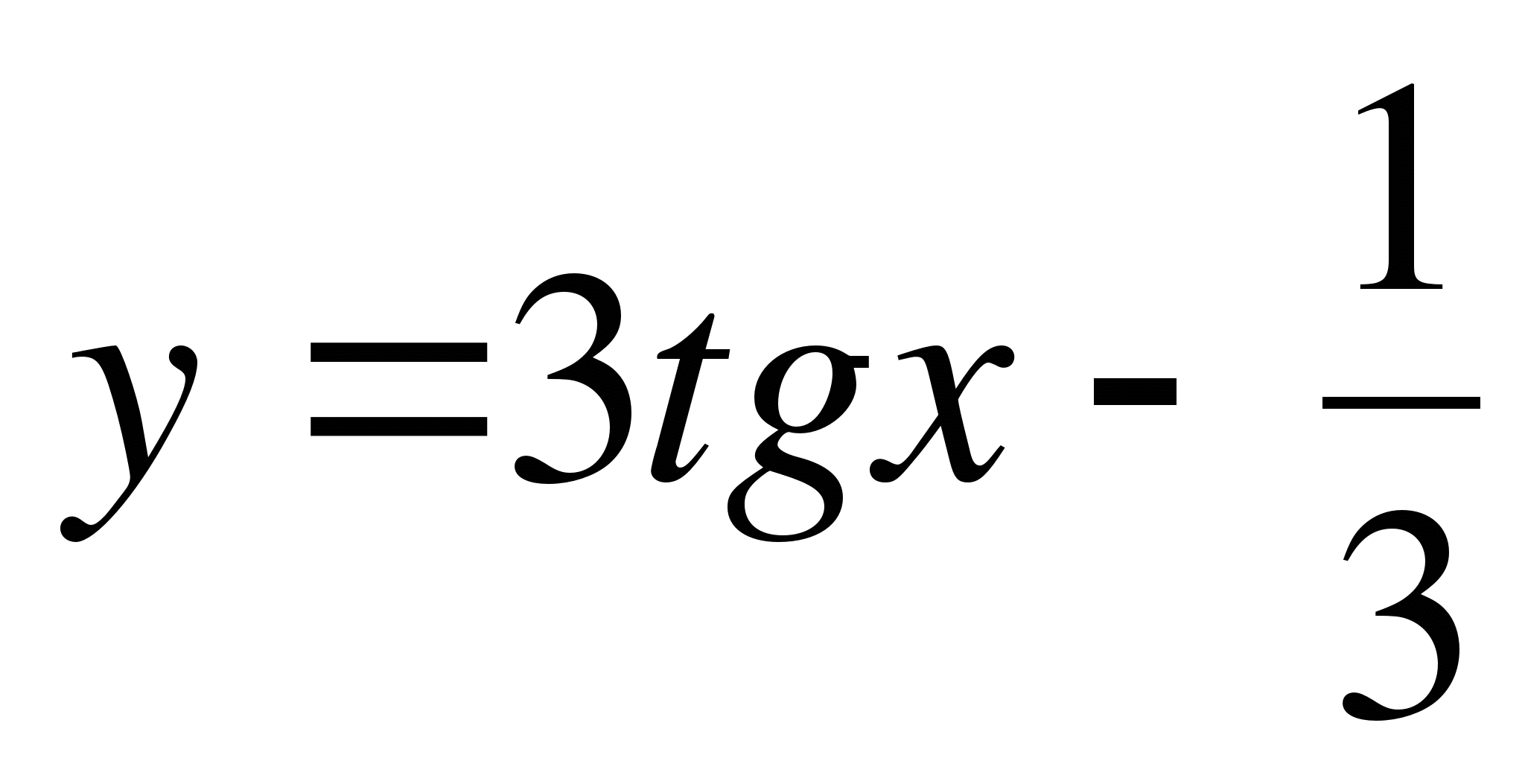
-
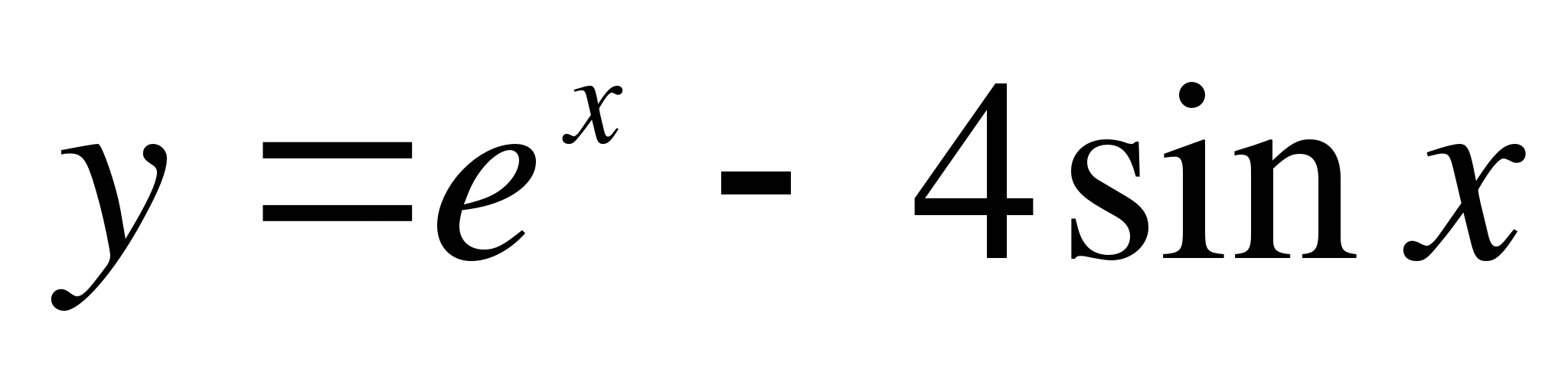
-
Тело движется по прямой по закону 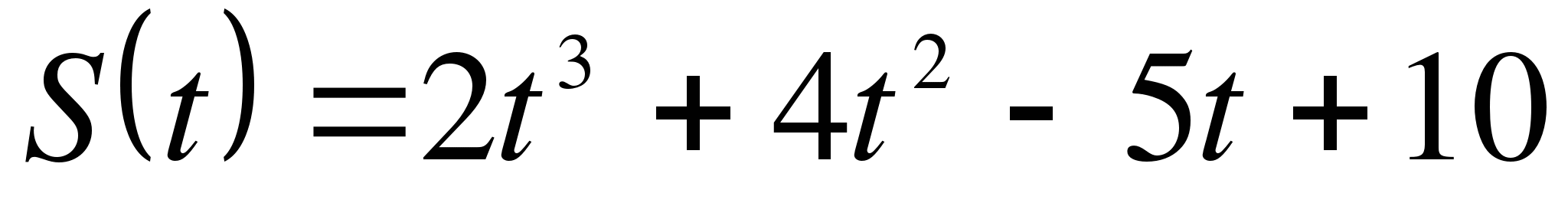
 Какую скорость приобретает тело в момент, когда его ускорение станет равным 10 м/с2.
Какую скорость приобретает тело в момент, когда его ускорение станет равным 10 м/с2.
-
Найдите тангенс угла наклона касательной, проведенной к графику функции 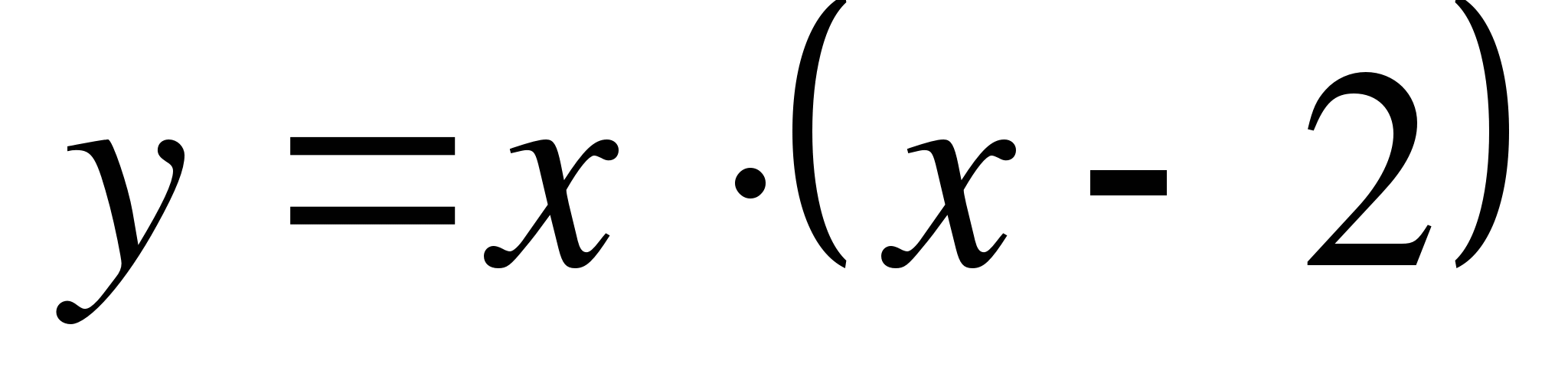 в точке
в точке 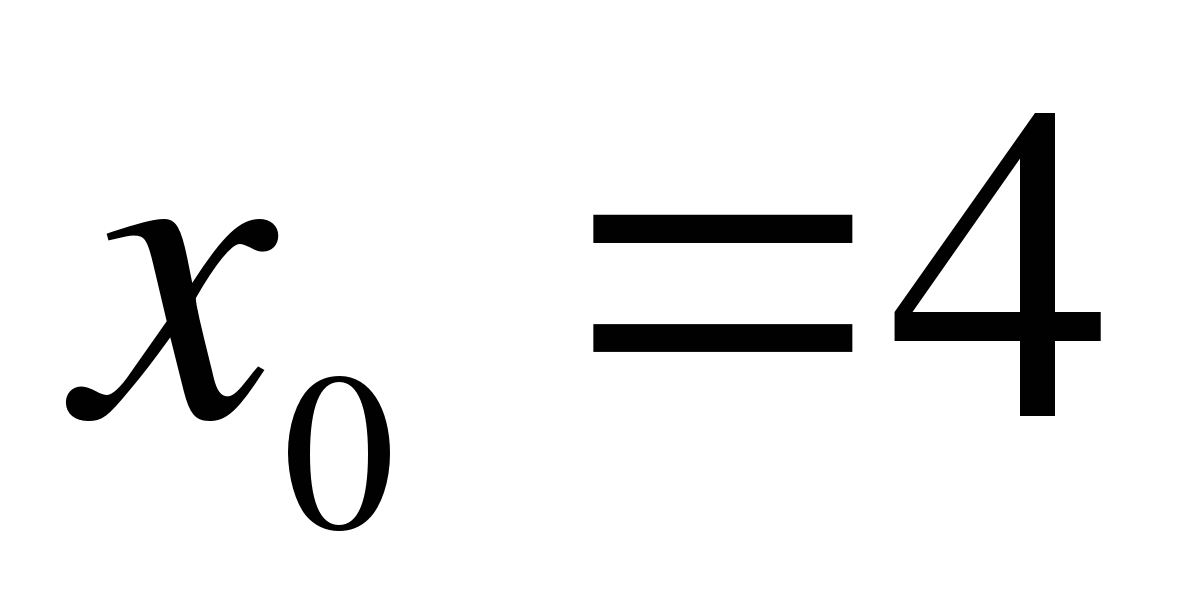 .
.
-
Найдите угловой коэффициент касательной к графику функции 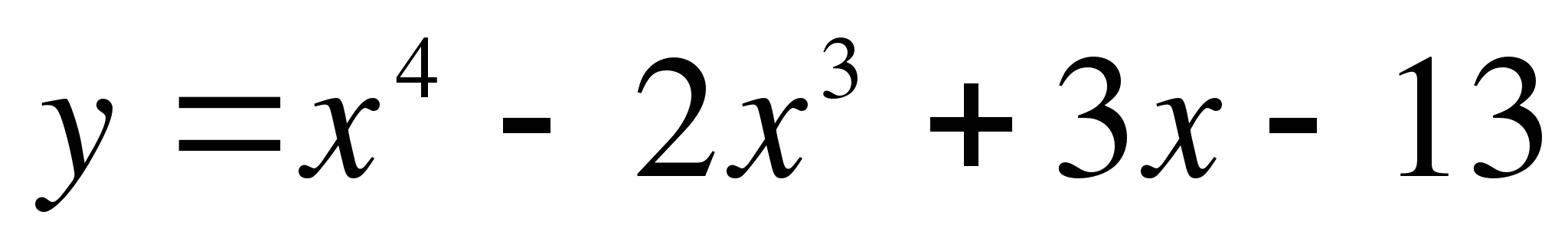 в точке
в точке 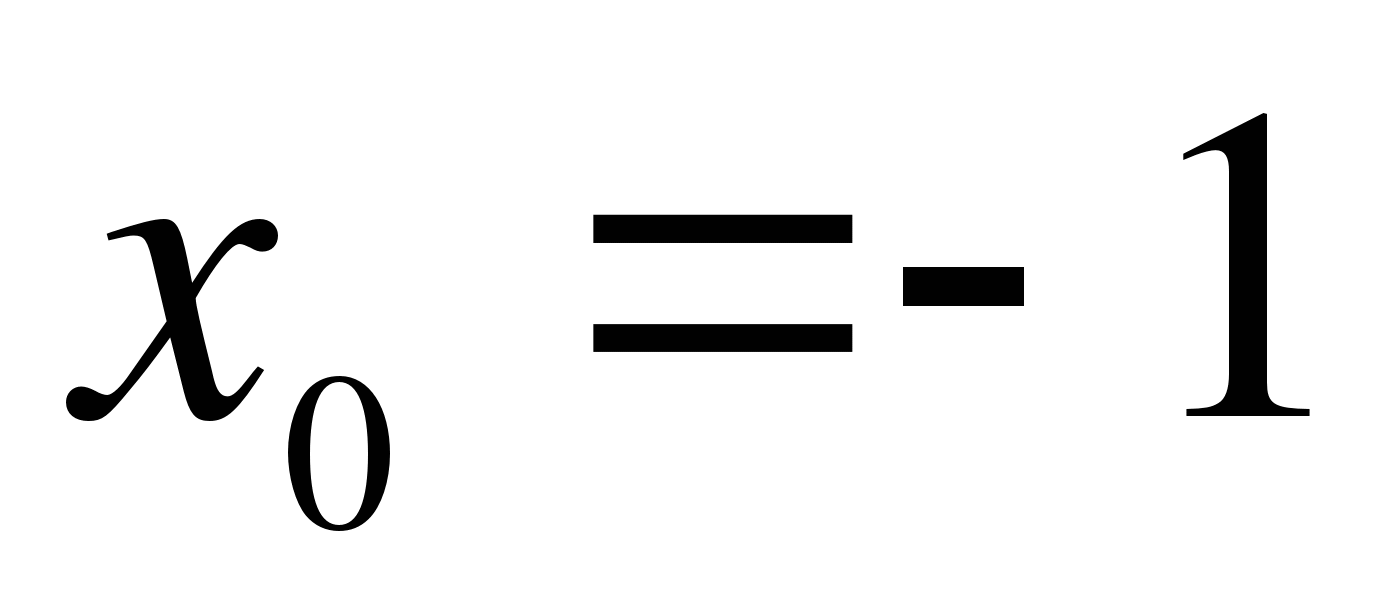 .
.
-
Найдите сумму угловых коэффициентов касательных к параболе 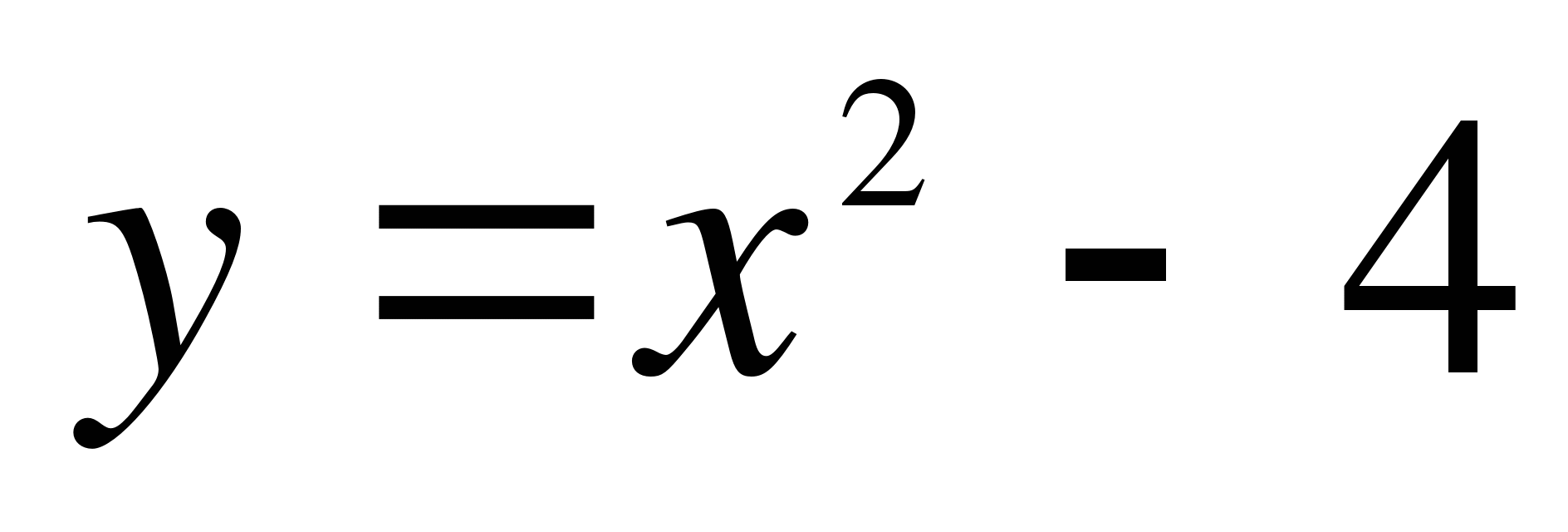 в точках пересечения параболы с осью абсцисс.
в точках пересечения параболы с осью абсцисс.
-
Тело движется прямолинейно в вертикальном направлении по закону  (t – время, h – расстояние от поверхности Земли до тела). Определите скорость в момент времени
(t – время, h – расстояние от поверхности Земли до тела). Определите скорость в момент времени 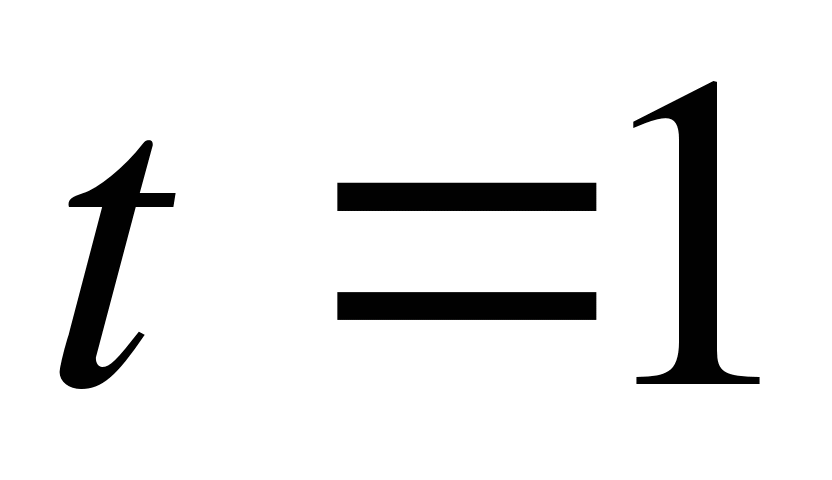 .
.
infourok.ru
"Производная" в формате ЕГЭ. страница 2
В5. Решите уравнение f ׳(х) = 0, где f(x) = sin6x + cos6x + 5
В 6. Найдите сумму корней уравнения , принадлежащих отрезку , если известно, что
Карточка-инструкция: Касательная к графику функции
Алгоритм написания уравнения касательной у=f(х0)+f'(х0) (х-х0)
1. Найти f(х0)
2. Найти f'(х)
3. Найти f'(х0)
4. Написать уравнение касательной у=f(х0)+f'(х0) (х-х0)
Алгоритм нахождения углового коэффициента касательной.
k=tga= f'(х0)
1. Найти f'(х)
2. Найти f'(х0)
Карточки-задания:
Написать уравнение касательной к графику функции
-
f(x) = x2-2x в точке с его абсциссой х0=2
-
f(x) = x2+1 в точке с его абсциссой х0=1
-
f(x) = -0,5x2+2x в точке с его абсциссой х0=0
Найти угловой коэффициент касательной, проведённой к графику
-
у = 5х4-0,5х+5 в точке х0=1
-
у = 5х3-7х в точке х0=2
-
у = х4-0,5х+5 в точке х0=1
Исследование функций
Алгоритм исследования функций
-
Найти область определения: D (f)
-
Найти производную функции, критические точки
-
Промежутки возрастания и убывания функции
-
Точки экстремума (max, min) и значения функции в этих точках
-
Точки пересечения графика с осями координат
-
Поведение функции в окрестности "особых точек"
Карточки-задания:
Исследовать функцию и построить её график
-
f(x) = x4 - 4x2
-
g(x) = -x3 + 3x - 2
-
h(x) = x3 + 6x - 15x - 3
-
f(x) = -x3 + 3x2 - 4
Наибольшее и наименьшее значения функции
Алгоритм нахождения наибольшего и наименьшего значения функции
-
Находим критические точки, т.е. f'(x) = 0
-
Вычислим значения функции во всех критических точках принадлежащих отрезку и на концах отрезка.
-
Из полученных чисел выбираем наибольшее и наименьшее.
Карточки-задания:
Найти наибольшее и наименьшее значение функции на отрезке:
-
f(x) = -3x2 + 6x - 10 [-2; 9]
-
g(x) = x3 + 3x2 - 45x - 2 [-6; 0]
-
h(x) = 2x2 - 8x + 6 [-1; 4]
-
y(x) = x3 - 3x2 - 9x - 4 [-4; 4]
-
u(x) = x3 -9x2 + 15x - 3 [3; 6]
-
g(x) = x4 - 8x3 + 10x2 + 1 [-1; 2]
Зачет № 1. Производная.
Перечень теоретических знаний:
Приращение аргумента, приращение функции Понятие о непрерывности функции, производная функции Производная с,x,x2, cu, xn Производная суммы, разности Производная произведения, частного Производная сложной функции Производная тригонометрических функций Решение примеров по теме «Производная»
Контрольная работа № 1 ПРОИЗВОДНАЯ.


Тест по теме производная:
1 Вариант.
1. Найдите производную функции
1) 2)
3) 4)
2. Найдите значение производной функции в точке
1) 1; 2) 0; 3) 0,5; 4) -1.
3. Для какой функции найдена производная
1) 2) 3) 4)
4. Найдите значение углового коэффициента касательной, проведенной к графику функции в точке с абсциссой
1) -3; 2) 0; 3) 3; 4) 5.
5. Найдите , если sin 1) 2) 3) 4) 0.
6. Напишите уравнение касательной к графику функции в точке
с абсциссой
1) у = - 3х – 3; 2) у = 8х+13; 3) у = - 8х – 3; 4) у = - 8х +13.
7. Найдите скорость и ускорение точки в момент времени c., если она движется прямолинейно по закону (координата измеряется метрах).
1) 2) 3) 4)
Контрольная работа по теме: Производная. Применение производной. 10 класс.
2 Вариант.
1. Найдите производную функции
1) 2) 3) 4)
infourok.ru
Контрольная работа по теме " Производная"
Контрольная работа по алгебре и началам математического анализа в 11 классе базового уровня по теме «Производная»
Предлагаются задания в 2 вариантах.
Каждый вариант состоит из трех частей, которые отличаются по сложности и форме содержания заданий.
В І части контрольной работы предложены четыре тестовых заданий с выбором одного правильного ответа. Задание считается выполненным правильно, если ученик указал только одну букву, которой соответствует правильный ответ. Правильный ответ оценивается одним баллом.
ІІ часть контрольной работы состоит из трёх заданий. Решение может иметь краткую запись решения без обоснования. Правильное решение каждого задания этого блока оценивается двумя баллами.
ІІІ часть контрольной работы состоит из одного задания. Решение должно иметь развернутую запись с обоснованием. Правильное решение оценивается тремя баллами.
Сумма баллов начисляется за правильно выполненные задания в соответствии максимально возможному количеству предложенных баллов для каждой части (5; 4; 3 – всего 12 баллов). При переводе в 5-и бальную систему оценивания предлагается следующая шкала перевода баллов в оценку:
11 - 13 баллов − «5»;
8 - 10 баллов − «4»;
4 - 7 баллов – «3»;
1 - 3 балла – «2».
При выполнении работы необходимо указать номер задания. Текст задания переписывать не обязательно.
Вариант 1
І часть (4 балла)
Задания 1-4 имеют по четыре варианта ответа, из которых только один верный. Выберите верный ответ. Верный ответ каждого задания оценивается одним баллом.
1.Найдите производную функции 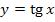 .
.
А) 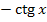 ; Г)
; Г) 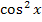 ;
;
Б) 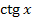 ; Д)
; Д) 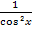 .
.
В) 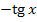 ;
;
2. Найдите производную функции 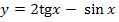 в точке с абсциссой
в точке с абсциссой 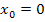 .
.
А) 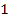 ; Г)
; Г) 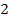 ;
;
Б) 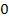 ; Д)
; Д) 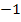 .
.
В) 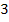 ;
;
3. Найдите тангенс угла наклона касательной, проведенной к графику функции 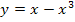 в точке с абсциссой
в точке с абсциссой 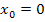 .
.
А) 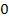 ; Г)
; Г) 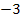 ;
;
Б) 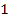 ; Д)
; Д) 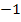 .
.
В) 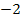 ;
;
4. Найдите производную функции 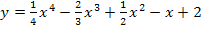 в точке с абсциссой
в точке с абсциссой 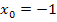 .
.
А) 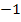 ; Г)
; Г)  ;
;
Б) 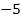 ; Д)
; Д) 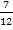 .
.
В) 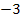 ;
;
ІІ часть (6 баллов)
Решение заданий 6-8
может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.
5. Составьте уравнение касательной к графику функции 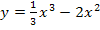 в точке с абсциссой
в точке с абсциссой 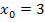 .
.
6. В какой момент времени скорость тела, движущегося по закону 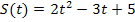 , равна нулю?
, равна нулю?
7.Найдите производную функции 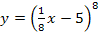 .
.
ІІІ часть (3 балла)
Решение 9 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.
8. При каких значениях х производная функции 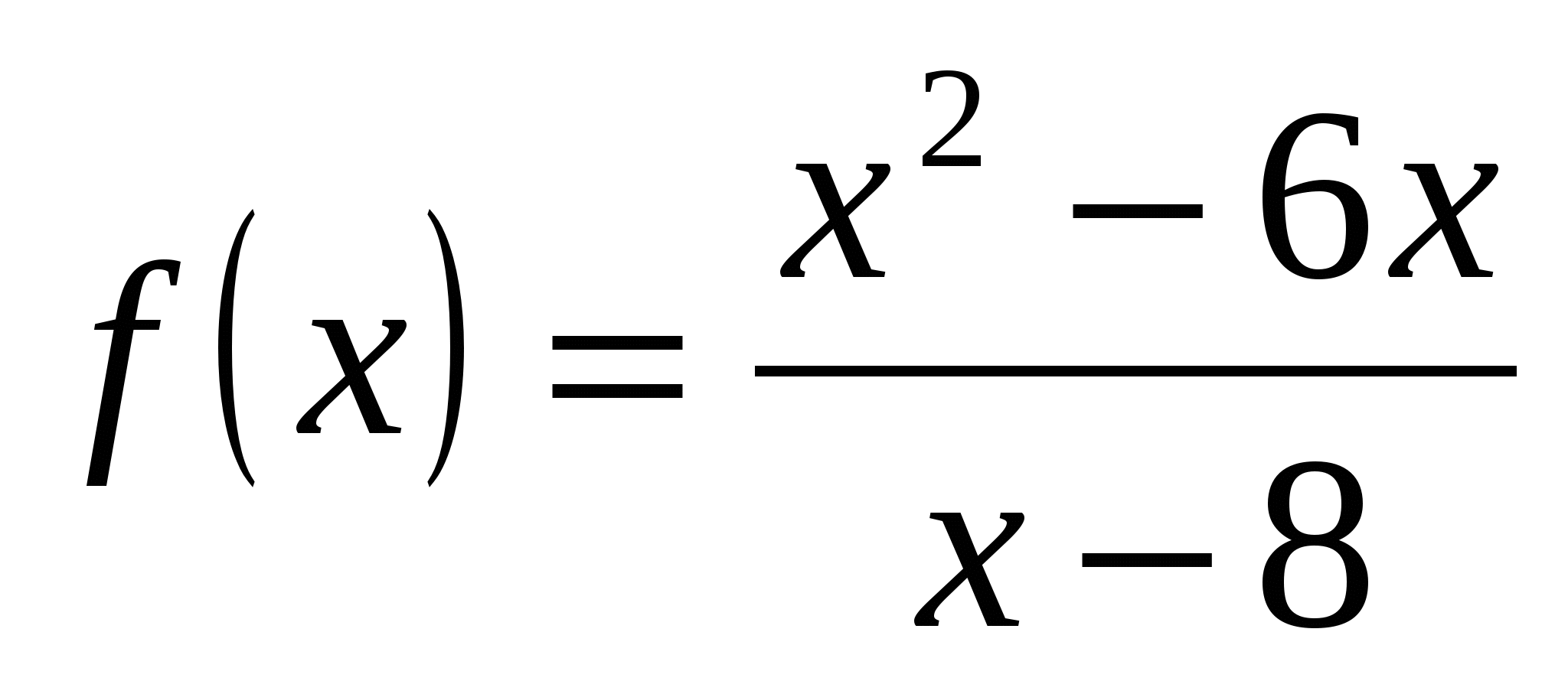 меньше нуля?
меньше нуля?
Вариант 2
І часть (4 балла)
Задания 1-4 имеют по четыре варианта ответа, из которых только один верный. Выберите верный ответ. Верный ответ каждого задания оценивается одним баллом.
1. Найдите производную функции 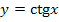 .
.
А) 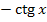 ; Г)
; Г) 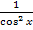 ;
;
Б) 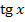 ; Д)
; Д) 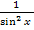 .
.
В) 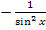 ;
;
2.Найдите производную функции 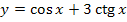 в точке с абсциссой
в точке с абсциссой 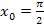 .
.
А) 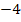 ; Г)
; Г) 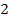 ;
;
Б) 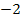 ; Д)
; Д) 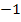 .
.
В) 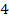 ;
;
3. Найдите производную функции 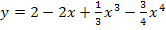 в точке с абсциссой
в точке с абсциссой 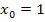 .
.
А) 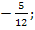 Г)
Г) 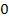 ;
;
Б) 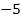 ; Д)
; Д)  .
.
В) 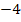 ;
;
4. Найдите производную функции 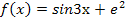 .
.
A) 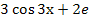 ; Г)
; Г) 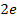 ;
;
Б) 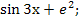 Д)
Д) 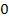 .
.
В) 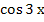 ;
;
ІІ часть (6 баллов)
Решение заданий 6-8
может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.
5. Составьте уравнение касательной к графику функции 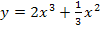 в точке с абсциссой
в точке с абсциссой 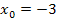 .
.
6. В какой момент времени скорость тела, движущегося по закону 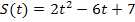 , равна нулю?
, равна нулю?
7. Найдите производную функции 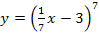 .
.
ІІІ часть (3 балла)
Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.
8. При каких значениях х производная функции 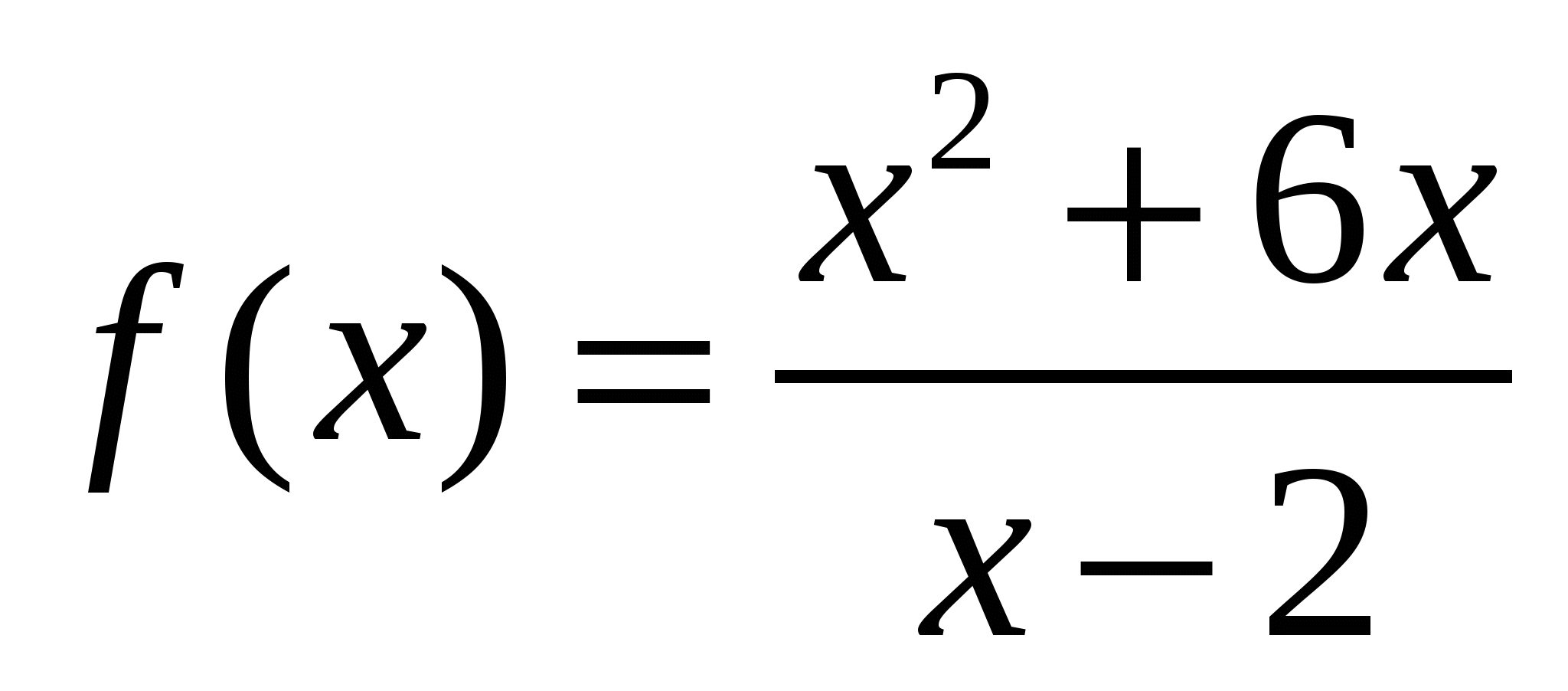 больше нуля?
больше нуля?
infourok.ru
Контрольная работа по теме "Производная"
Контрольная работа по математике по теме «Производная»
Вариант №1
№1-5. Найти значения производной функции в данной точке:
f(x) = 3ex + 2 tgx; f '(0) - ?
№2.
f(x) = 5x; f '(1) - ?
№3.
f(x) = ex · x3; f '(2) - ?
№4.
f(x) = ; f '(0) - ?
№5.
f(x) = e2x+3; f '(-1) - ?
№6. Написать уравнение касательной в точке x0 = 2:
f(x) = ex
№7. Исследуйте функцию на монотонность и экстремумы:
f(x) = x2 · ex
№8. Найдите наименьшее и наибольшее значения функции на [-1;1]:
f(x) = x2 · ex
Контрольная работа по математике по теме «Производная»
Вариант №2
№1-5. Найти значения производной функции в данной точке:
f(x) = 2 sinx – 4 · ex; f '()
№2.
f(x) = 9x; f '(0)
№3.
f(x) = ex · x5; f '(3)
№4.
f(x) = ; f '(0)
№5.
f(x) = e4-2x; f '(2)
№6. Написать уравнение касательной к графику функции в точке x0 = 1:
f(x) = 3x
№7. Исследуйте функцию на монотонность и экстремумы:
f(x) = x · x5x
№8. Найдите наименьшее и наибольшее значение функции на [-3; 1]:
f(x) = x2 · ex
Контрольная работа по математике по теме «Производная»
Вариант №3
№1-5. Найти значения производной функции в данной точке:
f(x) = 4x5 – 7 · ex; f '(-1) - ?
№2.
f(x) = ex + 3x; f '(0) - ?
№3.
f(x) = ex · x4; f '(1) - ?
№4.
f(x) = ; f '(0) - ?
№5.
f(x) = e6x-1; f '(2) - ?
№6. Написать уравнение касательной в точке x0 = 0:
f(x) = 2x + 11
№7. Исследуйте функцию на монотонность и экстремумы:
f(x) = 4x2 · ex
№8. Найдите наибольшее и наименьшее значения функции на [-2;2]:
f(x) = e-4x · x4
Контрольная работа по математике по теме «Производная»
Вариант №4
№1-5. Найти значения производной функции в данной точке:
f(x) = 2x + sinx – ex; f '(0) - ?
№2.
f(x) = 7 · 2x; f '(1) - ?
№3.
f(x) = 4x · xx; f '(2) - ?
№4.
f(x) = ; f '(-1) - ?
№5.
f(x) = 73-x; f '(2) - ?
№6. Написать уравнение касательной в точке x0=0:
f(x) = 4x – x2
№7. Исследуйте функцию на монотонность и экстремумы:
f(x) = x2 · ex+1
№8. Найдите наименьшее и наибольшее значения функции на [-4;1]:
f(x) = x3 · ex
Контрольная работа по математике по теме «Производная»
Вариант №5
№1-5. Найти значения производной функции в данной точке:
f(x) = cosx – x5 + 3ex; f '(0) - ?
№2.
f(x) = 4 · 7x; f '(2) - ?
№3.
f(x) = x3 · 5x; f '(1) - ?
№4.
f(x) = ; f '(1) - ?
№5.
f(x) = 32+6x; f '(0) - ?
№6. Написать уравнение касательной в точке x0 = 1:
f(x) = ex + x4
№7. Исследуйте функцию на монотонность и экстремумы:
f(x) = x · 3x
№8. Найдите наибольшее и наименьшее значения функции на [-1;1]:
f(x) = x2 · e2x
Контрольная работа по математике по теме «Производная»
Вариант №6
№1-5. Найти значения производной функции в данной точке:
f(x) = tgx – 5 · ex + 4; f '(3) - ?
№2.
f(x) = 2 · 8x; f '(3) - ?
№3.
f(x) = cosx · 3x; f '(1) - ?
№4.
f(x) = ; f '(1) - ?
№5.
f(x) = 23x-1; f '(0) - ?
№6. Написать уравнения касательныx в точке x0 = 1:
f(x) = 2ex – x
№7. Исследуйте функцию на монотонность и экстремумы:
f(x) = x · 2x
№8. Найдите наибольшее и наименьшее значения функции на [-2;2]:
f(x) = e3x · x3
infourok.ru
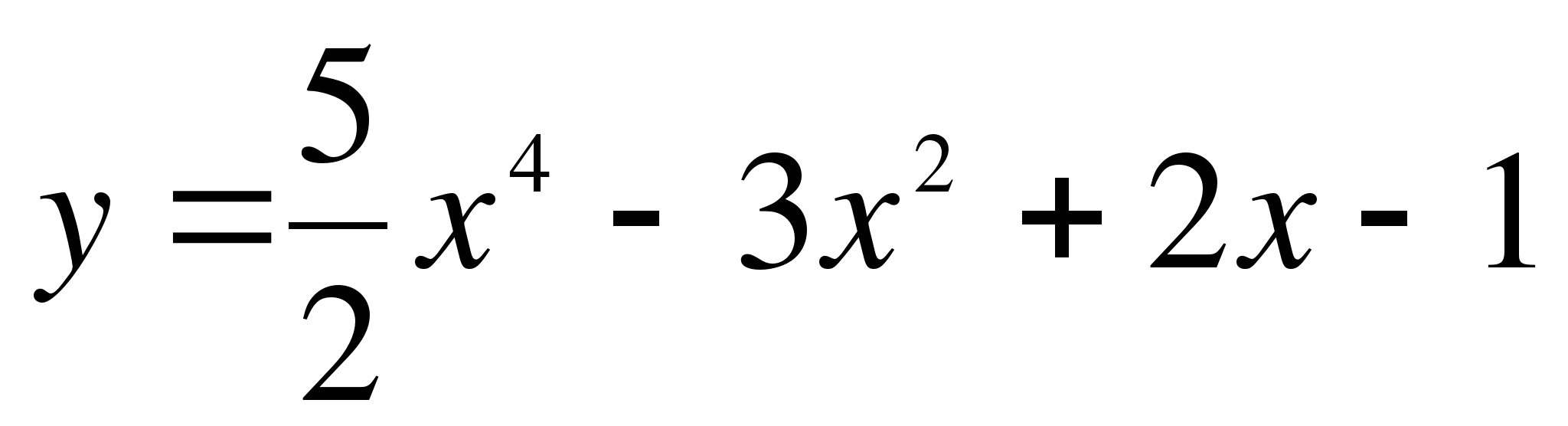
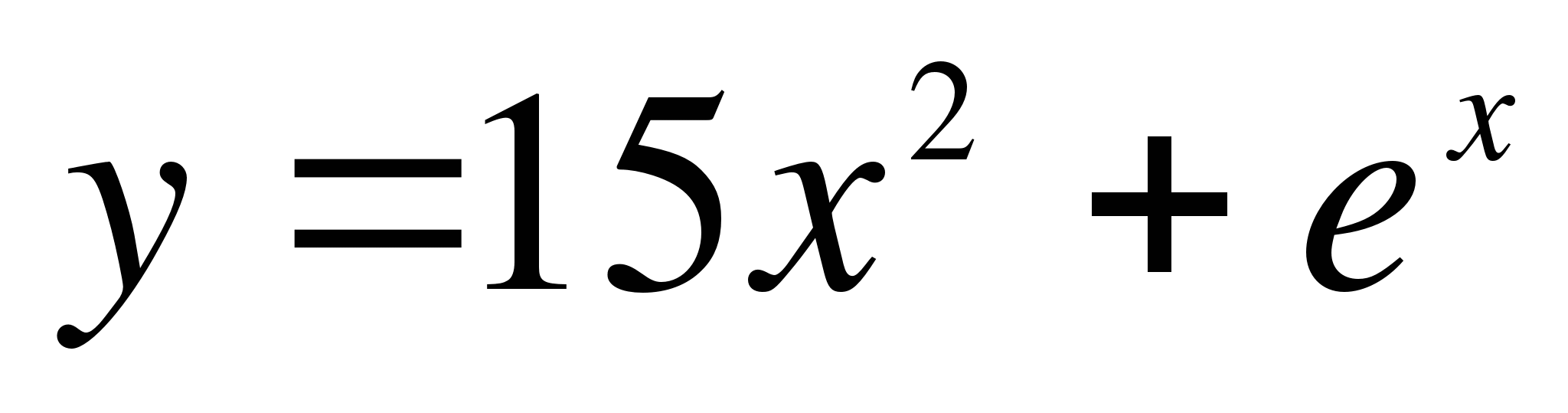
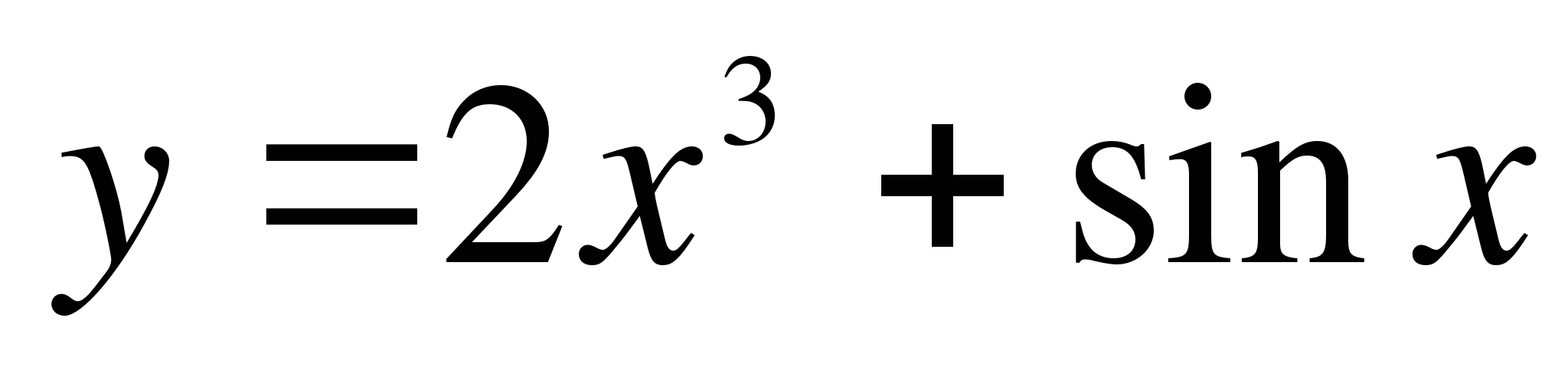
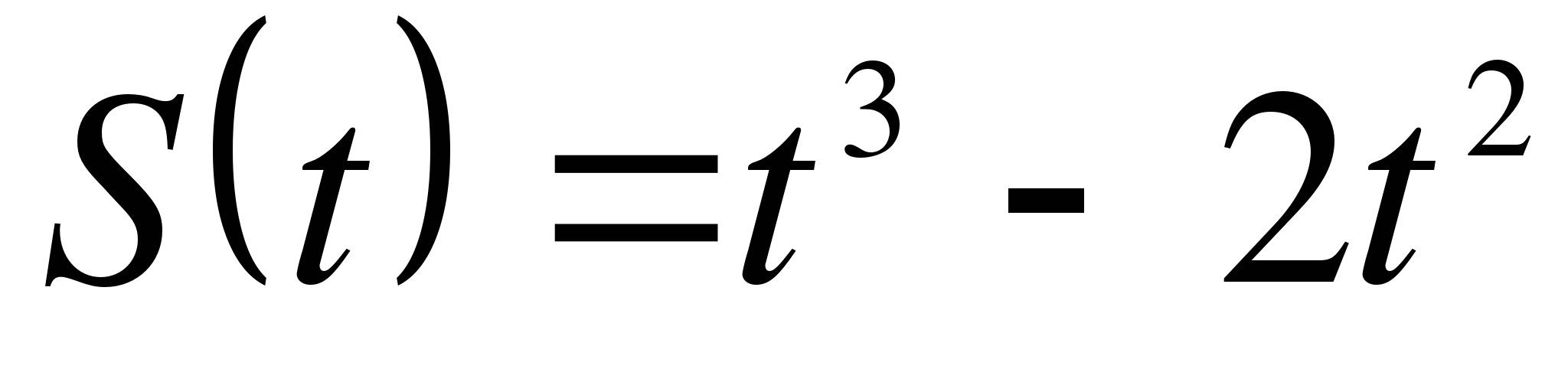 . Какой формулой задается скорость движения этой точки в момент времени t.
. Какой формулой задается скорость движения этой точки в момент времени t.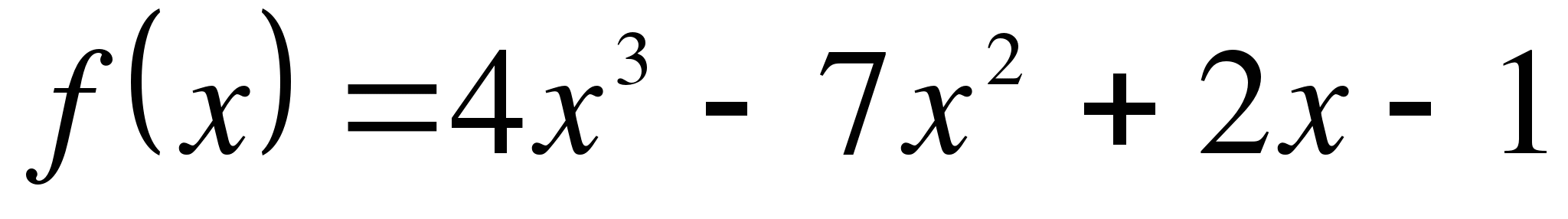 в точке с положительной абсциссой
в точке с положительной абсциссой 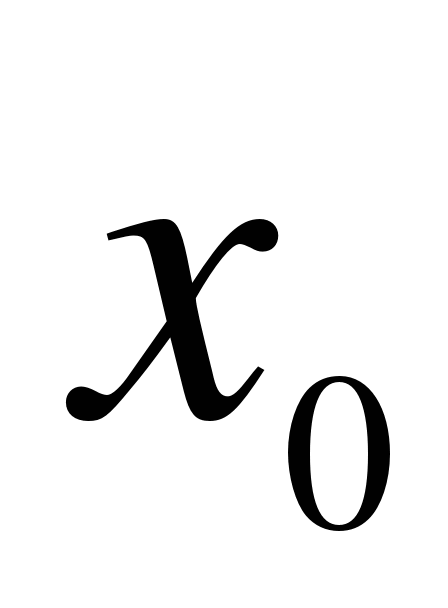 , равен 2. Найдите
, равен 2. Найдите 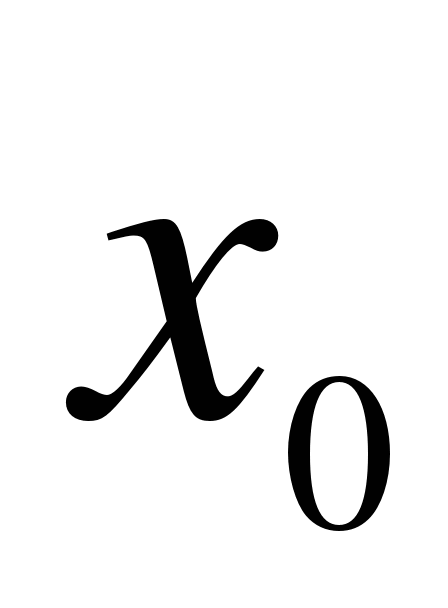 .
.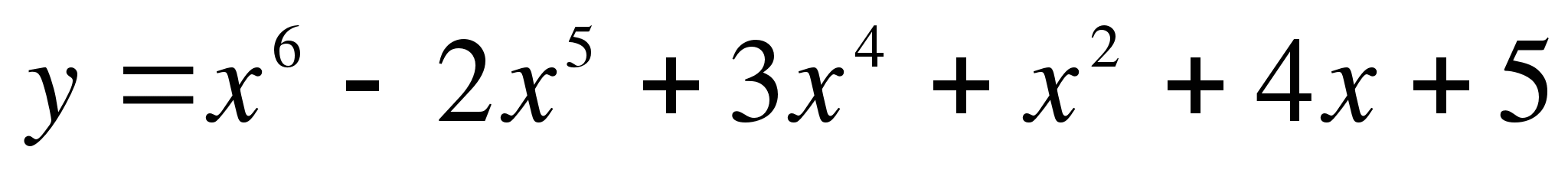 в точке
в точке 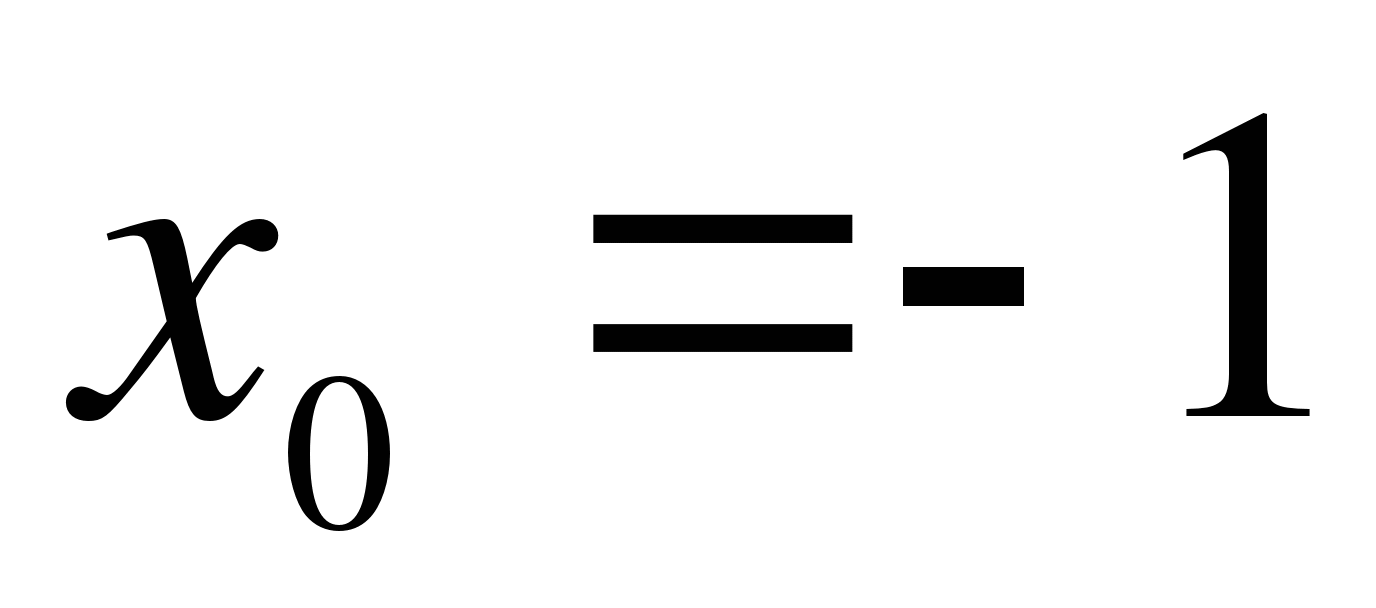 .
.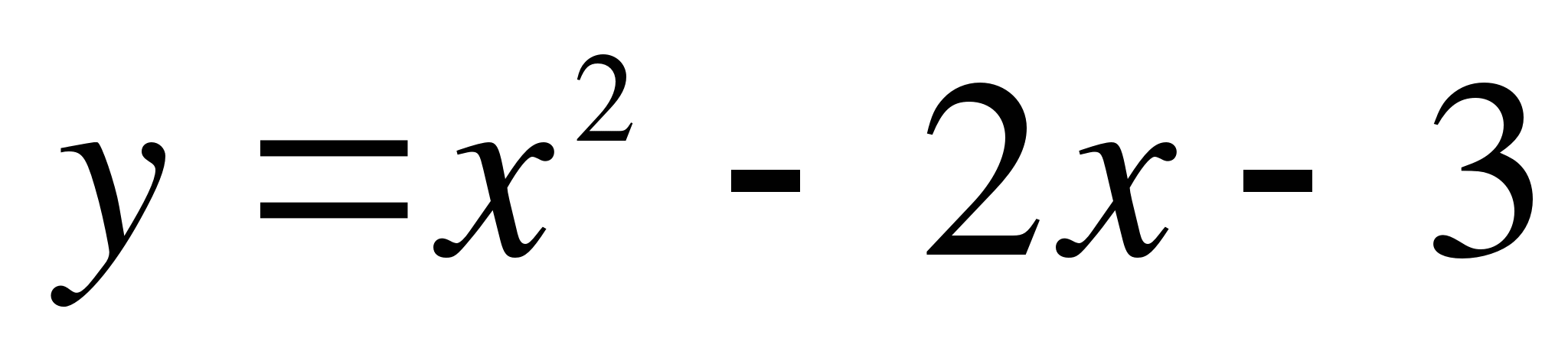 в точках пересечения параболы с осью абсцисс.
в точках пересечения параболы с осью абсцисс.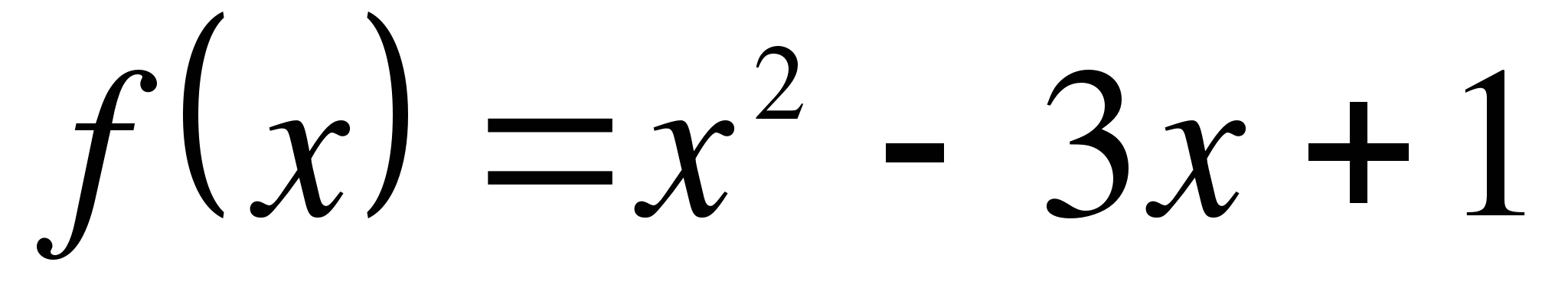 взята точка А, наклонена к оси абсцисс под углом, тангенс которого равен 7,2. Найдите абсциссу точки А.
взята точка А, наклонена к оси абсцисс под углом, тангенс которого равен 7,2. Найдите абсциссу точки А.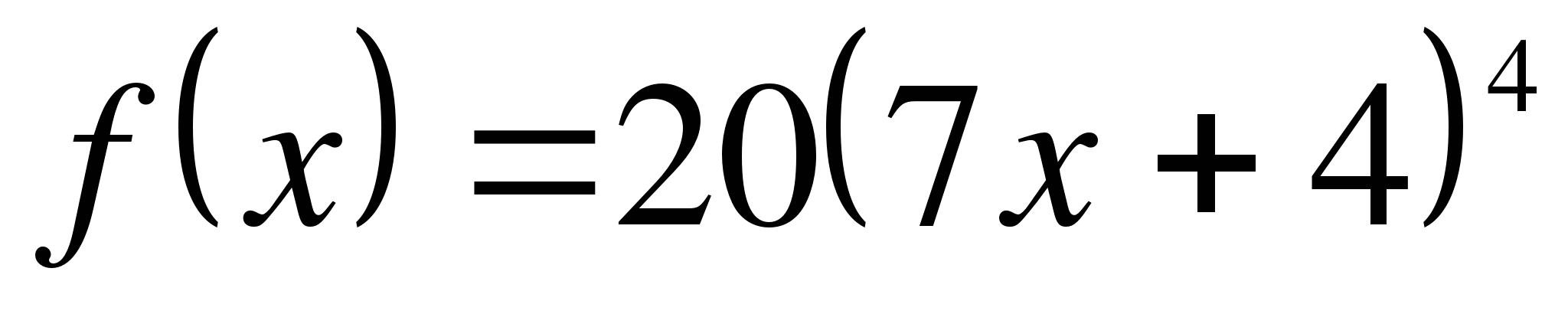
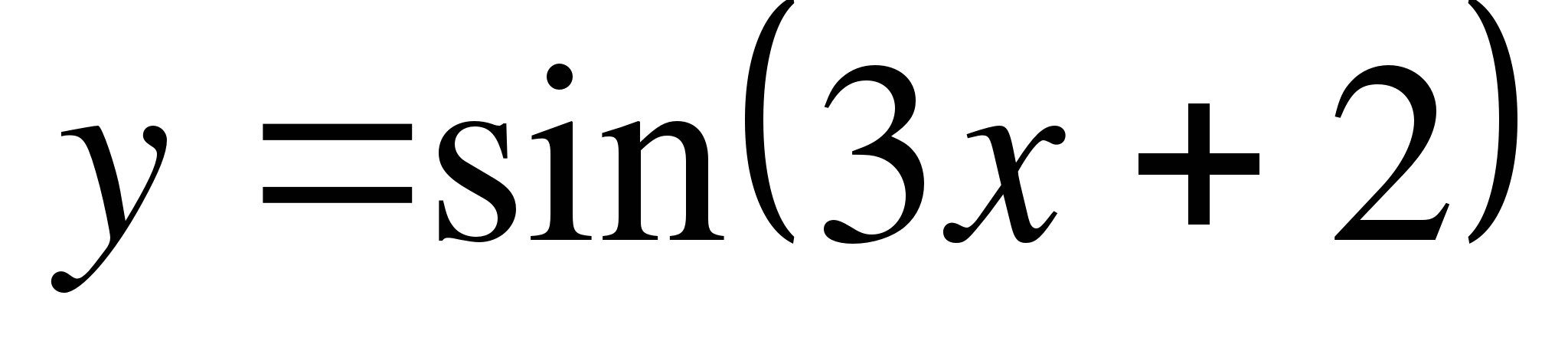

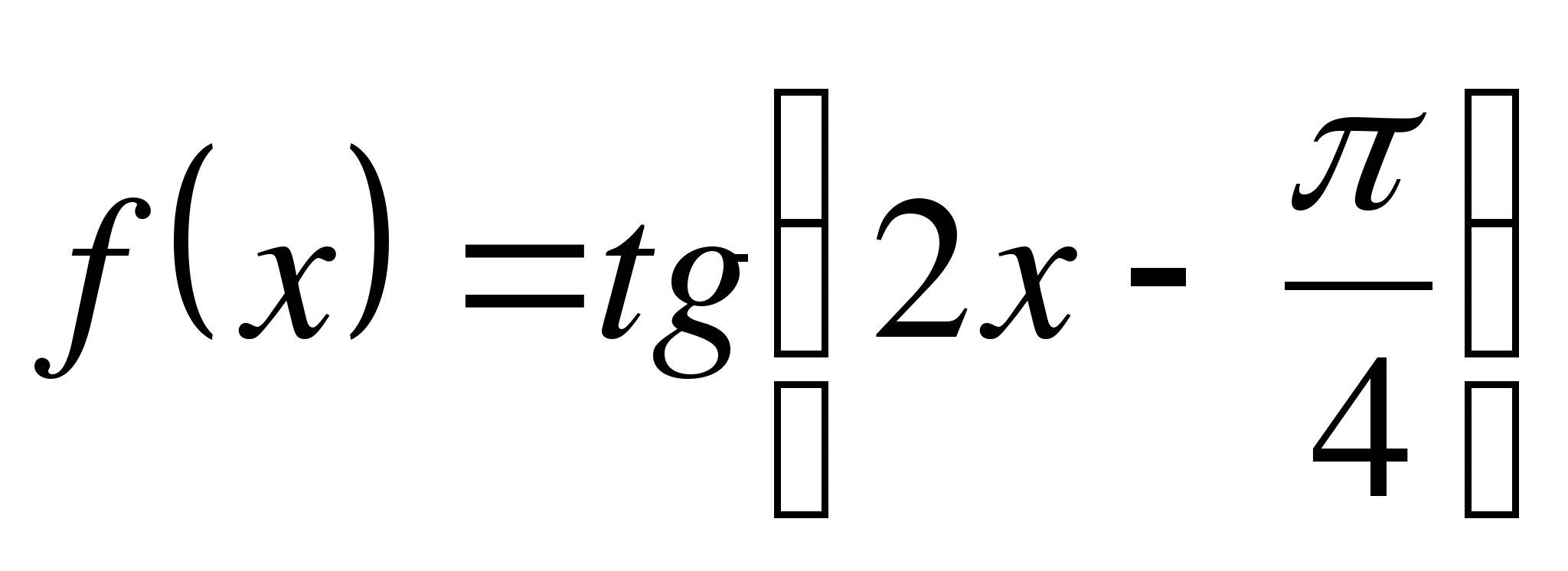 в точке
в точке 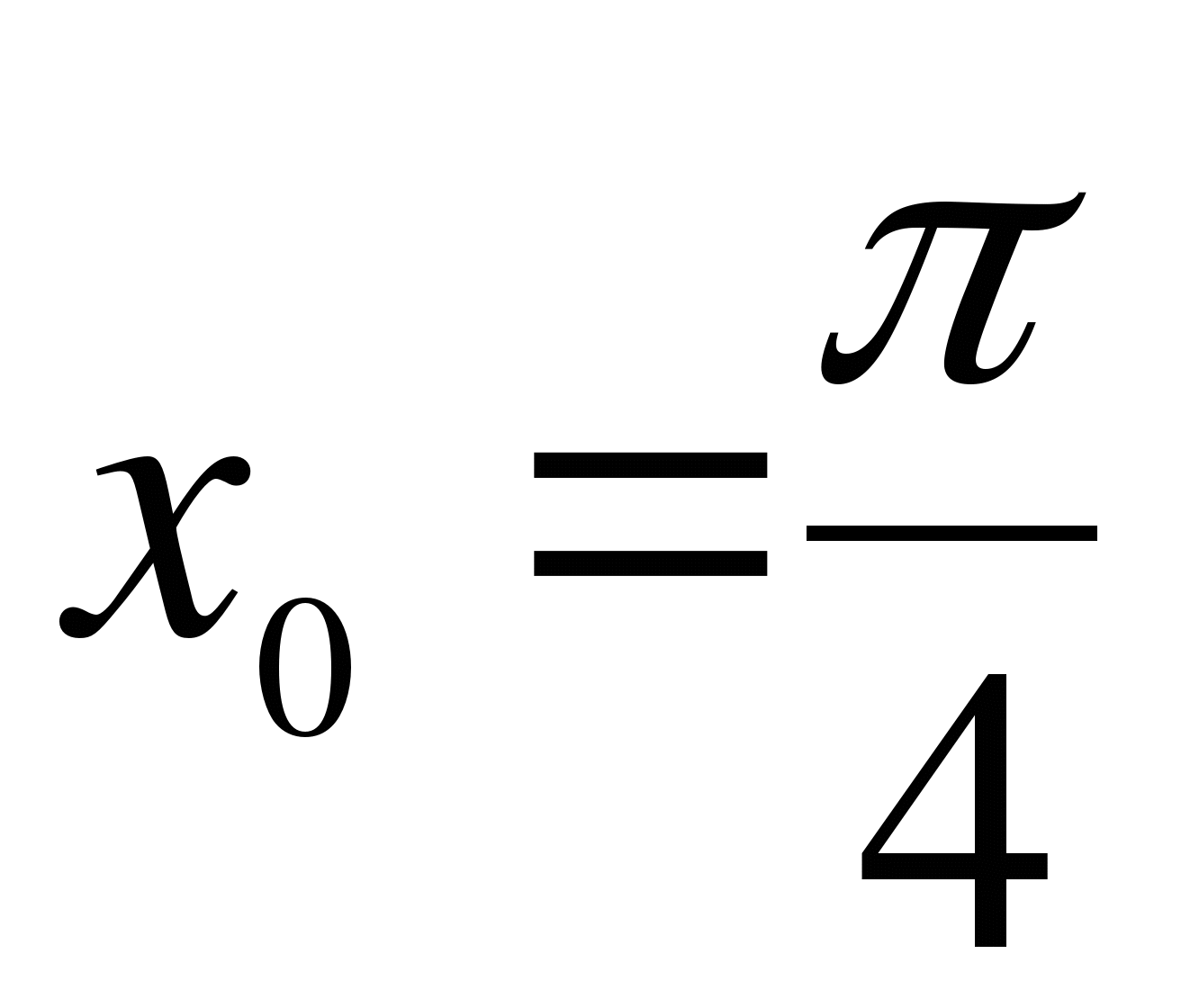 .
.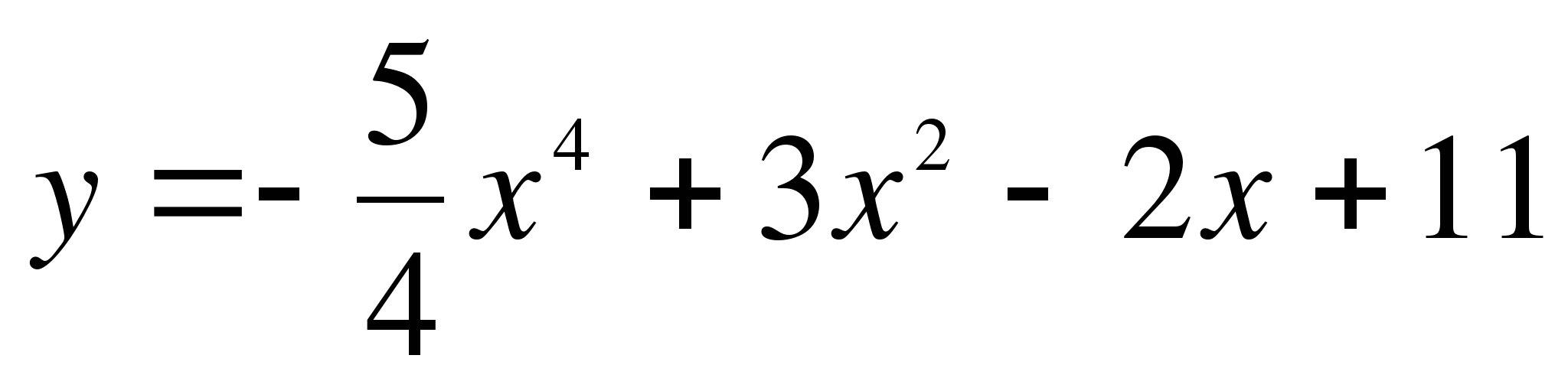
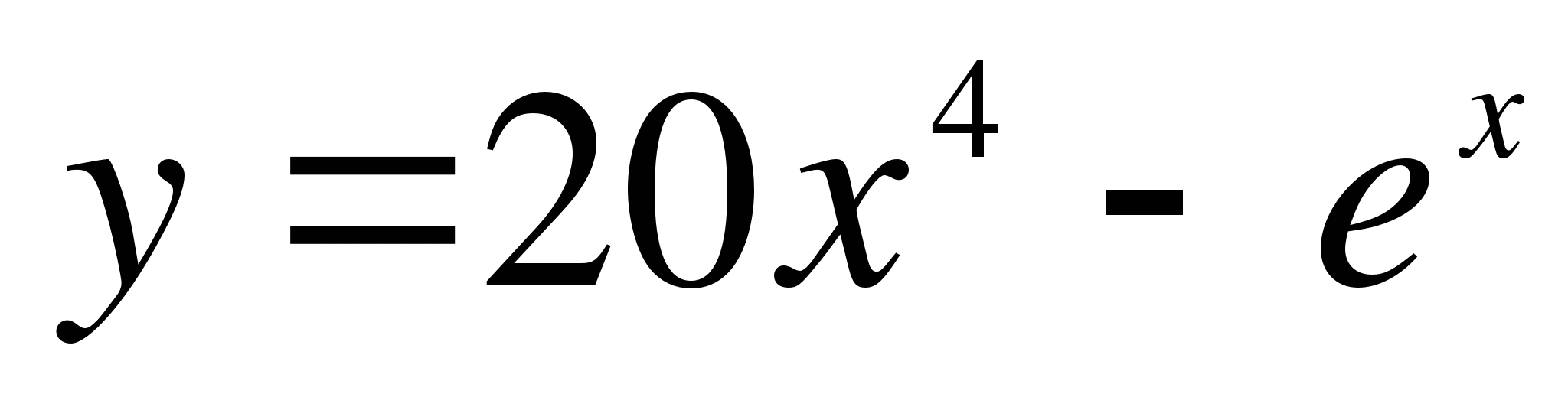
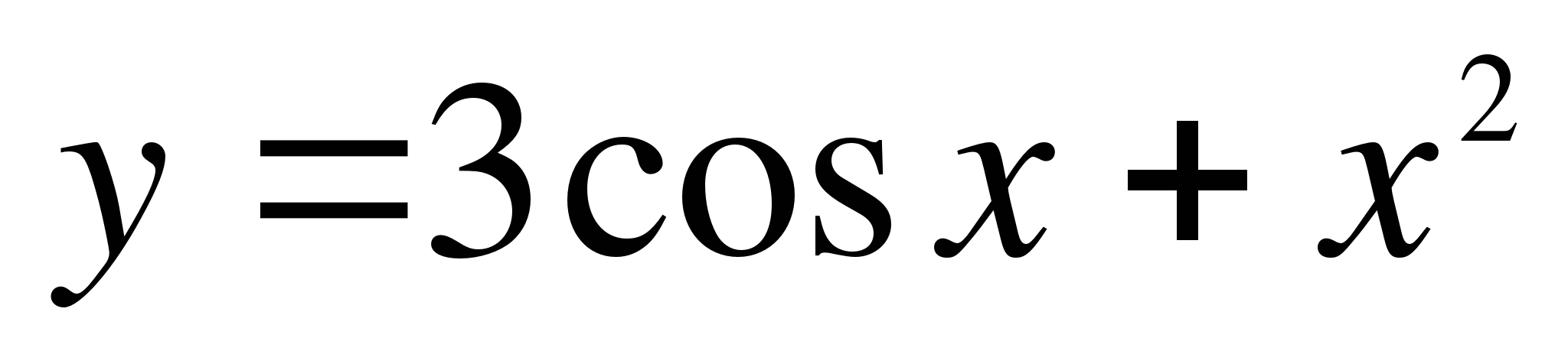
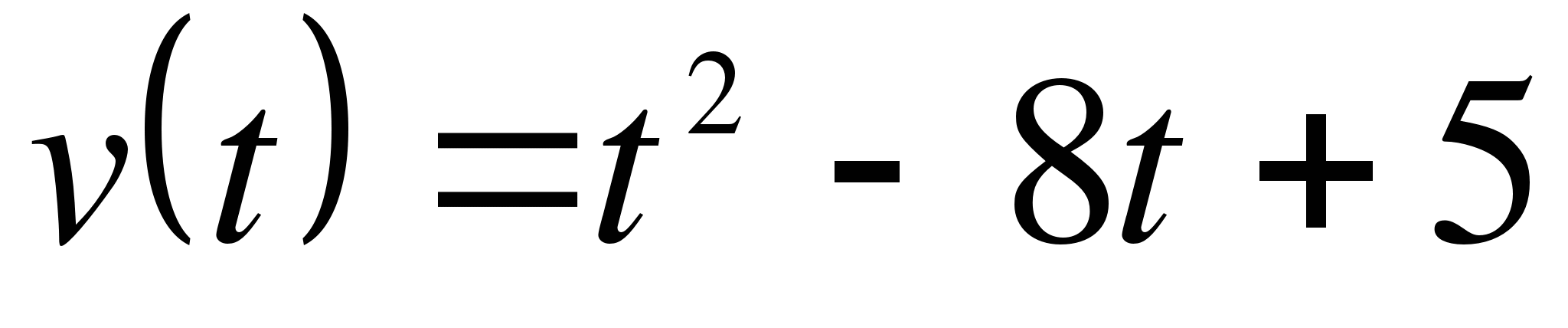 . Какую скорость приобретает тело в момент, когда его ускорение равно 12м/с2.
. Какую скорость приобретает тело в момент, когда его ускорение равно 12м/с2.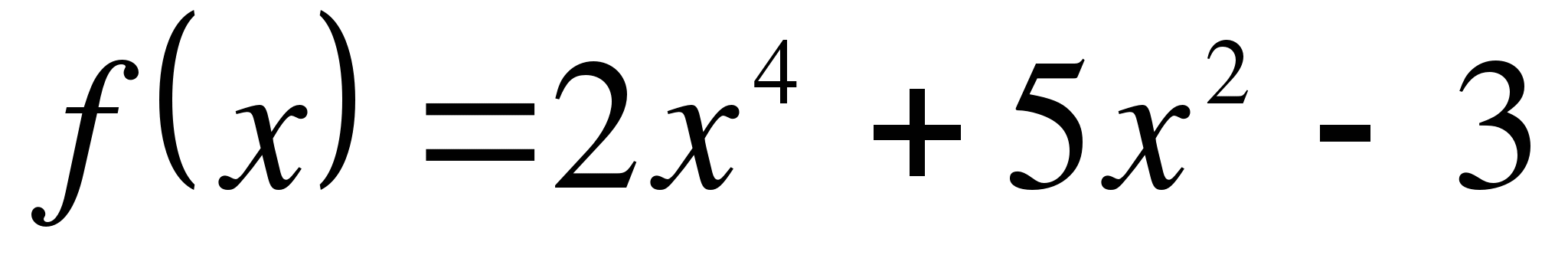 в точке с абсциссой
в точке с абсциссой 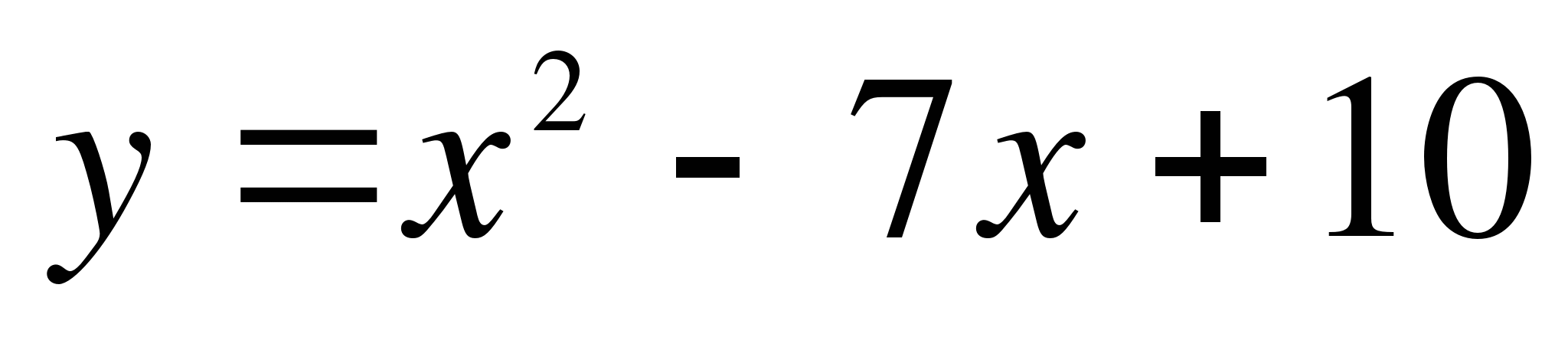 в точке с абсциссой
в точке с абсциссой 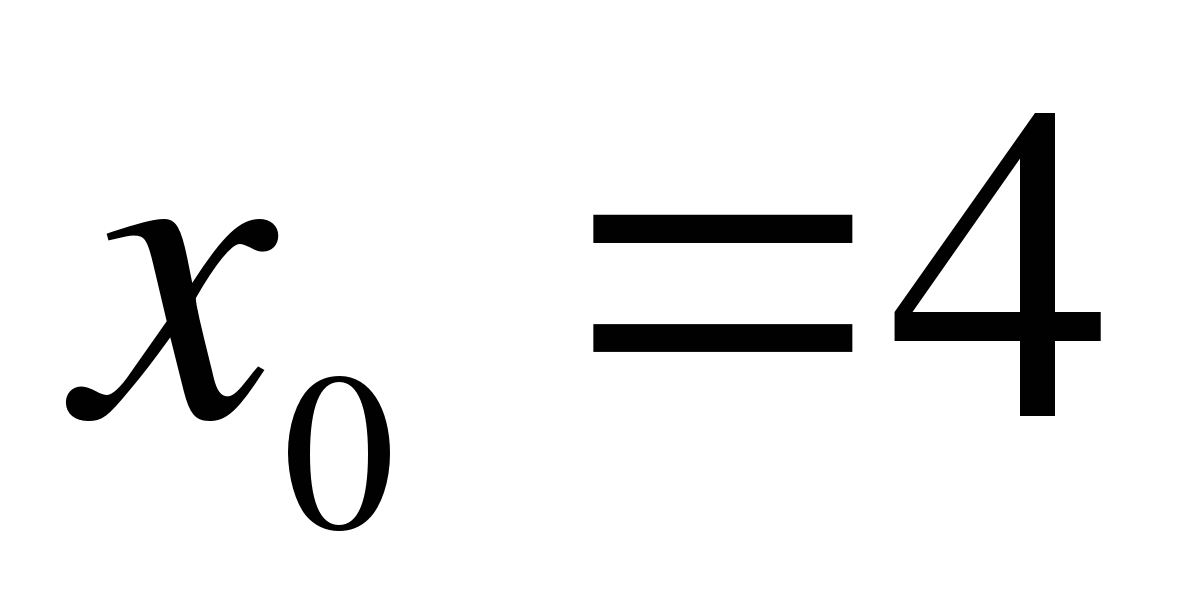 .
.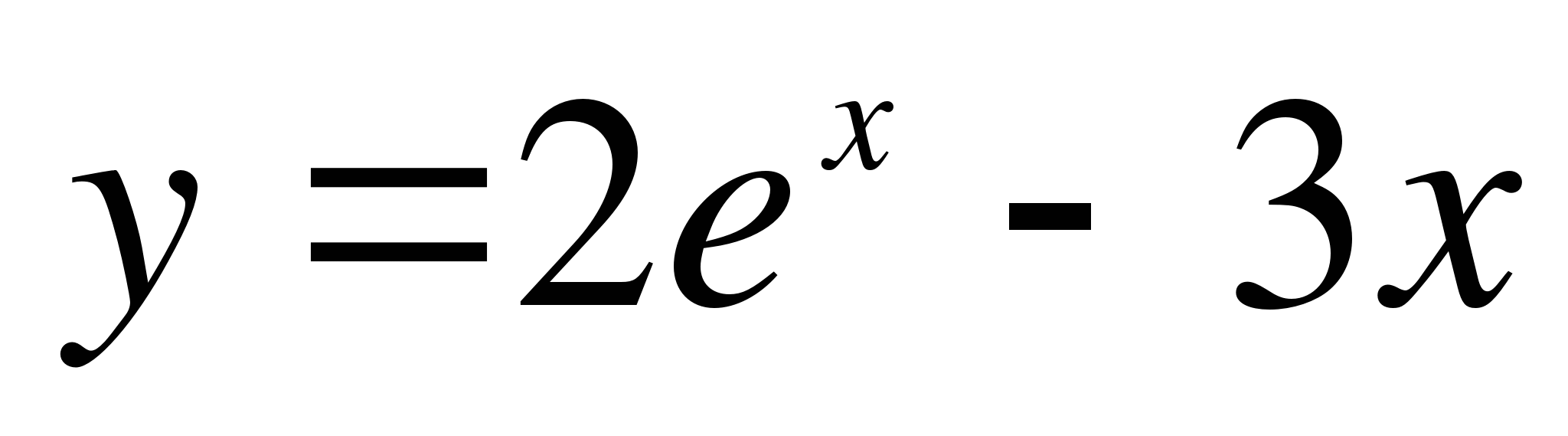 в точке
в точке 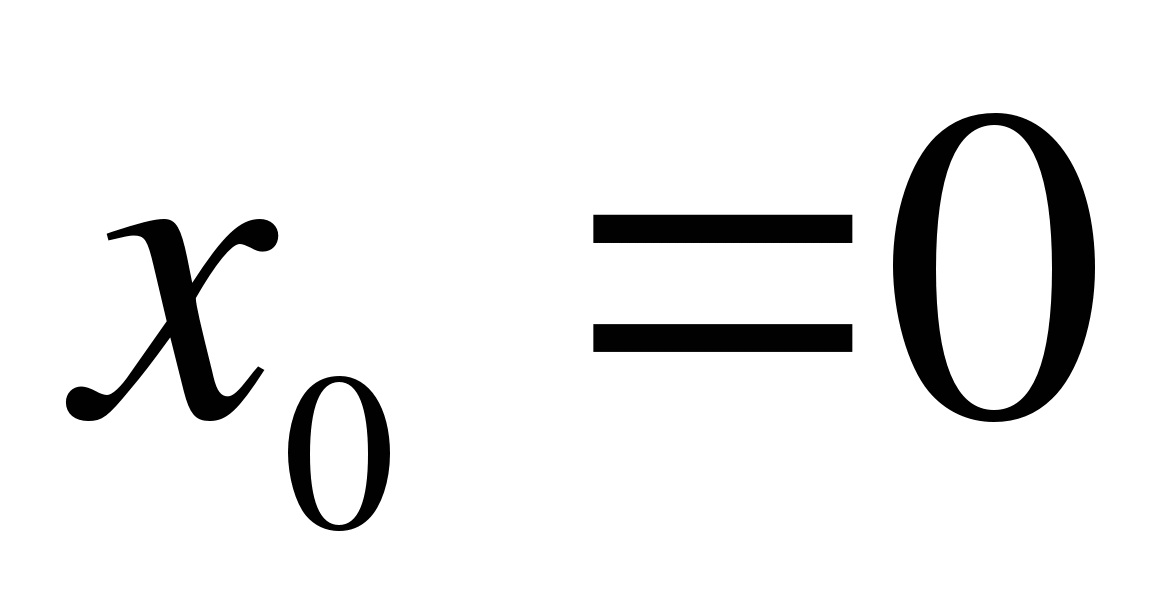
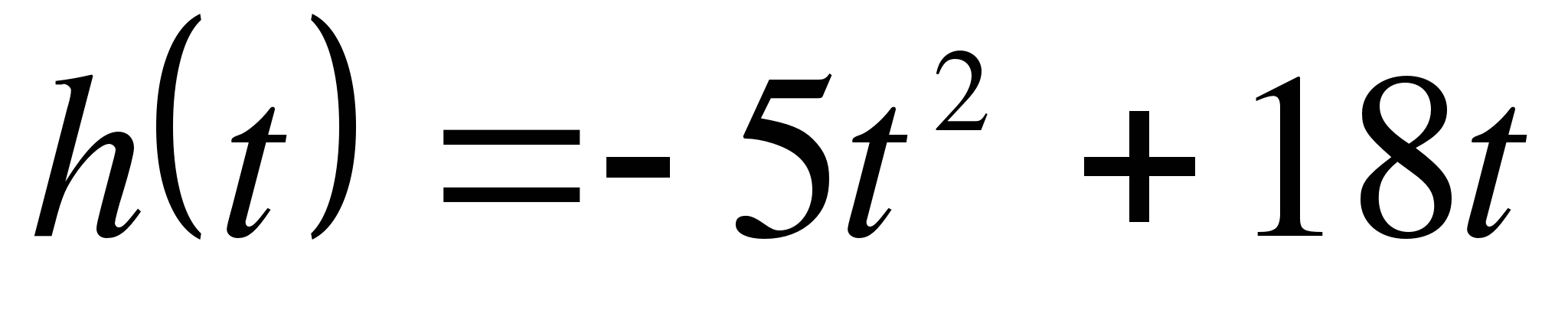 (t – время, h – расстояние от поверхности Земли до тела). В какой момент времени скорость будет равна 3?
(t – время, h – расстояние от поверхности Земли до тела). В какой момент времени скорость будет равна 3?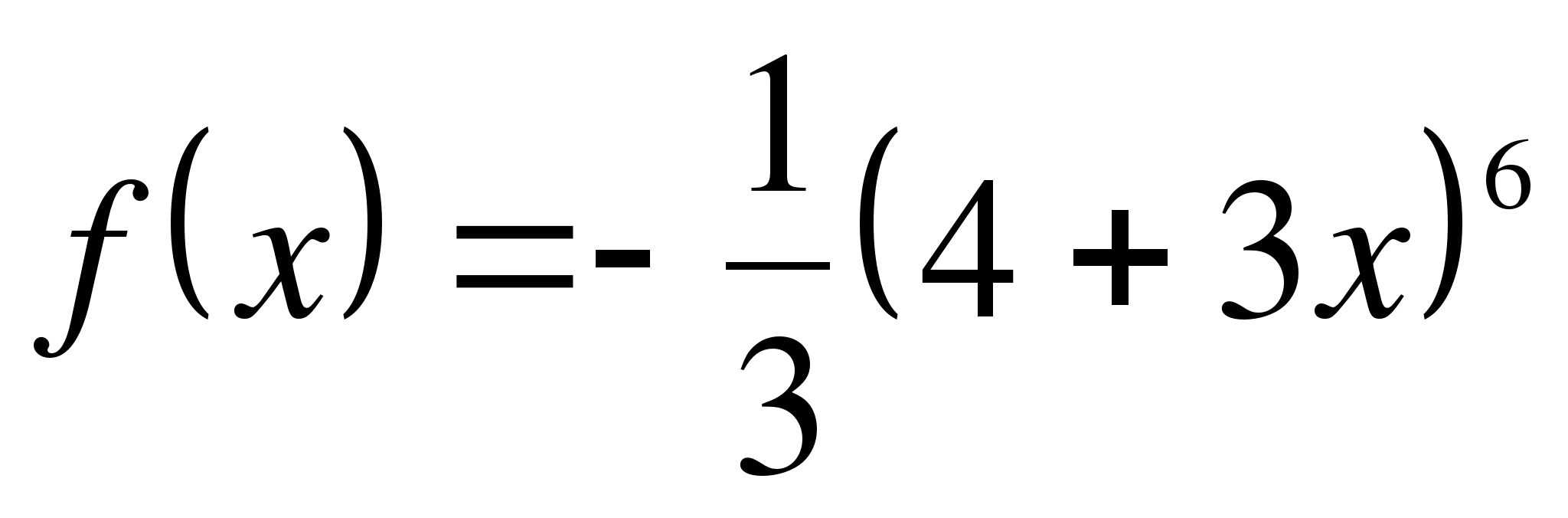
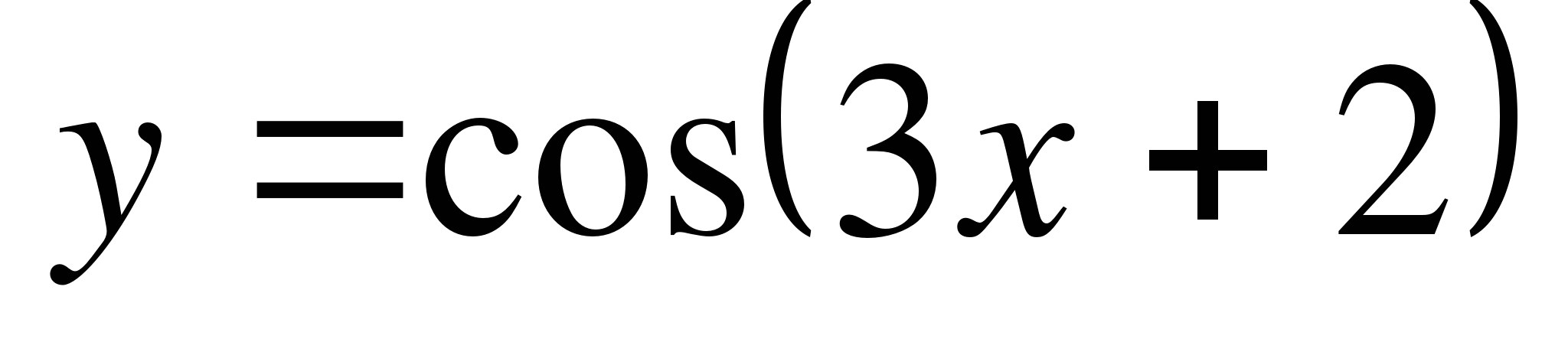
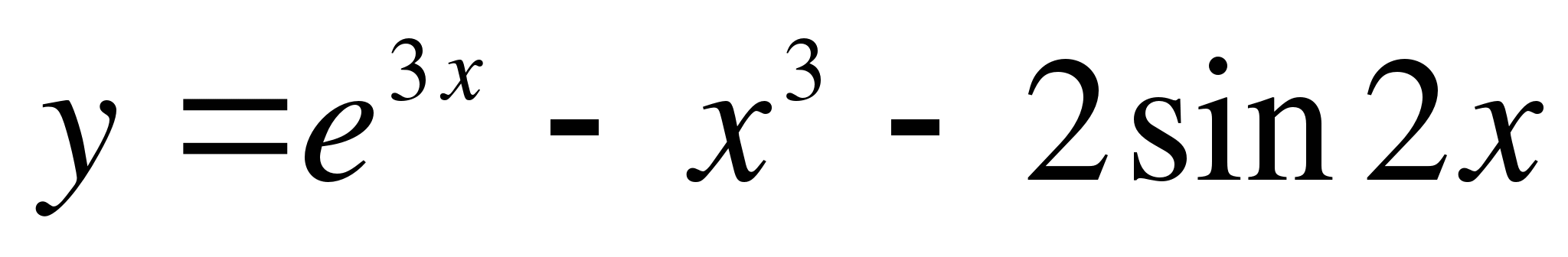
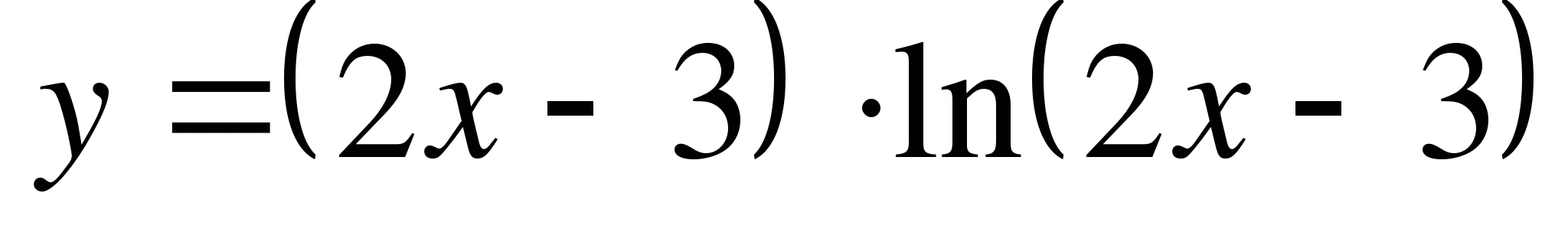 в точке
в точке 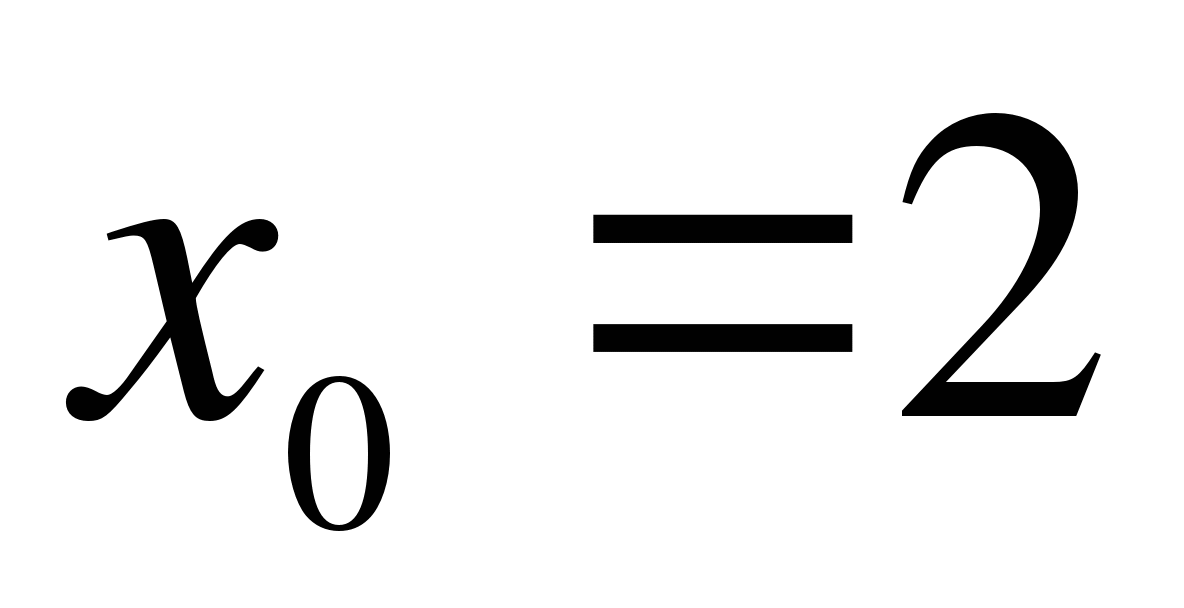 .
.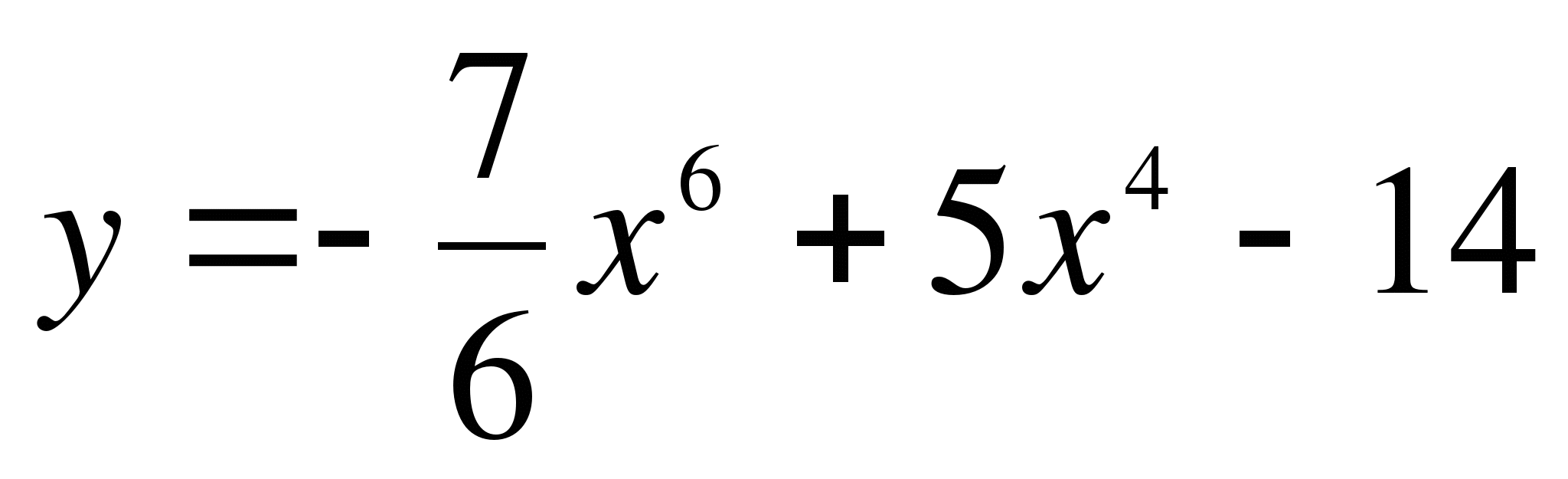
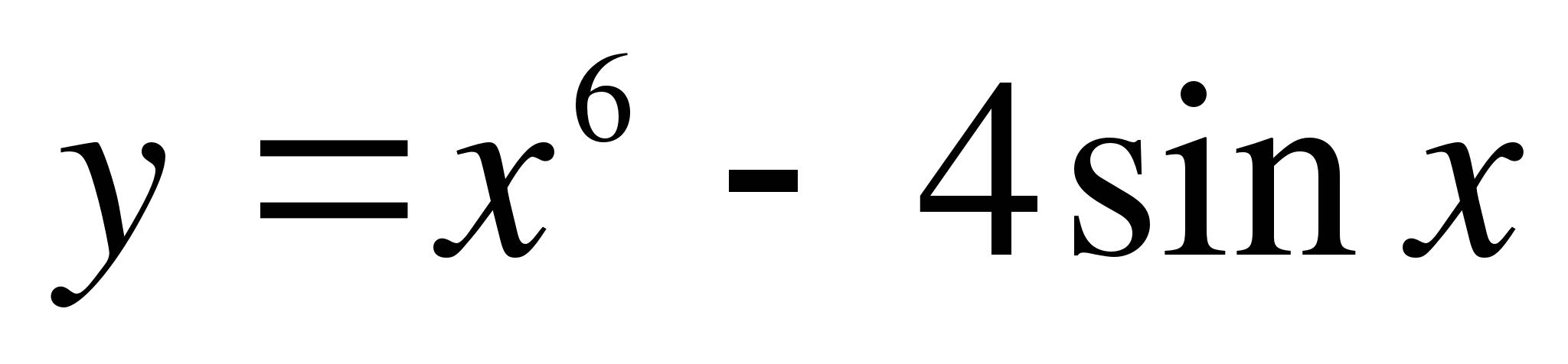
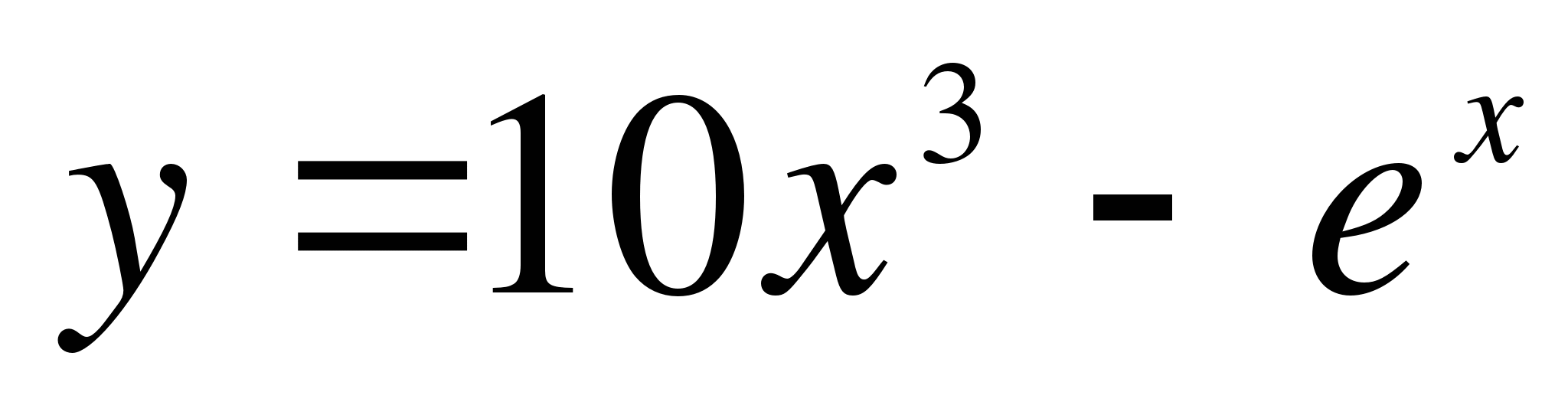
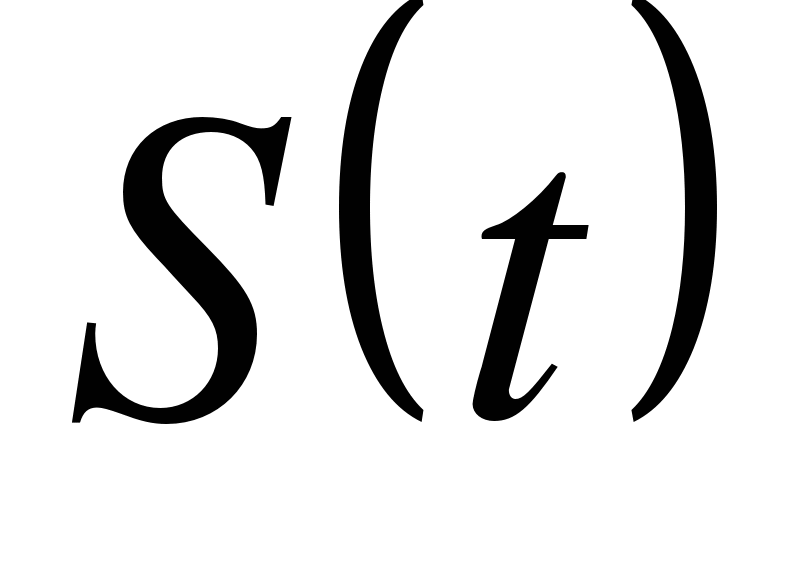 ( в метрах ) изменяется по закону
( в метрах ) изменяется по закону 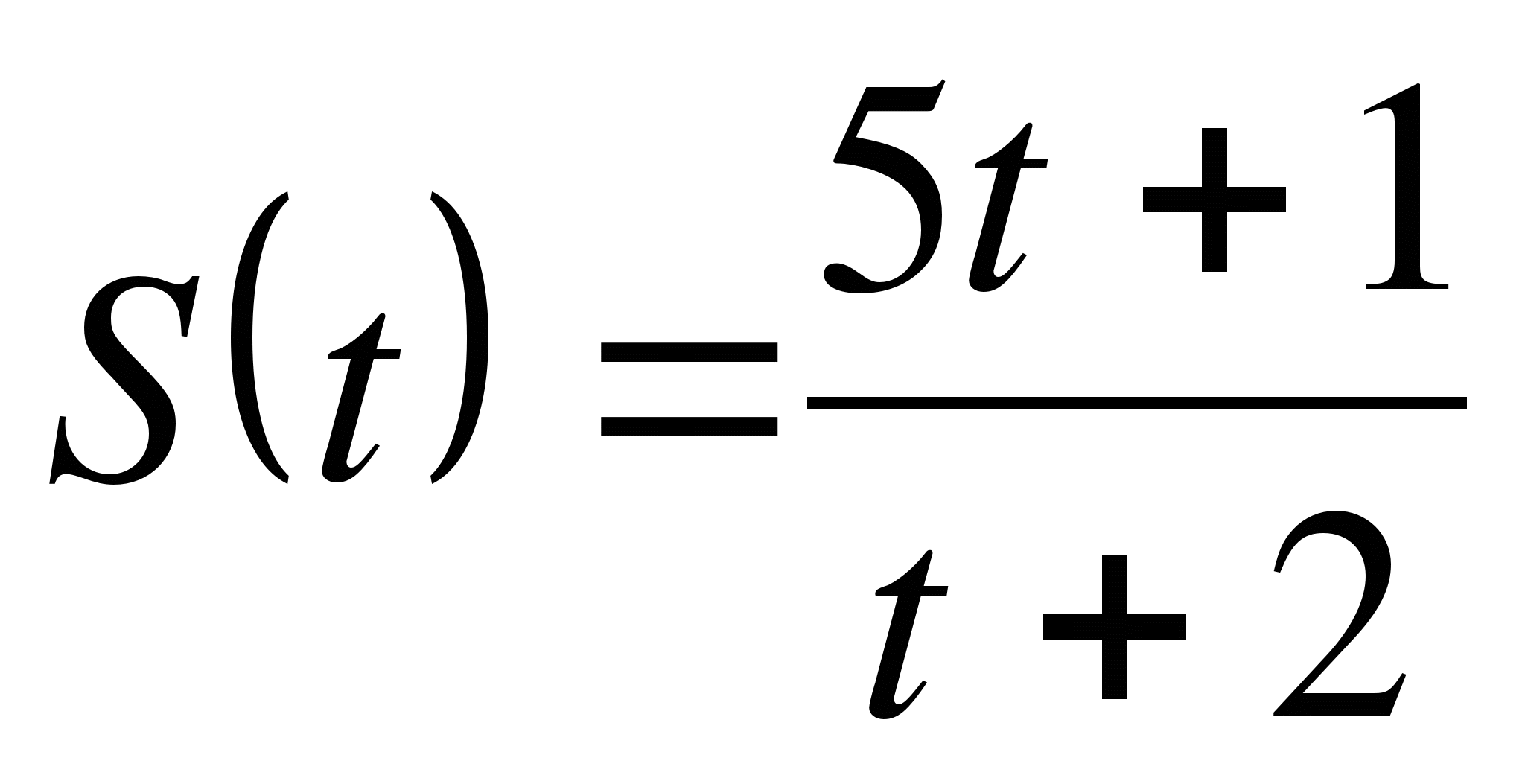 ( t – время в секундах ). Найдите скорость в момент
( t – время в секундах ). Найдите скорость в момент 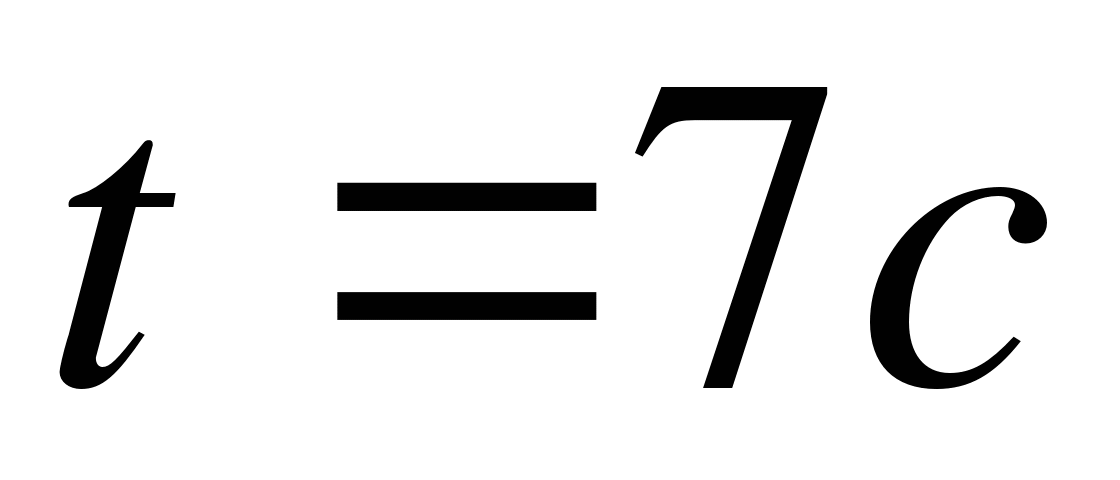 .
.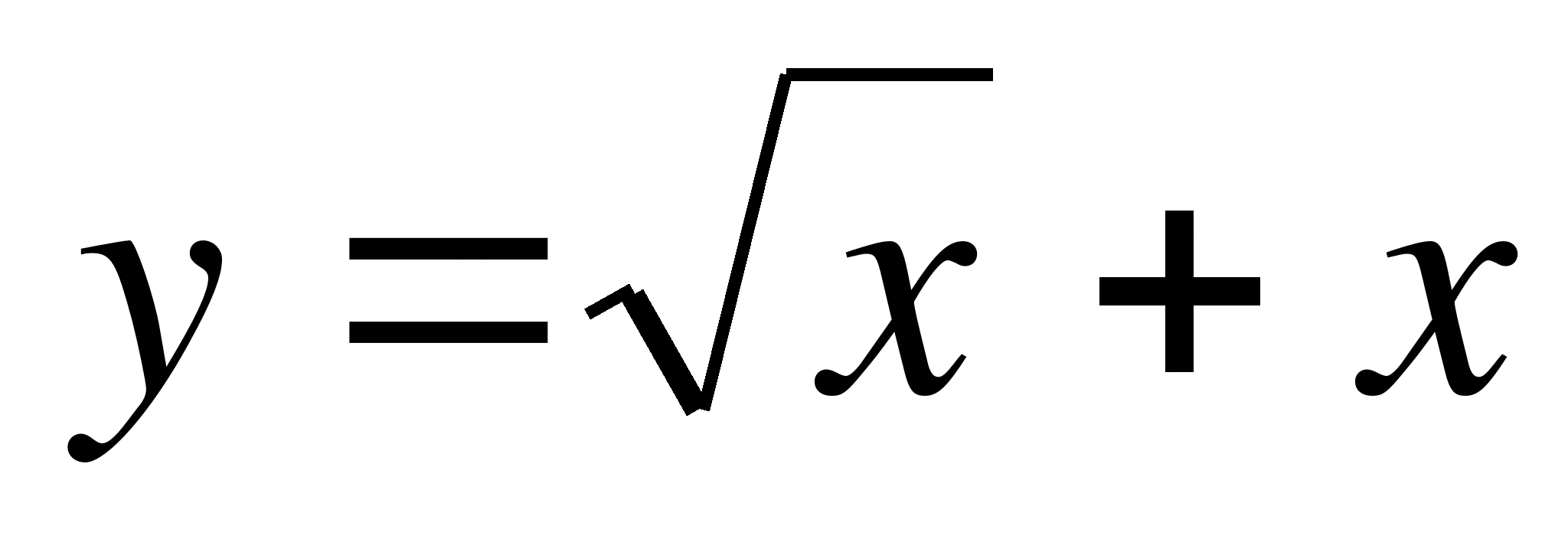 в точке
в точке 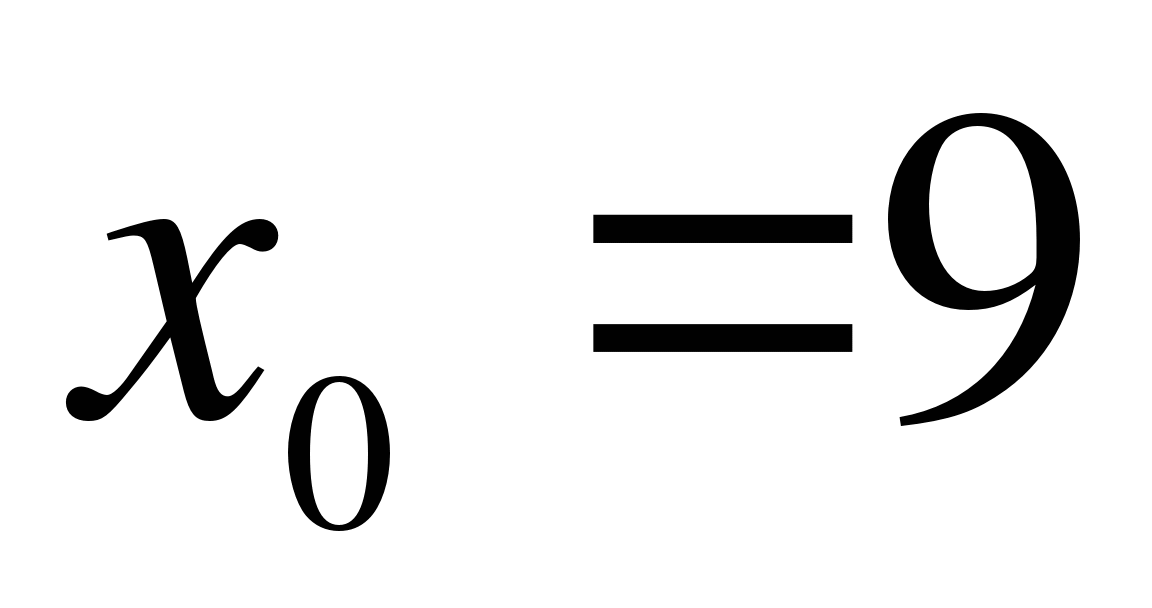 .
.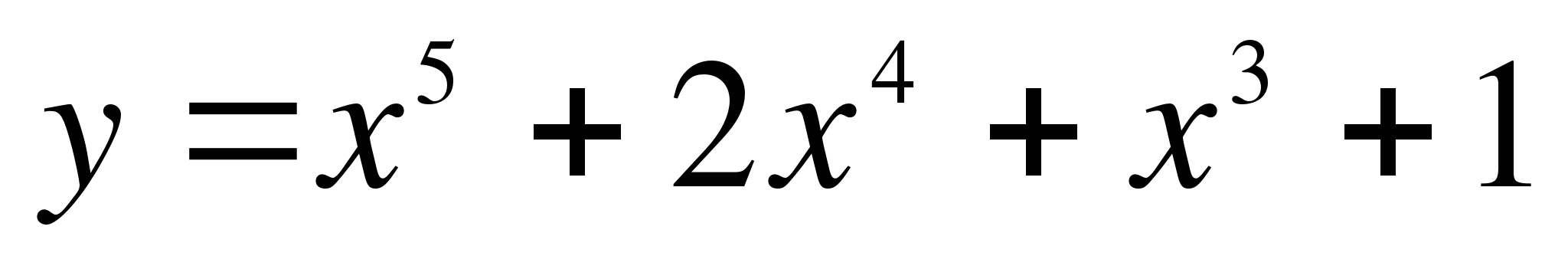 в точке
в точке 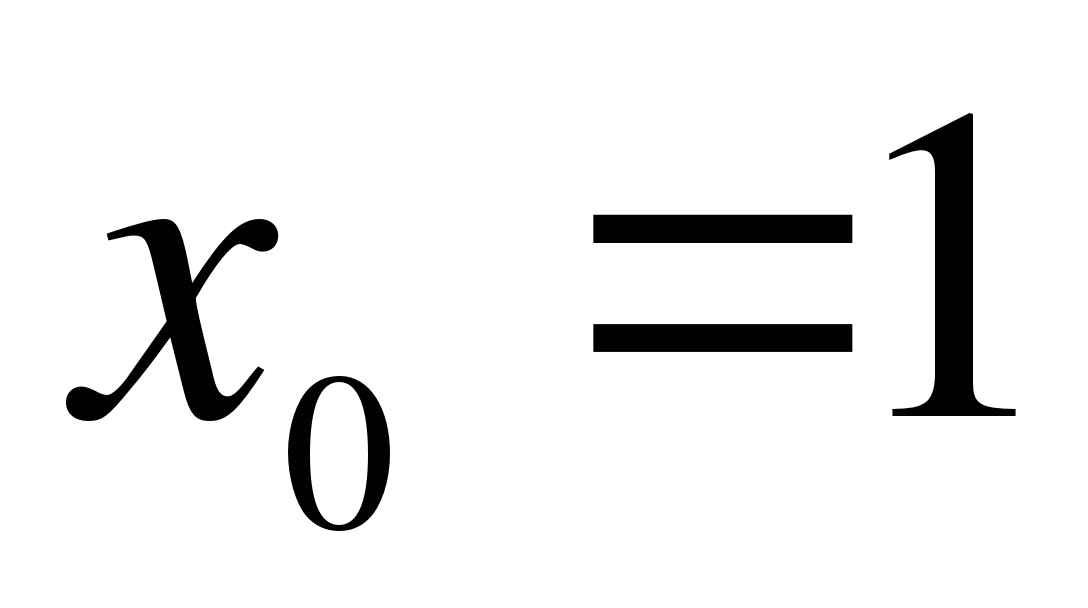 .
.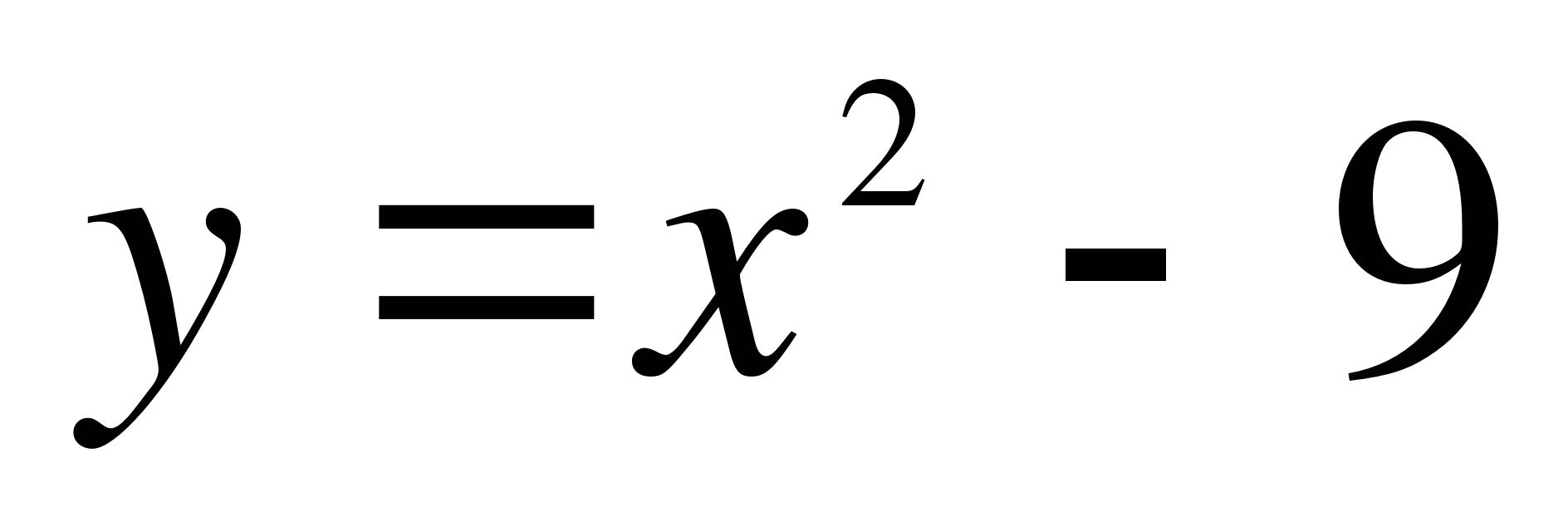 в точках пересечения параболы с осью абсцисс.
в точках пересечения параболы с осью абсцисс.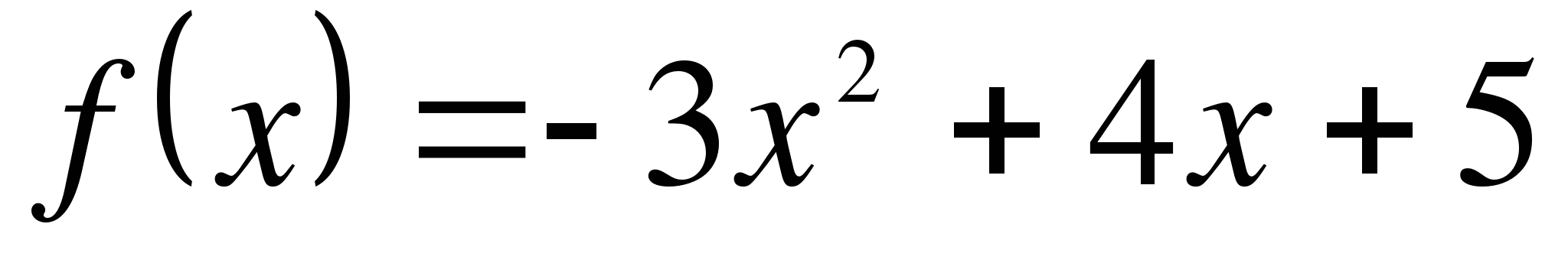 в которой угловой коэффициент касательной равен -8,6.
в которой угловой коэффициент касательной равен -8,6.
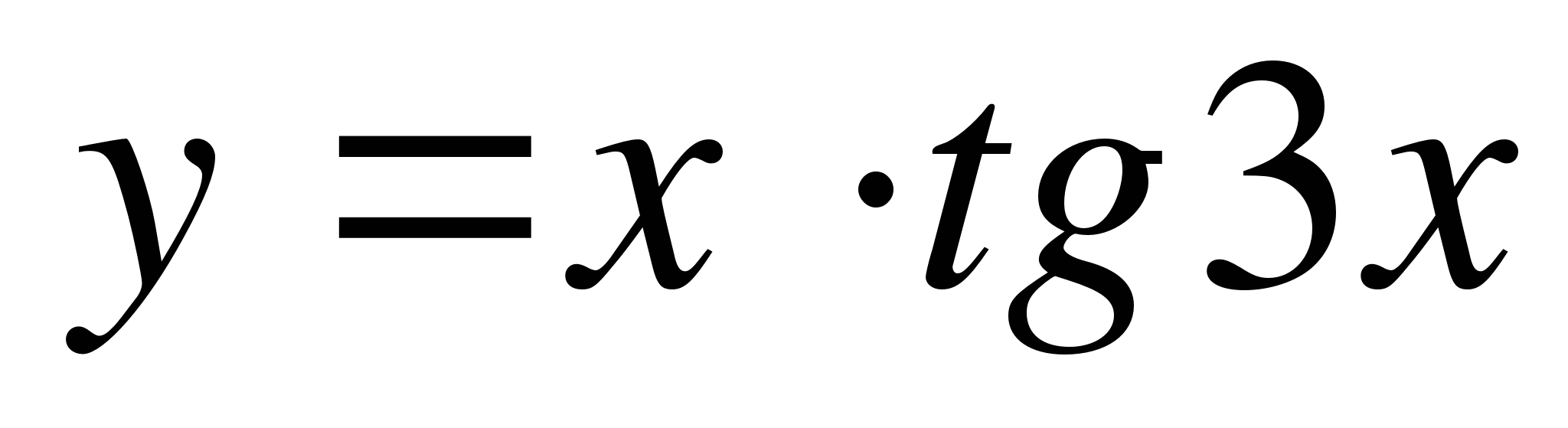
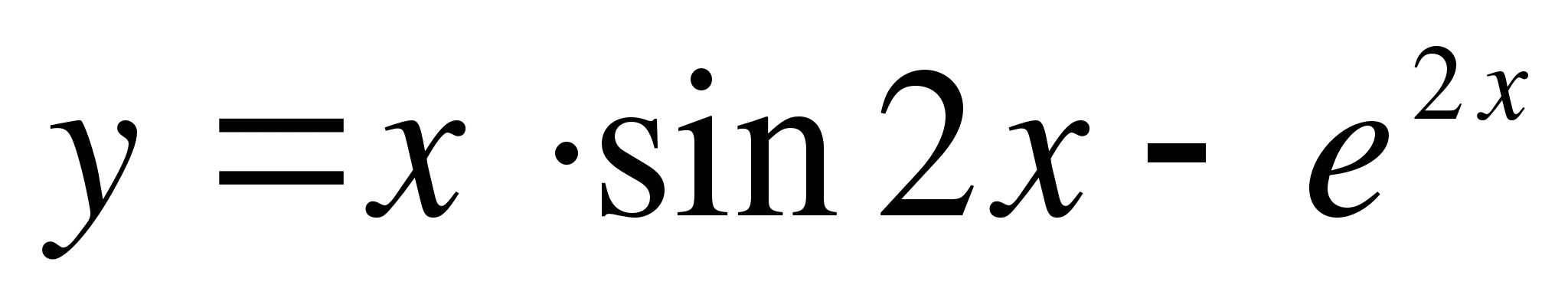
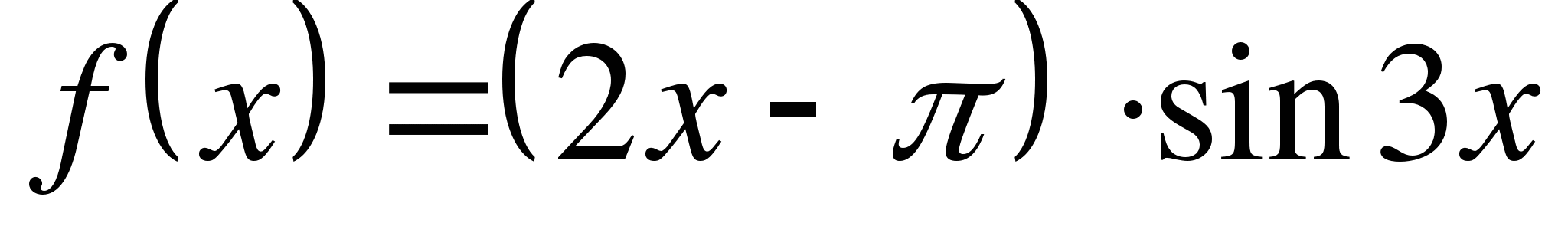 в точке
в точке 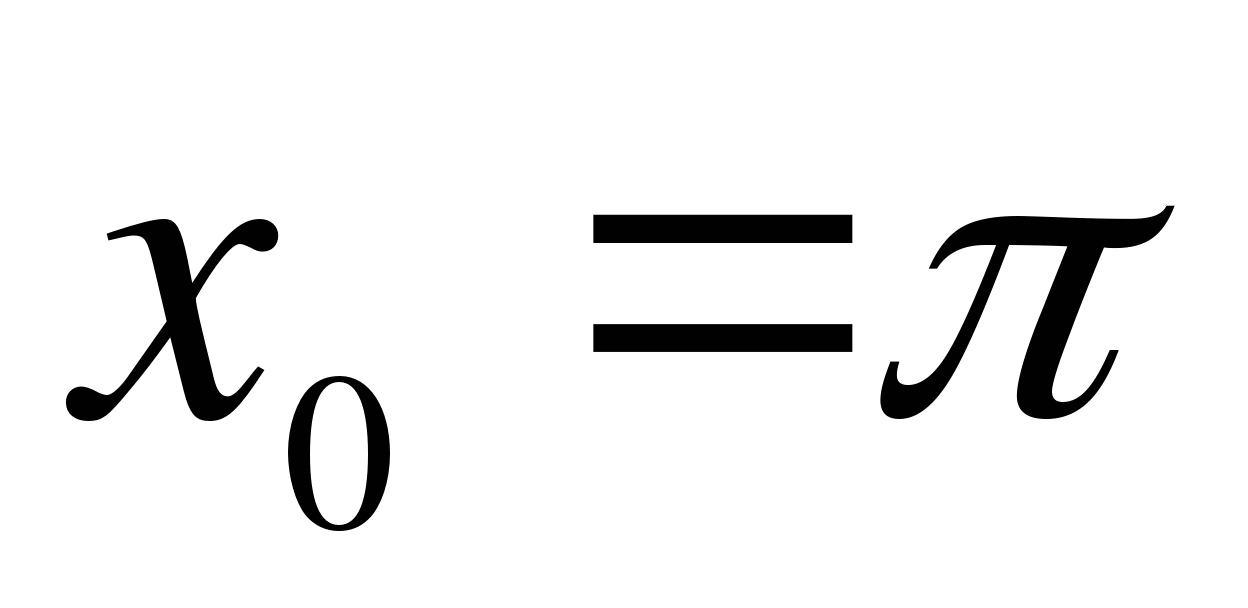 .
.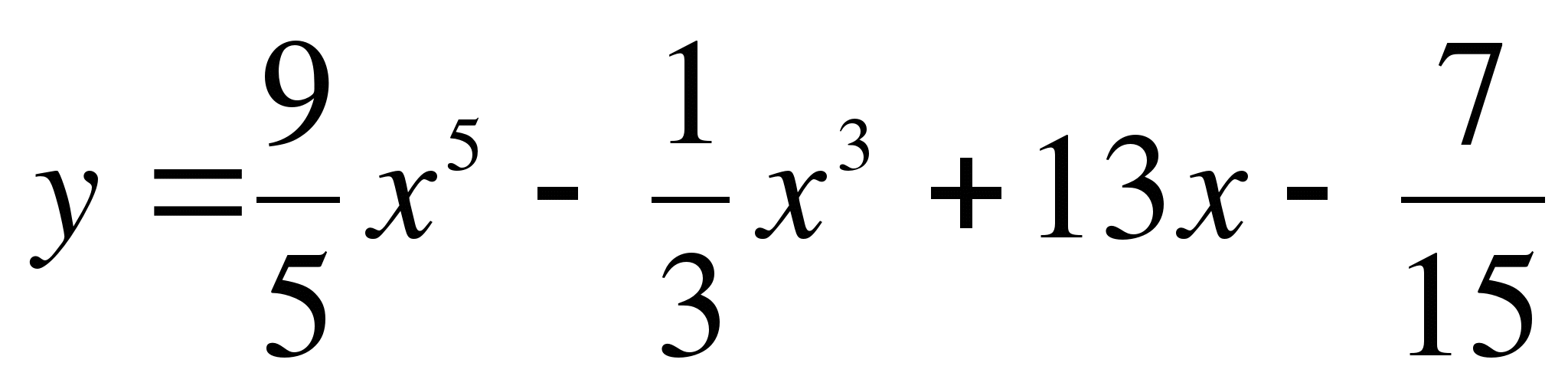
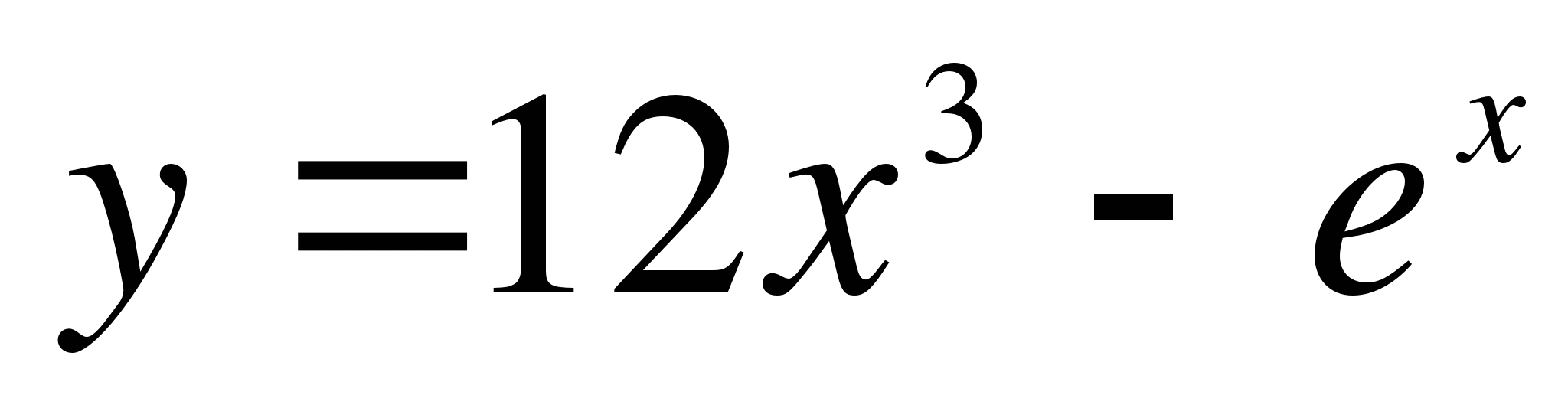
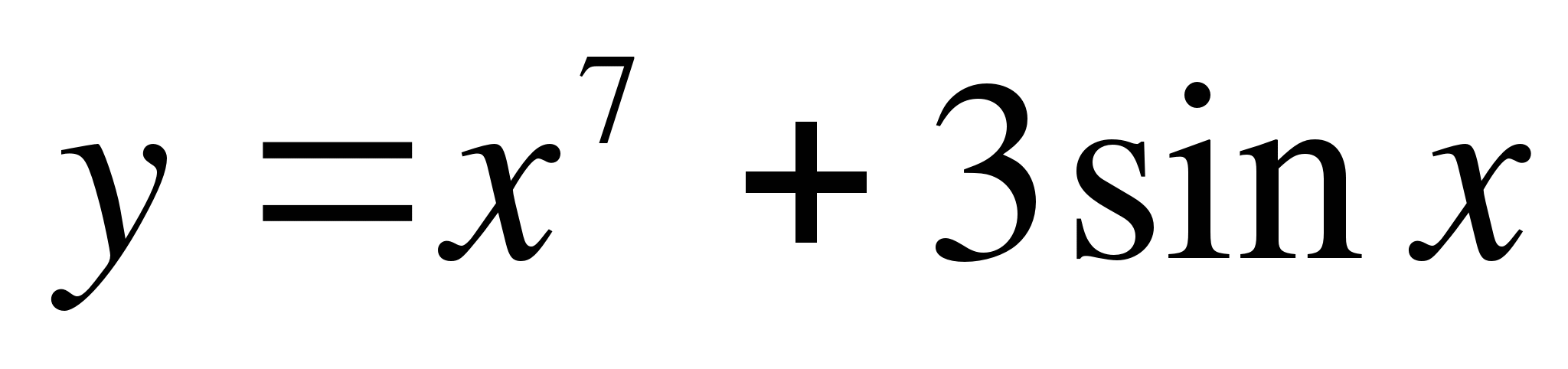
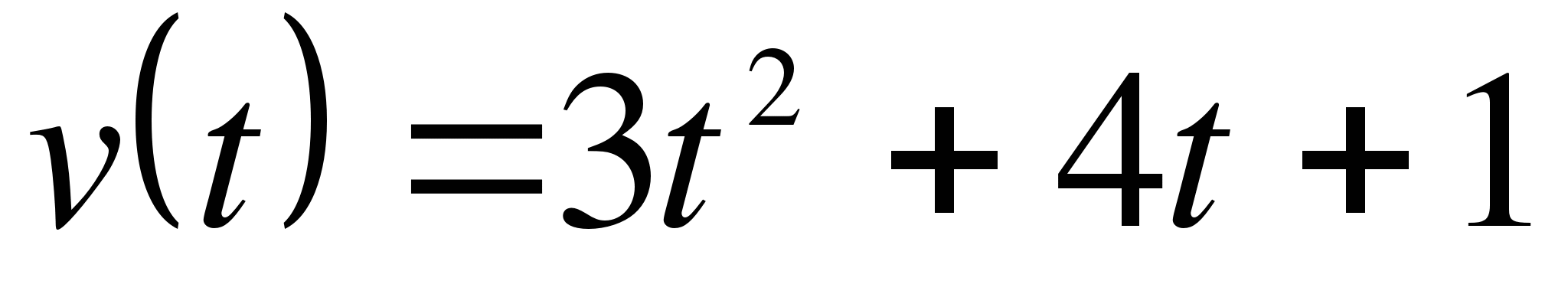 . Какую скорость приобретает тело в момент, когда его его ускорение станет равным 10 м/с2.
. Какую скорость приобретает тело в момент, когда его его ускорение станет равным 10 м/с2.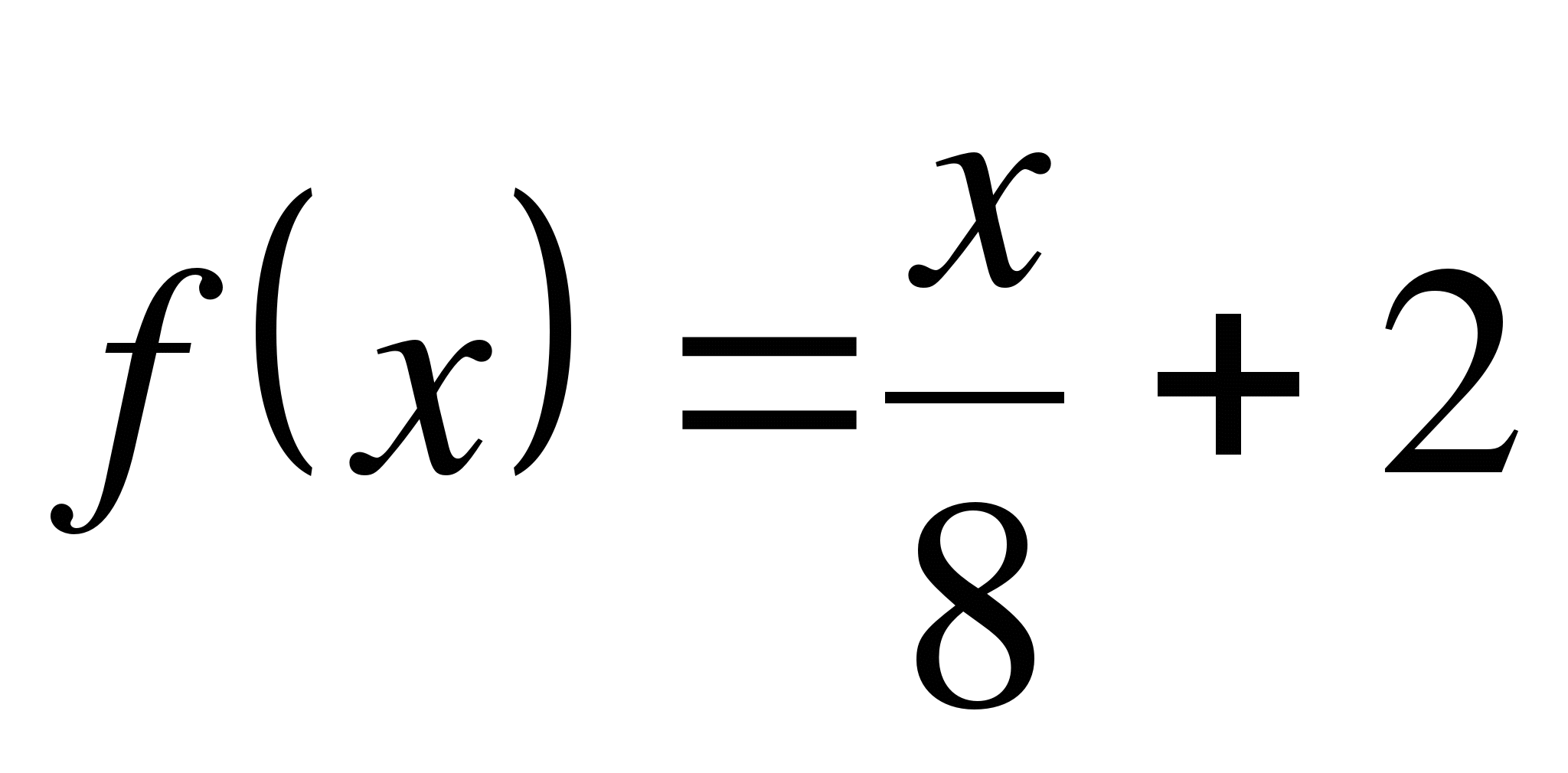 ;
; 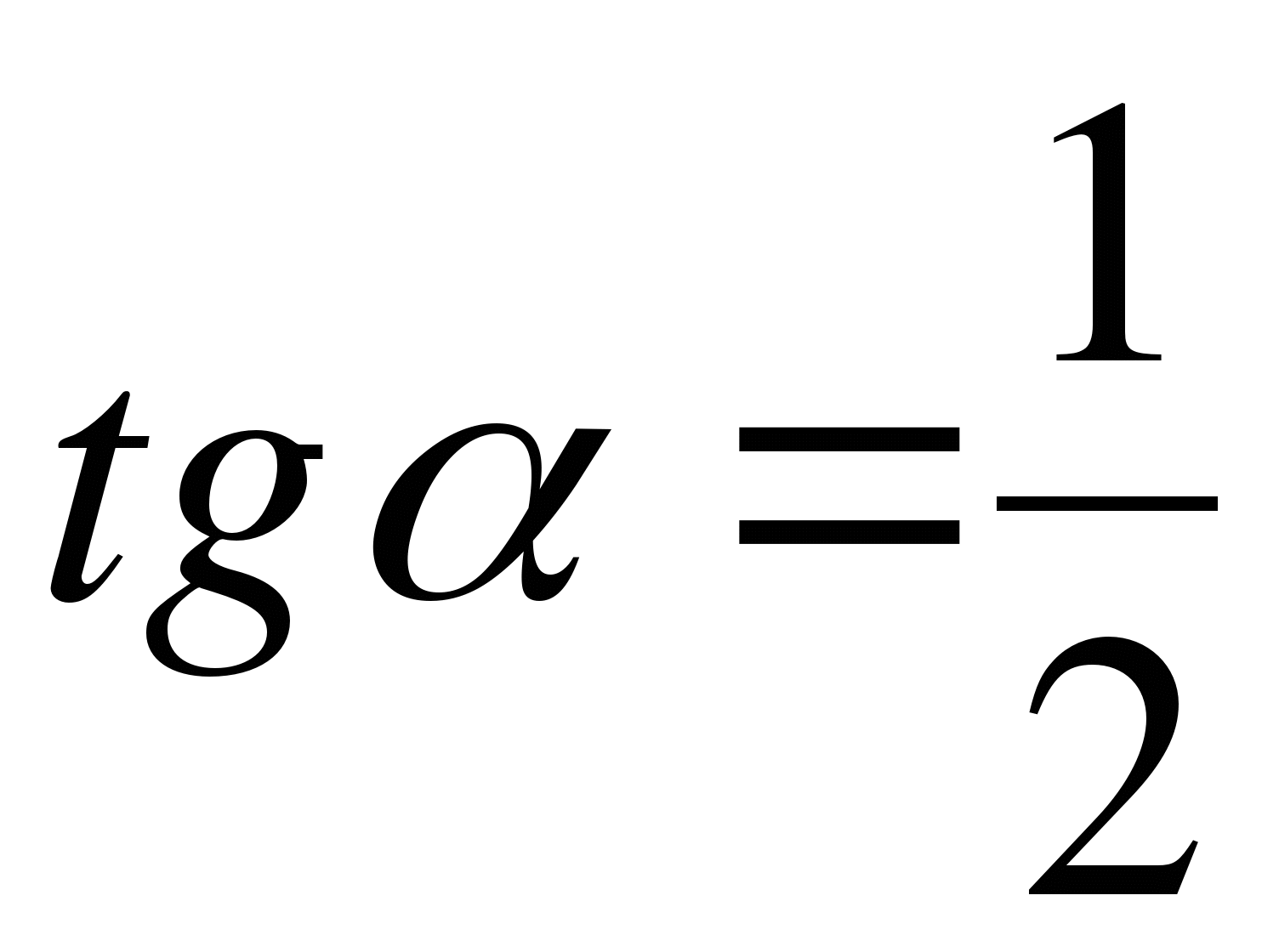 .
.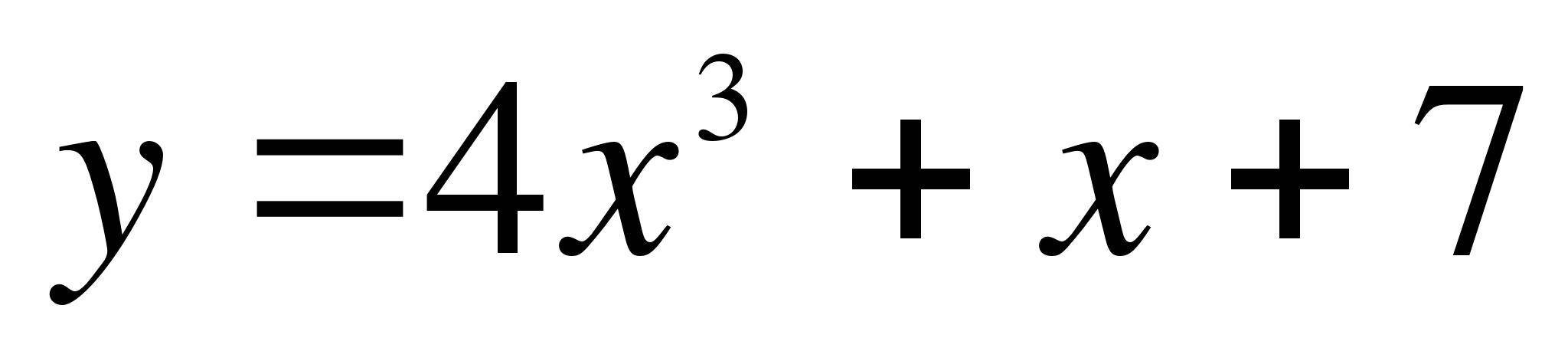 в точке
в точке 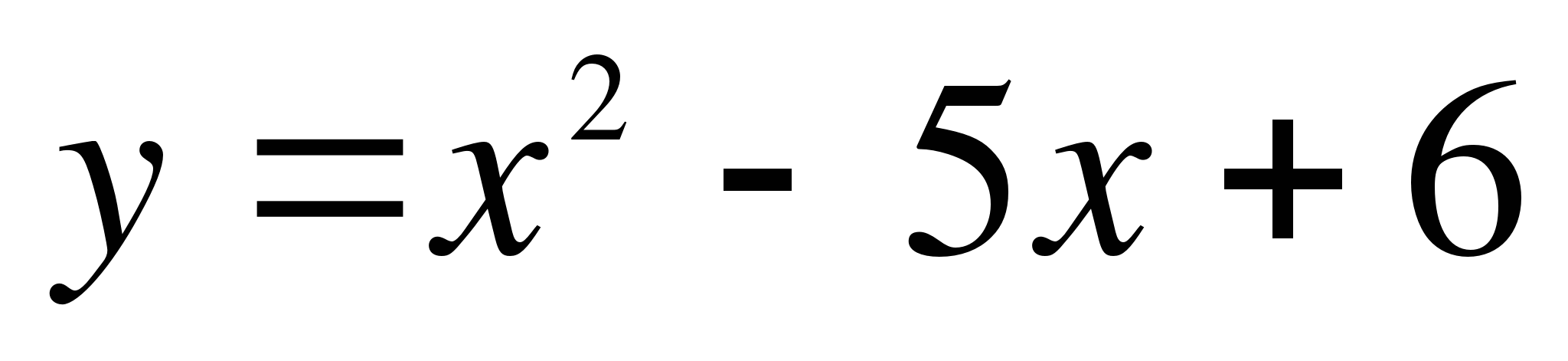 в точках пересечения параболы с осью абсцисс.
в точках пересечения параболы с осью абсцисс.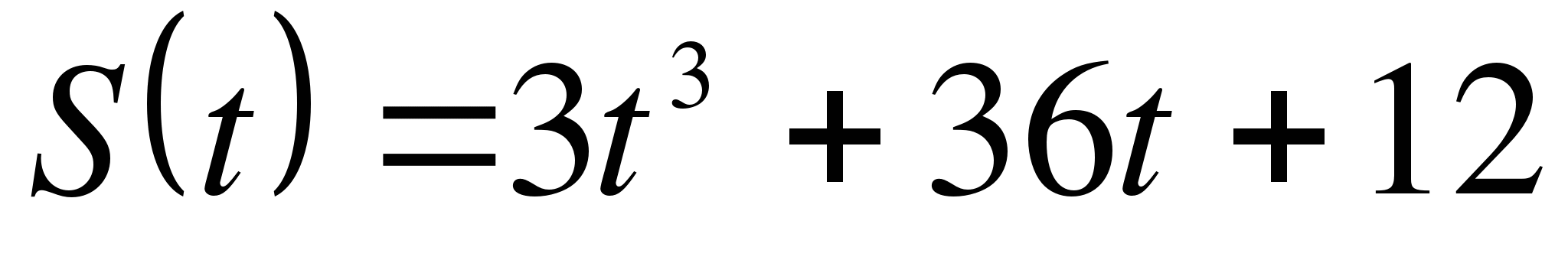 . В какой момент времени скорость точки будет равна 45?
. В какой момент времени скорость точки будет равна 45?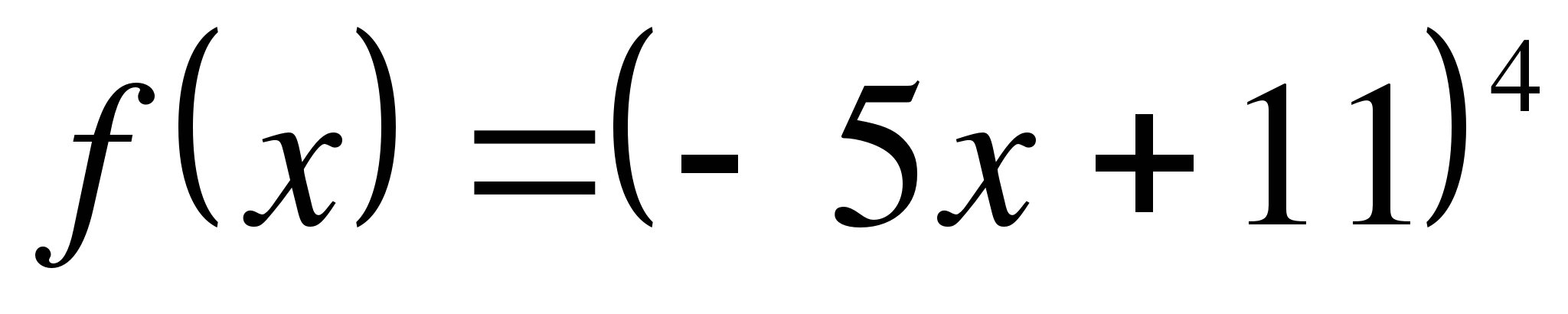
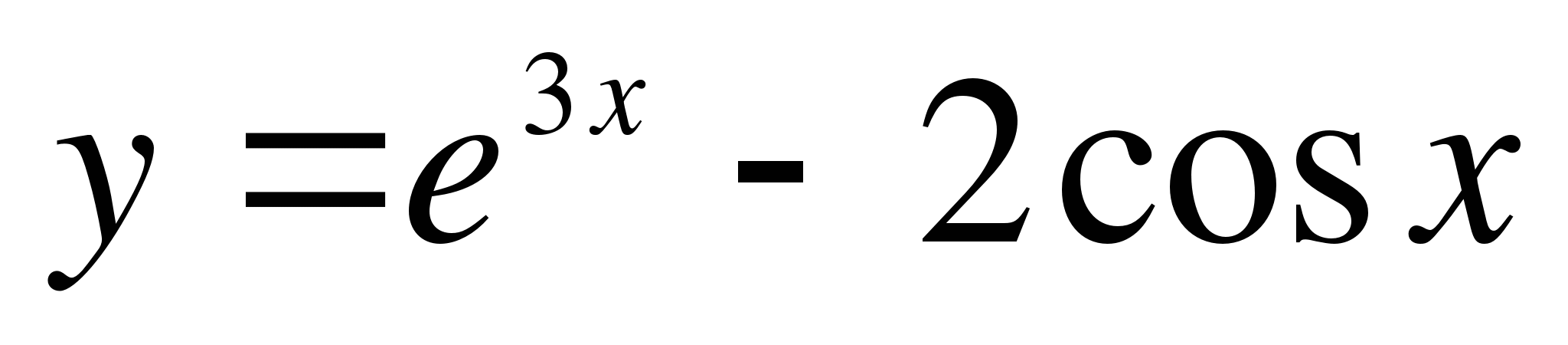
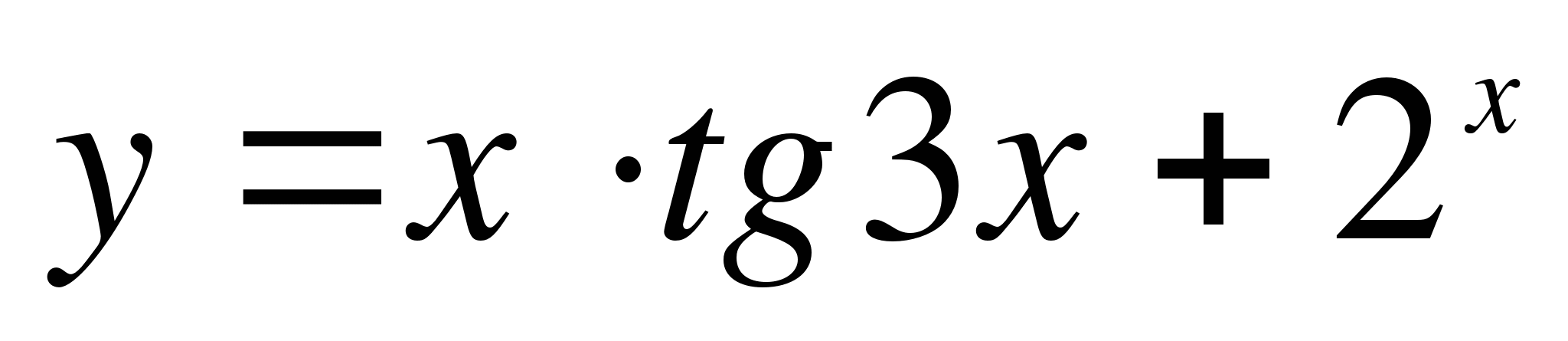
 в точке
в точке 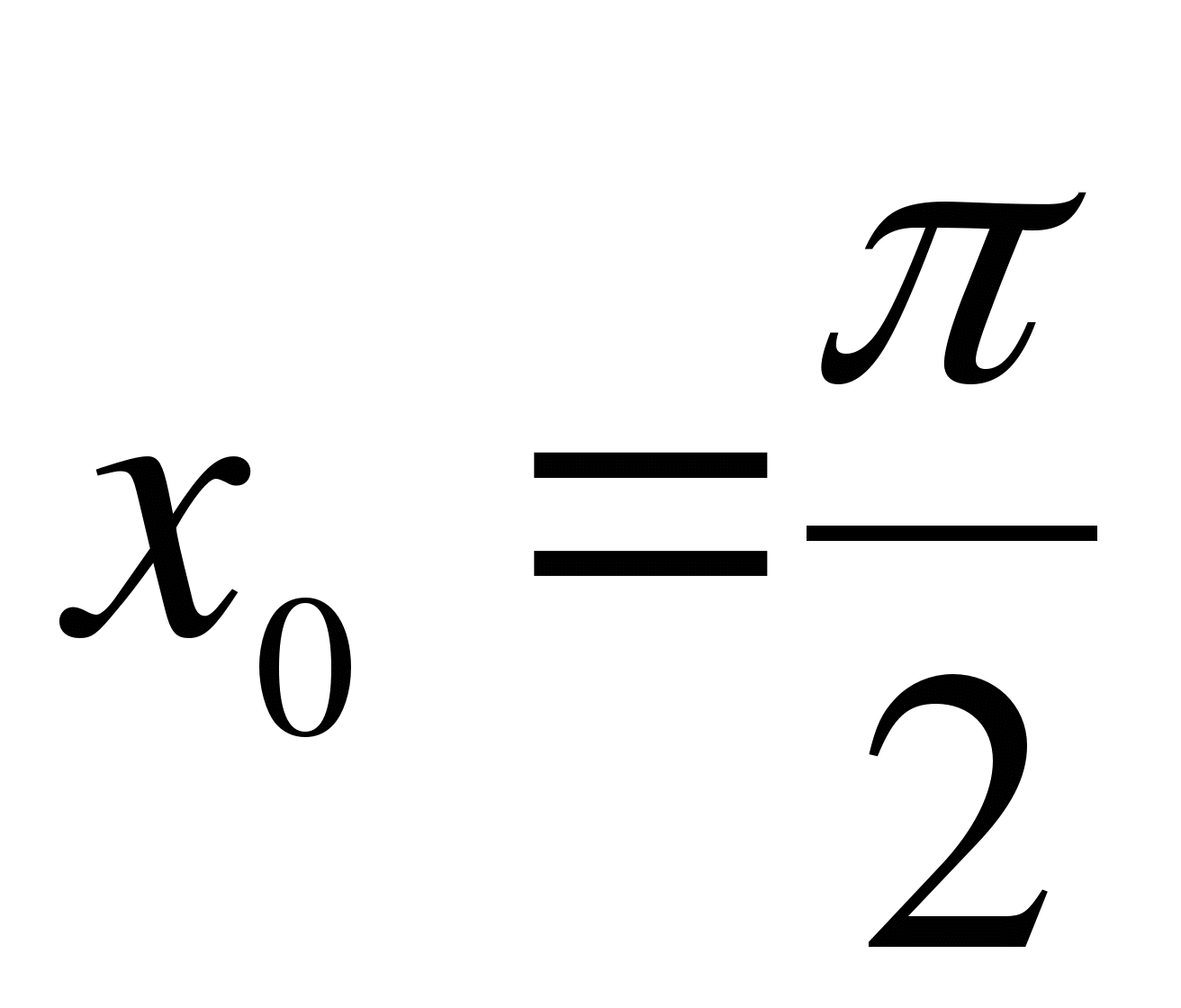 .
.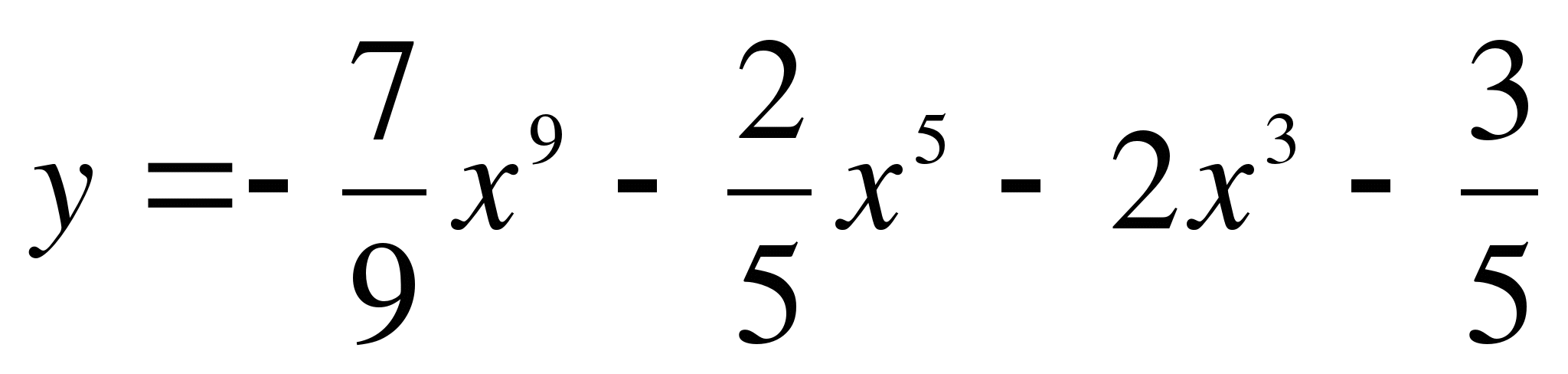
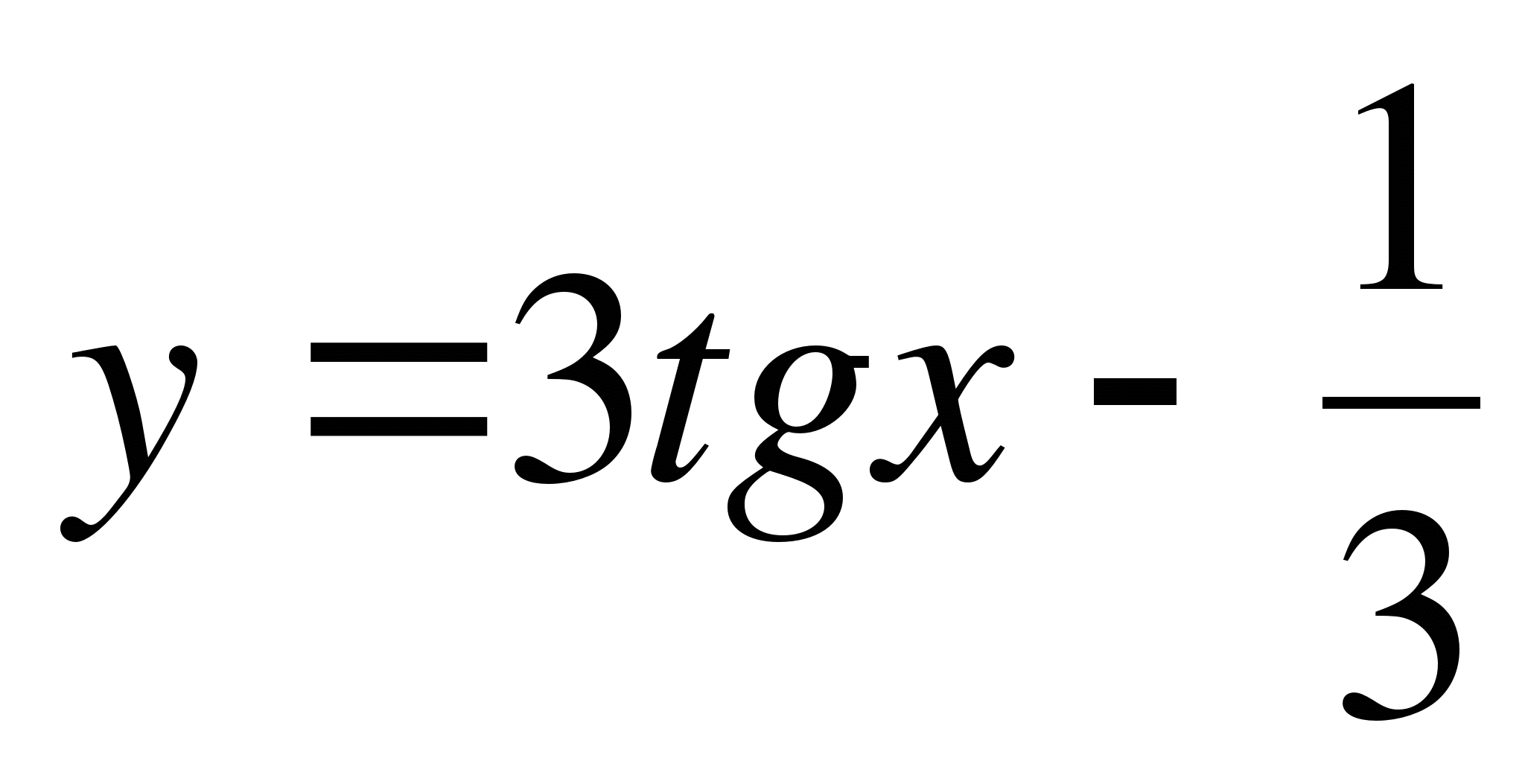
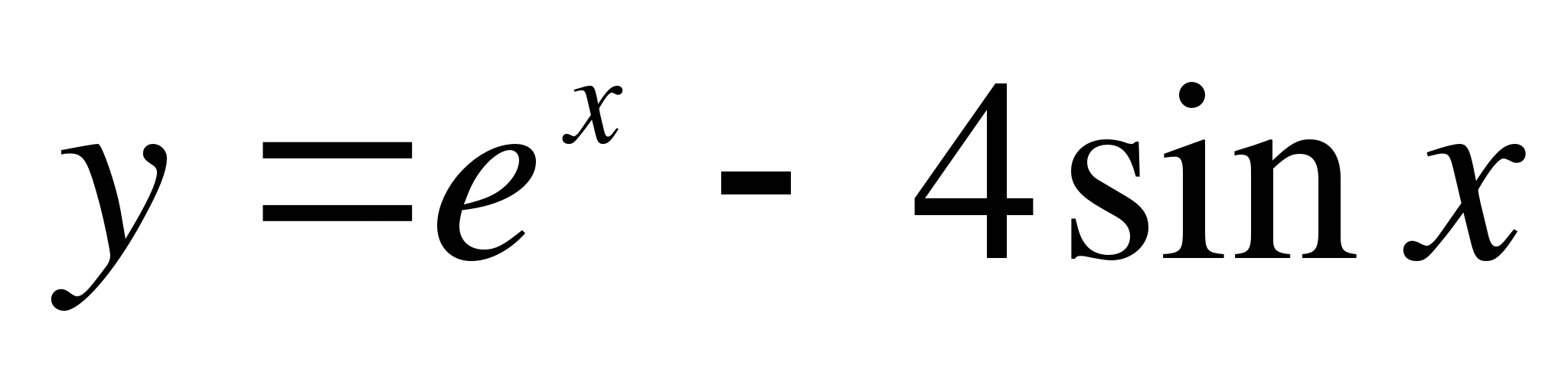
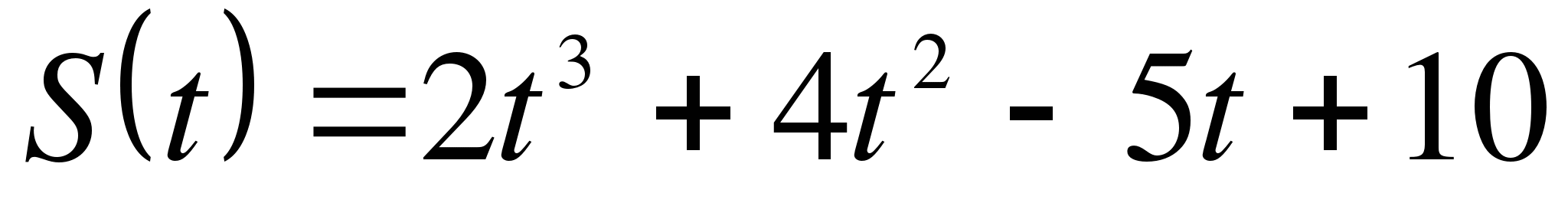
 Какую скорость приобретает тело в момент, когда его ускорение станет равным 10 м/с2.
Какую скорость приобретает тело в момент, когда его ускорение станет равным 10 м/с2.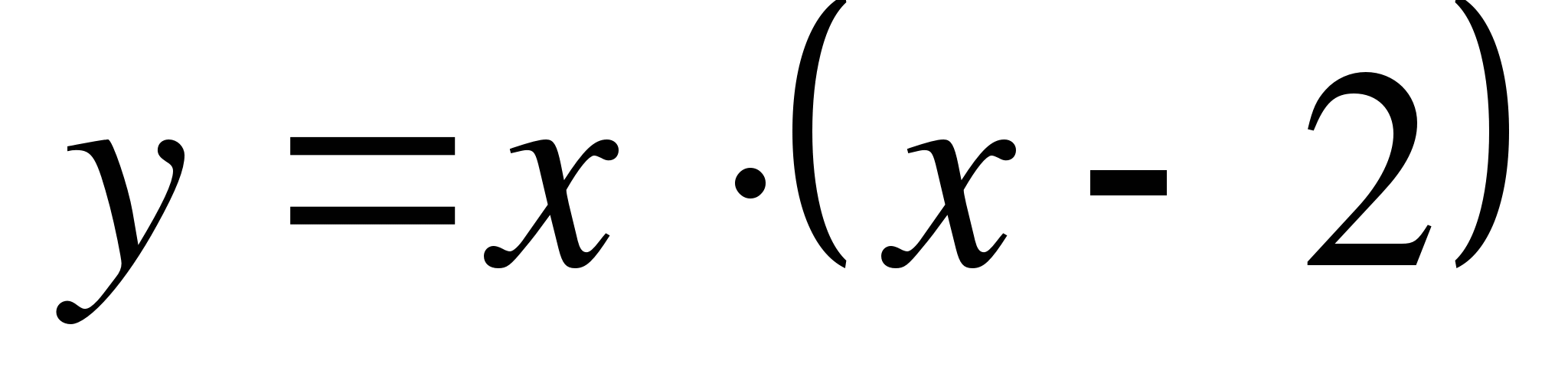 в точке
в точке 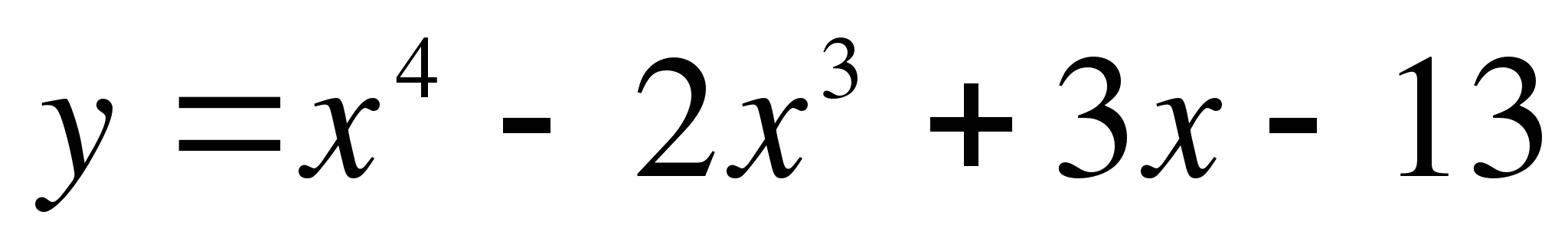 в точке
в точке 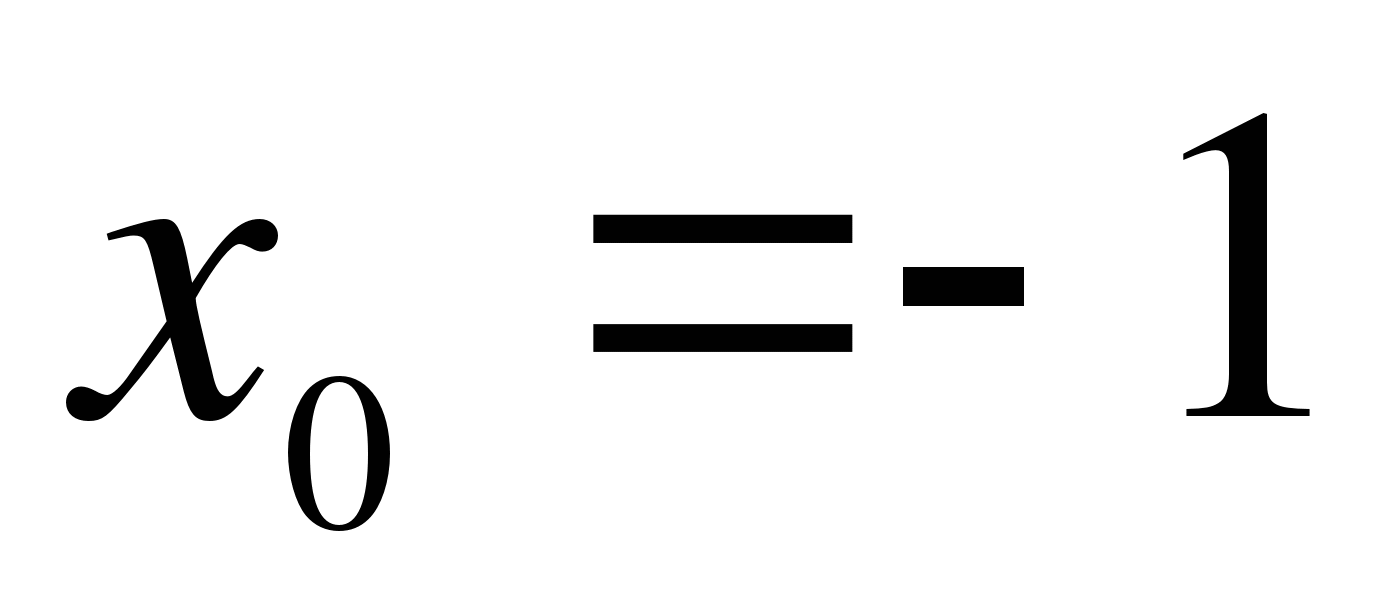 .
.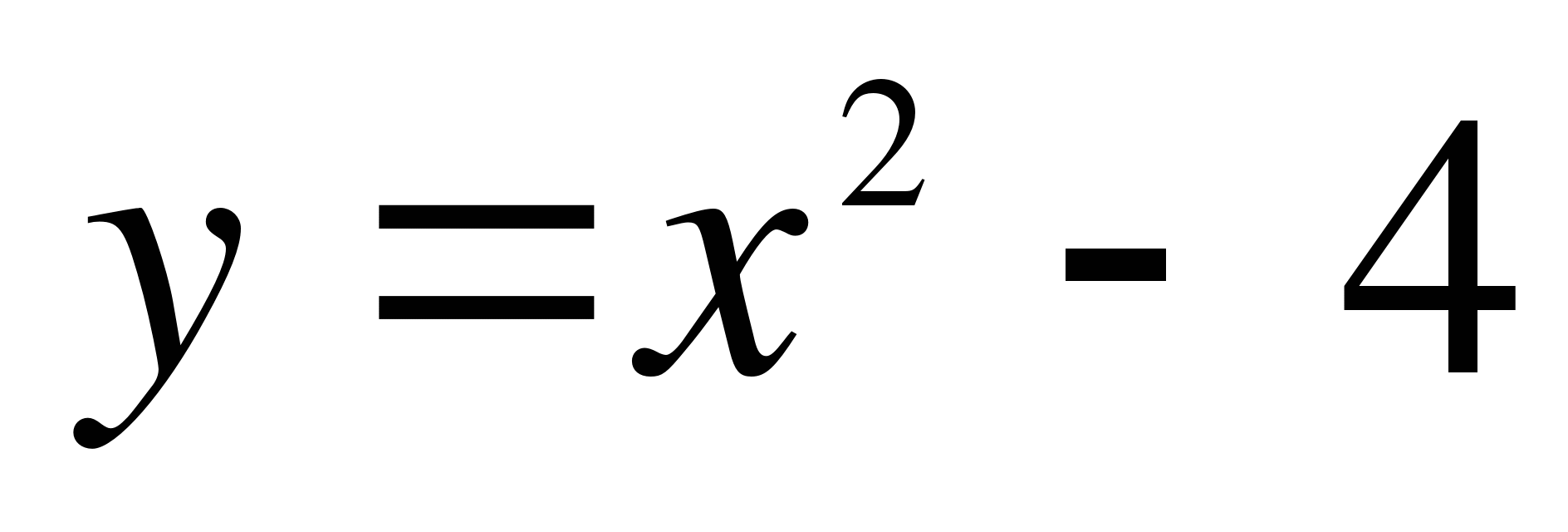 в точках пересечения параболы с осью абсцисс.
в точках пересечения параболы с осью абсцисс. (t – время, h – расстояние от поверхности Земли до тела). Определите скорость в момент времени
(t – время, h – расстояние от поверхности Земли до тела). Определите скорость в момент времени 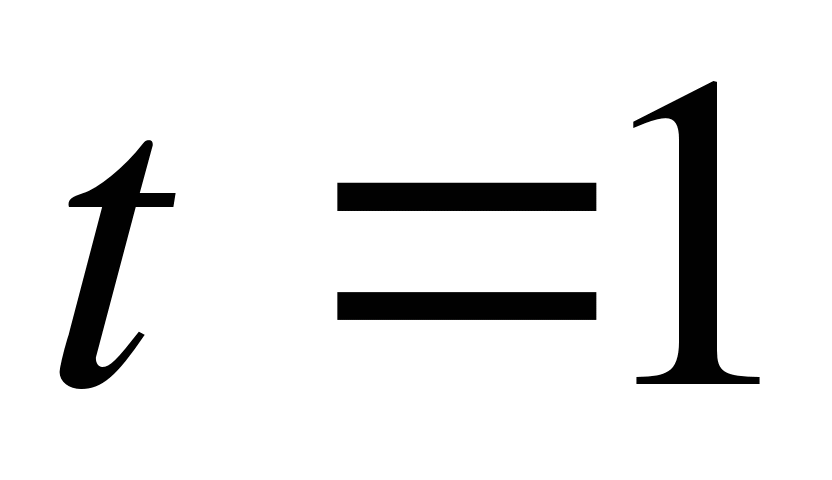 .
.

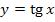 .
.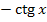 ; Г)
; Г) 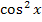 ;
;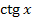 ; Д)
; Д) 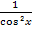 .
.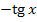 ;
;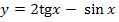 в точке с абсциссой
в точке с абсциссой 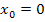 .
.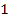 ; Г)
; Г) 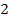 ;
;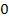 ; Д)
; Д) 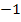 .
.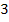 ;
;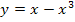 в точке с абсциссой
в точке с абсциссой 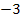 ;
;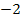 ;
;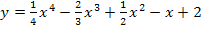 в точке с абсциссой
в точке с абсциссой 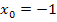 .
. ;
;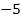 ; Д)
; Д) 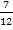 .
.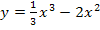 в точке с абсциссой
в точке с абсциссой 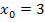 .
.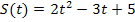 , равна нулю?
, равна нулю?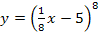 .
.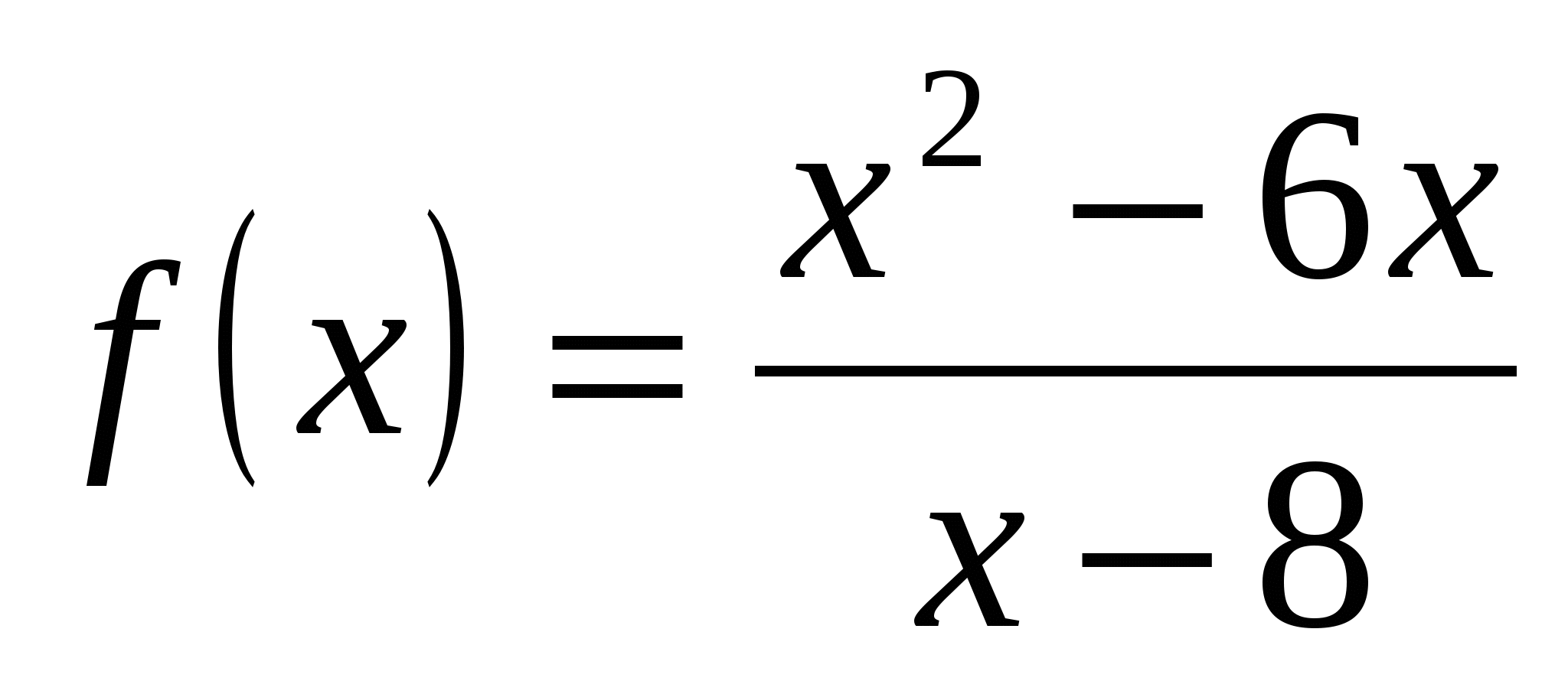 меньше нуля?
меньше нуля?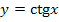 .
.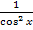 ;
;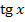 ; Д)
; Д) 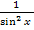 .
.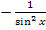 ;
;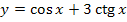 в точке с абсциссой
в точке с абсциссой 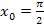 .
.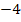 ; Г)
; Г) 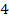 ;
;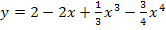 в точке с абсциссой
в точке с абсциссой 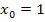 .
.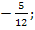 Г)
Г)  .
.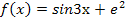 .
.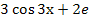 ; Г)
; Г) 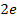 ;
;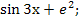 Д)
Д) 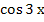 ;
;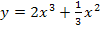 в точке с абсциссой
в точке с абсциссой 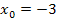 .
.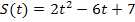 , равна нулю?
, равна нулю?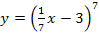 .
.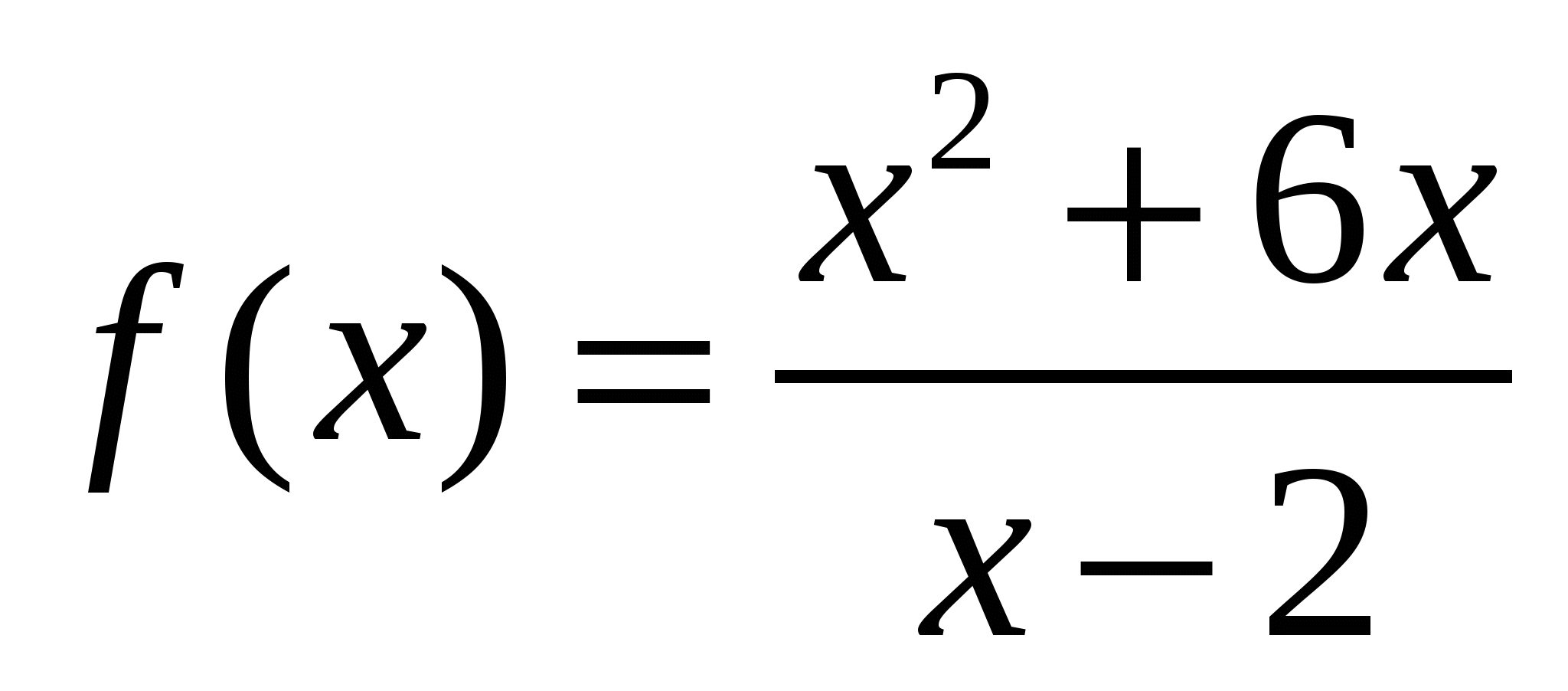 больше нуля?
больше нуля?







