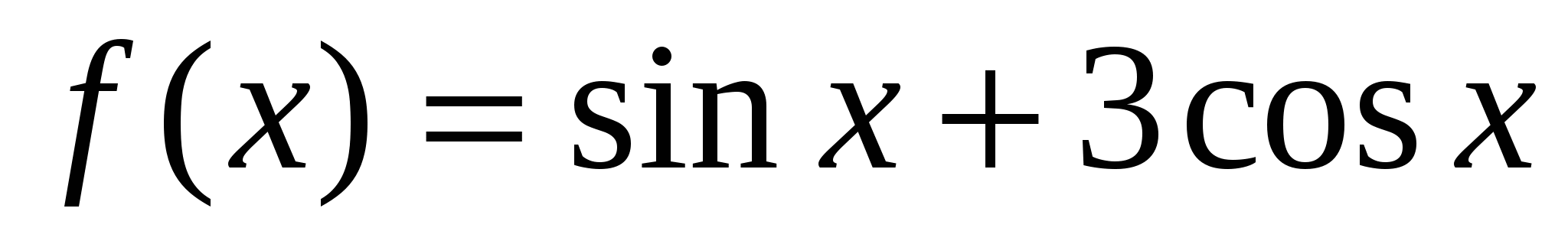 в точке
в точке 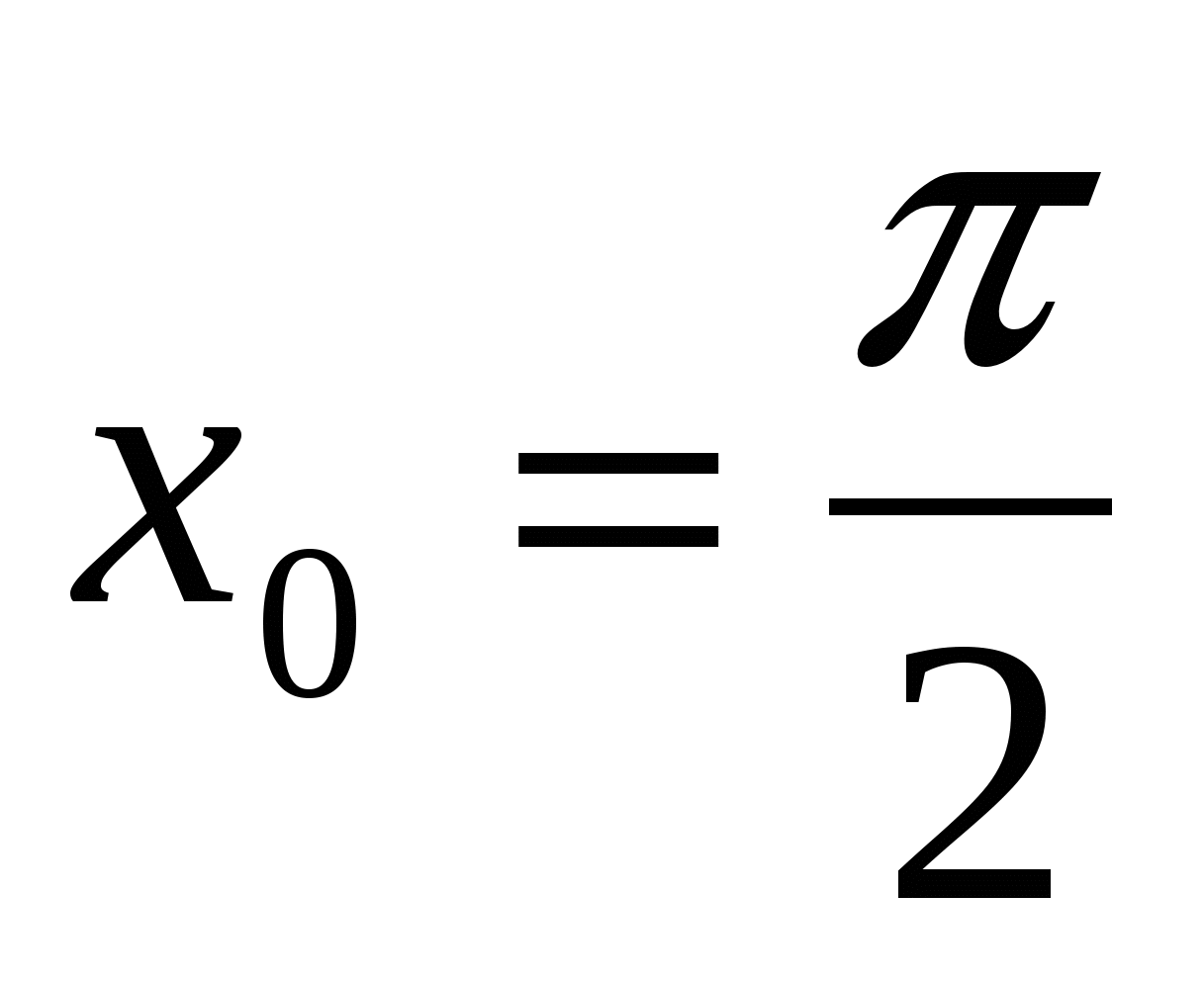 .
.
Контрольная работа по теме "Производная" в формате ЕГЭ.
№
I вариант
II вариант
1
Найдите значение производной функции 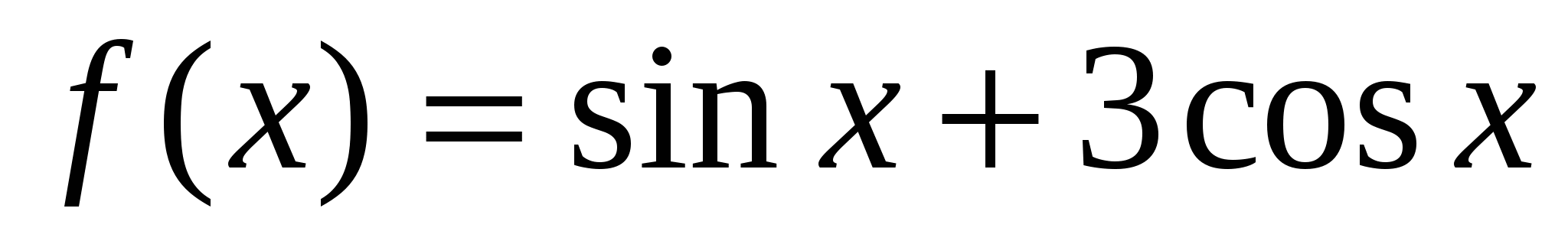 в точке
в точке 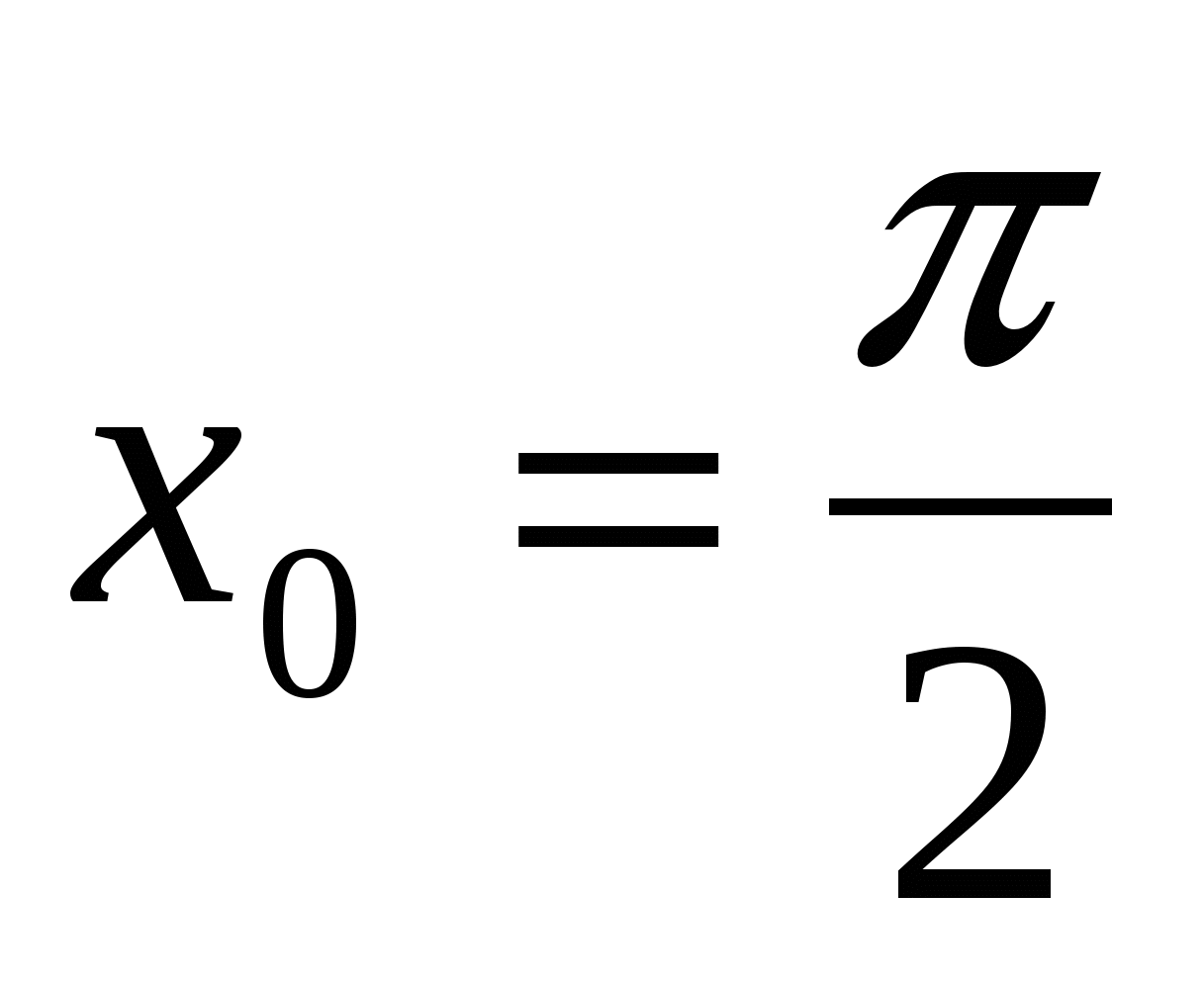 .
.
Найдите значение производной функции
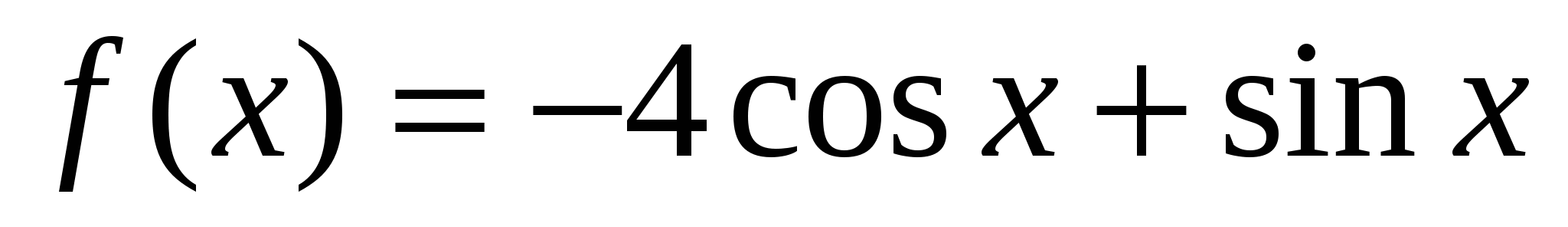 в точке
в точке 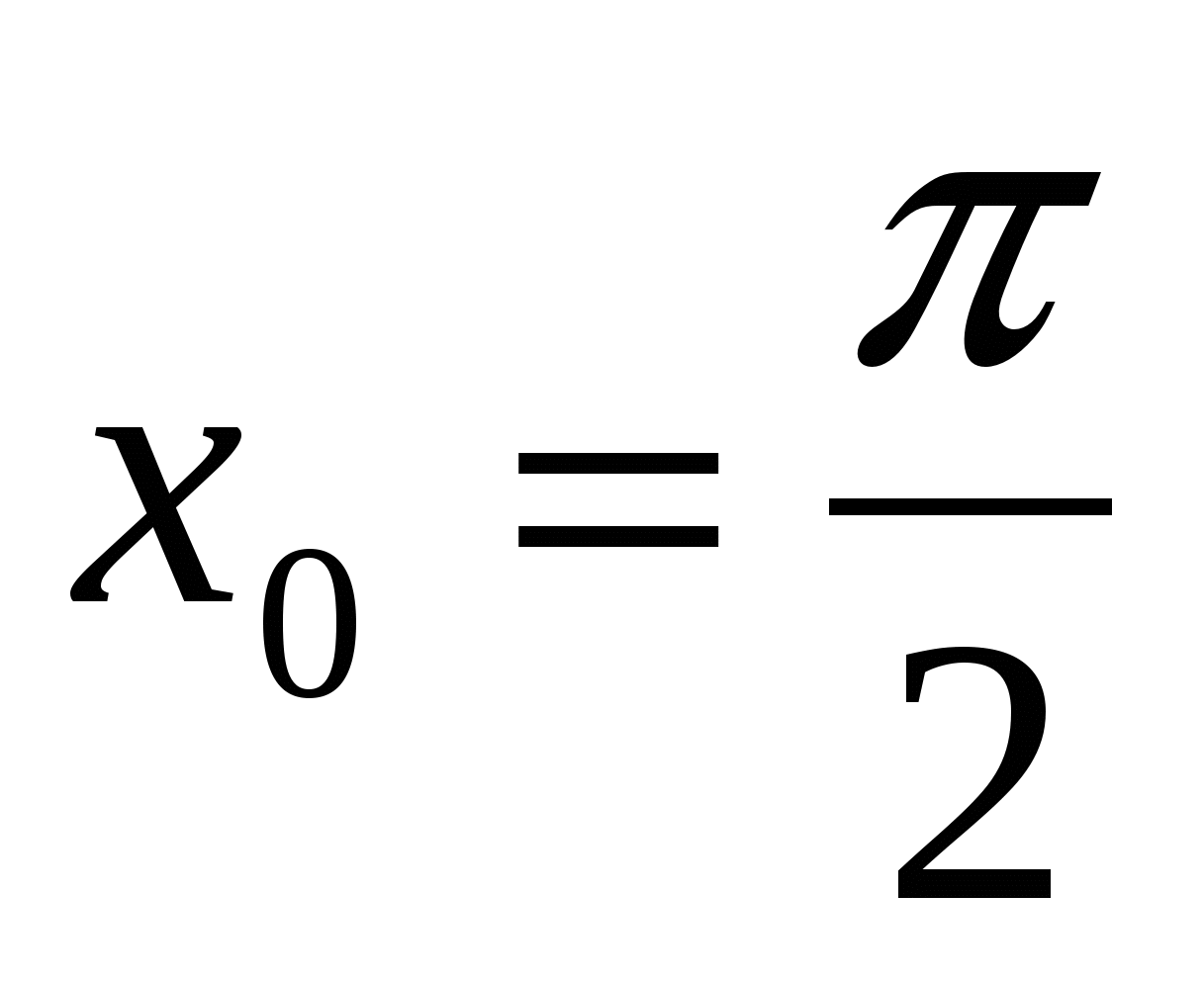 .
.
2
На рисунке изображён график функции 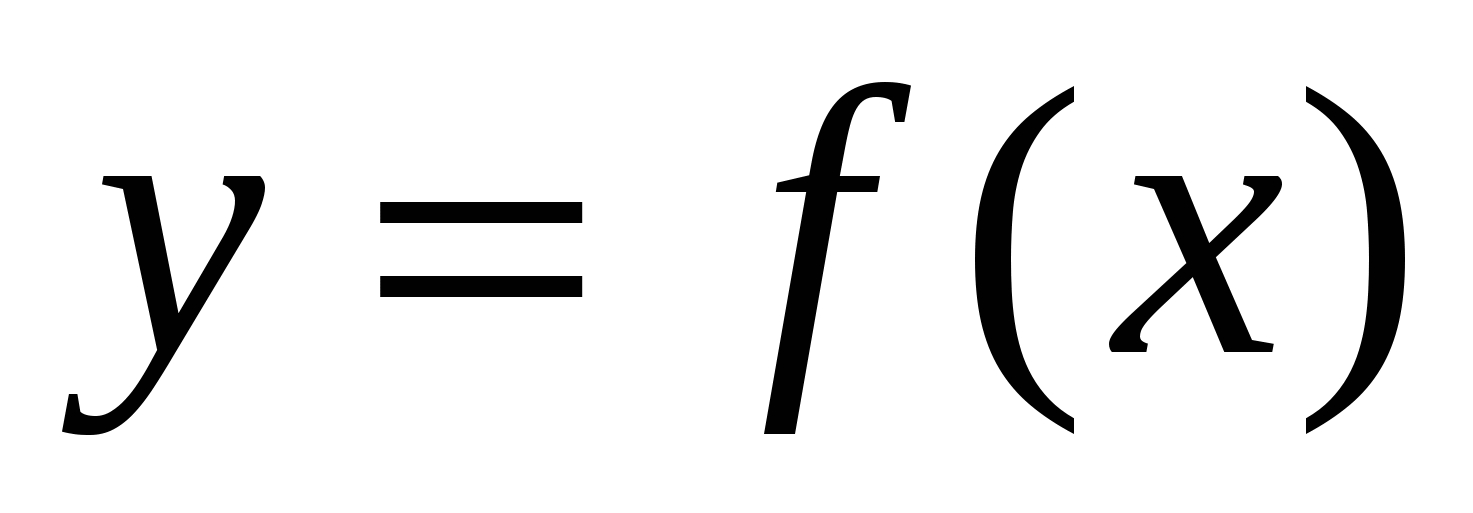 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 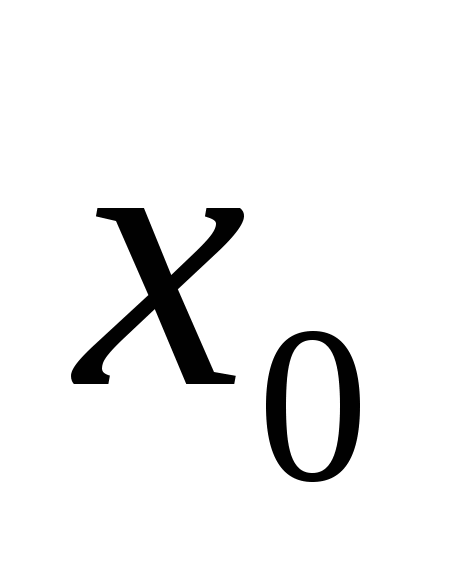 . Найдите значение производной функции
. Найдите значение производной функции 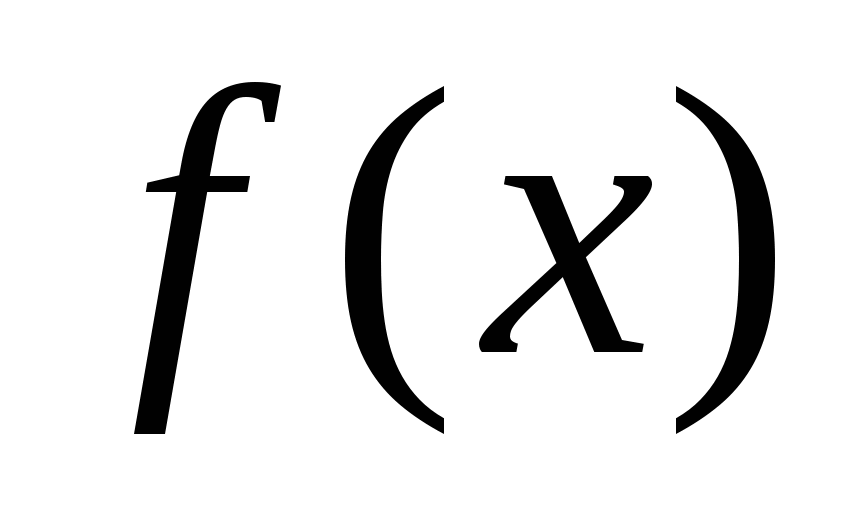 в точке
в точке 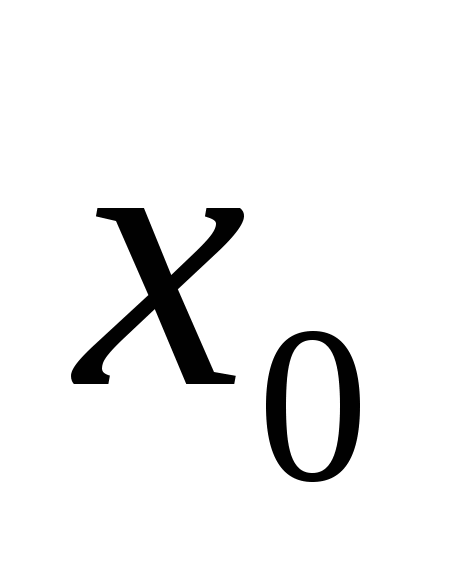 .
.
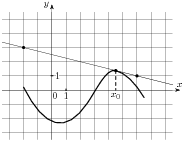
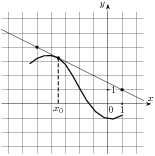
На рисунке изображён график функции 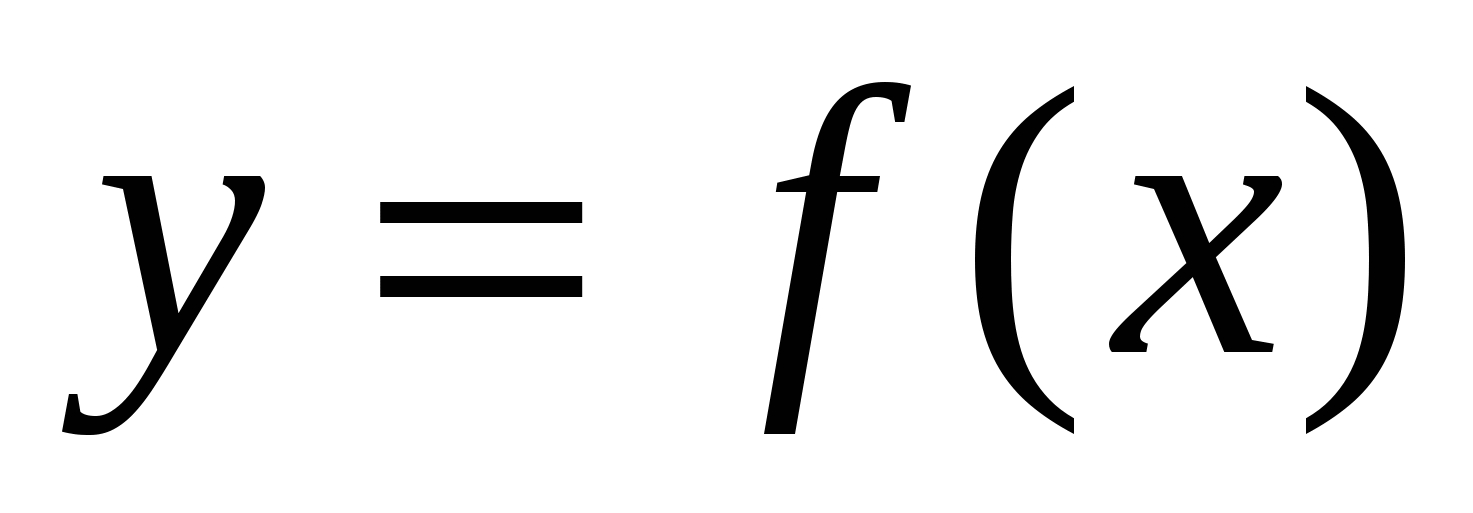 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой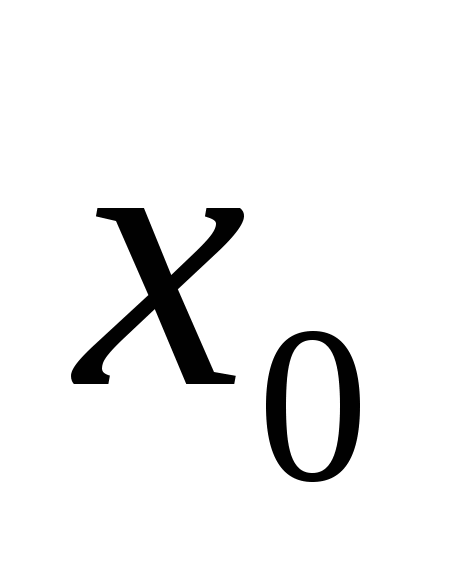 . Найдите значение производной функции
. Найдите значение производной функции 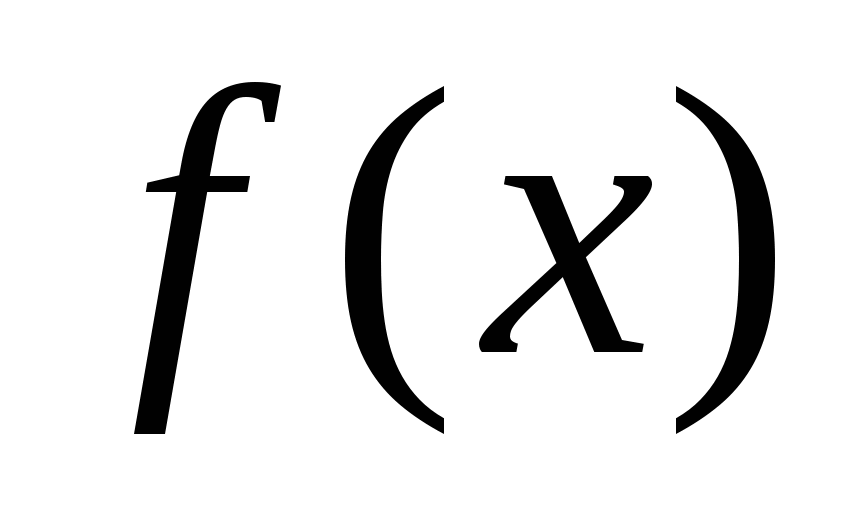 в точке
в точке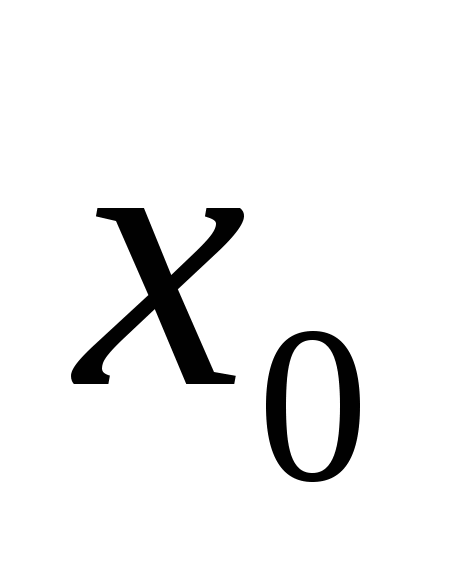 .
.
3
Найдите угловой коэффициент касательной к графику функции 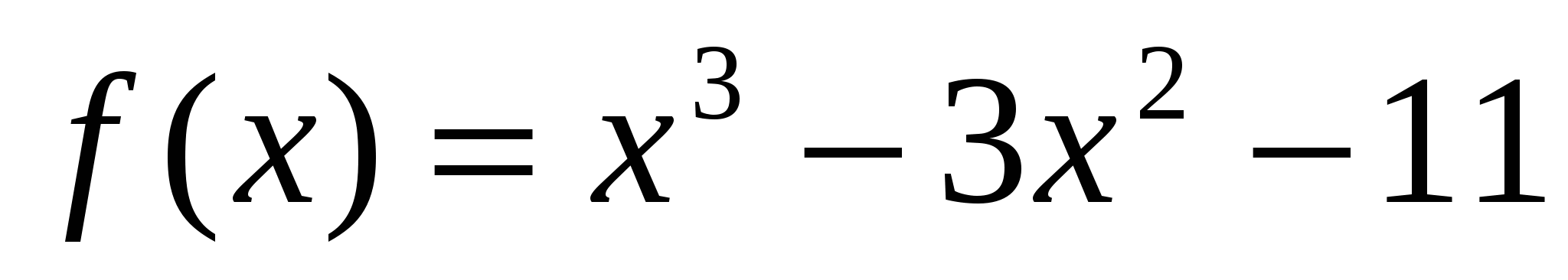
в точке с абсциссой 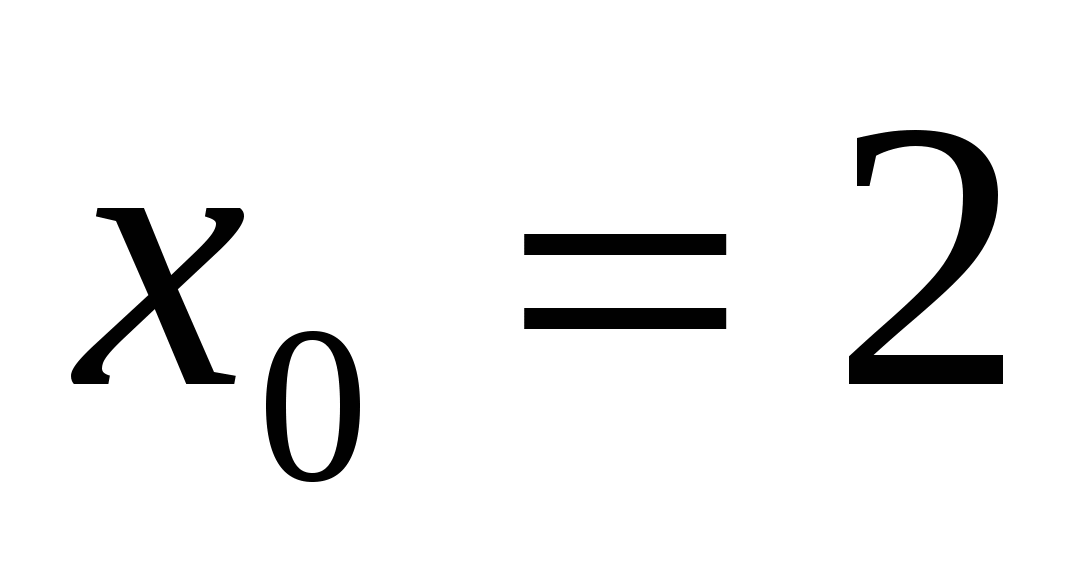 .
.
Найдите угловой коэффициент касательной к графику функции 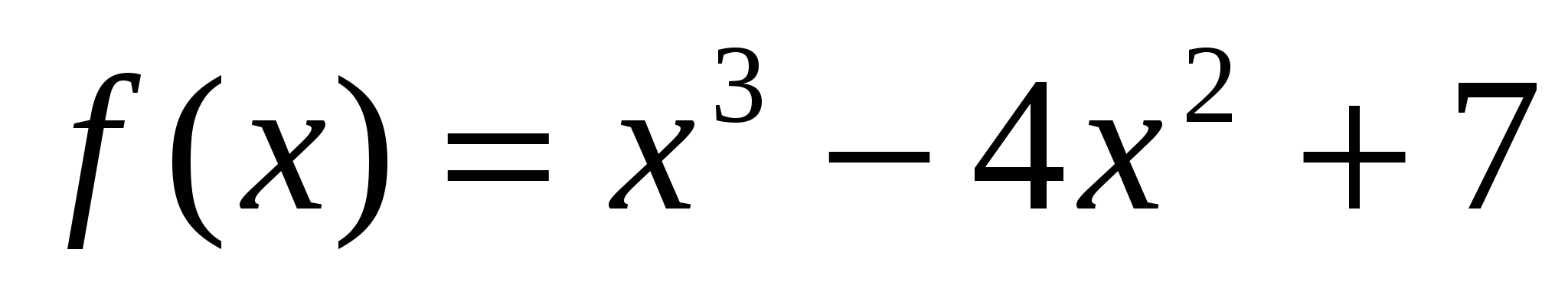
в точке с абсциссой 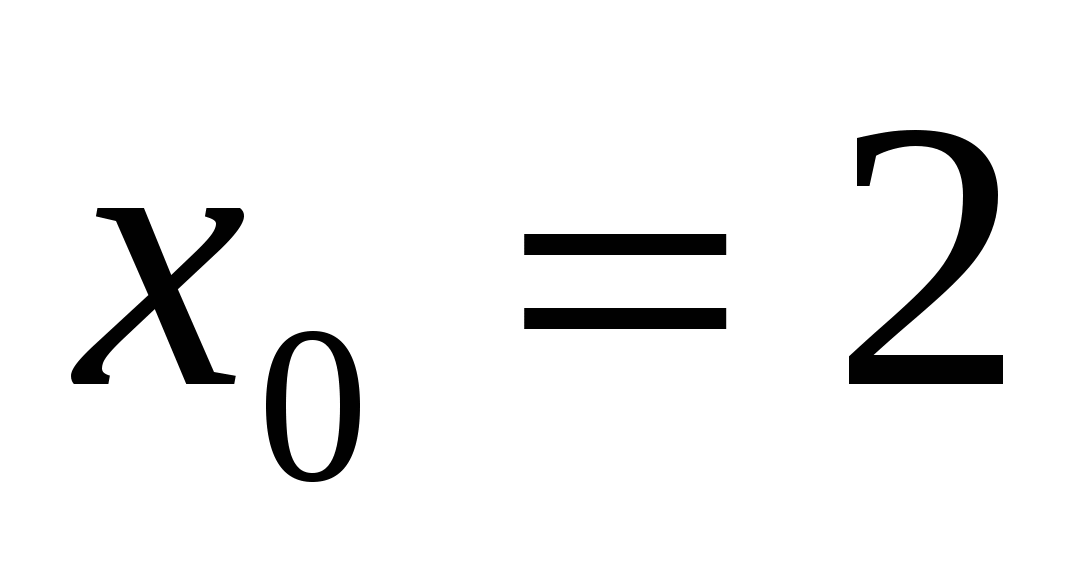 .
.
4
На рисунке изображен график функции 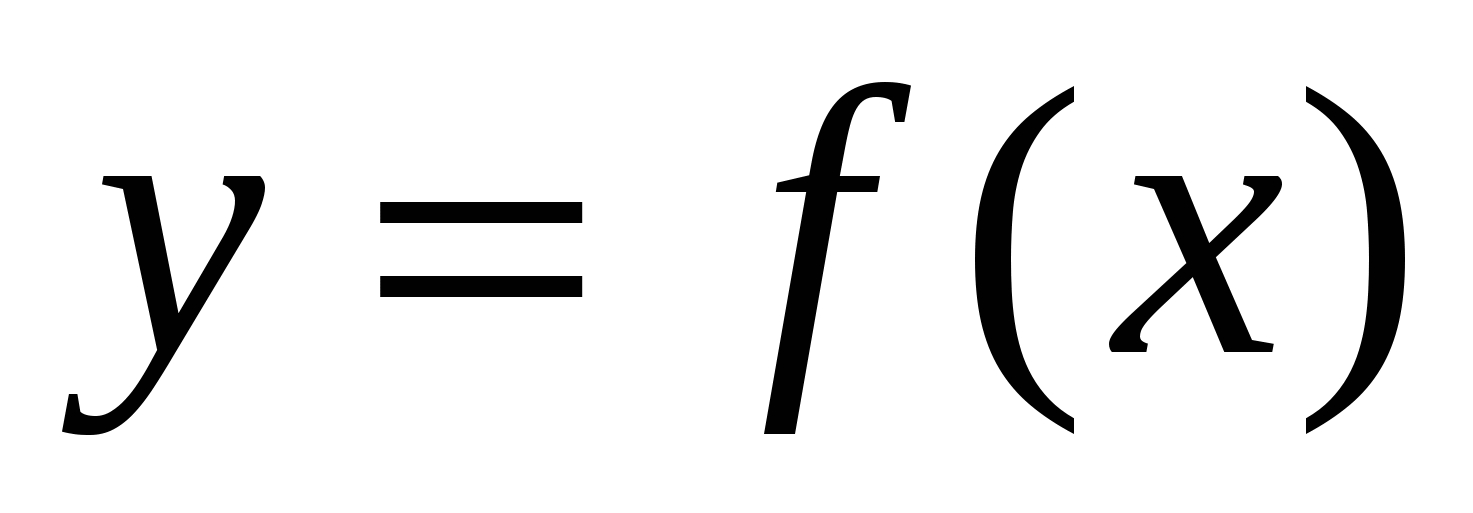 , определенной на интервале (-3;9). Найдите количество точек, в которых касательная к графику функции параллельна прямой
, определенной на интервале (-3;9). Найдите количество точек, в которых касательная к графику функции параллельна прямой 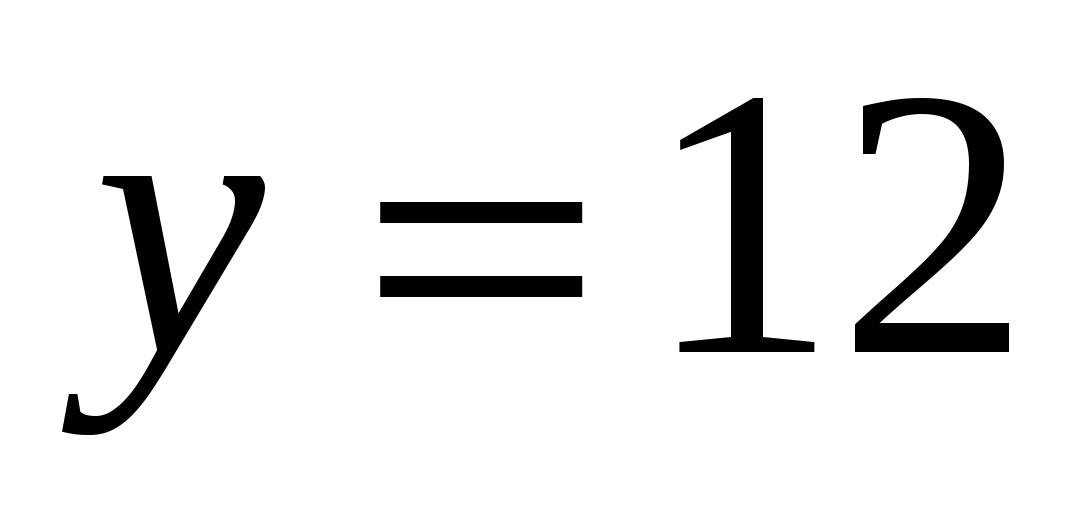 .
.
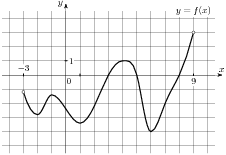
На рисунке изображен график функции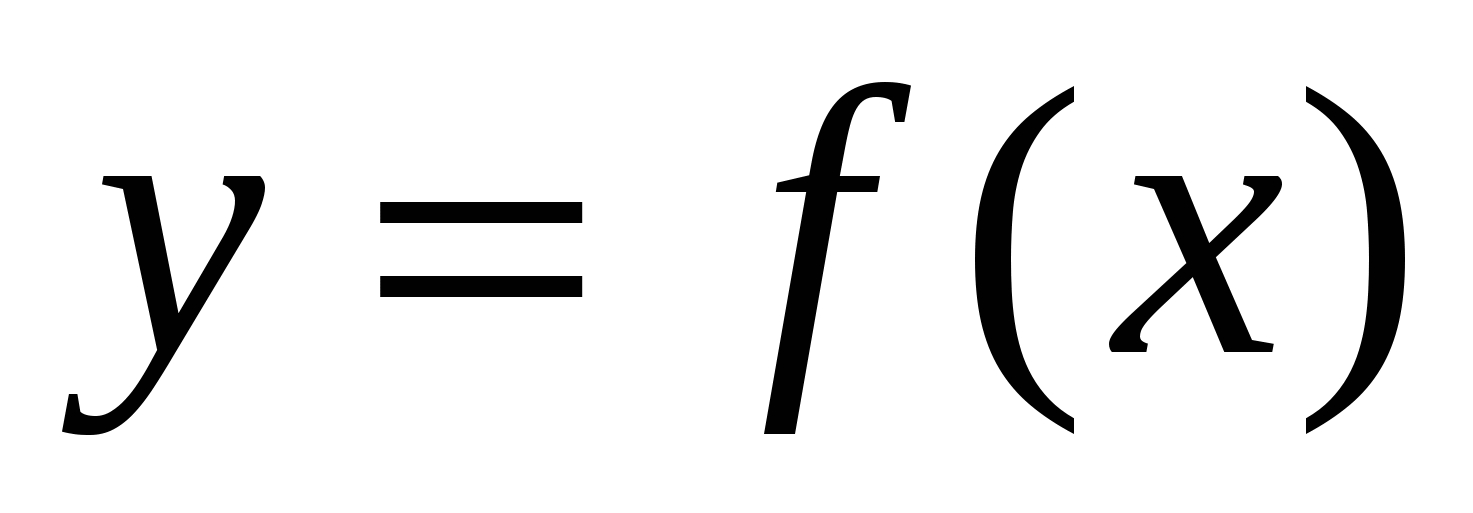 , определенной на интервале (-3;11). Найдите количество точек, в которых касательная к графику функции параллельна прямой
, определенной на интервале (-3;11). Найдите количество точек, в которых касательная к графику функции параллельна прямой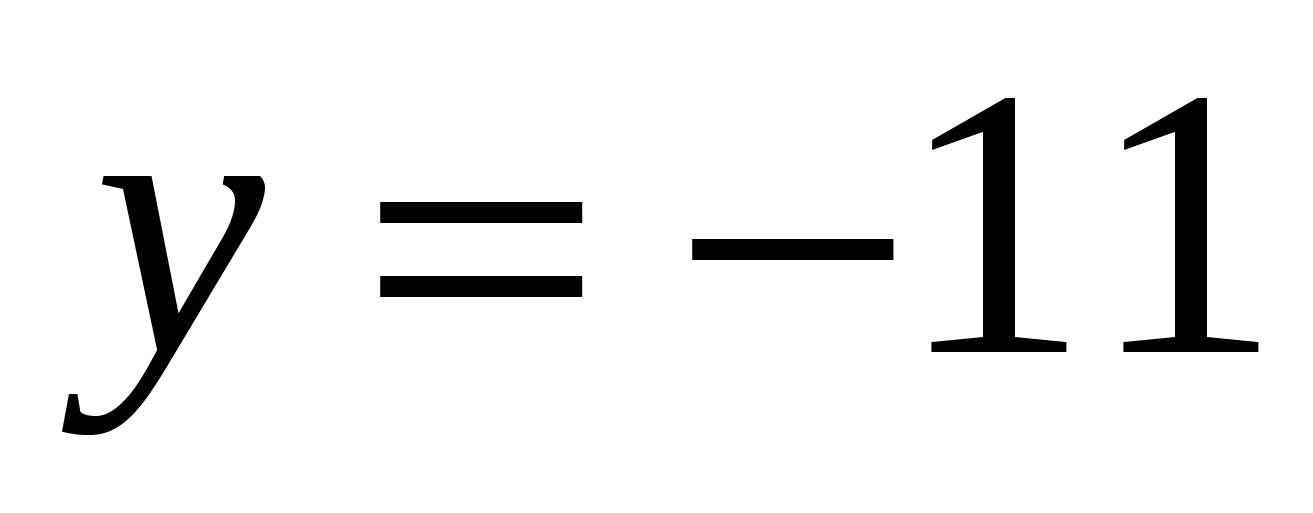 .
.

5
На рисунке изображен график производной функции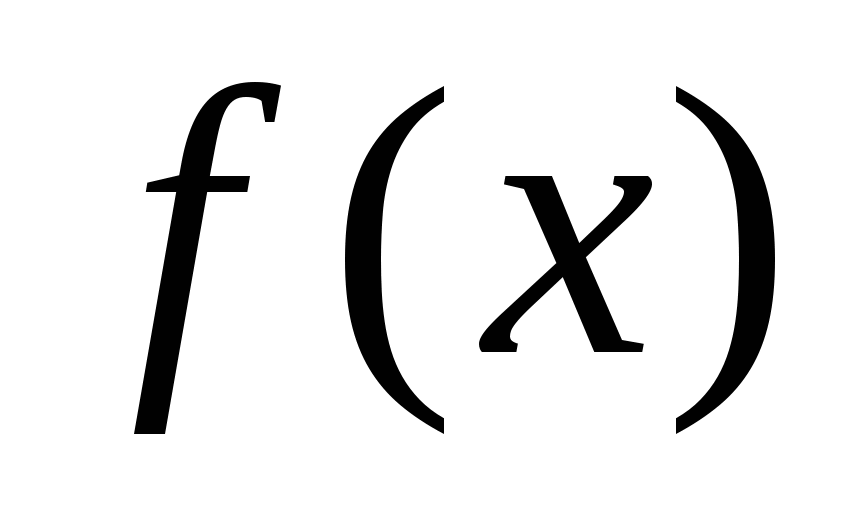 , определенной на интервале(-12;4). Найдите промежутки возрастания функции,
, определенной на интервале(-12;4). Найдите промежутки возрастания функции,
в ответе укажите длину наибольшего из них.

На рисунке изображен график производной функции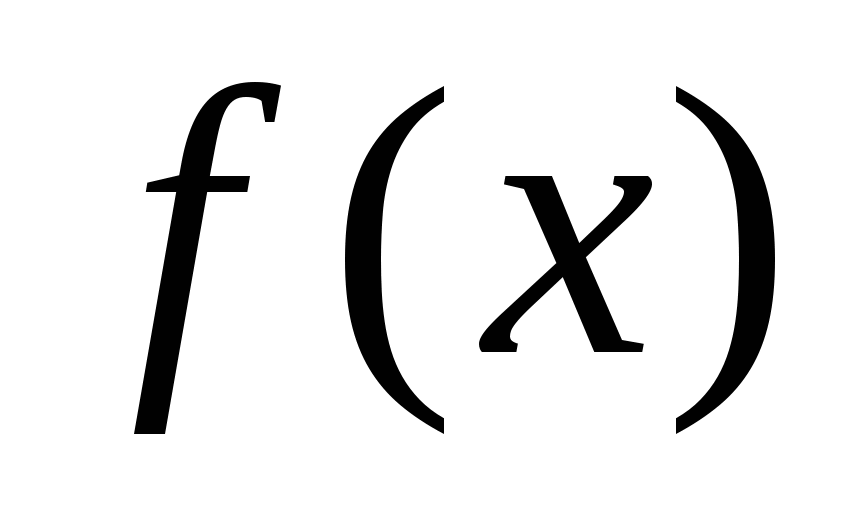 , определенной на интервале(-1;17). Найдите промежутки убывания функции,
, определенной на интервале(-1;17). Найдите промежутки убывания функции,
в ответе укажите длину наибольшего из них.

6
Укажите промежуток, на котором функция 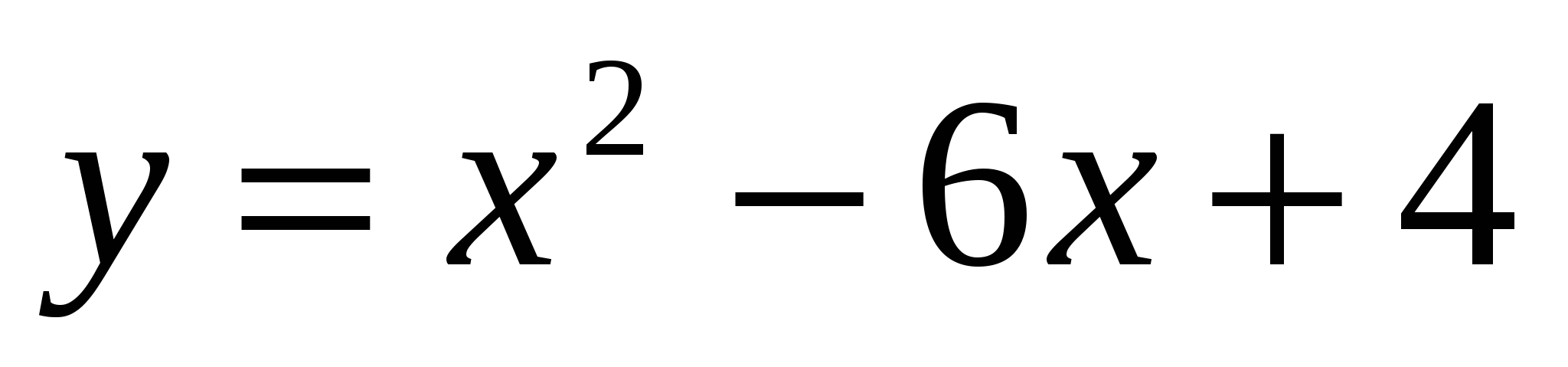 убывает.
убывает.
Укажите промежуток, на котором функция 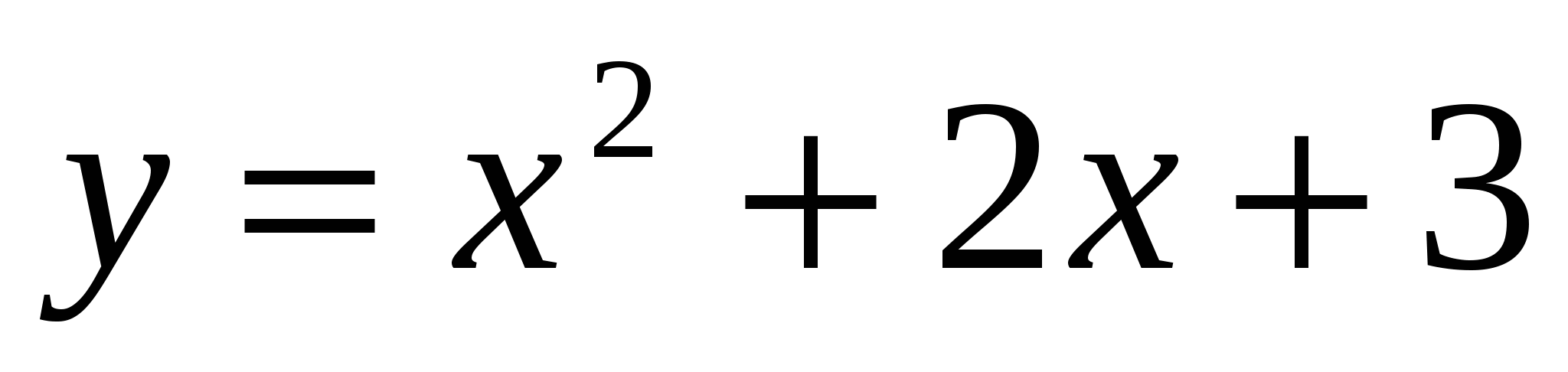 возрастает.
возрастает.
7
На рисунке изображен график функции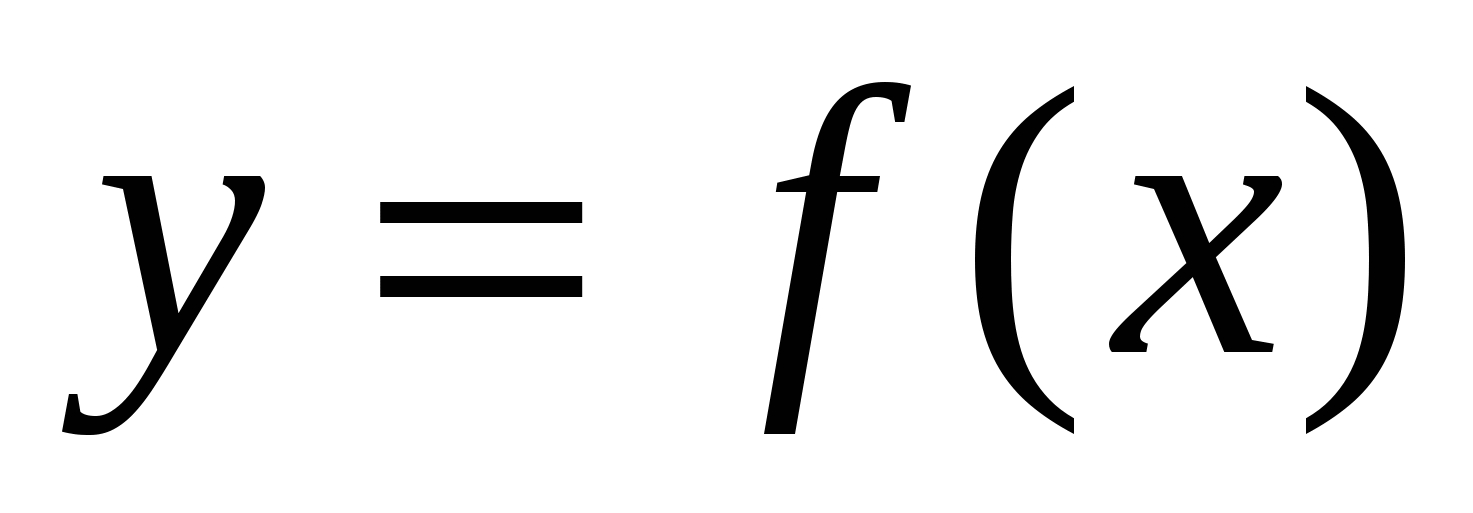 , определенной на интервале (-4;7).
, определенной на интервале (-4;7).
Найдите сумму точек экстремума функции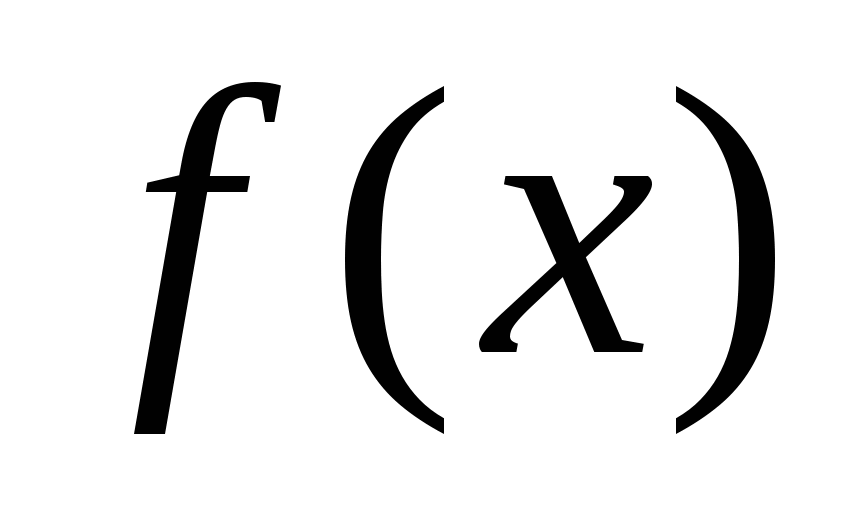 .
.

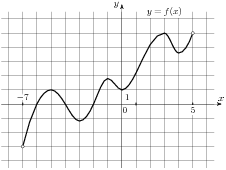
На рисунке изображен график функции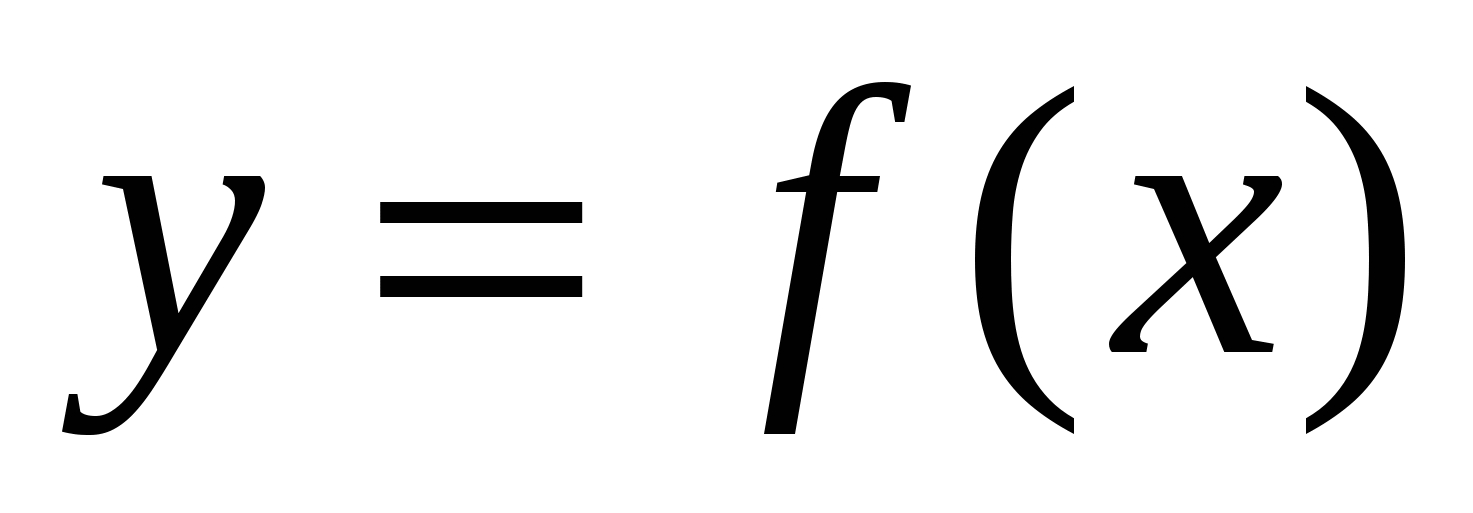 , определенной на интервале (-7;5).
, определенной на интервале (-7;5).
Найдите сумму точек экстремума функции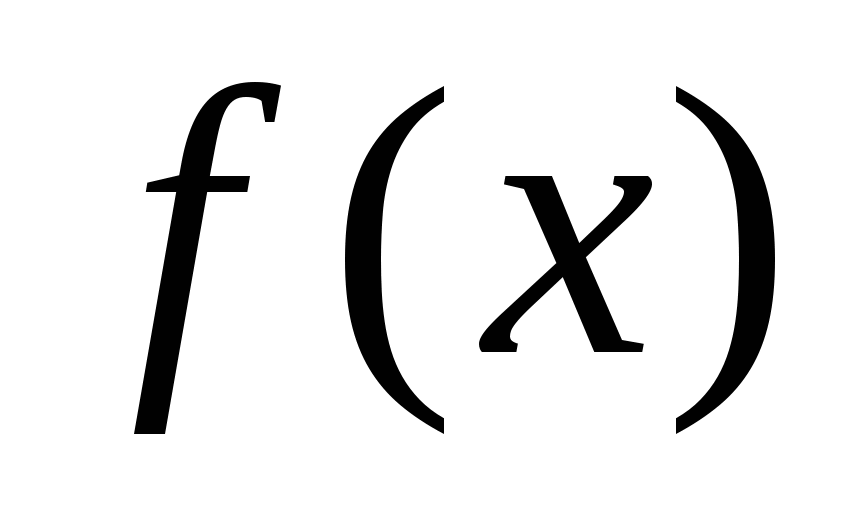 .
.
8
Найдите точки экстремума функции 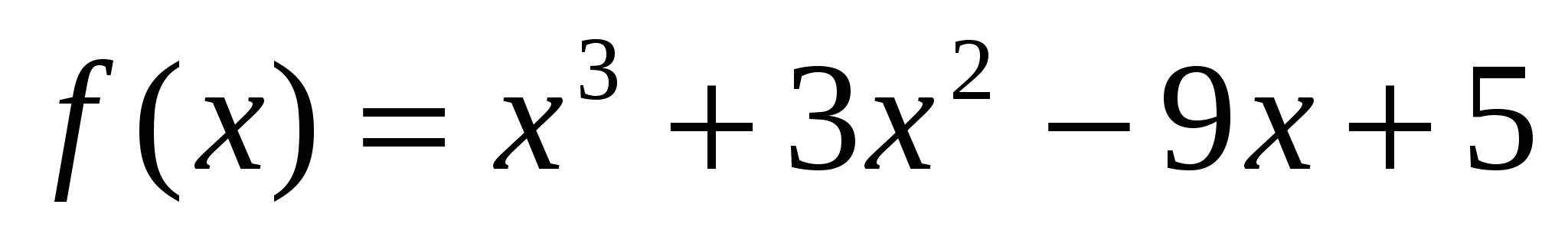 .
.
Найдите точки экстремума функции 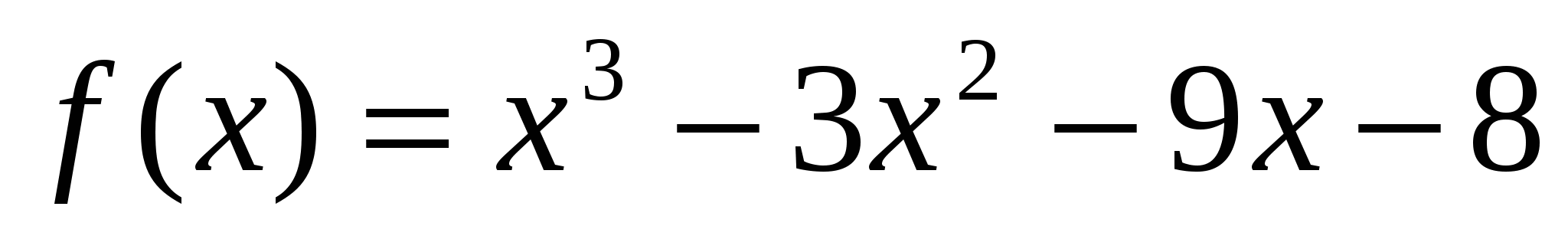 .
.
9
На рисунке изображен график производной функции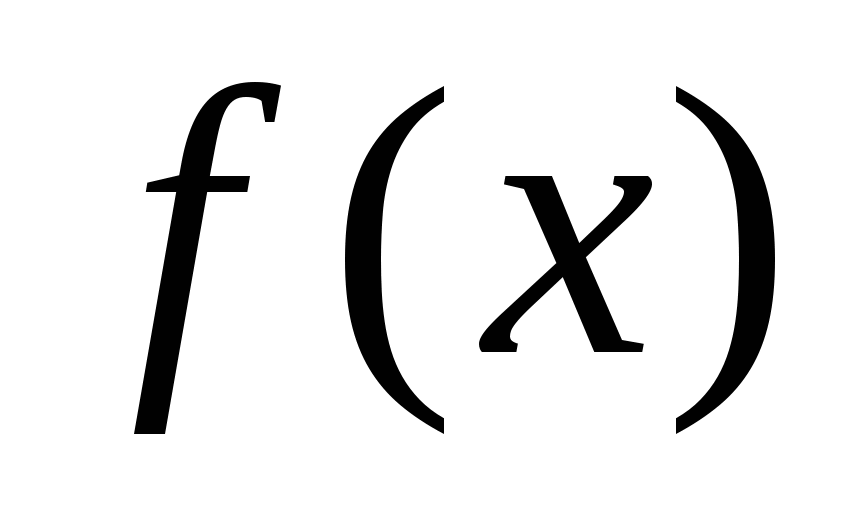 , определенной на интервале (-4;16). Найдите количество точек максимума функции на отрезке
, определенной на интервале (-4;16). Найдите количество точек максимума функции на отрезке 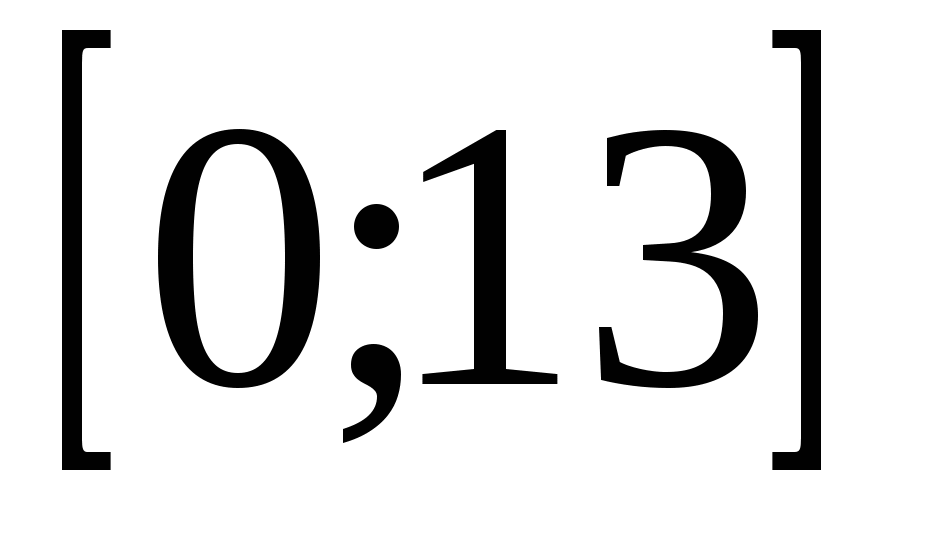 .
.

На рисунке изображен график производной функции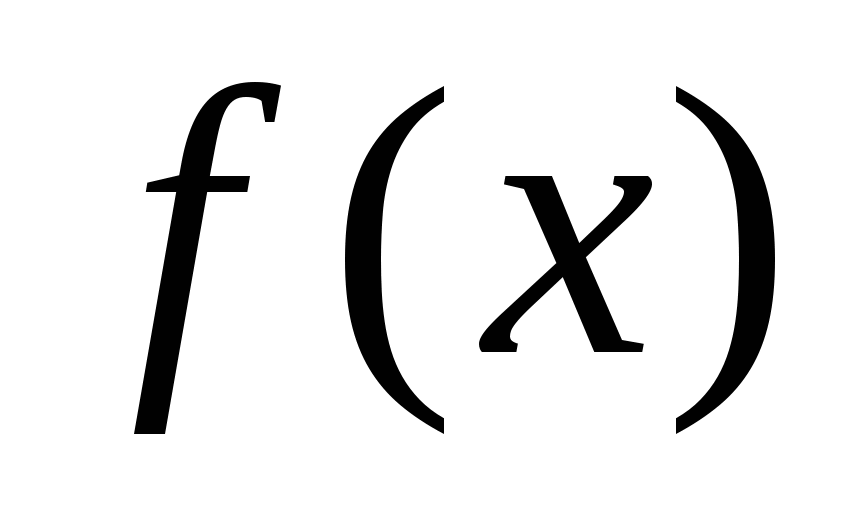 , определенной на интервале(-17;2). Найдите количество точек минимума функции на отрезке
, определенной на интервале(-17;2). Найдите количество точек минимума функции на отрезке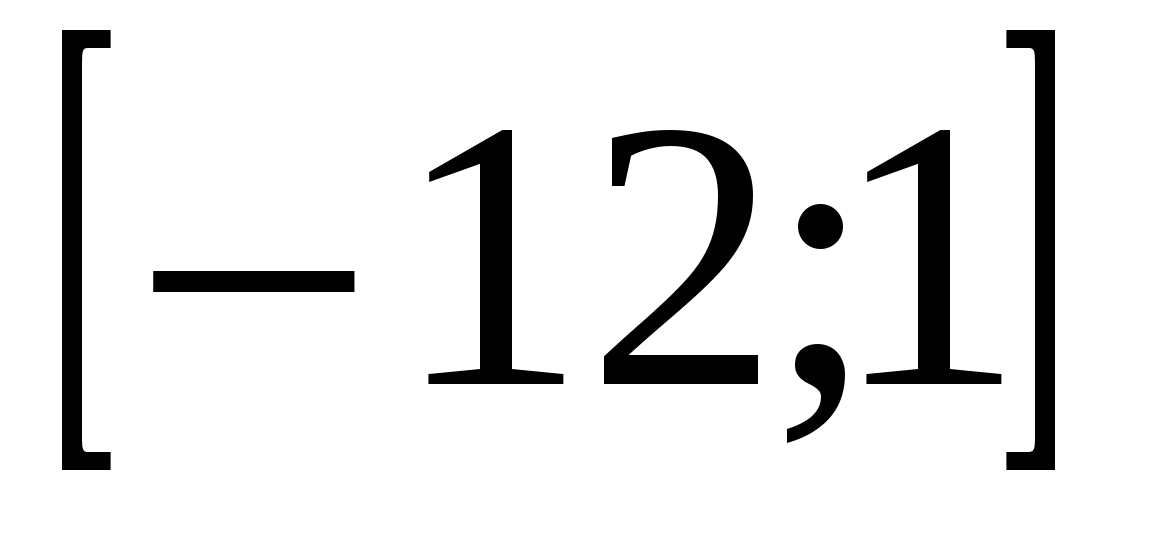 .
.

10
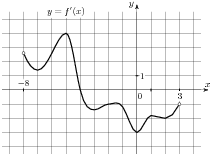
На рисунке изображен график производной функции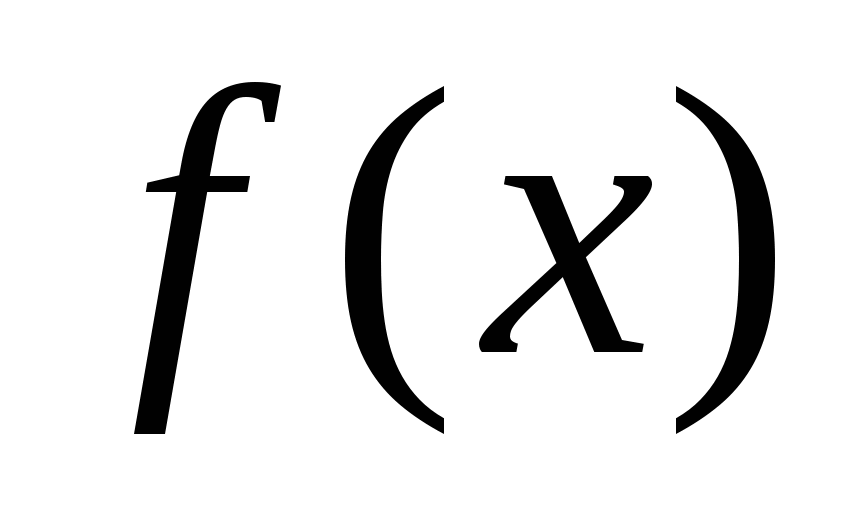 , определенной на интервале(-8; 4).
, определенной на интервале(-8; 4).
В какой точке отрезка 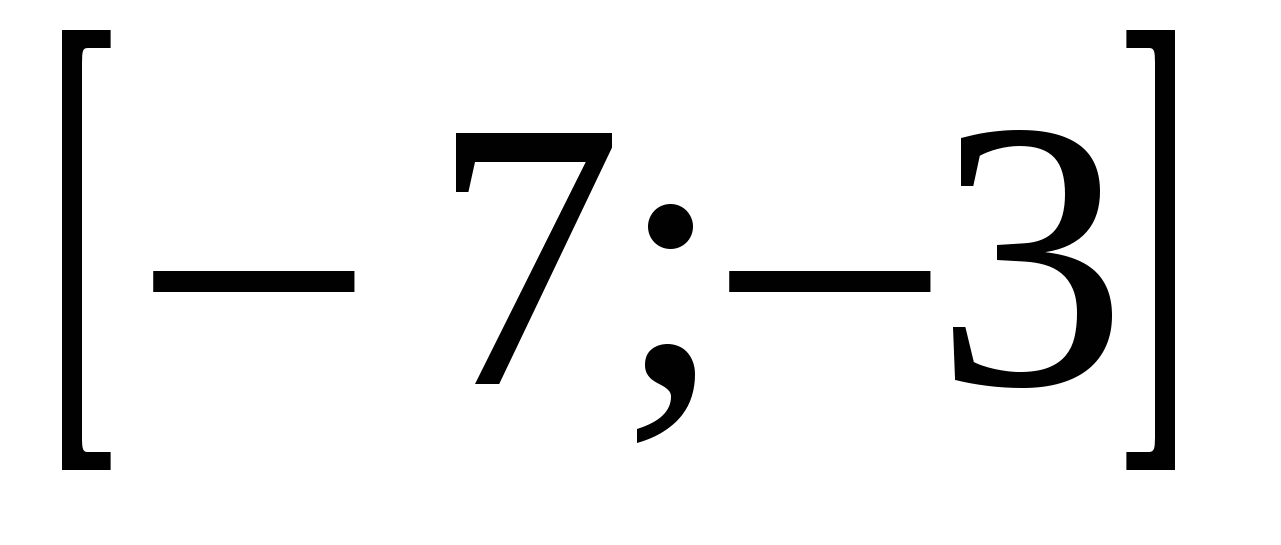 функция принимает наименьшее значение.
функция принимает наименьшее значение.
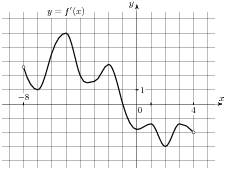
На рисунке изображен график производной функции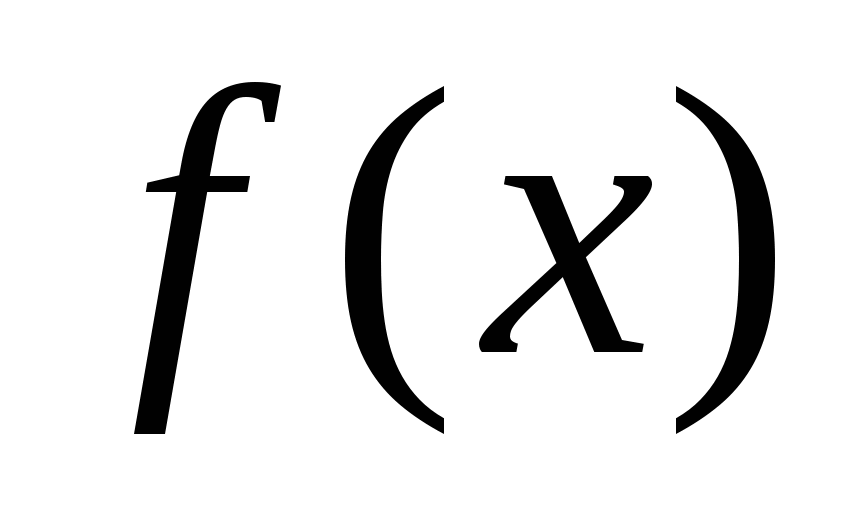 , определенной на интервале(-8;3). В какой точке отрезка
, определенной на интервале(-8;3). В какой точке отрезка 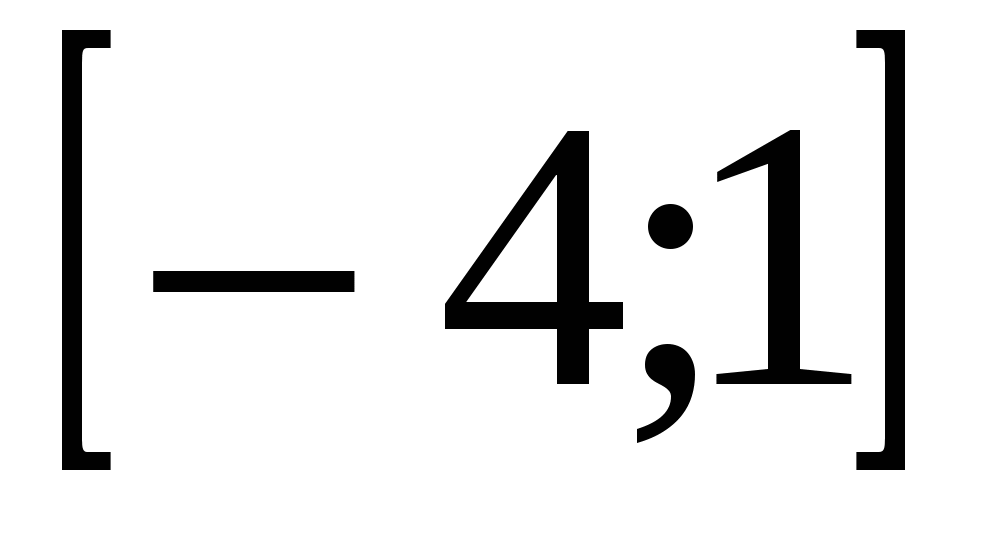 функция принимает наибольшее значение.
функция принимает наибольшее значение.
11
Прямая 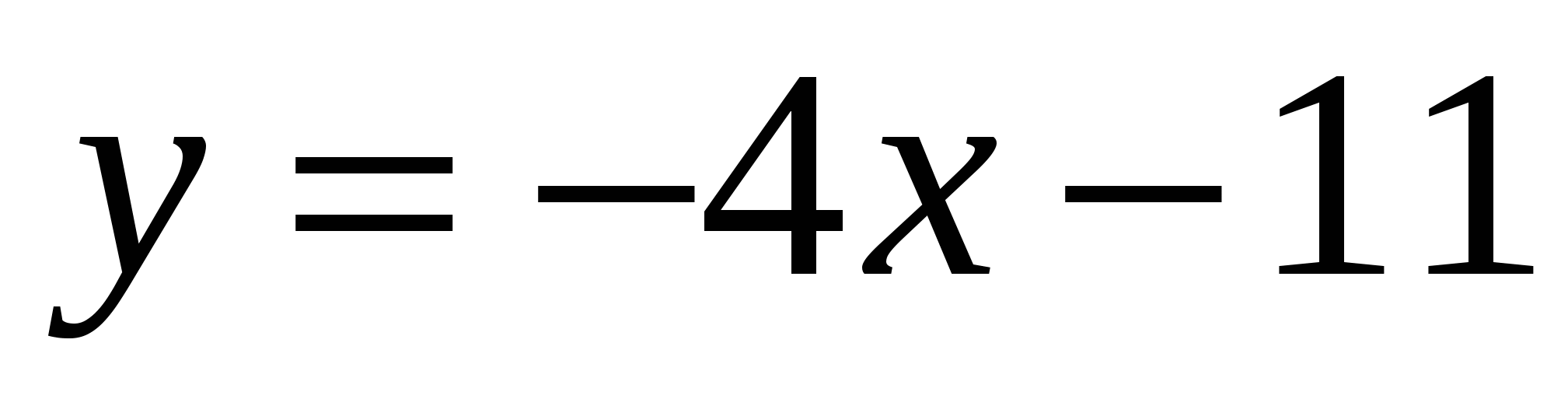 является касательной к графику функции
является касательной к графику функции 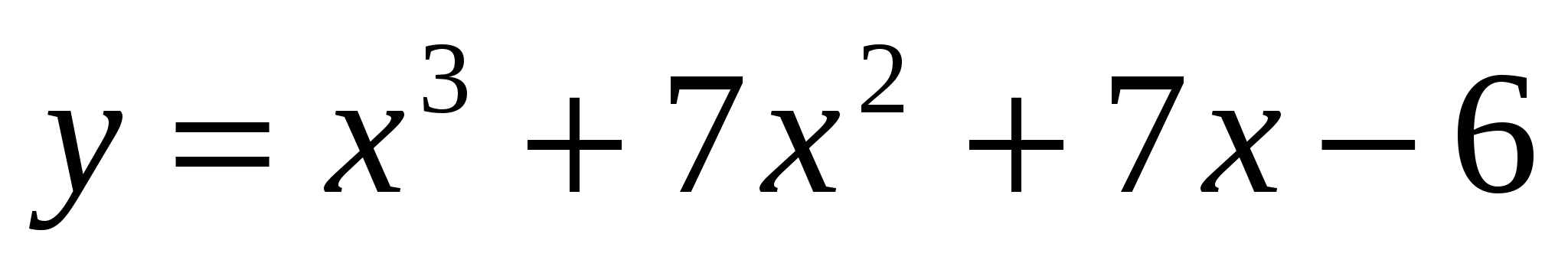 . Найдите абсциссу точки касания.
. Найдите абсциссу точки касания.
Прямая 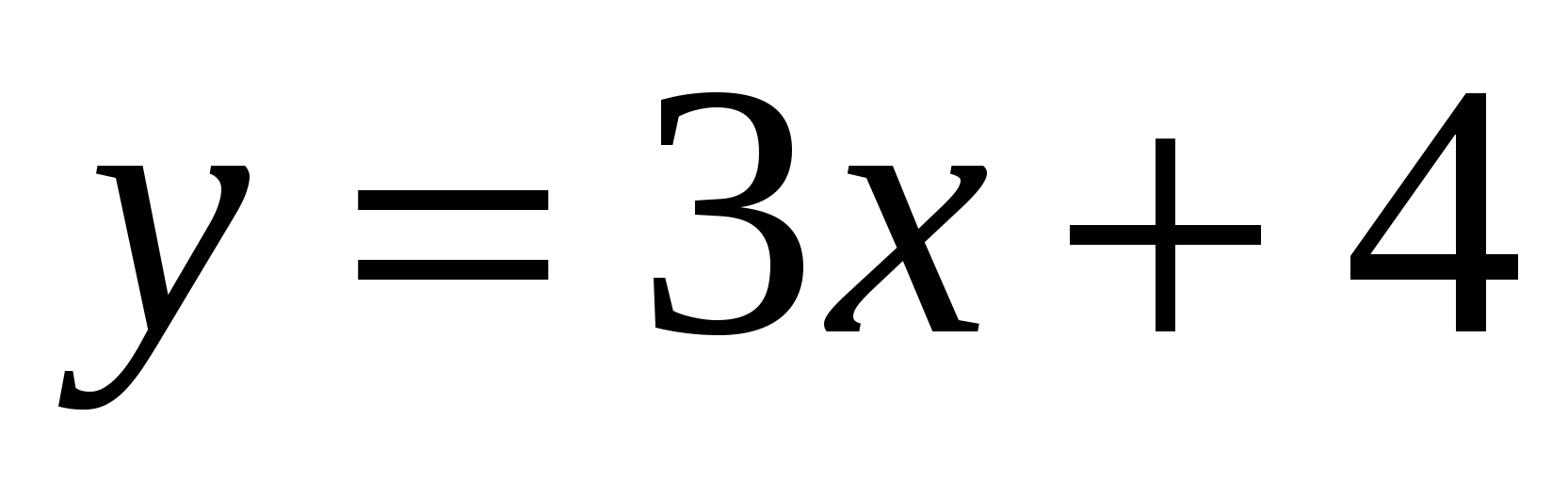 является касательной к графику функции
является касательной к графику функции  . Найдите абсциссу точки касания.
. Найдите абсциссу точки касания.
12
Точка движется прямолинейно по закону 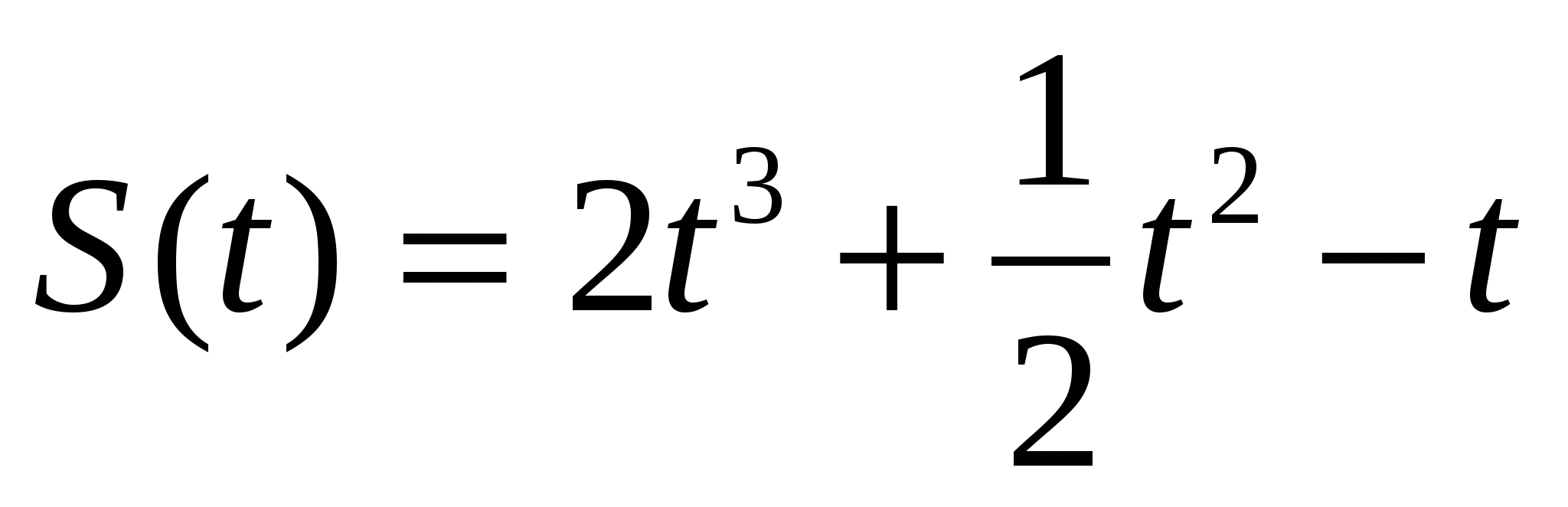 . Вычислите скорость и ускорение точки при t = 1.
. Вычислите скорость и ускорение точки при t = 1.
Точка движется прямолинейно по закону 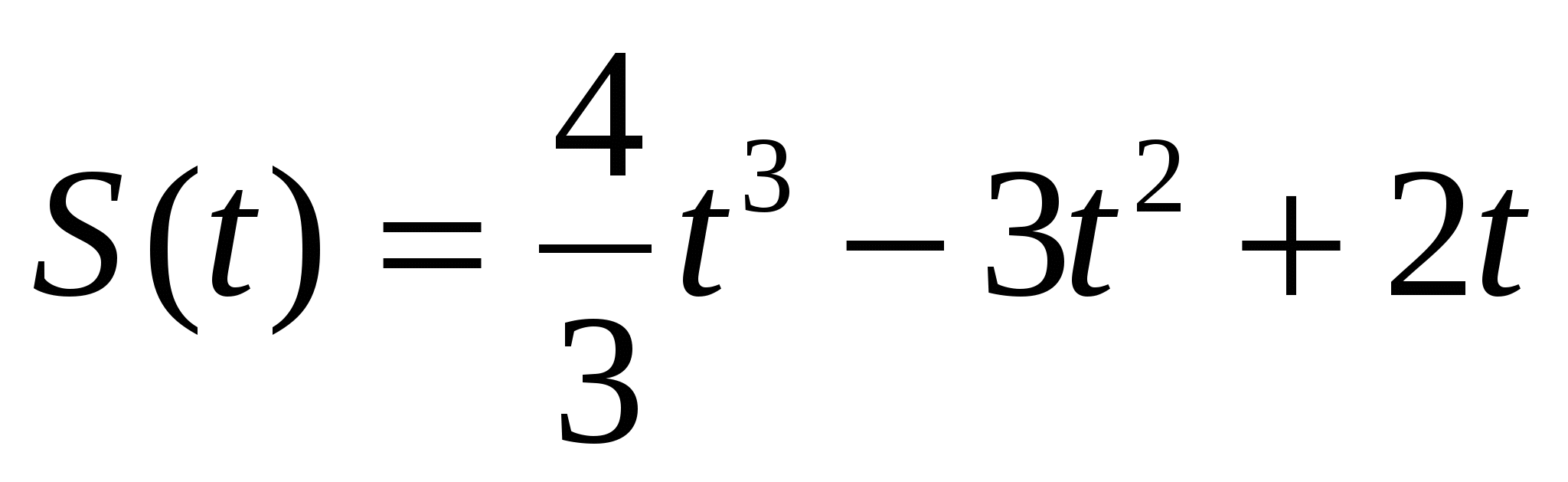 . Вычислите скорость и ускорение точки при t = 1.
. Вычислите скорость и ускорение точки при t = 1.
№
3 вариант
4 вариант
1
Найдите значение производной функции 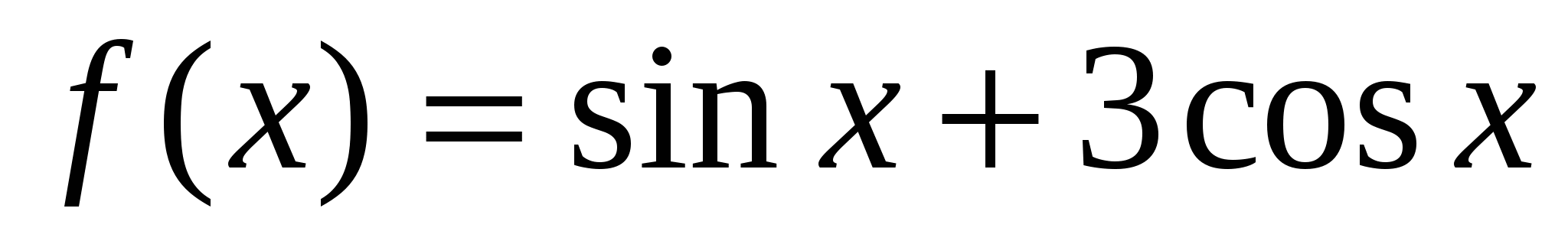 в точке
в точке 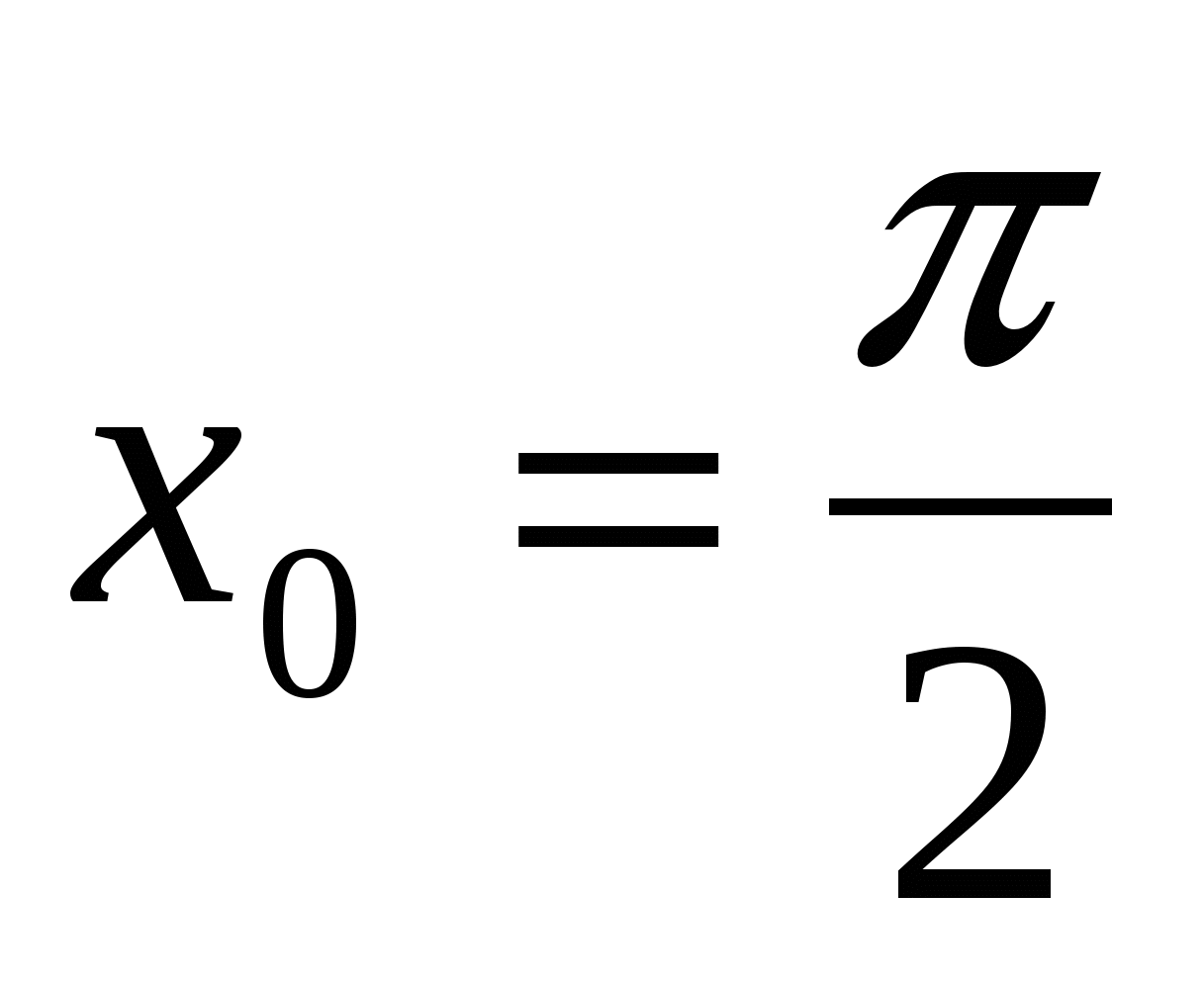 .
.
Найдите значение производной функции
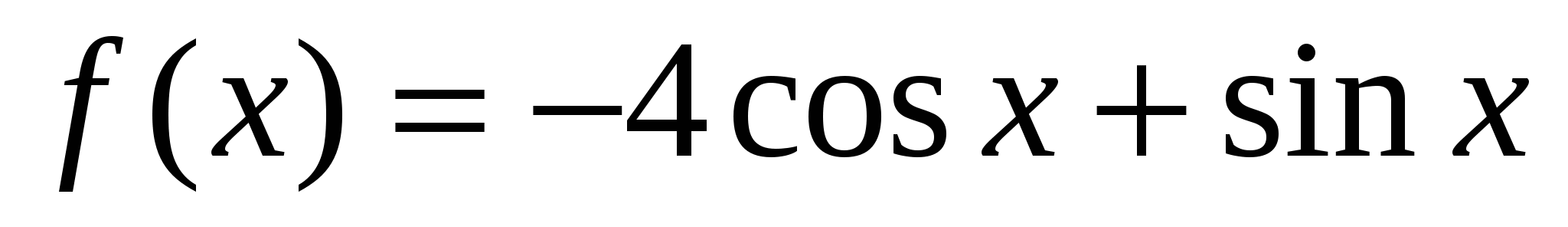 в точке
в точке 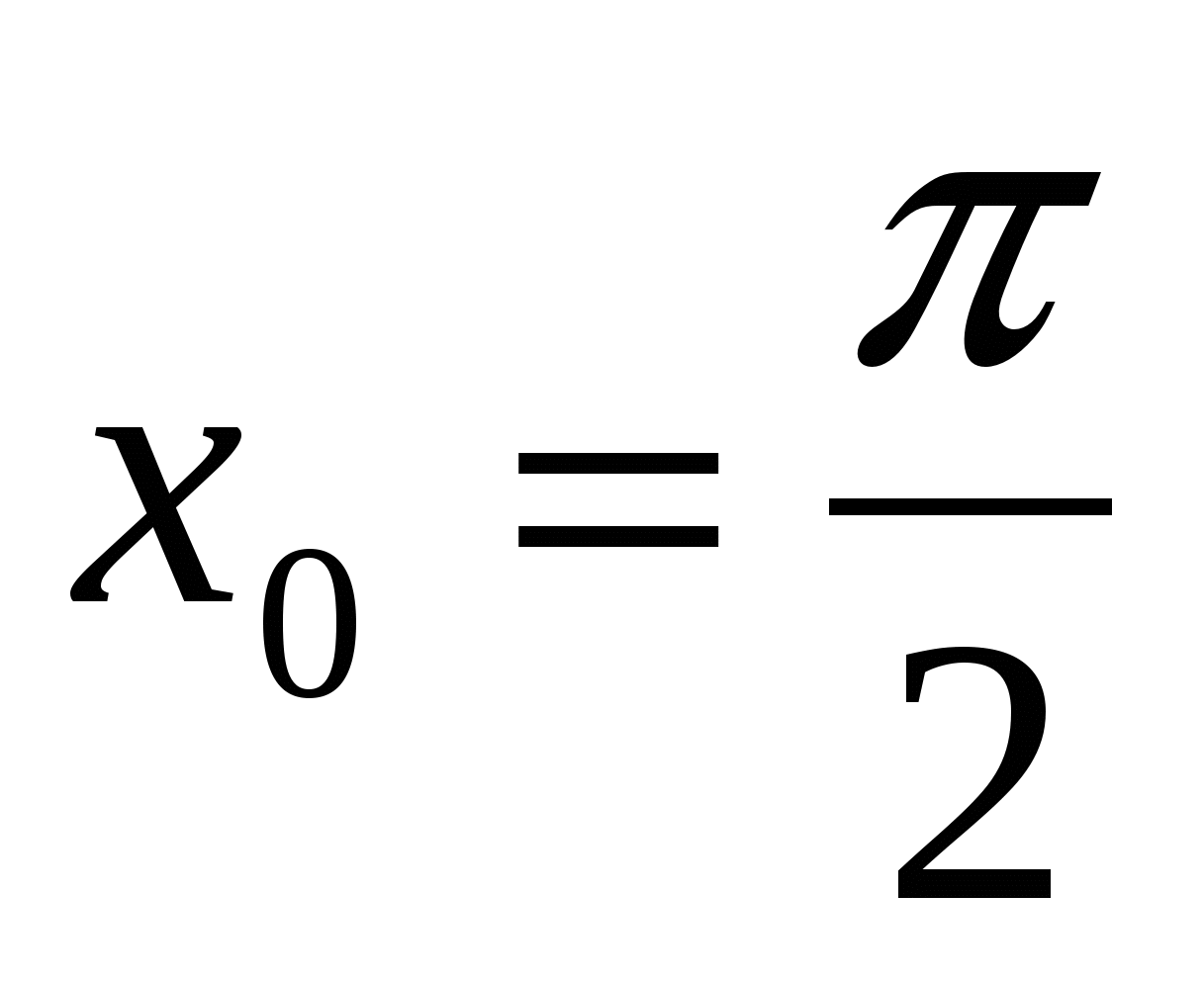 .
.
2
На рисунке изображён график функции 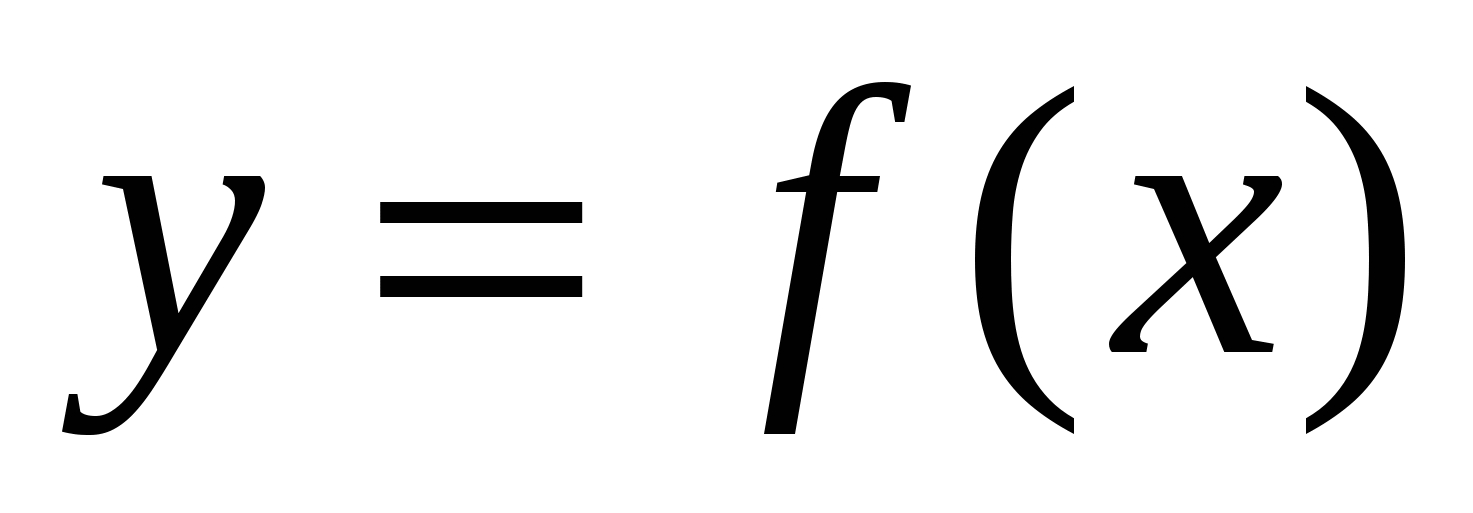 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 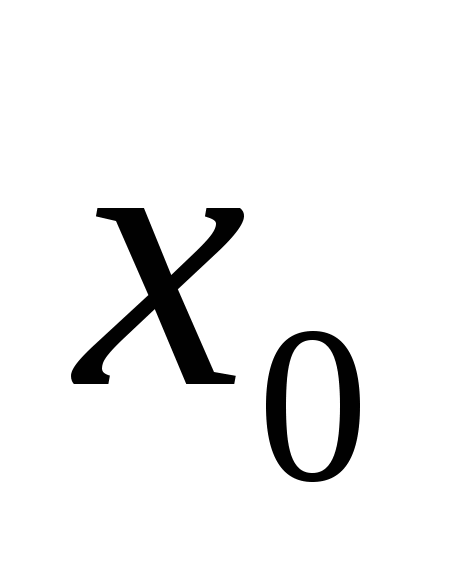 . Найдите значение производной функции
. Найдите значение производной функции 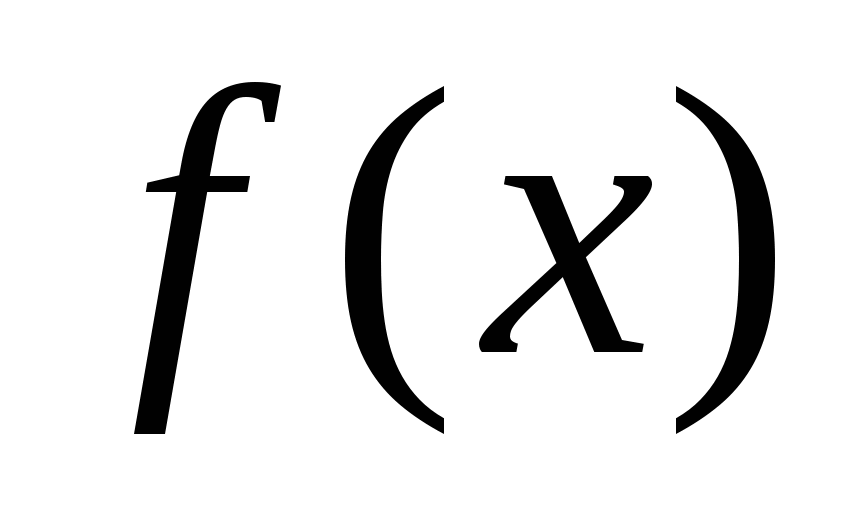 в точке
в точке 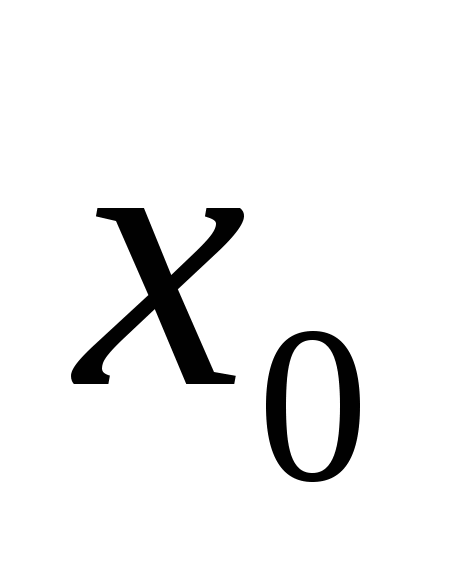 .
.

На рисунке изображён график функции 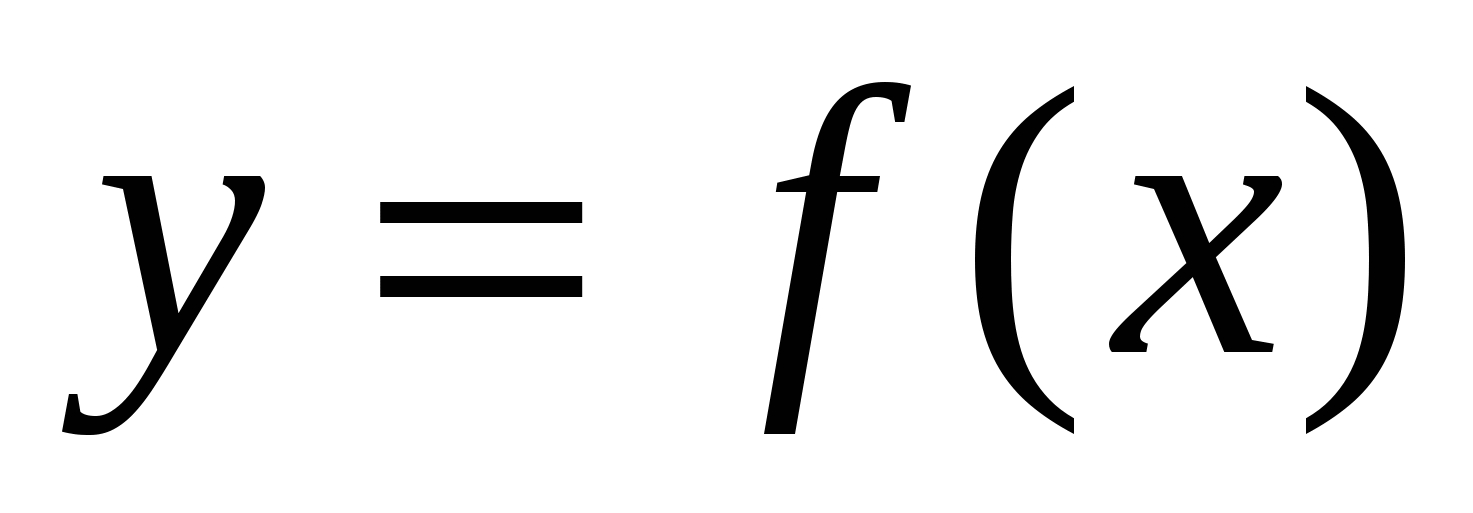 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой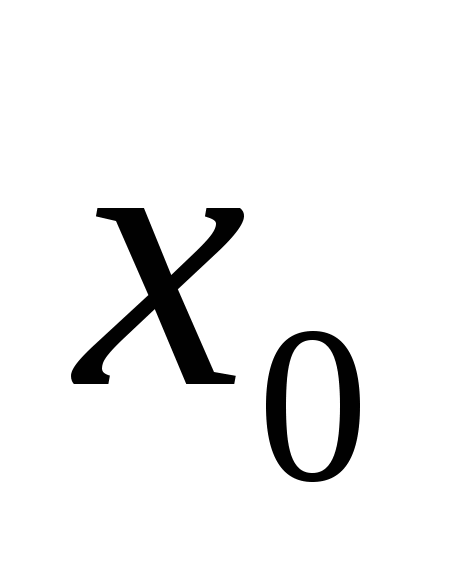 . Найдите значение производной функции
. Найдите значение производной функции 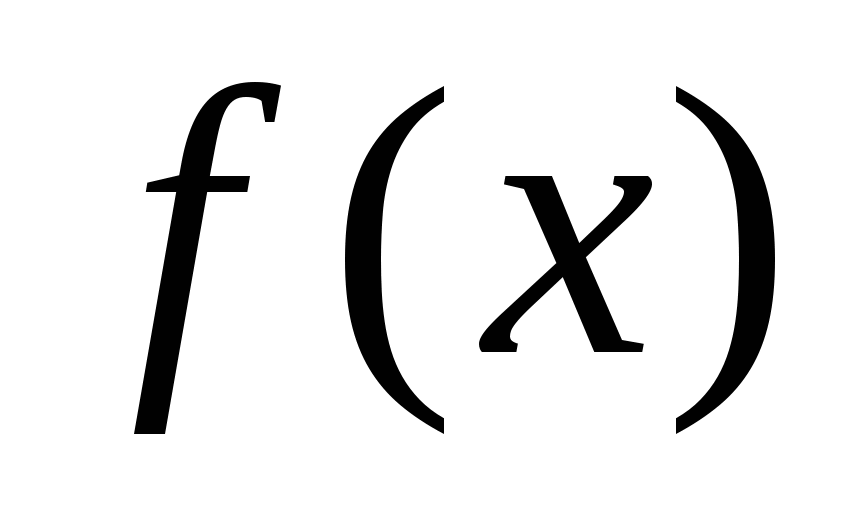 в точке
в точке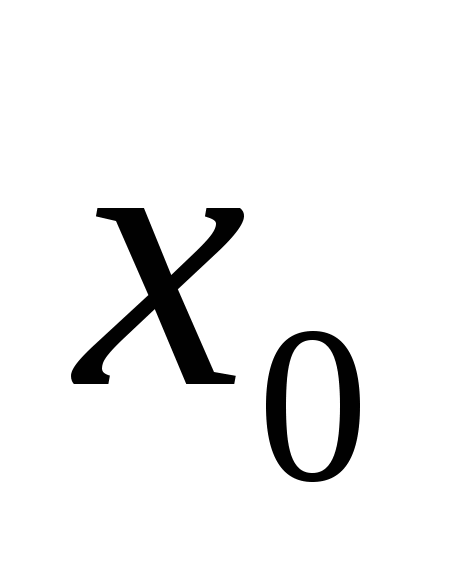 .
.

3
Найдите угловой коэффициент касательной к графику функции 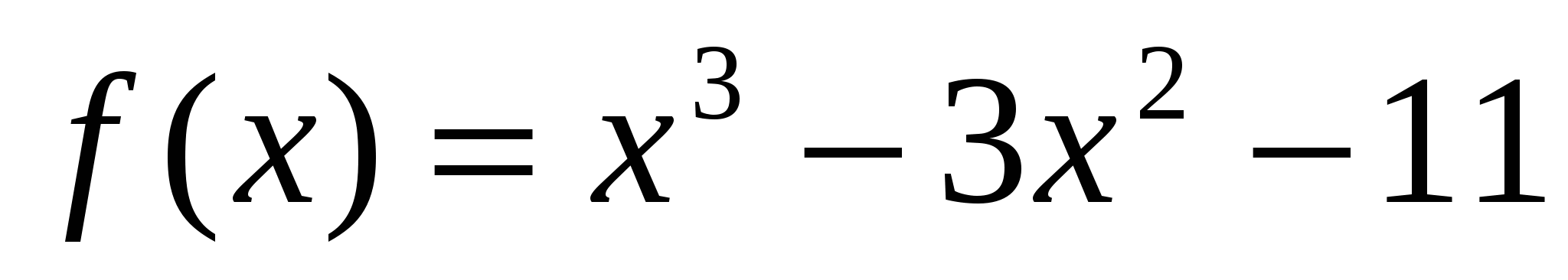
в точке с абсциссой 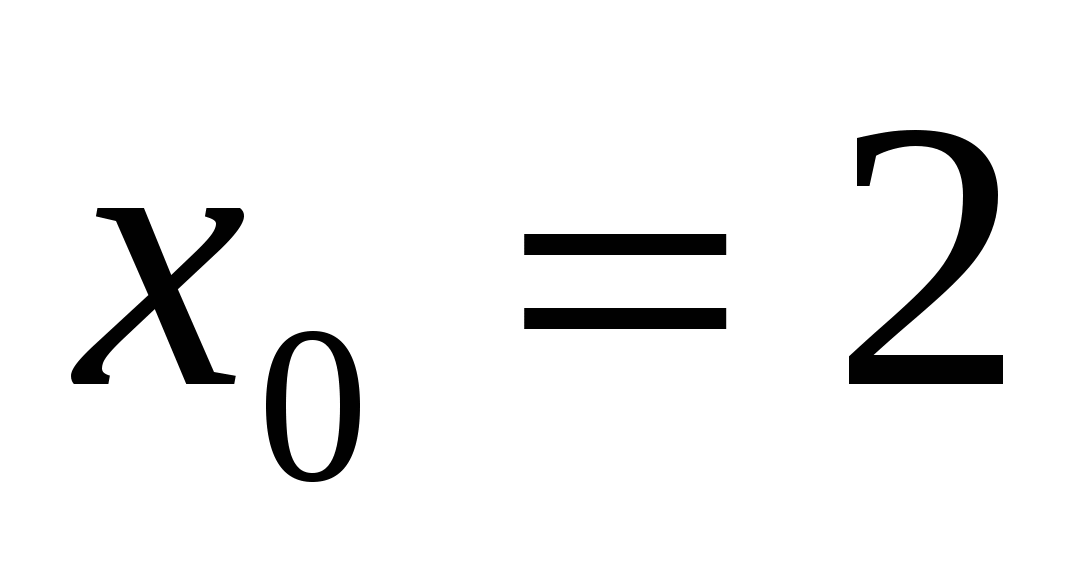 .
.
Найдите угловой коэффициент касательной к графику функции 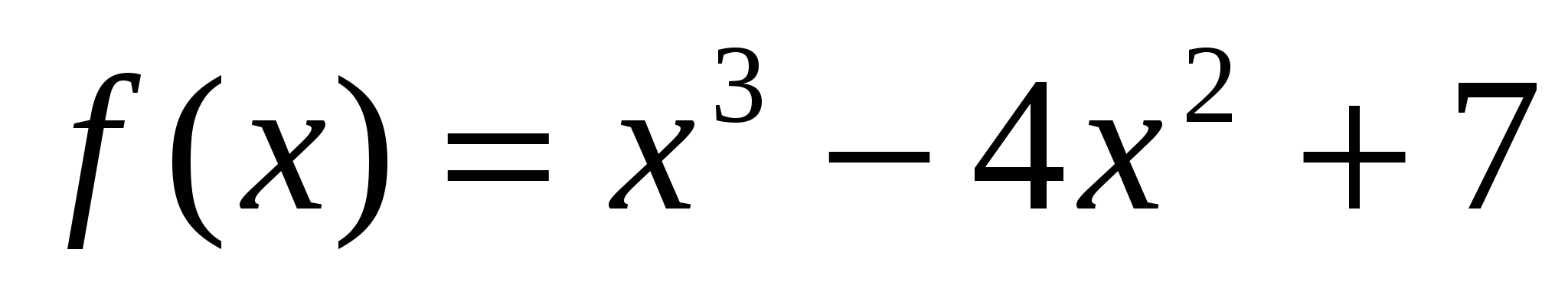
в точке с абсциссой 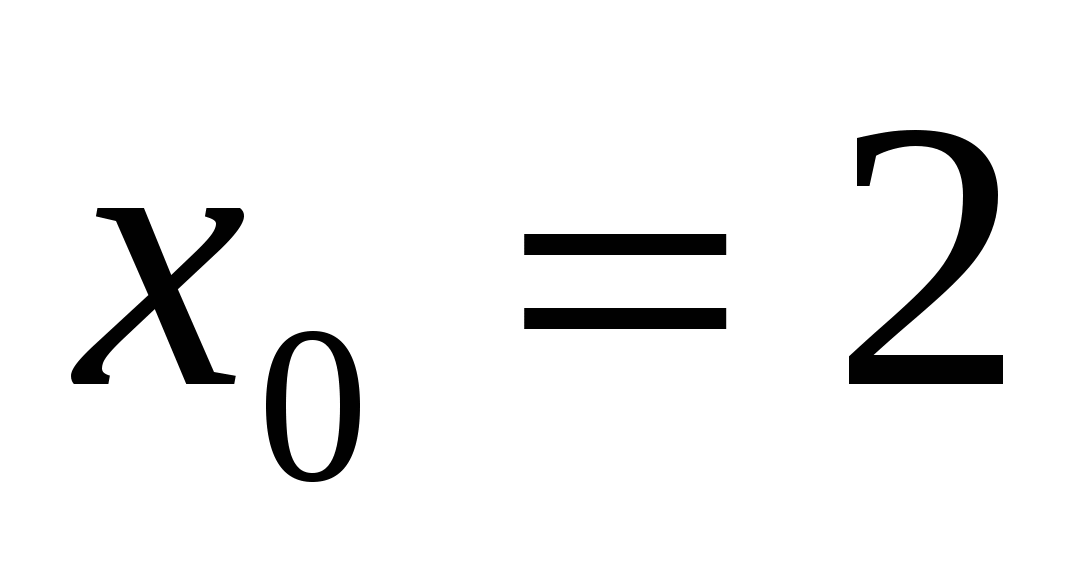 .
.
4
На рисунке изображен график функции 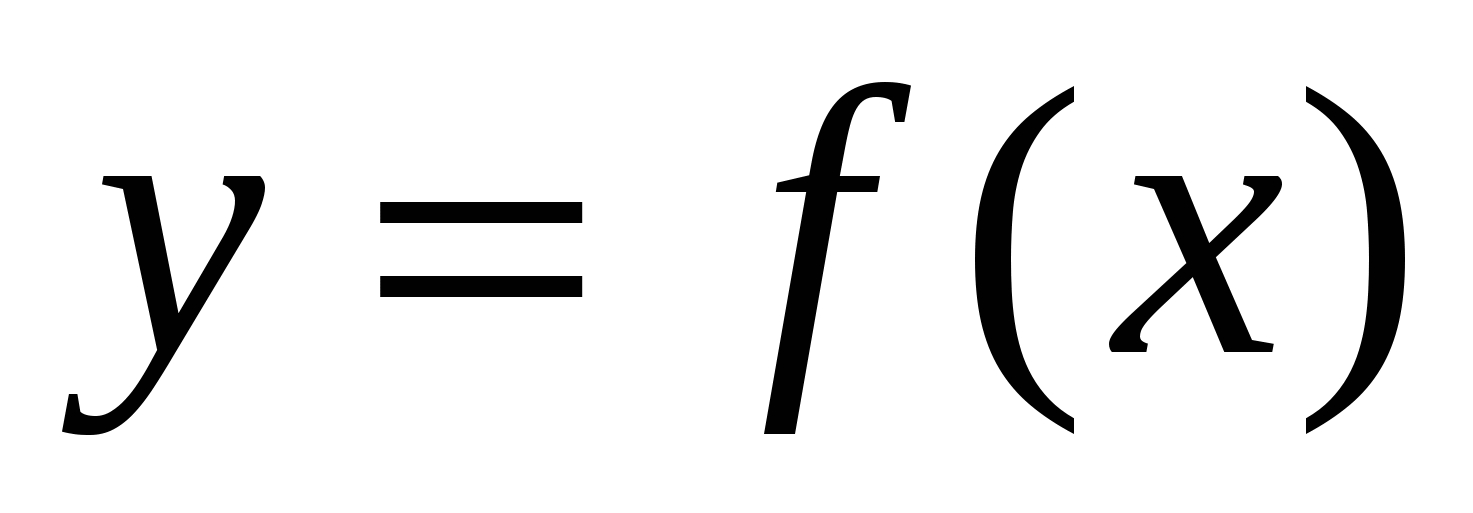 , определенной на интервале (-3;9). Найдите количество точек, в которых касательная к графику функции параллельна прямой
, определенной на интервале (-3;9). Найдите количество точек, в которых касательная к графику функции параллельна прямой 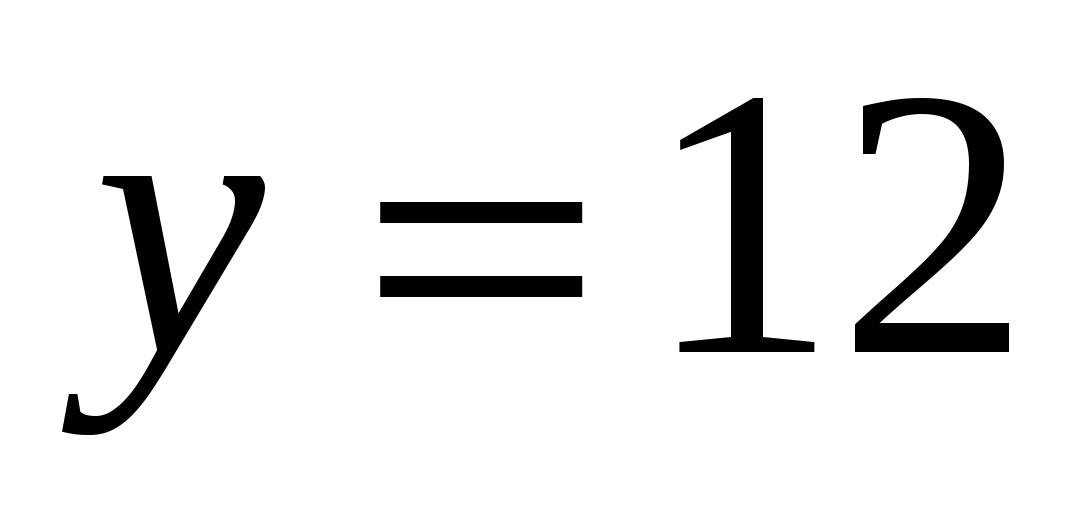 .
.

На рисунке изображен график функции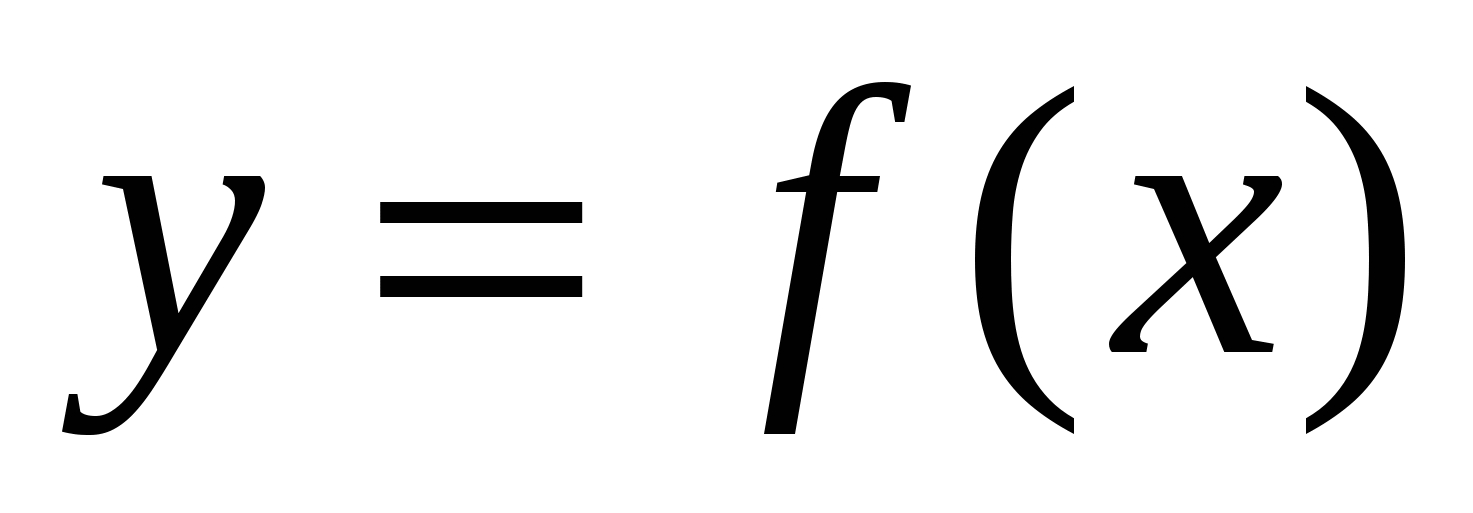 , определенной на интервале (-3;11). Найдите количество точек, в которых касательная к графику функции параллельна прямой
, определенной на интервале (-3;11). Найдите количество точек, в которых касательная к графику функции параллельна прямой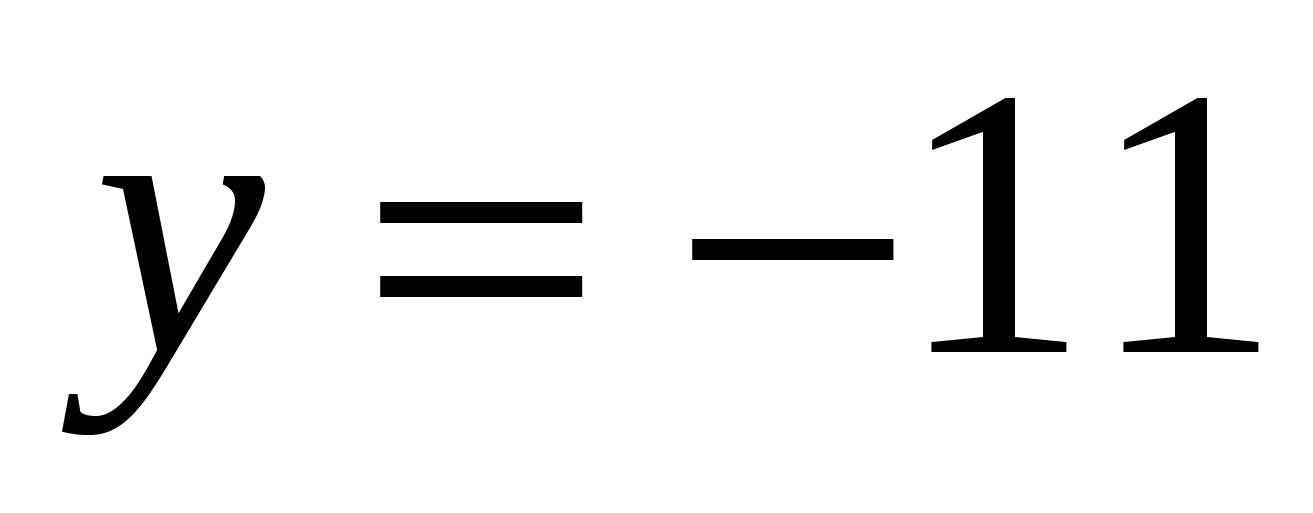 .
.

5
На рисунке изображен график производной функции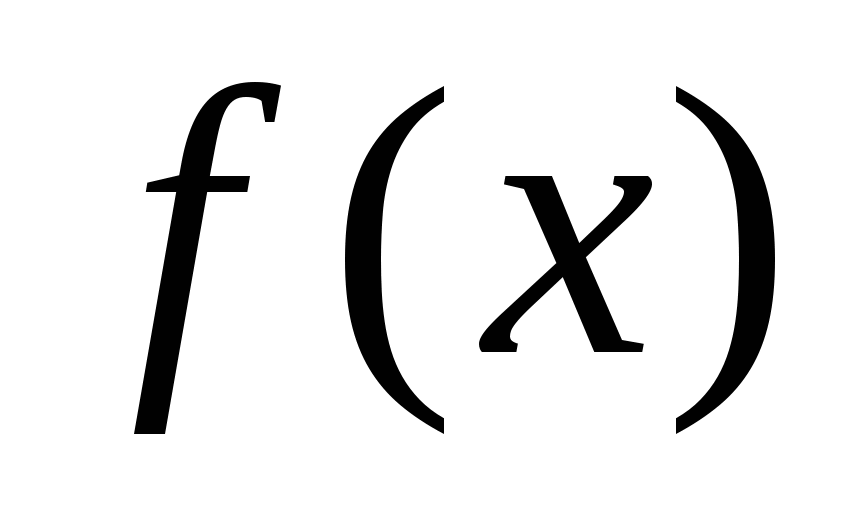 , определенной на интервале(-12;4). Найдите промежутки возрастания функции,
, определенной на интервале(-12;4). Найдите промежутки возрастания функции,
в ответе укажите длину наибольшего из них.

На рисунке изображен график производной функции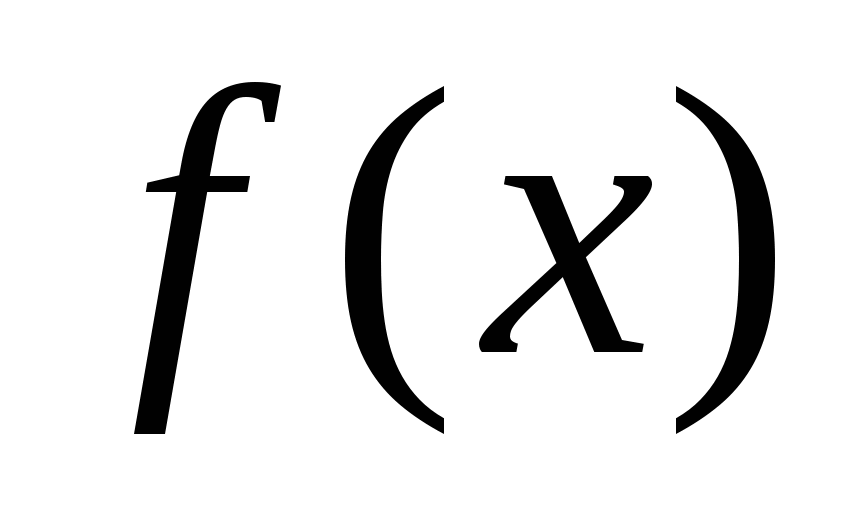 , определенной на интервале(-1;17). Найдите промежутки убывания функции,
, определенной на интервале(-1;17). Найдите промежутки убывания функции,
в ответе укажите длину наибольшего из них.

6
Укажите промежуток, на котором функция 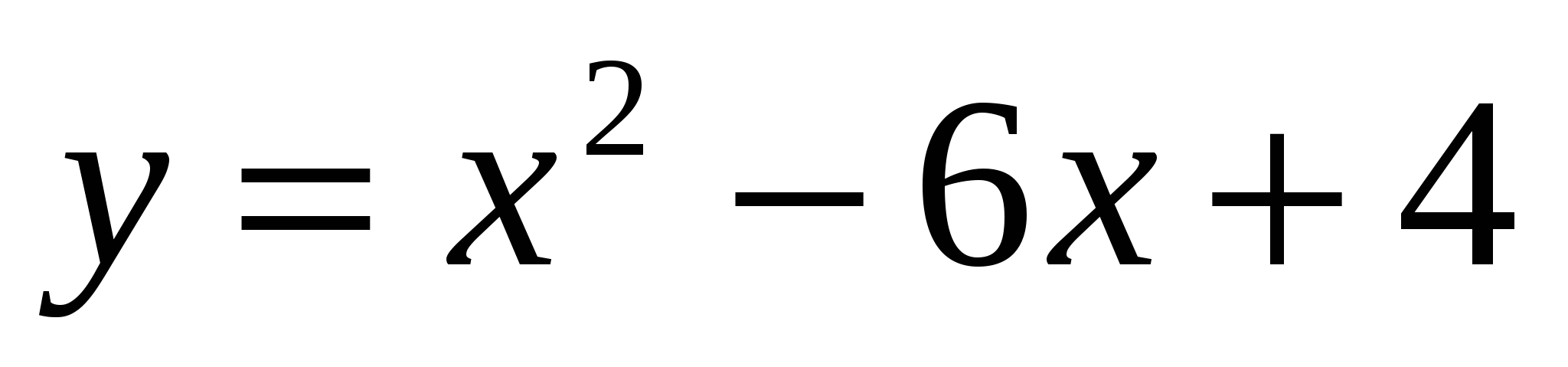 убывает.
убывает.
Укажите промежуток, на котором функция 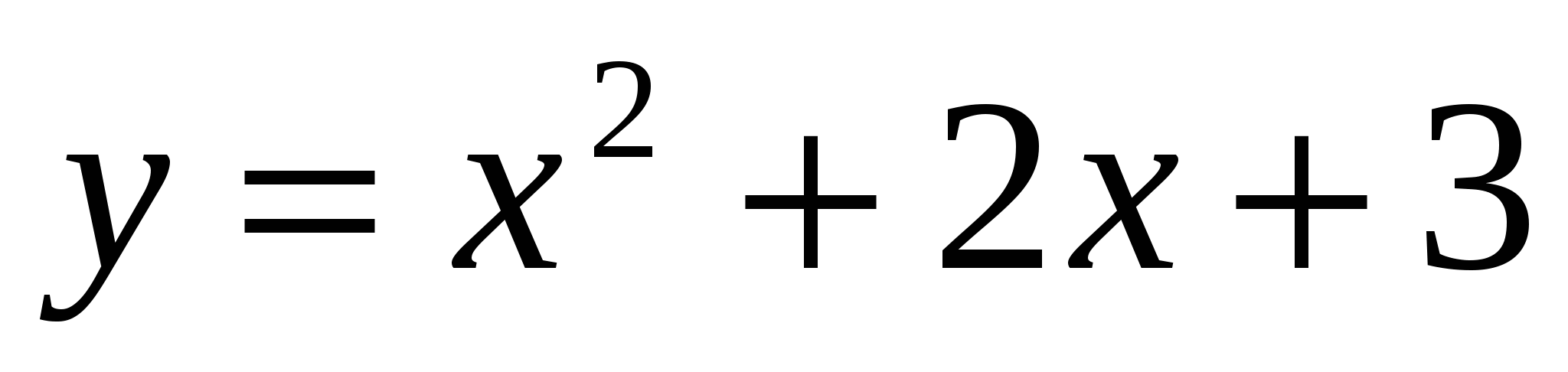 возрастает.
возрастает.
7
На рисунке изображен график функции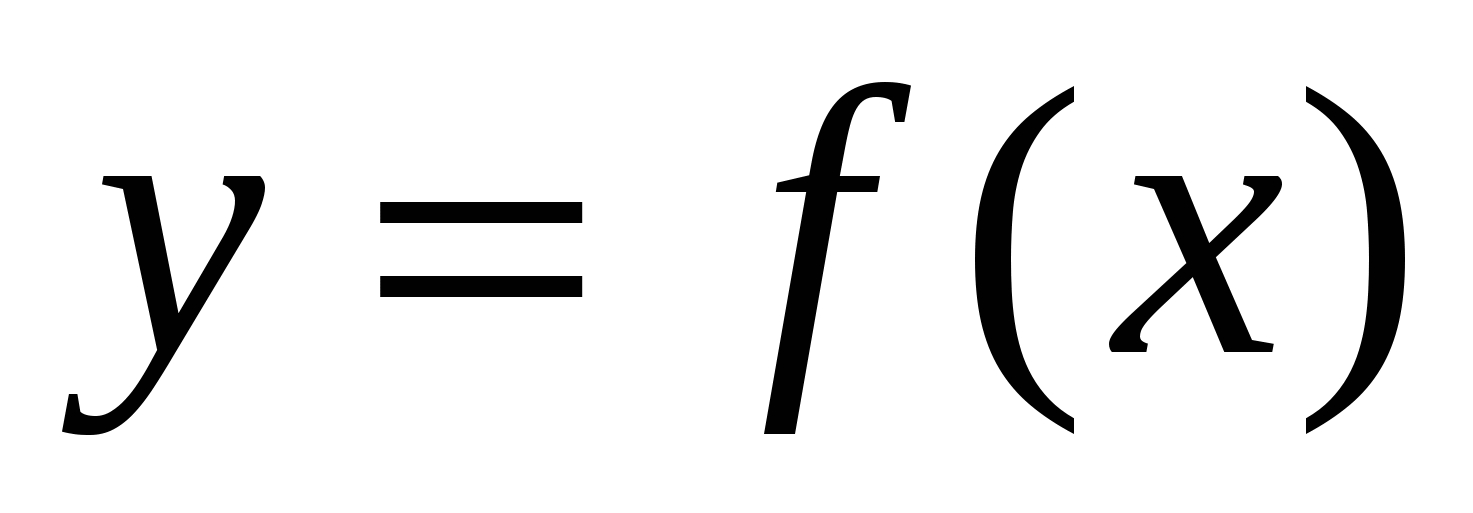 , определенной на интервале (-4;7).
, определенной на интервале (-4;7).
Найдите сумму точек экстремума функции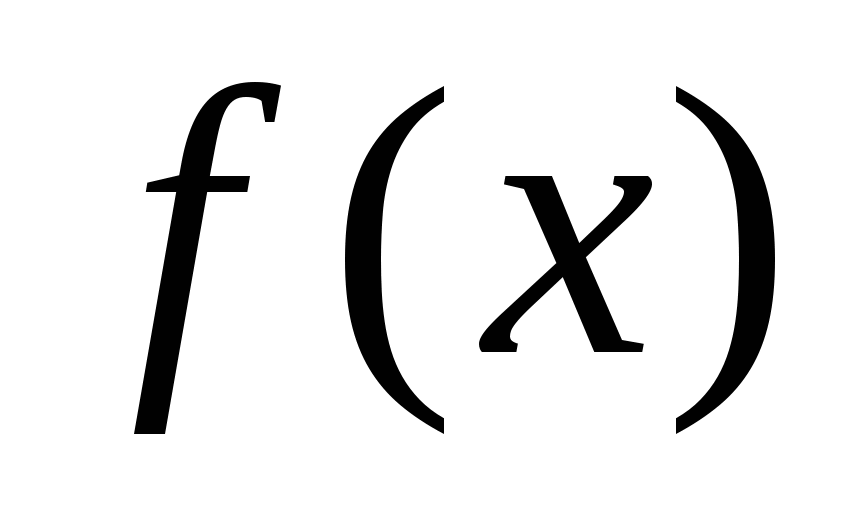 .
.

На рисунке изображен график функции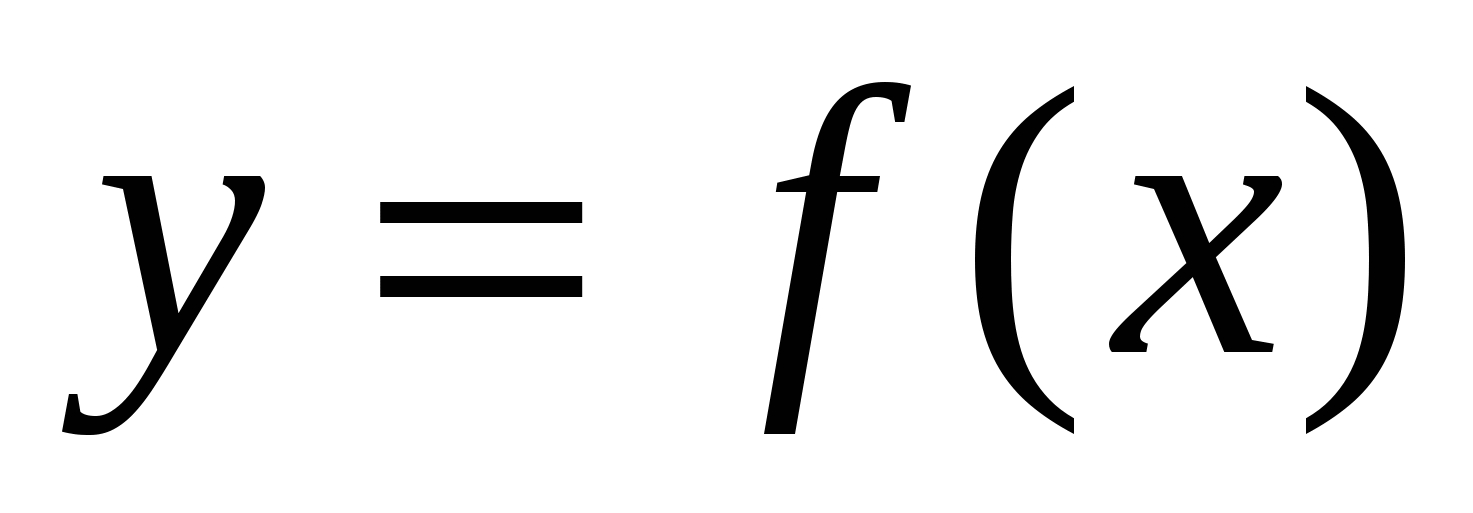 , определенной на интервале (-7;5).
, определенной на интервале (-7;5).
Найдите сумму точек экстремума функции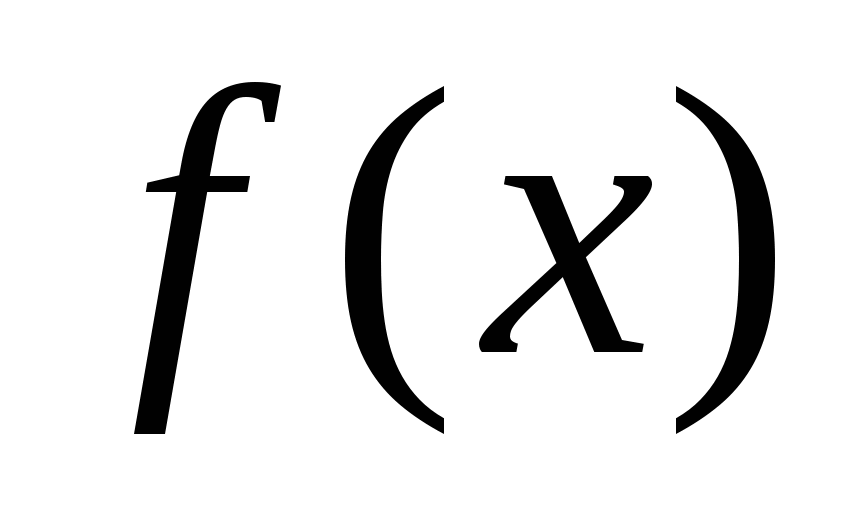 .
.

8
Найдите точки экстремума функции 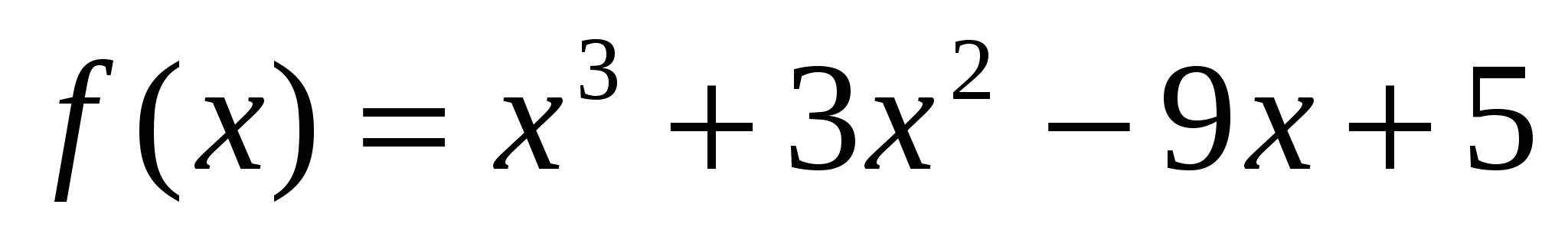 .
.
Найдите точки экстремума функции 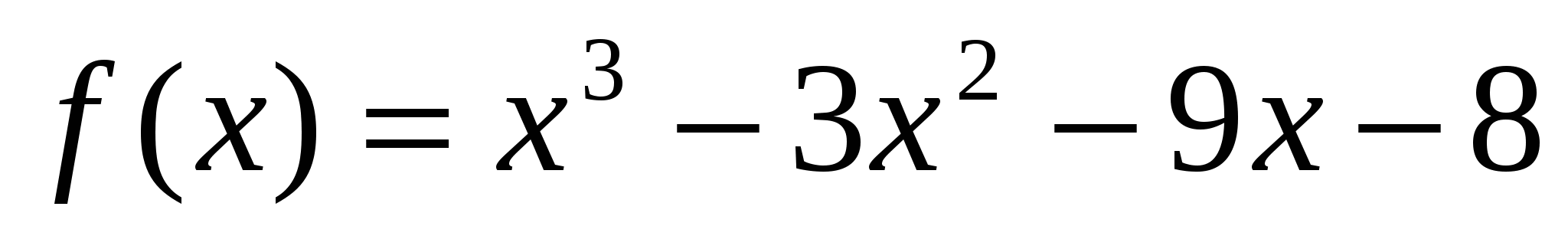 .
.
9
На рисунке изображен график производной функции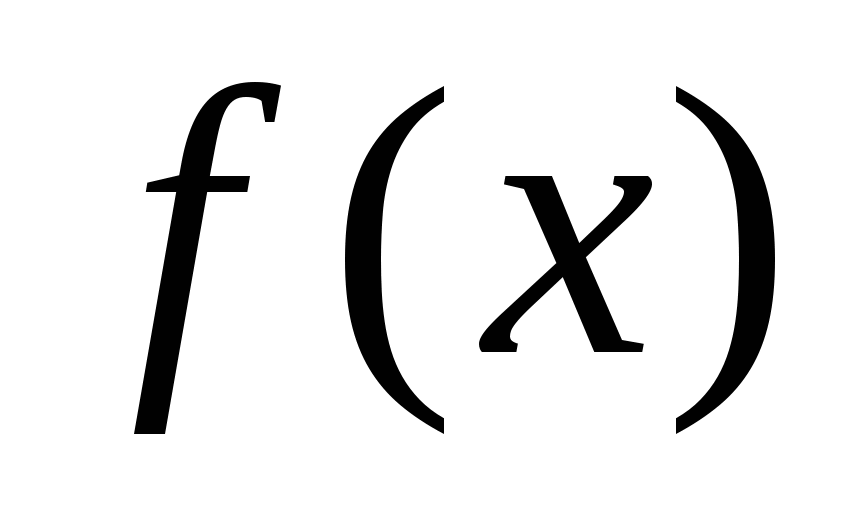 , определенной на интервале (-4;16). Найдите количество точек максимума функции на отрезке
, определенной на интервале (-4;16). Найдите количество точек максимума функции на отрезке 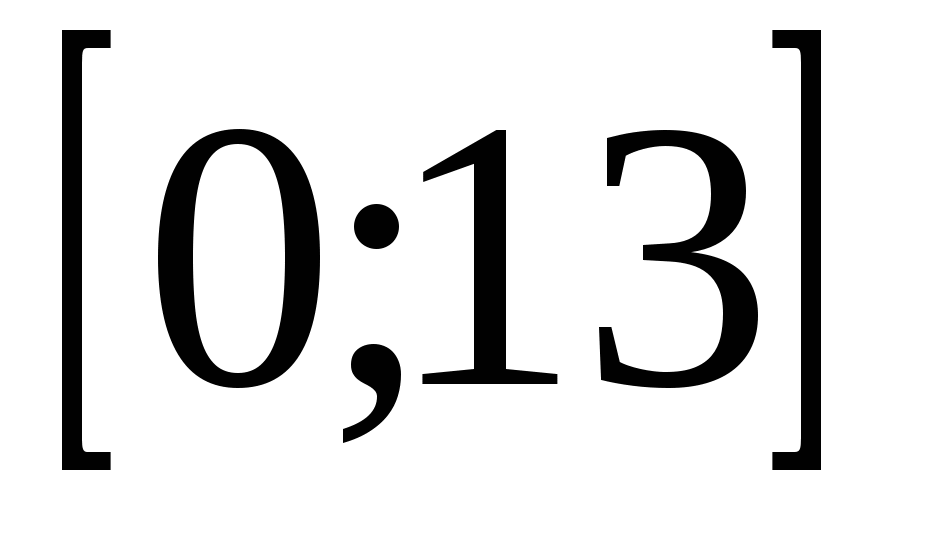 .
.

На рисунке изображен график производной функции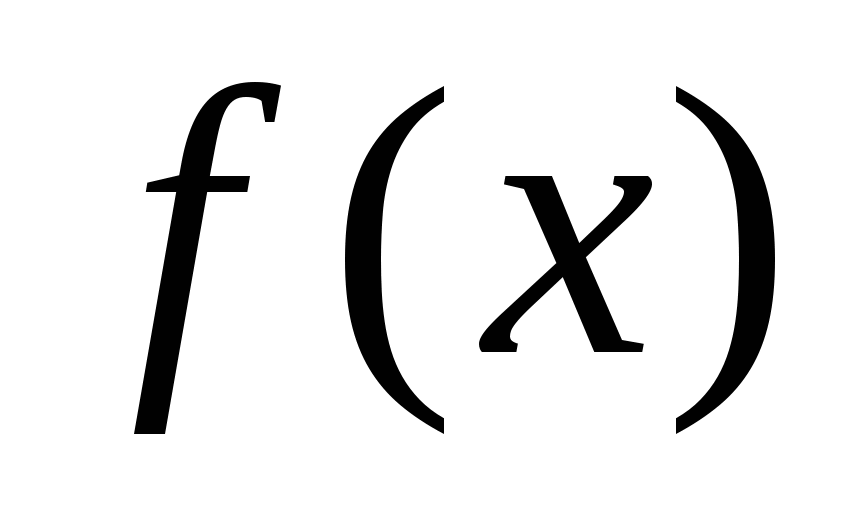 , определенной на интервале(-17;2). Найдите количество точек минимума функции на отрезке
, определенной на интервале(-17;2). Найдите количество точек минимума функции на отрезке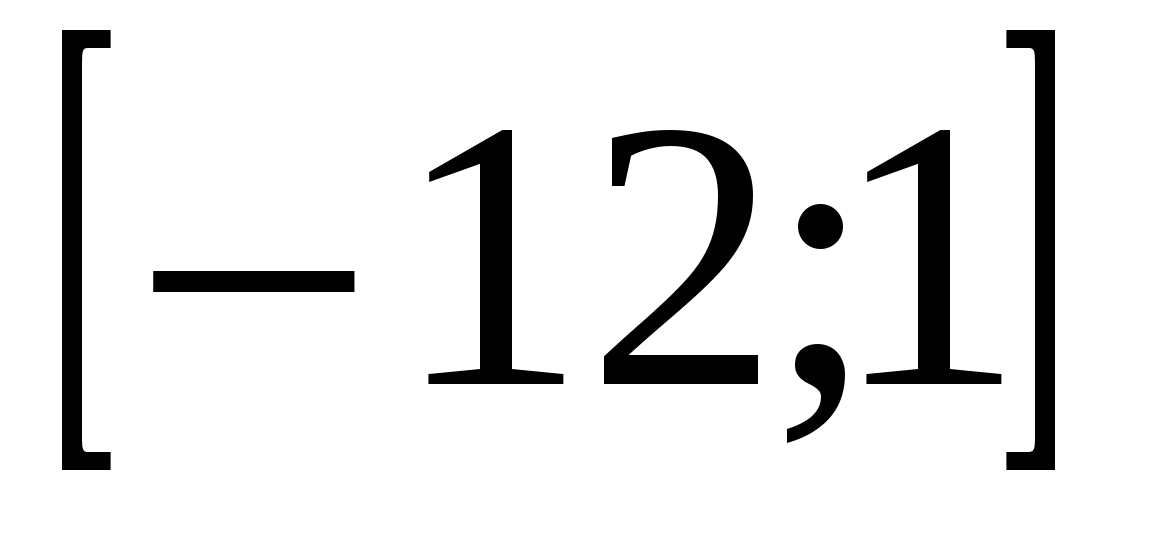 .
.

10
На рисунке изображен график производной функции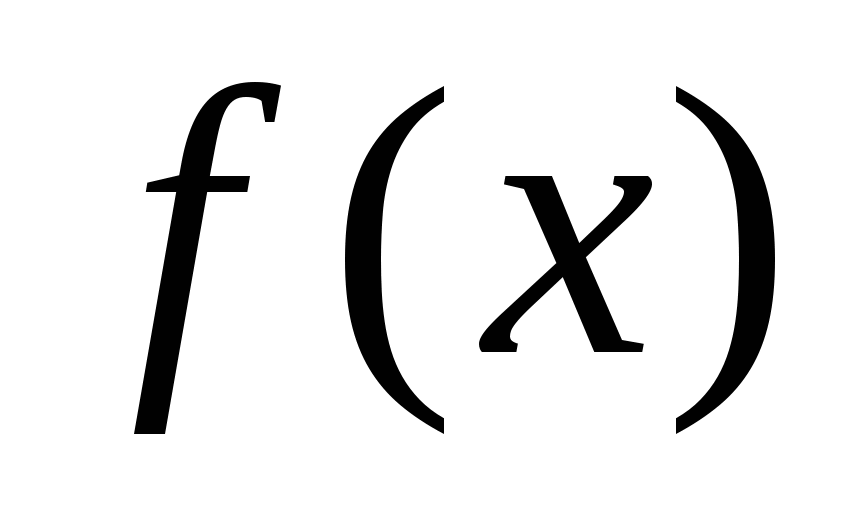 , определенной на интервале(-8; 4).
, определенной на интервале(-8; 4).
В какой точке отрезка 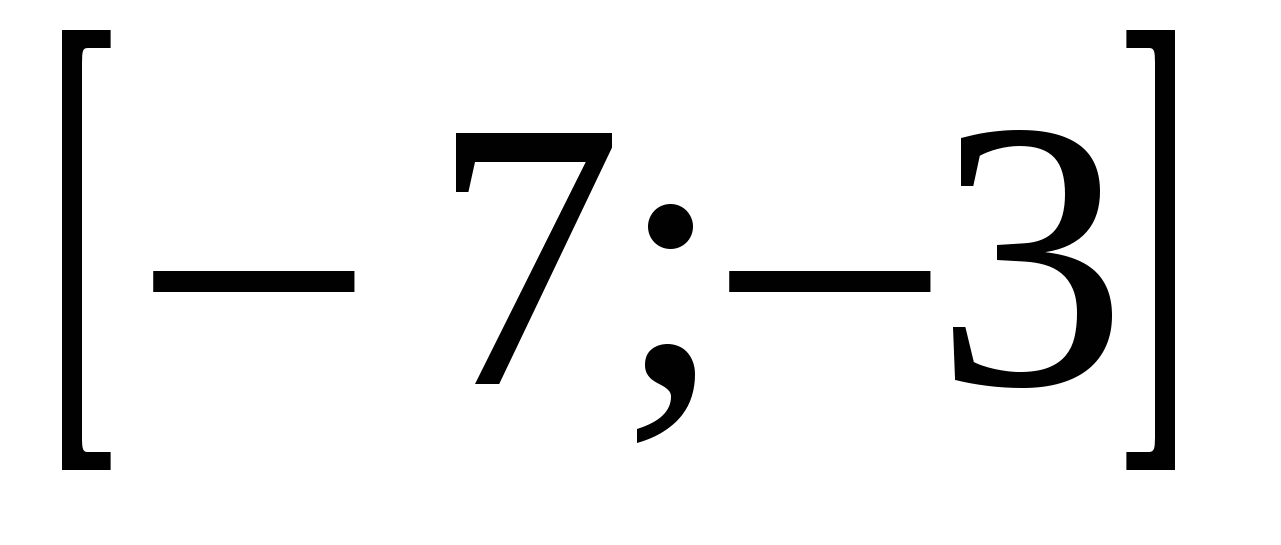 функция принимает наименьшее значение.
функция принимает наименьшее значение.

На рисунке изображен график производной функции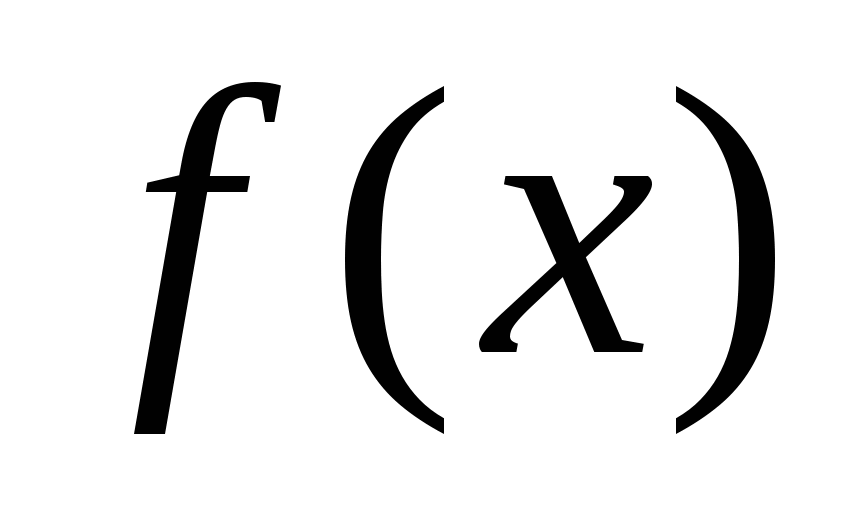 , определенной на интервале(-8;3). В какой точке отрезка
, определенной на интервале(-8;3). В какой точке отрезка 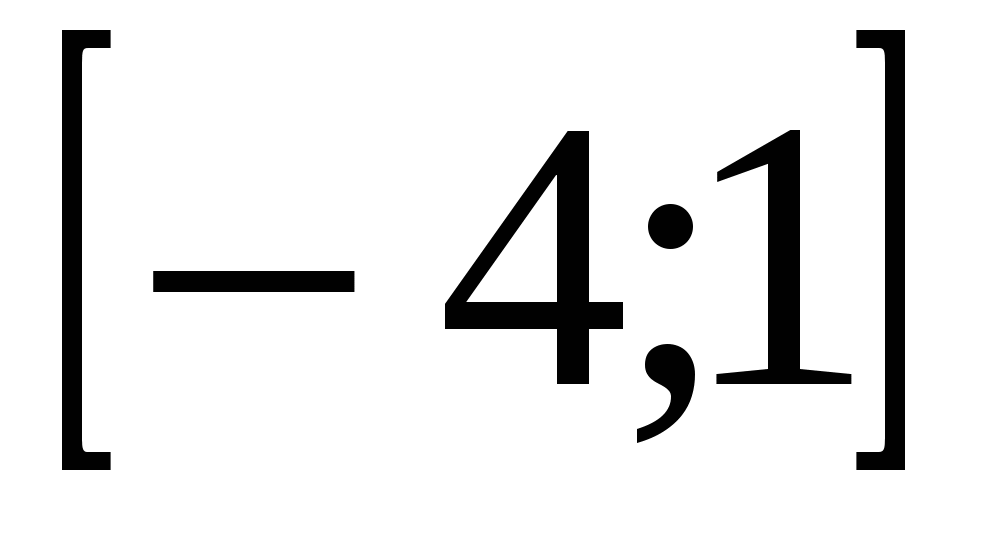 функция принимает наибольшее значение.
функция принимает наибольшее значение.

11
Прямая 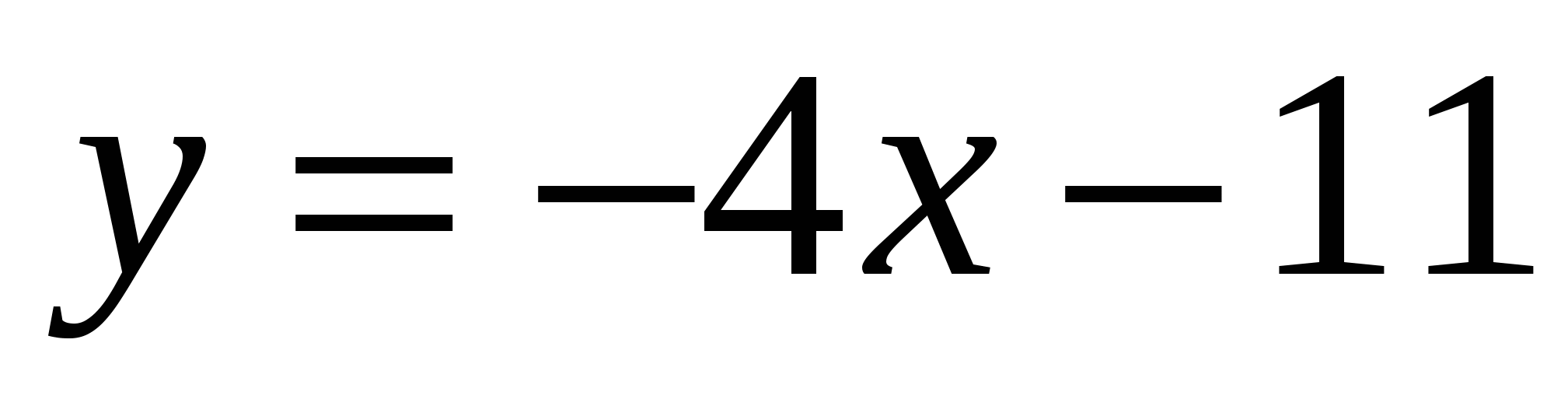 является касательной к графику функции
является касательной к графику функции 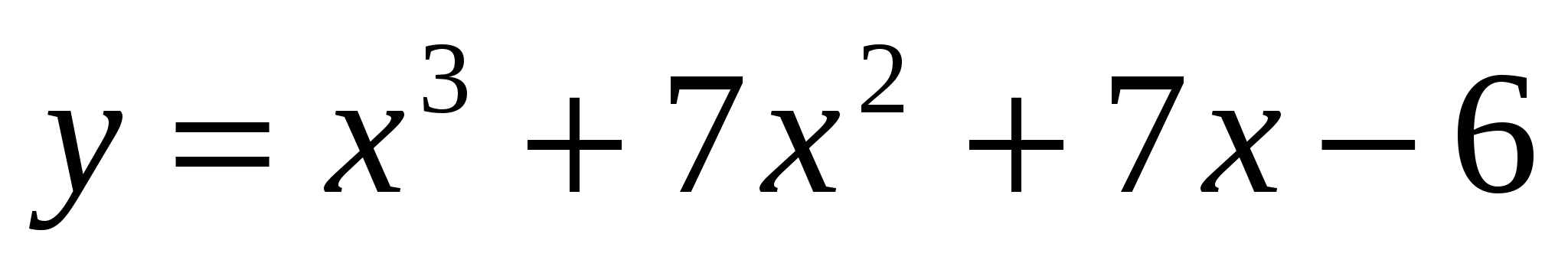 . Найдите абсциссу точки касания.
. Найдите абсциссу точки касания.
Прямая 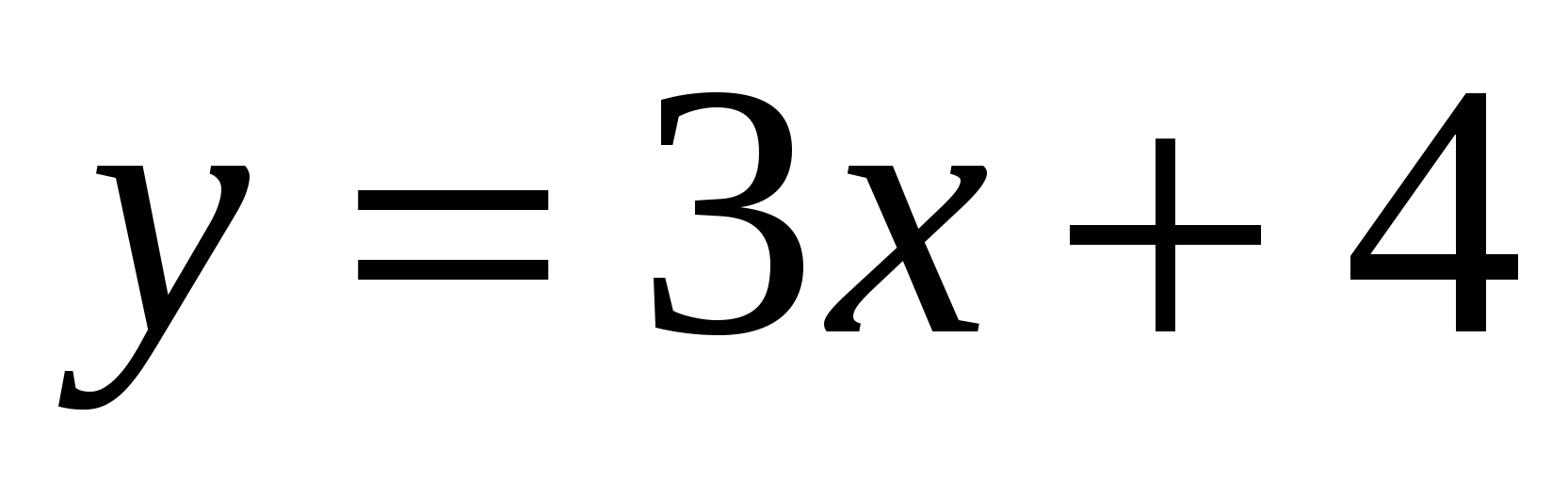 является касательной к графику функции
является касательной к графику функции  . Найдите абсциссу точки касания.
. Найдите абсциссу точки касания.
12
Точка движется прямолинейно по закону 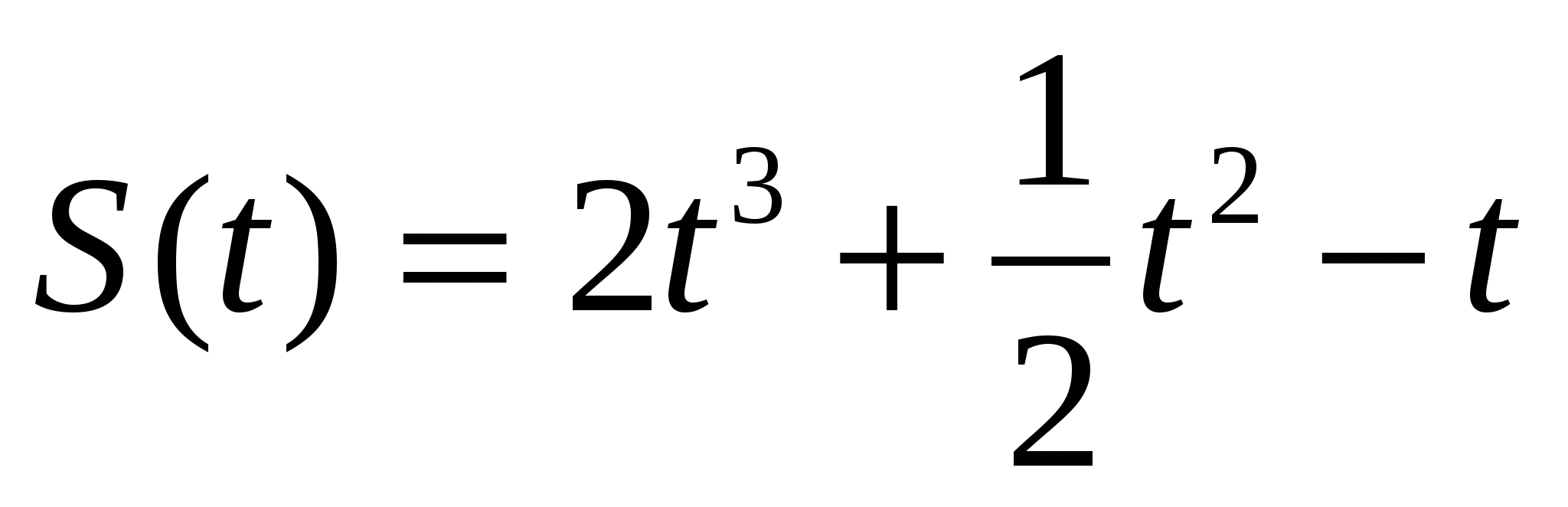 . Вычислите скорость и ускорение точки при t = 1.
. Вычислите скорость и ускорение точки при t = 1.
Точка движется прямолинейно по закону 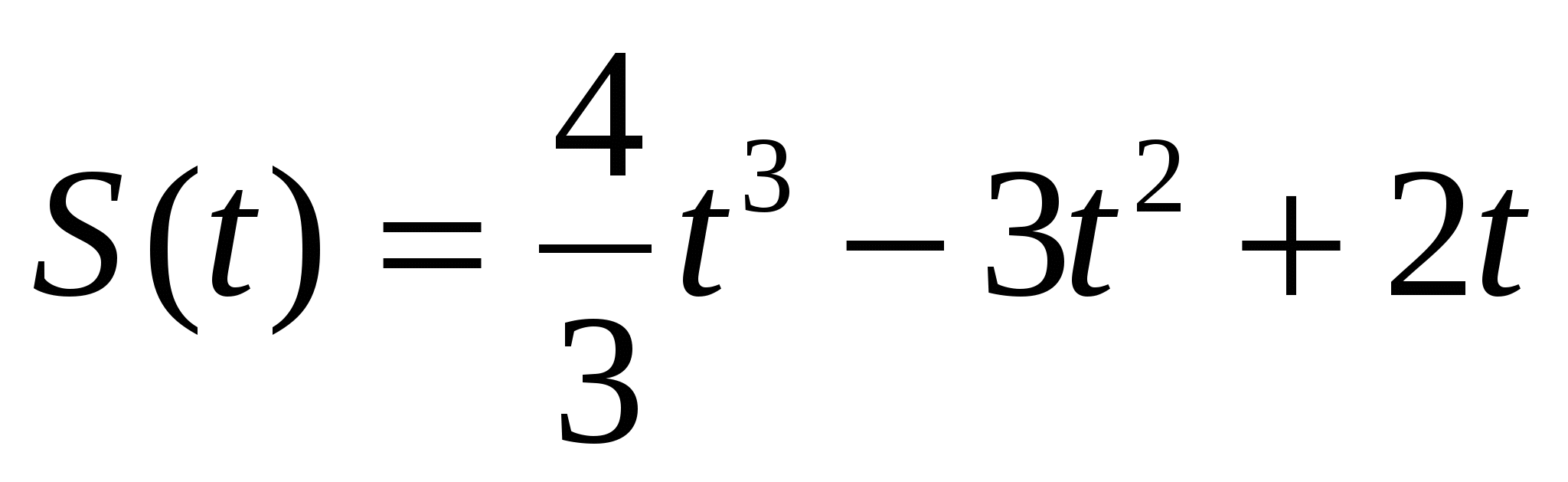 . Вычислите скорость и ускорение точки при t = 1.
. Вычислите скорость и ускорение точки при t = 1.
№
5 вариант
6 вариант
1
Найдите значение производной функции 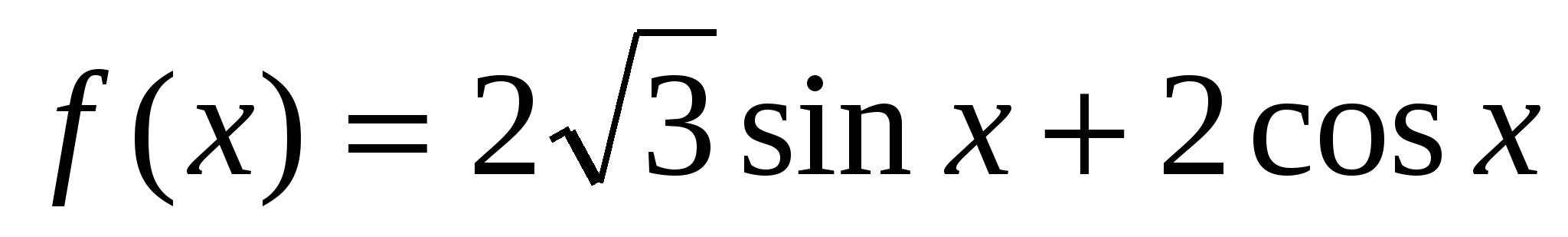 в точке
в точке 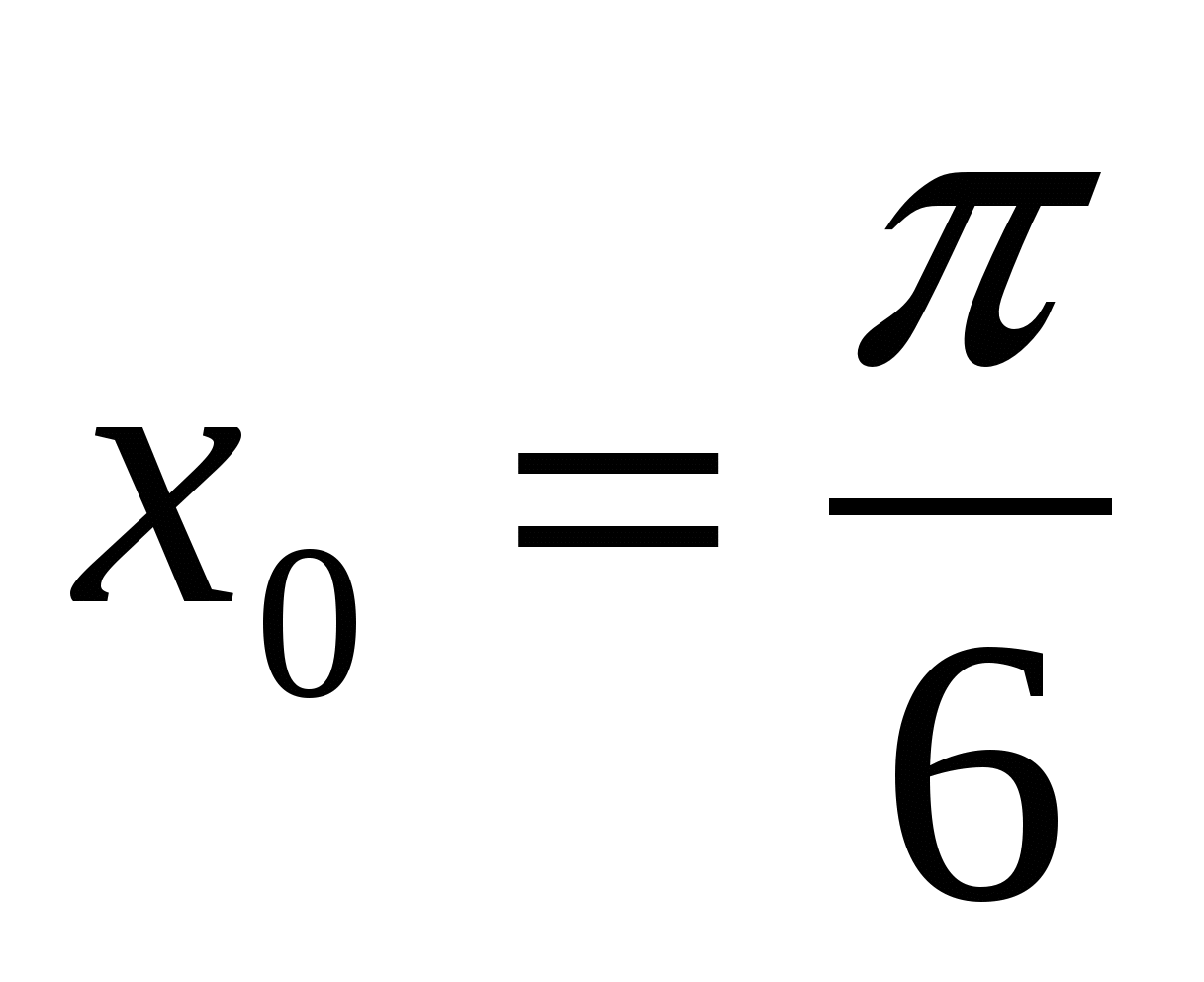 .
.
Найдите значение производной функции
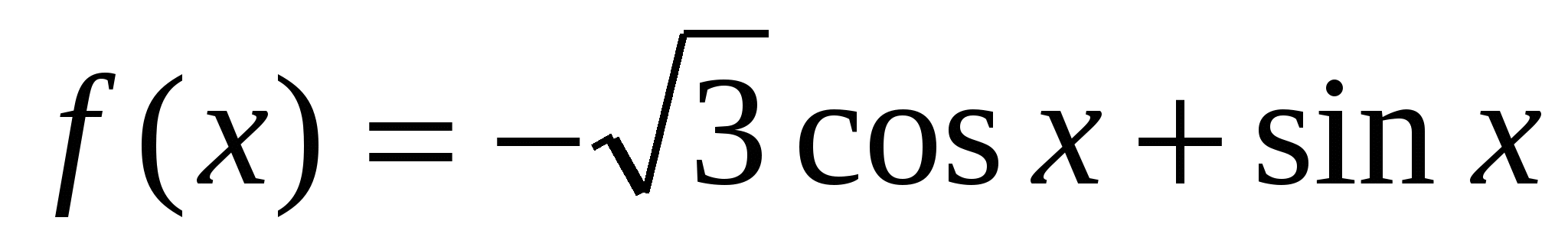 в точке
в точке 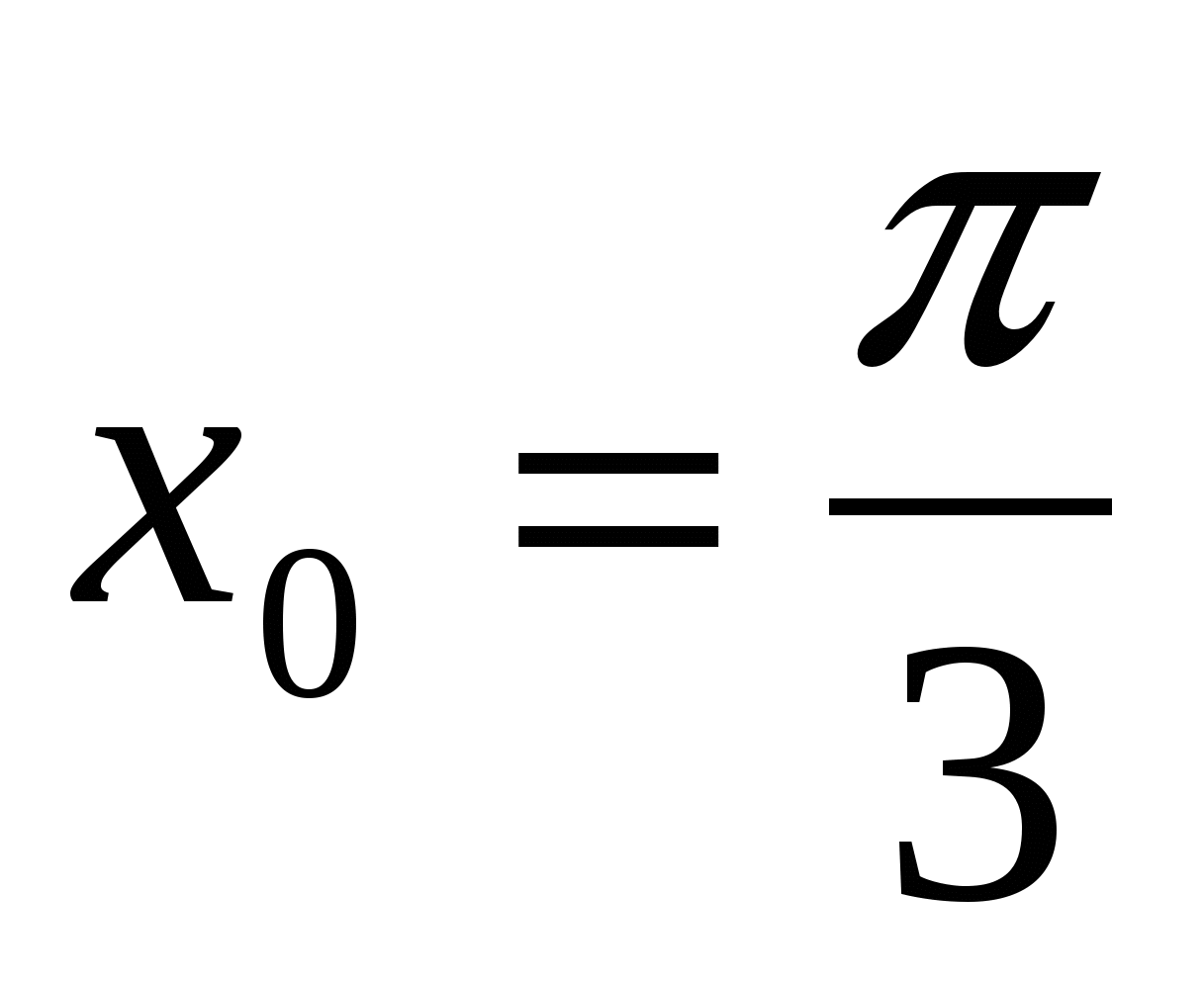 .
.
2
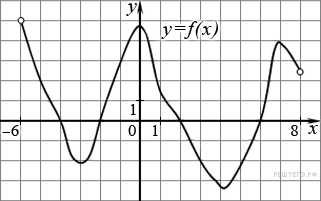 На рисунке изображен график функции
На рисунке изображен график функции 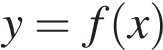 , определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
, определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
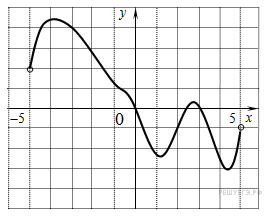 На рисунке изображен график функции
На рисунке изображен график функции 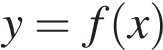 , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции
, определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции 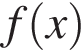 отрицательна.
отрицательна.
3
Найдите угловой коэффициент касательной к графику функции 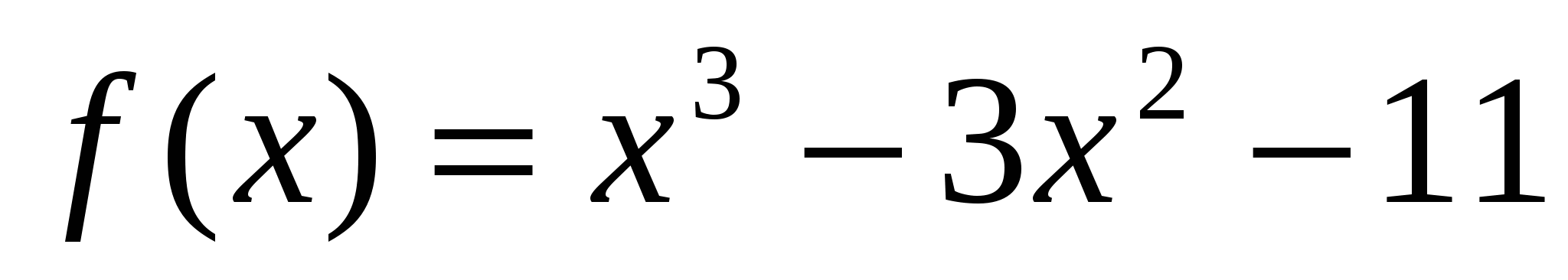
в точке с абсциссой 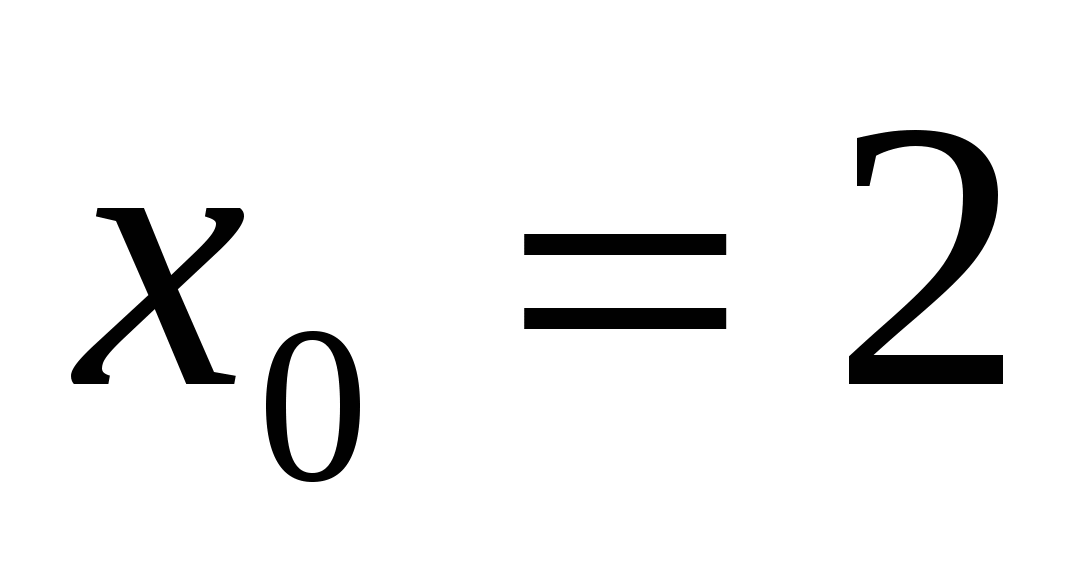 .
.
Найдите угловой коэффициент касательной к графику функции 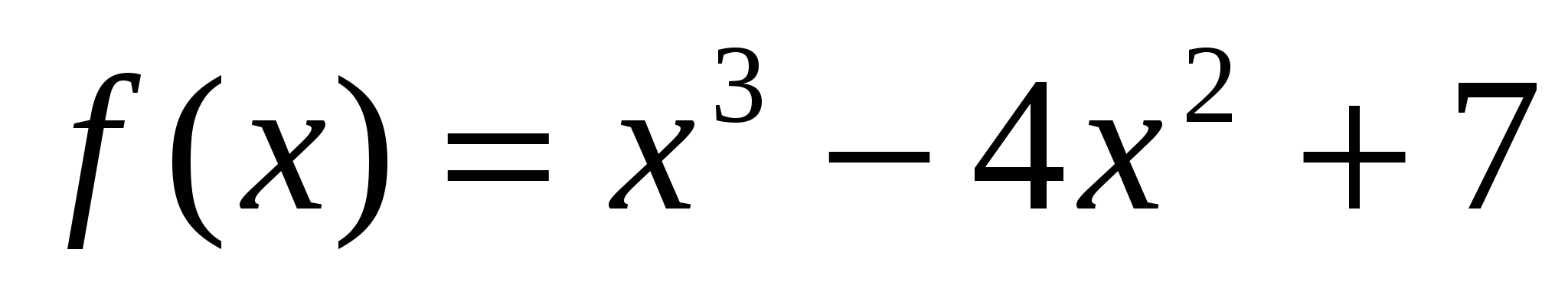
в точке с абсциссой 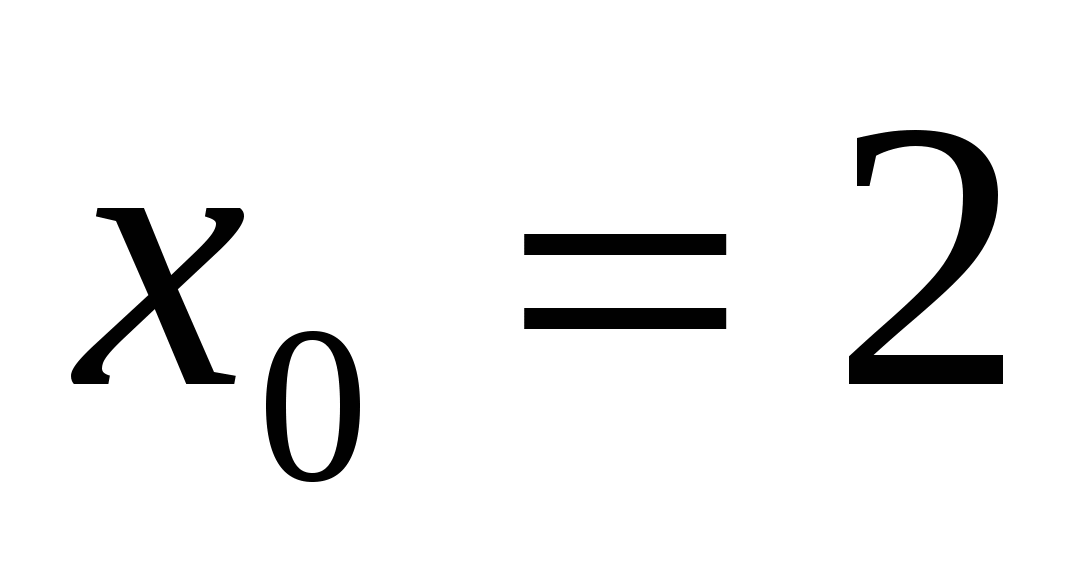 .
.
4
На рисунке изображен 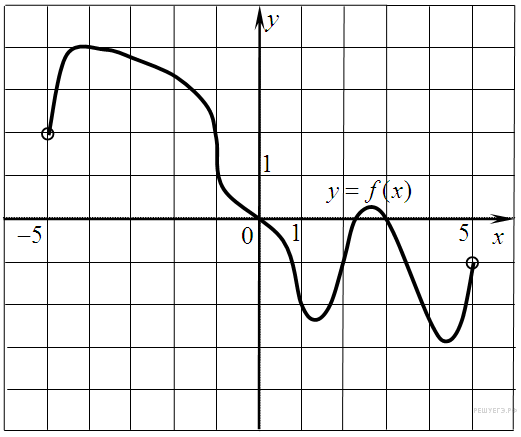 график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
4.
Н а рисунке изображен график функции y = f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x),.
а рисунке изображен график функции y = f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x),.
5
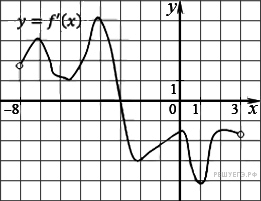 На рисунке изображен график производной функции
На рисунке изображен график производной функции 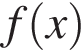 , определенной на интервале
, определенной на интервале 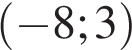 . В какой точке отрезка
. В какой точке отрезка 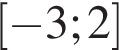 функция
функция 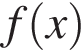 принимает наибольшее значение?
принимает наибольшее значение?
 На рисунке изображен график производной функции
На рисунке изображен график производной функции 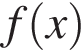 , определенной на интервале
, определенной на интервале 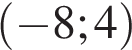 . В какой точке отрезка
. В какой точке отрезка 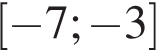
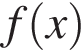 принимает наименьшее значение?
принимает наименьшее значение?
6
Укажите промежуток, на котором функция 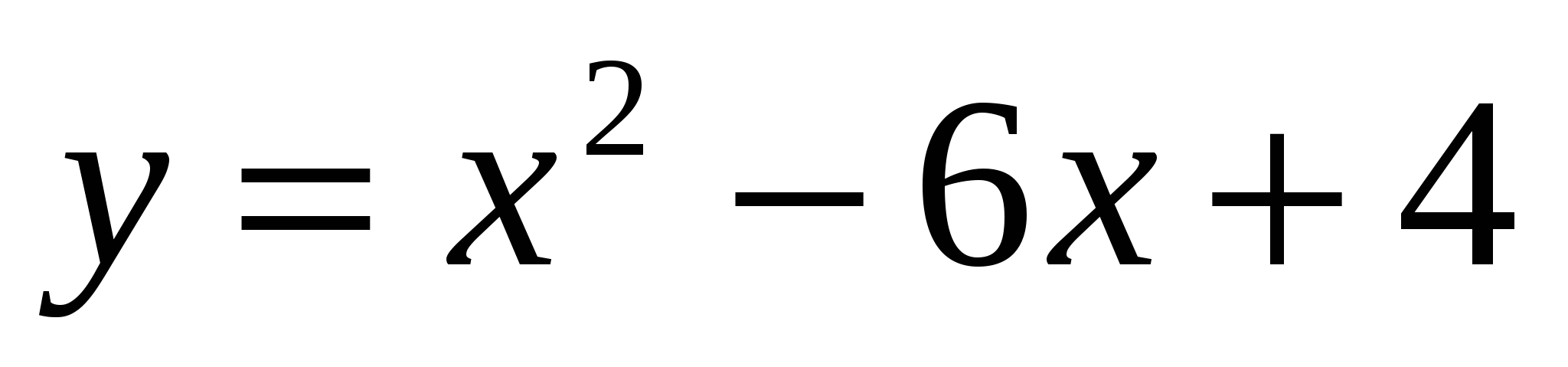 убывает.
убывает.
Укажите промежуток, на котором функция 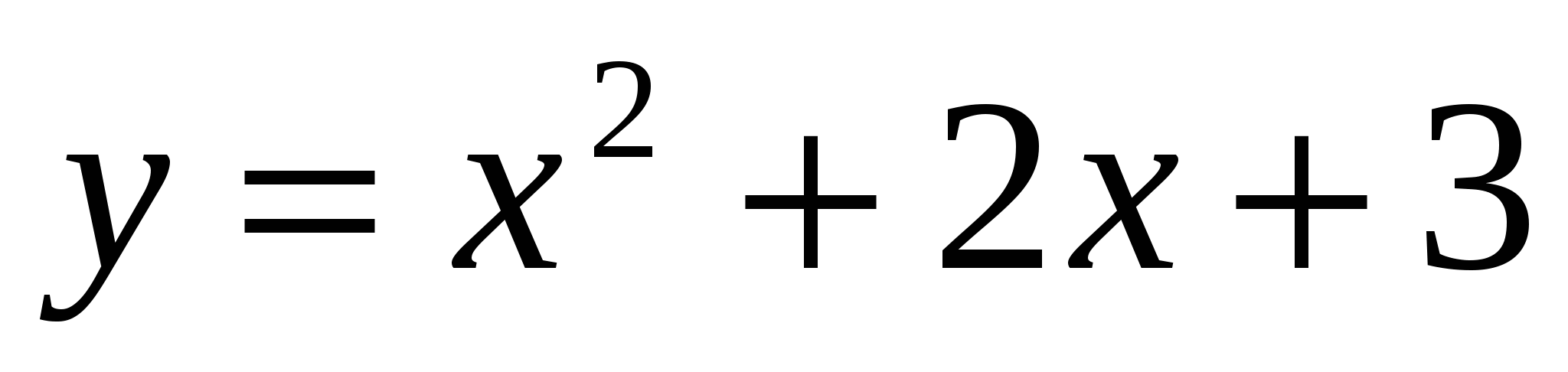 возрастает.
возрастает.
7
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].
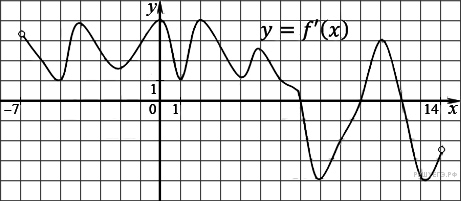
На рисунке изображен график производной функции 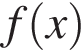 , определенной на интервале
, определенной на интервале 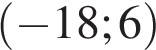 . Найдите количество точек минимума функции
. Найдите количество точек минимума функции 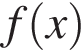 на отрезке
на отрезке 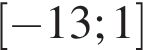 .
.
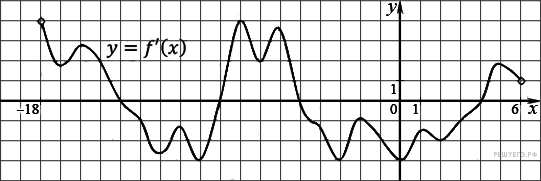
8
Найдите точку минимума функции 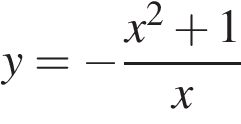
Найдите точку максимума функции 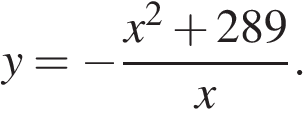
9
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
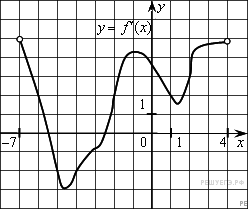
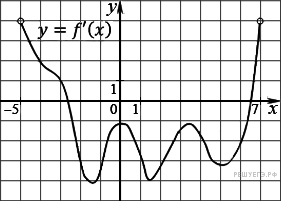 На рисунке изображен график производной функции f(x), определенной на интервале (−5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
На рисунке изображен график производной функции f(x), определенной на интервале (−5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
10
На рисунке изображен график производной функции f(x), определенной на интервале (−11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
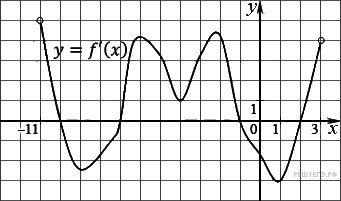
На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
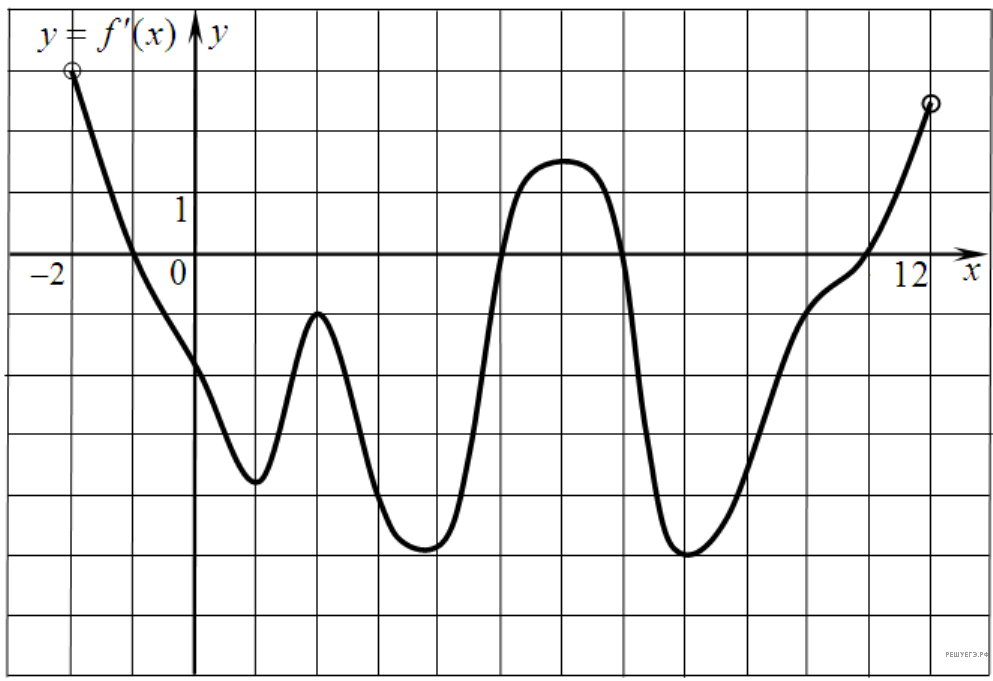
11
Найдите наибольшее значение функции 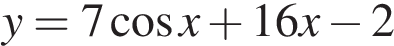 на отрезке
на отрезке 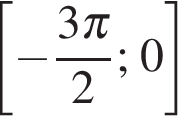 .
.
Найдите наименьшее значение функции  на отрезке
на отрезке 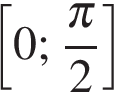 .
.
12
Найдите наименьшее значение функции 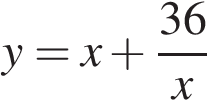 на отрезке
на отрезке 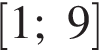 .
.
Найдите наибольшее значение функции 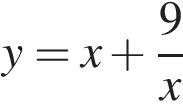 на отрезке
на отрезке 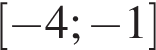 .
.
№
7вариант
8 вариант
1
Материальная точка движется прямолинейно по закону 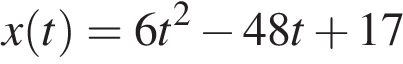 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
Материальная точка движется прямолинейно по закону 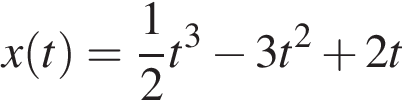 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
2
. 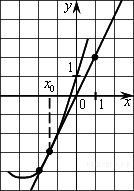 На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
. 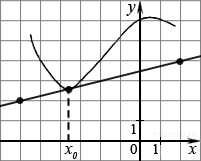 На рисунке изображён график функцииy=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
На рисунке изображён график функцииy=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
3
Найдите наименьшее значение функции 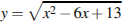 .
.
Найдите наибольшее значение функции 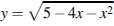 .
.
4
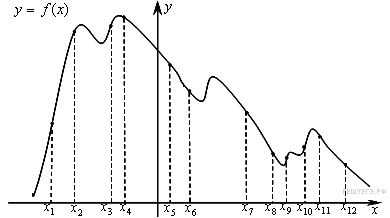
На рисунке изображён график функции 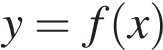 и двенадцать точек на оси абсцисс:
и двенадцать точек на оси абсцисс: 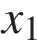 ,
, 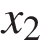 ,
, 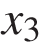 ,
,  ,
, 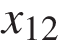 . В скольких из этих точек производная функции
. В скольких из этих точек производная функции 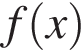 отрицательна?
отрицательна?
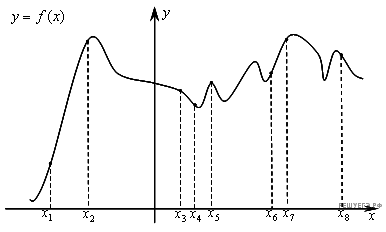
На рисунке изображён график функции 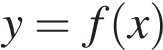 и восемь точек на оси абсцисс:
и восемь точек на оси абсцисс: 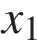 ,
, 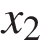 ,
, 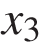 ,
,  ,
, 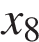 . В скольких из этих точек производная функции
. В скольких из этих точек производная функции 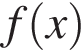 положительна?
положительна?
5
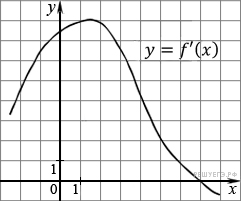 На рисунке изображен график производной функции
На рисунке изображен график производной функции 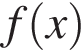 . Найдите абсциссу точки, в которой касательная к графику
. Найдите абсциссу точки, в которой касательная к графику 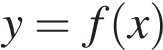 параллельна прямой
параллельна прямой 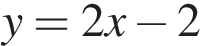 или совпадает с ней.
или совпадает с ней.
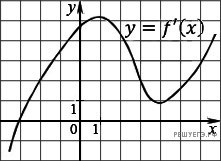 На рисунке изображен график производной функции
На рисунке изображен график производной функции 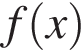 . Найдите абсциссу точки, в которой касательная к графику
. Найдите абсциссу точки, в которой касательная к графику 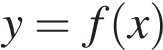 параллельна оси абсцисс или совпадает с ней.
параллельна оси абсцисс или совпадает с ней.
6
7
 На рисунке изображен график функции f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых производная функции f(x) равна 0.
На рисунке изображен график функции f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых производная функции f(x) равна 0.
На рисунке изображён график функции у = f'(x) — производной функцииf(x) определённой на интервале (1; 10). Найдите точку минимума функции f(x).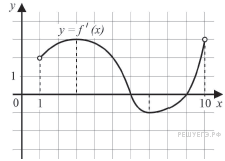
8
Найдите точку максимума функции 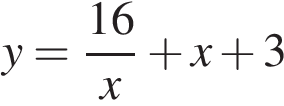 .
.
Найдите точку минимума функции 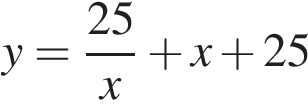 .
.
9
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

 На рисунке изображен график производной функции f(x), определенной на интервале (−5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
На рисунке изображен график производной функции f(x), определенной на интервале (−5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
10
На рисунке изображен график производной функции f(x), определенной на интервале (−11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

11
Найдите наибольшее значение функции 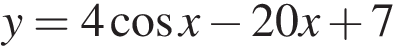 на отрезке
на отрезке 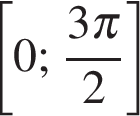 .
.
Найдите наибольшее значение функции 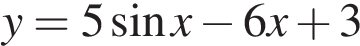 на отрезке
на отрезке 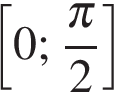 .
.
infourok.ru
Контрольная работа по теме: “Производная ” 10 класс (1 час)
Вариант 1 Часть 1
А1. Найдите производную функции 
1) ; 2)
; 2) ; 3)
; 3) ; 4)
; 4) ;
;
А2. Найдите значение производной функции  в точке
в точке 
1) 0; 2) -3; 3) 2; 4) -6;
А3. Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
А4. f(х) = (3х-2) . Найдите f ׳(1). 1) 1; 2) 0; 3) 15; 4) 5.
. Найдите f ׳(1). 1) 1; 2) 0; 3) 15; 4) 5.
А5. f(х) = 6sin x – 3. Решите уравнение f ׳(х) = 0
1) πk, k Z; 2)
Z; 2)  ; 3)
; 3)  ; 4) ±
; 4) ±
А6. f(х) = 5 Вычислите f ׳
Вычислите f ׳  . 1)
. 1)  ; 2)
; 2)  ; 3) 0; 4) 5.
; 3) 0; 4) 5.
Часть 2
В1. f(х) =  ctg 15x +
ctg 15x +  . Найдите f ׳
. Найдите f ׳
В2. Найдите значение производной функции  в точке
в точке 
В3. Найдите значение  , если
, если 
В4. Решите уравнение  , если f(x) =
, если f(x) =  ; g(x) =
; g(x) = 
В5. Решите уравнение f ׳(х) = 0, где f(x) = cos8x – sin8x – 1
В6. Найдите среднее арифметическое корней уравнения  , принадлежащих
, принадлежащих
отрезку  , если известно, что
, если известно, что 
Контрольная работа по теме: “Производная ” 10 класс (1 час)
Часть 1
Вариант 2
А1. Найдите производную функции 
1) ; 2)
; 2) ; 3)
; 3) ; 4)
; 4) ;
;
А2. Найдите значение производной функции  в точке
в точке 
1) 7; 2) -3; 3) 4; 4)  ;
;
А3 Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
А4. f(х) = (5х-4) . Найдите f ׳(1). 1) 6; 2) 1; 3) 30; 4) 0.
. Найдите f ׳(1). 1) 6; 2) 1; 3) 30; 4) 0.
А5. f(х) = 4cos x +2. Решите уравнение f ׳(х) = 0
1) πk, k Z; 2)
Z; 2)  ; 3) ±
; 3) ± 4)
4)  ;
;
А 6. f(х) = 3 Вычислите f ׳
Вычислите f ׳  . 1) 3; 2) 0; 3)
. 1) 3; 2) 0; 3)  ; 4)
; 4)  .
.
Часть 2
В1. f(х) =  tg 8x +
tg 8x +  . Найдите f ׳(
. Найдите f ׳( )
)
В2. Найдите значение производной функции  в точке
в точке 
В3. Найдите значение  , если
, если 
В4. Решите уравнение  , если f(x) =
, если f(x) =  ; g(x) = 2
; g(x) = 2
В5. Решите уравнение f ׳(х) = 0, где f(x) = sin6x + cos6x + 5
В6. Найдите наибольший отрицательный корень уравнения  , принадлежащий отрезку
, принадлежащий отрезку  , если известно, что
, если известно, что 
Контрольная работа по теме: “Производная ” 10 класс (1 час)
Часть 1
Вариант 3
А1. Найдите производную функции 
1) ; 2)
; 2) ;
;
3) ; 4)
; 4) ;
;
А2. Найдите значение производной функции  в точке
в точке 
1) 4; 2) -26; 3) -1; 4) 0;
А3 Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
А4. f(х) = (3х + 2) . Найдите f ׳(-1). 1) 1; 2) 0; 3) - 15; 4) 15.
. Найдите f ׳(-1). 1) 1; 2) 0; 3) - 15; 4) 15.
А5. f(х) = 12sin x – 6. Решите уравнение f ׳(х) = 0
1) πk, k Z; 2)
Z; 2)  ; 3)
; 3)  ; 4) ±
; 4) ±
А 6. f(х) = 5 Вычислите f ׳
Вычислите f ׳  . 1) 0; 2)
. 1) 0; 2)  ; 3) 5 4)
; 3) 5 4)  ;
;
Часть 2
В1. f(х) =  ctg 15x +
ctg 15x +  . Найдите f ׳
. Найдите f ׳
В2. Найдите значение производной функции  в точке
в точке 
В3. Найдите значение  , если
, если 
В4. Решите уравнение  , если f(x) =
, если f(x) =  ; g(x) =
; g(x) = 
В5. Решите уравнение f ׳(х) = 0, где f(x) = cos8x – sin8x – 1
В6. Найдите сумму наибольшего и наименьшего из корней уравнения  , принадлежащих отрезку
, принадлежащих отрезку  , если известно, что
, если известно, что 
Контрольная работа по теме: “Производная ” 10 класс (1 час)
Часть 1
Вариант 4
А1. Найдите производную функции 
1) ; 2)
; 2) ; 3)
; 3) ; 4)
; 4) ;
;
А2. Найдите значение производной функции  в точке
в точке 
1) 6; 2) -1; 3) -2; 4) 3;
А3. Найдите производную функции 
1)  2)
2)  3)
3)  4) -1;
4) -1;
А4. f(х) = (5х + 4) . Найдите f ׳(- 1). 1) 1; 2) - 30; 3) 30; 4) 6.
. Найдите f ׳(- 1). 1) 1; 2) - 30; 3) 30; 4) 6.
А5. f(х) = 8cos x + 4 . Решите уравнение f ׳(х) = 0
1)  ; 2) ±
; 2) ± ; 3)
; 3) ; 4) πk, k
; 4) πk, k Z;
Z;
А 6. f(х) = 3 Вычислите f ׳
Вычислите f ׳  . 1) 3; 2) 0; 3)
. 1) 3; 2) 0; 3)  ; 4)
; 4)  .
.
Часть 2
В1. f(х) =  tg 8x +
tg 8x +  . Найдите f ׳(
. Найдите f ׳( )
)
В3. Найдите значение  , если
, если 
В4. Решите уравнение  , если f(x) =
, если f(x) =  ; g(x) = 2
; g(x) = 2
В5. Решите уравнение f ׳(х) = 0, где f(x) = sin6x + cos6x + 5
В 6. Найдите сумму корней уравнения  , принадлежащих отрезку
, принадлежащих отрезку  , если известно, что
, если известно, что 
gigabaza.ru
Контрольная работа №3.
Вариант 1.
При прямолинейном движении тела путь S(t) (в метрах) изменяется по закону 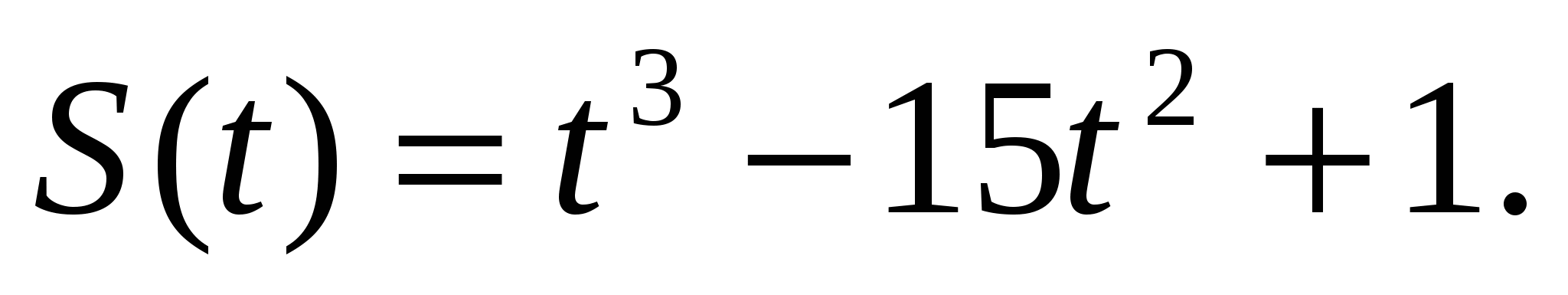
В какой момент времени ускорение тела будет равно нулю.
Исследовать функцию 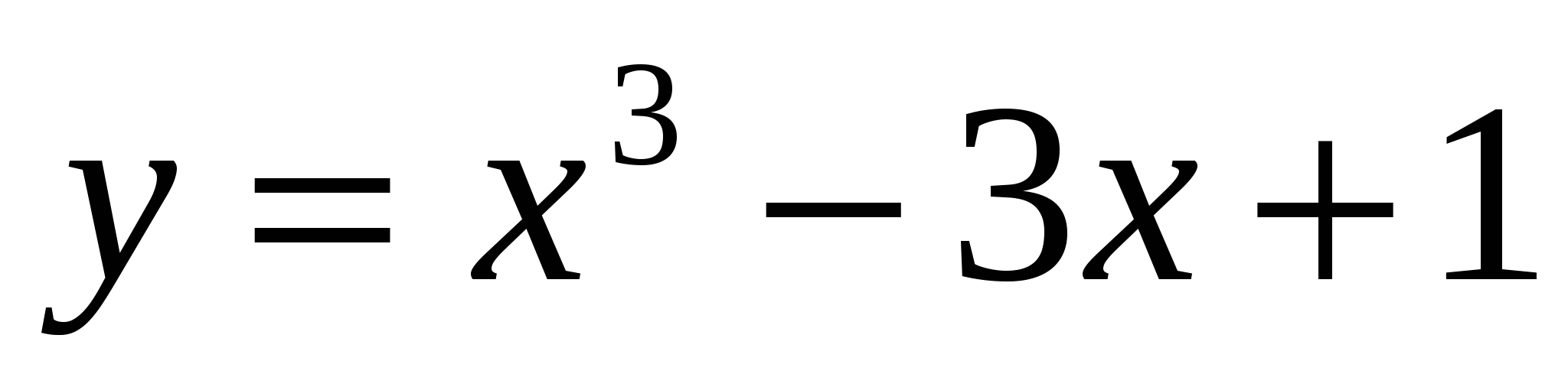 . Найти координаты точек экстремума и промежутки выпуклости функции.
. Найти координаты точек экстремума и промежутки выпуклости функции.
Найти производные функций:
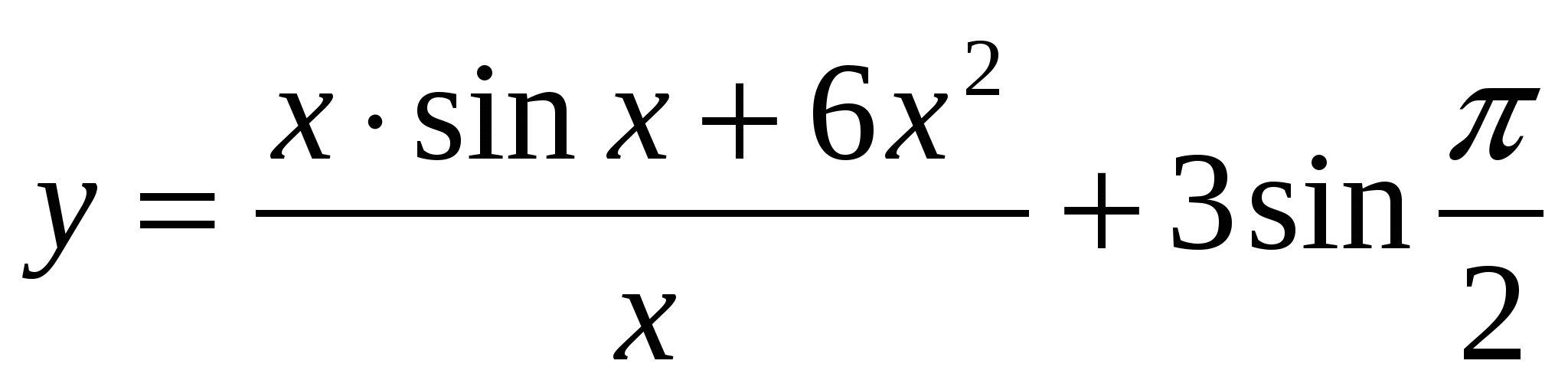
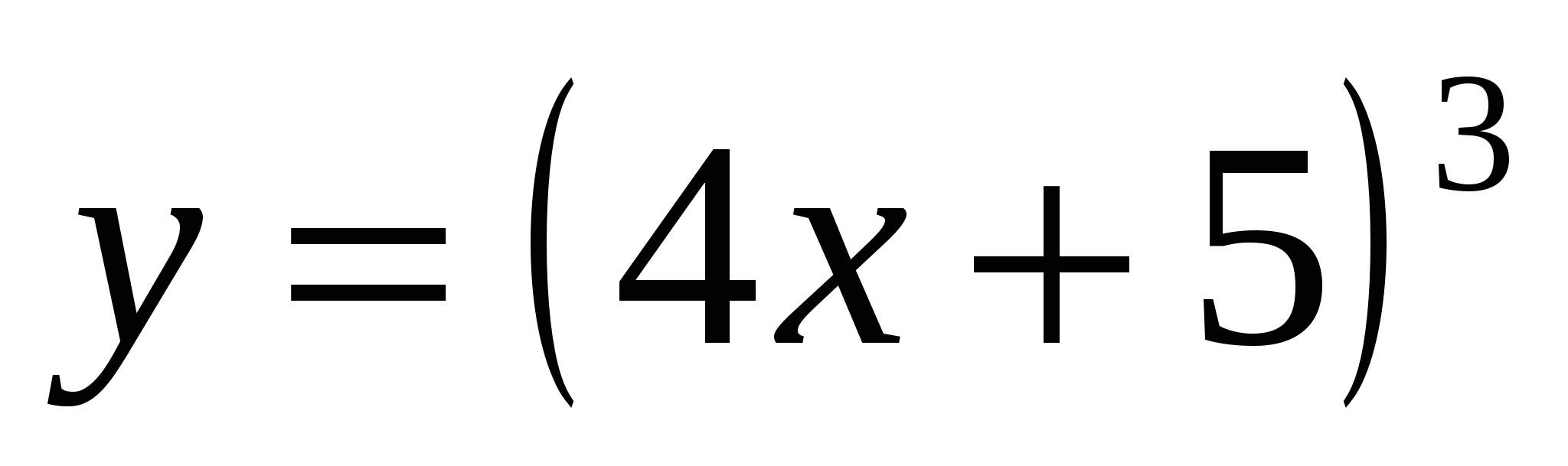
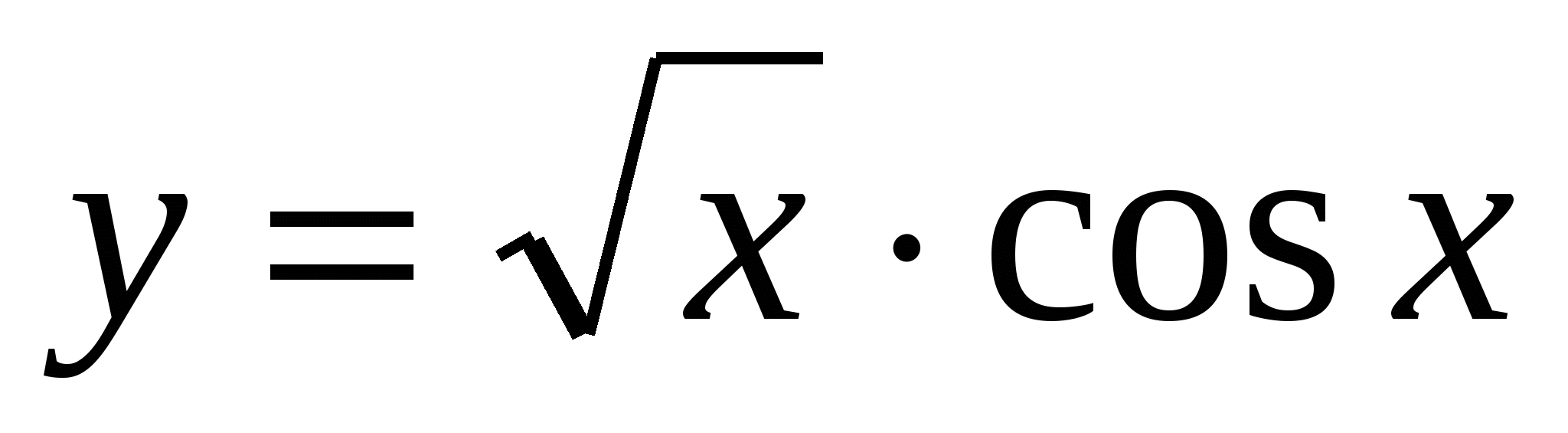
Контрольная работа №3.
Вариант 2.
При движении тела по прямой расстояние S(t) в метрах от начальной точки М изменяется по закону 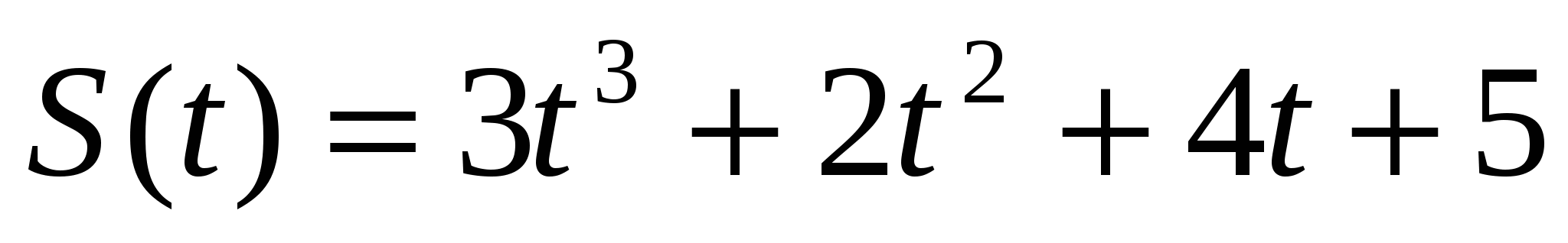 . (t – время в секундах). Через сколько секунд после начала движения мгновенное ускорение тела будет равно 58 м/с2.
. (t – время в секундах). Через сколько секунд после начала движения мгновенное ускорение тела будет равно 58 м/с2.
Исследовать функцию 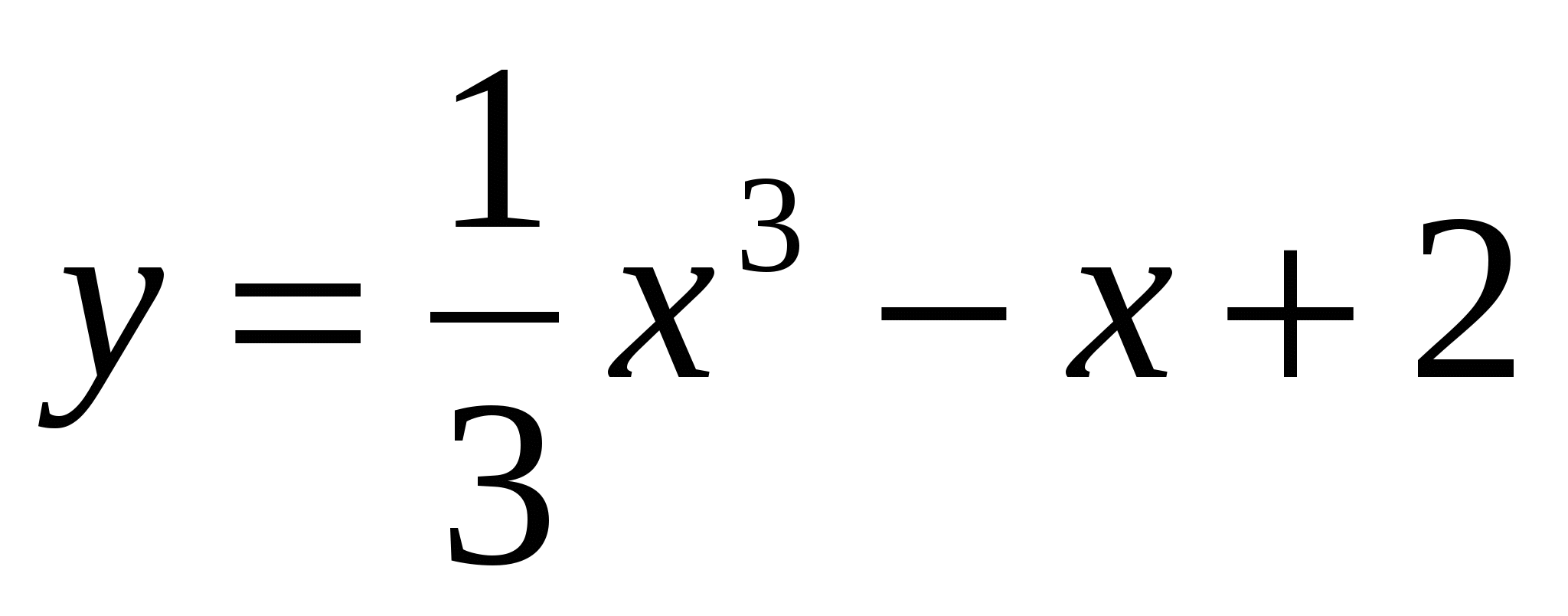 . Найти промежутки монотонности и координаты точек перегиба.
. Найти промежутки монотонности и координаты точек перегиба.
Найти производные функций:
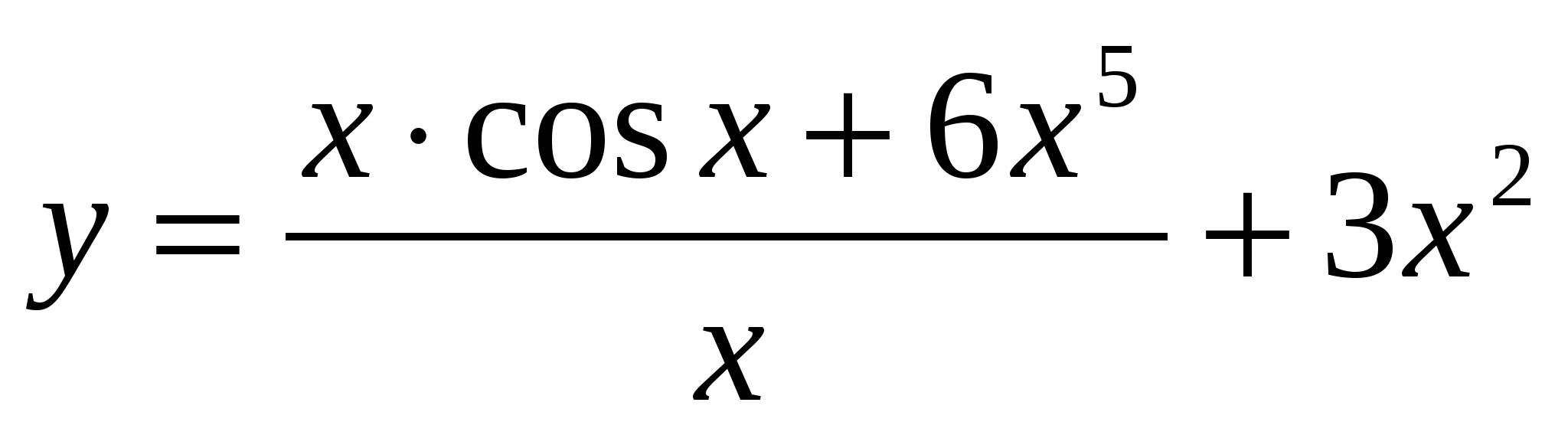
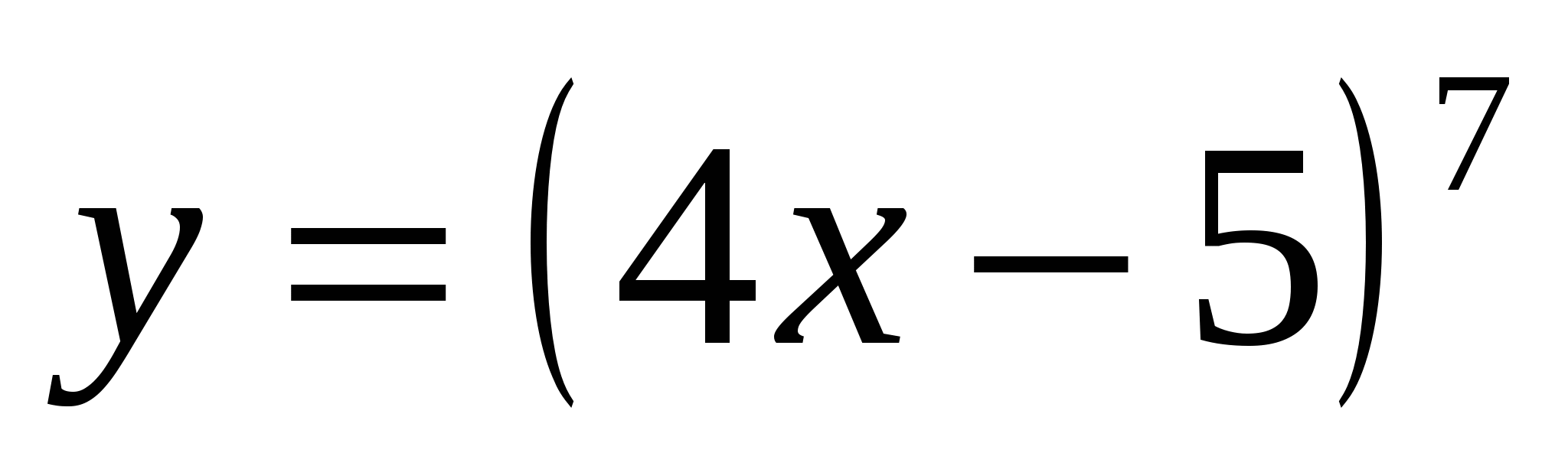
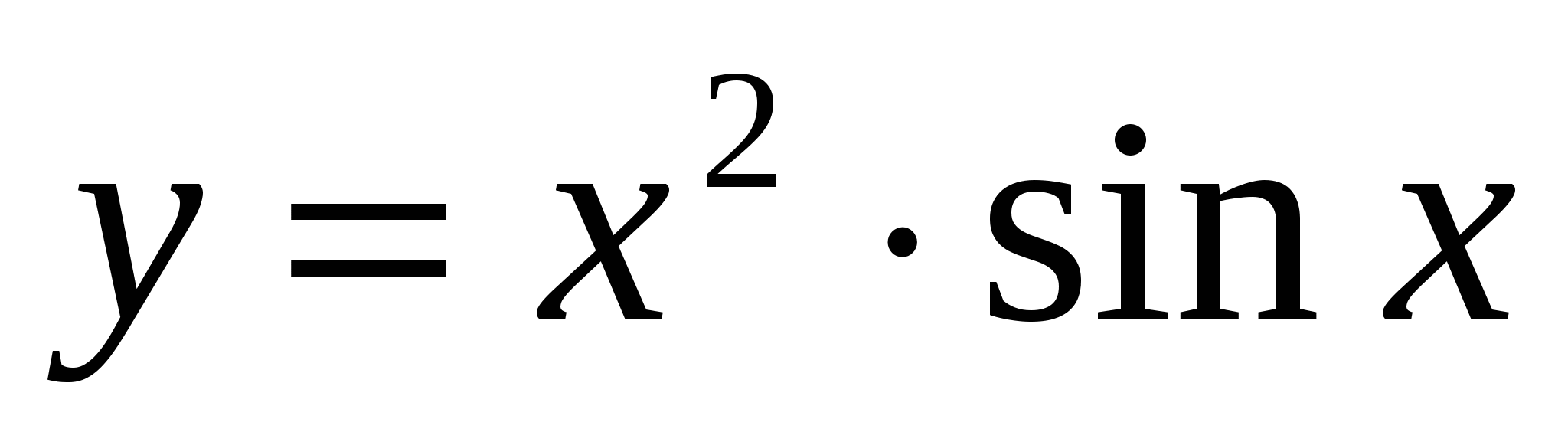
Контрольная работа №3.
Вариант 3.
При прямолинейном движении тела путь S(t) (в метрах) изменяется по закону 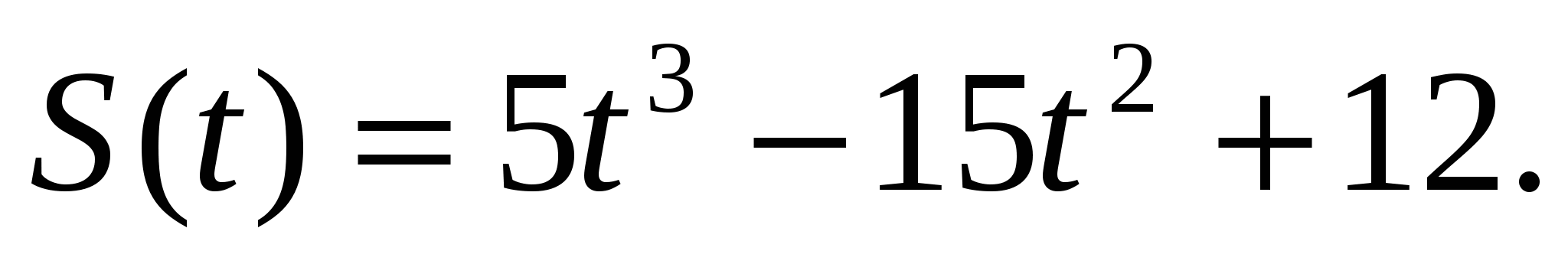 В какой момент времени ускорение тела будет равно нулю?
В какой момент времени ускорение тела будет равно нулю?
Исследовать функцию 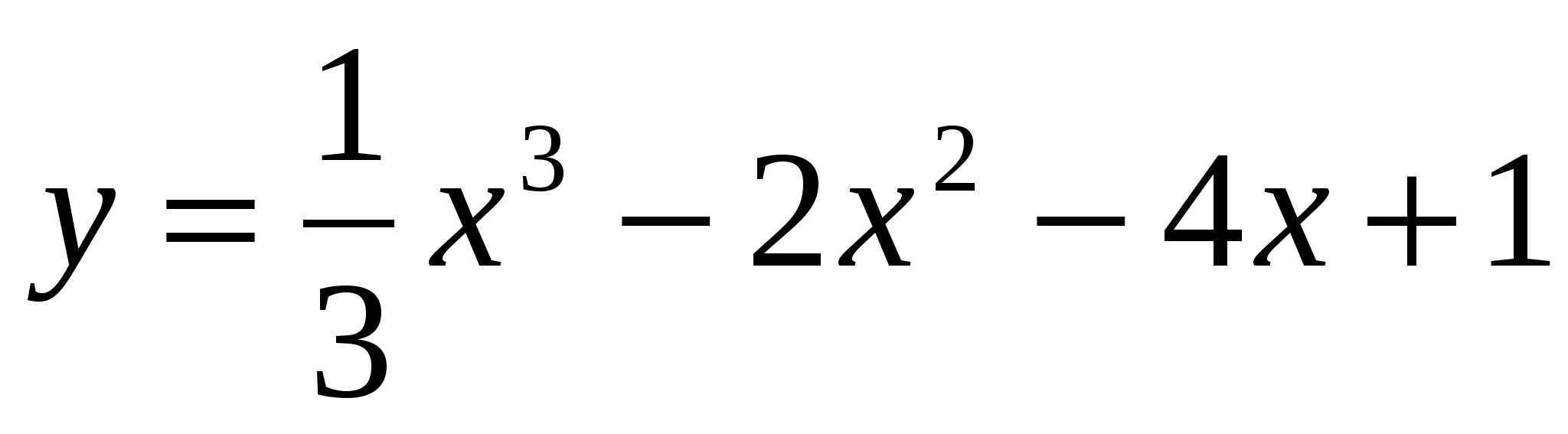 . Найти координаты точек экстремума и промежутки выпуклости функции.
. Найти координаты точек экстремума и промежутки выпуклости функции.
Найти производные функций:
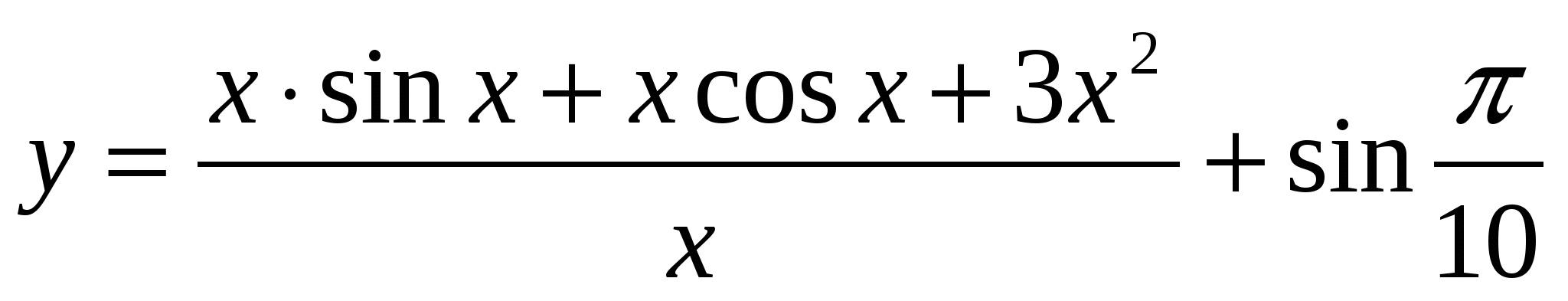
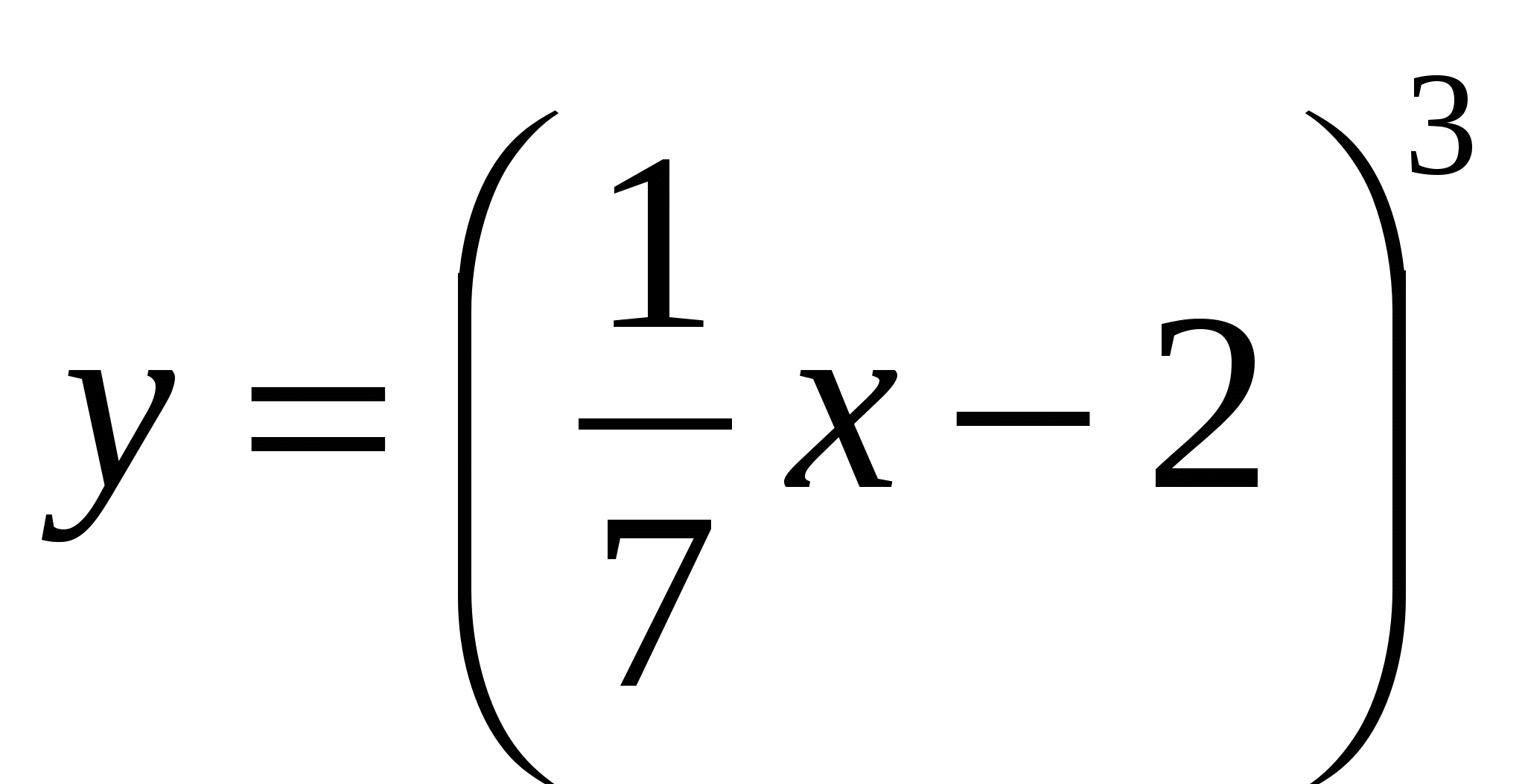
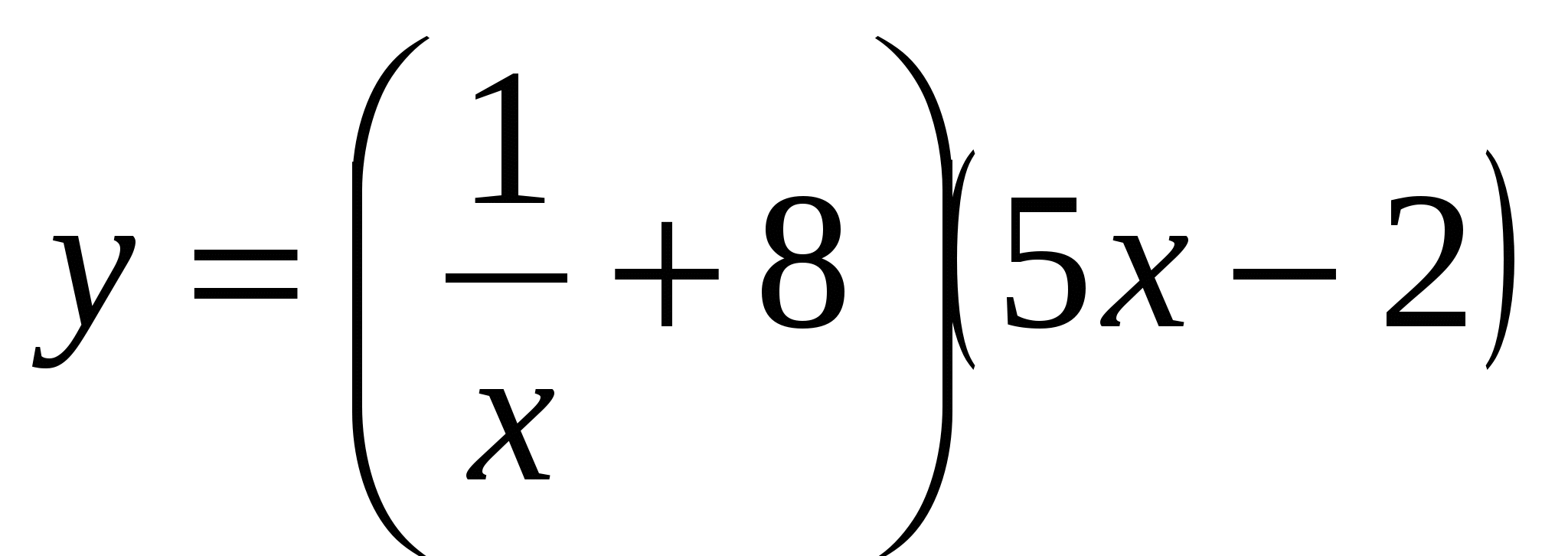
Контрольная работа №3.
Вариант 4.
Тело движется по прямой так, что его скорость  (в метрах в секунду) изменяется по закону
(в метрах в секунду) изменяется по закону 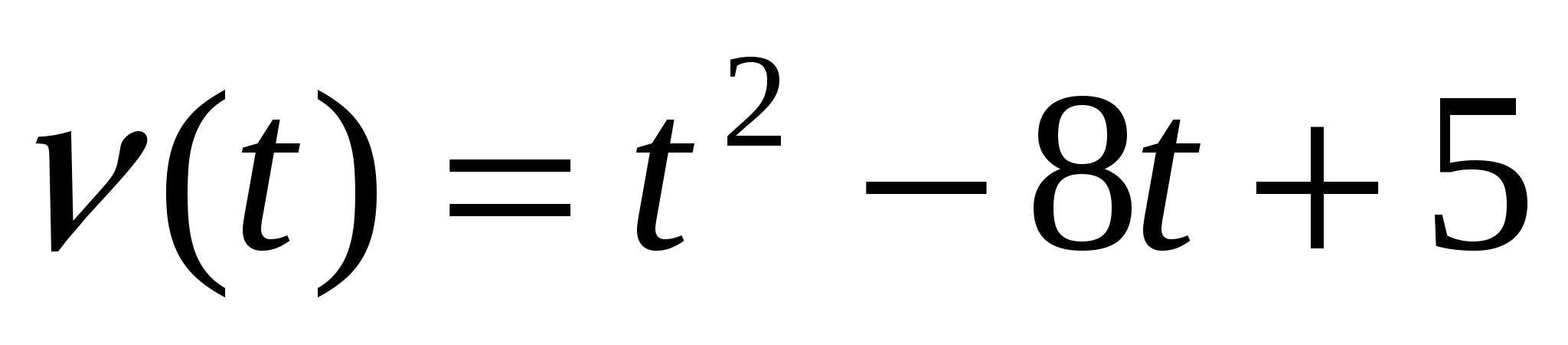 . Какую скорость приобретет тело в момент, когда его ускорение станет равным 12
. Какую скорость приобретет тело в момент, когда его ускорение станет равным 12 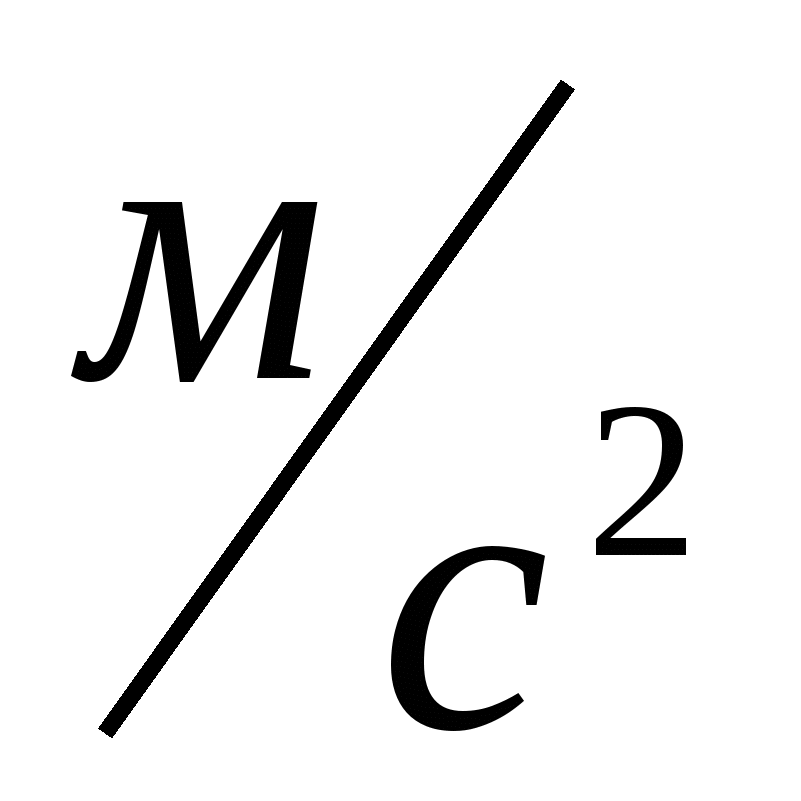
Исследовать функцию 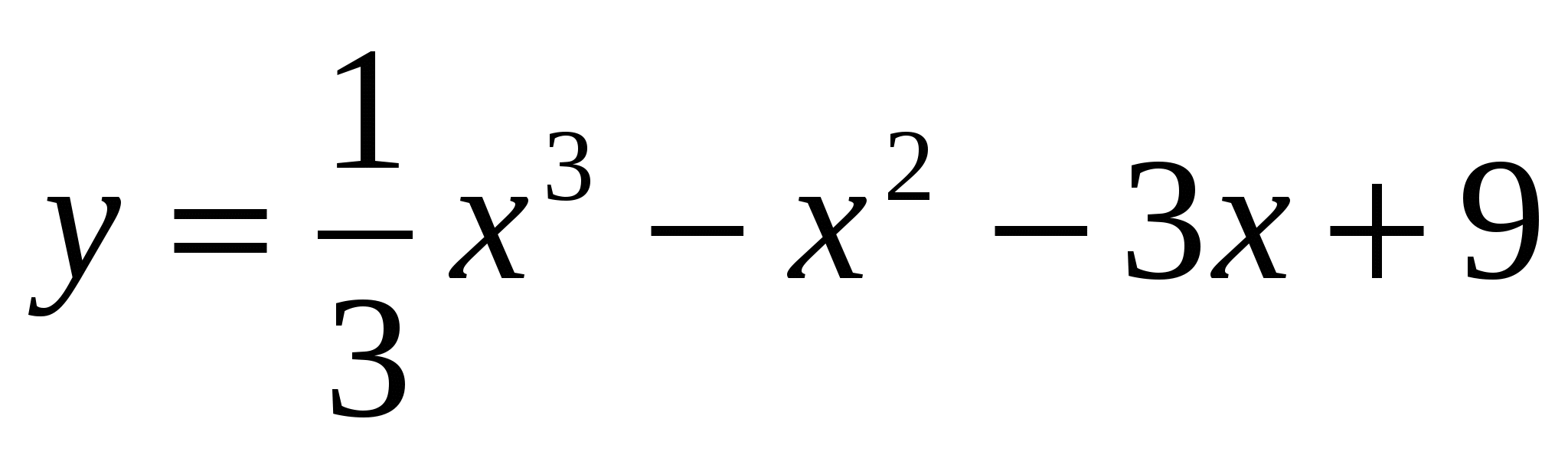 . Найти промежутки монотонности и координаты точек перегиба.
. Найти промежутки монотонности и координаты точек перегиба.
Найти производные функций:

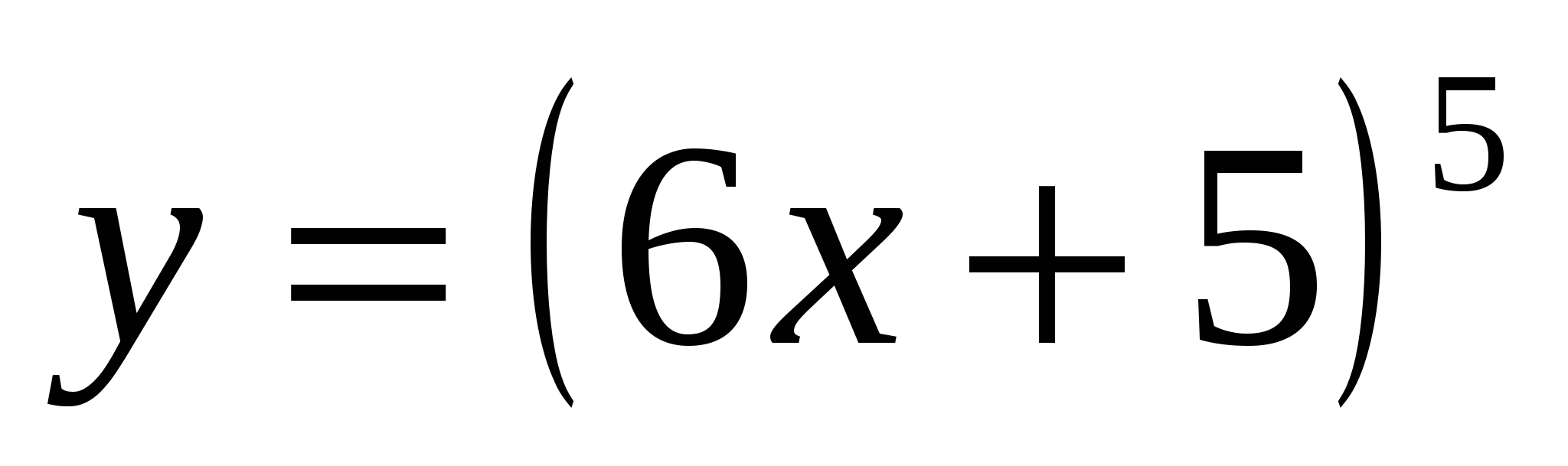
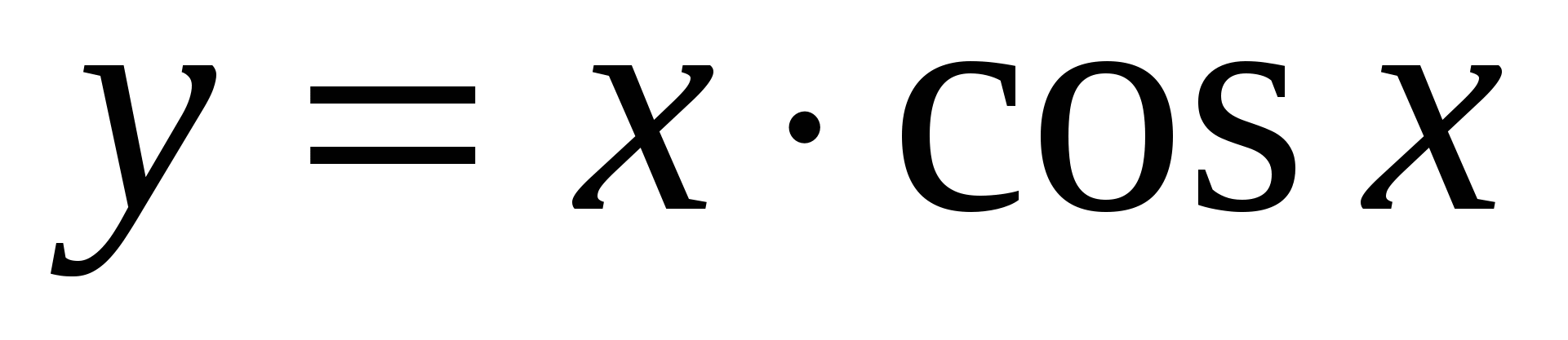
Контрольная работа №3.
Вариант 5.
Тело движется по прямой так, что его скорость  (в метрах в секунду) изменяется по закону
(в метрах в секунду) изменяется по закону 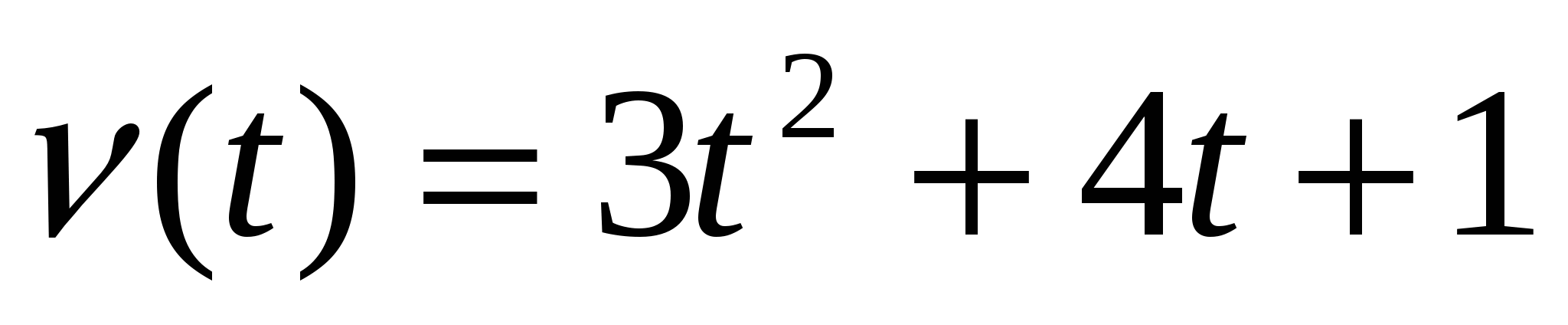 . Какую скорость приобретет тело в момент, когда его ускорение станет равным 10
. Какую скорость приобретет тело в момент, когда его ускорение станет равным 10 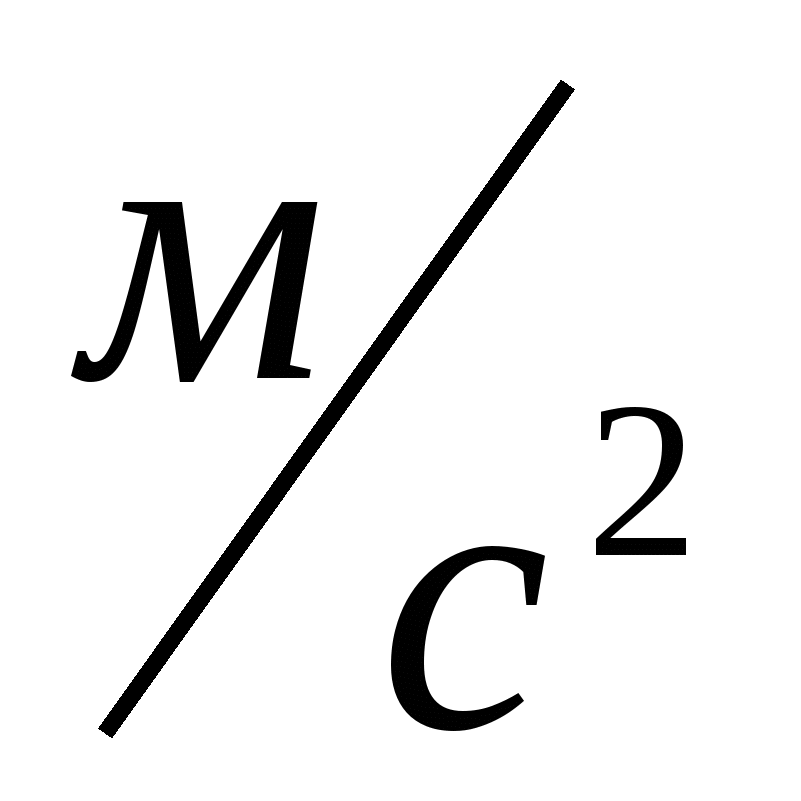
Исследовать функцию 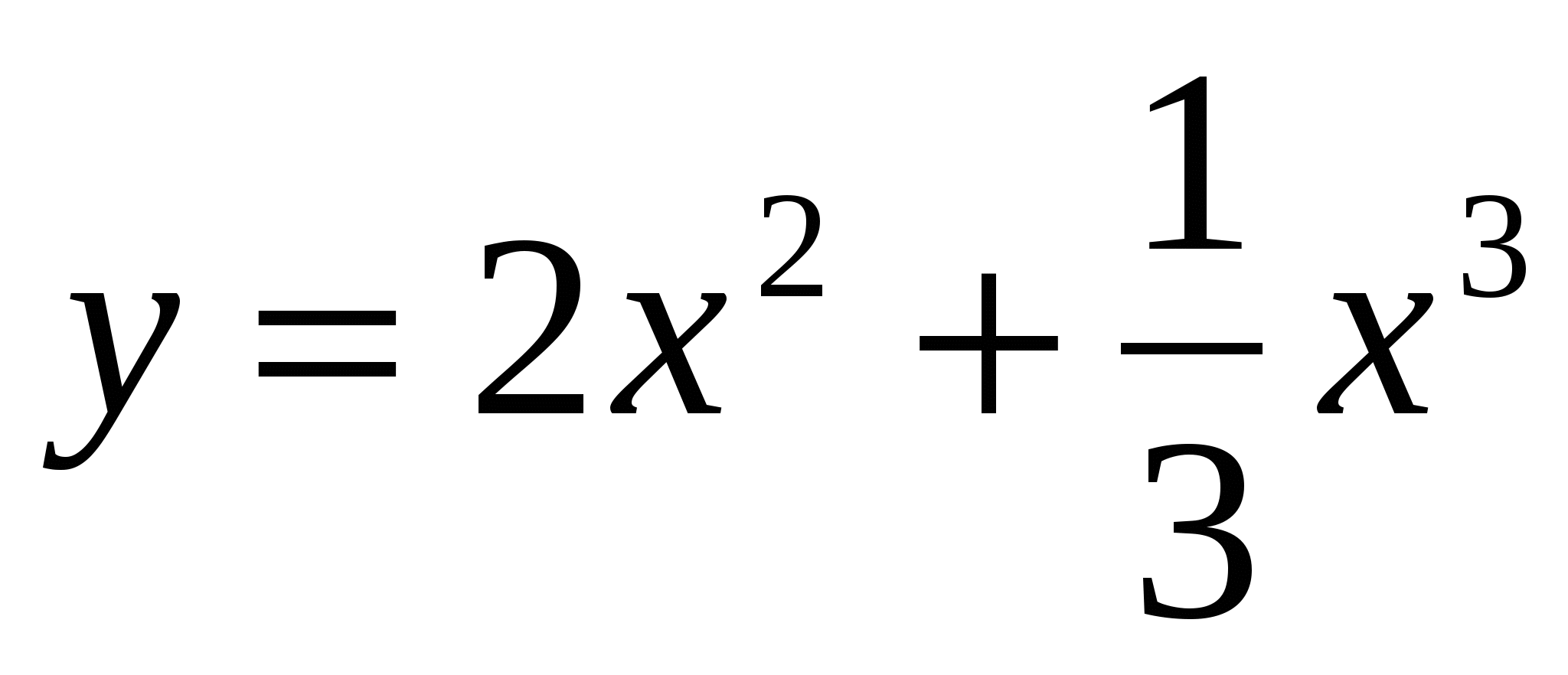 . Найти координаты точек экстремума и промежутки выпуклости функции.
. Найти координаты точек экстремума и промежутки выпуклости функции.
Найти производную функции:
Контрольная работа №3.
Вариант 6.
При прямолинейном движении тела путь S(t) (в метрах) изменяется по закону 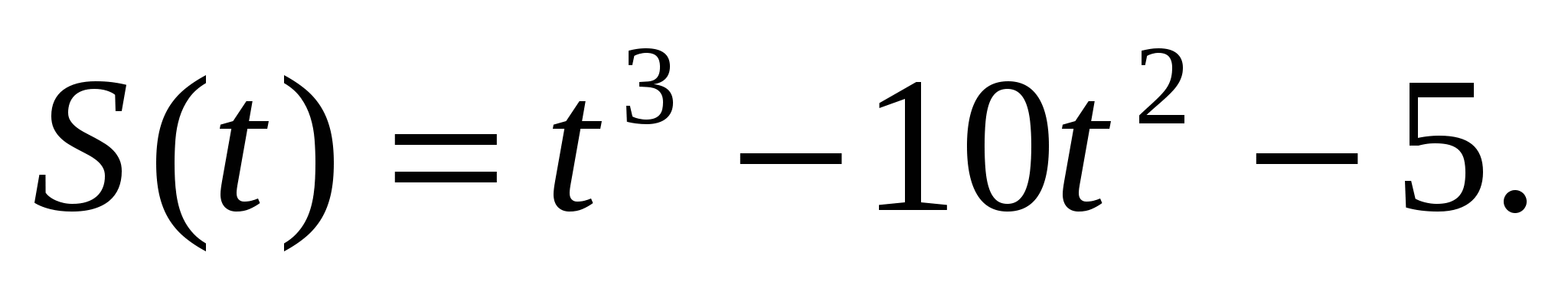 В какой момент времени ускорение тела будет равно нулю.
В какой момент времени ускорение тела будет равно нулю.
Исследовать функцию 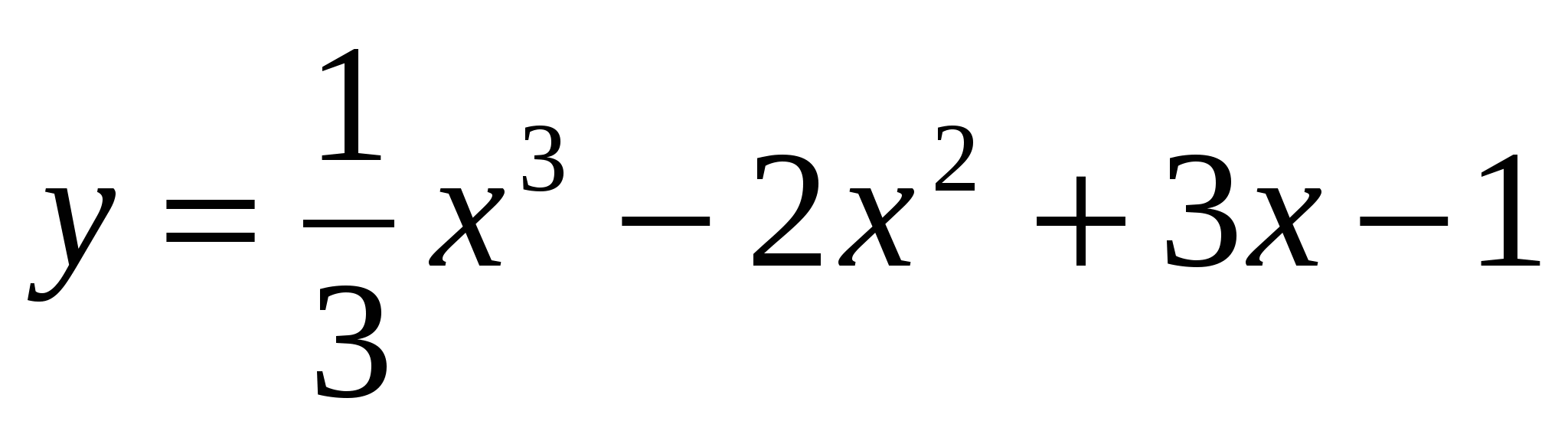 . Найти промежутки монотонности и координаты точек перегиба.
. Найти промежутки монотонности и координаты точек перегиба.
Найти производную функции:
Контрольная работа№3.
Вариант 7.
При прямолинейном движении тела путь S(t) (в метрах) изменяется по закону 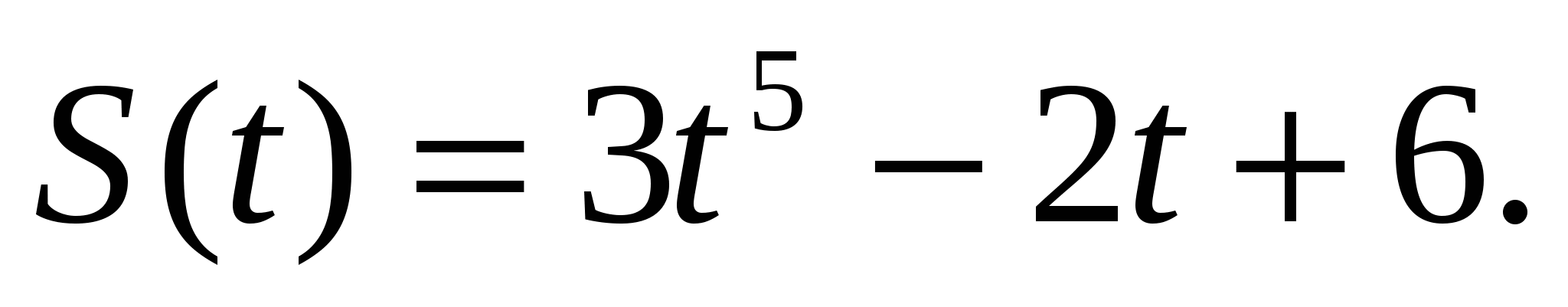 Вычислить ускорение движения в момент t=3 сек.
Вычислить ускорение движения в момент t=3 сек.
Исследовать функцию 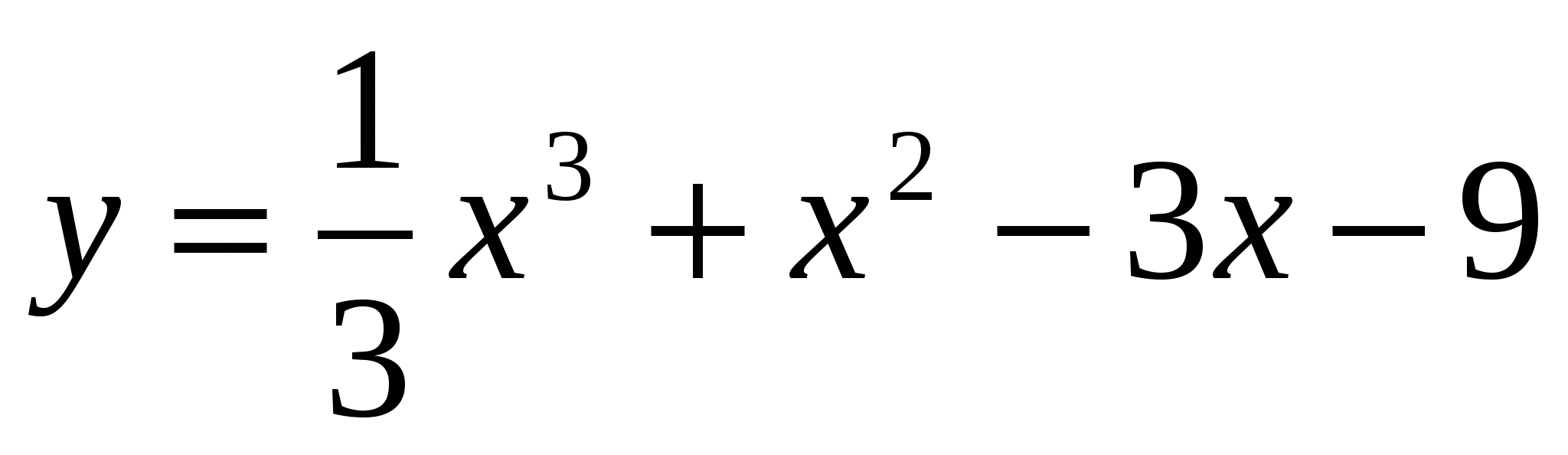 . Найти координаты точек экстремума и промежутки выпуклости функции.
. Найти координаты точек экстремума и промежутки выпуклости функции.
Найти производную функции:
Контрольная работа №3.
Вариант 8.
Две тела движутся по законам 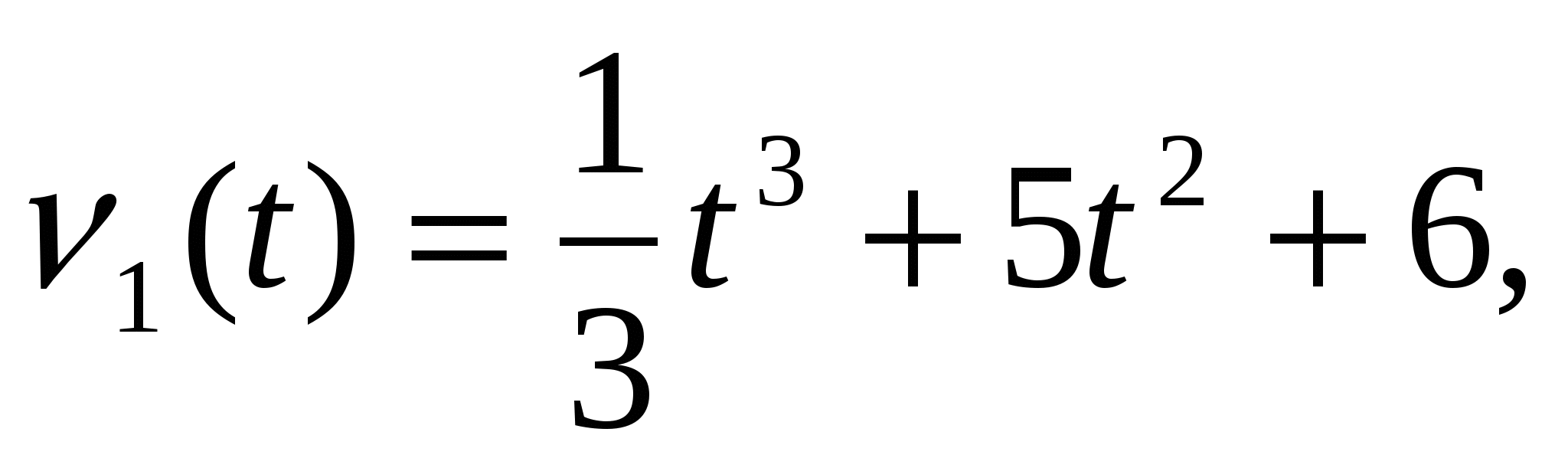
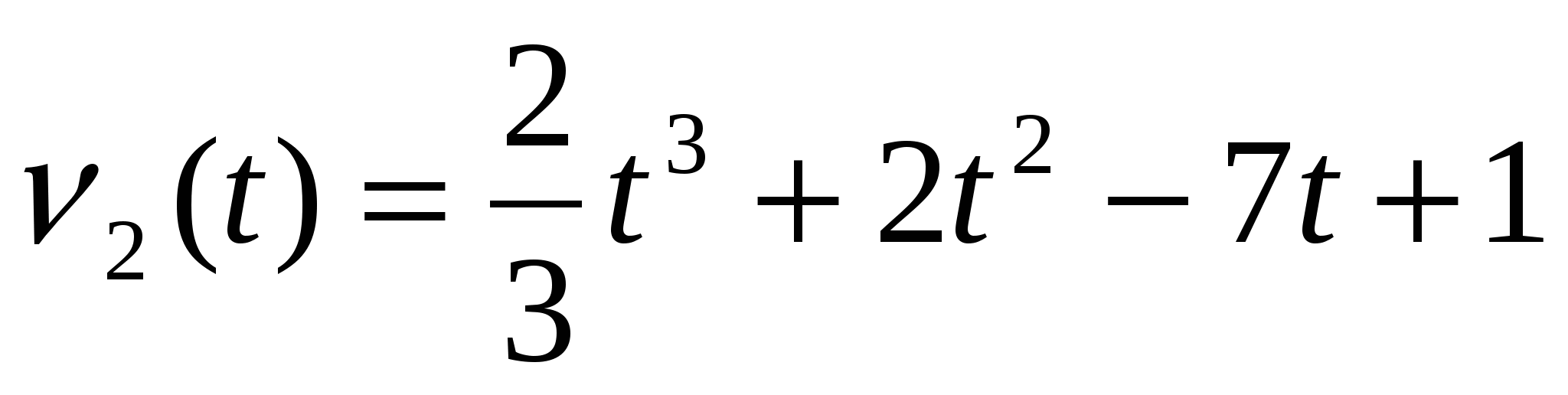 соответственно. В какой момент времени ускорения движения тел будут равны?
соответственно. В какой момент времени ускорения движения тел будут равны?
Исследовать функцию 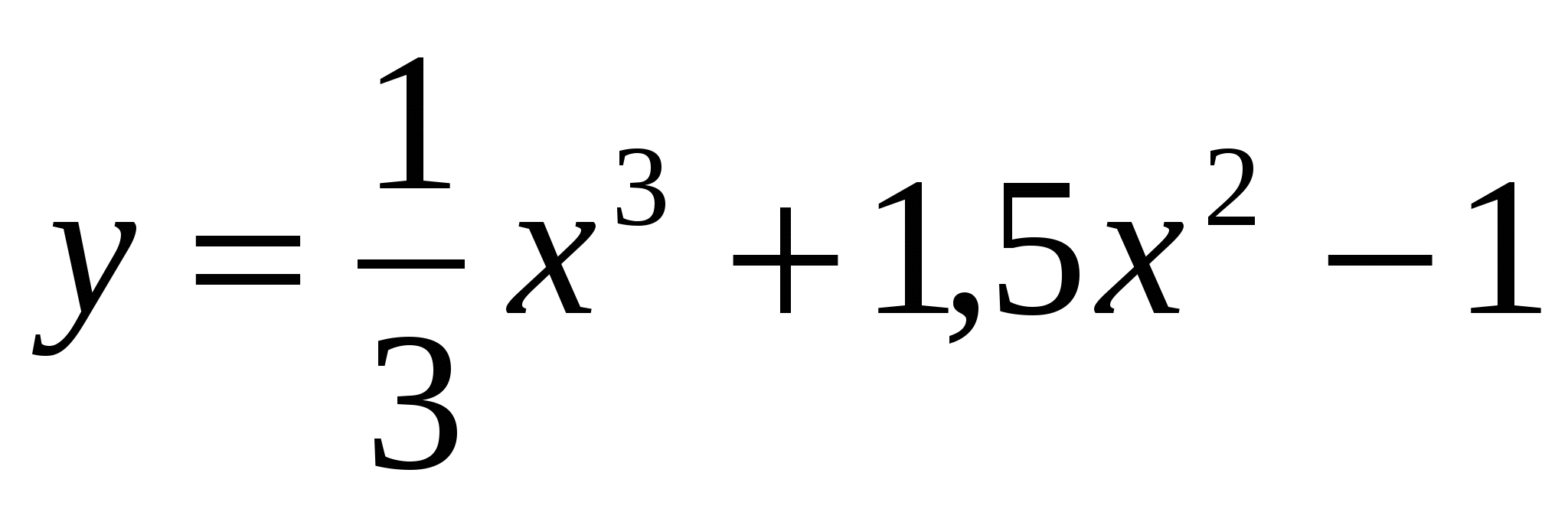 . Найти промежутки монотонности и координаты точек перегиба.
. Найти промежутки монотонности и координаты точек перегиба.
Найти производную функции:
Критерии оценок:
оценка «5» - при выполнении всех заданий
оценка «4» - при выполнении 1 и 3 задания и части 2 задания
оценка «3» - при выполнении 50% работы
Производная - одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств.
Это знакомство позволит:
- понимать суть несложных заданий с производной;
- успешно решать эти самые несложные задания;
- подготовиться к более серьёзным урокам по производной.
Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний!
Для успешного выполнения большинства заданий достаточно знать всего несколько терминов - чтобы понять задание, и всего несколько правил - чтобы его решить. И всё. Это радует.
В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование.
Важно понять, что дифференцирование - это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная.
Дифференцирование - действие над функцией.
Производная - результат этого действия.
Так же, как, например, сумма - результат сложения. Или частное - результат деления.
Зная термины, можно, как минимум, понимать задания. Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную и т.п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.
Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y' или f'(x) или S'(t) и так далее.
Штрих также может обозначать производную конкретной функции, например: (2х+3)', (x3)', (sinx)' и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем.
Нахождение производной - это преобразование функции по определённым правилам. Этих правил, на удивление, совсем немного.
Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. Вот они эти три кита:
1. Таблица производных (формулы дифференцирования).
2. Правила дифференцирования.
3. Производная сложной функции.
Начнём по порядку. В этом уроке рассмотрим таблицу производных.
В мире - бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Этот класс функций называется элементарные функции. Дифференцирование функций "с нуля", т.е. исходя из определения производной и теории пределов - штука достаточно трудоёмкая. Таблица производных самых популярных функций. Слева - элементарная функция, справа - её производная.
Функция y
Производная функции y'
1
C (постоянная величина)
C' = 0
2
x
x' = 1
3
xn (n - любое число)
(xn)' = nxn-1
x2 (n = 2)
(x2)' = 2x
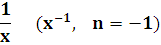
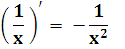
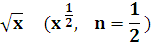
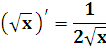
4
sin x
(sin x)' = cosx
cos x
(cos x)' = - sin x
tg x
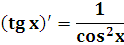
ctg x
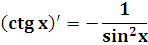
5
arcsin x
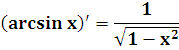
arccos x
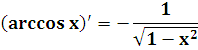
arctg x
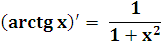
arcctg x
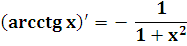
4
ax
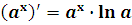
ex
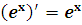
5
loga x
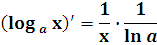
ln x (a = e)
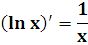
Рекомендую обратить внимание на третью группу функций в этой таблице производных. Производная степенной функции - одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице - вроде и нету...
Рассмотрим несколько примеров:
1. Найти производную функции y = x3
Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат:
(x3)' = 3·x3-1 = 3x2
Вот и все дела.
Ответ: y' = 3x2
2. Найти значение производной функции y = sinx в точке х = 0.
Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию... Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню - это уже новая функция.
По табличке находим синус и соответствующую производную:
y' = (sin x)' = cosx
Подставляем ноль в производную:
y'(0) = cos 0 = 1
Это и будет ответ.
3. Продифференцировать функцию:
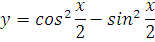
Что, внушает? ) Такой функции в таблице производных и близко нет.
Напомню, что продифференцировать функцию - это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает...
Но если увидеть, что наша функция - это косинус двойного угла, то всё сразу налаживается!
Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. По формуле косинуса двойного угла:
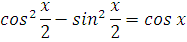
Т.е. наша хитрая функция есть не что иное, как y = cosx. А это - табличная функция. Сразу получаем:
Ответ: y' = - sin x.
Пример для продвинутых выпускников и студентов:
4. Найти производную функции:
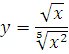
Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями... То вполне можно упростить эту функцию. Вот так:
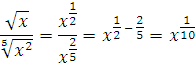
А икс в степени одна десятая - это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем:
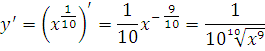
Вот и всё. Это будет ответ.
Надеюсь, что с первым китом дифференцирования - таблицей производных - всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования
Чтобы найти производную от любой функции, надо освоить всего три понятия:
1. Таблица производных.
2. Правила дифференцирования.
3. Производная сложной функции.
Дифференцирование - это операция нахождения производной. Более за этим термином ничего не кроется. Т.е. выражения "найти производную функции" и "продифференцировать функцию" - это одно и то же.
Выражение "правила дифференцирования" относится к нахождению производной от арифметических операций.
Вот они, правила дифференцирования:
Действие
Производная
1
Производная суммы
(U+V)' = U'+V'
2
Производная разности
(U-V)' = U'- V'
3
Производная произведения
(U·V)' = U'·V +U·V'
4
Производная от произведения на постоянное число
(C·V)' = CV'
5
Производная частного
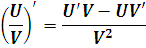
Под обозначениями U и V подразумеваются какие-то (совершенно любые!) функции U(x) и V(x).
Рассмотрим несколько примеров. Сначала - самые простые.
Найти производную функции y=sinx - x2
Здесь мы имеем разность двух элементарных функций. Применяем правило 2. Будем считать, что sinx - это функция U, а x2 - функция V. Имеем полное право написать:
y' = (sinx - x2)' = (sinx)'- (x2)'
Осталось найти производные от синуса и квадрата икса. Для этого существует таблица производных. Просто ищем в таблице нужные нам функции (sinx и x2), смотрим, какие у них производные и записываем ответ:
y' = (sinx)' - (x2)' = cosx - 2x
Правило 1 дифференцирования суммы работает точно так же.
А если у нас несколько слагаемых? Разбиваем функцию на слагаемые и ищем производную от каждого слагаемого независимо от остальных. Например:
Найти производную функции y=sinx - x2+cosx - x +3
Смело пишем:
y' = (sinx)' - (x2)' + (cosx)' - (x)' + (3)'
Опять находим в таблице производные синуса, квадрата икса, косинуса, чистого икса и тройки. Тройка - постоянная величина, в таблице обозначена буквой "С". Производная любой постоянной величины равна нулю. Можно сразу записать ответ:
y' = cosx - 2x - sinx - 1
Как видим, первые два правила дифференцирования просты и безотказны.)
Переходим к примерам на правило 3. Производная произведения чуть посложнее. Главное здесь - увидеть в исходной функции, что взять за U, а что - за V. Например:
Найти производную функции y=sinx · cosx.
Здесь всё очевидно. sinx - это U, cosx - это V. Пишем прямо по правилу:
y' = (sinx)' ·cosx + sinx · (cosx)' = cosx·cosx - sinx·sinx = cos2x - sin2x
Производную мы уже нашли. Обычно, если упрощение простое и очевидное, его нужно сделать. В нашем случае получилась формула косинуса двойного угла. Можно написать ответ:
y' = cos2x - sin2x = cos2x
Рассмотрим следствие из правила 3, т.е. правило 4. Эта формула получается прямо из производной для умножения функций. Если y=CU, где С - какое-то постоянное число, а U - любая функция, то:
y' =(C·U)' = C'·U + C·U' = 0·U + C·U' = C·U'
Словами говорят, что постоянную можно вынести из под знака производной.
Например, по этому правилу все производные от выражений, типа 5х, 3,4х, -2х и так далее, сразу же превращаются в постоянные числа:
(5х)' = 5·(x)' = 5·1 = 5
(-2х)' = -2·(x)' = -2·1 = -2
Пример посложнее:
Найти производную функции y=5sinx - 3x2.
Если расписывать подробно, получится вот так:
y' = (5sinx - 3x2)' = (5sinx)'- (3x2)'
В скобках - произведения функций (постоянное число - тоже функция!). К первой и второй скобкам надо бы использовать правило 3, но сокращённый вариант (правило 4) - куда приятнее! Просто выносим числа за знак производной:
y' = (5sinx)'- (3x2)' = 5(sinx)'- 3(x2)'
Далее находим в таблице значения производных и результат просто умножаем на эти числа:
y' = 5(sinx)'- 3(x2)' = 5cosx - 3·2x = 5cosx - 6x
Переходим к производной частного.
Правило 5.
Пример:
Найти производную функции
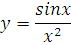
Расписываю по правилу 5. Подробно, со всеми скобочками и штрихами:
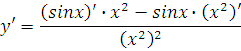
Берём производные (они табличные) в правой части:
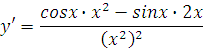
Приводим к приличному виду:
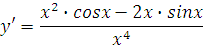
Если требуется дальнейшее упрощение, можно в числителе вынести икс за скобки и сократить с иксом в знаменателе. Получим ответ:
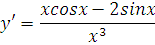
Вот мы и рассмотрели, как находить производные функций с помощью правил дифференцирования.
Разумеется, сумма, разность, частное и произведение могут комбинироваться в самых разных сочетаниях. Например:
Продифференцировать функцию:
y=(x2+2) · (x3-4)
Здесь под функцией U скрывается выражение (x2+2), а под функцией V - выражение (x3-4). Расписываем прямо по правилу:
y' = (x2+2)' · (x3-4) + (x2+2) · (x3-4)'
Теперь нужно довести дело до конца, т.е. вычислить производные от скобок. В первых скобках будет сумма функций:
(x2+2)' = (x2)' + 2' = 2x
Во вторых - разность функций:
(x3-4)' = (x3)' - 4' = 2x
Можно записать ответ:
y' = 2х · (x3-4) + (x2+2) · 3x2
Упрощаем, т.е. перемножаем и приводим подобные:
y' = 2x4-8х + 3x4+6x2 = 5x4+6x2-8х
Вот и всё. Достаточно производную от сложной функции расписать подробно, со всеми скобочками и штрихами, по подходящему правилу. Затем последовательно брать производные от скобок. Всё и получится.
Всё просто, но... могут случиться и сюрпризы. Попадётся, например, вот такое задание:
Найти производную функции y=x3· sinx · cosx.
Здесь у нас умножаются три функции. Нет подходящего правила. Мы вправе превратить умножение трёх функций в произведение двух, чтобы правило 3 в дело запустить. Просто возьмём за U и V то, что нам нужно. Например, пусть
U=x3· sinx
Тогда
V = cosx
Выделим эти U и V скобочками в исходной функции:
y=(x3· sinx) · (cosx).
Скобки никак не меняют исходную функцию, можно брать производную по правилу 3:
y'=((x3· sinx) · (cosx))'= (x3· sinx)'· (cosx)+(x3· sinx) · (cosx)'
Теперь видно, что в скобках (x3· sinx)' у нас опять произведение функций. Но уже двух. Можно расписать производную этих скобок отдельно. Теперь за U у нас пойдёт x3, а за V - sinx:
(x3· sinx)' = (x3)' · sinx +x3· (sinx)'= 3x2· sinx + x3· cosx
Вот практически и всё. Возвращаемся к исходной функции и вставляем наш результат промежуточного дифференцирования на своё место. Сразу же и производную от косинуса во втором слагаемом возьмём:
y'= (3x2· sinx + x3· cosx) · cosx + (x3· sinx) · (-sinx)
Производную нашли. Если требуется, перемножаем скобки и записываем ответ:
y'= 3x2· sinx · cosx + x3· cos2x - x3· sin2x
Замечу, что в этом примере U и V можно было выбрать по другому. За U взять x3, а за V - sinx · cosx. Это без разницы. Результат будет тот же самый.
В примерах постоянно приходится дифференцировать дроби. Но, если в знаменателе дроби - постоянное число, правила 5 можно избежать! Действия с дробями гласят, что деление можно заменить на умножение. Вот так:
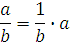
Это даёт возможность вместо правила 5 использовать куда более простое и удобное правило 4. Например:
Найти производную функции:
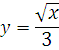
В процессе дифференцирования слегка преобразуем исходную функцию. Превратим деление в умножение:
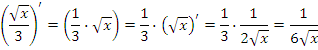
Кстати, преобразование исходной функции перед дифференцированием вполне возможно и, иногда, очень помогает. Скажем, производная от функции:
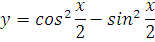
берётся достаточно хлопотно. Таблицы производных и правил дифференцирования здесь недостаточно. Это сложная функция. Но если её преобразовать до дифференцирования, применив формулу
cos2α, пример решается в уме.
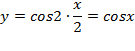
Практические советы:
1. Перед дифференцированием смотрим, нельзя ли упростить исходную функцию.
2. В замороченных примерах расписываем решение подробно, со всеми скобочками и штрихами.
3. При дифференцировании дробей с постоянным числом в знаменателе, превращаем деление в умножение и пользуемся правилом 4.
infourok.ru
Контрольная работа №3 по теме : « Производная»
Вариант №1

 определена на промежутке
определена на промежутке  . Используя изображенный на рисунке график производной
. Используя изображенный на рисунке график производной  , определите количество касательных к графику функции
, определите количество касательных к графику функции  , которые составляют угол
, которые составляют угол  с положительным направлением оси Ox.
с положительным направлением оси Ox. А1. Найдите производную функции 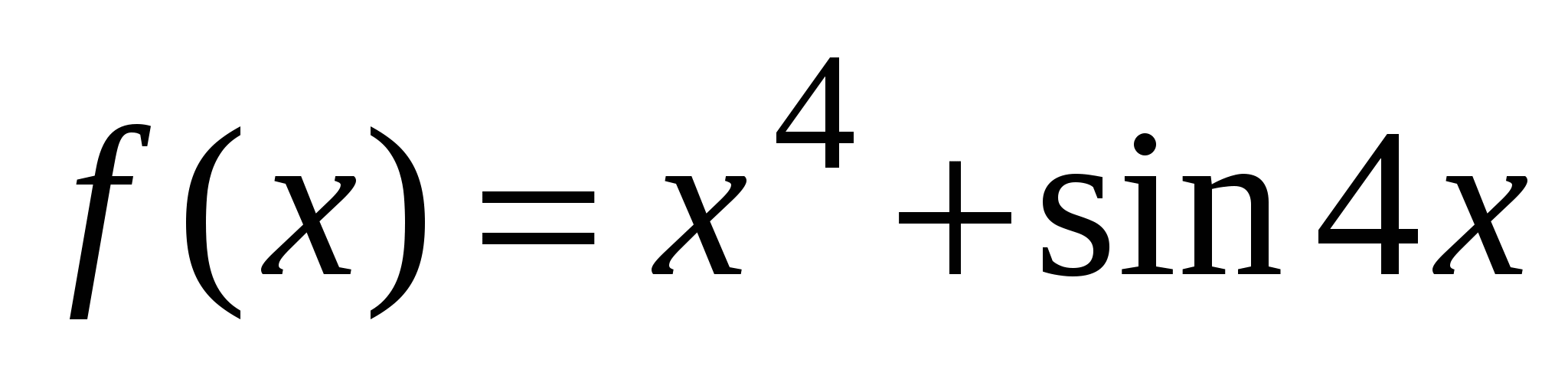 .
.
1) 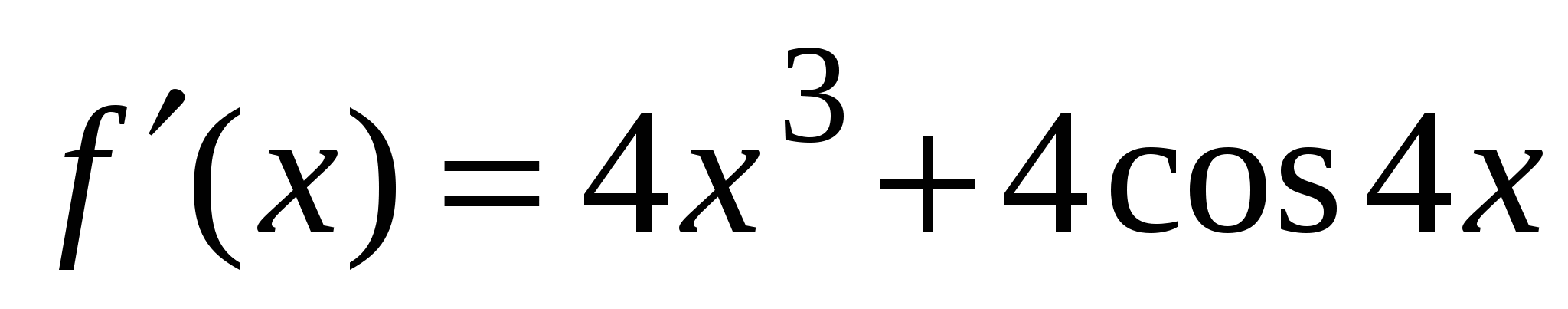
3) 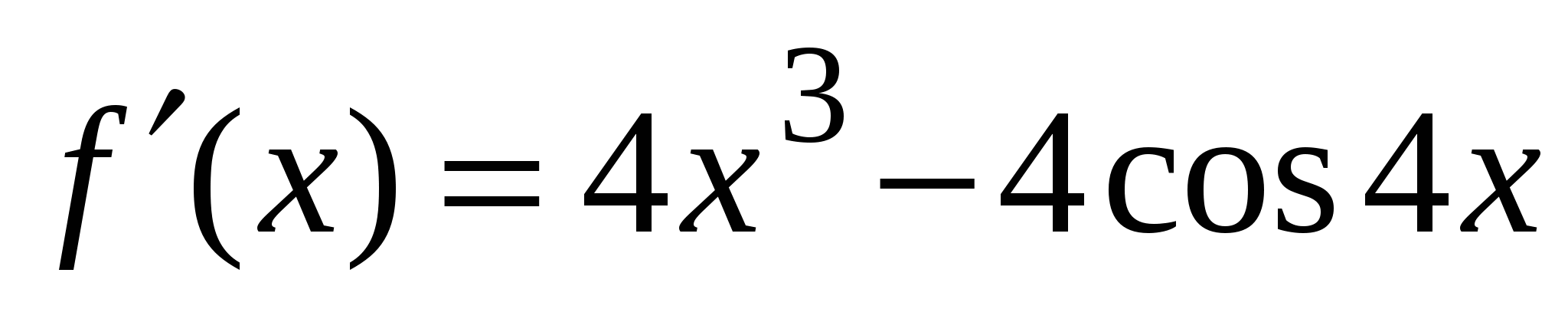
2) 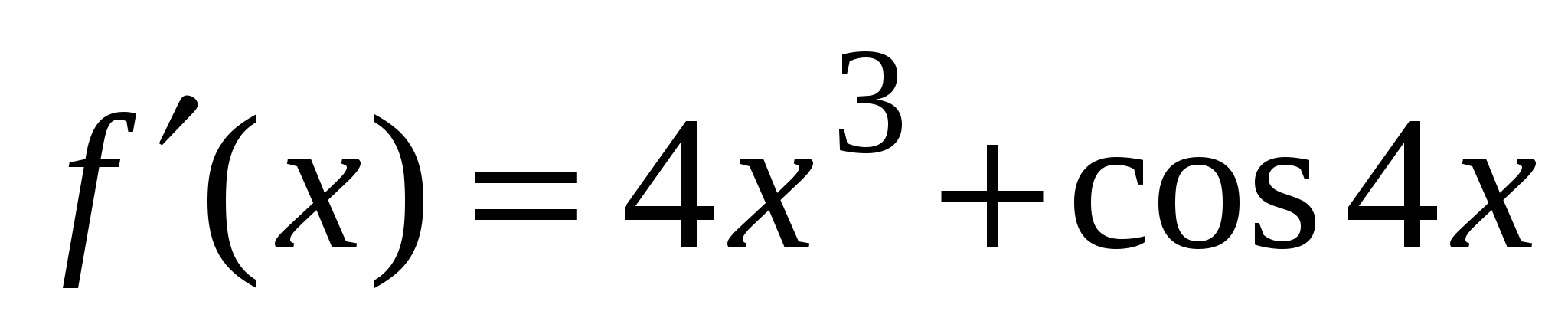
4) 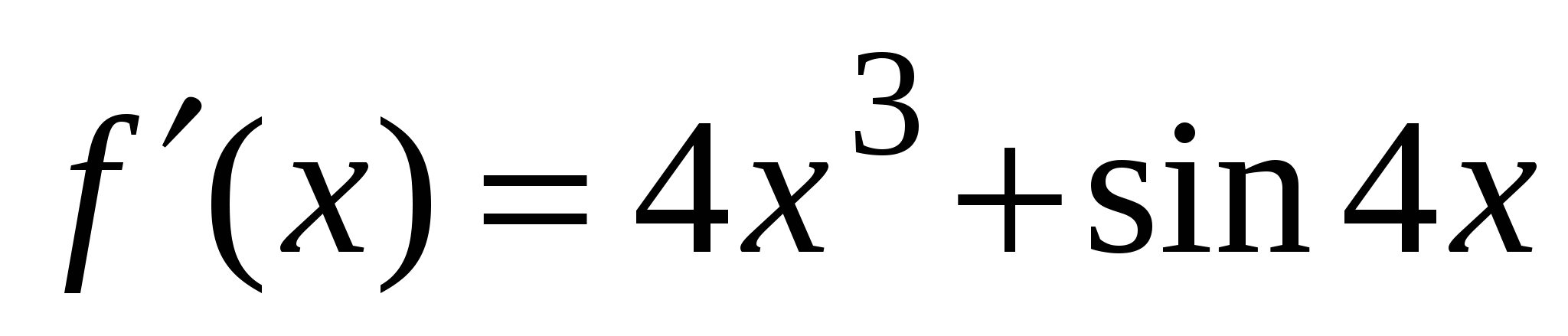
А2. Найдите производную функции 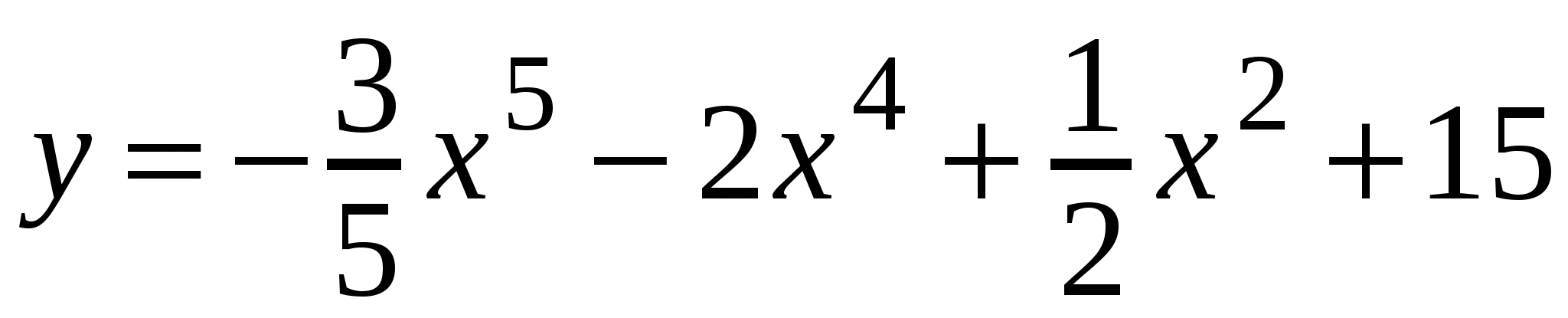 .
.
1)
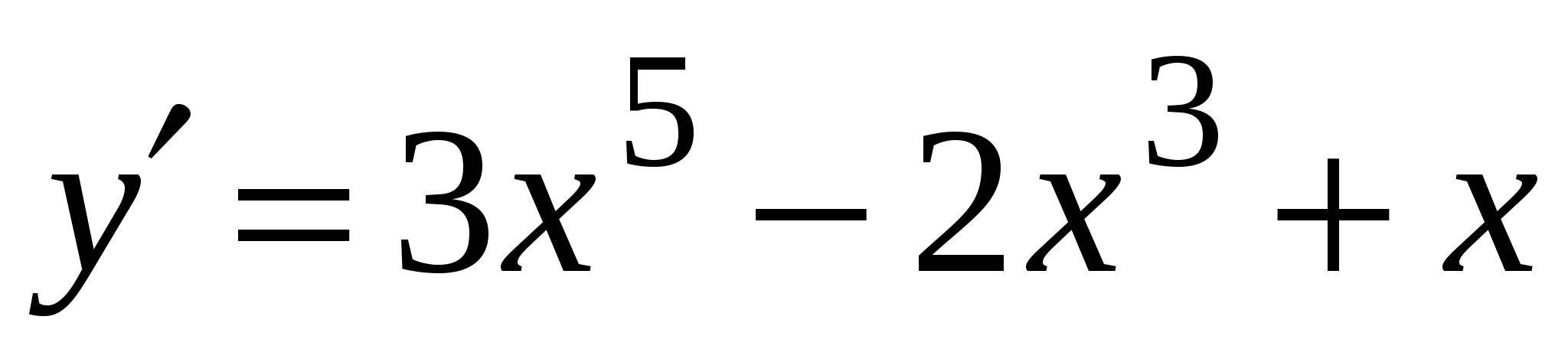
3)
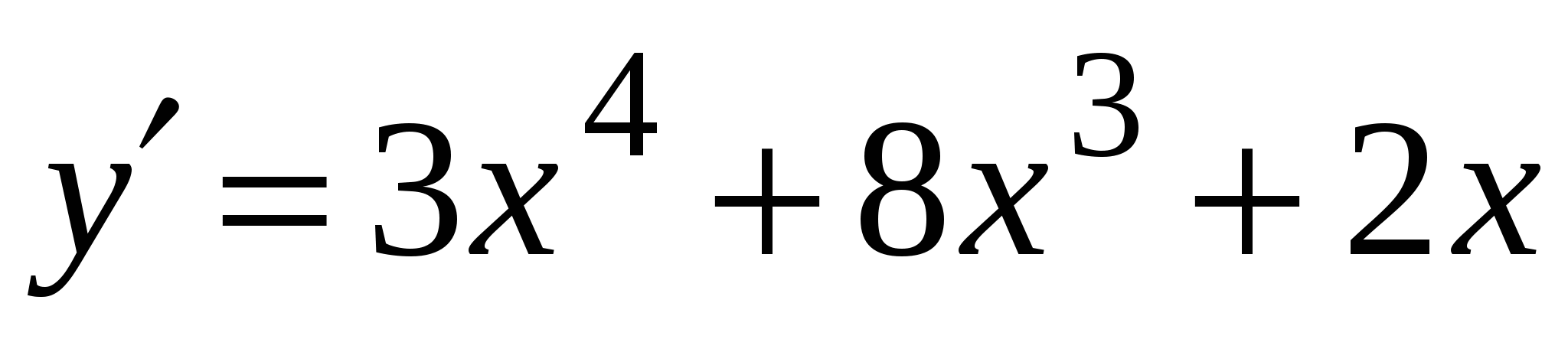
2)
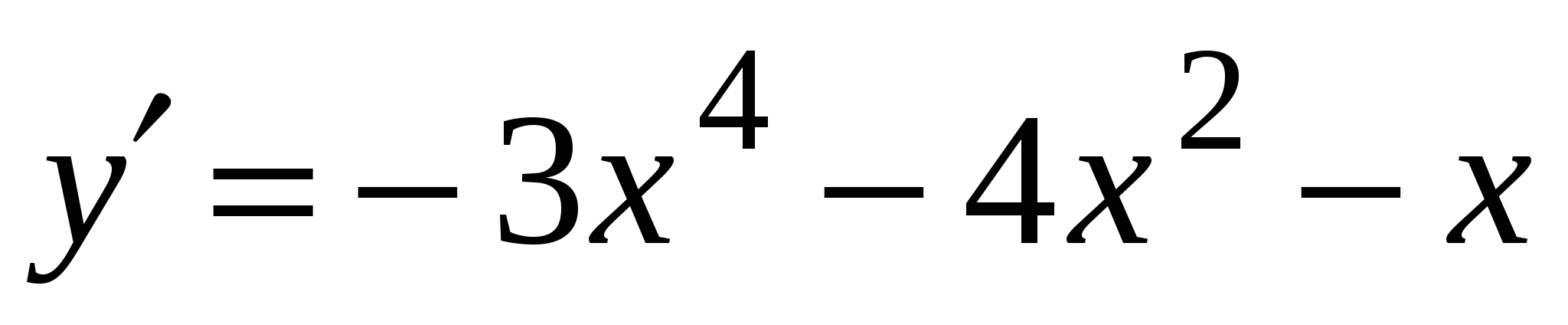
4)
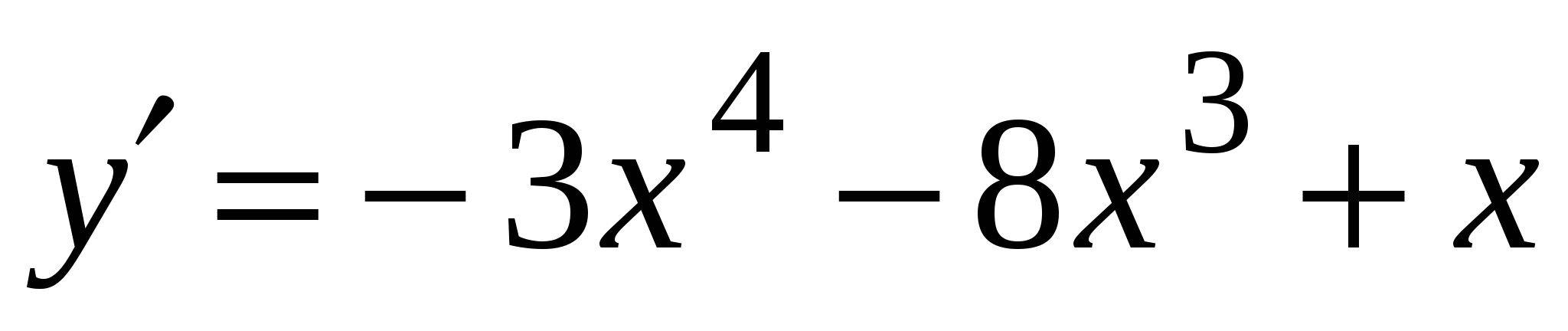
А3. Найдите производную функции 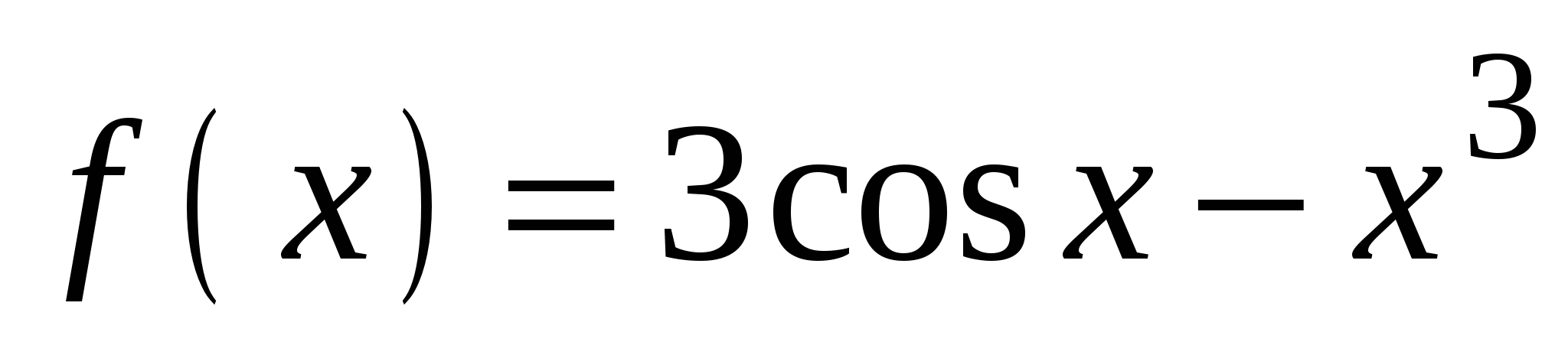 .
.
1)
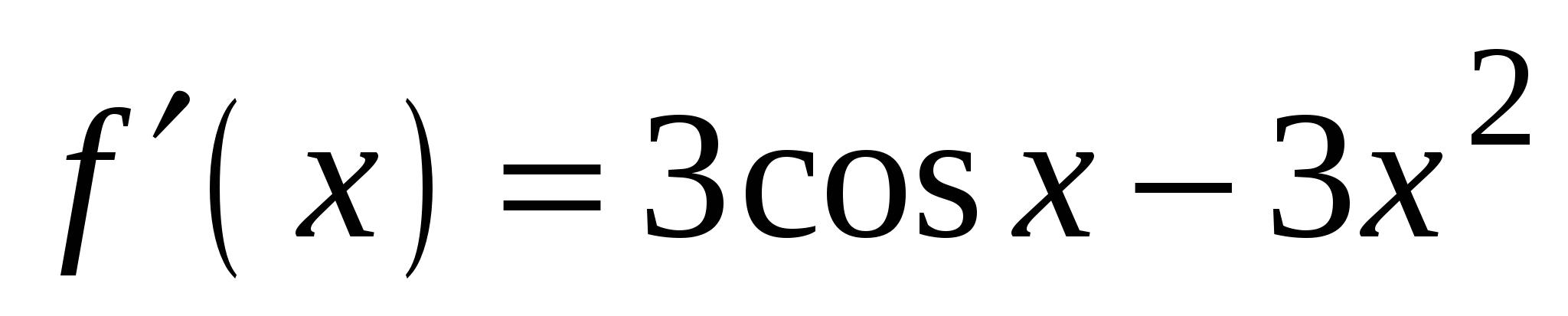
3)
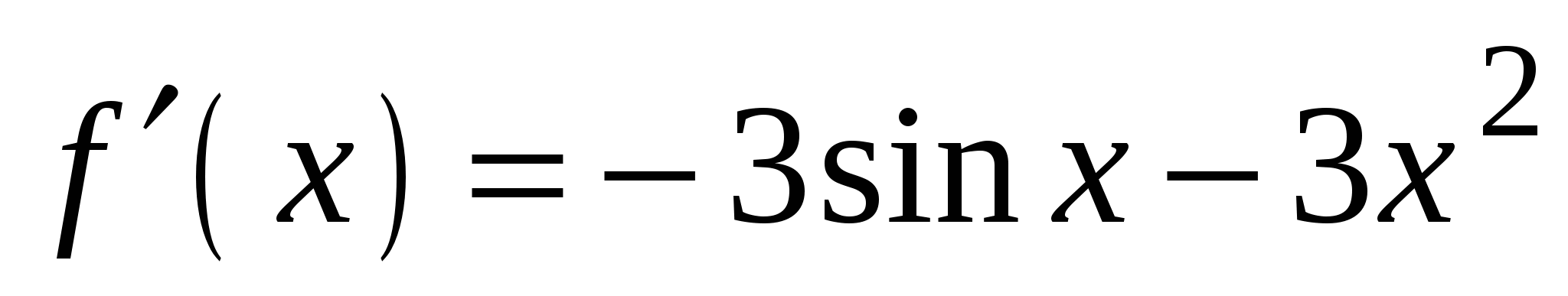
2)
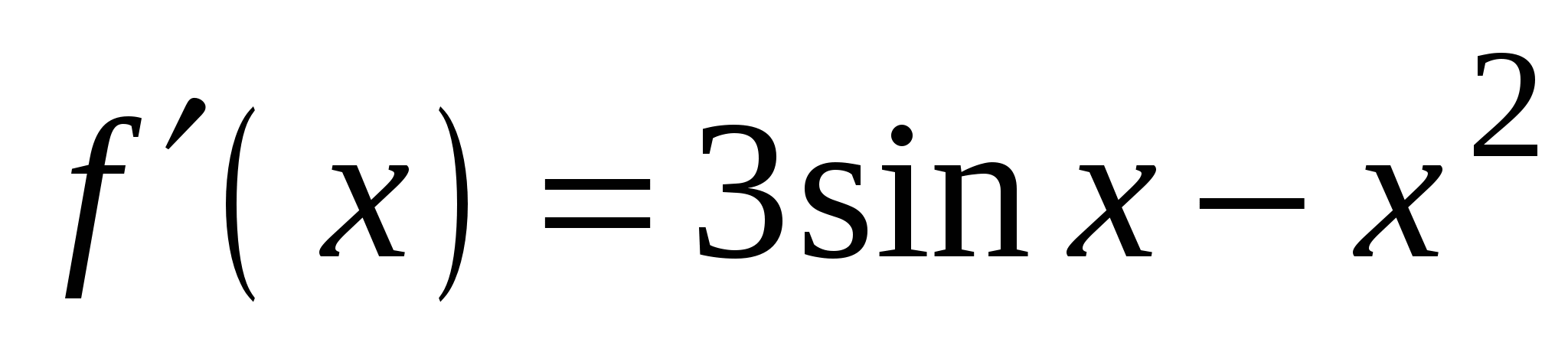
4)
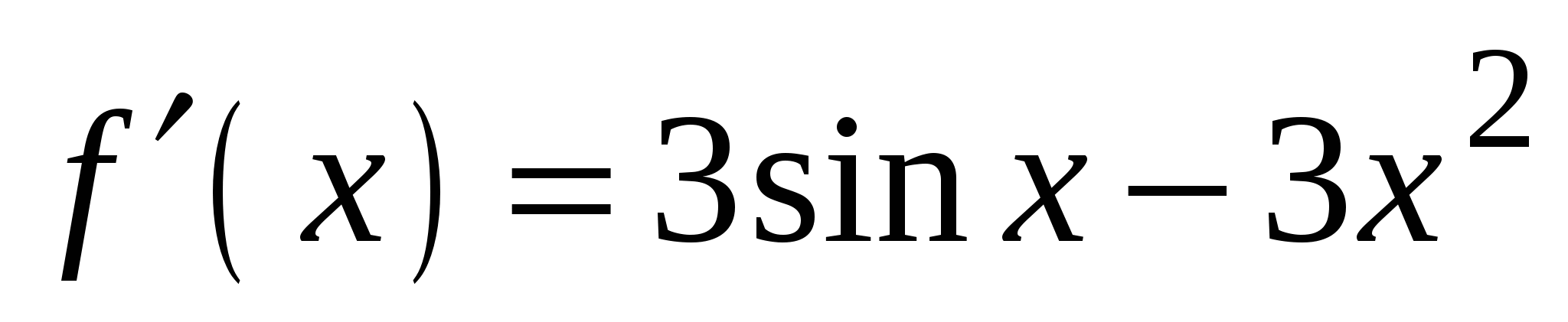
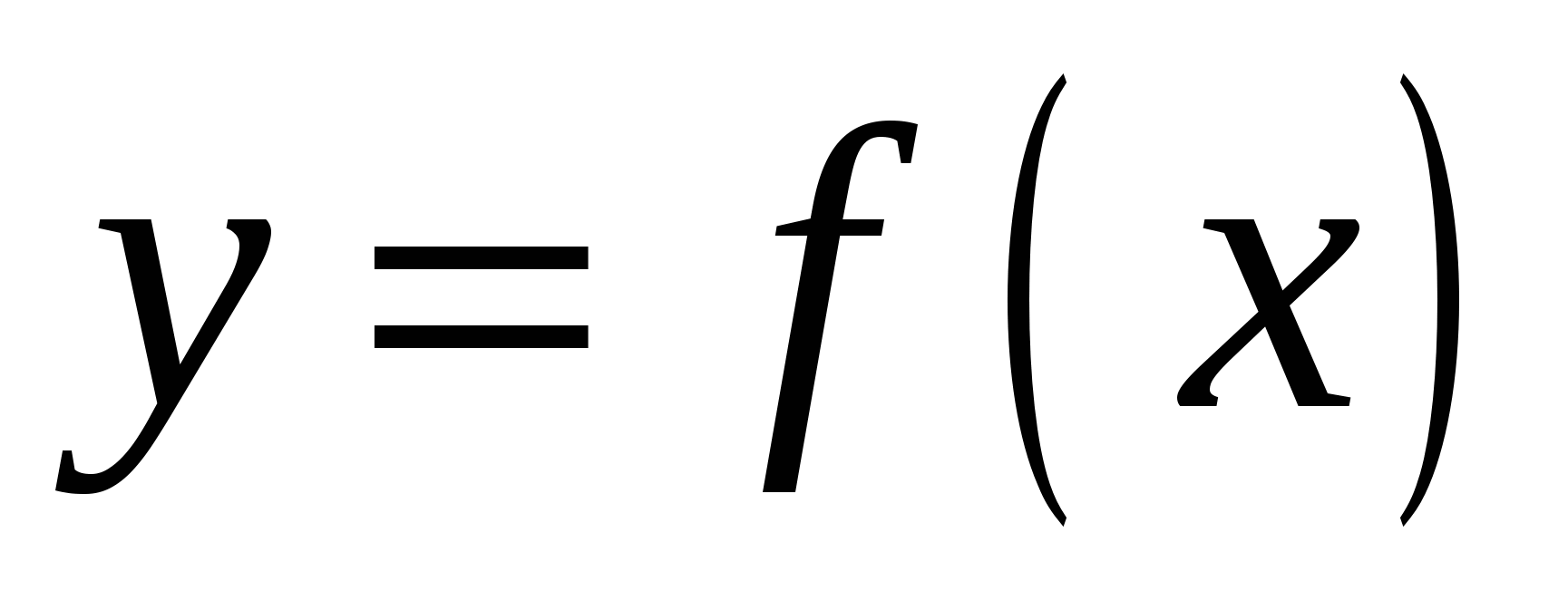 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
.
А4. Найдите производную функции 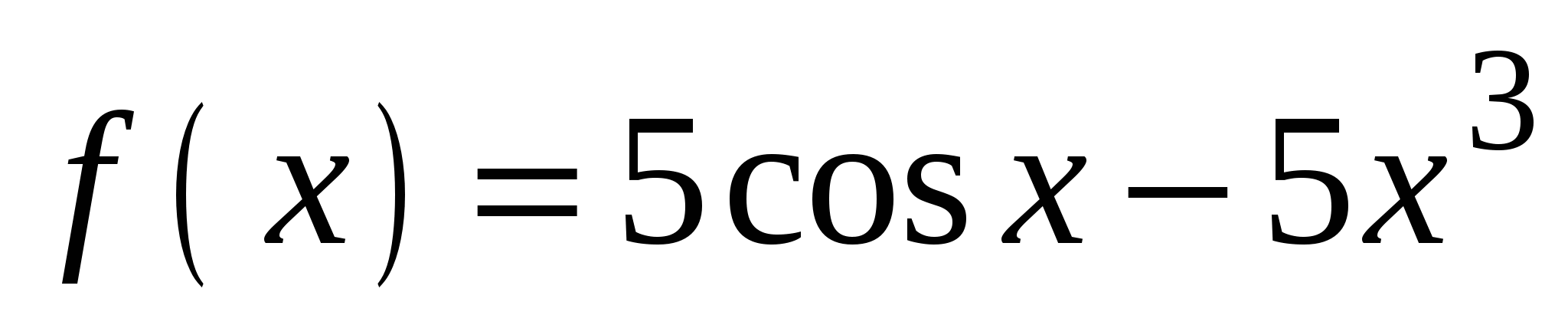 .
.
1)
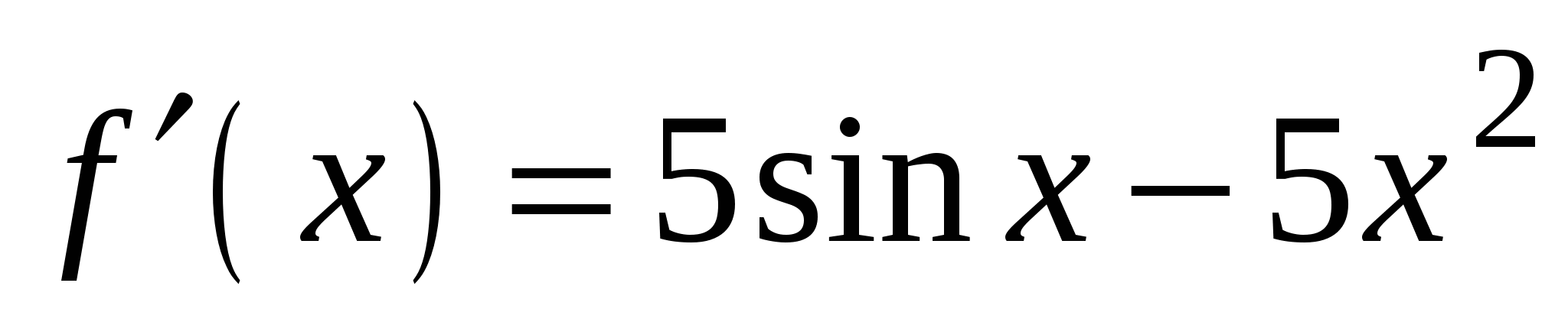
3)
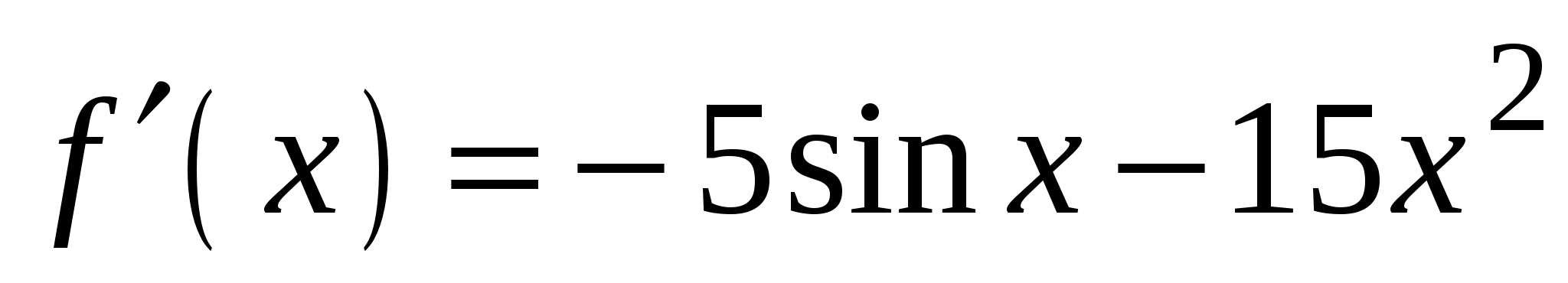
2)
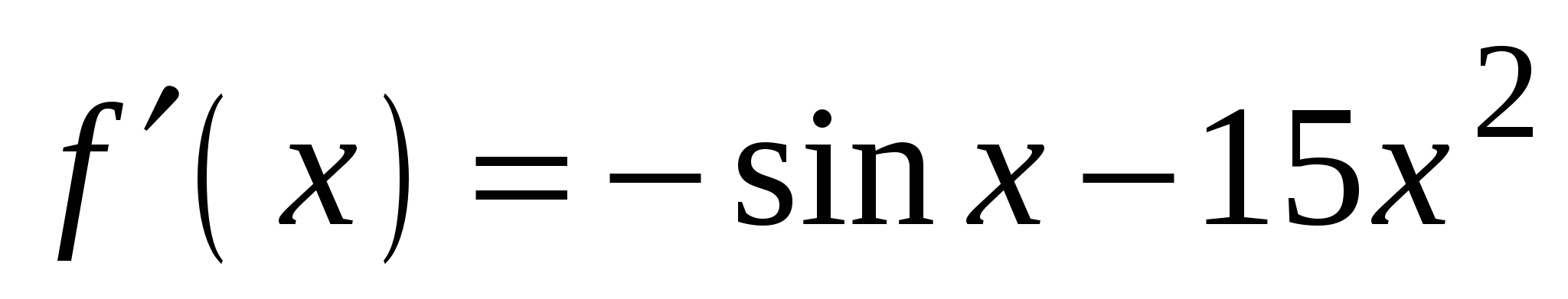
4)
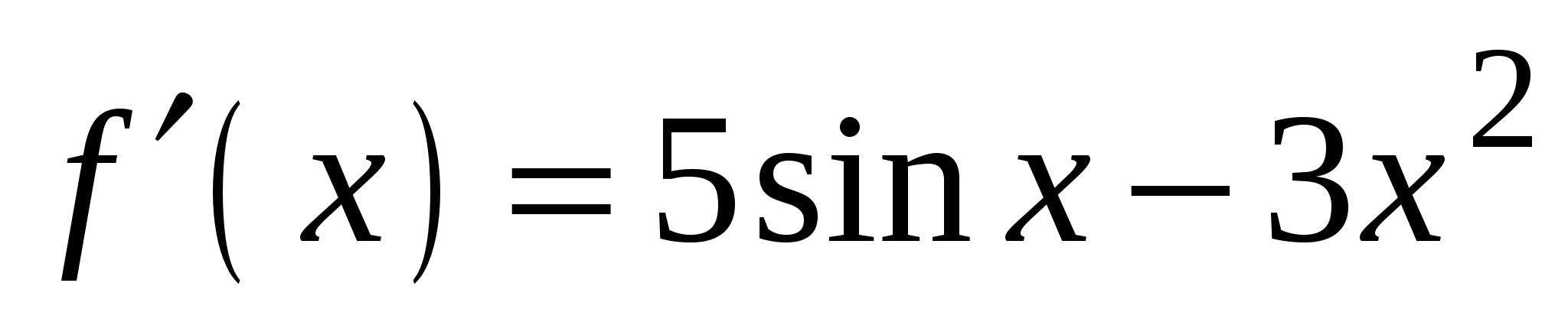
А5. Найдите производную функции  .
.
1)

3)

2)

4)


В3. На рисунке изображен график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
.
В4.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=t4+1/3t3-t2+8. Чему будет равна мгновенная скорость (м/с) через 3 с после начала движения?
В5.Материальная точка движется по закону х(t)= 1/3t3-t2+9t+11 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 10 м/с2 ?
В6. Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=5t2 - 3t+6. Через сколько секунд после начала движения произойдет остановка?
Контрольная работа №3 по теме: «Производная»
Вариант №2
B1 Функция  определена на промежутке
определена на промежутке  . На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции
. На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции  имеет наибольший угловой коэффициент.
имеет наибольший угловой коэффициент.
А1. Найдите производную функции 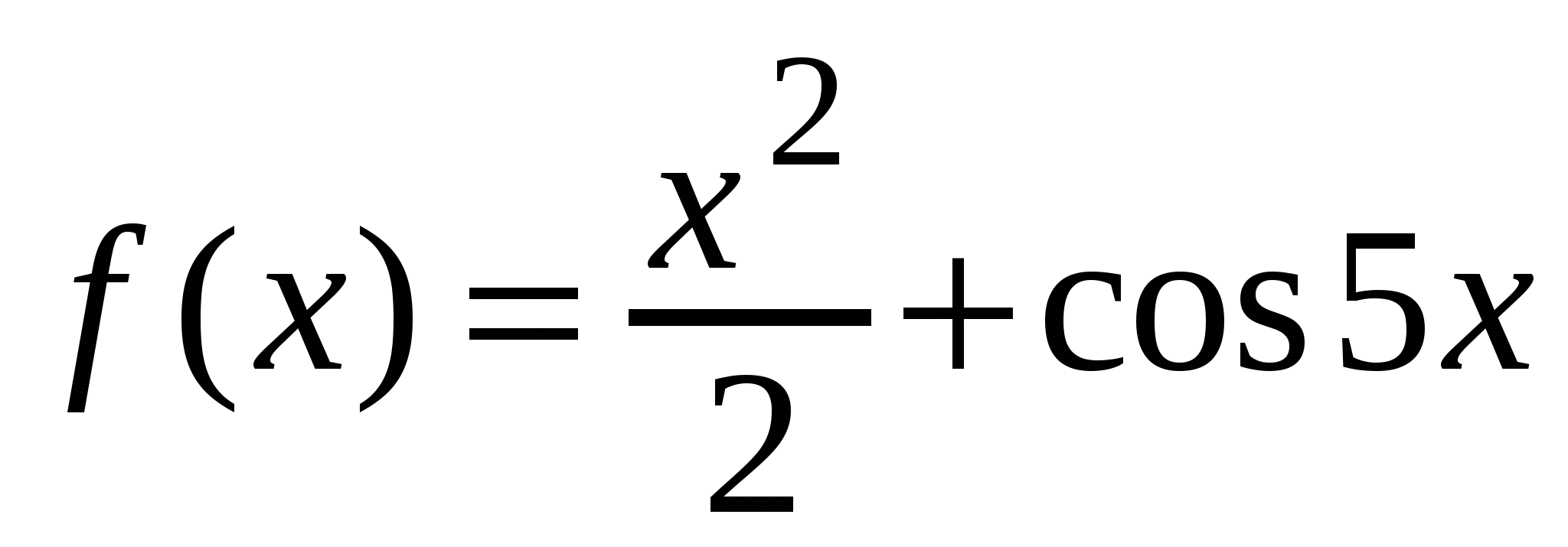 .
.
1) 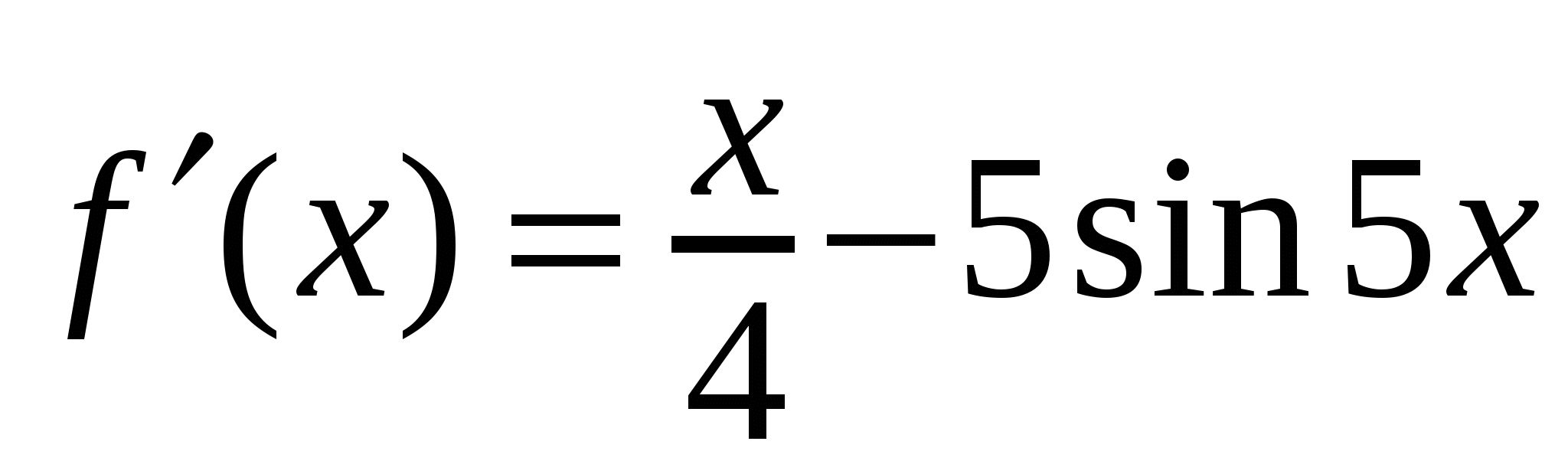
3) 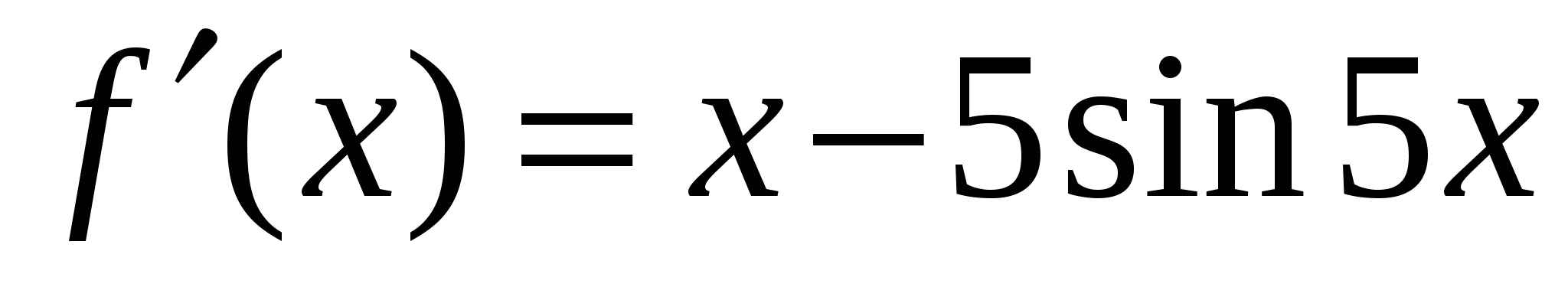
2) 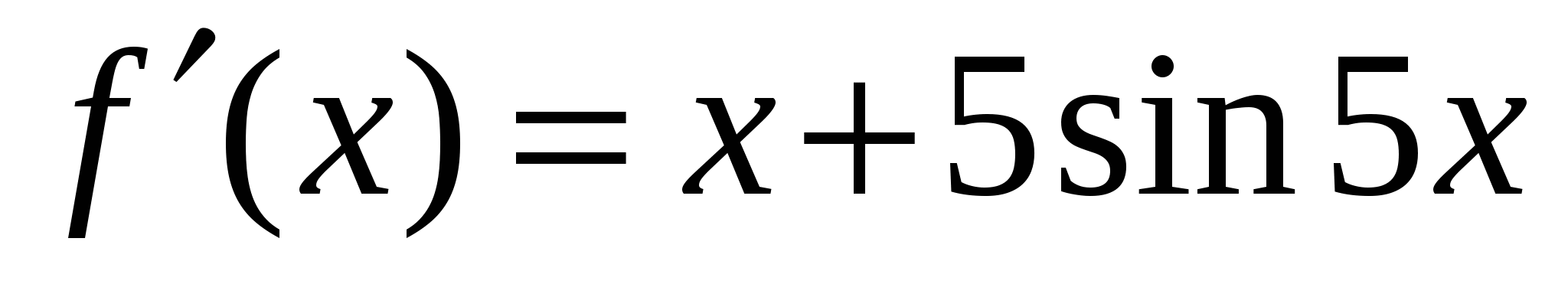
4) 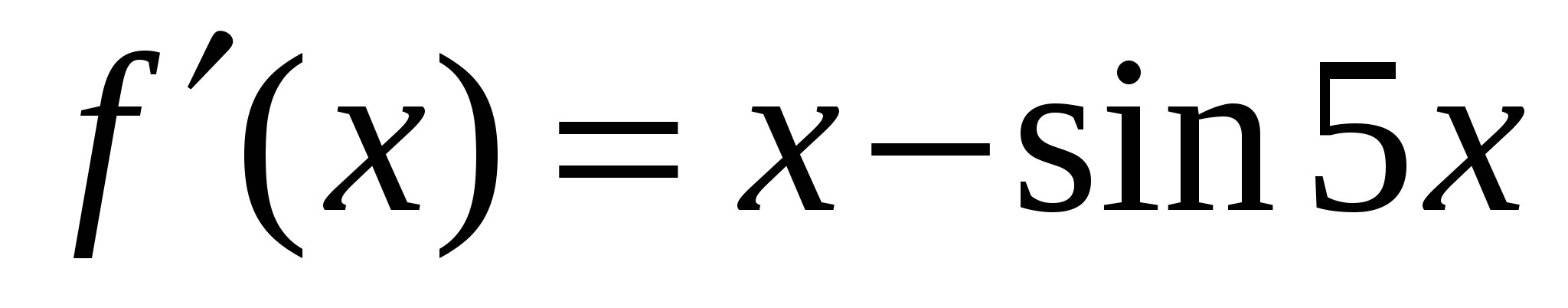
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Вычислите значение производной функции 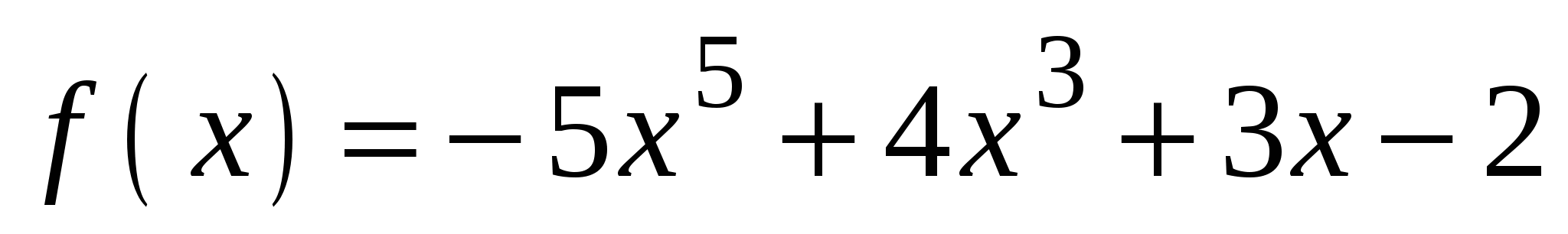 в точке
в точке 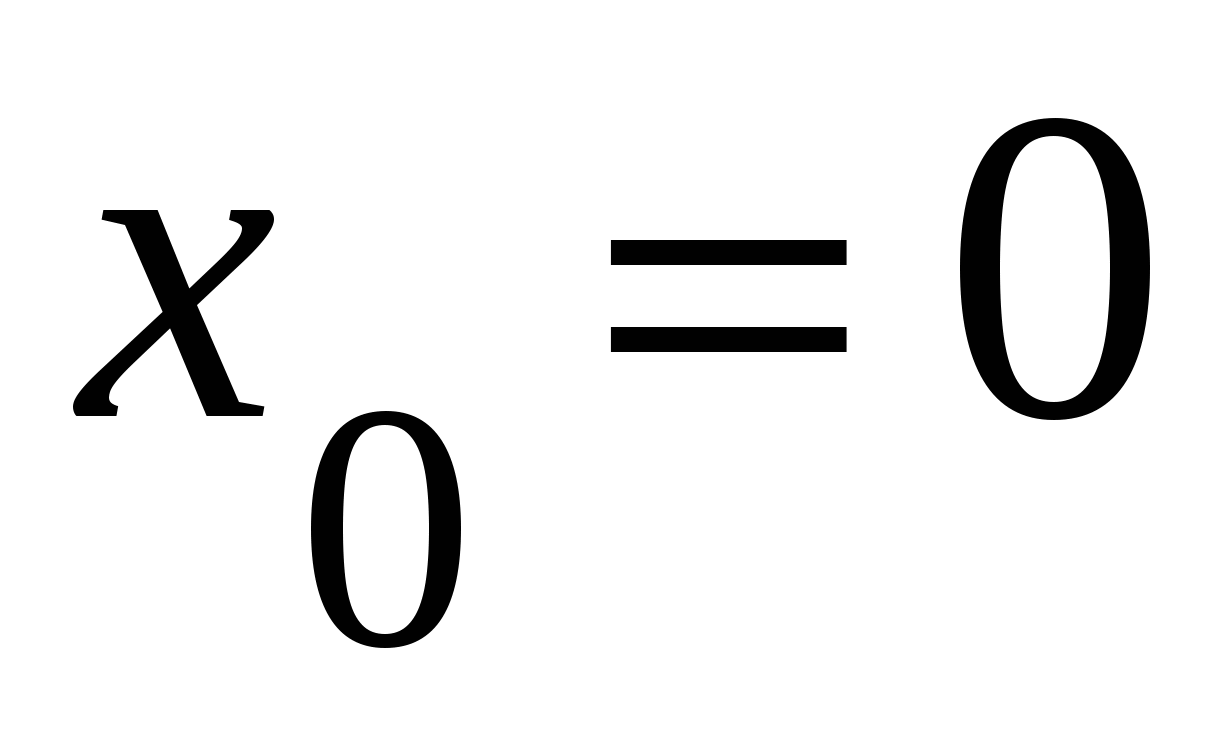 .
.
1)
3
2)
− 5
3)
− 3
4)
0
А4. Найдите производную функции 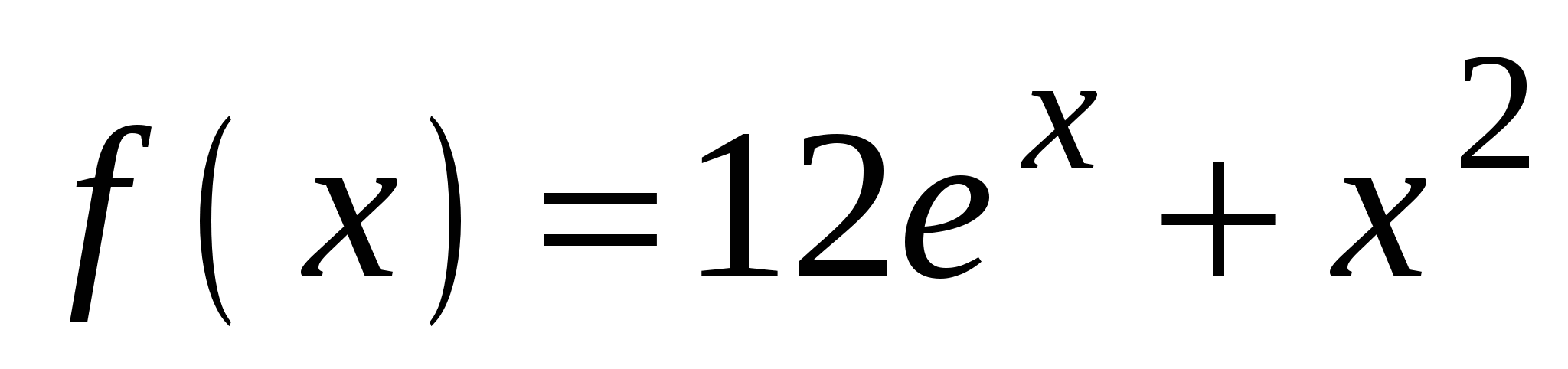 .
.
1)
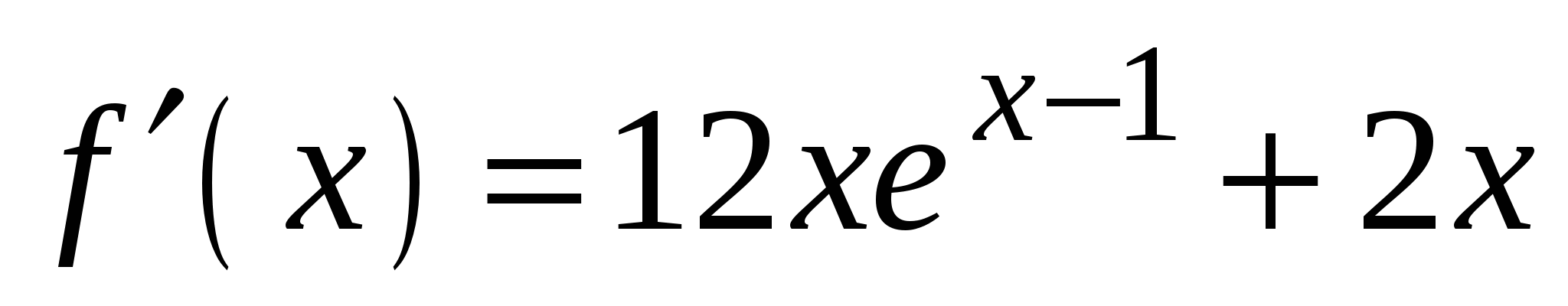
3)
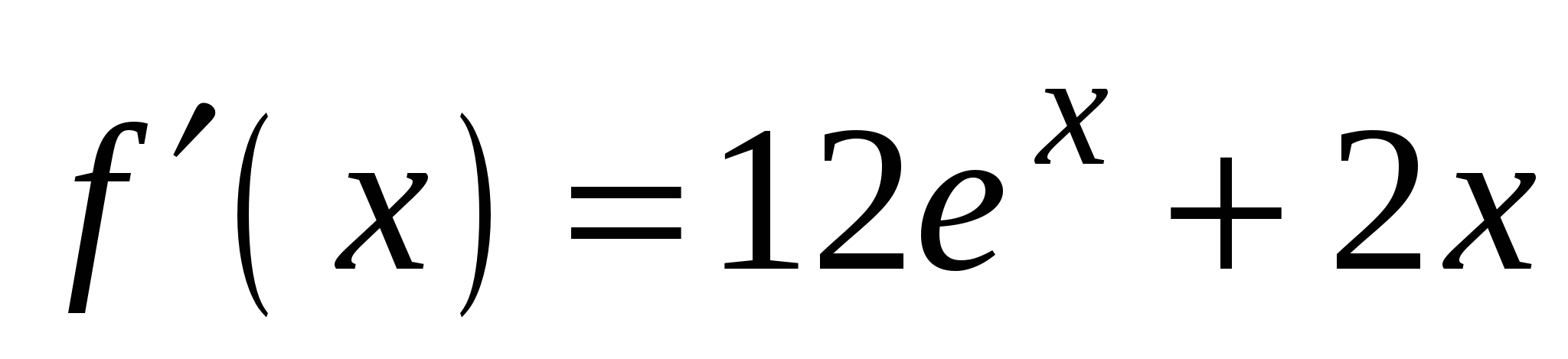
2)
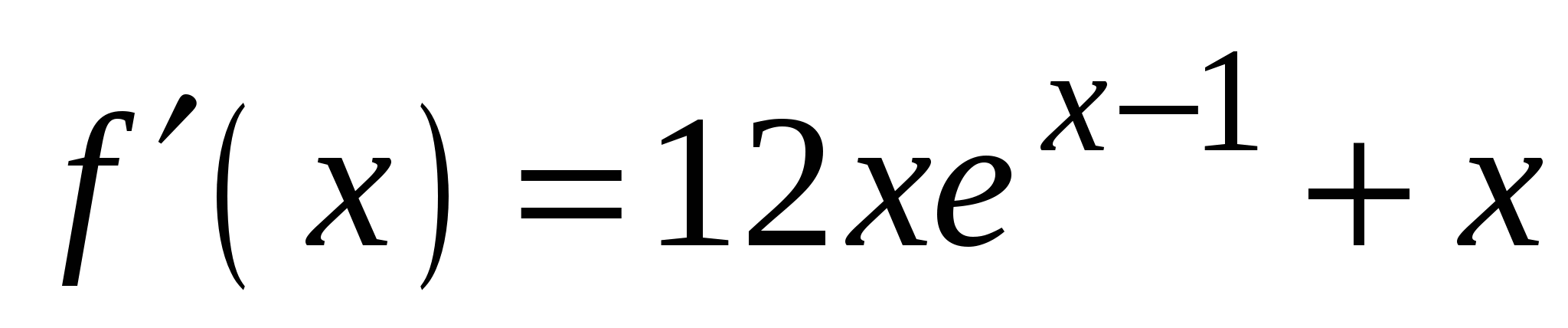
4)
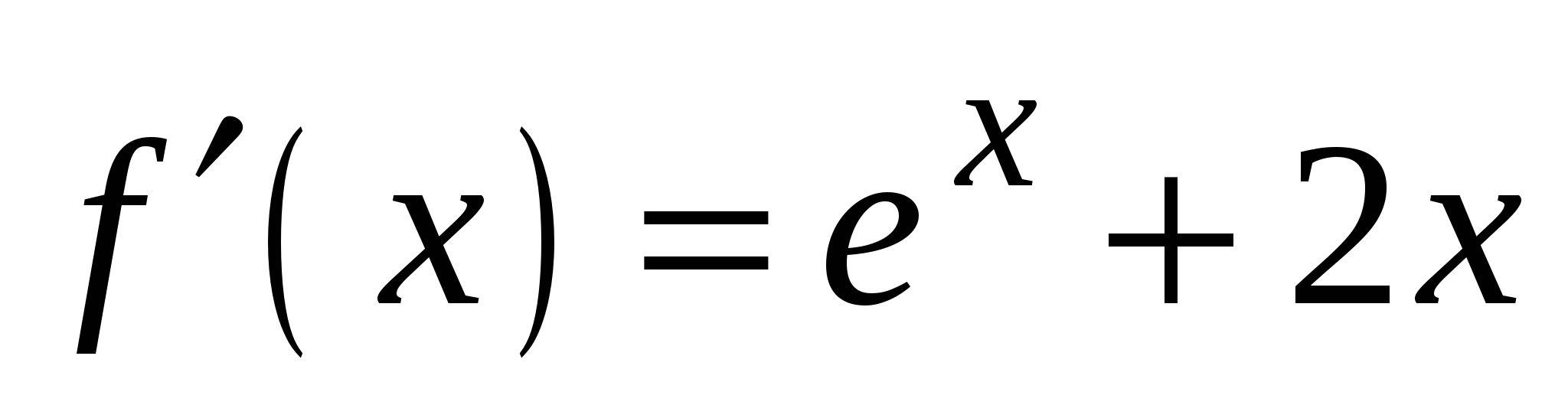

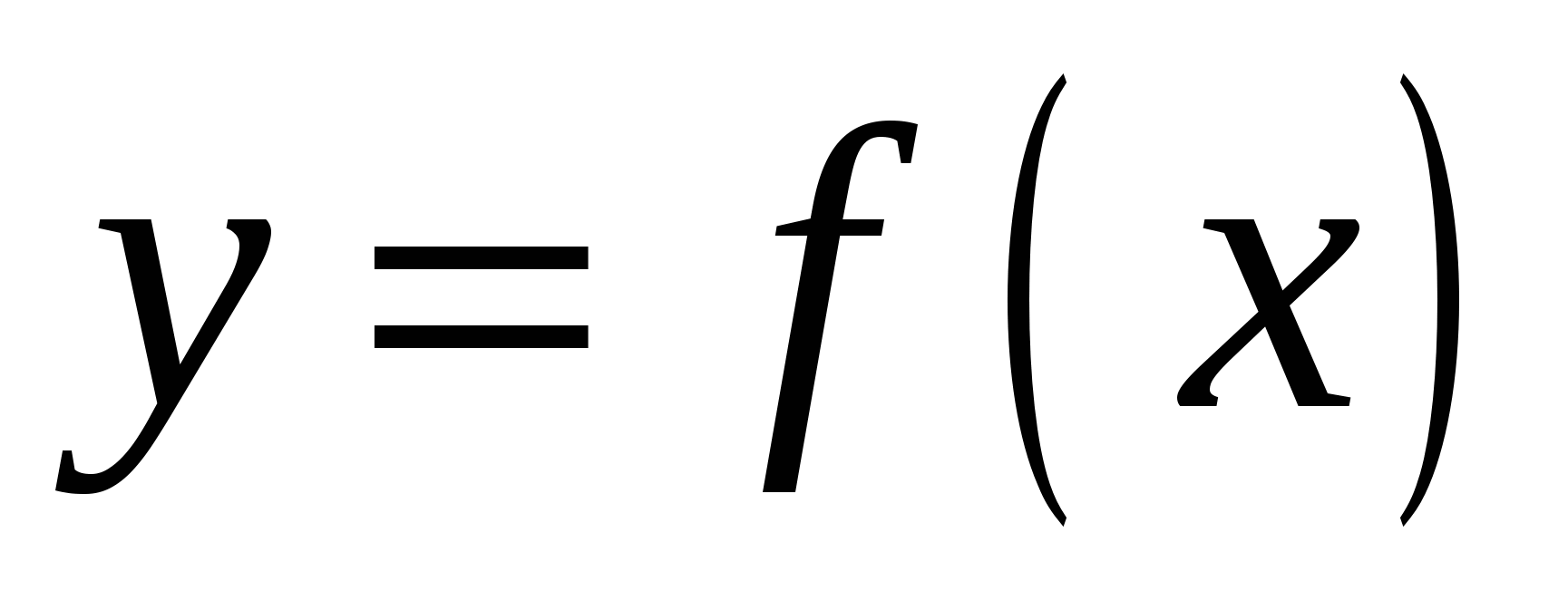 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. А5. Найдите производную функции 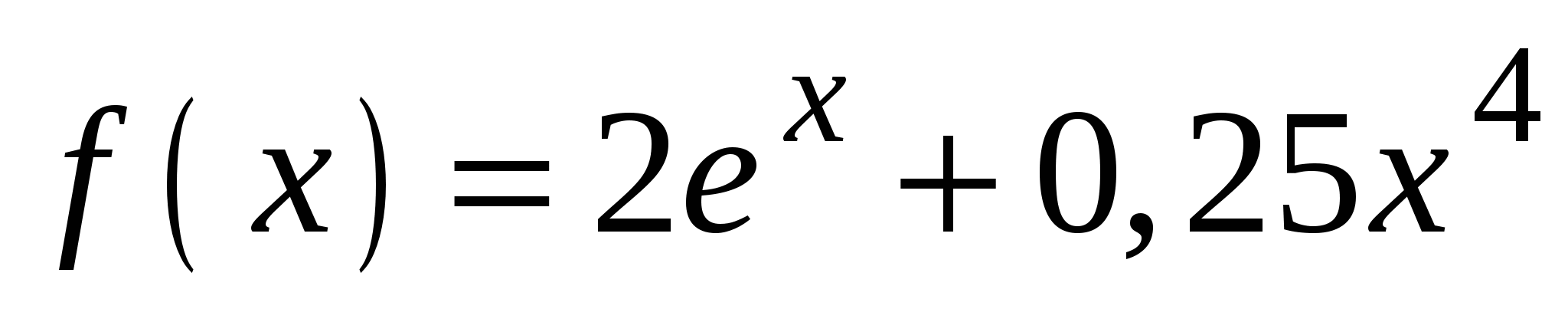 .
.
1)
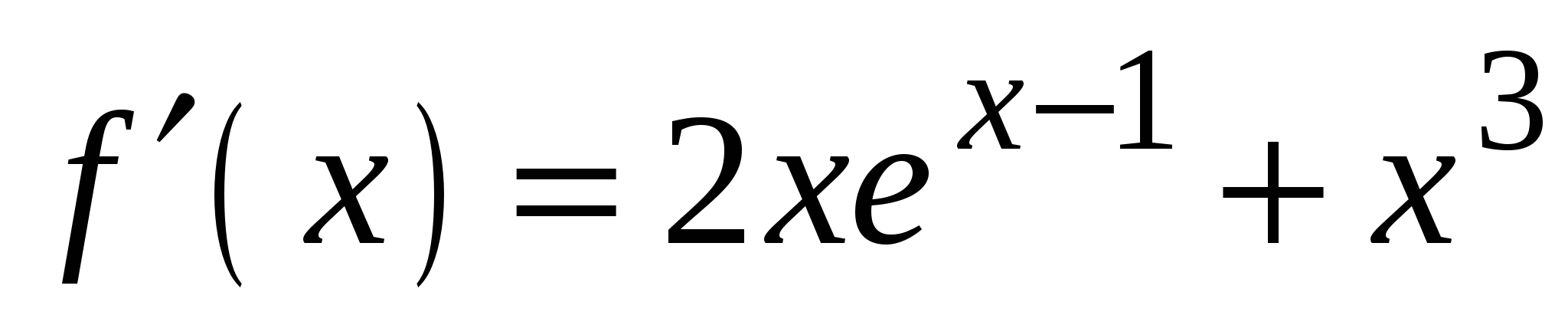
3)
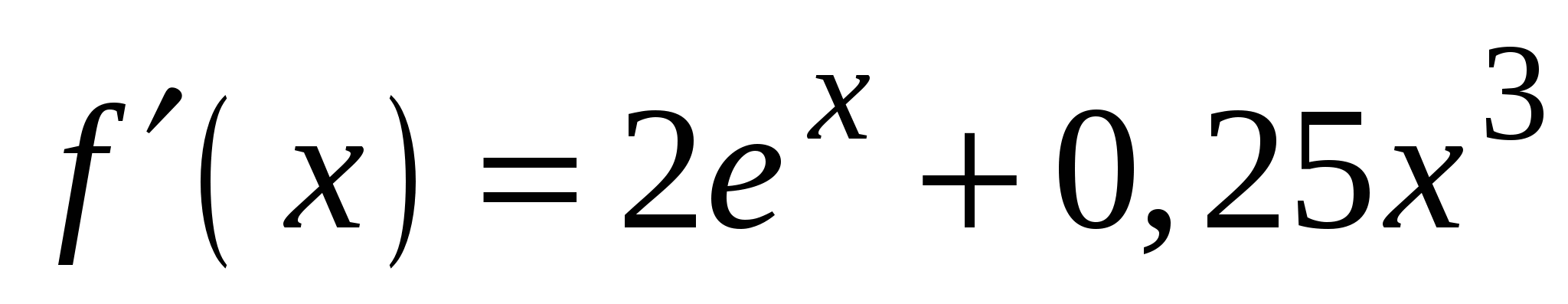
2)
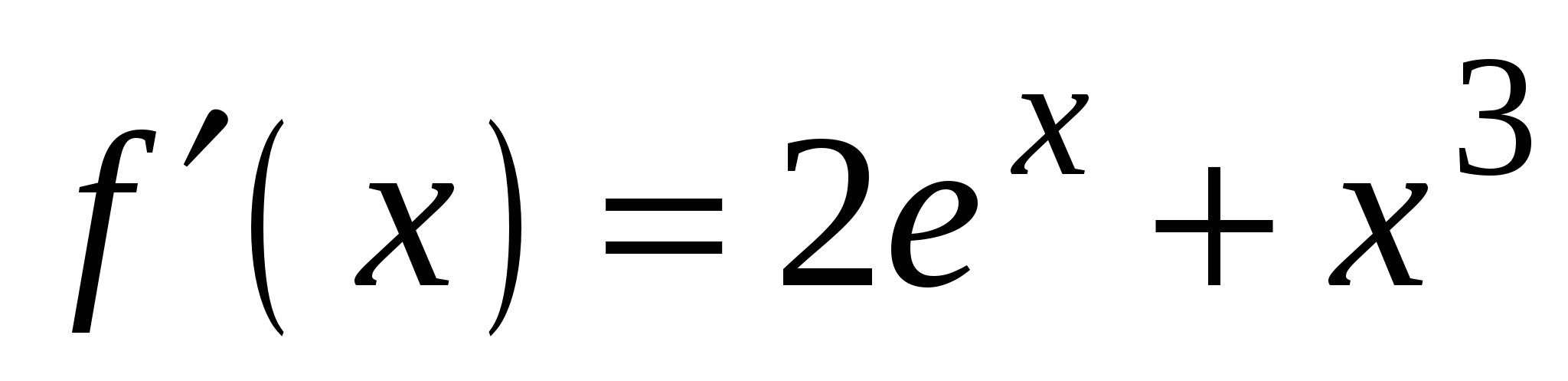
4)
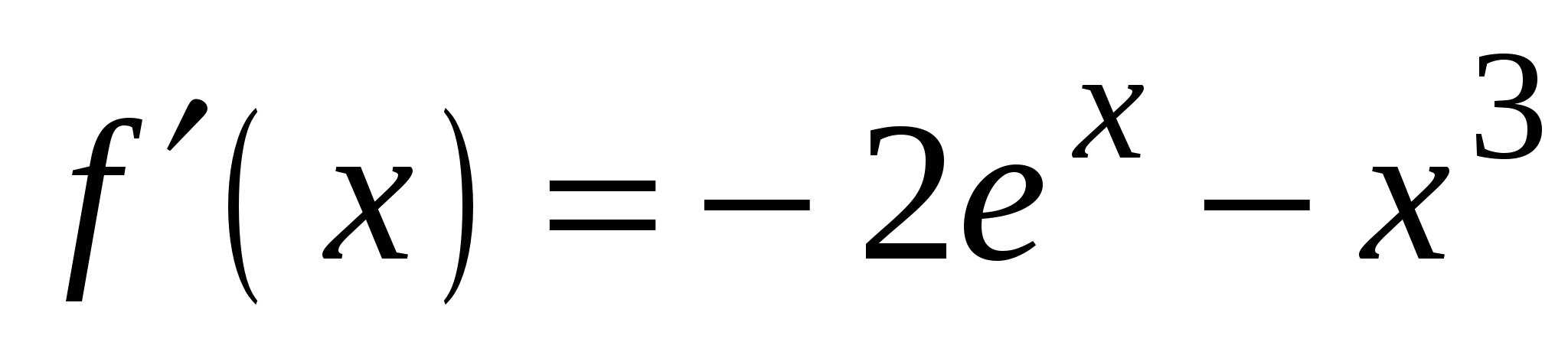

В3. На рисунке изображен график функции  и касательная к нему. Чему равно значение производной этой функции в точке с абсциссой
и касательная к нему. Чему равно значение производной этой функции в точке с абсциссой  ?
?
В4. Материальная точка движется по закону х(t)= t3-4t2+3t - 17 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 10 м/с2 ?
В5. Материальная точка движется по закону х(t)= t3-5t2+6t +7 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 8 м/с2 ?
В6. Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=1/4t4+t3-1/2t2+12. Чему будет равна мгновенная скорость (м/с) через 4 с после начала движения?
Контрольная работа №3 по теме: «Производная»
Вариант №3
.

B1. Функция  определена на промежутке. На рисунке изображен график ее производной
определена на промежутке. На рисунке изображен график ее производной  . Найдите количество точек экстремума функции
. Найдите количество точек экстремума функции  на данном промежутке.
на данном промежутке.
А1. Найдите производную функции 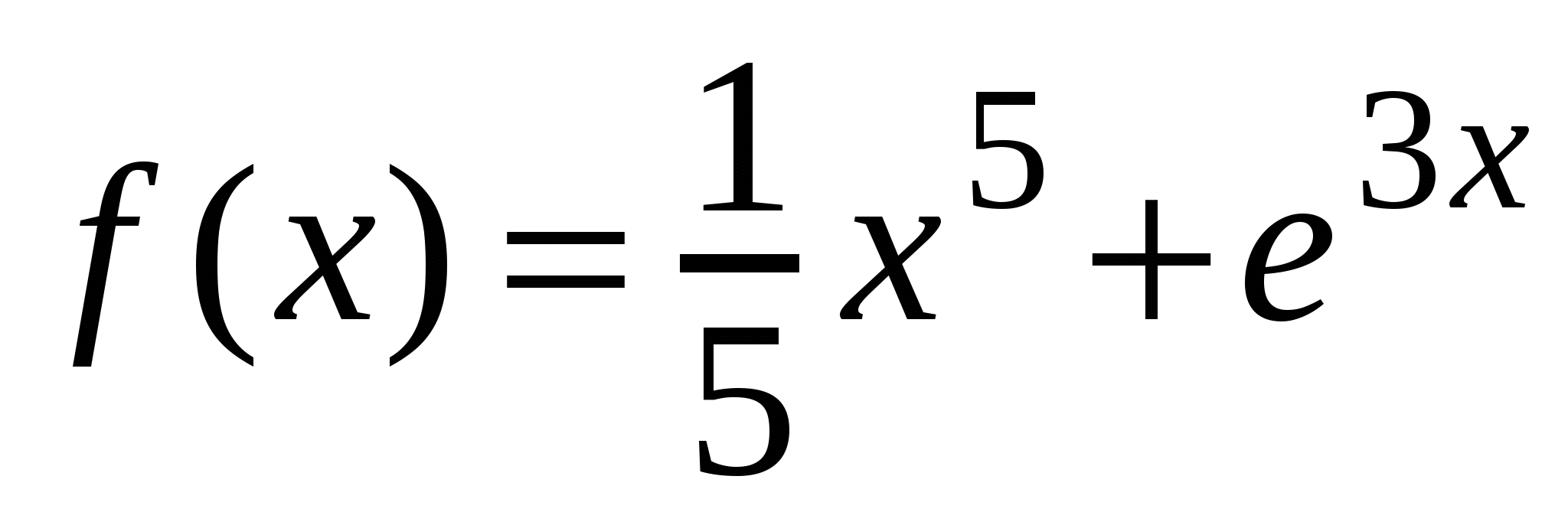 .
.
1) 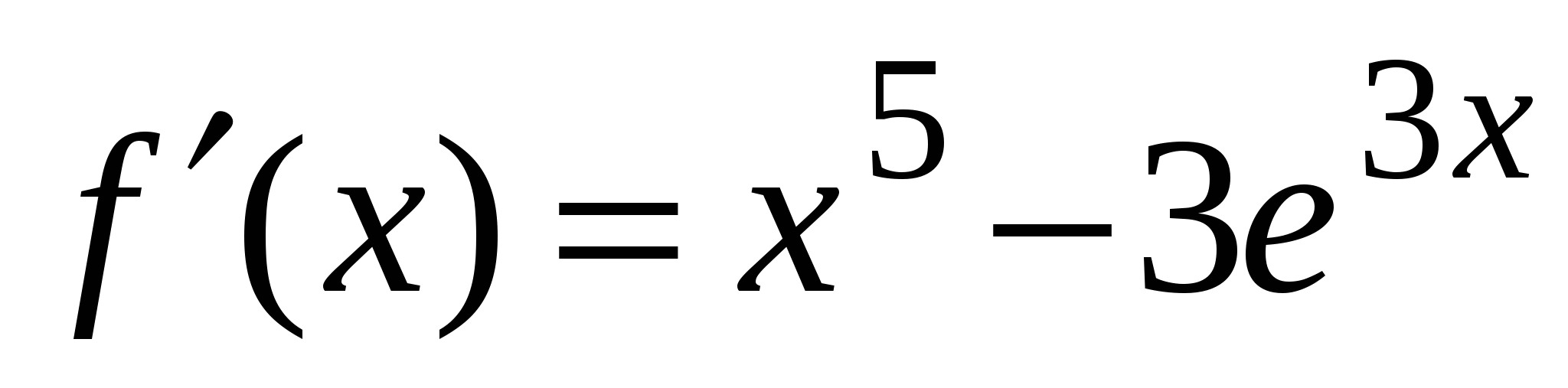
3) 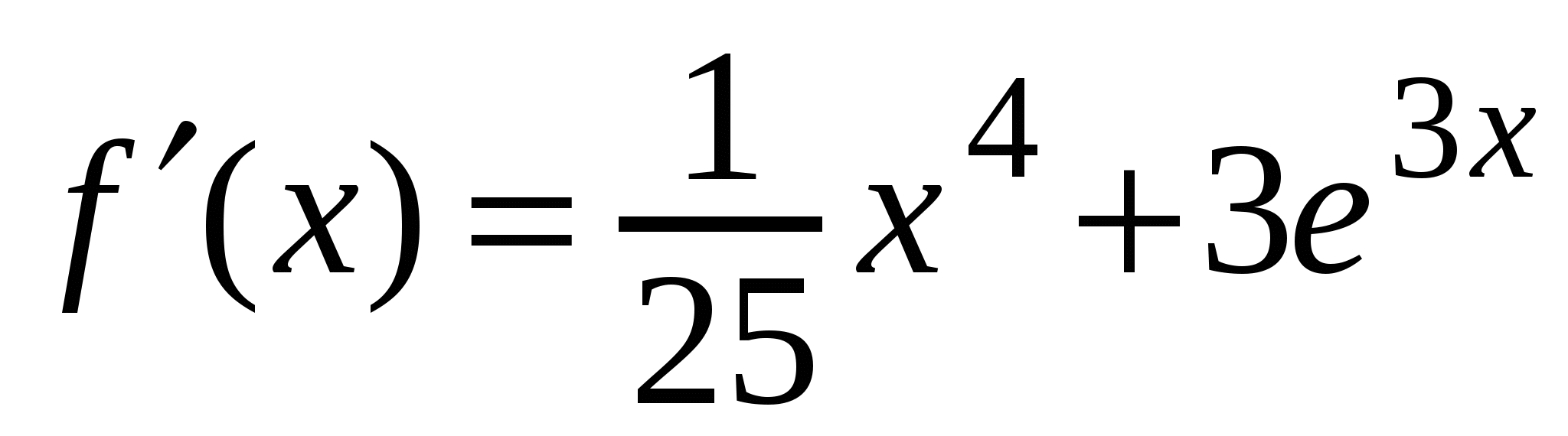
2) 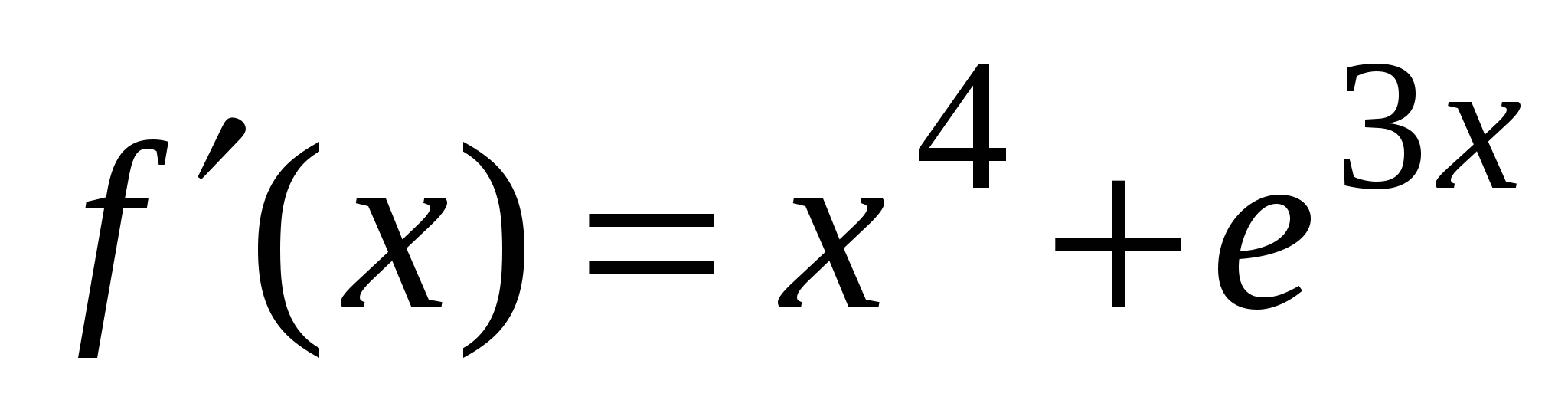
4) 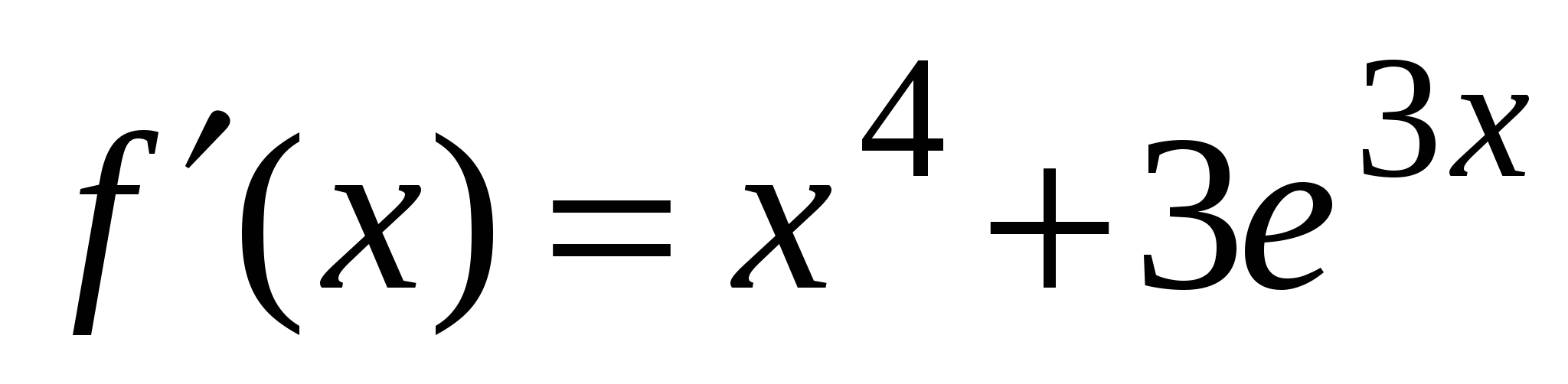
А2. Найдите производную функции 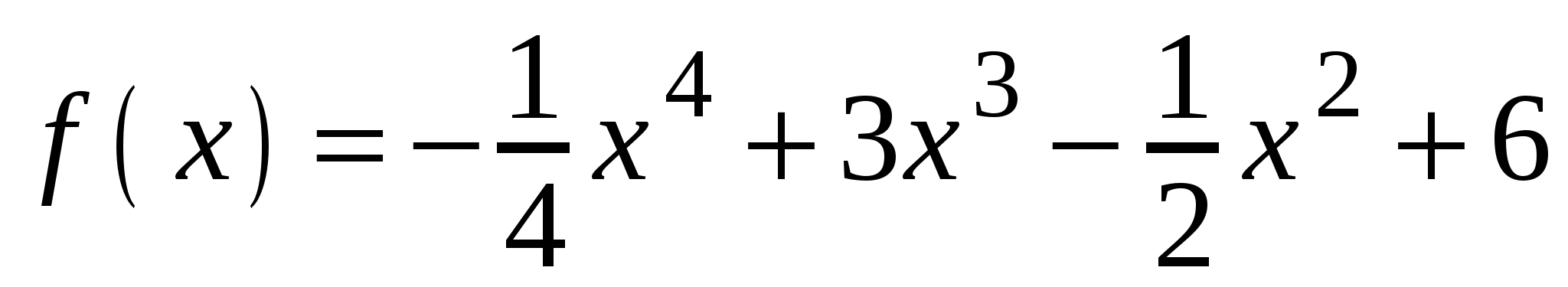 .
.
1)
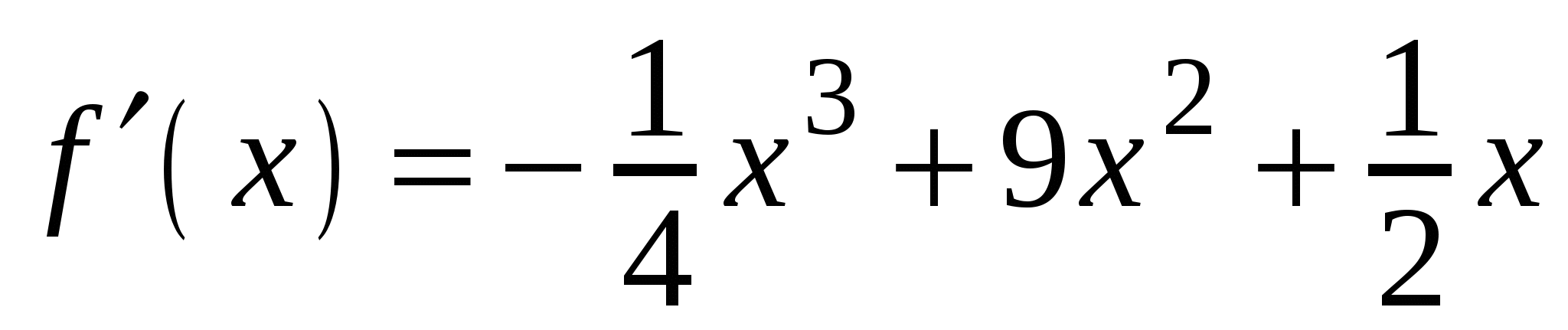
3)
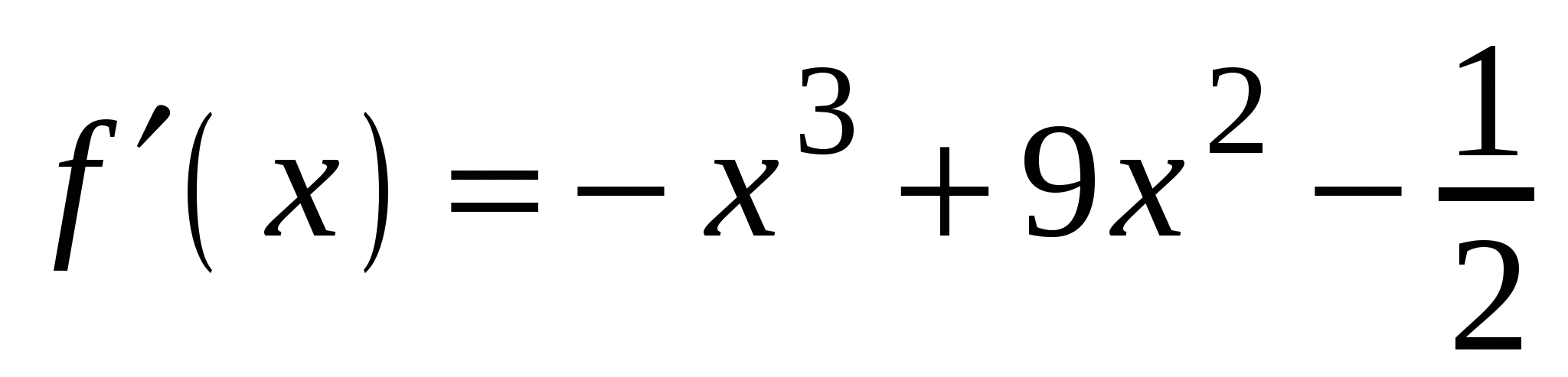
2)
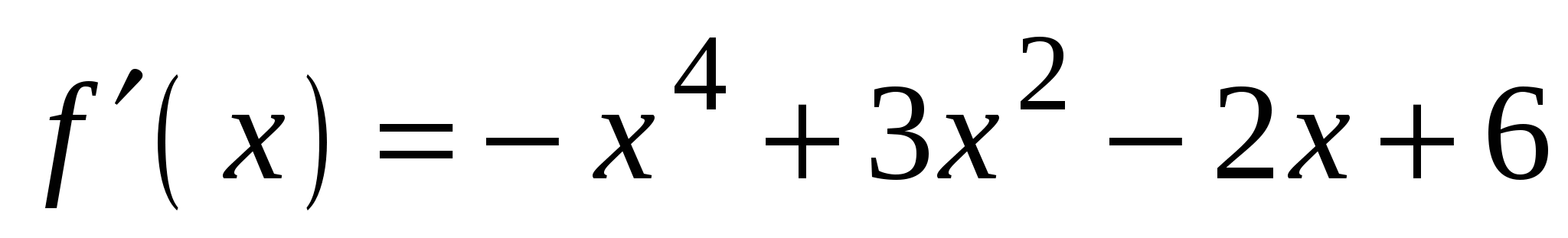
4)
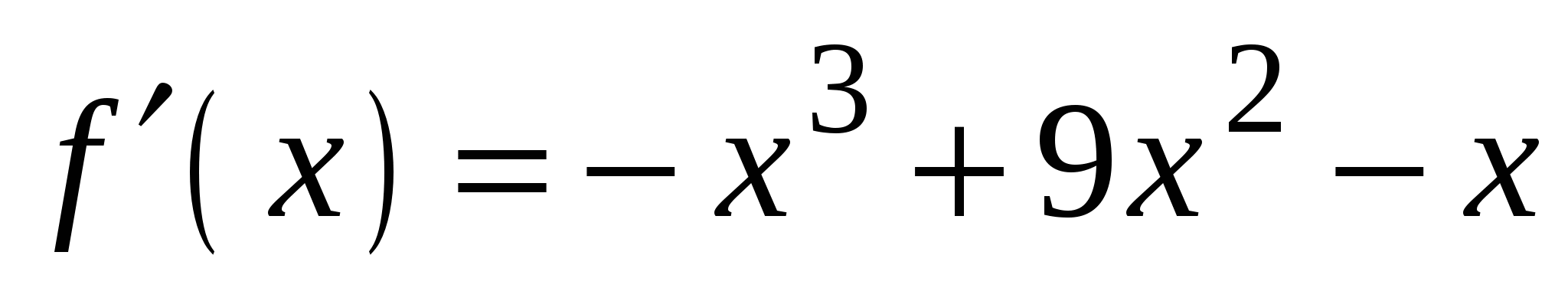
А3. Найдите производную функции 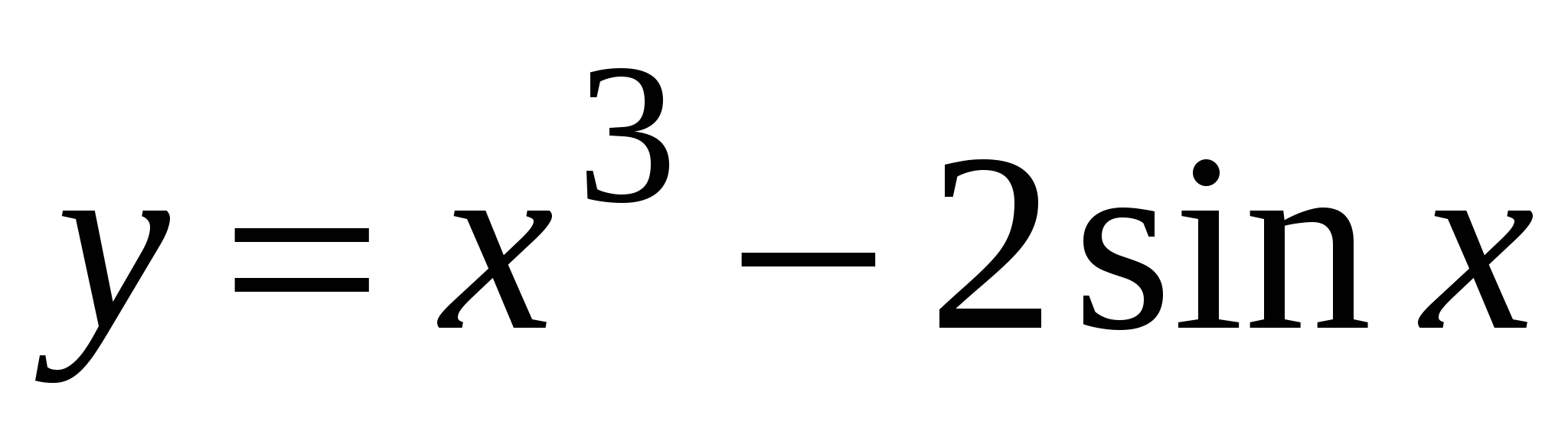 .
.
1)
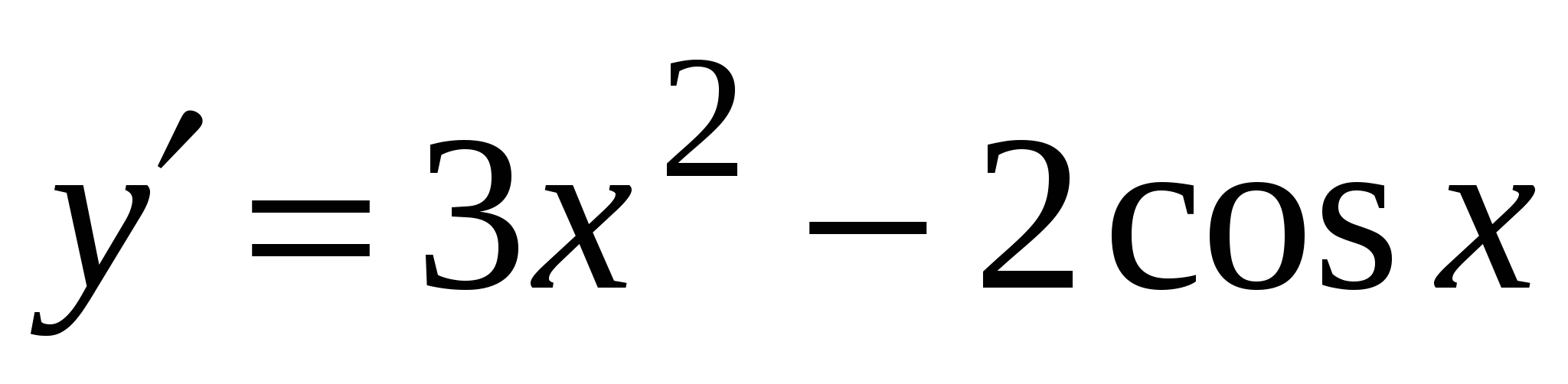
3)
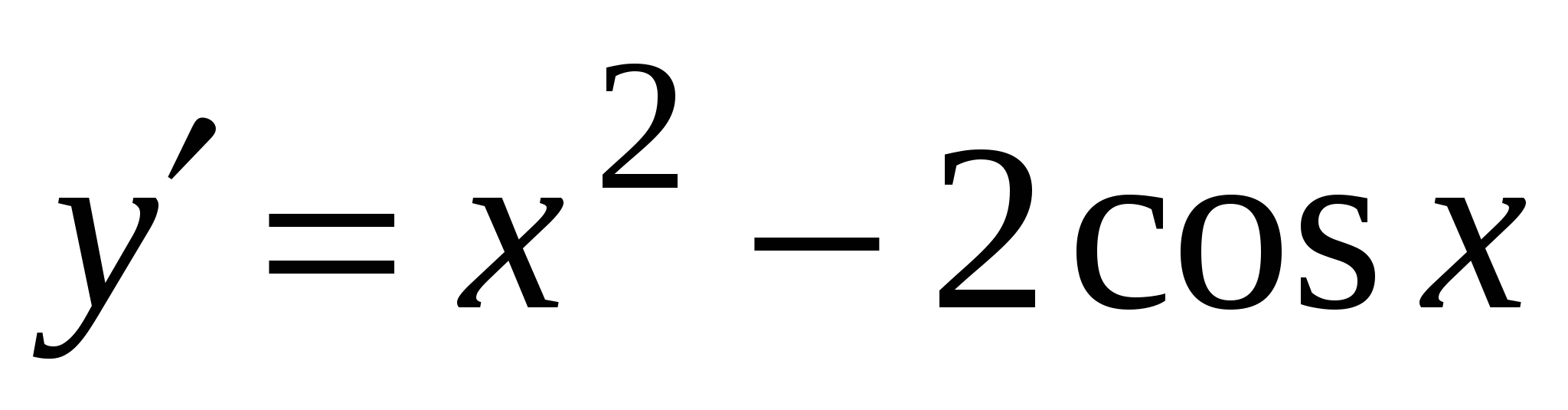
2)
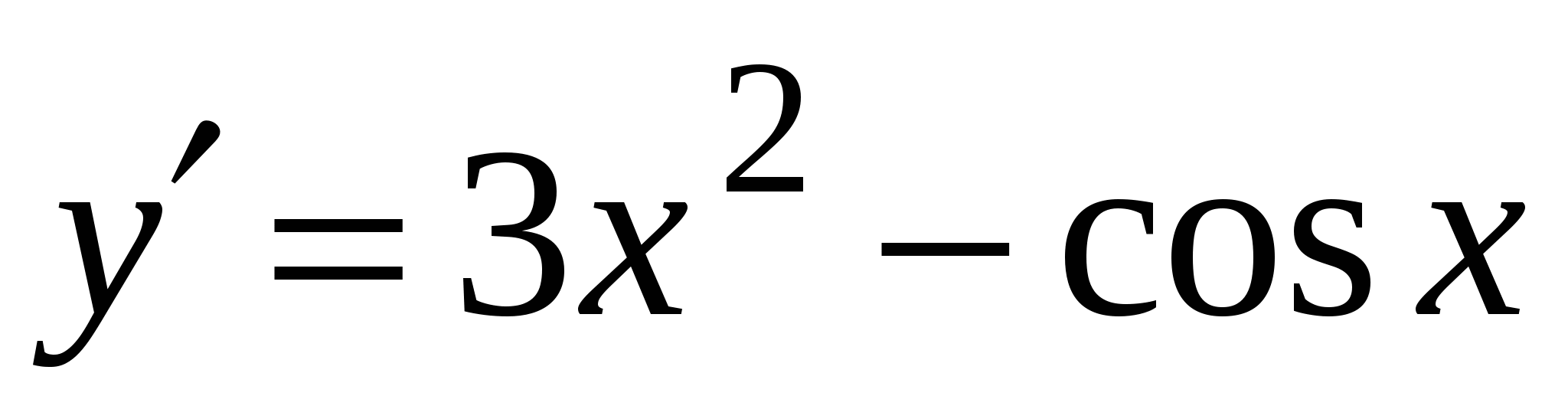
4)
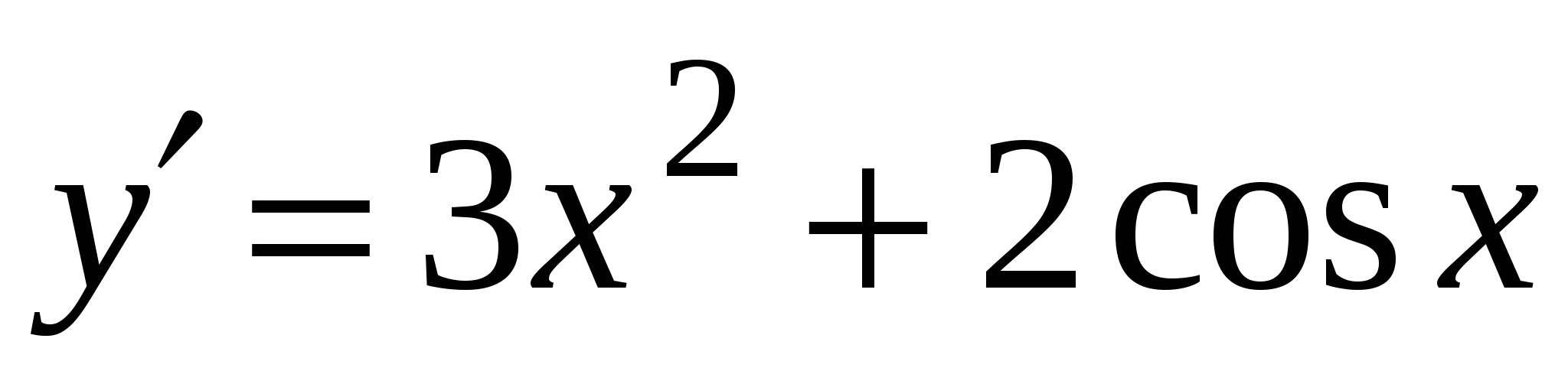

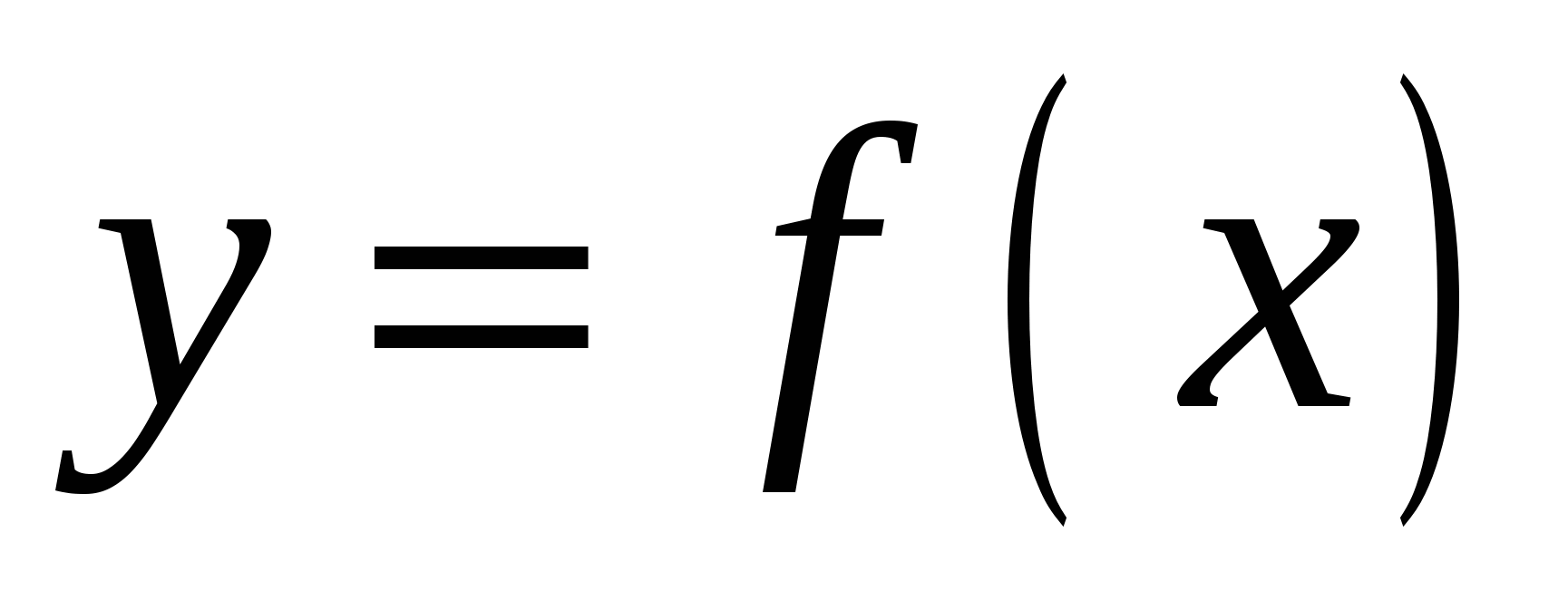 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. А4. Найдите производную функции 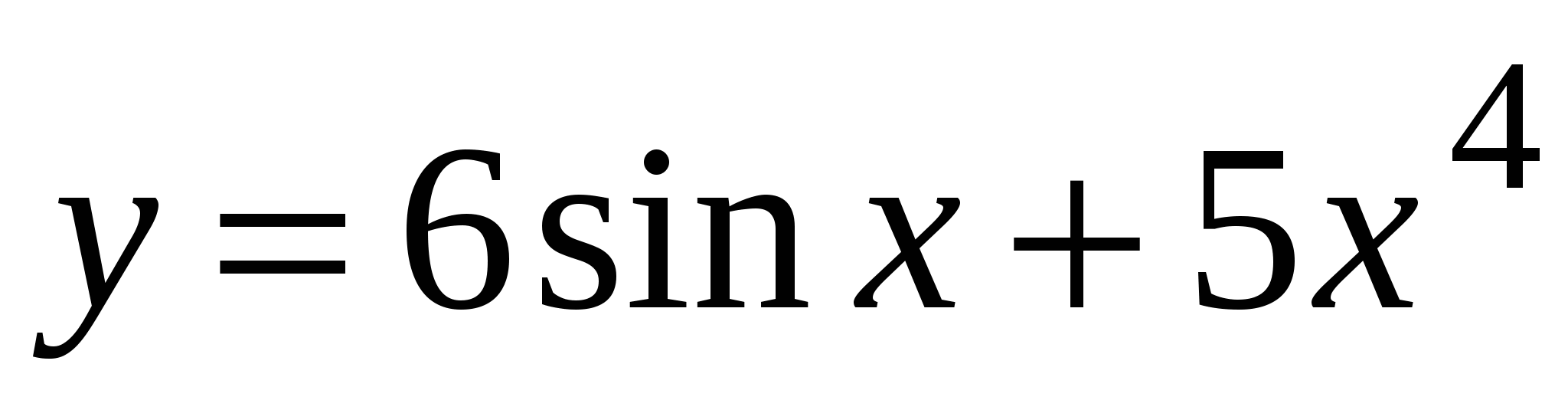 .
.
1)
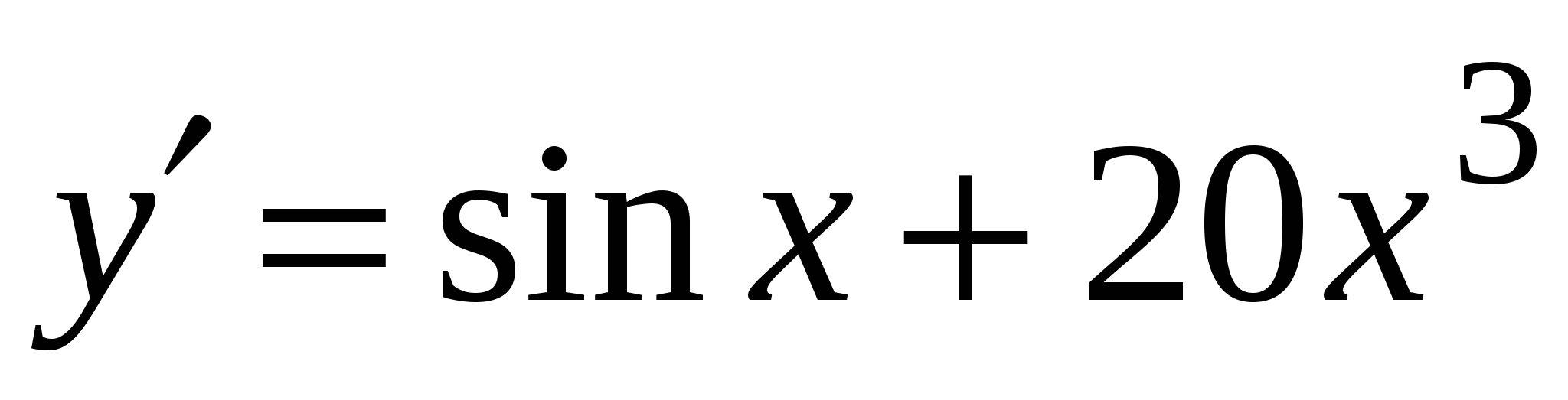
3)
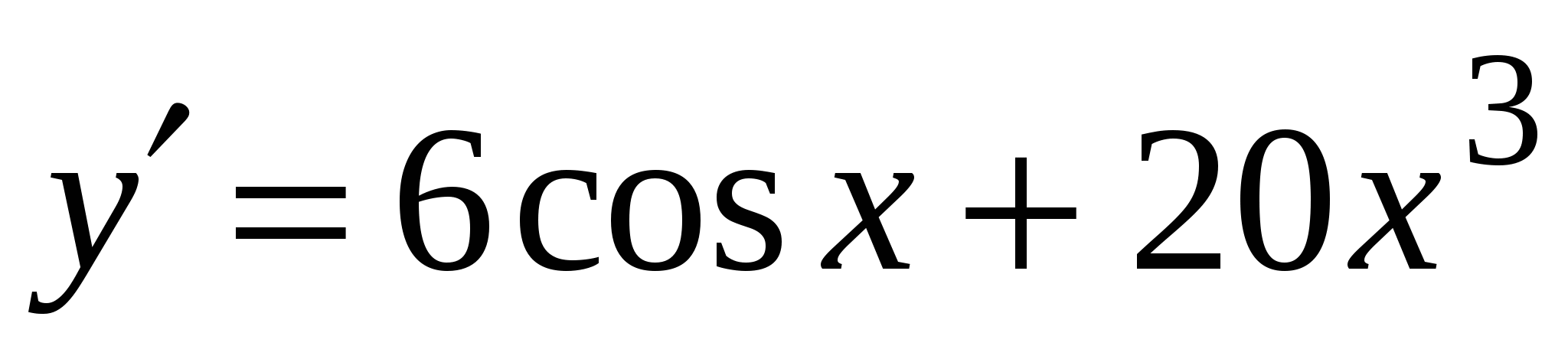
2)
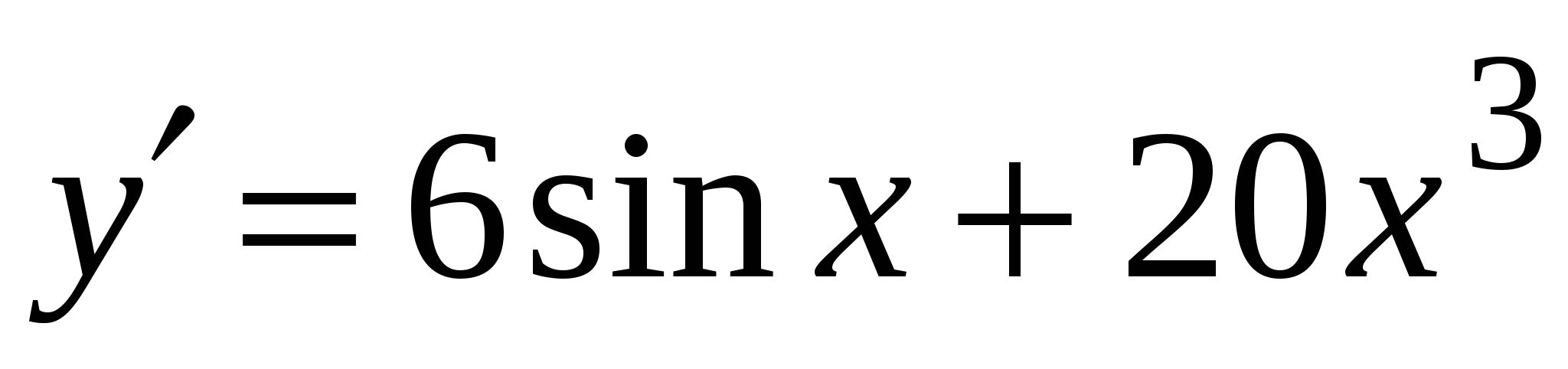
4)
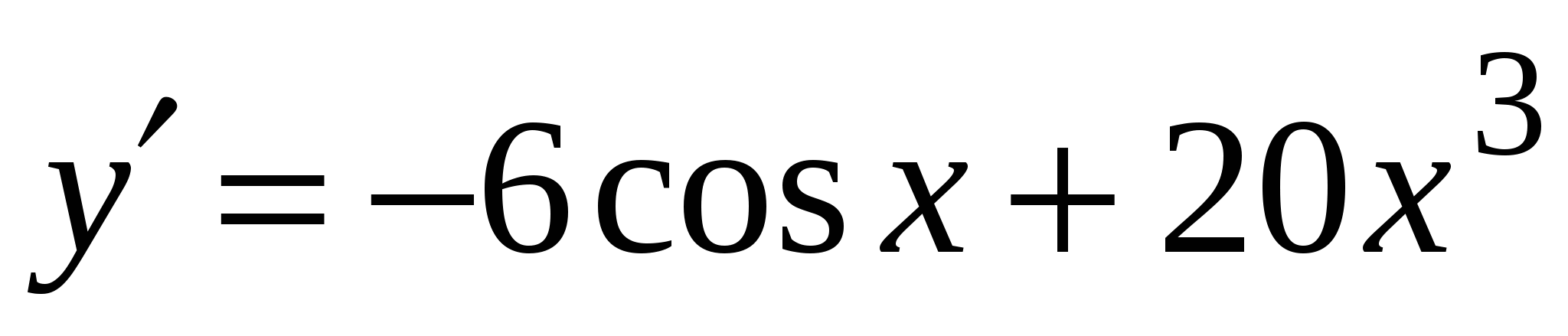
А5. Найдите производную функции  .
.
1)

3)

2)

4)


 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. В4. Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=6t2 - 24t-13. Через сколько секунд после начала движения произойдет остановка?
В5. Тело движется прямолинейно, его расстояние S (в м) от начала отсчета изменяется по закону S(t)=3t3-4t+5 м. Определите скорость движения тела через 2 с после начала движения.
В6.Материальная точка движется по закону х(t)=2 t3-3t2 -14t -27 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 6 м/с2 ?
Контрольная работа №3 по теме: «Производная»
Вариант №4
B1 Функция  задана на промежутке
задана на промежутке  . На рисунке изображен график ее производной
. На рисунке изображен график ее производной  . Найдите точку максимума функции
. Найдите точку максимума функции  на данном промежутке.
на данном промежутке.

А1. Найдите производную функции 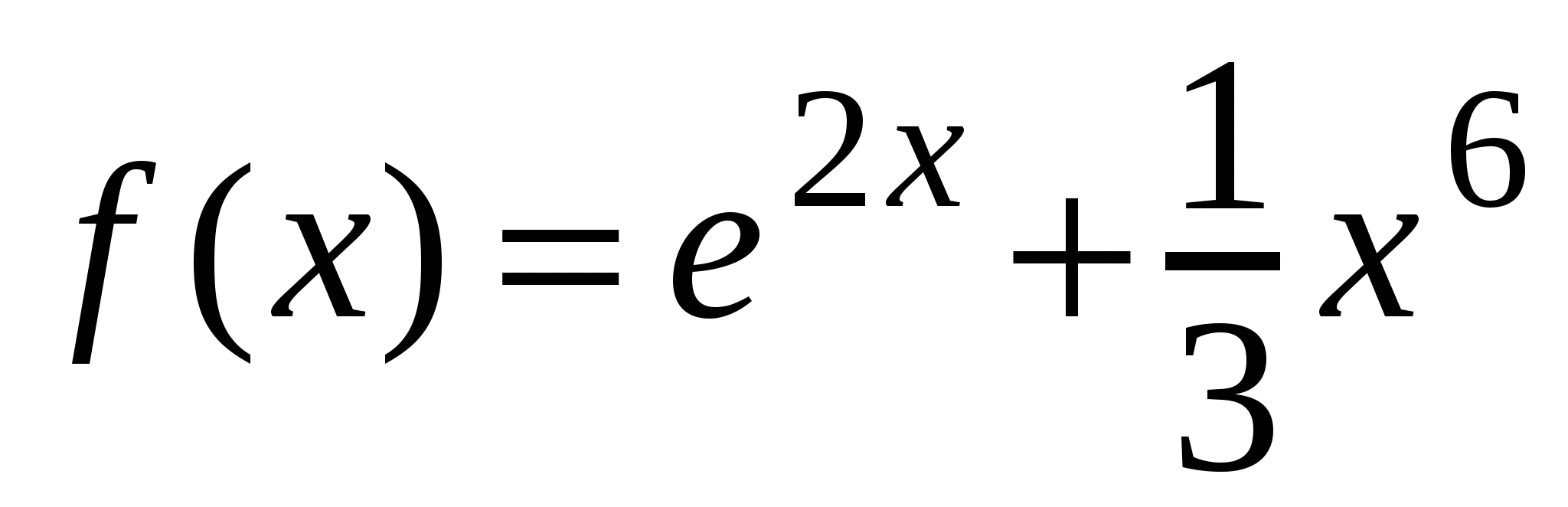 .
.
1) 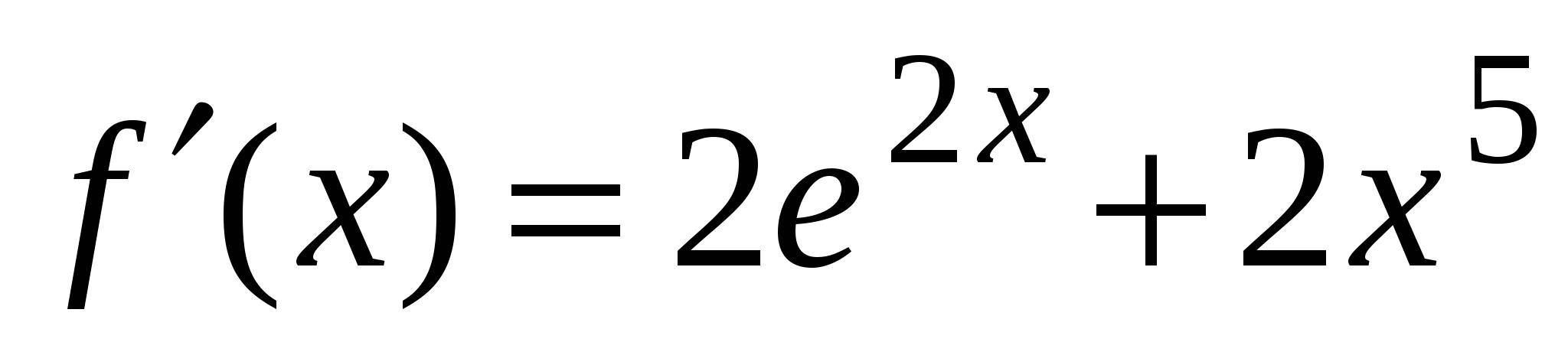
3) 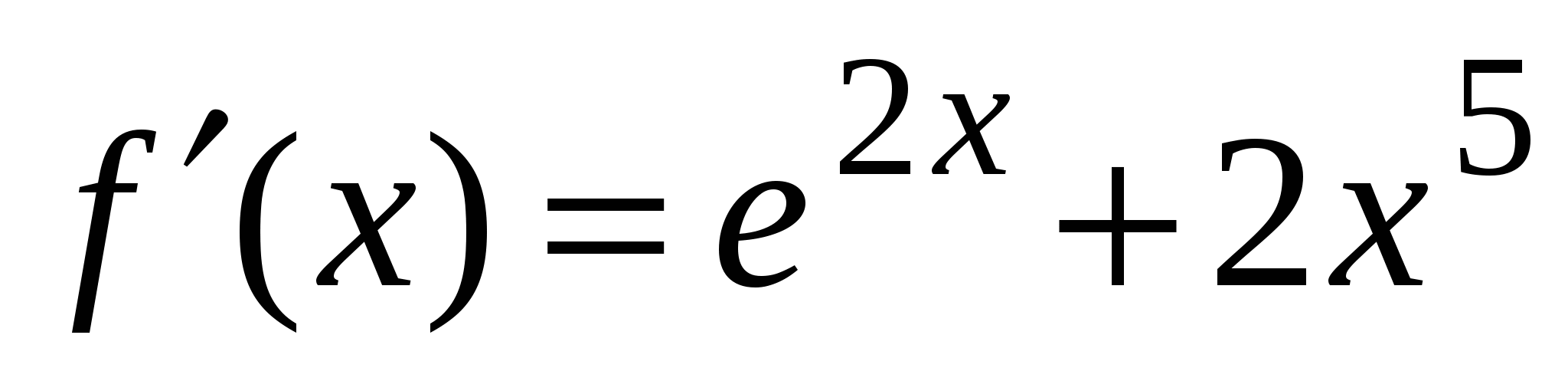
2) 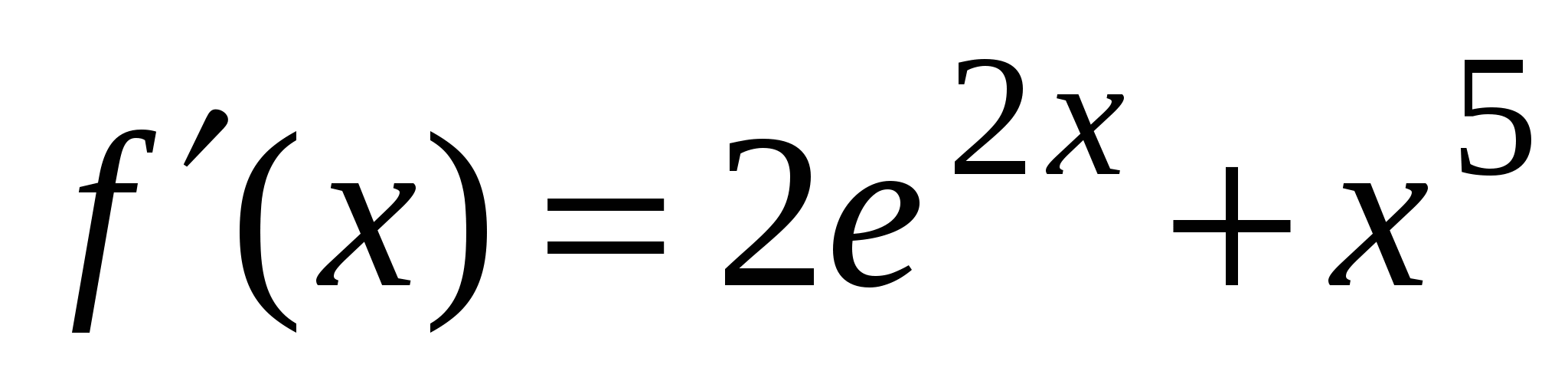
4) 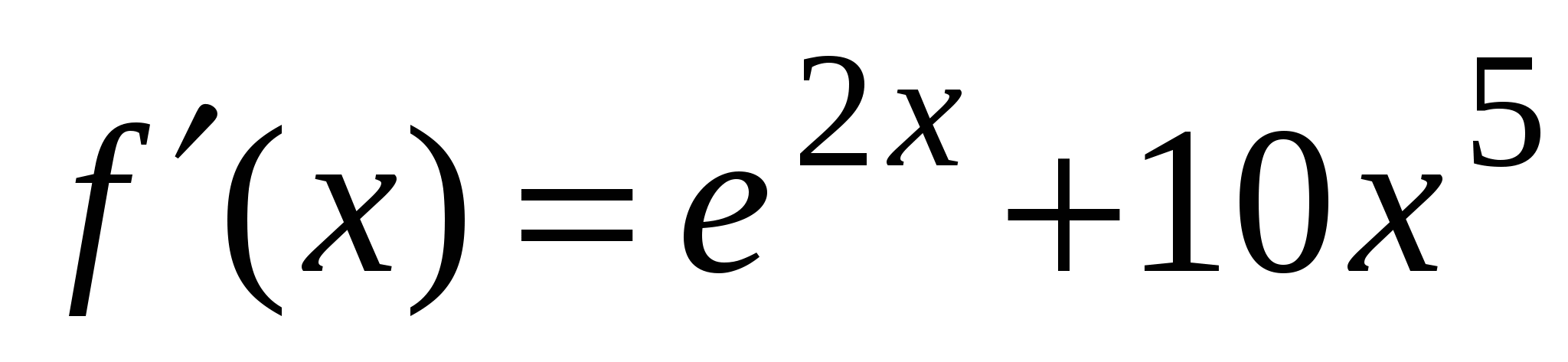
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Найдите производную функции 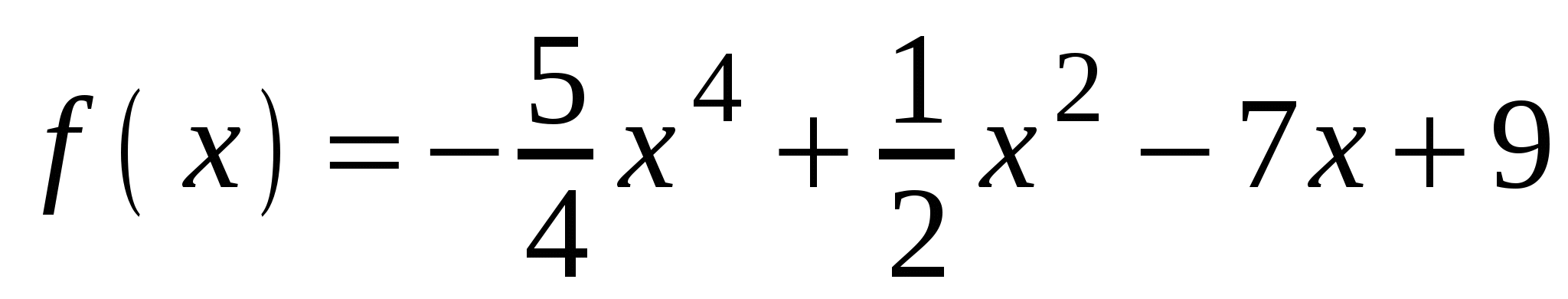 .
.
1)
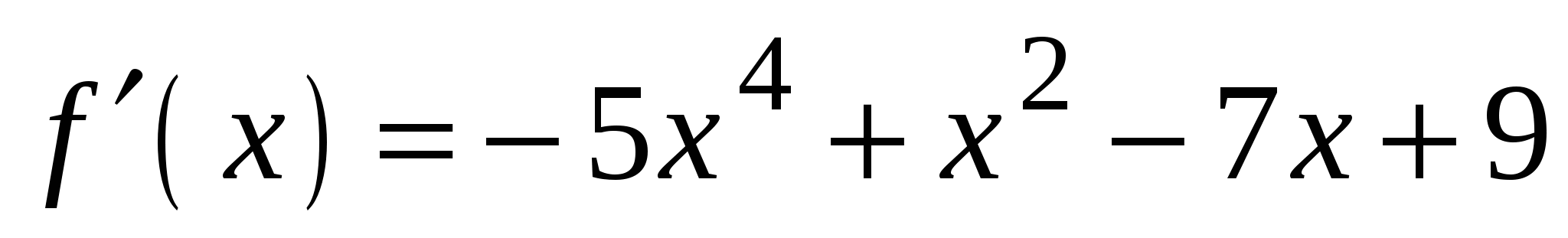
3)
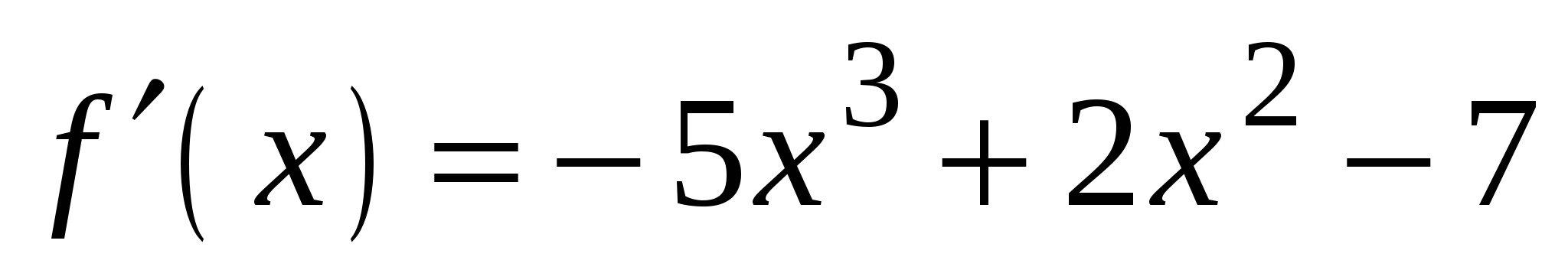
2)
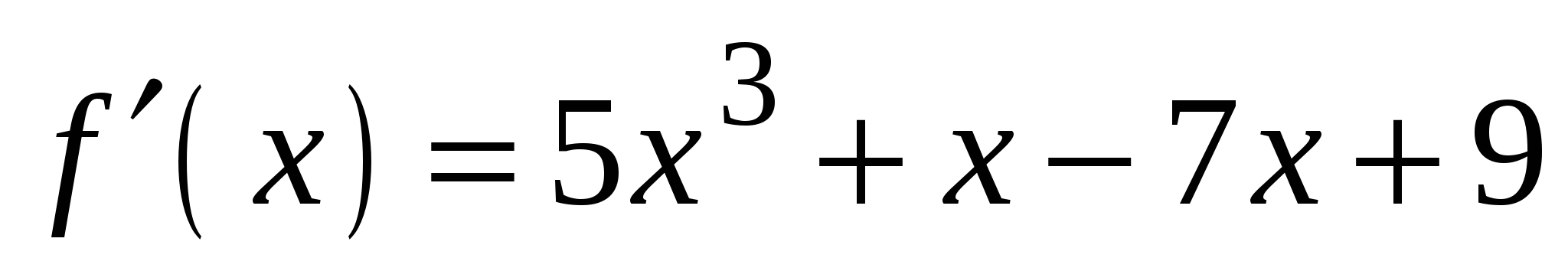
4)
А4. Найдите производную функции 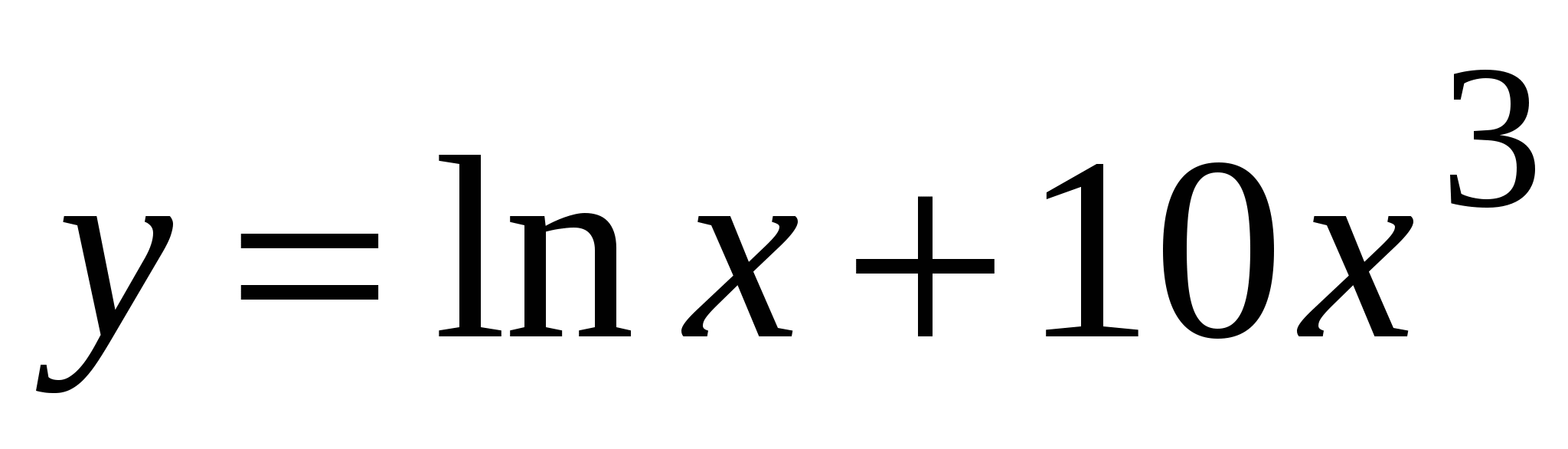 .
.
1)
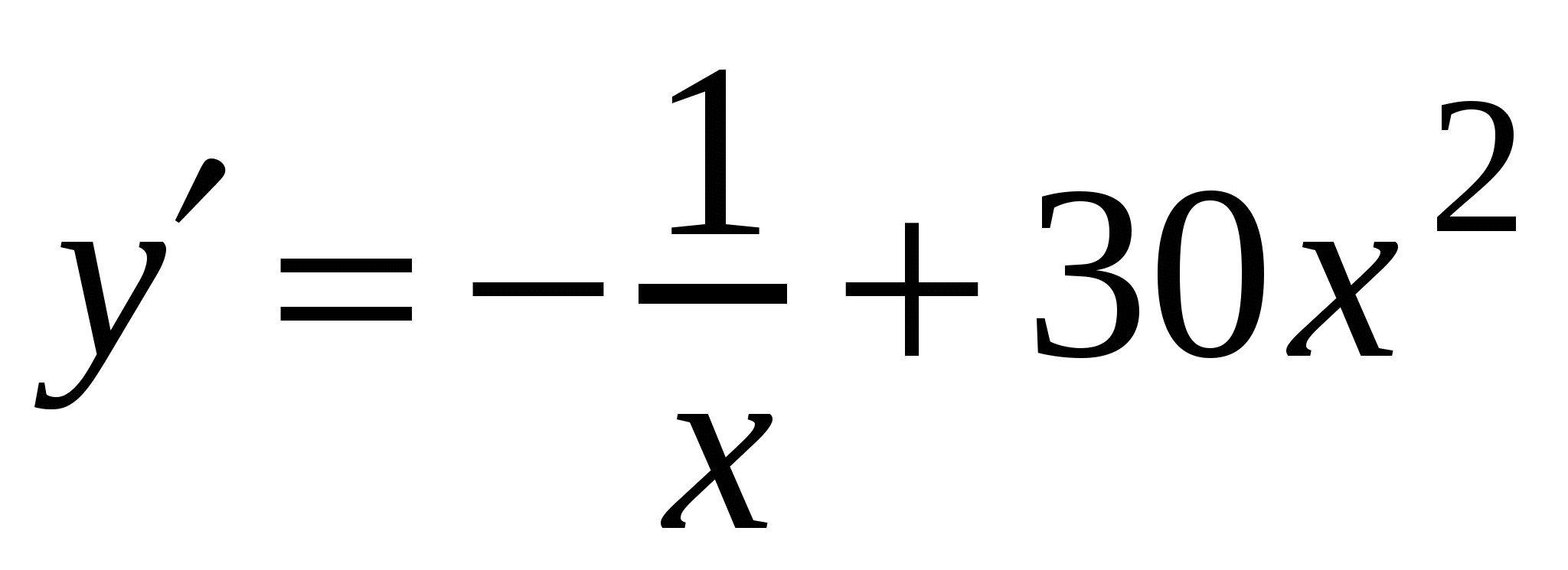
3)
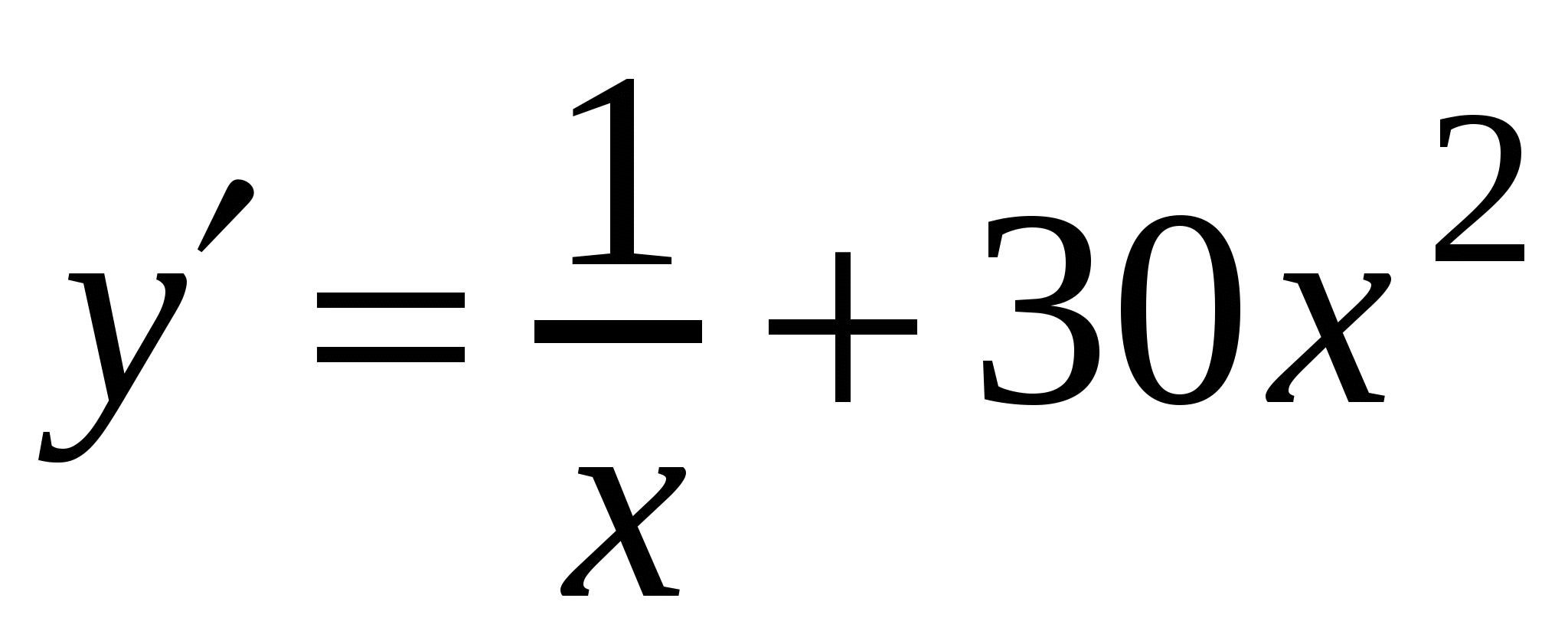
2)
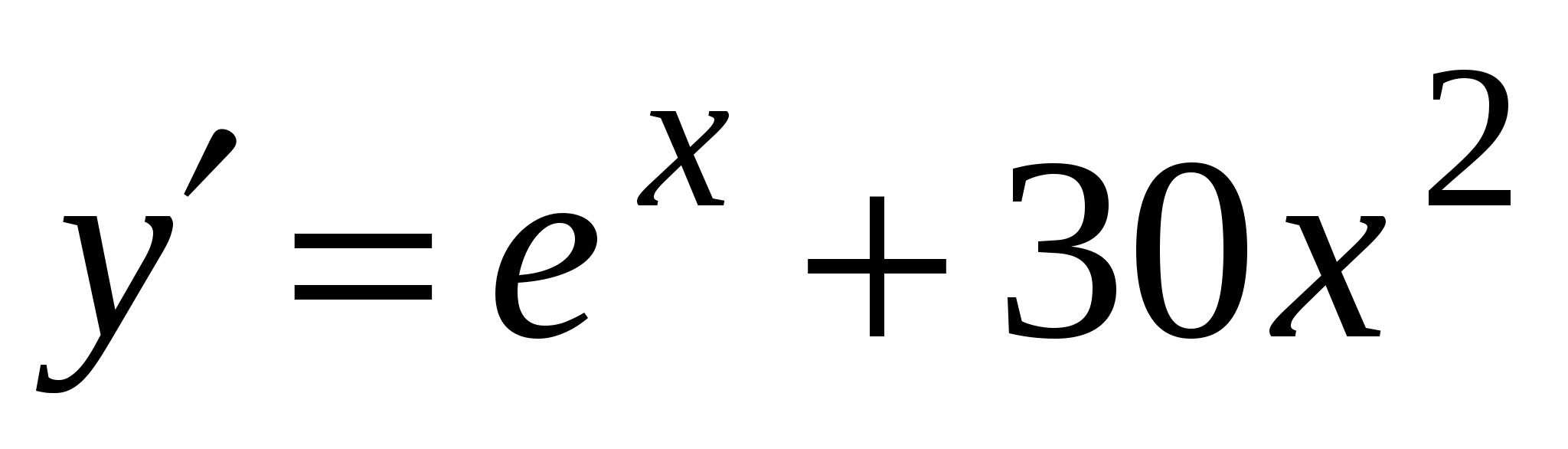
4)
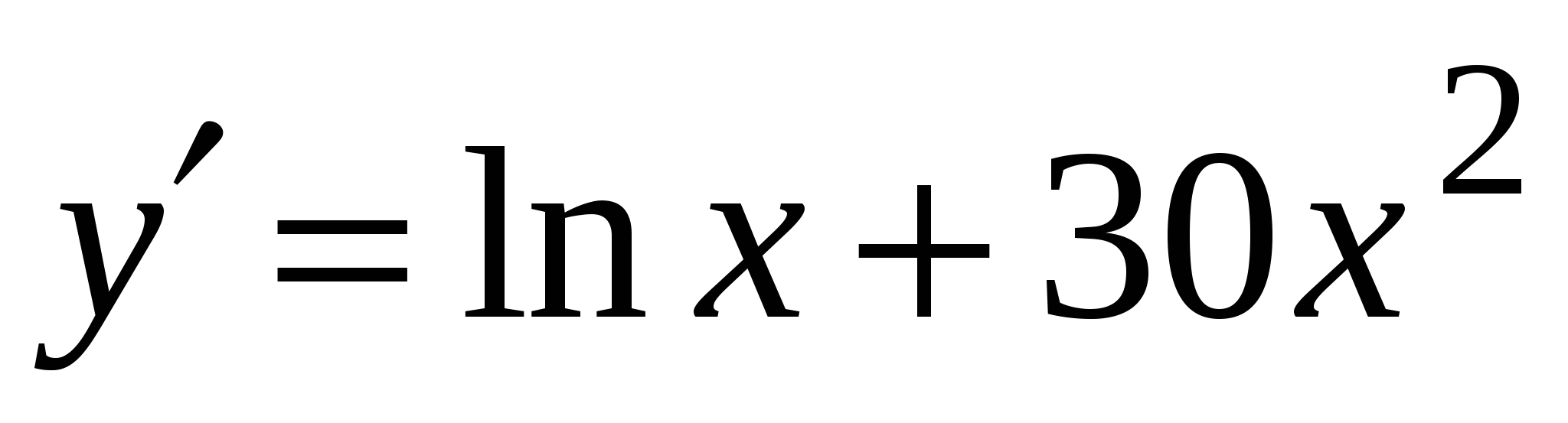

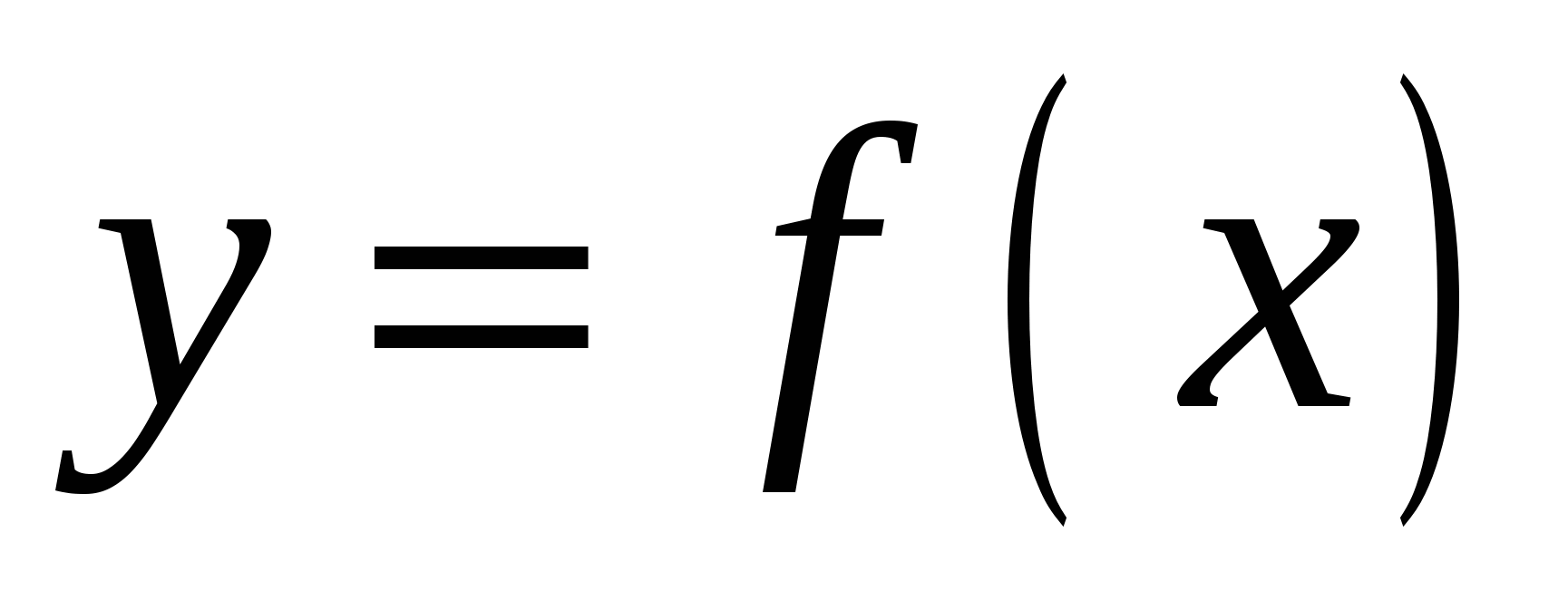 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
.
А5. Найдите производную функции 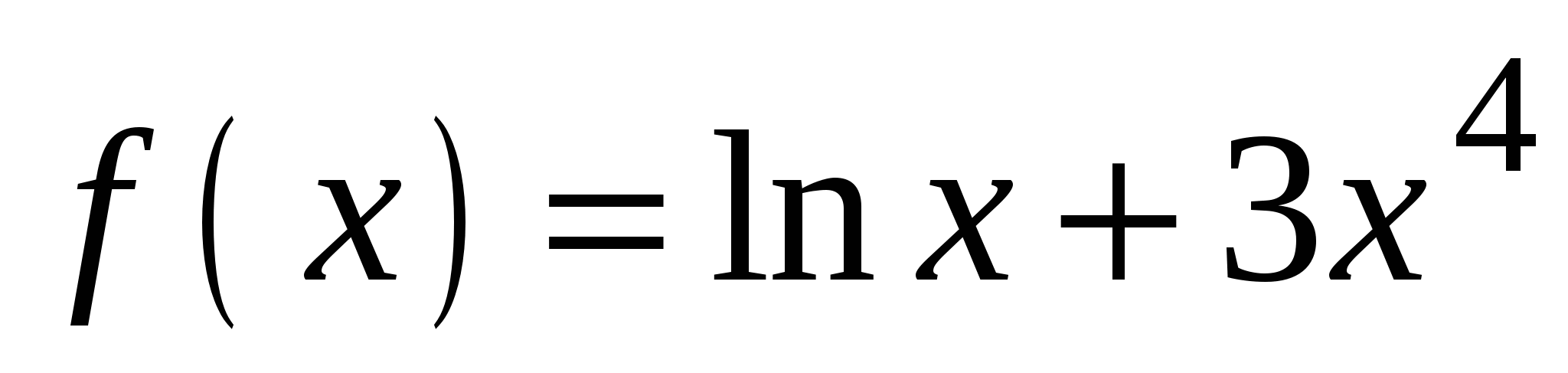 .
.
1)
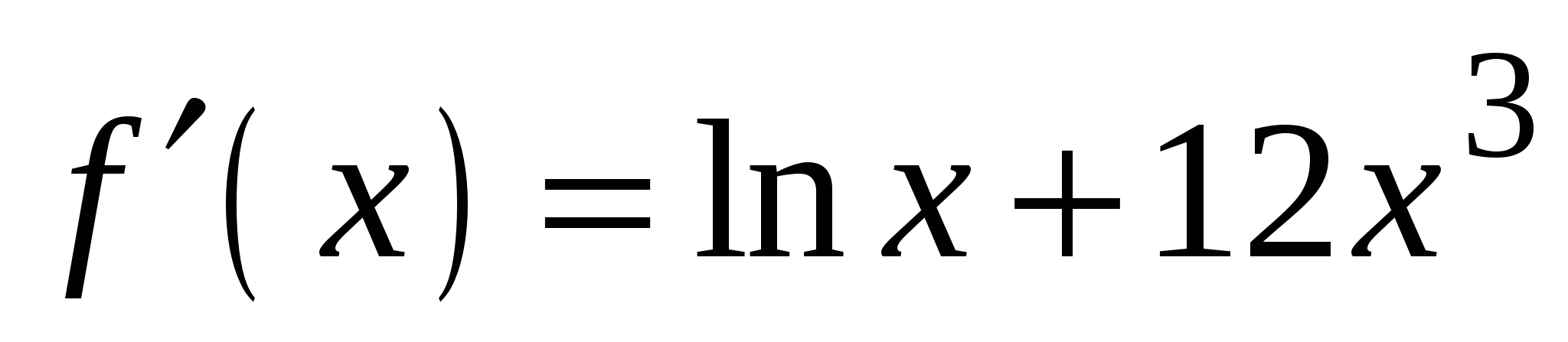
3)
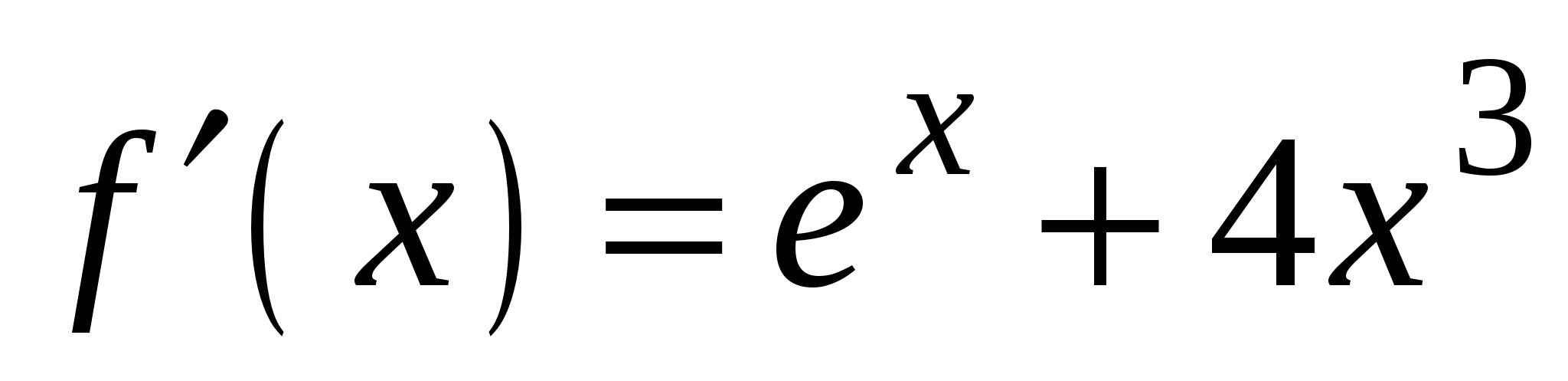
2)
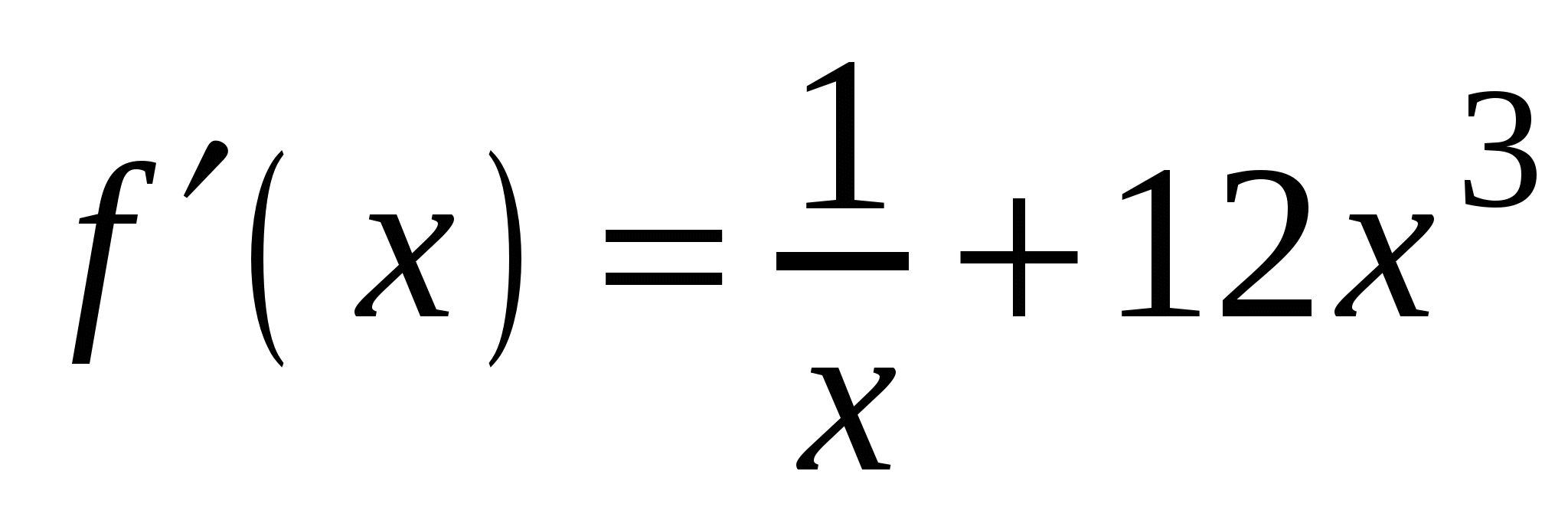
4)
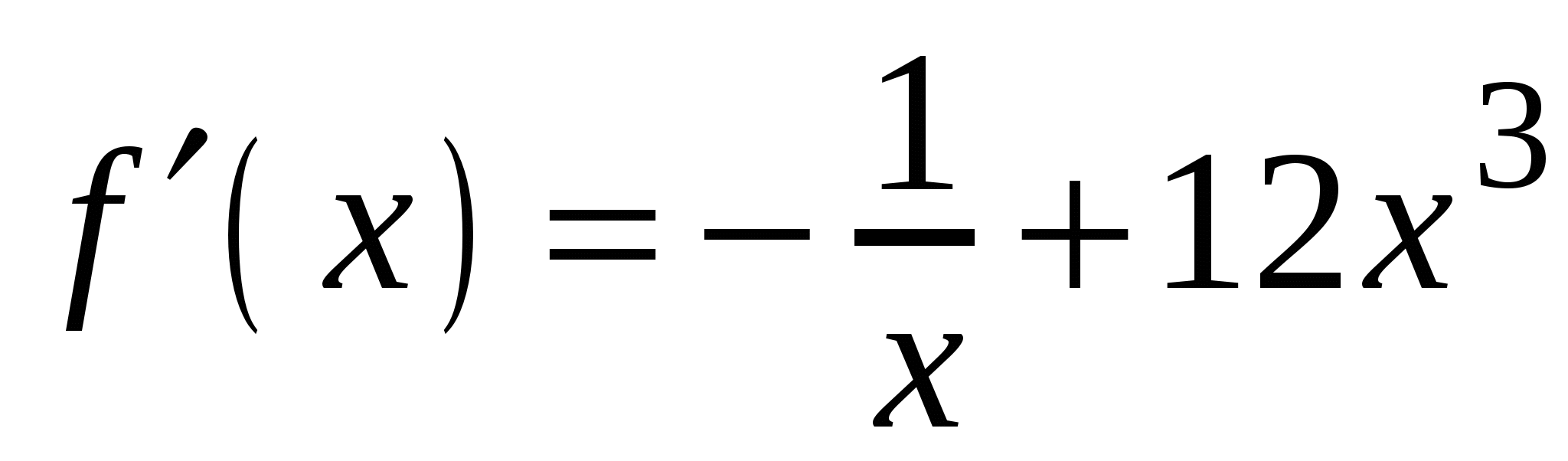

В3. . На рисунке изображен график функции
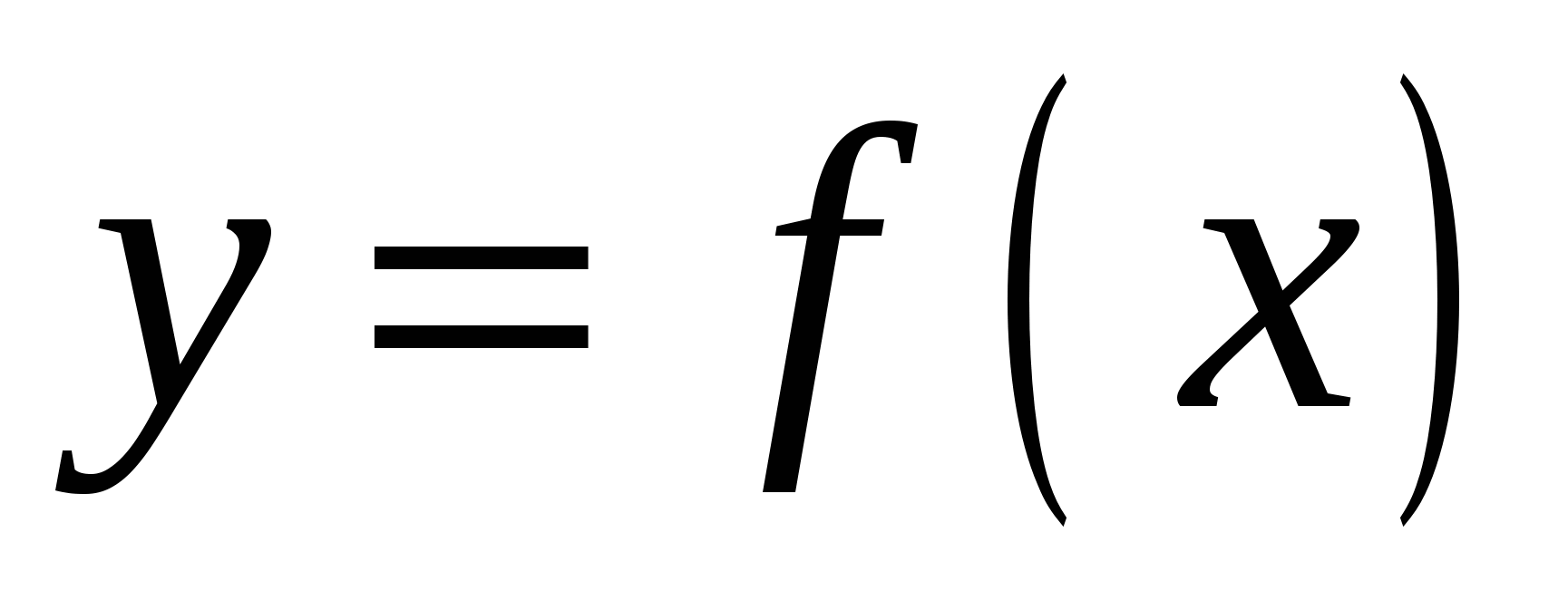 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
.
В4. Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=3/4t4-2/3t3+3t2-21. Чему будет равна мгновенная скорость (м/с) через 3 с после начала движения?
В5.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=3/4t4-2/3t3+3t2-21. Чему будет равна мгновенная скорость (м/с) через 3 с после начала движения?
В6.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=2t4-1/3t3+5t2-4. Чему будет равна мгновенная скорость (м/с) через 2 с после начала движения?
Контрольная работа №3 по теме: «Производная»
Вариант №5
B1 Функция  задана на промежутке
задана на промежутке  . На рисунке изображен график ее производной
. На рисунке изображен график ее производной  . Найдите количество точек минимума функции
. Найдите количество точек минимума функции  на данном промежутке
на данном промежутке

А1. Найдите производную функции 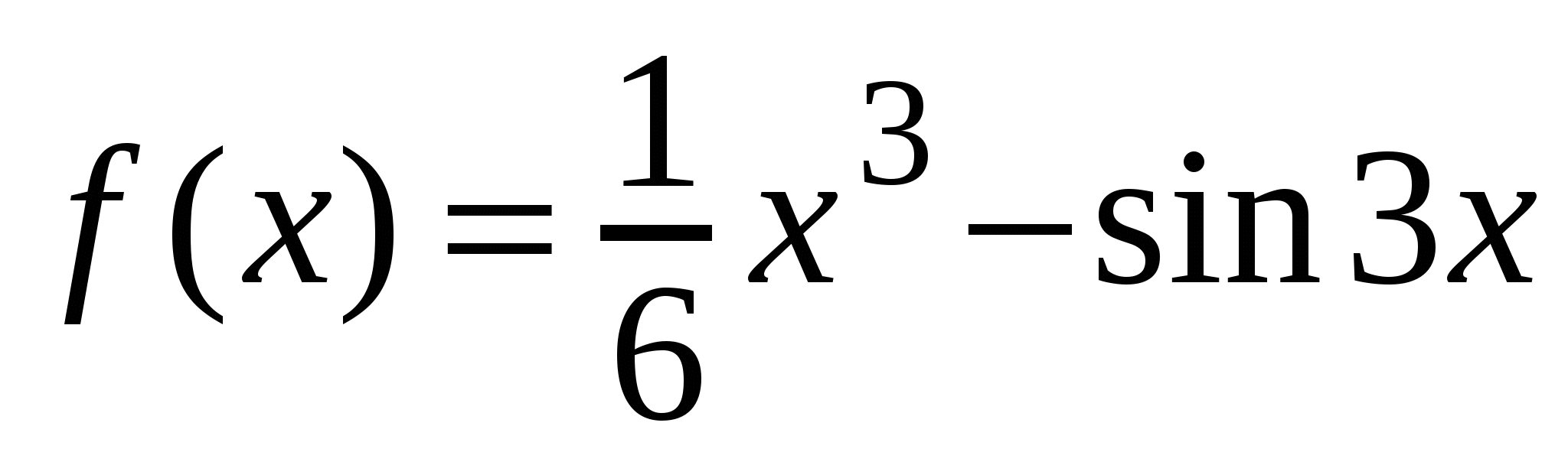 .
.
1) 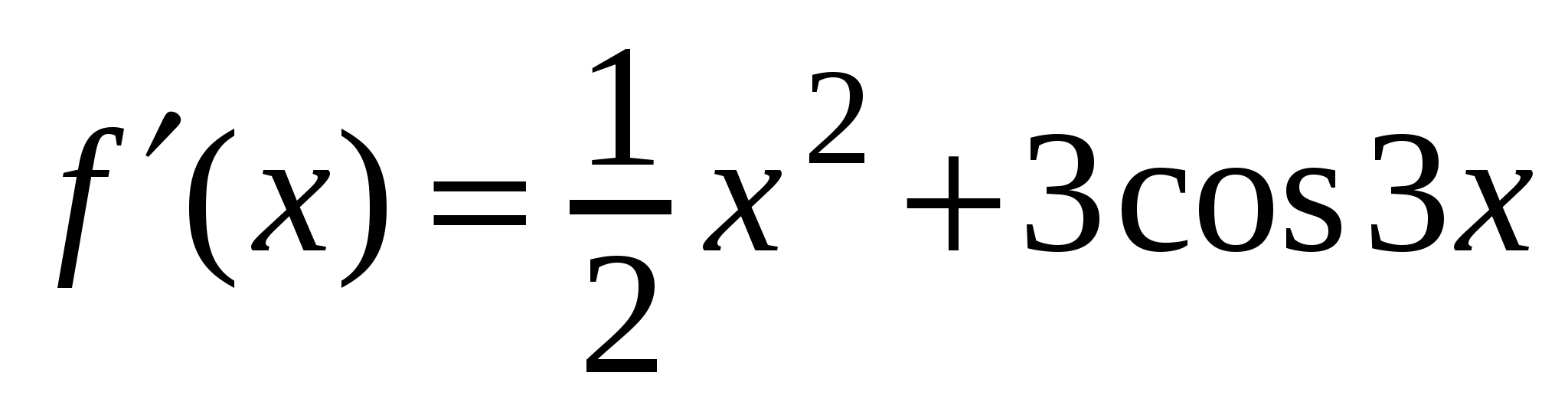
3) 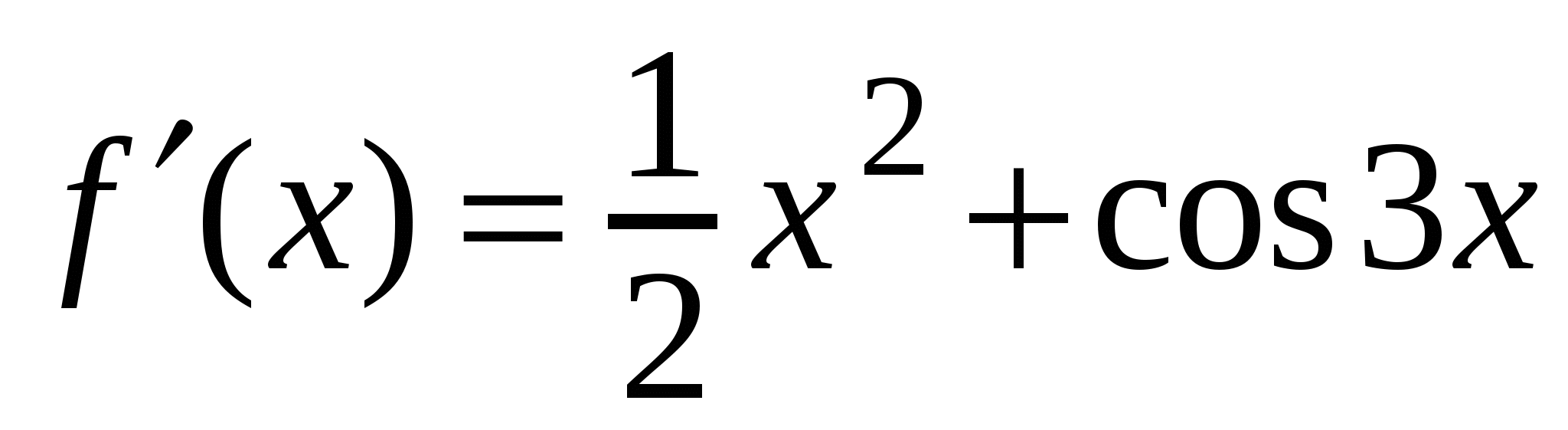
2) 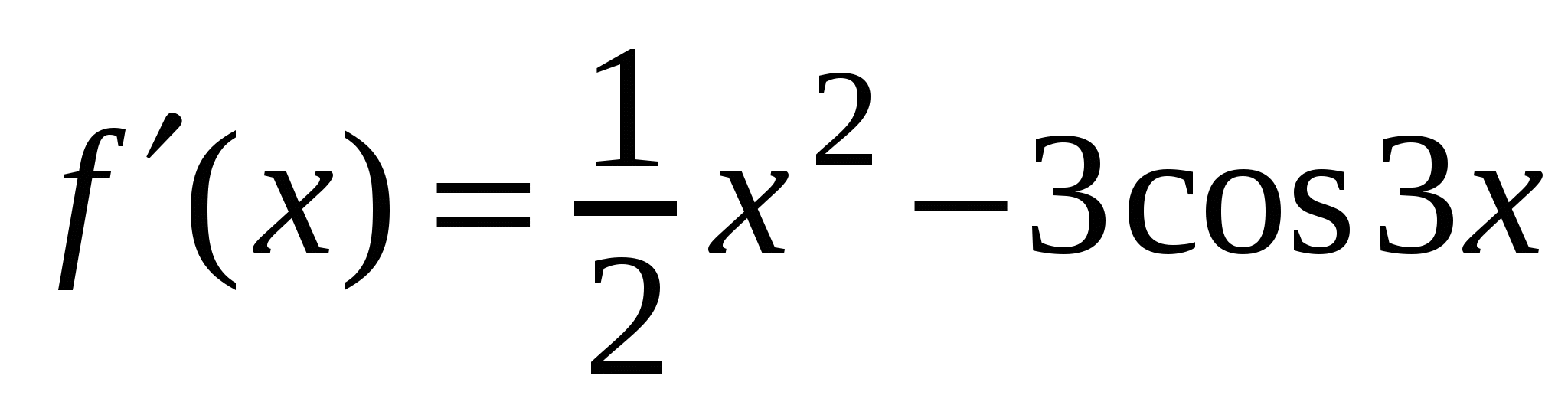
4) 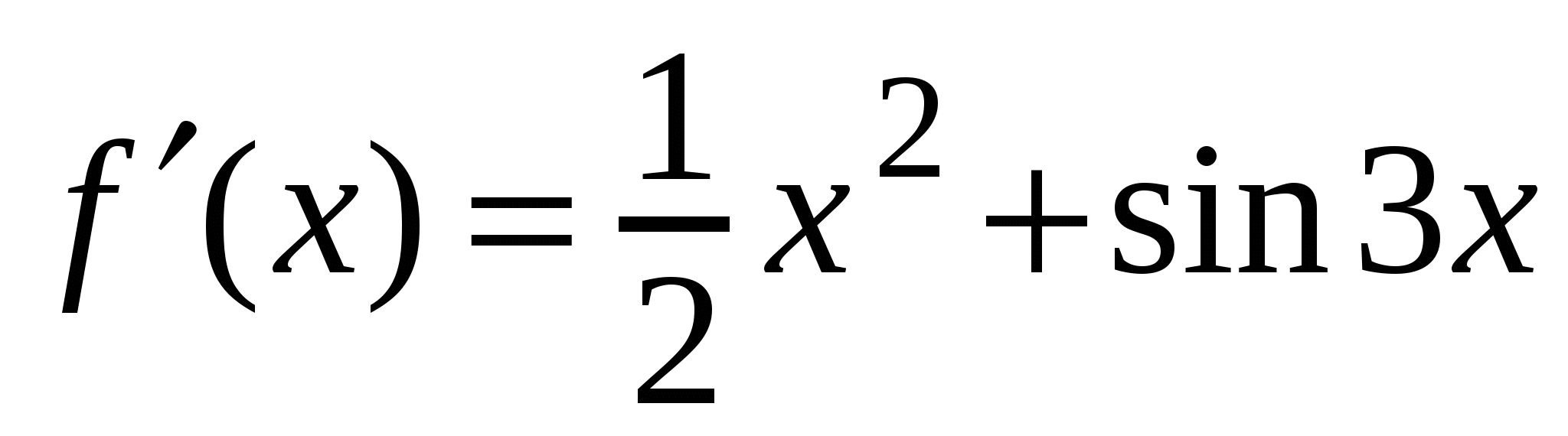
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Вычислите значение производной функции 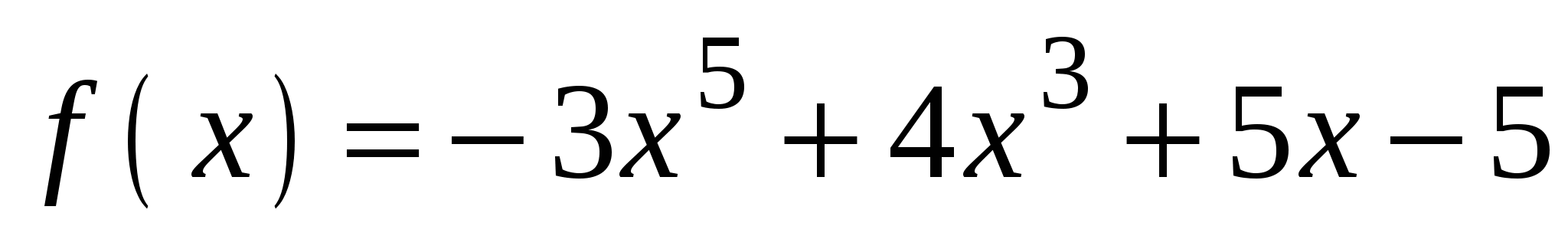 в точке
в точке 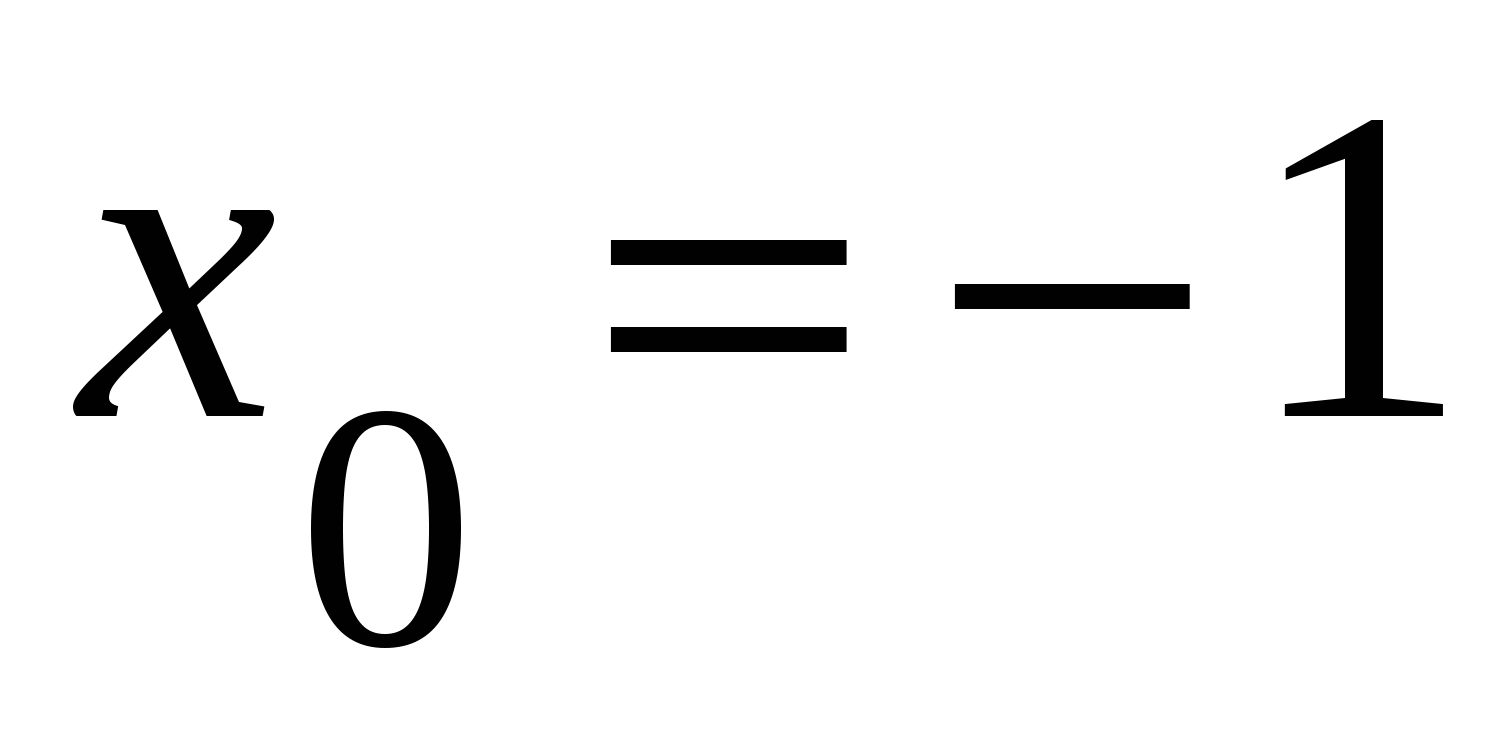 .
.
1)
8
2)
2
3)
3
4)
− 22
А4. Найдите производную функции 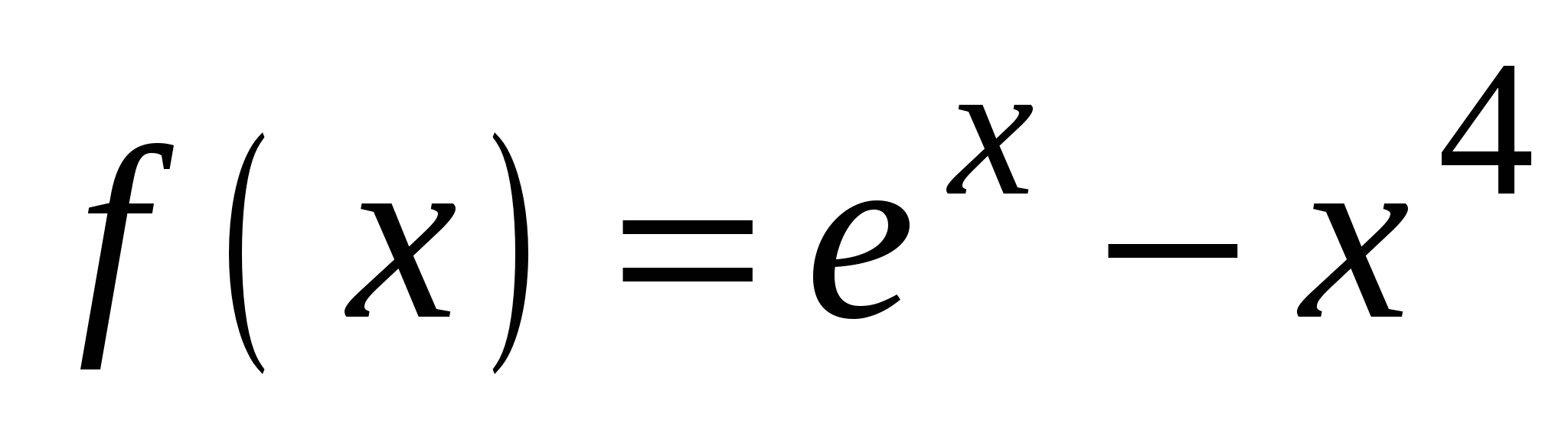 .
.
1)
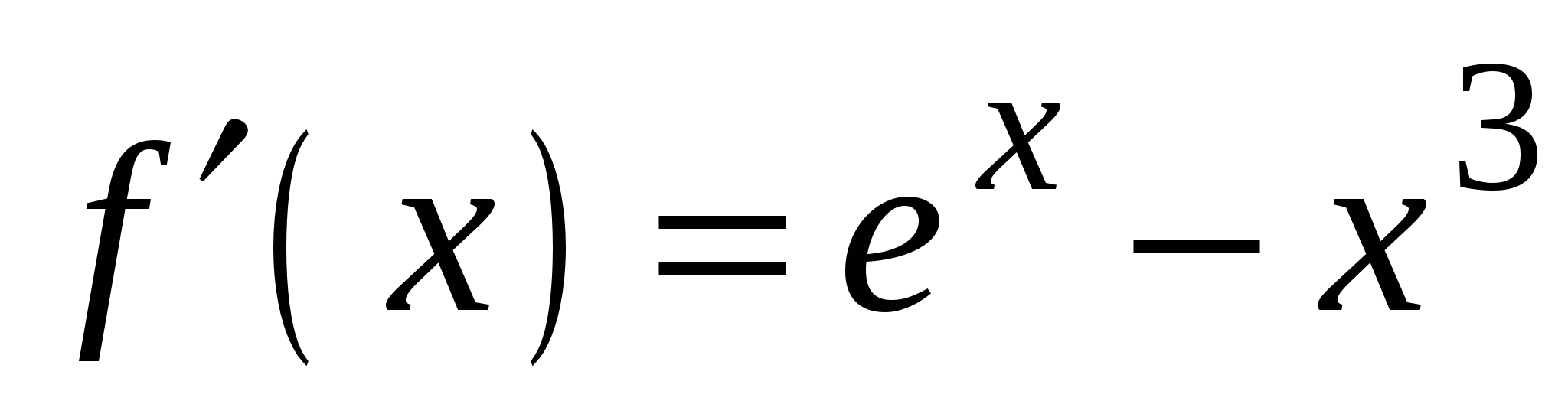
3)
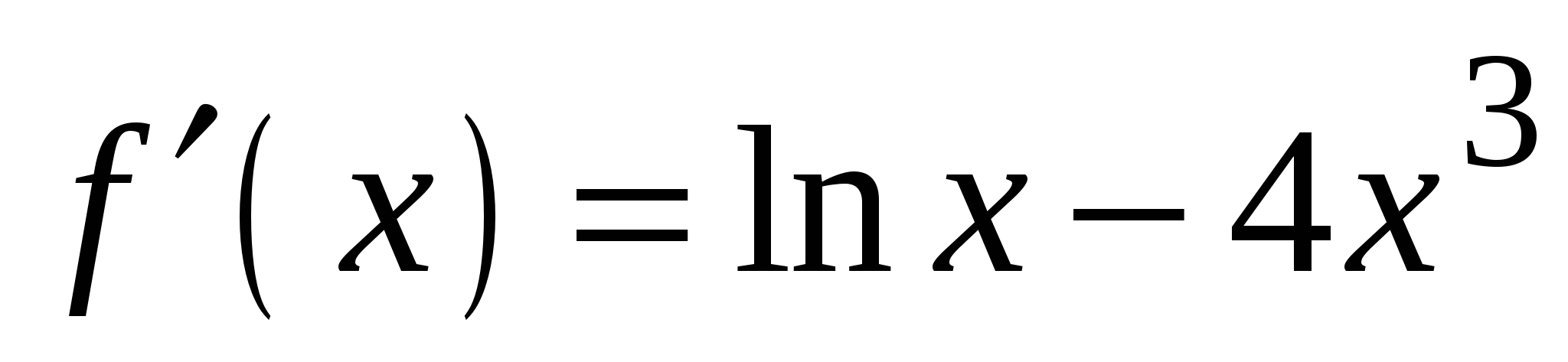
2)
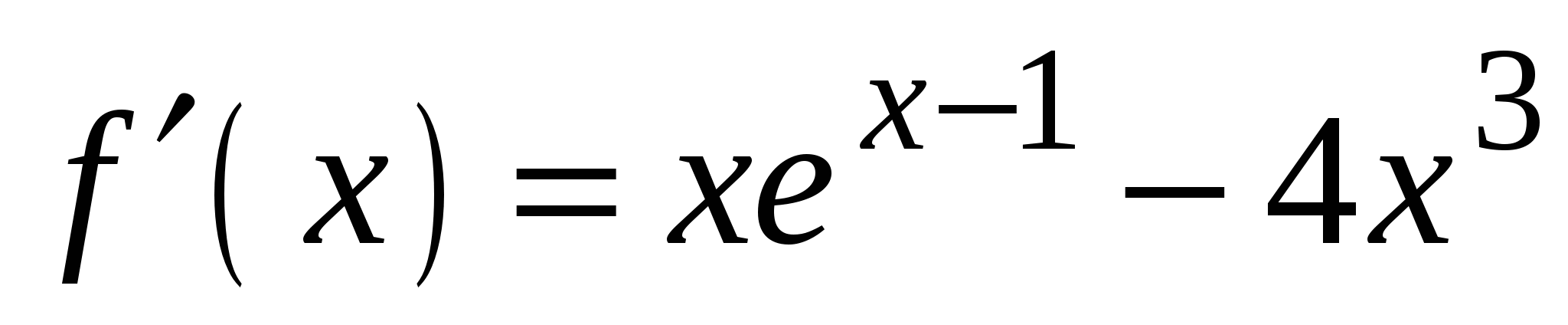
4)
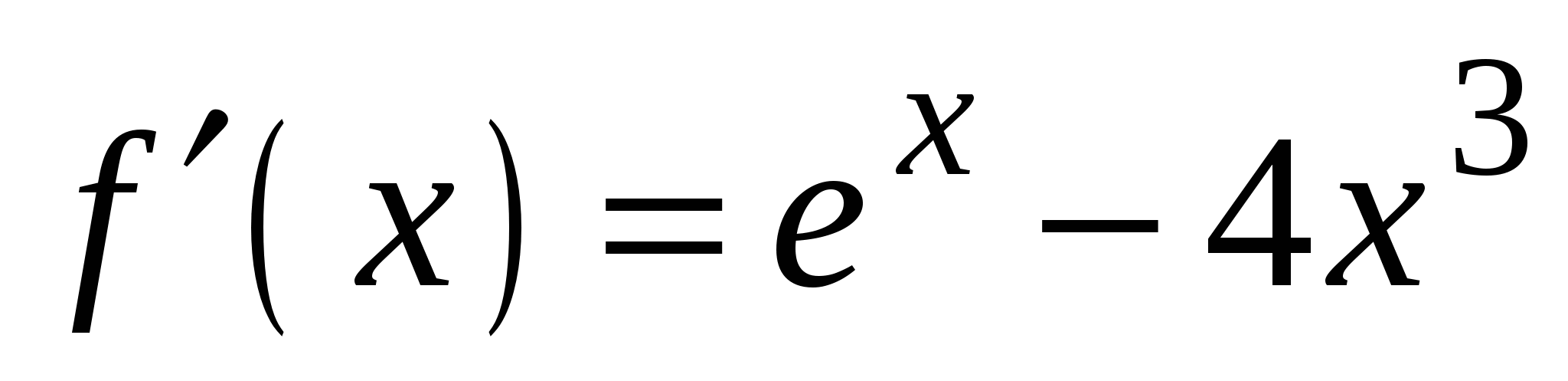

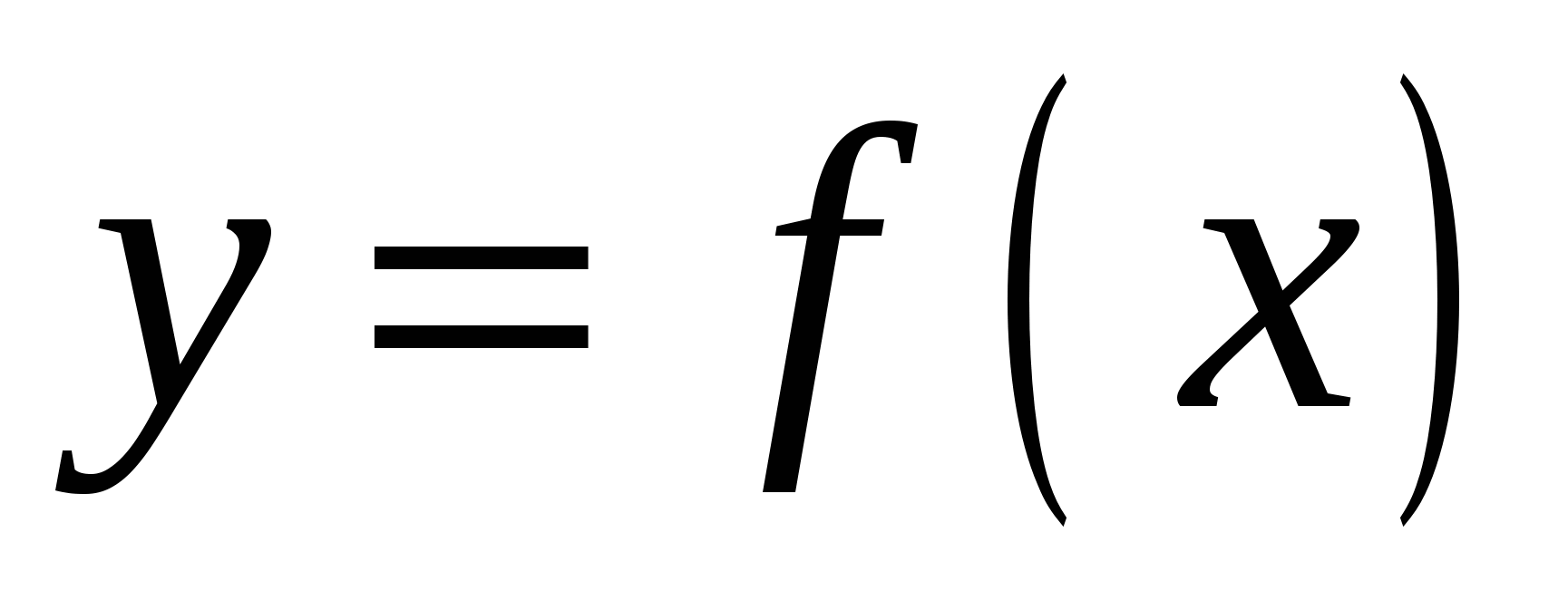 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. А5. Найдите производную функции 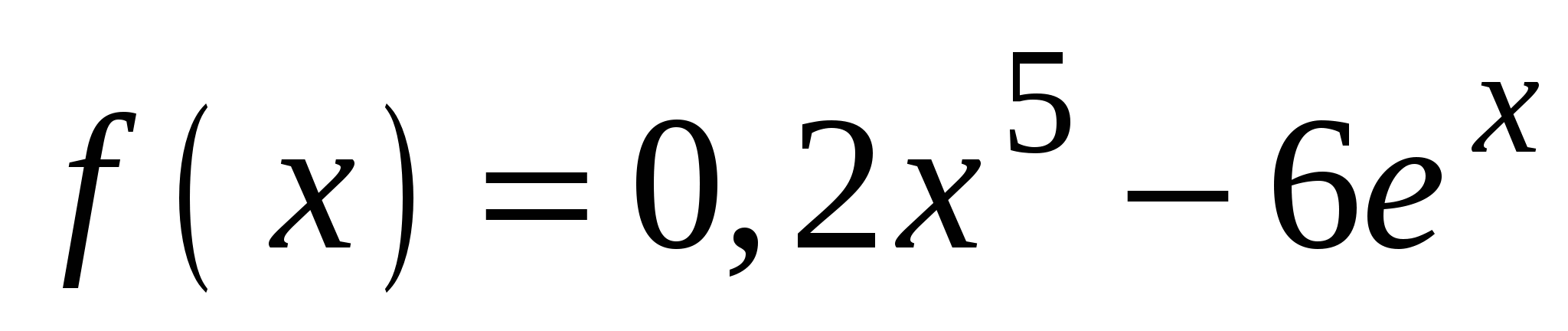 .
.
1)
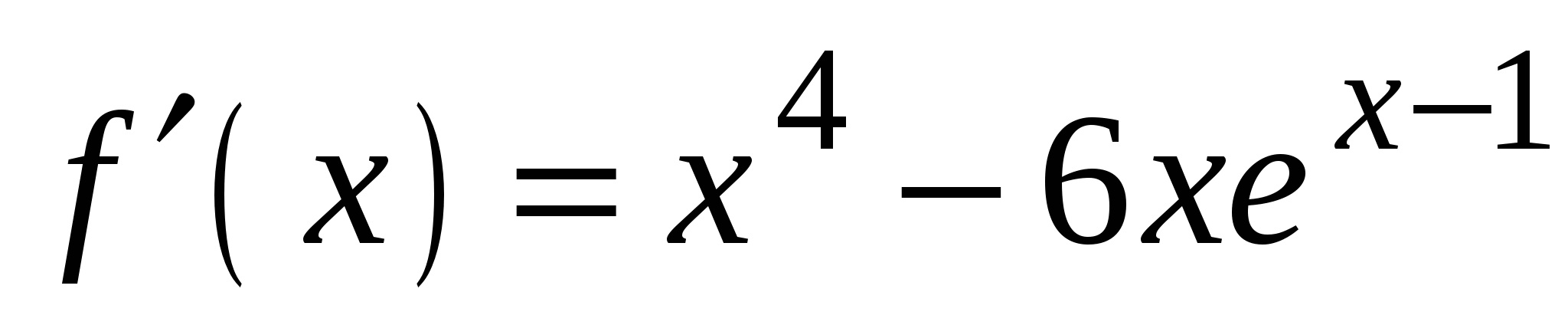
3)
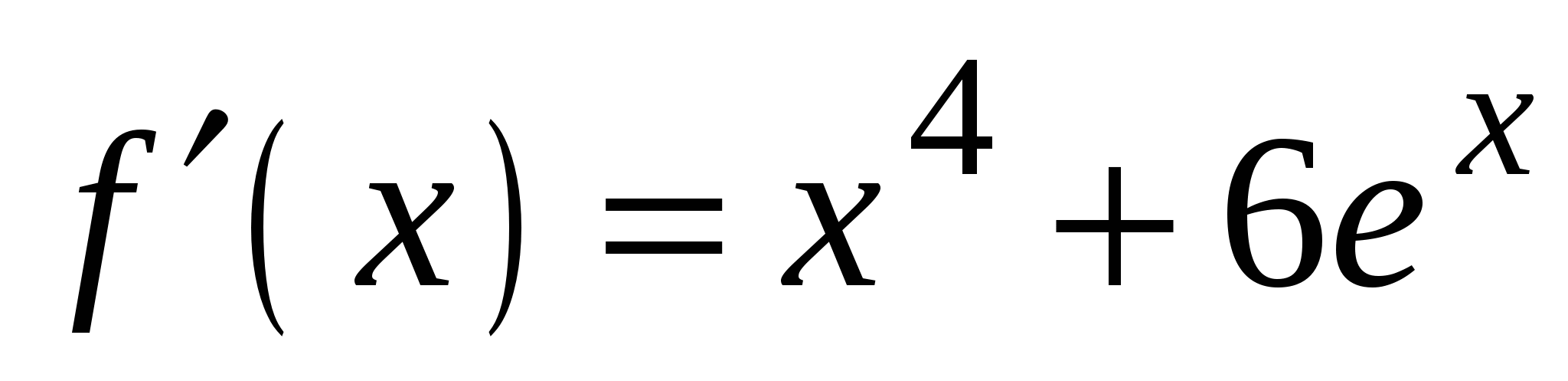
2)
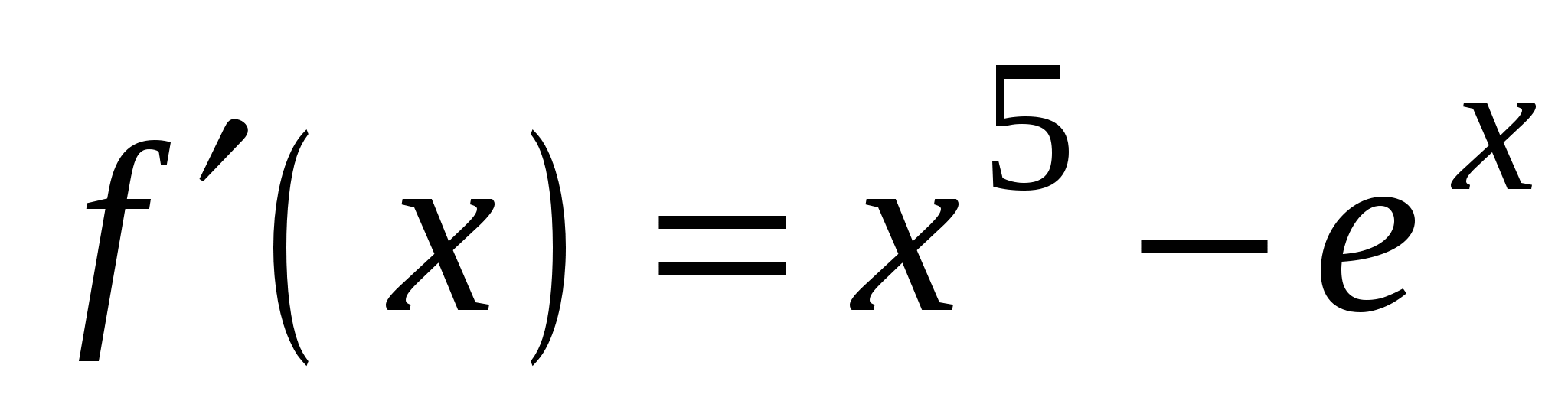
4)
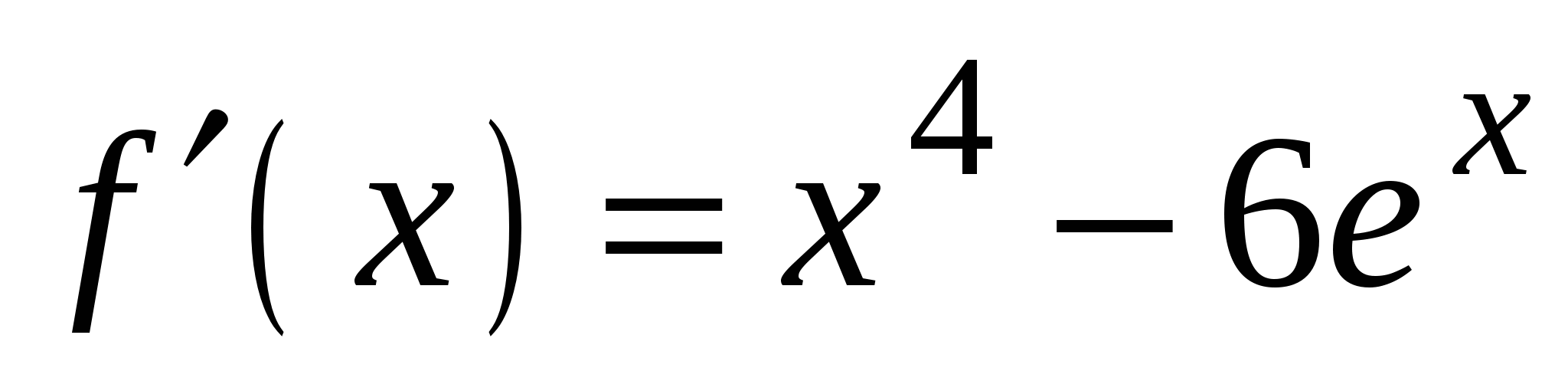

 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. В4. Материальная точка движется по закону х(t)=1/4 t3-3t2+21t - 18 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 3 м/с2 ?
В5.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=6t2 - 18t+19. Через сколько секунд после начала движения произойдет остановка?
В6. Материальная точка движется по закону х(t)=1/6 t3-4t2+35t - 11 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 2 м/с2 ?
Контрольная работа №3 по теме: «Производная»
Вариант №6

B1. Функция  определена на промежутке
определена на промежутке  . Используя изображенный на рисунке график производной
. Используя изображенный на рисунке график производной  , найдите угол наклона касательной к графику функции
, найдите угол наклона касательной к графику функции  в точке
в точке  . Ответ укажите в градусах
. Ответ укажите в градусах
А1. Найдите производную функции 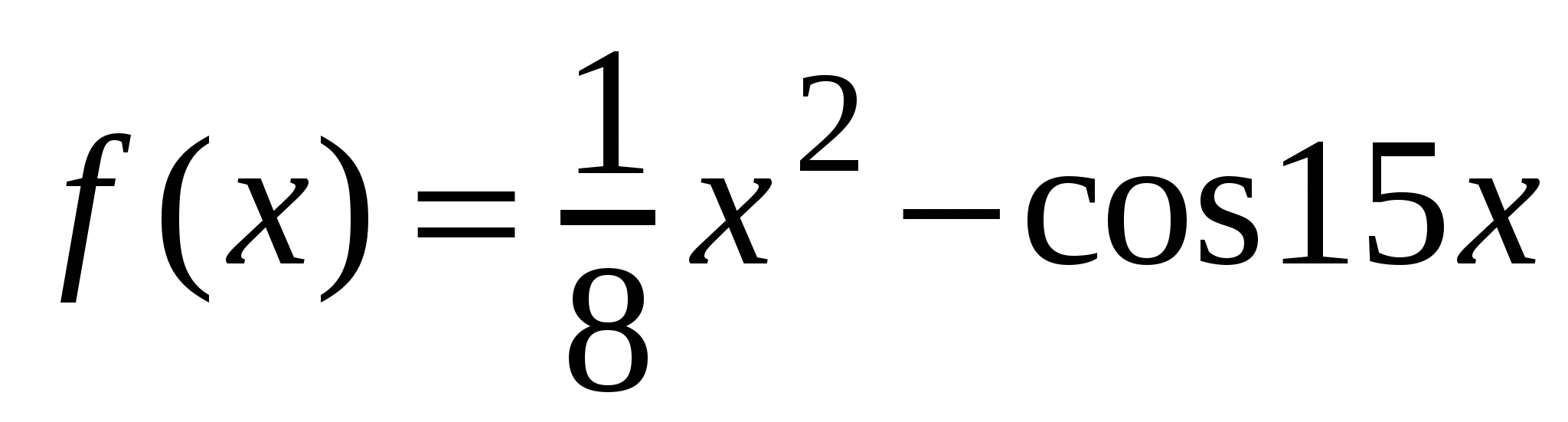 .
.
1) 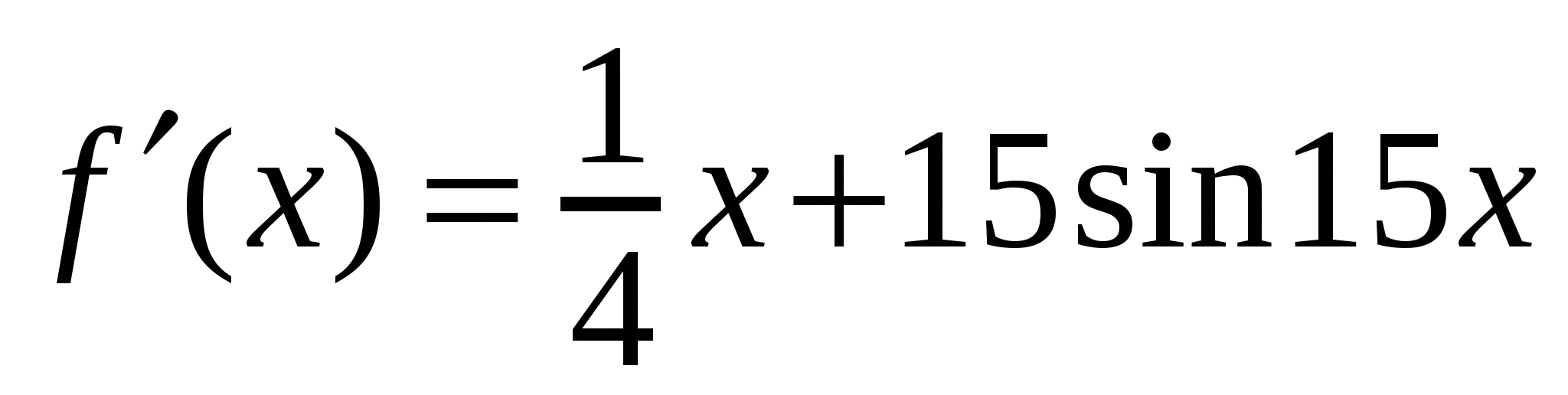
3) 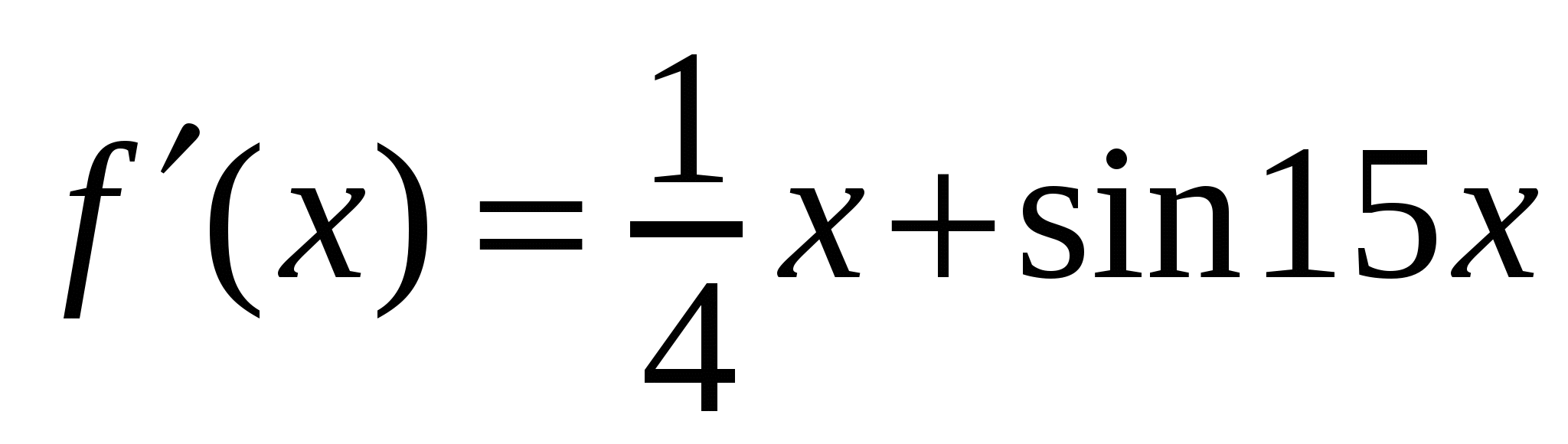
2) 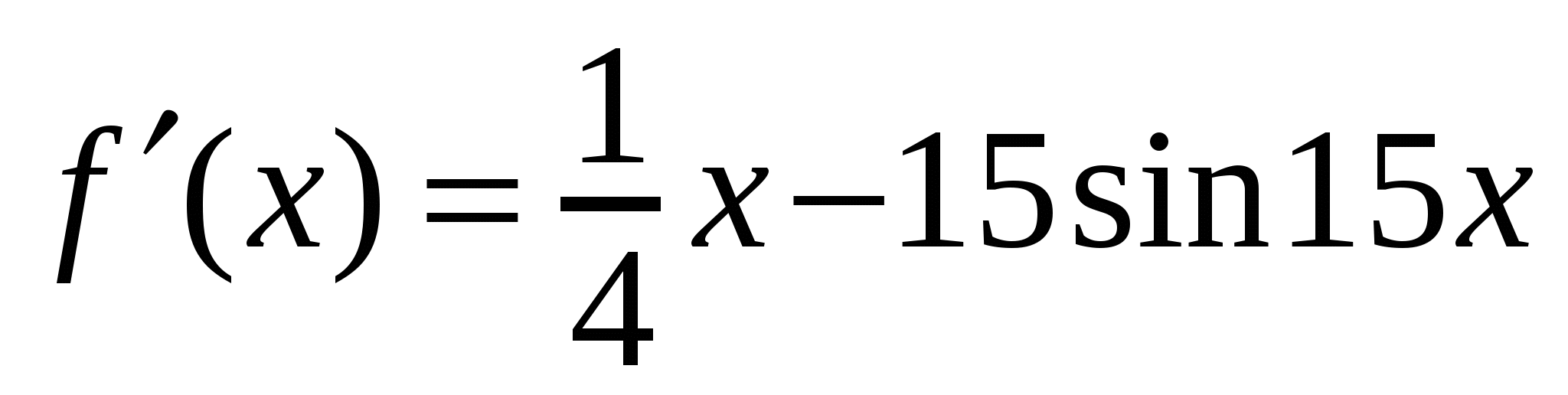
4) 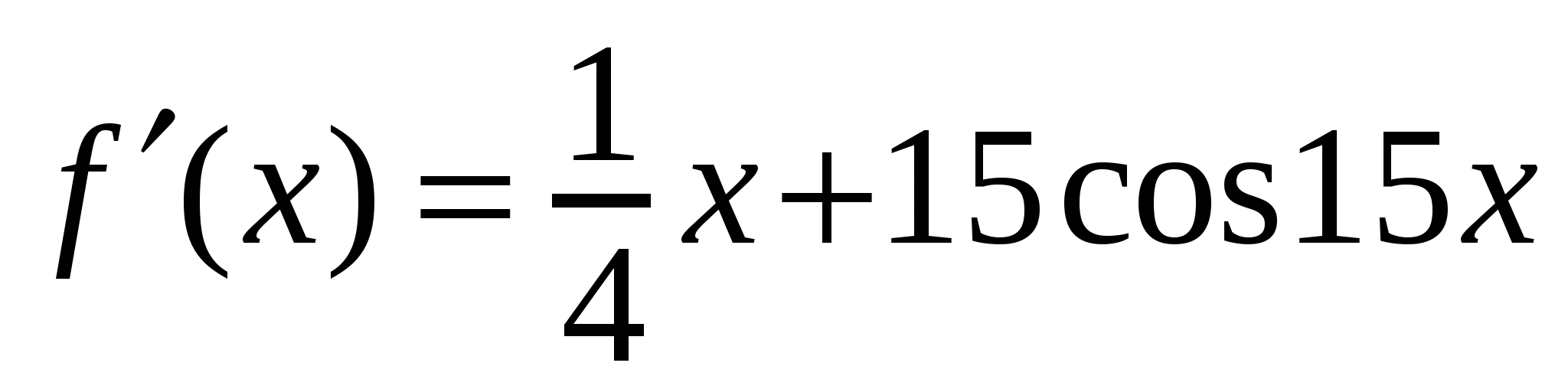
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Найдите производную функции 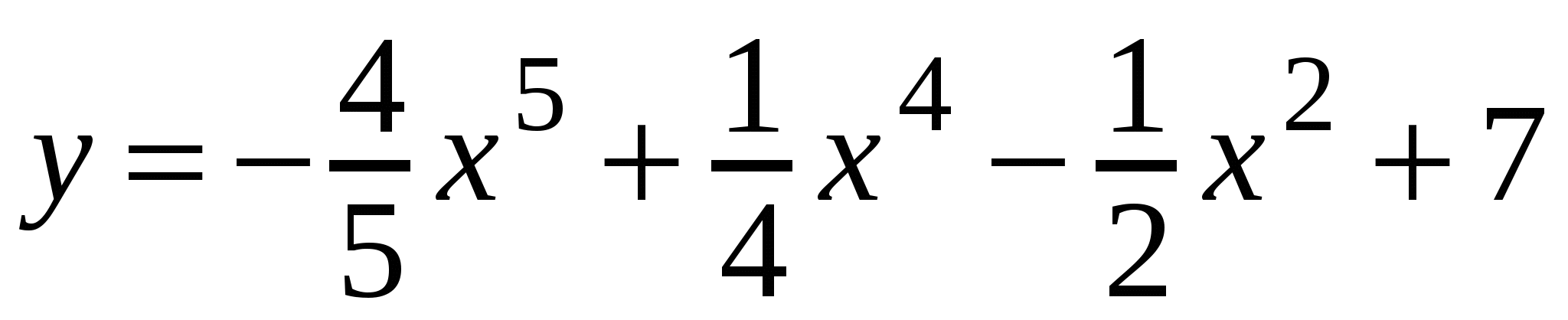 .
.
1)
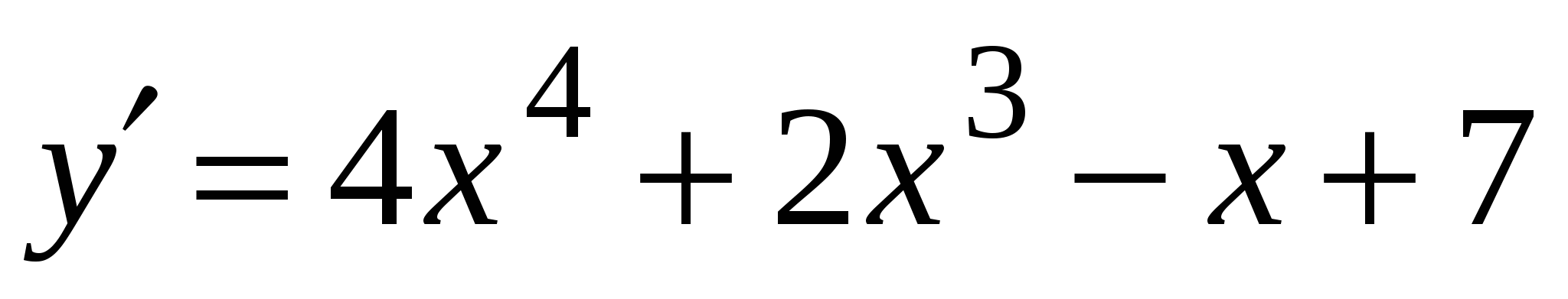
3)
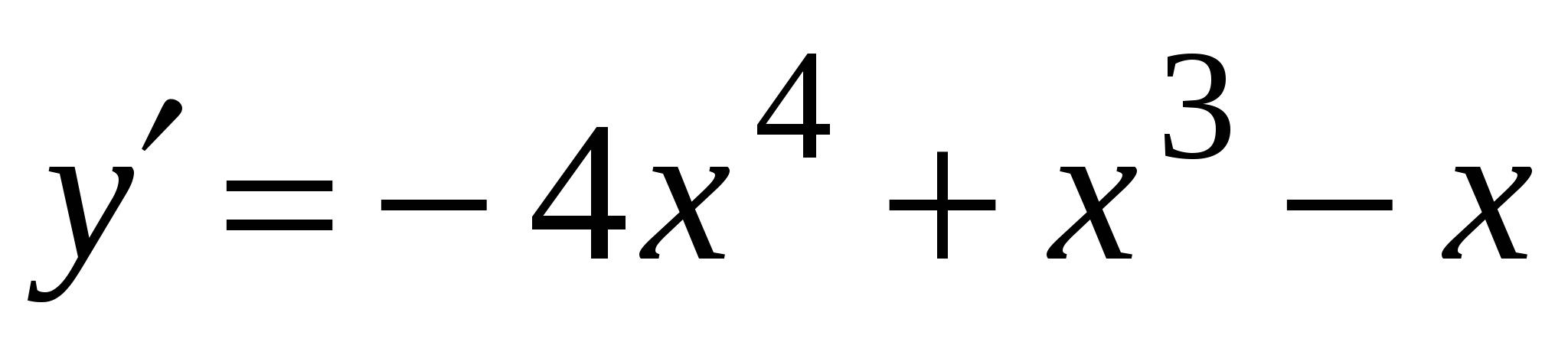
2)
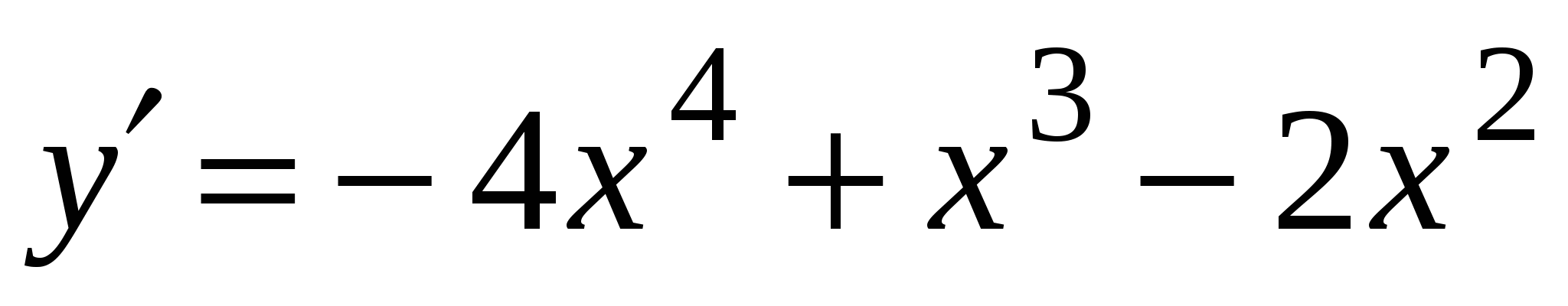
4)
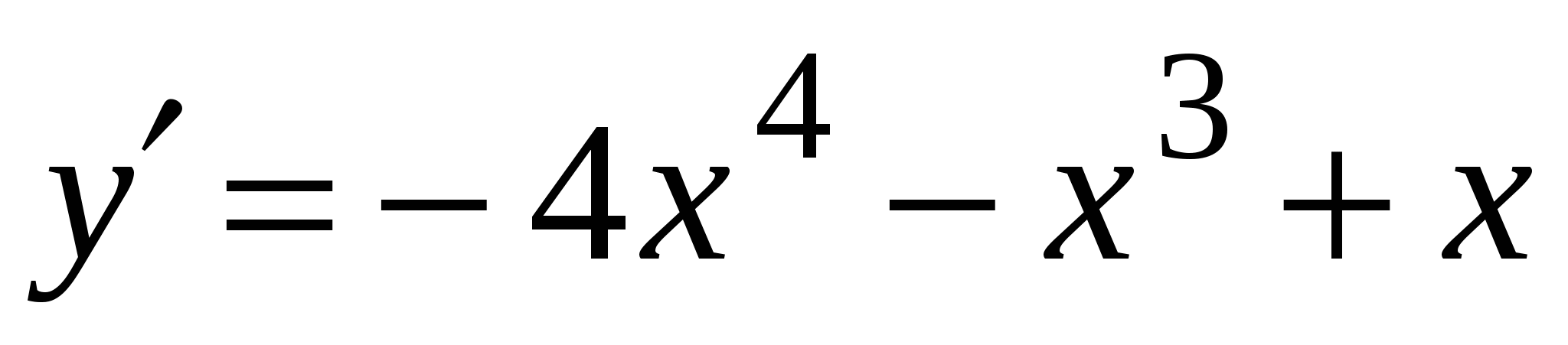
А4. Найдите производную функции 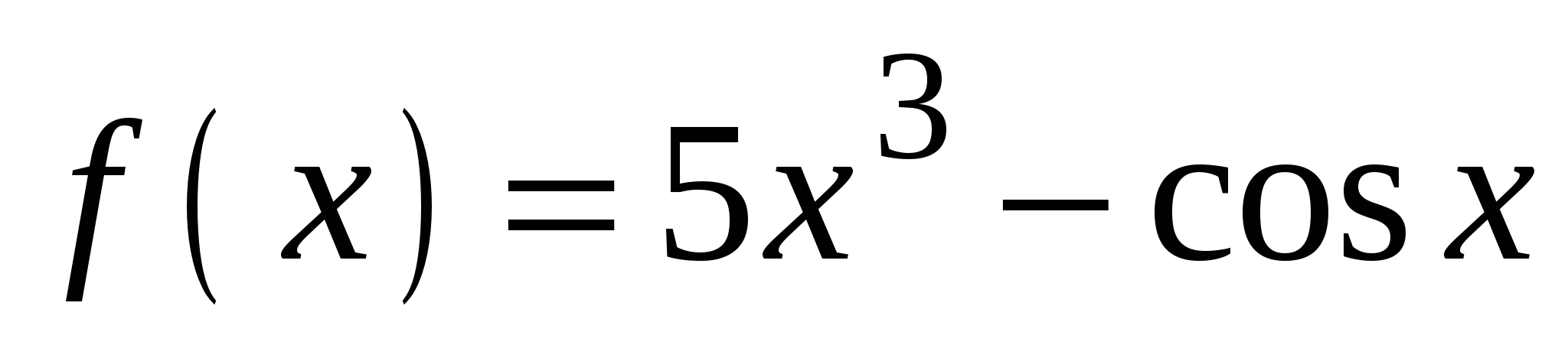 .
.
1)
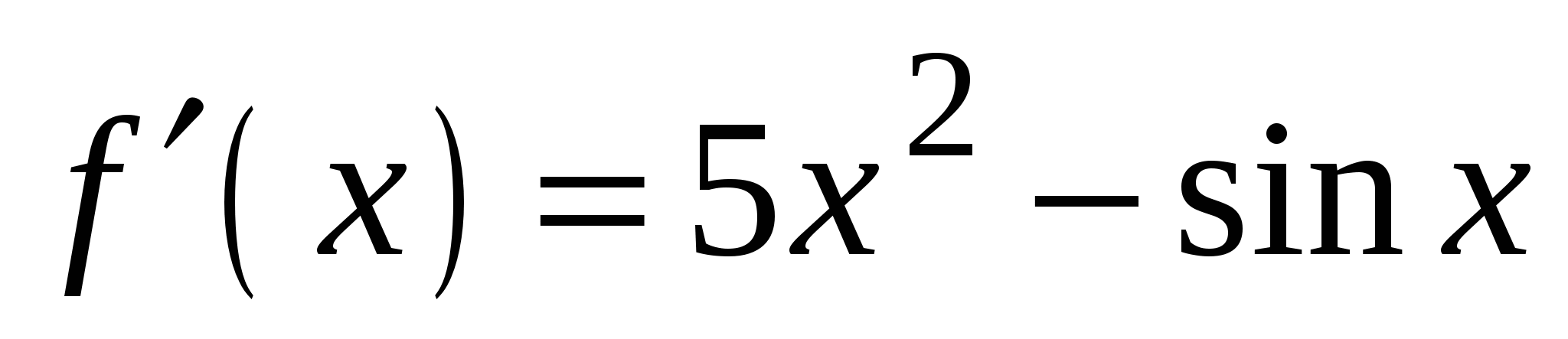
3)
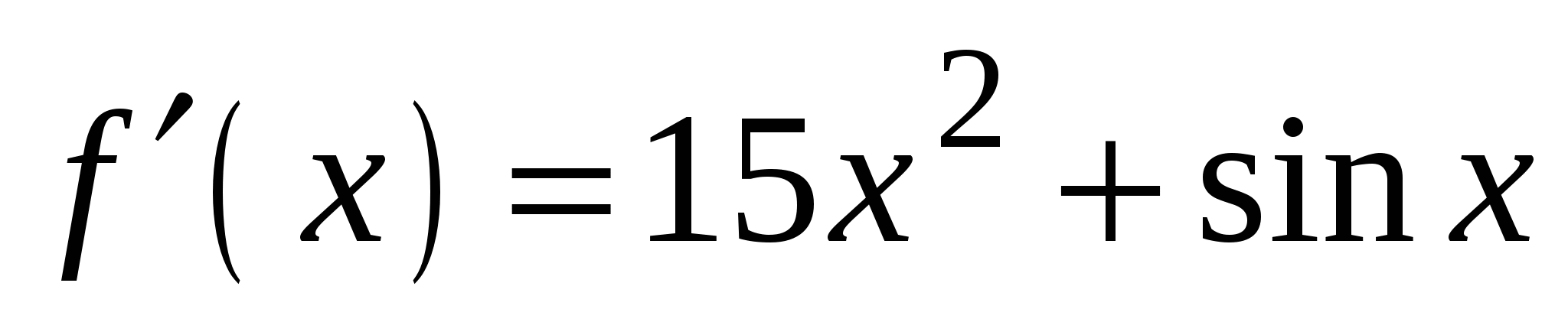
2)
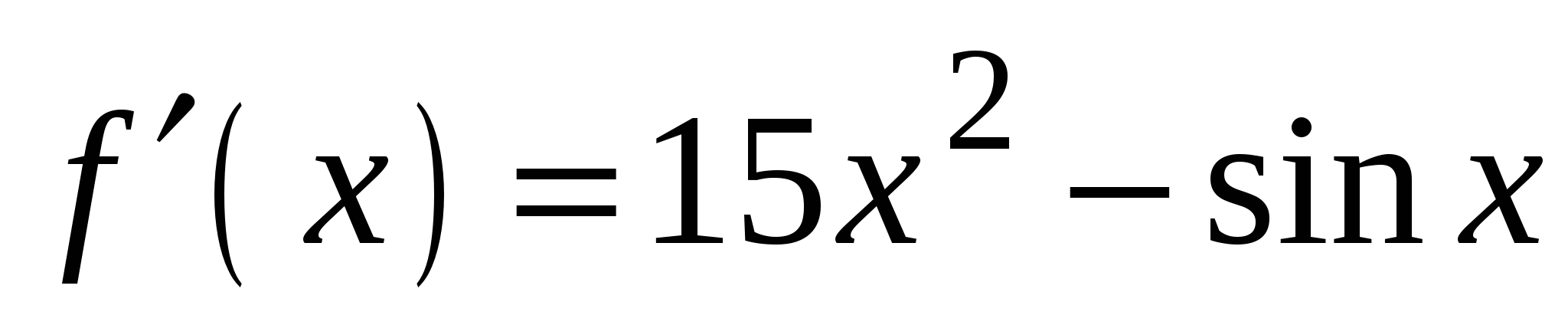
4)
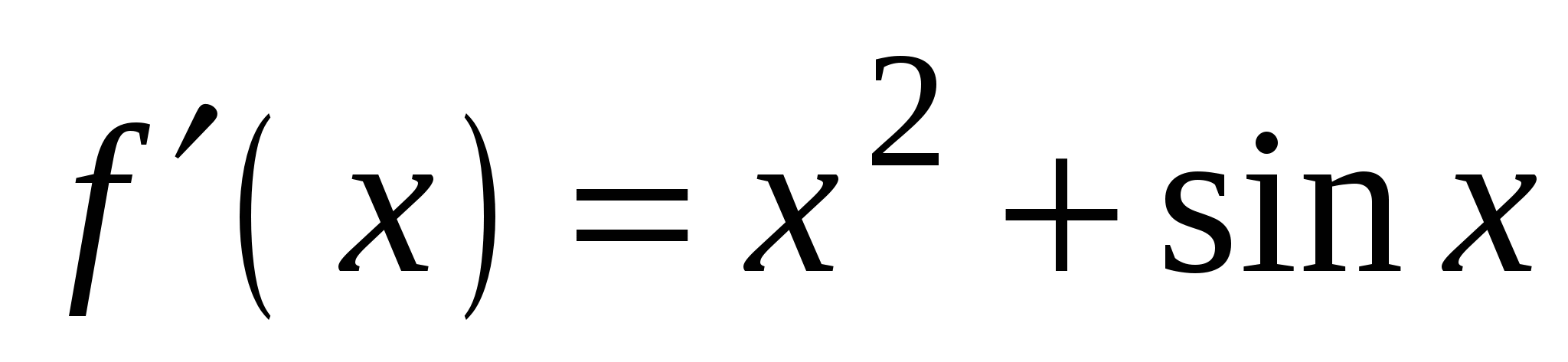

B2. На рисунке изображен график функции
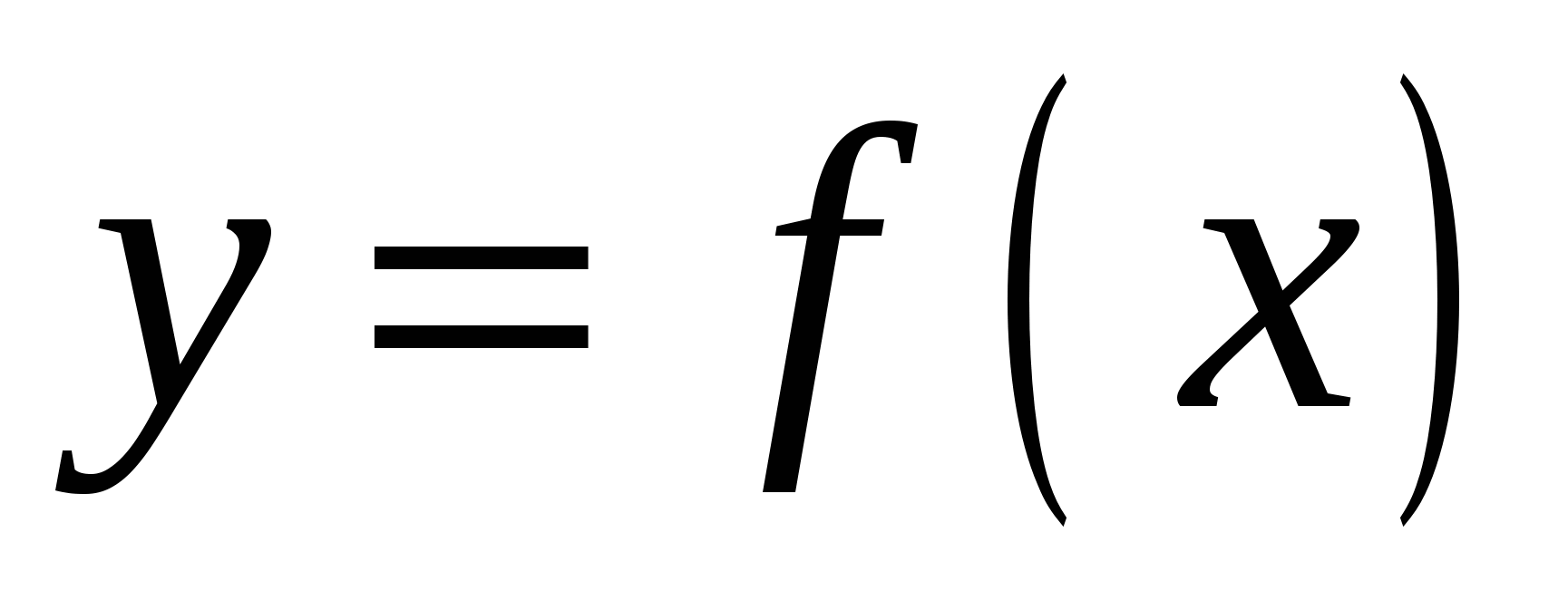 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
.
А5. Найдите производную функции 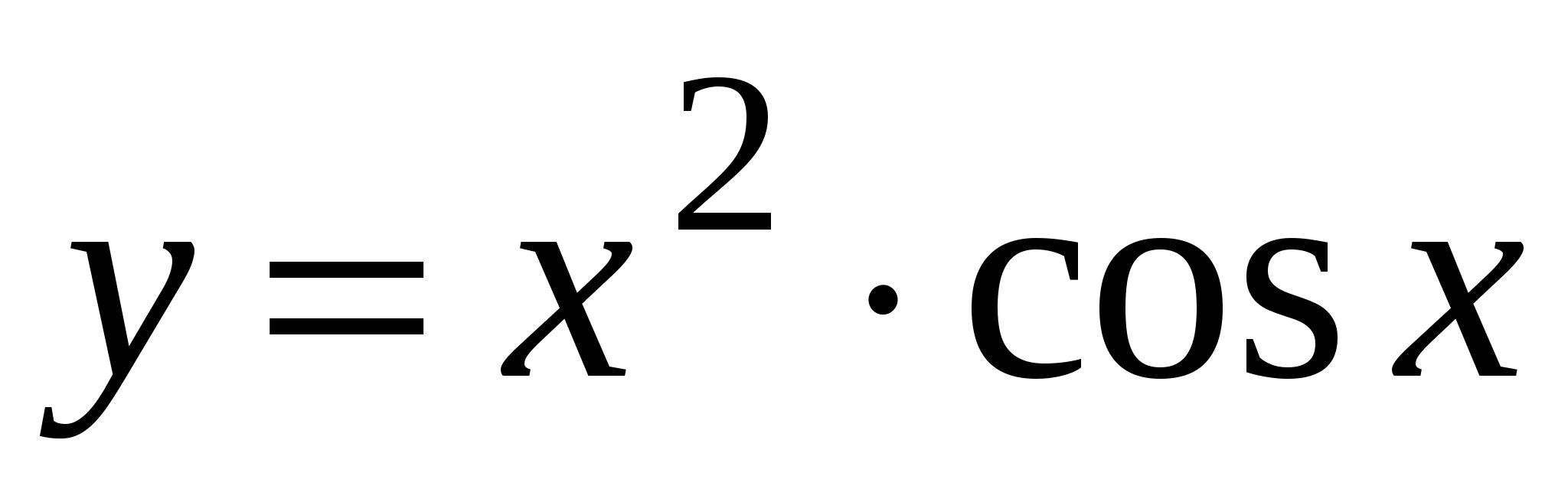 .
.
1)
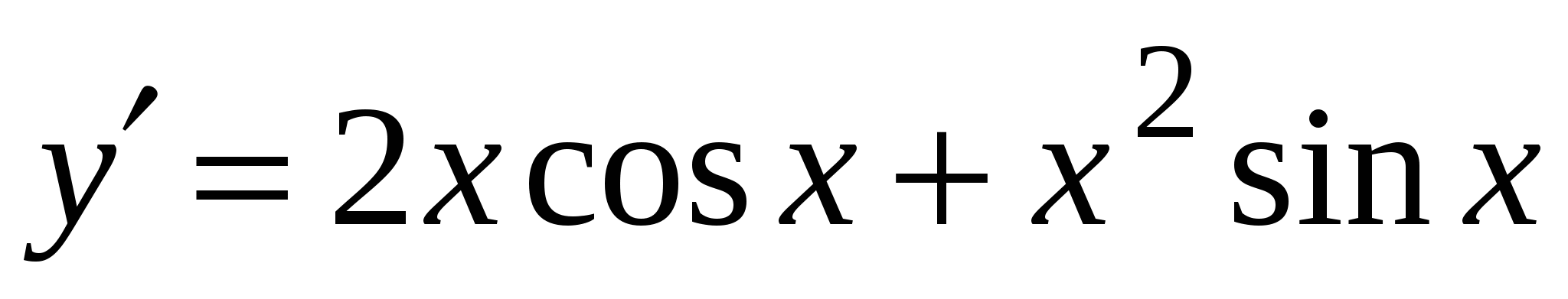
3)
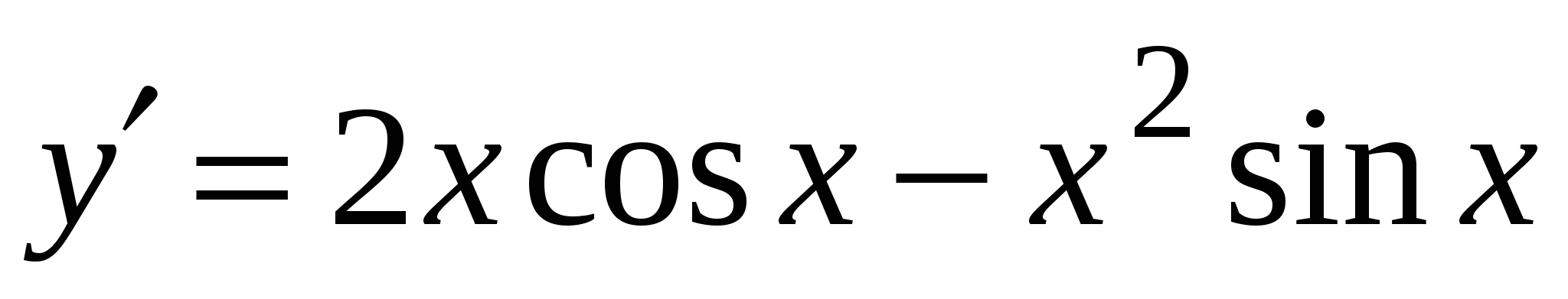
2)
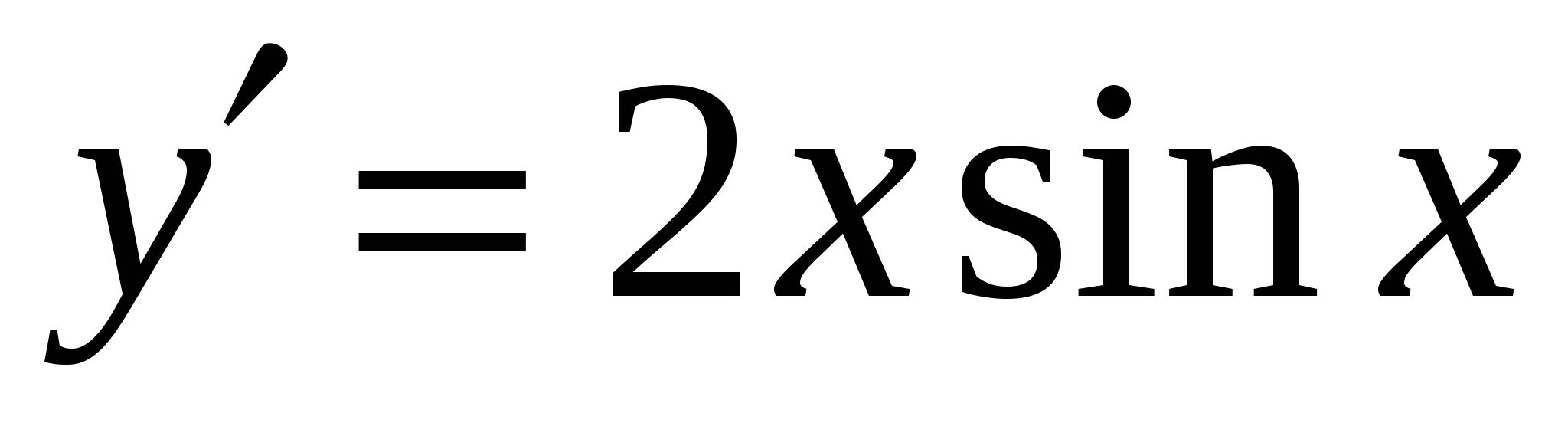
4)
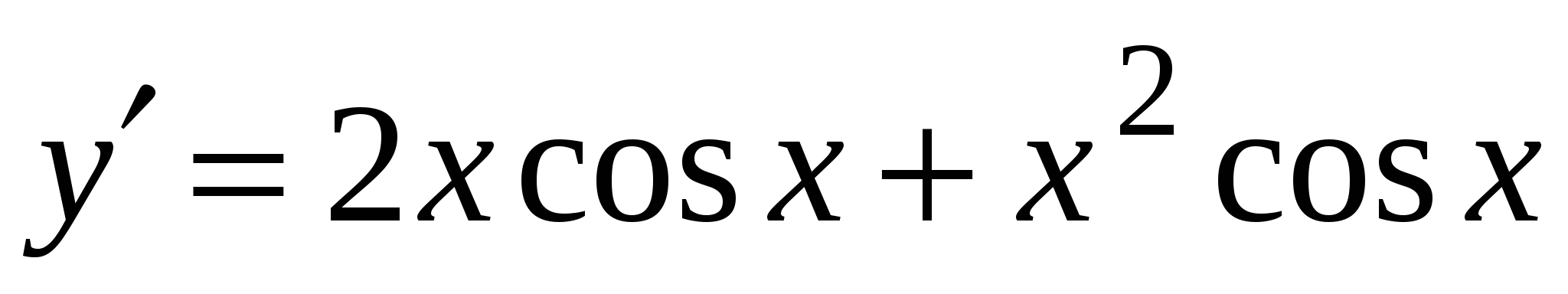
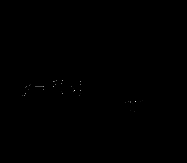
 и касательная к этому графику. Найдите значение выражения
и касательная к этому графику. Найдите значение выражения  .
. В4.Материальная точка движется по закону
х(t)=1/3 t3-6t2+35t +61 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 6 м/с2 ?
В5.Тело движется прямолинейно, его расстояние S (в м) от начала отсчета изменяется по закону S(t)=2t2+4 -9 м. Определите скорость движения тела через 4 с после начала движения.
В6.Материальная точка движется по закону х(t)=1/2 t3-7t2+16t -27 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 4 м/с2 ?
Контрольная работа №3 по теме: «Производная»
Вариант №7

B1 Функция  определена на промежутке
определена на промежутке  . Используя изображенный на рисунке график производной
. Используя изображенный на рисунке график производной  , определите количество касательных к графику функции
, определите количество касательных к графику функции  , которые составляют угол
, которые составляют угол  с положительным направлением оси Ox.
с положительным направлением оси Ox.
А1. Найдите производную функции 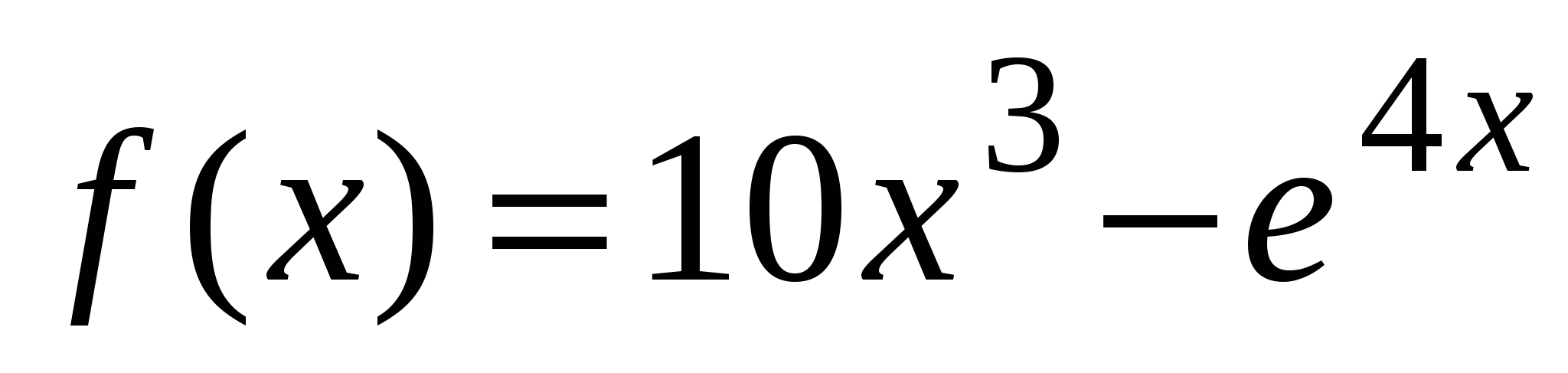 .
.
1) 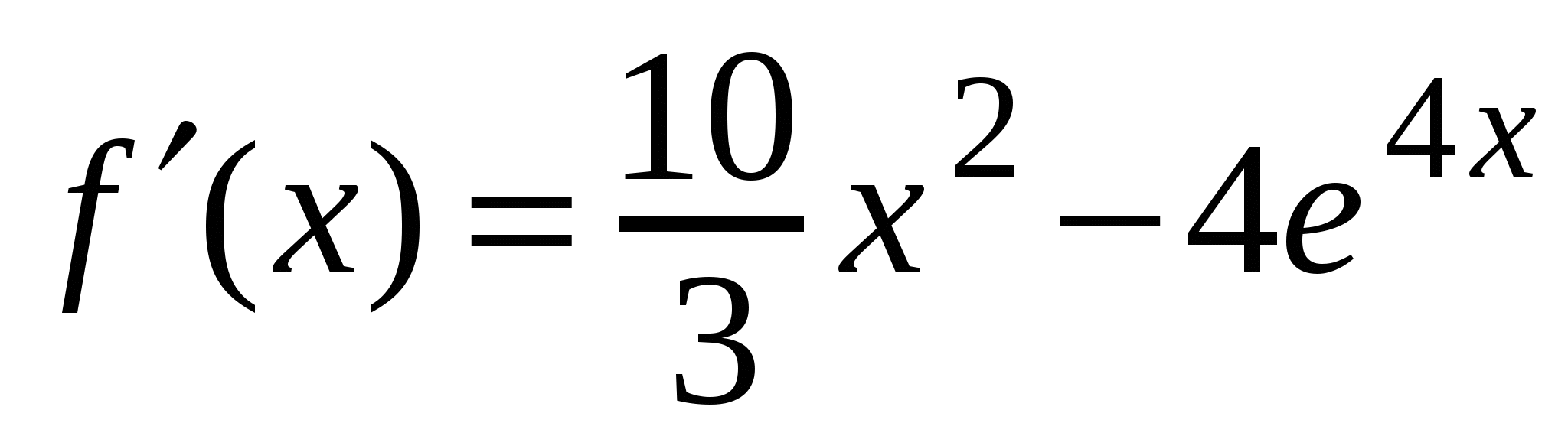
3) 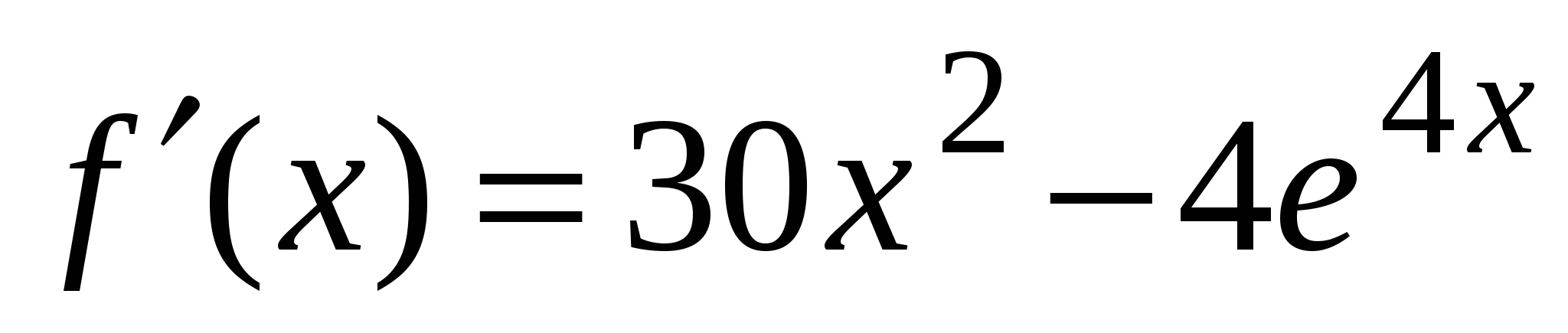
2) 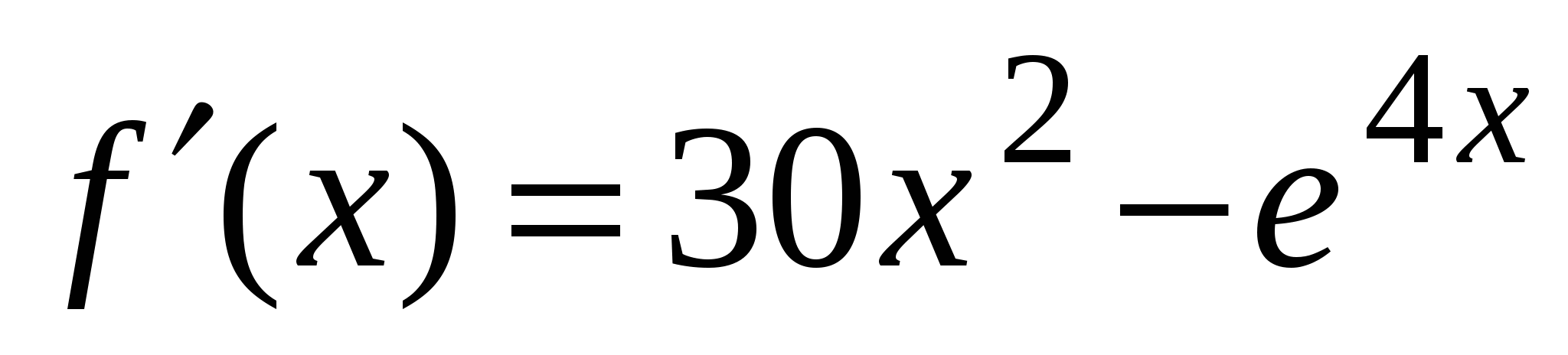
4) 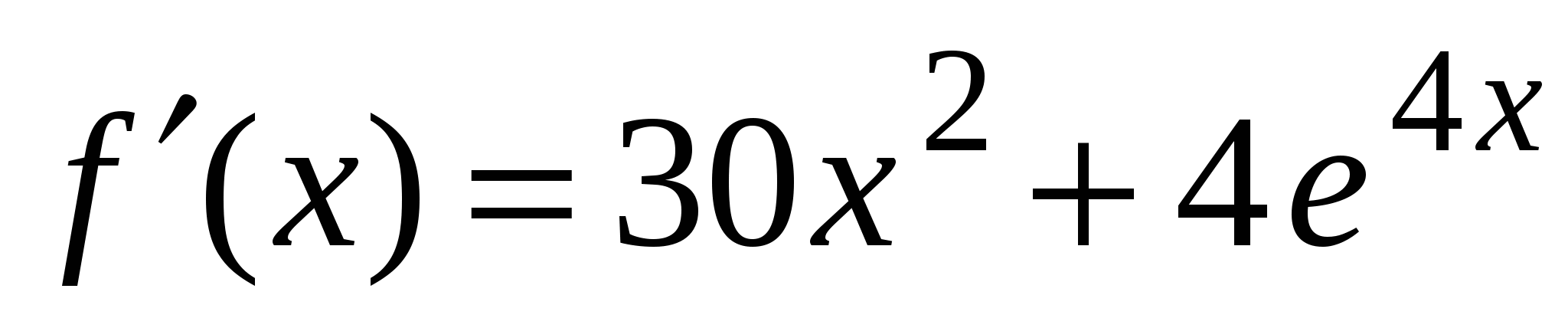
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Вычислите значение производной функции 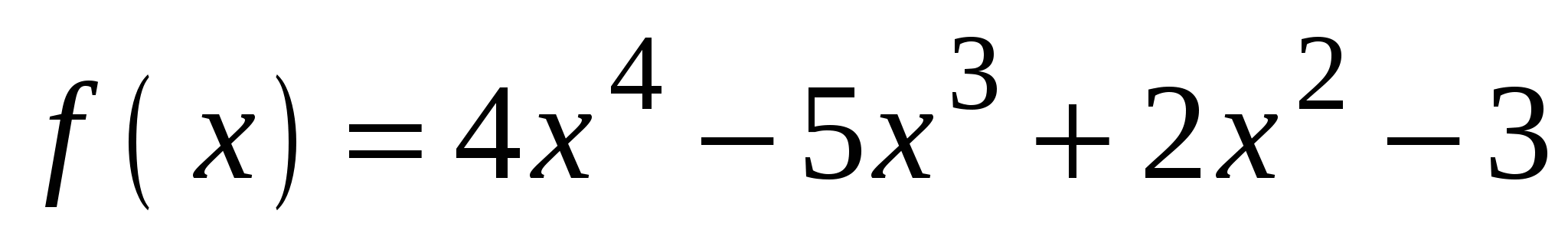 в точке
в точке 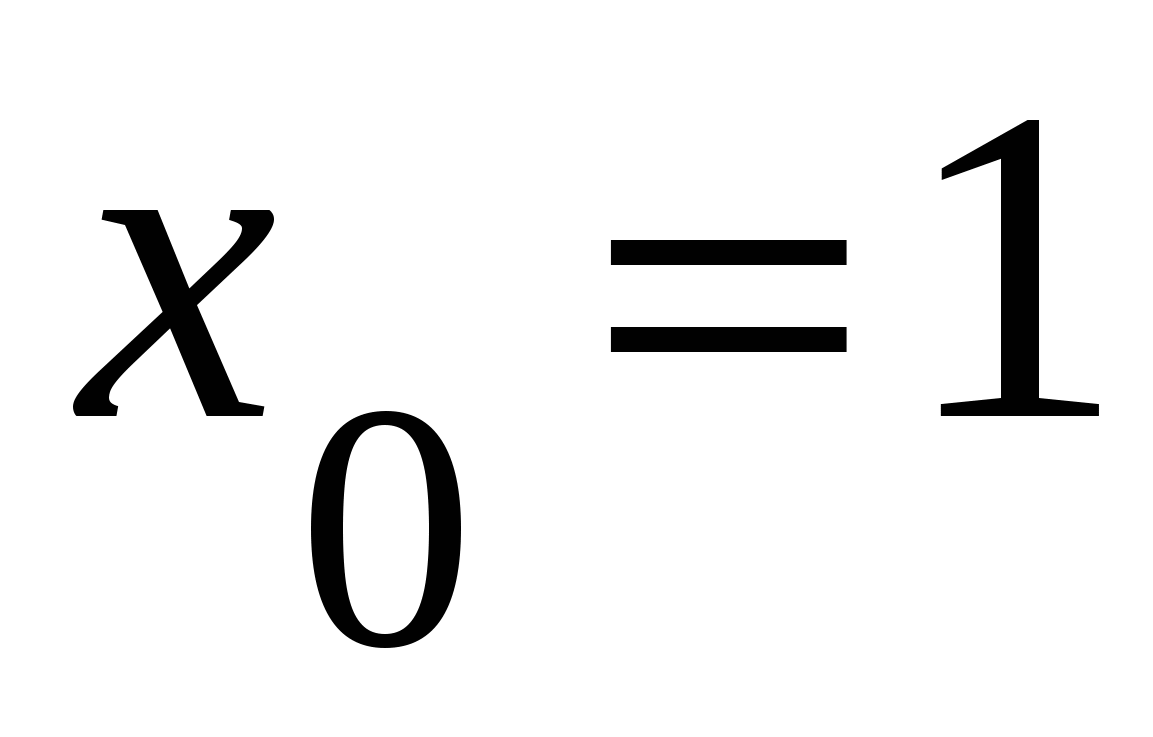 .
.
1)
5
2)
3
3)
27
4)
1
А4. Найдите производную функции 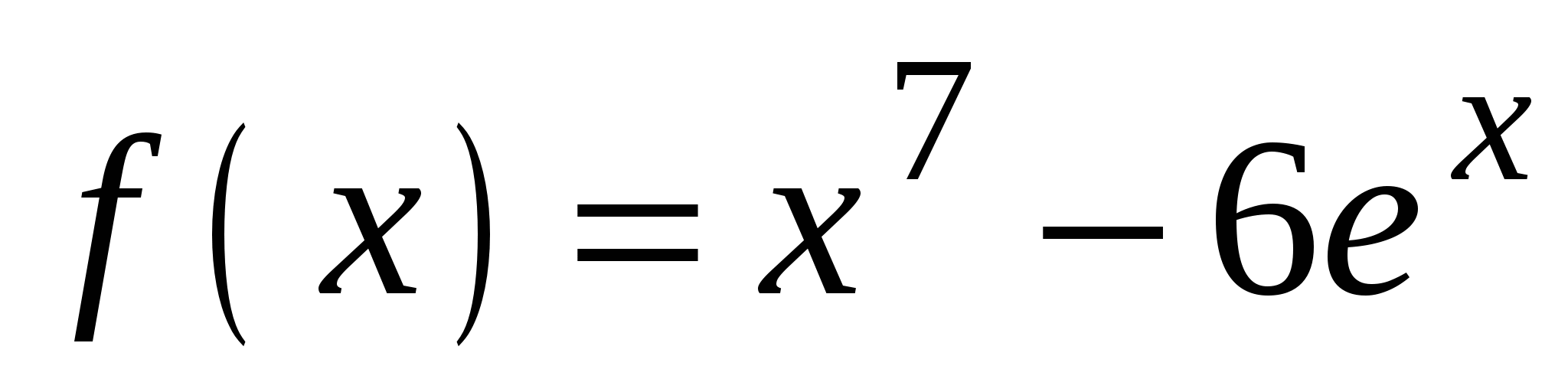 .
.
1)
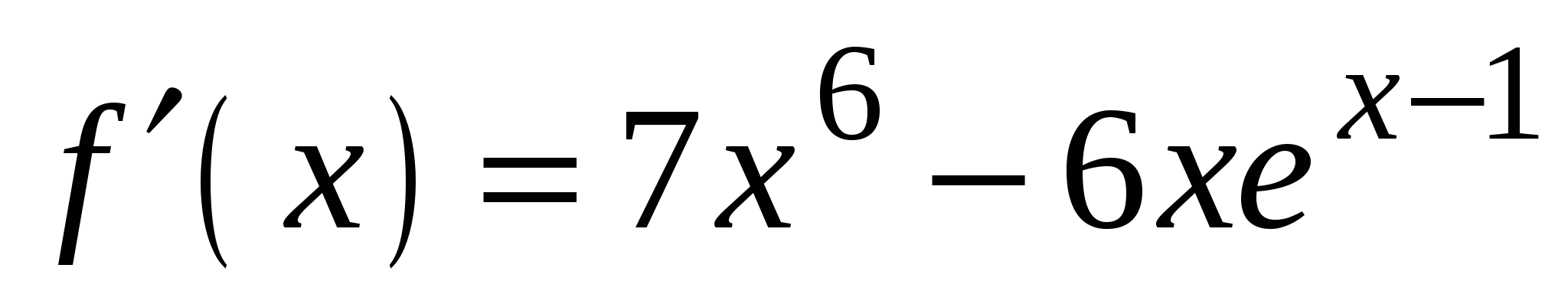
3)
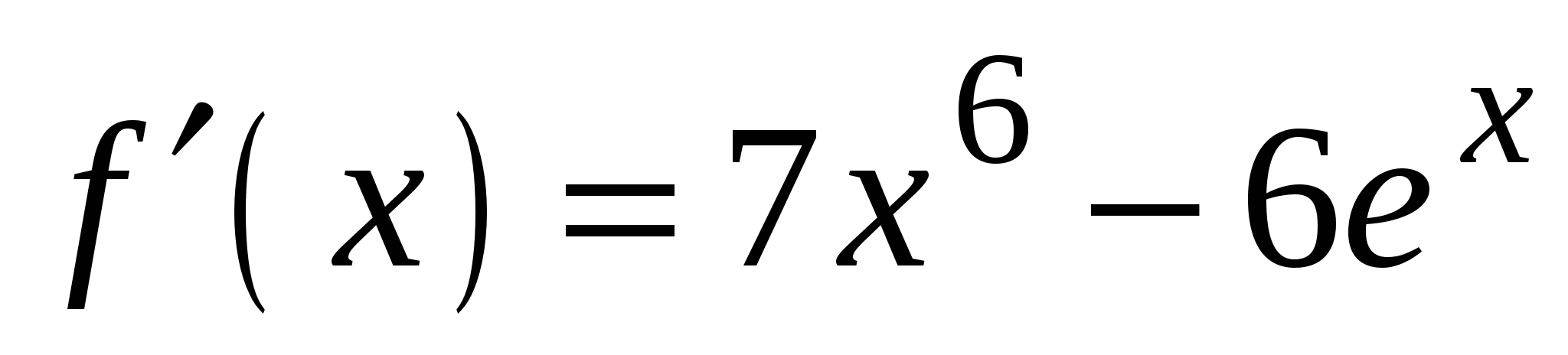
2)
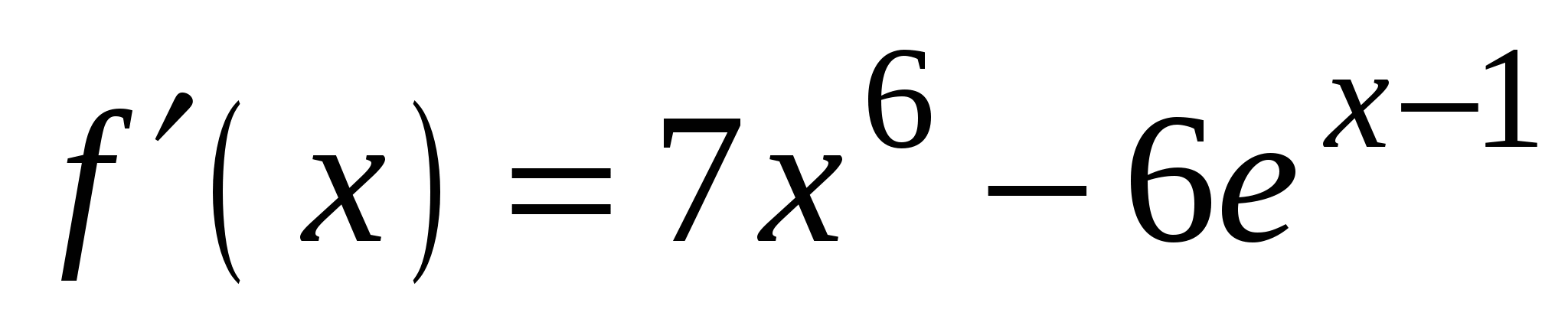
4)
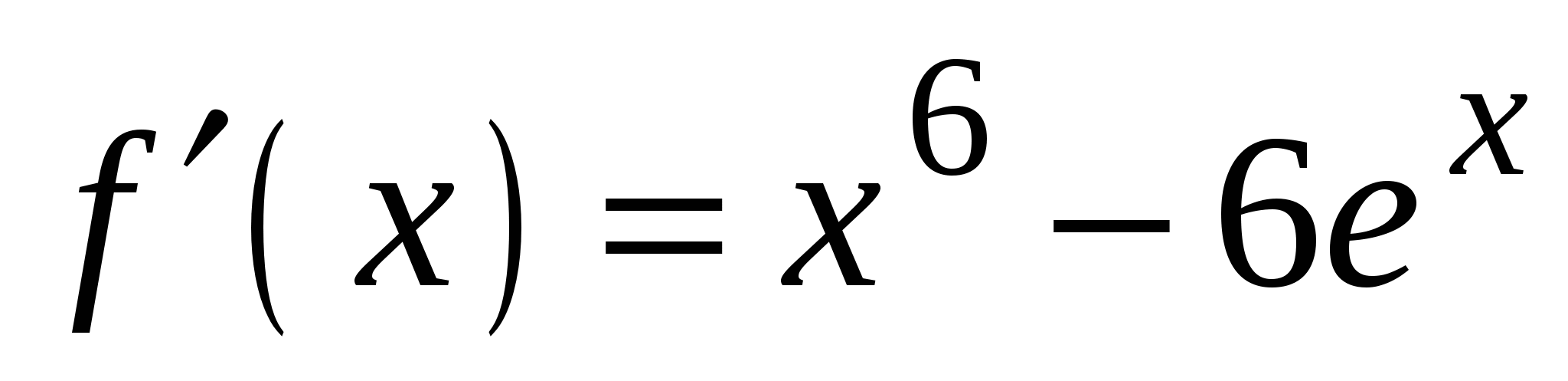

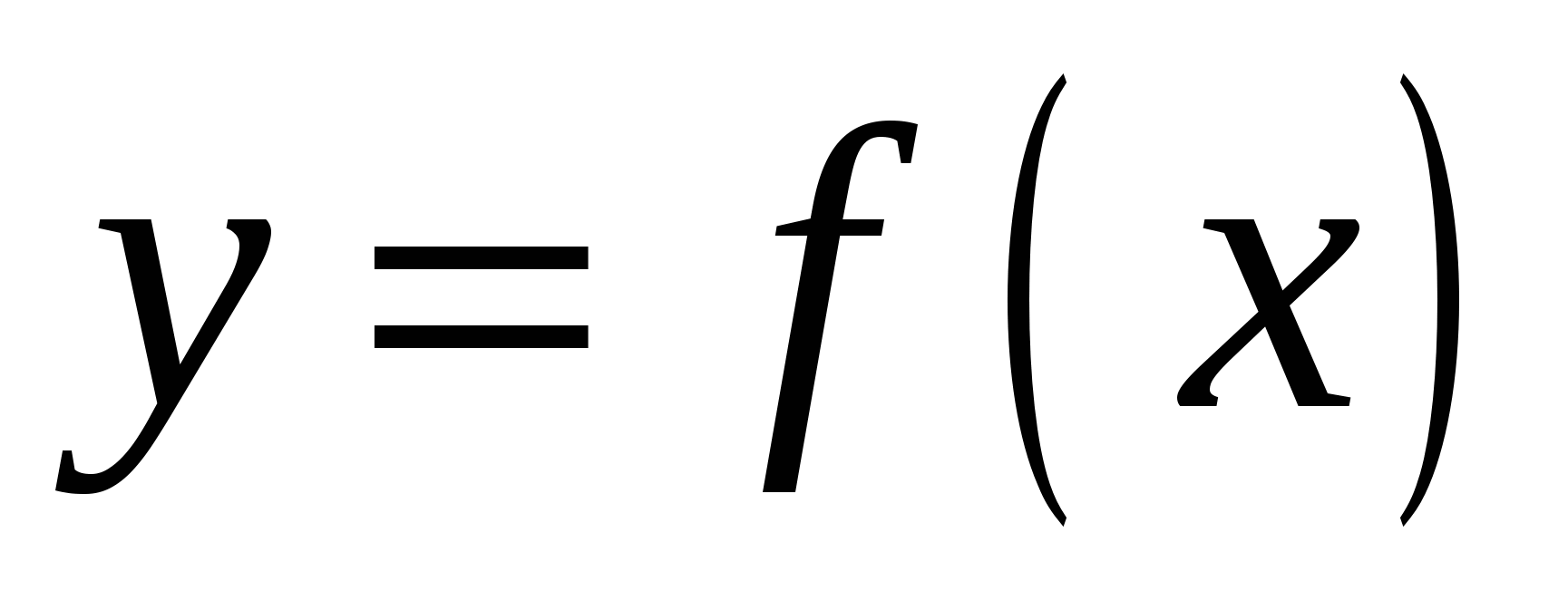 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. А5. Найдите производную функции 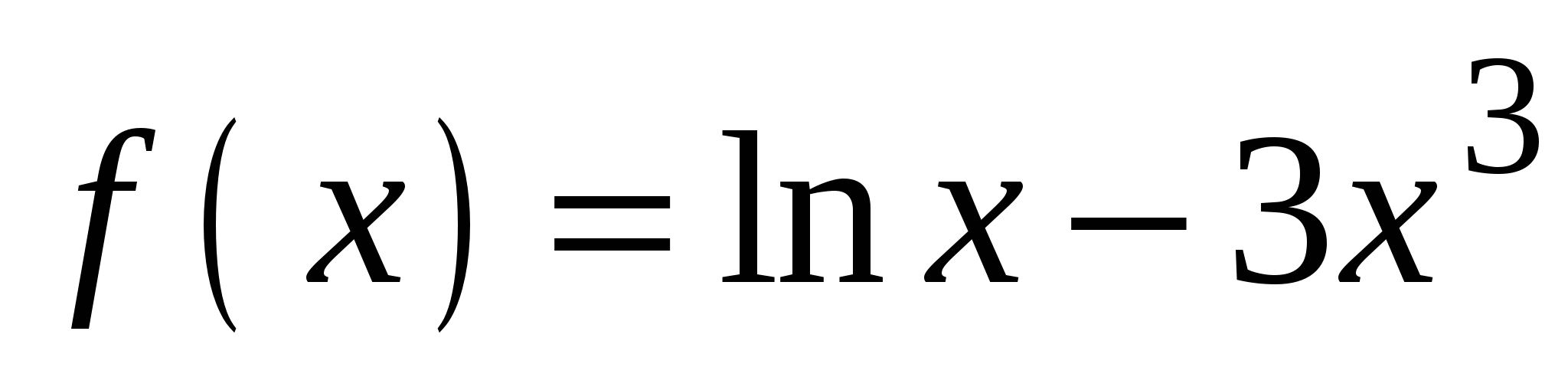 .
.
1)
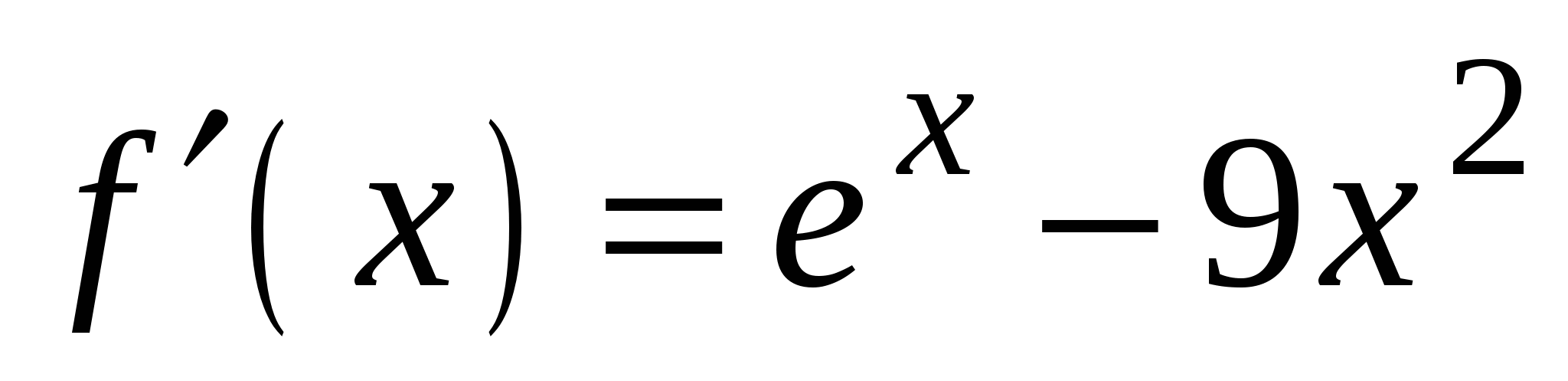
3)
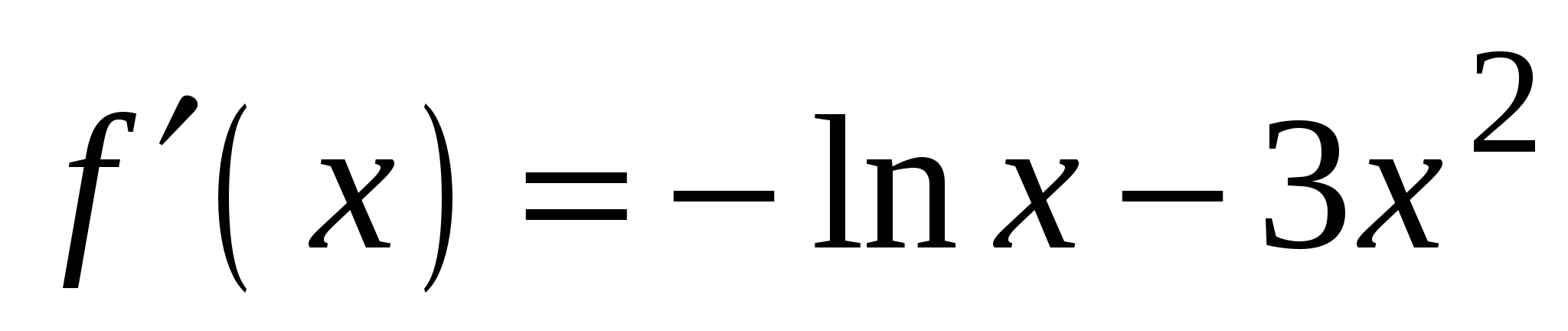
2)
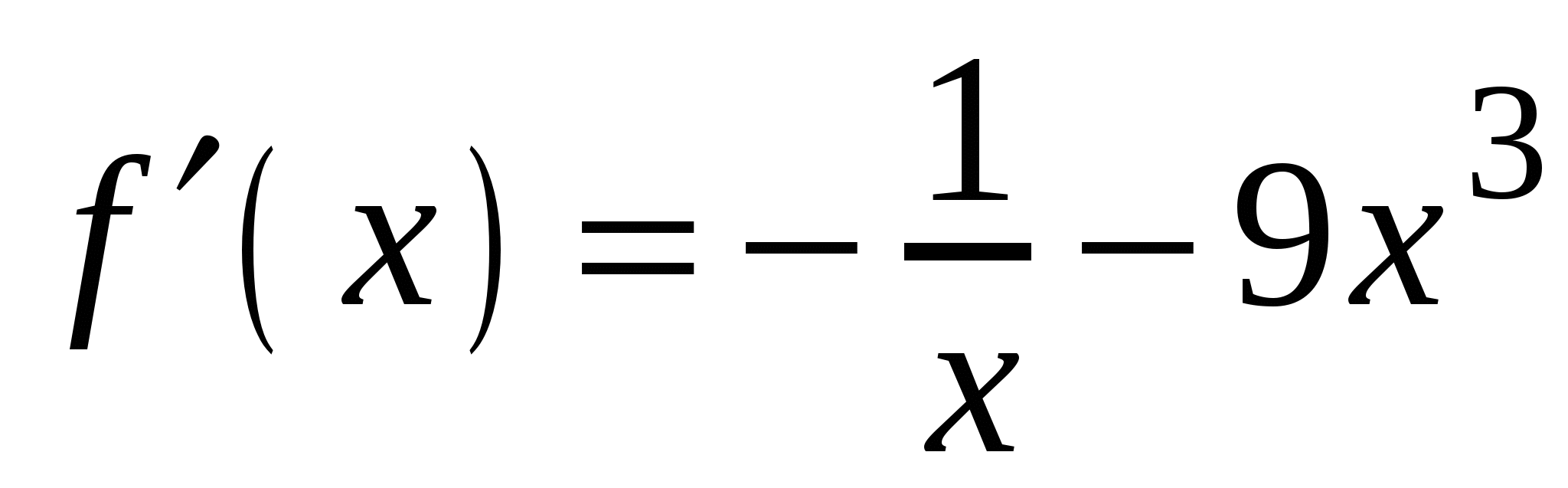
4)
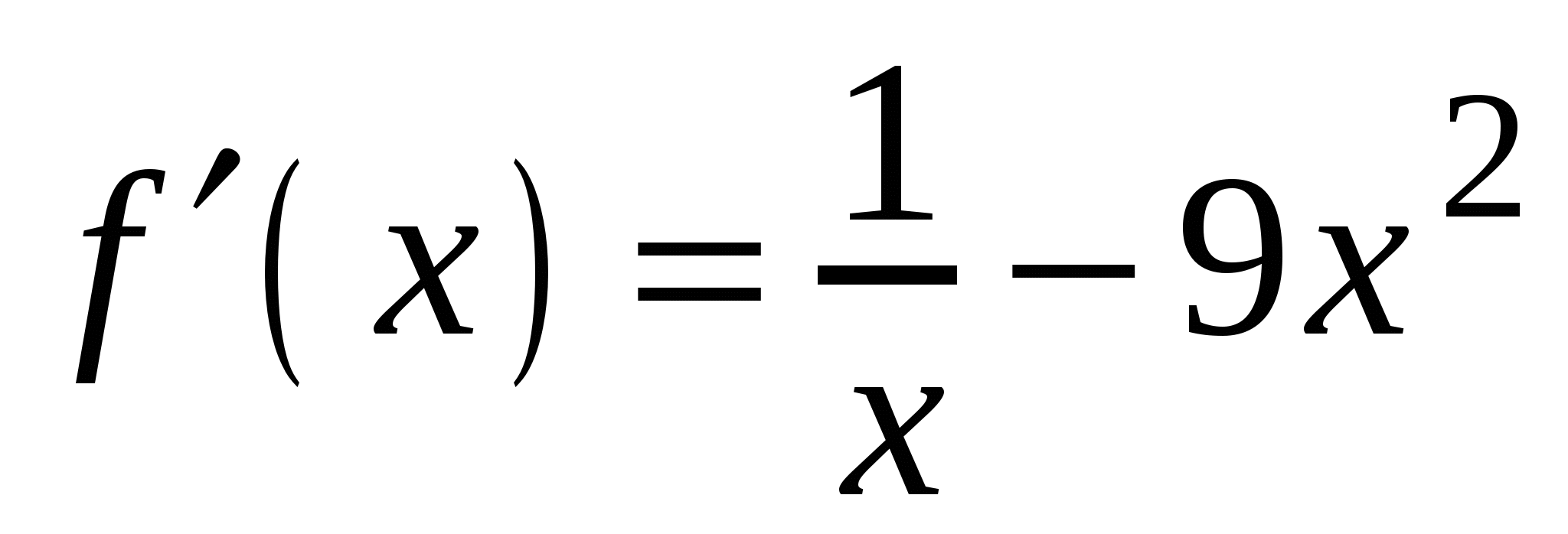

В3. На рисунке изображен график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
.
В4. Материальная точка движется по закону х(t)=1/4 t3-3t2+21t - 18 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 3 м/с2 ?
В5.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=6t2 - 18t+19. Через сколько секунд после начала движения произойдет остановка?
В6. Материальная точка движется по закону х(t)=1/6 t3-4t2+35t - 11 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 2 м/с2 ?
Контрольная работа №3 по теме: «Производная»
Вариант №8

B1 Функция  определена на промежутке
определена на промежутке  . Используя изображенный на рисунке график производной
. Используя изображенный на рисунке график производной  , определите количество касательных к графику функции
, определите количество касательных к графику функции  , параллельных оси Ox.
, параллельных оси Ox.
А1. Найдите производную функции 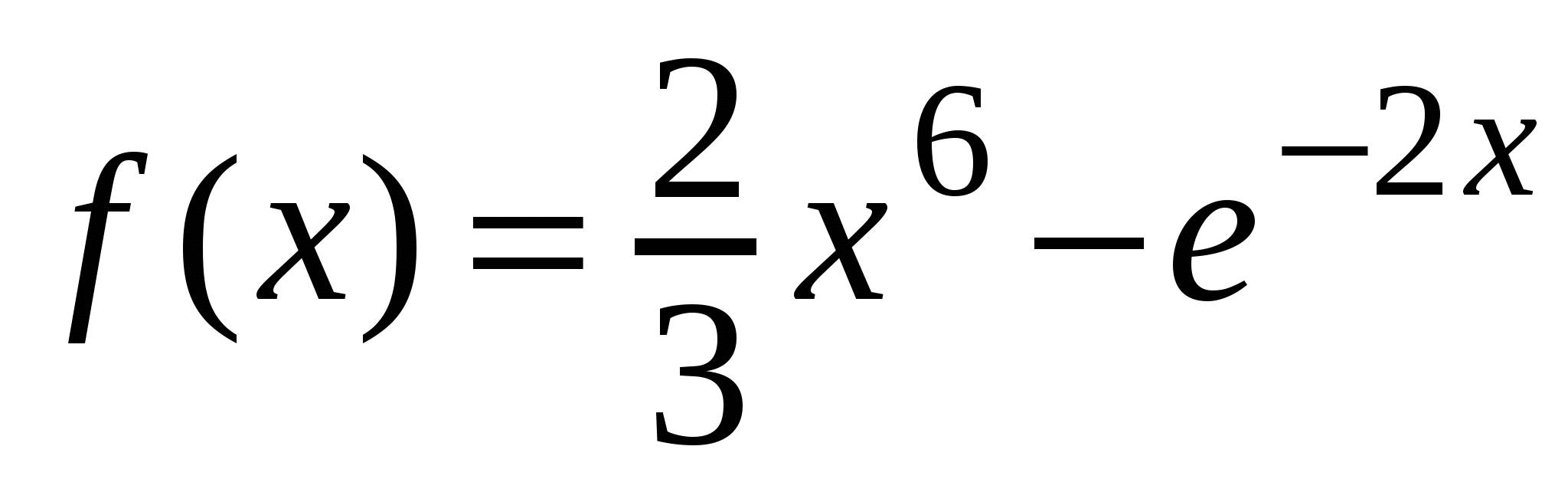 .
.
1) 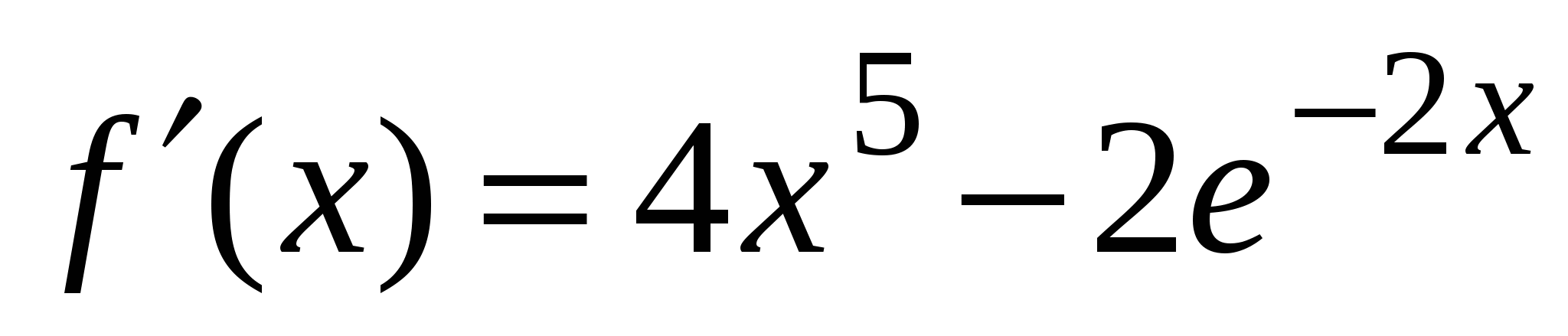
3) 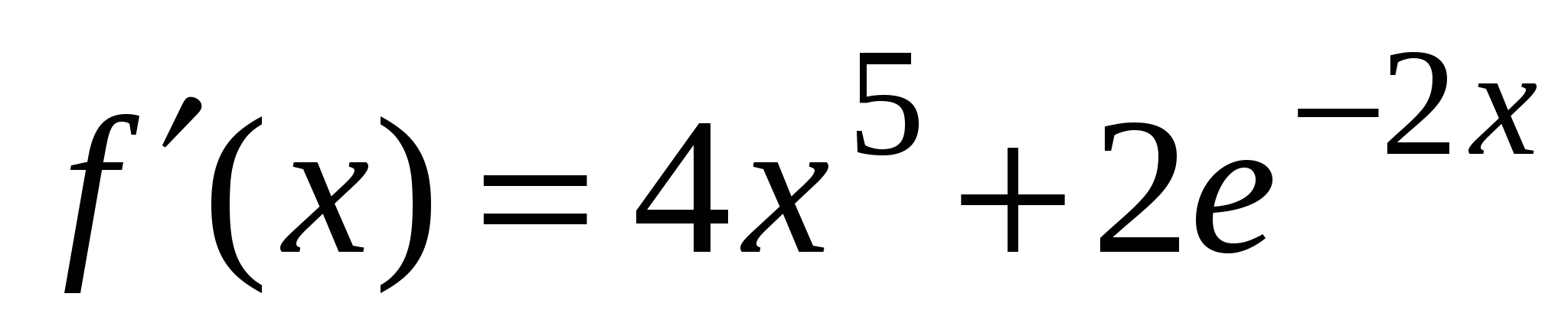
2) 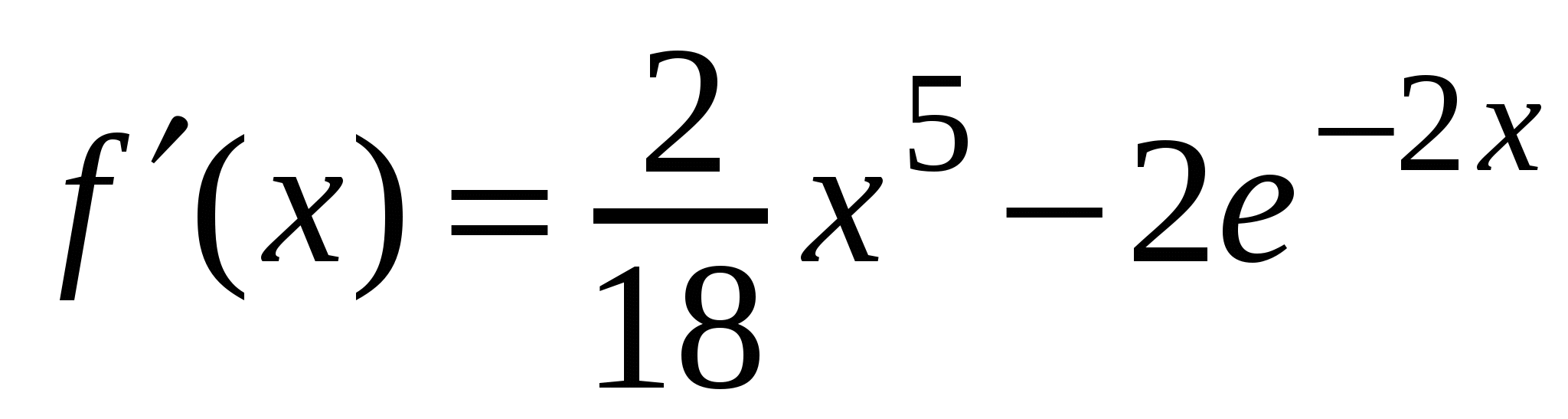
4) 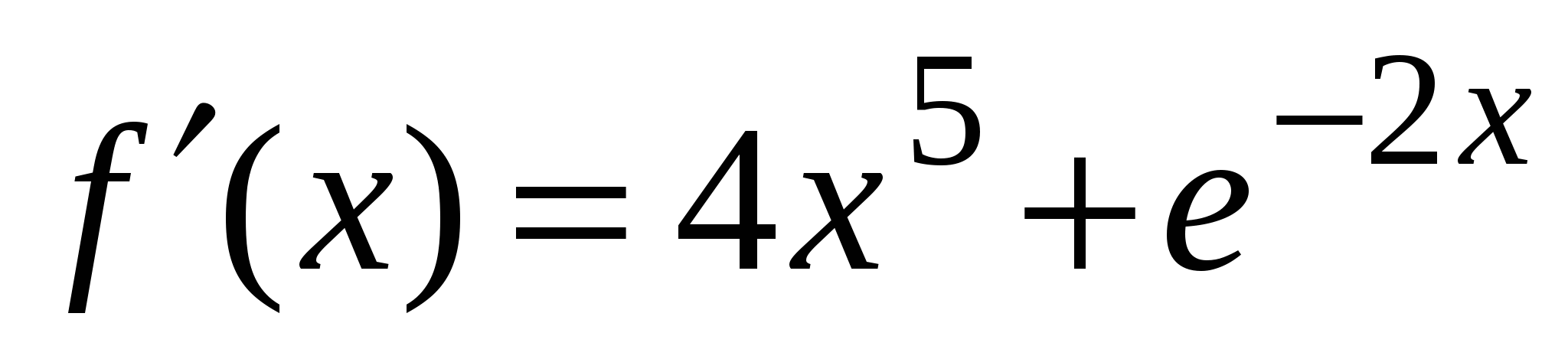
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Найдите производную функции 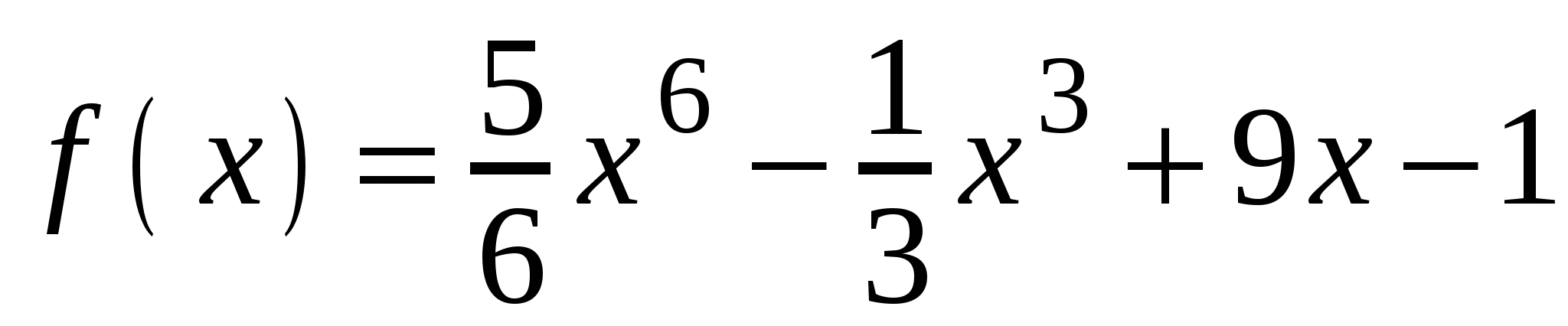 .
.
1)
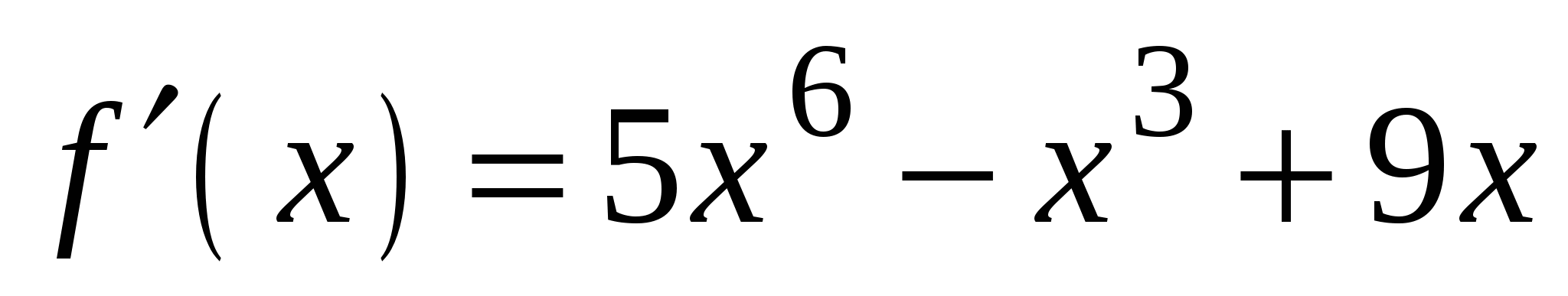
3)
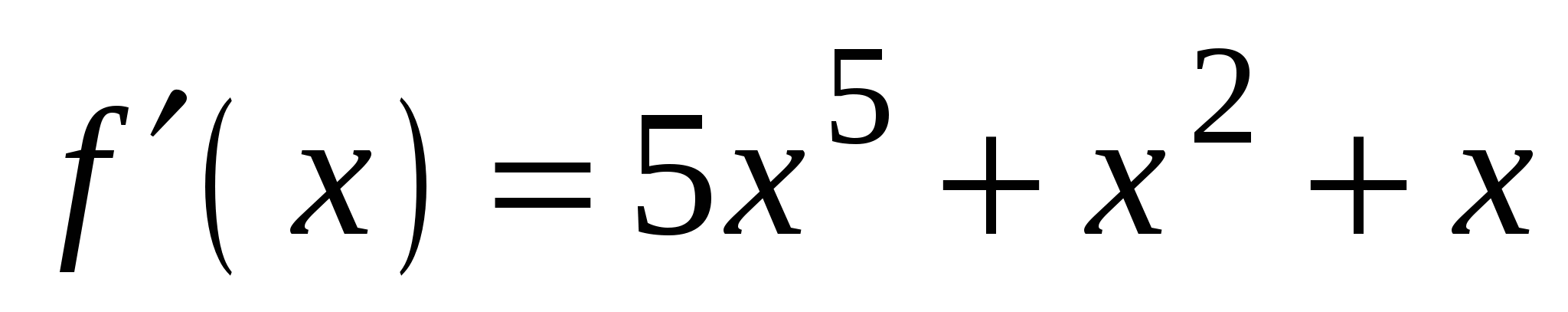
2)
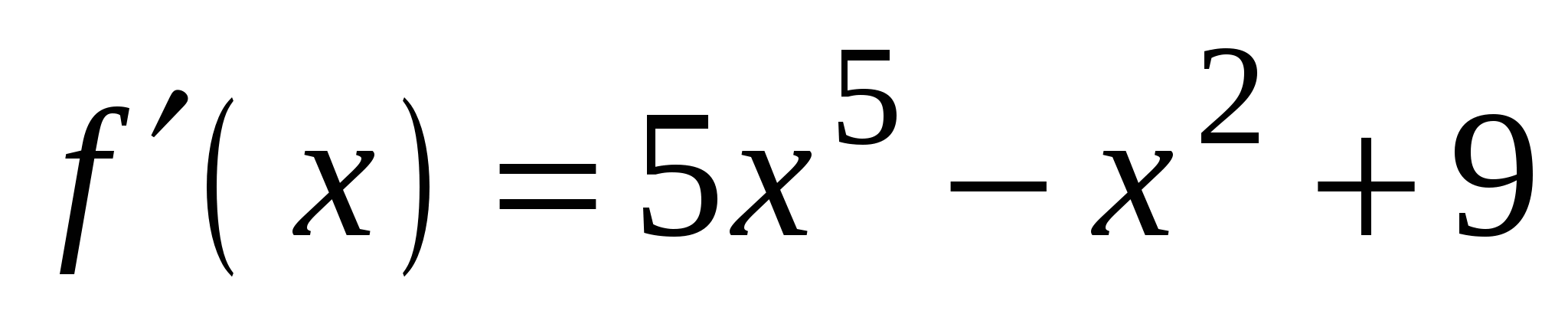
4)
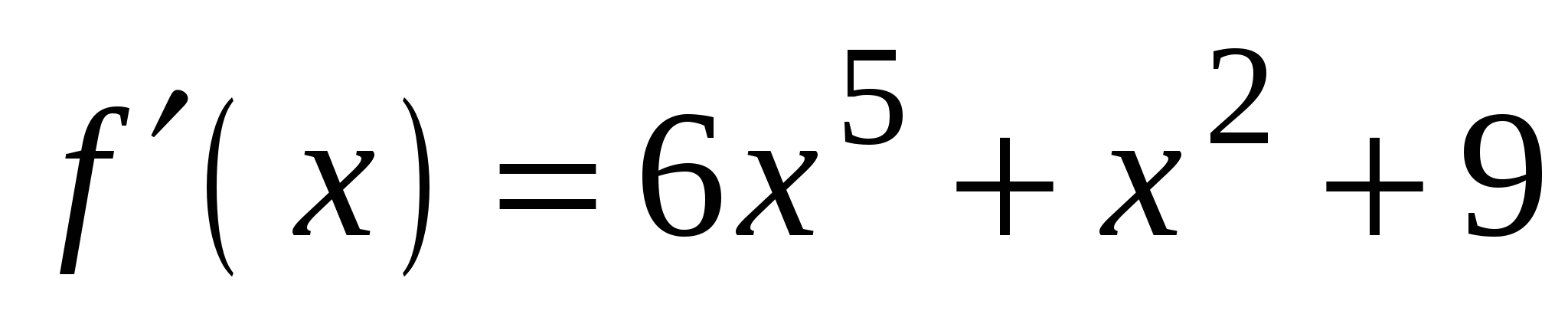
А4. Найдите производную функции 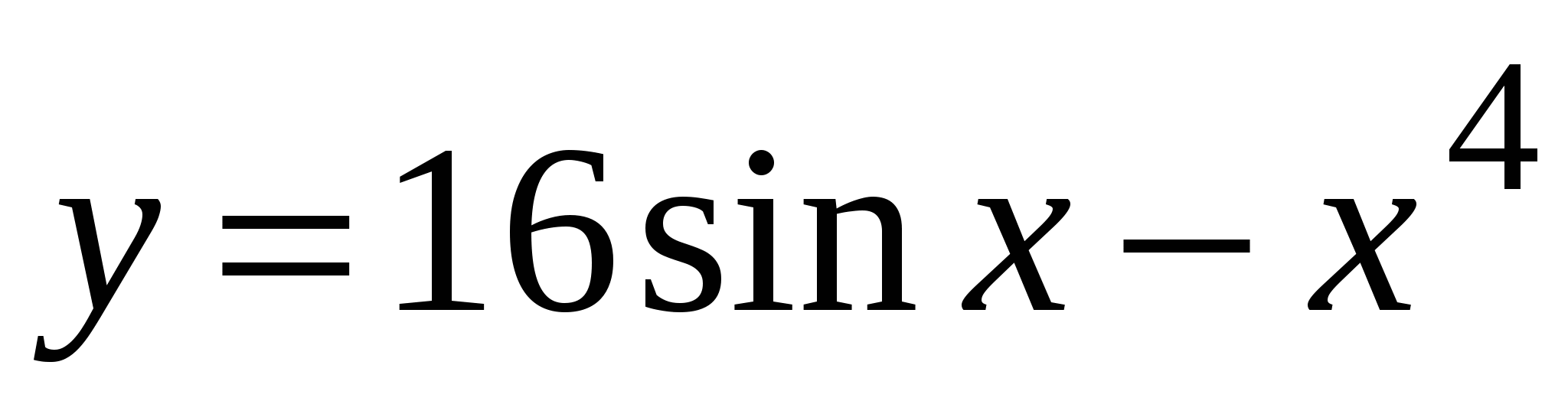 .
.
1)
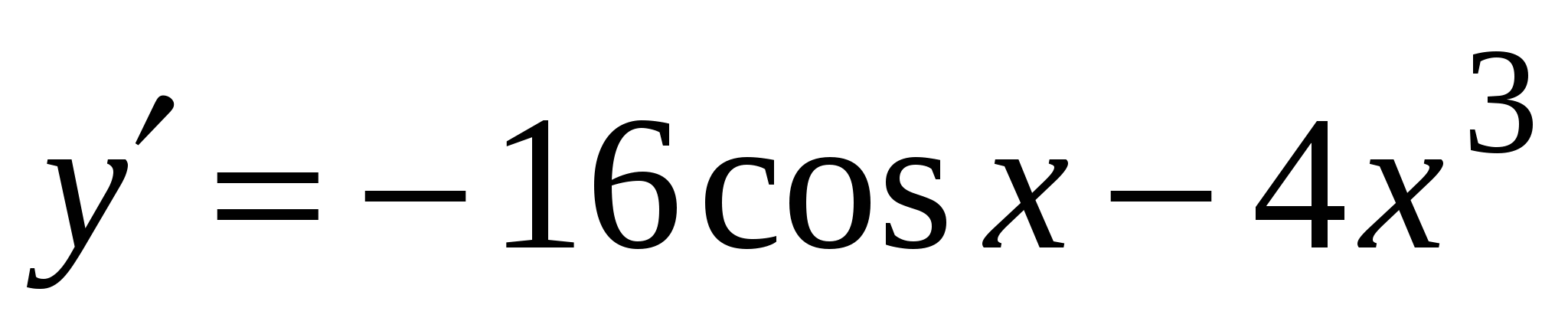
3)
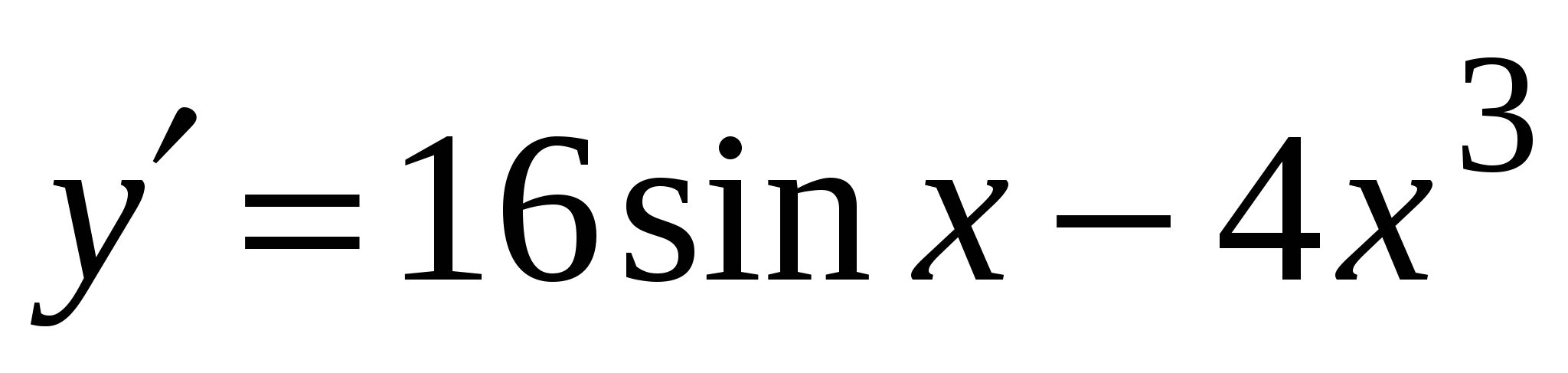
2)
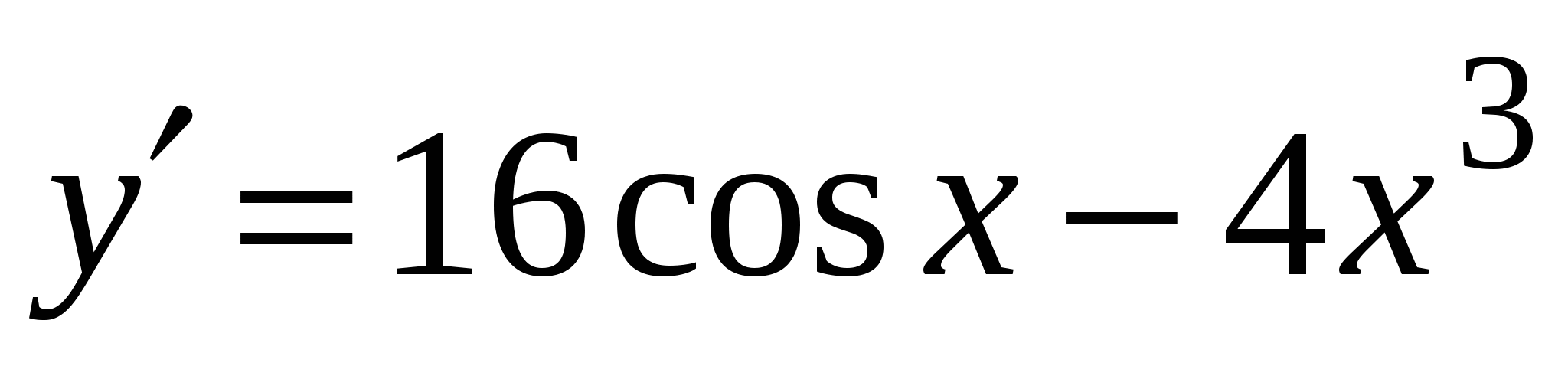
4)
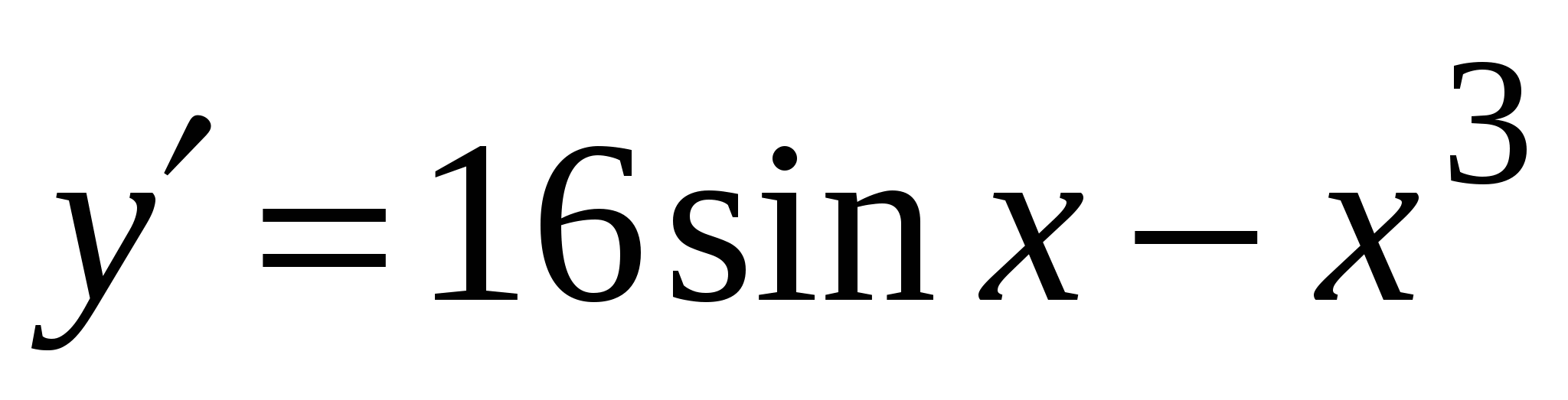

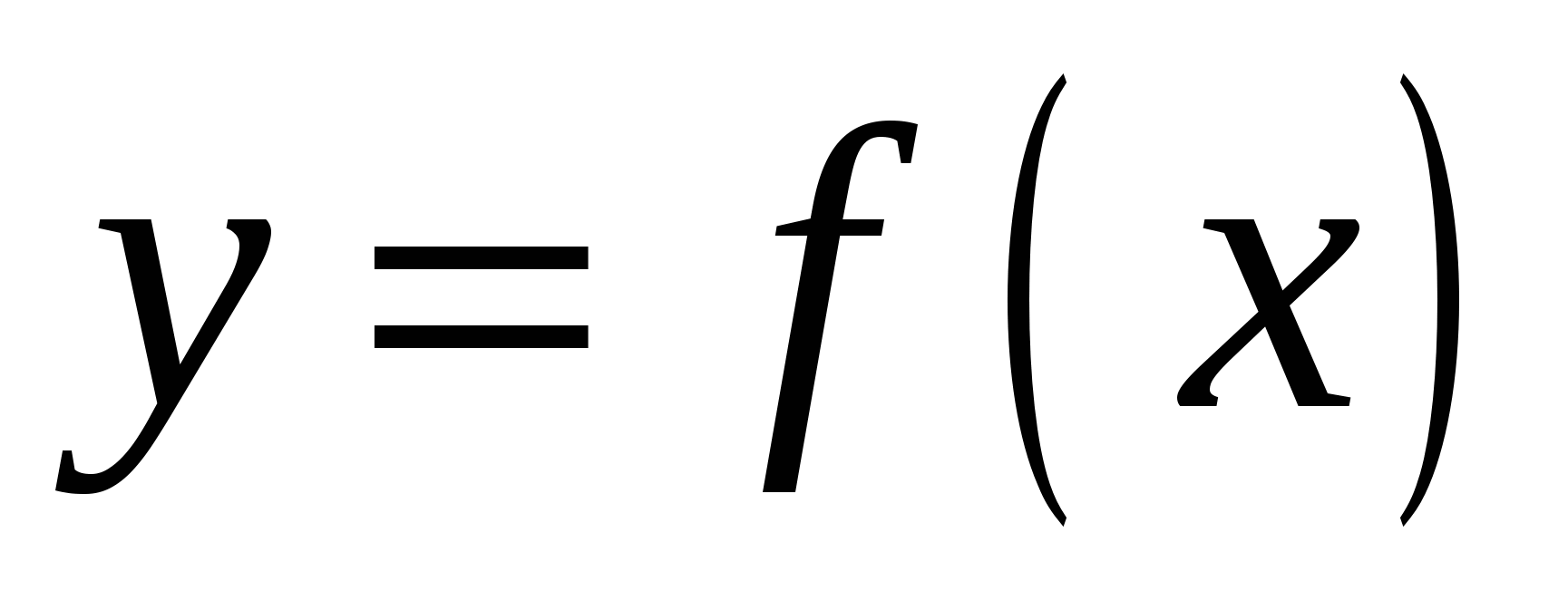 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. А5. Найдите производную функции 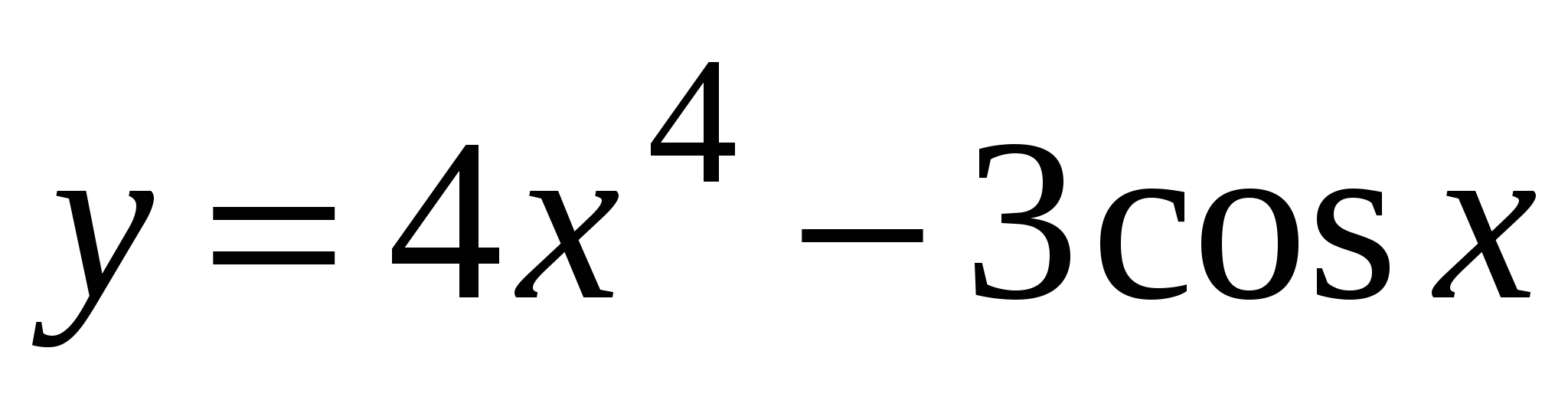 .
.
1)
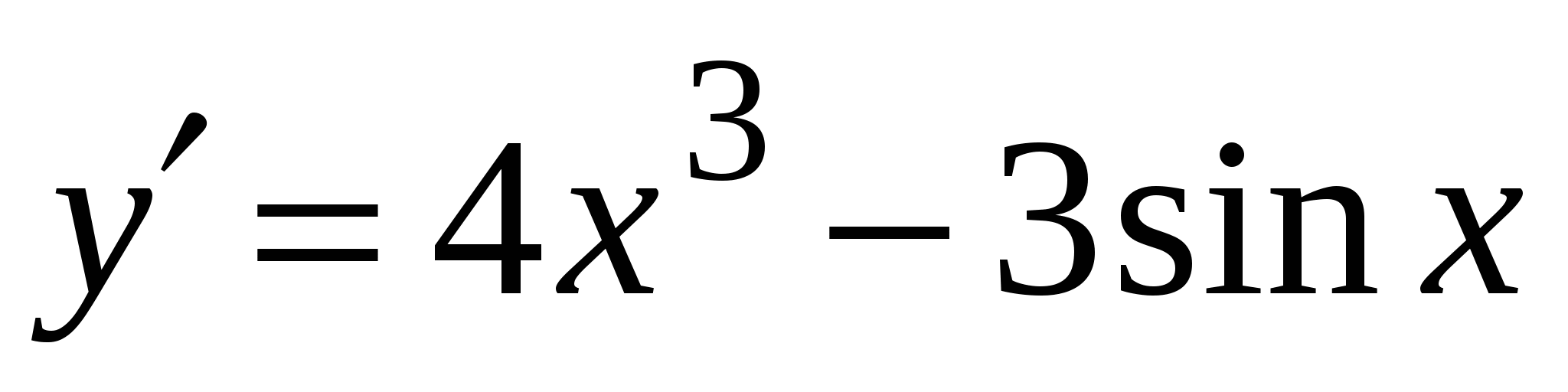
3)
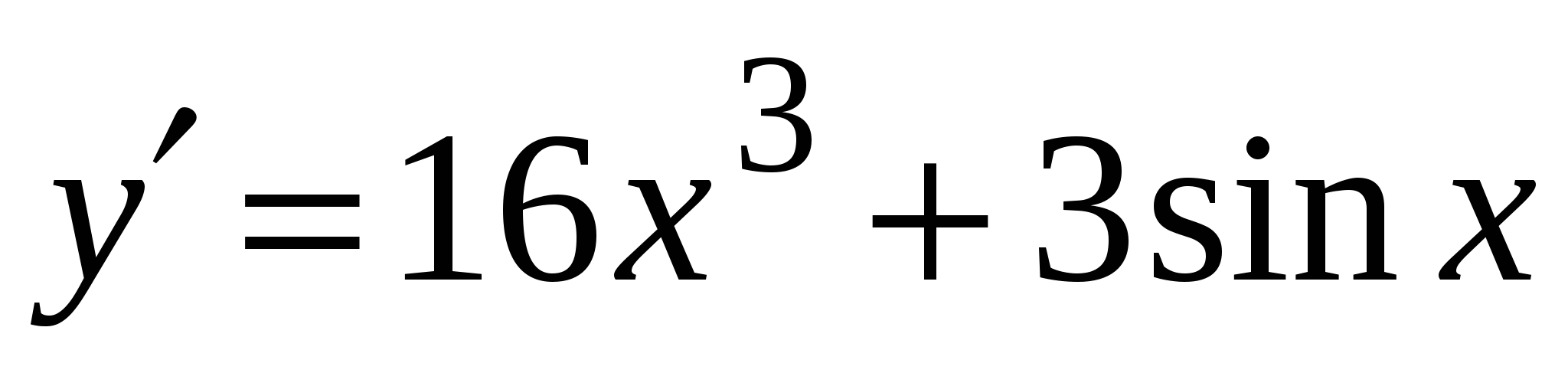
2)
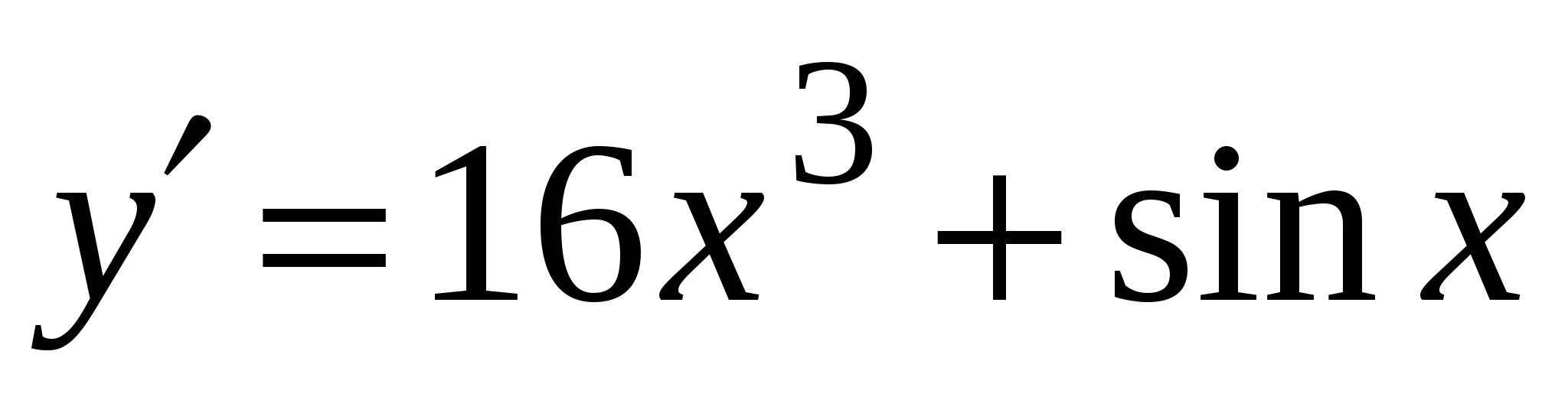
4)
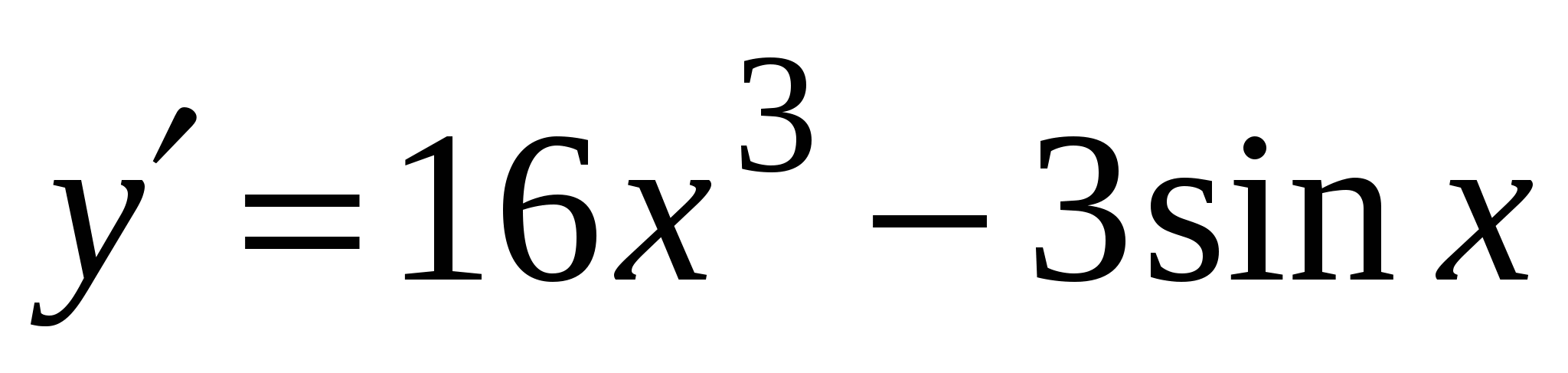

 и касательная к нему. Найдите значение производной
и касательная к нему. Найдите значение производной  .
. В4. Материальная точка движется по закону х(t)=1/4 t3-3t2+21t - 18 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 3 м/с2 ?
В5.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=6t2 - 18t+19. Через сколько секунд после начала движения произойдет остановка?
В6. Материальная точка движется по закону х(t)=1/6 t3-4t2+35t - 11 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 2 м/с2 ?
Контрольная работа №3 по теме: «Производная»
Вариант №9

B1. Функция  определена на промежутке
определена на промежутке  . На рисунке изображен график производной этой функции.
. На рисунке изображен график производной этой функции.
К графику функции провели касательные во всех точках, абсциссы которых целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент.
А1. Найдите производную функции 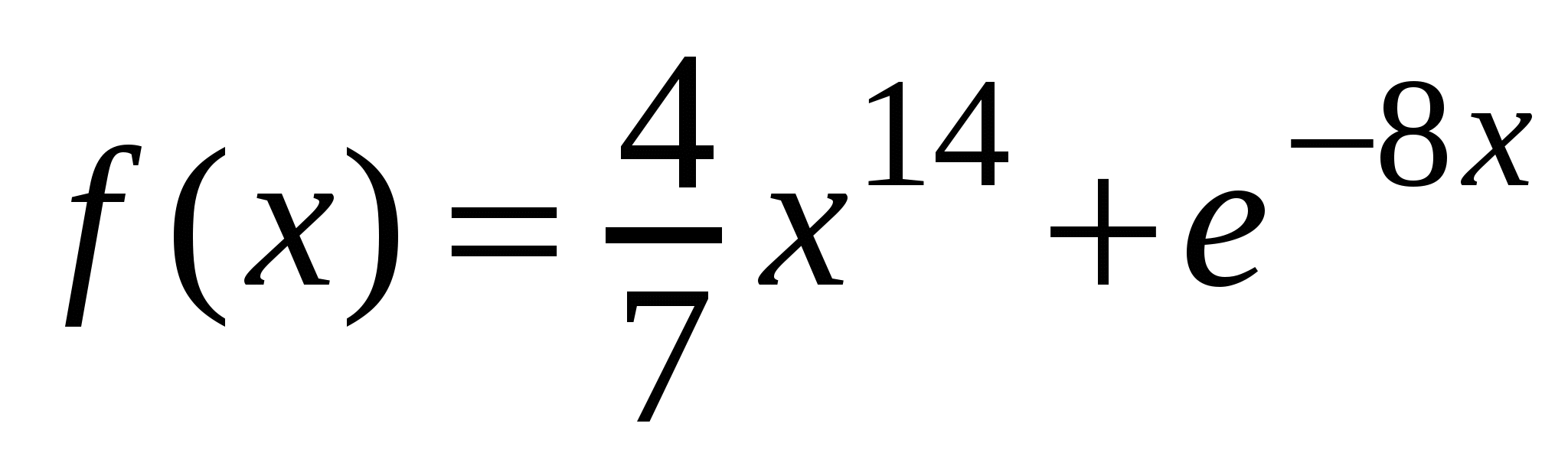 .
.
1) 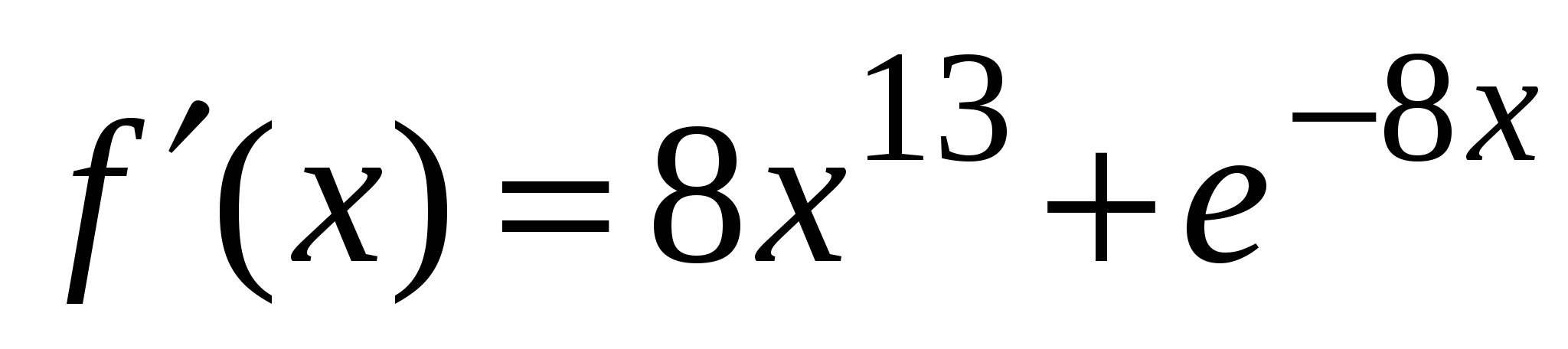
3) 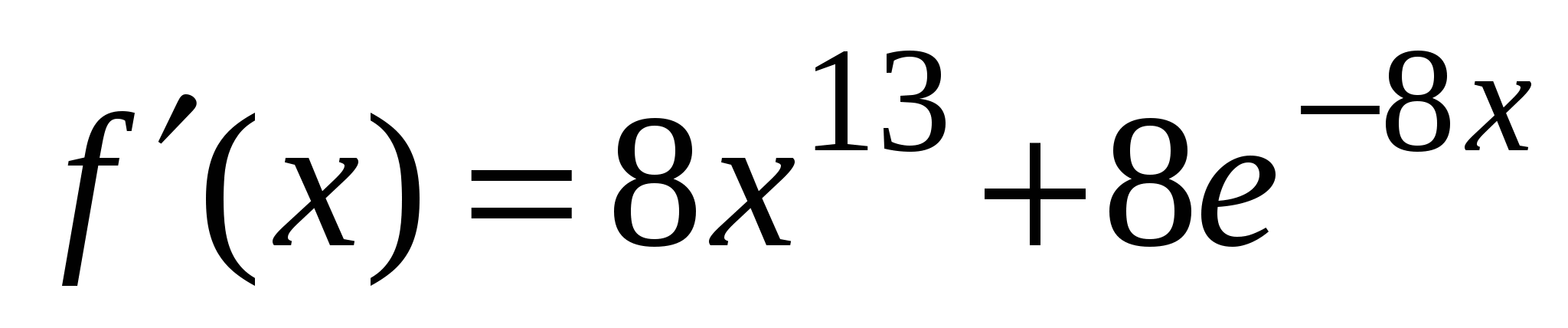
2) 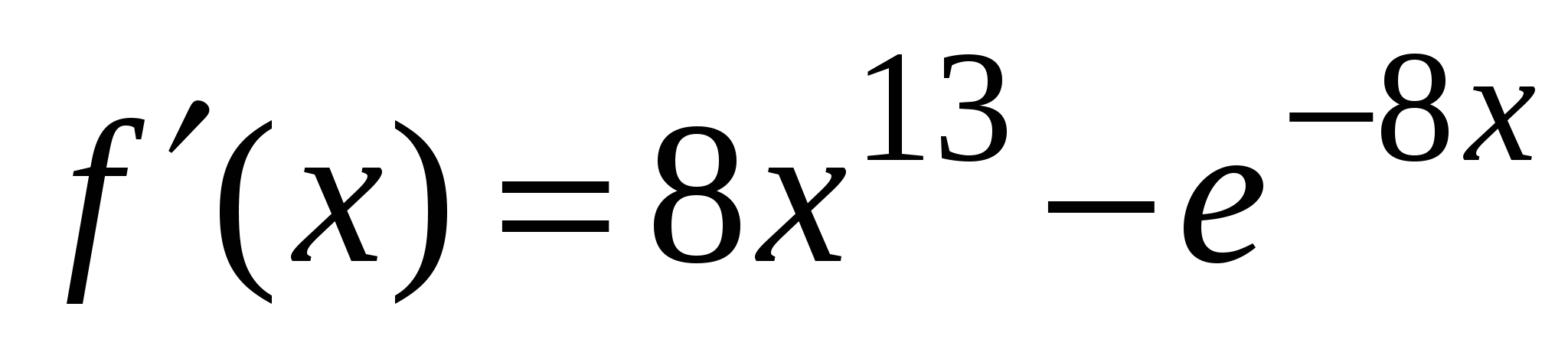
4) 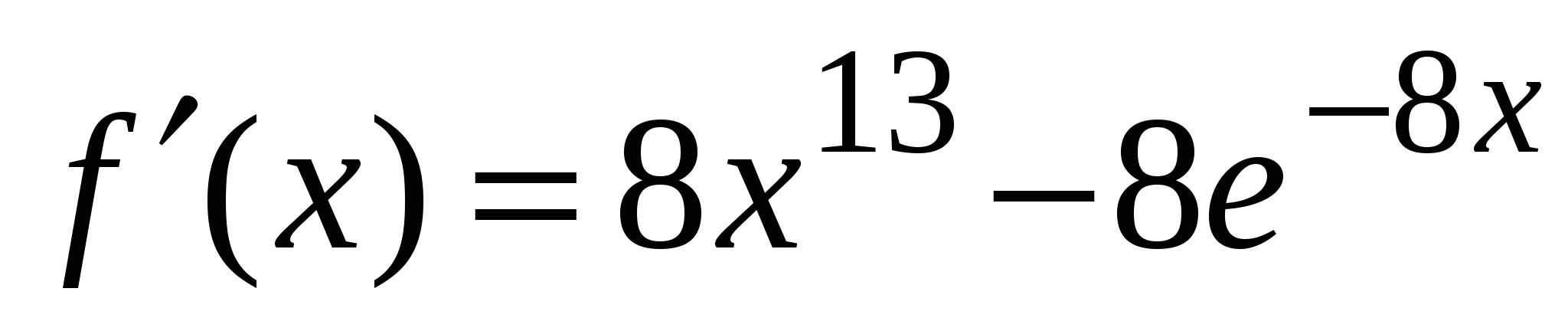
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Найдите производную функции 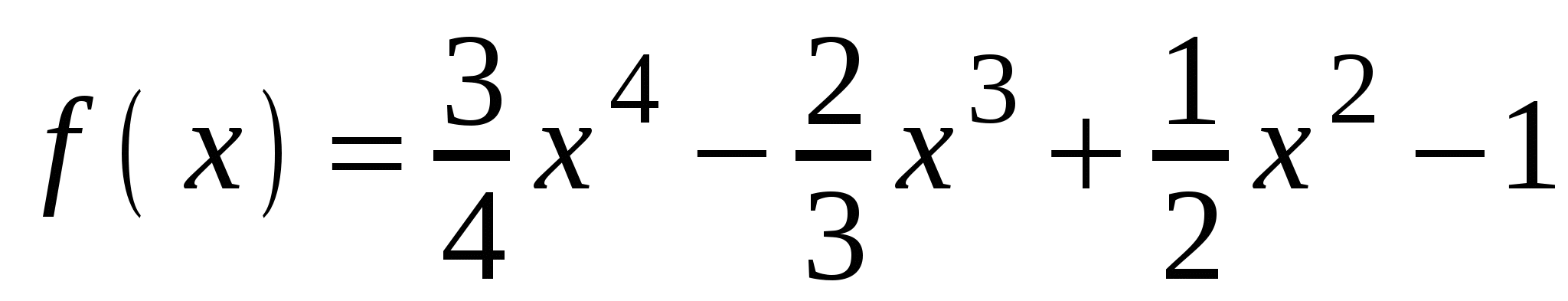 .
.
1)
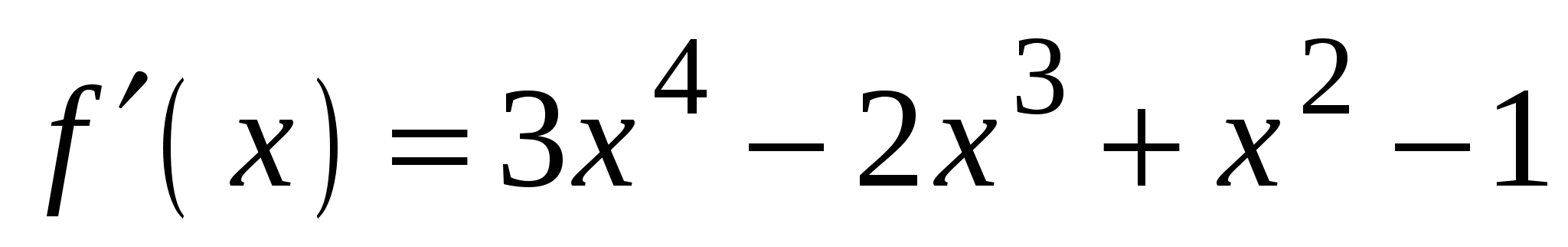
3)
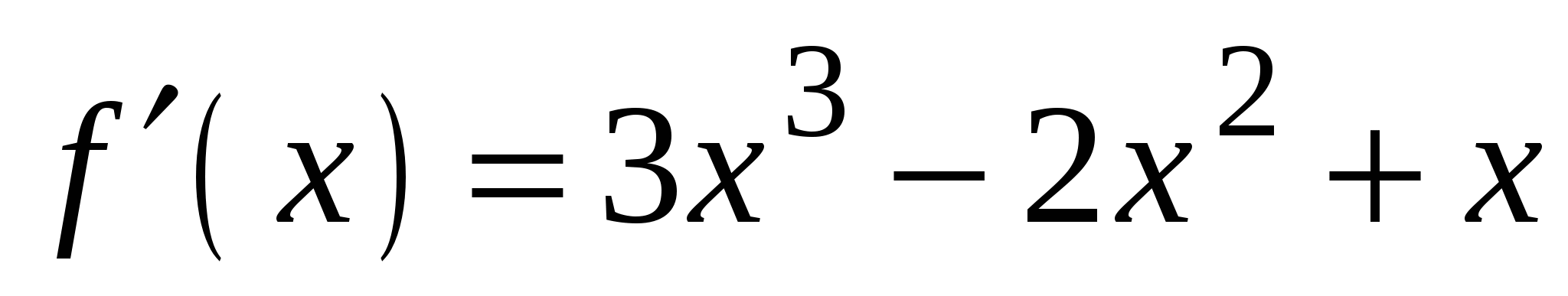
2)
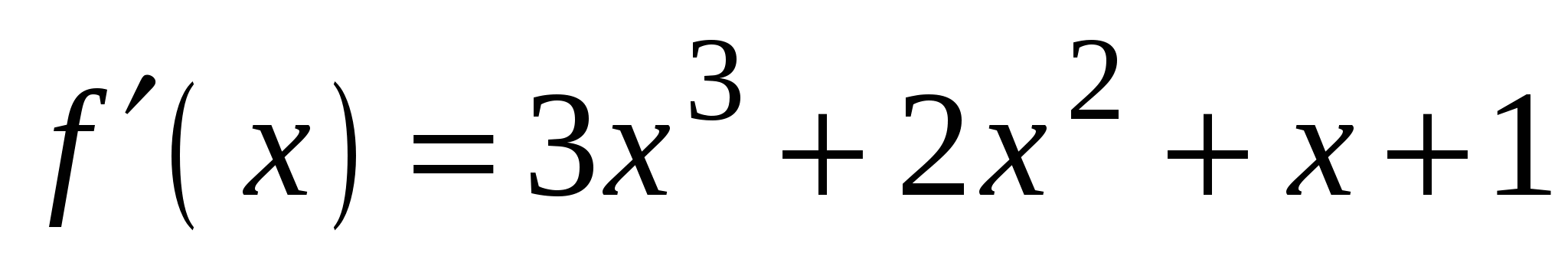
4)
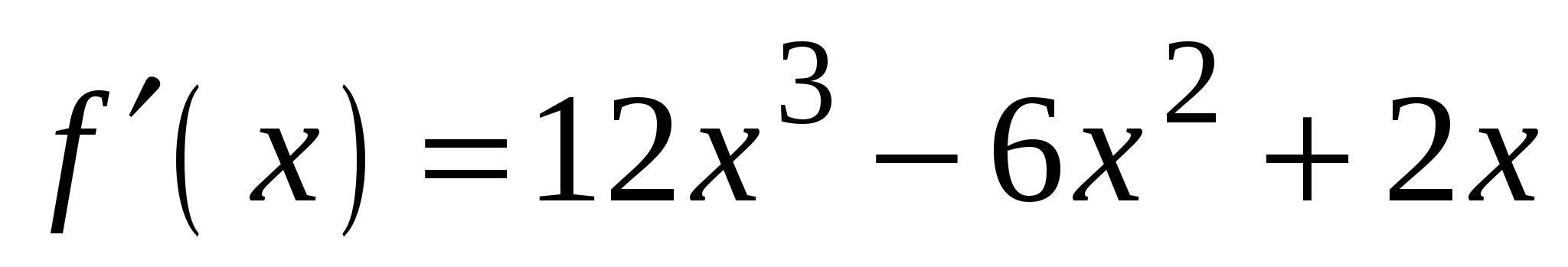
А4. Найдите производную функции 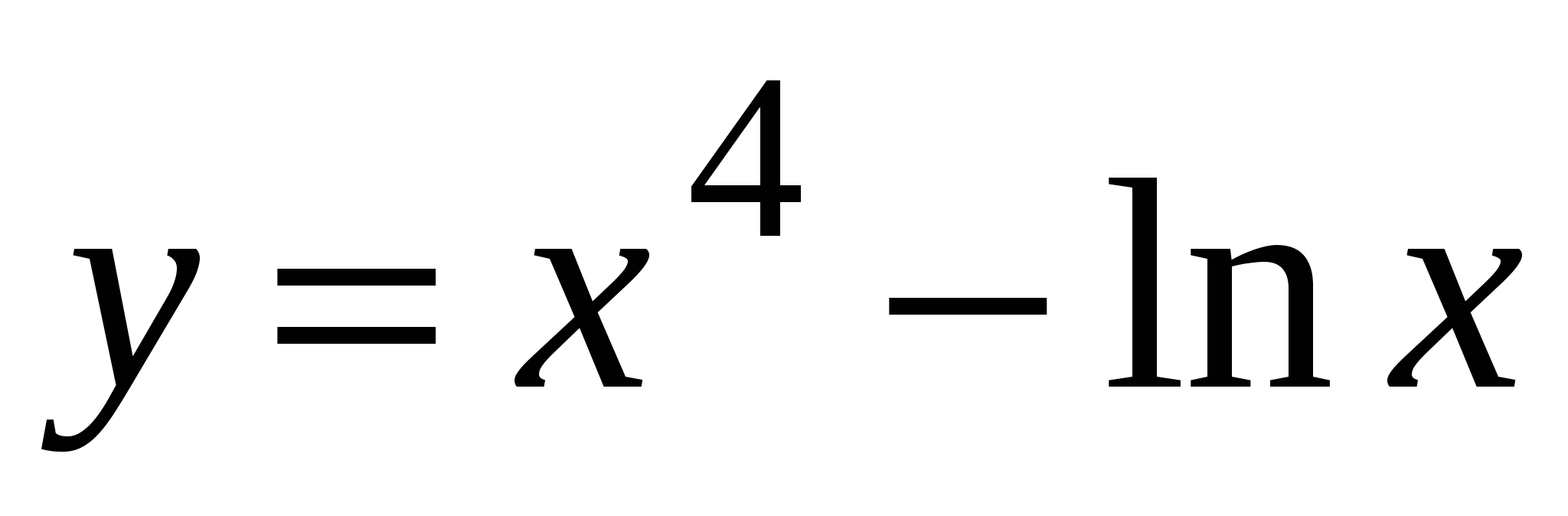 .
.
1)
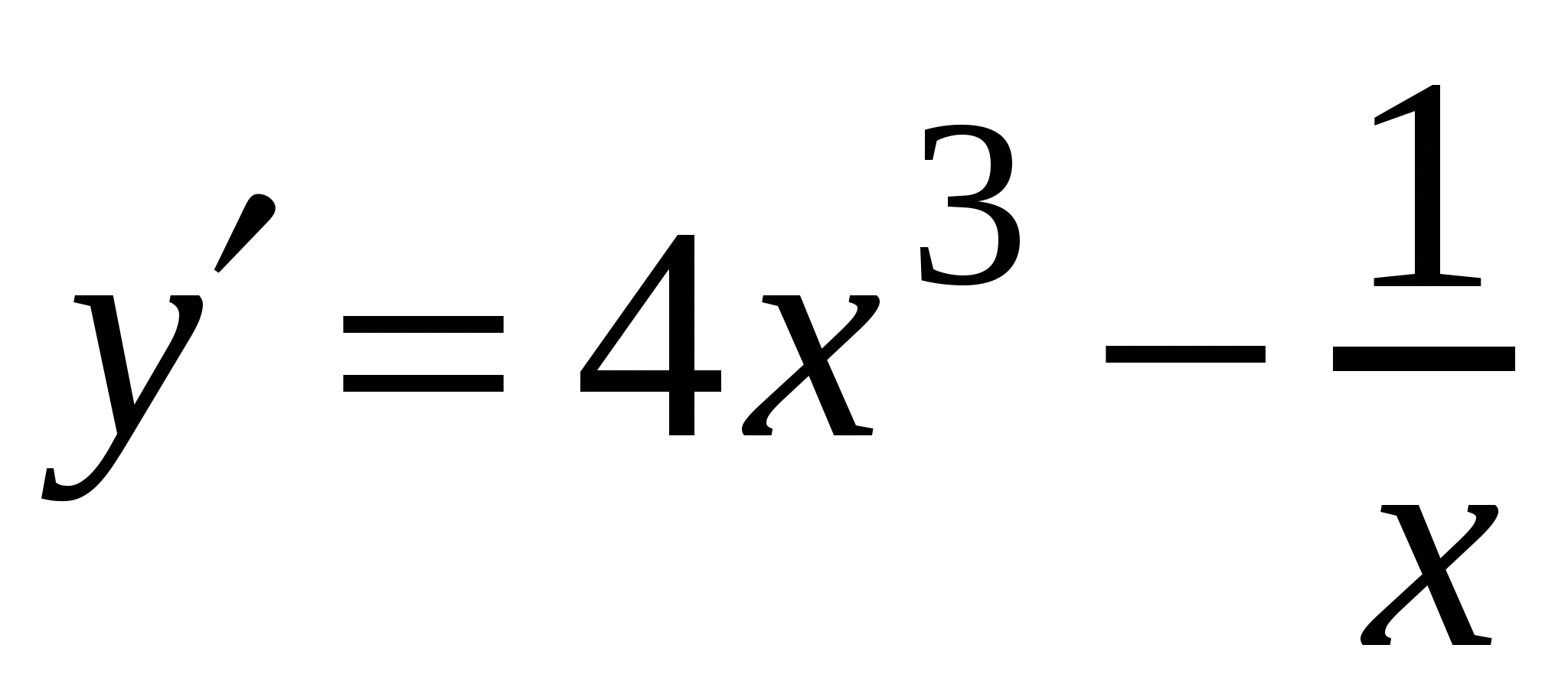
3)
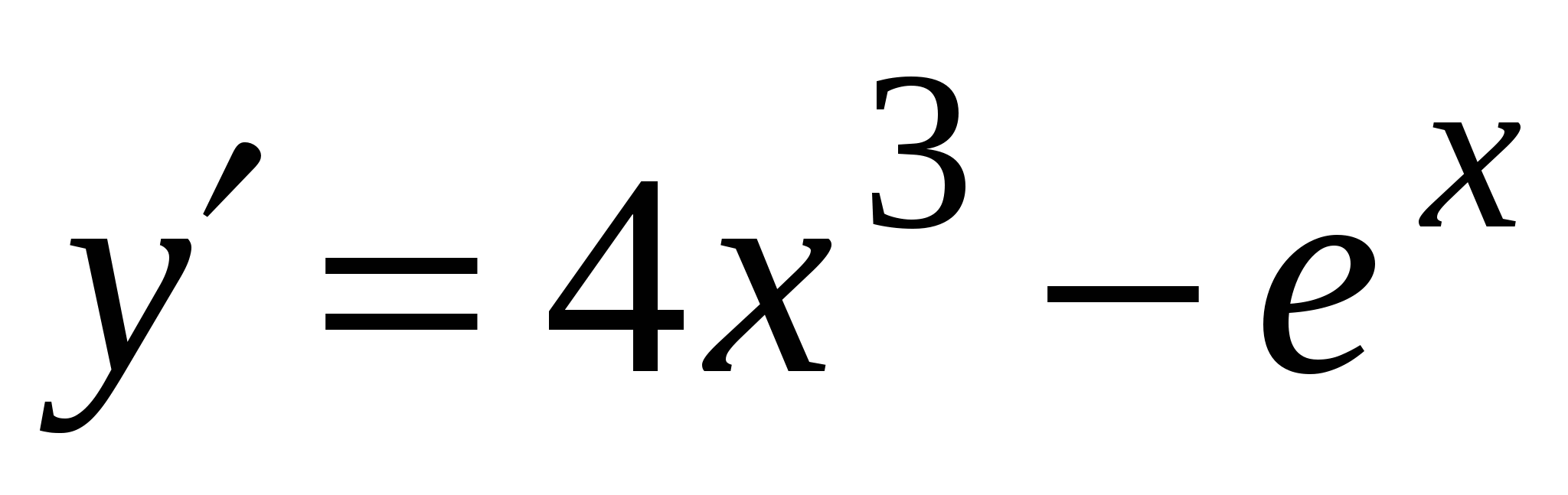
2)
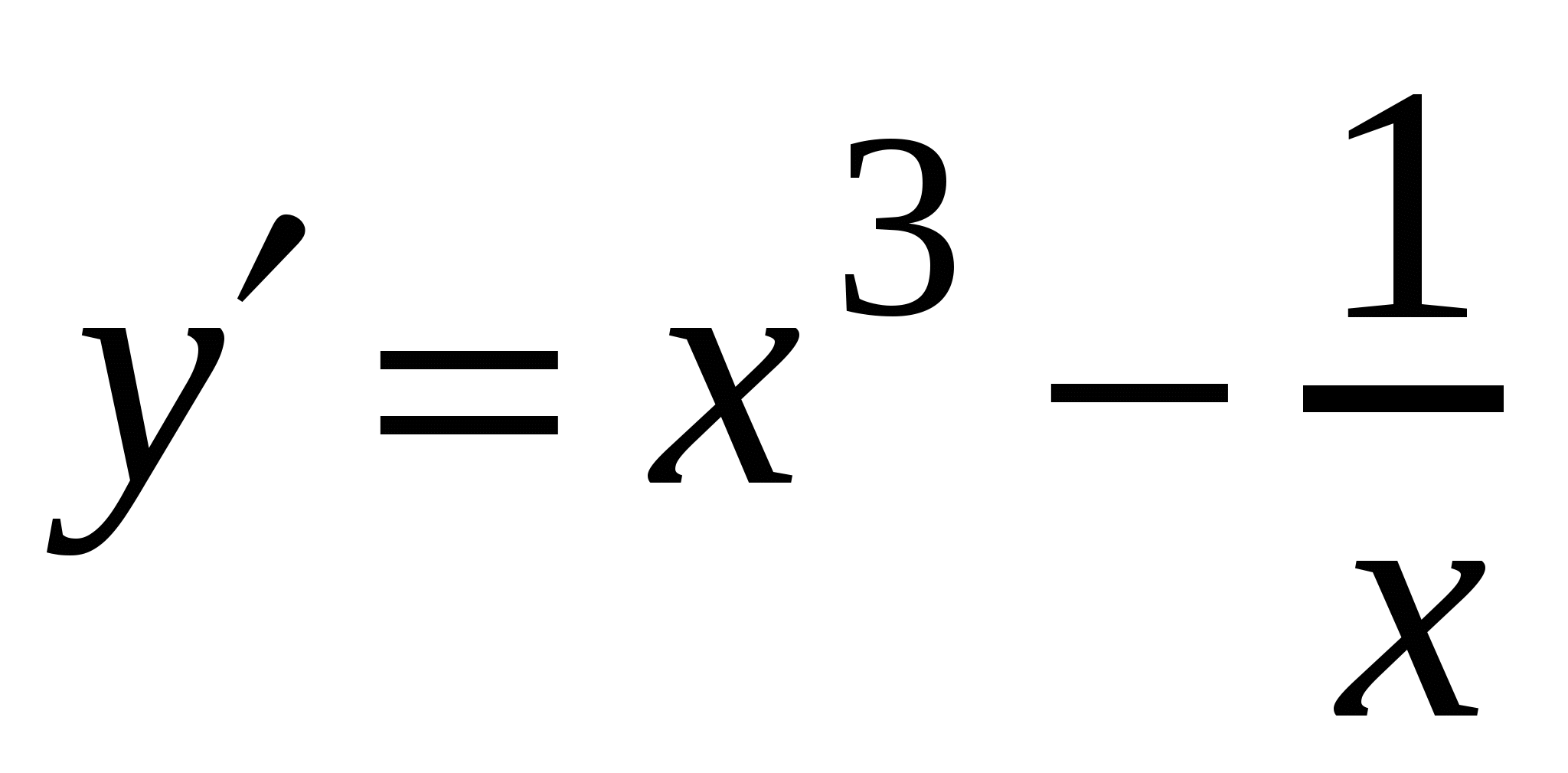
4)
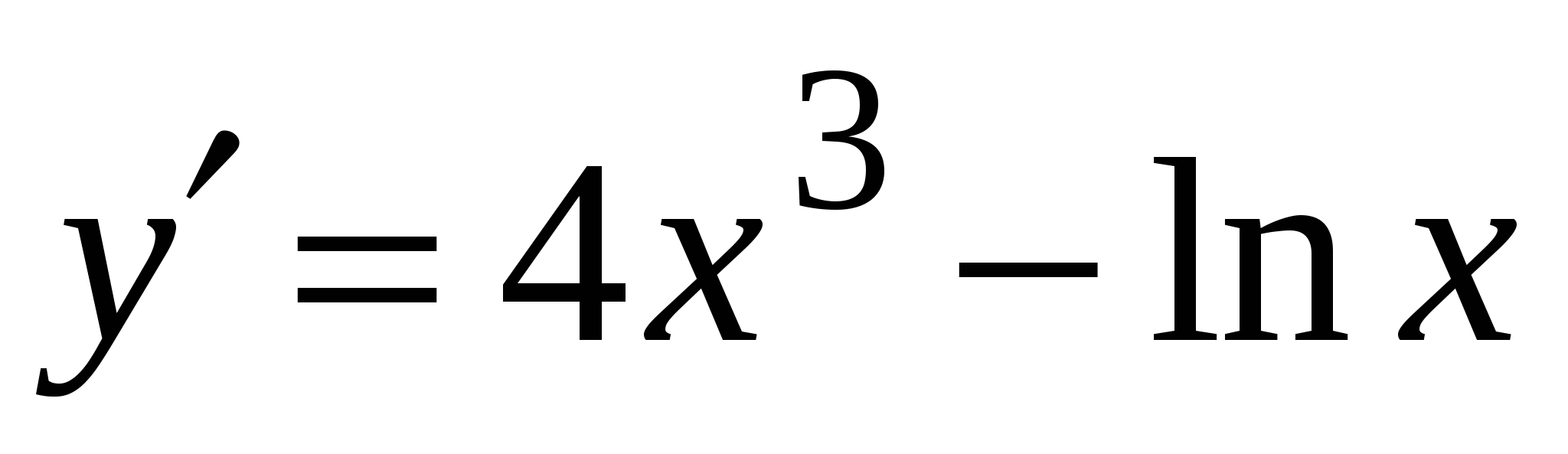

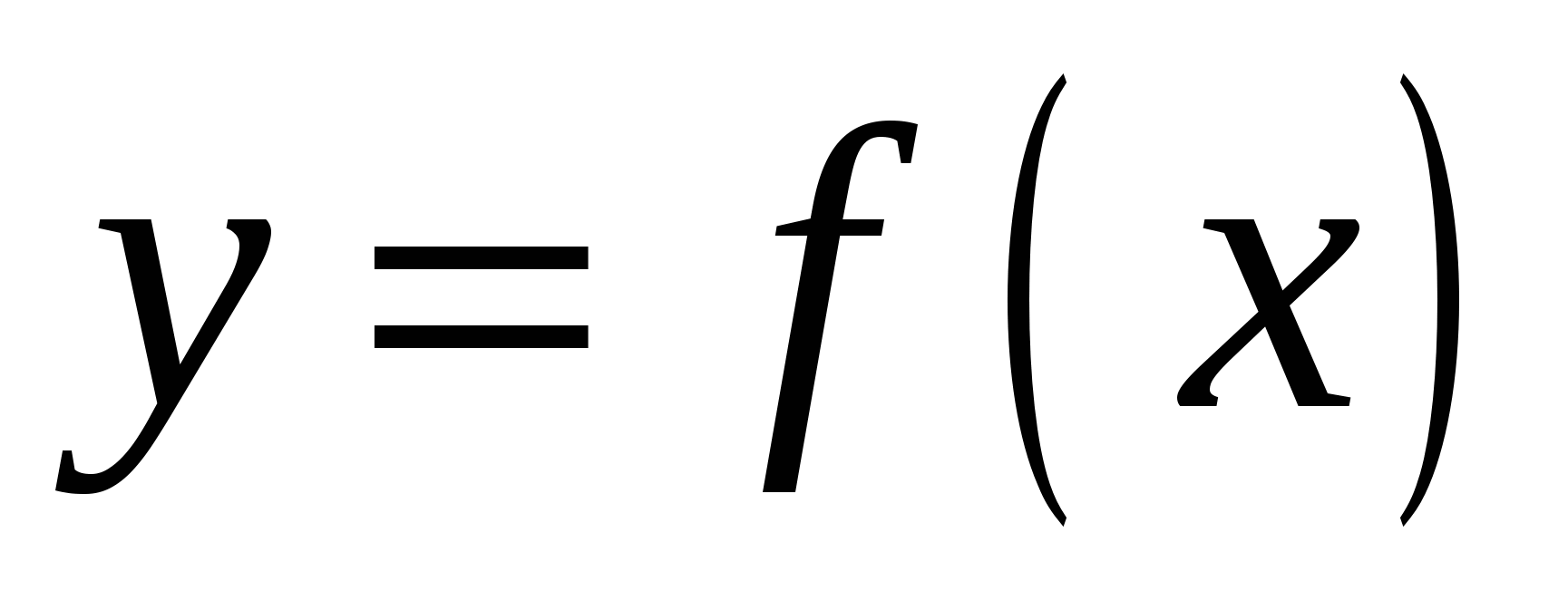 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. А5. Найдите производную функции 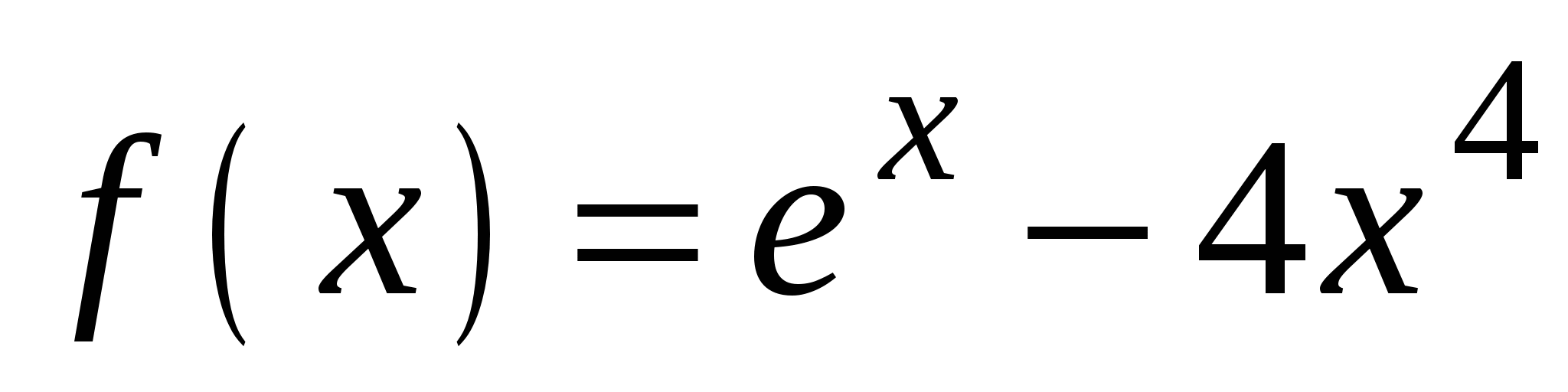 .
.
1)
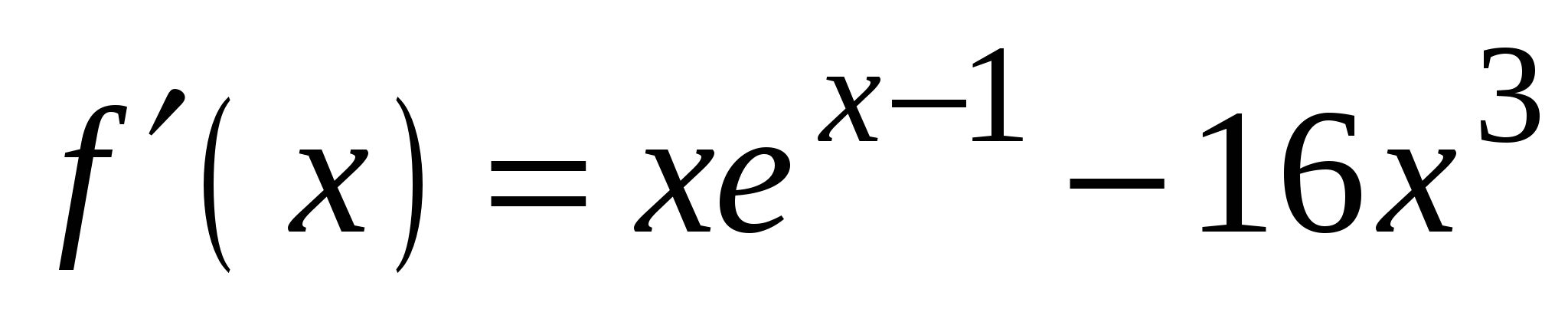
3)
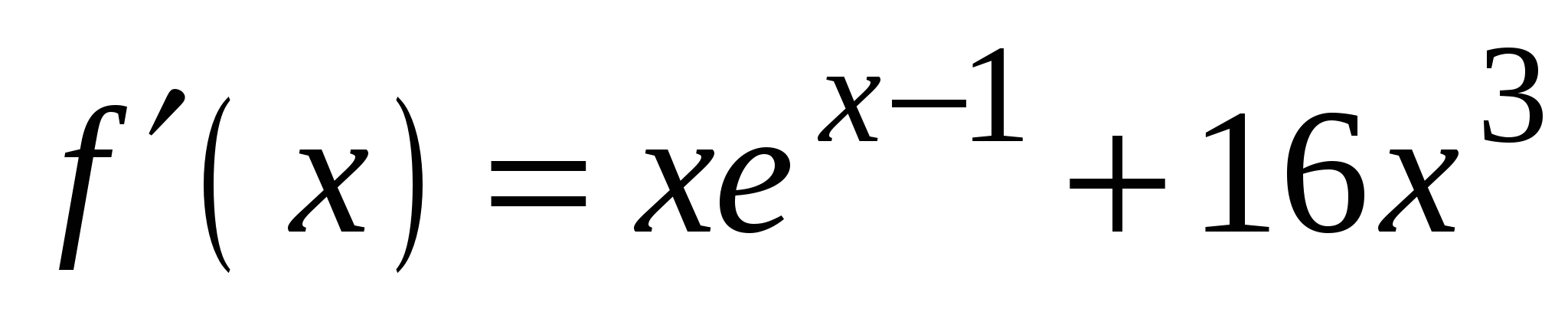
2)
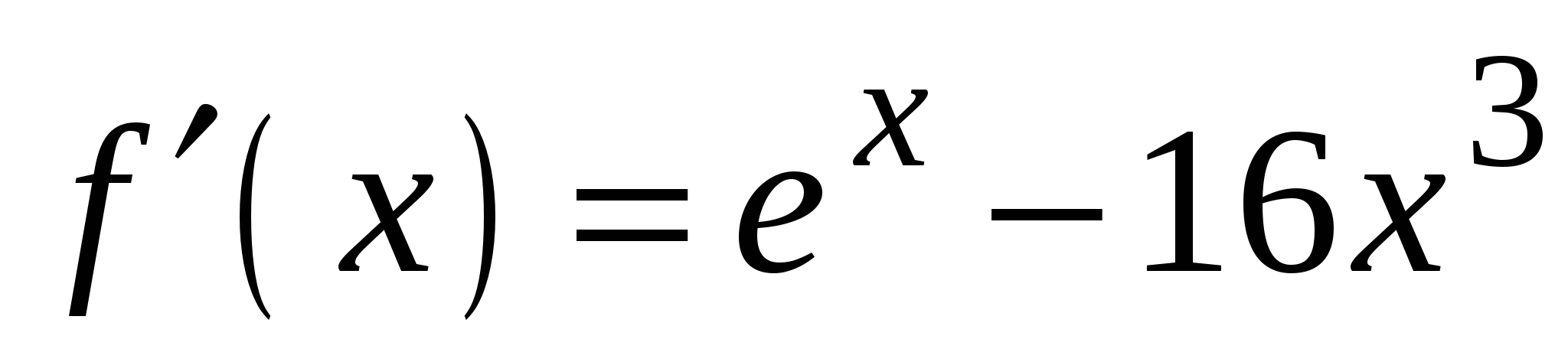
4)
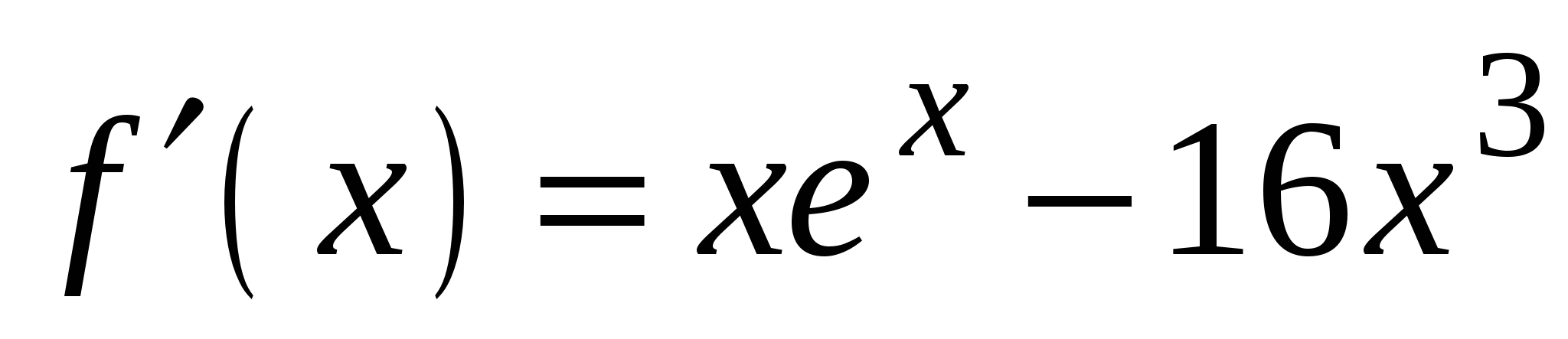

 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. В4.Материальная точка движется по закону
х(t)=1/3 t3-6t2+35t +61 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 6 м/с2 ?
В5.Тело движется прямолинейно, его расстояние S (в м) от начала отсчета изменяется по закону S(t)=2t2+4 -9 м. Определите скорость движения тела через 4 с после начала движения.
В6.Материальная точка движется по закону х(t)=1/2 t3-7t2+16t -27 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 4 м/с2 ?
Контрольная работа №3 по теме: «Производная»
Вариант №10

B1. Функция  определена на промежутке
определена на промежутке  . Используя изображенный на рисунке график производной
. Используя изображенный на рисунке график производной  , определите количество касательных к графику функции
, определите количество касательных к графику функции  , параллельных прямой
, параллельных прямой  .
.
А1. Найдите производную функции 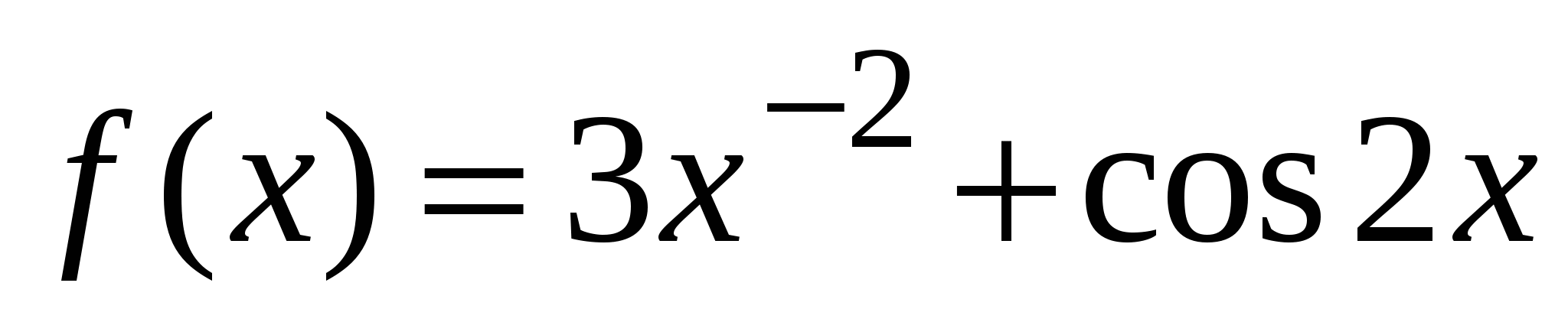 .
.
1) 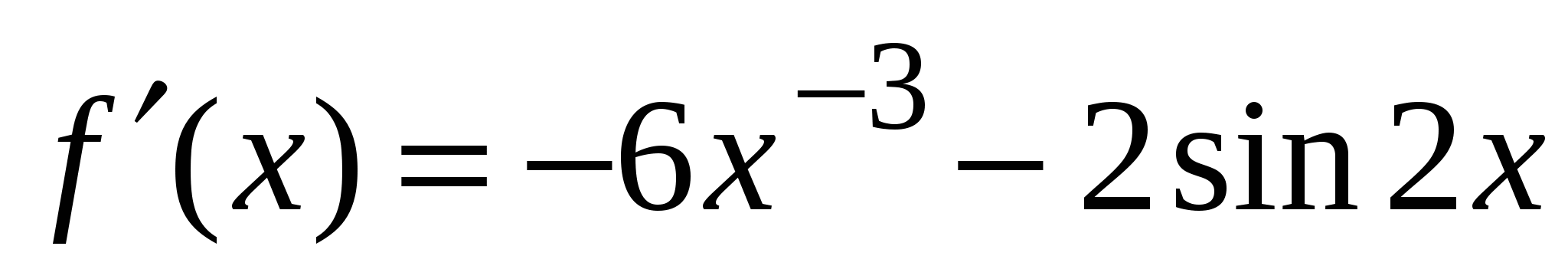
3) 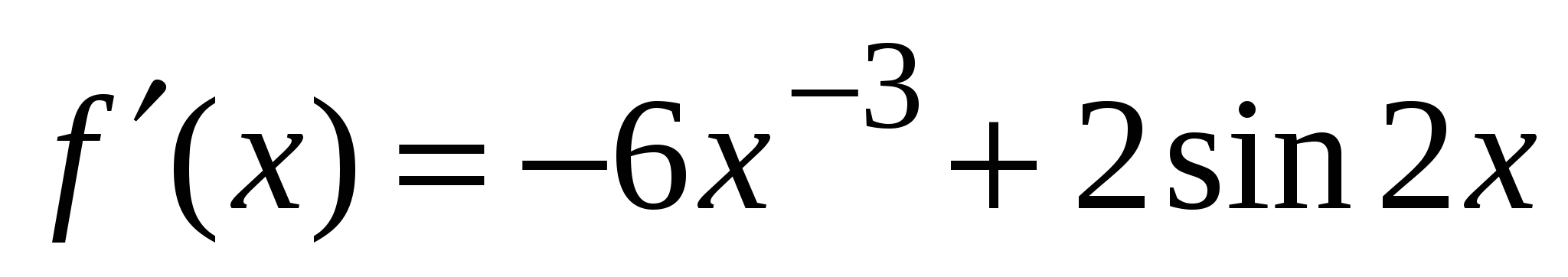
2) 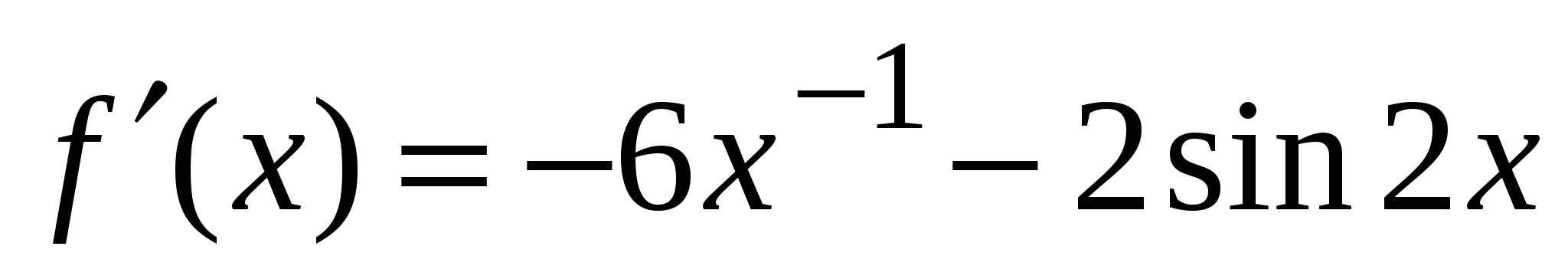
4) 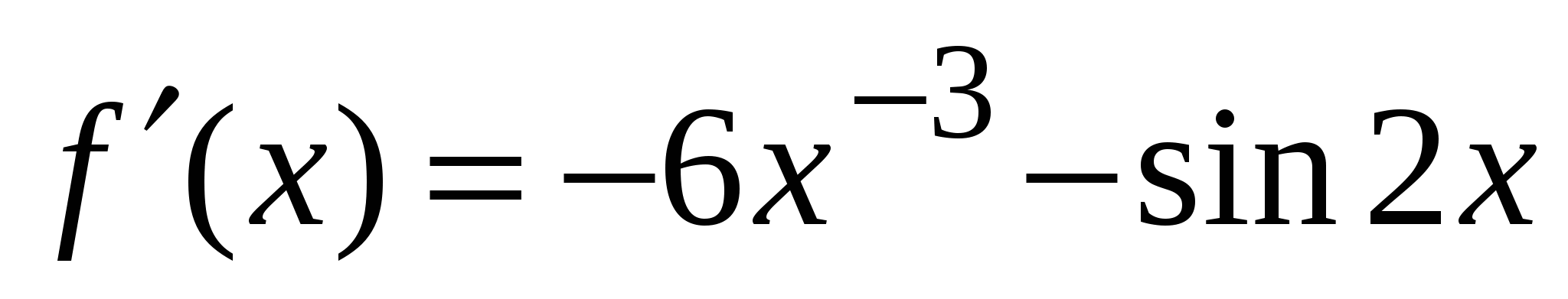
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Вычислите значение производной функции 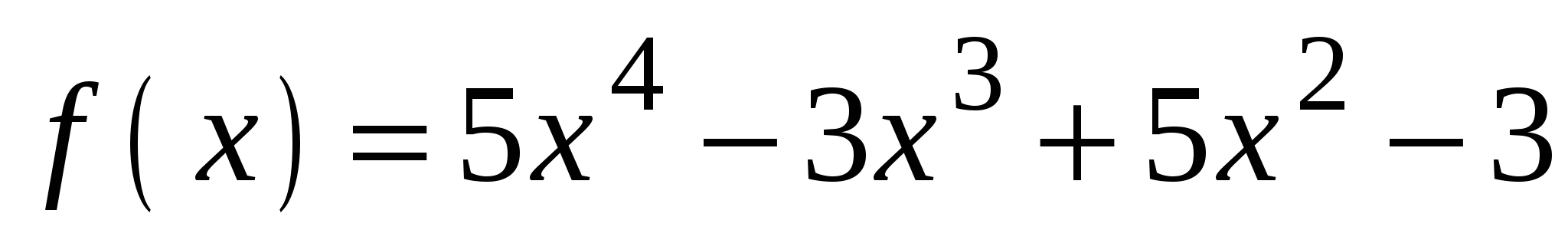 в точке
в точке 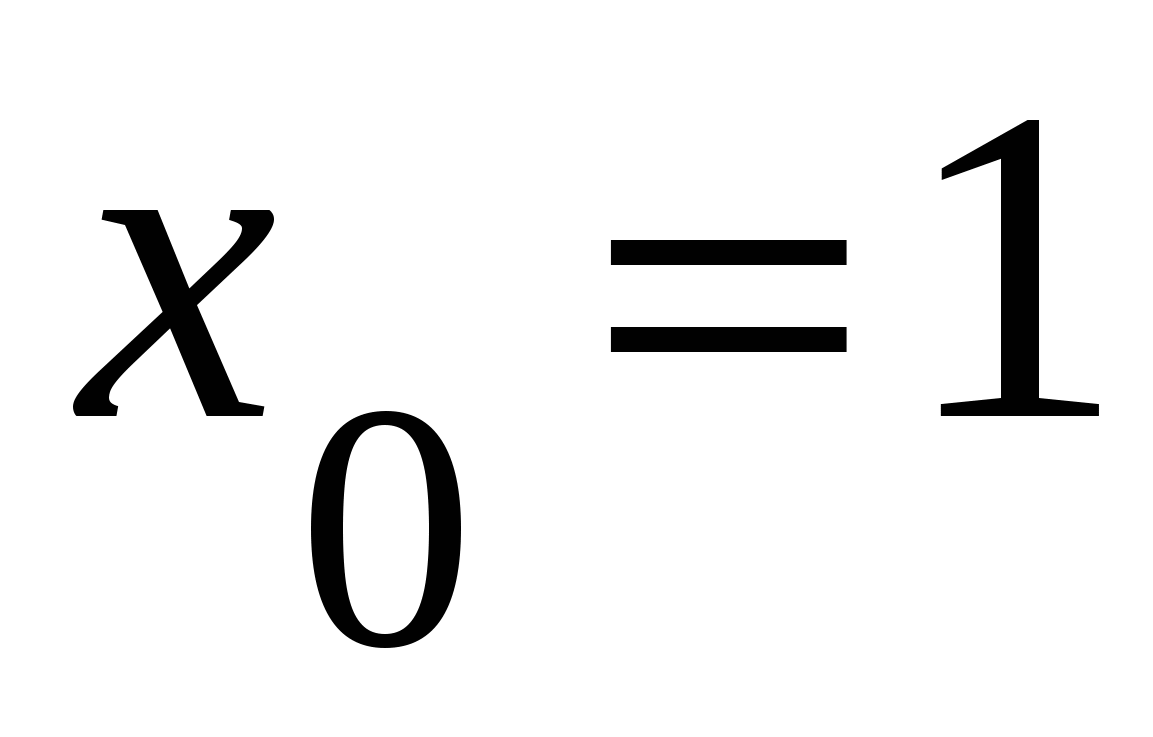 .
.
1)
21
2)
39
3)
− 1
4)
16
А4. Найдите производную функции 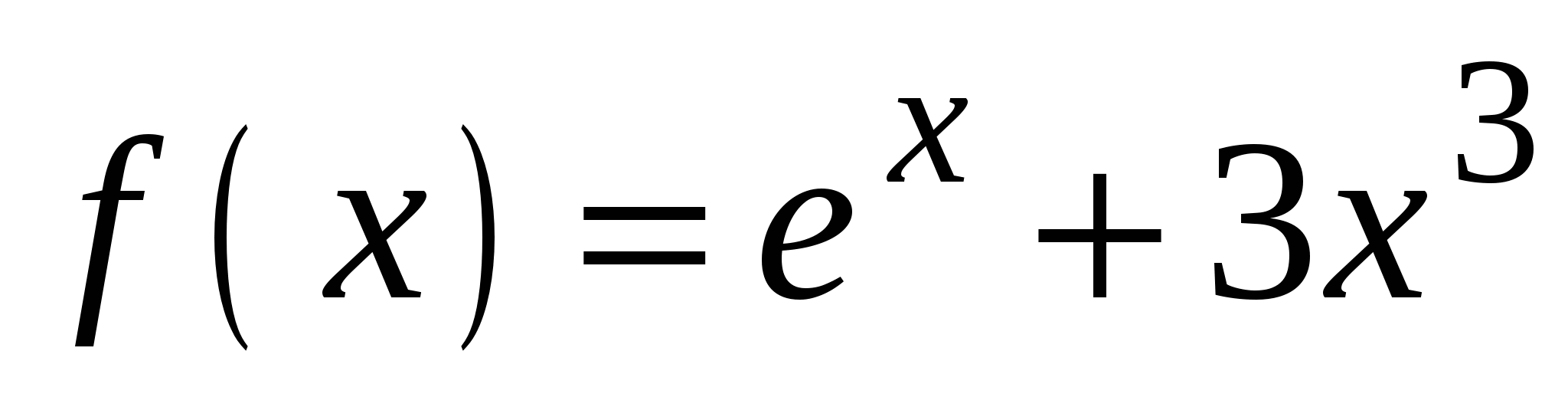 .
.
1)
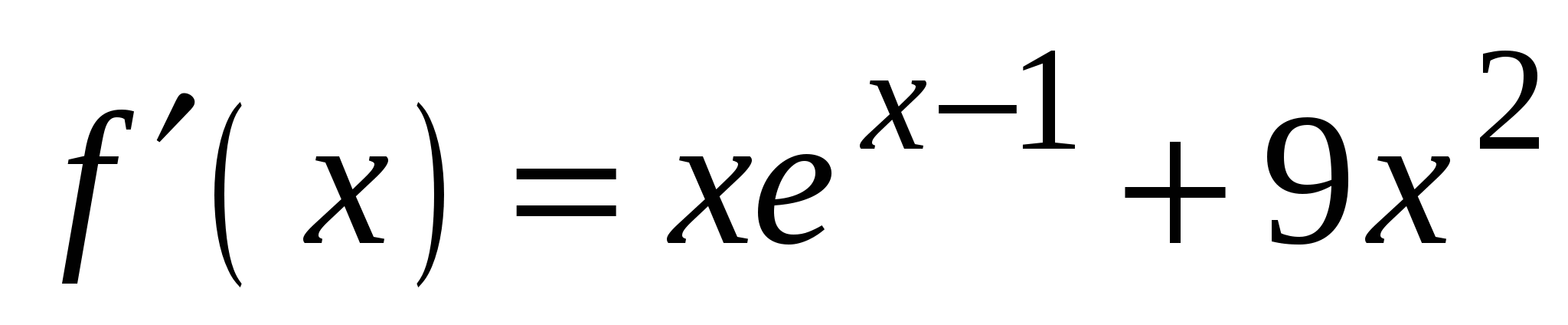
3)
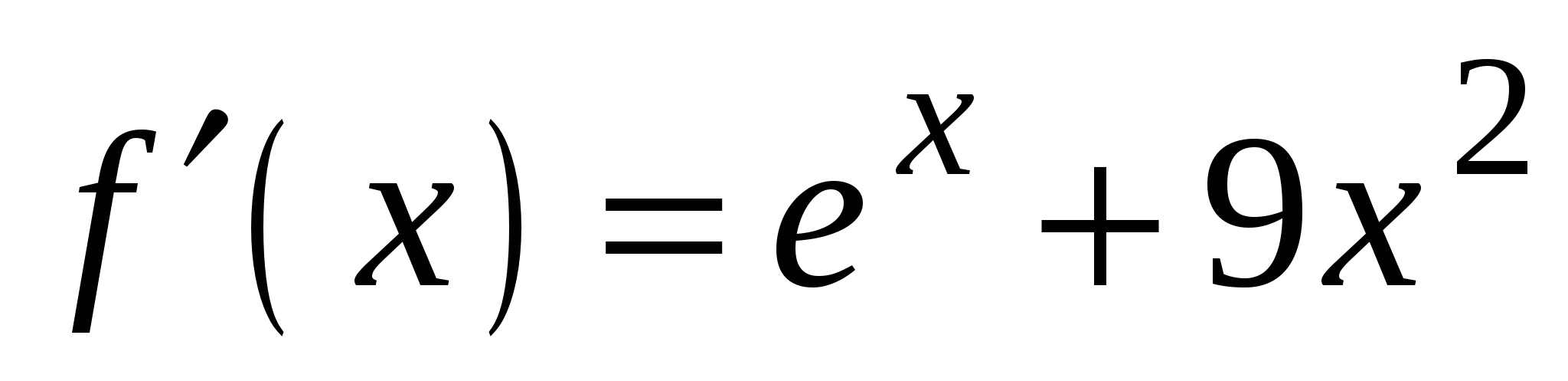
2)
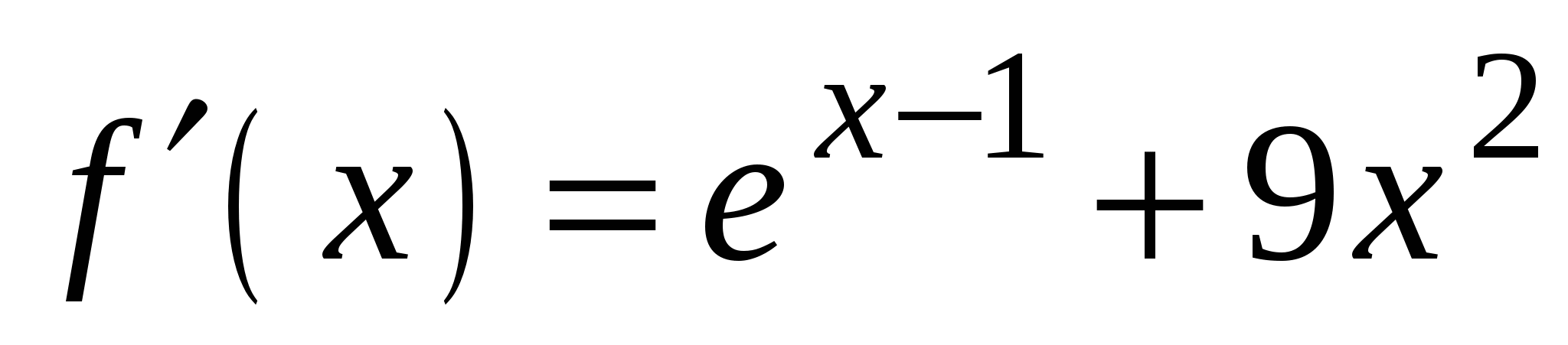
4)
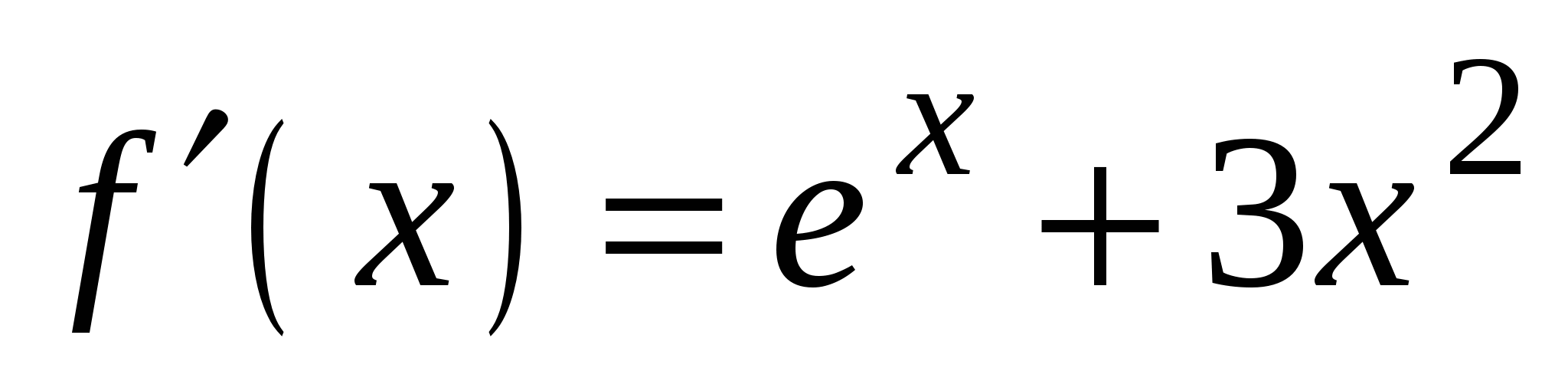

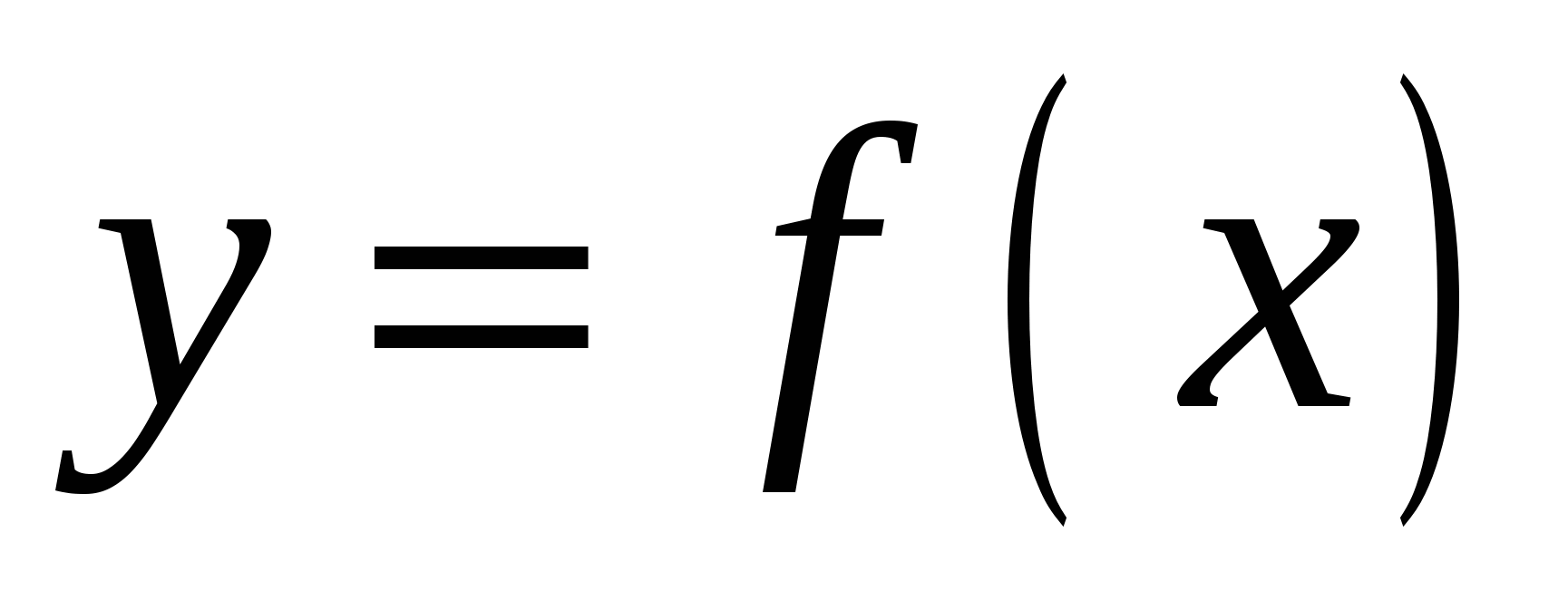 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. А5. Найдите производную функции 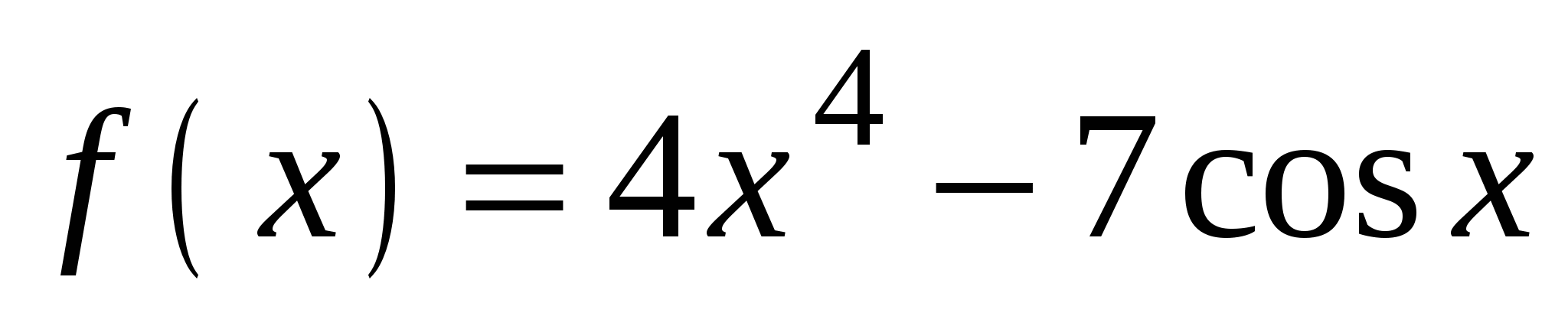 .
.
1)
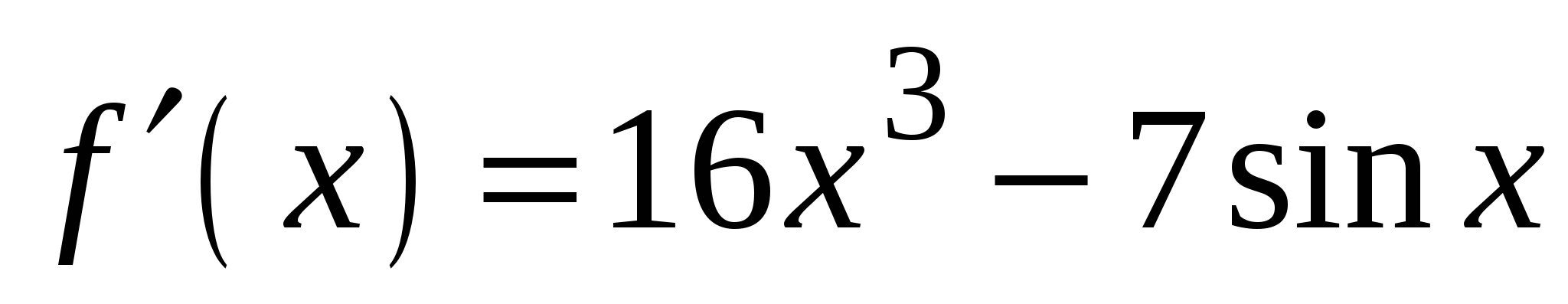
3)
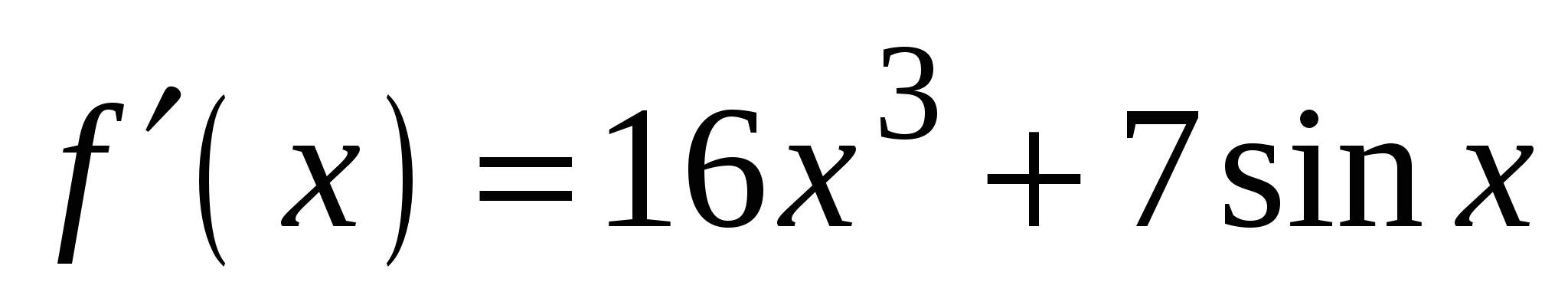
2)
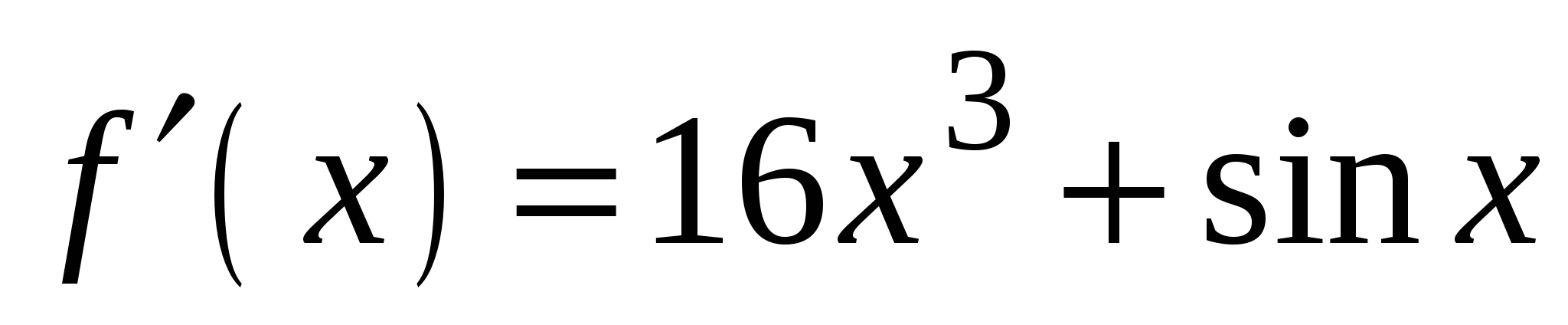
4)
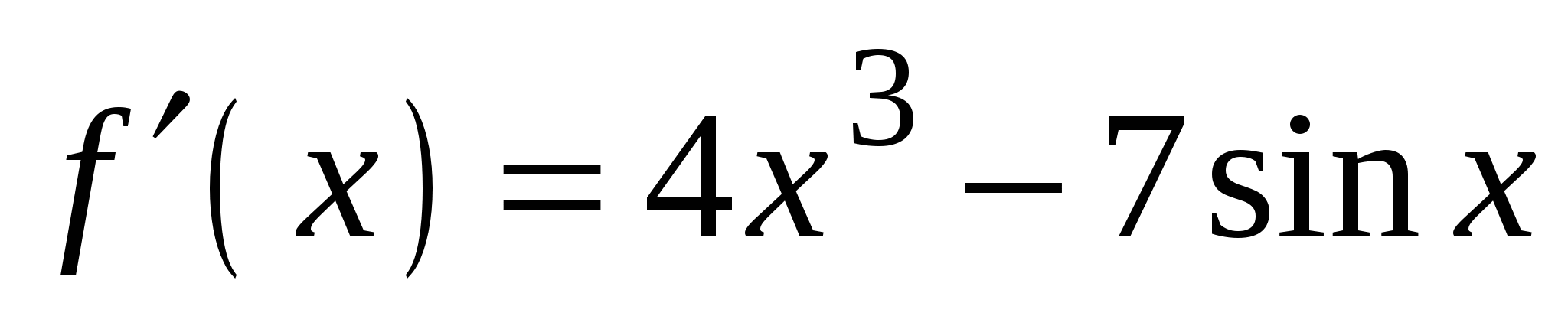

 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. В4.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=t4+1/3t3-t2+8. Чему будет равна мгновенная скорость (м/с) через 3 с после начала движения?
В5.Материальная точка движется по закону х(t)= 1/3t3-t2+9t+11 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 10 м/с2 ?
В6. Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=5t2 - 3t+6. Через сколько секунд после начала движения произойдет остановка?
Контрольная работа №3 по теме: «Производная»
Вариант №11

B1. На рисунке изображен график производной функции  . Найдите тангенс угла наклона касательной к графику функции
. Найдите тангенс угла наклона касательной к графику функции  в точке с абсциссой
в точке с абсциссой  .
.
А1. Найдите производную функции 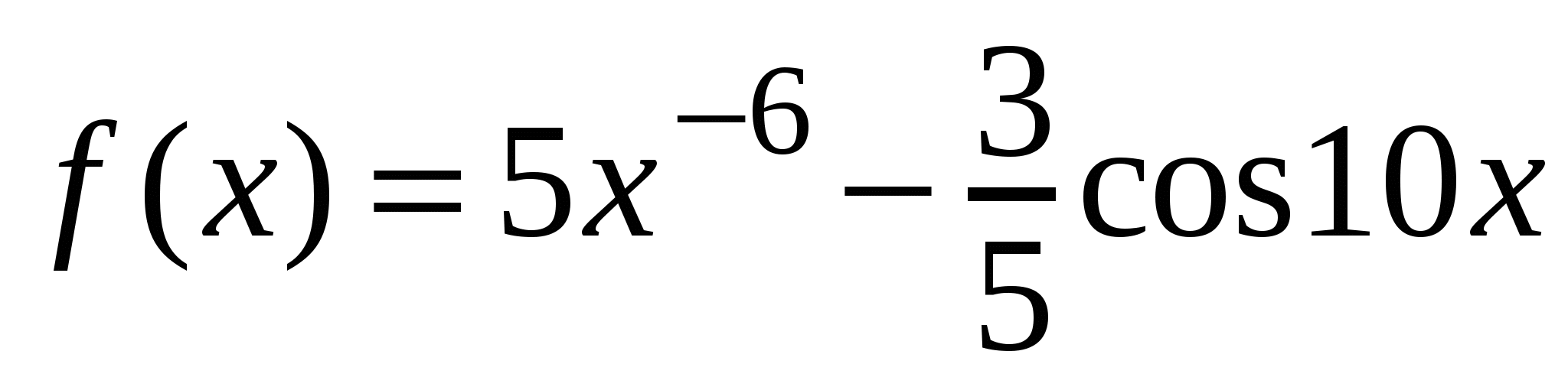 .
.
1) 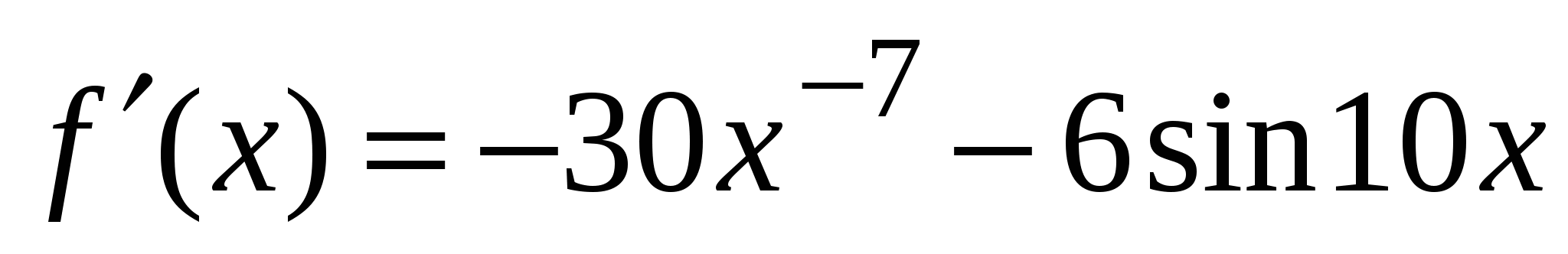
3) 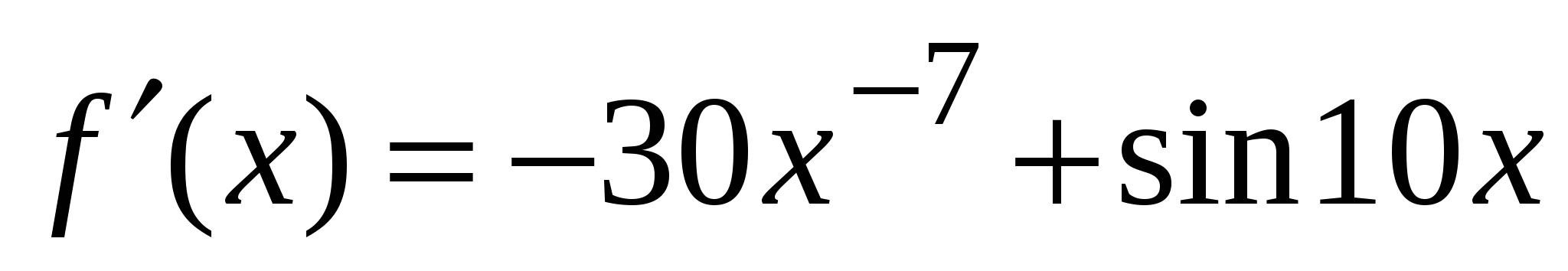
2) 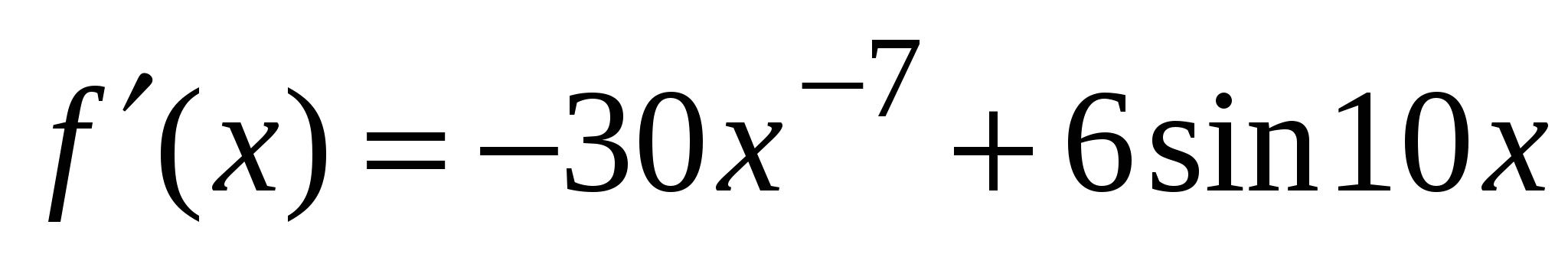
4) 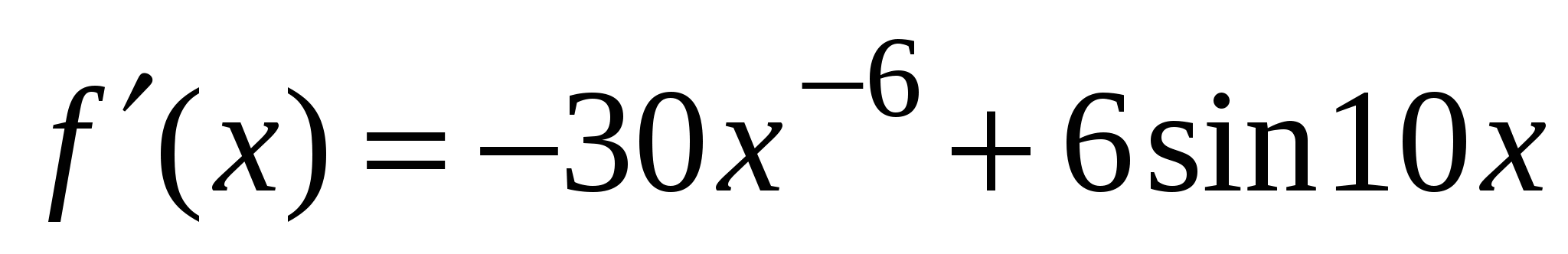
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Вычислите значение производной функции 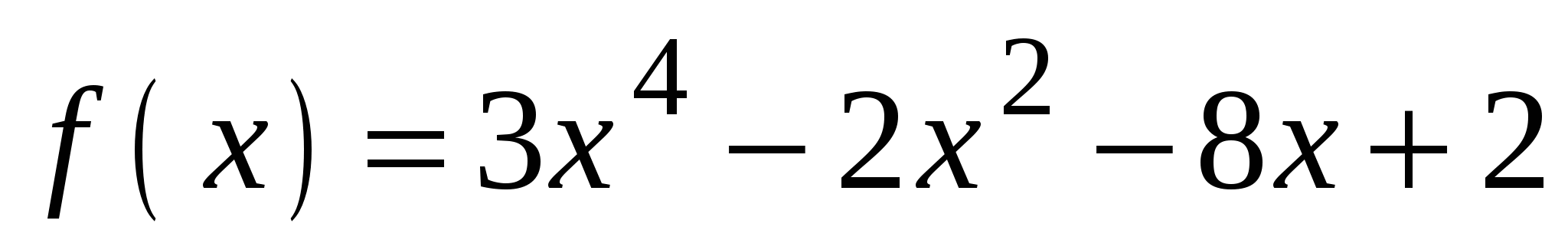 в точке
в точке 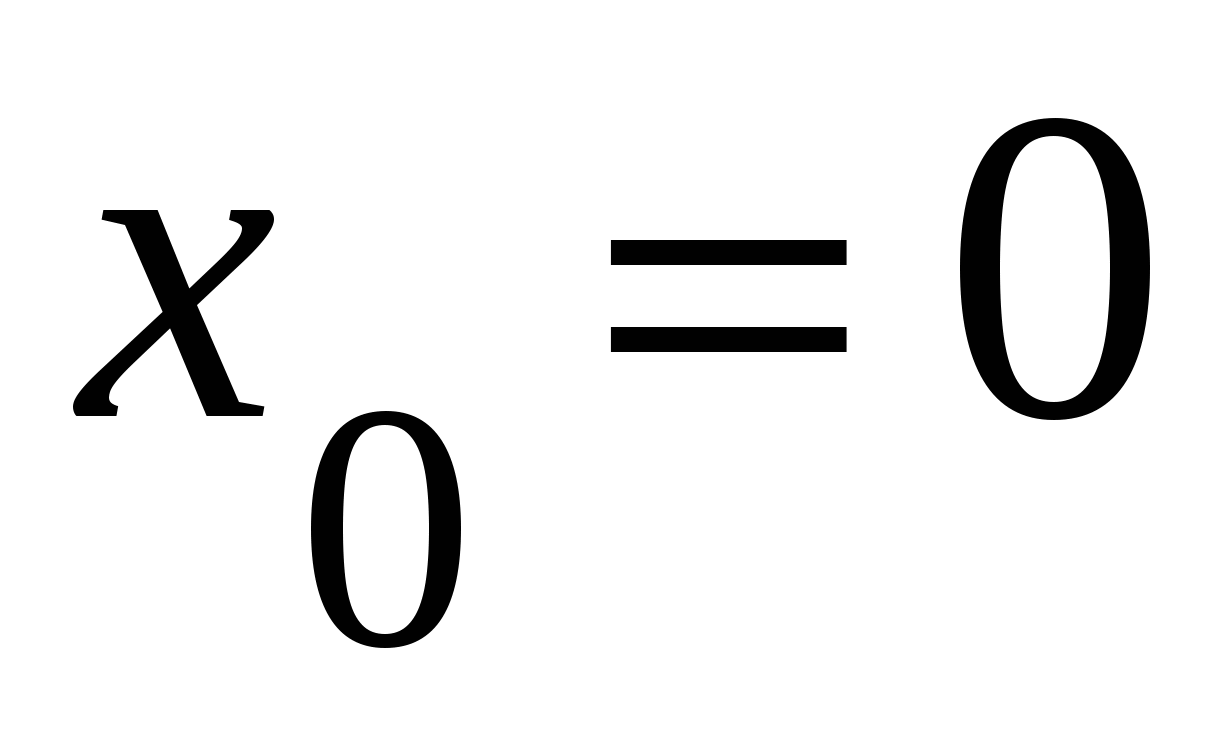 .
.
1)
8
2)
− 6
3)
0
4)
− 8
А4. Найдите производную функции 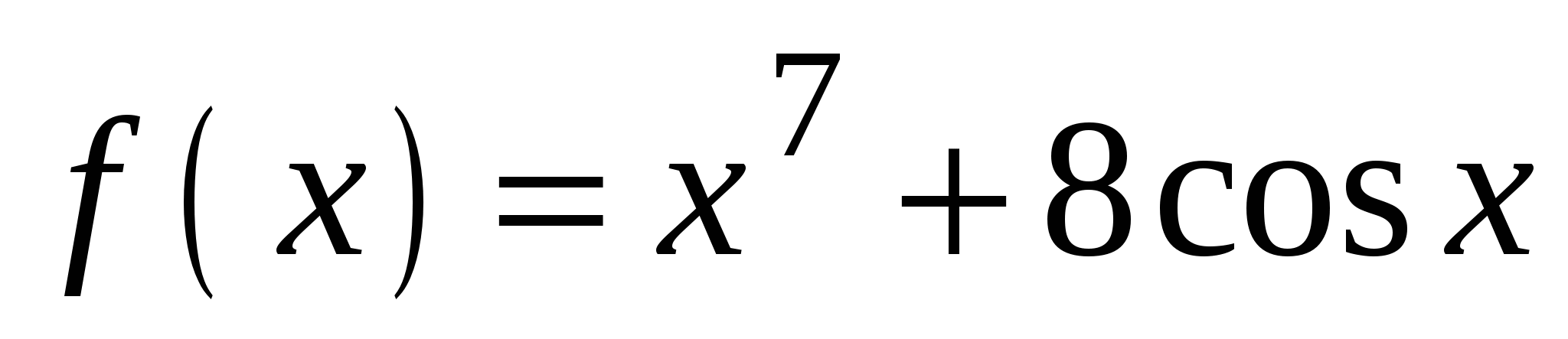 .
.
1)
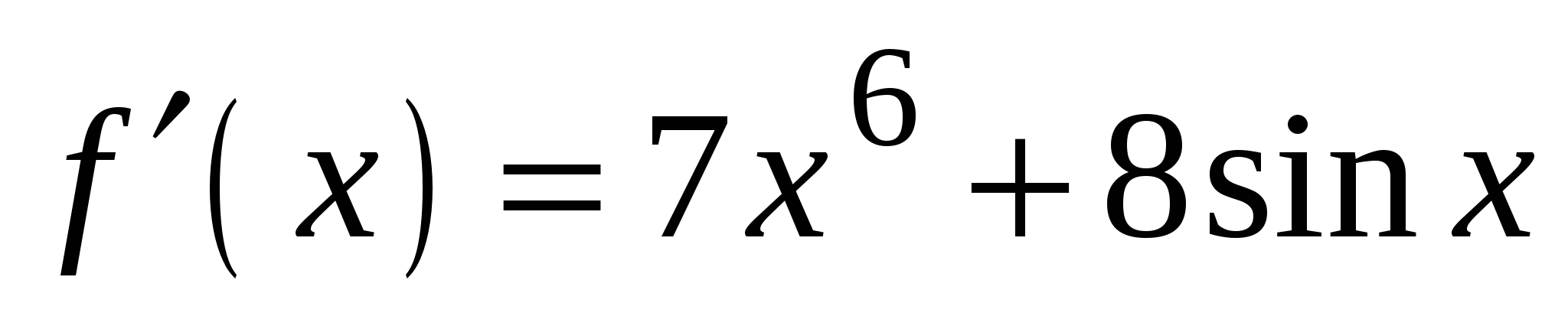
3)
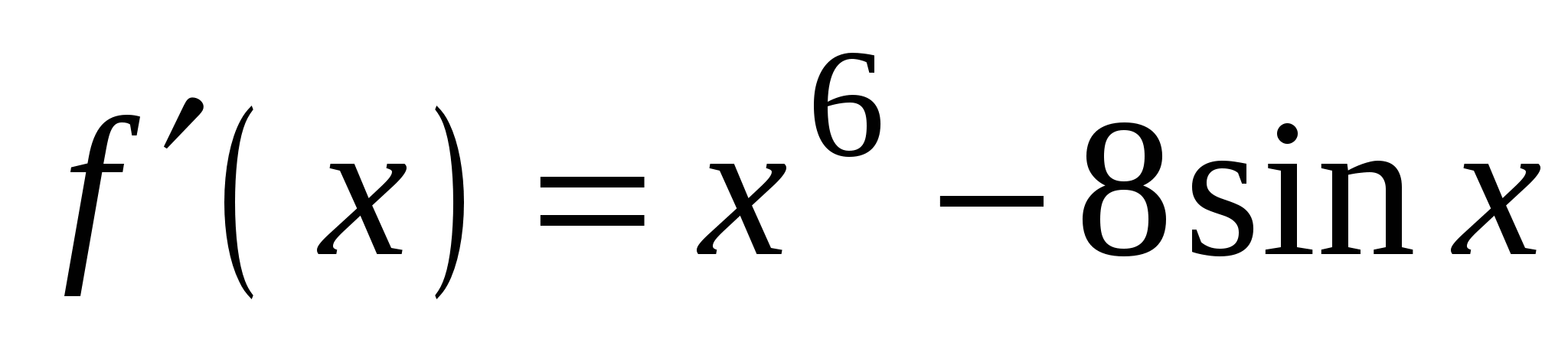
2)
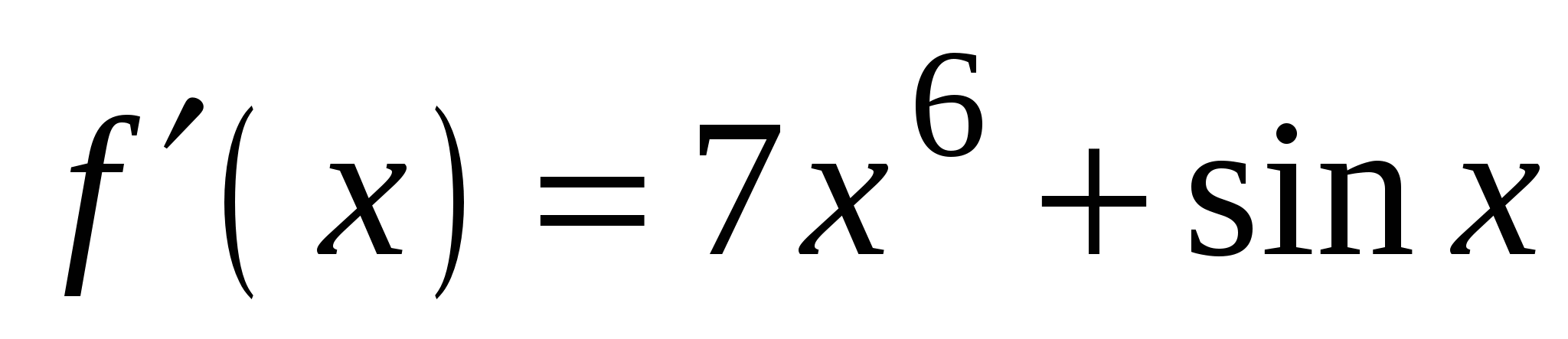
4)
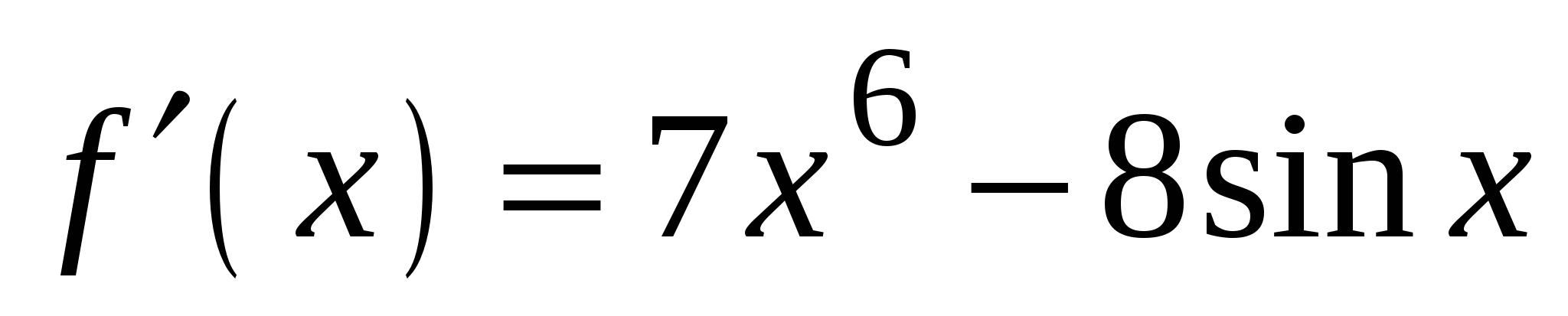

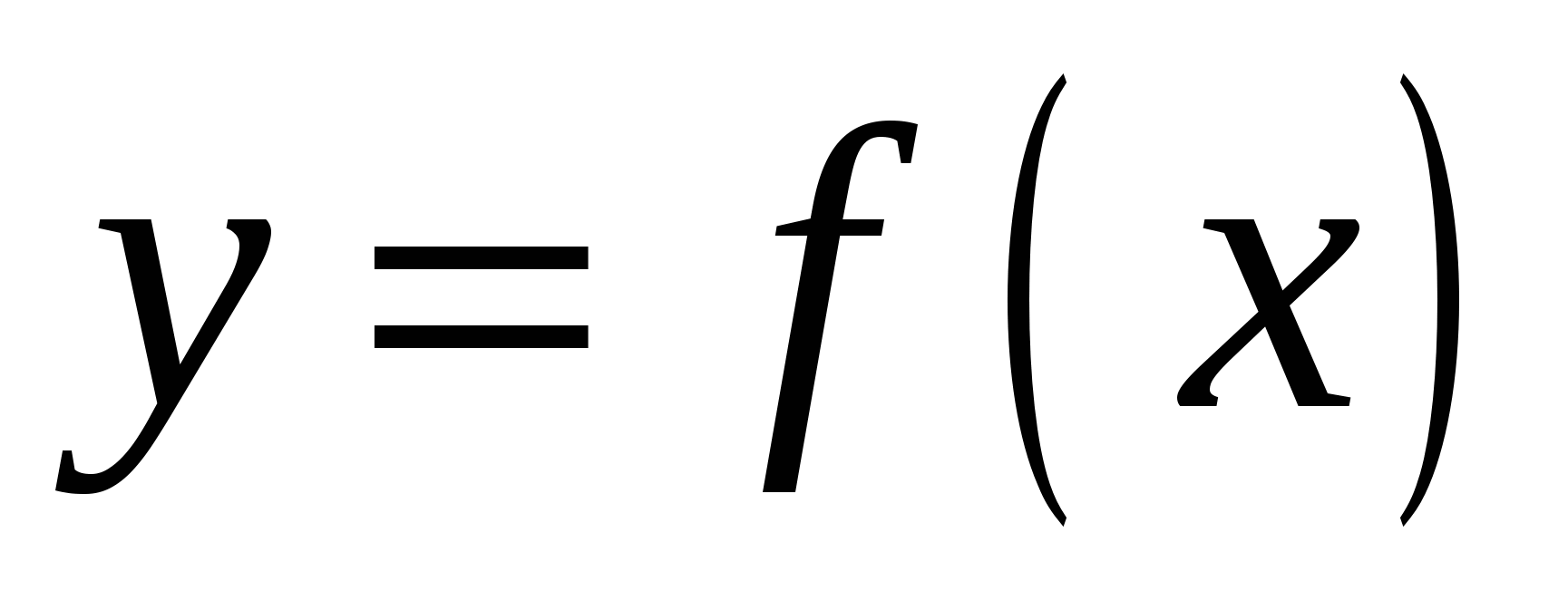 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. А5. Найдите производную функции 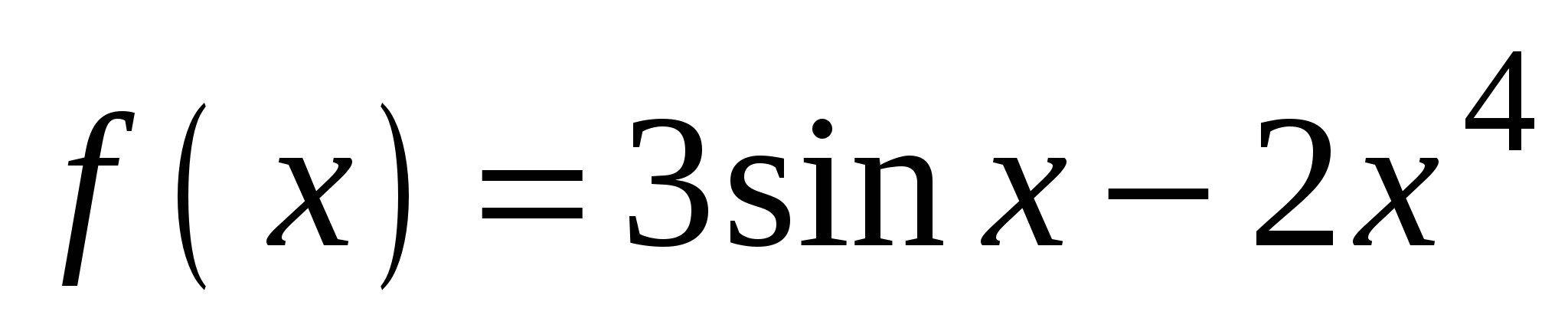 .
.
1)
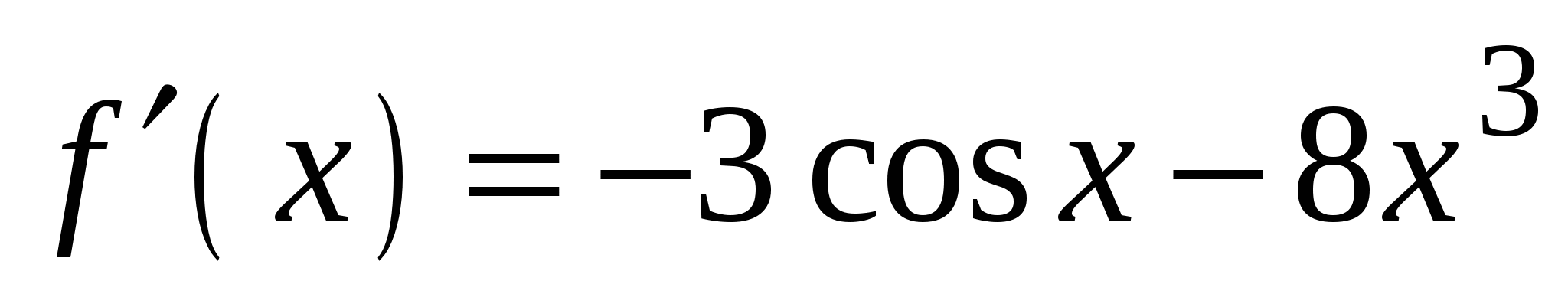
3)
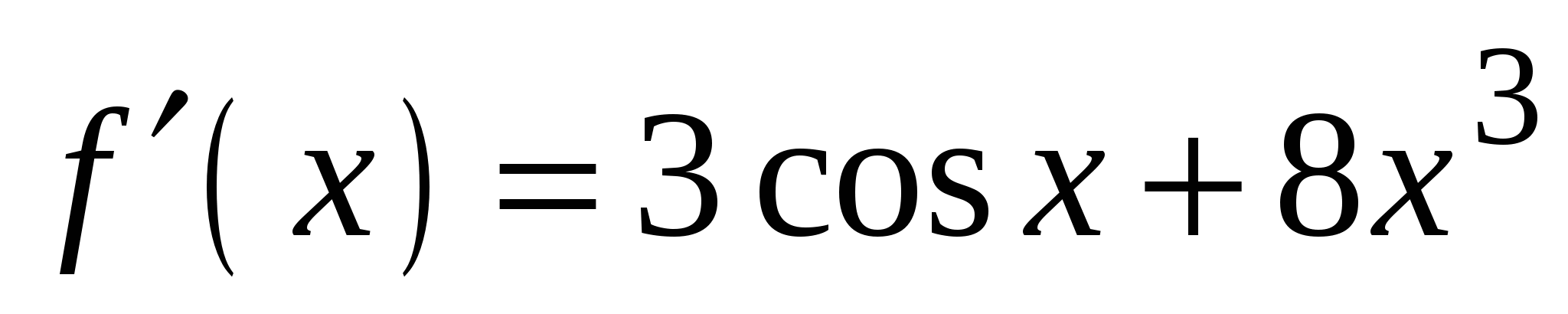
2)
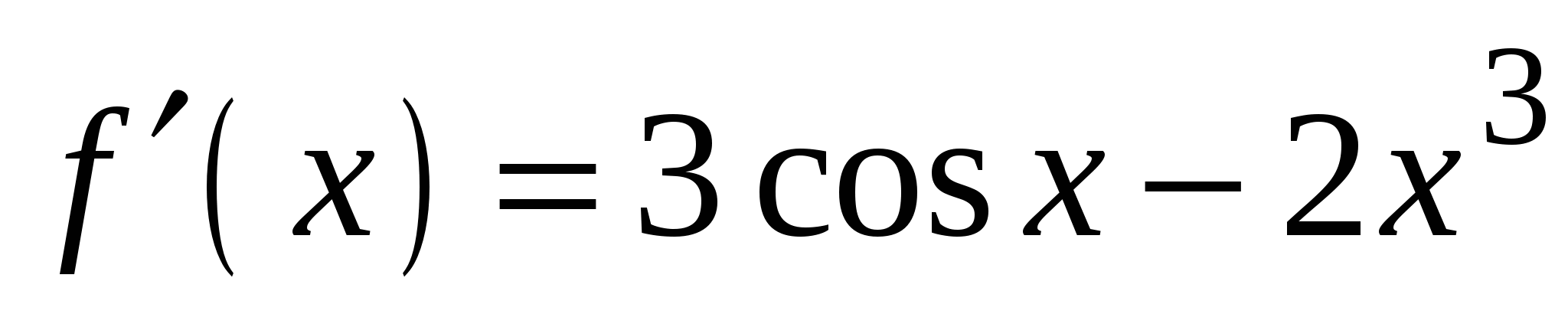
4)
В3. На рисунке изображен график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
.
В4. Материальная точка движется по закону х(t)= t3-4t2+3t - 17 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 10 м/с2 ?
В5. Материальная точка движется по закону х(t)= t3-5t2+6t +7 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 8 м/с2 ?
В6. Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=1/4t4+t3-1/2t2+12. Чему будет равна мгновенная скорость (м/с) через 4 с после начала движения?
Контрольная работа №3 по теме: «Производная»
Вариант №12

B1.Функция  определена на промежутке
определена на промежутке  . Используя изображенный на рисунке график производной
. Используя изображенный на рисунке график производной  , определите количество касательных к графику функции
, определите количество касательных к графику функции  , тангенс угла наклона которых к положительному направлению оси Ox равен
, тангенс угла наклона которых к положительному направлению оси Ox равен
А1. Найдите производную функции 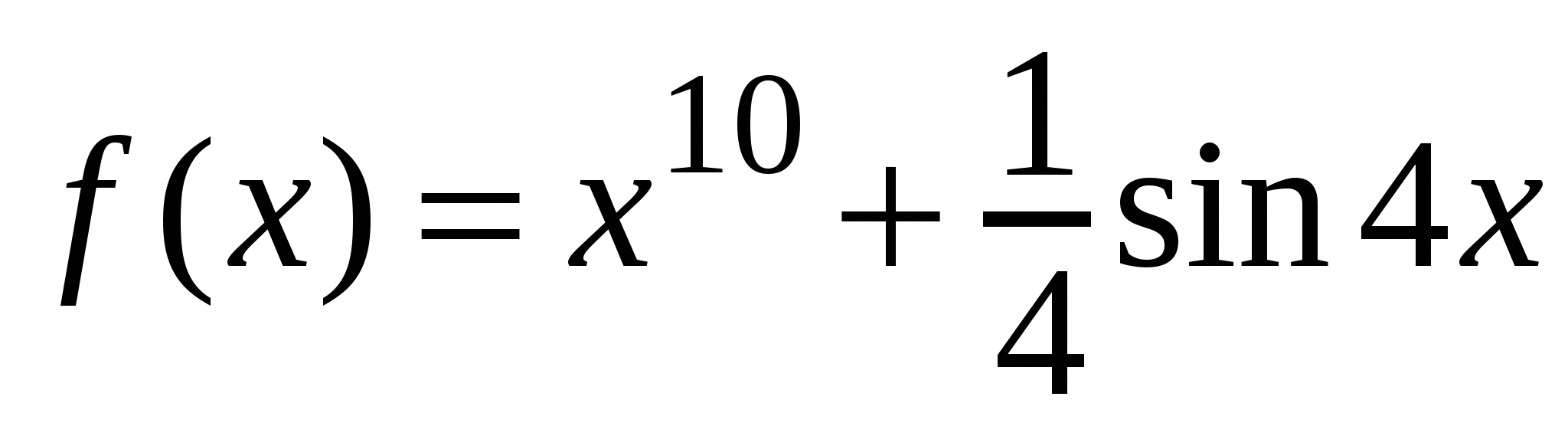 .
.
1) 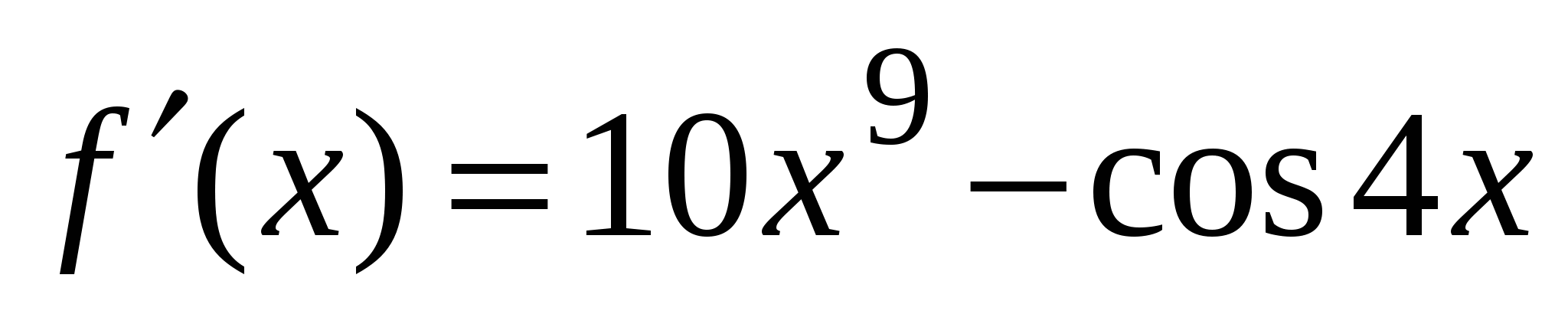
3) 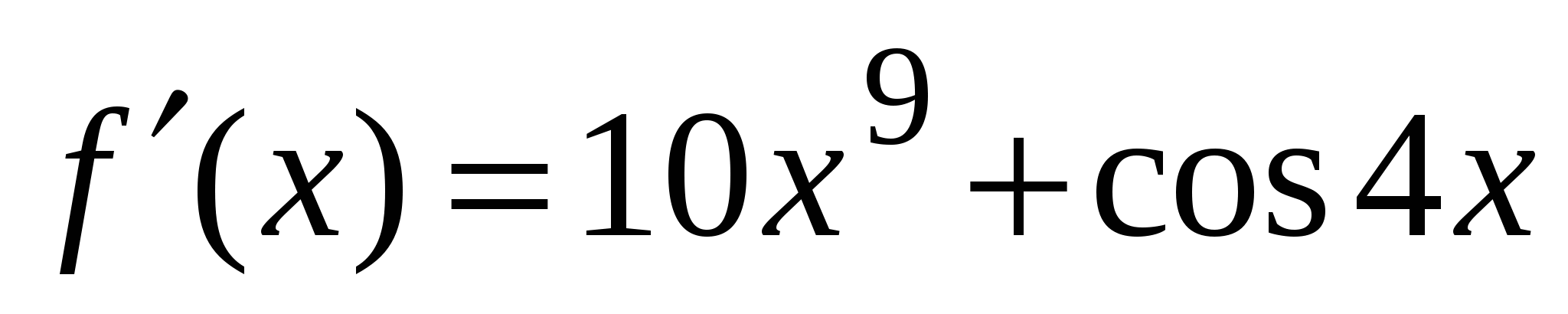
2) 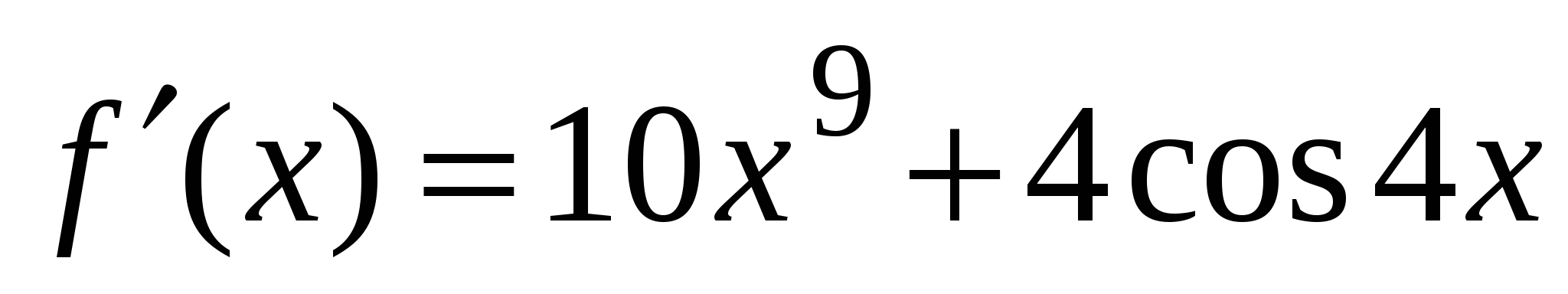
4) 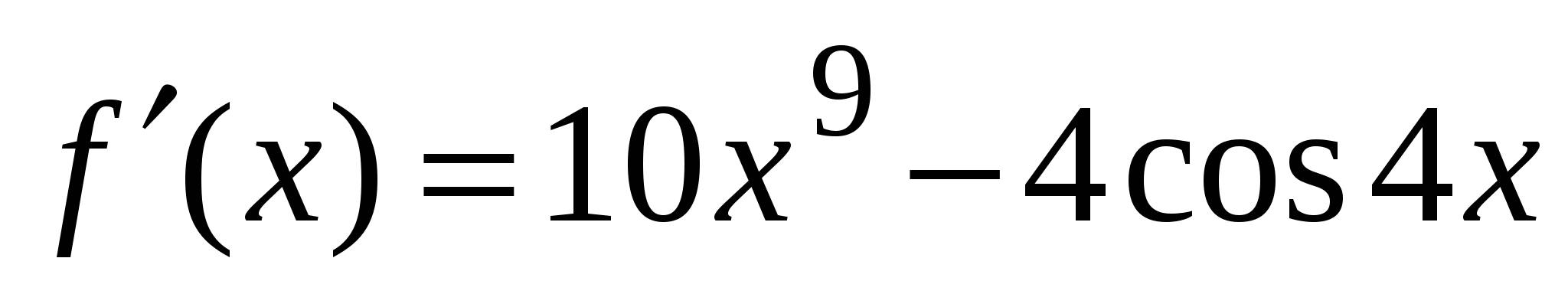
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Вычислите значение производной функции 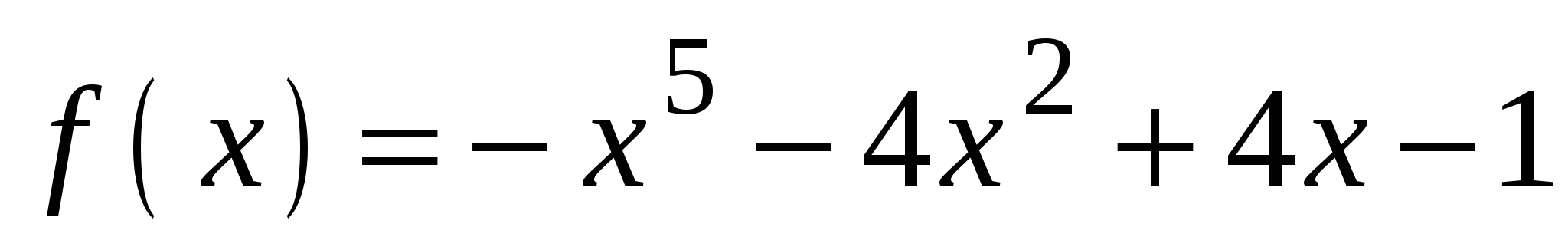 в точке
в точке 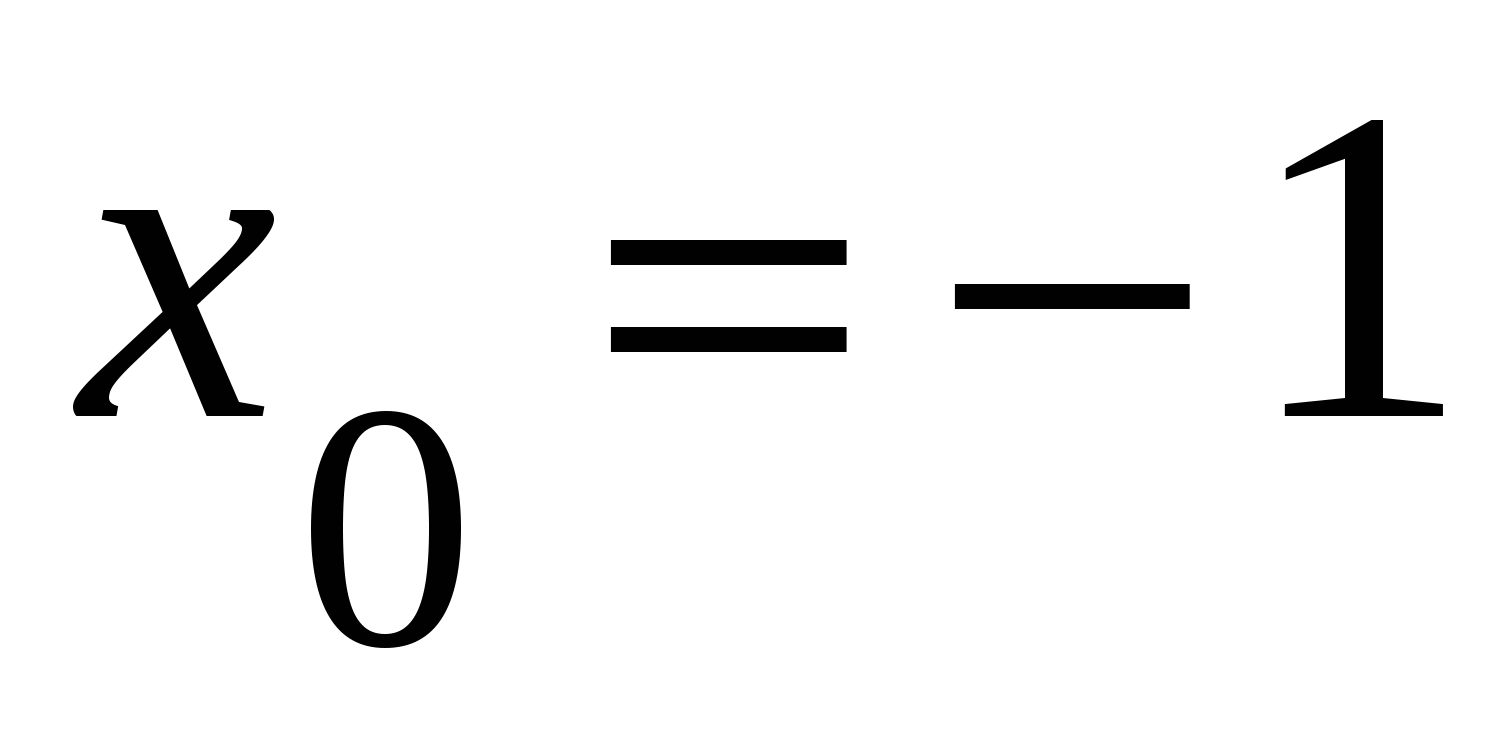 .
.
1)
− 9
2)
7
3)
1
4)
17
А4. Найдите производную функции 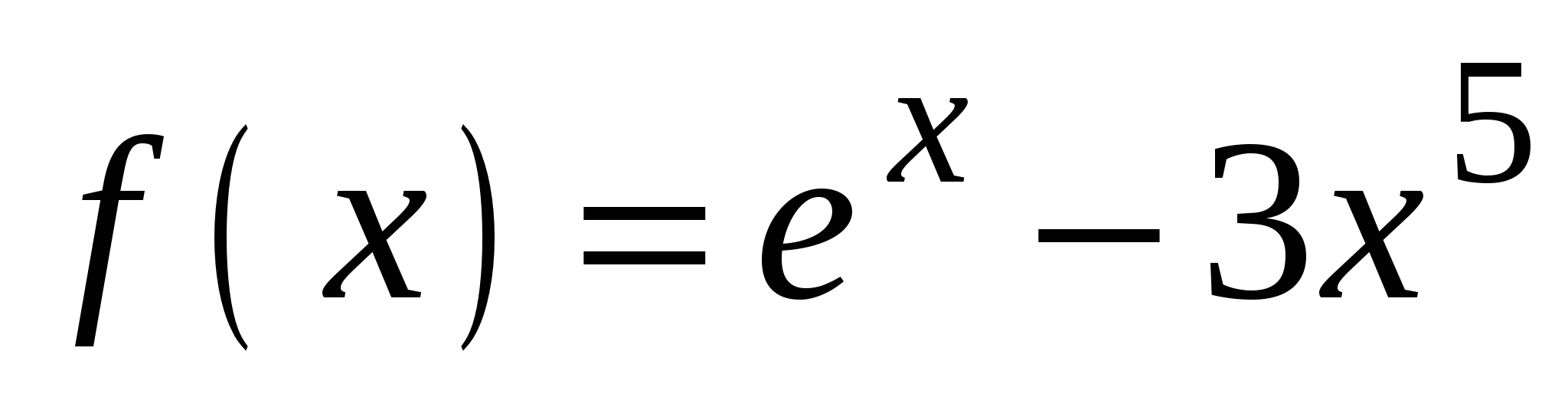 .
.
1)
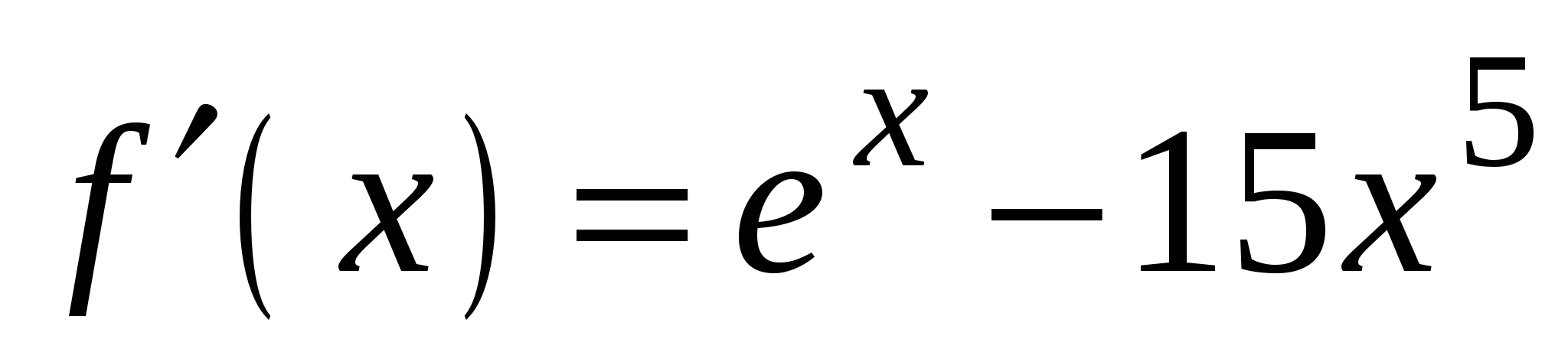
3)
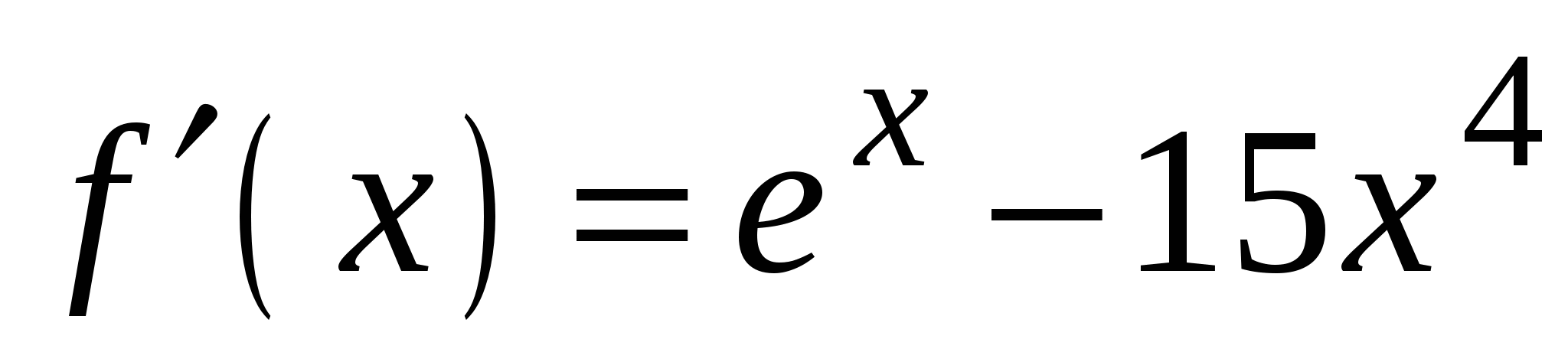
2)
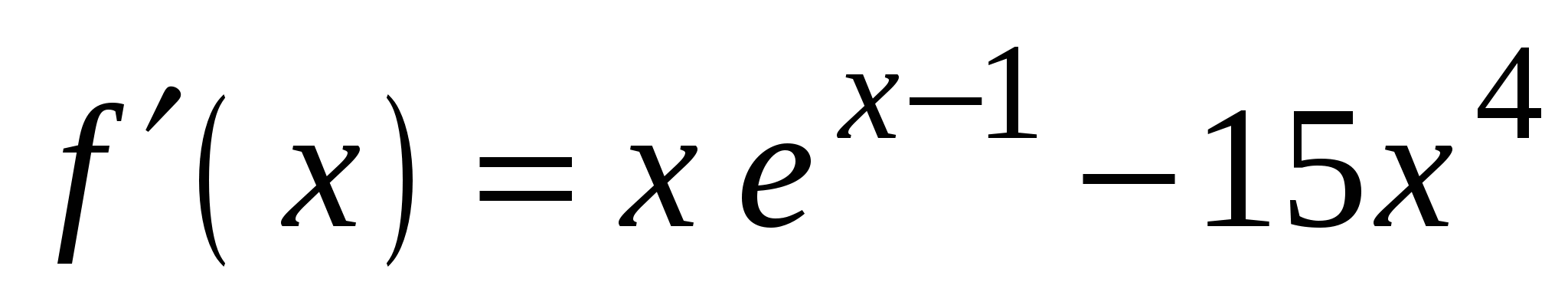
4)
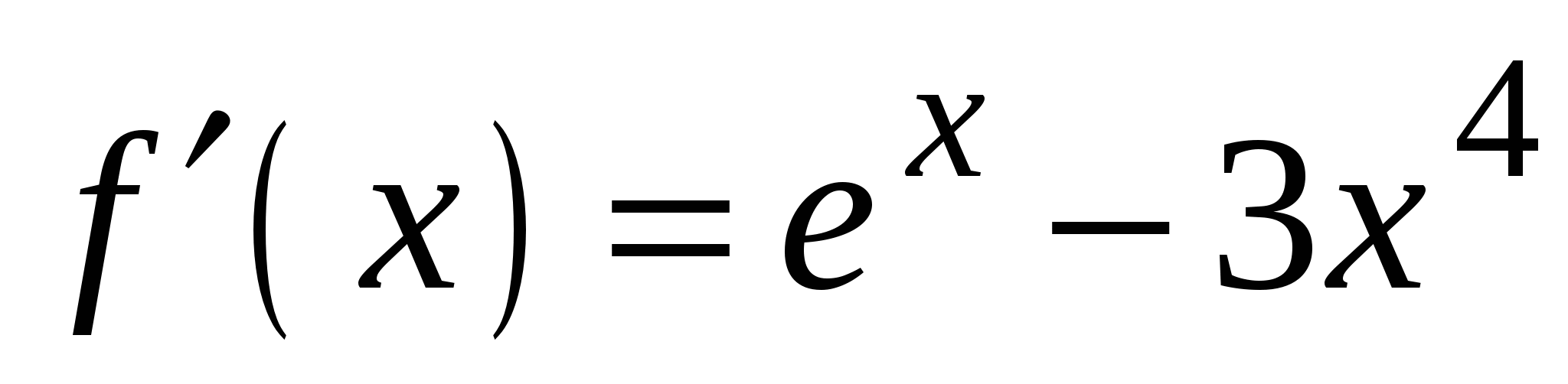

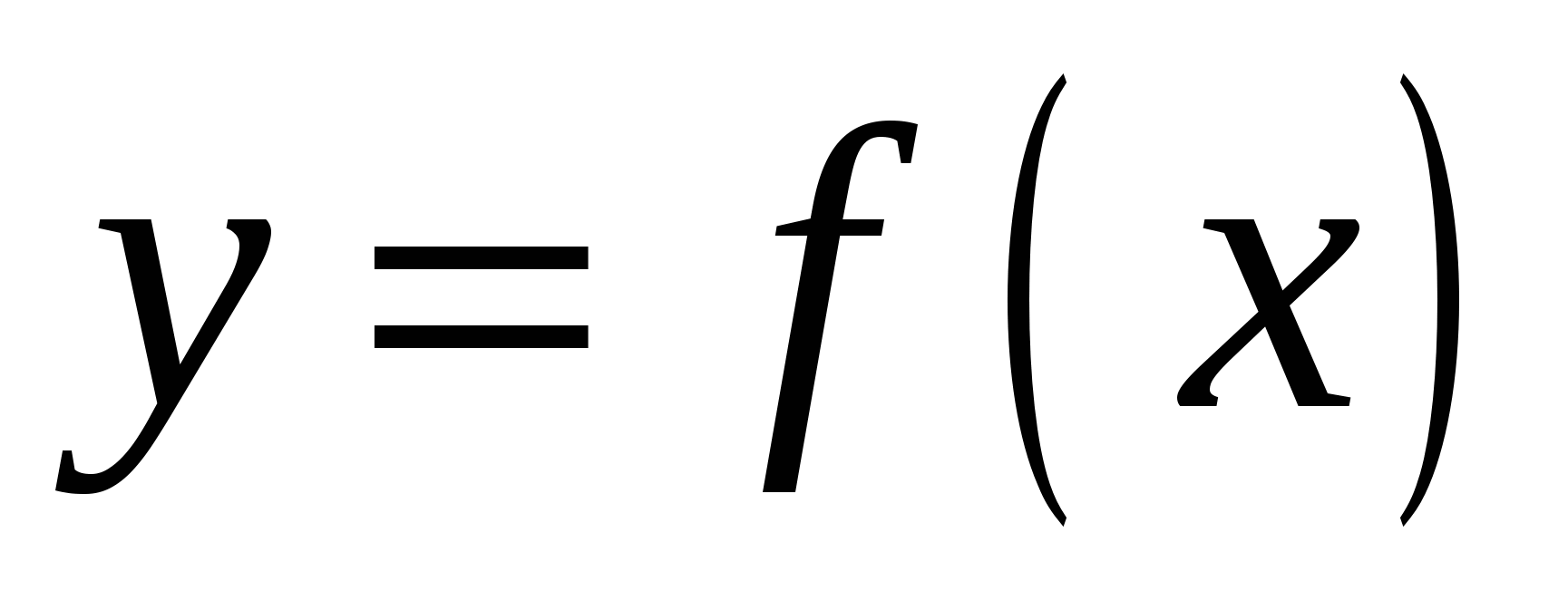 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. А5. Найдите производную функции 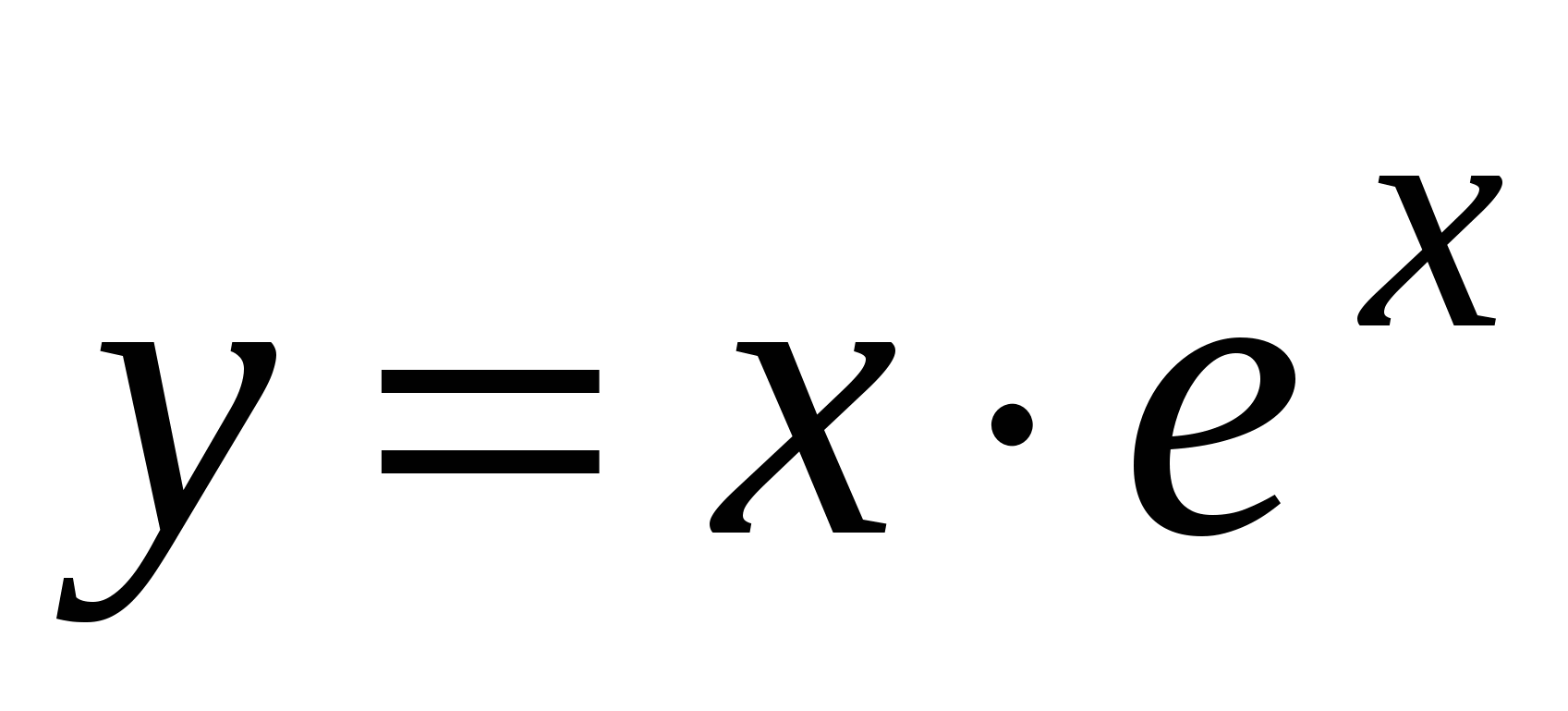 .
.
1)
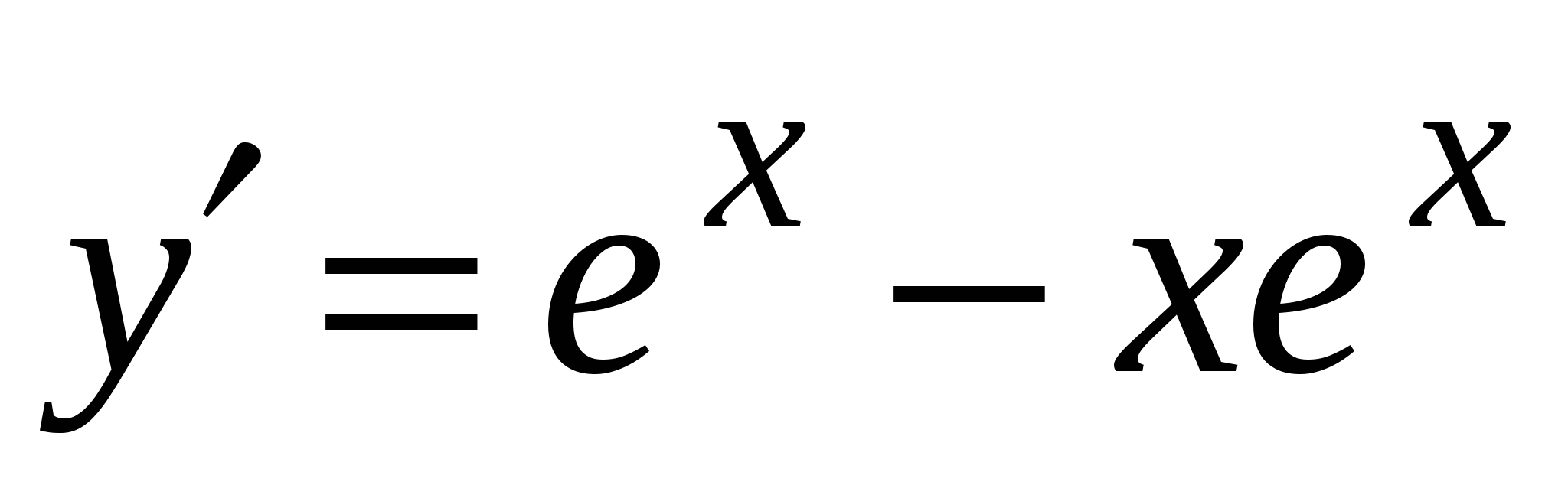
3)
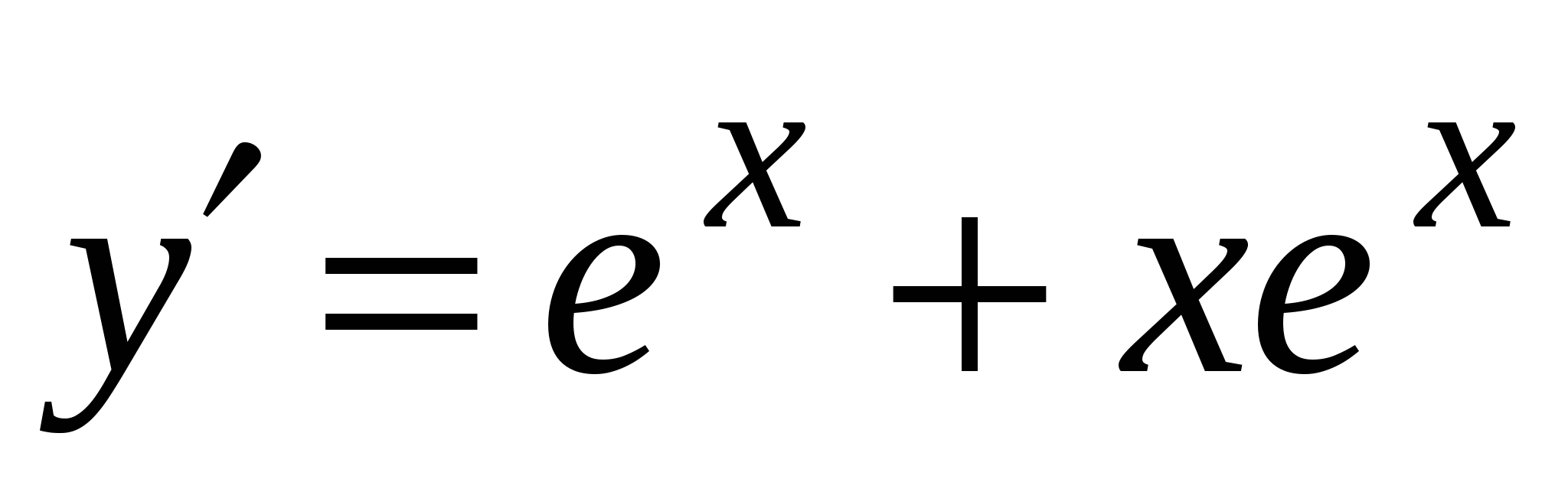
2)
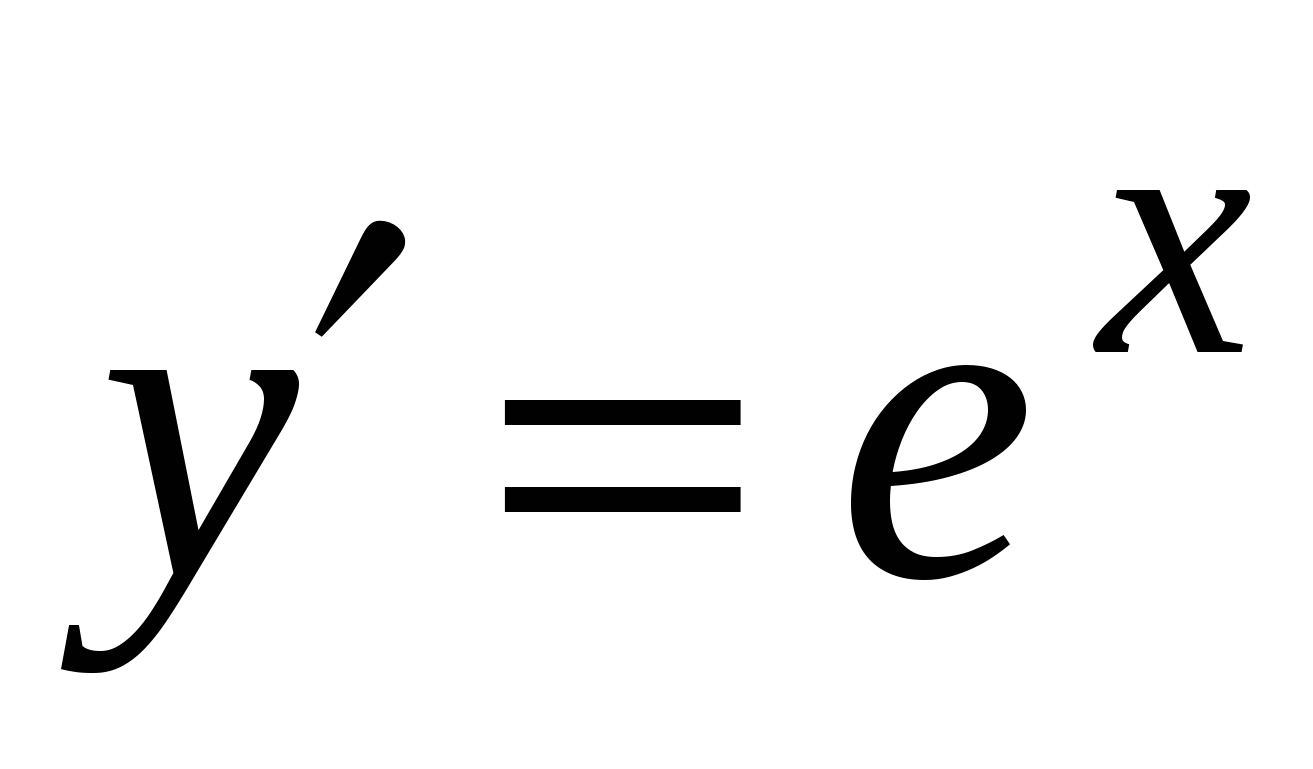
4)
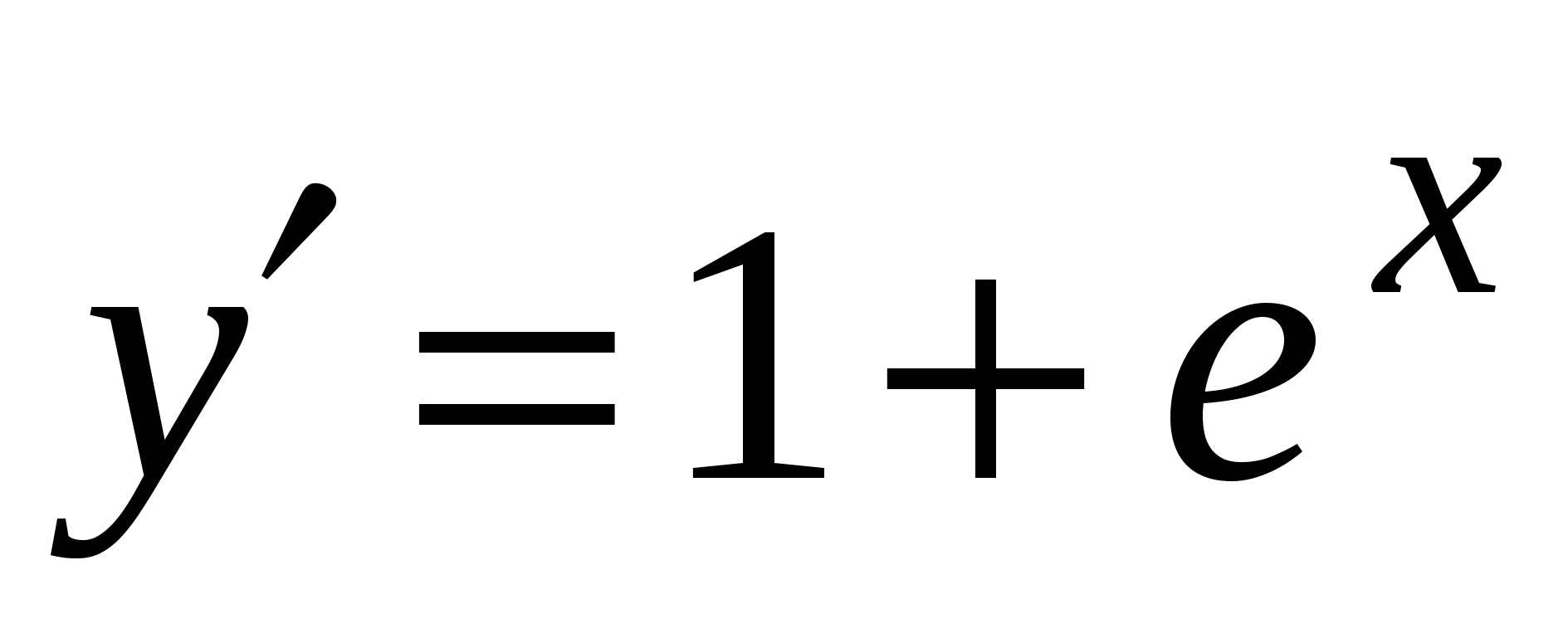

В3. На рисунке изображен график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
.
В4.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=t4+1/3t3-t2+8. Чему будет равна мгновенная скорость (м/с) через 3 с после начала движения?
В5.Материальная точка движется по закону х(t)= 1/3t3-t2+9t+11 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 10 м/с2 ?
В6. Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=5t2 - 3t+6. Через сколько секунд после начала движения произойдет остановка?
Контрольная работа №3 по теме: «Производная»
Вариант №13

B1. На рисунке изображен график производной  . Найдите тангенс угла наклона касательной к графику функции
. Найдите тангенс угла наклона касательной к графику функции  в точке с абсциссой
в точке с абсциссой  .
.
А1. Найдите производную функции 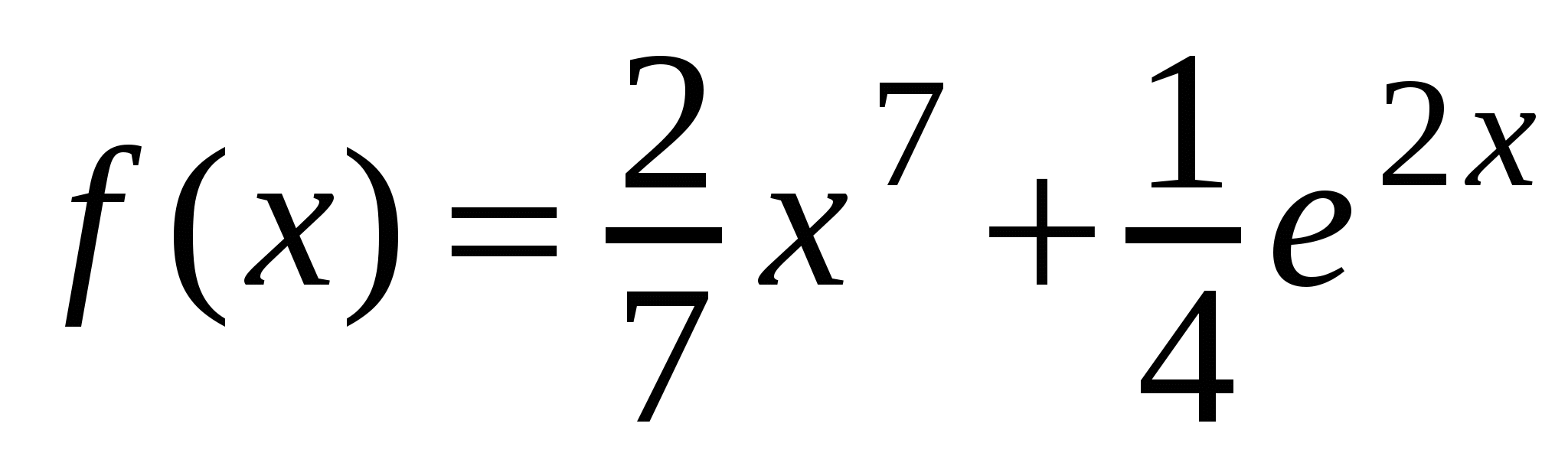 .
.
1) 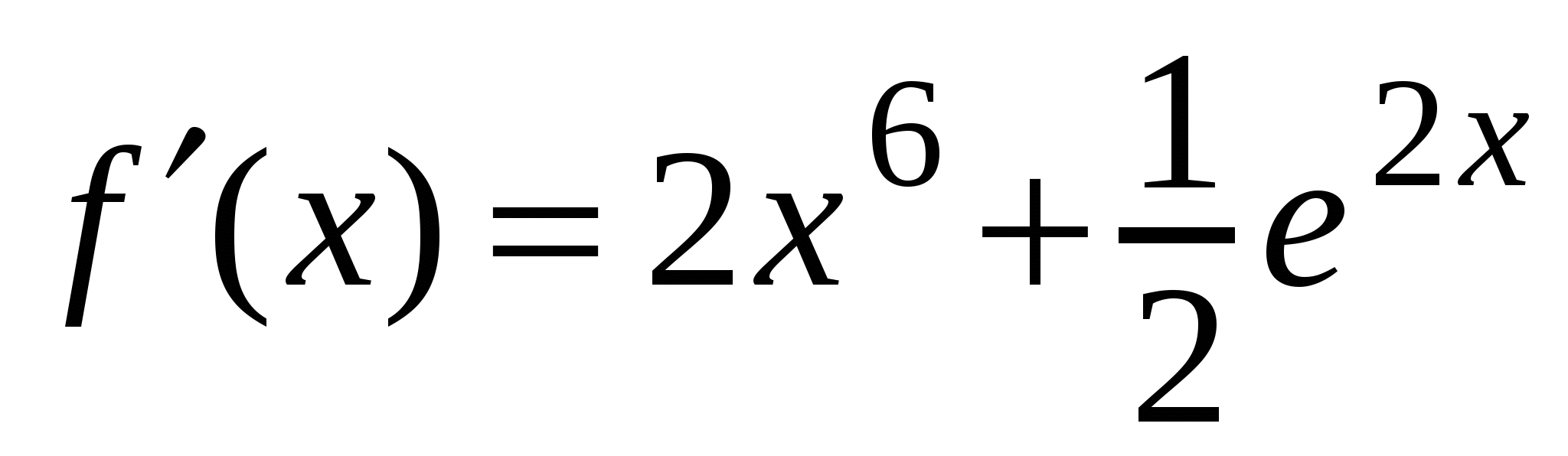
3) 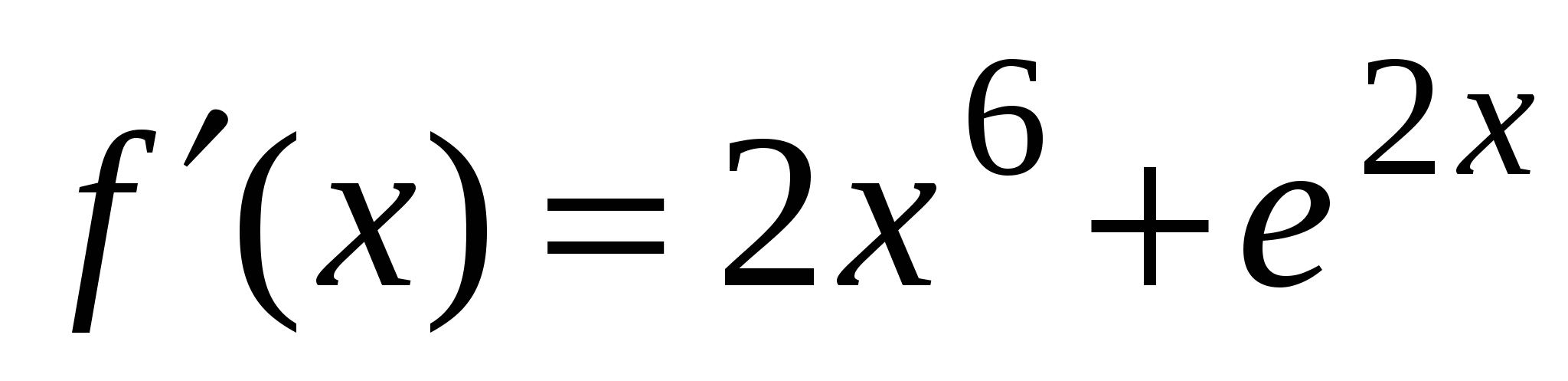
2) 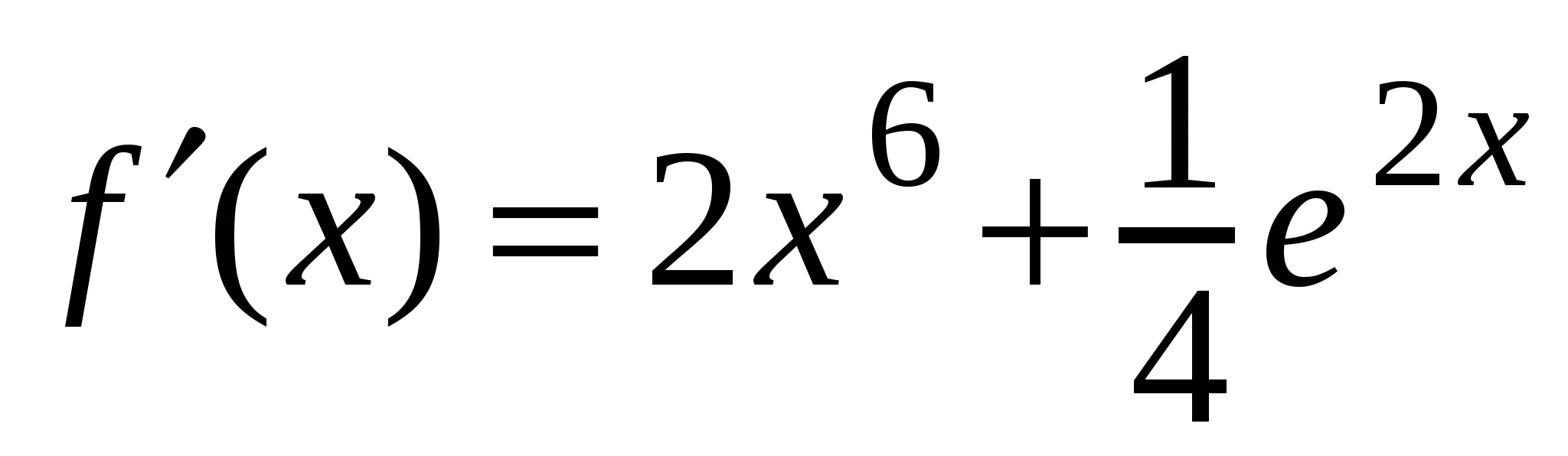
4) 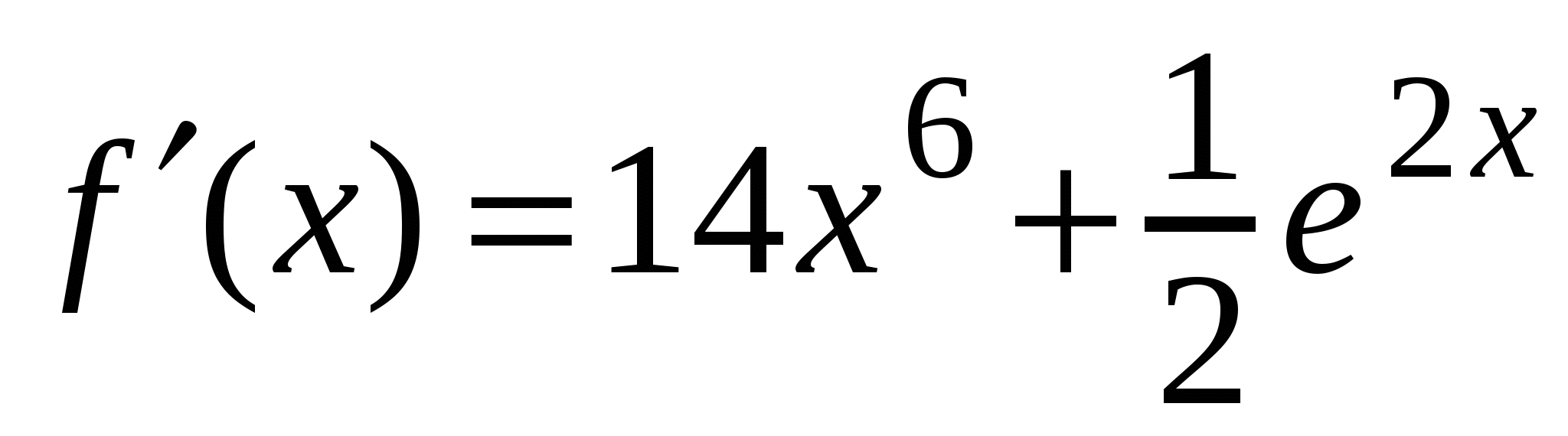
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Найдите производную функции 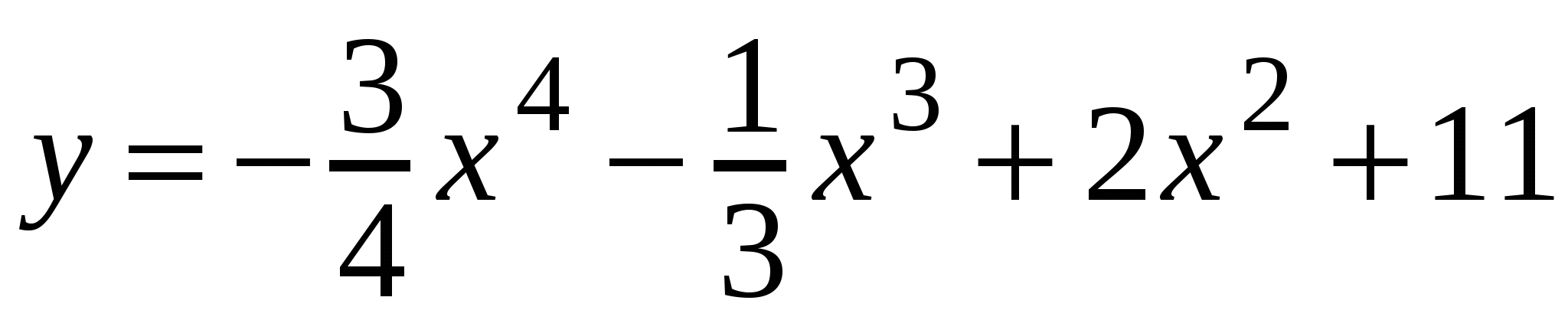 .
.
1)
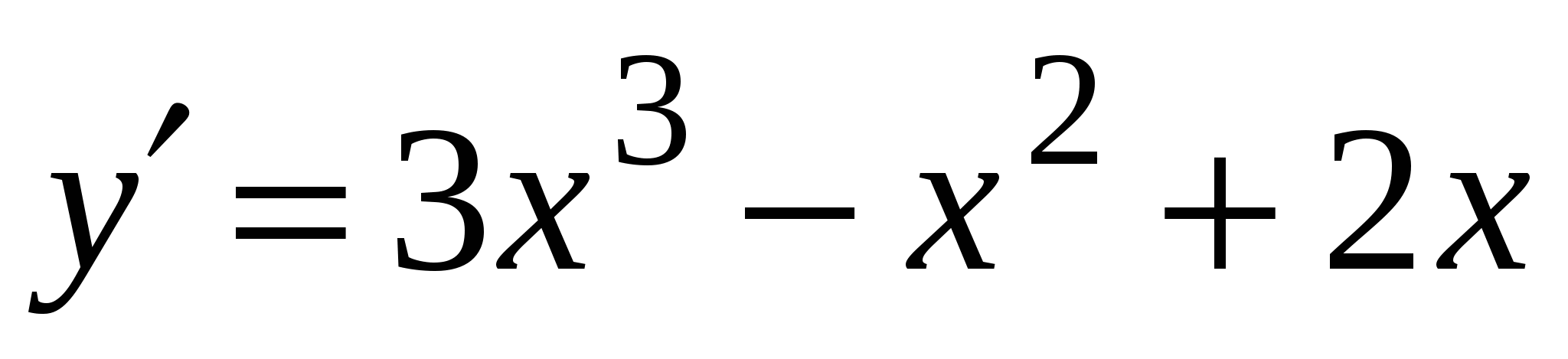
3)
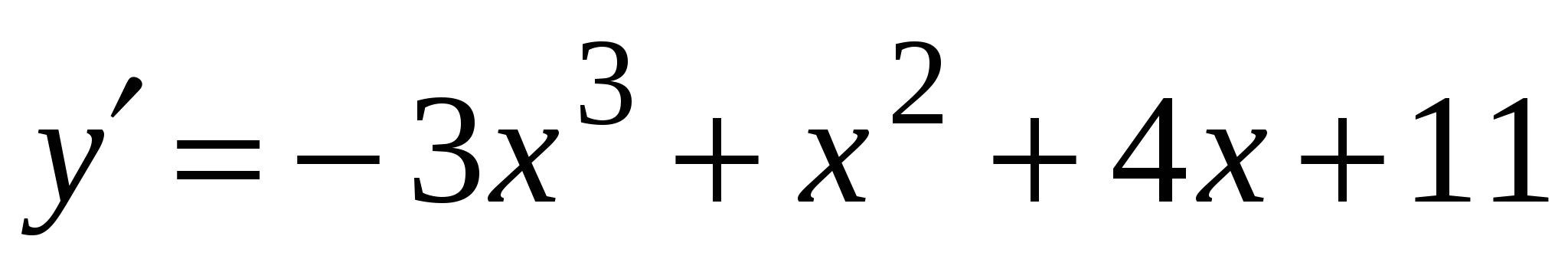
2)
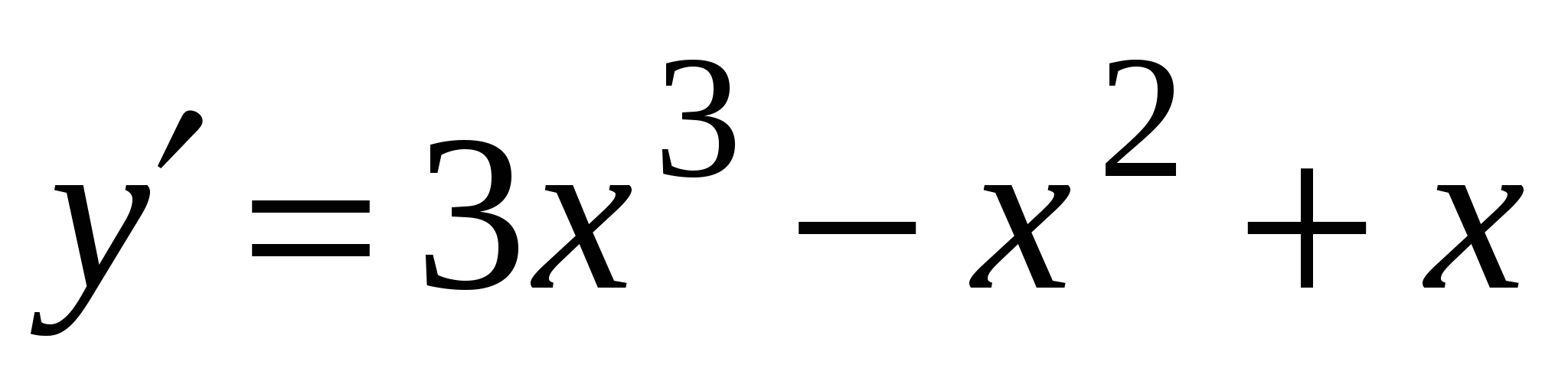
4)
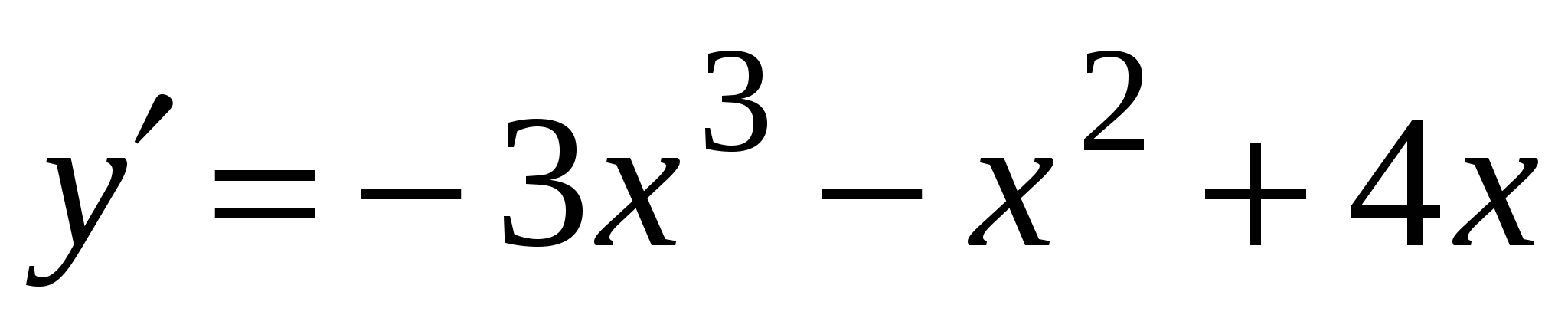
А4. Найдите производную функции 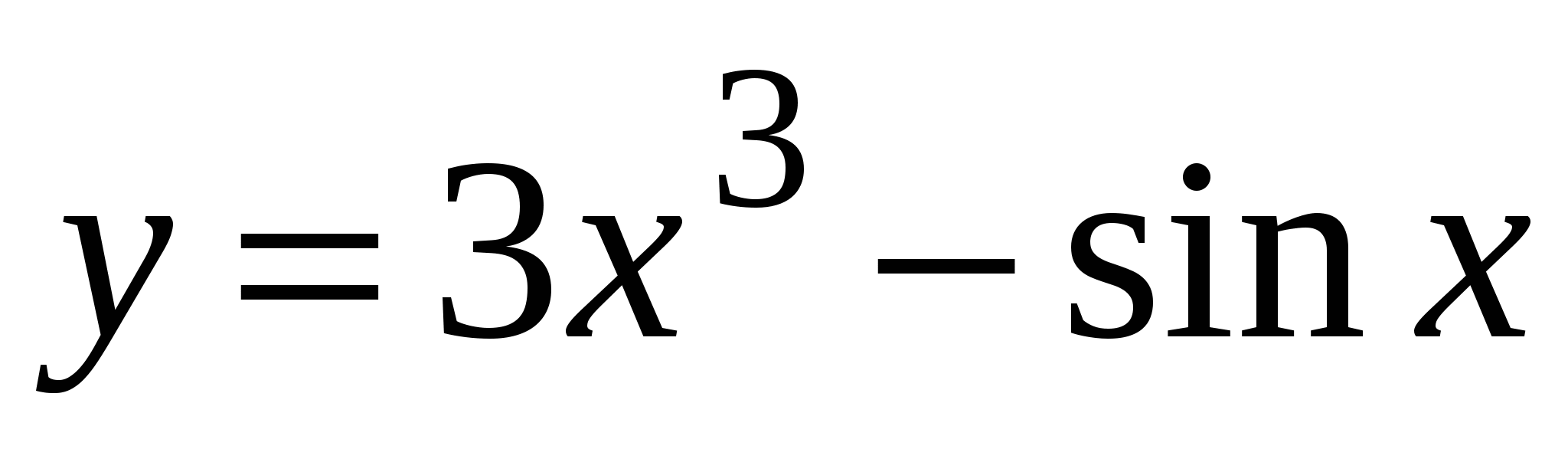 .
.
1)
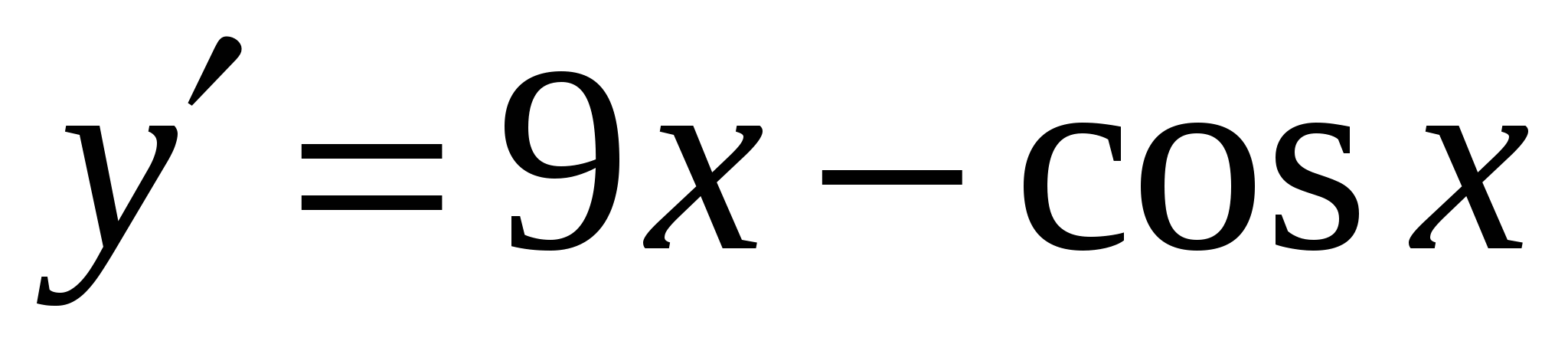
3)
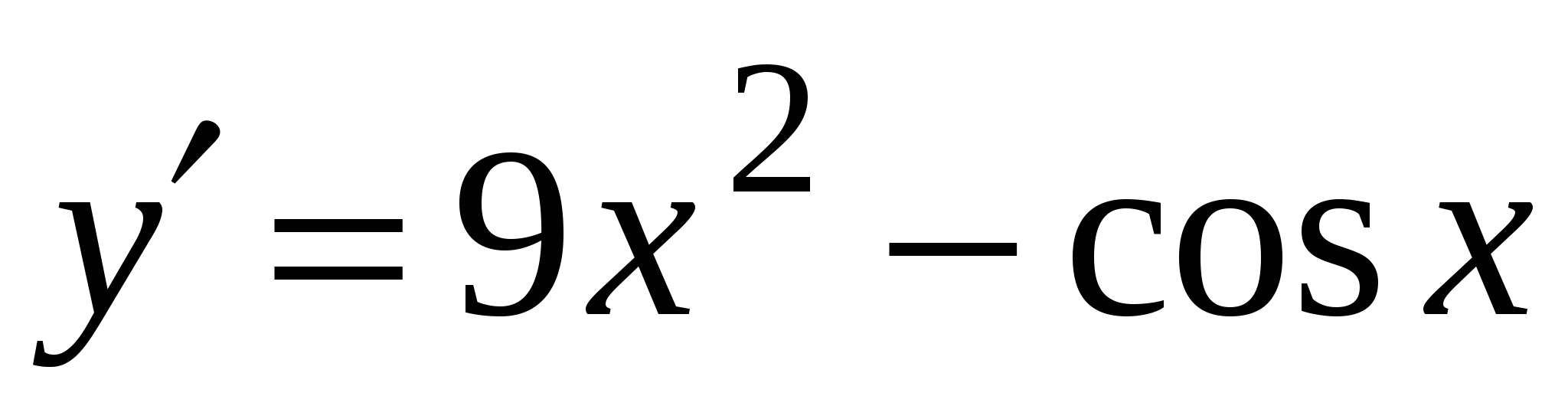
2)
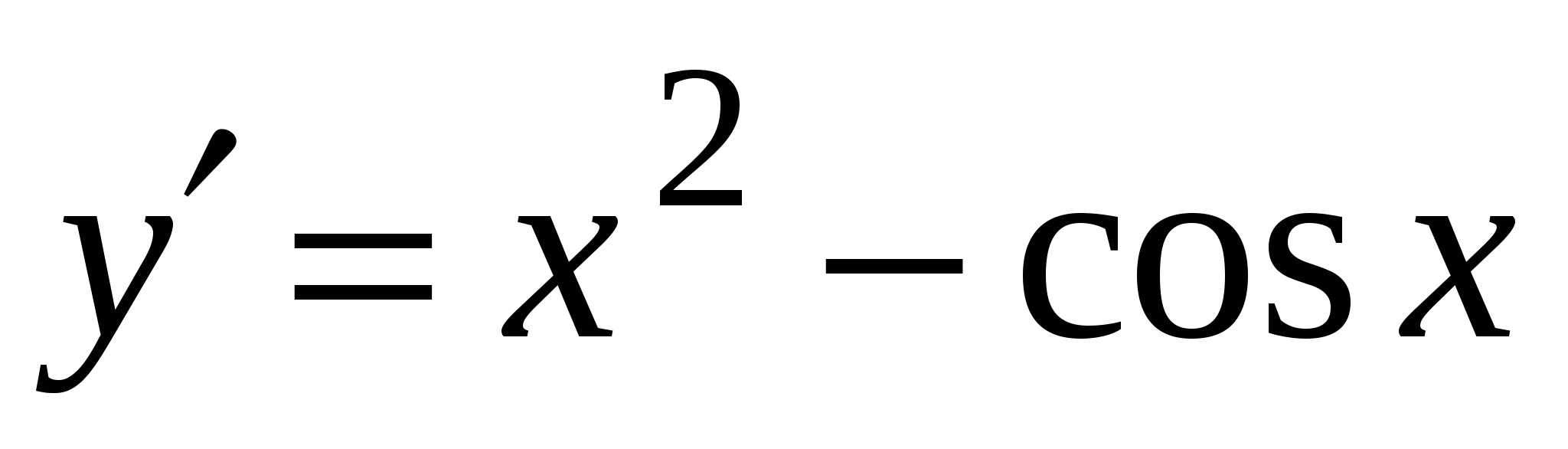
4)
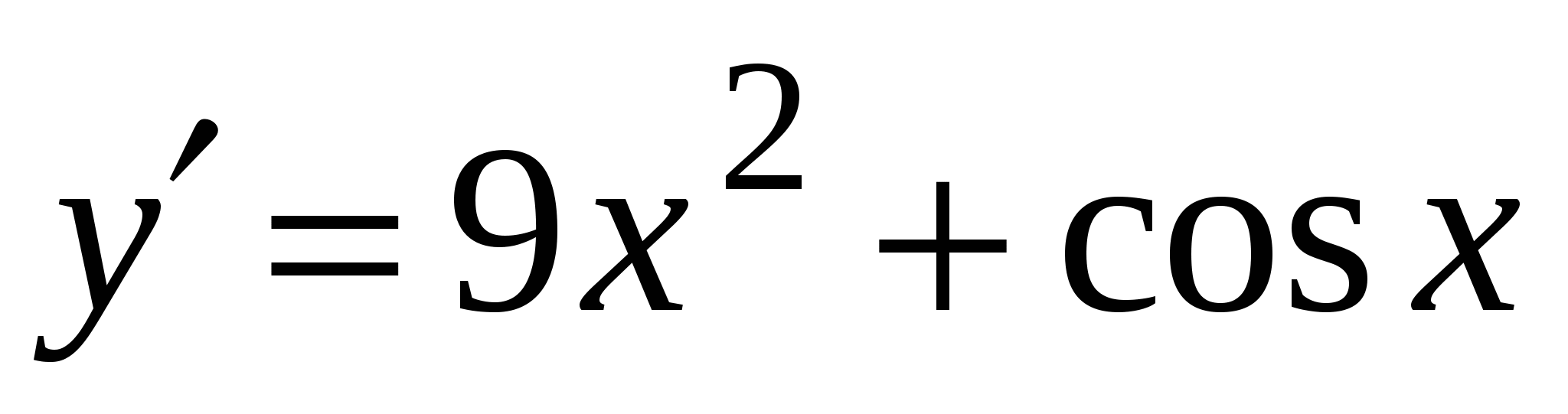

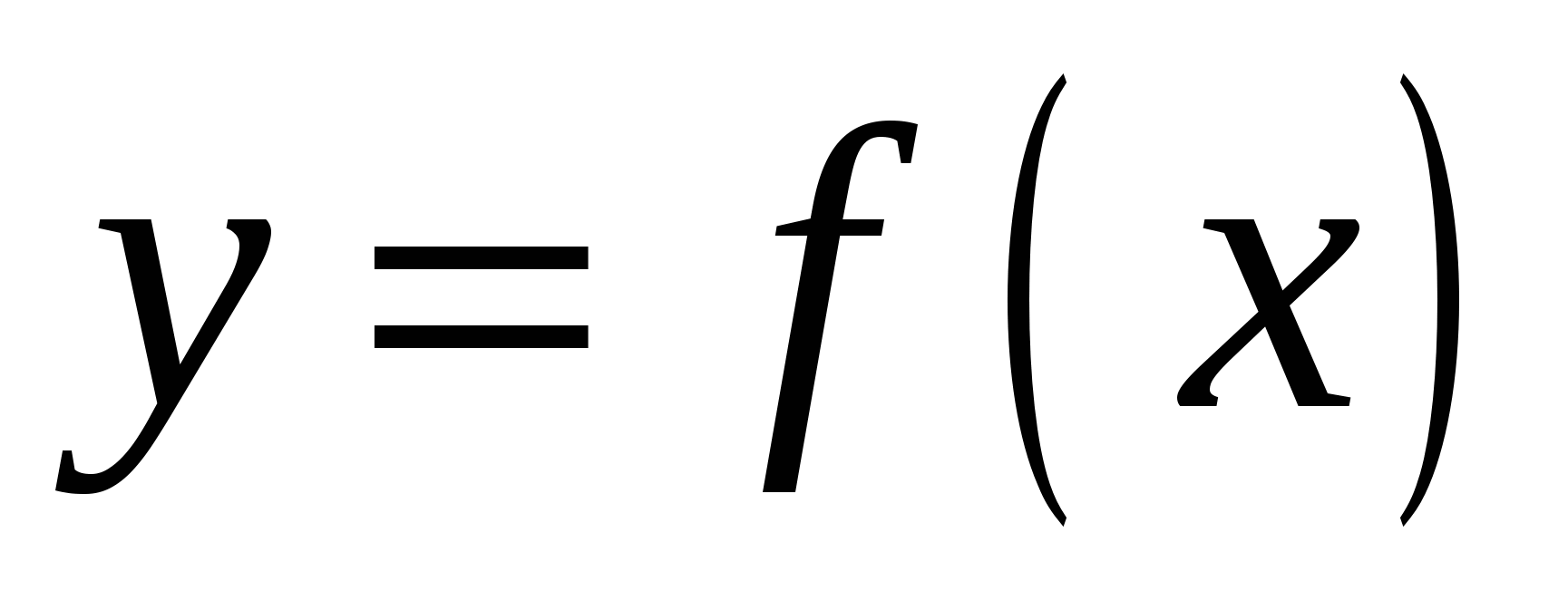 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. А5. Найдите производную функции 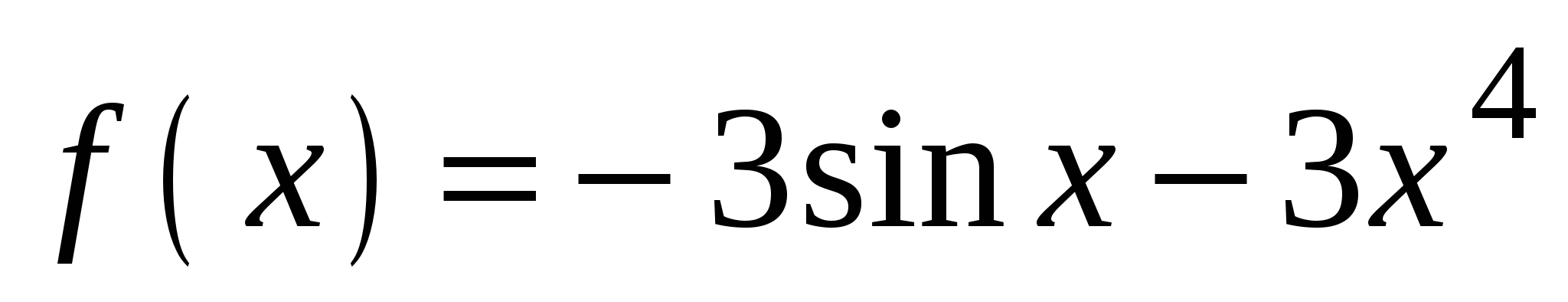 .
.
1)
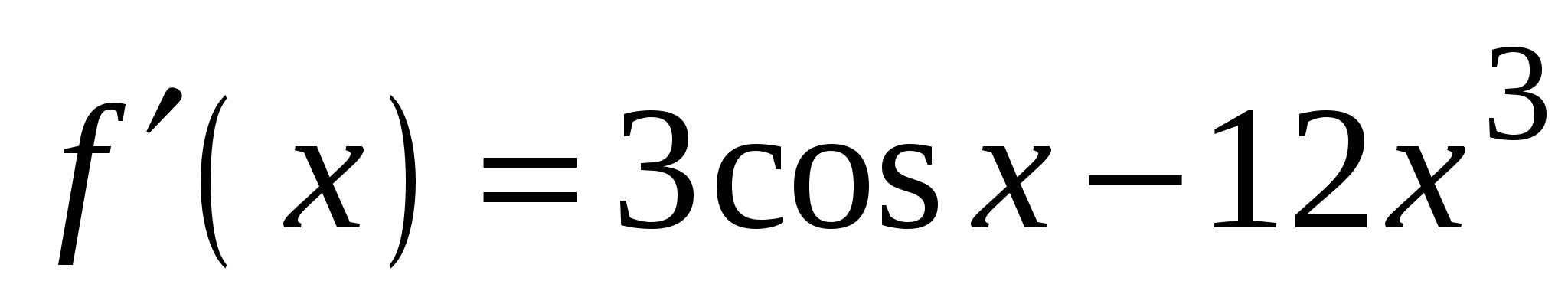
3)
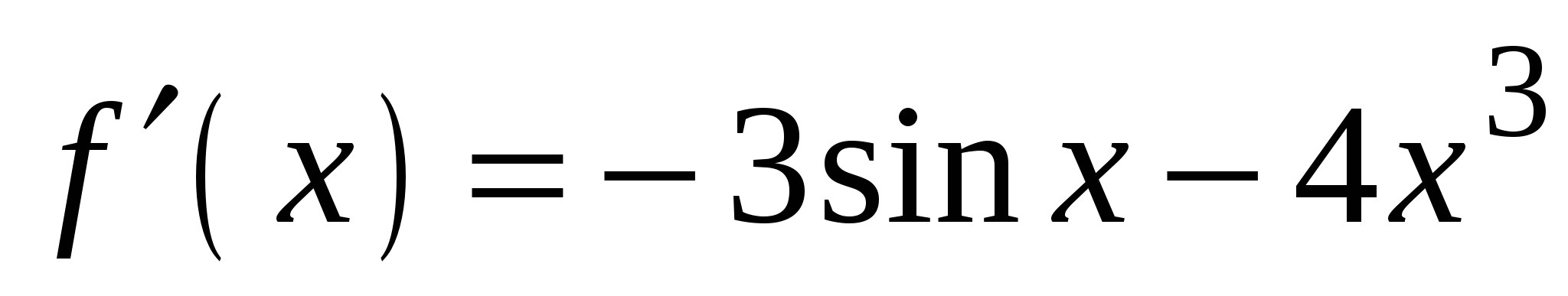
2)
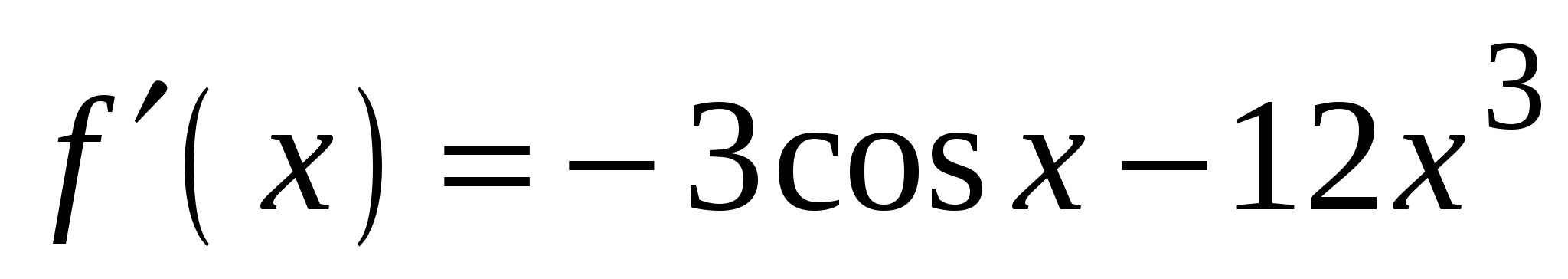
4)
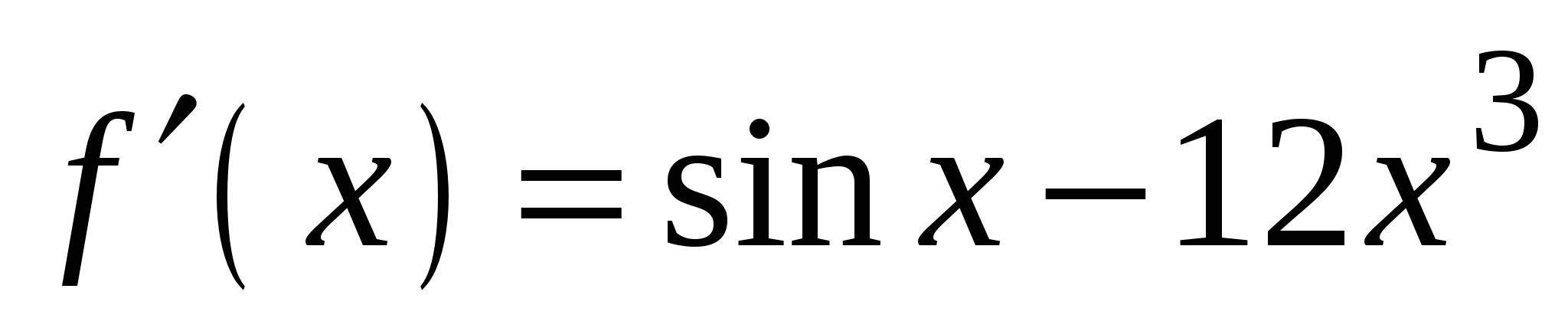

 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. В4. Материальная точка движется по закону
х(t)=1/4 t3-3t2+21t - 18 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 3 м/с2 ?
В5.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=6t2 - 18t+19. Через сколько секунд после начала движения произойдет остановка?
В6. Материальная точка движется по закону х(t)=1/6 t3-4t2+35t - 11 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 2 м/с2 ?
Контрольная работа №3 по теме: «Производная»
Вариант №14
B1.Функция  определена на промежутке
определена на промежутке  . Используя изображенный на рисунке график производной
. Используя изображенный на рисунке график производной  , определите количество касательных к графику функции
, определите количество касательных к графику функции  , которые составляют угол
, которые составляют угол  с положительным направлением оси Ox
с положительным направлением оси Ox

А1. Найдите производную функции 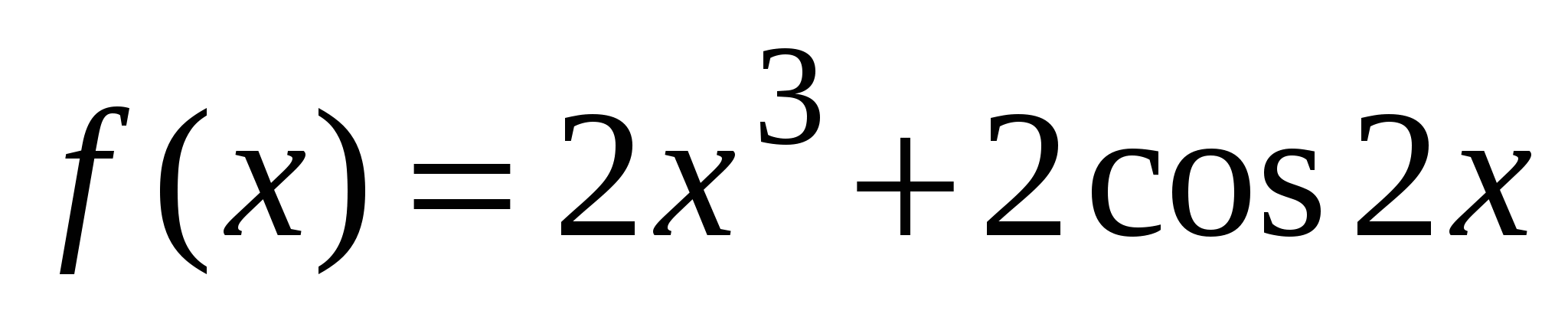 .
.
1) 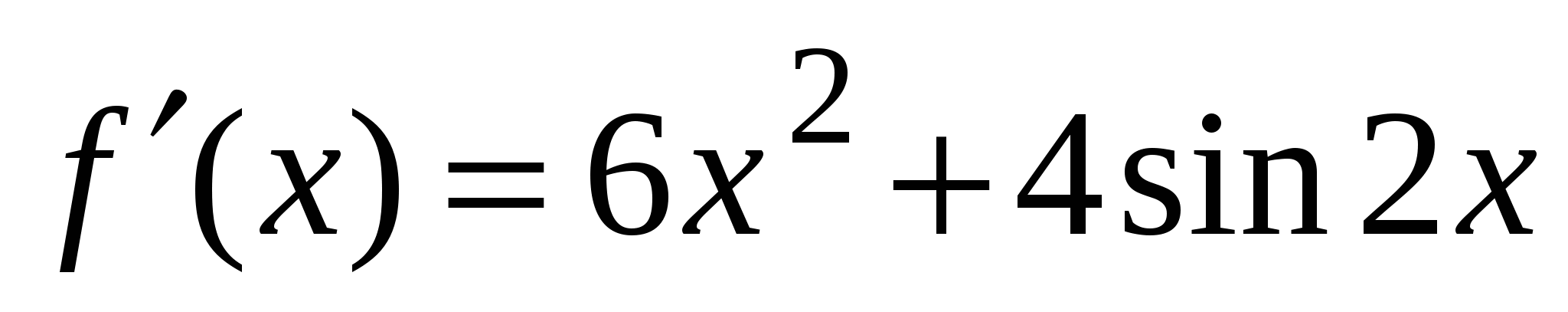
3) 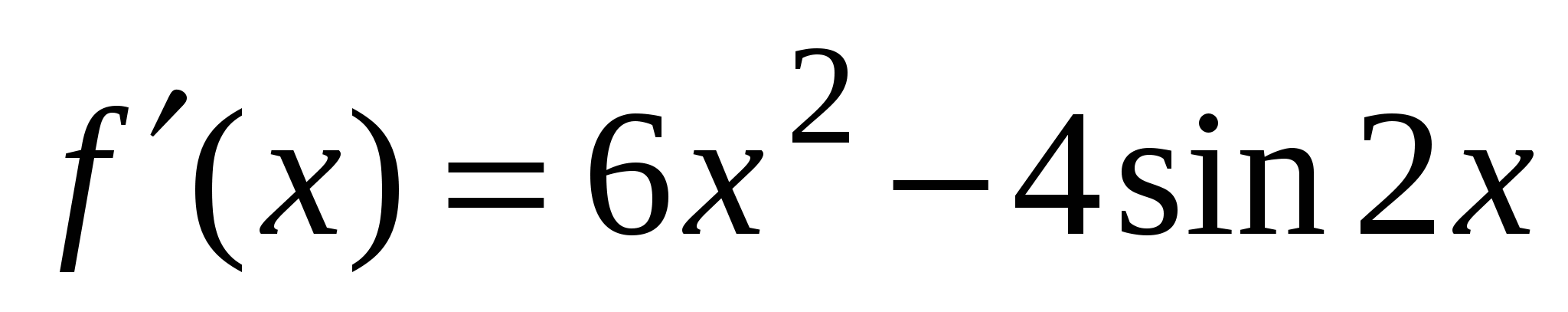
2) 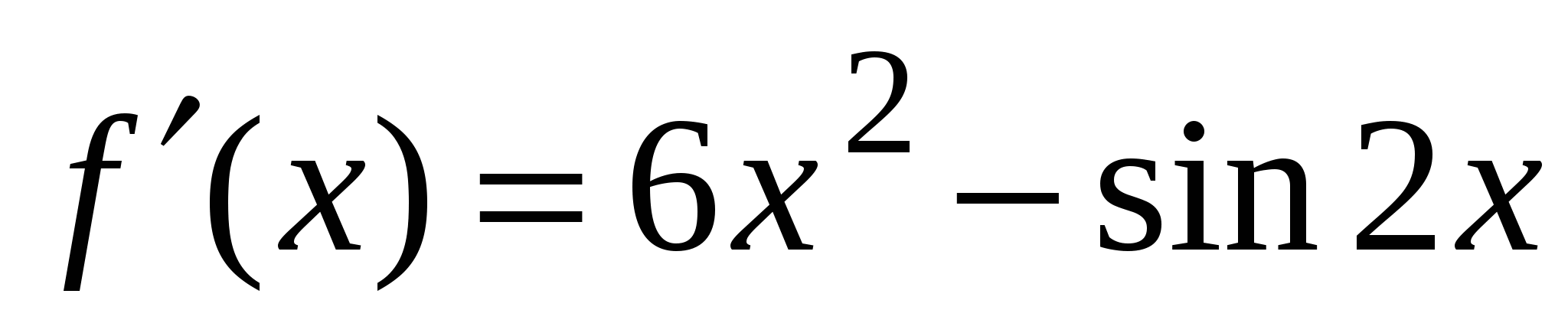
4) 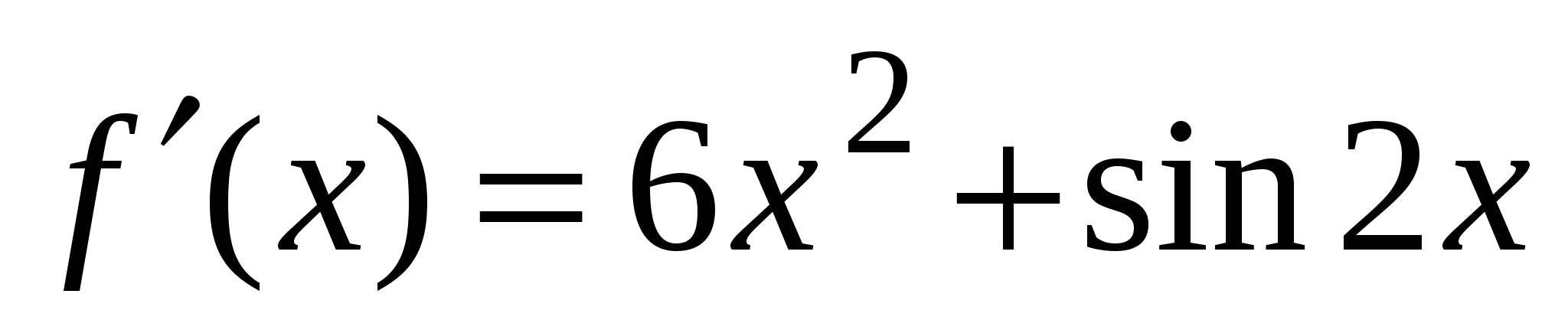
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Вычислите значение производной функции 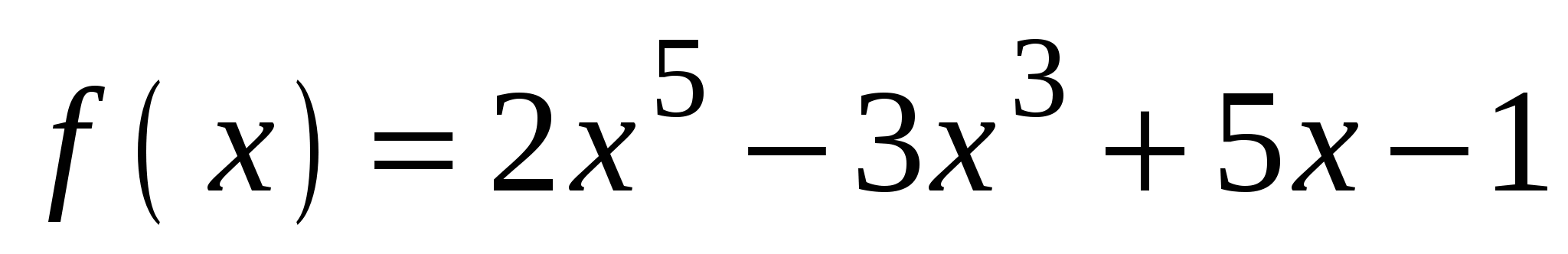 в точке
в точке 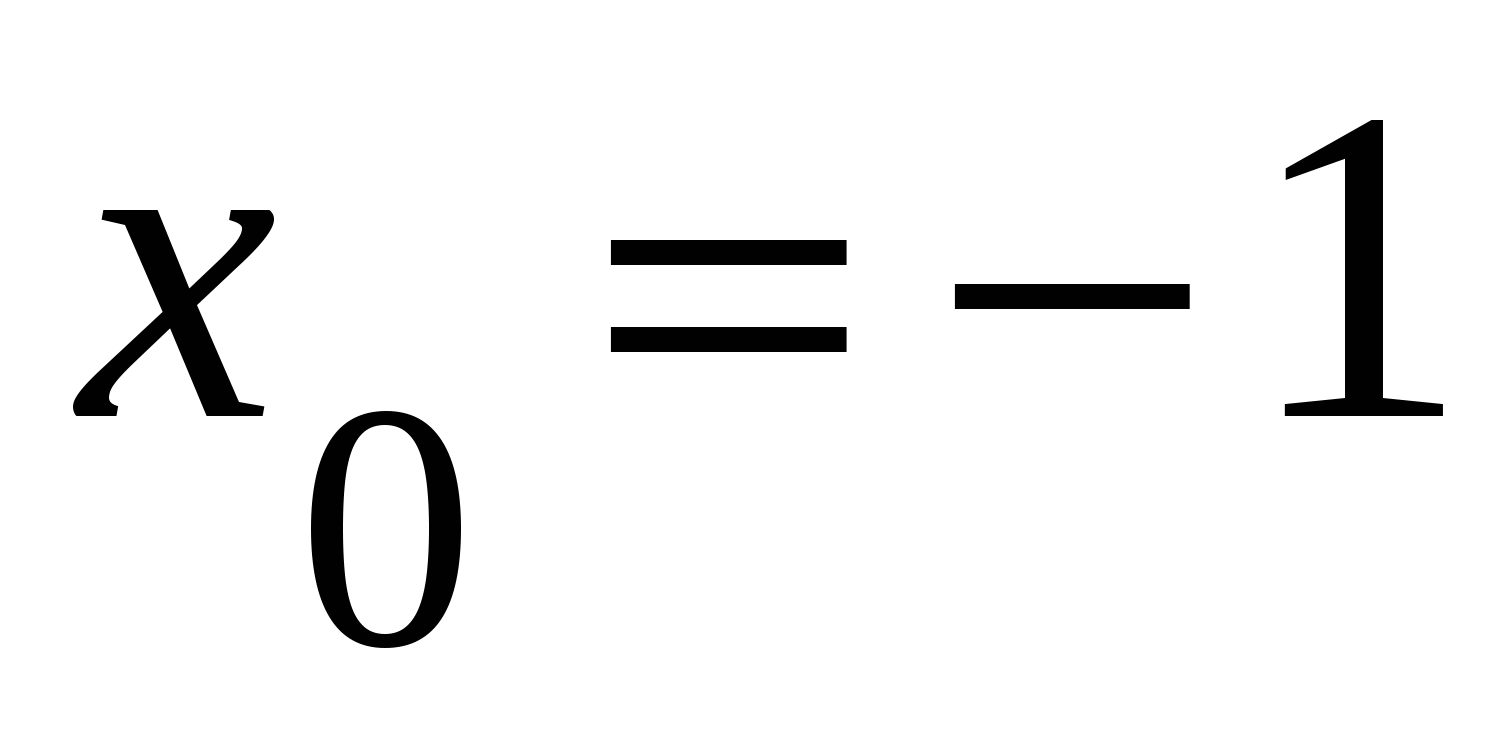 .
.
1)
6
2)
4
3)
− 14
4)
1
А4. Найдите производную функции 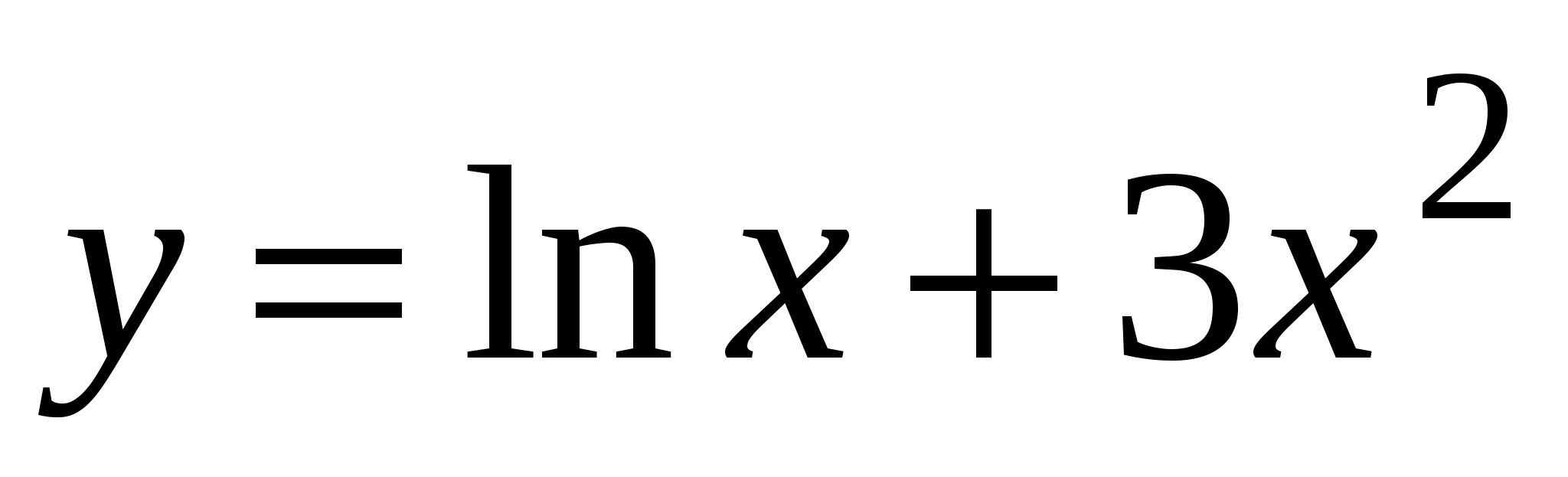 .
.
1)
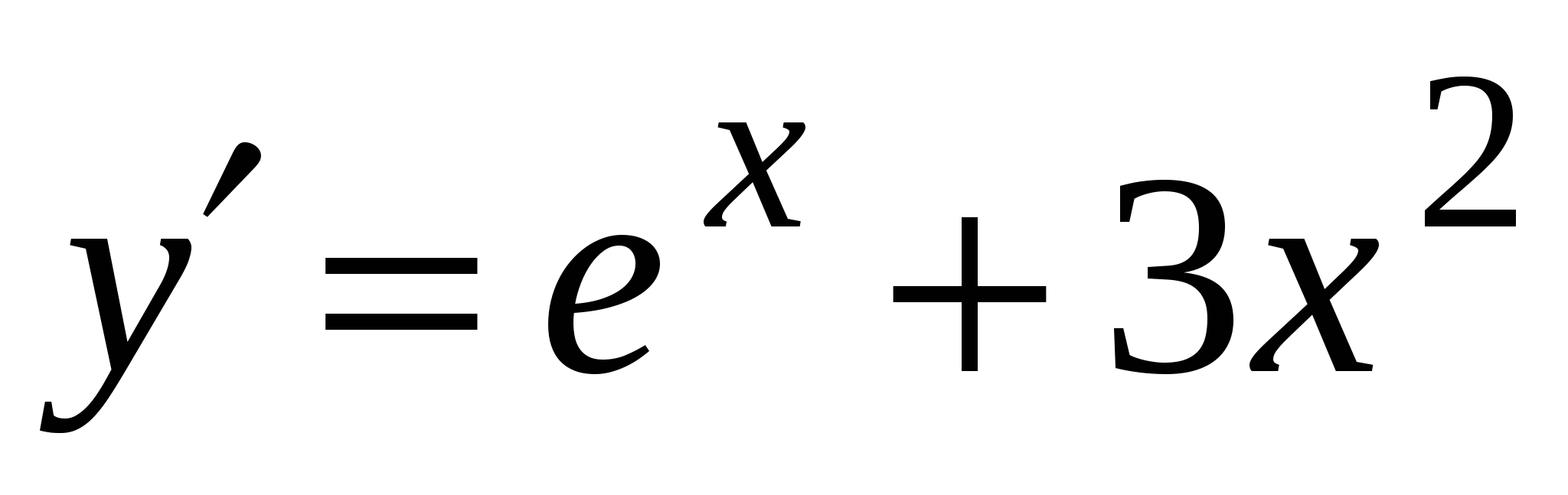
3)
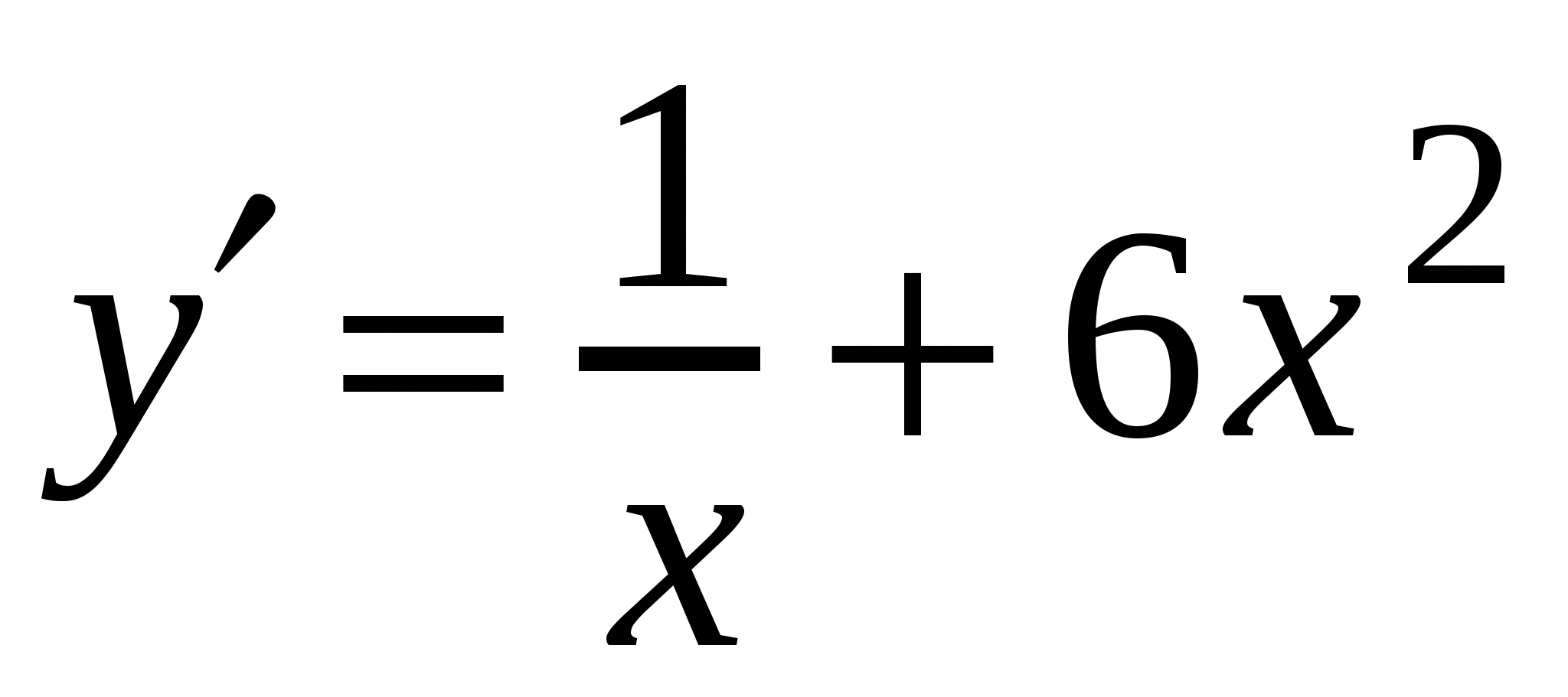
2)
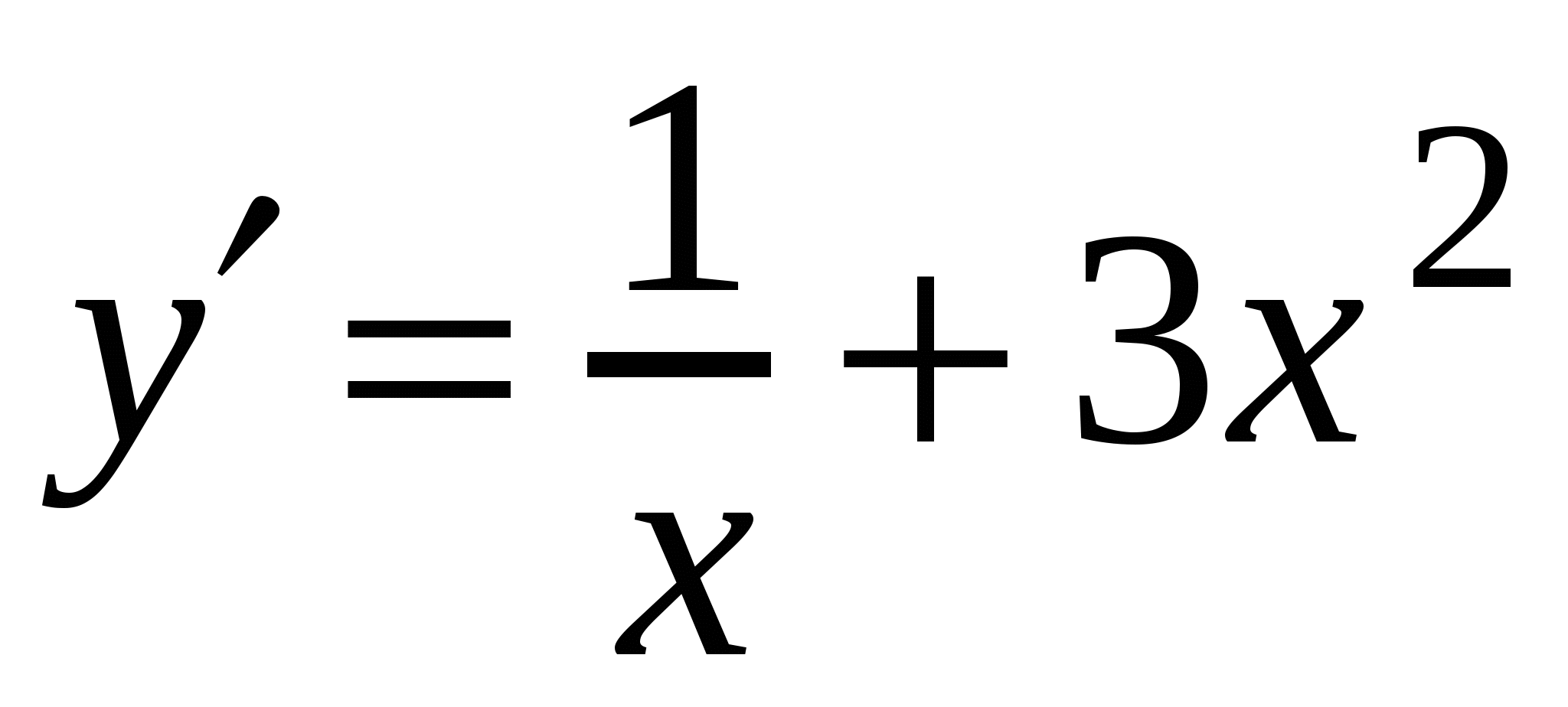
4)
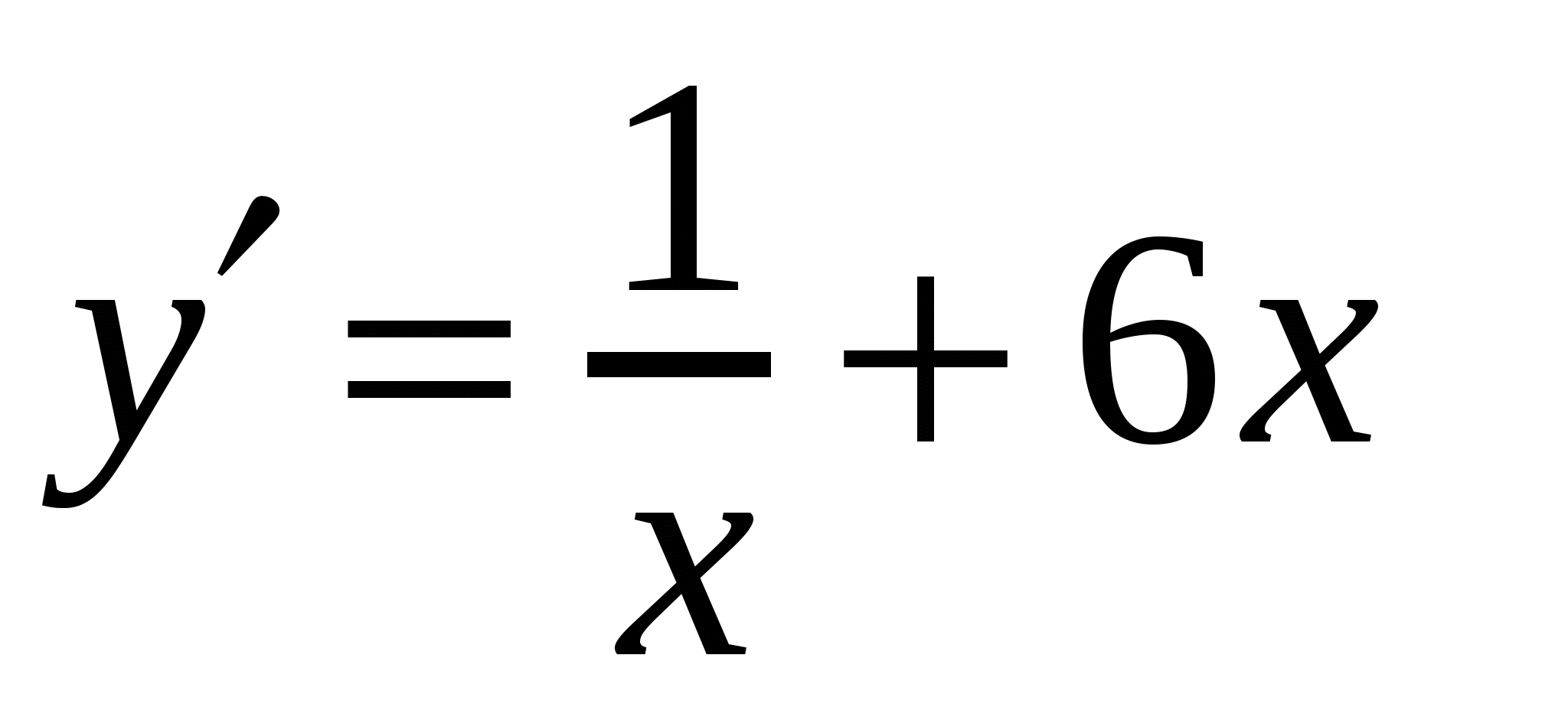

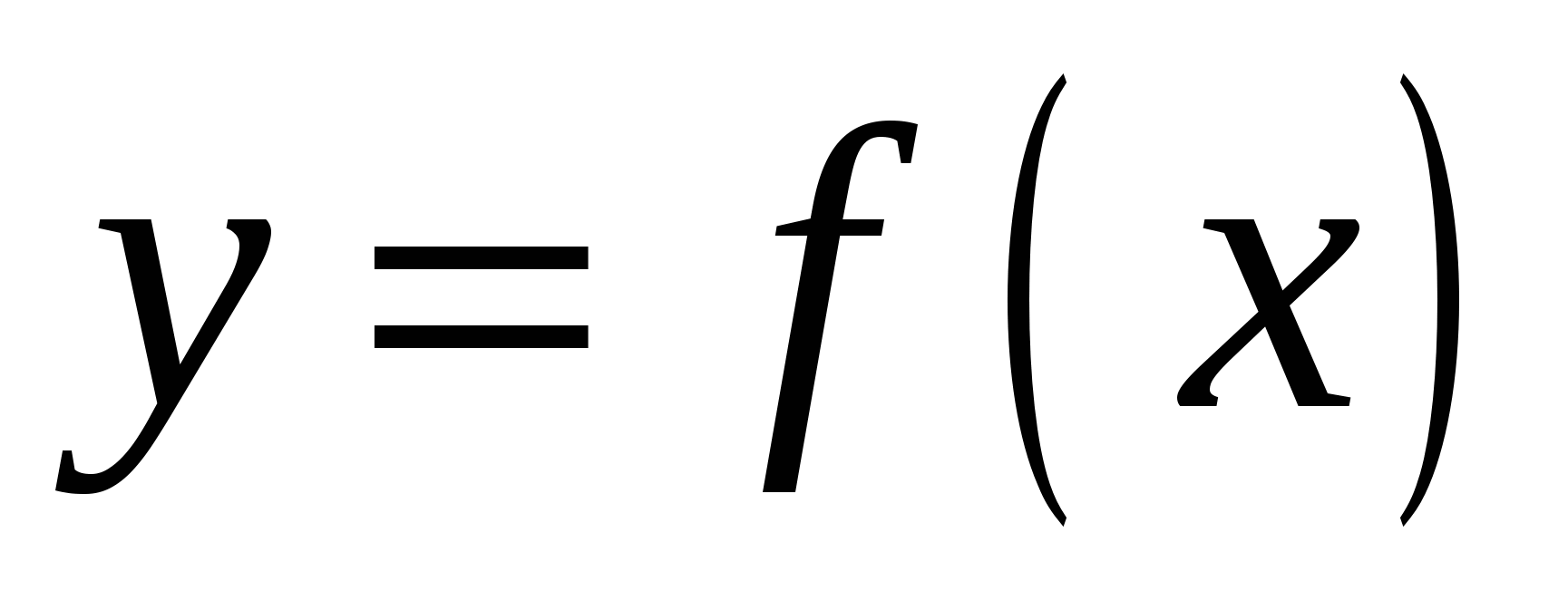 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
. А5. Найдите производную функции 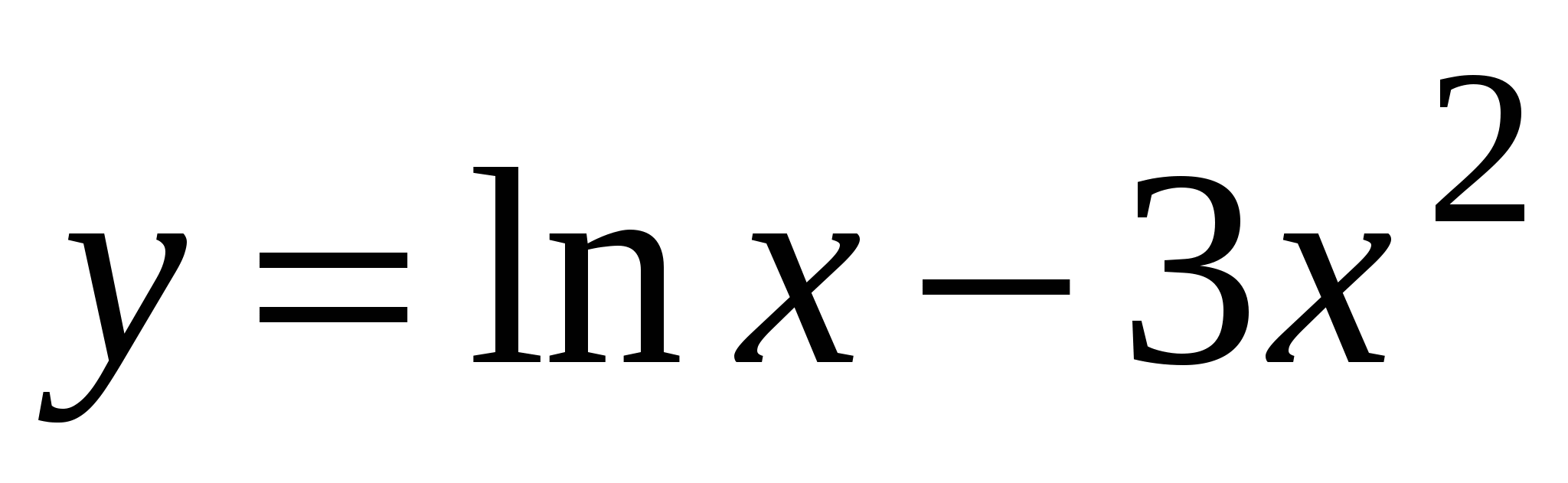 .
.
1)
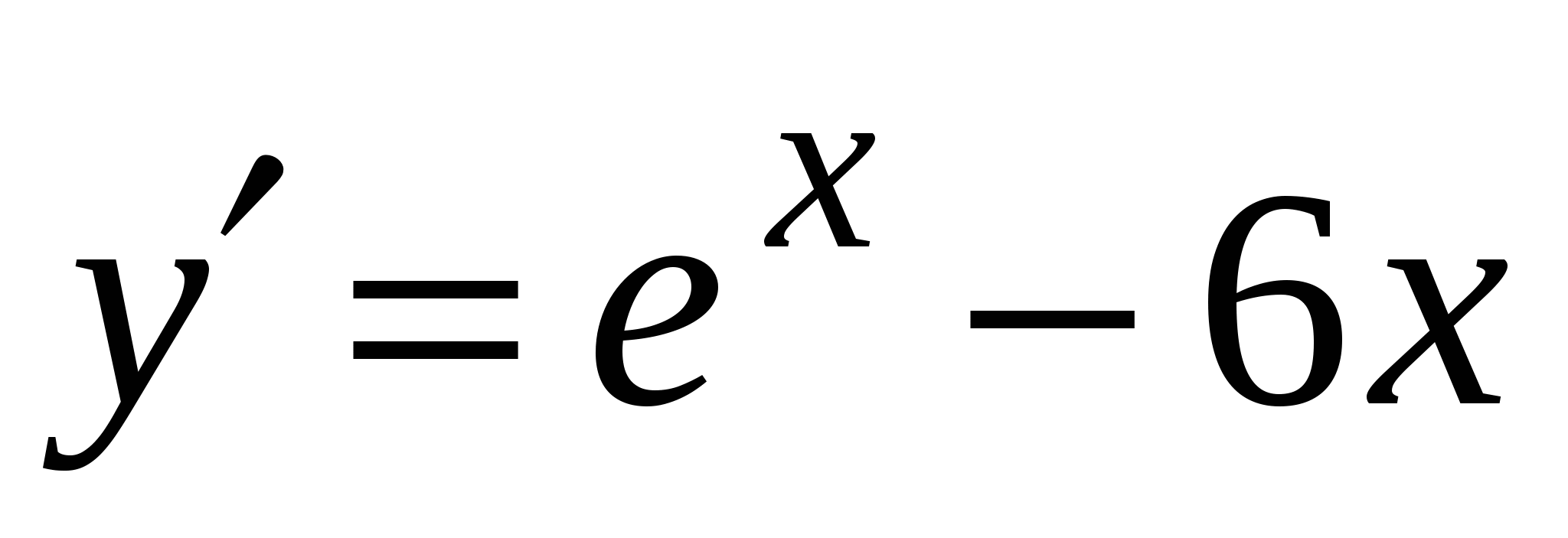
3)
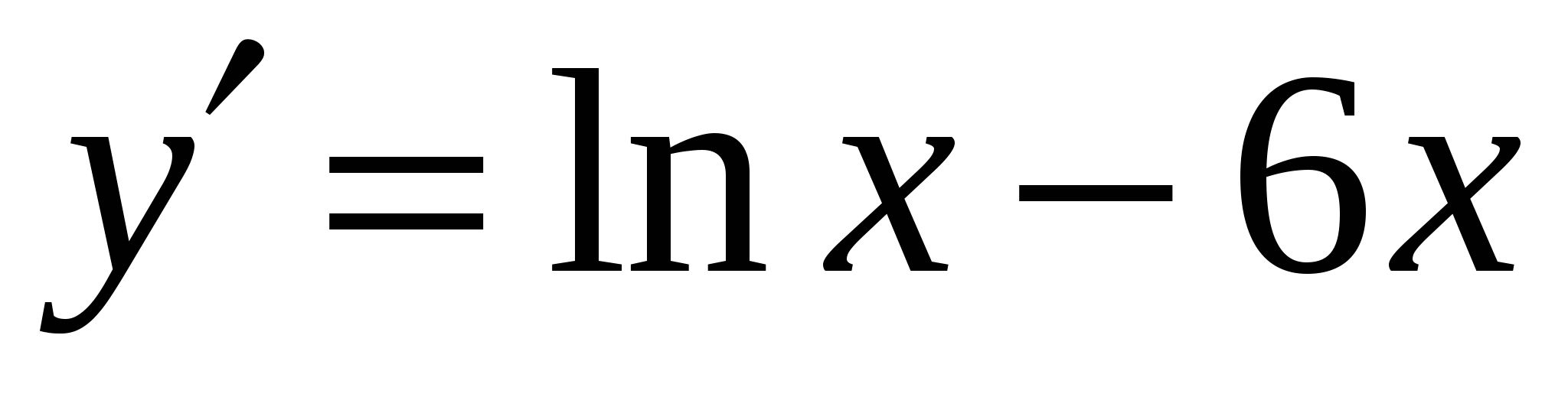
2)
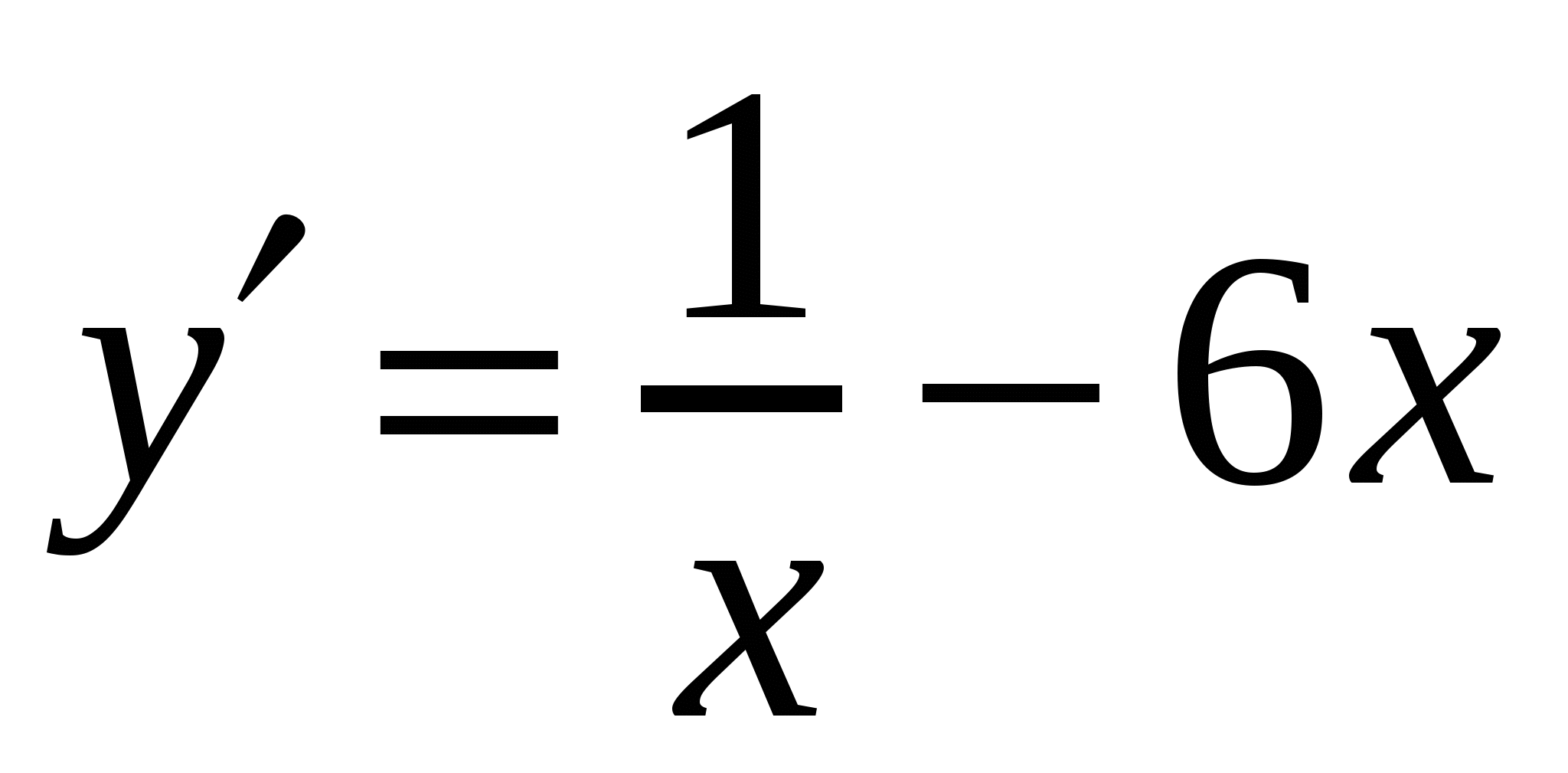
4)
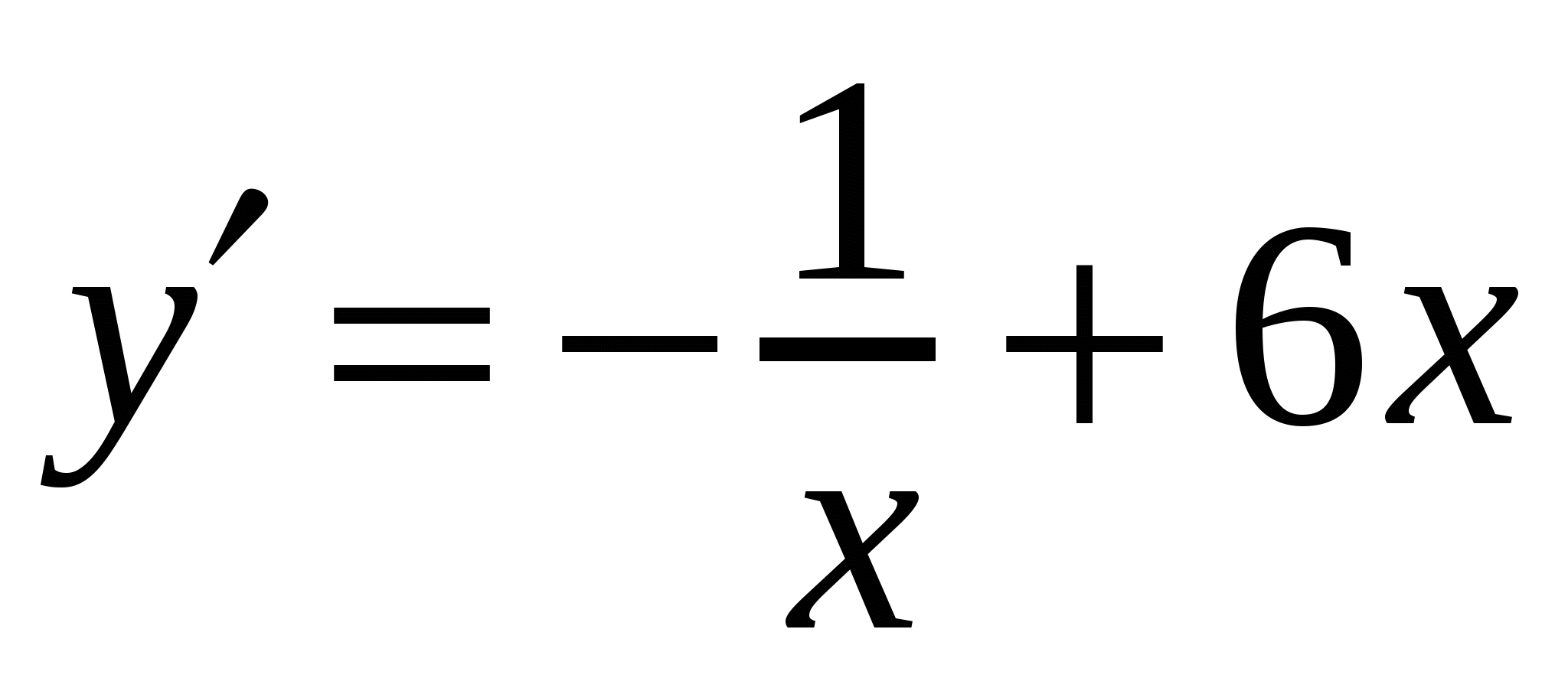

В3. На рисунке изображен график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
.
В4. Материальная точка движется по закону х(t)=1/4 t3-3t2+21t - 18 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 3 м/с2 ?
В5.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=6t2 - 18t+19. Через сколько секунд после начала движения произойдет остановка?
В6. Материальная точка движется по закону х(t)=1/6 t3-4t2+35t - 11 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 2 м/с2 ?
Контрольная работа №3 по теме: «Производная»
Вариант №15

B1 Функция  определена на промежутке
определена на промежутке  . На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции
. На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции  имеет наибольший угловой коэффициент.
имеет наибольший угловой коэффициент.
А1. Найдите производную функции 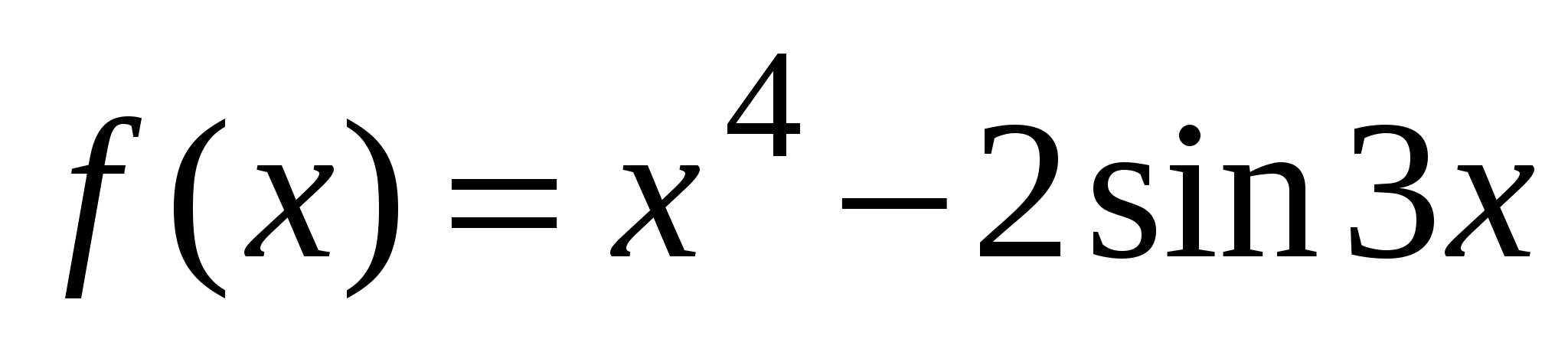 .
.
1) 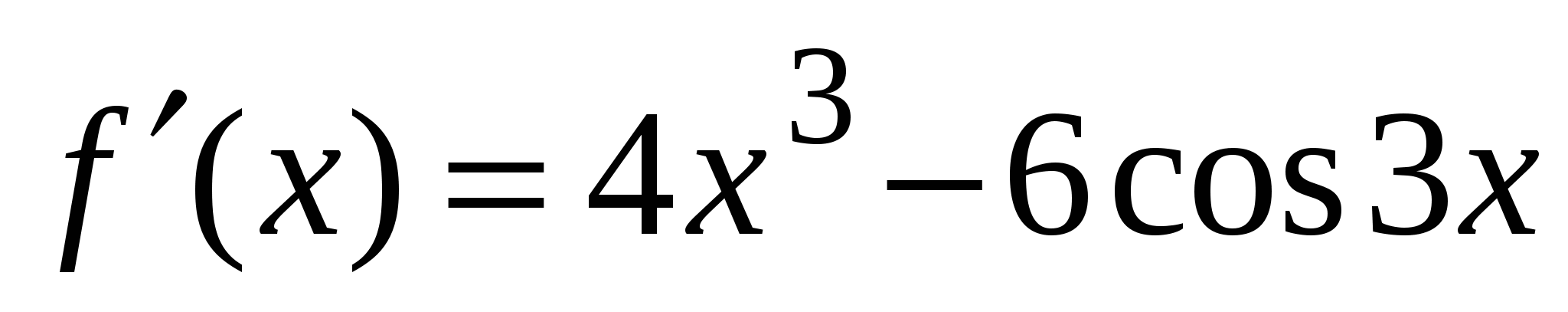
3) 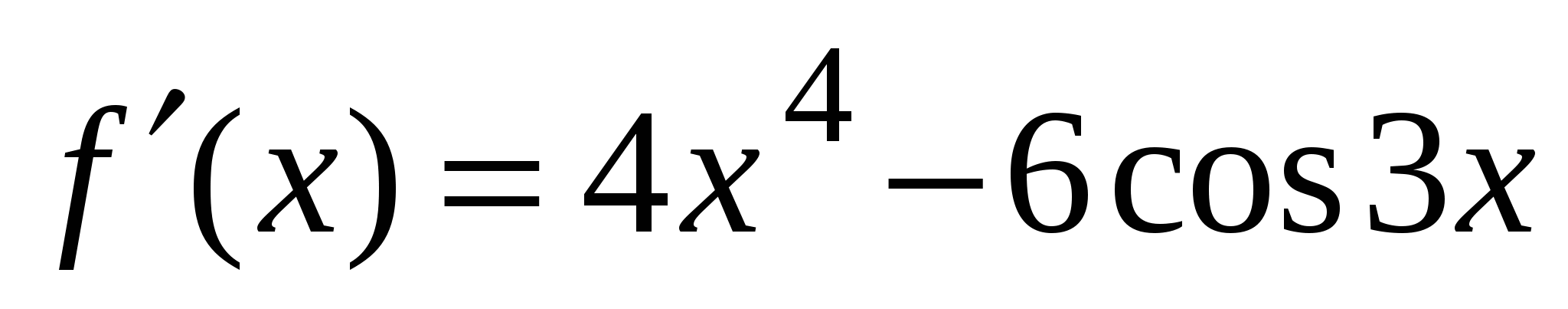
2) 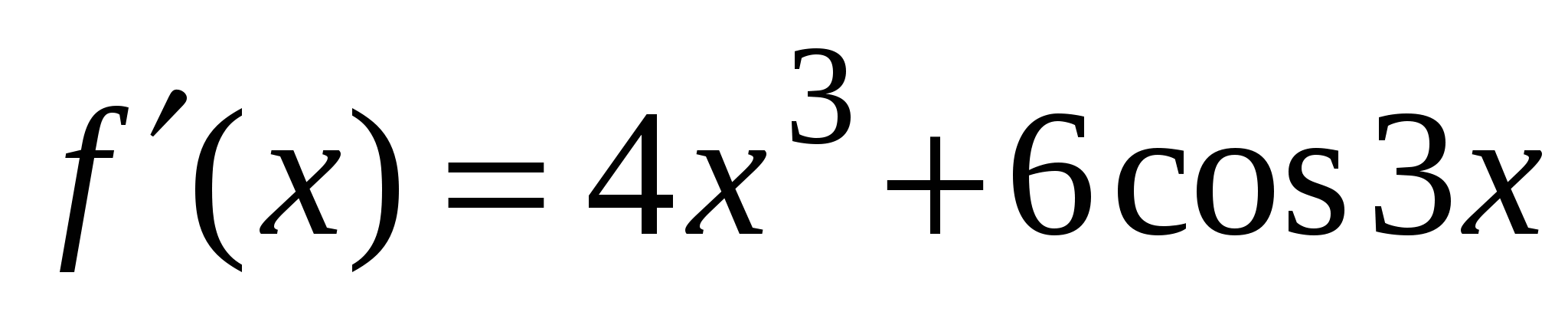
4) 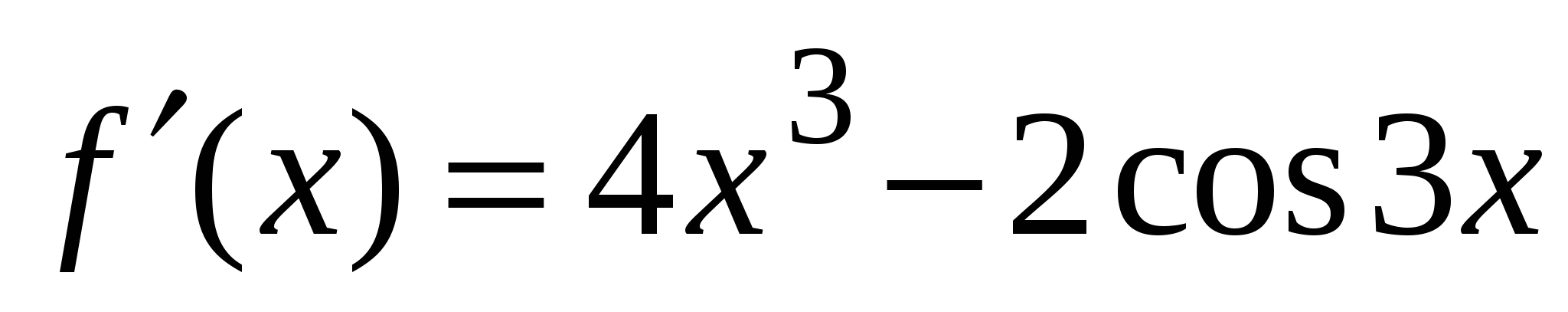
А2. Найдите производную функции  .
.
1)

3)

2)

4)

А3. Найдите производную функции 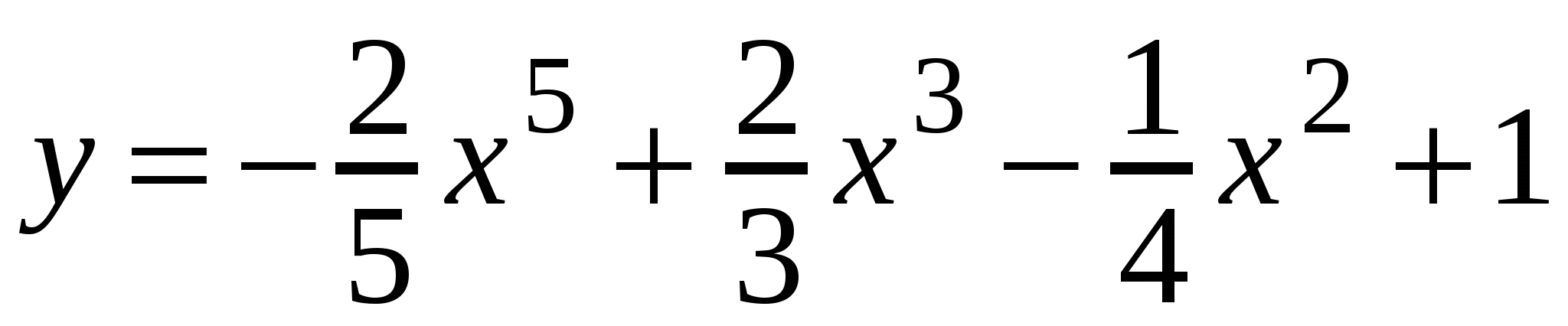 .
.
1)
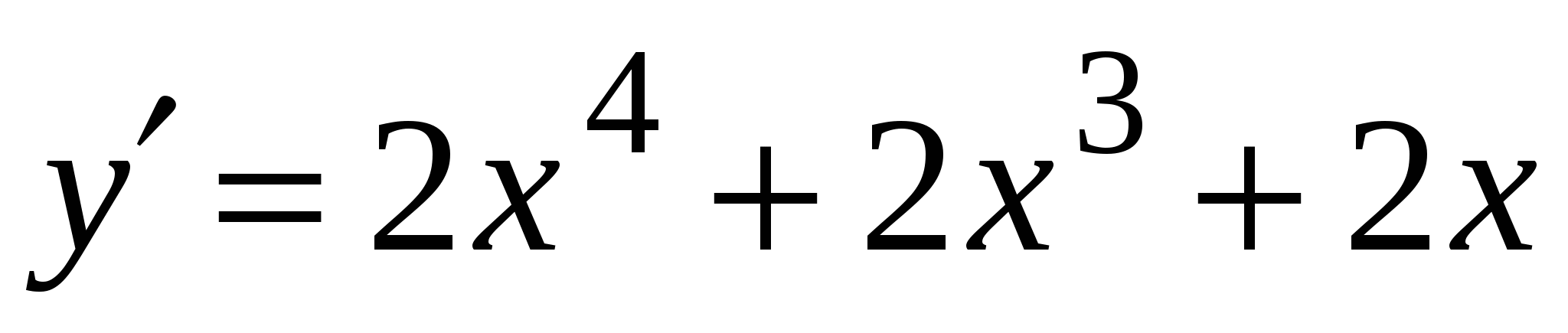
3)
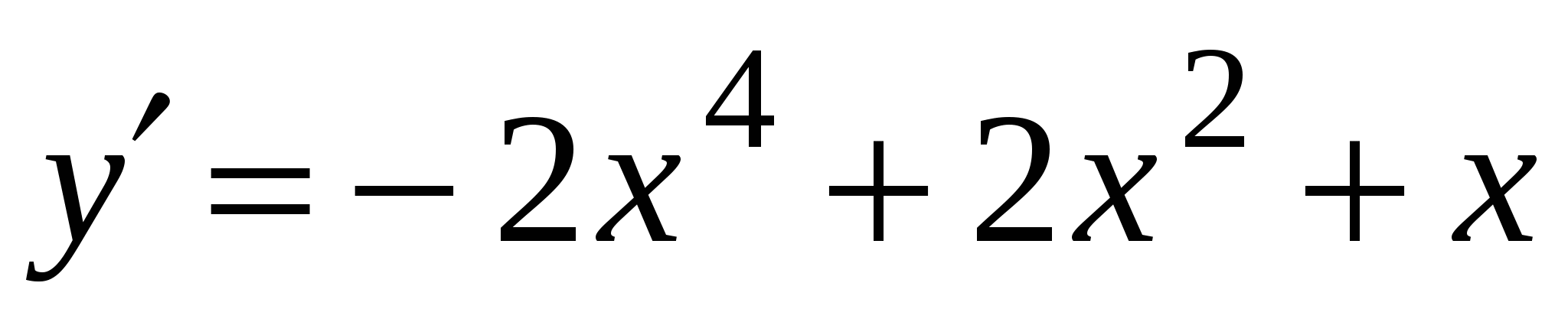
2)
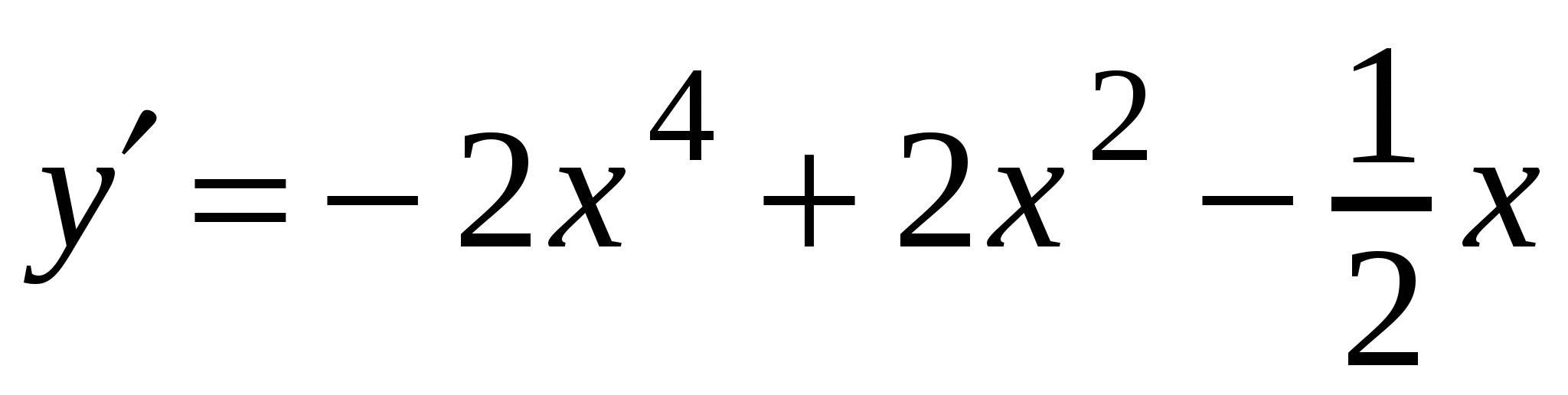
4)
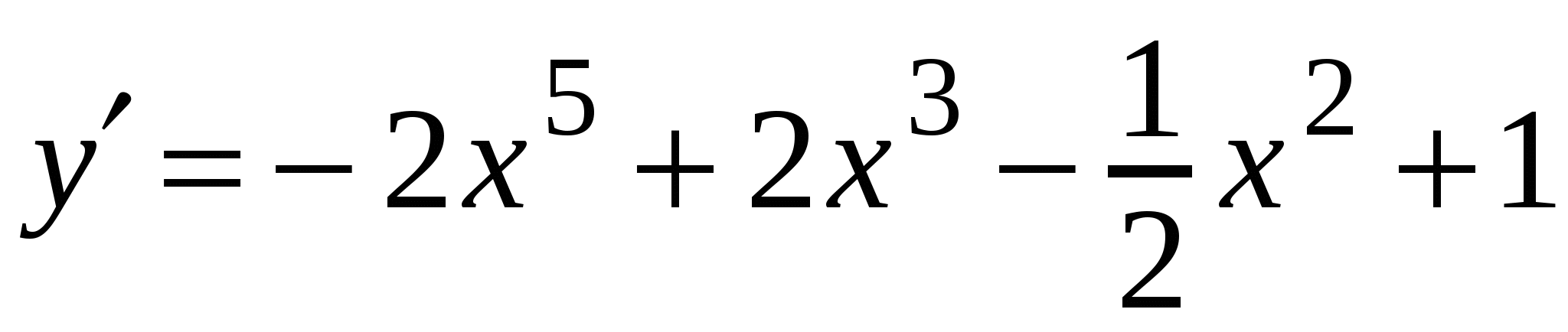
А4. Найдите производную функции 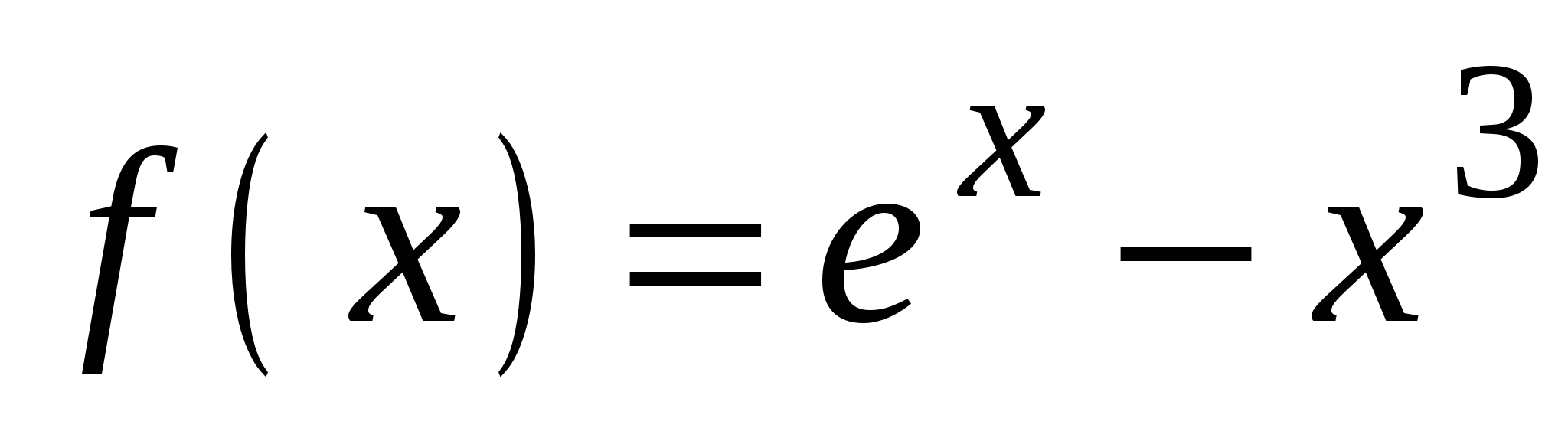 .
.
1)
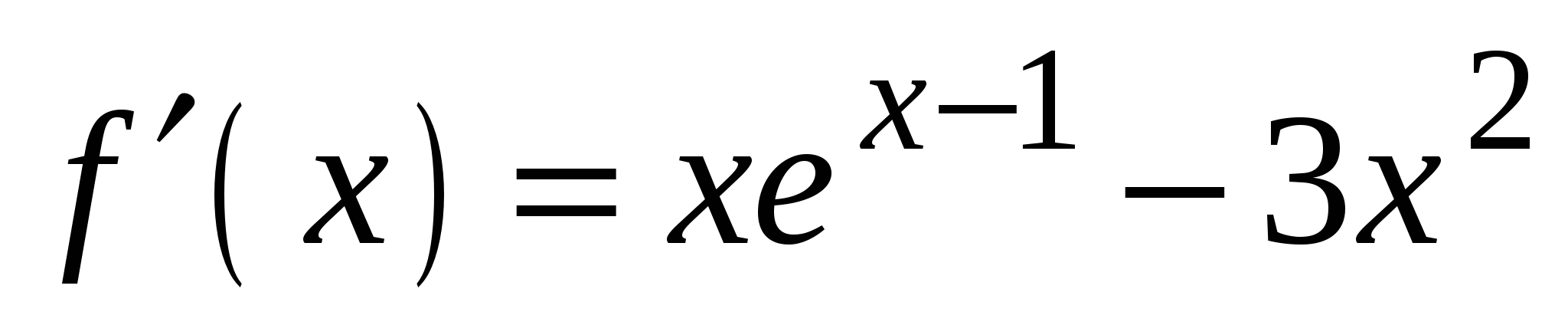
3)
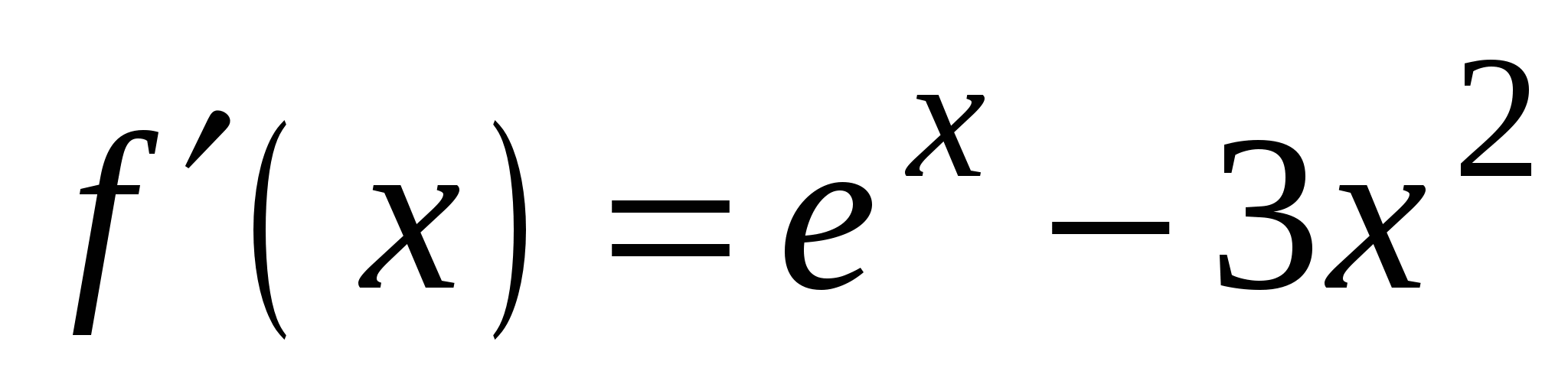
2)
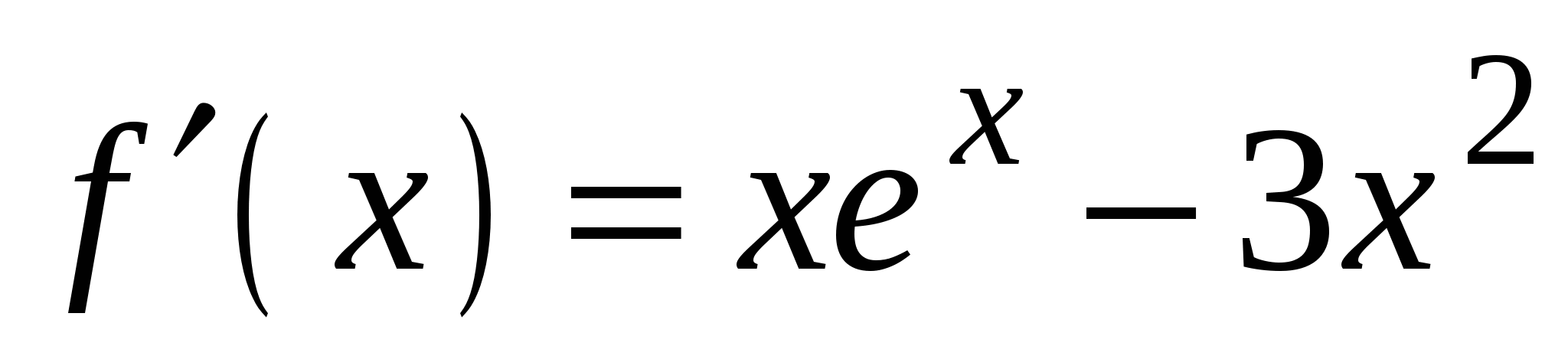
4)
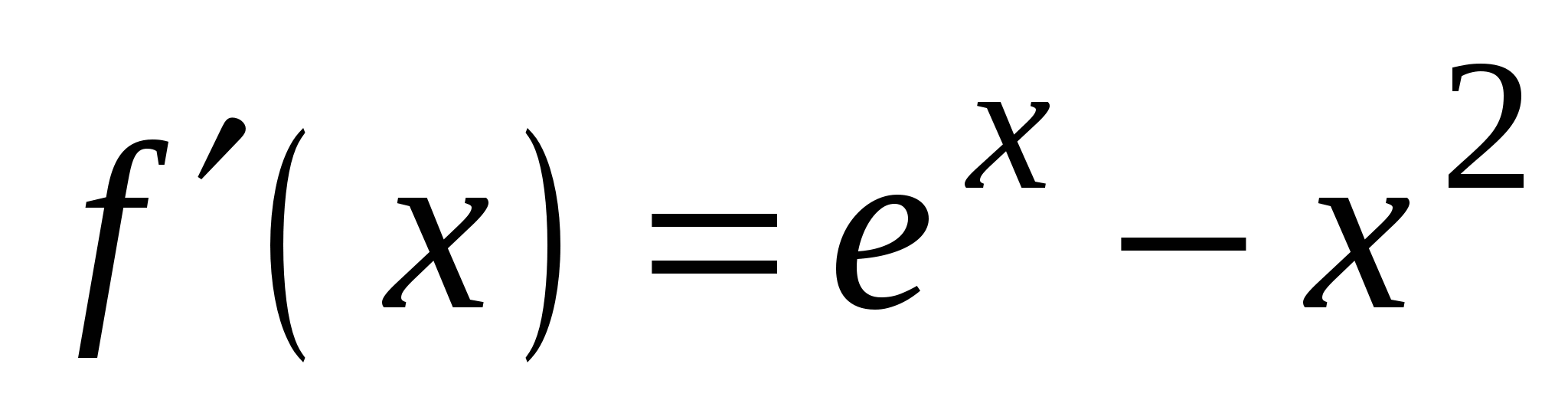

B2. На рисунке изображен график функции 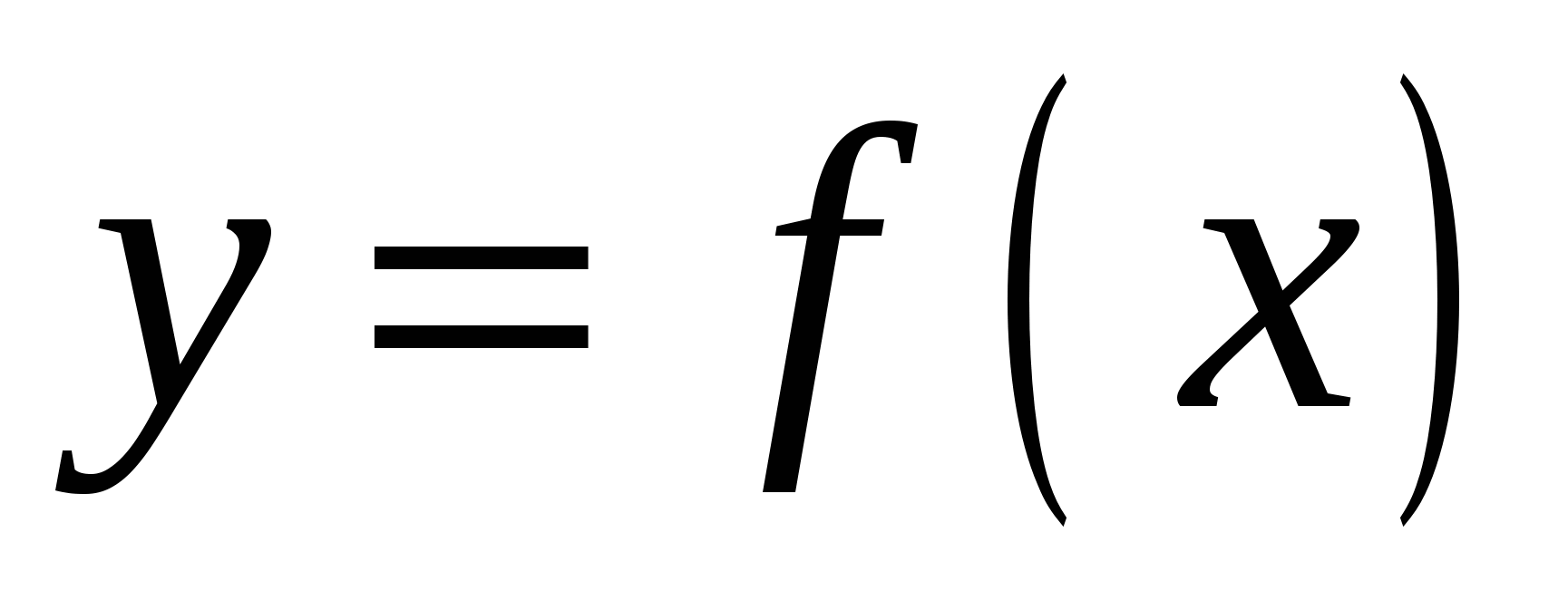 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
.
А5. Найдите производную функции 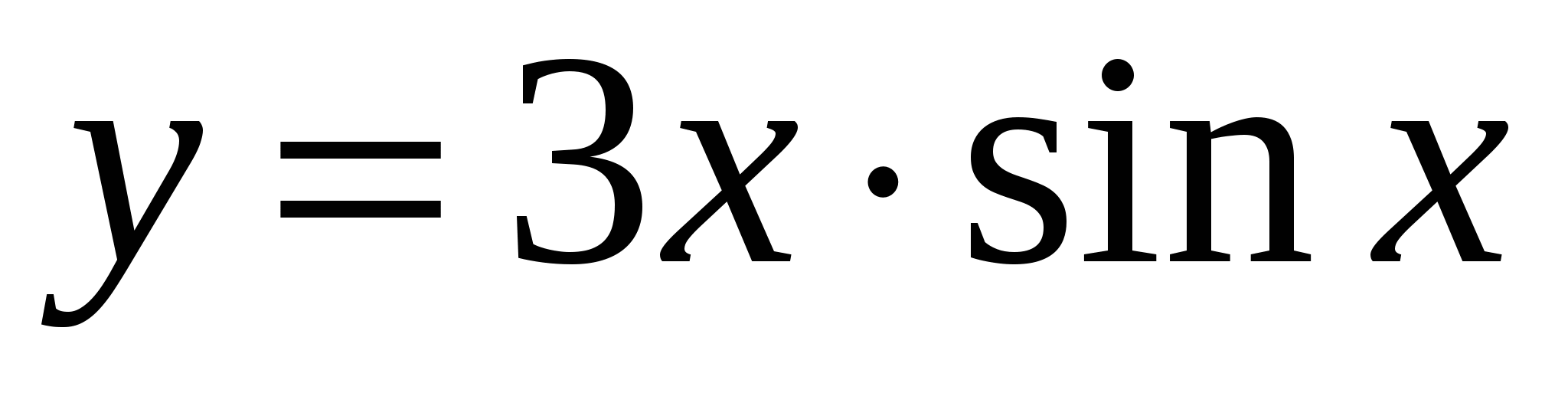 .
.
1)
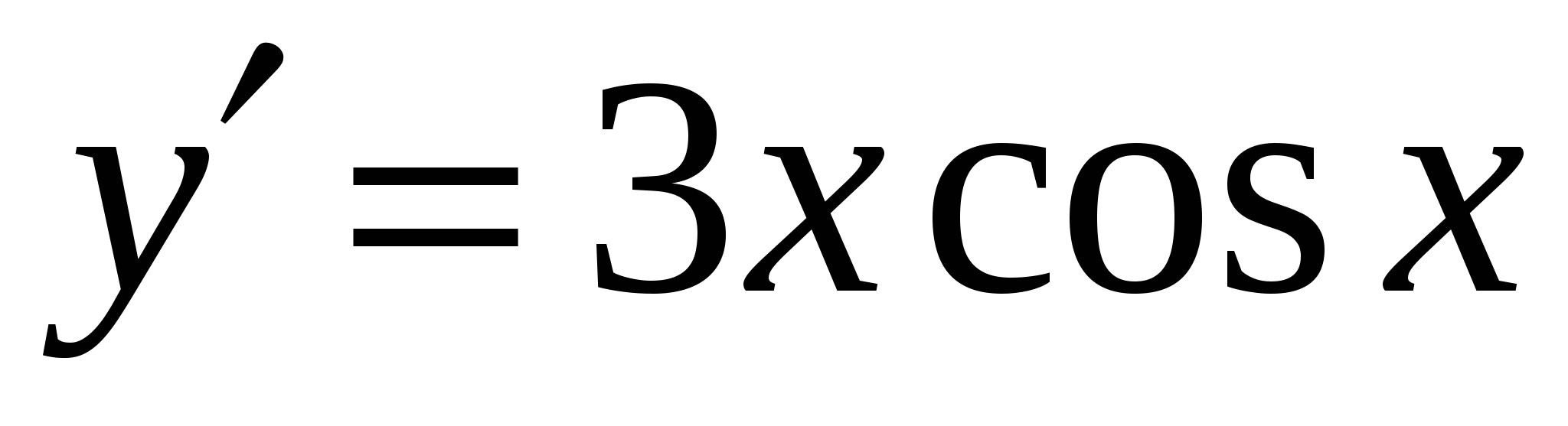
3)
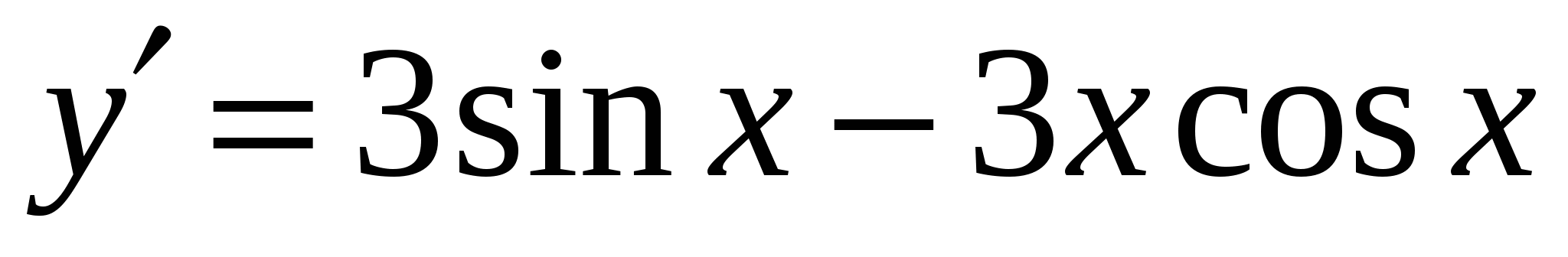
2)
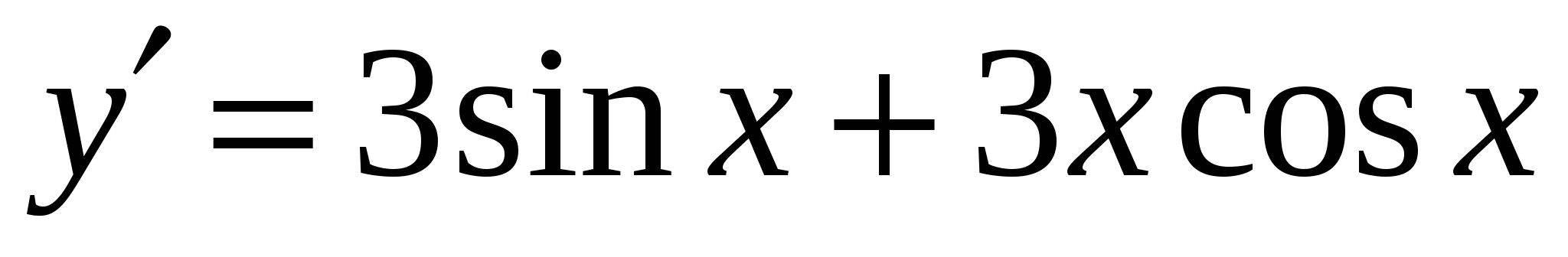
4)
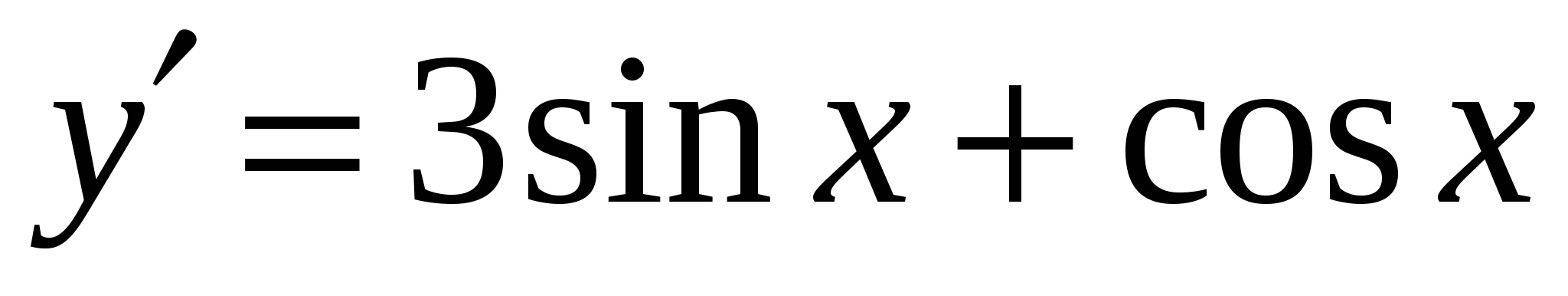

В3. На рисунке изображен график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной в точке
. Найдите значение производной в точке  .
.
В4. Материальная точка движется по закону
х(t)=1/4 t3-3t2+21t - 18 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 3 м/с2 ?
В5.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=6t2 - 18t+19. Через сколько секунд после начала движения произойдет остановка?
В6. Материальная точка движется по закону х(t)=1/6 t3-4t2+35t - 11 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 2 м/с2 ?
infourok.ru
Контрольная работа на тему «Производная» В-1
Задание 1. Вычислить пределы
а)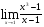
б)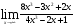
Задание 2.
Найти производную функции в точке x0=4
a)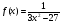 б)
б)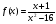
Задание 3. Найти производную функции
а) у = 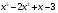 б) y =
б) y = 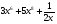 в) y =
в) y = 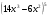
г) y = 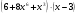 д) y =
д) y = 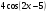 е) y =
е) y = 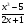
Задание 4. Найти вторую производную функции
а) у = 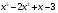 б)
б)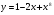
Задание 5. Составить уравнение касательной к графику функции y = f(x) в точке х0
а)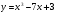 X0 =1
X0 =1
Задание 6. Исследовать функцию на монотонность и экстремумы:
а)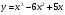
б)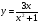
Задание 7. Найти скорость материальной точки в момент времени t
а)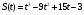
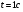
Правильное выполнение каждого примера оценивается 1 баллом. Максимально возможное количество баллов за контрольную работу – 16. Для того чтобы работа была зачтена, необходимо выполнить все задания и набрать не менее 8 баллов.
Контрольная работа на тему «Производная» В-2
Задание 1. Вычислить пределы
a)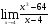
б) 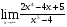
Задание 2.
Найти производную функции в точке x0=2
а) 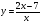 б)
б)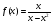
Задание 3. Найти производную функции
а) у = х3 + х б) у = 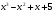 в) у =
в) у = 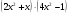
г) у = 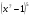 д) у =
д) у = 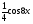 е) у =
е) у = 
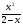
Задание 4. Найти вторую производную функции
а) 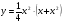 б)
б)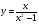
Задание 5. Составить уравнение касательной к графику функции y = f(x) в точке х0
а)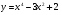
X0 = -1
Задание 6. Исследовать функцию на монотонность и экстремумы:
а)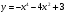
б)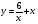
Задание 7. Найти скорость материальной точки в момент времени t
а)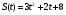
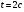
Правильное выполнение каждого примера оценивается 1 баллом. Максимально возможное количество баллов за контрольную работу – 16. Для того чтобы работа была зачтена, необходимо выполнить все задания и набрать не менее 8 баллов.
Контрольная работа на тему «Производная» В-3
Задание 1. Вычислить пределы
а)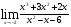
б)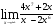
Задание 2.
Найти производную функции в точке x0=0
а) f (x) =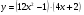 б)
б)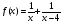
Задание 3. Найти производную функции
а) у = 6 – х – х2 б) 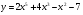 в)
в) 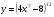
г) 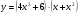 д)
д)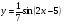 е)
е) 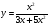
Задание 4. Найти вторую производную функции
а)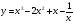 б)
б)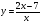
Задание 5. Составить уравнение касательной к графику функции y = f(x) в точке х0
а)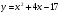
X0 = 0
Задание 6. Исследовать функцию на монотонность и экстремумы:
а)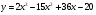
б)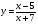
Задание 7. Найти скорость материальной точки в момент времени t
а)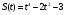
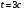
Правильное выполнение каждого примера оценивается 1 баллом. Максимально возможное количество баллов за контрольную работу – 16. Для того чтобы работа была зачтена, необходимо выполнить все задания и набрать не менее 8 баллов.
Контрольная работа на тему «Производная» В-4
Задание 1. Вычислить пределы
а)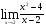
б)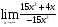
Задание 2.
Найти производную функции в точке x0=-1
а) f(x)=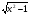 б)
б) 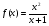
Задание 3. Найти производную функции
а) у = х2 + 4х б) 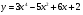 в)
в) 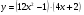
г) 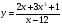 д)
д) 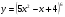 е)
е) 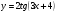
Задание 4. Найти вторую производную функции
а)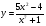 б)
б)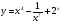
Задание 5. Составить уравнение касательной к графику функции y = f(x) в точке х0
а)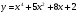
X0 = 1
Задание 6. Исследовать функцию на монотонность и экстремумы:
а)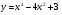
б)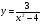
Задание 7. Найти скорость материальной точки в момент времени t
а)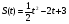
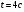
Правильное выполнение каждого примера оценивается 1 баллом. Максимально возможное количество баллов за контрольную работу – 16. Для того чтобы работа была зачтена, необходимо выполнить все задания и набрать не менее 8 баллов.
infourok.ru
1 вариант
Найдите производные функций:
а) f(x) = 5х4 + 3х2 – 8х – 9; б) g(x) = 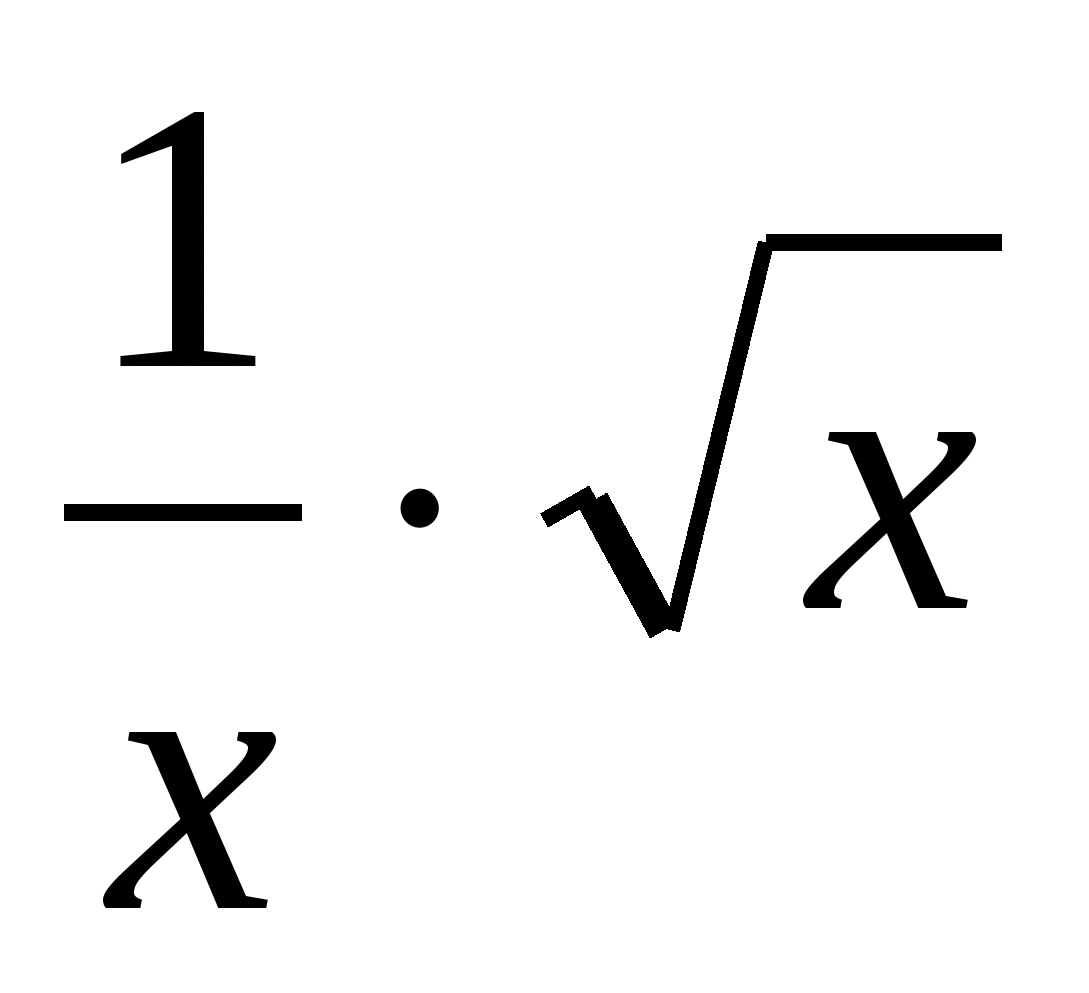 ;
;
в) q(x) = 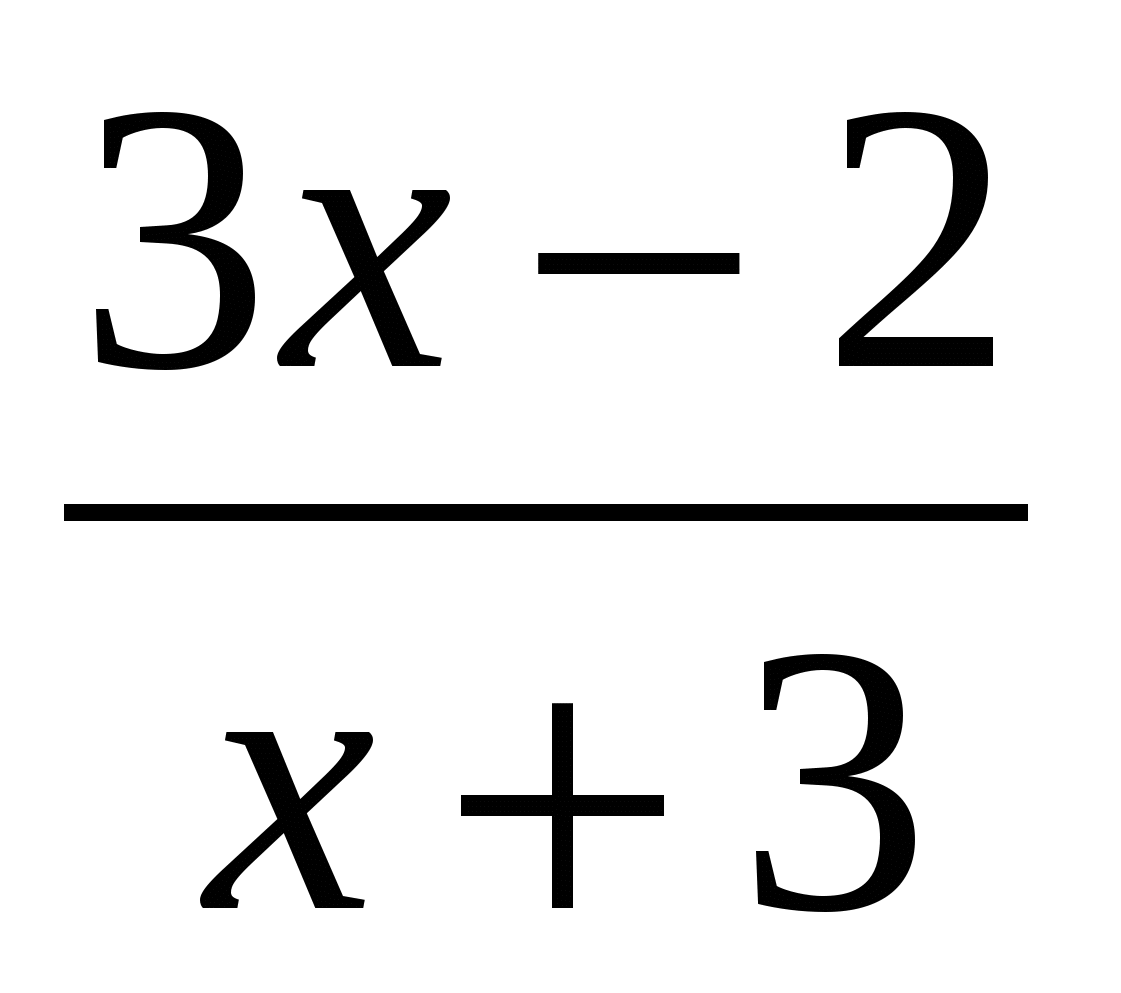 ; г) u(x) = sin 5x
; г) u(x) = sin 5x
2. Точка движется по закону х(t)=3t3+2t+1 Найдите ускорение точки в момент времени 2сек.
3. Найдите угол наклона касательной к графику функции f(x)=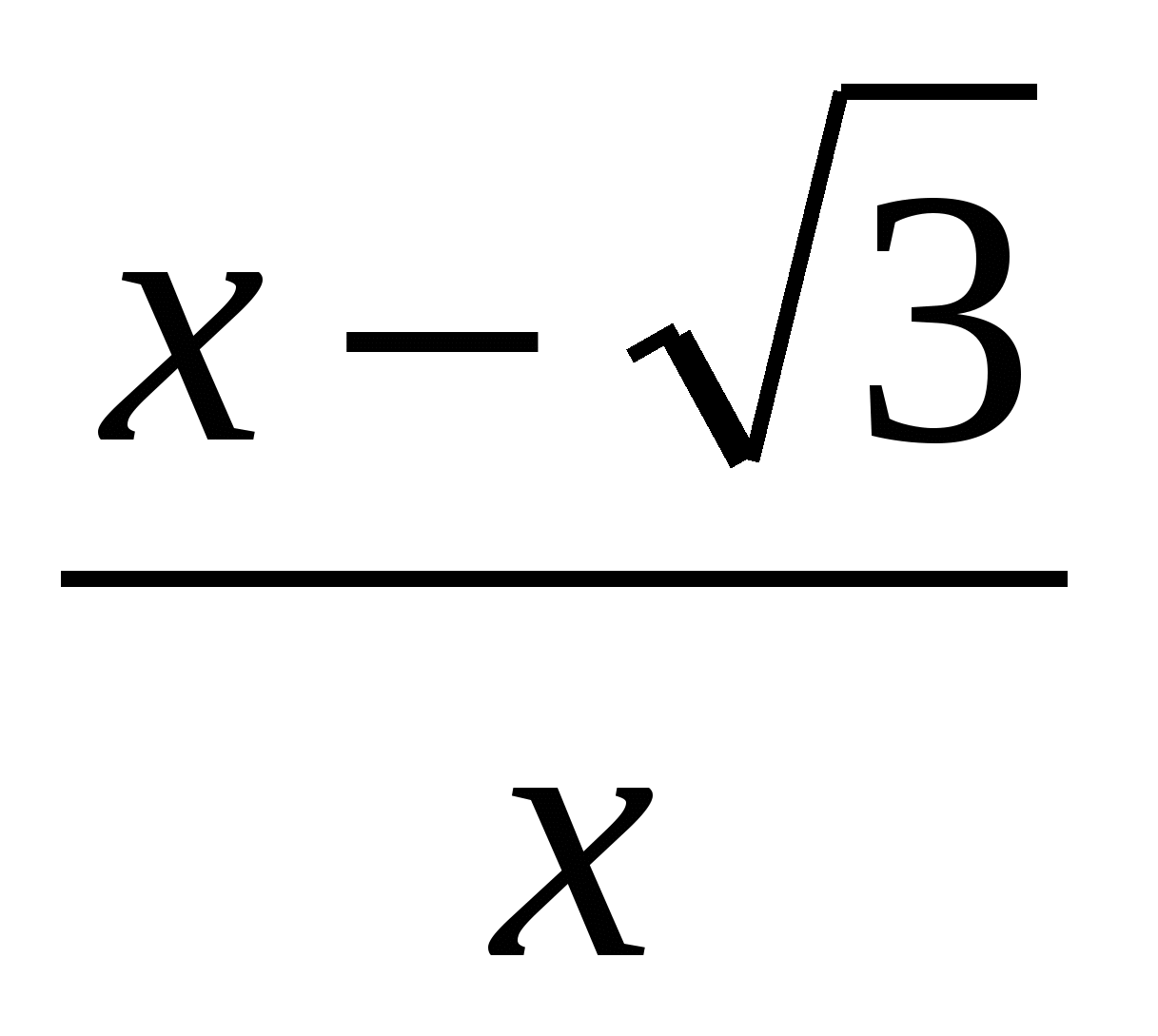 в точке х0=-1
в точке х0=-1
4. напишите уравнение касательной к графику функции f(x) = x2-2x в точке х0=2. Сделайте рисунок
5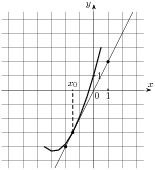 .На рисунке изображены график функции
.На рисунке изображены график функции 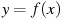 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 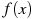 в точке
в точке 
6. Решите неравенство: 2х(х2-4)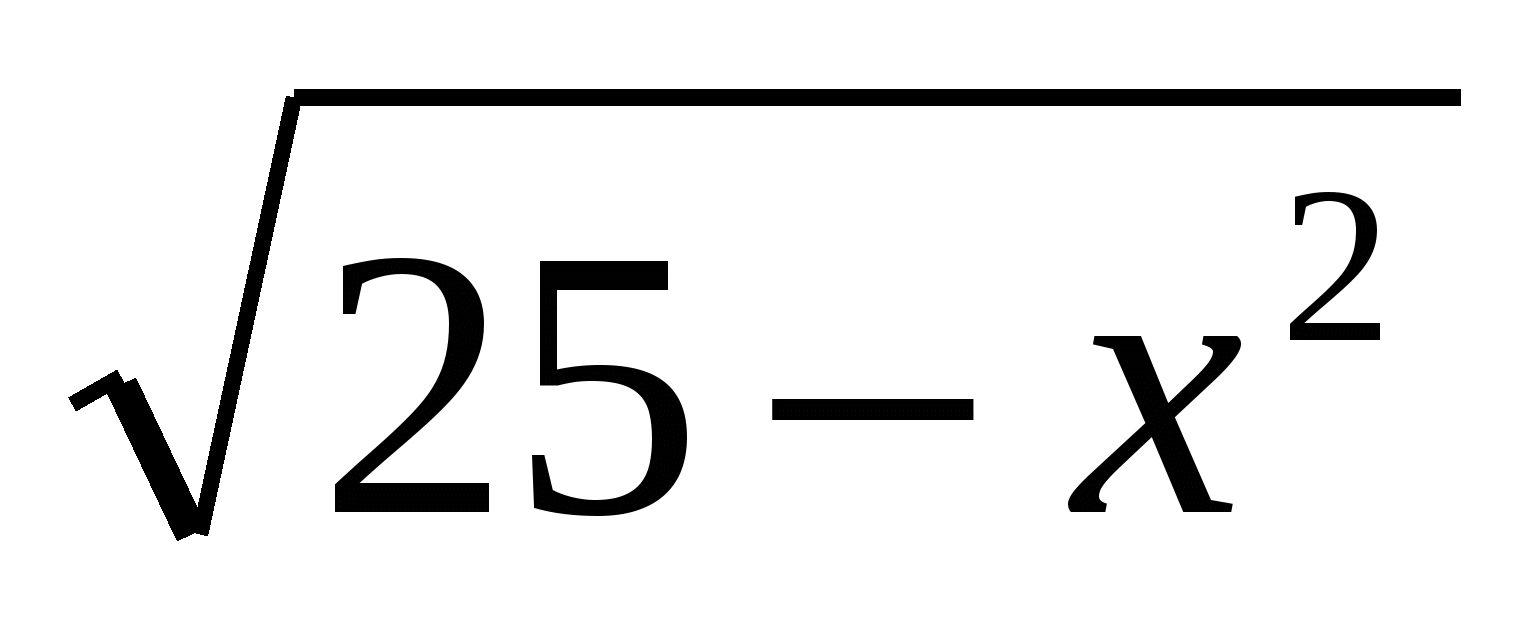 < 0
< 0
2 вариант
1. Найдите производные функций:
а) f(x) = 3х5 + 2х3 – 4х – 3; б)g(x) = 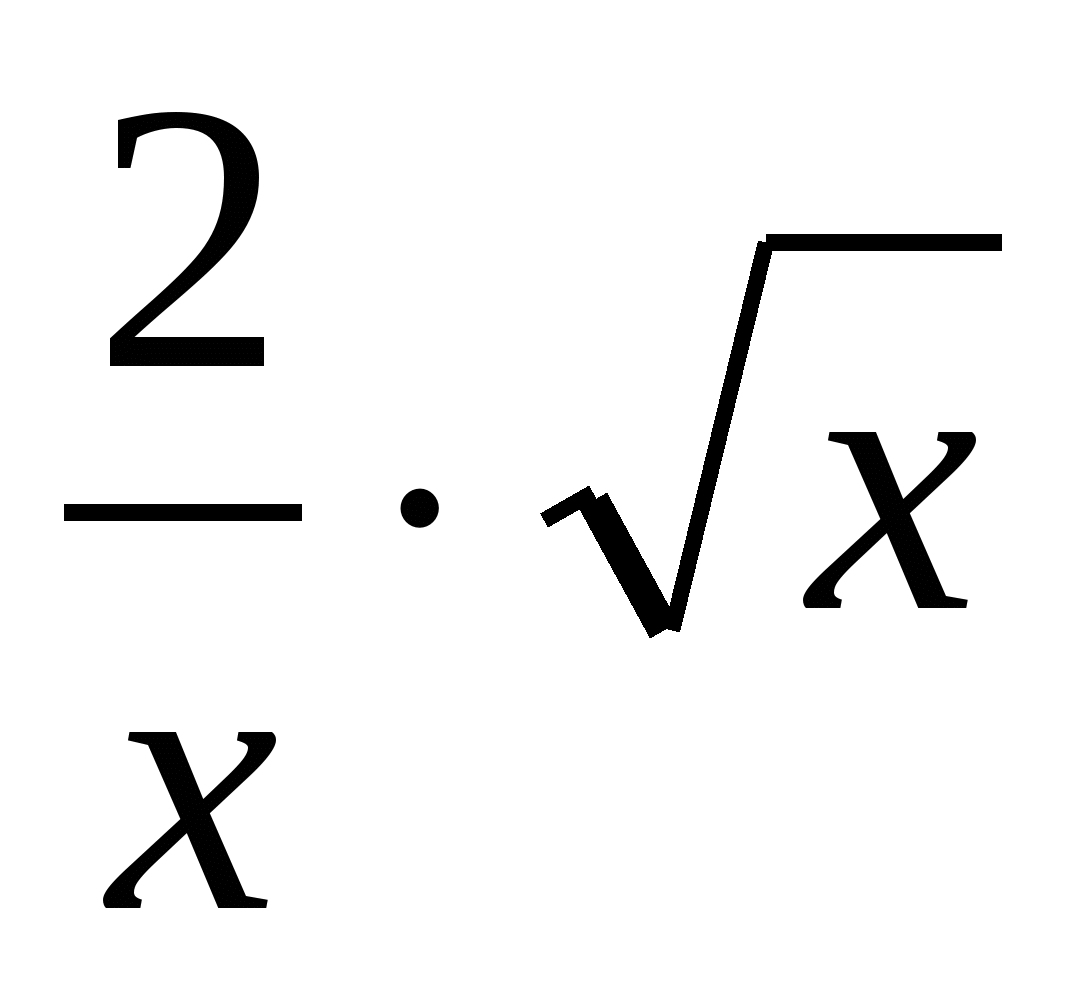 ;
;
в) q(x) = 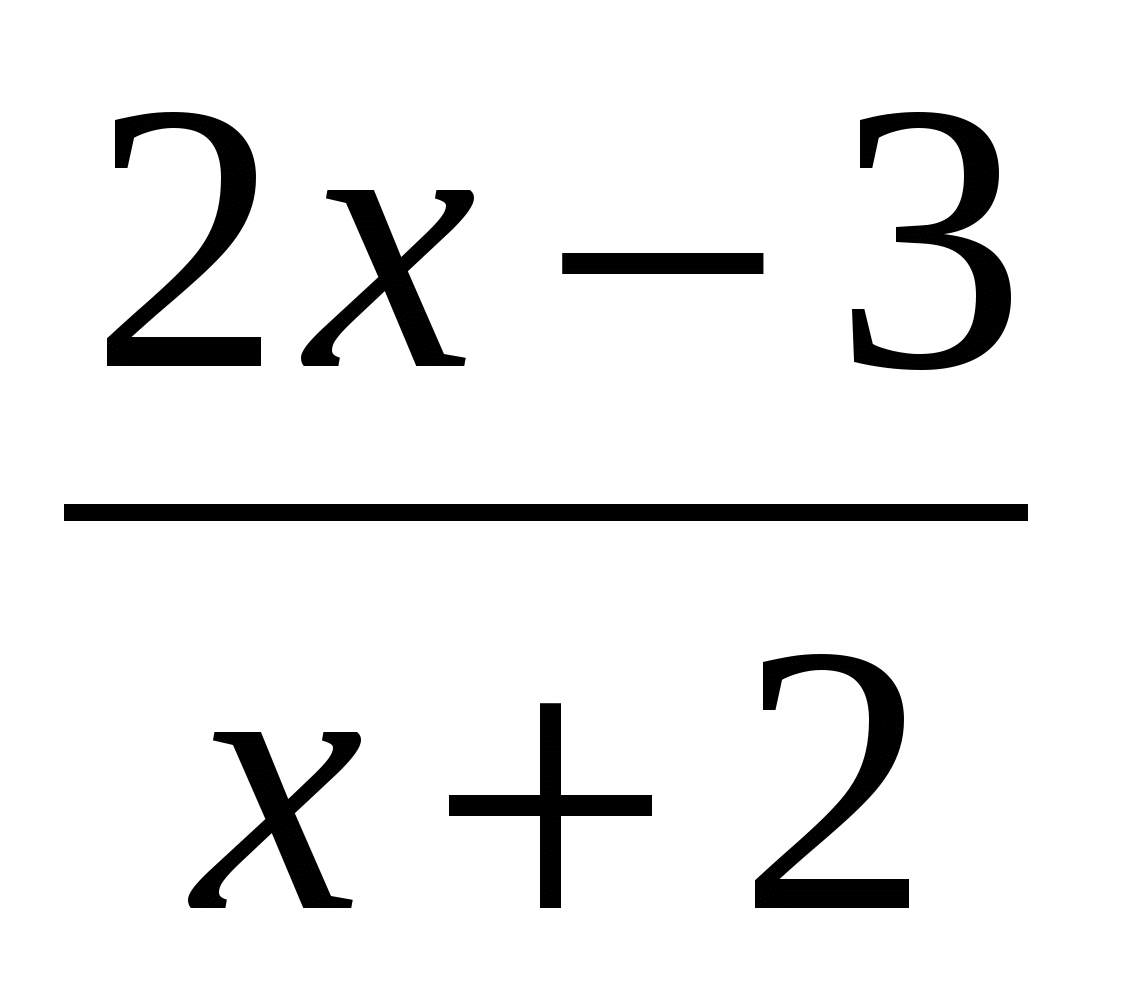 ; г) u(x) = cos 4x.
; г) u(x) = cos 4x.
2. Точка движется по закону х(t)=2t2+1 Найдите скорость точки в момент времени 2сек.
3. Найдите угол наклона касательной к графику функции f(x)=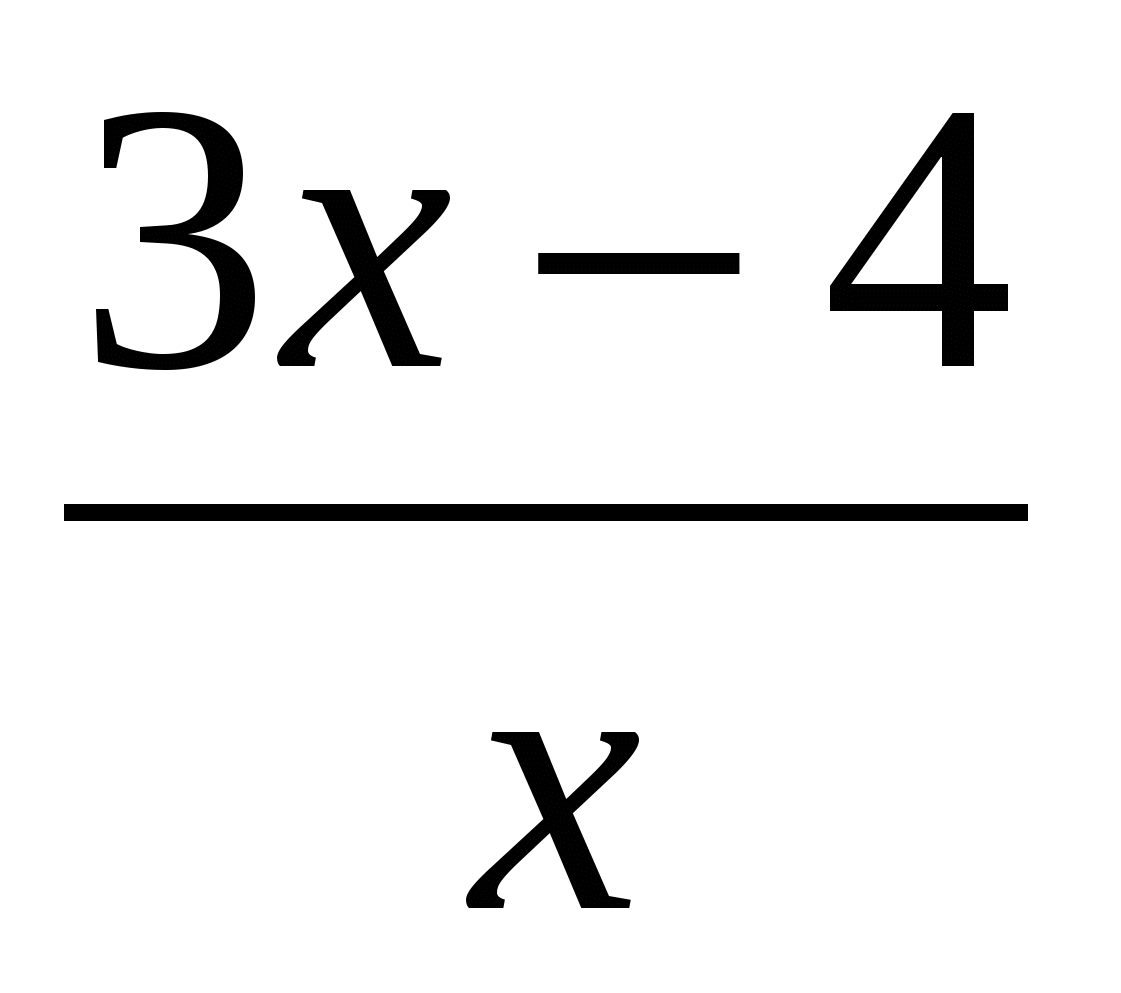 в точке х0=-2
в точке х0=-2
4. напишите уравнение касательной к графику функции f(x) = x2-1 в точке х0=-1. Сделайте рисунок
5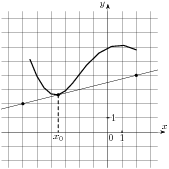 . На рисунке изображены график функции
. На рисунке изображены график функции 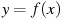 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 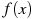 в точке
в точке 
6.Решите неравенство: х(х2-2х+1)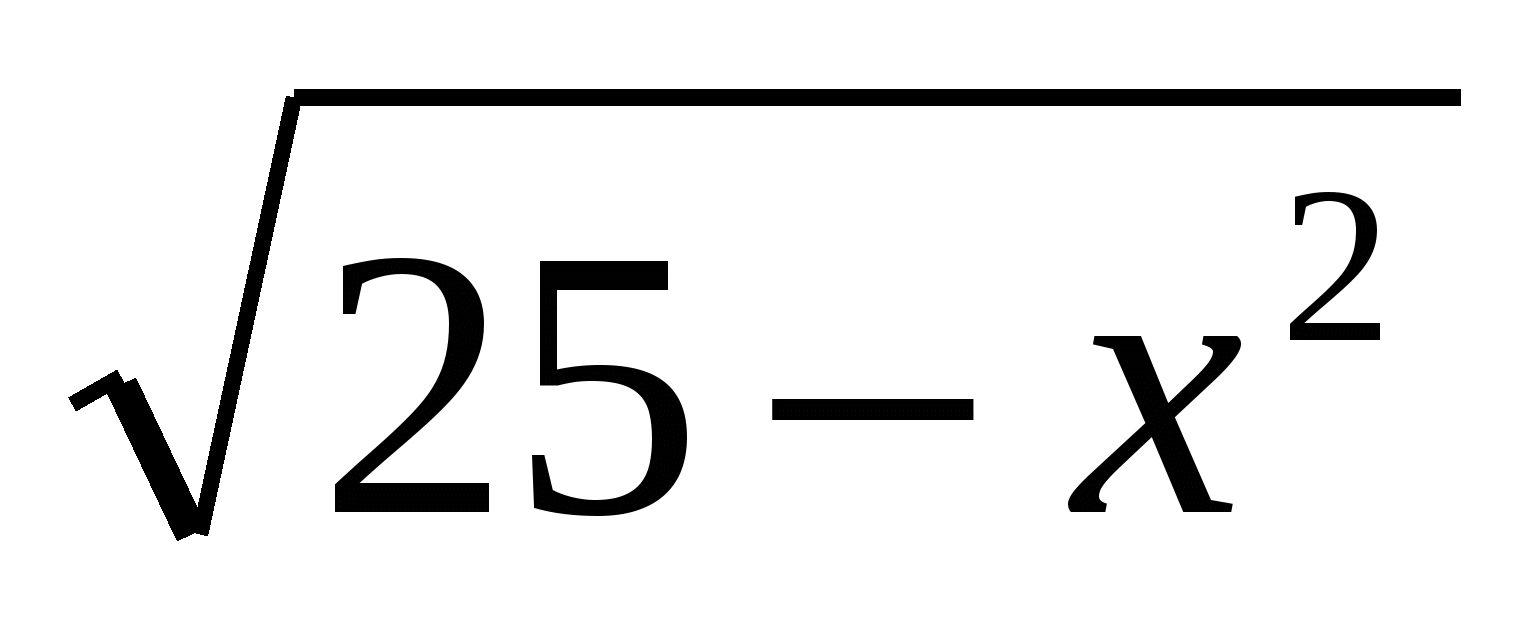 ≥ 0
≥ 0
3 вариант
1. Найдите производные функций:
а) f(x) = 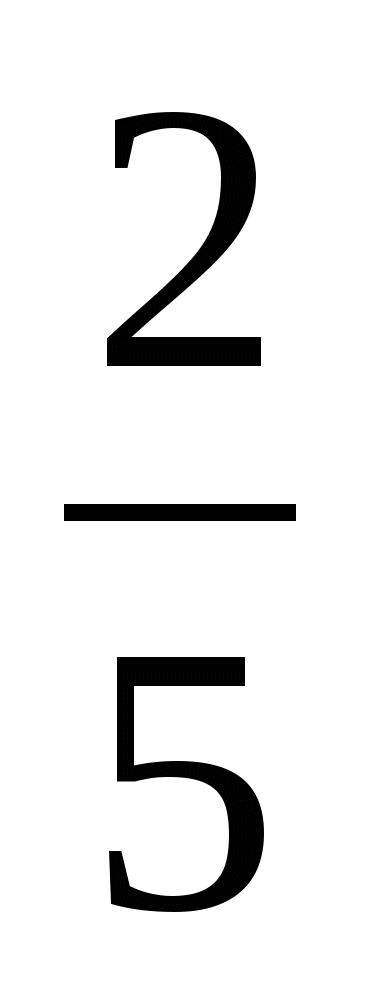 х5 + 3х3 – х – 4; б) g(x) =
х5 + 3х3 – х – 4; б) g(x) = 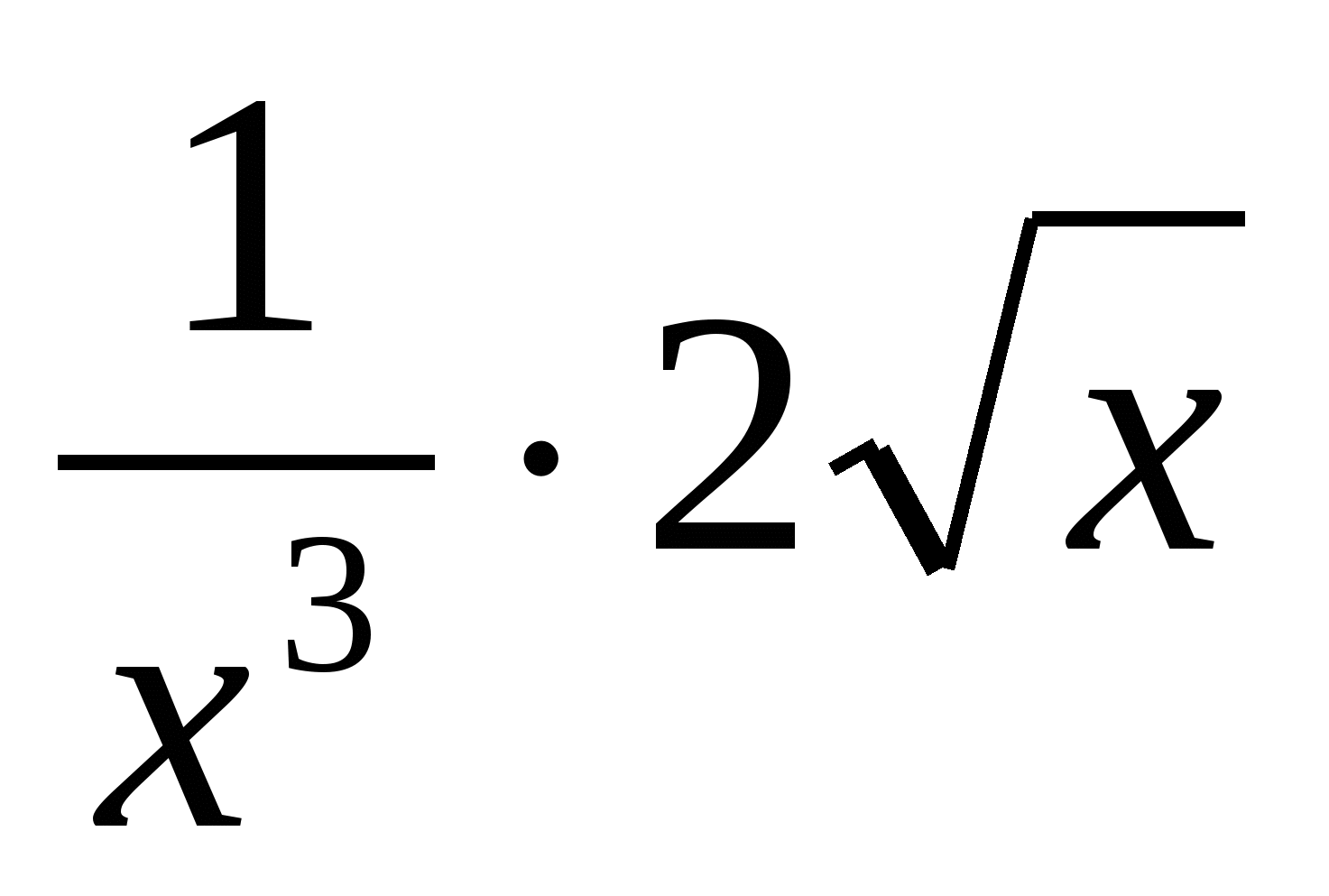 ;
;
в) q(x) = 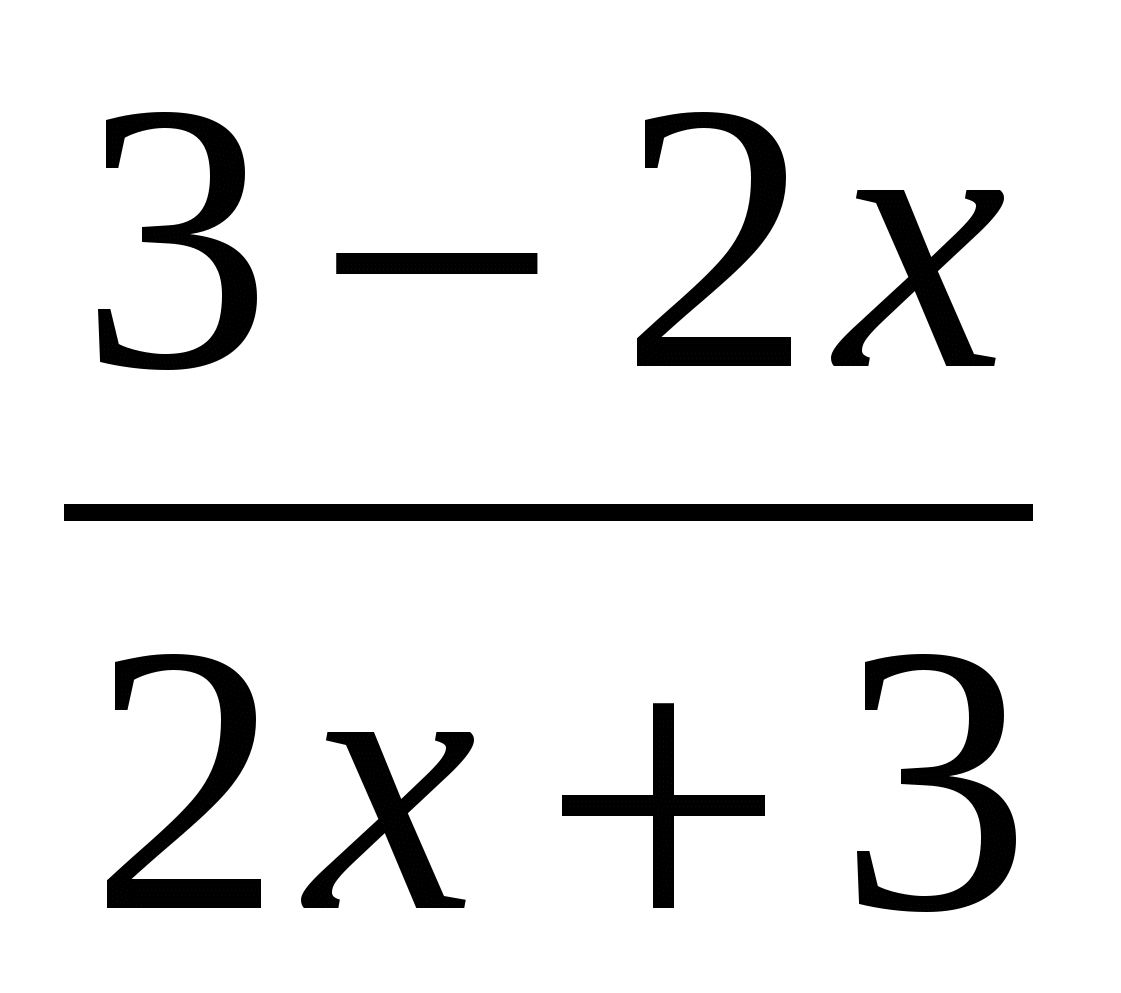 ; г) u(x) =
; г) u(x) = 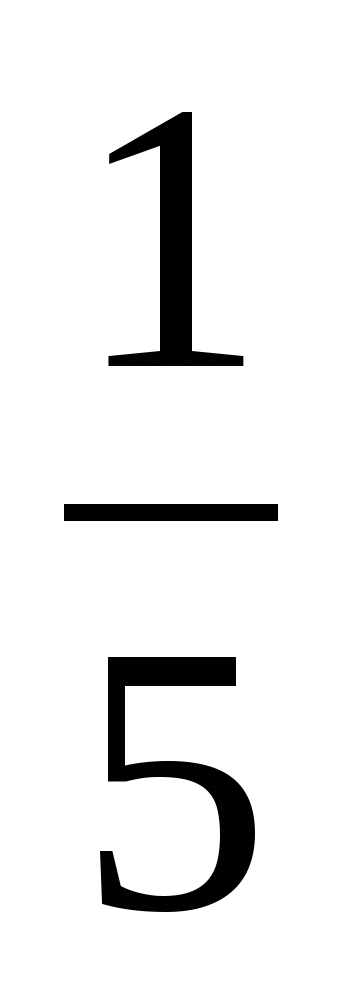 sin 5x
sin 5x
2. Точка движется по закону х(t)=2t3+4t Найдите ускорение точки в момент времени 2сек.
3. Найдите угол наклона касательной к графику функции f(x)=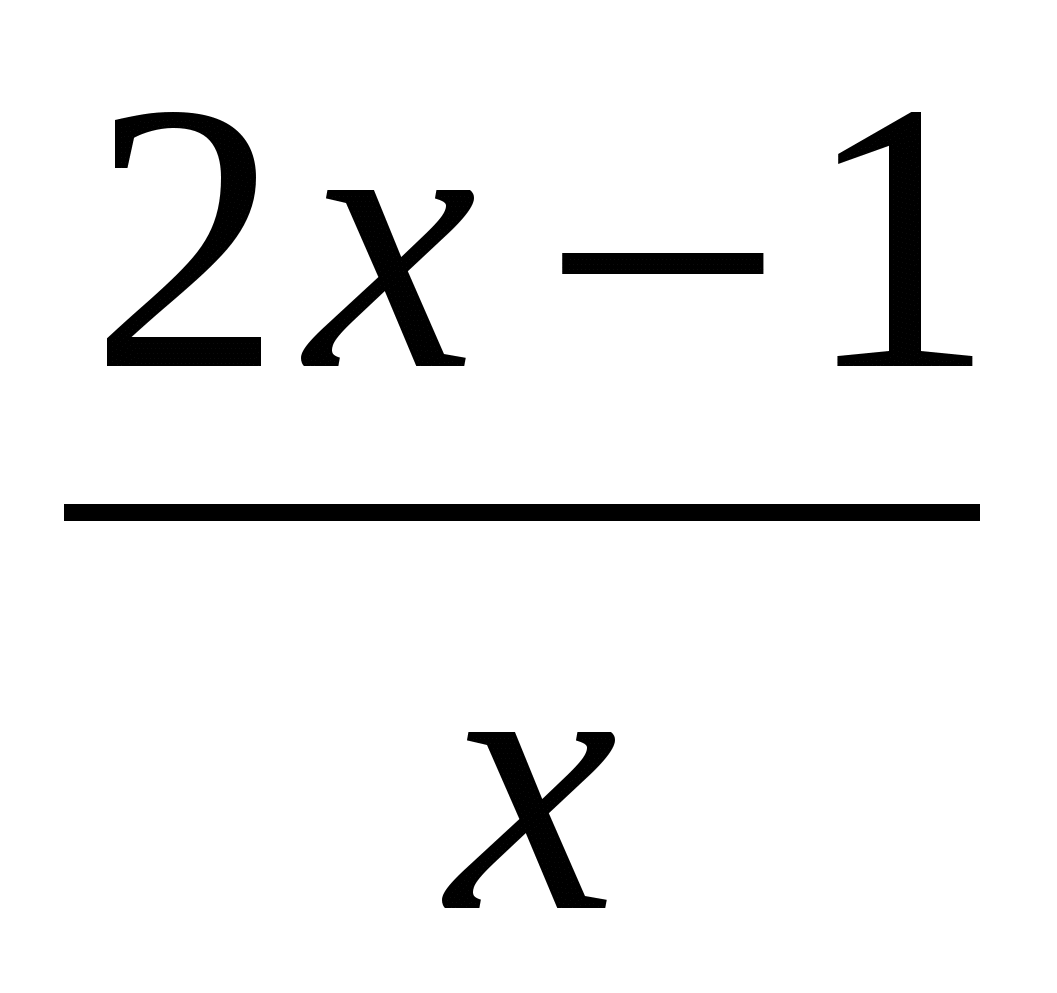 в точке х0=2
в точке х0=2
4. напишите уравнение касательной к графику функции f(x) = x2-4 в точке х0=3. Сделайте рисунок
5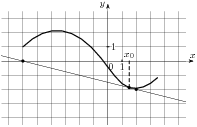 . На рисунке изображены график функции
. На рисунке изображены график функции 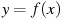 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 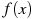 в точке
в точке 
6. Решите неравенство: (х2-2х)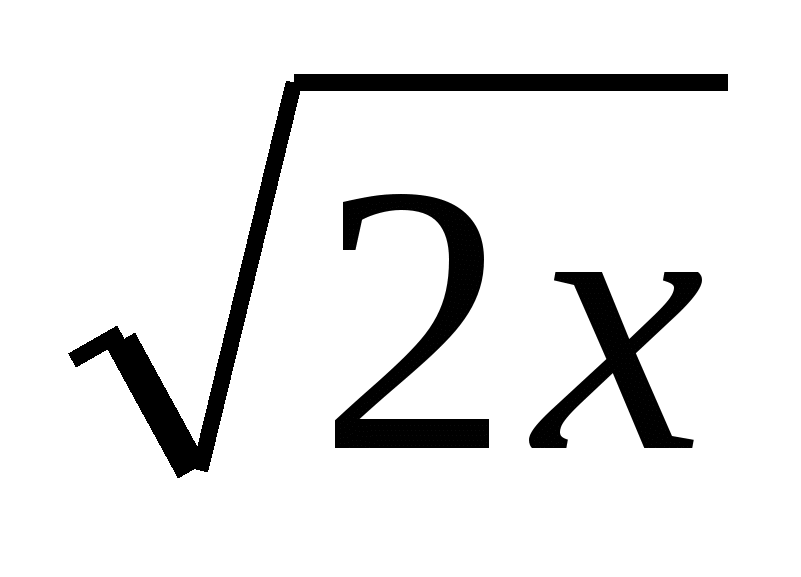 ≤ 0
≤ 0
4 вариант
1. Найдите производные функций:
а) f(x) = - 2х6 + 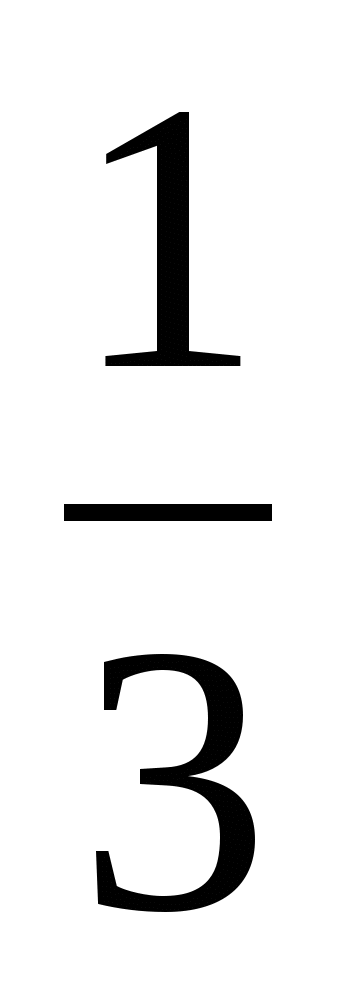 х9 – 3; б)g(x) =
х9 – 3; б)g(x) =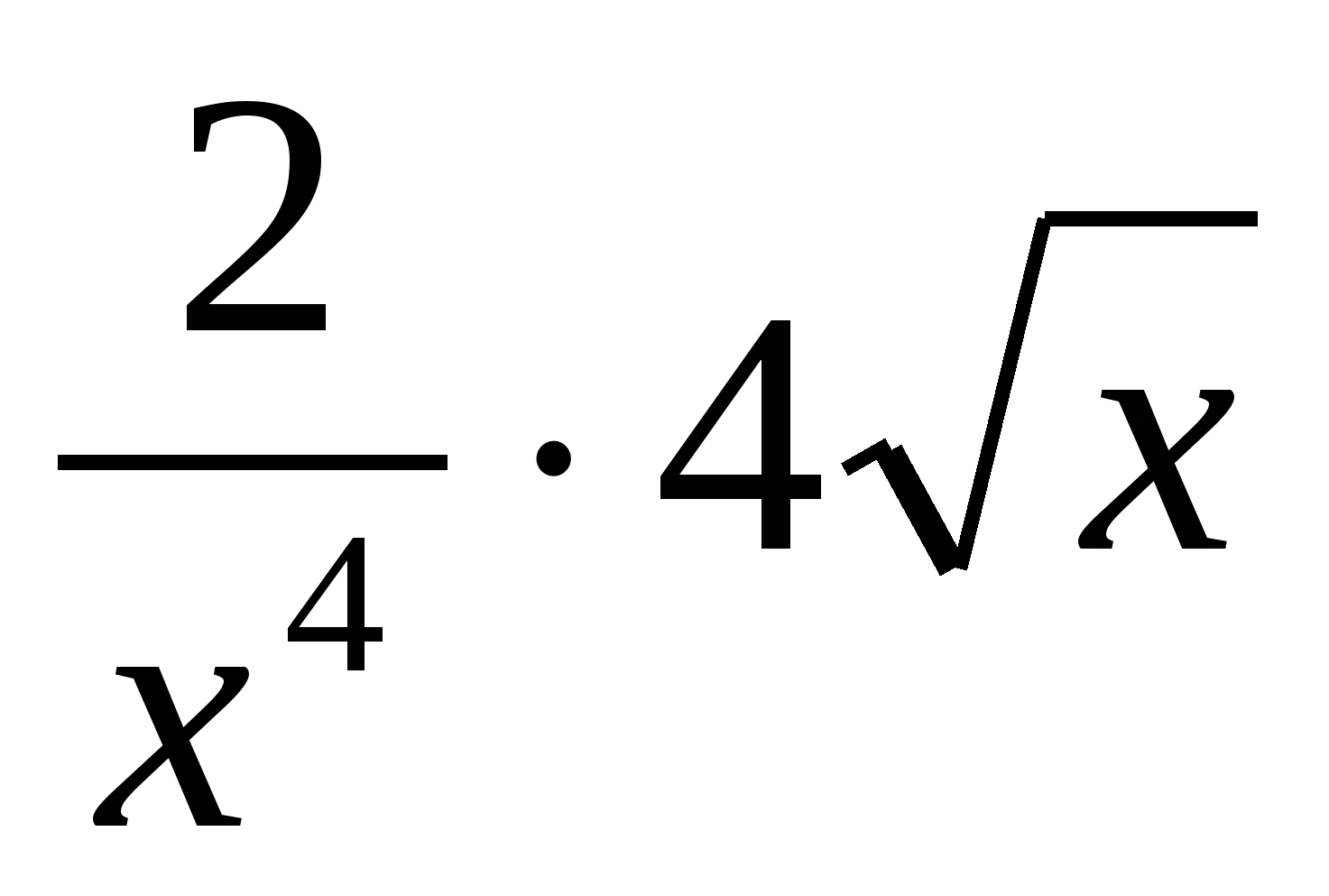 ;
;
в) q(x) = 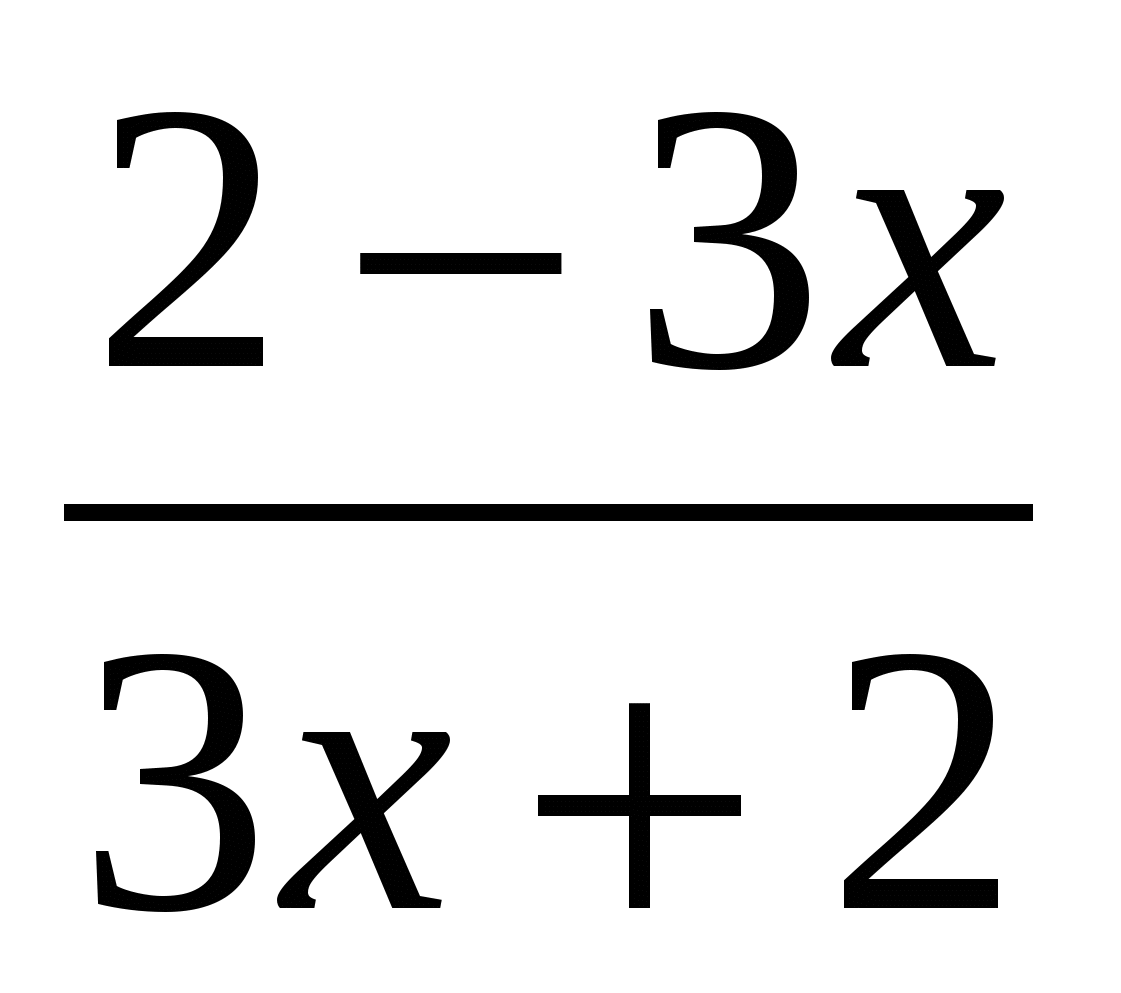 ; г) u(x) =
; г) u(x) = 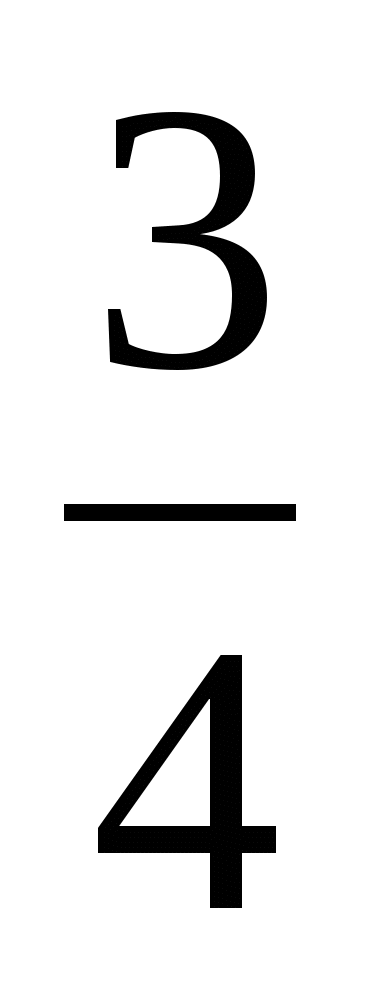 cos 4x.
cos 4x.
2. Точка движется по закону х(t)=t3+1 Найдите скорость точки в момент времени 3сек.
3. Найдите угол наклона касательной к графику функции f(x)=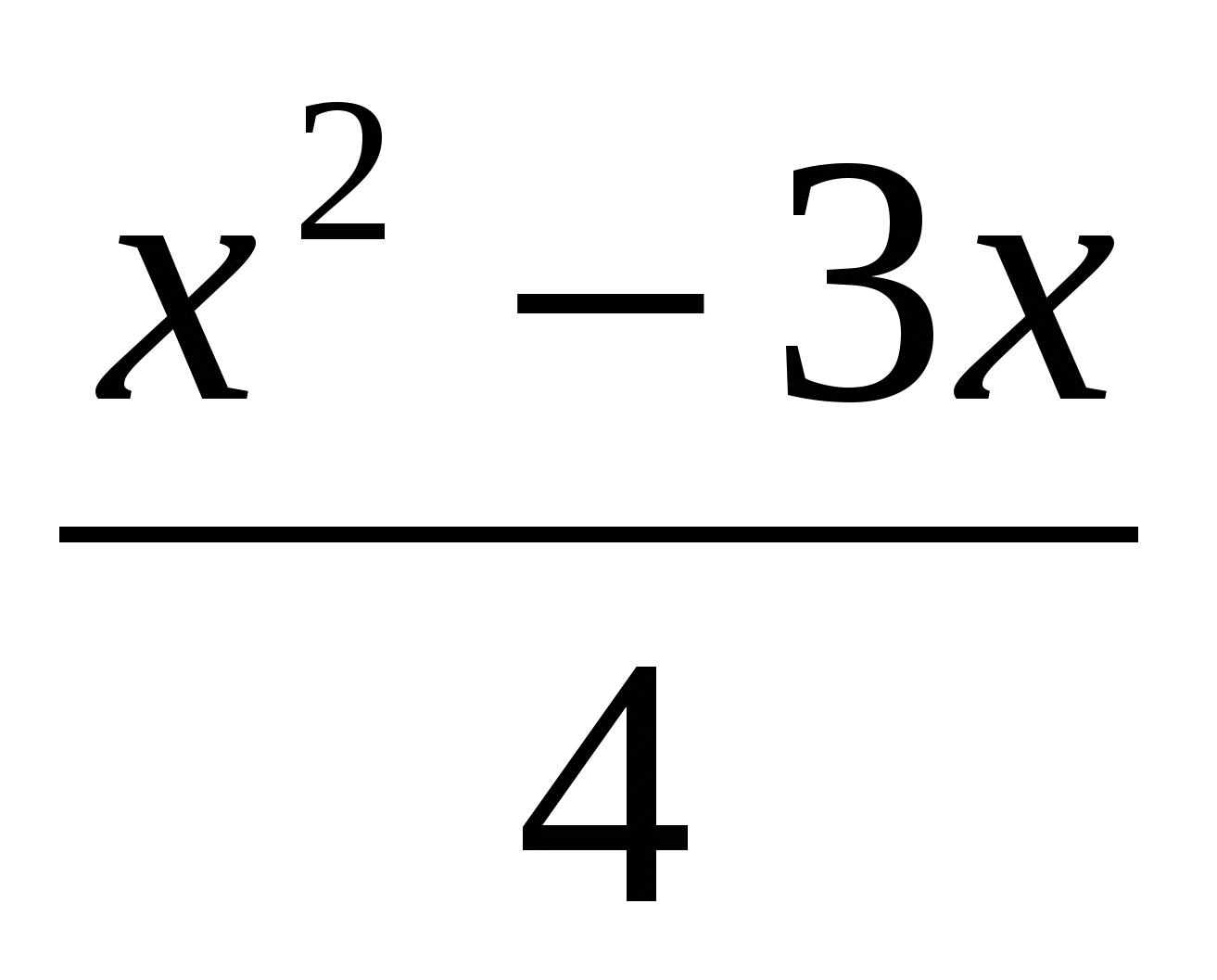 в точке х0=1
в точке х0=1
4. напишите уравнение касательной к графику функции f(x) = x2+5 в точке х0=2. Сделайте рисунок
5 . На рисунке изображены график функции
. На рисунке изображены график функции 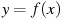 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 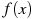 в точке
в точке 
6. Решите неравенство: (-х2+1)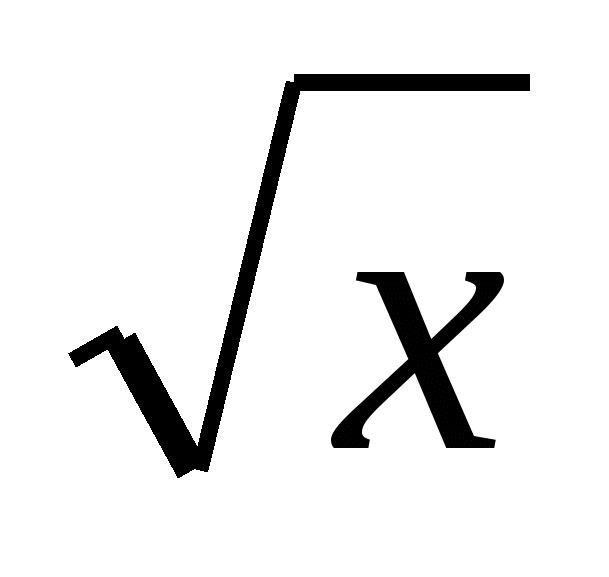 > 0
> 0
5 вариант
1. Найдите производные функций:
а) f(x) = 5х4 + 3х2 – 8х – 9; б) g(x) = 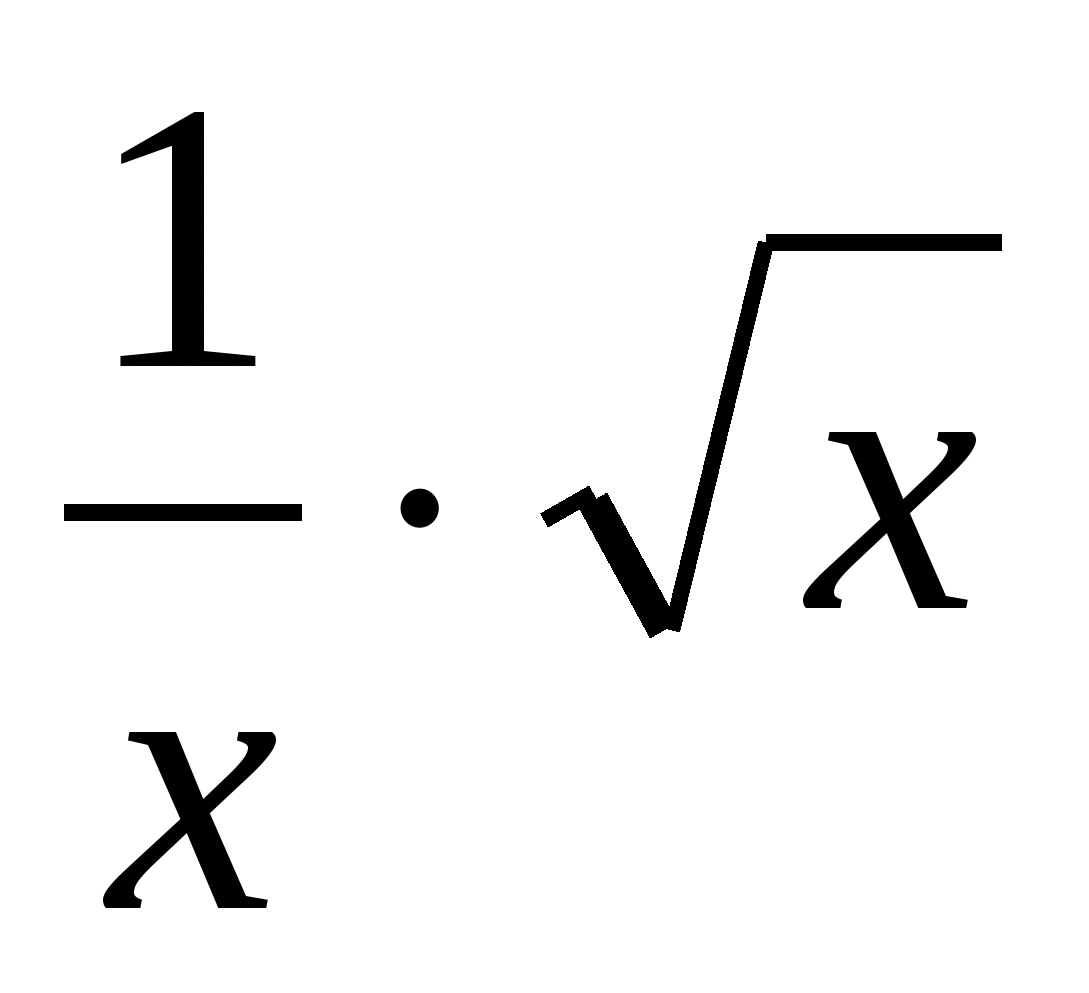 ;
;
в) q(x) = 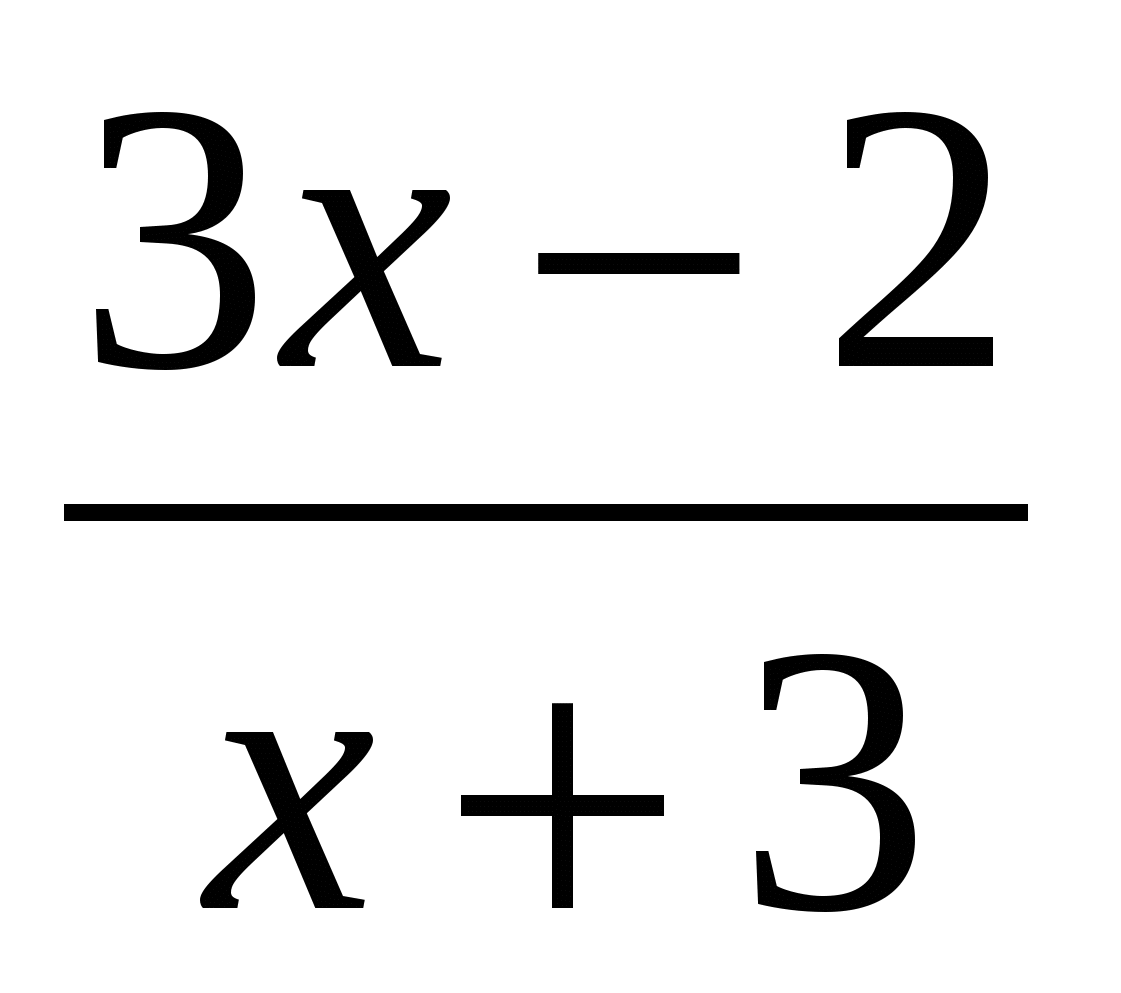 ; г) u(x) = sin 5x
; г) u(x) = sin 5x
2. Точка движется по закону х(t)=t3-1 Найдите ускорение точки в момент времени 2сек.
3. Найдите угол наклона касательной к графику функции f(x)=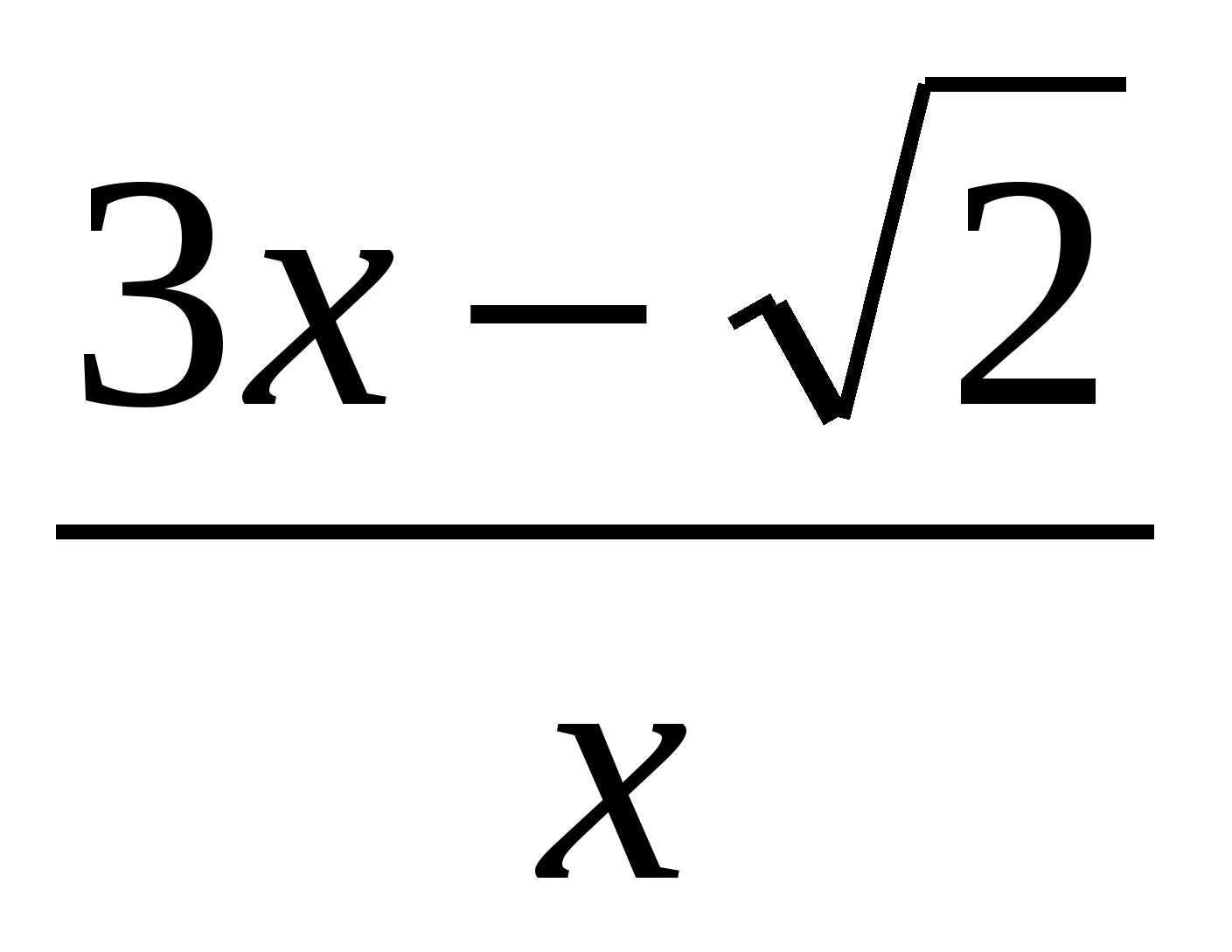 в точке х0=2
в точке х0=2
4. напишите уравнение касательной к графику функции f(x) = x2-1 в точке х0=-1. Сделайте рисунок
5 . На рисунке изображены график функции
. На рисунке изображены график функции 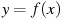 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 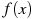 в точке
в точке 
6.Решите неравенство:(х2+х-6)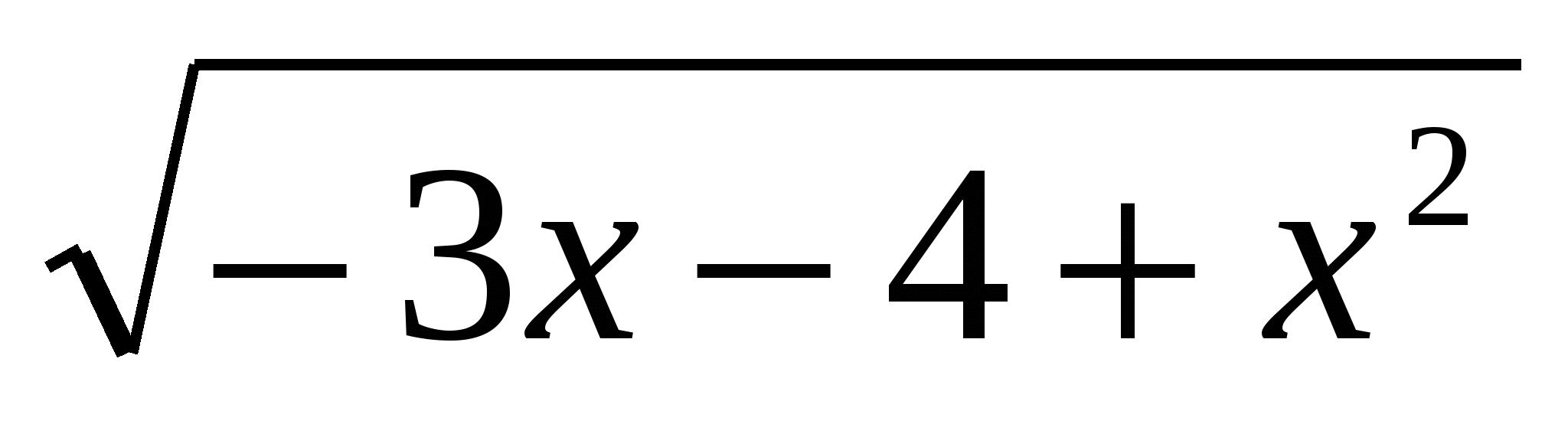 < 0
< 0
6 вариант
1. Найдите производные функций:
а) f(x) = 3х5 + 2х3 – 4х – 3; б)g(x) = 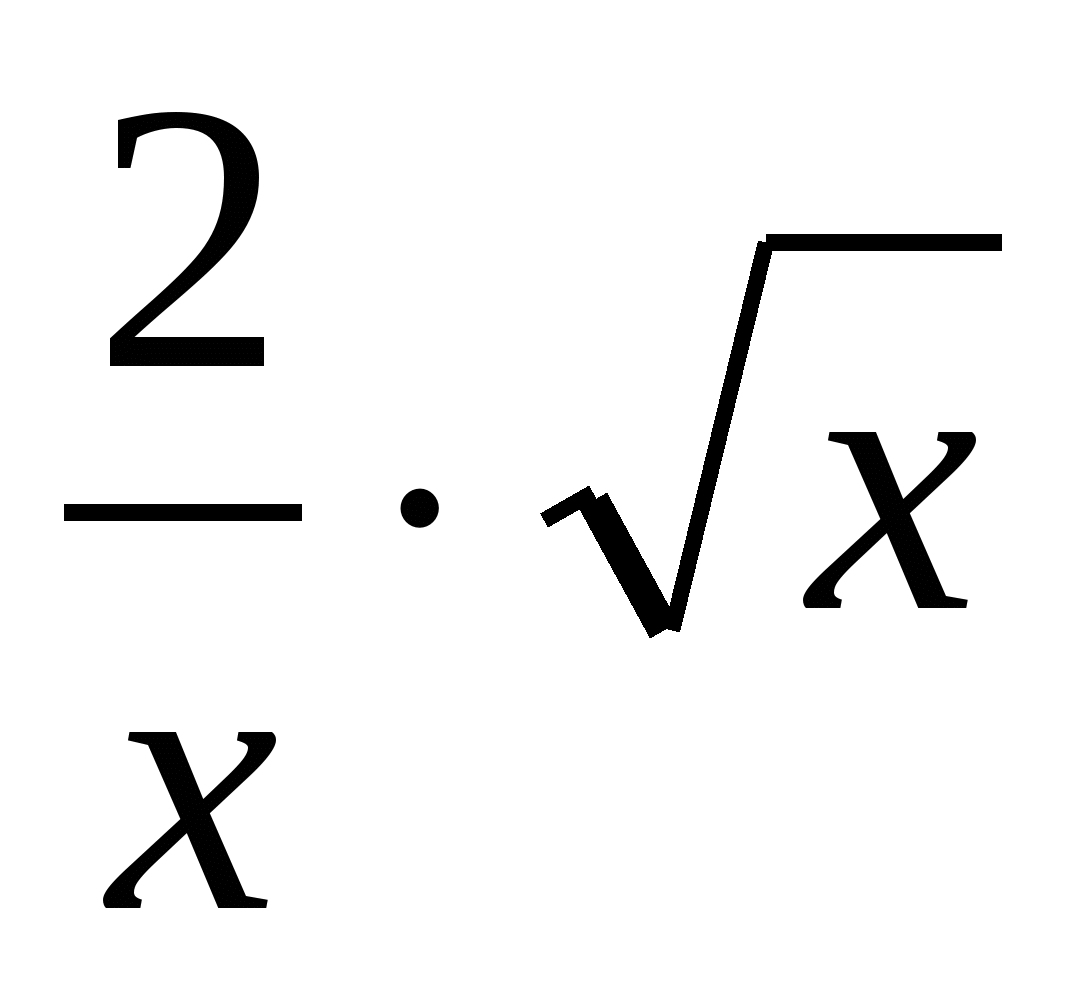 ;
;
в) q(x) = 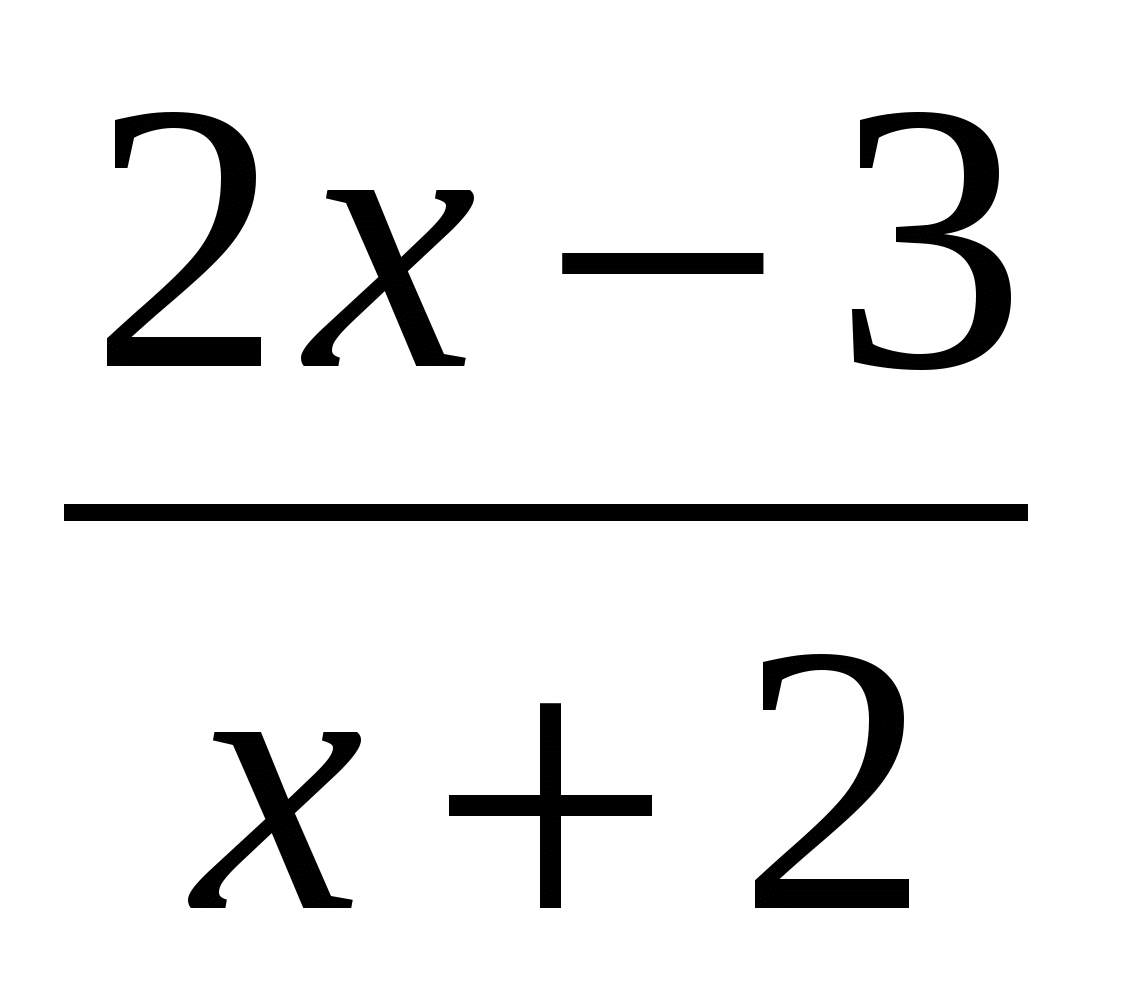 ; г) u(x) = cos 4x 2. Точка движется по закону х(t)= t3+5t Найдите, в какой момент времени скорость была равна 32м/с
; г) u(x) = cos 4x 2. Точка движется по закону х(t)= t3+5t Найдите, в какой момент времени скорость была равна 32м/с
3. Найдите угол наклона касательной к графику функции f(x)=sinx-7 в точке х0=2π
4. напишите уравнение касательной к графику функции f(x) = x2+2x в точке х0=1. Сделайте рисунок
5 . На рисунке изображены график функции
. На рисунке изображены график функции 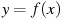 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 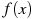 в точке
в точке 
6. Решите неравенство: (х2-1)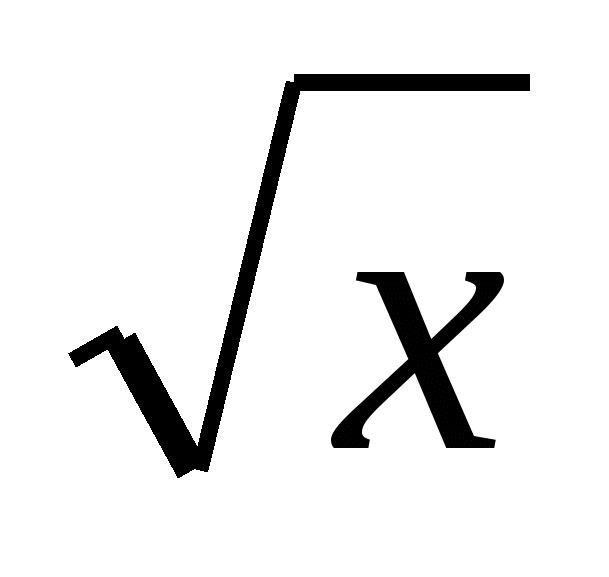 ≥ 0
≥ 0
7 вариант
1. Найдите производные функций:
а) f(x) = 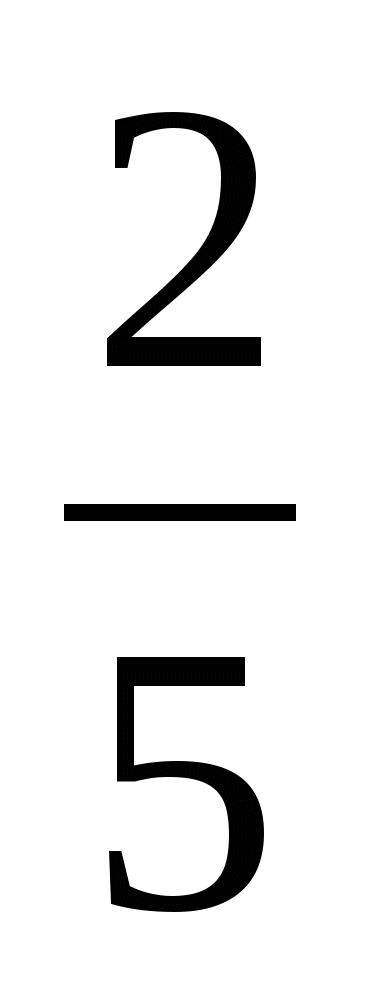 х5 + 3х3 – х – 4; б) g(x) =
х5 + 3х3 – х – 4; б) g(x) = 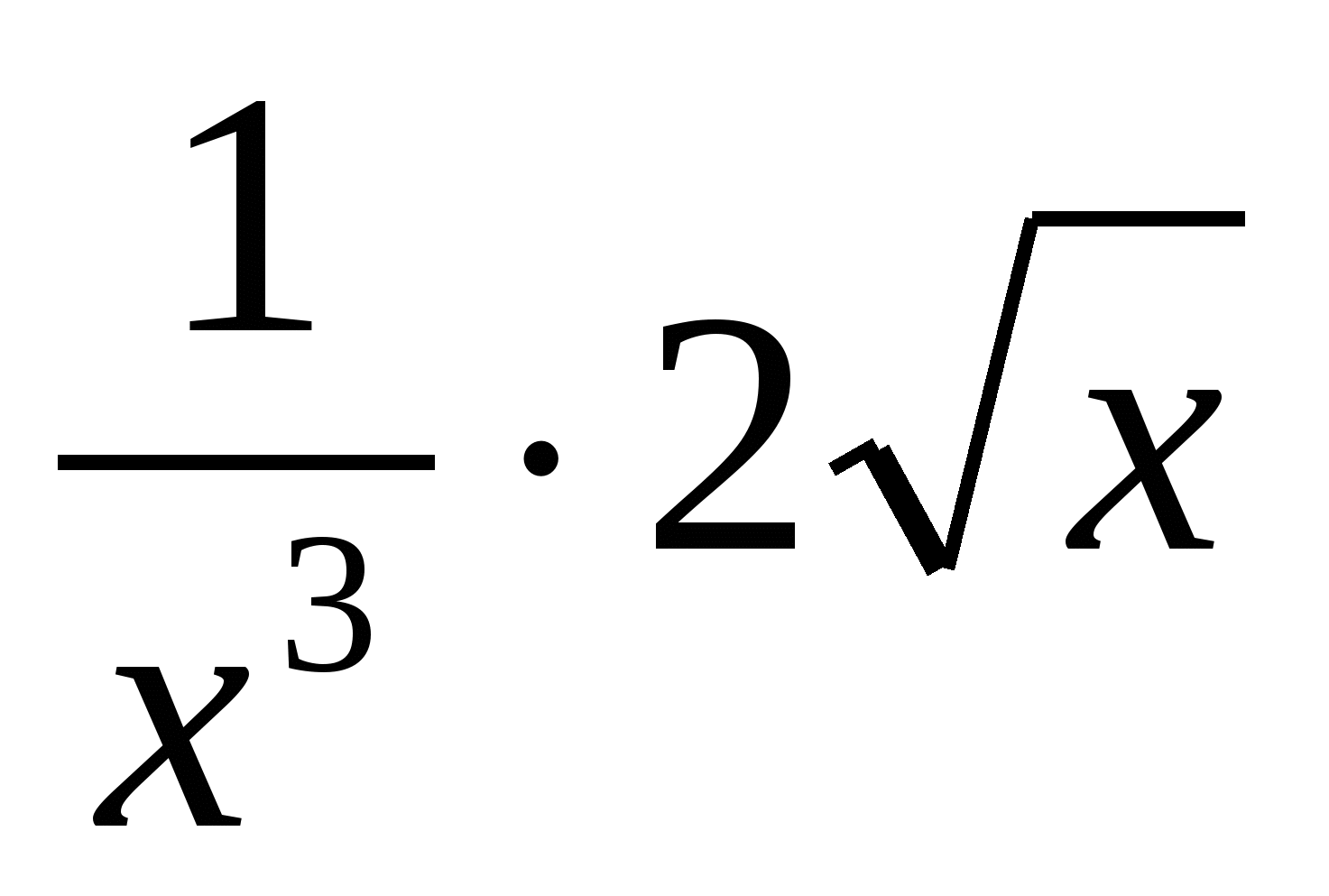 ;
;
в) q(x) = 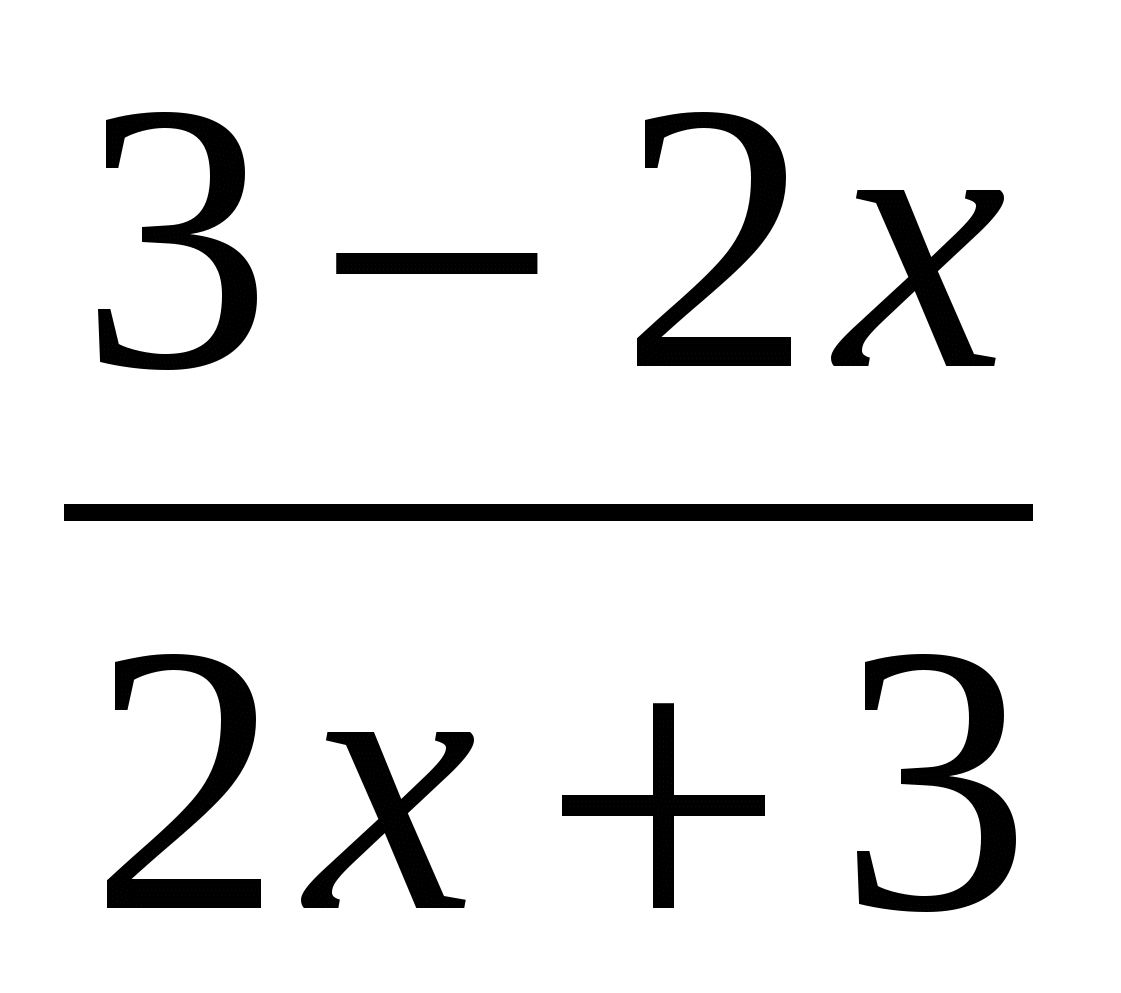 ; г) u(x) =
; г) u(x) = 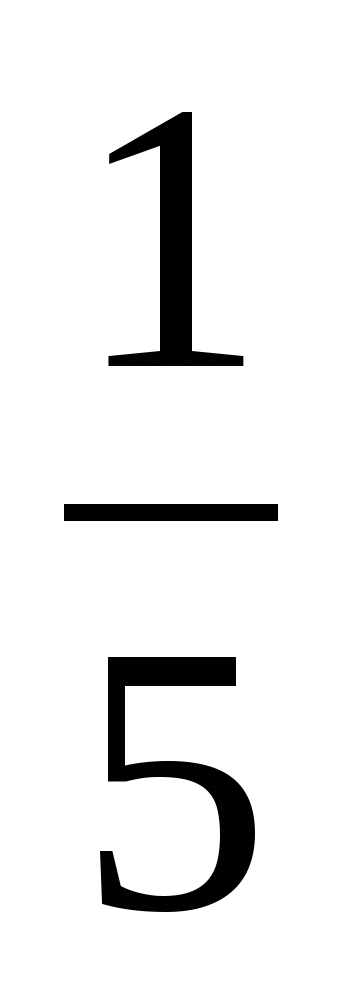 sin 5x
sin 5x
2. Точка движется по закону х(t)= t4+1 Найдите скорость точки в момент времени 1сек.
3. Найдите угол наклона касательной к графику функции f(x)=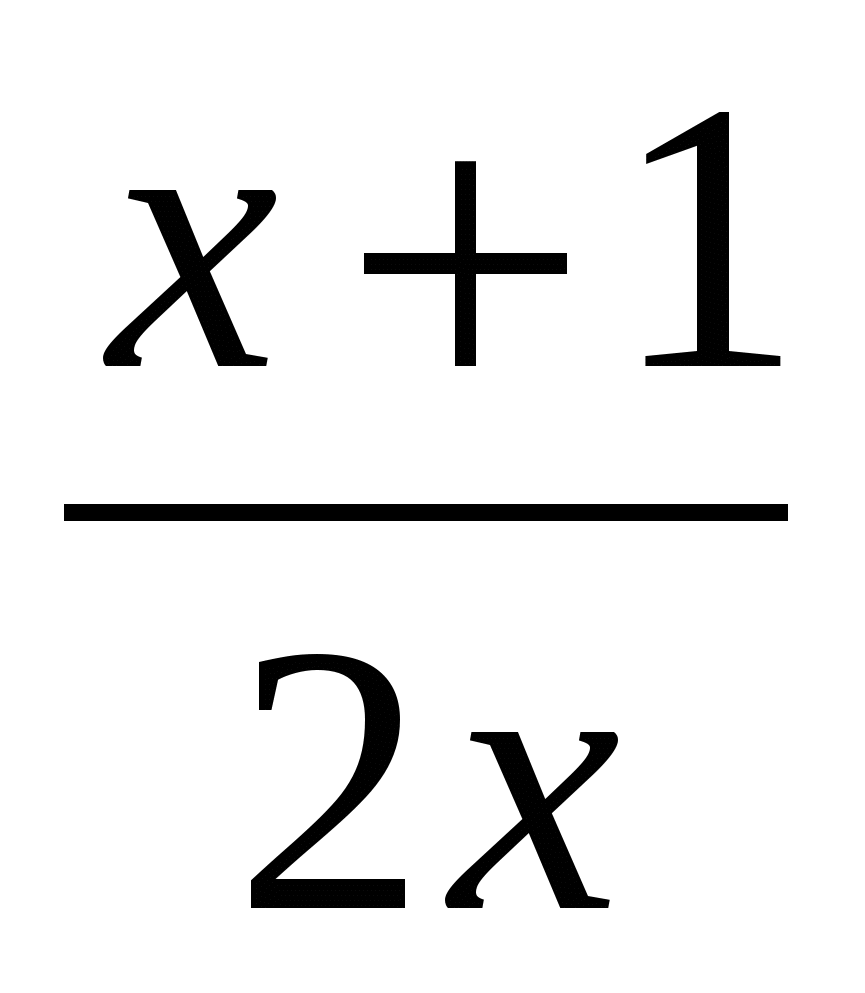 в точке х0=1
в точке х0=1
4. напишите уравнение касательной к графику функции f(x) = x2+3 в точке х0=1. Сделайте рисунок
5 . На рисунке изображены график функции
. На рисунке изображены график функции 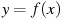 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 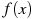 в точке
в точке 
6. Решите неравенство: (х+1)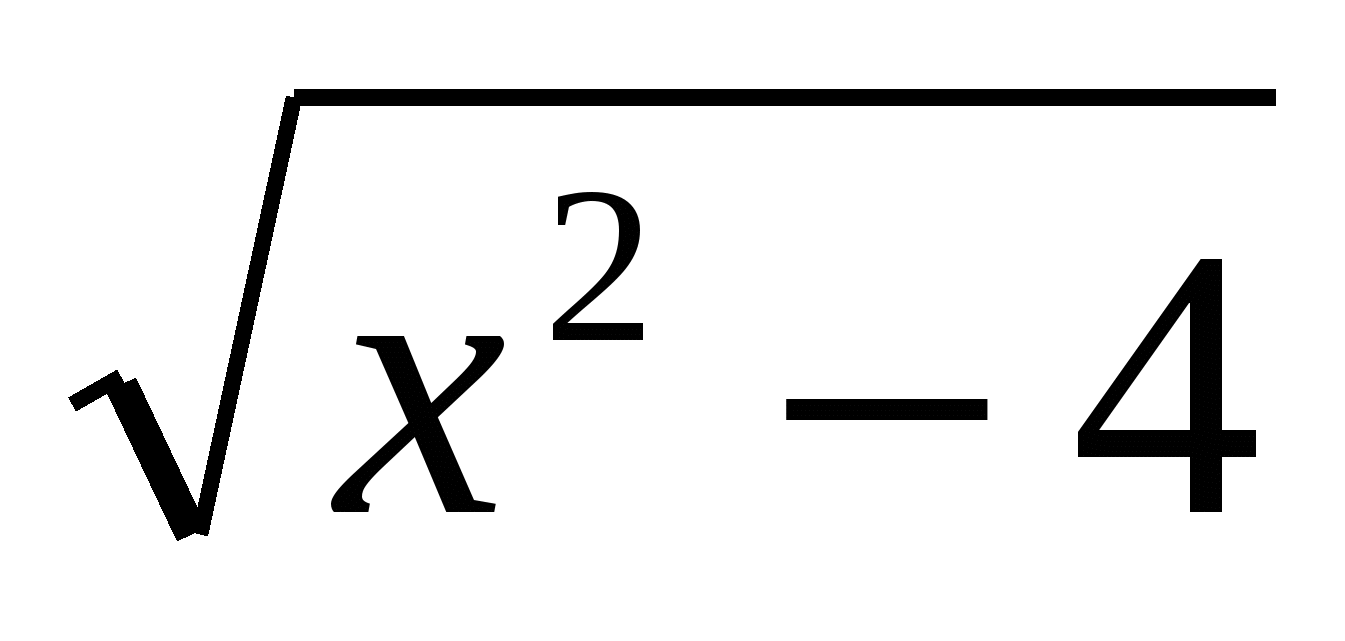 < 0
< 0
8 вариант
1. Найдите производные функций:
а) f(x) = - 2х6 + 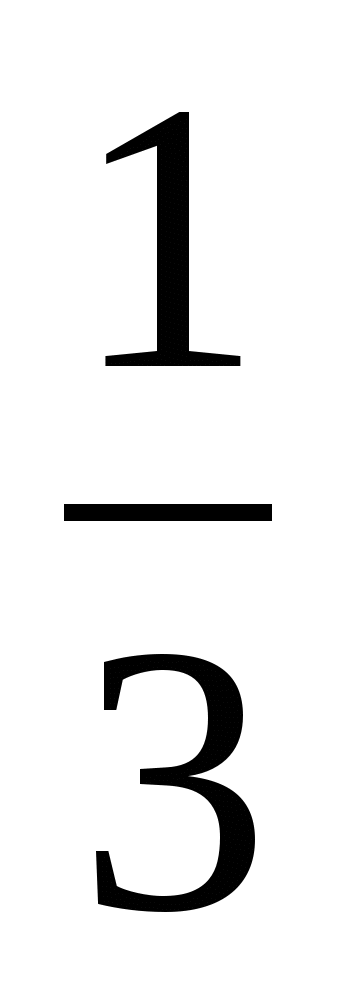 х9 – 3; б)g(x) =
х9 – 3; б)g(x) =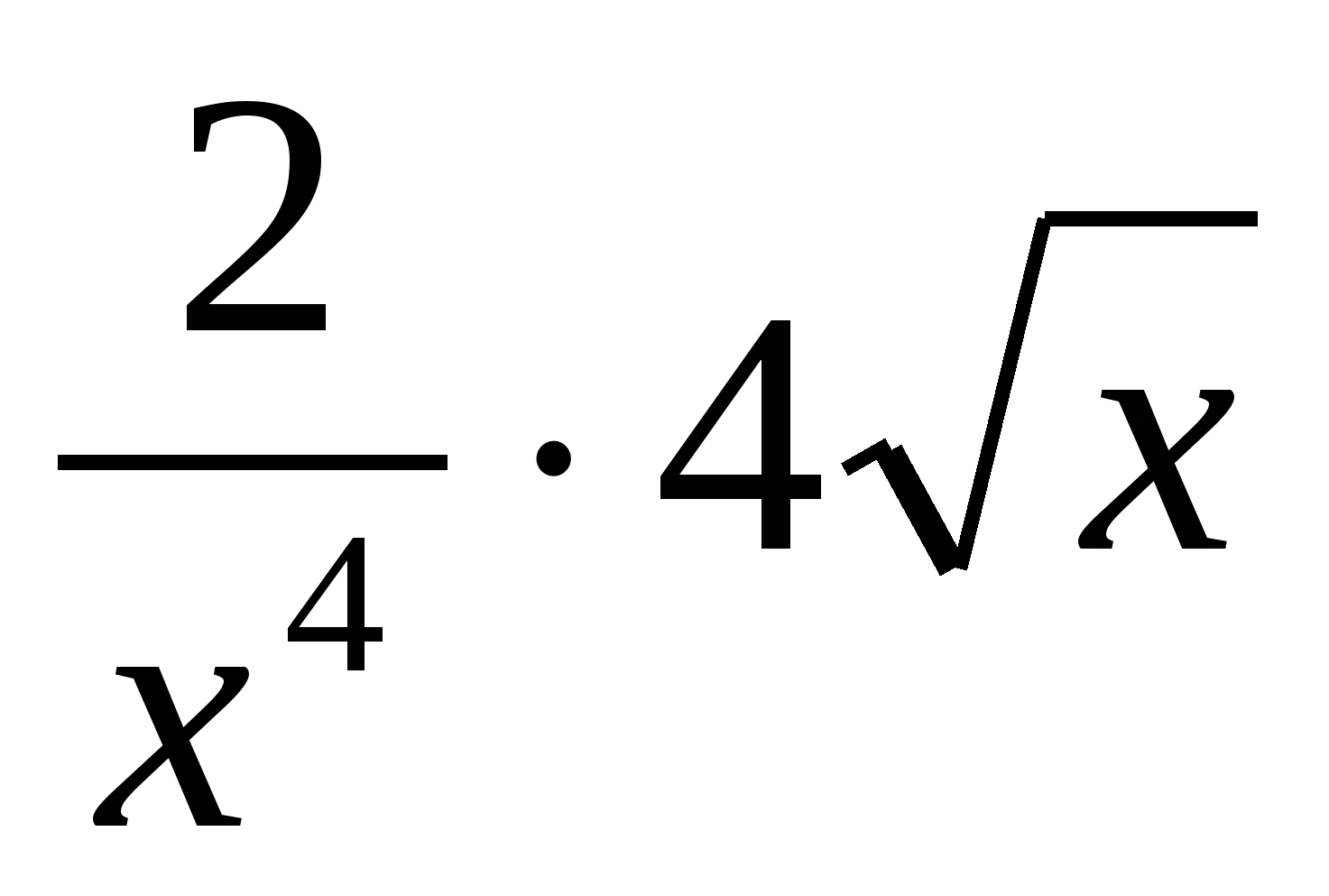 ;
;
в) q(x) = 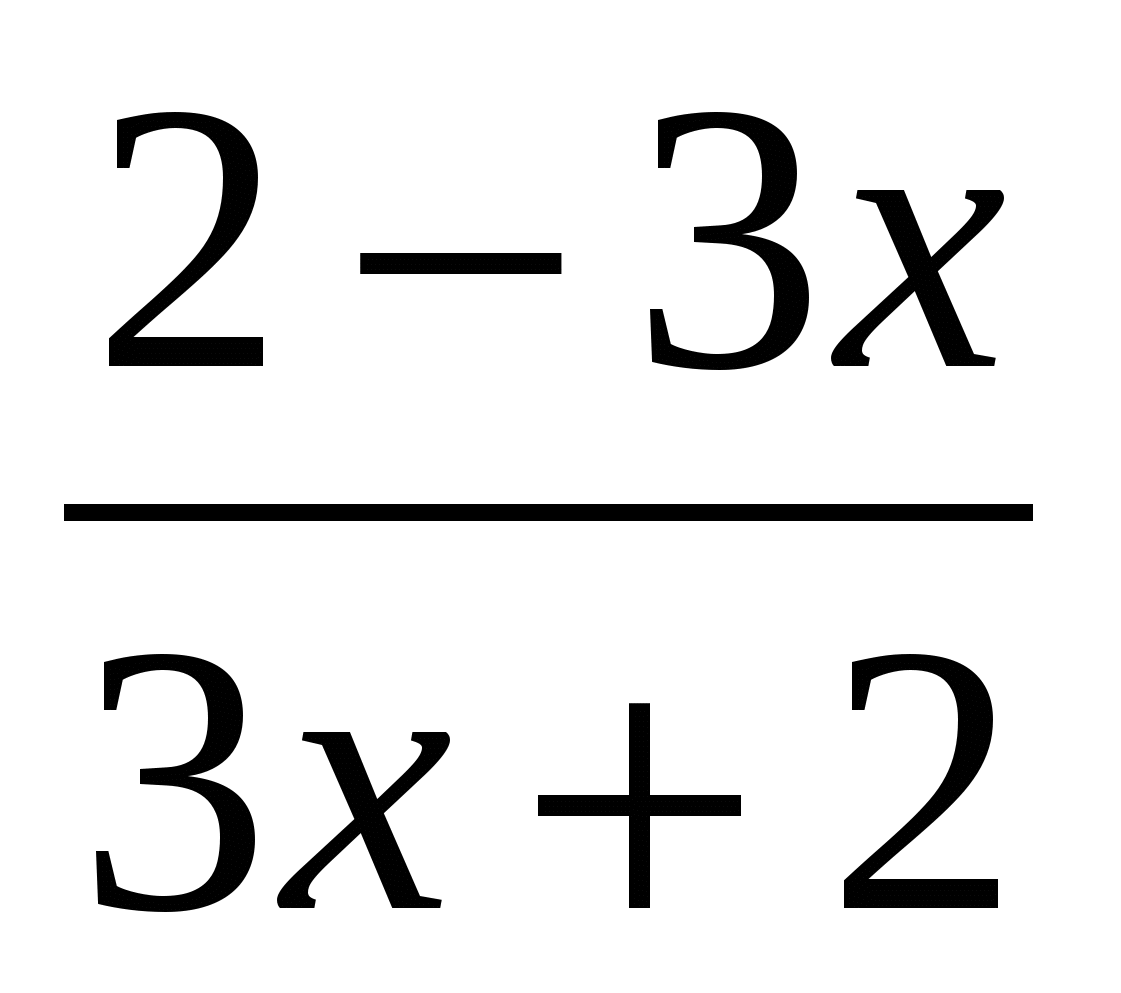 ; г) u(x) =
; г) u(x) = 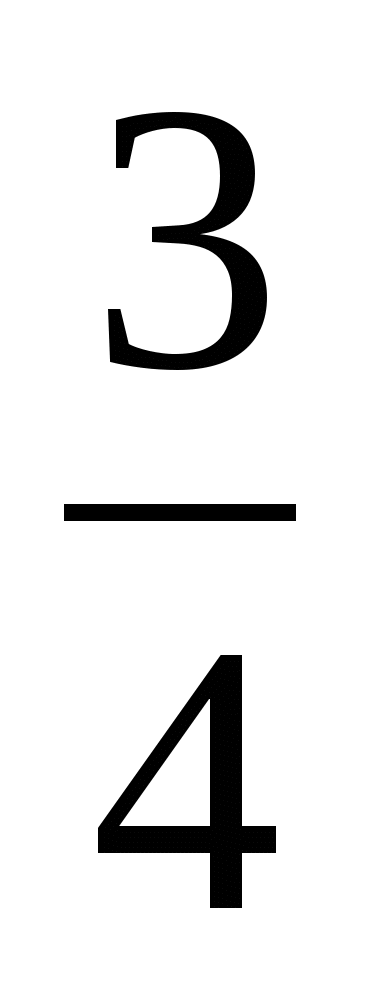 cos 4x
cos 4x
2. Точка движется по закону х(t)=2t3+1 Найдите в какой момент времени ускорение было 48м/с2
3. Найдите угол наклона касательной к графику функции f(x)=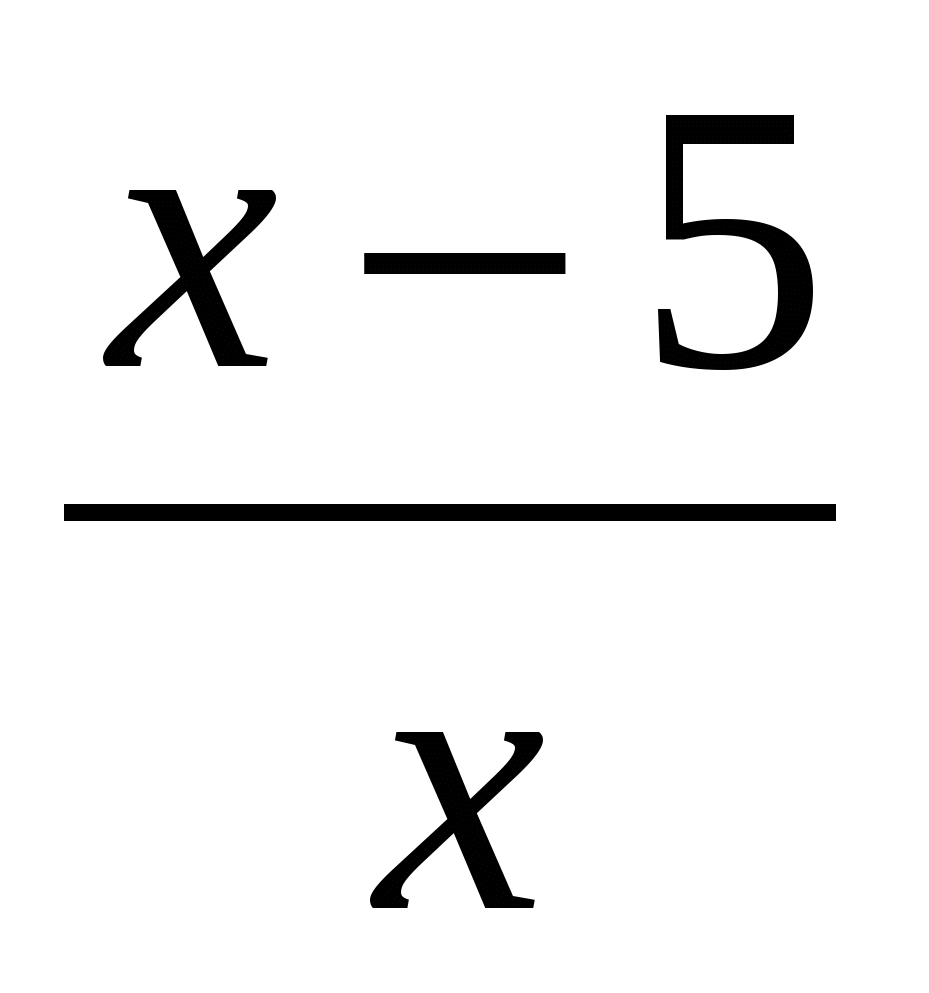 в точке х0=3
в точке х0=3
4. напишите уравнение касательной к графику функции f(x) = 0,5x2-2x в точке х0=1. Сделайте рисунок
5 . На рисунке изображены график функции
. На рисунке изображены график функции 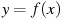 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 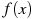 в точке
в точке 
6. Решите неравенство: (х+1)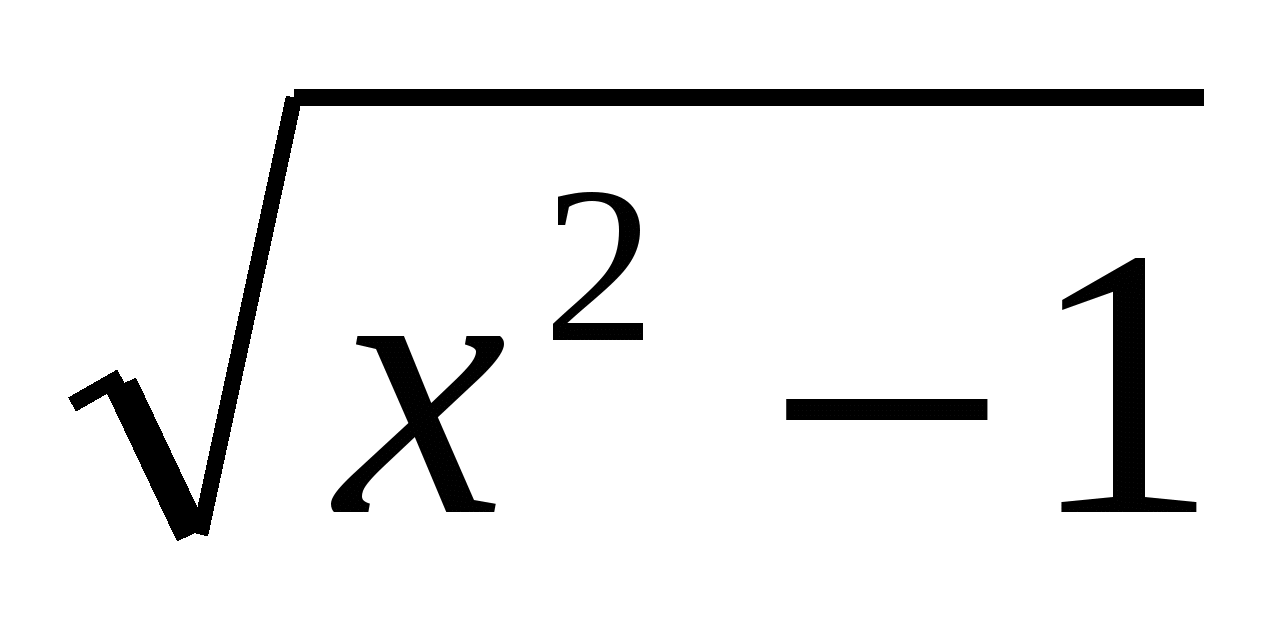 ≤ 0
≤ 0
9 вариант
1. Найдите производные функций:
а) f(x) = 5х4 + 3х2 – 8х – 9; б) g(x) = 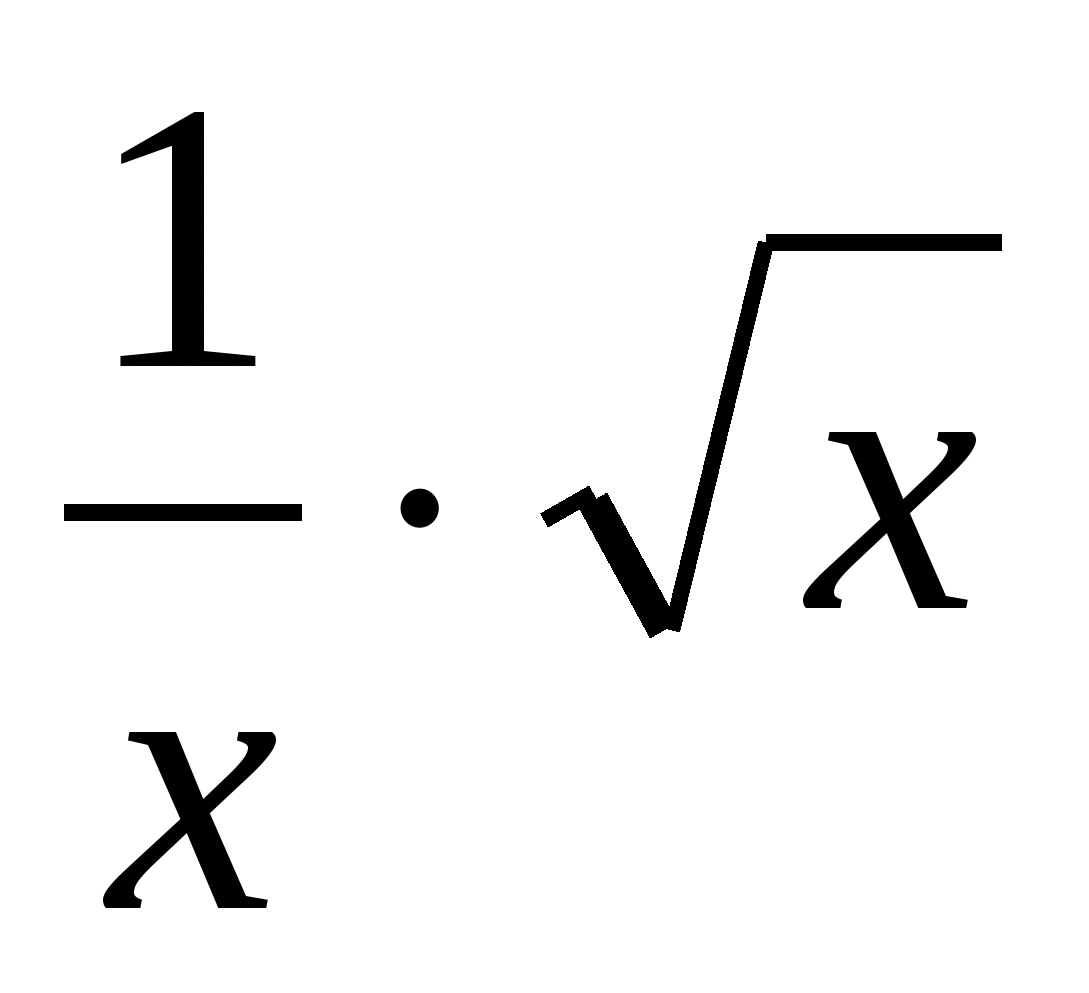 ;
;
в) q(x) = 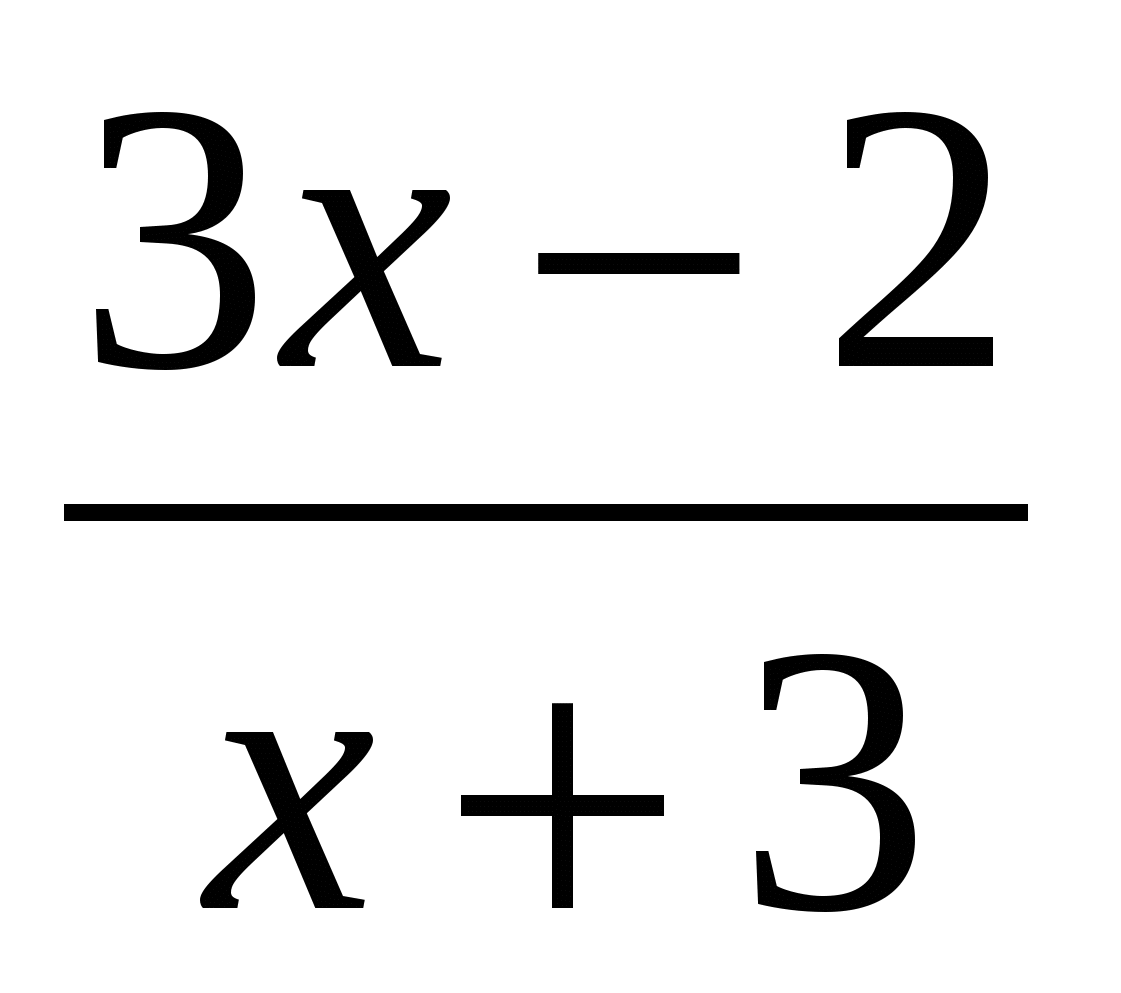 ; г) u(x) = sin 5x
; г) u(x) = sin 5x
2. Точка движется по закону х(t)=t3-4t Найдите скорость точки в момент времени 4сек.
3. Найдите угол наклона касательной к графику функции f(x)=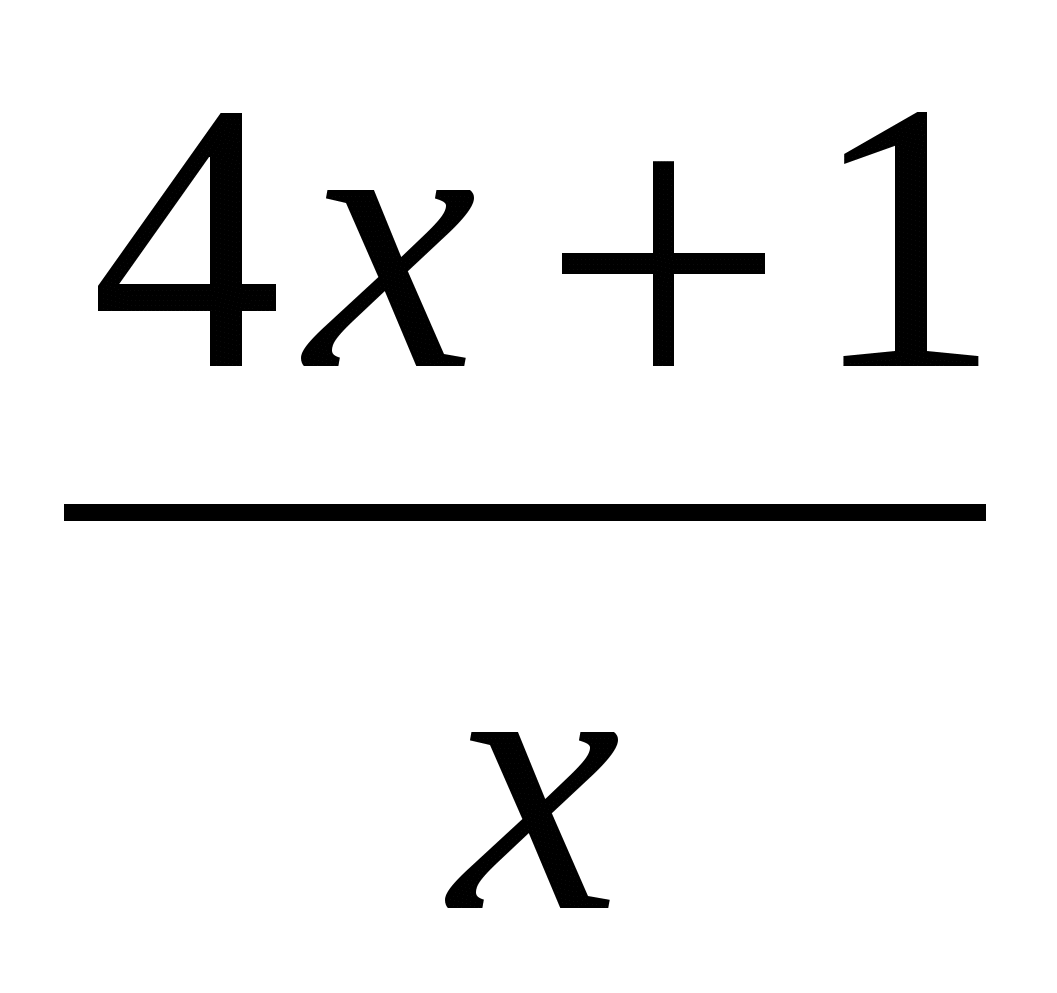 в точке х0=-1
в точке х0=-1
4 . напишите уравнение касательной к графику функции f(x) = 2x2+1 в точке х0=-1. Сделайте рисунок
. напишите уравнение касательной к графику функции f(x) = 2x2+1 в точке х0=-1. Сделайте рисунок
5. На рисунке изображены график функции 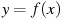 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 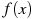 в точке
в точке 
6. Решите неравенство: х(х2+2х+1)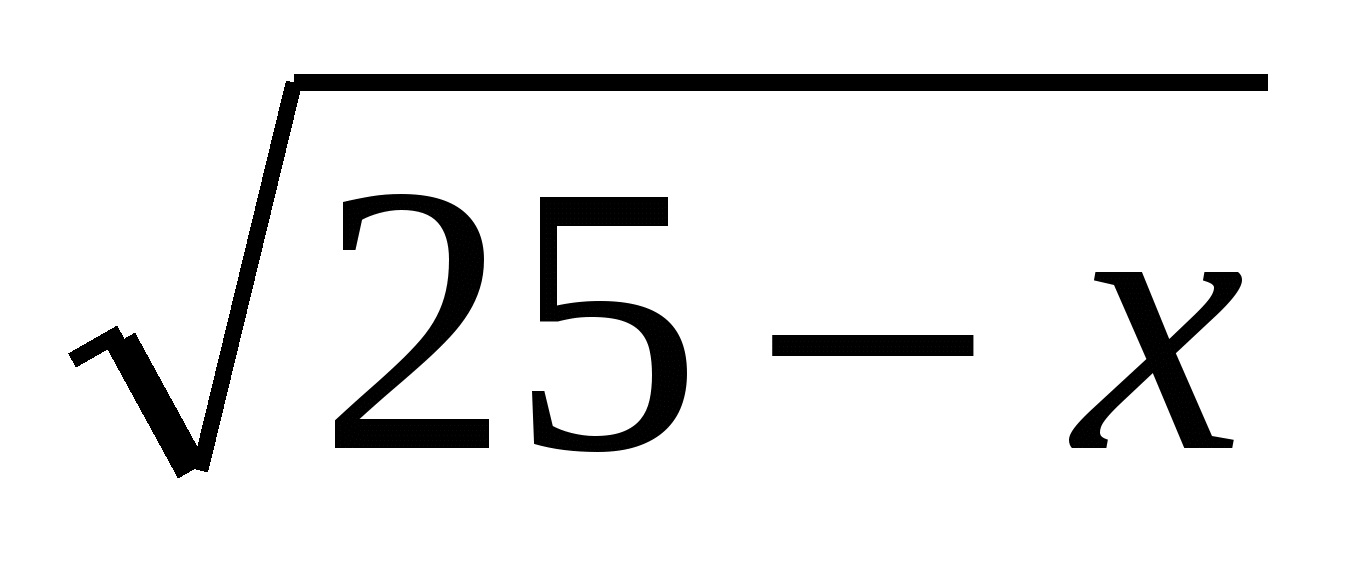 < 0
< 0
10 вариант
1. Найдите производные функций:
а) f(x) = 3х5 + 2х3 – 4х – 3; б)g(x) = 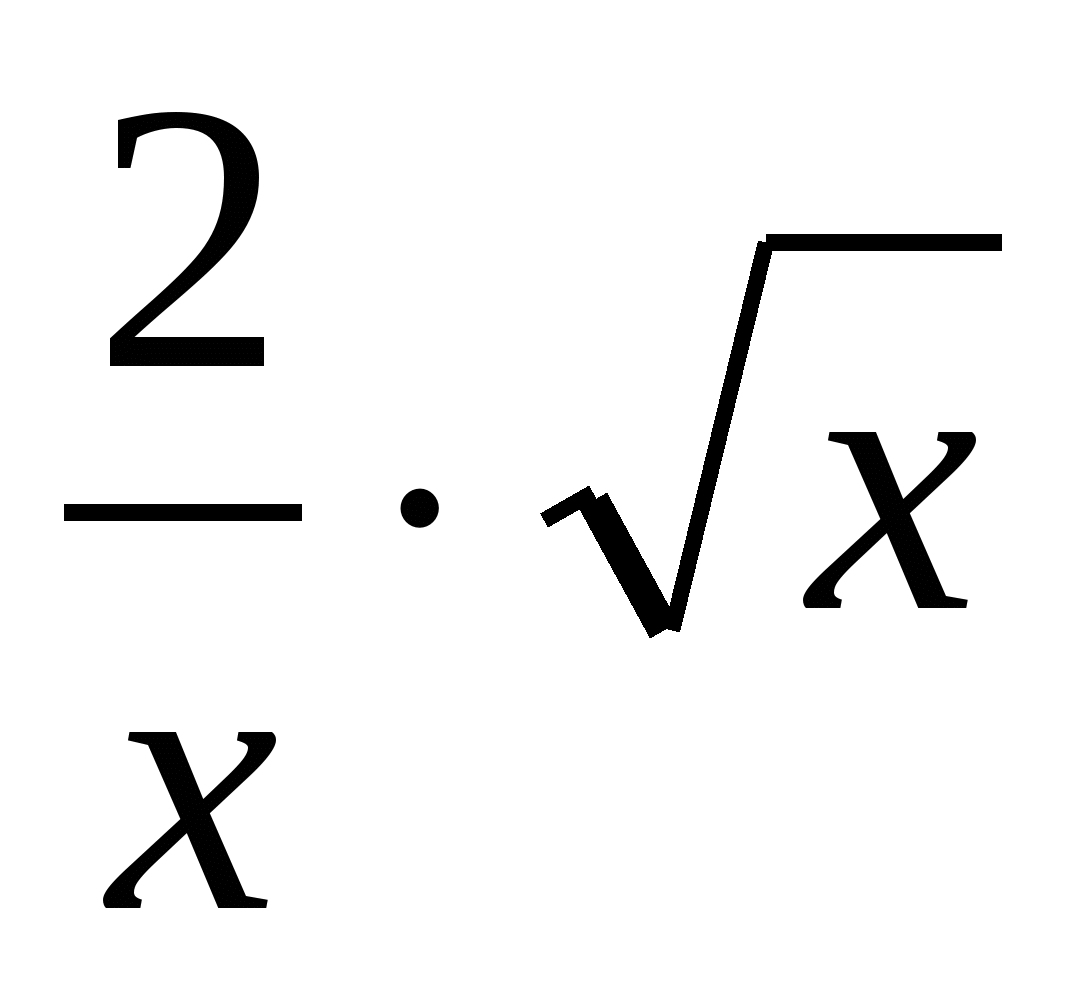 ;
;
в) q(x) = 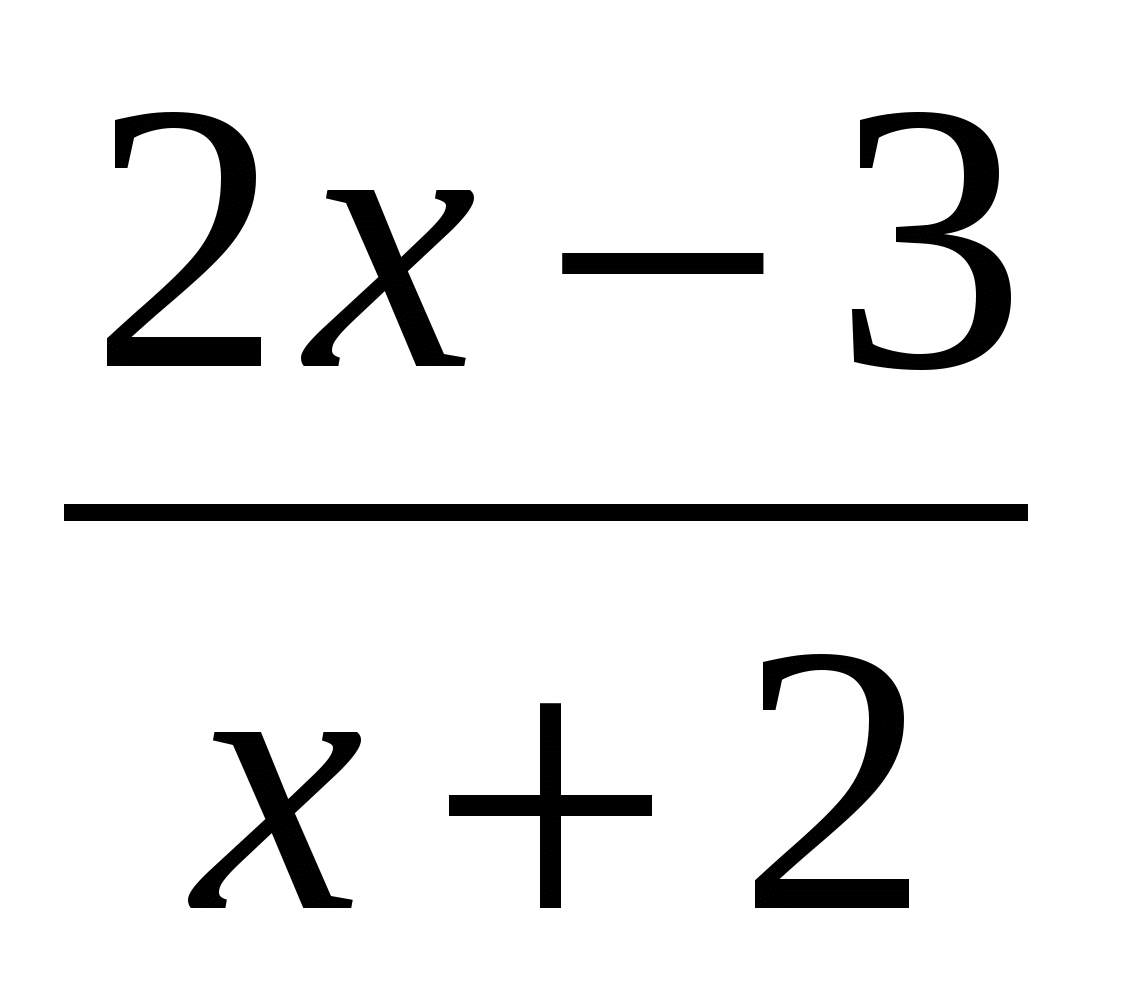 ; г) u(x) = cos 4x.
; г) u(x) = cos 4x.
2. Точка движется по закону х(t)=3t3+2. Найдите в какой момент времени ускорение было 27м/с2
3. Найдите угол наклона касательной к графику функции f(x)=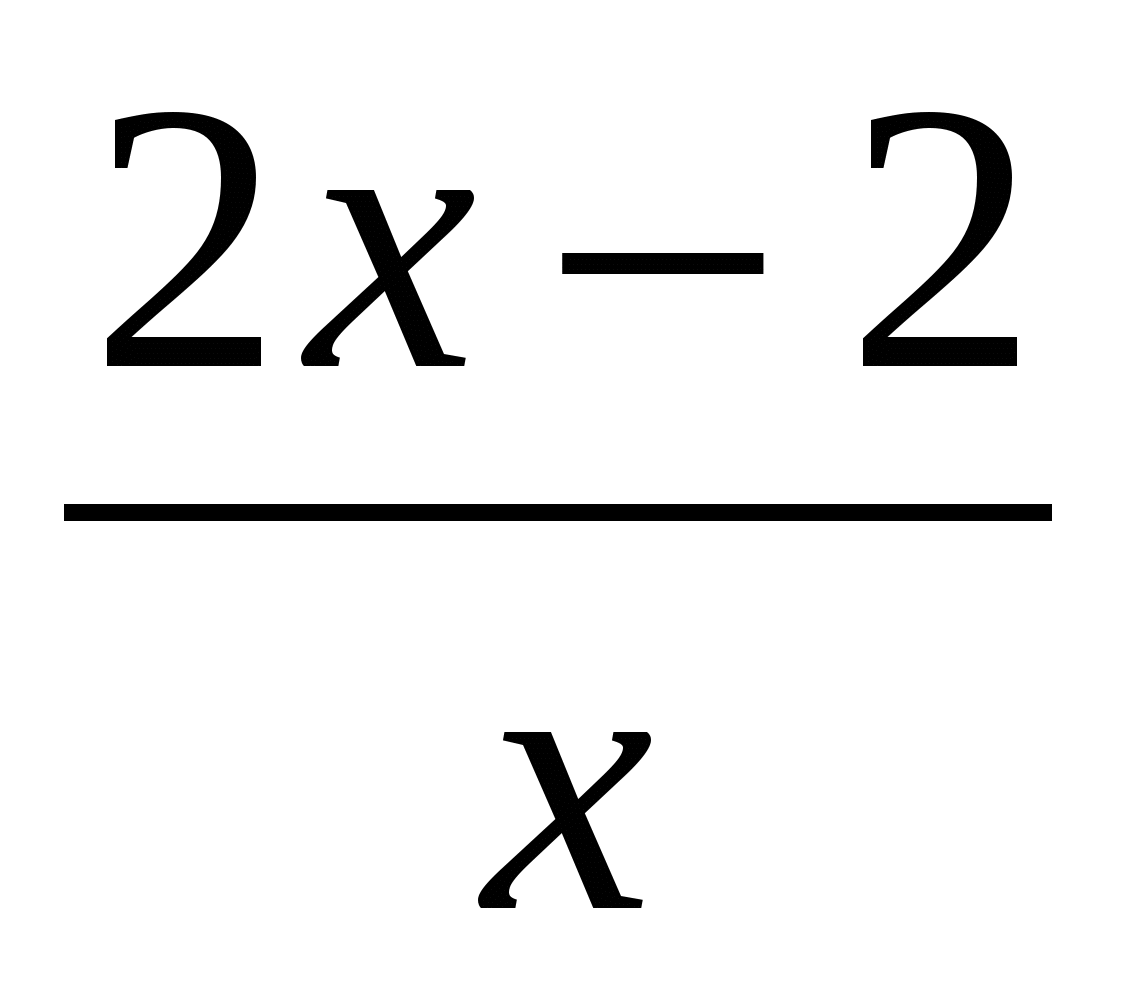 в точке х0=2
в точке х0=2
4. напишите уравнение касательной к графику функции f(x) = x2+x в точке х0=1. Сделайте рисунок
5 . На рисунке изображены график функции
. На рисунке изображены график функции 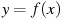 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 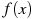 в точке
в точке 
6. Решите неравенство: (х+1)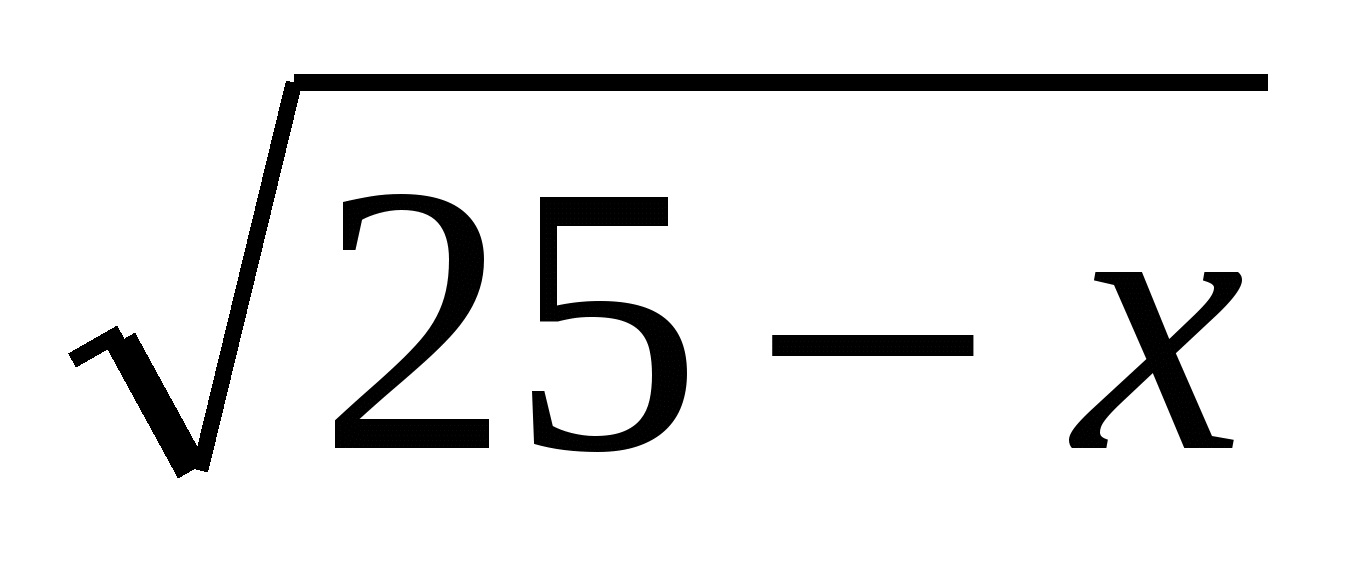 < 0
< 0
11 вариант
1. Найдите производные функций:
а) f(x) = 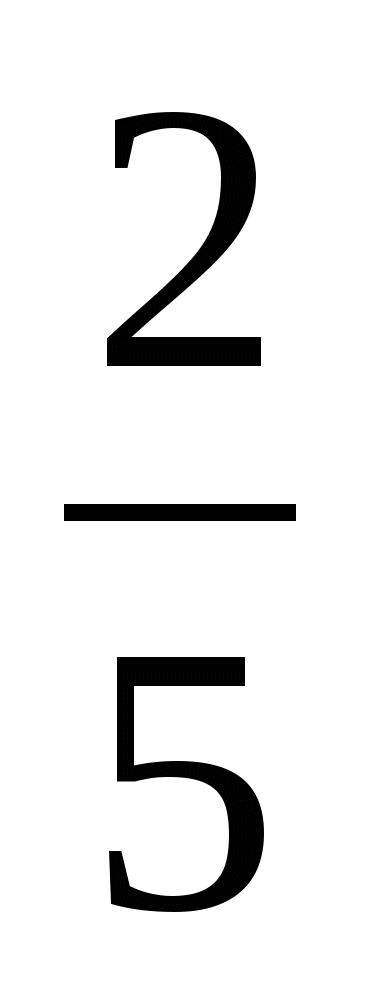 х5 + 3х3 – х – 4; б) g(x) =
х5 + 3х3 – х – 4; б) g(x) = 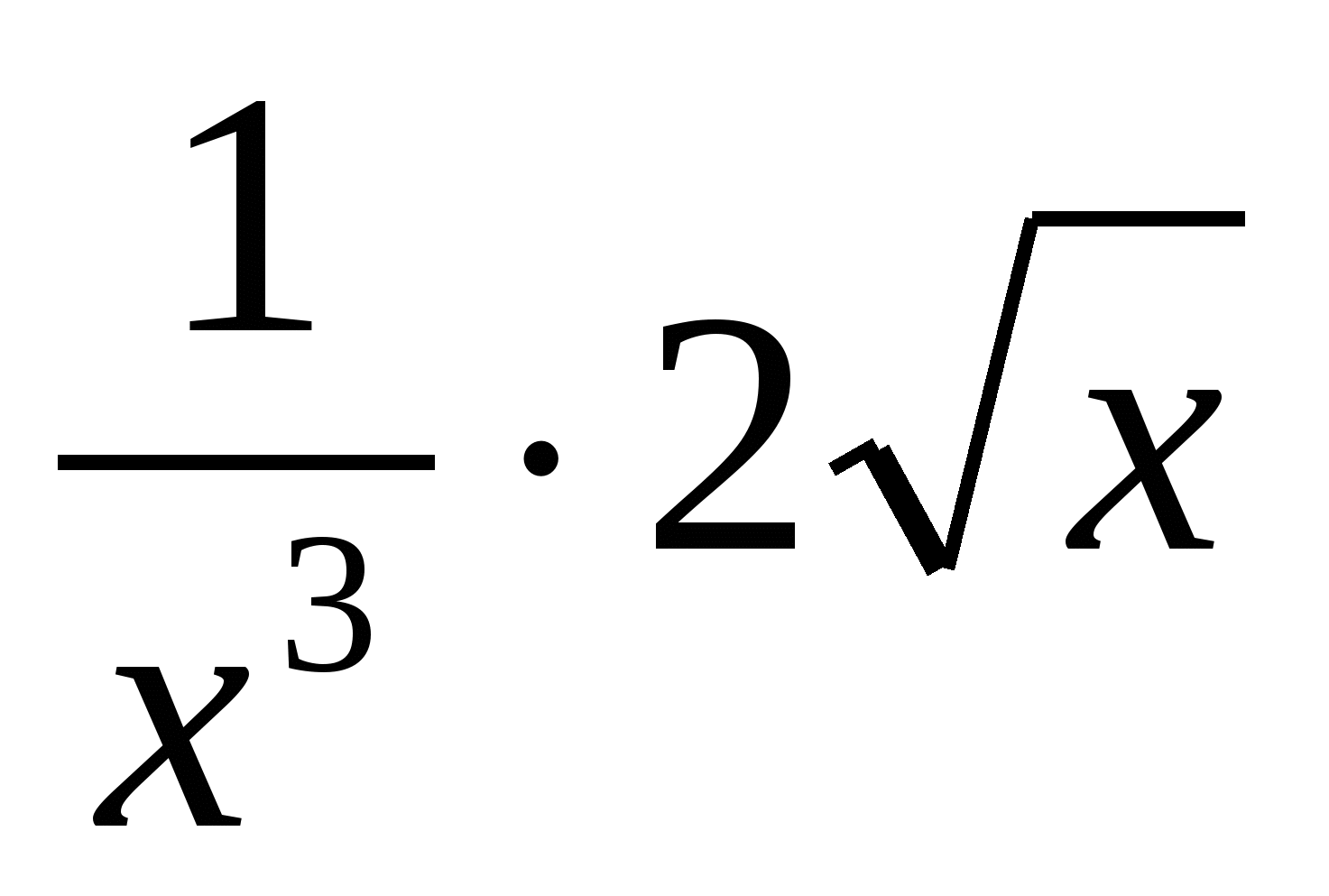 ;
;
в) q(x) = 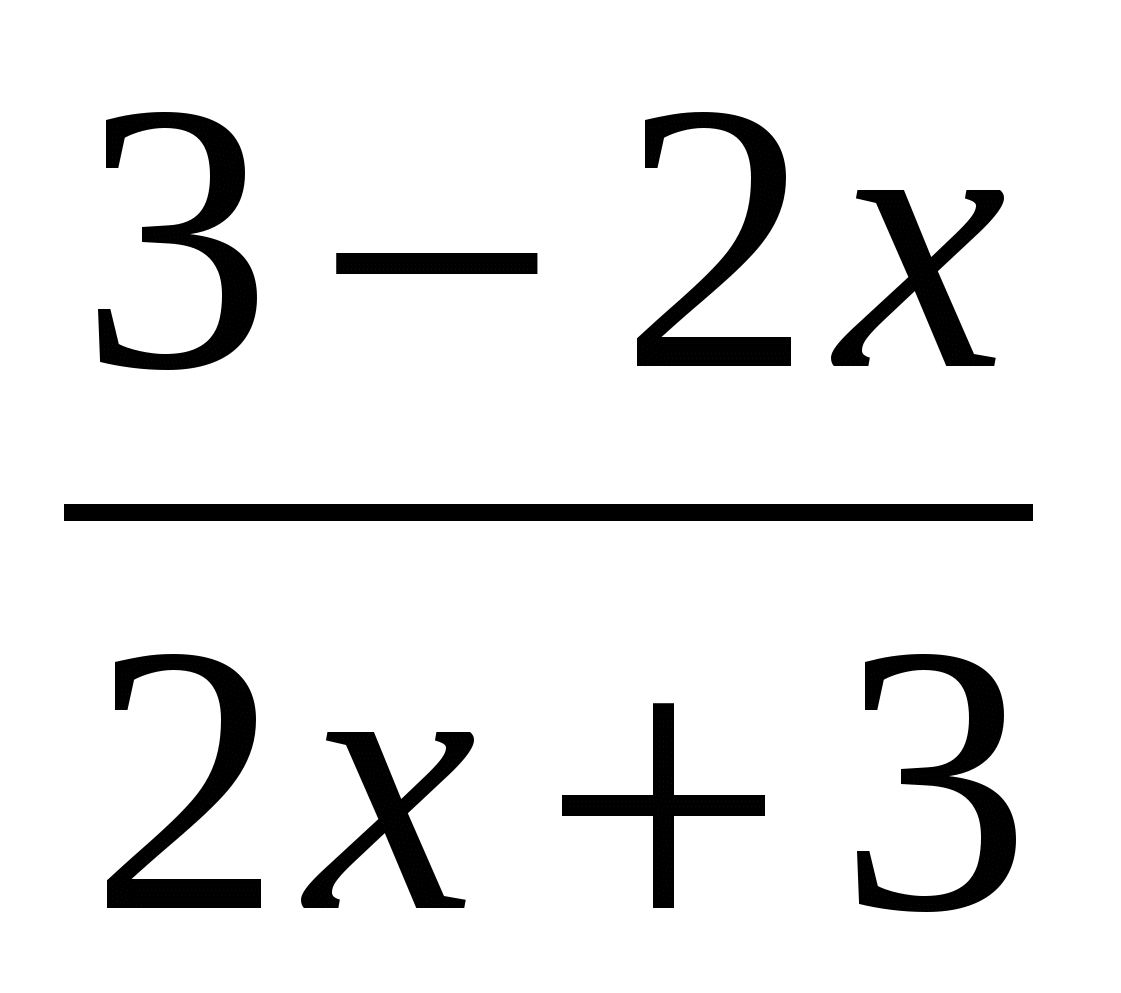 ; г) u(x) =
; г) u(x) = 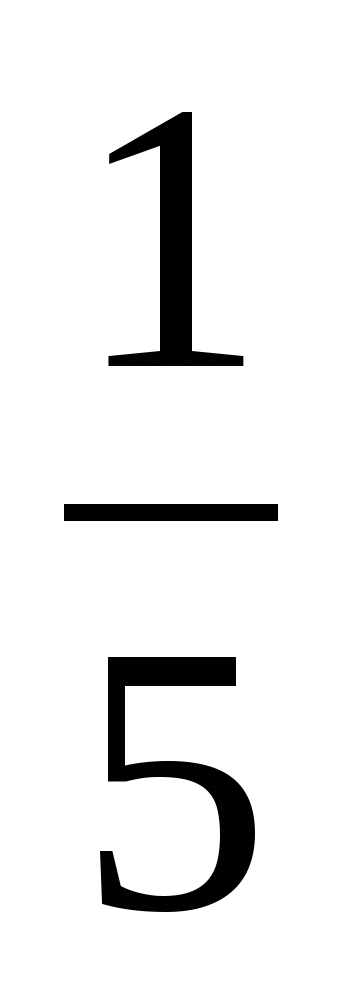 sin 5x
sin 5x
2. Точка движется по закону х(t)= t2+2t Найдите в какой момент времени скорость была 68м/с
3. Найдите угол наклона касательной к графику функции f(x)=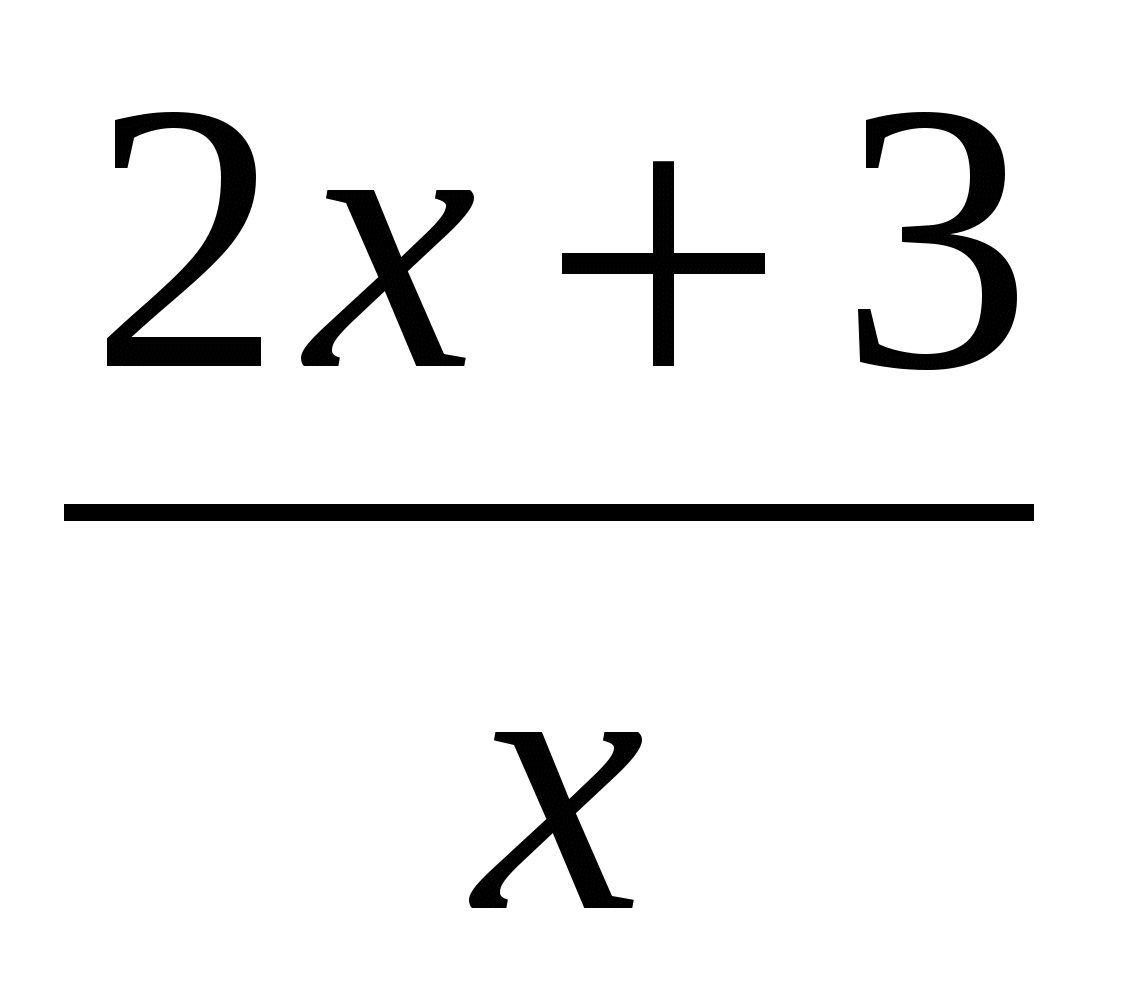 в точке х0=1
в точке х0=1
4. напишите уравнение касательной к графику функции f(x) = x2-x в точке х0=2. Сделайте рисунок
5 . На рисунке изображены график функции
. На рисунке изображены график функции 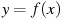 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 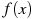 в точке
в точке 
6. Решите неравенство: (х2-4х+4)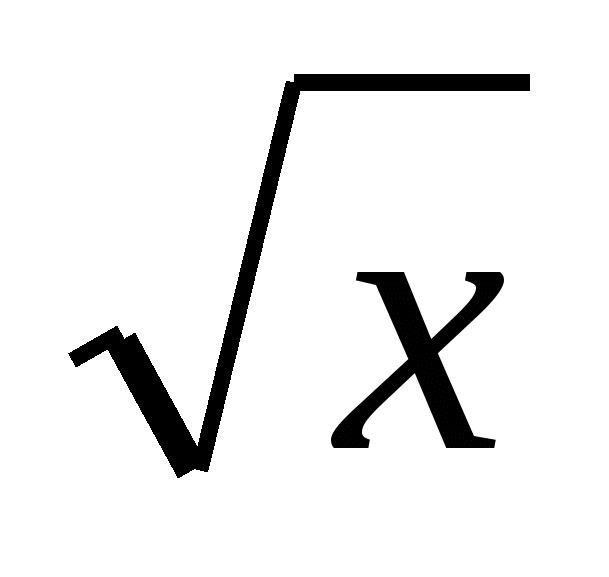 < 0
< 0
12 вариант
1. Найдите производные функций:
а) f(x) = - 2х6 + 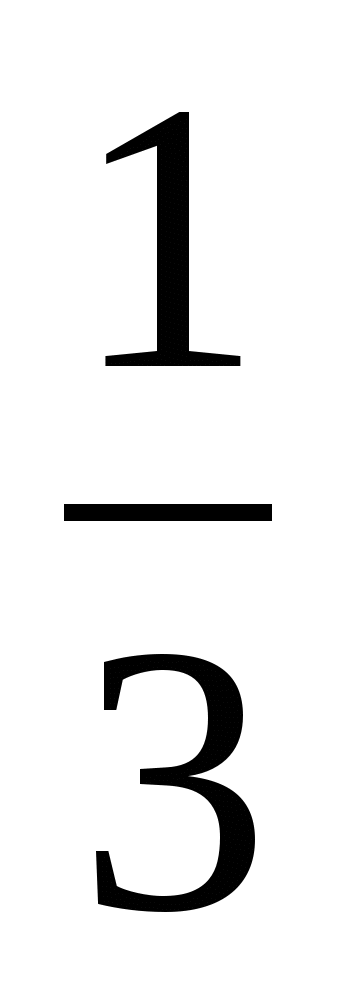 х9 – 3; б)g(x) =
х9 – 3; б)g(x) =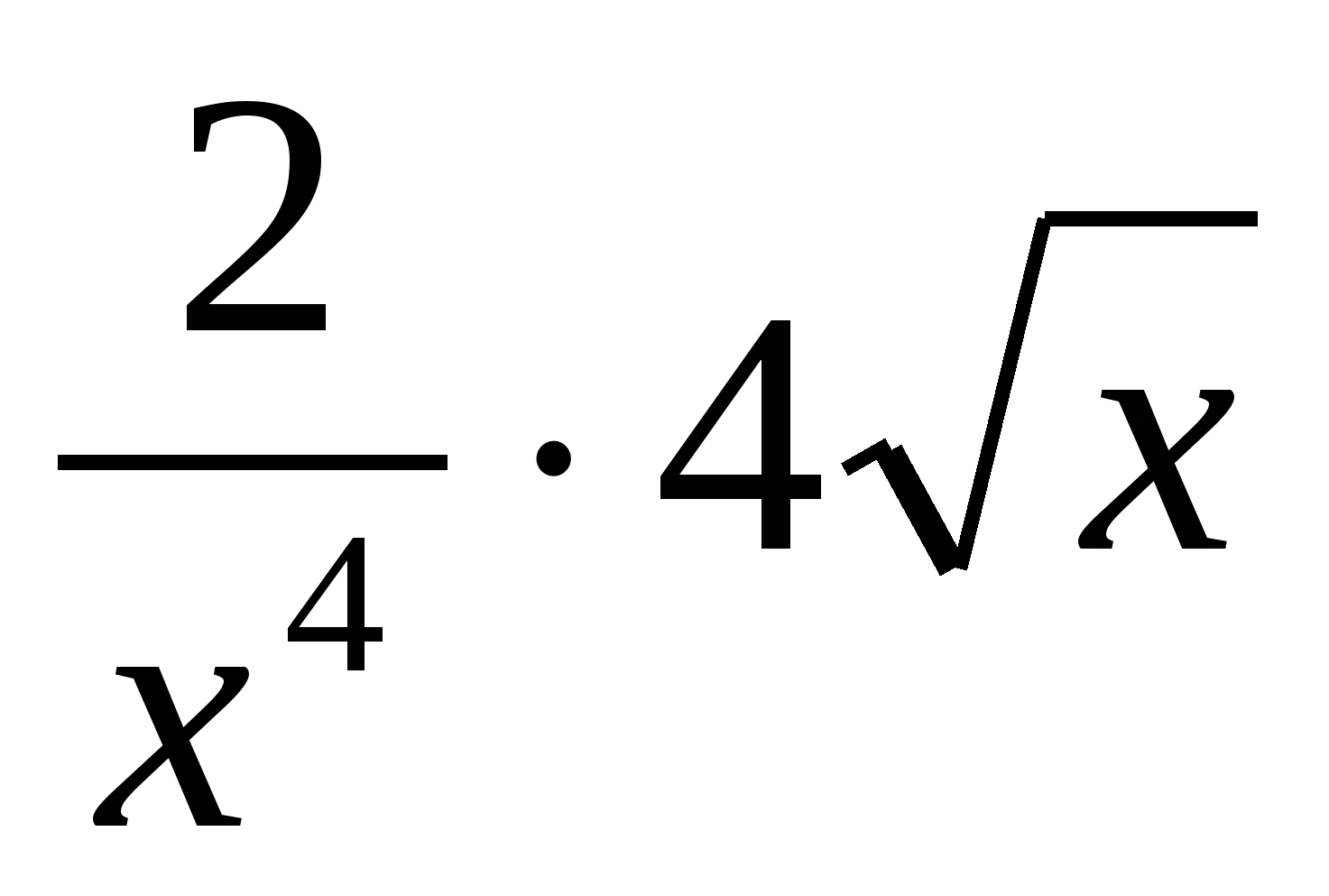 ;
;
в) q(x) = 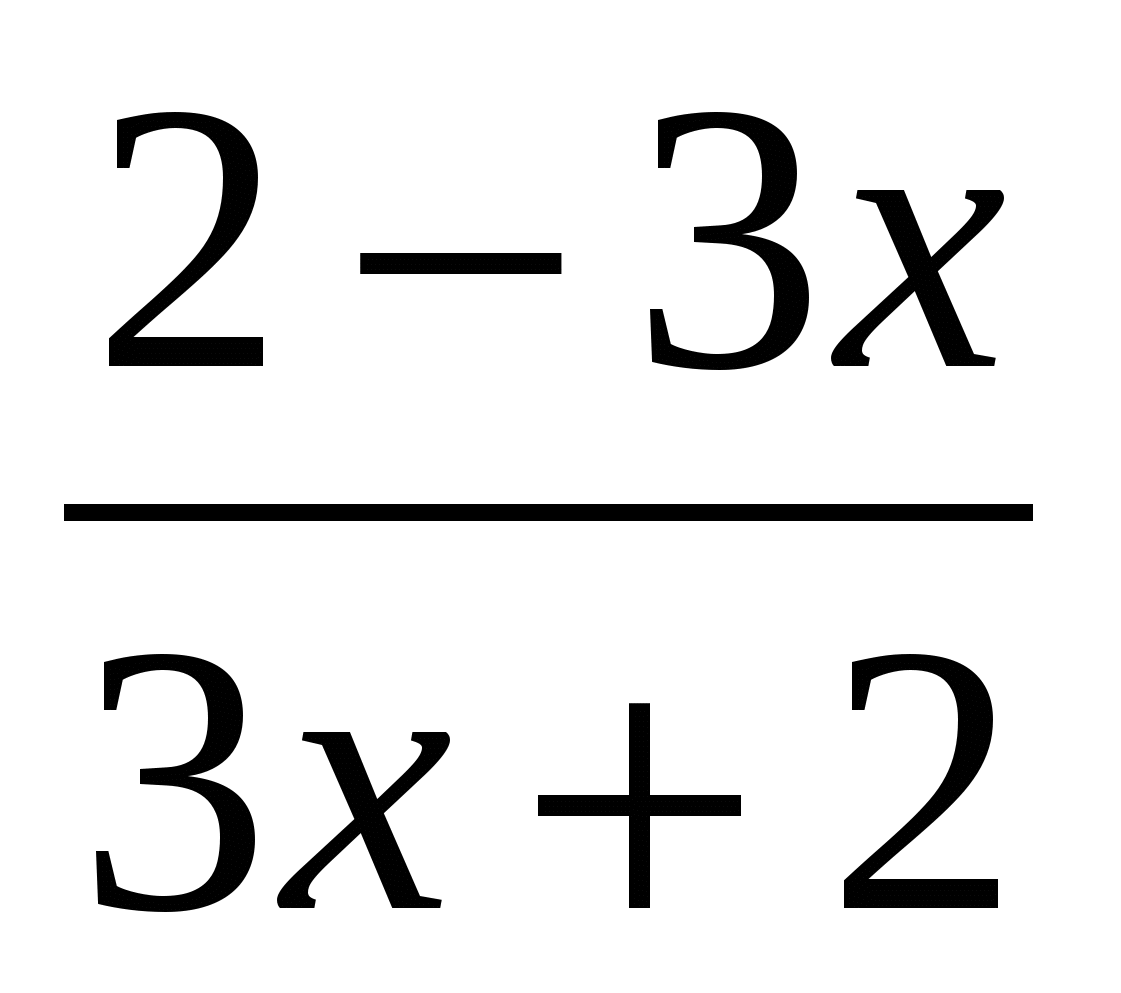 ; г) u(x) =
; г) u(x) = 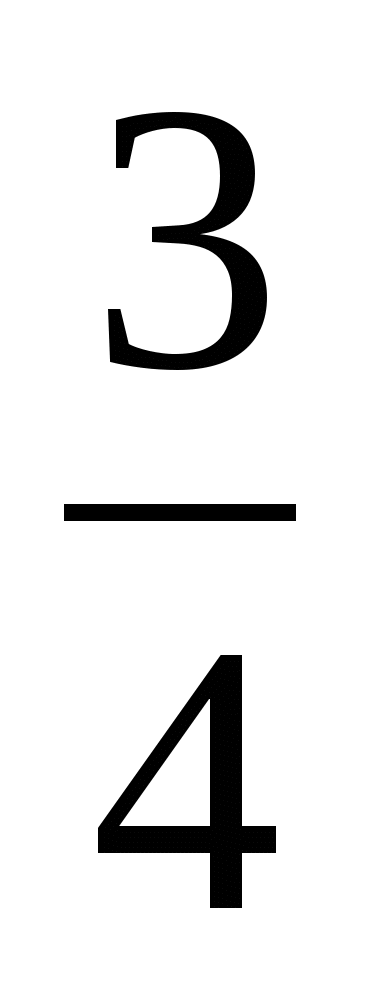 cos 4x 2. Точка движется по закону х(t)=t2+5. Найдите в какой момент времени скорость была 74м/с
cos 4x 2. Точка движется по закону х(t)=t2+5. Найдите в какой момент времени скорость была 74м/с
3. Найдите угол наклона касательной к графику функции f(x)=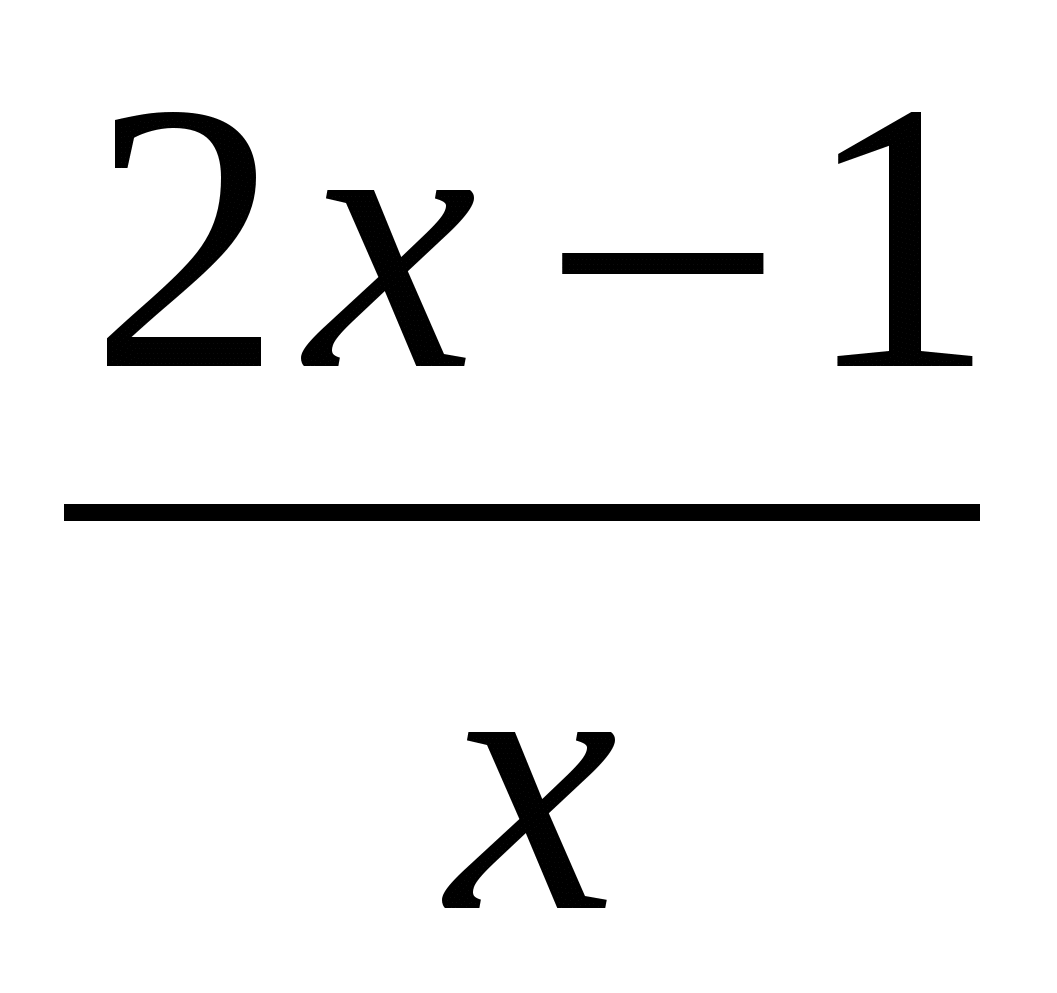 в точке х0=-1
в точке х0=-1
4. напишите уравнение касательной к графику функции f(x) = x2+1 в точке х0=1. Сделайте рисунок
5 . На рисунке изображены график функции
. На рисунке изображены график функции 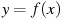 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 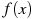 в точке
в точке 
6. Решите неравенство: х(х2+4х+4)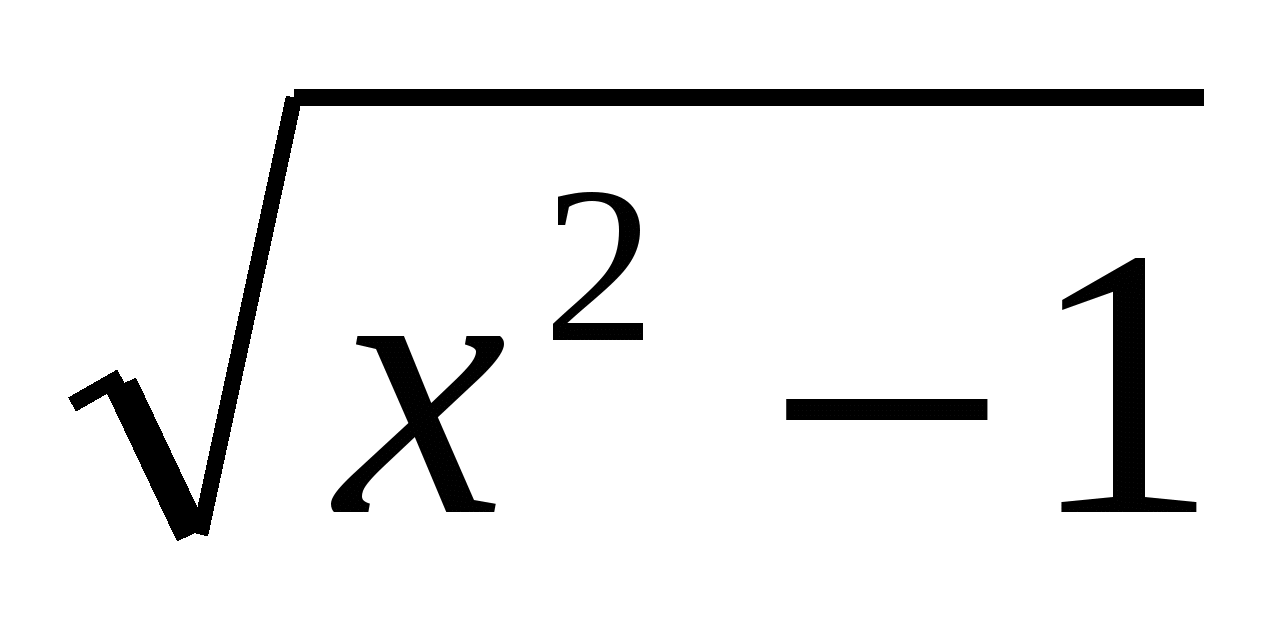 < 0
< 0
13 вариант
1. Найдите производные функций:
а) f(x) = 5х4 + 3х2 – 8х – 9; б) g(x) = 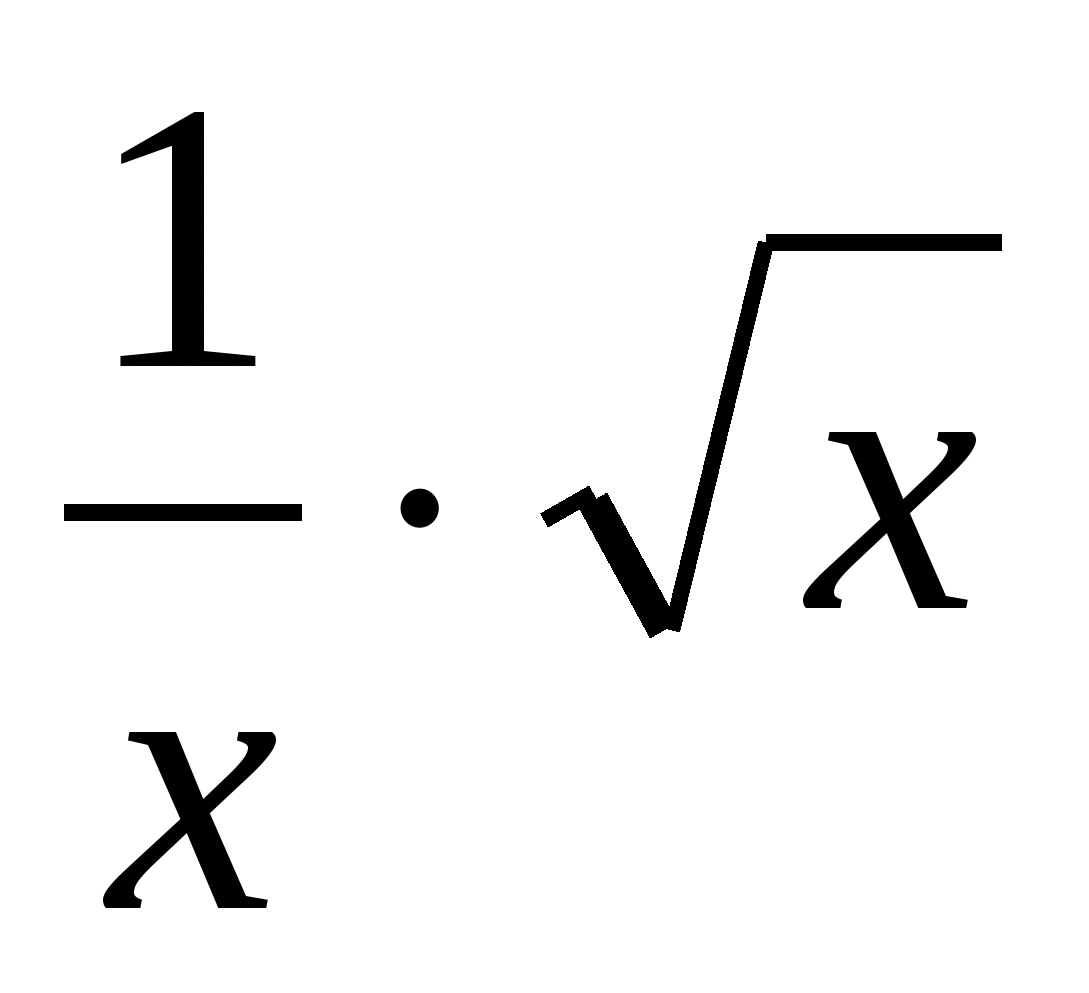 ;
;
в) q(x) = 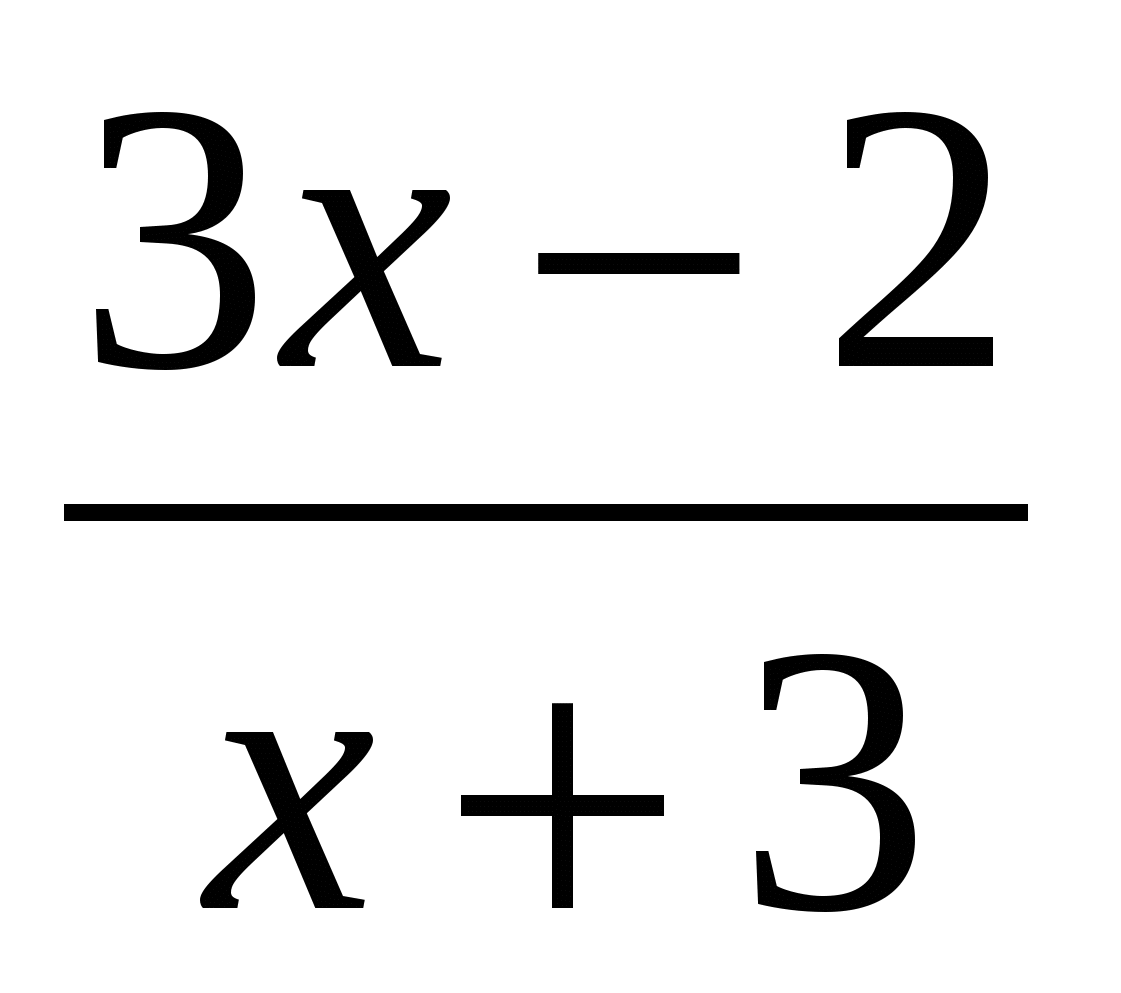 ; г) u(x) = sin 5x
; г) u(x) = sin 5x
2. Точка движется по закону х(t)=2t3+1 .Найдите в какой момент времени скорость точки была 54м/с
3. Найдите угол наклона касательной к графику функции f(x)=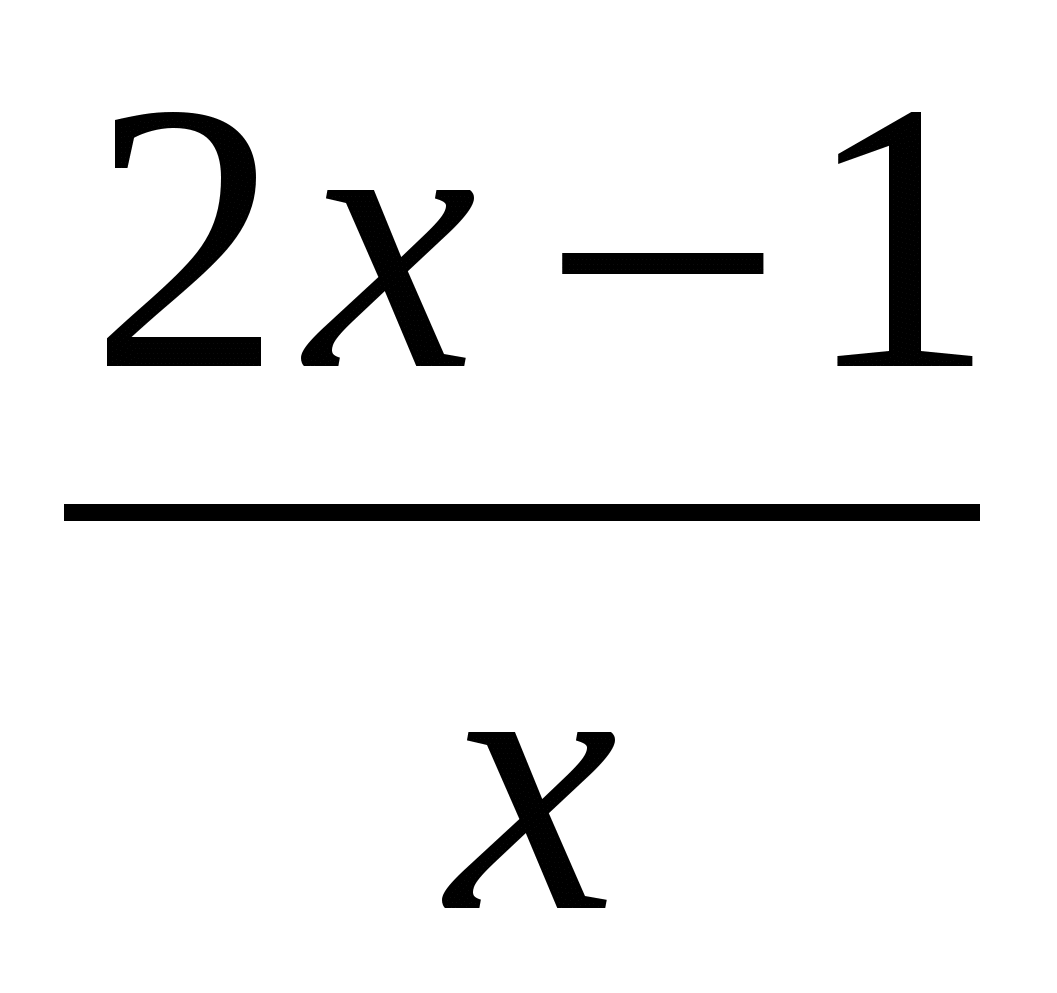 в точке х0=2
в точке х0=2
4. напишите уравнение касательной к графику функции f(x) = x2-3x в точке х0=-1. Сделайте рисунок
5 . На рисунке изображены график функции
. На рисунке изображены график функции 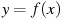 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 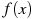 в точке
в точке 
6. Решите неравенство: (х+4)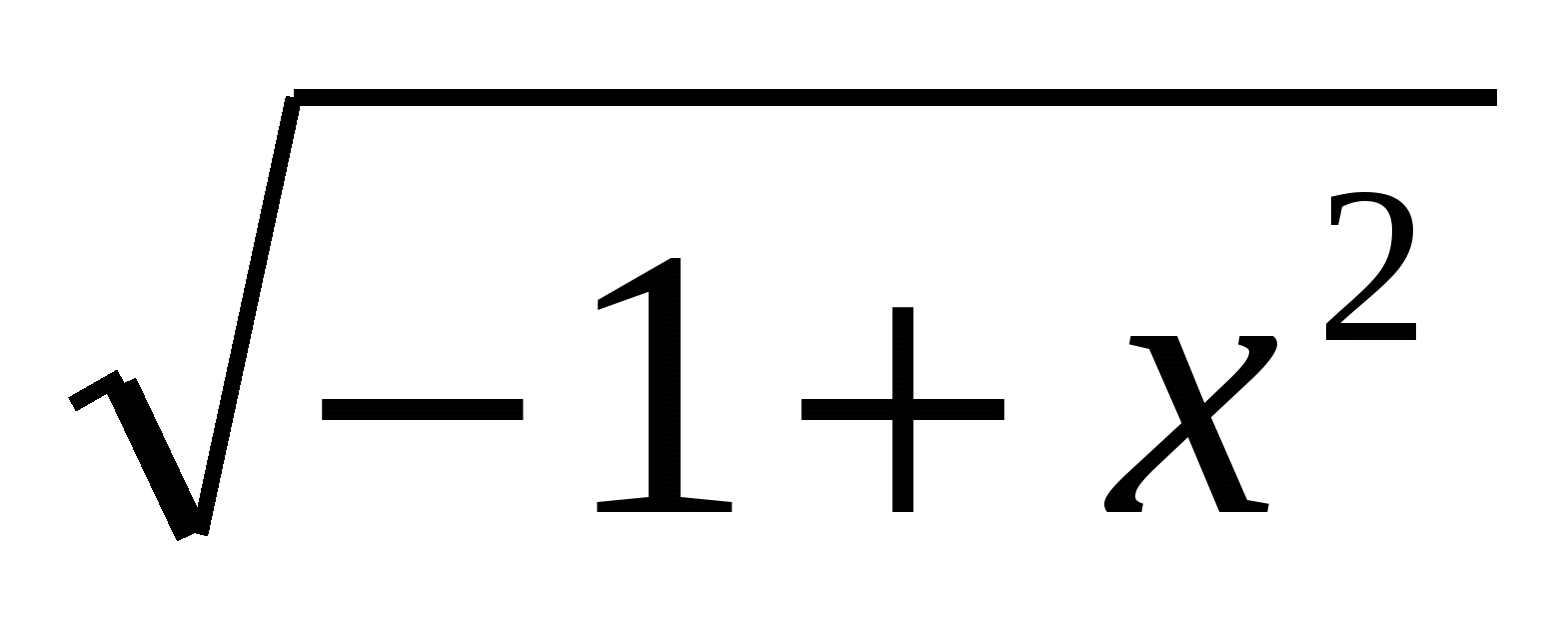 < 0
< 0
14 вариант
1. Найдите производные функций:
а) f(x) = 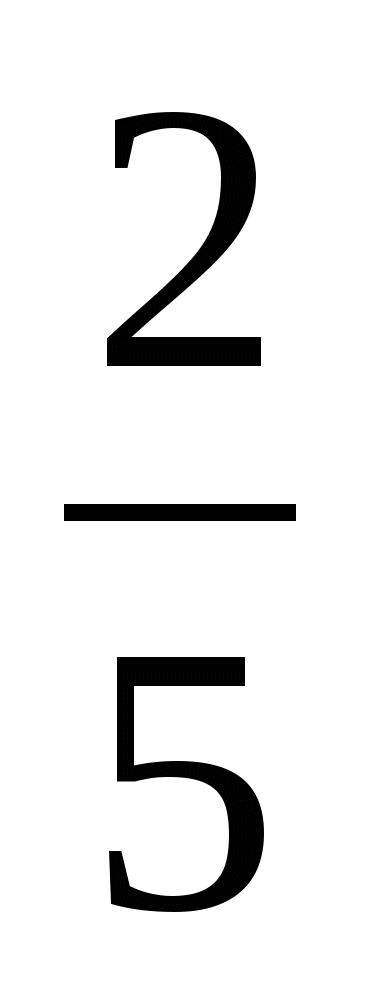 х5 + 3х3 – х – 4; б) g(x) =
х5 + 3х3 – х – 4; б) g(x) = 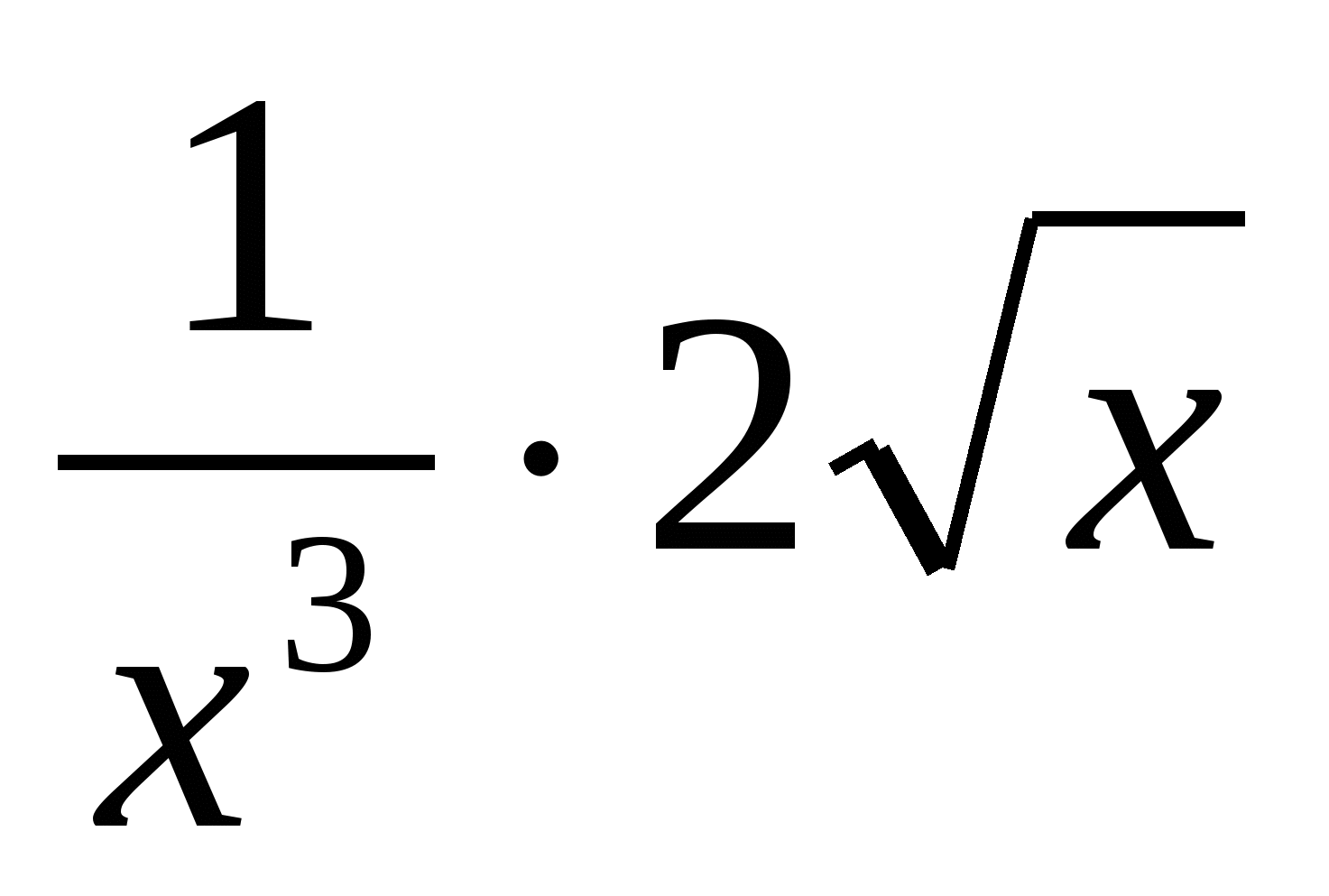 ;
;
в) q(x) = 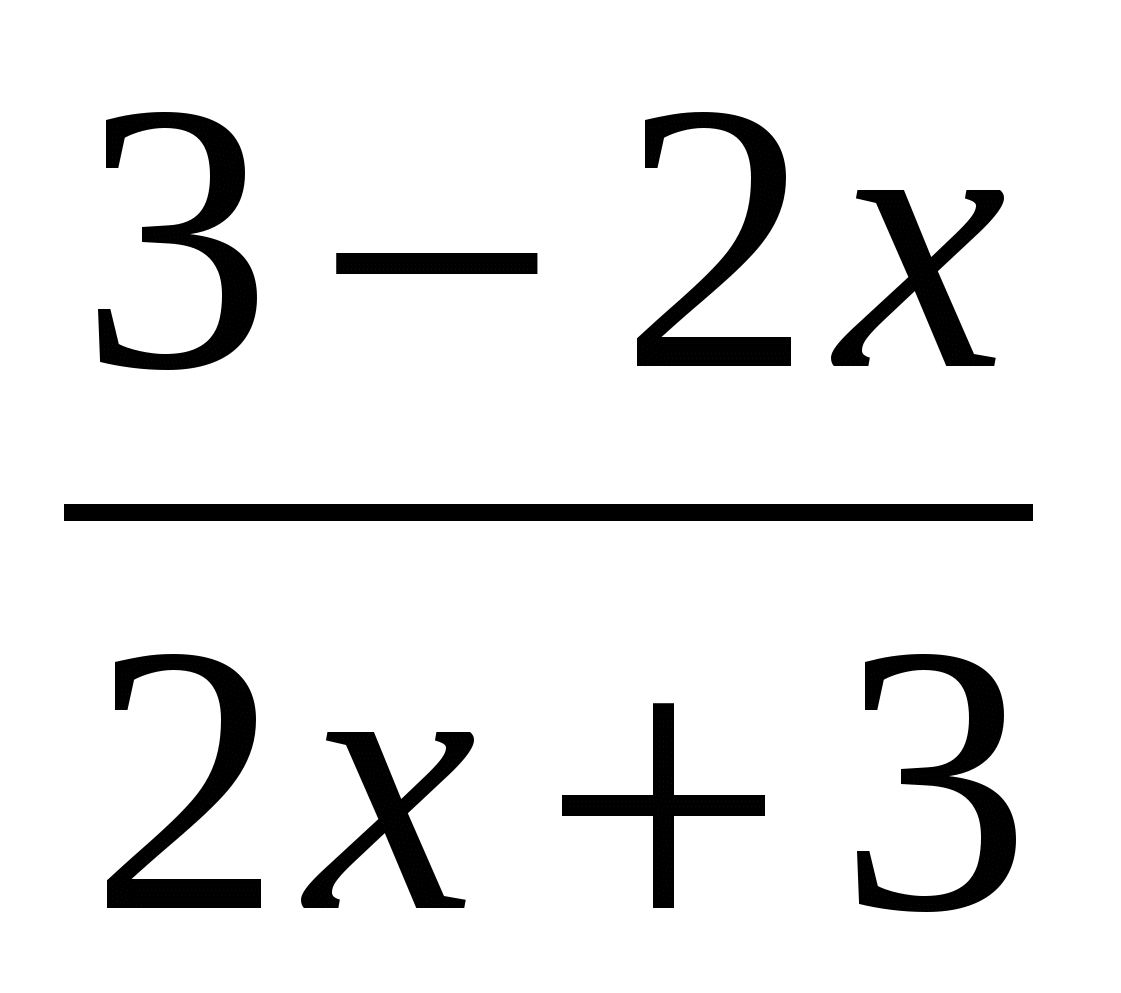 ; г) u(x) =
; г) u(x) = 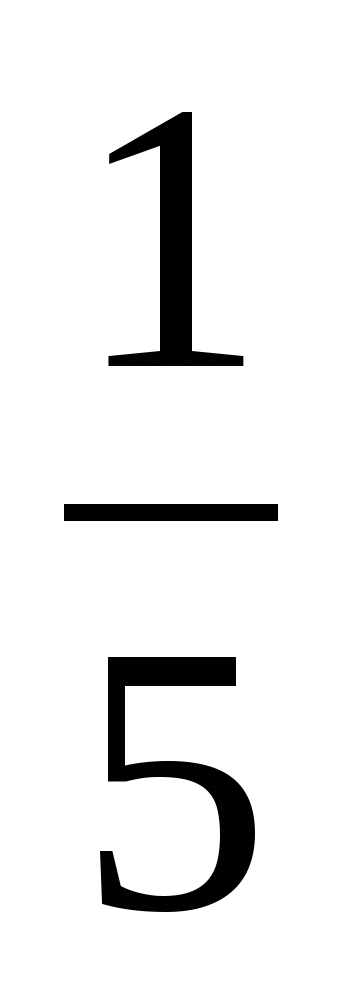 sin 5x
sin 5x
2. Точка движется по закону х(t)= t3+2t+3 Найдите ускорение точки в момент времени 1сек.
3. Найдите угол наклона касательной к графику функции f(x)=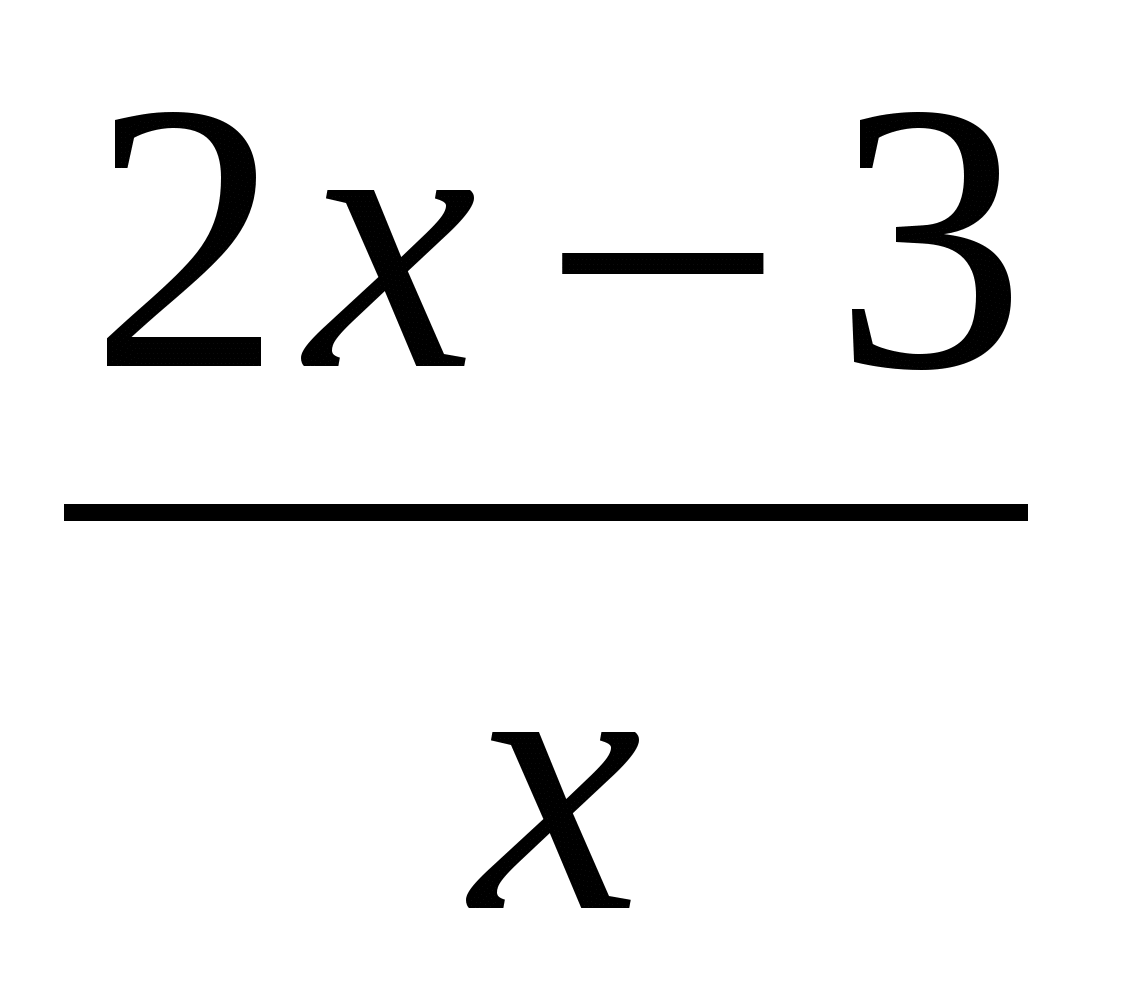 в точке х0=-1
в точке х0=-1
4. напишите уравнение касательной к графику функции f(x) = x2+2 в точке х0=-1. Сделайте рисунок
5 . На рисунке изображены график функции
. На рисунке изображены график функции 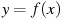 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 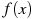 в точке
в точке 
6. Решите неравенство: х(х+4)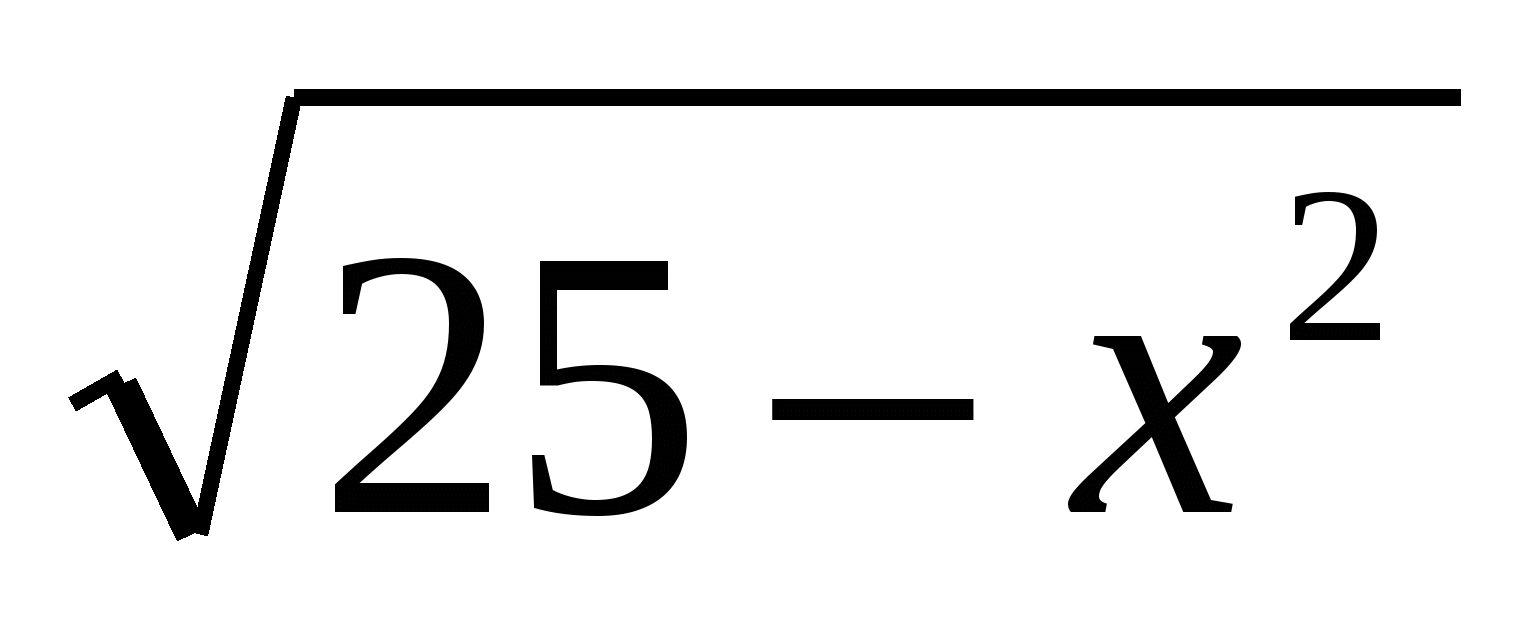 ≥ 0
≥ 0
infourok.ru
Контрольная работа № 2 ВАРИАНТ 1 А 11
Тема «Производная и ее геометрический смысл»
Найти производную функции:
а) 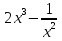 б)
б) 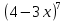
в) 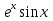 г)
г) 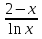
Найдите значение производной функции y = f(x) в точке х0, если 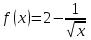 ,
, 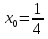
Записать уравнение касательной к графику функции 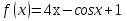 в точке
в точке 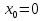
___________
Найти значения х, при которых значения производной функции 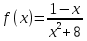 отрицательны.
отрицательны.
Найти точки графика функции 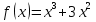 , в которых касательная к графику функции параллельна оси абсцисс.
, в которых касательная к графику функции параллельна оси абсцисс.
___________________________________________
Контрольная работа № 2 ВАРИАНТ 2 А 11
Тема «Производная и ее геометрический смысл»
Найти производную функции:
а) 3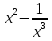 б)
б) 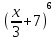
в) 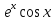 г)
г) 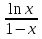
Найдите значение производной функции y = f(x) в точке х0, если 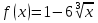 ,
, 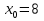
Записать уравнение касательной к графику функции 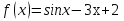 в точке
в точке 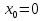
___________
Найти значения х, при которых значения производной функции 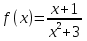 отрицательны.
отрицательны.
Найти точки графика функции 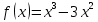 , в которых касательная к графику функции параллельна оси абсцисс.
, в которых касательная к графику функции параллельна оси абсцисс.
___________________________________________
Контрольная работа № 2 ВАРИАНТ 3 А 11
Тема «Производная и ее геометрический смысл»
Найти производную функции:
а) 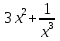 б)
б) 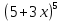
в) 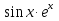 г)
г) 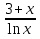
Найдите значение производной функции y = f(x) в точке х0, если 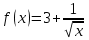 ,
, 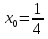
Записать уравнение касательной к графику функции 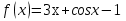 в точке
в точке 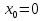
___________
Найти значения х, при которых значения производной функции 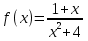 отрицательны.
отрицательны.
Найти точки графика функции 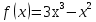 , в которых касательная к графику функции параллельна оси абсцисс.
, в которых касательная к графику функции параллельна оси абсцисс.
Контрольная работа № 2 ВАРИАНТ 4 А 11
Тема «Производная и ее геометрический смысл»
Найти производную функции:
а) 3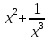 б)
б) 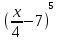
в) 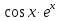 г)
г) 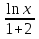
Найдите значение производной функции y = f(x) в точке х0, если 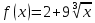 ,
, 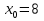
Записать уравнение касательной к графику функции 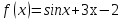 в точке
в точке 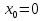
___________
Найти значения х, при которых значения производной функции 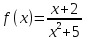 отрицательны.
отрицательны.
Найти точки графика функции 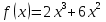 , в которых касательная к графику функции параллельна оси абсцисс.
, в которых касательная к графику функции параллельна оси абсцисс.
___________________________________________
Контрольная работа № 2 ВАРИАНТ 5 А 11
Тема «Производная и ее геометрический смысл»
Найти производную функции:
а) 4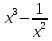 б)
б) 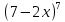
в) 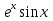 г)
г) 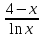
Найдите значение производной функции y = f(x) в точке х0, если 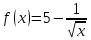 ,
, 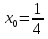
Записать уравнение касательной к графику функции 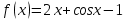 в точке
в точке 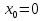
___________
Найти значения х, при которых значения производной функции 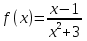 отрицательны.
отрицательны.
Найти точки графика функции 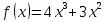 , в которых касательная к графику функции параллельна оси абсцисс.
, в которых касательная к графику функции параллельна оси абсцисс.
__________________________________________
Контрольная работа № 2 ВАРИАНТ 6 А 11
Тема «Производная и ее геометрический смысл»
Найти производную функции:
а) 5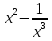 б)
б) 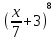
в) 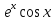 г)
г) 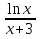
Найдите значение производной функции y = f(x) в точке х0, если 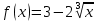 ,
, 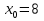
Записать уравнение касательной к графику функции 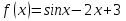 в точке
в точке 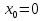
___________
Найти значения х, при которых значения производной функции 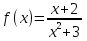 отрицательны.
отрицательны.
Найти точки графика функции  , в которых касательная к графику функции параллельна оси абсцисс.
, в которых касательная к графику функции параллельна оси абсцисс.
Контрольная работа № 2 ВАРИАНТ 7 А Тема «Производная и ее геометрический смысл»
Найти производную функции:
а) 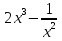 б)
б) 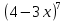
в) 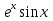 г)
г) 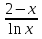
Найдите значение производной функции y = f(x) в точке х0, если 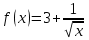 ,
, 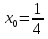
Записать уравнение касательной к графику функции 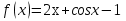 в точке
в точке 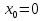
___________
Найти значения х, при которых значения производной функции 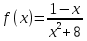 отрицательны.
отрицательны.
Найти точки графика функции 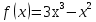 , в которых касательная к графику функции параллельна оси абсцисс.
, в которых касательная к графику функции параллельна оси абсцисс.
___________________________________________
Контрольная работа № 2 ВАРИАНТ 8 А 11
Тема «Производная и ее геометрический смысл»
Найти производную функции:
а) 3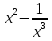 б)
б) 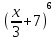
в) 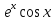 г)
г) 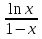
Найдите значение производной функции y = f(x) в точке х0, если 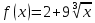 ,
, 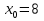
Записать уравнение касательной к графику функции 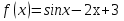 в точке
в точке 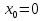
___________
Найти значения х, при которых значения производной функции 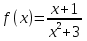 отрицательны.
отрицательны.
Найти точки графика функции 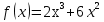 , в которых касательная к графику функции параллельна оси абсцисс.
, в которых касательная к графику функции параллельна оси абсцисс.
___________________________________________
Контрольная работа № 2 ВАРИАНТ 9 А 11
Тема «Производная и ее геометрический смысл»
Найти производную функции:
а) 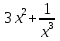 б)
б) 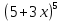
в) 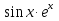 г)
г) 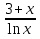
Найдите значение производной функции y = f(x) в точке х0, если 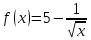 ,
, 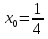
Записать уравнение касательной к графику функции 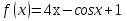 в точке
в точке 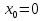
___________
Найти значения х, при которых значения производной функции 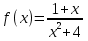 отрицательны.
отрицательны.
Найти точки графика функции 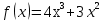 , в которых касательная к графику функции параллельна оси абсцисс.
, в которых касательная к графику функции параллельна оси абсцисс.
Контрольная работа № 2 ВАРИАНТ 10 А 11
Тема «Производная и ее геометрический смысл»
Найти производную функции:
а) 3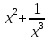 б)
б) 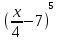
в) 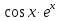 г)
г) 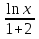
Найдите значение производной функции y = f(x) в точке х0, если 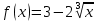 ,
, 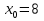
Записать уравнение касательной к графику функции 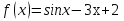 в точке
в точке 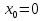
___________
Найти значения х, при которых значения производной функции 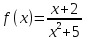 отрицательны.
отрицательны.
Найти точки графика функции 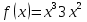 , в которых касательная к графику функции параллельна оси абсцисс.
, в которых касательная к графику функции параллельна оси абсцисс.
________________________________________
Контрольная работа № 2 ВАРИАНТ 11 А 11
Тема «Производная и ее геометрический смысл»
Найти производную функции:
а) 4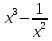 б)
б) 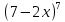
в) 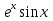 г)
г) 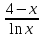
Найдите значение производной функции y = f(x) в точке х0, если 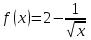 ,
, 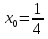
Записать уравнение касательной к графику функции 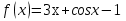 в точке
в точке 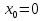
___________
Найти значения х, при которых значения производной функции 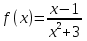 отрицательны.
отрицательны.
Найти точки графика функции 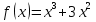 , в которых касательная к графику функции параллельна оси абсцисс.
, в которых касательная к графику функции параллельна оси абсцисс.
________________________________________
Контрольная работа № 2 ВАРИАНТ 12 А 11
Тема «Производная и ее геометрический смысл»
Найти производную функции:
а) 5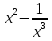 б)
б) 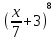
в) 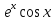 г)
г) 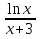
Найдите значение производной функции y = f(x) в точке х0, если 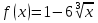 ,
, 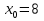
Записать уравнение касательной к графику функции 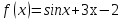 в точке
в точке 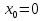
___________
Найти значения х, при которых значения производной функции 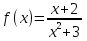 отрицательны.
отрицательны.
Найти точки графика функции 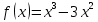 , в которых касательная к графику функции параллельна оси абсцисс.
, в которых касательная к графику функции параллельна оси абсцисс.
infourok.ru