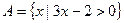.Домашняя контрольная работа по теме «Множества»
В - 1
1. Укажите множество действительных чисел, соответствующее записи .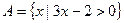
2. Дано множество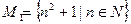 
.
а) Приведите три примера элементов множества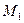 
.
б) Укажите, какие из чисел 3, 4, 5, 13, 25,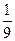 
, 
, 
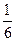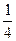принадлежат этому множеству.
в) Укажите, какие из чисел 3, 4, 5, 13, 25, 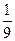, , 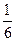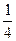не принадлежат этому множеству.
Запишите эти утверждения символически.
3. Дано множество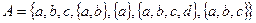 
. Какие из элементов этого множества являются множествами? Верна ли запись 
?
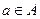4. На множестве U всех букв русского алфавита заданы множества А, В: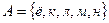 
; 
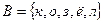. Найдите множество 
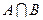и изобразите его кругами Эйлера.
5. Даны отрезки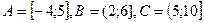 
. Найдите множество 
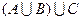и изобразите его кругами Эйлера.
6.В результате социологического опроса студентов факультета программирования о занятиях в свободное от уроков время выяснилось, что из 100 человек:
18 – любят только читать книги;
24 – читают книги, но не ходят в театр;
7 – читают книги и посещают театр;
38 – читают книги;
47 – ходят на дискотеки;
9 – посещают театр и дискотеки;
13 – лежат на диване перед телевизором, занимаются только просмотром всех возможных каналов телевидения.
Сколько студентов любят ходить в театр?
Домашняя контрольная работа по теме «Множества»
В - 2
1. Укажите множество действительных чисел, соответствующее записи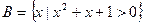 
.
2. Дано множество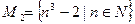 
.
а) Приведите три примера элементов множества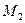 
.
б) Укажите, какие из чисел 3, 4, 5, 13, 25, 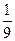, , 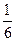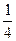принадлежат этому множеству.
в) Укажите, какие из чисел 3, 4, 5, 13, 25, 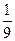, , 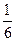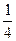не принадлежат этому множеству.
Запишите эти утверждения символически.
3. Дано множество 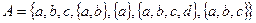. Какие из элементов этого множества являются множествами? Верна ли запись 
?
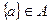4. На множестве U всех букв русского алфавита заданы множества А, В: 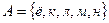; 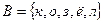. Найдите множество 
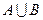и изобразите его кругами Эйлера.
5. Даны отрезки 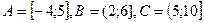. Найдите множество 
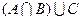и изобразите его кругами Эйлера.
6.В результате социологического опроса студентов факультета программирования о занятиях в свободное от уроков время выяснилось, что из 100 человек:
18 – любят только читать книги;
24 – читают книги, но не ходят в театр;
7 – читают книги и посещают театр;
38 – читают книги;
47 – ходят на дискотеки;
9 – посещают театр и дискотеки;
13 – лежат на диване перед телевизором, занимаются только просмотром всех возможных каналов телевидения.
Сколько студентов читают книги, посещают театр, но не дискотеки?
Домашняя контрольная работа по теме «Множества»
В - 3
1. Укажите множество действительных чисел, соответствующее записи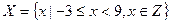 
.
2. Дано множество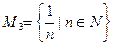 
.
а) Приведите три примера элементов множества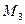 
.
б) Укажите, какие из чисел 3, 4, 5, 13, 25, 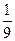, , 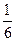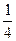принадлежат этому множеству.
в) Укажите, какие из чисел 3, 4, 5, 13, 25, 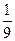, , 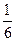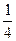не принадлежат этому множеству.
Запишите эти утверждения символически.
3. Дано множество 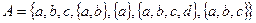. Какие из элементов этого множества являются множествами? Верна ли запись 
?
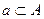4. На множестве U всех букв русского алфавита заданы множества А, В: ; ;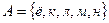 
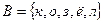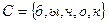Найдите множество 
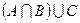и изобразите его кругами Эйлера.
5. Даны отрезки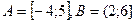 
. Найдите множество 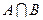и изобразите его кругами Эйлера.
6.В результате социологического опроса студентов факультета программирования о занятиях в свободное от уроков время выяснилось, что из 100 человек:
18 – любят только читать книги;
24 – читают книги, но не ходят в театр;
7 – читают книги и посещают театр;
38 – читают книги;
47 – ходят на дискотеки;
9 – посещают театр и дискотеки;
13 – лежат на диване перед телевизором, занимаются только просмотром всех возможных каналов телевидения.
Сколько студентов посещают либо дискотеки, либо театр?
megaobuchalka.ru
Контрольный тест «Множество»
Вариант 1
1.Дать определение: Множество – это….
2.Закончите определение:Множество, содержащее только те элементы, принадлежащие и множеству А и множеству В, называют …
а) пересечением множеств;
б) объединением множеств;
в) разностью множеств;
г) объединенностью множеств.
3.Соотнесите понятия из левого столбца с их символьными обозначениями из правого.
1. пустое множество; а) В Ì А;
2. пересечение множеств; б) Ç ;
3
. объединение множеств; в) ;
4. В – подмножество множества А. г) È
4. Даны множества: А – двузначные числа и В – нечетные числа. Укажите верный вариант ответа пересечения множеств А и В,
а) множество двузначных и нечетных чисел;
б) множество двузначных или нечетных чисел;
в) множество однозначных и нечетных чисел;
г) нет правильного ответа.
д) все варианты верны.
5. Укажите верный вариант записи объединения множеств:
А = {1;2;3;б} и В = {а;б;в;4;1}
а) А È В = {1;2;3;б;а;в;4};
б) А È В = { };
в) А È В = {а; б; в};
г) А È В = {1;б};
д) нет верного ответа;
е) все варианты верны.
6.Задано множество всех делителей числа 16 и множество всех делителей числа 30. Укажите для этих множеств их
А) общие лементы
Б)все элементы множеств
7. Покажите штриховкой множества АՈВ.
8. Пусть А – множество натуральных чисел, кратных 5 и В – множество натуральных чисел, кратных 10. Запишите любые шесть чисел, принадлежащих множеству А и шесть любых чисел, принадлежащих множеству В.
А: _________________ В: __________________
9. На схеме прямоугольник изображает всех учащихся 6 класса, круг Ч – те, кто любит чёрный шоколад, а круг Б – тех, кто любит белый шоколад. Штриховкой выделить
1) Те, кто не любит ни чёрный, ни белый шоколад.
2) Те, кто любит и чёрный и белый шоколад.
3) Те, кто любит какой-нибудь один вид шоколада: или чёрный или белый.
4) Те, кто любит белый и не любит чёрный шоколад
10. На схеме отражены результаты опроса учащихся 6 классов об их отношении к детективной литературе и фантастике. Прямоугольник отображает всех учащихся 6 класса, круг Д – множество учащихся, любящих детективы, круг Ф – шестиклассники, любящие фантастику.
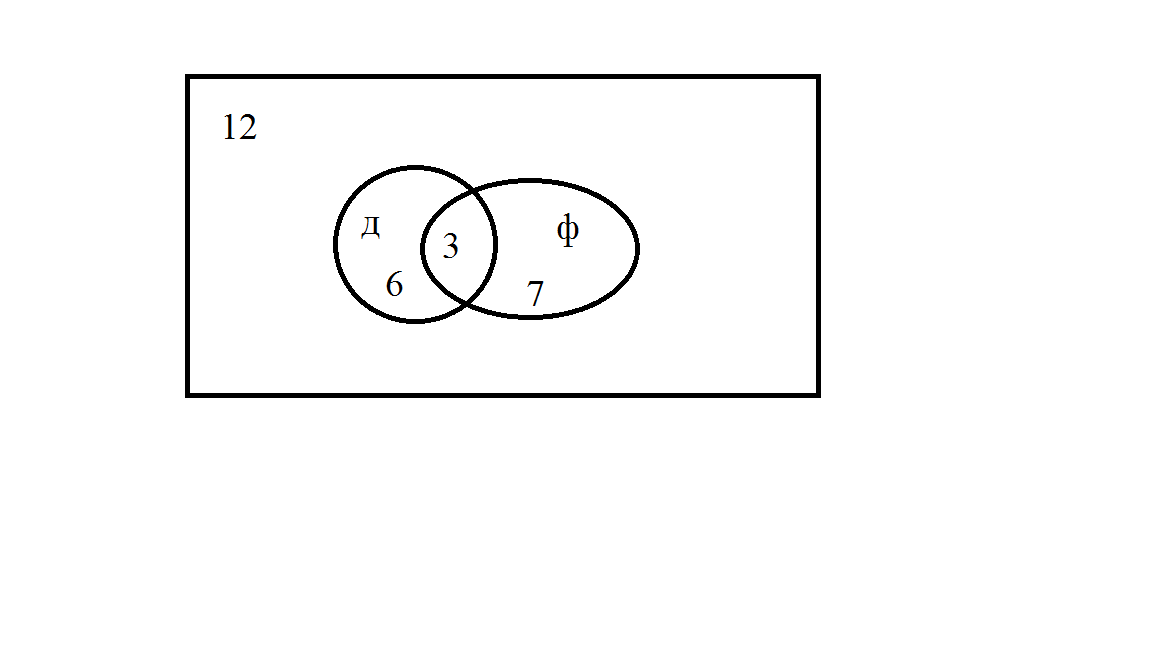
Ответьте на вопросы:
a) Сколько учеников не читают ни детективы, ни фантастику?
б) Сколько шестиклассников любят детективы, но не читают фантастику?
в) Сколько шестиклассников любят читать и детективы и фантастику?
г) Сколько учащихся любят фантастику и не любят детективы?
д) Сколько учащихся увлекается хотя бы одним из указанных видов литературы? е) Сколько учащихся всего было опрошено?
Контрольный тест «Множество»
Вариант 2
1.Дать определение: Подмножество – это….
2.Закончите определение:Множество, содержащее только те элементы, принадлежащие множеству А и не принадлежащие множеству В, называют …
а) пересечением множеств;
б) объединением множеств;
в) разностью множеств;
г) объединенностью множеств.
3.Соотнесите понятия из левого столбца с их символьными обозначениями из правого.
1. пустое множество; а) В Ì А;
2. пересечение множеств; б) Ç ;
3. объединение множеств; в) ;
4. В – подмножество множества А. г) È 
infourok.ru
РЕФЕРАТ
Множества.Операции над множествами
СОДЕРЖАНИЕ
Способы задания множества
Включение и равенство множеств
Диаграммы Эйлера-Венна
Операции над множествами
а) Объединение множеств
б) Пересечение множеств
в) Разность множеств
Дополнение множества
Понятие множествапринадлежит к числу основных, неопределяемых понятий математики. Оно несводится к другим, более простым понятиям. Поэтому его нельзя определить, аможно лишь пояснить, указывая синонимы слова «множество» и приводя примерымножеств: множество – набор, совокупность, собрание каких-либо объектов(элементов), обладающих общим для всех их характеристическим свойством.
Примеры множеств:
1) множествостудентов в данной аудитории;
2) множество людей,живущих на нашей планете в данный момент времени;
3) множество точекданной геометрической фигуры;
4) множество чётныхчисел;
5) множество корнейуравнения х2-5х+6=0;
6) множестводействительных корней уравнения х2+9=0;
Основоположниктеории множеств немецкий математик Георг Кантор (1845-1918) писал: «Множествоесть многое, мыслимое нами как единое». И хотя это высказывание учёного неявляется в полном смысле логическим определением понятия множества, но оноверно поясняет, что когда говорят о множестве, то имеют в виду некотороесобрание объектов, причём само это собрание рассматривается как единое целое,как один (новый) объект.
Объекты, составляющиеданное множество, называют его элементами.
Множество обычнообозначают большими латинскими буквами, а элементы множества − малымилатинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а />А, а если а непринадлежит А, то пишут: а />А.
Например, пусть N–множество натуральных чисел. Тогда 5/>N, но />/>N, />/>N. Если А — множество корней уравнения х2-5х+6=0,то 3 /> А, а4/>А.
В математикечасто исследуются так называемые числовые множества, т.е. множества, элементамикоторых являются числа. Для самых основных числовых множеств утвердилисьследующие обозначения:
N- множество всех натуральных чисел;
Z- множество всех целых чисел;
Q- множество всех рациональных чисел;
R- множество всех действительныхчисел.
Приняты также обозначенияZ+, Q+, R+ соответственно для множеств всех неотрицательных целых,рациональных и действительных чисел, и Z¯, Q¯, R¯ -для множеств всех отрицательных целых, рациональных идействительных чисел.
Способы заданиямножества
Множество Асчитается заданным, если относительно любого объекта а можно установить,принадлежит этот объект множеству А или не принадлежит; другими словами, еслиможно определить, является ли а элементом множества А или не является.Существуют два основных способа задания множества:
1) перечислениеэлементов множества;
2) указаниехарактеристического свойства элементов множества, т.е. такого свойства, которымобладают все элементы данного множества и только они.
Первым способом особенночасто задаются конечные множества. Например, множество студентов учебной группызадаётся их списком. Множество, состоящее из элементов a, b, c, … ,d, обозначают с помощью фигурных скобок: А={a; b; c; …;d}. Множество корней уравнения х2-5х+6=0состоит из двух чисел 2 и 3: А={2; 3}. Множество В целых решений неравенства -2< х < 3 состоит из чисел –1, 0, 1, 2, поэтому В={–1; 0; 1; 2}.
Второй способ заданиямножества является более универсальным. Множество элементов х, обладающихданным характеристическим свойством Р(х), также записывают с помощью фигурныхскобок: Х={х | Р (х)}, и читают: множество Х состоит из элементов х, таких, чтовыполняется свойство Р(х). Например, А={х | х2-5х+6=0}. Решивуравнение х2-5х+6=0, мы можем записать множество А первым способом:А={2; 3}.
Другой пример: Х={х | -1 ≤х < 4, х /> Z}, т.е. Х есть множество целых чиселх, таких, что –1 ≤ х < 4, значит, по-другому: Х={-1; 0; 1; 2; 3}.
Рассмотрим и такойпример: F={f | │f´(x)│≤ 1, 1 < x < 2}, т.е. F- множество функций f, производнаякоторых в интервале (1; 2) не превосходит по абсолютной величине числа 1.
Можетслучиться, что характеристическим свойством, определяющим множество А, необладает ни один объект. Тогда говорят, что множество А — пустое (не содержитни одного элемента) и пишут: А= Ø.
Например, А={х |х²+9=0, х/>R} –множество действительных чисел х, таких, что х²+9=0-пустое множество, т.к. таких действительных чисел нет.
Включение и равенствомножеств
Пусть Х и У – двамножества. Если каждый элемент х множества Х является элементом множества У, тоговорят, что множество Х содержится во множестве У и пишут: Х /> У или У />Х. Говорят также, что Хвключено в У или У включает Х, или что Х является подмножеством множества У.Знаки включения /> или /> относятся />только ко множествам иих не следует смешивать со знаками принадлежности Î и /> . Если, например, А — множествовсех студентов вуза, а В – множество студентов-первокурсников этого вуза, то Весть подмножество А, т.е. В /> А. Пустое множество считаютподмножеством любого множества Х, т.е. Ø /> Х, каким бы ни было множество Х.Ясно также, что каждое множество является подмножеством самого себя: Х />Х.
Если для двух множеств Хи У одновременно имеют место два включения Х />У и У /> Х, т.е. Х есть подмножествомножества У и У есть подмножество множества Х, то множества Х и У состоят изодних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У.Например, если А={2; 3}, а В={х | х² –5х+6=0}, то А=В.
Если Х />У, но Х≠ У, т.е.существует хотя бы один элемент множества У, не принадлежащий Х, то говорят,что Х есть собственное подмножество множества У, и пишут: Х /> У. Например: N/>Z, Z/>Q, Q/>R. Далее нам потребуется множество, которое содержит в качествесвоего подмножества любое другое множество. Такое «всеобъемлющее» множество будемназывать универсальным и обозначать буквой U .
Диаграммы Эйлера-Венна
Для наглядногопредставления множеств используют диаграммы Эйлера-Венна. В этом случаемножества обозначают областями на плоскости и внутри этих областей условнорасполагают элементы множества. Часто все множества на диаграмме размещаютвнутри прямоугольника, который представляет собой универсальное множество U. Если элемент принадлежит более чемодному множеству, то области, отвечающие таким множествам, должныперекрываться, чтобы общий элемент мог одновременно находиться всоответствующих областях. Выбор формы областей, изображающих множества надиаграммах, может быть произвольным (круги, внутренности эллипсов, многоугольникии т.п.). Покажем, например, с помощью диаграммы Эйлера-Венна, что множество Аявляется подмножеством множества В:
/>
С помощьютакой диаграммы становиться наглядным, например, такое утверждение:
если А/>В, а В />С, то А/>С.
/>
Строгое доказательство этогоутверждения, не опирающееся на диаграмму, можно провести так: пусть х />А; так как А /> В, то х /> В, а так как В/> С, то изх /> Вследует, что х /> С; значит, из того, что х /> А, следует х/>С, а поэтому А /> С.
Операции надмножествами
С помощьюнескольких множеств можно строить новые множества или, как говорят, производитьоперации над множествами. Мы рассмотрим следующие операции над множествами:объединение, пересечение, разность множеств, дополнение множества. Всерассматриваемые операции над множествами мы будем иллюстрировать на диаграммахЭйлера-Венна.
/>Объединение множеств
Объединением А/>В множеств А иВ называется множество, состоящее из всех элементов, принадлежащих хотя быодному из множеств А или В.
Символическая записьэтого определения: А />В={х | х/>А или х/>В}.
Здесь союз «или»понимается в смысле «неразделительного или», т.е. не исключается, что х можетпринадлежать и А и В. Отметим, что в таком случае элемент х, входящий в обамножества А и В, входит в их объединение только один раз (поскольку длямножества не имеет смысла говорить о том, что элемент входит в него несколькораз).
Пояснимопределение объединения множеств с помощью диаграммы Эйлера-Венна:
/>
На диаграмме объединениемножеств А и В выделено штриховкой.
Если множество Аопределяется характеристическим свойством Р (х), а множество В — характеристическим свойством Q(х),то А /> Всостоит из всех элементов, обладающих, по крайней мере, одним из этих свойств.
Примеры объединений двухмножеств:
1) Пусть А={2; 5; 7}, В={3;5; 6}. Тогда А /> В ={2; 3; 5; 6; 7}.
2) Пусть А=[-1/4; 2], В=[-2/3; 7/4]. Тогда А />В=[-2/3; 2] .
3) Пусть А= {х | х=8k, k /> Z}, B={x | x=8n-4, n /> Z}. Тогда A />B ={x | 4m, m/>Z}.
Операцияобъединения множеств может проводиться не только над двумя множествами.Определение объединения множеств можно распространить на случай любогоколичества множеств и даже – на систему множеств. Система множеств определяетсятак: если каждому элементу α множества М отвечает множество Аα,то совокупность всех таких множеств мы будем называть системой множеств.
Объединением системымножеств {Аα} называется множество />, состоящее из всех элементов,принадлежащих хотя бы одному из множеств Аα. При этом общиеэлементы нескольких множеств не различаются.
Таким образом, элемент х/>/>тогда и только тогда,когда найдется такой индекс α0 />М, что х />A α0.
В случае, когда М конечнои состоит из чисел 1, 2, …, n,применяется запись /> Если M=N, то имеемобъединение последовательности множеств />.
Рассмотрим ещё одинпример: пусть М=(1; 2) и для каждого α є М определим множество Аα=[0;α]; тогда />= [0;2).
Изопределения операции объединения непосредственно следует, что она коммутативна,т.е. А1/> A2 = A2/>А1, иассоциативна, т.е. (А1/> A2) /> А3 = А1/> (A2 /> А3).
Пересечение множеств
Пересечением А ∩ Вмножеств А и В называется множество, состоящее из всех элементов, принадлежащиходновременно каждому из множеств А и В.
Символическая записьэтого определения: А ∩ В={х | х/>А и х />В}.
Пояснимопределение пересечения множеств с помощью диаграммы Эйлера-Венна:
/>
А ∩ В
На диаграммепересечение множеств А и В выделено штриховкой.
Если множество А задаетсяхарактеристическим свойством Р(х), a множество В-свойством Q(х),то в А ∩ В входят элементы, одновременно обладающие и свойством Р(х), исвойством Q(х).
Примеры пересечений двухмножеств:
1) Пусть А={2; 5; 7;8}, В={3; 5; 6; 7}.Тогда А ∩ В={5; 7}.
2) Пусть А=[-1/4;7/4], В=[-2/3; 3/2]. Тогда А ∩ В= [-1/4; 3/2].
3) Пусть А= {х |х=2k, k є Z}, B={x | x=3n, n є Z}. Тогда А ∩ В ={x | x=6m, m /> Z}.
4) Пусть А-множество всех прямоугольников, В-множество всех ромбов. Тогда А ∩ В-множество фигур, одновременно являющихся и прямоугольниками, и ромбами, т.е.множество всех квадратов.
Операциюпересечения можно определить и для произвольной системы множеств {Аα},где α /> М.Пересечением системы множеств {Аα}, называется множество />, состоящее извсех элементов, принадлежащих одновременно каждому из множеств Аα,α />М, т.е./>= {x | x/>Аα для каждогоα /> М}.
В случае,когда М конечно и состоит из чисел 1, 2, …, n, применяется запись />. Если M=N, то имеемпересечение последовательности множеств />.
Врассмотренном выше примере системы множеств Аα =[0; α],α/>М=(1; 2) получим:/>=[0;1].
Операцияпересечения множеств, как и операция объединения, очевидно, коммутативна иассоциативна, т.е. А1∩A2 = A2 ∩А1 и (А1∩A2)∩<sub/>А3= А1∩(A2 ∩ А3).
Разностьмножеств
Разностью А\Вмножеств А и В называется множество, состоящее из всех элементов множества А,которые не принадлежат множеству В, т.е.
А\В={х | х />А и х/>В},
что можнопояснить на диаграмме Эйлера-Венна следующим образом:
/>
На диаграммеразность А\В выделена штриховкой.
Примерыразностей множеств:
1. Пусть А={1; 2; 5;7}, В={1; 3; 5; 6}. Тогда А\В ={2;7}, а В\А={3; 6}.
2. Пусть А=[-1/4;2],В=[-2/3; 7/4]. Тогда А\В=(7/4;2], а В\А=[-2/3; -1/4).
3. Пусть А — множествовсех четных целых чисел, В — множество всех целых чисел, делящихся на 3. тогдаА\В — множество всех четных целых чисел, которые не делятся на 3, а В\А–множество всех нечетных целых чисел, кратных трем.
Дополнениемножества
Пустьмножество А и В таковы, что А/>В. Тогда дополнением множества Адо множества В называется разность В\А. В этом случае применяется обозначение СBА=В\А. Если в качестве множества Вберётся универсальное множество U, топрименяется обозначение СА=СUА=U\А и такое множество просто называютдополнением множества А. Таким образом, символическая запись определениядополнения множества будет следующей: /> СА={x | x />A}.
На диаграммахЭйлера-Венна можно так пояснить определения СВА и СА:
/>
/>
www.ronl.ru
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ТАВРИЧЕСКОЕ ПРДСТАВИТЕЛЬСТВО ОТКРЫТОГО МЕЖДУНАРОДНОГО УНИВЕРСИТЕТА РАЗВИТИЯ ЧЕЛОВЕКА (УКРАИНА)
Реферат
По дисциплине
«Математические основы информационной деятельности»
Тема:
«Множества и операции над ними»
студентки 2 курса
З/0 Козловой Е.А.
Преподаватель:
Глушкова Л.В.
Факультет документации
и информационной деятельности
Симферополь, 2004
Множеством именуется некоторая совокупность элементов, объединенных по какому-либо признаку. Если есть такая совокупность, разумеется, как единое целое, говорят, что имеют дело с множеством.
Приведенное определение не может рассматриваться как математически строгое, поскольку понятие множества является исходным, на основе него строятся остальные понятия математики. Тем не менее, из при веденного определения ясно, как можно говорить с множестве, например, действительных чисел или множестве плоских фигур.
Если множество состоит из конечного числа элементов, оно называется конечным. Остальные множества называются бесконечными. Для множества используются следующие обозначения:
А = {а,b, с,d}
Приведенное обозначение записано для множества А, состоящего из элементов а, Ь, с, d.
Конечные множества можно задать перечнем их элементов, бесконечные — нельзя. Обычно бесконечное множество задают, указывая на свойства, которым обладают все элементы данного множества, при этом подчеркивают, что таким свойством не обладают никакие элементы, не входящие в это множество. Такое свойство называется характеристическим для рассматриваемого множества.
Множество, в котором не содержится ни одного элемента, называется пустым. Обозначается оно знаком Æ.
Множества, состоящие из одних и тех же элементов, называют совпадающими. Например, совпадают два конечных множества, которые отличаются друг от друга порядком их элементов. Если элемент а принадлежит множеству А, то пишут:
а Î А.
В противном случае пишут:
а Ï А.
Если одно множество является частью другого множества, говорят, что первое множество является подмножеством второго. Если первое множество обозначить А, а второе В, то обозначение такое:
А Ì В.
Для любого множества А справедливы высказывания: множество А является подмножеством самого себя. Пустое множество является подмножеством любого множества.
В качестве примера можно привести высказывание о том, что множество всех ромбов является подмножеством множества параллелограммов.
Над множествами определяют операции, во многом сходные с арифметическими. Рассмотрим понятие таких операций только над двумя множествами А и В, которые являются разнообразными подмножествами одного и того же множества U. Последнее назовем универсальным множеством. Операции над множествами удобно интерпретировать геометрически с помощью диаграмм Эйлера-Венна (рис. 1 — 4).
Определение 1. Пересечением множеств А и В называют их общую часть С. Другими словами, пересечение множеств А и В образуют элементы, принадлежащие равно как А, так и В
Такое множество обозначают:
С = А Ç В
Определение 2. Объединением множеств А и В, называют множество С, составленное из элементов, принадлежащих хотя бы одному из этих множеств
Определение 3. Разностью множеств А и В называют множество
С = В \ А,
составленное из элементов, принадлежащих множеству В, но не принадлежащих множеству А
Разность U \ A называется дополнением множества А до универсального множества U и обозначается:= U \ A
Геометрическая интерпретация множества дана на следующем рисунке:
Если применять операции объединения и пересечения- к подмножествам некоторого множества D, то снова получатся подмножества того же множества D.
Операции объединения и пересечения обладают многими свойствами, похожими на свойства операций сложения и умножения чисел. Например, пересечение и объединение множеств обладают свойствами коммутативности и ассоциативности. Пересечение дистрибутивно относительно объединения, то есть для любых множеств А, В и С верно соотношение:
А Ç (В и С) = (А Ç В)и (А Ç С).
В то же время операции над множествами имеют ряд свойств, у которых нет аналогов в операциях над числами. Так, для любого множества А верны равен ства:
А Ç А = А, а также А и А = А.
И также
А и (В Ç С) = (А и В) Ç (А и С)
С помощью свойств операции над множествами можно преобразовывать выражения, содержащие множества, подобно тому, как с помощью свойств операций над числами преобразовывают выражения в алгебре. Подобные действия над множествами и изучает булева алгебра, которая названа по имени английского исследователя Дж. Буля (1815 — 1864). Какими характеристиками можно описывать множества? Основной характеристикой конечного множества Является число его элементов.
Рассмотрим два множества А и В. Если в этих множествах находится одинаковое количество элементов, то из этих элементов можно составить пары таим образом, чтобы каждый элемент из множества, как и элемент из множества. В входил в одну и только в одну пару. Таким образом, между элементами множеств. А и В устанавливается так называемое взаимно однозначное соответствие. Считается истинным обратное утверждение: если между двумя конечными множествами А и В можно установить взаимно однозначное соответствие, то такие множества содержат равное количество элементов. Было предложено аналогичным образом сравнивать между собой бесконечные множества. Если между бесконечными множествами можно установить взаимно однозначное соответствие, значит, эти множества имеют одинаковую мощность. Один из создателей теории множеств немецкий математик Георг Кантор (1845 — 1918) сравнивал при помощи такого метода множества, составленные из чисел натуральных и чисел рациональных. Он показал, что между такими множествами существует взаимно однозначное соответствие, хотя множество натуральных чисел является лишь частью множества рациональных чисел. Таким образом, в теории бесконечных множеств утверждение «часть меньше целого» теряет свою силу. Множества, имеющие ту же мощность, что и множество натуральных чисел, называют счетными.
Таким образом, множество рациональных чисел счетно.
Есть несчетные множества. В качестве примера можно рассмотреть множество всех действительных чисел (это то же самое, что множество точек на прямой линии). Поскольку прямая непрерывна или континуальна, такую несчетную мощность называют мощностью континуума. Мощностью континуума обладает множество точек, например, прямоугольника, призмы, плоскости, всего пространства. Математики всего мира в течение долгих лет рассматривали проблему — существуют ли множества, мощность которых является промежуточной между счетной и мощностью континуума.
В 60-х годах нашего столетия американский математик П. Коэн и чешский математик П. Вопенко независимо друг от друга доказали, что как существование такого множества, так и его отсутствие не противоречат остальным аксиомам теории множеств.
Современная математическая наука вводит понятие дискретное множество и само понятие множества звучит так: под множеством понимается набор, совокупность, собрание каких-либо объектов (которые называются элементами множества).
Множество, все элементы которого изолированы друг от друга, называется дискретным. Для измерения степени изолированности элементов данного множества вводится понятие расстояния между элементами. Таким расстоянием для чисел может быть, например модуль разности между ними; для точек на плоскости — геометрическое расстояние; для двоичных наборов (чисел, кодов) одинаковой длины — число разрядов, в которых они различаются (например, расстояние между наборами 10110 и 11101). Дискретное множество определяется как множество объектов, расстояние между коне меньше некоторой наперед заданной величины e.
Конечное множество всегда дискретно (в качестве e берется минимальное из расстояний между элементами этого множества). Дискретно любое множество целых чисел (для них e = 1) и любое множество дробей, имеющих общий знаменатель m (для которых e=1/m ). Всякое дискретное множество счетно, т. е. его элементы можно пронумеровать целыми числами.
Однако не всякое счетное множество дискретно, например, счетное множество не дискретно, так как с ростом nрасстояние между соседними элементами стремится к нулю. Если задано дискретное множество точек прямой с минимальным расстоянием e любой отрезок длины l может содержать не более l/e +1 точек этого множества.
Понятие дискретного множества и связанные с понятия дискретного сигнала и дискретного времени чрезвычайно важны для информатики, как они лежат в основе разделения всех устройств и систем обработки информации на два основных класса — дискретные (цифровые) и непрерывные (аналоговые) устройства и системы.
Разница между дискретным и непрерывным представлением информации хорошо видна на примере часов. В электронных часах с цифровым циферблатом информация представляется дискретно — цифрами, каждая из которых четко отличает друг от друга. В механических часах со стрелочным циферблатом информация представляется непрерывно — положениями двух стрелок, причем два разных положения стрелки не всегда четко отличимы (особенно если на циферблате нет минутных делений).
Вообще любое представление информации с помощью конечного множества символов (букв, цифр, знаков препинания, математических знаков) дискретно; графическое представление (рисунок, чертеж) непрерывно.
Типичный пример дискретного устройства — ЭВМ, состояние памяти которой представляется последовательностью двоичных цифр — нулей и единиц, все операции в ней производятся с дискретными представлениями информации. Типичные примеры аналоговых устройств — измерительные приборы, представляющие информацию положением стрелки (вольтметр, спидометр), непрерывной кривой, выдаваемой на экран (осциллограф)или на бумагу (кардиограф) и т. д.
Переход от аналоговых представлений информации к цифровым (например, ввод результатов измерений ЭВМ) и обратно в технике осуществляется специальными устройствами: аналого-цифровыми и цифро-аналоговыми преобразователями.
Список использованных источников
1. Информатика/под общ. ред. Поспелова Д.А., М: Педагогика-пресс, 1994;
2. Математика и программирование (универсальная энциклопедия)/под ред. А.А. Щуплецова, — Мн: ТОО»Харвест», 1996;
3. Окно в мир информатики/под ред. Коляды М.Г., Днепропетровск: Сталкер, 1997.
www.ronl.ru
РЕФЕРАТ
Множества. Операции над множествами
СОДЕРЖАНИЕ
Способы задания множества
Включение и равенство множеств
Диаграммы Эйлера-Венна
Операции над множествами
а) Объединение множеств
б) Пересечение множеств
в) Разность множеств
Дополнение множества
Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Оно не сводится к другим, более простым понятиям. Поэтому его нельзя определить, а можно лишь пояснить, указывая синонимы слова «множество» и приводя примеры множеств: множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством.
Примеры множеств:
1) множество студентов в данной аудитории;
2) множество людей, живущих на нашей планете в данный момент времени;
3) множество точек данной геометрической фигуры;
4) множество чётных чисел;
5) множество корней уравнения х2 -5х+6=0;
6) множество действительных корней уравнения х2 +9=0;
Основоположник теории множеств немецкий математик Георг Кантор (1845-1918) писал: «Множество есть многое, мыслимое нами как единое». И хотя это высказывание учёного не является в полном смысле логическим определением понятия множества, но оно верно поясняет, что когда говорят о множестве, то имеют в виду некоторое собрание объектов, причём само это собрание рассматривается как единое целое, как один (новый) объект.
Объекты, составляющие данное множество, называют его элементами.
Множество обычно обозначают большими латинскими буквами, а элементы множества − малыми латинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а А, а если а не принадлежит А, то пишут: а А.
Например, пусть N–множество натуральных чисел. Тогда 5N, но N, N. Если А — множество корней уравнения х2 -5х+6=0, то 3 А, а 4А.
В математике часто исследуются так называемые числовые множества, т.е. множества, элементами которых являются числа. Для самых основных числовых множеств утвердились следующие обозначения:
N- множество всех натуральных чисел;
Z- множество всех целых чисел;
Q- множество всех рациональных чисел;
R- множество всех действительных чисел.
Приняты также обозначения Z+, Q+, R+ соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и ZЇ, QЇ, RЇ -для множеств всех отрицательных целых, рациональных и действительных чисел.
Способы задания множества
Множество А считается заданным, если относительно любого объекта а можно установить, принадлежит этот объект множеству А или не принадлежит; другими словами, если можно определить, является ли а элементом множества А или не является. Существуют два основных способа задания множества:
1) перечисление элементов множества;
2) указание характеристического свойства элементов множества, т.е. такого свойства, которым обладают все элементы данного множества и только они.
Первым способом особенно часто задаются конечные множества. Например, множество студентов учебной группы задаётся их списком. Множество, состоящее из элементов a, b, c, … ,d, обозначают с помощью фигурных скобок: А={a; b; c; …;d}. Множество корней уравнения х2 -5х+6=0 состоит из двух чисел 2 и 3: А={2; 3}. Множество В целых решений неравенства -2 < х < 3 состоит из чисел –1, 0, 1, 2, поэтому В={–1; 0; 1; 2}.
Второй способ задания множества является более универсальным. Множество элементов х, обладающих данным характеристическим свойством Р(х), также записывают с помощью фигурных скобок: Х={х | Р (х)}, и читают: множество Х состоит из элементов х, таких, что выполняется свойство Р(х). Например, А={х | х2 -5х+6=0}. Решив уравнение х2 -5х+6=0, мы можем записать множество А первым способом: А={2; 3}.
Другой пример: Х={х | -1 ≤ х < 4, х Z}, т.е. Х есть множество целых чисел х, таких, что –1 ≤ х < 4, значит, по-другому: Х={-1; 0; 1; 2; 3}.
Рассмотрим и такой пример: F={f | │fґ(x)│≤ 1, 1 < x < 2}, т.е. F- множество функций f, производная которых в интервале (1; 2) не превосходит по абсолютной величине числа 1.
Может случиться, что характеристическим свойством, определяющим множество А, не обладает ни один объект. Тогда говорят, что множество А — пустое (не содержит ни одного элемента) и пишут: А= Ш.
Например, А={х | хІ+9=0, хR} –множество действительных чисел х, таких, что хІ+9=0- пустое множество, т.к. таких действительных чисел нет.
Включение и равенство множеств
Пусть Х и У – два множества. Если каждый элемент х множества Х является элементом множества У, то говорят, что множество Х содержится во множестве У и пишут: Х У или У Х. Говорят также, что Х включено в У или У включает Х, или что Х является подмножеством множества У. Знаки включения или относятся только ко множествам и их не следует смешивать со знаками принадлежности Î и . Если, например, А — множество всех студентов вуза, а В – множество студентов-первокурсников этого вуза, то В есть подмножество А, т.е. В А. Пустое множество считают подмножеством любого множества Х, т.е. Ш Х, каким бы ни было множество Х. Ясно также, что каждое множество является подмножеством самого себя: Х Х.
Если для двух множеств Х и У одновременно имеют место два включения Х У и У Х, т.е. Х есть подмножество множества У и У есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У. Например, если А={2; 3}, а В={х | хІ –5х+6=0}, то А=В.
Если Х У, но Х≠ У, т.е. существует хотя бы один элемент множества У, не принадлежащий Х, то говорят, что Х есть собственное подмножество множества У, и пишут: Х У. Например: NZ, ZQ, QR. Далее нам потребуется множество, которое содержит в качестве своего подмножества любое другое множество. Такое «всеобъемлющее» множество будем называть универсальным и обозначать буквой U .
Диаграммы Эйлера-Венна
Для наглядного представления множеств используют диаграммы Эйлера-Венна. В этом случае множества обозначают областями на плоскости и внутри этих областей условно располагают элементы множества. Часто все множества на диаграмме размещают внутри прямоугольника, который представляет собой универсальное множество U. Если элемент принадлежит более чем одному множеству, то области, отвечающие таким множествам, должны перекрываться, чтобы общий элемент мог одновременно находиться в соответствующих областях. Выбор формы областей, изображающих множества на диаграммах, может быть произвольным (круги, внутренности эллипсов, многоугольники и т.п.). Покажем, например, с помощью диаграммы Эйлера-Венна, что множество А является подмножеством множества В:
С помощью такой диаграммы становиться наглядным, например, такое утверждение:
если АВ, а В С, то АС.
Строгое доказательство этого утверждения, не опирающееся на диаграмму, можно провести так: пусть х А; так как А В, то х В, а так как В С, то из х В следует, что х С; значит, из того, что х А, следует хС, а поэтому А С.
Операции над множествами
С помощью нескольких множеств можно строить новые множества или, как говорят, производить операции над множествами. Мы рассмотрим следующие операции над множествами: объединение, пересечение, разность множеств, дополнение множества. Все рассматриваемые операции над множествами мы будем иллюстрировать на диаграммах Эйлера-Венна.
Объединение множеств
Объединением АВ множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.
Символическая запись этого определения: А В={х | хА или хВ}.
Здесь союз «или» понимается в смысле «неразделительного или», т.е. не исключается, что х может принадлежать и А и В. Отметим, что в таком случае элемент х, входящий в оба множества А и В, входит в их объединение только один раз (поскольку для множества не имеет смысла говорить о том, что элемент входит в него несколько раз).
Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:
На диаграмме объединение множеств А и В выделено штриховкой.
Если множество А определяется характеристическим свойством Р (х), а множество В — характеристическим свойством Q(х), то А В состоит из всех элементов, обладающих, по крайней мере, одним из этих свойств.
Примеры объединений двух множеств:
1) Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда А В ={2; 3; 5; 6; 7}.
2) Пусть А=[-1/4; 2], В=[ -2/3; 7/4]. Тогда А В=[-2/3; 2] .
3) Пусть А= {х | х=8k, k Z}, B={x | x=8n-4, n Z}. Тогда A B ={x | 4m, mZ}.
Операция объединения множеств может проводиться не только над двумя множествами. Определение объединения множеств можно распространить на случай любого количества множеств и даже – на систему множеств. Система множеств определяется так: если каждому элементу α множества М отвечает множество Аα, то совокупность всех таких множеств мы будем называть системой множеств.
Объединением системы множеств {Аα } называется множество , состоящее из всех элементов, принадлежащих хотя бы одному из множеств Аα. При этом общие элементы нескольких множеств не различаются.
Таким образом, элемент хтогда и только тогда, когда найдется такой индекс α0 М, что х A α0.
В случае, когда М конечно и состоит из чисел 1, 2, …, n, применяется запись Если M=N, то имеем объединение последовательности множеств .
Рассмотрим ещё один пример: пусть М=(1; 2) и для каждого α є М определим множество Аα =[0;α]; тогда = [0;2).
Из определения операции объединения непосредственно следует, что она коммутативна, т.е. А1A2 = A2 А1, и ассоциативна, т.е. (А1A2 ) А3 = А1(A2 А3 ).
Пересечение множеств
Пересечением А ∩ В множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств А и В.
Символическая запись этого определения: А ∩ В={х | хА и х В}.
Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:
А ∩ В
На диаграмме пересечение множеств А и В выделено штриховкой.
Если множество А задается характеристическим свойством Р(х), a множество В-свойством Q(х), то в А ∩ В входят элементы, одновременно обладающие и свойством Р(х), и свойством Q(х).
Примеры пересечений двух множеств:
1) Пусть А={2; 5; 7; 8}, В={3; 5; 6; 7}.Тогда А ∩ В={5; 7}.
2) Пусть А=[-1/4; 7/4], В=[-2/3; 3/2]. Тогда А ∩ В= [-1/4; 3/2].
3) Пусть А= {х | х=2k, k є Z}, B={x | x=3n, n є Z}. Тогда А ∩ В ={x | x=6m, m Z}.
4) Пусть А- множество всех прямоугольников, В-множество всех ромбов. Тогда А ∩ В -множество фигур, одновременно являющихся и прямоугольниками, и ромбами, т.е. множество всех квадратов.
Операцию пересечения можно определить и для произвольной системы множеств {Аα }, где α М. Пересечением системы множеств {Аα }, называется множество , состоящее из всех элементов, принадлежащих одновременно каждому из множеств Аα, α М, т.е. = {x | xАα для каждого α М}.
В случае, когда М конечно и состоит из чисел 1, 2, …, n, применяется запись . Если M=N, то имеем пересечение последовательности множеств .
В рассмотренном выше примере системы множеств Аα =[0; α], αМ =(1; 2) получим:=[0;1].
Операция пересечения множеств, как и операция объединения, очевидно, коммутативна и ассоциативна, т.е. А1 ∩A2 = A2 ∩А1 и (А1 ∩A2 )∩ А3 = А1 ∩(A2 ∩ А3 ).
Разность множеств
Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.
А\В={х | х А и хВ},
что можно пояснить на диаграмме Эйлера-Венна следующим образом:
На диаграмме разность А\В выделена штриховкой.
Примеры разностей множеств:
1. Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда А\В ={2;7}, а В\А={3; 6}.
2. Пусть А=[-1/4;2], В=[-2/3; 7/4]. Тогда А\В=(7/4;2], а В\А=[-2/3; -1/4).
3. Пусть А — множество всех четных целых чисел, В — множество всех целых чисел, делящихся на 3. тогда А\В — множество всех четных целых чисел, которые не делятся на 3, а В\А –множество всех нечетных целых чисел, кратных трем.
Дополнение множества
Пусть множество А и В таковы, что АВ. Тогда дополнением множества А до множества В называется разность В\А. В этом случае применяется обозначение СB А=В\А. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СU А=U\А и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей: СА={x | x A}.
На диаграммах Эйлера-Венна можно так пояснить определения СВ А и СА:
www.ronl.ru
Министерство образования Российской Федерации
Вологодский государственный педагогический университет
Методические материалы
к практическим занятиям по математике
для студентов-гуманитариев
Вологда
“Русь”
2008
УДК Печатается по решению Ученого Совета ВГПУ от
В работе приведена подборка задач для практических занятий по математике со студентами гуманитарных факультетов (иностранных языков, исторического, отделения культурологии). Для каждого занятия составлены также контрольные вопросы и задачи для самостоятельного решения. Приведены примерные варианты контрольных работ.
Составители: и. о. доцента, кандидат технических наук А.Ю. Белянина,
доцент, кандидат физико-математических наук Т.В. Васильева,
ст. преподаватель М. А.Доброва
Рецензент: доцент, кандидат физико-математических наук Н. Г. Чернышева.
Ответственный за выпуск:
профессор, доктор пед. наук В.А. Тестов.
Вологодский государственный
педагогический университет,
издательство “Русь”, 2008 г.
Выписка из государственного стандарта.
Математика. Аксиоматический метод, основные математические структуры, вероятность и статистика, математические модели.
Выписка из учебного плана:
Факультет иностранных языков: лекции – 34 часа, практические занятия – 16 часов.
Исторический факультет: лекции – 12 часов, практические занятия – 18 часов.
Занятие 1.
1. Приведите примеры конечных и бесконечных множеств.
Перечислите способы задания множеств.
Назовите несколько подмножеств
а) множества натуральных чисел; б) множества геометрических фигур.
4. Какие множества называются равными? Какие из следующих множеств геометрических фигур на плоскости равны между собой:
A – множество всех квадратов;
B - множество всех прямоугольников;
C - множество всех четырехугольников с прямыми углами;
D - множество всех прямоугольников с равными сторонами;
F - множество всех ромбов с прямыми углами?
5. Перечислите основные операции над множествами. Для каждой операции сформулируйте определение и приведите простые примеры.
1. Запишите множество A, элементами которого являются натуральные делители числа 24, используя перечисление элементов множеств.
2. Даны множества: A={а, и, о, у, э, ы}, B={111, 222, 333, 444, 555, 666, 777, 888, 999}, C={0, 2, 4, 6, 8}. Задайте каждое из них описанием характеристического свойства.
Даны числа: 19; 
; 0; -27; 5,4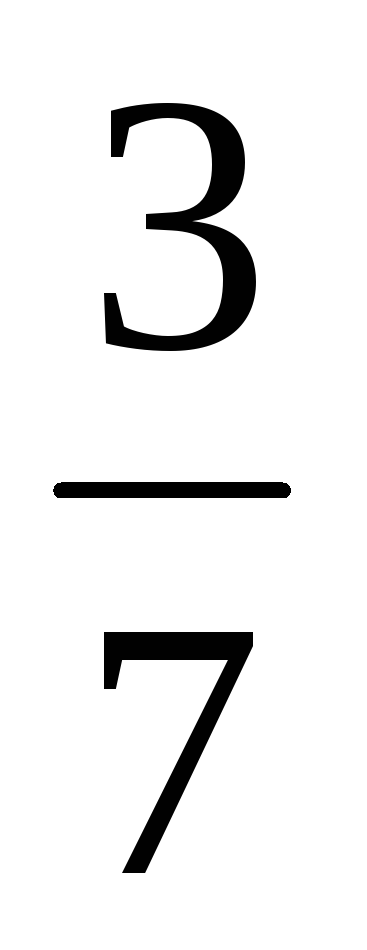
. Какие из них принадлежат множеству: а) целых чисел; б) целых неотрицательных чисел; в) рациональных чисел; г) действительных чисел?
Изобразите на координатной прямой множество Х, если
Х = {xxR, -2 x 7};
Х = {xxZ, -1 x 3};
Х = {xxN, -2 x 3}.
Изобразите на координатной прямой множество решений неравенства: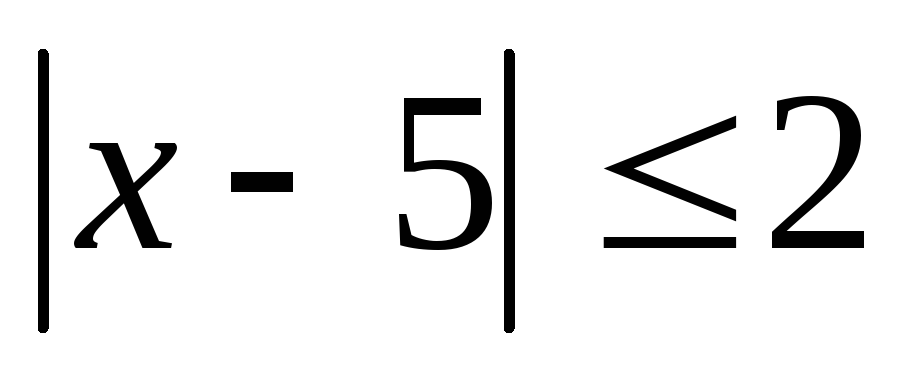 
.
Найдите множество решений уравнения, используя формулу для расстояния между двумя точками координатной прямой: а)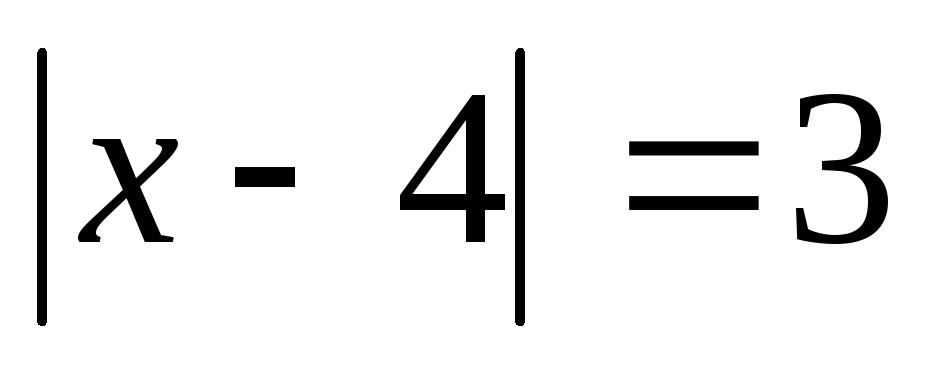 
; б)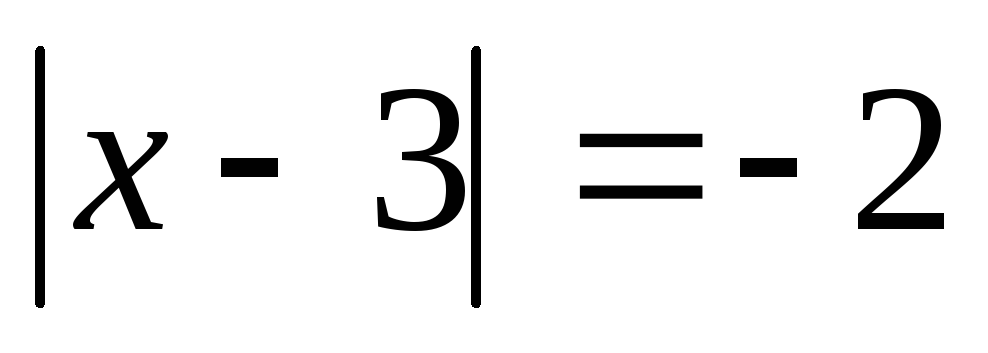 
.
Дано множество A={72, 56, 513, 117, 324}. Составьте подмножества данного множества, состоящие из чисел, которые:
а) делятся на 4;
б) делятся на 9;
в) делятся на 5;
г) не делятся на 10.
Изобразите при помощи кругов Эйлера множества P и Qi, если P – множество равнобедренных треугольников,
а) Q1 – множество остроугольных треугольников;
б) Q2 – множество прямоугольных треугольников;
в) Q3 – множество равносторонних треугольников.
Изобразите все четыре множества на одном чертеже.
Пусть A- множество натуральных чисел, запись которых оканчивается 0, B - множество натуральных чисел, кратных 10. Докажите, что множества A и B равны.
Известно, что N множество натуральных чисел, Z – множество целых чисел. Докажите, что высказывание Z N ложно.
11. Изобразите при помощи кругов Эйлера множества A, B и C, если:
а) А множество четных целых чисел,
B множество целых чисел, кратных 4;
b) А множество четных целых чисел,
В множество целых чисел, кратных 2;
с) А множество нечетных целых чисел,
В множество целых чисел, кратных 3,
С множество чисел, кратных 5.
Отношения между множествами всех выпуклых четырехугольников, параллелограммов, прямоугольников, ромбов и квадратов изображены на рисунке. Покажите каждое из множеств.
А D
F
Рис. 1
Установите, в каком отношении находятся множества А и В, если А = {a, b, c, d}, а множество В:
а) {k, l, m}; b) {b, c, o, f, k}; с) {b, d}.
Задания для самостоятельной работы.
I. Повторите теоретический материал по теме Множества. Операции над множествами. Попытайтесь ответить на контрольные вопросы к занятию 2.
II. Решите задачи:
1. Для каждого из слов “сосна“, “осколок“, “насос“, “колосс“, “сокол“ составьте множество его различных букв. Имеются ли среди полученных множеств равные?
2. Найдите все подмножества множества М =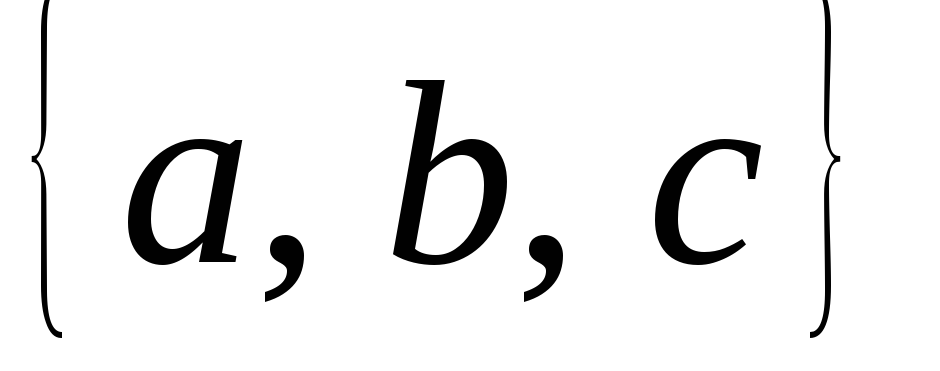 
. Сколько подмножеств получилось?
3. В каких отношениях находятся множества решений неравенств:
а)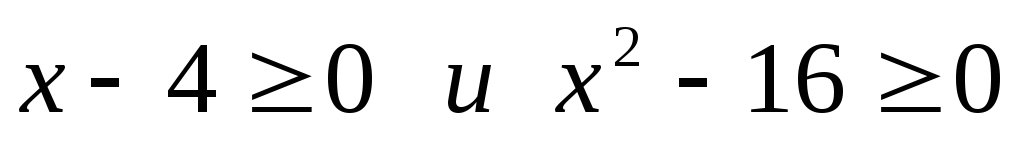 
; б)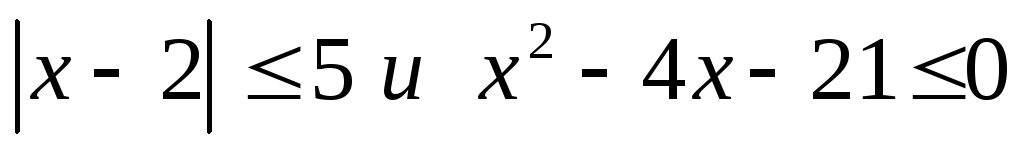 
?
4. А – множество двузначных чисел, В – множество четных натуральных чисел, С – множество чисел, кратных числу 4. В каком из случаев изображены данные множества? Приведите примеры множеств для двух других случаев.
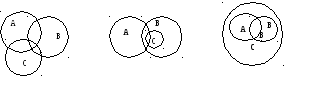
а) б) в)
5. Задайте множество D, элементами которого являются натуральные числа, меньшие семи.
studfiles.net
Контрольная работа по теме «Множества и операции над ними»
Вариант № 1
Даны два множества: А – множество четных цифр, В – множество нечетных цифр. Каким способом заданы множества? Задайте множества другим способом. В каком отношении находятся данные множества?
Для данных множеств: 
, 
, 
найдите и изобразите с помощью кругов Эйлера (декартово произведение – на плоскости) результаты операций:
;
;
Постройте три круга, представляющие попарно пересекающиеся множества А, В, С, и отметьте штриховкой области, изображающие множества:
Изобразите в прямоугольной системе координат множество 
, если
Из 53 студентов курса 28 человек занимаются по дополнительной программе «Математика», 32 человека – по программе «Информатика и ИКТ», 12 человек занимаются по обеим дополнительным общеобразовательным общеразвивающим программам. Сколько студентов не занимается ни по одной дополнительной программе?
Контрольная работа по теме «Множества и операции над ними»
Вариант № 2
Даны два множества: А – множество отрицательных целых чисел первого десятка, В – множество положительных целых чисел первого десятка. Каким способом заданы множества? Задайте множества другим способом. В каком отношении находятся данные множества?
Для данных множеств: 
, 
, 
найдите и изобразите с помощью кругов Эйлера (декартово произведение – на плоскости) результаты операций:
;
;
Постройте три круга, представляющие попарно пересекающиеся множества А, В, С, и отметьте штриховкой области, изображающие множества:
Изобразите в прямоугольной системе координат множество , если
В группе студентов 17 человек знает английский язык, 13 человек знает немецкий язык, 4 человека знает и английский и немецкий. Сколько человек в группе, если известно, что каждый студент знает хотя бы один язык?
videouroki.net
