Контрольная работа №1 по теме «Равномерное прямолинейное движение. Средний модуль скорости произвольного движения» Контрольная работа №. Контрольная равномерное прямолинейное движение
Примеры решения задач по теме «Равномерное прямолинейное движение»





«Физика - 10 класс»
При решении задач по данной теме необходимо прежде всего выбрать тело отсчёта и связать с ним систему координат. В данном случае движение происходит по прямой, поэтому для его описания достаточна одна ось, например ось ОХ. Выбрав начало отсчёта, записываем уравнения движения.
Задача I.
Определите модуль и направление скорости точки, если при равномерном движении вдоль оси ОХ её координата за время t1 = 4 с изменилась от х1 = 5 м до х2 = -3 м.
Р е ш е н и е.
Модуль и направление вектора можно найти по его проекциям на оси координат. Так как точка движется равномерно, то проекцию её скорости на ось ОХ найдём по формуле

Отрицательный знак проекции скорости означает, что скорость точки направлена противоположно положительному направлению оси ОХ. Модуль скорости υ = |υх| = |-2 м/с| = 2 м/с.
Задача 2.
Из пунктов А и В, расстояние между которыми вдоль прямого шоссе l0 = 20 км, одновременно навстречу друг другу начали равномерно двигаться два автомобиля. Скорость первого автомобиля υ1 = 50 км/ч, а скорость второго автомобиля υ2 = 60 км/ч. Определите положение автомобилей относительно пункта А спустя время t = 0,5 ч после начала движения и расстояние I между автомобилями в этот момент времени. Определите пути s1 и s2, пройденные каждым автомобилем за время t.

Р е ш е н и е.
Примем пункт А за начало координат и направим координатную ось ОХ в сторону пункта В (рис. 1.14). Движение автомобилей будет описываться уравнениями
x1 = х01 + υ1xt, x2 = х02 + υ2xt.
Так как первый автомобиль движется в положительном направлении оси ОХ, а второй — в отрицательном, то υ1x = υ1, υ2x = —υ2. В соответствии с выбором начала координат х01 = 0, х02 = l0. Поэтому спустя время t
x1 = υ1t = 50 км/ч • 0,5 ч = 25 км;
х2 = l0 — υ2t = 20 км - 60 км/ч • 0,5 ч = -10 км.
Первый автомобиль будет находиться в точке С на расстоянии 25 км от пункта А справа, а второй — в точке D на расстоянии 10 км слева. Расстояние между автомобилями будет равно модулю разности их координат: l = |х2 - x1| = |—10 км - 25 км| = 35 км. Пройденные пути равны:
s1 = υ1t = 50 км/ч • 0,5 ч = 25 км,
s2 = υ2t = 60 км/ч • 0,5 ч = 30 км.
Задача 3.
Из пункта А в пункт В выезжает первый автомобиль со скоростью υ1 Спустя время t0 из пункта В в том же направлении со скоростью υ2 выезжает второй автомобиль. Расстояние между пунктами A и В равно l. Определите координату места встречи автомобилей относительно пункта В и время от момента отправления первого автомобиля, через которое они встретятся.

Р е ш е н и е.
Примем пункт А за начало координат и направим координатную ось ОХ в сторону пункта В (рис. 1.15). Движение автомобилей будет описываться уравнениями
x1 = υ1t, х2 = l + υ2( t - t0).
В момент встречи координаты автомобилей равны: х1 = х2 = хв. Тогда υ1tв = l + υ2( tв - t0) и время до встречи 
Очевидно, что решение имеет смысл при υ1 > υ2 и l > υ2t0 или при υ1 < υ2 и l < υ2t0. Координата места встречи 
Задача 4.
На рисунке 1.16 представлены графики зависимости координат точек от времени. Определите по графикам: 1) скорости точек; 2) через какое время после начала движения они встретятся; 3) пути, пройденные точками до встречи. Напишите уравнения движения точек.

Р е ш е н и е.
За время, равное 4 с, изменение координаты первой точки: Δx1 = 4 - 2 (м) = 2 м, второй точки: Δх2 = 4 - 0 (м) = 4 м.
1) Скорости точек определим по формуле  υ1x = 0,5 м/с; υ2x = 1 м/с. Заметим, что эти же значения можно было получить по графикам, определив тангенсы углов наклона прямых к оси времени: скорость υ1x численно равна tgα1, а скорость υ2x численно равна tgα2.
υ1x = 0,5 м/с; υ2x = 1 м/с. Заметим, что эти же значения можно было получить по графикам, определив тангенсы углов наклона прямых к оси времени: скорость υ1x численно равна tgα1, а скорость υ2x численно равна tgα2.
2) Время встречи — это момент времени, когда координаты точек равны. Очевидно, что tв = 4 с.
3) Пути, пройденные точками, равны их перемещениям и равны изменениям их координат за время до встречи: s1 = Δх1= 2 м, s2 = Δх2 = 4 м.
Уравнения движения для обеих точек имеют вид х = х0 + υxt, где х0 = x01 = 2 м, υ1x = 0,5 м/с — для первой точки; х0 = х02 = 0, υ2x = 1 м/с — для второй точки.
Источник: «Физика - 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика - Физика, учебник для 10 класса - Класс!ная физика
Физика и познание мира --- Что такое механика --- Механическое движение. Система отсчёта --- Способы описания движения --- Траектория. Путь. Перемещение --- Равномерное прямолинейное движение. Скорость. Уравнение движения --- Примеры решения задач по теме «Равномерное прямолинейное движение» --- Сложение скоростей --- Примеры решения задач по теме «Сложение скоростей» --- Мгновенная и средняя скорости --- Ускорение --- Движение с постоянным ускорением --- Определение кинематических характеристик движения с помощью графиков --- Примеры решения задач по теме «Движение с постоянным ускорением» --- Движение с постоянным ускорением свободного падения --- Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» --- Равномерное движение точки по окружности --- Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение --- Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями --- Примеры решения задач по теме «Кинематика твёрдого тела»
Устали? - Отдыхаем!


Вверх
class-fizika.ru
Решение задач по теме "Равномерное прямолинейное движение"

Разделы: Физика
Тип урока: повторение и закрепление знаний, использую метод ключевых учебных ситуаций.
Образовательная цель: получение учащихся, усвоивших основные знания в данной теме:
- механическое движение – это изменение положения тела в пространстве относительно других тел с течением времени;
- основная задача механики – определение положения тела в любой момент времени;
- траектория движения – линия, вдоль которой движется тело;
- путь – физическая величина, равная длине траектории, пройденной телом за некоторый промежуток времени;
- перемещение – отрезок соединяющий начальное и конечное положение;
- при равномерном движении путь прямо пропорционален времени движения;
- график прямой пропорциональности – прямая, проходящая через начало координат;
- скорость равномерного движения – это физическая величина, характеризующая быстроту движения тела; она определяется отношением пути, пройденного телом, к отрезку времени, за которое был пройден этот путь.
Цель по развитию учащихся: подготовка учащихся, овладевших следующими видами деятельности:
- получать понятие “механическое движение”;
- получать понятие о физических величинах “путь”, “перемещение”, “координата”, “скорость”;
- получать график прямо пропорциональной зависимости пути от времени, координаты от времени с учетом погрешности;
- строить графики зависимости пути от времени, координаты от времени и скорости равномерного движения от времени;
- вычислять скорость, путь, перемещение и координату равномерного движения.
Задачи урока:
- повторить основные понятия и физические величины прямолинейного равномерного движения;
- создать условия для развития личности учеников в процессе их деятельности;
- способствовать развитию практических навыков и умений;
- научить выделять главное, сравнивать, развивать способности к обобщению, систематизации полученных знаний.
Этапы проведения урока:
- Организационный момент.
- Актуализация ранее усвоенных знаний.
- Системная актуализация.
- Контроль и самопроверка знаний.
- Рефлексия.
Ход урока
I. Актуализация раннее усвоенных знаний. (Решение качественных задач. Они позволяют учителю понять, как учащиеся усвоили теоретический материал по данной теме.)
1. Туристы перешли с одного берега озера, где располагалась их база, на другой и, посмотрев на часы, решили устроить краткий отдых. Стояла тихая погода, и им были хорошо слышны передачи радиоузла базы; поэтому последние известия они смогли прослушать, выключив свой транзистор. После этого один из туристов заявил, что расстояние до базы – почти 3 км. Каким образом он определил это расстояние? (Турист знал, что скорость звука воздухе при 20oС 340м/с. Он заметил, что сигналы точного времени, передаваемые по радио, слышны вначале из радиоприемника, а спусти некоторое время – с базы. Определив время запаздывания, он по формуле s = vзвt рассчитал расстояние до базы.)
2. Выехав рано утром из города на ровное и пустынное шоссе, шофер решил устроить первую остановку ровно через час. Как ему выполнить свое намерение, не смотря на часы? Радиоприёмник в автомобиле отсутствует. (В любом автомобиле есть счетчик пути и спидометр. Поэтому шофер должен поддерживать постоянной взятую скорость движения и дождаться увеличение километража пробега на величину, численно равную этой скорости.)
3. “Мировой рекорд” по прыжкам в высоту среди животных принадлежит маленькой южноафриканской антилопе. На какую высоту прыгнет антилопа, если она отталкивается от земли вверх со скоростью 12 м/с? (7,2 м.)
4. Человек, плывущий по реке на лодке, держится середины реки, если плывет по течению, и старается держаться около берега, если плывет против течения. Почему он так делает? (В первом случае скорость его перемещения возрастает благодаря значительной помощи течения, у которого скорость на середине реки наибольшая. Во втором случае течение реки будет мало мешать движению, поскольку у берегов скорость воды в реке всегда меньше, чем на середине.)
II. Решение задач
1. Даны уравнения движения трех различных тел, заданные в одной и той же системе координат: x1 = -20 +5t; x2 = 10 -4t; x3 = 2t. Все данные указаны в СИ.
Определите начальные координаты и проекции скоростей для каждого тела. Постройте графики зависимости координаты и проекции скорости от времени для каждого из движущихся тел.
| Деятельность учителя | Деятельность учеников |
| Запишите значения начальных координат для каждого из тел. | х01=______; х02=______; х03=______. |
| Запишите значения проекций скоростей для каждого из тел с учетом знака проекций. | vх1=______; vх2=______; vх3=______; |
| Заполните таблицы значений координат тел для двух выбранных моментов времени. | |
| Изобразите на графике координаты, которые занесены в таблицы для каждого из тел. Проведите через построенные точки графики зависимости координаты от времени для каждого из тел. | |
| Пользуясь результатами нахождения проекций скоростей, изобразите точки, соответствующие проекциям скоростей тел и постойте графики для каждого из тел. | |
Первую задачу решают учащиеся совместно с учителем. Потом предлагаем учащимся самим сформулировать задачи на нахождения начальной координаты, проекции скорости, координаты в определенный момент времени и построение графиков зависимости координаты и проекции скорости от времени.
2. Из двух пунктов А и В, расположенных на расстоянии S = 800 м друг от друга, одновременно навстречу друг другу начинают двигаться прямолинейно и равномерно два пешехода. Первый из них, вышедший из пункта А, движется равномерно со скоростью 4,5 км/ч. С какой скоростью движется второй пешеход, вышедший из пункта В, если встреча пешеходов произошла через 6 мин после начала движения? На каком расстоянии от пункта А встретились пешеходы?
| Деятельность учителя | Деятельность учеников |
| Выберете систему координат для описания движения пешеходов. | Координатную ось направим _________ Тело отчета поместим в точку ________ |
| Запишите уравнение движения пешехода, вышедшего из пункта А, в выбранной системе координат. | х1(t)=_______________________ |
| Чему равна начальная координата первого пешехода? | х01=______ |
| Чему равна конечная координата первого пешехода в момент времени со вторым пешеходом? | х1=______ |
| Чему равна величина проекции скорости первого пешехода? | vх1=______ |
| Запишите уравнение движения второго пешехода, вышедшего из пункта В, в выбранной системе координат. | х2(t)=_______ |
| Чему равна начальная координата второго пешехода? | х02=______ |
| Чему равна конечная координата второго пешехода в момент времени с первым пешеходом? | х2= ______ |
| Чему равна величина проекции скорости второго пешехода? | vх2=______; |
| Каков знак проекции скорости второго пешехода? | |
| Составьте систему из уравнений движения обоих пешеходов с учетом того, что в момент встречи координаты пешеходов одинаковы. | х1 = х2 |
| Проанализируйте данную систему уравнений и покажите, что она может быть решена относительно неизвестных v2 и х. | v2 __________ х _________ |
| Запишите ответ в общем виде для координаты точки встречи пешеходов. | |
| Проверьте наименование искомых величин по полученным формулам. | |
Вторую задачу решают учащиеся совместно с учителем. Потом предлагаем учащимся самим сформулировать задачи на определение скорости движения, место встречи и время встречи.
III. Решение теста по теме “равномерное прямолинейное движение” с последующий проверкой и разбором заданий 3 и 5. (15 минут)
1. Движутся три тела: улитка по стеблю растения (1), моторная лодка по поверхности воды (2) и реактивный самолет в небе (3). Движение тела можно характеризовать траекторией
1) только в случае 1
2) только в случае 2
3) только в случае 3
4) во всех трех случаях
2. Наблюдатель у палатки фиксирует с помощью прибора расстояние до всадников, которые скачут в степи с постоянной скоростью. Результаты его измерений представлены в таблице.
| t, с | 0 | 4 | 8 | 12 | 16 |
| S1, м | 430 | 410 | 390 | 370 | 350 |
| S2, м | 170 | 210 | 270 | 310 | 350 |
1) оба всадника удаляются от палатки
2) расстояние между всадниками постоянно сокращается
3) первый всадник приближается к палатке, второй – удаляется от нее
4) на шестнадцатой секунде всадники встретились
3. Муха равномерно переместилась по отрезку длиной 80 мм за 2 с. Чему равна скорость мухи?
Ответ: _________ м/с (0,04)
4. Уравнение движения тел имеют вид: x1 = -200 + t; x2 = -20t; x3 =0. Как и в каком направлении движутся тела?
К каждой позиции первого столбика подберите соответствующую позицию второго столбика. Цифры могут повторяться. (231)
| Тело | Вид движения |
| А) первое | 1) покоится |
| Б) второе | 2) равномерно по оси |
| В) третье | 3) равномерно против оси |
5. Тело движется прямолинейно вдоль оси ОX согласно зависимости координаты от времени x(t) = -8t + 3 (м). Чему равна координата этого тела через 5 с после начала движения?
После решения теста, учащиеся совместно с учителем проверяют ответы теста и разбирают у доски 3 и 5 задания.
3. Муха равномерно переместилась по отрезку длиной 80 мм за 2 с. Чему равна скорость мухи?
| Деятельность учителя | Деятельность учеников |
| Читаем внимательно условие задачи. | Читают условие и вникают в смысл задачи. |
| Выясняем что известно в данной задачи. | Путь, время. |
| Что необходимо найти в задании? | Скорость мухи. |
| Записываем условие задачи. | Записывают условие задачи. |
| Какая основная единица измерения пути? | м |
| Формула по которой вычисляется скорость? |  = =  |
| Все ли физические величины известны для вычисления скорости? | Да. |
| Вычисляем скорость равномерного движения. | Записывают решение задачи. |
5. Тело движется прямолинейно вдоль оси ОX согласно зависимости координаты от времени x(t) = -8t + 3 (м). Чему равна координата этого тела через 5 с после начала движения?
| Деятельность учителя | Деятельность учеников |
| Читаем внимательно условие задачи. | Читают условие и вникают в смысл задачи. |
| Выясняем что известно в данной задачи. | x0, v, t |
| Что необходимо найти в задании? | x |
| Записываем условие задачи. | Записывают условие задачи. |
| По какой формуле вычисляется координата тела равномерного движения. | x = x0 + vxt |
| Все ли физические величины известны для вычисления координаты? | Да. |
| Подставляем значения и вычисляем координату движения. | Записывают решение задачи. |
IV. Рефлексия. Подведение итогов урока. Домашнее задание.
Вспоминаем цель урока. Анализируем степень ее достижения. Формулируем выводы. Оцениваем успешность своей работы на уроке и уровень усвоения знаний.
xn--i1abbnckbmcl9fb.xn--p1ai
Равномерное прямолинейное движение
Равномерное прямолинейное движение -- это движение с постоянной скоростью, при котором ускорение отсутствует, а траектория движения представляет собой прямую линию.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена так же, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости: $\left\langle v\right\rangle =v$
Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.
Перемещение при равномерном прямолинейном движении определяется формулой:
$$ \overrightarrow{S} = \overrightarrow{v} \cdot t $$ Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна: $v_x = v$, то есть $v $>$ 0$
Проекция перемещения на ось ОХ равна: $s = v_t = x - x0$
где $x_0$ - начальная координата тела, $х$ - конечная координата тела (или координата тела в любой момент времени)
Уравнение движения, то есть зависимость координаты тела от времени $х = х(t)$, принимает вид: $х = x_0 + v_t$
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля ($v $
Зависимость проекции скорости тела от времени показана на рис. 1. Так как скорость постоянна ($v = const$), то графиком скорости является прямая линия, параллельная оси времени Ot.
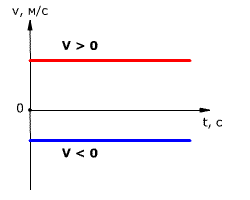
Рис. 1. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.
Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 2), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
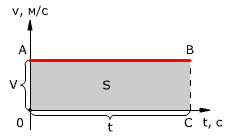
Рис. 2. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
График зависимости перемещения от времени показан на рис. 3. Из графика видно, что проекция скорости на ось Ot численно равна тангенсу угла наклона графика к оси времени:
\[v=\frac{S_1}{t_1}=tg\alpha \] 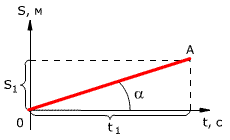
Рис. 3. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
Зависимость координаты от времени показана на рис. 4. Из рисунка видно, что
tg $\alpha $1 $>$ tg $\alpha $2, следовательно, скорость тела 1 выше скорости тела 2 (v1 $>$ v2).
tg $\alpha $3 = v3 $
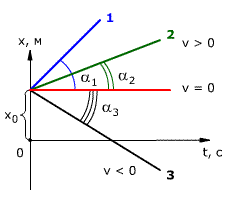
Рис. 4. Зависимость координаты тела от времени при равномерном прямолинейном движении.
Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть х = х0
Задача 2
Определить скорость течения реки и скорость катера в стоячей воде, если известно, что катер проходит расстояние 300 километров по течению за 4 часа, а против течения -- за 6 часов.
Дано: $L$=300000 м; $t_1$=14400 с; $t_2$=21600 с
Найти: $v_p$ - ?; $v_k$ - ?
Решение:
Скорость катера по течению реки относительно берега $v_1=v_k+v_p$, а против течения $v_2=v_k-v_p$ . Запишем закон движения для обоих случаев:
\[L=v_1t_1=\left(v_k+v_p\right)t_1; L=v_2t_2=\left(v_k-v_p\right)t_2\] Решив уравнения относительно vp и vk, получаем формулы для расчета скорости течения реки и скорости катера.
Скорость течения реки: $v_p=\frac{L\left(t_2-t_1\right)}{2t_1t_2}=\frac{300000\left(21600-14400\right)}{2\times 14400\times 21600}=3,47\ м/с$
Скорость катера: $v_к=\frac{L\left(t_2+t_1\right)}{2t_1t_2}=\frac{300000\left(21600+14400\right)}{2\times 14400\times 21600}=17,36\ м/с$
Ответ: скорость течения реки равна 3,47 метров в секунду, скорость катера равна 17,36 метров в секунду.
author24.ru
Контрольные вопросы
1. Как связан вектор перемещения тела с его координатами ?
2. В чем различие между перемещением и пройденным путем при прямолинейном движении ?
3. Какая имеется связь между скоростью тела и изменением его положения в пространстве ?
4. Зависит ли перемещение тела от выбора системы отсчета ?
5. Как определяется радиус-вектор и какова связь между радиусом-вектором некоторой точки и ее координатами ?
Равномерное прямолинейное движение Примеры решения задач
1. Два самолета одновременно вылетают из одного места по двум взаимно перпендикулярным направлениям. Один со скоростью v1 = 300 км/ч, другой со скоростью v2 = 400 км/ч. Как возрастает со временем расстояние между самолетами? Чему равно это расстояние S в момент, когда первый самолет пролетел путь S1 = 900 км?
Решение. Выберем декартову систему отсчета, ось x которой направлена параллельно скорости первого самолета, а ось y - параллельно скорости второго самолета. Пусть место вылета самолетов находится в начале координат. Тогда движение первого самолета происходит вдоль оси с постоянной скоростью v1, а второго - вдоль оси y с постоянной скоростью v2, и закон движения будет иметь вид:
x= v1t- для первого самолета,
y= v2t- для второго.
Очевидно, что расстояние между самолетами равно
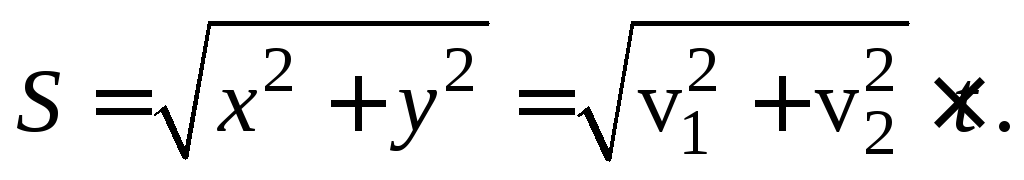
Первый самолет пролетел путь S1за время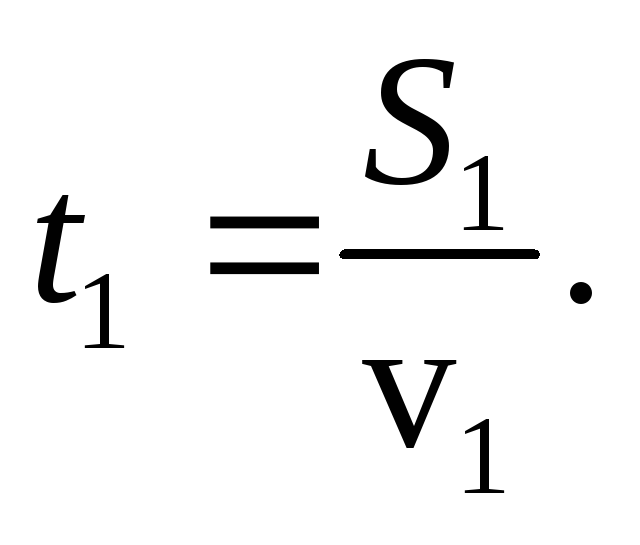 Расстояние между самолетами в этот момент, очевидно, будет равно:
Расстояние между самолетами в этот момент, очевидно, будет равно:
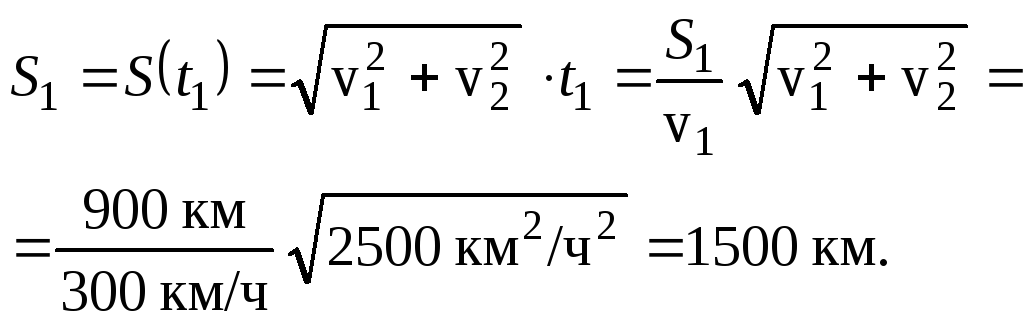
2.Из пунктовАиВ, расстояние между которымиl= 22 км, одновременно навстречу друг другу начали двигаться два автомобиля: первый со скоростью v1= 50 км/ч, а второй со скоростью v2= 60 км/ч. Определить, через сколько времени они встретятся и расстояние от точкиАдо места их встречи.
Р ешение. Выберем систему отсчета - осьx, начало отсчета которой совпадает с пунктомА(см. рис.).
ешение. Выберем систему отсчета - осьx, начало отсчета которой совпадает с пунктомА(см. рис.).
Запишем закон движения для каждого тела, т.е. зависимость координат от времени:
x1(t) = v1t- для первого тела,
x2(t) =l– v2t- для второго.
В момент встречи автомобилей t1их координаты равны, т.е. v1t1 =l– v2t1. Отсюда следует:
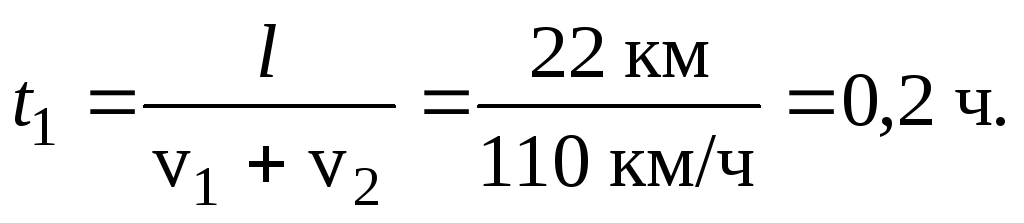
Расстояние от точки Адо места встречи равно:
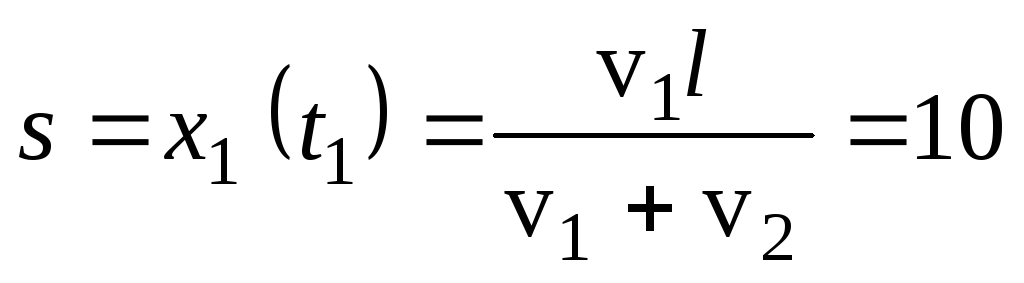 км.
км.
Задачи и упражнения
1.6.Движения двух велосипедистов заданы уравнениями:x1= 5t,x2 = 150 – 10t. Здесьx1иx2выражены в метрах, аt- в секундах. Найти время и место встречи.
1.7.Один автомобиль, двигаясь по прямой равномерно со скоростьюv1= 12 м/с в течениеt1= 10 с, проехал такой же путь, что и другой автомобиль заt2= 15 с. Какова скорость v2второго автомобиля ?
1.8.Из двух точек, расположенных на расстоянииl= 100 м друг от друга, одновременно в одном направлении начали движение два тела. Одно имело скорость v1= 2 м/с, а другое - v2= 7 м/с. Через какое время второе тело догонит первое? Какое перемещение совершит при этом каждое тело?
1.9.При равномерном движении двух тел навстречу друг другу вдоль одной прямой расстояние между ними уменьшается на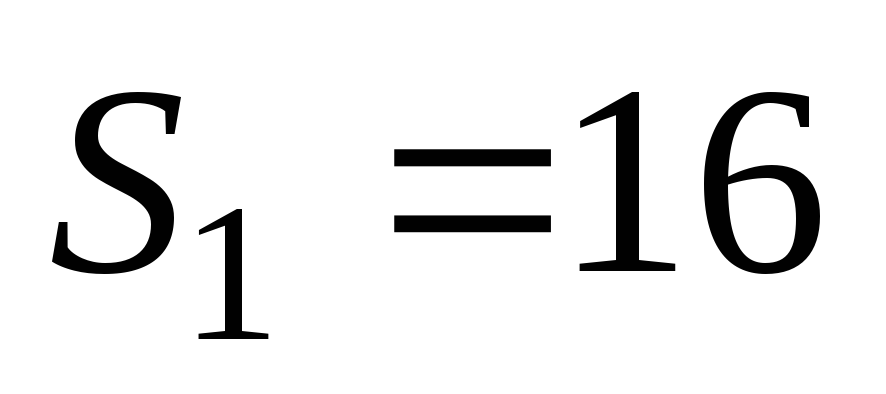 м за каждыеt1 = 10 c. При движении этих же тел с прежними по величине скоростями в одном направлении расстояние между ними увеличивается наS2=3 м за каждыеt2 = 5 c. Каковы скоростиv1иv2каждого из тел?
м за каждыеt1 = 10 c. При движении этих же тел с прежними по величине скоростями в одном направлении расстояние между ними увеличивается наS2=3 м за каждыеt2 = 5 c. Каковы скоростиv1иv2каждого из тел?
1.10.Катер береговой охраны догоняет корабль-нарушитель, движущийся со скоростьюv1 = 12 м/с к нейтральным водам. С какой минимальной скоростьюv2должен двигаться катер, чтобы догнать нарушителя в своих территориальных водах? Расстояние от катера до корабляS1 = 1800 м, а от катера до границы нейтральных водS2 = 5400 м.
studfiles.net
«Контрольная работа по теме «Равномерное и неравномерное прямолинейное движение»»
В11. Вертолет Ми-8 достигает скорости 250 км/ч. Какое время он затратит на перелет между двумя населенными пунктами, расположенными на расстоянии 100 км? 2. Во время подъема в гору скорость велосипедиста, двигающегося прямолинейно и равноускоренно, изменилась за 8 с от 18 км/ч до 10,8 км/ч. Найти ускорение велосипедиста. 2.Велосипедист съезжает с горки, двигаясь прямолинейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на 10 м/с. Ускорение велосипедиста 0,5 м/с2. Сколько времени длится спуск? 3. Лыжник съехал с горки за 6 с, двигаясь с постоянным ускорением 0,5 м/с2. Определите длину горки, если известно, что в начале спуска скорость лыжника была равна 18 км/ч. 4. Определить ускорение лодки, если, двигаясь из состояния покоя равноускоренно, за шестую секунду от начала движения она прошла 18 м. 5. Зависимость скорости материальной точки от времени задана формулой vх = 6t. Построить график этой зависимости. Написать уравнение х = x(t), если в начальный момент (t = 0) движущаяся точка находилась в начале координат (х = 0). Вычислить путь, пройденный материальной точкой за 10 с. В21. Тело, брошенное с поверхности земли вертикально вверх, достигло высоты 15 м и упало на землю. Определить путь, пройденный этим телом. 3.Аварийное торможение автомобиля происходило в течение 5 с. Определите, каким был тормозной путь, если начальная скорость автомобиля 90 км/ч, а модуль ускорения равен 5 м/с2. 4. Какую скорость приобретет автомобиль за 10 с, если, двигаясь из состояния покоя равноускоренно, он за 5 с проходит расстояние 25 м. 5.Уравнение движения по шоссе пешехода имеет вид: Х = 400 - 0,6t. Построить график этой зависимости. Найти координату в момент начала наблюдения, проекции на ось X начальной скорости и ускорения, а также направление и вид движения. В3 1. Тело переместилось из точки А с координатой Ха= 26 м в точку В с координатой ХВ= -4 м. Определите проекцию перемещения тела на ось ОХ. 2. Ускорение велосипедиста на одном из спусков трассы равно 1,2 м/с2. На этом спуске его скорость увеличилась на 18 м/с. Определить время, за которое велосипедист спускается с горки. 3. Какое расстояние пройдет автомобиль до полной остановки, если шофер резко тормозит при начальной скорости 72 км/ч с ускорением, равным по модулю 5 м/с2, а от начала торможения до остановки проходит 4 с? 4. Автомобиль, двигаясь равноускоренно из состояния покоя, за 4 с проходит 48 м. Какую скорость разовьет автомобиль к концу шестой секунды от начала движения? 5. Уравнение движения материальной точки имеет вид х = — 0,2t2. Построить график этой зависимости. Какое это движение? Найти координату точки через 5 с и путь, пройденный ею за это время. В41. Самолет пролетел по прямой 300 км, затем повернул под прямым углом и пролетел еще 400 км. Чему равен модуль вектора перемещения? 2. Санки съехали с одной горки и въехали на другую. Во время подъема на горку скорость санок, двигавшихся прямолинейно и равноускоренно, за 4 с изменилась от 12 м/с до 2 м/с. Найти модуль ускорения. 3. Во время игры девочка побежала без начальной скорости, прямолинейно с постоянным ускорением 1,2 м/с2. Определите ее путь за первые 5 с. 4. Тело, двигаясь с места равноускоренно, проходит за первые 4 с от начала движения 32 м. Какой скорости оно достигнет в конце десятой секунды?. 5. Уравнение движения по шоссе велосипедиста имеет вид: Х = -0,4t2 . Найти проекции на ось X начальной скорости и ускорения, а также направление и вид движения. Записать формулу зависимости проекции перемещения от времени. В5 1. Самолет пролетел по прямой 600 км, затем повернул под прямым углом и пролетел 800 км. Определите путь самолета. 2. Лыжник скатывается с горки, двигаясь прямолинейно и равноускоренно. За время спуска скорость лыжника увеличилась на 7,5 м/с. Ускорение лыжника 0,5 м/с2. Сколько времени длится спуск? 3. Вагонетка, имеющая скорость 7,2 км/ч, начинает двигаться с ускорением 0,25 м/с2. На каком расстоянии окажется вагонетка через 20 с? 4. Тело, двигаясь с места равноускоренно, проходит за четвертую секунду от начала движения 7 м. Какой путь пройдет тело за первые 10 с? 5. Уравнение движения материальной точки имеет вид х =15 + 0,4 t 2. Написать формулу зависимости Sx(t) и построить график. Определить координату точки через 5 с от начала движения, и путь, пройденный ею за это время.. В61. Стрела, выпущенная вертикально вверх, достигла максимальной высоты 15 м и упала на то же место, откуда была выпущена. Чему равен модуль ее перемещения? 2. Санки равноускоренно съехали со снежной горки. Их скорость в конце спуска 43,2 км/ч. Время спуска 6 с. С каким ускорением происходило движение, если спуск начинался из состояния покоя? 3. Подъезжая к станции, поезд тормозит в течение 20 с. Определите тормозной путь поезда, если его начальная скорость равна 72 км/ч, а модуль ускорения равен 1 м/с2. 4. Отходящий от станции поезд в течение первых 10 с движется прямолинейно и равноускоренно. Известно, что за третью секунду от начала движения поезд прошел 3,5 м. Определите модуль вектора ускорения, с которым он двигался. 5. Уравнение движения по шоссе бензовоза имеет вид: Х = -300 +0,5t2. Построить график этой зависимости. Найти координату в момент начала наблюдения, проекции на ось X начальной скорости и ускорения, а также направление и вид движения. В71. Материальная точка движется из пункта А в пункт В с координатой ХВ = 5 м. Определите координату пункта А, если проекция перемещения точки на ось ОХ равна SХ = 9 м. 2. Мотоцикл, трогаясь с места, движется с ускорением 3 м/с2. Какую скорость приобретет мотоцикл через 4 с? 3. Поезд, отойдя от станции, прошел путь 562,5 м. Сколько времени потребовалось для этого, если он двигался с ускорением 5 м/с2? 4. Автомобиль, двигаясь равноускоренно из состояния покоя, за пятую секунду разгона проходит 7,2 м. Какую скорость развил автомобиль к концу пятой секунды от начала движения? 5. Зависимость проекции перемещения от времени материальной точки имеет вид Sх=8t -3t2. Написать уравнение vx = vx (t) ; построить график этой зависимости; определить графически перемещение материальной точки за 3с, описать характер движения .В8 1. Два тела, брошенные с поверхности земли вертикально вверх, достигли высот 10 м и 20 м и упали на землю. Найти перемещения этих тел. 2. За какое время автомобиль, двигаясь с ускорением 1,6 м/с2, увеличит свою скорость с 11 м/с до 90 км/ч? 3. За какое время автомобиль, двигаясь из состояния покоя с ускорением 2 м/с2, пройдет путь 400 м? 4. Поезд начинает движение из состояния покоя и проходит за четвертую секунду 14 м. Какой путь пройдет тело за первые 10 с? 5. Движение материальной точки задано уравнением: x =40+ 2t - t2. Написать уравнение vx = vx (t) ; построить график этой зависимости; вычислить путь, пройденный материальной точкой за 10 с, определить характер движения . В91.За 6 минут равномерного движения мотоциклист проехал 3,6 км. Найти скорость мотоциклиста. 2. Лыжник начинает спускаться с горы из состояния покоя. Время спуска 30 с. Ускорение лыжника при спуске постоянно и равно 0,5 м/с2. Какова скорость лыжника в конце спуска? 3. К. Э. Циолковский в книге «Вне Земли», описывая полет ракеты, отмечал, что через 10 с после старта ракета находилась на расстоянии 5 км от поверхности Земли, С каким ускорением двигалась ракета? 4. Тело, двигаясь из состояния покоя, за пятую секунду прошло путь 27 м. С каким ускорением происходило движение? 5. Движение материальной точки задано уравнением: x =10 -4t + 2t2. Написать уравнение vx = vx (t) ; построить график этой зависимости; определить графически перемещение материальной точки за 3с, описать характер движения .В10 1. Тело переместилось из точки А с координатой ХА == -24 м в точку В с координатой ХВ = 14 м. Определите проекцию перемещения тела на ось ОХ. 2. Автомобиль, трогаясь с места, движется с ускорением 3 м/с2 .Определите скорость автомобиля в конце 7 с. 3. Подъезжая к остановке, автобус тормозит в течение 15 с. Определите тормозной путь автобуса, если его начальная скорость равна 54 км/ч, а модуль ускорения равен 1 м/с2. 4. Автомобиль начинает движение из состояния покоя. Какой путь пройдет автомобиль за третью секунду, двигаясь с ускорением 2 м/с2? 5. Движение материальной точки задано уравнением: x = -t - 6t2. Написать уравнение vx = vx (t) ; построить график этой зависимости; вычислить путь, пройденный материальной точкой за 5 с, определить характер движения .В11 1. Поезд движется из пункта А с координатой ХА = -435 км в пункт B. Определите координату пункта В, если проекция перемещения точки на ось ОХ равна SX = 165 км. 2. Велосипедист движется под уклон с ускорением 0,3 м/с . Через какое время он приобретет скорость 7,6 м/с, если его начальная скорость была 4 м/с? 3. Катер начал движение со скоростью 5 м/с и с постоянным ускорением 0,4 м/с2 . Определить путь, пройденный катером за 10 с. 4. Тело, двигаясь равноускоренно, в течение пятой секунды от начала движения прошло путь 45 м. Какой путь оно пройдет за 10 с от начала движения? 5. Движение материальной точки задано уравнением: х=10t+0,4t2. Написать уравнение vx = vx(t) ; построить график этой зависимости; определить графически перемещение материальной точки за 4с, описать характер движения . В12 1. Велосипедист, двигаясь равномерно по шоссе, проехал 1,8 км за 3 минуты. Найти скорость велосипедиста. 2. Каков модуль ускорения автомобиля при торможении, если при начальной скорости 54 км/ч время торможения до полной остановки 5 с? 3. Тело соскальзывает по наклонной плоскости, проходя за 10 с путь 2 м. Начальная скорость тела равна нулю. Определите модуль ускорения тела. 4. Автомобиль начинает движение из состояния покоя и проходит за четвертую секунду 3,5 м. С каким ускорением происходит движение? 5. Зависимость проекции перемещения от времени материальной точки имеет вид Sх= -4t +2t2. Написать уравнение vx = vx (t) ; построить график этой зависимости; вычислить путь, пройденный материальной точкой за 5 с, определить характер движения .schoolfiles.net
Контрольная работа №1 по теме «Равномерное прямолинейное движение. Средний модуль скорости произвольного движения» Контрольная работа №
скачать Контрольные работы физико-математический профиль стр. из Контрольные работы для классов физико-математического профиля СШ 10 класс- Контрольная работа № 1 по теме «Равномерное прямолинейное движение. Средний модуль скорости произвольного движения»
- Контрольная работа № 2 по теме «Прямолинейное равноускоренное движение»
- Контрольная работа № 3 по теме «Движение тела, брошенного под углом к горизонту»
- Контрольная работа № 4 по теме «Относительность движения»
- Контрольная работа № 5 по теме «Динамика точки»
- Контрольная работа № 6 по теме «Движение тела под действием нескольких сил»
- Контрольная работа № 7 по теме «Неинерциальные системы отсчета»
- Контрольная работа № 8 по теме «Закон сохранения импульса»
- Контрольная работа № 9 по теме «Механическая работа, мощность, энергия»
- Контрольная работа № 10 по теме «Статика»
- Контрольная работа № 11 по теме «Основные положения молекулярно-кинетической теории. Масса и размеры молекул»
- Контрольная работа № 12 по теме «Газовые законы. Молекулярно-кинетическая теория идеального газа»
- Контрольная работа № 13 по теме «Основы термодинамики»
- Контрольная работа № 14 по теме «Электростатика»
- Контрольная работа № 15 по теме «Постоянный электрический ток»
А.В.Авдеева, А.Б.Долицкий "Физика. Тематическое планирование к учебникам под редакцией Г.Я.Мякишева в 5 томах М., "Дрофа", 2005г.- там же см. ответы задач контрольных работ
Контрольная работа № 1 по теме «Равномерное прямолинейное движение. Средний модуль скорости произвольного движения» Вариант 1 - Автомобиль проехал первую половину пути со скоростью V1 = 40 км/ч, вторую — со cкоростью V2 = 60 км/ч. Найти среднюю скорость Vср на всем пути.
- Из города А в город В по прямой дороге отправляется грузовая машина со скоростью V1 = 40 км/ч. Спустя время τ0 = 1,5 ч из города В в город А выходит легковая машина со скоростью V2 = 80 км/ч. Через какое время τ после отправления легковой машины и на каком расстоянии d от пункта В встретятся машины, если в момент прибытия легковой машины в пункт А грузовая прошла путь s = 120 км?
3. По уравнениям координат написать уравнения скорости и построить графики зависимости скорости, пути и модуля перемещения от времени.х1 = -3 + t, х2 = 3 - t, х3 = -3 - t. 4. Даны графики изменения координаты прямолинейного движения трех точек: координата точки возрастает со временем, уменьшается, не меняется. Написать уравнения зависимости координат этих точек от времени и построить графики зависимости скорости и пути от времени 5. Два тела движутся по прямой в одну и ту же сторону со скоростями 5 м/с и 7 м/с. Начало движения второго тела запаздывает по сравнению с первым на 10 с. Когда и где встретятся тела? Вариант 2 - Автомобиль проехал первую половину пути со скоростью V1 = 60 км/ч, вторую — со скоростью V2 = 90 км/ч. Найти среднюю скорость Vср на всем пути.
- Из города А в город В по прямой дороге отправляется грузовая машина со скоростью V1 = 50 км/ч. Спустя время τ0 = 1 ч из города В в А выходит легковая машина со скоростью V2 = 80 км/ч. Через какое время τ после отправления легковой машины и на каком расстоянии d от пункта В встретятся машины, если в момент прибытия легковой машины в пункт А грузовая прошла путь s = 130 км?
3. По уравнению координат написать уравнения и построить графики зависимости скорости, пути и перемещения от времени.х1 = -5 + t, х2 = 5 – t, х3 = -5 - t. 4. Даны графики изменения координаты прямолинейного движения трех точек: координата точки возрастает со временем, уменьшается, не меняется. Написать уравнения зависимости координат этих точек от времени и построить графики зависимости скорости и пути от времени. 5 x, м . Два тела движутся вдоль одной прямой в одну и ту же сторону со скоростями 6 м/с и 10 м/с. Начало движения второго тела запаздывает по сравнению с первым на 15 с. Когда и где встретятся тела? . Два тела движутся вдоль одной прямой в одну и ту же сторону со скоростями 6 м/с и 10 м/с. Начало движения второго тела запаздывает по сравнению с первым на 15 с. Когда и где встретятся тела? 
вариант I вариант II Контрольная работа № 2 по теме «Прямолинейное равноускоренное движение» Вариант 1 1. Начертить графики зависимости скорости некоторых тел от времени, если графики зависимости ускорения этих тел от времени имеют вид, представленный на рисунке 1 (начальная скорость тел во всех случаях равна нулю). 2. По графику скорости V = V(t) (рис. 2) построить графики координаты х = x(t) и пути l = l(t). Начальная координата равна хо = -3м. Масштаб выбирается самостоятельно. Определить изменение координаты и пройденный путь за время движения. - За последнюю секунду свободно падающее без начальной скорости тело пролетело 3/4 всего
пути. Сколько времени падало тело?- Координата точки, движущейся прямолинейно вдоль оси X, меняется со временем по закону х = 11 – 35t + 40t2. Дать характеристику движения точки.
- Из точки А выходит тело, движущееся с начальной скоростью V01= 3 м/с и ускорением a1 = 2 м/с2. Спустя секунду из точки В ему навстречу выходит другое тело и движется с постоянной скоростью V2 = 5 м/с. Расстояние АВ равно I = 100 м. Сколько времени будет двигаться первое тело до встречи со вторым? Где они встретятся?
Вариант 21. Начертить графики зависимости скорости некоторых тел от времени, если графики зависимости ускорения этих тел от времени имеют вид, представленный на рисунке 1 (начальная скорость тел во всех случаях равна нулю). 2. По графику скорости V=V(t) (рис. 2) построить графики координаты х = x(t) и пути l = l(t). Начальная координата равна х0 = 2 м. Масштаб выбирается самостоятельно. Определить изменение координаты и пройденный путь за время движения. - Сколько секунд t свободно падало тело, если за последние две секунды оно прошло путь 60 м?
- Координата точки, движущейся прямолинейно вдоль оси Xу меняется со временем по закону х = -3-3t+4t2. Дать характеристику движения точки.
- Из точки А выходит тело, движущееся с начальной скоростью V01 = 2 м/с и ускорением
a1 = 2 м/с2. Спустя секунду из точки Б ему навстречу выходит другое тело и движется с постоянной скоростью V2= 10 м/с. Расстояние АВ равно I = 150 м. Сколько времени будет двигаться первое тело до встречи со вторым? Где они встретятся? 2 м/с2. Спустя секунду из точки Б ему навстречу выходит другое тело и движется с постоянной скоростью V2= 10 м/с. Расстояние АВ равно I = 150 м. Сколько времени будет двигаться первое тело до встречи со вторым? Где они встретятся?
вариант I __________________________________________________________________________________________________ 

вариант II Контрольная работа № 3 по теме «Движение тела, брошенного под углом к горизонту» Вариант 1 1. Камень, брошенный с поверхности Земли со скоростью V0, должен попасть в цель с известными координатами х и у. Чему должен быть равен угол бросания α? Какова траектория полета камня? Какова скорость V камня в точке расположения цели? Сопротивлением воздуха пренебречь. - Под каким углом α к горизонту следует бросить камень с вершины горы с уклоном (β = 45°), чтобы он упал на склон на максимальном расстоянии? Сопротивление воздуха не учитывать.
- Найти угол α, под которым атлету следует выпустить ядро, чтобы дальность полета ядра была максимальной. Рост атлета не учитывать. Сопротивлением воздуха пренебречь.
Вариант 2- Снаряд, выпущенный из пружинной пушки со скоростью V0, должен поразить цель с координатами х и у. Чему должен быть равен угол α возвышения ствола пушки? По какой траектории полетит снаряд? Какую скорость V будет иметь снаряд в точке расположения цели? Сопротивлением воздуха пренебречь.
- Минометная батарея расположена у подножия горы с наклоном к горизонту (β= 45°). Под каким углом α к горизонту надо установить ствол орудия, чтобы мина достигла склона на максимальной высоте? Сопротивление воздуха не учитывать.
- Найти угол α, под которым атлету следует выпустить копье, чтобы дальность полета была равна максимальной высоте подъема копья. Рост атлета не учитывать. Сопротивлением воздуха пренебречь.
Контрольная работа № 4 по теме «Относительность движения» Вариант 1 - Вагон движется со скоростью V0 = 36 км/ч. Наблюдатель в вагоне измерил угол α = 50° между вертикалью и направлением движения капель дождя относительно вагона. Относительно земли капли падают отвесно. Определить скорость капель V относительно земли и V' — относительно вагона.
- Катер, двигаясь по течению, из пункта А прибыл в пункт В за время t1 = 5 ч. Какое время t2 затратит катер на обратный путь, если скорость катера относительно воды в п = 5 раз превосходит скорость течения?
- Корабль выходит из пункта А со скоростью V и под углом а к линии АВ. Одновременно с выходом корабля из пункта В выпускается торпеда со скоростью и. Под каким углом β к линии АВ должна была выйти торпеда, чтобы поразить корабль?
- По взаимно перпендикулярным дорогам движутся равномерно два автомобиля со скоростями V1 = 54 км/ч и V2 = 72 км/ч соответственно. На каком расстоянии L друг от друга окажутся автомобили через время t = 10 мин после встречи у перекрестка?
Вариант 2 - Отвесно падающие капли дождя оставляют на боковых стеклах электрички, движущейся по горизонтальному пути со скоростью V = 72 км/ч, полосы под углом α = 40° к вертикали. Определить скорость и падения капель дождя на землю.
- Корабль идет курсом юго-восток со скоростью и узлов, при этом флюгер на мачте показывает восточный ветер. Корабль уменьшил ход до и/2 узлов, флюгер показывает северо-восточный ветер. Определить направление и скорость ветра V.
Примечание: направление курса указывает, куда идет корабль, направление ветра — откуда он дует.3. Корабль плывет на юг со скоростью V1 = 42 км/ч. Второй корабль идет курсом на юго-восток со скоростью V2 = 30 км/ч. Найти величину и и направление скорости второго корабля, определяемую наблюдателем, находящимся на палубе первого корабля. 4. Берега реки параллельны. Лодка вышла из точки ^ и, держа курс перпендикулярно берегам, достигла противоположного берега через время t1 = 10 мин после отправления. При этом она попала в точку С, лежащую на расстоянии s = 120 м ниже точки А по течению реки. Чтобы попасть из точки А в точку В, лежащую на прямой АВ, перпендикулярной берегам, лодке надо держать курс под некоторым углом к прямой АВ и против течения; в этом случае лодка достигнет противоположного берега через время t2 = 12,5 мин. Определить ширину L реки, скорость лодки относительно воды V и скорость течения реки и. Контрольная работа № 5 по теме «Динамика точки» Вариант 1 - На первоначально покоящееся тело массой т = 0,2 кг действует в течение времени
t = 5 с сила F = 0,1 Н. Какую скорость V приобретает тело и какой путь l пройдет оно за указанное время?- При каком минимальном коэффициенте трения между обувью и дорожкой спортсмен сможет пробегать стометровку за время t = 10 с, начиная движение с нулевой скоростью и ускоряясь только на первом участке s1 = 20 м?
- Какую скорость V может сообщить футболист мячу при ударе, если максимальная сила, с которой он может действовать на мяч, Fmax= 3,5 кН, время удара t0 = 8 • 10-3 с?
Считать, что сила во время удара нарастает и спадает по линейному закону (рис. 1). Масса мяча т = 0,5 кг.4. Два грузика массами т1 = 300 г и т2 = 200 г соединены нитью, перекинутой через блок, подвешенный на пружинных весах. Определить ускорение грузов, показание пружинных весов и силу натяжения нити. Трением в оси блока и его массой пренебречь. Вариант 2 1. На каком максимальном расстоянии 5 от вершины полусферы радиусом R = 45 см, отсчитанном вдоль ее поверхности, можно положить небольшое тело, чтобы оно не соскользнуло? Коэффициент трения тела о поверхность сферы μ = 0,75. 2. С какой силой нужно тянуть тело массой 60 кг по горизонтальной поверхности,чтобы оно двигалось равномерно? Сила приложена под углом 30° к горизонту. Коэффициент трения тела о поверхность 0,27. 3. Автомобиль массой т = 2 • 103 кг движется со скоростью V = 90 км/ч. В момент времени t = 0 на него начинает действовать горизонтальная тормозящая сила F, которая нарастает во времени по линейному закону (рис. 1). Через какое время автомобиль остановится? 4. На штанге укреплен невесомый неподвижный блок, через который перекинута нить с двумя грузами, массы которых т1 = 500 г и т2 = 100 г. В грузе т2 имеется отверстие, через которое проходит штанга (рис. 2). Сила трения груза т2 о штангу постоянна и равна F = 3 Н. Найтиускорение а грузов и силу натяжения Т нити. 

вариант I вариант II Контрольная работа № 6 по теме «Движение тела под действием нескольких сил» Вариант 1 - Тело пустили снизу вверх по наклонной плоскости с углом наклона α = 15°. Найти коэффициент трения μ, если время подъема тела оказалось в п = 2 раза больше времени спуска.
- Автомобиль массой т = 3 • 103 кг движется с постоянной скоростью V = 36 км/ч по мосту радиусом R = 60 м. С какой силой F давит автомобиль на мост в тот момент, когда линия, соединяющая центр кривизны моста с автомобилем, составляет угол α = 10° с вертикалью, если мост вогнутый?
- Какова первая космическая скорость V1 для планеты с такой же плотностью, как и у Земли, но радиус которой в п = 2 раза меньше, чем у Земли?
- Парашютист массой М = 80 кг падает при открытом парашюте с установившейся скоростью V1 = 5 м/с. Какой будет установившаяся скорость, если на том же парашюте спускается мальчик массой т = 40 кг? Сила сопротивления воздуха пропорциональна квадрату скорости.
Вариант 2- Тело пустили снизу вверх по наклонной плоскости с углом наклона α = 30°. Найти коэффициент трения μ, если время подъема тела оказалось в п = 3 раза больше времени спуска.
- Автомобиль массой т = 3 • 103 кг движется с постоянной скоростью V = 36 км/ч по мосту радиусом R = 60 м. С какой силой F давит автомобиль на мост в тот момент, когда линия, соединяющая центр кривизны моста с автомобилем, составляет угол α = 30° с вертикалью, если мост выпуклый?
3. На какую высоту Н надо запустить спутник в экваториальной плоскости, чтобы он все время находился над одной и той же точкой земной поверхности?4. Два одинаковых шарика связаны невесомой нитью, перекинутой через невесомый блок, причем один из шариков погружен в сосуд с жидкостью (рис. 1). С какой установившейся скоростью V будут двигаться шарики, если известно, что установившаяся скорость падения одиночного шарика в той же жидкости равна V0? Сила сопротивления жидкости пропорциональна скорости. Плотность жидкости равна ρж, плотность материала шариков равна ρ. 
Контрольная работа № 7 по теме «Неинерциальные системы отсчета» Вариант 1 - В лифте, поднимающемся с постоянным ускорением а, направленным вверх, колеблется математический маятник. Каков период его колебаний?
- В вагоне неподвижного поезда висит математический маятник. В некоторый момент поезд трогается и движется прямолинейно с постоянным ускорением а, вследствие чего маятник начинает отклоняться назад. Каков максимальный угол его отклонения от вертикали при колебании?
- Гладкая наклонная плоскость движется вправо с ускорением а. На плоскости лежит брусок массой т, удерживаемый нитью АВ (рис. 1) Найти силу натяжения нити и силу давления бруска на плоскость.
Вариант 2 1. В лифте, опускающемся с постоянным ускорением а, направленным вертикально вниз (а g),колеблется математический маятник. Каков период его колебаний? - В вагоне поезда, движущегося со скоростью 72 км/ч по закруглению радиусом 400 м, производится взвешивание тела на пружинных весах. Определите показания весов, если масса тела 100 кг.
- Г
 ладкая наклонная плоскость движется вправо с ускорением а. На плоскости лежит брусок массой т, удерживаемый нитью АВ (рис. 1). При каком ускорении aотн относительно наклонной плоскости нить оборвется? ладкая наклонная плоскость движется вправо с ускорением а. На плоскости лежит брусок массой т, удерживаемый нитью АВ (рис. 1). При каком ускорении aотн относительно наклонной плоскости нить оборвется?

. вариант I вариант I вариант II Контрольная работа № 8 по теме «Закон сохранения импульса» Вариант 1 - Снаряд, летящий горизонтально со скоростью и = 200 м/с, разрывается на две равные части, одна из которых после разрыва движется вертикально вниз со скоростью иг = 150 м/с. Какое расстояние по горизонтали пролетит второй осколок, если разрыв произошел на высоте Н = 500 м?
- Граната, летевшая со скоростью 10 м/с, разорвалась на два осколка. Больший осколок,масса которого составляла 60% массы всей гранаты, продолжал двигаться в прежнем направлении со скоростью 25 м/с. Найти скорость меньшего осколка.
- Призма 1, имеющая массу ml = m, была положена на призму 2, имеющую массу т2 = Зm (рис. 1). Верхняя призма начала скользить по нижней и в некоторый момент времени двигалась по ней со скоростью VOTH. Какую скорость и имела в этот момент нижняя призма? Призмы и горизонтальную плоскость считать гладкими. Какое расстояние s2 пройдет нижняя призма к моменту, когда верхняя призма коснется горизонтальной плоскости? Пусть между призмами 1 и 2 будет небольшое трение, а между призмой 2 и горизонтальной плоскостью трения не будет. Как это повлияет на ответ задачи?
Вариант 2 - Снаряд, находясь на высоте Н = 100 м и двигаясь в этот момент горизонтально со скоростью V = 400 м/с, разорвался на два одинаковых осколка. Какова дальность полета осколков, если один из них получил начальную скорость, направленную горизонтально под углом α = 45° к скорости снаряда? Сопротивлением воздуха пренебречь.
- Снаряд вылетает из орудия под углом α к горизонту, имея начальную скорость VQ. В некоторой точке траектории он разрывается на два осколка одинаковой массы, один из которых падает по вертикали, а другой начинает двигаться под углом β к горизонту. Какова скорость и второго осколка после разрыва? Сопротивление воздуха не учитывать.
- Призма 1, имеющая массу т1 =m, была положена на призму 2, имеющую массу
т2 = 4m (рис. 1). Верхняя призма начала скользить по нижней и в некоторый момент времени двигалась по ней со скоростью Vотн. Какую скорость и имела в этот момент нижняя призма? Призмы и горизонтальную плоскость считать гладкими. Какое расстояние s2 пройдет нижняя призма к моменту, когда верхняя призма коснется горизонтальной плоскости? Пусть между призмами 1 и 2 будет небольшое трение, а между призмой 2 и горизонтальной плоскостью трения не будет. Как это повлияет на ответ задачи?
Контрольная работа № 9 по теме «Механическая работа, мощность, энергия» Вариант 1 1. Пружинное ружье выстреливает шарик вертикально вверх на высоту 30 см, если пружина сжата на 1 см. Какова начальная скорость полета шарика? На какую высоту поднимется шарик, если эту пружину сжать на 3 см? 2. Конькобежец, разогнавшись до скорости V = 27 км/ч, въезжает на ледяную гору. На какую высоту Н от начального уровня въедет конькобежец, если подъем горы составляет h = 0,5 м на каждые s = 10 м по горизонтали и коэффициент трения коньков о лед μ = 0,02? 3. Тело массой т проходит мертвую петлю радиусом R, соскальзывая с наименьшей необходимой для этого высоты Н (рис. 1). Определить эту высоту, а также силу F, с которой тело давит на опору в точке петли А, радиус которой составляет угол а с вертикалью. Трением пренебречь. - Уклон участка шоссе α == 0,06. Спускаясь под уклон при выключенном двигателе,автомобиль движется равномерно со скоростью V = 60 км/ч. Какова должна быть мощность Р двигателя автомобиля, чтобы он мог преодолеть тот же уклон при подъеме с той же скоростью? Масса автомобиля т = 1,5 т.
Вариант 2 - Две пластины расположены горизонтально одна под другой и скреплены пружиной Массы пластин равны т1 и т2. С какой силой нужно надавить на верхнюю пластину, чтобы, двигаясь вверх после прекращения действия силы, верхняя пластина приподняла нижнюю?
- Санки съезжают с горы высотой Н и углом наклона а и движутся далее по горизонтальному участку. Коэффициент трения на всем пути саней одинаков и равен μ. Определить расстояние s, которое пройдут санки, двигаясь по горизонтальному участку до полной остановки.
- С высоты 2R соскальзывает небольшое тело по желобу, который образует мертвую петлю» радиусом R (рис. 1). На какой высоте h относительно уровня АВ тело оторвется от желоба? На какой высоте Н оно пройдет над точкой А?
4. Разогнавшись, конькобежец некоторое время движется по горизонтальной ледяной дорожке равномерно. Затем, перестав отталкиваться, он, двигаясь равнозамедленно, проезжает до остановки путь s = 60 м в течение t = 25 с. Масса конькобежца т = =50 кг. Определить коэффициент трения μ и мощность Р, затрачиваемую при равномерном движении.  
вариант I вариант II Контрольная работа № 10 по теме «Статика» Вариант 1 1. Груз весом Р удерживается на нитях АВ и ВС с помощью груза весом Q (рис. 1). Знаяуглы аир, найти силы натяжения нитей АВ и ВС. 2. Рельс длиной L = 10 м и массой т =100 кг поднимают на двух параллельных тросах. Найти силы натяжения Т1 и Т2 тросов, если один из них закреплен на конце рельса, а другой на расстоянии I = 1 м от другого конца. 3. Предохранительный клапан парового котла (рис. 2) должен открываться при давлении пара р. Площадь закрываемого паром отверстия S. На каком расстоянии х от оси вращения О надо поместить груз С массой М, чтобы удержать клапан в закрытом положении? Горизонтальный стержень имеет массу т и длину ОВ = I, а ОА = 0,25l.- Определить положение центра масс однородной пластины (рис. 3). Размеры выбрать произвольно.
- Однородный шар массой m = 20 кг удерживается на гладкой наклонной плоскости веревкой, привязанной к пружинным весам, укрепленным над плоскостью (рис. 4). Показания пружинных весов F = 100 Н. Угол наклона плоскости к горизонту
β=30°. Определить угол α, который составляет направление веревки с вертикалью, и силу давления Q шара на плоскость. Массой пружинных весов пренебречь.Вариант 2 - Груз весом Р удерживается с помощью нитей АВ и ВС (рис. 1). Зная угол α, найти натяжения этих нитей.
- Невесомый стержень АВ длиной L = 1 м подвешен на двух нитях (рис. 2). В точке С на расстоянии АС = 0,25 м к стержню подвешен груз весом Р = 120 Н. Вычислить силу натяжения нитей.
- Однородная балка весом Р = 600 Н и длиной L = 4 м опирается на гладкий пол и о выступ В, находящийся на высоте h = 3 м над полом (рис. 3). Балка образует угол α = 30° с вертикалью и удерживается веревкой АС, натянутой у самого пола. Вычислить силу натяжения Т веревки, силу реакции пола N и силу реакции N1 выступа B.
- Определить положение центра масс однородной пластины (рис. 4). Размеры выбрать произвольно.
- К вертикальной гладкой стене ^ подвешен однородный шар О на веревке АС (рис. 5). Веревка составляет со стеной угол а, вес шара Р. Определить силу натяжения Т веревки и силу давления Q шара на стену.
__________________________________________________________________________________________________вариант I 
 
  _ _ __________________________________________________________________________________________________ __________________________________________________________________________________________________
вариант II Контрольная работа № 11 по теме «Основные положения молекулярно-кинетической теории. Масса и размеры молекул» Вариант 1 - Сформулируйте основные положения МКТ.
- Сколько молекул содержится в углекислом газе (СО2) массой 1 г?
3. Определите массы молекул алюминия, газа метана СН4, метилового спирта СН3ОН и их концентрацию. Плотности алюминия, метана и метилового спирта соответственно равны 2700; 0,756 и 792 кг/м3. 4. Оцените размер атома алюминия. Вариант 2 - Какие эксперименты подтверждают основные положения МКТ?
- Какое количество вещества содержится в стакане воды объемом 250 см3? Плотность воды 1000 кг/м3.
- Определите массы молекул кремния, двуокиси углерода СО2, анилина C6H5Nh3 и их концентрацию. Плотности кремния, двуокиси углерода и анилина соответственно равны 2300; 1,977 и 1020 кг/м3.
- Оцените размер атома кремния.
Контрольная работа № 12 по теме «Газовые законы. Молекулярно-кинетическая теория идеального газа» Вариант 1 - Какое давление на стенки сосуда производит кислород, если средняя квадратичная скорость его молекул 400 м/с, а концентрация равна 2,7 · 1021м -3?
- Какова разница в массе воздуха, заполняющего помещение объемом 50 м3, зимой и летом, если температура помещения летом достигает 40 °С, а зимой падает до 0 °С? Давление нормальное. Молярная масса воздуха 0,029 г/моль.
- Открытую стеклянную трубку длиной 1 м наполовину погружают в ртуть. Затем трубку закрывают сверху и вынимают из ртути. Какой длины столбик ртути останется, в трубке? Атмосферное давление равно 750 мм рт. ст.
Вариант 2 - Какое давление на стенки сосуда производят молекулы газа, если масса газа 3 г, объем 0,0005 м3, а средняя квадратичная скорость молекул 500 м/с?
- В сосуде объемом 1 л заключено 0,28 г азота. Азот нагрет до температуры 1500 °С. При этой температуре 30% молекул азота диссоциировало на атомы. Определить давление в сосуде.
- Воздух в стакане высотой 10 см с площадью дна S = 25 см2 нагрет до температуры t1 = 87 °С. Стакан погружен вверх дном в воду так, что его дно находится на уровне поверхности воды. Какой объем воды войдет в стакан, когда воздух в стакане примет температуру воды t2 = 17 °С?
Контрольная работа №13 по теме «Основы термодинамики» Вариант 1 1. Кислород нагревают при постоянном давлении от температуры О °С. Какое количество теплоты необходимо сообщить газу, чтобы его объем удвоился? Количество вещества 1 моль. - В калориметр с теплоемкостью 63 Дж/К было налито 250 г масла при температуре 12 °С. После опускания в масло медного тела массой 500 г при температуре 100 °С установилась общая температура 33 °С. Какова удельная теплоемкость масла по данным опыта? Удельная теплоемкость меди 380Дж/(кг·К).
- Температура нагревателя идеальной тепловой машины 117 °С, а холодильника 27 °С. Машина получает от нагревателя за 1 с количество теплоты, равное 200 Дж. Определить КПД машины, количество теплоты, отдаваемое холодильнику в 1 с, работу, совершаемую машиной
за 1 с.- При передаче газу количества теплоты 17 кДж он совершает работу, равную 50 кДж. Чему равно изменение внутренней энергии газа? Охладился газ или нагрелся?
Вариант 2 - В сосуде находится одноатомный газ при температуре 17 °С и давлении 100 кПа. Объем сосуда 3 л. Газ изохорно нагревают на 100 °С. Определить изменение внутренней энергии газа. Какое количество теплоты было передано газу в этом процессе?
- В идеальной тепловой машине за счет каждого килоджоуля энергии, получаемой от нагревателя, совершается работа 300 Дж. Определить КПД машины и температуру нагревателя, если температура холодильника 280 К.
- Свинцовая пуля, летящая со скоростью 200 м/с, попадает в земляной вал. На сколько повысилась температура пули, если 78% кинетической энергии пули превратилось во внутреннюю энергию? Удельная теплоемкость свинца — 130 Дж/(кг • К).
- В каком из процессов газ совершает большую работу: 1—3—2—1 или 1—4—3—1(рис. 1)?

Контрольная работа № 14 по теме «Электростатика» Вариант 1 1. Обкладки плоского конденсатора имеют заряды +q и +2q соответственно. Чему равна напряженность поля в конденсаторе, если площадь пластин S? Каково напряжение между обкладками, если расстояние между ними d? Определить заряды, скопившиеся на внутренних и внешних сторонах обкладок. 2. Три одинаковых конденсатора емкостью С каждый соединили в батарею, как показано на рисунке 1. Определить заряд батареи и каждого конденсатора; напряжение на каждом конденсаторе, если на батарею подано напряжение U. 3. Внутрь полого металлического шара радиусом r, с зарядом q, поместили такой же точечный заряд. Найти напряженность и потенциал поля в точке А, лежащей вне сферы на расстоянии d от ее поверхности. - Два точечных заряда q и -Зq расположили на расстоянии d друг от друга. Какой третий заряд Q и где надо расположить, чтобы первые два заряда находились в равновесии? Что произойдет, если третий заряд освободить?
- Между двумя плоскими параллельными пластинами, расстояние между которыми d много меньше размеров пластин, находится во взвешенном состоянии пылинка массой m, несущая на себе заряд q. До какой разности потенциалов заряжены пластины?
Вариант 2 1. Рассчитать, с какой силой притягиваются друг к другу пластины плоского заряженного конденсатора, емкость которого С, а разность потенциалов между пластинами U. Расстояние между пластинами d. 2. Три одинаковых конденсатора емкостью С каждый соединили в батарею, как показано на рисунке 1. Определить заряд батареи и каждого конденсатора; напряжение на каждом конденсаторе, если на батарею подано напряжение U. - Металлический шар радиусом 2 см имеет заряд 1,33·10 -8 Кл. Шар окружен концентрической металлической оболочкой радиусом 5 см, заряд которой равен -2 • 10-8 Кл. Определить напряженность и потенциал поля на расстояниях L1 = 1 см, L2 = 4 см, L3 = 6 см от центра шара.
- Одинаковые по модулю, но разные по знаку заряды 18 нКл расположены в двух вершинах равностороннего треугольника. Сторона треугольника 2 м. Определить напряженность поля в третьей вершине треугольника.
- Какой угол с вертикалью составляет нить, на которой висит заряженный шарик массой 0,25 г, помещенный в горизонтальное однородное электростатическое поле напряженностью
106 В/м? Заряд шарика равен 2,5 нКл. 
вариант I вариант II Контрольная работа № 15 по теме «Постоянный электрический ток» Вариант 1 1. Определить силу тока через амперметр (рис. 1). ЭДС источника равна ε. Внутренними сопротивлениями амперметра и источника тока пренебречь. R1 = R2 = R3 = r, RA = 2r. 2. Электромотор включен в цепь постоянного тока напряжением U = 220 В. Сопротивление обмотки мотора R = 2 Ом, потребляемая сила тока I = 10 А. Найти потребляемую мощность и КПД мотора. - Имеется прибор с ценой деления 10 мкА.Шкала прибора содержит 100 делений. Внутреннее сопротивление прибора 50 Ом. Как из этого прибора сделать вольтметр для измерения напряжения до 200 В или миллиамперметр для измерения силы тока до 800 мА?
- Определить заряд на конденсаторе (рис. 2), если R1 = R2 = R3 = R4= 20 Ом, ε =500 В,
r = 10 Ом и С = 10 мкФ.- Электрический чайник имеет два нагревательных элемента. При включении одного из них вода в чайнике закипает за 15 мин, при включении другого — за 30 мин. Через какое время закипит вода в чайнике, если включить оба элемента: последовательно, параллельно?
Вариант 21. Определить силу тока через амперметр (рис. 1). ЭДС источника равна ε. Внутренними сопротивлениями амперметра и источника тока пренебречь. R1=R4 = r, R2 =R3 = 2r. 2. Электромотор включен в цепь постоянного тока напряжением U = 120 В. Сопротивление обмотки мотора R = 2 Ом, потребляемая сила тока / = 5 А. Найти потребляемую мощность и КПД мотора. 3. Вольтметр, соединенный последовательно с резистором сопротивлением 10 кОм, при включении в сеть напряжением 220 В показывает 70 В, а соединенный последовательно с другим резистором показывает 20 В. Найти сопротивление этого резистора. - До какого потенциала зарядится конденсатор ^ , присоединенный к источнику тока, ЭДС которого ε = 3,6 В, по схеме, изображенной на рисунке 2? Какой заряд будет при этом на обкладках конденсатора, если его емкость равна 2 мкФ?
- Какой длины надо взять никелиновую проволоку с площадью поперечного сечения
0,84 мм2, чтобы изготовить нагреватель с КПД 80%, при помощи которого можно было бы нагреть воду объемом 2 л от 20 °С до кипения за 10 мин при напряжении 200 В?Вариант I 

__________________________________________________________________________________________________ Вариант II  
База данных защищена авторским правом © kursovaya-referat.ru 2017При копировании материала укажите ссылку | kursovaya-referat.ru
Контрольная работа №1 по теме «Равномерное прямолинейное движение. Средний модуль скорости произвольного движения» Контрольная работа №
скачать Контрольные работы физико-математический профиль стр. из Контрольные работы для классов физико-математического профиля СШ 10 класс- Контрольная работа № 1 по теме «Равномерное прямолинейное движение. Средний модуль скорости произвольного движения»
- Контрольная работа № 2 по теме «Прямолинейное равноускоренное движение»
- Контрольная работа № 3 по теме «Движение тела, брошенного под углом к горизонту»
- Контрольная работа № 4 по теме «Относительность движения»
- Контрольная работа № 5 по теме «Динамика точки»
- Контрольная работа № 6 по теме «Движение тела под действием нескольких сил»
- Контрольная работа № 7 по теме «Неинерциальные системы отсчета»
- Контрольная работа № 8 по теме «Закон сохранения импульса»
- Контрольная работа № 9 по теме «Механическая работа, мощность, энергия»
- Контрольная работа № 10 по теме «Статика»
- Контрольная работа № 11 по теме «Основные положения молекулярно-кинетической теории. Масса и размеры молекул»
- Контрольная работа № 12 по теме «Газовые законы. Молекулярно-кинетическая теория идеального газа»
- Контрольная работа № 13 по теме «Основы термодинамики»
- Контрольная работа № 14 по теме «Электростатика»
- Контрольная работа № 15 по теме «Постоянный электрический ток»
А.В.Авдеева, А.Б.Долицкий "Физика. Тематическое планирование к учебникам под редакцией Г.Я.Мякишева в 5 томах М., "Дрофа", 2005г.- там же см. ответы задач контрольных работ
Контрольная работа № 1 по теме «Равномерное прямолинейное движение. Средний модуль скорости произвольного движения» Вариант 1 - Автомобиль проехал первую половину пути со скоростью V1 = 40 км/ч, вторую — со cкоростью V2 = 60 км/ч. Найти среднюю скорость Vср на всем пути.
- Из города А в город В по прямой дороге отправляется грузовая машина со скоростью V1 = 40 км/ч. Спустя время τ0 = 1,5 ч из города В в город А выходит легковая машина со скоростью V2 = 80 км/ч. Через какое время τ после отправления легковой машины и на каком расстоянии d от пункта В встретятся машины, если в момент прибытия легковой машины в пункт А грузовая прошла путь s = 120 км?
3. По уравнениям координат написать уравнения скорости и построить графики зависимости скорости, пути и модуля перемещения от времени.х1 = -3 + t, х2 = 3 - t, х3 = -3 - t. 4. Даны графики изменения координаты прямолинейного движения трех точек: координата точки возрастает со временем, уменьшается, не меняется. Написать уравнения зависимости координат этих точек от времени и построить графики зависимости скорости и пути от времени 5. Два тела движутся по прямой в одну и ту же сторону со скоростями 5 м/с и 7 м/с. Начало движения второго тела запаздывает по сравнению с первым на 10 с. Когда и где встретятся тела? Вариант 2 - Автомобиль проехал первую половину пути со скоростью V1 = 60 км/ч, вторую — со скоростью V2 = 90 км/ч. Найти среднюю скорость Vср на всем пути.
- Из города А в город В по прямой дороге отправляется грузовая машина со скоростью V1 = 50 км/ч. Спустя время τ0 = 1 ч из города В в А выходит легковая машина со скоростью V2 = 80 км/ч. Через какое время τ после отправления легковой машины и на каком расстоянии d от пункта В встретятся машины, если в момент прибытия легковой машины в пункт А грузовая прошла путь s = 130 км?
3. По уравнению координат написать уравнения и построить графики зависимости скорости, пути и перемещения от времени.х1 = -5 + t, х2 = 5 – t, х3 = -5 - t. 4. Даны графики изменения координаты прямолинейного движения трех точек: координата точки возрастает со временем, уменьшается, не меняется. Написать уравнения зависимости координат этих точек от времени и построить графики зависимости скорости и пути от времени. 5 x, м . Два тела движутся вдоль одной прямой в одну и ту же сторону со скоростями 6 м/с и 10 м/с. Начало движения второго тела запаздывает по сравнению с первым на 15 с. Когда и где встретятся тела? . Два тела движутся вдоль одной прямой в одну и ту же сторону со скоростями 6 м/с и 10 м/с. Начало движения второго тела запаздывает по сравнению с первым на 15 с. Когда и где встретятся тела? 
вариант I вариант II Контрольная работа № 2 по теме «Прямолинейное равноускоренное движение» Вариант 1 1. Начертить графики зависимости скорости некоторых тел от времени, если графики зависимости ускорения этих тел от времени имеют вид, представленный на рисунке 1 (начальная скорость тел во всех случаях равна нулю). 2. По графику скорости V = V(t) (рис. 2) построить графики координаты х = x(t) и пути l = l(t). Начальная координата равна хо = -3м. Масштаб выбирается самостоятельно. Определить изменение координаты и пройденный путь за время движения. - За последнюю секунду свободно падающее без начальной скорости тело пролетело 3/4 всего
пути. Сколько времени падало тело?- Координата точки, движущейся прямолинейно вдоль оси X, меняется со временем по закону х = 11 – 35t + 40t2. Дать характеристику движения точки.
- Из точки А выходит тело, движущееся с начальной скоростью V01= 3 м/с и ускорением a1 = 2 м/с2. Спустя секунду из точки В ему навстречу выходит другое тело и движется с постоянной скоростью V2 = 5 м/с. Расстояние АВ равно I = 100 м. Сколько времени будет двигаться первое тело до встречи со вторым? Где они встретятся?
Вариант 21. Начертить графики зависимости скорости некоторых тел от времени, если графики зависимости ускорения этих тел от времени имеют вид, представленный на рисунке 1 (начальная скорость тел во всех случаях равна нулю). 2. По графику скорости V=V(t) (рис. 2) построить графики координаты х = x(t) и пути l = l(t). Начальная координата равна х0 = 2 м. Масштаб выбирается самостоятельно. Определить изменение координаты и пройденный путь за время движения. - Сколько секунд t свободно падало тело, если за последние две секунды оно прошло путь 60 м?
- Координата точки, движущейся прямолинейно вдоль оси Xу меняется со временем по закону х = -3-3t+4t2. Дать характеристику движения точки.
- Из точки А выходит тело, движущееся с начальной скоростью V01 = 2 м/с и ускорением
a1 = 2 м/с2. Спустя секунду из точки Б ему навстречу выходит другое тело и движется с постоянной скоростью V2= 10 м/с. Расстояние АВ равно I = 150 м. Сколько времени будет двигаться первое тело до встречи со вторым? Где они встретятся? 2 м/с2. Спустя секунду из точки Б ему навстречу выходит другое тело и движется с постоянной скоростью V2= 10 м/с. Расстояние АВ равно I = 150 м. Сколько времени будет двигаться первое тело до встречи со вторым? Где они встретятся?
вариант I __________________________________________________________________________________________________ 

вариант II Контрольная работа № 3 по теме «Движение тела, брошенного под углом к горизонту» Вариант 1 1. Камень, брошенный с поверхности Земли со скоростью V0, должен попасть в цель с известными координатами х и у. Чему должен быть равен угол бросания α? Какова траектория полета камня? Какова скорость V камня в точке расположения цели? Сопротивлением воздуха пренебречь. - Под каким углом α к горизонту следует бросить камень с вершины горы с уклоном (β = 45°), чтобы он упал на склон на максимальном расстоянии? Сопротивление воздуха не учитывать.
- Найти угол α, под которым атлету следует выпустить ядро, чтобы дальность полета ядра была максимальной. Рост атлета не учитывать. Сопротивлением воздуха пренебречь.
Вариант 2- Снаряд, выпущенный из пружинной пушки со скоростью V0, должен поразить цель с координатами х и у. Чему должен быть равен угол α возвышения ствола пушки? По какой траектории полетит снаряд? Какую скорость V будет иметь снаряд в точке расположения цели? Сопротивлением воздуха пренебречь.
- Минометная батарея расположена у подножия горы с наклоном к горизонту (β= 45°). Под каким углом α к горизонту надо установить ствол орудия, чтобы мина достигла склона на максимальной высоте? Сопротивление воздуха не учитывать.
- Найти угол α, под которым атлету следует выпустить копье, чтобы дальность полета была равна максимальной высоте подъема копья. Рост атлета не учитывать. Сопротивлением воздуха пренебречь.
Контрольная работа № 4 по теме «Относительность движения» Вариант 1 - Вагон движется со скоростью V0 = 36 км/ч. Наблюдатель в вагоне измерил угол α = 50° между вертикалью и направлением движения капель дождя относительно вагона. Относительно земли капли падают отвесно. Определить скорость капель V относительно земли и V' — относительно вагона.
- Катер, двигаясь по течению, из пункта А прибыл в пункт В за время t1 = 5 ч. Какое время t2 затратит катер на обратный путь, если скорость катера относительно воды в п = 5 раз превосходит скорость течения?
- Корабль выходит из пункта А со скоростью V и под углом а к линии АВ. Одновременно с выходом корабля из пункта В выпускается торпеда со скоростью и. Под каким углом β к линии АВ должна была выйти торпеда, чтобы поразить корабль?
- По взаимно перпендикулярным дорогам движутся равномерно два автомобиля со скоростями V1 = 54 км/ч и V2 = 72 км/ч соответственно. На каком расстоянии L друг от друга окажутся автомобили через время t = 10 мин после встречи у перекрестка?
Вариант 2 - Отвесно падающие капли дождя оставляют на боковых стеклах электрички, движущейся по горизонтальному пути со скоростью V = 72 км/ч, полосы под углом α = 40° к вертикали. Определить скорость и падения капель дождя на землю.
- Корабль идет курсом юго-восток со скоростью и узлов, при этом флюгер на мачте показывает восточный ветер. Корабль уменьшил ход до и/2 узлов, флюгер показывает северо-восточный ветер. Определить направление и скорость ветра V.
Примечание: направление курса указывает, куда идет корабль, направление ветра — откуда он дует.3. Корабль плывет на юг со скоростью V1 = 42 км/ч. Второй корабль идет курсом на юго-восток со скоростью V2 = 30 км/ч. Найти величину и и направление скорости второго корабля, определяемую наблюдателем, находящимся на палубе первого корабля. 4. Берега реки параллельны. Лодка вышла из точки ^ и, держа курс перпендикулярно берегам, достигла противоположного берега через время t1 = 10 мин после отправления. При этом она попала в точку С, лежащую на расстоянии s = 120 м ниже точки А по течению реки. Чтобы попасть из точки А в точку В, лежащую на прямой АВ, перпендикулярной берегам, лодке надо держать курс под некоторым углом к прямой АВ и против течения; в этом случае лодка достигнет противоположного берега через время t2 = 12,5 мин. Определить ширину L реки, скорость лодки относительно воды V и скорость течения реки и. Контрольная работа № 5 по теме «Динамика точки» Вариант 1 - На первоначально покоящееся тело массой т = 0,2 кг действует в течение времени
t = 5 с сила F = 0,1 Н. Какую скорость V приобретает тело и какой путь l пройдет оно за указанное время?- При каком минимальном коэффициенте трения между обувью и дорожкой спортсмен сможет пробегать стометровку за время t = 10 с, начиная движение с нулевой скоростью и ускоряясь только на первом участке s1 = 20 м?
- Какую скорость V может сообщить футболист мячу при ударе, если максимальная сила, с которой он может действовать на мяч, Fmax= 3,5 кН, время удара t0 = 8 • 10-3 с?
Считать, что сила во время удара нарастает и спадает по линейному закону (рис. 1). Масса мяча т = 0,5 кг.4. Два грузика массами т1 = 300 г и т2 = 200 г соединены нитью, перекинутой через блок, подвешенный на пружинных весах. Определить ускорение грузов, показание пружинных весов и силу натяжения нити. Трением в оси блока и его массой пренебречь. Вариант 2 1. На каком максимальном расстоянии 5 от вершины полусферы радиусом R = 45 см, отсчитанном вдоль ее поверхности, можно положить небольшое тело, чтобы оно не соскользнуло? Коэффициент трения тела о поверхность сферы μ = 0,75. 2. С какой силой нужно тянуть тело массой 60 кг по горизонтальной поверхности,чтобы оно двигалось равномерно? Сила приложена под углом 30° к горизонту. Коэффициент трения тела о поверхность 0,27. 3. Автомобиль массой т = 2 • 103 кг движется со скоростью V = 90 км/ч. В момент времени t = 0 на него начинает действовать горизонтальная тормозящая сила F, которая нарастает во времени по линейному закону (рис. 1). Через какое время автомобиль остановится? 4. На штанге укреплен невесомый неподвижный блок, через который перекинута нить с двумя грузами, массы которых т1 = 500 г и т2 = 100 г. В грузе т2 имеется отверстие, через которое проходит штанга (рис. 2). Сила трения груза т2 о штангу постоянна и равна F = 3 Н. Найтиускорение а грузов и силу натяжения Т нити. 

вариант I вариант II Контрольная работа № 6 по теме «Движение тела под действием нескольких сил» Вариант 1 - Тело пустили снизу вверх по наклонной плоскости с углом наклона α = 15°. Найти коэффициент трения μ, если время подъема тела оказалось в п = 2 раза больше времени спуска.
- Автомобиль массой т = 3 • 103 кг движется с постоянной скоростью V = 36 км/ч по мосту радиусом R = 60 м. С какой силой F давит автомобиль на мост в тот момент, когда линия, соединяющая центр кривизны моста с автомобилем, составляет угол α = 10° с вертикалью, если мост вогнутый?
- Какова первая космическая скорость V1 для планеты с такой же плотностью, как и у Земли, но радиус которой в п = 2 раза меньше, чем у Земли?
- Парашютист массой М = 80 кг падает при открытом парашюте с установившейся скоростью V1 = 5 м/с. Какой будет установившаяся скорость, если на том же парашюте спускается мальчик массой т = 40 кг? Сила сопротивления воздуха пропорциональна квадрату скорости.
Вариант 2- Тело пустили снизу вверх по наклонной плоскости с углом наклона α = 30°. Найти коэффициент трения μ, если время подъема тела оказалось в п = 3 раза больше времени спуска.
- Автомобиль массой т = 3 • 103 кг движется с постоянной скоростью V = 36 км/ч по мосту радиусом R = 60 м. С какой силой F давит автомобиль на мост в тот момент, когда линия, соединяющая центр кривизны моста с автомобилем, составляет угол α = 30° с вертикалью, если мост выпуклый?
3. На какую высоту Н надо запустить спутник в экваториальной плоскости, чтобы он все время находился над одной и той же точкой земной поверхности?4. Два одинаковых шарика связаны невесомой нитью, перекинутой через невесомый блок, причем один из шариков погружен в сосуд с жидкостью (рис. 1). С какой установившейся скоростью V будут двигаться шарики, если известно, что установившаяся скорость падения одиночного шарика в той же жидкости равна V0? Сила сопротивления жидкости пропорциональна скорости. Плотность жидкости равна ρж, плотность материала шариков равна ρ. 
Контрольная работа № 7 по теме «Неинерциальные системы отсчета» Вариант 1 - В лифте, поднимающемся с постоянным ускорением а, направленным вверх, колеблется математический маятник. Каков период его колебаний?
- В вагоне неподвижного поезда висит математический маятник. В некоторый момент поезд трогается и движется прямолинейно с постоянным ускорением а, вследствие чего маятник начинает отклоняться назад. Каков максимальный угол его отклонения от вертикали при колебании?
- Гладкая наклонная плоскость движется вправо с ускорением а. На плоскости лежит брусок массой т, удерживаемый нитью АВ (рис. 1) Найти силу натяжения нити и силу давления бруска на плоскость.
Вариант 2 1. В лифте, опускающемся с постоянным ускорением а, направленным вертикально вниз (а g),колеблется математический маятник. Каков период его колебаний? - В вагоне поезда, движущегося со скоростью 72 км/ч по закруглению радиусом 400 м, производится взвешивание тела на пружинных весах. Определите показания весов, если масса тела 100 кг.
- Г
 ладкая наклонная плоскость движется вправо с ускорением а. На плоскости лежит брусок массой т, удерживаемый нитью АВ (рис. 1). При каком ускорении aотн относительно наклонной плоскости нить оборвется? ладкая наклонная плоскость движется вправо с ускорением а. На плоскости лежит брусок массой т, удерживаемый нитью АВ (рис. 1). При каком ускорении aотн относительно наклонной плоскости нить оборвется?

. вариант I вариант I вариант II Контрольная работа № 8 по теме «Закон сохранения импульса» Вариант 1 - Снаряд, летящий горизонтально со скоростью и = 200 м/с, разрывается на две равные части, одна из которых после разрыва движется вертикально вниз со скоростью иг = 150 м/с. Какое расстояние по горизонтали пролетит второй осколок, если разрыв произошел на высоте Н = 500 м?
- Граната, летевшая со скоростью 10 м/с, разорвалась на два осколка. Больший осколок,масса которого составляла 60% массы всей гранаты, продолжал двигаться в прежнем направлении со скоростью 25 м/с. Найти скорость меньшего осколка.
- Призма 1, имеющая массу ml = m, была положена на призму 2, имеющую массу т2 = Зm (рис. 1). Верхняя призма начала скользить по нижней и в некоторый момент времени двигалась по ней со скоростью VOTH. Какую скорость и имела в этот момент нижняя призма? Призмы и горизонтальную плоскость считать гладкими. Какое расстояние s2 пройдет нижняя призма к моменту, когда верхняя призма коснется горизонтальной плоскости? Пусть между призмами 1 и 2 будет небольшое трение, а между призмой 2 и горизонтальной плоскостью трения не будет. Как это повлияет на ответ задачи?
Вариант 2 - Снаряд, находясь на высоте Н = 100 м и двигаясь в этот момент горизонтально со скоростью V = 400 м/с, разорвался на два одинаковых осколка. Какова дальность полета осколков, если один из них получил начальную скорость, направленную горизонтально под углом α = 45° к скорости снаряда? Сопротивлением воздуха пренебречь.
- Снаряд вылетает из орудия под углом α к горизонту, имея начальную скорость VQ. В некоторой точке траектории он разрывается на два осколка одинаковой массы, один из которых падает по вертикали, а другой начинает двигаться под углом β к горизонту. Какова скорость и второго осколка после разрыва? Сопротивление воздуха не учитывать.
- Призма 1, имеющая массу т1 =m, была положена на призму 2, имеющую массу
т2 = 4m (рис. 1). Верхняя призма начала скользить по нижней и в некоторый момент времени двигалась по ней со скоростью Vотн. Какую скорость и имела в этот момент нижняя призма? Призмы и горизонтальную плоскость считать гладкими. Какое расстояние s2 пройдет нижняя призма к моменту, когда верхняя призма коснется горизонтальной плоскости? Пусть между призмами 1 и 2 будет небольшое трение, а между призмой 2 и горизонтальной плоскостью трения не будет. Как это повлияет на ответ задачи?
Контрольная работа № 9 по теме «Механическая работа, мощность, энергия» Вариант 1 1. Пружинное ружье выстреливает шарик вертикально вверх на высоту 30 см, если пружина сжата на 1 см. Какова начальная скорость полета шарика? На какую высоту поднимется шарик, если эту пружину сжать на 3 см? 2. Конькобежец, разогнавшись до скорости V = 27 км/ч, въезжает на ледяную гору. На какую высоту Н от начального уровня въедет конькобежец, если подъем горы составляет h = 0,5 м на каждые s = 10 м по горизонтали и коэффициент трения коньков о лед μ = 0,02? 3. Тело массой т проходит мертвую петлю радиусом R, соскальзывая с наименьшей необходимой для этого высоты Н (рис. 1). Определить эту высоту, а также силу F, с которой тело давит на опору в точке петли А, радиус которой составляет угол а с вертикалью. Трением пренебречь. - Уклон участка шоссе α == 0,06. Спускаясь под уклон при выключенном двигателе,автомобиль движется равномерно со скоростью V = 60 км/ч. Какова должна быть мощность Р двигателя автомобиля, чтобы он мог преодолеть тот же уклон при подъеме с той же скоростью? Масса автомобиля т = 1,5 т.
Вариант 2 - Две пластины расположены горизонтально одна под другой и скреплены пружиной Массы пластин равны т1 и т2. С какой силой нужно надавить на верхнюю пластину, чтобы, двигаясь вверх после прекращения действия силы, верхняя пластина приподняла нижнюю?
- Санки съезжают с горы высотой Н и углом наклона а и движутся далее по горизонтальному участку. Коэффициент трения на всем пути саней одинаков и равен μ. Определить расстояние s, которое пройдут санки, двигаясь по горизонтальному участку до полной остановки.
- С высоты 2R соскальзывает небольшое тело по желобу, который образует мертвую петлю» радиусом R (рис. 1). На какой высоте h относительно уровня АВ тело оторвется от желоба? На какой высоте Н оно пройдет над точкой А?
4. Разогнавшись, конькобежец некоторое время движется по горизонтальной ледяной дорожке равномерно. Затем, перестав отталкиваться, он, двигаясь равнозамедленно, проезжает до остановки путь s = 60 м в течение t = 25 с. Масса конькобежца т = =50 кг. Определить коэффициент трения μ и мощность Р, затрачиваемую при равномерном движении.  
вариант I вариант II Контрольная работа № 10 по теме «Статика» Вариант 1 1. Груз весом Р удерживается на нитях АВ и ВС с помощью груза весом Q (рис. 1). Знаяуглы аир, найти силы натяжения нитей АВ и ВС. 2. Рельс длиной L = 10 м и массой т =100 кг поднимают на двух параллельных тросах. Найти силы натяжения Т1 и Т2 тросов, если один из них закреплен на конце рельса, а другой на расстоянии I = 1 м от другого конца. 3. Предохранительный клапан парового котла (рис. 2) должен открываться при давлении пара р. Площадь закрываемого паром отверстия S. На каком расстоянии х от оси вращения О надо поместить груз С массой М, чтобы удержать клапан в закрытом положении? Горизонтальный стержень имеет массу т и длину ОВ = I, а ОА = 0,25l.- Определить положение центра масс однородной пластины (рис. 3). Размеры выбрать произвольно.
- Однородный шар массой m = 20 кг удерживается на гладкой наклонной плоскости веревкой, привязанной к пружинным весам, укрепленным над плоскостью (рис. 4). Показания пружинных весов F = 100 Н. Угол наклона плоскости к горизонту
β=30°. Определить угол α, который составляет направление веревки с вертикалью, и силу давления Q шара на плоскость. Массой пружинных весов пренебречь.Вариант 2 - Груз весом Р удерживается с помощью нитей АВ и ВС (рис. 1). Зная угол α, найти натяжения этих нитей.
- Невесомый стержень АВ длиной L = 1 м подвешен на двух нитях (рис. 2). В точке С на расстоянии АС = 0,25 м к стержню подвешен груз весом Р = 120 Н. Вычислить силу натяжения нитей.
- Однородная балка весом Р = 600 Н и длиной L = 4 м опирается на гладкий пол и о выступ В, находящийся на высоте h = 3 м над полом (рис. 3). Балка образует угол α = 30° с вертикалью и удерживается веревкой АС, натянутой у самого пола. Вычислить силу натяжения Т веревки, силу реакции пола N и силу реакции N1 выступа B.
- Определить положение центра масс однородной пластины (рис. 4). Размеры выбрать произвольно.
- К вертикальной гладкой стене ^ подвешен однородный шар О на веревке АС (рис. 5). Веревка составляет со стеной угол а, вес шара Р. Определить силу натяжения Т веревки и силу давления Q шара на стену.
__________________________________________________________________________________________________вариант I 
 
  _ _ __________________________________________________________________________________________________ __________________________________________________________________________________________________
вариант II Контрольная работа № 11 по теме «Основные положения молекулярно-кинетической теории. Масса и размеры молекул» Вариант 1 - Сформулируйте основные положения МКТ.
- Сколько молекул содержится в углекислом газе (СО2) массой 1 г?
3. Определите массы молекул алюминия, газа метана СН4, метилового спирта СН3ОН и их концентрацию. Плотности алюминия, метана и метилового спирта соответственно равны 2700; 0,756 и 792 кг/м3. 4. Оцените размер атома алюминия. Вариант 2 - Какие эксперименты подтверждают основные положения МКТ?
- Какое количество вещества содержится в стакане воды объемом 250 см3? Плотность воды 1000 кг/м3.
- Определите массы молекул кремния, двуокиси углерода СО2, анилина C6H5Nh3 и их концентрацию. Плотности кремния, двуокиси углерода и анилина соответственно равны 2300; 1,977 и 1020 кг/м3.
- Оцените размер атома кремния.
Контрольная работа № 12 по теме «Газовые законы. Молекулярно-кинетическая теория идеального газа» Вариант 1 - Какое давление на стенки сосуда производит кислород, если средняя квадратичная скорость его молекул 400 м/с, а концентрация равна 2,7 · 1021м -3?
- Какова разница в массе воздуха, заполняющего помещение объемом 50 м3, зимой и летом, если температура помещения летом достигает 40 °С, а зимой падает до 0 °С? Давление нормальное. Молярная масса воздуха 0,029 г/моль.
- Открытую стеклянную трубку длиной 1 м наполовину погружают в ртуть. Затем трубку закрывают сверху и вынимают из ртути. Какой длины столбик ртути останется, в трубке? Атмосферное давление равно 750 мм рт. ст.
Вариант 2 - Какое давление на стенки сосуда производят молекулы газа, если масса газа 3 г, объем 0,0005 м3, а средняя квадратичная скорость молекул 500 м/с?
- В сосуде объемом 1 л заключено 0,28 г азота. Азот нагрет до температуры 1500 °С. При этой температуре 30% молекул азота диссоциировало на атомы. Определить давление в сосуде.
- Воздух в стакане высотой 10 см с площадью дна S = 25 см2 нагрет до температуры t1 = 87 °С. Стакан погружен вверх дном в воду так, что его дно находится на уровне поверхности воды. Какой объем воды войдет в стакан, когда воздух в стакане примет температуру воды t2 = 17 °С?
Контрольная работа №13 по теме «Основы термодинамики» Вариант 1 1. Кислород нагревают при постоянном давлении от температуры О °С. Какое количество теплоты необходимо сообщить газу, чтобы его объем удвоился? Количество вещества 1 моль. - В калориметр с теплоемкостью 63 Дж/К было налито 250 г масла при температуре 12 °С. После опускания в масло медного тела массой 500 г при температуре 100 °С установилась общая температура 33 °С. Какова удельная теплоемкость масла по данным опыта? Удельная теплоемкость меди 380Дж/(кг·К).
- Температура нагревателя идеальной тепловой машины 117 °С, а холодильника 27 °С. Машина получает от нагревателя за 1 с количество теплоты, равное 200 Дж. Определить КПД машины, количество теплоты, отдаваемое холодильнику в 1 с, работу, совершаемую машиной
за 1 с.- При передаче газу количества теплоты 17 кДж он совершает работу, равную 50 кДж. Чему равно изменение внутренней энергии газа? Охладился газ или нагрелся?
Вариант 2 - В сосуде находится одноатомный газ при температуре 17 °С и давлении 100 кПа. Объем сосуда 3 л. Газ изохорно нагревают на 100 °С. Определить изменение внутренней энергии газа. Какое количество теплоты было передано газу в этом процессе?
- В идеальной тепловой машине за счет каждого килоджоуля энергии, получаемой от нагревателя, совершается работа 300 Дж. Определить КПД машины и температуру нагревателя, если температура холодильника 280 К.
- Свинцовая пуля, летящая со скоростью 200 м/с, попадает в земляной вал. На сколько повысилась температура пули, если 78% кинетической энергии пули превратилось во внутреннюю энергию? Удельная теплоемкость свинца — 130 Дж/(кг • К).
- В каком из процессов газ совершает большую работу: 1—3—2—1 или 1—4—3—1(рис. 1)?

Контрольная работа № 14 по теме «Электростатика» Вариант 1 1. Обкладки плоского конденсатора имеют заряды +q и +2q соответственно. Чему равна напряженность поля в конденсаторе, если площадь пластин S? Каково напряжение между обкладками, если расстояние между ними d? Определить заряды, скопившиеся на внутренних и внешних сторонах обкладок. 2. Три одинаковых конденсатора емкостью С каждый соединили в батарею, как показано на рисунке 1. Определить заряд батареи и каждого конденсатора; напряжение на каждом конденсаторе, если на батарею подано напряжение U. 3. Внутрь полого металлического шара радиусом r, с зарядом q, поместили такой же точечный заряд. Найти напряженность и потенциал поля в точке А, лежащей вне сферы на расстоянии d от ее поверхности. - Два точечных заряда q и -Зq расположили на расстоянии d друг от друга. Какой третий заряд Q и где надо расположить, чтобы первые два заряда находились в равновесии? Что произойдет, если третий заряд освободить?
- Между двумя плоскими параллельными пластинами, расстояние между которыми d много меньше размеров пластин, находится во взвешенном состоянии пылинка массой m, несущая на себе заряд q. До какой разности потенциалов заряжены пластины?
Вариант 2 1. Рассчитать, с какой силой притягиваются друг к другу пластины плоского заряженного конденсатора, емкость которого С, а разность потенциалов между пластинами U. Расстояние между пластинами d. 2. Три одинаковых конденсатора емкостью С каждый соединили в батарею, как показано на рисунке 1. Определить заряд батареи и каждого конденсатора; напряжение на каждом конденсаторе, если на батарею подано напряжение U. - Металлический шар радиусом 2 см имеет заряд 1,33·10 -8 Кл. Шар окружен концентрической металлической оболочкой радиусом 5 см, заряд которой равен -2 • 10-8 Кл. Определить напряженность и потенциал поля на расстояниях L1 = 1 см, L2 = 4 см, L3 = 6 см от центра шара.
- Одинаковые по модулю, но разные по знаку заряды 18 нКл расположены в двух вершинах равностороннего треугольника. Сторона треугольника 2 м. Определить напряженность поля в третьей вершине треугольника.
- Какой угол с вертикалью составляет нить, на которой висит заряженный шарик массой 0,25 г, помещенный в горизонтальное однородное электростатическое поле напряженностью
106 В/м? Заряд шарика равен 2,5 нКл. 
вариант I вариант II Контрольная работа № 15 по теме «Постоянный электрический ток» Вариант 1 1. Определить силу тока через амперметр (рис. 1). ЭДС источника равна ε. Внутренними сопротивлениями амперметра и источника тока пренебречь. R1 = R2 = R3 = r, RA = 2r. 2. Электромотор включен в цепь постоянного тока напряжением U = 220 В. Сопротивление обмотки мотора R = 2 Ом, потребляемая сила тока I = 10 А. Найти потребляемую мощность и КПД мотора. - Имеется прибор с ценой деления 10 мкА.Шкала прибора содержит 100 делений. Внутреннее сопротивление прибора 50 Ом. Как из этого прибора сделать вольтметр для измерения напряжения до 200 В или миллиамперметр для измерения силы тока до 800 мА?
- Определить заряд на конденсаторе (рис. 2), если R1 = R2 = R3 = R4= 20 Ом, ε =500 В,
r = 10 Ом и С = 10 мкФ.- Электрический чайник имеет два нагревательных элемента. При включении одного из них вода в чайнике закипает за 15 мин, при включении другого — за 30 мин. Через какое время закипит вода в чайнике, если включить оба элемента: последовательно, параллельно?
Вариант 21. Определить силу тока через амперметр (рис. 1). ЭДС источника равна ε. Внутренними сопротивлениями амперметра и источника тока пренебречь. R1=R4 = r, R2 =R3 = 2r. 2. Электромотор включен в цепь постоянного тока напряжением U = 120 В. Сопротивление обмотки мотора R = 2 Ом, потребляемая сила тока / = 5 А. Найти потребляемую мощность и КПД мотора. 3. Вольтметр, соединенный последовательно с резистором сопротивлением 10 кОм, при включении в сеть напряжением 220 В показывает 70 В, а соединенный последовательно с другим резистором показывает 20 В. Найти сопротивление этого резистора. - До какого потенциала зарядится конденсатор ^ , присоединенный к источнику тока, ЭДС которого ε = 3,6 В, по схеме, изображенной на рисунке 2? Какой заряд будет при этом на обкладках конденсатора, если его емкость равна 2 мкФ?
- Какой длины надо взять никелиновую проволоку с площадью поперечного сечения
0,84 мм2, чтобы изготовить нагреватель с КПД 80%, при помощи которого можно было бы нагреть воду объемом 2 л от 20 °С до кипения за 10 мин при напряжении 200 В?Вариант I 

__________________________________________________________________________________________________ Вариант II  
База данных защищена авторским правом © kursovaya-referat.ru 2017При копировании материала укажите ссылку | www.kursovaya-referat.ru












 υ1x = 0,5 м/с; υ2x = 1 м/с. Заметим, что эти же значения можно было получить по графикам, определив тангенсы углов наклона прямых к оси времени: скорость υ1x численно равна tgα1, а скорость υ2x численно равна tgα2.
υ1x = 0,5 м/с; υ2x = 1 м/с. Заметим, что эти же значения можно было получить по графикам, определив тангенсы углов наклона прямых к оси времени: скорость υ1x численно равна tgα1, а скорость υ2x численно равна tgα2. 


 =
= 




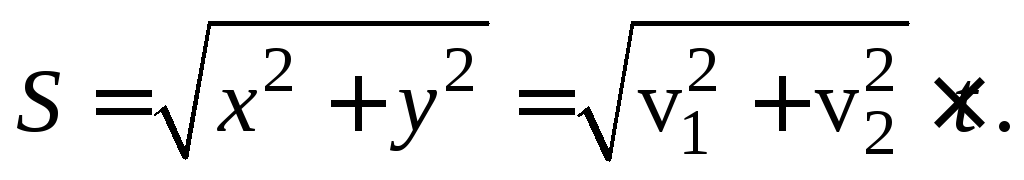
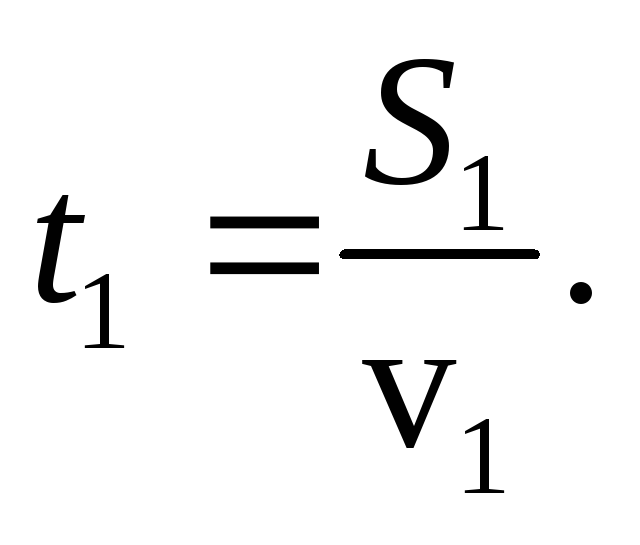 Расстояние между самолетами в этот момент, очевидно, будет равно:
Расстояние между самолетами в этот момент, очевидно, будет равно: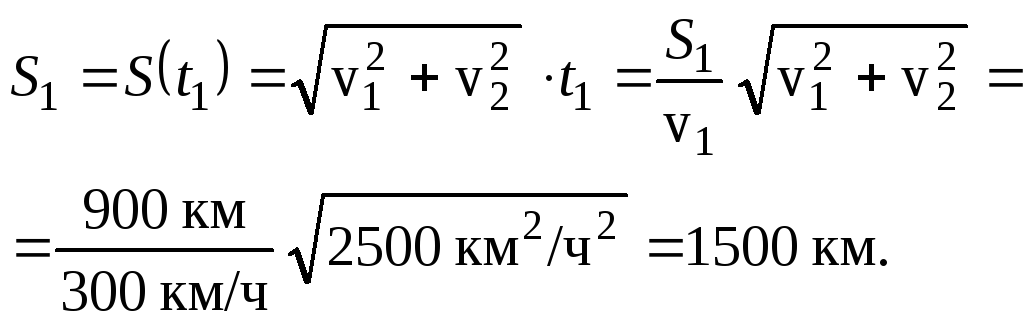
 ешение. Выберем систему отсчета - осьx, начало отсчета которой совпадает с пунктомА(см. рис.).
ешение. Выберем систему отсчета - осьx, начало отсчета которой совпадает с пунктомА(см. рис.).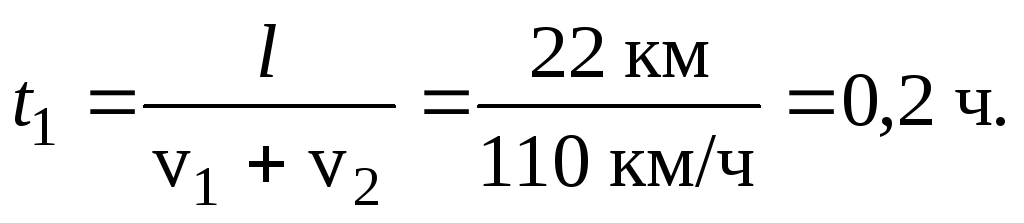
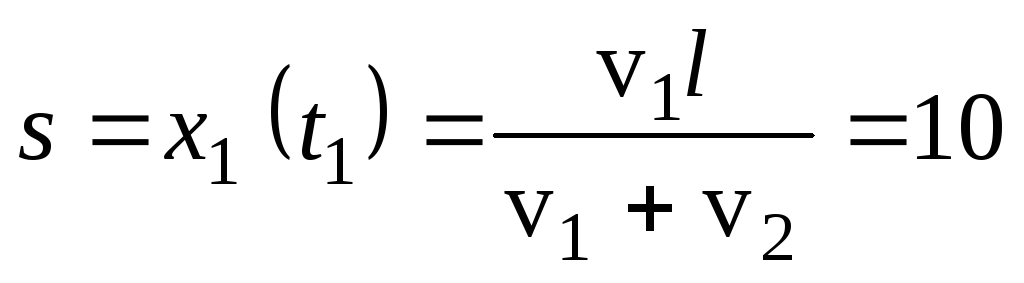 км.
км.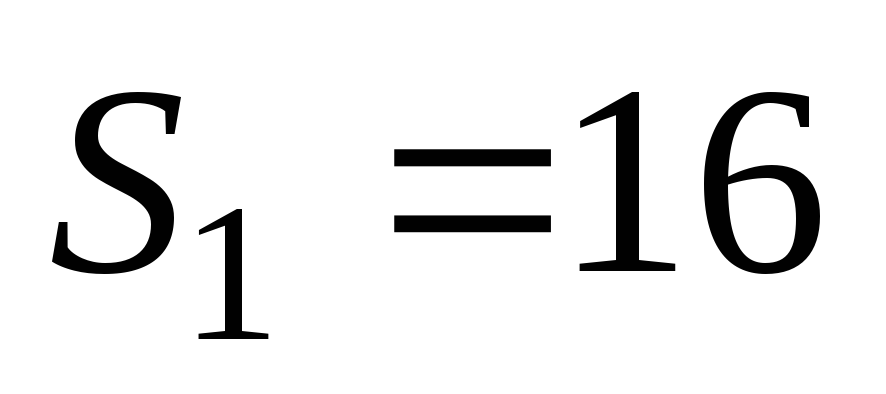 м за каждыеt1 = 10 c. При движении этих же тел с прежними по величине скоростями в одном направлении расстояние между ними увеличивается наS2=3 м за каждыеt2 = 5 c. Каковы скоростиv1иv2каждого из тел?
м за каждыеt1 = 10 c. При движении этих же тел с прежними по величине скоростями в одном направлении расстояние между ними увеличивается наS2=3 м за каждыеt2 = 5 c. Каковы скоростиv1иv2каждого из тел? . Два тела движутся вдоль одной прямой в одну и ту же сторону со скоростями 6 м/с и 10 м/с. Начало движения второго тела запаздывает по сравнению с первым на 15 с. Когда и где встретятся тела?
. Два тела движутся вдоль одной прямой в одну и ту же сторону со скоростями 6 м/с и 10 м/с. Начало движения второго тела запаздывает по сравнению с первым на 15 с. Когда и где встретятся тела? 
 2 м/с2. Спустя секунду из точки Б ему навстречу выходит другое тело и движется с постоянной скоростью V2= 10 м/с. Расстояние АВ равно I = 150 м. Сколько времени будет двигаться первое тело до встречи со вторым? Где они встретятся?
2 м/с2. Спустя секунду из точки Б ему навстречу выходит другое тело и движется с постоянной скоростью V2= 10 м/с. Расстояние АВ равно I = 150 м. Сколько времени будет двигаться первое тело до встречи со вторым? Где они встретятся?





 ладкая наклонная плоскость движется вправо с ускорением а. На плоскости лежит брусок массой т, удерживаемый нитью АВ (рис. 1). При каком ускорении aотн относительно наклонной плоскости нить оборвется?
ладкая наклонная плоскость движется вправо с ускорением а. На плоскости лежит брусок массой т, удерживаемый нитью АВ (рис. 1). При каком ускорении aотн относительно наклонной плоскости нить оборвется?







 _
_ __________________________________________________________________________________________________
__________________________________________________________________________________________________






 . Два тела движутся вдоль одной прямой в одну и ту же сторону со скоростями 6 м/с и 10 м/с. Начало движения второго тела запаздывает по сравнению с первым на 15 с. Когда и где встретятся тела?
. Два тела движутся вдоль одной прямой в одну и ту же сторону со скоростями 6 м/с и 10 м/с. Начало движения второго тела запаздывает по сравнению с первым на 15 с. Когда и где встретятся тела? 
 2 м/с2. Спустя секунду из точки Б ему навстречу выходит другое тело и движется с постоянной скоростью V2= 10 м/с. Расстояние АВ равно I = 150 м. Сколько времени будет двигаться первое тело до встречи со вторым? Где они встретятся?
2 м/с2. Спустя секунду из точки Б ему навстречу выходит другое тело и движется с постоянной скоростью V2= 10 м/с. Расстояние АВ равно I = 150 м. Сколько времени будет двигаться первое тело до встречи со вторым? Где они встретятся?





 ладкая наклонная плоскость движется вправо с ускорением а. На плоскости лежит брусок массой т, удерживаемый нитью АВ (рис. 1). При каком ускорении aотн относительно наклонной плоскости нить оборвется?
ладкая наклонная плоскость движется вправо с ускорением а. На плоскости лежит брусок массой т, удерживаемый нитью АВ (рис. 1). При каком ускорении aотн относительно наклонной плоскости нить оборвется?







 _
_ __________________________________________________________________________________________________
__________________________________________________________________________________________________





