Контрольная работа по геометрии за 1 полугодие, (7 класс). Контрольная работа по геометрии 1

Урок геометрии: контрольные работы. 8-й класс

1 вариант

1. Найдите sin, tg, если cos=.

2. Стороны двух треугольников равны 75 см, 60 см, 72 см и 2,5 см, 2 см, 2,4 см. Подобны ли эти треугольники?

3. В АВС С=90. Найдите sinA, cosA, tgA, если АС=4, ВС=3.

4. Точки M и N – середины сторон АВ и ВС АВС. Найдите , если АВ=4, ВС=5, АС=6.

2 вариант

1. Найдите sin, tg, если cos=0,6.

2. Стороны треугольника равны 5 см, 4,6 см и 2,5 см. Найдите две стороны подобного ему треугольника, если вторая его сторона равна 2,3 см.

3. В АВС С=90. Найдите sinA, cosA, tgA, если АС=5, ВС=12.

4. Точки M и N – середины сторон АВ и ВС АВС. Найдите , если MN=3, MВ=4, BN=5.

1 вариант

1.Найдите sin, tg, если cos=.

2.Стороны двух треугольников равны 75 см, 60 см, 72 см и 2,5 см, 2 см, 2,4 см. Подобны ли эти треугольники?

3.В АВС С=90. Найдите sinA, cosA, tgA, если АС=4, ВС=3.

4.Точки M и N – середины сторон АВ и ВС АВС. Найдите , если АВ=4, ВС=5, АС=6.

2 вариант

1. Найдите sin, tg, если cos=0,6.

2. Стороны треугольника равны 5 см, 4,6 см и 2,5 см. Найдите две стороны подобного ему треугольника, если вторая его сторона равна 2,3 см.

3. В АВС С=90. Найдите sinA, cosA, tgA, если АС=5, ВС=12.

4. Точки M и N – середины сторон АВ и ВС АВС. Найдите , если MN=3, MВ=4, BN=5.

1 вариант

1.Найдите sin, tg, если cos=.

2.Стороны двух треугольников равны 75 см, 60 см, 72 см и 2,5 см, 2 см, 2,4 см. Подобны ли эти треугольники?

3.В АВС С=90. Найдите sinA, cosA, tgA, если АС=4, ВС=3.

4.Точки M и N – середины сторон АВ и ВС АВС. Найдите , если АВ=4, ВС=5, АС=6.

2 вариант

1. Найдите sin, tg, если cos=0,6.

2. Стороны треугольника равны 5 см, 4,6 см и 2,5 см. Найдите две стороны подобного ему треугольника, если вторая его сторона равна 2,3 см.

3. В АВС С=90. Найдите sinA, cosA, tgA, если АС=5, ВС=12.

4. Точки M и N – середины сторон АВ и ВС АВС. Найдите , если MN=3, MВ=4, BN=5.

1 вариант

1.Найдите sin, tg, если cos=.

2.Стороны двух треугольников равны 75 см, 60 см, 72 см и 2,5 см, 2 см, 2,4 см. Подобны ли эти треугольники?

3.В АВС С=90. Найдите sinA, cosA, tgA, если АС=4, ВС=3.

4.Точки M и N – середины сторон АВ и ВС АВС. Найдите , если АВ=4, ВС=5, АС=6.

2 вариант

1. Найдите sin, tg, если cos=0,6.

2. Стороны треугольника равны 5 см, 4,6 см и 2,5 см. Найдите две стороны подобного ему треугольника, если вторая его сторона равна 2,3 см.

3. В АВС С=90. Найдите sinA, cosA, tgA, если АС=5, ВС=12.

4. Точки M и N – середины сторон АВ и ВС АВС. Найдите , если MN=3, MВ=4, BN=5.

1 вариант

1. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки 6 и 8, считая от основания. Найдите периметр треугольника.

2. Стороны угла А касаются окружности в точках В и С. Найдите ОА, если ОВ=3, ВАС=600.

3. Хорда АВ стягивает дугу, равную 2000, а хорда АС – дугу в 800. Найдите ВАС. Рассмотрите два случая.

2 вариант

1. Сумма двух противоположных сторон описанного четырехугольника равна 30 см. Найдите периметр четырехугольника.

2. Серединный перпендикуляр к стороне ВС треугольника АВС пересекает сторону АС в т.М и СМ, если ВМ=11,6 см, АС=23,4см.

3. Хорды АВ и СК пересекаются в т.О. Найдите СК, если АО=4, ВО=6, СО=3.

1 вариант

1. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки 6 и 8, считая от основания. Найдите периметр треугольника.

2. Стороны угла А касаются окружности в точках В и С. Найдите ОА, если ОВ=3, ВАС=600.

3. Хорда АВ стягивает дугу, равную 2000, а хорда АС – дугу в 800. Найдите ВАС. Рассмотрите два случая.

2 вариант

1. Сумма двух противоположных сторон описанного четырехугольника равна 30 см. Найдите периметр четырехугольника.

2. Серединный перпендикуляр к стороне ВС треугольника АВС пересекает сторону АС в т.М и СМ, если ВМ=11,6 см, АС=23,4см.

3. Хорды АВ и СК пересекаются в т.О. Найдите СК, если АО=4, ВО=6, СО=3.

1 вариант

1. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки 6 и 8, считая от основания. Найдите периметр треугольника.

2. Стороны угла А касаются окружности в точках В и С. Найдите ОА, если ОВ=3, ВАС=600.

3. Хорда АВ стягивает дугу, равную 2000, а хорда АС – дугу в 800. Найдите ВАС. Рассмотрите два случая.

2 вариант

1. Сумма двух противоположных сторон описанного четырехугольника равна 30 см. Найдите периметр четырехугольника.

2. Серединный перпендикуляр к стороне ВС треугольника АВС пересекает сторону АС в т.М и СМ, если ВМ=11,6 см, АС=23,4см.

3. Хорды АВ и СК пересекаются в т.О. Найдите СК, если АО=4, ВО=6, СО=3.

1 вариант

1. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки 6 и 8, считая от основания. Найдите периметр треугольника.

2. Стороны угла А касаются окружности в точках В и С. Найдите ОА, если ОВ=3, ВАС=600.

3. Хорда АВ стягивает дугу, равную 2000, а хорда АС – дугу в 800. Найдите ВАС. Рассмотрите два случая.

2 вариант

1. Сумма двух противоположных сторон описанного четырехугольника равна 30 см. Найдите периметр четырехугольника.

2. Серединный перпендикуляр к стороне ВС треугольника АВС пересекает сторону АС в т.М и СМ, если ВМ=11,6 см, АС=23,4см.

3. Хорды АВ и СК пересекаются в т.О. Найдите СК, если АО=4, ВО=6, СО=3.

xn--i1abbnckbmcl9fb.xn--p1ai

Контрольная работа по геометрии за 1 полугодие, (7 класс)

Контрольная работа по геометрии за 1 полугодие

(7 класс)

Цель: проверить уровень усвоения ГОСО по темам «Простейшие геометрические фигуры и их свойства», «Смежные и вертикальные углы», «Признаки равенства треугольников»:

- уметь находить длину отрезков, градусные меры смежных и вертикальных углов,

- уметь использовать определение равных треугольников для нахождения длин сторон и градусных мер углов треугольников,

- уметь строить прямой угол,

- понятие биссектриса, медиана треугольника,

- понятие равнобедренный треугольник и его свойства,

- знание признаков равенства треугольников,

- правильно записывать обозначения фигур, оформление задач и рисунков.

Содержание контрольной работы

Технологическая матрица.

Критерии оценивания.

Нормы оценки:

«5» - 29 – 26 балла

«4» - 25 – 21

«3» - 20 - 16

«2» - 15 и менее

xn--j1ahfl.xn--p1ai

контрольная работа по геометрии

Контрольная работа №1 (1 четверть). "Начальные геометрические сведения"

Вариант I. 

1. На отрезке KN отмечены две точки L и M. Найдите длину отрезка LM, если известно, что KN= 12 см, MN = 3,5 см, KL = 4,6 см. Укажите, какая точка лежит на отрезке KM? 

2. На заданном рисунке OM биссектриса угла NOL.- Найдите угол KON, если угол NOM равен 60°.- Постройте угол KOP, который будет вертикальный LOM. Рассчитаете его градусную меру.- Сколько градусов будет в угле LOP?

3. Угол COD равен 135°. Лучами OE и OF, угол разделёна на 3 равных угла. Сколько прямых углов получилось?

Вариант II 

1. На отрезке KM отмечены две точки L и N. Найдите длину отрезка LN, если известно, что KM= 8,6 см, NM = 1,5 см, KL = 2,6 см. Укажите, какая точка лежит на отрезке KN? 

2. На заданном рисунке OB биссектриса угла AOC.- Найдите угол DOA, если угол AOB равен 70°.- Постройте угол DOE, который будет вертикальный COB. Рассчитаете его градусную меру.- Сколько градусов будет в угле DOE?

3. Угол EOF равен 120°. Лучами OA и OB, угол разделён на 4 равных угла. Сколько углов по 60° получилось?

Вариант III 

1. На отрезке LK отмечены две точки N и M. Найдите длину отрезка NM, если известно, что LK= 13,8 см, LN = 4,5 см, MK = 1,6 см. Укажите, какая точка лежит на отрезке NK? 

2. На заданном рисунке OG биссектриса угла FOH.- Найдите угол EOF, если угол FOG равен 30°.- Постройте угол EOI, который будет вертикальный GOH. Рассчитаете его градусную меру.- Сколько градусов будет в угле EOI?

3. Угол BOD равен 140°. Лучами OA, OC и OE угол разделён на 4 равных угла. Сколько углов по 70° получилось?

Контрольная работа №2 (2 четверть). "Треугольник и окружность"

Вариант I 

1. Задан равнобедренный треугольник ABC. Известно, что угол ABE равен углу CBD.Докажите, что треугольник DBE является равнобедренным треугольником. Найдите угол AEB, если известно, что угол BDE равен 65°. 

2. Задан отрезок AB равный 4 см и прямой угол. Постройте на биссектрисе угла точку, где расстояние от вершины угла до точки равно длине отрезка. 

3. Задана окружность с центром О и с хордой CD. Радиус OE проведен перпендикулярно хорде CD. Докажите, что хорды CE и DE равны.

Вариант II 

1. Задан равнобедренный треугольник MNP. Известно, что угол MND равен углу ENP.Докажите, что треугольник DNE является равнобедренным треугольником. Найдите угол MDN, если известно, что угол MEN равен 70°. 

2. Задан отрезок AB равный 3 см и острый угол. Постройте на биссектрисе угла точку, где расстояние от вершины угла до точки равно удвоенной длине отрезка. 

3. Задана окружность с центром О и с хордой EF. Радиус OD проведен перпендикулярно хорде EF. Докажите, что хорды DE и DF равны.

Вариант III 

1. Задан равнобедренный треугольник XYZ. Известно, что угол XYD равен углу ZYE.Докажите, что треугольник DYE является равнобедренным треугольником. Найдите угол XDY, если известно, что угол XEY равен 50°. 

2. Задан отрезок AB равный 4 см и угол равный 50°. Постройте на биссектрисе угла точку, где расстояние от вершины угла до точки равно половине длине отрезка. 

3. Задана окружность с центром О и с хордой LM. Радиус OK проведен перпендикулярно хорде LM. Докажите, что хорды LK и MK равны.

Контрольная работа №3 (3 четверть). "Параллельные прямые"

Вариант I 

1. На данном рисунке угол 1 равен 120°, угол 2 равен 110°, угол 3 равен 65#176;. Найдите, чему равен угол 4 и сколько ещё таких углов есть на рисунке? 

2. Задан острый угол. На одной из сторон отмечены 2 точки K и L. ОТ этих точек проведены перпендикулярные прямые к другой стороне угла, соответственно KM и LN. Докажите, что эти прямые параллельны друг другу. Чему равен угол KLN, если угол MKL равен 120°? 

3. Задан треугольник XYZ. На его двух сторонах XY и YZ, указаны точки A и B соответственно. Докажите, что если угол YAB равен углу YXZ, то угол ABY равен углу XZY. 

Вариант II 

1. На данном рисунке угол 1 равен 65°, угол 2 равен 105°, угол 3 равен 65°. Найдите, чему равен угол 4 и сколько ещё таких углов есть на рисунке? 

2. Задан острый угол. На одной из сторон отмечены 2 точки С и D. От этих точек проведены перпендикулярные прямые к другой стороне угла, соответственно CE и DF. Докажите, что эти прямые параллельны друг другу. Чему равен угол CDF, если угол ECD равен 135°? 

3. Задан треугольник MNL. На его двух сторонах MN и NL, указаны точки A и B соответственно. Докажите, что если угол NAB равен углу NML, то угол ABN равен углу MNL. 

Вариант III 

1. На данном рисунке угол 1 равен 80°, угол 2 равен 110°, угол 3 равен 80°. Найдите, чему равен угол 4 и сколько ещё таких углов есть на рисунке? 

2. Задан острый угол. На одной из сторон отмечены 2 точки E и F. ОТ этих точек проведены перпендикулярные прямые к другой стороне угла, соответственно EG и FI. Докажите, что эти прямые параллельны друг другу. Чему равен угол EFI, если угол GEF равен 105°? 

3. Задан треугольник DEF. На его двух сторонах DE и EF, указаны точки A и B соответственно. Докажите, что если угол EAB равен углу EDF, то угол ABE равен углу DFE.

Контрольная работа №4 (4 четверть). "Треугольник. Соотношение между углами и сторонами"

Вариант I 

1. Задан треугольник DEF. Угол D меньше угла F на 40°, а угол E меньше угла В в 3 раза. Найдите все углы треугольника. Какая сторона больше DE или EF? 

2. Задан прямоугольный треугольник XYZ, где YZ гипотенуза. Внешний угол при вершине Z равен 120°, сторона XY равна 7 см. Чему равна длина гипотенузы? 

3. В равнобедренном треугольнике KLM, на основании KM указана точка P. От этой точки проведены перпендикуляры к двум боковым сторонам, соответственно PA и PB. Докажите, что эти отрезки PA и PB равны друг другу. 

Вариант II 

1. Задан треугольник KLM. Угол K меньше угла L в 2 раза, а угол М больше угла L на 30°. Найдите все углы треугольника. Какая сторона больше KL или LM? 

2. Задан прямоугольный треугольник CDE, где DE гипотенуза. Внешний угол при вершине E равен 120°, сторона CD равна 5 см. Чему равна длина гипотенузы? 

3. В равнобедренном треугольнике CDE, на основании CE указана точка N. От этой точки проведены перпендикуляры к двум боковым сторонам, соответственно NA и NB. Докажите, что эти отрезки NA и NB равны друг другу. 

Вариант III 

1. Задан треугольник ABC. Угол A меньше угла B в 3 раза, а угол B больше угла C на 70°. Найдите все углы треугольника. Какая сторона больше AB или BC? 

2. Задан прямоугольный треугольник EFD, где FD гипотенуза. Внешний угол при вершине D равен 150°, сторона AB равна 10 см. Чему равна длина гипотенузы? 

3. В равнобедренном треугольнике XYZ, на основании XZ указана точка М. От этой точки проведены перпендикуляры к двум боковым сторонам, соответственно MA и MB. Докажите, что эти отрезки MA и MB равны друг другу. 

videouroki.net

Годовая контрольная работа по геометрии для 8 общеобразовательного класса

Годовая контрольная работа по геометрии для 8 общеобразовательного класса.

Цель проведения: проверка знаний учащихся и подготовка к ОГЭ.

( Предусмотрена для УМК любого автора).

Время выполнения работы – 1 урок. Задание состоит из двух частей по степени сложности:

1 часть – базовый уровень, 2 часть – повышенный.

Система оценивания:

за каждое верно выполненное задание 1 части ставится - 1 балл;

за верно выполненное задание 2-ой части - 2 балла.

Максимальное число баллов – 10

Оценивание работы: отметка «5» – 10 баллов

отметка «4» – 8 – 9 баллов

отметка «3» – 5 – 7 баллов

отметка «2» – менее 5 баллов.

Ответы:

1 вариант

1 часть:

1. Один из углов параллелограмма равен 24°. Найти больший угол параллелограмма.

1) 66° 2) 114° 3) 136° 4) 156°

2. В треугольнике АВС основание АС равно 18 см, а высота, проведенная к нему, равна

7 см. Найти площадь треугольника.

1) 56 2) 63 3) 72 4) 84

3. Вписанный угол АВС окружности с центром в точке О равен 37°. Найти центральный угол, опирающийся на эту же дугу окружности.

1) 18,5° 2) 40° 3) 74° 4) 124°

4. Окружность радиусом 8 см вписана в квадрат. Найти площадь этого квадрата.

1) 256 2) 196 3) 144 4) 64

5. Катеты прямоугольного треугольника равны 8 см и 15 см. Найти гипотенузу треугольника.

1) 7 2) 23 3) 17 4) 120

6. Найти площадь ромба, если его диагонали равны 8 см и 6 см.

1) 48 2) 24 3) 14 4) 7

7. К окружности с центром в точке О проведены две касательные, пересекающиеся под углом 76° в точке Р и касающиеся окружности в точках А и В. Найти величину угла АОВ.

1) 104 2) 52 3) 76 4) 26

8. В прямоугольном треугольнике АВС ∟А = 30°, катет ВС = 4,5 см. Найти АВ.

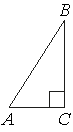
1) 4,5 2) 6 3) 9 4) 18

2 часть

9. На стороне AC  треугольника ABC отмечена точка D так, что AD = 5, DC = 7. Площадь треугольника ABC  равна 60 см². Найдите площадь треугольника ABD.

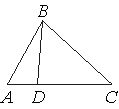
1) 12 2) 25 3) 15 4) 35

2 вариант

1 часть:

1. Один из углов параллелограмма равен 127°. Найти меньший угол параллелограмма.

1) 27° 2) 53° 3) 36° 4) 63°

2. В треугольнике АВС основание АС равно 12 см, а высота, проведенная к нему, равна

4 см. Найти площадь треугольника.

1) 16 2) 18 3) 24 4) 48

3. Центральный угол окружности с центром в точке О равен 116°. Найти вписанный угол, опирающийся на эту же дугу окружности.

1) 58° 2) 40° 3) 74° 4) 64°

4. Окружность радиусом 6 см вписана в квадрат. Найти периметр этого квадрата.

1) 36 2) 48 3) 24 4) 64

5. Катеты прямоугольного треугольника равны 24 см и 7 см. Найти гипотенузу треугольника.

1) 25 2) 31 3) 50 4) 64

6. Найти площадь ромба, если его диагонали равны 18 см и 10 см.

1) 180 2) 90 3) 360 4) 28

7. К окружности с центром в точке О проведены две касательные, пересекающиеся под углом 84° в точке Р и касающиеся окружности в точках А и В. Найти величину

угла АОВ.

1) 48 2) 84 3) 96 4) 124

8. В прямоугольном треугольнике АВС ∟А = 30°, АВ= 13см. Найти катет ВС.

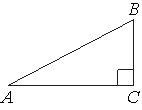
1) 26 2) 4,5 3) 9 4) 6,5

2 часть

9. Окружность пересекает луч АС в точках В и С так, что АВ = 4 см, ВС= 12 см. Найти длину касательной АК.

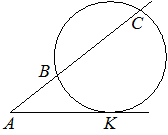
1) 8 2) 24 3) 48 4) 4

xn--j1ahfl.xn--p1ai

Смотрите также

• 
  Входная контрольная работа по истории
• 
  Контрольная работа лексика 6 класс
• Контрольная работа по теме лексика
• Контрольная по биологии 8 класс
• 
  Контрольные по русскому 2 класс
• 
  Контрольная работа 1 класс 8
• 
  Контрольная по биологии 7 класс
• 
  Контрольная по биологии 5 класс
• 
  Реформа контрольной и надзорной деятельности
• Анализ контрольной работы по математике
• 
  1 контрольная работа по физике