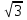Контрольная работа по теме "Комплексные числа". Комплексные числа контрольная

Контрольная работа по теме "Комплексные числа"

Практическая работа №

«Действия над комплексными числами»

Вариант № 1

1. Записать алгебраическую форму записи комплексного числа.

2. Перевести число из алгебраической формы записи в тригонометрическую:

Z= - 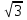-i

3. Дано комплексное число Z = 5 – 4 i

Записать число противоположное и сопряженное исходному.

4. Выполнить действие

Z = (- 6 + 2 i) + (- 6 - 2 i )

5. Выполнить умножение

Z = (3 + 4 i) (3 - 4 i)

6. Выполнить деление

Z = ( 3 - 2 i ) : ( 1 + 3 i )

7. Выполнить действия

Z = ( 5 + 2 i ) : ( 2 - 5 i ) - ( 3 - 4 i ) : ( 4 + 3 i )

8. Найти z1-z2, z1+z3, z2*z3, z3/z4, 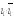если: z1=3-5i,z2=0.3+0.2i, z3=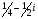, z4=-0.4+3i.

9. Выполнить в тригонометрической форме записи следующие операции: z4*z3, z4/z2, 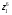, , 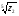если: z1=2√3+2i; z2=6-6i; z3=-√3/2-1,5i; z4=3.

10. Решить уравнение: z2-10z+34=0

_________________________________________________________________________

Практическая работа №

«Действия над комплексными числами»

Вариант № 2

1. Записать тригонометрическую форму записи комплексного числа.

2. Перевести число из алгебраической формы записи в показательную форму:

Z= -1 + 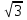i

3.Дано комплексное число

Z = 7 + 9 i

Записать число противоположное и сопряженное исходному.

4. Выполнить действие

Z = (5 + 3 i) + (- 2 - 5 i)

5.Выполнить умножение

Z = (-2 + 3 i) (-1 - 6 i)

6.Выполнить деление

Z = (4 +- 3 i): (-2 - 5 i)

7.Выполнить действия

Z = ( -1 + 3 i ) : ( 5 + i ) + (7 + 3 i ) : ( 1 - 2 i )

8. Найти z2-z1, z2+z3, z1*z3, z2/z4, 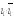если: z1=-3-5i,z2=0.3+0.2i, z3=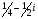, z4=-0.4+3i.

9. Выполнить в тригонометрической форме записи следующие операции: z1*z3, z3/z2, 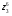, , 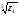если: z1=2√3+2i; z2=6-6i; z3=-√3/2-1,5i; z4=3.

10.Решить уравнение: z2-10z+26=0

infourok.ru

Комплексные числа. Контрольная работа. | Социальная сеть работников образования

Контрольная работа по математике №1 «Комплексные числа».

Вариант 1.

1. Найти z1-z2, z1+z3, z2*z3, z3/z4,  если: z1=3-5i,z2=0.3+0.2i, z3=, z4=-0.4+3i.
2. Выполнить в тригонометрической форме записи следующие операции: z4*z3, z4/z2, , , если: z1=2√3+2i, z2=6-6i, z3=-√3/2-1.5i, z4=3.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 2.

1. Найти z1-z2, z1+z3, z2*z3, z3/z4,  если: z1=4+2i, z2=0.5-0,1i, z3=, z4=-3-0,5i.
2. Выполнить в тригонометрической форме записи следующие операции: z4*z2, z4/z3, , , если: z1=4-4√3i, z2=-3+3i, z3=√6+√2i, z4=4i.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 3.

1. Найти z1-z3, z2+z3, z2*z1, z1/z4,  если: z1=3-5i,z2=0.3+0.2i, z3=, z4=-0.4+3i.
2. Выполнить в тригонометрической форме записи следующие операции: z2*z3, z4/z1, , , если: z1=2√3+2i, z2=6-6i, z3=-√3/2-1.5i, z4=3.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 4.

1. Найти z4-z2, z2+z3, z1*z3, z3/z2,  если: z1=4+2i, z2=0.5-0,1i, z3=, z4=-3-0,5i.
2. Выполнить в тригонометрической форме записи следующие операции: z1*z2, z2/z4, , , если: z1=4-4√3i, z2=-3+3i, z3=√6+√2i, z4=4i.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 5.

1. Найти z2-z1, z2+z3, z1*z3, z2/z4,  если: z1=-3-5i,z2=0.3+0.2i, z3=, z4=-0.4+3i.
2. Выполнить в тригонометрической форме записи следующие операции: z1*z3, z3/z2, , , если: z1=2√3+2i, z2=6-6i, z3=-√3/2-1.5i, z4=3.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 6.

1. Найти z3-z2, z1+z3, z2*z3, z3/z4,  если: z1=-4+2i, z2=0.5+0,1i, z3=, z4=-3-0,5i.
2. Выполнить в тригонометрической форме записи следующие операции: z4*z2, z4/z3, , , если: z1=4+4√3i, z2=-3+3i, z3=√6-√2i, z4=4i.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 7.

1. Найти z1-z3, z2+z3, z2*z4, z1/z4,  если: z1=-3-5i,z2=-0.3+0.2i, z3=, z4=-0.4-3i.
2. Выполнить в тригонометрической форме записи следующие операции: z2*z3, z4/z1, , , если: z1=2√3-2i, z2=6+6i, z3=-√3/2+1.5i, z4=3.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 8.

1. Найти z4-z2, z2+z3, z1*z3, z3/z2,  если: z1=-4+2i, z2=-0.5-0,1i, z3=, z4=-3+0,5i.
2. Выполнить в тригонометрической форме записи следующие операции: z1*z2, z2/z4, , , если: z1=4+4√3i, z2=3+3i, z3=√6- √2i, z4=-4i.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 9.

1. Найти z1-z2, z1+z3, z2*z3, z3/z4,  если: z1=-3-5i,z2=-0.3+0.2i, z3=, z4=0.4+3i.
2. Выполнить в тригонометрической форме записи следующие операции: z4*z3, z4/z2, , , если: z1=-2√3+2i, z2=-6-6i,               z3=- √3/2+1.5i, z4=3.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 10.

1. Найти z1-z2, z1+z3, z2*z3, z3/z4,  если: z1=-4+2i, z2=-0.5-0,1i, z3=, z4=3-0,5i.
2. Выполнить в тригонометрической форме записи следующие операции: z4*z2, z4/z3, , , если: z1=-4-4√3i, z2=3+3i, z3=- √6+√2i, z4=4i.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 11.

1. Найти z1-z3, z2+z3, z2*z1, z1/z4,  если: z1=-3-5i,z2=-0.3+0.2i, z3=, z4=0.4+3i.
2. Выполнить в тригонометрической форме записи следующие операции: z2*z3, z4/z1, , , если: z1=-2√3+2i, z2=-6-6i,               z3=- √3/2+1.5i, z4=3.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 12.

1. Найти z4-z2, z2+z3, z1*z3, z3/z2,  если: z1=-4+2i, z2=-0.5-0,1i, z3=, z4=3-0,5i.
2. Выполнить в тригонометрической форме записи следующие операции: z1*z2, z2/z4, , , если: z1=- 4- 4√3i, z2=3+3i, z3=- √6+√2i, z4=4i.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 13.

1. Найти z2-z1, z2+z3, z1*z3, z2/z4,  если: z1=-3+5i,z2=0.3-0.2i, z3=, z4=-0.4-3i.
2. Выполнить в тригонометрической форме записи следующие операции: z1*z3, z3/z2, , , если: z1=2√3-2i, z2=6+6i, z3=- √3/2+1.5i, z4=3.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 14.

1. Найти z3-z2, z1+z3, z2*z3, z3/z4,  если: z1=-4-2i, z2=0.5-0,1i, z3=, z4=-3+0,5i.
2. Выполнить в тригонометрической форме записи следующие операции: z4*z2, z4/z3, , , если: z1=4-4√3i, z2=-3-3i, z3=√6+√2i, z4=4i.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 15.

1. Найти z1-z3, z2+z3, z2*z4, z1/z4,  если: z1=-3+5i,z2=-0.3-0.2i, z3=, z4=-0.4+3i.
2. Выполнить в тригонометрической форме записи следующие операции: z2*z3, z4/z1, , , если: z1=2√3+2i, z2=6-6i, z3=-√3/2-1.5i, z4=3.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 16.

1. Найти z4-z2, z2+z3, z1*z3, z3/z2,  если: z1=-4-2i, z2=-0.5+0,1i, z3=, z4=-3-0,5i.
2. Выполнить в тригонометрической форме записи следующие операции: z1*z2, z2/z4, , , если: z1=4-4√3i, z2=-3+3i, z3=√6+√2i, z4=-4i.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 17.

3. Найти z1-z2, z1+z3, z2*z3, z3/z4,  если: z1=3-5i,z2=0.3+0.2i, z3=, z4=-0.4+3i.
4. Выполнить в тригонометрической форме записи следующие операции: z4*z3, z4/z2, , , если: z1=2√3+2i, z2=6-6i, z3=-√3/2-1.5i, z4=3.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 18.

3. Найти z1-z2, z1+z3, z2*z3, z3/z4,  если: z1=4+2i, z2=0.5-0,1i, z3=, z4=-3-0,5i.
4. Выполнить в тригонометрической форме записи следующие операции: z4*z2, z4/z3, , , если: z1=4-4√3i, z2=-3+3i, z3=√6+√2i, z4=4i.

Контрольная работа по математике №1 «Комплексные числа».

Вариант 19.

3. Найти z1-z3, z2+z3, z2*z1, z1/z4,  если: z1=3-5i,z2=0.3+0.2i, z3=, z4=-0.4+3i.
4. Выполнить в тригонометрической форме записи следующие операции: z2*z3, z4/z1, , , если: z1=2√3+2i, z2=6-6i, z3=-√3/2-1.5i, z4=3.

nsportal.ru

контрольная (комплексные числа) 4вариант

Вариант 4

Задача 1. Записать комплексное число в тригонометрической и в показательной формах; построить вектор, соответствующий данному числу:

z 82 82i

Решение: Вычислим модуль комплексного числа по формуле:

r x2 y2

Получим r 822 822 128 128

Вычислим аргумент комплексного числа. Так как

arctg y x

Запишем число в тригонометрической форме:

и в показательной форме

i

z 16e4

256 16

x 0, то воспользуемся формулой:

Построим вектор, соответствующий данному числу:

для этого на действительной оси выберем единичный отрезок, построим луч,

образующий с действительной осью угол 4 , так как положительный отсчет ведется

против часовой стрелки, а 0, то луч откладываем по часовой стрелке. На построенном луче отложим отрезок, длина которого равна модулю данного комплексного числа, то есть длины 16. Получаем требуемый вектор.

Imz

Rez

4

r 16

Задача 2. Вычислить, используя формулу Муавра. Ответ записать в алгебраической форме:

Решение: Степень комплексного числа вычисляется по формуле Муавра, для этого сначала надо найти модуль и аргумент этого числа.

Вычислим модуль комплексного числа по формуле: r x2 y2

Вычислим аргумент комплексного числа. Так как x 0, то воспользуемся формулой:

Задача 3. Найти все различные значения корняn-ойстепени; построить векторы, соответствующие этим значениям. Ответы записать в алгебраической форме:

2 23i

Решение: Значения корнейn-ойиз комплексного числа вычисляются по формуле:

Поэтому сначала нужно найти модули и аргументы чисел.

z 2 23i

Вычислим модуль комплексного числа по формуле: r x2 y2 r 2 2 23 2 4 12 16 4

Вычислим аргумент комплексного числа. Так как x 0,y 0, то воспользуемся

два, найдем их:

Построим векторы, соответствующие найденным значениям, для этого сначала построим окружность радиуса 2 , числу w0 соответствует вектор длины 2, образующий с

Imz

w1

w0

Задача 4. Решить уравнения:

а) z3 8 0

б) z2 3 4i z2 6i0

Решение:

а) z3 8 0

Для решения этого уравнения можно воспользоваться формулой сокращенного умножения: a3 b3 a b a2 ab b2 .

Левую часть уравнения преобразуем, используя эту формулу:

z 2 z2 2z 4 0. Это уравнение равносильно совокупности двух уравнений:

z 2 0

z2 2z 4 0

Из первого уравнения получаем корень z1 2

Второе уравнение является квадратным. Корни квадратного уравнения находятся по

б) z2 3 4i z2 6i0

Уравнение имеет следующие коэффициенты: a 1,b 3 4i,c 2 6i Тогда

D3 4i 2 4 1 2 6i 32 2 3 4i 4i 2 8 24i

9 24i 16 8 24i 1

studfiles.net

Контрольная работа по теме "Комплексные числа" для первого курса.

Контрольная работа по теме «Комплексные числа» 1 курс

Вариант 1

Выполнить действия

1) 1 +2(4+8i)- (3i-2)(4+i)

2) 3+8i

i-4

3) (2+2i)2

4) Изобразить z-(1+2i)=3

5)Решить уравнение х2+25=9

Вариант 2

Выполнить действия

1) 1 +2(4+9i)- (3i-1)(5-i)

2) 3+9i

3i-8

3) (1+4i)2

4) Изобразить z-(1-2i)=1

5)Решить уравнение х2+26=1

Вариант 3

Выполнить действия

1) 2 +2(4+8i)- (3i-2)(3+i)

2) 1+8i

2i-4

3) (3-2i)2

4) Изобразить z-(1+3i)=2

5)Решить уравнение х2+55=9

Вариант 4

Выполнить действия

1) 3 +1(-4+8i)- (3i+4)(4+i)

2) 7+8i

-3i-4

3) (5+2i)2

4) Изобразить z-(-1+2i)=4

5)Решить уравнение х2+11=9

Вариант 5

Выполнить действия

1) 3(4-8i)-(3i-2)(4+7i) +3

2) 3+8i

3i+2

3) (-1-4i)2

4) Изобразить z-(-1-3i)=5

5)Решить уравнение х2+44=9

Вариант 6

Выполнить действия

1) 5 +1(4-7i)+(4i-2)(4+2i)

2) 3-2i

3i-7

3) (9-2i)2

4) Изобразить z-(-1+3i)=2

5)Решить уравнение х2+56=12

Вариант 7

Выполнить действия

1) 1-2(4-3i)- (3i-2)(3-2i)

2) 3+8i

7+7i

3) (1+i)2

4) Изобразить z-(1+1i)=5

5)Решить уравнение х2+45=13

Вариант 8

Выполнить действия

1) 1 +2(4+5i)- (3i-2)(4+2i)

2) 1+1i

2i-5

3) (2+i)2

4) Изобразить z-(4+2i)=1

5)Решить уравнение х2+25=9

Вариант 9

Выполнить действия

1) 4 +4(4+4i)- (3i-1)(4+i)

2) 8+8i

3i-6

3) (4-i)2

4) Изобразить z-(1-5i)=3

5)Решить уравнение 56-x2=111

Вариант 10

Выполнить действия

1) 1 +3(9-8i)- (3i-9)(4-3i)

2) 1+8i

2i-6

3) (2+i)2

4) Изобразить z-(3+7i)=2

5)Решить уравнение 54-x2=156

Вариант 11

Выполнить действия

1) 1 +2(4+8i)+(3i-1)(4+i)

2) 3-5i

i-1

3) (2-i)2

4) Изобразить z+(3+5i)=3

5)Решить уравнение х2+446=9

Вариант 12

Выполнить действия

1) -4+5(4+8i)+(3i-2)(5+2i)

2) 1-2i

3i-1

3) (7-5i)2

4) Изобразить z-(1+2i)=3

5)Решить уравнение 76-x2=111

Вариант 13

Выполнить действия

1) 4 -2(4+4i)- (3i-1)(5+3i)

2) 1-8i

3i+2

3) (5+8i)2

4) Изобразить z-(1+5i)=3

5)Решить уравнение х2+87=9

Вариант 14

Выполнить действия

1)5 +2(4+8i)+(3i-2)(9+2i)

2) 3+8i

4i-6

3) (3-i)2

4) Изобразить z-(7-2i)=3

5)Решить уравнение х2+89=5

Вариант 15

Выполнить действия

1) 1 +6(6+8i)-(7i-7)(4+i)

2) 9-4i

5+7i

3) (9-3i)2

4) Изобразить z-(-7+1i)=5

5)Решить уравнение78+ х2=9

Вариант 16

Выполнить действия

1) 9+7(5+7i)+(1i-2)(4+i)

2) 9+9i

I+4

3) (5+2i)2

4) Изобразить z-(4+2i)=2

5)Решить уравнение х2+890=456

Вариант 17

Выполнить действия

1) 9 -2(4+8i)+ (3i+2)(4+i)

2) 8+8i

3i+4

3) (7-i)2

4) Изобразить z-(1+2i)=3

5)Решить уравнение х2+444=56

Вариант 18

Выполнить действия

1) 1 -5(4+8i)- (3i-2)(4+i)

2) 3+8i

i-4

3) (6+4i)2

4) Изобразить z-(1+2i)=3

5)Решить уравнение х2+2=-95

Вариант 19

Выполнить действия

1) 10 +5(4+8i)+(3i+6)(1+5i)

2) 1-8i

5i+4

3) (2-5i)2

4) Изобразить z-(7+2i)=4

5)Решить уравнение х2+2=-954

Вариант 20

Выполнить действия

1) 1-2(4+7i)- (3i-3)(3+i)

2) 3+3i

4i+9

3) (16-i)2

4) Изобразить z-(4+2i)=3

5)Решить уравнение х2+98=-2

Вариант 21

Выполнить действия

1) 2 +2(4+8i)+ (2i-2)(4+5i)

2) 8+8i

8i-4

3) (3+3i)2

4) Изобразить z+(1+2i)=4

5)Решить уравнение х2+25=-91

Вариант 22

Выполнить действия

1) 1 +2(9-8i)- (3i-1)(4+i)

2) 3+1i

2i-9

3) (1-5i)2

4) Изобразить z-(1+7i)=3

5)Решить уравнение х2+25=9

Вариант 23

Выполнить действия

1) 1 +2(5+8i)+ (3i-2)(1-i)

2) 3+8i

3i-4

3) (3-i)2

4) Изобразить z-(4+2i)=3

5)Решить уравнение х2+38=2

Вариант 24

Выполнить действия

1) 4-2(4+4i)+(1i-3)(4+i)

2) 3+8i

i-4

3) (2+i)2

4) Изобразить z-(-5+2i)=1

5)Решить уравнение х2+25=9

Вариант 25

Выполнить действия

1) 1 +2(4+6i)+(3i+2)(4+i)

2) 3+8i

i-4

3) (2+i)2

4) Изобразить z-(3-2i)=6

5)Решить уравнение х2+25=9

Вариант 26

Выполнить действия

1) 1 +2(4+8i)- (3i-2)(4+i)

2) 3+8i

i-4

3) (2+i)2

4) Изобразить z-(1+2i)=3

5)Решить уравнение х2+25=9

Вариант 27

Выполнить действия

1) -1+2(4+6i)+(3i+2)(4+i)

2) -3+8i

6i-8

3) (-2+8i)2

4) Изобразить z-(3-9i)=2

5)Решить уравнение х2+77=4

Вариант 28

Выполнить действия

1) 7+4(4+7i)+(3i+2)(4+i)

2) 3+8i

6i+4

3) (-2+5i)2

4) Изобразить z-(3-2i)=3

5)Решить уравнение х2+25=-68

Вариант 29

Выполнить действия

1) -6(4+6i)+(3i+7)(4-i)+8

2) -3+8i

3i-5

3) (2+i)2

4) Изобразить z-(3-1i)=2

5)Решить уравнение х2+25=-66

Вариант 30

Выполнить действия

1) 1 +2(4+6i)+(3i+2)(4+i)

2) 1+3+8i

4i+6

3) (2+8i)2

4) Изобразить z-(-5+2i)=2

5)Решить уравнение х2+25=-89

multiurok.ru

Смотрите также

• 
  Обязательная контрольная работа
• 
  Проект контрольная работа
• 
  Spotlight 3 контрольные
• 
  Контрольные spotlight 5
• 
  Spotlight 5 контрольные
• 
  Мой контрольный журнал
• 
  План контрольной работы
• 
  Контрольная работа введение
• 
  Введение контрольная работа
• 
  Контрольные работы канакина
• 
  Задачи контрольной работы