ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ М
2407
инистерство транспорта Российской ФедерацииФедеральное агентство железнодорожного транспорта
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Самарский государственный университет путей сообщения
Кафедра механики
Методические указания и задания
к выполнению контрольных и расчетно-графических работ
для студентов технических специальностей
очной и заочной форм обучения
Составители: Ю. Д. Карышев
Л. В. Кудюров
Самара
УДК 531/534
Теоретическая механика. Кинематика : методические указания и задания к выполнению контрольных и расчетно-графических работ для студентов технических специальностей очной и заочной форм обучения / составители : Ю. Д. Карышев, Л. В. Кудюров. – Самара : СамГУПС, 2009. – 34 с.
Утверждены на заседании кафедры 03.06.2009 г., протокол № 11.
Печатаются по решению редакционно-издательского совета СамГУПС.
Приведены методические указания и задания к выполнению контрольных и расчетно-графических работ по кинематике курса теоретической механики, предназначенные для студентов технических специальностей Самарского государственного университета путей сообщения всех форм обучения.
Составители: Ю. Д. Карышев
Л. В. Кудюров
Рецензенты: к.т.н., доцент кафедры «Механика» СамГУПС Е. В. Глобенко;
к.ф-м.н., доцент кафедры «Механика» СамГТУ В. А. Бруяка
Редактор И. М. Егорова
Компьютерная верстка Е. А. Самсонова
Подписано в печать 08.10.2009. Формат 60×90 1/16.
Усл. печ. л. 2,1. Тираж 200 экз. Заказ № 188.
© Самарский государственный университет путей сообщения, 2009
Перечень задач, входящих в контрольные и расчетно-графические работы, выдается преподавателем в зависимости от специальности студента. Номер рисунка к задаче определяется по последней цифре шифра студента (номера зачетной книжки), а номер условия в таблице – по предпоследней.
При выполнении работ записи, чертежи, схемы должны быть выполнены в определенном масштабе, аккуратно. Условие задачи и величины, подлежащие определению, приводятся в краткой записи. Решение задач должно сопровождаться всеми необходимыми пояснениями и обосновываться ссылками на соответствующие теоремы или иные теоретические положения, на основе которых производится решение.
На рисунках должны быть указаны направления векторов, которые определены в результате решения задачи.
Защита проводится в часы консультаций. Студент должен знать основы теории по теме работы, владеть методикой решения задач данного типа.
Кинематикой называется раздел механики, в котором изучается движение материальных тел в пространстве с чисто геометрической точки зрения, то есть вне связи с силами, определяющими это движение.
Под движением в механике понимается изменение с течением времени положения данного тела в пространстве по отношению к другому телу, которое называют телом отсчета. С телом отсчета можно связать некоторую систему координат, которую называют системой отсчета, и изучать движение тела по отношению к ней. Если тело не перемещается по отношению к выбранной системе координат, то говорят, что оно находится в покое. При движении тела все его точки в общем случае совершают различные движения. Поэтому изучению движения тела должно предшествовать изучение движения точки.
studfiles.net
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ
Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Мехатроника» Г. В. Васильева ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Екатеринбург Издательство УрГУПС 2014
Министерство образования РФ Сибирская государственная автомобильно-дорожная академия Кафедра теоретической механики ТЕОРЕТИЧЕСКАЯ МЕХАНИКА СТАТИКА Часть I Методические указания для решения задач и контрольные
Министерство образования и науки Российской Федерации Уральский федеральный университет имени первого Президента России Б. Н. Ельцина А.А. Мироненко МЕХАНИКА СБОРНИК ЗАДАНИЙ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Самарский государственный архитектурно-строительный университет» Кафедра сопротивления
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА 1.. Кинематика. Кинематика это часть теоретической механики, в которой изучается механическое движение материальных точек и твердых тел. Механическое движение это перемещение
Е. А. Митюшов, С. А. Берестова ТЕОРЕТИЧЕСКАЯ МЕХАНИКА: СТАТИКА. КИНЕМАТИКА. ДИНАМИКА КОНСПЕКТ ЛЕКЦИЙ Издание второе. Исправленное и дополненное Москва Ижевск 2005 УДК 531.1 Интернет-магазин http://shop.rcd.ru
Министерство образования Республики Беларусь Учреждение образования «Полоцкий государственный университет» В. Н. КОРОВКИН, Н. А. КУЛИК ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Учебно-методический комплекс для студентов
Министерство образования и науки России Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Казанский национальный исследовательский технологический
Министерство образования и науки Российской Федерации Елабужский государственный педагогический университет В.Ю. Шурыгин, Р.М. Тимербаев ОСНОВЫ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ F тр r α R a ϕ x m g α Елабуга 9 УДК
Министерство образования и науки Российской Федерации Ивановский государственный химико-технологический университет С.Г. Сахарова, В.П. Зарубин, М.Ю. Колобов ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. Статика Учебное пособие
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕТУРНО - СТРОИТЕЛЬНЫЙ
Экзаменационный билет 9.6.6 ч. мин. Вопрос. Теорема о скоростях точек неизменяемого отрезка. Вопрос. Центральный удар. Косой удар. Соударение двух тел. Удар по неподвижному телу Невесомый стержень B длиной
Федеральное агентство по образованию Южно-уральский Государственный Университет Кафедра теоретической механики 531(07) Т338 Теоретическая механика Рабочая программа и контрольные задания. Часть I. Статика
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ СЫКТЫВКАРСКИЙ ЛЕСНОЙ ИНСТИТУТ ФИЛИАЛ ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКАЯ ГОСУДАРСТВЕННАЯ ЛЕСОТЕХНИЧЕСКАЯ
Министерство образования и науки Российской Федерации Уральский федеральный университет имени первого Президента России Б. Н. Ельцина Ю. В. Денисов Н. А. Клинских ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Допущено учебно-методическим
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «Ульяновский государственный технический университет» В. К. МАНЖОСОВ, О. Д. НОВИКОВА,
Министерство образования и науки Российской Федерации Федеральное агентство по образованию Южно-Уральский государственный университет Кафедра «Технология обработки материалов» 53(07) П408 Н.И. Пневская
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» В.В. Дробчик,
. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА.3. Динамика. Динамика это часть теоретической механики, в которой рассматривается движение материальной точки или тела под действием приложенных сил, а также устанавливается связь
СРЕДНЕЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕ А. А. ЭРДЕДИ, Н. А. ЭРДЕДИ ТЕХНИЧЕСКАЯ МЕХАНИКА УЧЕБНИК Рекомендовано Федеральным государственным автономным учреждением «Федеральный институт развития образования»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ РАСЧЕТНО-ГРАФИЧЕСКИХ И КОНТРОЛЬНЫХ РАБОТ ПО ТЕОРЕТИЧЕСКОЙ
Министерство образования и науки РФ Федеральное агенство по образованию Пермский государственный технический университет Кафедра теоретической механики ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Учебно-методическое пособие
Федеральное агентство по образованию Архангельский государственный технический университет TEOРИЯ МЕХАНИЗМОВ И МАШИН Методические указания и задания к контрольной роботе Архангельск 2009 В соответствии
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Владимирский государственный университет А.И. НОВОЖИЛОВ КРАТКИЙ КУРС ТЕОРЕТИЧЕСКОЙ
РАСЧЕТ ТРЕХШАРНИРНЫХ СИСТЕМ Хабаровск 4 Министерство образования Российской Федерации Государственное образовательное учреждение высшего профессионального образования «Хабаровский государственный технический
Министерство образования Республики Беларусь УО «Витебский государственный технологический университет» Тема6. «Определенный интеграл» Кафедра теоретической и прикладной математики. разработана доц. Е.Б.Дуниной
Решение задач по теме «Магнетизм» Магнитное поле- это особая форма материи, которая возникает вокруг любой заряженной движущейся частицы. Электрический ток- это упорядоченное движение заряженных частиц
ФИЗИЧЕСКАЯ МЕХАНИКА И ЕЕ РАЗДЕЛЫ Физическая механика или просто механика раздел физики, в котором описывается наиболее простая форма движения материи: механическое движение, состоящее из изменения взаимного
Примеры решений контрольных работ Л.И. Терехина, И.И. Фикс 1 Контрольная работа 3. Аналитическая геометрия на плоскости 1. Составить уравнения прямых, проходящих через точку A(4; 1) a) параллельно прямой
Львов Геннадий Иванович ОСНОВЫ ТЕОРИИ ПЛАСТИН И ОБОЛОЧЕК Учебник ВВЕДЕНИЕ Основные уравнения теории упругости В теории упругости существуют три группы формул которые образуют основные уравнения теории
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НИЗКОТЕМПЕРАТУРНЫХ И ПИЩЕВЫХ ТЕХНОЛОГИЙ
И В Яковлев Материалы по физике MathUsru Равноускоренное движение Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное
РЫЛЬСКИЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ КОЛЛЕДЖ ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ГОУ ВПО «ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС По дисциплине «Теоретическая Механика» Для направления 151000 «Технологические
. ПОТЕНЦИАЛ. РАБОТА СИЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ Потенциал, создаваемый точечным зарядом в точке A, находящейся на, если положить потенциал на бесконечности равным нулю: φ( ). Потенциал, создаваемый в
docplayer.ru
Депобразования и молодежи Югры
бюджетное учреждение профессионального образования
Ханты-Мансийского автономного округа – Югры
«Мегионский политехнический колледж»
(БУ «Мегионский политехнический колледж»)
Преподаватель физики и технической механики
Магомедов А.М.
Учебный материал по теоретической механике.
часть 2.
Кинематика. Динамика.
Методические указания (для изучения теоретического курса, практических и лабораторных занятий) для студентов очной и заочной форм обучения.
Направление: Специальность 131018 Разработка и эксплуатация нефтяных и газовых месторождений.
Мегион, 2016
Депобразования и молодежи Югры
бюджетное учреждение профессионального образования
Ханты-Мансийского автономного округа – Югры
«Мегионский политехнический колледж»
(БУ «Мегионский политехнический колледж»)
Преподаватель физики и технической механики
Магомедов А.М.
Учебный материал по теоретической механике
часть 2
Кинематика. Динамика.
методические указания (для изучения теоретического курса, практических и лабораторных занятий) для студентов очной и заочной форм обучения.
Направление: Специальность 131018 Разработка и эксплуатация нефтяных и газовых месторождений.
Мегион,2016
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
Одной из ведущих дисциплин высшей технической школы является теоретическая механика - наука о механическом движении и взаимодействии материальных тел. Законы теоретической механики лежат в основе фундаментальных, прикладных и специальных наук.
Теоретическая механика включает в себя три основных раздела: статика, кинематика и динамика.
Кинематика - раздел теоретической механики, в котором изучают геометрические свойства движения тел без учета их масс и действующих на них сил.
Динамика - это основной завершающий раздел теоретической механики, изучающий движение материальных точек и тел с учетом сил, вызывающих это движение.
В общем курсе теоретической механики изучают механику материальной точки, механику твердого тела и механику системы материальных точек. Роль и значение теоретической механики состоит в том, что ее законы и методы позволяют изучить ряд важных явлений в окружающем мире.
В пособии рассматриваются основные теоретические вопросы разделов механики, а так же дано подробное решение наиболее важных задач из контрольных работ по кинематике и динамике, при этом, следует уделить особое внимание тем задачам, которые будут предложены студентам на экзамене.
По каждому разделу теоретической механики представлены контрольные задания по ряду задач для расчетно-графических работ, которые могут выполняться на практических занятиях или выдаваться как домашние задания, а так же могут быть использованы в качестве контрольных заданий для заочного обучения.
Выбор задач осуществляется по вариантам, указанным преподавателем (для очного обучения), или по двум последним цифрам личного шифра (для заочного обучения).
Пособие содержит по 30 вариантов заданий по 4 темам кинематики и задачу по динамике, охватывающую при решении ее различными способами 4 темы.
Цель работы - закрепить теоретический материал программы и приобрести твердые навыки решения задач по теоретической механике.
1. КИНЕМАТИКА
1.1 Основные понятия и определения
В задачах данного раздела определяются координаты, скорость, ускорение точки в любой назначенный момент времени при различных способах задания движения. Из всех способов задания движения точки наибольшее распространение получили координатный и естественный способы.
Рассмотрим координатный способ задания движения точки. Положение в пространстве движущейся точки определяется тремя координатами в декартовой системе координат. Эти координаты задаются как функции времени:
; 
; 
.
Скорость точки представляет собой вектор, характеризующий быстроту и направление движения точки в данный момент времени.
При задании движения точки уравнениями проекции скорости на оси декартовых координат равны:
; 
; 
.
Модуль скорости
.
Характеристикой быстроты изменения скорости является ускорение а. При задании движения точки уравнениями проекции ускорения на координатные оси равны:
; 
; 
.
Модуль ускорения:
.
Далее рассмотрим естественный способ задания движения точки.
Считается, что движение точки задано естественным способом, если указаны ее траектория и закон изменения криволинейной координаты 
. Модуль скорости точки определяется по формуле
.
Вектор скорости V направлен по касательной к траектории.
Ускорение точки определяется как векторная сумма касательного и нормального ускорений точки:
.
Модуль касательного ускорения определяется по формуле
.
Модуль нормального ускорения определяется по формуле
,
где 
– радиус кривизны траектории в данной точке.
Вектор нормального ускорения 
всегда направлен по главной нормали в сторону центра кривизны траектории.
Модуль полного ускорения
.
ω = π·n/ 30
Касательное ускорение
Неравномерное
aτ = dV / dt
aτ = R·ε
Равнопеременное
aτ = (V-V0) / t
Ускорение нормальное
Неравномерное
an = V2 / ρ
an = ω2· R
Равнопеременное
Полное ускорение
Неравномерное
a = √ an2 + aτ2
a = R·√ε2 + ω4
Равнопеременное
Ускорение
угловое
Неравномерное
ε = 0
ε = dω / dt
Равнопеременное
ε = (ω- ω0) / t
Исследование движения точек фигуры при плоскопараллельном движении
1. Для определения мгновенного центра скоростей достаточно знать направление скоростей двух любых точек фигуры, мгновенный центр скоростей находится в точке пересечения перпендикуляров, опущенных из этих точек к их скоростям.
2. Скорости точек плоской фигуры пропорциональны их расстояниям до мгновенного центра скоростей: VA/PA=VB/PB, где P – мгновенный центр скоростей, A и B – любые точки плоской фигуры.
При сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей,
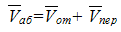
α – угол между векторами относительной и переносной скоростей.
При сложном движении ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений. Кориолисово ускорение равно удвоенному векторному произведению переносной угловой скорости и относительной скорости точки: 
Направлен вектор перпендикулярно плоскости, проходящей через векторы переносной угловой скорости и относительной скорости точки в сторону поворота вектора переносной угловой скорости к вектору относительной скорости против хода часовой стрелки.
1.2. Кинематика точки
1.2.1. Пример выполнения расчетно-графической работы
Пример 1
1. Исходные данные. По заданным уравнениям движения точки М
, 
(где x, y - в см)
установить вид ее траектории и для момента времени 
сек. найти положение точки на траектории, ее скорость, ускорение.
2. Решение.
Определяем вид траектории. Исключая время 
из уравнений движения, найдем вид траектории точки М в координатной форме.
Так как время входит в аргументы тригонометрических функций синуса и косинуса, то, используя формулу 
, получим
Траекторией движения точки М является эллипс. Центр эллипса имеет координаты XC = 0, YC = 4, gолуоси эллипса а=2 см, b=3 см.
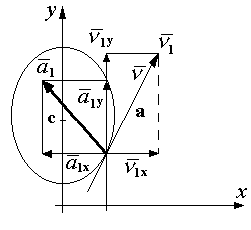
Определяем положение точки на траектории при сек. Подставляя время сек. в 34, получим
,
.
Точку с координатами 
, 
обозначим на траектории через М1.
Скорость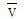
точки М определим через ее проекции на координатные оси.
, 
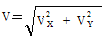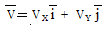, где
,
.
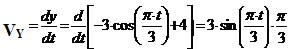Тогда
.
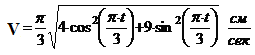Так как величина скорости 
зависит от времени , то движение точки неравномерное.
При сек.
,
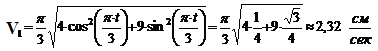
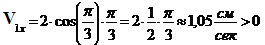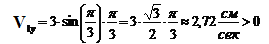
Построим вектор скорости точки М1. 1
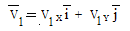или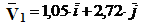
.
В точке М1 параллельно осям x, y, в выбранном масштабе, откладываем
.
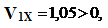
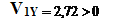Вектор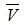 
- диагональ прямоугольника, построенного на V1X и V1Y, как на сторонах.
Пример 2.
1. Исходные данные.
Даны уравнения движения точки М в плоскости xy:
, 
(где x, y - в сантиметрах, - в секундах).
Найти уравнение траектории точки М; для момента времени сек., найти положение точки на траектории, ее скорость, полное ускорение, касательное и нормальное ускорения, а также радиус кривизны в соответствующей точке.
2. Решение.
Из второго уравнения, подставляя значение в первое уравнение, получим уравнение траектории X = Y2 + 2 – уравнение параболы.
Заметим, что траекторией движения является только верхняя ветвь параболы, т.к. время t>0 .
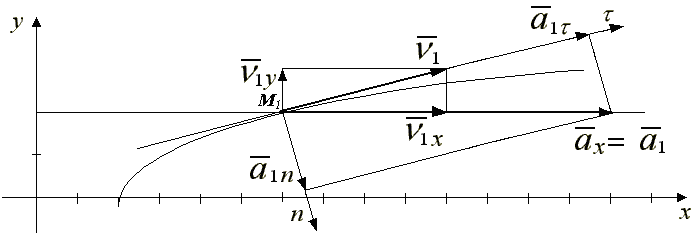
Полагая время сек., найдем координаты, определяющие положение точки на траектории в этот момент времени.
.
Точку с координатами =6, =2 на траектории обозначим М1.
Величину скорости точки М найдем по ее проекциям на координатные оси:
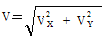, где
VX = (4t2 + 2)' = 8tсм/с, VY = (2t)' = 2см/с.
Тогда, поскольку величина скорости зависит от времени , то движение точки неравномерное.
В момент времени сек: V1X = 8см/с, V1Y = 2 см/с, V1 = 8,2 см/с.
Выберем масштаб и построим вектор скорости в положении М1 по составляющим V1X и V1Y
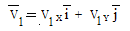
Модуль ускорения точки М определяем аналогично
, где
,
.
Полное ускорение
является постоянным во все время движения точки.
Выберем масштаб, построим вектор ускорения:
, 
.
Разложим полное ускорение на составляющие вдоль этих осей
, где
- касательное ускорение точки М;
- нормальное ускорение точки М.
Из рисунка 
, 
Касательное ускорение определяется по формуле aτ = dV/dt.
Если dV/dt >0 – движение ускоренное,
если dV/dt <0 – движение замедленное.
Найдем 
Т.к. время t > 0, aτ >0, следовательно, движение точки М ускоренное.
, что соответствует значению на рисунке.
Нормальное ускорение характеризует изменение скорости по направлению. В случае криволинейного движения, оно всегда существует и определяется по формуле an = V2/ρ, где ρ - радиус кривизны траектории в соответствующей точке. Т.к. радиус кривизны параболы в точке М1 неизвестен, то величину нормального ускорения можно определить следующим образом:
, что соответствует значению на рисунке.
Радиус кривизны параболы в точке М1 найдем из выражения
ρ1 = V21/a1n = 68/1,8 = 37,8см
Ответ: точка М совершает криволинейное ускоренное движение, т.к. вектор касательного ускорения во все время движения совпадает с направлением вектора скорости.
1.2.2. Варианты заданий
Точка М движется в плоскости xOy согласно уравнениям: x=x(t), y=y(t).
Определить траекторию движения точки, для заданного момента времени t найти положение точки на траектории, ее скорость и ускорение и показать их на рисунке, а также определить радиус кривизны траектории в данной точке.
Исходные данные для расчета
вар.
X, см
Y, см
t, с
№
вар.
X, см
Y, см
t, с
1
4t2 + 3t + 7
8t2 + 6t + 1
2
16
t2 + 4t + 3
t2 + 8t + 1
2
2
3t2 + 6t + 2
3t
1
17
-t - 1
-2/(t + 1)
1
3
3cos(πt/3)
5sin(πt/3)
3
18
t2
3t - 2
2
4
3/(t+1)
3t+3
1
19
2sin(πt/8) +2
2cos(πt/8) - 1
2
5
2sin(πt/3) +1
3cos(πt/3)
2
20
2t3 + 3
6t3 + 12
1
6
3t2 + 2t + 5
9t2 + 6t + 11
1
21
-3/(t + 1)
-3t - 3
2
7
2t2 + 6t + 2
2t
2
22
t4 + 1
t4 - 2
2
8
t2 - 4t + 1
t + 1
1
23
3cos(t)
3sin(t)
π/6
9
-4/(t + 1)
-2t - 2
0
24
10/(5t + 1)
2,5t
1
10
2t2 + 4
3t + 1
2
25
2cos(πt/6)
3sin(πt/6) + 3
2
11
3sin(πt/4) +2
4cos(πt/4) - 1
1
26
3cos(πt/3) + 2
3sin(πt/3) - 2
1
12
7t + 1
-8/(7t + 1)
1/7
27
3t2 + 3t + 3
8t2 + 8t + 5
1
13
3cos(πt/6) + 1
2sin(πt/6) - 2
3
28
t2 + 6t + 2
2t
1
14
4t + 5
5t2 + 1
1
29
5/(t+1)
5t+5
2
15
4cos(πt/4)
4sin(πt/4) - 2
1
30
2cos(πt/3)
3sin(πt/3) + 2
2
1.3. Простейшие виды движения твердого тела
1.3.1. Пример выполнения расчетно-графической работы
1. Исходные данные.
Определить скорость и ускорение точки М, а также скорость и ускорение груза 1 в заданный момент времени.
Дано: x(t) = 7t2, R2 = 25см, r2 = 15см, R3 = 20см, r3 = 10см, t1 = 1c
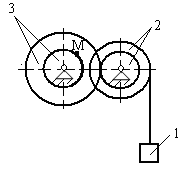
2. Решение
V1 = x´(t) = 14t; a1 = 14м/с2;
V1(t1) = 14м/с
VМ = V1(r2· r3)/( R2· R3) ; VМ =4,2t ;
VM(t1) = 4,2м/с
aM = √aτ2 + an2;
aτ = VМ´ = 4,2м/с2; an = VМ2/ r3 = 1,76 м/с2;
aM =4,55 м/с2
1.4. Плоскопараллельное движение твердого тела
1.4.1. Пример выполнения расчетно-графической работы
1. Исходные данные. Определить VA, VB, aA, aB, ωAB.
Дано: OA = 25см, АВ = 25см, ωOA = 2рад/с, εOA = 4рад/с2
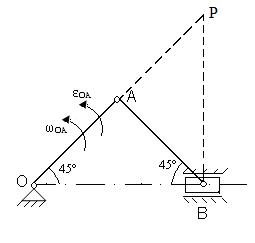
2. Решение
VA = ωOA· OA; VA = 50см/с; aA = ОА√ ωOA4 + εOA2; aA = 140 см/с2. Для нахождения VB необходимо найти положение мгновенного центра скоростей (точку P) и воспользоваться VB= VABP/AP; ωAB= VA/AP. Для вычисления ускорения точки В необходимо воспользоваться теоремой о сложении ускорений, взяв точку А в качестве полюса.
1.5. Сложное движение точки
1.5.1. Пример выполнения расчетно-графической работы
1. Исходные данные. ОМ(t) = t2 +t; φ(t) = t2 – t; R =4м, t=1c.
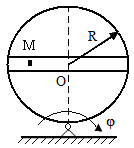
2. Решение. Определяем первоначально положение точки в заданный момент времени OM = 2м. Для нахождения абсолютной скорости необходимо найти относительную и переносную скорости:
Vот= ОМ(t)´=2t+1=3м/с; Vпер=ω∙OM=φ(t)´∙OM=(2t-1)∙OM=2м/с. Vабс=√V2от+V2пер-2Vот∙Vперcosβ. Угол β - угол между вектором относительной скорости и вектором переносной скорости. cosβ=OM/√R2+OM2=2/√20=0,48. Тогда Vабс=7,23м/с. Абсолютное ускорение находим согласно теореме Кориолиса.
2. ДИНАМИКА
2.1. Основные понятия и определения
Общие теоремы динамики
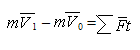
Теорема об изменении кинетической энергии
mV12/2 – mV02/2 = ∑Ai=FS
Кинетическая энергия тела зависит от характера его движения.
Момент инерции однородных тел
СтерженьL – длина
m- масса
Ось А -перпендикулярна стержню и проходит через его конец
JА = 1/3mL2
Тонкое круглое кольцо
R – радиус
m - масса
Ось С - перпендикулярна плоскости кольца и проходит через его центр
JC = mR2
Круглая пластина или цилиндр
R – радиус
m- масса
Ось С - перпендикулярна плоскости пластины и проходит через его центр
JC = 1/2mR2
Сплошная прямоугольная пластина
m – масса
А и В - стороны
Ось X – вдоль стороны, длиной А, ось Y – вдоль стороны, длиной В
JX = 1/3mВ2
JY = 1/3mА2
Принцип Даламбера. Основой для построения теоретической механики служат законы Ньютона. Однако на основе законов Ньютона можно получить некоторые другие общие законы, позволяющие составить уравнения, описывающие движение механической системы. Такие законы получили название принципов аналитической механики. Одним из них является принцип Даламбера.
Пусть мы имеем систему, состоящих из n материальных точек. Выделим какую-нибудь из точек системы с массой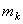 
. Под действием приложенных к ней внешних и внутренних сил 
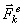и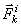 
(в которые входят и активные силы, и реакции связи) точка получает по отношению к инерциальные системе отсчета некоторое ускорение 
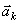. Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам 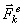и 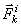прибавить силу инерции 
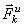, то полученная система сил будет уравновешенной, т.е. будет
.
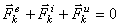Это выражение отображает принцип Даламбера для одной материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает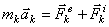 
. Перенесем здесь член 
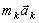в правую часть равенства и придем к последнему соотношению.
Принцип Даламбера для системы: если в любой момент времени к каждой из точек системы, кроме фактически действующих на ней внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики.
Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систему. Тогда на основании принципа Даламбера должно быть:
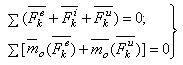
2.2. Динамика механических систем с одной степенью свободы
2.2.1. План выполнения расчетно-графической работы
Задачу, представленную в пункте 3.2.2 необходимо решать по следующему плану:
1. Найти ускорение тела 1, используя теорему об изменении кинетической энергии. T – T0 = ∑Aie + ∑Aii.
2. Найти ускорение тела 1, используя принцип Даламбера.
3. Найти ускорение тела 1, используя общее уравнение динамики.
4.Найденные ускорения, при правильном решении должны совпадать, возможна небольшая погрешность.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Теоретическая механика. Терминология [Текст]. Вып. 90. М.: Наука, 2016.-40с.
2. Тарг, С.М. Краткий курс теоретической механики [Текст]: учеб. для втузов/ С. М. Тарг. 14-е изд, стер.-М.: Высш. шк., 2014.-416с.
3. Попов, М.В. Теоретическая механика. Краткий курс [Текст]: учеб. для втузов/ М. В. Попов. - М.: Наука, 1016.-336с.
4. Вебер, Г.Э. Лекции по теоретической механике [Текст]: учеб. пособие/ Г. Э. Вебер, С. А. Ляпцев. Екатеринбург: УГГГА, 2008.-272с.
infourok.ru
