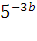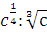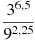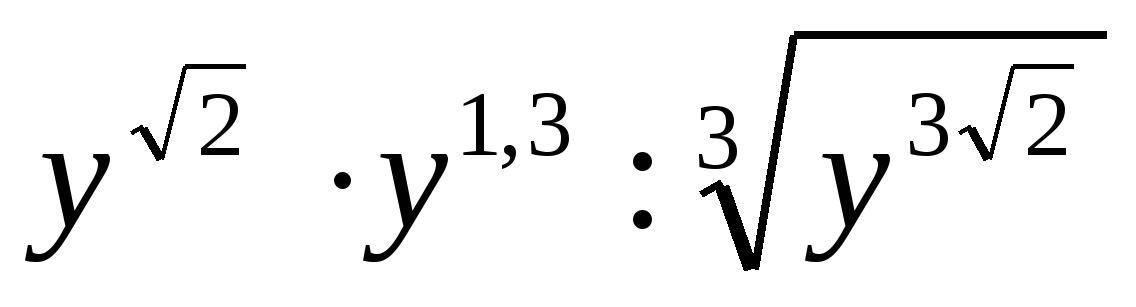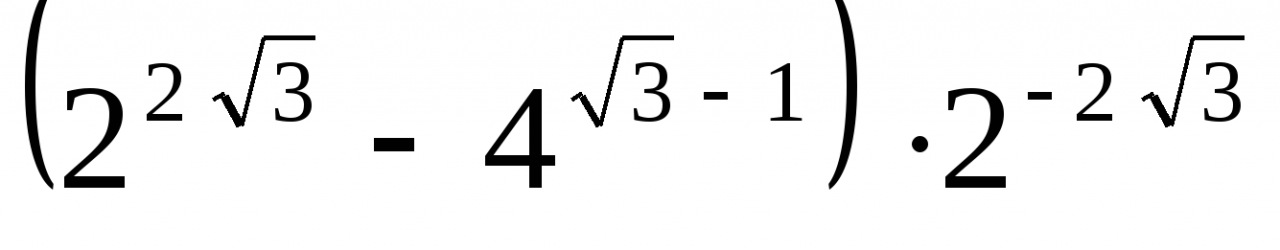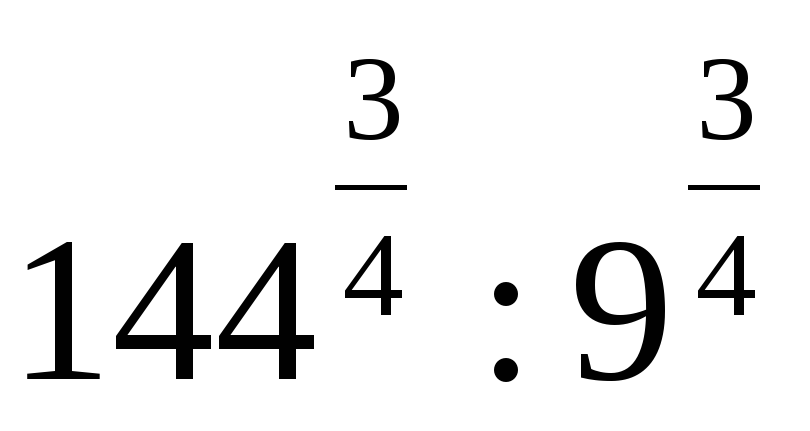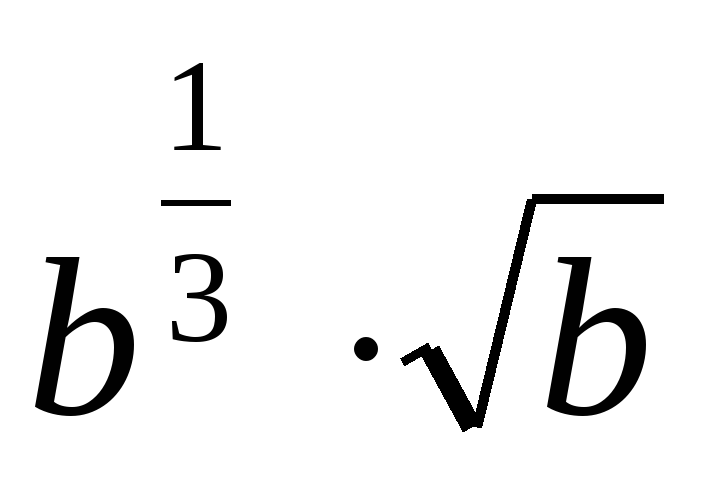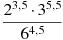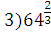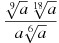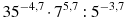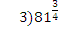Главная »
Реферат »
Реферат на тему степень с действительным показателем
Урок по теме "Степень с действительным показателем" в 11-м классе. Реферат на тему степень с действительным показателем
Степени с действительным показателем
Самостоятельная работа студента 1 курс по теме Степени с действительным показателем. Свойства степени с действительным показателем (6 часов)
ЗАДАНИЕ:
Изучить теоретический материал и сделать конспект (2 часа)
Разгадать кроссворд (2 часа)
Выполнить домашнюю контрольную работу (2 часа)
Справочный и дидактический материал представлен ниже
О понятии степени с рациональным показателем
Некоторые наиболее часто встречающиеся
Виды трансцендентных функций, прежде
Всего показательные, открывают доступ ко
Многим исследованиям.
Л. Э й л е р
Из практики решения-все более сложных алгебраических задач и оперирования со степенями возникла необходимость обобщения понятия степени и расширения его посредством введения в качестве показателя нуля, отрицательных и дробных чисел.
Равенство а0 = 1 (для  ) применял в своих трудах в начале XV в. самаркандский ученый ал-Каши. Независимо от него нулевой показатель был введен Н. Шюке в XV в. Последний ввел и отрицательные показатели степени. Идея дробных показателей содержится у французского математика Н. Орема (XIV в.) в его
) применял в своих трудах в начале XV в. самаркандский ученый ал-Каши. Независимо от него нулевой показатель был введен Н. Шюке в XV в. Последний ввел и отрицательные показатели степени. Идея дробных показателей содержится у французского математика Н. Орема (XIV в.) в его
труде «Алгоризм пропорций». Вместо нашего знака  он писал
он писал  , вместо
, вместо  он писал
он писал  4. Орем словесно формулирует правила действий со степенями, например (в современной записи):
4. Орем словесно формулирует правила действий со степенями, например (в современной записи):  ,
,  и т.п.
и т.п.
Позже дробные, как и отрицательные, показатели встречаются в «Полной арифметике» (1544) немецкого математика М. Штифеля и у С. Стевина. Последний пишет о том, что корень степени п из числа а можно считать как степень а с дробным показателем  .
.
О целесообразности введения нулевого, отрицательных и дробных показателей и современных символов впервые подробно писал в 1665 г, английский математик Джон Валлис. Его дело завершил И. Ньютон, который стал систематически применять новые символы, после чего они вошли в общий обиход.
Введение степени с рациональным показателем является одним из многих примеров обобщения понятия математического действия. Степень с нулевым, отрицательным и дробным показателями определяется таким образом, чтобы к ней были применимы те же правила действий, которые имеют место для степени с натуральным показателем, т. е. чтобы сохранились основные свойства первоначально определенного понятия степени, а именно:





Новое определение степени с рациональным показателем не противоречит старому определению степени с натуральным показателем, т. е. смысл нового определения степени с рациональным показателем сохраняется и для частного случая степени с натуральным показателем. Этот принцип, соблюдаемый при обобщении математических понятий, называется принципом перманентности (сохранения, постоянства). В несовершенной форме его высказал в 1830 г. английский математик Дж. Пикок, полностью и четко его установил немецкий математик Г. Ганкель в 1867 г. Принцип перманентности соблюдается и при обобщении понятии числа и расширении его до понятия действительного числа, а до этого — при введении понятия умножения на дробь и т. п.
Степенная функция и графическое решение уравнений и неравенств
Благодаря открытию метода координат и аналитической геометрии начинай с XVII в. стало возможным общеприменимое графическое исследование функций и графическое решение уравнений.
Степенной функцией называют функцию вида
 , (1)
, (1)
где α— постоянное вещественное число. Вначале мы ограничимся, однако, лишь рациональными значениями α и вместо равенства (1) запишем:
 , (2)
, (2)
где  — рациональное число. Для
— рациональное число. Для  и
и  по определению соответственно имеем:
по определению соответственно имеем:
у =1, у =х.
Графиком первой из этих функций на плоскости является прямая, параллельная оси Ох, а второй — биссектриса 1-го и 3-го координатных углов.
При  графиком функций является парабола
графиком функций является парабола  . Декарт, который первое неизвестное обозначал через z, второе — через у, третье — через x:, записывал уравнение параболы так:
. Декарт, который первое неизвестное обозначал через z, второе — через у, третье — через x:, записывал уравнение параболы так:  (z— абсцисса). Параболой он часто пользовался для решения уравнений. Чтобы решить, например, уравнение 4-й степени
(z— абсцисса). Параболой он часто пользовался для решения уравнений. Чтобы решить, например, уравнение 4-й степени
 (3)
(3)
Декарт с помощью подстановки
 (4)
(4)
получил квадратное уравнение с двумя неизвестными:
 (5)
(5)
изображающее окружность, расположенную в одной плоскости (zх) с параболой (4). Таким образом, Декарт, вводя вторую неизвестную (х), разбивает уравнение (3) на два уравнения (4) и (5), каждое из которых представляет определенное геометрическое место точек. Ординаты точек их пересечения и дают корни уравнения (3).
Притча:
«Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному замку. «Кто первым откроет, тот и будет первым помощником». Никто даже не притронулся к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ.
Тогда царь сказал: «Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, а надеешься на собственные силы и не боишься сделать попытку».
И мы сегодня будем пытаться, пробовать, чтобы прийти к правильному решению.
1. С каким математическим понятием связаны слова:
Основание
Показатель (Степень)
Какими словами можно объединить слова:
Рациональное число
Целое число
Натуральное число
Иррациональное число (Действительное число)
Сформулируйте тему урока. (Степень с действительным показателем)
Задачи:
– повторить свойства степени
– рассмотреть применение свойств степени при вычислениях и упрощениях выражений
– отработка вычислительных навыков.
Итак, ар, где р – число действительное.
Приведите примеры (выберете из выражений 5–2,  , 43,
, 43,  ) степени
) степени
– с натуральным показателем
– с целым показателем
– с рациональным показателем
– с иррациональным показателем
При каких значениях а имеет смысл выражение
аn, где n  (а – любое)
(а – любое)
аm, где m  (а не равно 0) Как от степени с отрицательным показателем перейти к степени с положительным показателем?
(а не равно 0) Как от степени с отрицательным показателем перейти к степени с положительным показателем?
 , где p
, где p  , q
, q  (а > 0)
(а > 0)
Какие действия (математические операции) можно выполнять со степенями?
Установите соответствие:
| При умножении степеней с равными основаниями | Основания умножаются, а показатель остаётся прежним |
| При делении степеней с равными основаниями | Основания делятся, а показатель остаётся прежним |
| При возведении степени в степень | Основание остаётся прежним, а показатели умножаются |
| При умножении степеней с равными показателями | Основание остаётся прежним, а показатели вычитаются |
| При делении степеней с равными показателями | Основание остаётся прежним, а показатели складываются |
«Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей»
– Так сказал американский математик Морис Клайн.






Вариант 1

Вариант 2

Домашняя контрольная работа «Степень с действительным показателем».
Вариант №1 [Вариант №2].
1)Вычислить:

2) Упростить выражение при а

 ;
;
3) Сократить дробь 
4) Сравнить числа  и
и 
10
studfiles.net
Степень с действительным показателем | Бесплатные курсовые, рефераты и дипломные работы
Степень с действительным показателем
Вариант 1
№1. Укажите рисунок, на котором изображен график функции 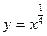 :
:
№2. Представьте выражение 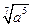 в виде степени с рациональным показателем:
в виде степени с рациональным показателем:
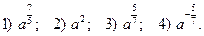
№3. Найдите … значение выражения  .
.
№4. Решите уравнение 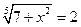 .
.
№5. Вынесите множитель из-под знака корня в выражении 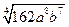 , если
, если 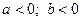 .
.
№6. Сократите дробь: 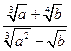
№7.Найдите значение выражения 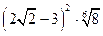 .
.
№8. Решите неравенство 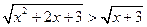 .
.
№9. Сумма членов бесконечной геометрической прогрессии 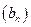 в три раза больше ее первого члена. Найдите отношение
в три раза больше ее первого члена. Найдите отношение 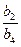 .
.
№10. Решите уравнение 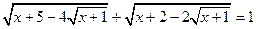
Вариант 2
№1. Укажите рисунок, на котором изображен график функции 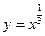 :
:
№2. Представьте выражение 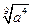 в виде степени с рациональным показателем:
в виде степени с рациональным показателем:
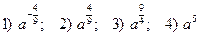 .
.
№3. Найдите значение выражения 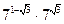 .
.
№4. Решите уравнение 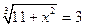 .
.
№5. Вынесите множитель из-под знака корня в выражении 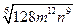 , если
, если 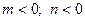 .
.
№6. Сократите дробь: 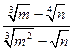
№7.Найдите значение выражения 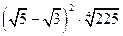 .
.
№8. Решите неравенство 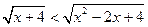 .
.
№9. Сумма членов бесконечной геометрической прогрессии 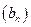 в полтора раза меньше ее первого члена. Найдите отношение
в полтора раза меньше ее первого члена. Найдите отношение 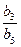 .
.
№10. Решите уравнение 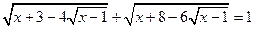 .
.
Контрольная работа №2
(для классов физико-математического направления)
Степень с действительным показателем
Вариант 1
№1. Укажите функцию, график которой изображен на рисунке: 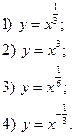 | 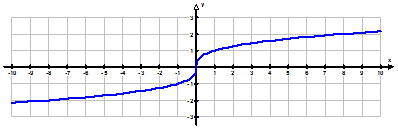 |
№2. Представьте число 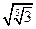 в виде степени с рациональным показателем:
в виде степени с рациональным показателем:
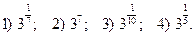
№3. Найдите значение выражения 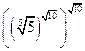 .
.
№4. Представьте в виде обыкновенной дроби число 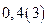 .
.
№5. Упростите выражение 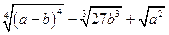 , если
, если 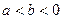 .
.
№6. Решите уравнение: 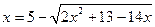 .
.
№7.Упростите выражение 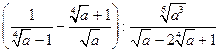 .
.
№8. Найдите значение выражения 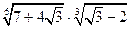 .
.
№9. Решите неравенство 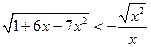 .
.
№10. Решите уравнение 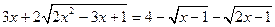 .
.
Вариант 2
№1. Укажите функцию, график которой изображен на рисунке: 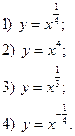 | 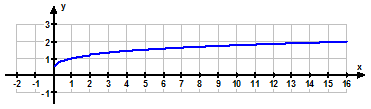 |
№2. Представьте число 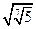 в виде степени с рациональным показателем:
в виде степени с рациональным показателем:
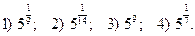
№3. Найдите значение выражения 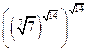 .
.
№4. Представьте в виде обыкновенной дроби число 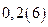 .
.
№5. Упростите выражение 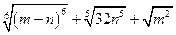 , если
, если 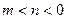 .
.
№6. Решите уравнение: 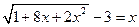 .
.
№7.Упростите выражение 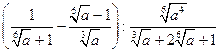 .
.
№8. Найдите значение выражения 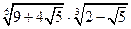 .
.
№9. Решите неравенство 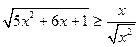 .
.
№10. Решите уравнение 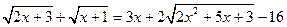 .
.
refac.ru
Персональный сайт - Свойства степени
Степень с натуральным показателем.
Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен a:
an = 
В выражении an :
- число а (повторяющийся множитель) называют основанием степени
- число n (показывающее сколько раз повторяется множитель) – показателем степени
Например:25 = 2·2·2·2·2 = 32,здесь:2 – основание степени,5 – показатель степени,32 – значение степени
Отметим, что основание степени может быть любым числом.
Вычисление значения степени называют действием возведения в степень. Это действие третьей ступени. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание).
Для записи больших чисел часто применяются степени числа 10. Так, расстояние от земли до солнца примерно равное 150 млн. км, записывают в виде 1,5 · 108
Каждое число больше 10 можно записать в виде: а · 10n , где 1 ≤ a < 10 и n – натуральное число. Такая запись называется стандартным видом числа.
Например: 4578 = 4,578 · 103 ;
103000 = 1,03 · 105.
Свойства степени с натуральным показателем:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней складываются
a m · a n = a m + n
например: 71.7 · 7 - 0.9 = 71.7+( - 0.9) = 71.7 - 0.9 = 70.8
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней вычитаются
a m / a n = a m — n ,
где, m > n, a ≠ 0
например: 133.8 / 13 -0.2 = 13(3.8 -0.2) = 133.6
3. При возведении степени в степень основание остается прежним, а показатели степеней перемножаются.
(a m ) n = a m · n
например: (23)2 = 2 3·2 = 26
4. При возведении в степень произведения в эту степень возводится каждый множитель
(a · b)n = an·bm,
например:(2·3) 3 = 2 n · 3 m ,
5. При возведении в степень дроби в эту степень возводятся числитель и знаменатель
(a / b)n = an / bn
например: (2 / 5)3=(2 / 5)·(2 / 5)·(2 / 5) = 23/53
Степенью числа а > 0 с рациональным показателем  , где m – целое число, а n – натуральное (n > 1), называется число
, где m – целое число, а n – натуральное (n > 1), называется число 
Итак: 
Например:
Степень числа 0 определена только для положительных показателей;
по определению 0r = 0 , для любого r > 0
Замечания
- Из определения степени с рациональным показателем следует, что для любого положительного а и любого рационального r число ar положительно.
- Любое рациональное число допускает различные записи его в виде дроби, поскольку
 для любого натурального k. Значение аr также не зависит от формы записи рационального числа r.
для любого натурального k. Значение аr также не зависит от формы записи рационального числа r. - При а < 0 рациональная степень числа а не определяется.
Для степеней с рациональным показателем сохраняются основные свойства степеней, верные для любых показателей (при условии, что основание степени будет положительным).
Итак, для любого действительного числа мы определили операцию возведения в натуральную степень; для любого числа 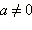 мы определили возведения в нулевую и целую отрицательную степень; для любого
мы определили возведения в нулевую и целую отрицательную степень; для любого 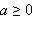 мы определили операцию возведения в положительную дробную степень; для любого
мы определили операцию возведения в положительную дробную степень; для любого 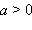 мы определили операцию возведения в отрицательную дробную степень.
мы определили операцию возведения в отрицательную дробную степень.
Возникает естественный вопрос: можно ли каким-либо образом определить операцию возведения в иррациональную степень, а, следовательно, определить смысл выражения ax и для любого действительного числа x? Оказывается, что для положительных чисел a можно придать смысл записи aα , где α - иррациональное число. Для этого нужно рассмотреть три случая: a = 1, a > 1, 0 < a < 1.
- Если a = 1, то по определению полагают, что 1α = 1.
- Если a > 1, то выберем любое рациональное число r1 < α и любое рациональное число r2 > α. Тогда, очевидно, r1 < r2 и, следовательно:
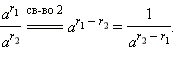
Но 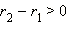 и потому (так как a > 1)
и потому (так как a > 1) 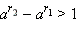 и, наконец,
и, наконец, 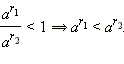
Под 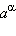 понимают такое число, которое лежит между
понимают такое число, которое лежит между 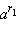 и
и 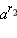 при любом выборе чисел
при любом выборе чисел 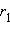 и
и 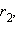 обладающих свойством
обладающих свойством 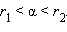 Можно доказать, что число
Можно доказать, что число 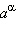 существует и единственно для любого a > 1 и любого иррационального α.
существует и единственно для любого a > 1 и любого иррационального α. - Если 0 < a < 1, то выберем любое рациональное число
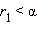 и любое рациональное число
и любое рациональное число 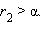 Тогда, очевидно,
Тогда, очевидно, 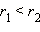 и, следовательно,
и, следовательно, 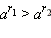 (это неравенство доказывается аналогично приведённому выше для a > 1). Под
(это неравенство доказывается аналогично приведённому выше для a > 1). Под 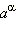 понимают такое число, которое лежит между
понимают такое число, которое лежит между 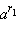 и
и 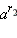 при любом выборе чисел
при любом выборе чисел 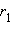 и
и 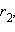 обладающих свойством
обладающих свойством 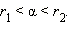 Можно доказать, что число
Можно доказать, что число 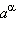 существует и единственно для любого 0 < a < 1 и любого иррационального α.
существует и единственно для любого 0 < a < 1 и любого иррационального α.
Итак, для a > 0 мы определили степень с любым действительным показателем.
hystory-for-vki.narod.ru
Степени с действительным показателем. Свойства степени с действительным показателем
Самостоятельная работа студента 1 курс по теме Степени с действительным показателем. Свойства степени с действительным показателем (6 часов)
ЗАДАНИЕ:
- Изучить теоретический материал и сделать конспект (2 часа)
- Разгадать кроссворд (2 часа)
- Выполнить домашнюю контрольную работу (2 часа)
Справочный и дидактический материал представлен ниже
О понятии степени с рациональным показателем
Некоторые наиболее часто встречающиеся
Виды трансцендентных функций, прежде
Всего показательные, открывают доступ ко
Многим исследованиям.
Л. Э й л е р
Из практики решения-все более сложных алгебраических задач и оперирования со степенями возникла необходимость обобщения понятия степени и расширения его посредством введения в качестве показателя нуля, отрицательных и дробных чисел.
Равенство а0 = 1 (для ) применял в своих трудах в начале XV в. самаркандский ученый ал-Каши. Независимо от него нулевой показатель был введен Н. Шюке в XV в. Последний ввел и отрицательные показатели степени. Идея дробных показателей содержится у французского математика Н. Орема (XIV в.) в его
труде «Алгоризм пропорций». Вместо нашего знака он писал , вместо он писал 4. Орем словесно формулирует правила действий со степенями, например (в современной записи): , и т.п.
Позже дробные, как и отрицательные, показатели встречаются в «Полной арифметике» (1544) немецкого математика М. Штифеля и у С. Стевина. Последний пишет о том, что корень степени п из числа а можно считать как степень а с дробным показателем .
О целесообразности введения нулевого, отрицательных и дробных показателей и современных символов впервые подробно писал в 1665 г, английский математик Джон Валлис. Его дело завершил И. Ньютон, который стал систематически применять новые символы, после чего они вошли в общий обиход.
Введение степени с рациональным показателем является одним из многих примеров обобщения понятия математического действия. Степень с нулевым, отрицательным и дробным показателями определяется таким образом, чтобы к ней были применимы те же правила действий, которые имеют место для степени с натуральным показателем, т. е. чтобы сохранились основные свойства первоначально определенного понятия степени, а именно:
Новое определение степени с рациональным показателем не противоречит старому определению степени с натуральным показателем, т. е. смысл нового определения степени с рациональным показателем сохраняется и для частного случая степени с натуральным показателем. Этот принцип, соблюдаемый при обобщении математических понятий, называется принципом перманентности (сохранения, постоянства). В несовершенной форме его высказал в 1830 г. английский математик Дж. Пикок, полностью и четко его установил немецкий математик Г. Ганкель в 1867 г. Принцип перманентности соблюдается и при обобщении понятии числа и расширении его до понятия действительного числа, а до этого — при введении понятия умножения на дробь и т. п.
Степенная функция и графическое решение уравнений и неравенств
Благодаря открытию метода координат и аналитической геометрии начинай с XVII в. стало возможным общеприменимое графическое исследование функций и графическое решение уравнений.
Степенной функцией называют функцию вида
, (1)
где α— постоянное вещественное число. Вначале мы ограничимся, однако, лишь рациональными значениями α и вместо равенства (1) запишем:
, (2)
где — рациональное число. Для и по определению соответственно имеем:
у =1, у =х.
Графиком первой из этих функций на плоскости является прямая, параллельная оси Ох, а второй — биссектриса 1-го и 3-го координатных углов.
При графиком функций является парабола . Декарт, который первое неизвестное обозначал через z, второе — через у, третье — через x:, записывал уравнение параболы так: (z— абсцисса). Параболой он часто пользовался для решения уравнений. Чтобы решить, например, уравнение 4-й степени
(3)
Декарт с помощью подстановки
(4)
получил квадратное уравнение с двумя неизвестными:
(5)
изображающее окружность, расположенную в одной плоскости (zх) с параболой (4). Таким образом, Декарт, вводя вторую неизвестную (х), разбивает уравнение (3) на два уравнения (4) и (5), каждое из которых представляет определенное геометрическое место точек. Ординаты точек их пересечения и дают корни уравнения (3).
Притча:
«Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному замку. «Кто первым откроет, тот и будет первым помощником». Никто даже не притронулся к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ.
Тогда царь сказал: «Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, а надеешься на собственные силы и не боишься сделать попытку».
И мы сегодня будем пытаться, пробовать, чтобы прийти к правильному решению.
1. С каким математическим понятием связаны слова:
Основание
Показатель (Степень)
Какими словами можно объединить слова:
Рациональное число
Целое число
Натуральное число
Иррациональное число (Действительное число)
Сформулируйте тему урока. (Степень с действительным показателем)
Задачи:
– повторить свойства степени
– рассмотреть применение свойств степени при вычислениях и упрощениях выражений
– отработка вычислительных навыков.
Итак, ар, где р – число действительное.
Приведите примеры (выберете из выражений 5–2, , 43, ) степени
– с натуральным показателем
– с целым показателем
– с рациональным показателем
– с иррациональным показателем
При каких значениях а имеет смысл выражение
аn, где n (а – любое)
аm, где m (а не равно 0) Как от степени с отрицательным показателем перейти к степени с положительным показателем?
, где p , q (а > 0)
Какие действия (математические операции) можно выполнять со степенями?
Установите соответствие:
При умножении степеней с равными основаниями | Основания умножаются, а показатель остаётся прежним |
При делении степеней с равными основаниями | Основания делятся, а показатель остаётся прежним |
При возведении степени в степень | Основание остаётся прежним, а показатели умножаются |
При умножении степеней с равными показателями | Основание остаётся прежним, а показатели вычитаются |
При делении степеней с равными показателями | Основание остаётся прежним, а показатели складываются |
«Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей»
– Так сказал американский математик Морис Клайн.
Вариант 1
Вариант 2
Домашняя контрольная работа «Степень с действительным показателем».
Вариант №1 [Вариант №2].
1)Вычислить:
2) Упростить выражение при а
;
3) Сократить дробь
4) Сравнить числа и
referat911.ru
Урок по теме "Степень с действительным показателем" в 11-м классе
Разделы: Математика
Тема урока: Степень с действительным
показателем.
Задачи:
- Образовательные:
- обобщить понятие степени;
- отработать умение находить значение степени с
действительным показателем;
- закрепить умения использовать свойства степени
при упрощении выражений;
- выработать навык использования свойств степени
при вычислениях.
- Развивающие:
- интеллектуальное, эмоциональное, личностное
развитие ученика;
- развивать умение обобщать, систематизировать
на основе сравнения, делать вывод;
- активизировать самостоятельную деятельность;
- развивать познавательный интерес.
- Воспитательные:
- воспитание коммуникативной и информационной
культуры обучающихся;
- эстетическое воспитание осуществляется через
формирование умения рационально, аккуратно
оформлять задание на доске и в тетради.
Учащиеся должны знать: определение и
свойства степени с действительным показателем.
Учащиеся должны уметь:
- определять имеет ли смысл выражение со
степенью;
- использовать свойства степени при вычислениях
и упрощении выражений;
- решать примеры, содержащие степень;
- сравнивать, находить сходства и отличия.
Форма урока: семинар – практикум, с
элементами исследования. Компьютерная
поддержка.
Форма организации обучения: индивидуальная,
групповая.
Тип урока: урок исследовательской и
практической работы.
ХОД УРОКА
Организационный момент
Притча:
«Однажды царь решил выбрать из своих
придворных первого помощника. Он подвёл всех к
огромному замку. «Кто первым откроет, тот и будет
первым помощником». Никто даже не притронулся к
замку. Лишь один визирь подошёл и толкнул замок,
который открылся. Он не был закрыт на ключ.
Тогда царь сказал: «Ты получишь эту должность,
потому что полагаешься не только на то, что
видишь и слышишь, а надеешься на собственные силы
и не боишься сделать попытку».
И мы сегодня будем пытаться, пробовать, чтобы
прийти к правильному решению.
1. С каким математическим понятием
связаны слова:
Основание
Показатель (Степень)
Какими словами можно объединить слова:
Рациональное число
Целое число
Натуральное число
Иррациональное число (Действительное
число)
Сформулируйте тему урока. (Степень с
действительным показателем)
2. Какая наша стратегическая
цель? (ЕГЭ)
Какие цели нашего урока?
– Обобщить понятие степени.
Задачи:
– повторить свойства степени
– рассмотреть применение свойств степени при
вычислениях и упрощениях выражений
– отработка вычислительных навыков.
3. Итак, ар, где р – число
действительное.
Приведите примеры (выберете из выражений 5–2,
 , 43,
, 43,  ) степени
) степени
– с натуральным показателем
– с целым показателем
– с рациональным показателем
– с иррациональным показателем
4. При каких значениях а имеет
смысл выражение
аn, где n  (а
– любое)
аm, где m
(а
– любое)
аm, где m  (а
(а  0) Как от степени с
отрицательным показателем перейти к степени с
положительным показателем?
0) Как от степени с
отрицательным показателем перейти к степени с
положительным показателем? , где
, где  (а
(а 0)
0)
5. Из данных выражений выберете те,
которые смысла не имеют:
( –3)2,  ,
,  , 0–3,
, 0–3,  , ( –3)–1,
, ( –3)–1,  .6. Вычислите. Ответы в каждом столбике
обладают одним общим свойством. Укажите лишний
ответ (этим свойством не обладающий)
.6. Вычислите. Ответы в каждом столбике
обладают одним общим свойством. Укажите лишний
ответ (этим свойством не обладающий)
 =
2
=
2
 =
=

 =
= 
 =
6
=
6
 =
=  (неправ.
др.)
(неправ.
др.)
 =
=  (нельзя записать дес. др.)
(нельзя записать дес. др.) =
=  (дробь)
(дробь)
 =
= 
 =
= 
7. Какие действия (математические
операции) можно выполнять со степенями?
Установите соответствие:
| При умножении степеней с равными
основаниями |
Основания умножаются, а показатель остаётся
прежним |
| При делении степеней с равными основаниями |
Основания делятся, а показатель остаётся
прежним |
| При возведении степени в степень |
Основание остаётся прежним, а показатели
умножаются |
| При умножении степеней с равными показателями |
Основание остаётся прежним, а показатели
вычитаются |
| При делении степеней с равными показателями |
Основание остаётся прежним, а показатели
складываются |
Один ученик записывает формулы (свойства) в
общем виде.
8. Дополнить степени из п.3 так, чтобы к
полученному примеру можно было применить
свойства степени.
(Один человек работает у доски, остальные в
тетрадях. Для проверки обменяться тетрадями, а
ещё один выполняет действия на доске)
9. На доске (работает ученик):
Вычислите  :
:  =
=
Самостоятельно (с проверкой на листах)
 =
=  =
=
Какой из ответов не может получиться в части
«В» на ЕГЭ? Если в ответе получилось  , то как записать такой
ответ в части «В»?
, то как записать такой
ответ в части «В»?
10. Самостоятельное выполнение задания
(с проверкой у доски – несколько человек)
Задание с выбором ответа
| |
|
1 |
2 |
3 |
4 |
| 1 |
 |

|
25 –   |
19 |

|
| 2 |
 : :  |

|

|
–7  |
–9 |
| 3 |
0,3  |
9,1 |
2,9 |
89,9 |
8,9 |
| 4 |
 |
1 |
0 |
2,5 |
4 |
11. Задание с кратким ответом (решение у
доски):
 +
+  + (60)5
+ (60)5  2 – 3–4
2 – 3–4 

 27 =
27 =
Самостоятельно с проверкой на скрытой доске:
 –
–  – 32
– 32 2– 4
2– 4
 + (30)4
+ (30)4  4 =
4 =
12. Сократите дробь (на доске):
 =
=
В это время один человек решает на доске
самостоятельно:  =
(класс проверяет)
=
(класс проверяет)
13. Самостоятельное решение (на
проверку)
На отметку «3»: Тест с выбором ответа:
1. Укажите выражение, равное степени 
2. Представьте в виде степени произведение: 
3. Упростите выражение  :
:  и
найдите его значение при х = 2
и
найдите его значение при х = 2
1.  |
2. 8 |
3.  |
4. – 8 |
4. Чему равно значение выражения  при а =
при а = 
| 1. – 9 |
2.  |
3.  |
4. 9 |
5. Вычислите 
1.  |
2.  |
3. 16 |
4. – 16 |
На отметку «4»: № 439 (1, 2, 4, 5, 6)
На отметку «5»:
1. 
2. Упростите выражение 
14. Дополнительно (индивидуально) тем,
кто быстрее справится с заданиями:
Сравните числа  и
и

15. Дома: №438, придумать
по 2 примера на свойства степени.
В заключение урока:
«Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать
материальную сторону жизни людей,А математика способна достичь всех этих целей»
– Так сказал американский математик Морис
Клайн.
– Спасибо за урок!
xn--i1abbnckbmcl9fb.xn--p1ai
Урок «Свойства степени с действительным показателем»
Сообщение цели, темы и задач урока; показ его практической значимости. 1)Заменить корень степенью: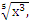 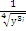 ; ; 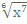 ; ; 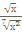 ; ;
2)Вычислить значение выражения: ( трое выполнивших первыми все задания, сдают работу): 1) 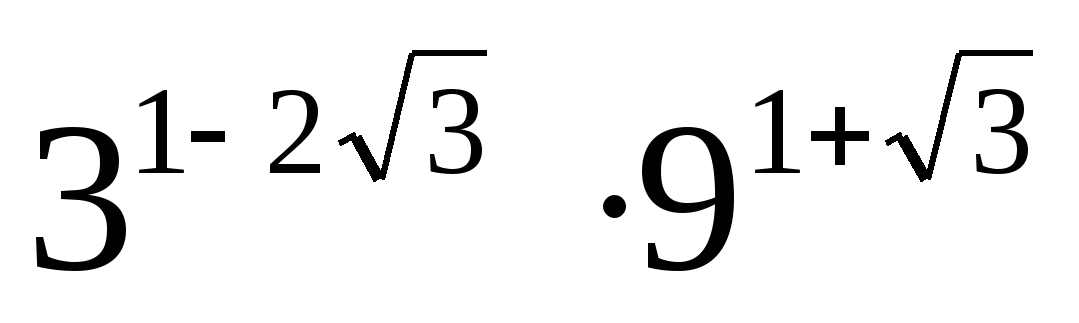 2) 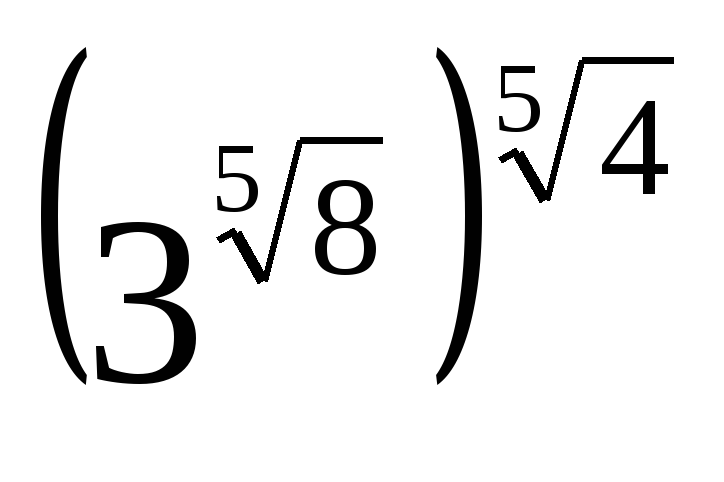 3) 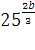 * * 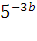 4) 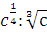 5) 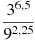 3) Работа в группах: ! группа: 1)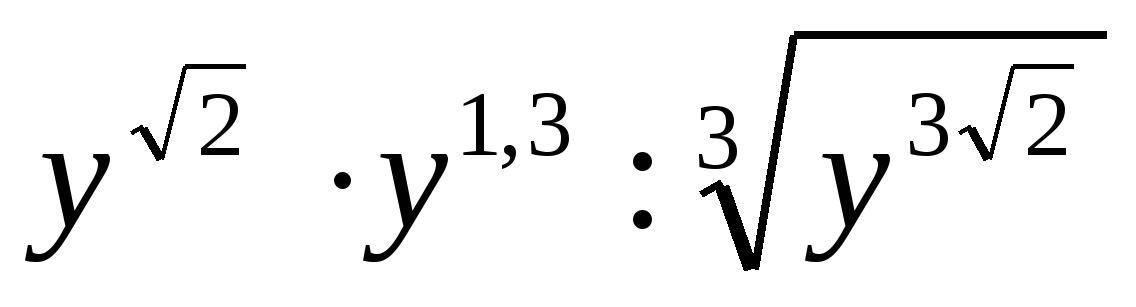 2)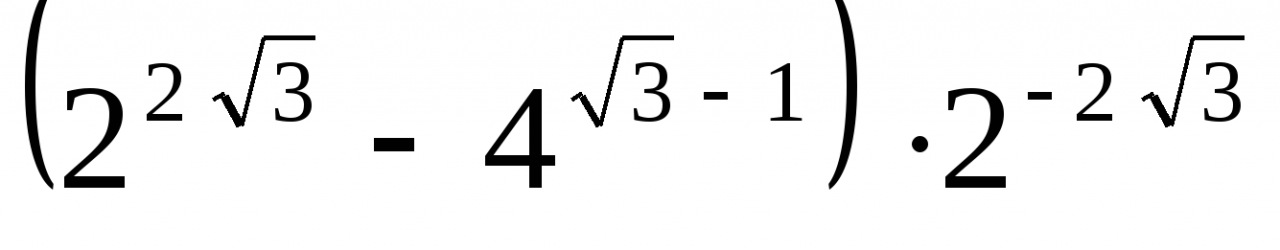 3)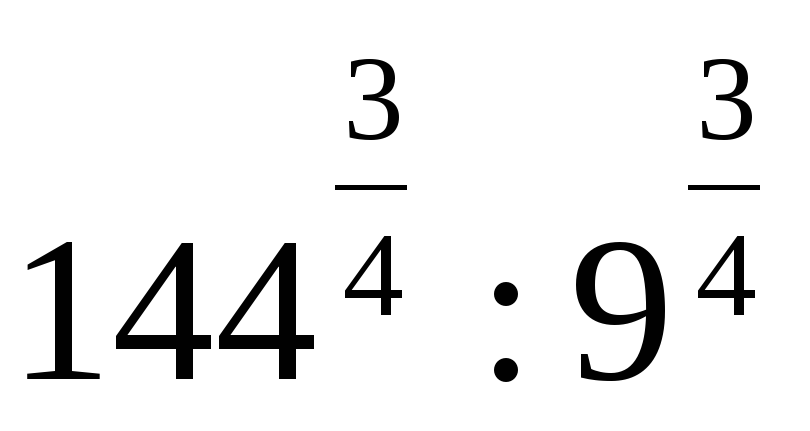 2группа: 1)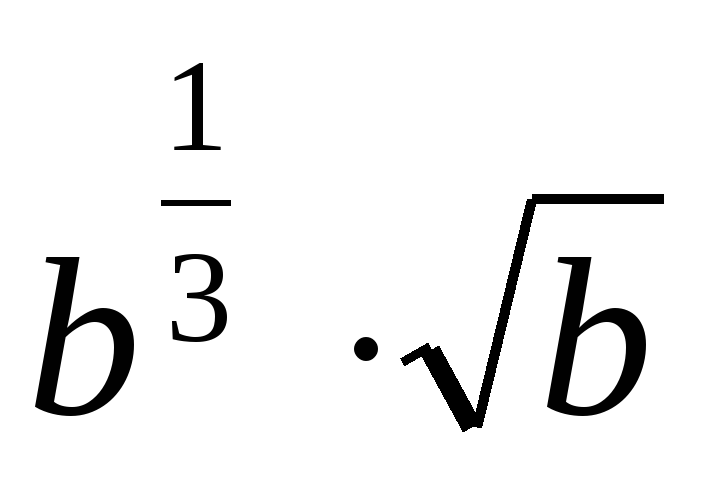 2)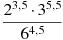 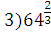
3 группа: 1) 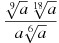 2)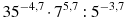 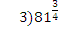
-Формирует пары с различной степенью знаний и мотивацией, организует их работу по заданному плану. -Контролирует работу, консультирует при необходимости. -Задает вопросы . -Организует индивидуально-групповую форму работы студентов, создает ситуацию общения. -Осуществляет контроля и помощь при возникших затруднениях. -С помощью вопросов помогает найти объяснение. -Вызывает к доске из каждой группы « слабого» студента решить по одному заданию из карточки. | Отвечают на вопросы преподавателя.. Отвечают устно Решают данные примеры в тетрадях , после того как сданы 3 работы проверяют на доске. Работают по группам: вычисляют пять различных интегралов в течении 10 минут. Решают в тетрадях «не свои» задания и проверяют свое задание. | - усвоение содержания нового материала в основном на репродуктивном уровне, который связан с осмыслением полученных данных и выявлением его связей с другими; - развиваются логическое мышление, умение рассуждать, анализировать, - развиваются умения применять теоретические знания при расчете, -продолжают формироваться коммуникативные и регулятивные учебные умения | xn--j1ahfl.xn--p1ai
 ) применял в своих трудах в начале XV в. самаркандский ученый ал-Каши. Независимо от него нулевой показатель был введен Н. Шюке в XV в. Последний ввел и отрицательные показатели степени. Идея дробных показателей содержится у французского математика Н. Орема (XIV в.) в его
) применял в своих трудах в начале XV в. самаркандский ученый ал-Каши. Независимо от него нулевой показатель был введен Н. Шюке в XV в. Последний ввел и отрицательные показатели степени. Идея дробных показателей содержится у французского математика Н. Орема (XIV в.) в его он писал
он писал  , вместо
, вместо  он писал
он писал  4. Орем словесно формулирует правила действий со степенями, например (в современной записи):
4. Орем словесно формулирует правила действий со степенями, например (в современной записи):  ,
,  и т.п.
и т.п. .
.




 , (1)
, (1) , (2)
, (2) — рациональное число. Для
— рациональное число. Для  и
и  по определению соответственно имеем:
по определению соответственно имеем: графиком функций является парабола
графиком функций является парабола  . Декарт, который первое неизвестное обозначал через z, второе — через у, третье — через x:, записывал уравнение параболы так:
. Декарт, который первое неизвестное обозначал через z, второе — через у, третье — через x:, записывал уравнение параболы так:  (z— абсцисса). Параболой он часто пользовался для решения уравнений. Чтобы решить, например, уравнение 4-й степени
(z— абсцисса). Параболой он часто пользовался для решения уравнений. Чтобы решить, например, уравнение 4-й степени (3)
(3) (4)
(4) (5)
(5) , 43,
, 43,  ) степени
) степени  (а – любое)
(а – любое) (а не равно 0) Как от степени с отрицательным показателем перейти к степени с положительным показателем?
(а не равно 0) Как от степени с отрицательным показателем перейти к степени с положительным показателем? , где p
, где p  , q
, q  (а > 0)
(а > 0)










 ;
;
 и
и 
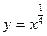 :
: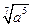 в виде степени с рациональным показателем:
в виде степени с рациональным показателем: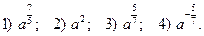
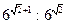 .
.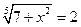 .
.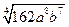 , если
, если 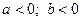 .
.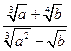
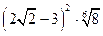 .
.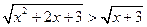 .
.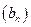 в три раза больше ее первого члена. Найдите отношение
в три раза больше ее первого члена. Найдите отношение 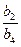 .
.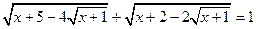
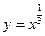 :
: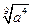 в виде степени с рациональным показателем:
в виде степени с рациональным показателем: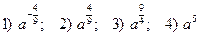 .
.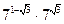 .
.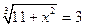 .
.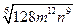 , если
, если 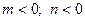 .
.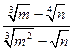
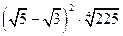 .
.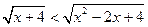 .
.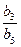 .
.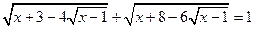 .
.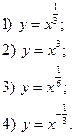

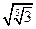 в виде степени с рациональным показателем:
в виде степени с рациональным показателем: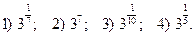
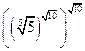 .
.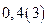 .
.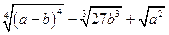 , если
, если 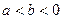 .
.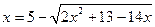 .
.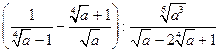 .
.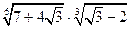 .
.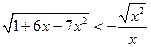 .
.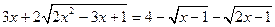 .
.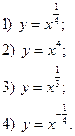

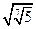 в виде степени с рациональным показателем:
в виде степени с рациональным показателем: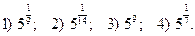
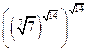 .
.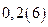 .
.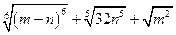 , если
, если 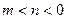 .
.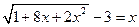 .
.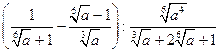 .
.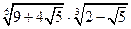 .
.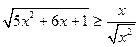 .
.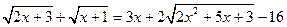 .
.
 , где m – целое число, а n – натуральное (n > 1), называется число
, где m – целое число, а n – натуральное (n > 1), называется число 


 для любого натурального k. Значение аr также не зависит от формы записи рационального числа r.
для любого натурального k. Значение аr также не зависит от формы записи рационального числа r.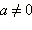 мы определили возведения в нулевую и целую отрицательную степень; для любого
мы определили возведения в нулевую и целую отрицательную степень; для любого 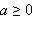 мы определили операцию возведения в положительную дробную степень; для любого
мы определили операцию возведения в положительную дробную степень; для любого 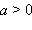 мы определили операцию возведения в отрицательную дробную степень.
мы определили операцию возведения в отрицательную дробную степень.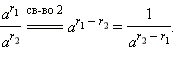
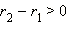 и потому (так как a > 1)
и потому (так как a > 1) 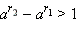 и, наконец,
и, наконец, 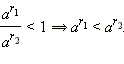
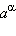 понимают такое число, которое лежит между
понимают такое число, которое лежит между 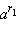 и
и 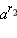 при любом выборе чисел
при любом выборе чисел 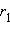 и
и 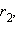 обладающих свойством
обладающих свойством 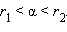 Можно доказать, что число
Можно доказать, что число 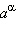 существует и единственно для любого a > 1 и любого иррационального α.
существует и единственно для любого a > 1 и любого иррационального α.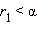 и любое рациональное число
и любое рациональное число 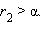 Тогда, очевидно,
Тогда, очевидно, 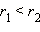 и, следовательно,
и, следовательно, 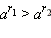 (это неравенство доказывается аналогично приведённому выше для a > 1). Под
(это неравенство доказывается аналогично приведённому выше для a > 1). Под 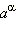 понимают такое число, которое лежит между
понимают такое число, которое лежит между 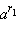 и
и 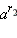 при любом выборе чисел
при любом выборе чисел 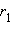 и
и 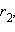 обладающих свойством
обладающих свойством 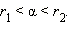 Можно доказать, что число
Можно доказать, что число 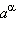 существует и единственно для любого 0 < a < 1 и любого иррационального α.
существует и единственно для любого 0 < a < 1 и любого иррационального α. , 43,
, 43,  ) степени
) степени  (а
– любое)
аm, где m
(а
– любое)
аm, где m  (а
(а  0) Как от степени с
отрицательным показателем перейти к степени с
положительным показателем?
0) Как от степени с
отрицательным показателем перейти к степени с
положительным показателем? , где
, где  (а
(а 0)
0) ,
,  , 0–3,
, 0–3,  , ( –3)–1,
, ( –3)–1,  .6. Вычислите. Ответы в каждом столбике
обладают одним общим свойством. Укажите лишний
ответ (этим свойством не обладающий)
.6. Вычислите. Ответы в каждом столбике
обладают одним общим свойством. Укажите лишний
ответ (этим свойством не обладающий) =
2
=
2
 =
=

 =
= 
 =
6
=
6
 =
=  (неправ.
др.)
(неправ.
др.)
 =
=  (нельзя записать дес. др.)
(нельзя записать дес. др.) =
=  (дробь)
(дробь)
 =
= 
 =
= 
 :
:  =
=  =
=  =
=  , то как записать такой
ответ в части «В»?
, то как записать такой
ответ в части «В»?




 :
: 





 +
+  + (60)5
+ (60)5  2 – 3–4
2 – 3–4 
 –
–  – 32
– 32 + (30)4
+ (30)4  =
= =
(класс проверяет)
=
(класс проверяет)









 :
:  и
найдите его значение при х = 2
и
найдите его значение при х = 2

 при а =
при а = 






 и
и

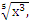
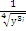 ;
;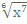 ;
; 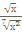 ;
;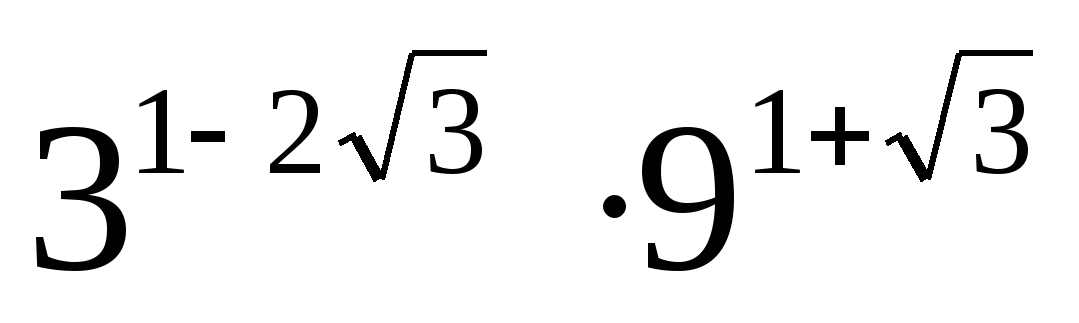
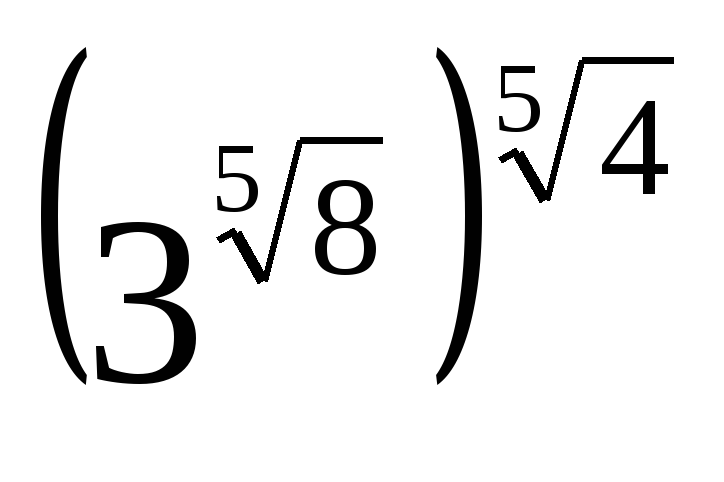
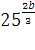 *
*