Реферат по математике "Отношение величин" (6 класс). Реферат 6 класс по математике

Реферат по математике "Отношение величин" (6 класс)

МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №3

КАРАСУКСКОГО РАЙОНА

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

«ОТНОШЕНИЕ ВЕЛИЧИН»

Выполнили:

ученицы 6 класса

МОУ СОШ № 3

Афанасьева Елена

Скрыпник Александра

Шнайдер Лина

Руководитель:

учитель математики

Сердюков

Валентин Иванович

КАРАСУК 2010

Содержание

Актуальность…………………………………………………………….…....3

Что такое отношение?........................................................................................4

Что такое число π?..............................................................................................4

Практическая работа…………………………………………………………..5

Результаты исследования…………..………………………………………....6

Метод Бюффона……..………………………………………………………....6

Что такое прямая пропорциональная зависимость?........................................7

Масштаб.………………………………………………………………………..7

Исследовательская работа…………………………………………………......8

Что такое обратная пропорциональная зависимость………………………...9

Практическая работа……………………………………………….……..........9

Что такое «золотое сечение»…………………………………………...……..10

Отношение в фотографиях….……….…………………………………..……12

Отношение в процентах…………………………………………………….…12

Вывод…………………………………………………………………………...12

Список литературы………………………………………………………….....12

Актуальность

На уроках математики мы познакомились с отношением величин. Нам захотелось узнать об этом побольше. Отношения величин человек в своей жизни использует постоянно. Это в науках: математике, физике, химии и т. п., и в практической деятельности: проценты, масштаб, диаграммы и многое другое. И поэтому мы выбрали эту тему.

Цель

Познакомиться с понятием отношения величин и его применением в математике и в жизни людей.

Задачи.

Изучить использование отношений величин в :

Гипотеза

Предположим, отношение величин - это только математическое понятие. И в жизни мы его не используем.

Что такое отношение

Частное двух чисел называют отношением этих чисел.

Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.

Как используется отношения?

Учение об отношениях особенно успешно развивалось в IV в. до н.э. в Древней Греции, а сейчас они чаще используются в жизни и в практике людей. Теперь рассмотрим использование отношений в математике на примере числа π.

Что такое число π

Число π – математическая константа, выражающая отношение длины окружности к длине её диаметра. В цифровом выражении c:d=π начинается как 3,141592… и имеет бесконечную математическую продолжительность.

Как считают специалисты, это число было открыто вавилонскими магами. Возможно, что эта математическая константа лежала в основе строительства легендарного Храма царя Соломона.

Практическое вычисление числа π

Для вычисления числа π мы выполнили практическую работу. Для этого взяли несколько предметов цилиндрической формы: скотч,

2 цилиндра,

infourok.ru

Реферат по математике "Отношение величин" (6 класс) страница 3

Пример обратной пропорциональной зависимости является правило равновесия рычага.

Практическая работа

Для нашей практической работы нам понадобился рычаг. Рычаг представляет собой твердое тело, которое может вращаться вокруг неподвижной опоры.

Как мы работали с рычагом

Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называют плечом силы. Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.

Результат работы

Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил. Так это правило можно записать в виде формулы: F1:F2=L2:L1

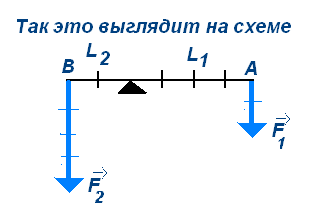
Выводы

Применяя правило рычага, можно большей силой уравновесить меньшую силу. При этом плечо меньшей силы должно быть длиннее плеча большей силы.

«Золотое сечение»

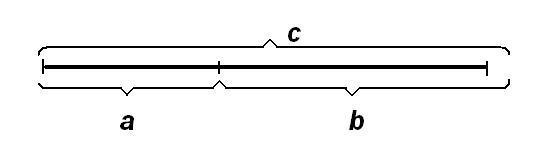
«Золотое сечение»- это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей c:b=b:а

Где наблюдается «золотое сечение»

Принцип золотого сечения находит свое отражение в природе, искусстве, науке, архитектуре, технике, в пропорциях человеческого тела.

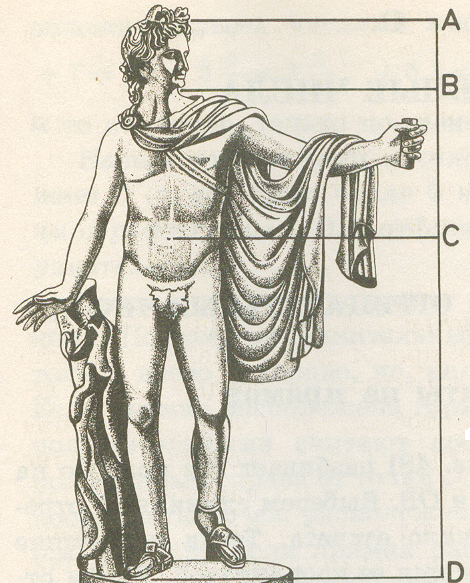
Золотое сечение в природе

Расположение листьев на некоторых растениях, тело ящерицы, тело человека – все это подчинено правилу золотого сечения.

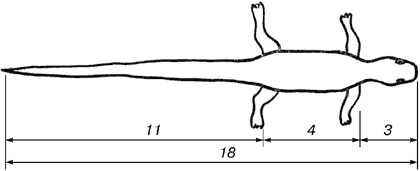
Золотое сечение в архитектуре и искусстве

Храм Парфенон, храм Василия Блаженного, Смольной собор в Санкт -Петербурге построены по правилам золотого сечения. Тоже самое мы видим в картинах «Корабельная роща», «Пушкин на акте в Лицее», «Пушкин в селе Михайловском».

Отношение в фотографиях

Все мы когда-нибудь фотографировались. В процессе фотографирования объекта происходит изменение его размеров в отношении k=Ro:Rф, где Ro-размеры объекта , а Rф- соответствующие размеры фотографии. Учитель математики нам сказал , что k называется коэффициентом подобия.

Отношение и проценты

Отношение одной величины к другой, умноженное на сто - это и есть отношение в процентах. А проценты мы используем всюду.

заключение

Наша гипотеза, выдвинутая в начале проекта оказалась неверна. Отношение мы используем не только в математике, но и в разных отраслях нашей деятельности.

Литература

infourok.ru

Реферат по математике "Отношение величин" (6 класс) страница 2

2 катушки.

Инструменты для измерения и вычисления:

мерная лента, штангенциркуль, калькулятор.

Практическая работа

Мы измерили диаметры и длины окружностей выбранных нами предметов. Сначала мы измерили цилиндры, затем катушки и скотч. Потом поделили длину окружности на диаметр.

c:d=π

Результаты измерений и вычислений занесли в таблицу.

Результаты исследования

c:d

Модуль разности

c:d - π

1

Скотч

27, 6см

8см

3,4500

0,3085

2

Малый цилиндр

15.3см

4,4см

3,4800

0,3385

3

Большой цилиндр

30,7см

9,8см

3,1326

0,0089

4

Малая катушка

17см

5,09см

3,3398

0,1983

5

Большая катушка

30,8см

9,7см

3,1752

0,0337

Анализ результатов

Из диаграммы видно, что ближе всего к числу π=3,1415… мы подошли, когда измеряли большой цилиндр и большую катушку

Метод Бюффона

Наш способ вычисления числа π очень приближенный и далеко не единственный. Еще в далеком 1777 году французский ученый Жорж Бюффон(1707- 1788) опубликовал работу, в которой предложил оценить число π, бросая иголку на специально разрисованную поверхность. Если при бросании обыкновенной иголки на разлинованную доску замечать сколько раз она попадет на одну из прямых, затем результаты поставить в открытую Бюффоном формулу р=2L:aπ, можно вычислить число π с большой точностью.

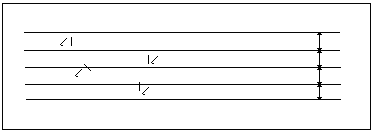
Результаты исследования

3,1415

Вольф

1850

5000

3,1596

0,0181

Смит

1855

3204

3,1553

0,0138

Фокс

1884

1120

3,1419

0,0004

Лаццарини

1901

3408

3,1415929

0,0000929

Что такое прямая пропорциональная зависимость

Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.

Т.е. отношение двух значений одной величины равно отношению двух соответствующих значений другой величины

Примером прямой пропорциональной зависимости является масштаб.

Масштаб

Понятие масштаба тоже связанно с отношением величин.

Масштаб это – отношение длины отрезка на карте к длине соответствующего отрезка на местности.

Для чего используется масштаб

Все мы пользуемся картами местности, но на ней невозможно отобразить натуральную величину объектов. Для этого нам нужен масштаб. С его помощью мы можем уменьшить величину в нужное нам количество раз.

Исследовательская работа

Нам нужно нарисовать на обычном листе комнату площадью 3мx3м. Но мы не сможем передать точную величину комнаты 3мx3м, поэтому ее нужно уменьшить, т.е. мы воспользуемся масштабом. Чтобы воспользоваться масштабом, уменьшим длину и ширину комнаты в одинаковое количество раз. Длину и ширину уменьшим в 20 раз. т.е. 3м:20=15см. 3м:20=15см

Итог работы

В итоге нашей работы мы получили план комнаты размером 15x15cм

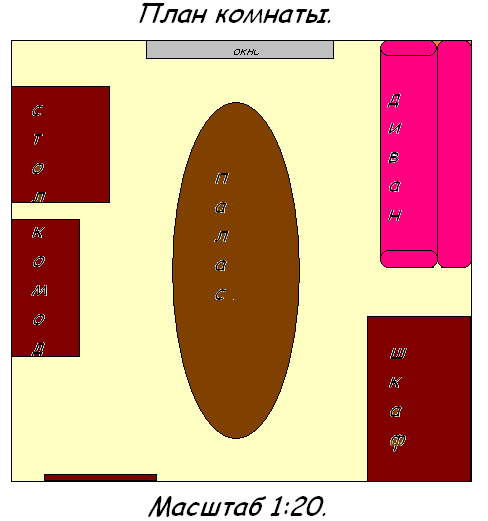
Что такое обратная пропорциональная зависимость

Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них другая уменьшается (увеличивается) во столько же раз.

Иначе, две величины называют обратно пропорциональными, если отношение двух значений одной величины равно обратному отношению двух соответствующих значений другой величины

infourok.ru

Реферат - Программа «Математика-6 класс»

Пояснительная записка.

Учебная программа «Математика-6 класс» составлена на основе «Примерной программы основного общего образования по математике»(2004г.) и содержит обязательный минимум содержания образовательной программы по математике. Программа конкретизирует содержание предметных тем образовательного стандарта и дает примерное распределение учебных часов по разделам курса.

Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации, учебному плану МОУ в 6 классе на 2009-2010 учебный год на изучение математики отводится 5 ч в неделю, 170 ч. в год.

Изучение математики в 6 классе направлено на достижение следующих целей:

овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

Учебная программа включает 10 основных разделов:

Делимость натуральных чисел(20ч)

Сложение и вычитание дробей с разными знаменателями(22ч)

Умножение и деление обыкновенных дробей(32ч)

Отношения и пропорции(19ч)

Положительные и отрицательные числа(13ч)

Сложение и вычитание положительных и отрицательных чисел(11ч)

Умножение и деление положительных и отрицательных чисел(13ч)

Решение уравнений(14ч)

Координаты на плоскости(13ч)

Повторение (13ч).

Содержание учебного материала.

Делимость натуральных чисел (20ч).

Основное содержание раздела: делители и кратные числа; общий делитель и общее кратное; признаки делимости на 2,3,5,9,10; простые и составные числа; разложение натурального числа на простые множители.

^ Основная цель раздела – завершить изучение натуральных чисел, подготовить основу для освоения действия с обыкновенными дробями.

Сложение и вычитание дробей с разными знаменателями (22ч).

Основное содержание раздела: основное свойство дроби; сокращение дробей; приведение дробей к общему знаменателю; понятие о наименьшем общем знаменателе дробей; сравнение дробей; сложение и вычитание дробей; решение текстовых задач.

^ Основная цель раздела- выработать прочные навыки преобразования дробей, сравнения, сложения и вычитания дробей.

Умножение и деление обыкновенных дробей (32ч).

Основное содержание раздела: умножение и деление дробей; основные задачи на дроби (нахождение дроби от числа; нахождение числа по его дроби).

^ Основная цель раздела – выработать прочные навыки арифметических действий с обыкновенными дробями и решения основных задач на дроби.

Отношения и пропорции (19ч)

Основное содержание раздела: пропорция; основное свойство пропорции; решение задач с помощью пропорции; понятие о прямой и обратной пропорциональностях величин; задачи на пропорции; масштаб; формулы длины окружности и площади круга; шар.

^ Основная цель раздела – сформировать понятия пропорции; прямой и обратной пропорциональности величин.

Положительные и отрицательные числа (13ч).

Основное содержание раздела: положительные и отрицательные числа; противоположные числа; модуль числа и его геометрический смысл; сравнение чисел; целые числа; изображение чисел на прямой; координаты точек.

^ Основная цель раздела – расширить представления учащихся о числе путем введения отрицательных чисел.

Сложение и вычитание положительных и отрицательных чисел (11ч).

Основное содержание раздела: сложение и вычитание положительных и отрицательных чисел.

^ Основная цель раздела – выработать прочные навыки сложения и вычитания положительных и отрицательных чисел.

Умножение и деление положительных и отрицательных чисел (13ч).

Основное содержание раздела: умножение и деление положительных и отрицательных чисел; понятие о рациональном числе; десятичное приближение обыкновенной дроби; применение законов арифметических действий для рационализации вычислений.

^ Основная цель раздела – выработать прочные навыки арифметических действий с положительными и отрицательными числами.

Решение уравнений (14ч)

Основное содержание раздела: простейшие преобразования выражений -раскрытие скобок, приведение подобных слагаемых; решение линейных уравнений; примеры решения текстовых задач с помощью линейных уравнений

^ Основная цель раздела – подготовить учащихся к выполнению преобразований выражений, решению уравнений.

Координаты на плоскости (13ч).

Основное содержание раздела: построение перпендикуляра к прямой и параллельных прямых c помощью угольника и линейки; прямоугольная система координат на плоскости; абсцисса и координата точки; примеры графиков и диаграмм.

^ Основная цель раздела –познакомить учащихся с прямоугольной системой координат на плоскости.

Повторение (13ч).

Основная цель раздела – повторить основные темы курса математики 6 класса.

^ Общеучебные умения, навыки и способы деятельности.

В ходе преподавания математики в основной школе, работы над формированием перечисленных в программе знаний и умений, учащиеся должны овладеть умениями общеучебного характера, разнообразными способами деятельности, приобрести опыт:

планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;

решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;

проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

www.ronl.ru

темы пректов по математике для учащихся 6 класса

Примерные темы проектов по математике для шестиклассников на 2014/2015 уч.год.

1. Магические фигуры (квадраты и не только). История, теория, как самому составить магический квадрат. Магические треугольники, шестиугольники, пространственные тела или что-то еще – на ваш выбор.

2. Задача со спичками: сколько квадратов можно составить из 24 спичек, чтобы не осталось лишних спичек?

3. Рациональные приёмы счета. Приёмы, которые позволяют нам считать быстрее и делать меньше ошибок. В чем они заключаются? Почему приводят к правильным ответам?

4. Невозможные фигуры (альбом изображений с комментариями, почему такую фигуру невозможно построить в действительности).

5. Старинные меры длины в пословицах и поговорках.

6. Отрицательные числа в математике и не только.

7. Геометрическая интерпретация формул сокращенного умножения. Как можно, используя площади прямоугольников, обосновать формулы, например, (а+в)2=а2+2ав+в2 и многие другие?

8. Квадраты на клетчатой бумаге. Легко изобразить на ней квадрат, площадь которого равняется 4 клеткам, сложнее – с площадью 13 клеток, а вот квадрат площадью 31 клетка изобразить уже не получится. Какие квадраты можно изобразить, а какие нельзя?

9. Игра «Ферзь». На поле f8 стоит ферзь. Играют двое и ходят по очереди. Каждый из игроков за один ход может передвинуть ферзя либо на несколько клеток вниз по вертикали (на сколько угодно), либо на несколько клеток влево по горизонтали, либо на несколько клеток влево – вниз по диагонали. Проигрывает тот, кому некуда ходить. Значит, выигрывает тот, кому удастся загнать ферзя в левый нижний угол – на поле а1. Кто выигрывает при правильной игре - первый или второй игрок, и как он должен играть?

10. Геометрические фигуры в картинах известных художников. Составить альбом.

11. Головоломки своими руками. Должна получиться небольшая игротека головоломок собственного изготовления и приложение - правила и решения к ним.

12. Многогранники- трансформеры. Можно воспользоваться многочисленными роликами на youtube (вот пример: http://www.youtube.com/watch?v=-d4IQT_phlQ), или из других источников, можно придумать что-то самостоятельно. Необходимо подробно зафиксировать процесс изготовления. Можно и ролик снять.

13. Геометрические фигуры и вышивка в технике «изонить».

14. Задачник по математике как исторический документ. Вам дан задачник для деревенской школы 1929 года. Какие выводы о жизни в деревне в то уже далекое время вы можете сделать? Больше или меньше знали и умели по математике те школьники по сравнению с вами? И как думаете, какие выводы сделают историки в 2114 году, анализируя современный нам учебник математики?

15. Можно ли вычеркнуть из произведения 1!·2! ·3! ·…·100! Один из факториалов так, чтобы произведение оставшихся было квадратом натурального числа?

16. Клетки на клетчатом листе бумаги назовем соседними, если они имеют общую сторону. Будем рассматривать фигуры из клеток, у которых каждая клетка имеет четное число соседок (но не равное нулю) и фигуры, у которых каждая клетка имеет нечетное число соседок. Называть такие фигуры будем «фигура четного типа» и «фигура нечетного типа» соответственно. Заметим, что в фигуре любого типа каждая клетка должна иметь минимум одну соседку! Вопрос для исследования: из какого количества клеток можно составить фигуры четного типа? А нечетного?

17. Математические задачи в литературных произведениях.

18. Обманы в рекламе с точки зрения математики. В газетах часто появляется рекламные объявления типа: «Мы ищем счастливчика, чтобы вручить ему миллион! Задумайте число, умножьте его на 5, потом умножьте на 2. Разделите полученный результат на задуманное число. У вас получилось 10? Вы и есть счастливчик!». Далее следует предложение что-нибудь купить. Тот, кто хорошо знает математику, не попадется на эти уловки. Найдите несколько подобных объявлений (одно из них перед вами) и объясните, на чем основаны эти фокусы.

19. Задачи с пентамино.

Имеются 12 фигурок, каждая из которых состоит из 5 равных квадратиков (на рисунке каждая фигура обозначена похожей на неё буквой латинского алфавита). С ними связаны много задач. Вот некоторые из них.

19.1. Из 11 элементов пентамино можно собрать прямоугольник 5х11. Двенадцатый элемент останется лишним. На рисунке это фигура Z. Сложите как можно больше прямоугольников, каждый раз оставляя лишним какой-нибудь другой элемент.

19.2. Из 12 элементов пентамино сложите прямоугольник 5х13 так, чтобы внутри прямоугольника (по центру) образовалось отверстие в виде одной из фигурок (на рисунке отверстие имеет форму фигуры Z). Сложите как можно больше таких прямоугольников с отверстием в виде разных фигур пентамино.

19.3. Если принять длину клеточки пентамино за 10 м, то симметричная башня, изображенная на рисунке, имеет высоту 290 м. Постройте её из 12 элементов пентамино. Попробуйте построить симметричную башню высотой 310 м. Наивысшее достижение – 320 м, оно принадлежит Елене Жуковой из Московской области. Сможете ли вы его повторить? А превзойти?

19.4. На рисунке из фигурок пентамино выложен замкнутый «забор» таким образом, что соседние фигуры имеют общую сторону. Площадь «внутреннего дворика» равна 126 квадратных единиц. Сможете ли вы выложить «забор» так, чтобы увеличить площадь «внутреннего дворика»?

19.5. Раскрасим фигурки пентамино двумя цветами в шахматном порядке (см рис.). Сложите из них шахматную доску. Одно решение приведено здесь. Попробуйте найти хотя бы еще одно (известны еще три).

infourok.ru

Реферат по математике "Отношение величин" (6 класс)

МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №3

КАРАСУКСКОГО РАЙОНА

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

«ОТНОШЕНИЕ ВЕЛИЧИН»

Выполнили:ученицы 6 класса

МОУ СОШ № 3

Афанасьева Елена

Скрыпник Александра

Шнайдер ЛинаРуководитель:

учитель математики

Сердюков

Валентин Иванович

КАРАСУК 2010

Содержание

Актуальность…………………………………………………………….…....3

Что такое отношение?........................................................................................4

Что такое число π?..............................................................................................4

Практическая работа…………………………………………………………..5

Результаты исследования…………..………………………………………....6

Метод Бюффона……..………………………………………………………....6

Что такое прямая пропорциональная зависимость?........................................7

Масштаб.………………………………………………………………………..7

Исследовательская работа…………………………………………………......8

Что такое обратная пропорциональная зависимость………………………...9

Практическая работа……………………………………………….……..........9

Что такое «золотое сечение»…………………………………………...……..10

Отношение в фотографиях….……….…………………………………..……12

Отношение в процентах…………………………………………………….…12

Вывод…………………………………………………………………………...12

Список литературы………………………………………………………….....12

Актуальность

На уроках математики мы познакомились с отношением величин. Нам захотелось узнать об этом побольше. Отношения величин человек в своей жизни использует постоянно. Это в науках: математике, физике, химии и т. п., и в практической деятельности: проценты, масштаб, диаграммы и многое другое. И поэтому мы выбрали эту тему.

ЦельПознакомиться с понятием отношения величин и его применением в математике и в жизни людей.

Задачи.Изучить использование отношений величин в :

• математике;
• географии;
• физике;
• искусстве;
• пропорциях человеческого тела;
• жизнедеятельности людей;

Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.

Как используется отношения?

Учение об отношениях особенно успешно развивалось в IV в. до н.э. в Древней Греции, а сейчас они чаще используются в жизни и в практике людей. Теперь рассмотрим использование отношений в математике на примере числа π.Что такое число πЧисло π – математическая константа, выражающая отношение длины окружности к длине её диаметра. В цифровом выражении c:d=π начинается как 3,141592… и имеет бесконечную математическую продолжительность.

Как считают специалисты, это число было открыто вавилонскими магами. Возможно, что эта математическая константа лежала в основе строительства легендарного Храма царя Соломона.Практическое вычисление числа πДля вычисления числа π мы выполнили практическую работу. Для этого взяли несколько предметов цилиндрической формы: скотч,

2 цилиндра,

2 катушки.

Инструменты для измерения и вычисления:

мерная лента, штангенциркуль, калькулятор.

ekonnom.ru

ГДЗ по математике 6 класс Виленкин.

16.10.2011/шпаргалка

ГДЗ к учебнику Математика 3 класс Моро М.И. и др.; Части 1 и 2. 2006-2009 годы.

Домашняя работа по математике к учебнику "Математика. 3 класс." Моро М.И. и др. (М., Просвещение, 2006 - 2009 гг.).

На первый взгляд думается, что при изучении математики в 3 классе не может возникнуть никаких проблем. Однако, не всё так радужно и элементарно просто -  огромное количество и школьников и родителей круглосуточно ищут в интернет готовые домашние задания по математике 3 класс Моро М.И.

В данном ГДЗ приведенены решения обычных математических действий: сложение и вычитание, умножение и деление, простые уравнения, площадь и единицы площади и т.п. Уважаемому М.И. Моро удалось создать действительно интересный и занимательный учебник по математике, который позволяет ным школьникам эффективно развивать навыки математического мышления. А ГДЗ за 3 класс по учебнику Моро поможет тем ученикам и родителям, у которых возникнут сложности с решением домашних заданий. 

16.10.2011/шпаргалка

Домашняя работа по математике за 1 класс к учебнику Л.Г. Петерсон «Математика. I класс. В 3-х частях» / М.И. Петрова. — М.: Издательство «Экзамен», 2012. — 158, [2] с. (Серия «Решебник»)

ISBN 978-5-377-04I82-5

Предлагаемое учебное пособие содержит образцы выполнения всех заданий и упражнений из учебника «Математика. I класс. В 3-х частях / Л.Г. Петерсон. — 2-е изд., перераб. — М.: Издательство «Ювента», 2010».

Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы но математике.

ГДЗ по математике за 1 класс к учебнику Л.Г. Петерсон 2010

Домашняя работа по математике за 1 класс к учебнику Л.Г. Петерсон «Математика. I класс. В 3-х частях» / М.И. Петрова. — М.: Издательство «Экзамен», 2012. — 158, [2] с. (Серия «Решебник»)

Данный решебник содержит образцы выполнения всех заданий и упражнений из учебника «Математика. I класс. В 3-х частях / Л.Г. Петерсон. — 2-е изд., перераб. — М.: Издательство «Ювента», 2010».

Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы но математике. Иноогда кажется, что в 1 классе уж точно нет ничего сложного, однако статистика запросов говорит о том, что это востребованный решебник.

Запросы:

• математика 1 класс петерсон        

• уроки математики петерсон 1 класс      

• петерсон математика 1 класс скачать    

• математика 1 класс л петерсон     

• учебник математики 1 класс петерсон   

• математика петерсон 1 класс программа        

• петерсон математика 1 класс планирование   

• ответы петерсон математика 1 класс     

• математика петерсон 1 класс перспектива      

• петерсон математика 1 класс контрольные    

• петерсон математика 1 класс задачи

referatwork.ru

Смотрите также

• 
  Реферат по математике 5 класс
• 
  Реферат теория государства и права
• 
  Реферат по биологии 6 класс
• 
  Реферат по истории 5 класс
• 
  Реферат на тему healthy food
• 
  Работа секретаря в офисе реферат
• 
  Я хочу стать судьей реферат
• 
  Реферат праздник как феномен культуры
• 
  Реферат на тему индийская музыка
• 
  Праздник как феномен культуры реферат
• 
  Искусственное освещение реферат по бжд