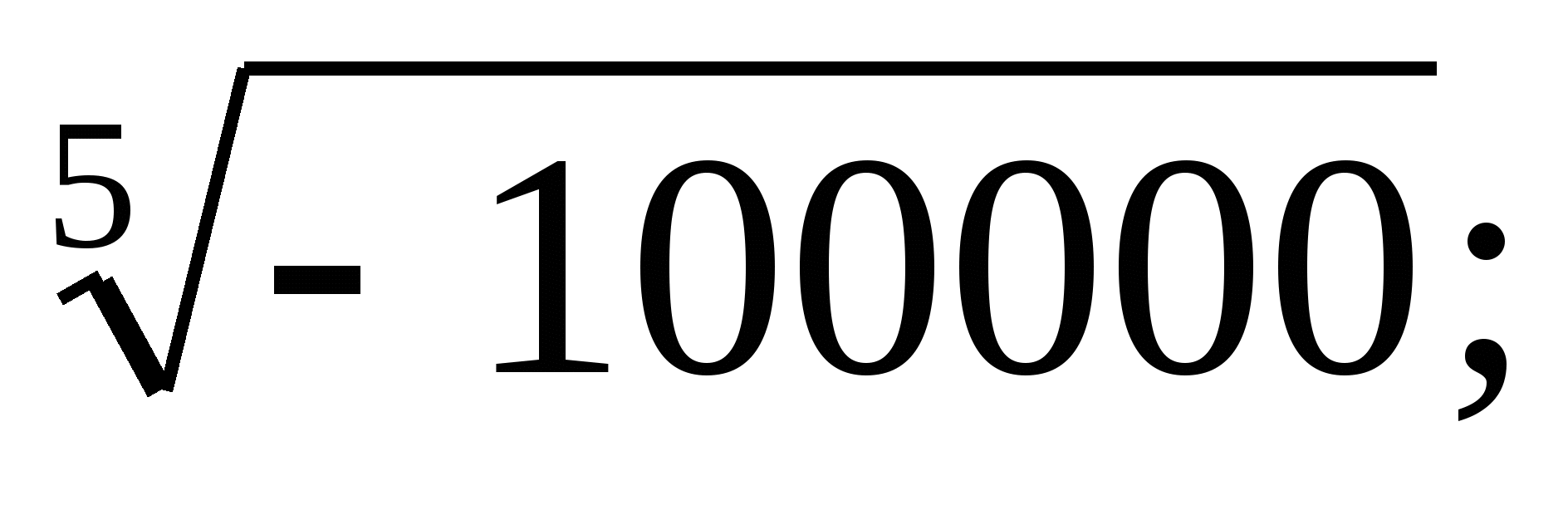 б)
б) 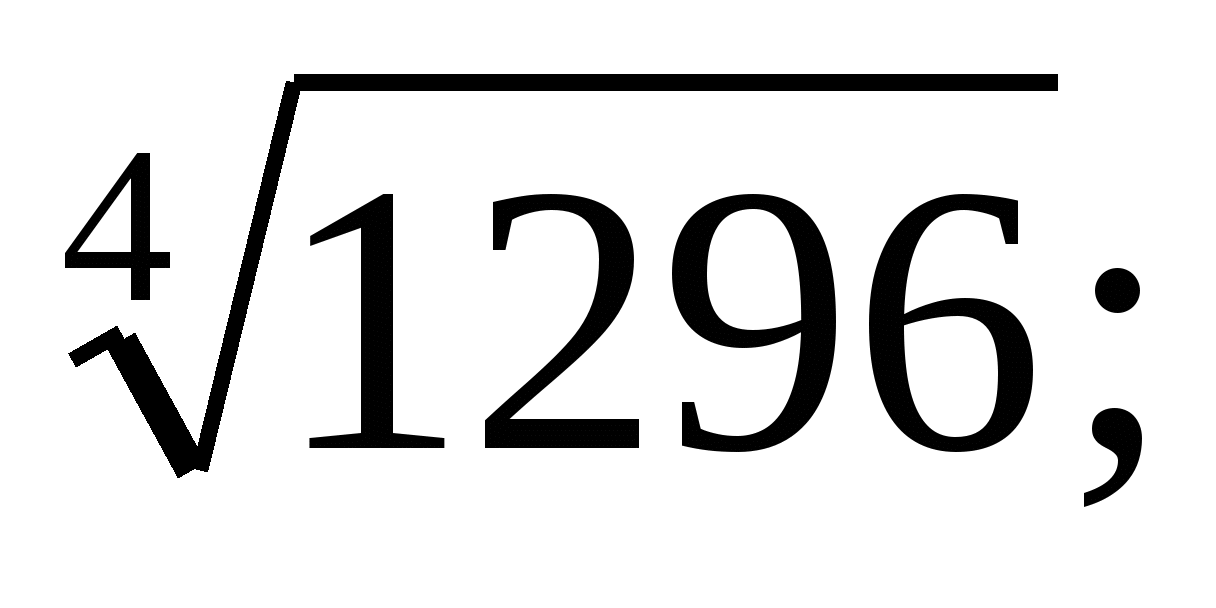 в)
в) 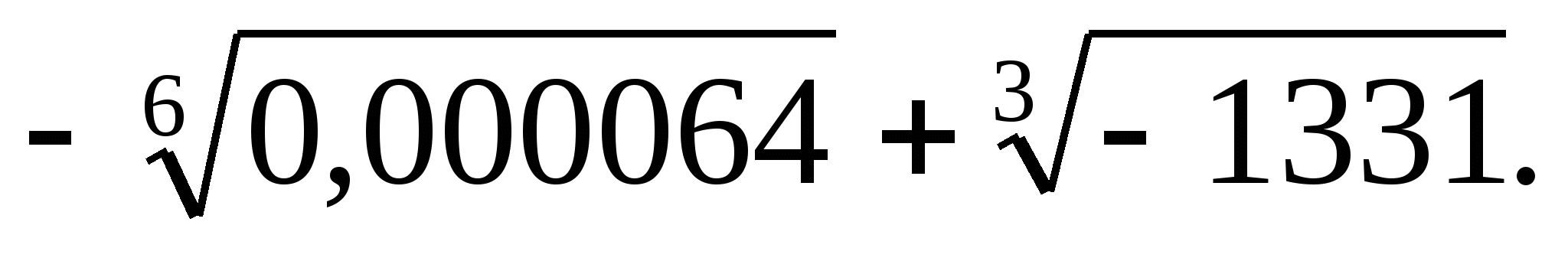
Контрольная работа №1
Вариант 1
Вычислите:
а) 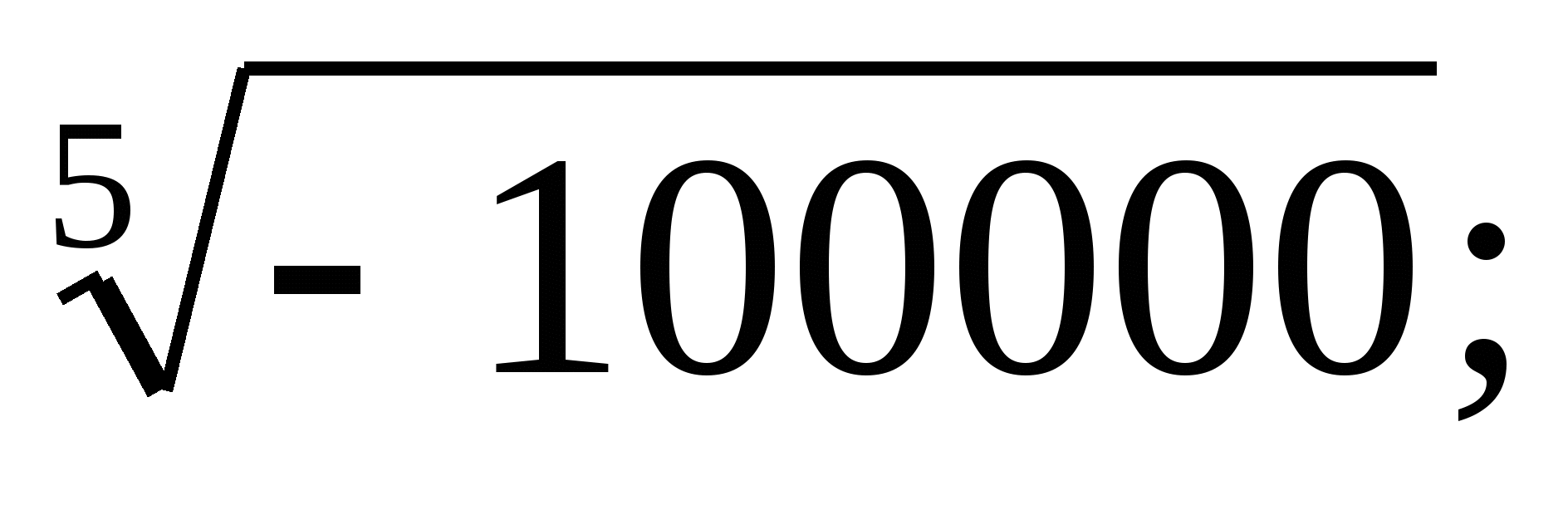 б)
б) 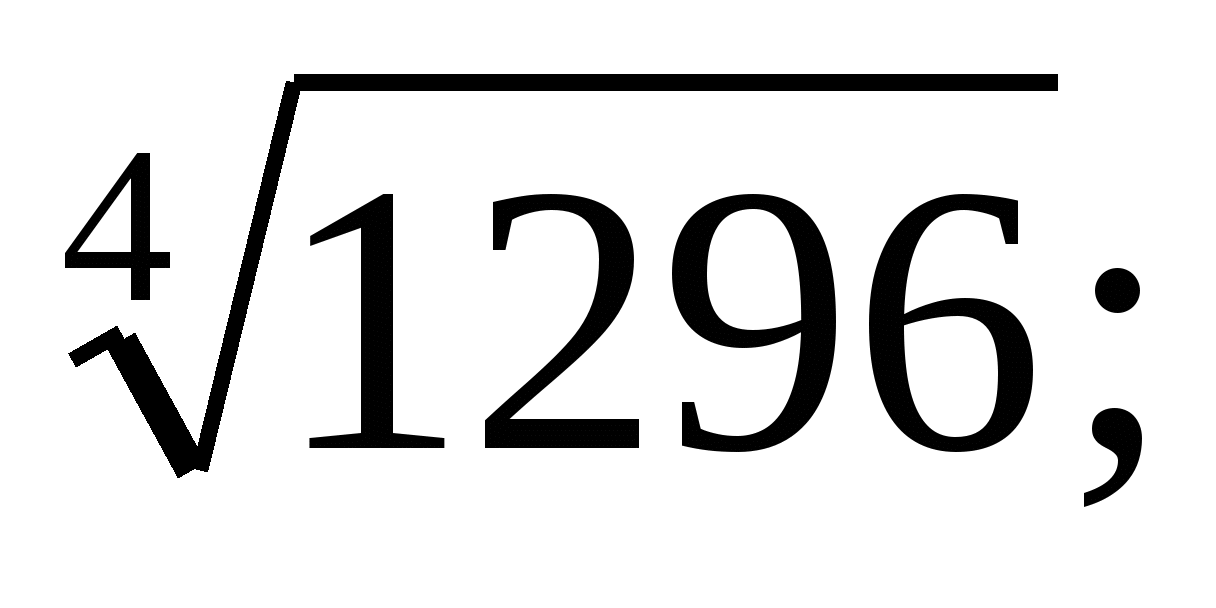 в)
в) 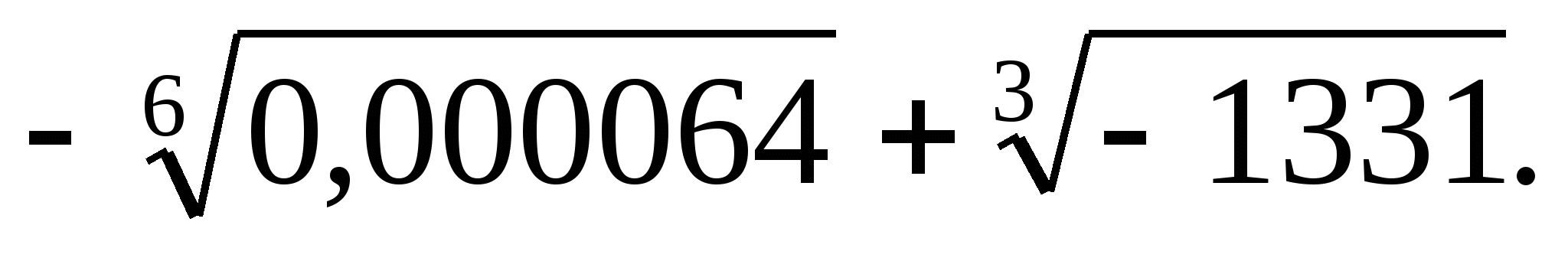
Расположите числа в порядке убывания: 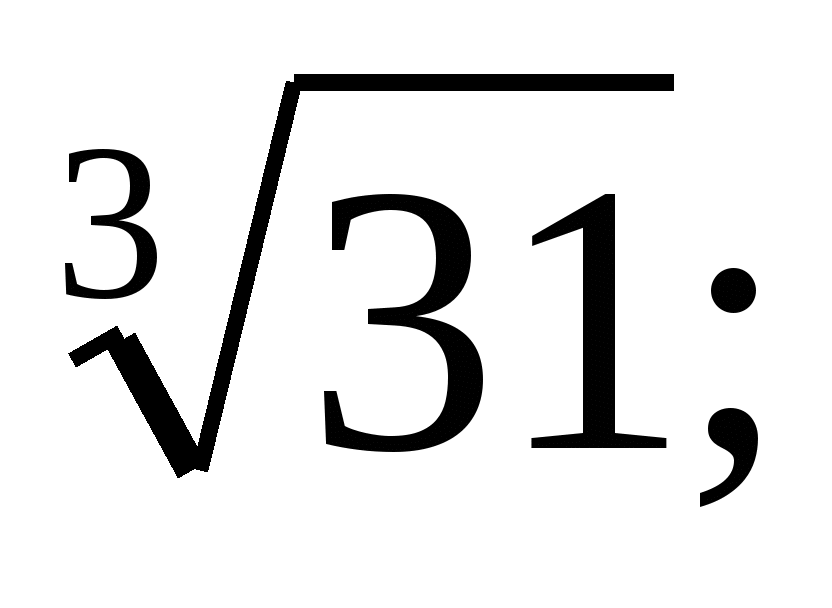
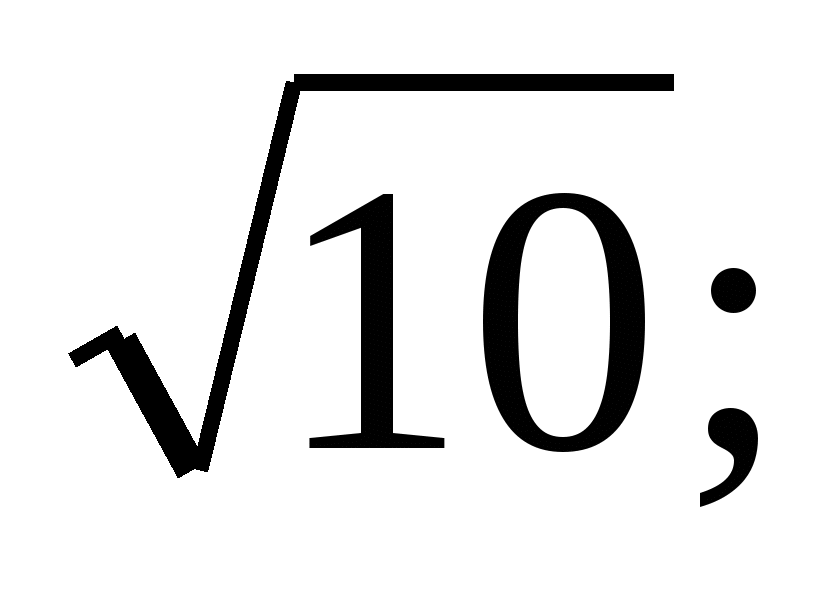
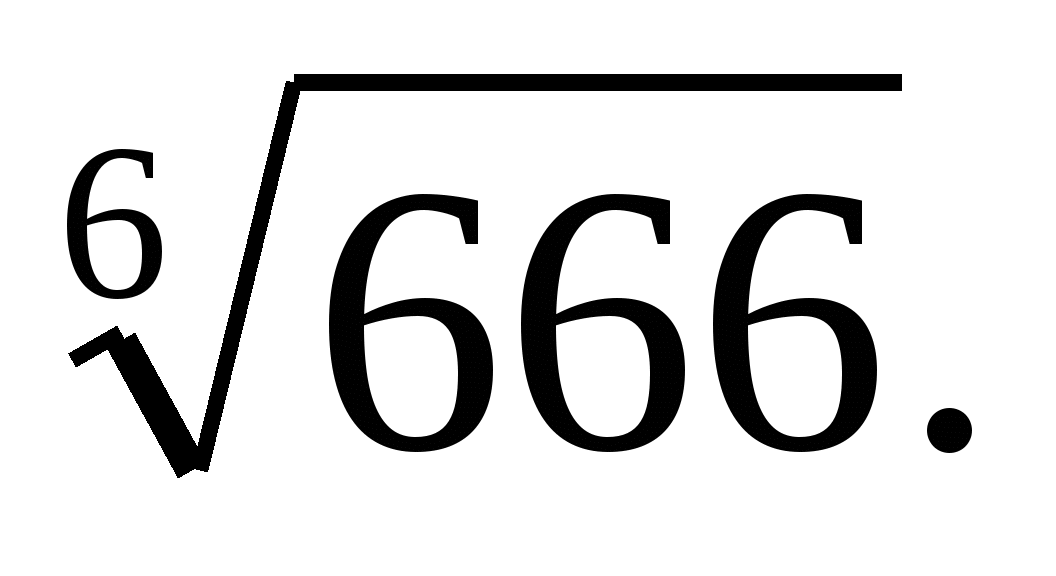
Постройте график функции:
а) 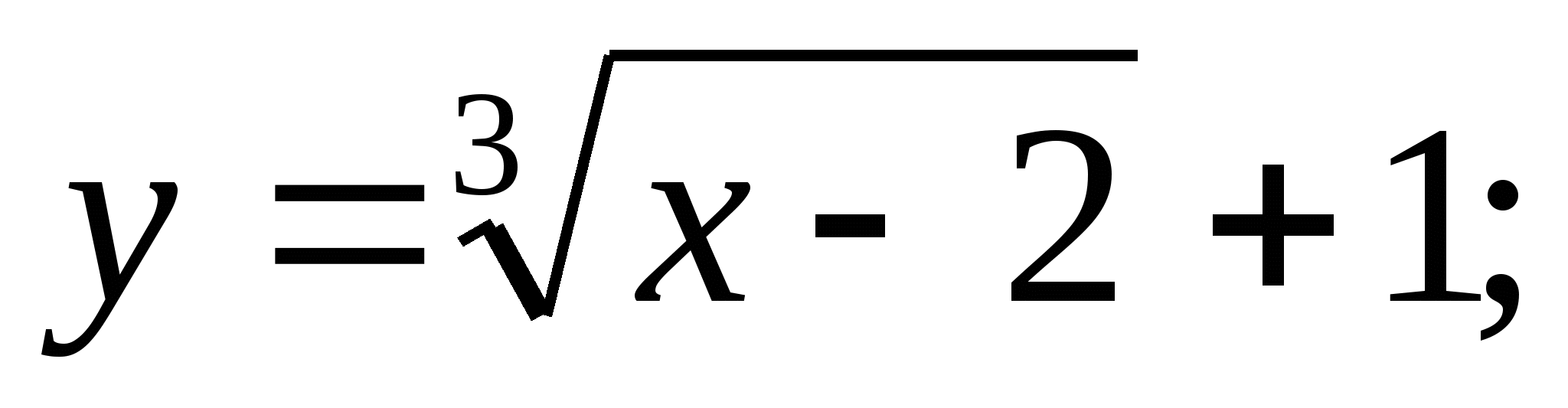 б)
б) 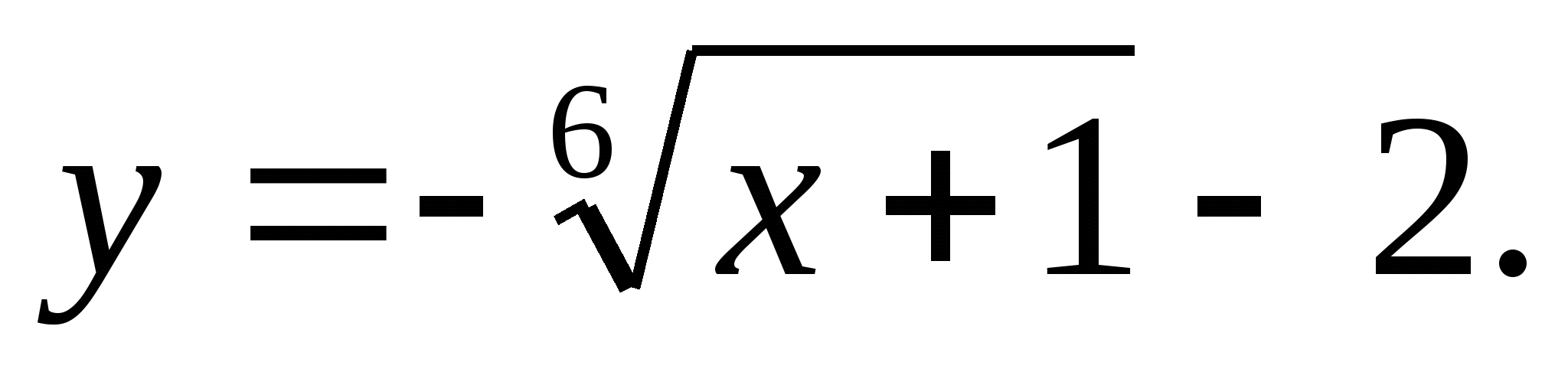
Вычислите: 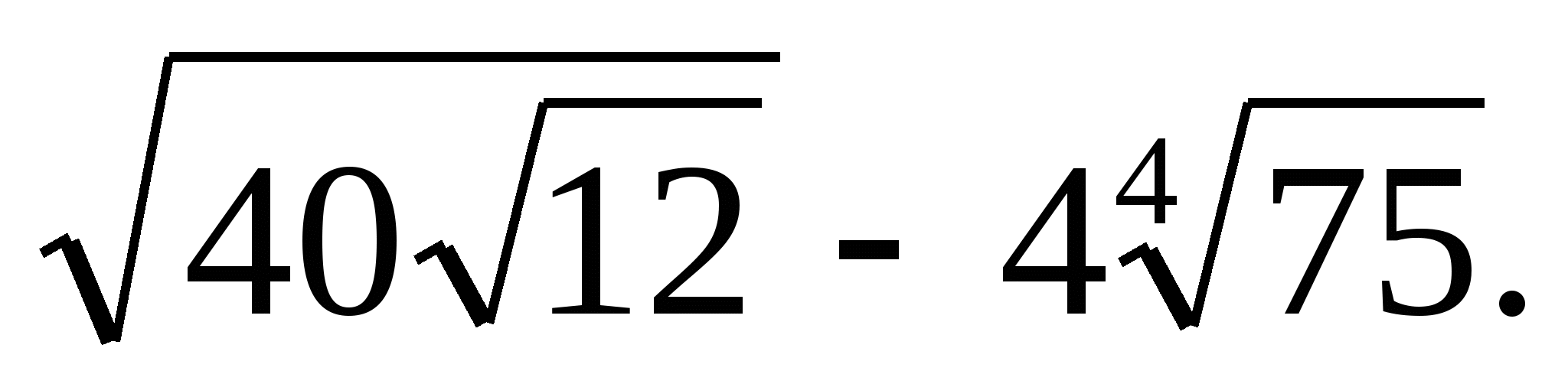
Найдите значение выражения: 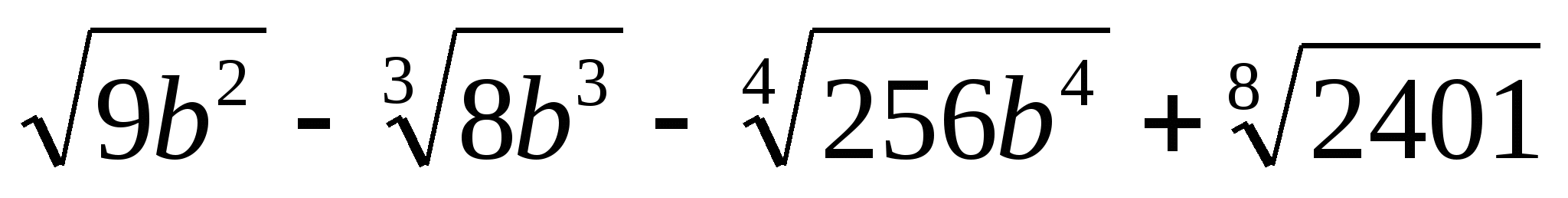 при
при 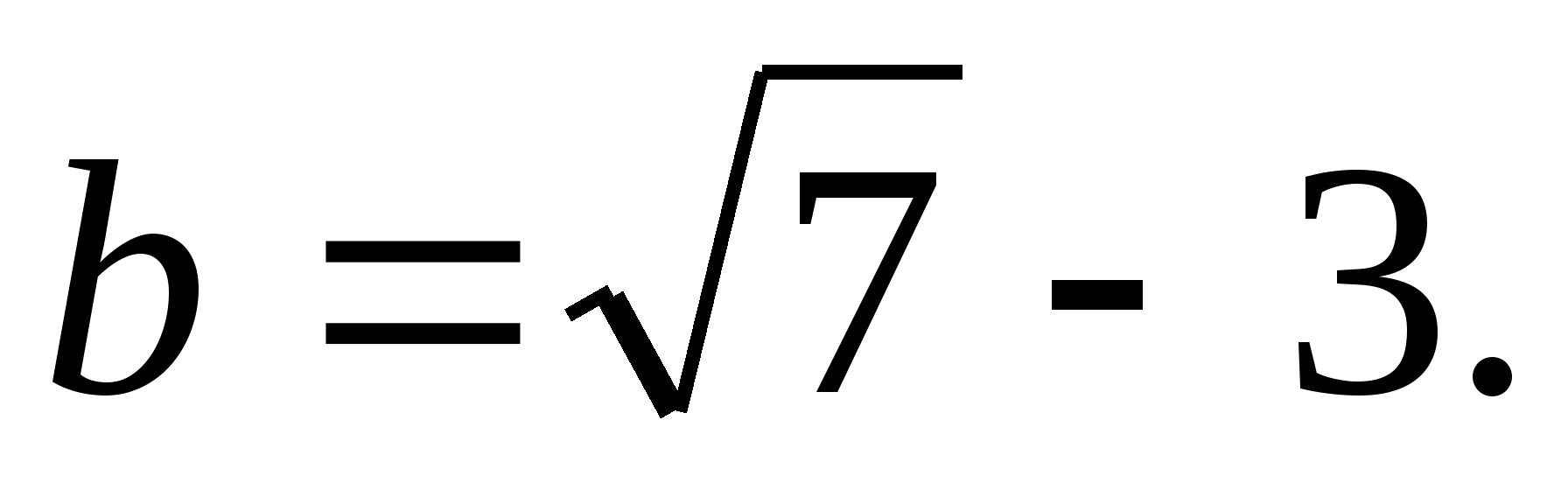
Решите уравнение: 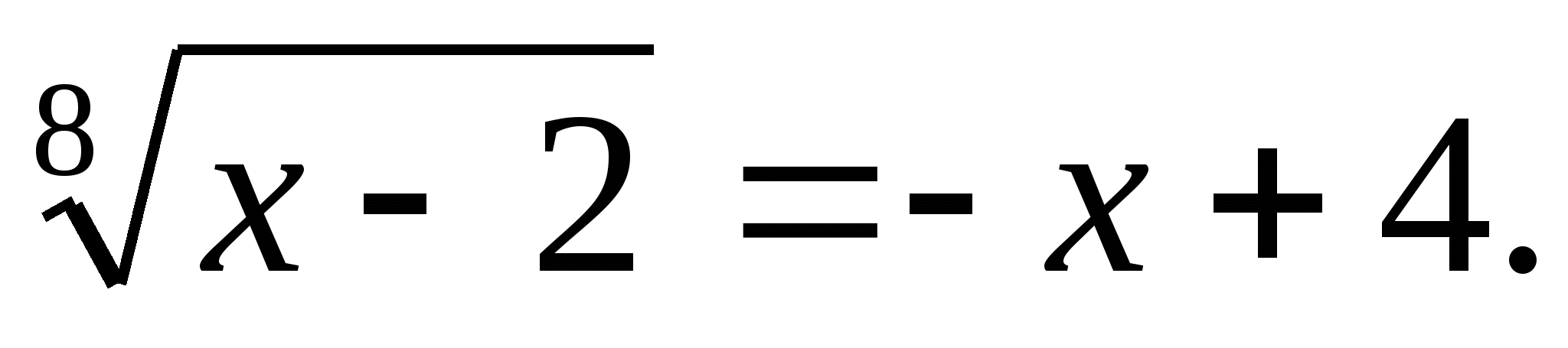
Контрольная работа №1
Вариант 2
Вычислите:
а) 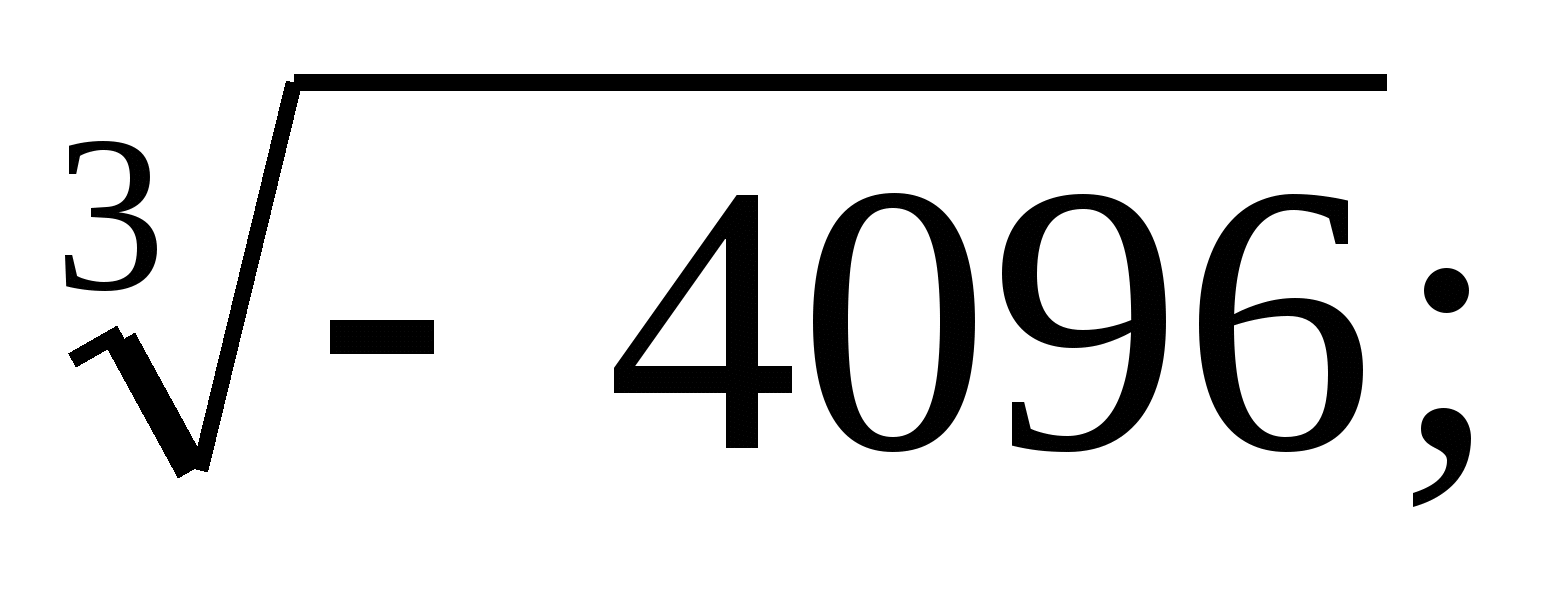 б)
б) 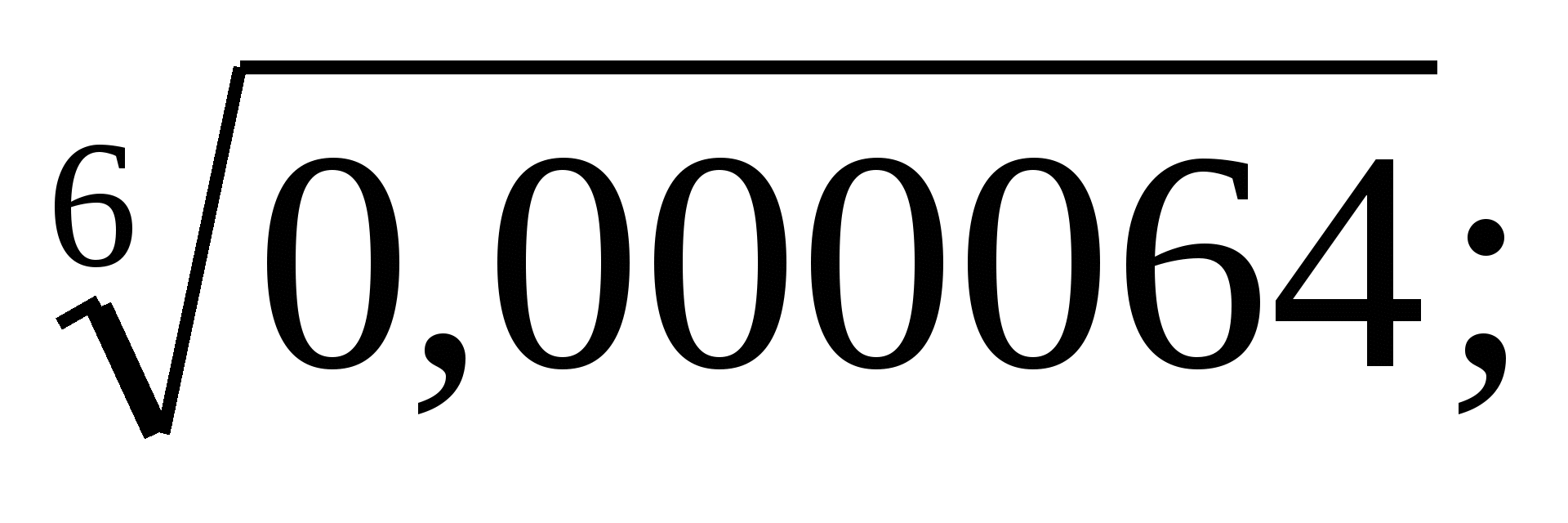 в)
в) 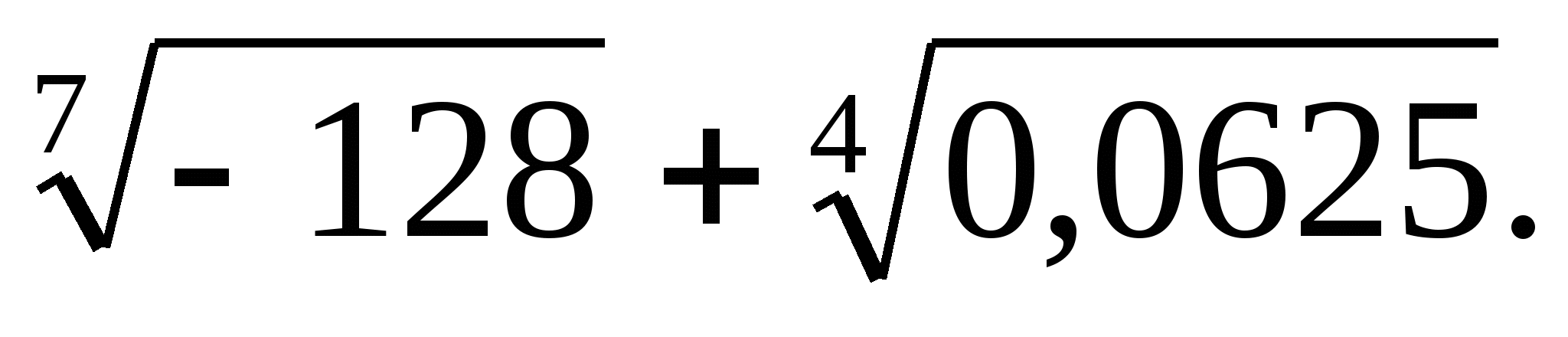
Расположите числа в порядке возрастания: 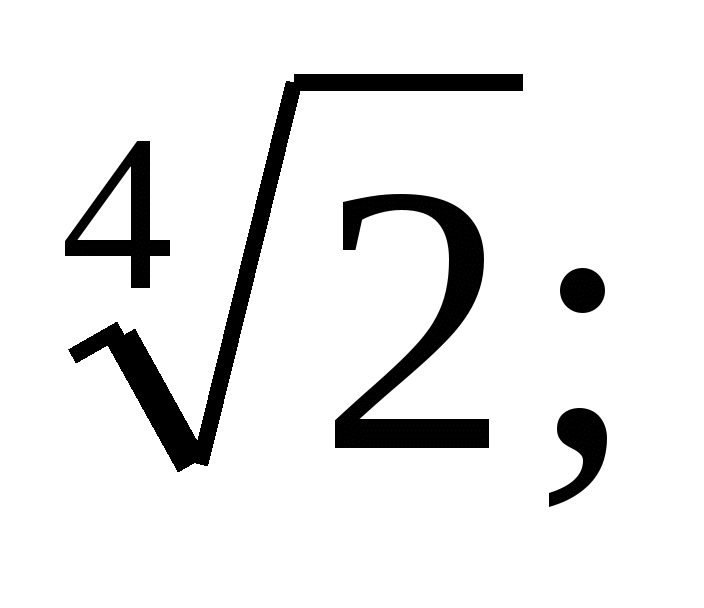
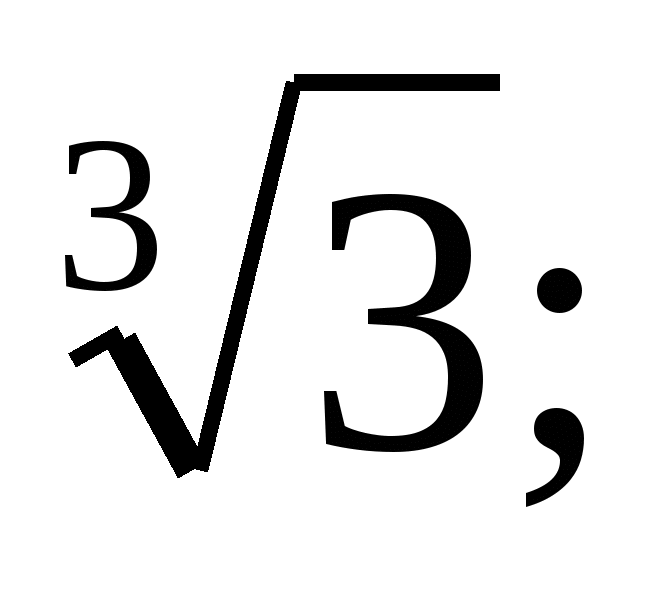
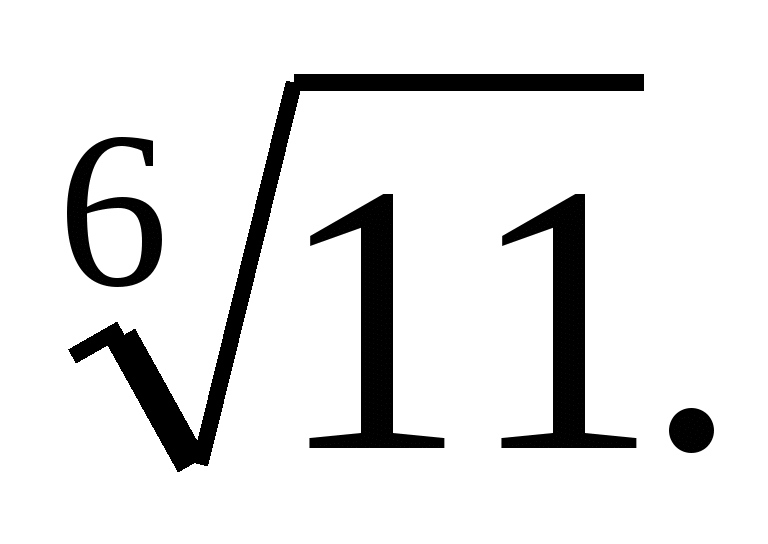
Постройте график функции:
а) 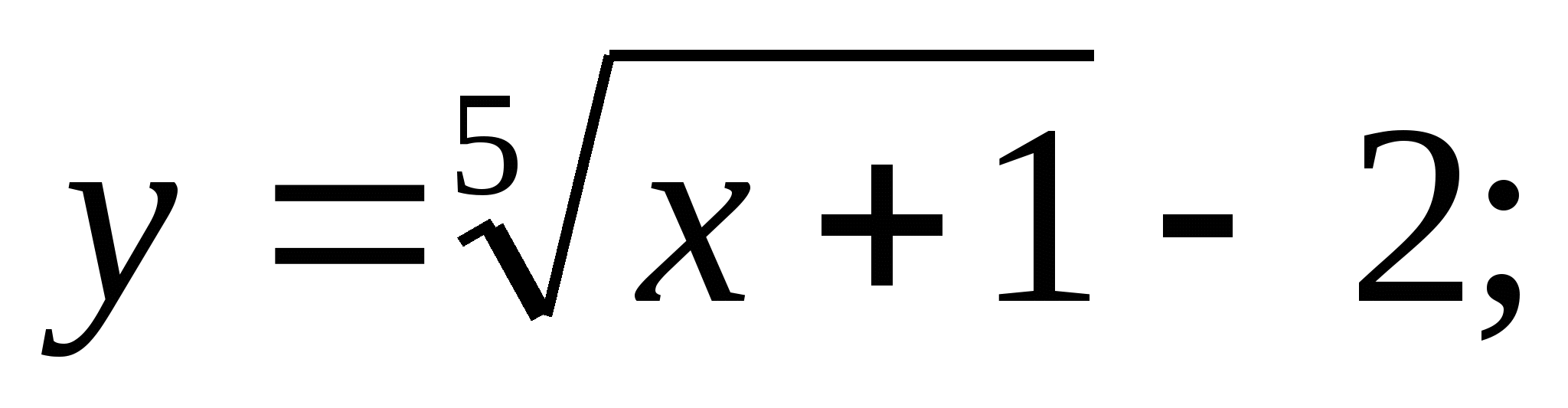 б)
б) 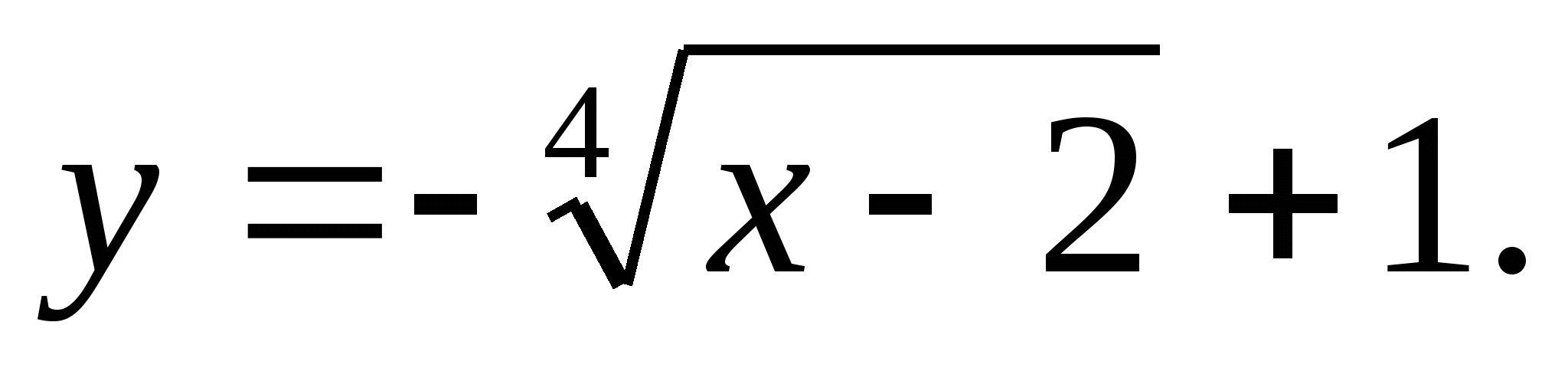
Вычислите: 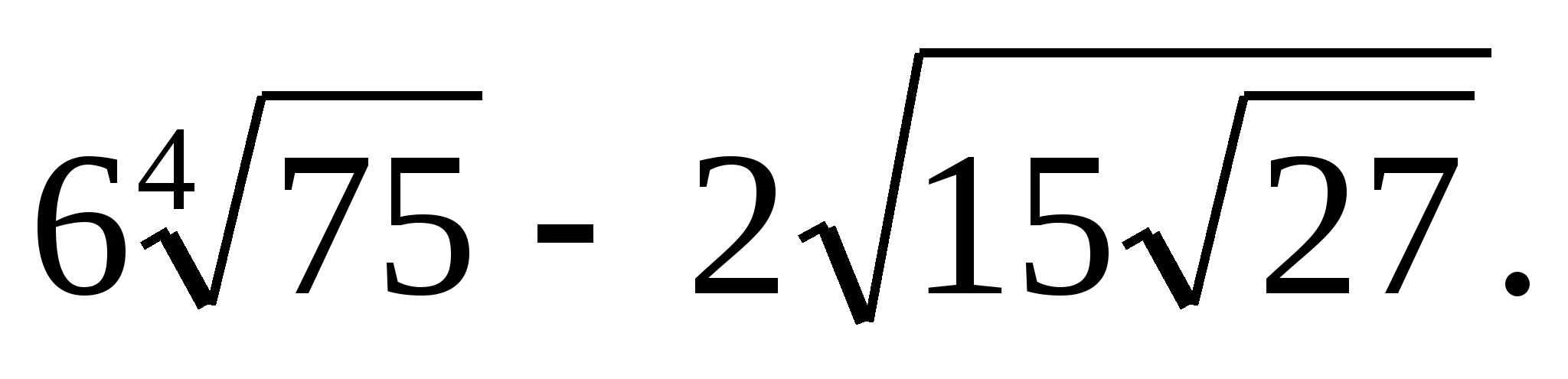
Найдите значение выражения: 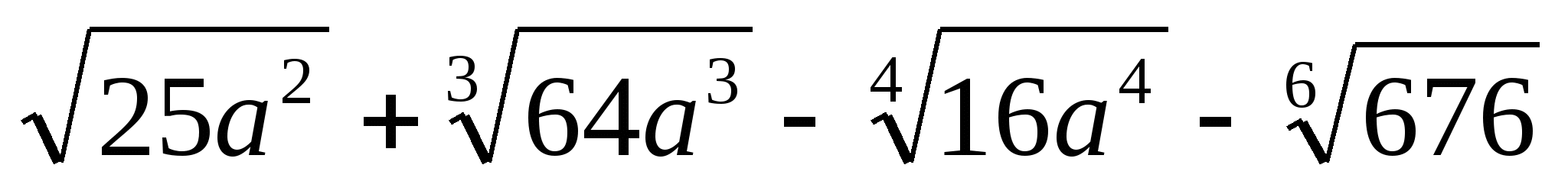 при
при 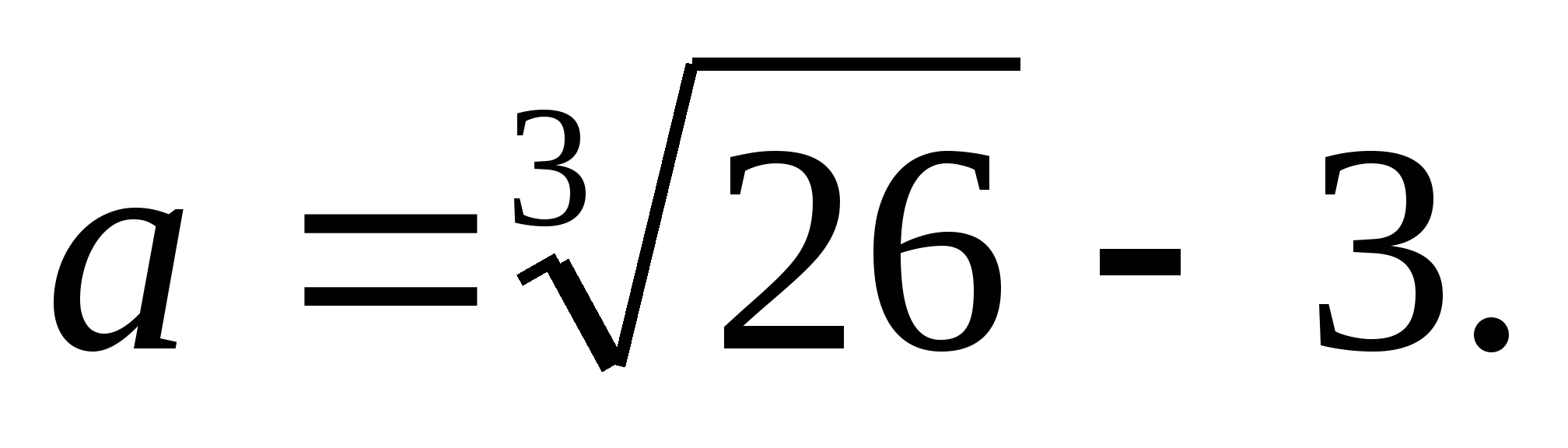
Решите уравнение: 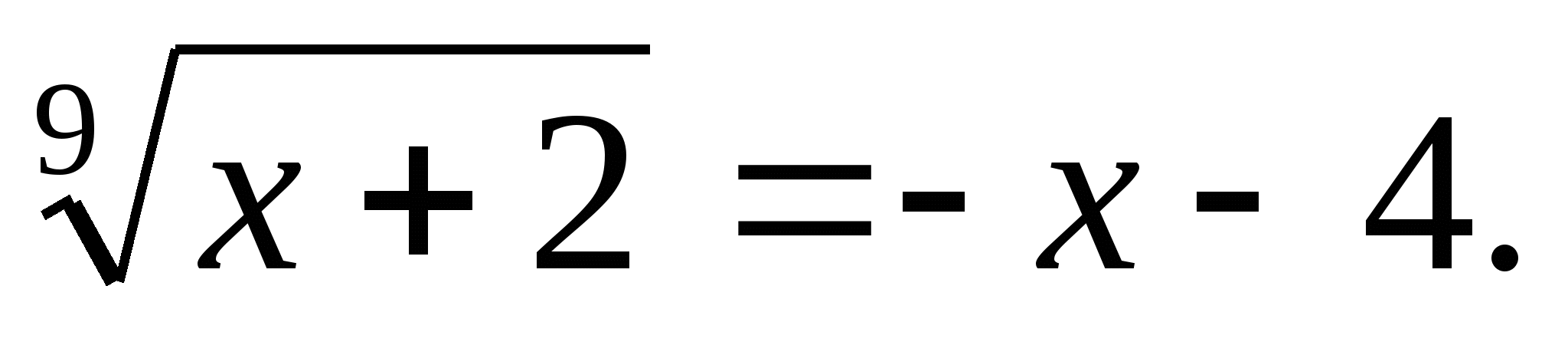
Контрольная работа №1
Вариант 3
Вычислите:
а) 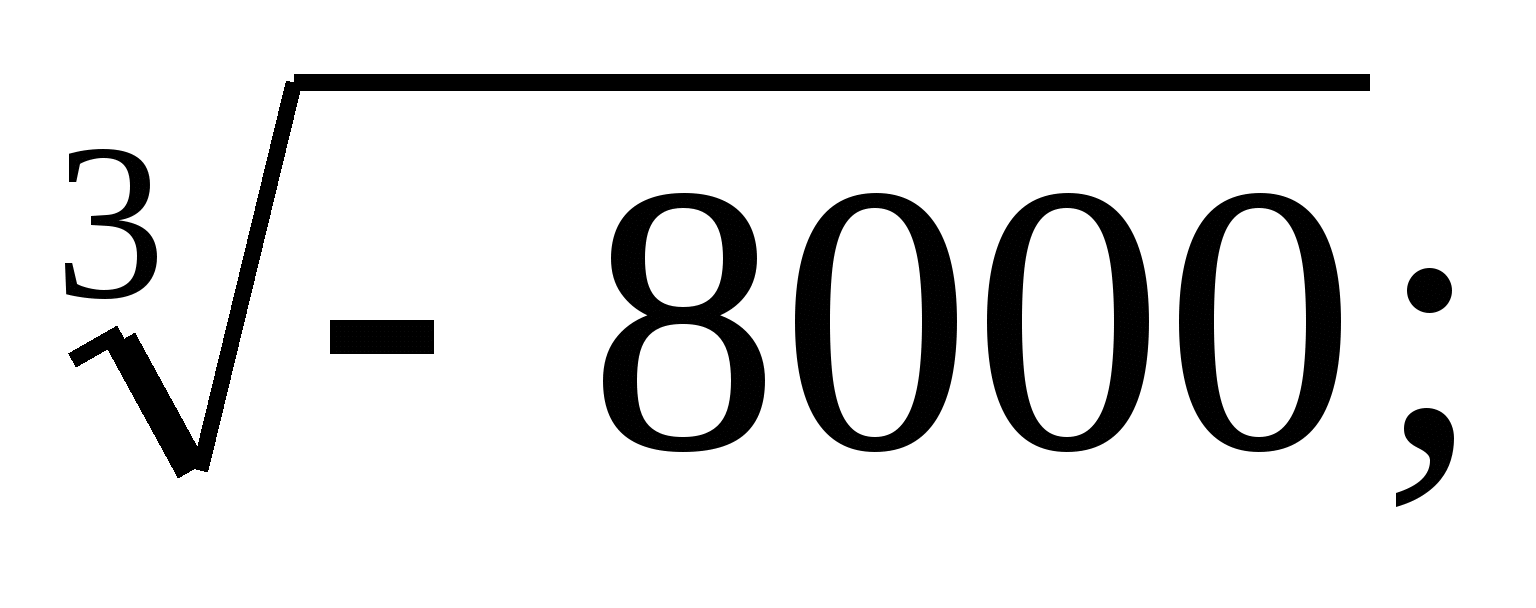 б)
б) 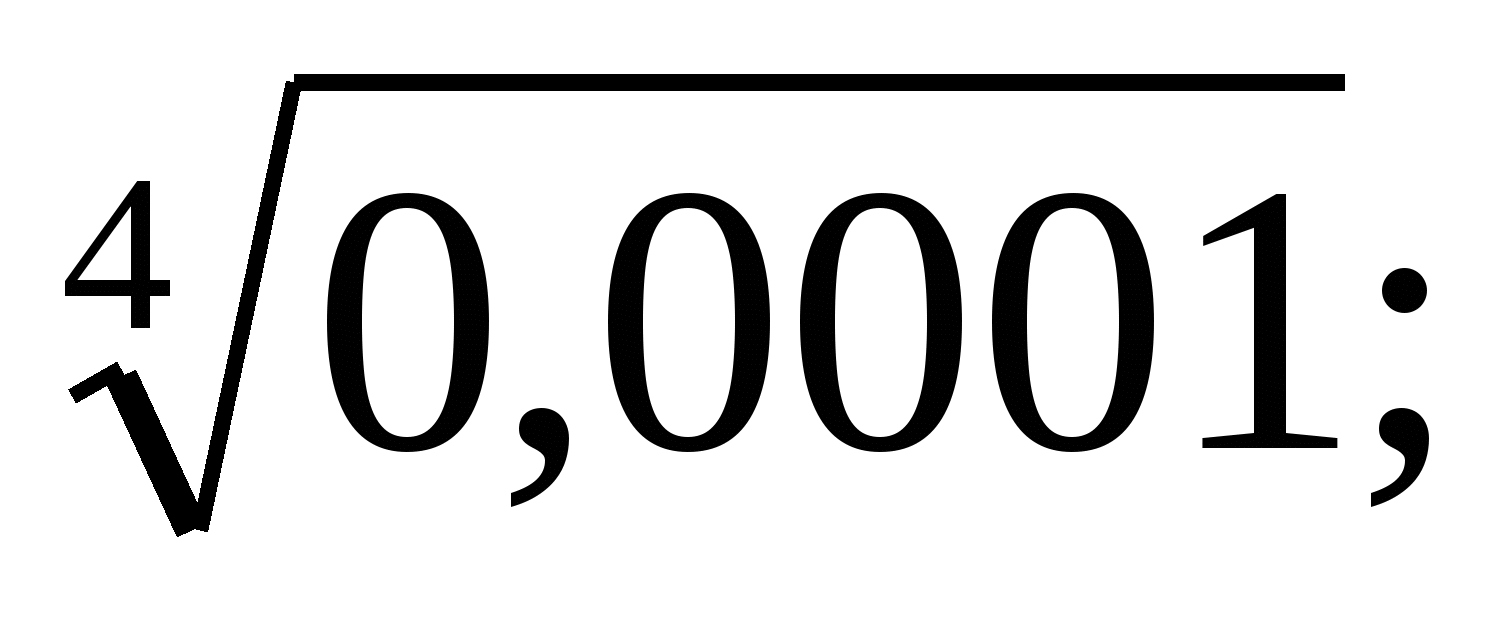 в)
в) 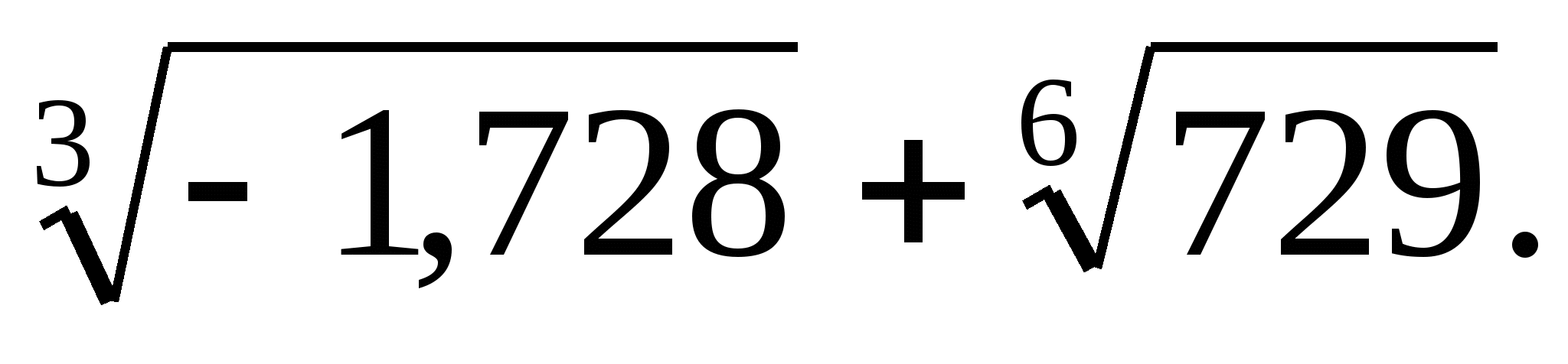
Расположите числа в порядке убывания: 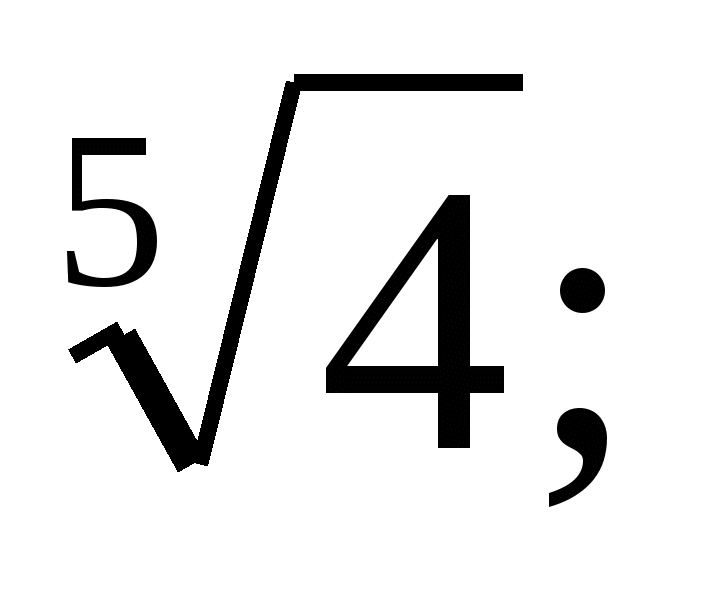
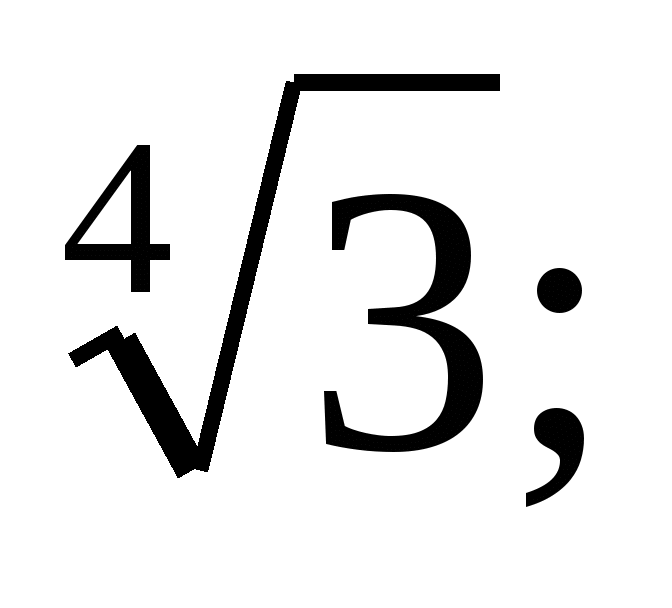
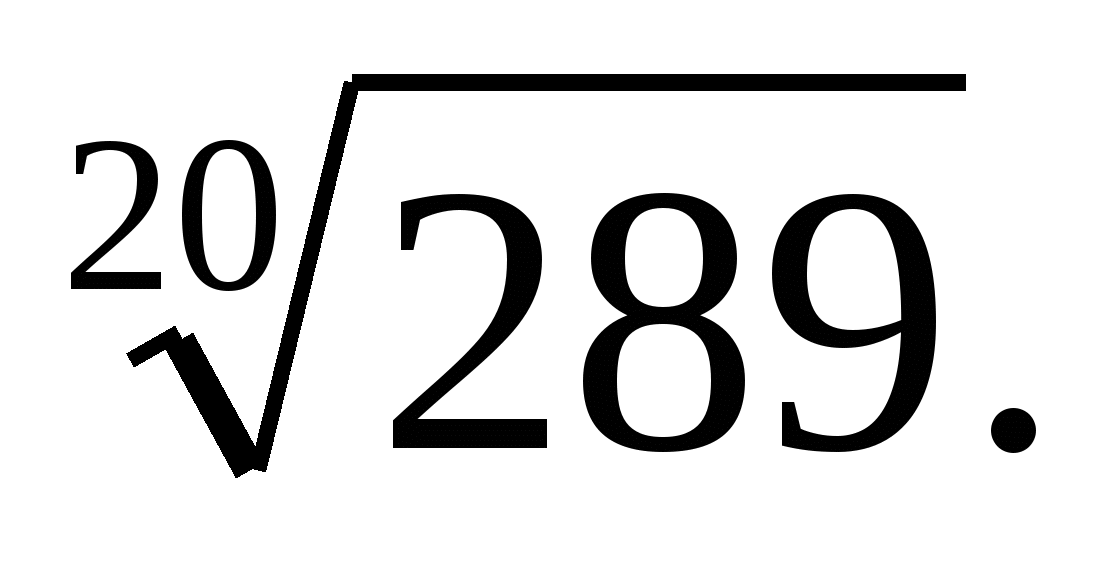
Постройте график функции:
а) 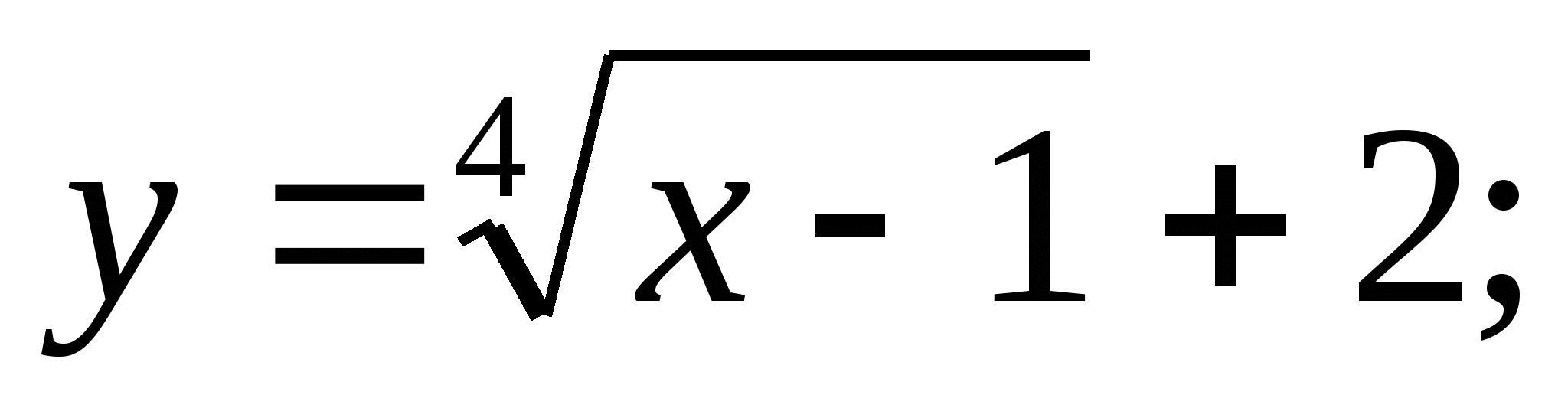 б)
б) 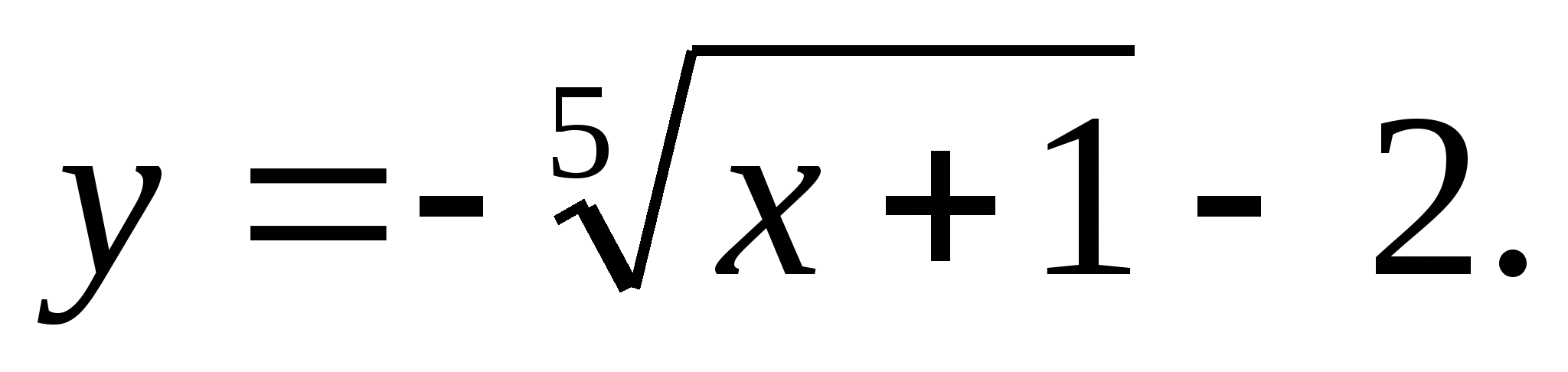
Вычислите: 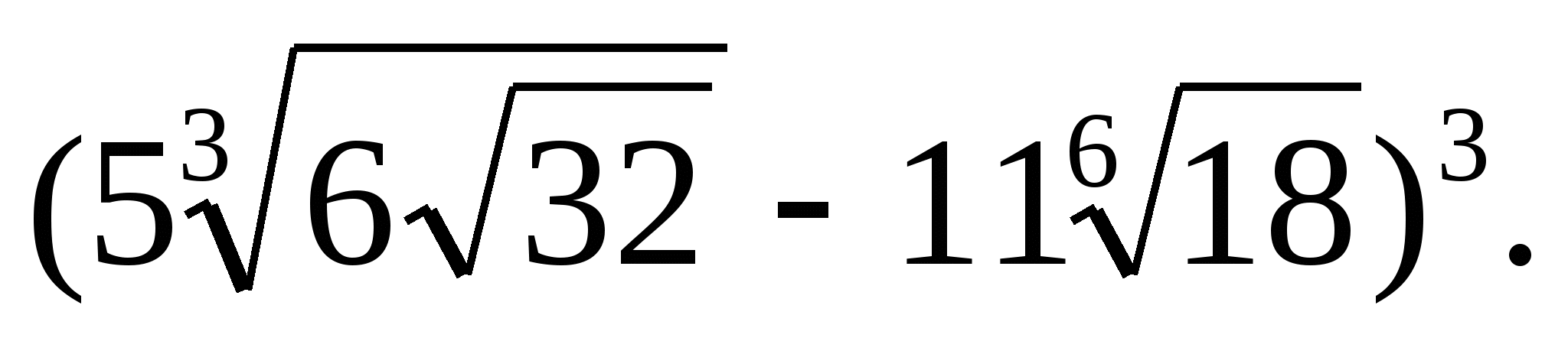
Найдите значение выражения: 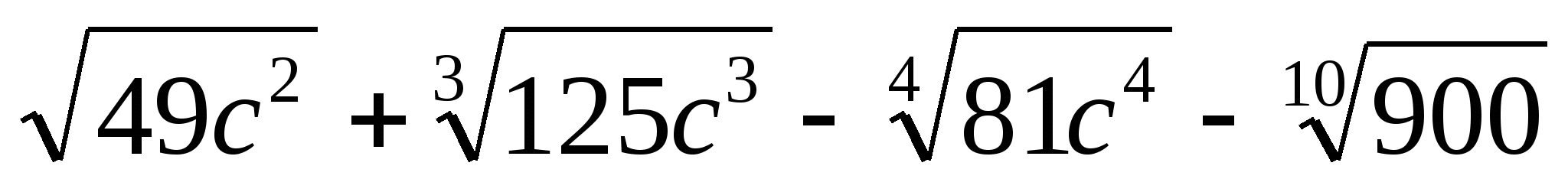 при
при 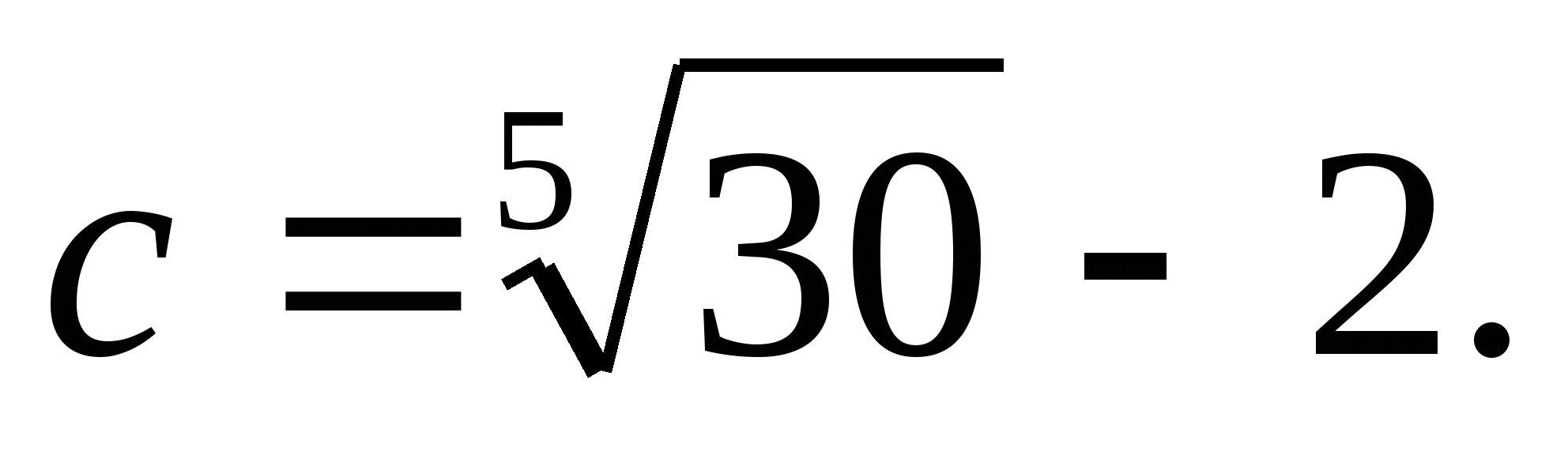
Решите уравнение: 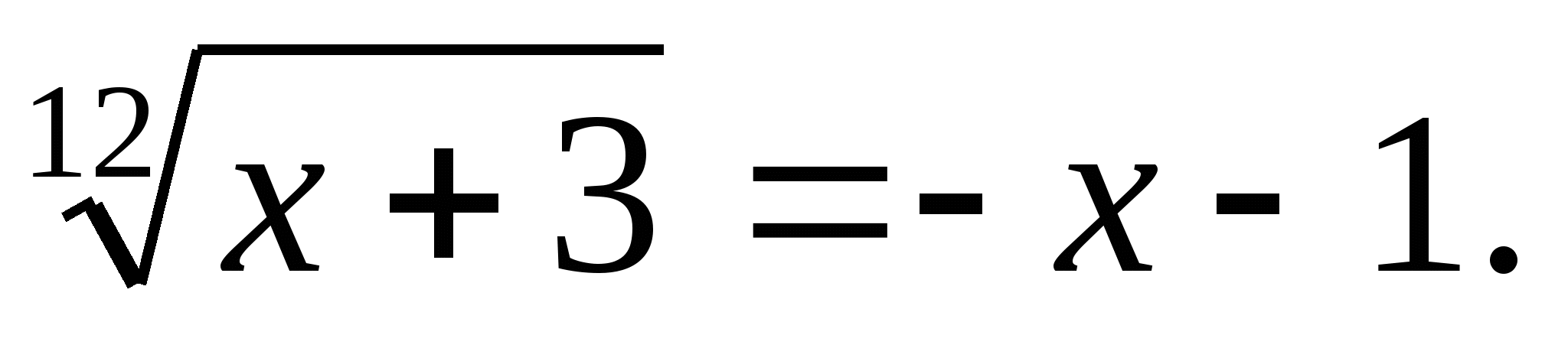
Контрольная работа №1
Вариант 4
Вычислите:
а) 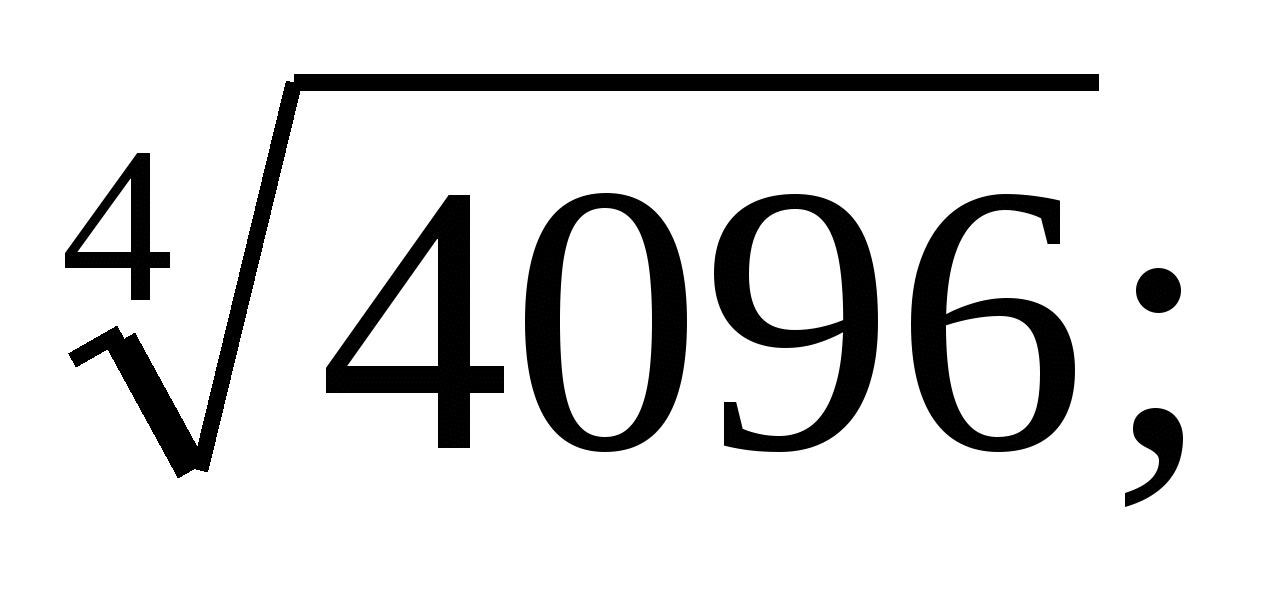 б)
б) 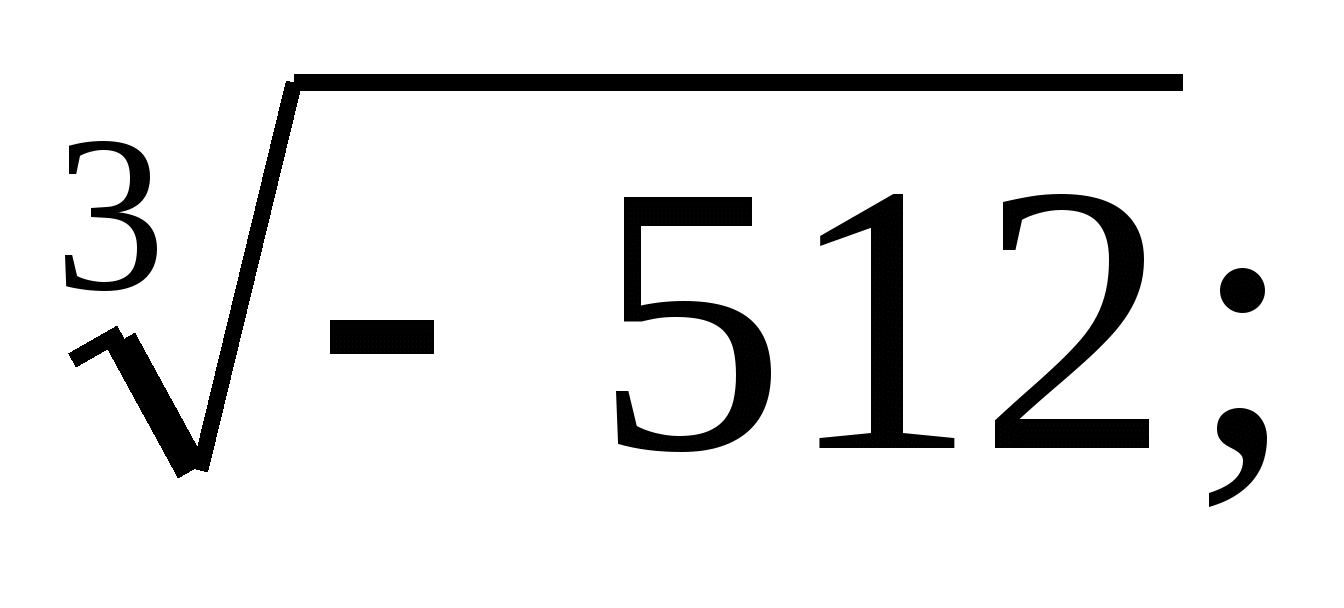 в)
в) 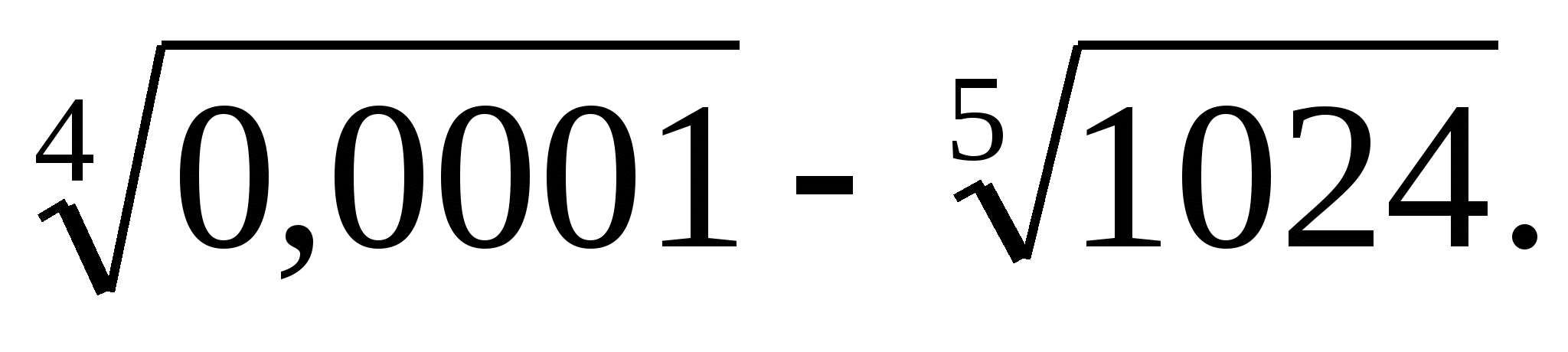
Расположите числа в порядке возрастания: 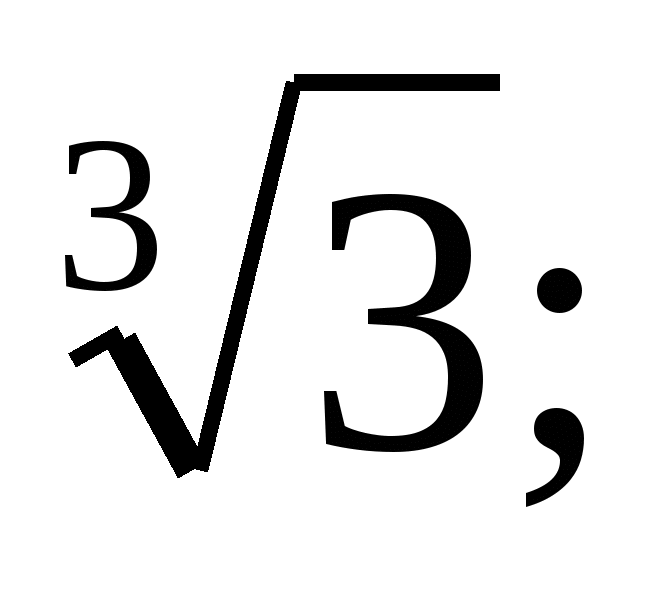
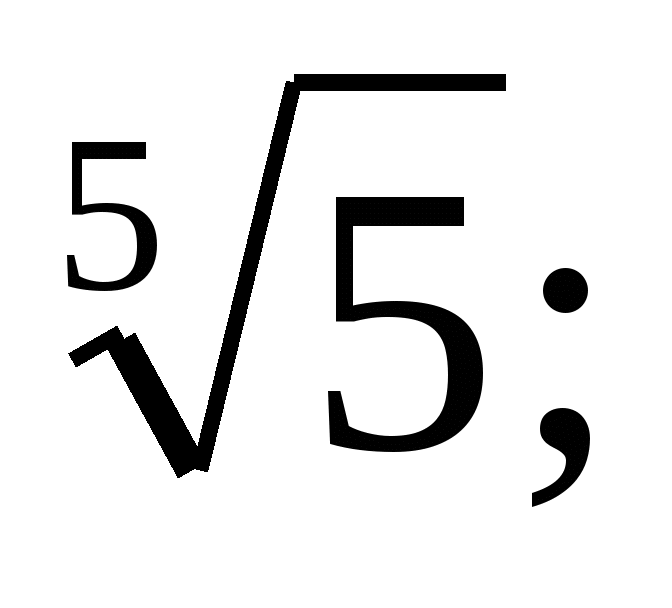
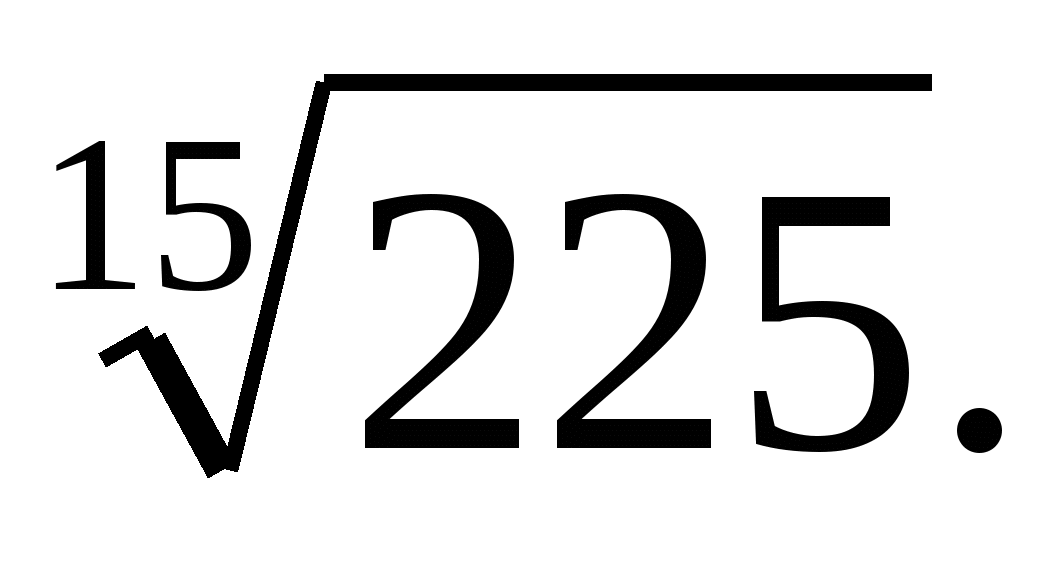
Постройте график функции:
а) 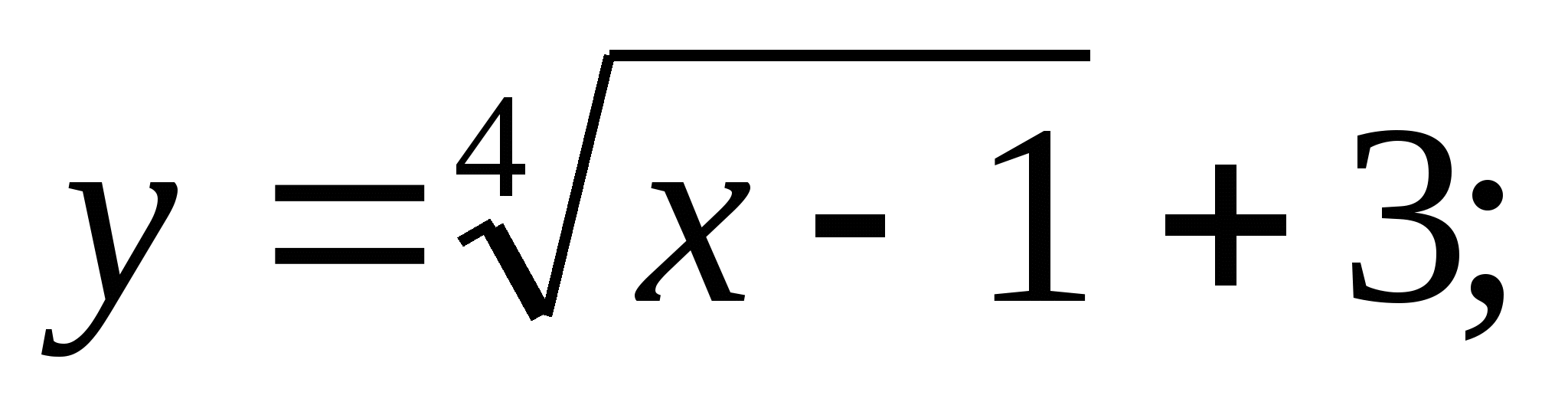 б)
б) 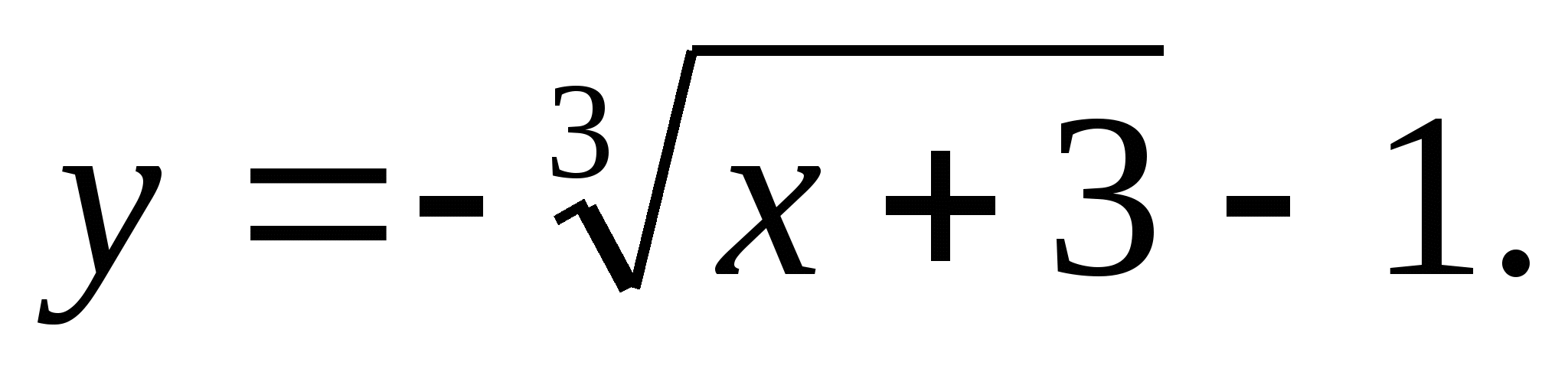
Вычислите: 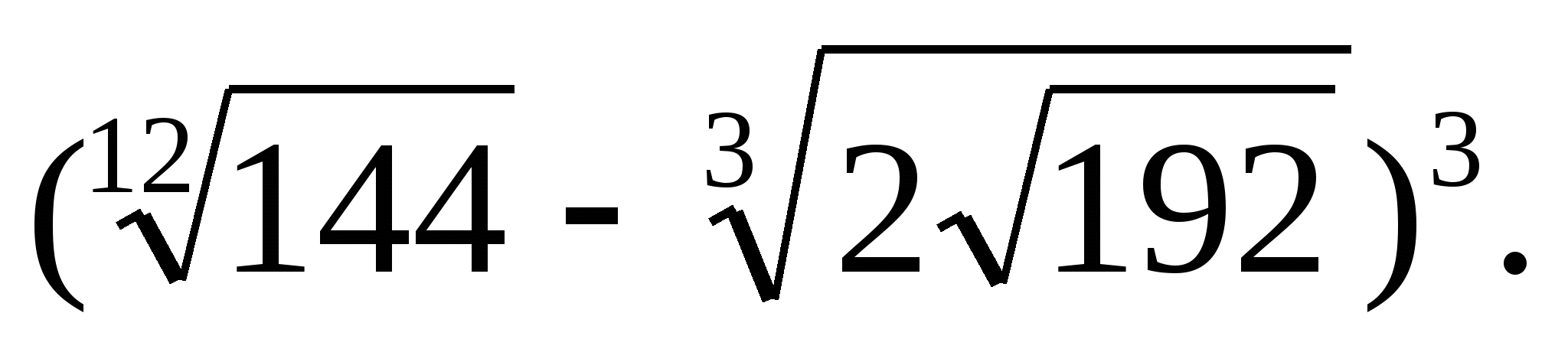
Найдите значение выражения: 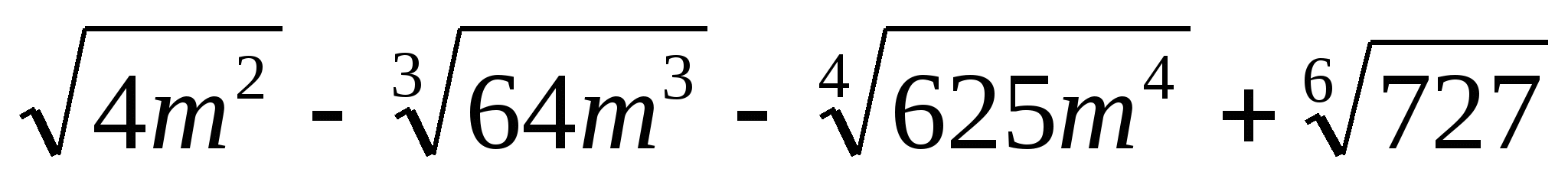 при
при 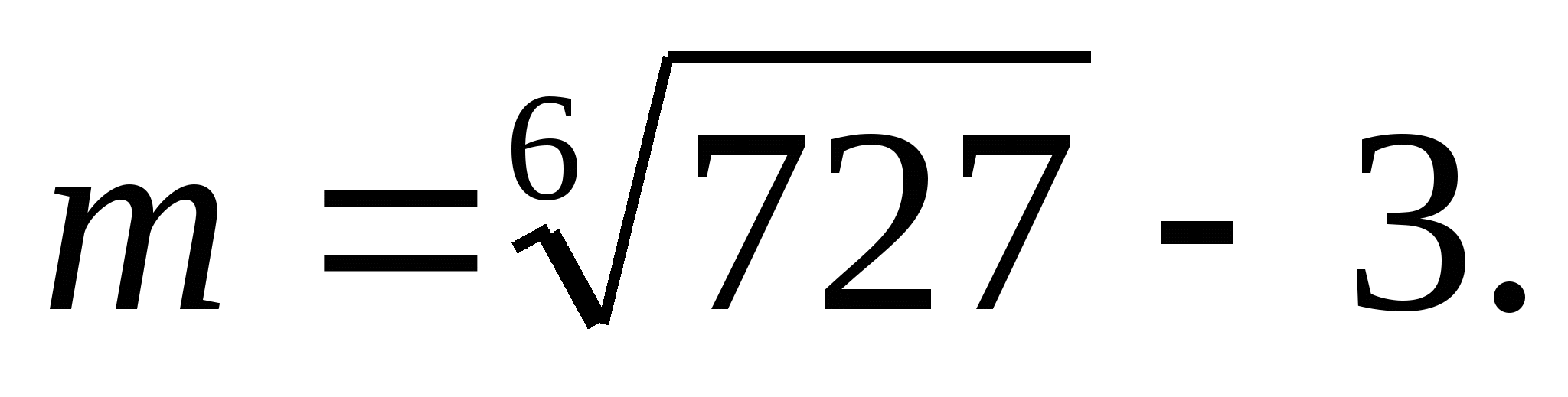
Решите уравнение: 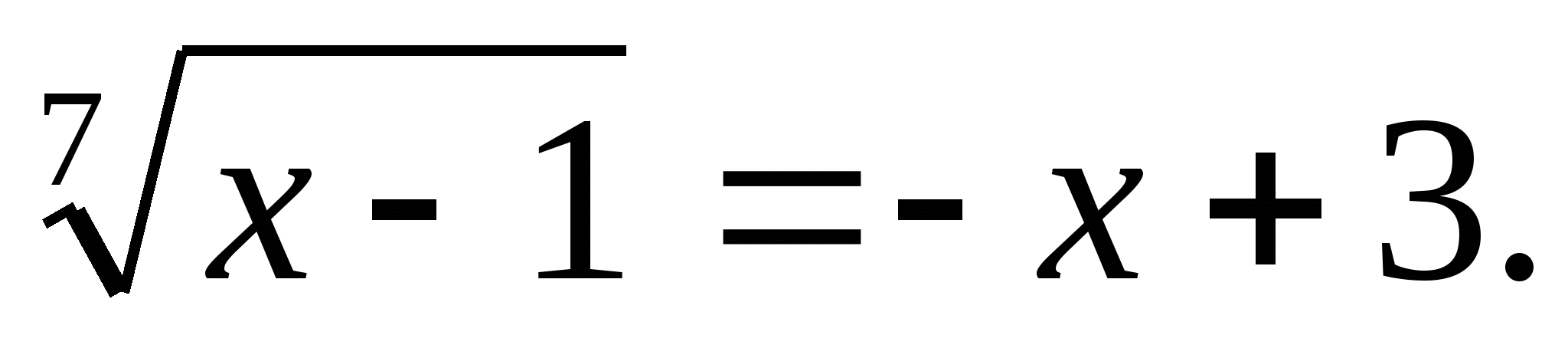
Контрольная работа №2
Вариант 1
Вычислите:
а) 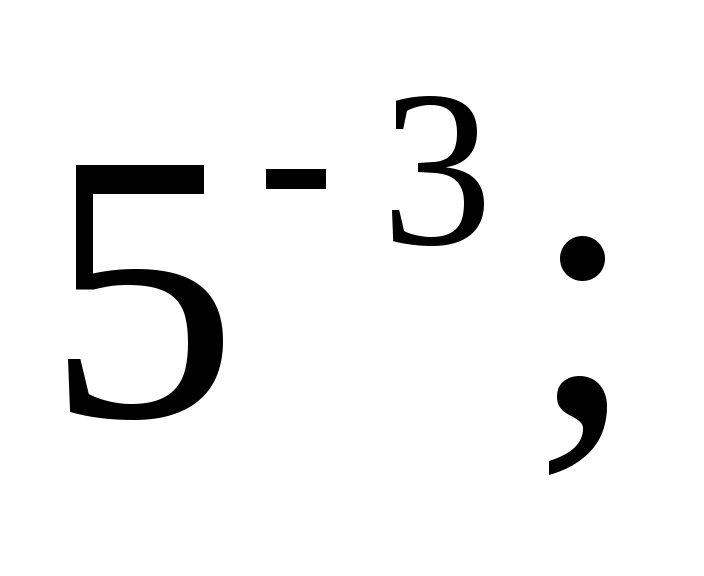 б)
б) 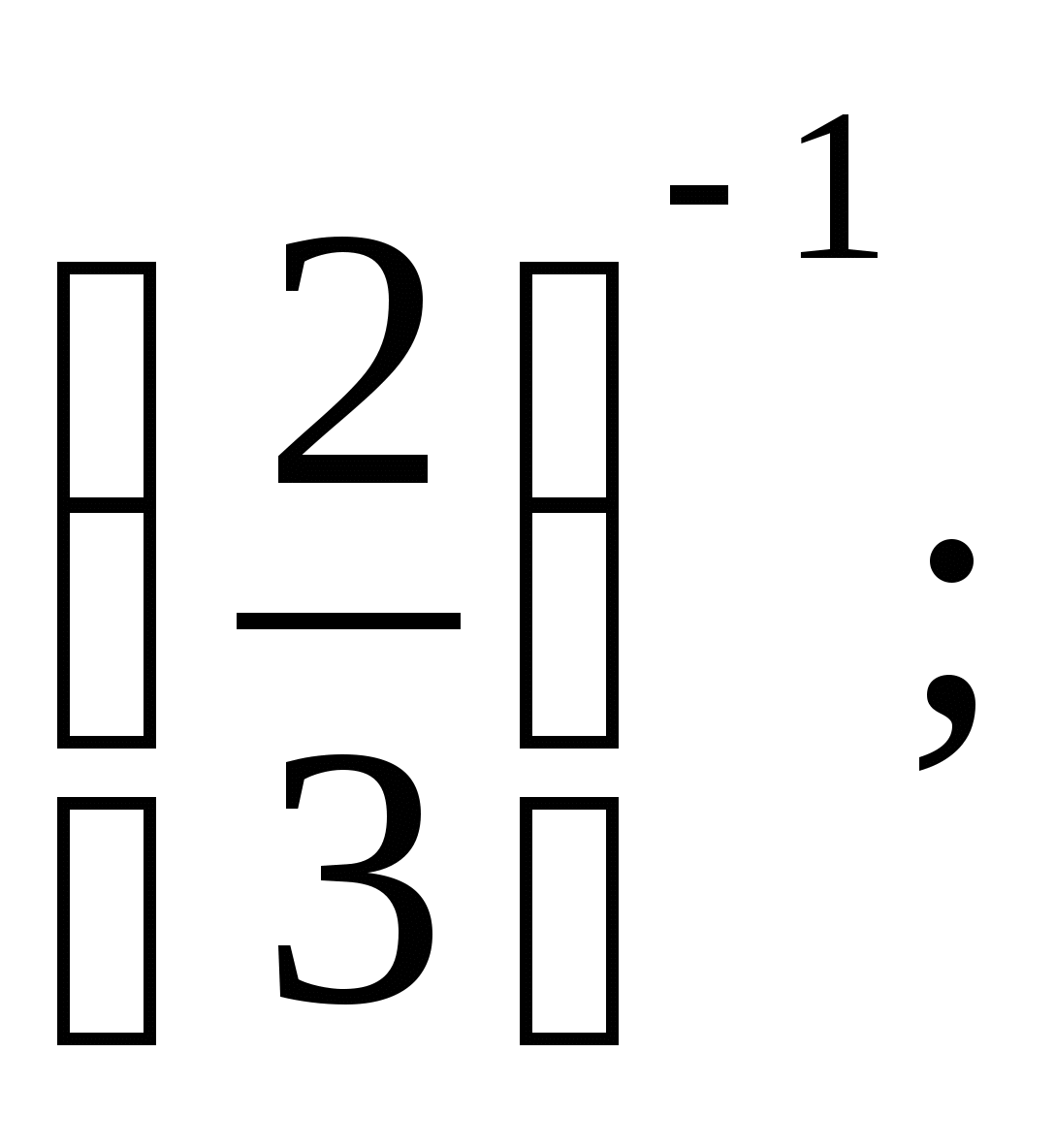 в)
в) 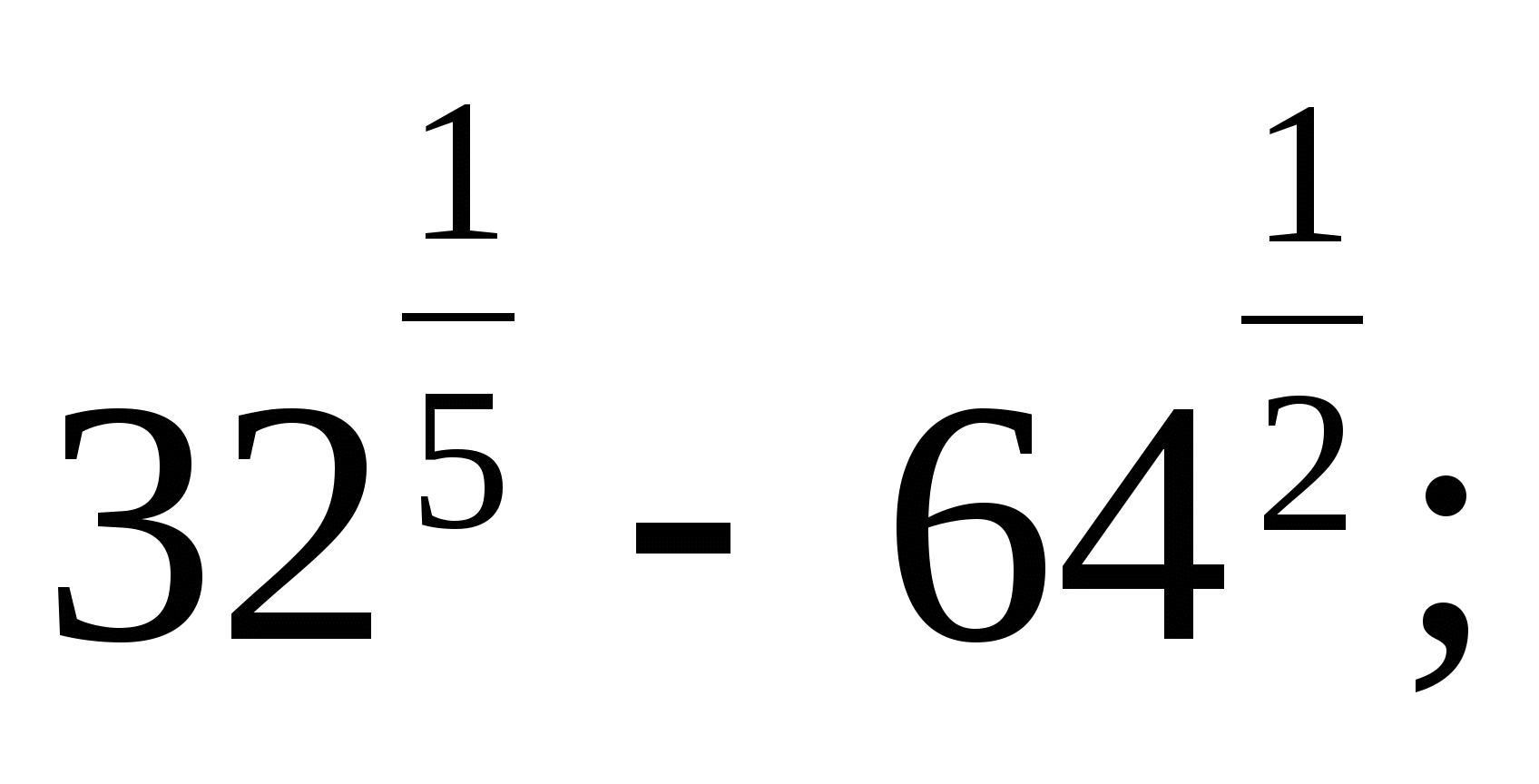 г)
г) 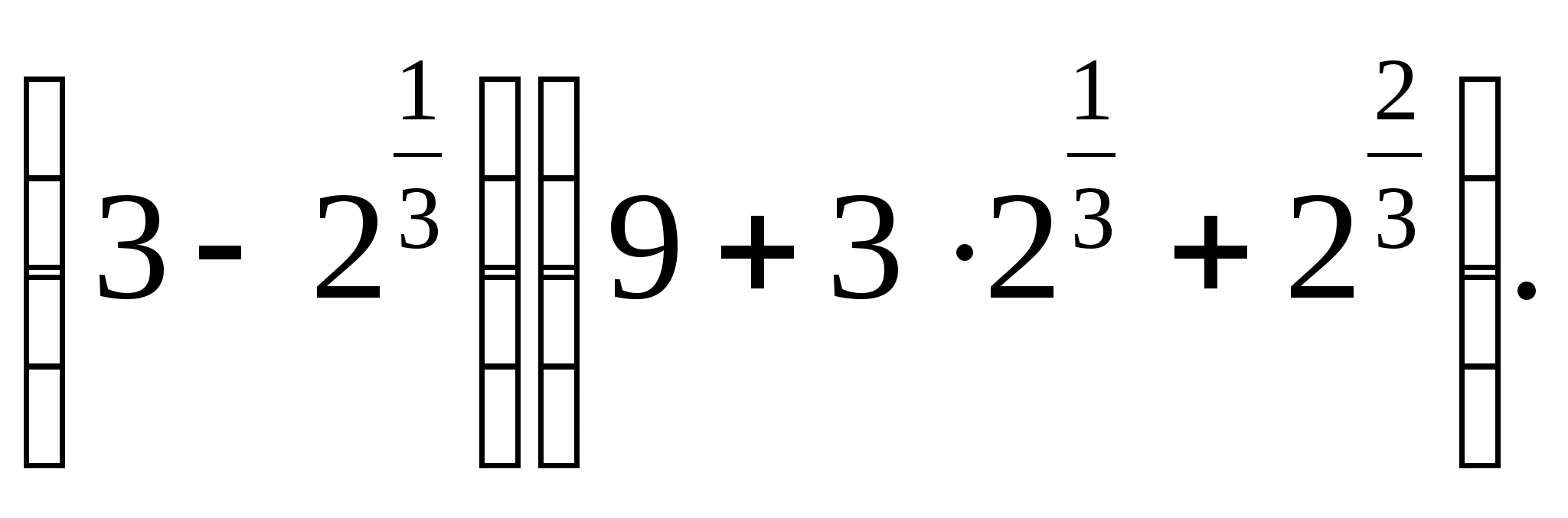
Постройте график функции: а) 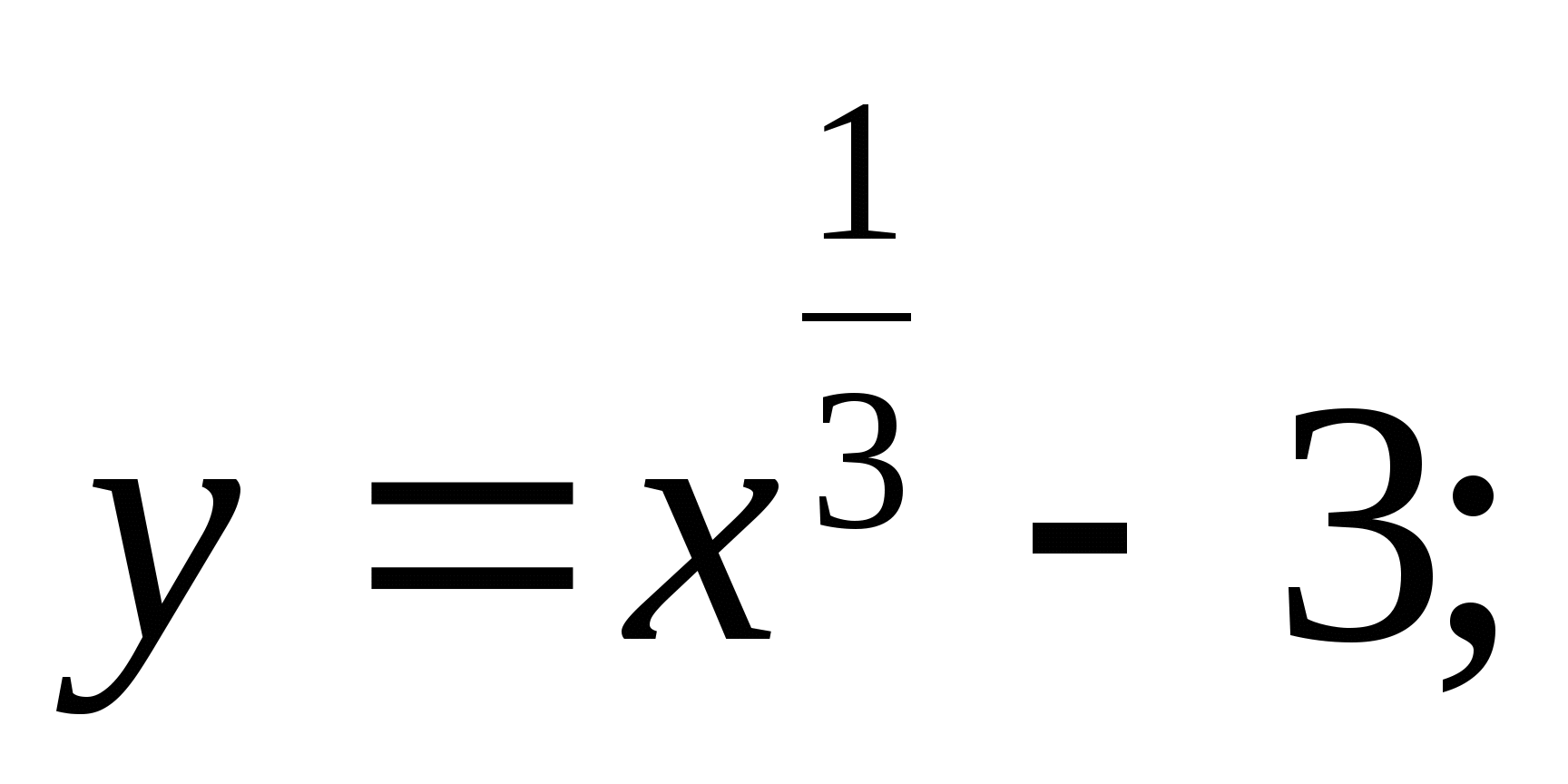 б)
б) 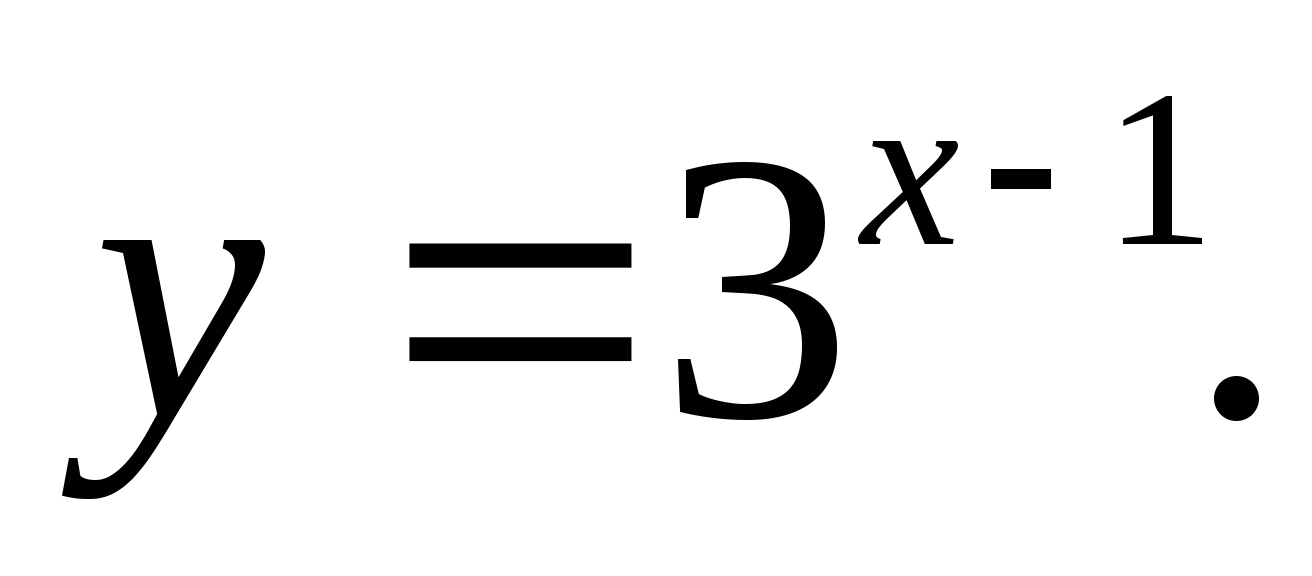
Решите уравнение: а) 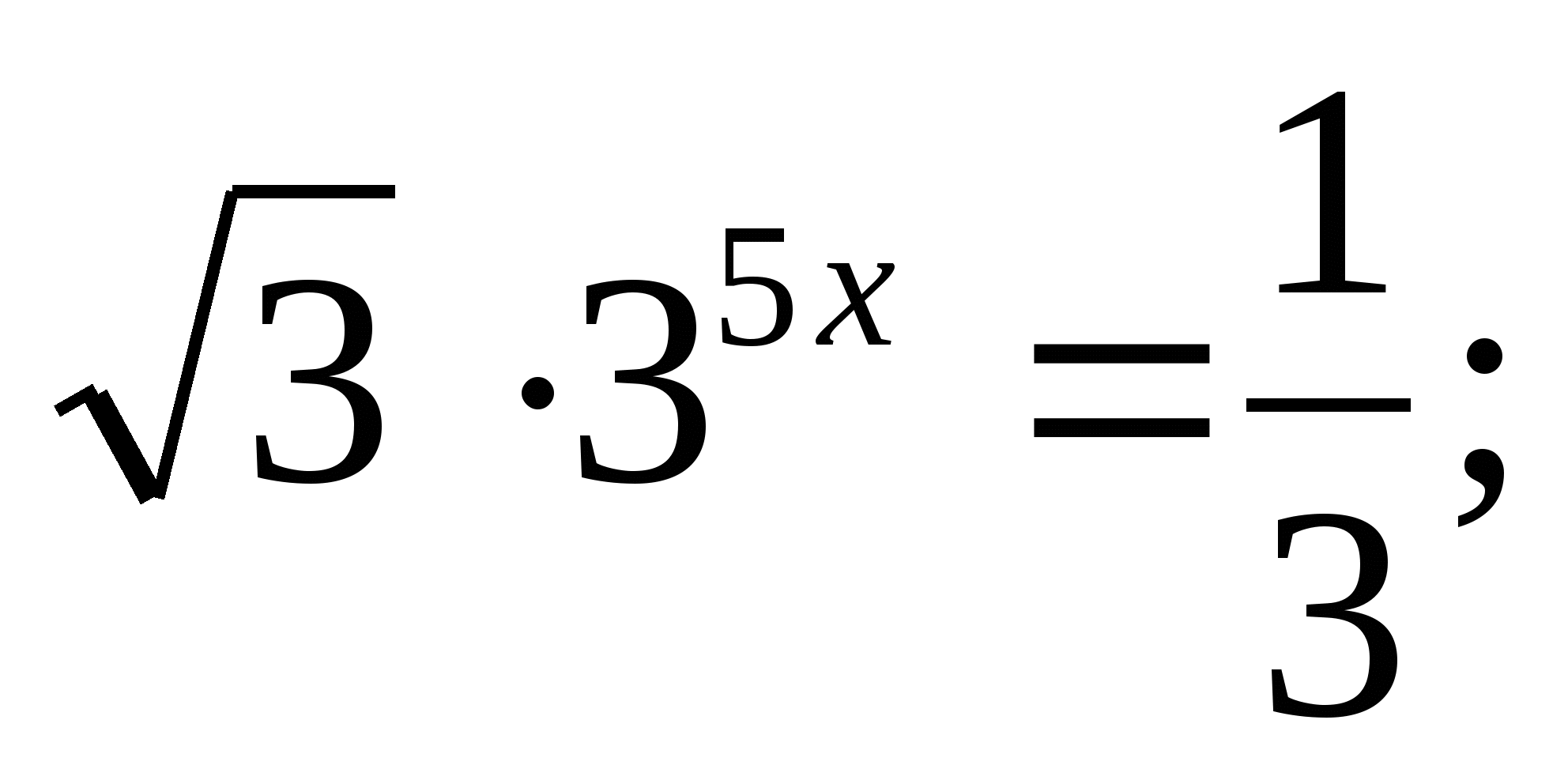 б)
б) 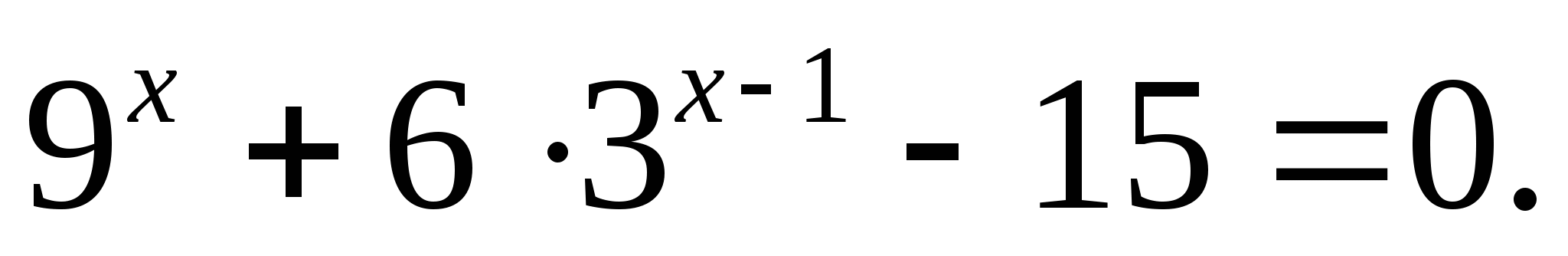
Решите неравенство: 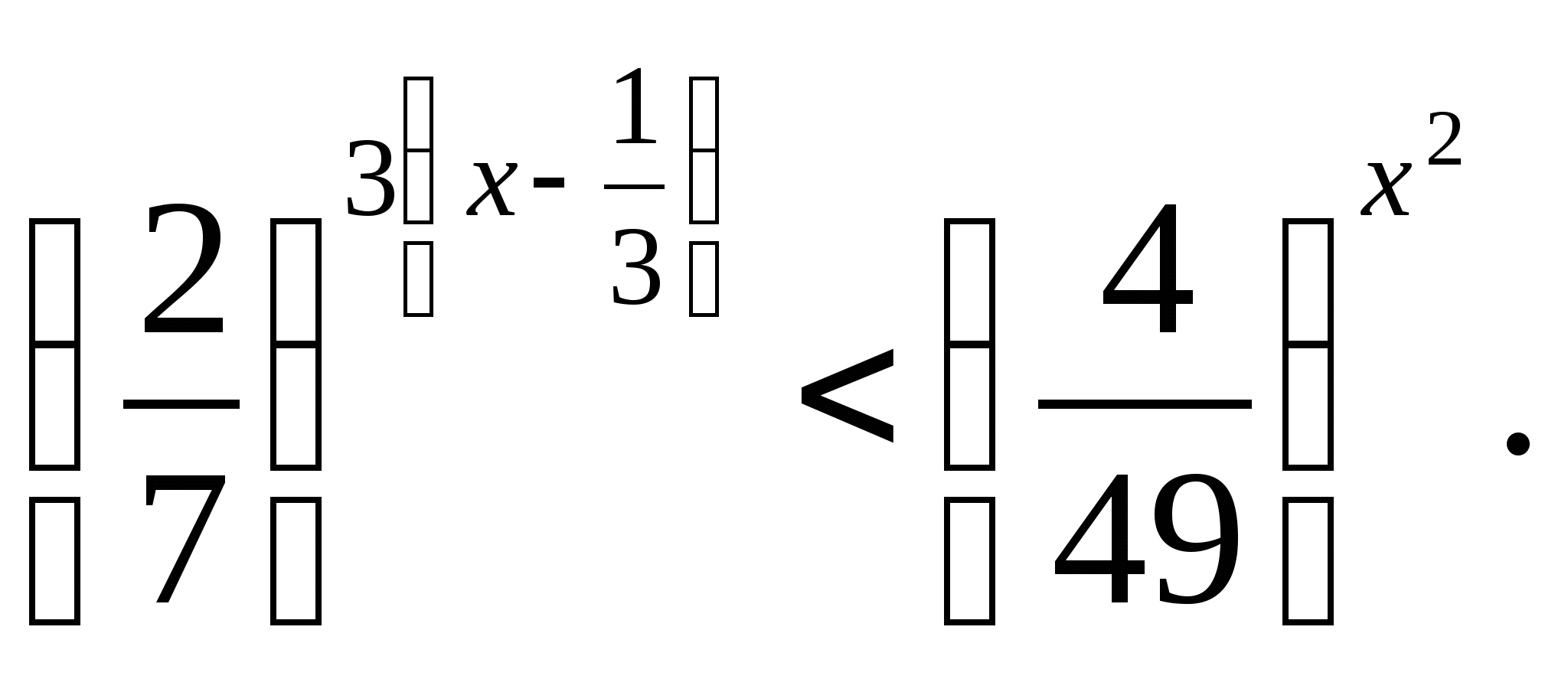
Составьте уравнение касательной к графику функции 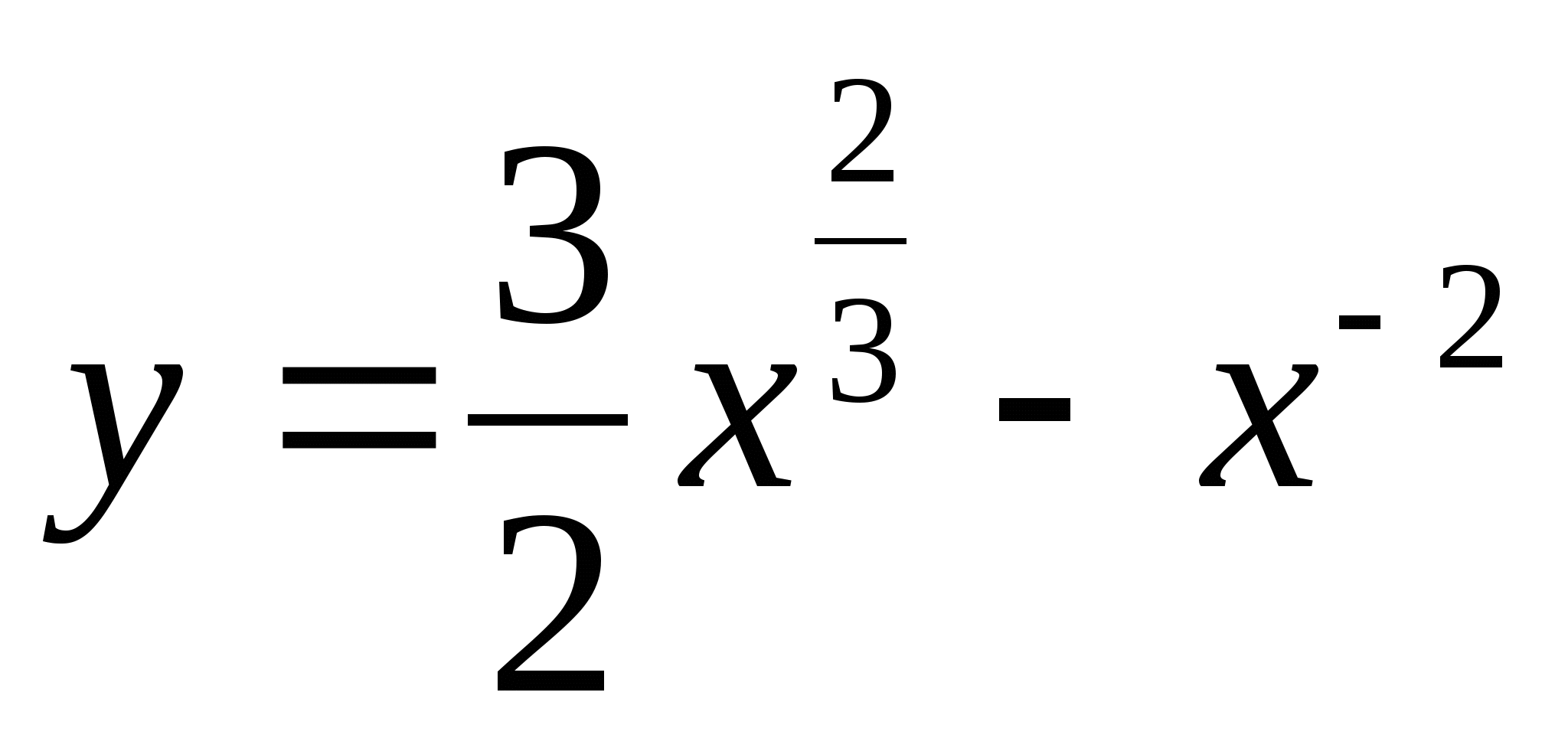 в точке х=1.
в точке х=1.
Дана функция 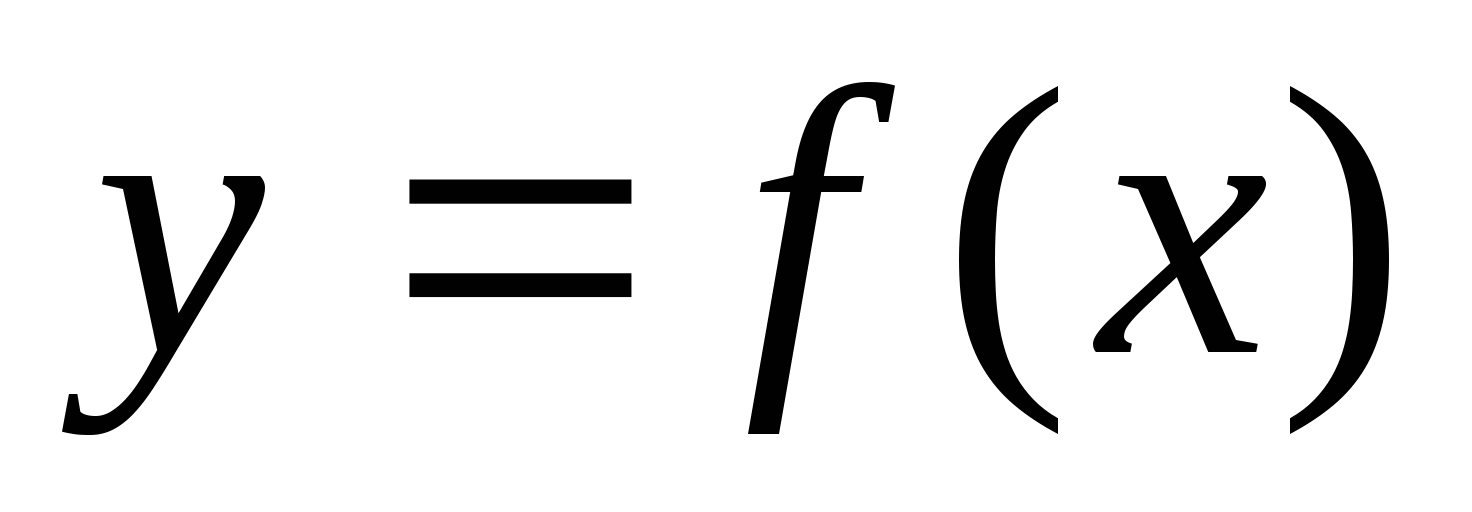 , где
, где 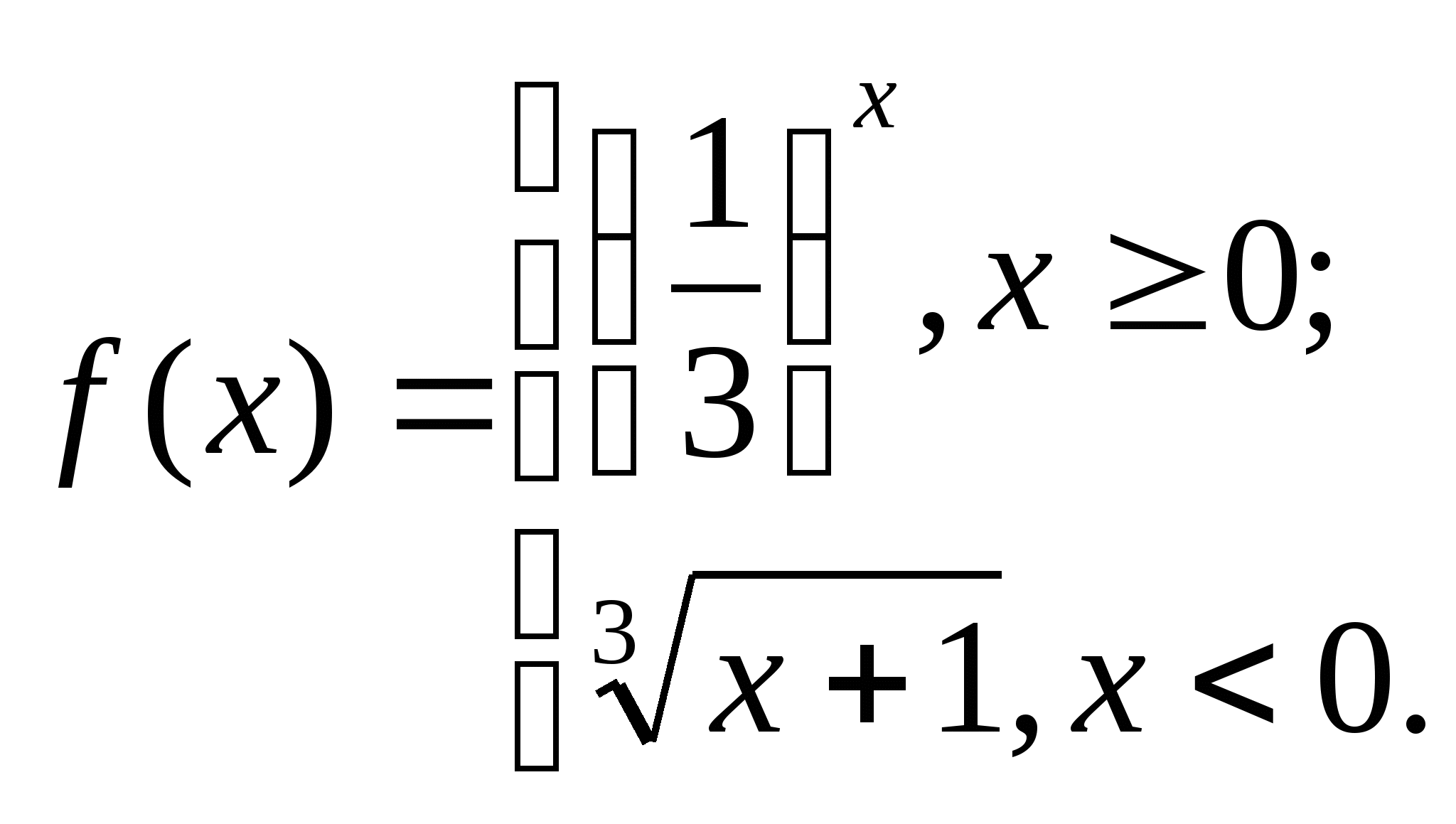
а) Вычислите: f(-1), f (3).
б) Постройте график функции.
в) Найдите область значений функции.
г) Выясните, при каких значениях параметра  уравнение
уравнение 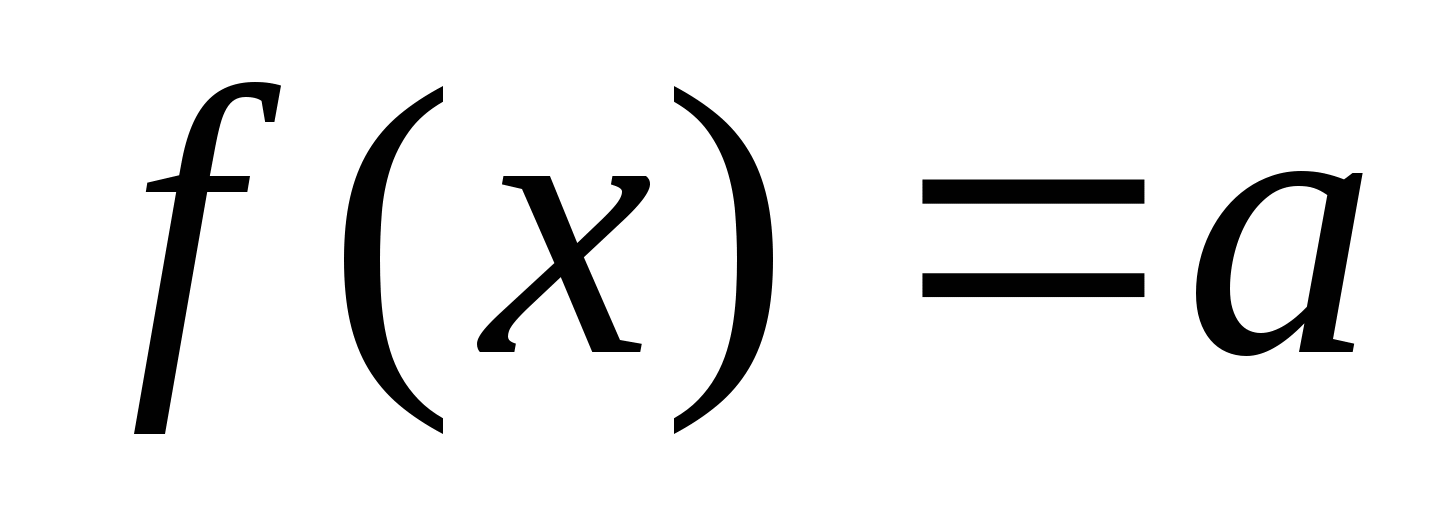 имеет два корня.
имеет два корня.
Контрольная работа №2
Вариант 2
Вычислите:
а) 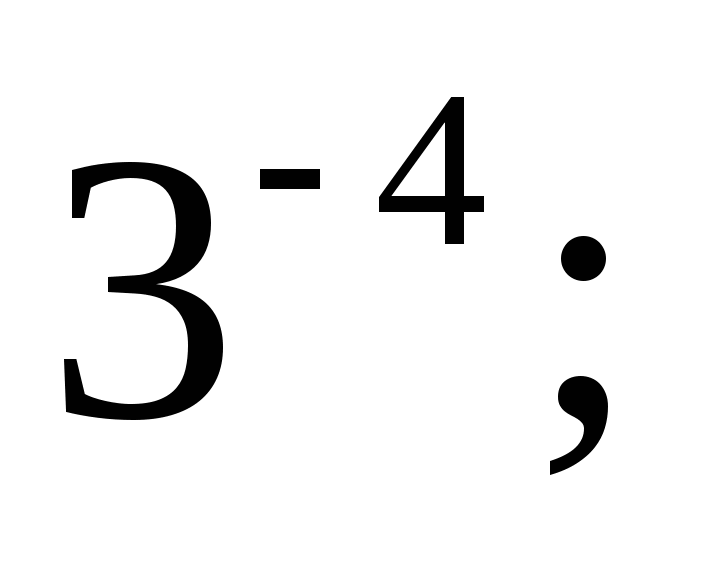 б)
б) 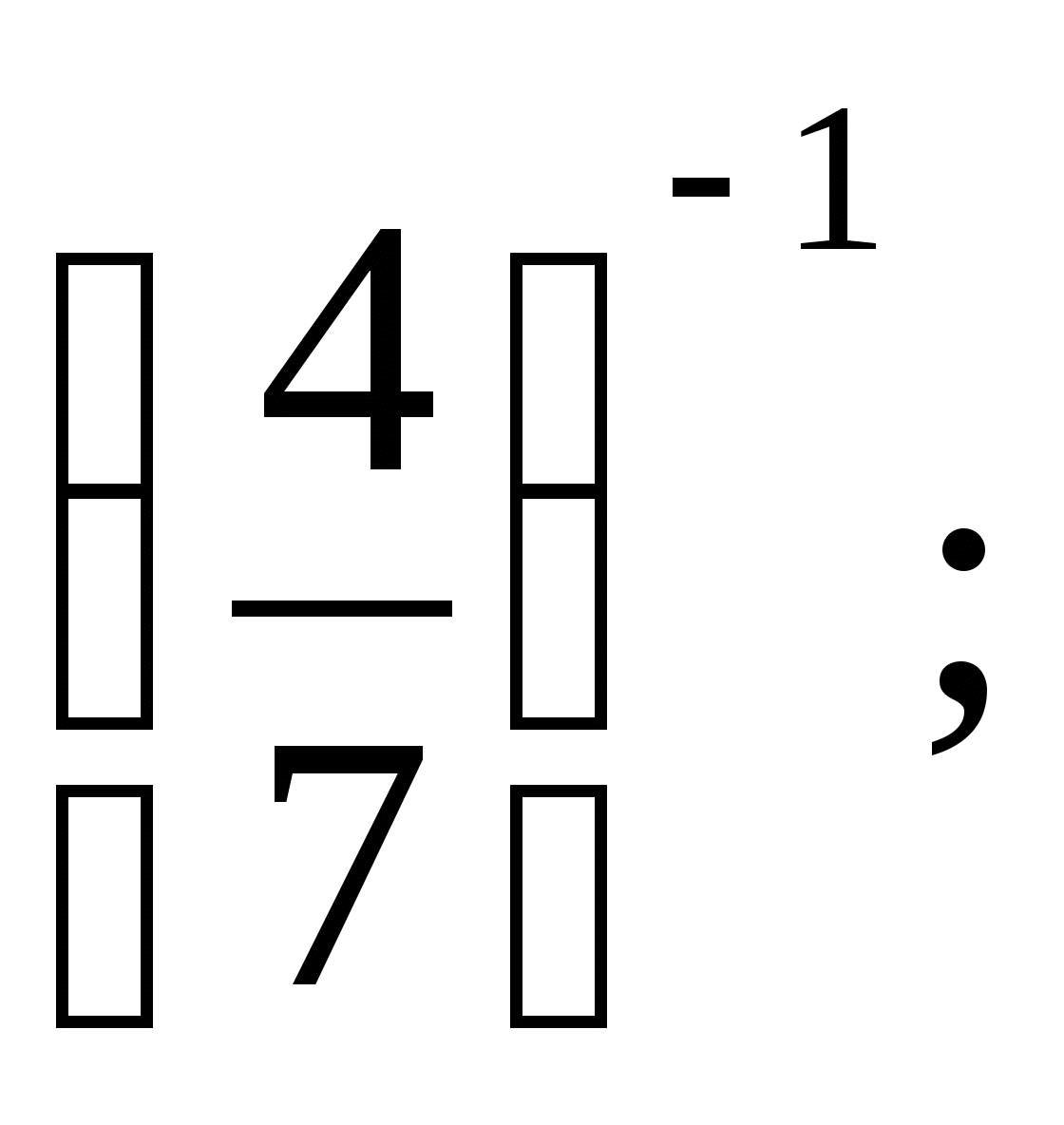 в)
в) 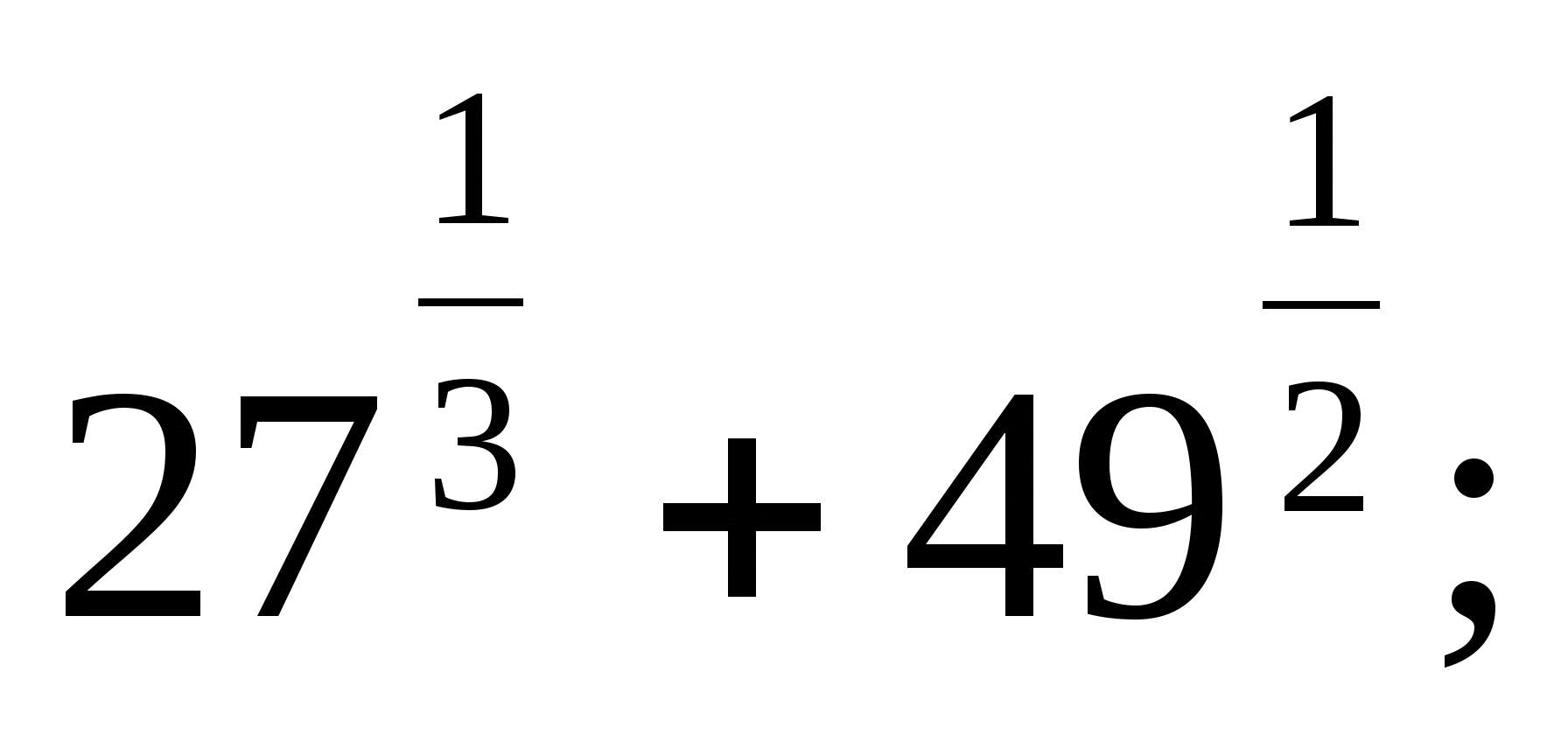 г)
г) 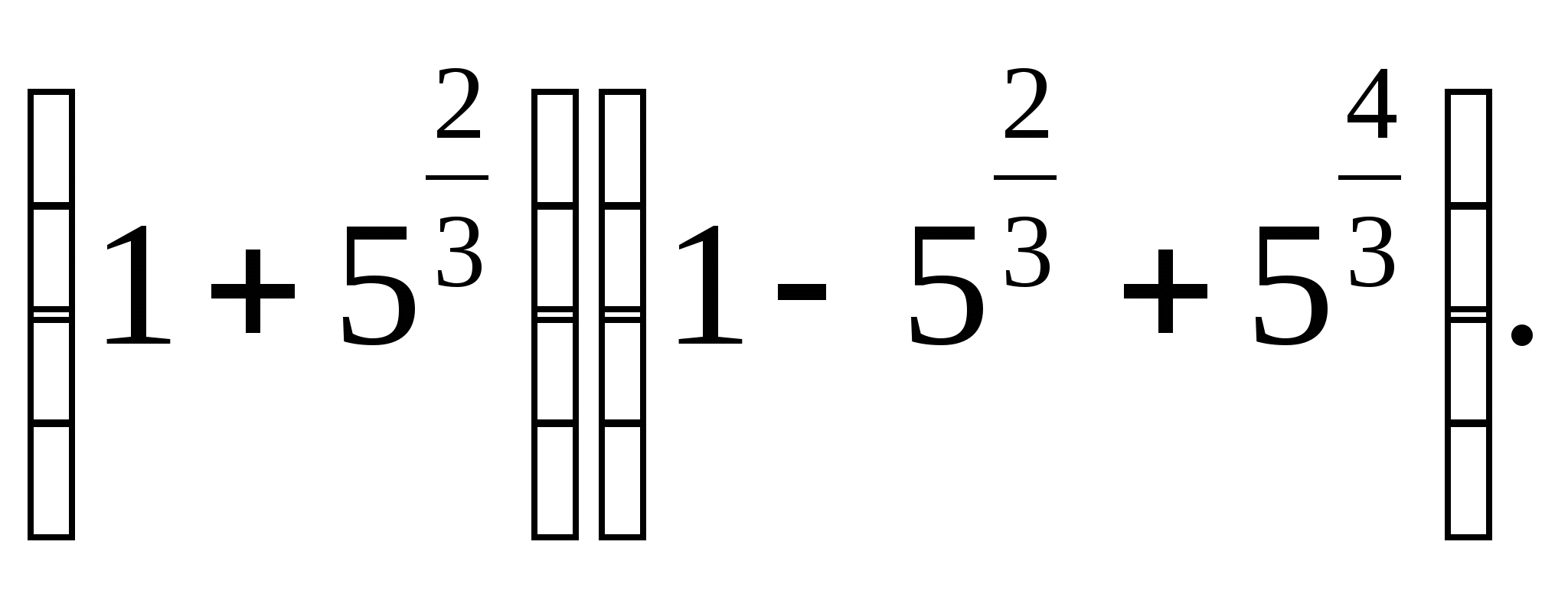
Постройте график функции: а) 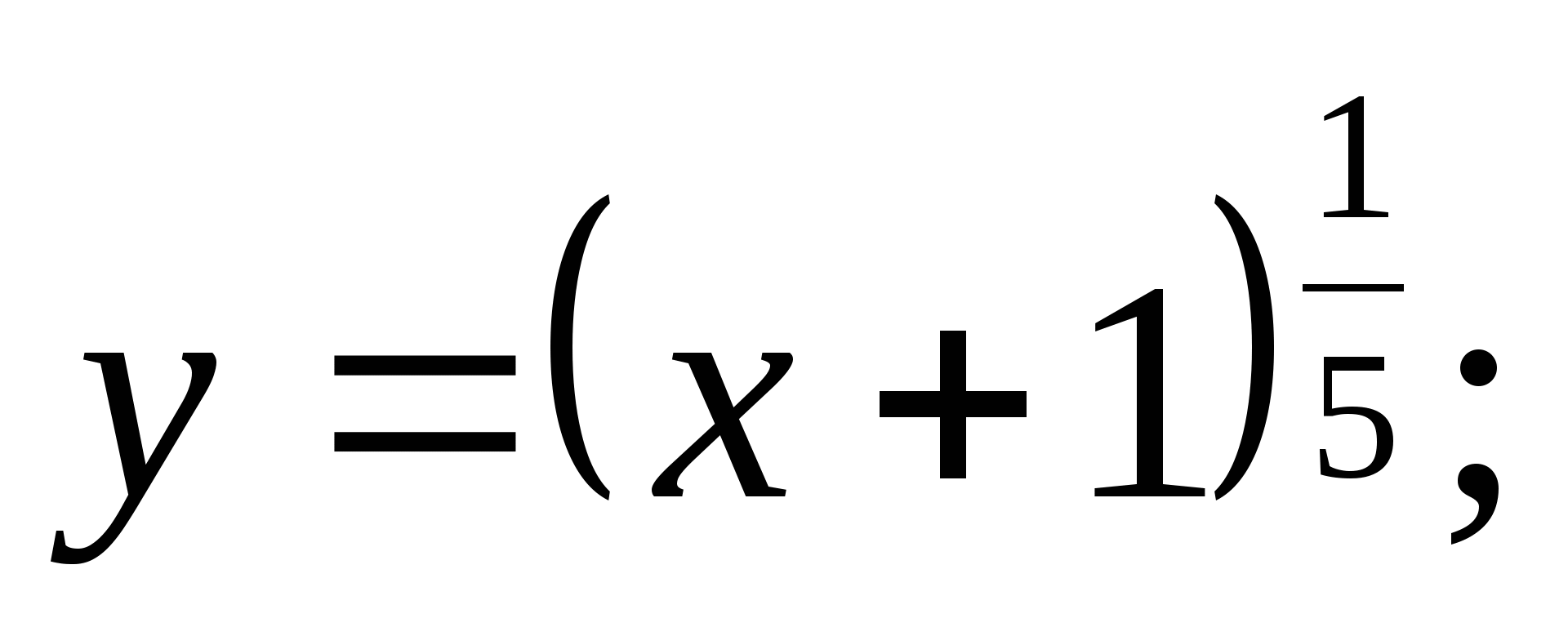 б)
б) 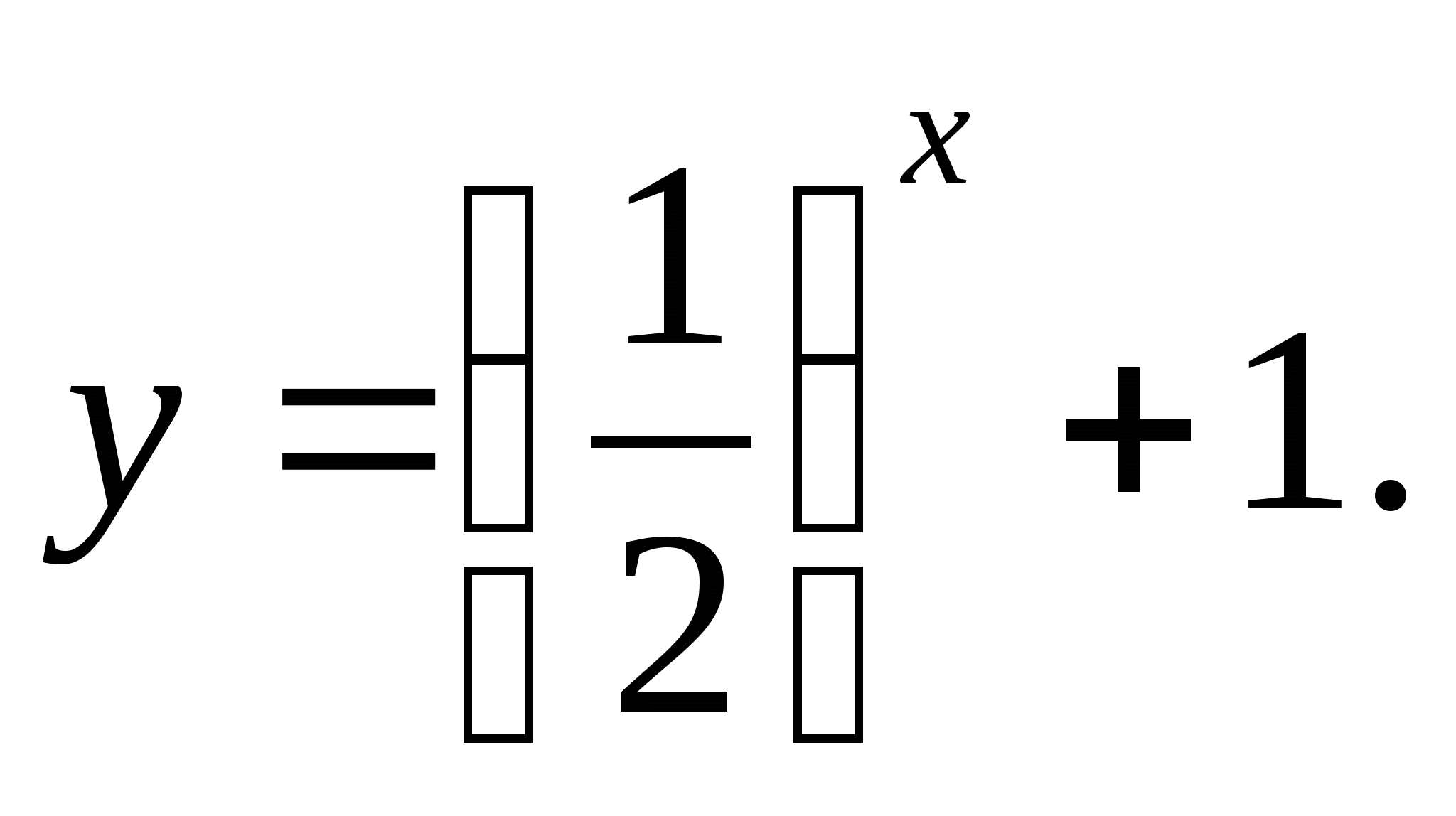
Решите уравнение: а) 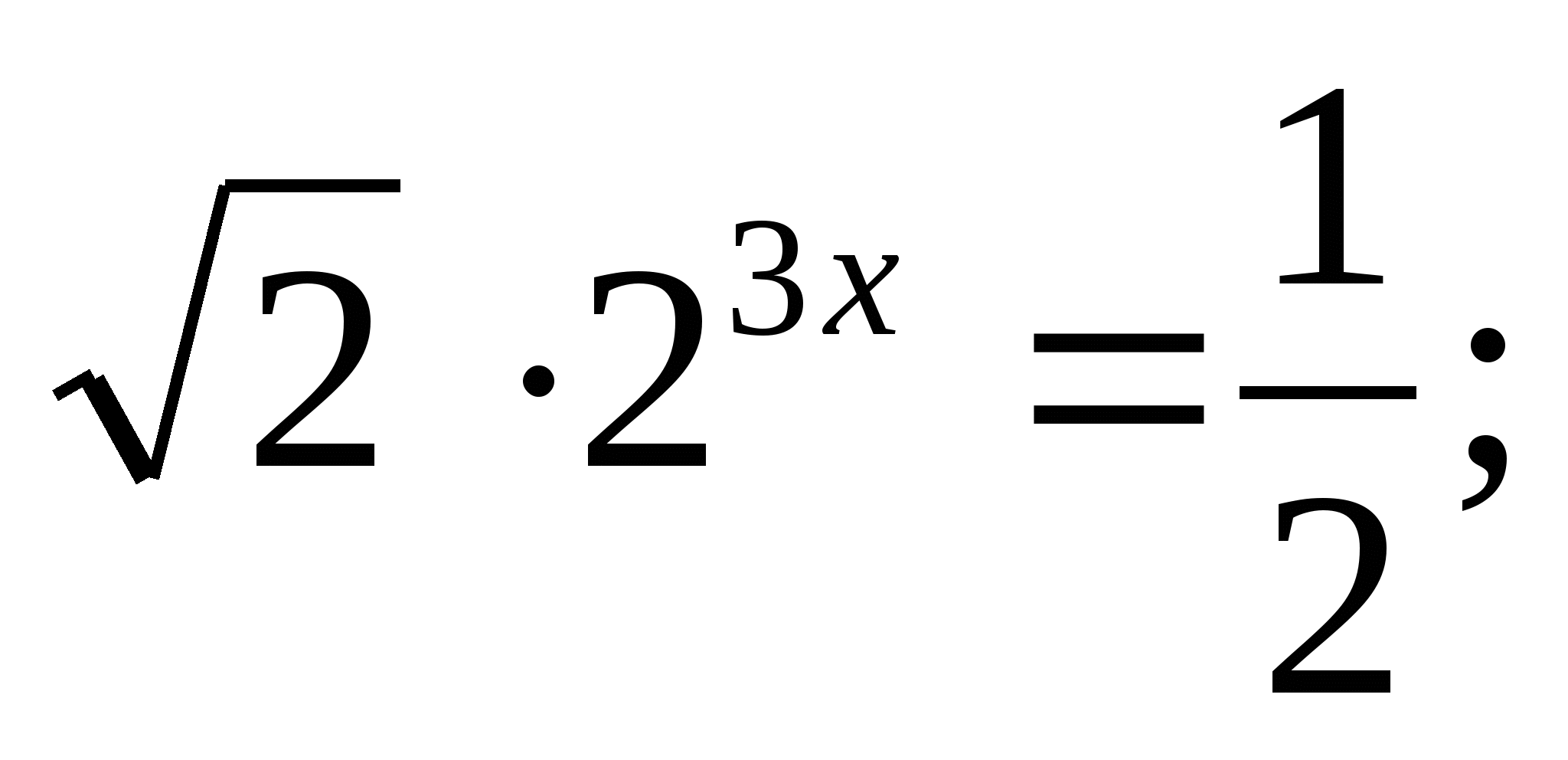 б)
б) 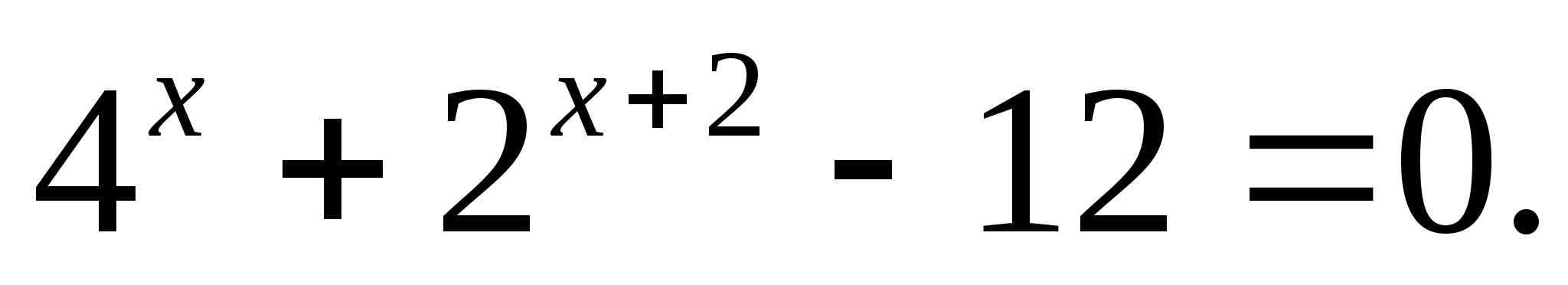
Решите неравенство: 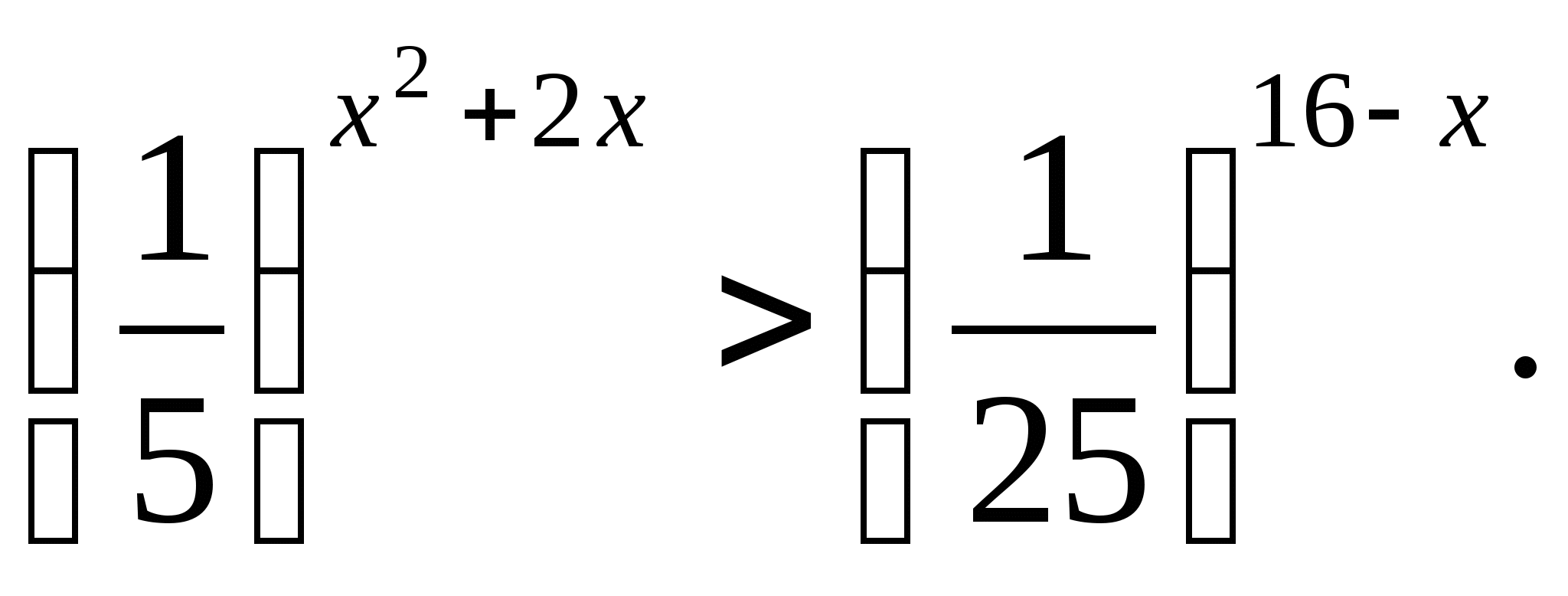
Найдите наибольшее и наименьшее значения функции 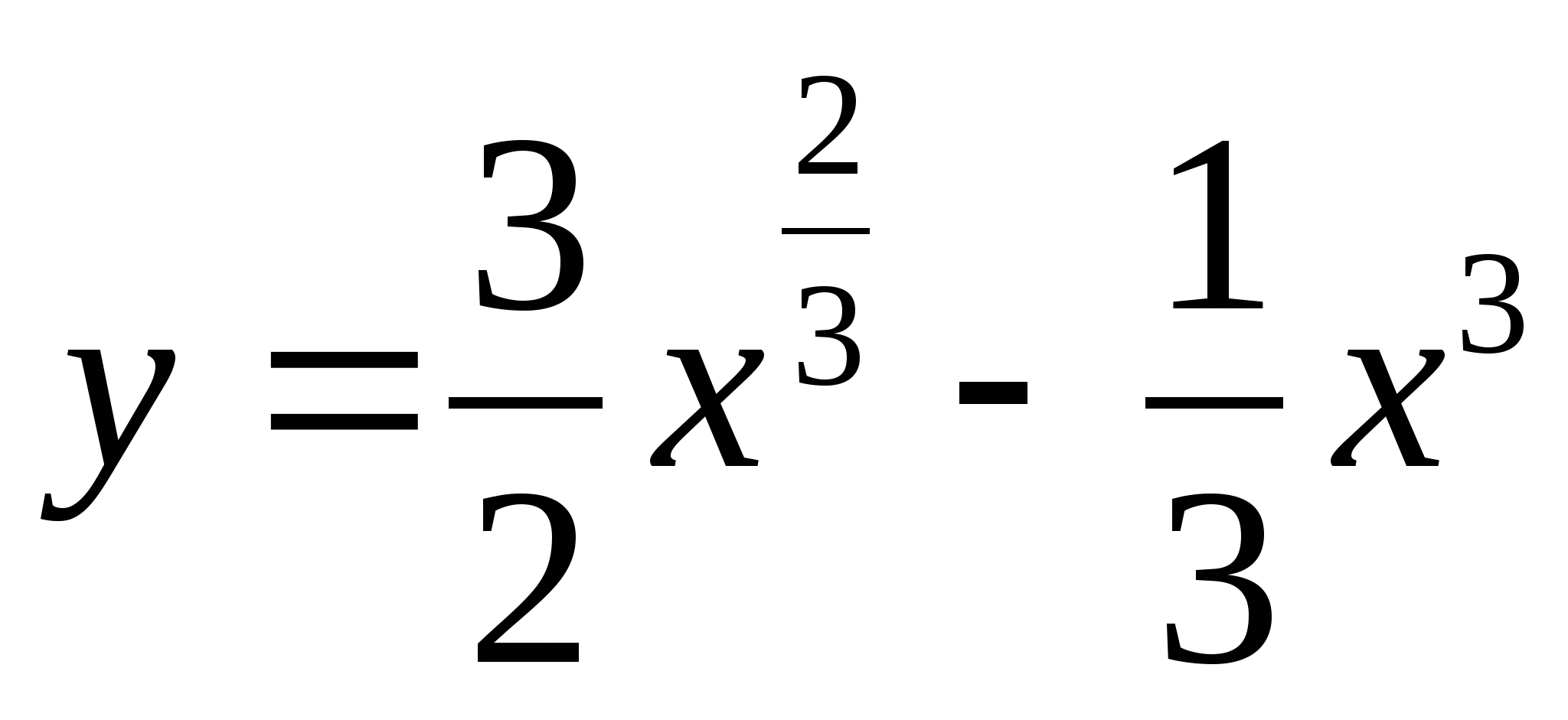 на отрезке [0;8].
на отрезке [0;8].
Дана функция 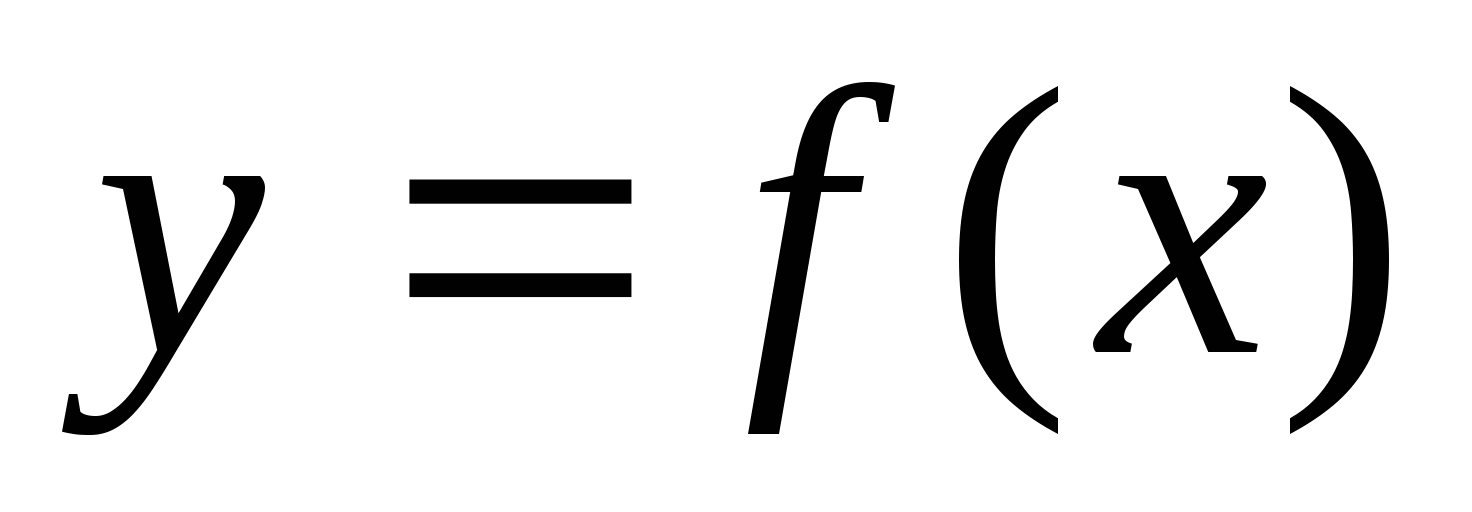 , где
, где 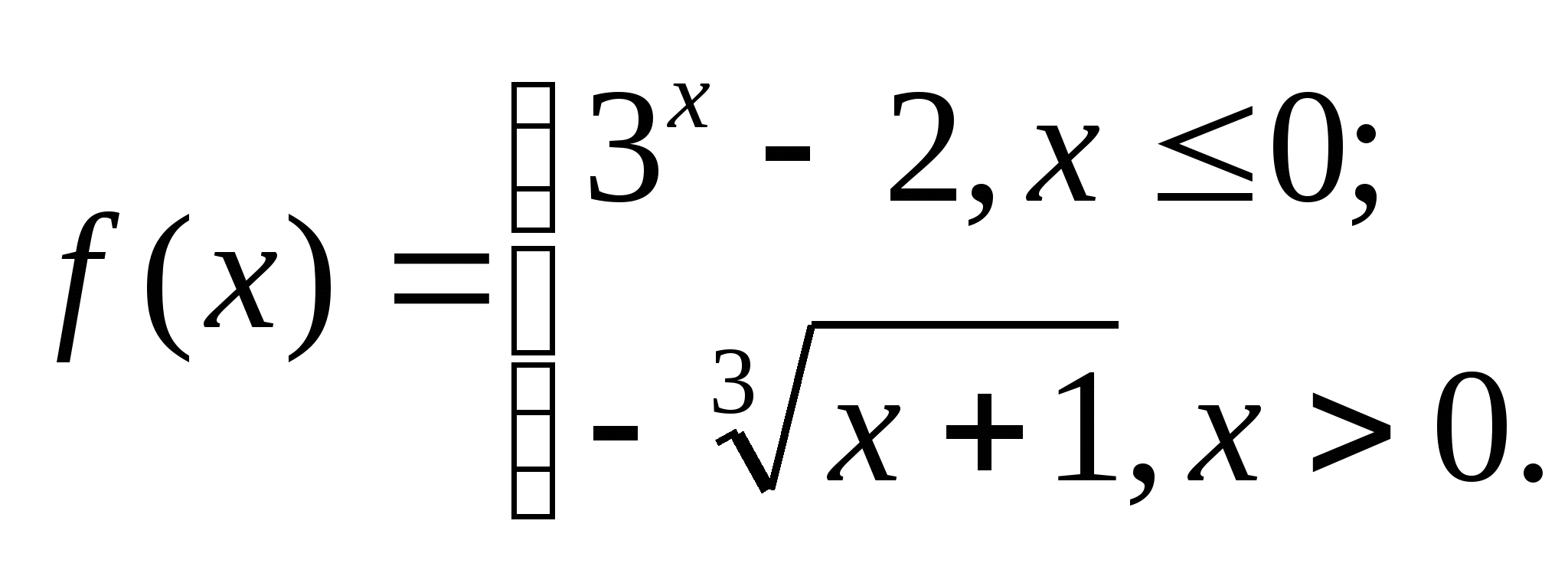 а) Вычислите: f(-2), f (7).
а) Вычислите: f(-2), f (7).
б) Постройте график функции.
в) Найдите область значений функции.
г) Выясните, при каких значениях параметра  уравнение
уравнение 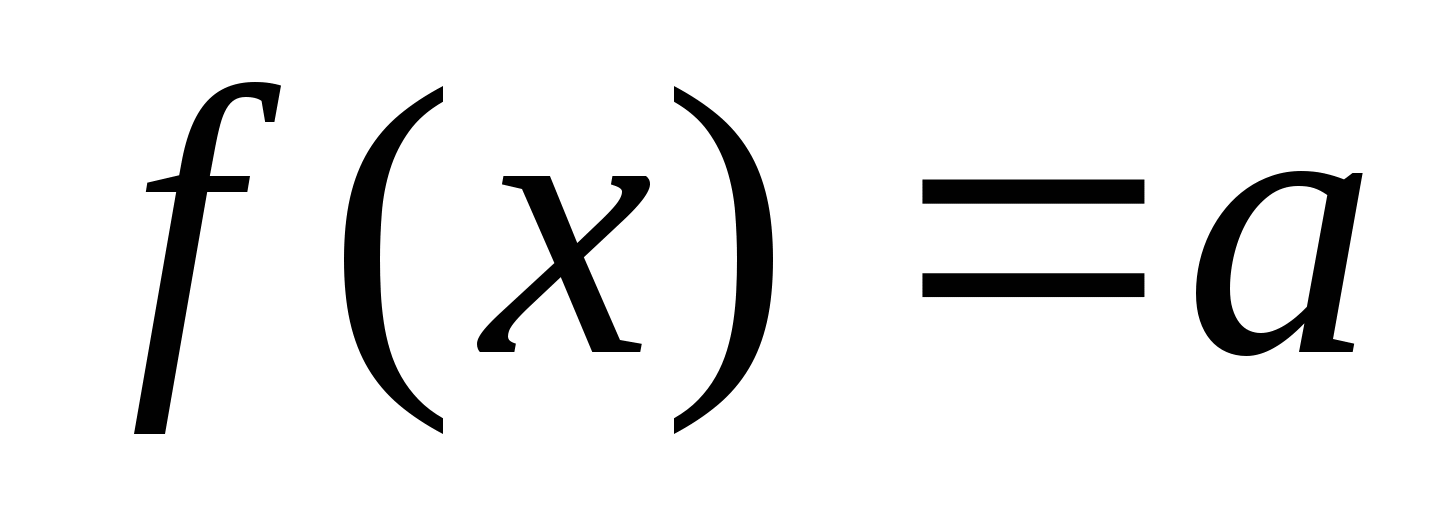 имеет два корня.
имеет два корня.
Контрольная работа №2
Вариант 3
Вычислите:
а) 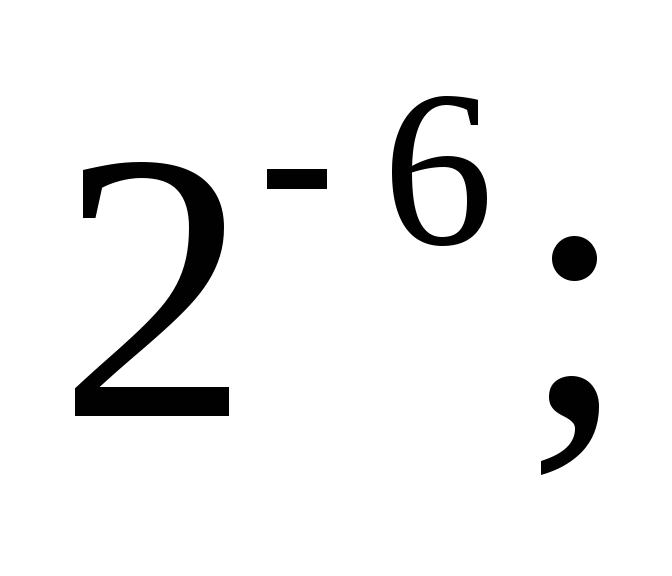 б)
б) 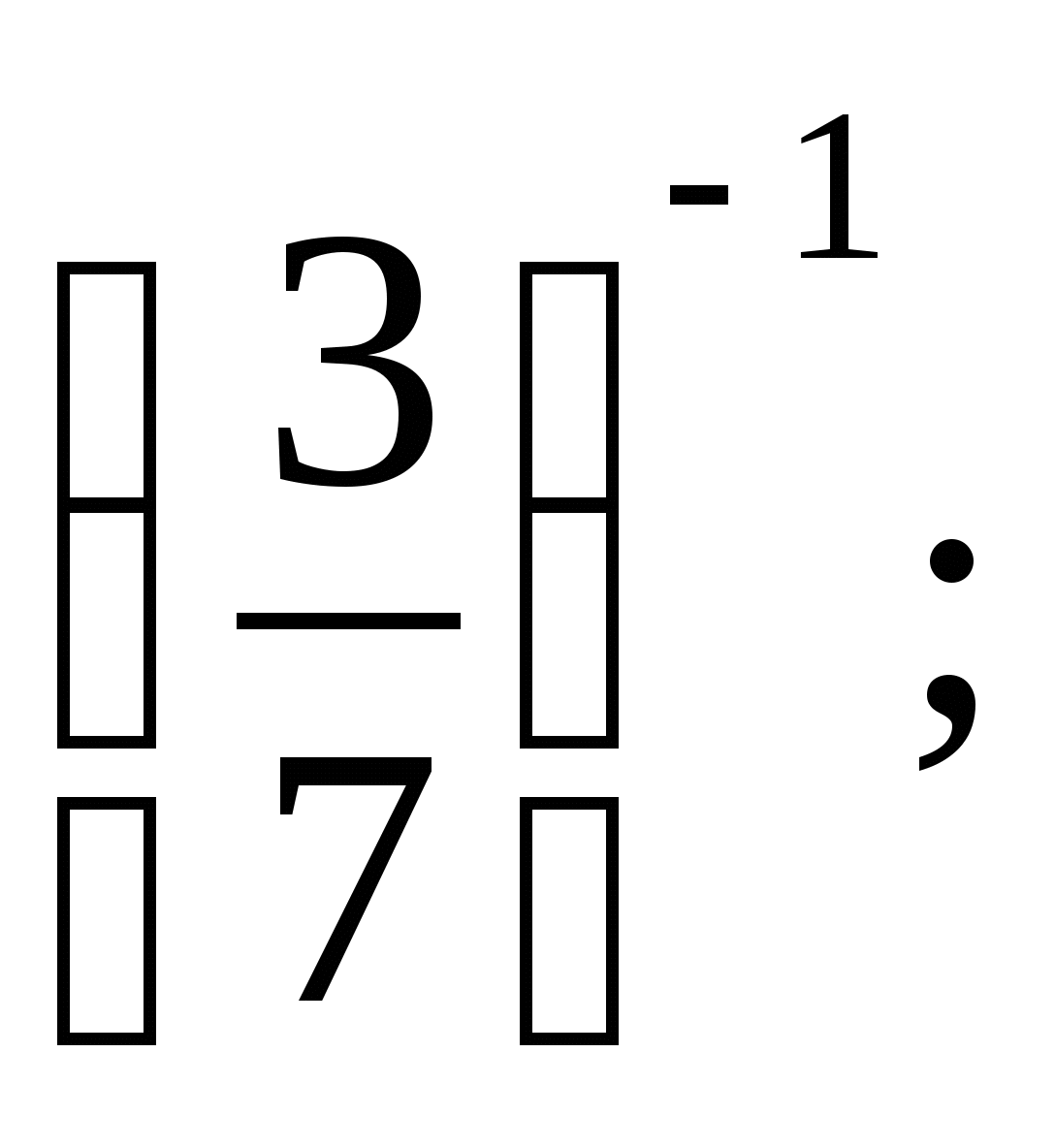 в)
в) 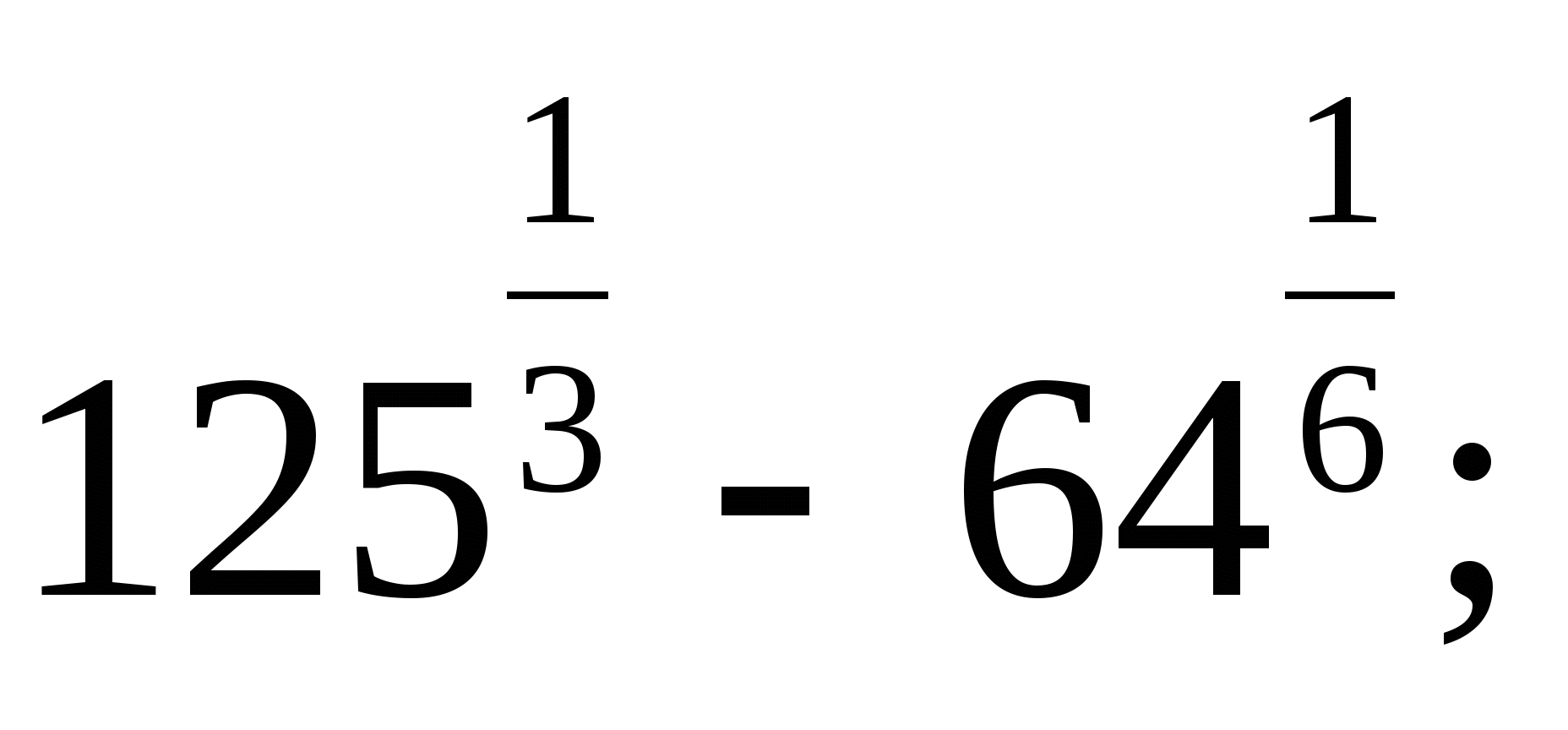 г)
г) 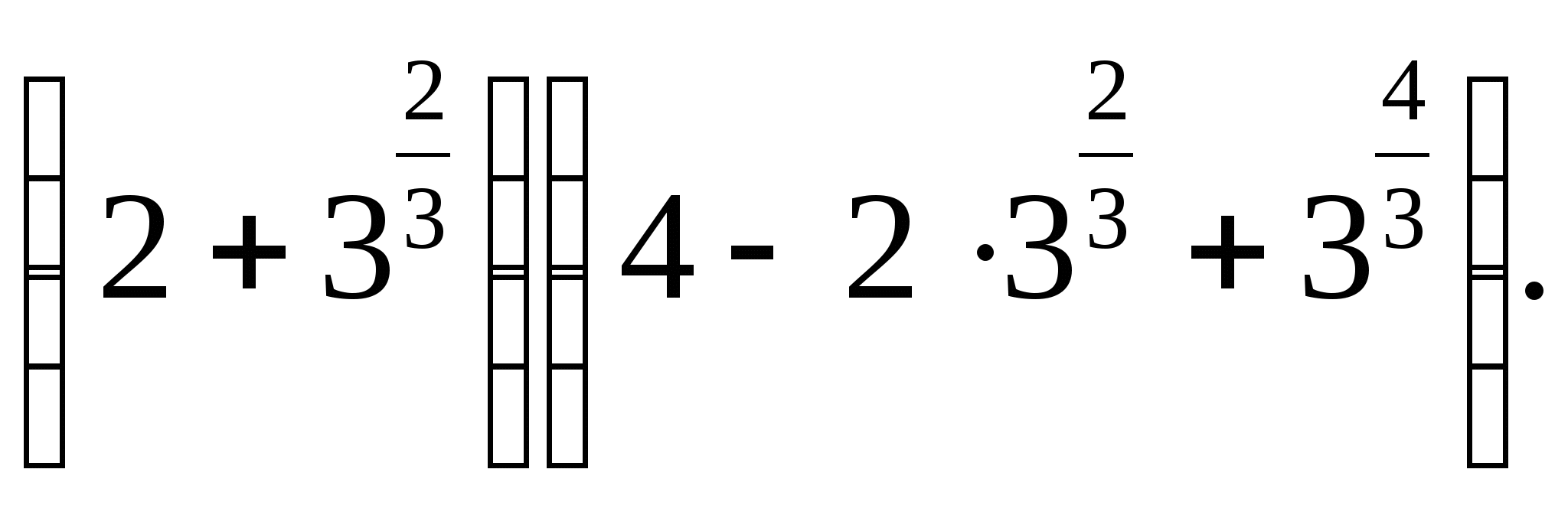
Постройте график функции: а) 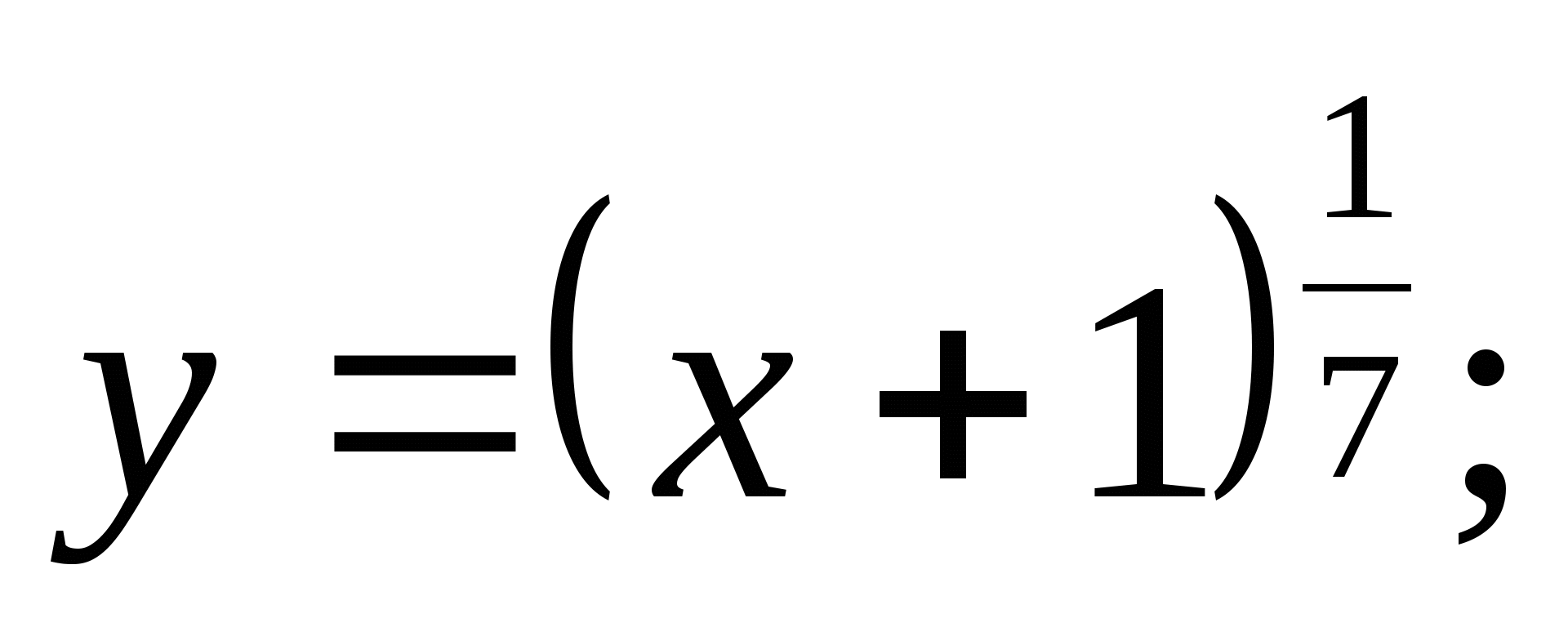 б)
б) 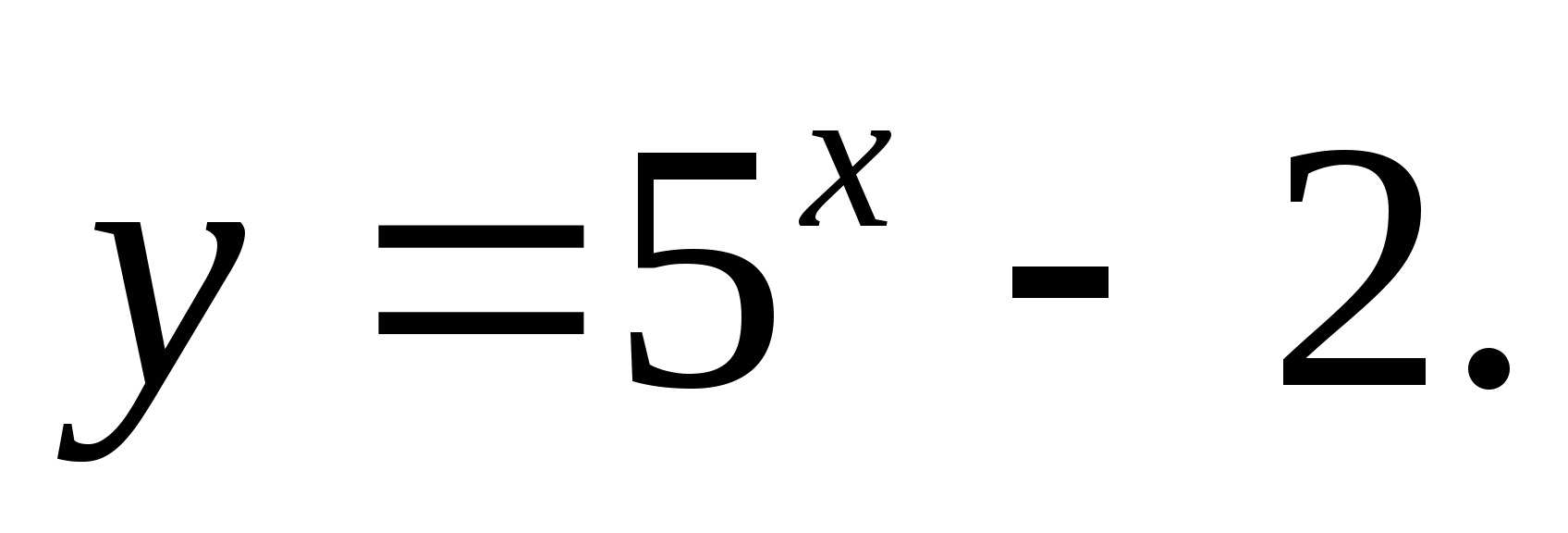
Решите уравнение: а) 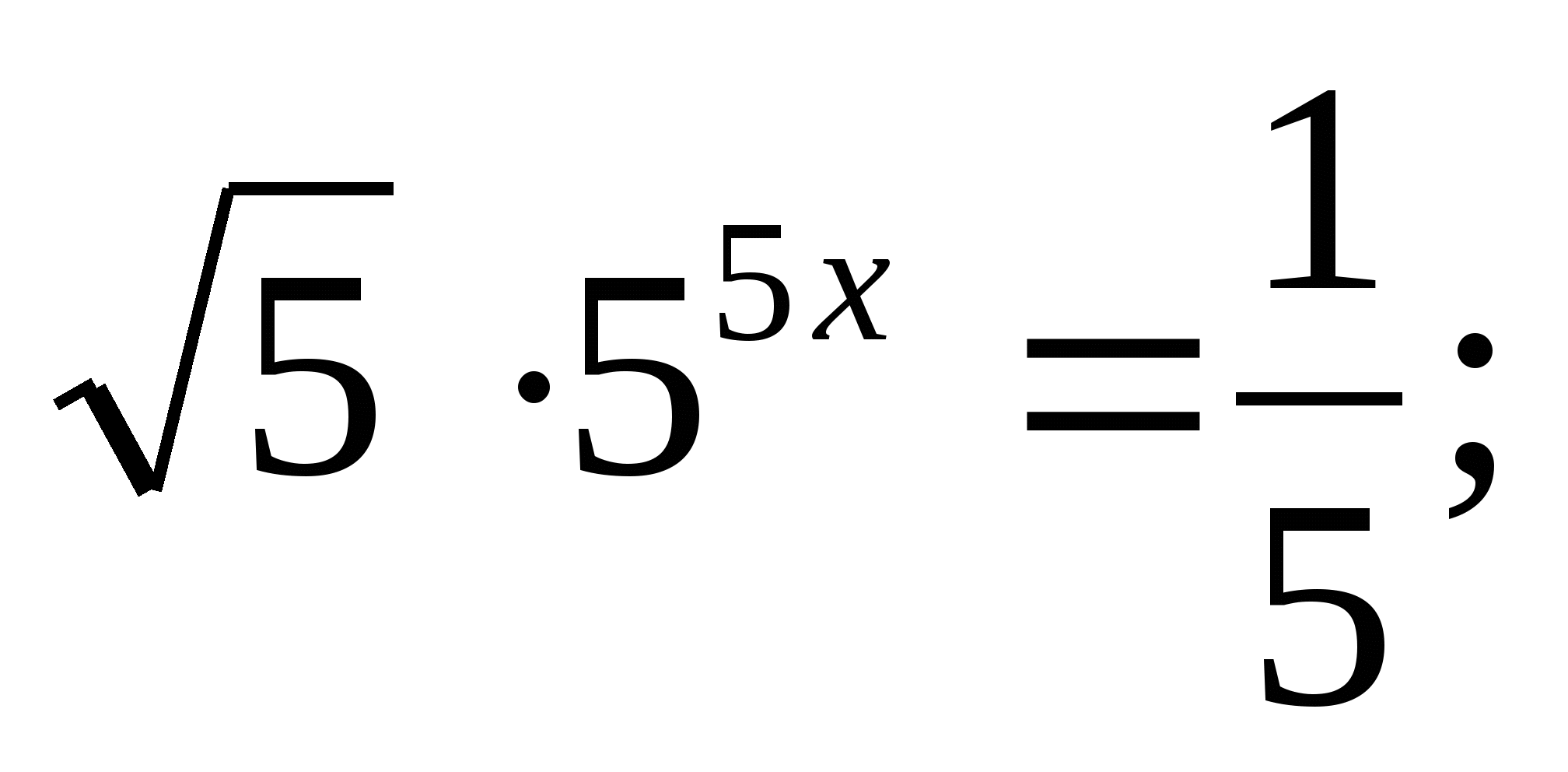 б)
б) 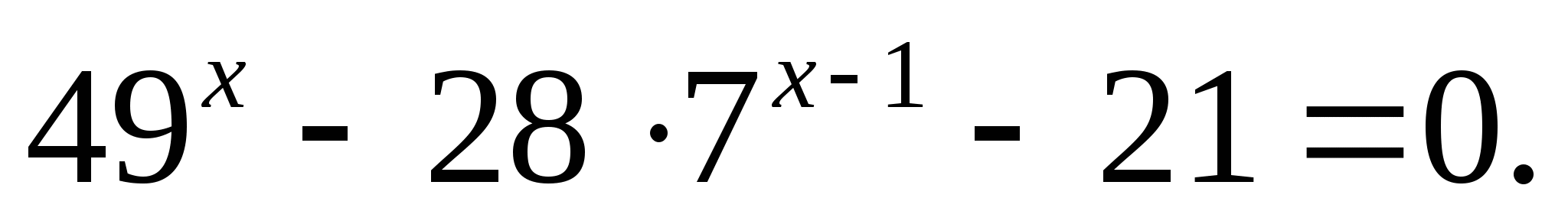
Решите неравенство: 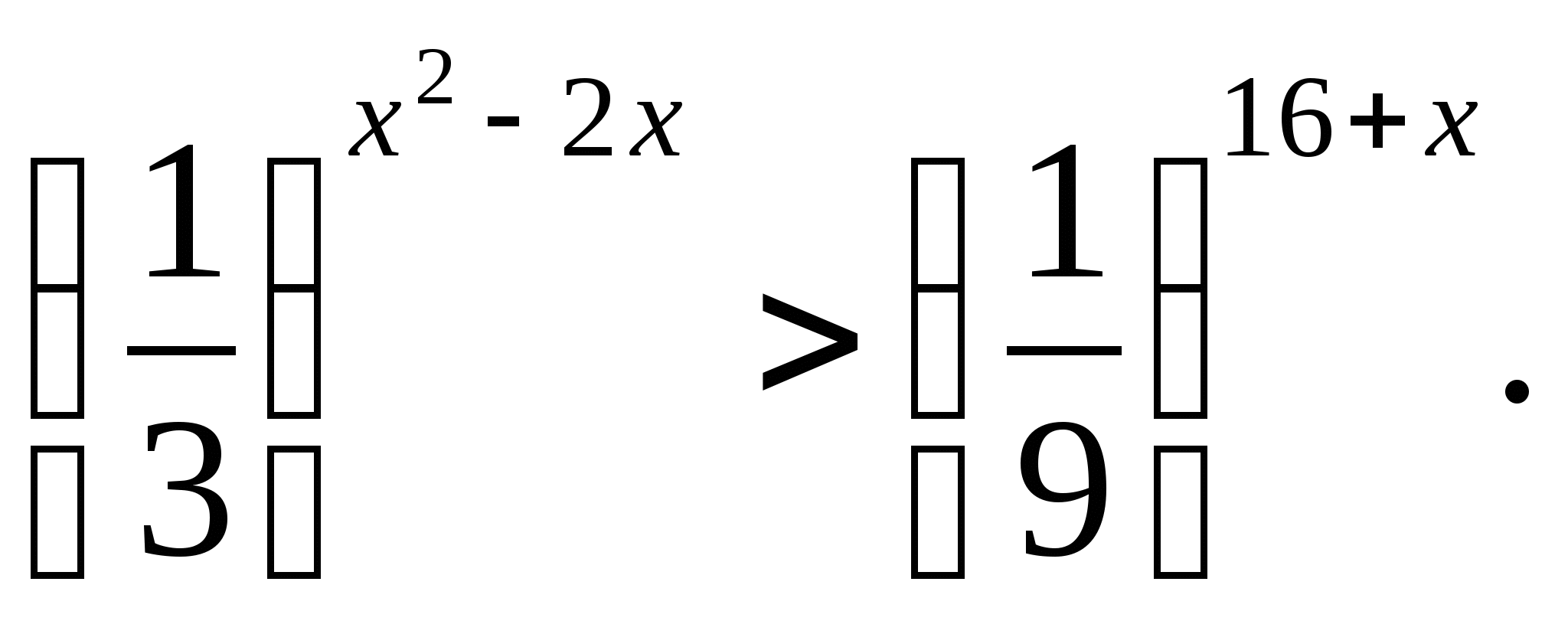
Составьте уравнение касательной к графику функции 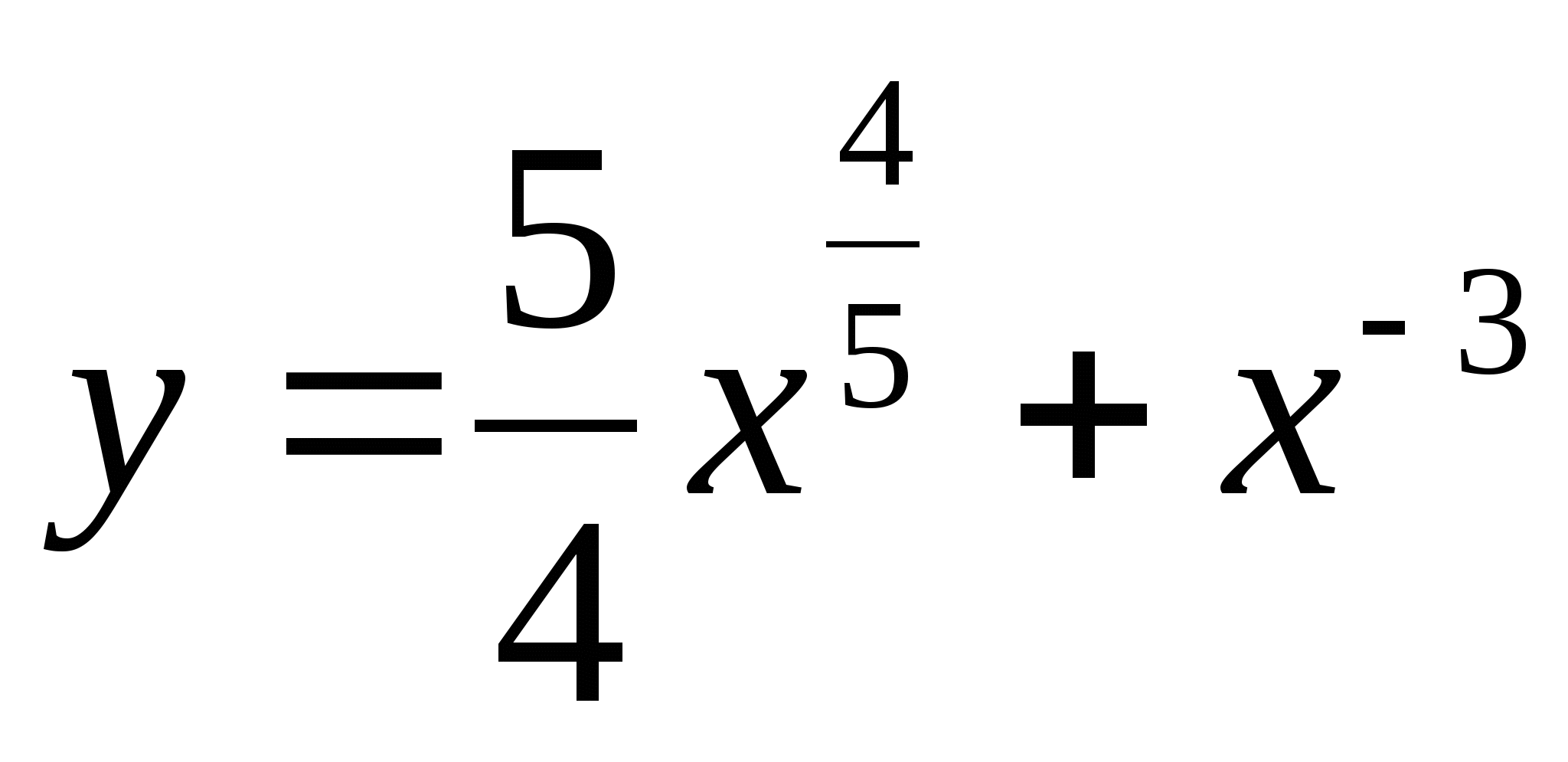 в точке х=1.
в точке х=1.
Дана функция 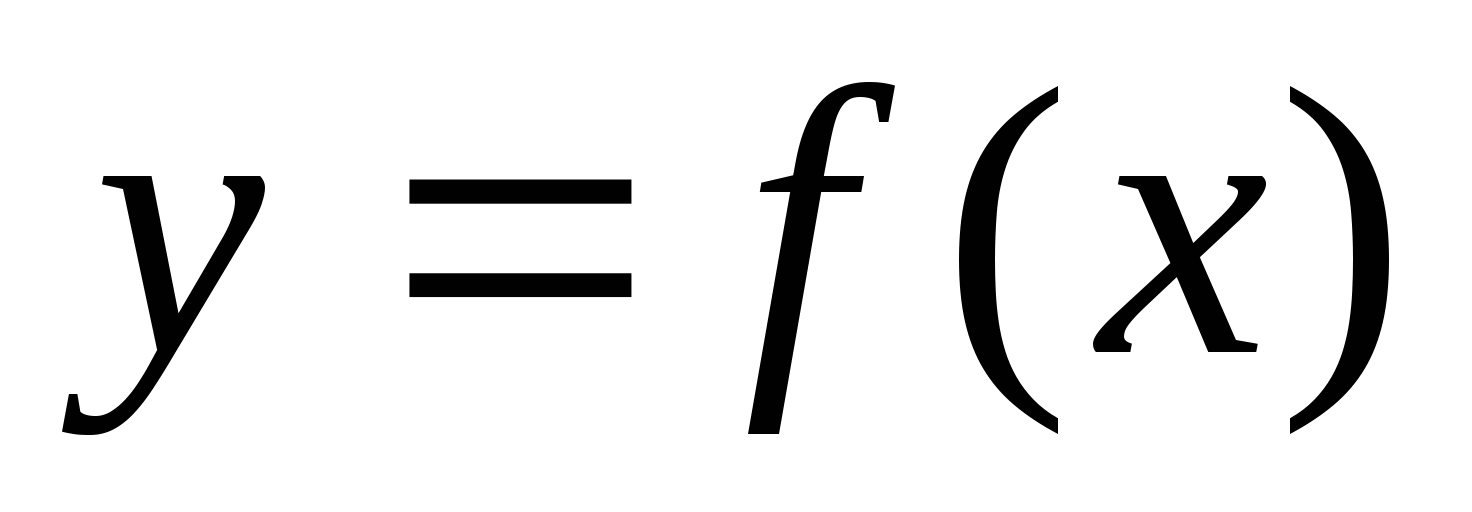 , где
, где 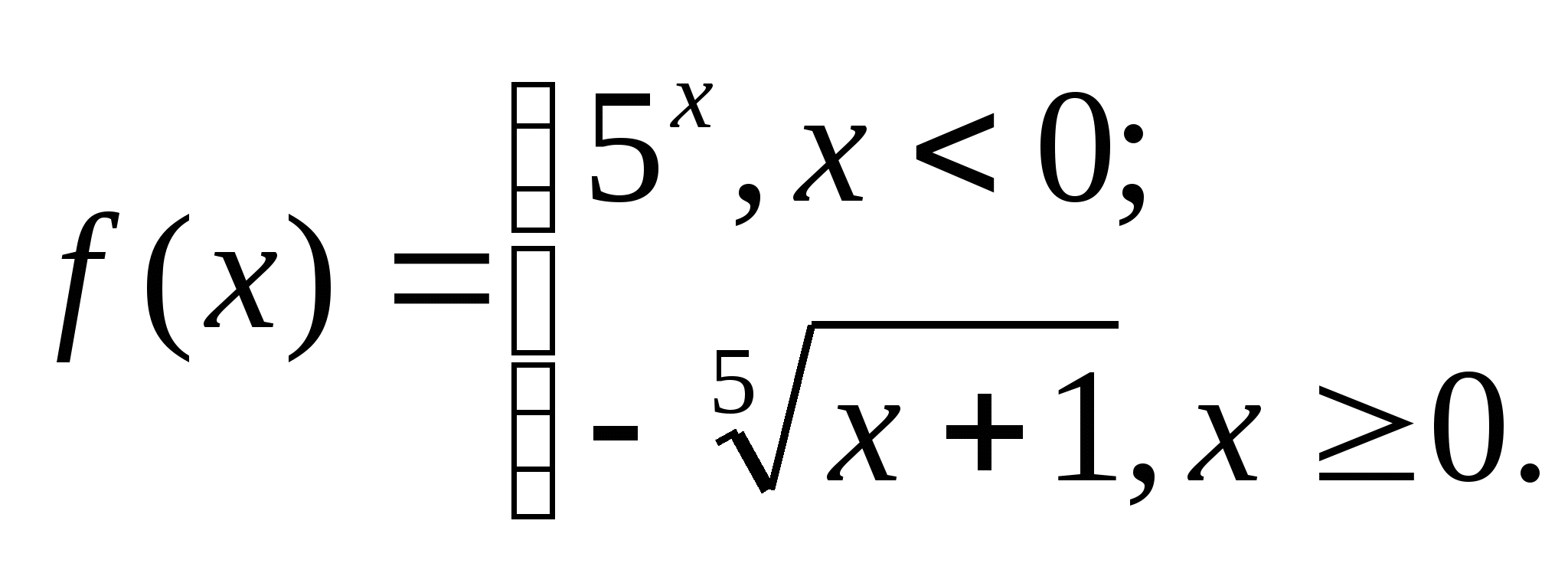
а) Вычислите: f(-4), f (31).
б) Постройте график функции.
в) Найдите область значений функции.
г) Выясните, при каких значениях параметра  уравнение
уравнение 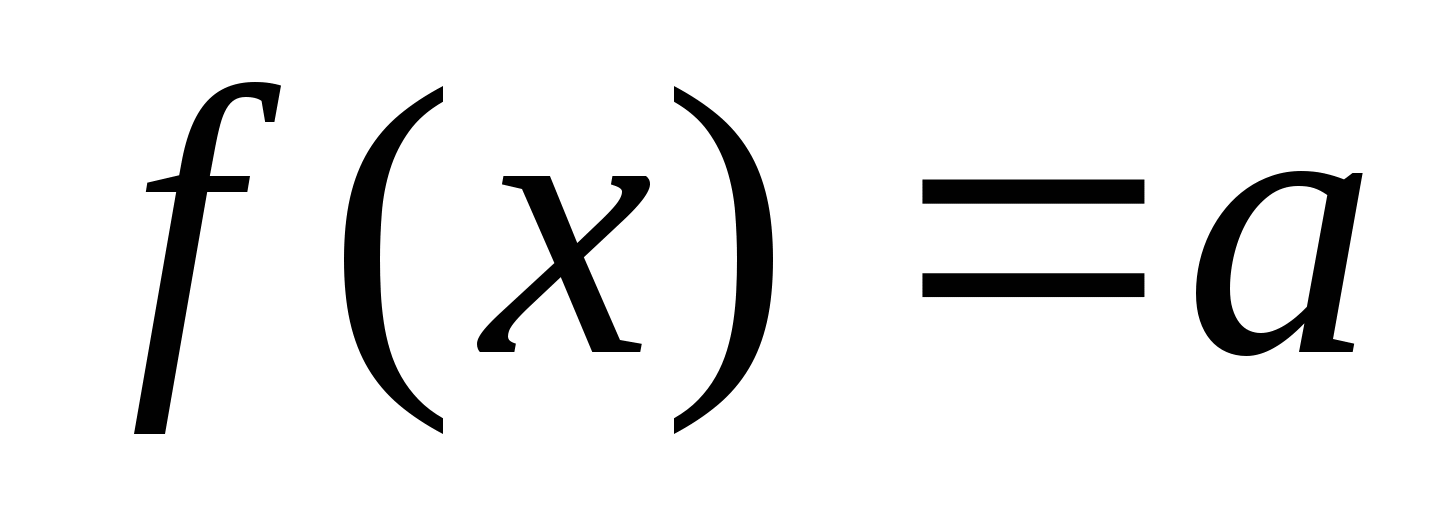 имеет два корня.
имеет два корня.
Контрольная работа №2
Вариант 4
Вычислите:
а) 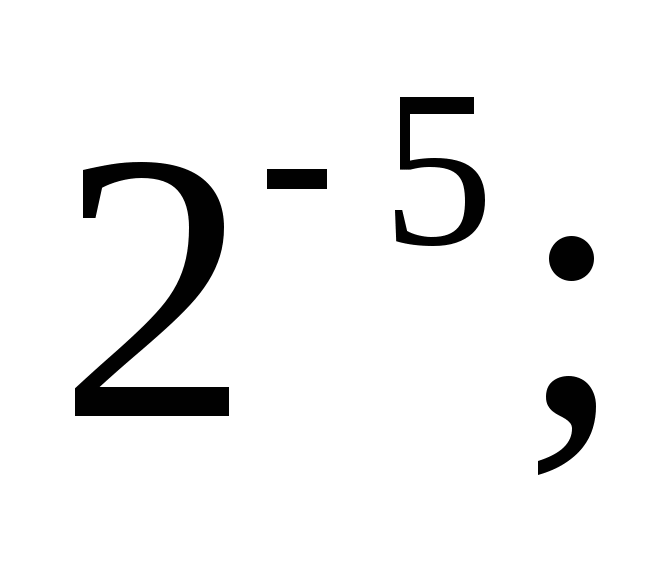 б)
б) 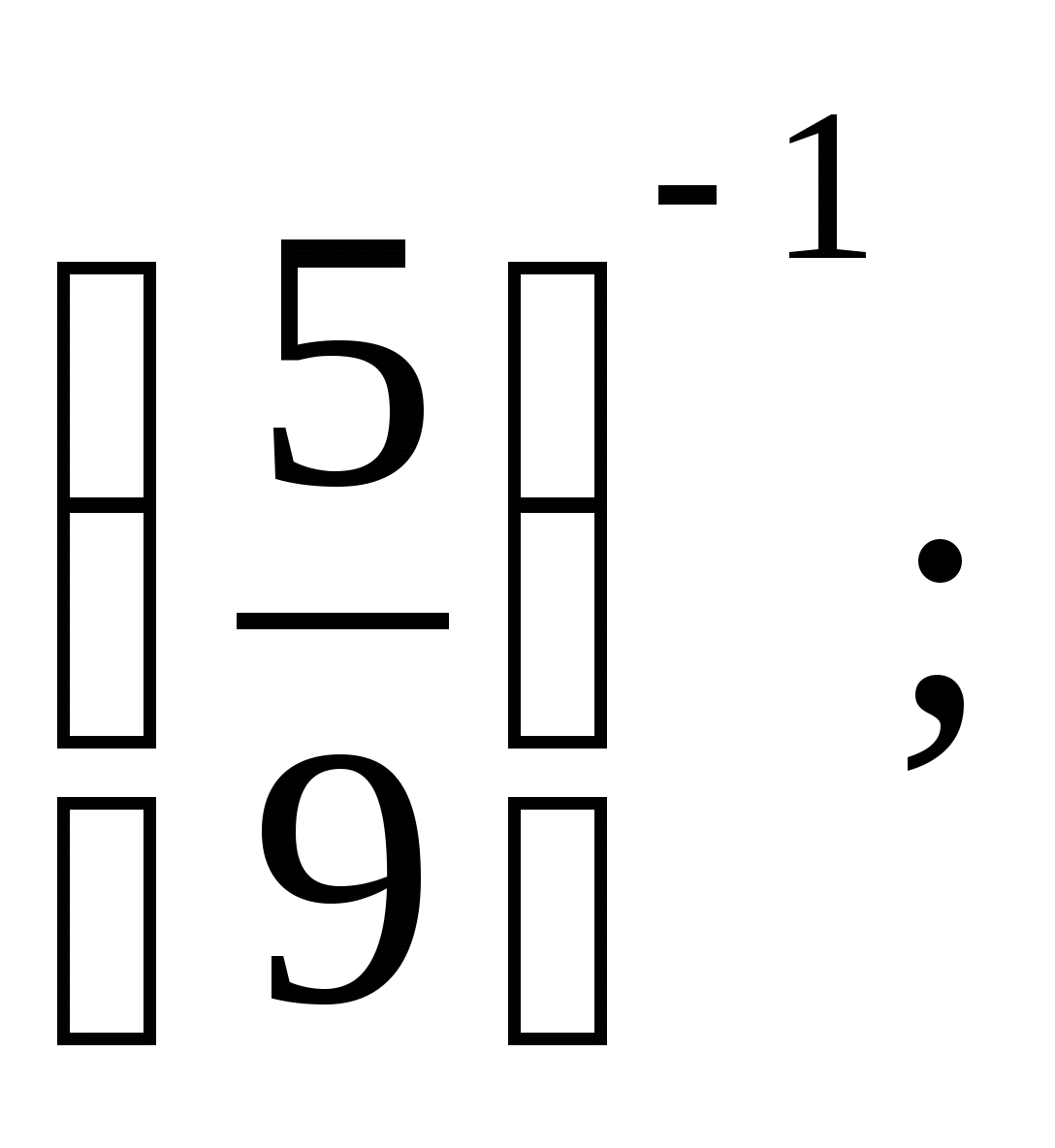 в)
в) 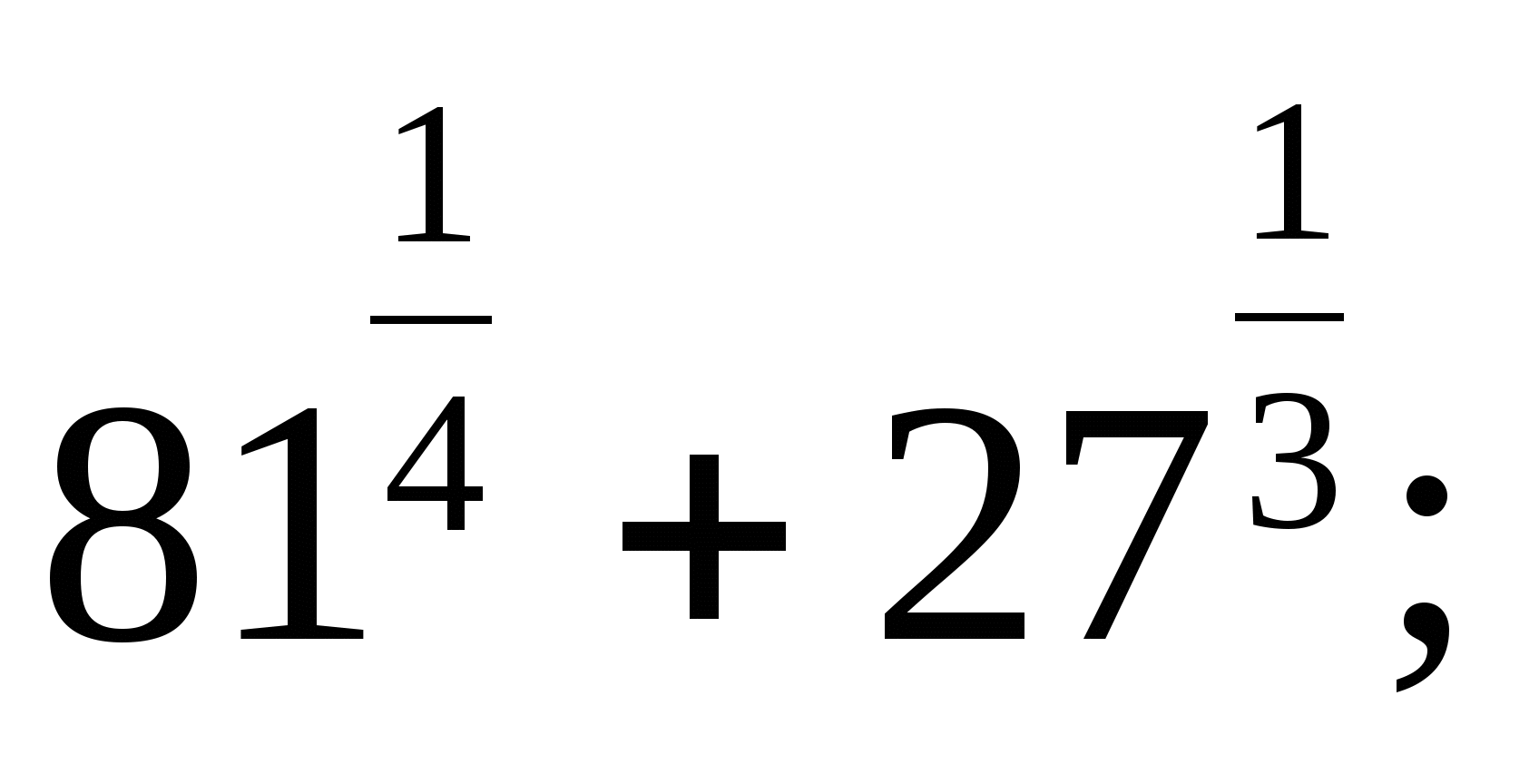 г)
г) 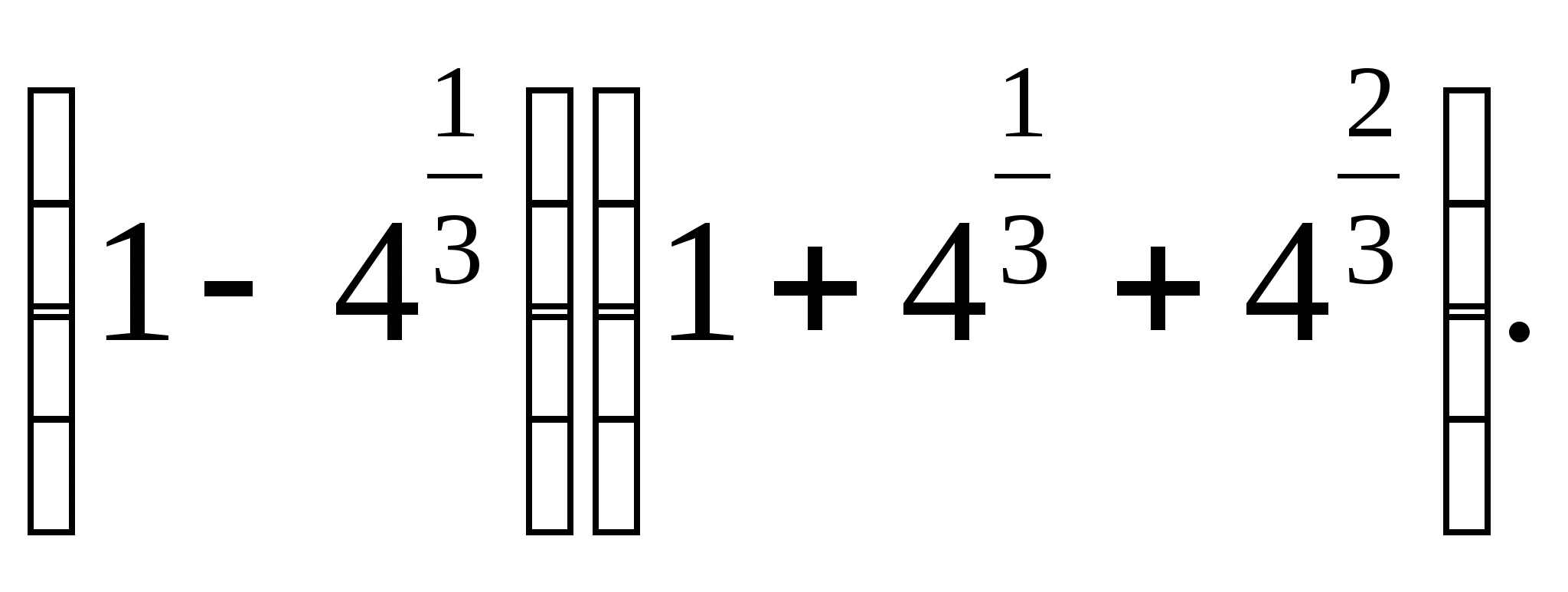
Постройте график функции: а) 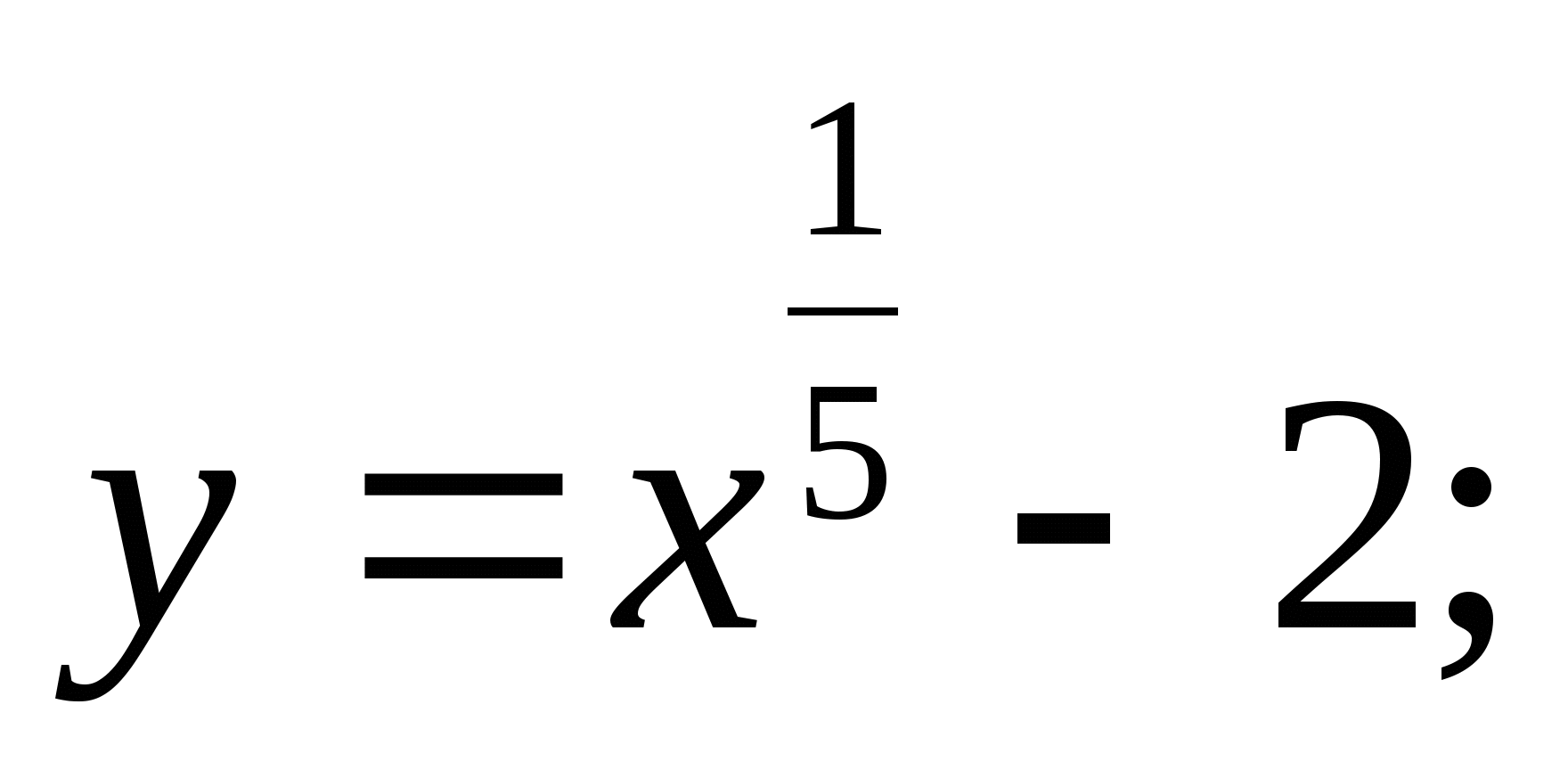 б)
б) 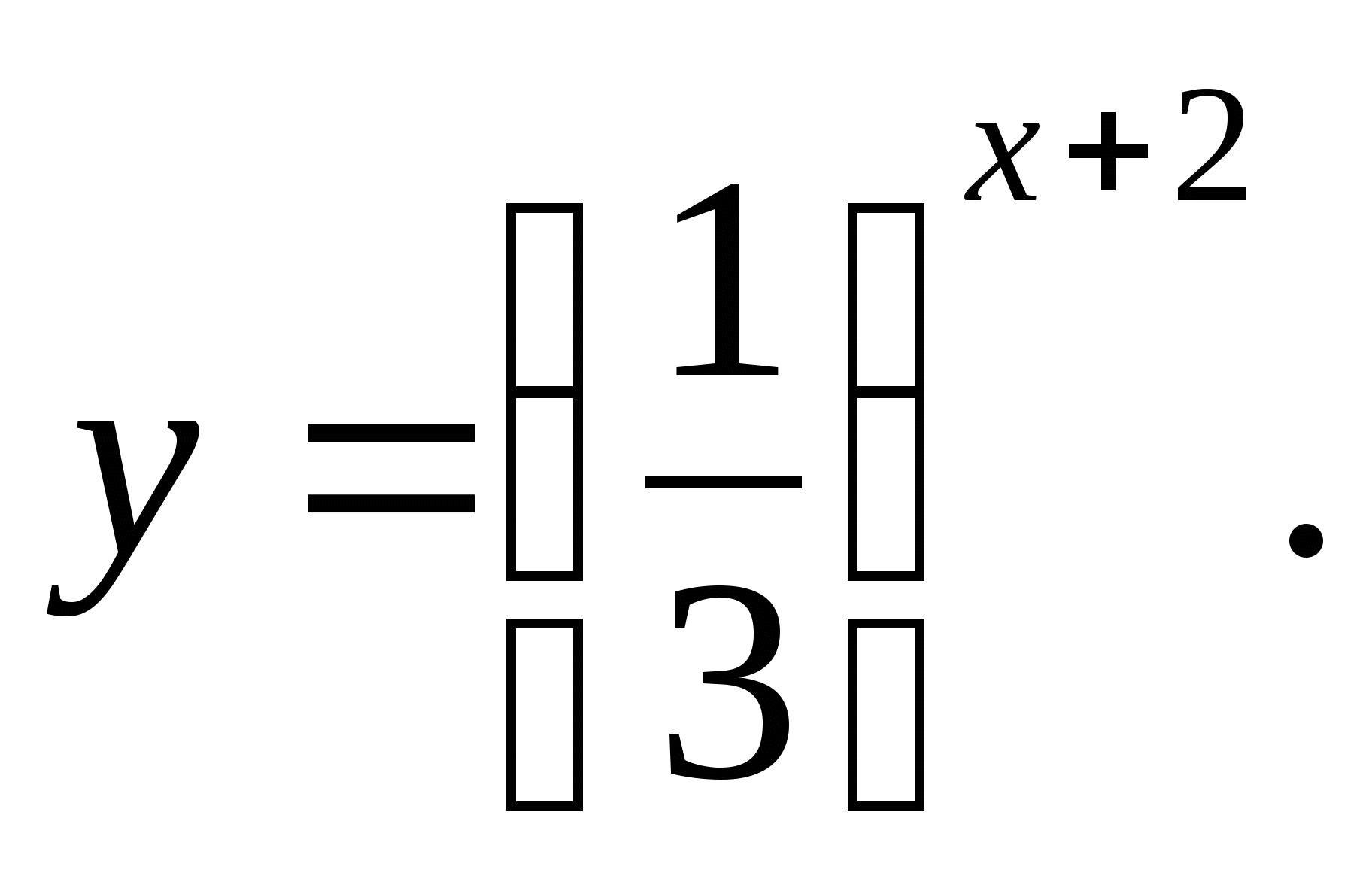
Решите уравнение: а) 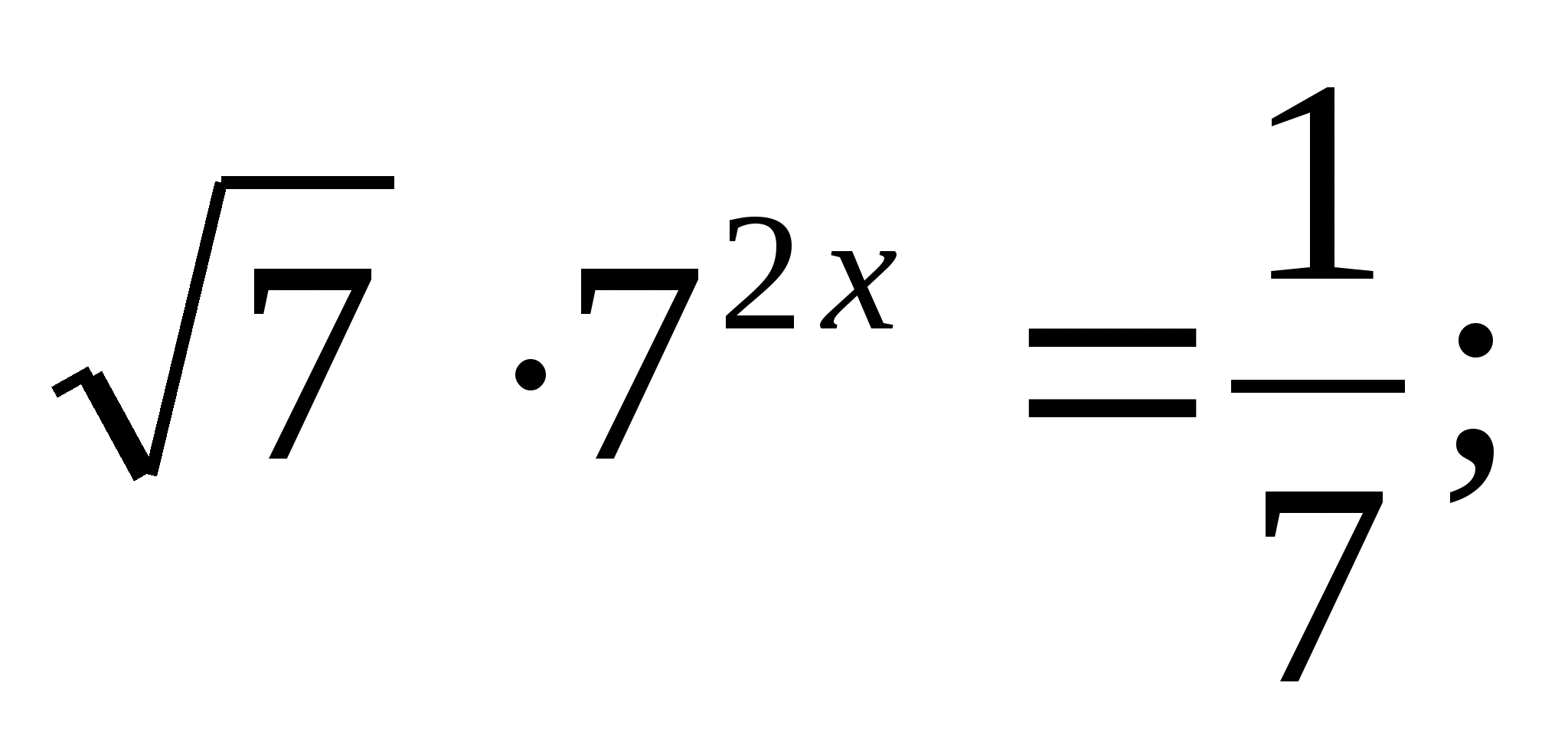 б)
б) 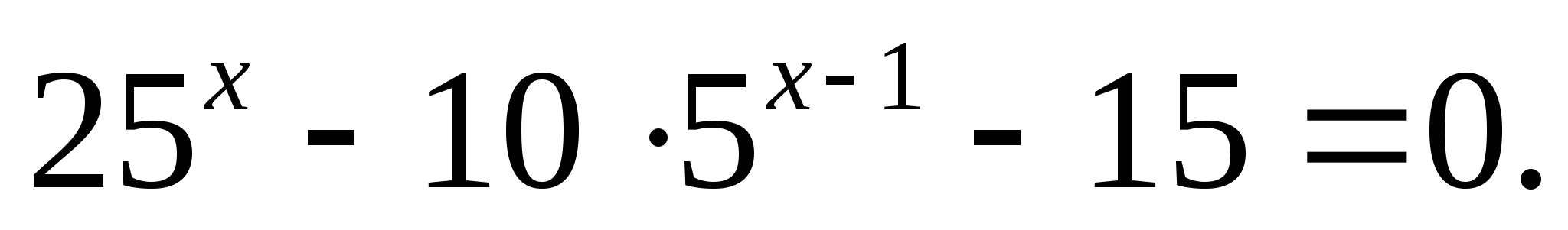
Решите неравенство: 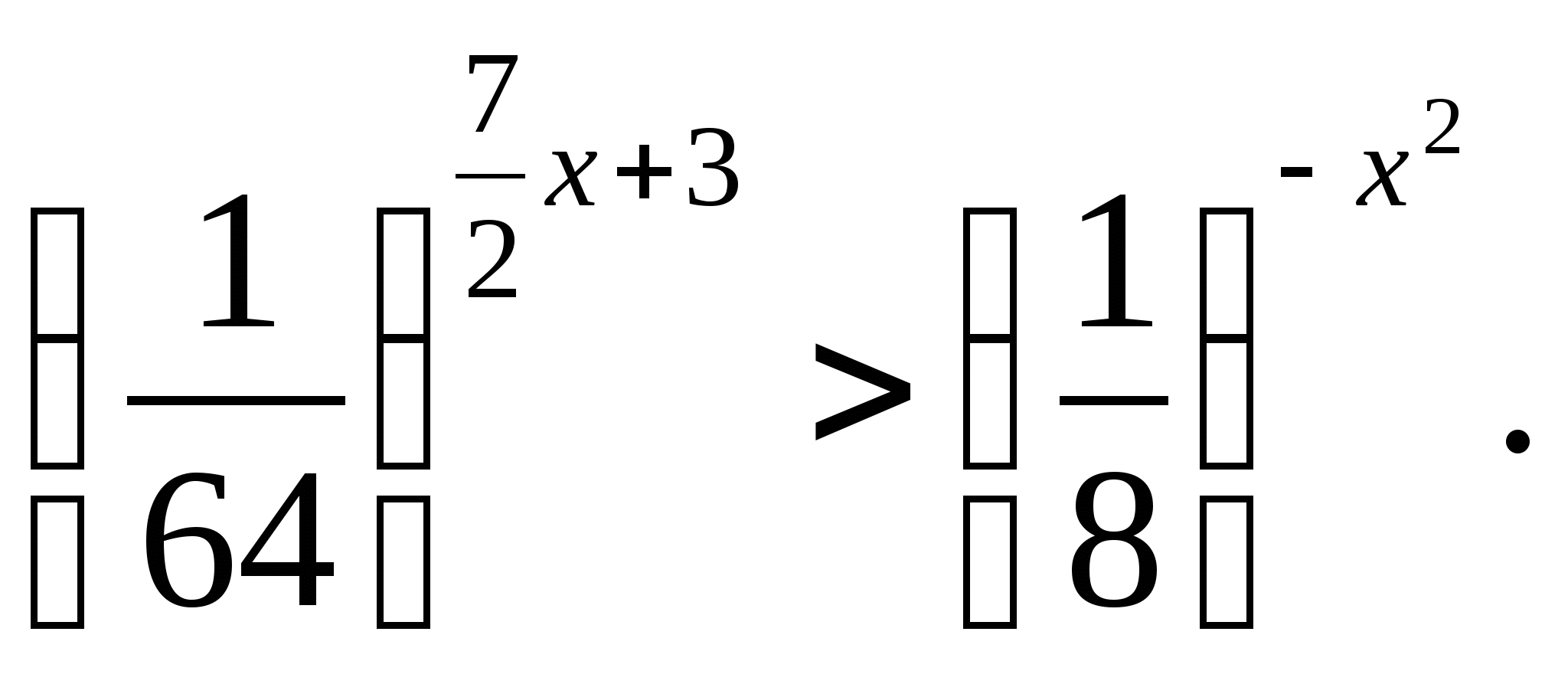
Найдите наибольшее и наименьшее значения функции 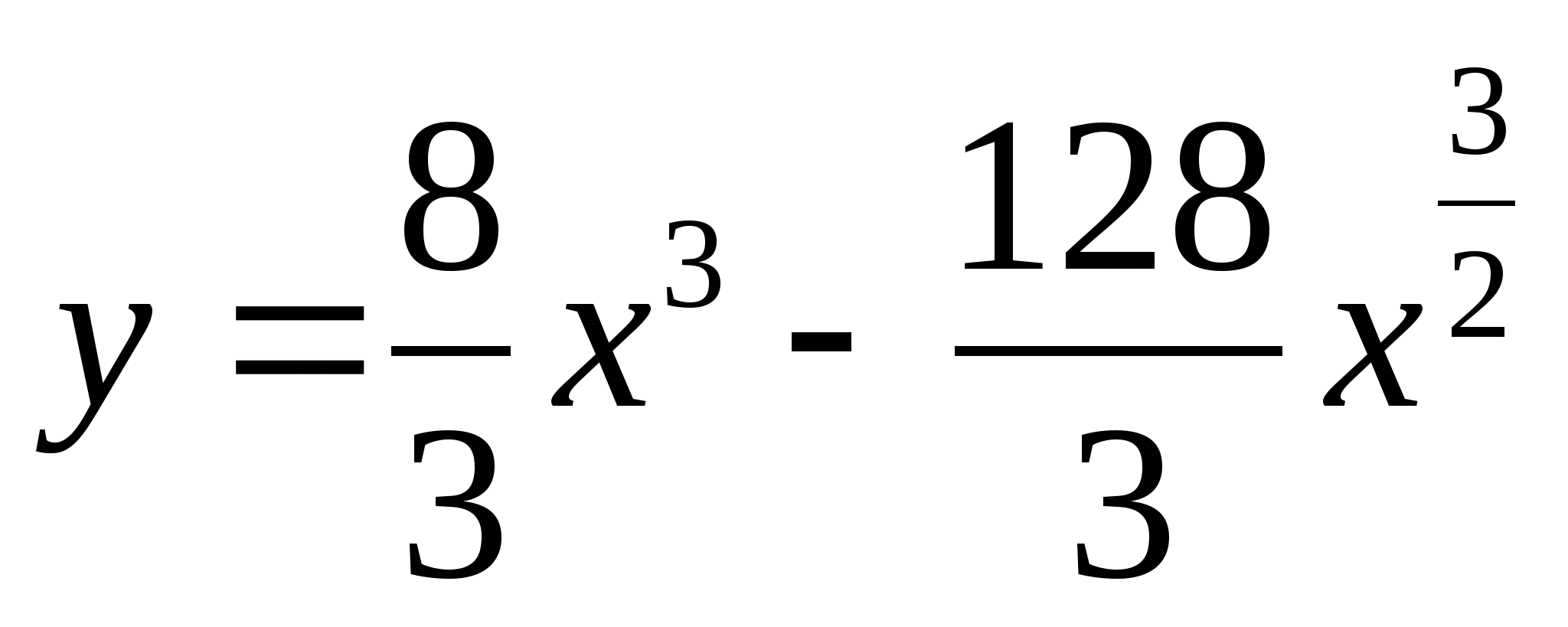 на отрезке [1;9].
на отрезке [1;9].
Дана функция 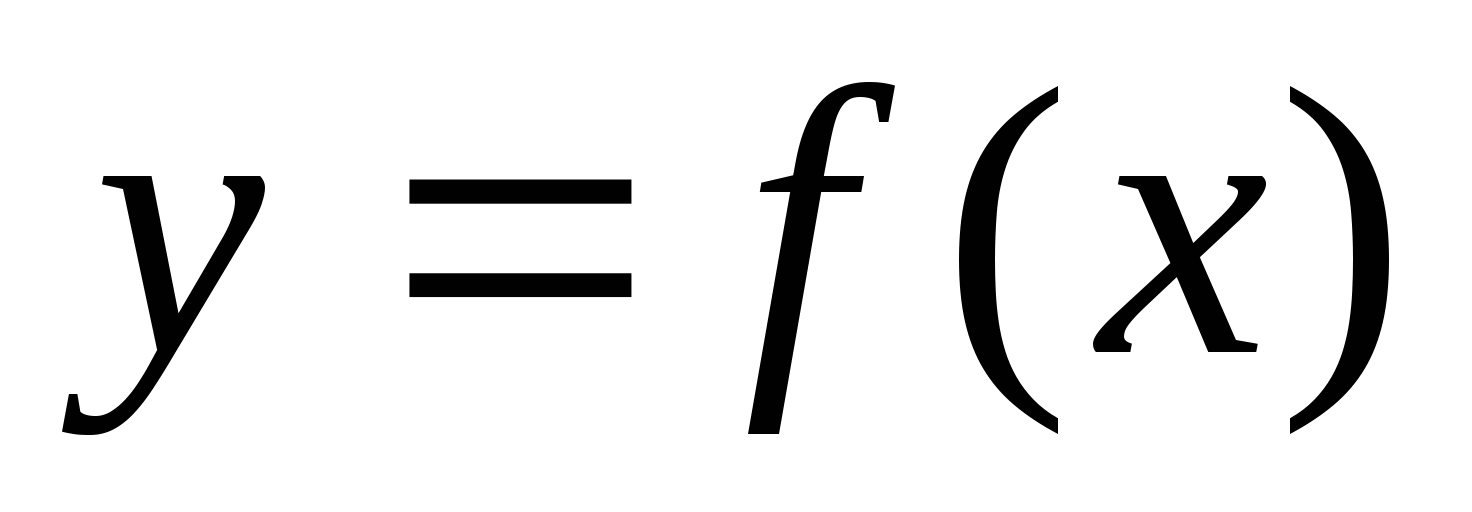 , где
, где 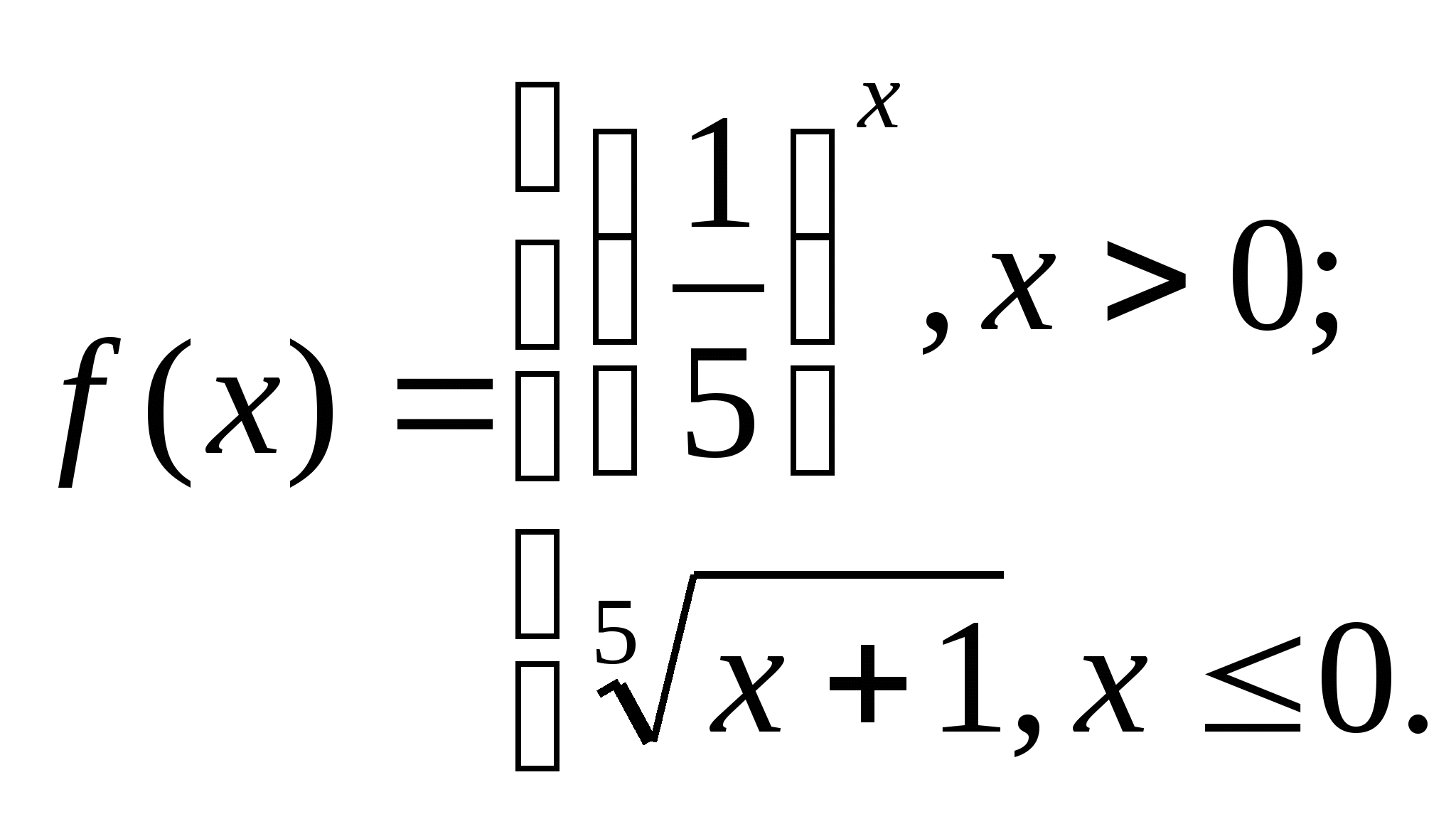
а) Вычислите: f(-1), f (4).
б) Постройте график функции.
в) Найдите область значений функции.
г) Выясните, при каких значениях параметра  уравнение
уравнение 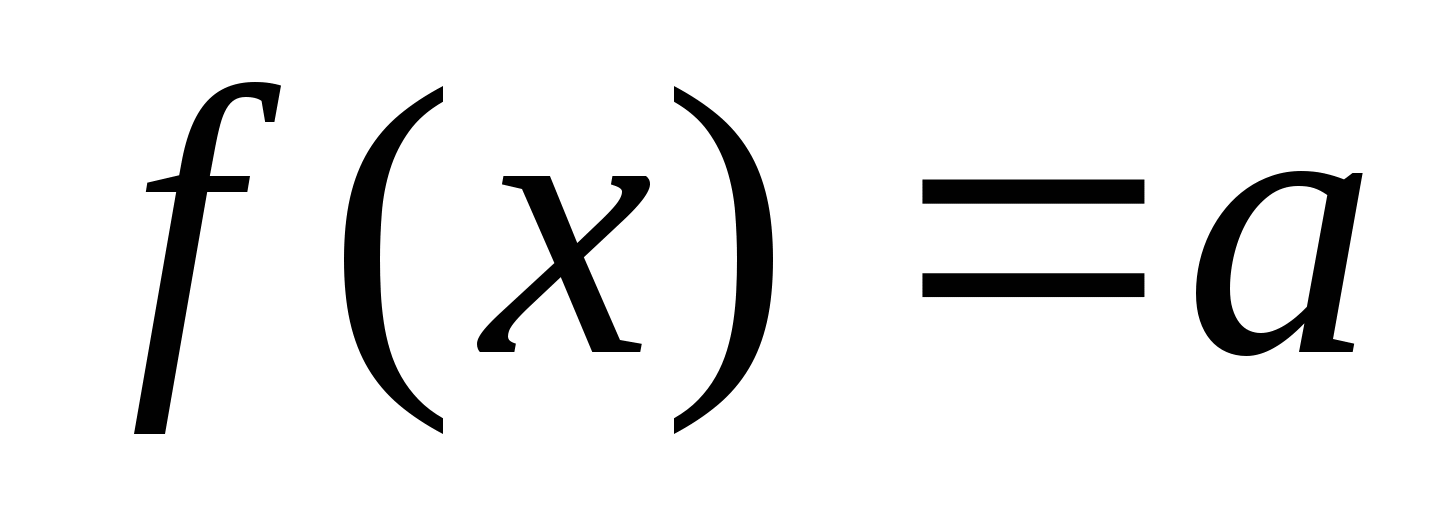 имеет два корня.
имеет два корня.
Контрольная работа №3
Вариант 1
Вычислите: а) 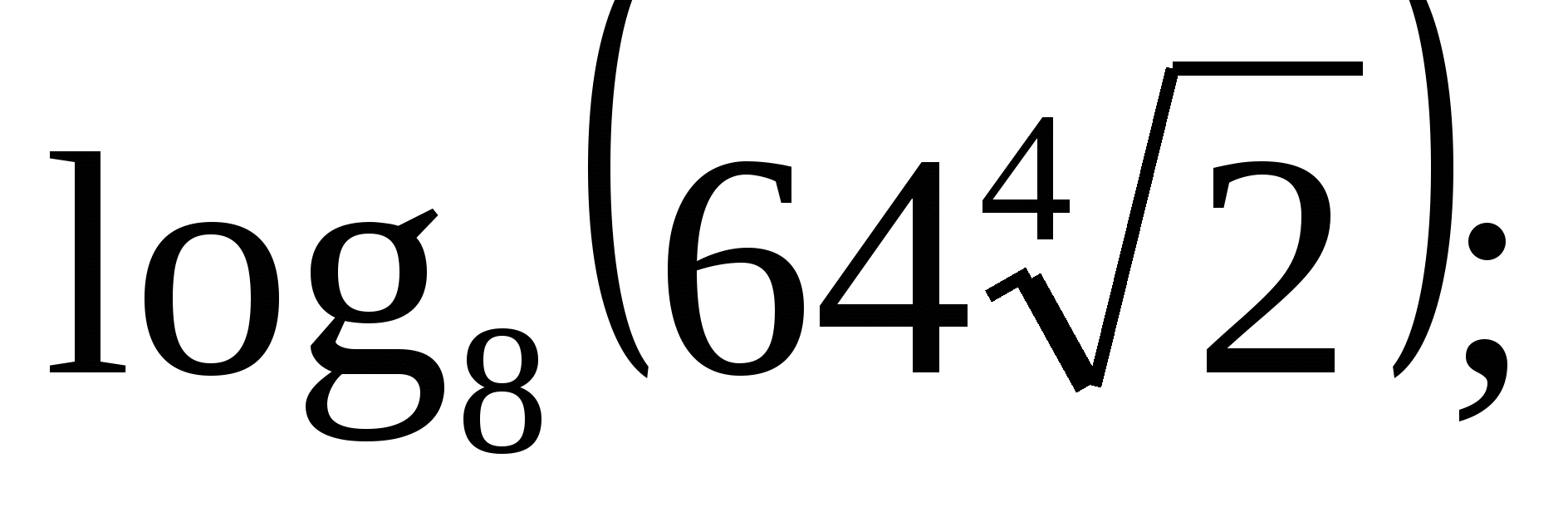 б)
б) 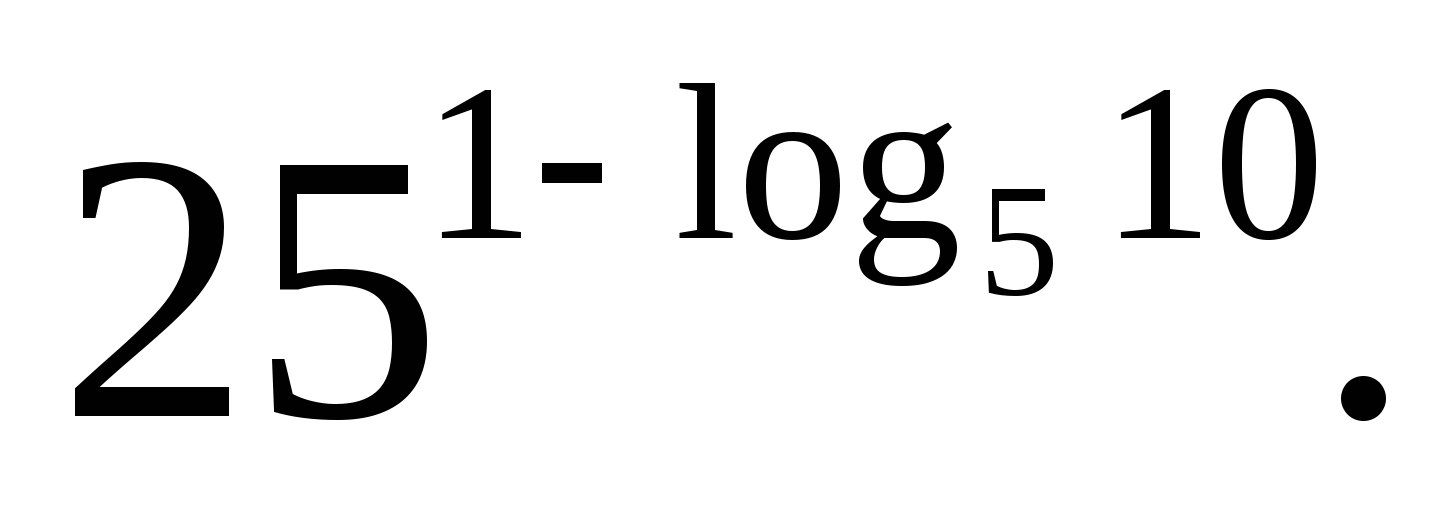
Постройте график функции: а) 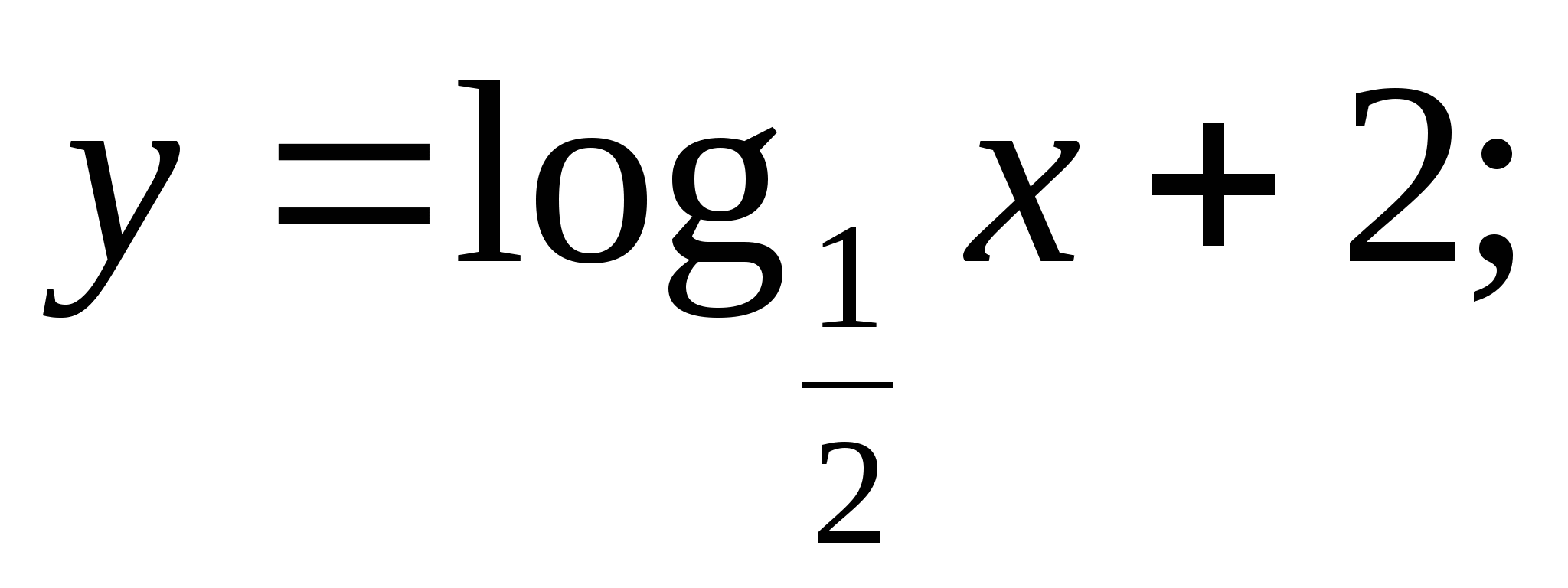 б)
б) 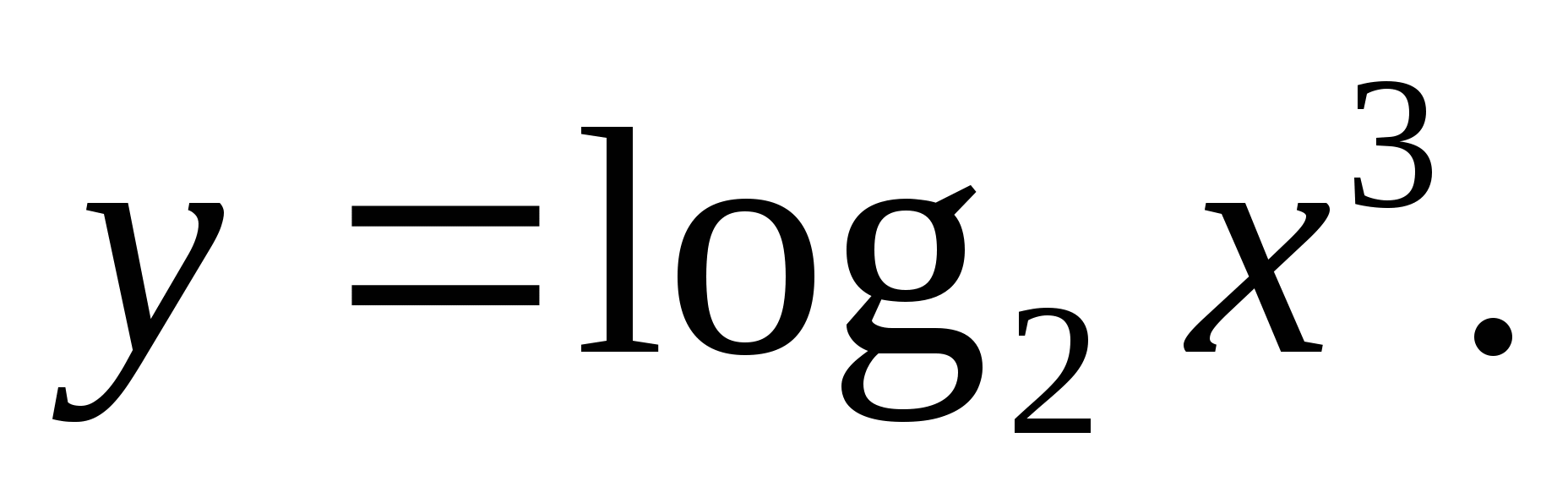
Решите уравнение: а) 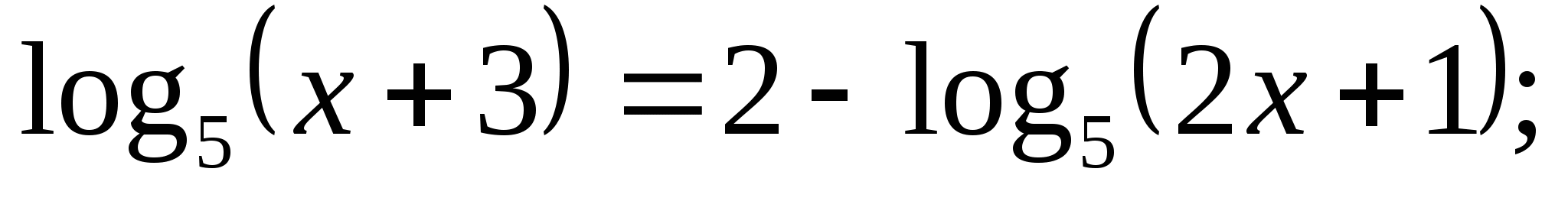 б)
б) 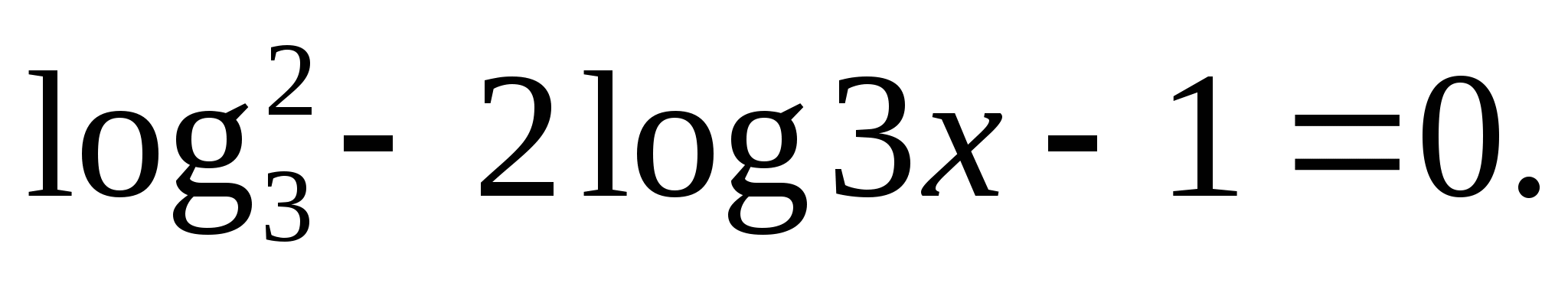
Решите неравенство: 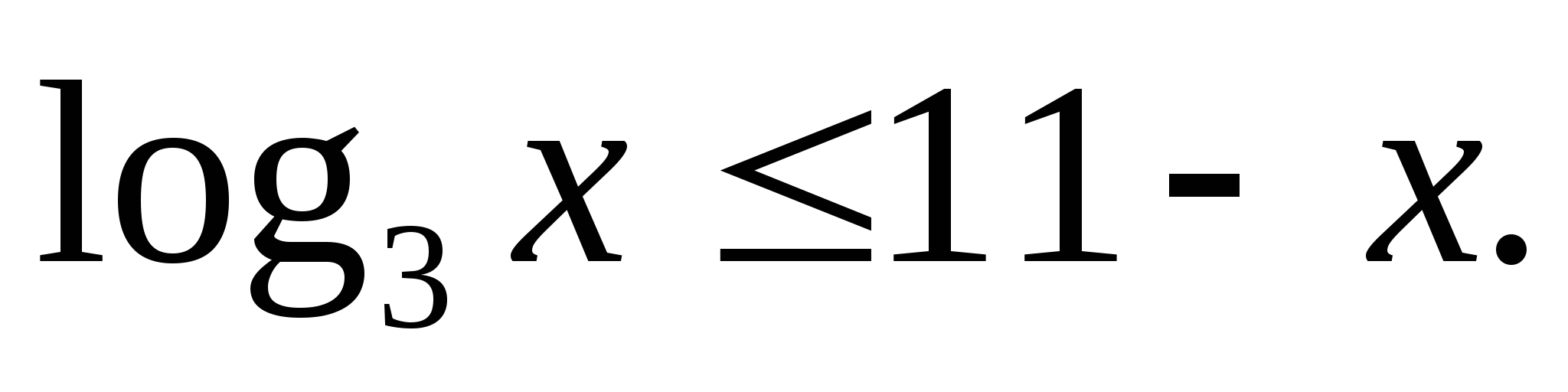
Решите уравнение: 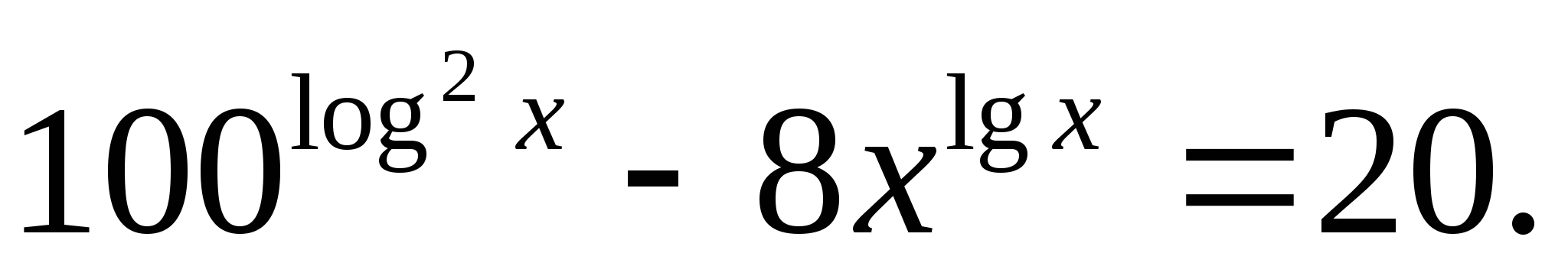
Контрольная работа №3
Вариант 2
Вычислите: а) 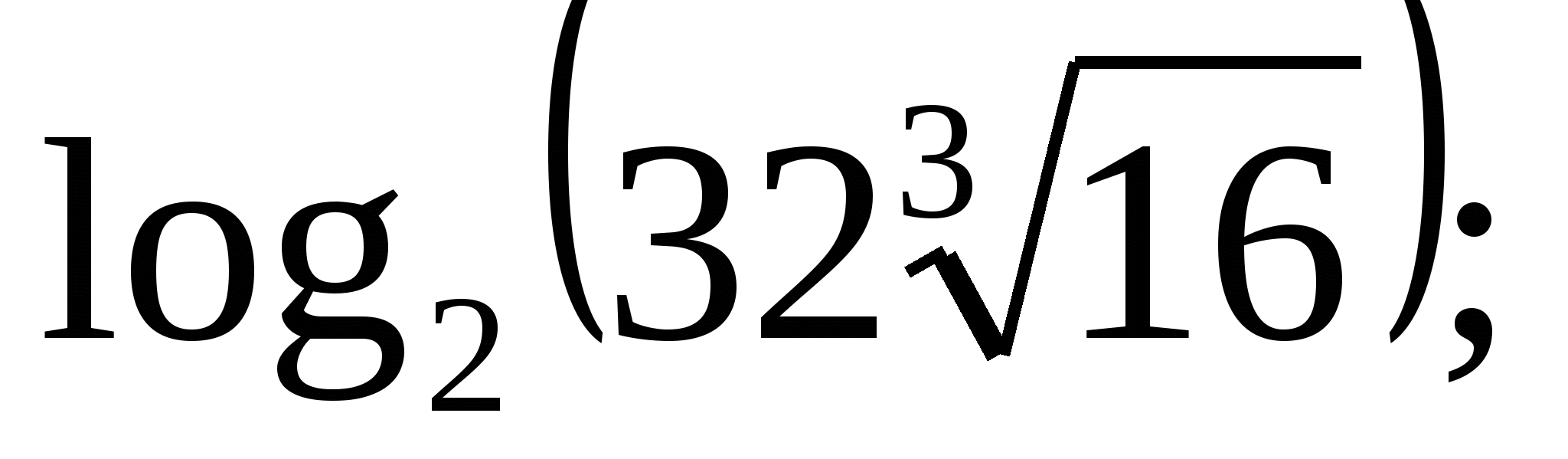 б)
б) 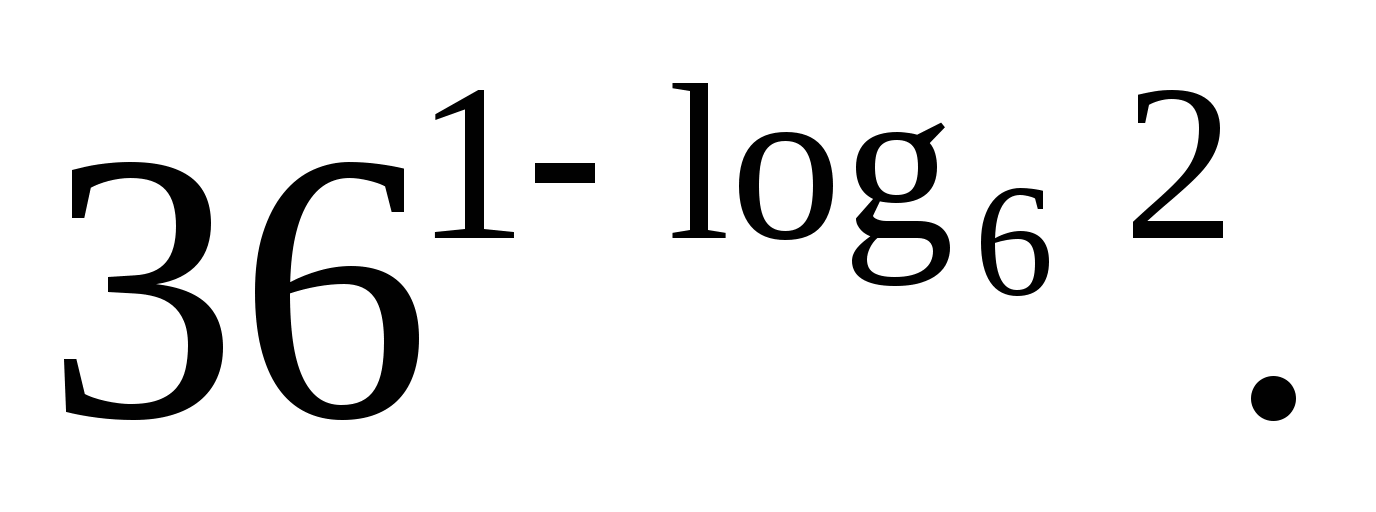
Постройте график функции: а) 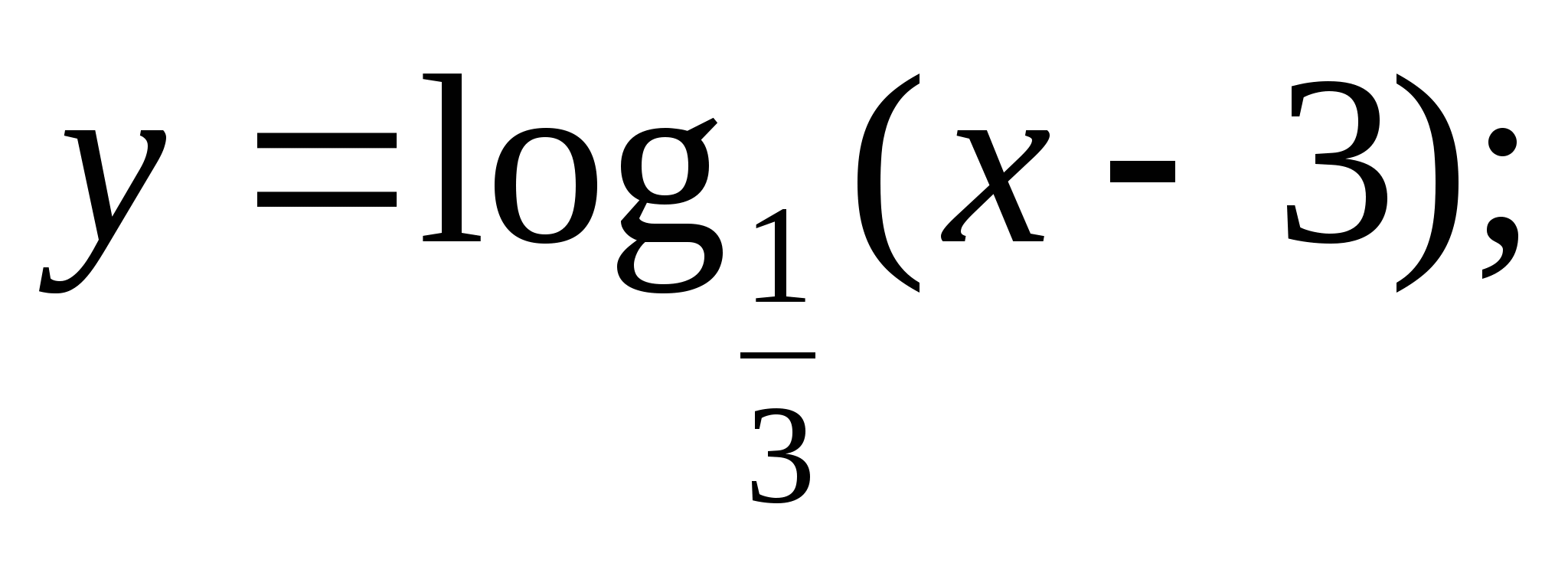 б)
б) 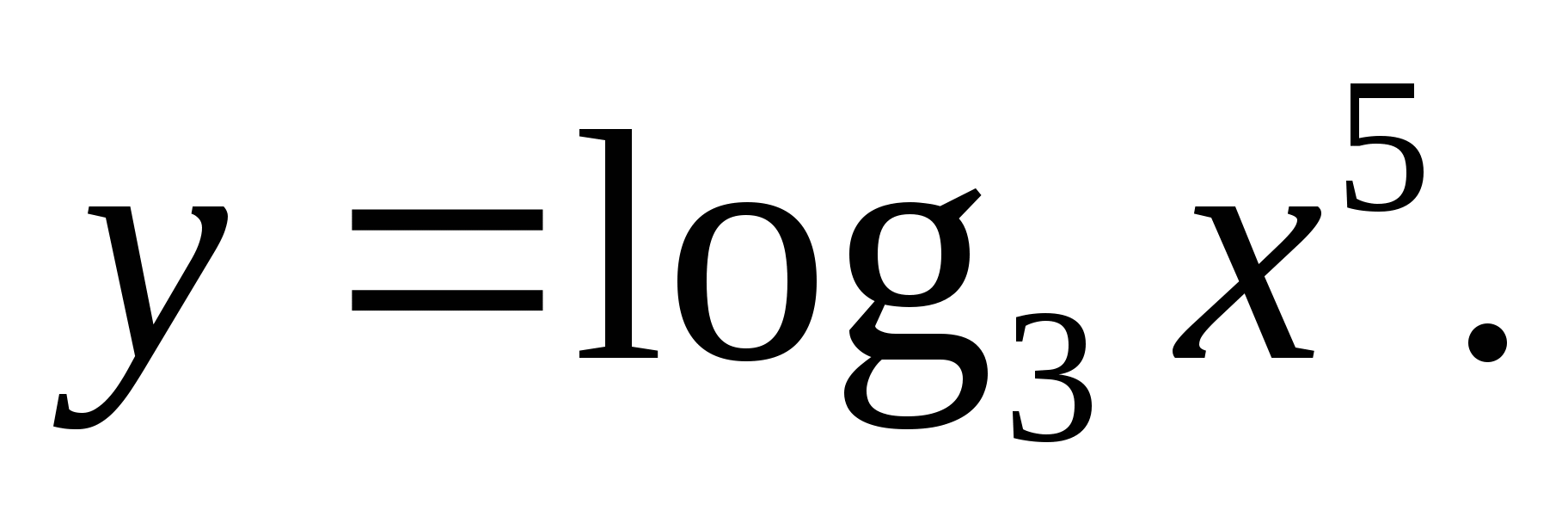
Решите уравнение: а) 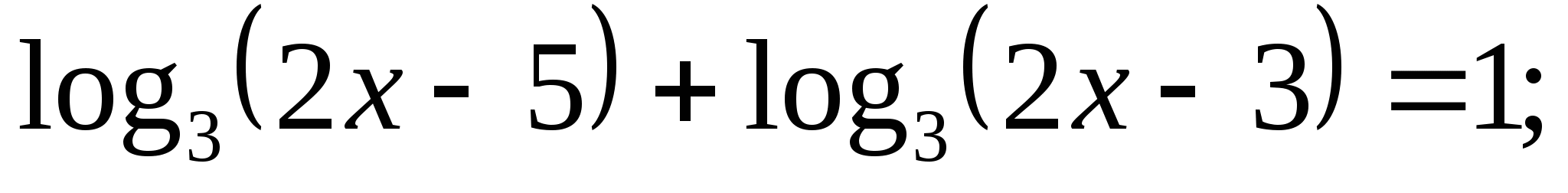 б)
б) 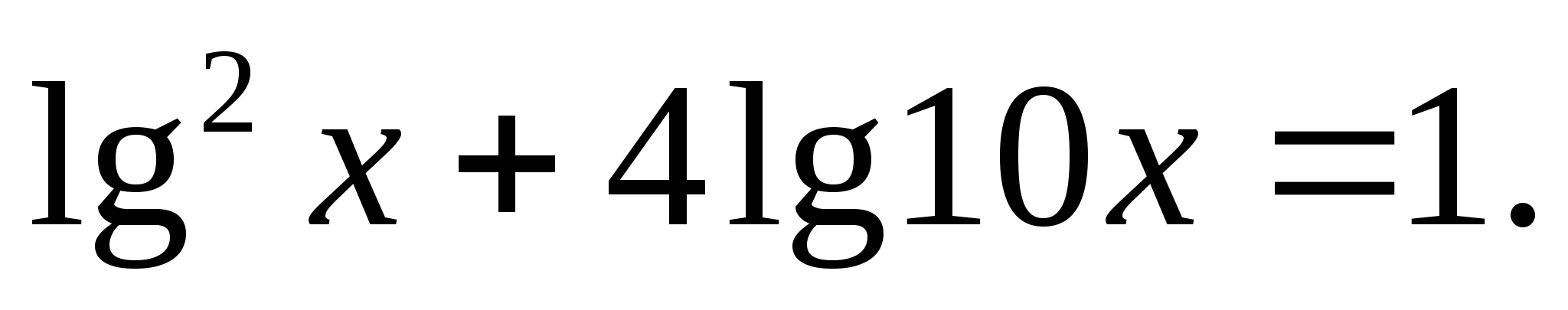
Решите неравенство: 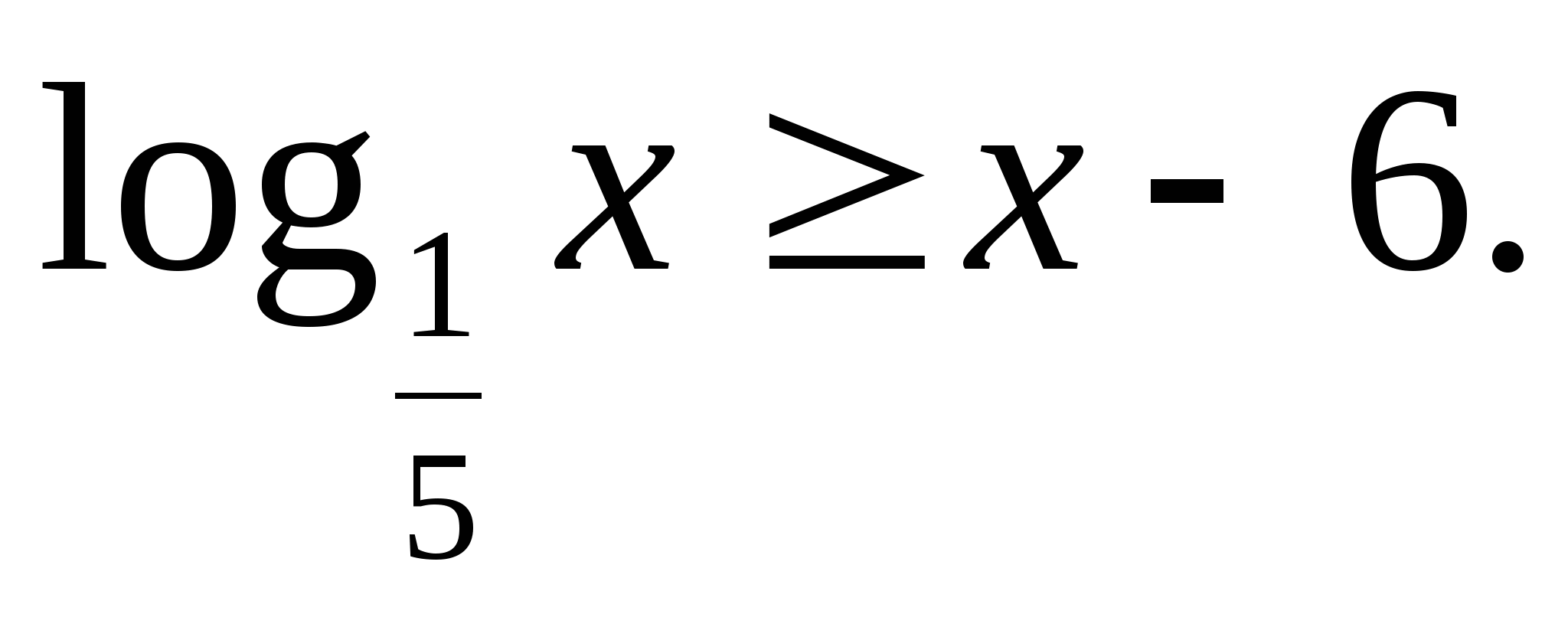
Решите уравнение: 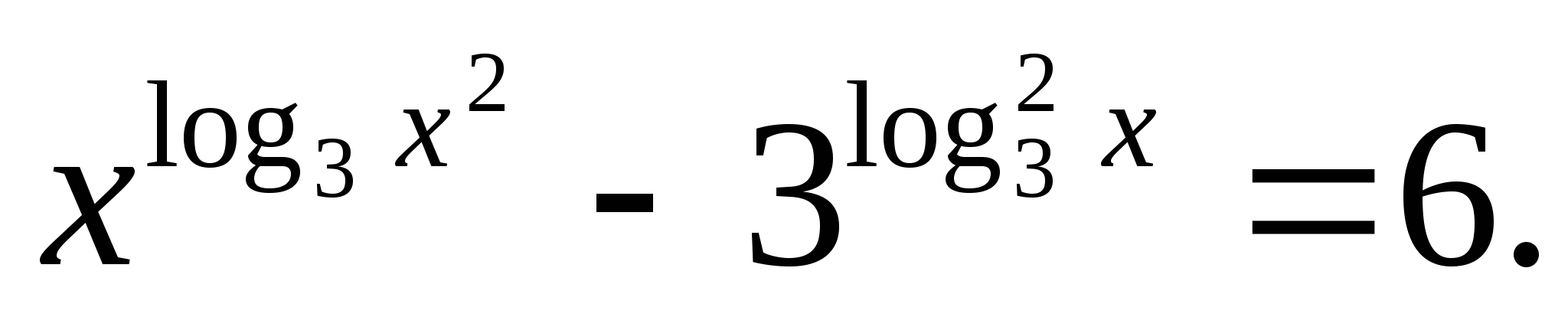
Контрольная работа №3
Вариант 3
Вычислите: а) 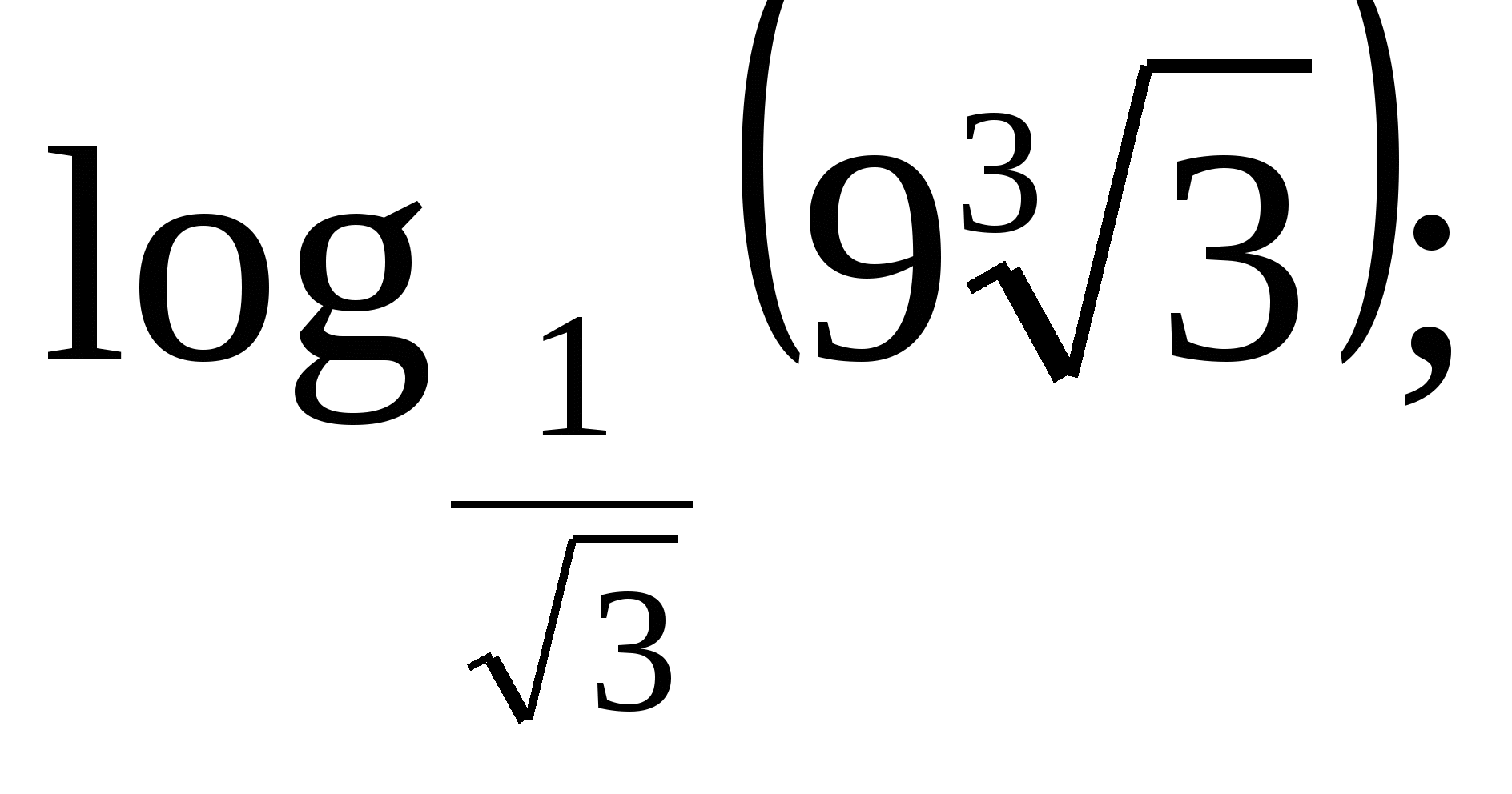 б)
б) 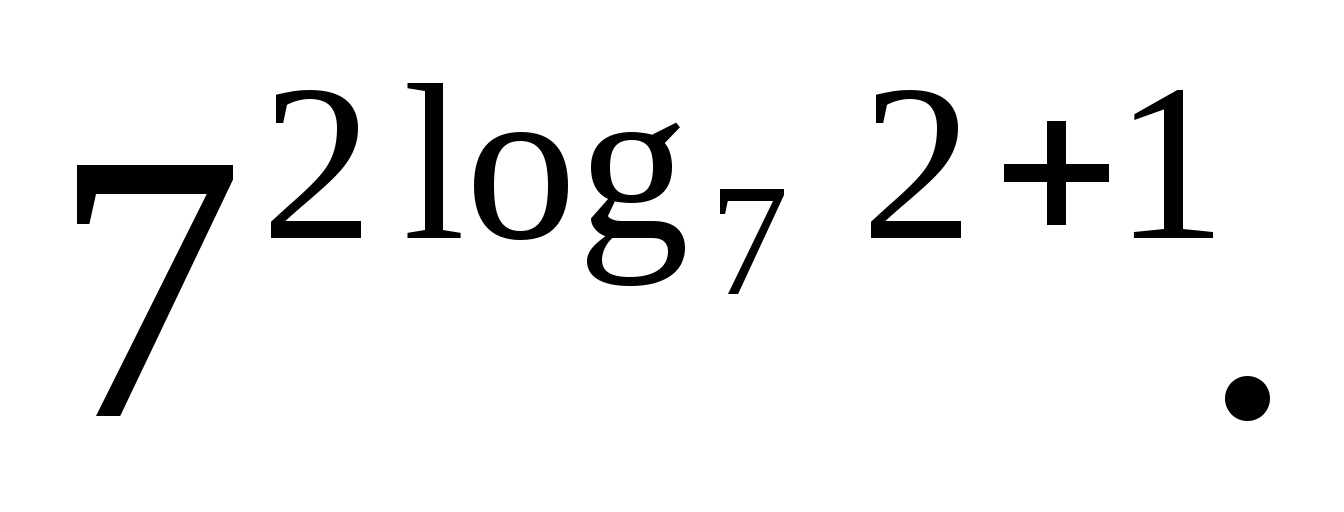
Постройте график функции: а) 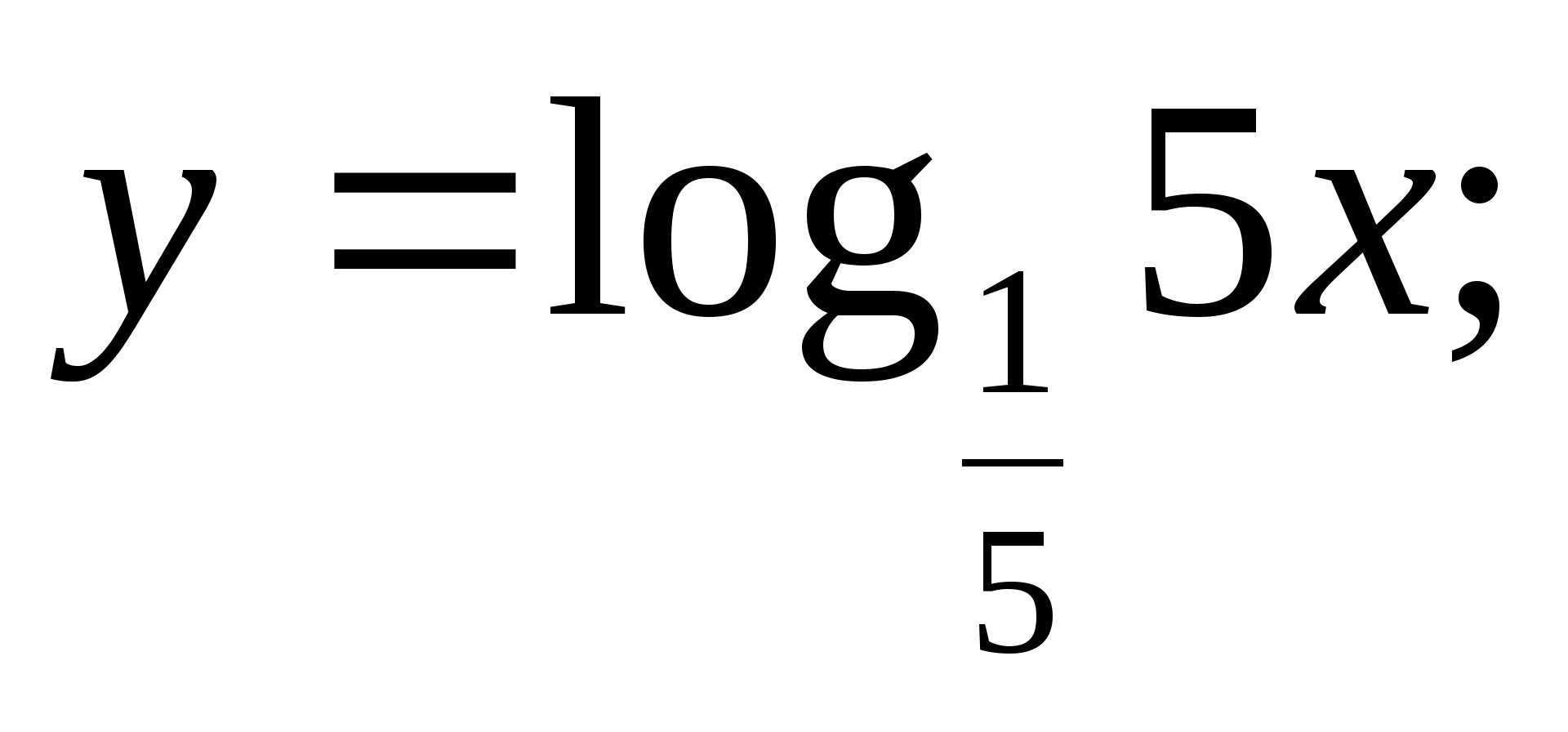 б)
б) 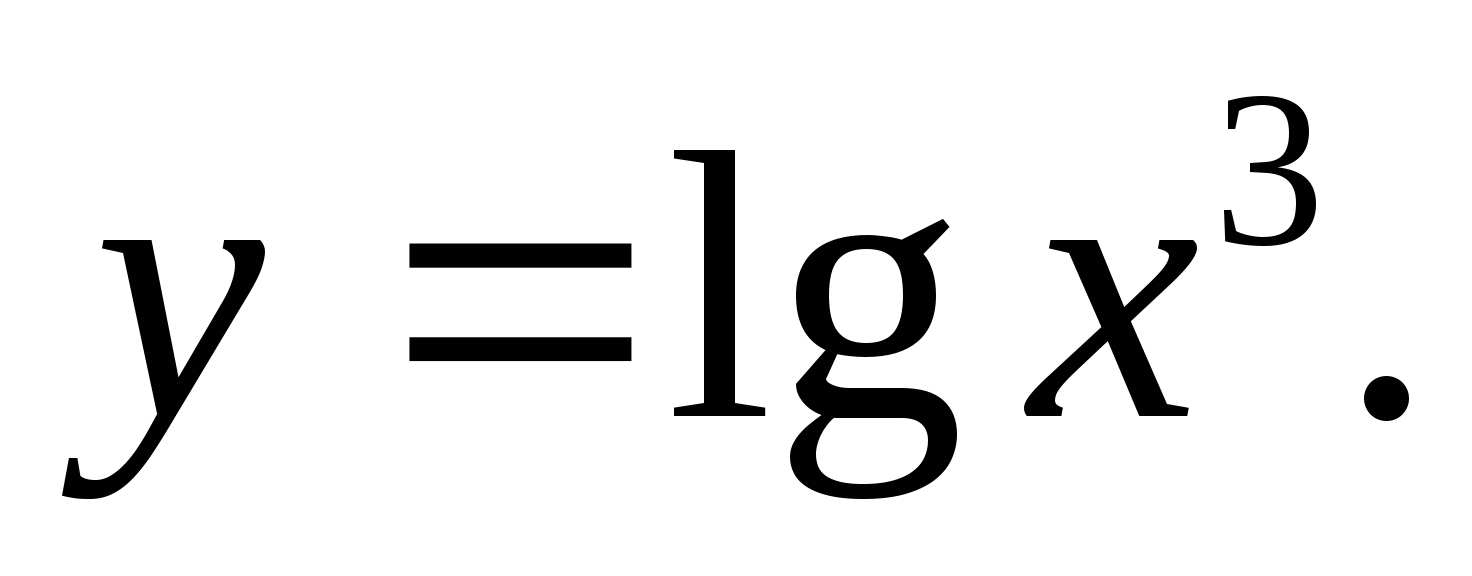
Решите уравнение: а) 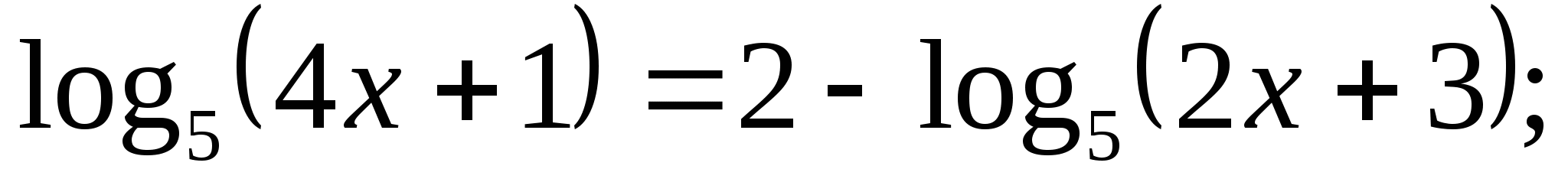 б)
б) 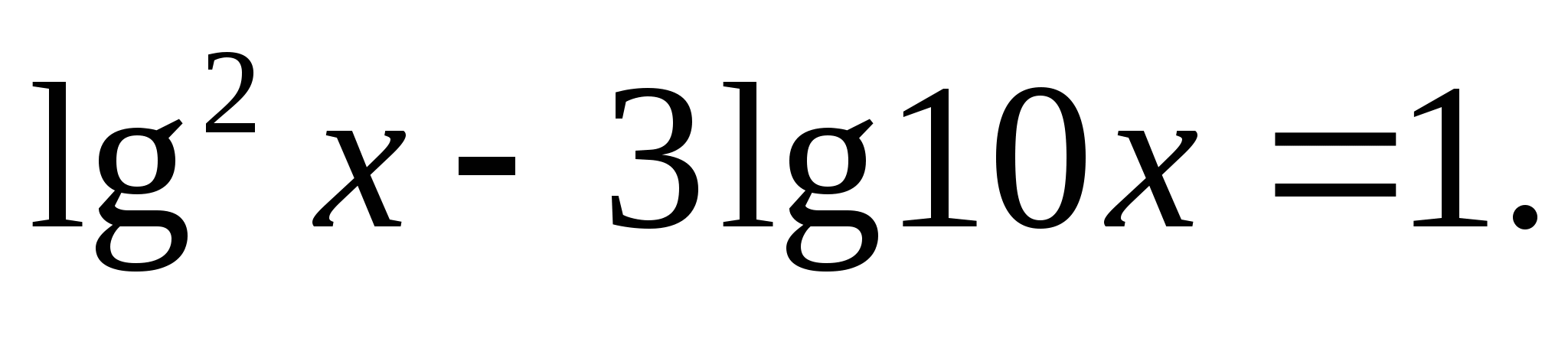
Решите неравенство: 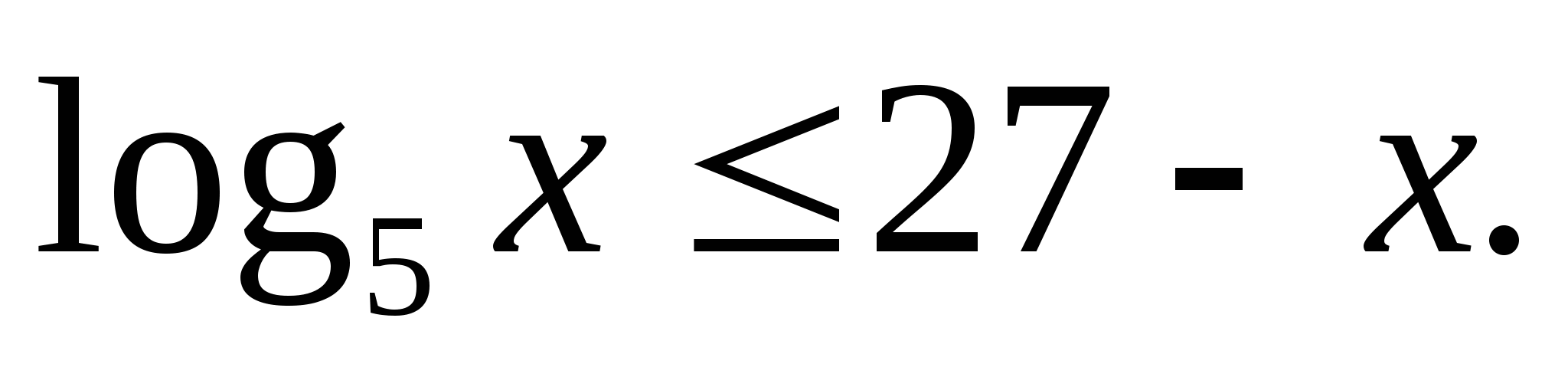
Решите уравнение: 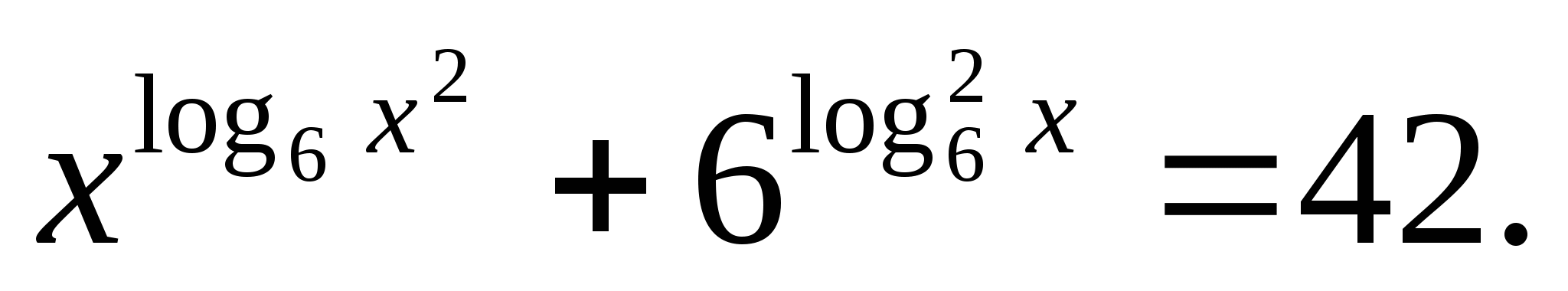
Контрольная работа №3
Вариант 4
Вычислите: а) 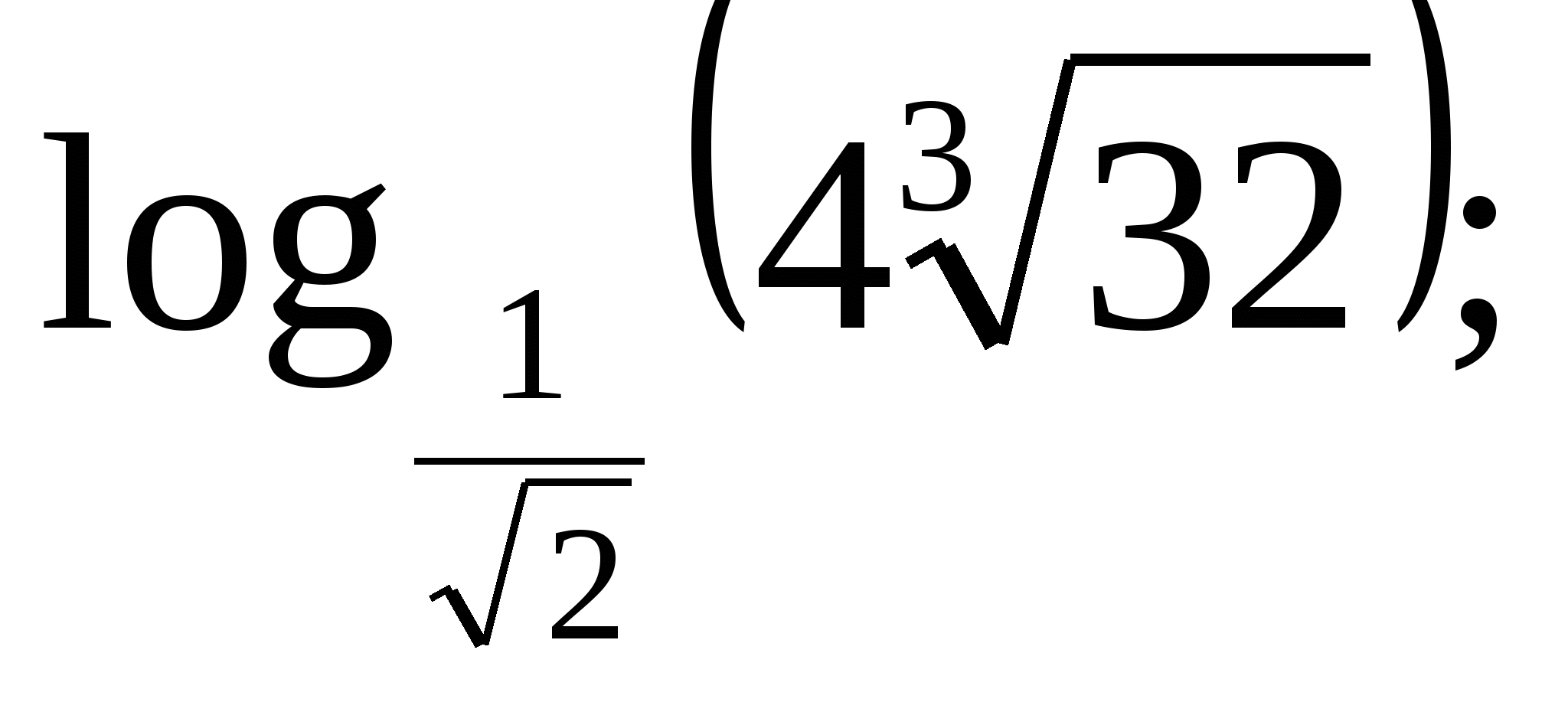 б)
б) 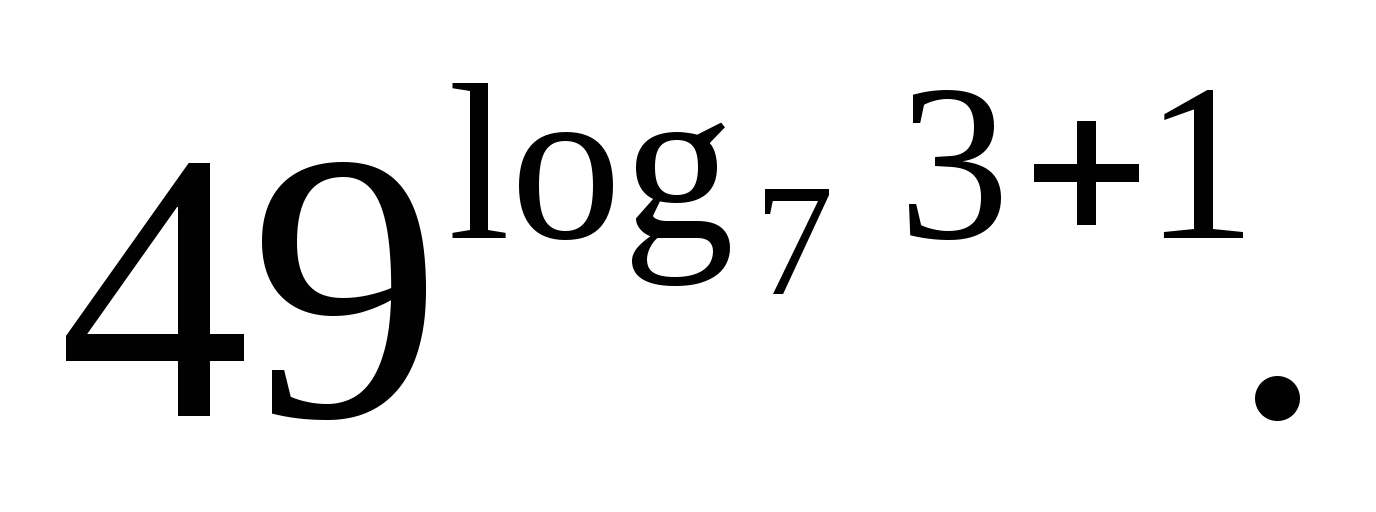
Постройте график функции: а) 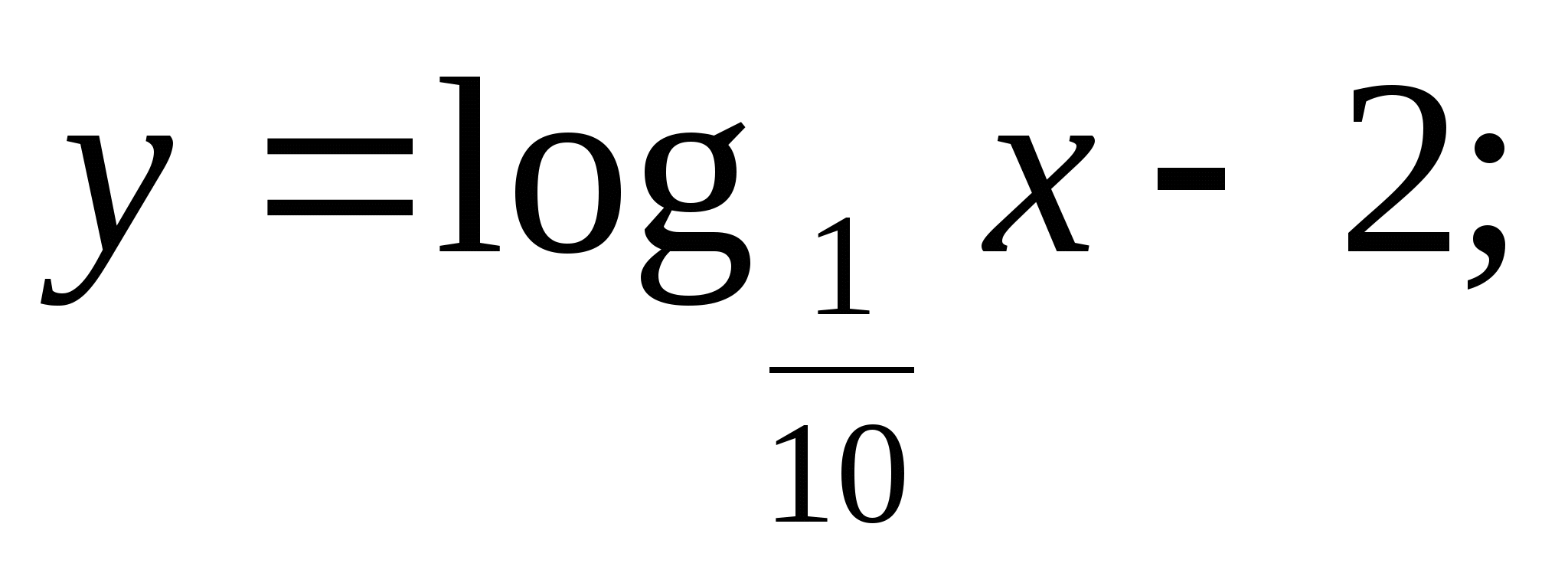 б)
б) 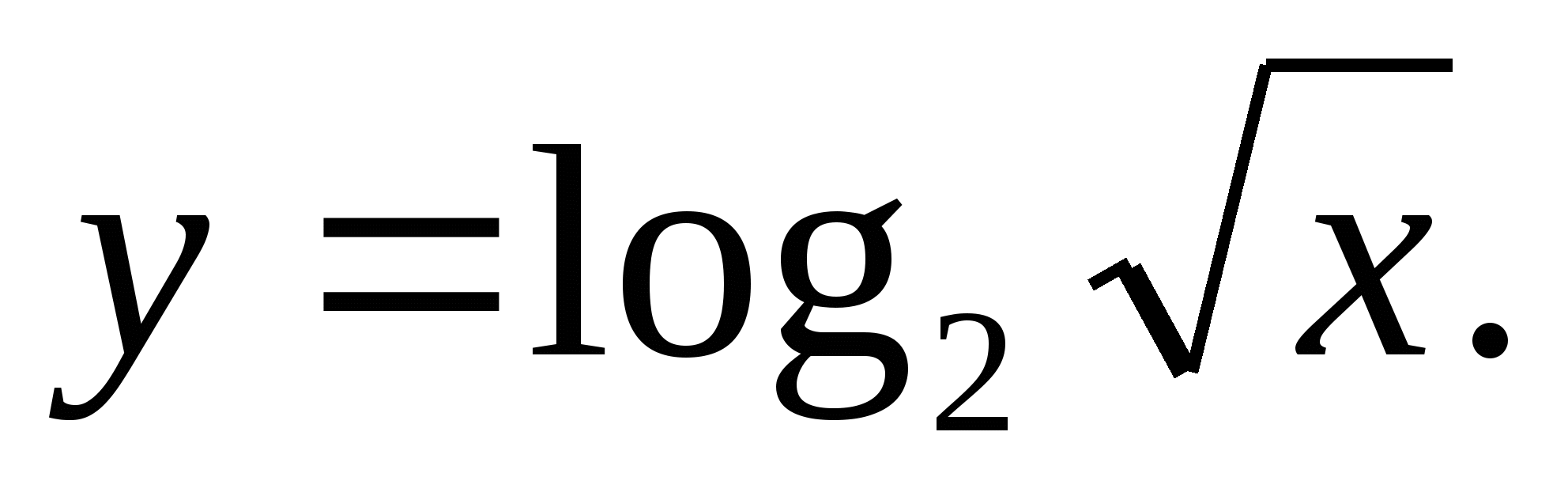
Решите уравнение: а) 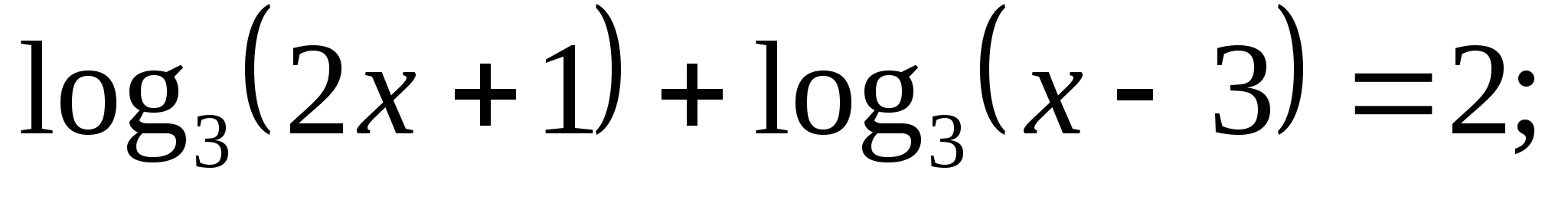 б)
б) 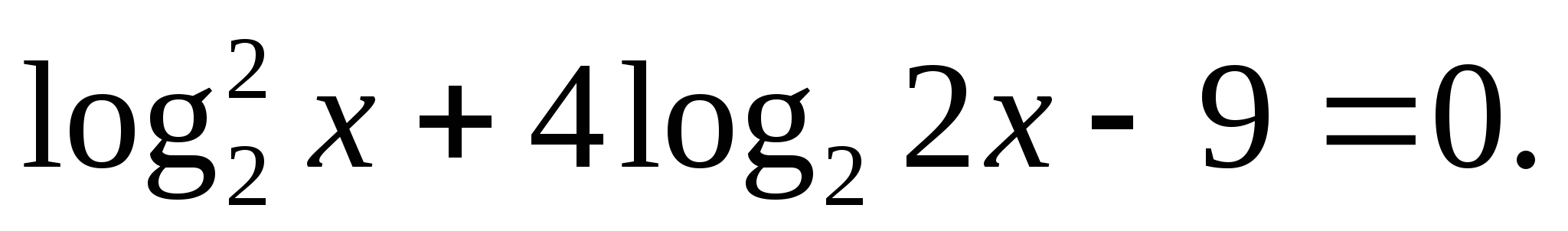
Решите неравенство: 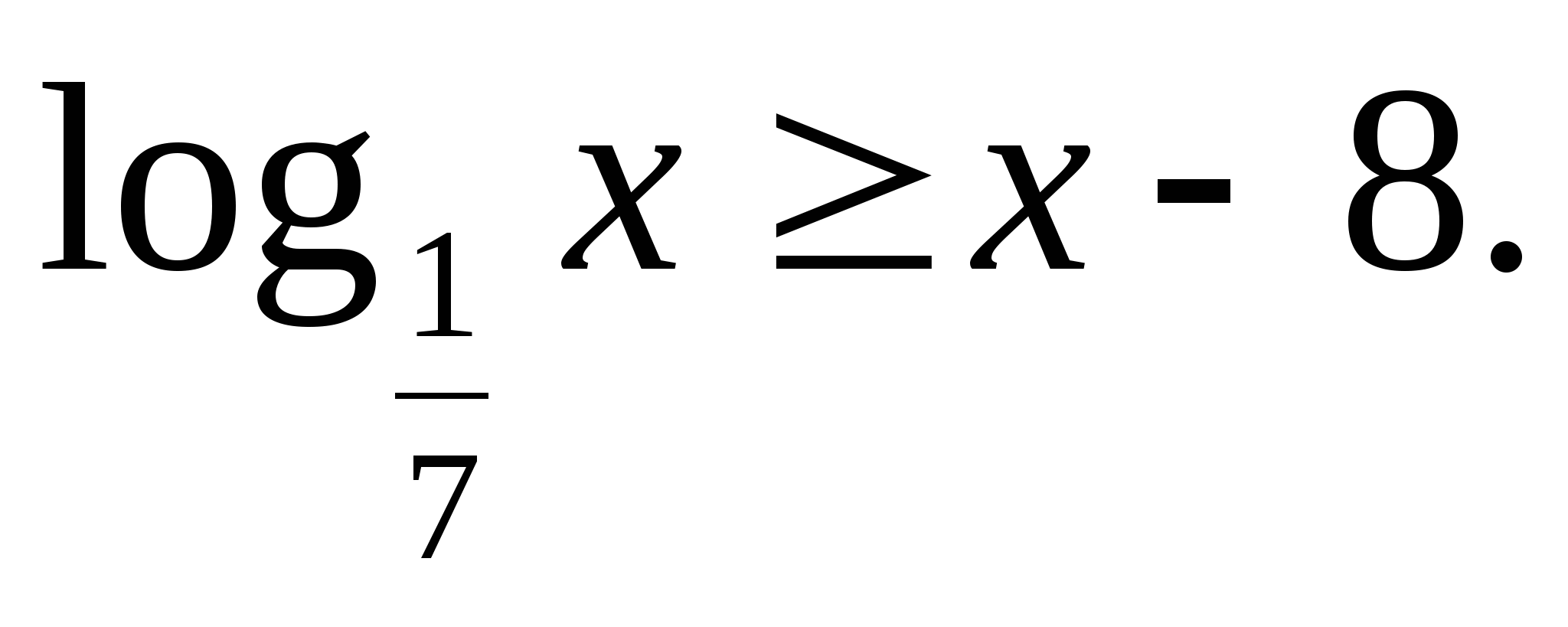
Решите уравнение: 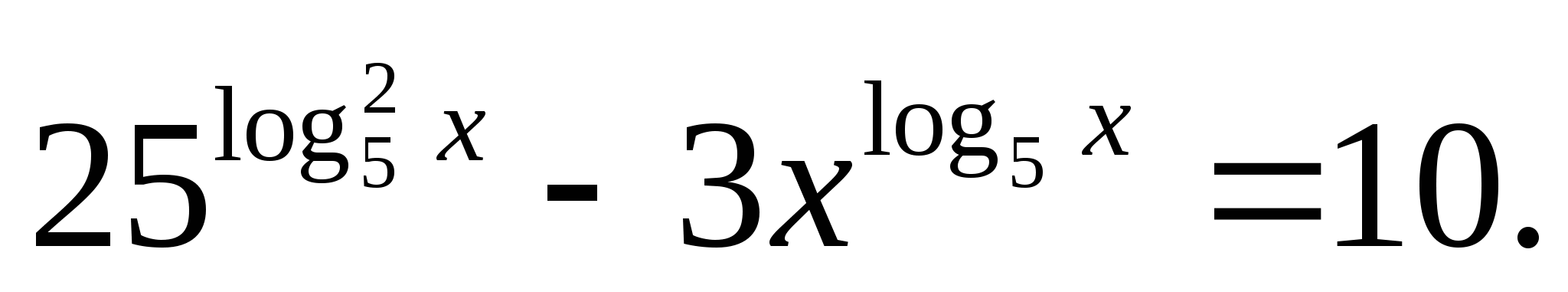
Контрольная работа №4
Вариант 1
Решите неравенство: 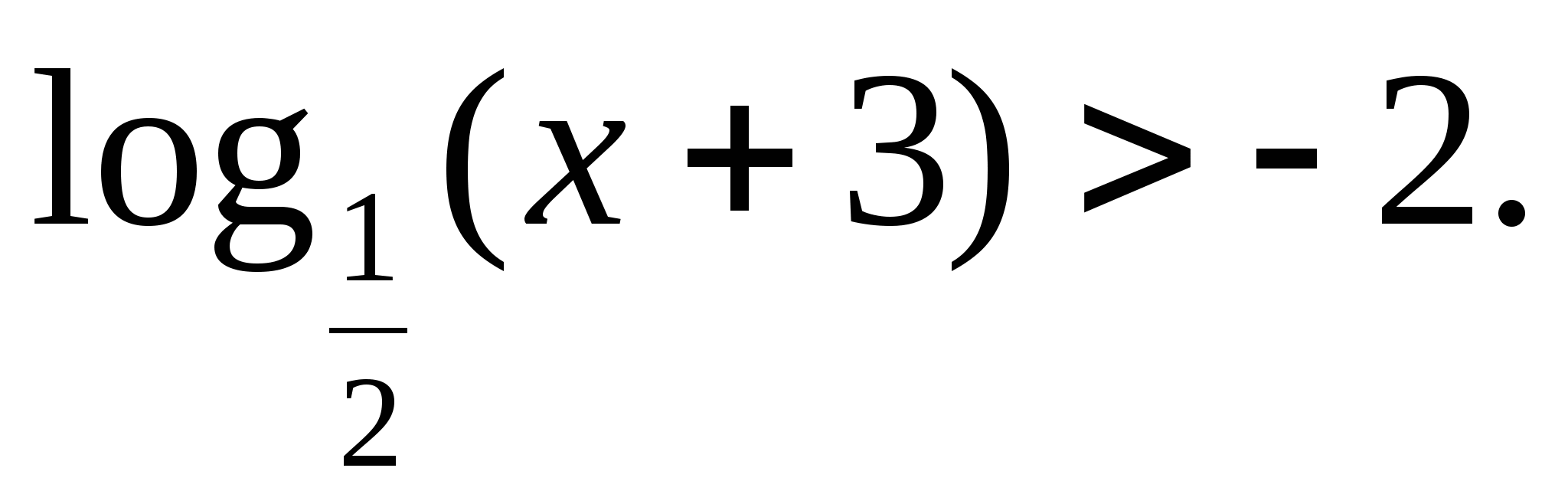
Исследуйте функцию 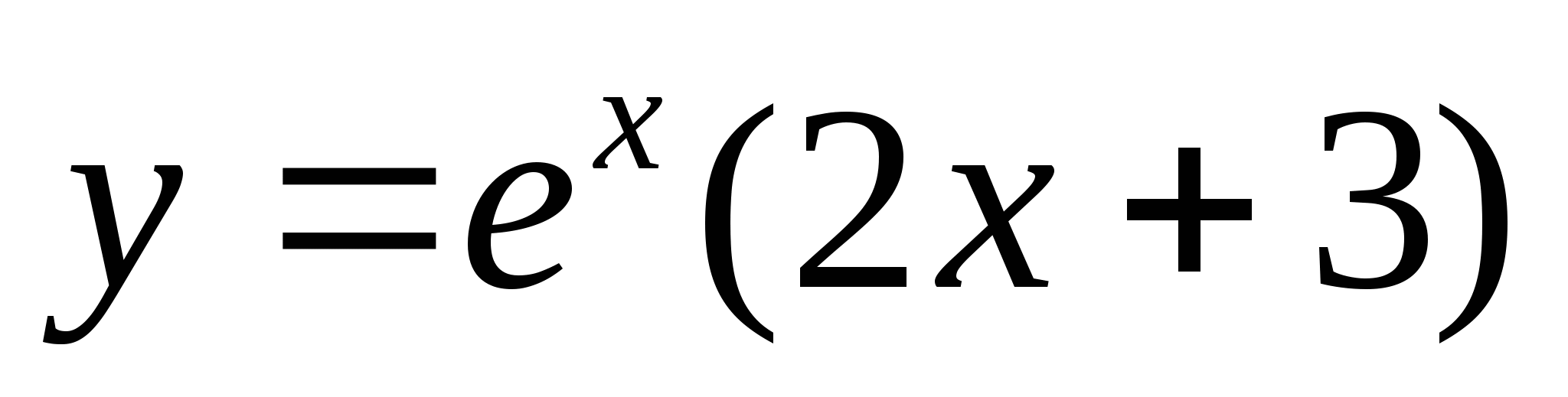 на монотонность и экстремумы.
на монотонность и экстремумы.
Напишите уравнение касательной к графику функции 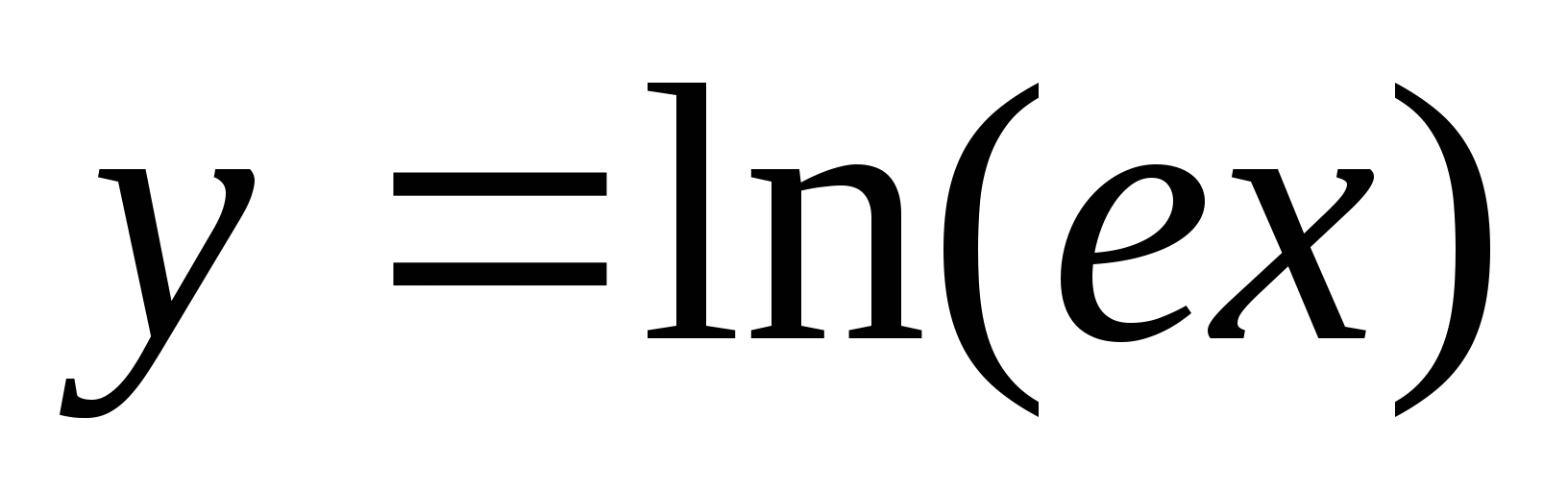
в точке x=1.
Решите уравнение: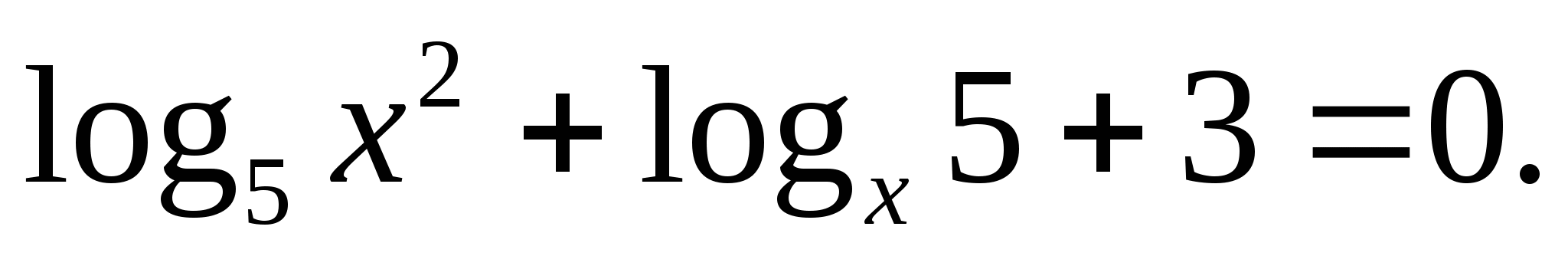
Решите систему уравнений 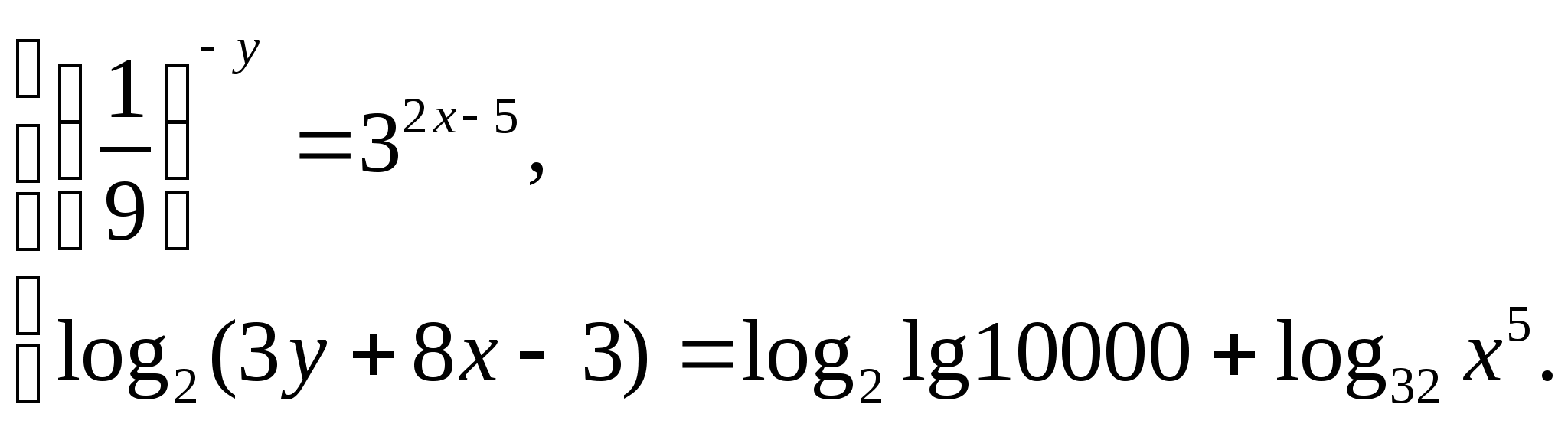
Контрольная работа №4
Вариант 2
Решите неравенство: 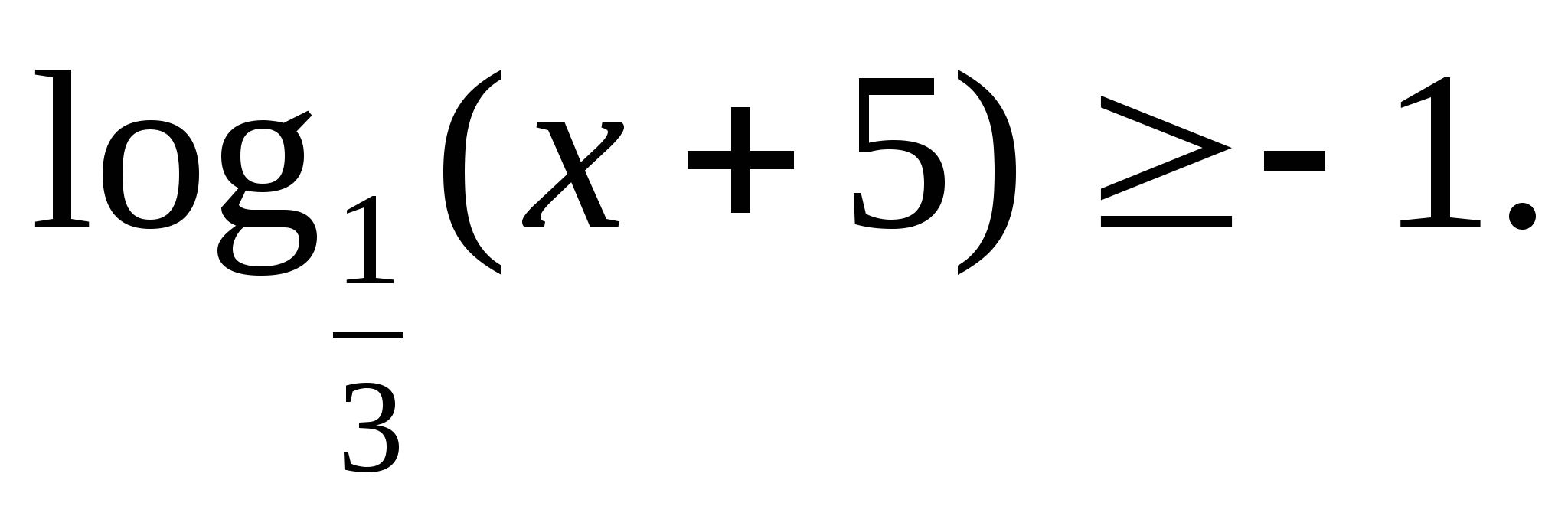
Исследуйте функцию 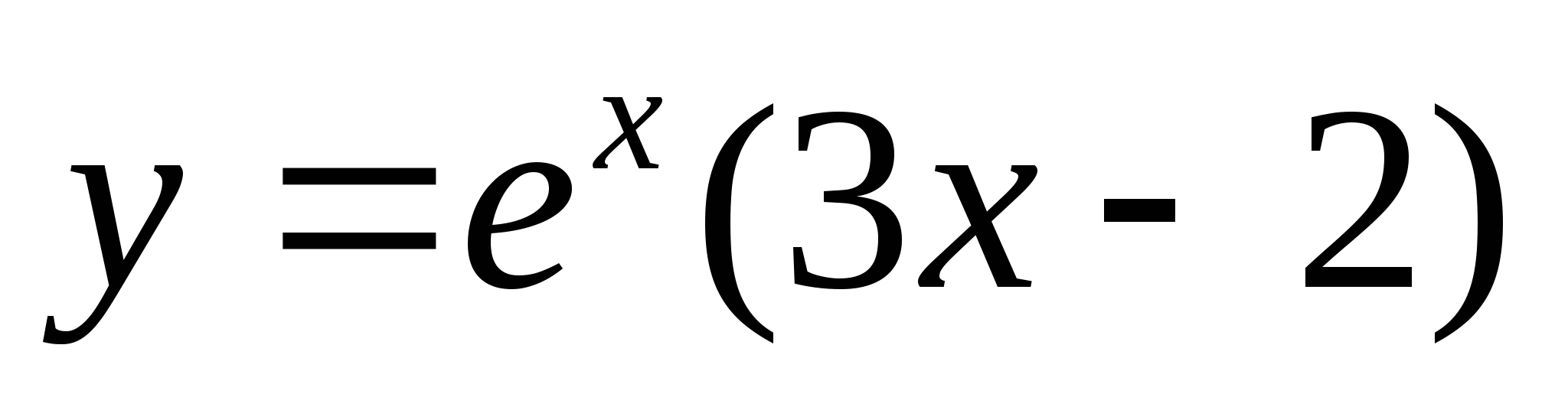 на монотонность и экстремумы.
на монотонность и экстремумы.
Напишите уравнение касательной к графику функции 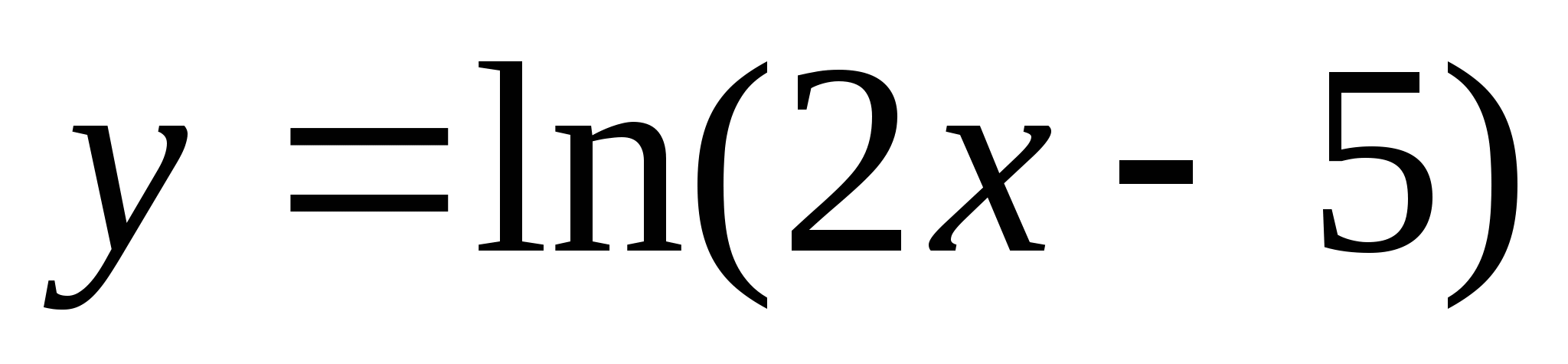
в точке x=3.
Решите уравнение: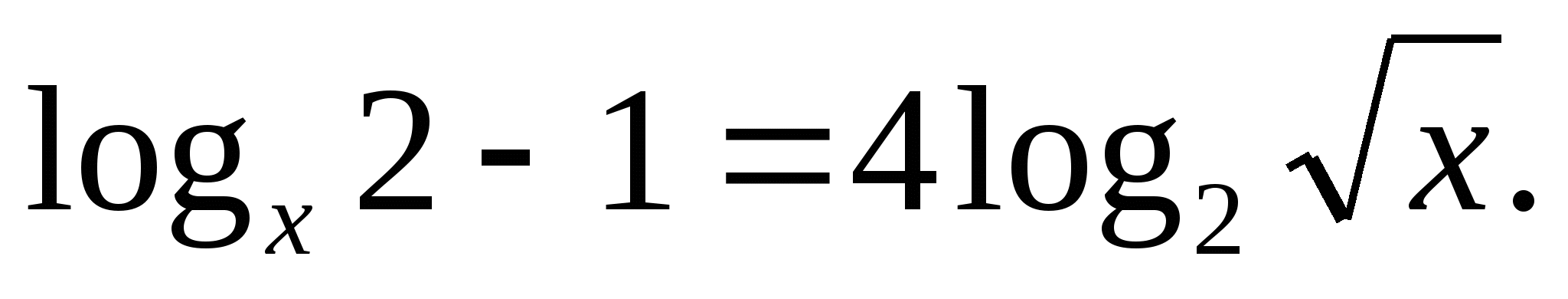
Решите систему уравнений 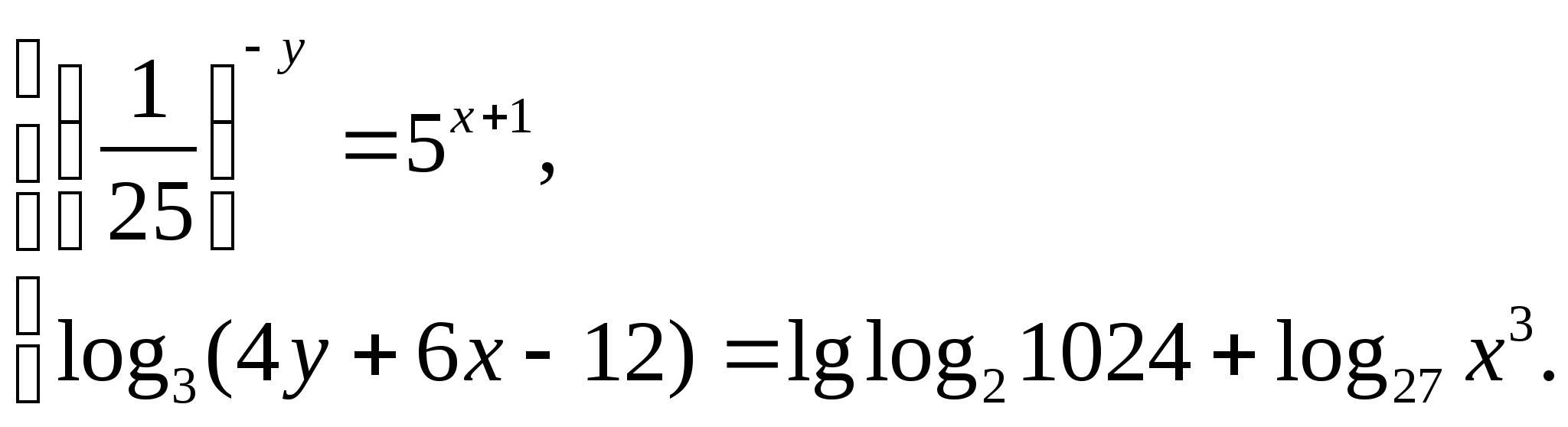
Контрольная работа №4
Вариант 3
Решите неравенство: 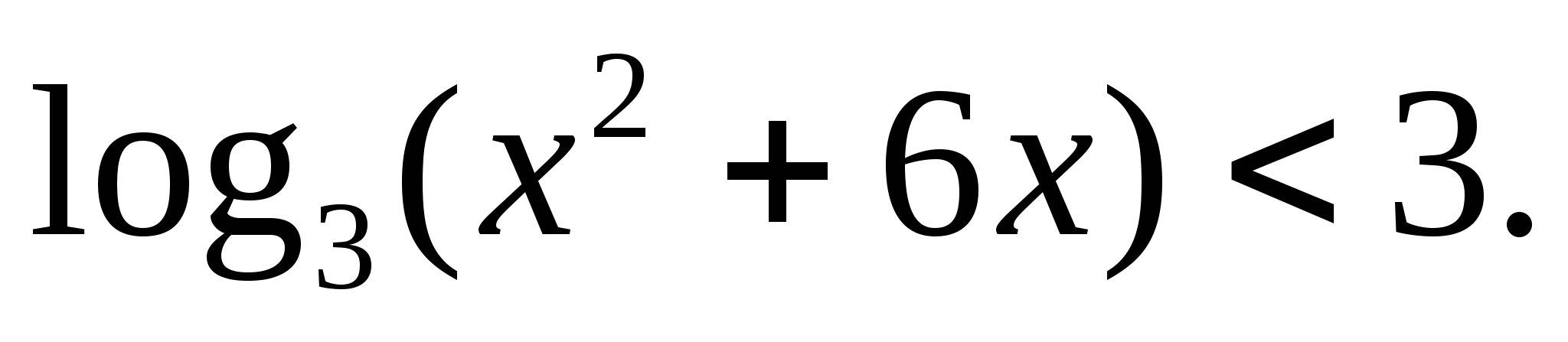
Исследуйте функцию 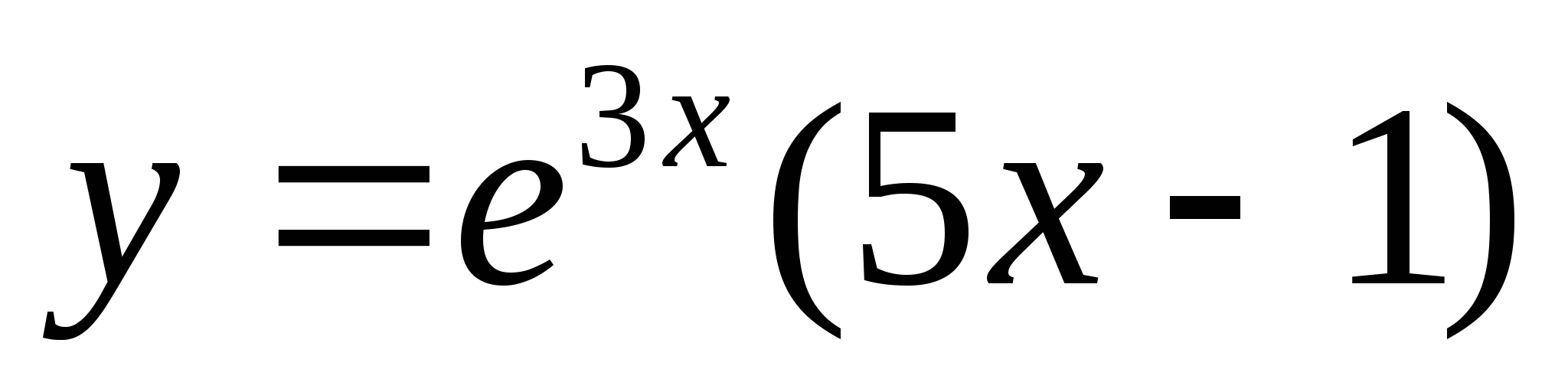 на монотонность и экстремумы.
на монотонность и экстремумы.
Напишите уравнение касательной к графику функции 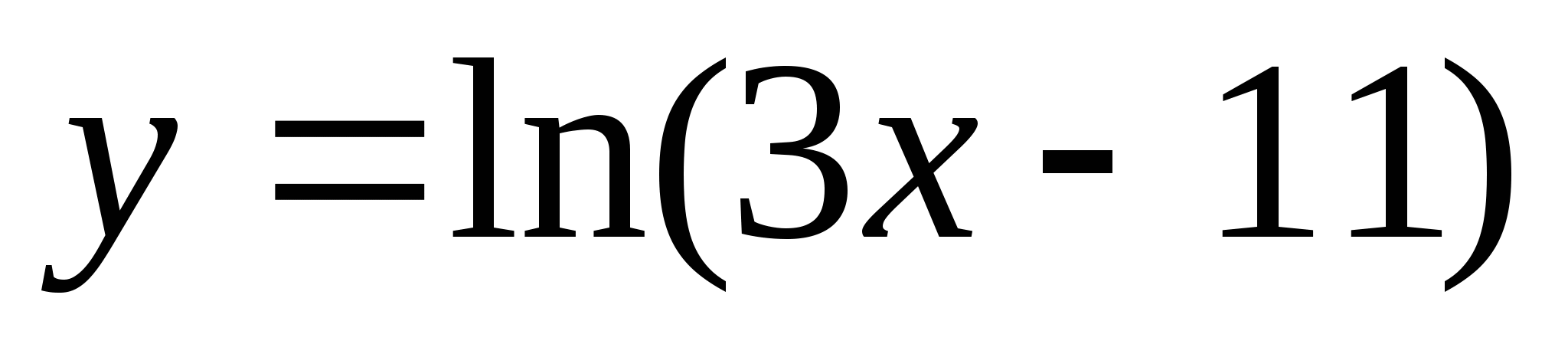
в точке x=4.
Решите уравнение: 2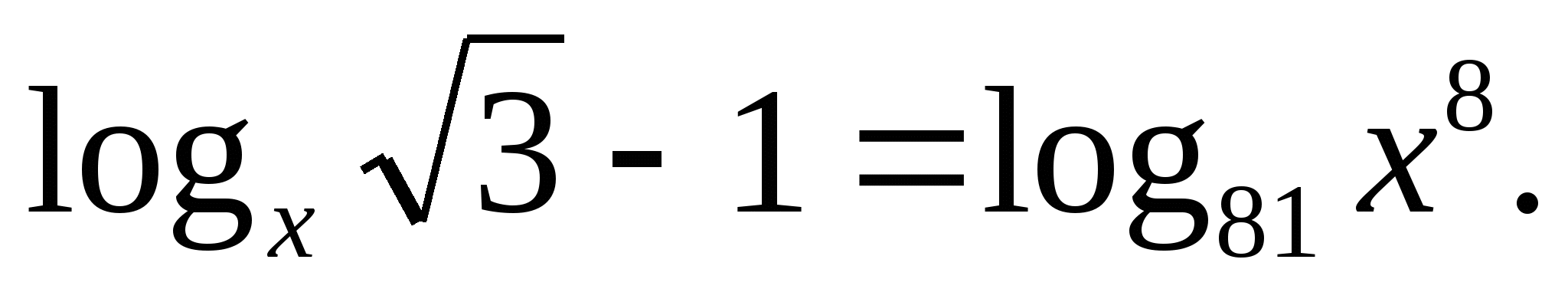
Решите систему уравнений 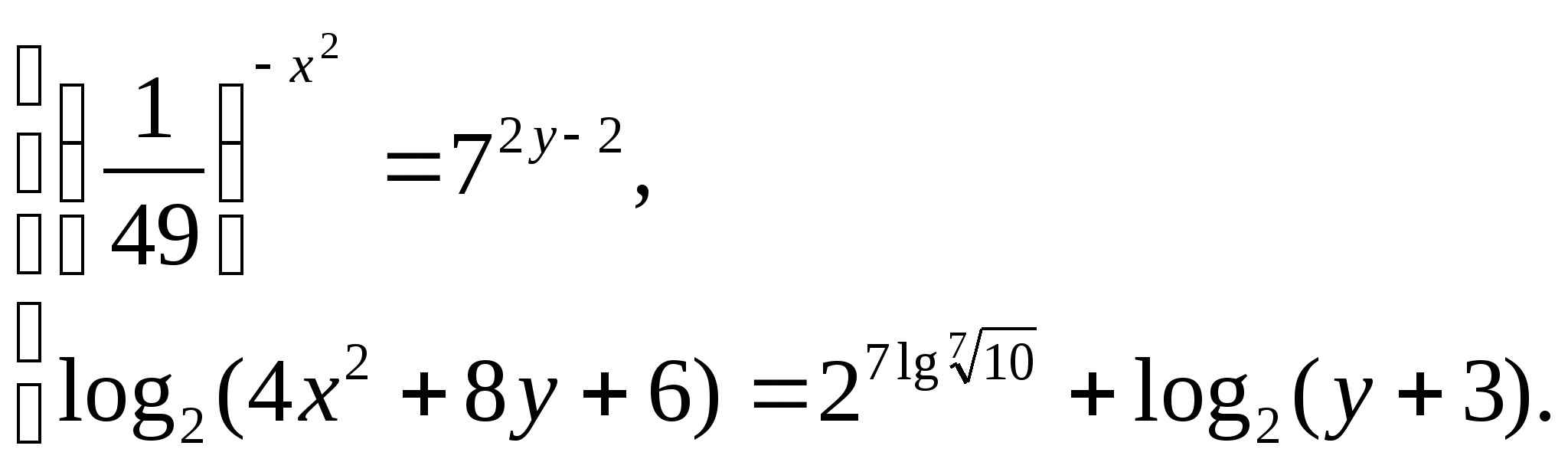
Контрольная работа №4
Вариант 4
Решите неравенство: 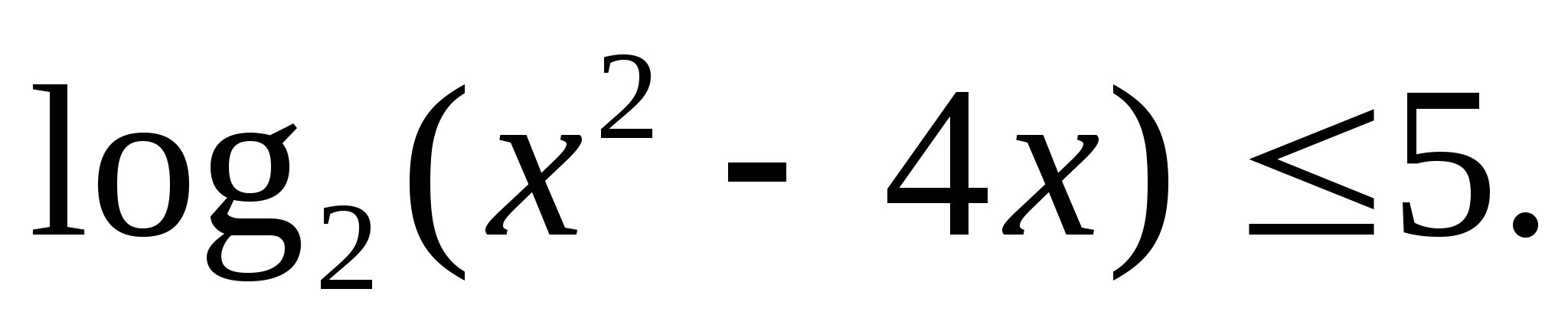
Исследуйте функцию 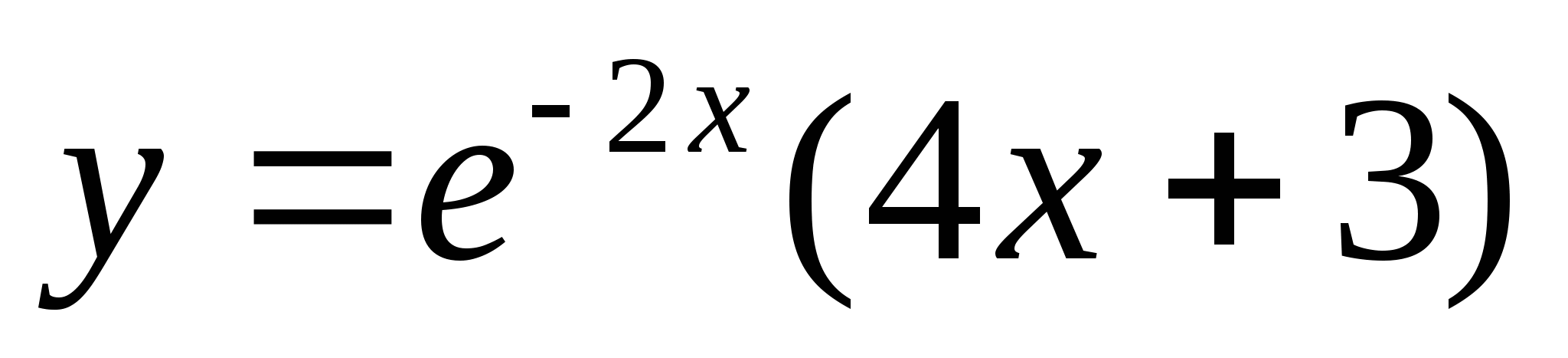 на монотонность и экстремумы.
на монотонность и экстремумы.
Напишите уравнение касательной к графику функции 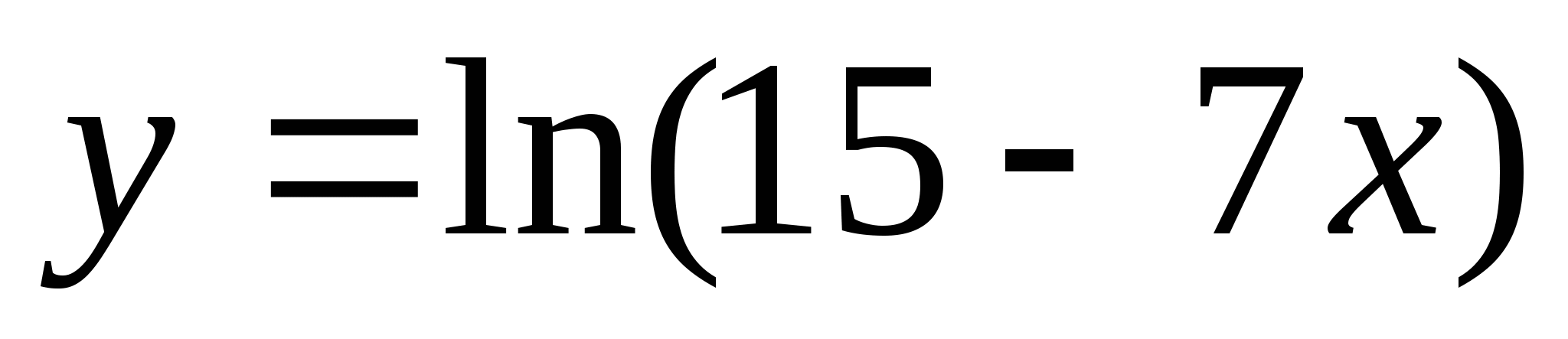
в точке x=2.
Решите уравнение: 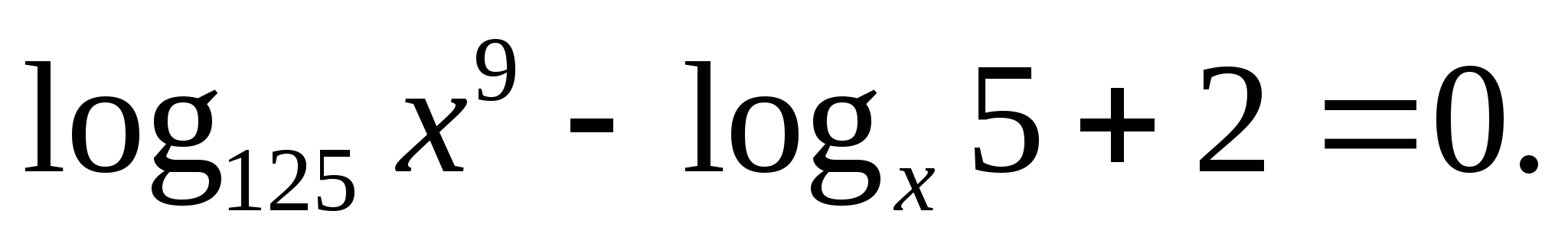
Решите систему уравнений 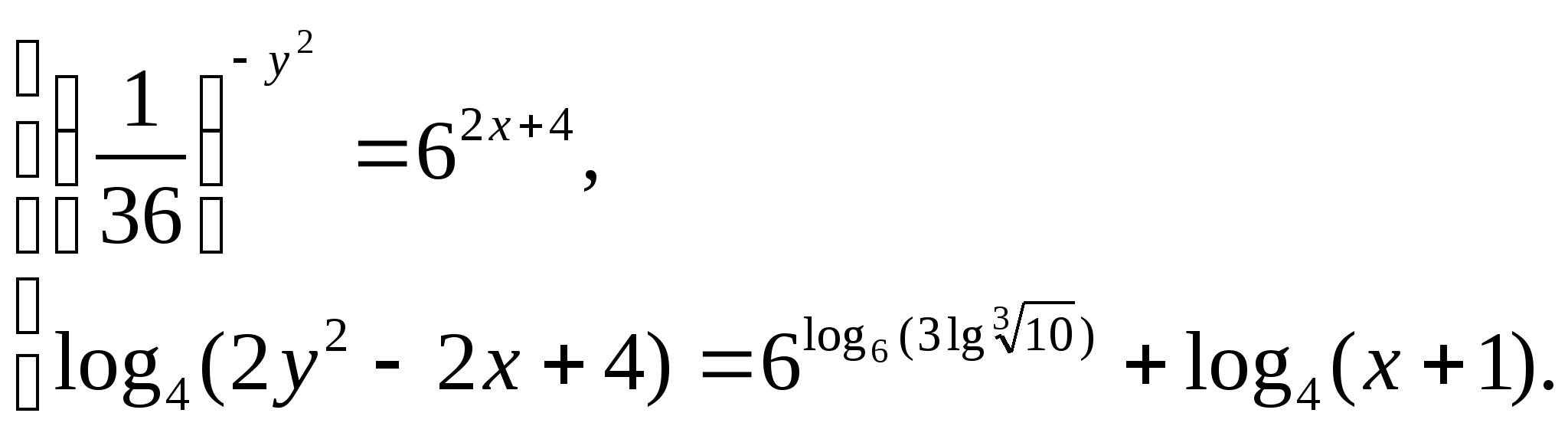
Контрольная работа №5
Вариант 1
Докажите, что функция 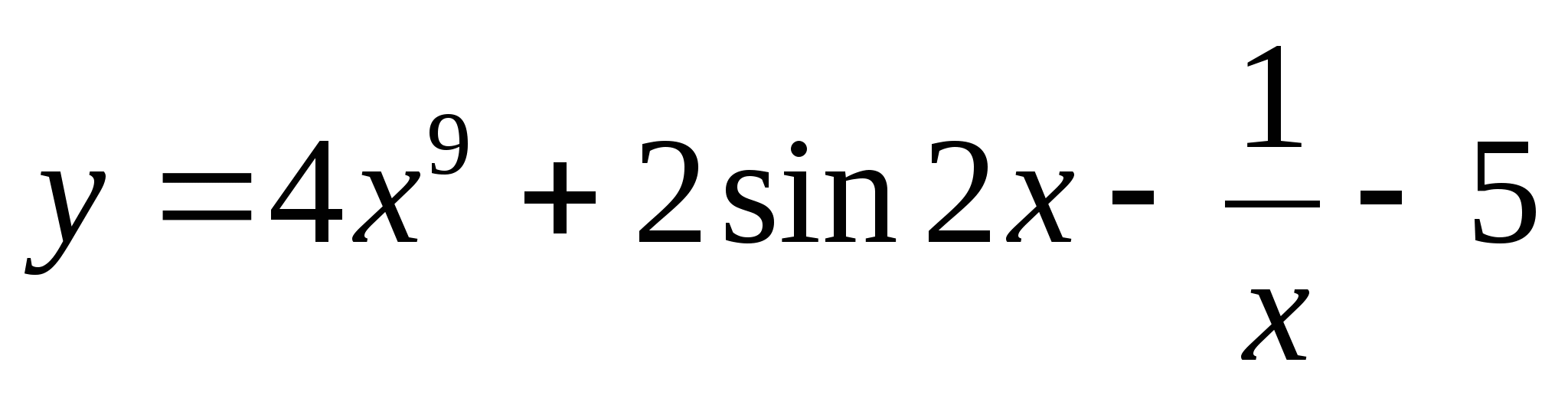 является первообразной для функции
является первообразной для функции 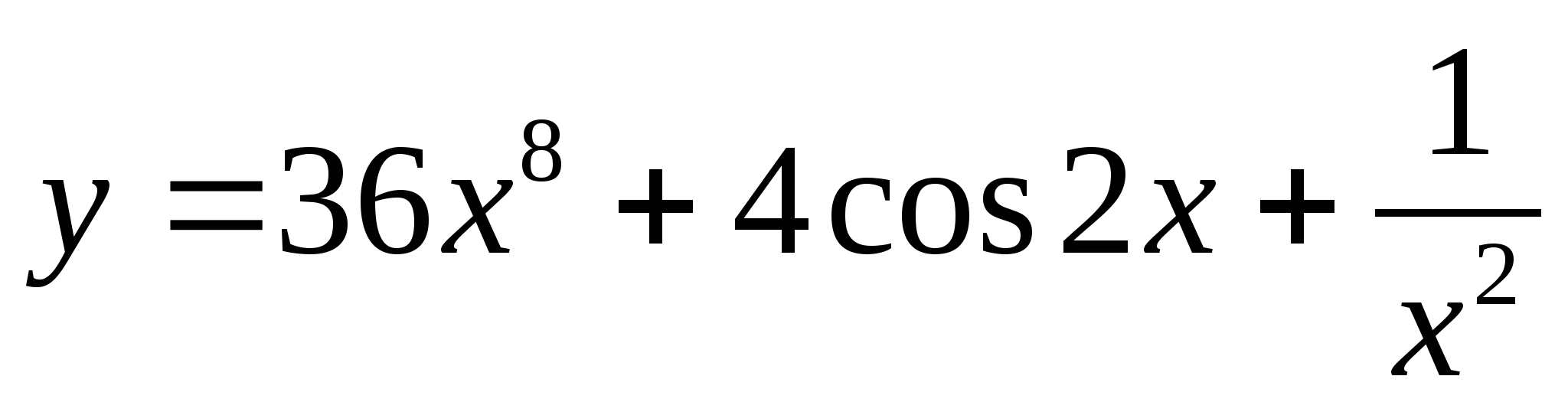 .
.
Для данной функции 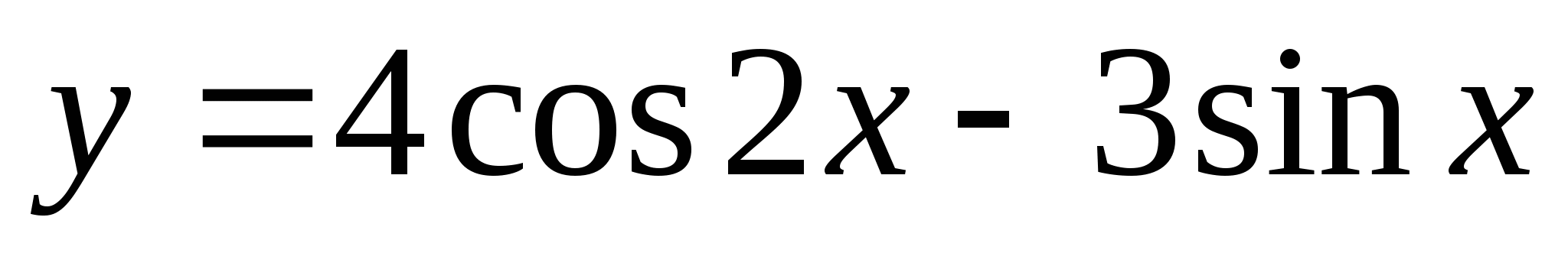 найдите ту первообразную, график которой проходит через заданную точку А (-π;0).
найдите ту первообразную, график которой проходит через заданную точку А (-π;0).
Вычислите интеграл: а) 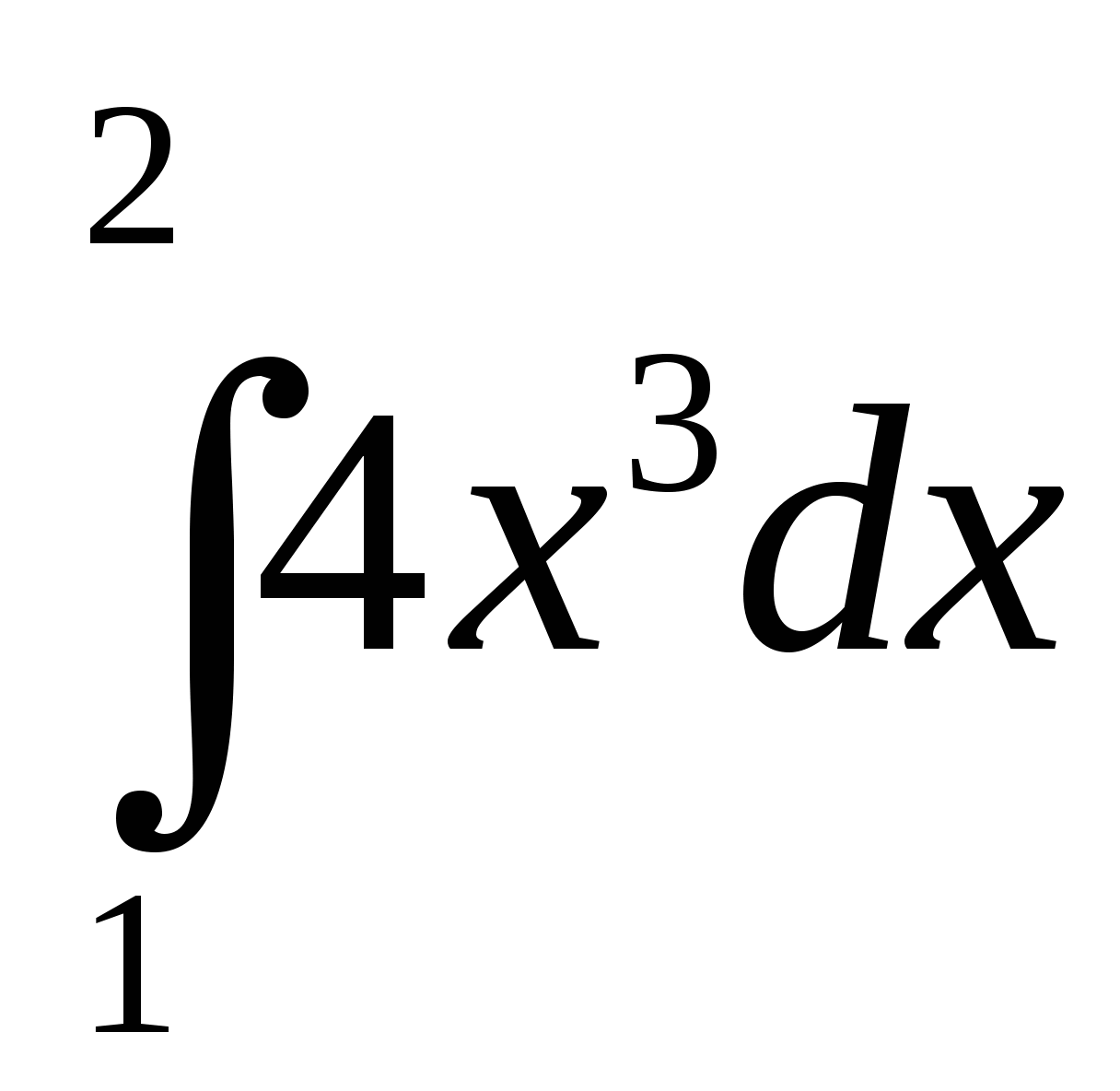 ; б)
; б) 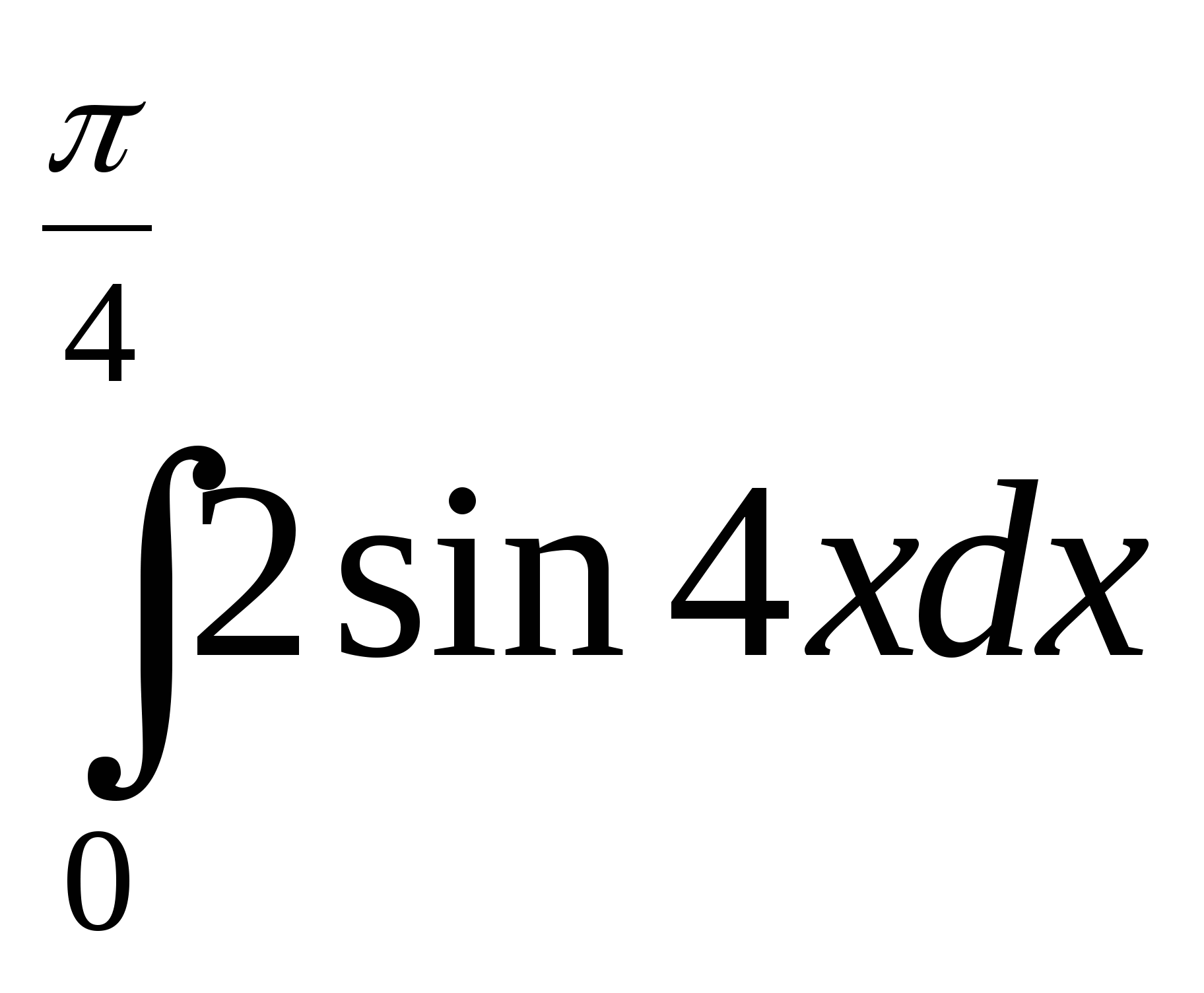 .
.
Вычислите площадь фигуры, ограниченной линиями 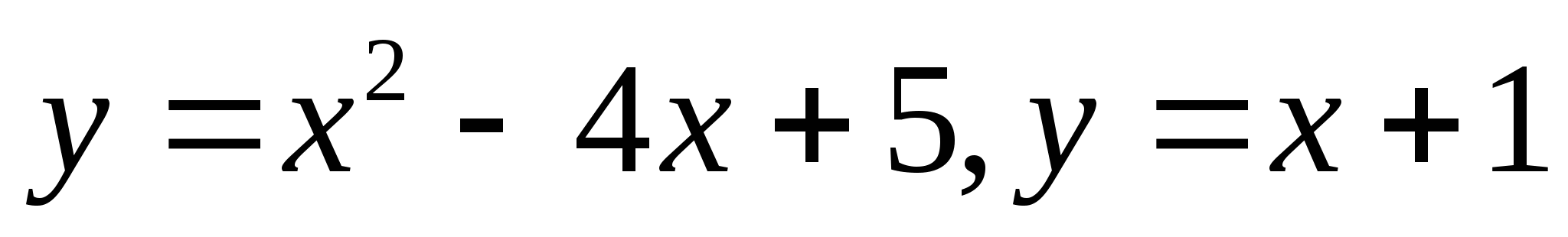 .
.
Известно, что функция 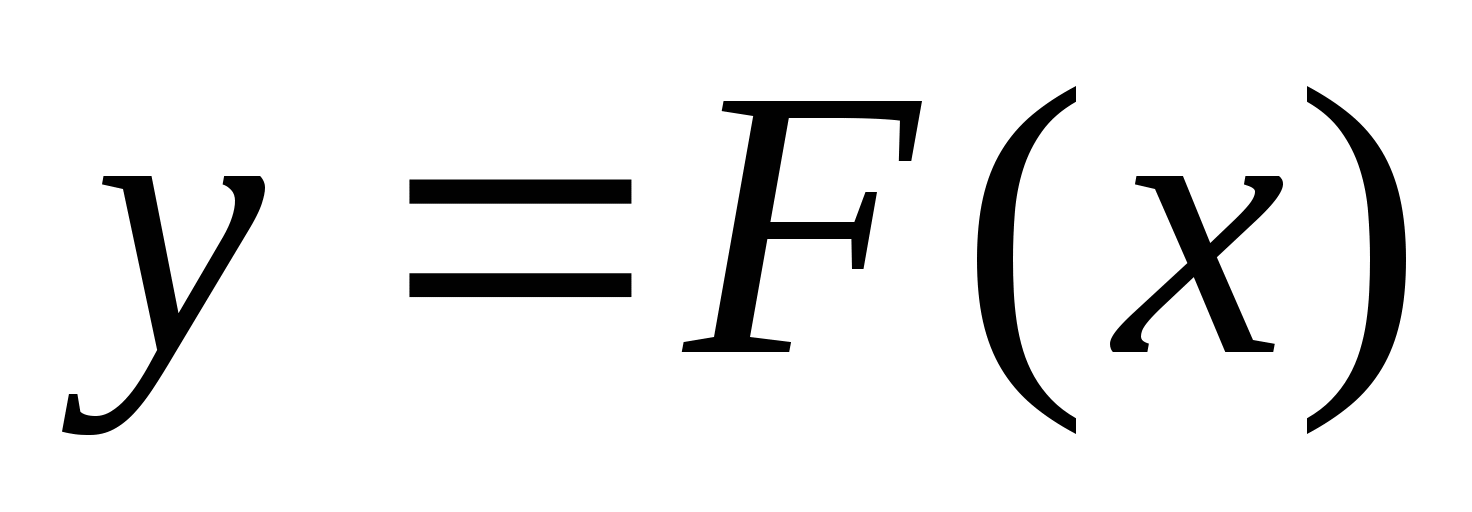 – первообразная для функции
– первообразная для функции 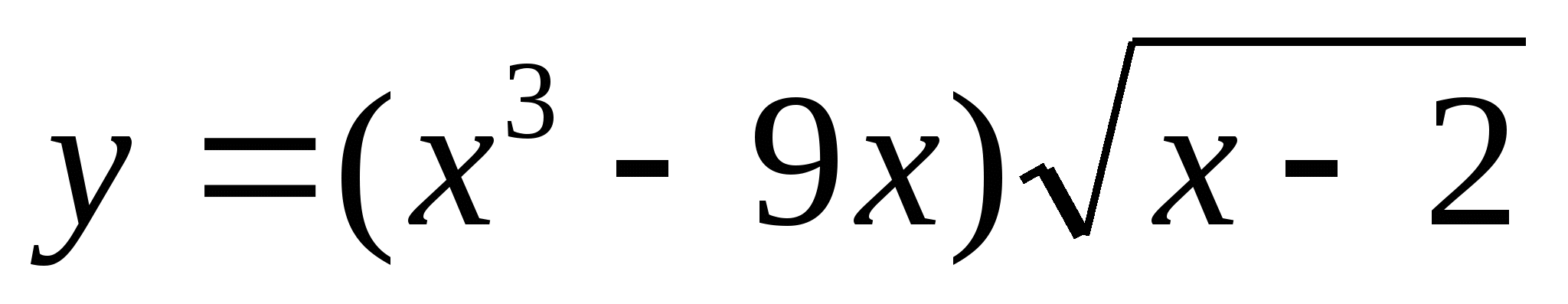 . Исследуйте функцию
. Исследуйте функцию 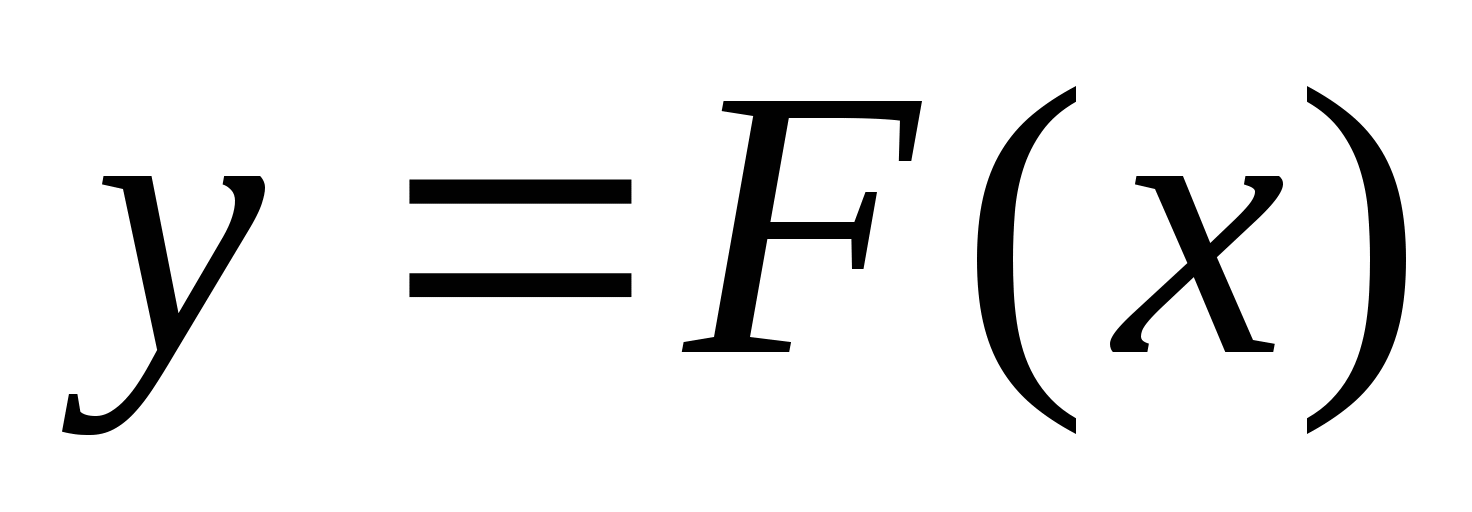 на монотонность и экстремумы.
на монотонность и экстремумы.
Контрольная работа №5
Вариант 2
Докажите, что функция  является первообраз-ной для функции
является первообраз-ной для функции 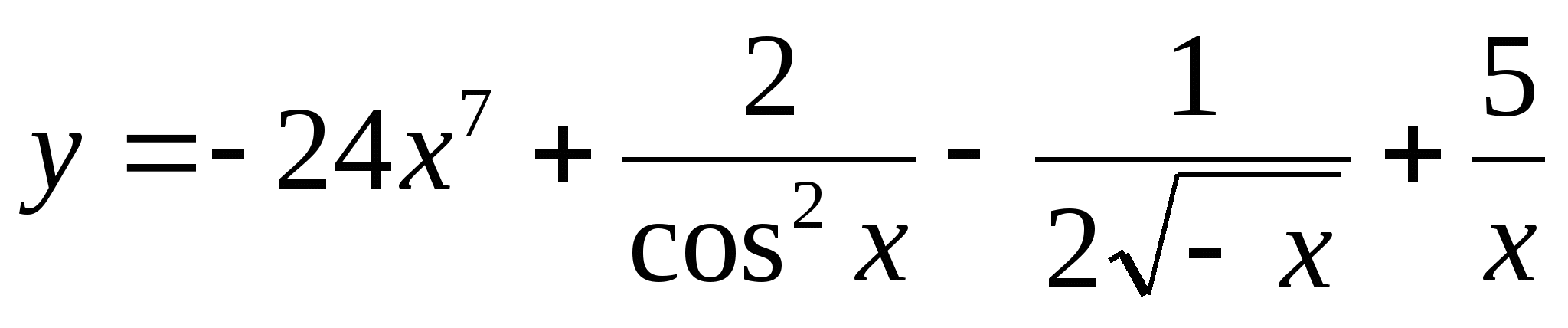 .
.
Для данной функции 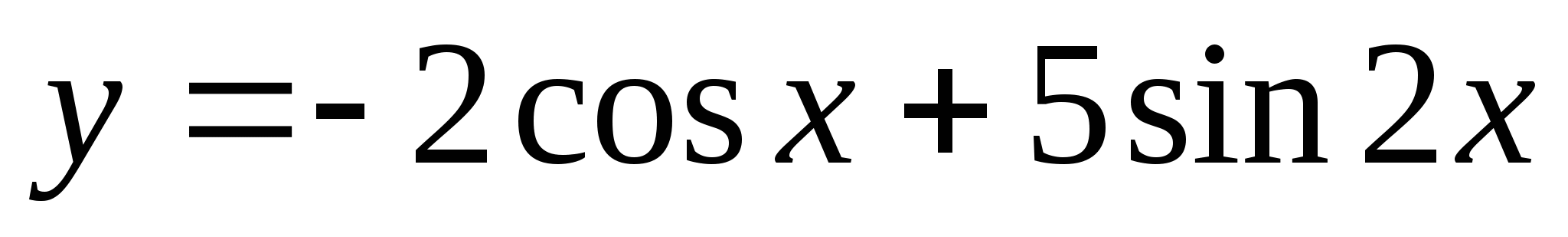 найдите ту первообразную, график которой проходит через заданную точку А (-
найдите ту первообразную, график которой проходит через заданную точку А (-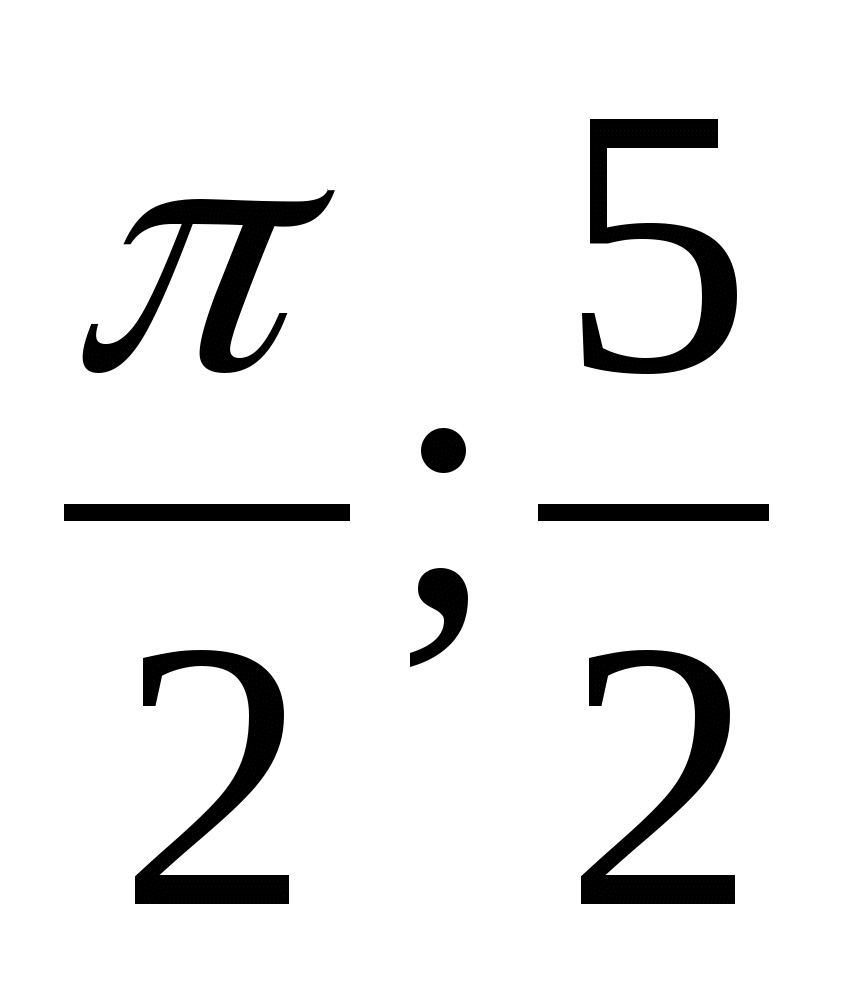 ).
).
Вычислите интеграл: а) 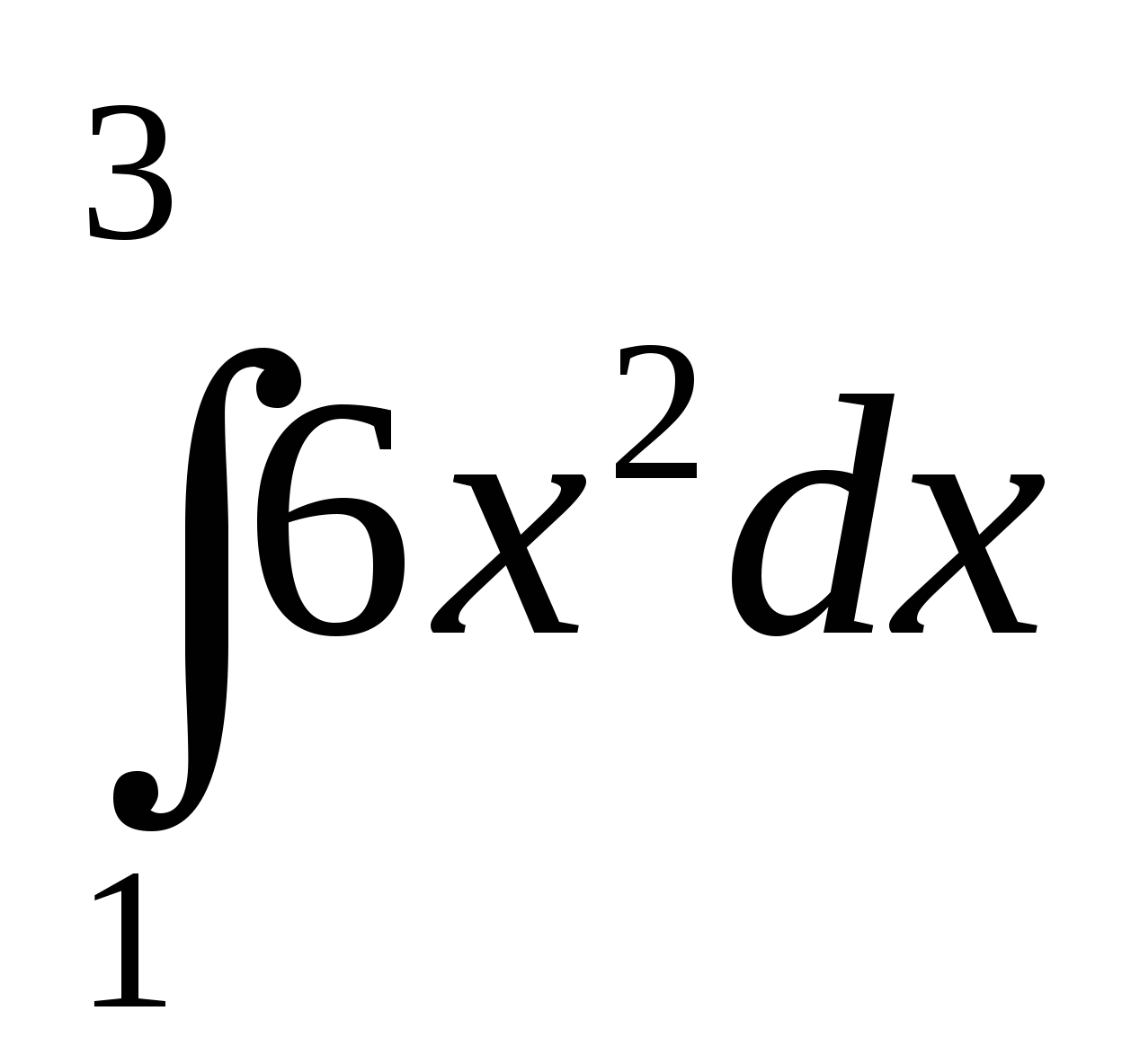 ; б)
; б) 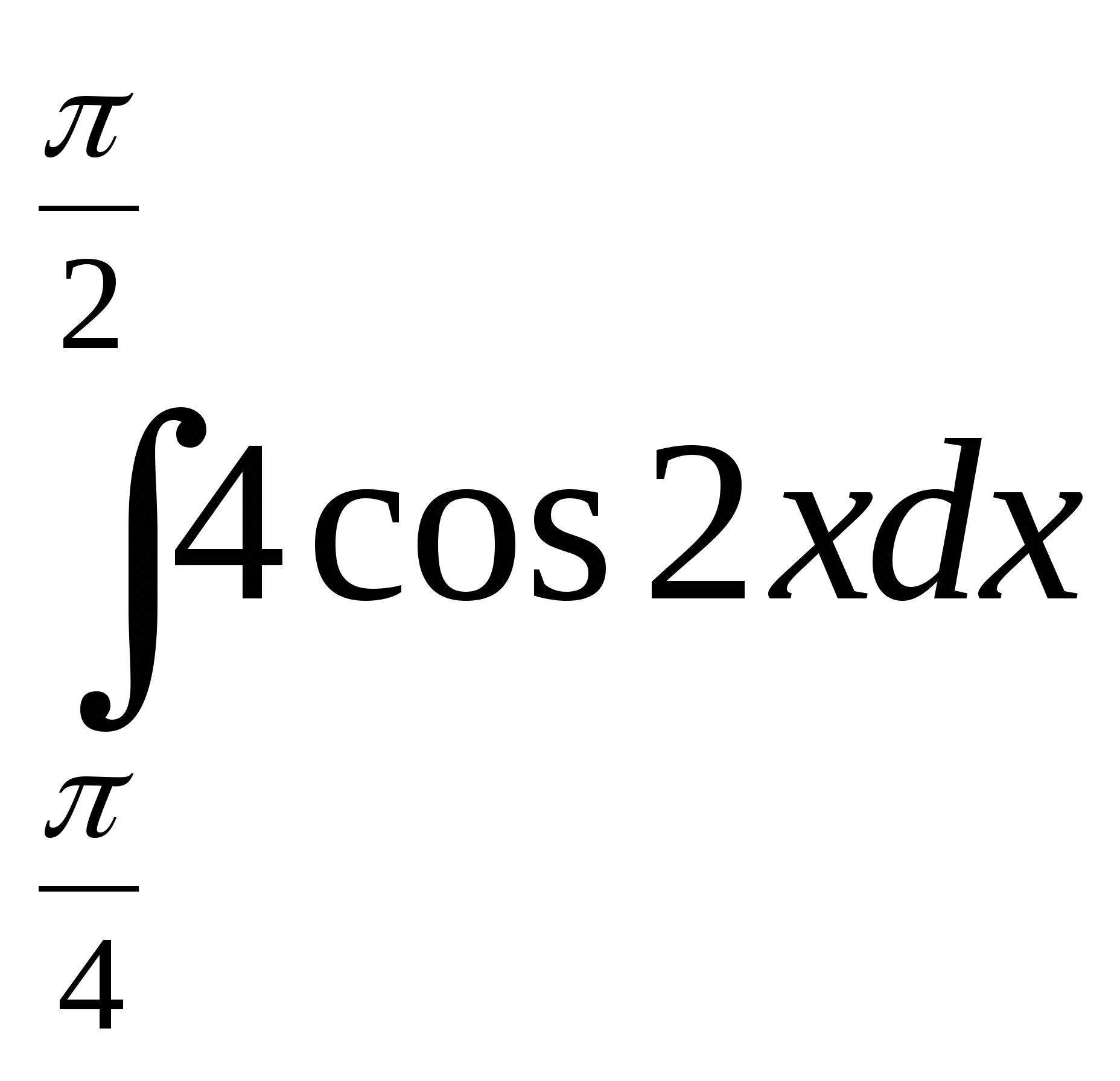 .
.
Вычислите площадь фигуры, ограниченной линиями 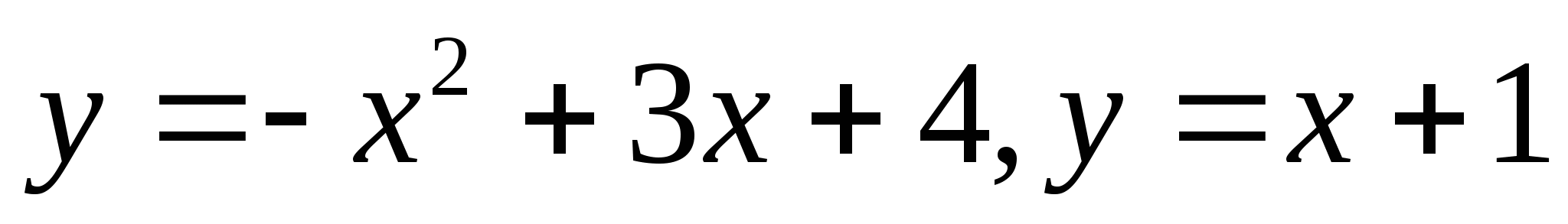 .
.
Известно, что функция 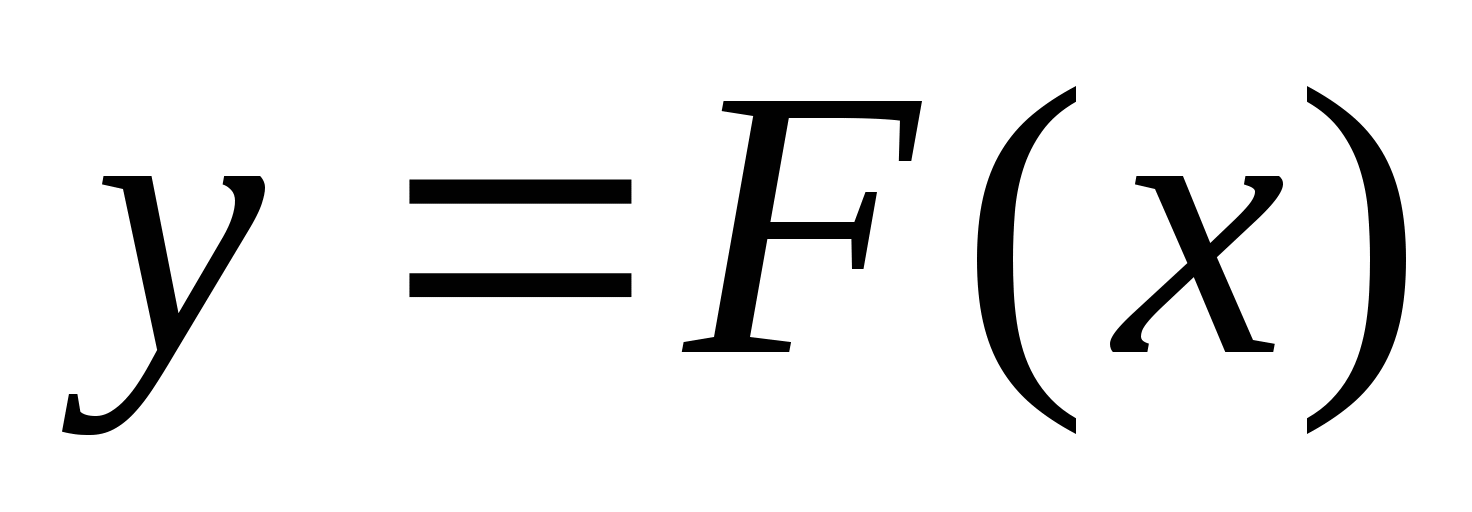 – первообразная для функции
– первообразная для функции 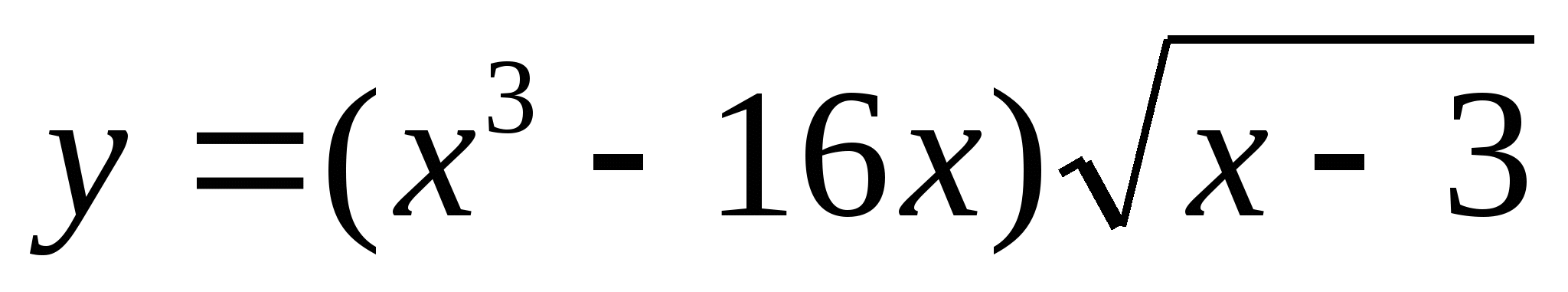 . Исследуйте функцию
. Исследуйте функцию 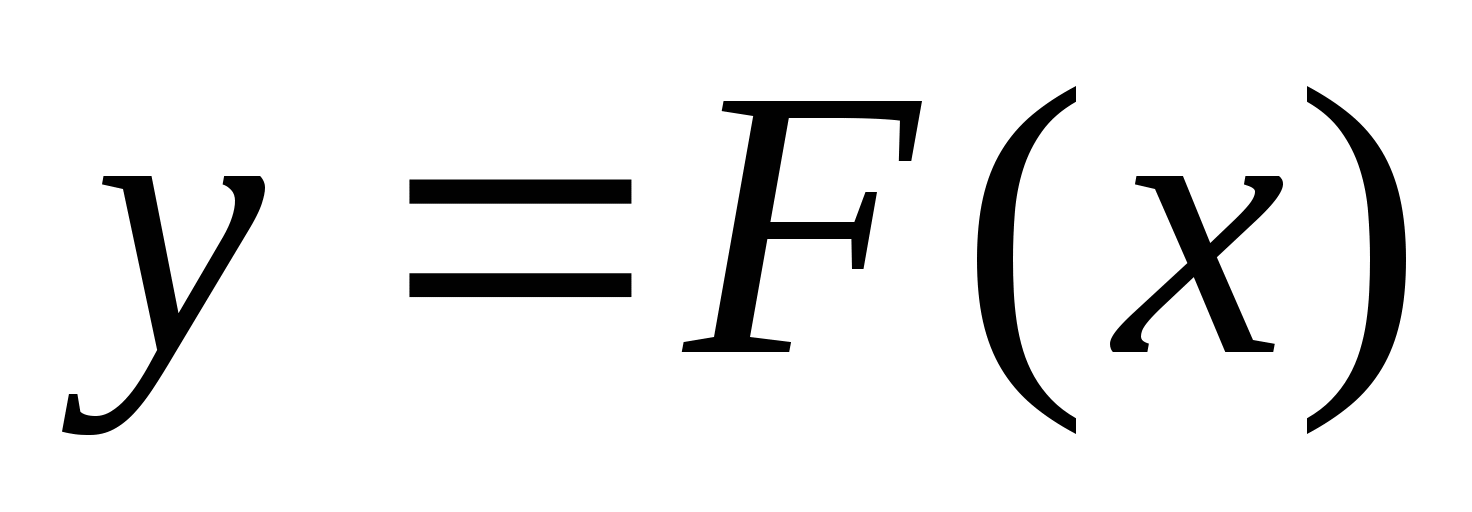 на монотонность и экстремумы.
на монотонность и экстремумы.
Контрольная работа №5
Вариант 3
Докажите, что функция 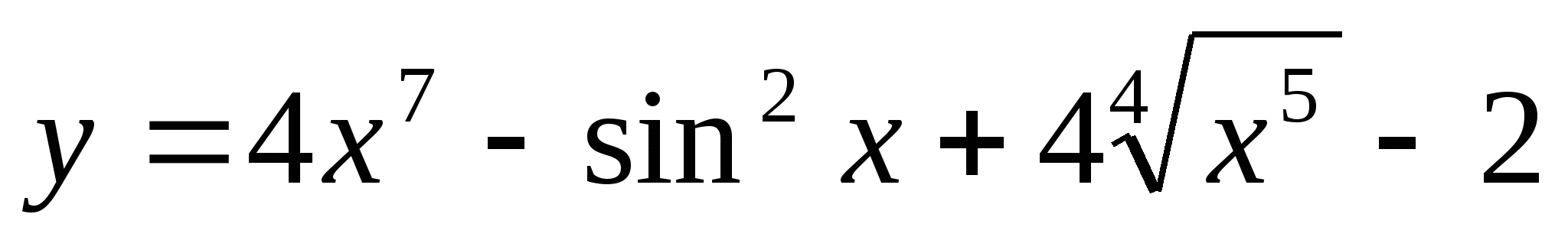 является первообразной для функции
является первообразной для функции 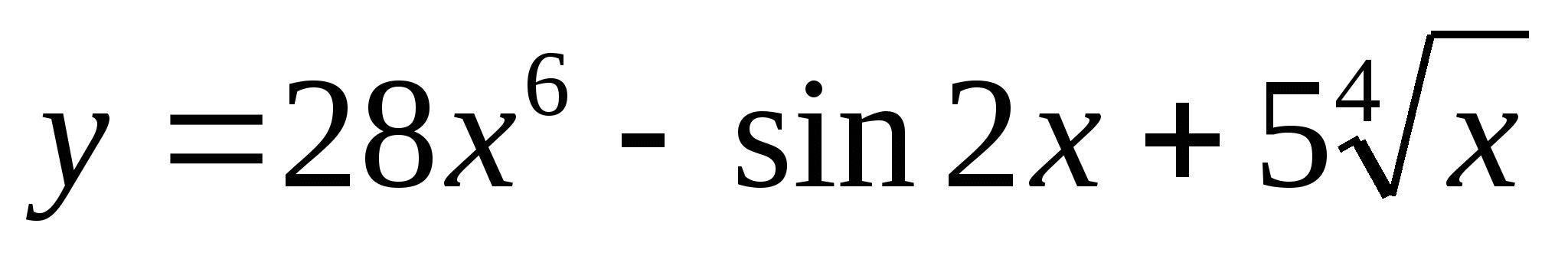 .
.
Для данной функции 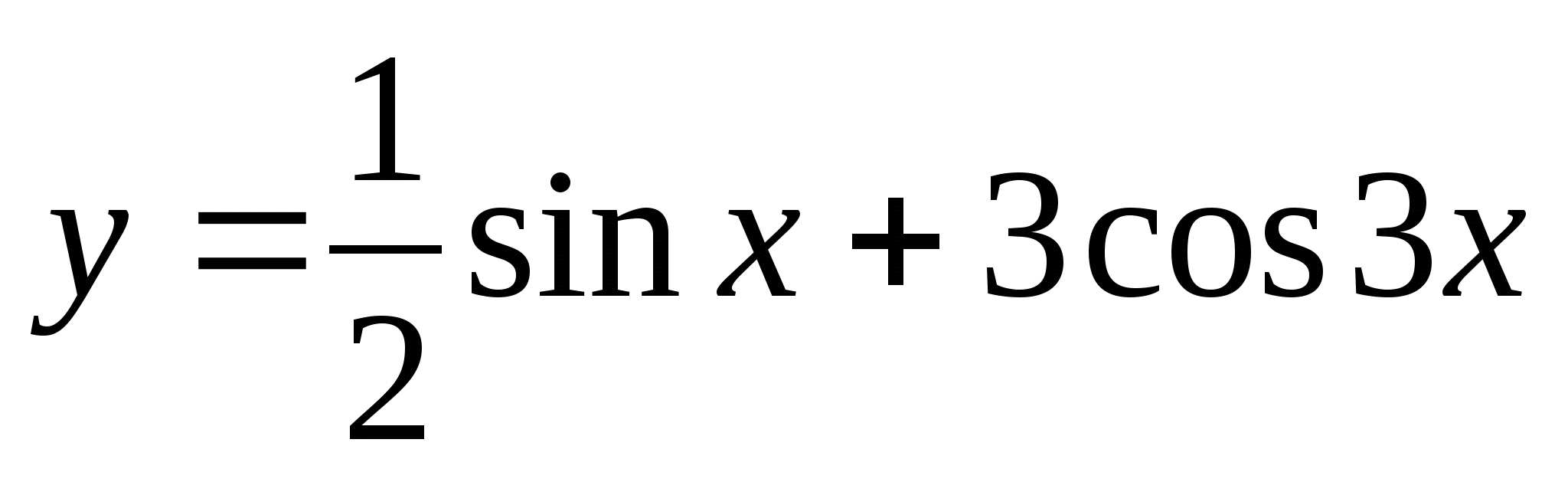 найдите ту первообразную, график которой проходит через заданную точку А (
найдите ту первообразную, график которой проходит через заданную точку А (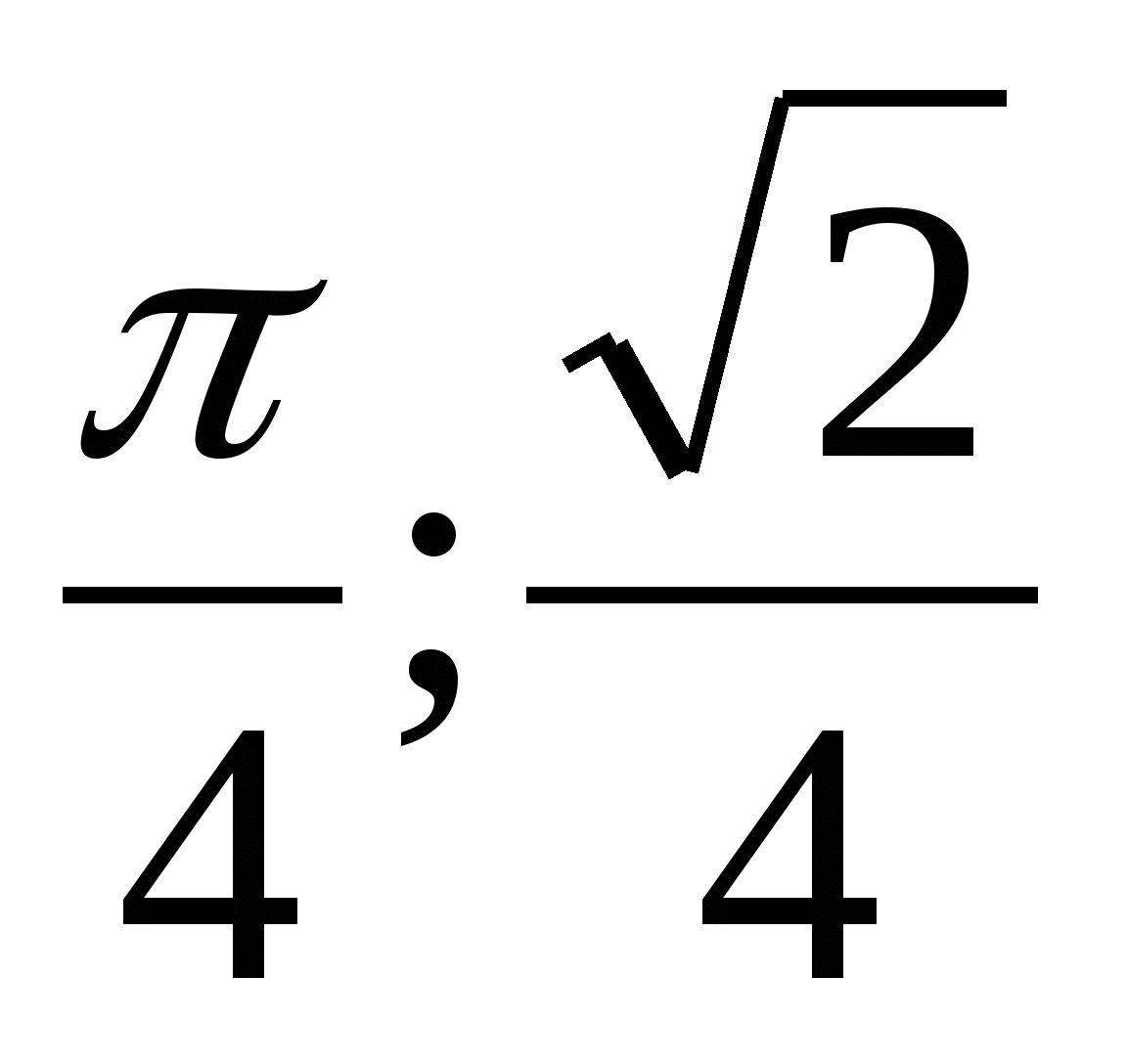 ).
).
Вычислите интеграл: а) 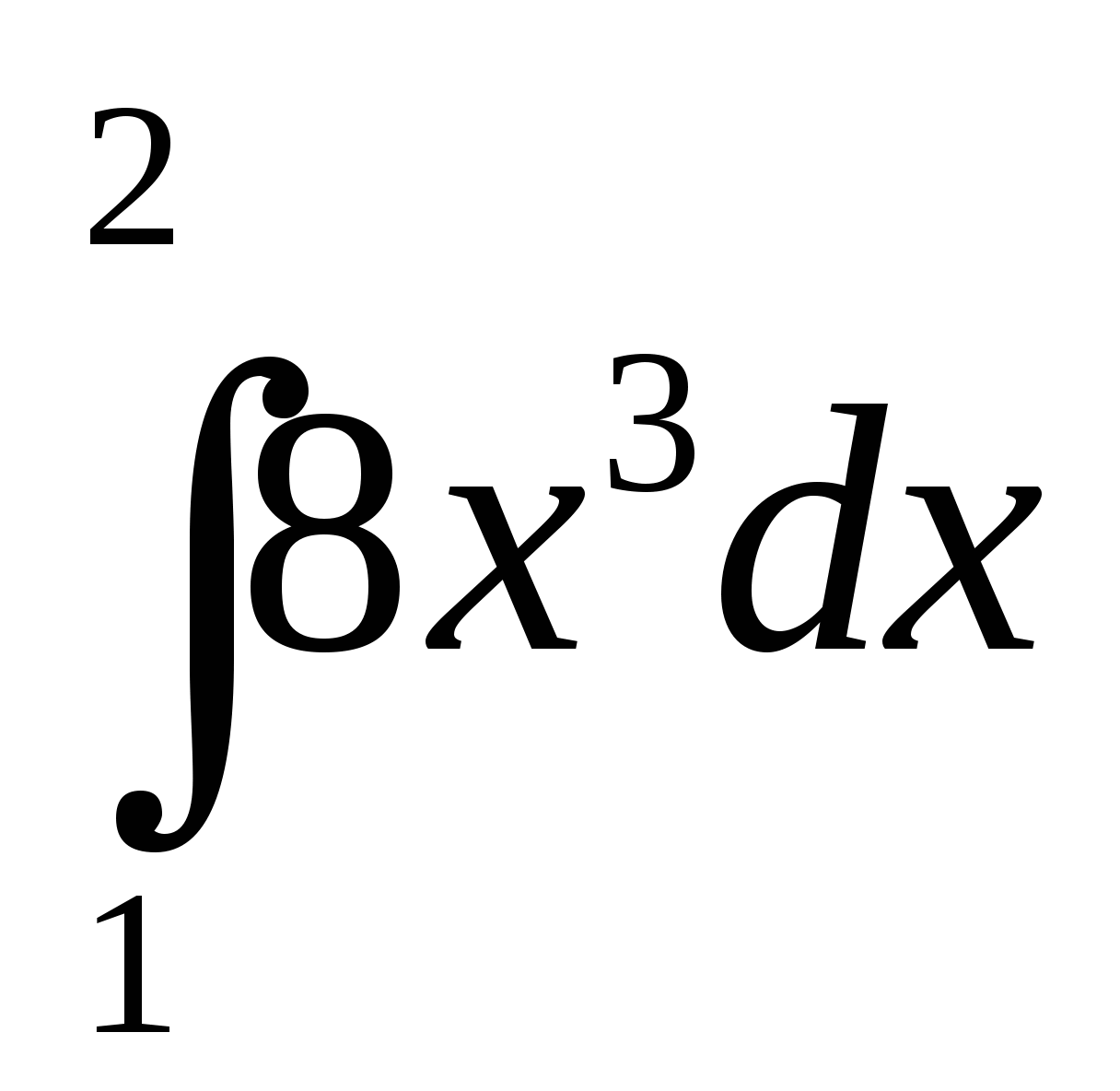 ; б)
; б) 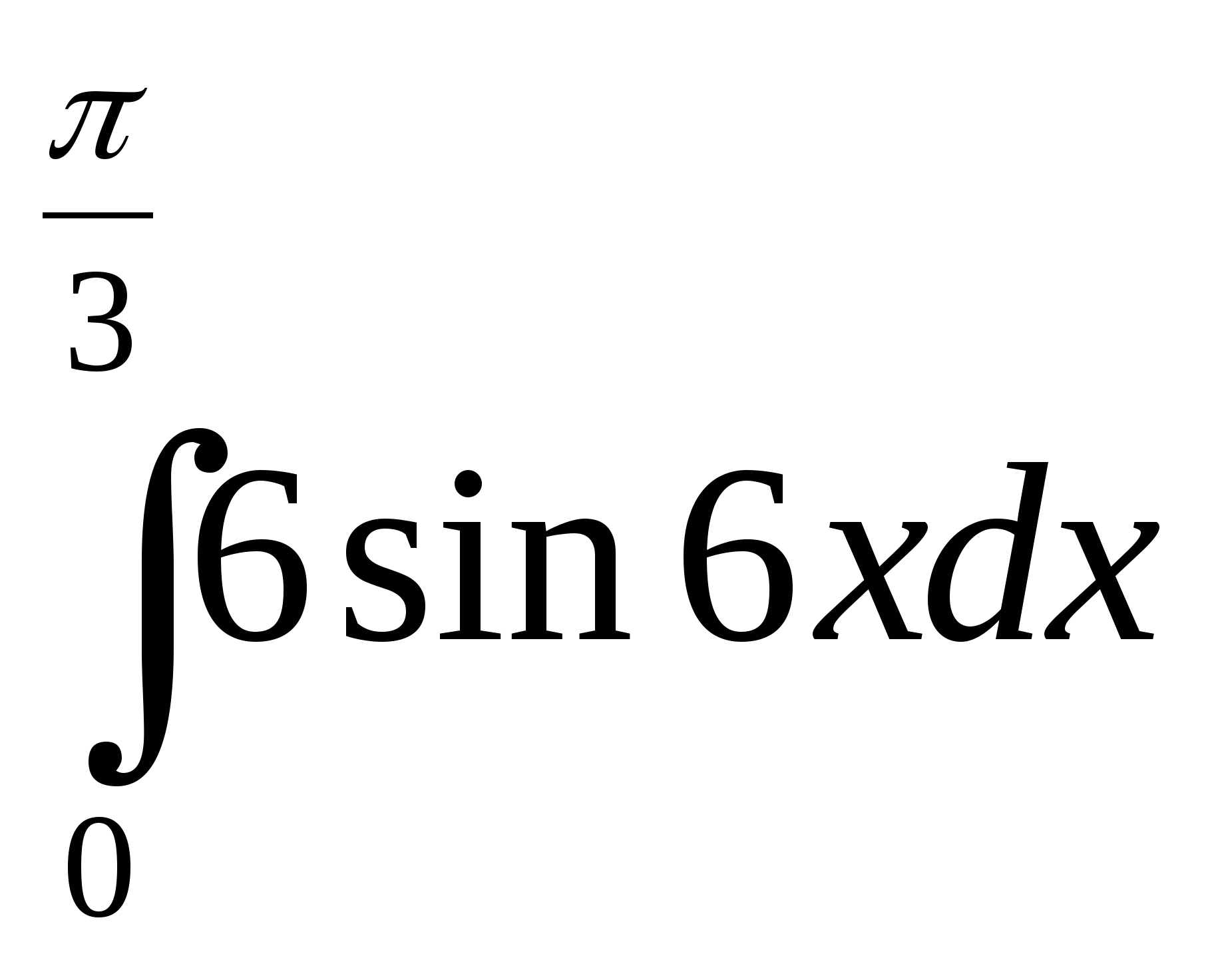 .
.
Вычислите площадь фигуры, ограниченной линиями 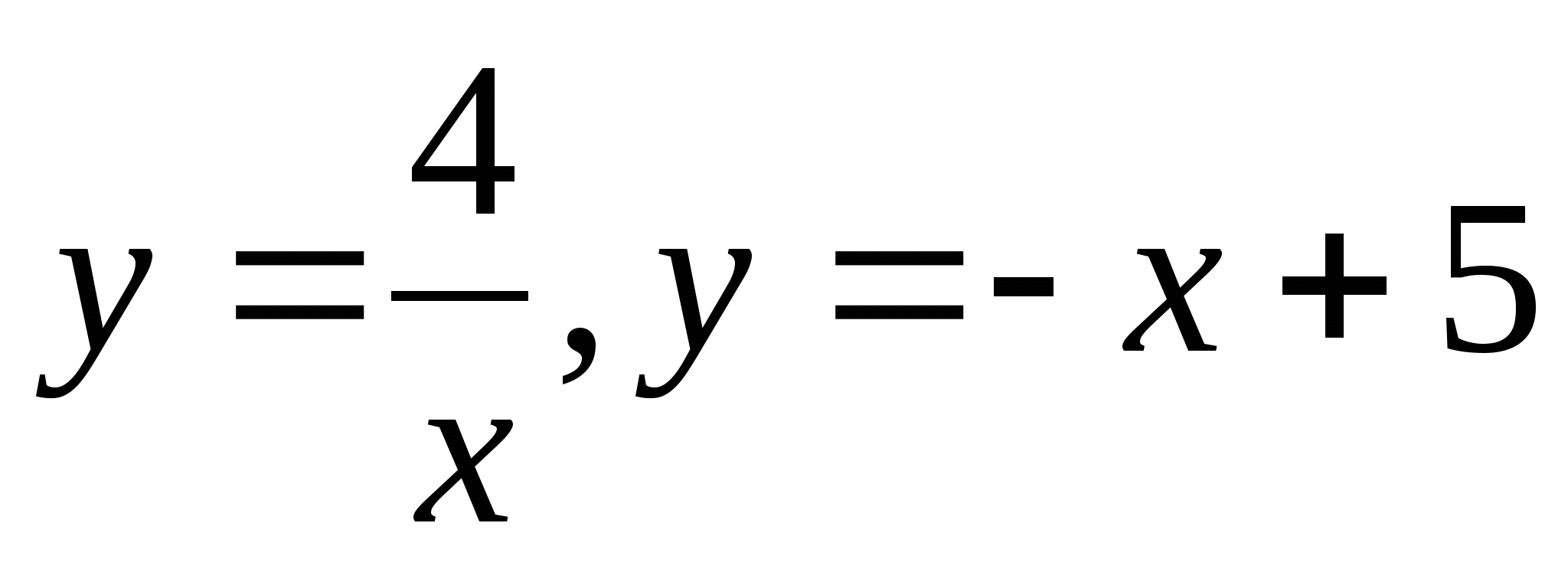 .
.
Известно, что функция 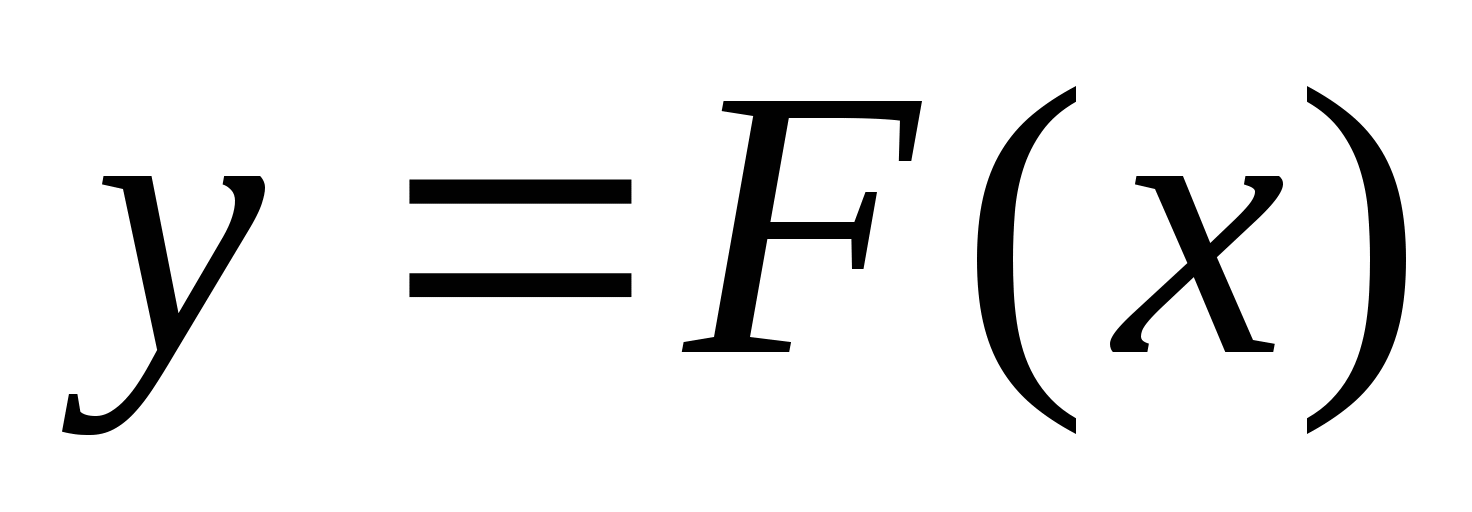 – первообразная для функции
– первообразная для функции 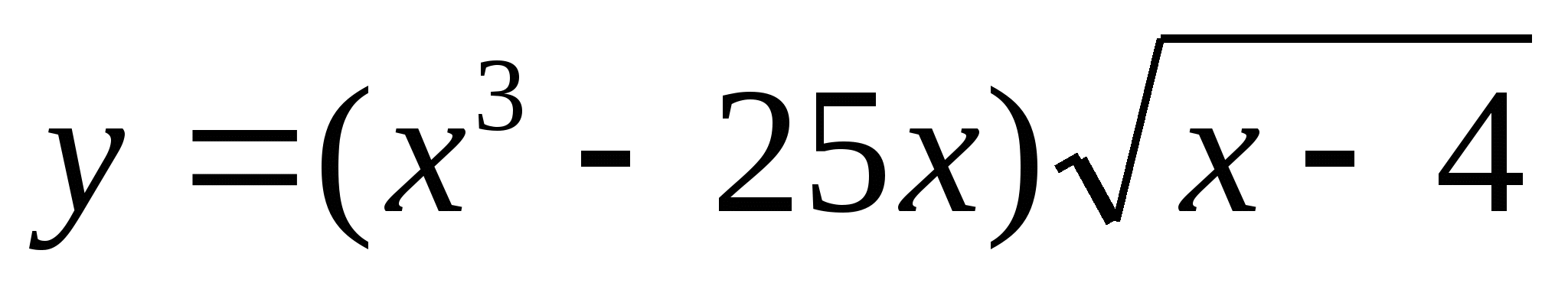 . Сравните числа F (6) и F (7).
. Сравните числа F (6) и F (7).
Контрольная работа №5
Вариант 4
Докажите, что функция 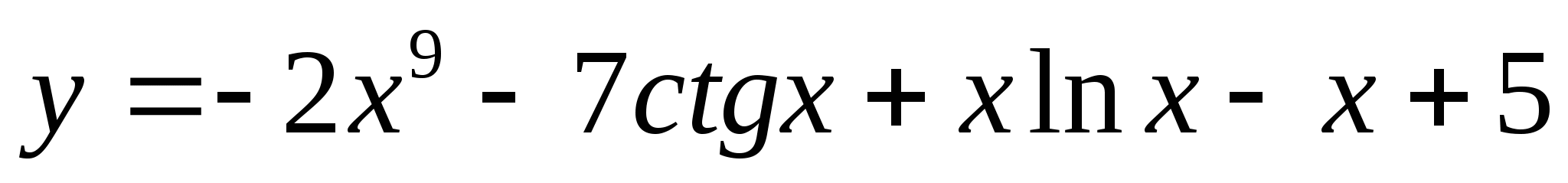 является первообразной для функции
является первообразной для функции 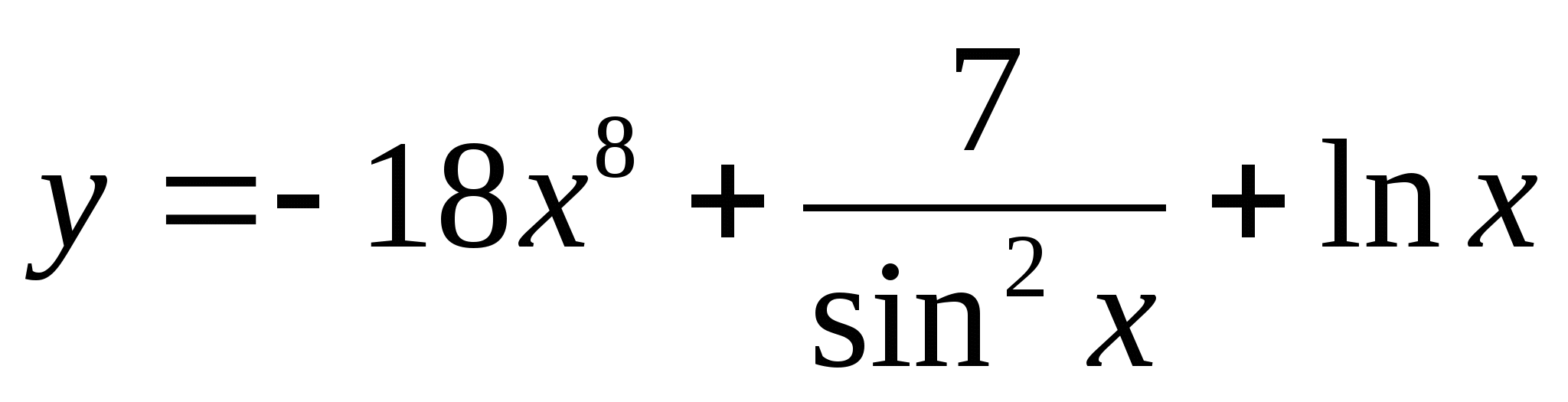 .
.
Для данной функции 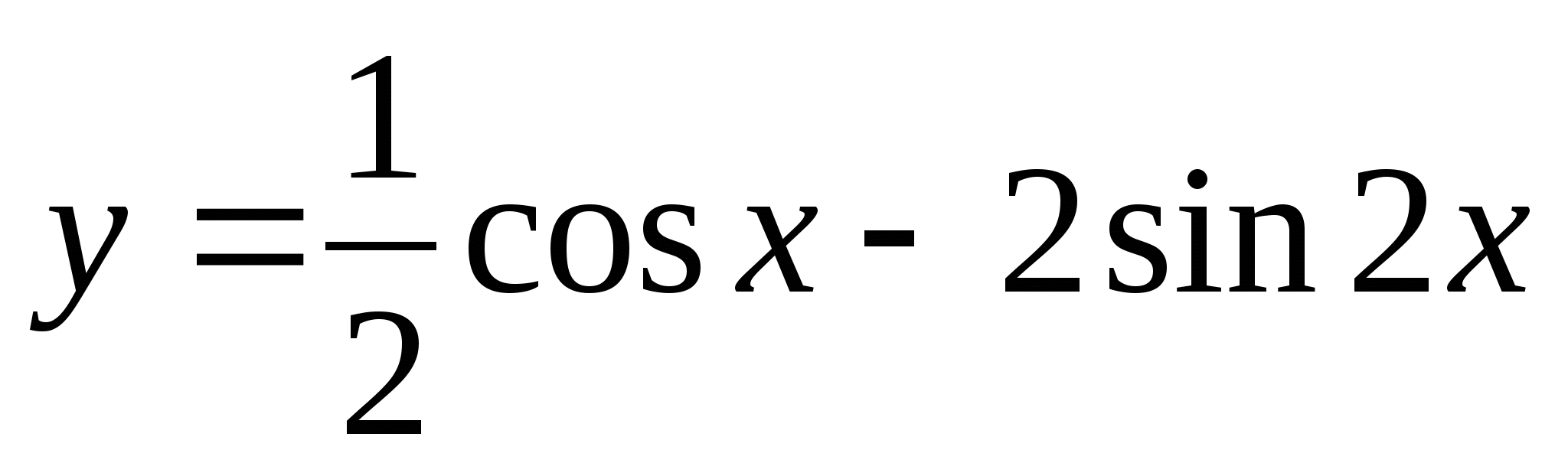 найдите ту первообразную, график которой проходит через заданную точку А (
найдите ту первообразную, график которой проходит через заданную точку А (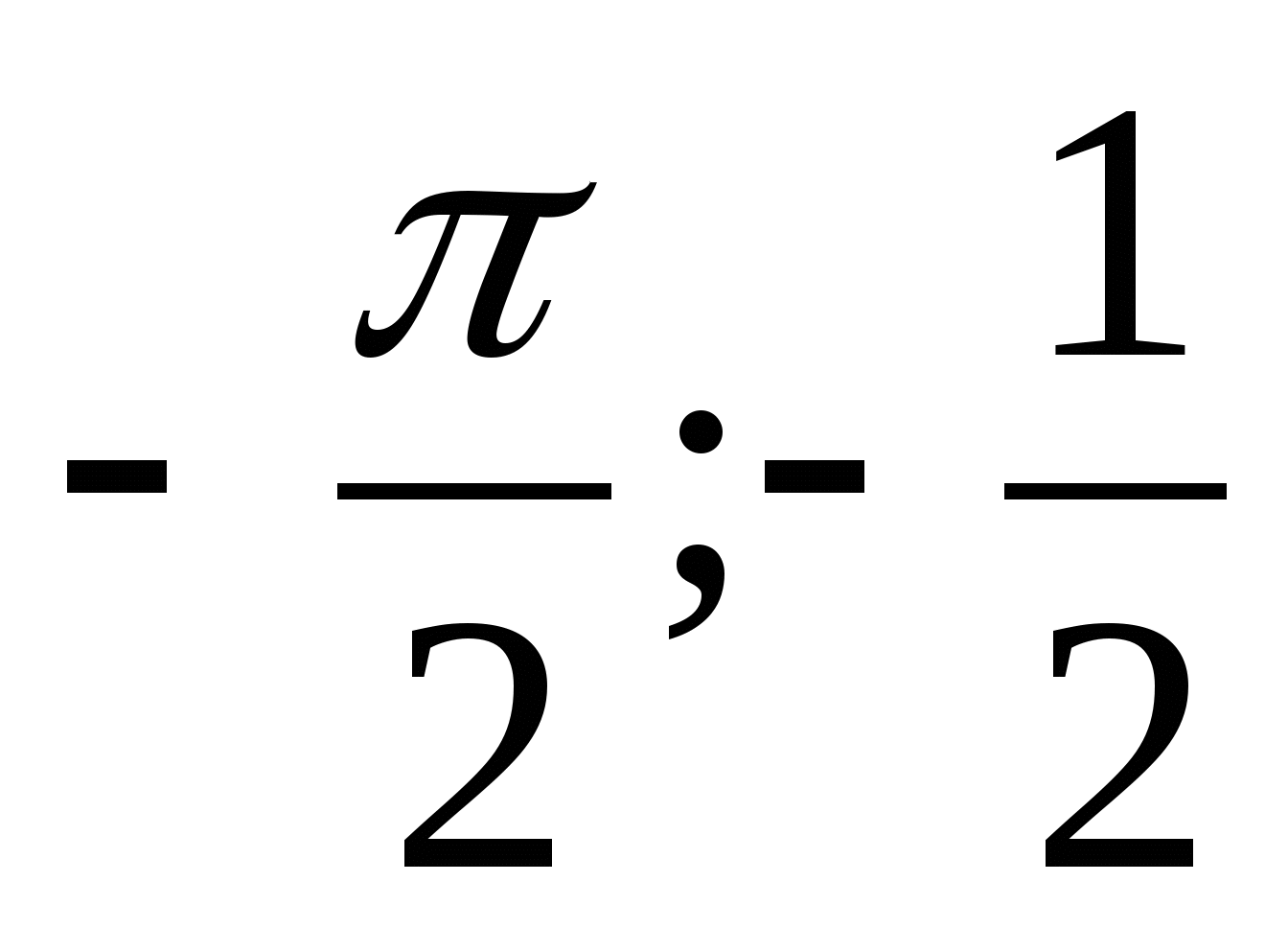 ).
).
Вычислите интеграл: а) 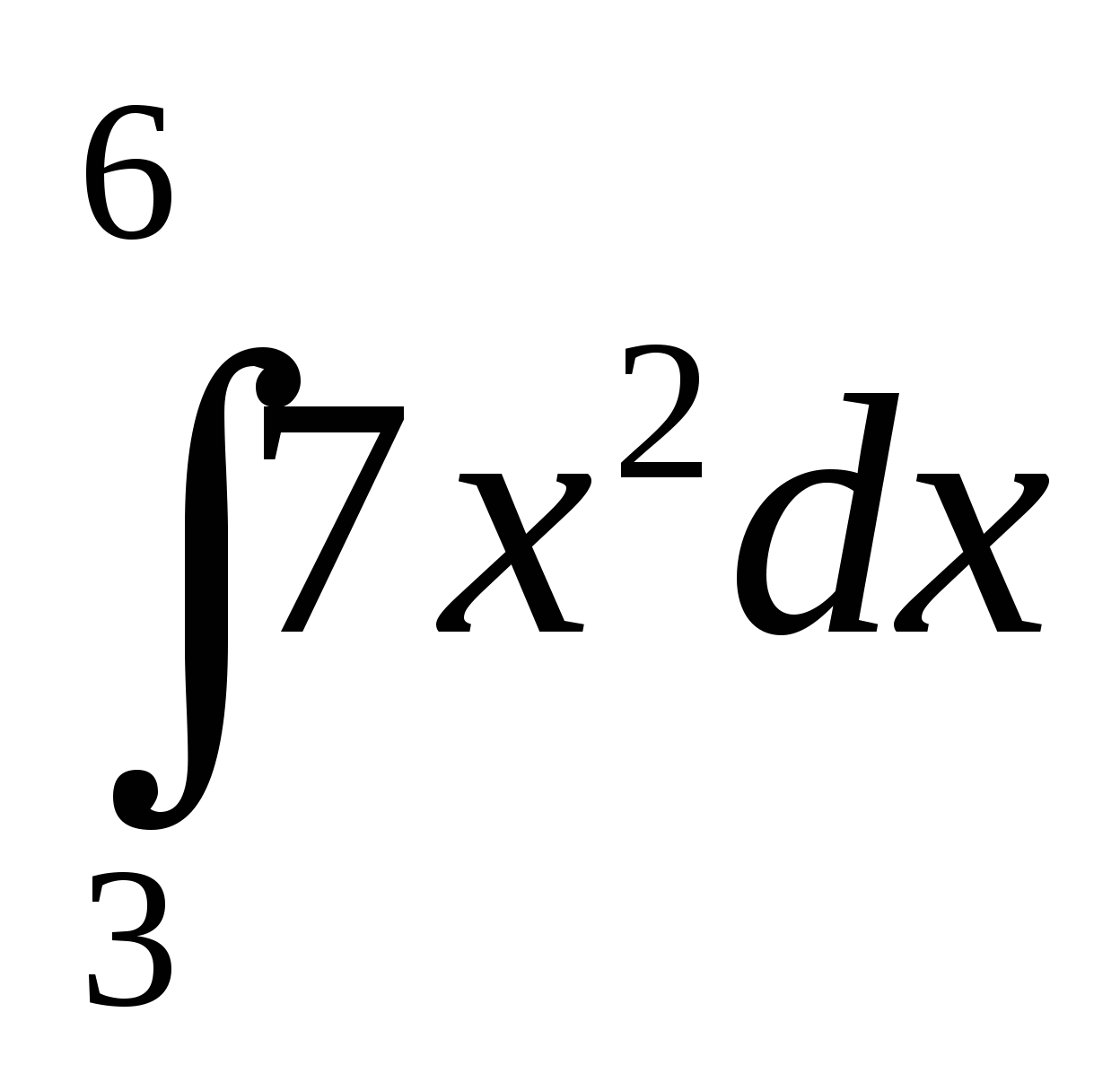 ; б)
; б) 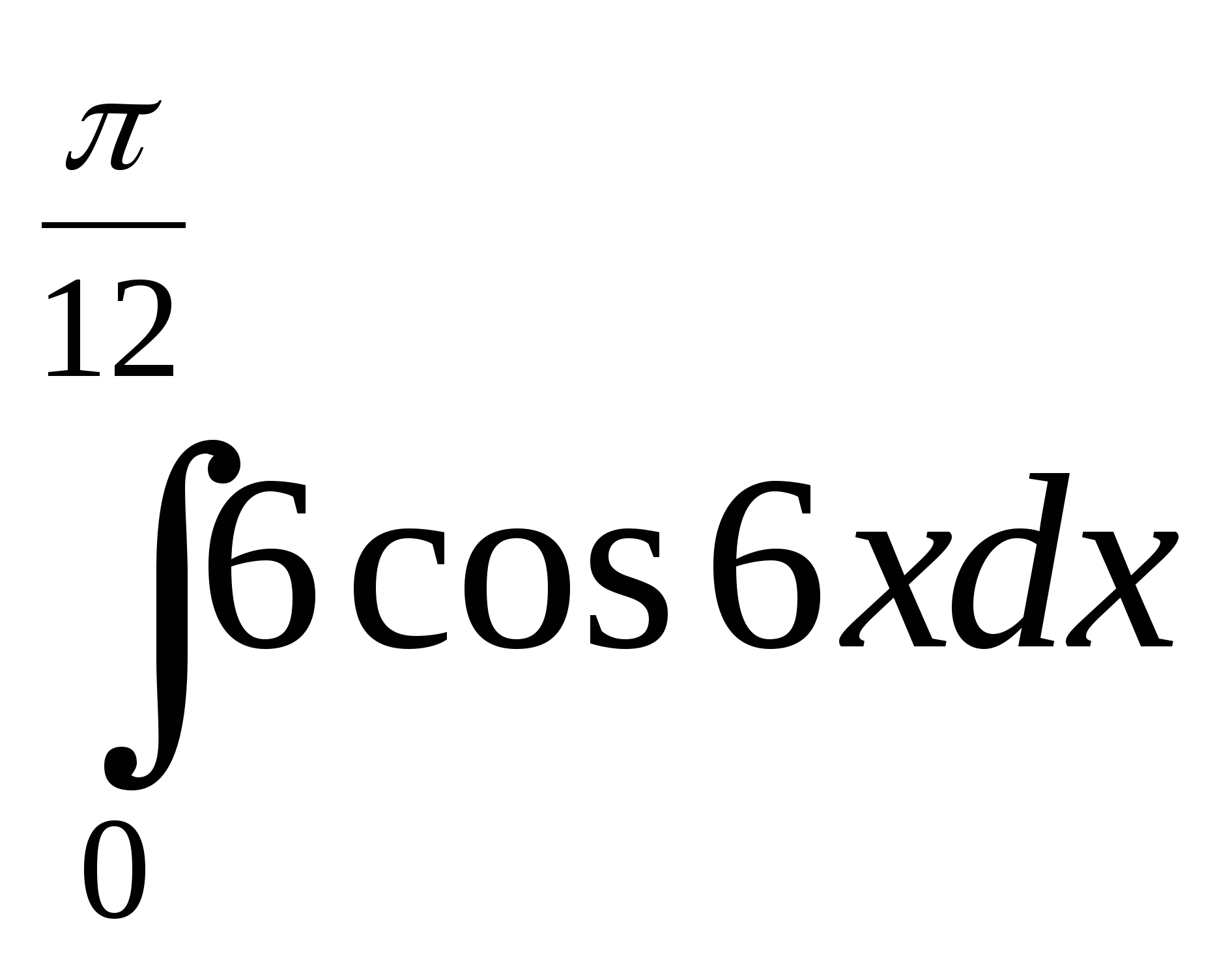 .
.
Вычислите площадь фигуры, ограниченной линиями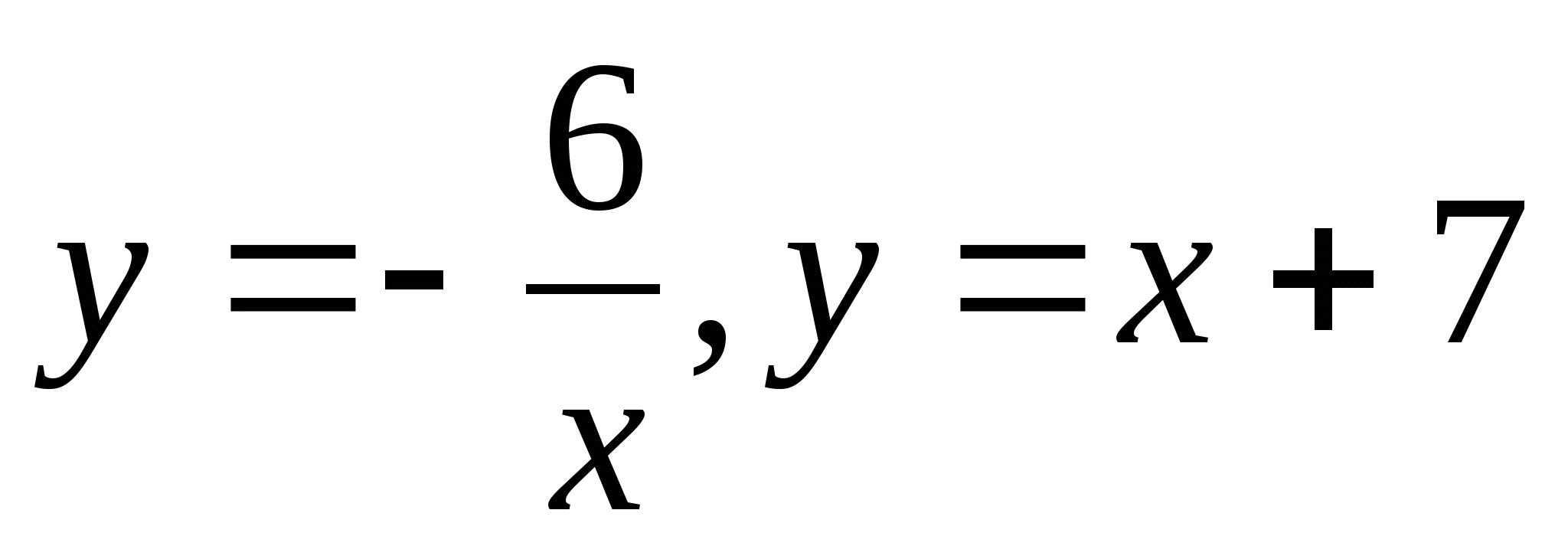 .
.
Известно, что функция 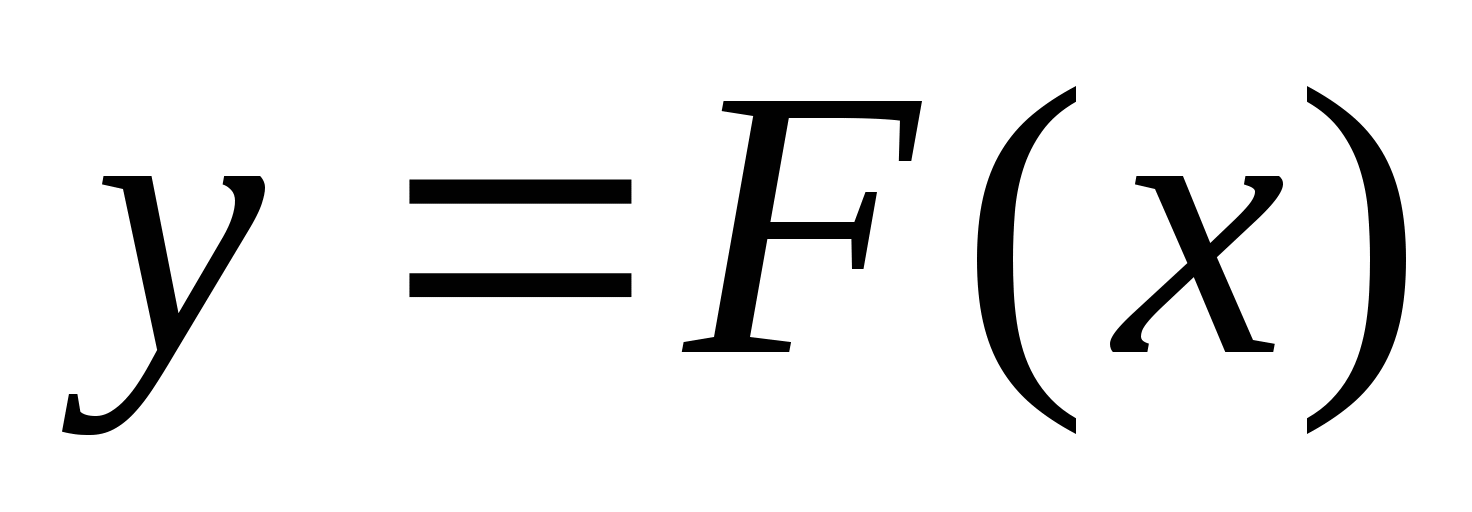 – первообразная для функции
– первообразная для функции 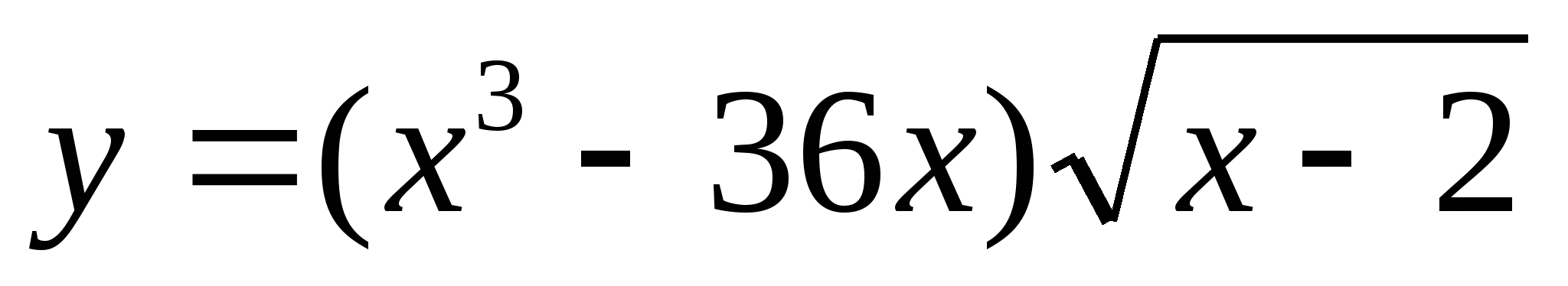 . Сравните числа F (3) и F (4).
. Сравните числа F (3) и F (4).
Контрольная работа №6
Вариант 1
В клубе 25 спортсменов. Сколькими способами из них можно составить команду из четырёх человек для участия в четырёхэтапной эстафете с учётом порядка пробега этапов?
Сколько трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 0 при условии, что каждая цифра может встретиться в записи числа один раз?
Решите уравнение 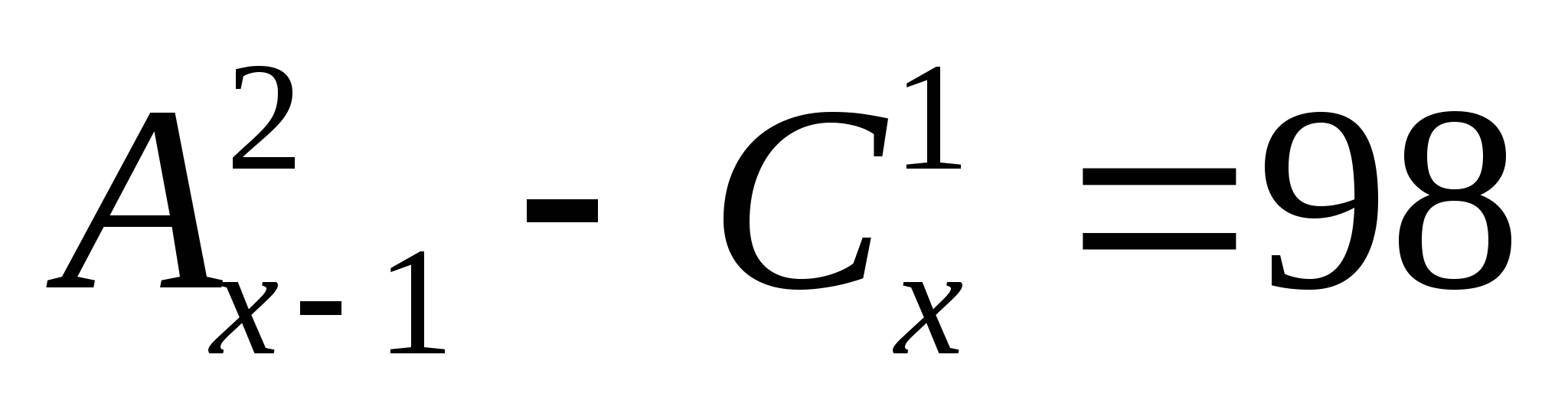 .
.
Напишите разложение степени бинома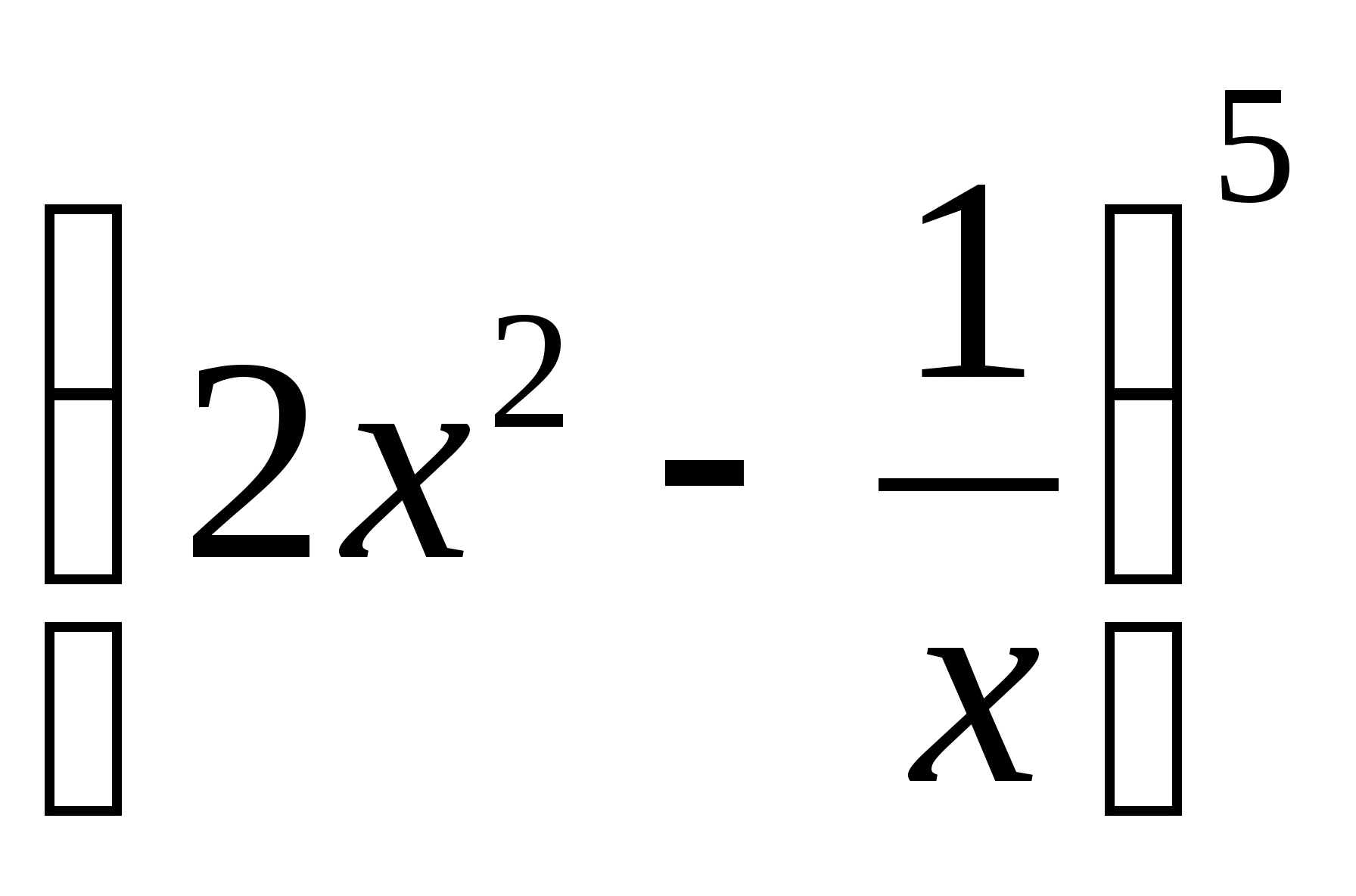 .
.
Из колоды в 36 карт вытаскивают две карты. Какова вероятность извлечь при этом карты одинаковой масти?
На прямой взяты шесть точек, а на параллельной ей прямой – 7 точек. Сколько существует треугольников, вершинами которых являются данные точки?
Контрольная работа №6
Вариант 2
Сколькими способами можно составить трёхцветный полосатый флаг, если имеется ткань пяти различных цветов?
Сколько различных трёхзначных чисел можно составить из цифр 1, 2, 3 при условии, что цифры могут повторяться?
Решите уравнение 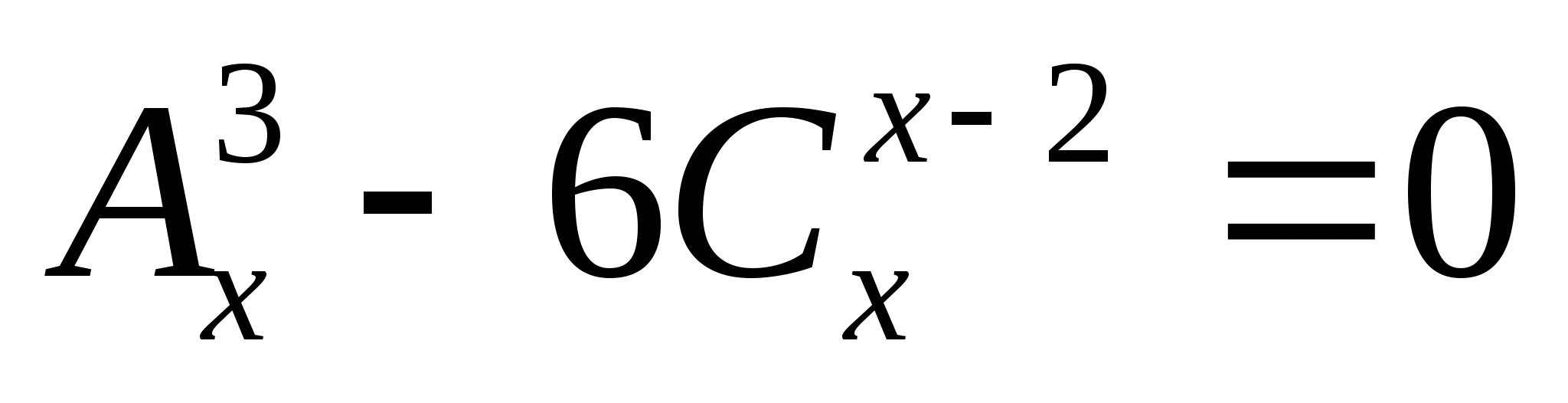 .
.
Напишите разложение степени бинома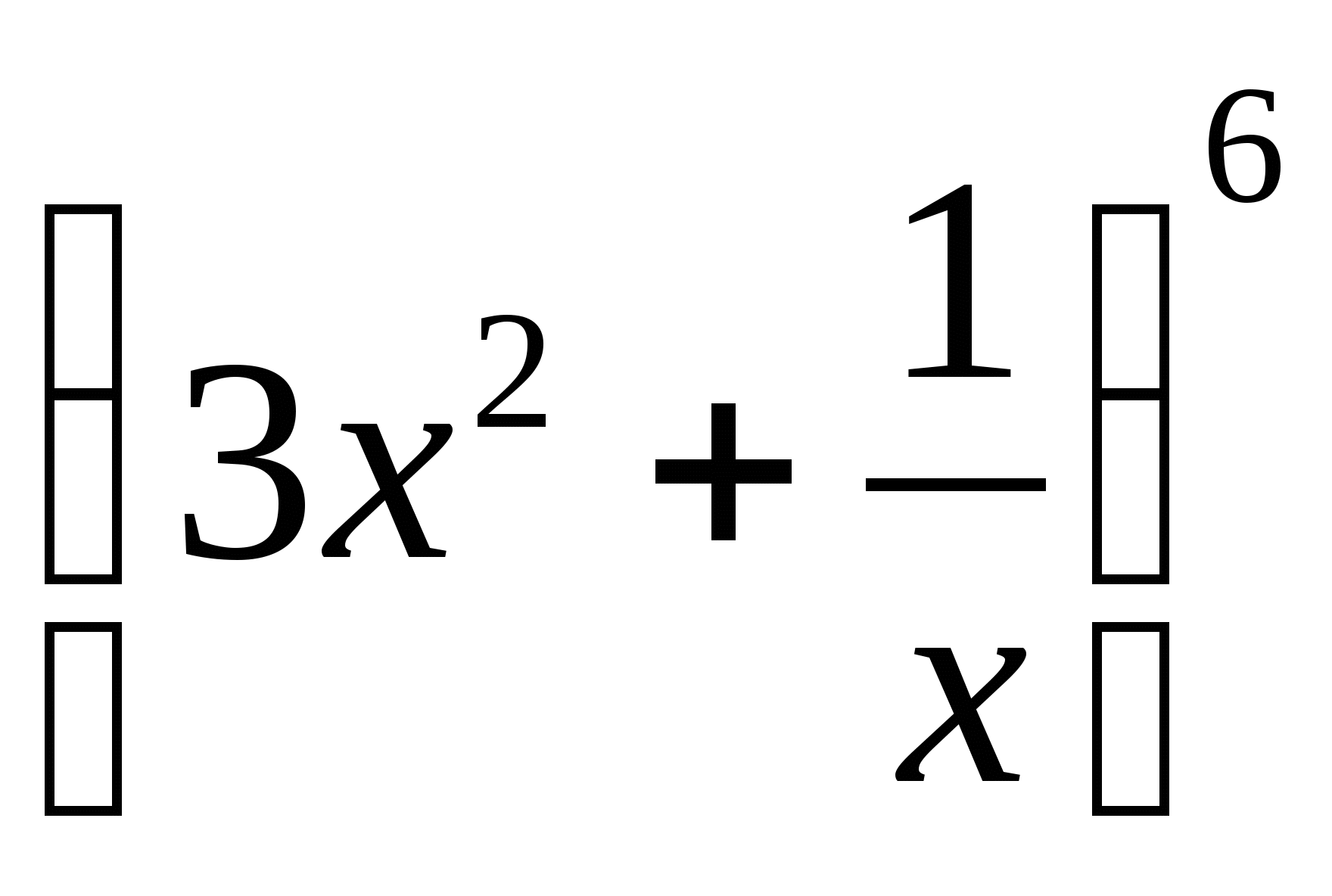 .
.
Из колоды в 36 карт вытаскивают три карты. Какова вероятность того, что все они тузы?
Сколько существует треугольников, вершины которых являются вершинами данного выпуклого 10-угольника?
Контрольная работа №6
Вариант 3
В городской думе 30 человек. Из них на общем заседании надо выбрать председателя, а также его первого, второго и третьего заместителей. Сколькими способами это можно сделать?
Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6 при условии, что цифры могут повторяться?
Решите уравнение 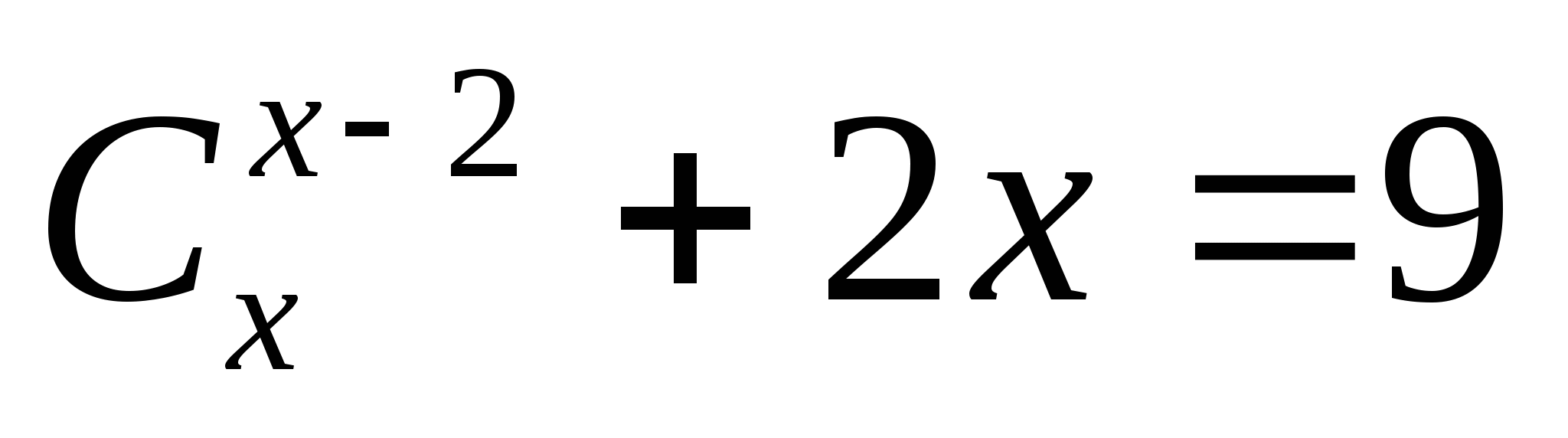 .
.
Напишите разложение степени бинома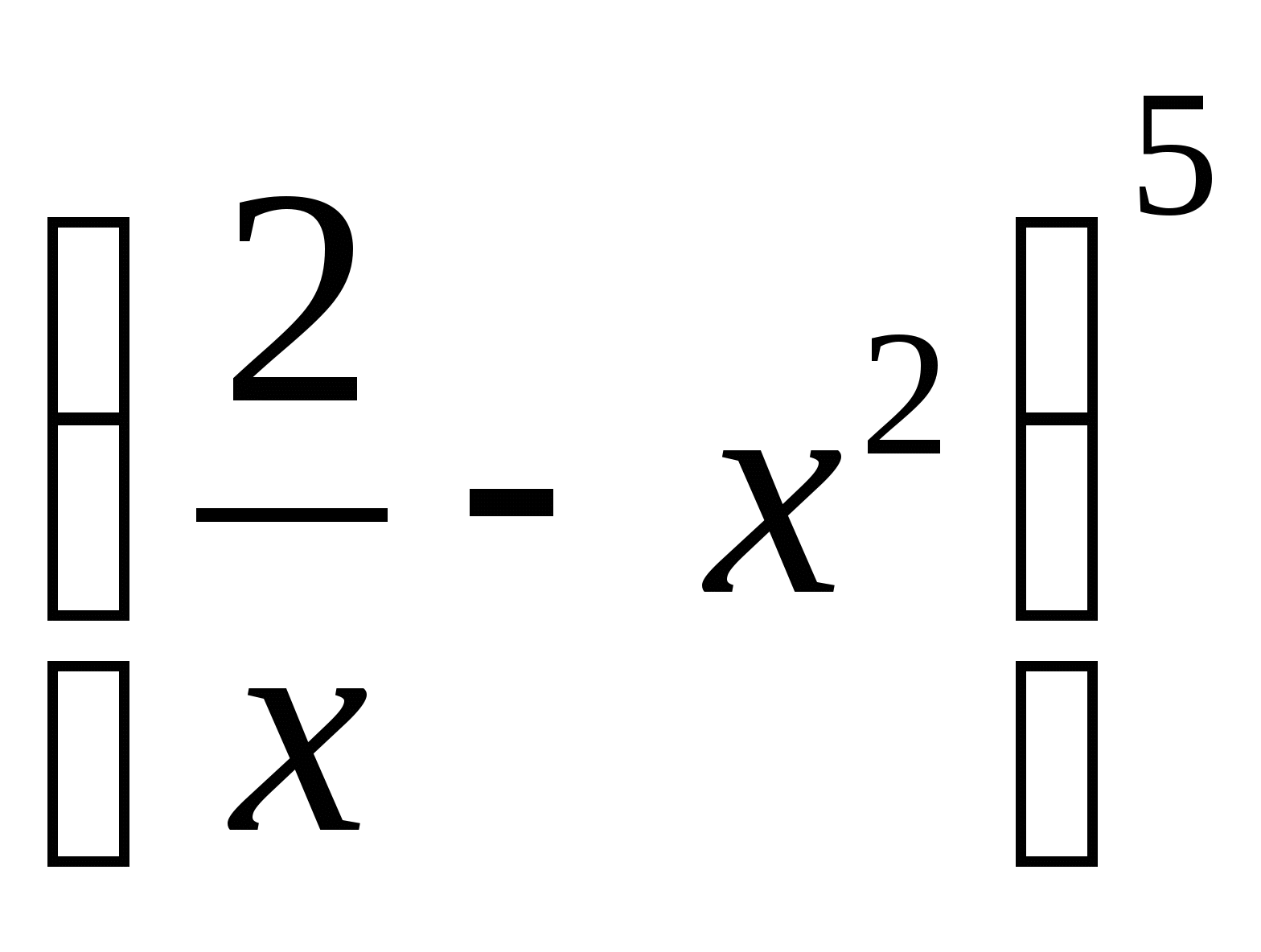 .
.
В урне находятся 3 белых и 4 чёрных шара. Какова вероятность того, что вынутые из неё наудачу два шара окажутся белыми?
На прямой взяты 8 точек, а на параллельной ей прямой – 5 точек. Сколько существует треугольников, вершинами которых являются данные точки?
Контрольная работа №6
Вариант 4
В яхт-клубе состоит 9 человек. Из них на общем собрании надо выбрать председателя, заместителя, секретаря и казначея. Сколькими способами это можно сделать?
Сколько четырёхзначных чисел можно составить из цифр 1, 2, 3, 0 при условии, что каждая цифра может встретиться в записи числа один раз?
Решите уравнение 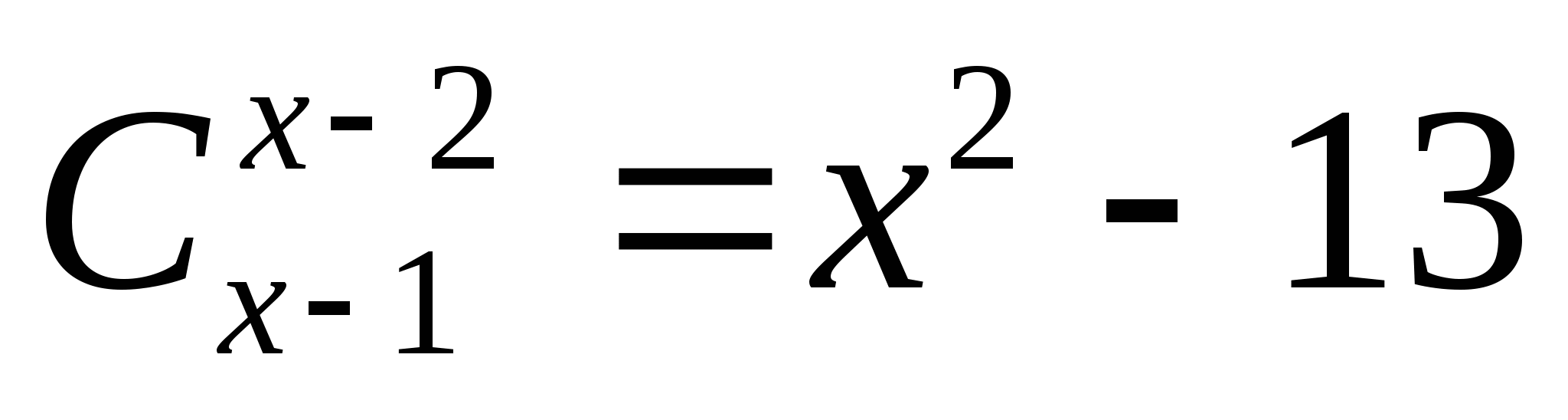 .
.
Напишите разложение степени бинома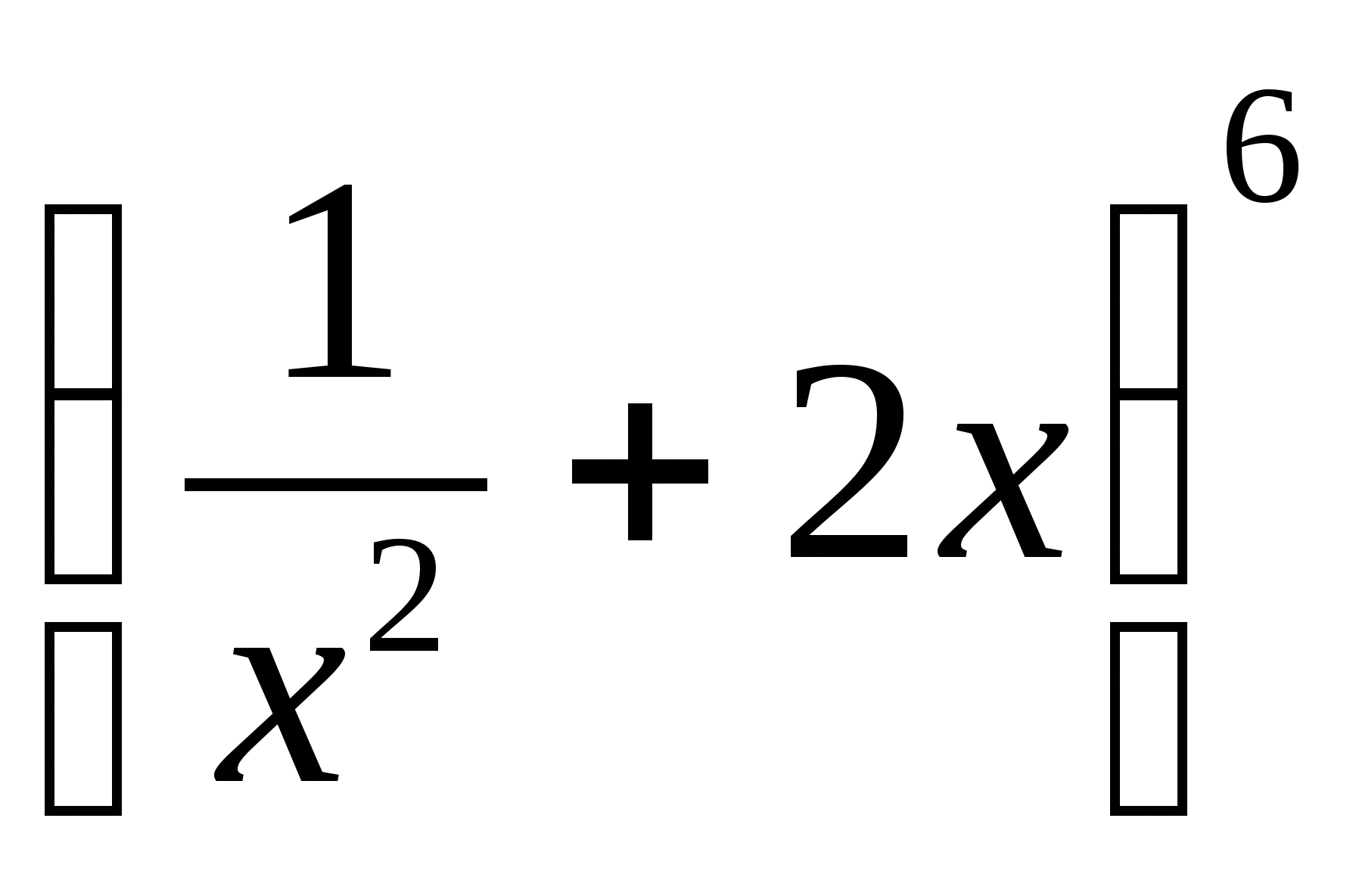 .
.
В урне находятся 2 белых, 3 красных и 16 чёрных шаров. Какова вероятность того, что из вынутых наудачу двух шаров один окажется белым, а другой красным?
Сколько существует треугольников, вершины которых являются вершинами данного выпуклого 8-угольника, а стороны не совпадают со сторонами этого многоугольника?
Контрольная работа №7 (2 часа)
Вариант 1
Решите уравнение: а) 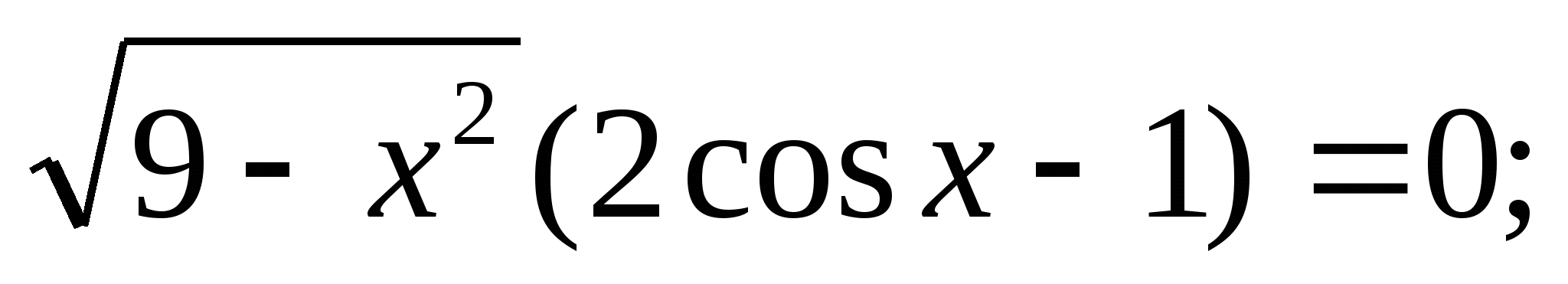 б)
б) 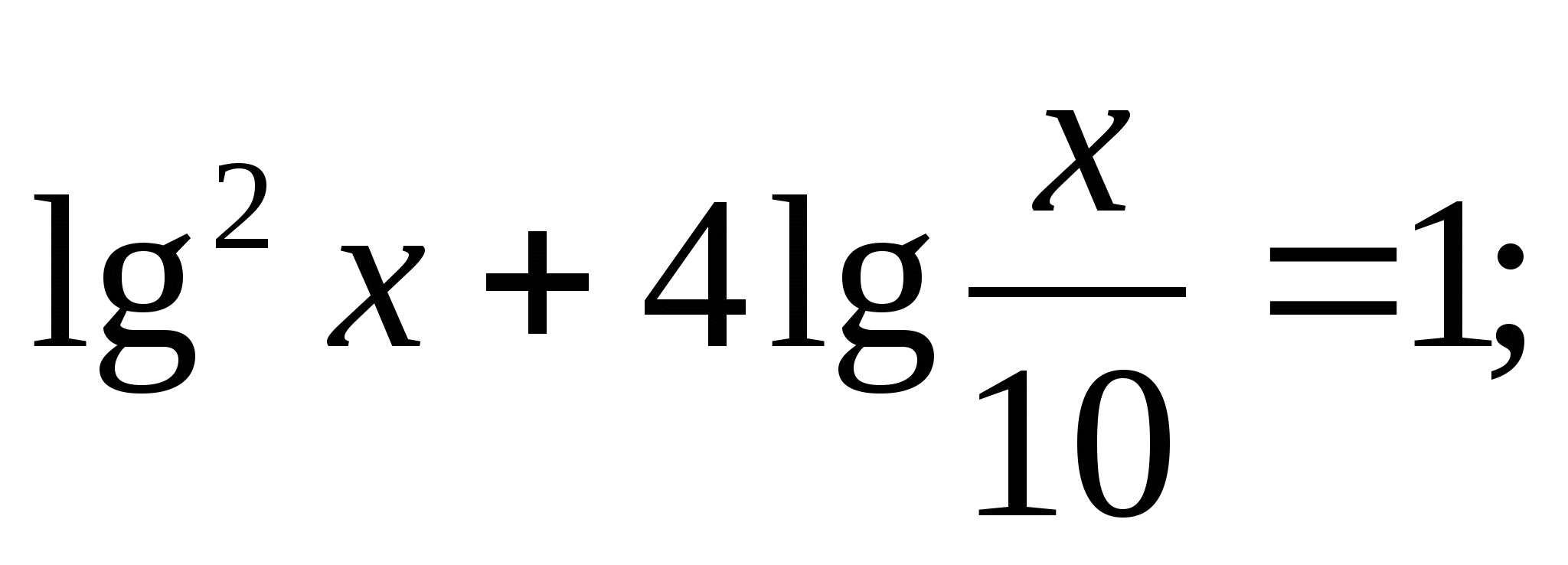
в) 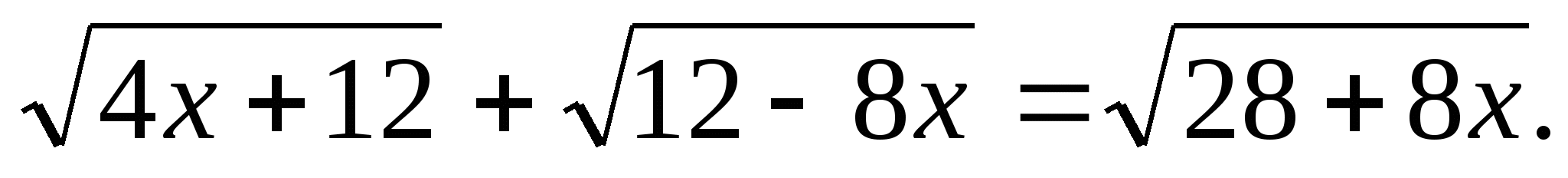
Решите неравенство: а) 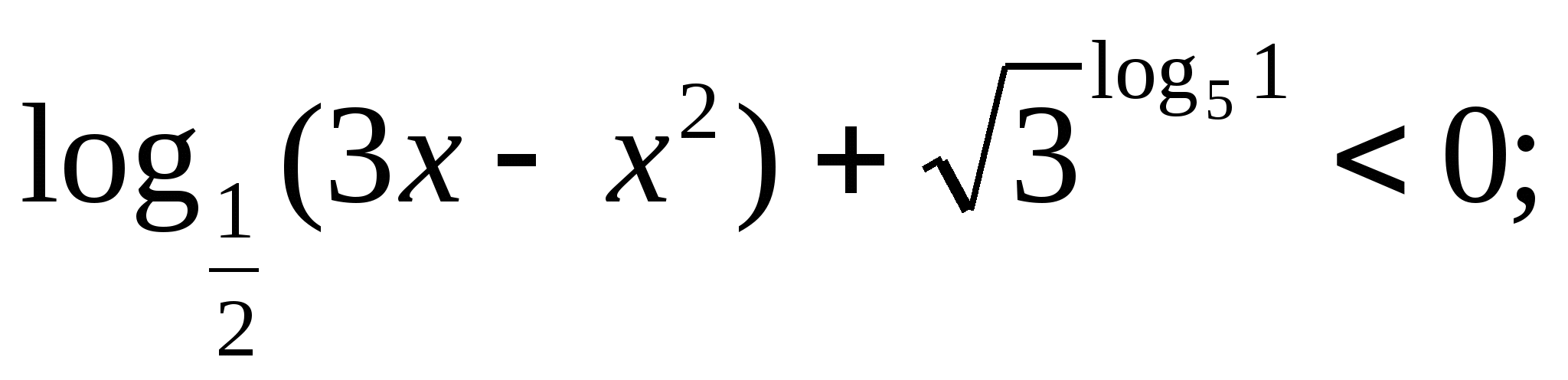 б)
б) 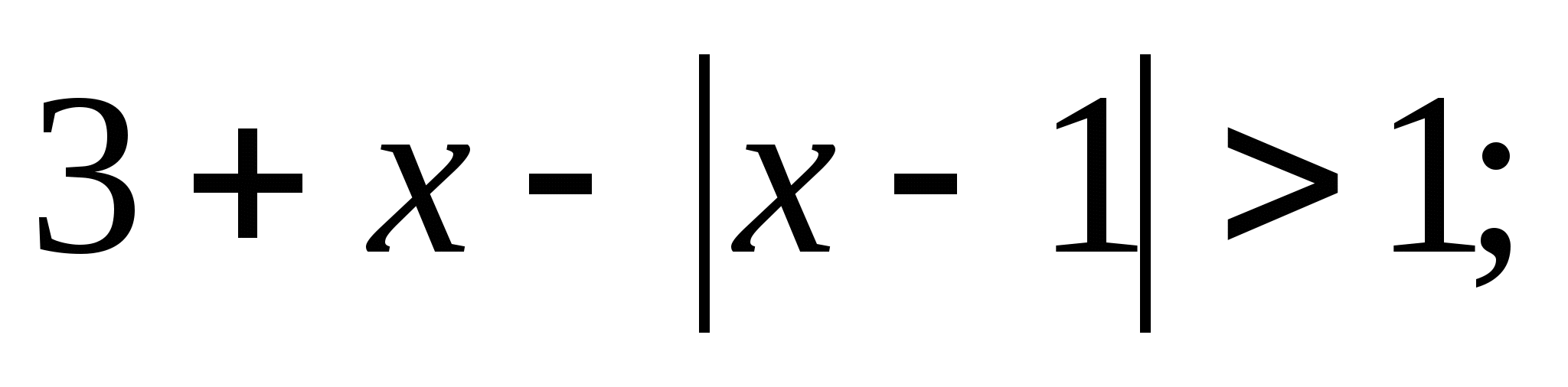
в) 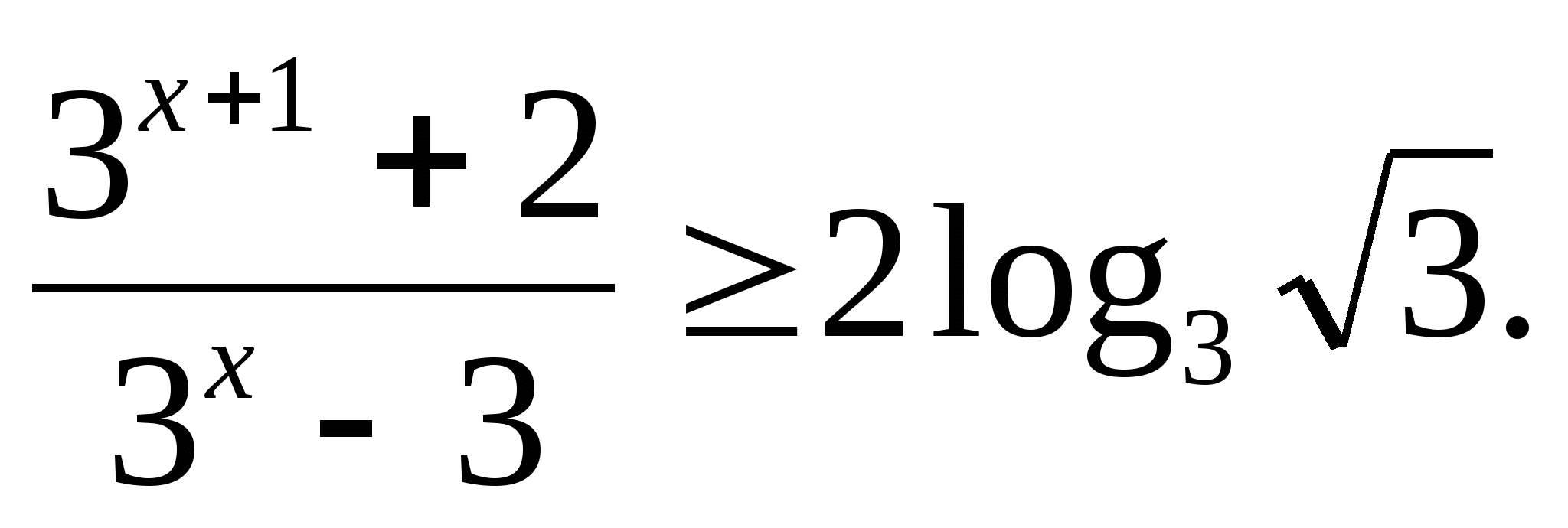
Решите уравнение в целых числах: 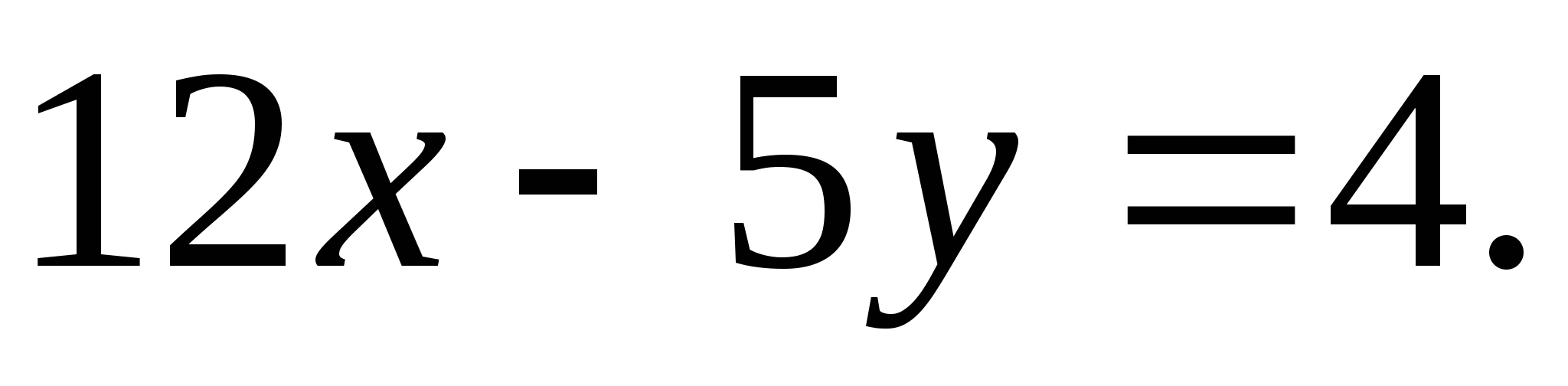
Решите систему уравнений: 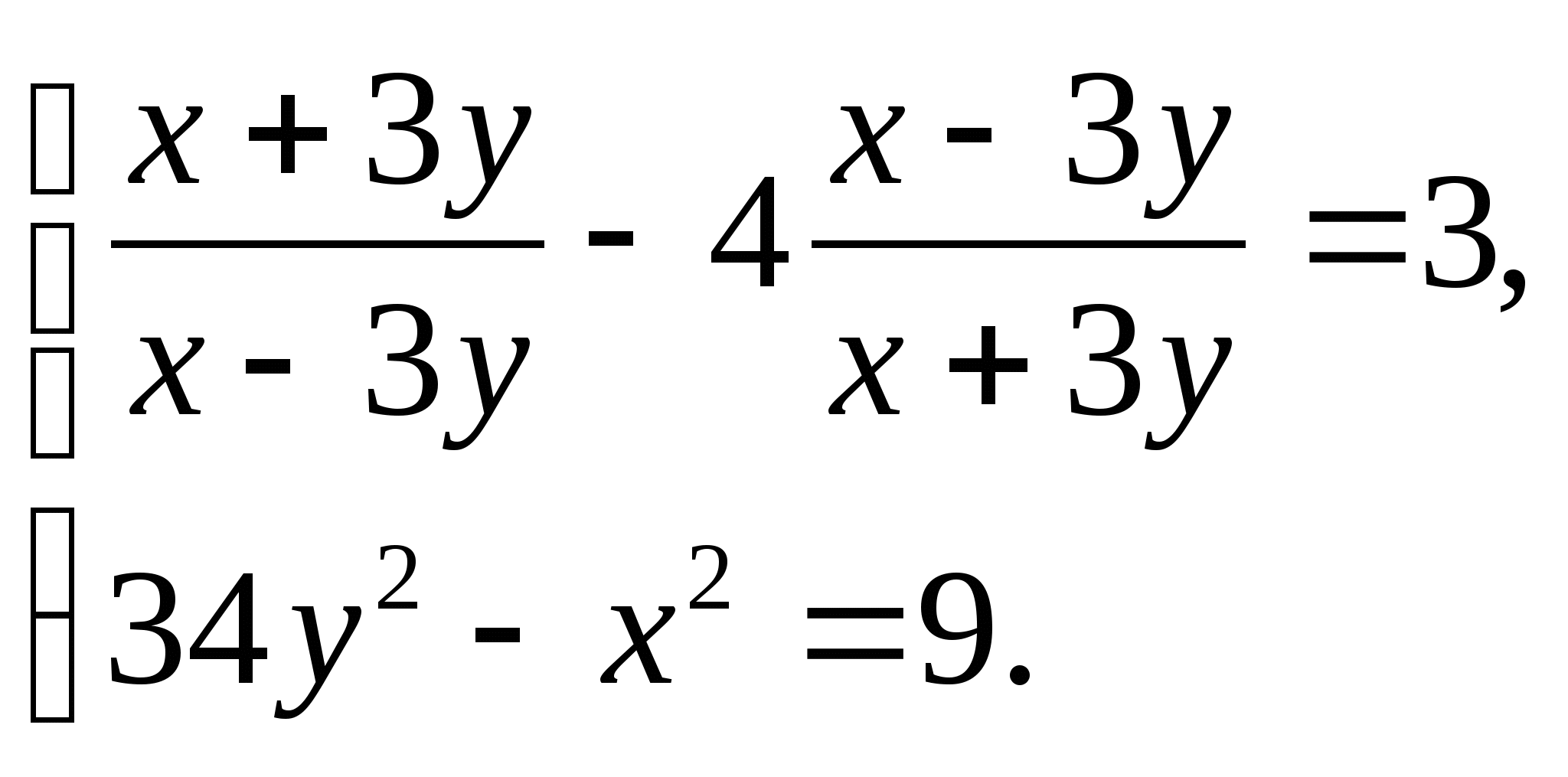
Решите уравнение: 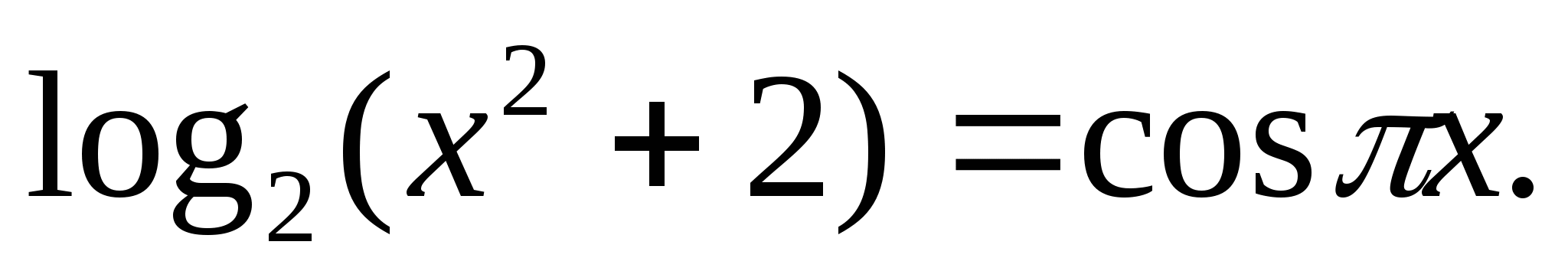
Контрольная работа №7 (2 часа)
Вариант 2
Решите уравнение: а) 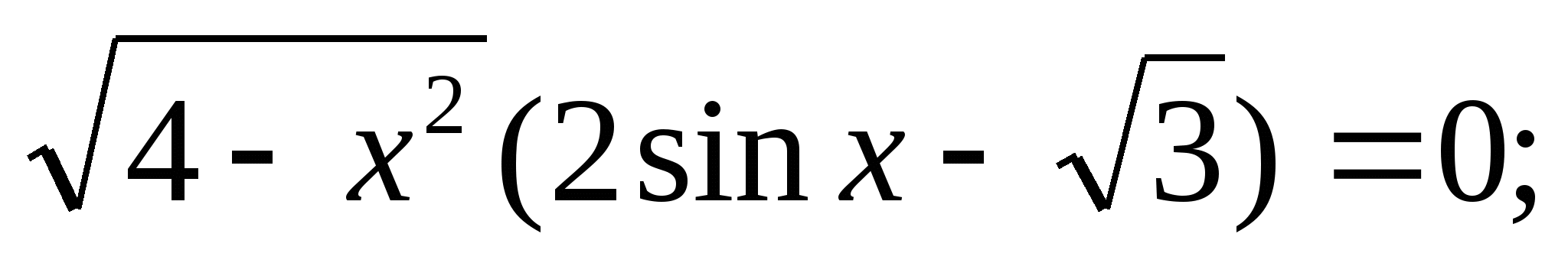 б)
б) 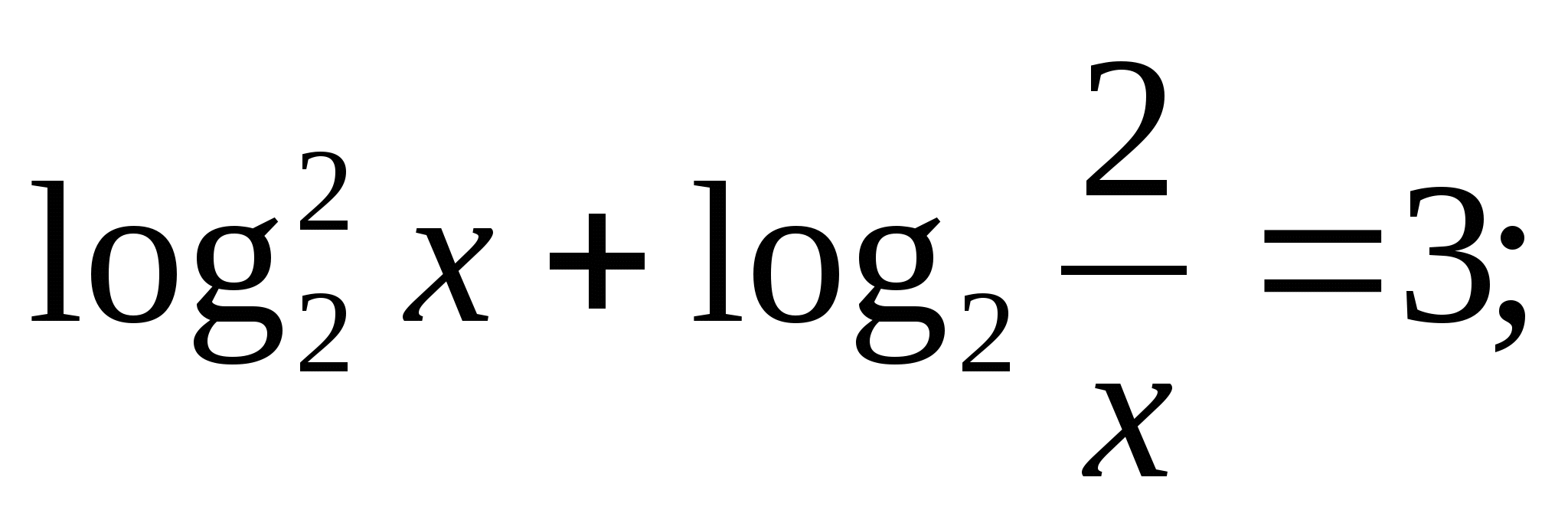
в) 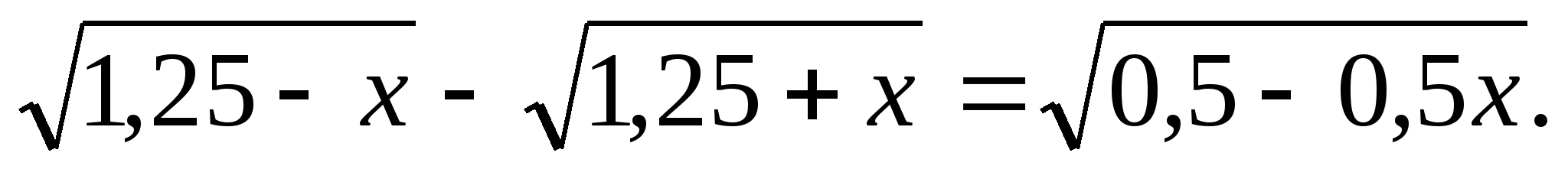
Решите неравенство: а) 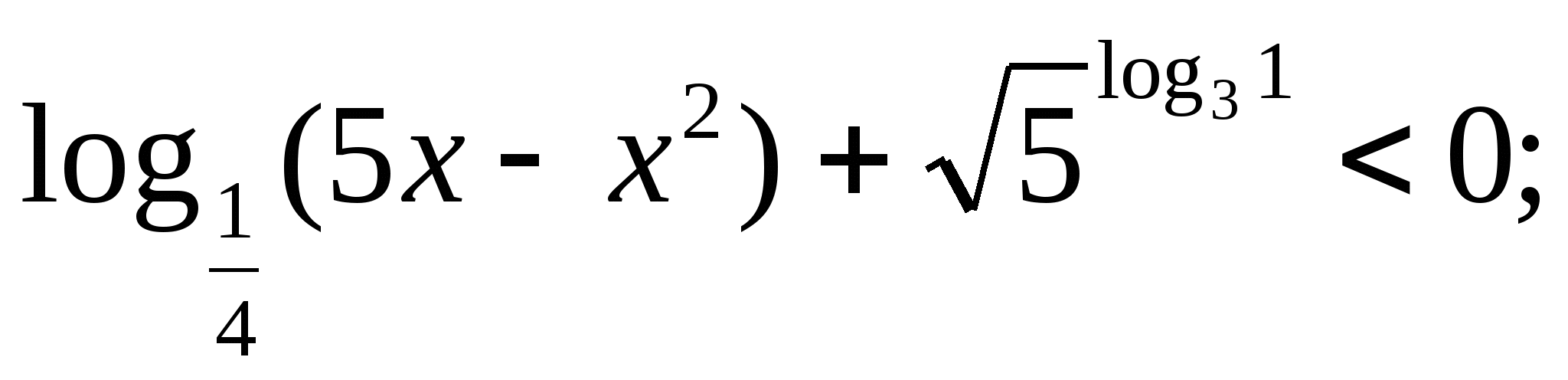 б)
б) 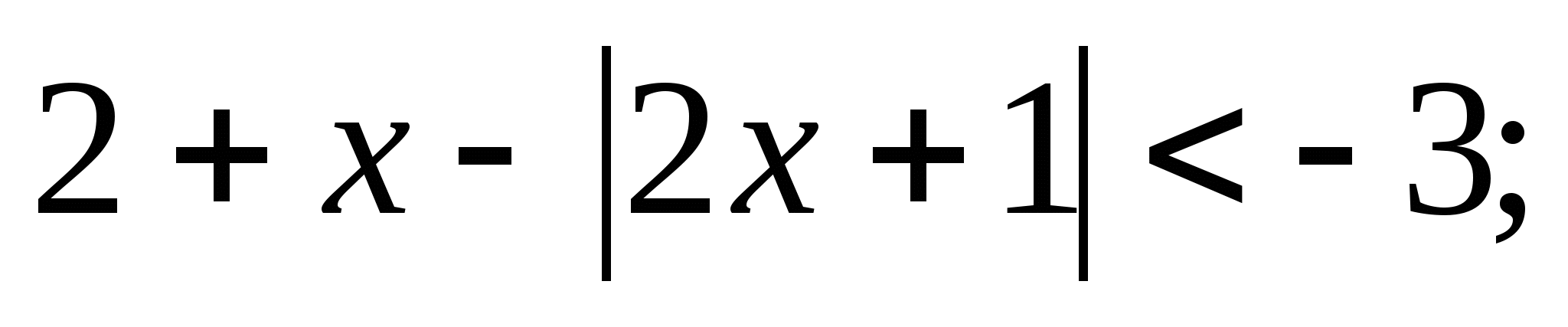
в) 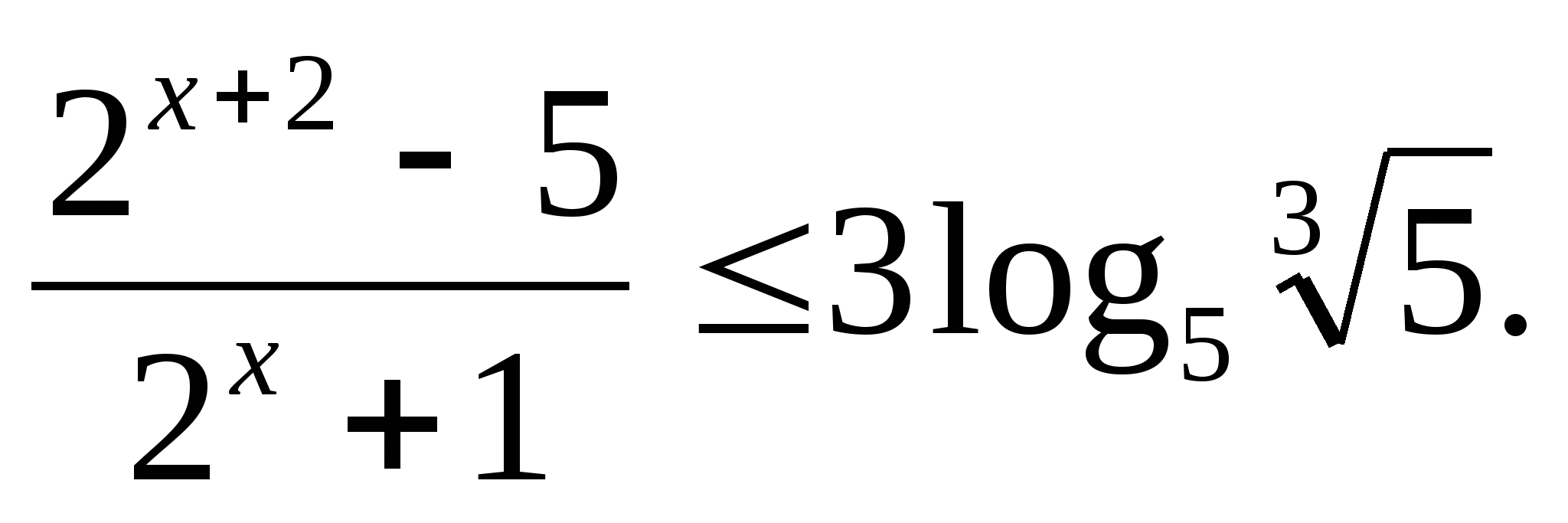
Решите уравнение в целых числах: 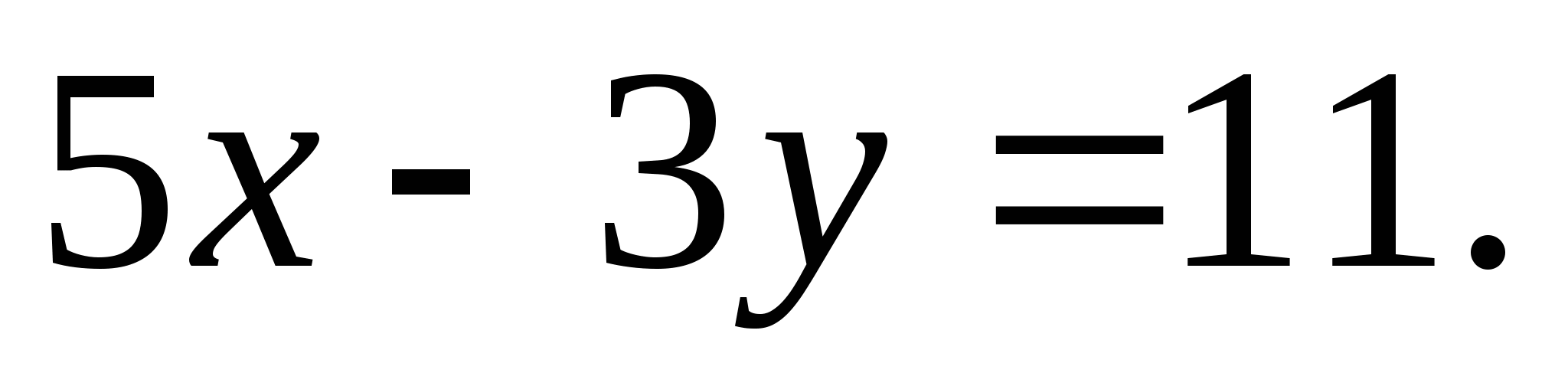
Решите систему уравнений: 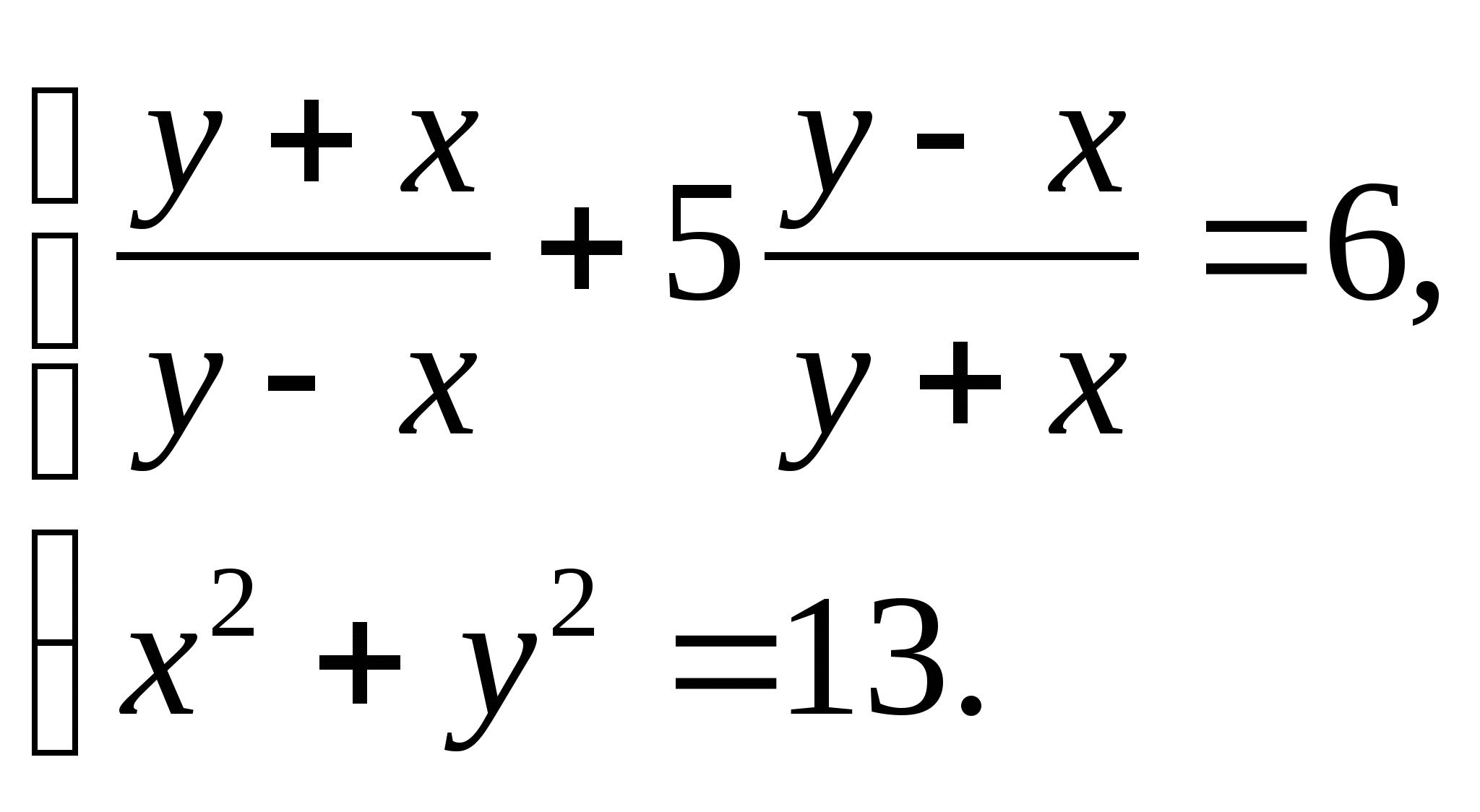
Решите уравнение: 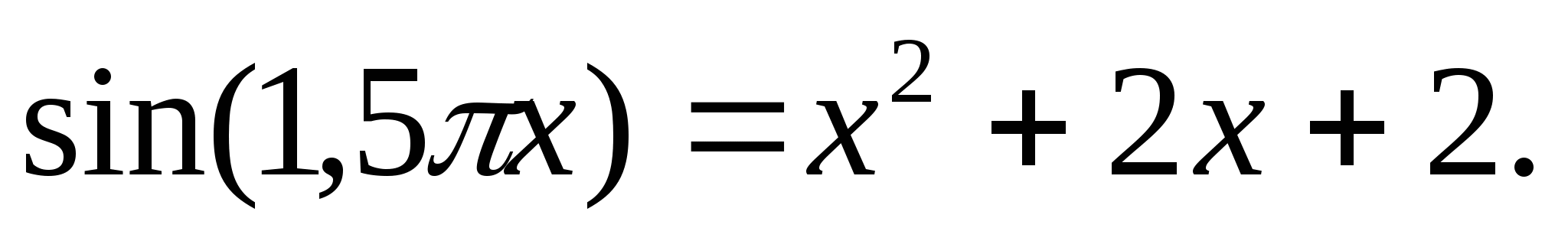
Контрольная работа №7 (2 часа)
Вариант 3
Решите уравнение: а) 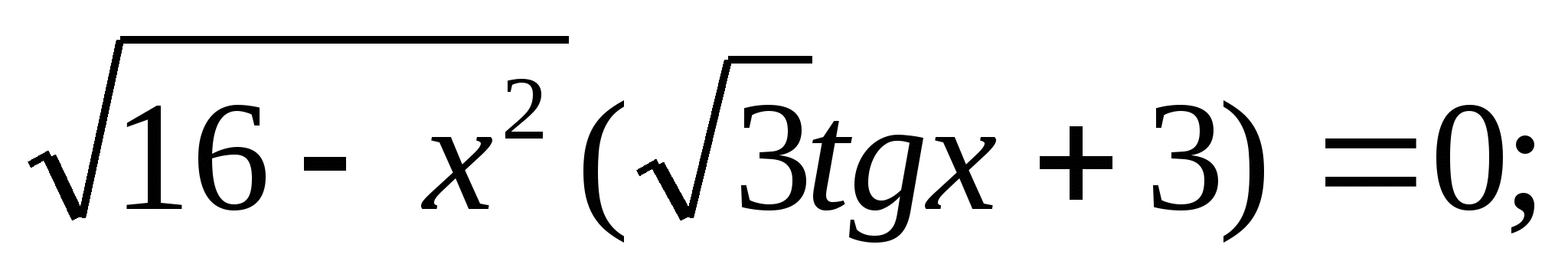 б)
б) 
в) 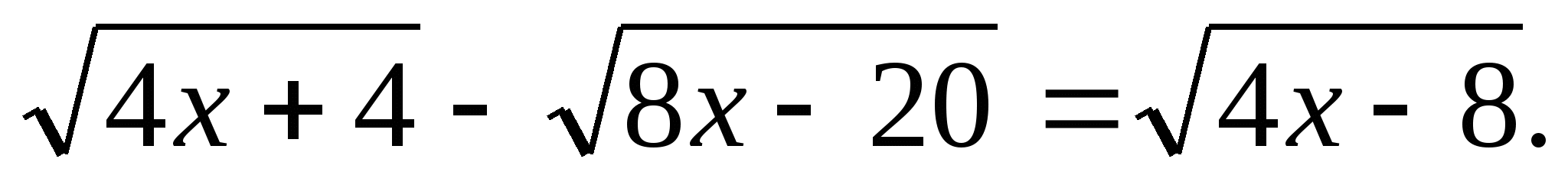
Решите неравенство: а) 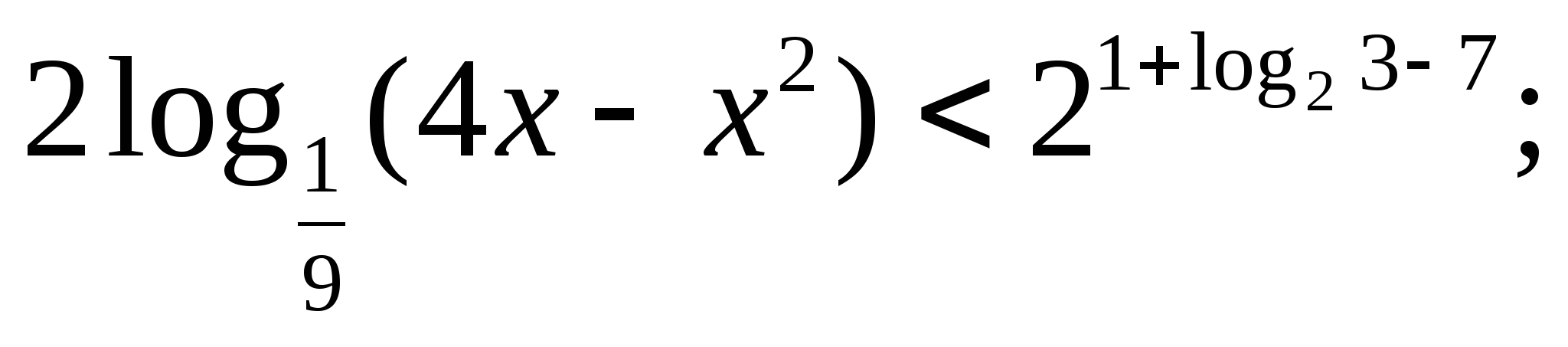 б)
б) 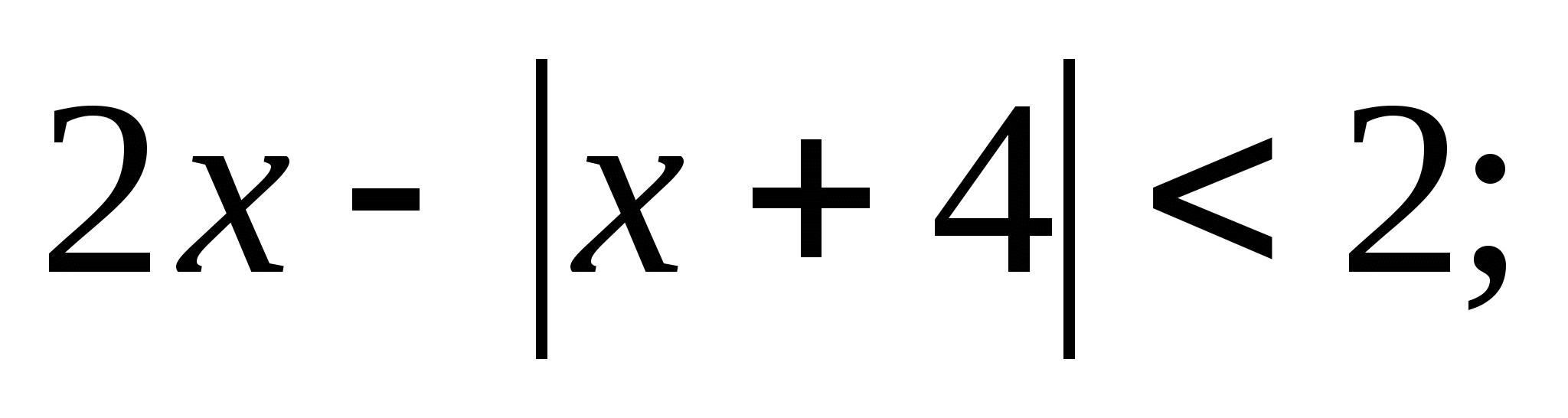
в) 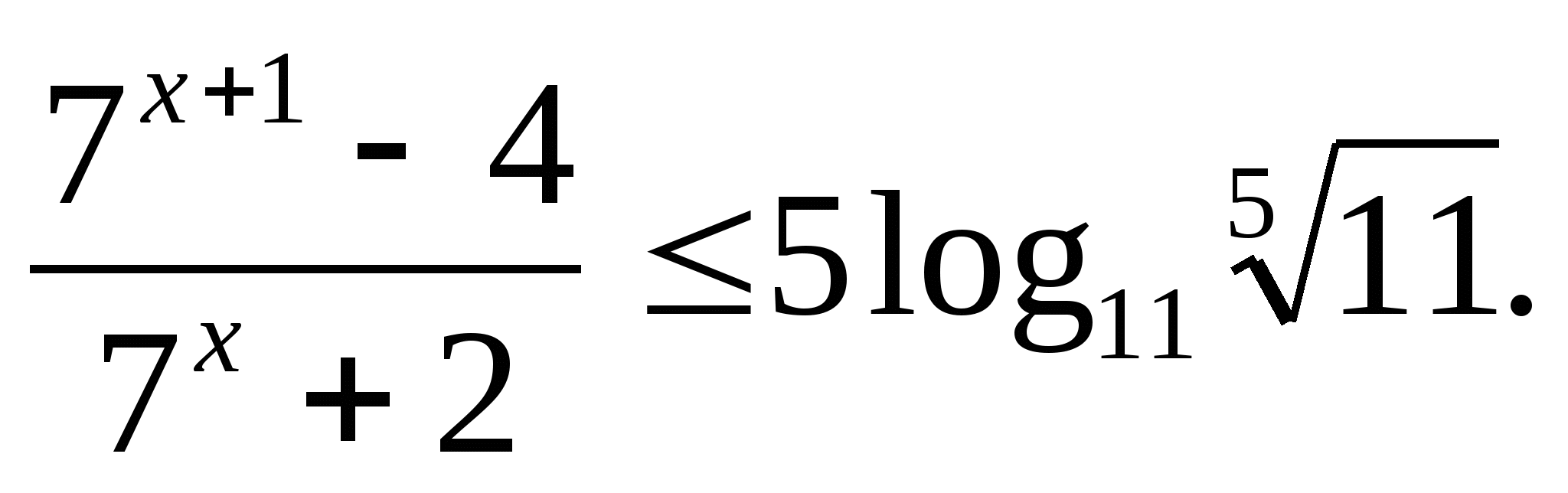
Решите уравнение в целых числах: 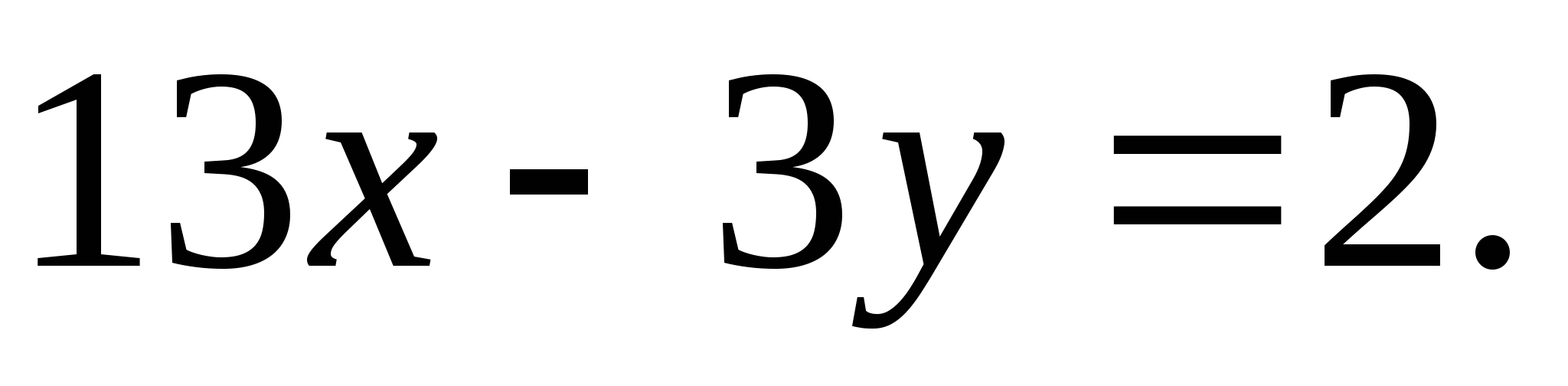
Решите систему уравнений: 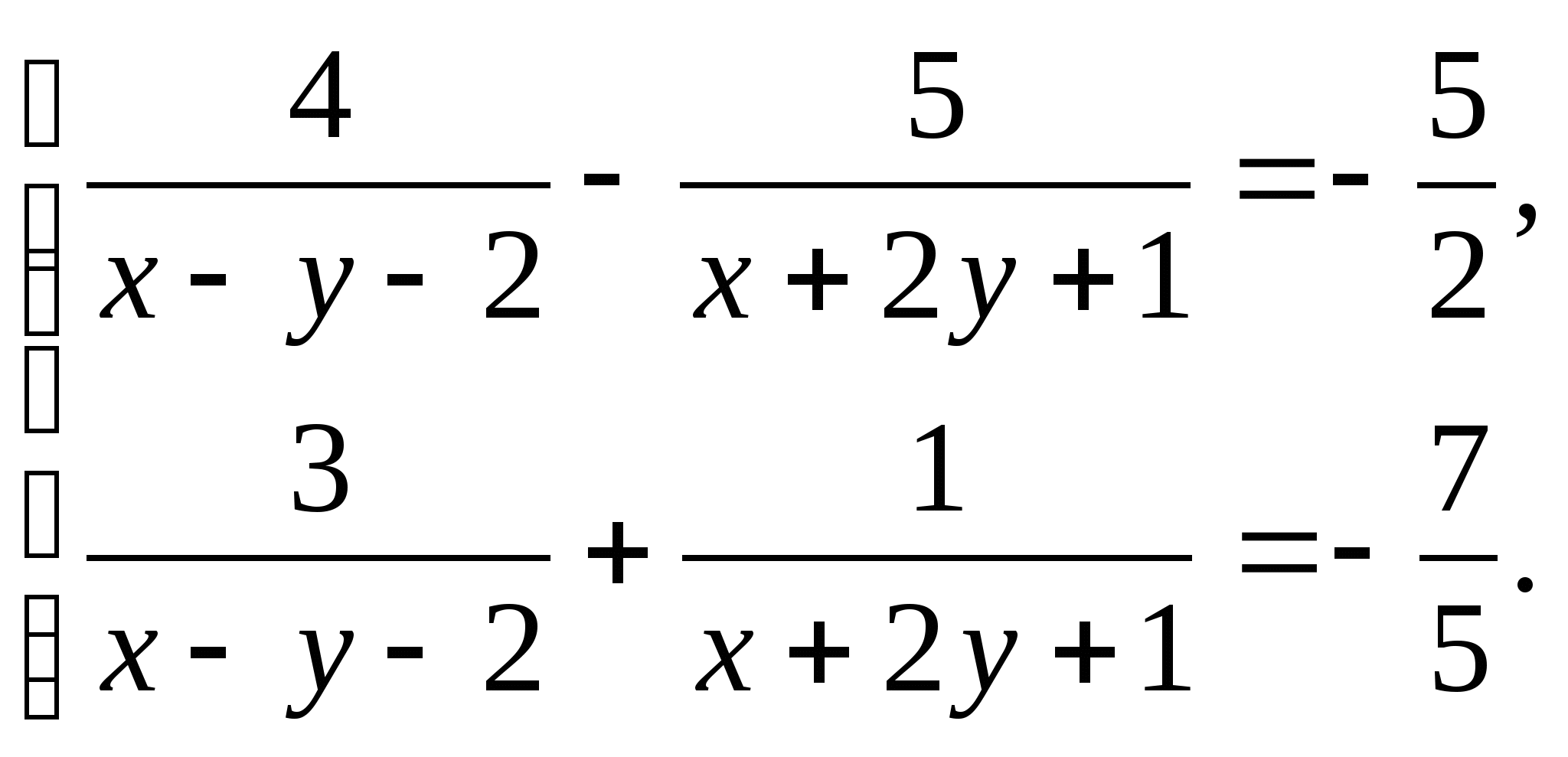
Решите уравнение: 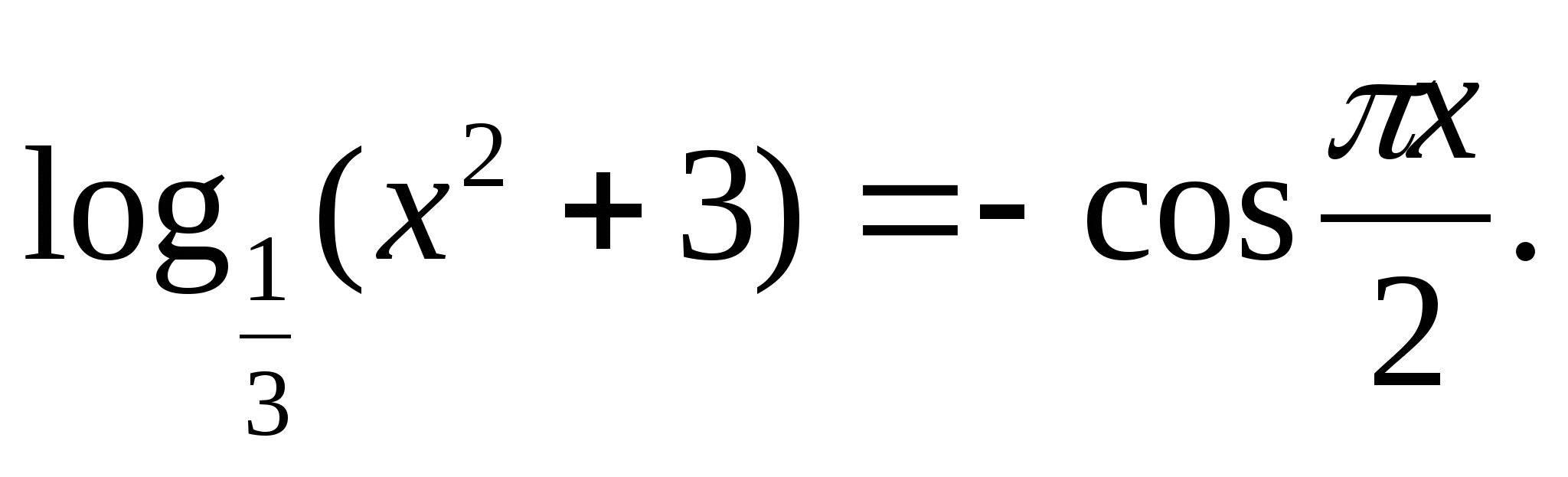
Контрольная работа №7 (2 часа)
Вариант 4
Решите уравнение: а) 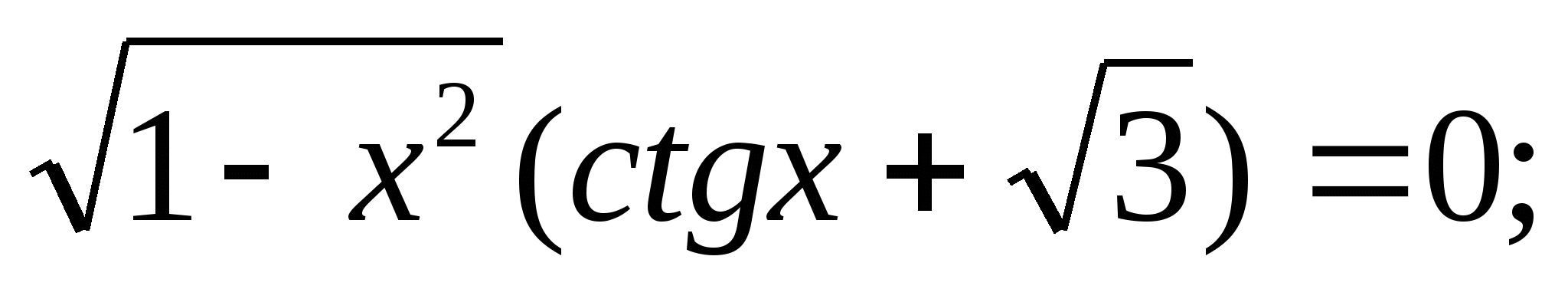 б)
б) 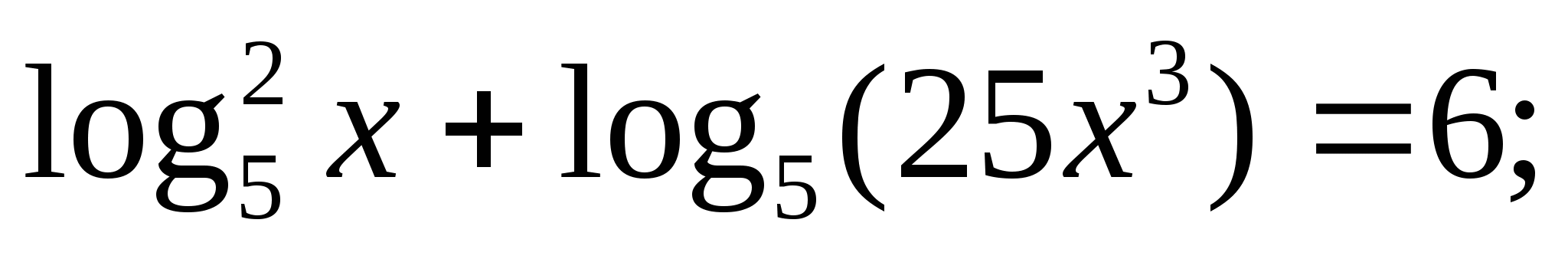
в) 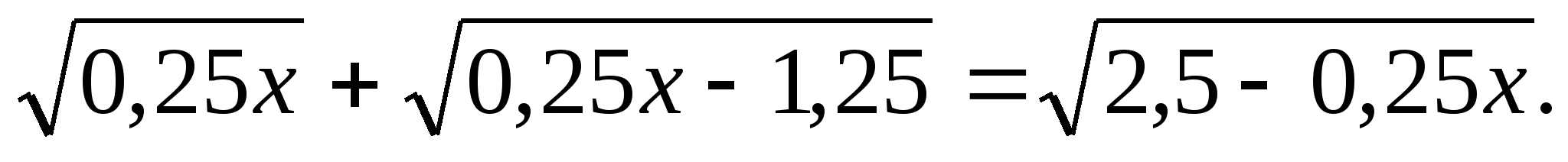
Решите неравенство: а) 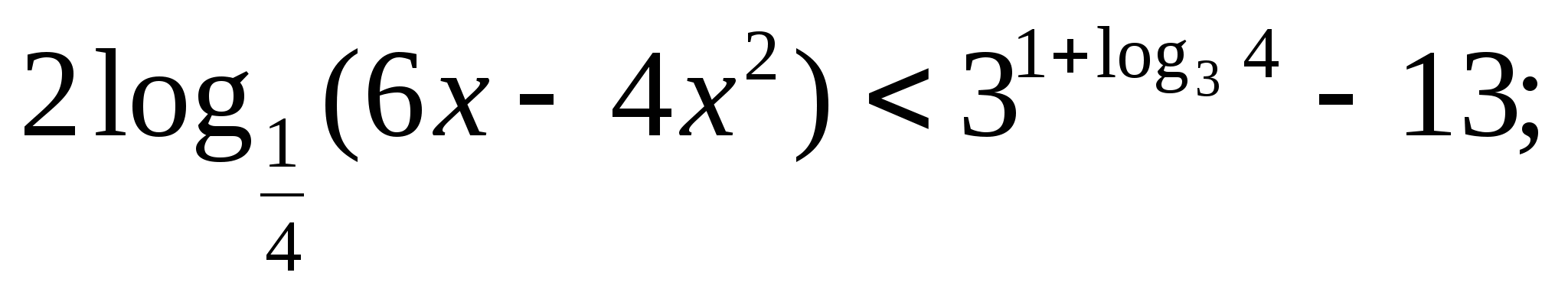 б)
б) 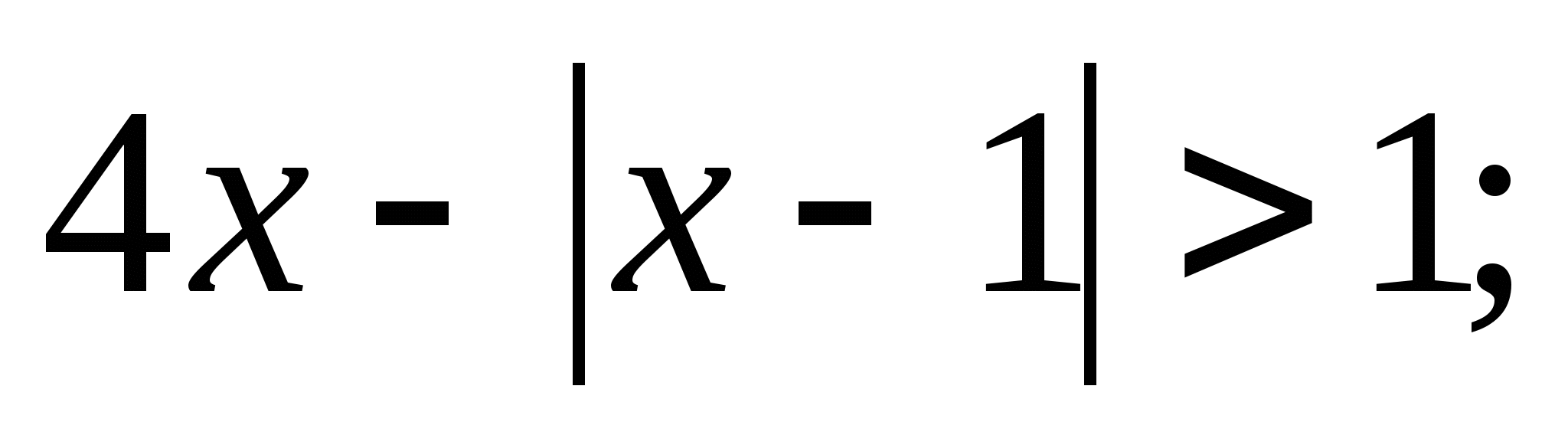
в) 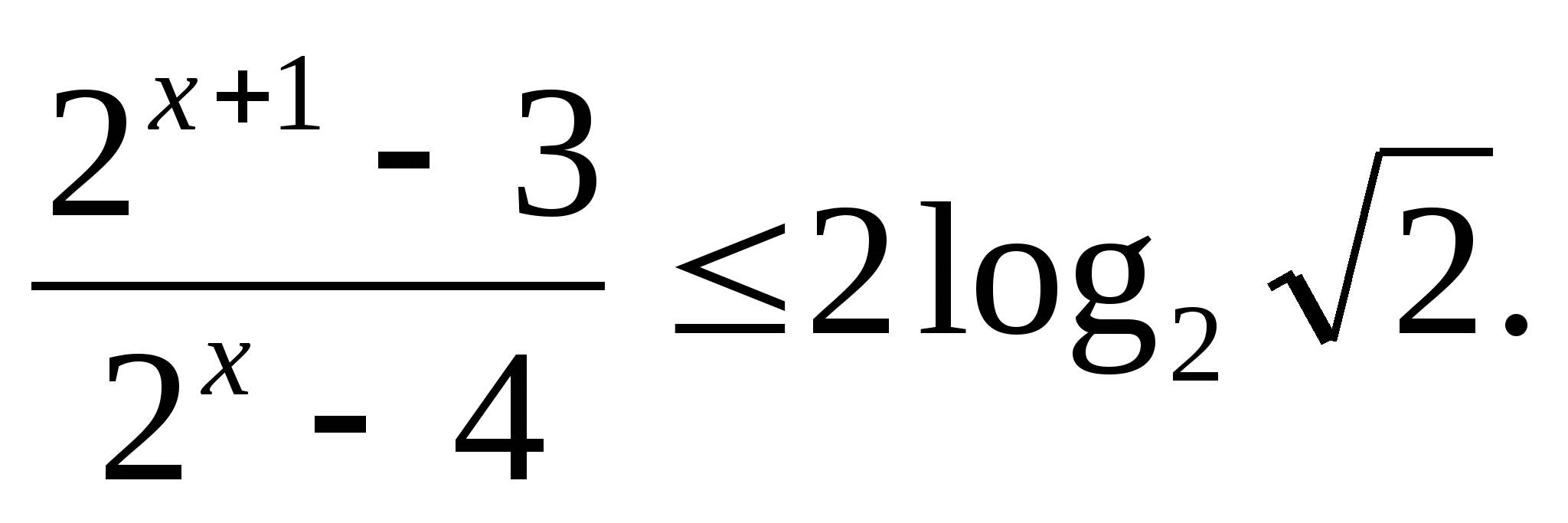
Решите уравнение в целых числах: 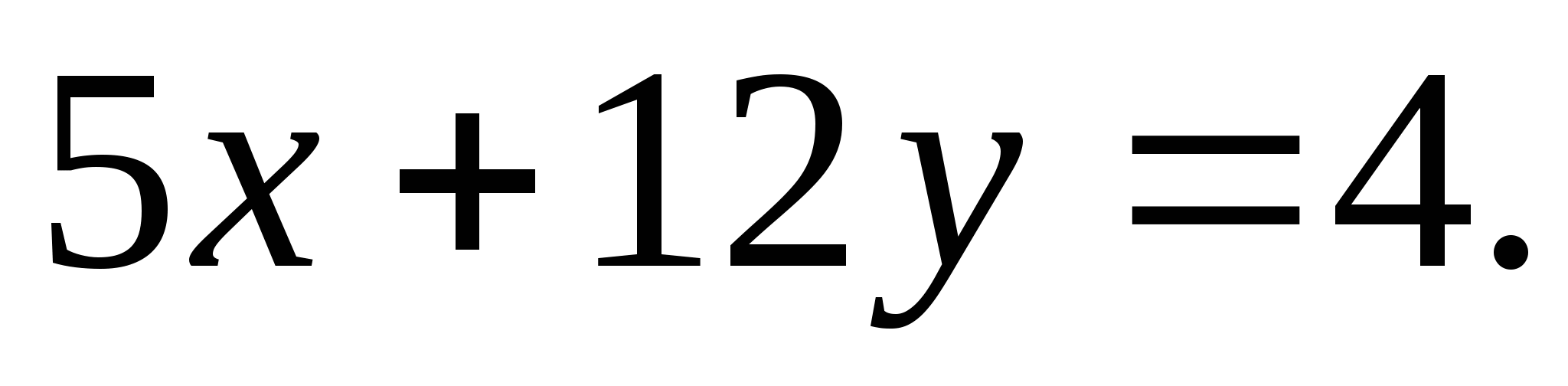
Решите систему уравнений: 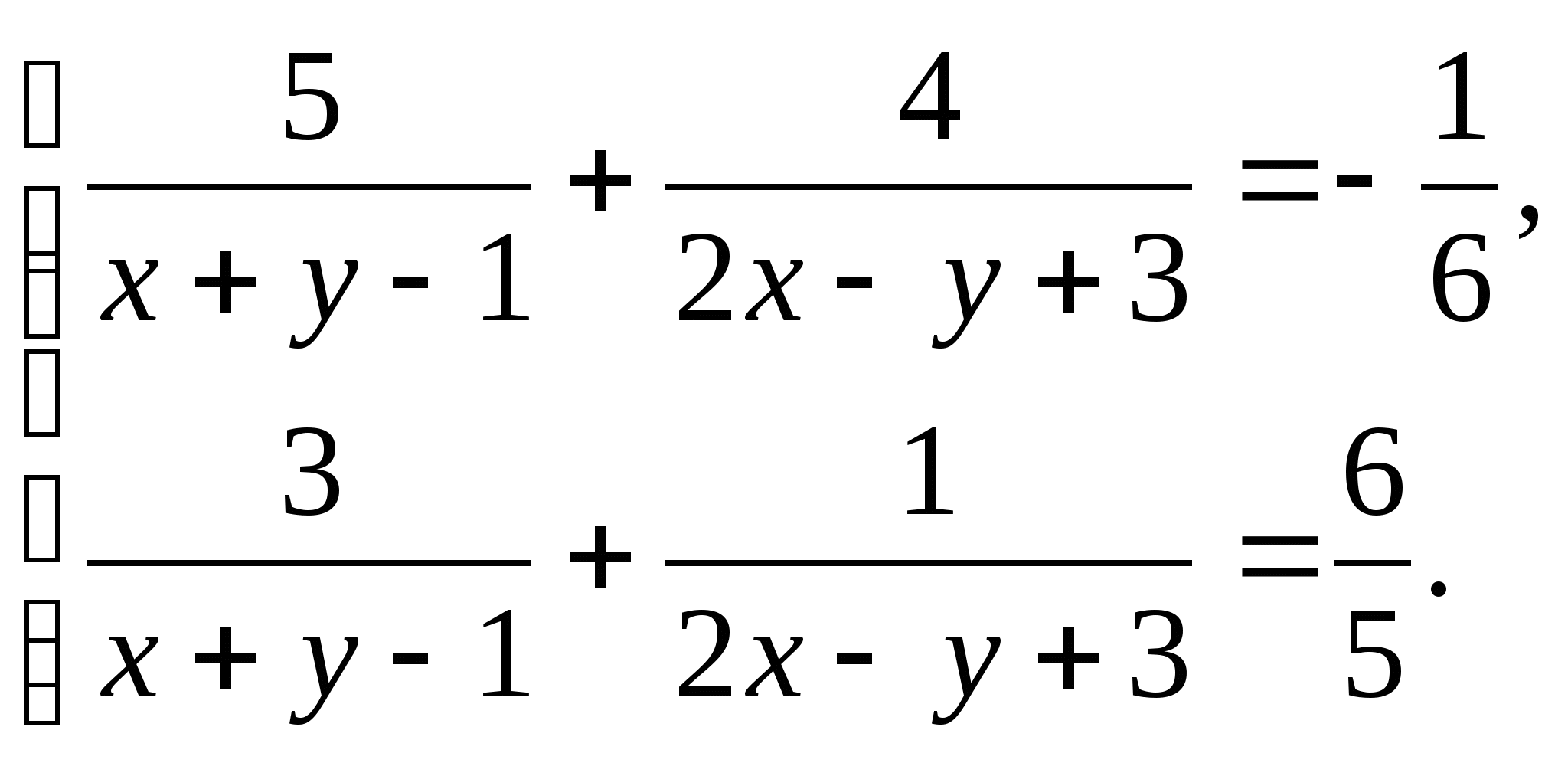
Решите уравнение: 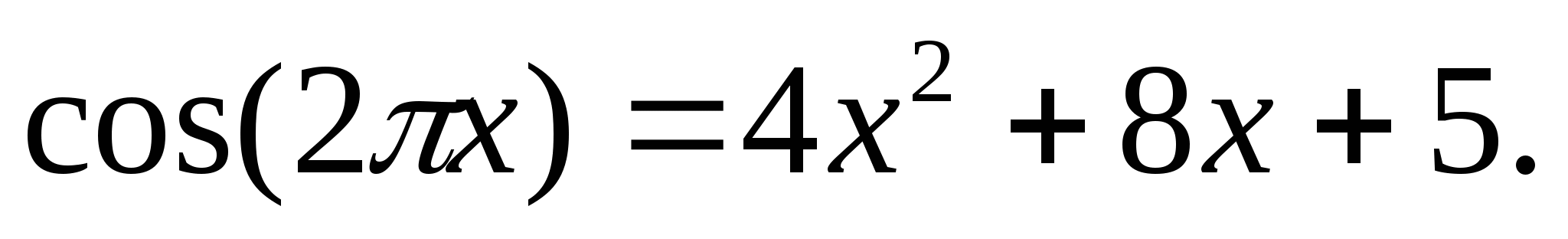
infourok.ru
Контрольная работа по теме «Корни, степени и логарифмы» (28 ч)
I вариант
1. Вычислите:
а)  в)
в) 
б)  г)
г) 
2. Сравните числа:
а)  и
и  б) log20,9 и 0,1 в) 221 и 314
б) log20,9 и 0,1 в) 221 и 314
3. Решите уравнения:
а)  в) log5(x2 – 10x) = 2 + log52x
в) log5(x2 – 10x) = 2 + log52x
б) 7x + 2 – 14 7x = 5II вариант
1. Вычислите:
а)  в)
в) 
б)  г)
г) 
2. Сравните числа:
а)  и
и  б)
б)  и 0,5 в) 542 и 739
и 0,5 в) 542 и 739
3. Решите уравнения:
а)  в) lg (3x2 – 2x) = 1 + lg (x 2)
в) lg (3x2 – 2x) = 1 + lg (x 2)
б) 10 5x – 1 + 5x + 1 = 7Контрольная работа № 1 по теме «Прямые и плоскости» (28 ч)
I вариант
1. ABCDA1B1C1D1 – прямоугольный параллелепипед. Докажите:а) DC A1D;
б) CD || плоскости ABB1A1;
в) DC AA1.
2. Треугольник ABC прямоугольный и равнобедренный с прямым углом C и гипотенузой 8 см. Отрезок CM перпендикулярен плоскости треугольника и равен 3 см. Отрезок MN прямой AB. Вычислите длину отрезка MN.| 3. На рисунке 3.1 прямые SA, SC, SB не лежат в одной плоскости. Среди отрезков EN, EF, KL, KM, FL, MN найдите пересекающиеся, не выходящие из одной точки, и лежащие на скрещивающихся прямых. Ответ обоснуйте. |  |
II вариант
1. ABCDA1B1C1D1 – прямоугольный параллелепипед. Докажите:
а) AD AB1;
б) AD || плоскости BB1C1C;
в) AD C1C.
2. Треугольник ABC равносторонний со стороной  см. Отрезок AE перпендикулярен плоскости треугольника ABC, отрезок EK прямой BC, длина отрезка AE =
см. Отрезок AE перпендикулярен плоскости треугольника ABC, отрезок EK прямой BC, длина отрезка AE =  см. Вычислите длину отрезка EK.
см. Вычислите длину отрезка EK.
3. Через прямую a проходят две различные плоскости и . В плоскости взята прямая a, в плоскости – прямая b. Могут ли прямые a и b быть:
а) параллельными,б) пересекающимися,
в) скрещивающимися?
Для каждого случая сделайте рисунок и обоснуйте ответ.Контрольная работа № 2 по теме «Прямые и плоскости» (28 ч)
I вариант
1. Плоскости равностороннего треугольника ABC и квадрата BCDE перпендикулярны. Найдите расстояние от точки A до стороны DE, если AB = 4 см.
2. ABCDA1B1C1D1 – прямоугольный параллелепипед. AB = AD = 8 дм, AA1 = 2 дм. M – середина B1C1, K – середина C1D1. Постройте сечение параллелепипеда плоскостью BMK, определите его вид и найдите его площадь.
3. Плоскости и параллельны. Через точку O, вне этих плоскостей, проведены две пересекающиеся прямые a и b. Прямая a пересекает плоскость в точке A, плоскость – в точке A1, а прямая b пересекает плоскости и в точках B и B1 соответственно. OA : OA1 = 2 : 3, AB = 10 см.
Найдите A1B1.
Рассмотрите все возможные случаи.II вариант
1. Плоскости равнобедренного треугольника ABC и квадрата ABDE перпендикулярны. Найдите расстояние от точки C до стороны DE, если AB = 6 см и ABC = 90.
2. ABCDA1B1C1D1 – прямоугольный параллелепипед. AB = AD = 12 см, AA1 = 3 см. Постройте сечение параллелепипеда плоскостью AKE, где K – середина A1B1 и E – середина B1C1. Определите вид сечения и найдите его площадь.
3. Плоскости и параллельны. На плоскости взяты точки C и D, так что CD = 8 см. На плоскости взята точка A и проведена прямая AC. Через точку D и точку M AC и лежащую вне плоскостей и проведена прямая DM, которая пересекает плоскость в точке K.
Найдите длину отрезка AC, если AK = 4 см, а AM = 3 см.
Рассмотрите все возможные случаи.
Контрольная работа по теме «Комбинаторика» (12 ч)
I вариант
1. Сколько слагаемых (до приведения подобных членов) получится, если раскрыть скобки в произведении
(x + y)(x2 + xy + y2)(x3 + y3 – x2y)?
2. Антон и Борис набирают на компьютере последовательность символов. Антон набирает подряд 15 символов, Борис – 3 символа. При этом Антон может использовать 4 различных символа, а Борис – 10. Кто из них может набрать больше последовательностей?
3. Из пяти букв А, Б, В, Г, Е составляют шестибуквенное слово, начинающееся с гласной буквы. Сколько можно составить таких слов, используя каждую букву любое число раз?
4. Чему равно число способов, которыми можно из класса в 15 человек выбрать группу из трех человек и назначить в ней старшего?
5. В слове ТЕОРЕМА переставили буквы всеми возможными способами. Сколько получилось различных вариантов?II вариант
1. Сколько слагаемых (до приведения подобных членов) получится, если раскрыть скобки в произведении
(a – b)(a2 + b2)(a3 – a2b + ab2 – b3)?
2. Антон и Борис набирают на компьютере последовательность символов. Антон набирает подряд 4 символа, Борис – 5 символов. При этом Антон может использовать 8 различных символов, а Борис – 5. Кто из них может набрать больше последовательностей?
3. Из пяти букв А, Б, В, Г, Е составляют шестибуквенное слово, начинающееся с согласной буквы. Сколько можно составить таких слов, используя каждую букву любое число раз?
4. Чему равно число способов, которыми можно из класса в 20 человек выбрать группу из четырех человек и назначить в ней старшего?
5. В слове ВАРИАНТ переставили буквы всеми возможными способами. Сколько получилось различных вариантов?
Контрольная работа по теме «Координаты и векторы» (12 ч)
I вариант
1. Дан тетраэдр DABC, K – середина ребра AC, M – середина отрезка KD,  ,
,  ,
,  . Разложите вектор
. Разложите вектор  по векторам
по векторам  ,
,  ,
,  .
.
2. Даны векторы  {1; –2; 0},
{1; –2; 0},  {3; –6; 0} и
{3; –6; 0} и  {0; –3; 4}.
{0; –3; 4}.
Найдите координаты и длину вектора  .
.
3. Найдите скалярное произведение  , если
, если  = 2,
= 2,  = 3,
= 3,  = 120.
= 120.
4. Даны точки C(3; –2; 1), D(–1; 2; 1), M(2; –3; 3), N(–1; 1; –2). Найдите
а) cos ;
;б) длину вектора  .
.
 ;
;б) длину вектора  .
.
Контрольная работа № 1 по теме «Основы тригонометрии» (28 ч)
I вариант
1. Изобразите на числовой окружности точки Pt, соответствующие числам
t =  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 
и сравните значения косинусов этих чисел.
2. Вычислите  , если sin =
, если sin =  и угол лежит во второй четверти.
и угол лежит во второй четверти.
3. Докажите тождество
 = tg2
= tg2
4. Преобразуйте в произведение
cos – cos 3 + cos 5 – cos 7
5. Упростите выражение и найдите его значение:
 при
при  .
.
6. Сравните числа, используя тригонометрическую окружность:
sin 12 и cos 13.
7*. Докажите тождество
sin 10° + 2 sin 5° cos 15° + cos 50° = cos 10°.II вариант
1. Изобразите на числовой окружности точки Pt, соответствующие числам
t =  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 
и сравните значения синусов этих чисел.
2. Вычислите  , если cos = –0,6 и угол лежит в третьей четверти.
, если cos = –0,6 и угол лежит в третьей четверти.
3. Докажите тождество
(tg + ctg )(1 – cos 4) = 4 sin 2
4. Преобразуйте в произведение
sin – sin 3 – sin 5 + sin 7
5. Упростите выражение и найдите его значение:
 при
при  .
.
6. Сравните числа, используя тригонометрическую окружность:
sin 14 и cos 9.
7*. Докажите тождество
sin 40° – 2 cos 10° sin2 15° + sin 20° =  cos 10°.Контрольная работа № 2 по теме «Основы тригонометрии» (28 ч)
cos 10°.Контрольная работа № 2 по теме «Основы тригонометрии» (28 ч)
I вариант
1. Решите тригонометрические уравнения:
а)  г) 2 cos2x + 9 sin x + 3 = 0
г) 2 cos2x + 9 sin x + 3 = 0
б) cos 2x = sin  д) sin 6x + sin 2x = sin 4x
д) sin 6x + sin 2x = sin 4x
в) sin x =  cos x
cos x
2. Найдите корни уравнения, принадлежащие промежутку
а)  , 0 x 2
, 0 x 2
б) cos 2x + sin2x = cos x, – x II вариант
1. Решите тригонометрические уравнения:
а)  г) 5 – 2 sin2x + 7 cos x = 0
г) 5 – 2 sin2x + 7 cos x = 0
б) sin 2x – 1 = 0 д) cos 3x – cos 5x = sin 4x
в) sin x + cos x = 0
2. Найдите корни уравнения, принадлежащие промежутку
а)  , – x
, – x
б) cos 2x + sin x = cos2x, 0 x 2
Контрольная работа № 1 по теме «Функции и графики» (28 ч)
I вариант
1. Проведите полное исследование функции и постройте ее график:
y = x2 – 2x – 3.
По графику определите, при каких a уравнение f(x) = a имеет два положительных корня.
2. Дана функция y = f(x), где  .
.
Постройте графики функций:
а) y = f(x) в) y = f(|x|)
б) y = |f(x)| + 1 г) y = f(x + 2)
и выделите среди них те, которые обладают свойствами четности или нечетности (выбор обоснуйте).
3. Найдите область определения функции
lg  .II вариант
.II вариант
1. Проведите полное исследование функции и постройте ее график:
y = –x2 + 4x + 5.
По графику определите, при каких a уравнение f(x) = a имеет два положительных корня.
2. Дана функция y = f(x), где  .
.
Постройте графики функций:
а) y = f(x) в) y = f(|x|)
б) y = |f(x)| + 1 г) y = f(x + 2)
и выделите среди них те, которые обладают свойствами четности или нечетности (выбор обоснуйте).
3. Найдите область определения функции
ln  .
.
Контрольная работа № 2 по теме «Функции и графики» (28 ч)
I вариант
1. Постройте график функции

и опишите ее свойства.
2. Сравните числа, используя свойства монотонности функции:
а)  и
и  б) 5–8,1 и 5–9 в)
б) 5–8,1 и 5–9 в)  и
и 
Ответы обоснуйте.
3. Решите неравенство
 .
.
4. Решите уравнения
а) log2(x + 2) = 15 – 2x в) lg (x2 – 6x + 9) = lg 3(x + 3)
б) 2 4x – 3 2x – 2 = 0II вариант
1. Постройте график функции

и опишите ее свойства.
2. Сравните числа, используя свойства монотонности функции:
а) 2816 и 7916 б) 0,3–12 и 0,3–11 в)  и
и 
Ответы обоснуйте.
3. Решите неравенство
 .
.
4. Решите уравнения
а) 0,5x – 1 = 3x + 14 в) log6 (2x2 – x) = log6 3x
б) 3 25x – 14 5x – 5 = 0
netnado.ru
Контрольные работы по теме «Степени и корни» в 11 классе по учебнику А.Г.Мордкович (профильный уровень).
Литература :
Дидактический материал 11класс Б.М.Ивлев, просвещение 2000г.
Дидактический материал 10-11класс А.П.Ершова, Москва «Илекса» 2007г.
Дидактический материал 7-11класс Б.Г.Зив, С.Петербург 2004г.
Задания ЕГЭ.
Контрольная работа №3
по теме «Степень с рациональным показателем»
1.Вычислите:
а)(-1)21 – 813/4 + (22/3  21/2) – 165/4 + (- 0,25)-3
21/2) – 165/4 + (- 0,25)-3
б) (302/3  21/3) : (52/3
21/3) : (52/3  811/6 )
811/6 )
2. Найти значение выражения при а = -5
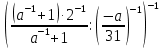
3.Упростить:
а). 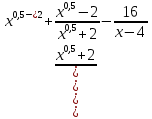
б). 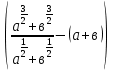 :
: 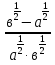
в).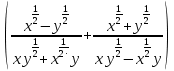
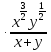
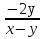
Контрольная работа №2
по теме «Преобразование выражений, содержащих радикалы»
1.Вычислить:
а)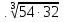 -
- 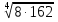 +
+ 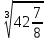
б)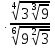 в)
в)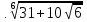
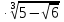
2.Сравнить значения выражений:
а)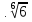 и
и 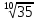
б)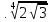 и
и 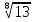
3.Сократи дробь:
а).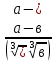 б).
б). 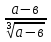
4.Установить область определения выражения:
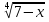 +
+ 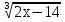
5.Найти значение выражения при в = 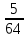
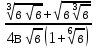
6. Упростить выражение:
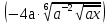 3 + ( -10
3 + ( -10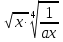 )2 – 5
)2 – 5 (
(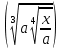 3)2
3)2
infourok.ru