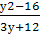Контрольная работа по математике для 11 класса. Контрольная по математике 11
Проверочная работа по математике для 11 класса
Проверочная работа по математике в 11 классе
Инструкция по выполнению работы
На выполнение работы отводится 90 минут.
Работа состоит из двух частей, включающих в себя 15 заданий.
Часть 1 (1-12 задание) содержит задания базового уровня с кратким ответом.
Часть 2 (13-15 задание) содержат задания повышенного уровня. При выполнении этих заданийнеобходимо записать полное обоснованное решение и ответ.
Советуем выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удаѐтся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
При выполнении работы запрещается пользоваться вычислительной техникой.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
| Вариант 1 Часть 1 Ответами к заданиям 1–12 являются цифра, число или последовательность цифр, которые следует записать в специальном поле |
| 1 | Для ремонта квартиры требуется 37 рулонов обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов? |
| 2 | На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 2003 году. Ответ дайте в градусах Цельсия. 
|
| 3 4 | Найдите значение выражения  Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 
|
| 5 | В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси. |
| 6 | Решите уравнение:  = 5 = 5 |
| 7 | Упростите выражение  и найдите его значение при  . . |
| 8 9 10 11 12 | В треугольнике АВС угол С равен 90°, АС=9,sinА=  . Найдите АВ. . Найдите АВ. 
Найдите значение выражения  Площадь поверхности куба равна 18.  Найдите его диагональ. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути – со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле:  , где l — длина ребра куба в метрах, , где l — длина ребра куба в метрах,  — плотность воды, а g — ускорение свободного падения — плотность воды, а g — ускорение свободного падения (считайте  Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 153125 Н? Ответ выразите в метрах. Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 153125 Н? Ответ выразите в метрах. |
| Часть 2 При выполнении заданий 13 –15 необходимо записать полное обоснованное решение и ответ. 13 а) Решите уравнение  б) Найдите все корни уравнения, принадлежащие отрезку  14 В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми SB и AD. |
| 15 | Решите неравенство:  |
| | |
| |
| | |
Проверочная работа в 11 классе
Инструкция по выполнению работы
На выполнение работы отводится 90 минут.
Работа состоит из двух частей, включающих в себя 15 заданий.
Часть 1 (1-12 задание) содержит задания базового уровня с кратким ответом.
Часть 2 (13-15 задание) содержат задания повышенного уровня. При выполнении этих заданий необходимо записать полное обоснованное решение и ответ.
Советуем выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удаѐтся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
При выполнении работы запрещается пользоваться вычислительной техникой.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
| Вариант 2 Часть 1 Ответами к заданиям 1–12 являются цифра, число или последовательность цифр, которые следует записать в специальном поле |
| 1 | Для ремонта квартиры требуется 63 рулона обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов? |
| 2 | На диаграмме показана среднемесячная температура в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия. 
|
| 3 4 | Найдите значение выражения  Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 
|
| 5 | В фирме такси в данный момент свободно 16 машин: 4 черных, 3 синих и 9 белых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет черное такси. |
| 6 | Решите уравнение: = 7 = 7 |
| 7 | Упростите выражение  и найдите его значение при  . . |
| 8 9 10 11 12 | В треугольнике АВС угол С равен 90°, АС=4,sinА=  . Найдите АВ. . Найдите АВ. 
Найдите значение выражения: 
Площадь поверхности куба равна 8. Найдите его диагональ. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 27 км/ч, а вторую половину пути — со скоростью, на 18 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле:  , где , где  – длина ребра куба в метрах, – длина ребра куба в метрах,  кг/м3 – плотность воды, а кг/м3 – плотность воды, а  – ускорение свободного падения (считайте – ускорение свободного падения (считайте  Н/кг). Какой может быть Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах. |
| Часть 2 При выполнении заданий 13 –15 необходимо записать полное обоснованное решение и ответ. |
| 13 | а) Решите уравнение  б) Укажите корни этого уравнения, принадлежащее отрезку  |
| 14 | В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 12, а боковые ребра равны 36, найдите косинус угла между прямыми SB и AD. |
| |
| 15 | Решите неравенство:  |
Ответы и решения
Вариант 1
Часть 1:
| № п/п | Ответ |
| 1 | 7 |
| 2 | 20 |
| 3 | -1,3 |
| 4 | 6 |
| 5 | 0,4 |
| 6 | 5 |
| 7 | 5 |
| 8 | 15 |
| 9 | 6 |
| 10 | 3 |
| 11 | 32 |
| 12 | 2,5 |
Часть 2:
13. а) Решите уравнение 
б) Найдите все корни уравнения, принадлежащие отрезку 
Решение.
а) Преобразуем уравнение:


Получаем  или
или  откуда
откуда 
 или
или  где
где 
б) На отрезке  корни отберём с помощью единичной окружности.
корни отберём с помощью единичной окружности.
Получаем  и
и 
Ответ: а) 
б) 
| Баллы | Критерии оценки выполнения задания |
| 3 | Обоснованно получен правильный ответ |
| 2 | Тригонометрическое уравнение решено верно, но неверно указаны или не указаны корни, принадлежащие отрезку |
| 1 | Тригонометрическое уравнение решено, но допущена вычислительная ошибка |
| 0 | Решение не соответствует ни одному из критериев |
14. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми SB и AD.
Решение.
Прямая AD параллельна прямой BC. Следовательно, искомый угол — SBC. В равнобедренном треугольнике SBC проведём медиану и высоту SM. Имеем:
Из прямоугольного треугольника SBM
получаем:
Ответ: 
| Баллы | Критерии оценки выполнения задания |
| 2 | Обоснованно получен верный ответ |
| 1 | Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно |
| 0 | Другие случаи, не соответствующие указанным критериям |
| 2 | Максимальный балл |
15. Решите неравенство: 
Решение.
Перепишем неравенство в виде:
Множество решений исходного
неравенства:
Ответ:
| Баллы | Критерии оценки выполнения задания |
| 2 | Обоснованно получен верный ответ |
| 1 | Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно |
| 0 | Другие случаи, не соответствующие указанным критериям |
| 2 | Максимальный балл |
Вариант 2
Часть 1:
| № п/п | Ответ |
| 1 | 11 |
| 2 | -14 |
| 3 | 4 |
| 4 | 6 |
| 5 | 0,25 |
| 6 | 45 |
| 7 | 3 |
| 8 | 5 |
| 9 | 2 |
| 10 | 2 |
| 11 | 36 |
| 12 | 2 |
Часть 2:
13. а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащее
отрезку 
Решение.
Сведём уравнение к квадратному относительно синуса, используя
формулу Имеем:
б) С помощью числовой окружности отберём корни, принадлежащие
отрезку , получим число
Ответ:
а) б)
| Баллы | Критерии оценки выполнения задания |
| 3 | Обоснованно получен правильный ответ |
| 2 | Тригонометрическое уравнение решено верно, но неверно указаны или не указаны корни, принадлежащие отрезку |
| 1 | Тригонометрическое уравнение решено, но допущена вычислительная ошибка |
| 0 | Решение не соответствует ни одному из критериев |
14. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 12, а боковые ребра равны 36, найдите косинус угла между прямыми SB и AD.
Решение.
Прямая  параллельна прямой
параллельна прямой  Следовательно, искомый угол — В равнобедренном треугольнике
Следовательно, искомый угол — В равнобедренном треугольнике  проведём
проведём
медиану и высоту 
Имеем:
Из прямоугольного треугольника
получаем:
Ответ: 
| Баллы | Критерии оценки выполнения задания |
| 2 | Обоснованно получен верный ответ |
| 1 | Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно |
| 0 | Другие случаи, не соответствующие указанным критериям |
| 2 | Максимальный балл |
15. Решите неравенство: 
Решение.
Перепишем неравенство в виде:
Таким образом, множество решений исходного неравенства:
Ответ:
| Баллы | Критерии оценки выполнения задания |
| 2 | Обоснованно получен верный ответ |
| 1 | Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно |
| 0 | Другие случаи, не соответствующие указанным критериям |
| 2 | Максимальный балл |
Критерии оценки выполнения
Общий балл формируется путем суммирования баллов, полученных учащимися за выполнение заданий. За каждое верно выполненное задание части 1 начисляется 1 балл, за каждое задание части 2 – 2 балла.
Оценка работы:
| Балл | Отметка |
| 14-18 | 5 |
| 9-13 | 4 |
| 6-8 | 3 |
| 0-5 | 2 |
kopilkaurokov.ru
Контрольные работы по математике 11 класс
Контрольные работы по алгебре и началам анализа в 11 классе
Контрольная работа № 1 «Тригонометрические функции»
1. Найдите область определения и множество значений функции у = sin2x+1.
2. Выясните, является ли функция у = sin x – tg x четной или нечетной.
3. Сравните числа:
А) sin  и ) sin
и ) sin  ; Б) cos
; Б) cos  и cos
и cos  ; В) sin 2 и cos 2,3
; В) sin 2 и cos 2,3
4. Найдите все числа из отрезка [-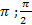 ], для которых выполняется равенство sin x= -
], для которых выполняется равенство sin x= - 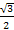 .
.
5. Постройте график функции у = -2 cos (х -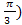 .
.
Контрольная работа № 2 «Производная и ее геометрический смысл»
1. Найдите производную функции: а) 4 х 3+ 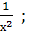 б)
б) 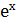 sin х; в)
sin х; в) 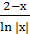 ; г)
; г) 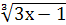
2.Найдите значения х, при которых значения производной функции f(x) = 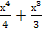 -3
-3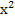 равны нулю.
равны нулю.
3. Запишите уравнение касательной к графику функции f(x) = 1+4х-sin x в точке с абсциссой х0 = 0.
4. На графике функции f(x)=х3 -3х2+2 найдите все такие точки, в которых касательная, проведенная к графику, параллельна прямой у=3х.
Контрольная работа № 3 «Применение производной к исследованию функции»
-
Найдите интервалы возрастания и убывания функции у=1+2х2-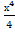 .
.
-
Постройте график функции у=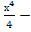 2х2.
2х2.
-
Найдите ромб наибольшей площади,если известно, что сумма его диагоналей равна 10.
-
Найдите направления выпуклости графика функции у=х+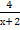
Контрольная работа № 4 «Интеграл»
1. Докажите, что функция F(x) = ех+х3-cos х является первообразной функции f (x) = 2е2х+3х2+sin х на всей числовой оси.
2. Найдите первообразную F функции f (x) = 3х2+2х-3 , график которой проходит через точку М(1;-2).
3. Вычислите площадь фигуры, ограниченной параболой у=х2+х-6 и осью Ох.
4. Найдите площадь фигуры, ограниченной линиями у=2+4х-х2 и у=х2-2х+2.
5. Найдите площадь фигуры, ограниченной параболой у=х2-12 и касательными к ней, проведенными из точки А (0;3).
Контрольная работа № 5 «Комплексные числа»
-
На комплексной плоскости постройте точки –i, -2+2i.
-
Выполните действия: а) i4+i5-2i; б) 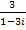 -
-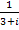 .
.
-
Решите уравнение 2z2-6z+5=0/
-
Найдите все аргументы комплексного числа z=-2-2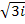 и запишите его в тригонометрической форме.
и запишите его в тригонометрической форме.
-
Пользуясь формулой Муавра, возведите в степень (1+i)6и результат запишите в алгебраической форме.
-
Решите уравнение z3=-27.
Контрольная работа № 6 «Элементы комбинаторики»
-
Упростите 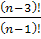 , где n€N, n>4.
, где n€N, n>4.
-
Найдите значение выражения 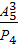 +
+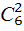 .
.
-
Сколько различных трехзначных чисел можно записать с помощью цифр 0,1,2,3 при условии, что цифры в числе могут повторяться?
-
Сколькими способами можно составить букет из трех цветков, выбирая цветы из девяти имеющихся?
-
Запишите разложение бинома (1+х)6.
Контрольная работа № 6 «Теория вероятности»
-
В ящике находится 3 белых, 5 черных, 6 красных шаров. Наугад вынимают один шар. Какова вероятность того, что вынутый шар: а) белый или черный; б) желтый; в) не белый?
-
Брошены 2 игральные кости. Какова вероятность того, что на одной кости выпало 3 очка, а на другой – четное число очков?
-
В корзине лежат 5 яблок и 3 апельсина. Наугад дважды из корзины вынимают по одному плоду (не возвращая их в корзину). Какова вероятность того, что вторым было взято яблоко, при условии, что первым был апельсин?
-
Имеется 13 карт черной масти и 5 карт красной масти. Какова вероятность того, что среди двух карт, вынутых наугад, хотя бы одна будет красной?
infourok.ru
Контрольная работа по математике для 11 класса
Контрольная работа по математике для 11 класса
На выполнение контрольной работы по математике дается 2 часа. Работа состоит из двух частей. Первая часть содержит 10. К каждому заданию В1-В10 требуется дать краткий ответ. Задания С1, С2 выполняются на отдельном листе и ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В10 оцениваются в 1 балл, С1 – 2 балла, С2 – 3 балла.
Таблица перевода тестовых баллов в школьные отметки.
Тестовый балл
Школьная отметка | | 0-4 | 2 |
| 5-8 | 3 |
| 9-11 | 4 |
| 12-15 | 5 |
Вариант 1
Часть I
В1. Найдите значение выражения  log
log
В2. Найдите остаток от деления многочлена  13
13  + 67
+ 67 - 3x + 4 на многочлен P(x) =
- 3x + 4 на многочлен P(x) = +5 x +1.
+5 x +1.
В3. На рисунке изображен график первообразной y = F (x) некоторой функции y = f(x), определенной на интервале ( - 16; - 2). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-15; -8]. 
В4. Валя выбирает случайное трехзначное число. Найдите вероятность того, что оно делится на 51.
В5. Решите уравнение = 0,04.
= 0,04.
В6 Высота конуса равна 30, а длина образующей - 34. Найдите диаметр основания конуса.

В7. Коэффициент полезного действия некоторого двигателя определяется формулой  . При каком наименьшем значении температура нагревателя
. При каком наименьшем значении температура нагревателя  ( в градусах Кельвина) КПД этого двигателя будет не меньше 80%, если температура холодильника
( в градусах Кельвина) КПД этого двигателя будет не меньше 80%, если температура холодильника  = 200 К?
= 200 К?
В8. Объем цилиндра равен 12см . Чему равен объем конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр?
. Чему равен объем конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр?
В9. Два автомобиля отправляются в 420 – километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 1 час раньше второго. Найти скорость автомобиля, пришедшего к финишу вторым.
В10. Найдите наименьшее значение функции y = ( на отрезке [6; 8].
на отрезке [6; 8].
Часть II
С1. Радиус основания конуса равен 8, а его высота равна 15. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 14. Найдите расстояние от центра основания конуса до плоскости сечения.
С2. Решите систему неравенств

.
МАТЕМАТИКА, 11 класс
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 2 часа. Работа состоит из двух частей. Первая часть содержит 10 заданий. К каждому заданию В1-В10 требуется дать краткий ответ. Задания С1, С2 выполняются на отдельном листе и ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В10 оцениваются в 1 балл, С1 – 2 балла, С2 – 3 балла.
Таблица перевода тестовых баллов в школьные отметки.
Тестовый балл
Школьная отметка | | 0-4 | 2 |
| 5-8 | 3 |
| 9-11 | 4 |
| 12-15 | 5 |
Вариант 2
Часть I
В1. 
В2. Найдите остаток от деления многочлена 
 - 11
- 11 + x + 7 на многочлен P(x) =
+ x + 7 на многочлен P(x) = +3.
+3.
В3. На рисунке изображен график первообразной
некоторой функции y = f(x). Одна из первообразных этой функции равна F( x) =  . Найдите площадь заштрихованной фигуры.
. Найдите площадь заштрихованной фигуры.

В4. В фирме такси в данный момент свободно 10 машин: 5 черных, 1 желтая и 4 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
В5. Решите уравнение = 0,25.
= 0,25.
В6. В сосуд, имеющий форму конуса, налили 25 мл жидкости до половины высоты сосуда (см. рис.) Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?

В7. Коэффициент полезного действия некоторого двигателя определяется формулой  ,
,  - температура нагревателя ( в градусах Кельвина) ,
- температура нагревателя ( в градусах Кельвина) , - температура холодильника ( в градусах Кельвина) При какой температуре нагревателя
- температура холодильника ( в градусах Кельвина) При какой температуре нагревателя  КПД двигателя будет 45%, если температура холодильника
КПД двигателя будет 45%, если температура холодильника  = 275 К? Ответ выразите в градусах Кельвина.
= 275 К? Ответ выразите в градусах Кельвина.
В8. Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 6. Найдите объем параллелепипеда.

В9. Из пункта А круговой трассы, длина которой равна 30 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого равна 92 км/ч, скорость второго — 77 км/ч. Через сколько минут первый автомобилист будет опережать второго ровно на 1 круг?
В10. Найдите набольшее значение функции y = ( на отрезке [19; 21].
на отрезке [19; 21].
Часть II
С1. Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра.
С2. Решите систему неравенств

МАТЕМАТИКА, 11 класс
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 2 часа. Работа состоит из двух частей. Первая часть содержит 10. К каждому заданию В1-В10 требуется дать краткий ответ. Задания С1, С2 выполняются на отдельном листе и ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В10 оцениваются в 1 балл, С1 – 2 балла, С2 – 3 балла.
Таблица перевода тестовых баллов в школьные отметки.
Тестовый балл
Школьная отметка | | 0-4 | 2 |
| 5-8 | 3 |
| 9-11 | 4 |
| 12-15 | 5 |
Вариант 3
Часть I
В1 
В2. Найдите остаток от деления многочлена 
 + x на многочлен р(x) =
+ x на многочлен р(x) = + x + 1
+ x + 1
В3. На рисунке изображен график некоторой функции у = Пользуясь рисунком, вычислите определенный интеграл
Пользуясь рисунком, вычислите определенный интеграл 
 dx
dx 
В4. В сборнике билетов по биологии всего 25 билетов, в 12 из них встречается вопрос по круглым червям. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику попадется вопрос по круглым червям.
В5. Решите уравнение  = 36.
= 36.
В6 Высота конуса равна 4, а длина образующей - 5. Найдите диаметр основания конуса.

В7. Температуру нагревательного элемента (в градусах Кельвина) в зависимости от времени (вминутах) можно вычислять по формуле Т(t) = Т0 + аt + b t2, где Т0 = 760 К, а = 34 К/мин, b = -0,2 К/мин2. Известно, что при температурах нагревателя свыше 1600 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время (в минутах) после начала работы нужно отключать прибор.
В8. Площадь боковой поверхности цилиндра равна  , а высота — 8 . Найдите диаметр основания.
, а высота — 8 . Найдите диаметр основания.
В9. Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
В10. Найдите наимбольшее значение функции  на отрезке [-4,5; 0].
на отрезке [-4,5; 0].
Часть II
С1. Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Найдите угол между этой плоскостью и плоскостью основания цилиндра.
С2. Решите систему неравенств

.
МАТЕМАТИКА, 11 класс
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 2 часа. Работа состоит из двух частей. Первая часть содержит 10 заданий. К каждому заданию В1-В10 требуется дать краткий ответ. Задания С1, С2 выполняются на отдельном листе и ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В10 оцениваются в 1 балл, С1 – 2 балла, С2 – 3 балла.
Таблица перевода тестовых баллов в школьные отметки.
Тестовый балл
Школьная отметка | | 0-4 | 2 |
| 5-8 | 3 |
| 9-11 | 4 |
| 12-15 | 5 |
Вариант 4
Часть I
В1. Найдите значение выражения  .
.
В2. Найдите остаток от деления многочлена 
 - 2
- 2 - 5 на многочлен р(x) =
- 5 на многочлен р(x) = – 9х.
– 9х.
В3. На рисунке изображён график функции y = F(x) и одной из первообразных некоторой функции f(x), определённой на интервале (−3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−2;4].

В4.. На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 7 прыгунов из Голландии и 2 прыгуна из Боливии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первым будет выступать прыгун из Боливии.
В5. Найдите корень уравнения:  .
.
В6. Длина окружности основания цилиндра равна 7. Площадь боковой поверхности равна 105. Найдите высоту цилиндра.
В7 На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле:  , где
, где  – постоянная,
– постоянная,  – радиус аппарата в метрах,
– радиус аппарата в метрах,  м3 – плотность воды, а
м3 – плотность воды, а  – ускорение свободного падения (считайте
– ускорение свободного падения (считайте  Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.
Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.
В8 Диаметр основания конуса равен 136, а длина образующей — 85 . Найдите высоту конуса.
В9. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
В10. Найдите наименьшее значение функции  на отрезке [0; 2].
на отрезке [0; 2].
Часть II
С1. Две параллельные плоскости, находящиеся на расстоянии 12 друг от друга, пересекают шар. Получившиеся сечения одинаковы, и площадь каждого из них равна 64л. Найдите площадь поверхности шара.
С3. Решите систему неравенств

globuss24.ru



 = 5
= 5
 .
. . Найдите АВ.
. Найдите АВ. 


 , где l — длина ребра куба в метрах,
, где l — длина ребра куба в метрах,  — плотность воды, а g — ускорение свободного падения
— плотность воды, а g — ускорение свободного падения  Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 153125 Н? Ответ выразите в метрах.
Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 153125 Н? Ответ выразите в метрах.





 = 7
= 7
 . Найдите АВ.
. Найдите АВ. 
 – длина ребра куба в метрах,
– длина ребра куба в метрах,  кг/м3 – плотность воды, а
кг/м3 – плотность воды, а  – ускорение свободного падения (считайте
– ускорение свободного падения (считайте 



 или
или  откуда
откуда 
 или
или  где
где 
 корни отберём с помощью единичной окружности.
корни отберём с помощью единичной окружности.
 и
и 


 и ) sin
и ) sin  ; Б) cos
; Б) cos  и cos
и cos  ; В) sin 2 и cos 2,3
; В) sin 2 и cos 2,3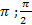 ], для которых выполняется равенство sin x= -
], для которых выполняется равенство sin x= - 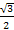 .
.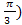 .
.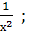 б)
б) 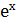 sin х; в)
sin х; в) 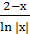 ; г)
; г) 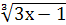
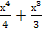 -3
-3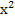 равны нулю.
равны нулю.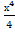 .
.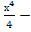 2х2.
2х2.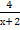
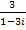 -
-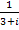 .
.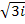 и запишите его в тригонометрической форме.
и запишите его в тригонометрической форме.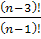 , где n€N, n>4.
, где n€N, n>4.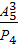 +
+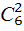 .
. log
log
 13
13  + 67
+ 67 - 3x + 4 на многочлен P(x) =
- 3x + 4 на многочлен P(x) =
 = 0,04.
= 0,04.
 . При каком наименьшем значении температура нагревателя
. При каком наименьшем значении температура нагревателя  ( в градусах Кельвина) КПД этого двигателя будет не меньше 80%, если температура холодильника
( в градусах Кельвина) КПД этого двигателя будет не меньше 80%, если температура холодильника  = 200 К?
= 200 К? . Чему равен объем конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр?
. Чему равен объем конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр? на отрезке [6; 8].
на отрезке [6; 8].

 +3.
+3.  . Найдите площадь заштрихованной фигуры.
. Найдите площадь заштрихованной фигуры.
 = 0,25.
= 0,25. 

 на отрезке [19; 21].
на отрезке [19; 21].

 Пользуясь рисунком, вычислите определенный интеграл
Пользуясь рисунком, вычислите определенный интеграл 
 dx
dx 
 = 36.
= 36. , а высота — 8 . Найдите диаметр основания.
, а высота — 8 . Найдите диаметр основания. на отрезке [-4,5; 0].
на отрезке [-4,5; 0].
 .
. - 5 на многочлен р(x) =
- 5 на многочлен р(x) =
 .
. , где
, где  – постоянная,
– постоянная,  – радиус аппарата в метрах,
– радиус аппарата в метрах,  м3 – плотность воды, а
м3 – плотность воды, а  – ускорение свободного падения (считайте
– ускорение свободного падения (считайте  Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.
Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах. на отрезке [0; 2].
на отрезке [0; 2].