 правильной четырехугольной пирамиде SABCD точка O – центр
правильной четырехугольной пирамиде SABCD точка O – центрКонтрольная работа по теме «Многогранники. Тела вращения»
I - вариант
№ задания
Баллы
Содержание задания
1
Отрезок, соединяющий две вершины, не принадлежащие одной грани называются ….
2
Площадь боковой поверхности прямой пирамиды равна …
4
Изобразите усеченную четырехугольную пирамиду
3
Изобразите осевое сечение цилиндра
6
Пусть радиус цилиндра 2 см, высота 4 см . Найдите площадь полной поверхности цилиндра
5
Высота конуса равна 5 см, а образующая конуса 7 см.
Найдите радиус основания
6
В шар диаметром D вписан цилиндр с диаметром основания d.
Вычислите площадь осевого сечения цилиндра
3
В правильной четырехугольной пирамиде SABCD точка O – центр
правильной четырехугольной пирамиде SABCD точка O – центр
основания, S – вершина, SD=30, BD=36. Найдите длину отрезка SO.
7
Дан прямоугольный параллелепипед ABCDA1B1C1D 1. AB = 3, AA1= 4, AD = 2. Найдите площадь поверхности треугольной призмы AA1BDD1C.
7
Найдите
а ) расстояние между вершинами C и B2 многогранника, изображенного на рисунке;
) расстояние между вершинами C и B2 многогранника, изображенного на рисунке;
Все двугранные углы многогранника
прямые.
Всего
44
Контрольная работа по теме «Многогранники. Тела вращения»
II - вариант
№ задания
Баллы
Содержание задания
1
Стороны граней многогранника называются …..
2
Площадь боковой поверхности прямой призмы равна…
4
Нарисуйте наклонную треугольную призму
3
Изобразите сечение конуса плоскость, параллельной основанию
6
Пусть радиус цилиндра 2 см, высота 4 см . Найдите площадь боковой поверхности цилиндра
5
Высота конуса равна 8 см, а радиус основания 6 см. найдите образующую конуса
6
В шар диаметром D вписан цилиндр с диаметром основания d.
Вычислите высоту цилиндра
3
В правильной четырехугольной пирамиде SABCD O – центр
правильной четырехугольной пирамиде SABCD O – центр
основания, S – вершина, SD=17, BD=16. Найдите длину отрезка SO.
7
Дан прямоугольный параллелепипед ABCDA 1B 1C 1D1. , AB =4, BB 1= 3, BC =1. Найдите площадь поверхности треугольной призмы ABB1DCC1.
7
Найдите расстояние между вершинами B2 и C многогранника,
изображенного на рисунке. Все двугранные углы многогранника прямые.

Всего
44
Лист эталонов
I - вариант
№ задания
Баллы
Примерное решение
1
диагональ
2
Половине произведения периметра основания на апофему
4,3
Усеченная Осевое
четырехугольная пирамида сечение цилиндра


6
Дано:
радиус цилиндра 2 см,
высота 4 см
Найдите
площадь полной
поверхности цилиндра

Решение
АО=2см, ОО1=4см.
Длина окружности в основании L==4π, Sбок=2πRh=16π
Sосн=πR2=4π
Sполн=2 Sосн++ Sбок=24π
Ответ: Sполн=24π
5
Дано:
Высота конуса равна 5 см,
образующая конуса 7 см.
Найдите
радиус основания
Р
О
А

Решение:
РО=5 см, РА=7см.
По т. Пифагора в треугольнике РОА найдем катет ОА:

6
Дано:
В шар диаметром D
вписан цилиндр
с диаметром основания d.
Вычислите
п лощадь осевого сечения цилиндра
лощадь осевого сечения цилиндра
Решение:
АО=D/2 ВО1=d./2
Площадь осевого сечения цилиндра
Sсе= КВ*ВН, но КВ=d, а
ВН= 2ВР.
ВР найдем из треугольника ВОР по т. Пифагора: ВР2=ОВ2-ОР2, т.е. ВР=

Sсе=d
Ответ: Sсеч=d
3
SABCD - правильная четырехугольная пирамида
O – центр основания,
S – вершина, SD=30, BD=36. Найдите длину отрезка SO.

Решение:
DO=½BD=18
По т.Пифагора из треугольника SOD имеем: SO=
Ответ: SO=24
7
Дано:
прямоугольный параллелепипед A1B1C1.
AB = 3, AА1= 4 , AD = 2. Найдите площадь поверхности треугольной призмы
AA1BD1C.

Решение:
Площадь поверхности треугольной призмы
AA1BDD1C складывается из двух площадей оснований и площади боковой поверхности.
Найдем площадь основания АА1В: Sосн = ½ AА1 * AB =2*3 =6
Sбок =( AА1 +AB + A1B) *AD
Найдем A1B по т. Пифагора из треугольника AА1B:
A1B= , тогда
, тогда
Sбок = (4+3 +5)*2 =24.
S = 2 Sосн +Sбок =12+24 = 36
Ответ: площадь поверхности треугольной призмы AA1BDD1C равна 36 кв. ед.
7
Найдите
а) расстояние между вершинами C и B2
многогранника, изображенного на рисунке;
 Все двугранные углы многогранника
Все двугранные углы многогранника
прямые.
Решение:
Проведем дополнительные построения: из точки В2 и С2 опустим перпендикуляры соответственно на стороны АВ и СD, точки обозначим как В3 и С3.
Проведем прямые А2В2, D2С2 до пресечения с прямыми ВВ1 и СС1 соответственно, получим точки В2 и С2
Получим новый параллелепипед В3В2С2С3ВСВ2С2, для которых расстояние от точки В2 до С есть длина диагонали.
Измерения нового параллелограмма 13, 18, 6, поэтому =
Ответ: В2 С = 23 ед.
Всего
44
Лист эталонов
II - вариант
№ задания
Баллы
Содержание задания
1
ребрами
2
Произведению периметра основания на высоту
4
Нарисуйте наклонную треугольную призму

Изобразите сечение конуса плоскость, параллельной основанию

3
6
Дано:
радиус цилиндра 2 см,
высота 4 см .
Найдите
площадь боковой поверхности цилиндра

Решение:
Ответ: Sбок = 16 π
5
Дано:
Высота конуса равна 8 см,
радиус основания 6 см.
найдите:
образующую конуса

Решение:
Из треугольника SОА по т.Пифагора имеем:
 (см0
(см0
Ответ: образующая конуса равна 10 см.
6
Дано:
шар диаметром D
вписан цилиндр
диаметр основания d.
Вычислите в ысоту цилиндра
ысоту цилиндра
Решение:
АО=D/2 ВО1=d./2
Высота цилиндра ВН= 2ВР.
ВР найдем из треугольника ВОР по т. Пифагора: ВР2=ОВ2-ОР2, т.е. ВР=
ВН= 
Ответ: высота цилиндра равна 
3
Дано:
пирамида SABCD- правильная
O – центр основания,
S – вершина,
SD=17, BD=16.
Найдите длину отрезка SO.

Решение:
DO=½BD=8
По т.Пифагора из треугольника SOD имеем: SO=
Ответ: SO=15
7
Дано:
прямоугольный параллелепипед ABCDA1B1C1D1. ,
AB =4, BB 1= 3, BC =1.
Найдите
площадь поверхности
треугольной призмы ABB1DCC1.

Решение:
Площадь поверхности треугольной призмы AA1BDD1C складывается из двух площадей оснований и площади боковой поверхности.
Найдем площадь основания АА1В:
Sосн = ½ ВВ1 * AB =6
Sбок =( ВВ1 +AB + A1B) *AD
Найдем A1B по т. Пифагора из треугольника AАВ1B:
A1B= , тогда
, тогда
Sбок = (3+4 +5)*2 =24.
S = 2 Sосн +Sбок =12+24 = 36
Ответ: площадь поверхности треугольной призмы AA1BDD1C равна 36 кв. ед.
7
Найдите
а) расстояние между вершинами
B2и C многогранника;
б) объем фигуры,
изображенной на рисунке.
Все двугранные углы
м ногогранника прямые.
ногогранника прямые.
Решение:
Проведем дополнительные построения: из точки В2 и С2 опустим перпендикуляры соответственно на стороны АВ и СD, точки обозначим как В3 и С3.
Проведем прямые А2В2, D2С2 до пресечения с прямыми ВВ1 и СС1 соответственно, получим точки В2 и С2
Получим новый параллелепипед В3В2С2С3ВСВ2С2, для которых расстояние от точки В2 до С есть длина диагонали.
Измерения нового параллелограмма 13, 18, 6, поэтому =
Ответ: В2 С = 23 ед.
Всего
44
www.metod-kopilka.ru
Контрольная работа №2 по теме «Многогранники»
Вариант 1
1. Стороны основания прямого параллелепипеда равны 6 см и 4 см, угол между ними равен  . Диагональ большей боковой грани равна 10 см. Найдите площадь боковой и площадь полной поверхности параллелепипеда.
. Диагональ большей боковой грани равна 10 см. Найдите площадь боковой и площадь полной поверхности параллелепипеда.
2. Основание прямой призмы – прямоугольный треугольник с катетами 6 см и 8 см. Найти площадь боковой поверхности призмы, если её наибольшая боковая грань – квадрат.
3. Боковое ребро правильной четырёхугольной пирамиды составляет с плоскостью основания угол  . Найдите площадь боковой и площадь полной поверхности пирамиды, если сторона основания равна 7 см.
. Найдите площадь боковой и площадь полной поверхности пирамиды, если сторона основания равна 7 см.
4. Апофема правильной четырёхугольной пирамиды равна  , высота пирамиды равна
, высота пирамиды равна  . Найдите:
. Найдите:
а) Сторону основания пирамиды.
б) Угол между боковой гранью и основанием.
в) Площадь поверхности пирамиды.
г) Расстояние от центра основания пирамиды до плоскости боковой грани.
Вариант 2
1. Ребро правильного тетраэдра DАВС равно 9 см. Постройте сечение тетраэдра, проходящее через середину ребра DА, параллельно плоскости DВС, и найдите площадь этого сечения.
2. Найдите площадь полной поверхности куба, если расстояние от вершины верхнего основания куба до центра нижнего основания равно 18 см.
3. Найдите площадь полной поверхности правильной треугольной пирамиды, если её апофема равна 8 см, а угол между апофемой и высотой пирамиды равен  .
.
4. Сторона основания правильной четырёхугольной призмы равна р, диагональ призмы образует с плоскостью основания угол  . Найдите:
. Найдите:
а) Диагональ призмы.
б) Угол между диагональю призмы и плоскостью боковой грани.
в) Площадь боковой поверхности призмы.
г) Площадь сечения призмы плоскостью, проходящей через сторону нижнего основания и противоположную сторону верхнего основания.
Вариант 3
1. В основании прямого параллелепипеда лежит ромб со стороной 12 см и углом  . Меньшая диагональ параллелепипеда равна 13 см. Найдите площадь боковой и площадь полной поверхности параллелепипеда.
. Меньшая диагональ параллелепипеда равна 13 см. Найдите площадь боковой и площадь полной поверхности параллелепипеда.
2. Основание прямой призмы – треугольник со сторонами 8 см и 3 см и углом между ними  . Высота призмы равна 15 см. Найдите площадь боковой и площадь полной поверхности призмы.
. Высота призмы равна 15 см. Найдите площадь боковой и площадь полной поверхности призмы.
3. Найдите площадь полной поверхности правильной треугольной пирамиды, если её апофема равна 4 см, а угол между апофемой и высотой пирамиды равен  .
.
4. Боковое ребро правильной четырехугольной пирамиды равно 4 см и образует с плоскостью основания пирамиды угол 450.
а) Найдите высоту пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
Вариант 4
1. Найдите площадь полной поверхности правильного тетраэдра, высота которого равна 16 см.
2. Основание прямой призмы – треугольник со сторонами 8 см и 15 см и углом между ними  . Высота призмы равна 11 см. Найдите площадь боковой и площадь полной поверхности призмы.
. Высота призмы равна 11 см. Найдите площадь боковой и площадь полной поверхности призмы.
3. Боковое ребро правильной треугольной пирамиды составляет с высотой угол  . Найдите площадь боковой и площадь полной поверхности пирамиды, если сторона основания равна 10 см.
. Найдите площадь боковой и площадь полной поверхности пирамиды, если сторона основания равна 10 см.
4. Диагональ правильной четырёхугольной призмы равна р и образует с плоскостью боковой грани угол  . Найдите:
. Найдите:
а) Сторону основания призмы.
б) Угол между диагональю призмы и плоскостью основания.
в) Площадь боковой поверхности призмы.
г) Площадь сечения призмы плоскостью, проходящей через диагональ основания параллельно диагонали призмы.
Критерии оценки:
«5» - задание выполнено полностью.
«4» - выполнено три задания.
«3» - выполнено два задания.
multiurok.ru
Контрольная работа №4
Многогранники
Вариант1
Основание прямой призмы - равнобедренный треугольник, в котором высота, проведенная к основанию, равна 8см. Высота призмы равна 12см. Найдите полную поверхность призмы, если боковая грань, содержащая основание треугольника, - квадрат.
2. Основание пирамиды – правильный треугольник с площадью 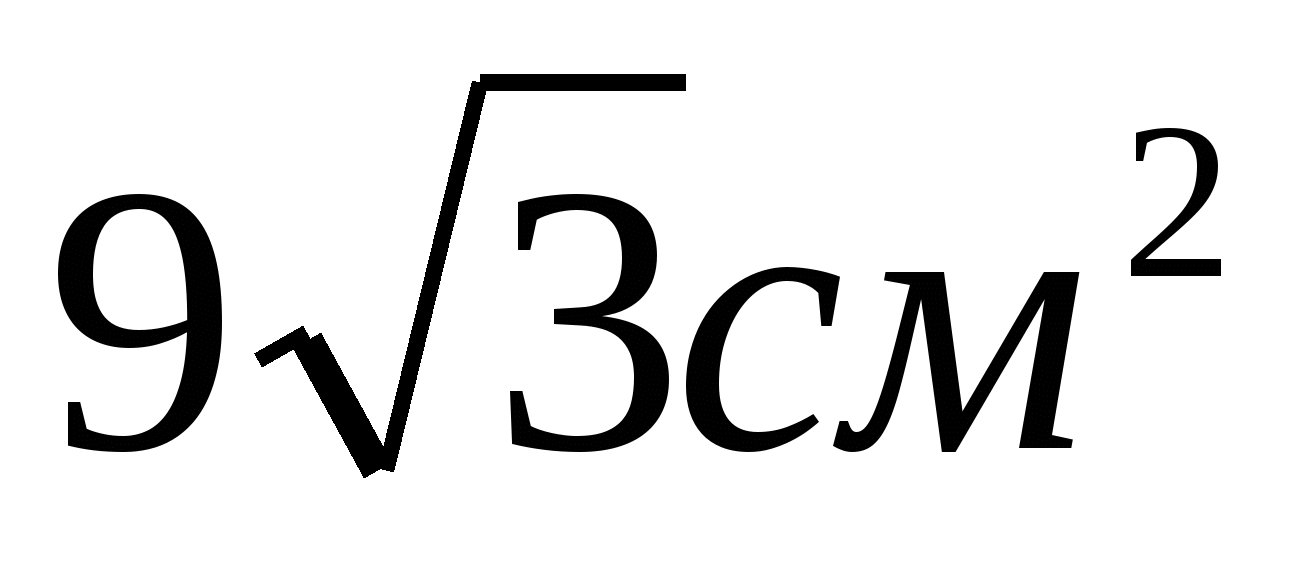 . Две боковые грани пирамиды перпендикулярны к плоскости основания, а третья – наклонена к ней под углом 300.
. Две боковые грани пирамиды перпендикулярны к плоскости основания, а третья – наклонена к ней под углом 300.
а) Найдите длины боковых ребер пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
3. Стороны оснований правильной треугольной усеченной пирамиды равны 2 и 6 см, а боковая грань образует с плоскостью большего основания угол 600. Найдите боковую поверхность данной пирамиды и высоту полной пирамиды, из которой получена данная усеченная пирамида.
4. Равнобедренные треугольники АВС и ADС имеют общее основание АС, а двугранный угол BACD – прямой. Найдите углы, образуемые прямой BD с плоскостями треугольников, если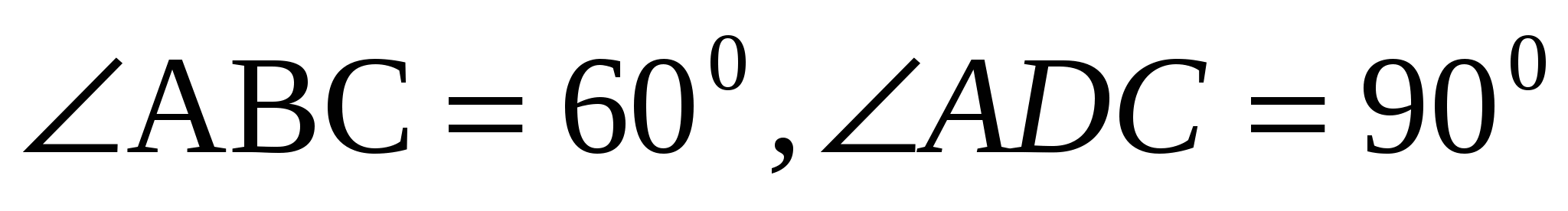
Контрольная работа №4
Многогранники
Вариант1
Основание прямой призмы - равнобедренный треугольник, в котором высота, проведенная к основанию, равна 8см. Высота призмы равна 12см. Найдите полную поверхность призмы, если боковая грань, содержащая основание треугольника, - квадрат.
2. Основание пирамиды – правильный треугольник с площадью 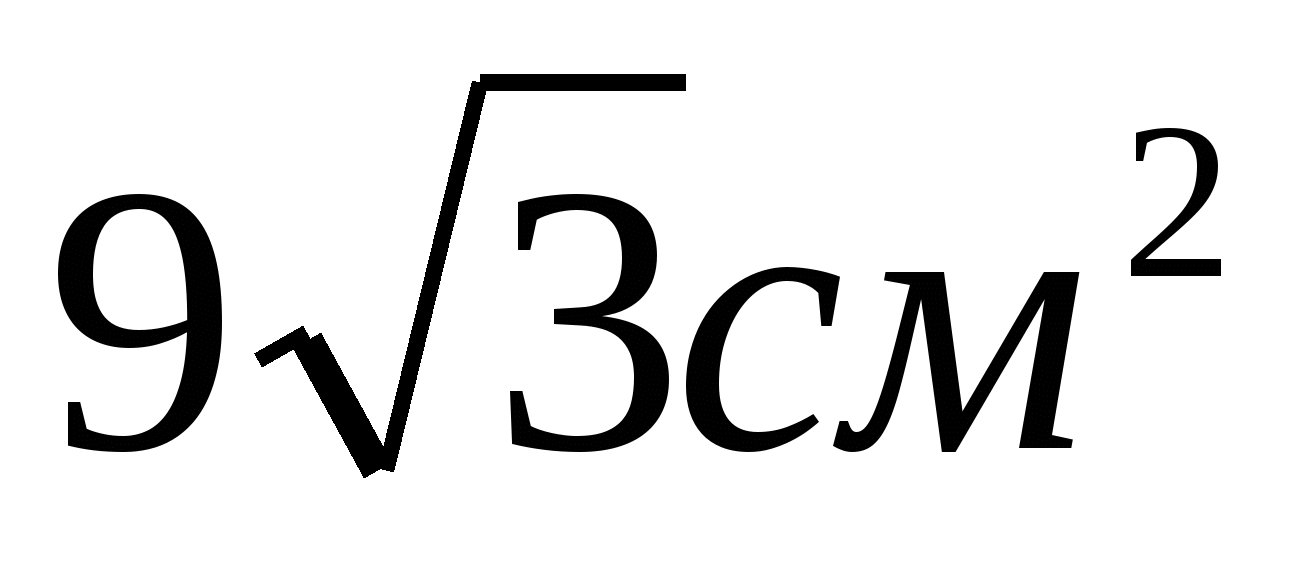 . Две боковые грани пирамиды перпендикулярны к плоскости основания, а третья – наклонена к ней под углом 300.
. Две боковые грани пирамиды перпендикулярны к плоскости основания, а третья – наклонена к ней под углом 300.
а) Найдите длины боковых ребер пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
3. Стороны оснований правильной треугольной усеченной пирамиды равны 2 и 6 см, а боковая грань образует с плоскостью большего основания угол 600. Найдите боковую поверхность данной пирамиды и высоту полной пирамиды, из которой получена данная усеченная пирамида.
4. Равнобедренные треугольники АВС и ADС имеют общее основание АС, а двугранный угол BACD – прямой. Найдите углы, образуемые прямой BD с плоскостями треугольников, если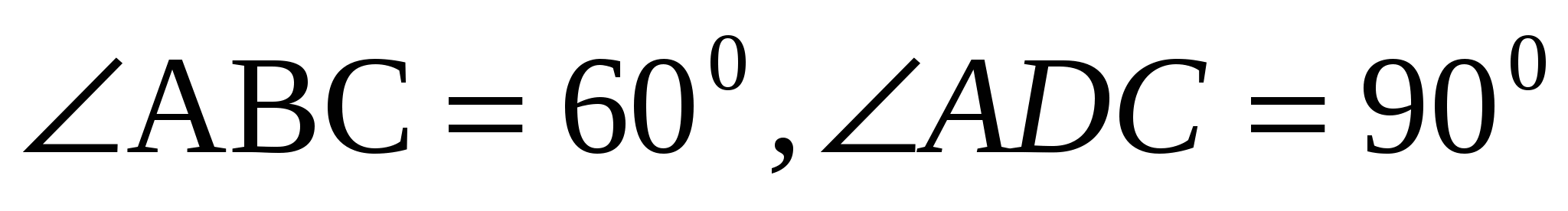
Контрольная работа №4
Многогранники
Вариант2
1. Основание прямой призмы – прямоугольный треугольник, с катетом 12 см и гипотенузой 13 см. Найдите полную поверхность призмы, если боковая грань, содержащая неизвестный катет основания является квадратом.
2. Основание пирамиды – равнобедренный прямоугольный треугольник с гипотенузой 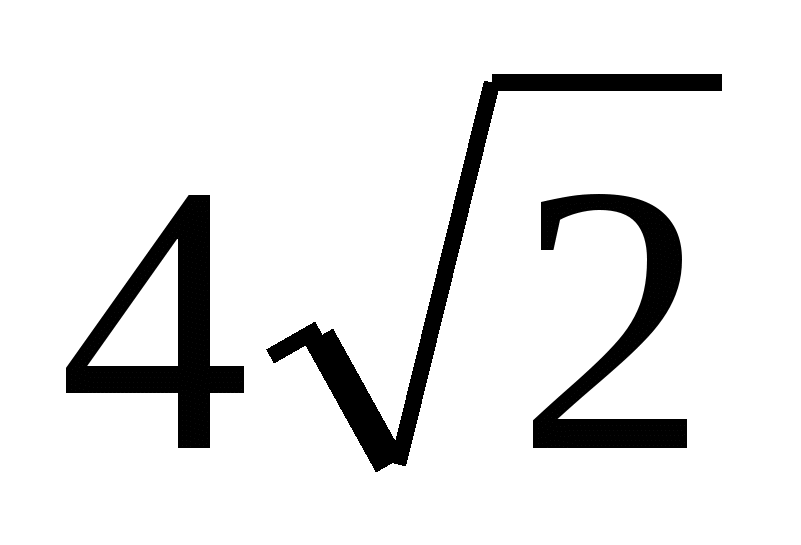 см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 450.
см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 450.
а) Найдите длины боковых ребер пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
3. Стороны оснований правильной усеченной четырехугольной пирамиды равны 2 и 8 см, а боковое ребро пирамиды образует с плоскостью большего основания угол 450. Найдите высоту данной пирамиды и боковую поверхность полной пирамиды, из которой получена данная усеченная пирамида.
4. Равнобедренные треугольники АВС и ADС имеют общее основание АС, а двугранный угол BACD – прямой. Найдите углы, образуемые прямой BD с плоскостями треугольников, если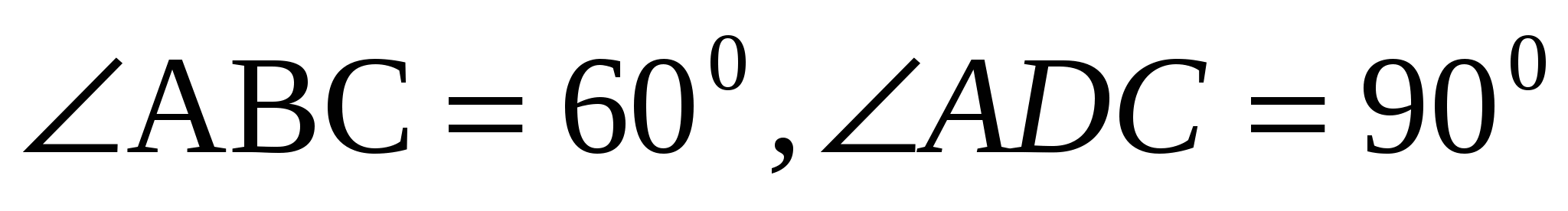
Контрольная работа №4
Многогранники
Вариант2
1. Основание прямой призмы – прямоугольный треугольник, с катетом 12 см и гипотенузой 13 см. Найдите полную поверхность призмы, если боковая грань, содержащая неизвестный катет основания является квадратом.
2. Основание пирамиды – равнобедренный прямоугольный треугольник с гипотенузой 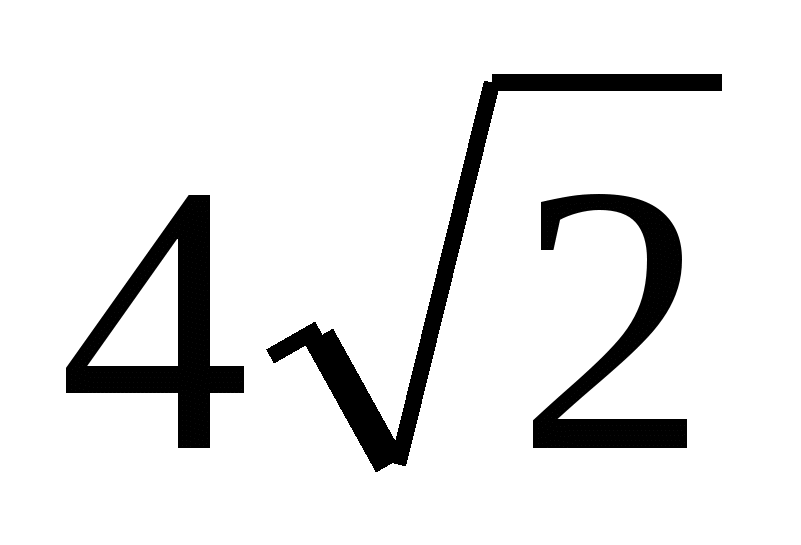 см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 450.
см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 450.
а) Найдите длины боковых ребер пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
3. Стороны оснований правильной усеченной четырехугольной пирамиды равны 2 и 8 см, а боковое ребро пирамиды образует с плоскостью большего основания угол 450. Найдите высоту данной пирамиды и боковую поверхность полной пирамиды, из которой получена данная усеченная пирамида.
4. Равнобедренные треугольники АВС и ADС имеют общее основание АС, а двугранный угол BACD – прямой. Найдите углы, образуемые прямой BD с плоскостями треугольников, если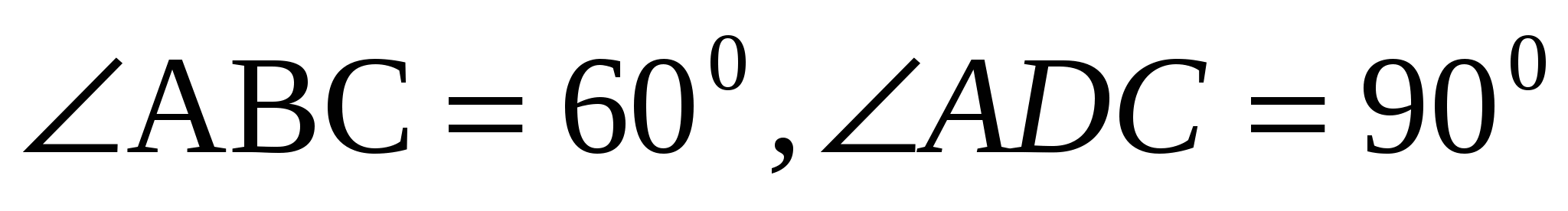
infourok.ru
Контрольная работа
Площади поверхностей многогранников.
Цель: проверка знаний и практических умений обучающихся.
1 вариант
Уровень А.
А1. Выберите верное утверждение
а) параллелепипед состоит из шести треугольников;
б) противоположные грани параллелепипеда имеют общую точку;
в) диагонали параллелепипеда пересекаются и точкой пересечения делятся пополам.
А2. Количество ребер шестиугольной призмы
а) 18; б) 6; в) 24; г) 12; д) 15.
А3.Наименьшее число граней призмы
а) 3; б) 4; в) 5; г) 6; д) 9.
А4. Не является правильным многогранником
а) правильный тетраэдр; б) правильная призма; в) правильный додекаэдр; г) правильный октаэдр.
А5. Выберите верное утверждение:
а) выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер;
б) правильная треугольная пирамида и правильный тетраэдр – это одно и то же;
в) площадь боковой поверхности пирамиды равна произведению периметра основания на высоту.
А6. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется
а) диагональю; б) медианой; в) апофемой.
А7. Диагональ многогранника – это отрезок, соединяющий
а) любые две вершины многогранника; б) две вершины, не принадлежащие одной грани;
в) две вершины, принадлежащие одной грани.
Уровень В.
В8. Найдите диагонали прямоугольного параллелепипеда, если стороны его основания 3 см ,
4 см, а высота равна 10 см .
Уровень С.
С9. В правильной четырёхугольной пирамиде со стороной основания 8 м, боковая грань
наклонена к плоскости основания под углом 60 0. Найдите:
а) высоту пирамиды; б) площадь боковой поверхности.
2 вариант
Уровень А.
А1. Выберите верное утверждение
а) тетраэдр состоит из четырех параллелограммов;
б) отрезок, соединяющий противоположные вершины параллелепипеда, называется его
диагональю;
в) параллелепипед имеет всего шесть ребер.
А2. Количество граней шестиугольной призмы
а) 6; б) 8; в) 10; г) 12; д) 16.
А3.Наименьшее число рёбер призмы
а) 9; б) 8; в) 7; г) 6; д) 5.
А4. Не является правильным многогранником
а) правильный тетраэдр; б) правильный додекаэдр; в) правильная пирамида; г) правильный октаэдр.
А5. Выберите верное утверждение:
а) правильный додекаэдр состоит из восьми правильных треугольников;
б) правильный тетраэдр состоит из восьми правильных треугольников;
в) правильный октаэдр состоит из восьми правильных треугольников.
А6. Апофема – это
а) высота пирамиды; б) высота боковой грани пирамиды;
в) высота боковой грани правильной пирамиды.
А7. Усеченная пирамида называется правильной, если
а) ее основания – правильные многоугольники;
б) она получена сечением правильной пирамиды плоскостью, параллельной основанию;
в) ее боковые грани – прямоугольники.
Уровень В.
В8. Найдите боковое ребро правильной четырёхугольной, пирамиды, у которой сторона
основания 8 м, а высота равна 10 м.
Уровень С.
С9. В прямоугольном параллелепипеде стороны основания 5 м и 12 м, а диагональ
infourok.ru
10класс. Контрольная работа по геометрии по теме «Многогранники»
1вариант
1.Основание прямой призмы – прямоугольный треугольник с катетами 10 и 24 см. Найдите площадь боковой поверхности призмы, если ее наибольшая грань - квадрат.
2. Боковое ребро правильной четырехугольной пирамиды равно 4 см и образует с плоскостью основания пирамиды угол 45 ̊ .
А) Найдите высоту пирамиды.
Б) Найдите площадь боковой поверхности пирамиды.
2вариант
1.Основание прямой призмы – прямоугольный треугольник с катетом 12см и гипотенузой 13 см. Найдите площадь боковой поверхности призмы, если ее наименьшая грань - квадрат.
2. Высота правильной четырехугольной пирамиды равна см , а боковое ребро наклонено к плоскости основания под углом 60 ̊ .
см , а боковое ребро наклонено к плоскости основания под углом 60 ̊ .
А) Найдите боковое ребро пирамиды.
Б) Найдите площадь боковой поверхности пирамиды.
10класс. Контрольная работа по геометрии по теме «Многогранники»
1вариант
1.Основание прямой призмы – прямоугольный треугольник с катетами 10 и 24 см. Найдите площадь боковой поверхности призмы, если ее наибольшая грань - квадрат.
2. Боковое ребро правильной четырехугольной пирамиды равно 4 см и образует с плоскостью основания пирамиды угол 45 ̊ .
А) Найдите высоту пирамиды.
Б) Найдите площадь боковой поверхности пирамиды.
2вариант
1.Основание прямой призмы – прямоугольный треугольник с катетом 12см и гипотенузой 13 см. Найдите площадь боковой поверхности призмы, если ее наименьшая грань - квадрат.
2. Высота правильной четырехугольной пирамиды равна см , а боковое ребро наклонено к плоскости основания под углом 60 ̊ .
см , а боковое ребро наклонено к плоскости основания под углом 60 ̊ .
А) Найдите боковое ребро пирамиды.
Б) Найдите площадь боковой поверхности пирамиды.
10класс. Контрольная работа по геометрии по теме «Многогранники»
1вариант
1.Основание прямой призмы – прямоугольный треугольник с катетами 10 и 24 см. Найдите площадь боковой поверхности призмы, если ее наибольшая грань - квадрат.
2. Боковое ребро правильной четырехугольной пирамиды равно 4 см и образует с плоскостью основания пирамиды угол 45 ̊ .
А) Найдите высоту пирамиды.
Б) Найдите площадь боковой поверхности пирамиды.
2вариант
1.Основание прямой призмы – прямоугольный треугольник с катетом 12см и гипотенузой 13 см. Найдите площадь боковой поверхности призмы, если ее наименьшая грань - квадрат.
2. Высота правильной четырехугольной пирамиды равна см , а боковое ребро наклонено к плоскости основания под углом 60 ̊ .
см , а боковое ребро наклонено к плоскости основания под углом 60 ̊ .
А) Найдите боковое ребро пирамиды.
Б) Найдите площадь боковой поверхности пирамиды.
multiurok.ru