.КОНТРОЛЬНАЯ РАБОТА (Многогранники) – 11 кл.
Параллелепипед. Куб. Призма. Пирамида.
1) Найдите площадь полной поверхности куба и его объём, если расстояние от вершины верхнего основания куба до центра нижнего основания равно .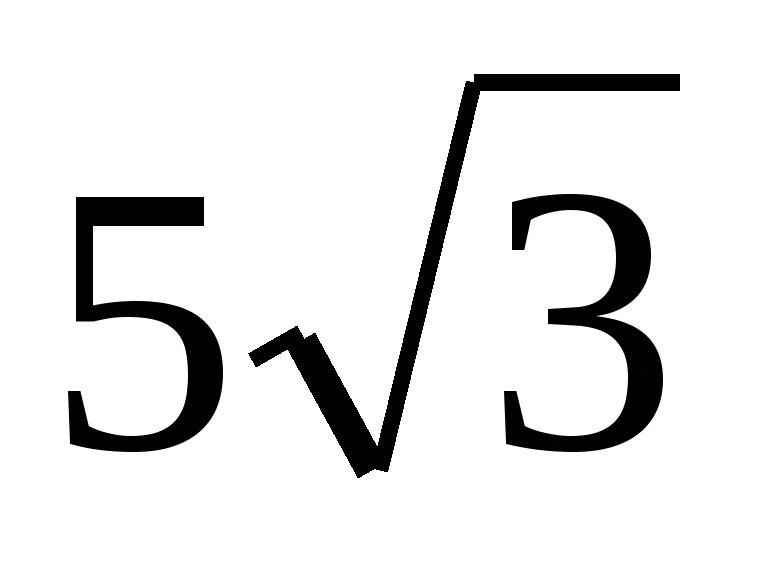
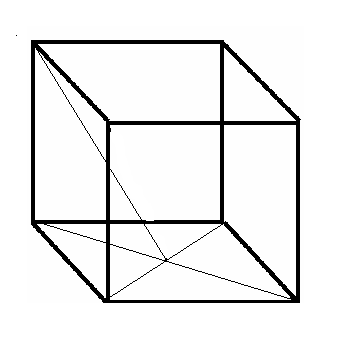
Указания к решению задачи: в данной задаче надо помнить:
1) что площадь поверхности куба – это сумма площадей всех его граней, т.е. квадратов;
2) что грани куба – квадраты; если ребро куба неизвестная величина Х, то диагональ квадрата нижнего основания Х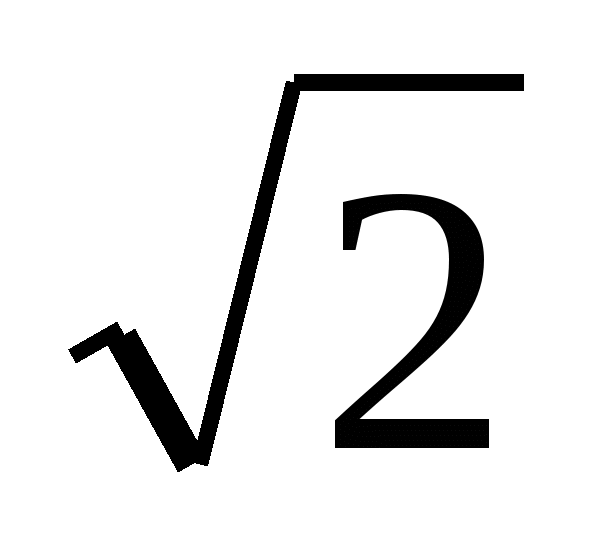
. Следует рассмотреть прямоугольный треугольник и воспользоваться теоремой Пифагора для нахождения ребра куба.
2) Основание прямой призмы – треугольник со сторонами 8см и 15см и углом между ними 
. Высота призмы 11см. Найдите:
А) площадь боковой и площадь полной поверхности призмы;
Б) объём призмы.
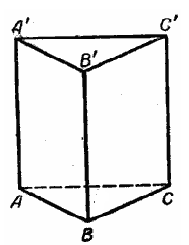
У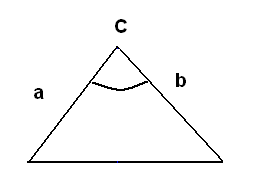
казания к решению задачи: существует формула площади полной поверхности призмы – найдите её. Воспользуйтесь формулой площади треугольника 
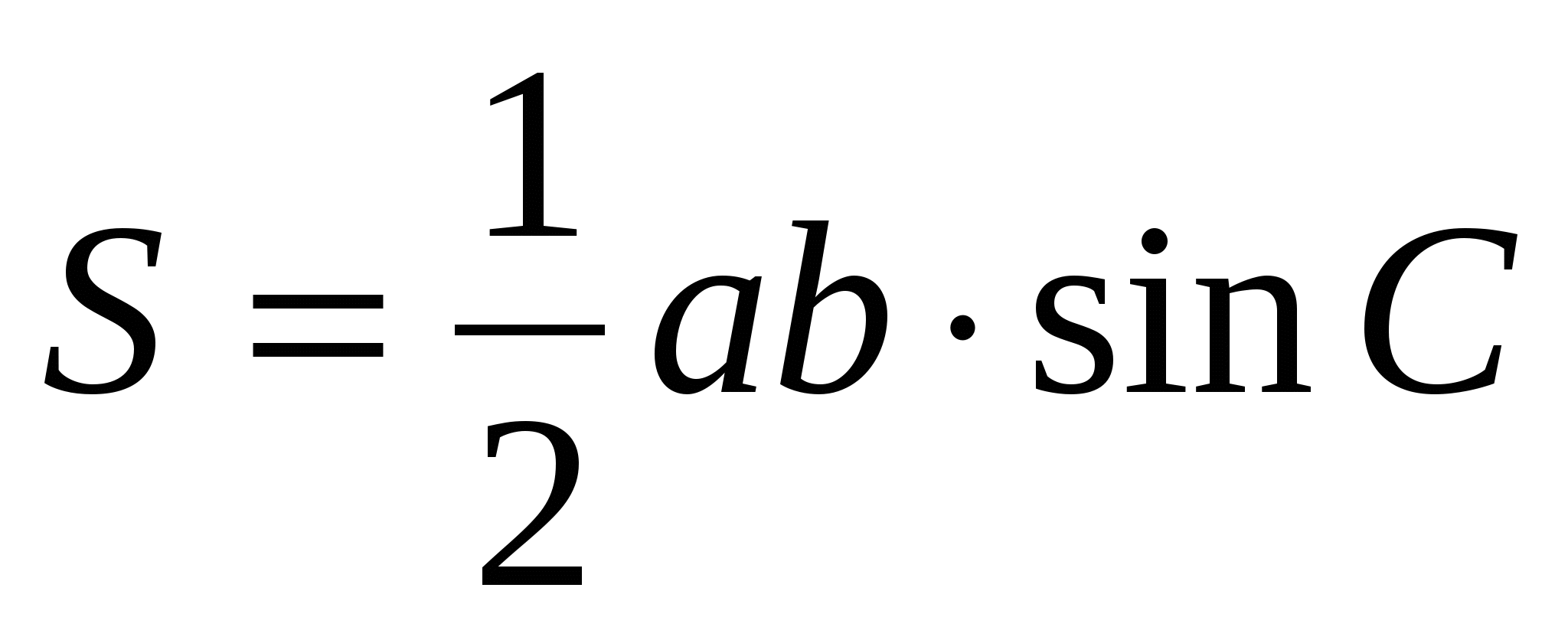, где a и b – стороны треугольника, С – угол между ними.
Сторону АС можно найти разными способами: по теореме косинусов
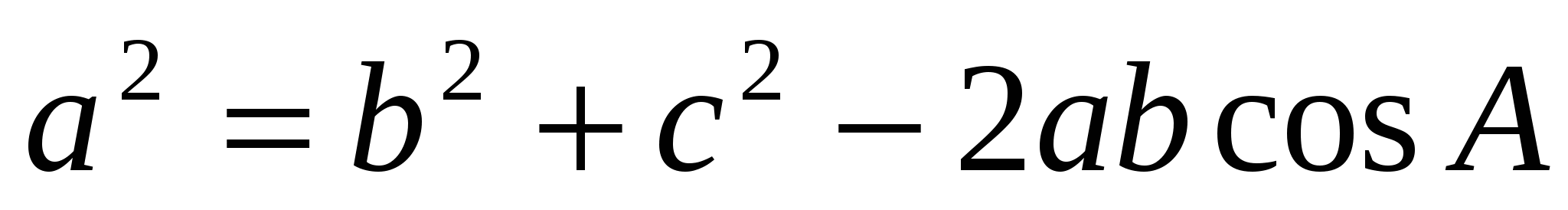или по формуле Герона 
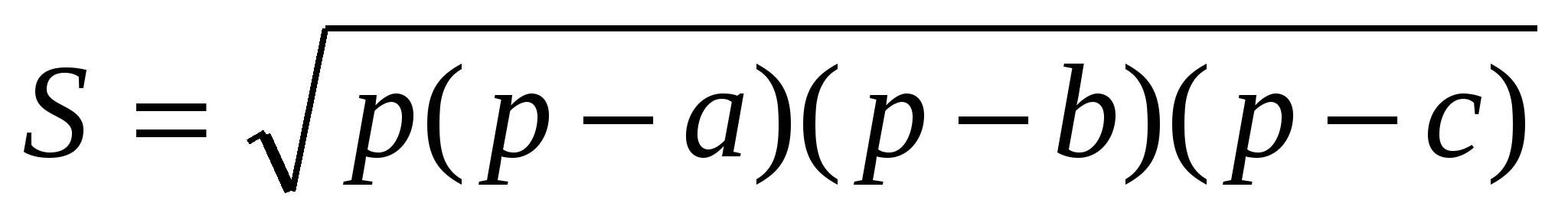, где p-полупериметр треугольника.
3) Найдите:
а) объём правильного тетраэдра, высота которого равна 5;
б)٭ площадь полной поверхности правильного тетраэдра, высота которого равна 5.
У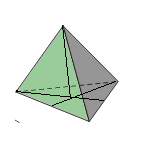
казания к решению задачи: Три медианы треугольника ( AD, BE, CF, см.рис.) пересекаются в одной точке O, всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины. Т.Е отрезок АО = 
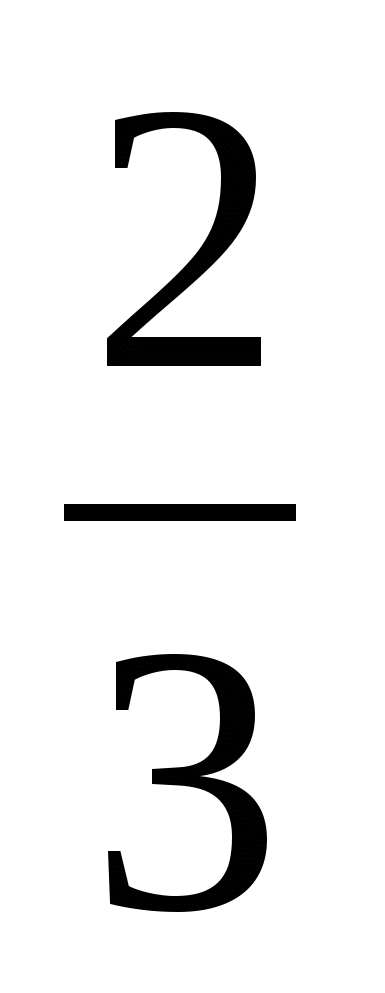, отрезок ОD = 
.
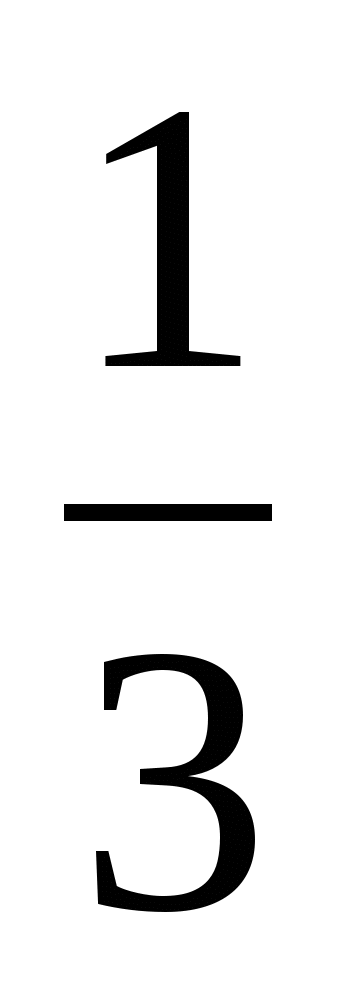Площадь равностороннего треугольника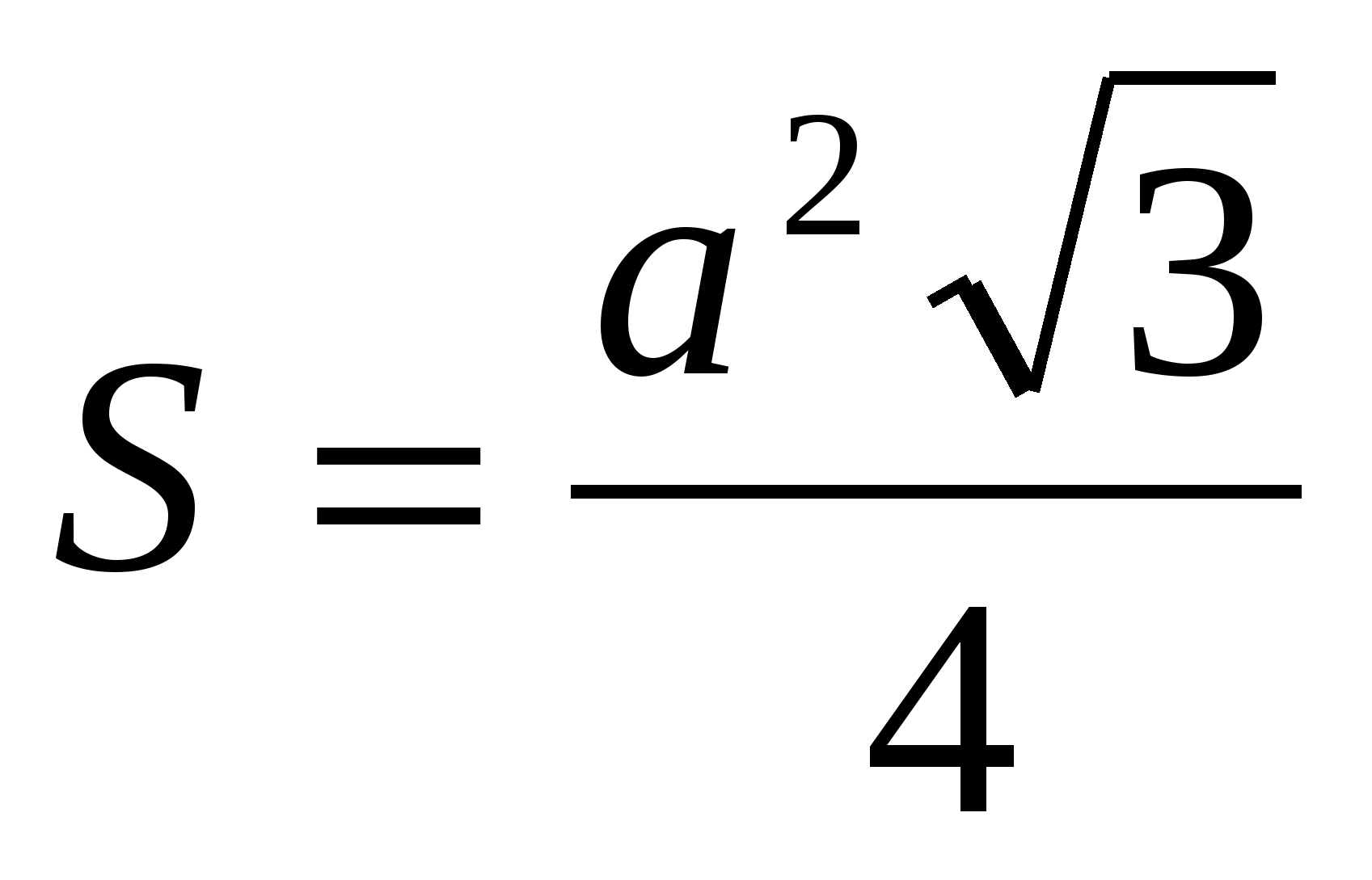 
КОНТРОЛЬНАЯ РАБОТА (Многогранники) – 11 кл.
Параллелепипед. Куб. Призма. Пирамида.
1) Найдите площадь полной поверхности куба и его объём, если расстояние от вершины верхнего основания куба до центра нижнего основания равно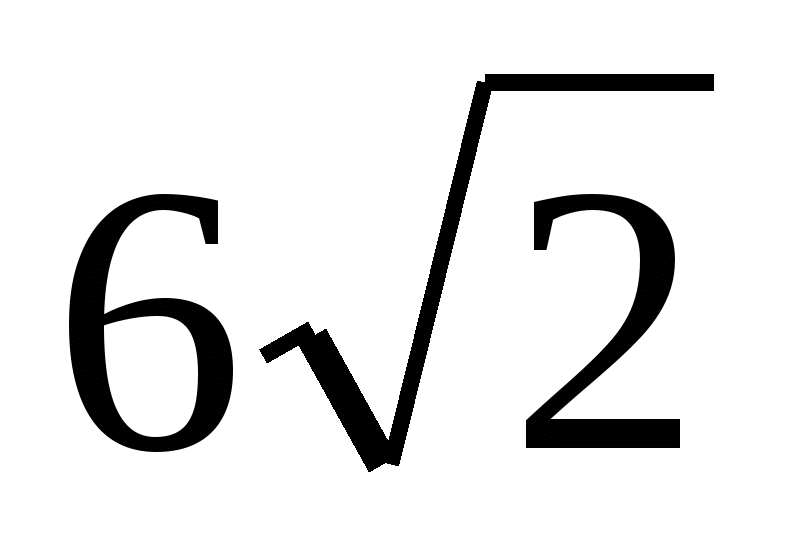 
.
У
казания к решению задачи: в данной задаче надо помнить:
1) что площадь поверхности куба – это сумма площадей всех его граней, т.е. квадратов;
2) что грани куба – квадраты; если ребро куба неизвестная величина Х, то диагональ квадрата нижнего основания Х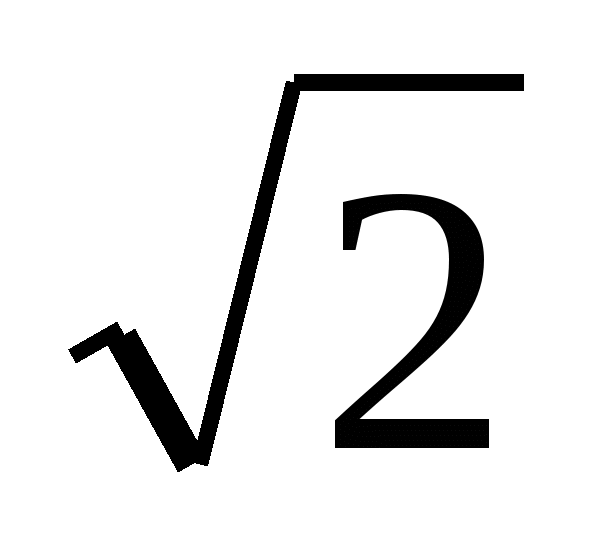. Следует рассмотреть прямоугольный треугольник и воспользоваться теоремой Пифагора для нахождения ребра куба.
2) Основание прямой призмы – треугольник со сторонами 8см и 3см и углом между ними . Высота призмы 15см. Найдите:
А) площадь боковой и площадь полной поверхности призмы;
Б) объём призмы.
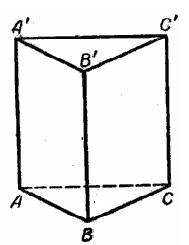
Указания к решению задачи: существует формула площади полной поверхности призмы – найдите её. Воспользуйтесь формулой площади треугольника 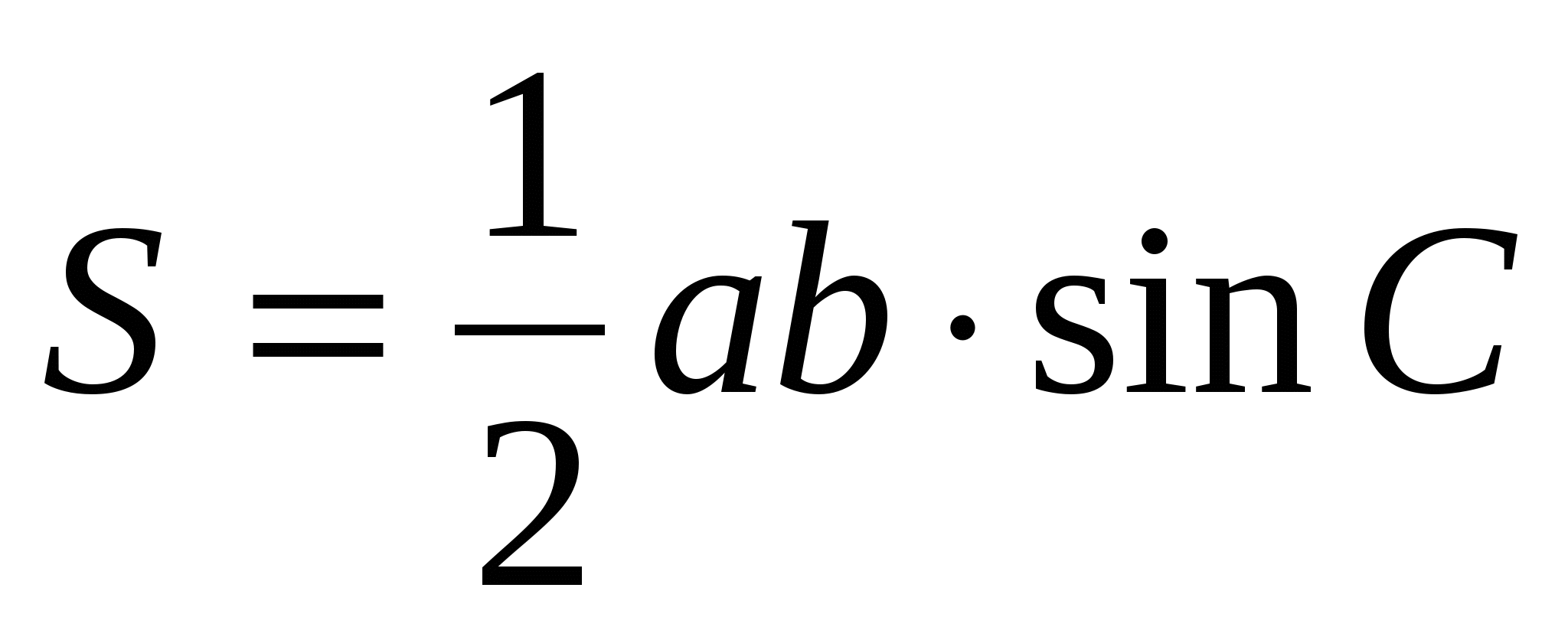, где a и b – стороны треугольника, С – угол между ними.
Сторону АС можно найти разными способами: по теореме косинусов
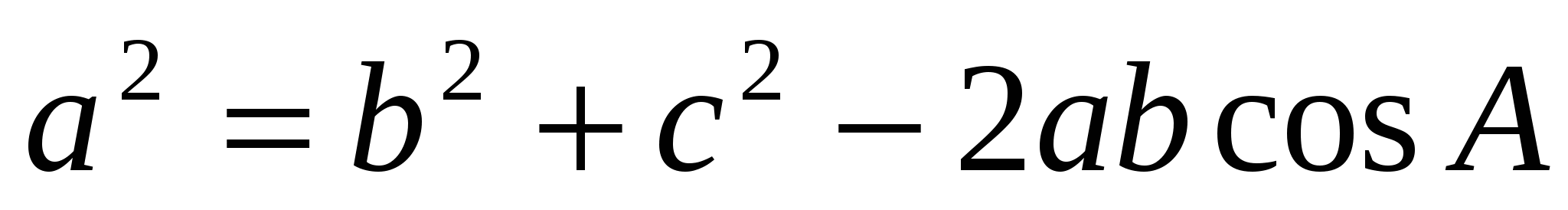или по формуле Герона 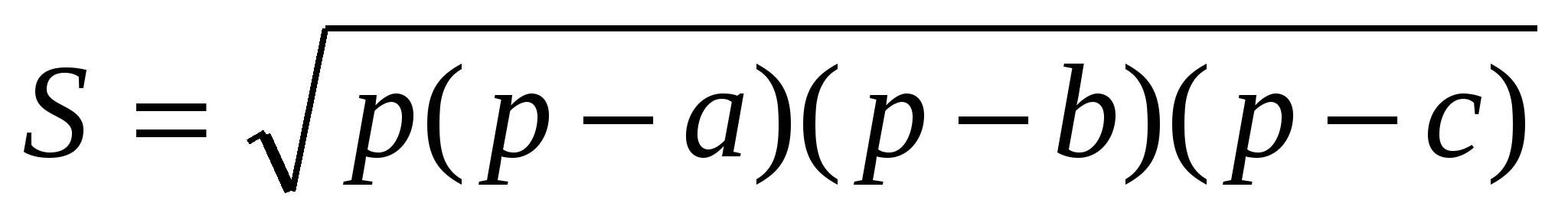, где p-полупериметр треугольника.
3) Найдите:
а) объём правильного тетраэдра, высота которого равна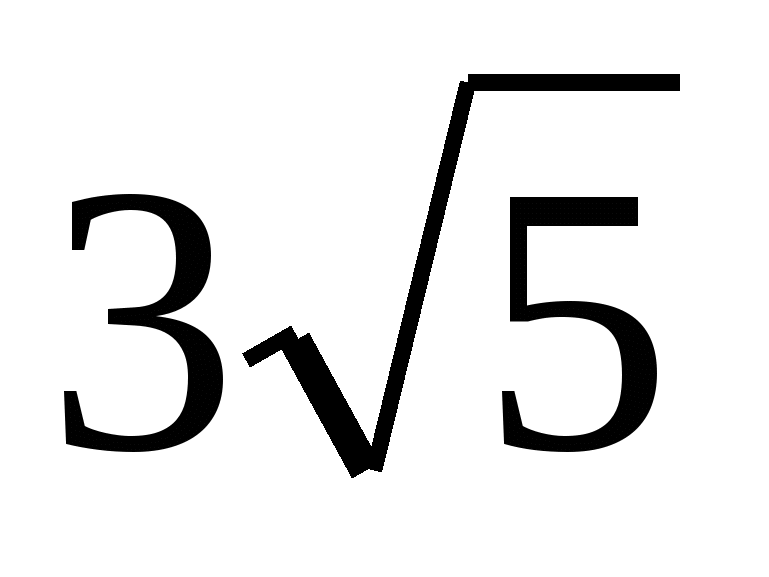 
;
б)٭ площадь полной поверхности правильного тетраэдра, высота которого равна .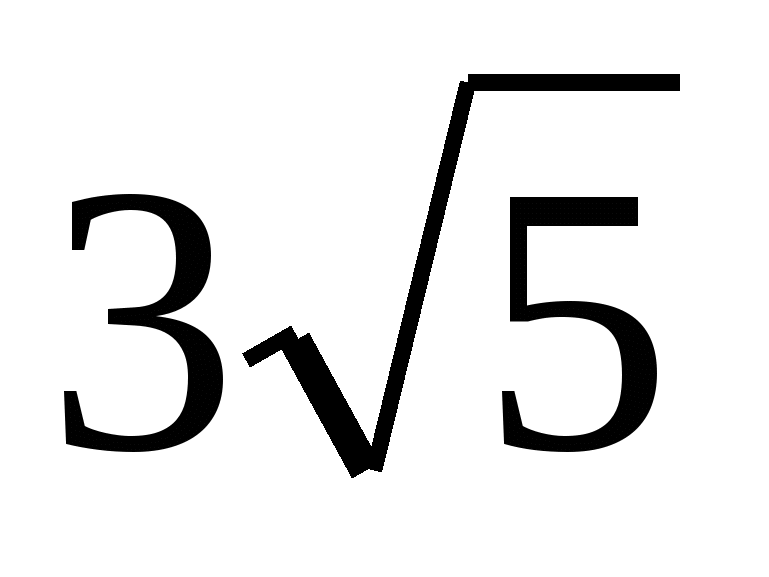
Указания к решению задачи: Три медианы треугольника ( AD, BE, CF, см.рис.) пересекаются в одной точке O, всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины. Т.Е отрезок АО = 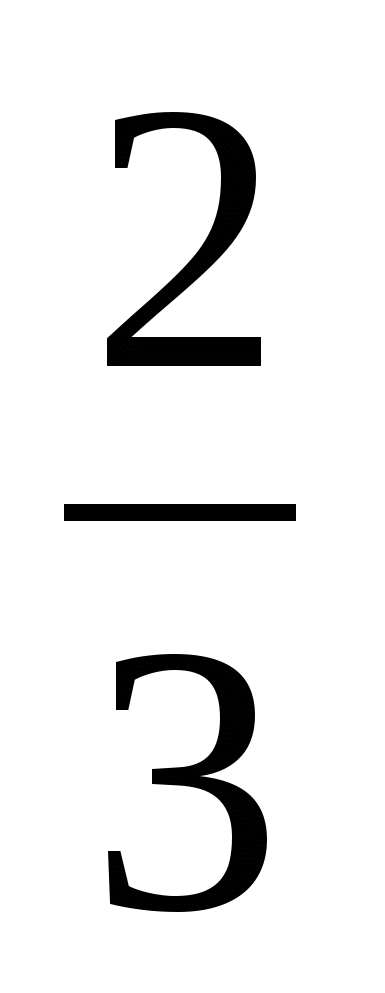, отрезок ОD = .
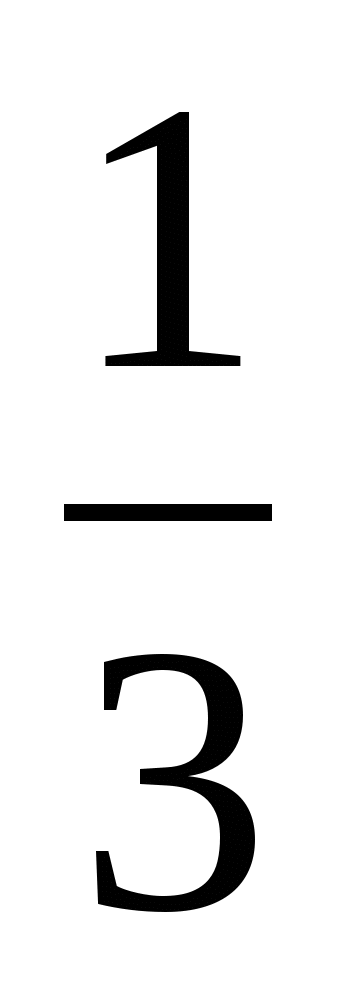Площадь равностороннего треугольника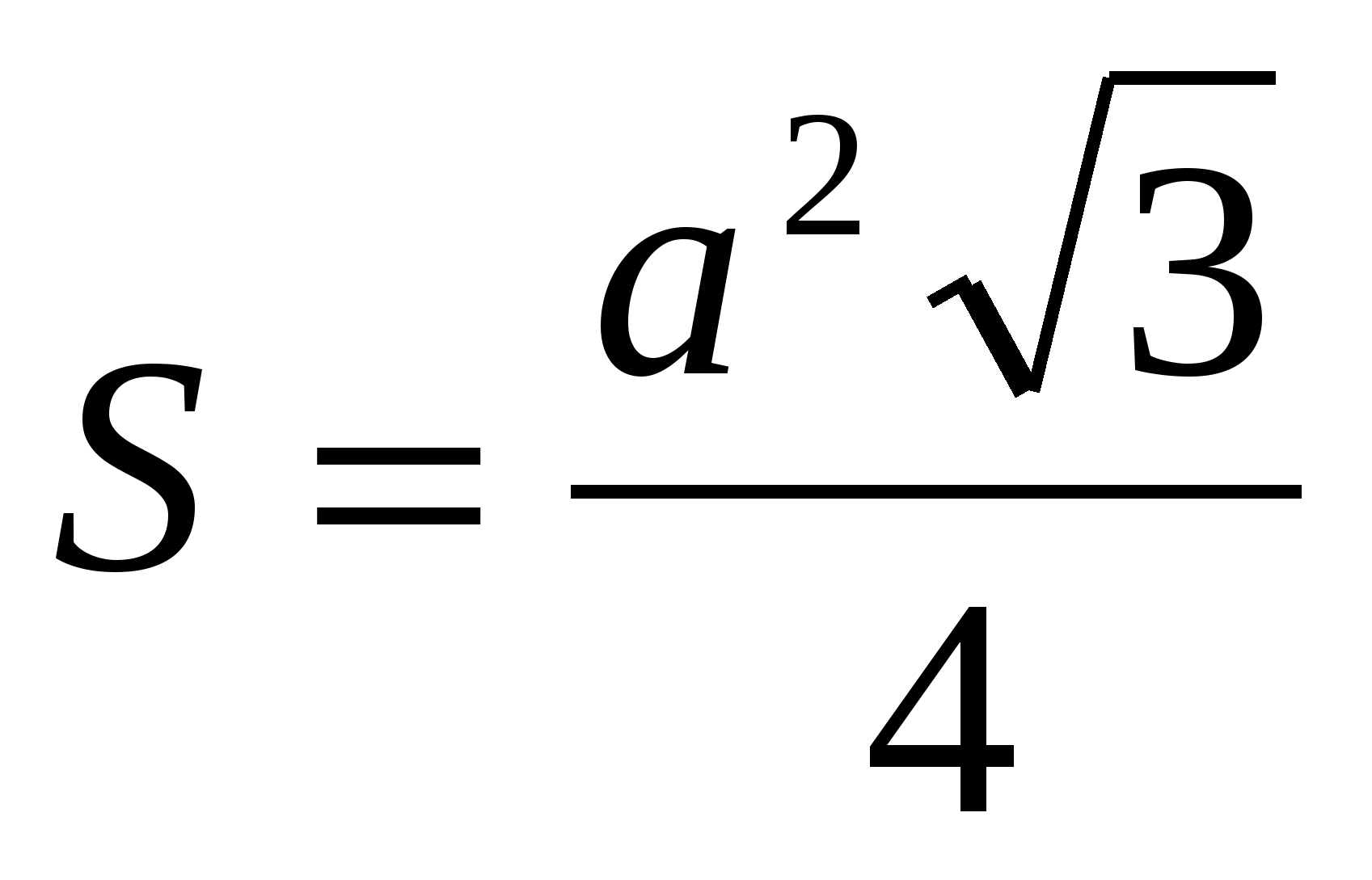
Элементы пирамиды
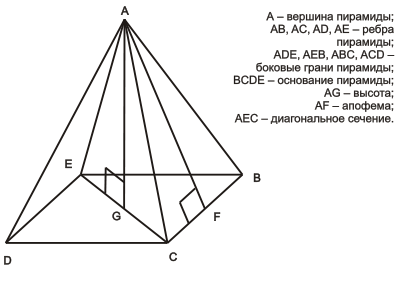
Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему (высоту боковой грани).
Объем пирамиды равен одной трети произведения площади основания на высоту
infourok.ru
Контрольная работа по теме «Многогранники».
1 вариант
Уровень А.
А1. Выберите верное утверждение
а) параллелепипед состоит из шести треугольников;
б) противоположные грани параллелепипеда имеют общую точку;
в) диагонали параллелепипеда пересекаются и точкой пересечения делятся пополам.
А2. Количество ребер шестиугольной призмы
а) 18; б) 6; в) 24; г) 12; д) 15.
А3.Наименьшее число граней призмы
а) 3; б) 4; в) 5; г) 6; д) 9.
А4. Не является правильным многогранником
а) правильный тетраэдр; б) правильная призма; в) правильный додекаэдр;
г) правильный октаэдр.
А5. Выберите верное утверждение:
а) выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер;
б) правильная треугольная пирамида и правильный тетраэдр – это одно и то же;
в) площадь боковой поверхности пирамиды равна произведению периметра
основания на высоту.
А6. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется
а) диагональю; б) медианой; в) апофемой.
А7. Диагональ многогранника – это отрезок, соединяющий
а) любые две вершины многогранника;
б) две вершины, не принадлежащие одной грани;
в) две вершины, принадлежащие одной грани.
Уровень В.
В8. Найдите диагонали прямоугольного параллелепипеда, если стороны его основания 3 см , 4 см, а высота равна 10 см.
Уровень С.
С9. В правильной четырёхугольной пирамиде со стороной основания 8 м, боковая грань наклонена к плоскости основания под углом 60 0.
Найдите: а) высоту пирамиды; б) площадь боковой поверхности.
Контрольная работа по теме «Многогранники».
2 вариант
Уровень А.
А1. Выберите верное утверждение
а) тетраэдр состоит из четырех параллелограммов;
б) отрезок, соединяющий противоположные вершины параллелепипеда,
называется его диагональю;
в) параллелепипед имеет всего шесть ребер.
А2. Количество граней шестиугольной призмы
а) 6; б) 8; в) 10; г) 12; д) 16.
А3.Наименьшее число рёбер призмы
а) 9; б) 8; в) 7; г) 6; д) 5.
А4. Не является правильным многогранником
а) правильный тетраэдр; б) правильный додекаэдр; в) правильная пирамида;
г) правильный октаэдр.
А5. Выберите верное утверждение:
а) правильный додекаэдр состоит из восьми правильных треугольников;
б) правильный тетраэдр состоит из восьми правильных треугольников;
в) правильный октаэдр состоит из восьми правильных треугольников.
А6. Апофема – это
а) высота пирамиды; б) высота боковой грани пирамиды;
в) высота боковой грани правильной пирамиды.
А7. Усеченная пирамида называется правильной, если
а) ее основания – правильные многоугольники;
б) она получена сечением правильной пирамиды плоскостью, параллельно
основанию;
в) ее боковые грани – прямоугольники.
Уровень В.
В8. Найдите боковое ребро правильной четырёхугольной, пирамиды, у которой сторона основания 8 м, а высота равна 10 м.
Уровень С.
С9. В прямоугольном параллелепипеде стороны основания 5 м и 12 м, а диагональ параллелепипеда наклонена к плоскости основания под углом 30 0. Найдите: а) высоту параллелепипеда; б) площадь боковой поверхности.
Критерии оценки контрольной работы
Максимальный балл за работу – 12 баллов
Шкала перевода баллов в отметки
Ответы к контрольной работе
а)в)
А6
в)
в)
А7
б)
б)
В8
5м
м
С9
h = 4 м ; Sб.п. = 128 м2
h = ; Sб.п. = м2
infourok.ru
Контрольная работа по теме: «Многогранники».
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Контрольная работа по геометрии «Многогранники», включает в себя задания базового уровня сложности, 2 варианта. Время выполнения – 1урок (45 мин.).
Цель: проверка знаний, умений и навыков учащихся при решении задач по теме «Многогранники».
Контрольная работе по теме «Многогранники»
Вариант 1
Часть А:
Из четырех вариантов ответов выберете один верный
Среди изображенных тел выберите номера тех, которые являются призмами?
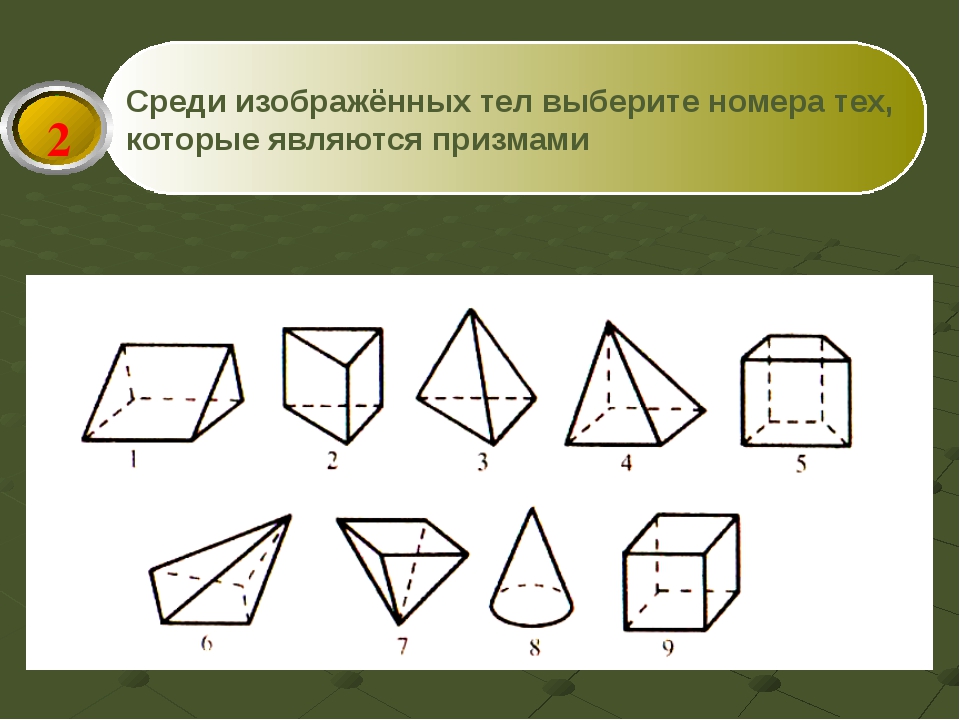
3, 4, 6, 7
1, 2, 5, 9
1, 2, 4, 5
6, 7, 8, 9
Найдите площадь поверхности куба, если длина ребра равна 4 см.
56 см2
72 см2
96 см2
112 см2
В прямоугольном параллелепипеде три измерения равны 6 дм, 9 дм, 15 дм. Найдите площадь поверхности прямоугольного параллелепипеда.
558 см2
358 см2
279 см2
423 см2
Сколько граней имеет восьмиугольная призма?
10
12
16
20
Сколько ребер имеет четырехугольная усеченная пирамида?
8
10
12
14
Сколько вершин имеет прямоугольный параллелепипед?
6
8
10
14
Часть В:
Запишите пропущенное слово
Параллелепипед называется ____, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
В прямоугольном параллелепипеде все шесть граней - _______.
______ - длины трех ребер, имеющих общую вершину.
Многогранник, гранями которого являются n – угольники (верхнее и нижнее основание), расположенные в параллельных плоскостях, и n – четырехугольников (боковые грани), называется _______.
Основания правильной усеченной пирамиды – правильные многоугольники, а боковые грани - _____.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется _____ усеченной пирамиды.
Часть С:
Решить задачу
Объем прямоугольного параллелепипеда равен 60 см3. Площадь одной его грани равна 12 см2. Найдите ребро прямоугольного параллелепипеда, перпендикулярное этой грани.
Контрольная работе по теме «Многогранники»
Вариант 2
Часть А:
Из четырех вариантов ответов выберете один верный
Среди изображенных тел выберите номера тех, которые являются пирамидами?
3, 4, 6, 7
1, 2, 5, 9
1, 2, 4, 5
6, 7, 8, 9
Найдите объем куба, если длина ребра равна 7 см.
243 см3
333 см3
343 см3
443 см3
В прямоугольном параллелепипеде три измерения равны 6 дм, 9 дм, 15 дм. Найдите объем прямоугольного параллелепипеда.
420 дм3
510 дм3
624 дм3
810 дм3
Сколько ребер имеет восьмиугольная призма?
15
18
24
32
Сколько вершин имеет четырехугольная усеченная пирамида?
4
8
12
16
Сколько граней имеет прямоугольный параллелепипед?
10
12
14
6
Часть В:
Запишите пропущенное слово
_______ - многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой.
Призма, у которой боковое ребро перпендикулярно плоскости основания, называется ____.
Призма, у которой боковое ребро не будет перпендикулярно к основаниям, называется ___.
Пирамида называется ____, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является высотой.
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными ____.
Высота боковой грани правильной пирамиды, проведенная из вершины, называется ____.
Часть С:
Решить задачу
Объем прямоугольного параллелепипеда равен 24 см3. Одно из его ребер равно 3 см. найдите площадь грани прямоугольного параллелепипеда, перпендикулярной этому ребру.
Расчетное время выполнения практической работы: 45 минут
Контрольная работа оценивается по 21 – бальной системе.
Максимальное количество баллов по заданиям:
Часть А
infourok.ru
Контрольная работа по теме «Многогранники. Тела вращения» II - вариант
образующую конуса, 2) полную поверхность конуса, 3) объем конуса.Плоскость проходит на расстоянии 8 см от центра шара, радиус сечения шара равен 6 см. Найдите его площадь поверхности и объем.
В правильной четырехугольной пирамиде SABCD точка O – центр
основания, S – вершина, SD=17, BD=16. Найдите:
длину отрезка SO,
площадь полной поверхности,
объем 
Найдите объем и площадь полной поверхности прямой призмы, в основании которой лежит параллелограмм со сторонами 7 см и 9 см, угол между этими сторонами равен 600, а высота призмы равна 12 см.
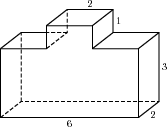
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Выполните чертеж в соответствии с приведенным на рисунке и постройте сечение многогранника плоскостью, проходящей через указанные три точки. Опишите построение.
Контрольная работа по теме «Многогранники. Тела вращения» I - вариант
Высота конуса равна 5 см, а образующая конуса 7 см.Найдите: 1) радиус основания, 2) площадь полной поверхности, 3) объем конуса.
Плоскость проходит на расстоянии 4 см от центра шара, радиус сечения шара равен 3 см. Найдите его объем и площадь поверхности.
В правильной четырехугольной пирамиде SABCD точка O – центр основания, S – вершина, SD=30, BD=36. Найдите:
длину отрезка SO,
площадь полной поверхности,
объем
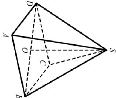
Найдите объем и площадь полной поверхности прямой призмы, в основании которой лежит параллелограмм со сторонами 6,7 см и 8 см, угол между этими сторонами равен 300, а высота призмы равна 10 см.
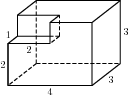
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Выполните чертеж в соответствии с приведенным на рисунке и постройте сечение многогранника плоскостью, проходящей через указанные три точки. Опишите построение.
Контрольная работа по теме «Многогранники. Тела вращения» III - вариант
Высота конуса равна 4 см, а радиус основания 3 см.Найдите: 1) образующую конуса, 2) полную поверхность конуса, 3) объем конуса.
Плоскость проходит на расстоянии 6 см от центра шара, радиус сечения шара равен см. Найдите его площадь поверхности и объем.
В правильной четырехугольной пирамиде SABCD точка O – центр
основания, S – вершина, SD=17, BD=30. Найдите:
длину отрезка SO,
площадь полной поверхности,
объем
Найдите объем и площадь полной поверхности прямой призмы, в основании которой лежит прямоугольный треугольник с катетами 4 см и 3 см, а высота призмы равна 8 см.
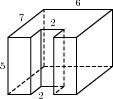
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Выполните чертеж в соответствии с приведенным на рисунке и постройте сечение многогранника плоскостью, проходящей через указанные три точки. Опишите построение.
Контрольная работа по теме «Многогранники. Тела вращения» IV - вариант
Высота конуса равна 10 см, а образующая конуса 26 см.Найдите: 1) радиус основания, 2) площадь полной поверхности, 3) объем конуса.
Плоскость проходит на расстоянии 21 см от центра шара, радиус сечения шара равен 20 см. Найдите его объем и площадь поверхности.
infourok.ru
Вариант №1
В правильной четырехугольной пирамиде SABCD точка О – центр основания, S - вершина , SC = 13, АС = 10. Найти высоту пирамиды.
В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол 
. Найти площадь боковой и полной поверхности параллелепипеда.
В основании четырехугольной пирамиды SABCD точка О – центр основания, S - вершина лежит прямоугольник со сторонами 6 см и 8 см . SO = 4. Найти площадь боковой и полной поверхности пирамиды.
В основании прямой призмы лежит треугольник АВС со сторонами АВ = 10, ВС = 21, АС = 17. Боковое ребро А
= 15. Точка М 
А и АМ : М = 2 : 3. Найти площадь сечения ВМС.
Вариант №2
В правильной четырехугольной пирамиде SABCD точка О – центр основания, S - вершина , SC = 13, SO = 5. Найти длину отрезка BD.
В прямоугольном параллелепипеде стороны основания равны 15 см и 8 см. Диагональ параллелепипеда образует с плоскостью основания угол . Найти площадь боковой и полной поверхности параллелепипеда.
В основании четырехугольной пирамиды SABCD точка О – центр основания, S - вершина лежит прямоугольник со сторонами 12 см и 5 см . SO = 8. Найти площадь боковой и полной поверхности пирамиды.
В основании прямой призмы лежит треугольник АВС со сторонами АВ = 13, ВС = 14, АС = 15. Боковое ребро А = 28. Точка М А и АМ : М = 4 : 3. Найти площадь сечения ВМС.
Вариант №1
В правильной четырехугольной пирамиде SABCD точка О – центр основания, S - вершина , SC = 13, АС = 10. Найти высоту пирамиды.
В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол . Найти площадь боковой и полной поверхности параллелепипеда.
В основании четырехугольной пирамиды SABCD точка О – центр основания, S - вершина лежит прямоугольник со сторонами 6 см и 8 см . SO = 4. Найти площадь боковой и полной поверхности пирамиды.
В основании прямой призмы лежит треугольник АВС со сторонами АВ = 10, ВС = 21, АС = 17. Боковое ребро А = 15. Точка М А и АМ : М = 2 : 3. Найти площадь сечения ВМС.
Вариант №2
В правильной четырехугольной пирамиде SABCD точка О – центр основания, S - вершина , SC = 13, SO = 5. Найти длину отрезка BD.
В прямоугольном параллелепипеде стороны основания равны 15 см и 8 см. Диагональ параллелепипеда образует с плоскостью основания угол . Найти площадь боковой и полной поверхности параллелепипеда.
В основании четырехугольной пирамиды SABCD точка О – центр основания, S - вершина лежит прямоугольник со сторонами 12 см и 5 см . SO = 8. Найти площадь боковой и полной поверхности пирамиды.
В основании прямой призмы лежит треугольник АВС со сторонами АВ = 13, ВС = 14, АС = 15. Боковое ребро А = 28. Точка М А и АМ : М = 4 : 3. Найти площадь сечения ВМС.
multiurok.ru
Контрольная работа по теме «Многогранники» с элементами ЕГЭ. Вариант 5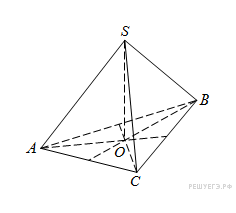
№ 1 (B9). В правильной треугольной пирамиде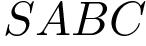 
медианы основания 
пересекаются в точке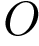 
. Площадь треугольника равна 4; объем пирамиды равен 6. Найдите длину отрезка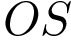 
.
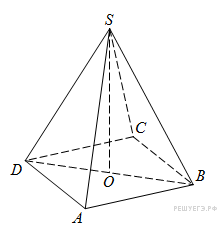
№ 2 (B9). В правильный четырехугольной пирамиде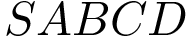 
точка 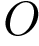– центр основания, 
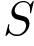– вершина, 
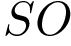=12,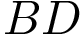 
=18. Найдите боковое ребро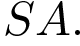 
№ 3 (В9). В правильной треугольной пирамиде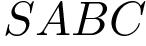 
– середина ребра 
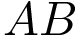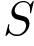, – вершина. Известно, что 
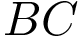=7, а площадь боковой поверхности пирамиды равна 42. Найдите длину отрезка 
.
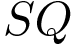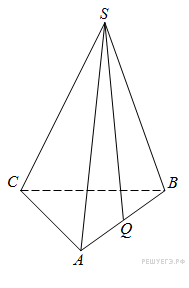
№4 (B9). В правильной четырехугольной пирамиде 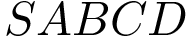точка 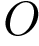— центр основания, 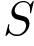вершина, 
, 
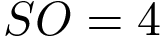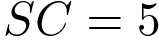. Найдите длину отрезка 
.
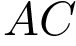№ 5 (В9). Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.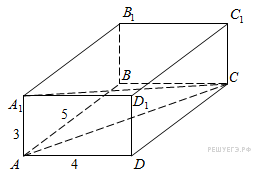
№ 6 (B9). Найдите квадрат расстояния между вершинам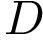и 
и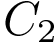 
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
№ 7 (B11). Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
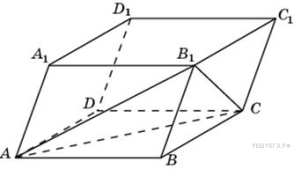
№ 8 (B11). Объем параллелепипеда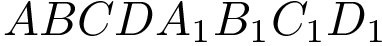 
равен 12. Найдите объем треугольной пирамиды 
.
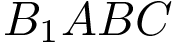infourok.ru
Контрольная работа №4 «Многогранники»Вариант 1
1) Изобразите произвольный многогранник. Обозначьте его вершины и перечислите его элементы:
грани, вершины, ребра, диагональ.
2) Продолжите определение:
а) «площадь полной поверхности призмы – это сумма…»;
б) «площадь боковой поверхность пирамиды – это…».
3) В прямоугольном параллелепипеде стороны основания равны 12 и 5 сантиметров. Диагональ параллелепипеда образует с плоскостью образования угол в 45º. Найти боковое ребро параллелепипеда.
4) В правильной четырехугольной призме площадь основания равна 144 см2; высота призмы 8 см. Найти диагональ призмы.
5) Дан куб АВСDА1В1С1D1, ребро которого равно 3 см. Найти площадь сечения, проходящего через ребро АВ и вершину D.
____________________________________________________________________________________________
Контрольная работа №4 «Многогранники»Вариант 2
1) Изобразите произвольную призму. Обозначьте ее вершины и перечислите ее элементы:
Боковые грани, вершины, основания, диагональ.
2) Продолжите определение:
а) «площадь боковой поверхности призмы – это сумма…»;
б) «площадь полной поверхность пирамиды – это…».
3) Основанием прямого параллелепипеда является ромб с диагоналями 10 см и 24 см, а высота параллелепипеда равна 10 см. Найти бо́льшую диагональ параллелепипеда.
4) В основании пирамиды SABCD лежит прямоугольник ABCD со сторонами 6 см и 8 см.. Боковые ребра пирамиды равны 5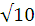
см. Найти высоту пирамиды.
5) Дан куб АВСDА1В1С1D1, ребро которого равно 3 см. Найти площадь сечения, проходящего через диагонали ВА1 и DА1.
____________________________________________________________________________________________
Контрольная работа №4 «Многогранники»Вариант 1
1) Изобразите произвольный многогранник. Обозначьте его вершины и перечислите его элементы:
грани, вершины, ребра, диагональ.
2) Продолжите определение:
а) «площадь полной поверхности призмы – это сумма…»;
б) «площадь боковой поверхность пирамиды – это…».
3) В прямоугольном параллелепипеде стороны основания равны 12 и 5 сантиметров. Диагональ параллелепипеда образует с плоскостью образования угол в 45º. Найти боковое ребро параллелепипеда.
4) В правильной четырехугольной призме площадь основания равна 144 см2; высота призмы 8 см. Найти диагональ призмы.
5) Дан куб АВСDА1В1С1D1, ребро которого равно 3 см. Найти площадь сечения, проходящего через ребро АВ и вершину D.
Контрольная работа №4 «Многогранники»Вариант 1
1) Изобразите произвольный многогранник. Обозначьте его вершины и перечислите его элементы:
грани, вершины, ребра, диагональ.
2) Продолжите определение:
а) «площадь полной поверхности призмы – это сумма…»;
б) «площадь боковой поверхность пирамиды – это…».
3) В прямоугольном параллелепипеде стороны основания равны 12 и 5 сантиметров. Диагональ параллелепипеда образует с плоскостью образования угол в 45º. Найти боковое ребро параллелепипеда.
4) В правильной четырехугольной призме площадь основания равна 144 см2; высота призмы 8 см. Найти диагональ призмы.
5) Дан куб АВСDА1В1С1D1, ребро которого равно 3 см. Найти площадь сечения, проходящего через ребро АВ и вершину D.
____________________________________________________________________________________________
Контрольная работа №4 «Многогранники»Вариант 2
1) Изобразите произвольную призму. Обозначьте ее вершины и перечислите ее элементы:
Боковые грани, вершины, основания, диагональ.
2) Продолжите определение:
а) «площадь боковой поверхности призмы – это сумма…»;
б) «площадь полной поверхность пирамиды – это…».
3) Основанием прямого параллелепипеда является ромб с диагоналями 10 см и 24 см, а высота параллелепипеда равна 10 см. Найти бо́льшую диагональ параллелепипеда.
4) В основании пирамиды SABCD лежит прямоугольник ABCD со сторонами 6 см и 8 см.. Боковые ребра пирамиды равны 5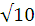 см. Найти высоту пирамиды.
5) Дан куб АВСDА1В1С1D1, ребро которого равно 3 см. Найти площадь сечения, проходящего через диагонали ВА1 и DА1.
____________________________________________________________________________________________
Контрольная работа №4 «Многогранники»Вариант 2
1) Изобразите произвольную призму. Обозначьте ее вершины и перечислите ее элементы:
Боковые грани, вершины, основания, диагональ.
2) Продолжите определение:
а) «площадь боковой поверхности призмы – это сумма…»;
б) «площадь полной поверхность пирамиды – это…».
3) Основанием прямого параллелепипеда является ромб с диагоналями 10 см и 24 см, а высота параллелепипеда равна 10 см. Найти бо́льшую диагональ параллелепипеда.
4) В основании пирамиды SABCD лежит прямоугольник ABCD со сторонами 6 см и 8 см.. Боковые ребра пирамиды равны 5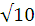 см. Найти высоту пирамиды.
5) Дан куб АВСDА1В1С1D1, ребро которого равно 3 см. Найти площадь сечения, проходящего через диагонали ВА1 и DА1.
infourok.ru
