
Контрольная работа
«Предел функции»
Найти предел функции
1
а)
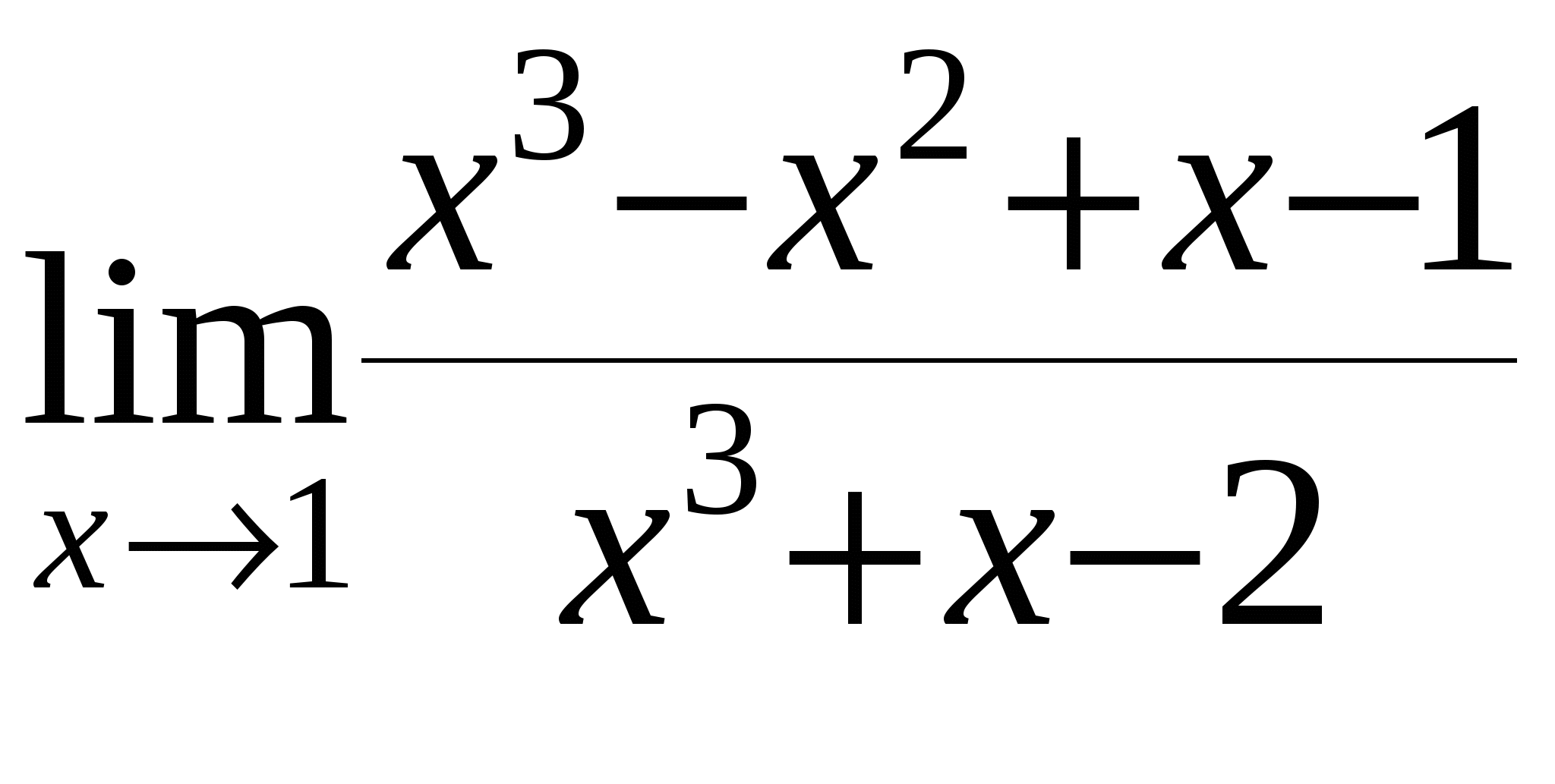
б)
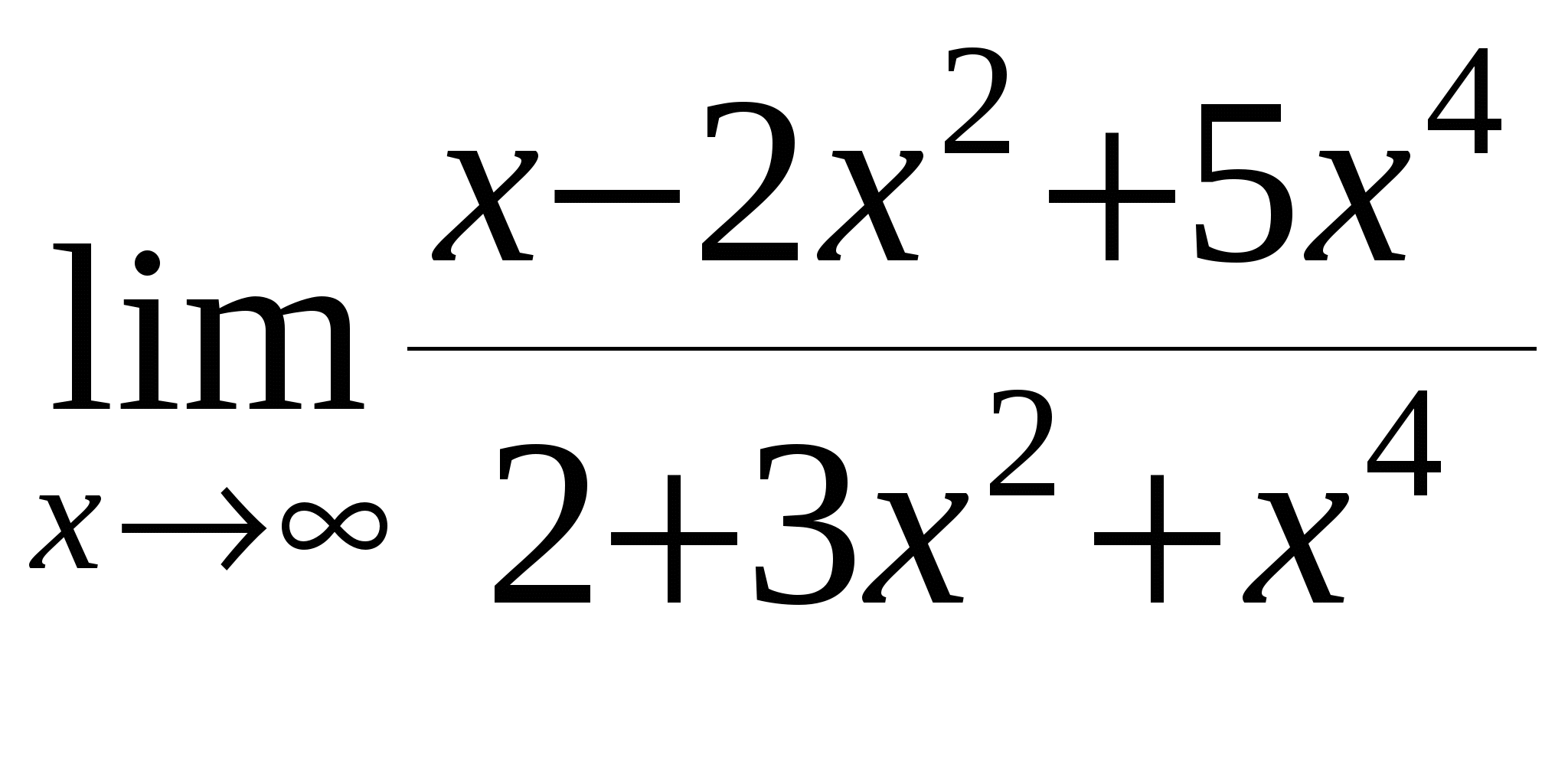
в)
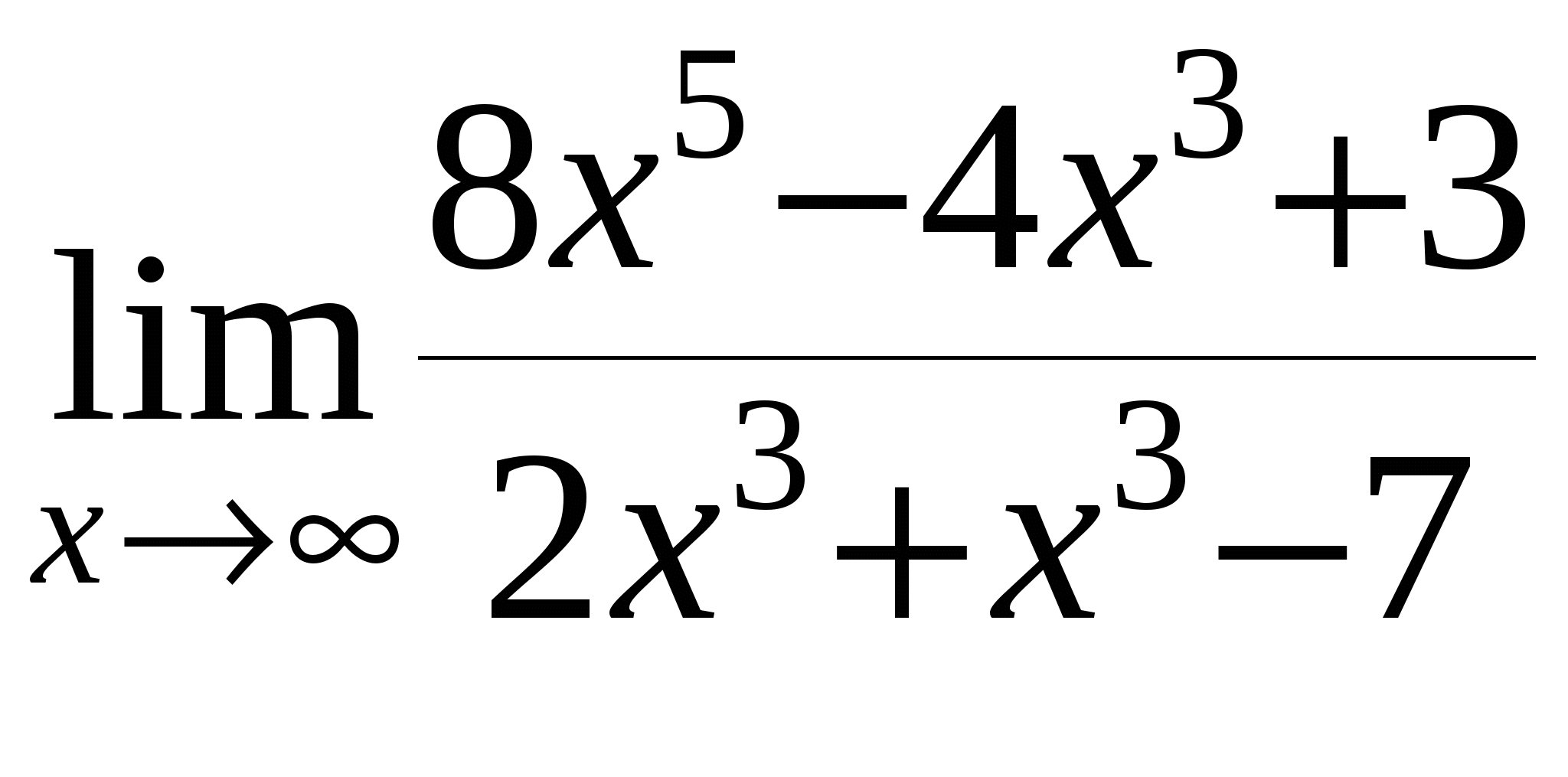
г)
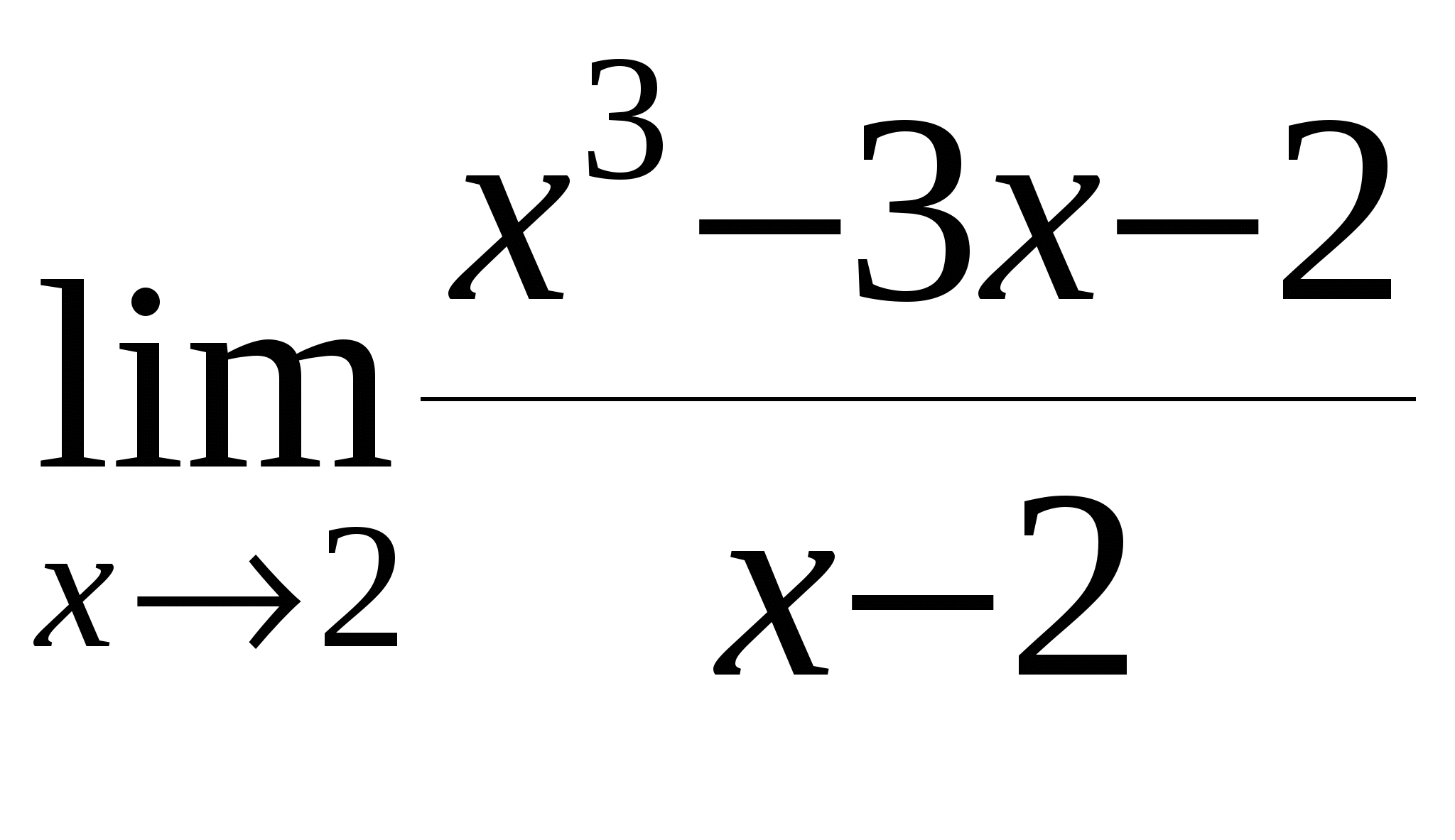
д)
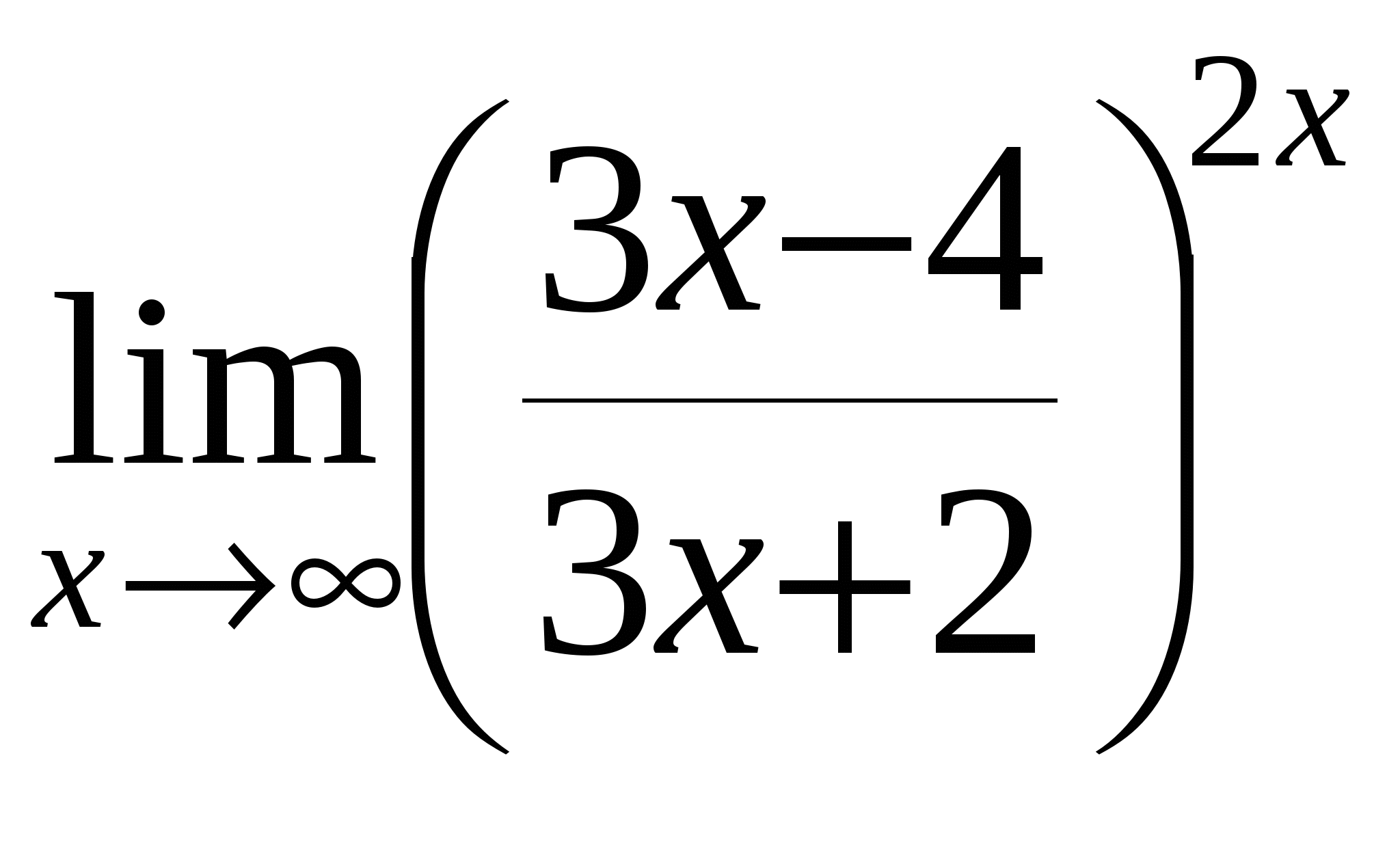
е)
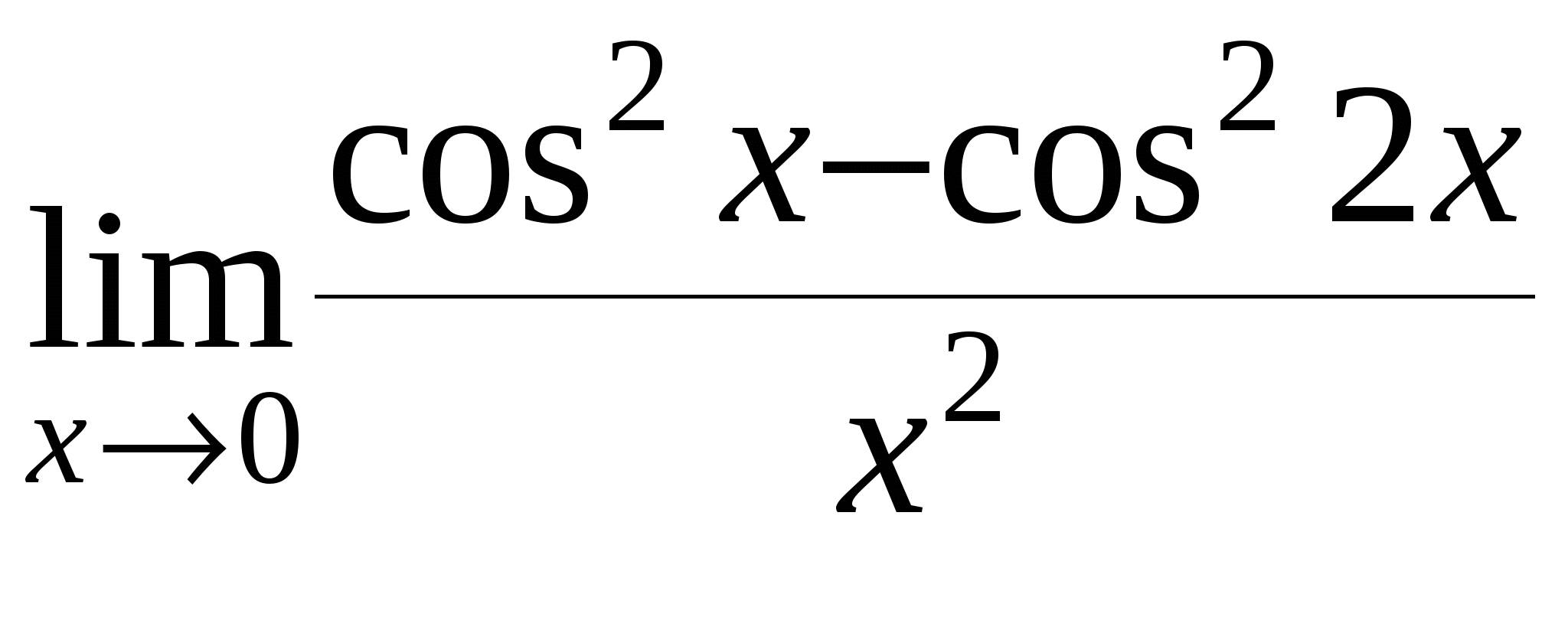
Найти предел функции
2
а)
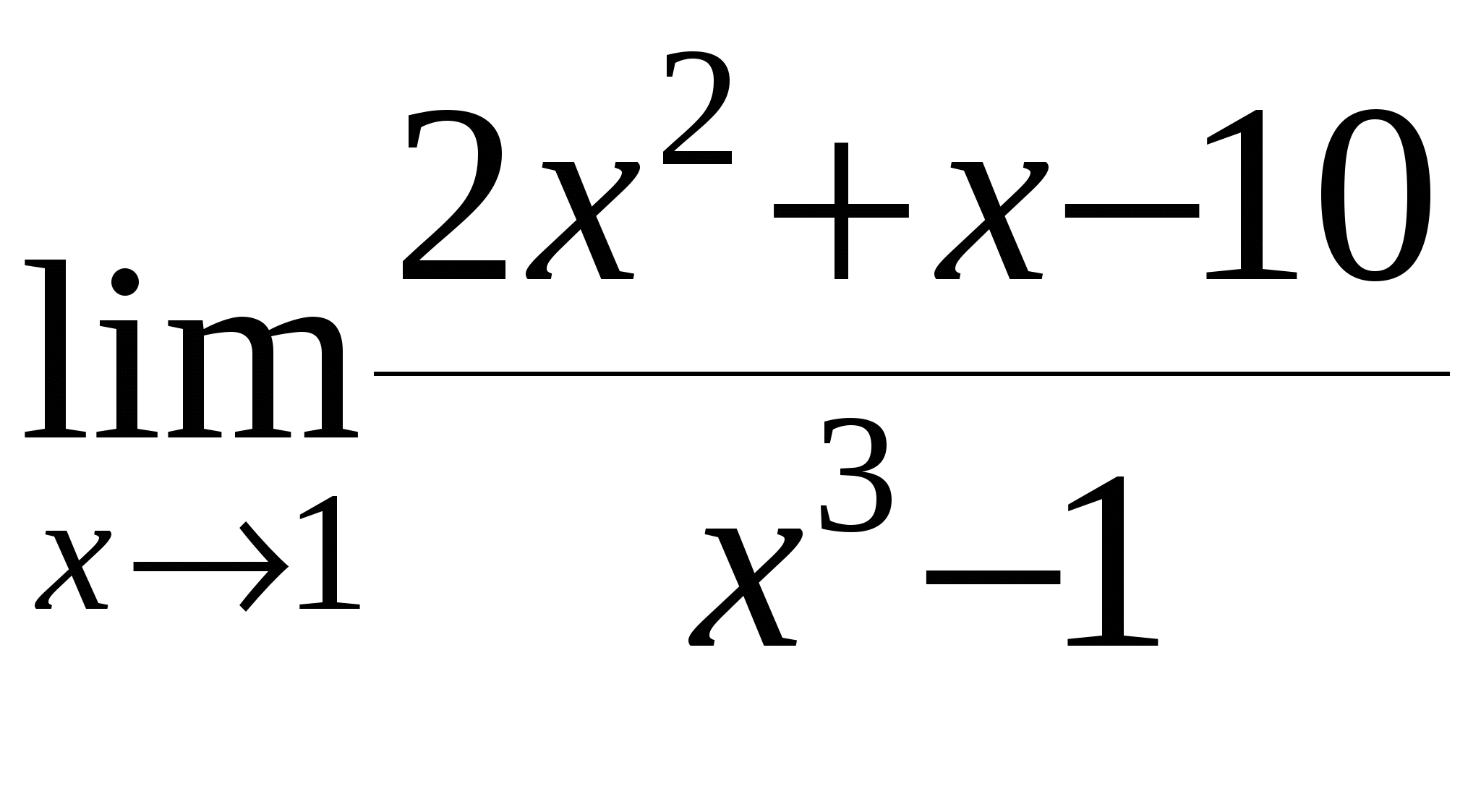
б)
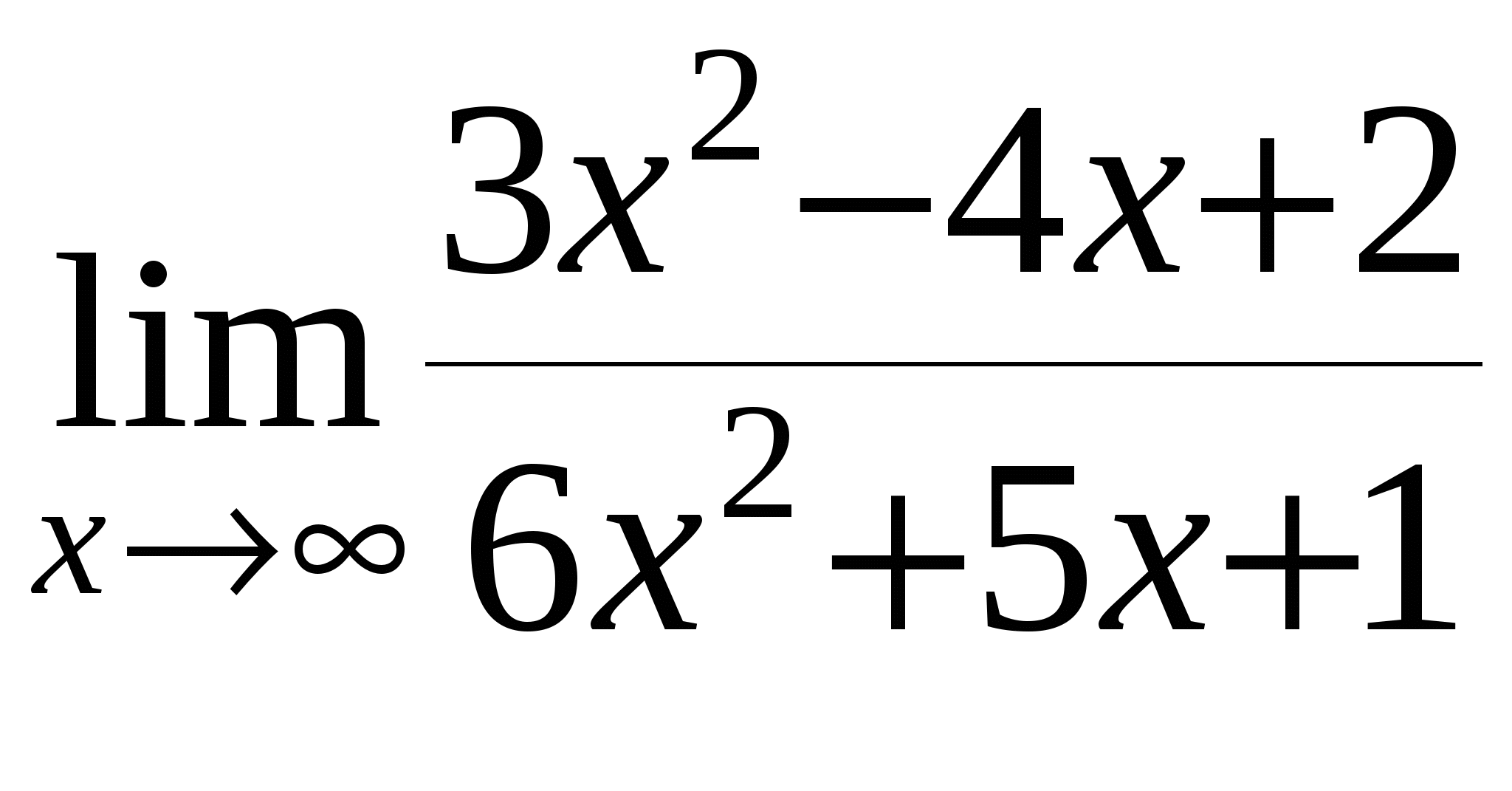
в)

г)
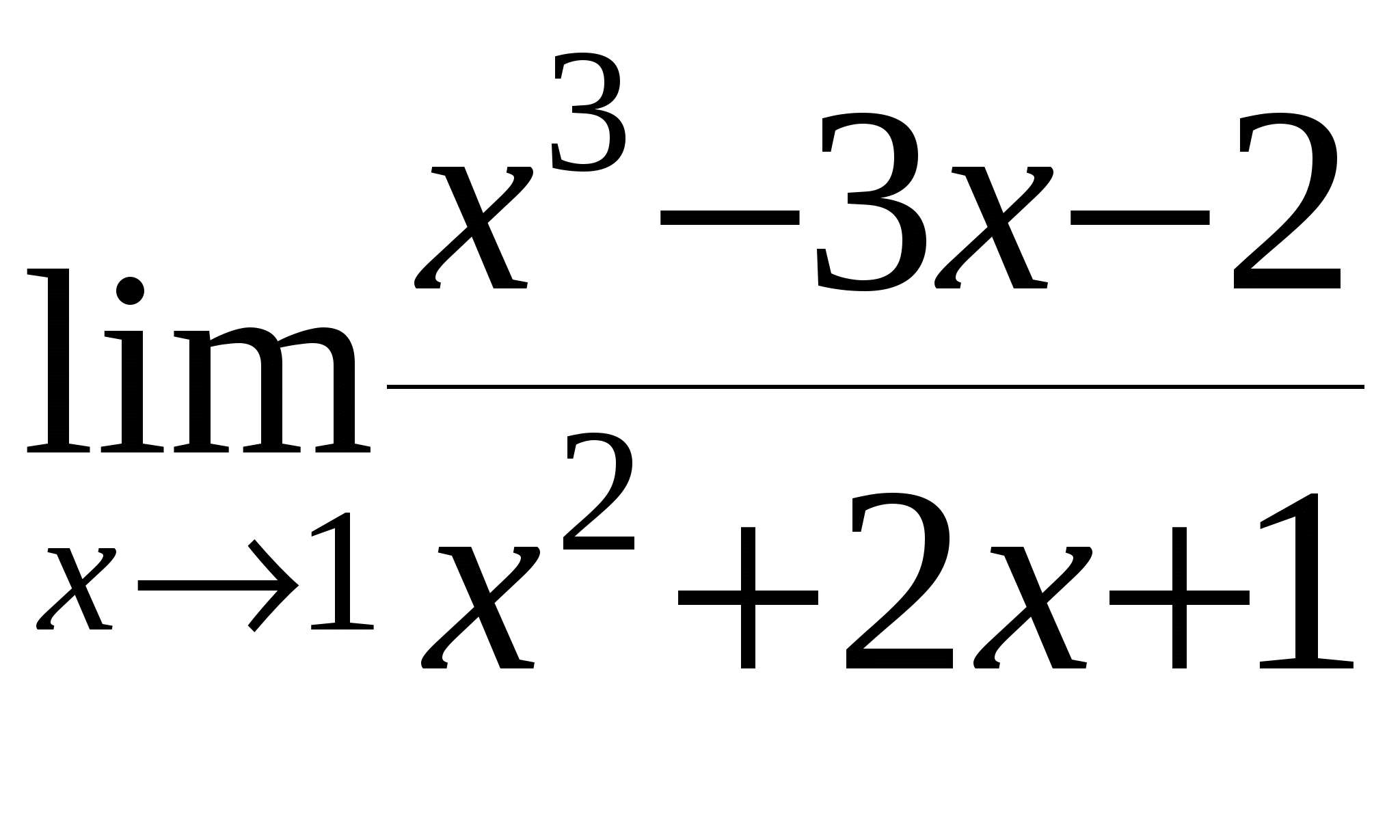
д)
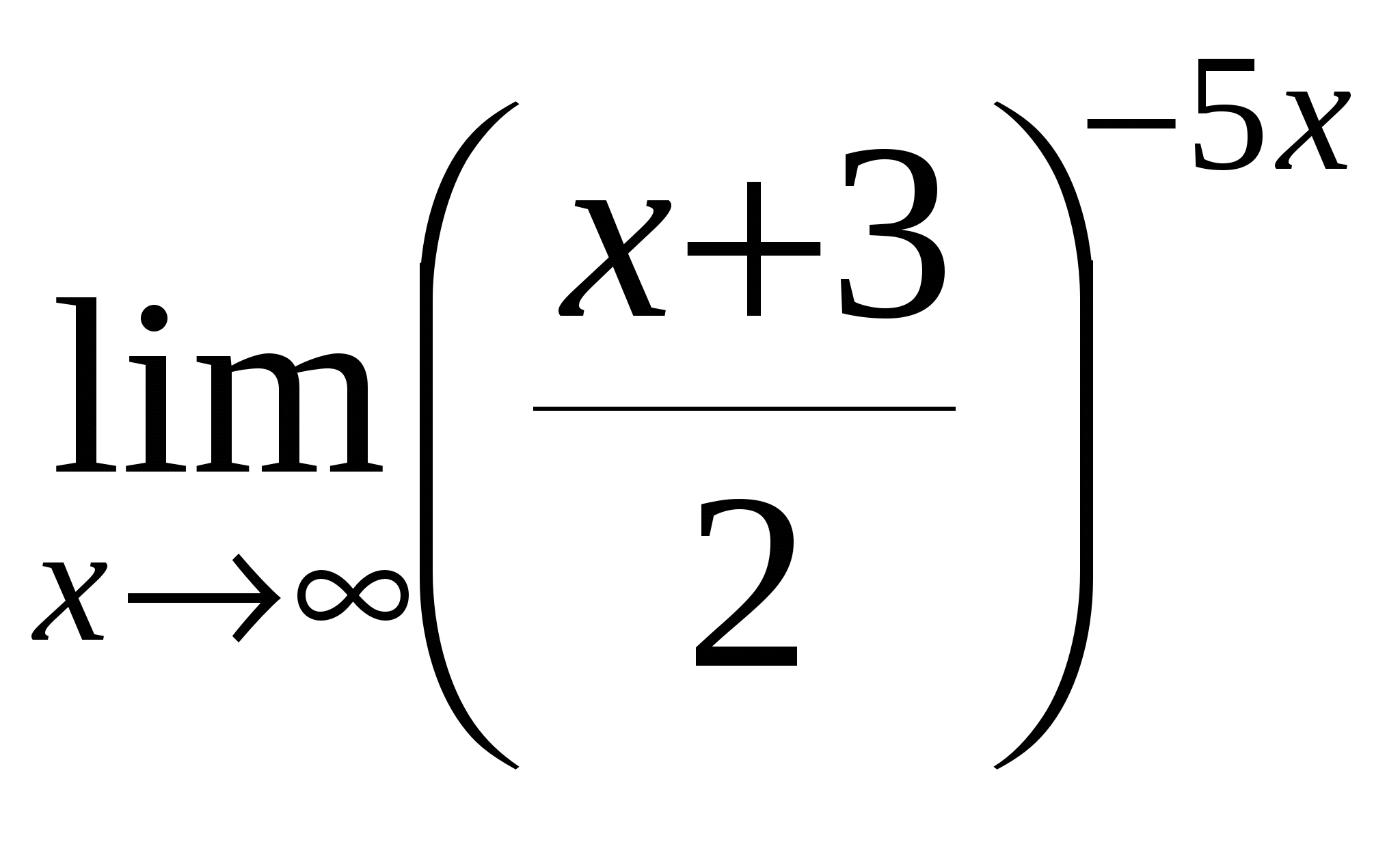
е)
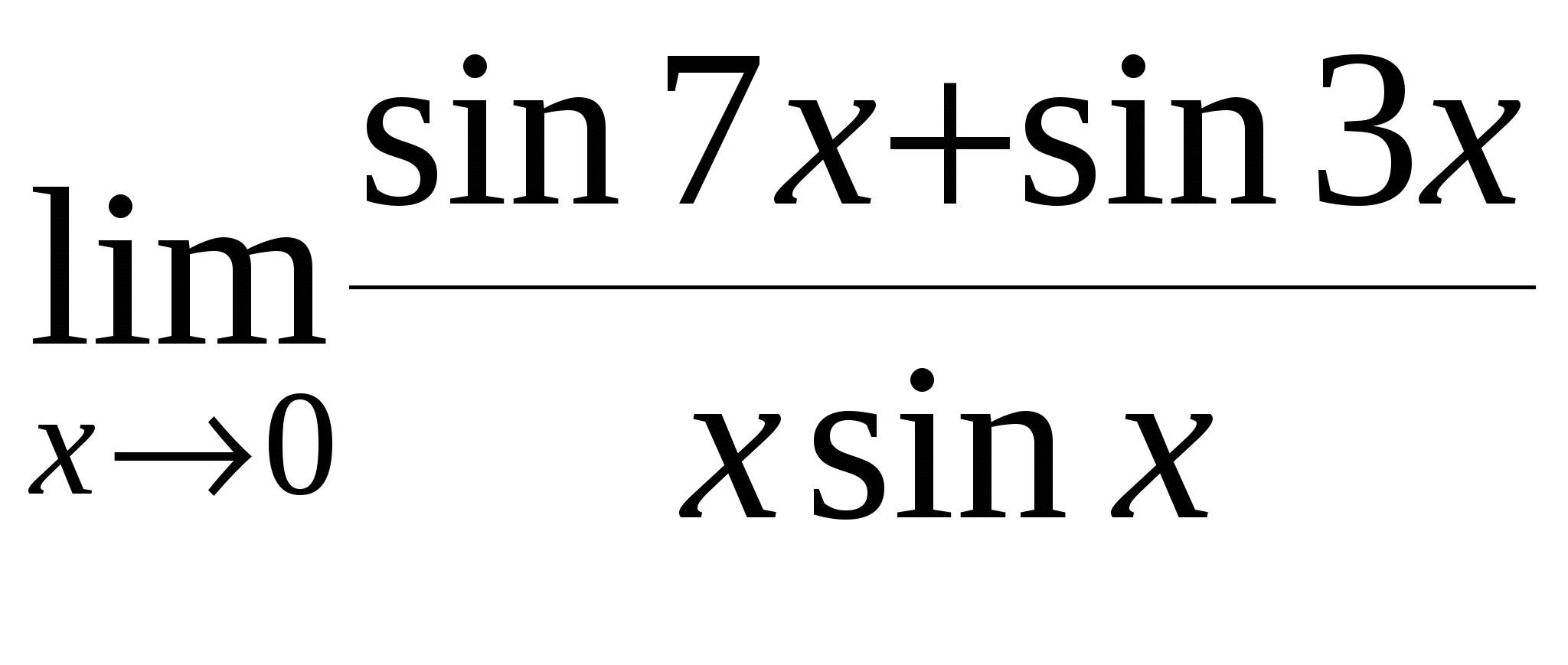
Найти предел функции
3
а)
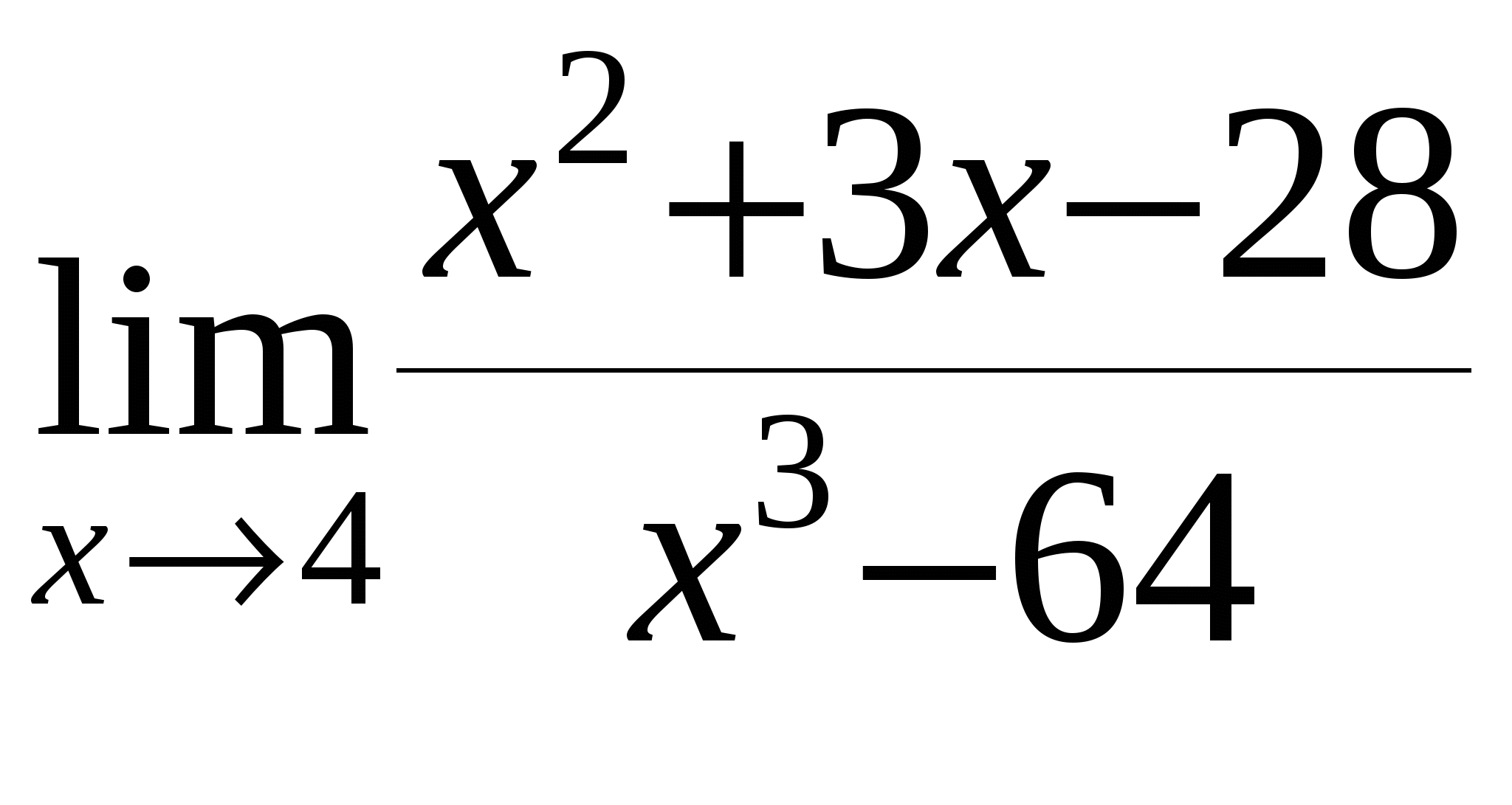
б)
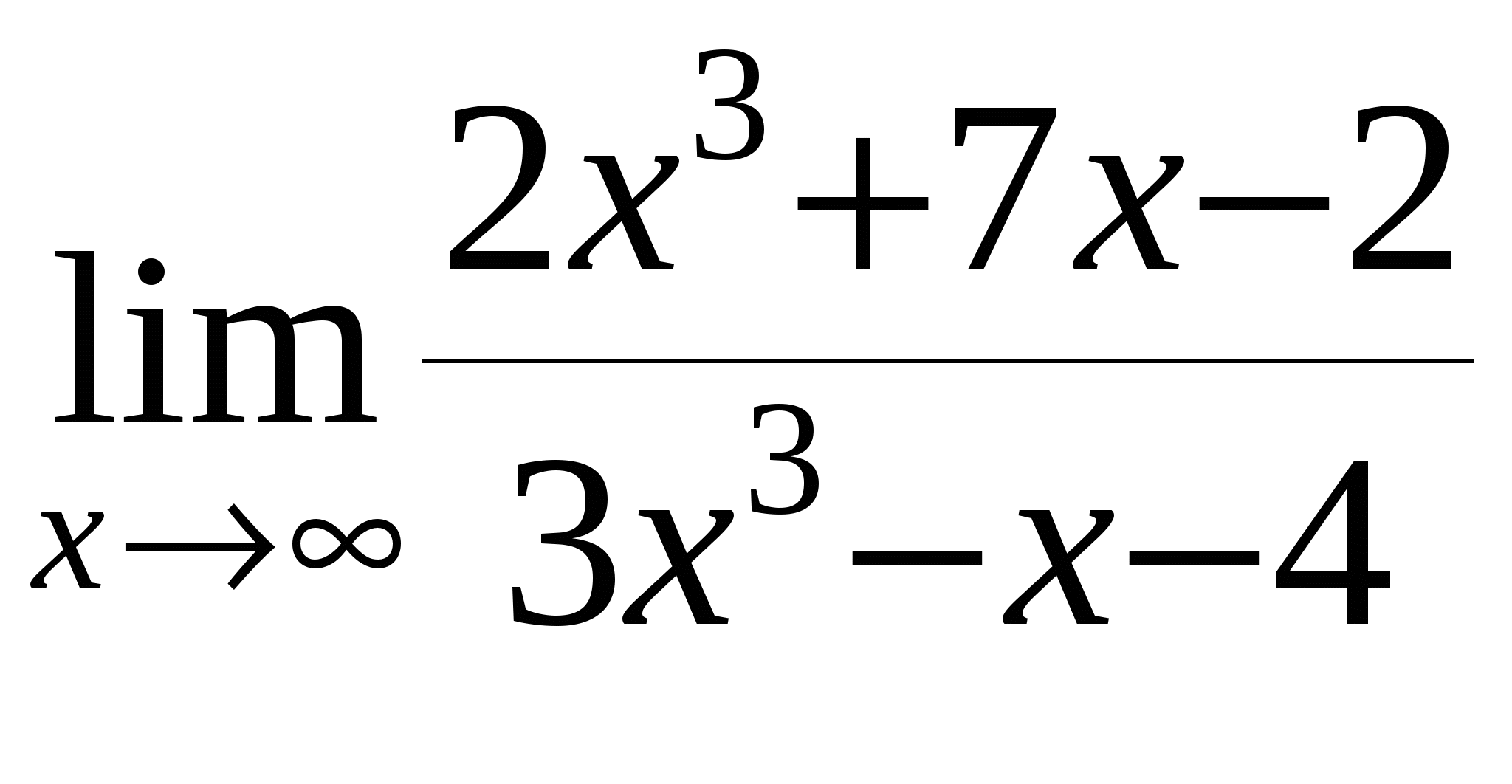
в)
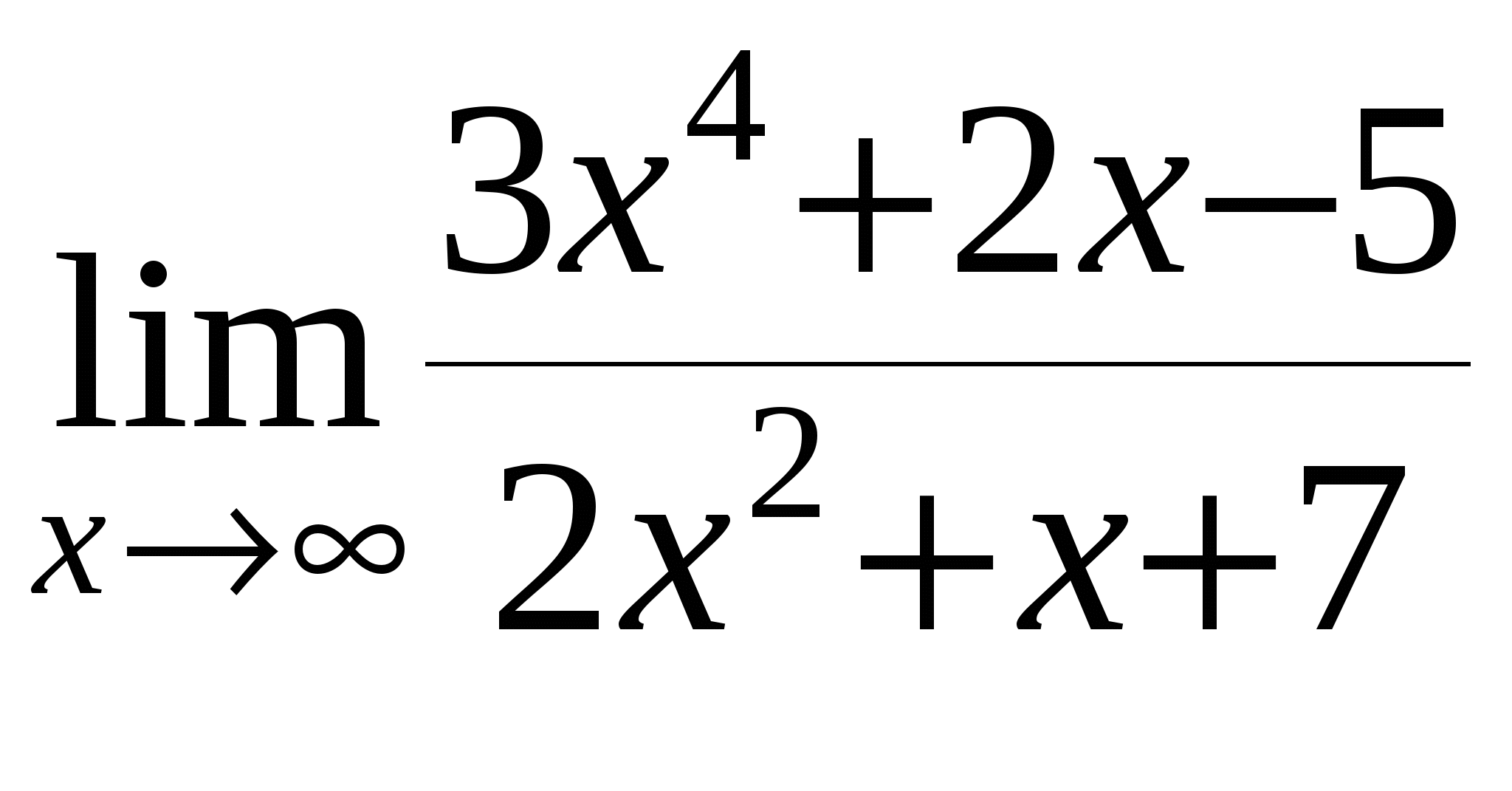
г)
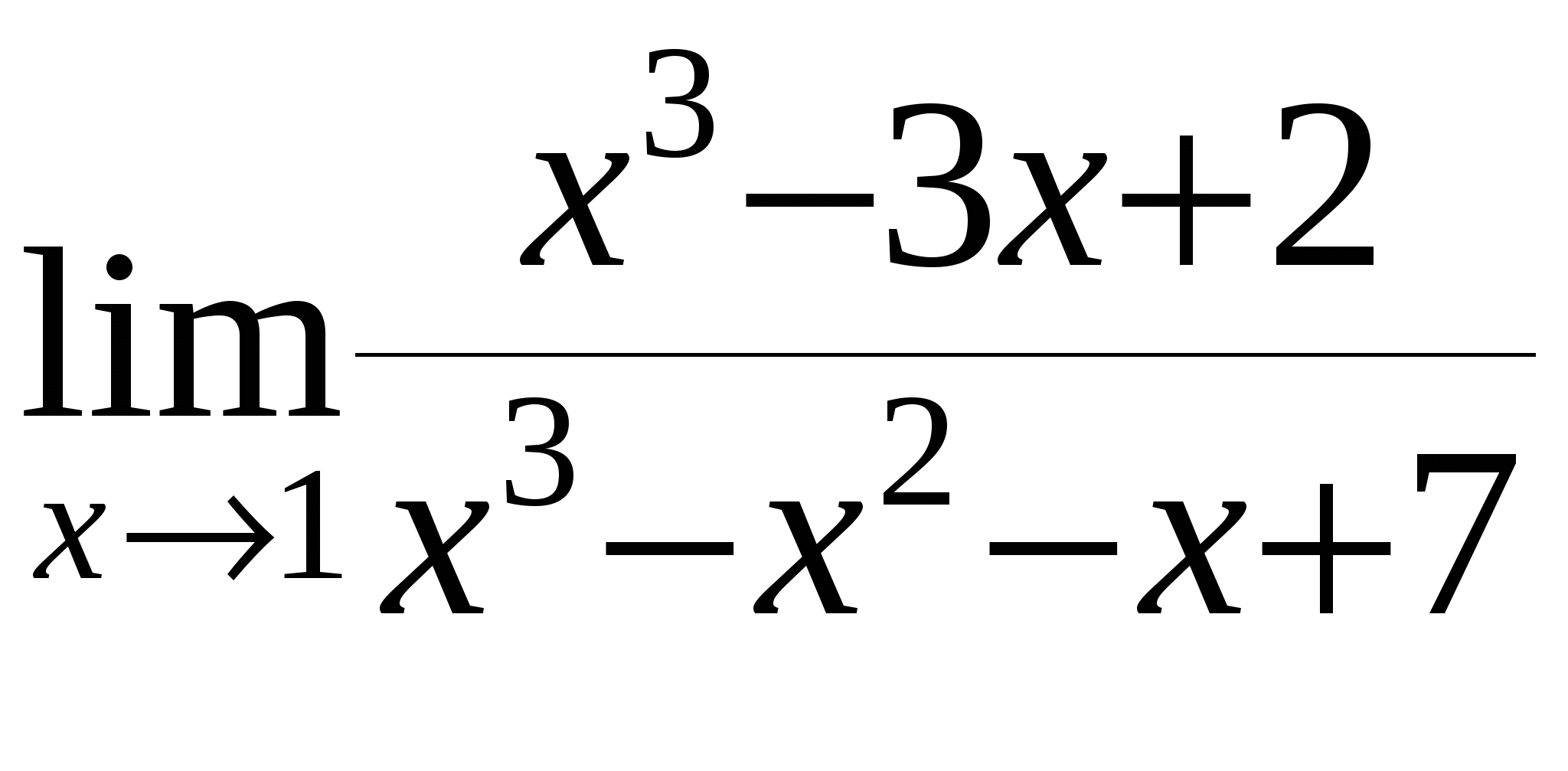
д)
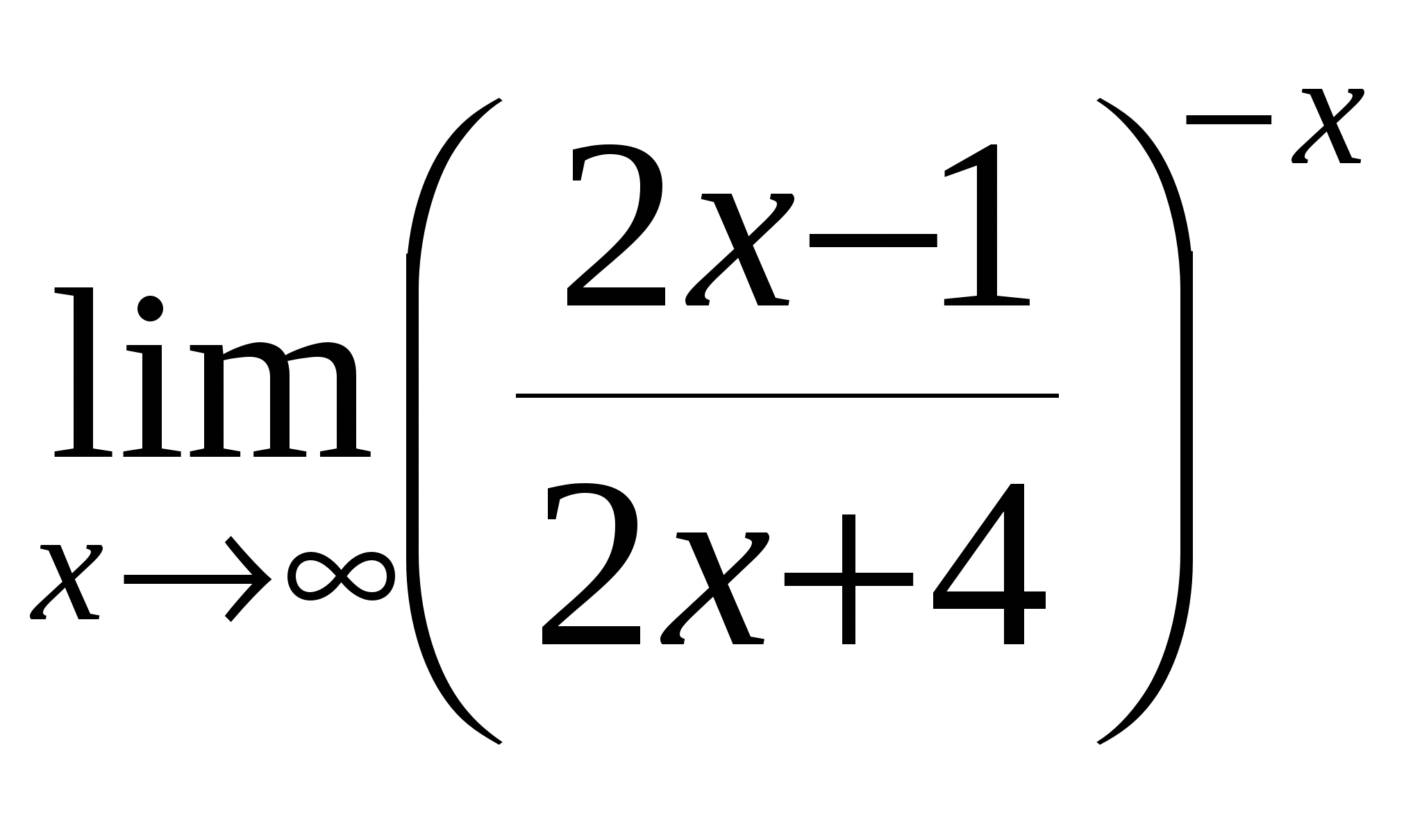
е)
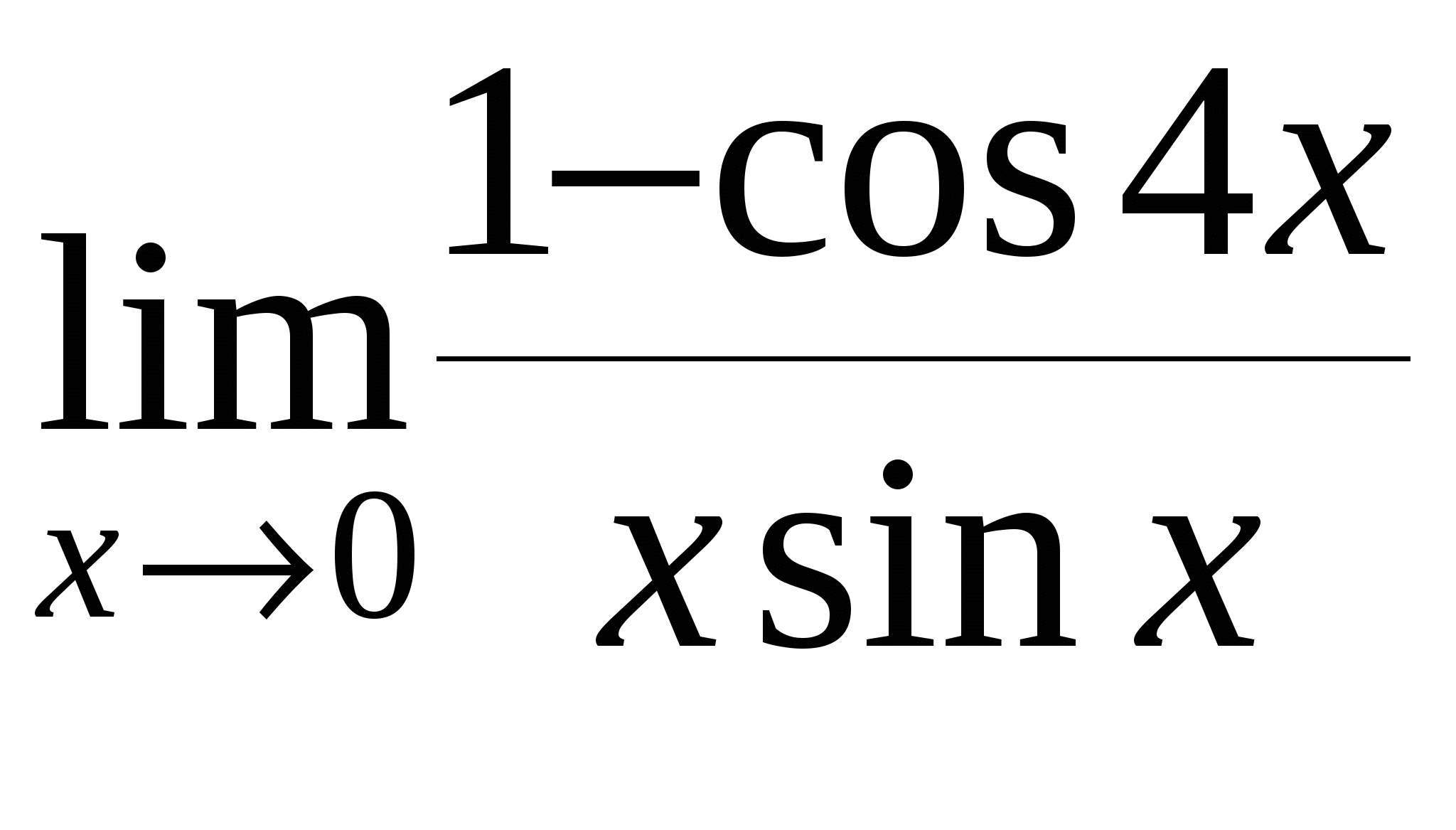
Контрольная работа № 5
Найти предел функции
4
а)
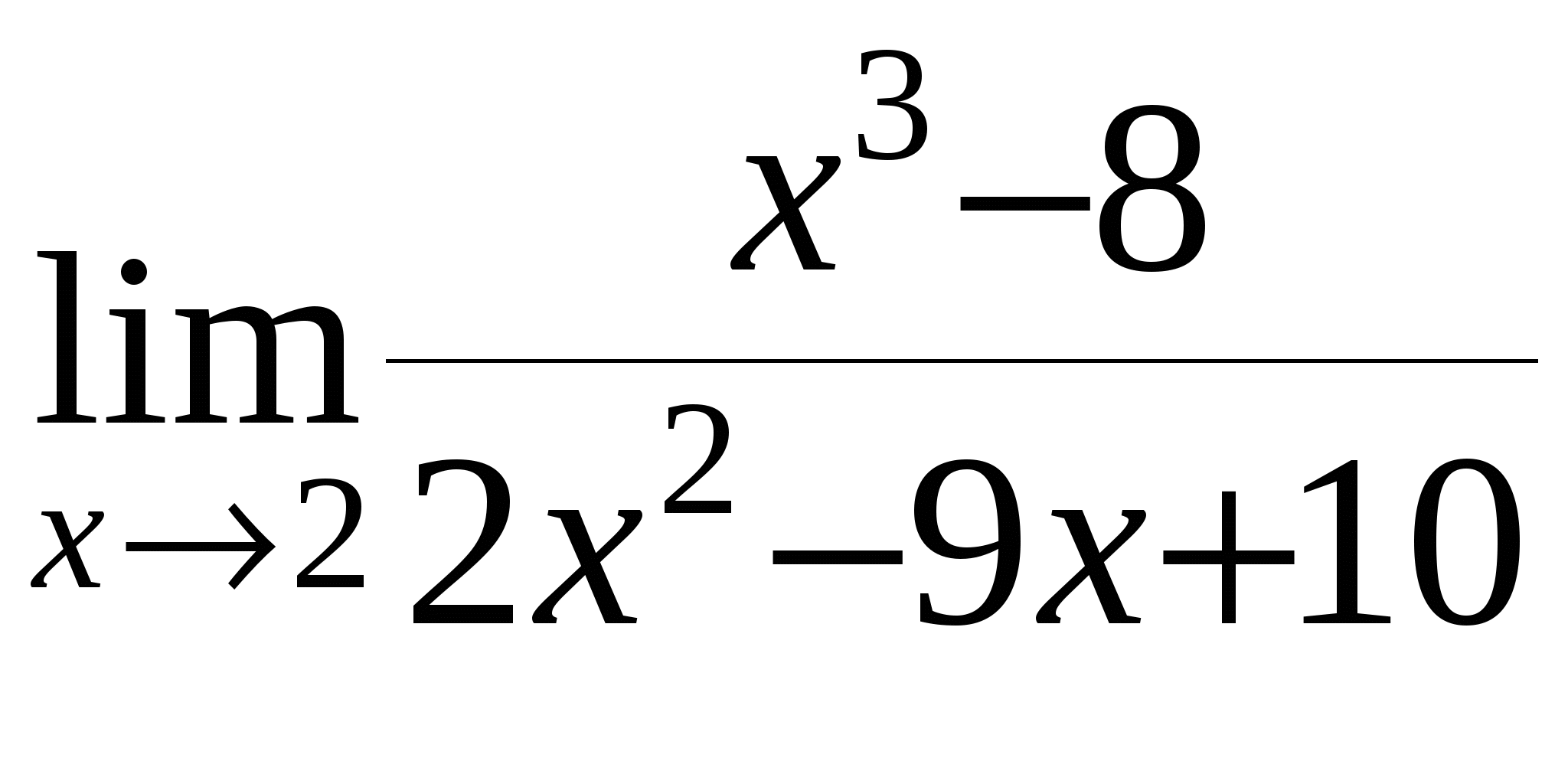
б)
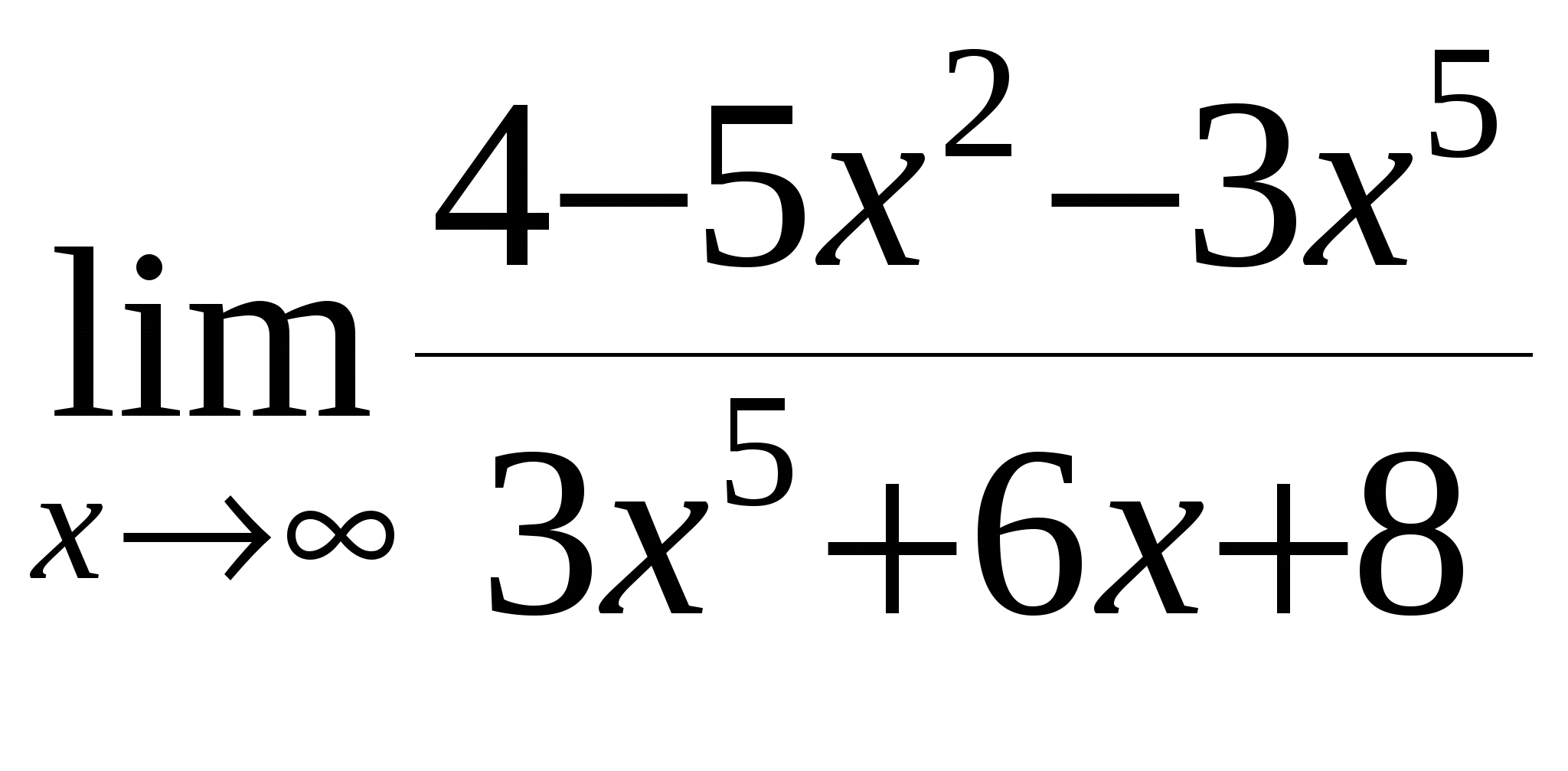
в)
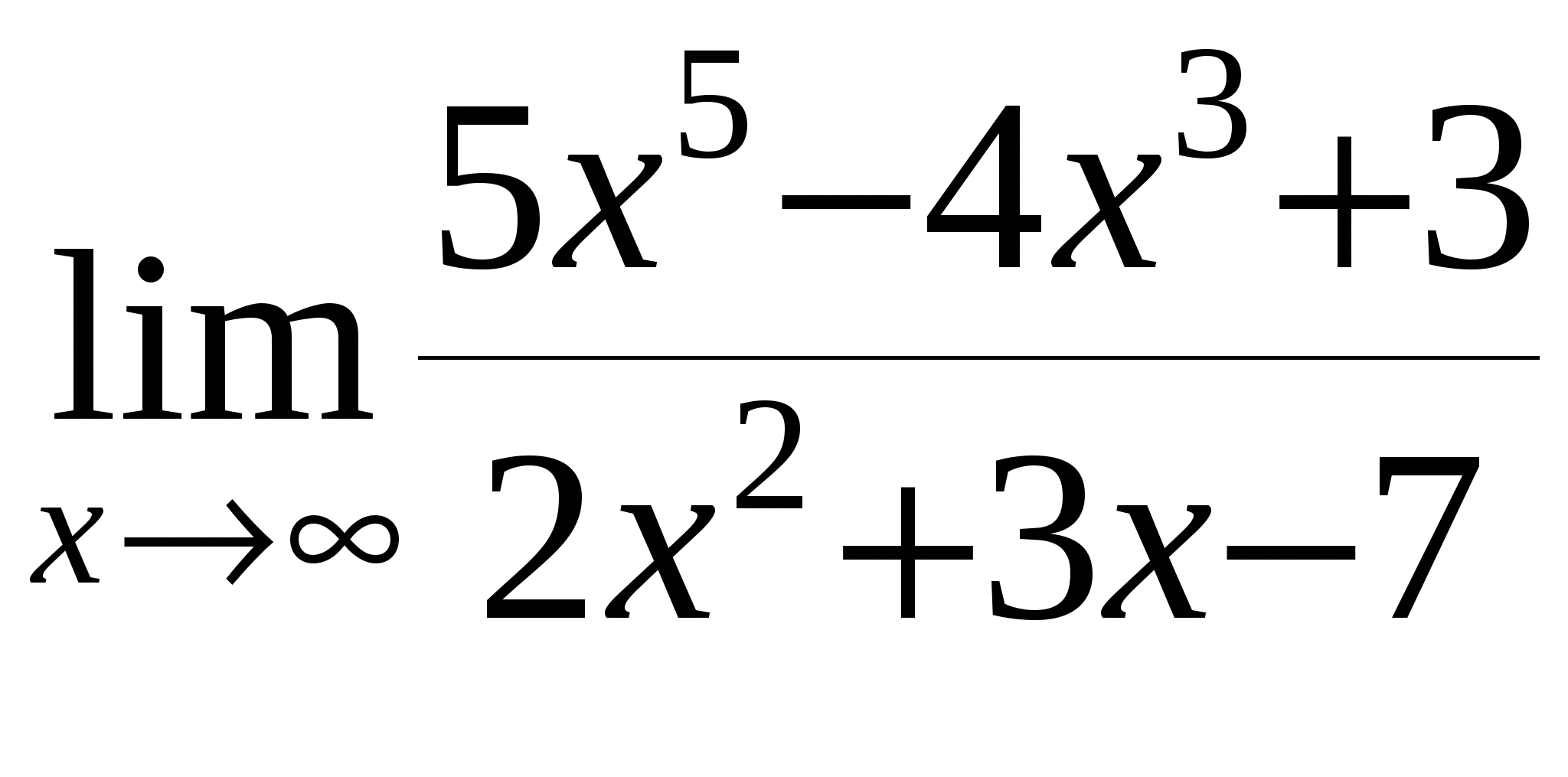
г)
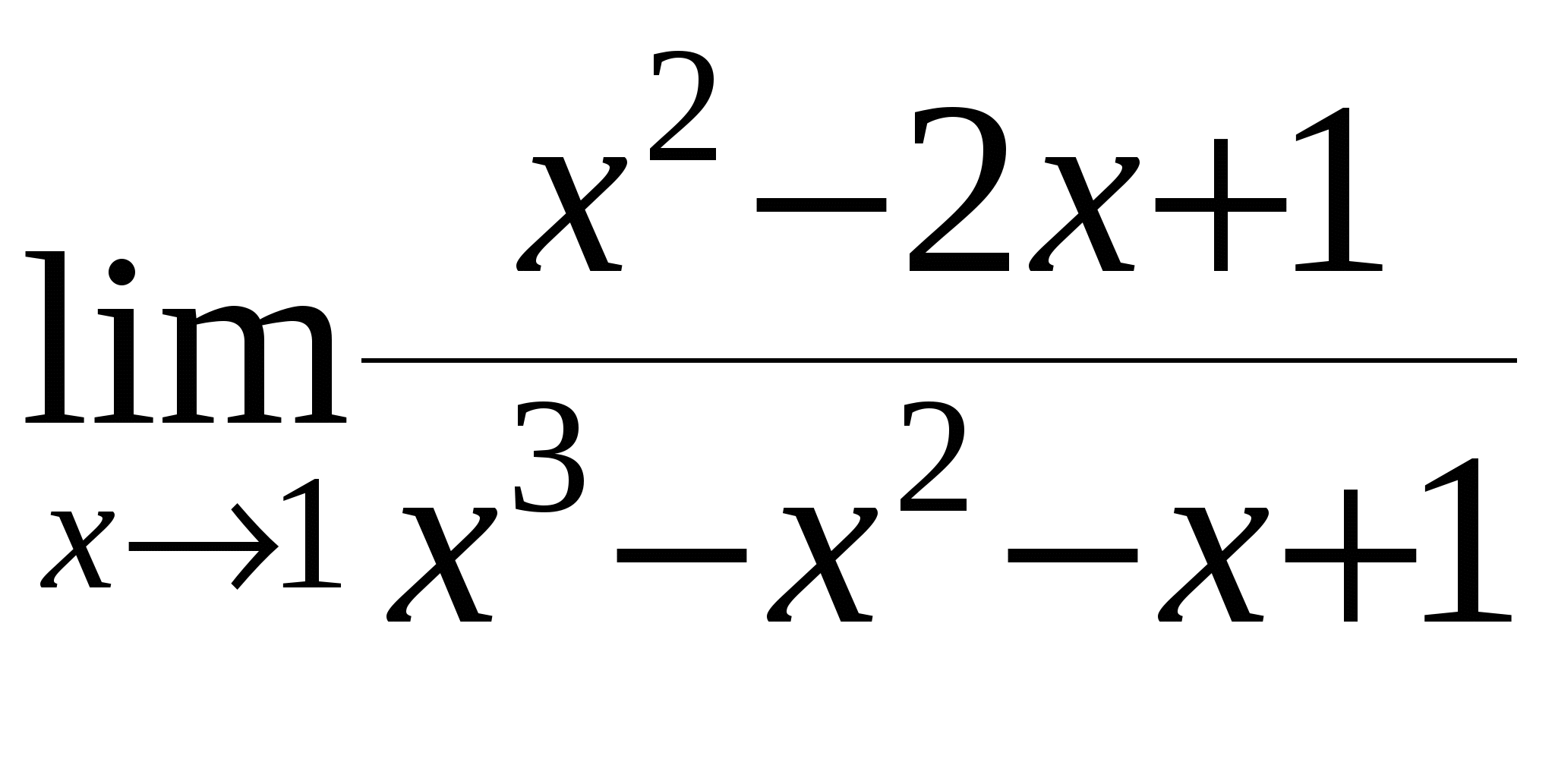
д)

е)
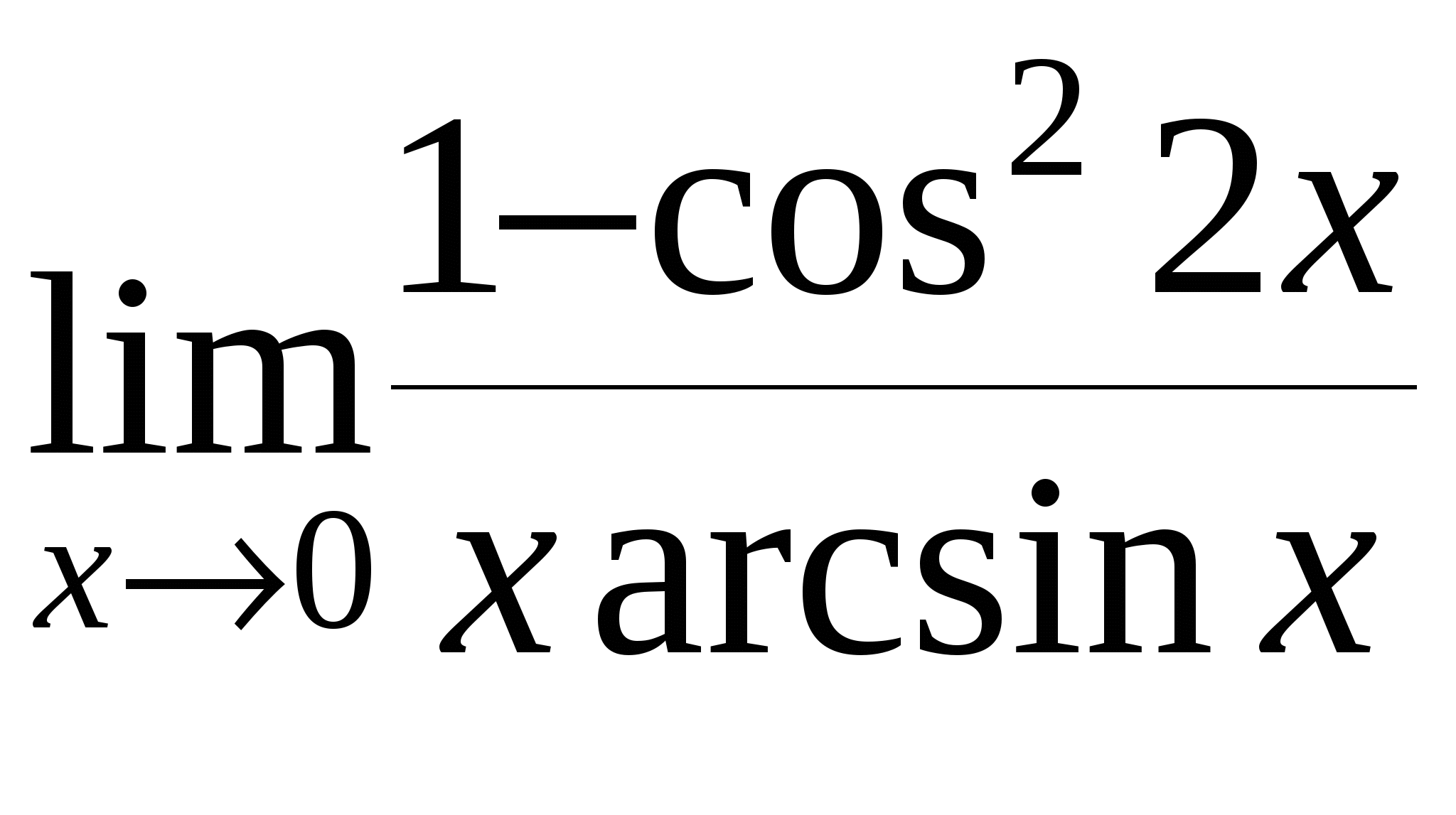
Найти предел функции
5
а)
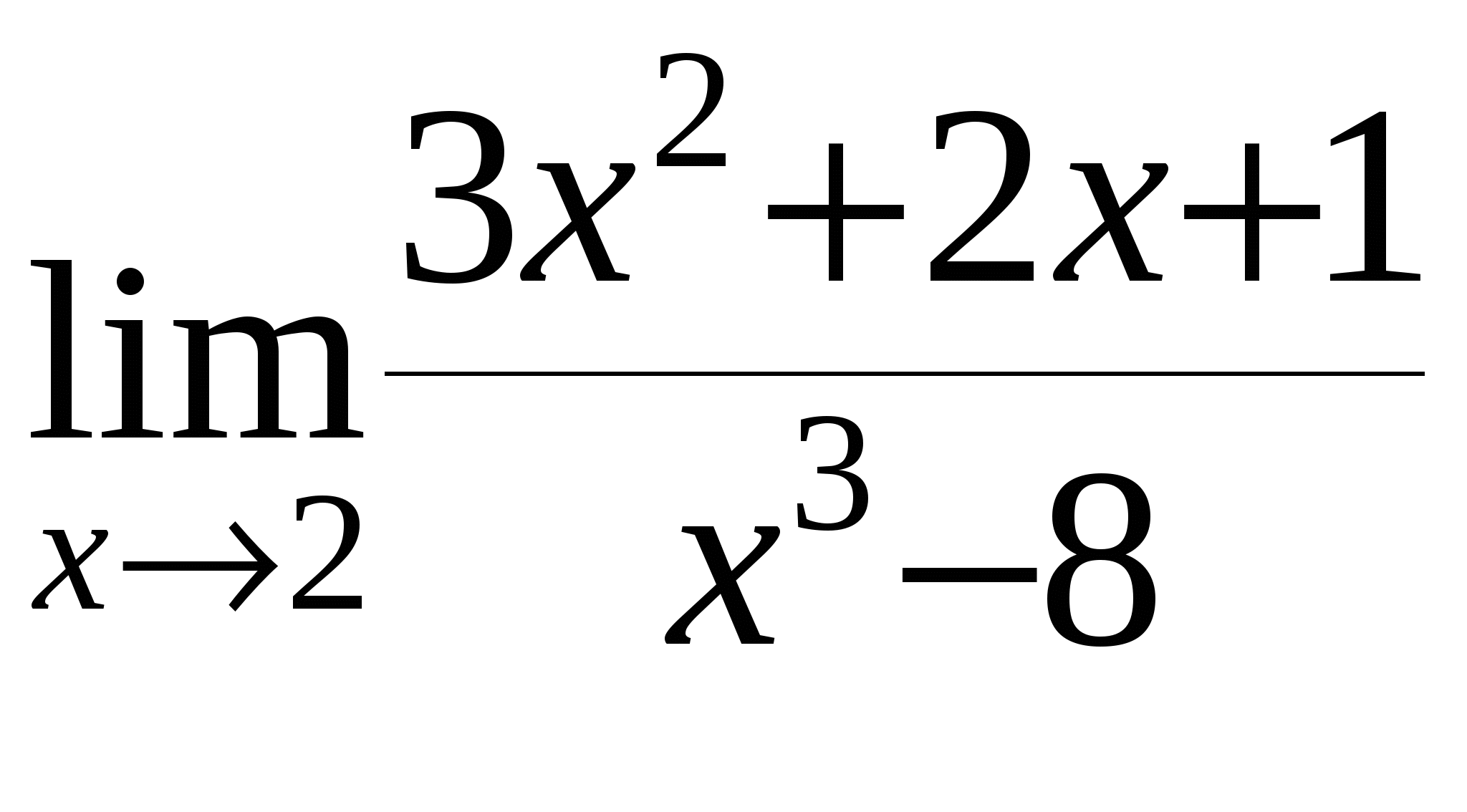
б)
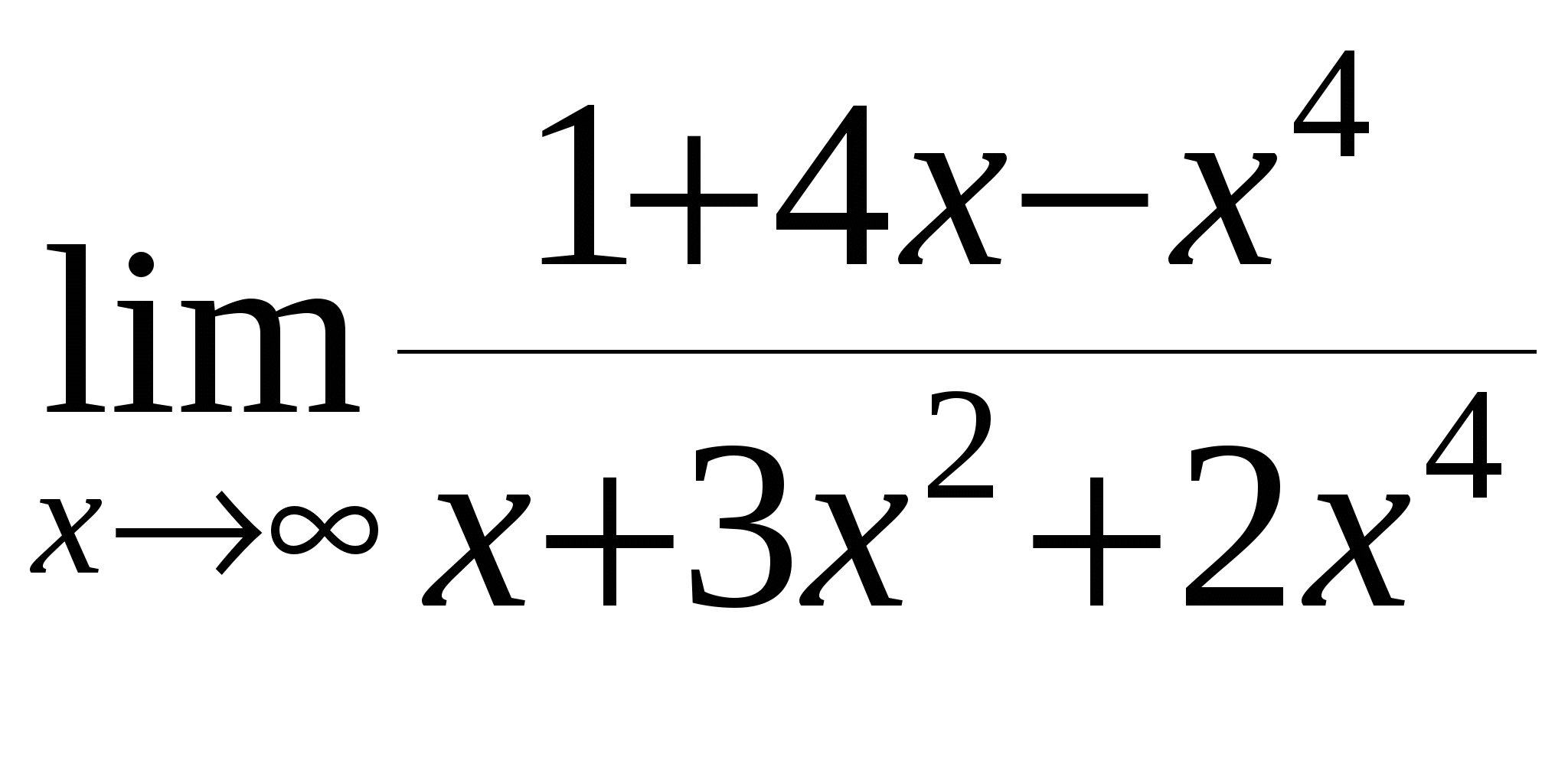
в)
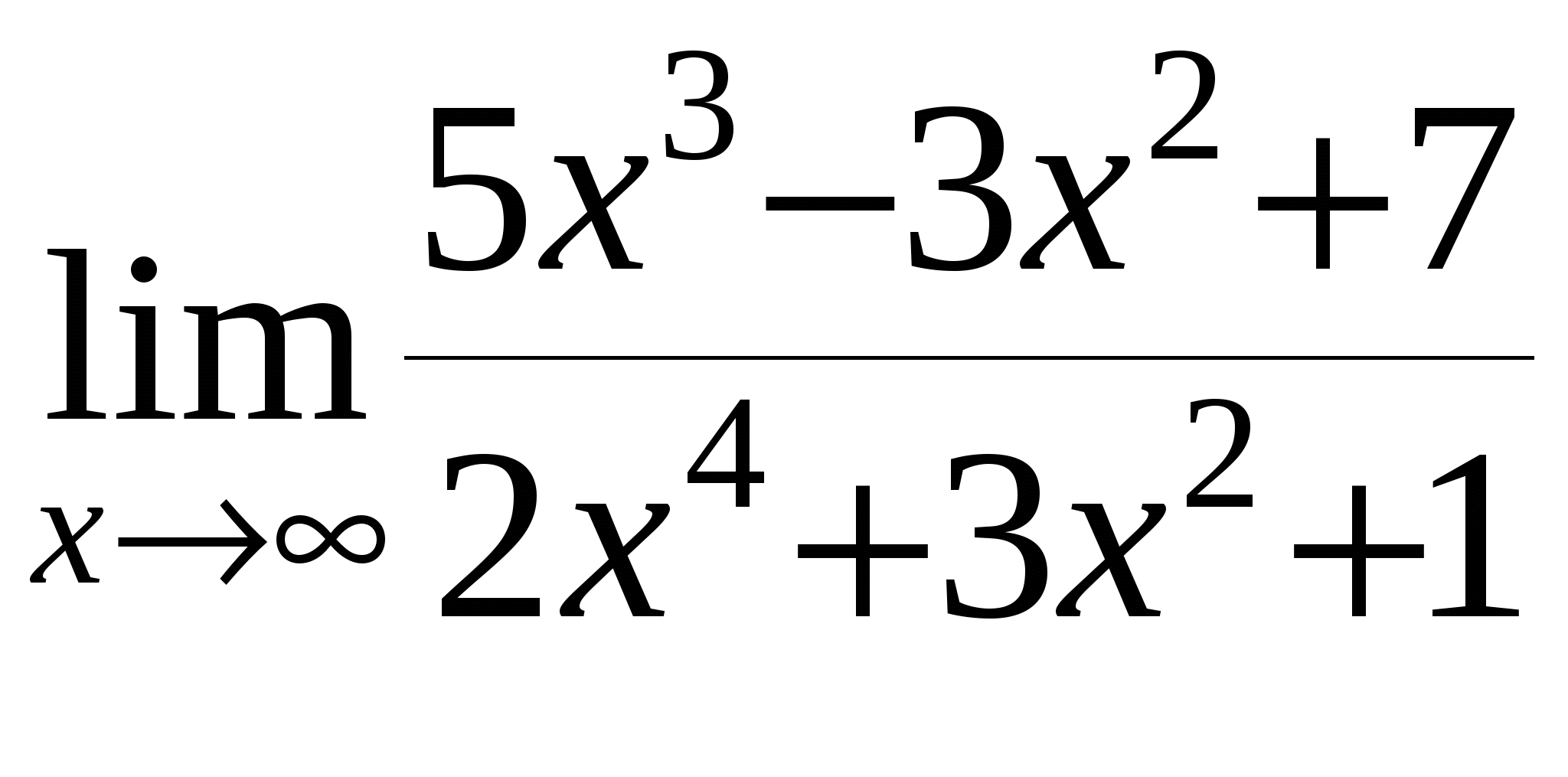
г)
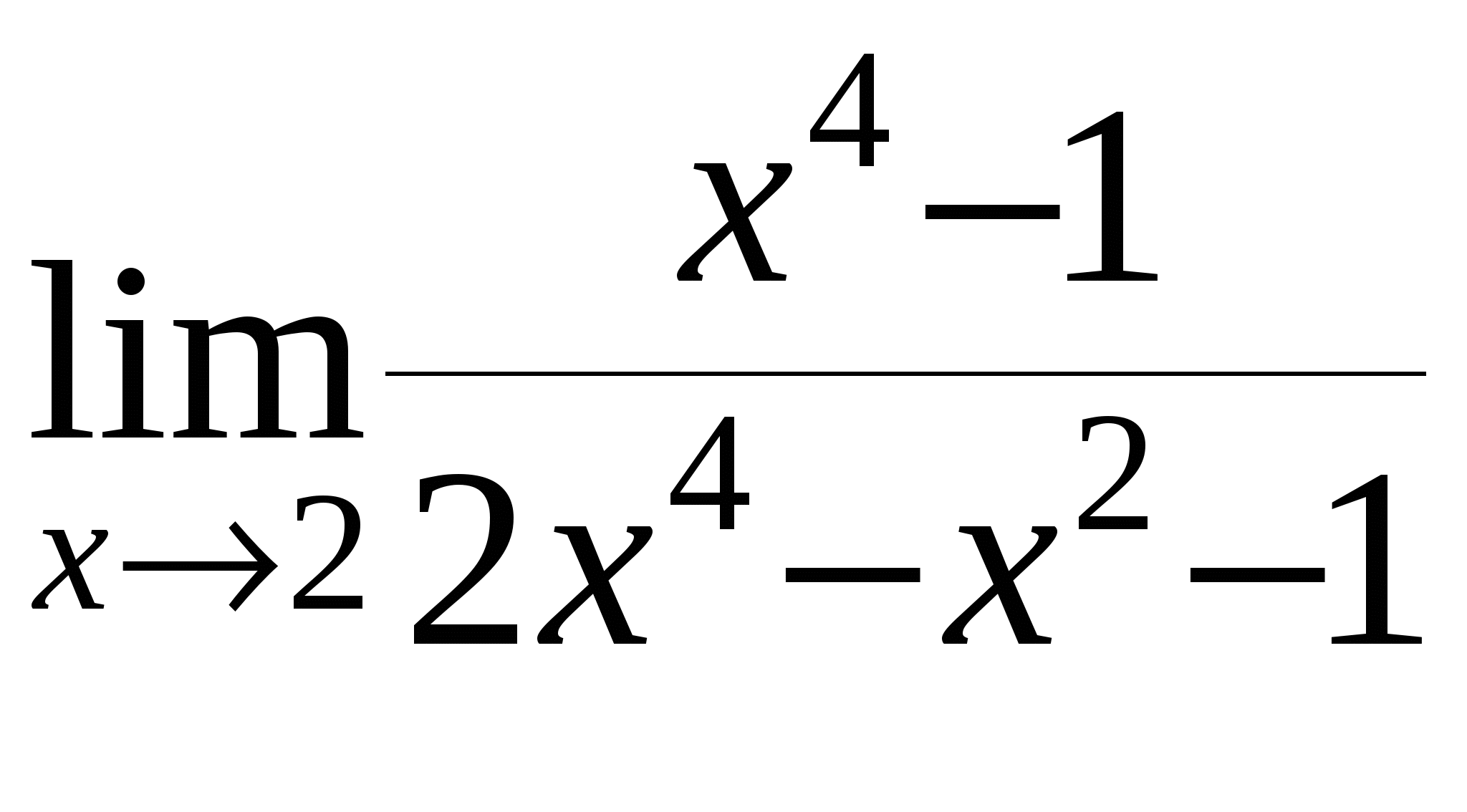
д)
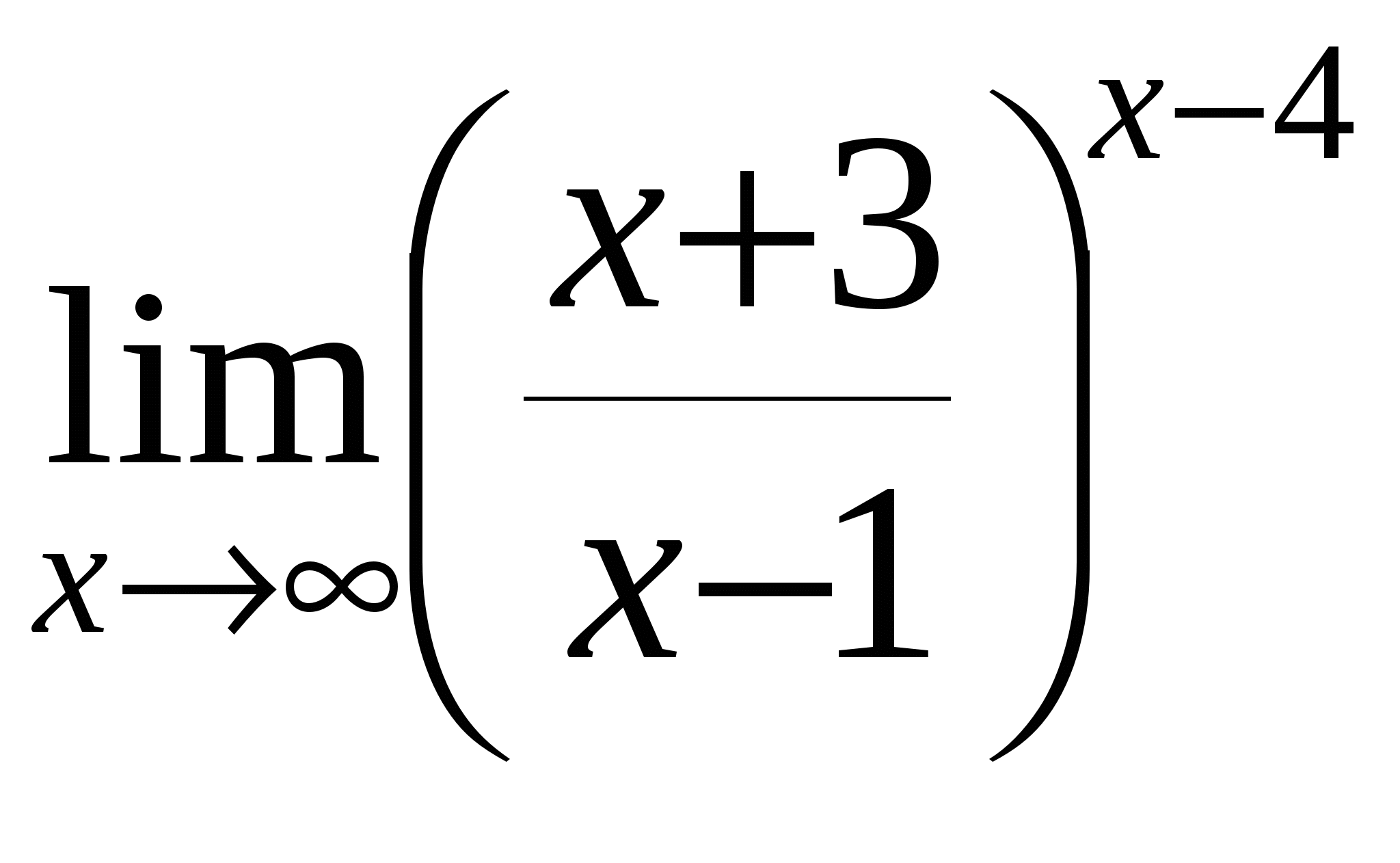
е)
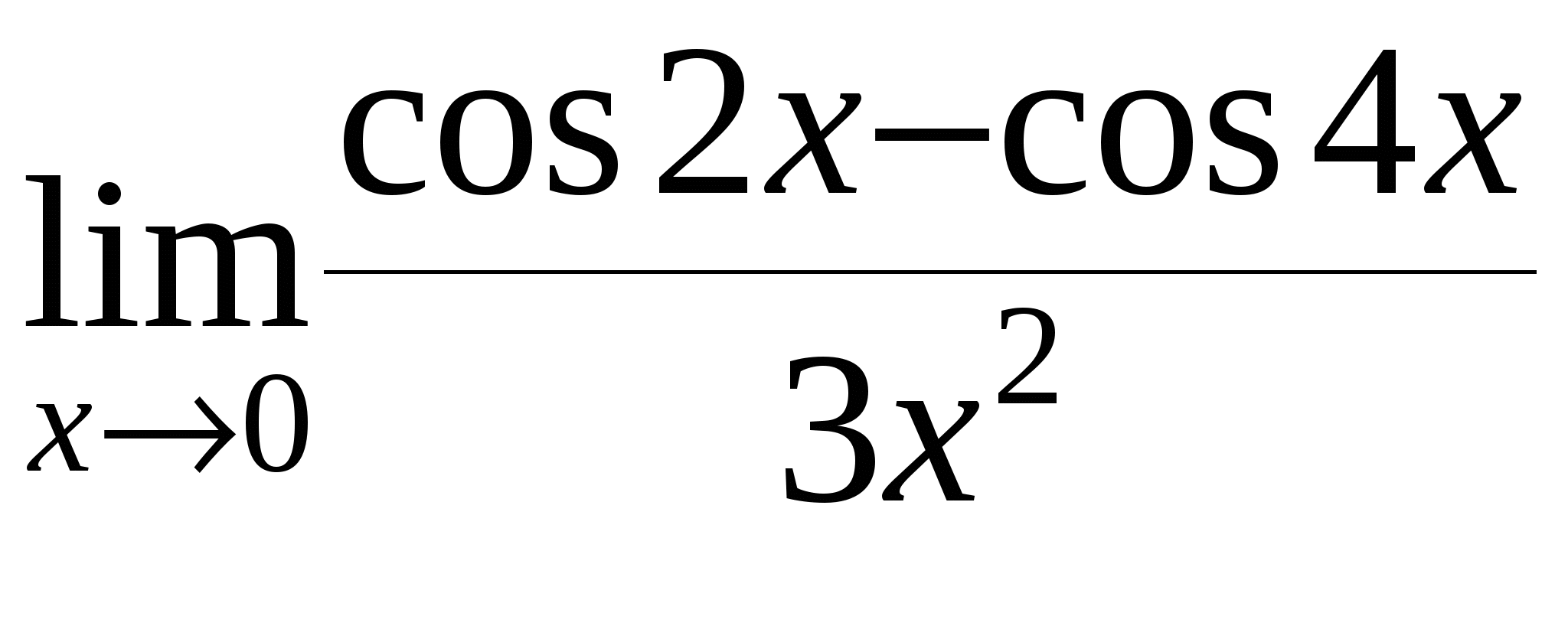
Найти предел функции
6
а)
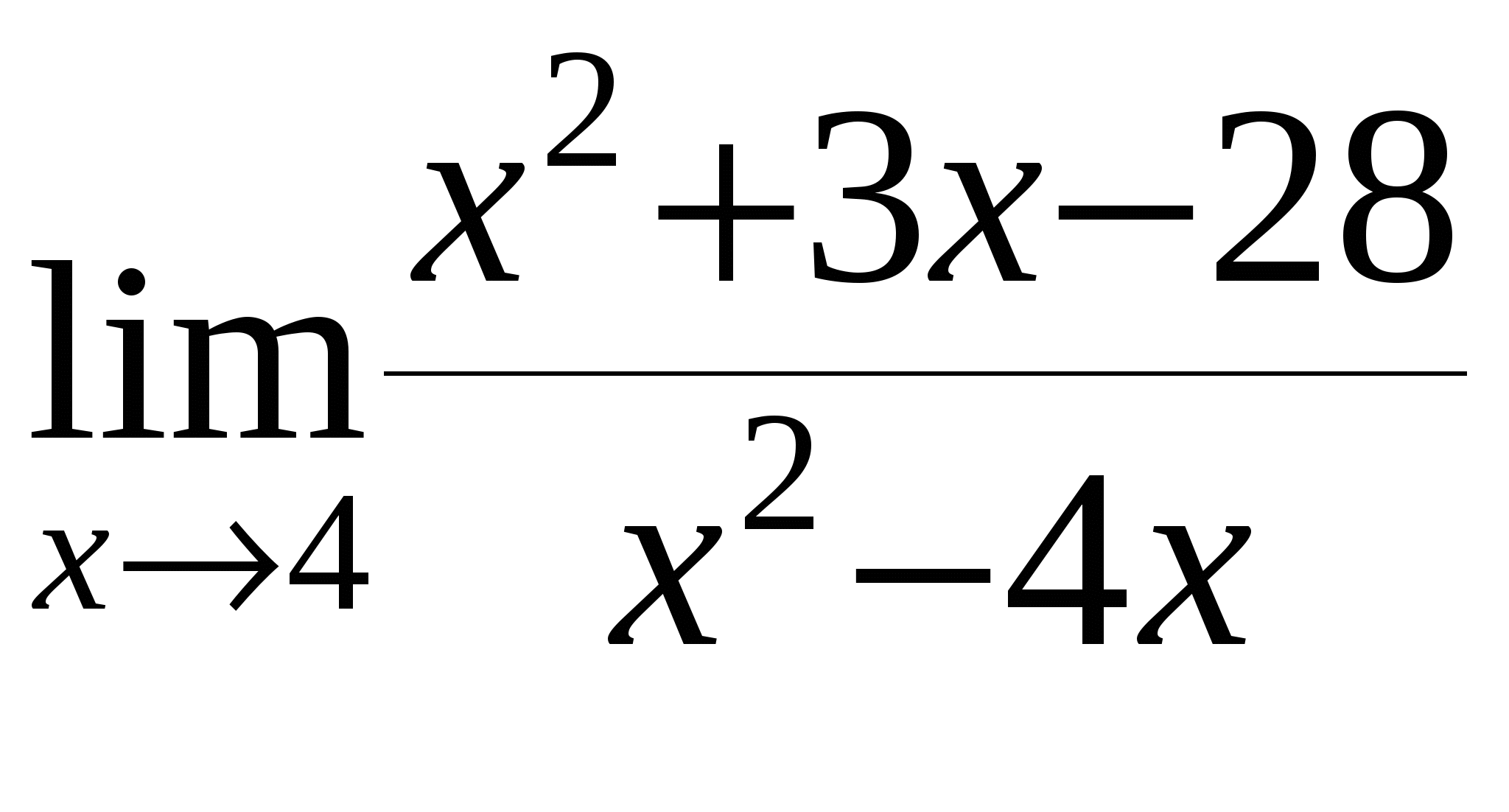
б)
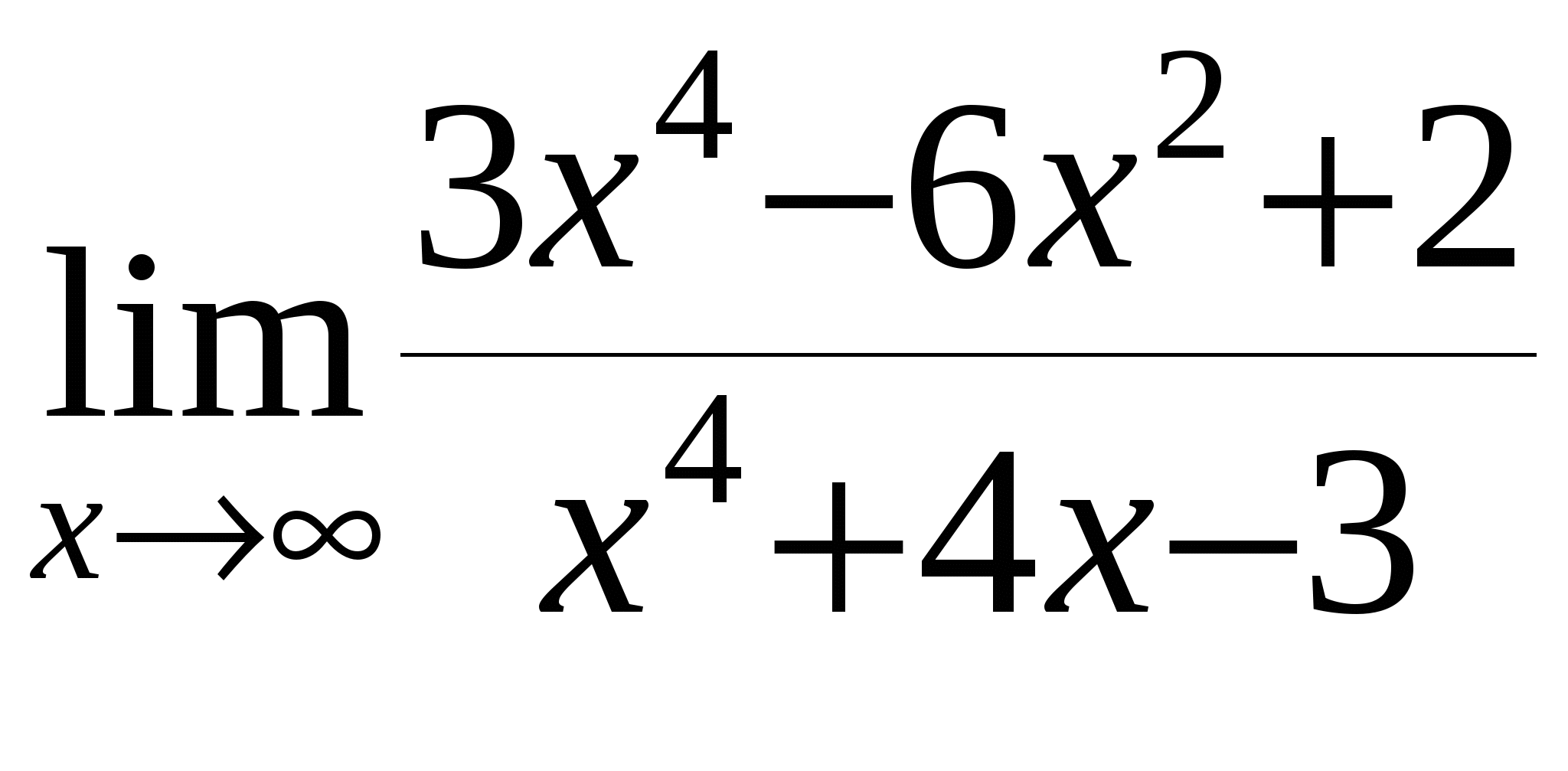
в)
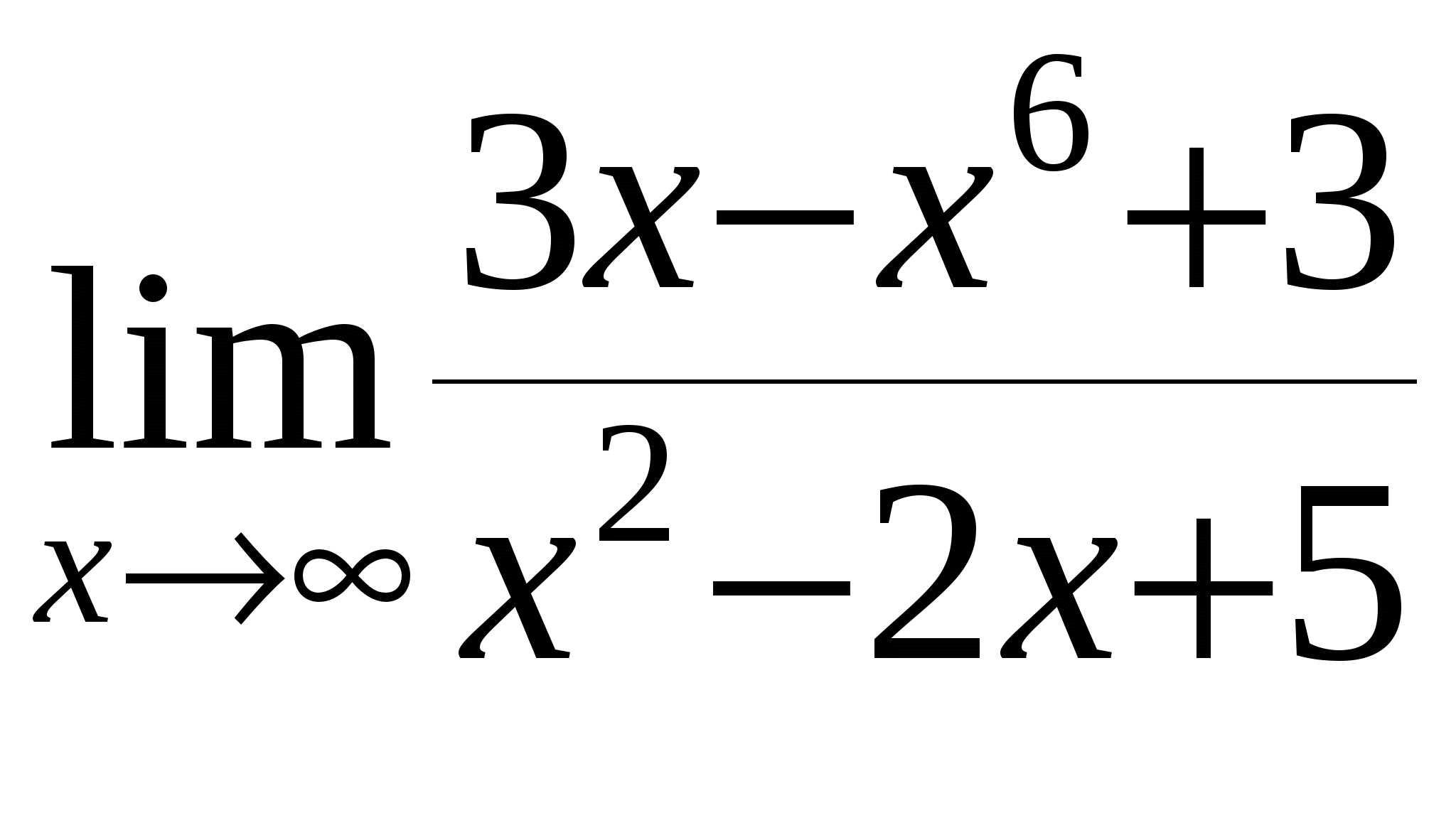
г)
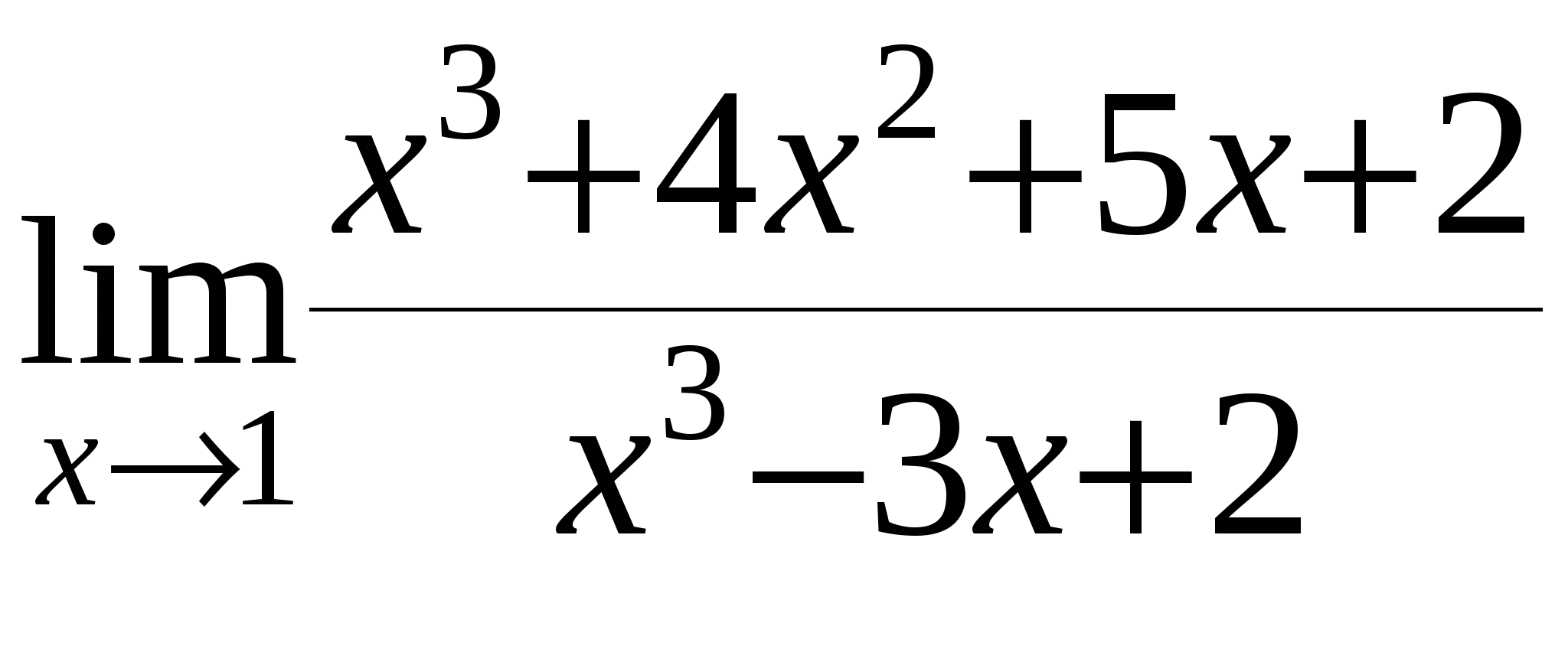
д)
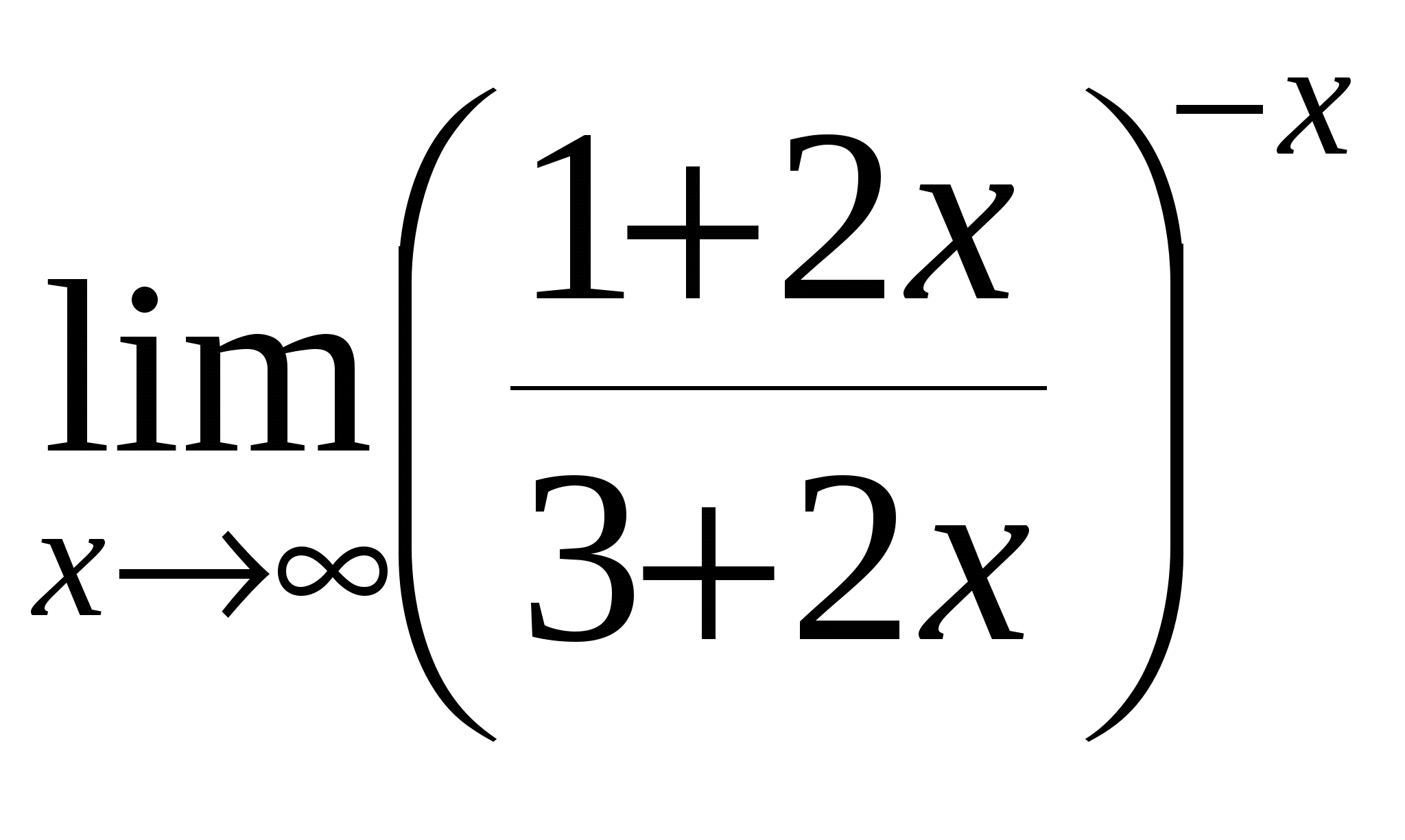
е)
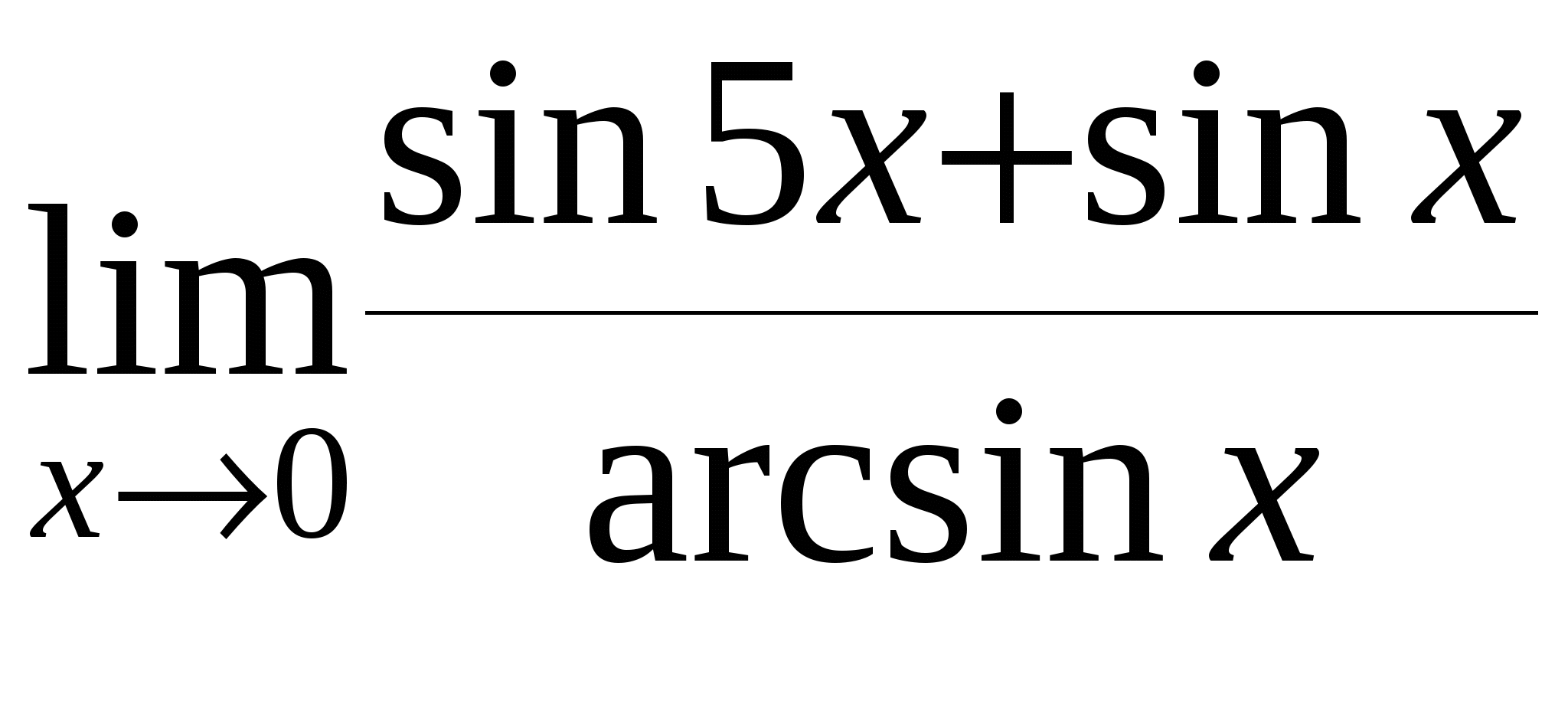
Контрольная работа № 5
Найти предел функции
7
а)
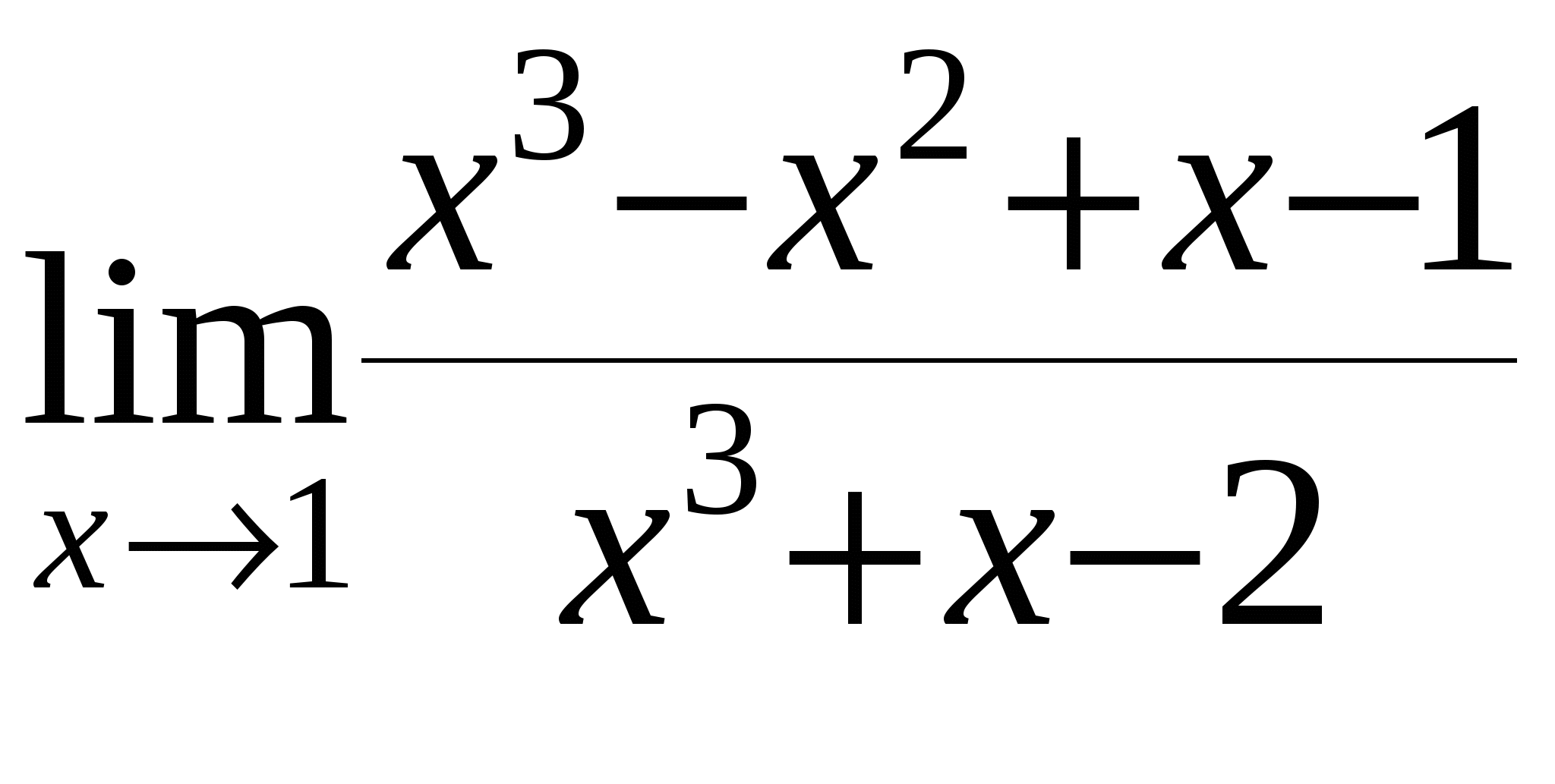
б)
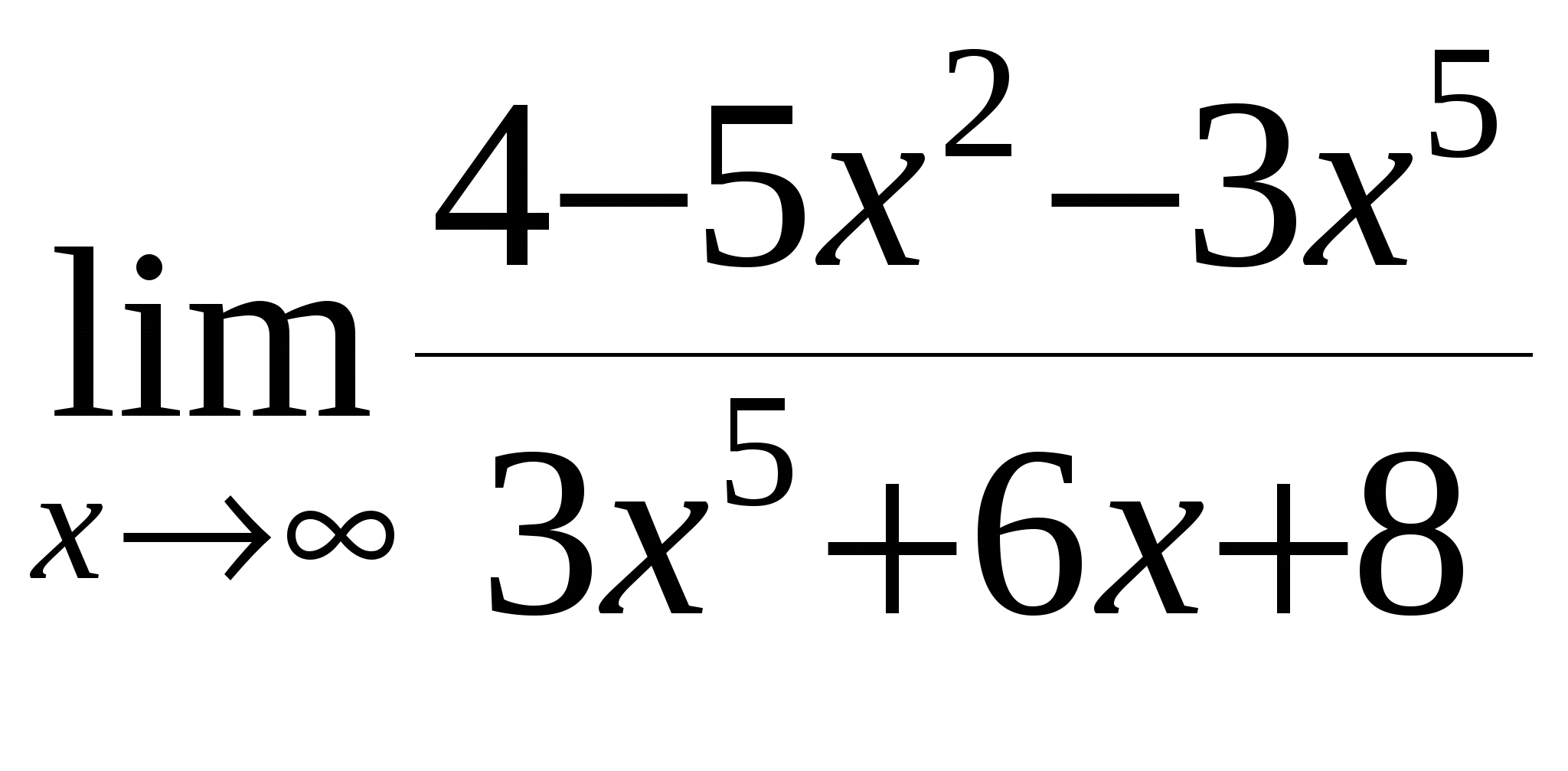
в)
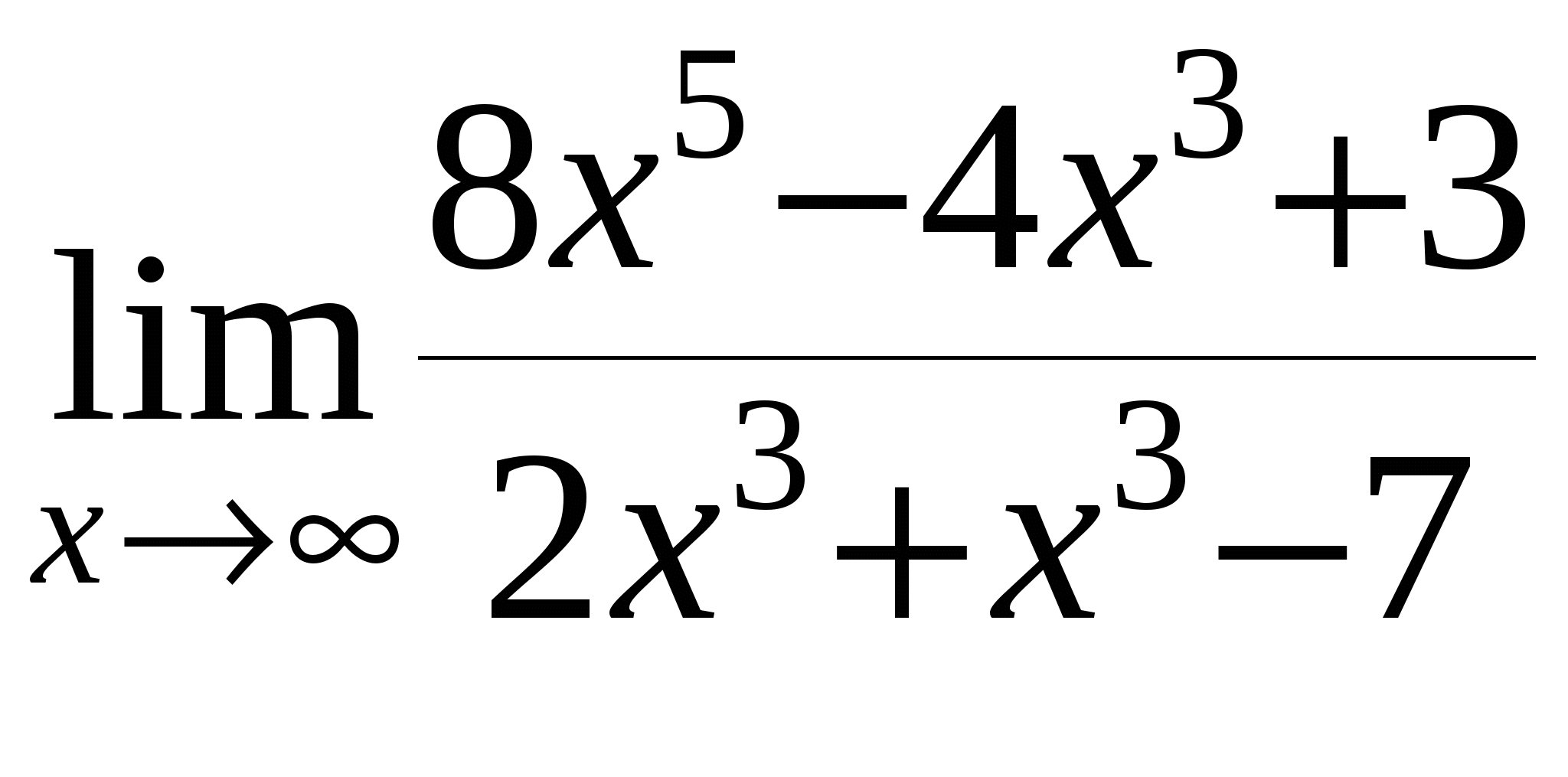
г)
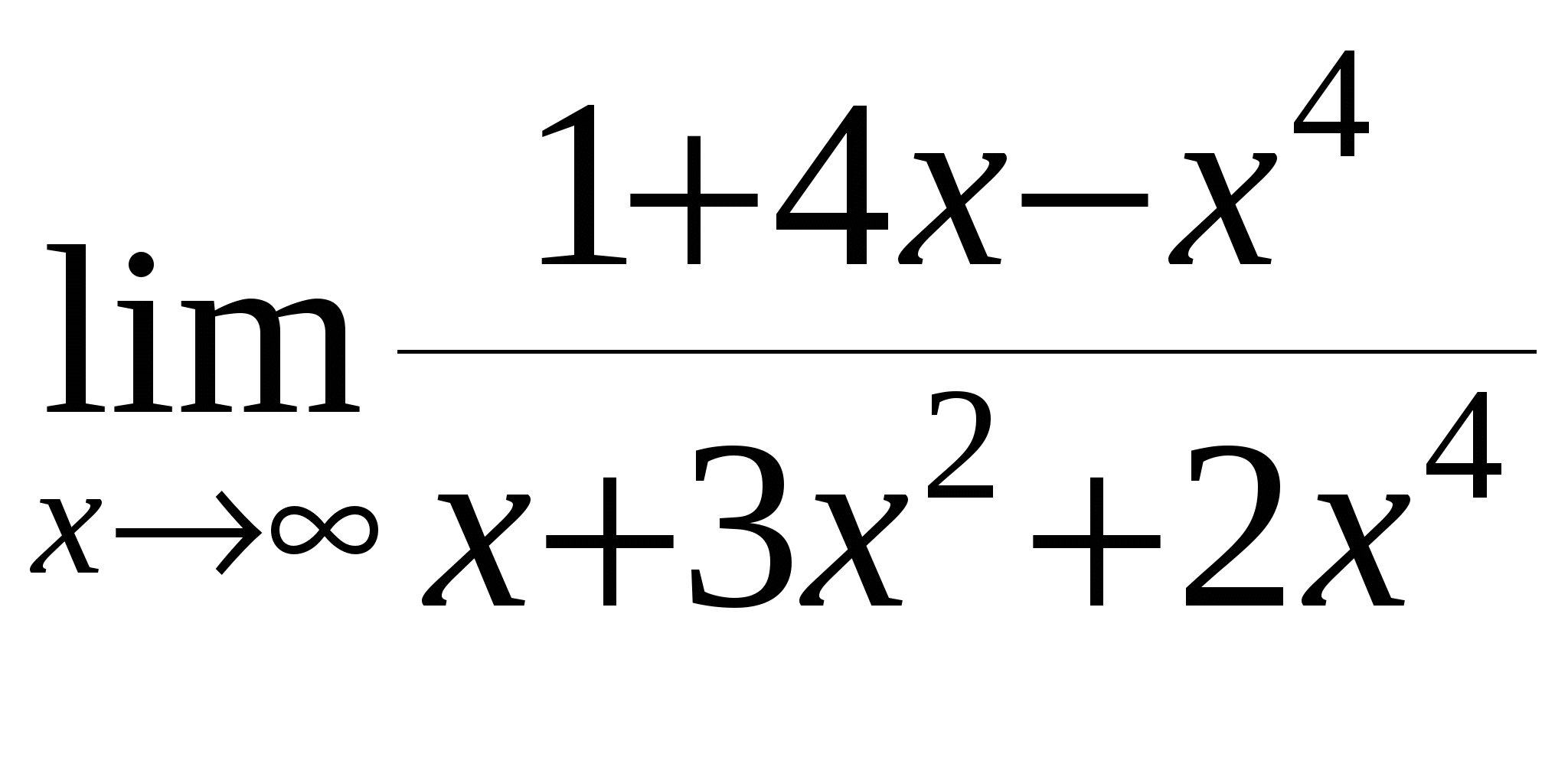
д)
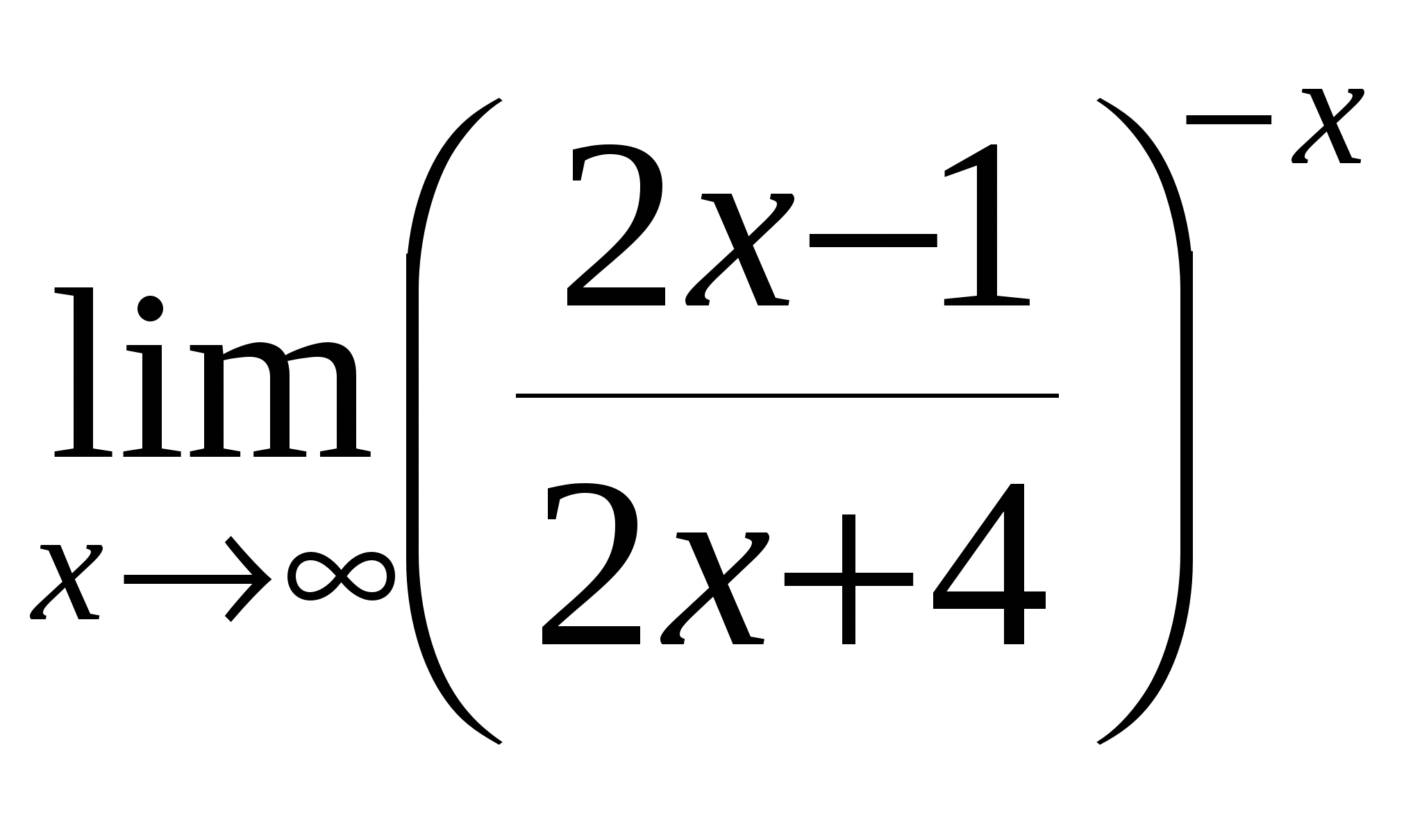
е)
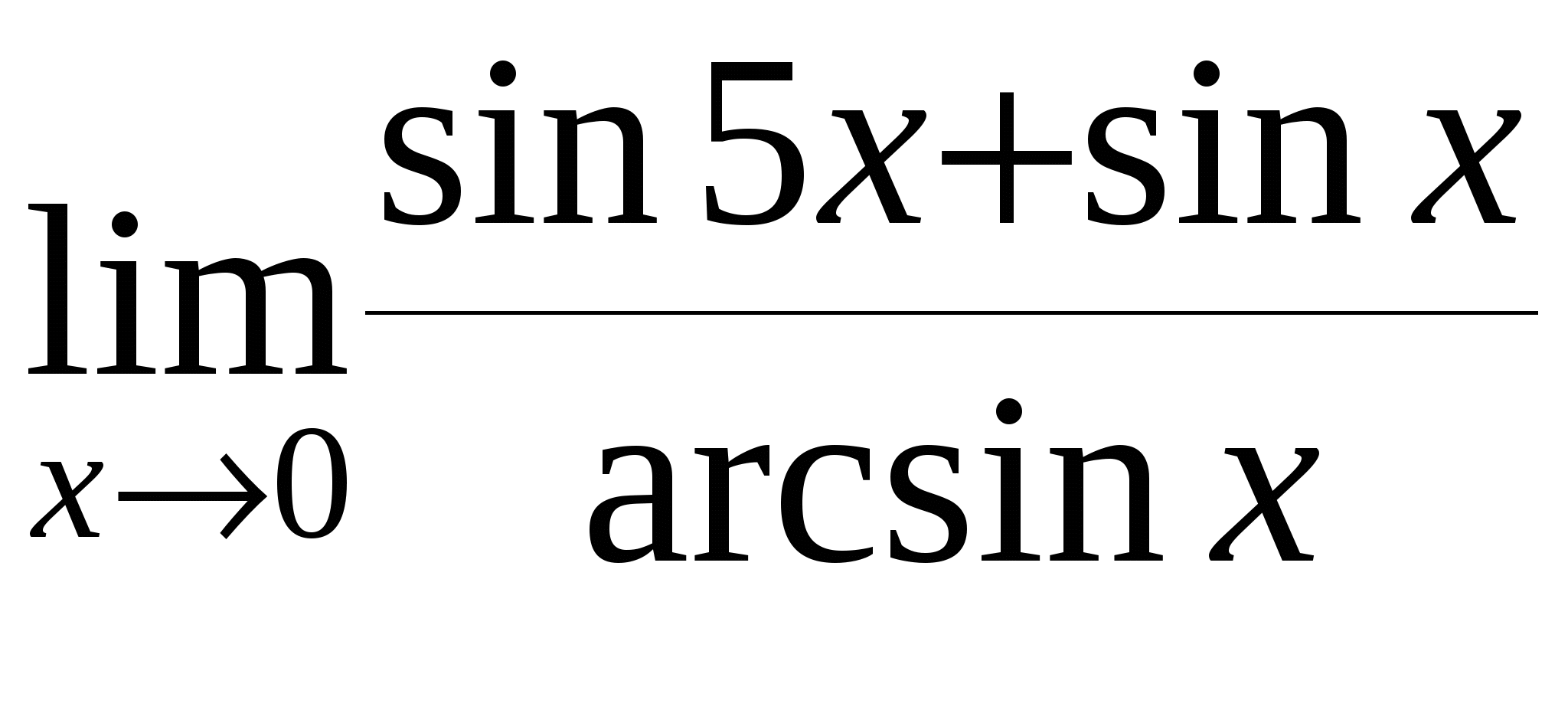
Найти предел функции
8
а)
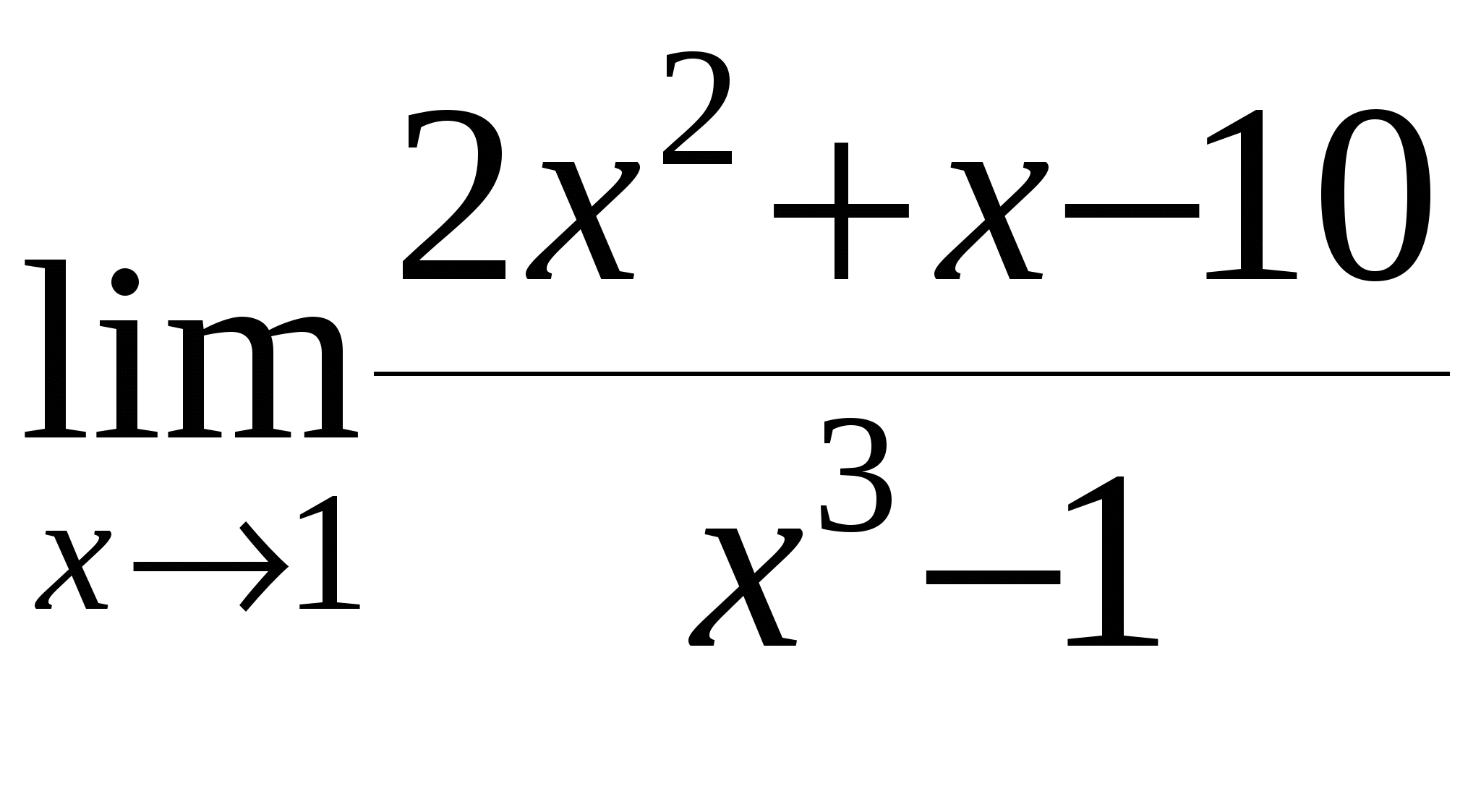
б)
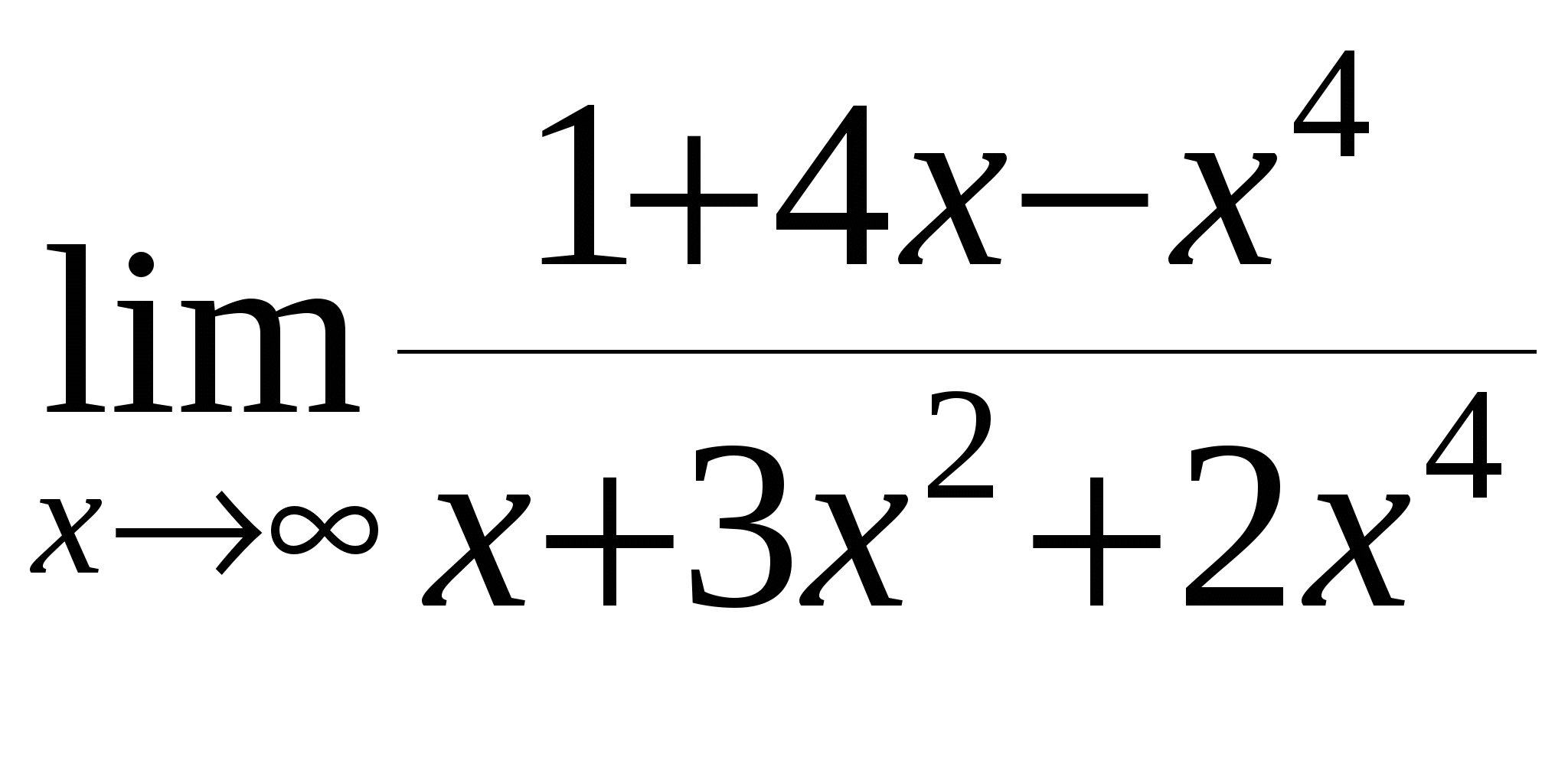
в)
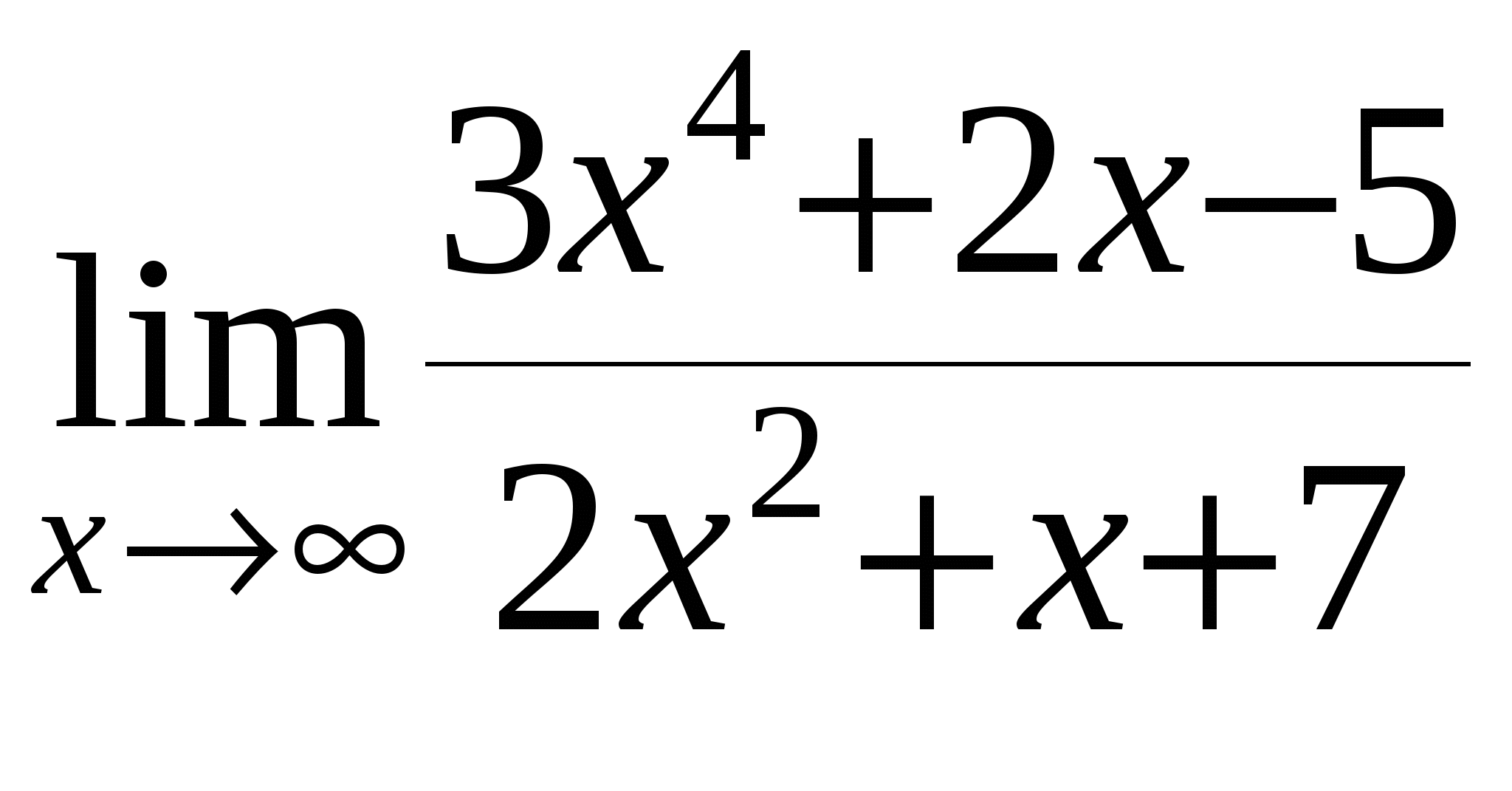
г)
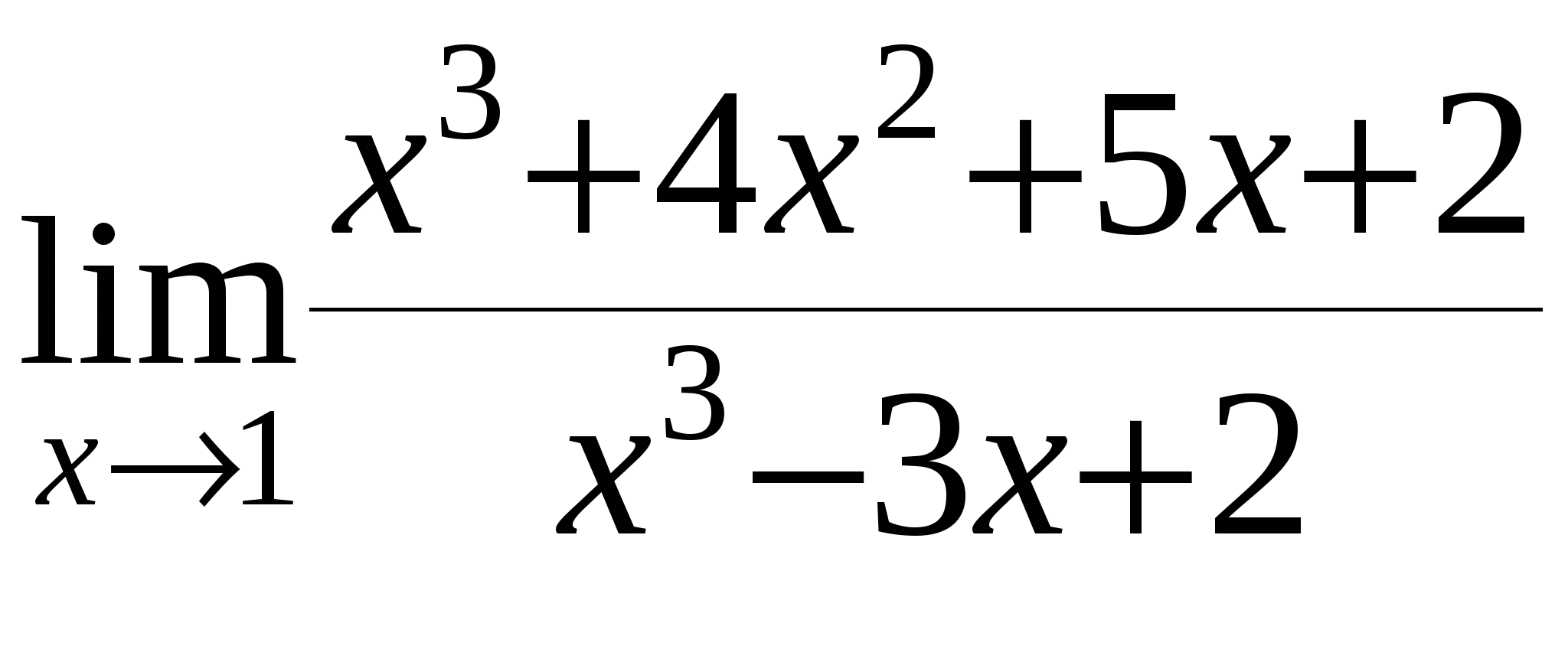
д)

е)
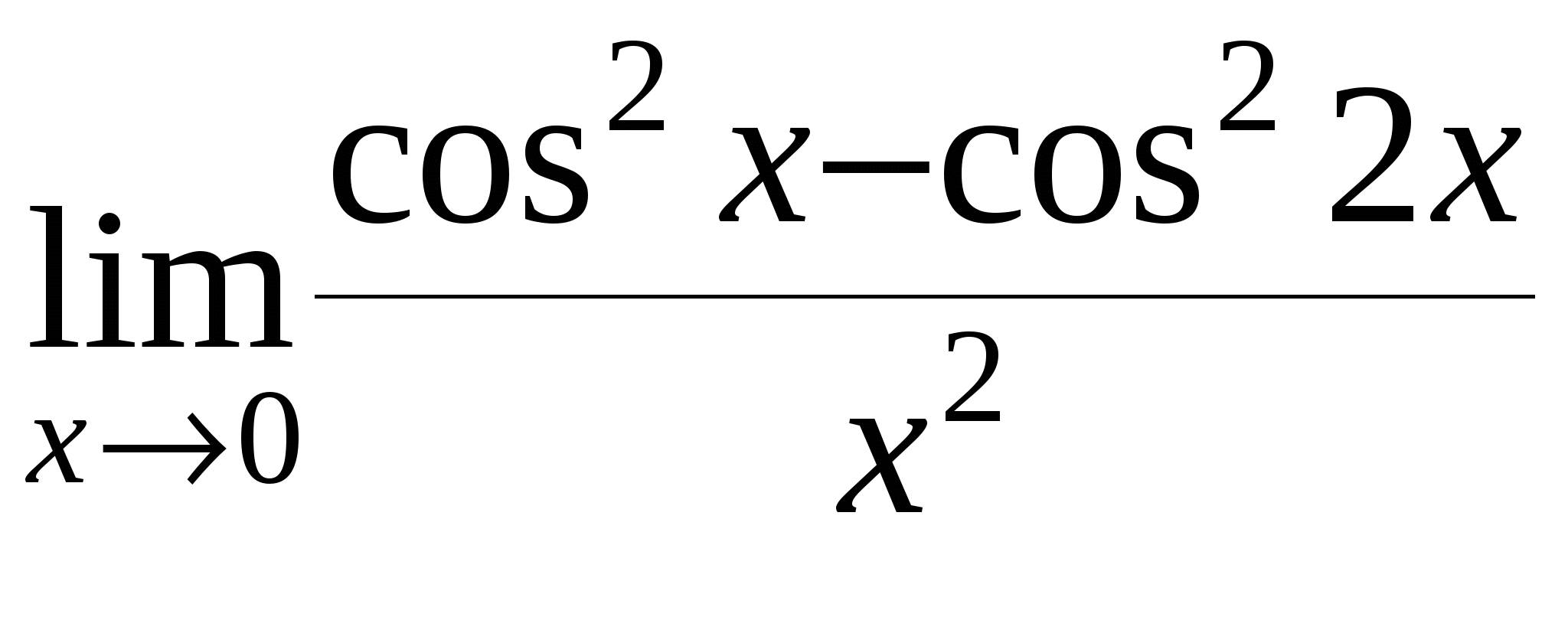
Найти предел функции
9
а)
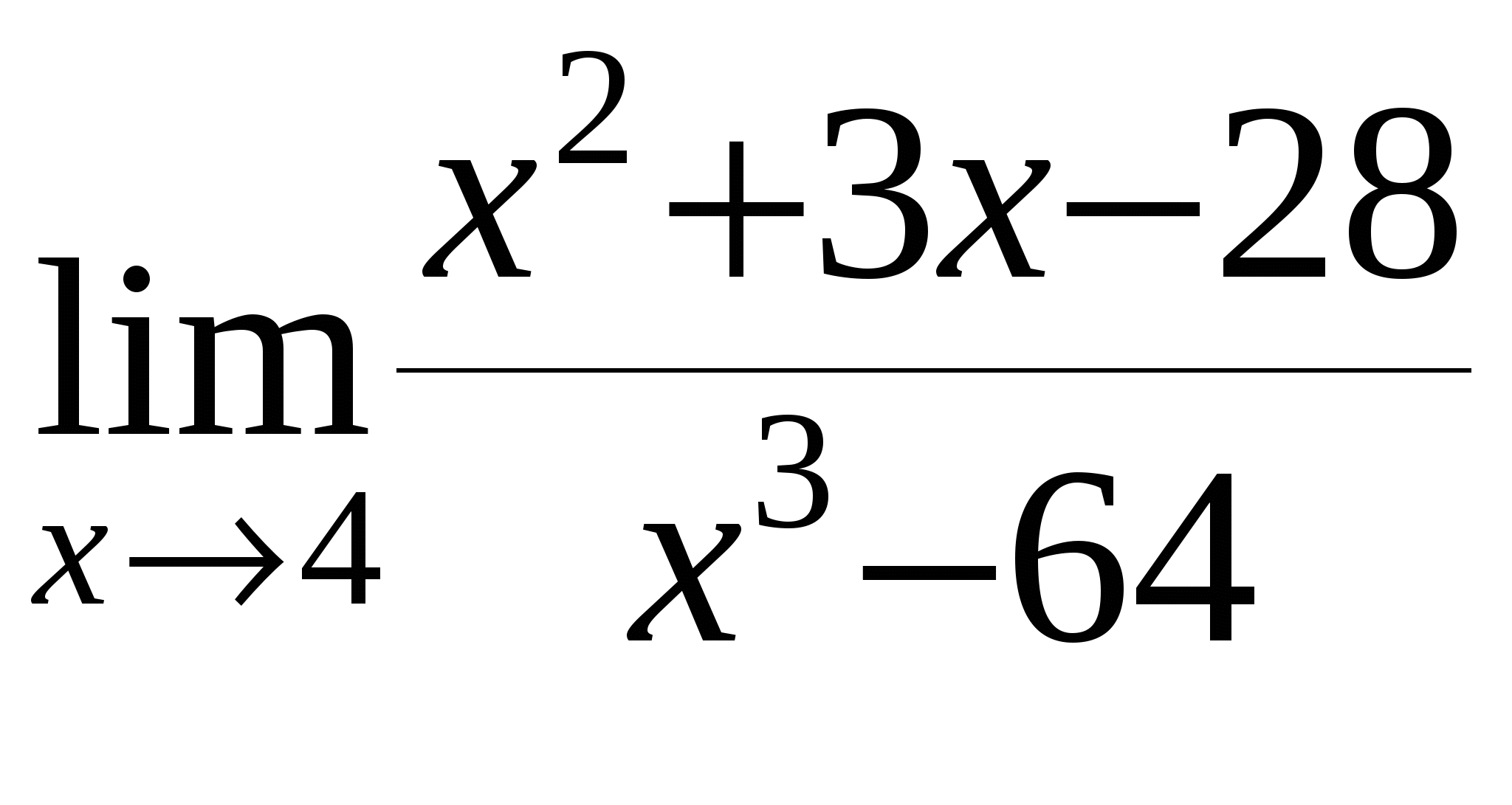
б)
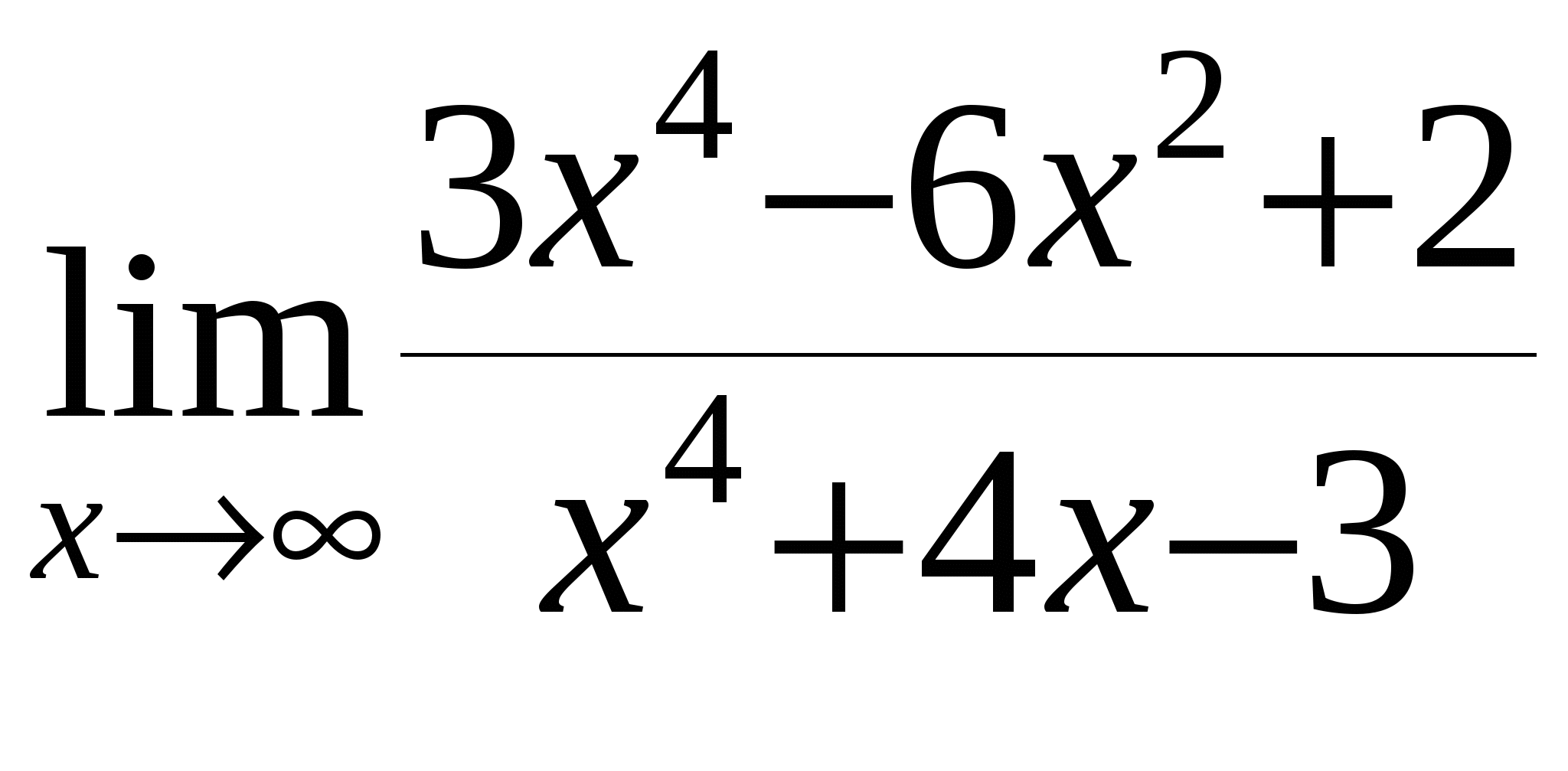
в)
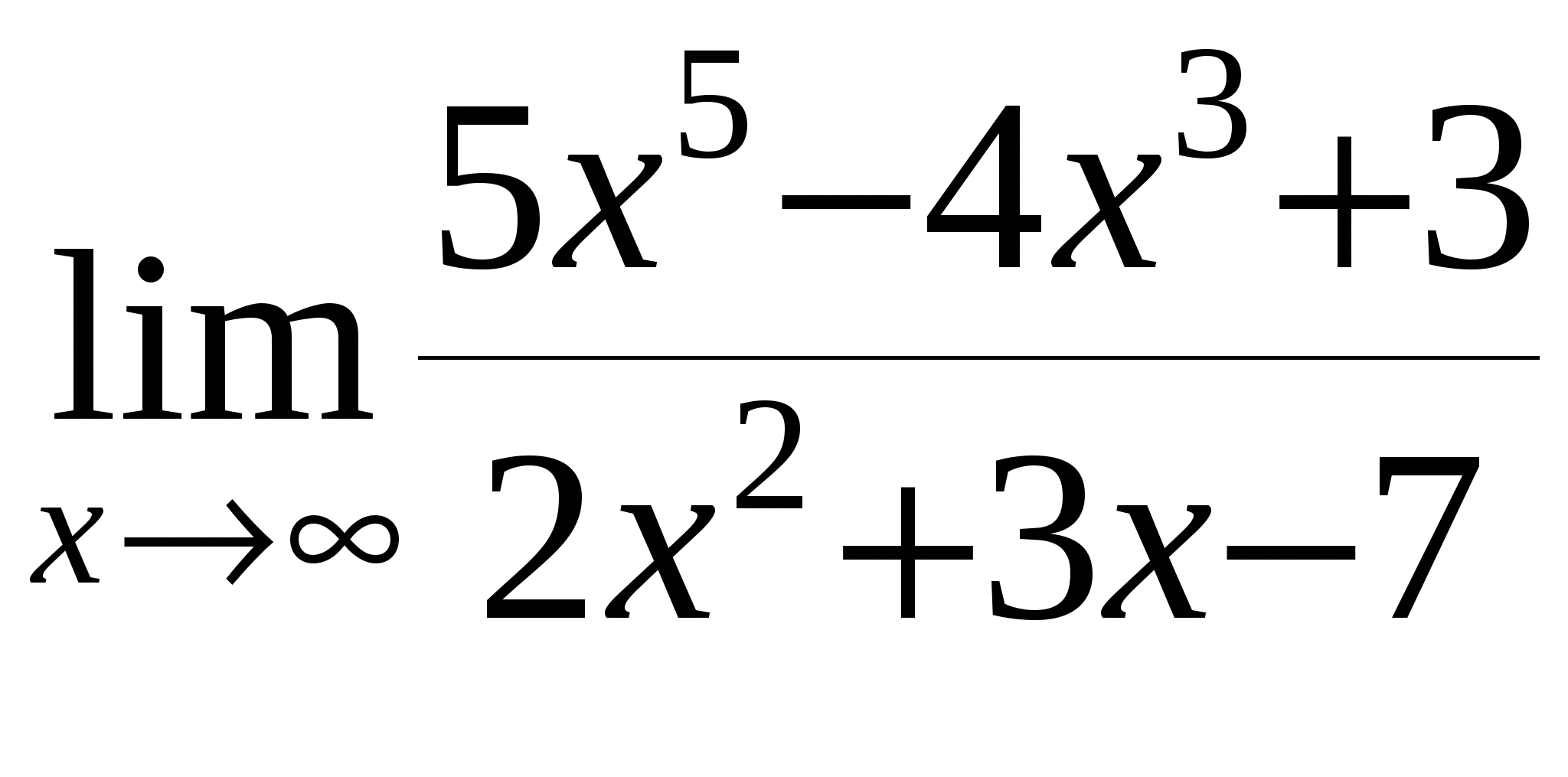
г)
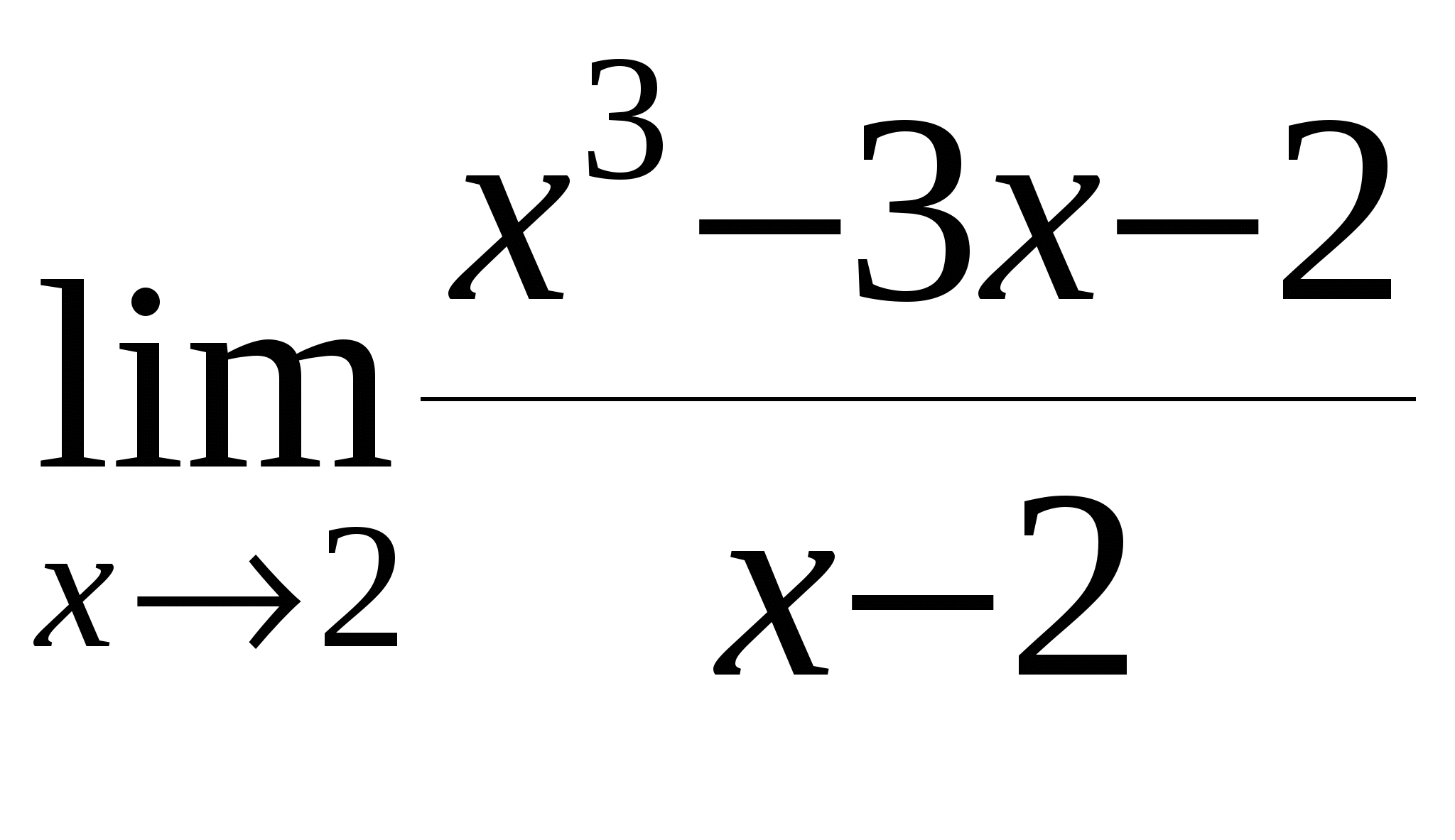
д)
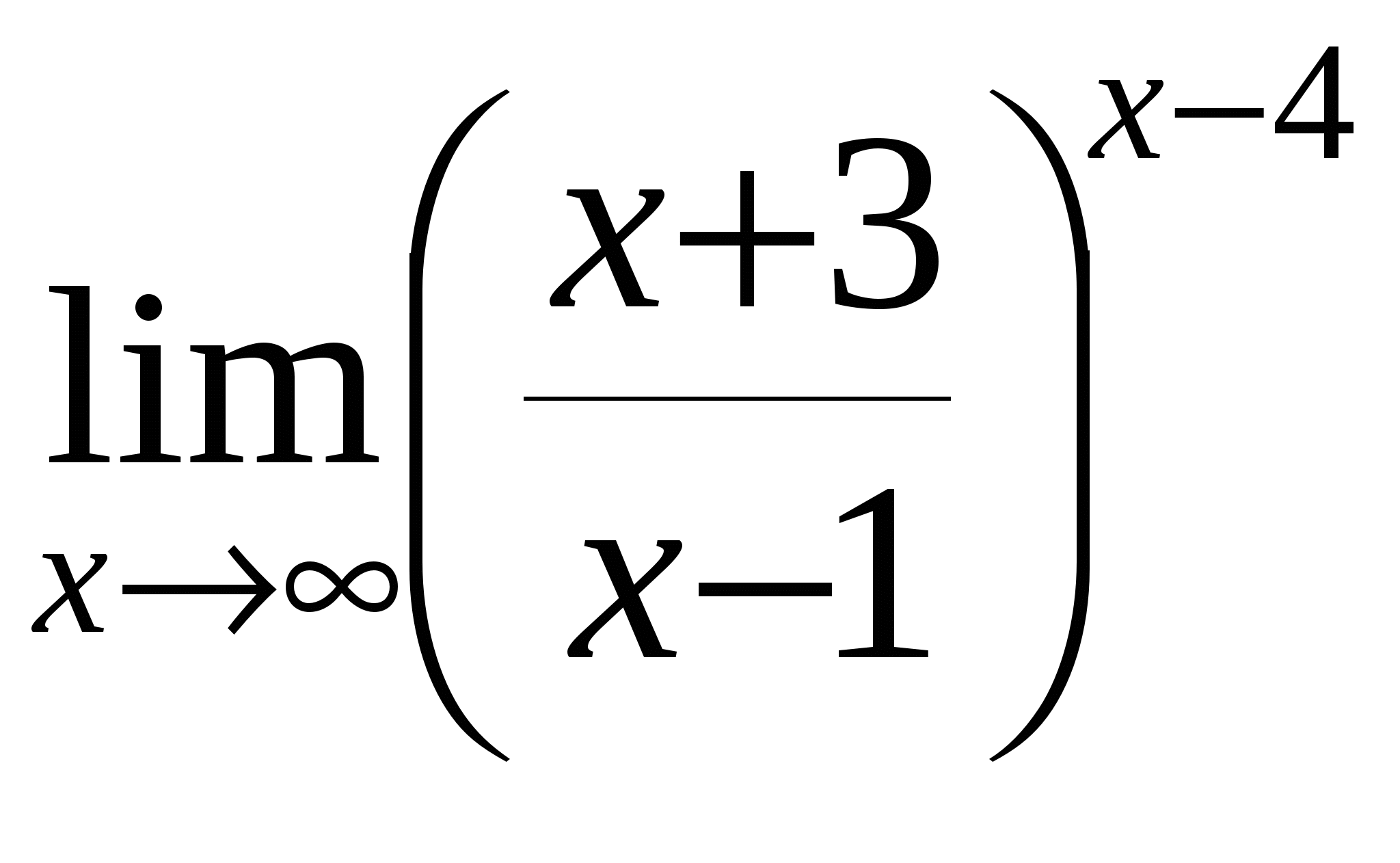
е)
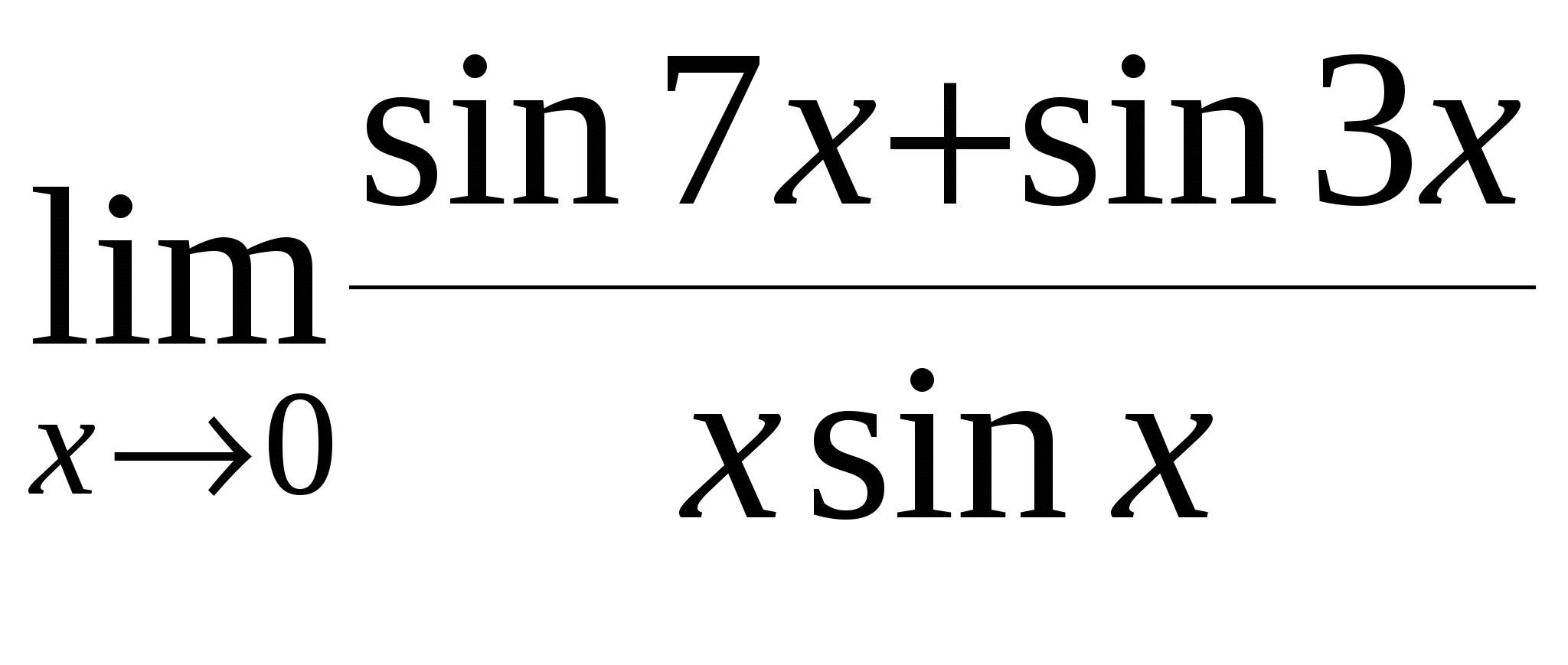
Контрольная работа № 5
Найти предел функции
10
а)
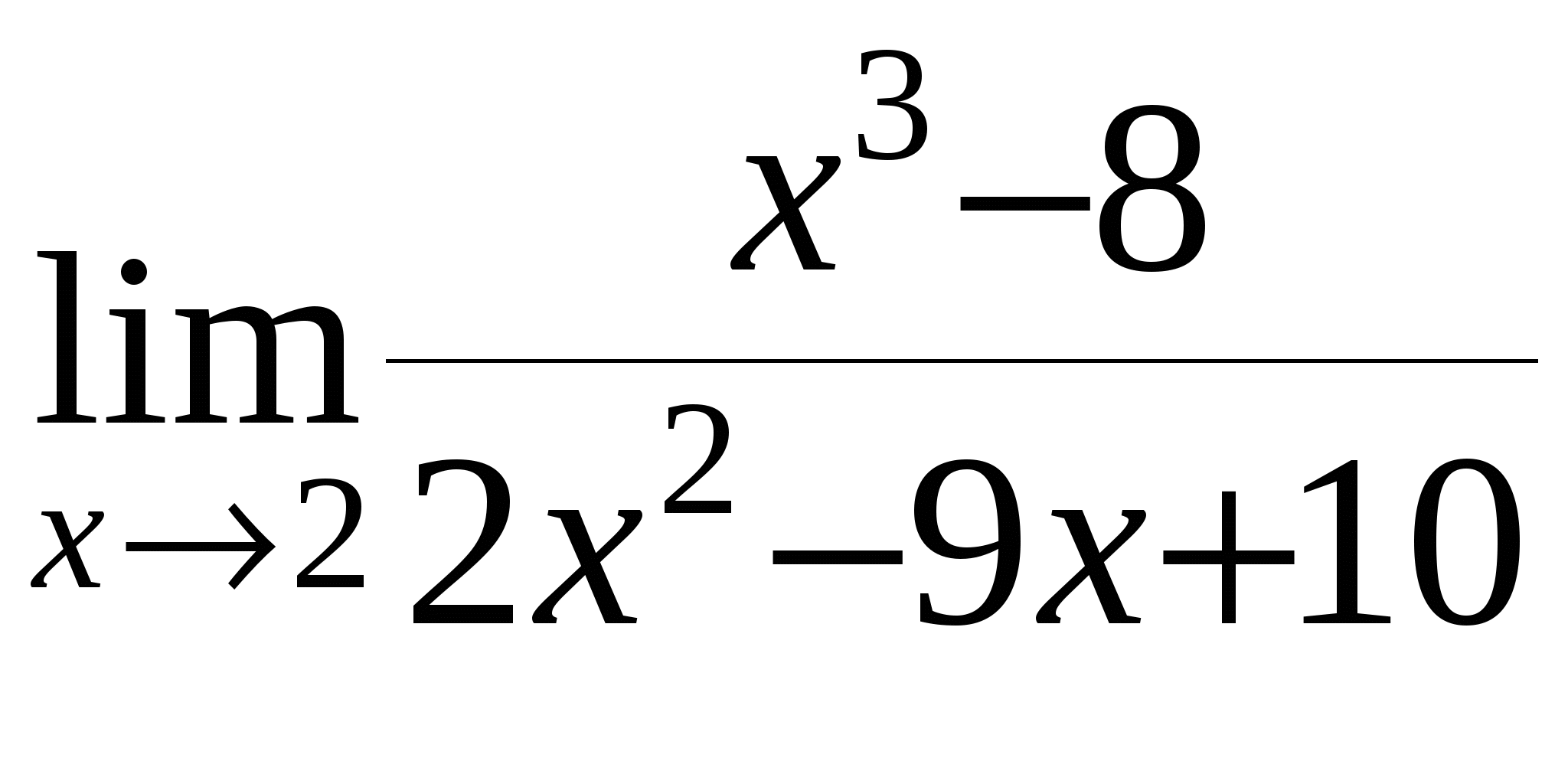
б)
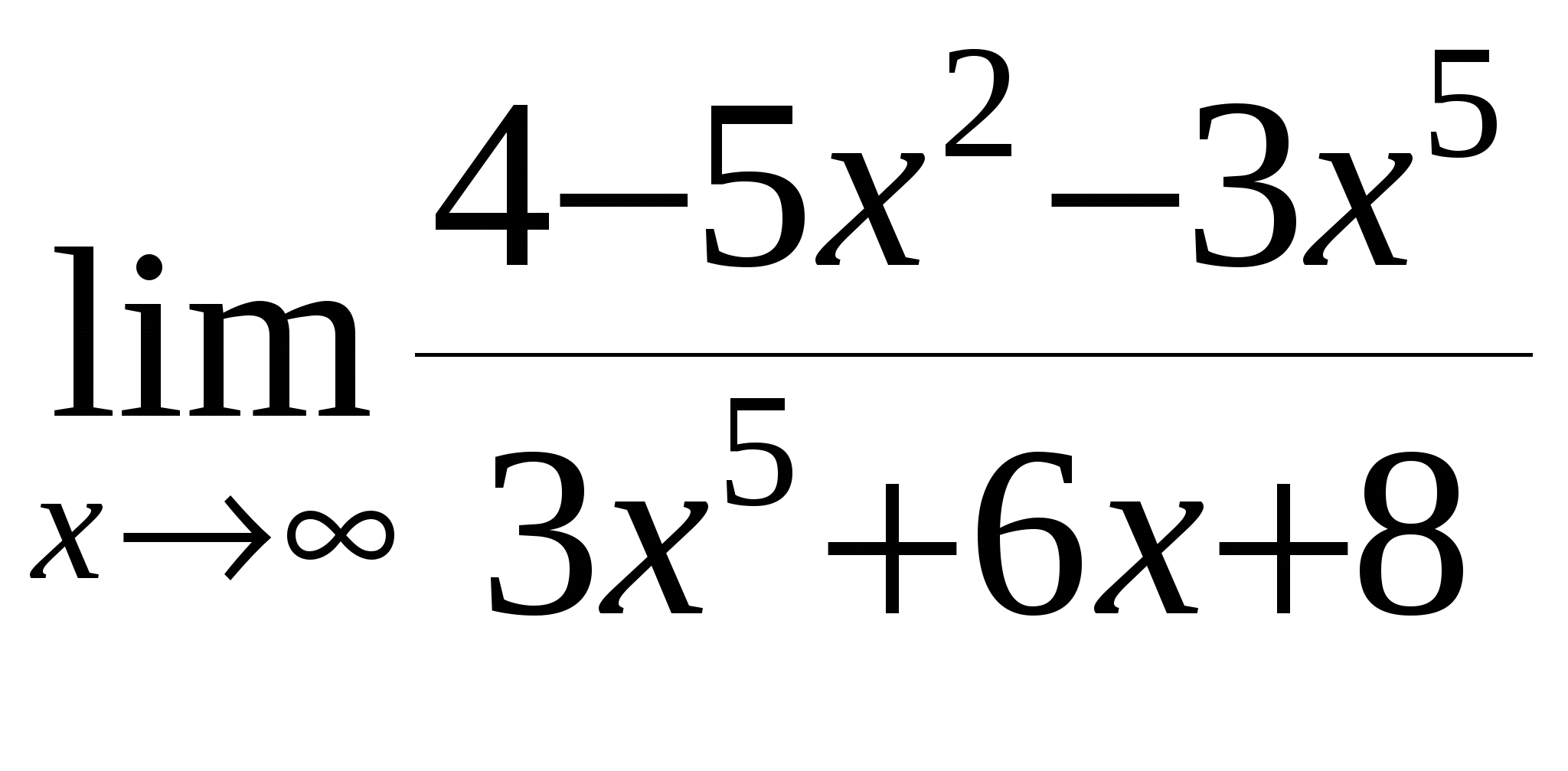
в)
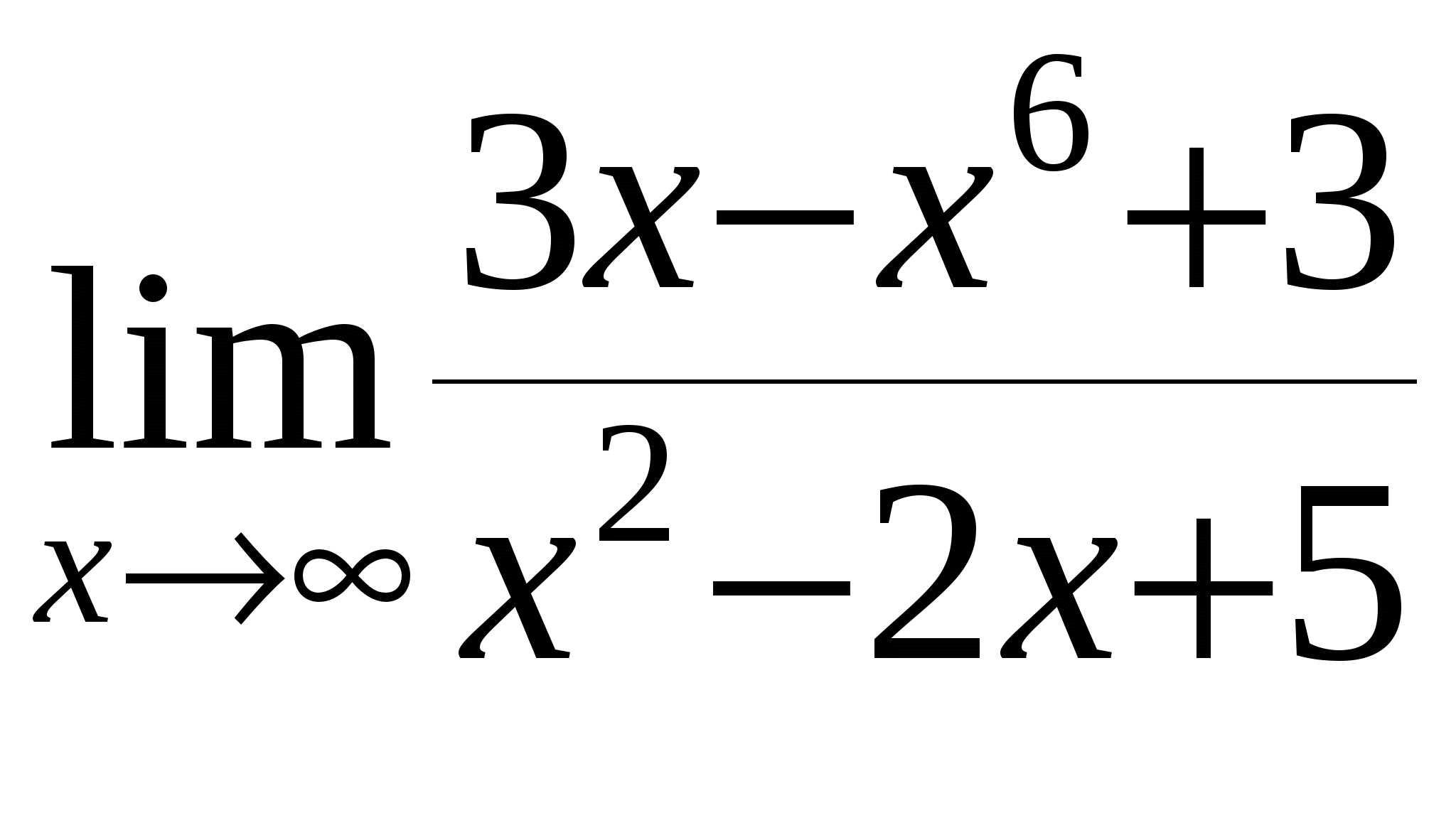
г)
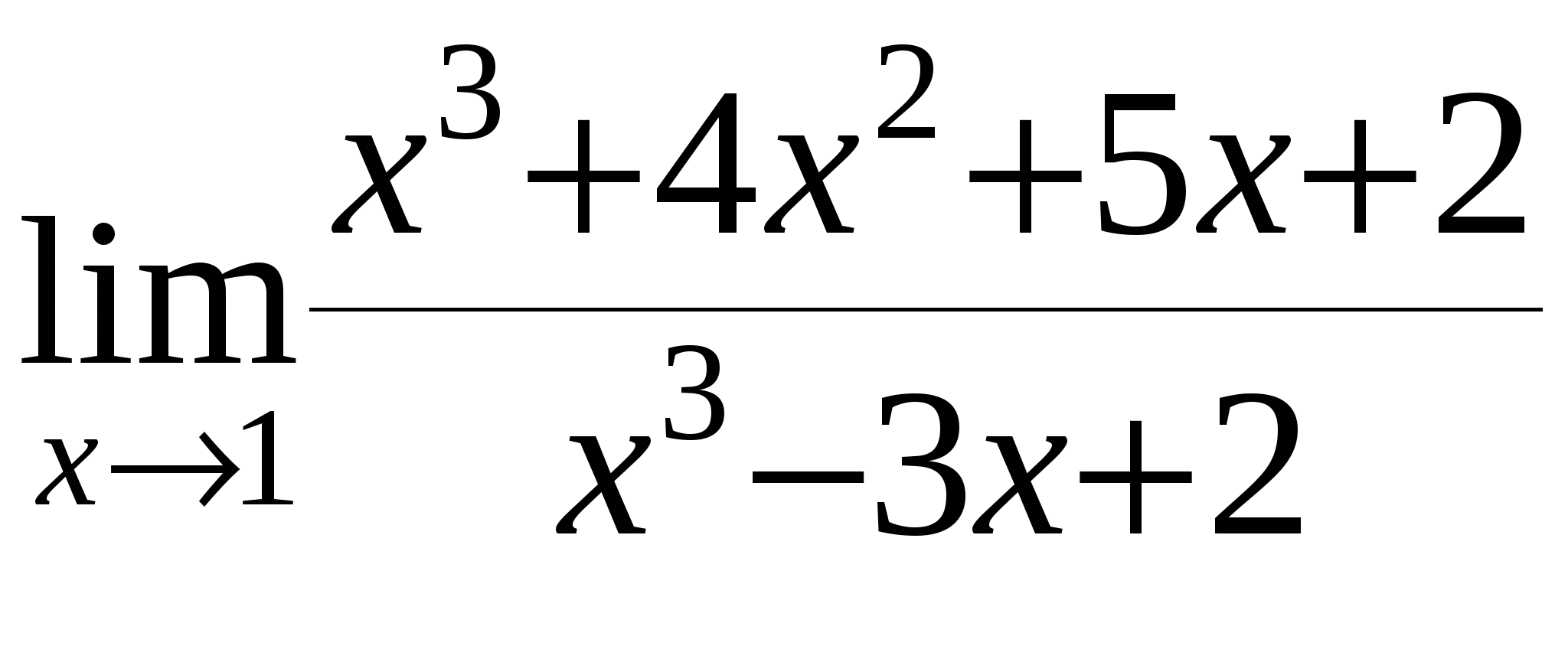
д)

е)
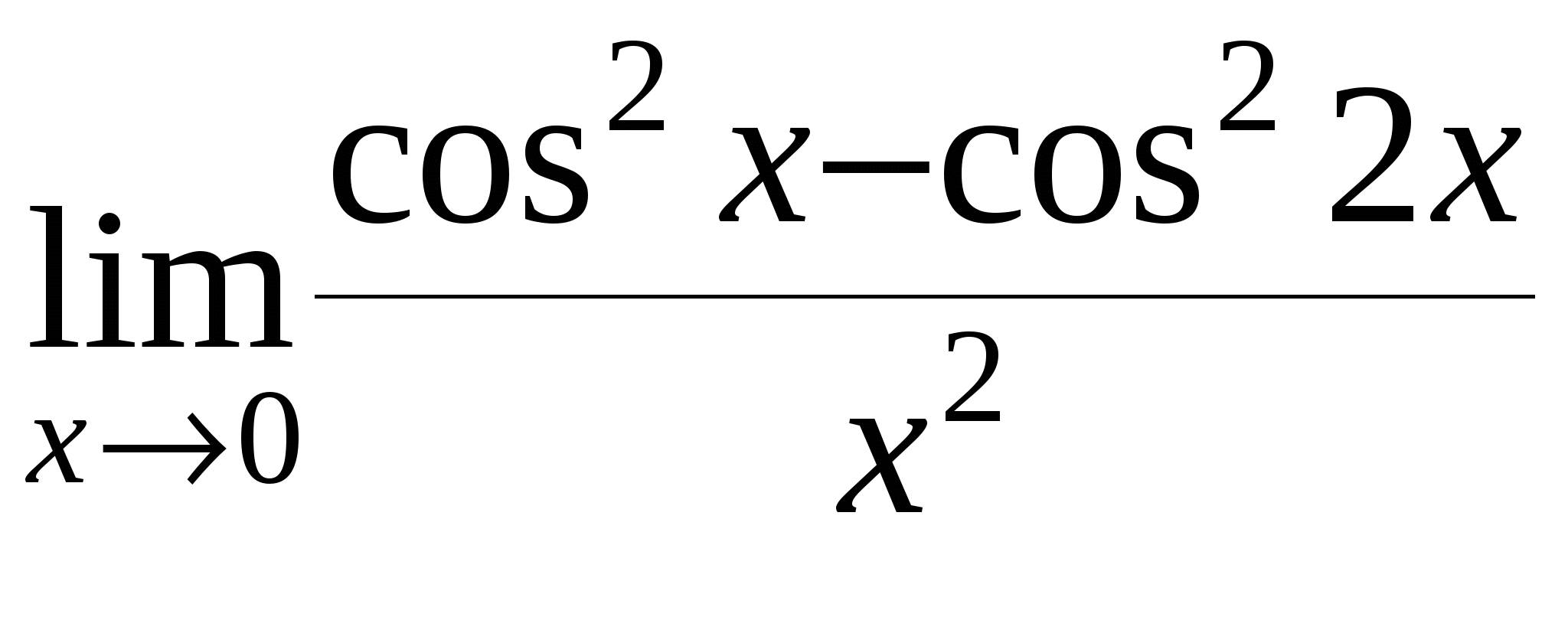
Найти предел функции
11
а)
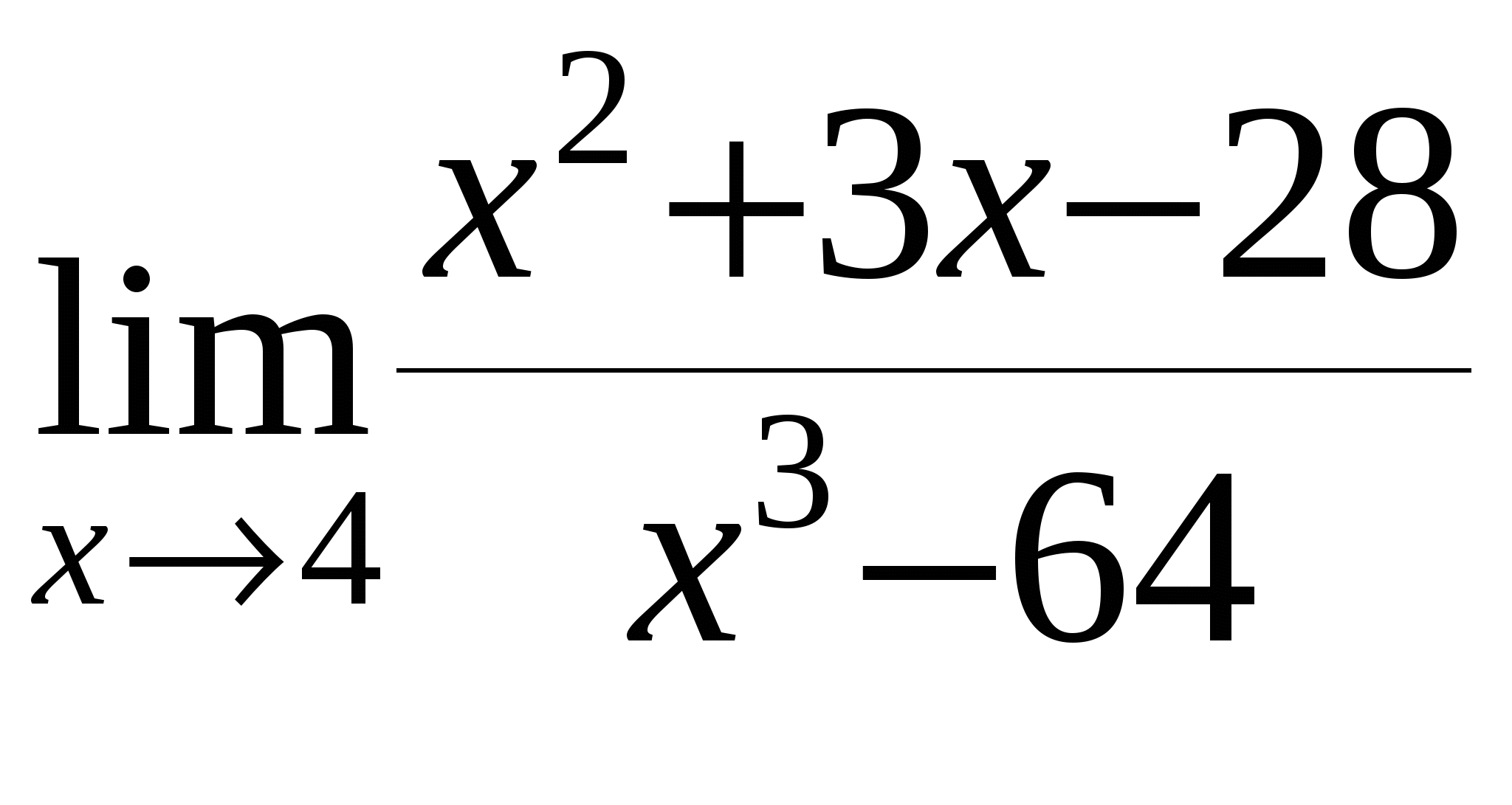
б)
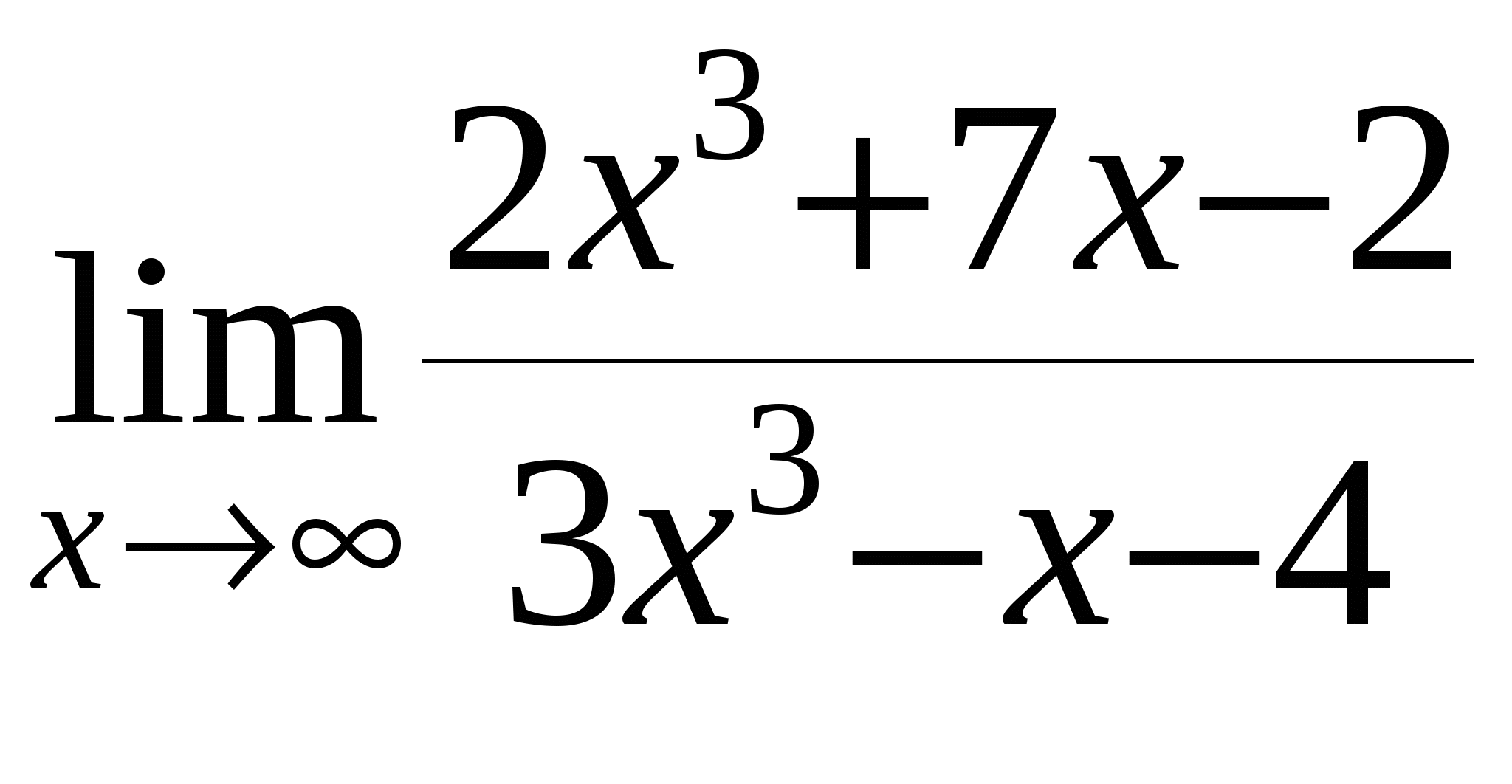
в)
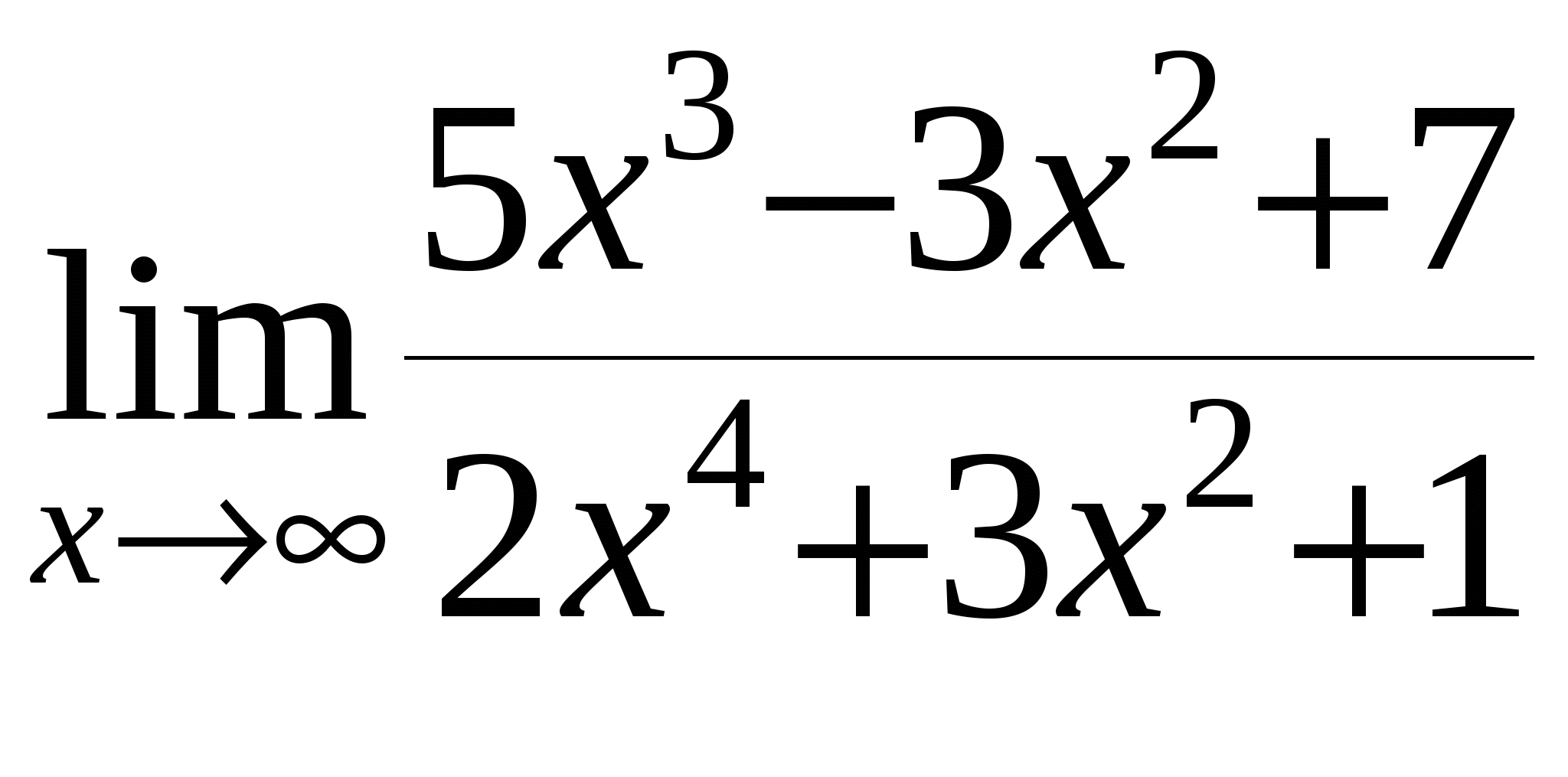
г)
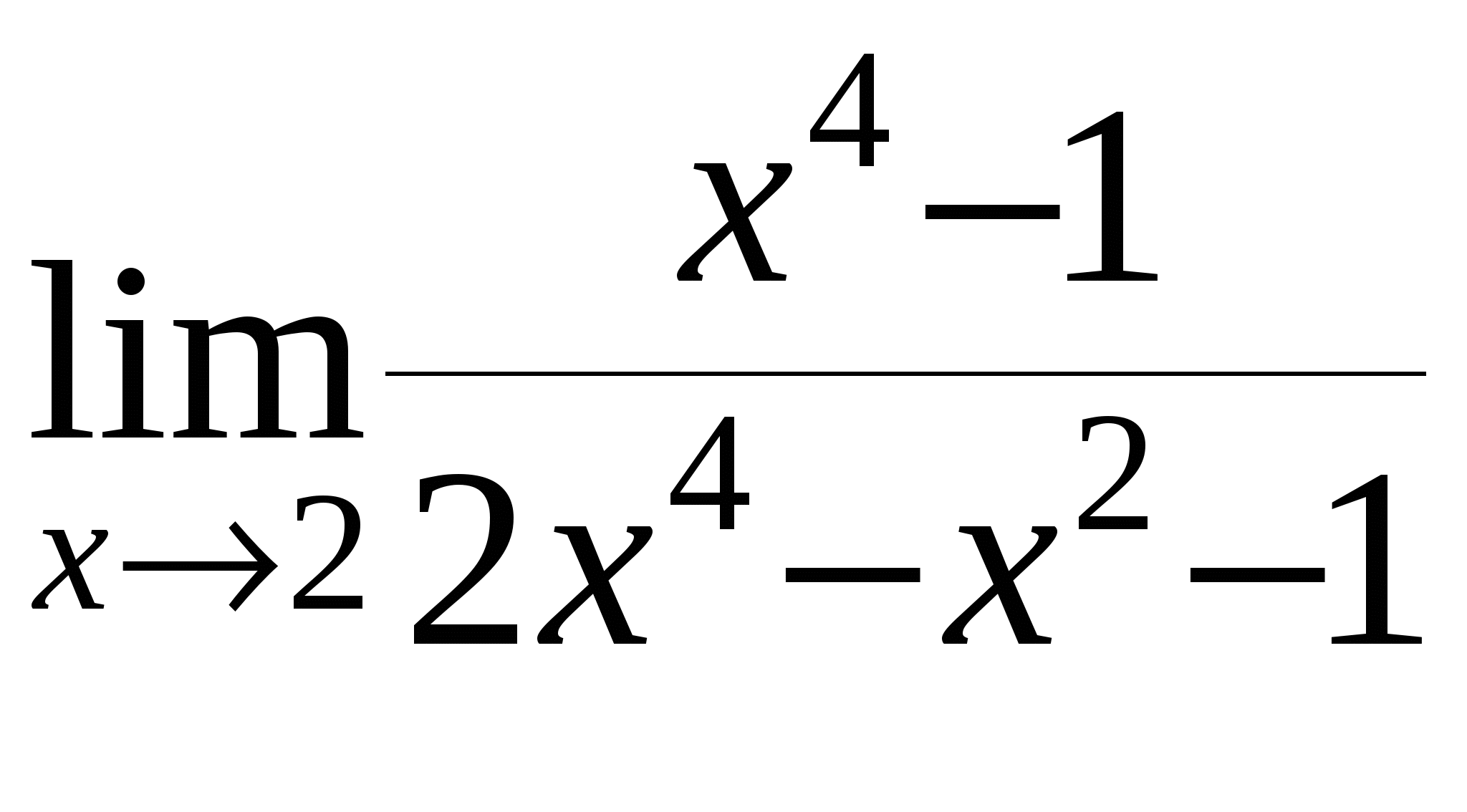
д)
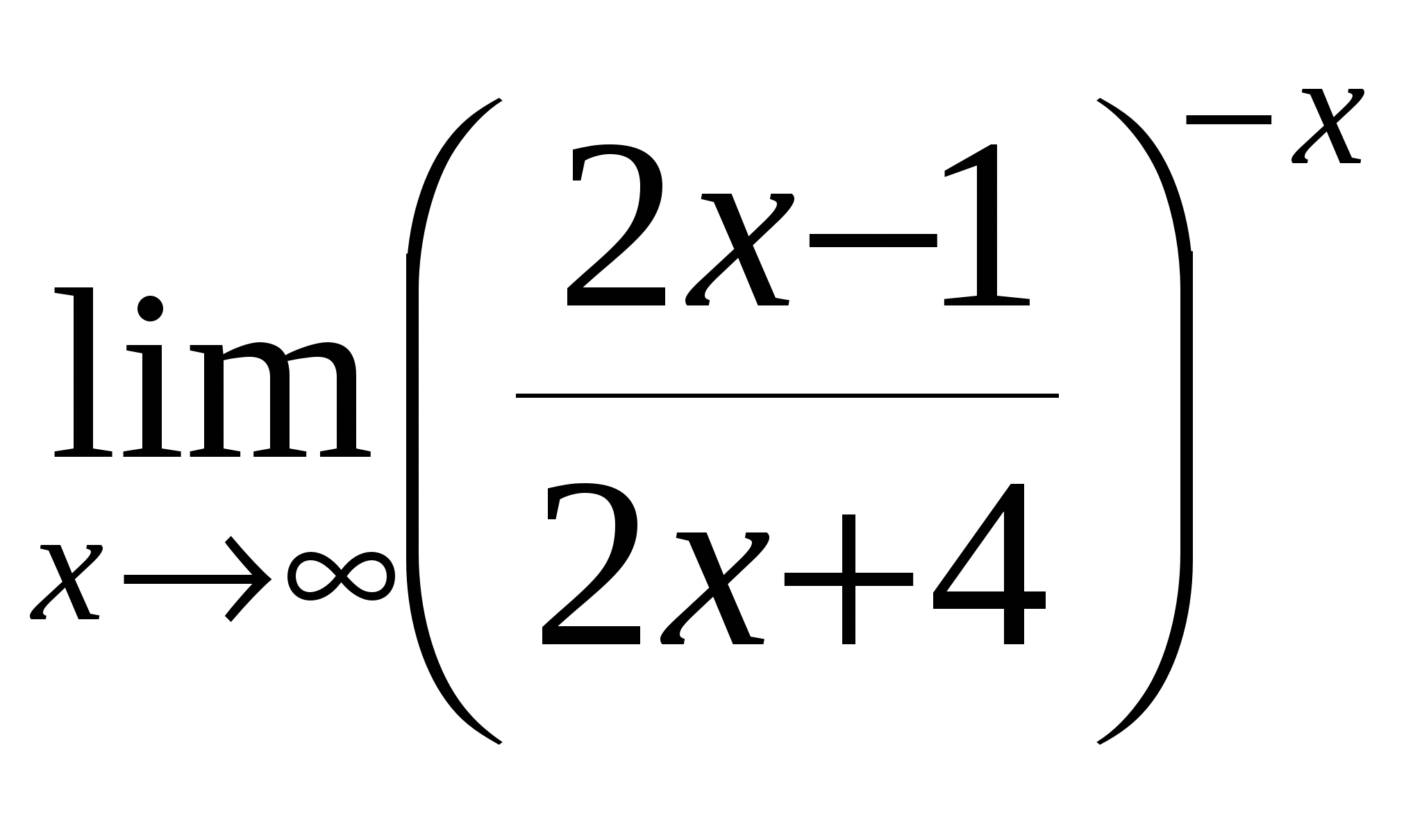
е)
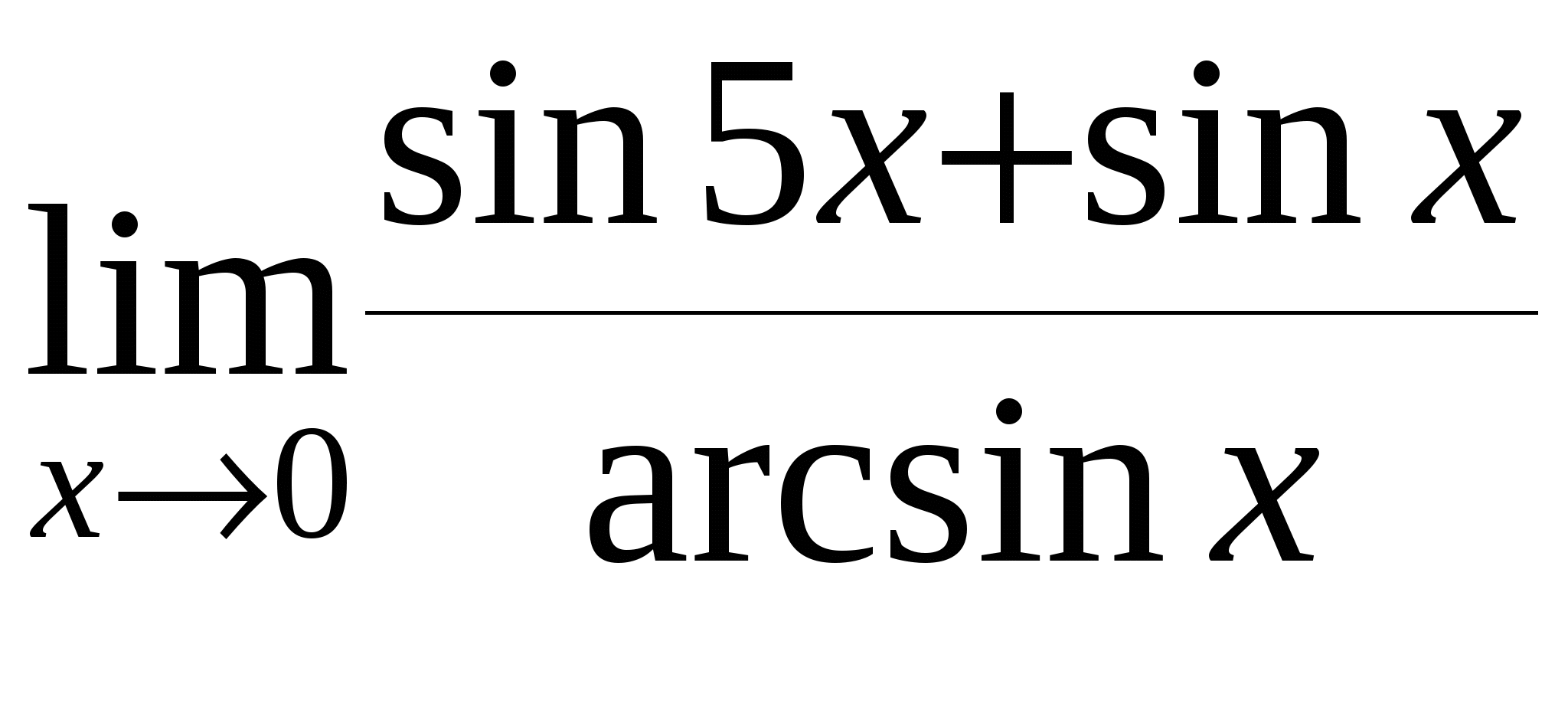
Найти предел функции
12
а)
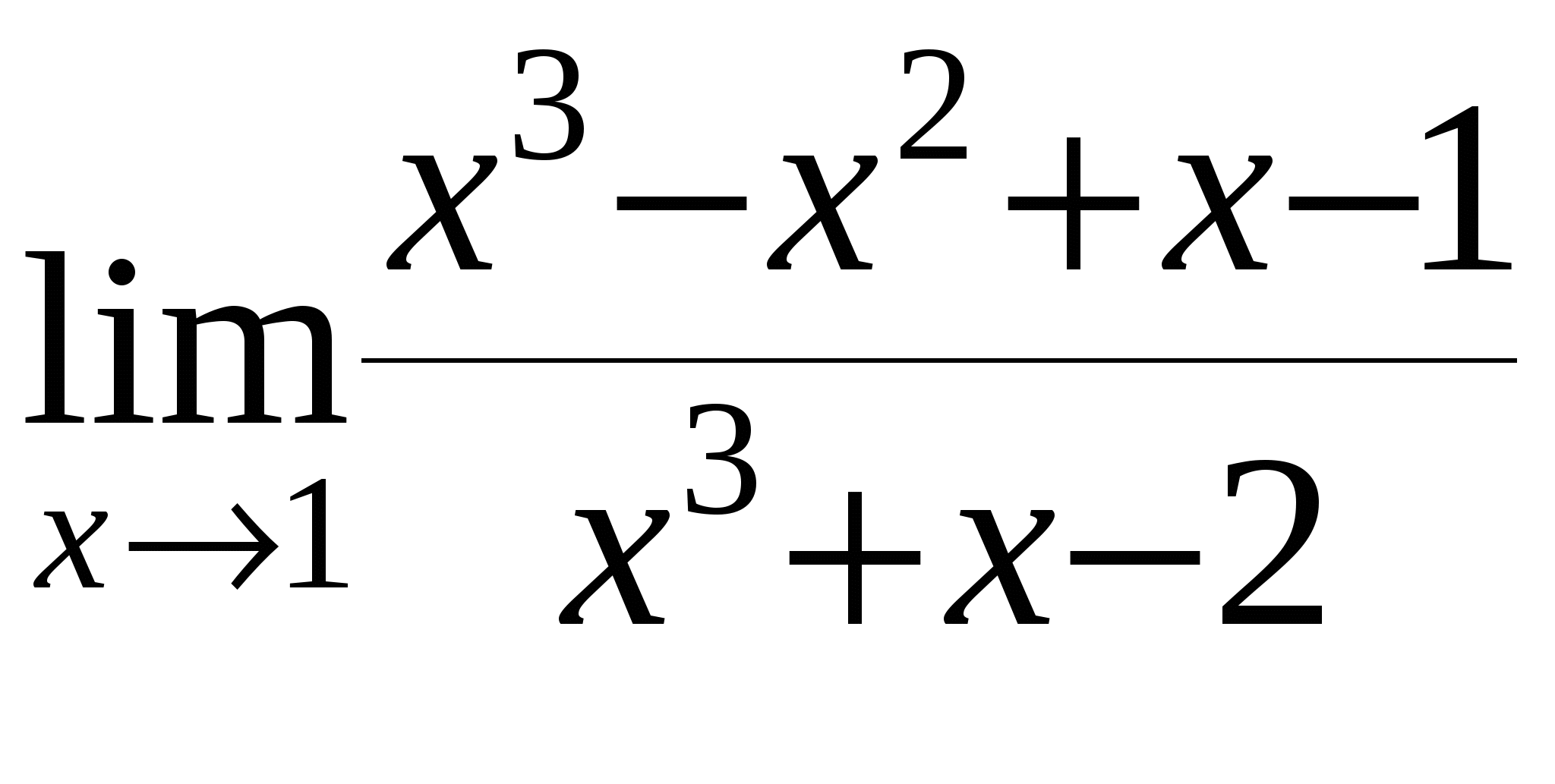
б)
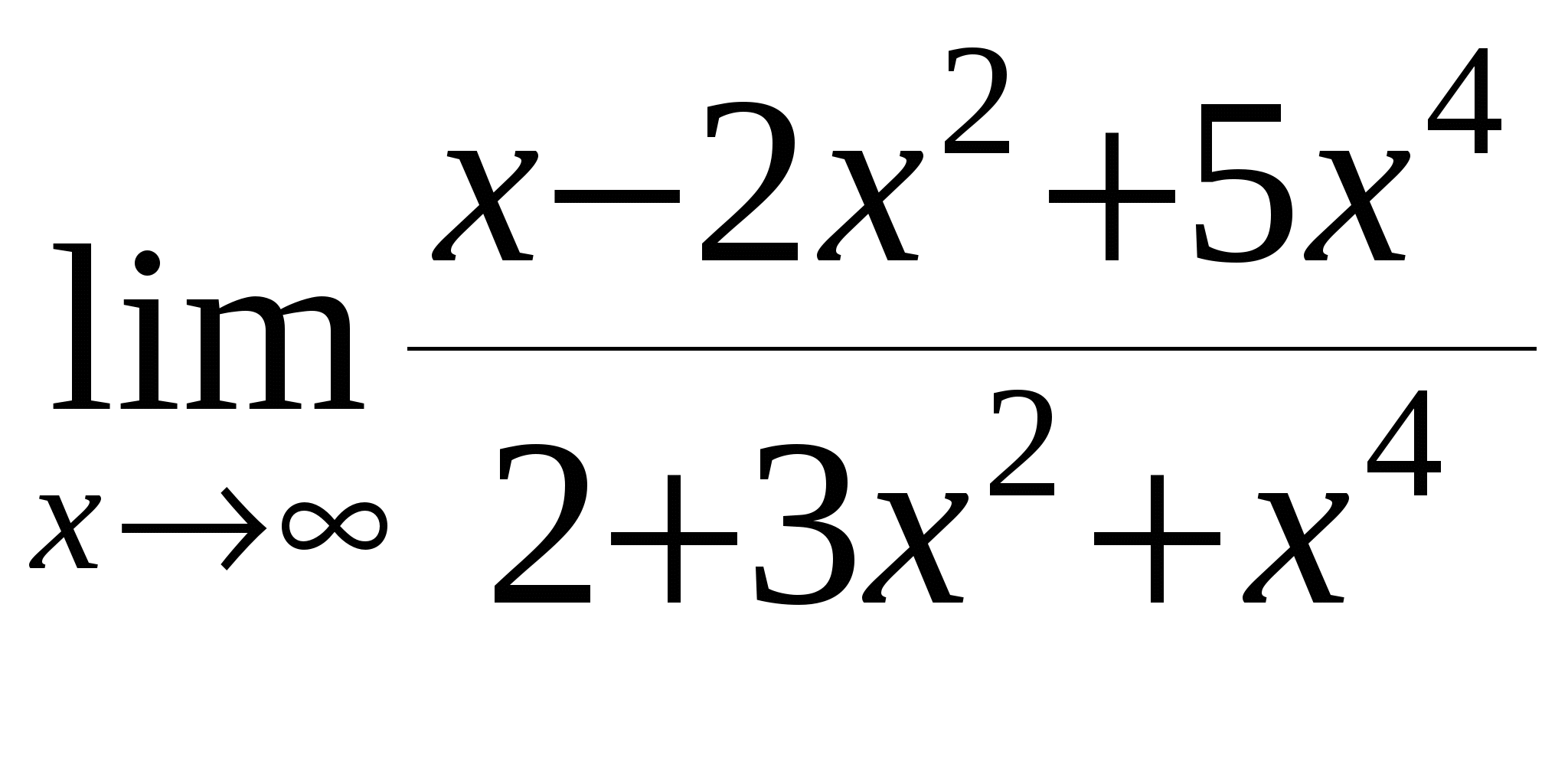
в)
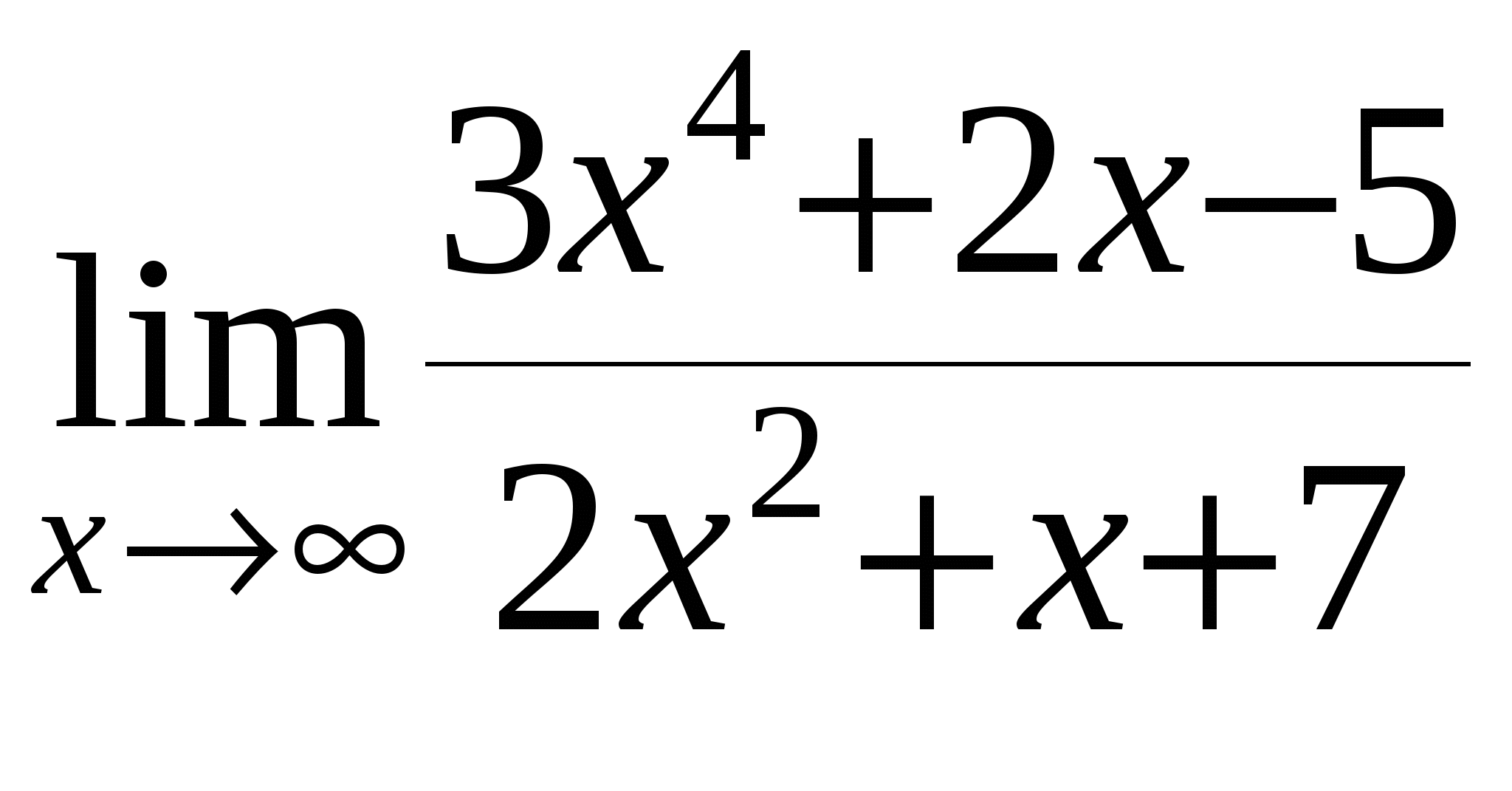
г)
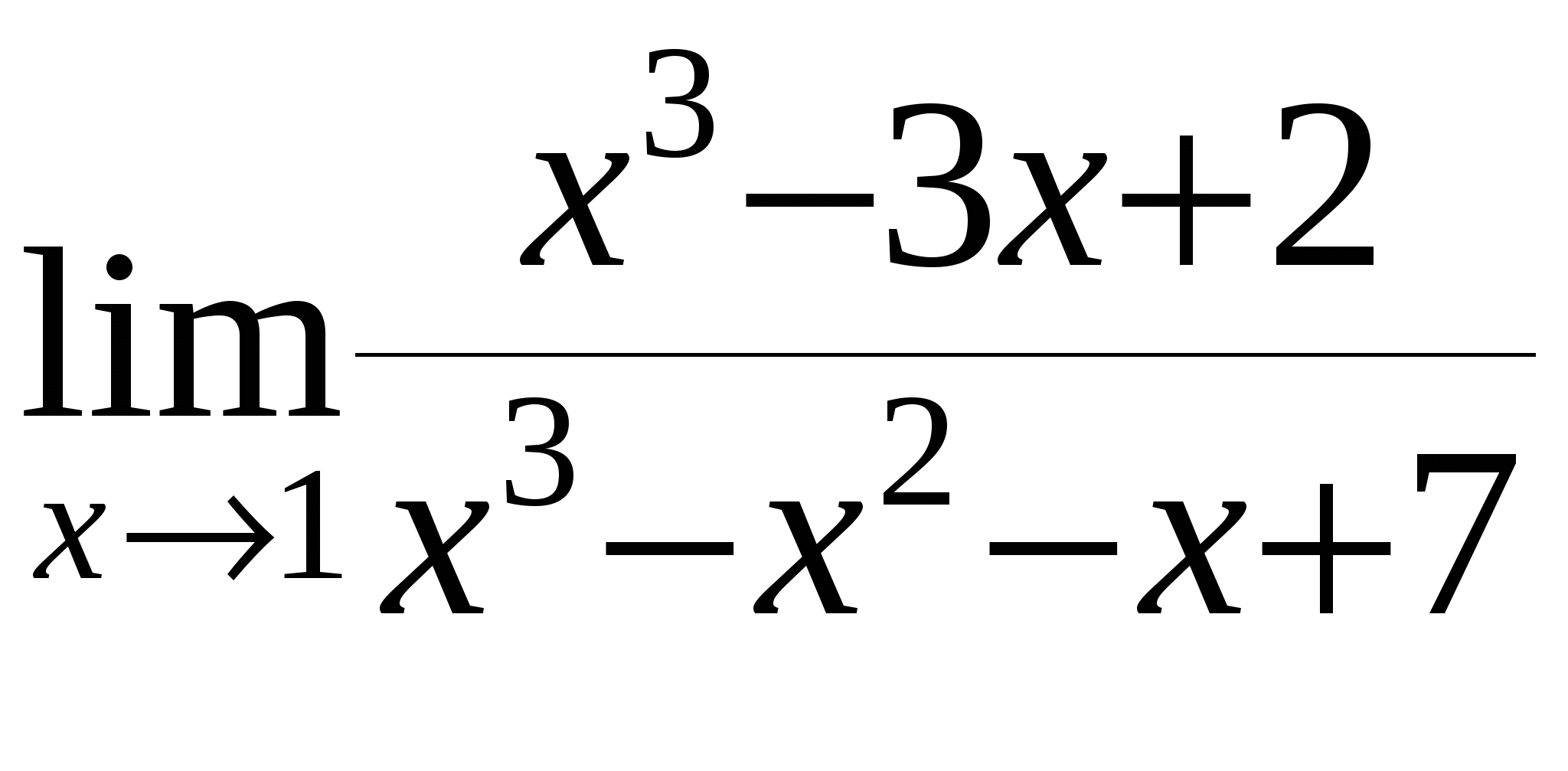
д)
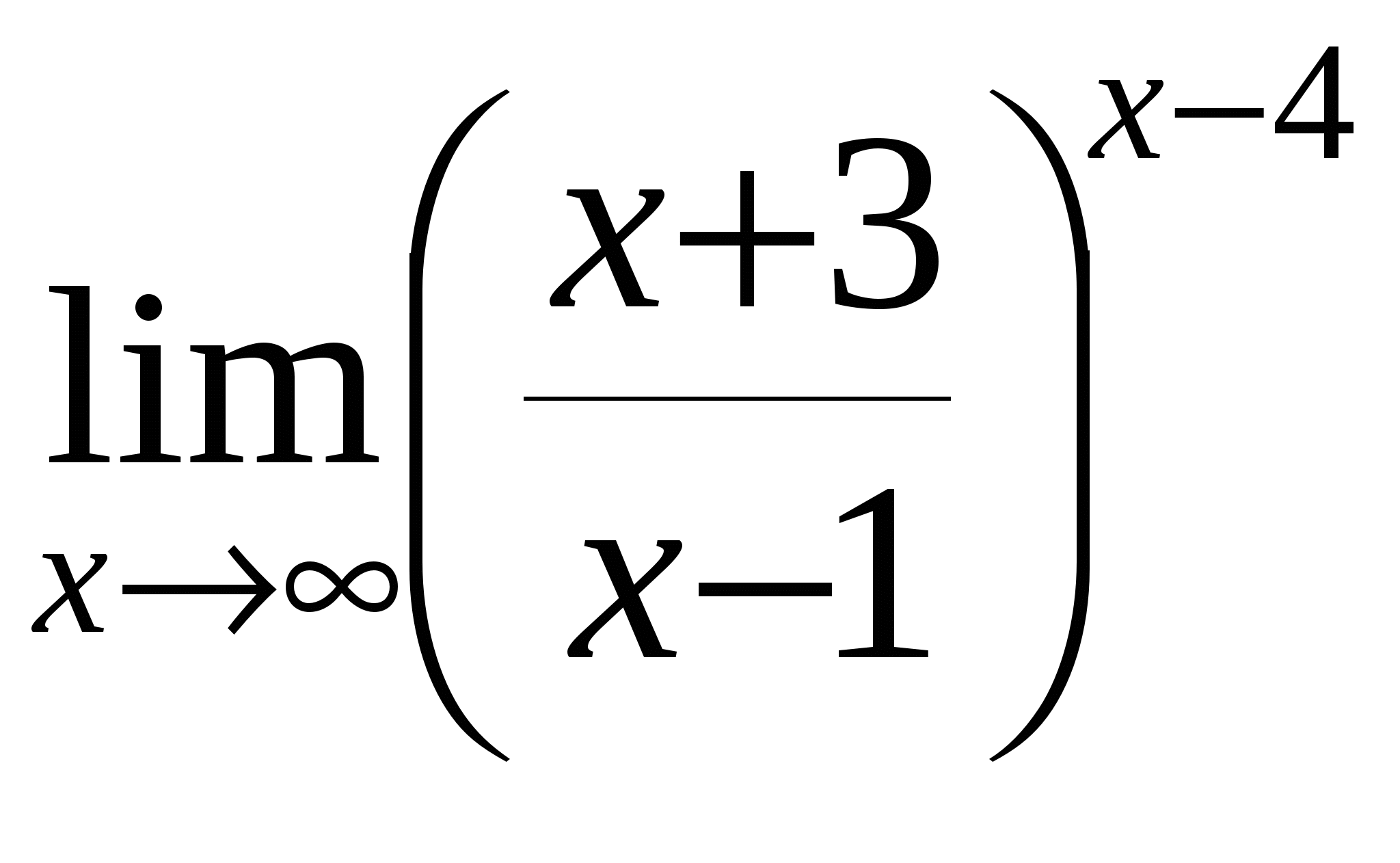
е)
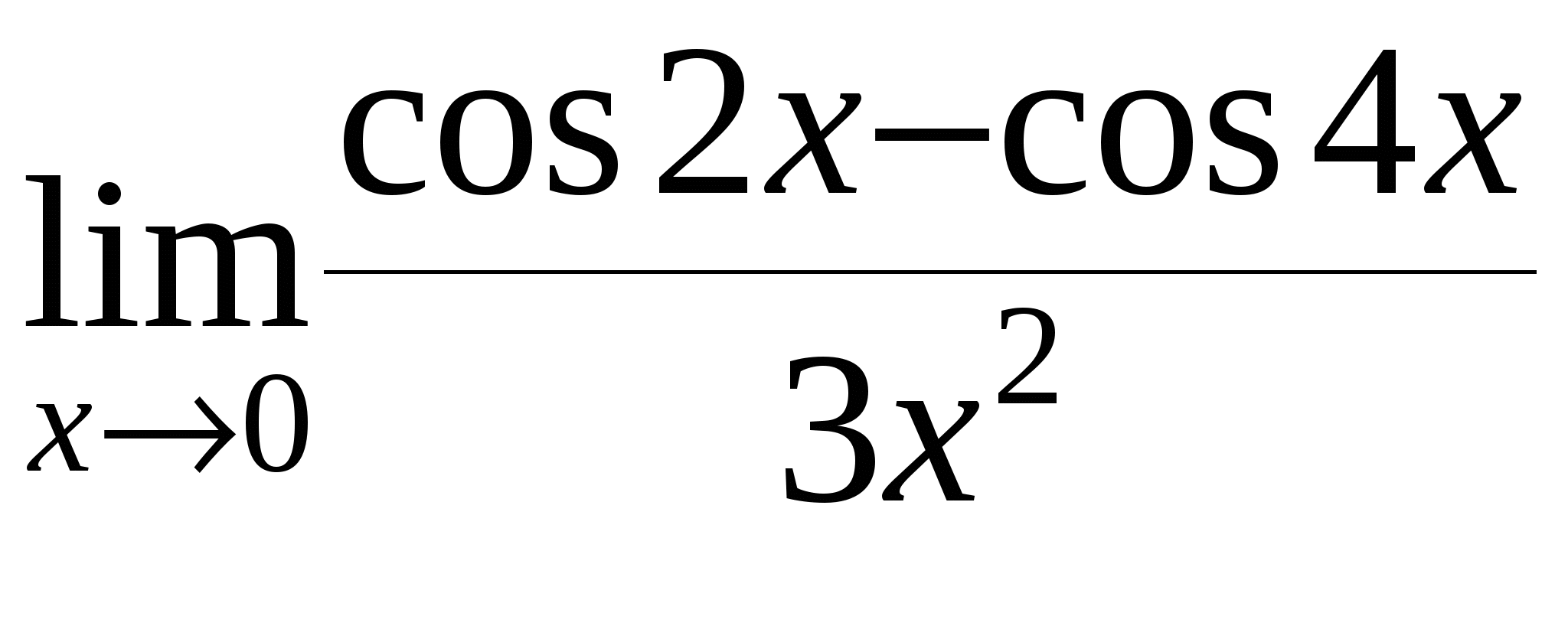
Контрольная работа № 5
Найти предел функции
13
а)
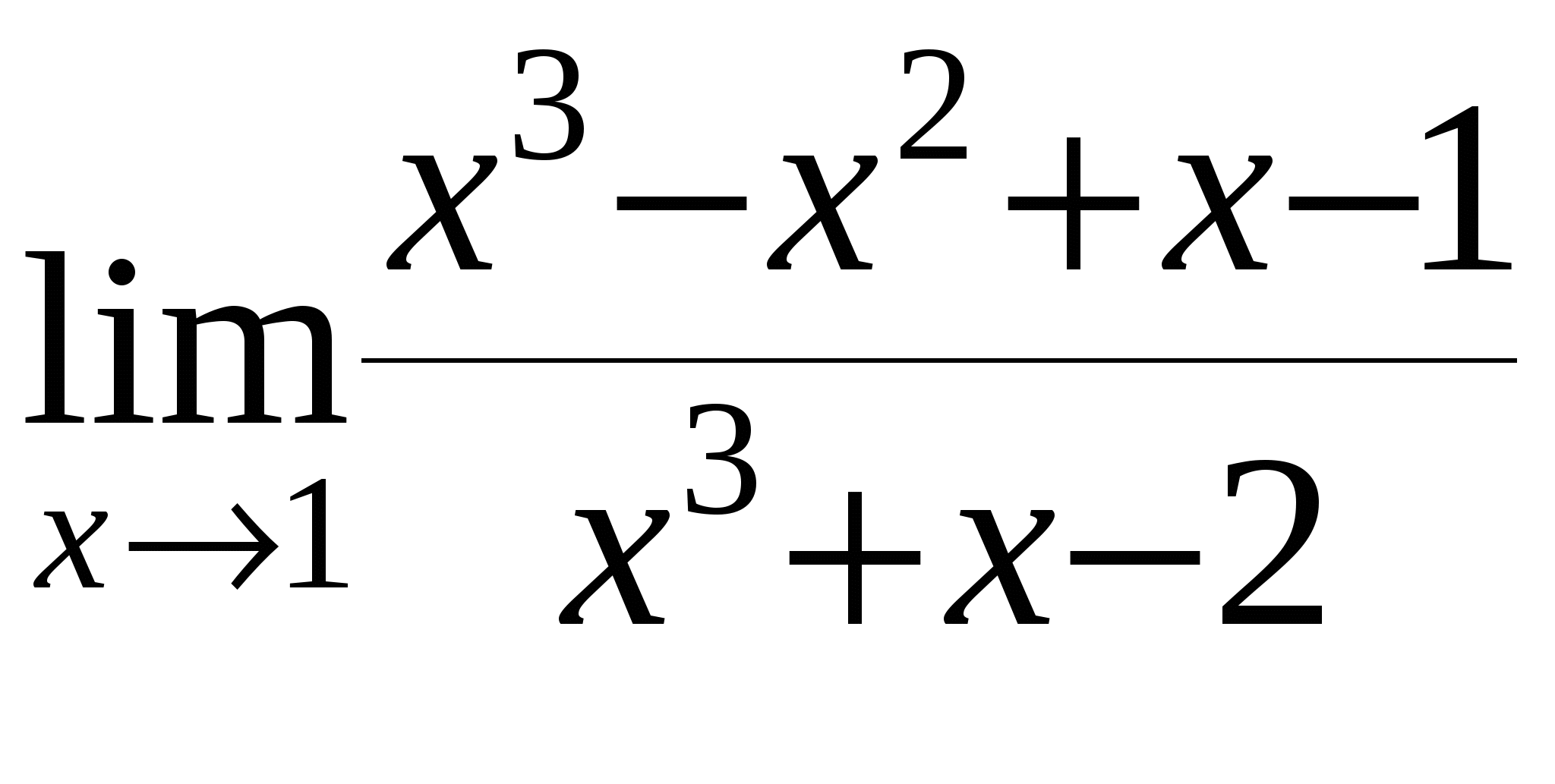
б)
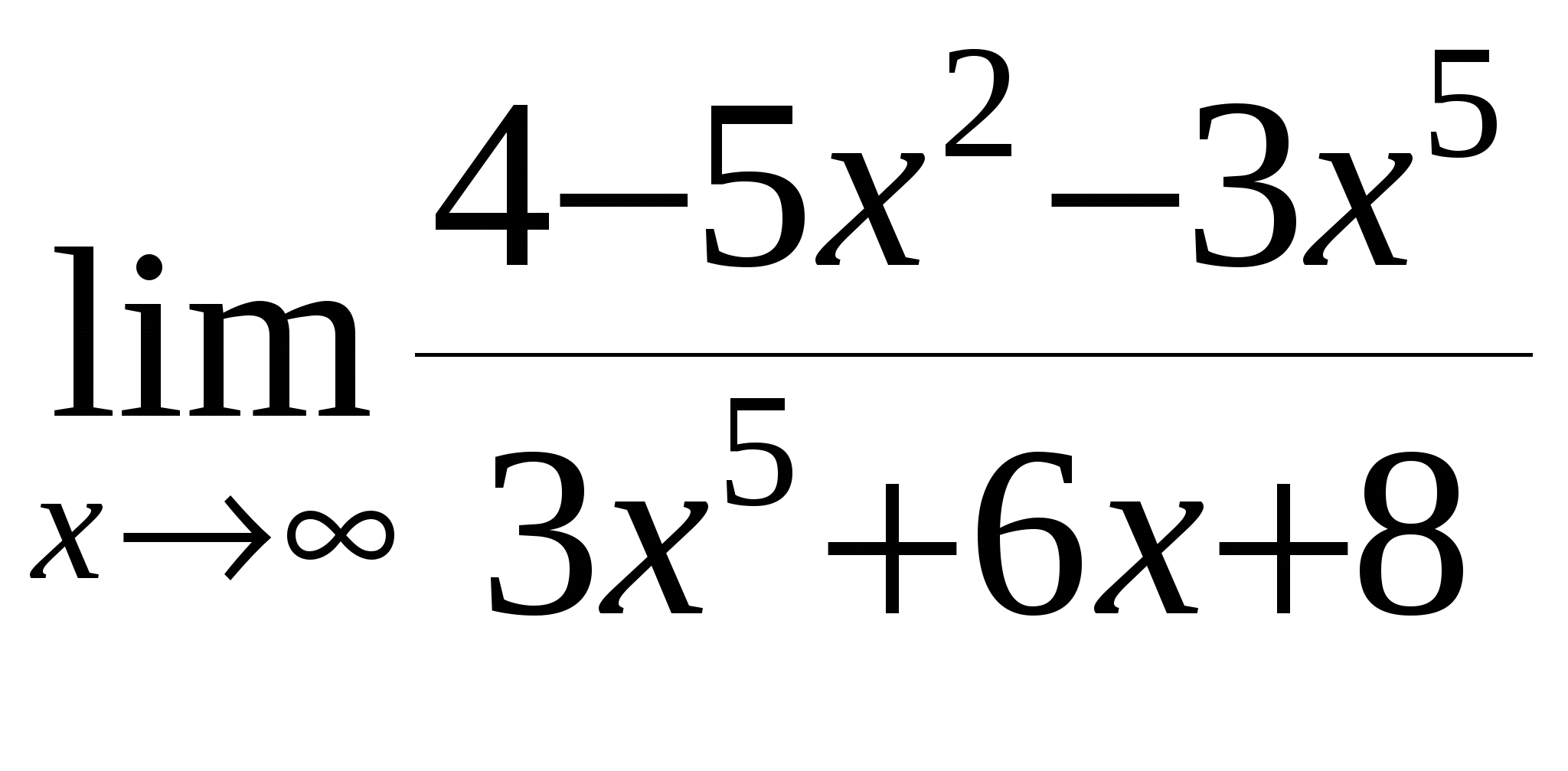
в)
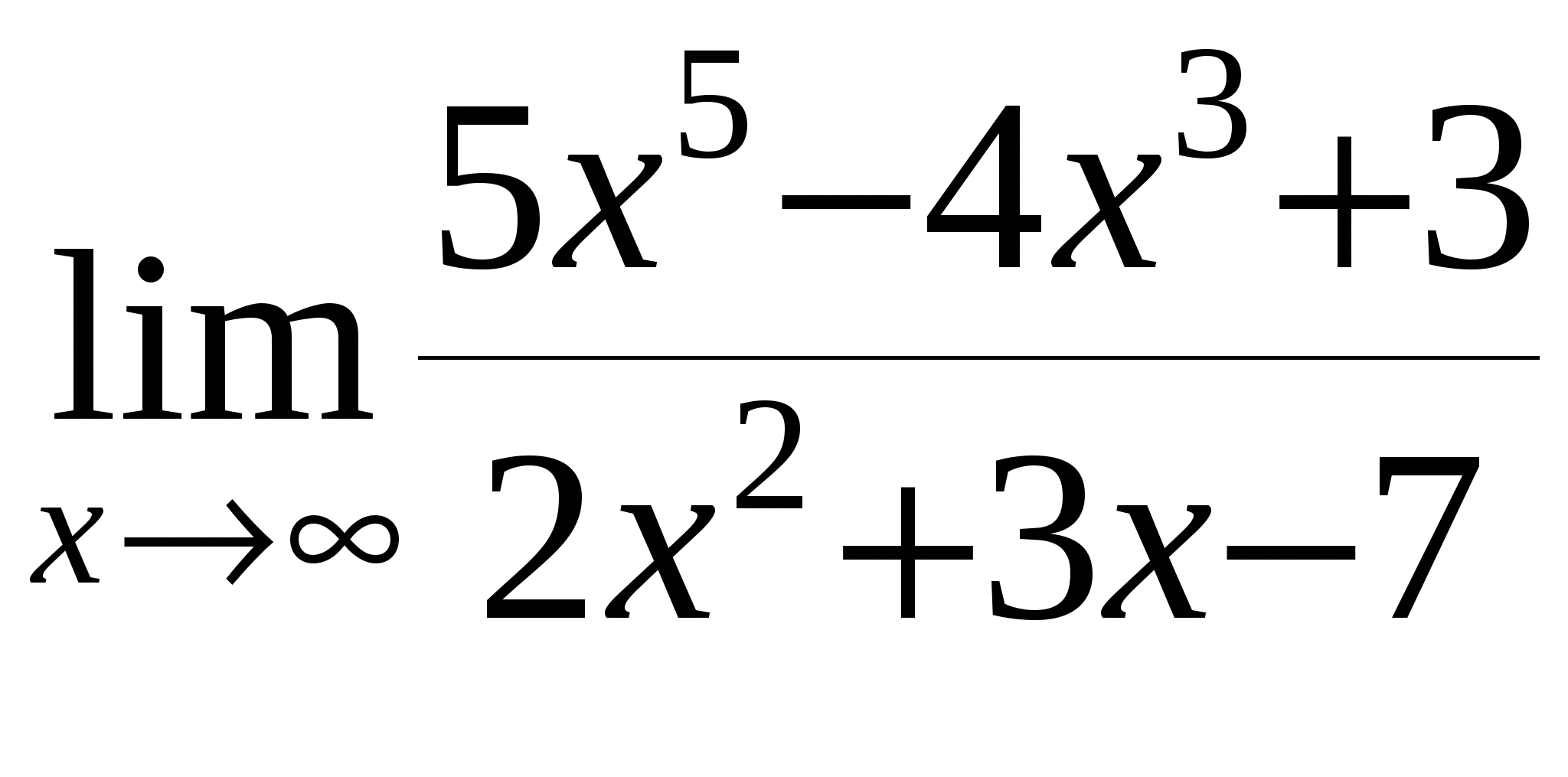
г)
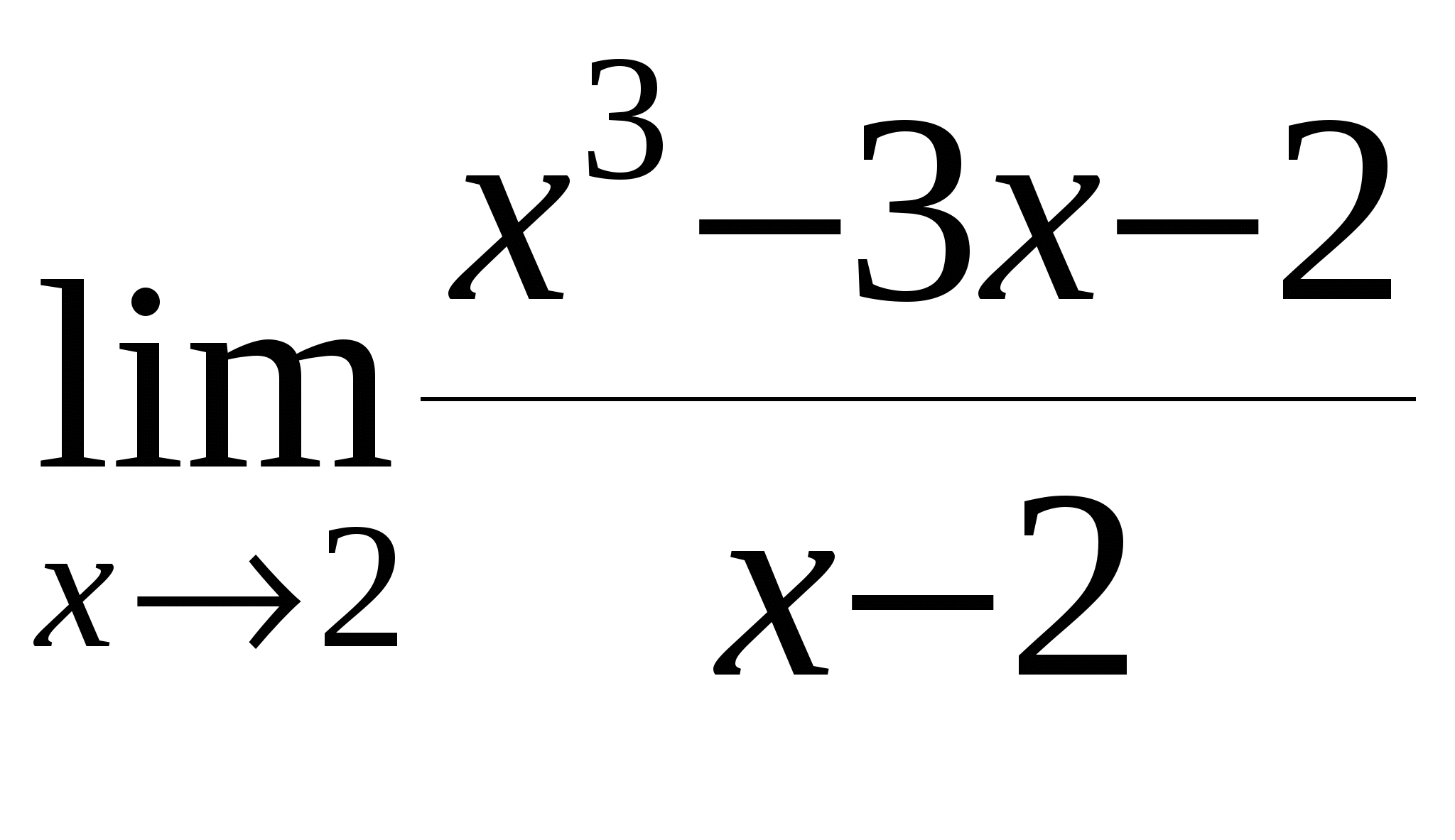
д)
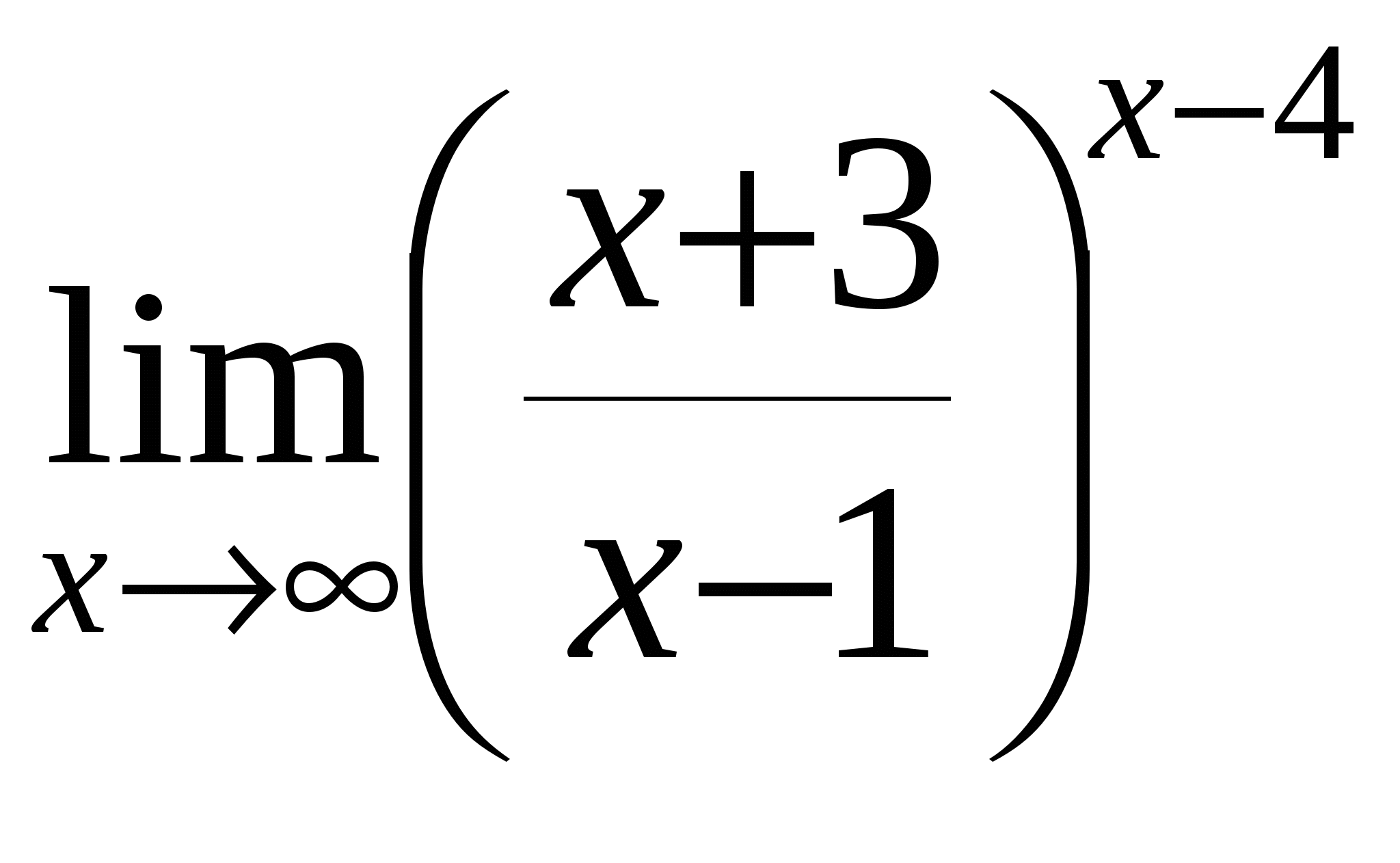
е)
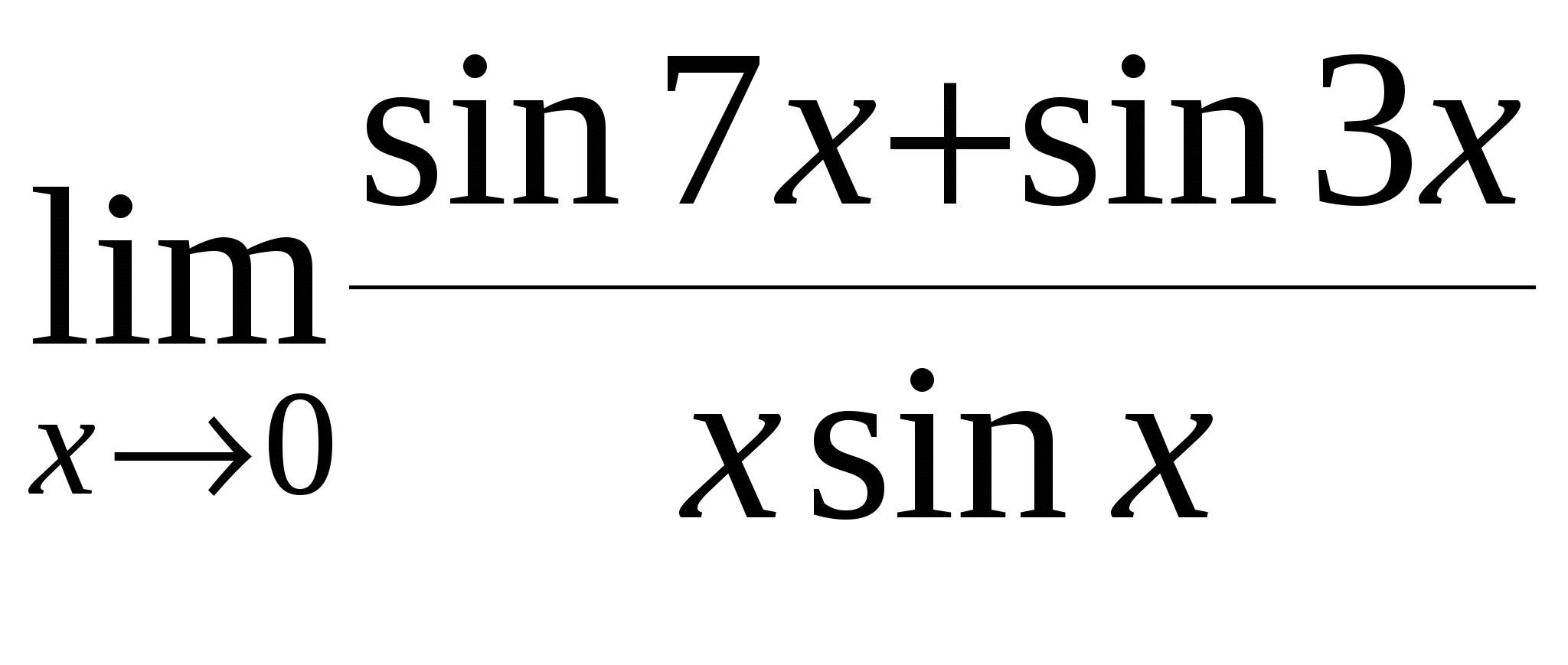
Найти предел функции
14
а)
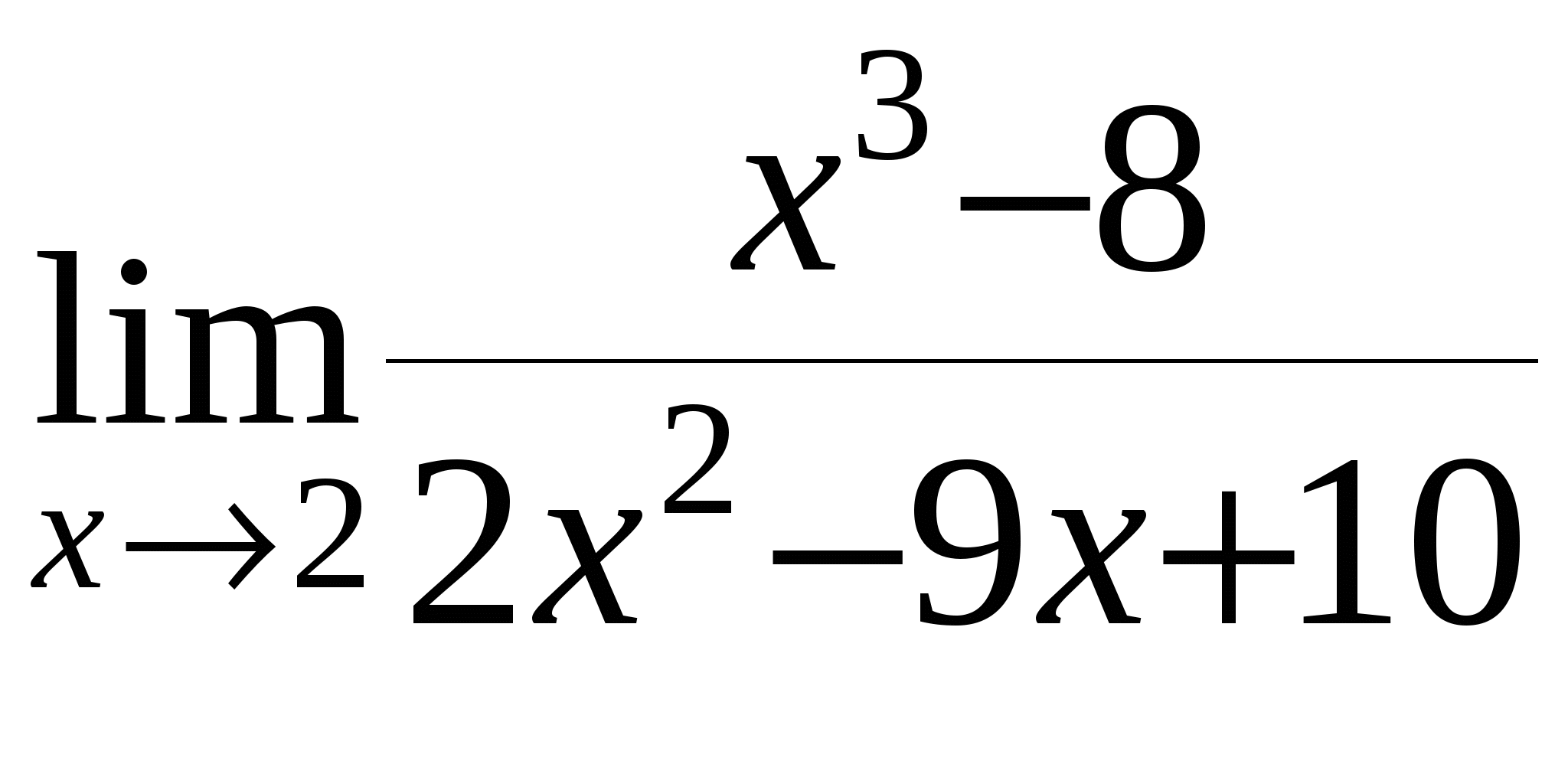
б)
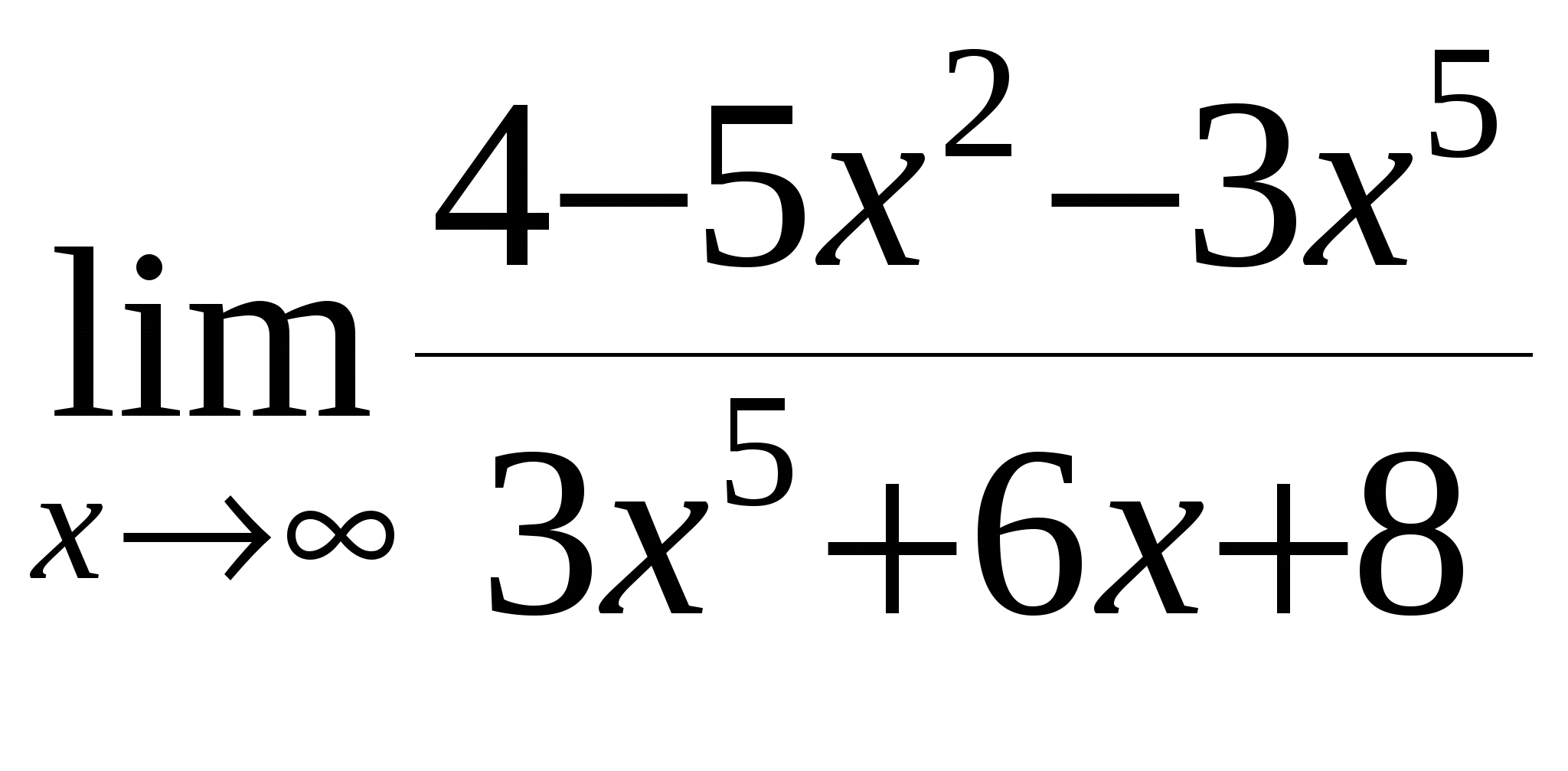
в)
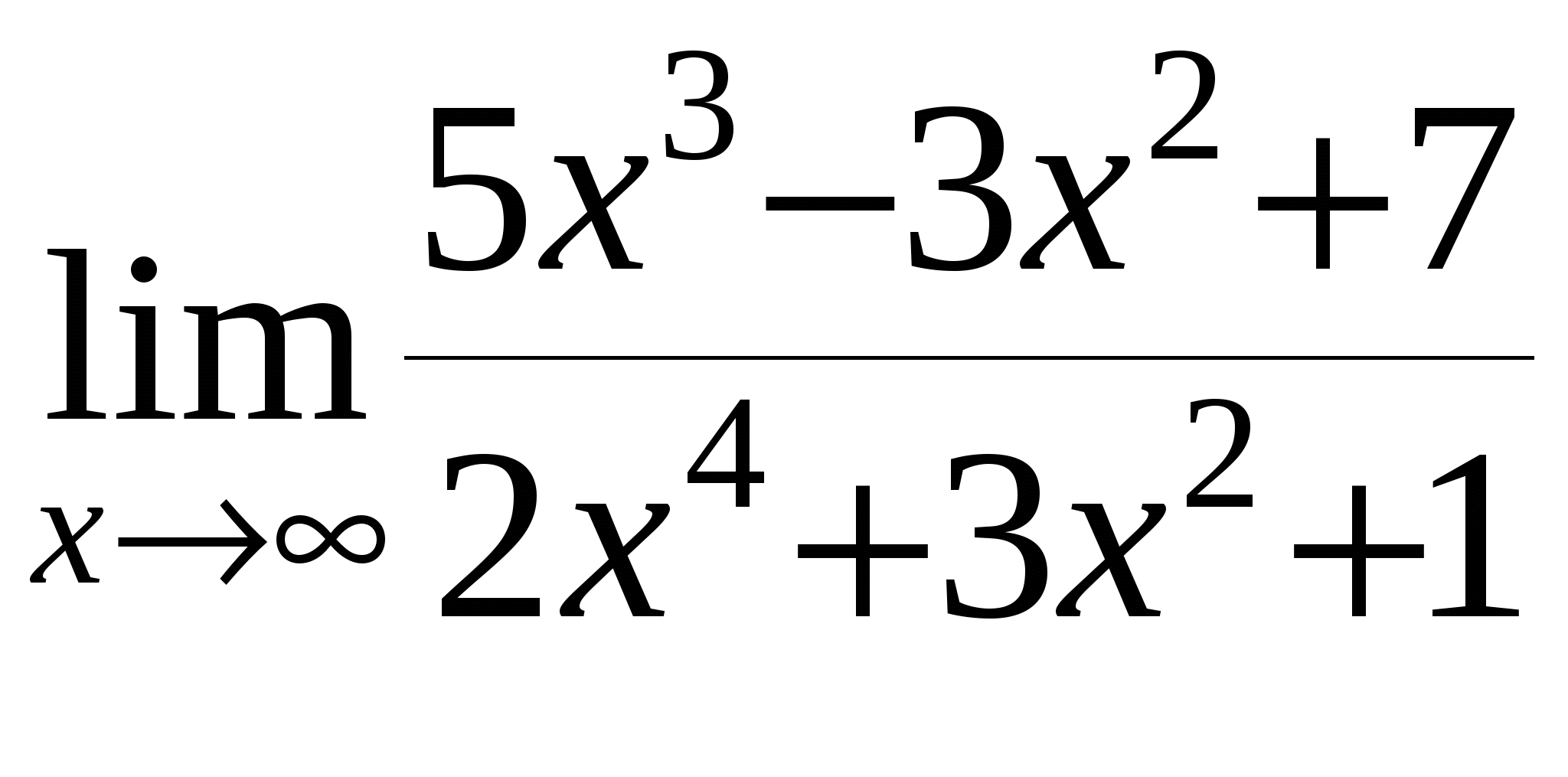
г)
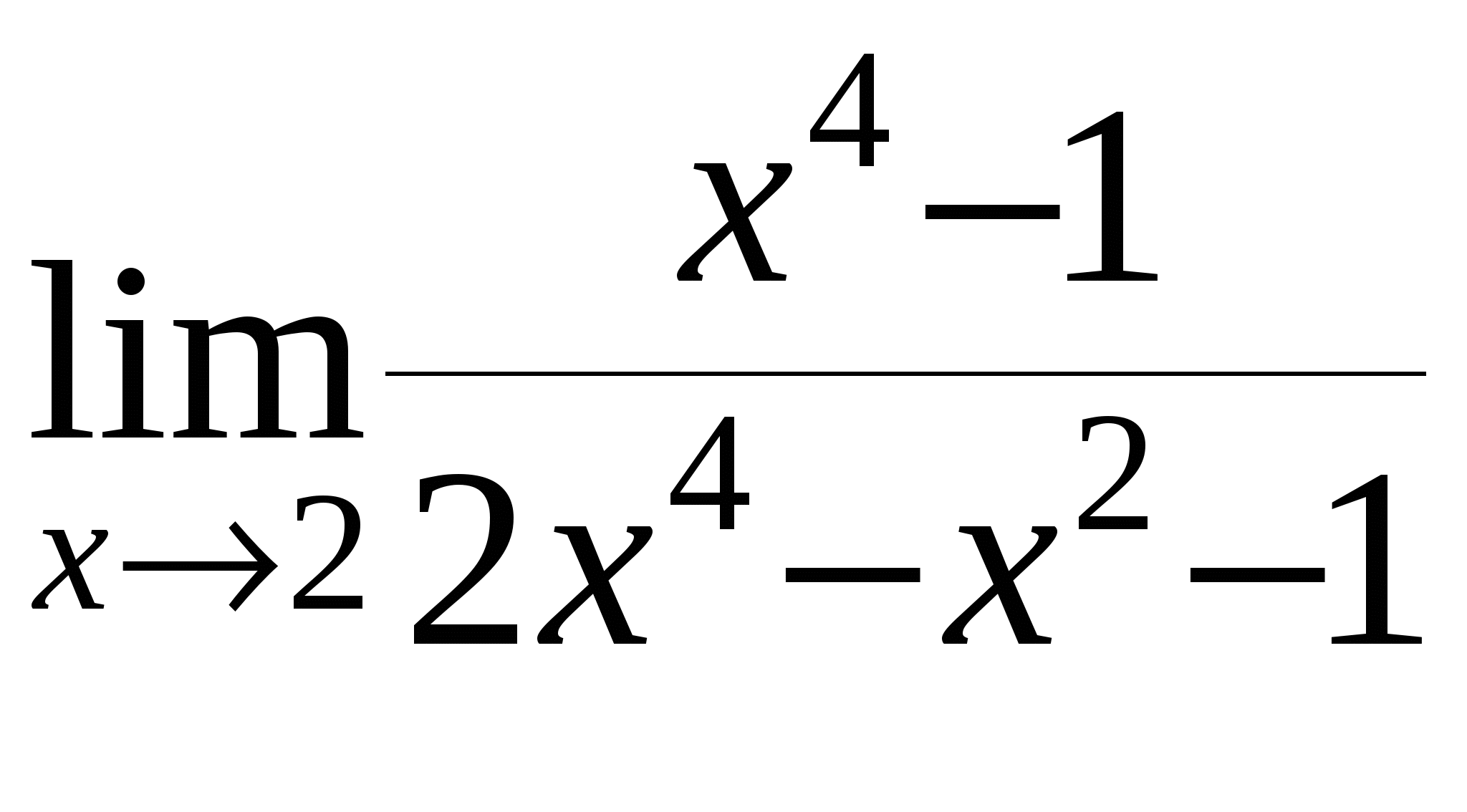
д)
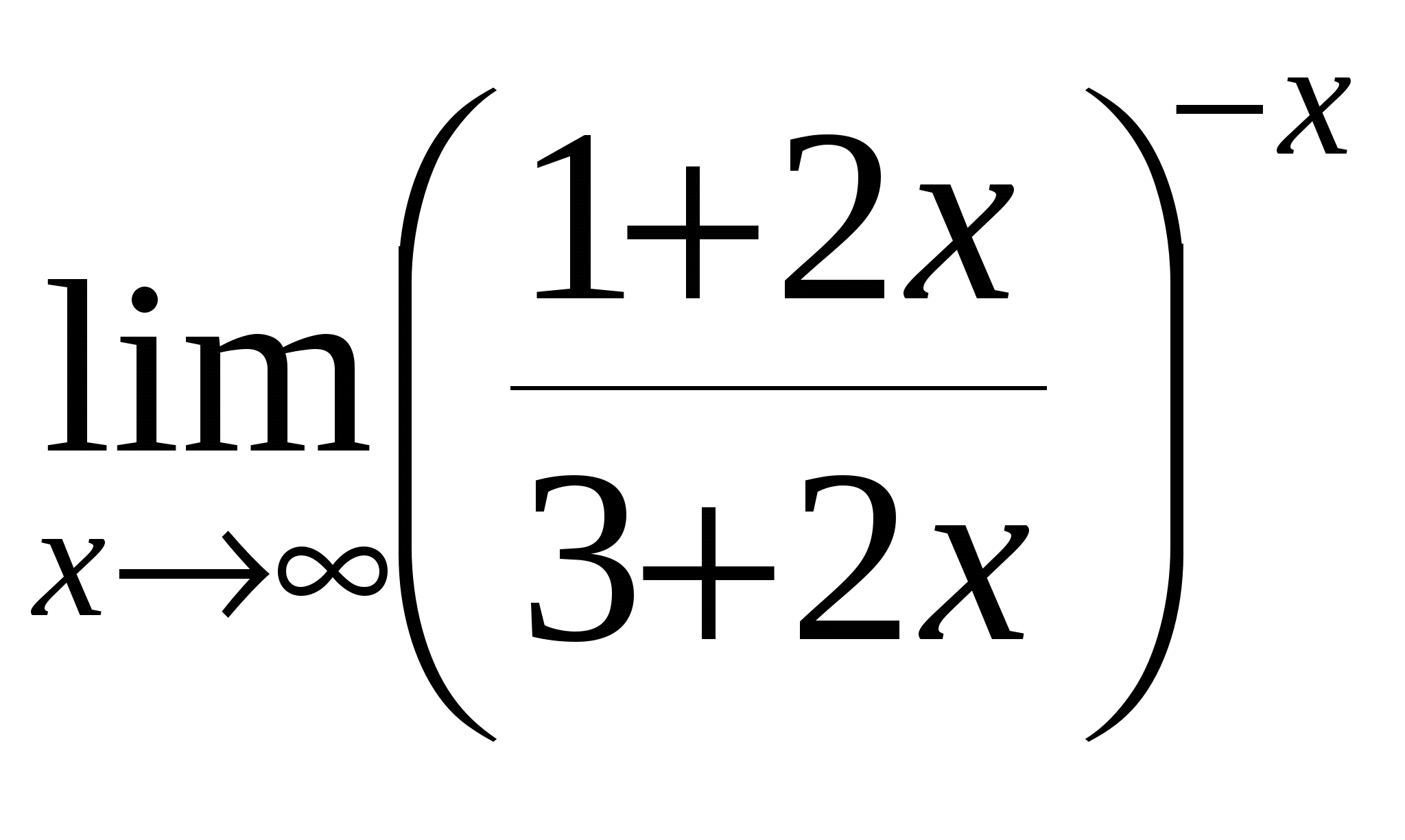
е)
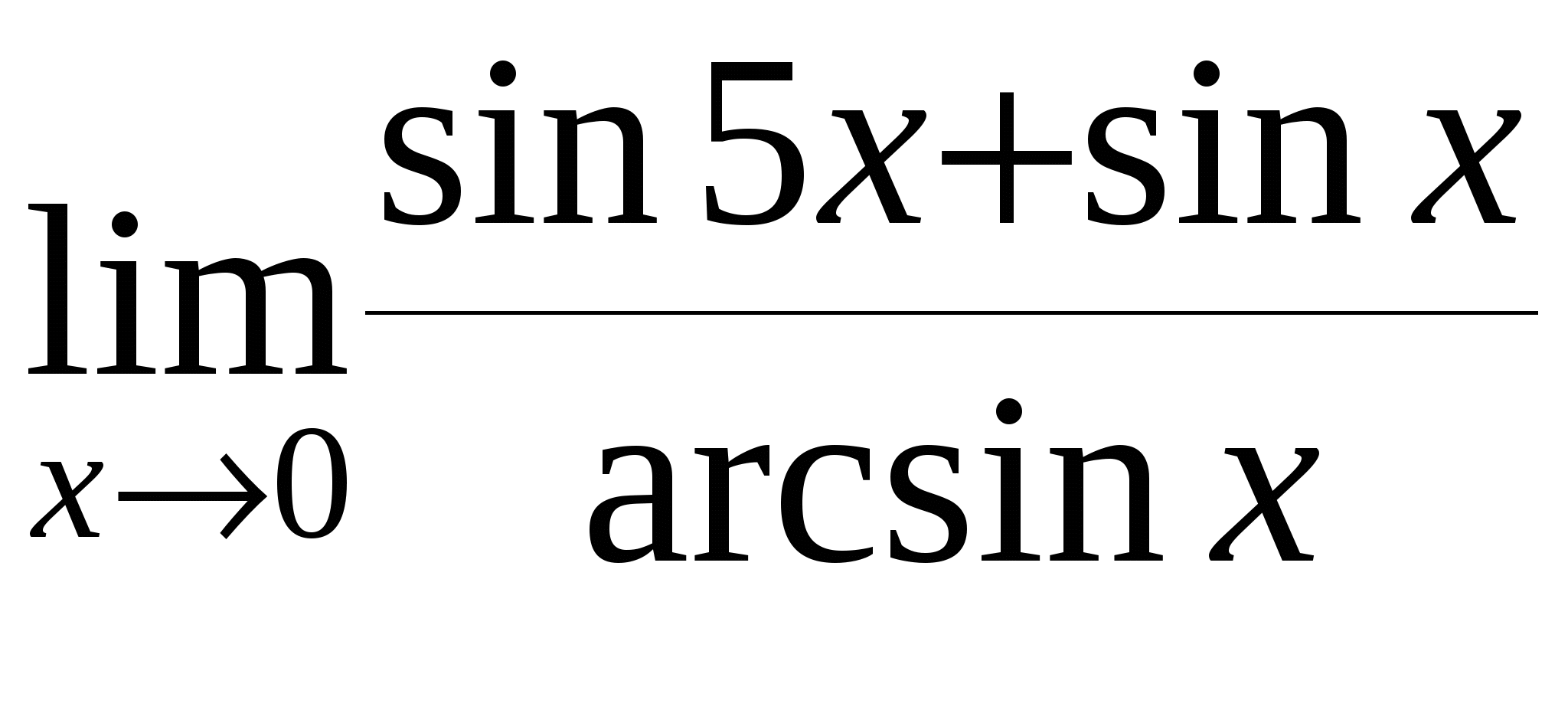
Найти предел функции
15
а)
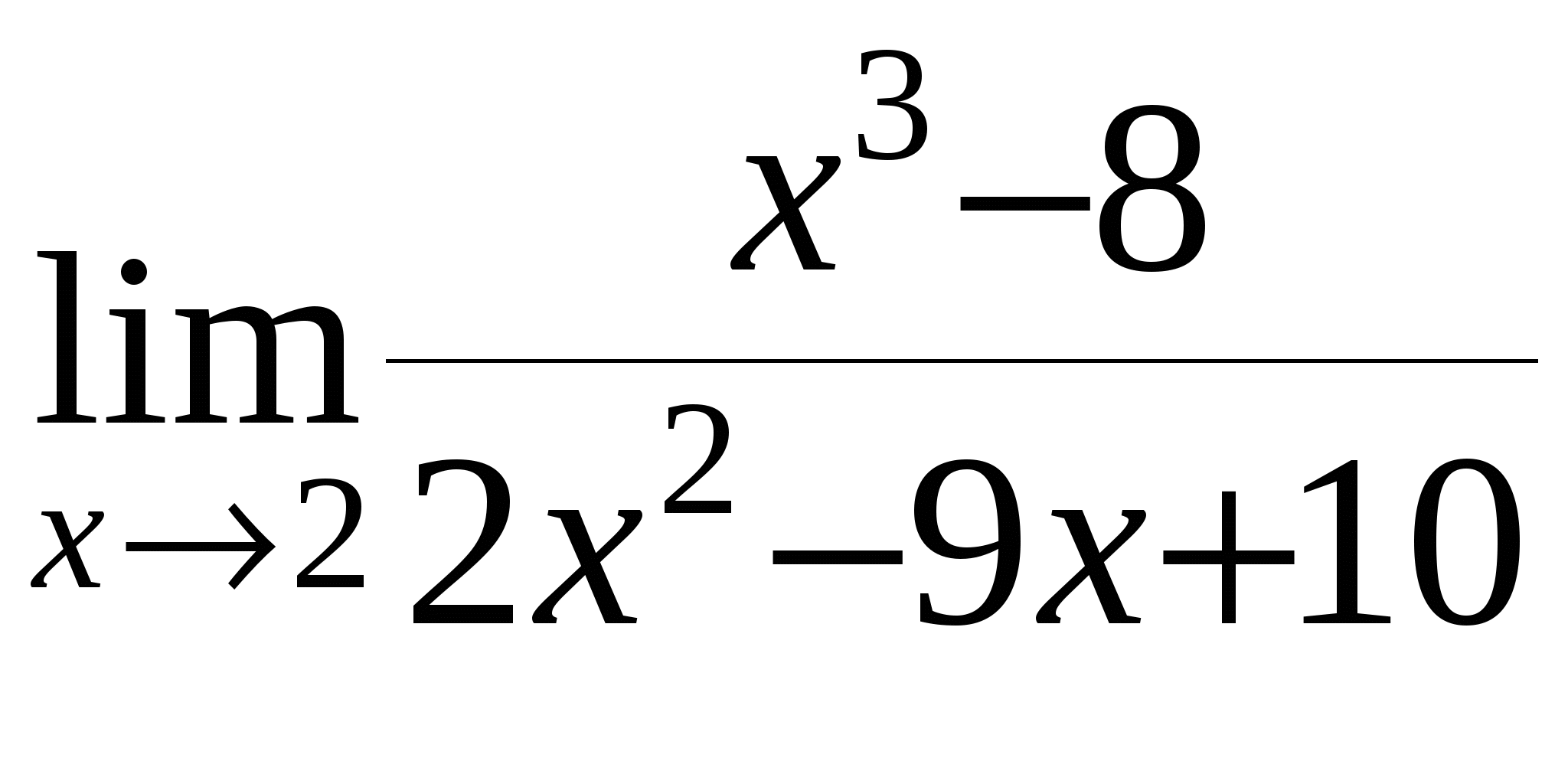
б)
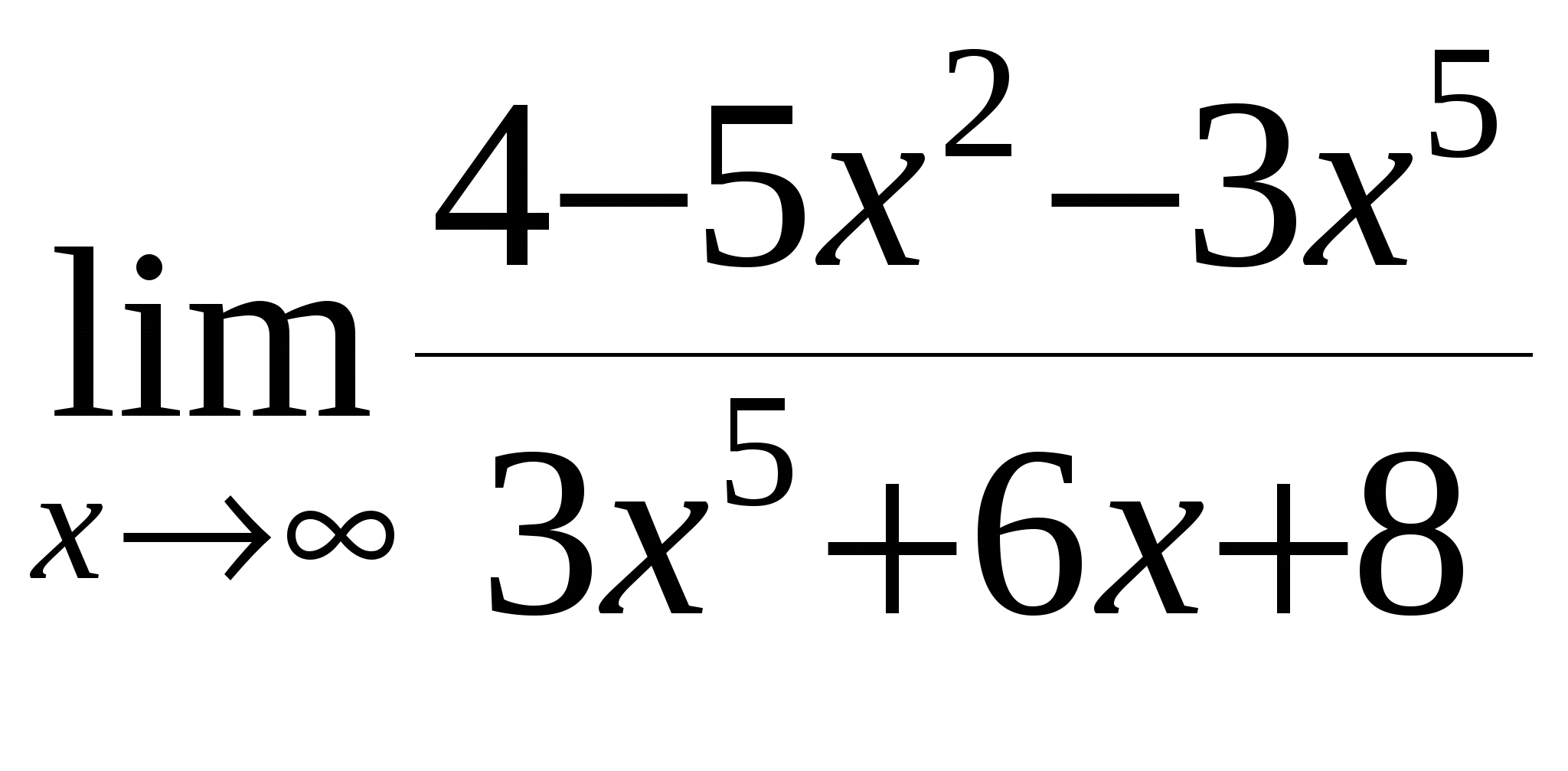
в)
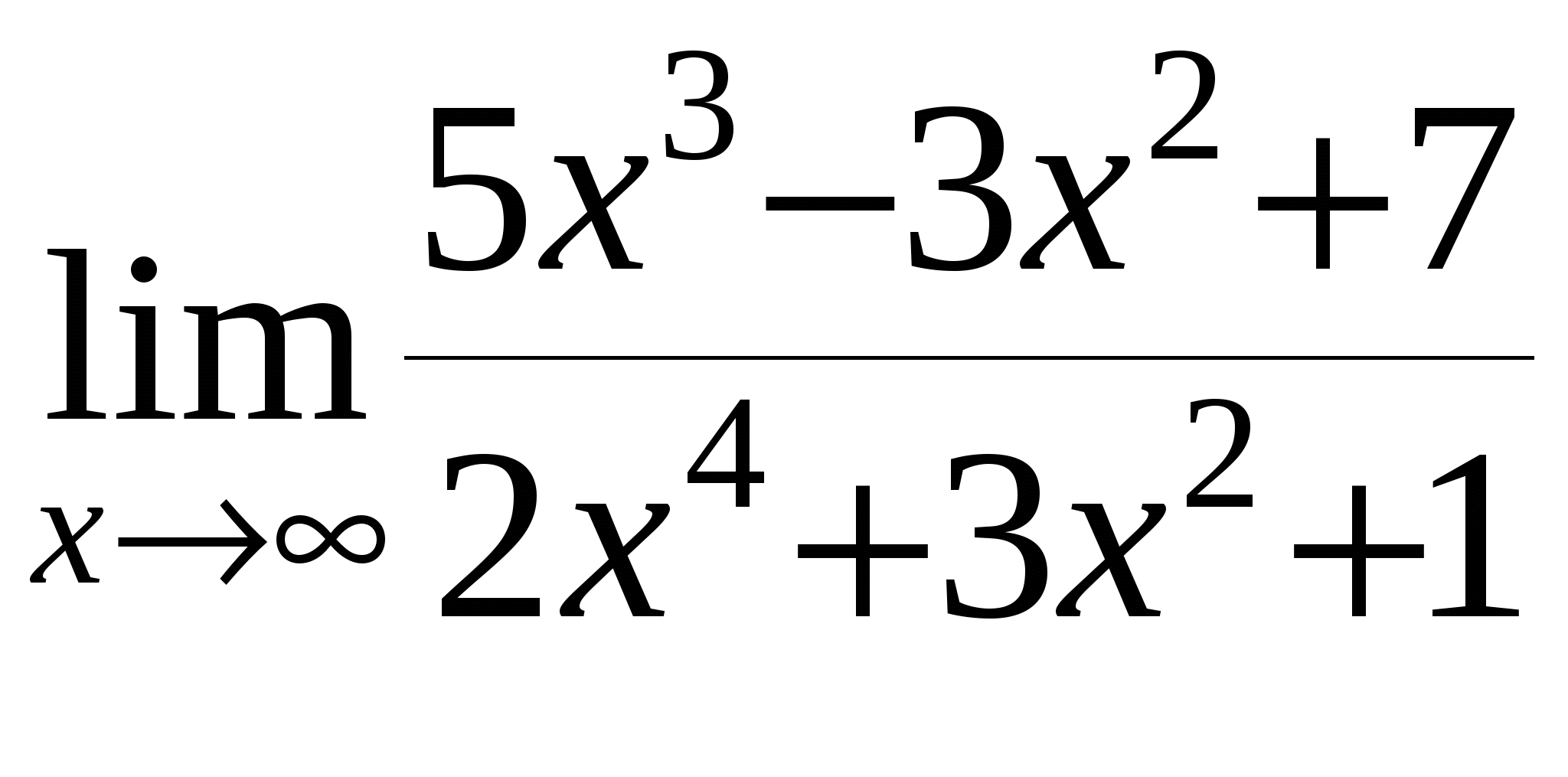
г)
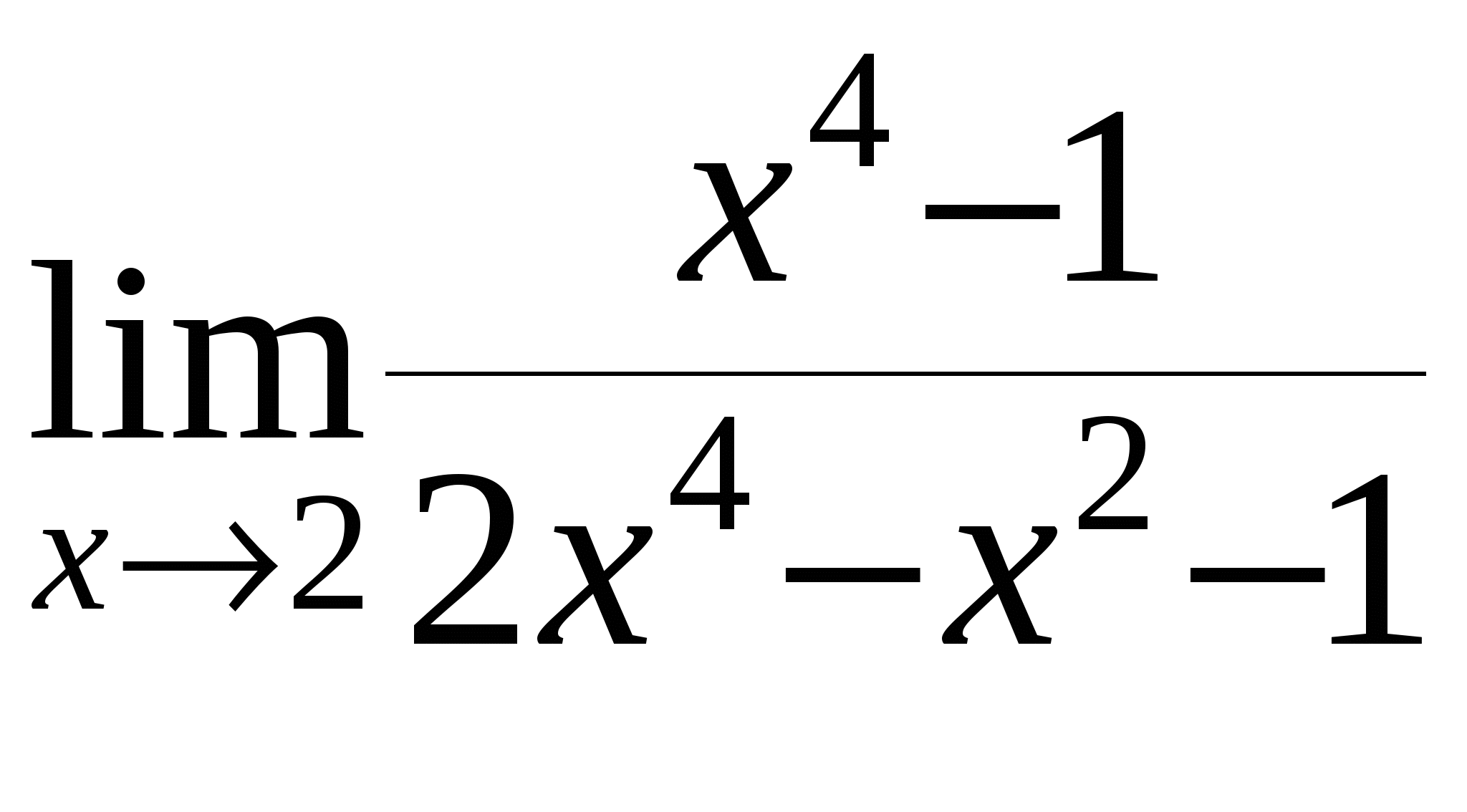
д)
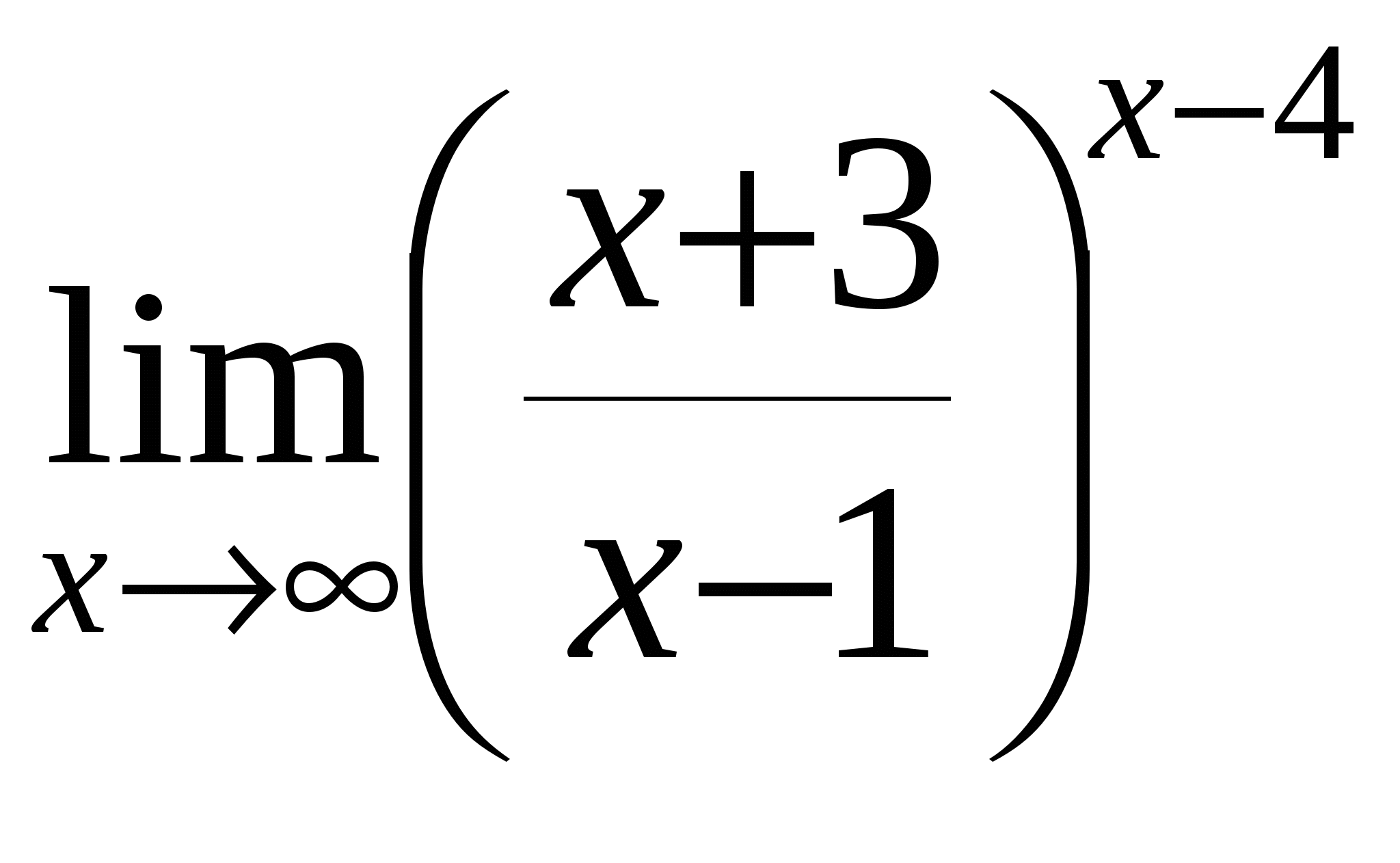
е)
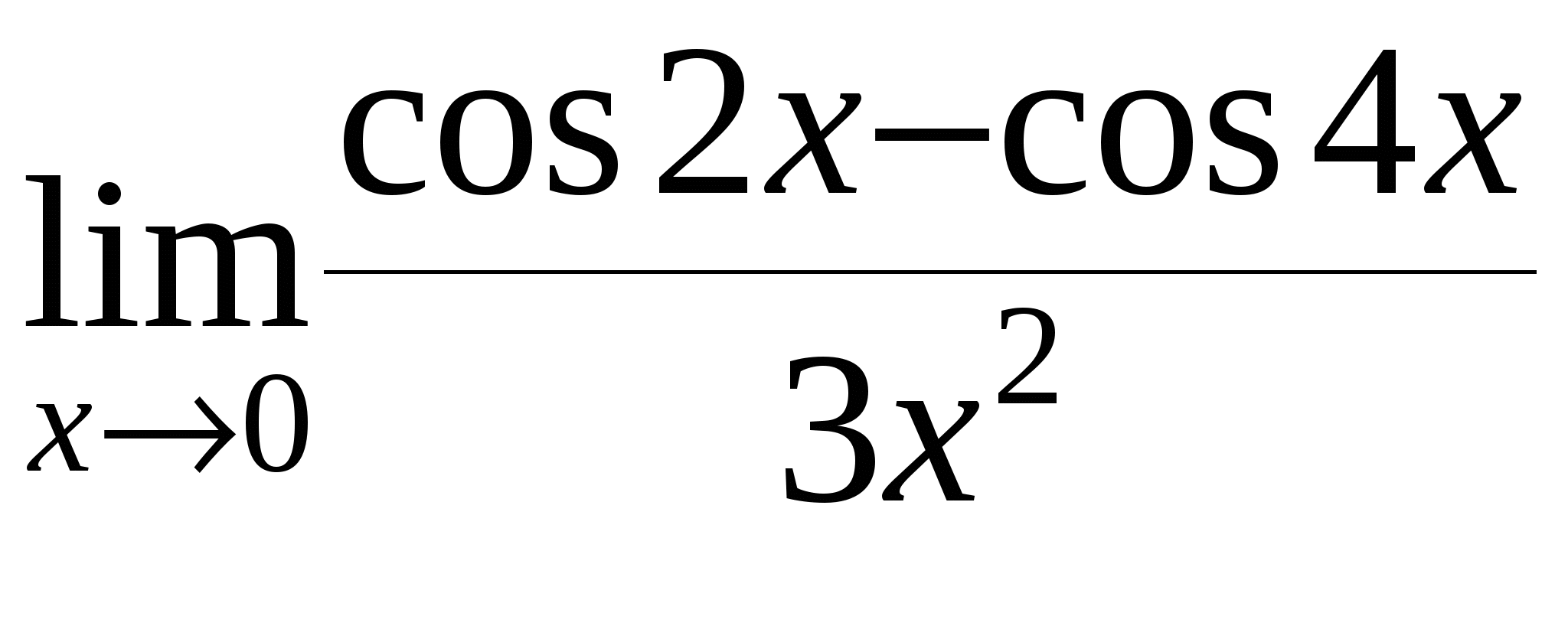
Контрольная работа № 5
Найти предел функции
16
а)
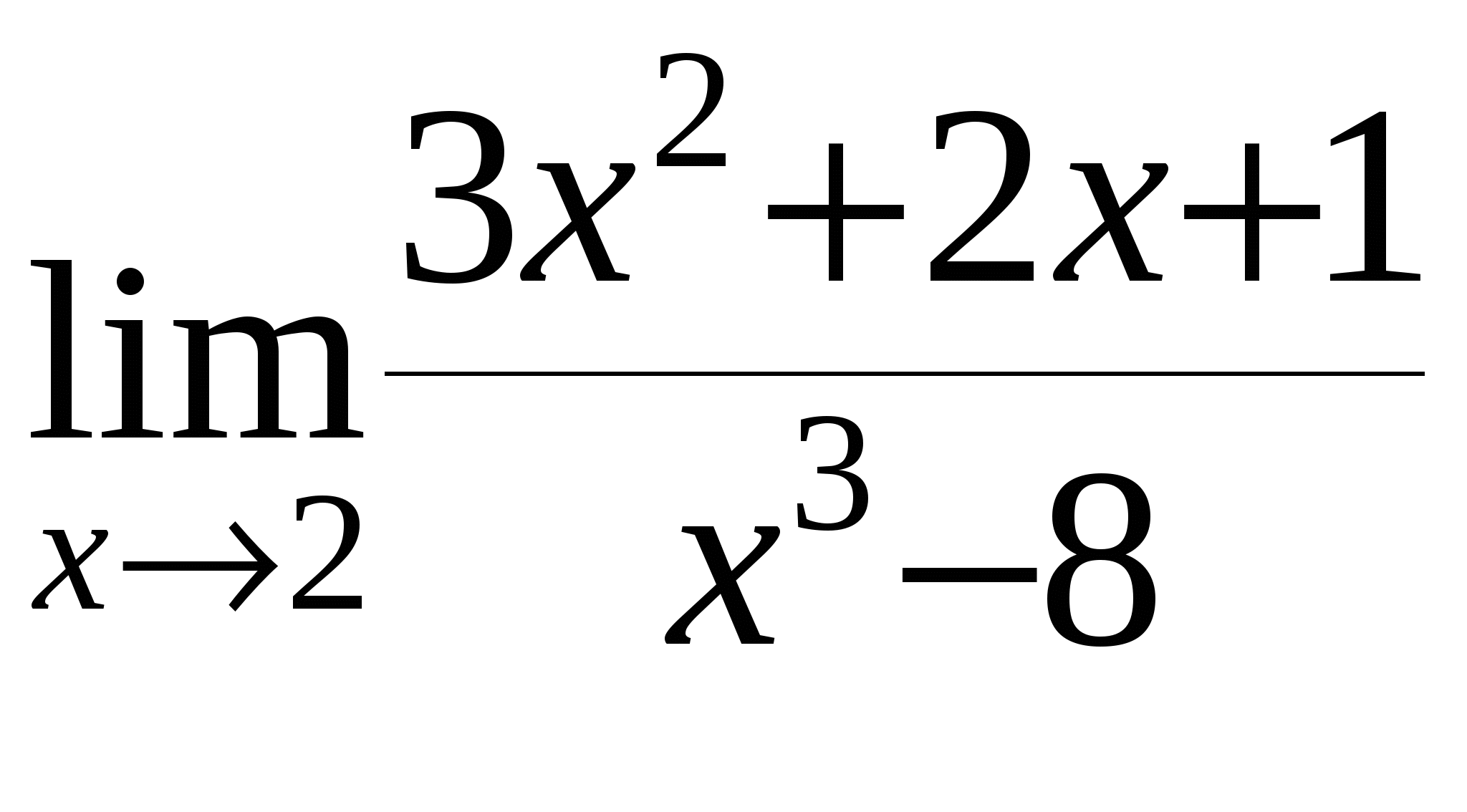
б)
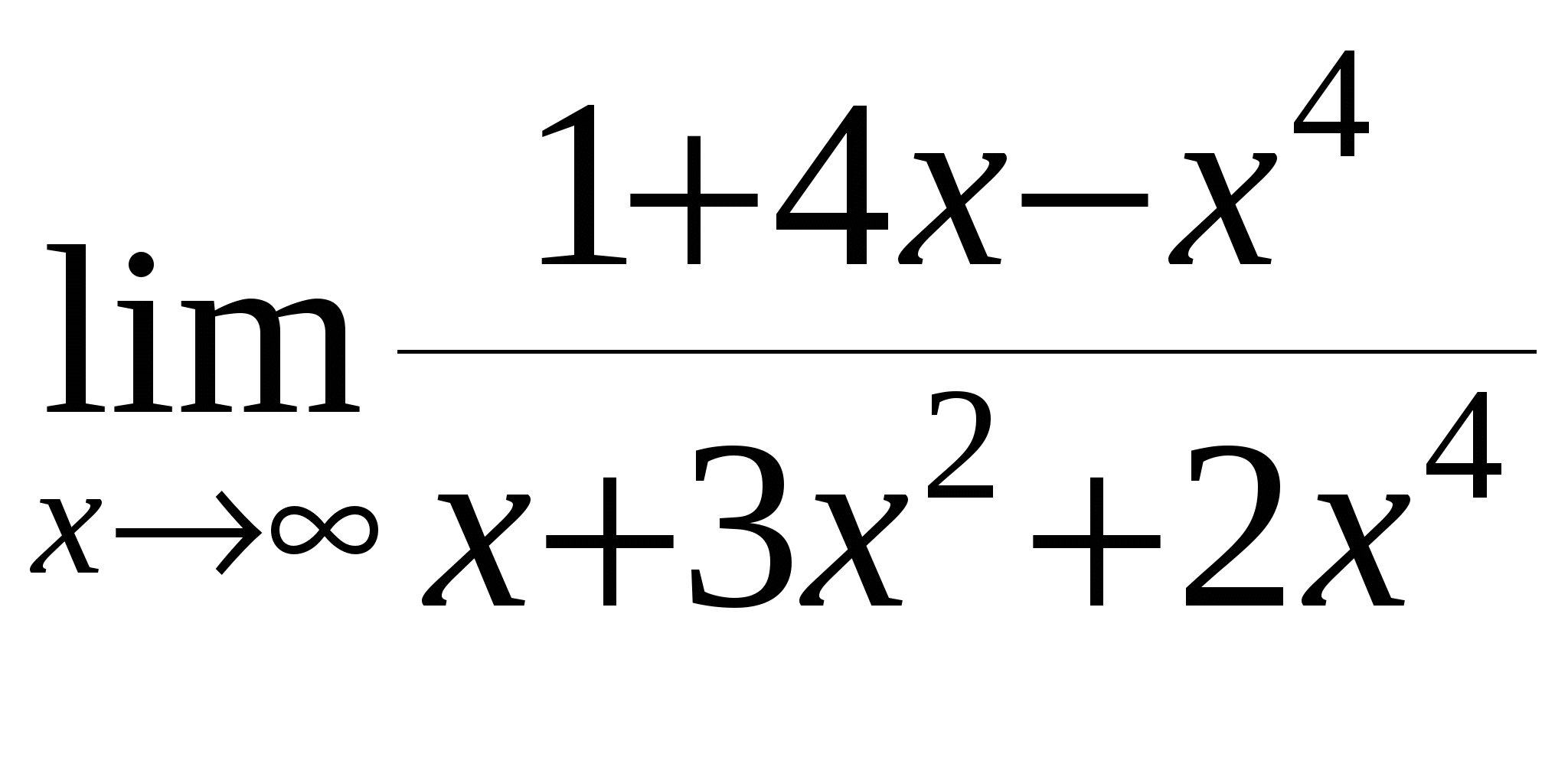
в)
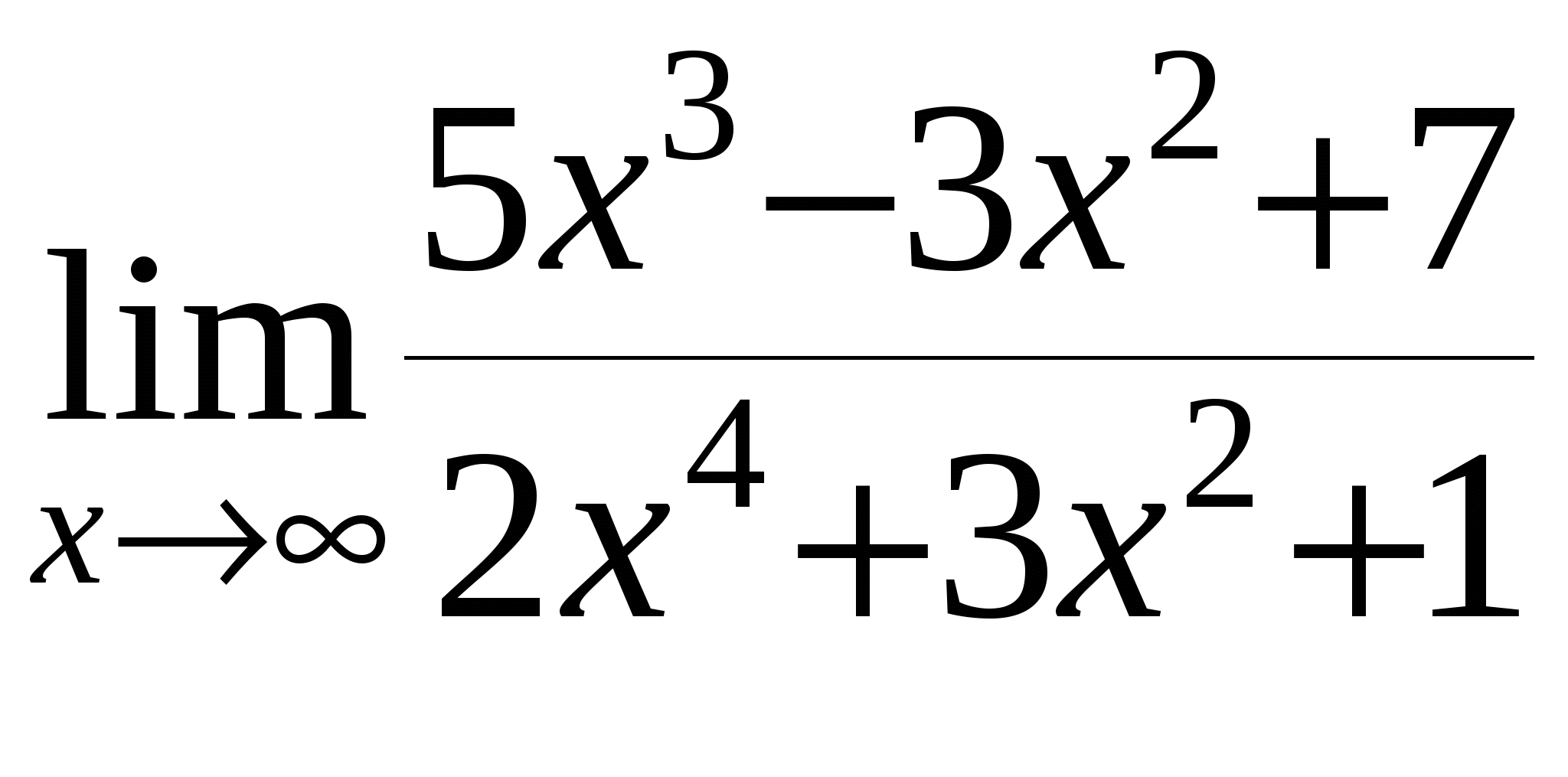
г)
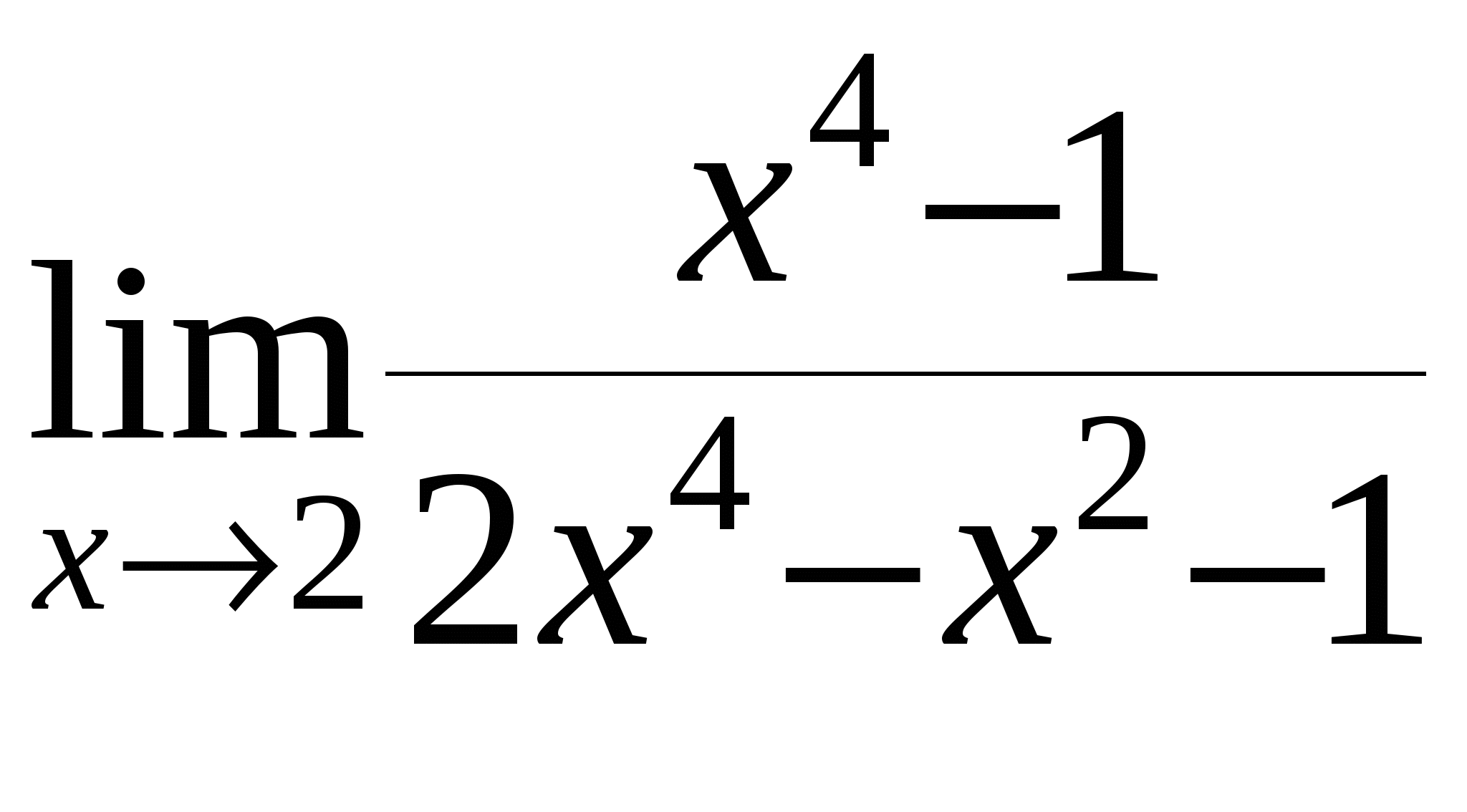
д)
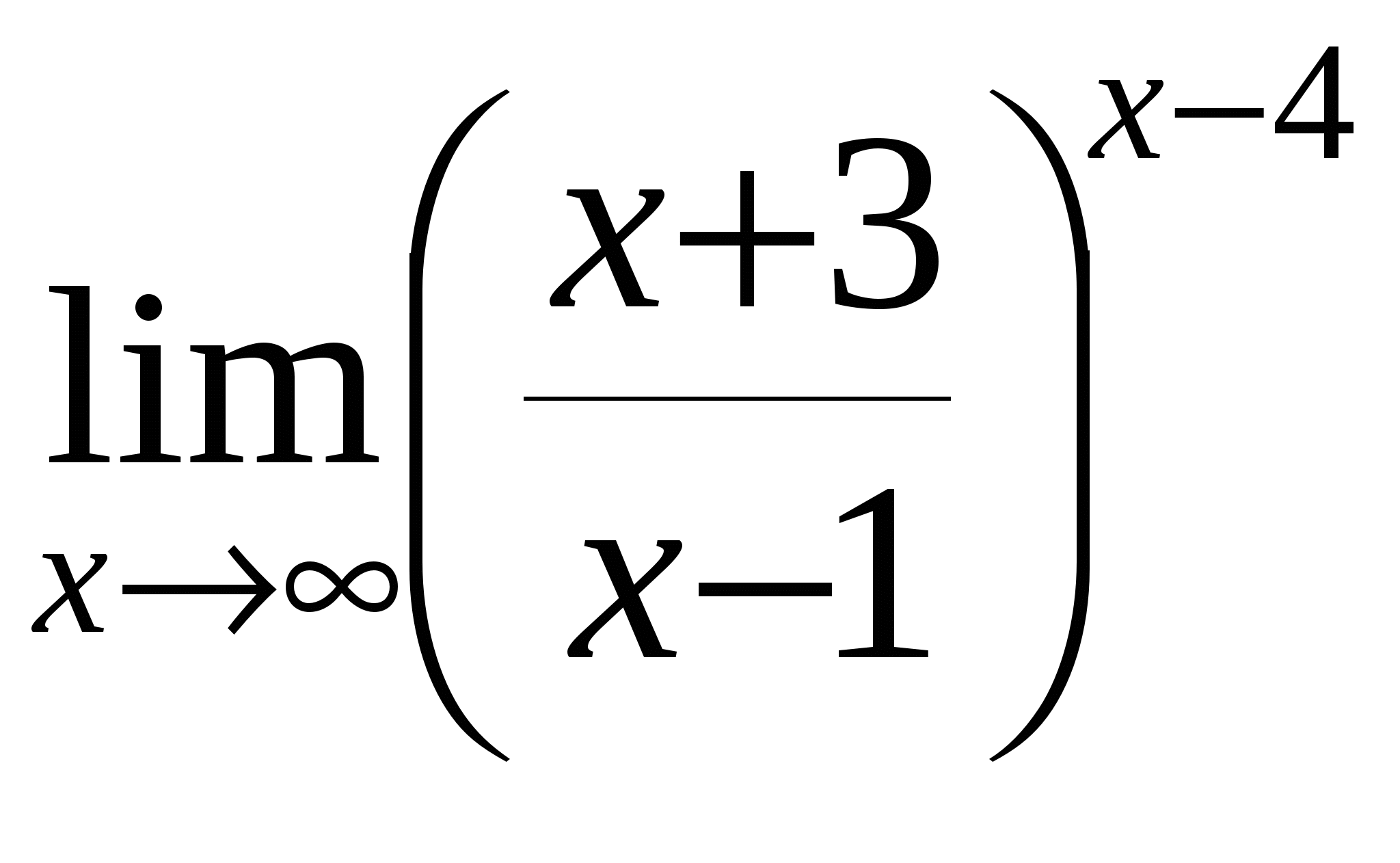
е)
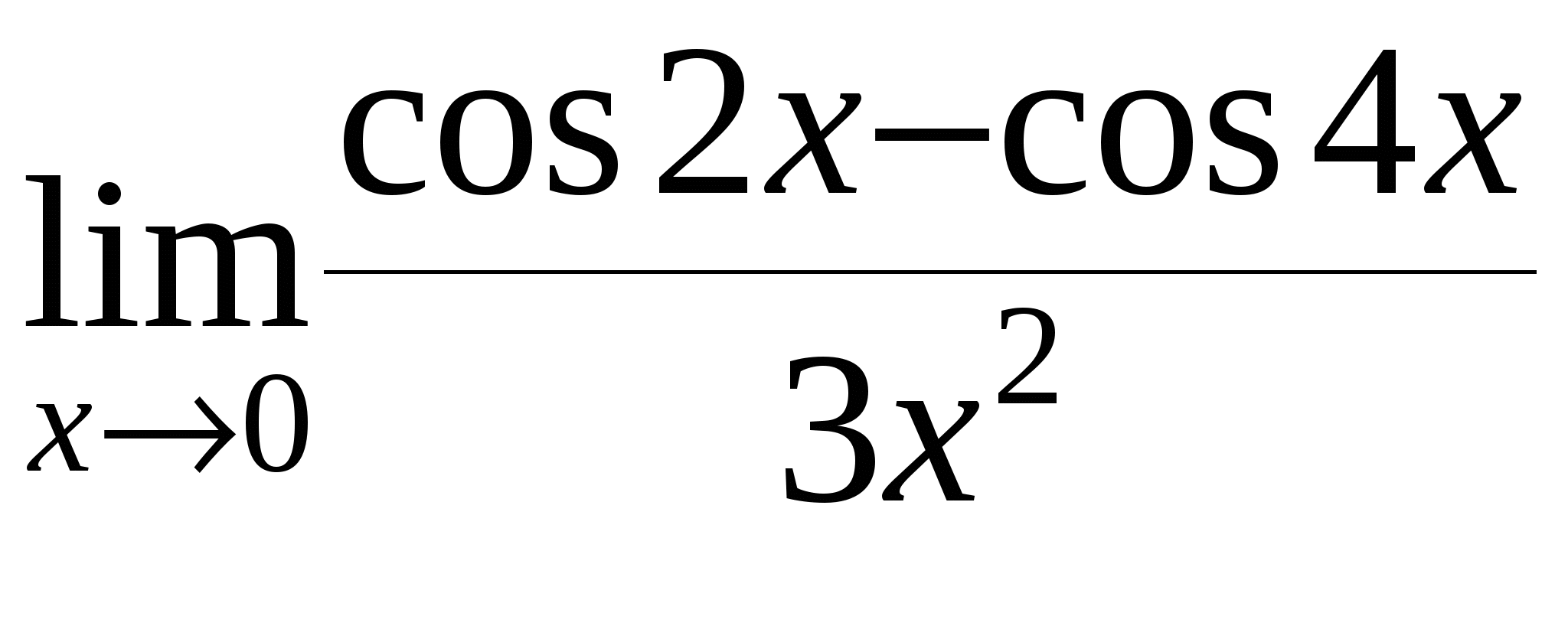
Найти предел функции
17
а)
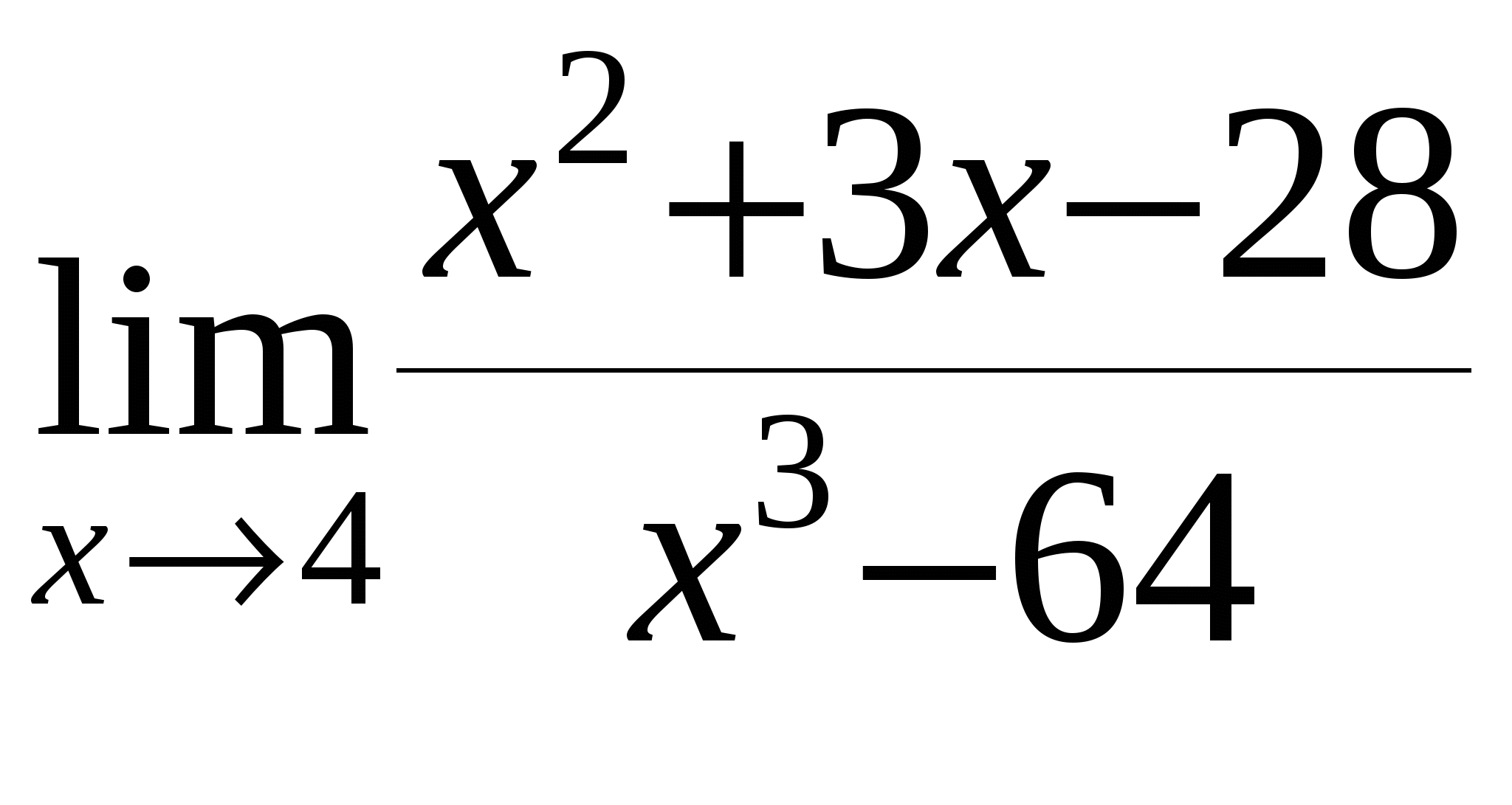
б)
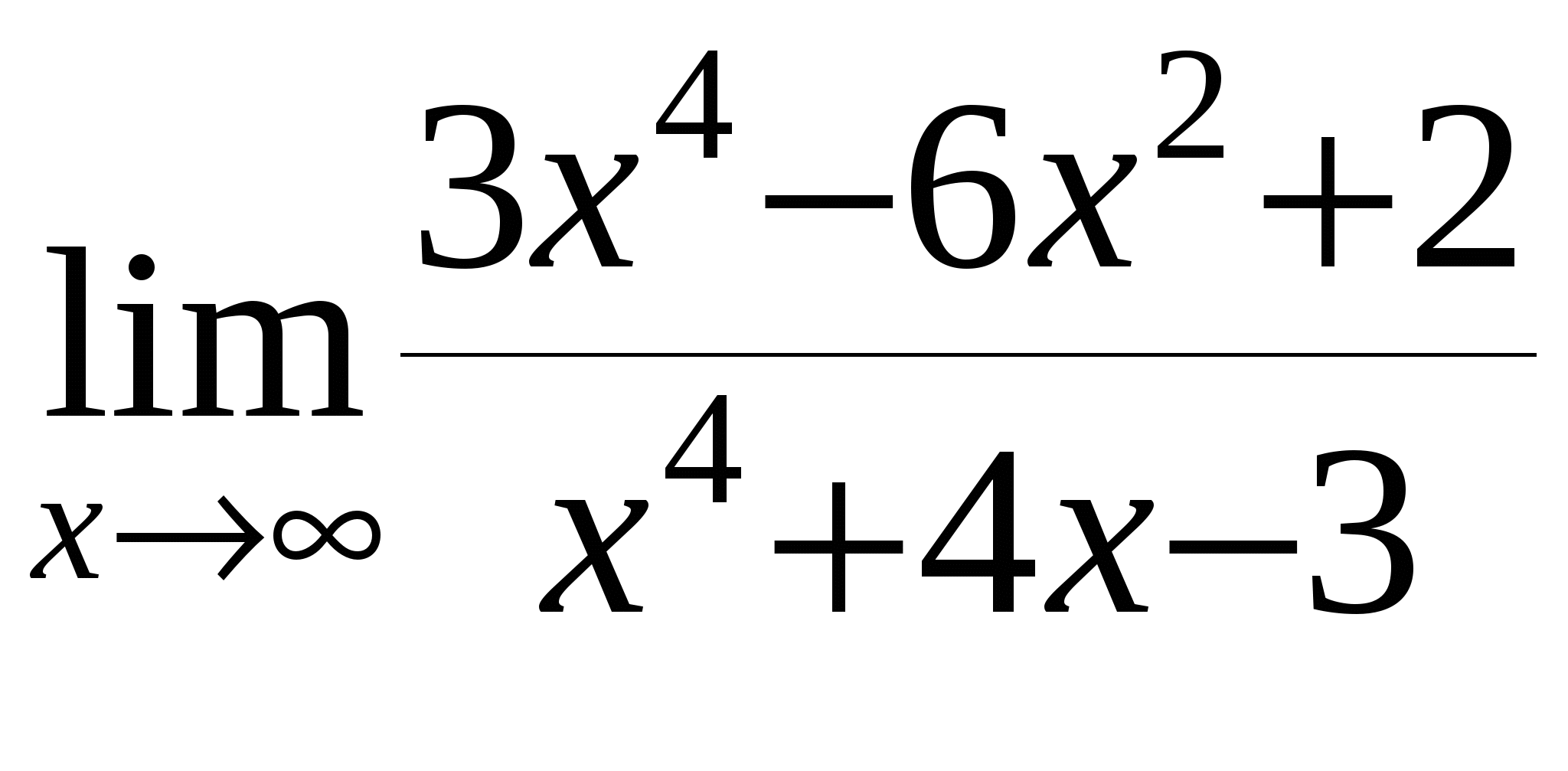
в)
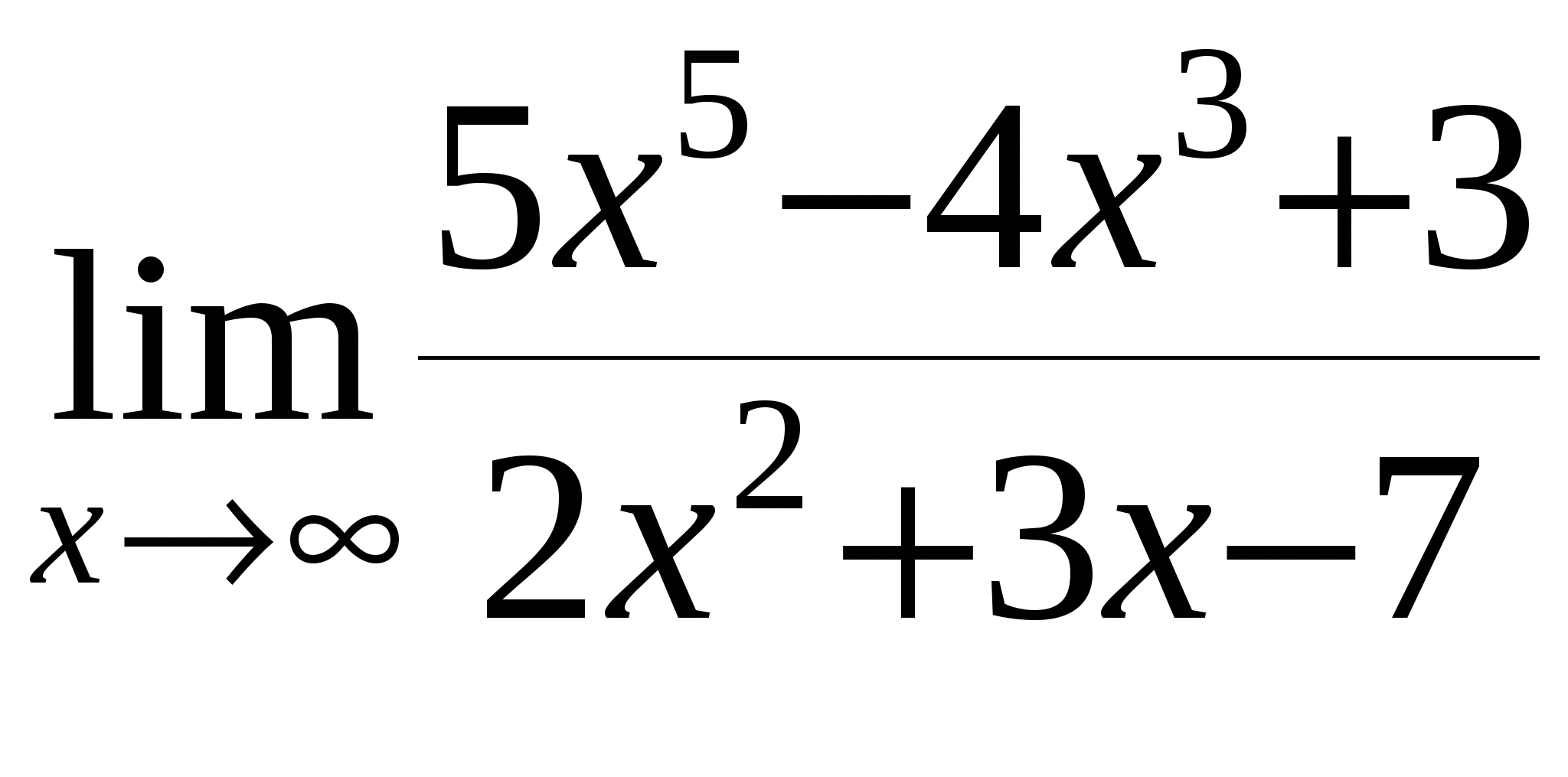
г)
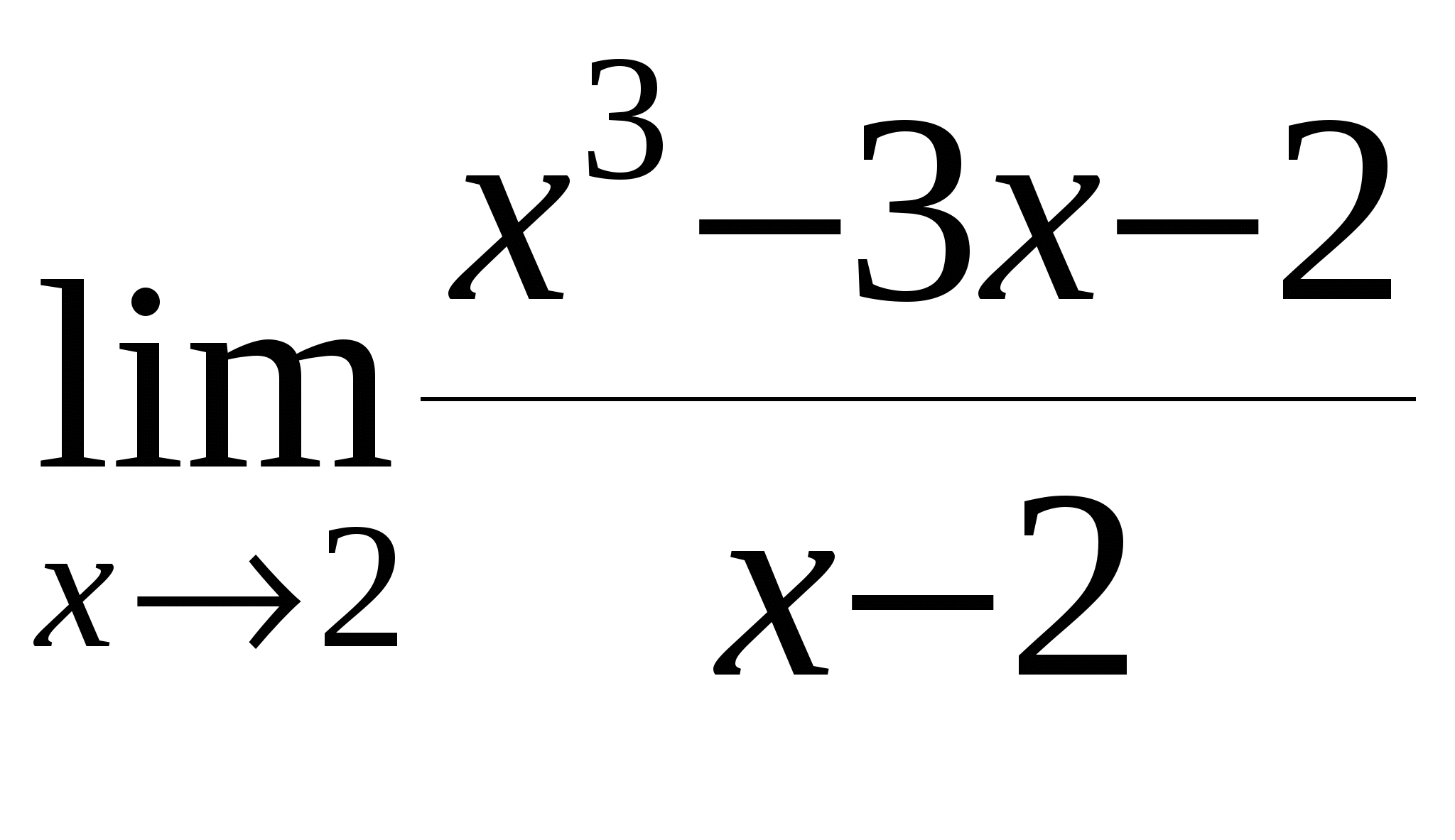
д)
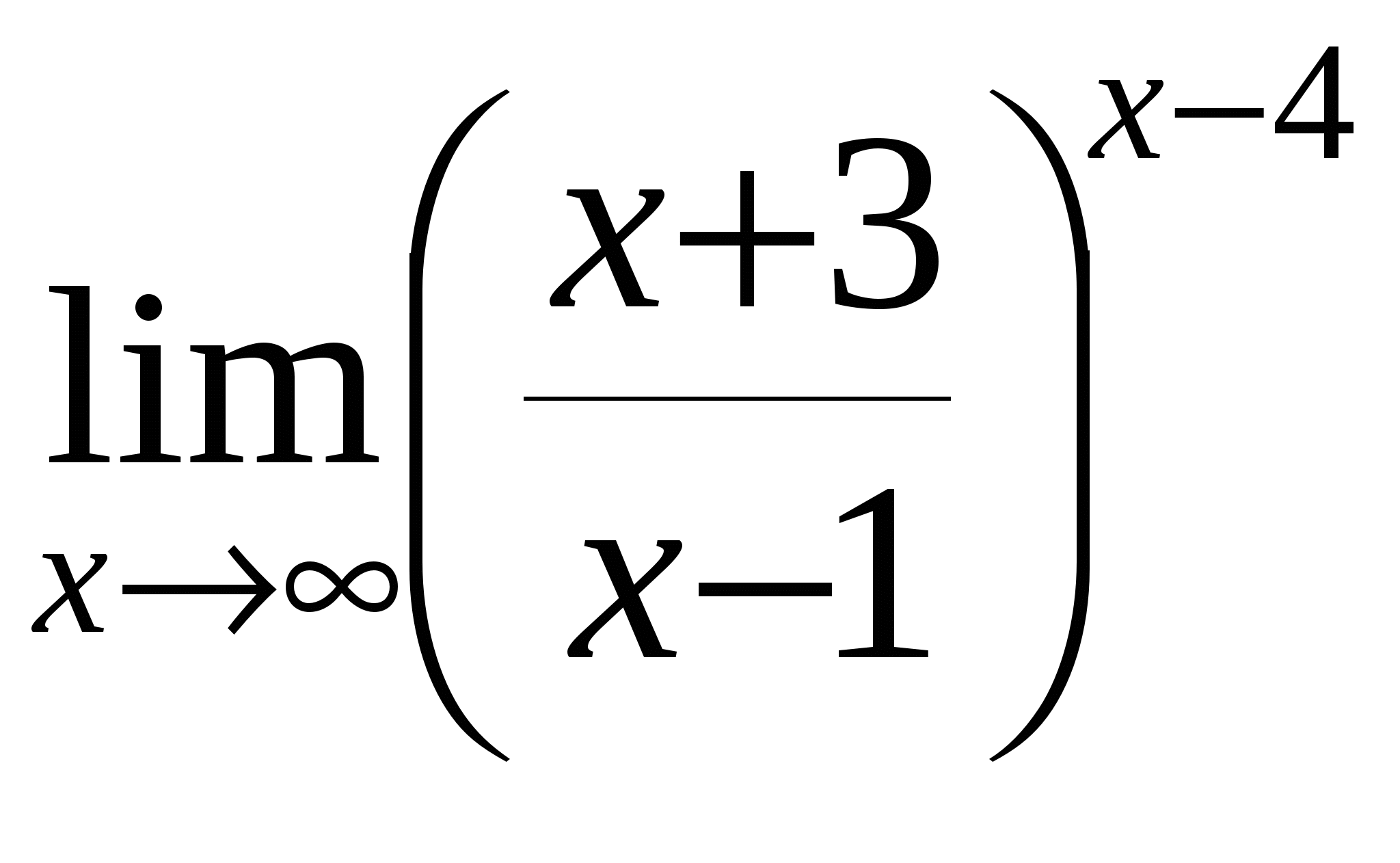
е)
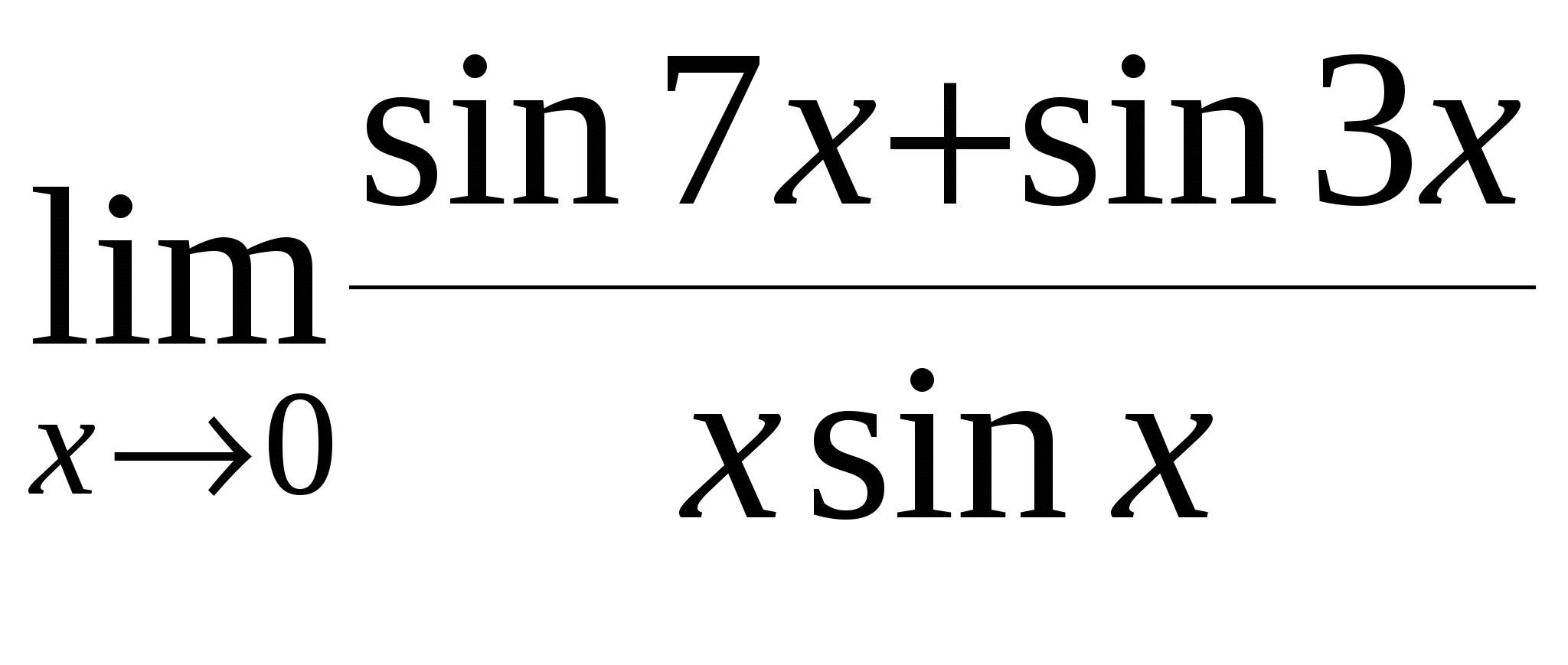
Найти предел функции
18
а)
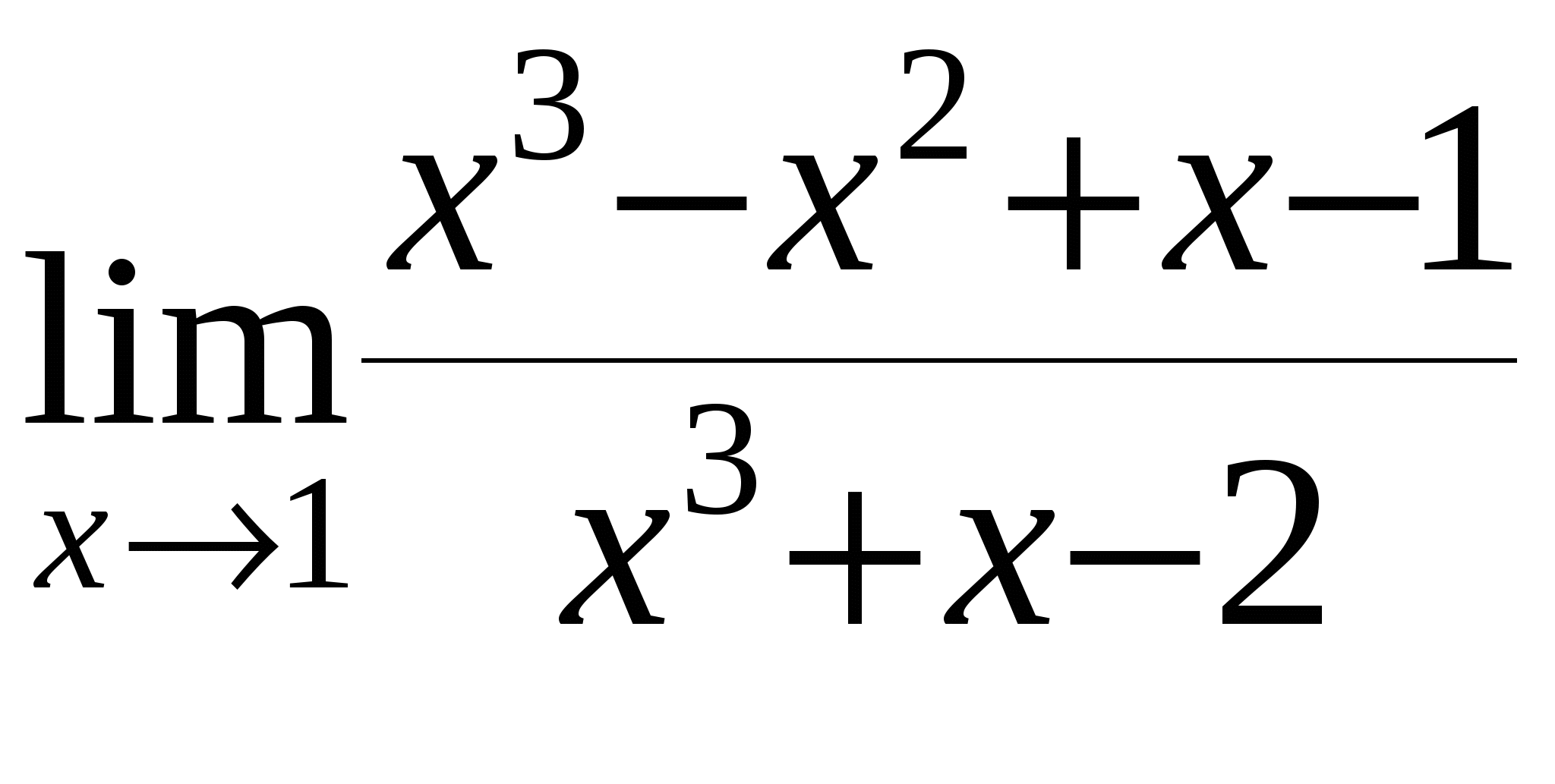
б)
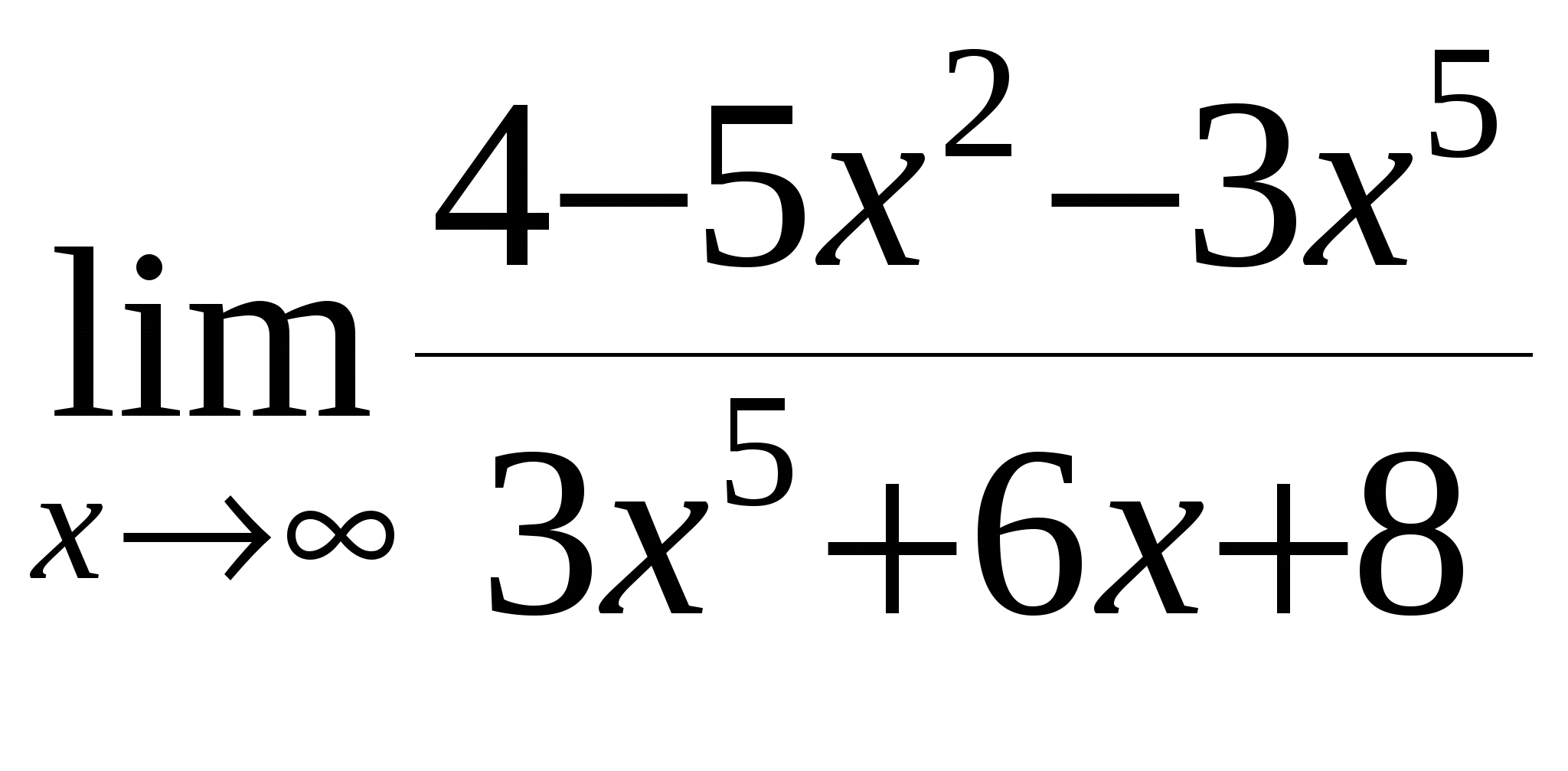
в)
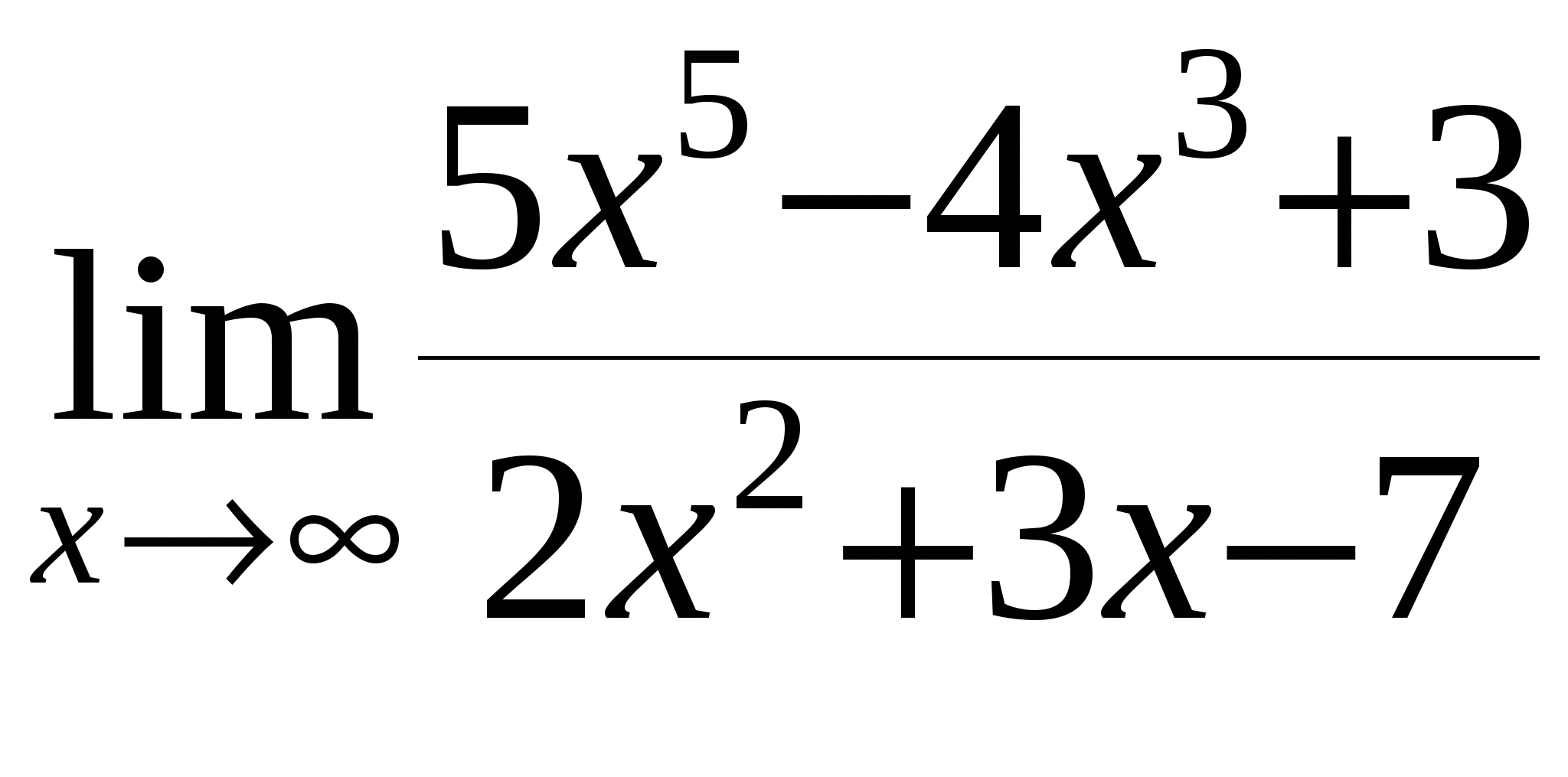
г)
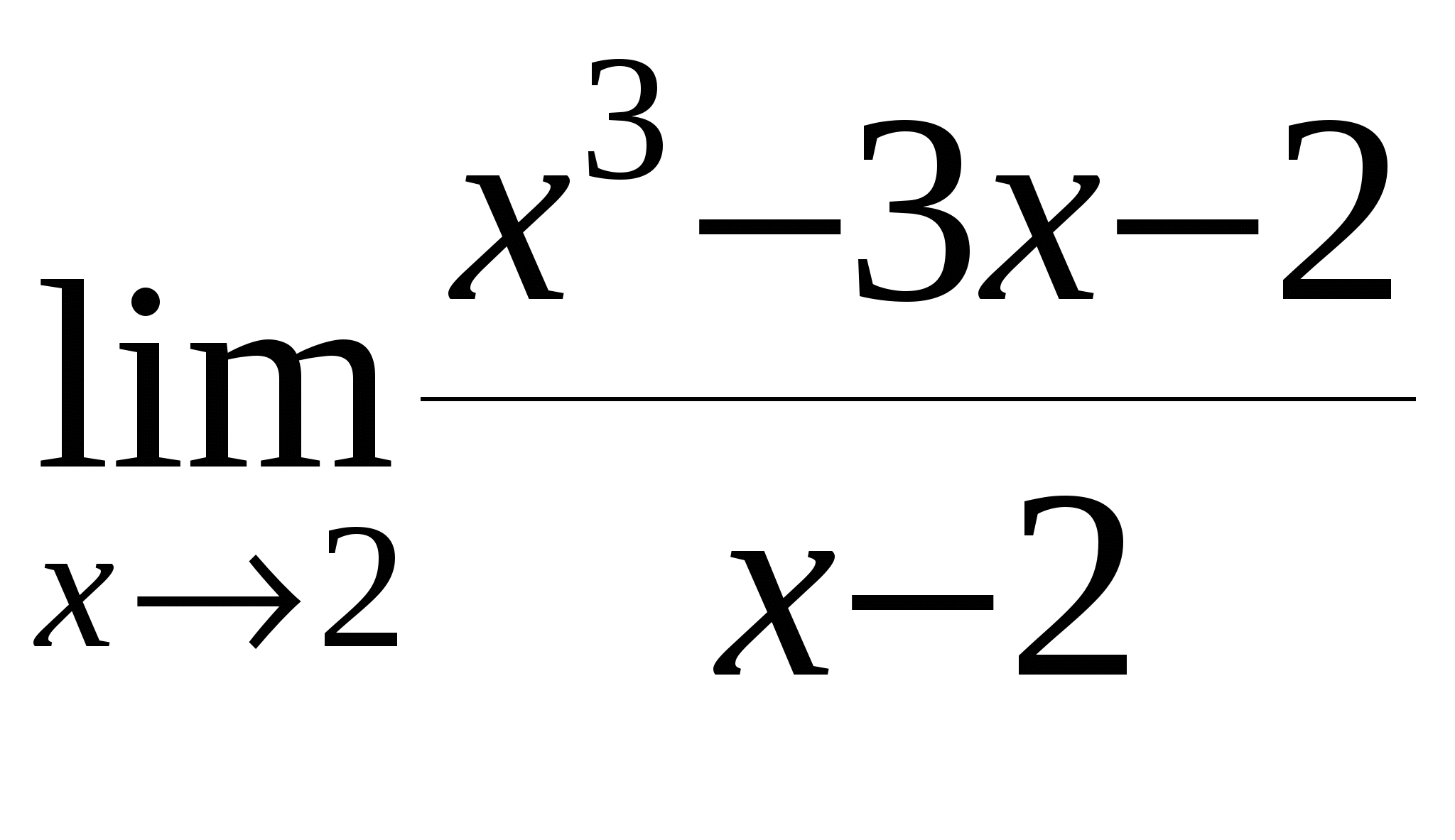
д)
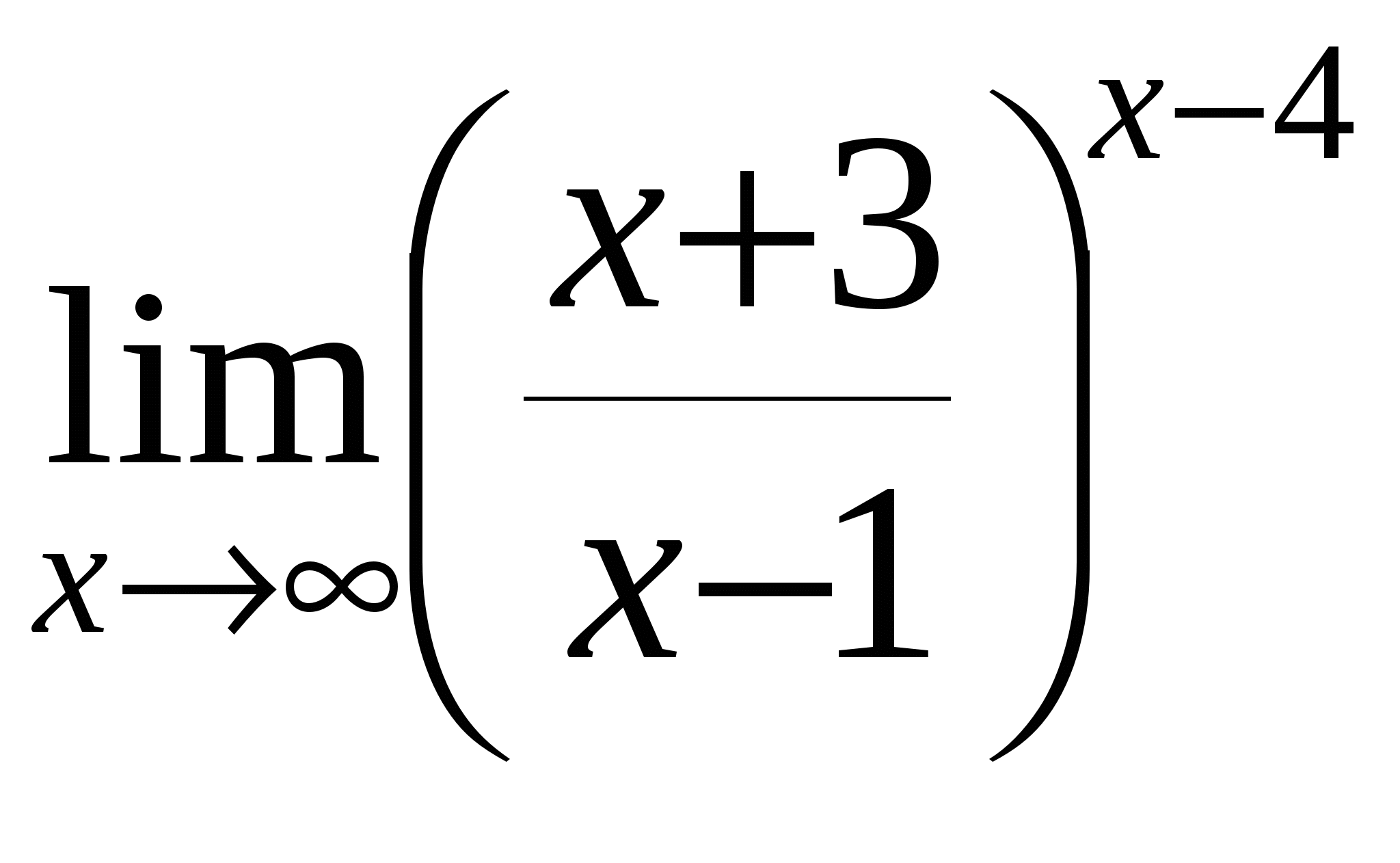
е)
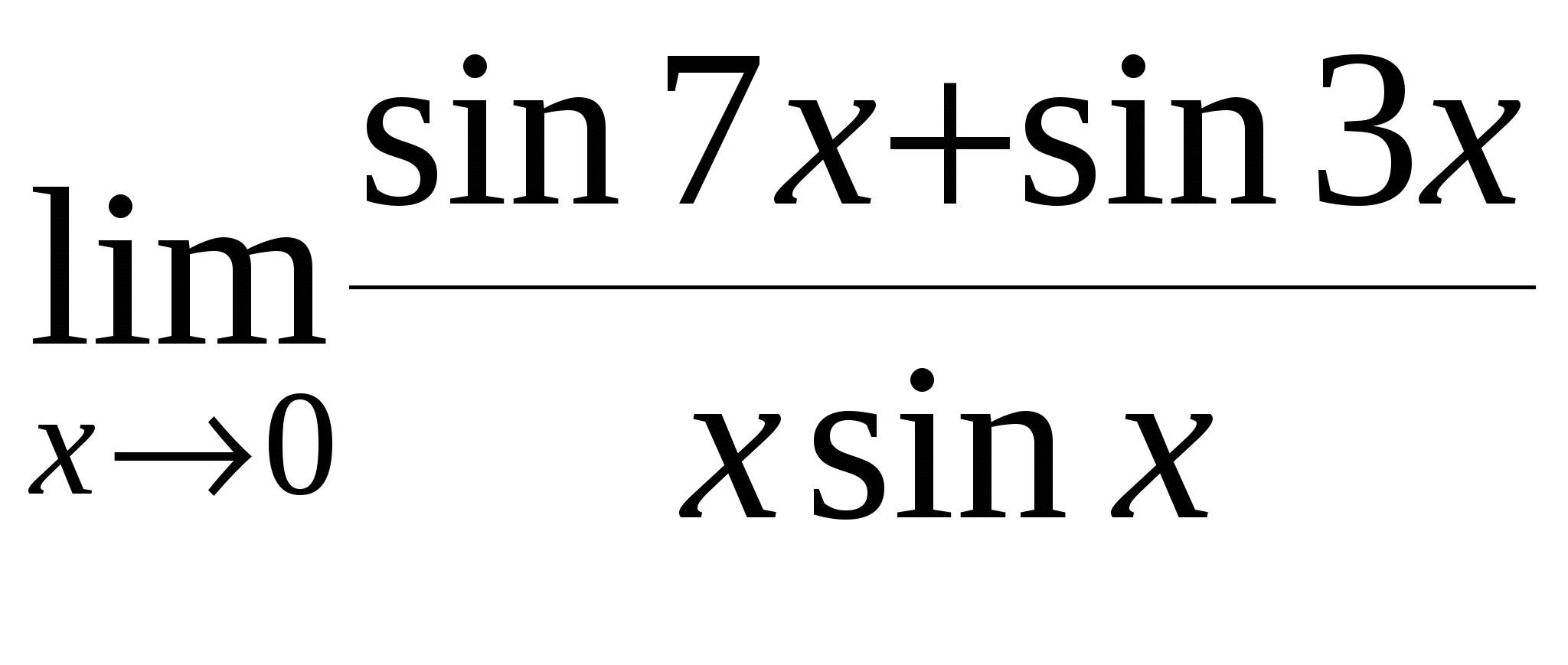
Контрольная работа № 5
Найти предел функции
19
а)
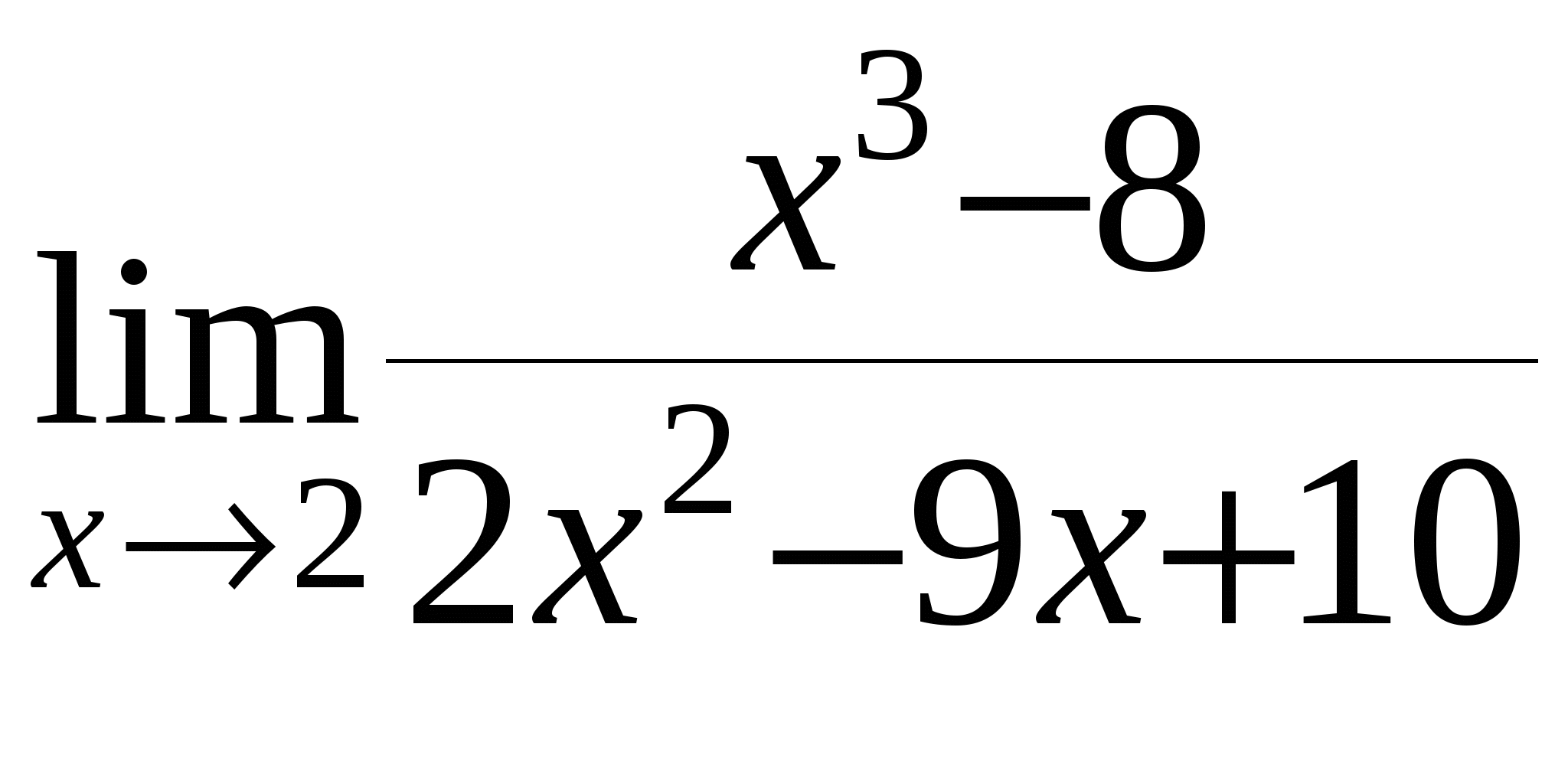
б)
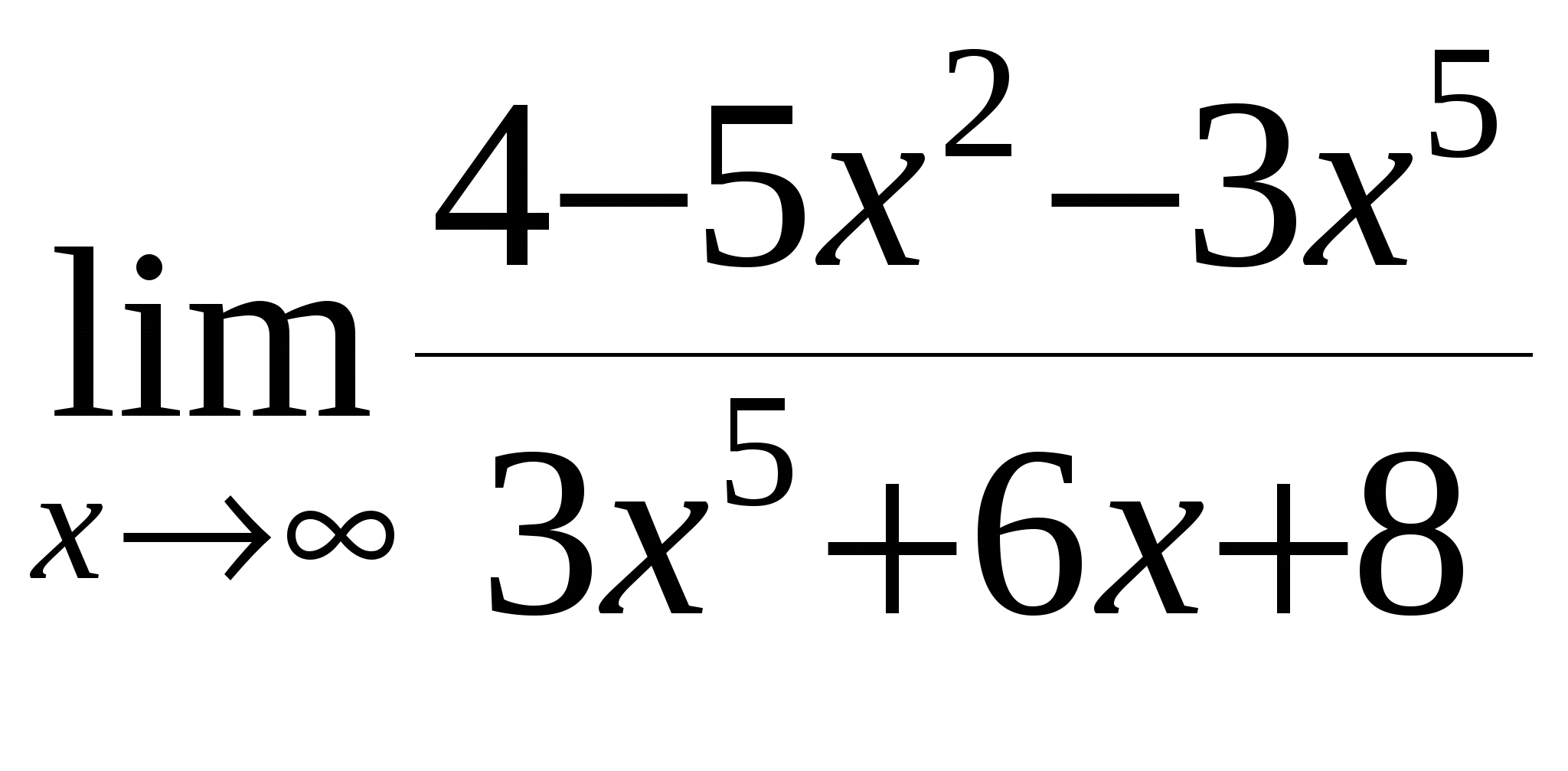
в)
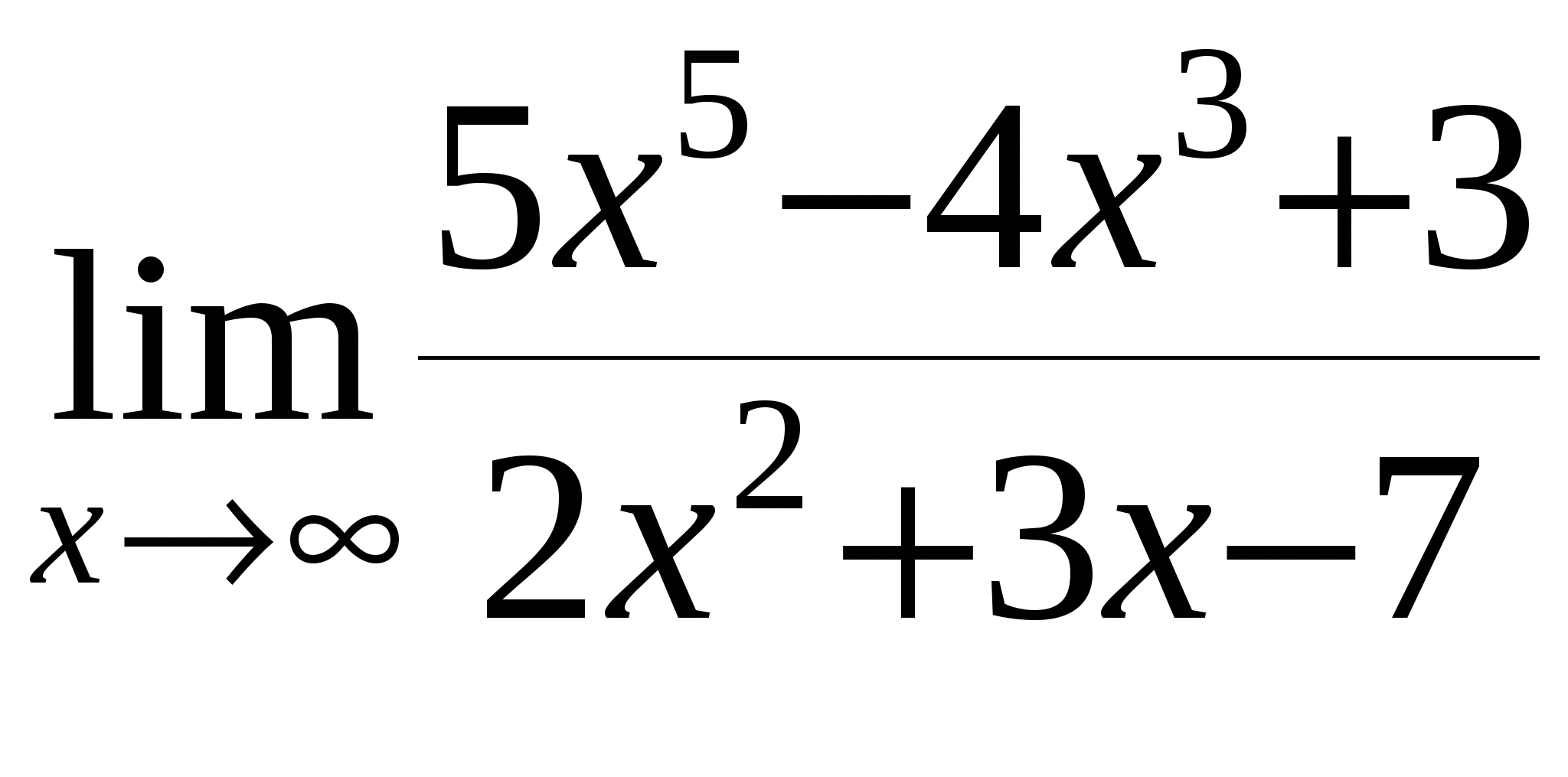
г)
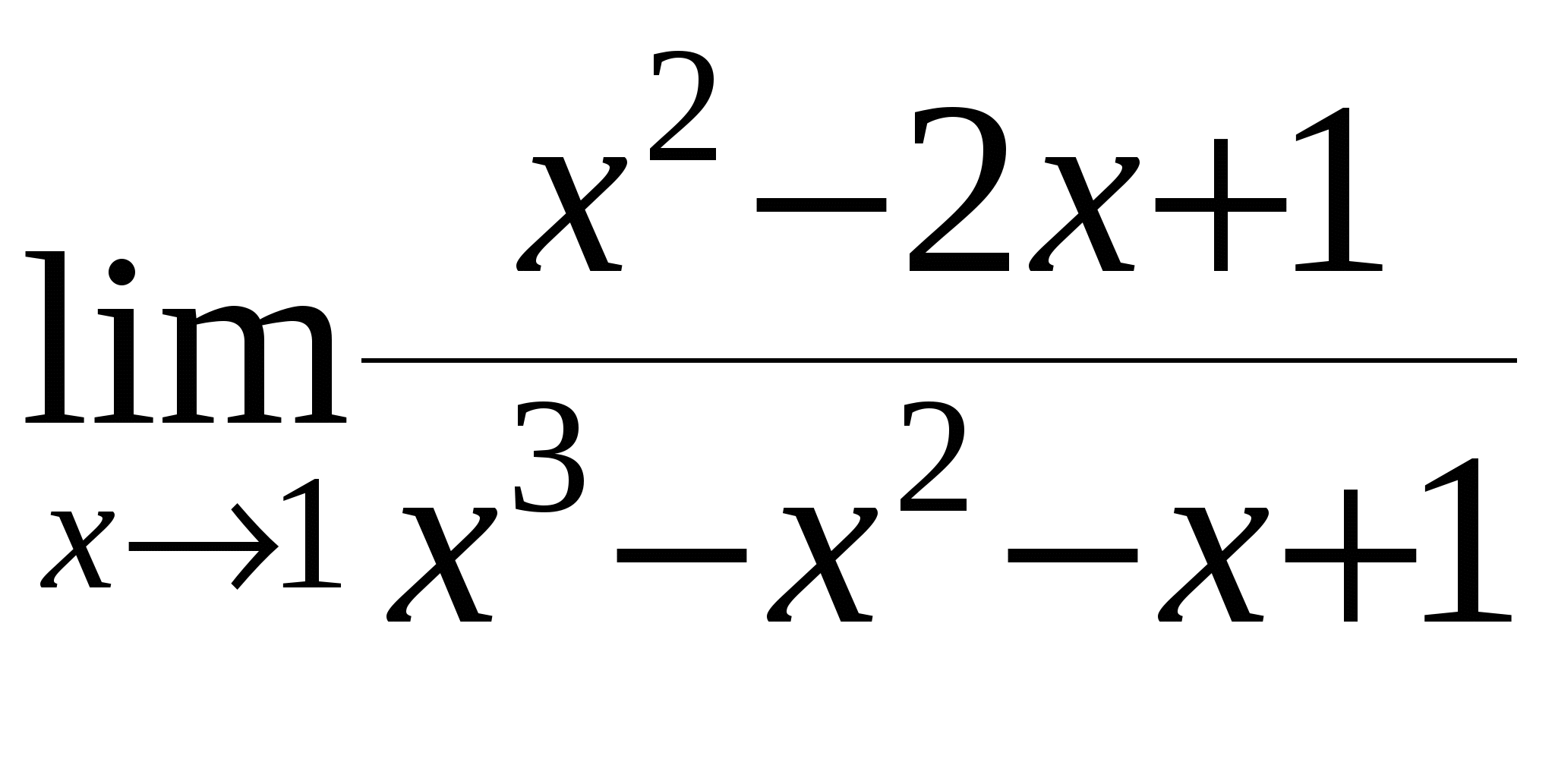
д)

е)
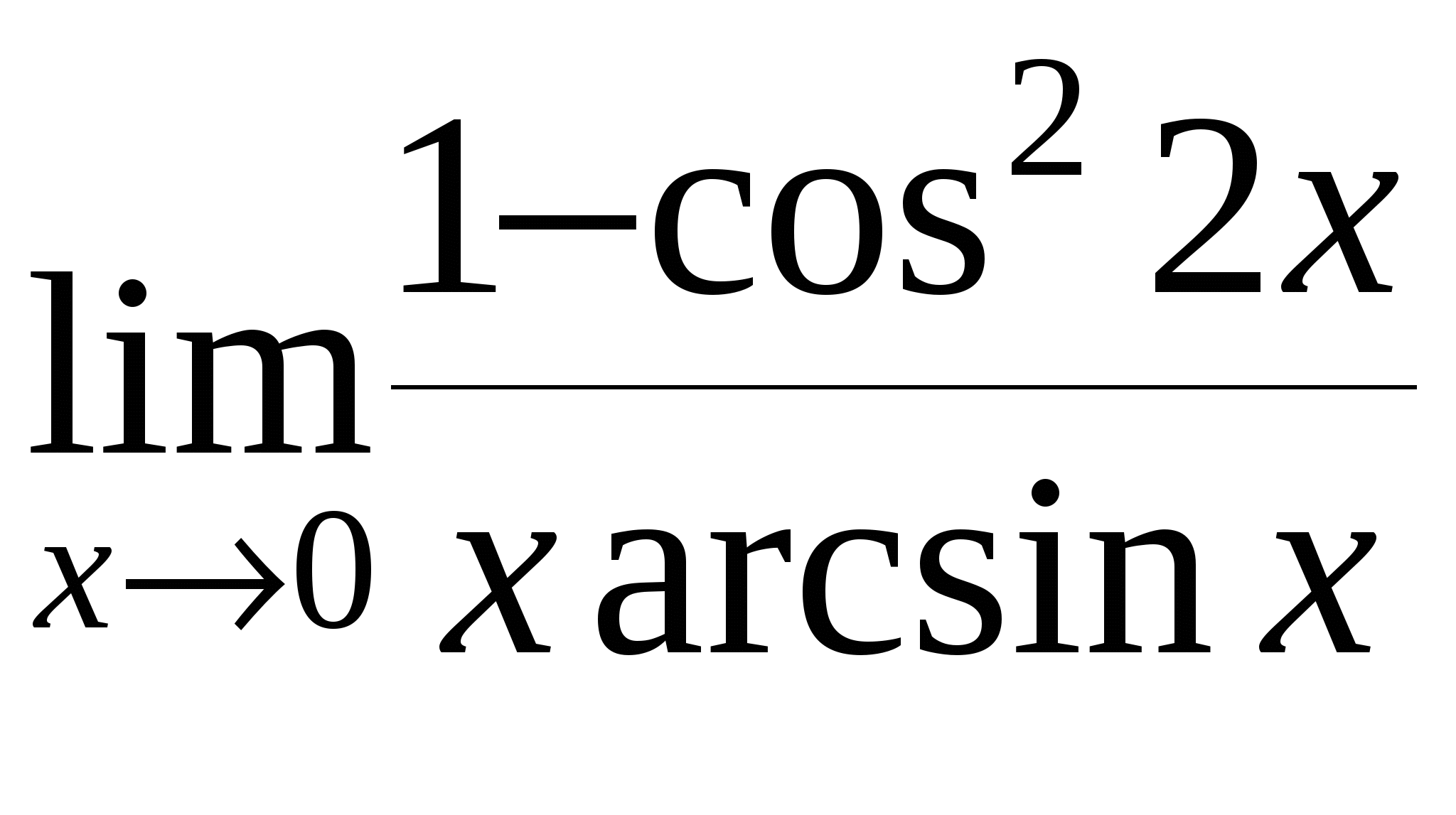
Найти предел функции
20
а)
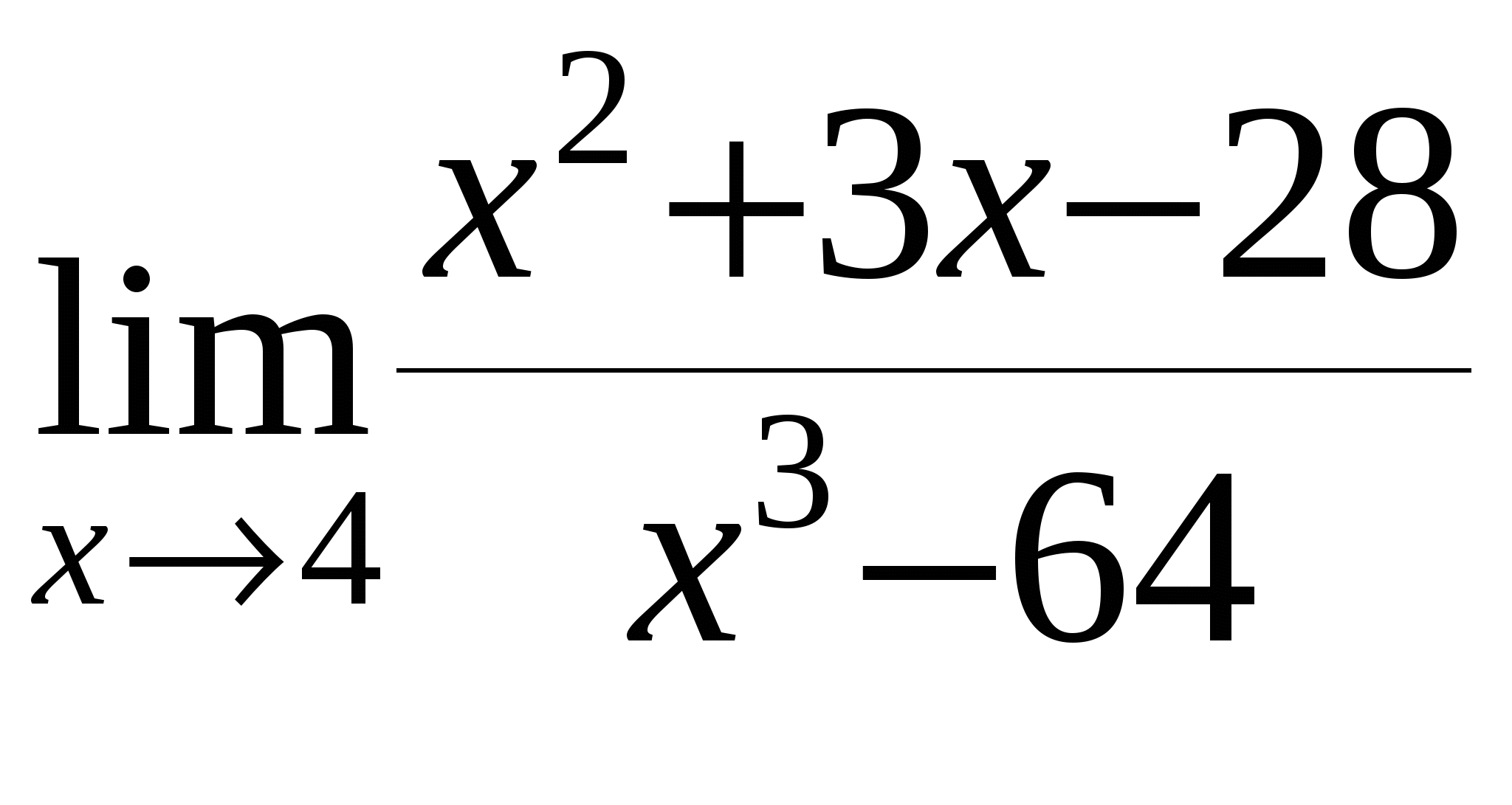
б)
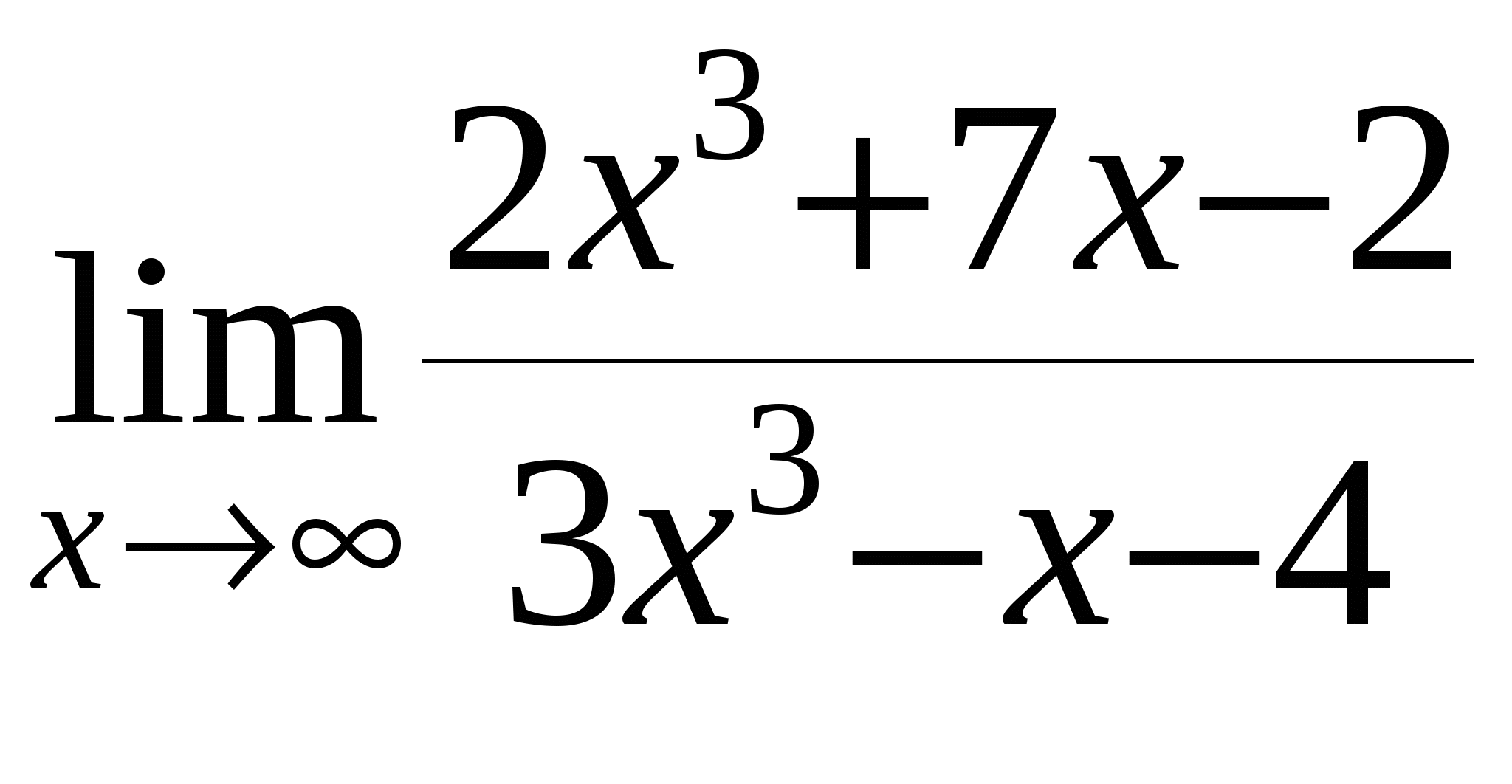
в)
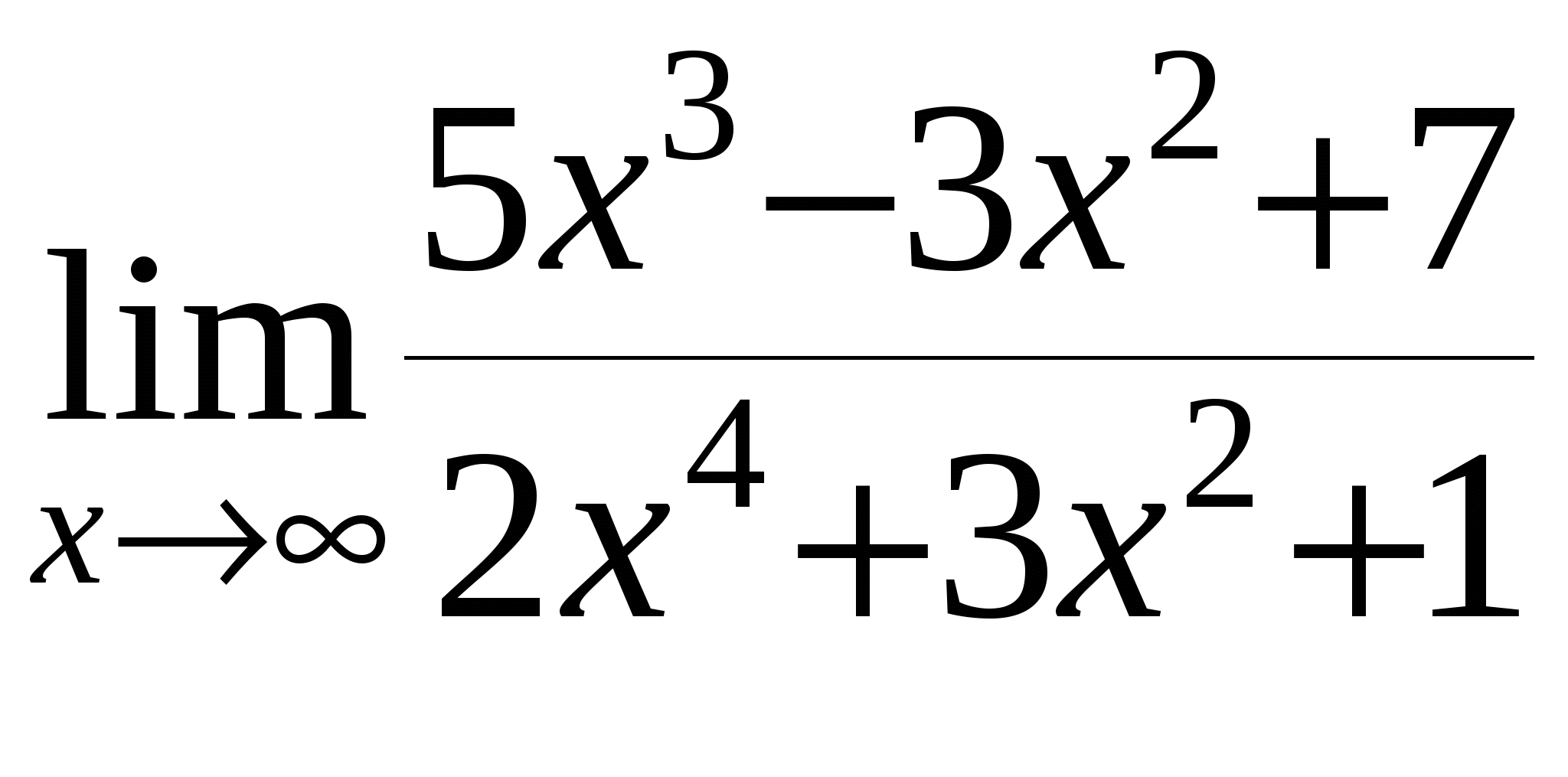
г)
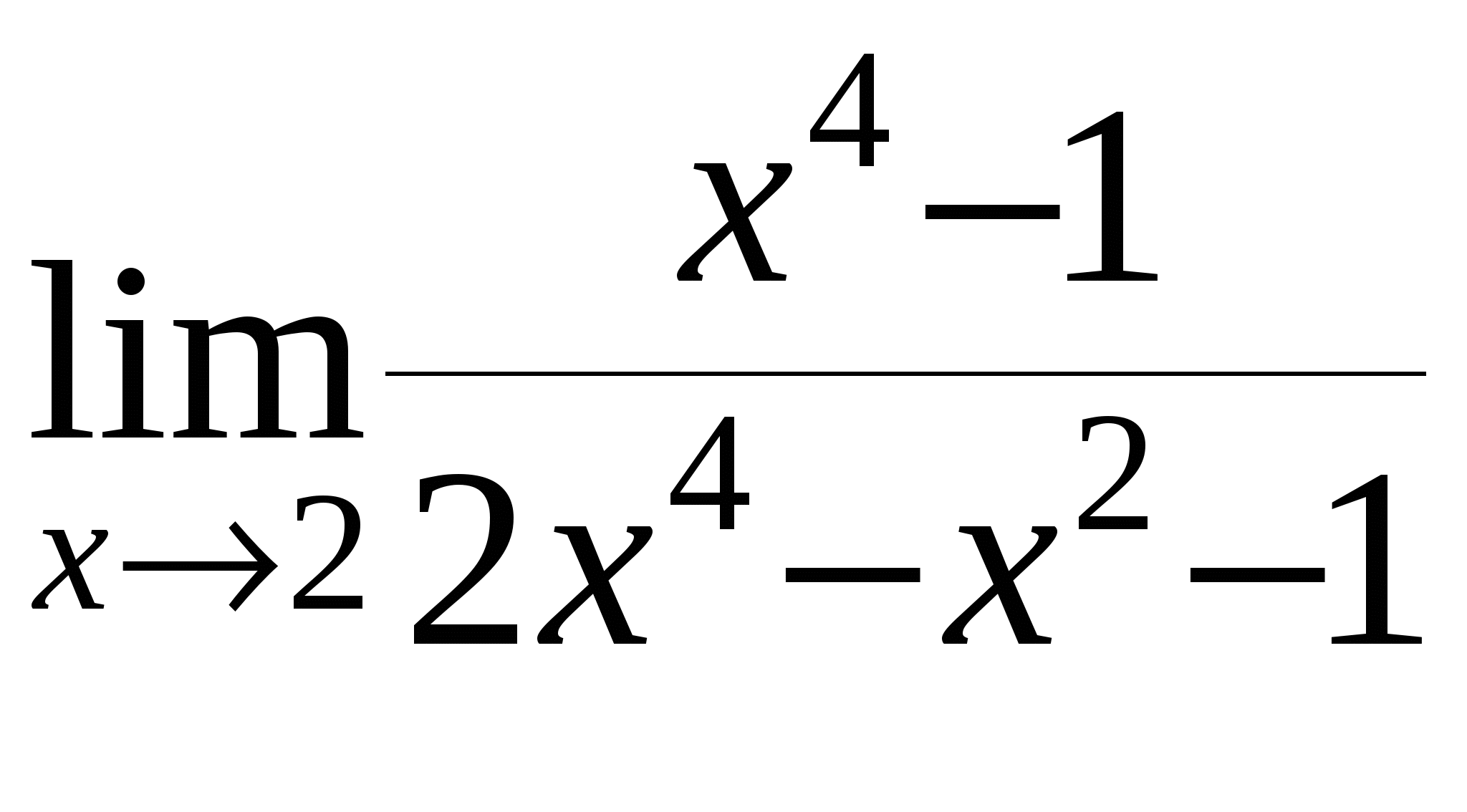
д)
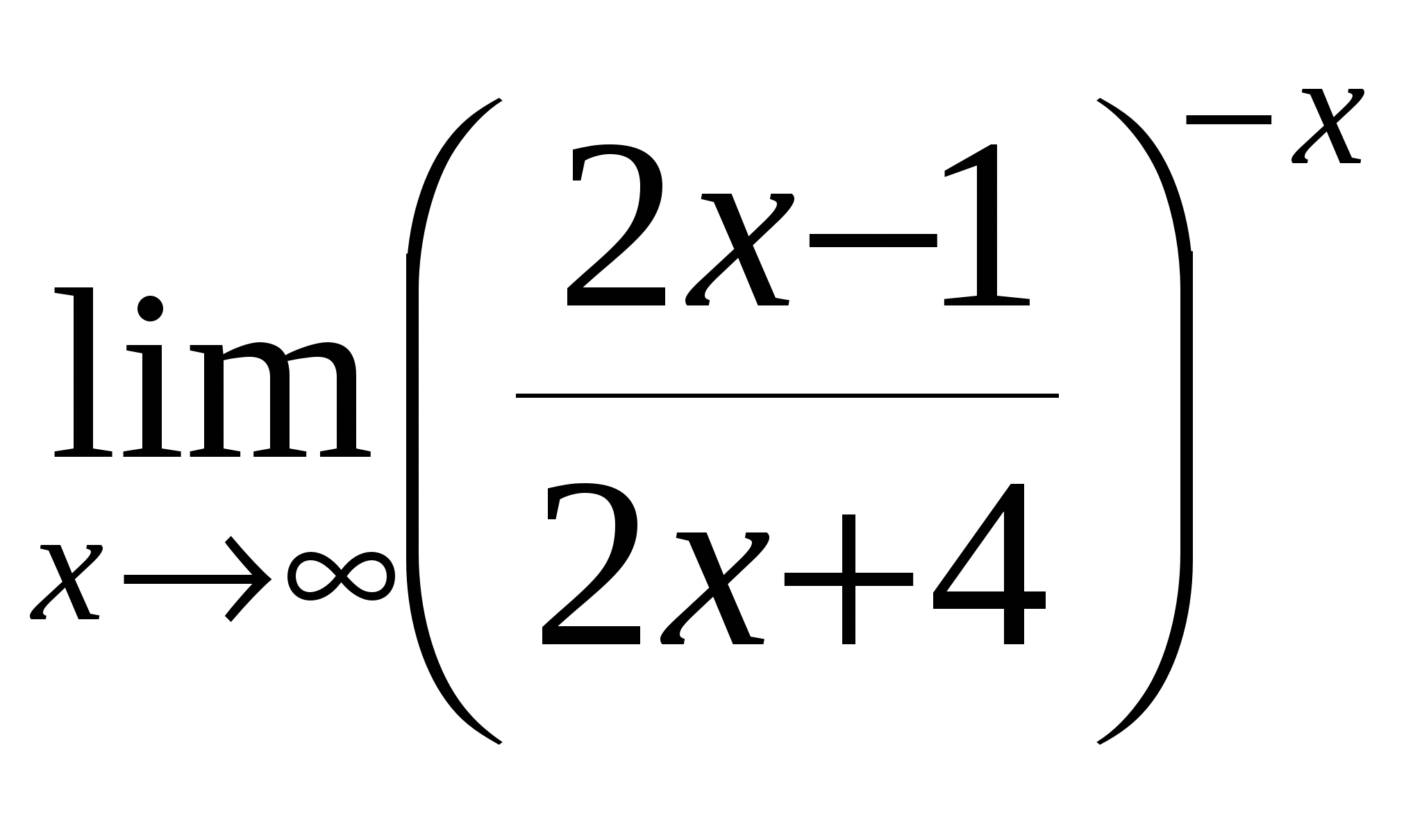
е)
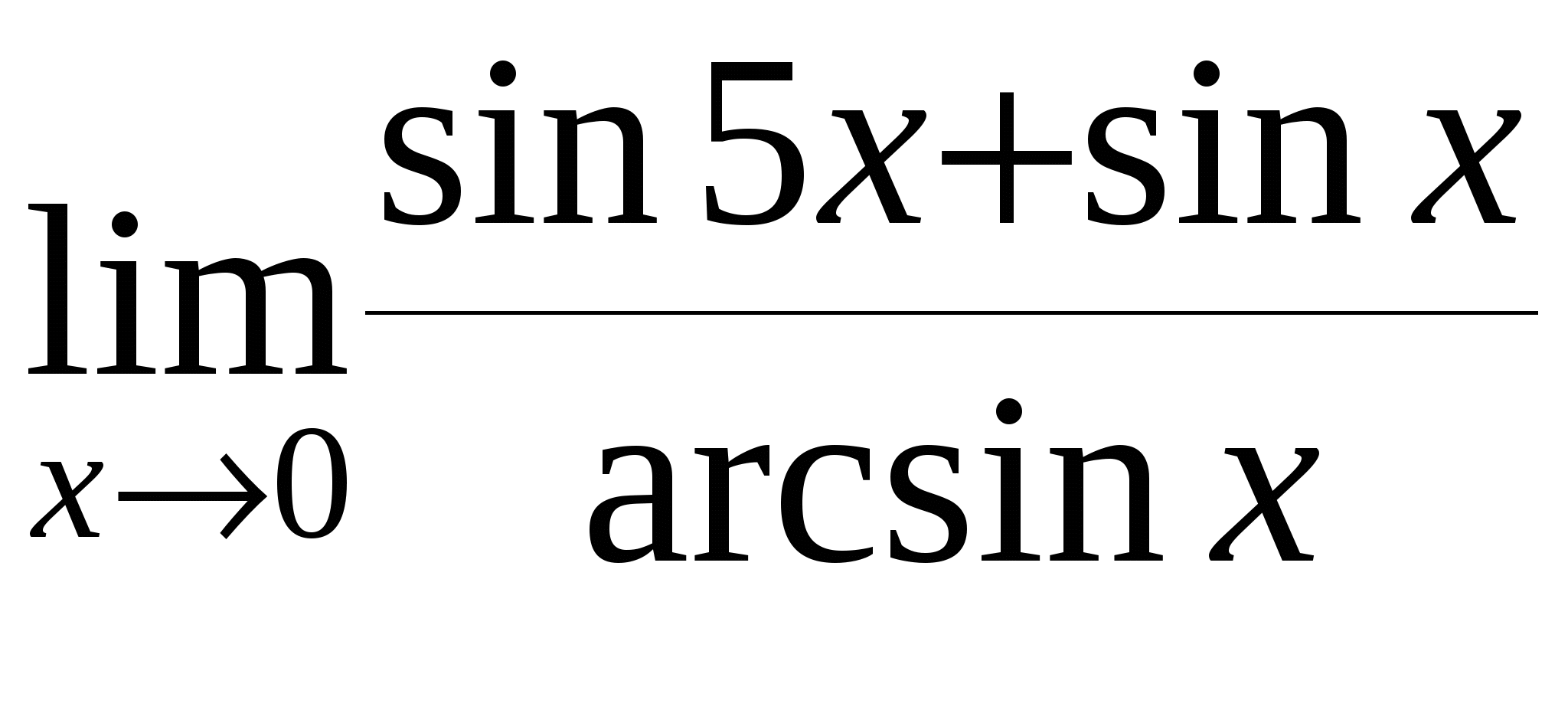
infourok.ru
 Вопросы для экзамена 1-й курс (1-й семестр) 1. Определения основных операций над множествами. 2. Законы дистрибутивности для операций над множествами. 3. Произведение множеств, простейшие свойства произведений
Вопросы для экзамена 1-й курс (1-й семестр) 1. Определения основных операций над множествами. 2. Законы дистрибутивности для операций над множествами. 3. Произведение множеств, простейшие свойства произведений
 7 «Архитектура» семестр Очная форма обучения. Бакалавры. I курс, семестр. Направление 7 «Архитертура». Дисциплина - «Математика» Содержание Содержание... Балльно - рейтинговая система... Самостоятельная
7 «Архитектура» семестр Очная форма обучения. Бакалавры. I курс, семестр. Направление 7 «Архитертура». Дисциплина - «Математика» Содержание Содержание... Балльно - рейтинговая система... Самостоятельная
 ВОПРОСЫ И ТИПОВЫЕ ЗАДАЧИ к итоговому экзамену по дисциплине «Математический анализ» Прикладная математика На устном экзамене студент получает два теоретических вопроса и две задачи Всего 66 вопросов год
ВОПРОСЫ И ТИПОВЫЕ ЗАДАЧИ к итоговому экзамену по дисциплине «Математический анализ» Прикладная математика На устном экзамене студент получает два теоретических вопроса и две задачи Всего 66 вопросов год
 Аннотация дисциплины «Математический анализ» Направления подготовки: 01.03.02 «Прикладная математика и информатика» Профиль подготовки: Системное программирование и компьютерные технологии" Квалификация
Аннотация дисциплины «Математический анализ» Направления подготовки: 01.03.02 «Прикладная математика и информатика» Профиль подготовки: Системное программирование и компьютерные технологии" Квалификация
 Математика для направления 8..6 торговое дело Контрольные вопросы по курсу Математика семестр. п мерные векторы. п мерное векторное пространство.. Матрицы. Линейные операции над матрицами. Умножение матриц..
Математика для направления 8..6 торговое дело Контрольные вопросы по курсу Математика семестр. п мерные векторы. п мерное векторное пространство.. Матрицы. Линейные операции над матрицами. Умножение матриц..
 ОГЛАВЛЕНИЕ Предисловие... 15 Глава I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 1. Матрицы... 16 1.1. Основные понятия... 16 1.2. Действия над матрицами... 17 2. Определители... 20 2.1. Основные понятия... 20 2.2. Свойства
ОГЛАВЛЕНИЕ Предисловие... 15 Глава I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 1. Матрицы... 16 1.1. Основные понятия... 16 1.2. Действия над матрицами... 17 2. Определители... 20 2.1. Основные понятия... 20 2.2. Свойства
 1. Цель и задачи дисциплины Математический анализ Целью освоения дисциплины «Математический анализ» является формирование у будущих специалистов знаний и умения применять математический аппарат и математические
1. Цель и задачи дисциплины Математический анализ Целью освоения дисциплины «Математический анализ» является формирование у будущих специалистов знаний и умения применять математический аппарат и математические
 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ КИБЕРНЕТИКИ, ИНФОРМАТИКИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ КИБЕРНЕТИКИ, ИНФОРМАТИКИ
 Государственное автономное образовательное учреждение высшего профессионального образования города Москвы «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ИНДУСТРИИ ТУРИЗМА ИМЕНИ ЮАСЕНКЕВИЧА» МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Государственное автономное образовательное учреждение высшего профессионального образования города Москвы «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ИНДУСТРИИ ТУРИЗМА ИМЕНИ ЮАСЕНКЕВИЧА» МАТЕМАТИЧЕСКИЙ АНАЛИЗ
 Федеральное государственное образовательное учреждение высшего профессионального образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» (ФИНУНИВЕРСИТЕТ) Кафедра «Математика» ГАПостовалова
Федеральное государственное образовательное учреждение высшего профессионального образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» (ФИНУНИВЕРСИТЕТ) Кафедра «Математика» ГАПостовалова
 Функция. 1 1. Какие числа образуют множество действительных чисел? 2. Что называется числовой осью? 3. Что называется интервалом? 4. Определить понятие окрестности точки. 5. Что называется абсолютной величиной?
Функция. 1 1. Какие числа образуют множество действительных чисел? 2. Что называется числовой осью? 3. Что называется интервалом? 4. Определить понятие окрестности точки. 5. Что называется абсолютной величиной?
 2 3 1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА В связи с возросшей ролью математики в современной науке и технике будущие экологи, инженеры нуждаются в серьезной математической подготовке. Изучение математики развивает
2 3 1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА В связи с возросшей ролью математики в современной науке и технике будущие экологи, инженеры нуждаются в серьезной математической подготовке. Изучение математики развивает
 МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»
 ОГЛАВЛЕНИЕ Предисловие 3 Введение 5 Часть первая. Математический анализ функций одной переменной 10 Глава I. Вещественные числа 10 1. Множества. Обозначения. Логические символы 10 2. Вещественные числа
ОГЛАВЛЕНИЕ Предисловие 3 Введение 5 Часть первая. Математический анализ функций одной переменной 10 Глава I. Вещественные числа 10 1. Множества. Обозначения. Логические символы 10 2. Вещественные числа
 . Цели и задачи дисциплины Целями освоения дисциплины «Математический анализ» являются: - получение базовых знаний и формирование основных навыков по математическому анализу, необходимых для решения задач,
. Цели и задачи дисциплины Целями освоения дисциплины «Математический анализ» являются: - получение базовых знаний и формирование основных навыков по математическому анализу, необходимых для решения задач,
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждениевысшего образования «УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждениевысшего образования «УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
 Направление: «Строительство» Вопросы и задачи к экзамену семестр. Матрицы: определение, виды. Действия с матрицами: транспонирование, сложение, умножение на число, умножение матриц. 2. Элементарные преобразования
Направление: «Строительство» Вопросы и задачи к экзамену семестр. Матрицы: определение, виды. Действия с матрицами: транспонирование, сложение, умножение на число, умножение матриц. 2. Элементарные преобразования
 Уметь: Тема 1. Предел и непрерывность функции Вычислять пределы функций и числовых последовательностей, используя различные приемы, в том числе, замечательные пределы, проводить сравнение бесконечно малых
Уметь: Тема 1. Предел и непрерывность функции Вычислять пределы функций и числовых последовательностей, используя различные приемы, в том числе, замечательные пределы, проводить сравнение бесконечно малых
 2 ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Учебная программа по дисциплине «Математический анализ» разработана для специальности «Прикладная информатика» шифр 1-31 03 07-03 высших учебных заведений. Целью изучения дисциплины
2 ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Учебная программа по дисциплине «Математический анализ» разработана для специальности «Прикладная информатика» шифр 1-31 03 07-03 высших учебных заведений. Целью изучения дисциплины
 Алгебра и начала анализа, ХI АЛГЕБРА И НАЧАЛА АНАЛИЗА По Положению о государственной (итоговой) аттестации выпускников XI(XII) классов общеобразовательных учреждений Российской Федерации учащиеся сдают
Алгебра и начала анализа, ХI АЛГЕБРА И НАЧАЛА АНАЛИЗА По Положению о государственной (итоговой) аттестации выпускников XI(XII) классов общеобразовательных учреждений Российской Федерации учащиеся сдают
 МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Воронежский государственный аграрный университет имени императора
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Воронежский государственный аграрный университет имени императора
 Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» (ФИНАНСОВЫЙ УНИВЕРСИТЕТ) Кафедра «Математика-1»
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» (ФИНАНСОВЫЙ УНИВЕРСИТЕТ) Кафедра «Математика-1»
 Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» (ФИНАНСОВЫЙ УНИВЕРСИТЕТ) Кафедра «Математика-»
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» (ФИНАНСОВЫЙ УНИВЕРСИТЕТ) Кафедра «Математика-»
 3.2 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПРЕПОДАВАТЕЛЯМ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ Семестр I Раздел 1. Векторная и линейная алгебра. Практическое занятие 1 1. Цель: Рассмотреть задачи на вычисление определителей второго
3.2 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПРЕПОДАВАТЕЛЯМ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ Семестр I Раздел 1. Векторная и линейная алгебра. Практическое занятие 1 1. Цель: Рассмотреть задачи на вычисление определителей второго
 2 1. ЦЕЛЬ И ЗАДАЧИ ДИСЦИПЛИНЫ Целью дисциплины является формирование представлений о понятиях и методах математического анализа, его месте и роли в системе математических наук, использовании в естественных
2 1. ЦЕЛЬ И ЗАДАЧИ ДИСЦИПЛИНЫ Целью дисциплины является формирование представлений о понятиях и методах математического анализа, его месте и роли в системе математических наук, использовании в естественных
 СЫКТЫВКАРСКИЙ ЛЕСНОЙ ИНСТИТУТ Кафедра высшей математики МАТЕМАТИЧЕСКИЙ АНАЛИЗ САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ Методические указания для подготовки дипломированных специалистов по направлению 654700 «Информационные
СЫКТЫВКАРСКИЙ ЛЕСНОЙ ИНСТИТУТ Кафедра высшей математики МАТЕМАТИЧЕСКИЙ АНАЛИЗ САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ Методические указания для подготовки дипломированных специалистов по направлению 654700 «Информационные
 МАТЕМАТИЧЕСКИЙ АНАЛИЗ Ориентировочный план семинаров, 1 семестр 1. Вещественные числа. 1.1. Аксиоматика вещественных чисел. «Школьное» представление о числе как модель поля действительных чисел. 33 1.2.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ Ориентировочный план семинаров, 1 семестр 1. Вещественные числа. 1.1. Аксиоматика вещественных чисел. «Школьное» представление о числе как модель поля действительных чисел. 33 1.2.
docplayer.ru
Контрольная работа №1
«Введение в математический анализ»
ВАРИАНТ 0
1. 2.
2.
3. 4.
4. 5.
5.
6. 7.
7.
8. 9.
9.
10. Вычислить односторонние пределы функции в точках :
:
 .
.
Нарисовать график функции в окрестности этих точек.
11.  12.
12.
Примеры решения задач
Пример 1.
Доказать, пользуясь определением по Коши предела функции в точке, что  .
.
Решение.
По определению предела функции в точке ( по Коши):

 >0>0:x: 0<|x-1|<
>0>0:x: 0<|x-1|< .
.
Выберем произвольное число >0. Найдем для него число>0, такое, что для всехх, удовлетворяющих условию 0<|x-1|<выполнено неравенство . Преобразуем левую часть:
. Преобразуем левую часть:

 .
.
Значит, неравенство  равносильно неравенству
равносильно неравенству . Отсюда
. Отсюда . Поэтому в качестве можно взять число
. Поэтому в качестве можно взять число . При таком из условия 0<|x-1|<будет следовать неравенство
. При таком из условия 0<|x-1|<будет следовать неравенство .
.
Таким образом, показано, что >0= :x: 0<|x-1|<
:x: 0<|x-1|< . Это значит, что
. Это значит, что .
.
Пример 2.
Вычислить предел  .
.
Решение.
Для раскрытия имеющейся здесь неопределенности вида  применим следующий прием:разделим числитель и знаменатель дроби на старшую степень n. В данном случае надо разделить наn3. Получим
применим следующий прием:разделим числитель и знаменатель дроби на старшую степень n. В данном случае надо разделить наn3. Получим

 .
.
Использовали тот факт, что величины  ,
, ,
, ,
, ,
, являются бесконечно малыми приn, следовательно, их предел равен нулю.
являются бесконечно малыми приn, следовательно, их предел равен нулю.
Пример 3.
Вычислить предел  .
.
Решение.
В этом примере в скобке имеем неопределенность вида -. Чтобы избавиться от нее, применим следующий прием:умножим и разделим на выражение, сопряженное выражению в скобках. В данном случае умножим на и в числителе получим разность квадратов. Упростив, придем к неопределенности вида
и в числителе получим разность квадратов. Упростив, придем к неопределенности вида , которую раскроем, как в предыдущем примере, делением на старшую степеньn(на
, которую раскроем, как в предыдущем примере, делением на старшую степеньn(на ).
).
 =
= ==
== =
= =
= =
= .
.
Пример 4.
Вычислить предел  .
.
Решение.
В данном примере используется определение факториала натурального числа. Факториаломчислаn называется произведение всех натуральных чисел от 1 доnвключительно:n!=123n. Например, 1!=1, 2!=12=2, 3!=123=6 и т. д. По определению 0!=1.
называется произведение всех натуральных чисел от 1 доnвключительно:n!=123n. Например, 1!=1, 2!=12=2, 3!=123=6 и т. д. По определению 0!=1.
В пределах такого вида приходится выражать факториалы бóльших чисел через факториал меньшего числа. В данном случае меньшим числом является (3n-1). По определению факториала можем записать:
 .
.
Значит, (3n+1)!=(3n-1)!(3n)(3n+1), а (3n)!=(3n-1)!(3n).
Выразим факториалы указанным образом через (3n-1)! и сократим дробь на (3n-1)! Затем раскроем скобки в числителе и знаменателе и разделим на старшую степеньn(наn3).
 =
= =
= =
= =
= .
.
Пример 5.
Вычислить предел  .
.
Решение.
Применим следующий прием: разделим числитель и знаменатель на старшую степень бóльшего по модулю числа. Заметим, что в данном примере можно делить на 5n+2или на 5n+1или на 5n. При этом используется известный предел:

Удобнее делить числитель и знаменатель на 5n.
 =
= =
= .
.
Пример 6.
Вычислить предел  .
.
Решение.
Так как предел основания  , а предел показателя степени
, а предел показателя степени , то в данном случае имеем неопределенность 1. При вычислении пределов такого вида используется второй замечательный предел:
, то в данном случае имеем неопределенность 1. При вычислении пределов такого вида используется второй замечательный предел: . Вместоnздесь может стоять любая бесконечно большая величина, то есть
. Вместоnздесь может стоять любая бесконечно большая величина, то есть , где
, где .
.
Выделим вначале в основании целую часть. Для этого получим в числителе выражение, равное знаменателю и разделим почленно числитель на знаменатель.
 =
= =
= .
.
В нашем случае  . В показателе выделим выражение
. В показателе выделим выражение и затем используем свойство
и затем используем свойство .
.
 =
= =
= =
=
 =
= .
.
Пример 7.
Вычислить предел  .
.
Решение.
Числитель и знаменатель данной дроби стремятся к нулю при х10. Для раскрытия имеющейся здесь неопределенности разложим числитель и знаменатель на множители и разделим на выражение (х-10). Для этого в числителе применим формулу разности кубов:
разложим числитель и знаменатель на множители и разделим на выражение (х-10). Для этого в числителе применим формулу разности кубов: , а в знаменателе вынесемх за скобки и свернем квадрат разности:
, а в знаменателе вынесемх за скобки и свернем квадрат разности:
 .
.
Числитель получившейся дроби стремится к 300, а знаменатель – к нулю, т. е. является бесконечно малой величиной. Значит, дробь является бесконечно большой величиной и
 .
.
Пример 8.
Вычислить предел  .
.
Решение.
В данном случае имеется неопределенность  . Умножим числитель и знаменатель дроби на выражение, сопряженное числителю, и на выражение, сопряженное знаменателю:
. Умножим числитель и знаменатель дроби на выражение, сопряженное числителю, и на выражение, сопряженное знаменателю:


 .
.
Пример 9.
Вычислить предел  .
.
Решение.
Прих0sinx0, 3xsinx0,x20. Значит, можно заменить числитель и знаменатель дроби эквивалентными бесконечно малыми: ,
, . Тогда получим
. Тогда получим
 .
.
Пример 4.
Вычислить предел  .
.
Решение.
В данном случае выражение, стоящее под знаком синуса, не является бесконечно малым:  . Поэтому вначале необходимо раскрыть в этом выражении скобки и затем применить формулу приведения:
. Поэтому вначале необходимо раскрыть в этом выражении скобки и затем применить формулу приведения: . Получим
. Получим
 .
.
Теперь можно заменить числитель и знаменатель эквивалентными бесконечно малыми:  ,
, прих0. Тогда
прих0. Тогда
 .
.
Пример 10.
Вычислить предел .
.
Решение.

Пример 11.
Вычислить предел  .
.
Решение.
Выражение, стоящее под знаком предела, является показательно-степенной функцией  , где
, где ,
, . Вычислим пределы основания и степени:
. Вычислим пределы основания и степени:
 ,
, .
.
Тогда используя правило предел степени равен степени пределов(в данном случае нет неопределенности), получим

 .
.
Пример 12.
Вычислить предел  .
.
Решение.
В этом примере предел основания  , предел показателя
, предел показателя . Значит, имеется неопределенность 1. Воспользуемся вторым замечательным пределом в следующей форме записи:
. Значит, имеется неопределенность 1. Воспользуемся вторым замечательным пределом в следующей форме записи: . Выполним преобразования, как в примере 5 из задания 2:
. Выполним преобразования, как в примере 5 из задания 2:


 .
.
Пример 13.
Исследовать на непрерывность функцию  .
.
Решение.
Функция является элементарной как отношение двух многочленов, значит, она непрерывна во всех точках своей области определения. Областью определения является множество всех точек числовой прямой, за исключением тех, в которых знаменатель обращается в нуль. Найдем нули знаменателя: x2-6x+5=0x=1 иx=5.
Итак,  , данная функция непрерывна на
, данная функция непрерывна на . Точких=1 их=5 являются точками разрыва. Исследуем характер разрыва. Для этого найдем односторонние пределы функции в точкахх=1 их=5.
. Точких=1 их=5 являются точками разрыва. Исследуем характер разрыва. Для этого найдем односторонние пределы функции в точкахх=1 их=5.
 ,
,
 ,
,
 ,
,
 ,
,
В точках х=1 их=5 функция имеет бесконечные односторонние пределы. Следовательно, эти точки являются точками разрыва второго рода.
studfiles.net
Контрольная работа
«Предел последовательности»
Вычислить предел последовательности
1
а)

б)
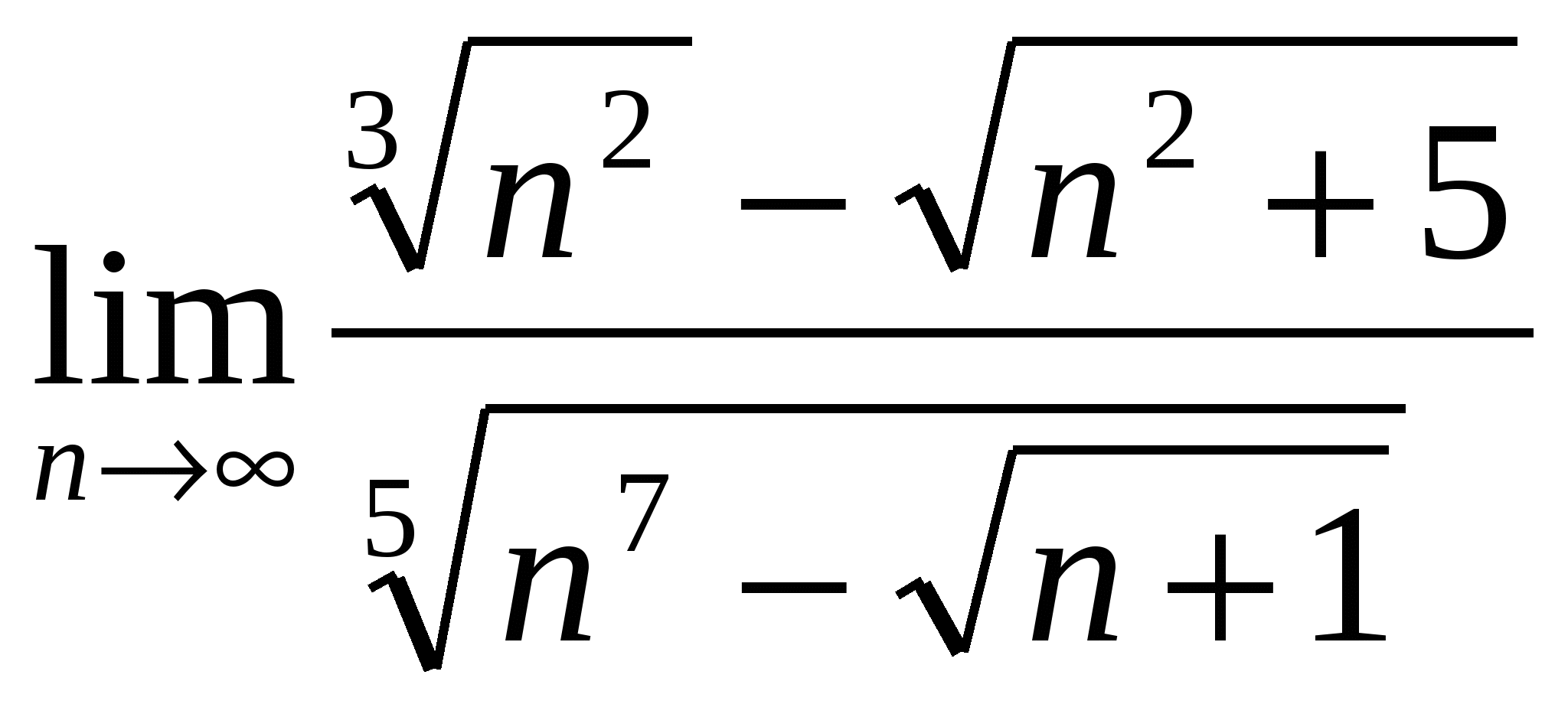
в)
 n
n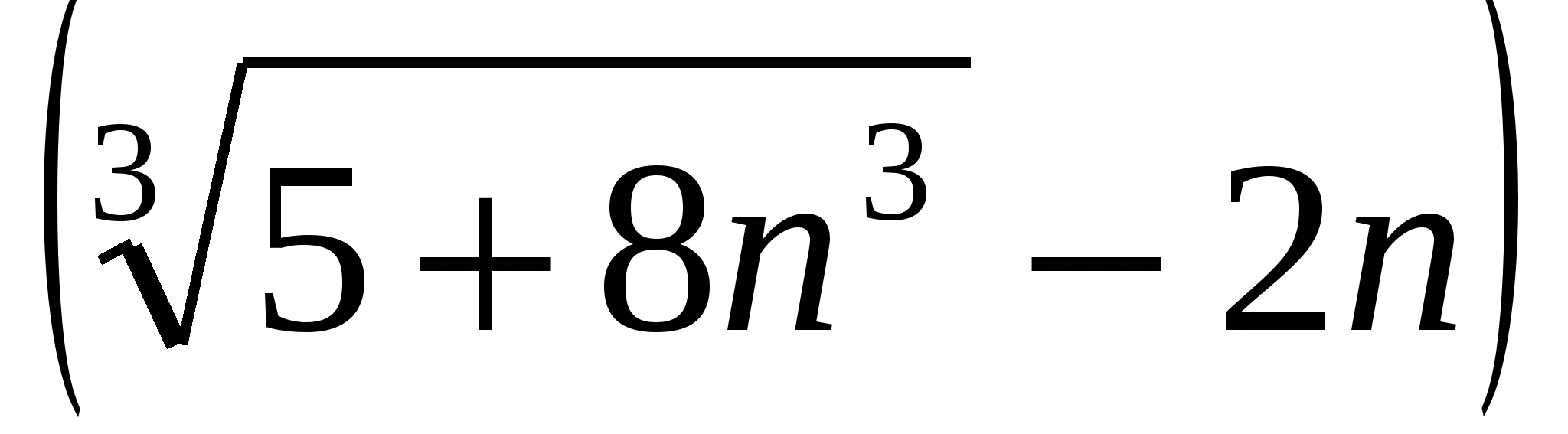
г)

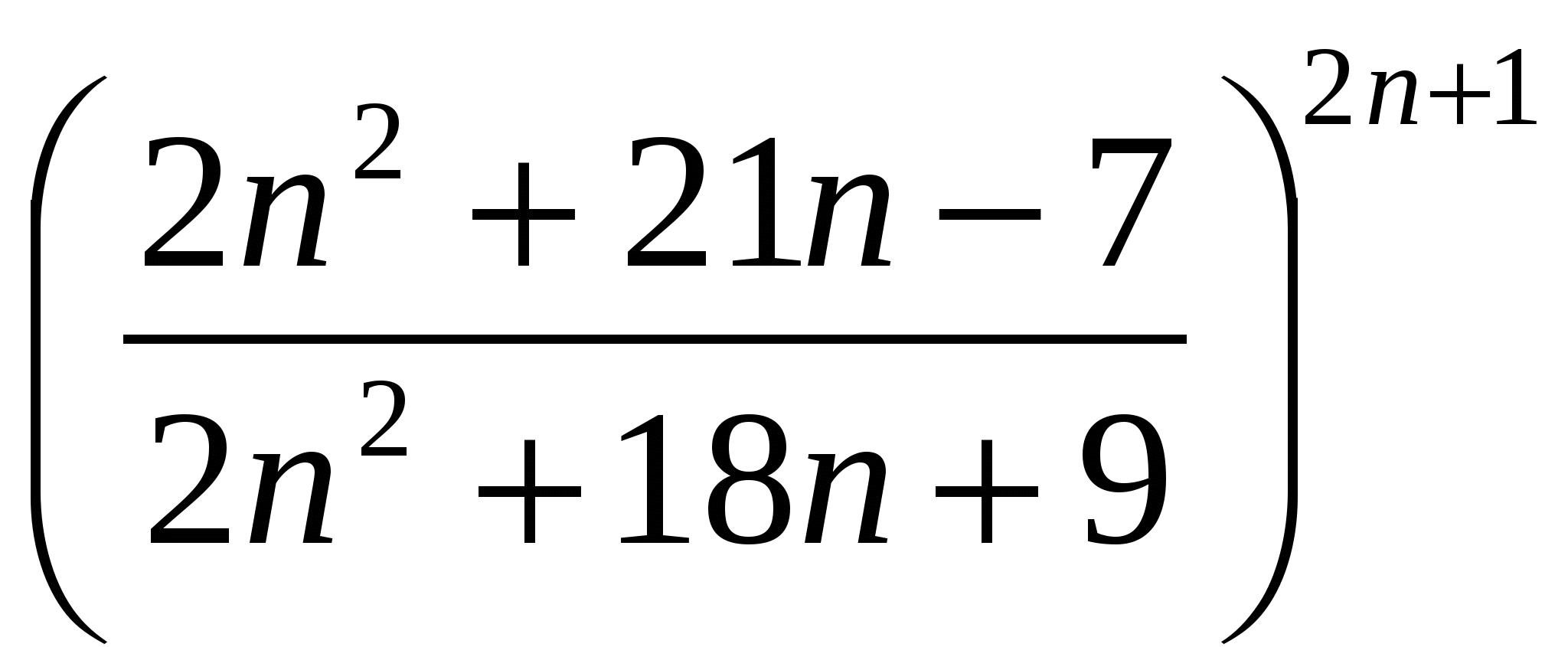
Вычислить предел последовательности
2
а)
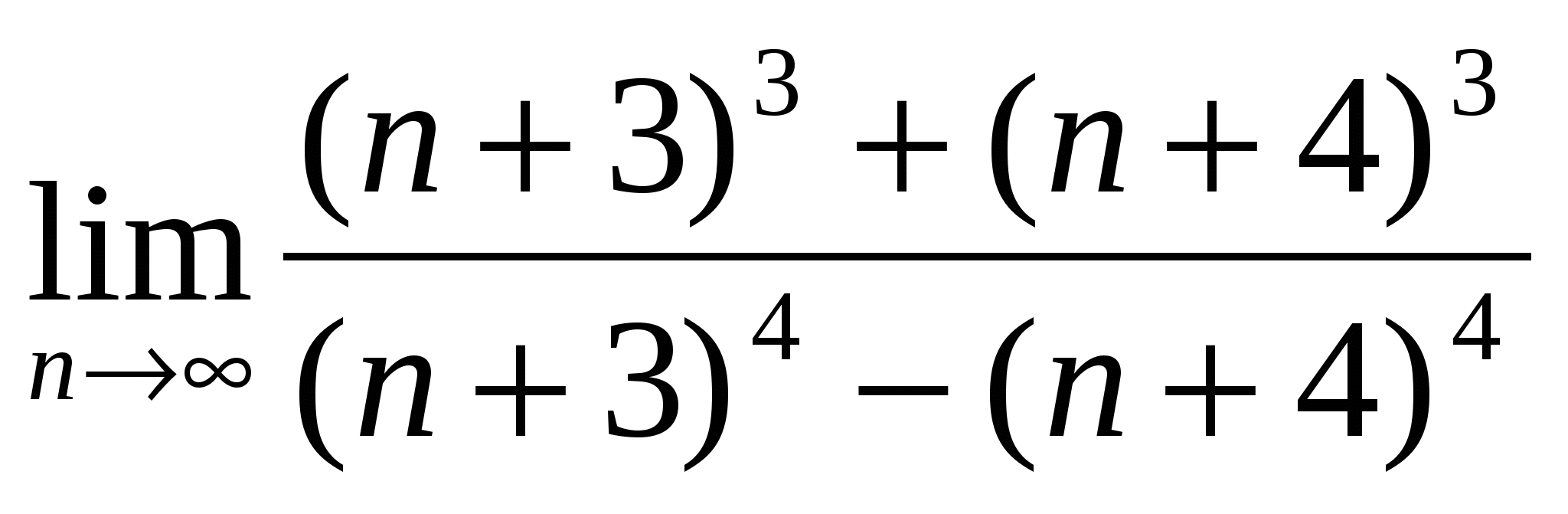
б)
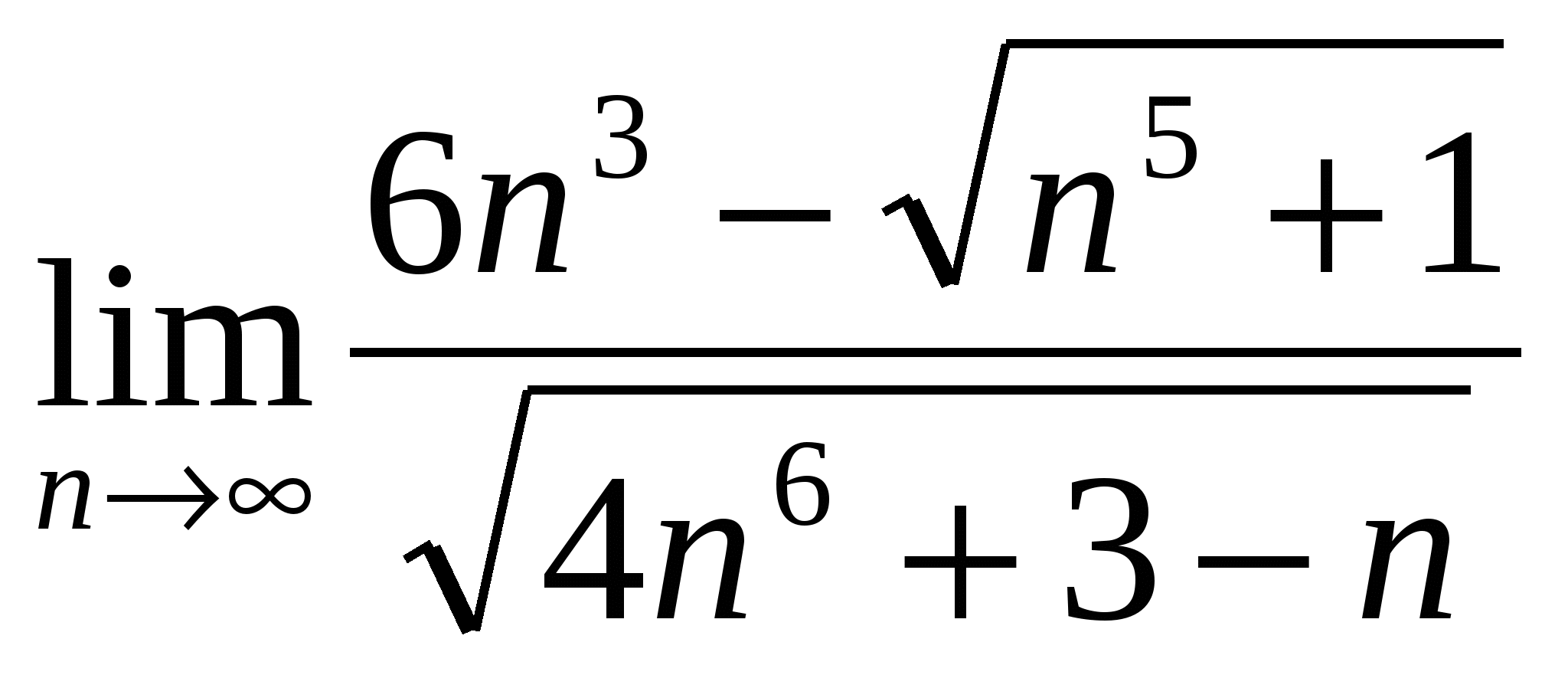
в)

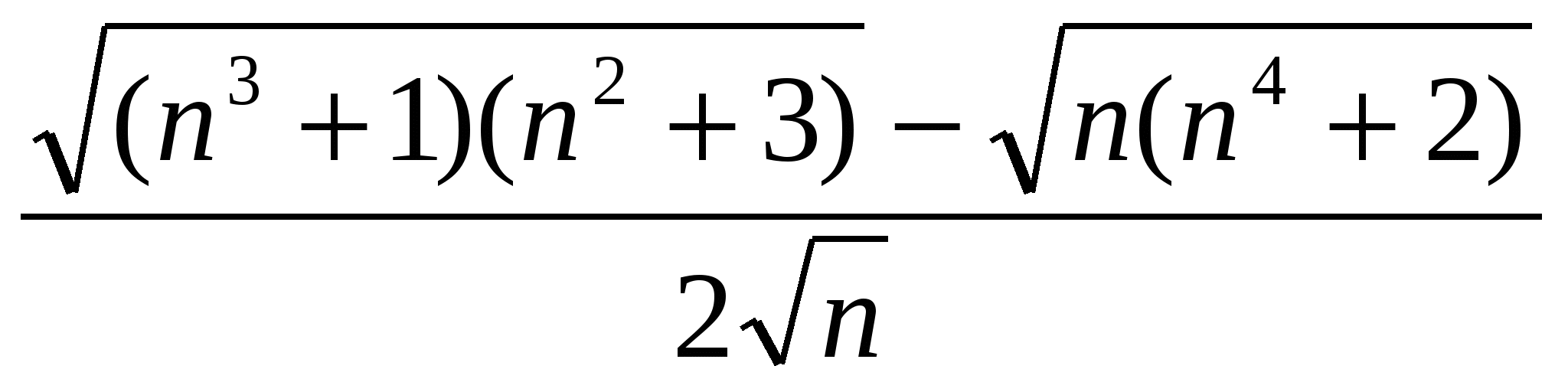
г)

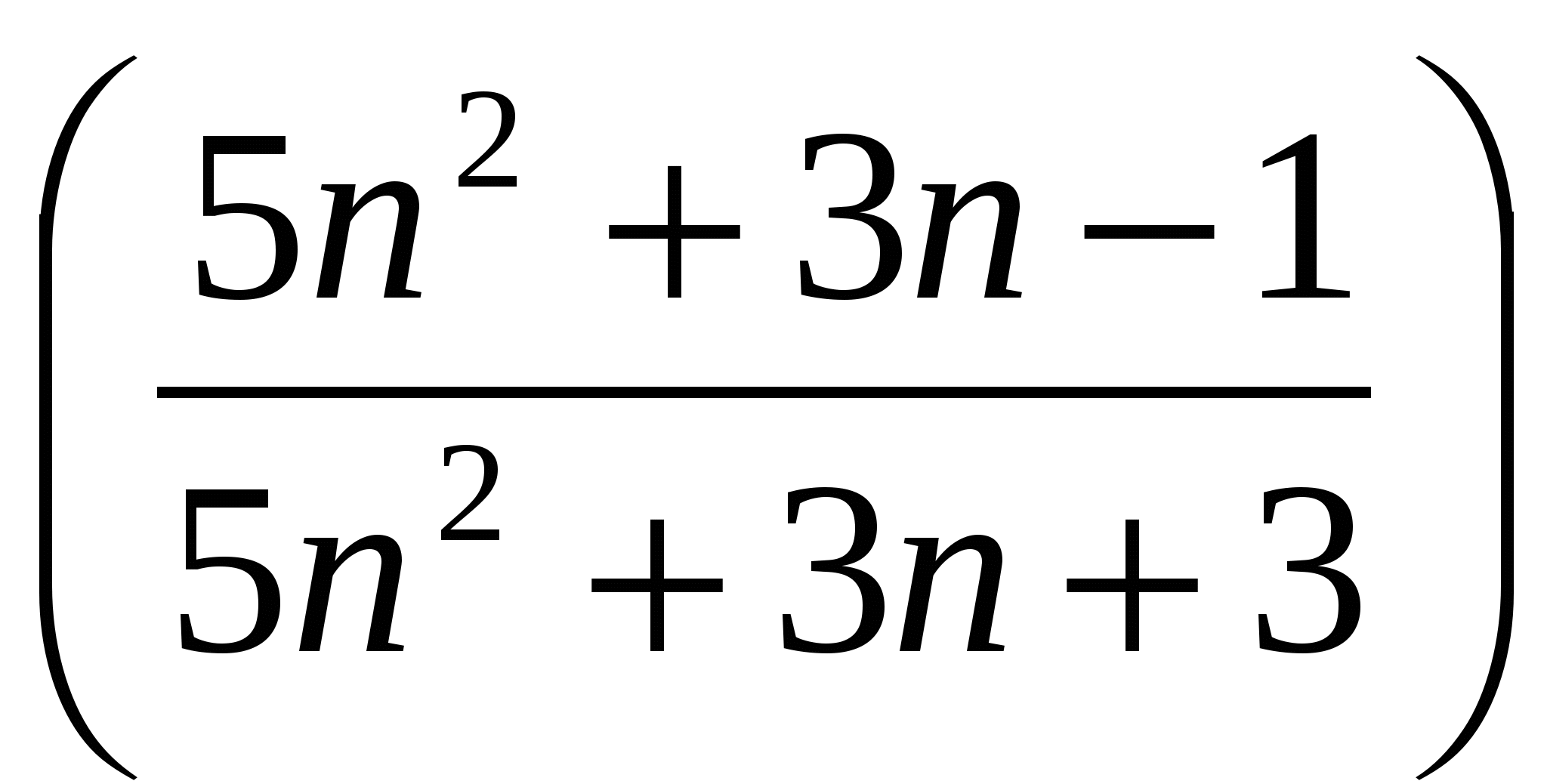
Вычислить предел последовательности
3
а)
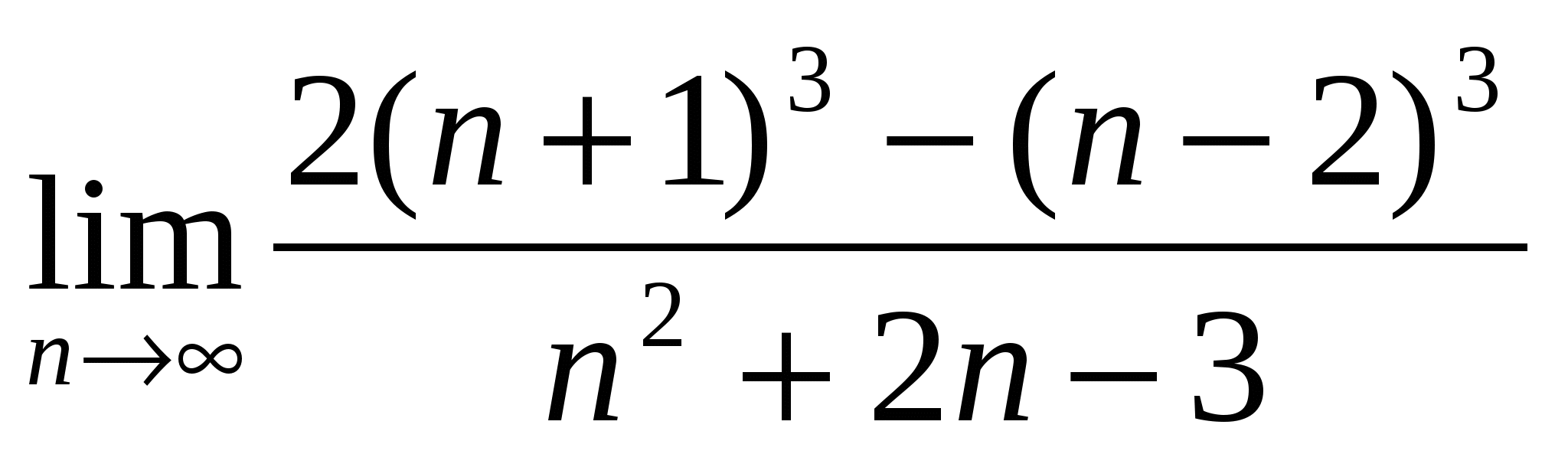
б)
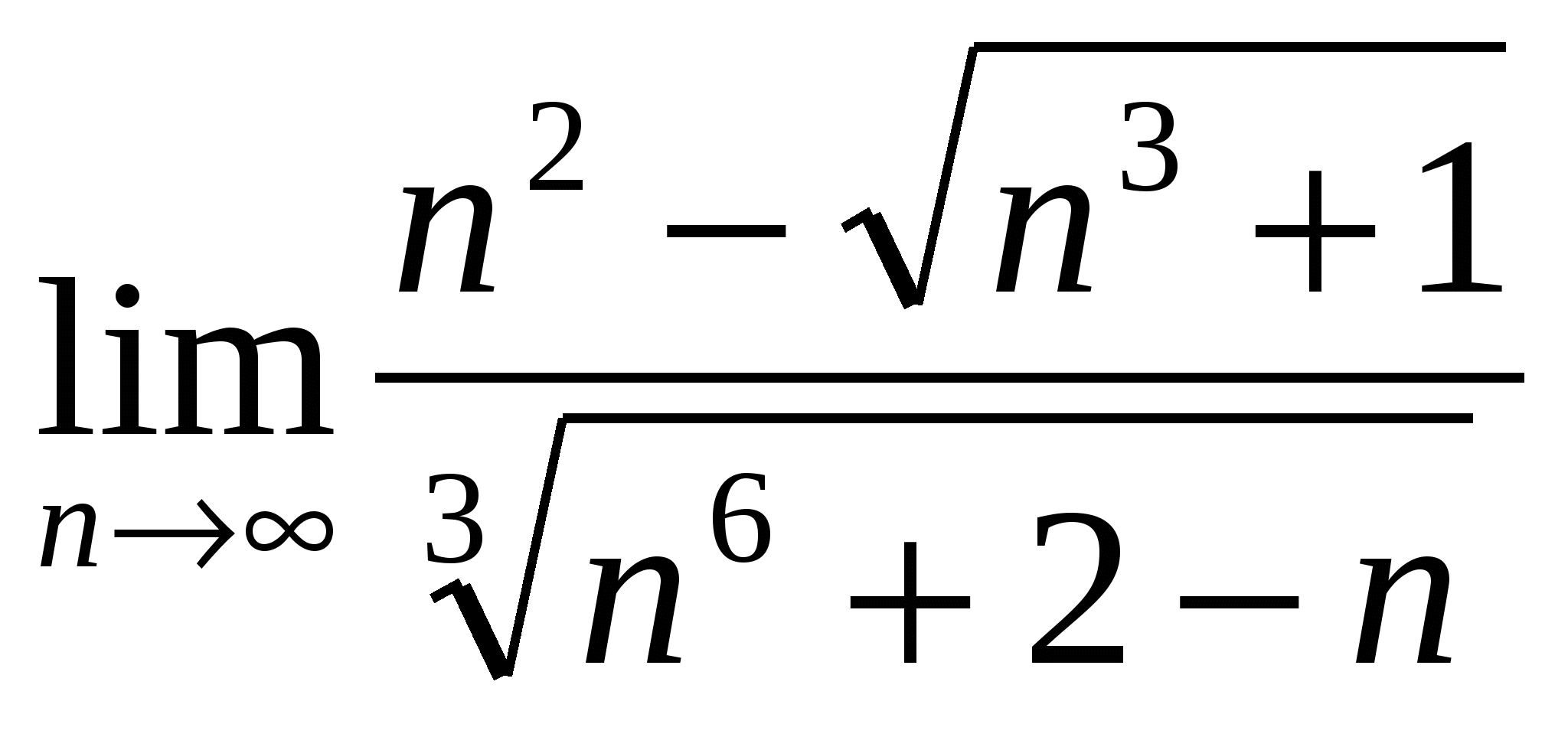
в)

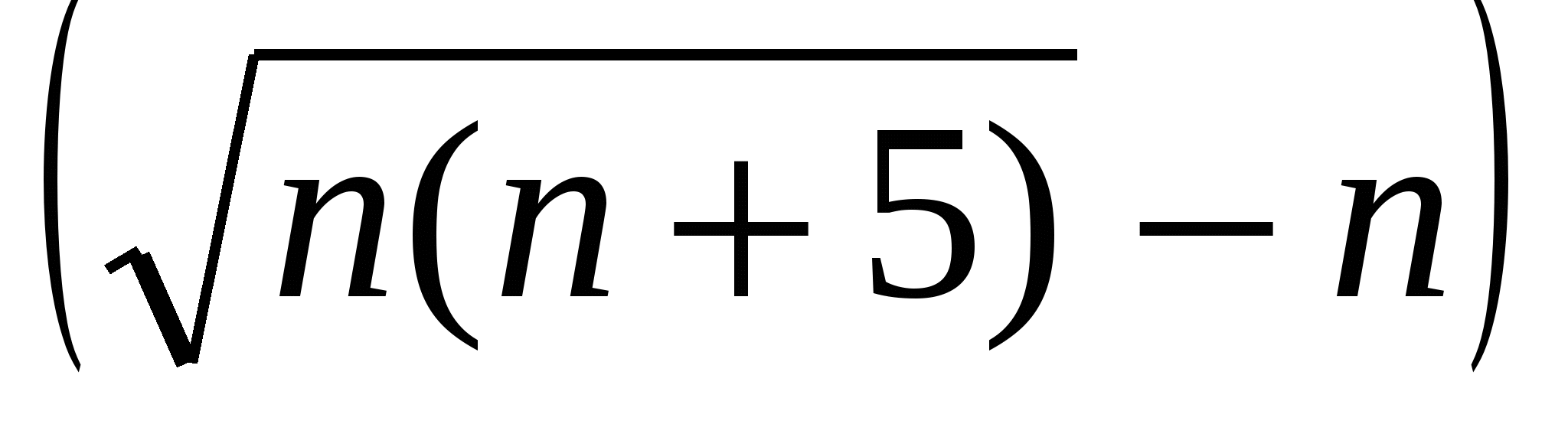
г)

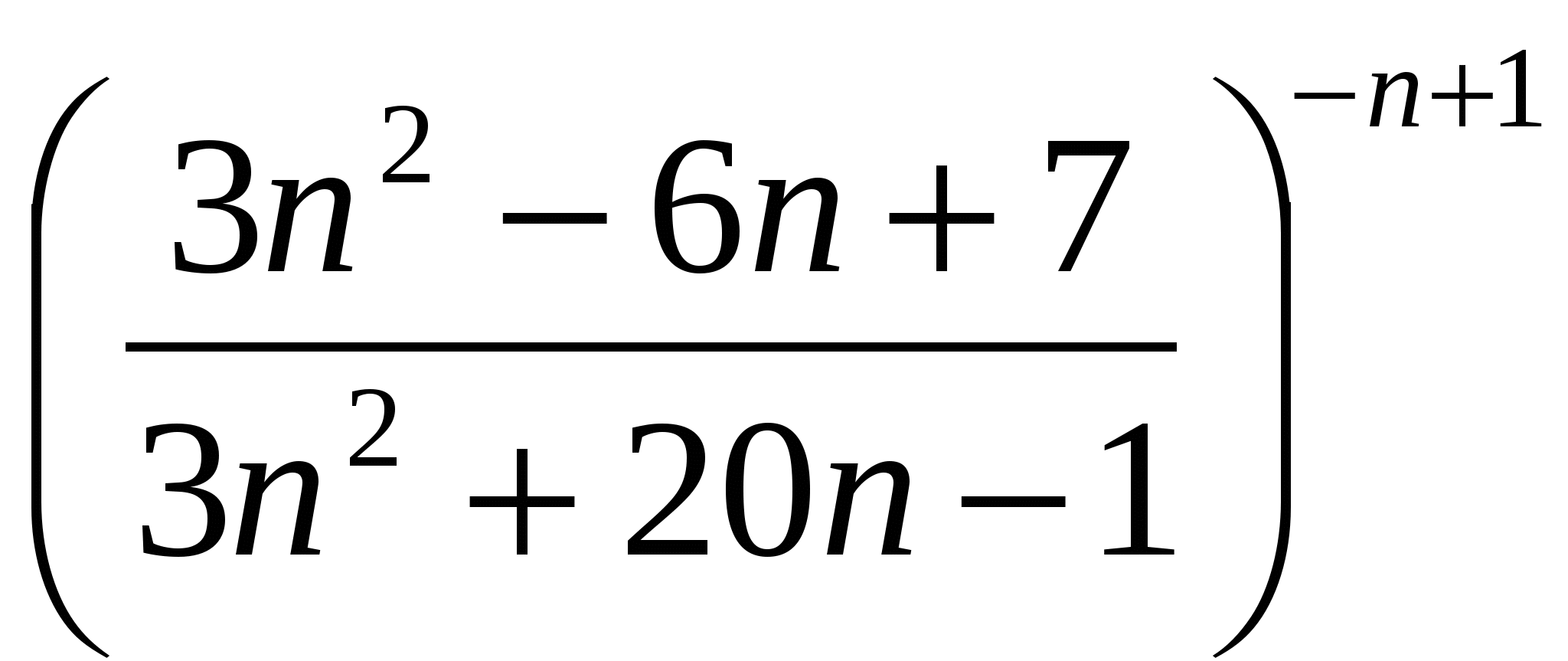
Вычислить предел последовательности
4
а)
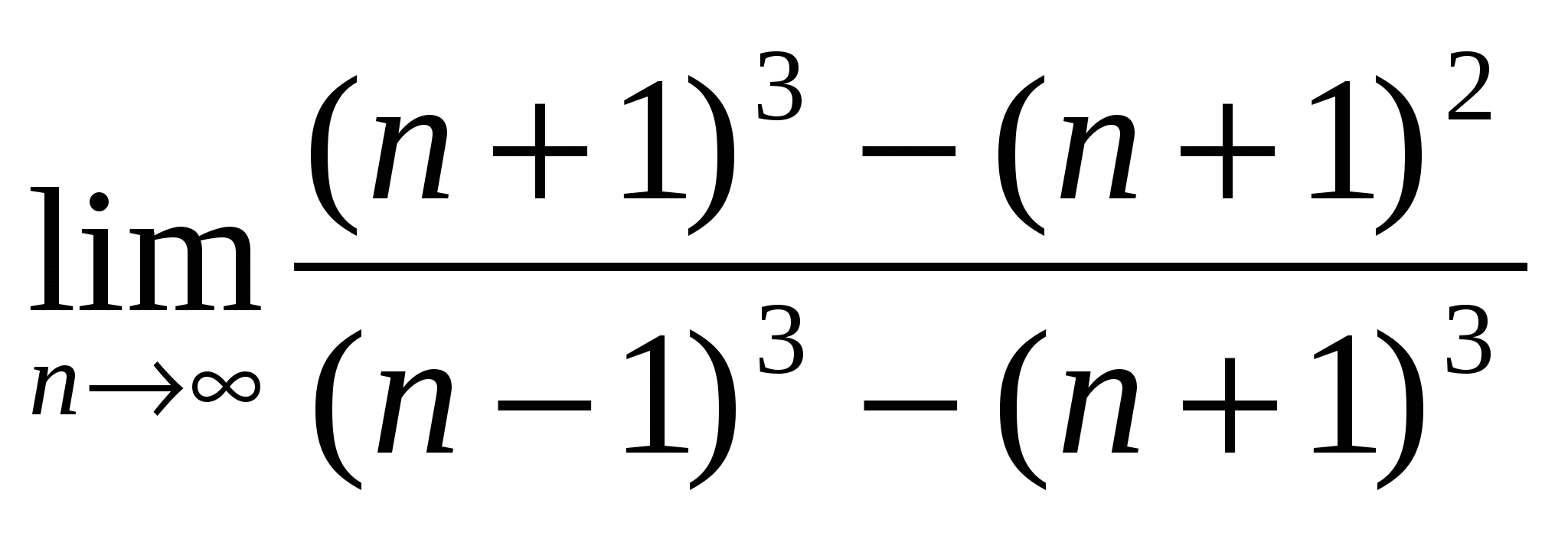
б)
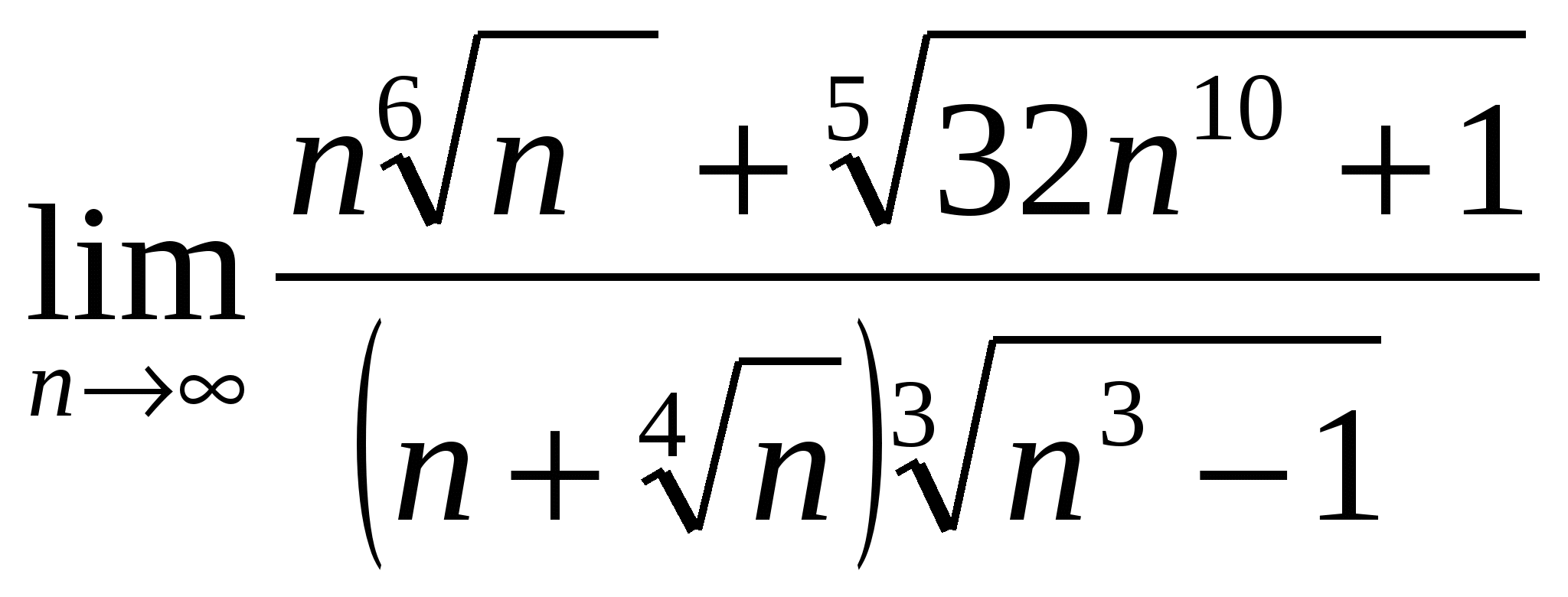
в)

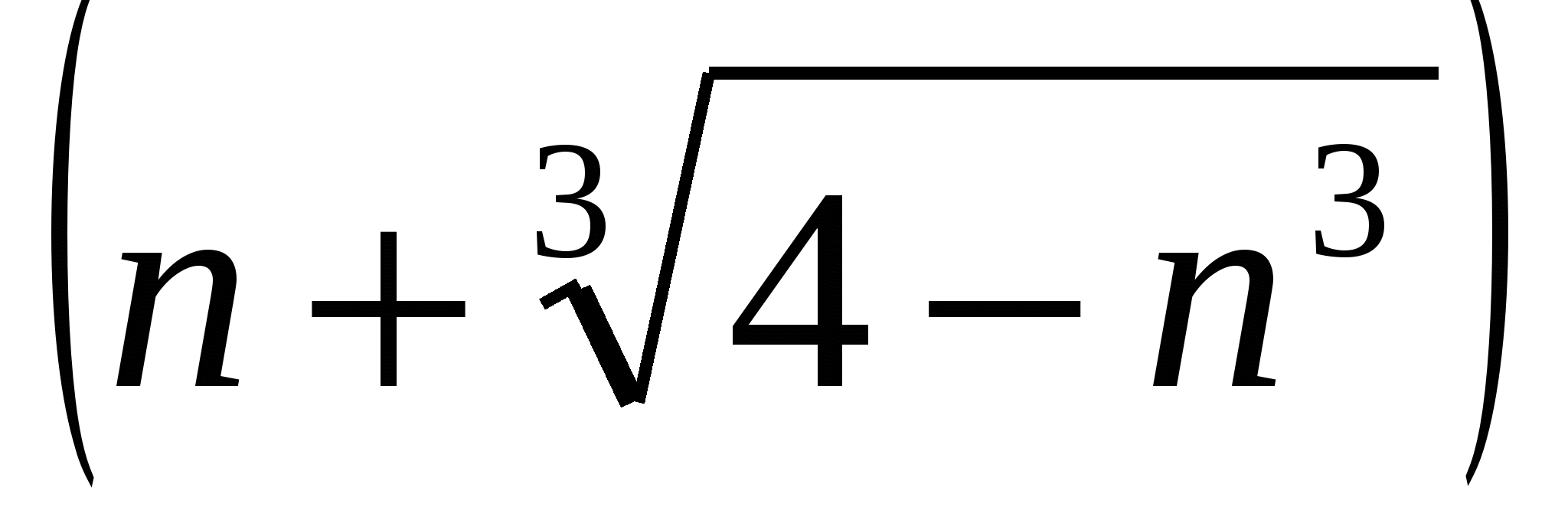
г)

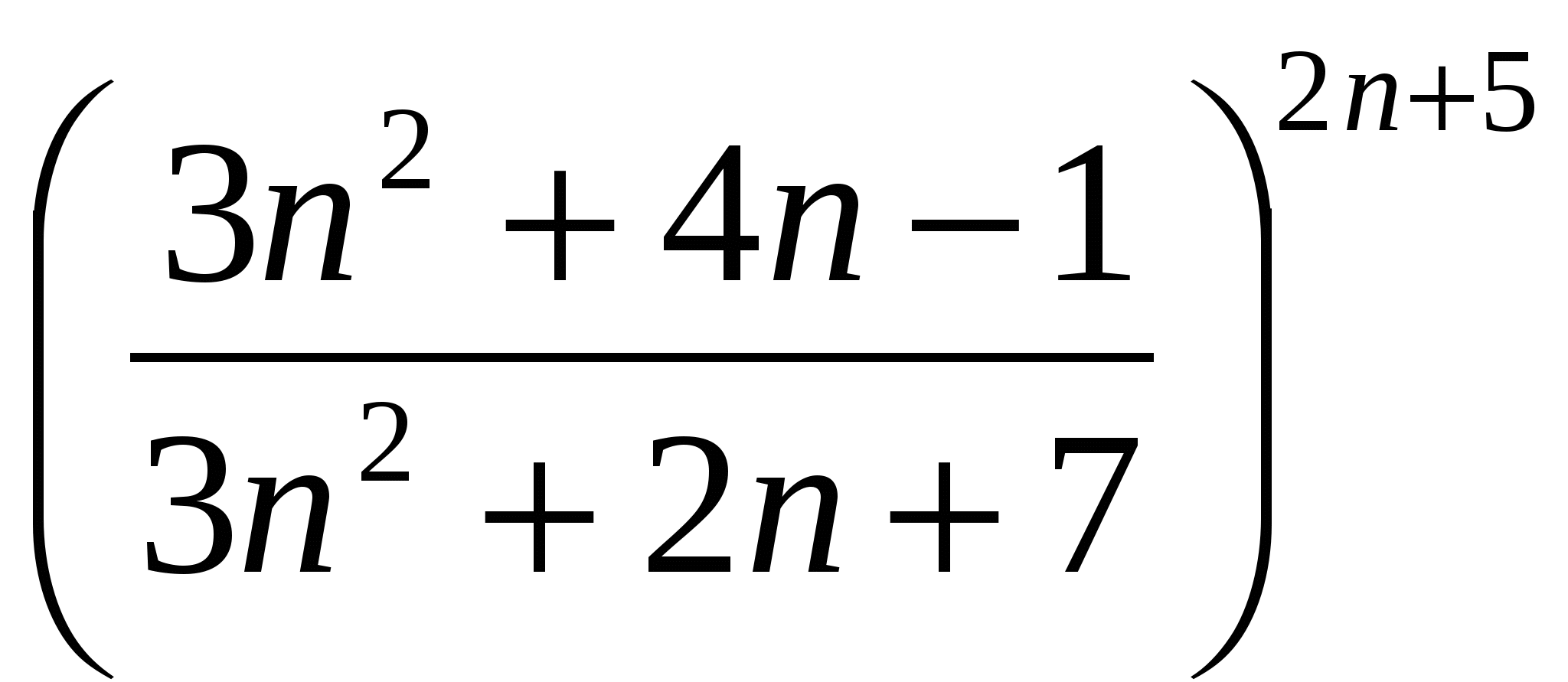
Вычислить предел последовательности
5
а)
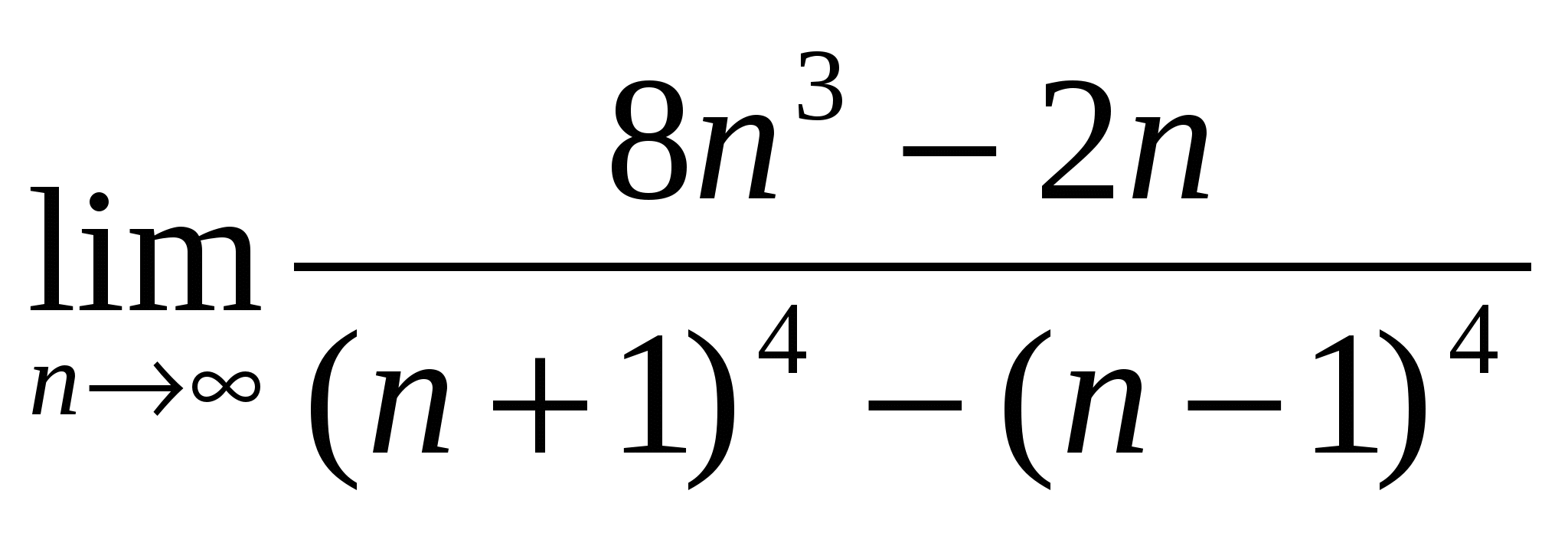
б)
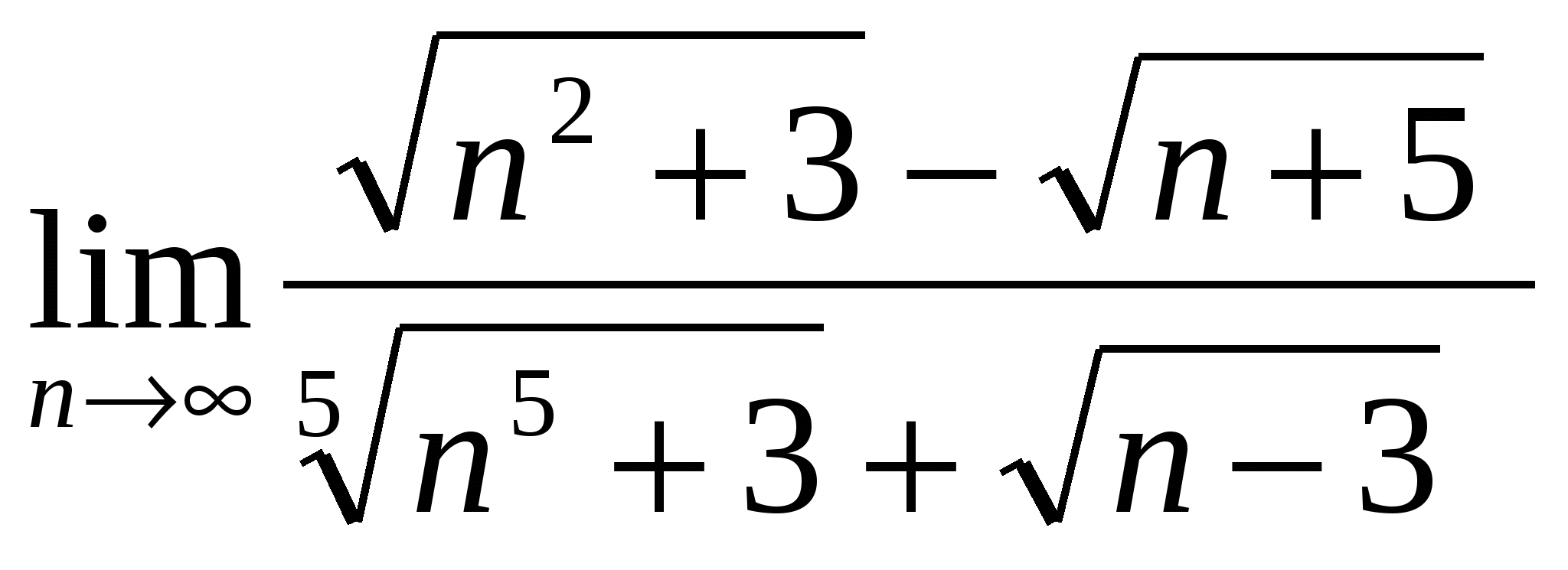
в)

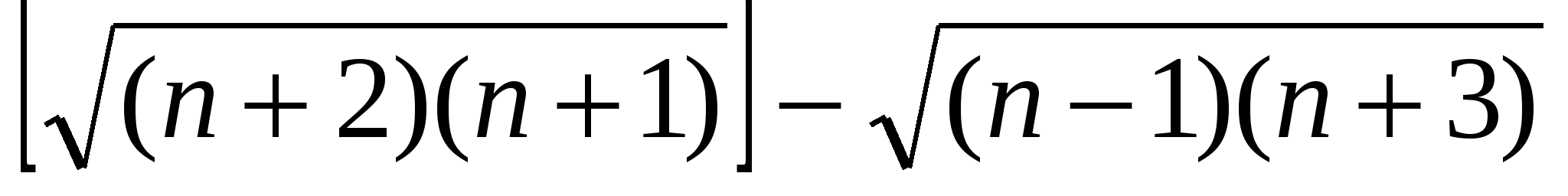
г)

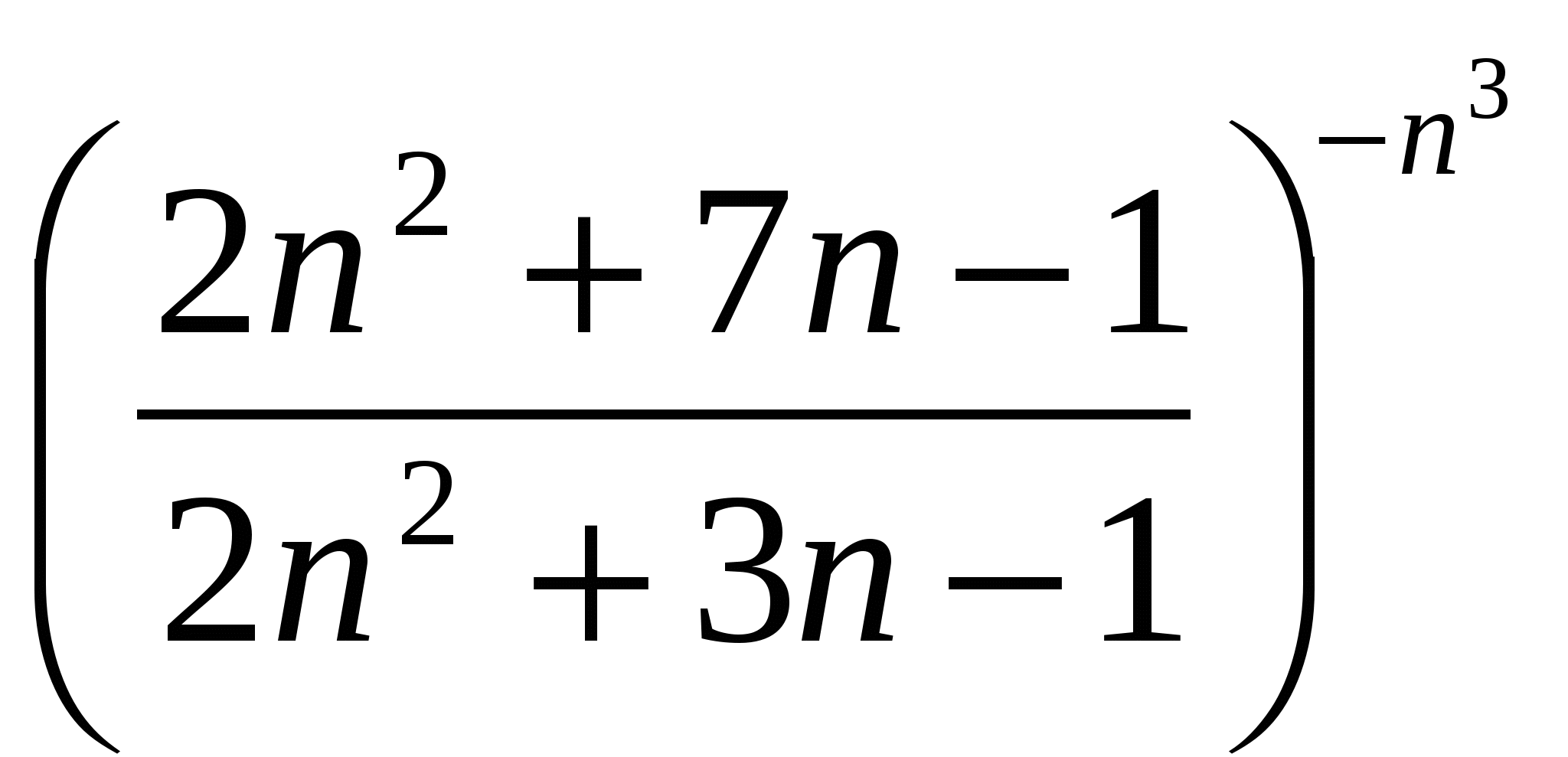
Контрольная работа № 4
Вычислить предел последовательности
6
а)
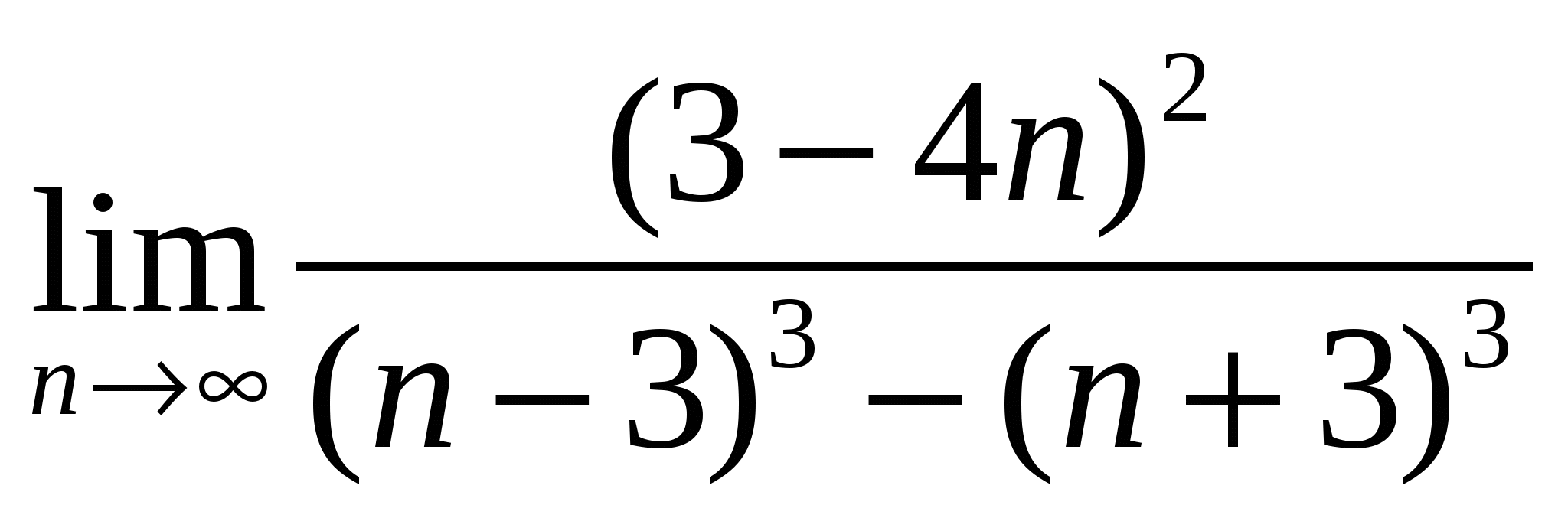
б)
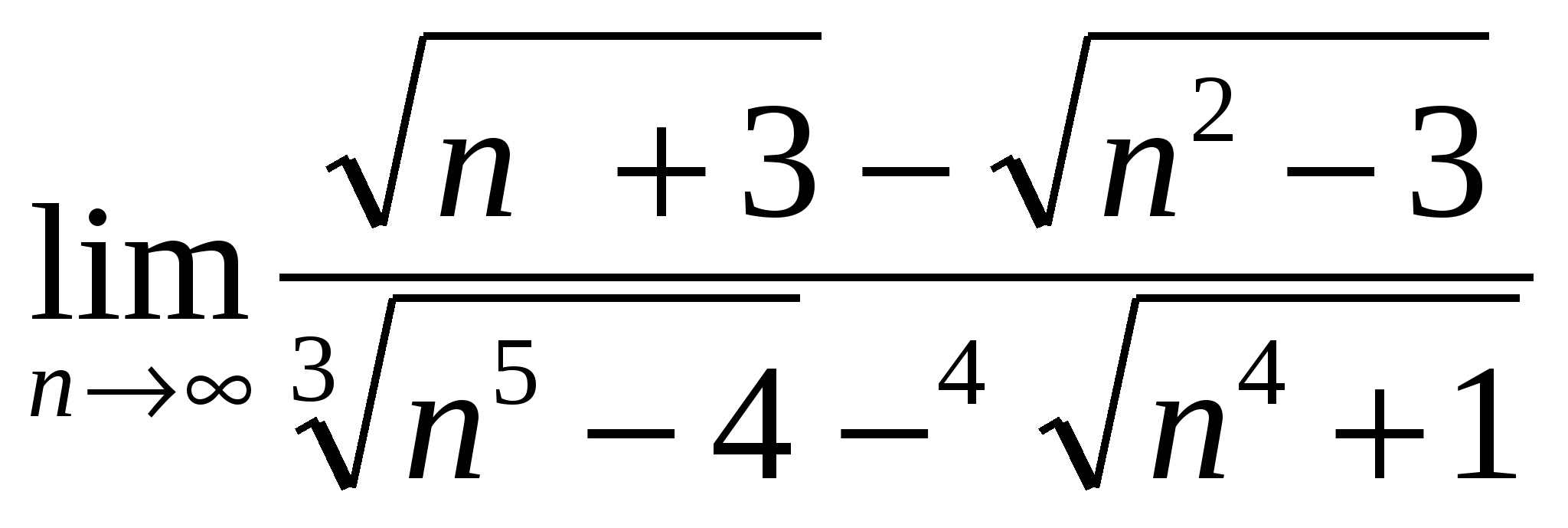
в)

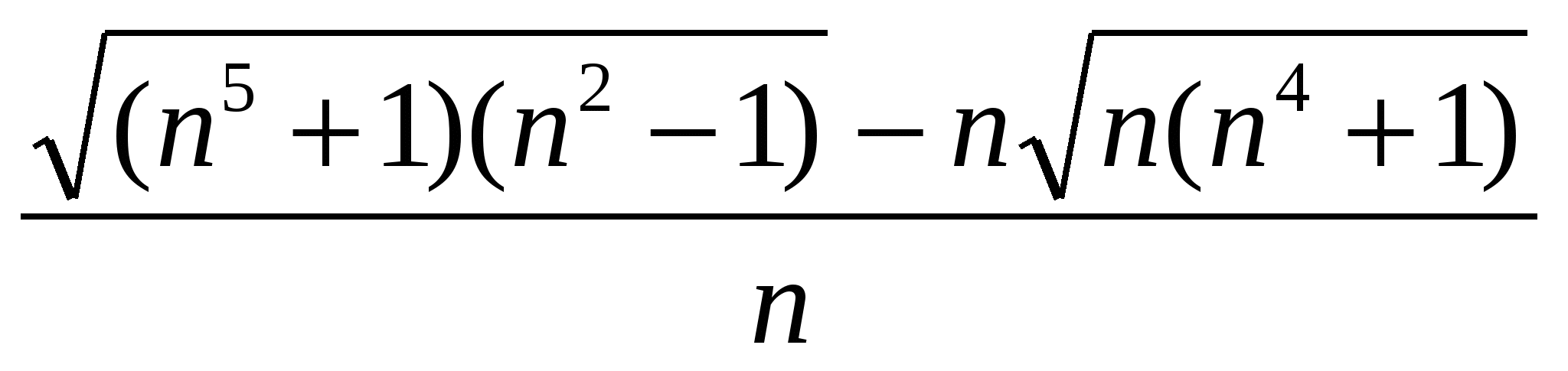
г)

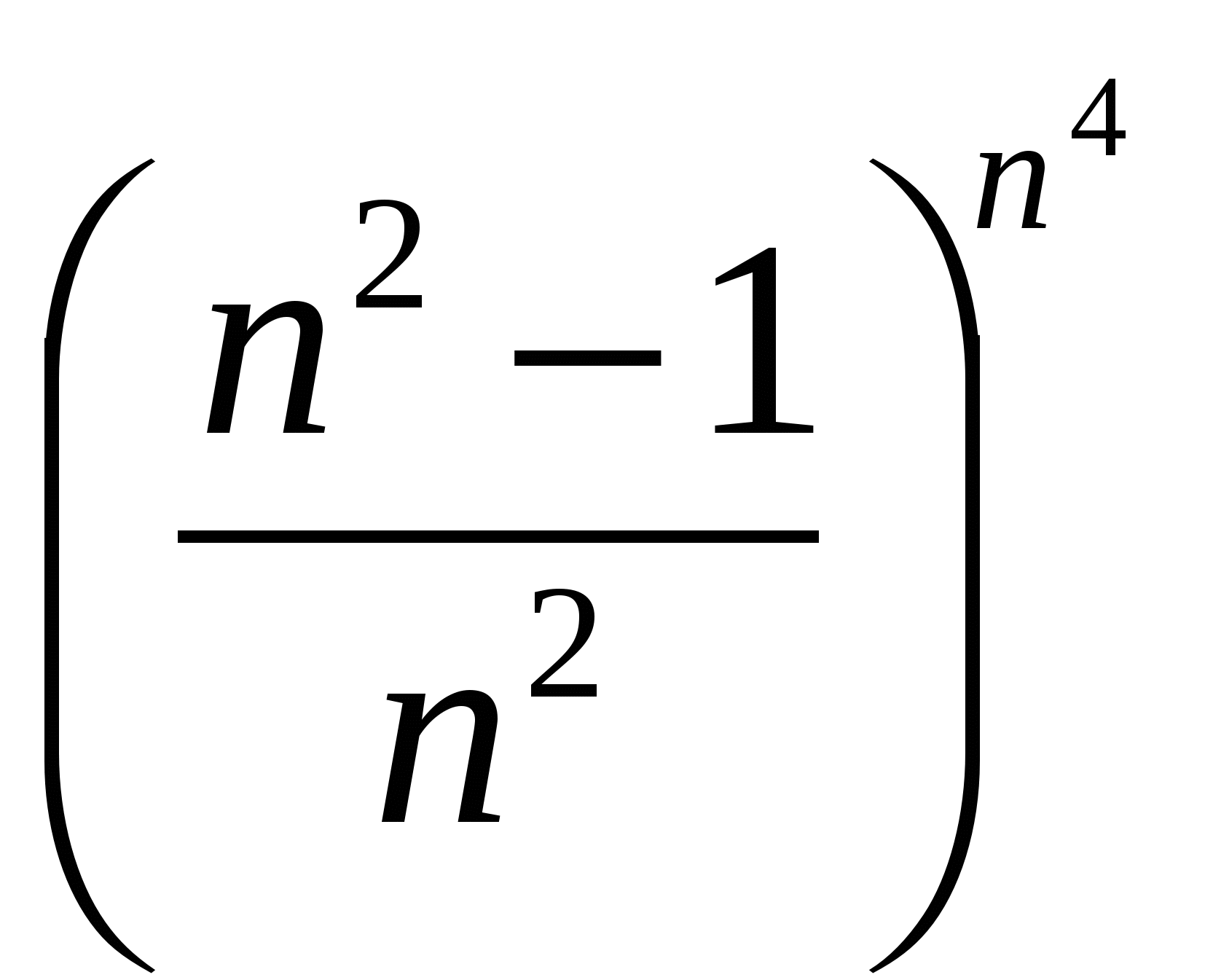
Вычислить предел последовательности
7
а)
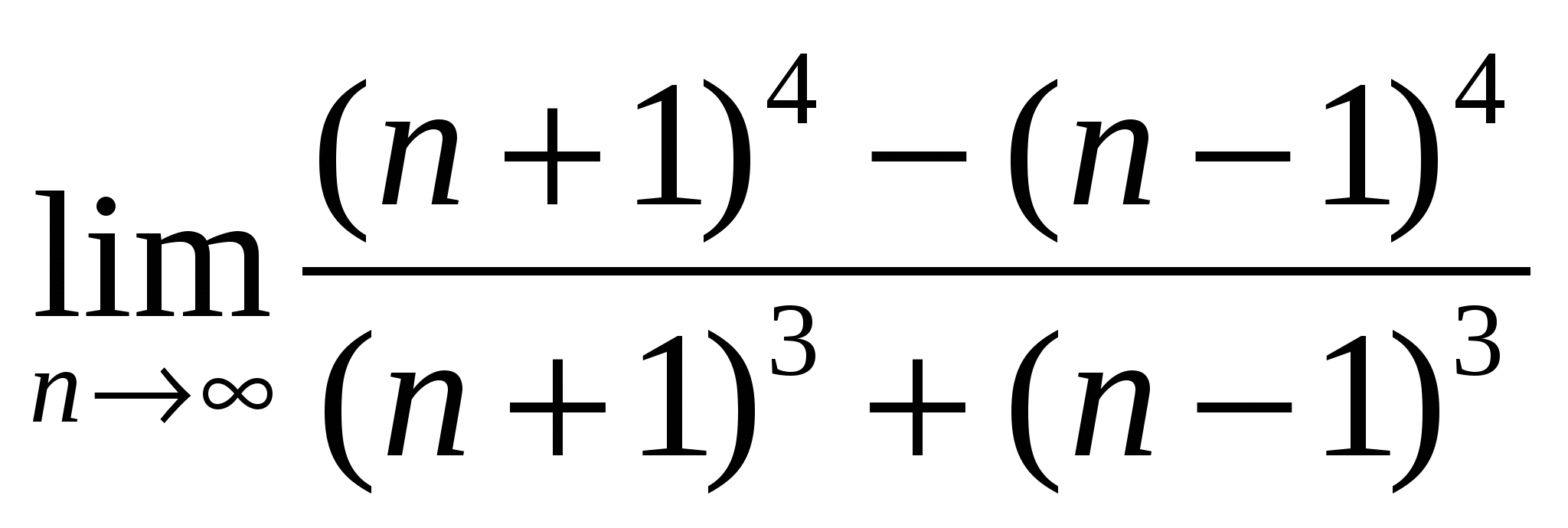
б)
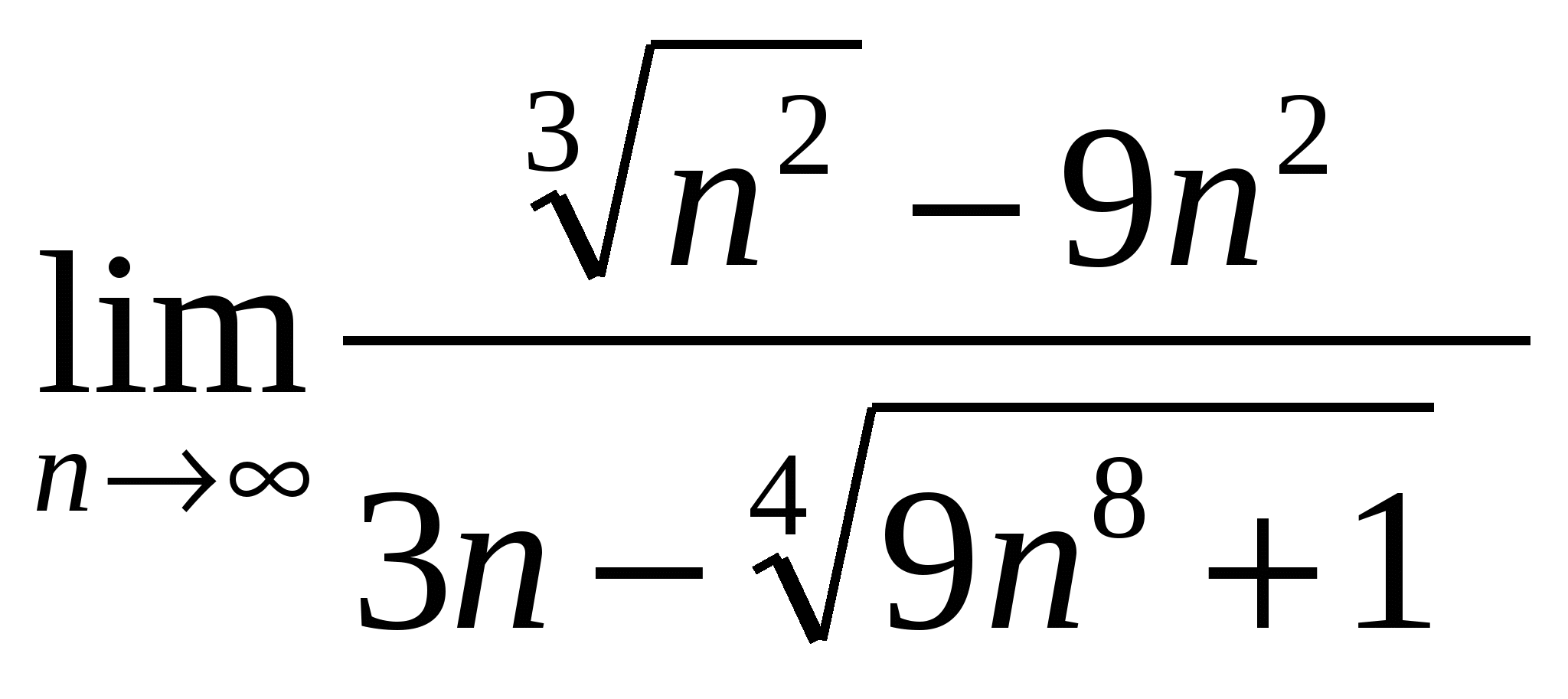
в)

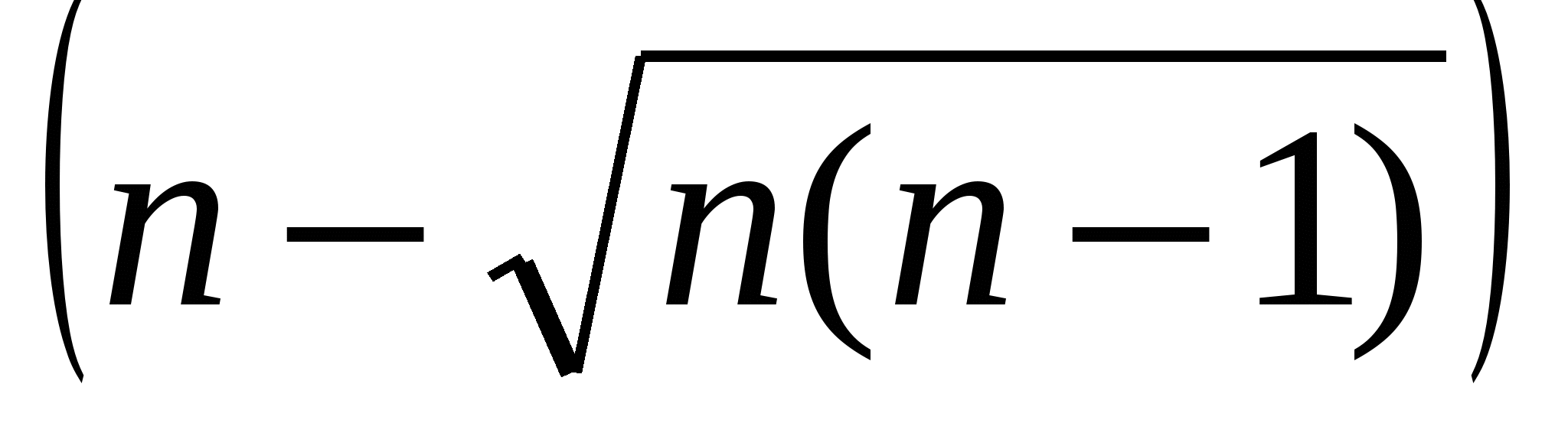
г)

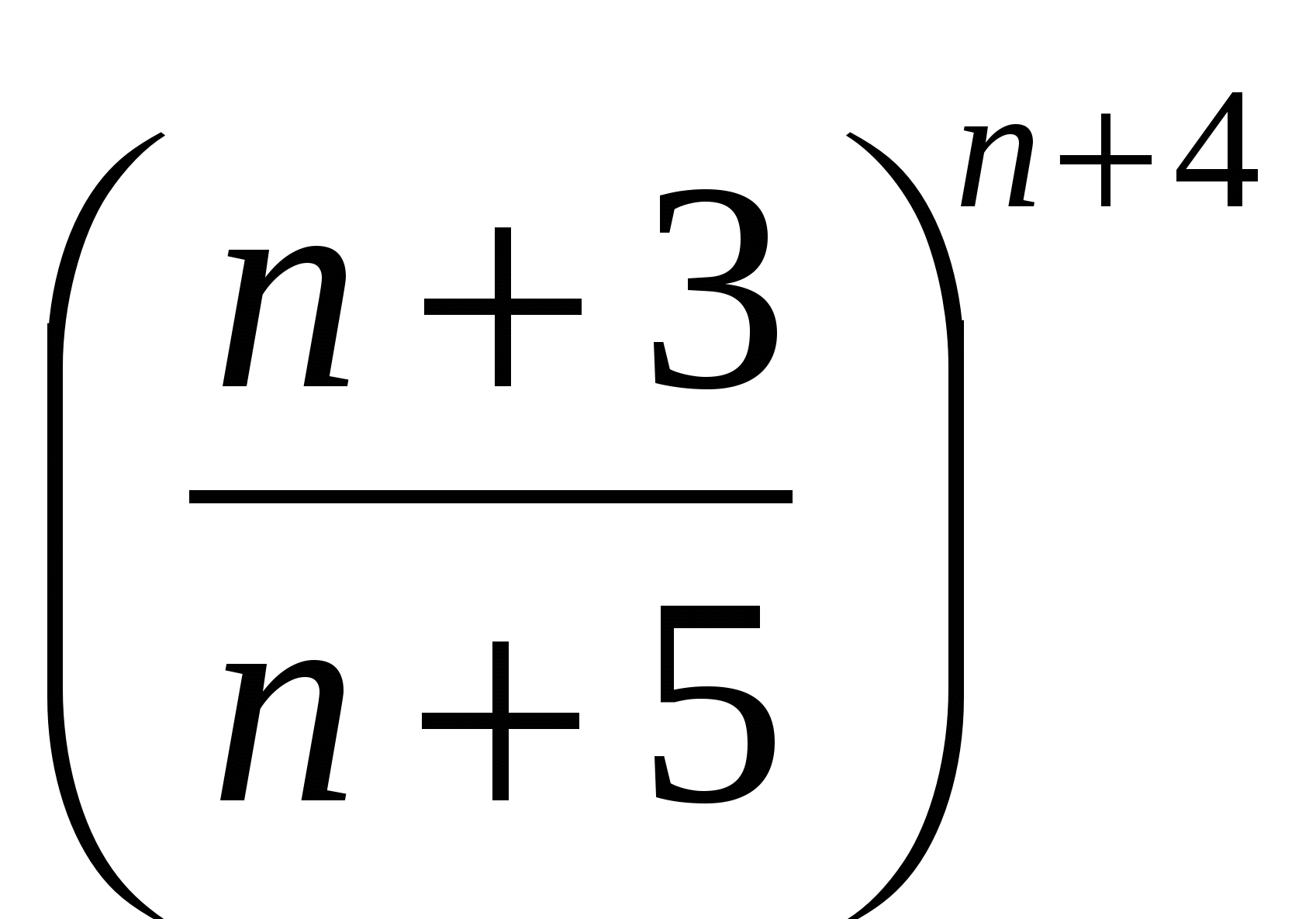
Вычислить предел последовательности
8
а)
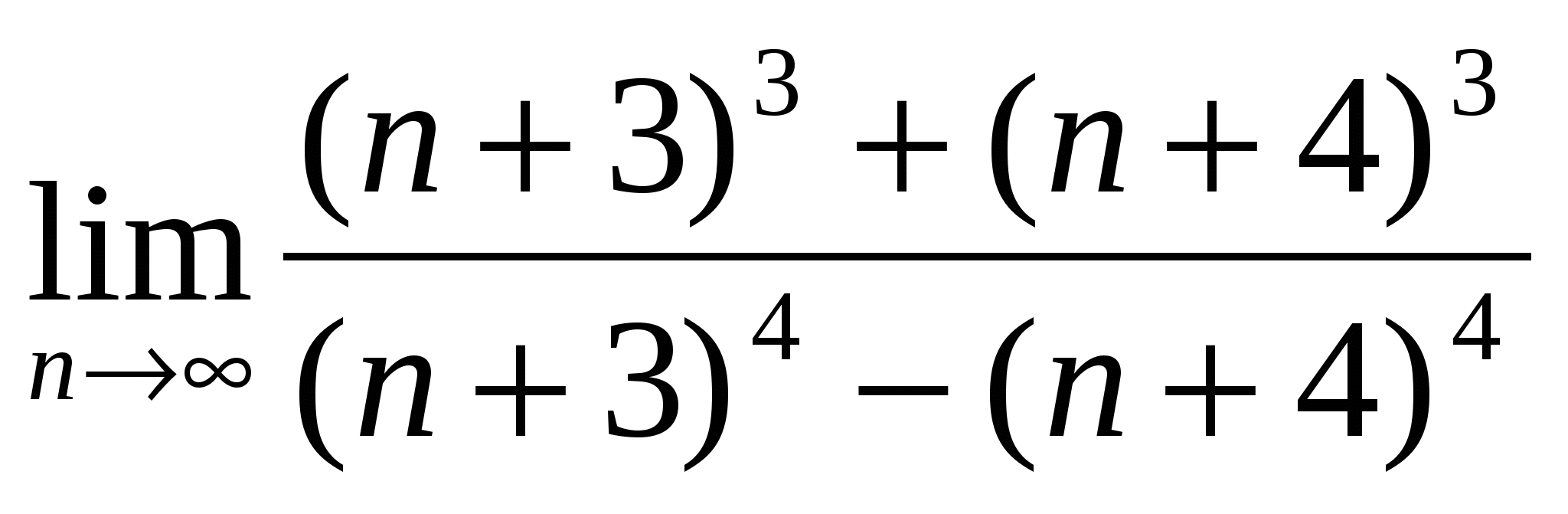
б)
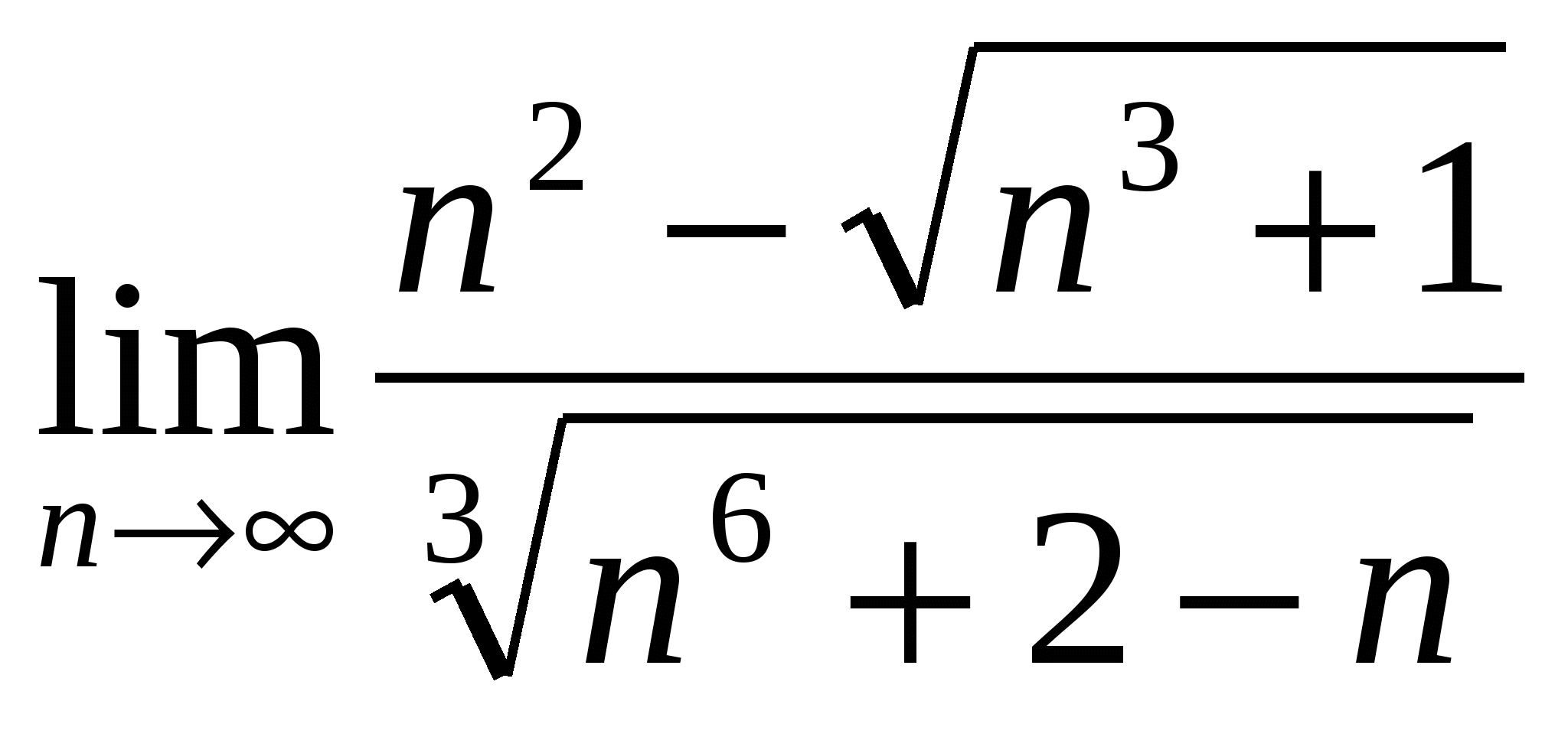
в)

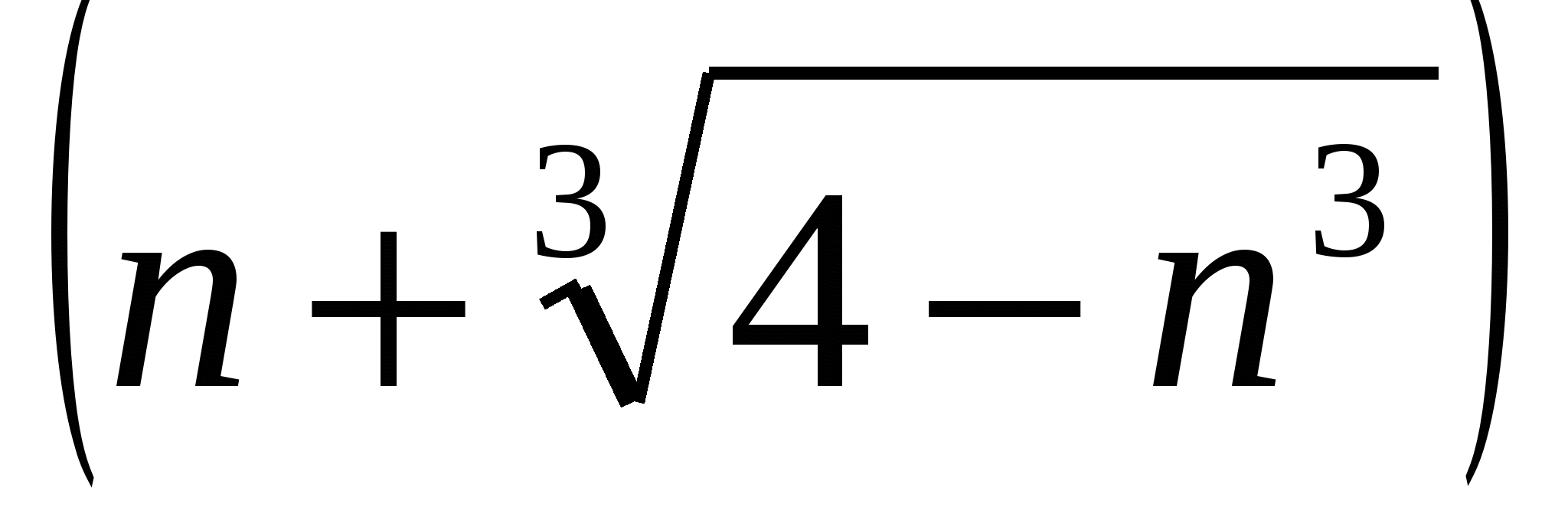
г)

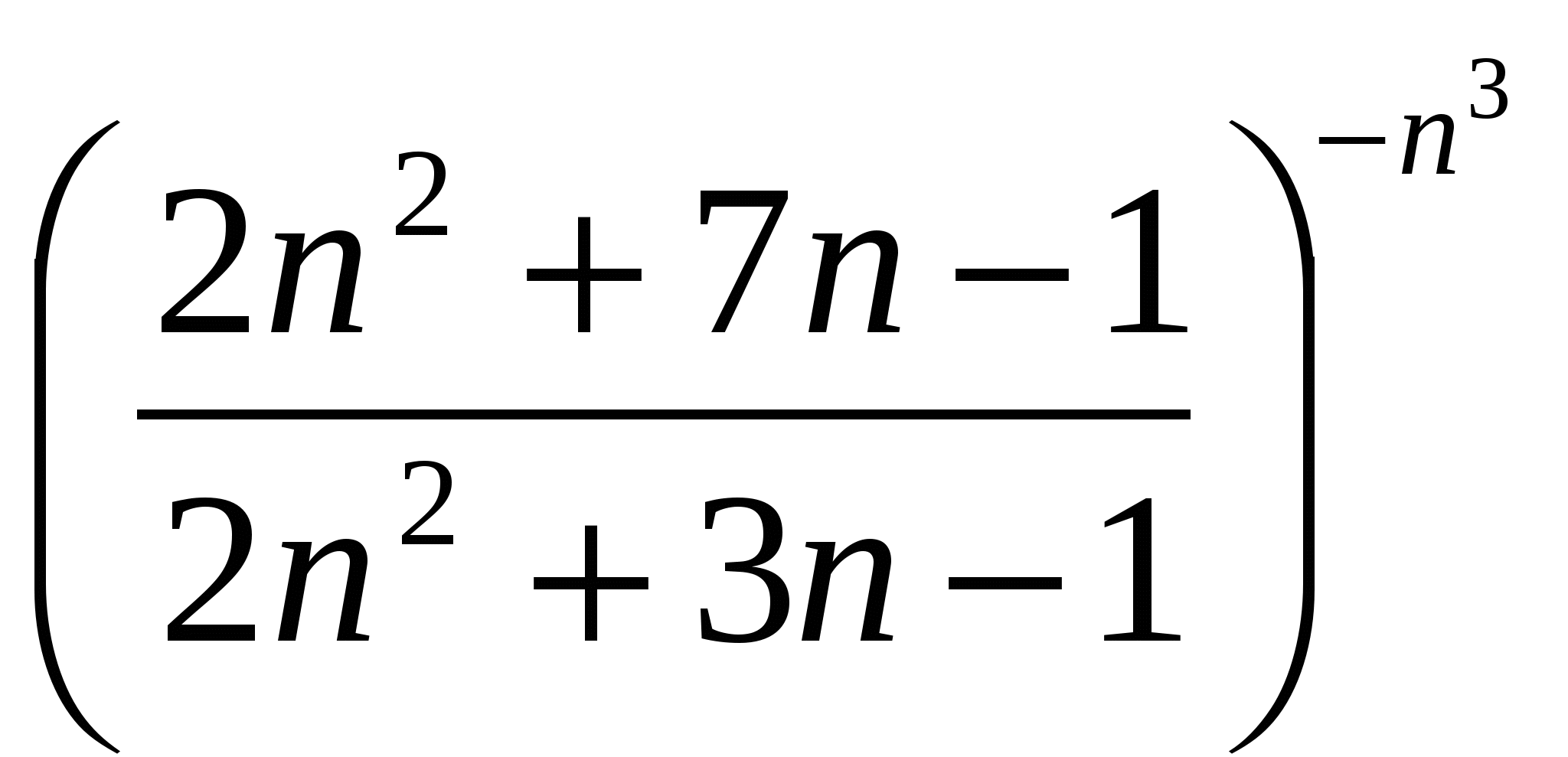
Вычислить предел последовательности
9
а)
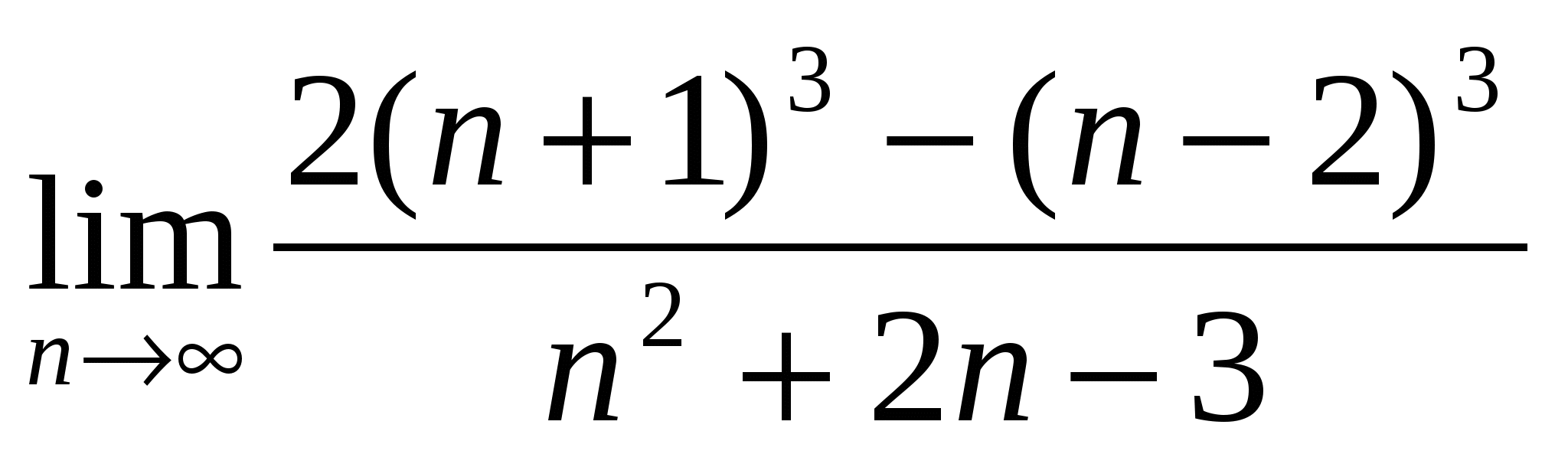
б)
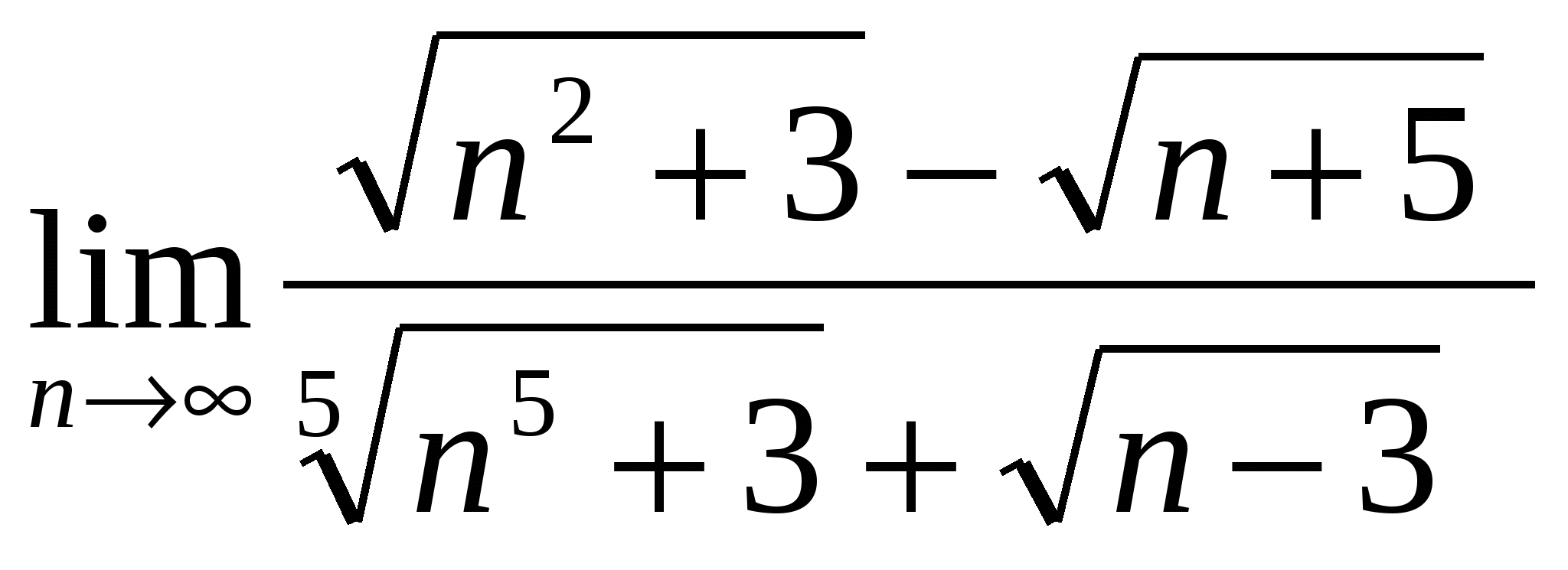
в)

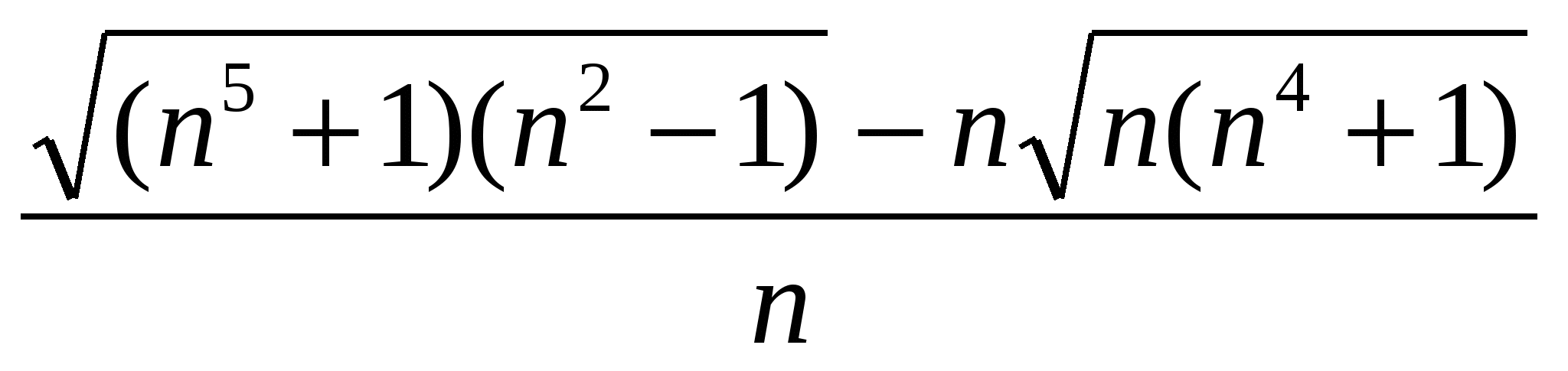
г)

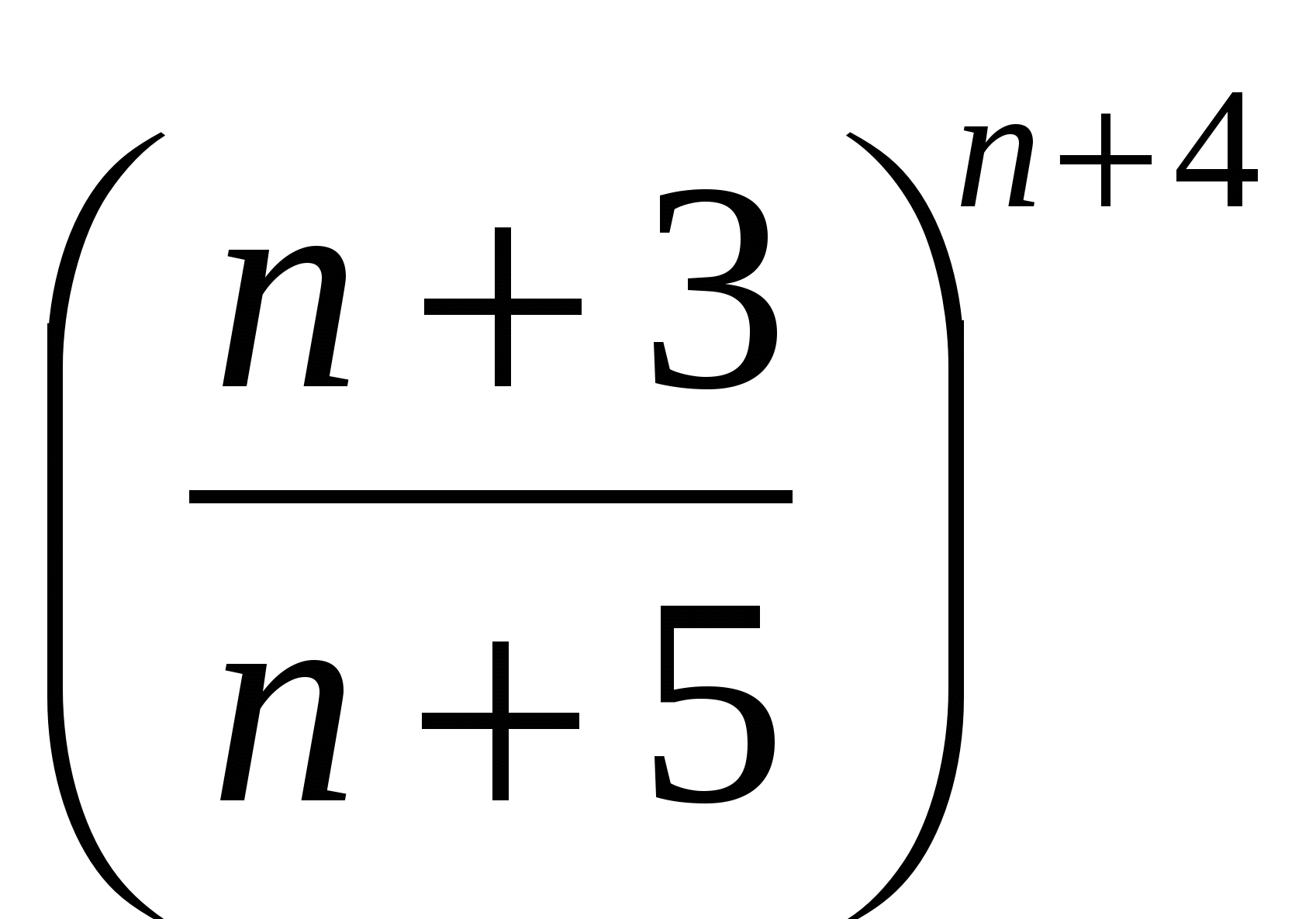
Вычислить предел последовательности
10
а)

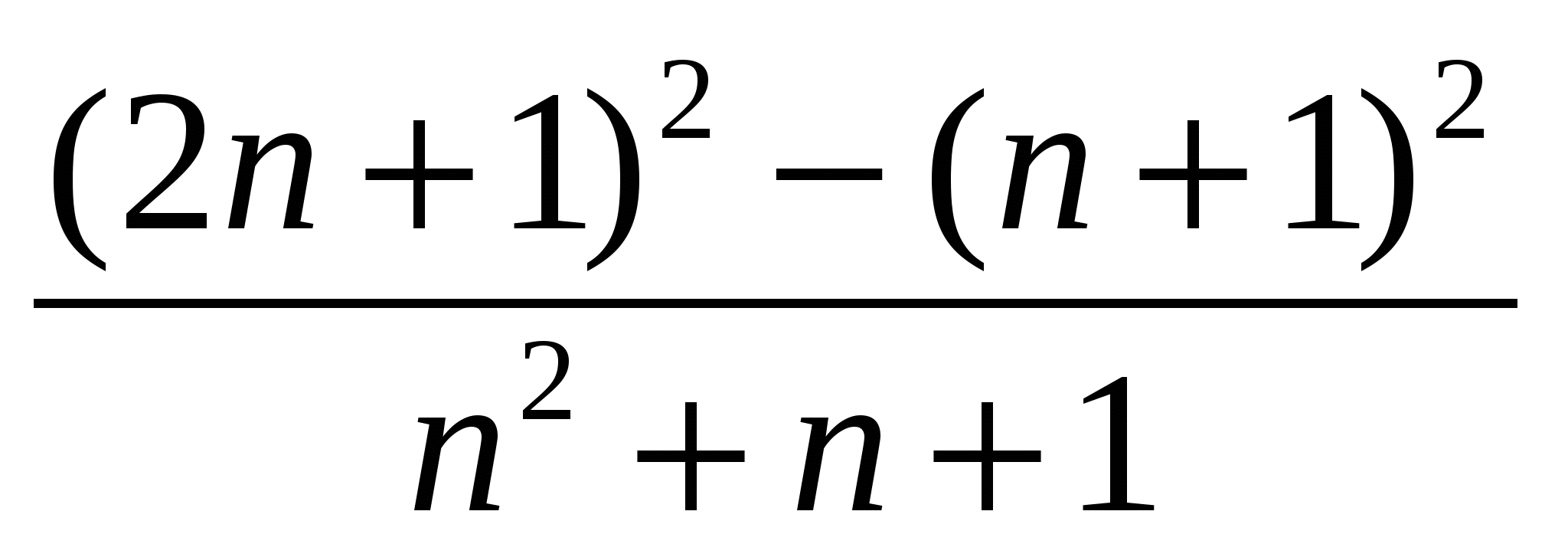
б)
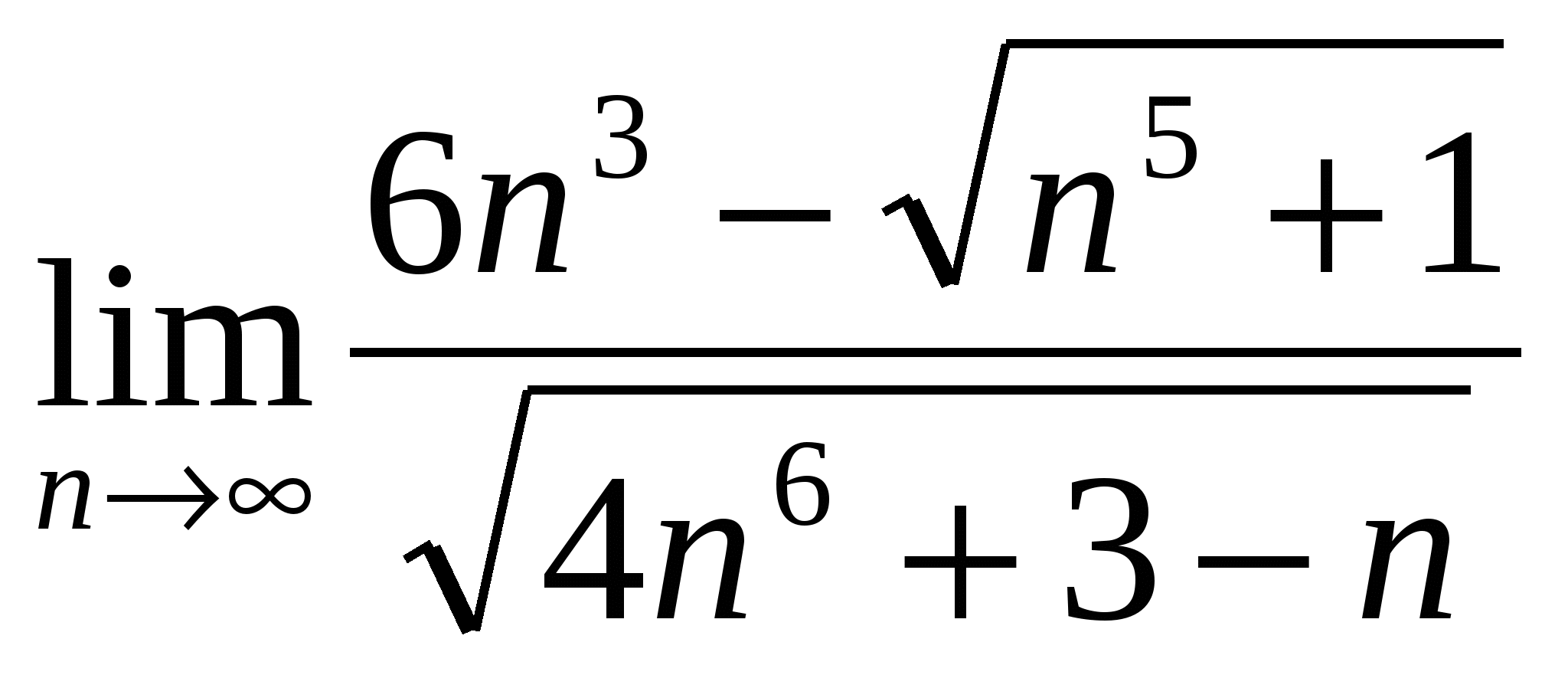
в)

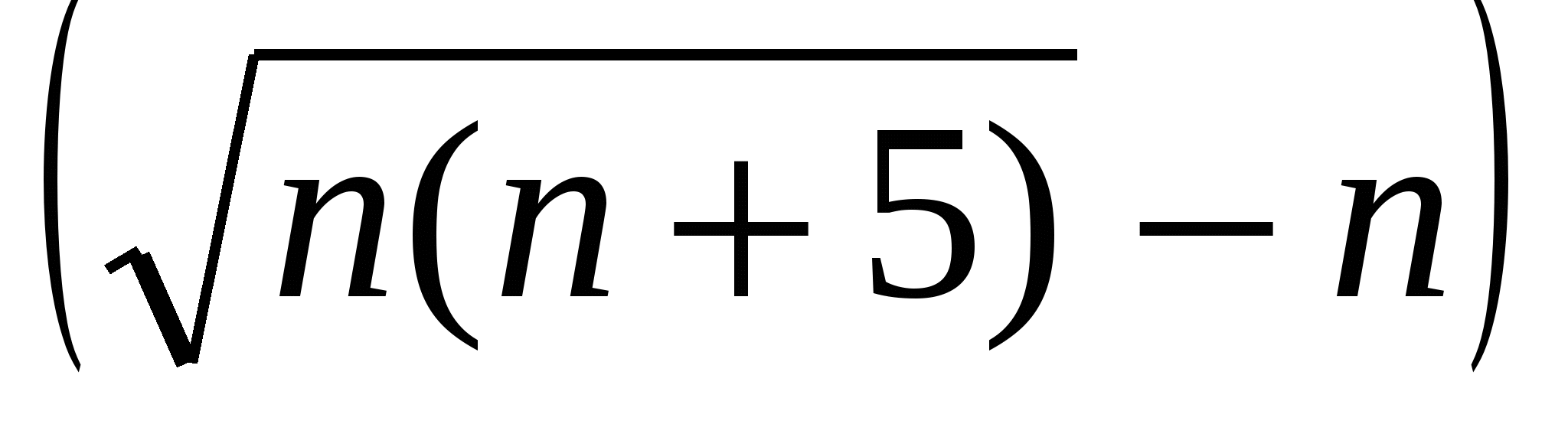
г)

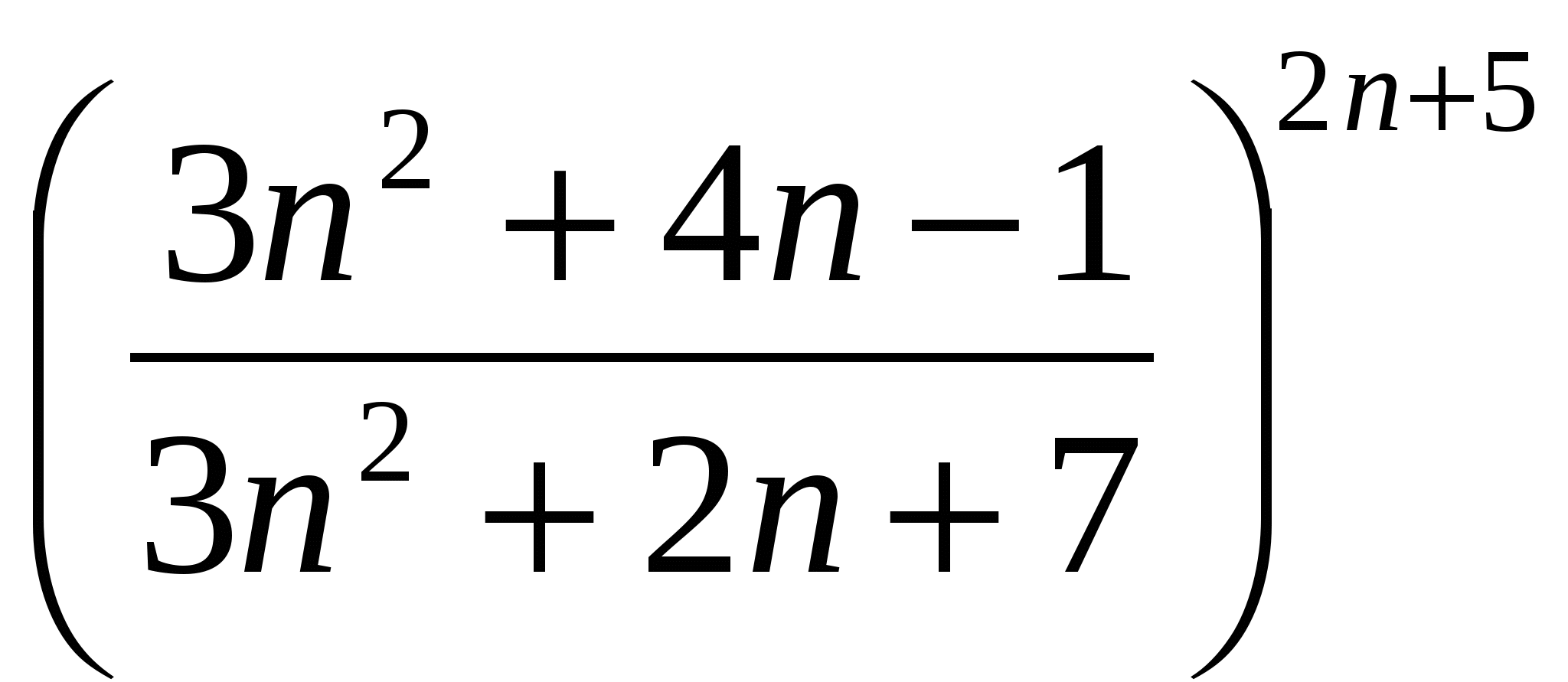
Контрольная работа № 4
Вычислить предел последовательности
11
а)
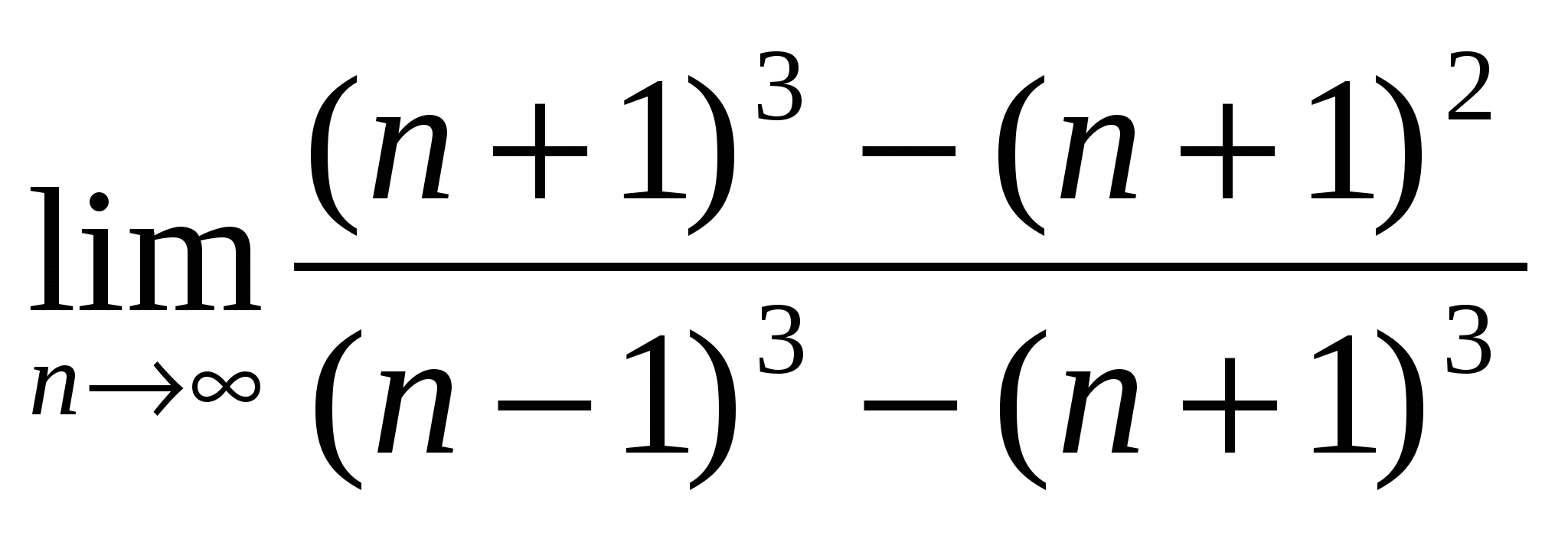
б)
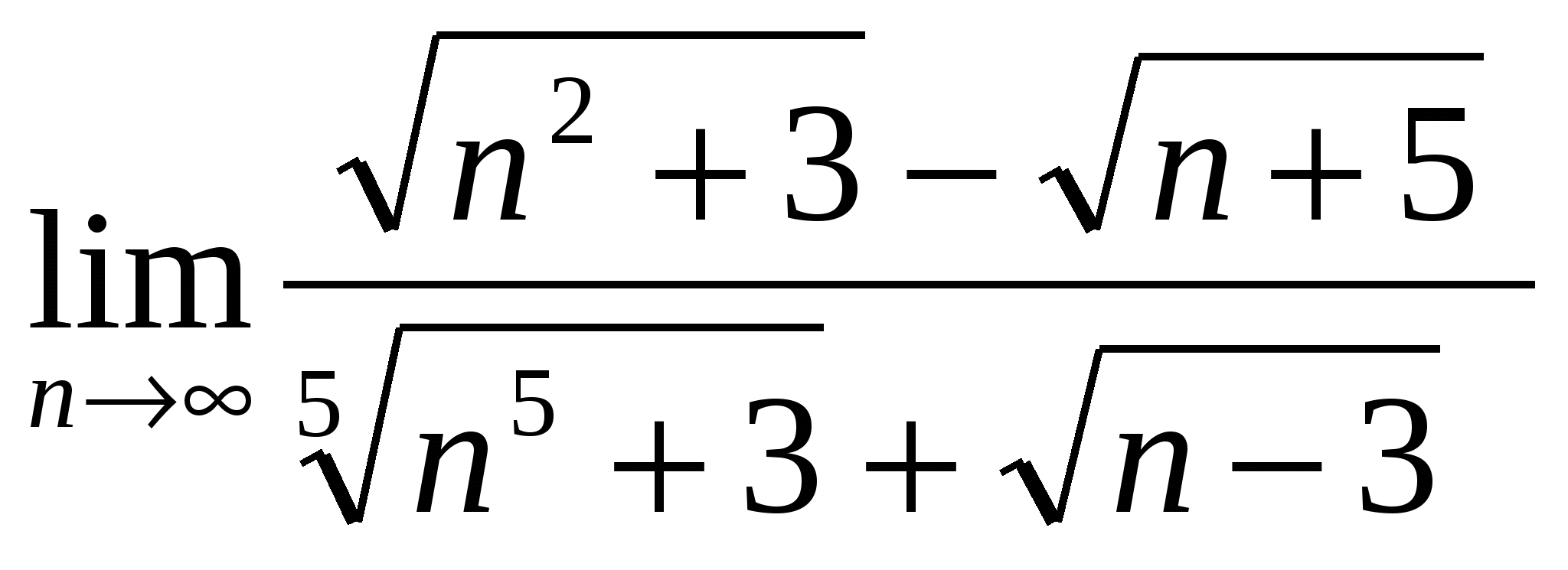
в)

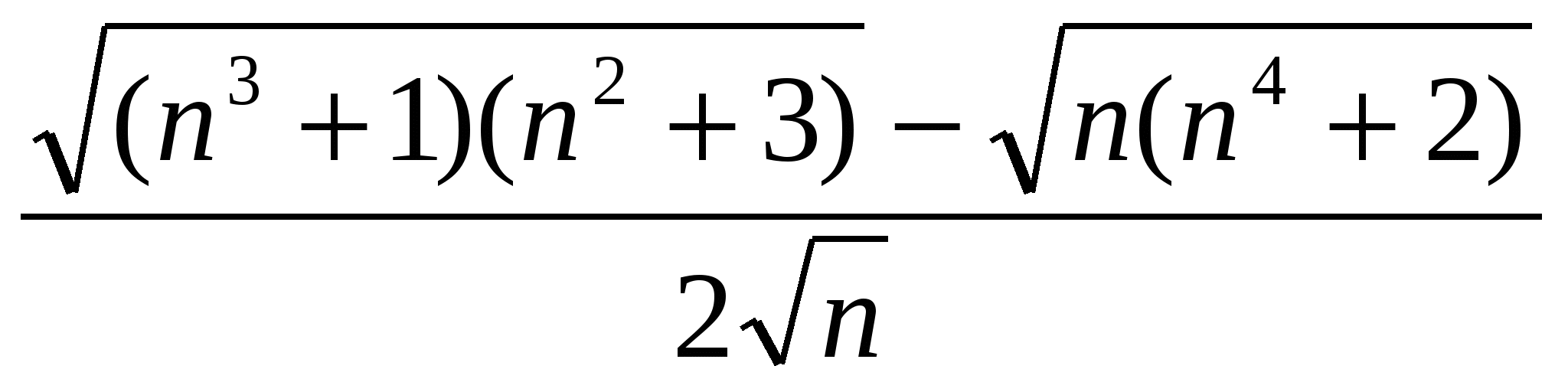
г)

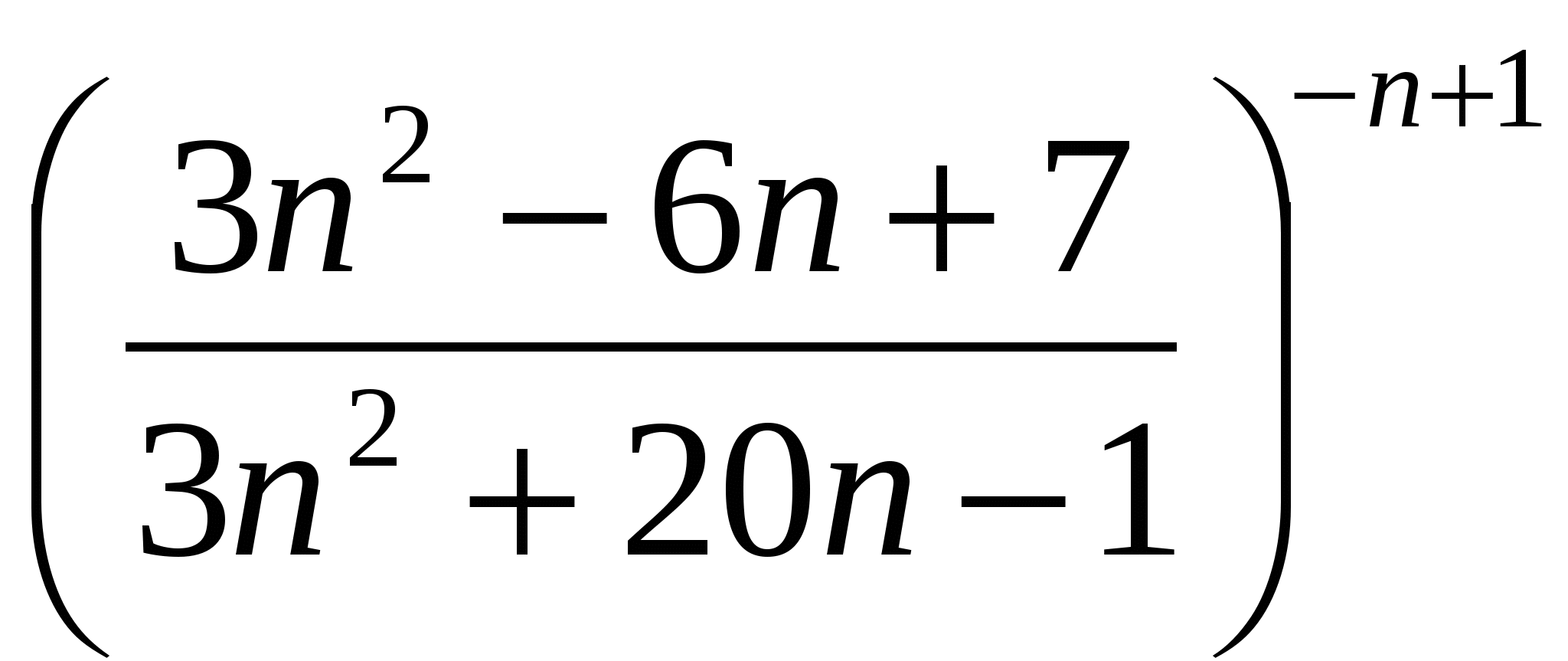
Вычислить предел последовательности
12
а)

б)
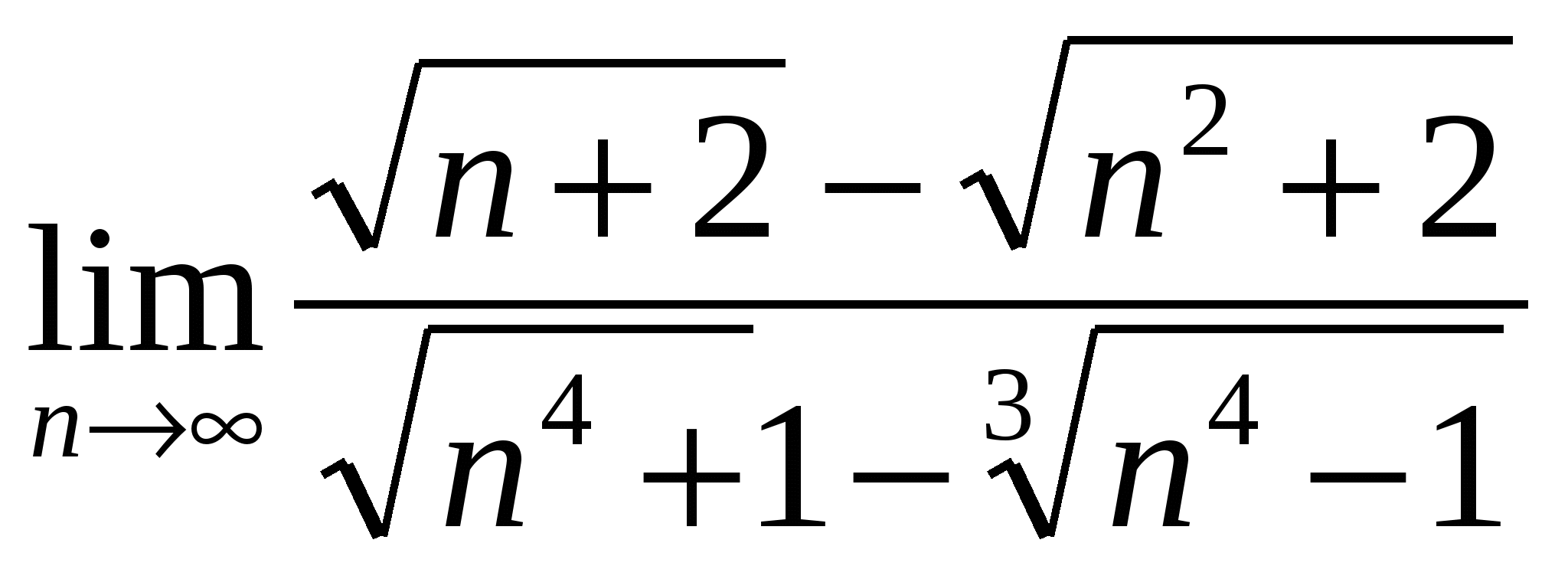
в)

г)
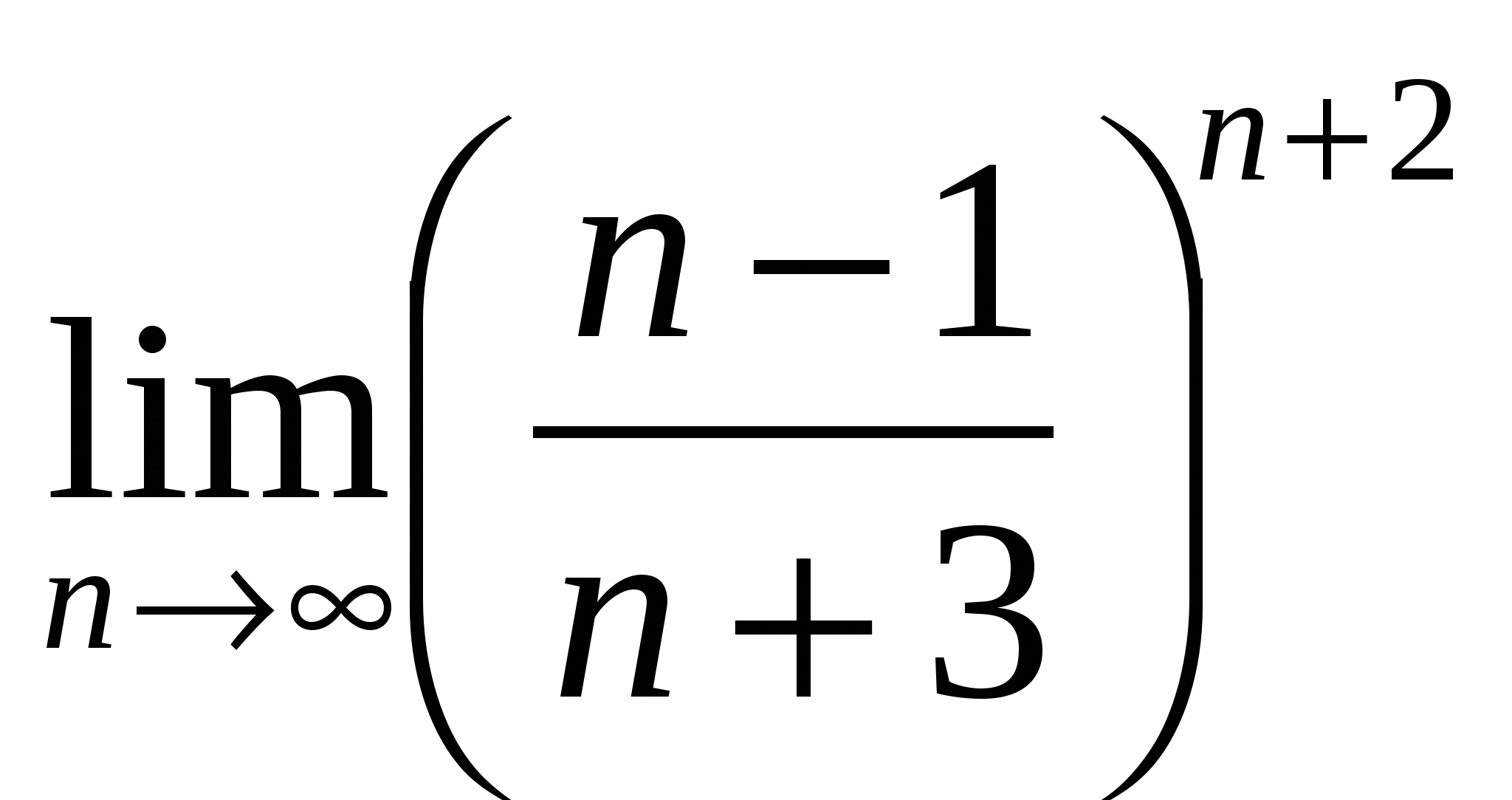
Вычислить предел последовательности
13
а)
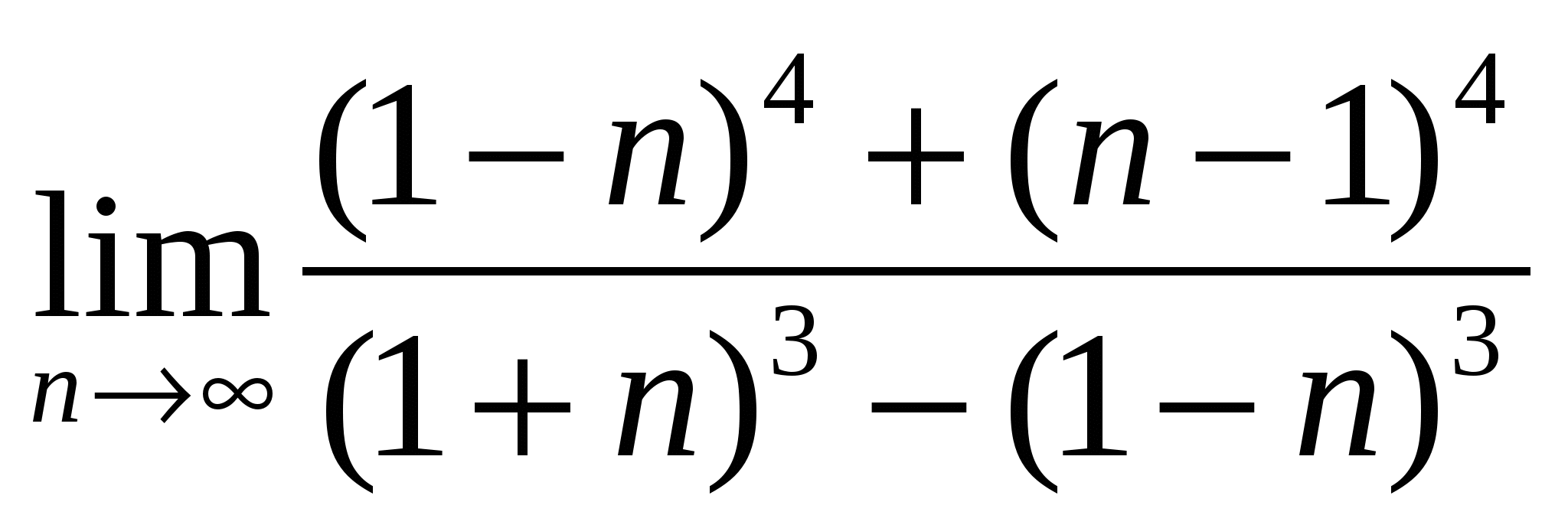
б)
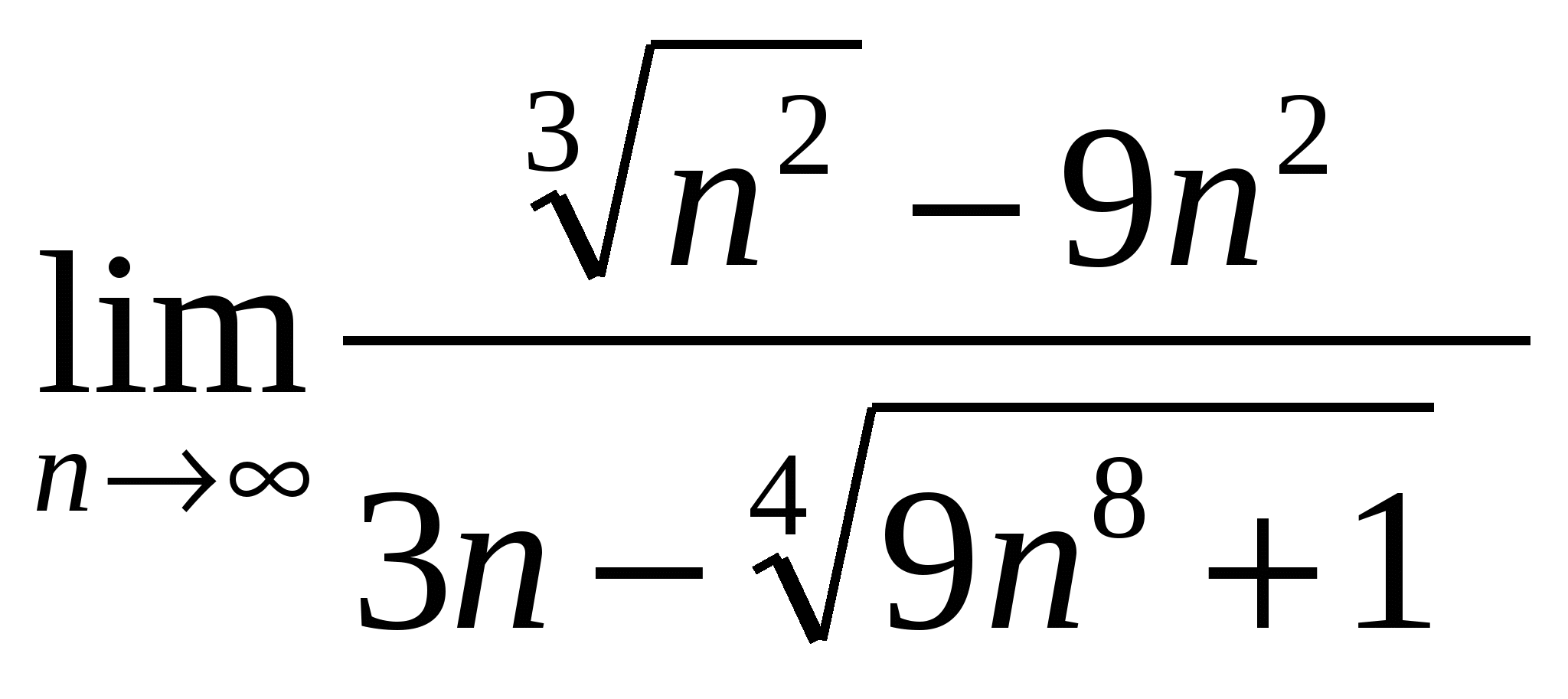
в)


г)

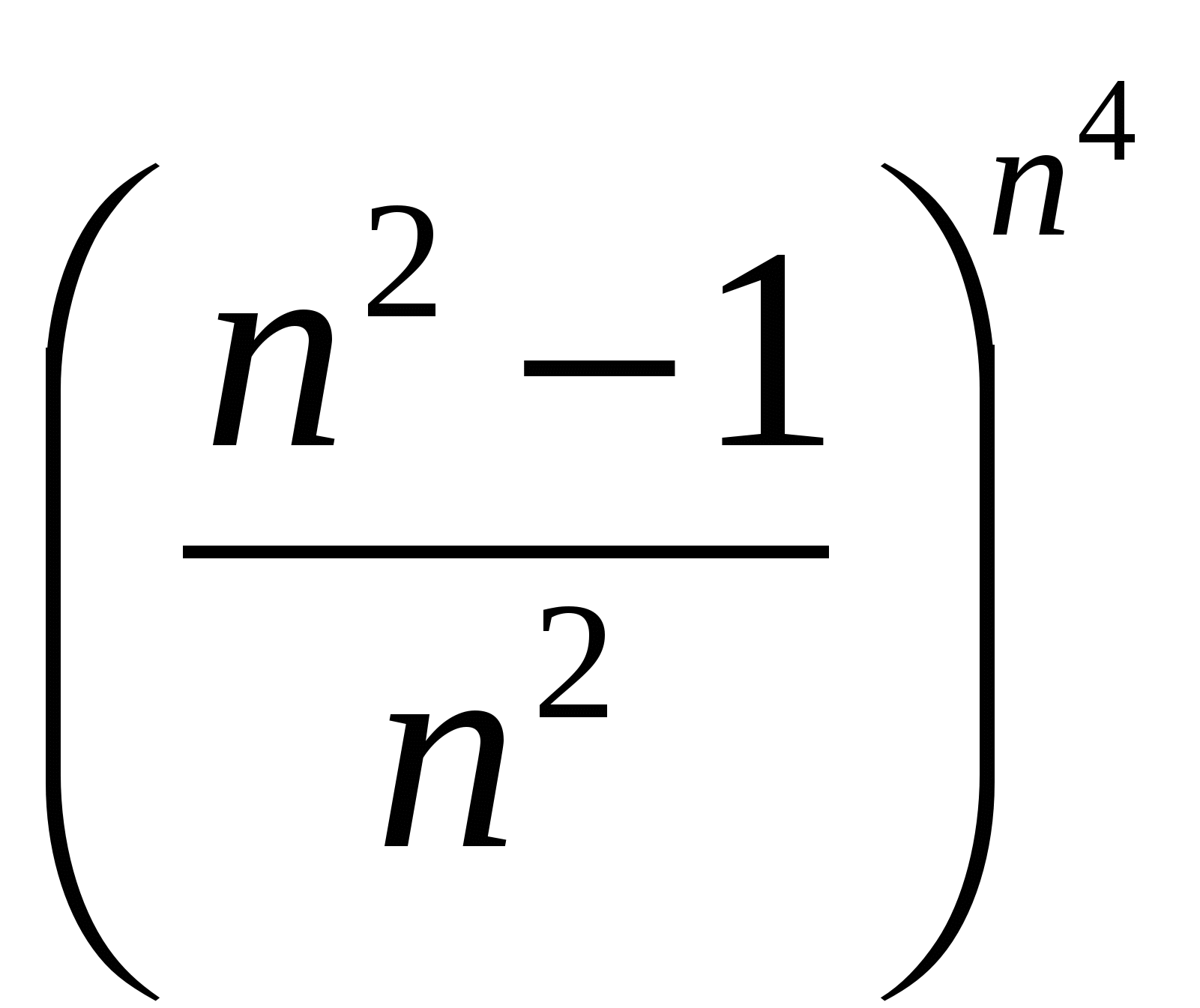
Вычислить предел последовательности
14
а)
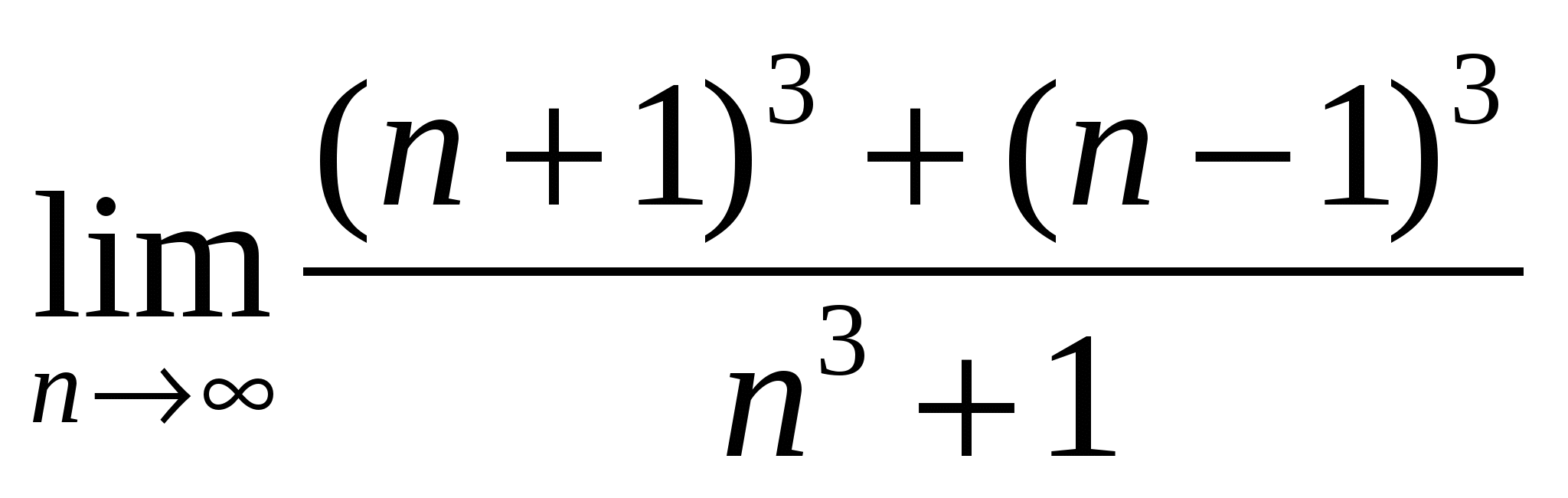
б)
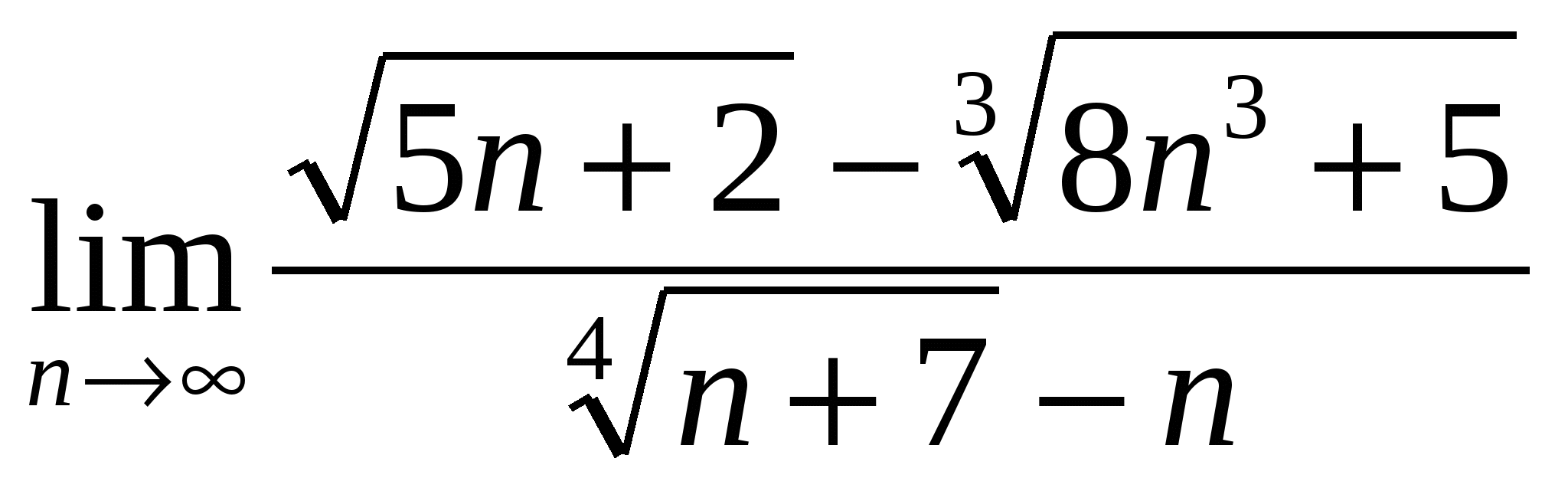
в)
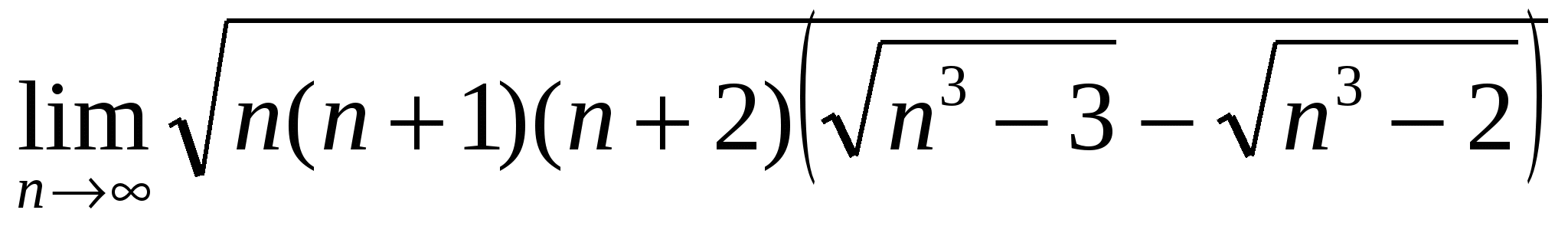
г)
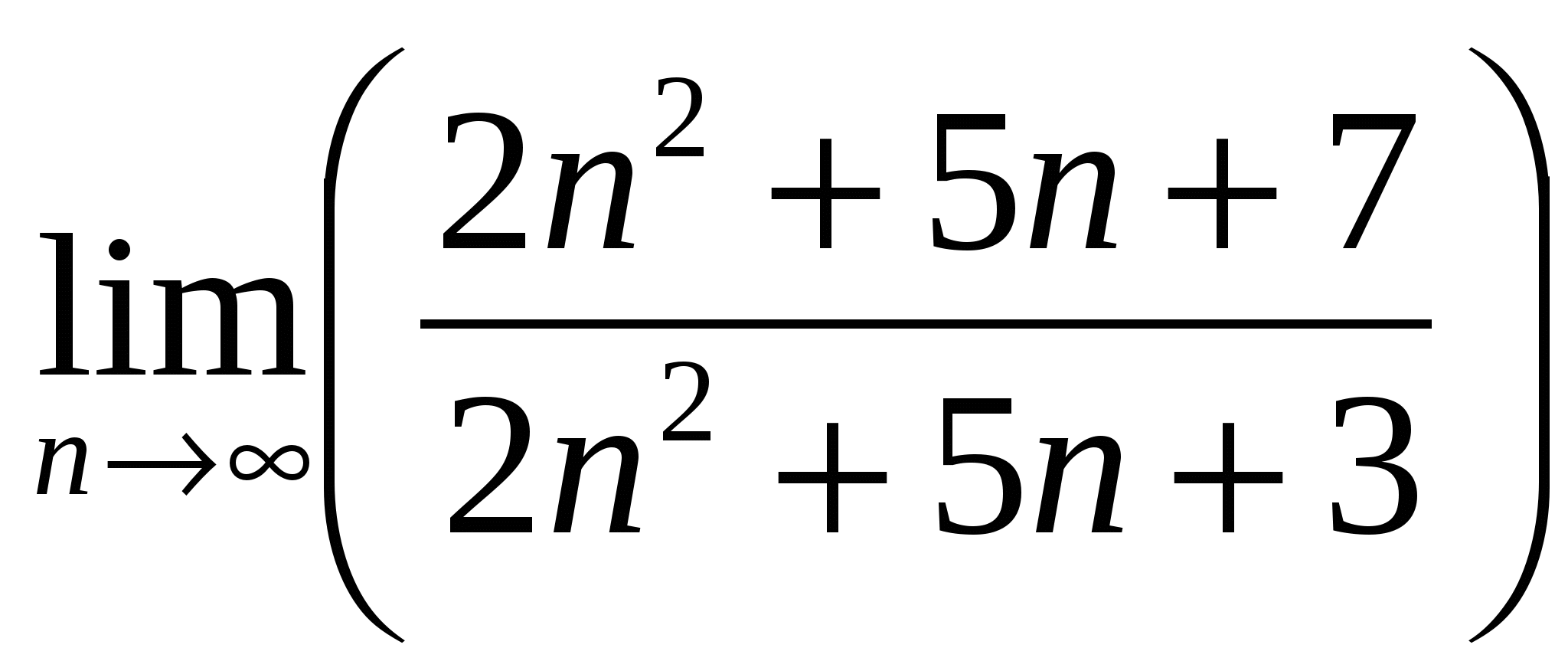
Вычислить предел последовательности
15
а)
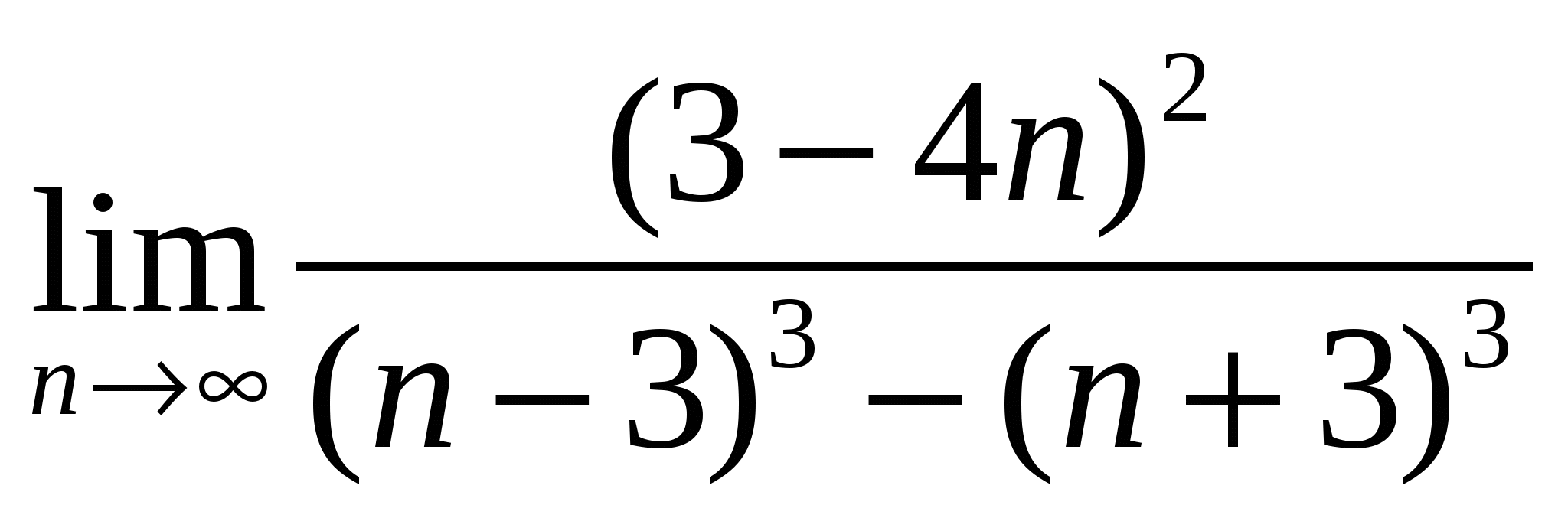
б)
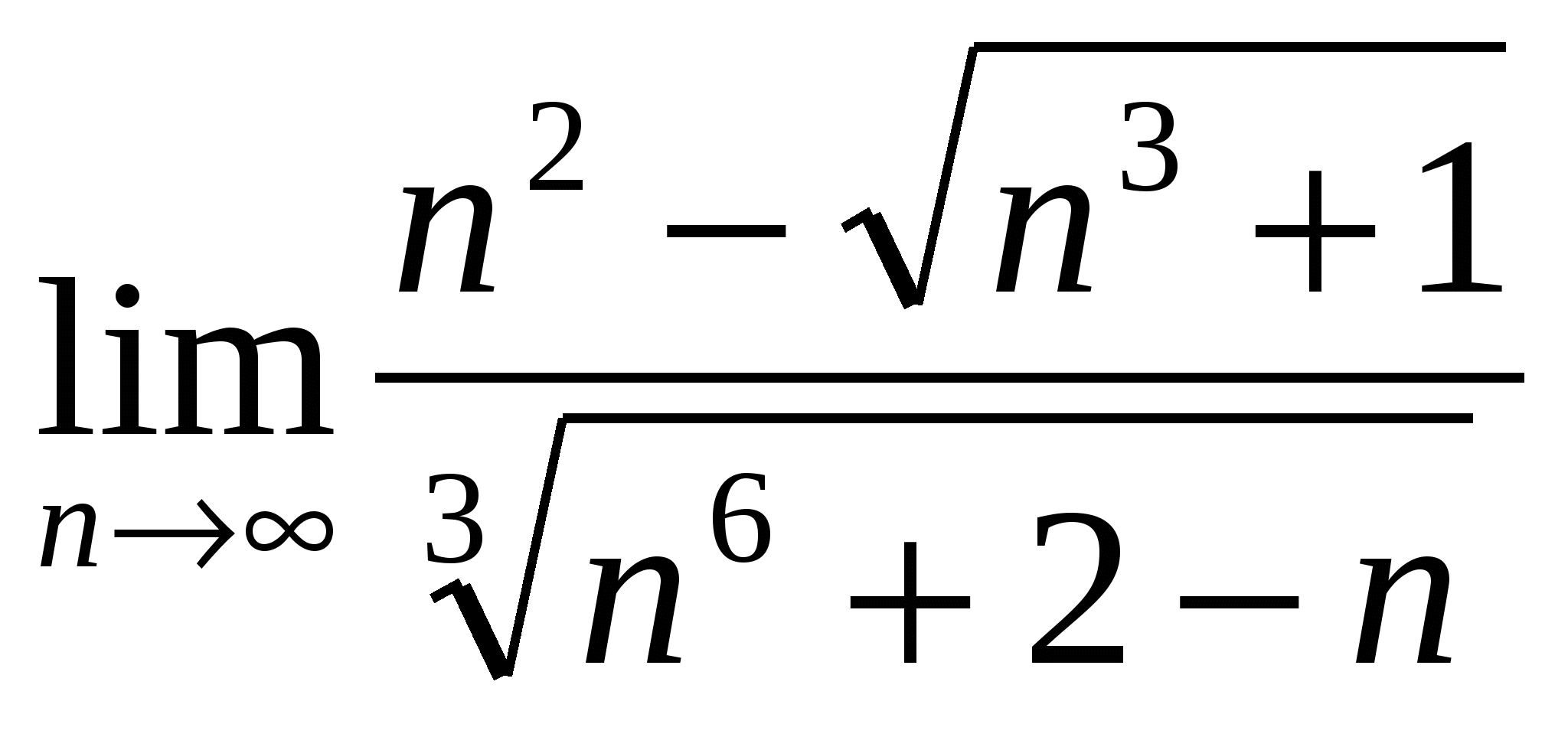
в)
 n
n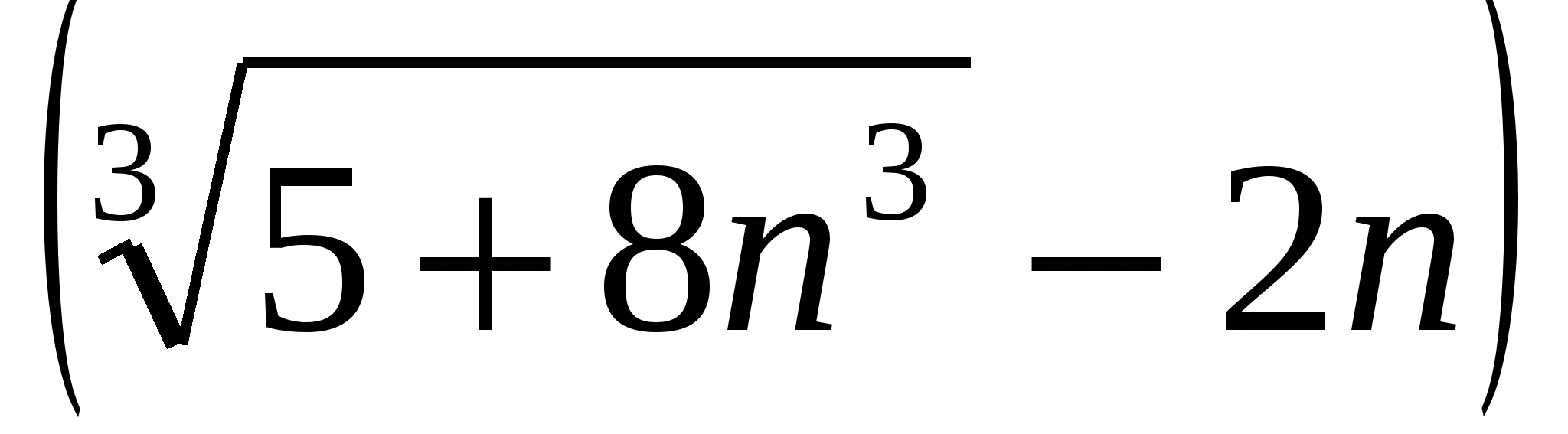
г)
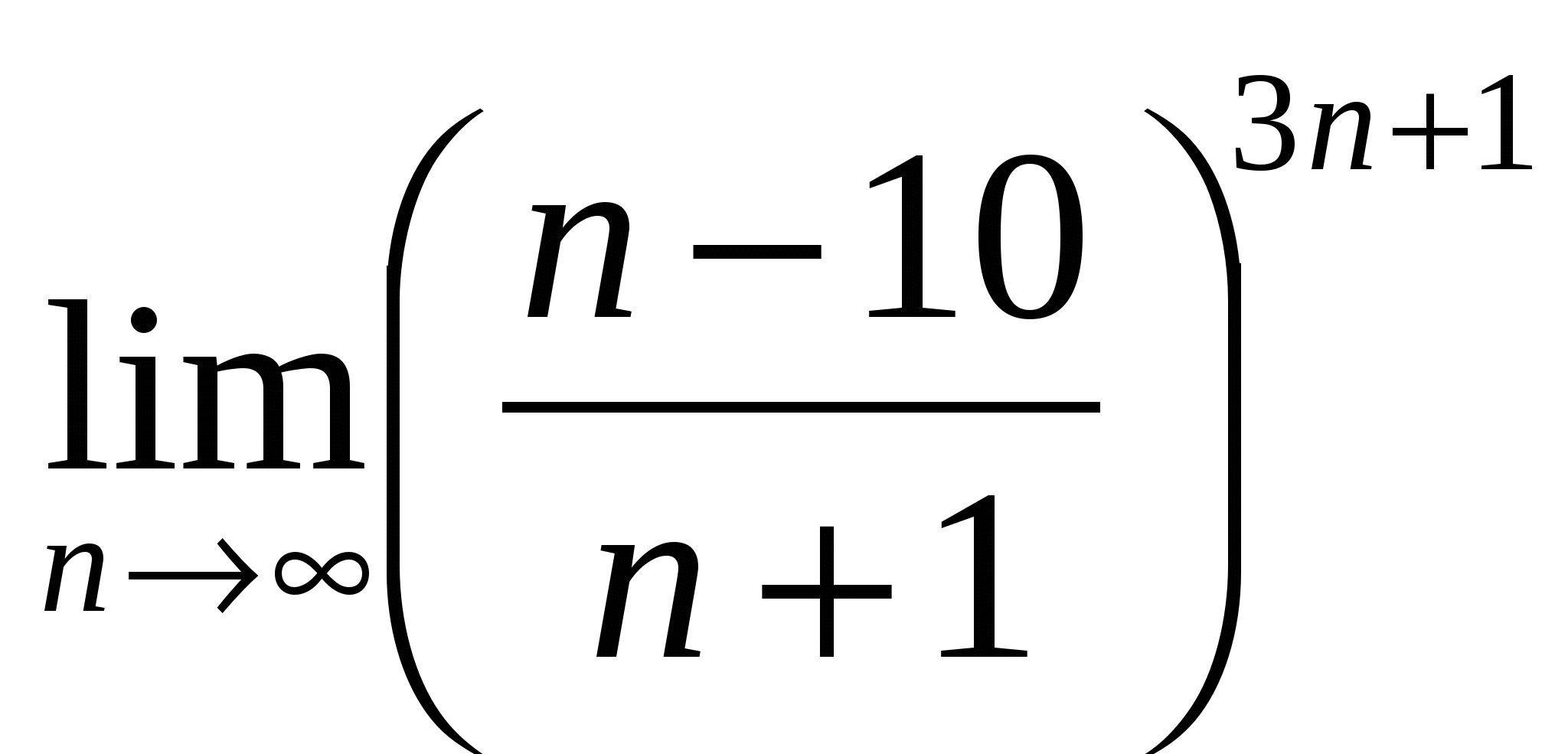
Вычислить предел последовательности
16
а)
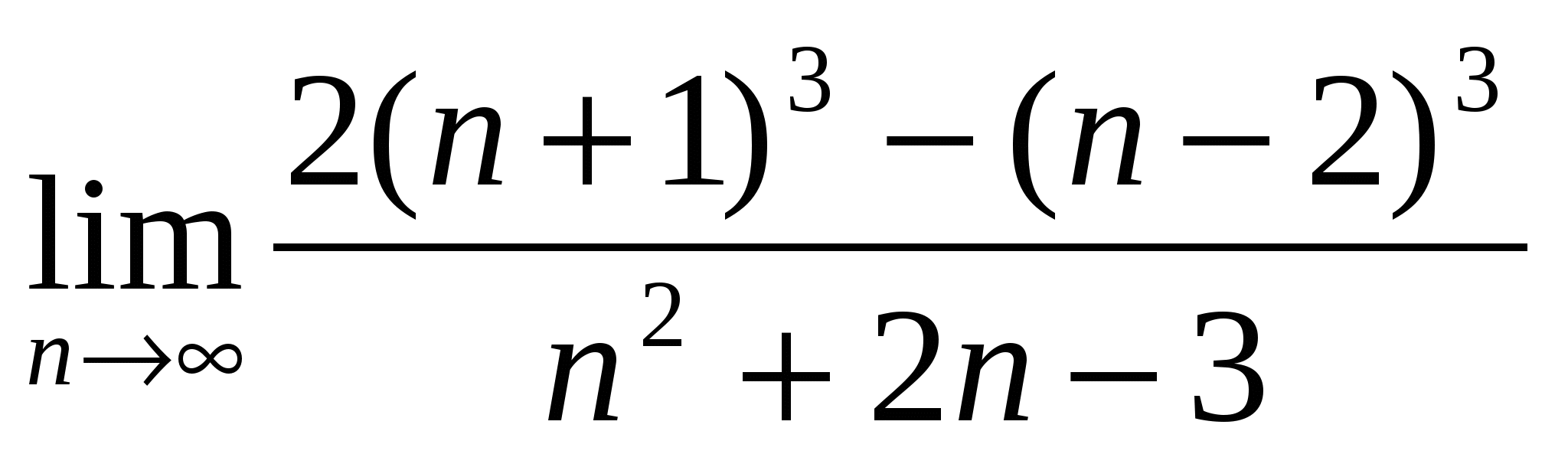
б)
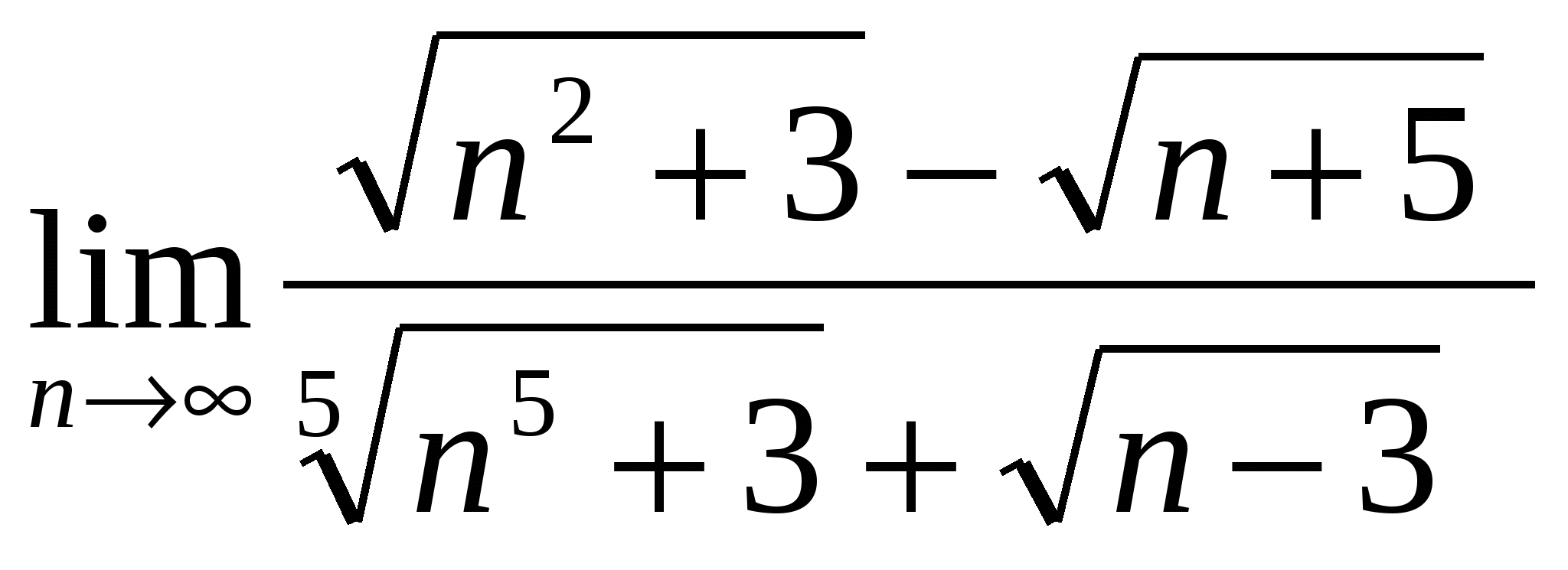
в)

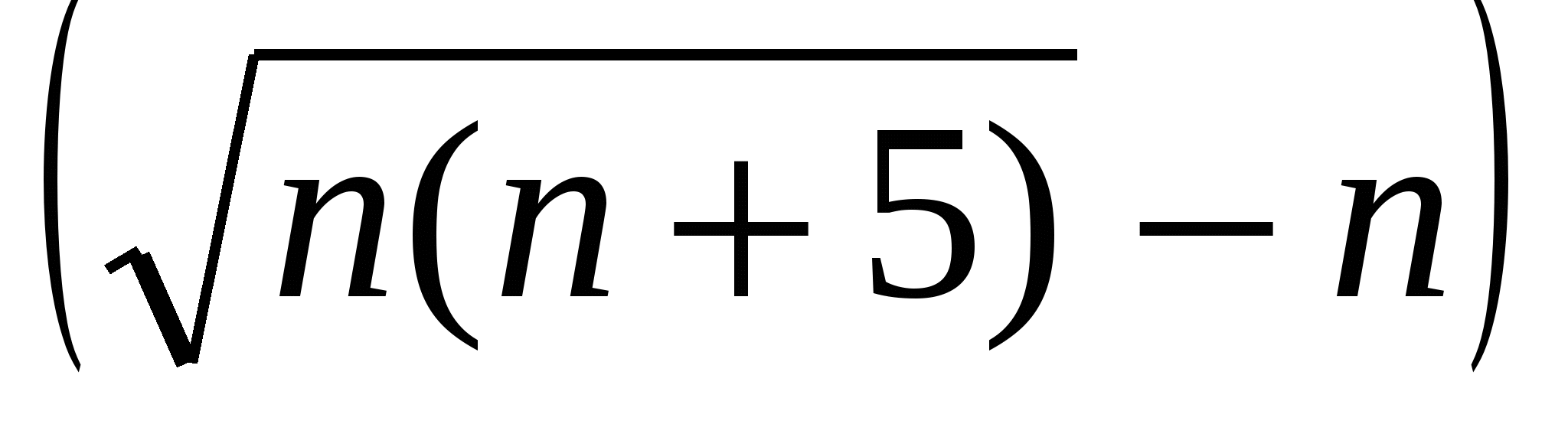
г)

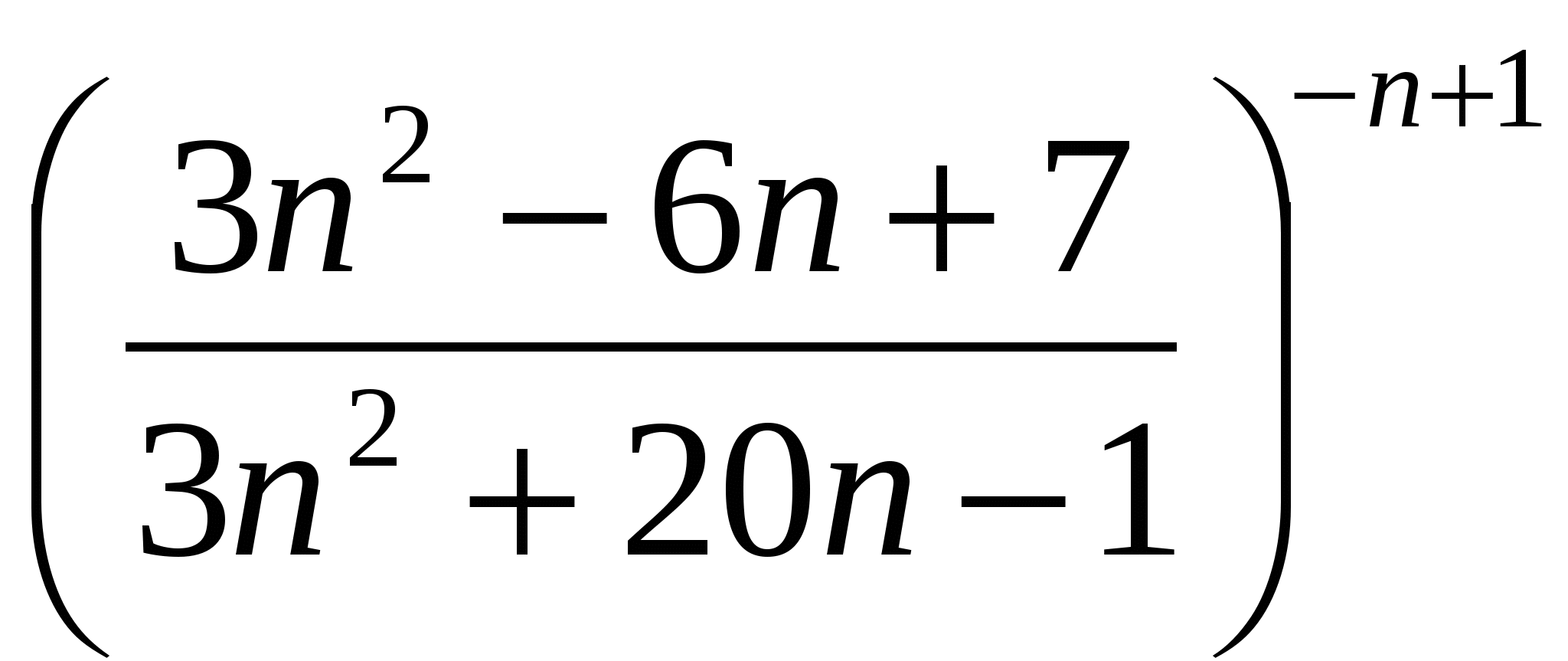
Вычислить предел последовательности
17
а)
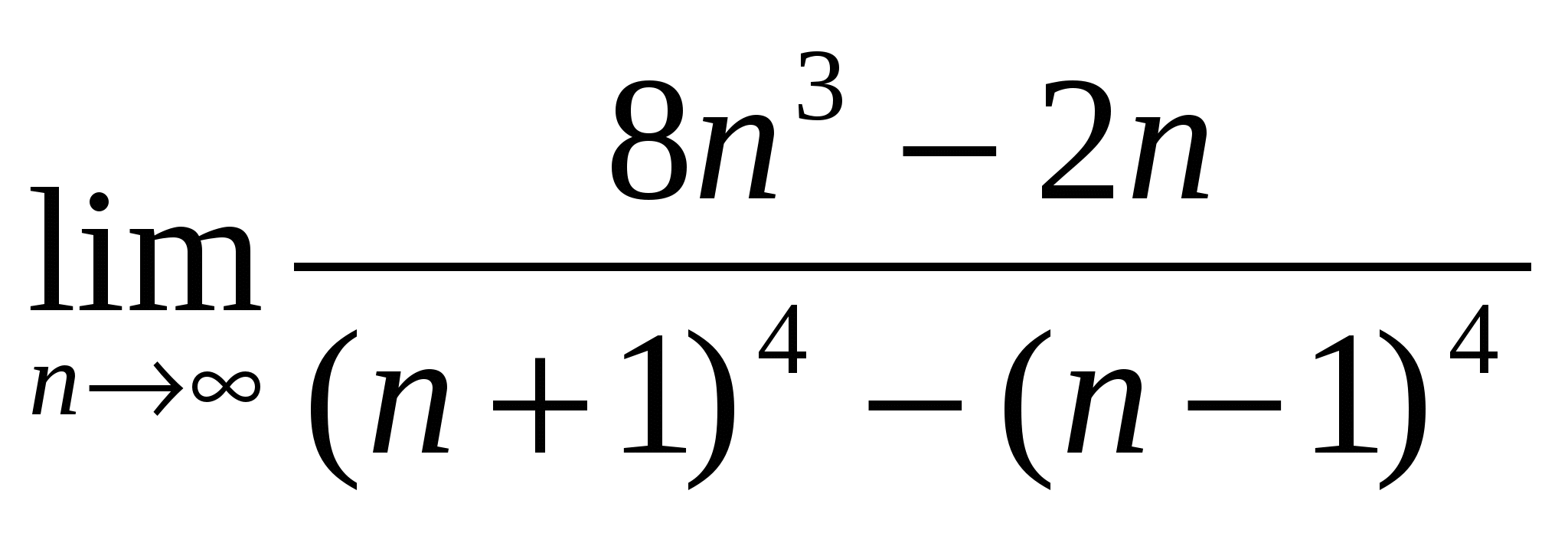
б)
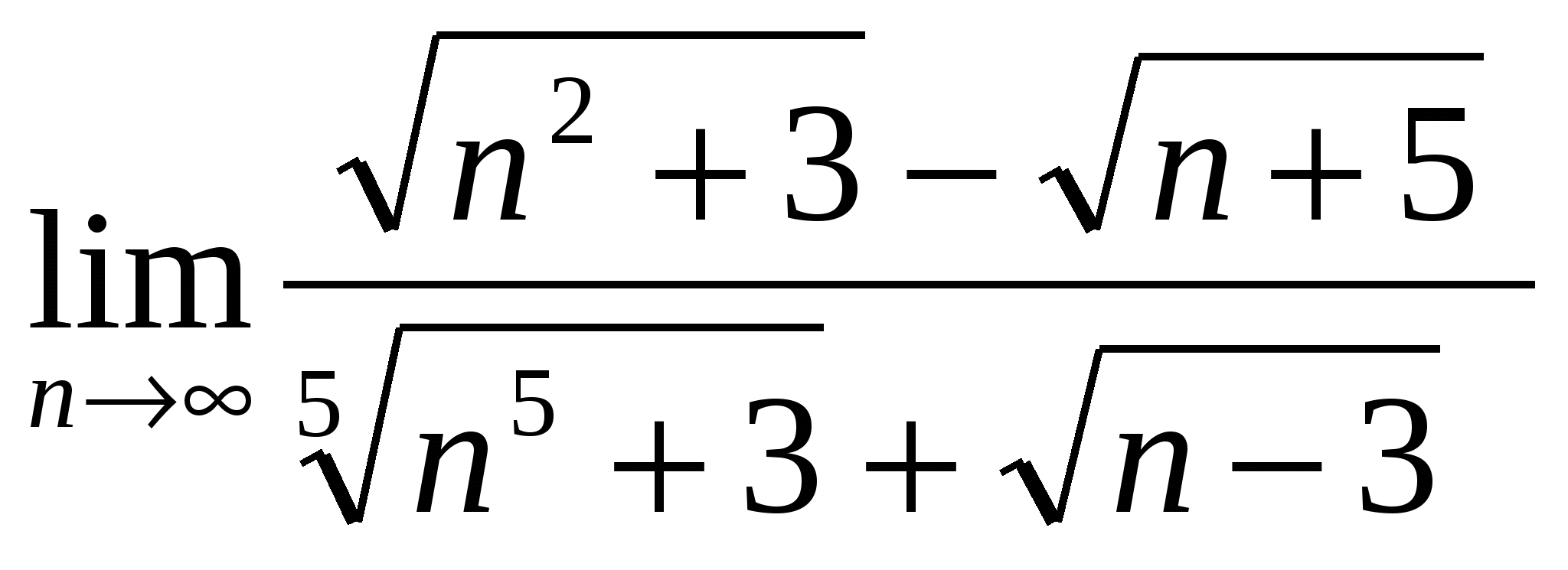
в)

г)
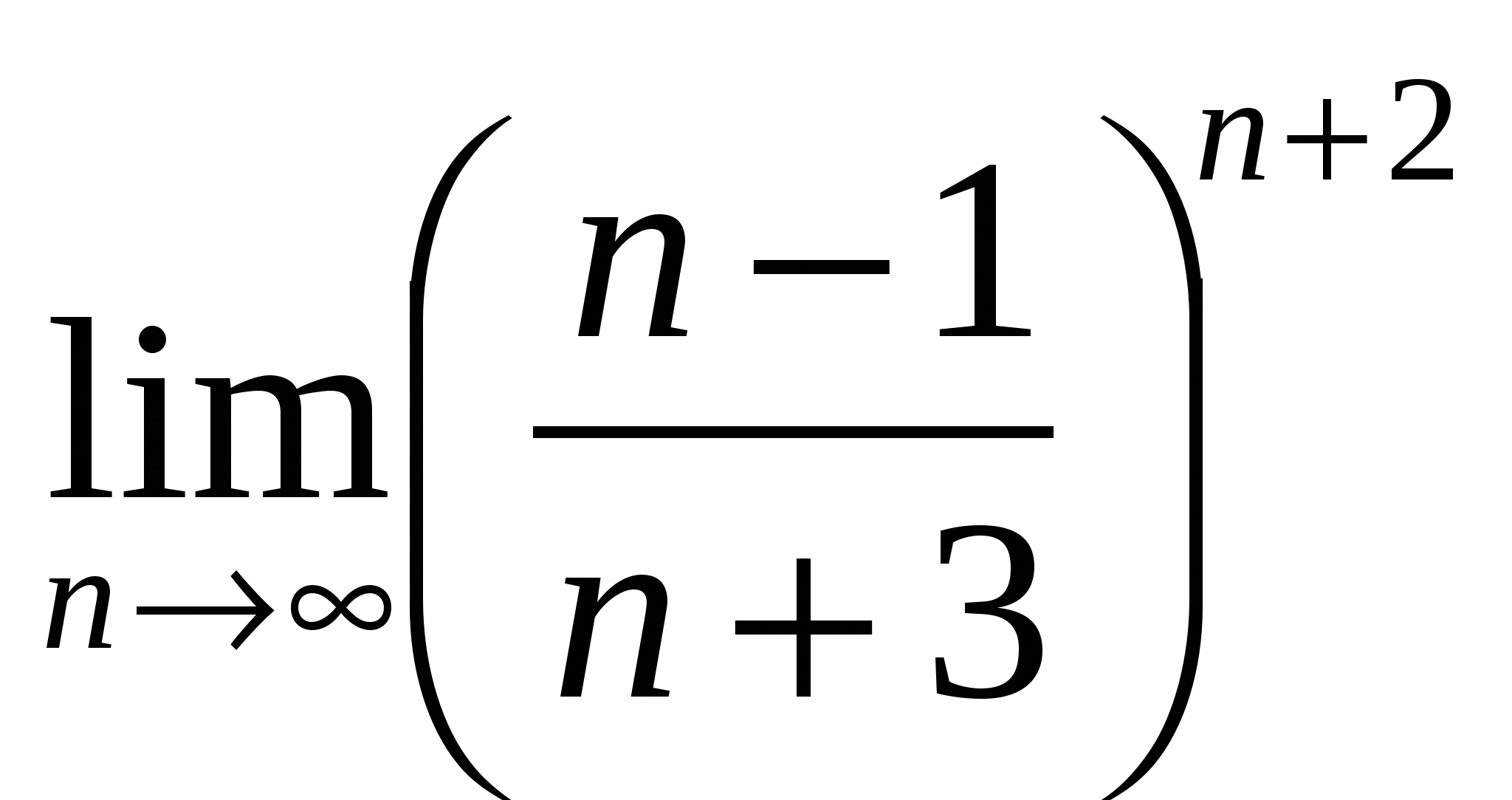
Вычислить предел последовательности
18
а)
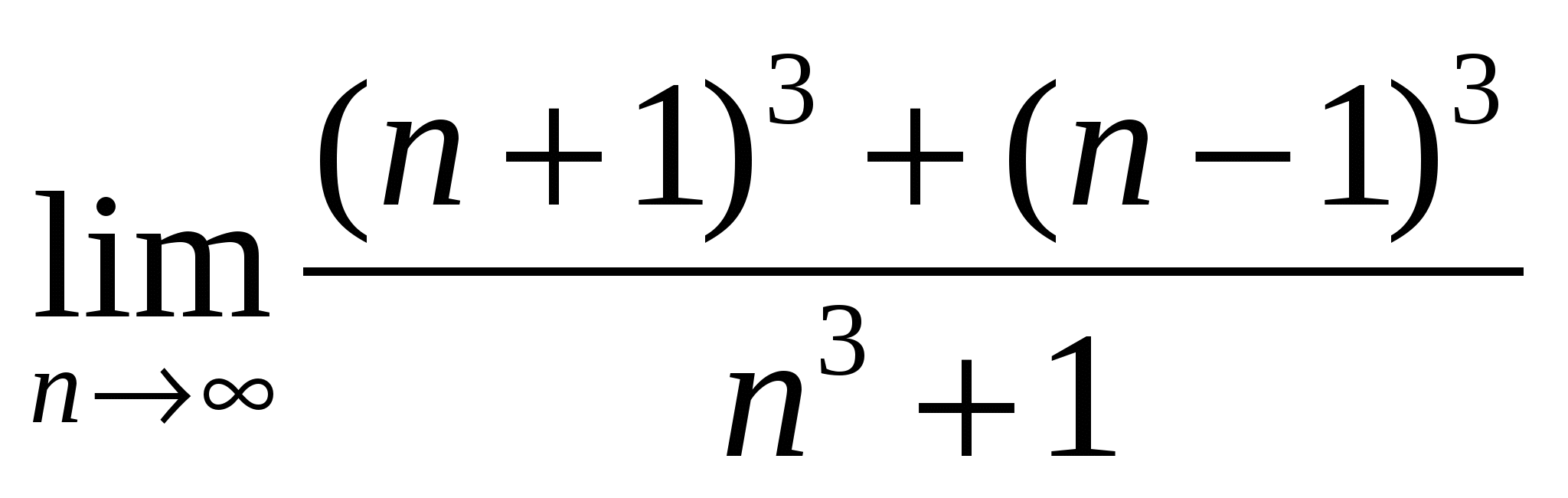
б)
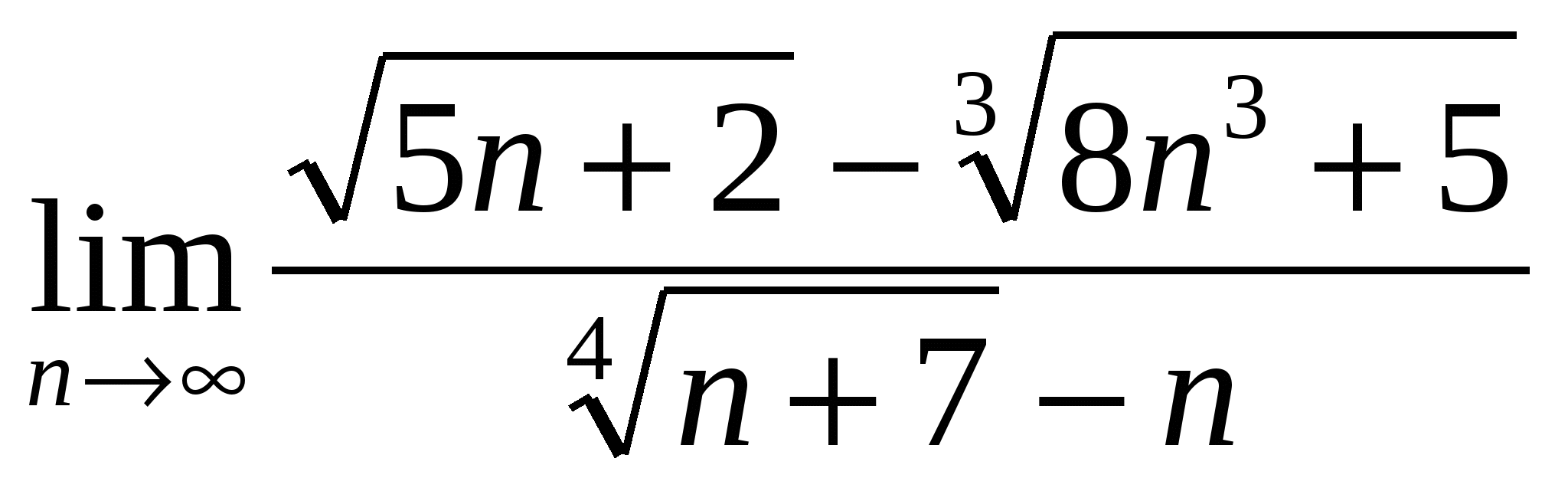
в)

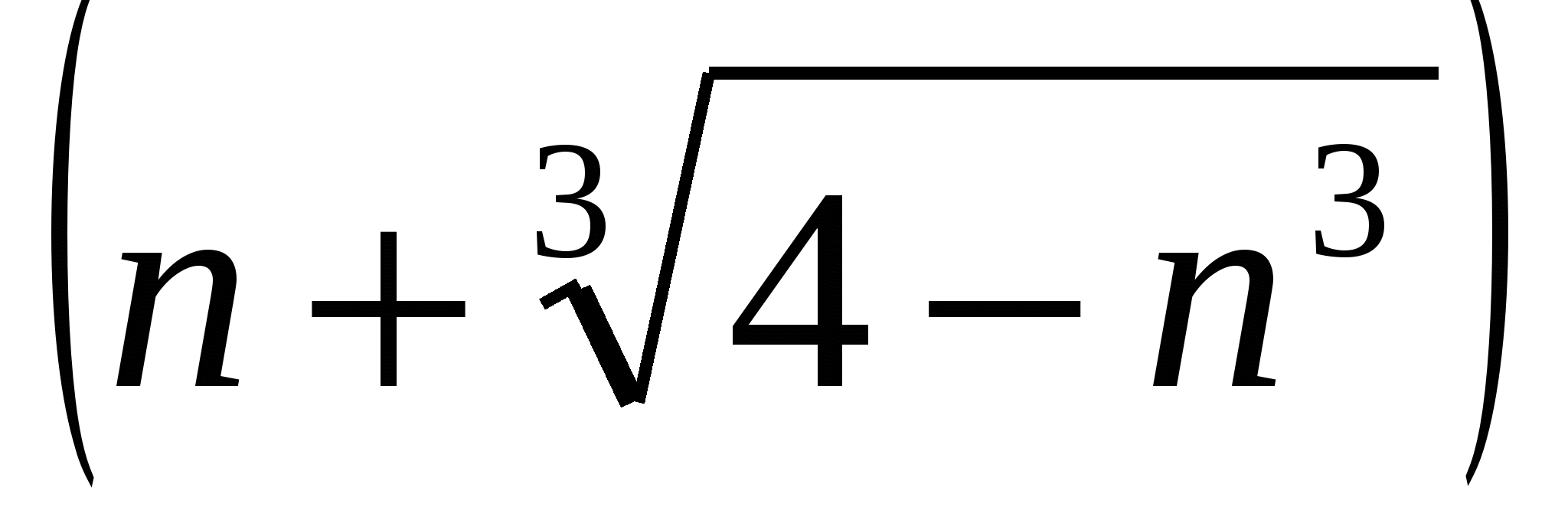
г)

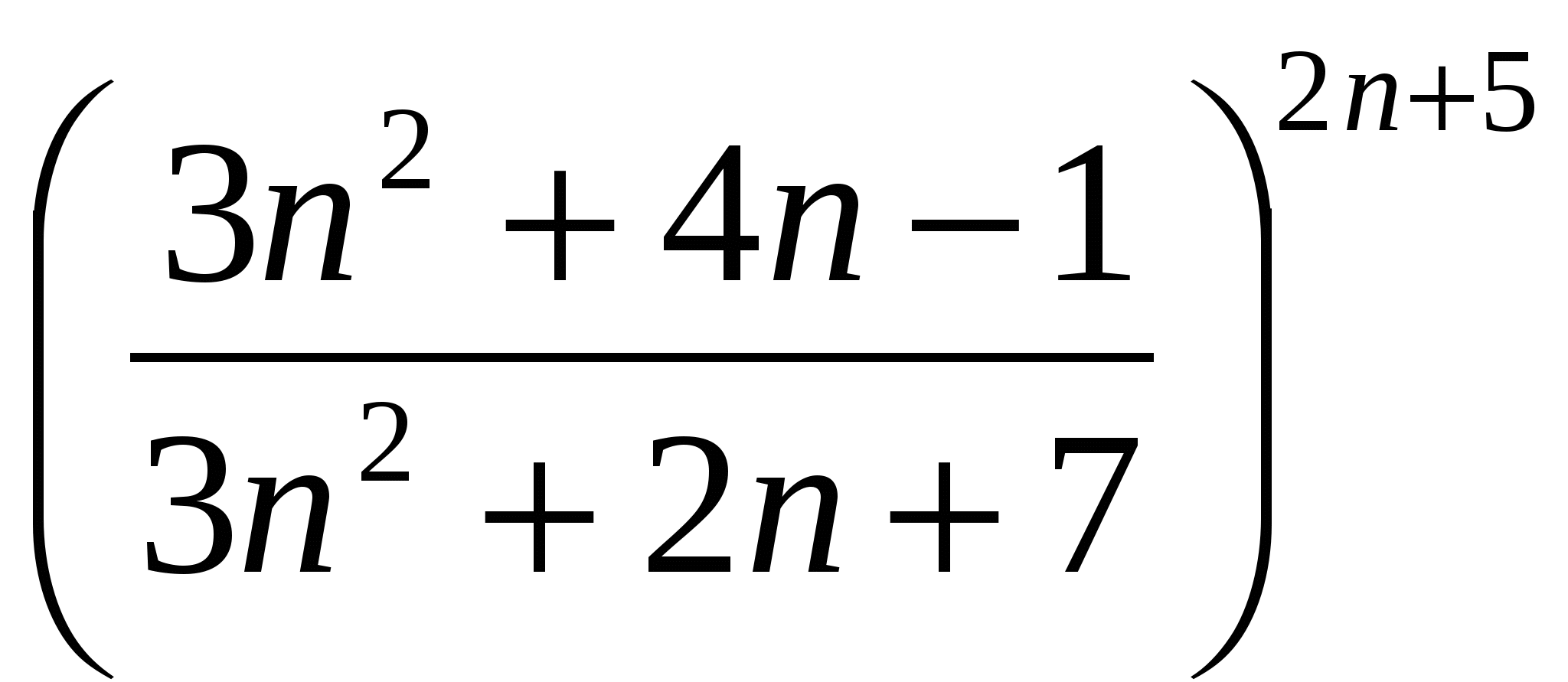
Вычислить предел последовательности
19
а)
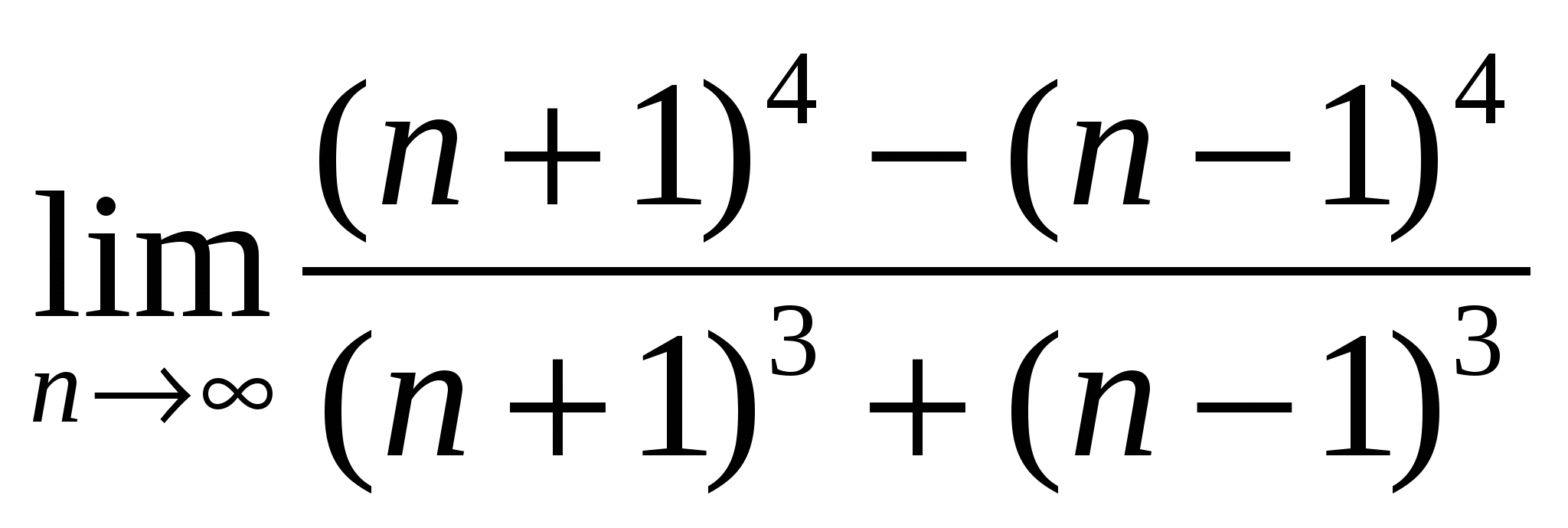
б)
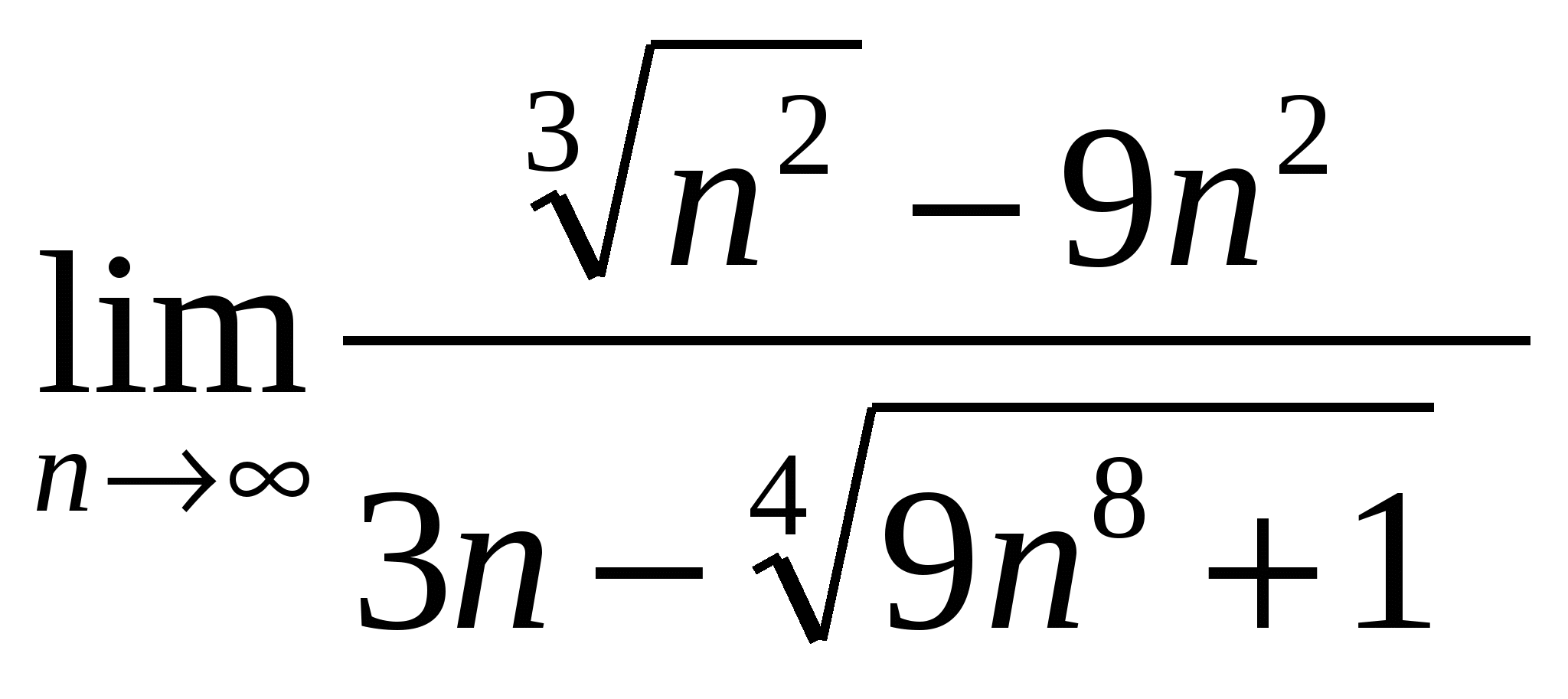
в)


г)

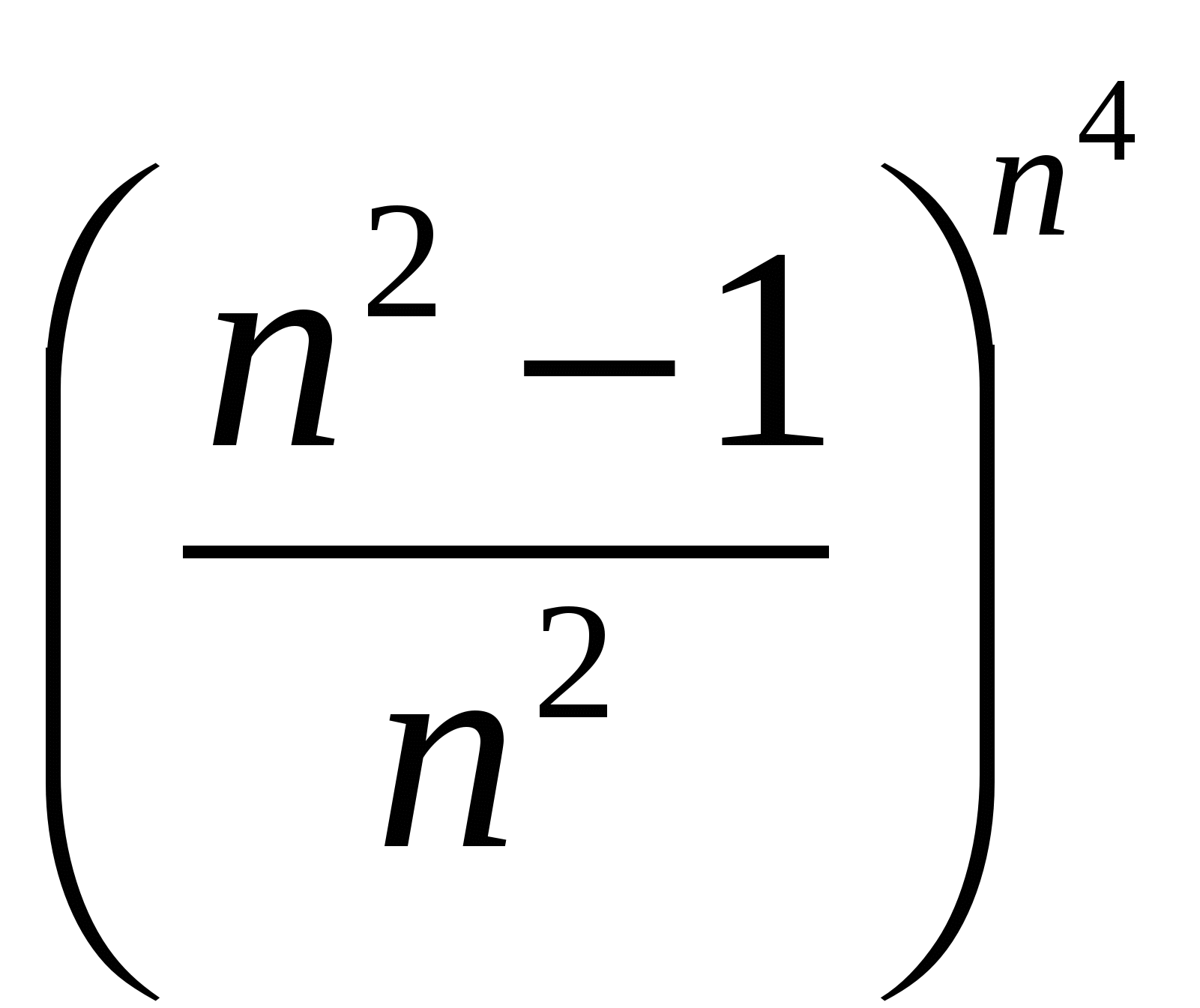
Вычислить предел последовательности
20
а)

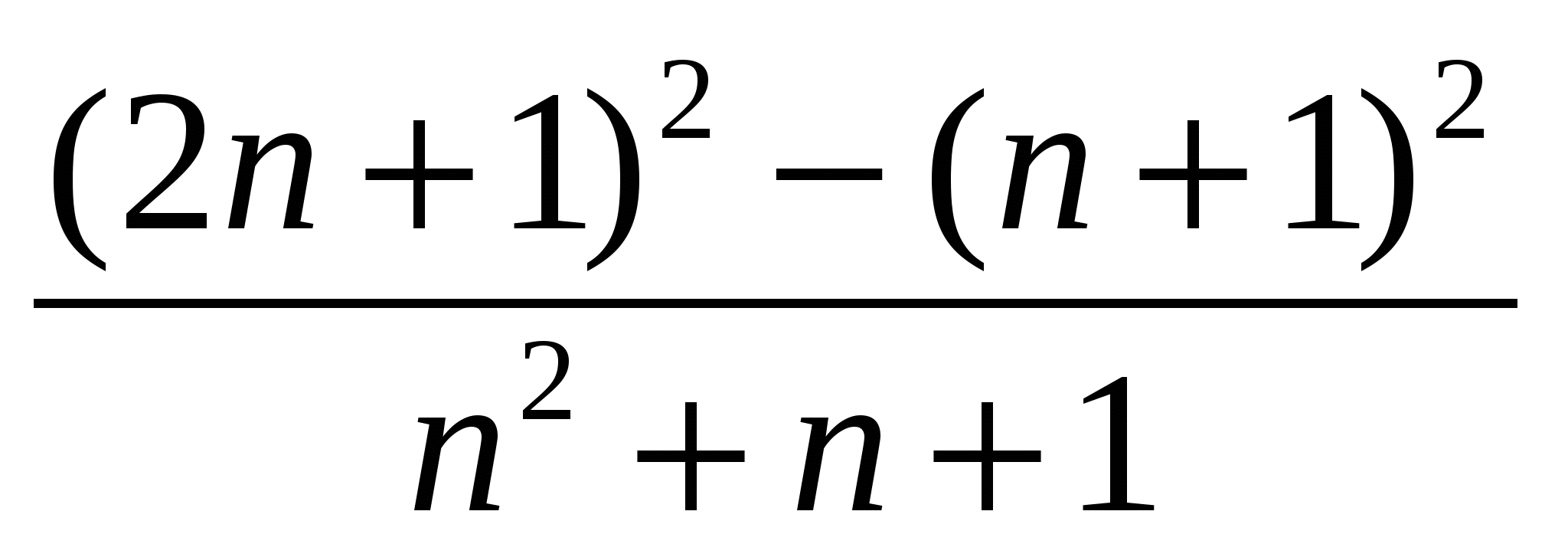
б)
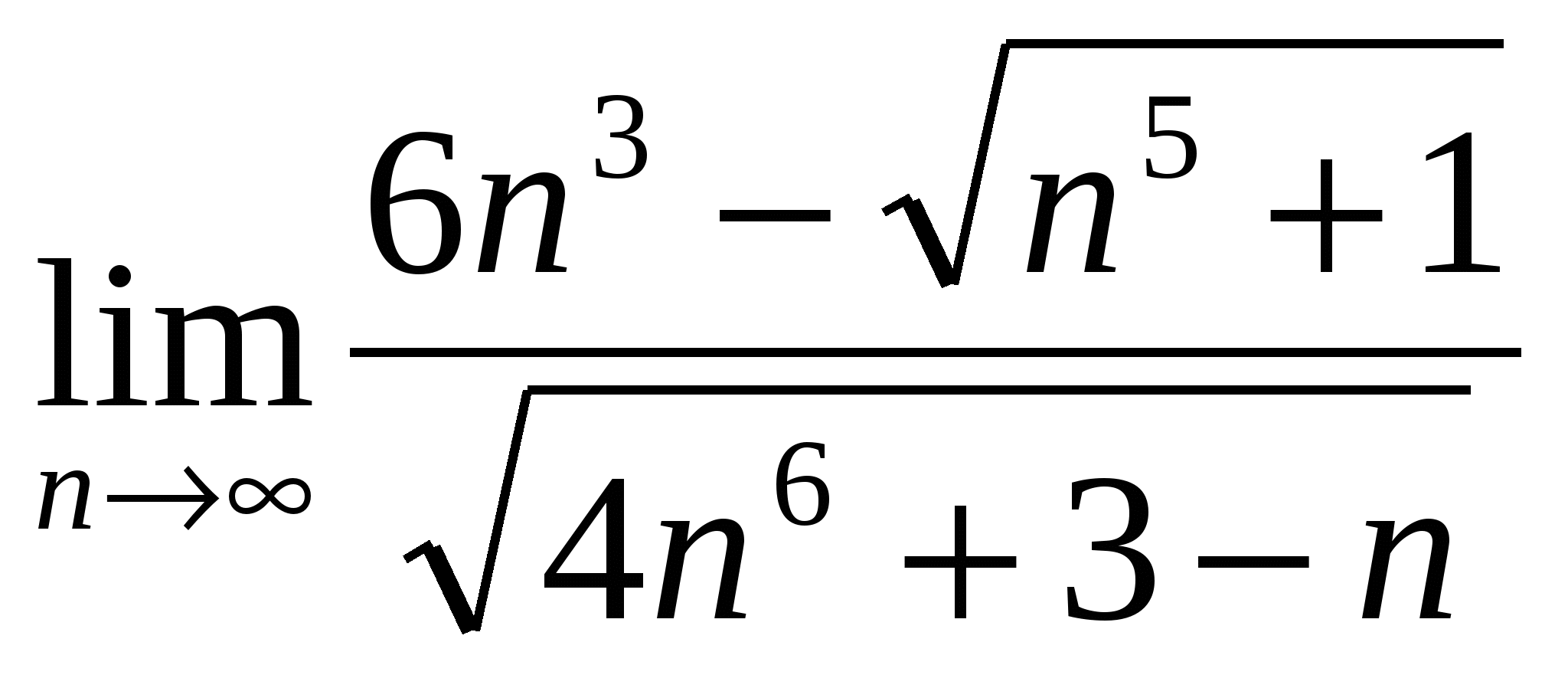
в)

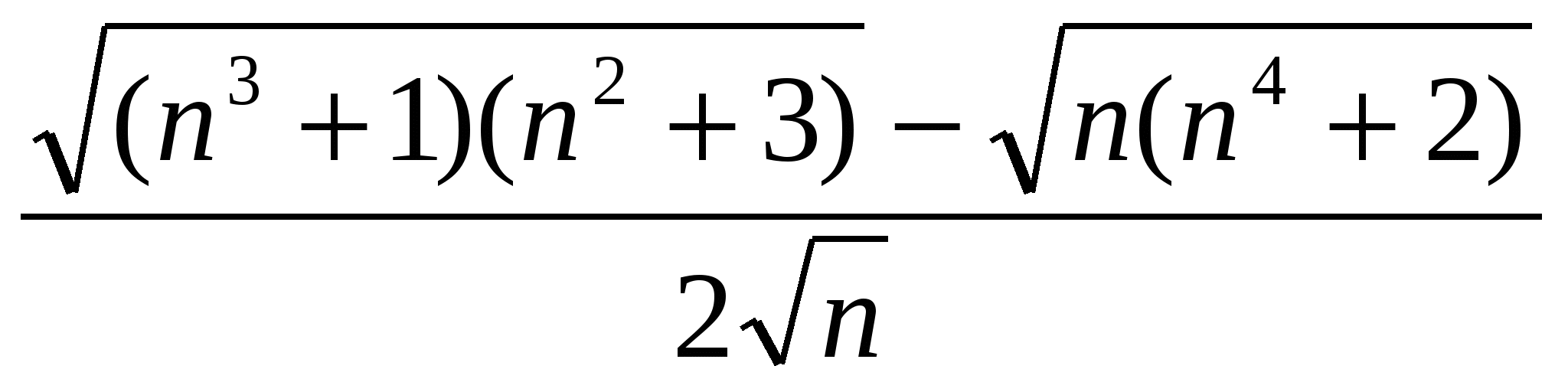
г)

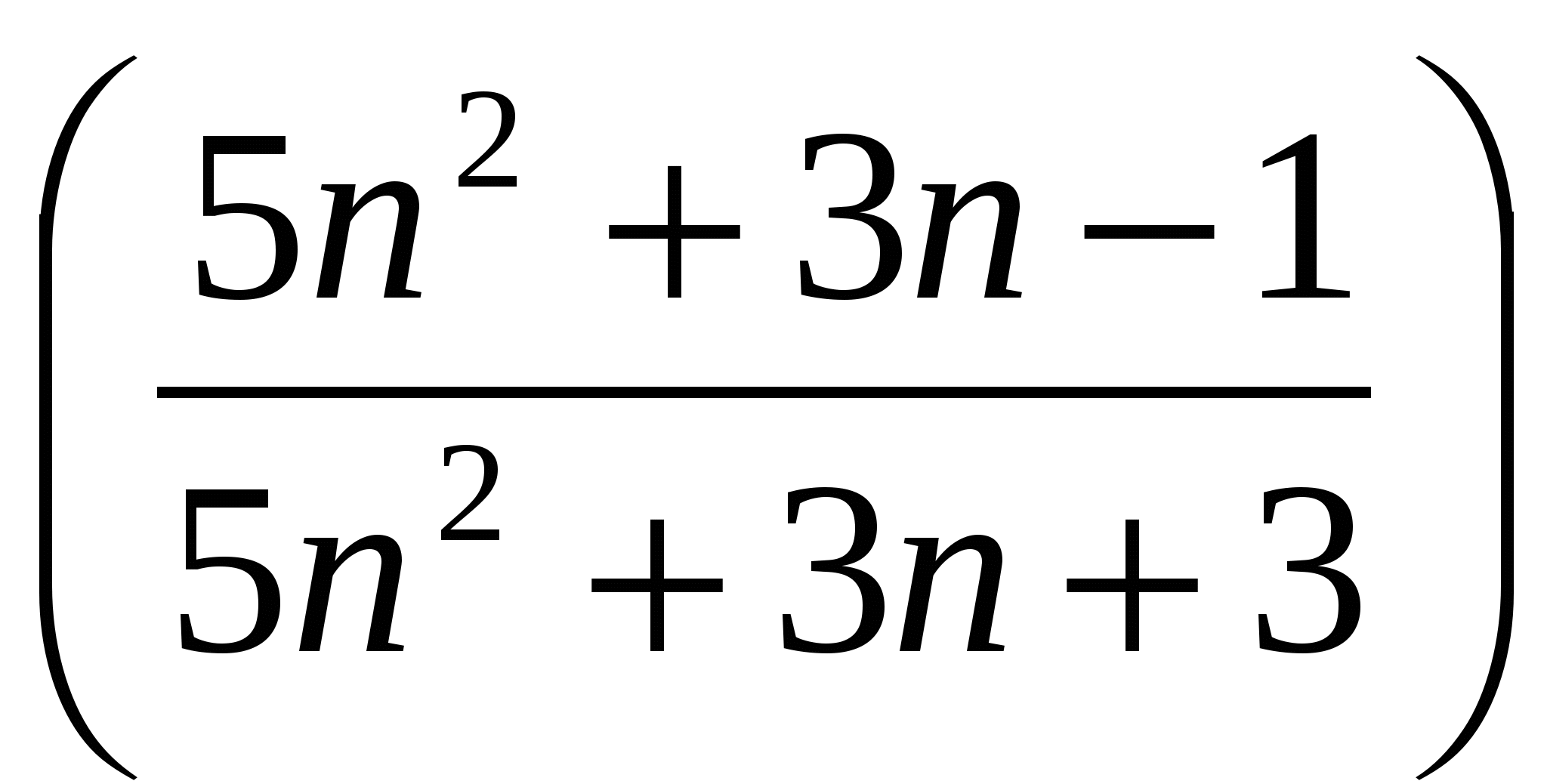
Контрольная работа № 4
infourok.ru
Число, переменная, функция.
Предел функции.
Основные виды неопределенностей.
Бугров Я.С., Никольский С.М. Высшая математика: Учеб.для вузов:в 3т.-5-е изд.,стер.-М.:Дрофа .- (Высшее образование. Современный учебник).т.2. Дифференциальное и интегральное исчисление.-2003.-509 с.
Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. пособие: в 2-х т.- Изд. стер. –М.: Интеграл – Пресс.Т.1. -2001.- 415 с.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Учеб. для вузов: в 3-х томах. – 8-е изд.-М.: Физматлит. т.1 – 2001. -697 с.
Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие. -22-е изд., перераб.- СПб: Профессия, 2003.-432 с.
Кудрявцев Л.Д. Курс математического анализа. Учеб. для вузов: В 3-х томах. – 5-е изд., перераб. и доп. –М.: Дрофа. Т.1. – 2003.-703 с.
Ильин В.А., Позняк Э.Г. Основы математического анализа. Учеб. для вузов в 2-х частях. – 6-е изд. стер. –М. Физматлит, 2002, -646 с.
Данко П.Е. и др. Высшая математика в упражнениях и задачах (с решениями): в 2 ч./ Данко П.Е., Попов А.Г., Кожевникова Т.Я.-6-е изд..-М.: ОНИКС 21 век, ч.2. -2002.-416 с.
Вычислить пределы функций.
а) Найти  .
.
Решение. Прежде всего, проверим, применимы ли к данной дроби теоремы о пределах, или мы имеем дело с неопределенностью. Для этого найдем пределы числителя и знаменателя дроби. Функции  и
и являются бесконечно большими. Поэтому,
являются бесконечно большими. Поэтому, ,
, .
.
Следовательно, имеем дело с неопределенностью вида  .
.
Для раскрытия этой неопределенности и использовании теоремы о пределе отношения двух функций выделим в числителе и в знаменателе  в старшей для числителя и знаменателя степени в качестве сомножителя и сократим дробь.
в старшей для числителя и знаменателя степени в качестве сомножителя и сократим дробь.

Ответ. 0.
б) Найти  .
.
Решение. Для раскрытия неопределенности  в этом случае, нужно разложить числитель и знаменатель на множители и сократить дробь на общий множитель.
в этом случае, нужно разложить числитель и знаменатель на множители и сократить дробь на общий множитель.

Ответ. -9.
Найти  .
.
Решение. Для вычисления данного предела подставим значение  в функцию, стоящую под знаком предела. Получим,
в функцию, стоящую под знаком предела. Получим,
 .
.
Ответ. -3.
в) Найти  .
.
Решение. Для раскрытия неопределенности  в этом случае, нужно умножить числитель и знаменатель на выражение, сопряженное числителю, а затем сократить дробь на общий множитель.
в этом случае, нужно умножить числитель и знаменатель на выражение, сопряженное числителю, а затем сократить дробь на общий множитель.

Ответ.  .
.
г) Найти  .
.
Решение. Для раскрытия неопределенности  в этом случае, нужно выделить первый замечательный предел:
в этом случае, нужно выделить первый замечательный предел: 

Ответ. k
д) Найти  .
.
Решение. Для раскрытия неопределенности  в этом случае, нужно произведение преобразовать в частное, то есть неопределенность
в этом случае, нужно произведение преобразовать в частное, то есть неопределенность свести к неопределенности
свести к неопределенности или
или .
.

Выделяем первый замечательный предел, то есть, умножаем числитель и знаменатель на  . Получаем,
. Получаем,
 .
.
Ответ.  .
.
е) Найти  .
.
Решение. Для раскрытия неопределенности  в этом случае, нужно выделить второй замечательный предел:
в этом случае, нужно выделить второй замечательный предел: .
.

Ответ.  .
.
ж) Найти 
Решение. Для раскрытия неопределенности  в этом случае, нужно выделить второй замечательный предел:
в этом случае, нужно выделить второй замечательный предел: .
.

Ответ.  .
.
Найти 
Решение. Подставим значение  в функцию, стоящую под знаком предела. Получим,
в функцию, стоящую под знаком предела. Получим,

Ответ.  .
.
Задана функция  и два значения аргумента
и два значения аргумента  .
.
Требуется:
найти пределы функции при приближении к каждому из данных значений  слева и справа;
слева и справа;
установить является ли данная функция непрерывной или разрывной для каждого из данных значений  ;
;
сделать схематический чертеж.
Решение. Найдем левый и правый пределы в точке  .
.


Левый предел конечен и равен 0, а правый предел бесконечен. Следовательно, по определению  точка разрыва второго рода.
точка разрыва второго рода.
Найдем левый и правый пределы в точке  .
.

 , т.е.
, т.е.  точка непрерывности функции
точка непрерывности функции  .
.
Сделаем схематический чертеж.

Рис. 1
3. Функция задается различными аналитическими выражениями для различных областей независимой переменной.
Требуется:
найти точки разрыва функции, если они существуют;
найти скачок функции в каждой точке разрыва;
сделать схематический чертеж.

Решение. Функция  непрерывна для
непрерывна для , функция
, функция непрерывна в каждой точке из
непрерывна в каждой точке из , функция
, функция непрерывна в каждой точке интервала
непрерывна в каждой точке интервала .
.
Точки, в которых функция может иметь разрыв, это точки  и
и , где функция меняет свое аналитическое выражение.
, где функция меняет свое аналитическое выражение.
Исследуем точку  .
.
 ,
,  ,
, . Таким образом, точка
. Таким образом, точка есть точка непрерывности функции
есть точка непрерывности функции .
.
Исследуем точку  .
.
 ,
,  ,
, . Таким образом, односторонние пределы существуют, конечны, но не равны между собой. По определению, исследуемая точка – точка разрыва первого рода. Величина скачка функции в точке разрыва
. Таким образом, односторонние пределы существуют, конечны, но не равны между собой. По определению, исследуемая точка – точка разрыва первого рода. Величина скачка функции в точке разрыва равен
равен .
.
Сделаем схематический чертеж

Рис. 2
studfiles.net
Вариант №1
Найти пределы указанных функций
1)  2)
2)  3)
3)  4)
4) 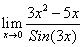
Вариант №2
Найти пределы указанных функций
1)  2)
2) 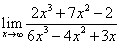 3)
3)  4)
4) 
Вариант №3
Найти пределы указанных функций
1)  2)
2)  3)
3)  4)
4) 
Вариант №4
Найти пределы указанных функций
1)  2)
2)  3)
3) 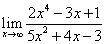 4)
4) 
Вариант №5
Найти пределы указанных функций
1)  2)
2)  3)
3)  4)
4) 
Вариант №6
Найти пределы указанных функций
1)  2)
2)  3)
3)  4)
4) 
Вариант №7
Найти пределы указанных функций
1)  2)
2)  3)
3)  4)
4) 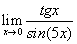
Вариант №8
Найти пределы указанных функций
1) 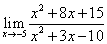 2)
2)  3)
3) 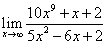 4)
4) 
Вариант №9
Найти пределы указанных функций
1)  2)
2) 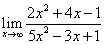 3)
3)  4)
4) 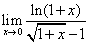
Вариант №10
Найти пределы указанных функций
1)  2)
2)  3)
3)  4)
4) 
Вариант №11
Найти пределы указанных функций
1)  2)
2)  3)
3) 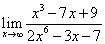 4)
4) 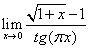
Вариант №12
Найти пределы указанных функций
1)  2)
2)  3)
3) 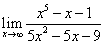 4)
4) 
Вариант №13
Найти пределы указанных функций
1)  2)
2) 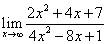 3)
3)  4)
4) 
Вариант №14
Найти пределы указанных функций
1)  2)
2)  3)
3)  4)
4) 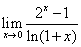
Вариант №15
Найти пределы указанных функций
1)  2)
2) 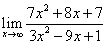 3)
3) 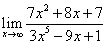 4)
4) 
Вариант №16
Найти пределы указанных функций
1)  2)
2) 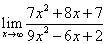 3)
3)  4)
4) 
Вариант №17
Найти пределы указанных функций
1)  2)
2)  3)
3) 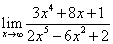 4)
4) 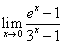
Вариант №18
Найти пределы указанных функций
1)  2)
2) 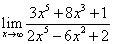 3)
3)  4)
4) 
Вариант №19
Найти пределы указанных функций
1)  2)
2)  3)
3)  4)
4) 
Вариант №20
Найти пределы указанных функций
1) 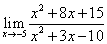 2)
2)  3)
3)  4)
4) 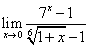
| Вариант | ФИО |
|
| 1 | Байгузина | |
| 2 | Богатова Наталья Викторовна |
|
| 3 | Вильданова Альбина Айратовна |
|
| 4 | Гайзуллина Регина Ильвировна |
|
| 5 | Гордеева Камила Александровна |
|
| 6 | Жданова Лидия Алексеевна |
|
| 7 | Зайнуллина Галина Игоревна |
|
| 8 |
| |
| 9 | Козлова Калерия Александровна |
|
| 10 | Кочкина Елена Алесандровна |
|
| 11 | Луценко Наталья Олеговна |
|
| 12 | Перевалова Маргарита Вячаславовна |
|
| 13 | Плеханова Ольга Сергеевна |
|
| 14 | Садовникова Ольга Владимировна |
|
| 15 | Самигуллина Алина Рифкатовна |
|
| 16 | Сидорова |
|
| 17 | Ступин Марк Олегович |
|
| 18 | Ташкеева Мария Сергеевна |
|
| 19 | Филипова Елена Петровна |
|
| 20 | Хамитова Альбина Ринатовна |
|
pandia.ru
Санкт-Петербургское государственное образовательное учреждение среднего профессионального образования
Согласовано:
Предметной (цикловой) комиссией Председатель
____________/_____________
(Подпись) (ФИО)
«_____» __________200__г.
__________/______________/
(Подпись) (ФИО)
«____»________200___г.
Указания по проведению
практической работы № ___1____
Задачи на вычисление пределов
(Название работы)
Специальность __080110, 080112, 080501__
_____________(___................. __)
(Подпись) (ФИО)
«_______» _________________200___г.
Цель работы:
1. Формировать умения и навыки вычисления пределов
2. Формировать умения и навыки самостоятельного умственного труда
3. Прививать умения и навыки работы со справочным материалом
4. Определить уровень остаточных знаний студентов по данной теме
Перечень справочной литературы :
1. Богомолов Н.В. «Практические занятия по математике», М: Высшая школа, 2004
2. Письменный Д. «Конспект лекций по высшей математике», ч.1., Москва, Айрис-Пресс, 2004
3. Шипачев В.С. «Задачник по высшей математике», М: Высшая школа, 2003
4. Выгодский М.Я. «Справочник по высшей математике», Росткнига, 2001
Краткие теоретические сведения:
Предел последовательности
Определение. Число  называется пределом последовательности
называется пределом последовательности  , если для любого положительно
, если для любого положительно  го числа найдется такое натуральное число
го числа найдется такое натуральное число  , что при всех
, что при всех  >
> выполняется неравенство
выполняется неравенство 
Пишут: 

Графически это выглядит так:
 n -
n -


Т.е. элемент  находится в
находится в  - окрестности точки а. При этом последовательности
- окрестности точки а. При этом последовательности  называется сходящейся, в противном случае – расходящейся.
называется сходящейся, в противном случае – расходящейся.
Основные свойства сходящихся последовательностей
1)Сходящаяся последовательность ограничена.
2)Пусть  ,
,  , тогда а)
, тогда а)  б)
б)  в)
в) 
3)Если  и для всех
и для всех  выполняется неравенства
выполняется неравенства  , то
, то  .
.
4) Если  и последовательность {уn } - ограниченная, то
и последовательность {уn } - ограниченная, то 
| №1. Найти пределы: | |
|
|
|
Бесконечно большие и бесконечно малые функции
Определение. Функция  называется бесконечно малой при
называется бесконечно малой при  , если
, если 
Например: 1)  при
при  б. м. ф. т.к.
б. м. ф. т.к.  2)
2)  при
при  б. м. ф. т. к
б. м. ф. т. к 
Определение. Функция  называется бесконечно большой при
называется бесконечно большой при  , если
, если  ,
,  или
или 
Например,  есть б. б. Ф при
есть б. б. Ф при  ;
; 
 если б. б. ф. при
если б. б. ф. при  действительно
действительно  и
и 
Теорема (о связи между функций, ее приделом и бесконечно малой функцией ). Если функция  имеет придел, равный
имеет придел, равный  , то ее можно представить как сумму числа
, то ее можно представить как сумму числа  и бесконечно малой функции
и бесконечно малой функции  , т.е. если
, т.е. если 
Теорема (обратная). Если функцию  можно представить в виде суммы числа А и б.м.ф.
можно представить в виде суммы числа А и б.м.ф.  (x), то число А является пределом функции
(x), то число А является пределом функции , т.е если
, т.е если  , то
, то 
Например, требуется вычислить  . Представим числитель и знаменатель в виде суммы числа и б.м.ф.
. Представим числитель и знаменатель в виде суммы числа и б.м.ф. 
Функции  при
при  есть б.м.ф. таким образом
есть б.м.ф. таким образом 
Основные теоремы о пределах
Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:

Теорема справедлива для алгебраической суммы любого конечного числа функций.
Теорема 2. Функция может иметь только один предел при  .
.


Теорема 3. Предел произведения двух функций равен произведению их пределов:
 .
.
Следствие 1. Постоянный множитель можно выносить за знак предела: 
Следствие 2. Предел степени с натуральным показателем равен той же степени предела:  .
.
Теорема 4. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю.

Примеры:
1)
 =
= =
=
 =
=
 =
=
=

 =
= =
=
2)  =
=
=
3) 
Первый замечательный предел

Второй замечательный предел
 или
или 
Примеры:
Вычислить:
1)  .
.
2)  .
.
3) 

4)  =
=
 =
= =
=
№2. Найти пределы: 




№3. Найти пределы:
Порядок проведения работы:
1. Используя теоретические сведения выполнить предложенное преподавателем задание
2. Соответствующим образом оформить работу
| Лист 1. Практическая работа по теме «Вычисление пределов» Выполнил:__________ (ФИО) группа:_____________ Проверил:__________ Оценка:____________ | Лист 2. № примера Решение: Ответ: |
Оформление работы:
www.yurii.ru