Контрольная работа по теме "Основные тригонометрические формулы". Контрольная тригонометрия
Контрольная работа по теме "Основные тригонометрические формулы"
| Самостоятельная работа №1 по теме «Основные тригонометрические формулы». Вариант 1. 1.Вычислите: 2 cos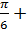 tg tg 2.Упростите выражение: 1- cos²α·tg²α 3.Найдите sinα, если известно, что cosα = -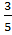 , π˂α˂ , π˂α˂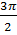 4. Упростите выражение: 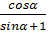 + +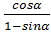 5.Докажите тождество: (1+tg²α+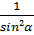 )·sin²α·cos²α=1 )·sin²α·cos²α=1 | Самостоятельная работа №1 по теме «Основные тригонометрические формулы». Вариант 2. 1.Вычислите: sin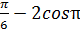 2.Упростите выражение: 1- sinα·cosα·tgα 3.Найдите sinα, если известно, что cosα = 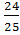 , , 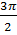 ˂α˂2π ˂α˂2π 4. Упростите выражение: 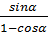 - -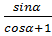 5.Докажите тождество: (1-cos²α)·(1+ctg²α)=1 |
| Самостоятельная работа №1 по теме «Основные тригонометрические формулы». Вариант 1. 1.Вычислите: 2 cos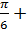 tg tg 2.Упростите выражение: 1- cos²α·tg²α 3.Найдите sinα, если известно, что cosα = -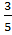 , π˂α˂ , π˂α˂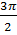 4. Упростите выражение: 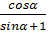 + +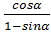 5.Докажите тождество: (1+tg²α+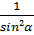 )·sin²α·cos²α=1 )·sin²α·cos²α=1 | Самостоятельная работа №1 по теме «Основные тригонометрические формулы». Вариант 2. 1.Вычислите: sin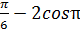 2.Упростите выражение: 1- sinα·cosα·tgα 3.Найдите sinα, если известно, что cosα = 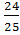 , , 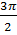 ˂α˂2π ˂α˂2π 4. Упростите выражение: 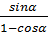 - -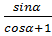 5.Докажите тождество: (1-cos²α)·(1+ctg²α)=1 |
Тема «Основные тригонометрические формулы».
Вариант 1.
1.Вычислите: 2 cos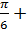 tg
tg
2.Упростите выражение: 1- cos²α·tg²α
3.Найдите sinα, если известно, что cosα= -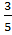 , π˂α˂
, π˂α˂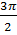
4. Упростите выражение:
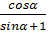 +
+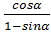
5.Докажите тождество:
(1+tg²α+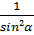 )·sin²α·cos²α=1
)·sin²α·cos²α=1
Вариант 2.
1.Вычислите: sin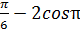
2.Упростите выражение: 1- sinα·cosα·tgα
3.Найдите sinα, если известно, что cosα= 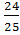 ,
, 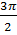 ˂α˂2π
˂α˂2π
4. Упростите выражение:
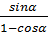 -
-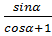
5.Докажите тождество:
(1-cos²α)·(1+ctg²α)=1
Контрольная работа №1 по теме: «Формулы сложения и их следствия».
Вариант 1.
1.Докажите тождество: sin2α+ctg2α+cos2α=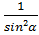
2.Вычислите: 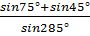
3.Найдите sin x, если cos x=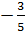 ,
,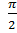 ˂x˂π
˂x˂π
4.Упростите выражение: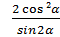
5.Найдите значение выражения:
а) 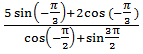 ;
;
б) 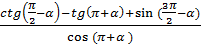
Контрольная работа №1 по теме: «Формулы сложения и их следствия».
Вариант 2.
1.Докажите тождество: sin2α+tg2α+cos2α=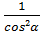
2.Вычислите: 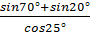
3.Найдите cos x, если sin x=-0,8; -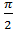 ˂x˂0
˂x˂0
4.Упростите выражение: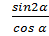 - sinα
- sinα
5.Найдите значение выражения:
а) 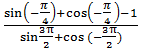 ;
;
б) 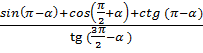
Контрольная работа №1 по теме: «Формулы сложения и их следствия».
Вариант 1.
1.Докажите тождество: sin2α+ctg2α+cos2α=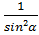
2.Вычислите: 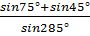
3.Найдите sin x, если cos x=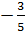 ,
,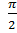 ˂x˂π
˂x˂π
4.Упростите выражение: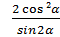
5.Найдите значение выражения:
а) 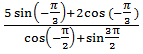 ;
;
б) 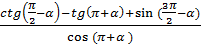
Контрольная работа №1 по теме: «Формулы сложения и их следствия».
Вариант 2.
1.Докажите тождество: sin2α+tg2α+cos2α=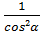
2.Вычислите: 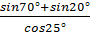
3.Найдите cos x, если sin x=-0,8; -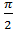 ˂x˂0
˂x˂0
4.Упростите выражение: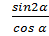 - sinα
- sinα
5.Найдите значение выражения:
а) 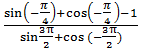 ;
;
б) 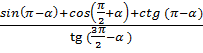
Тема «Формулы сложения и их следствия».
Вариант 1.
1.Докажите тождество: sin2α+ctg2α+cos2α=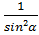
2.Вычислите: 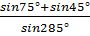
3.Найдите sin x, если cos x=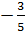 ,
,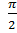 ˂x˂π
˂x˂π
4.Упростите выражение: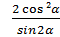
5.Найдите значение выражения:
а) 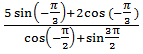 ; б)
; б) 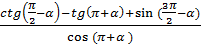
Вариант 2.
1.Докажите тождество: sin2α+tg2α+cos2α=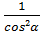
2.Вычислите: 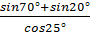
3.Найдите cos x, если sin x=-0,8; -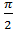 ˂x˂0
˂x˂0
4.Упростите выражение: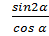 - sinα
- sinα
5.Найдите значение выражения:
а) 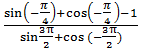 ; б)
; б) 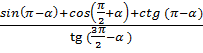
Контрольная работа №1 по теме «Основные тригонометрические формулы».
Вариант 1.
1.Вычислите: 2 cos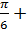 tg
tg
2.Упростите выражение: 1- cos²α·tg²α
3.Найдите sinα, если известно, что cosα = -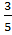 , π˂α˂
, π˂α˂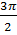
4. Докажите тождество:
sin2α+ctg2α+cos2α=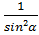
5. Найдите значение выражения:
а) 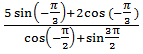 ;
;
б) 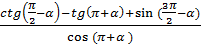
Контрольная работа №1 по теме «Основные тригонометрические формулы».
Вариант 2.
1.Вычислите: sin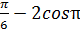
2.Упростите выражение: 1- sinα·cosα·tgα
3.Найдите sinα, если известно, что cosα = 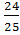 ,
, 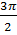 ˂α˂2π
˂α˂2π
4. Докажите тождество:
sin2α+tg2α+cos2α=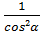
5. Найдите значение выражения:
а) 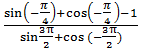 ;
;
б) 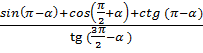
Контрольная работа №1 по теме «Основные тригонометрические формулы».
Вариант 1.
1.Вычислите: 2 cos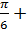 tg
tg
2.Упростите выражение: 1- cos²α·tg²α
3.Найдите sinα, если известно, что cosα = -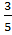 , π˂α˂
, π˂α˂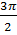
4. . Докажите тождество:
sin2α+ctg2α+cos2α=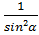
5. Найдите значение выражения:
а) 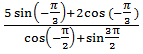 ;
;
б) 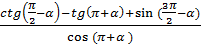
Контрольная работа №1 по теме «Основные тригонометрические формулы».
Вариант 2.
1.Вычислите: sin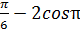
2.Упростите выражение: 1- sinα·cosα·tgα
3.Найдите sinα, если известно, что cosα = 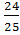 ,
, 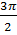 ˂α˂2π
˂α˂2π
4. Докажите тождество:
sin2α+tg2α+cos2α=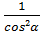
5. Найдите значение выражения:
а) 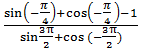 ;
;
б) 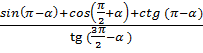
infourok.ru
Контрольная работа в 10 классе «Основные тригонометрические формулы"
Тема «Основные тригонометрические формулы».
Вариант 1.
1.Вычислите: 2 cos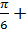 tg
tg
2.Упростите выражение: 1- cos²α·tg²α
3.Найдите sinα, если известно, что cosα= -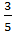 , π˂α˂
, π˂α˂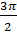
4. Упростите выражение:
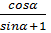 +
+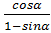
5.Докажите тождество:
(1+tg²α+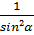 )·sin²α·cos²α=1
)·sin²α·cos²α=1
Вариант 2.
1.Вычислите: sin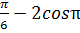
2.Упростите выражение: 1- sinα·cosα·tgα
3.Найдите sinα, если известно, что cosα= 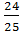 ,
, 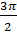 ˂α˂2π
˂α˂2π
4. Упростите выражение:
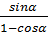 -
-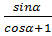
5.Докажите тождество:
(1-cos²α)·(1+ctg²α)=1
Контрольная работа №1 по теме «Основные тригонометрические формулы».
Вариант 3.
1.Вычислите: 2 cos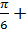 tg
tg
2.Упростите выражение: 1- cos²α·tg²α
3.Найдите sinα, если известно, что cosα = -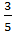 , π˂α˂
, π˂α˂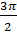
4. Докажите тождество:
sin2α+ctg2α+cos2α=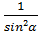
5. Найдите значение выражения:
а) 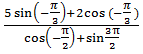 ;
;
б) 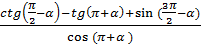
Вариант 4.
1.Вычислите: sin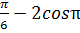
2.Упростите выражение: 1- sinα·cosα·tgα
3.Найдите sinα, если известно, что cosα = 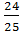 ,
, 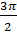 ˂α˂2π
˂α˂2π
4. Докажите тождество:
sin2α+tg2α+cos2α=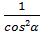
5. Найдите значение выражения:
а) 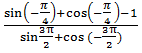 ;
;
б) 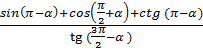
infourok.ru
Контрольная работа по Математике "Тригонометрические уравнения" 10-11 класс
Контрольная работа по теме «Тригонометрические уравнения»
Вариант 1
1. Решить уравнения, сводящиеся к квадратным:
а) 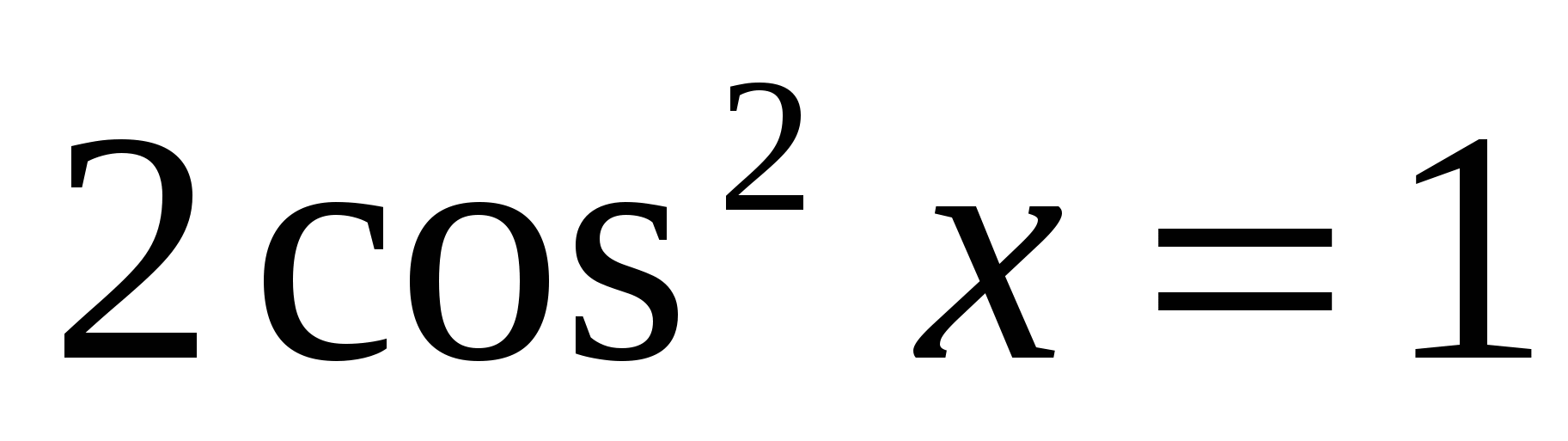 ; б)
; б) 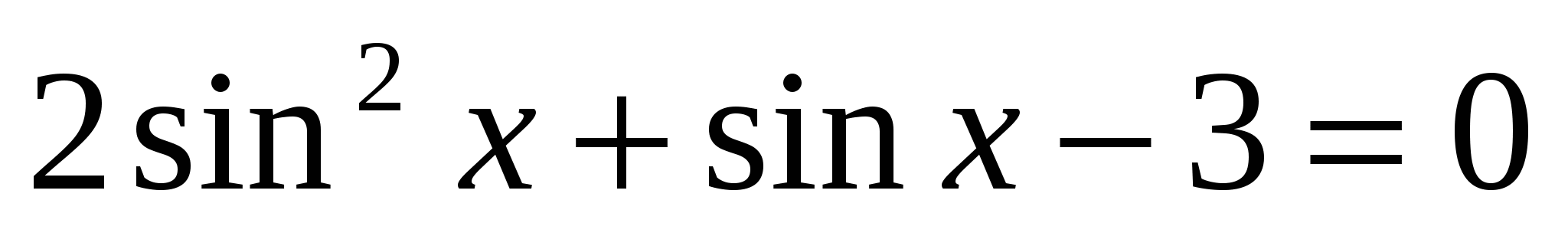 ;
;
в) 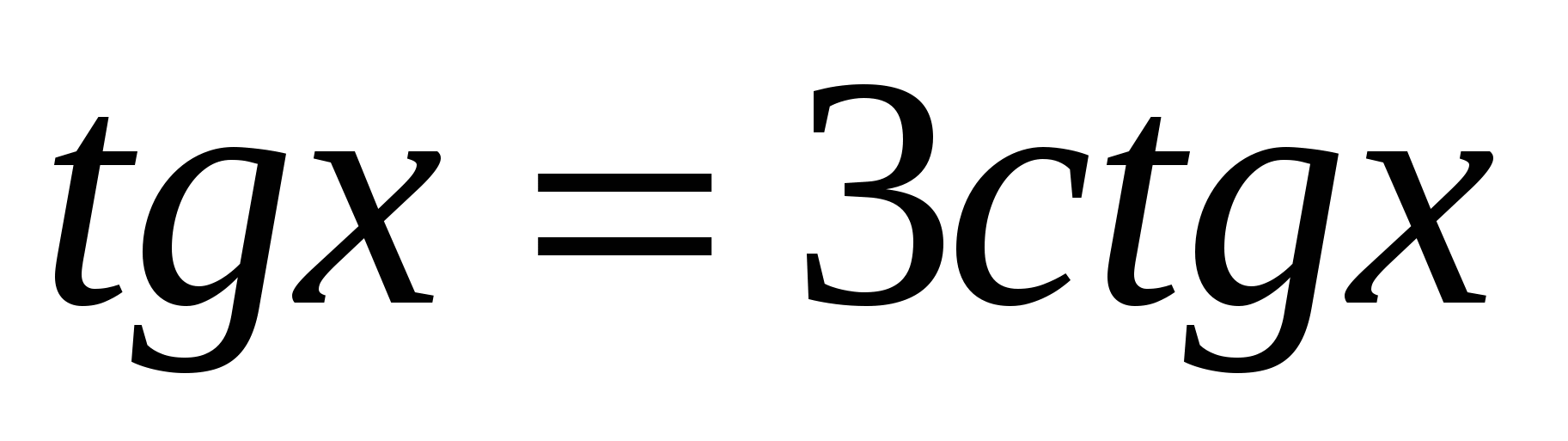 ; г)
; г) 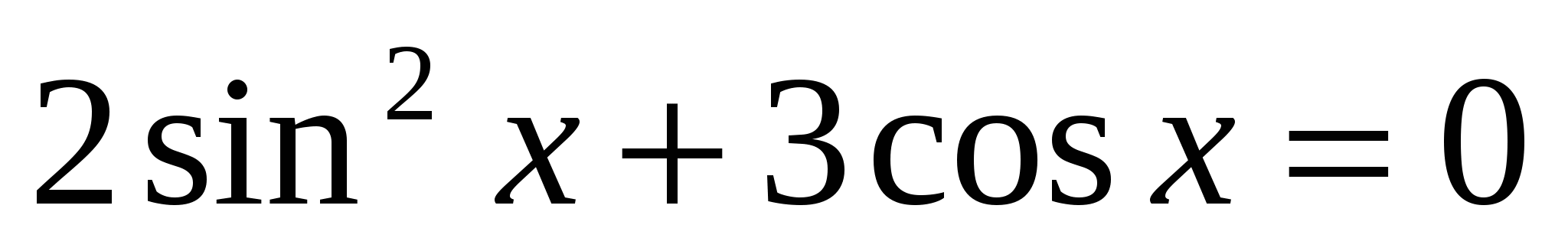 .
.
2. Решить уравнение разложением на множители:
а) 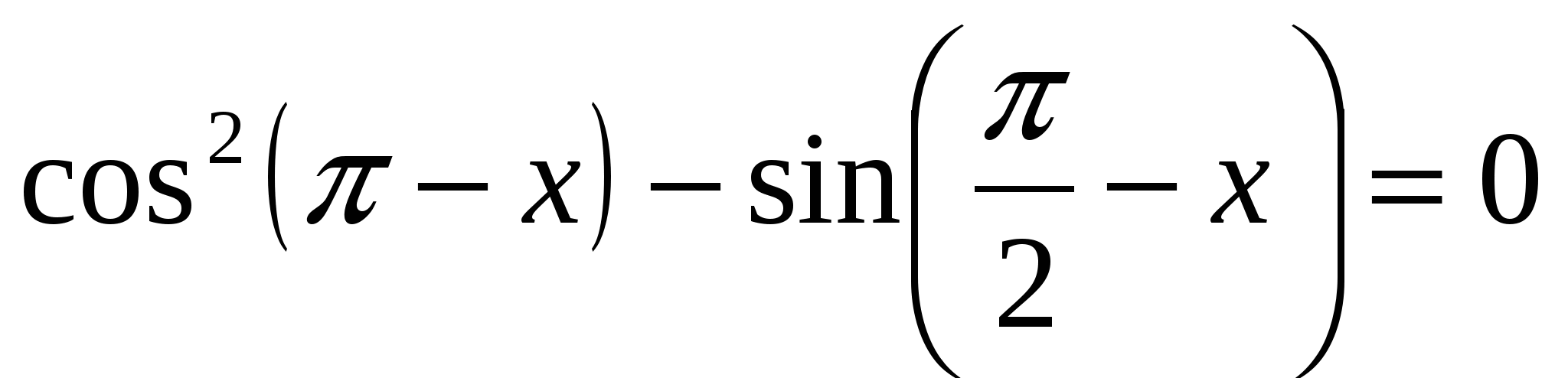 ; б)
; б) 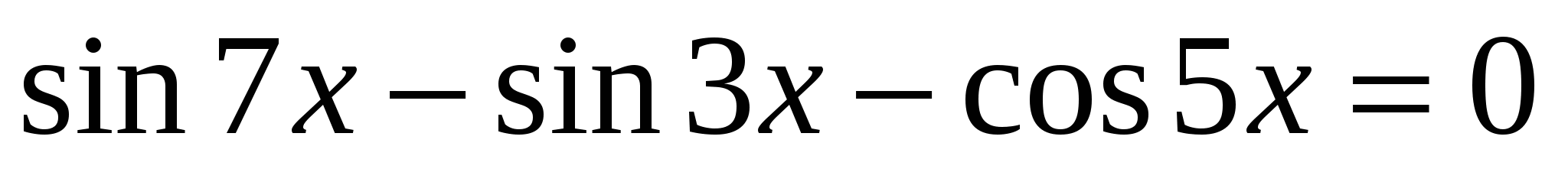 .
.
3. Решить однородное уравнение первой степени:
а) 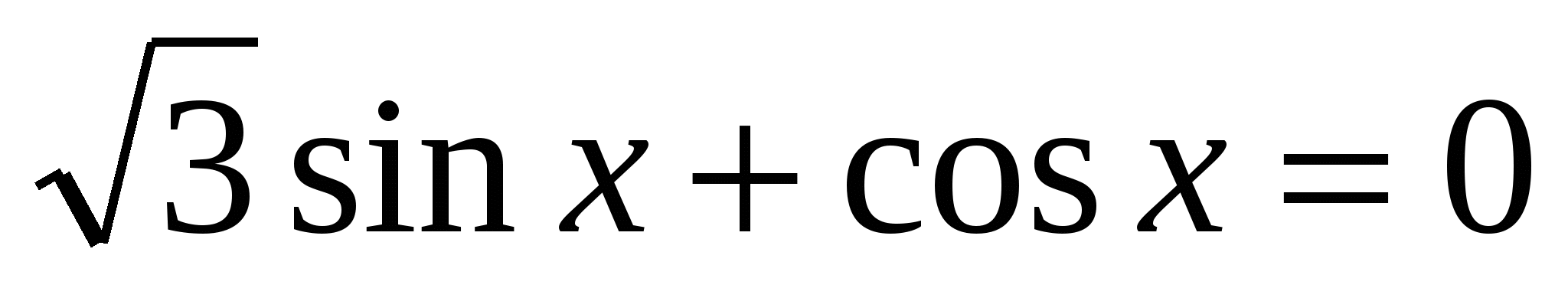 ; б)
; б) 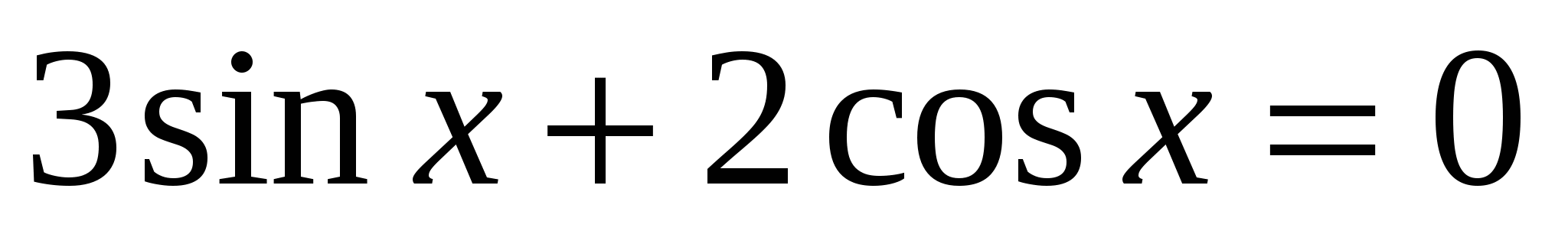 .
.
4. Решить однородное уравнение второй степени:
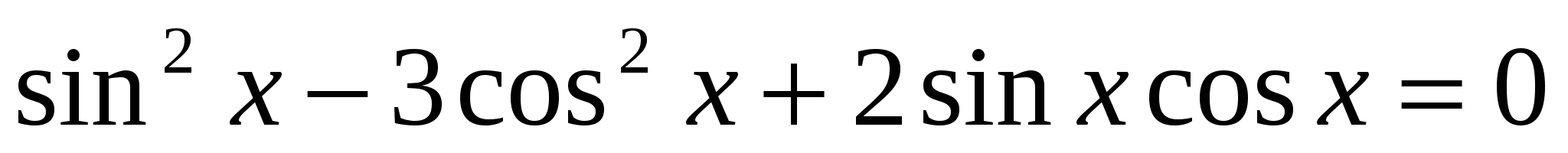 .
.
5. Решить неоднородное уравнение:
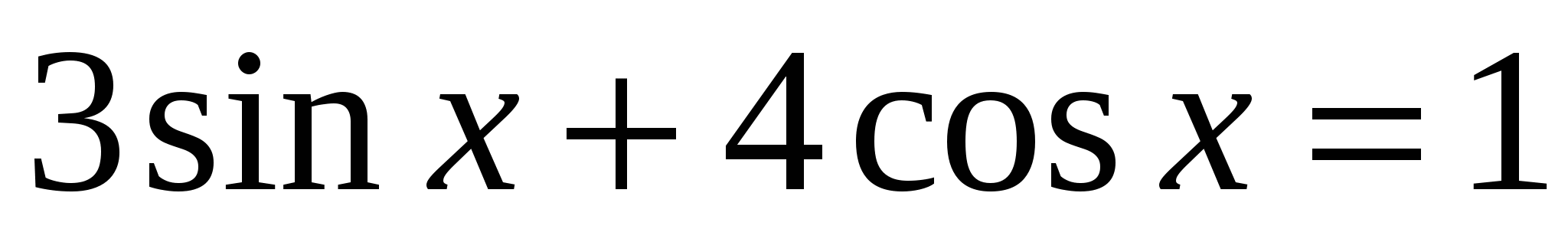 .
.
Контрольная работа по теме «Тригонометрические уравнения»
Вариант 2
1. Решить уравнения, сводящиеся к квадратным:
а) 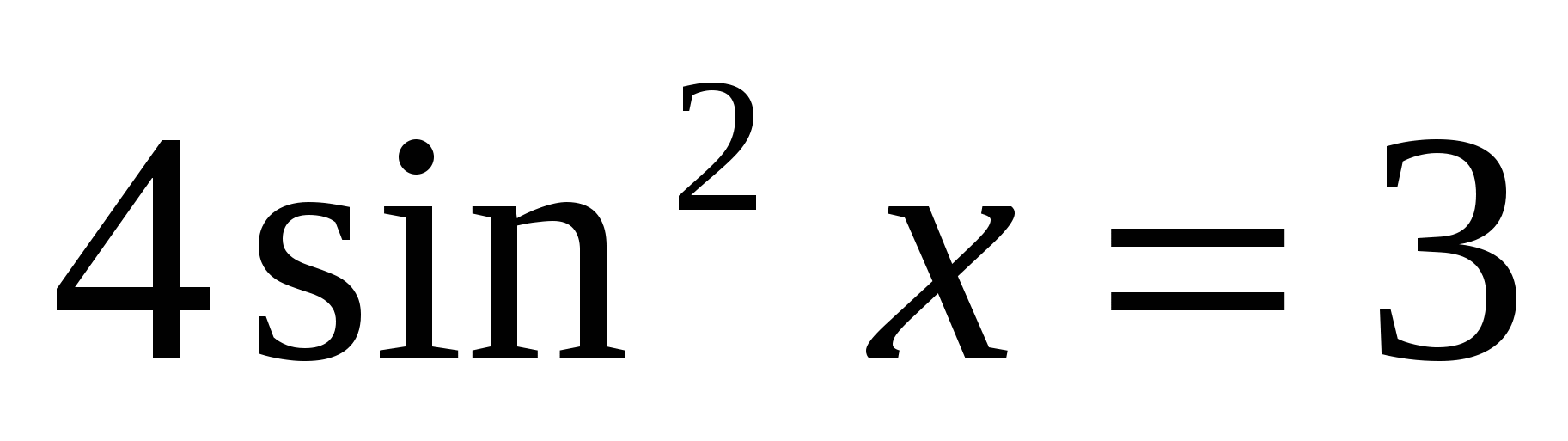 ; б)
; б) 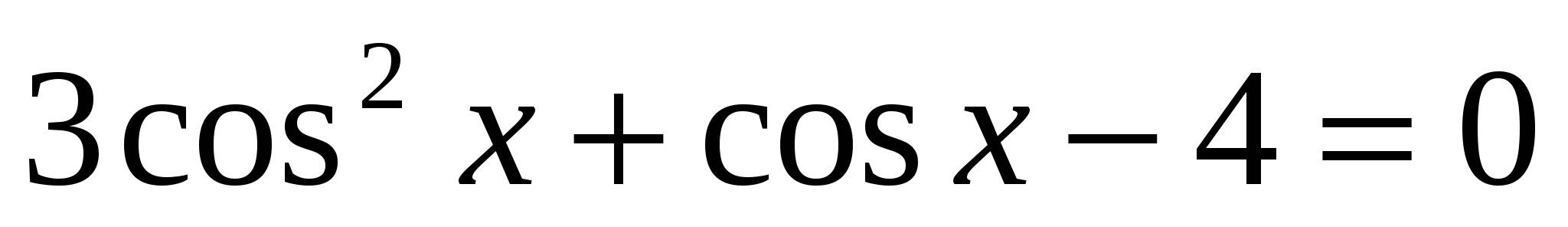 ;
;
в) 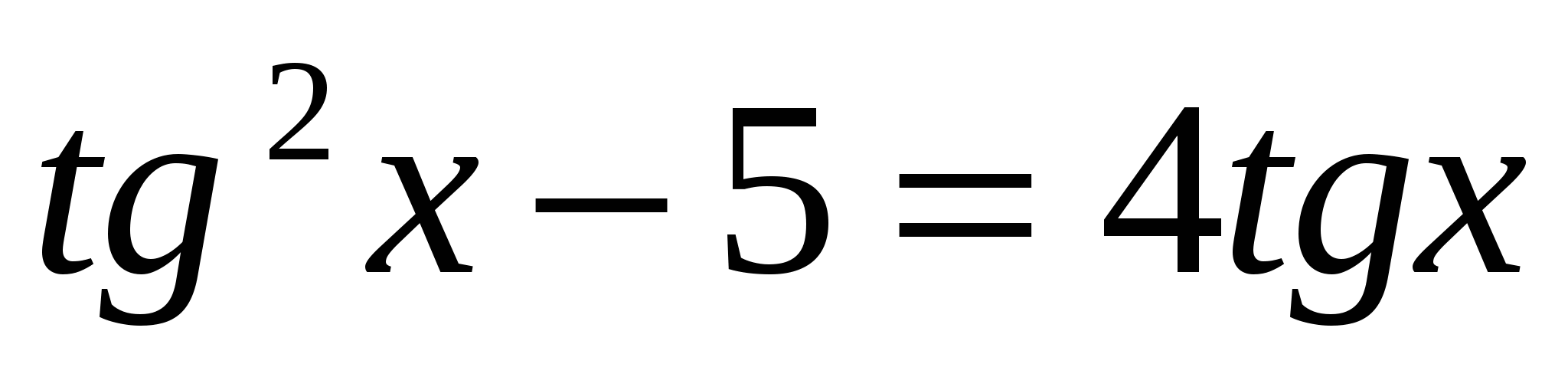 ; г)
; г) 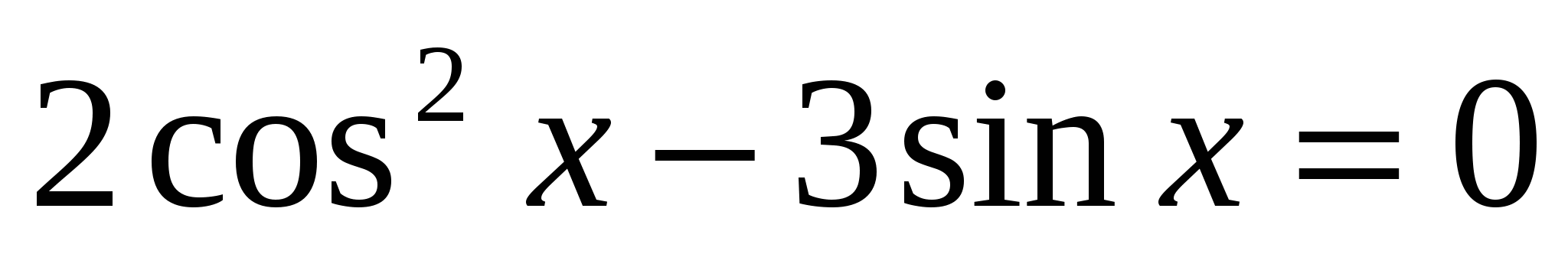 .
.
2. Решить уравнение разложением на множители:
а) 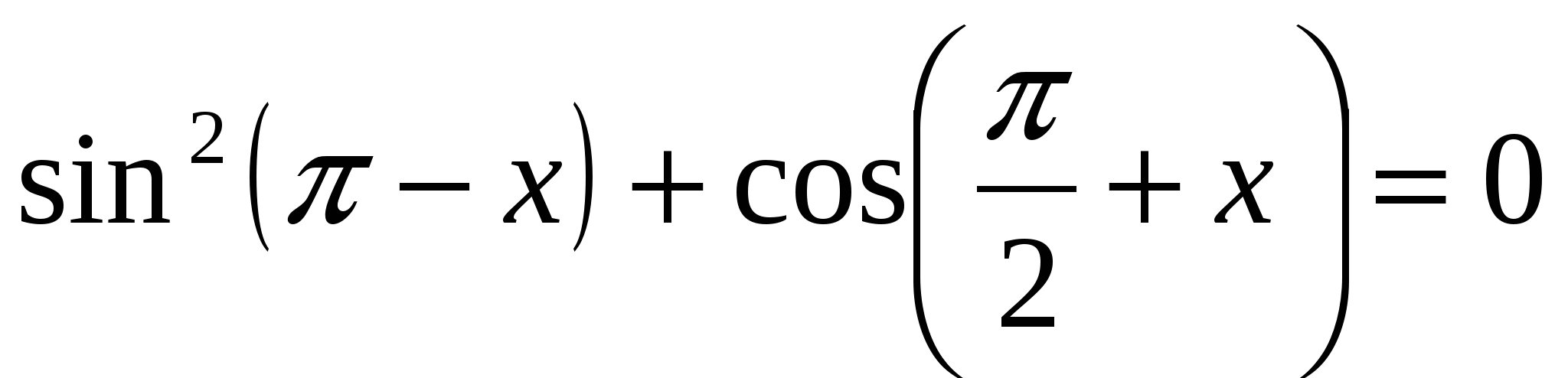 ; б)
; б) 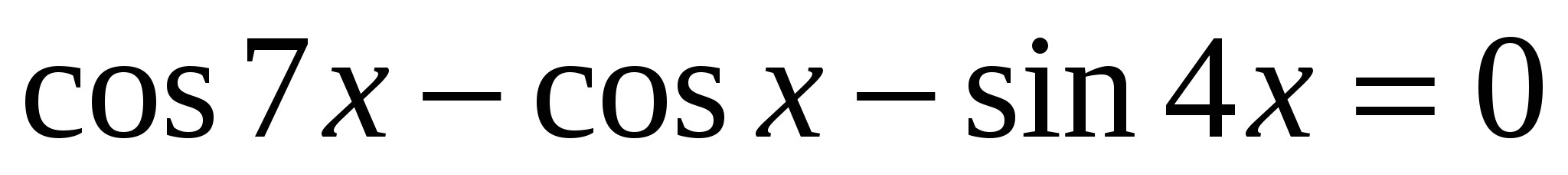 .
.
3. Решить однородное уравнение первой степени:
а) 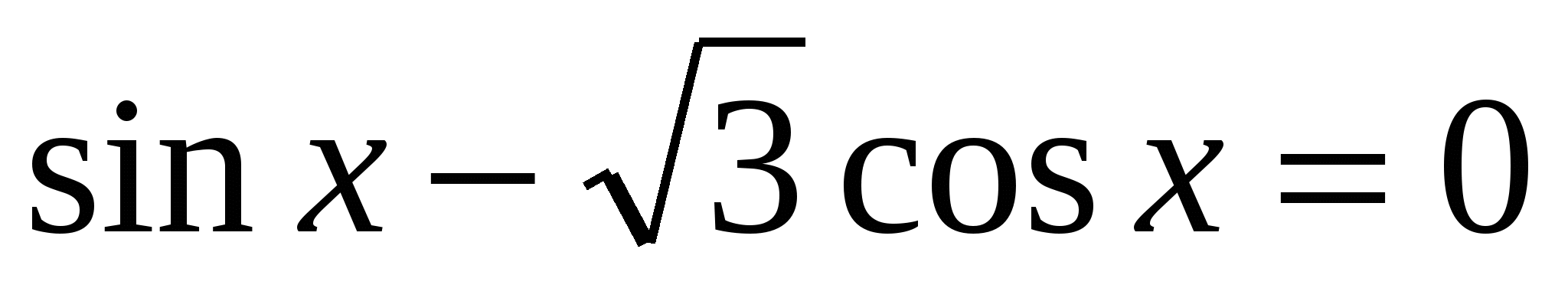 ; б)
; б) 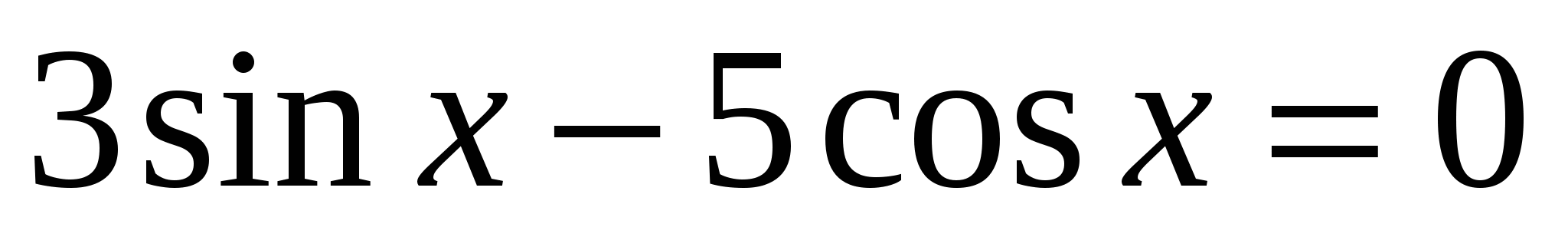 .
.
4. Решить однородное уравнение второй степени:
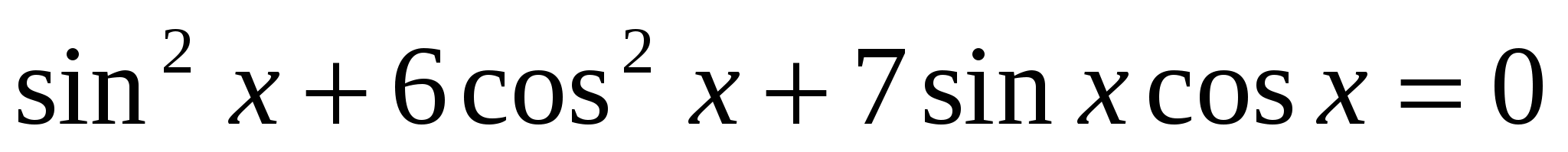 .
.
5. Решить неоднородное уравнение:
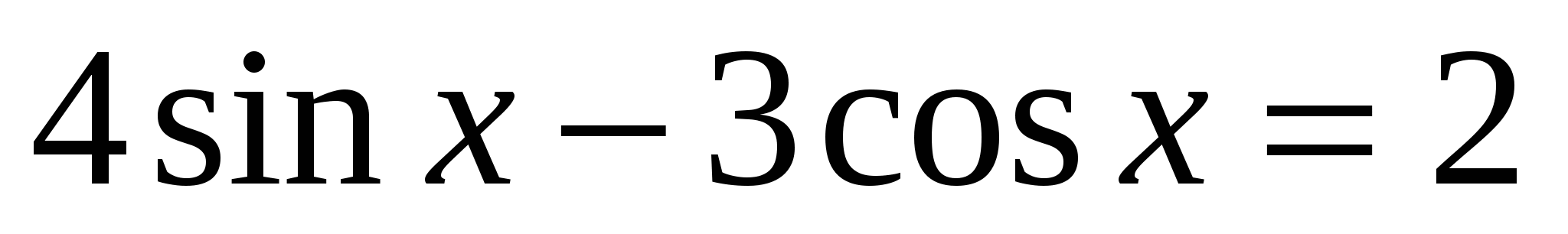 .
.
Контрольная работа по теме «Тригонометрические уравнения»
Вариант 1
1. Решить уравнения, сводящиеся к квадратным:
а) 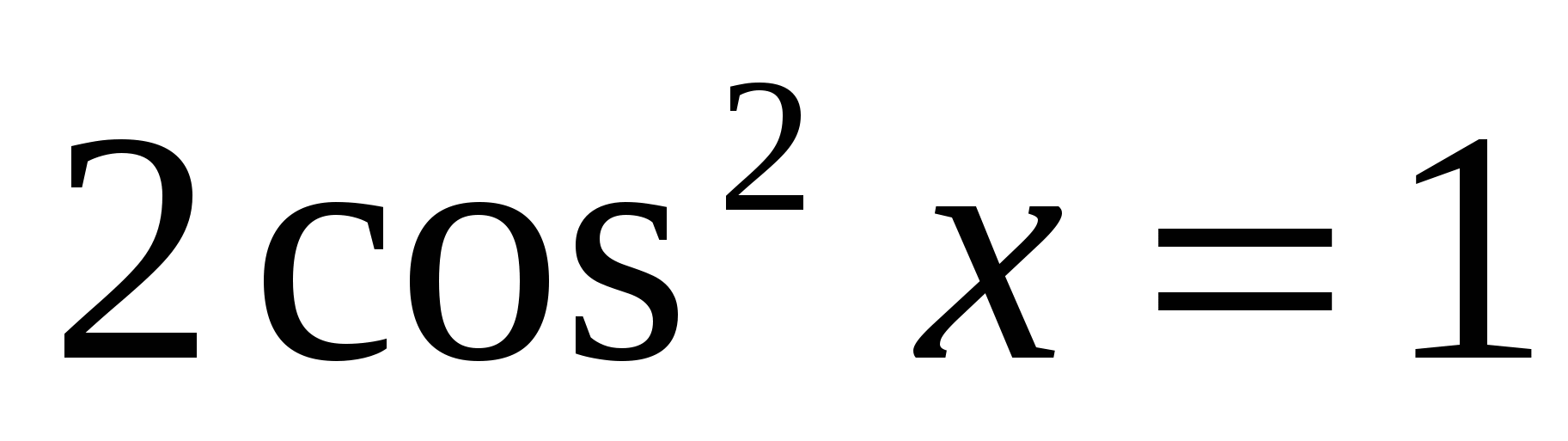 ; б)
; б) 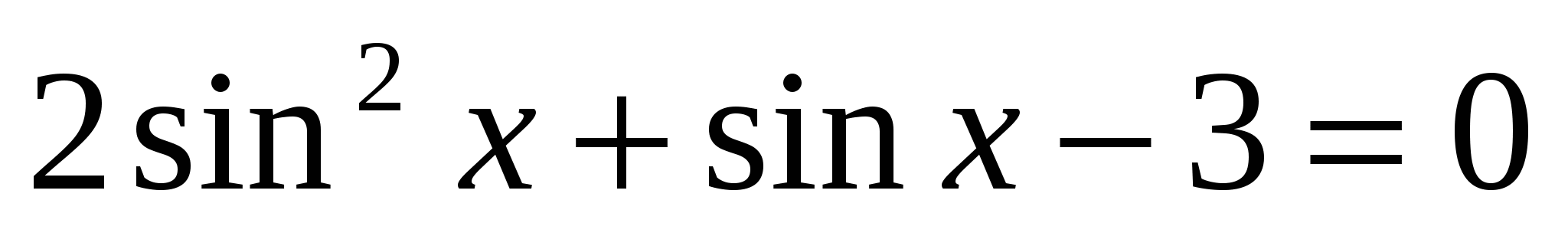 ;
;
в) 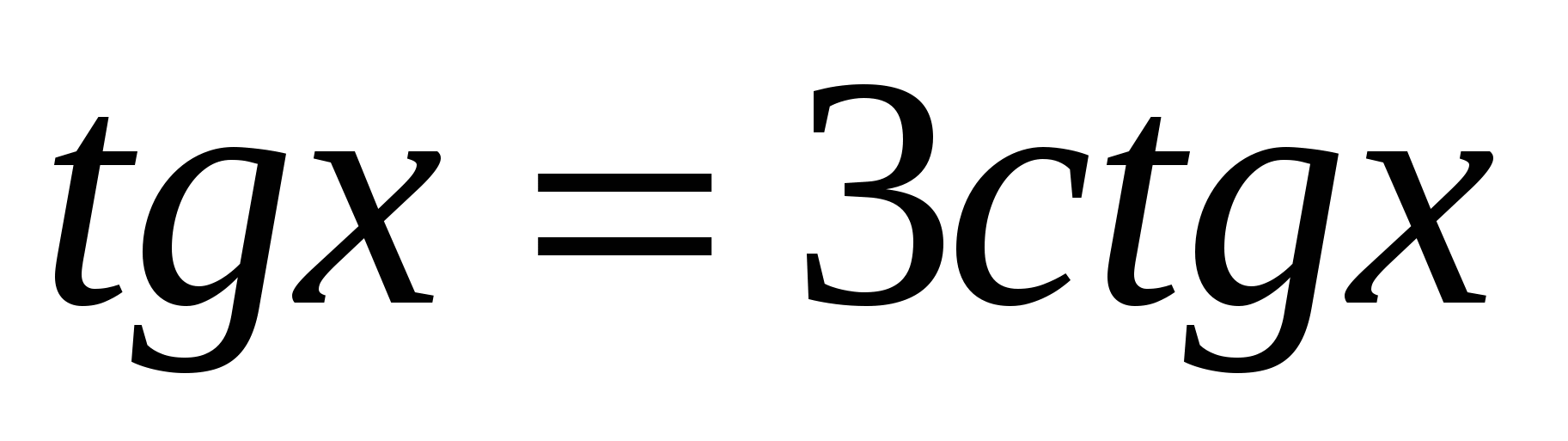 ; г)
; г) 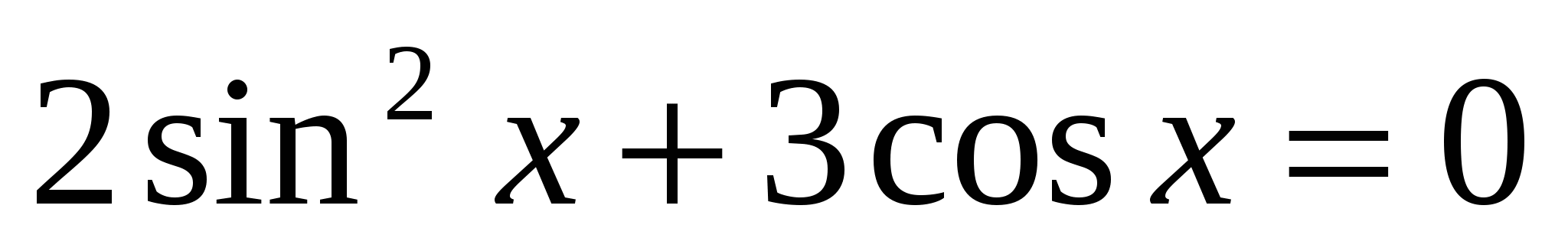 .
.
2. Решить уравнение разложением на множители:
а) 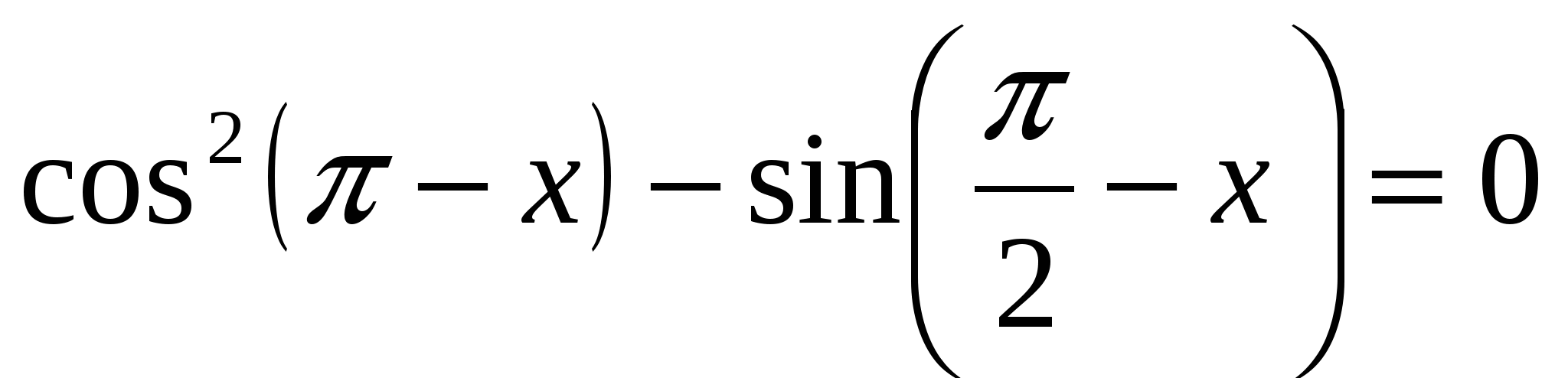 ; б)
; б) 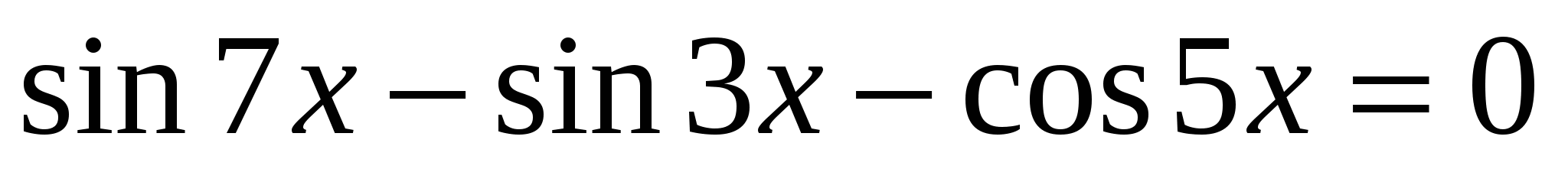 .
.
3. Решить однородное уравнение первой степени:
а) 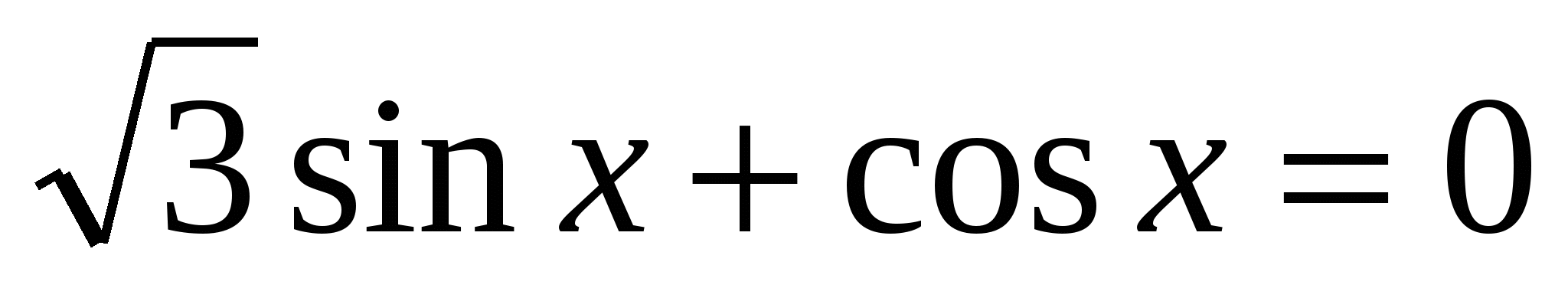 ; б)
; б) 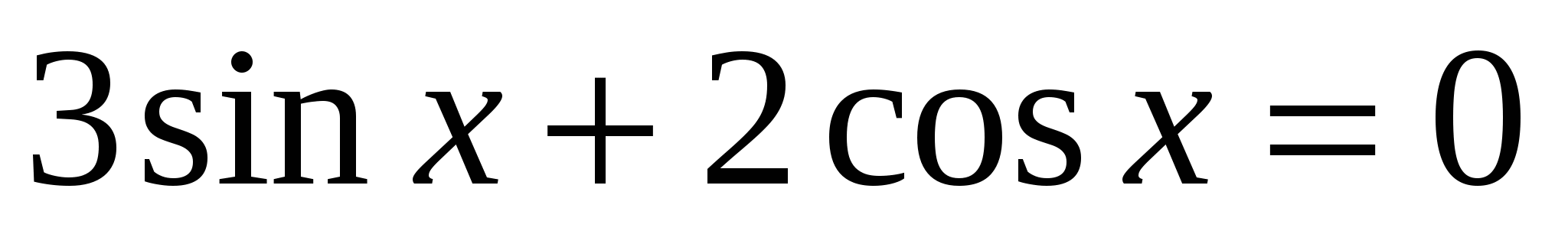 .
.
4. Решить однородное уравнение второй степени:
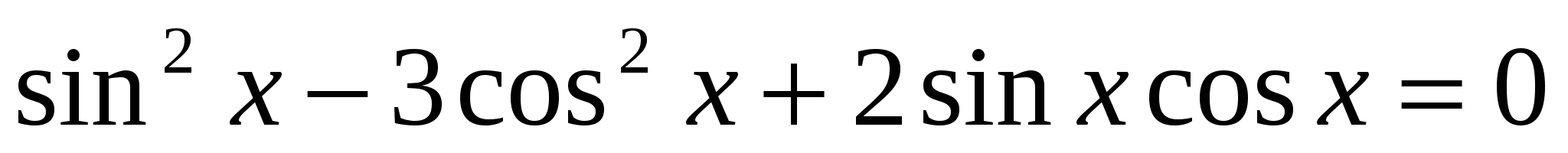 .
.
5. Решить неоднородное уравнение:
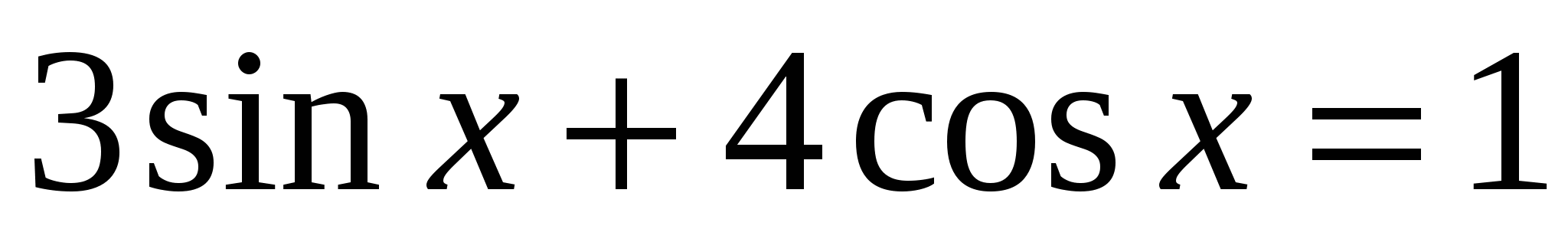 .
.
Контрольная работа по теме «Тригонометрические уравнения»
Вариант 2
1. Решить уравнения, сводящиеся к квадратным:
а) 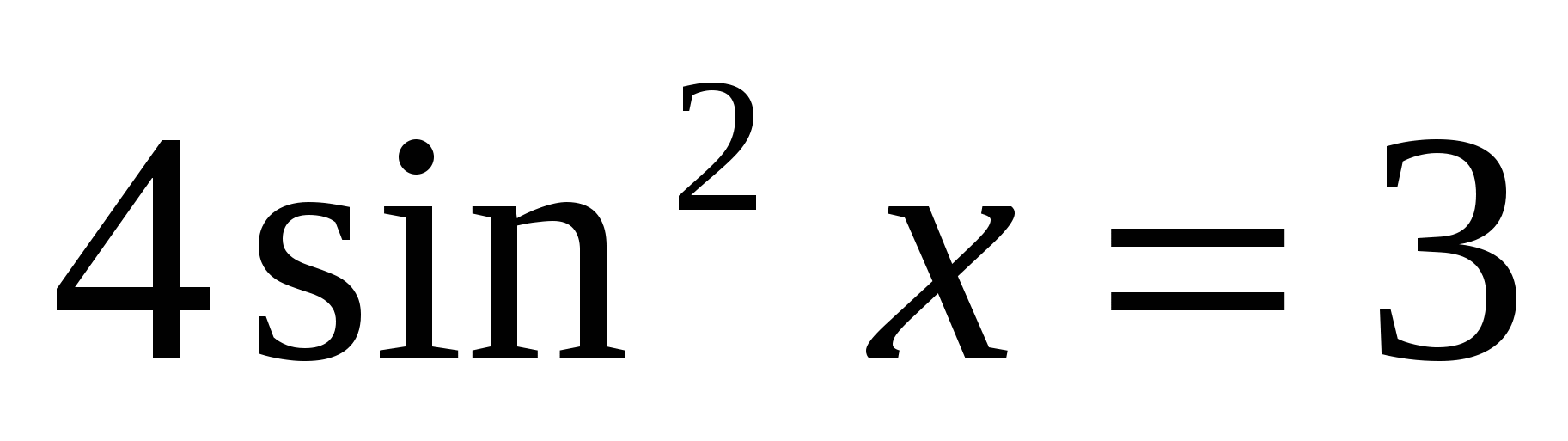 ; б)
; б) 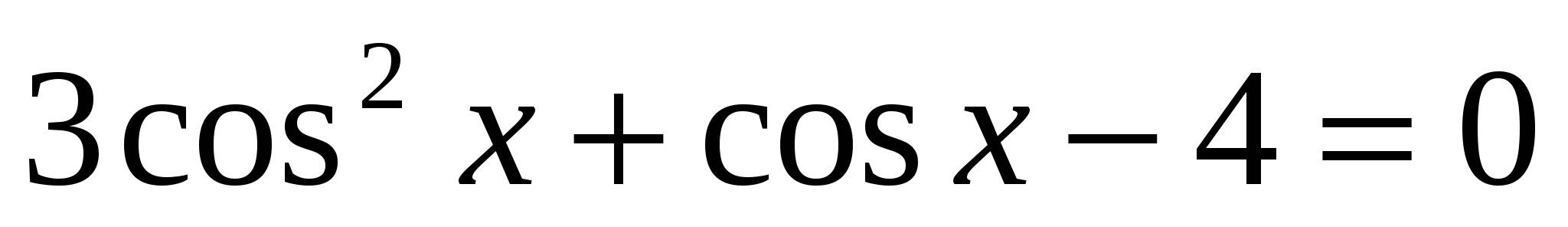 ;
;
в) 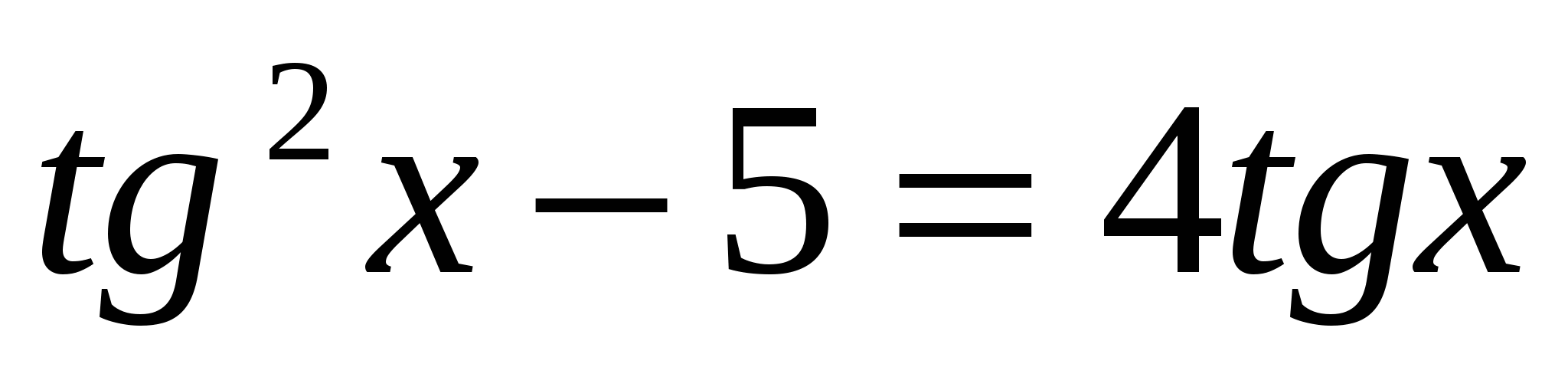 ; г)
; г) 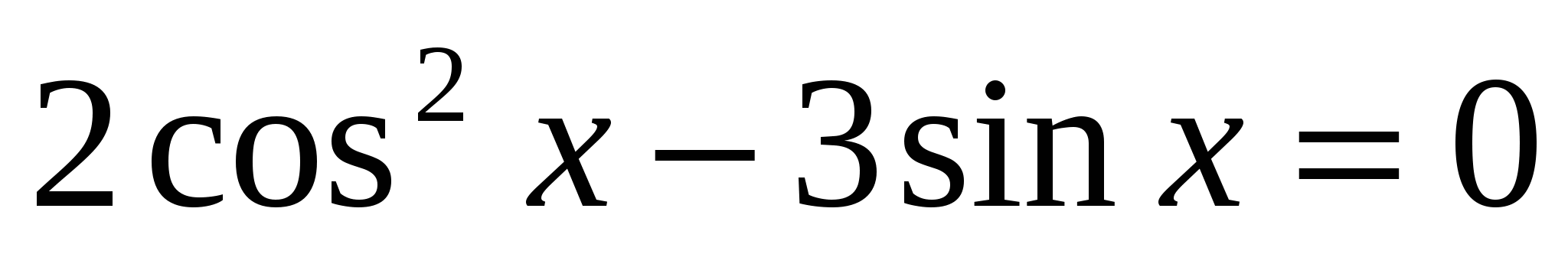 .
.
2. Решить уравнение разложением на множители:
а) 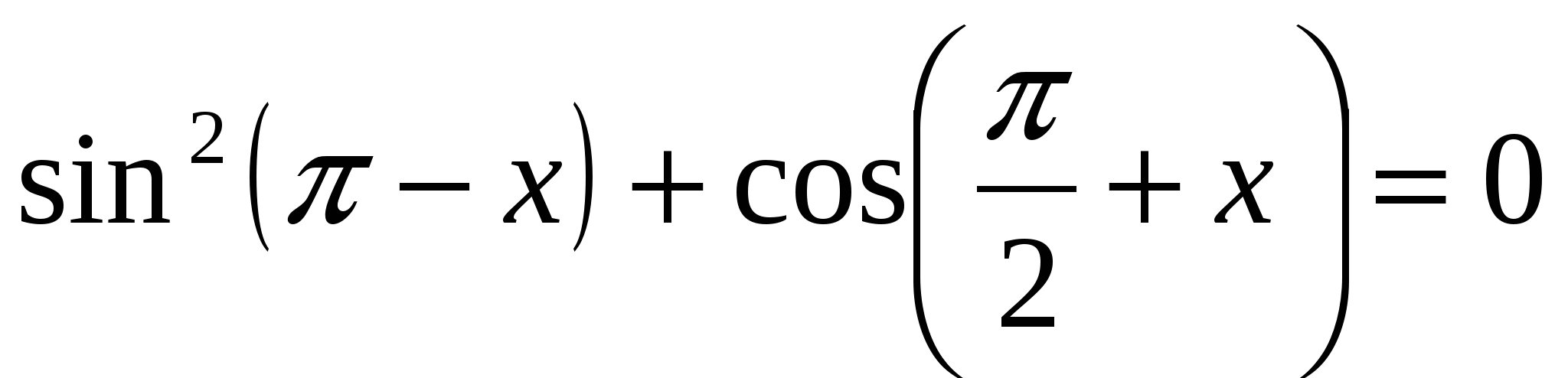 ; б)
; б) 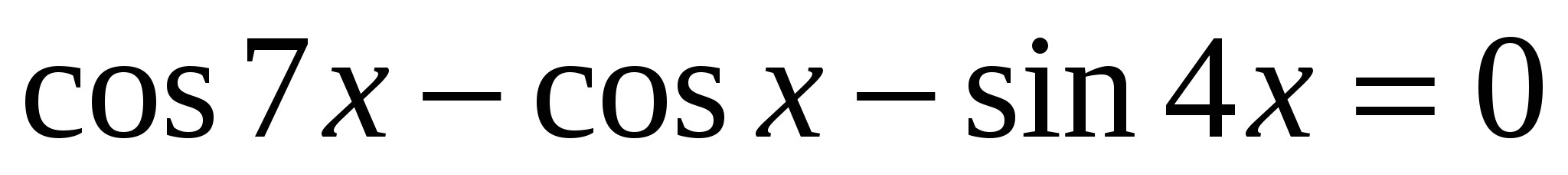 .
.
3. Решить однородное уравнение первой степени:
а) 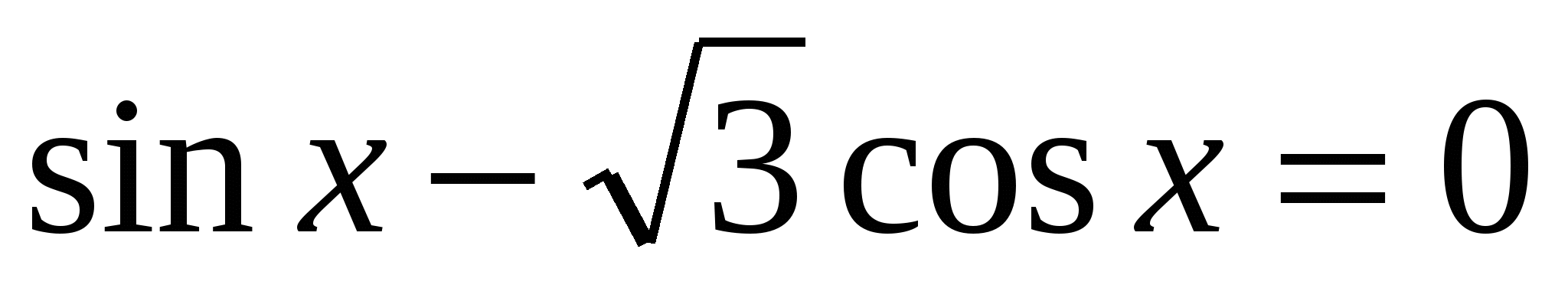 ; б)
; б) 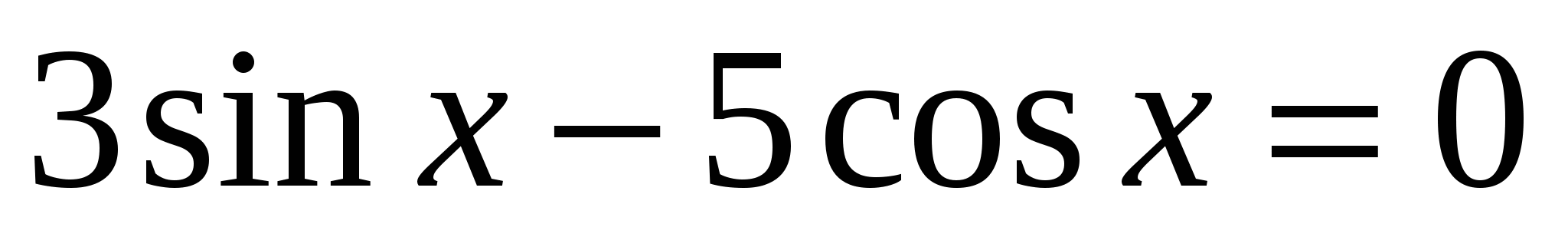 .
.
4. Решить однородное уравнение второй степени:
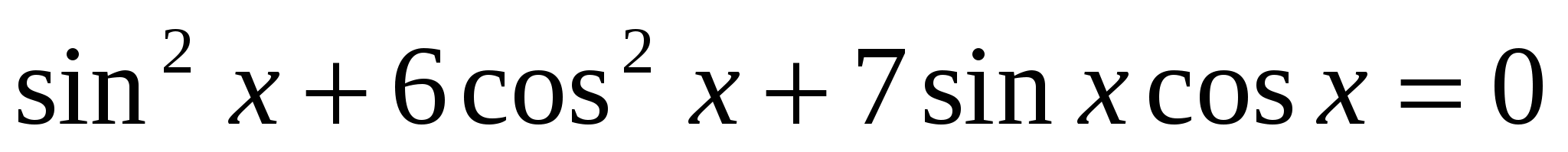 .
.
5. Решить неоднородное уравнение:
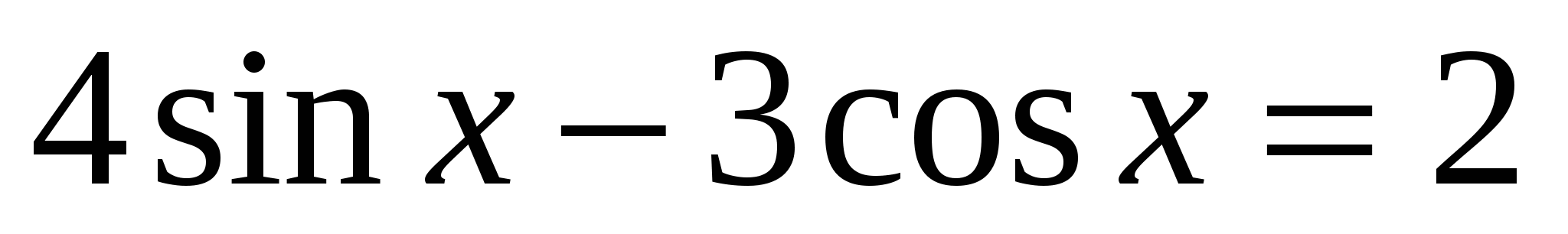 .
.
doc4web.ru
Контрольная работа по математике "Тригонометрия"
Контрольная работа по математике, раздел «Тригонометрия»
Вариант 1
№1. Выразите в радианной мере величины углов: 1500, 900, 2700.
№2. Выразите в градусной мере величины углов: 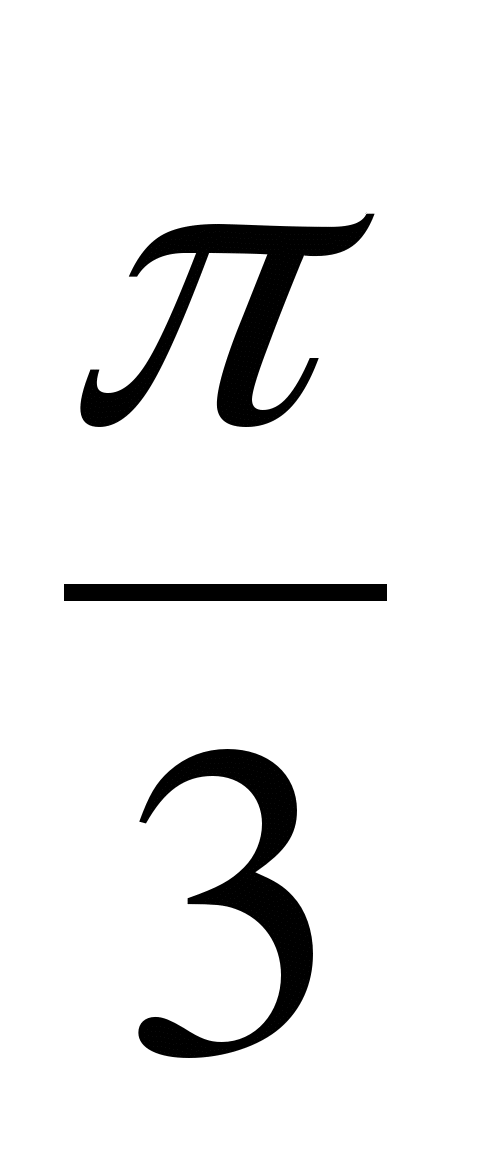 ,
, 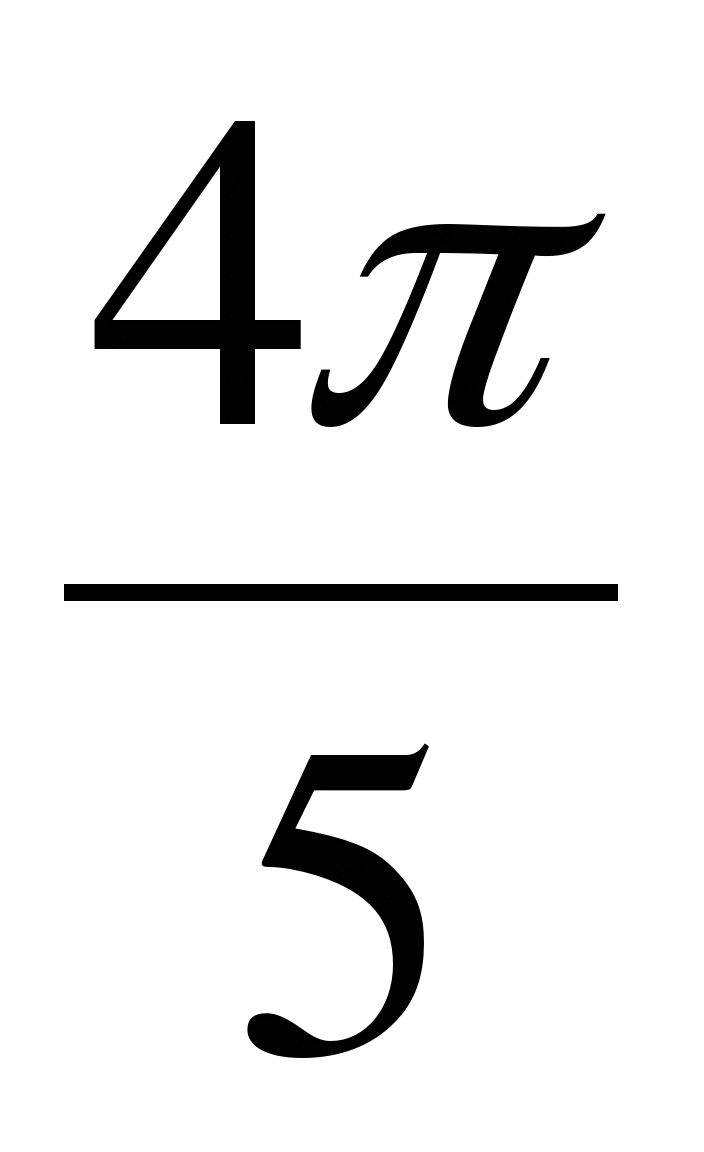 ,
, 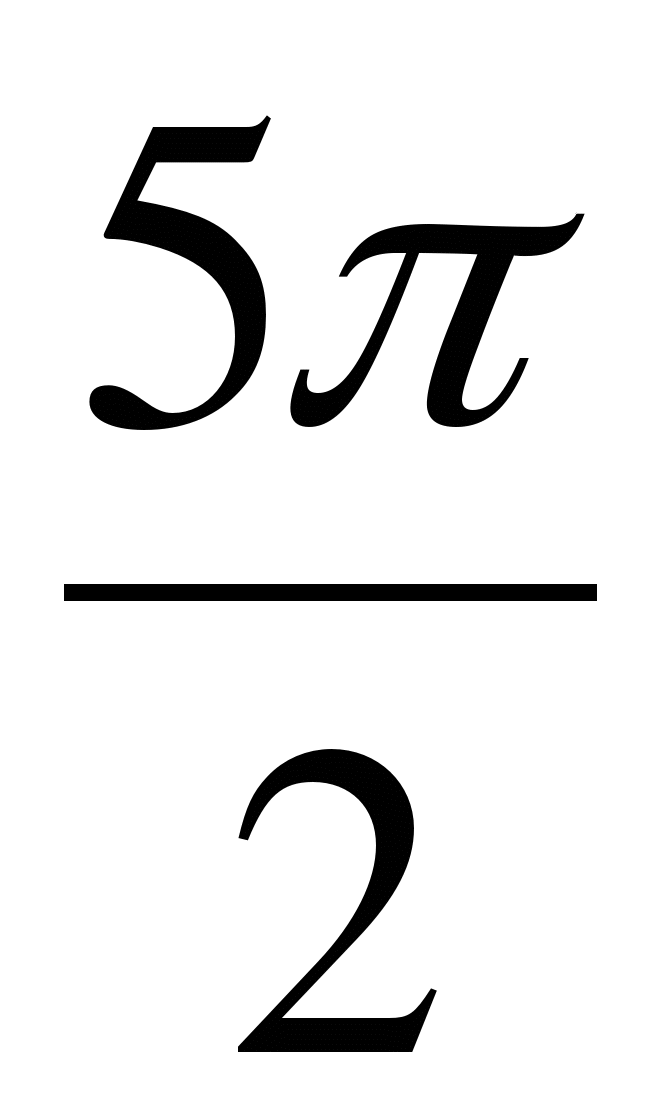 .
.
№3. Найдите числовое значение выражения 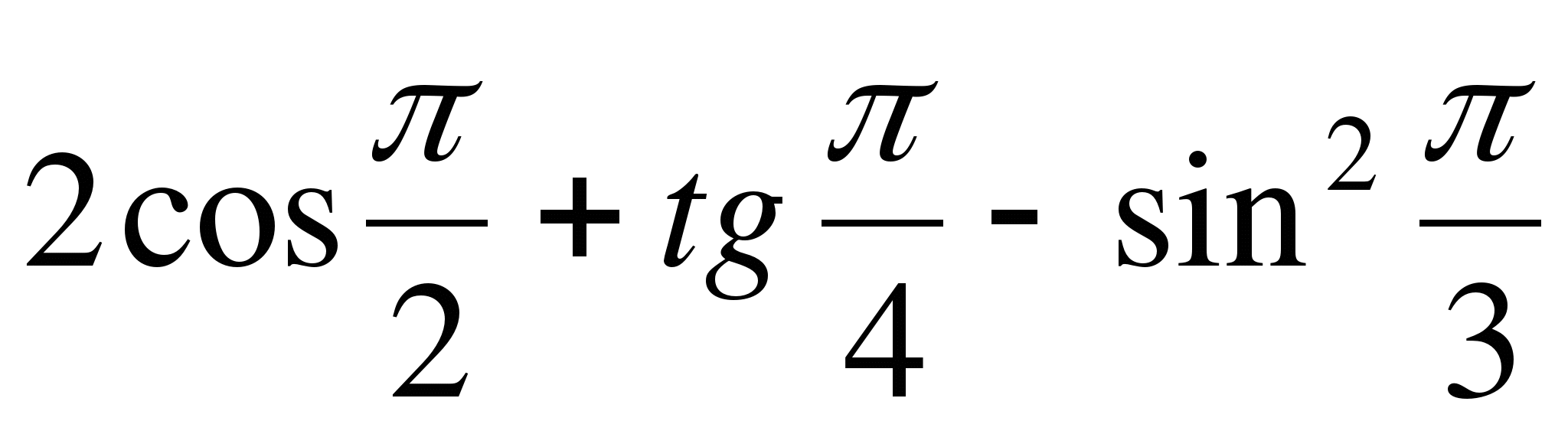 .
.
№4. Могут ли синус и косинус одного и того же числа быть равными соответственно: 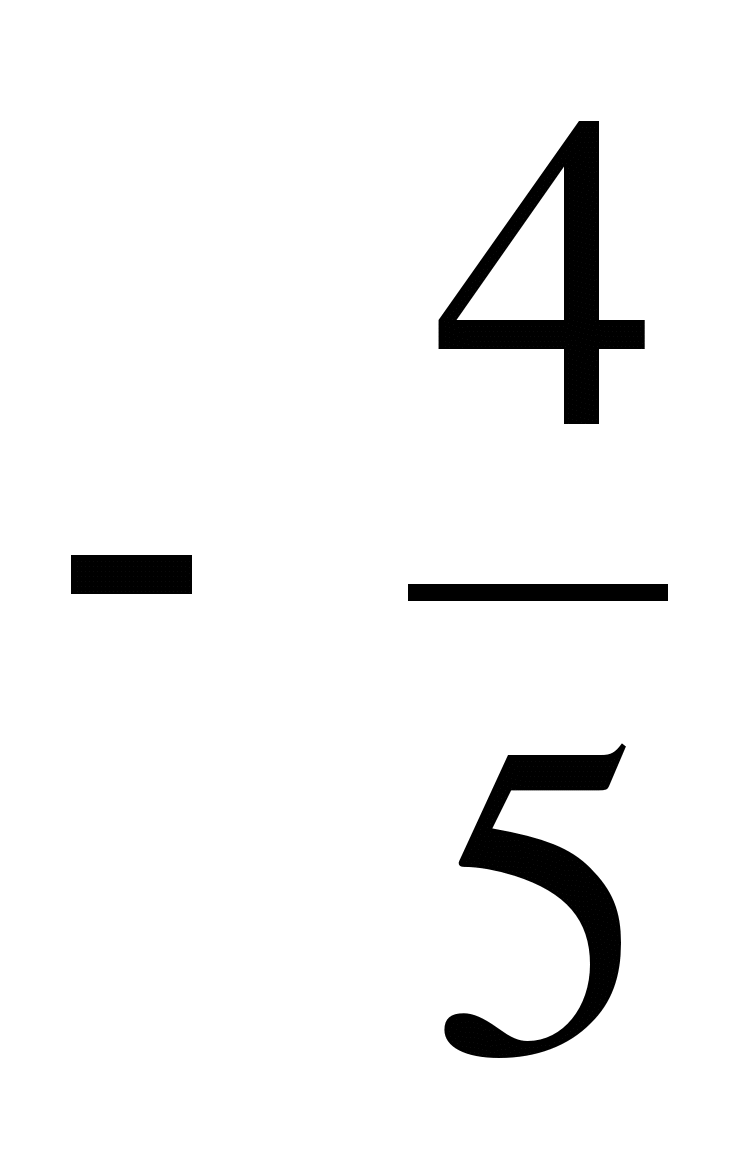 и
и 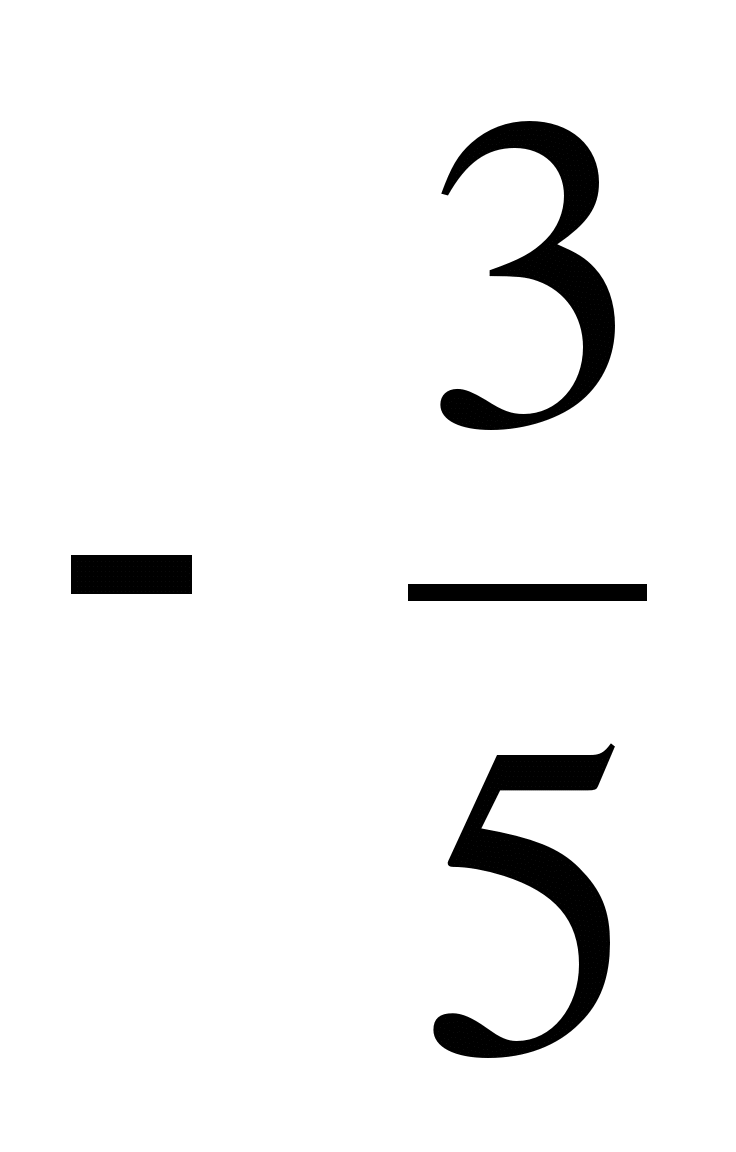 ?
?
№5. Могут ли тангенс и котангенс одного и того же числа быть равными соответственно: 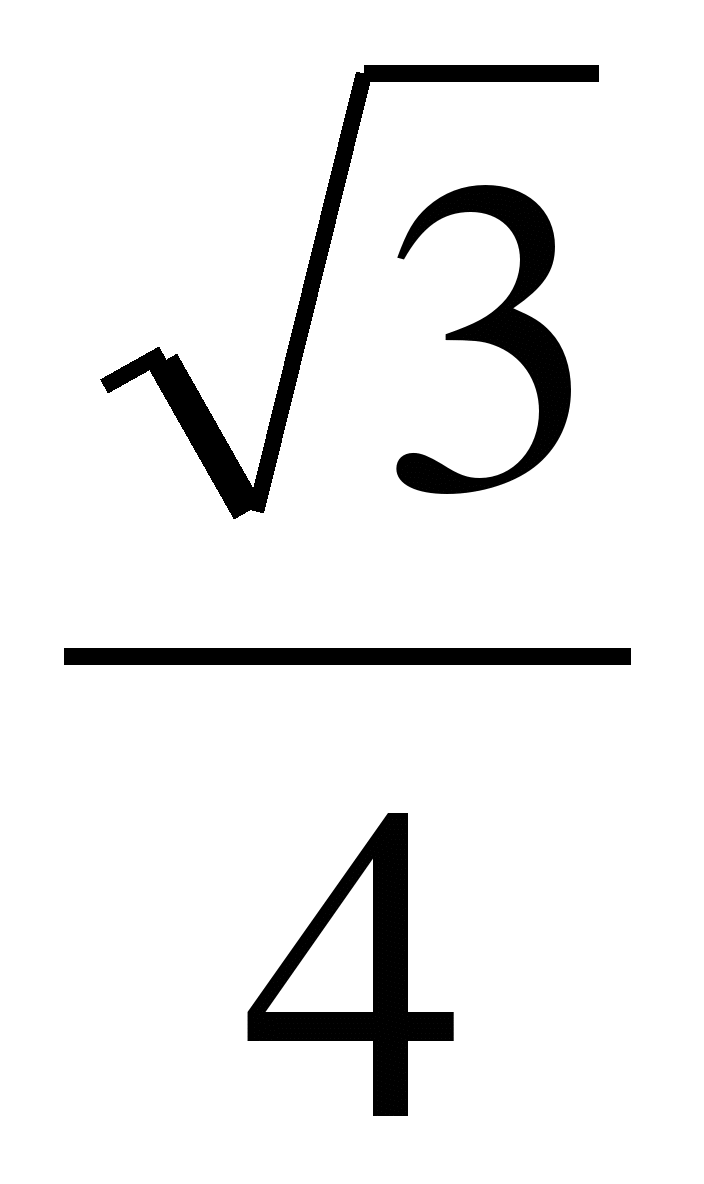 и
и 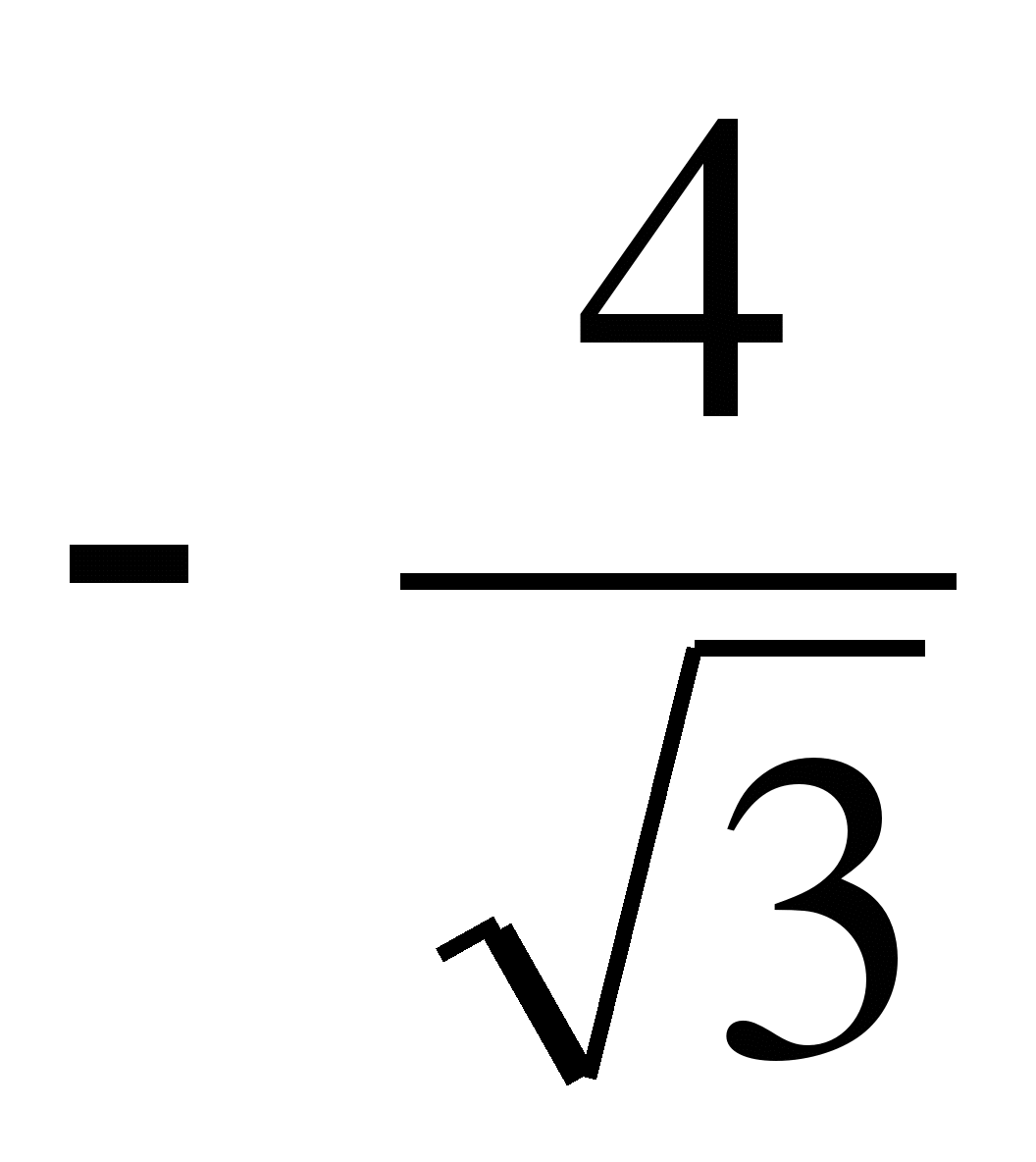 ?
?
№6. Найдите значения других трёх основных тригонометрических функций, если: 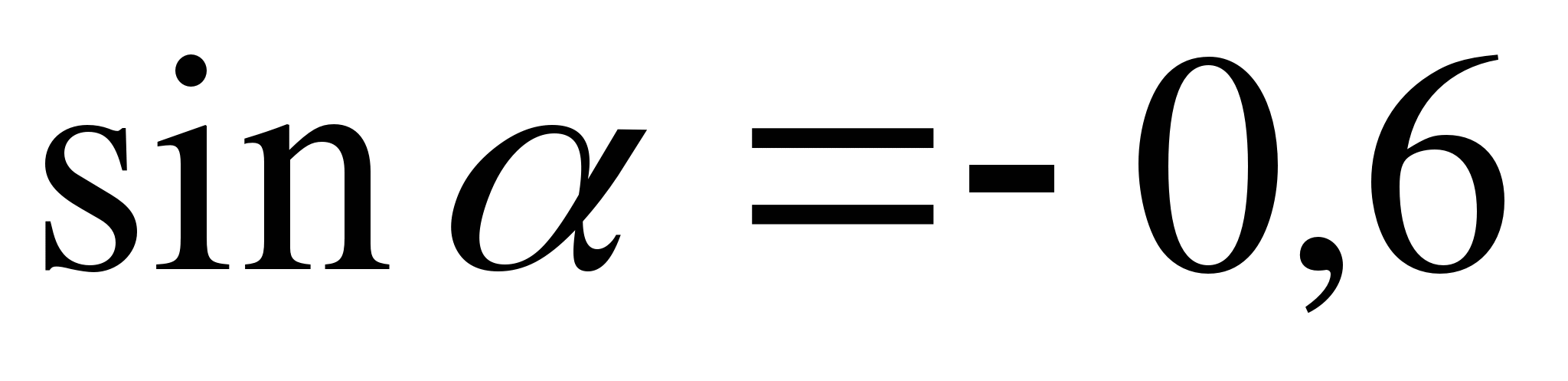 ,
, 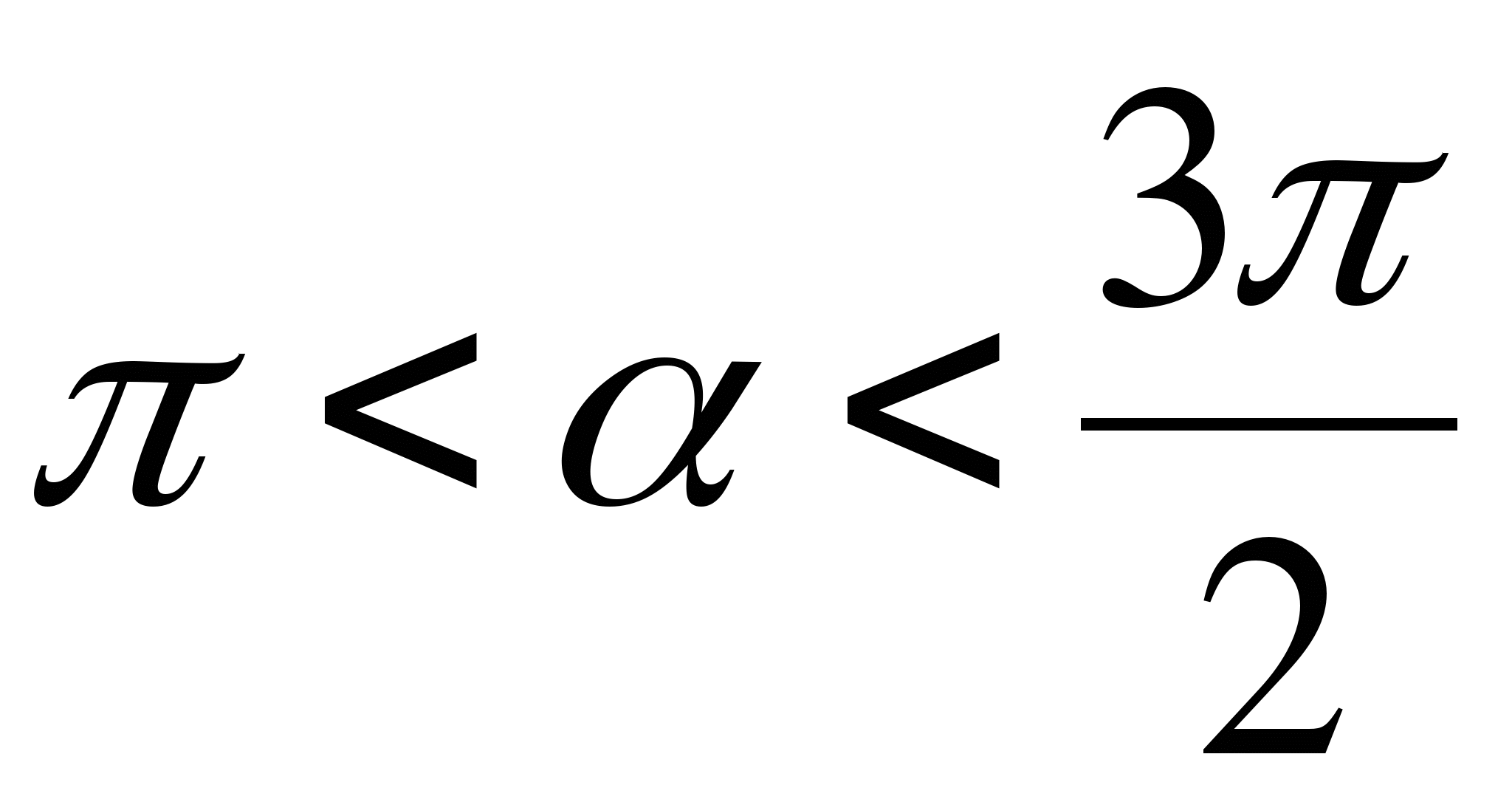 .
.
№7. Вычислите 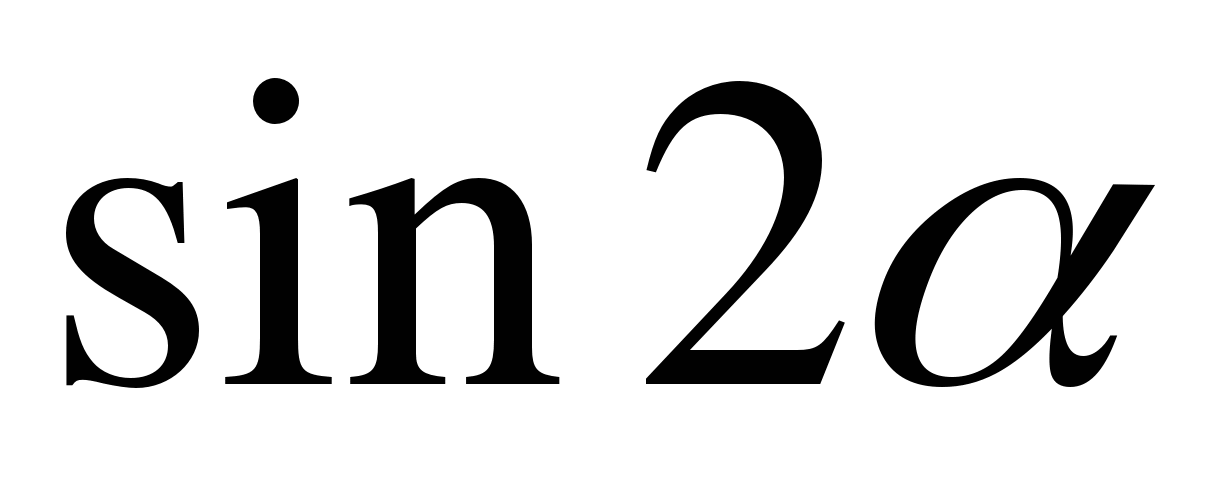 , если
, если 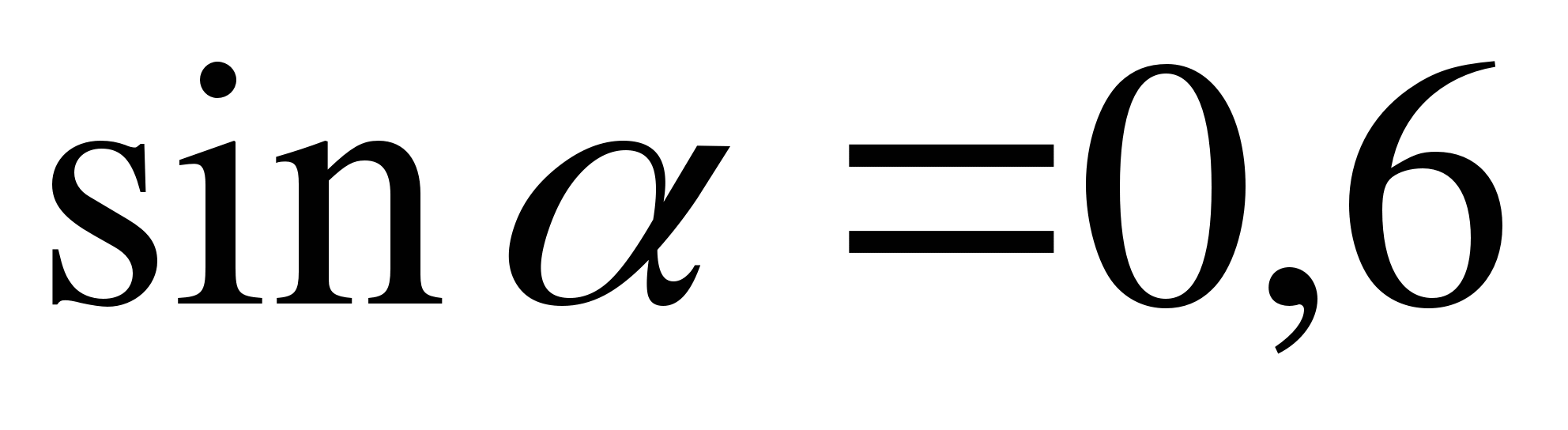 ,
, 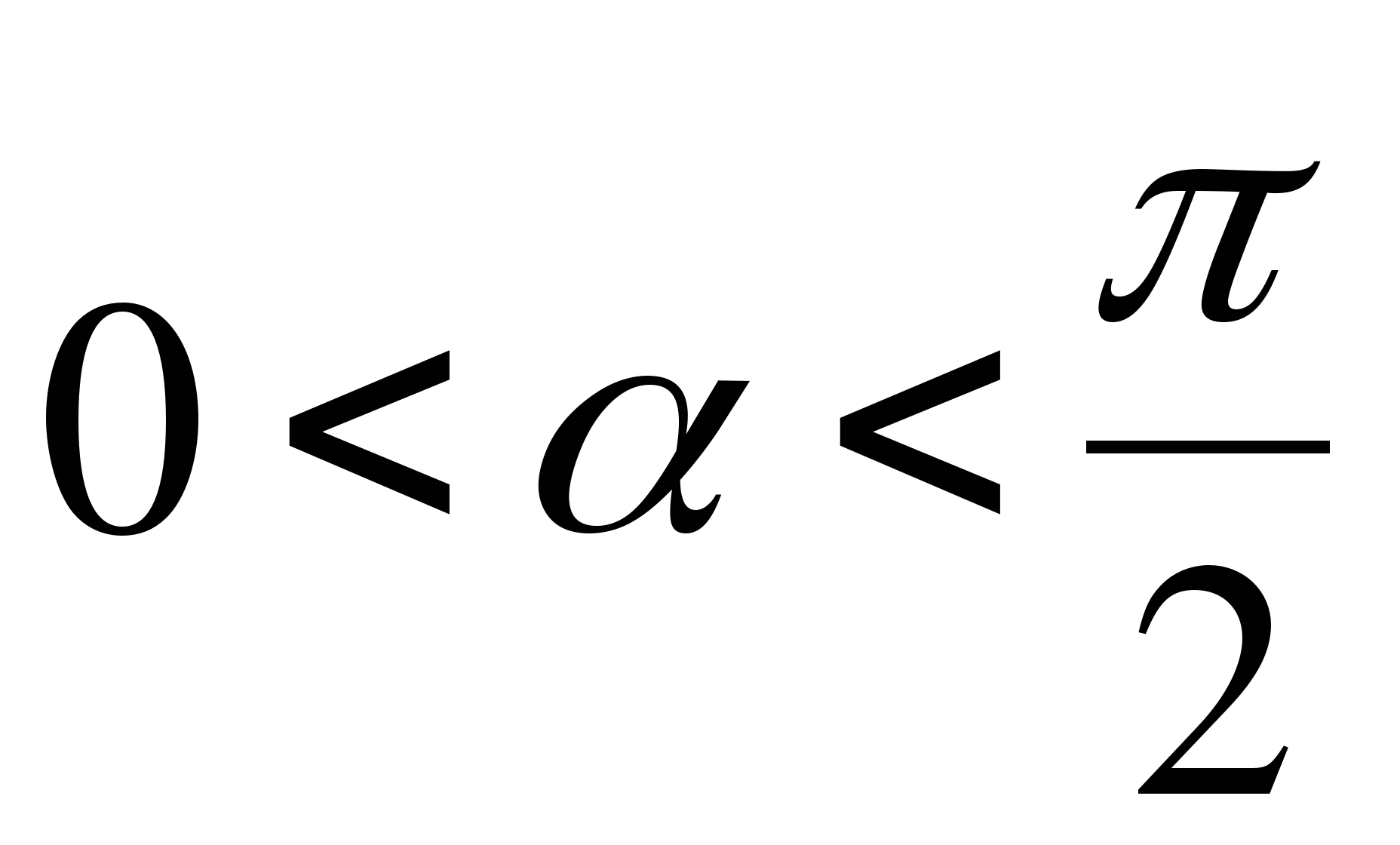 .
.
№8. Вычислите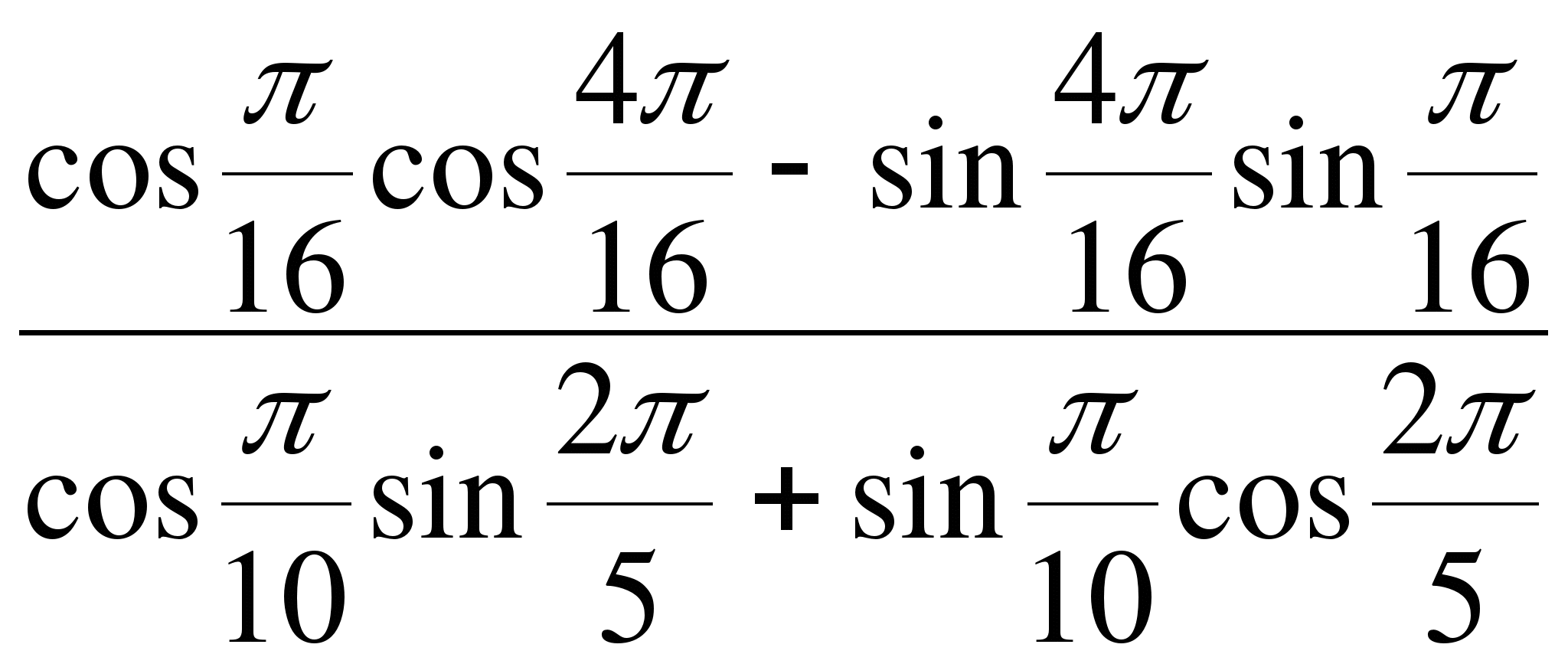
Контрольная работа по математике, раздел «Тригонометрия»
Вариант 2
№1. Выразите в радианной мере величины углов: 2160, 720, 3100.
№2. Выразите в градусной мере величины углов: 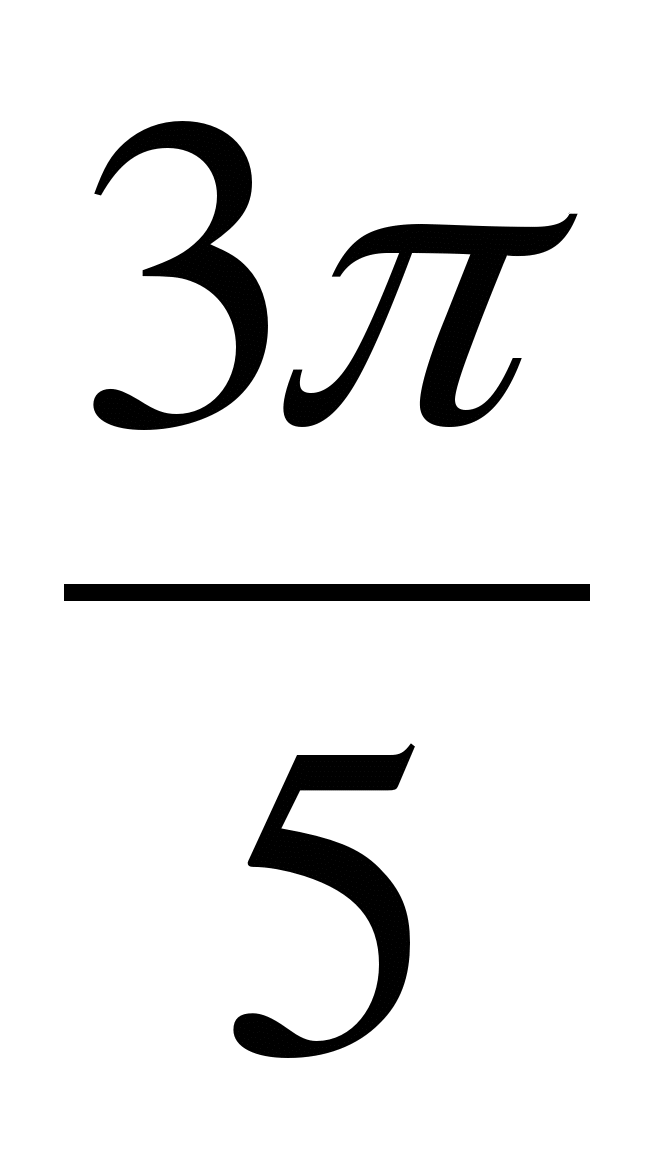 ,
, 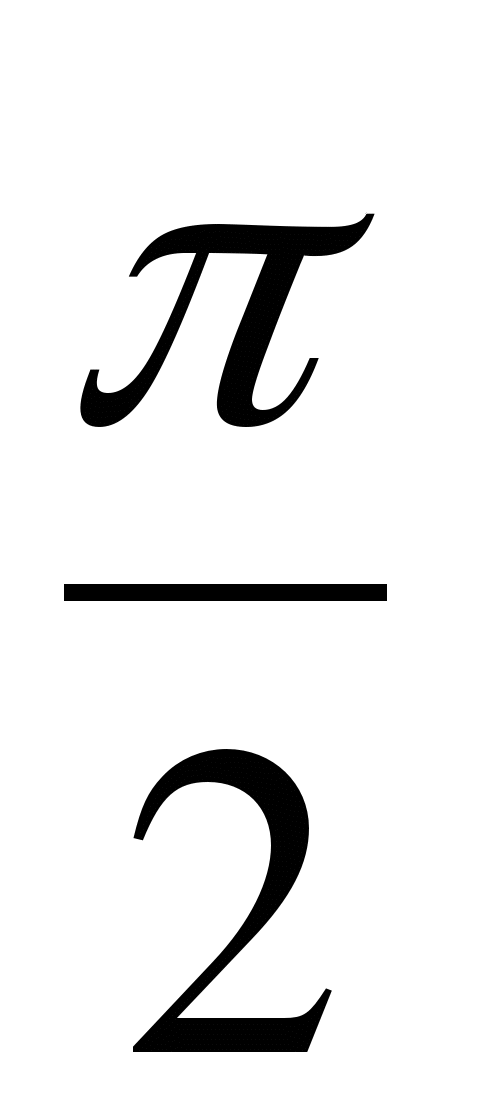 ,
,  .
.
№3. Найдите числовое значение выражения 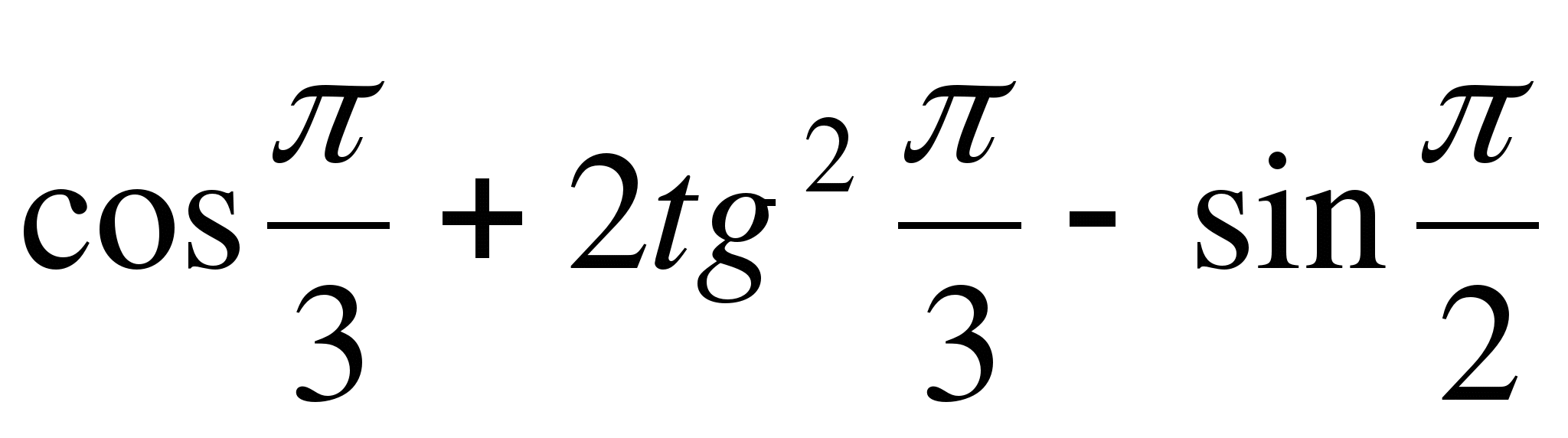 .
.
№4. Могут ли синус и косинус одного и того же числа быть равными соответственно: 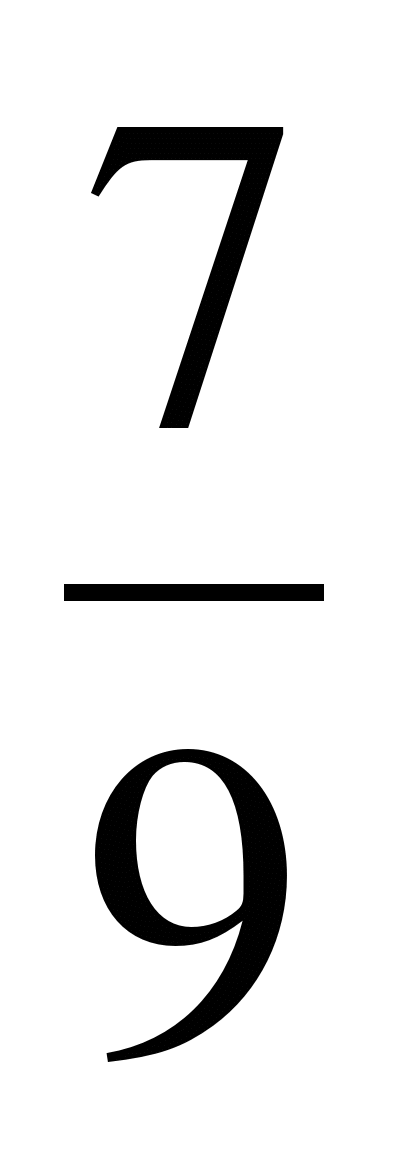 и
и 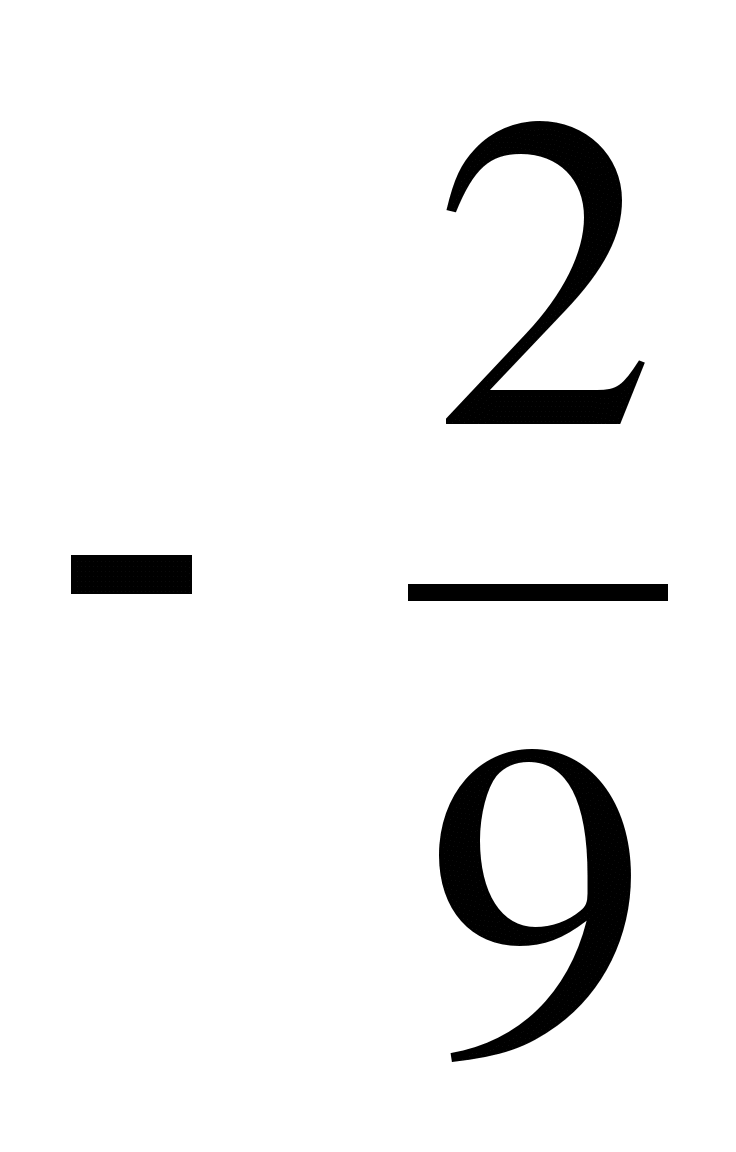 ?
?
№5. Могут ли тангенс и котангенс одного и того же числа быть равными соответственно: 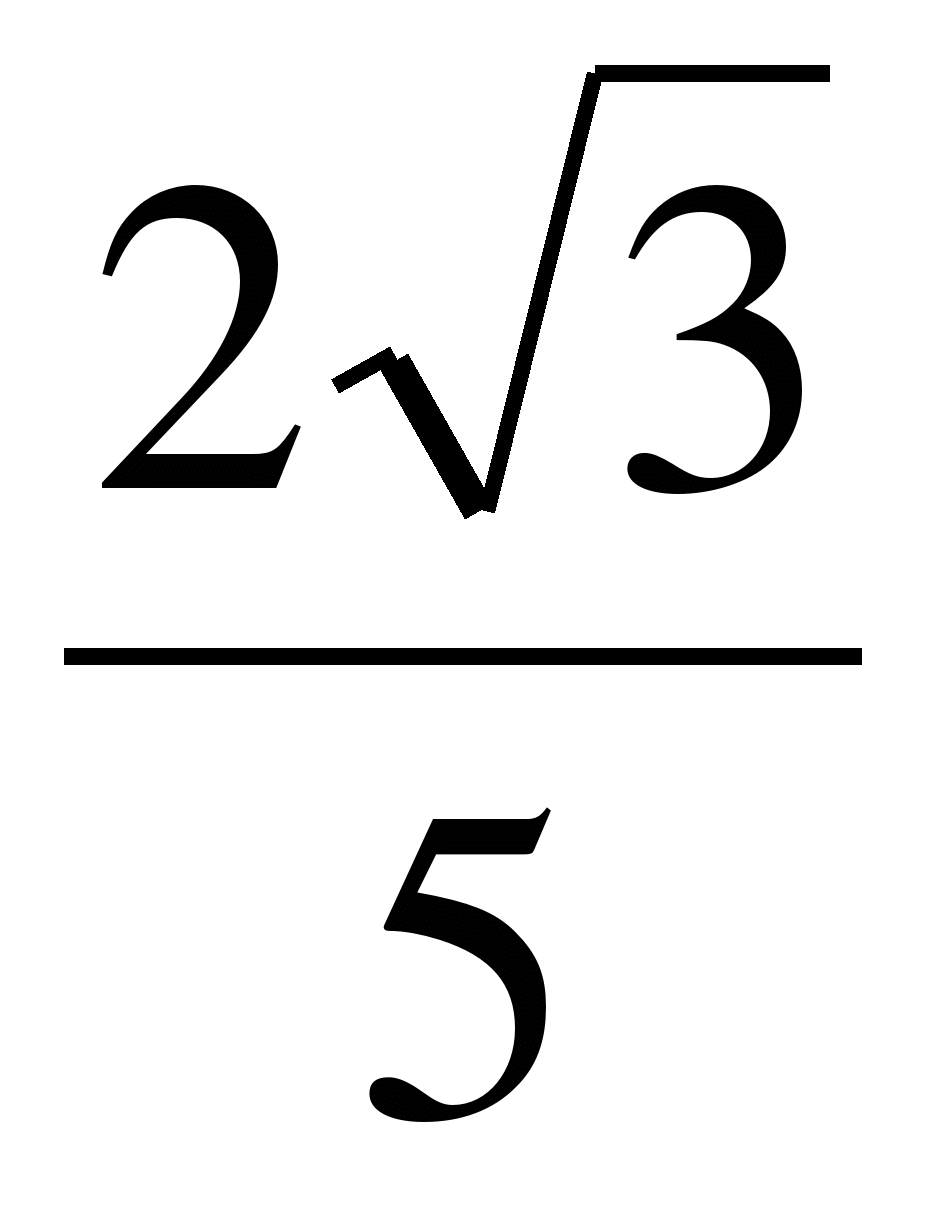 и
и 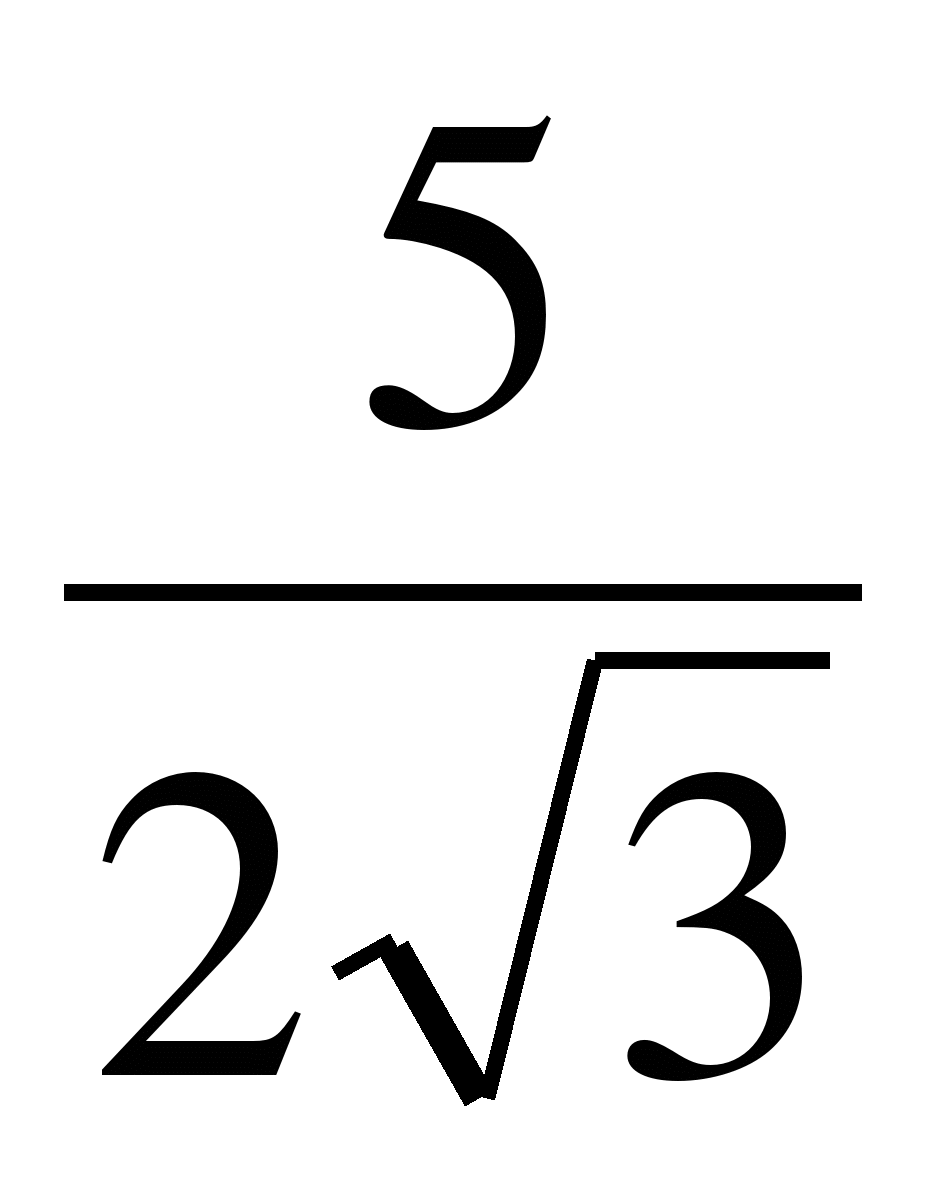 ?
?
№6. Найдите значения других трёх основных тригонометрических функций, если: 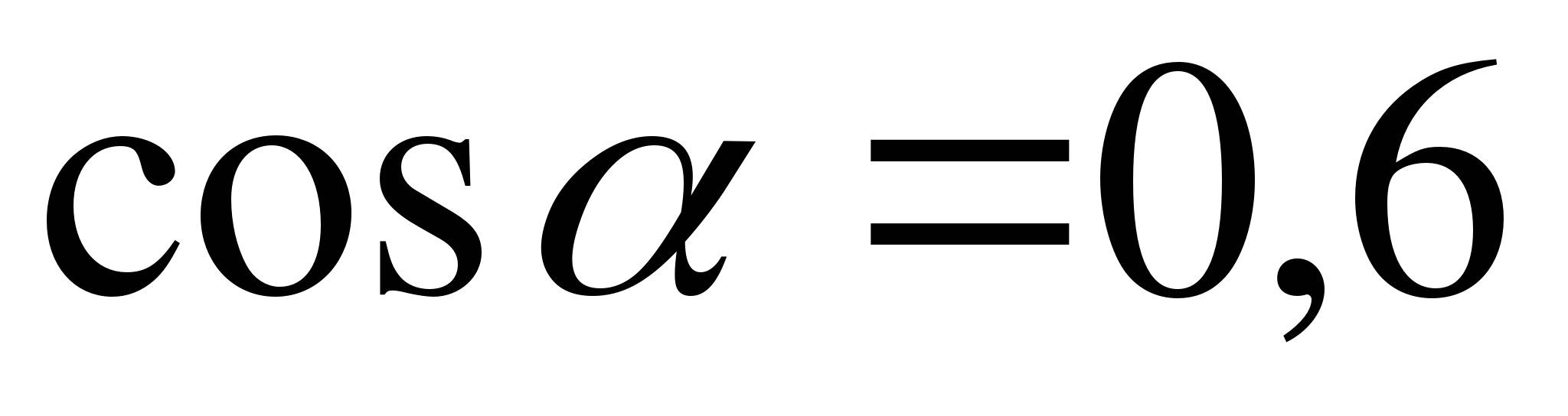 ,
, 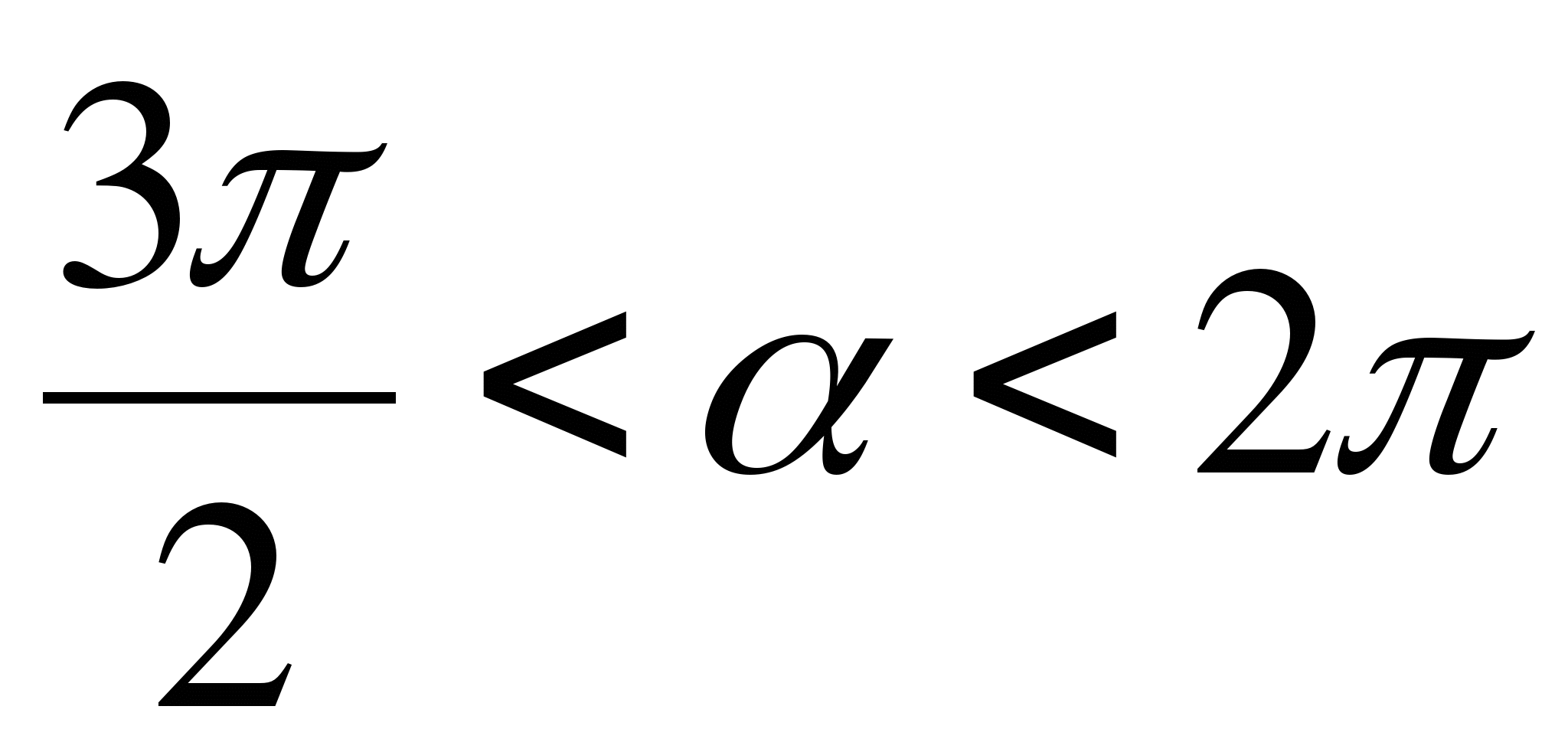 .
.
№7. Вычислите 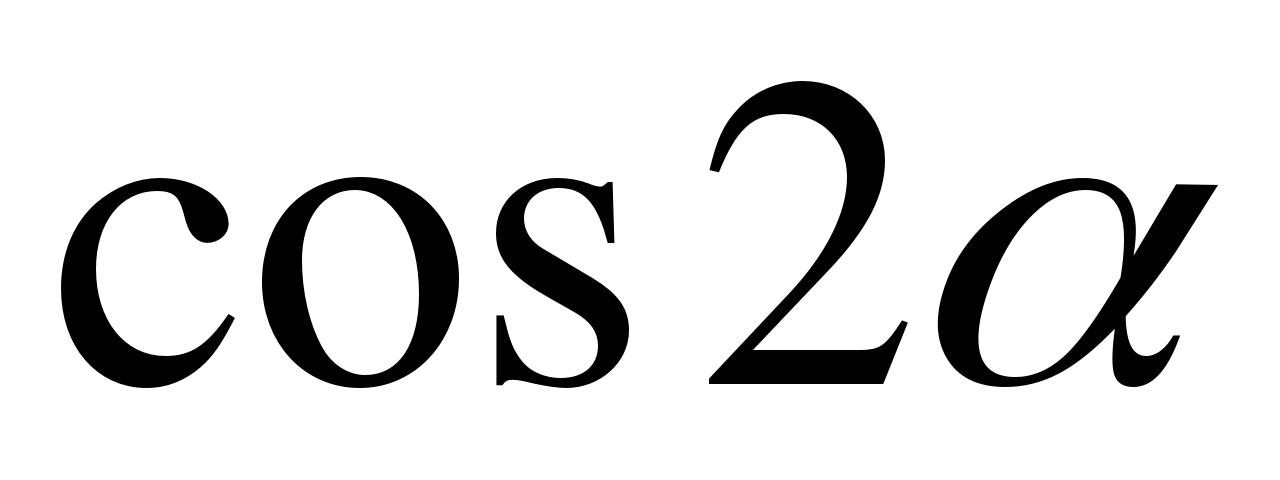 , если
, если 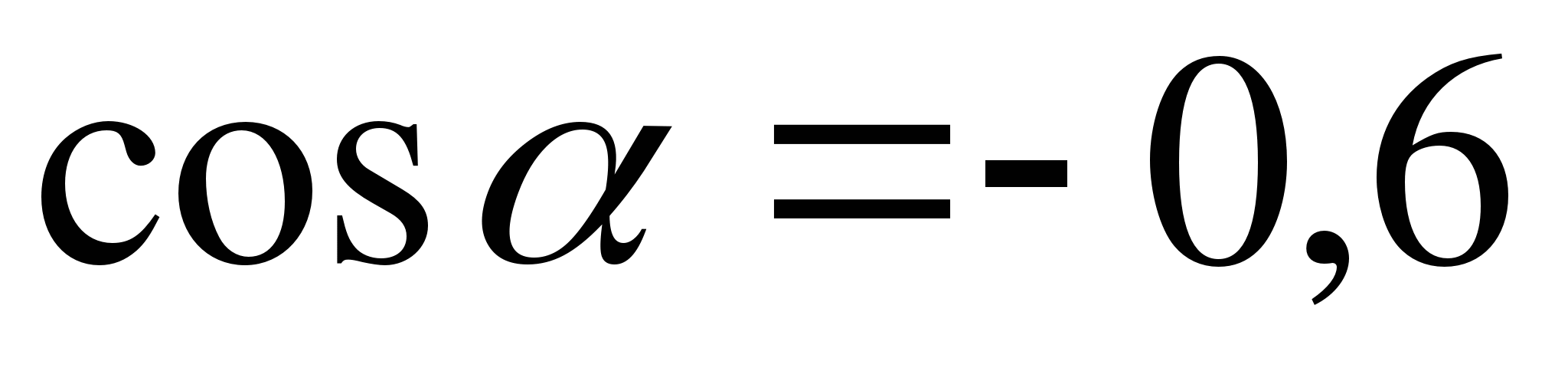 ,
, 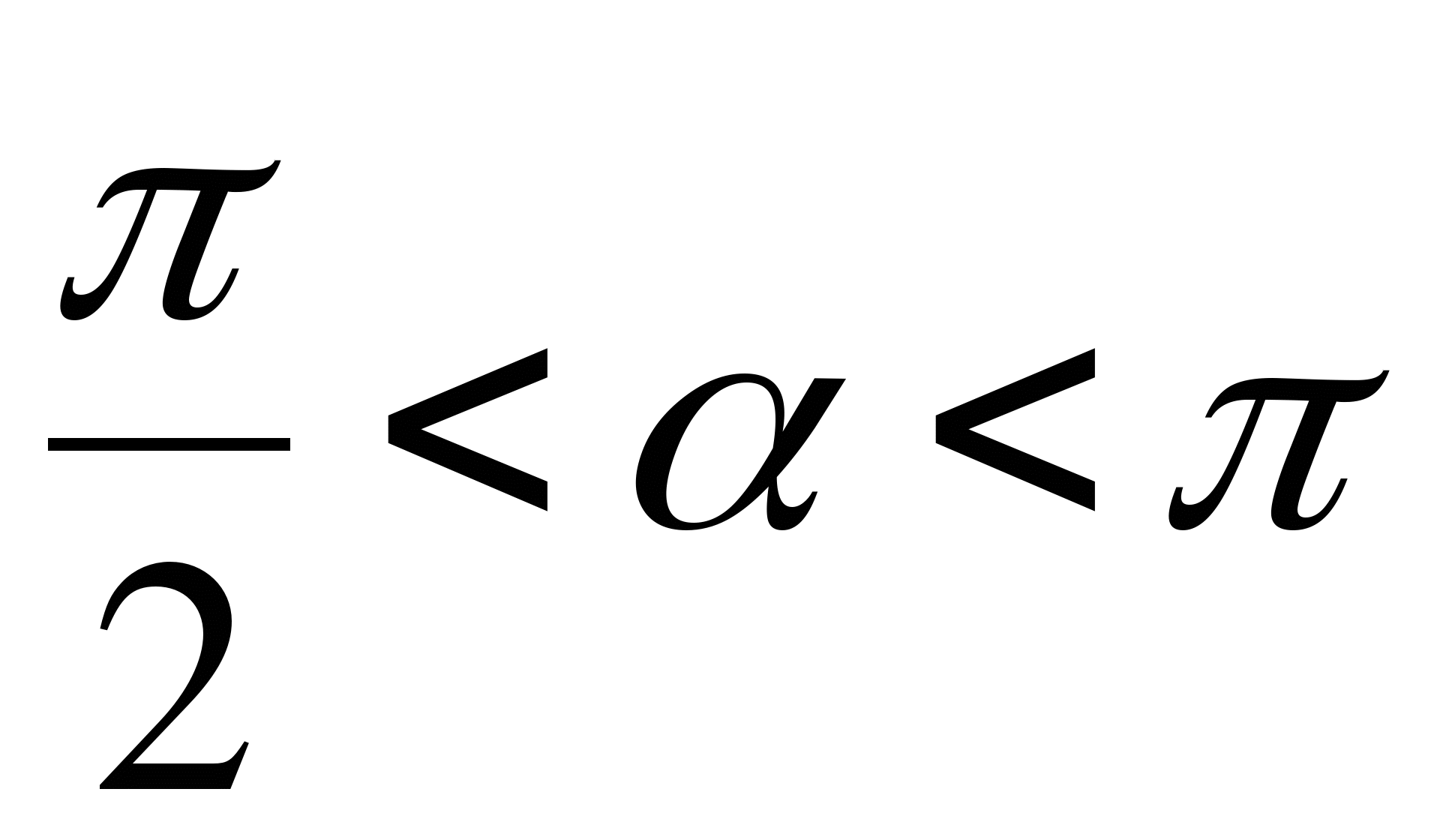 .
.
№8. Вычислите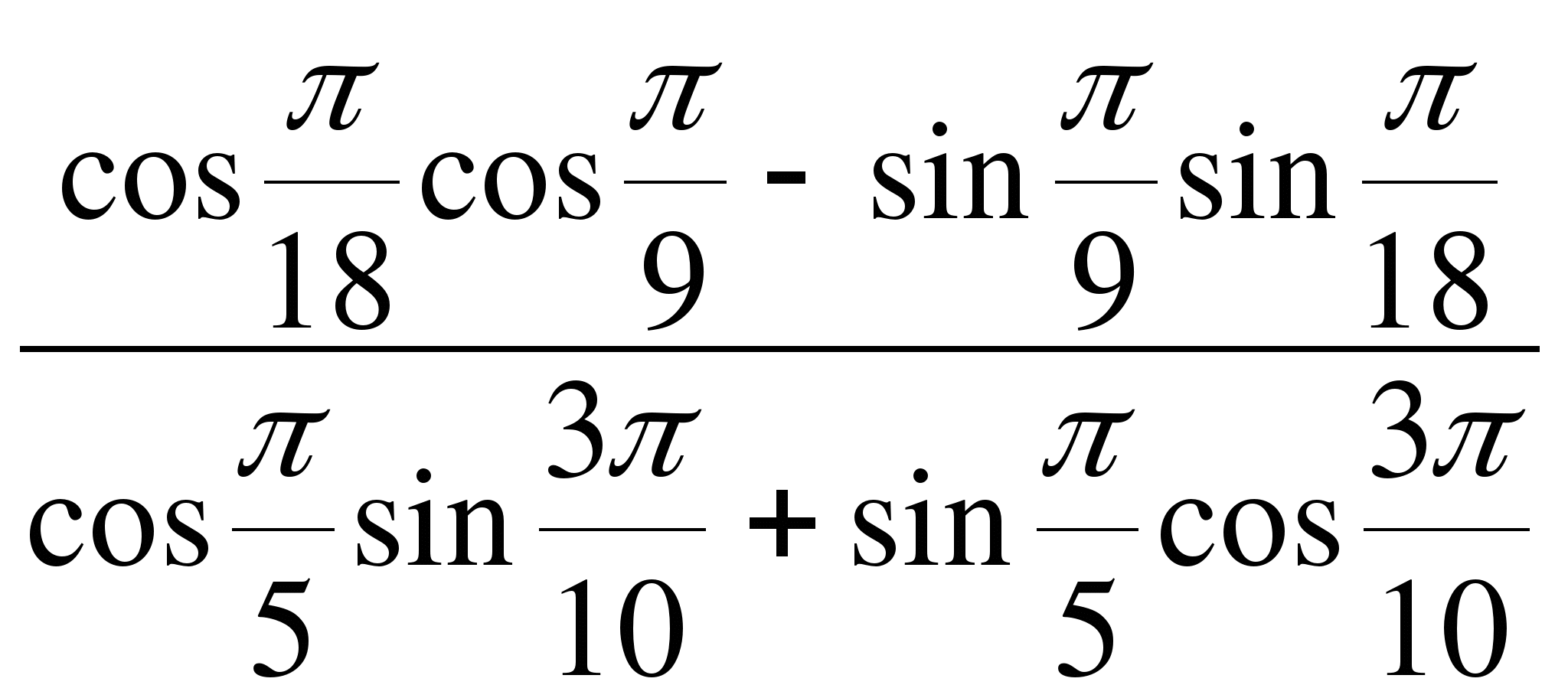
infourok.ru
КИМы по математике по теме "Основы тригонометрии"
Контрольно-измерительные материалы
по учебной дисциплине МАТЕМАТИКА
для обучающихся 1 курса (10 класс)
Тема программы: «Основы тригонометрии»
Всего заданий 5. Время выполнения 45 минут.
ТРЕБОВАНИЯ К ЗНАНИЯМ И УМЕНИЯМ
| Знания | Умения |
| Учебные элементы (УЭ), подлежащие усвоению | Уровень усвоения | Действия, подлежащие освоению | Уровень усвоения |
| Тригонометрические функции числового аргумента - определения синуса, косинуса, тангенса и котангенса произвольного угла и числа; - радианная и градусная мера угла. | 1 2 | - находить синус, косинус, тангенс и котангенс произвольного угла и числа; - находить радианную и градусную меру угла. | 2 2 |
| Основные формулы тригонометрии -основное тригонометрическое тождество; -формулы приведения; - синус, косинус, тангенс суммы и разности двух углов; - синус, косинус, тангенс двойного угла. | 1 1 1 1 | - выполнять тригонометрические преобразования выражений. | 2 |
Контрольная работа
по теме «Основы тригонометрии»
Вариант №1.
| № п/п | Задание | Способ выполнения |
| 1 | Записать в других единицах измерения углы: 225˚ 315˚  | Переведите данные углы в другие единицы измерения, запишите решение и ответ |
| 2 | Вычислить:   | Вычислите значение выражения, запишите решение и ответ |
| 3 | Найти четверти четверти | Вычислите значенияфункций, запишите решение и ответ |
| 4 | Вычислить: sin 75˚ | Вычислите значение выражения, запишите решение и ответ |
| 5 | Упростить:   | Вычислите значение выражения, запишите решение и ответ |
Вариант №2.
| № п/п | Задание | Способ выполнения |
| 1 | Записать в других единицах измерения углы: 165˚ 225˚  | Переведите данные углы в другие единицы измерения, запишите решение и ответ |
| 2 | Вычислить:   | Вычислите значение выражения, запишите решение и ответ |
| 3 | Найти  четверти четверти | Вычислите значения функций, запишите решение и ответ |
| 4 | Вычислить: tg75˚ | Вычислите значение выражения, запишите решение и ответ |
| 5 | Упростить:   | Вычислите значение выражения, запишите решение и ответ |
Контрольная карта к контрольной работе
по теме «Основы тригонометрии»
Вариант №1.
| № п/п | Задание | Эталон правильного ответа | Оценка в баллах |
| 1 | Записать в других единицах измерения углы: 225˚ 315˚  |  = = 



| 4 |
| 2 | Вычислить:  
| 
| 4 |
| 3 | Найти:  четверти четверти
|  ; ;  ; ; 
| 6 |
| 4 | Вычислить: sin 75˚ | 
| 6 |
| 5 | Упростить:   | 
| 8 |
| Всего баллов | 28 |
Вариант №2.
| № п/п | Задание | Эталон правильного ответа | Оценка в баллах |
| 1 | Записать в других единицах измерения углы: 165˚ 225˚  |  = = 



| 4 |
| 2 | Вычислить:  
| | 4 |
| 3 | Найти: четверти четверти |  ; ;  ; ; 
| 6 |
| 4 | Вычислить: tg75˚ | 
| 6 |
| 5 | Упростить:   | 
| 8 |
| Всего баллов | 28 |
| КОЛ-ВО БАЛЛОВ | ОЦЕНКА |
| 19-22 | 3 |
| 23-25 | 4 |
| 26-28 | 5 |
videouroki.net
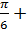 tg
tg
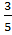 , π˂α˂
, π˂α˂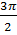
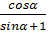 +
+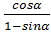
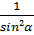 )·sin²α·cos²α=1
)·sin²α·cos²α=1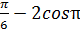
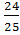 ,
, 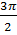 ˂α˂2π
˂α˂2π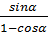 -
-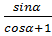
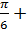 tg
tg
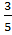 , π˂α˂
, π˂α˂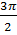
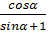 +
+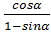
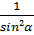 )·sin²α·cos²α=1
)·sin²α·cos²α=1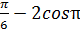
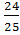 ,
, 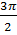 ˂α˂2π
˂α˂2π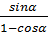 -
-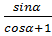
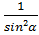
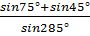
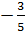 ,
,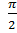 ˂x˂π
˂x˂π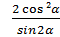
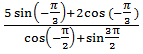 ;
; 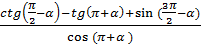
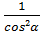
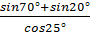
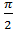 ˂x˂0
˂x˂0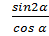 - sinα
- sinα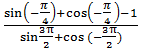 ;
; 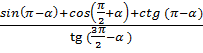
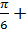 tg
tg
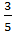 , π˂α˂
, π˂α˂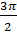
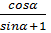 +
+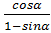
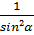 )·sin²α·cos²α=1
)·sin²α·cos²α=1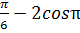
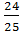 ,
, 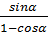 -
-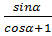
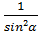
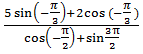 ;
;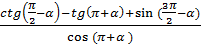
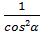
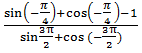 ;
;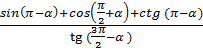
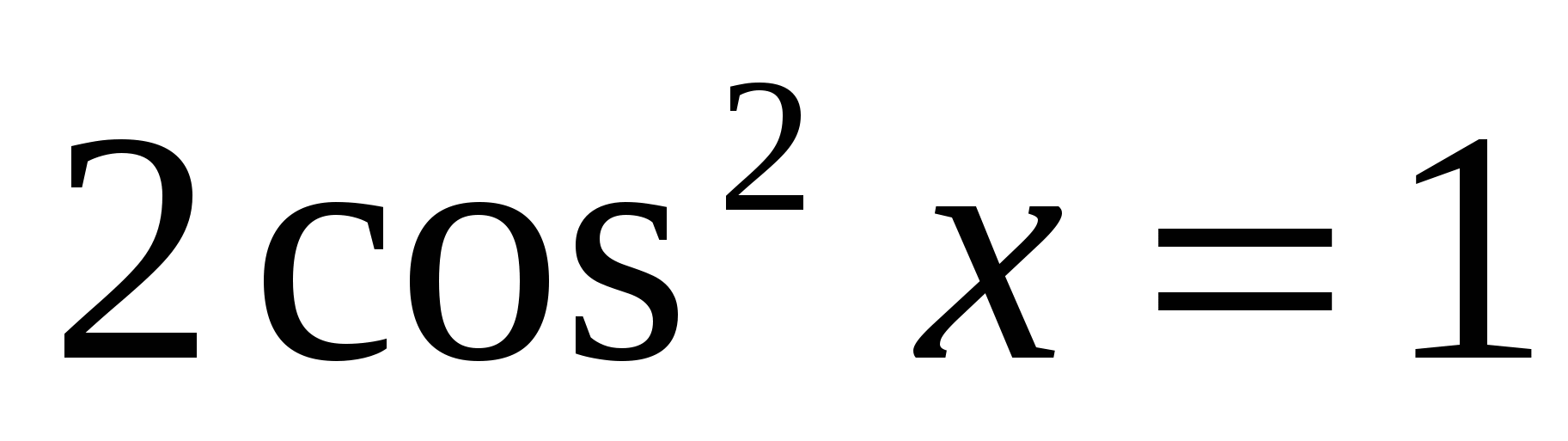 ; б)
; б) 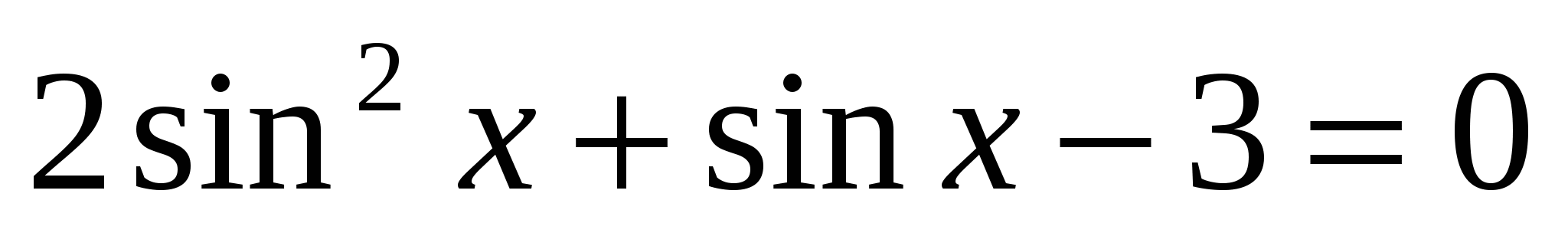 ;
; 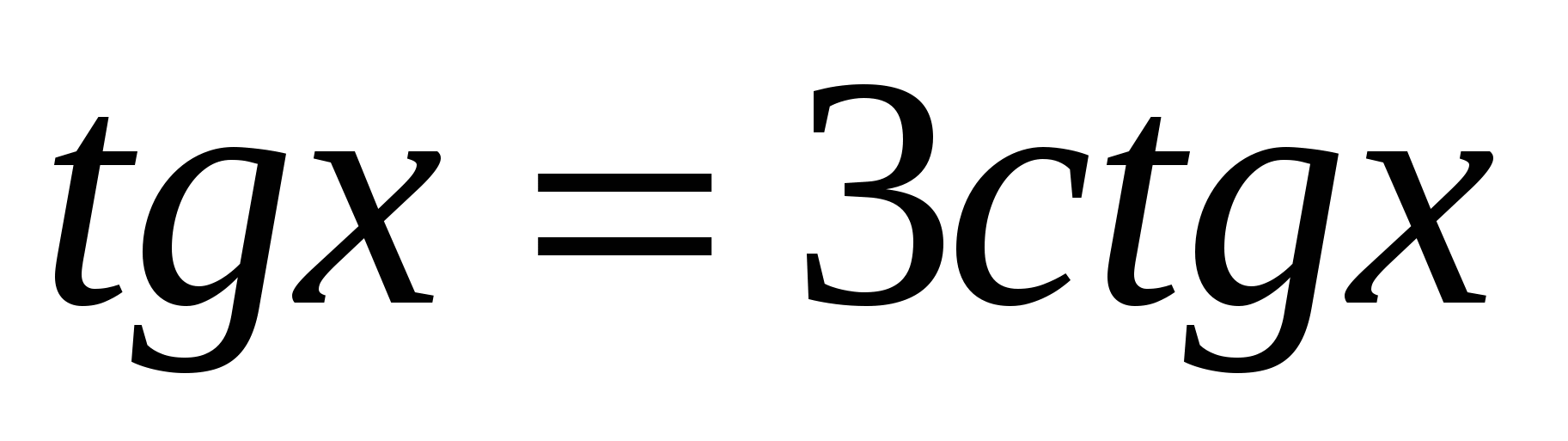 ; г)
; г) 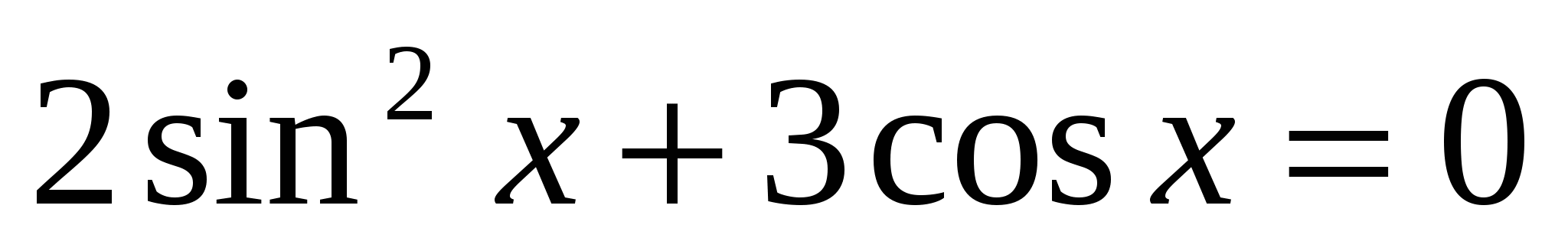 .
.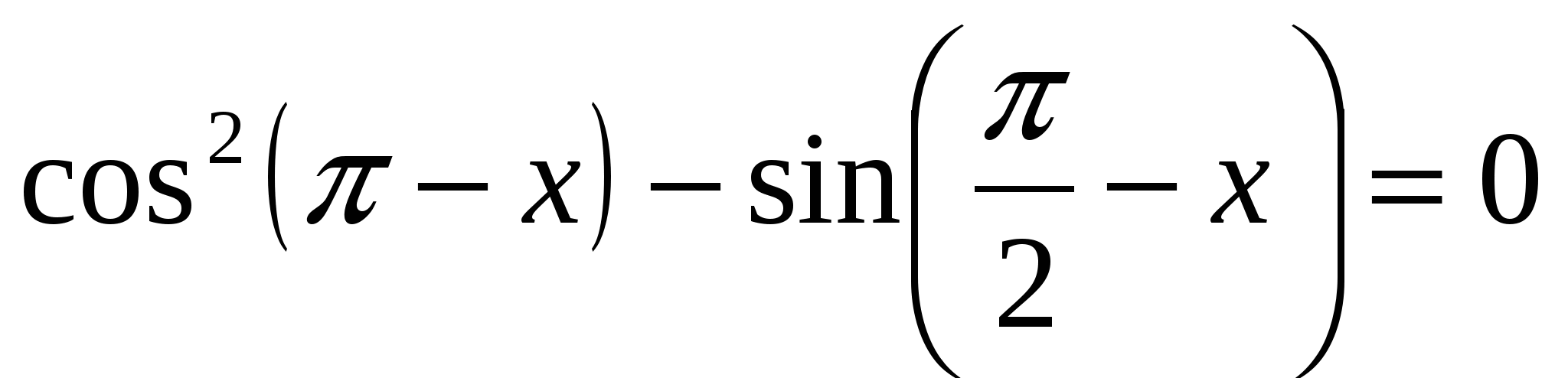 ; б)
; б) 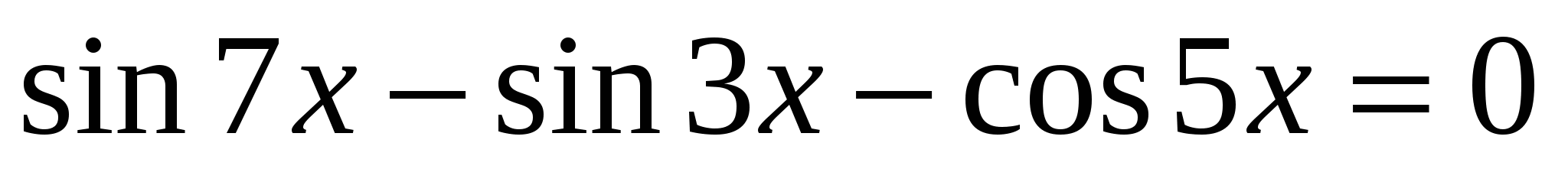 .
.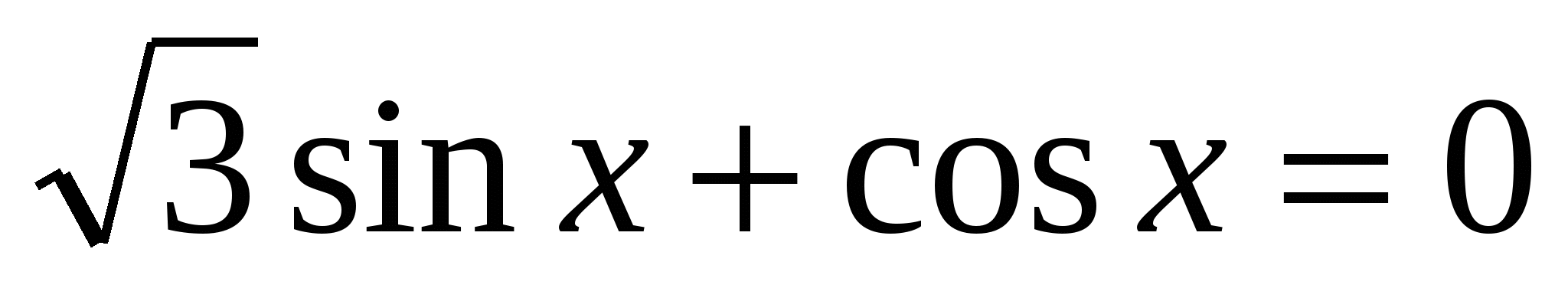 ; б)
; б) 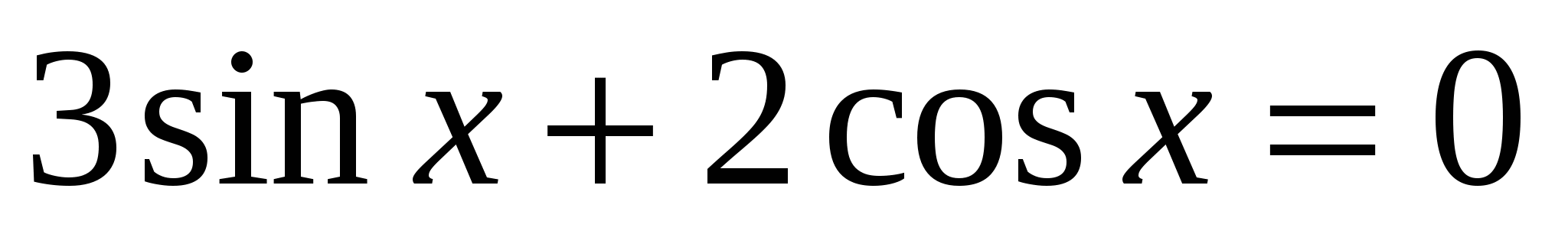 .
.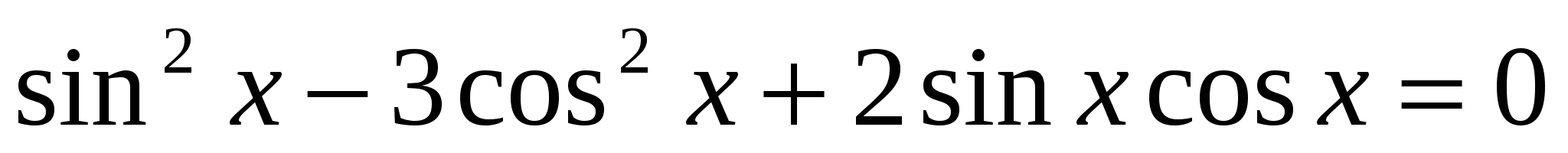 .
.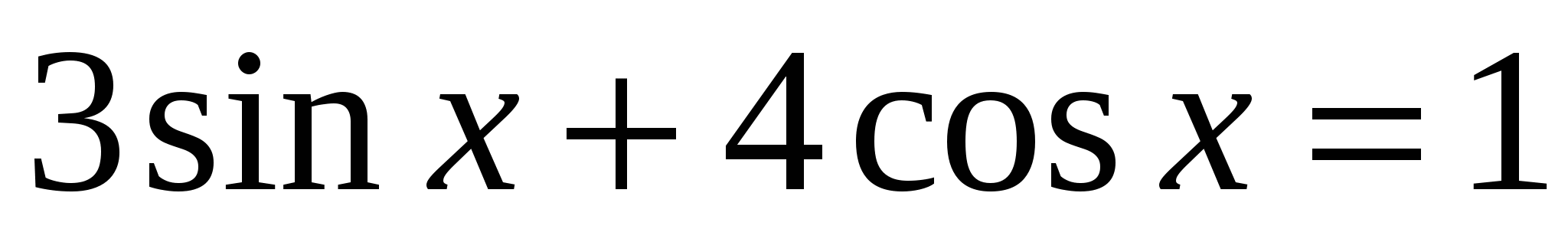 .
.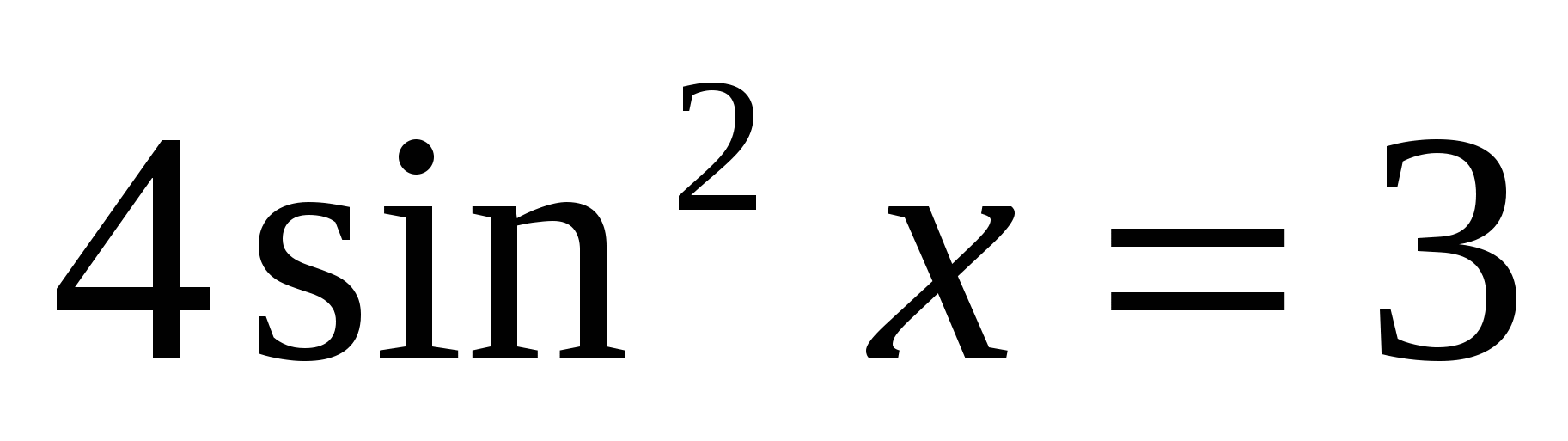 ; б)
; б) 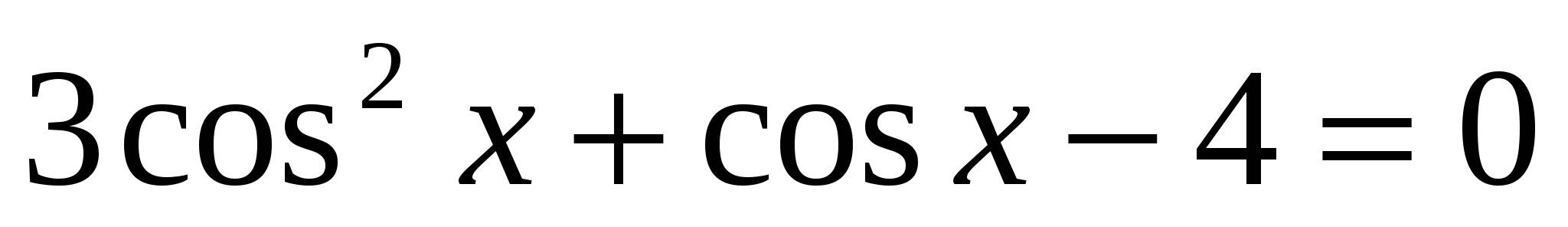 ;
; 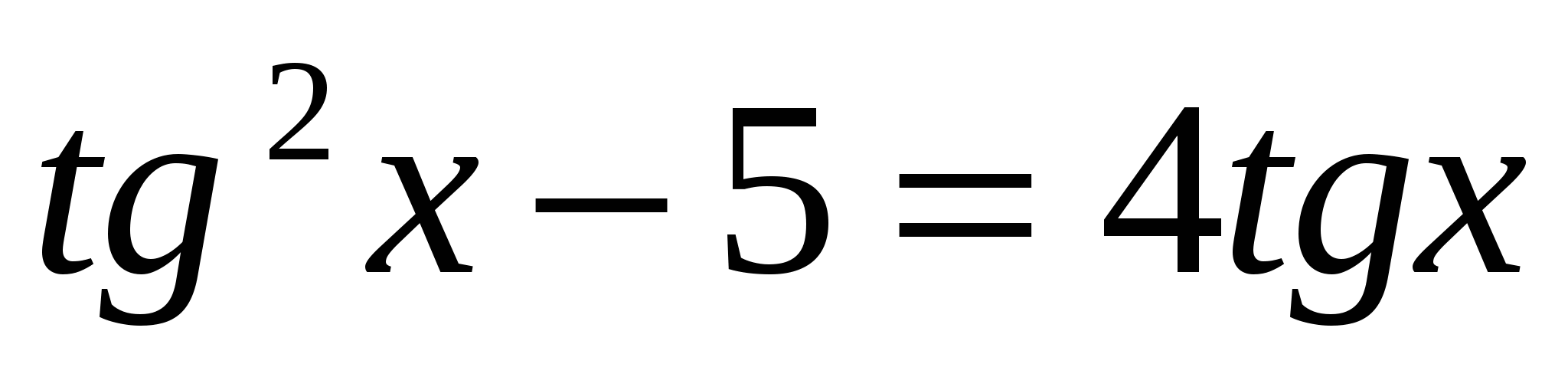 ; г)
; г) 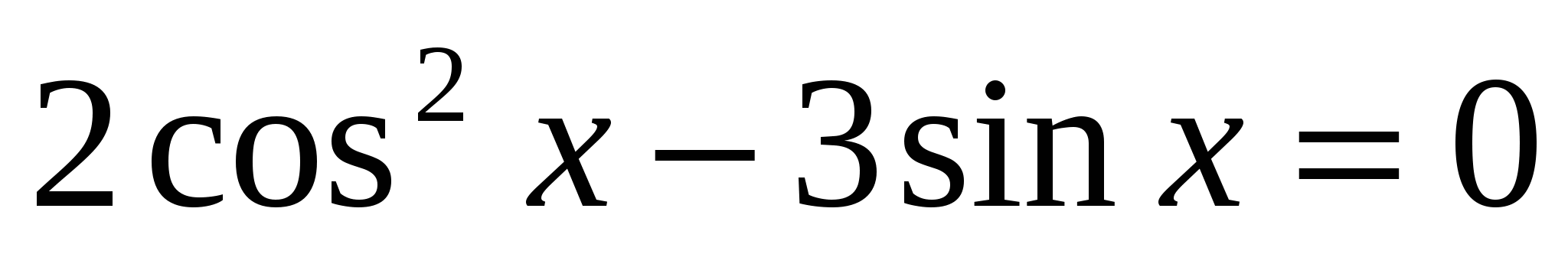 .
.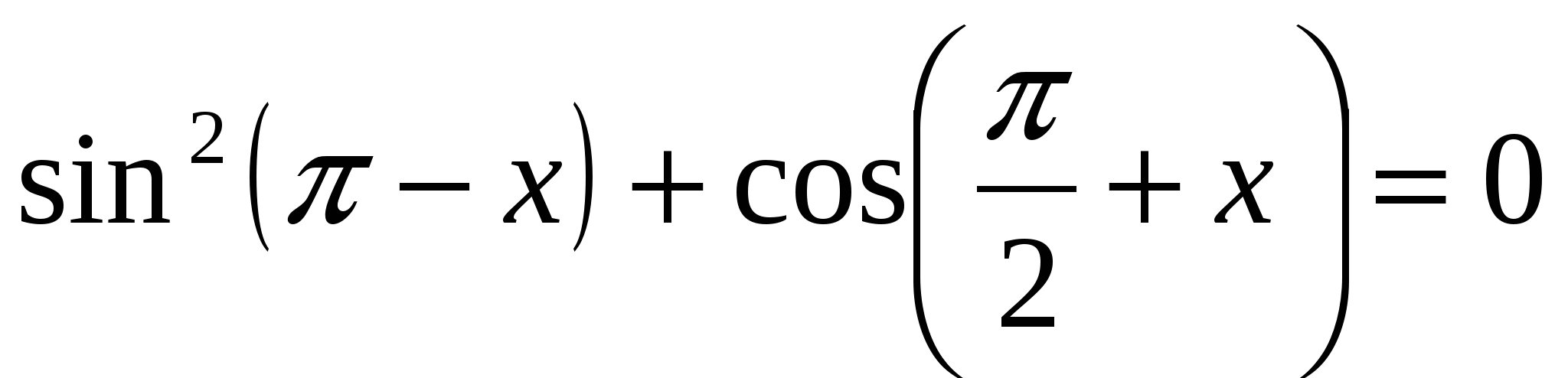 ; б)
; б) 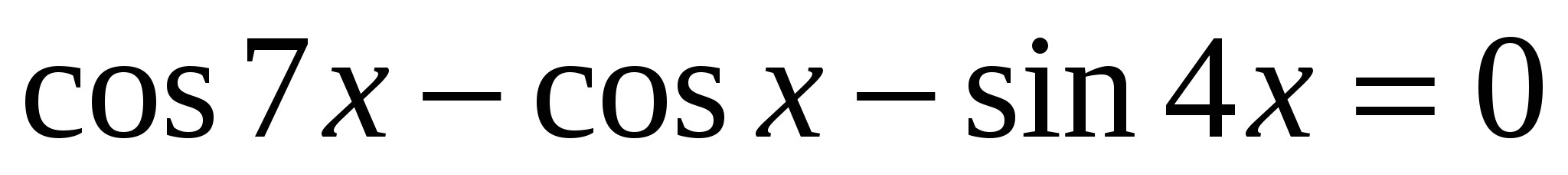 .
.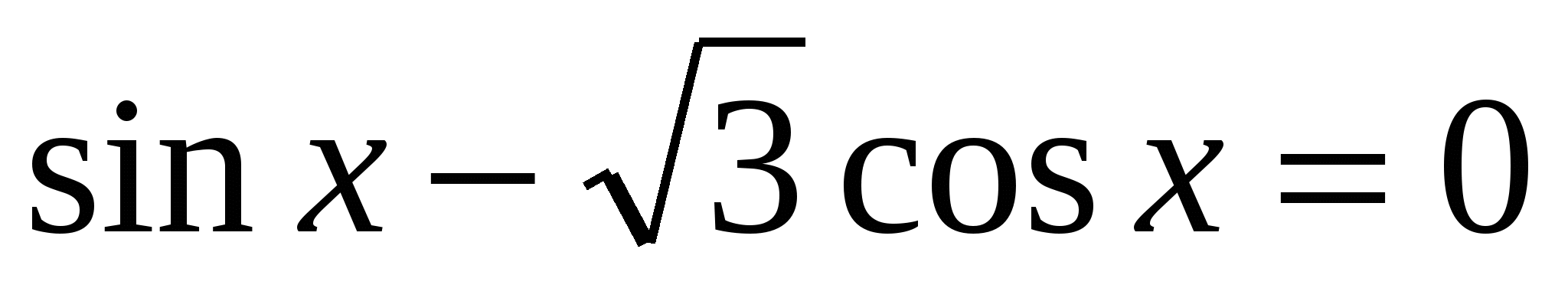 ; б)
; б) 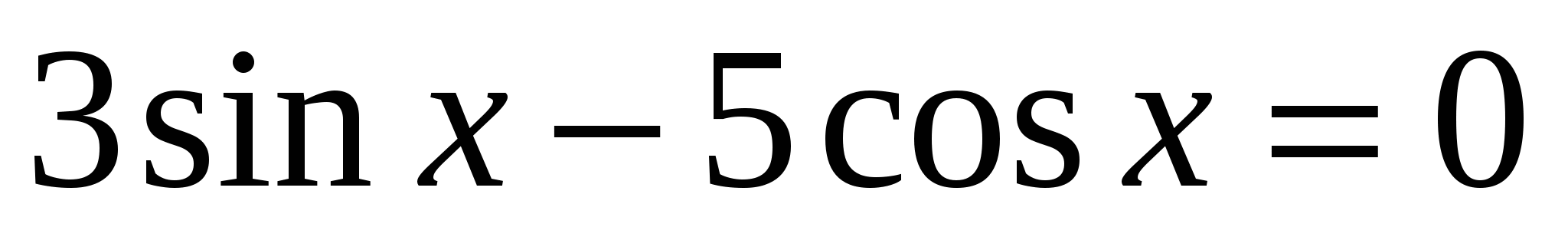 .
.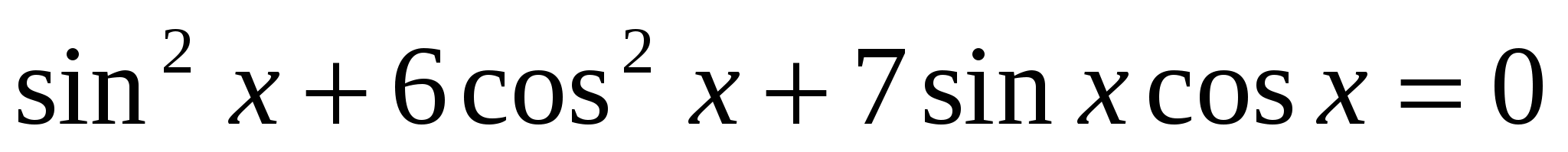 .
.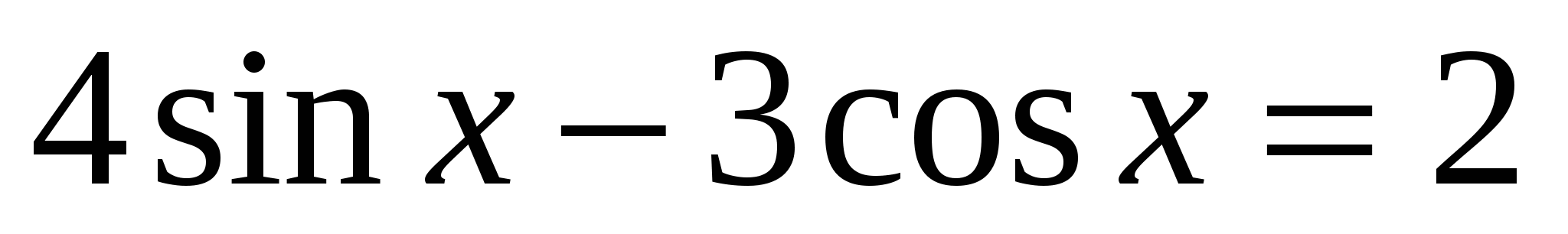 .
.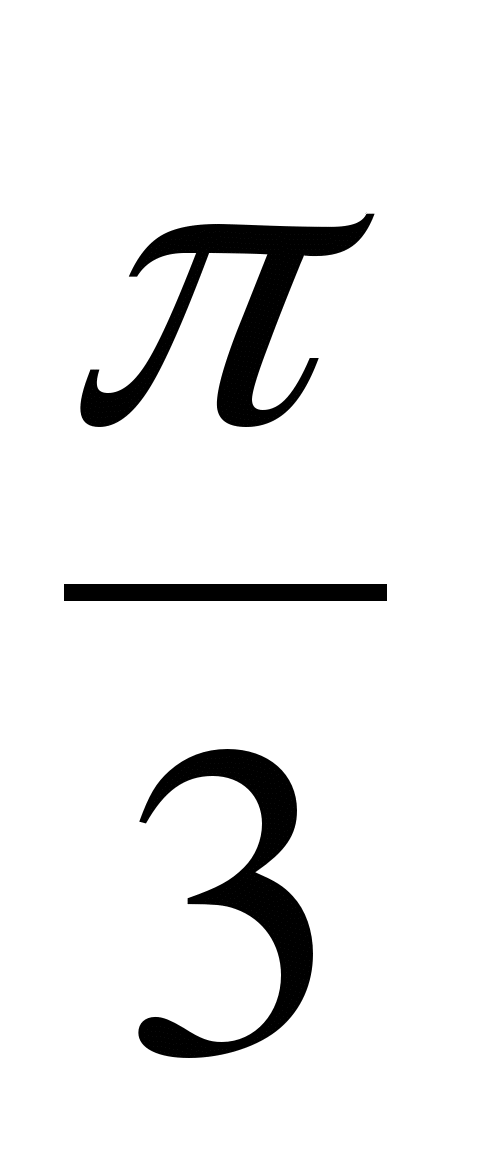 ,
, 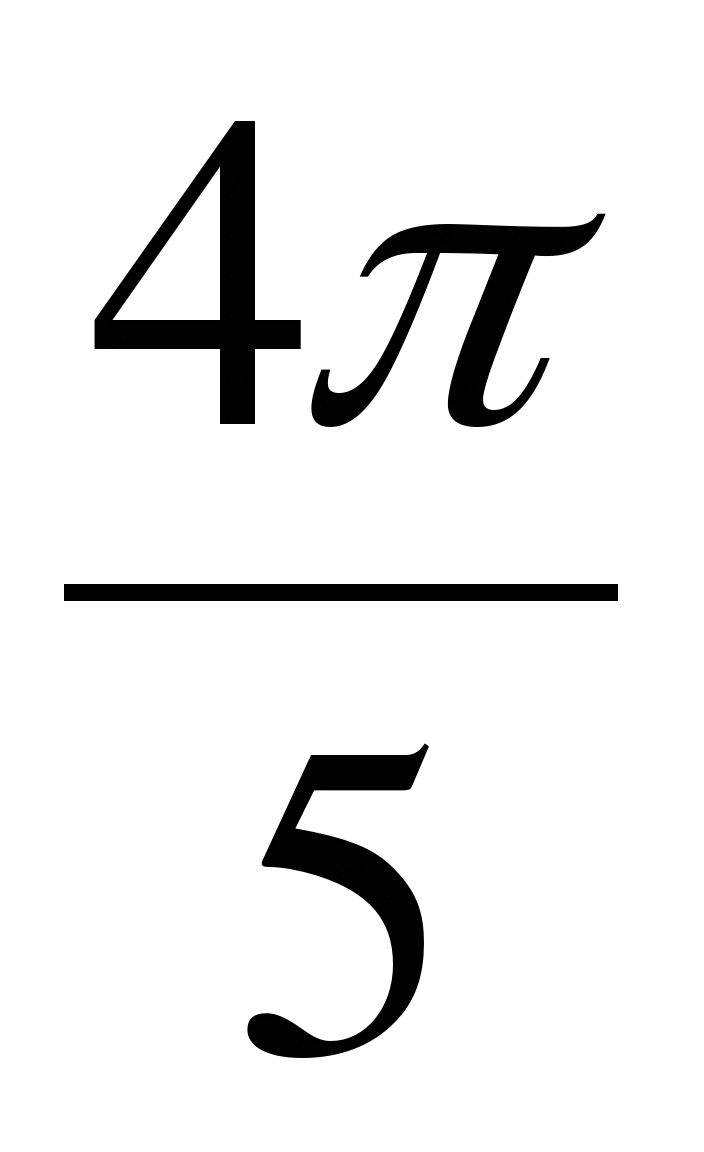 ,
, 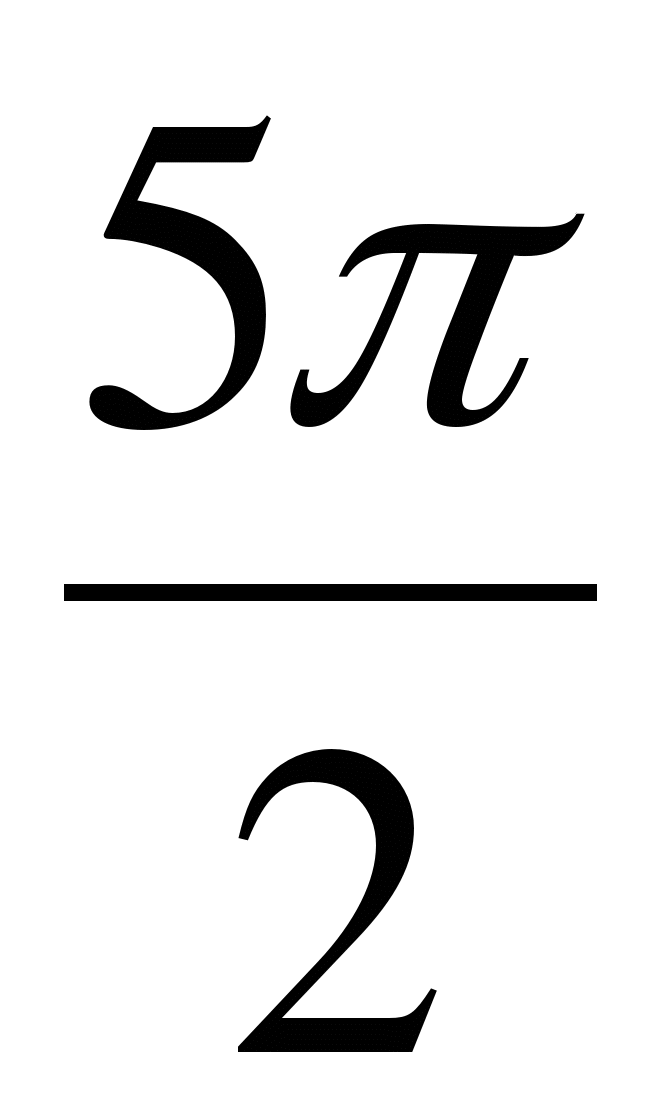 .
.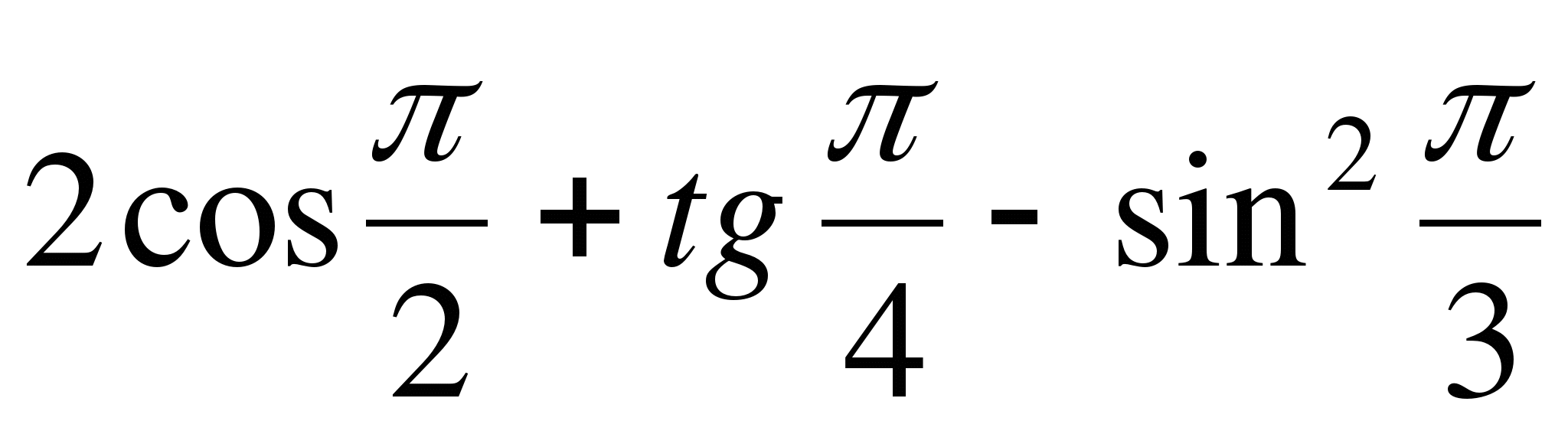 .
.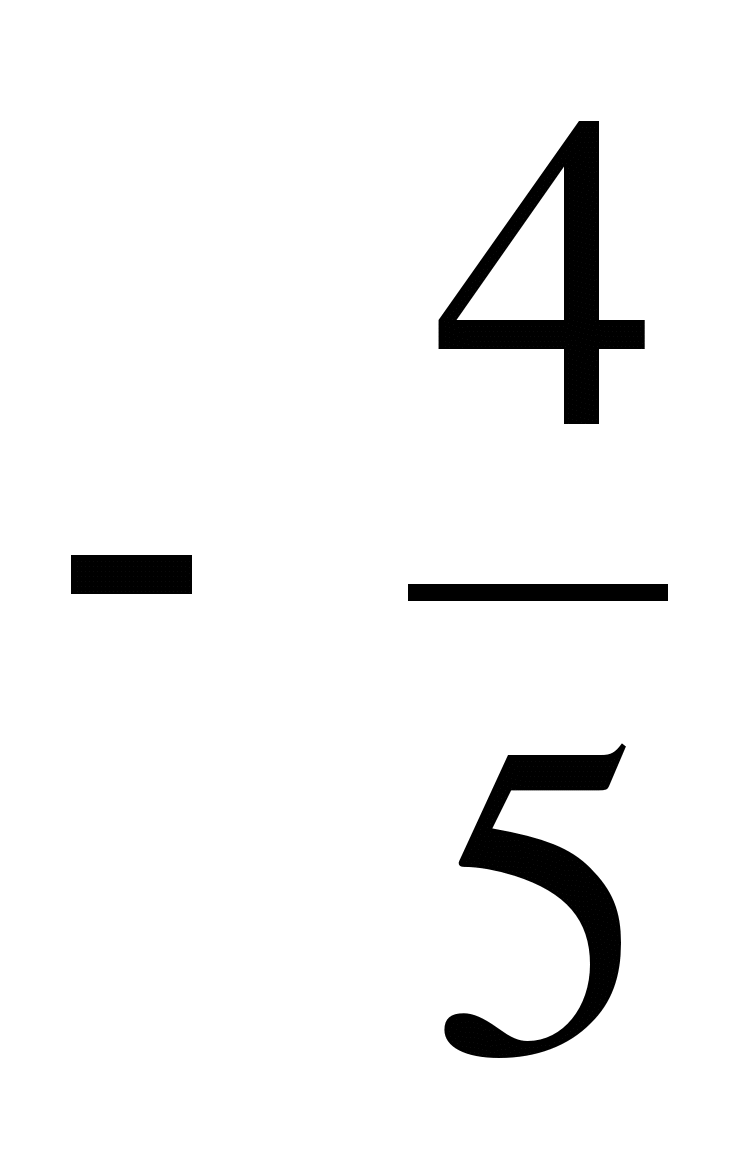 и
и 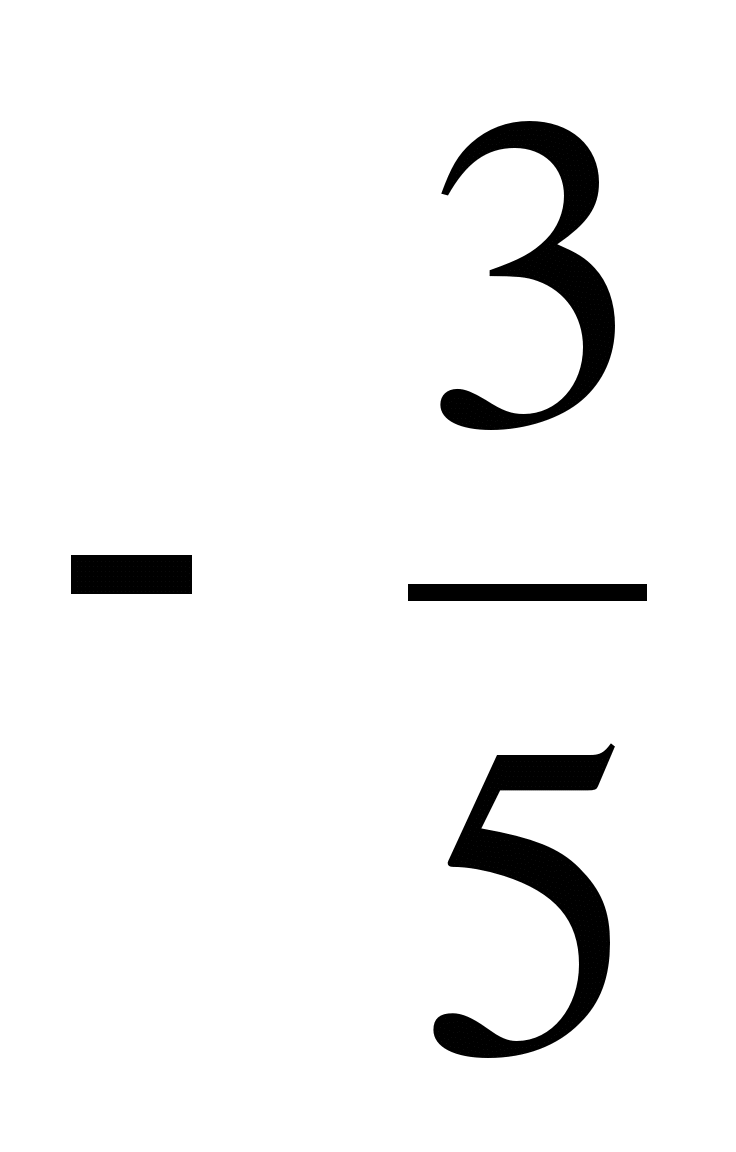 ?
?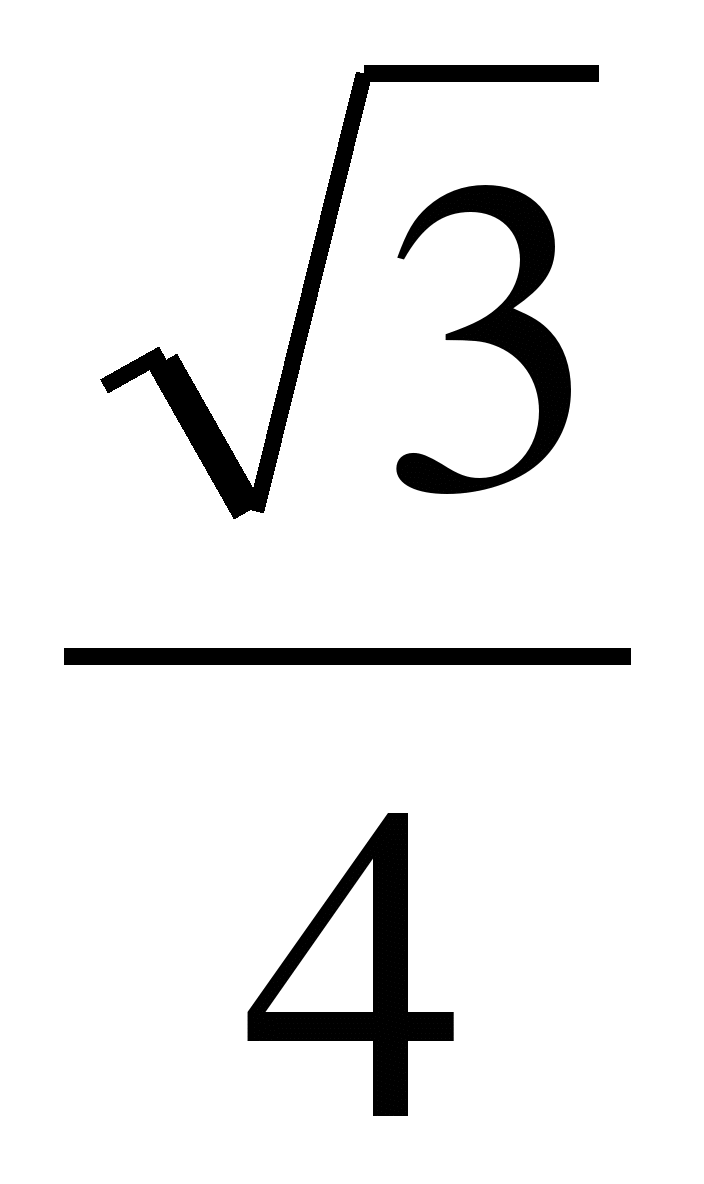 и
и 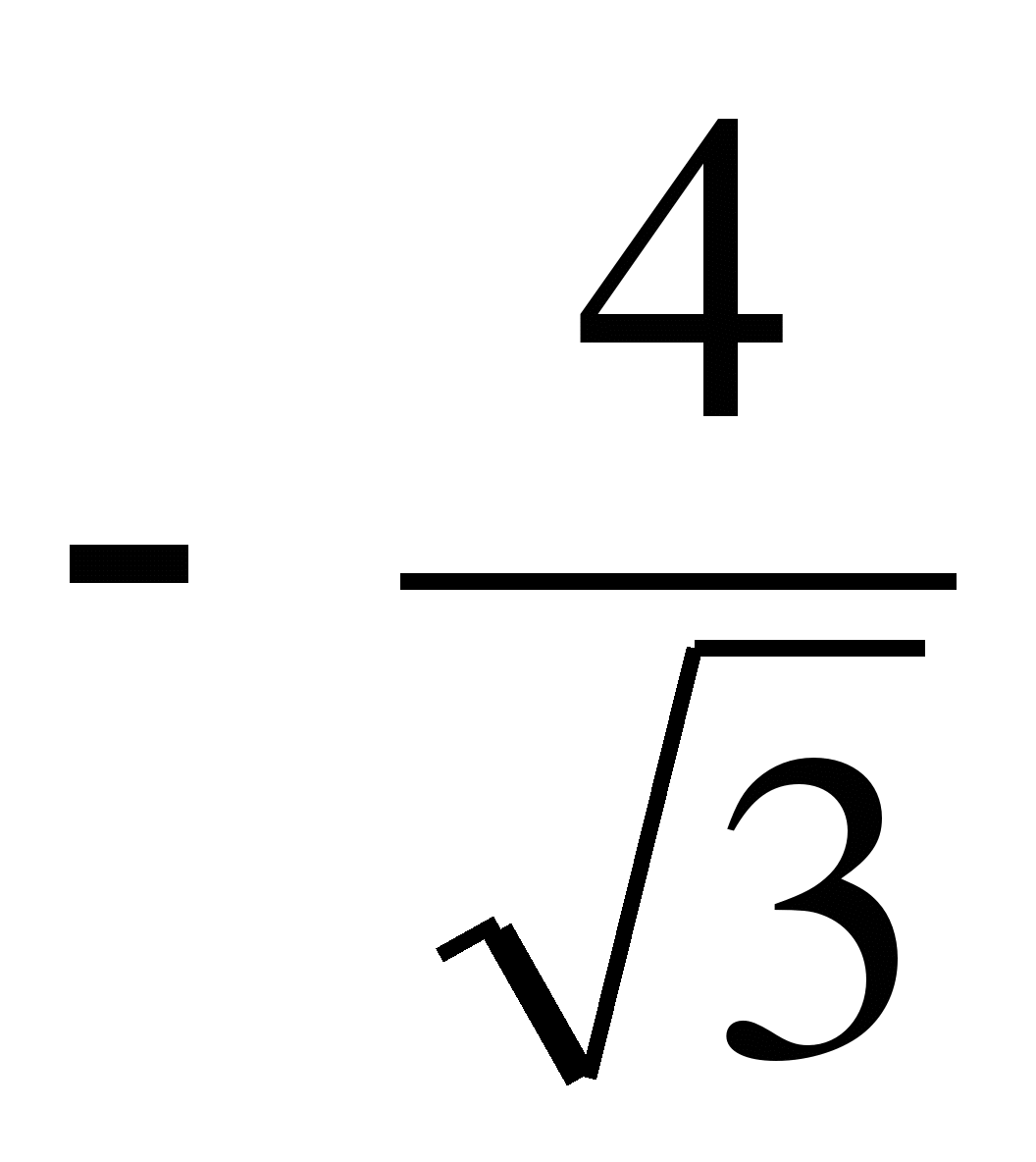 ?
?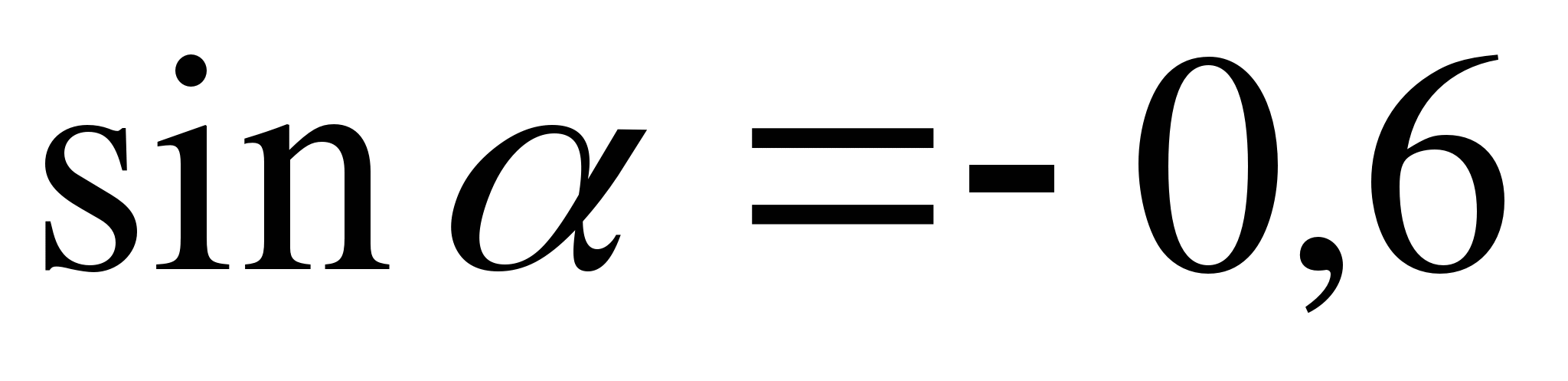 ,
, 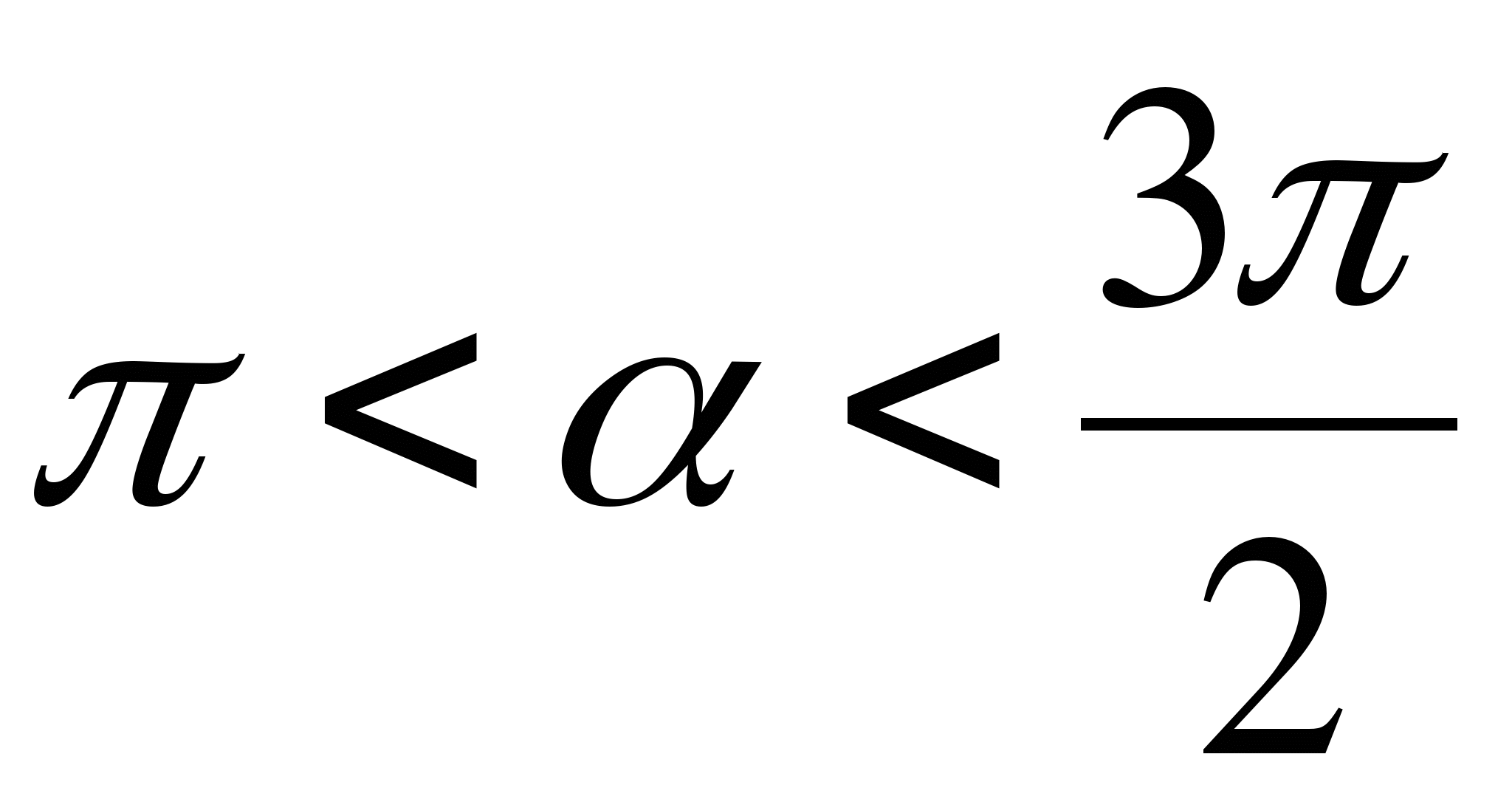 .
.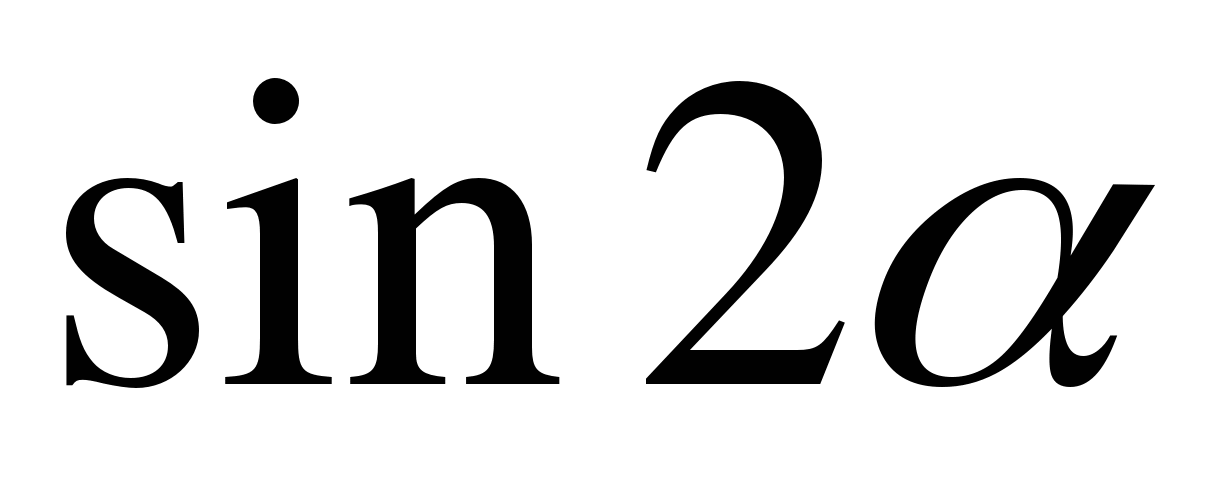 , если
, если 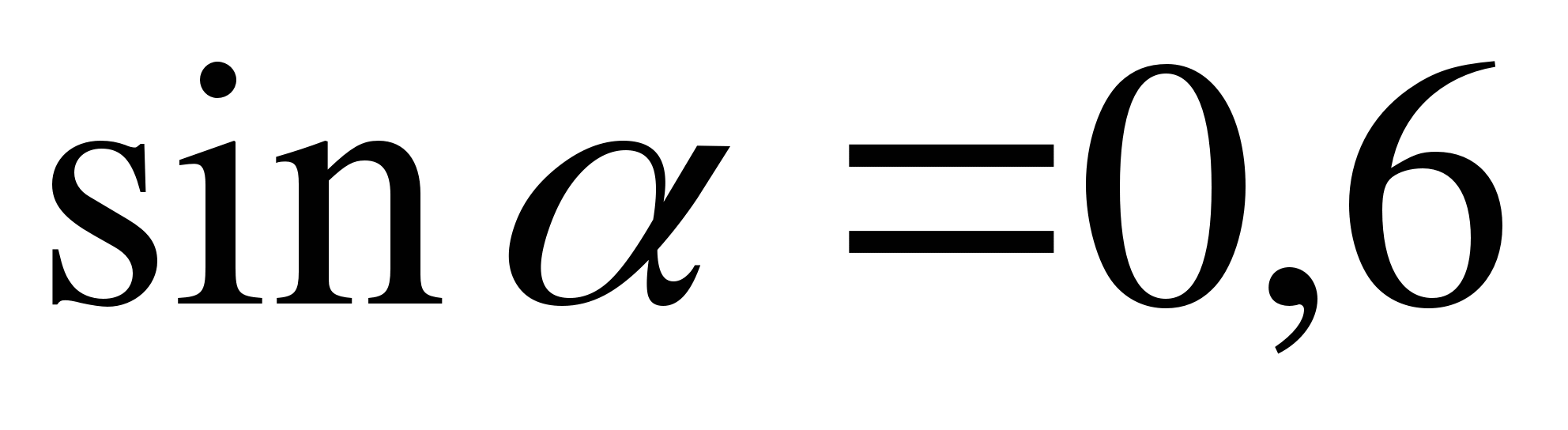 ,
, 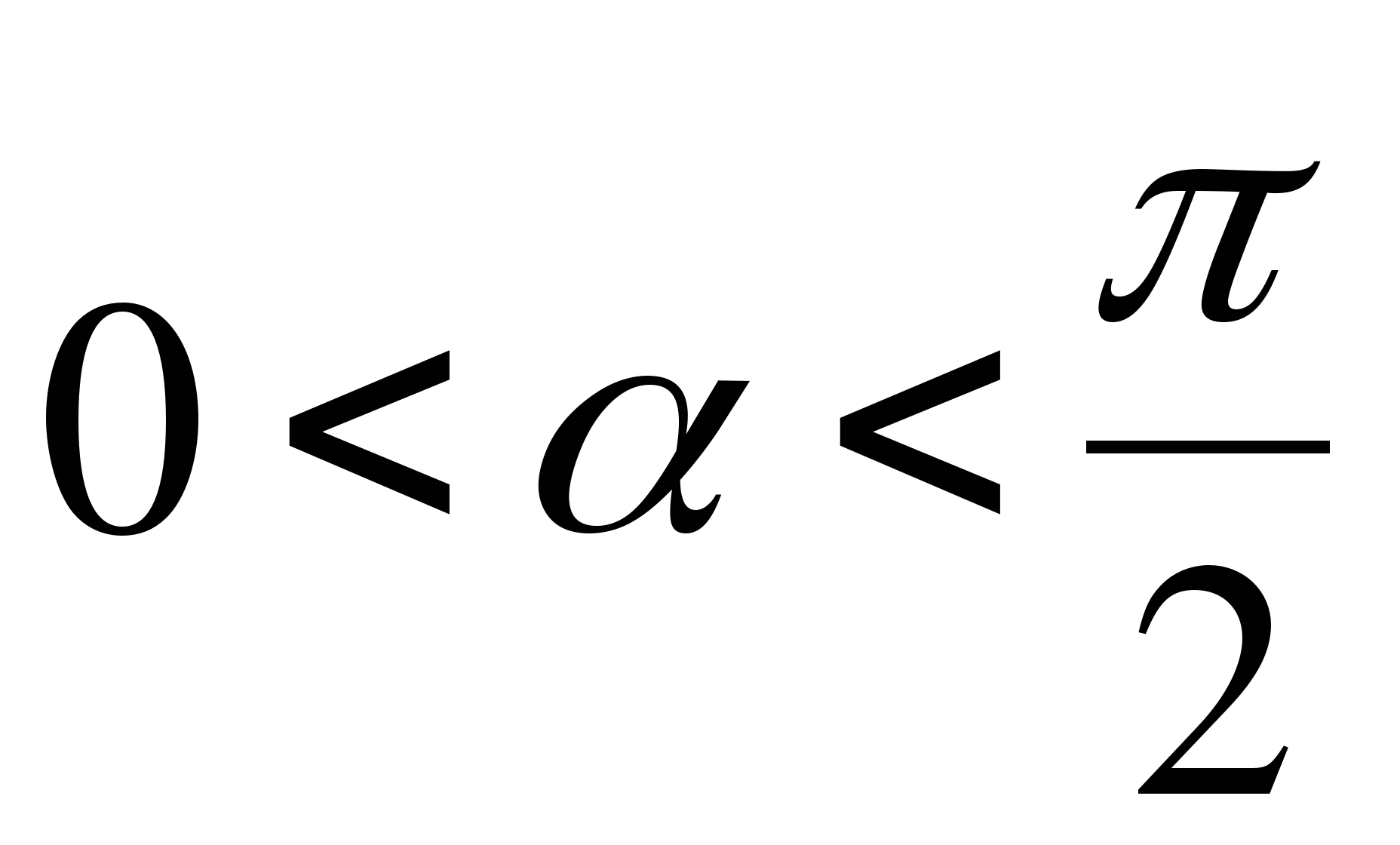 .
.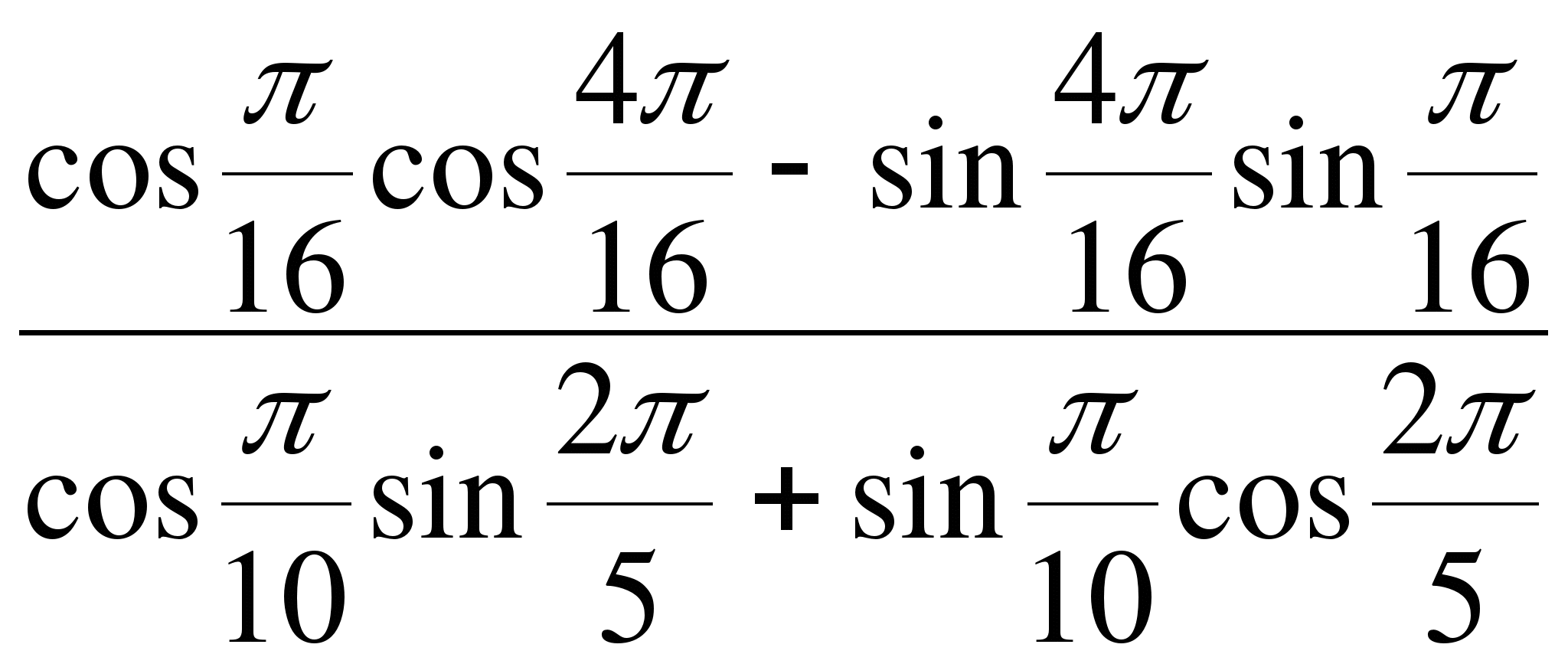
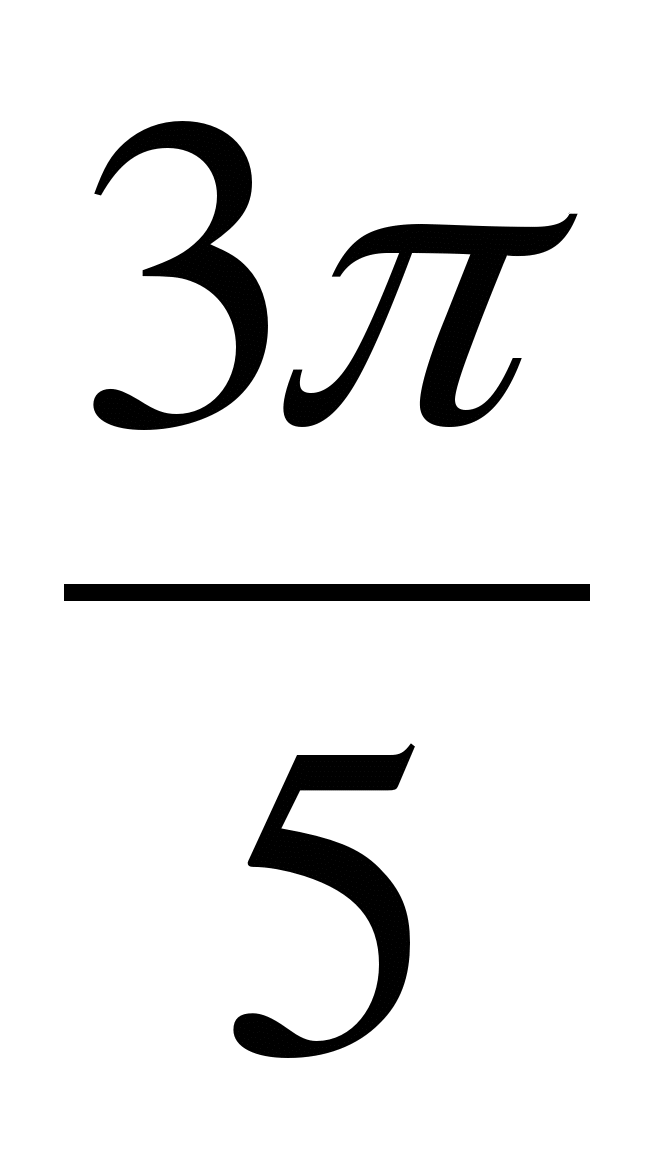 ,
, 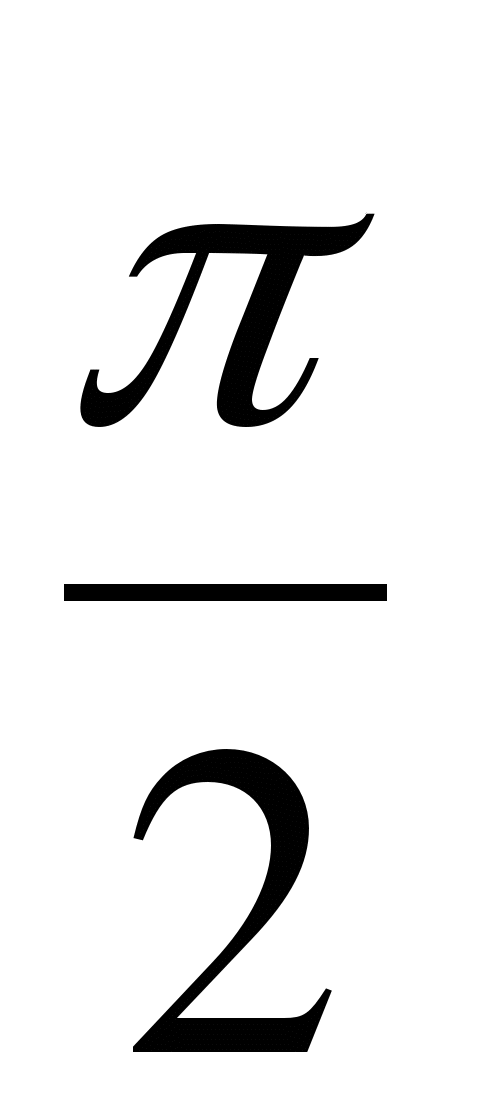 ,
,  .
.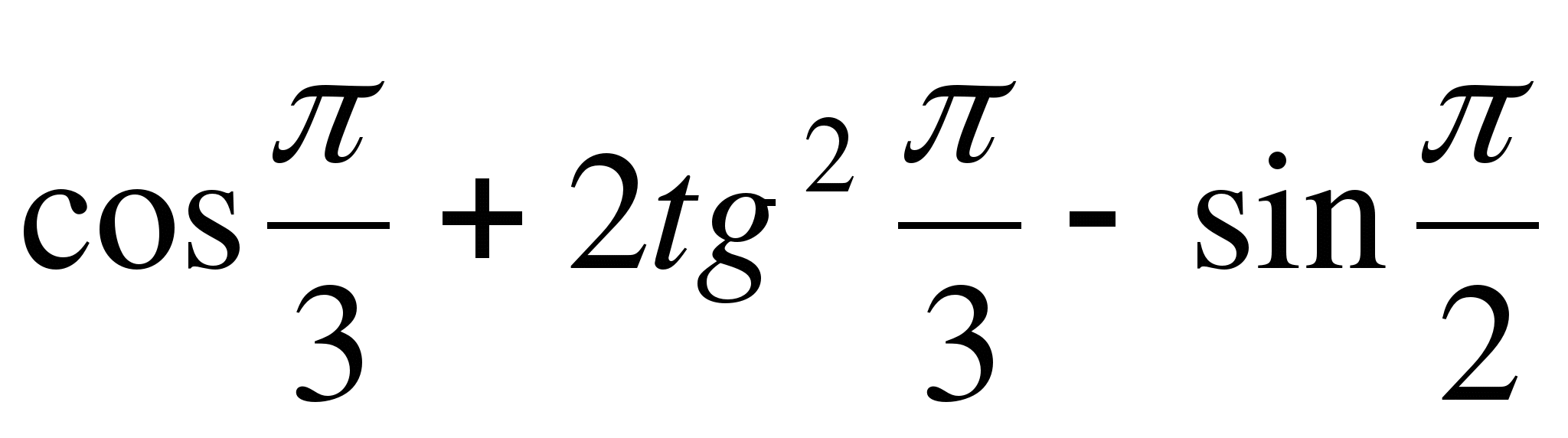 .
.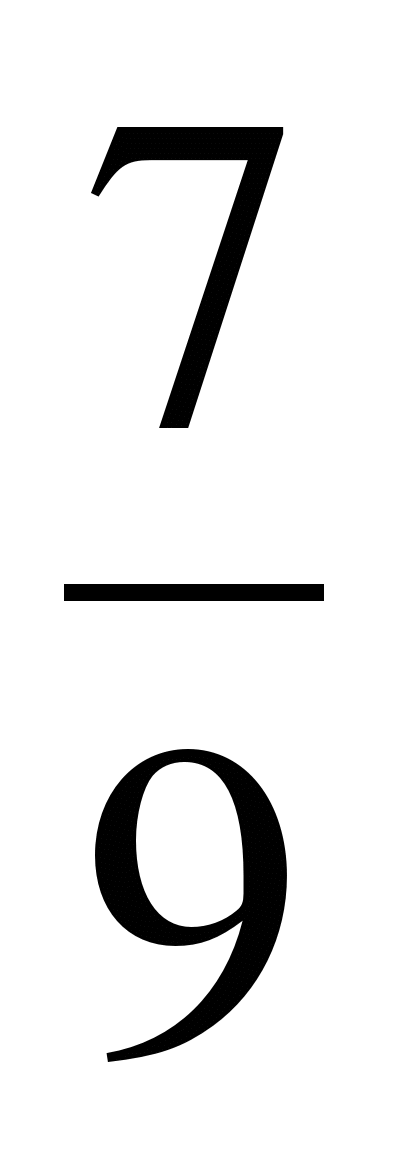 и
и 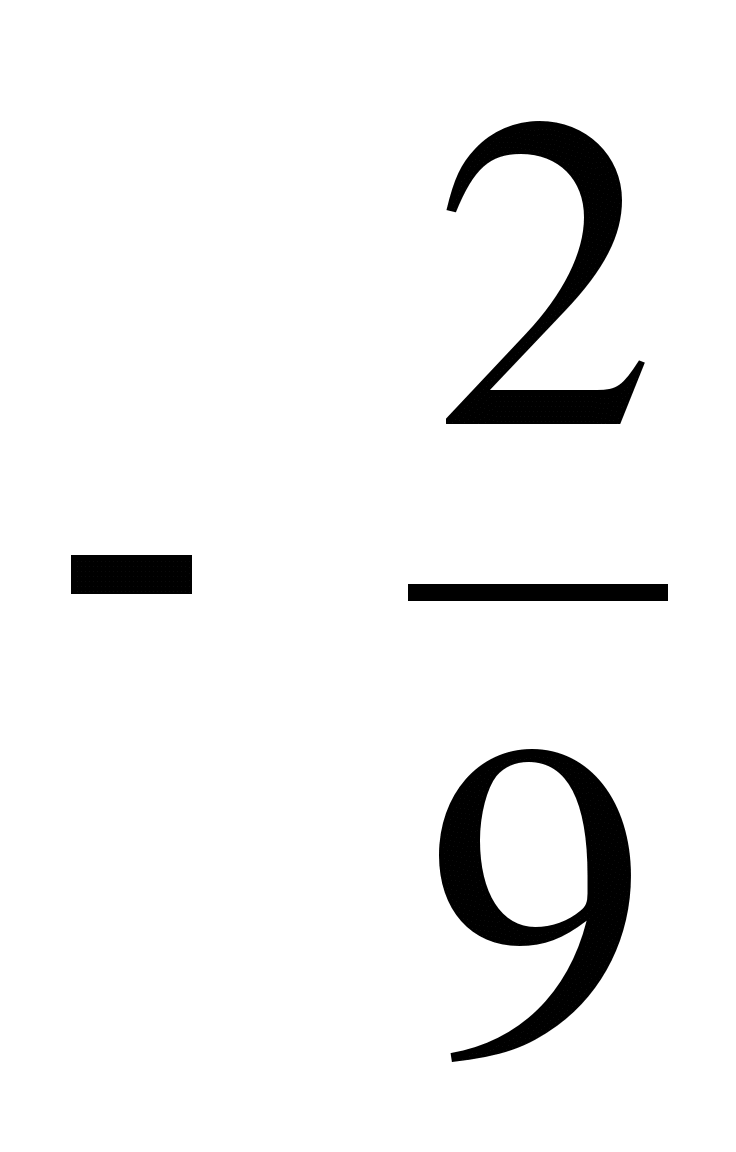 ?
?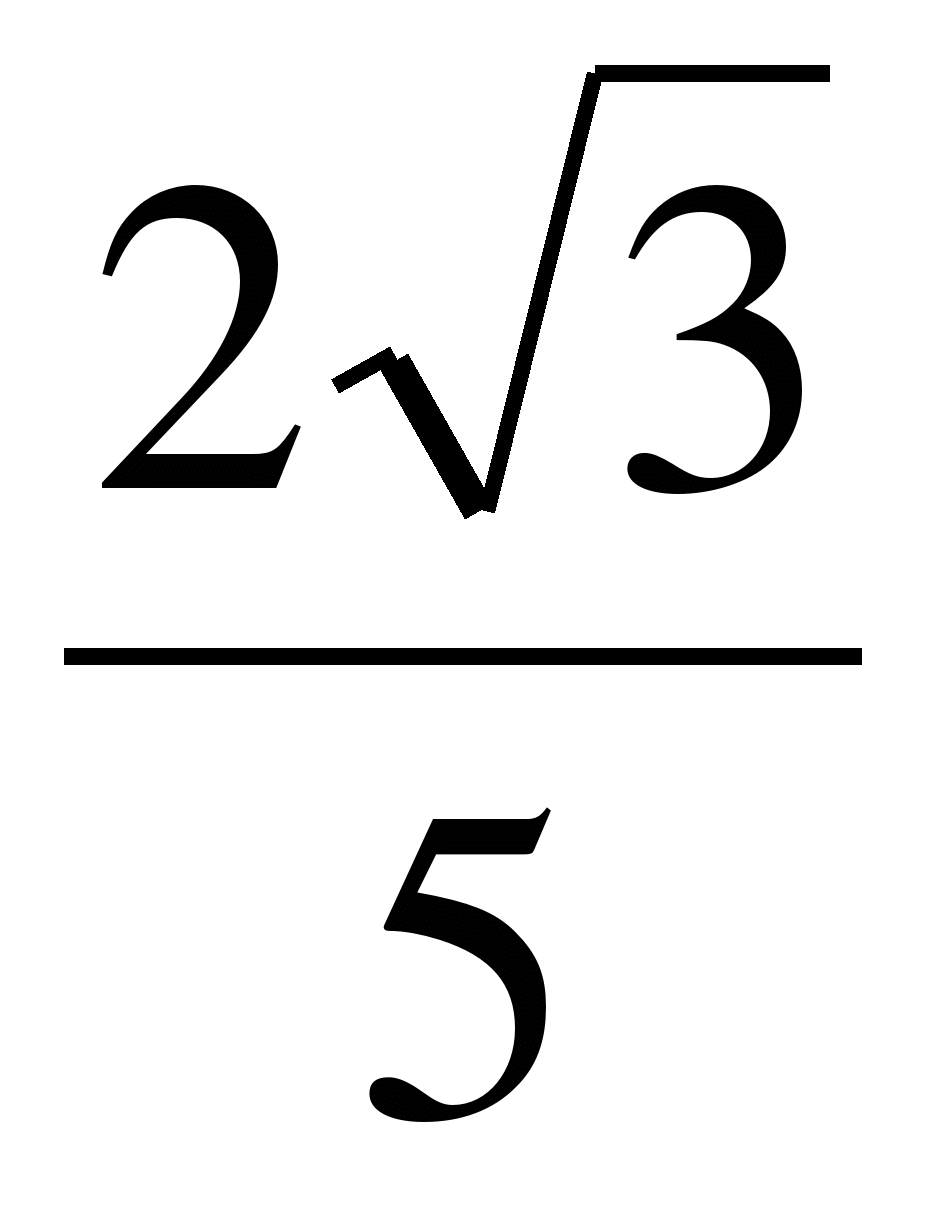 и
и 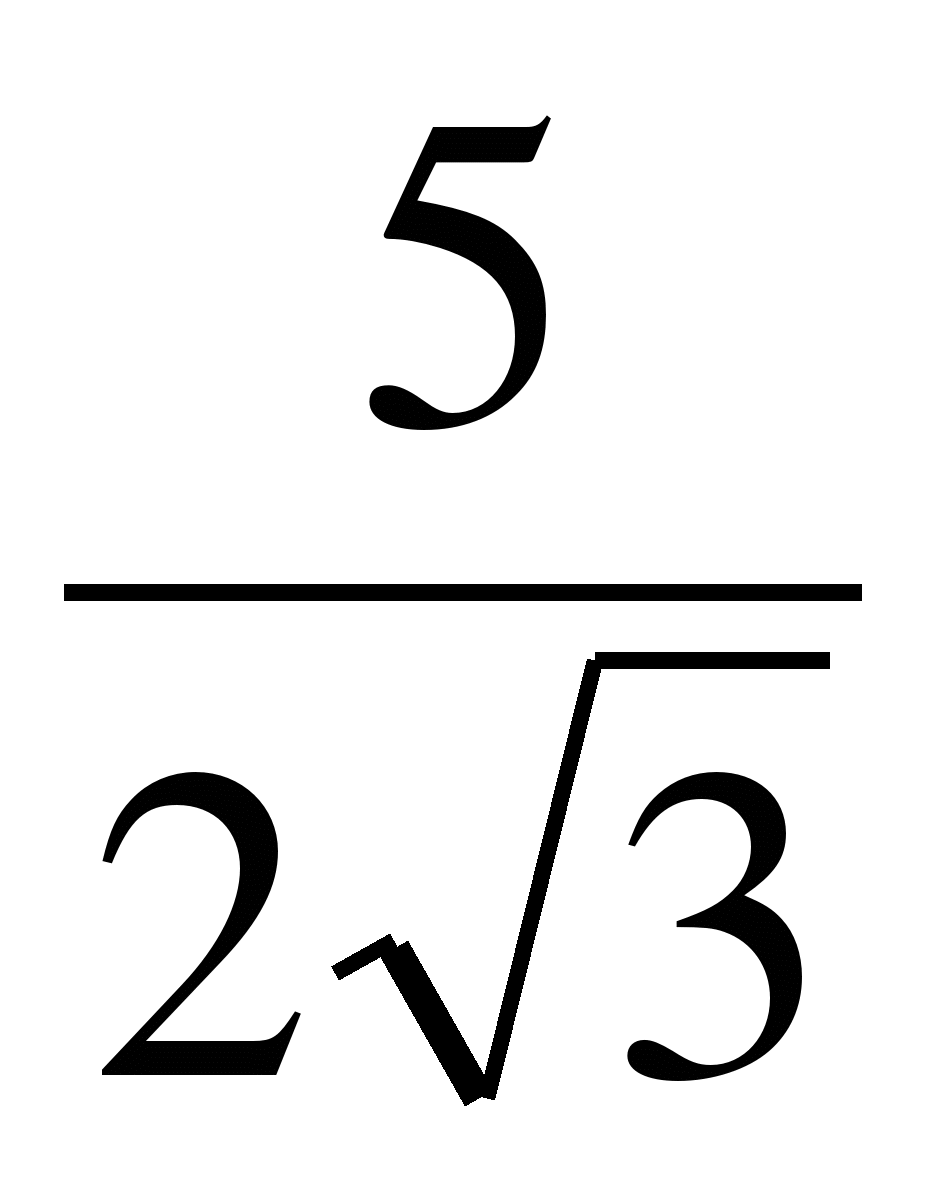 ?
?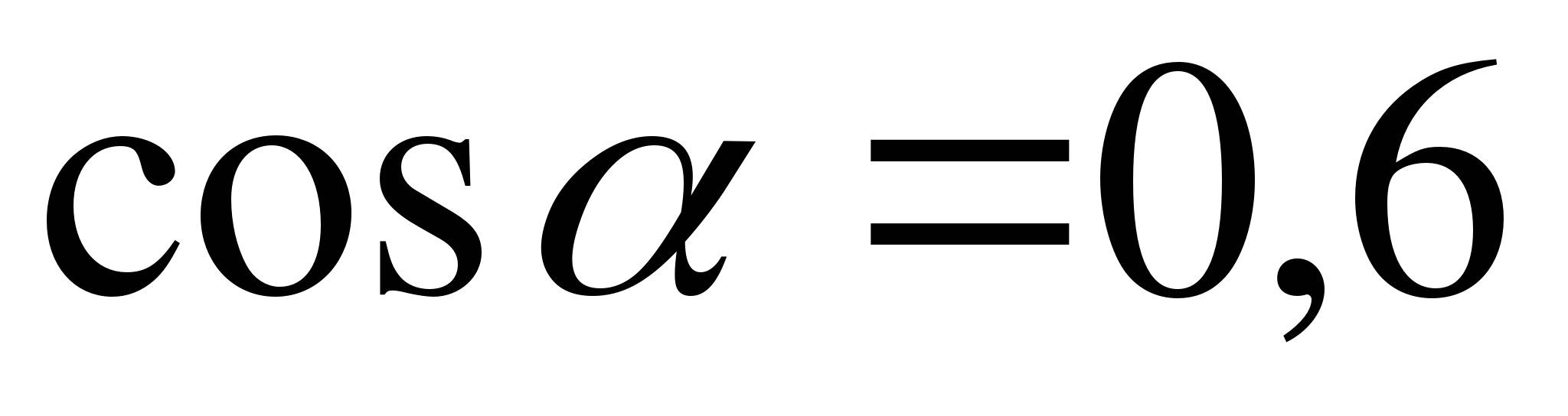 ,
, 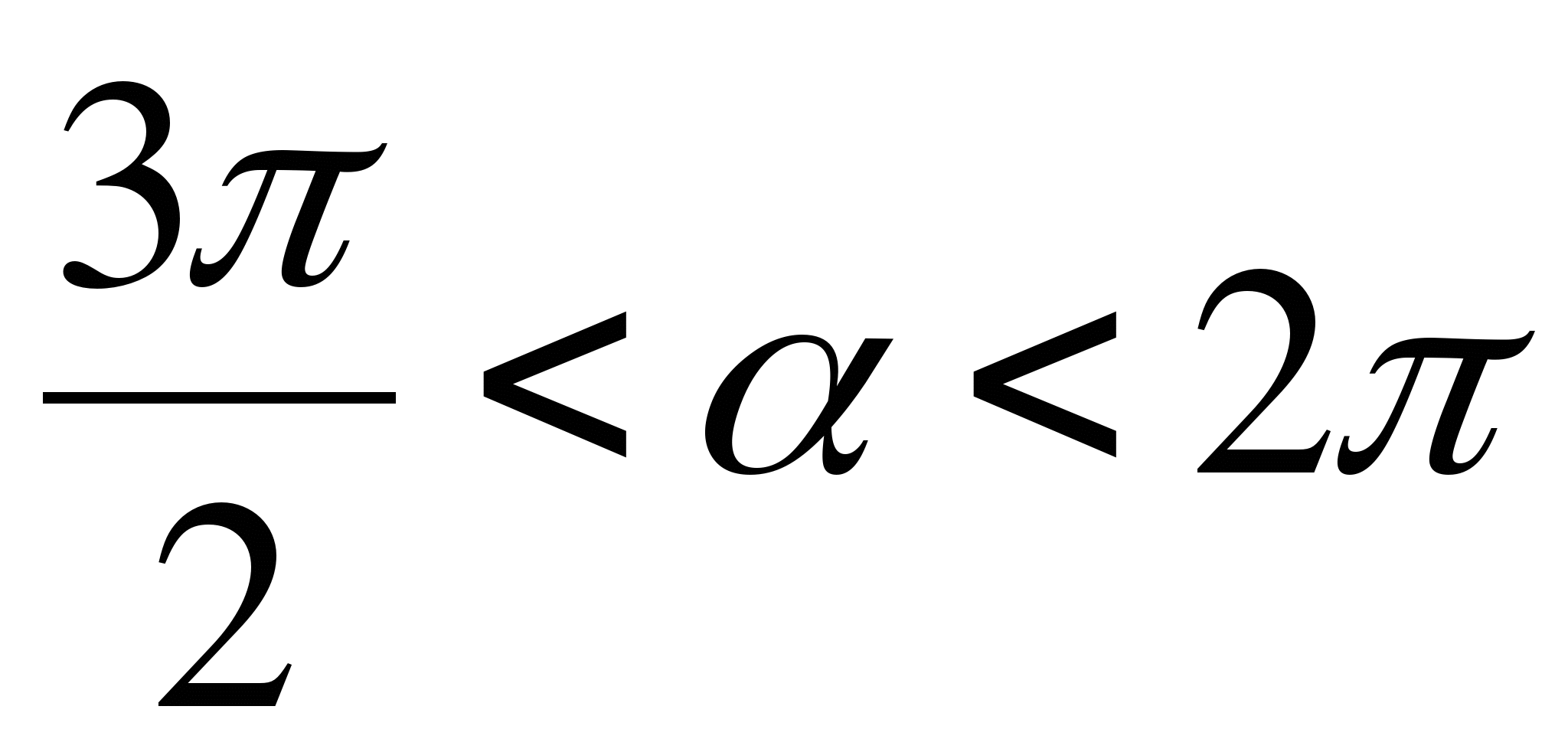 .
.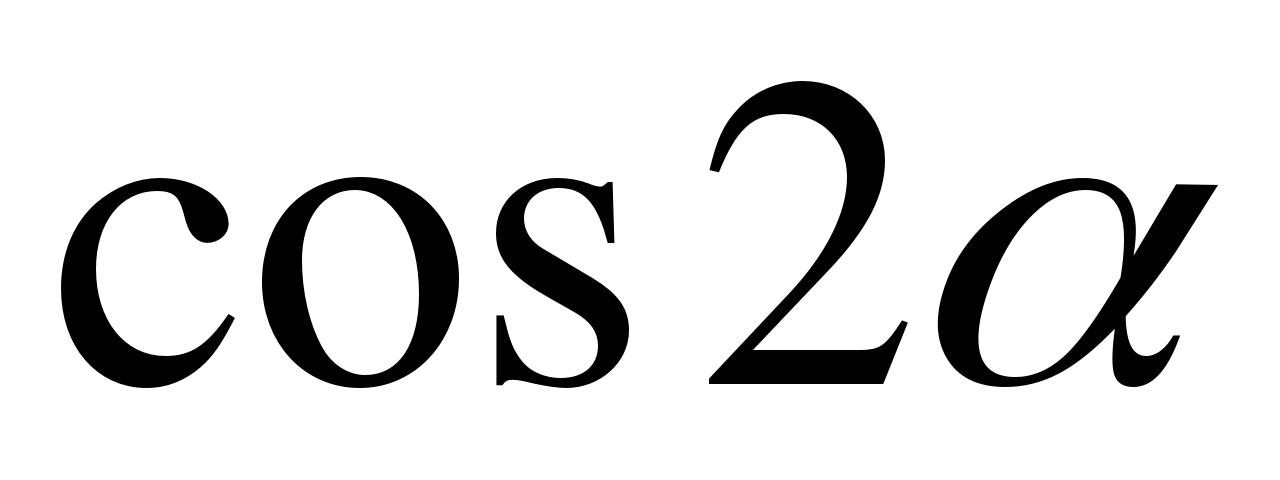 , если
, если 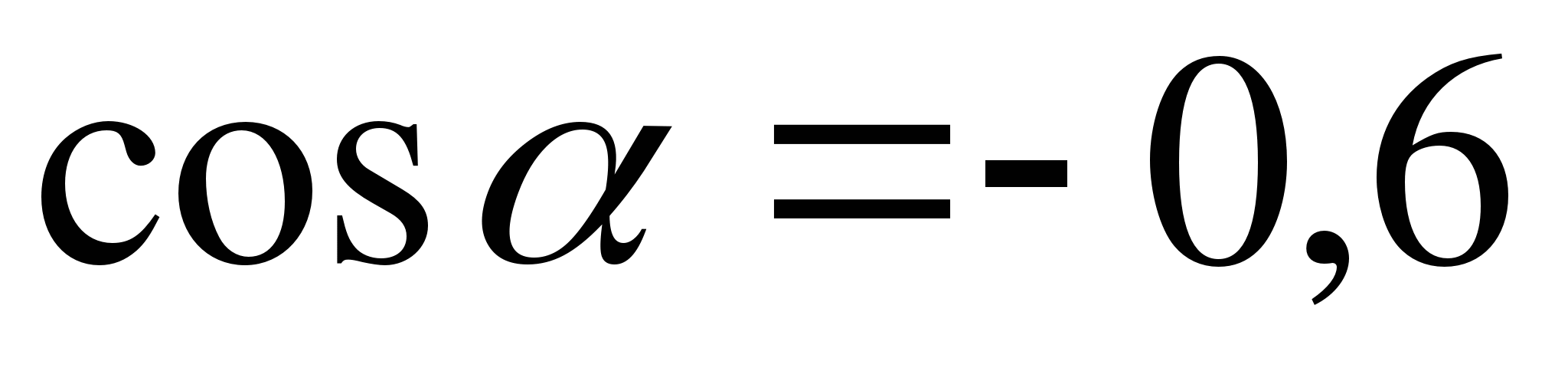 ,
, 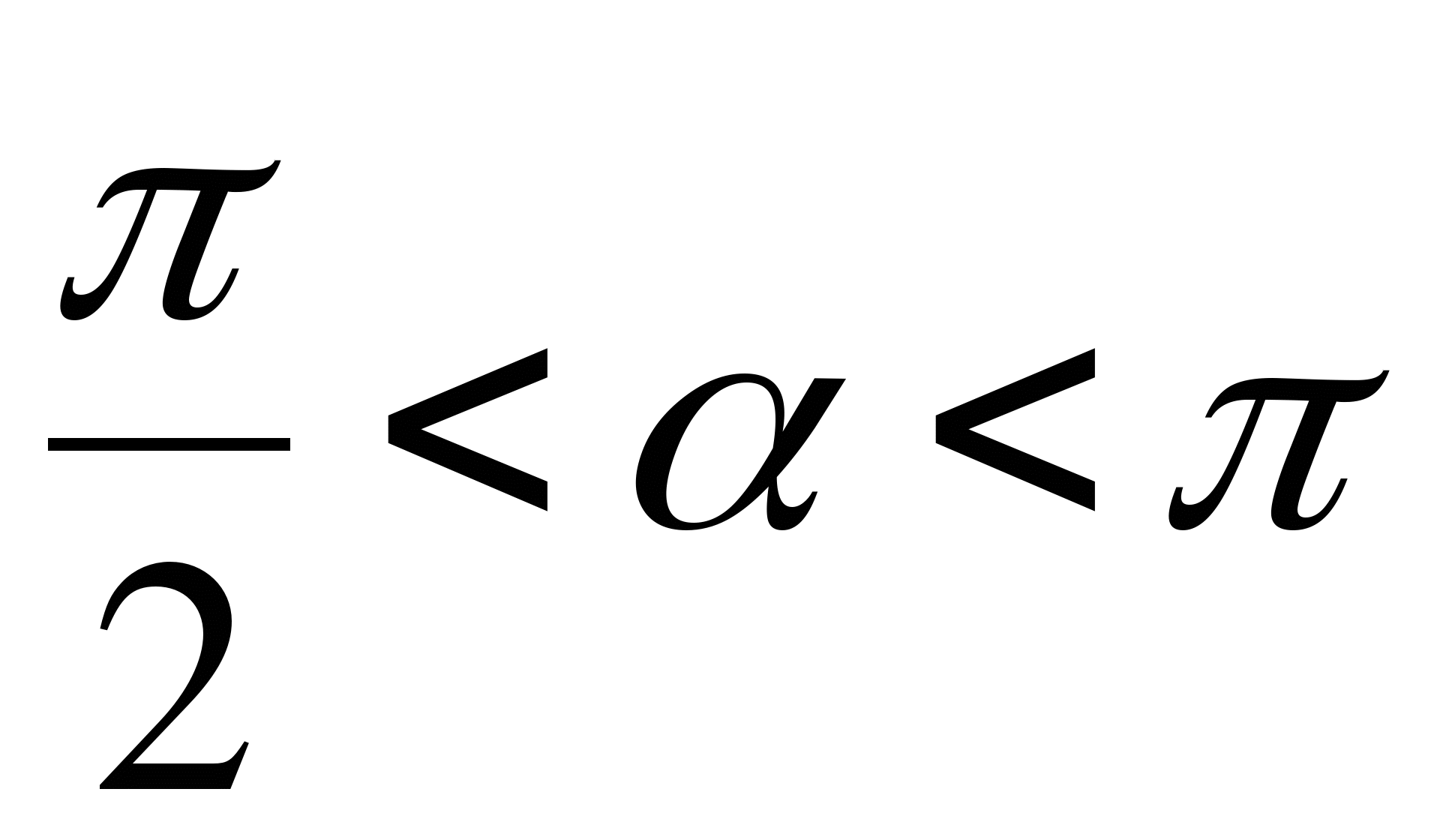 .
.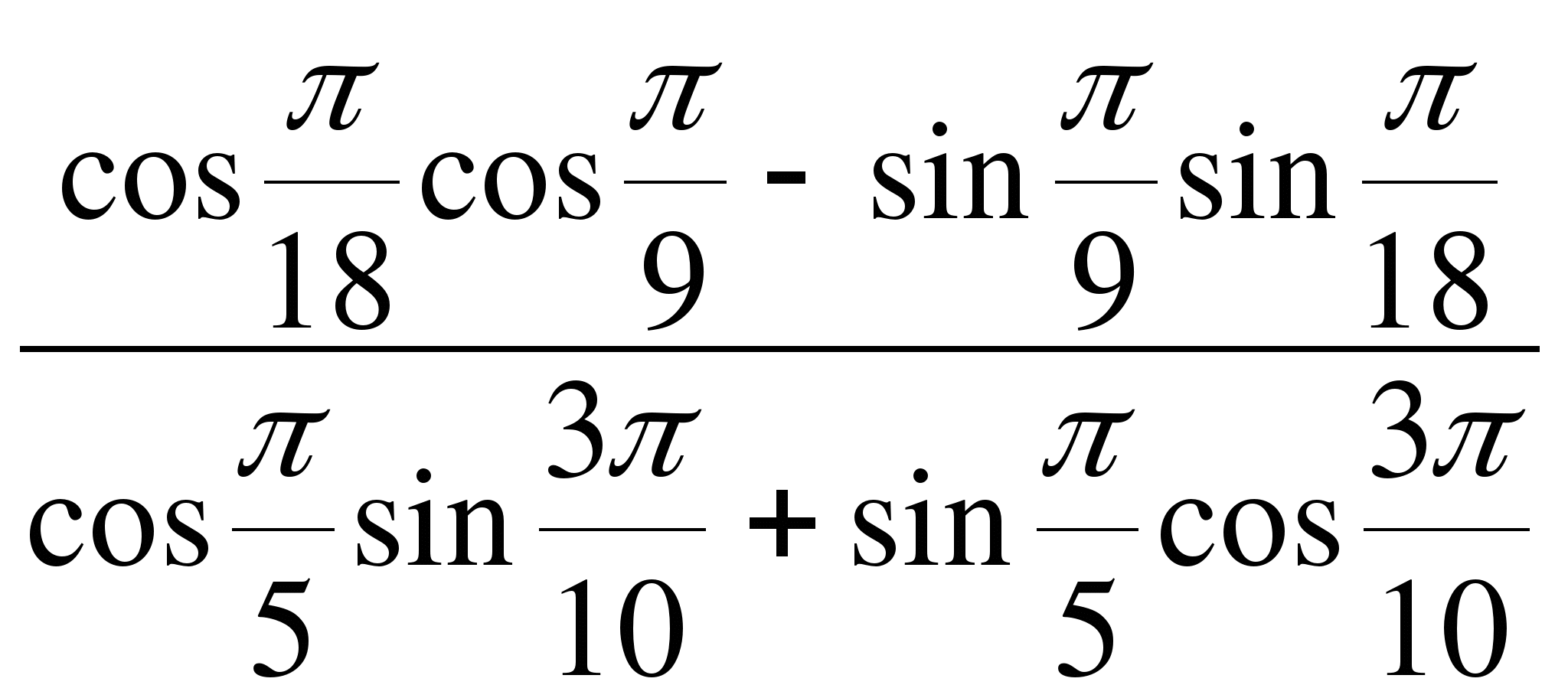



 четверти
четверти



 четверти
четверти

 =
= 





 четверти
четверти ;
;  ;
; 







