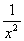 ; д) у =
; д) у = 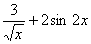 .
.
ВАРИАНТ 1.
1. Найдите общий вид первообразных F(х) для функции f (х):
а) f (х) = х + 2; б) f (х) = х3 – 2х + 1; в) f (х) = х2 + соs х; г) f (х) = 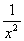 ; д) у =
; д) у = 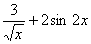 .
.
2. Найдите ту первообразную функции, график которой проходит через начало координат
f (х) = 2х2 – 3х + 1.
3. Пусть F(х) – первообразная функции f (х) = х2 – х . Найдите промежутки монотонности и точки экстремума.
4. (дополнительно) Является ли функция F(х) первообразной для функции f (х)
а) F(х) = 2 sin2х cos2х, f (х) = sin 4х; б) F(х) = (х + 2)4, f (х)= 4х3 + 24х2 + 48х + 32.
КОНТРОЛЬНАЯ РАБОТА № 2 по теме «Первообразная»
ВАРИАНТ 2.
1. Найдите общий вид первообразных F(х) для функции f (х):
а) f (х) = 3х – 1; б) f (х) = х4 – 3х2 + 7; в) f (х) = х5 + sin х; г) f (х) =  ; д) у =
; д) у = 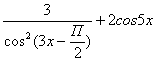 .
.
2. Найдите ту первообразную функции f (х) = 1 – 4х, график которой проходит через точку М (-1; 9)
3. Пусть F(х) – первообразная функции f (х) = х2+3х. Найдите промежутки монотонности и точки экстремума
4. (дополнительно) Является ли функция F(х) первообразной для функции f (х)
а) F(х) = 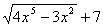 , f (х) =
, f (х) = 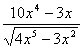 ; б) F(х) =
; б) F(х) =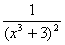 , f (х)=
, f (х)= 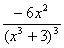 .
.
КОНТРОЛЬНАЯ РАБОТА № 2 по теме «Первообразная»
ВАРИАНТ 3.
1. Найдите общий вид первообразных F(х) для функции f (х):
а) f (х) = 3х2 – х + 8; б) f (х) = 4х3 + 6х3 + 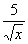 ; в) f (х) =
; в) f (х) = 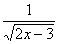 +
+ 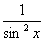 ; г) f (х) =
; г) f (х) = 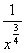 ; д) у =
; д) у =
2. Найдите ту первообразную функции f (х) = 2х + 4 график которой проходит через точку М (-1; 1)
3. Пусть F(х) – первообразная функции f (х) = 4х3 -16 . Найдите промежутки монотонности и точки экстремума
4. (дополнительно) Является ли функция F(х) первообразной для функции f (х)
а) F(х) = 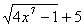 , f (х) =
, f (х) = 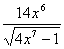 ; б) F(х) =
; б) F(х) =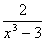 , f (х)=
, f (х)= 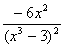 .
.
КОНТРОЛЬНАЯ РАБОТА № 2 по теме «Первообразная»
ВАРИАНТ 4.
1. Найдите общий вид первообразных F(х) для функции f (х):
а) f (х) = -2х4 – 3х3 -2; б) f (х) =  + 6х6 +
+ 6х6 + 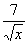 ; в) f (х) =
; в) f (х) = 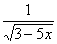 +
+ 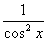 ; г) f (х) =
; г) f (х) = 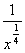 ; д) у =
; д) у =
2. Найдите ту первообразную функции f (х) = – х +1, график которой проходит через точку М (-2; -3).
3. Пусть F(х) – первообразная функции f (х) = 256 – 4х3 . Найдите промежутки монотонности и точки экстремума
4. (дополнительно) Является ли функция F(х) первообразной для функции f (х)
а) F(х) = 2 – sin2х + cos2х, f (х) = -2sin 2х; б) F(х) = (х – 1)4, f (х)= 4х3 – 12х2 + 12х – 1.
КОНТРОЛЬНАЯ РАБОТА № 2 по теме «Первообразная»
ВАРИАНТ 4.
1. Найдите общий вид первообразных F(х) для функции f (х):
а) f (х) = -2х4 – 3х3 -2; б) f (х) =  + 6х6 +
+ 6х6 + 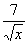 ; в) f (х) =
; в) f (х) = 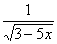 +
+ 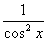 ; г) f (х) =
; г) f (х) = 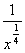 ; д) у =
; д) у =
2. Найдите ту первообразную функции f (х) = – х +1, график которой проходит через точку М (-2; -3).
3. Пусть F(х) – первообразная функции f (х) = 256 – 4х3 . Найдите промежутки монотонности и точки экстремума
4. (дополнительно) Является ли функция F(х) первообразной для функции f (х)
а) F(х) = 2 – sin2х + cos2х, f (х) = -2sin 2х; б) F(х) = (х – 1)4, f (х)= 4х3 – 12х2 + 12х – 1.
КОНТРОЛЬНАЯ РАБОТА № 2 по теме «Первообразная»
ВАРИАНТ 4.
1. Найдите общий вид первообразных F(х) для функции f (х):
а) f (х) = -2х4 – 3х3 -2; б) f (х) =  + 6х6 +
+ 6х6 + 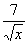 ; в) f (х) =
; в) f (х) = 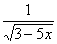 +
+ 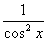 ; г) f (х) =
; г) f (х) = 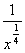 ; д) у =
; д) у =
2. Найдите ту первообразную функции f (х) = – х +1, график которой проходит через точку М (-2; -3).
3. Пусть F(х) – первообразная функции f (х) = 256 – 4х3 . Найдите промежутки монотонности и точки экстремума
4. (дополнительно) Является ли функция F(х) первообразной для функции f (х)
а) F(х) = 2 – sin2х + cos2х, f (х) = -2sin 2х; б) F(х) = (х – 1)4, f (х)= 4х3 – 12х2 + 12х – 1.
А– 11 К – 2
КОНТРОЛЬНАЯ РАБОТА № 2
по теме «Первообразная».
(Колмогоров)
pandia.ru
Контрольная работа по теме:
«Производная. Первообразная и интеграл»
| Раздел. Начала математического анализа. | |||
| Тема. Производная. Первообразная и интеграл | Знание свойств производной и умение находить производную функции | 2 | К.р.№5(1,2,3) |
| Умение находить угловой коэффициент касательной к графику функции. Знание формулы углового коэффициента касательной к графику функции | 2 | К.р.№5(3) | |
| Умение находить критические точки | 2 | К.р.№5(1,2) | |
| Умение находить промежутки монотонности | 2 | К.р.№5(2) | |
| Знание алгоритма нахождения наибольшего и наименьшего значений функции на отрезке. Умение его применить | 2 | К.р.№5(2) | |
| Умение находить все первообразные функции. Знание свойств первообразной функции | 2 | К.р.№5(4,5) | |
| Умение находить абсциссу точки графика функции. Знание формулы углового коэффициента касательной к графику функции | 2 | К.р.№5(3) | |
| Умение находить площадь фигуры через производную. Знание формулы Ньютона-Лейбница | 2 | К.р.№5(4) | |
Контрольная работа по теме:
«Производная. Первообразная и интеграл»
Вариант № 1
Найдите критические (стационарные) точки функции f(x)=2x3-9x2-60x+127.
Найдите наибольшее и наименьшее значение функции y=2x3-3x2-12x+24 на отрезке [-2;1].
Составьте уравнение касательной к графику функции f(x)=2x2-5x+1, в точке графика с абсциссой x0=2.
Найдите площадь криволинейной трапеции, ограниченной графиком функции f(x)=x2+3x и прямыми x=0, x=1.
Первообразная функции f(x)=3x2+2x при x=1 принимает значение 81. Найдите ее значение при x=-1.
Контрольная работа по теме:
«Производная. Первообразная и интеграл»
Вариант № 2
Найдите критические (стационарные) точки функции f(x)=2x3+3x2-72x-213.
Найдите наибольшее и наименьшее значение функции y=x3-9x2+24x-15 на отрезке [1;3].
Составьте уравнение касательной к графику функции f(x)=3x2-4x-2, в точке графика с абсциссой x0=-1.
Найдите площадь криволинейной трапеции, ограниченной графиком функции f(x)=2x2+x и прямыми x=0, x=1.
Первообразная функции f(x)=4x3+2x при x=1 принимает значение 25. Найдите ее значение при x=2.
Эталоны ответов
Вариант № 1
f(x)=2x3-9x2-60x+127
Решение:
f’(x)=6x2-18x-60
f’(x)=0 => 6x2-18x-60=0
x2-3x-10=0
По теореме, обратной теореме Виета:
x1+x2=3
x1*x2=-10
x1=-2, x2=5
Ответ: x1=-2, x2=5
y=2x3-3x2-12x+24, [-2;1]
Решение:
y’=6x2-6x-12
y’=0 => 6x2-6x-12=0
x2-x-2=0
По теореме, обратной теореме Виета:
x1+x2=1
x1*x2=-2
x1=-1, x2=2
Отрезку [-2;1] принадлежит только точка x1=-1.
y(-2)=-16-12+24+24=20
y(-1)=-2-3+12+24=31
y(1)=2-3-12+24=11
Ответ: yнаиб=31 при x=-1, yнаим=11 при x=1
f(x)=2x2-5x+1, в точке графика с абсциссой x0=2
Решение:
f’(x)=4x-5
f(2)=8-10+1=-1, f’(2)=8-5=3
y=f(x0)+f’(x0)(x-x0)
y=-1+3(x-2)
y=3x-7
Ответ: y=3x-7
f(x)=x2+3x, x=0, x=1
Решение:
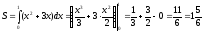
Ответ: 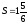
f(x)=3x2+2x, F(1)=81. F(-1)=?
Решение:
F(x)=x3+x2+C
F(1)=1+1+C, F(1)=81 => C=79
F(-1)=-1+1+79=79
Ответ: F(-1)=79
Вариант № 2
f(x)=2x3+3x2-72x-213
Решение:
f’(x)=6x2+6x-72
f’(x)=0 => 6x2+6x-72=0
x2+x-12=0
По теореме, обратной теореме Виета:
x1+x2=-1
x1*x2=-12
x1=-4, x2=3
Ответ: x1=-4, x2=3
y=x3-9x2+24x-15, [1;3]
Решение:
y’=3x2-18x+24
y’=0 => 3x2-18x+24=0
x2-6x+8=0
По теореме, обратной теореме Виета:
x1+x2=6
x1*x2=8
x1=2, x2=4
Отрезку [1;3] принадлежит точка x1=2.
y(1)=1-9+24-15=1
y(2)=8-36+48-15=5
y(3)=27-81+72-15=3
Ответ: yнаиб=5 при x=2, yнаим=1 при x=1
f(x)=3x2-4x-2, в точке графика с абсциссой x0=-1
Решение:
f’(x)=6x-4
f(-1)=3+4-2=5, f’(-1)=-6-4=-10
y=f(x0)+f’(x0)(x-x0)
y=5-10(x+1)
y=-10x-5
Ответ: y=-10x-5
f(x)=2x2+x, x=0, x=1
Решение:

Ответ: 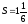
f(x)=4x3+2x, F(1)=25. F(2)=?
Решение:
F(x)=x4+x2+C
F(1)=1+1+C, F(1)=25 => C=23
F(2)=16+4+25=45
Ответ: F(2)=45
xn--j1ahfl.xn--p1ai
Задания для подготовки к контрольной работе по теме: «Первообразная и интеграл.»
Контрольная работа по теме: «Первообразная и интеграл.» Вариант1
1. Докажите, что F(x) = х4 - 3sin x является первообразной для f(x) = 4х3 - 3cos х
2. Для функции f(x) =  + 3 sin x найдите какую-нибудь первообразную, значение которой в точке х = p — отрицательное число.
+ 3 sin x найдите какую-нибудь первообразную, значение которой в точке х = p — отрицательное число.
3. Вычислите интегралы: a) ; б)
; б) ;
;
4. Вычислите площадь фигуры, ограниченной линиями: у=1- х3, у = 0 (ось Ох),
х = -1.
5. Найти площадь фигуры, ограниченной прямой  и линией
и линией  .
.
6. Вычислите площадь фигуры, ограниченной графиком функции у = 0,5х2 + 2, касательной к этому графику в точке с абсциссой х = -2 и прямой х = 0.
7. Дана функция
Известно, что график некоторой ее первообразной проходит через точку (0; -1). Чему равно значение этой первообразной в точке  ?
?
Контрольная работа по теме: «Первообразная и интеграл.» Вариант2
1. Докажите, что F(х) = х5 + cos x является первообразной для f(x) = 5х4 – sin х.
2. Для функции f(x) =  - 2 cos x найдите какую-нибудь первообразную, значение которой в точке
- 2 cos x найдите какую-нибудь первообразную, значение которой в точке — положительное число.
— положительное число.
3. Вычислите интегралы: а)  б)
б) 
4. Вычислите площадь фигуры, ограниченной линиями: у=2- х2, у = 0 (ось Ох),
х = -1, х = 0.
5. Найти площадь фигуры, ограниченной прямой  , линией
, линией  и осью абсцисс.
и осью абсцисс.
6. Вычислите площадь фигуры, ограниченной графиком функции у = х3 + 2, касательной к этому графику в точке с абсциссой х = 1 и прямой х = 0; фигура расположена в правой координатной полуплоскости.
7. Дана функция
Известно, что график некоторой ее первообразной проходит через точку ( ; 0). Чему равно значение этой первообразной в точке
; 0). Чему равно значение этой первообразной в точке  ?
?
Критерии оценки: полностью и правильно выполнены:
6 заданий– «5»; 5 задания – «4»; 4-3 задания – «3»
gigabaza.ru
Контрольная работа по теме: «Первообразная и интеграл».
(заочная форма обучения)
12 класс
Методические рекомендации к контрольной работе.
Необходимо знать: таблицу первообразных, уметь применять первообразную для вычисления площадей криволинейных трапеций, основные правила интегрирования, формулы простейших интегралов.
Справочный материал.
Определение: функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для всех х из этого промежутка F’(x)=f(x).
Правила вычисления первообразных:
1.f(x)+h(x) = F(x)+H(x)
2.k f (x) = k F(x), k – постоянная
3.f ( kx+b) = 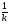 F(kx+b), если k≠0, b – постоянная.
F(kx+b), если k≠0, b – постоянная.
Таблица первообразных.
Функция f(x)
Первообразная F(x) для f(x)
k≠0
k x
хn, где n є Z, n≠-1
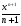
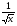
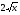
sin x
сos x
sin x
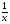 , х ≠ 0
, х ≠ 0
ln |x|
ex
ex
ax
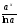
Определение: интегралом от а до b функции f называется приращение первообразной F этой функции, т.е. 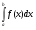 . (читается: «Интеграл от а до б эф от икс дэ икс»).
. (читается: «Интеграл от а до б эф от икс дэ икс»).
∫ - знак интеграла; а и b – пределы интегрирования; а – нижний предел; b- верхний предел; f – подынтегральная функция; х – переменная интегрирования.
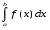 = F(b) – F(a) - формула Ньютона – Лейбница.
= F(b) – F(a) - формула Ньютона – Лейбница.
Определение: фигуру ограниченную графиком непрерывной функции f, отрезком [a,b] и прямыми х=а и х=b называют криволинейной трапецией.
Примеры.
Найдите первообразную функции f(x)=x3+2, график которой проходит через данную точку Р (2;15).
РЕШЕНИЕ:
F(x) =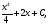
Т.к. график одной из первообразных проходит через точку (2;15), то составим и решим уравнение F(2)=15.
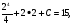 4+4+C=15, 8+C=15, C=7.
4+4+C=15, 8+C=15, C=7.
F(x) =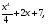
Ответ: F(x)=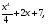
Найдите площадь криволинейной трапеции, ограниченной линиями у=х4; у=1.
Решение.
у=х4 – графиком данной функции является парабола ветви которой направлены вверх с вершиной в точке (0;0).
у=1 – уравнение прямой параллельной оси ОХ.
2. Строим график функции у=х4
х
-1
1
у
1
1
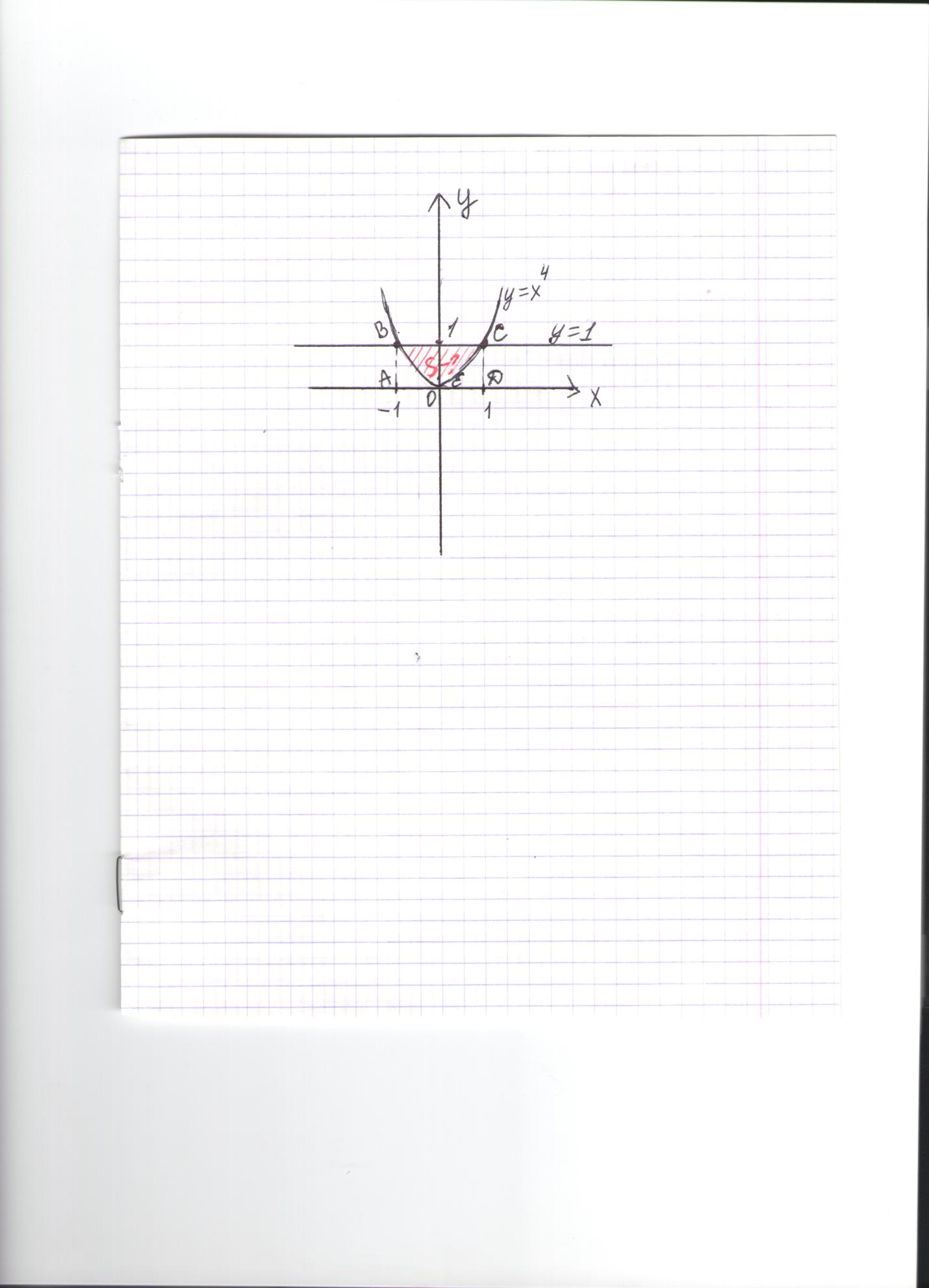
3Найдем пределы интегрирования из уравнения х4=1
х1 = -1; х2 =1 отметим их на графике
4. Вычисляем площадь
Искомая площадь может быть получена как разность площадей прямоугольника АВСД и криволинейной трапеции АВЕСД
S ВCЕ = S АВСД – S АВЕСД
S АВСД = АВ ×ВС = 1× 2 = 2 кв. ед.
S АВЕСД = 
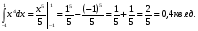
S ВCЕ = 2 – 0, 4 = 1,6 кв. ед.


Ответ: 1,6 кв.ед.
Примечание: для удобства записи разность F(b) – F(a) в формуле Ньютона – Лейбница принято сокращенно обозначать 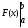 . Пользуясь этим обозначением, формулу Ньютона – Лейбница запишем в виде:
. Пользуясь этим обозначением, формулу Ньютона – Лейбница запишем в виде: 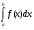 =
=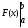
Контрольная работа
Тема Первообразная и интеграл .
Найти все первообразные функции 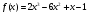 .
.
Вычислите интеграл
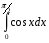
Докажите справедливость равенства
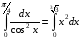
Найдите первообразную функции 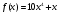 значение которой при х=0 равно 6.
значение которой при х=0 равно 6.
Является ли функция 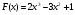 первообразной для каждой из следующих функций:
первообразной для каждой из следующих функций: 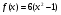 ,
, 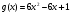 ,
, 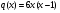 ?
?
Найти площадь криволинейной трапеции 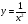 , y = 0, x = 2, x = 4.
, y = 0, x = 2, x = 4.
Найдите первообразную функции 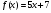 , график которой проходит через данную точку Q (-2;4).
, график которой проходит через данную точку Q (-2;4).
8.Вычислить площадь фигуры ограниченной линиями
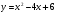 , y = 2, x = 4.
, y = 2, x = 4.
Применяя правила первообразных вычислите все первообразные функций:
а) 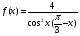 б)
б) 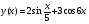
Варианты выполнения контрольной
Начальная буква фамилии
Номера заданий
А Б Ю Я
1, 3, 5, 8
Г Д Щ Ш
2, 4, 6, 9
Ж З Ц Ч Э
1, 2, 5, 7
И Е Ф Х К
3, 4, 5, 9
Л М Н Т У
1, 3, 4, 7
В О П Р С
2, 3, 6, 8
infourok.ru
Контрольная работа № 4 по теме«Первообразная и интеграл»
Вариант 1
1. Найти все первообразные следующих функций:
а) f(x) = sin 3x + 4x – 8
б) f(x) = 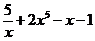
в) f(x) = cos (2x + 1) – eх +x
2. Вычислить:
а) 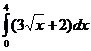
б) 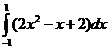
в) 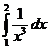
г) 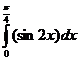
4.Вычислить площадь фигуры ограниченной линиями у=х2-4х+5 и осью ОХ.
Контрольная работа №4 по теме «Первообразная и интеграл»
Вариант 2
Найти все первообразные следующих
функций:
а) f(x) = sin (2x – 3) + 4x5 + 2
б) f(x) = 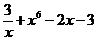
в) f(x) = cos 2x – eх+1 +x
2. Вычислить:
а) 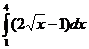
б) 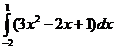
в) 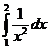
г) 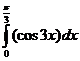 \
\
3. Найти первообразную, график которой проходит
через т. А
Вычислить площадь фигуры ограниченной
линиями у=х2-х-12 и осью ОХ.
Контрольная работа № 4 по теме«Первообразная и интеграл»
Вариант3
1.Найти все первообразные следующих функций:
а) f(x) = cos3x + x – 6
б) f(x) = 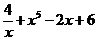
в) f(x) = sin (2x + 1) – eх – 1 +2x
2. Вычислить:
а) 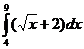
б) 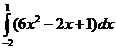
в) 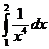
г) 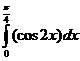
4. Вычислить площадь фигуры ограниченной линиями у=х2+х-6 и осью ОХ.
Вариант 4
1. Найти все первообразные следующих функций:
а) f(x) = cos (2x – 3) + x4 + 7
б) f(x) = 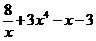
в) f(x) = sin 2x – eх – 2 +5x
2. Вычислить:
а) 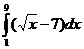
б) 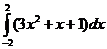
в) 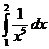
г) 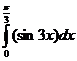
3. . Найти первообразную, график которой
проходит через т.А
4. Вычислить площадь фигуры ограниченной линиями у=х2+3х-4 и осью ОХ.
infourok.ru
ГБПОУ Строгановский колледж
Контрольная работа по алгебре и началам математического анализа
Тема «Первообразная функции и интеграл»
2 курс системы НПО и 1 курс СПО
на базе основного образования
Разработано преподавателем математики
Пешковой Ольгой Алексеевной
Контрольная работа по теме «Первообразная функции и интеграл. Применение интеграла» ориентирована на учебник Ш.А.Алимова и др. «Алгебра и начала анализа» 1 и 2 курса колледжей по профессиям технического и естественно-математического профилей.
Контрольная работа предназначена для самостоятельной внеаудиторной работы.
Контрольная работа включает в себя 10 вариантов заданий одинакового уровня сложности. Вариант определяется последними цифрами номера зачетной книжки студента /или порядкового номера в журнале теоритических занятий/.
Работа выполняется студентом в отдельной тетради с соответствующим оформлением титульного листа. На титульном листе указывается дисциплина, название контрольной работы, номер варианта, фамилия, имя и отчество студента, группа.
Оформление работы должно соответствовать «Единым требованиям оформления письменных работ по математике».
Правильное выполнение каждого задания оценивается 1 баллом. Максимально возможное количество баллов за контрольную работу – 12. Для того чтобы работа была зачтена, необходимо выполнить все задания и набрать не менее 8 баллов.
Задание 1. Найти первообразные следующих функций
1 вариант
а) у = 1 б)  в) у =3sin x г)
в) у =3sin x г)  д)
д)  е) y = sin 2x + 2cos 3x
е) y = sin 2x + 2cos 3x
2 вариант
 б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
3 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
4 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
5 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
6 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
7 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
8 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
9 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
10 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
Задание 2 Вычислить площадь фигуры ограниченной линиями
1 вариант
а) x = -1 x = 2 y = 0 y = x2 – 1
б) y = 0 y = 1 – x2
2 вариант
x = 0 x = 3 y = 0 y = - x2 + 1
 y = x - 2
y = x - 2
3 вариант
a) x = 1 x = 2 y = 0 y = x2 + 1
b)
4 вариант
x = -1 x = 1 y = 0 y = x2 - 2
5 вариант
x = 1 x = 4 y = 0 y = x - 1
6 вариант
x = 1 x = 4 y = 0 y = 
7 вариант
x = 0 x = 2 y = 0 y = x3
8 вариант
x = 1 x = 2 y = 0 y = 2x2
9 вариант
x = -1 x = 2 y = 0 y = 
10 вариант
x = 1 x = 2 y = 0 y = 2x
Задание 3 Вычислить определенный интеграл
1 вариант
а)  б)
б)  в)
в)  г)
г) 
2 вариант
а)  б)
б)  в)
в)  г)
г) 
3 вариант
а)  б)
б)  в)
в)  г)
г) 
4 вариант
а)  б)
б)  в)
в)  г)
г) 
5 вариант
а)  б)
б)  в)
в)  г)
г) 
6 вариант
а)  б)
б)  в)
в)  г)
г) 
7 вариант
а)  б)
б)  в)
в)  г)
г) 
8 вариант
а)  б)
б)  в)
в)  г)
г) 
9 вариант
а)  б)
б)  в)
в)  г)
г) 
10 вариант
а)  б)
б)  в)
в)  г)
г) 
Задание 4 Найти общее решение дифференциального уравнения
1 вариант а)  ’=x2 б) y’= y
’=x2 б) y’= y
2 вариант а) y’=  б) y’= 2y
б) y’= 2y
3 вариант а) y’= sin x б) y’=
4 вариант а) y’ =  б) y’ = y2
б) y’ = y2
5 вариант а) y’ = 2x + 1 б) y’ = -5y
6 вариант а) y’ = x2 + x б) y’ = = y
7 вариант а) y’ = sin x б) y’ = 5y
8 вариант а) y’ = 2 cos x б) y’ = 6y
9 вариант а) y’ = 5x4 б) y’ = 
10 вариант а) y’ = -6x б) y’ = - y
Задание 5 Найти частное решение дифференциального уравнения
1 вариант а) y’ = x2 y(2 ) = 1
2 вариант а) y’ =  y(e ) = 1
y(e ) = 1
3 вариант а) y’ = e-x y(0) = -2
4 вариант а) y’ = 2cos x y( ) = 3
) = 3
5 вариант а) y’ = 3x + 2 y(1) = 4
6 вариант а) y’ = x3 y(1) = 3
7 вариант а) y’ =  y(-1) = 2
y(-1) = 2
8 вариант а) y’ = x + 2x2 y(1) = 1
9 вариант а) y’ = x3 + 1 y(-1) = 2
10 вариант а) y’ = 2 – 3x y(1) = 6
Задание 6 Вычислить значения скорости V(t) м/с и перемещения S(t) м материальной точки за время t c, если ускорение
1 вариант a(t) = 3t + 2 t = 3 c
2 вариант a(t) = - 3t + t2 t = 1 c
3 вариант a(t) =  t = 2 c
t = 2 c
4 вариант a(t) = -2t3 + 4 t = 2 c
5 вариант a(t) = 2t2 – 3 t = 1 c
6 вариант a(t) = -6 + t3 t = 4 c
7 вариант a(t) =  t = 5 c
t = 5 c
8 вариант a(t) = 3x5+2 t = 1 c
9 вариант a(t) = -2x3 – 4 t = 4 c
10 вариант a(t) = 3 + 4t3 t = 2 c
Задание 7 Вычислить объем тела, полученного вращением графика функции y = f (x) вокруг оси Ох
1 вариант f(x) = x3 + 2 a = 0 b = 2
2 вариант f(x) = - x2 + 1 a = 1 b = 2
3 вариант f(x) = 2 – 2x3 a = - 1 b = 0
4 вариант f (x) =  a = 1 b = 4
a = 1 b = 4
5 вариант f(x) = x2 + 1 a = 1 b = 3
6 вариант f(x) =  a = 2 b = 3
a = 2 b = 3
7 вариант f(x) =  a = 1 b = 4
a = 1 b = 4
8 вариант f(x) = cos x a =  b =
b = 
9 вариант f(x) = sin x a = 0 b = 
10 вариант f(x) = x + 1 a = 2 b = 4
Задание 8 Найти неопределённые интегралы
1 вариант
а)  б)
б)  в)
в)  г)
г) 

2 вариант
а) 
 б)
б)  в)
в)  г)
г) 
3 вариант
а)  б)
б)  в)
в)  г)
г) 
4 вариант
а)  б)
б)  в)
в)  г)
г) 
5 вариант
а)  б)
б)  в)
в)  г)
г) 
6 вариант
а)  б)
б)  в)
в)  г)
г) 
7 вариант
а)  б)
б)  в)
в)  г)
г) 
8 вариант
а)  б)
б)  в)
в)  г)
г) 
9 вариант
а)  б)
б)  в)
в)  г)
г) 
10 вариант
а)  б)
б)  в)
в)  г)
г) 
globuss24.ru
Здесь Вы можете скачать Контрольная работа по Алгебре "Первообразная функции и интеграл" для предмета : Алгебра. Данный документ поможет вам подготовить хороший и качественный материал для урока.
ГБПОУ Строгановский колледж
Контрольная работа по алгебре и началам математического анализа
Тема «Первообразная функции и интеграл»
2 курс системы НПО и 1 курс СПО
на базе основного образования
Разработано преподавателем математики
Пешковой Ольгой Алексеевной
Контрольная работа по теме «Первообразная функции и интеграл. Применение интеграла» ориентирована на учебник Ш.А.Алимова и др. «Алгебра и начала анализа» 1 и 2 курса колледжей по профессиям технического и естественно-математического профилей.
Контрольная работа предназначена для самостоятельной внеаудиторной работы.
Контрольная работа включает в себя 10 вариантов заданий одинакового уровня сложности. Вариант определяется последними цифрами номера зачетной книжки студента /или порядкового номера в журнале теоритических занятий/.
Работа выполняется студентом в отдельной тетради с соответствующим оформлением титульного листа. На титульном листе указывается дисциплина, название контрольной работы, номер варианта, фамилия, имя и отчество студента, группа.
Оформление работы должно соответствовать «Единым требованиям оформления письменных работ по математике».
Правильное выполнение каждого задания оценивается 1 баллом. Максимально возможное количество баллов за контрольную работу – 12. Для того чтобы работа была зачтена, необходимо выполнить все задания и набрать не менее 8 баллов.
Задание 1. Найти первообразные следующих функций
1 вариант
а) у = 1 б)  в) у =3sin x г)
в) у =3sin x г)  д)
д)  е) y = sin 2x + 2cos 3x
е) y = sin 2x + 2cos 3x
2 вариант
 б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
3 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
4 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
5 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
6 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
7 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
8 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
9 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
10 вариант
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
Задание 2 Вычислить площадь фигуры ограниченной линиями
1 вариант
а) x = -1 x = 2 y = 0 y = x2 – 1
б) y = 0 y = 1 – x2
2 вариант
x = 0 x = 3 y = 0 y = - x2 + 1
 y = x - 2
y = x - 2
3 вариант
a) x = 1 x = 2 y = 0 y = x2 + 1
b)
4 вариант
x = -1 x = 1 y = 0 y = x2 - 2
5 вариант
x = 1 x = 4 y = 0 y = x - 1
6 вариант
x = 1 x = 4 y = 0 y = 
7 вариант
x = 0 x = 2 y = 0 y = x3
8 вариант
x = 1 x = 2 y = 0 y = 2x2
9 вариант
x = -1 x = 2 y = 0 y = 
10 вариант
x = 1 x = 2 y = 0 y = 2x
Задание 3 Вычислить определенный интеграл
1 вариант
а)  б)
б)  в)
в)  г)
г) 
2 вариант
а)  б)
б)  в)
в)  г)
г) 
3 вариант
а)  б)
б)  в)
в)  г)
г) 
4 вариант
а)  б)
б)  в)
в)  г)
г) 
5 вариант
а)  б)
б)  в)
в)  г)
г) 
6 вариант
а)  б)
б)  в)
в)  г)
г) 
7 вариант
а)  б)
б)  в)
в)  г)
г) 
8 вариант
а)  б)
б)  в)
в)  г)
г) 
9 вариант
а)  б)
б)  в)
в)  г)
г) 
10 вариант
а)  б)
б)  в)
в)  г)
г) 
Задание 4 Найти общее решение дифференциального уравнения
1 вариант а)  ’=x2 б) y’= y
’=x2 б) y’= y
2 вариант а) y’=  б) y’= 2y
б) y’= 2y
3 вариант а) y’= sin x б) y’=
4 вариант а) y’ =  б) y’ = y2
б) y’ = y2
5 вариант а) y’ = 2x + 1 б) y’ = -5y
6 вариант а) y’ = x2 + x б) y’ = = y
7 вариант а) y’ = sin x б) y’ = 5y
8 вариант а) y’ = 2 cos x б) y’ = 6y
9 вариант а) y’ = 5x4 б) y’ = 
10 вариант а) y’ = -6x б) y’ = - y
Задание 5 Найти частное решение дифференциального уравнения
1 вариант а) y’ = x2 y(2 ) = 1
2 вариант а) y’ =  y(e ) = 1
y(e ) = 1
3 вариант а) y’ = e-x y(0) = -2
4 вариант а) y’ = 2cos x y( ) = 3
) = 3
5 вариант а) y’ = 3x + 2 y(1) = 4
6 вариант а) y’ = x3 y(1) = 3
7 вариант а) y’ =  y(-1) = 2
y(-1) = 2
8 вариант а) y’ = x + 2x2 y(1) = 1
9 вариант а) y’ = x3 + 1 y(-1) = 2
10 вариант а) y’ = 2 – 3x y(1) = 6
Задание 6 Вычислить значения скорости V(t) м/с и перемещения S(t) м материальной точки за время t c, если ускорение
1 вариант a(t) = 3t + 2 t = 3 c
2 вариант a(t) = - 3t + t2 t = 1 c
3 вариант a(t) =  t = 2 c
t = 2 c
4 вариант a(t) = -2t3 + 4 t = 2 c
5 вариант a(t) = 2t2 – 3 t = 1 c
6 вариант a(t) = -6 + t3 t = 4 c
7 вариант a(t) =  t = 5 c
t = 5 c
8 вариант a(t) = 3x5+2 t = 1 c
9 вариант a(t) = -2x3 – 4 t = 4 c
10 вариант a(t) = 3 + 4t3 t = 2 c
Задание 7 Вычислить объем тела, полученного вращением графика функции y = f (x) вокруг оси Ох
1 вариант f(x) = x3 + 2 a = 0 b = 2
2 вариант f(x) = - x2 + 1 a = 1 b = 2
3 вариант f(x) = 2 – 2x3 a = - 1 b = 0
4 вариант f (x) =  a = 1 b = 4
a = 1 b = 4
5 вариант f(x) = x2 + 1 a = 1 b = 3
6 вариант f(x) =  a = 2 b = 3
a = 2 b = 3
7 вариант f(x) =  a = 1 b = 4
a = 1 b = 4
8 вариант f(x) = cos x a =  b =
b = 
9 вариант f(x) = sin x a = 0 b = 
10 вариант f(x) = x + 1 a = 2 b = 4
Задание 8 Найти неопределённые интегралы
1 вариант
а)  б)
б)  в)
в)  г)
г) 

2 вариант
а) 
 б)
б)  в)
в)  г)
г) 
3 вариант
а)  б)
б)  в)
в)  г)
г) 
4 вариант
а)  б)
б)  в)
в)  г)
г) 
5 вариант
а)  б)
б)  в)
в)  г)
г) 
6 вариант
а)  б)
б)  в)
в)  г)
г) 
7 вариант
а)  б)
б)  в)
в)  г)
г) 
8 вариант
а)  б)
б)  в)
в)  г)
г) 
9 вариант
а)  б)
б)  в)
в)  г)
г) 
10 вариант
а)  б)
б)  в)
в)  г)
г) 
docbase.org