.Контрольная работа по теме «Функции и графики»
1 вариант
1. Найдите область определения функции .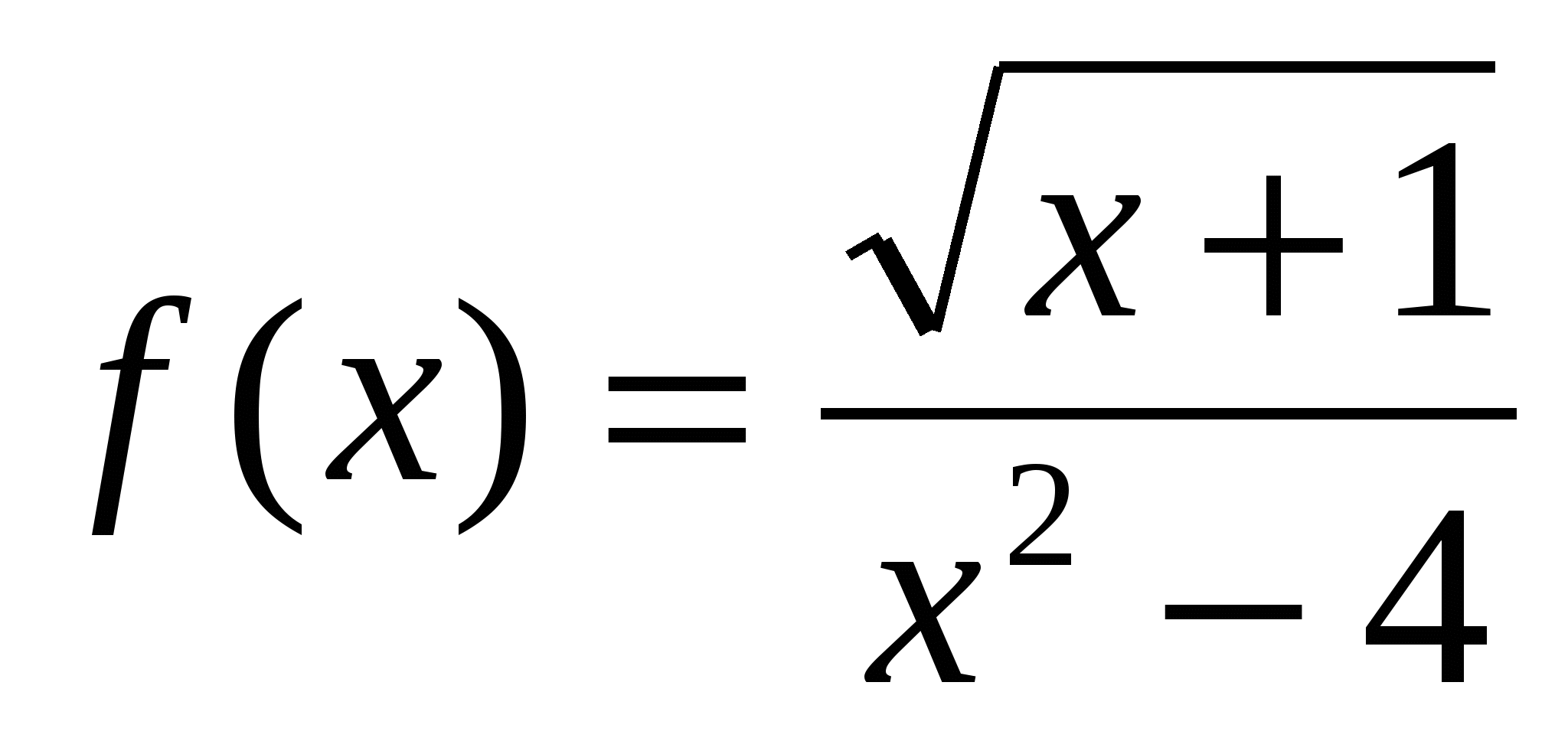
2. Найдите область значений функции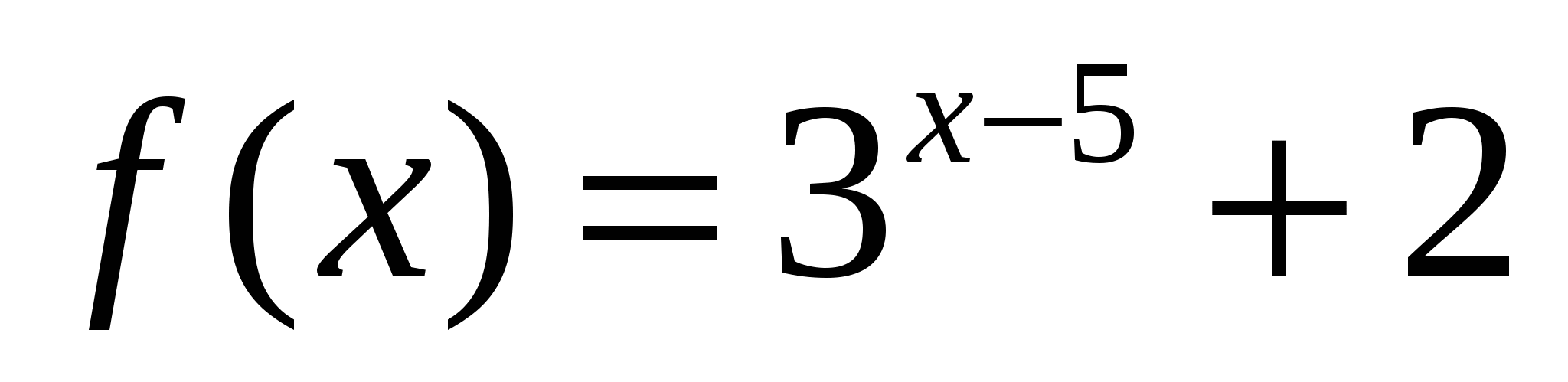 
.
3. Найдите наименьшее значение функции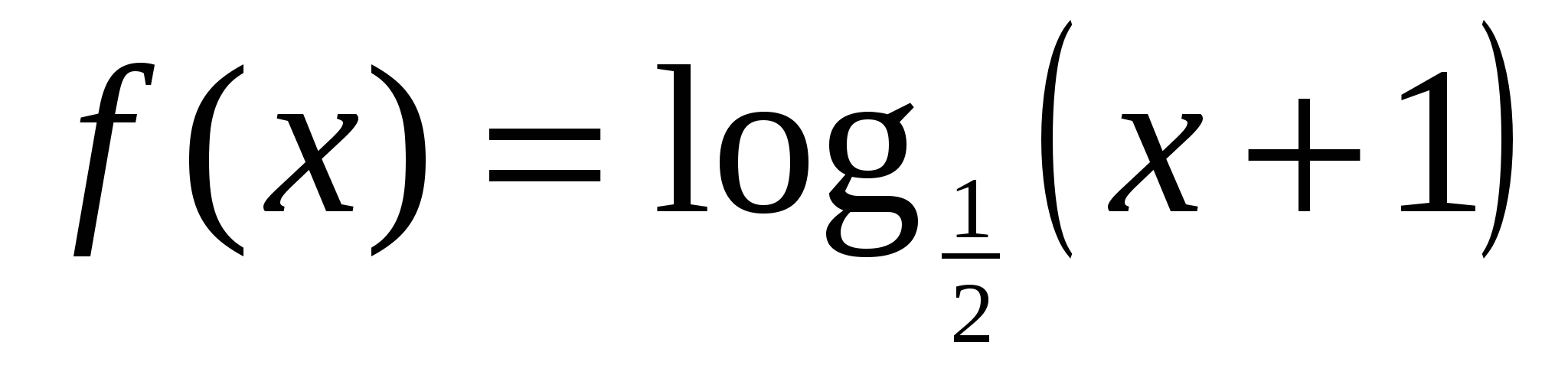 
на отрезке 
.
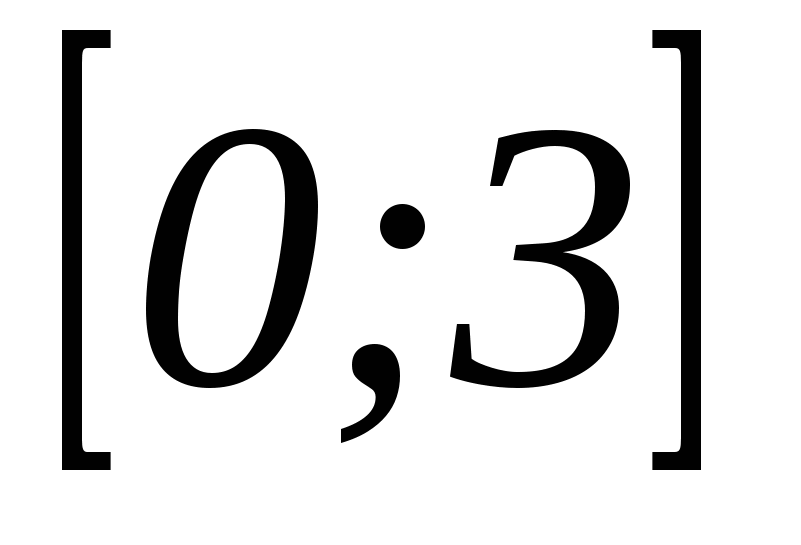4. Исследуйте на чётность и нечетность функцию
а)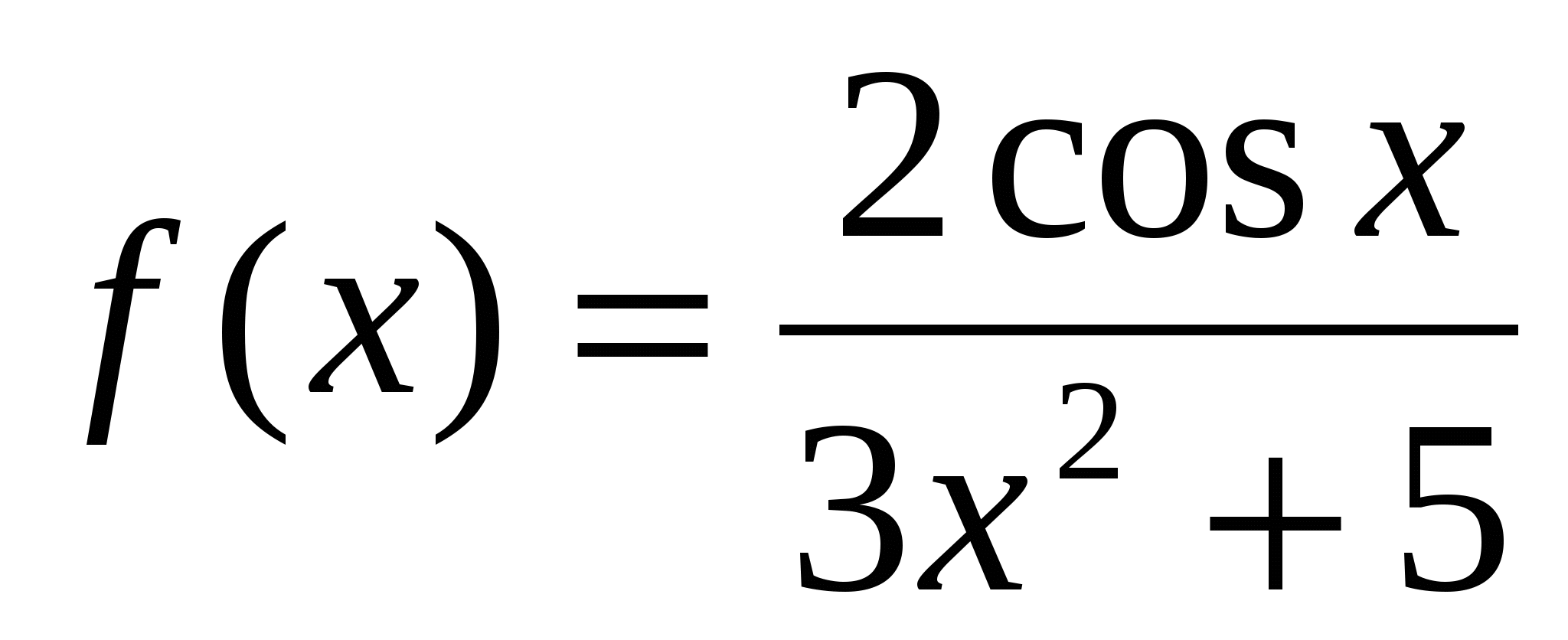 
; б) 
.
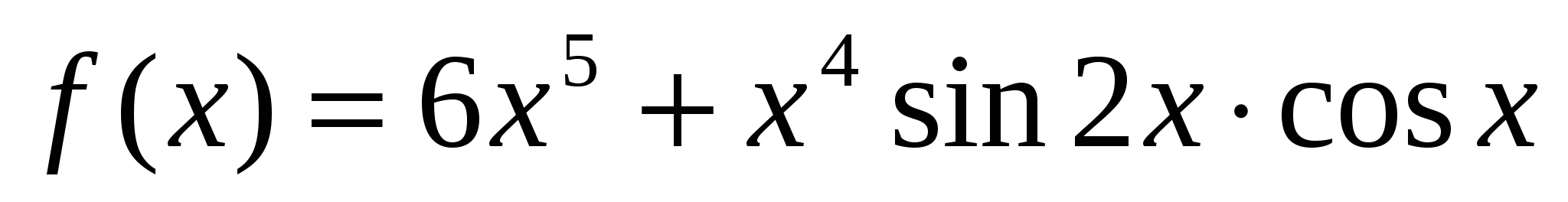5. Постройте график функции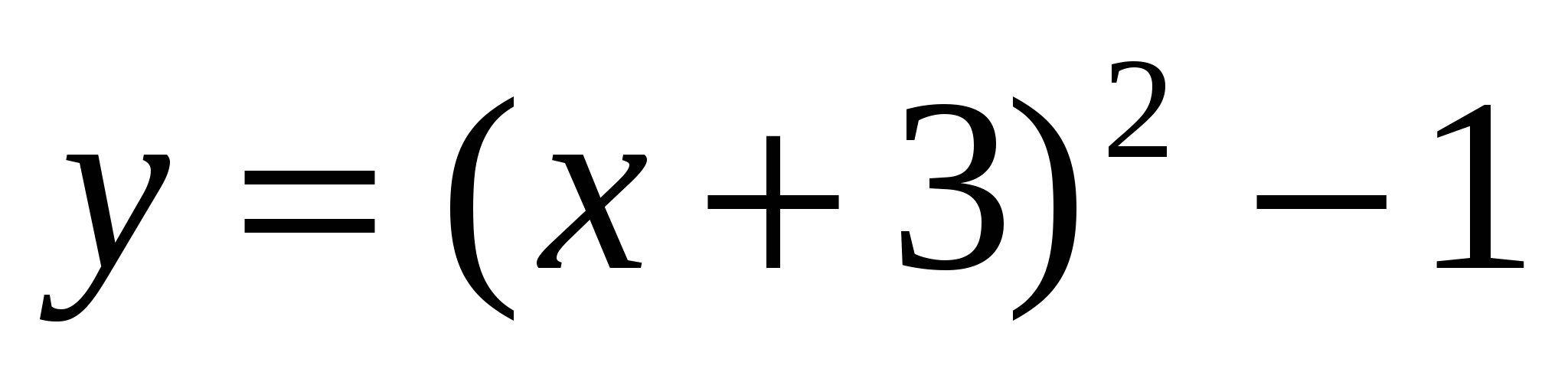 
. Пользуясь графиком, найдите
промежутки возрастания и убывания функции, экстремум функции.
6. Найдите функцию, обратную к функции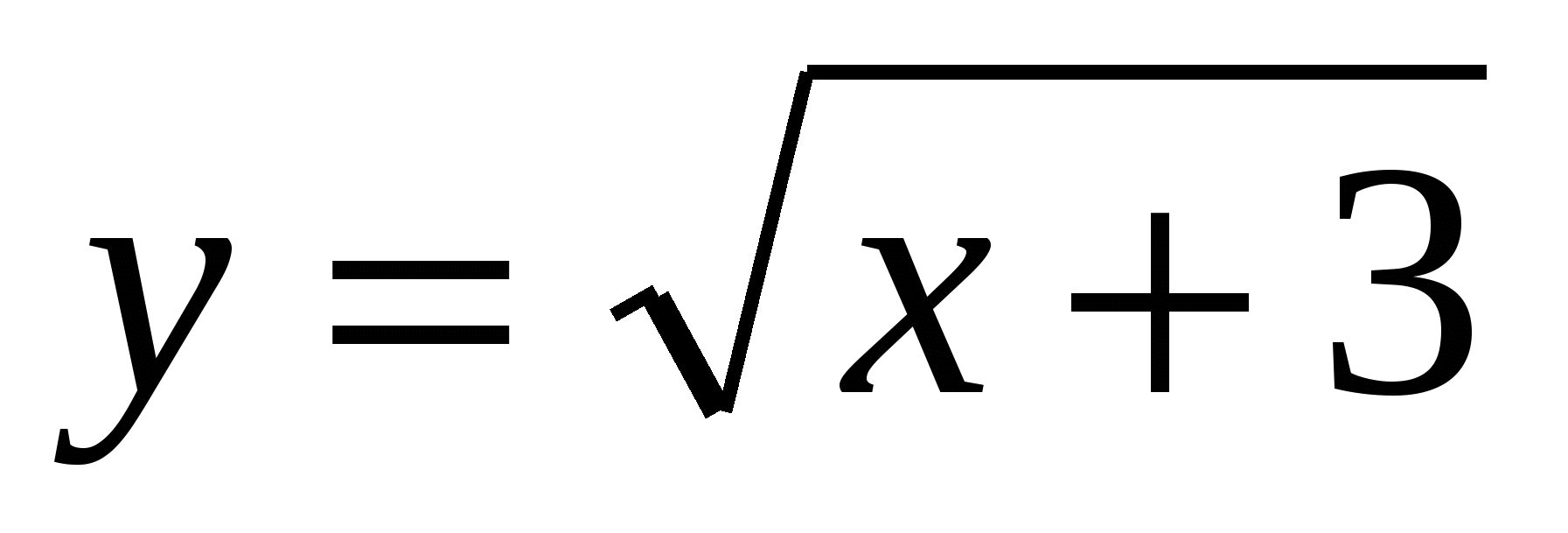 
.
Постройте график данной функции и график обратной к данной функции;
укажите область определения и множество значений каждой из них.
__________________________________________________________________________________________________
Контрольная работа по теме «Функции и графики»
2 вариант
1. Найдите область определения функции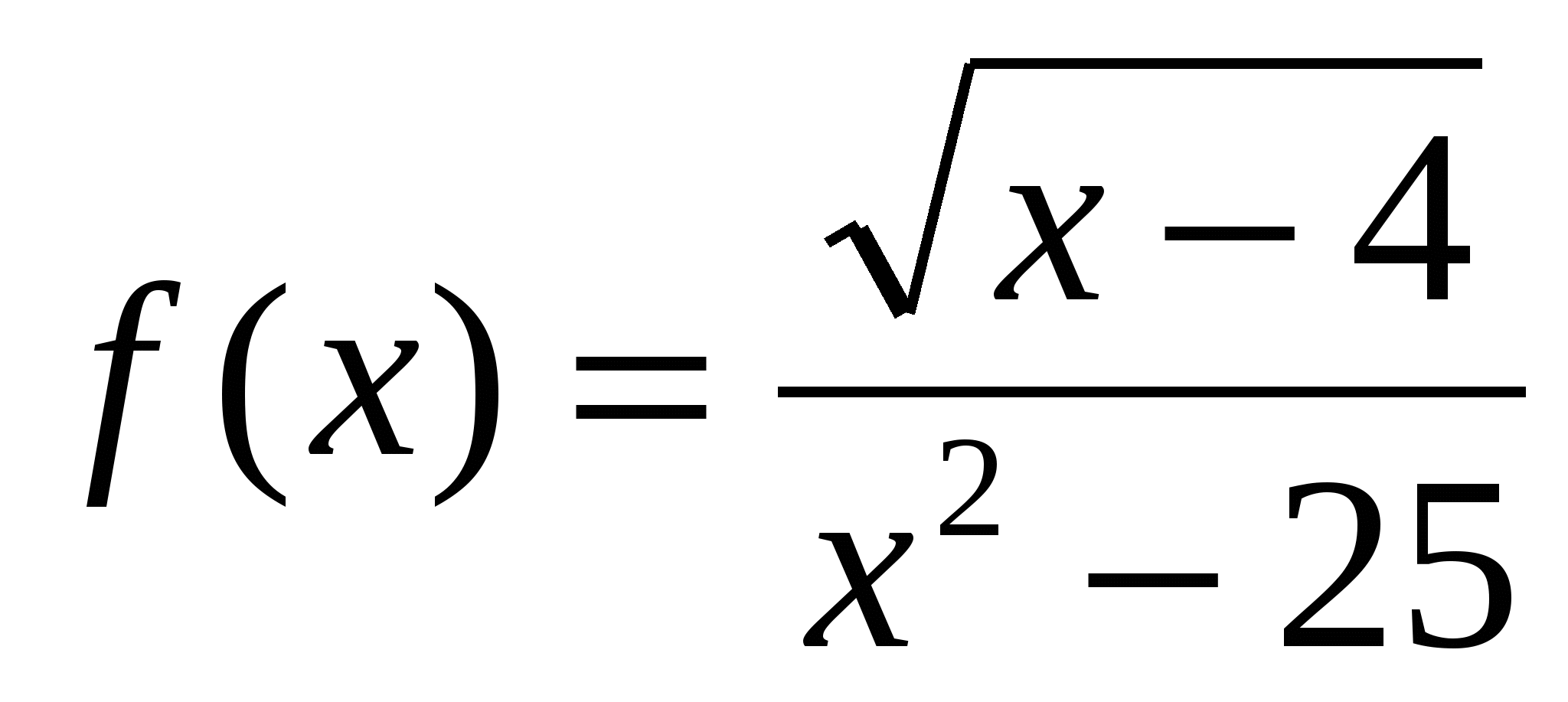 
.
2. Найдите область значений функции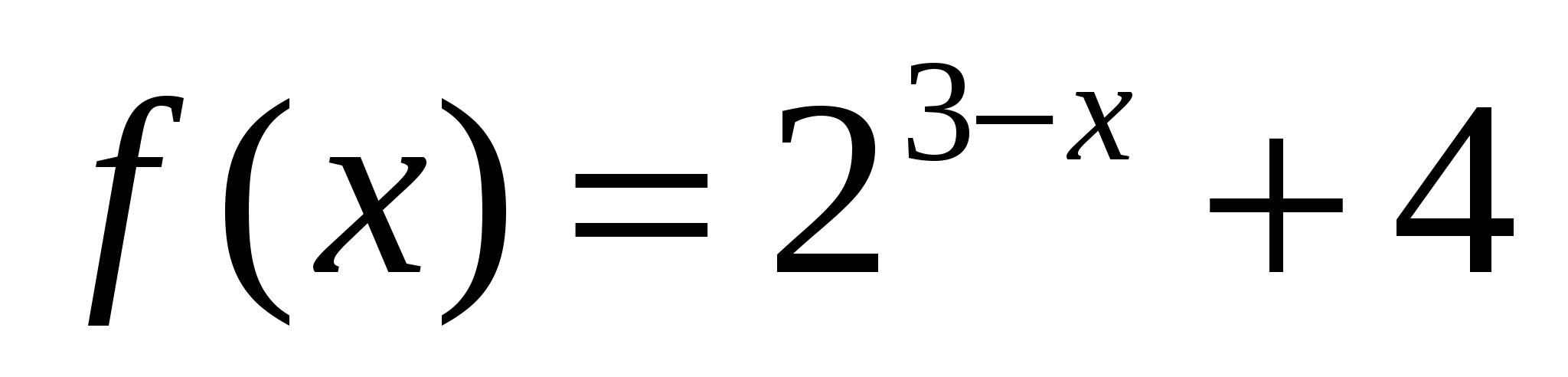 
.
3. Найдите наибольшее значение функции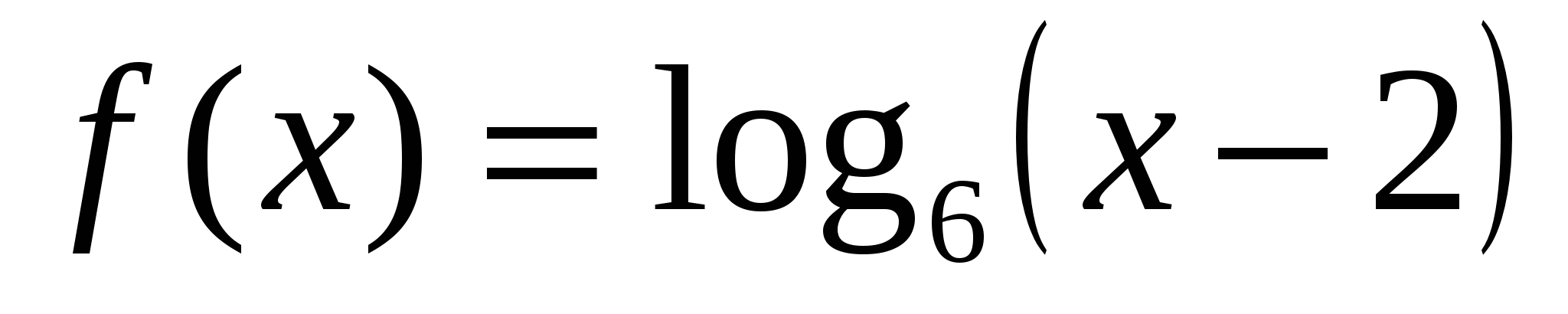 
на отрезке 
.
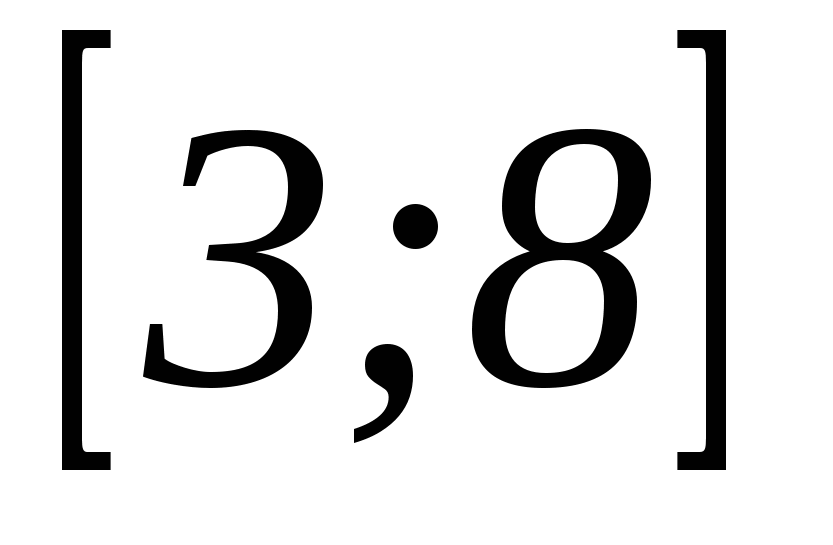4. Исследуйте на чётность и нечетность функцию
а)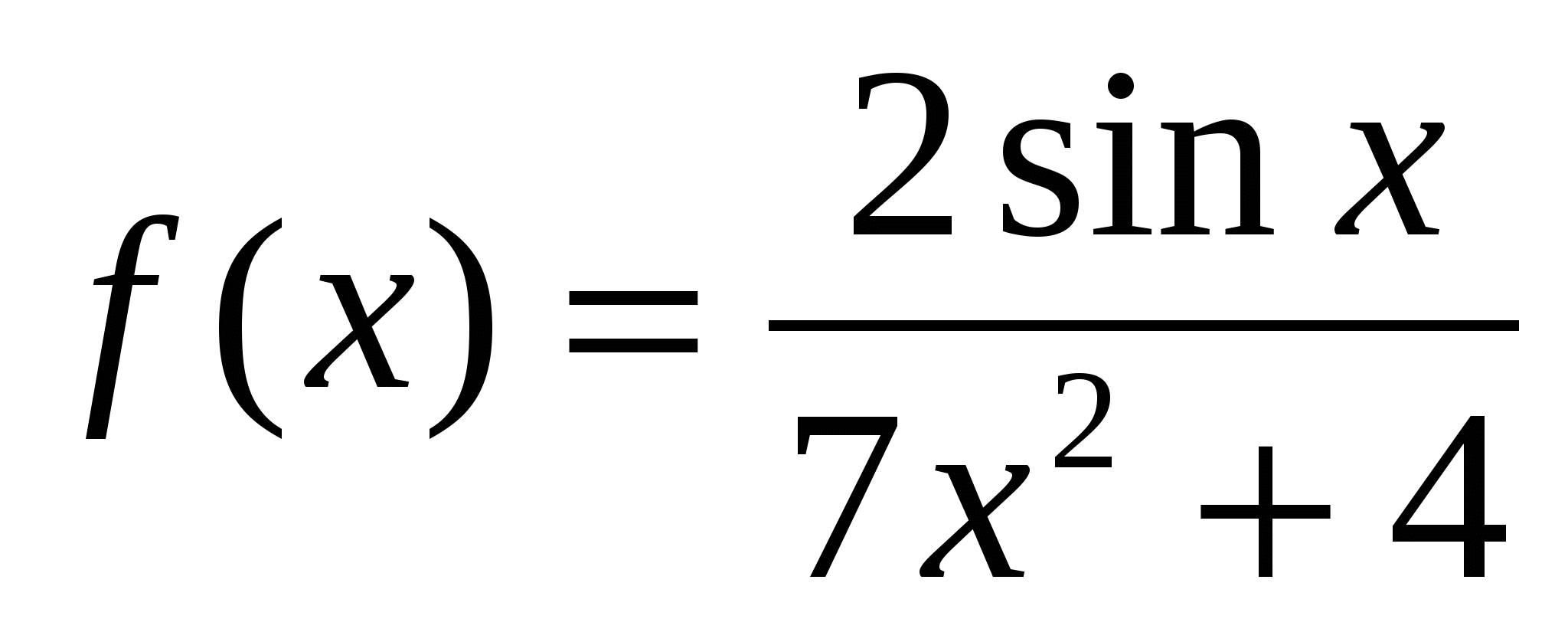 
; б)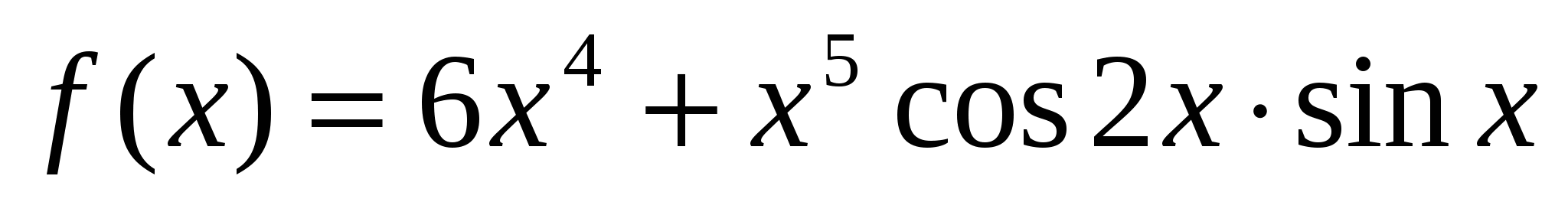 
.
5. Постройте график функции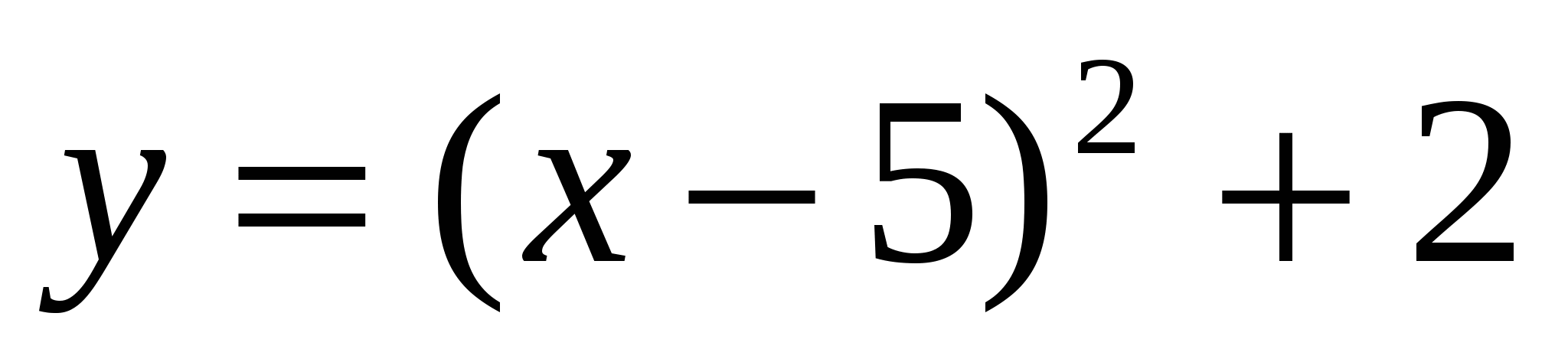 
. Пользуясь графиком, найдите
промежутки возрастания и убывания функции, экстремум функции.
6. Найдите функцию, обратную к функции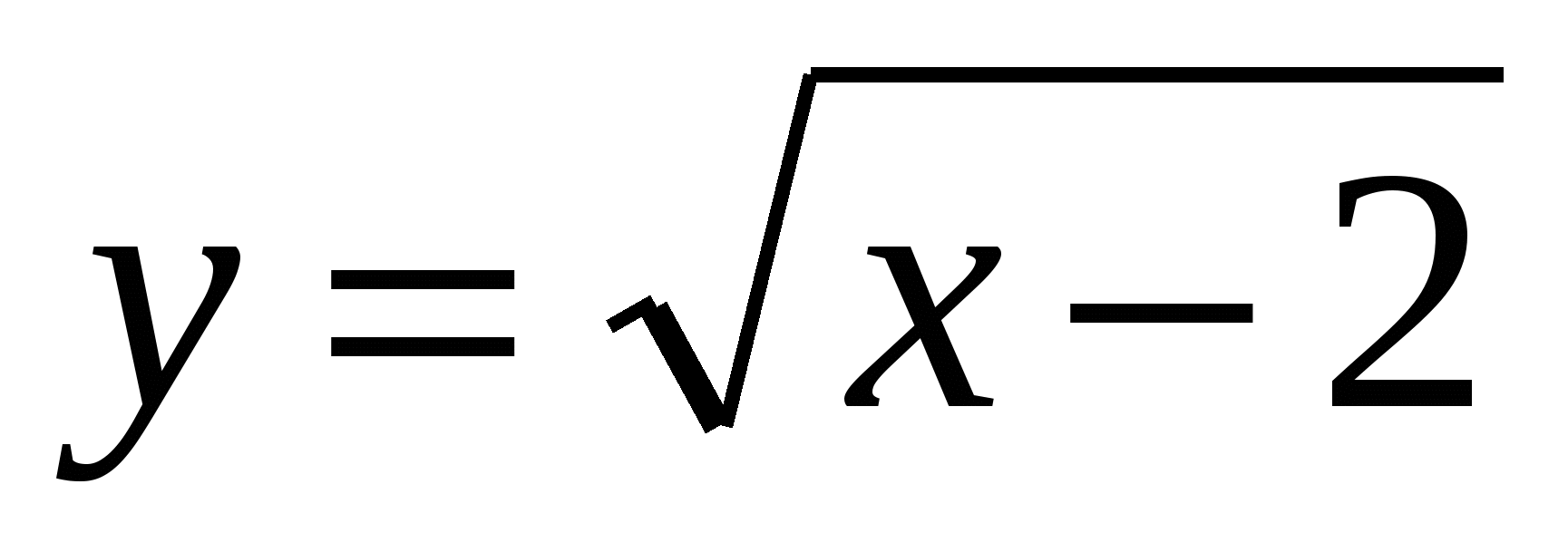 
.
Постройте график данной функции и график обратной к данной функции;
укажите область определения и множество значений каждой из них.
Контрольная работа по теме «Функции и графики»
3 вариант
1. Найдите область определения функции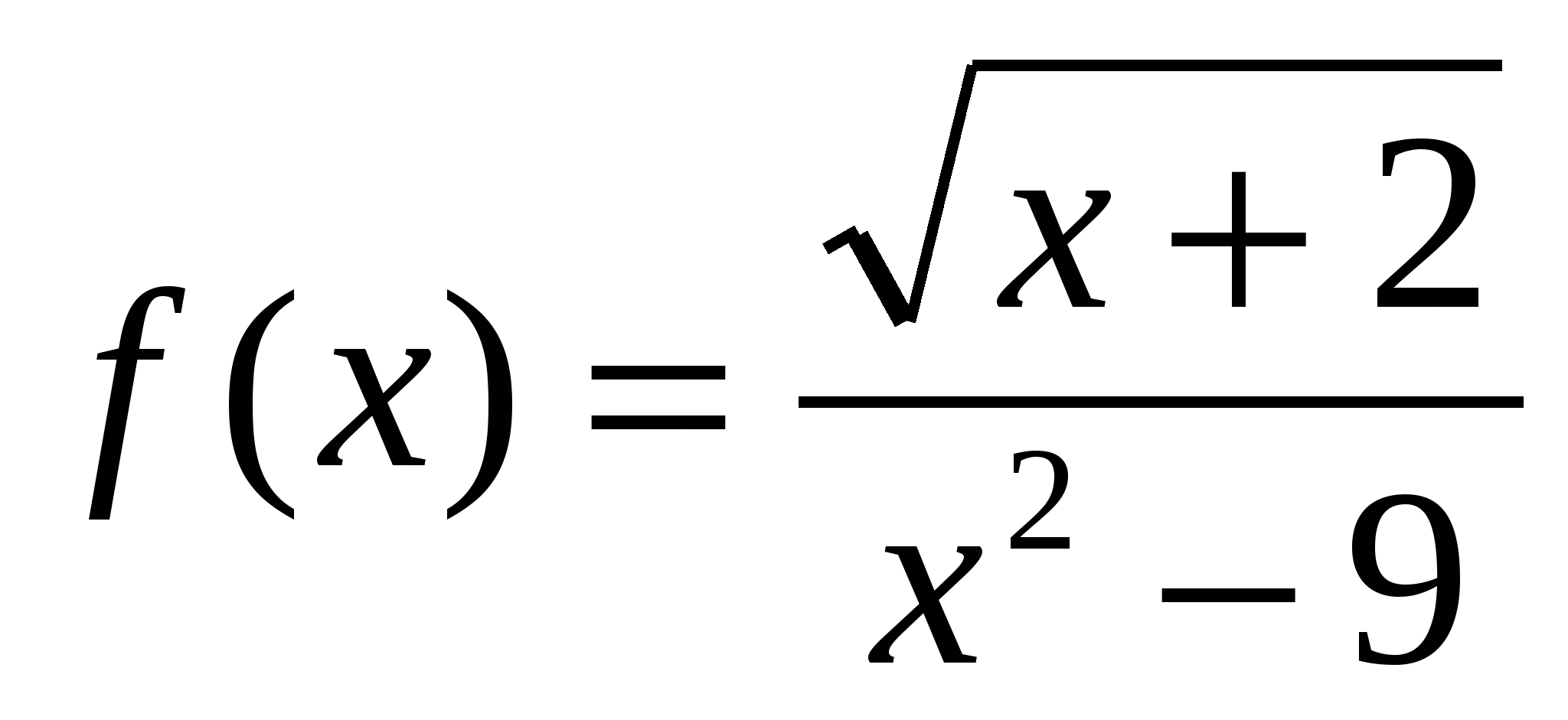 
.
2. Найдите область значений функции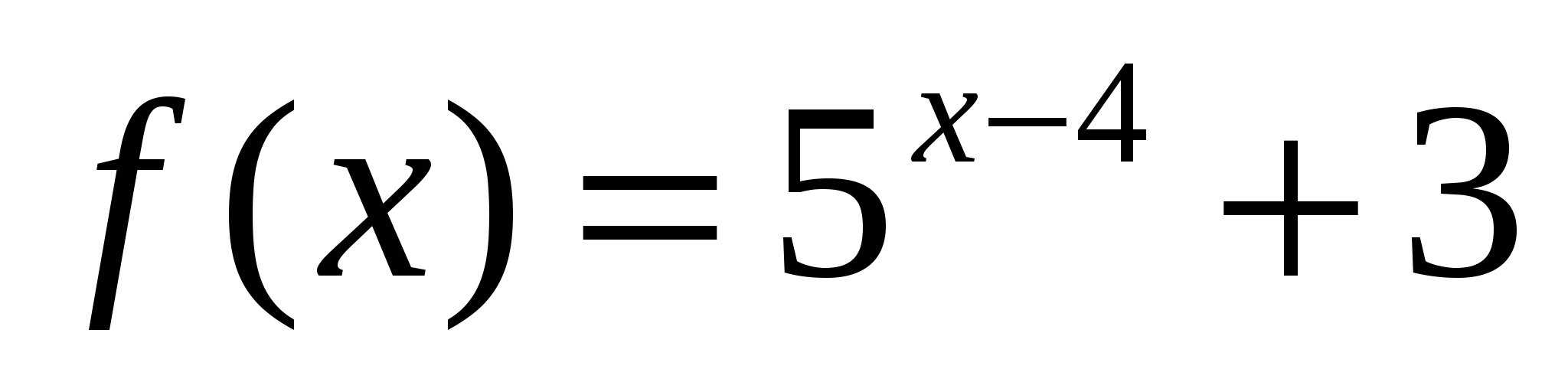 
.
3. Найдите наименьшее значение функции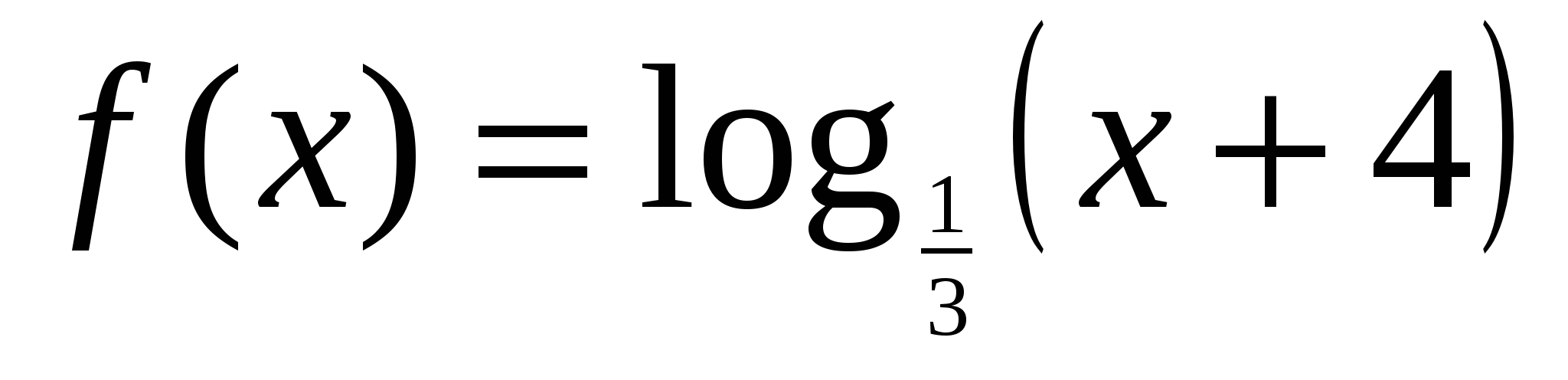 
на отрезке 
.
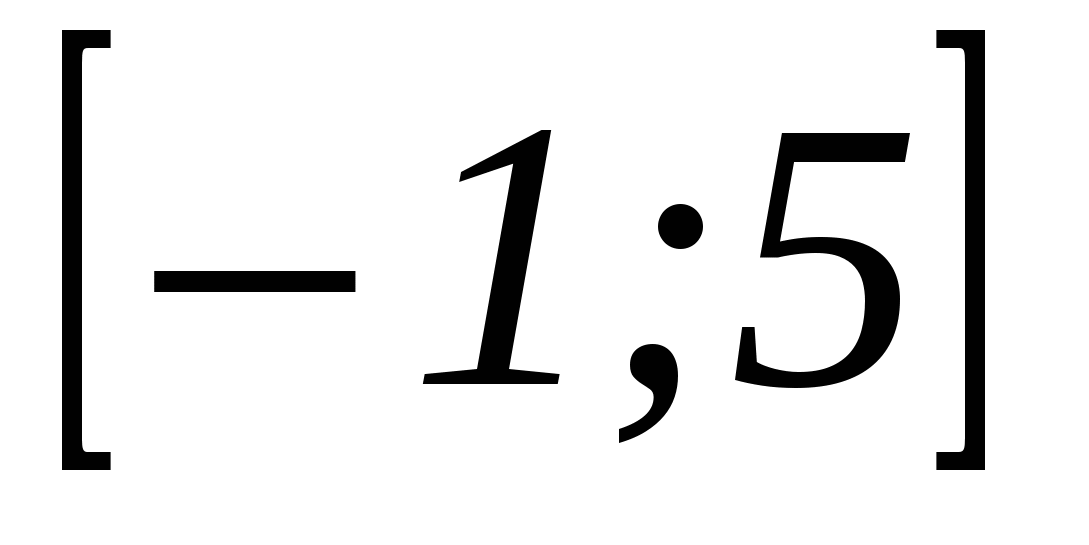4. Исследуйте на чётность и нечетность функцию
а)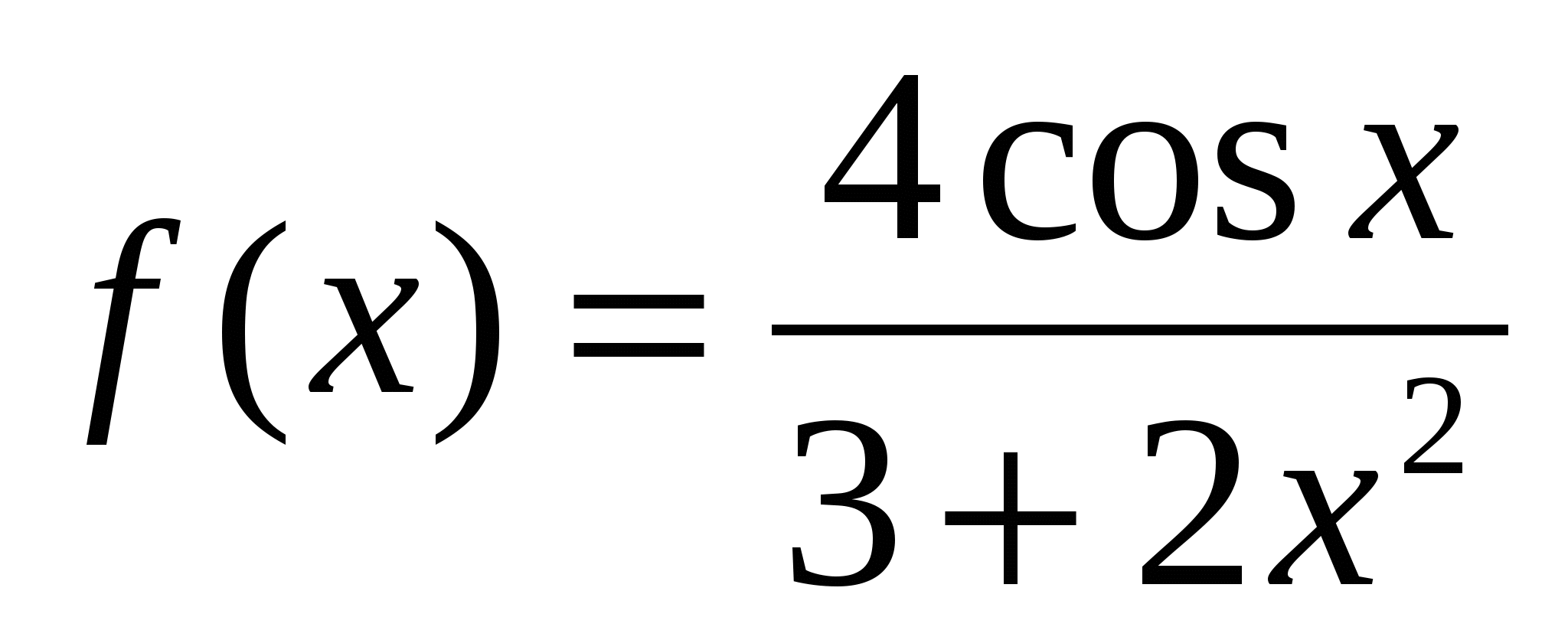 
; б)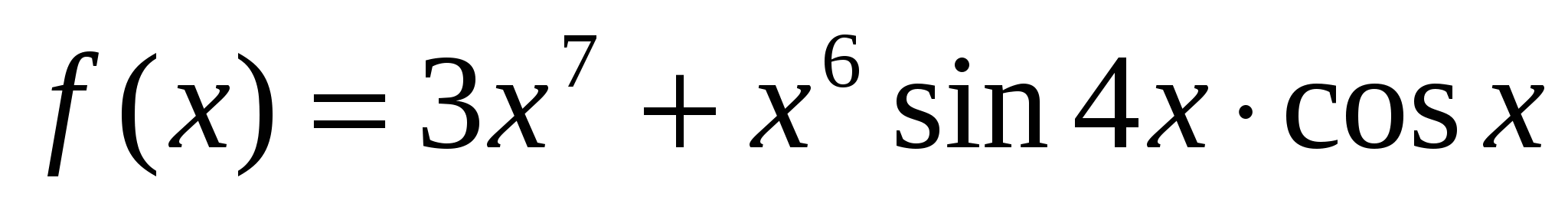 
.
5. Постройте график функции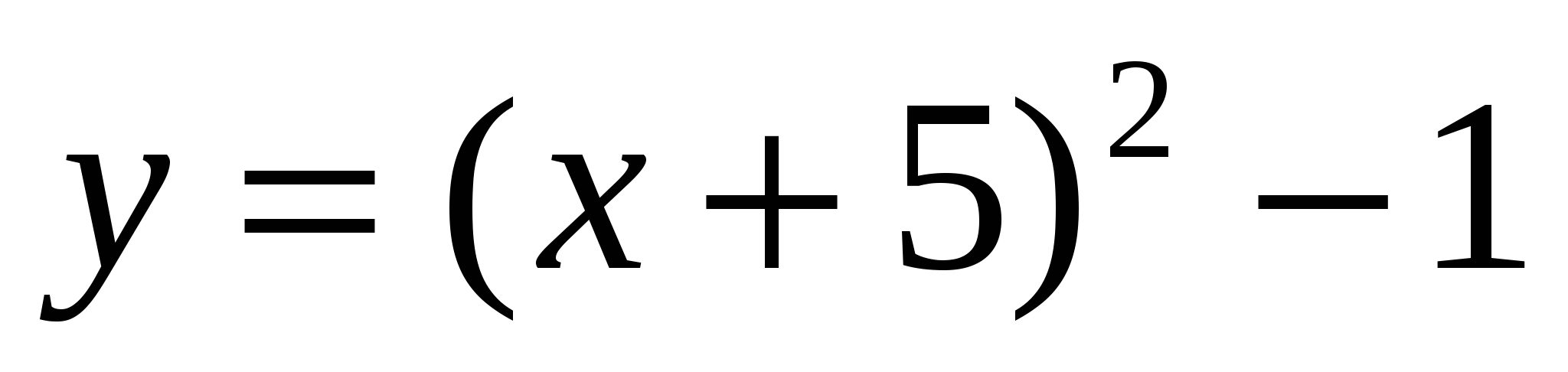 
. Пользуясь графиком, найдите
промежутки возрастания и убывания функции, экстремум функции.
6. Найдите функцию, обратную к функции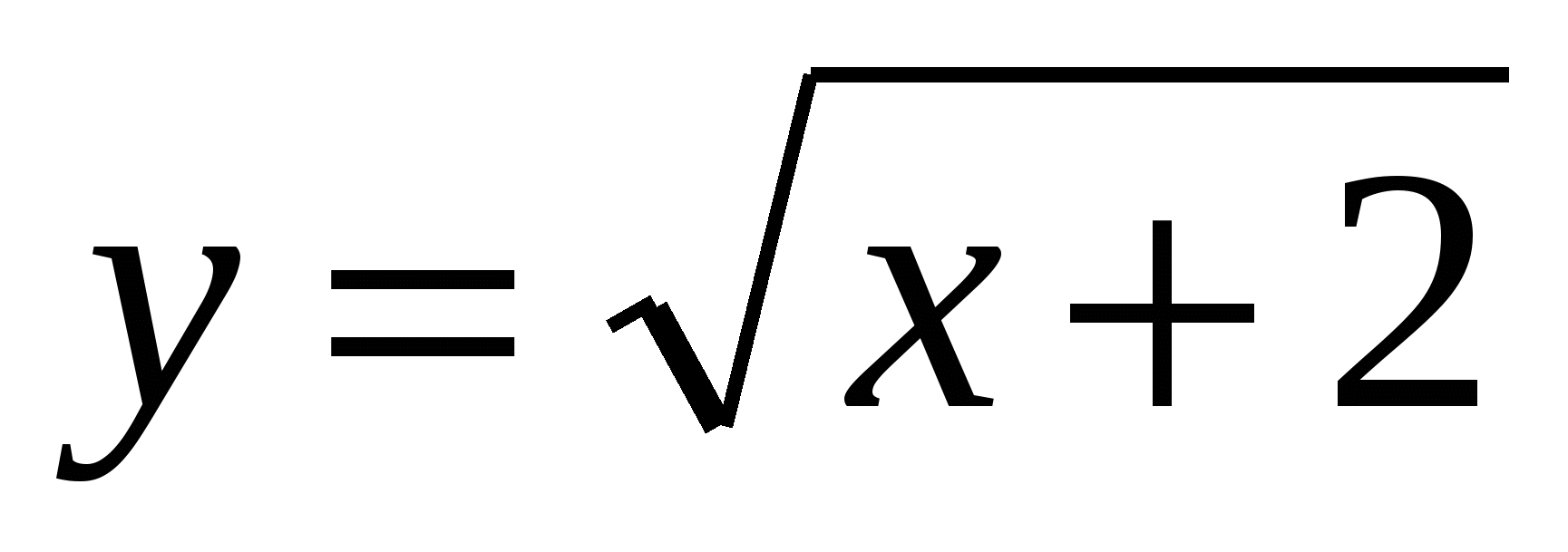 
.
Постройте график данной функции и график обратной к данной функции;
укажите область определения и множество значений каждой из них.
__________________________________________________________________________________________________
Контрольная работа по теме «Функции и графики»
4 вариант
1. Найдите область определения функции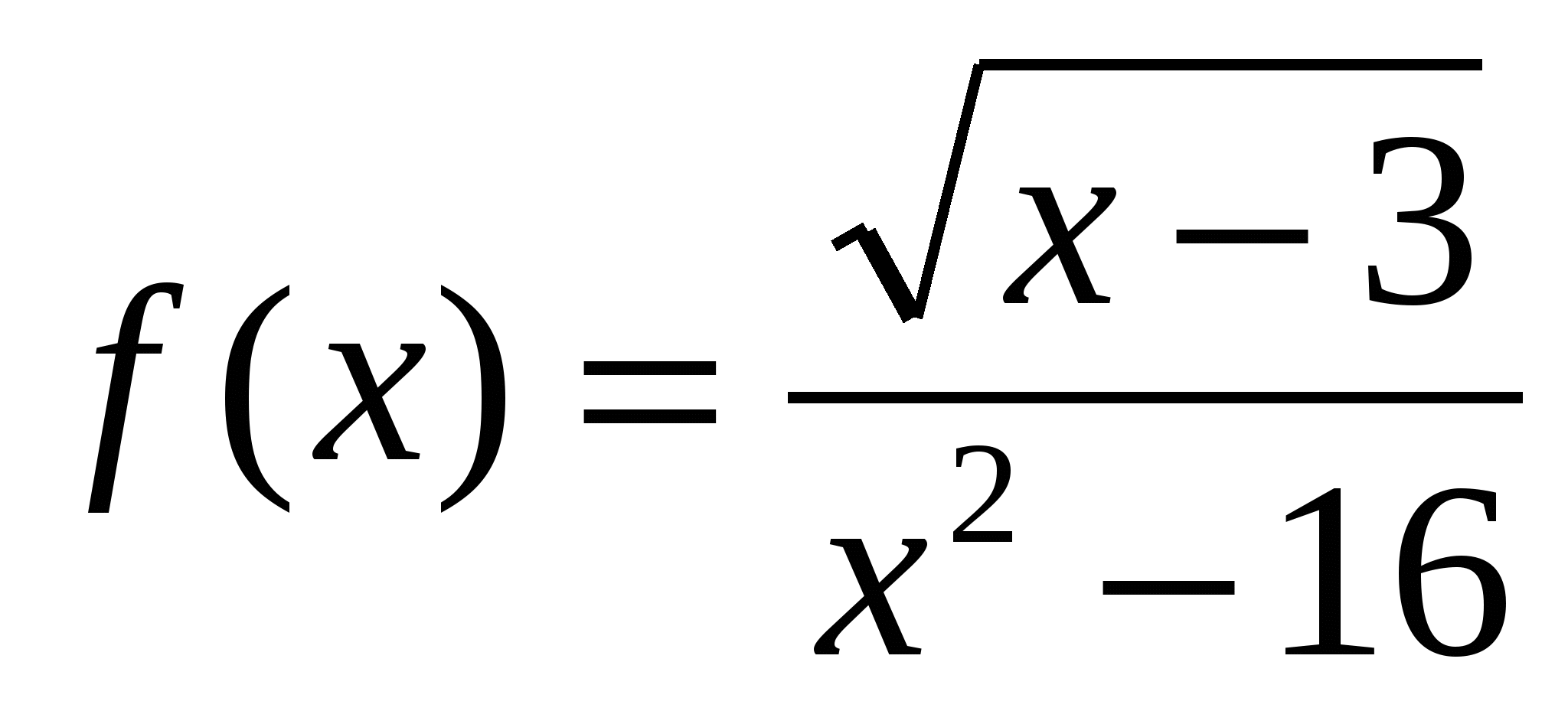 
.
2. Найдите область значений функции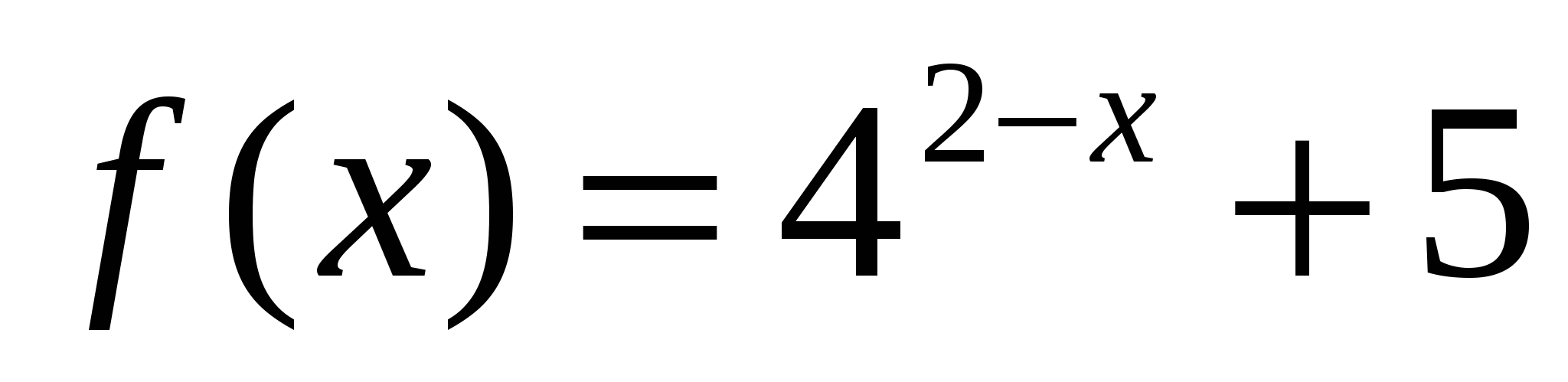 
.
3. Найдите наибольшее значение функции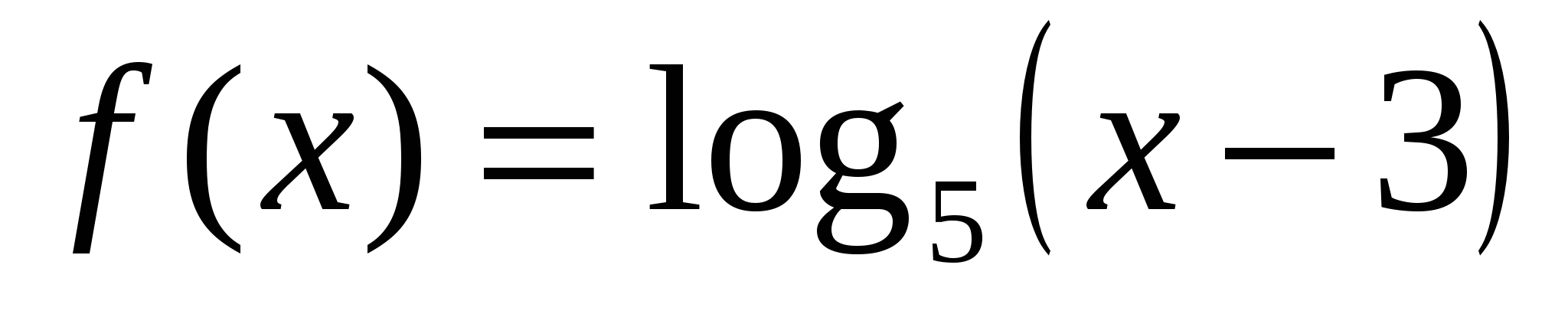 
на отрезке 
.
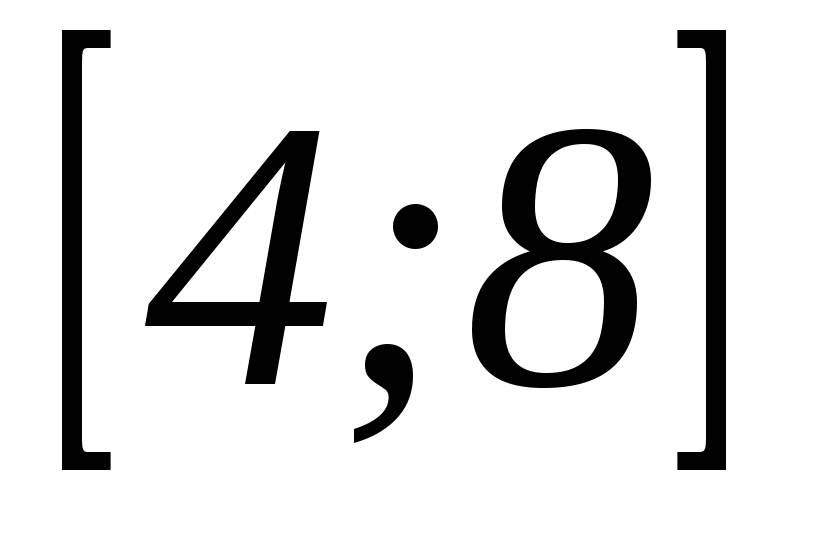4. Исследуйте на чётность и нечетность функцию
а)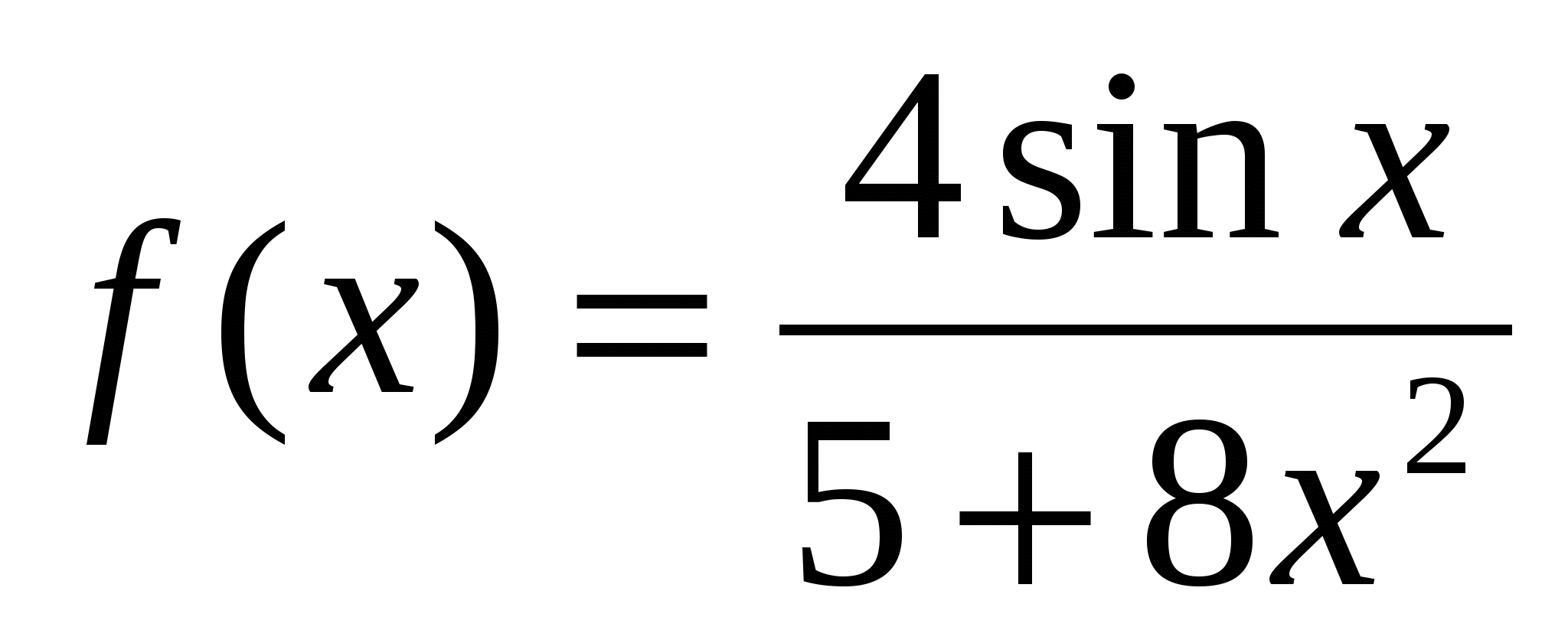 
; б)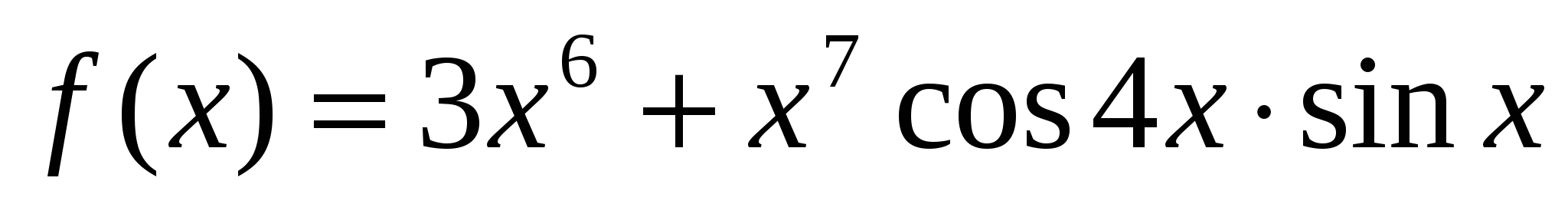 
.
5. Постройте график функции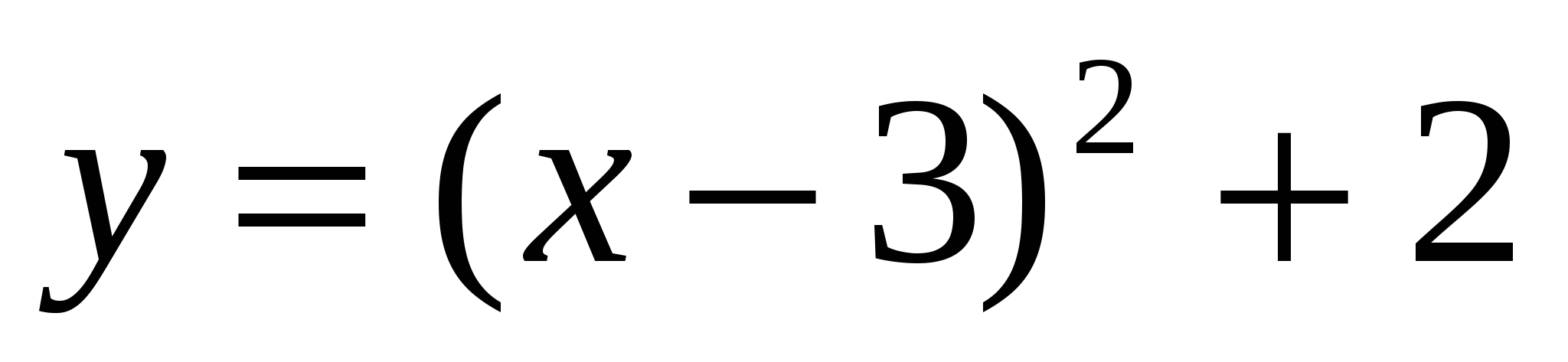 
. Пользуясь графиком, найдите
промежутки возрастания и убывания функции, экстремум функции.
6. Найдите функцию, обратную к функции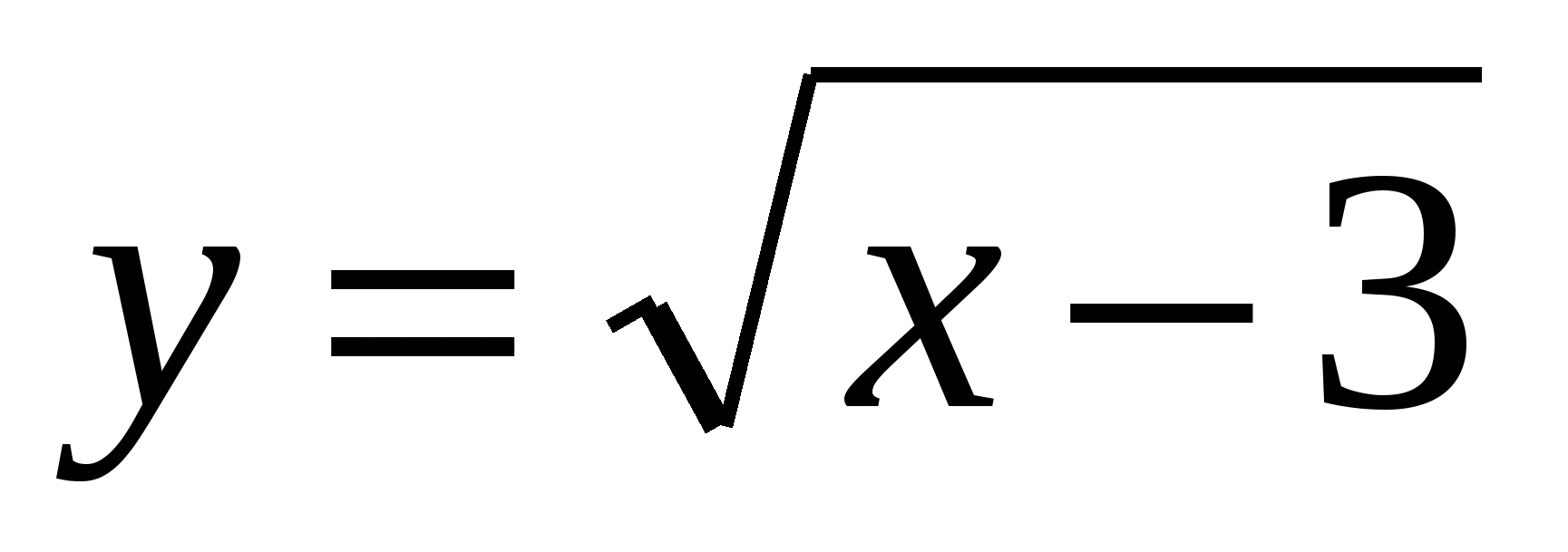 
.
Постройте график данной функции и график обратной к данной функции;
укажите область определения и множество значений каждой из них.
Контрольная работа по теме «Функции и графики»
ОТВЕТЫ
№
задания
1вариант
2 вариант
3 вариант
4 вариант
1
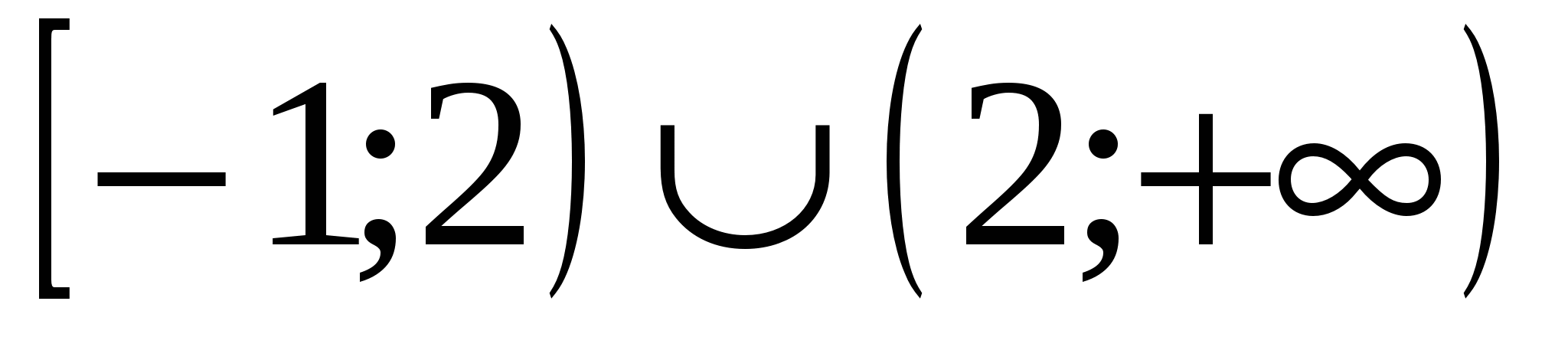
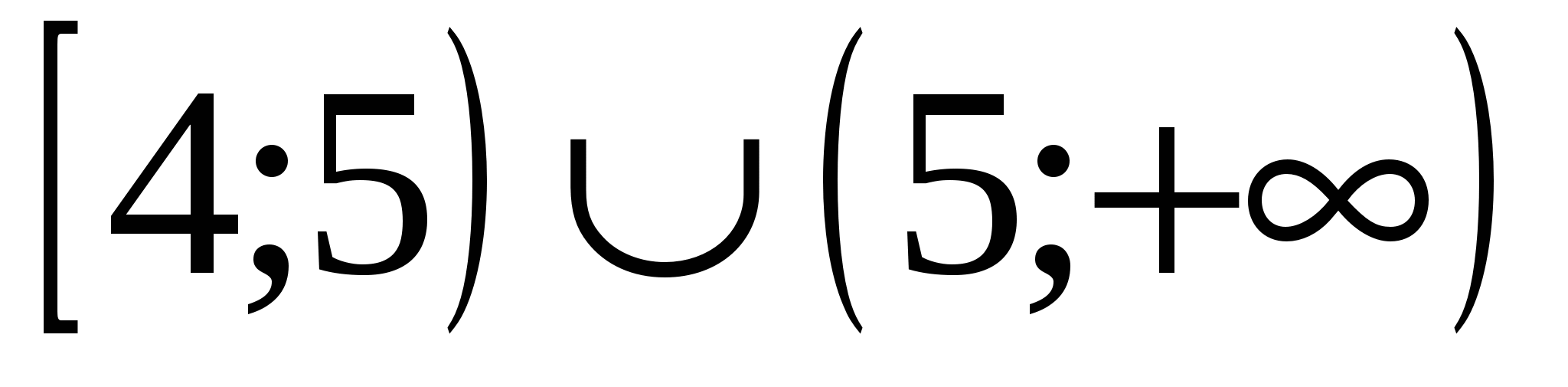
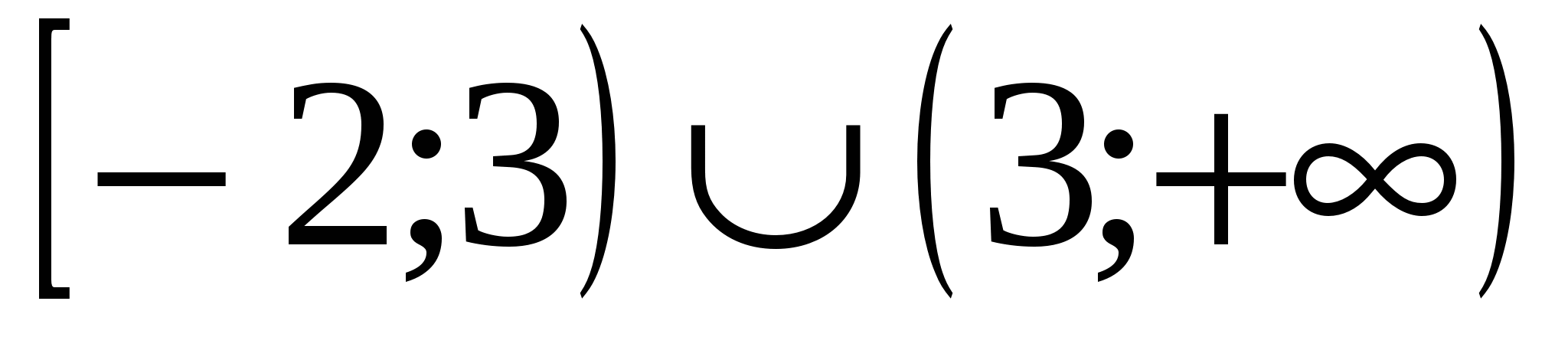
2
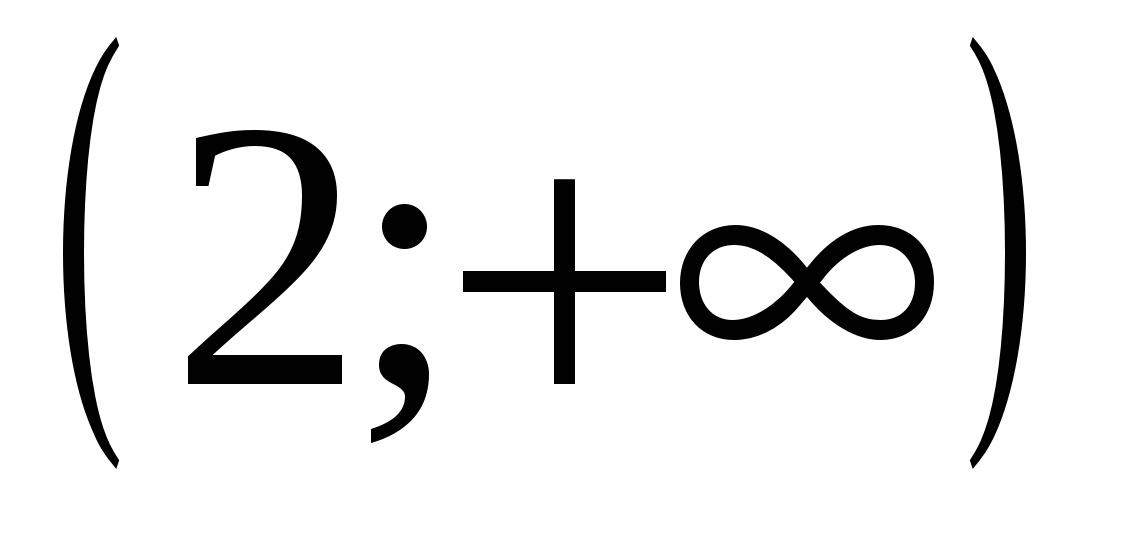
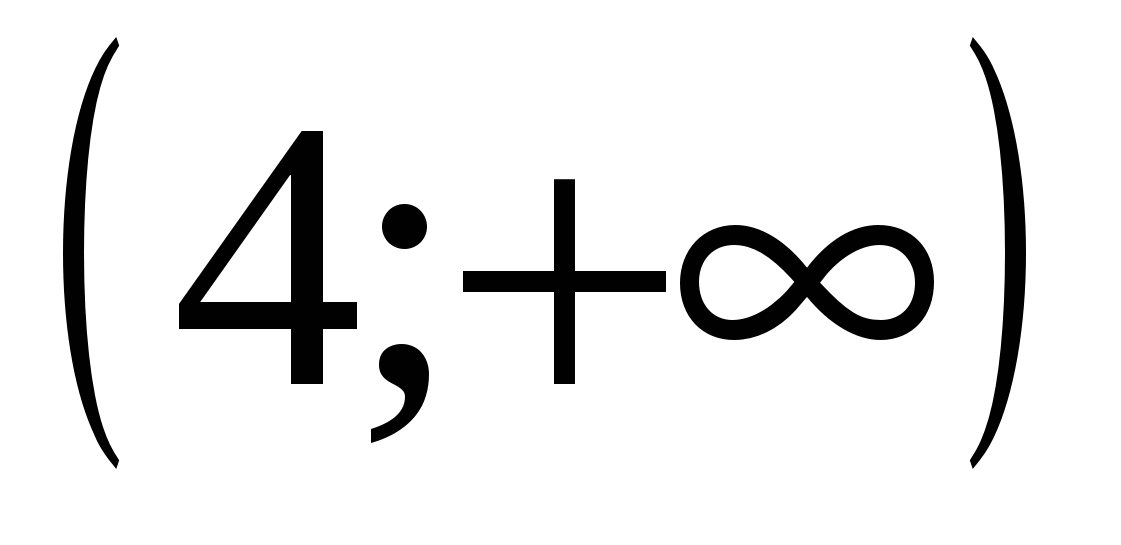
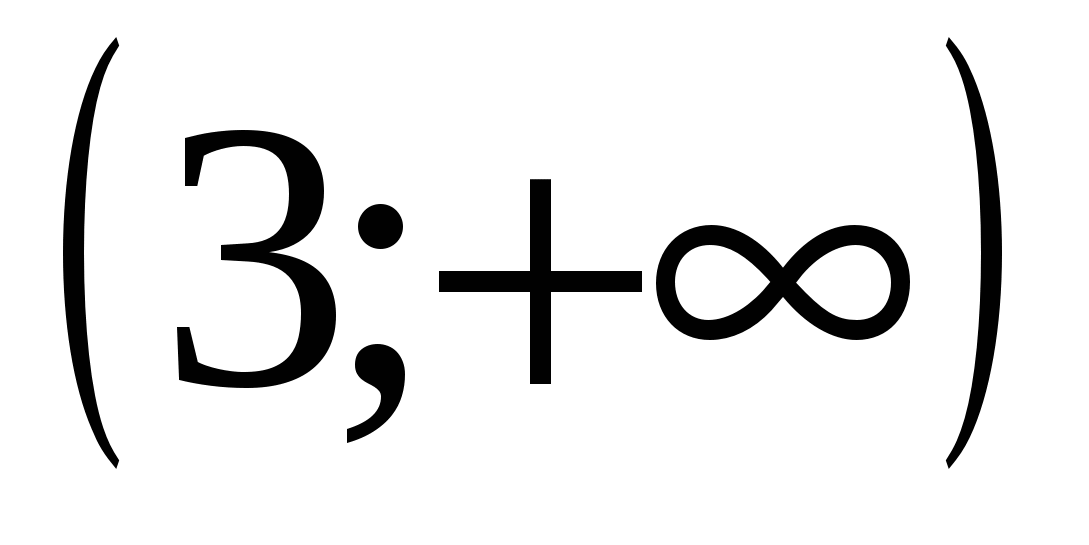
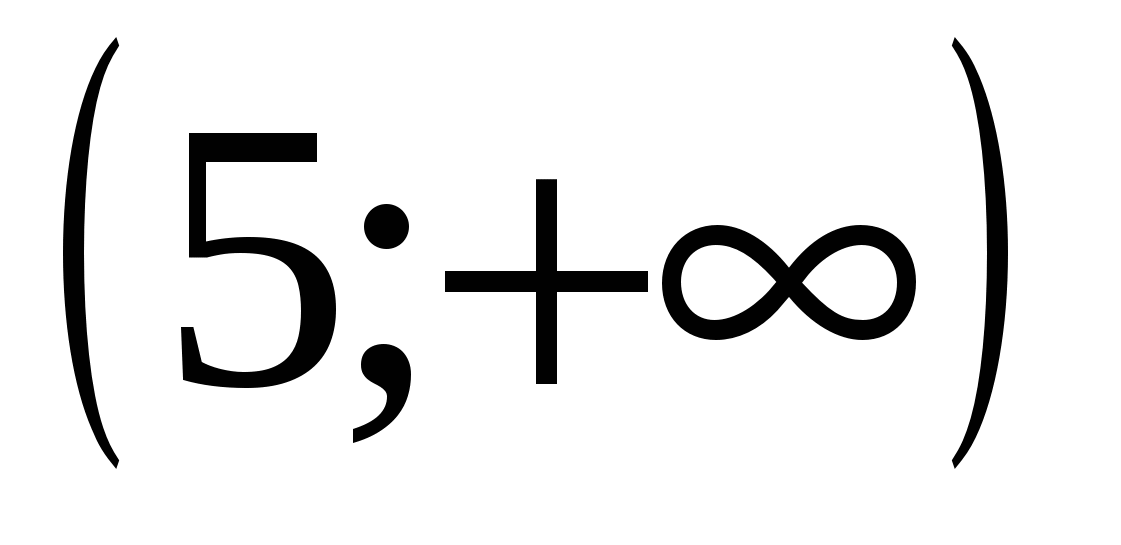
3
-2
1
-2
1
4а)
чётная
нечётная
чётная
нечётная
4б)
нечётная
чётная
нечётная
чётная
5
убывает
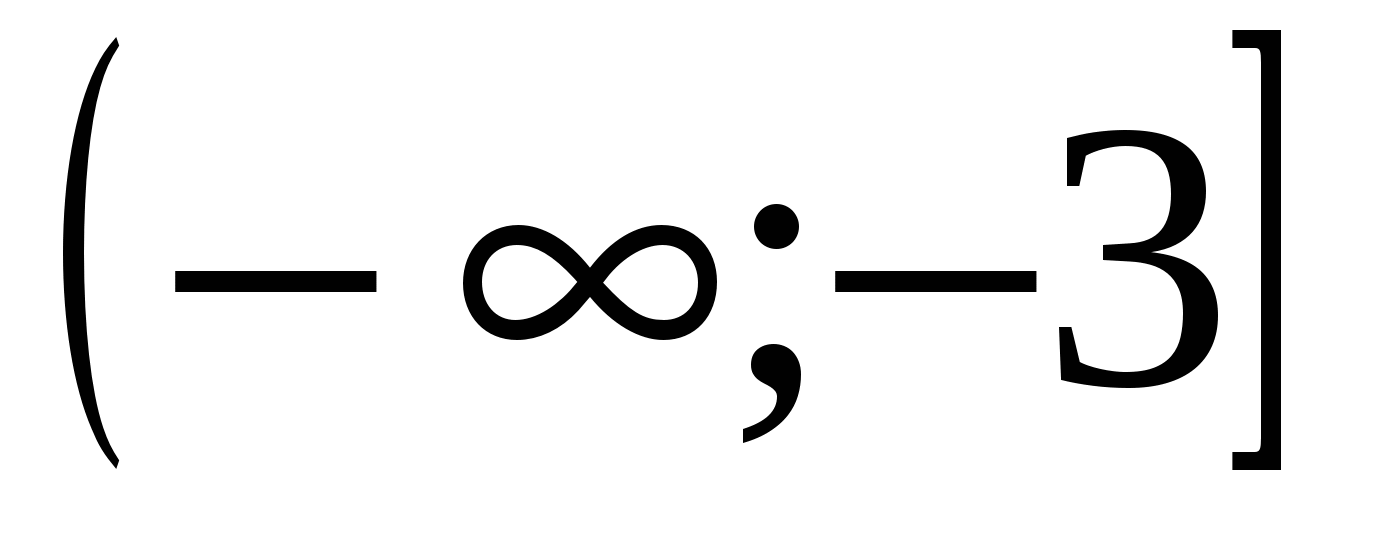
возрастает
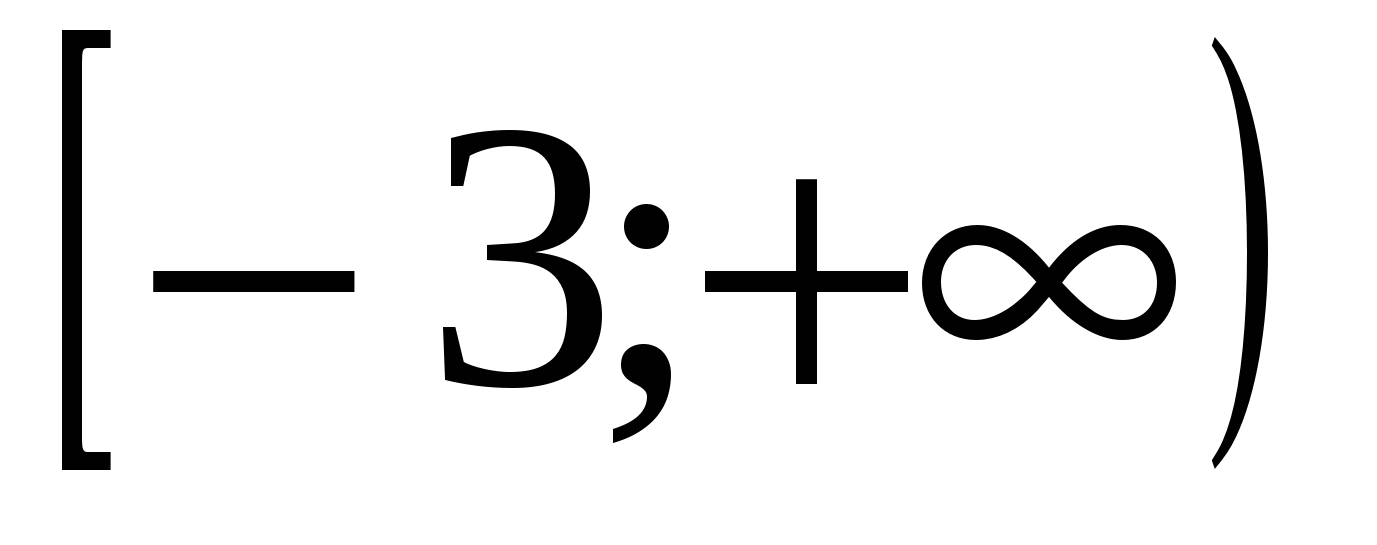
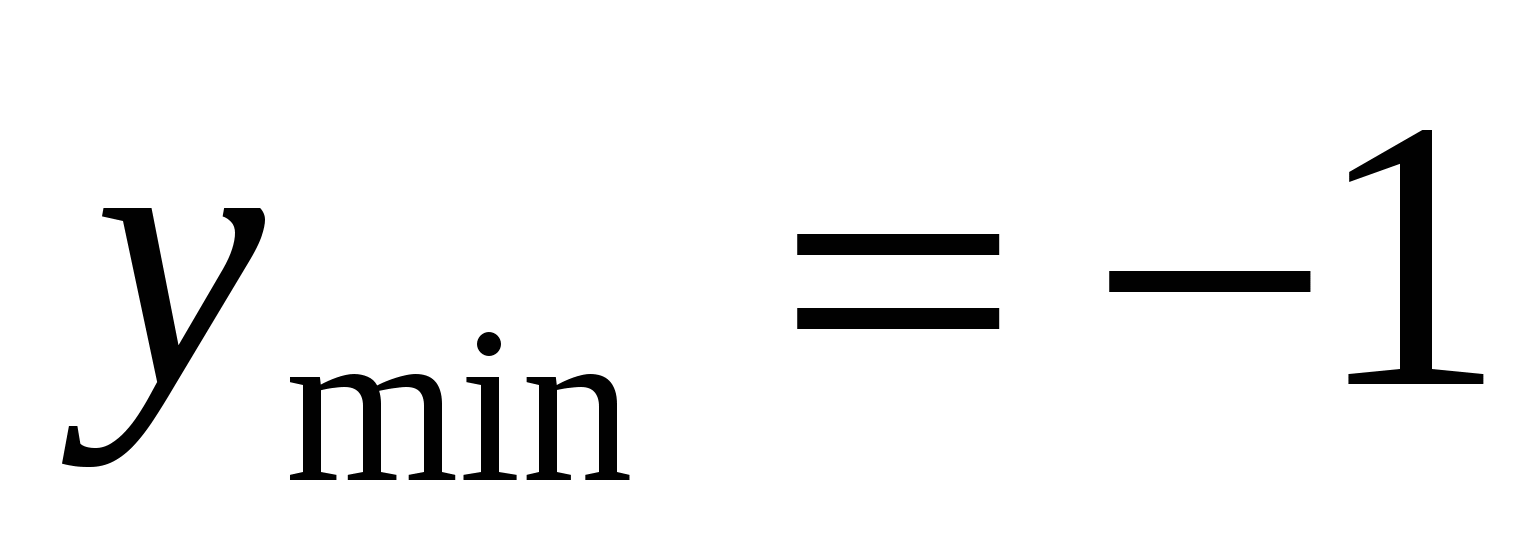
убывает
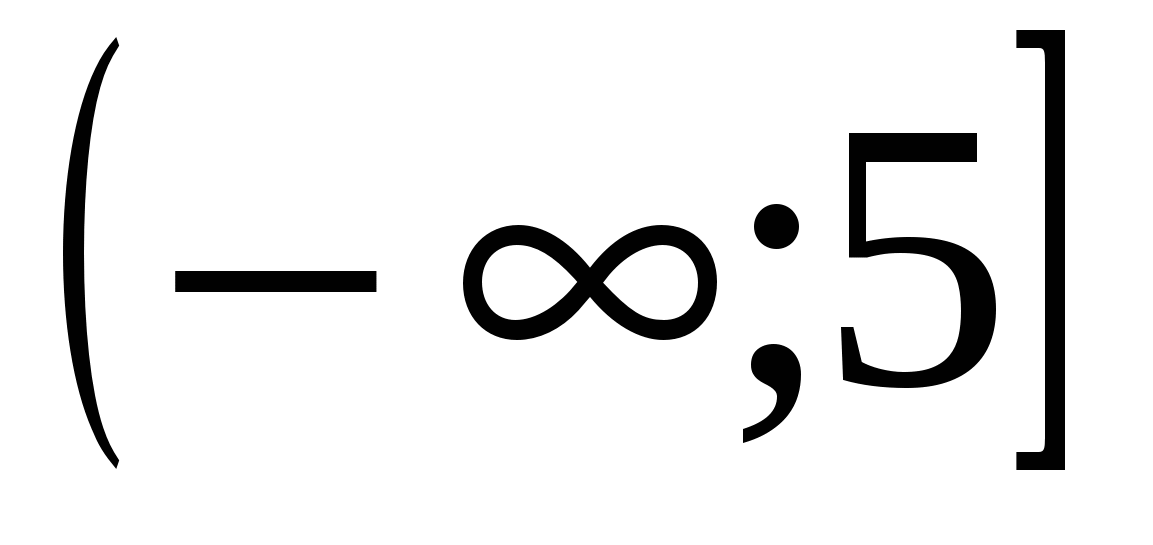
возрастает
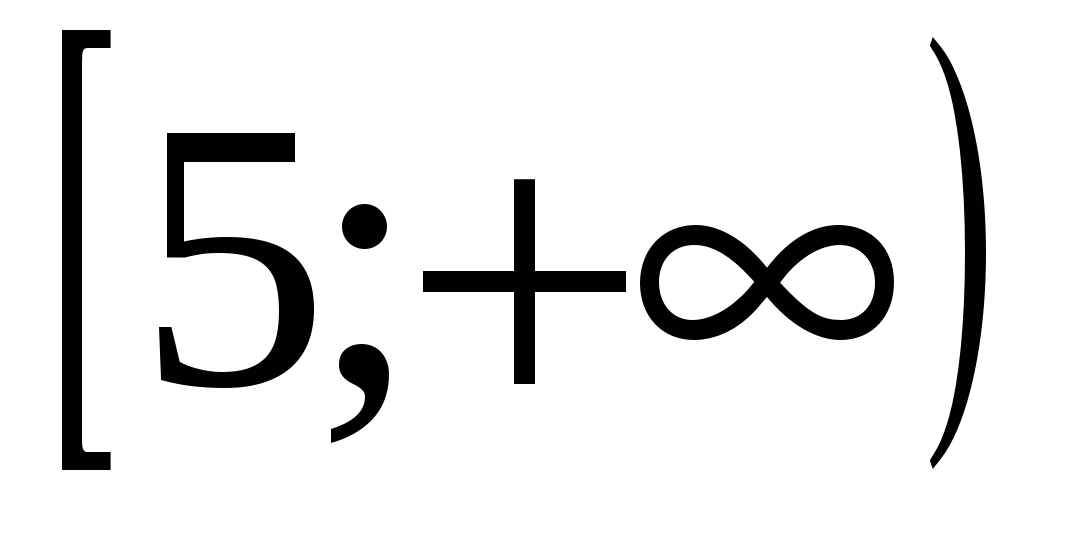
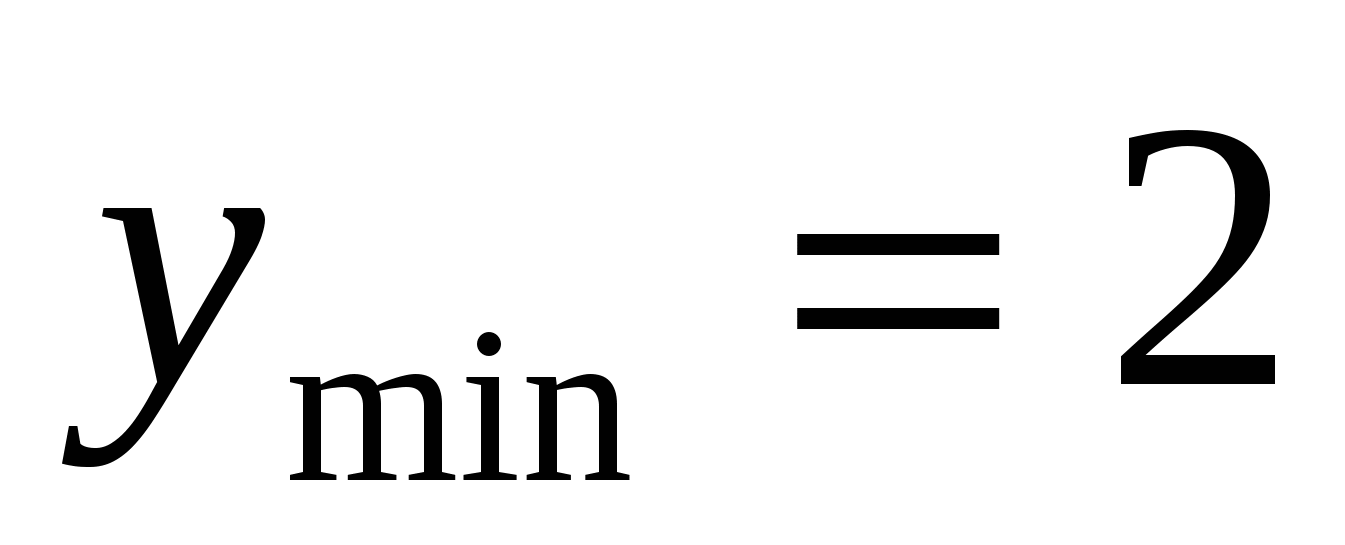
убывает
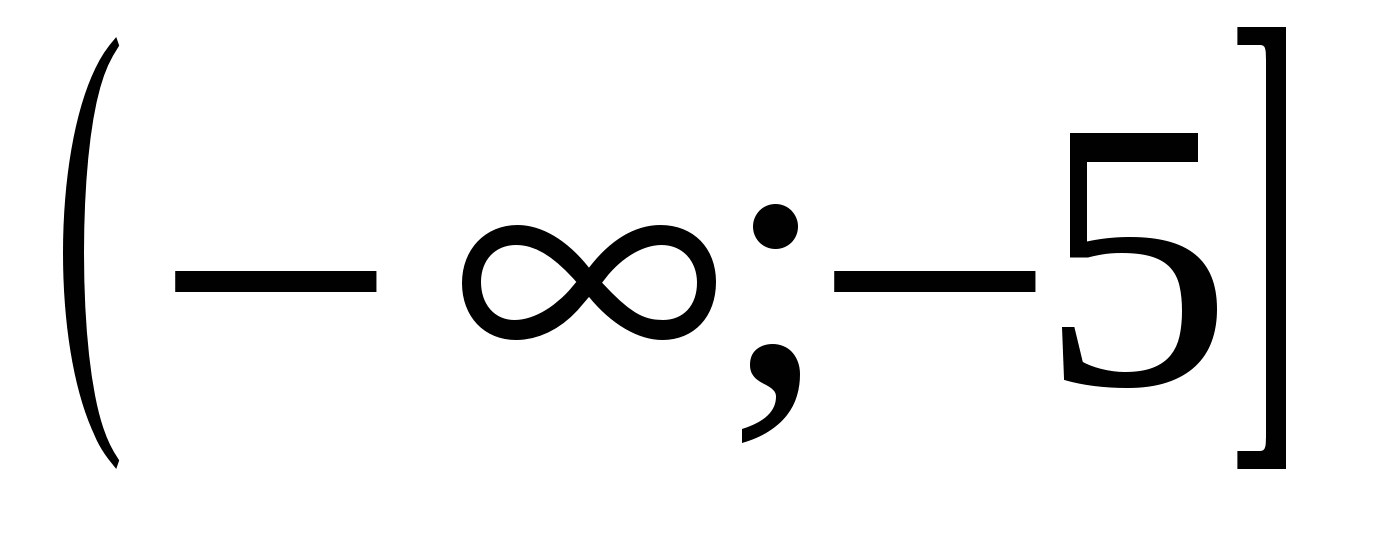
возрастает
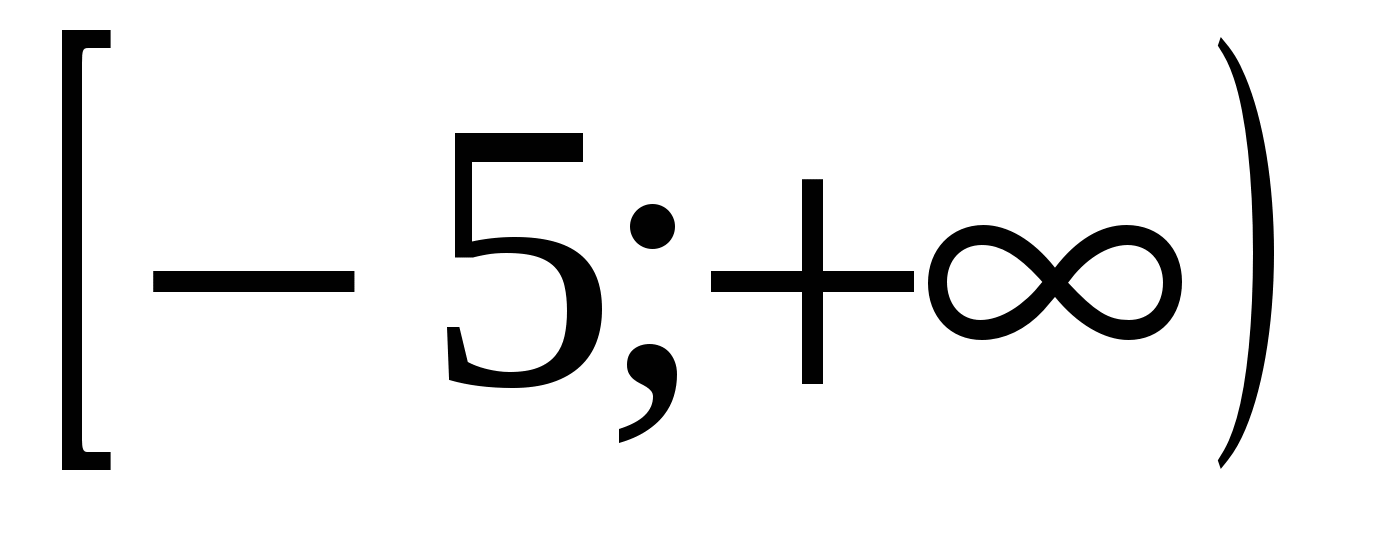
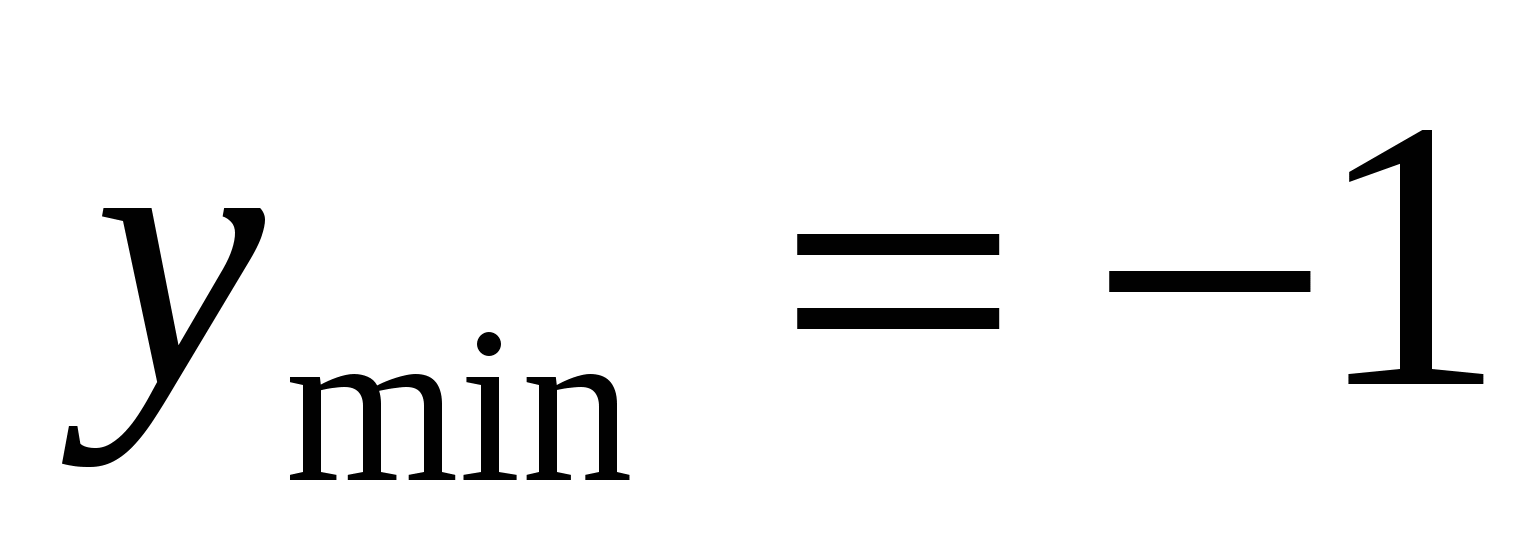
убывает
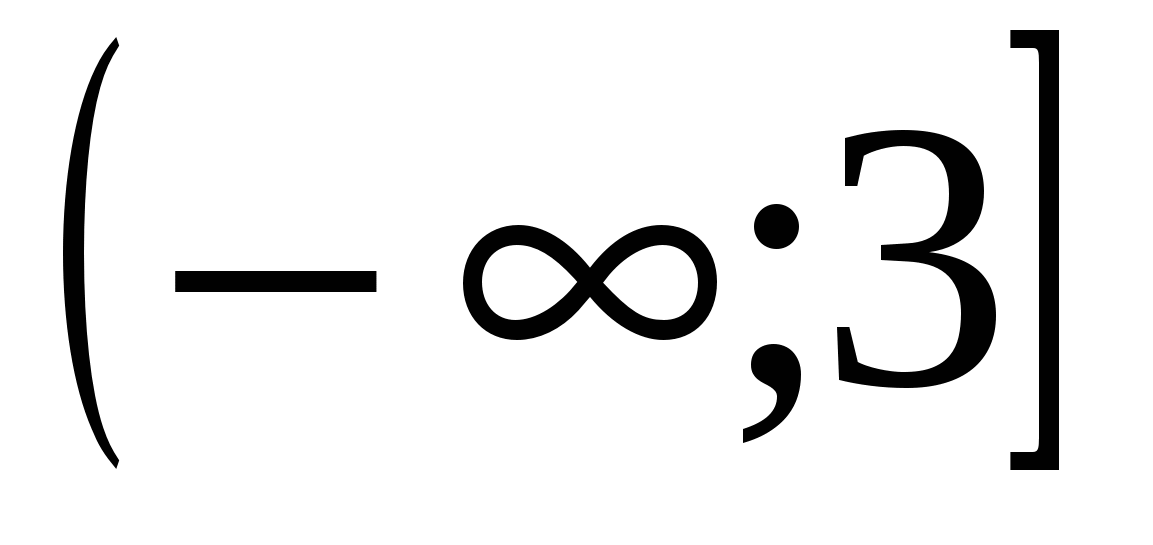
возрастает
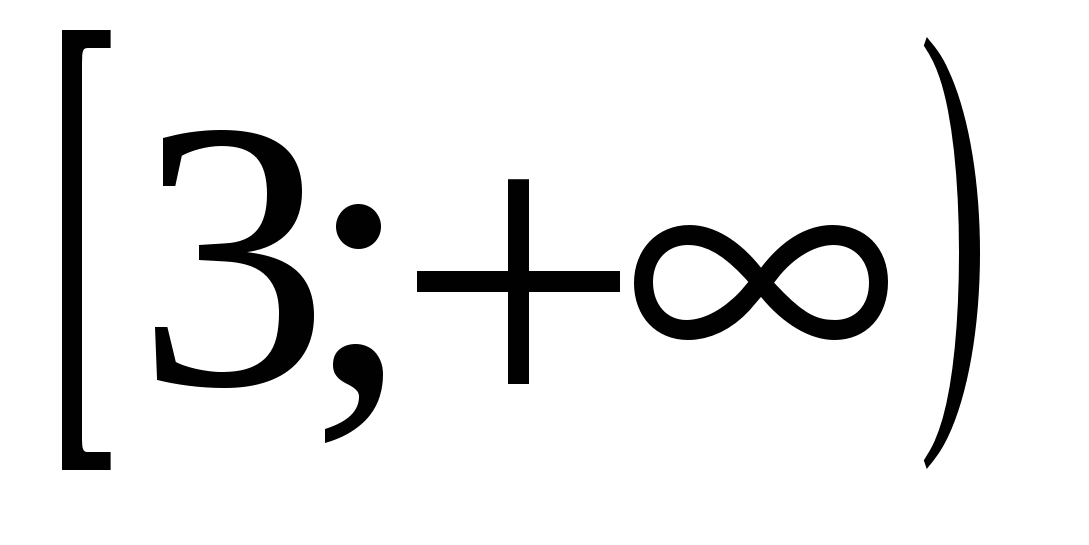
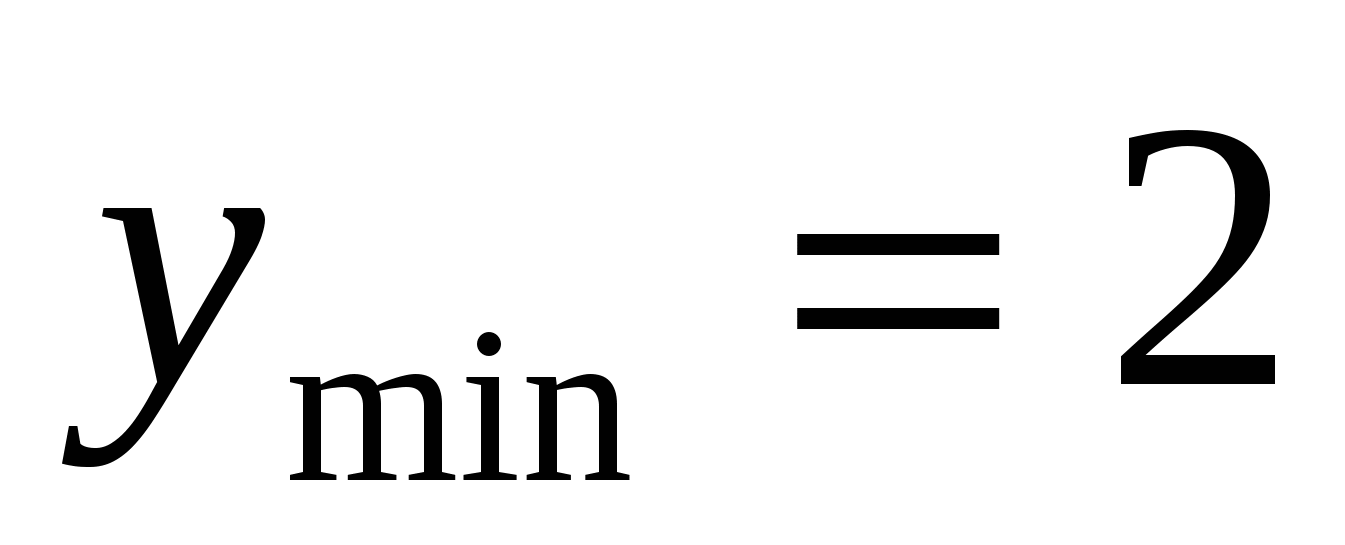
6
, 
,
,
,
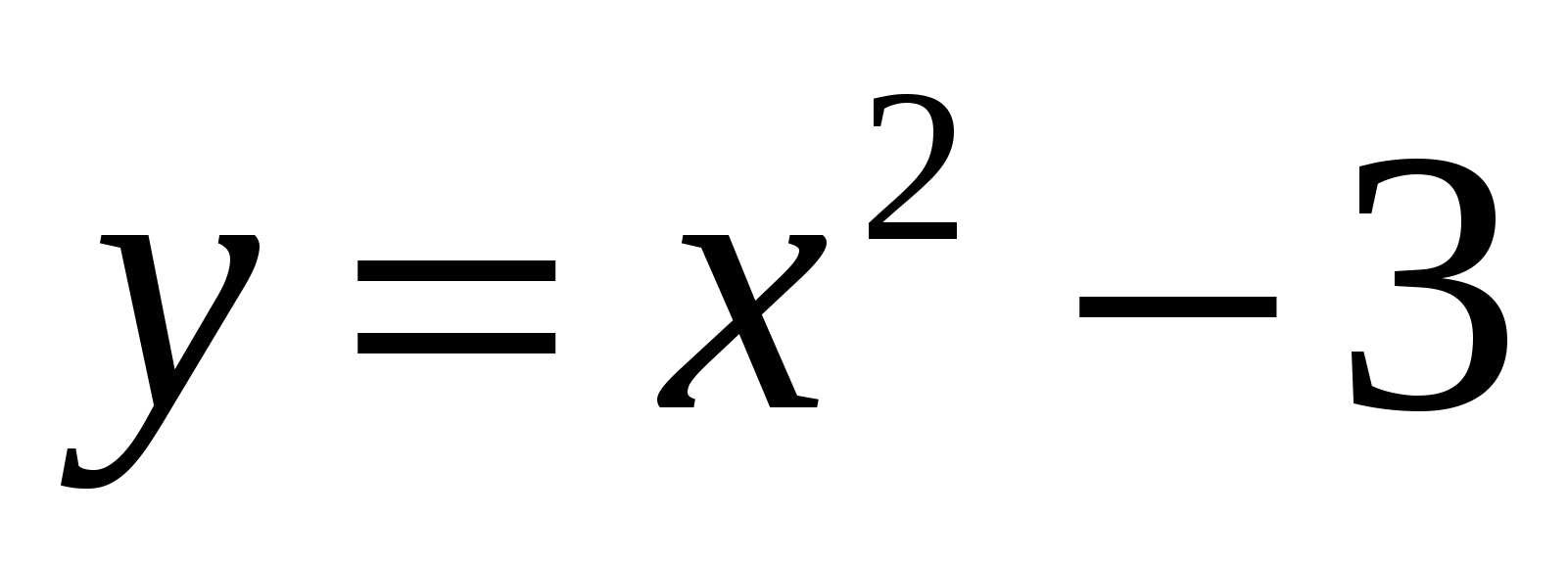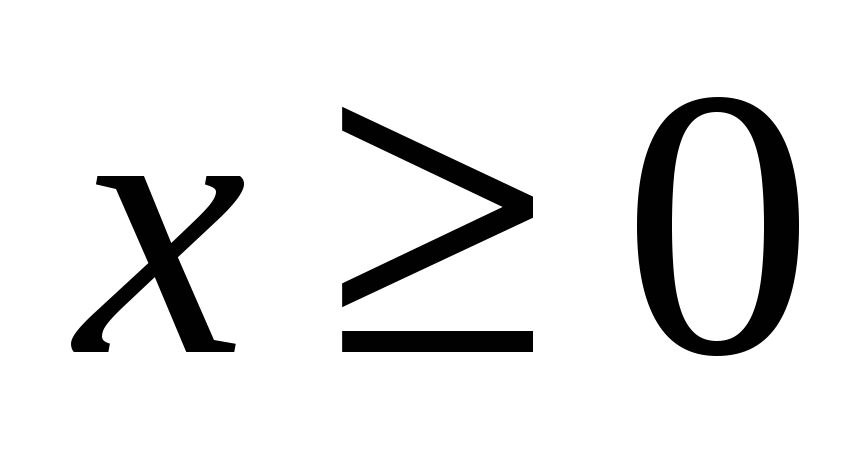
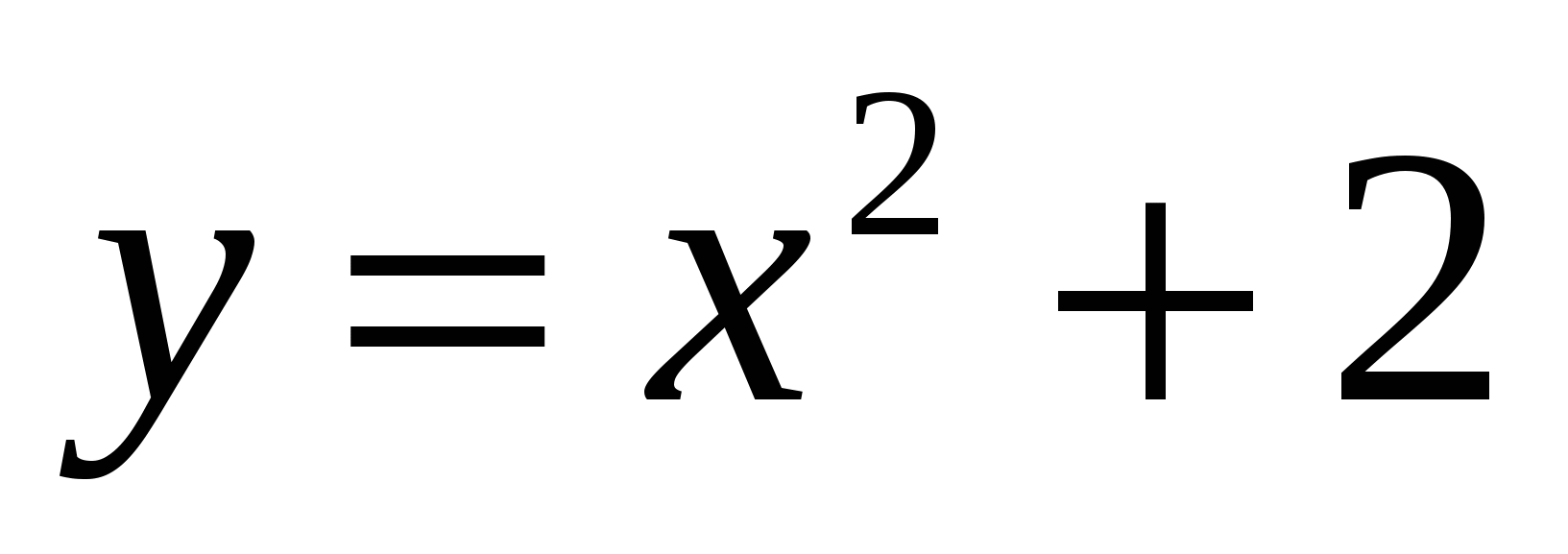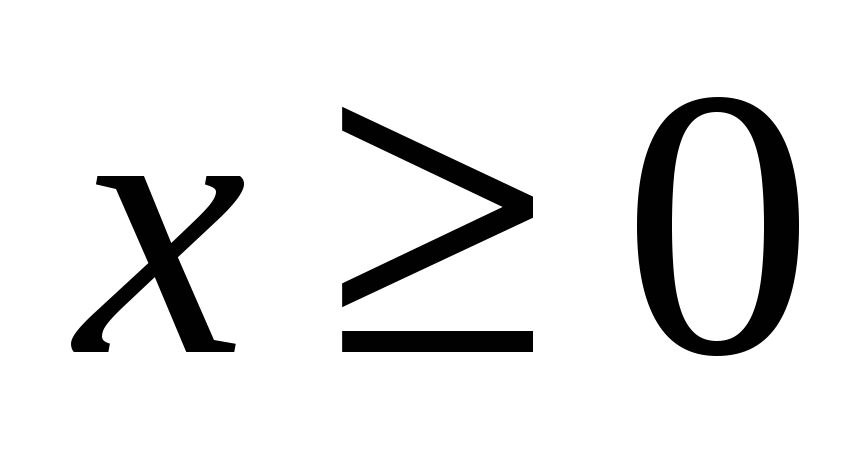
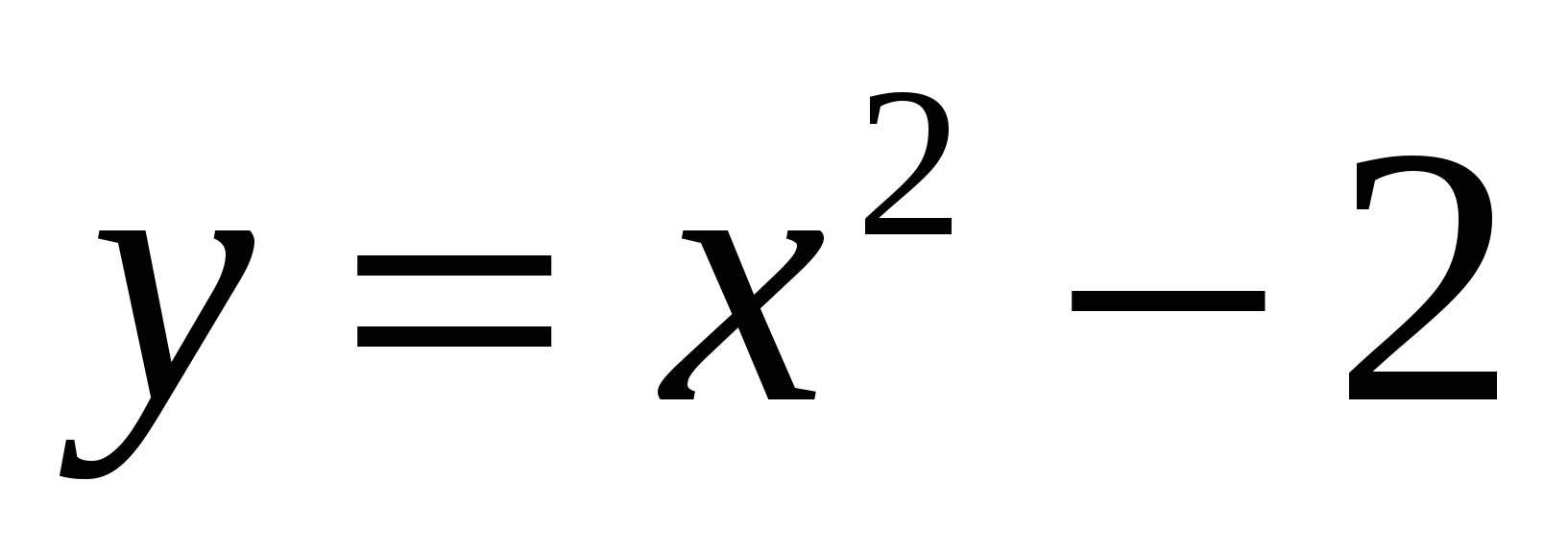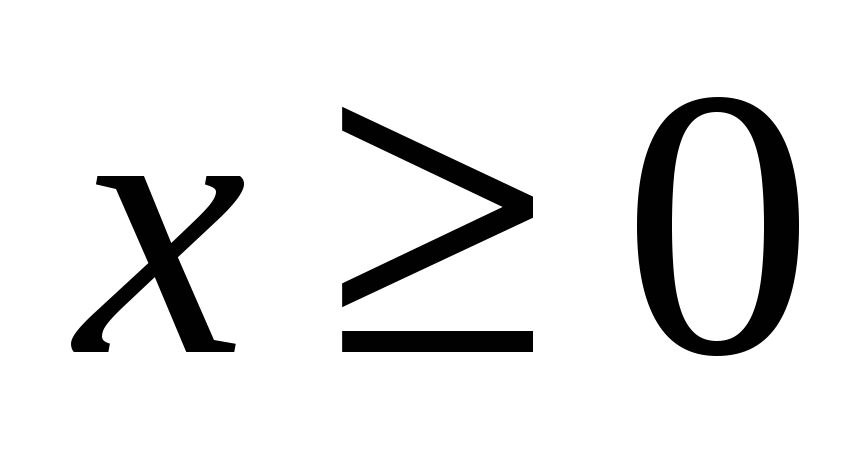
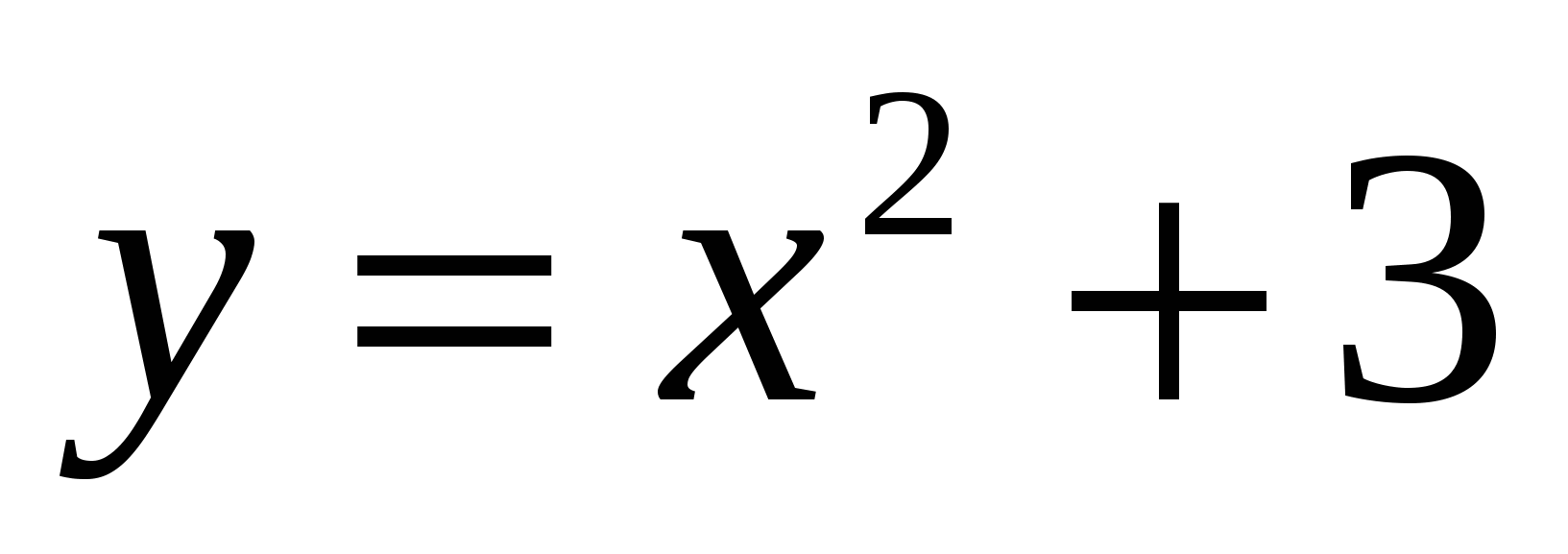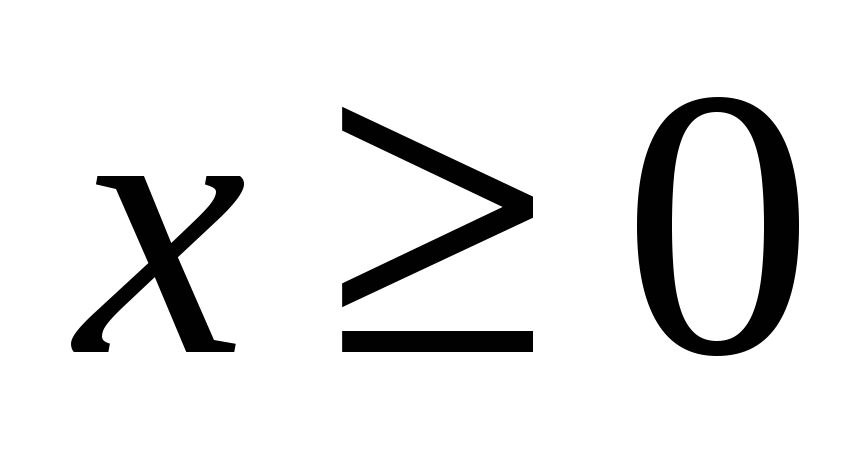
infourok.ru
Контрольная работа №6
Исследование функций
ТЕМА 6. Исследование функций.
Функция, основные свойства.
Наибольшее и наименьшее значение функции, заданной на ограниченном промежутке.
СПИСОК ЛИТЕРАТУРЫ
Бугров Я.С., Никольский С.М. Высшая математика: Учеб.для вузов:в 3т.-5-е изд.,стер.-М.:Дрофа .- (Высшее образование. Современный учебник).т.2. Дифференциальное и интегральное исчисление.-2003.-509 с.
Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. пособие: в 2-х т.- Изд. стер. –М.: Интеграл – Пресс. Т.1. -2001.- 415 с.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Учеб. для вузов: в 3-х томах. – 8-е изд.-М.: Физматлит. т.1 – 2001. -697 с.
Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие. -22-е изд., перераб.- СПб: Профессия, 2003.-432 с.
Кудрявцев Л.Д. Курс математического анализа. Учеб. для вузов: В 3-х томах. – 5-е изд., перераб. и доп. –М.: Дрофа. Т.1. – 2003.-703 с.
Ильин В.А., Позняк Э.Г. Основы математического анализа. Учеб. для вузов в 2-х частях. – 6-е изд. стер. –М. Физматлит, 2002, -646 с.
Данко П.Е. и др. Высшая математика в упражнениях и задачах (с решениями): в 2 ч./ Данко П.Е., Попов А.Г., Кожевникова Т.Я.-6-е изд..-М.: ОНИКС 21 век, ч.2. -2002.-416 с.
Решение типового варианта контрольной работы
Пример 1.
Найти наибольшее и наименьшее значение функции 
на отрезке
Решение. Функция достигает наибольшего и наименьшего значения либо в критических точках, принадлежащих заданному отрезку, либо на концах этого отрезка. Найдем критические точки (т.е. точки в которых производная равна нулю или не существует):
при 
и
Найдем значение функции в этих точках и на концах отрезка
Выберем из предложенных значений наибольшее и наименьшее.
Итак, наибольшее значение функции на заданном отрезке равно 2 и достигается при 
,
, а наименьшее значение равно -18 при
,
Пример 2.
Исследовать функцию 
и построить ее график.
Решение.
Общая схема исследования функций:
Найти область определения функции.
Исследовать поведение функции на концах области определения. Найти точки разрыва функции и ее односторонние пределы в этих точках. Найти вертикальные асимптоты.
Выяснить, является функция четной, нечетной, периодической.
Найти точки пересечения графика функции с осями координат и интервалы знакопостоянства функции.
Найти наклонные асимптоты графика функции.
Найти точки экстремума и интервалы возрастания и убывания функции.
Найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.
Построить схематический график функции, используя все полученные результаты.
1. Функция не определена, если 
Область определения: 
2. Т.к. 
- точка разрыва функции исследуем поведение функции в этой точке слева и справа
Т.к. пределы равны 
значит
точка разрыва второго рода.
Следовательно, прямая 
- вертикальная асимптота.
Проверим функцию на четность, нечетность. Напомним, что функция 
называется четной (нечетной) если выполнены два условия:
Область определения симметрична относительно начала координат
Если 
четная, то график симметричен относительно оси ординат, а для нечетной – относительно начала координат.
Функция не является ни четной, ни нечетной, т.е. общего вида.
Функция не является периодической
4. Найдем точки пересечения графика функции с осями координат
Найдем промежутки знакопостоянства функции
5. Найдем наклонные асимптоты 
где
Для 
k и b вычисляются аналогично
6. Найдем точки экстремума функции и промежутки монотонности.
Возрастание и убывание функции 
характеризуется знаком ее производной
: если в некотором интервале
, то в этом интервале функция возрастает, а если
, то функция убывает в этом интервале.
Функция 
может иметь экстремум только в тех точках, которые принадлежат области определения и в которых ее производная равна нулю или не существует. Если
меняет знак с “+” на “-” при переходе через исследуемую точку, то эта точка максимума, если
меняет знак с “-” на “+” при переходе через исследуемую точку, то эта точка является точкой минимума. Если
не меняет знак при переходе через точку
, в этой точке экстремума нет.
Найдем все точки из области определения функции 
, в которых производная
обращается в ноль или не существует.
Составим таблицу
|
|
| -2 |
| 1 |
| 7 |
|
|
| + | 0 | + | не существует | - | 0 | + |
|
|
| 0 |
| не существует |
|
|
|
| возрастает | возрастает | убывает | min | возрастает |
Функция возрастает на интервалах 
,
,
и убывает на интервале
. Точка
есть точка минимума
7. Найдем точки перегиба и промежутки выпуклости и вогнутости функции
Напомним, что график функции 
называется выпуклым на интервале
, если в каждой точке этого интервала график лежит ниже любой своей касательной. График функции
называется вогнутым на интервале
, если в каждой точке этого интервала график лежит выше любой своей касательной.
Точки, в которых функция меняет выпуклость на вогнутость или наоборот, называются точками перегиба.
Перегиб возможен в точках, в которых 
равна нулю или не существует. Если
на интервале
, то график функции является выпуклым
на этом интервале, если же
, то на интервале
график вогнутый
.
Найдем точки перегиба 
Составим таблицу
|
|
| -2 |
| 1 |
|
|
| - | 0 | + | не существует | + |
|
|
| 0 |
| не существует |
|
Точка 
- точка перегиба.
Дополнительные точки:
8. Построим график функции, используя результаты исследования.
Замечание:
При построении графика масштабы по оси OX и OY могут не совпадать.
Вариант 1
1. Найти наибольшее и наименьшее значение функции на отрезке:
2. Исследовать функцию и построить ее график:
Вариант 2
1. Найти наибольшее и наименьшее значение функции на отрезке: 
2. Исследовать функцию и построить ее график:
Вариант 3
1. Найти наибольшее и наименьшее значение функции на отрезке: 
2. Исследовать функцию и построить ее график:
Вариант 4
1. Найти наибольшее и наименьшее значение функции на отрезке: 
2. Исследовать функцию и построить ее график:
Вариант 5
1. Найти наибольшее и наименьшее значение функции на отрезке: 
2. Исследовать функцию и построить ее график:
Вариант 6
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 7
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 8
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 9
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 10
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 11
1. Найти наибольшее и наименьшее значение функции на отрезке:
; 
2. Исследовать функцию и построить ее график:
Вариант 12
1. Найти наибольшее и наименьшее значение функции на отрезке:
; 
2. Исследовать функцию и построить ее график:
Вариант 13
1. Найти наибольшее и наименьшее значение функции на отрезке:
; 
2. Исследовать функцию и построить ее график:
Вариант 14
1. Найти наибольшее и наименьшее значение функции на отрезке:
; 
2. Исследовать функцию и построить ее график:
Вариант 15
1. Найти наибольшее и наименьшее значение функции на отрезке:
; 
2. Исследовать функцию и построить ее график:
Вариант 16
1. Найти наибольшее и наименьшее значение функции на отрезке:
; 
2. Исследовать функцию и построить ее график:
Вариант 17
1. Найти наибольшее и наименьшее значение функции на отрезке:
; 
2. Исследовать функцию и построить ее график:
Вариант 18
1. Найти наибольшее и наименьшее значение функции на отрезке:
; 
2. Исследовать функцию и построить ее график:
Вариант 19
1. Найти наибольшее и наименьшее значение функции на отрезке:
; 
2. Исследовать функцию и построить ее график:
Вариант 20
1. Найти наибольшее и наименьшее значение функции на отрезке:
;
2. Исследовать функцию и построить ее график:
Вариант 21
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 22
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 23
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 24
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 25
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 26
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 27
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 28
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 29
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
Вариант 30
Найти наибольшее и наименьшее значение функции на отрезке: 
Исследовать функцию и построить ее график: 
studfiles.net
Контрольная работа по алгебре.
« Функция»
Вариант 1.
1. Постройте график функции, если её область определения [-5;4], значения функции составляют отрезок [-3;5]. Функция убывает на [-5;-1] и [2;4], а возрастает на [-1;2].
Нулями функции являются точки -2 и 1.
2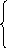
. Постройте график функции: 
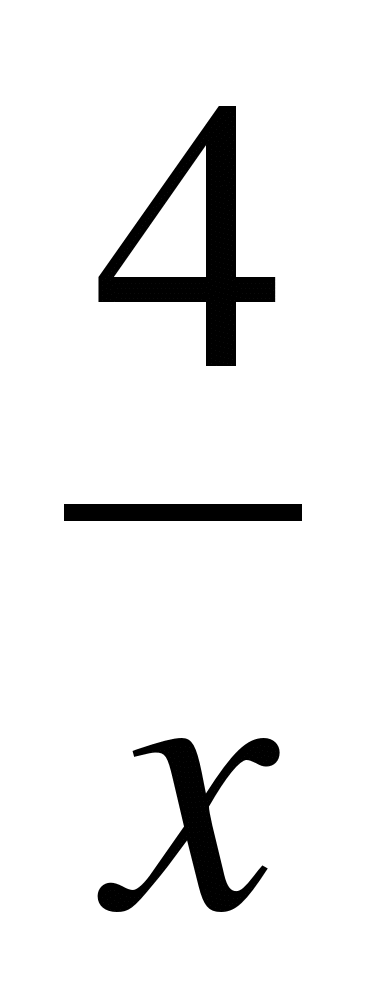, при х 
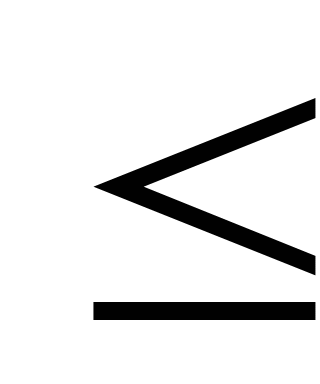-2 ;
f(x)= х, при -2< х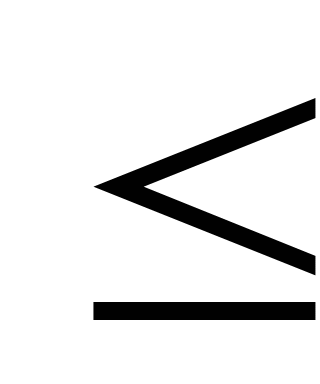 3 ;
-2(х-4)2 +5, при х > 3 .
Исследуйте эту функцию по графику, используя план:
Область определения;Область значения;
Нули функции;
Промежутки знакопостоянства;
Промежутки монотонности;
Наибольшее и наименьшее значение функции.
Характеристика функции.
3. Исследуйте функцию на чётность (нечётность):
а) f(x) =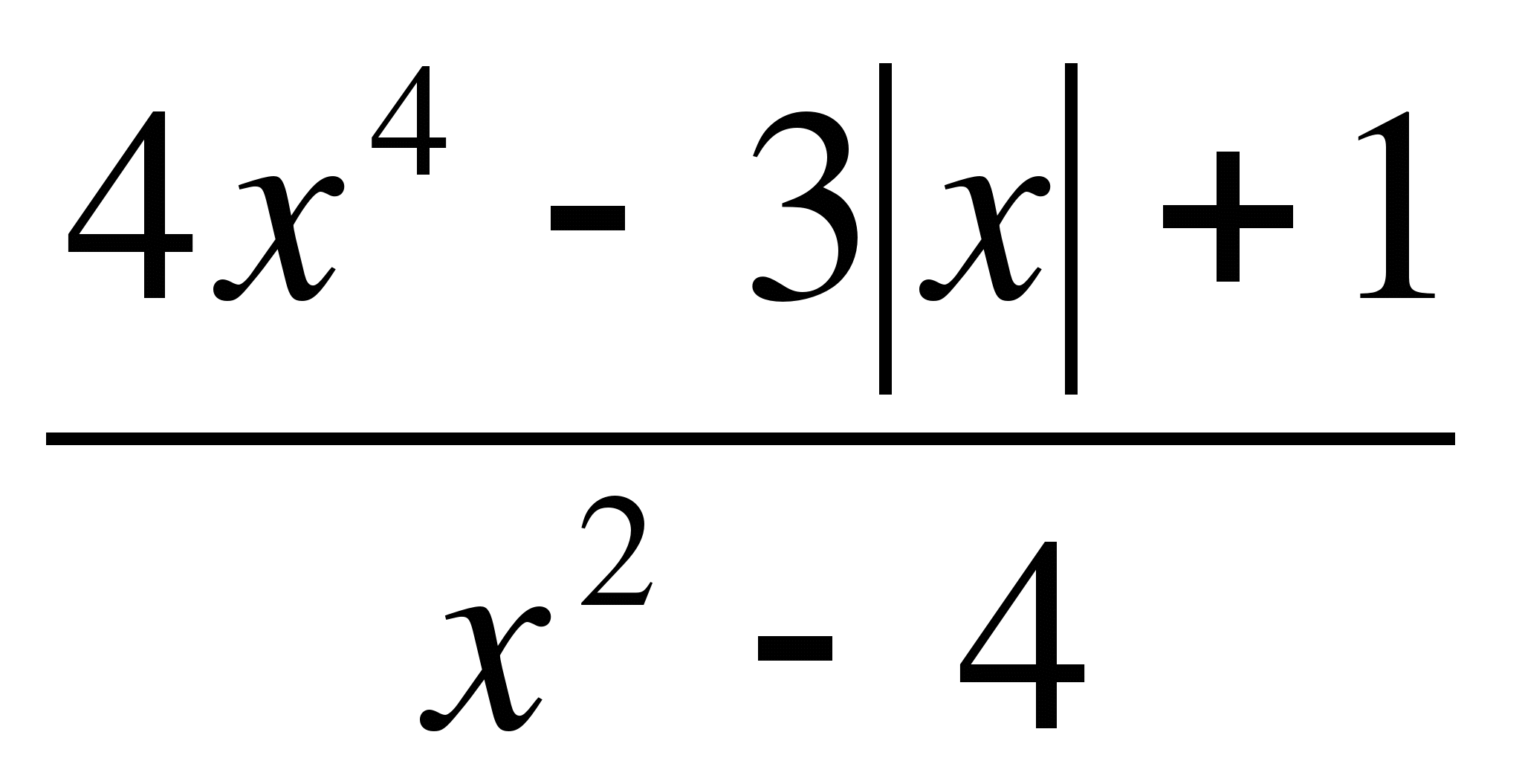 
; б) f(x) =
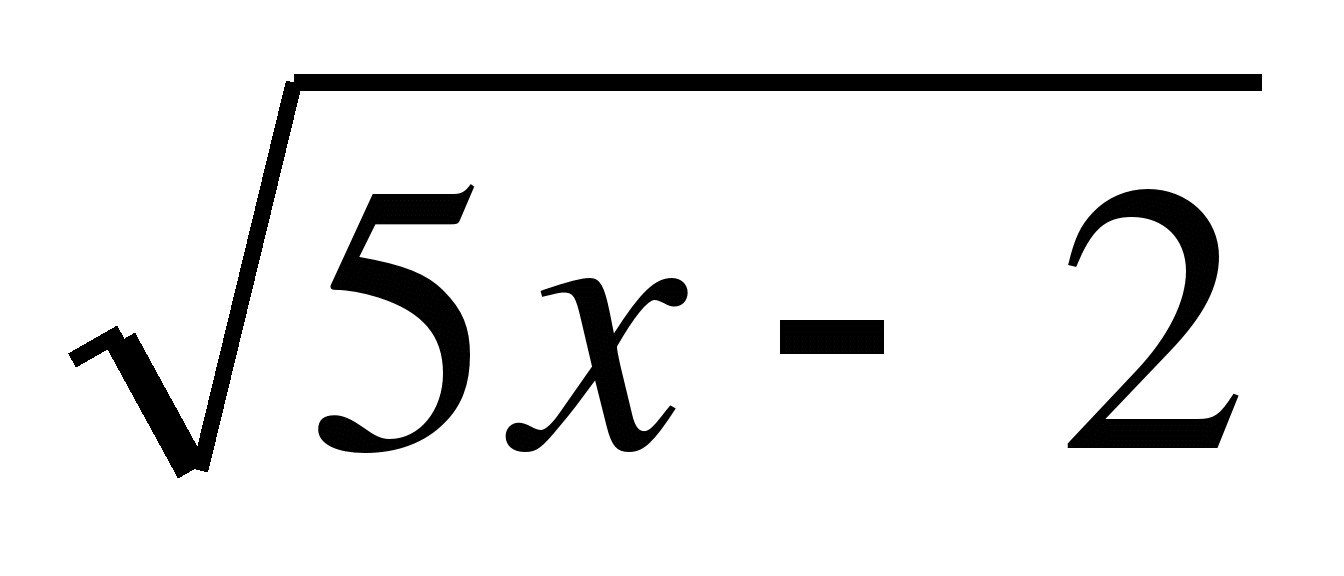; в) f(x) = 
.
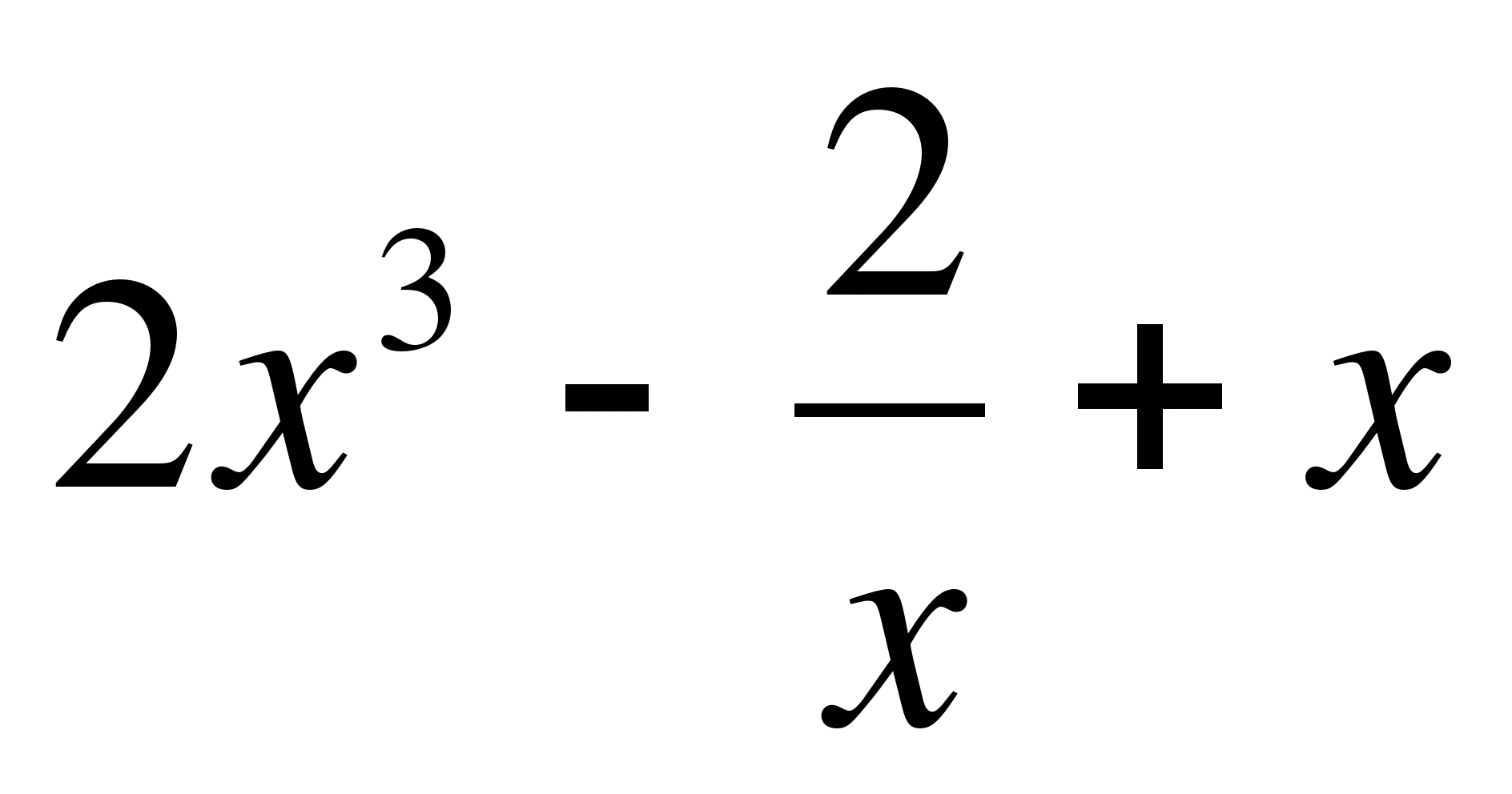4. Функция у=f(x) является чётной и при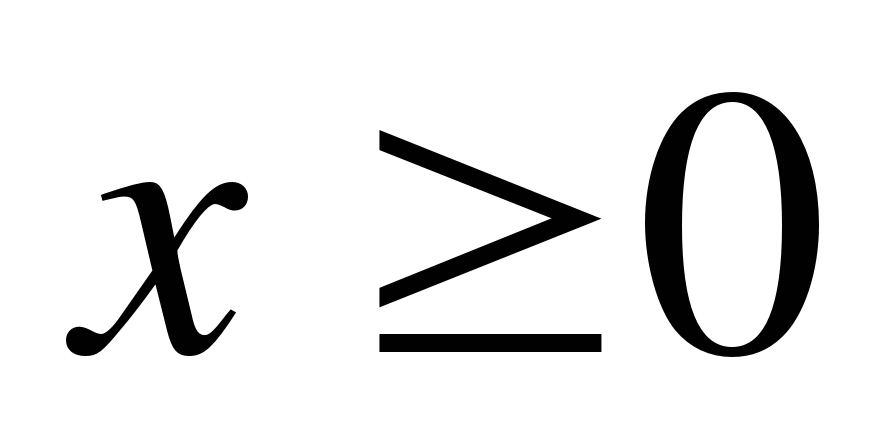 
совпадает с функцией у=2
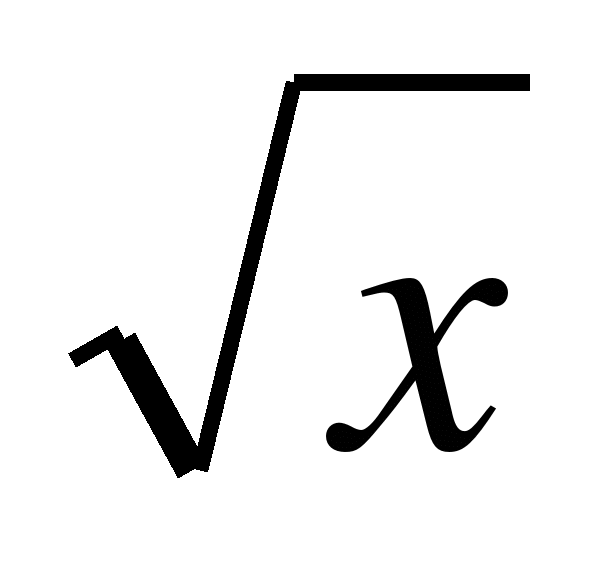. Постройте график этой функции.
5. Используя движение графика в системы координат, постройте график функции
f(x) =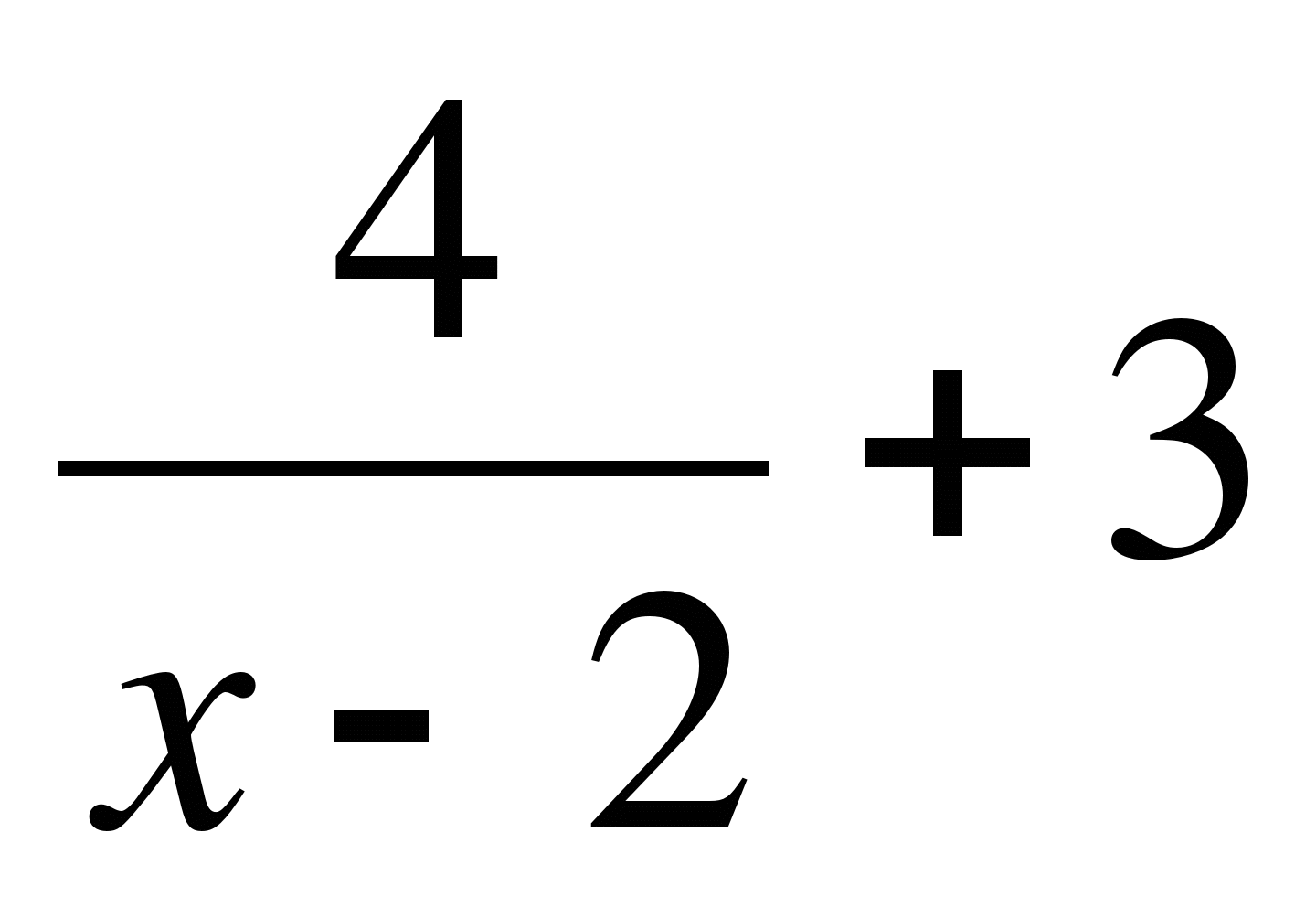
Используя график, дайте краткую характеристику функции по плану:
1. Непрерывность; ( если есть асимптоты, то укажите их уравнения)
2. Монотонность;
3. Ограниченность;
4. Чётность ( нечётность).
6. Проведите аналитическое исследование функции у =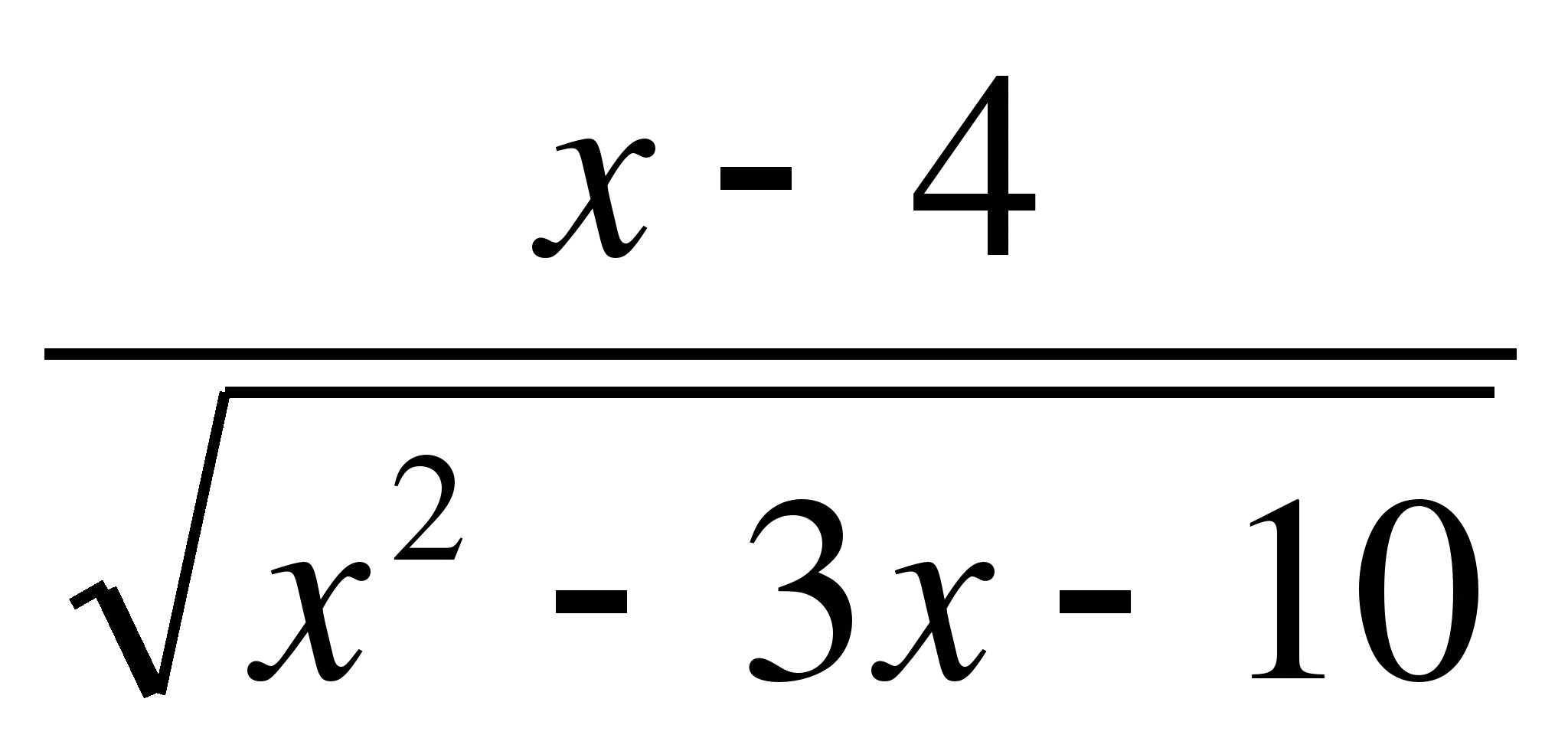 
, ответив на вопросы: 1) Dy; 2) Нули функции; 3) Промежутки знакопостоянства функции.
7
. Найдите аналитически область значения функции у= -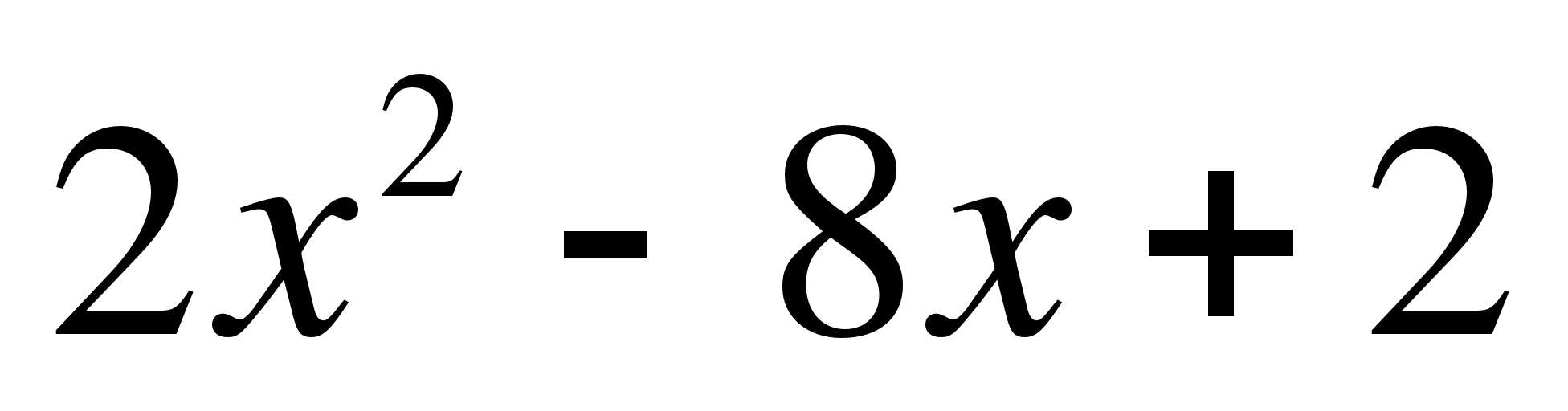
.
Постройте график функции а) f (x) =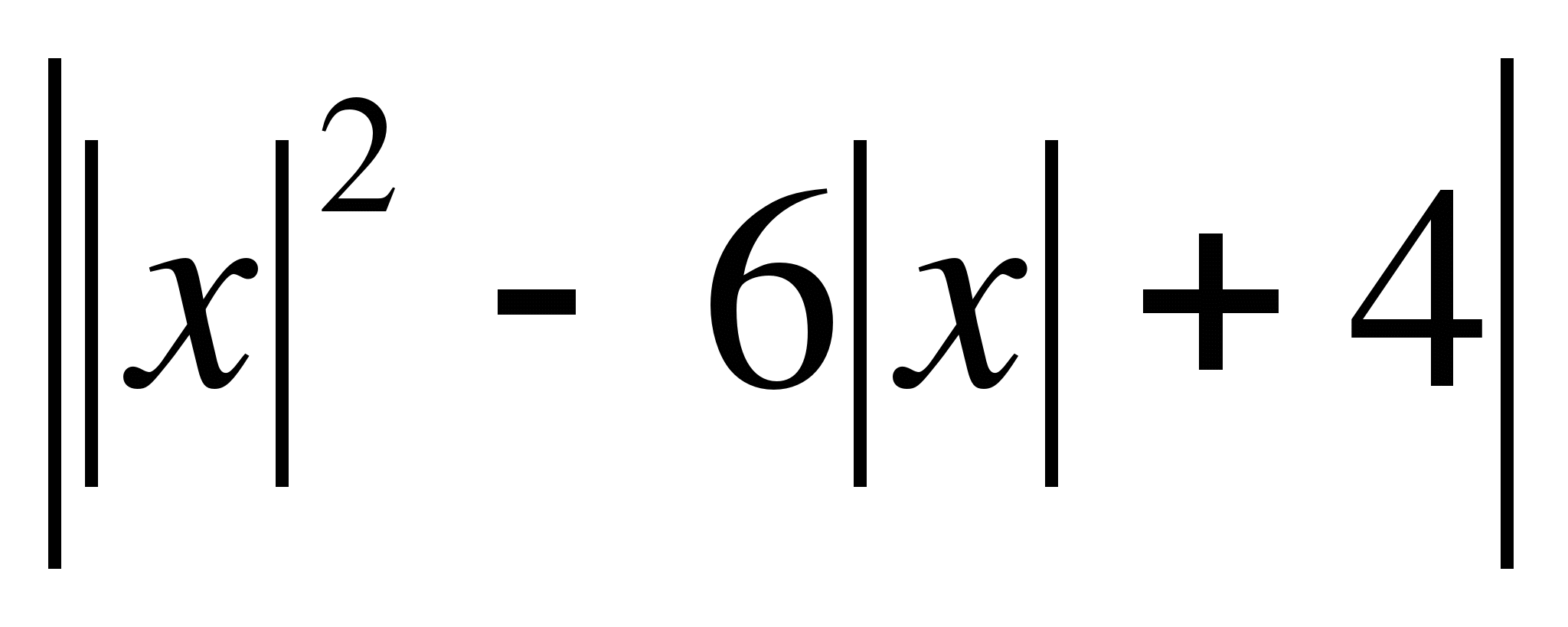 
; б)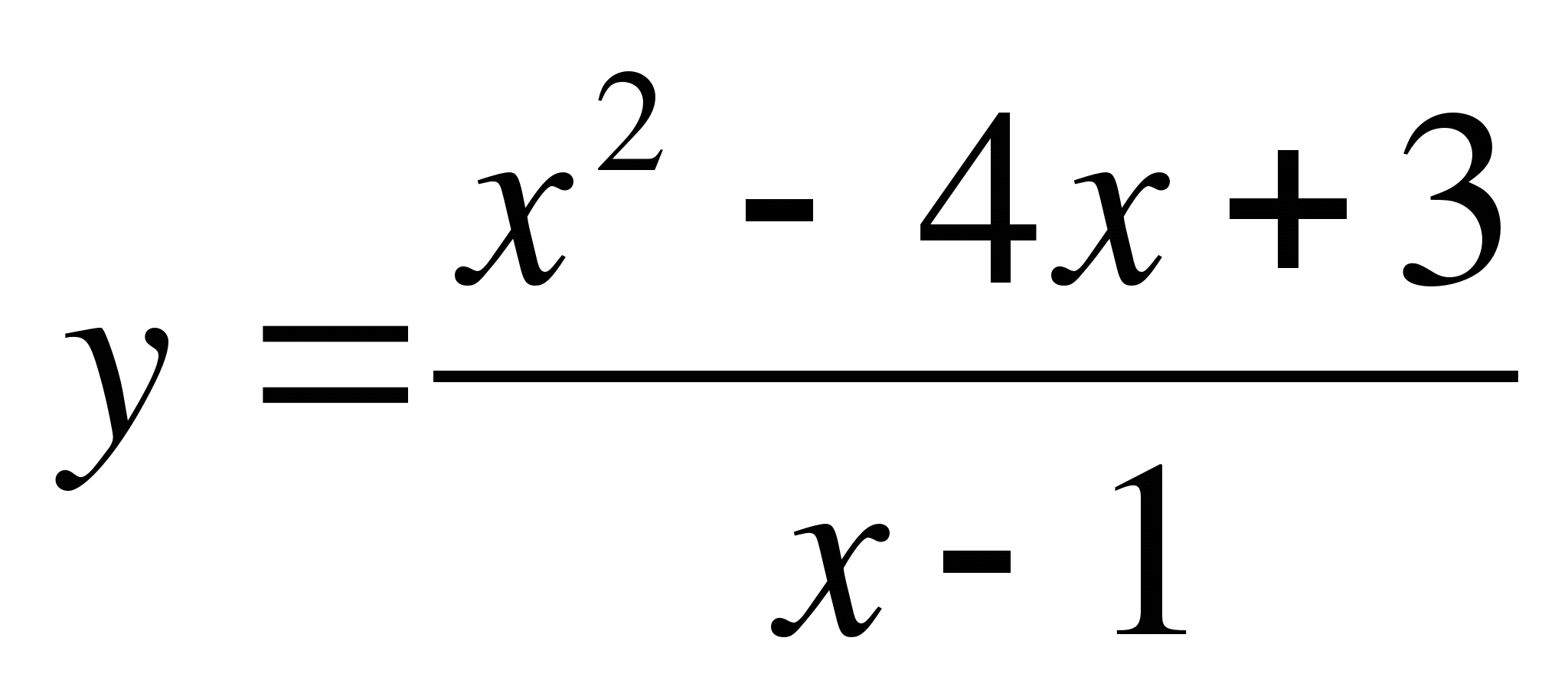 
.
Контрольная работа по алгебре.
« Функция»
Вариант 2
1. Постройте график функции, если её область определения [-3;4], значения функции составляют отрезок [-3;5]. Функция возрастает на [-3;-1] и [2;4], а убывает на [-1;2].
Н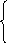
улями функции являются точки с абсциссами -2 и 2.
2. Постройте график функции: f(x)=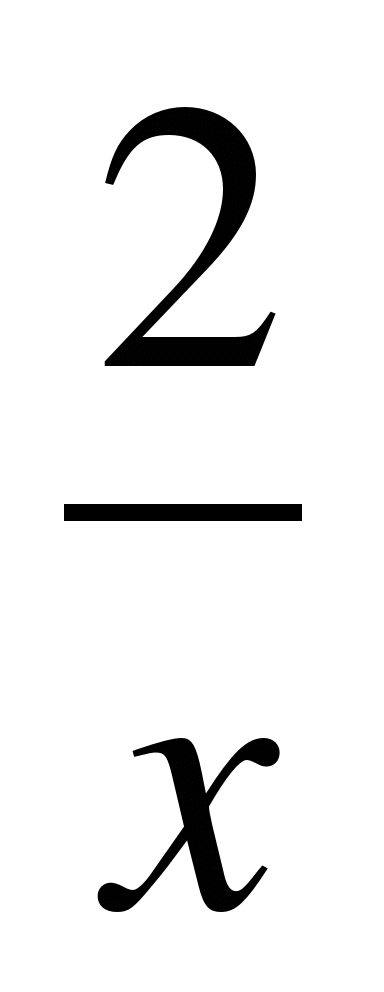 
, при х 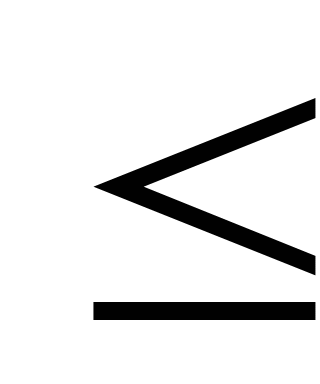-1 ;
х-1, при х > -1
Исследуйте эту функцию по графику, используя план:
1.Область определения;Область значения;
Нули функции;
Промежутки знакопостоянства;
Промежутки монотонности;
Наибольшее и наименьшее значение функции.
Характеристика функции.
3. Исследуйте функцию на чётность (нечётность):
а) f(x) =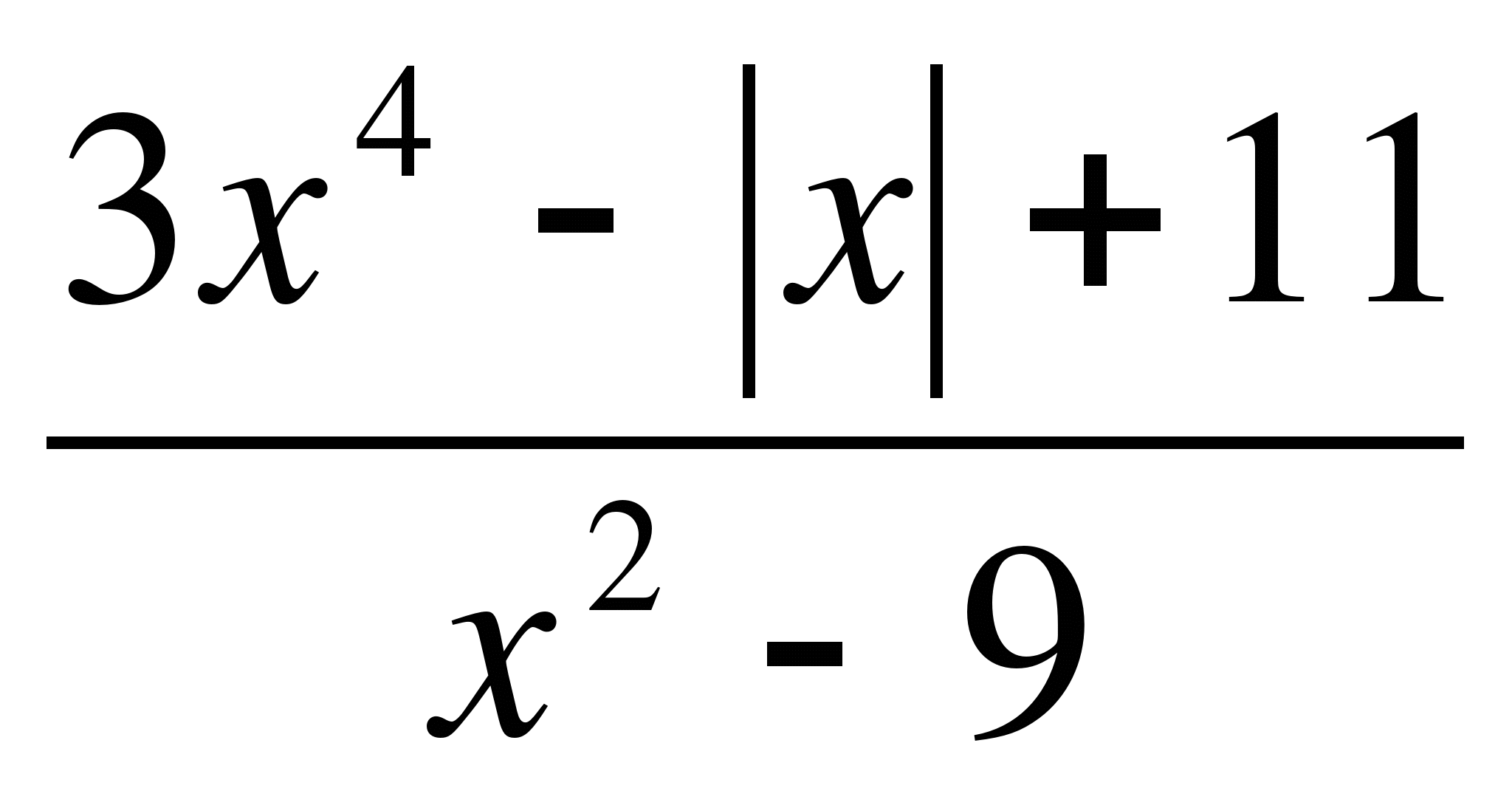 
; б) f(x) =
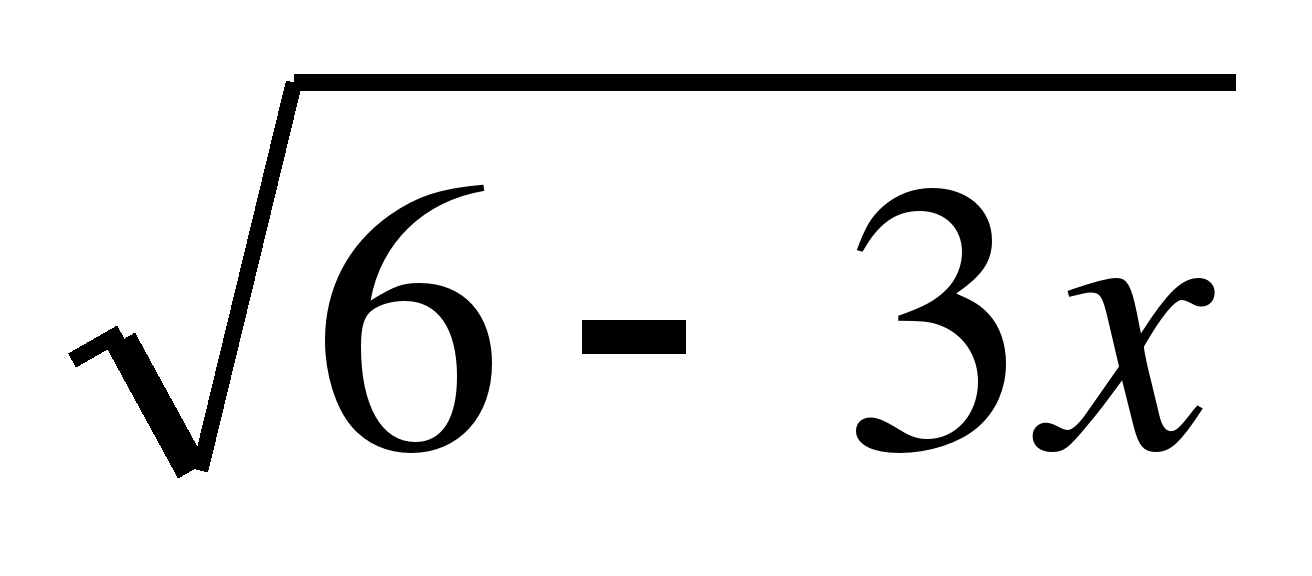; в) f(x) = 4x3 -
.
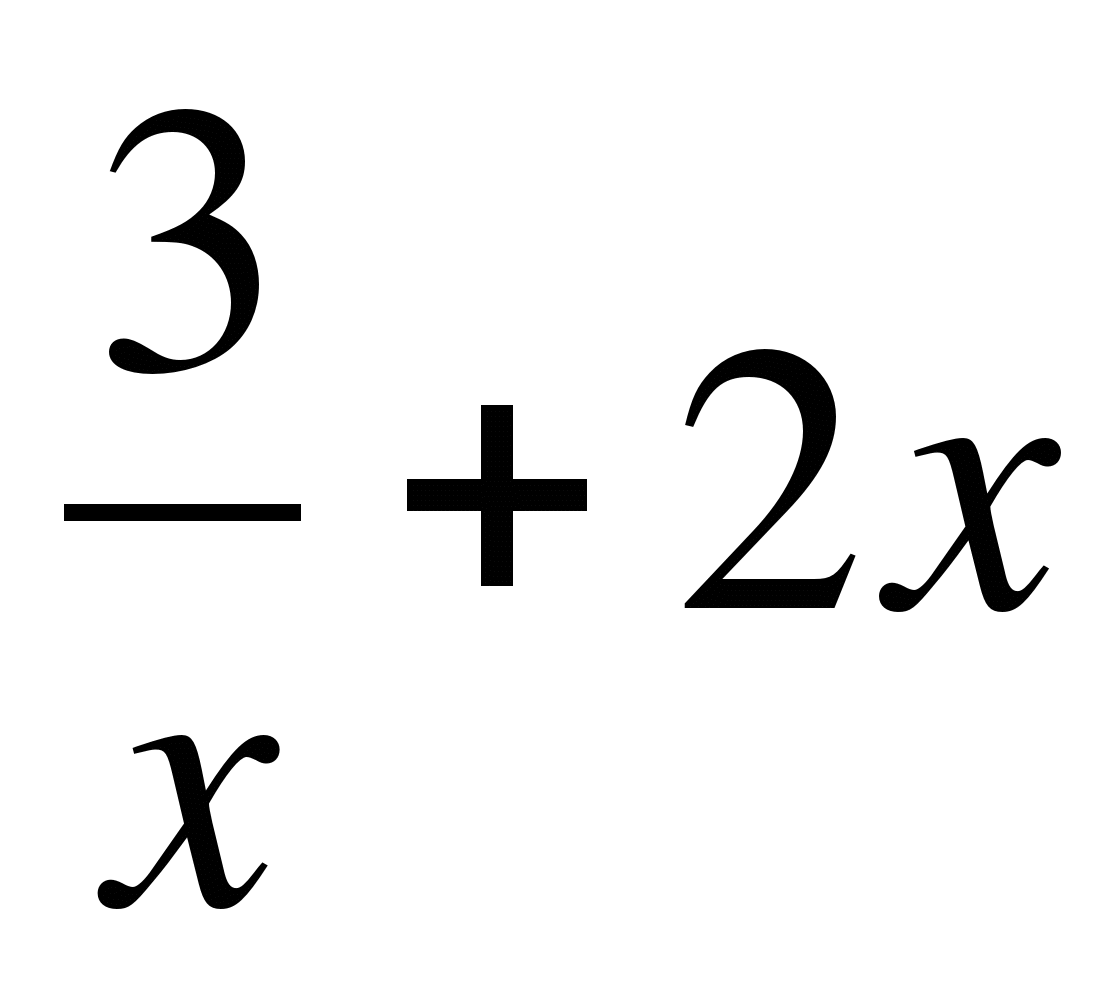4. Функция у=f(x) является нечётной и при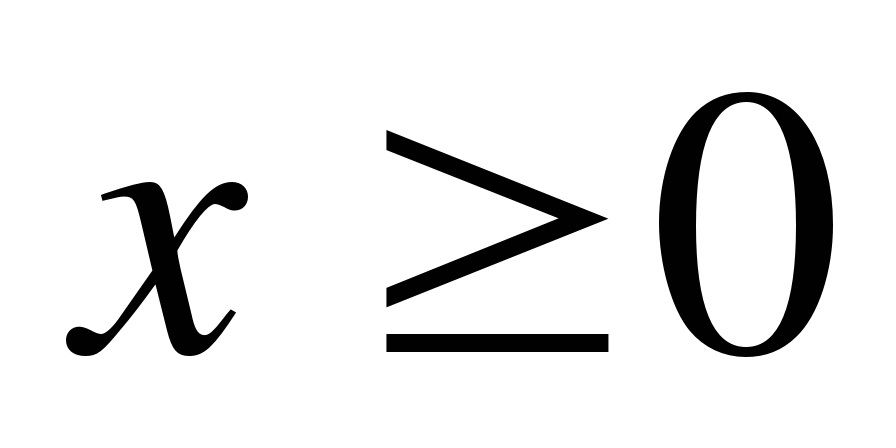 
совпадает с функцией у=2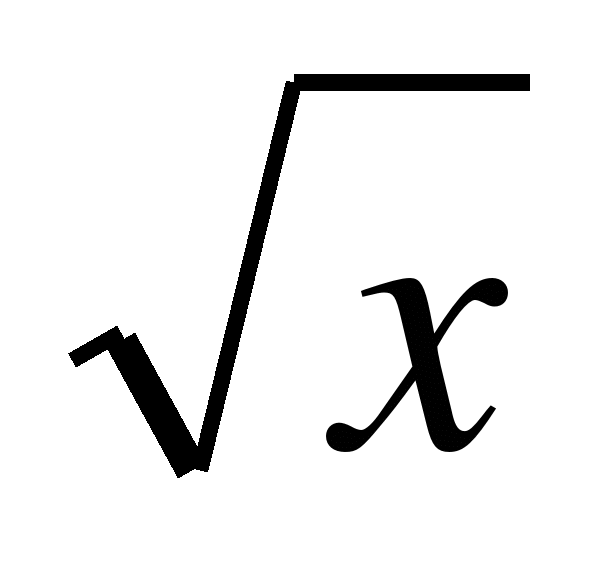. Постройте график этой функции.
5. Используя движение графика в системы координат, постройте график функции
f(x) =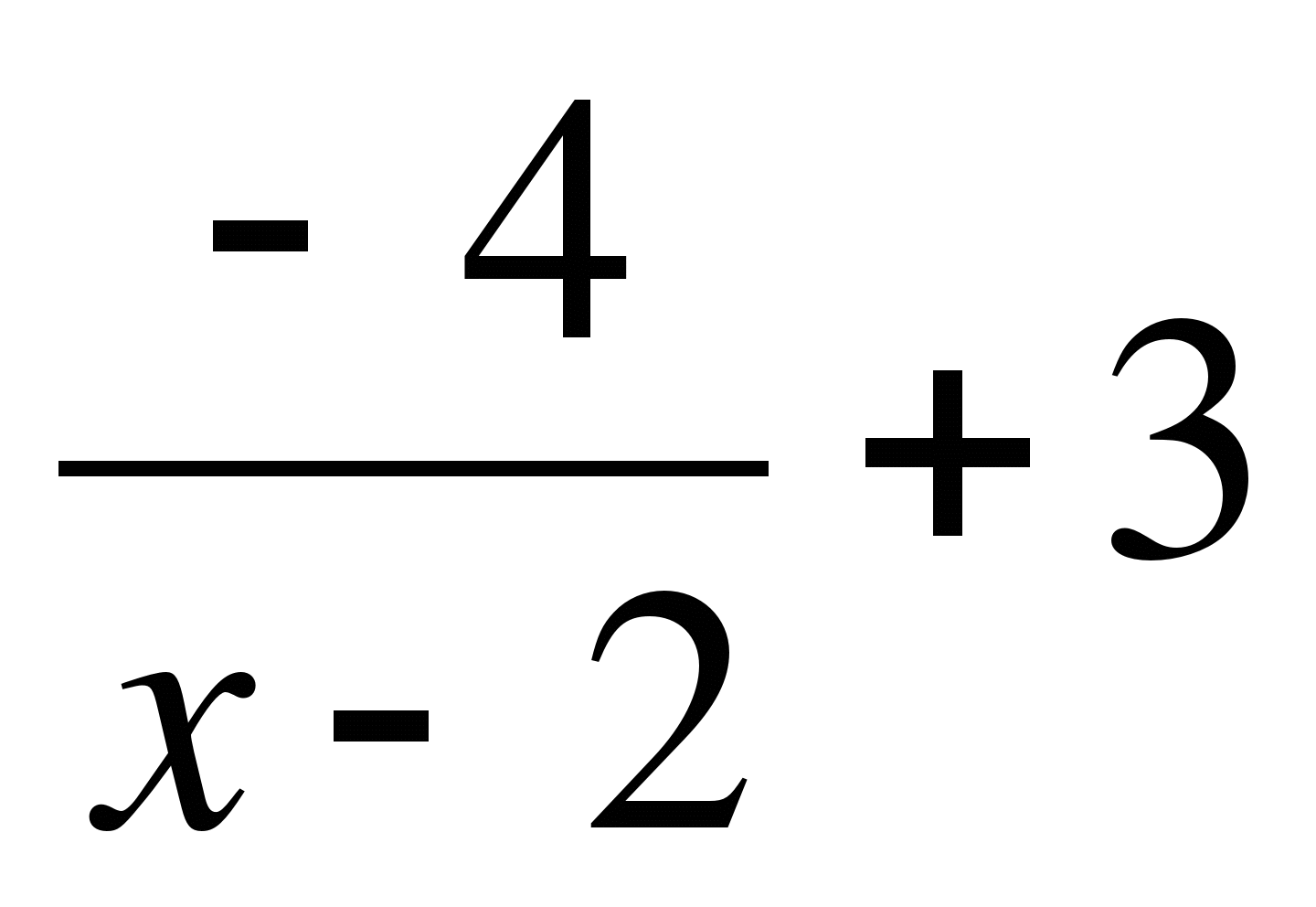 
.
Используя график, дайте краткую характеристику функции по плану:
1. Непрерывность; ( если есть асимптоты, то укажите их уравнения)
2. Монотонность;
3. Ограниченность;
4. Чётность (нечётность).
6. Проведите аналитическое исследование функции у =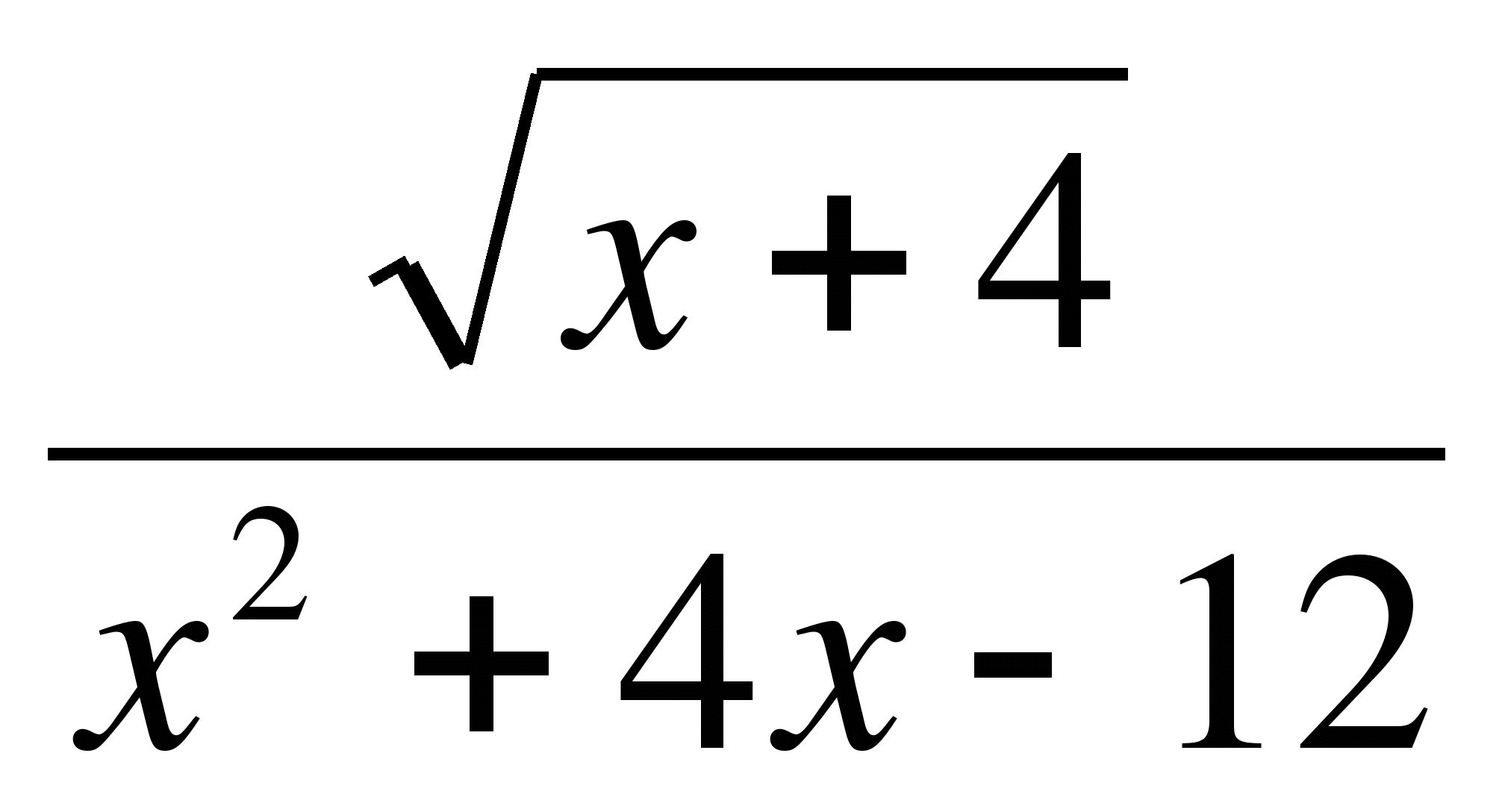
, ответив на вопросы: 1) Dy; 2) Нули функции; 4) Промежутки знакопостоянства функции.
7. Найдите аналитически область значения функции у=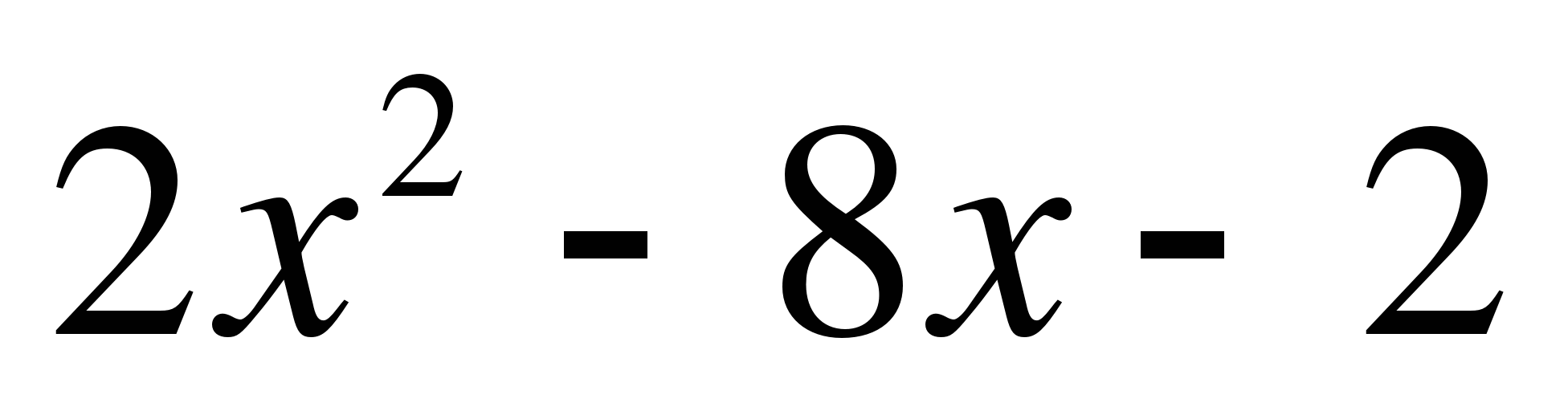
.
8. Постройте график функции f(x) =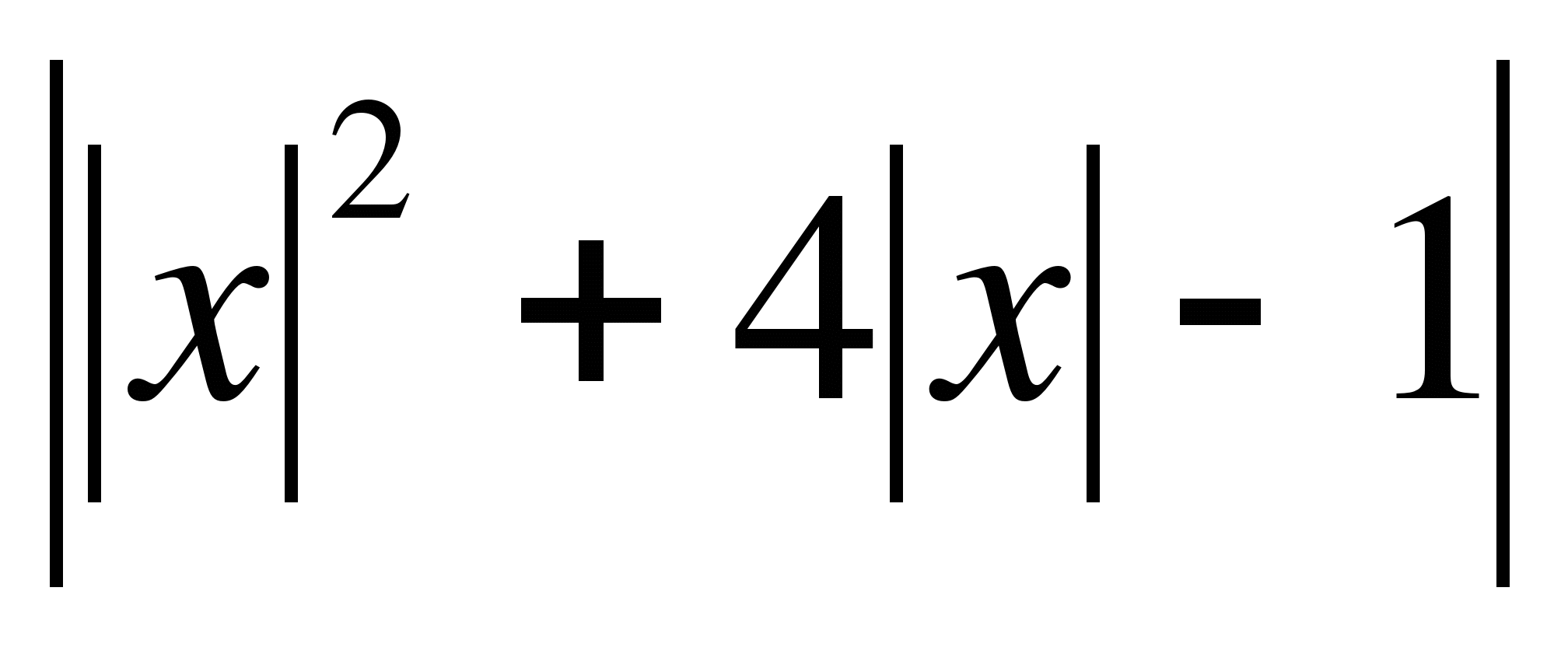
; 
.
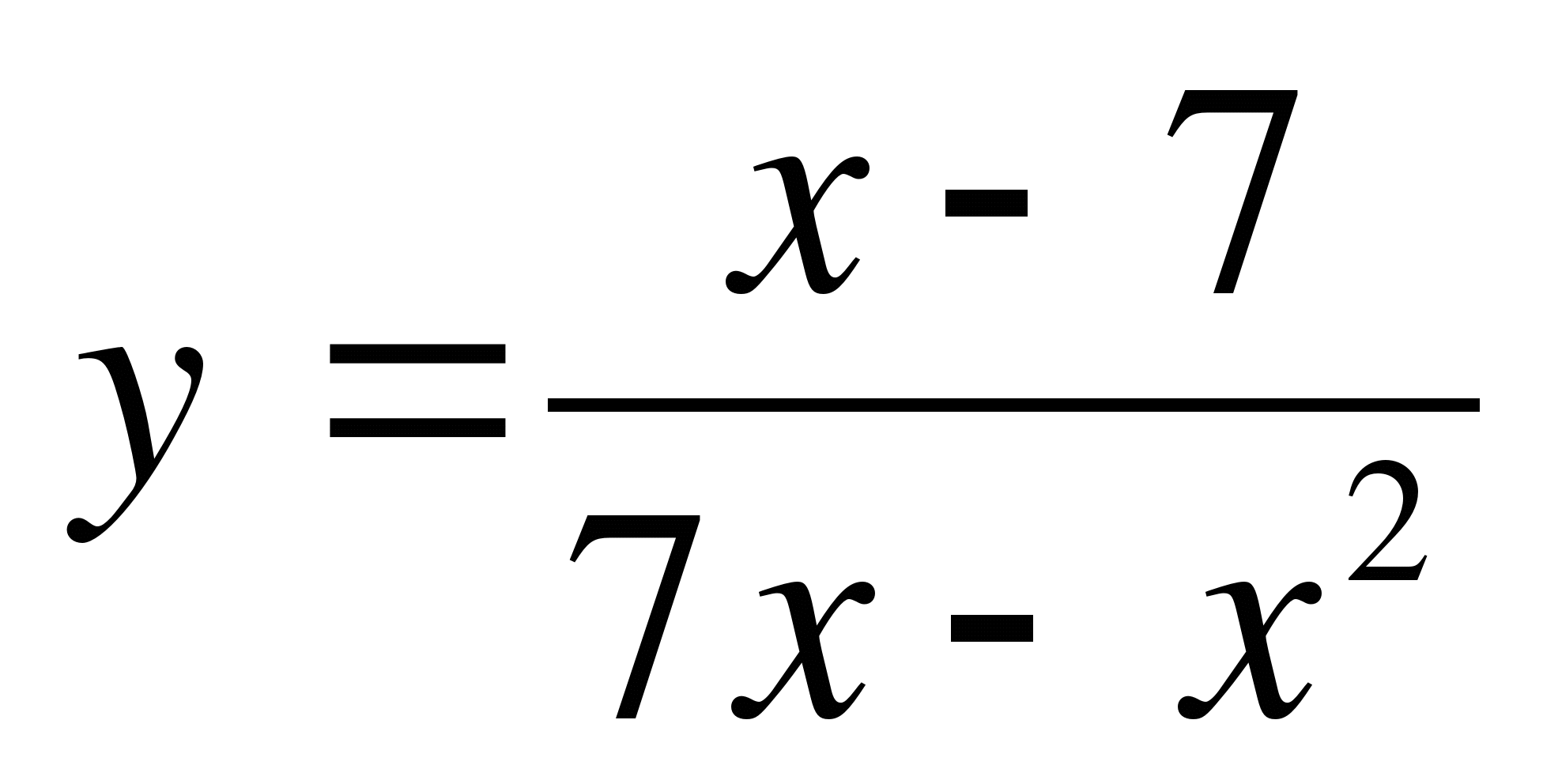infourok.ru
Контрольная работа № 1
по теме «Функции и их свойства»
Цель: проверить уровень усвоение ГОСО
- умение находить значение функции в точке;
- умение находить область определения функции;
- умения строить эскиз графика функции и находить по эскизу промежутки
возрастания и убывания , экстремумы функции, точки пересечения с осями
координат;
- знания свойств четных и нечетных функций.
1. Вычислите:
y = f(x) является нечетной y = f(x) является четной
2 f(-4) + f(3) f(-3) + 2 f(1)
eсли f(4)=1, f(-3)=2 eсли f(3)=4, f(-1)=2
2. Найдите значение функции в точке X0.
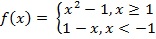
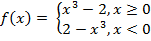
X0 = -2 и X0 = 4 X0 = -3 и X0 = 1
3. Постройте эскиз функции и найдите координаты точек его пересечения с осями координат.
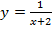
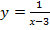
4. Найдите область определения функции
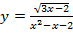
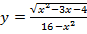
5. Найдите промежутки возрастания и убывания и экстремумы функции.
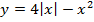
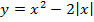
Критерии оценки.
0-10 баллов – «2»
11-14баллов – «3»
15-19 баллов – «4»
20-21 баллов – «5»
Распределение заданий по содержанию и видам деятельности.
Содержательные линии
Воспроизведение знаний
Применение знаний
Интеграция знаний
Процентное
Соотношение в тексте
Четные и нечетные функции.
№1
20%
Значения функции в точке
№2
20%
График функции и ее свойства
№3,4
№5
40%
Процентное
Соотношение в тексте
40%
40%
20%
100%
Критерии оценивания
№
задания
Характеристика задания
Проверяемые элементы
Балл за выполнение проверяемого элемента
Балл за выполнение задания
1
Свойства четных и нечетных функций.
Знания свойств четных и нечетных функций
2
3
Запись ответа
1
2
Значение функции в точке
Правильно подставил
2
3
Вычисления
1
3
График функции и ее свойства
Построение эскиза графика
2
5
Пересечение с осью абсцисс
1
Пересечение с осью ординат
2
Запись ответа
1
4
Область определения функции
Составление условий для нахождения области определения
2
5
Решение неравенства
1
Запись ответа
2
5
Промежутки возрастания , убывания и экстремумы функции
Вершина параболы
1
5
Свойства модуля
1
Эскиз графика
2
Запись ответа
1
infourok.ru
1 вариант
А1. Какая из функций имеет область определения промежуток (-3;3)?
А2.Найдите область значения функции
А3 На рисунке изображён график функции у=f(x). Найдите неверное утверждение.
|
|
|
|||||||||||
А4. Найдите функцию, обратную функции у= 4х – 3
А5. На каком рисунке изображён график нечётной функции?
1. у 2. у 3. у 4. у
х х
х х
А6. Найдите наименьшее значение функции
1. -2 2. 1 3. -1 4. 2
В1 Найдите область определения функции:
В2. Область значения функции у= f(х) промежуток [-4; 8]. Найдите область значения функций:
В3. Постройте график функции
1) Найдите f(-2), f(3), f(4). 2) Опишите свойства этой функции по графику.
С1. Постройте график функции у=|x-3|+|x+2|-|2x+8| и определите область её значения.
С2. Найдите нули функции у=||x-8| -3x+1|-x.
C3. При каком значении параметра а, уравнение |||x+4|-3|-2|=aимеет четыре корня, восемь корней?
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ
а) |3-x| + |2+x| - |16-2x|=2x-11 б) |2+|x+3|-2|x+5|-x|=x+10
2. Постройте график функции у=f(x) и опишите её свойства
3 вариант
А1. Какая из функций имеет область определения промежуток [-3;3]?
А2.Найдите область значения функции
А3 На рисунке изображён график функции у=f(x). Найдите неверное утверждение.
|
|
|
|||||||||||
А4. Найдите функцию, обратную функции у= 4х + 3
А5. На каком рисунке изображён график нечётной функции?
1. у 2. у 3. у 4. у
х х
х х
А6. Найдите наименьшее значение функции
1. -2 2. 1 3. -1 4. 2
В1 Найдите область определения функции:
В2. Область значения функции у= f(х) промежуток [-5; 4]. Найдите область значения функций:
В3. Постройте график функции
1) Найдите f(-2), f(-1), f(2). 2) Опишите свойства этой функции по графику.
С1. Постройте график функции у=|х+2|-|x-4|+|2x+8| и определите область её значения.
С2. Найдите нули функции у=||3-x|+2x-1|-x.
C3. При каком значении параметра а, уравнение |||x+1|-2|-3|=aимеет два корня, пять корней?
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ
а) |3-x| + |2+x| - |16-2x|=2x-11 б) |2+|x+3|-2|x+5|-x|=x+10
2. Постройте график функции у=f(x) и опишите её свойства
2 вариант
А1. Какая из функций имеет область определения промежуток [-4;4)?
А2.Найдите область значения функции
А3 На рисунке изображён график функции у=f(x). Найдите неверное утверждение.
|
|
|
|||||||||||
А4. Найдите функцию, обратную функции у= 2х +5
А5. На каком рисунке изображён график чётной функции?
1. у 2. у 3. у 4. у
х х
х х
А6. Найдите наибольшее значение функции
1. -5 2. 11 3. 1 6 4. 3
В1 Найдите область определения функции:
В2. Область значения функции у= f(х) промежуток [-4; 7]. Найдите область значения функций:
В3. Постройте график функции
1) Найдите f(-3), f(-2), f(0). 2) Опишите свойства этой функции по графику.
С1. Постройте график функции у=|2x-8|-|x+2|+|x+6| и определите область её значения.
С2. Найдите нули функции у=||x+6|-x+2|-x.
C3. При каком значении параметра а, уравнение |||x+3|-2|-3|=aимеет два корня, четыре корня?
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ
а) |2+x| + |5-x| - |18-3x|= -3x-11 б) |1+|x-3|-5|x-+2|-x|=x-8
2. Постройте график функции у=f(x) и опишите её свойства
4 вариант
А1. Какая из функций имеет область определения промежуток (-4;4)?
А2.Найдите область значения функции
А3 На рисунке изображён график функции у=f(x). Найдите неверное утверждение.
|
|
|
|||||||||||
А4. Найдите функцию, обратную функции у= 2х- 4
А5. На каком рисунке изображён график чётной функции?
1. у 2. у 3. у 4. у
х х
х х
А6. Найдите наибольшее значение функции
1. -2 2. 7 3. -9 4. 3
В1 Найдите область определения функции:
В2. Область значения функции у= f(х) промежуток [-4; -1]. Найдите область значения функций:
В3. Постройте график функции
1) Найдите f(-2), f(2), f(4). 2) Опишите свойства этой функции по графику.
С1. Постройте график функции у=|2x+6|-|x-3|-|x+6| и определите область её значения.
С2. Найдите нули функции у=||x-5|+x-2|+x.
C3. При каком значении параметра а, уравнение |||x-2|-1|-3|=aимеет четыре корня, пять корней?
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ
а) |2+x| + |5-x| - |18-3x|= -3x-11 б) |1+|x-3|-5|x-+2|-x|=x-8
2. Постройте график функции у=f(x) и опишите её свойства
obrazbase.ru
КОНТРОЛЬНЫЕ РАБОТЫ
ПО МАТЕМАТИКЕ
ГБОУ СПО «Новокуйбышевский
нефтехимический техникум»
преподаватель математики
Шипилова Людмила Александровна
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
Показательная функция
Сравнить: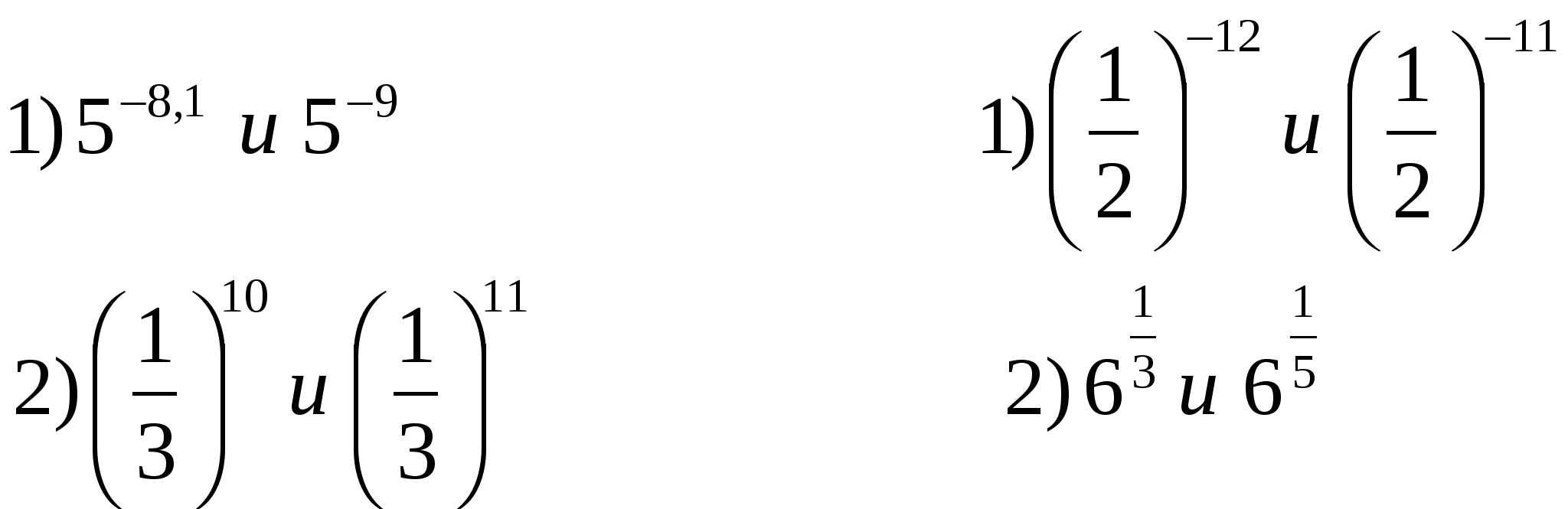 
Решить уравнения: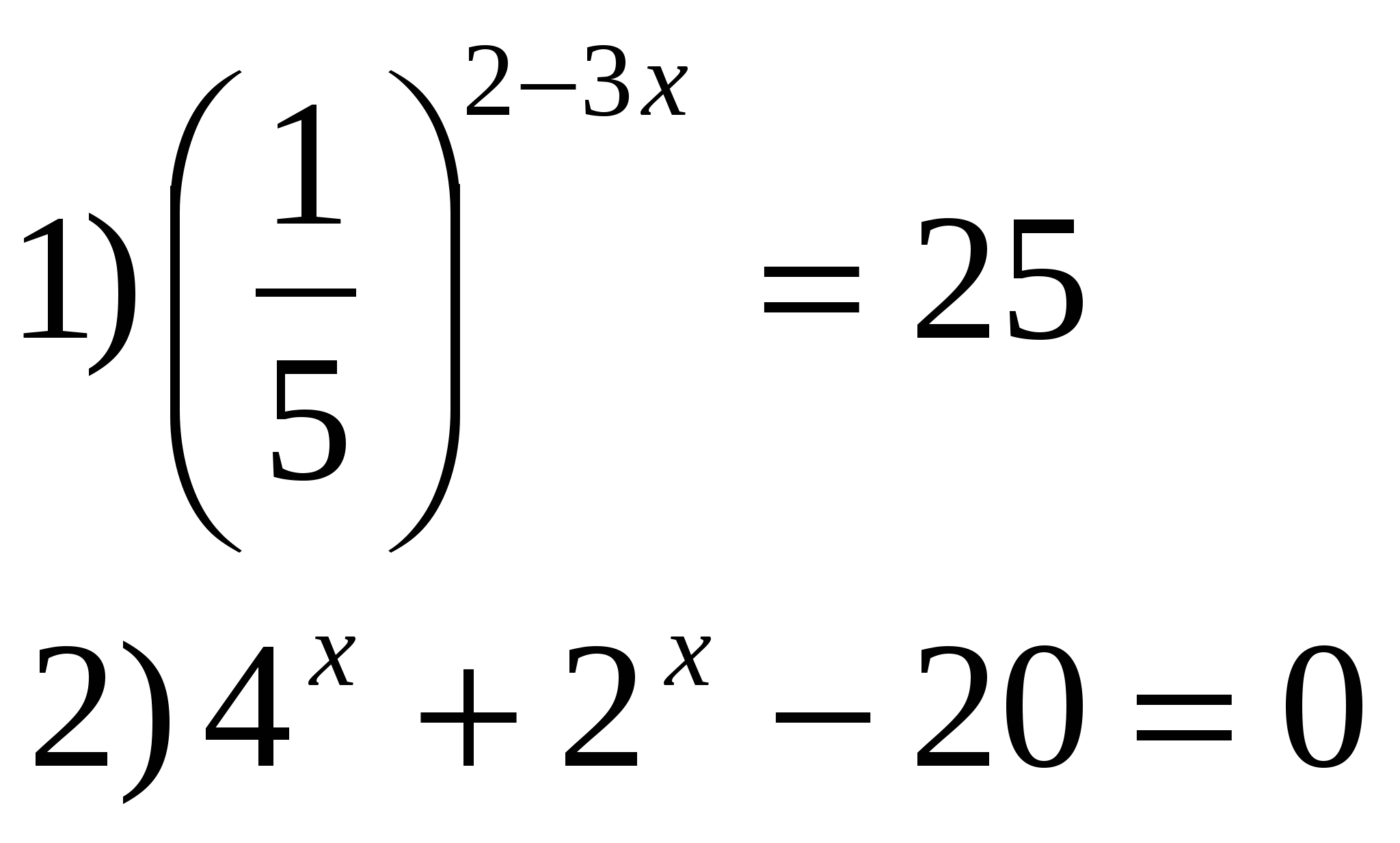 
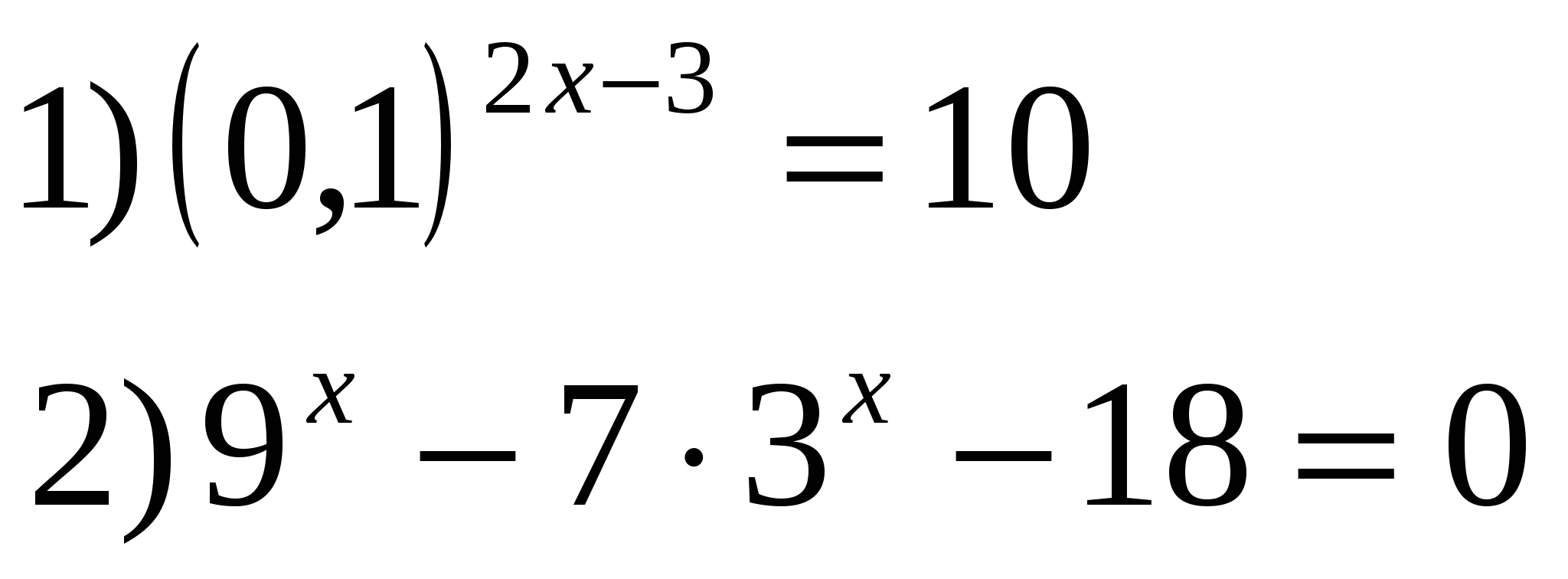
3) Решить неравенства: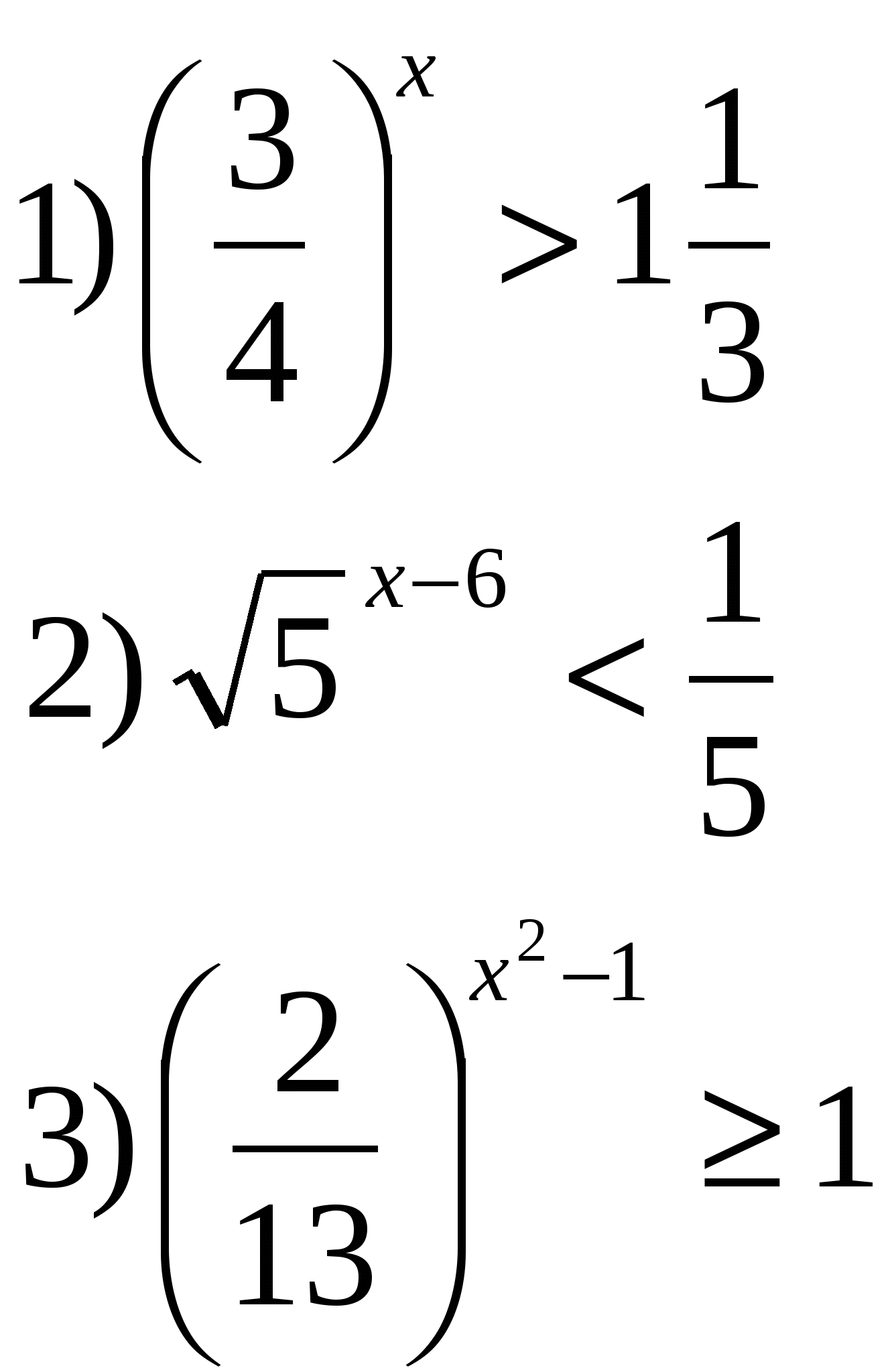 
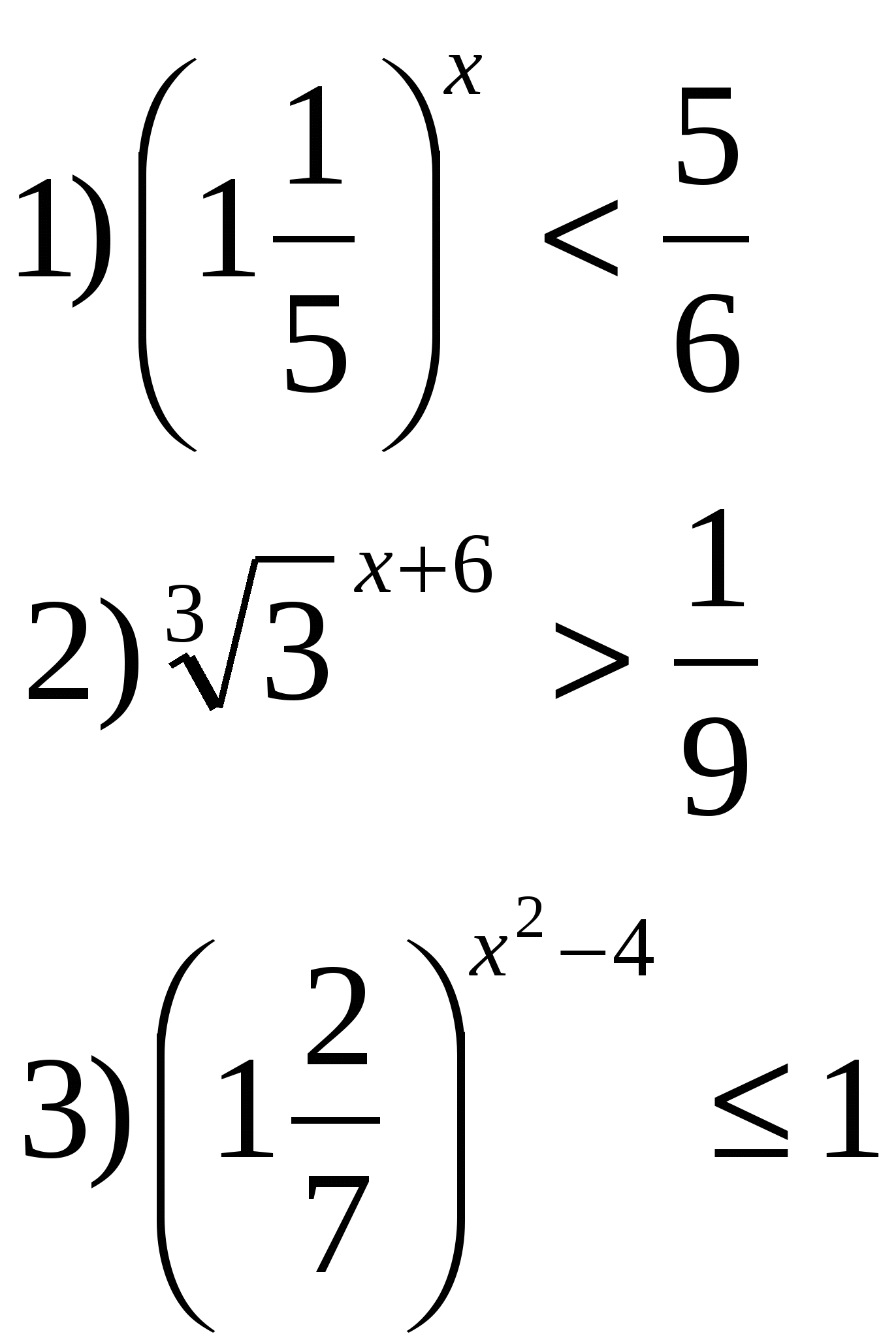
4*) Решить систему уравнений: 
5*) Решить уравнение: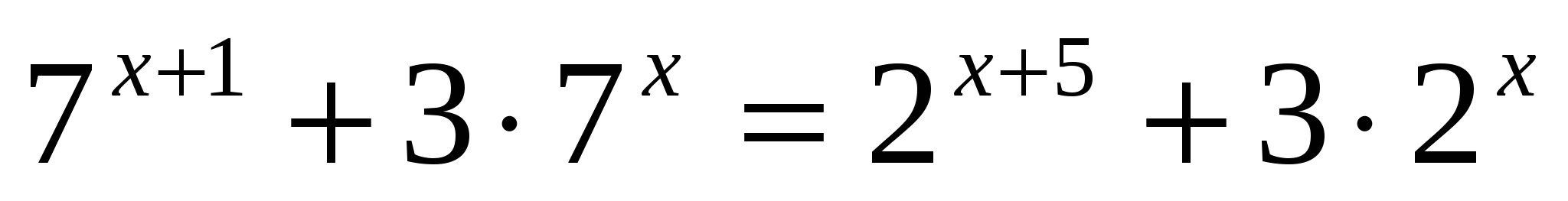 
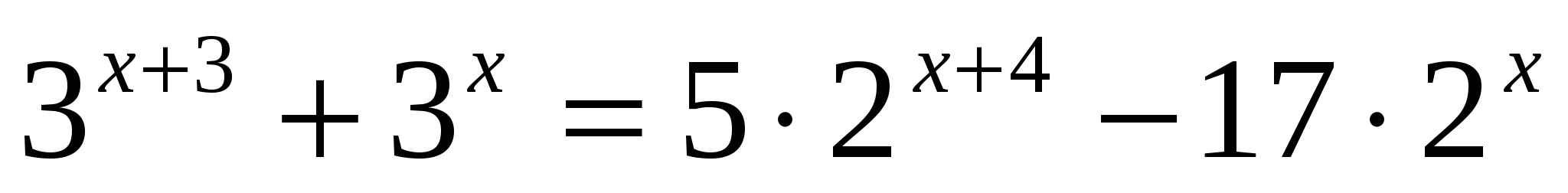
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
Логарифмическая функция
Вариант № 1 Вариант № 2
1) Вычислить: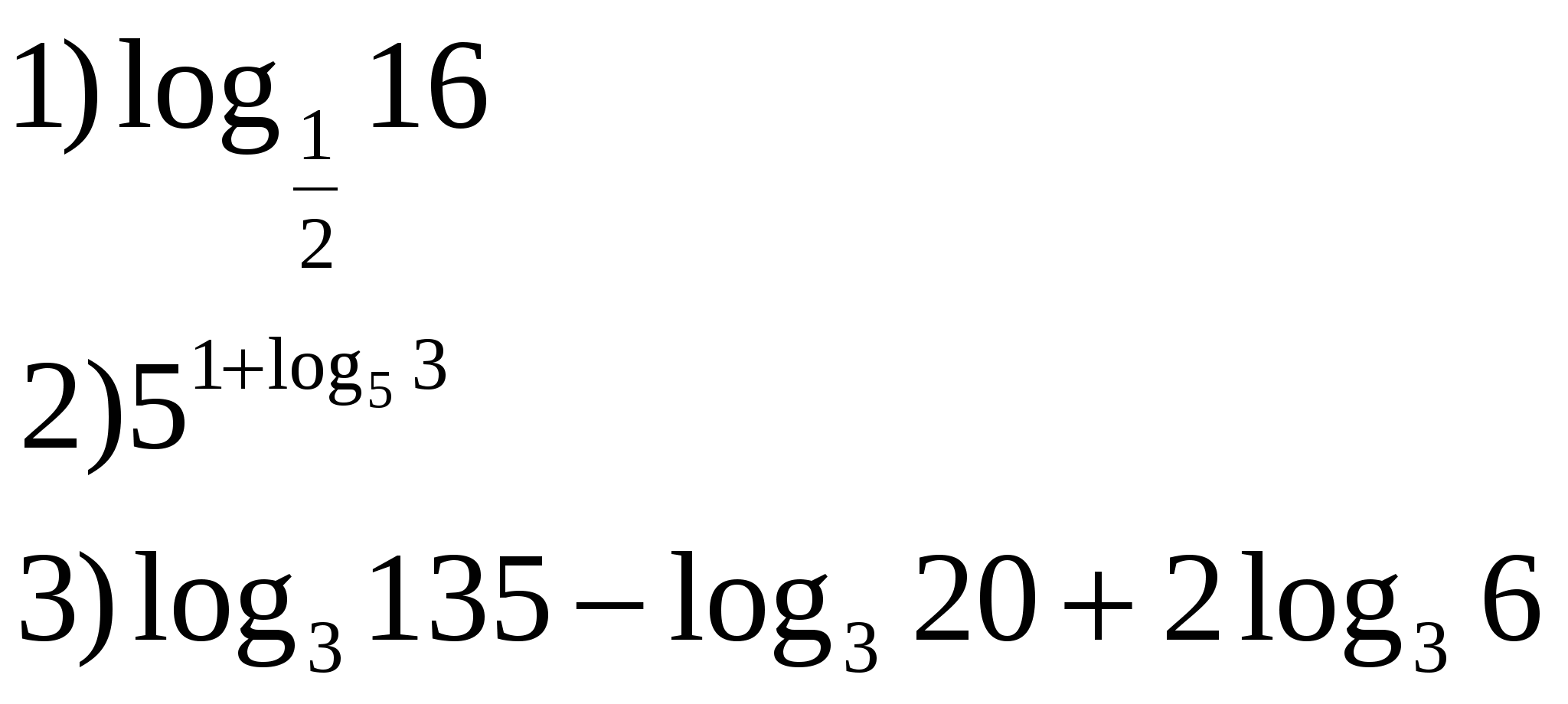 
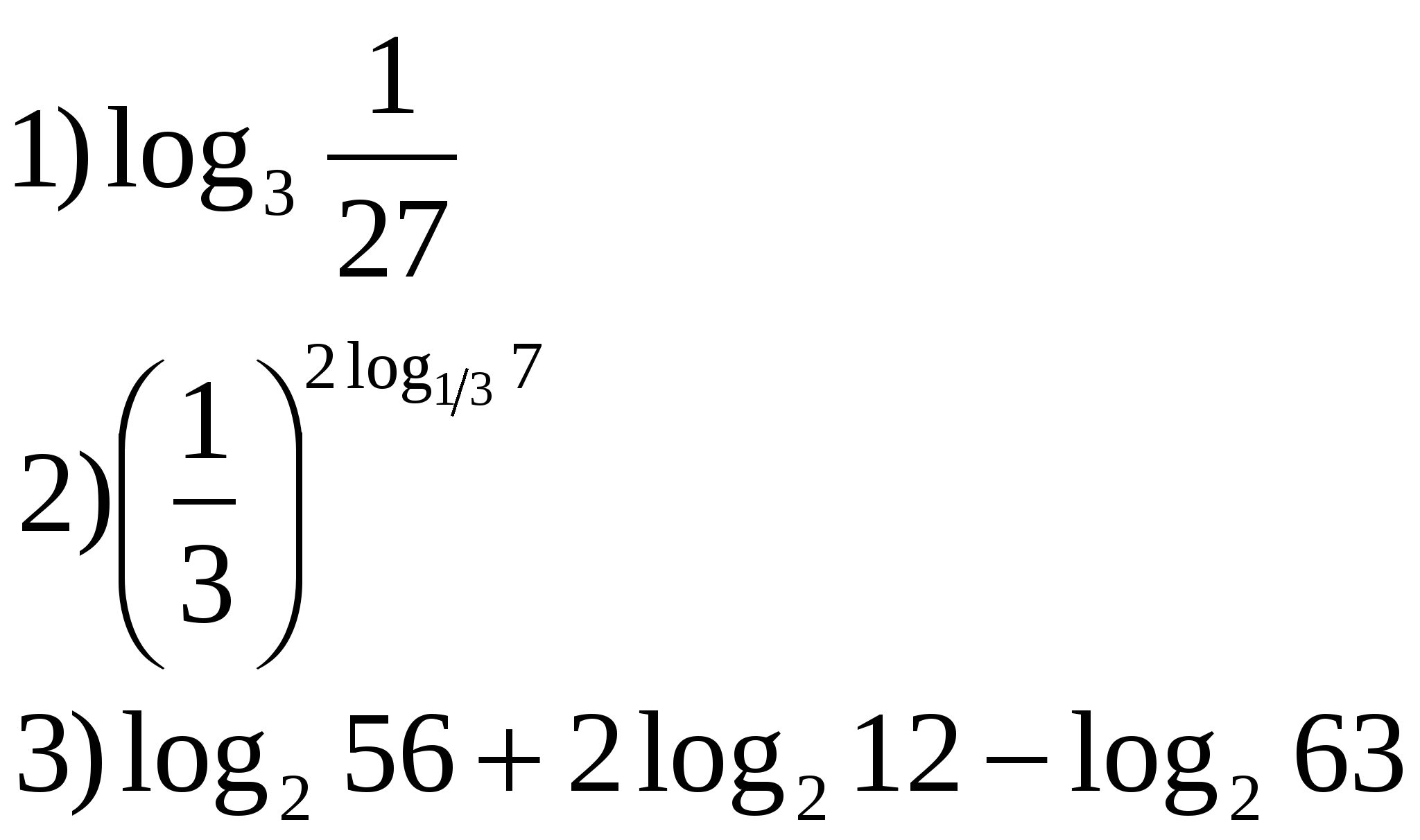
2) Сравнить: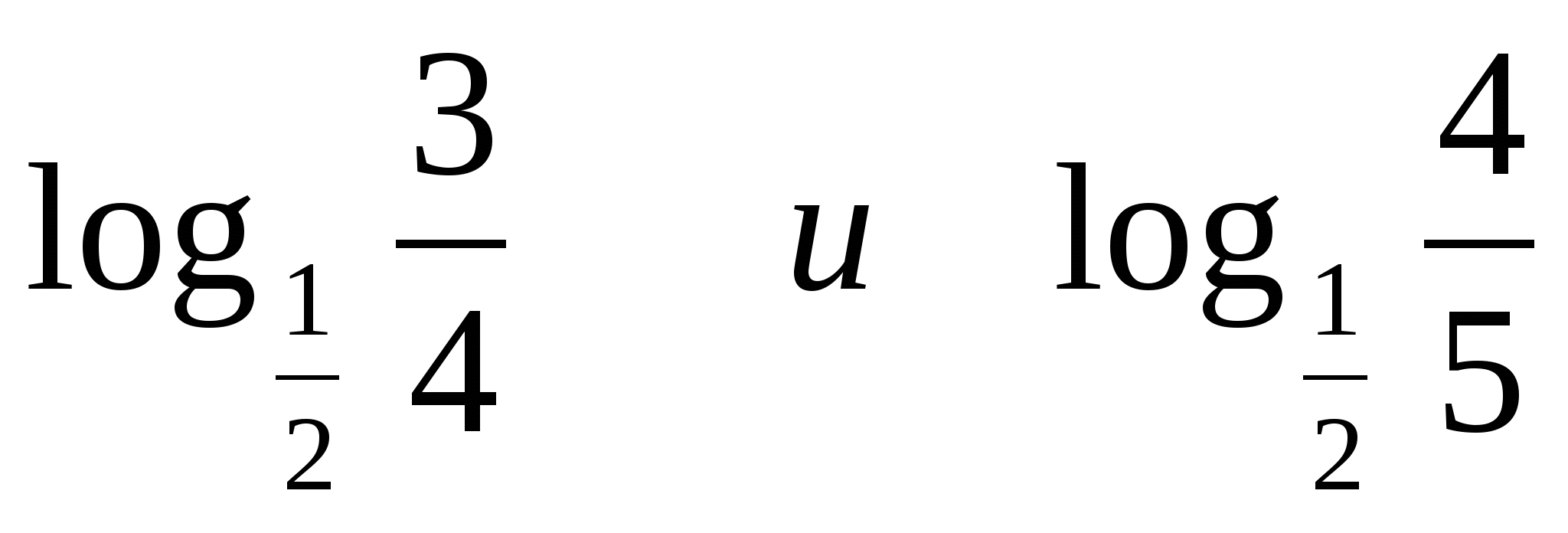 
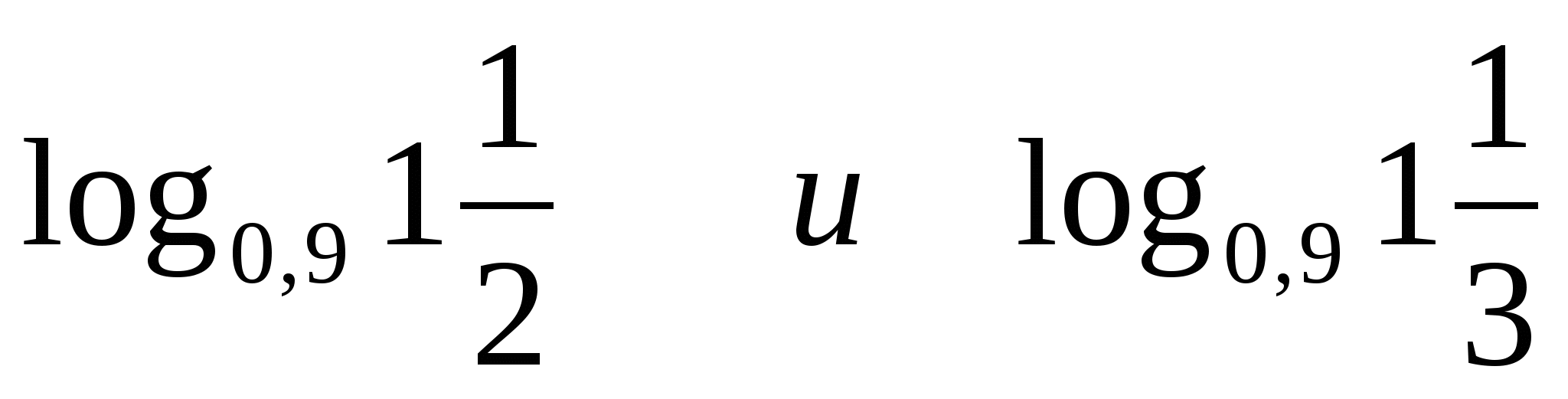
Решить уравнение: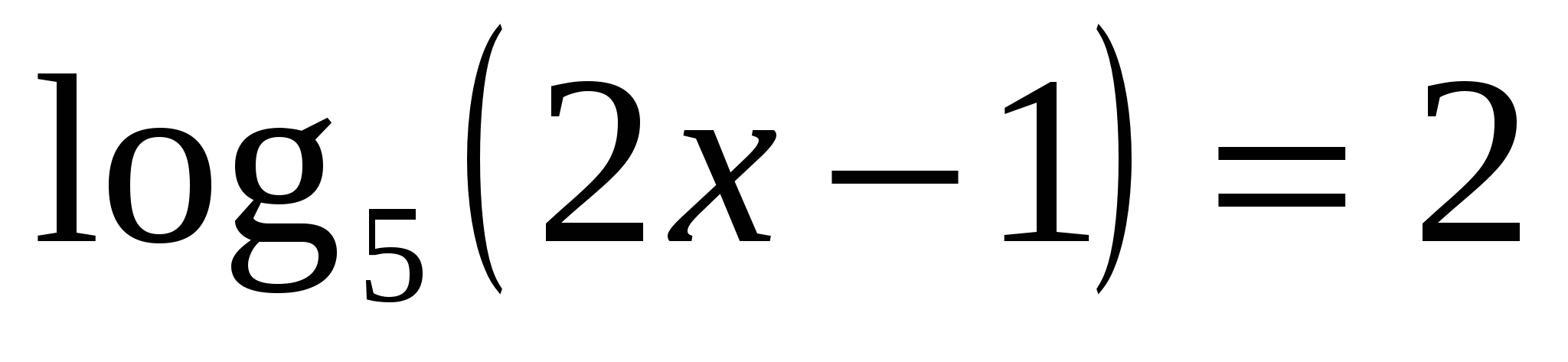 
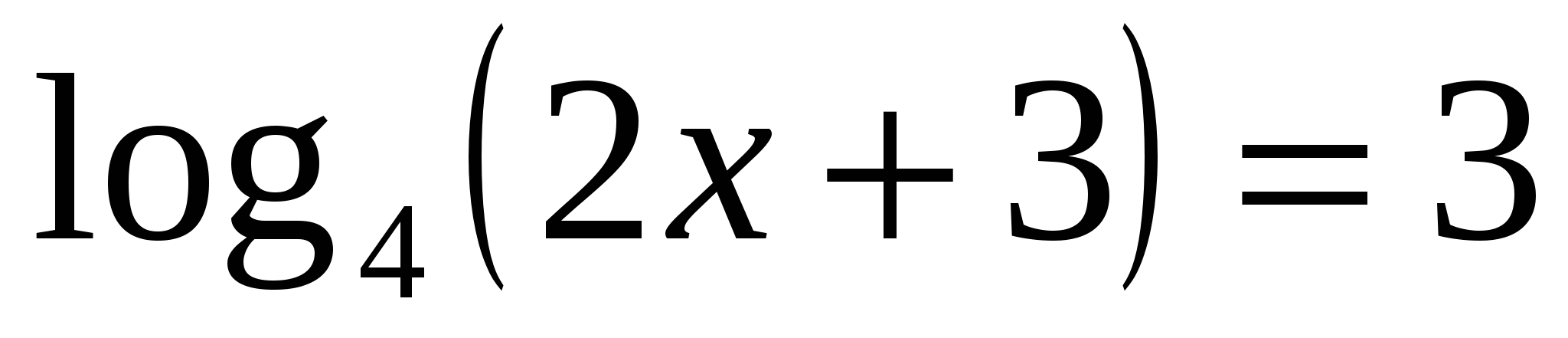
Решить неравенство: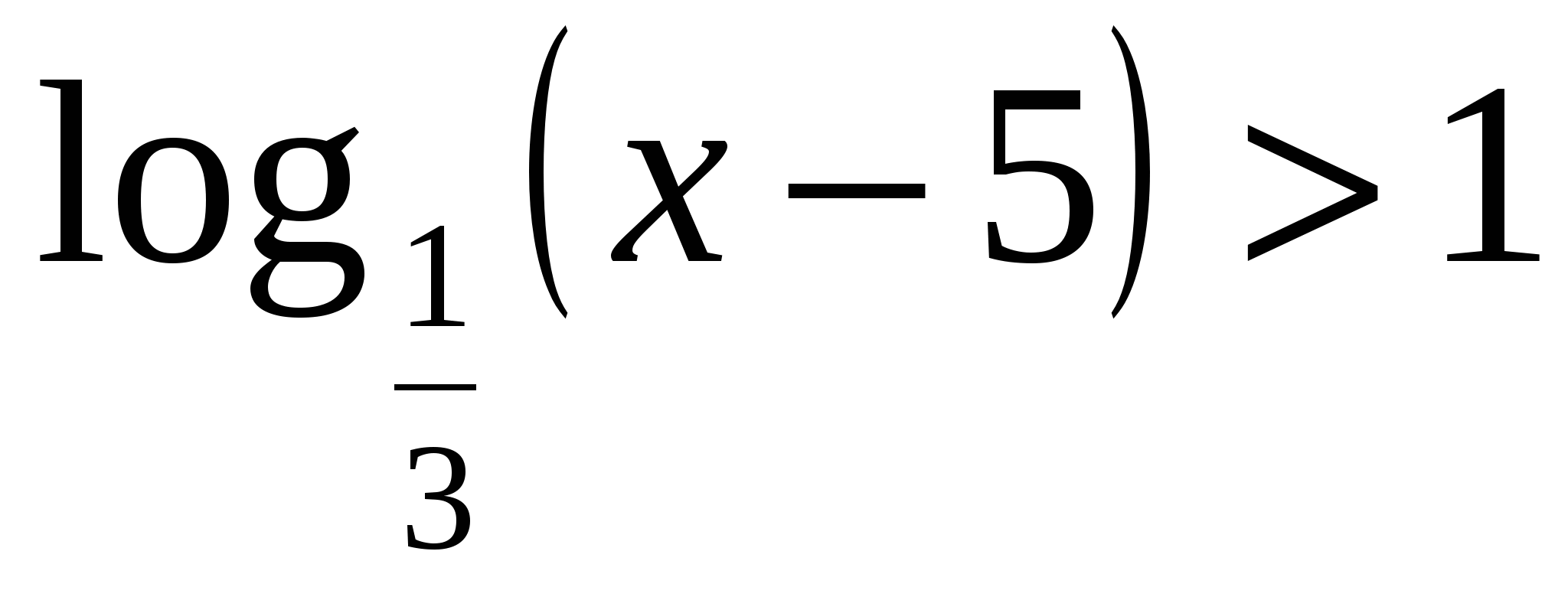 
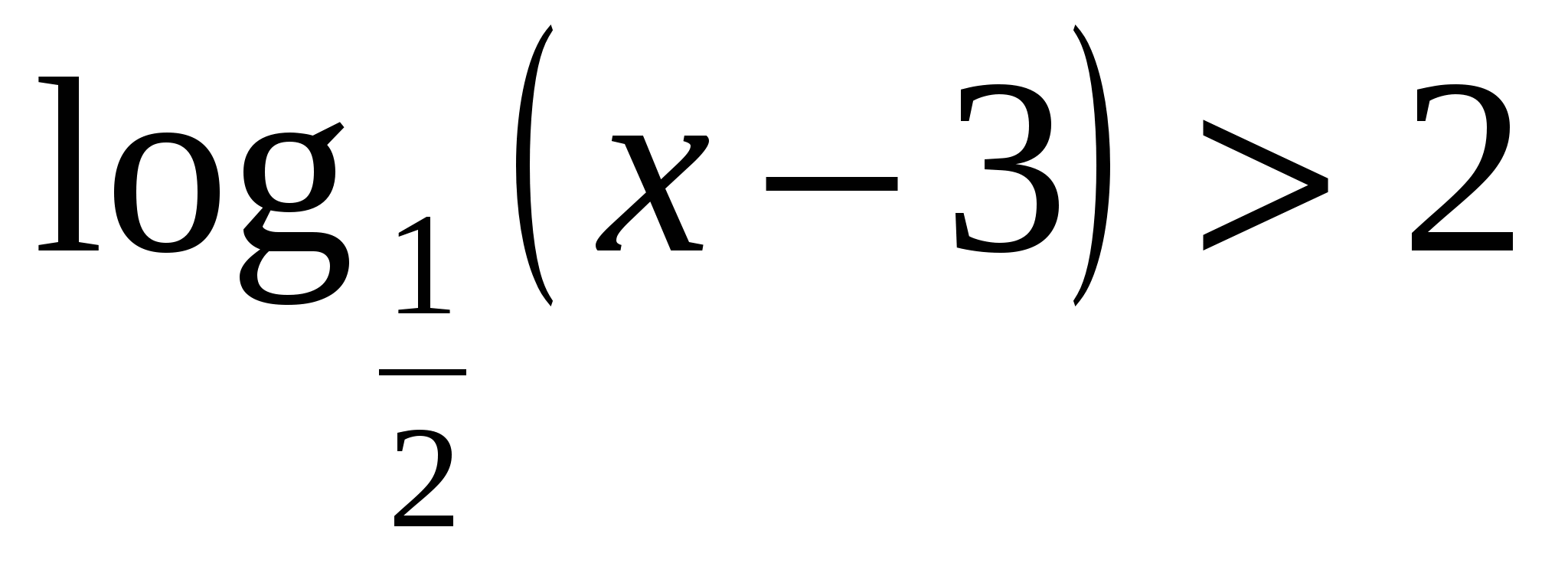
5*) Решить уравнение: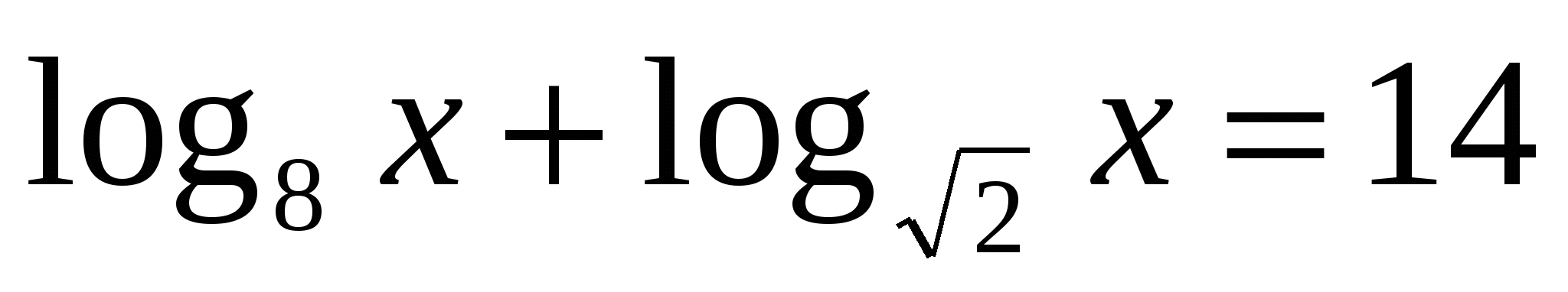 
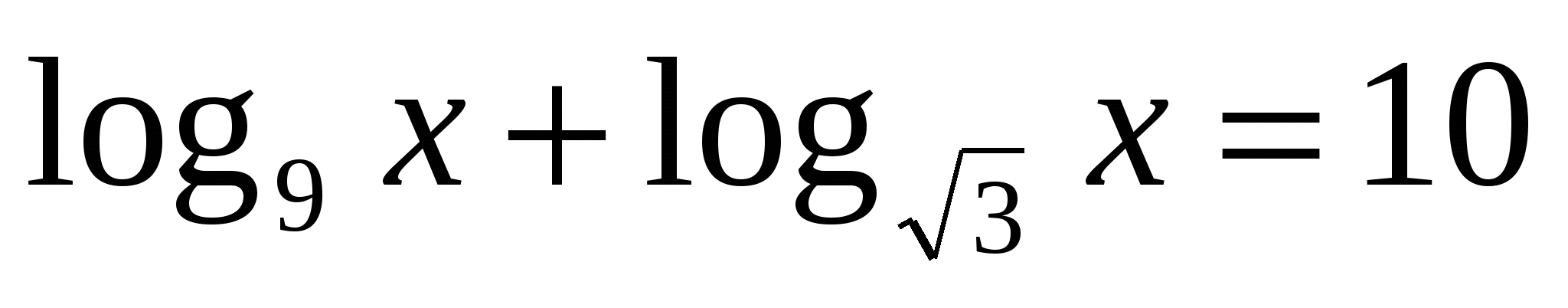
6*) Решить нерав-во: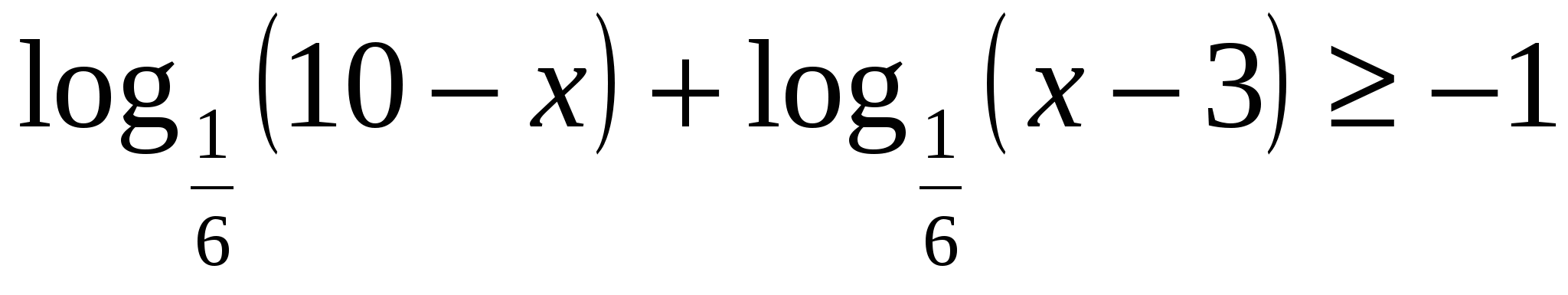 
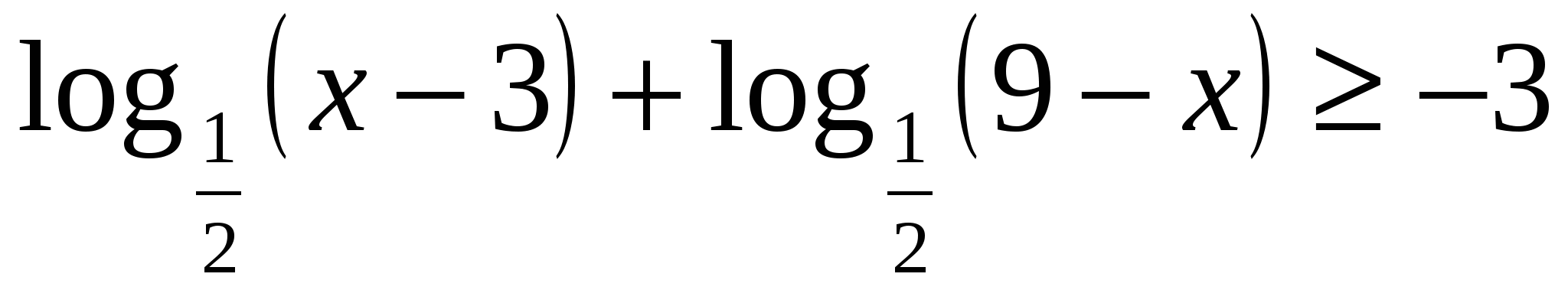
7*) Решить неравенство: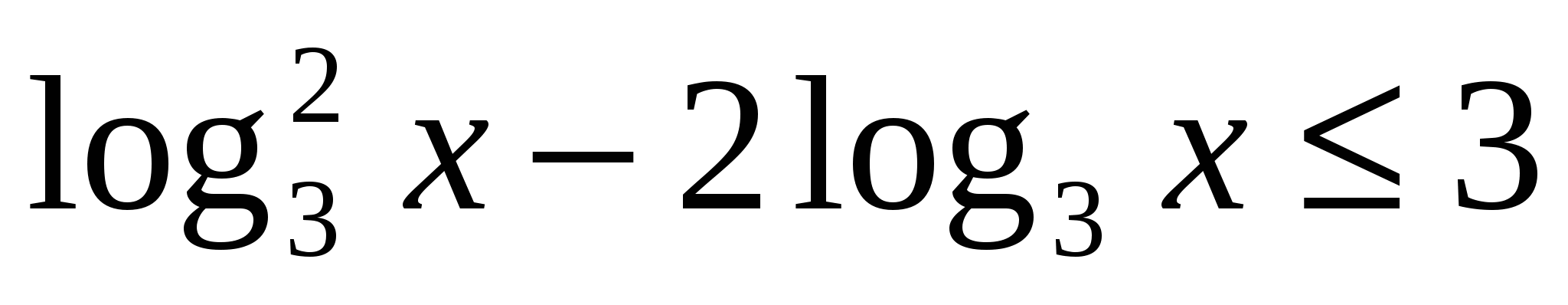 
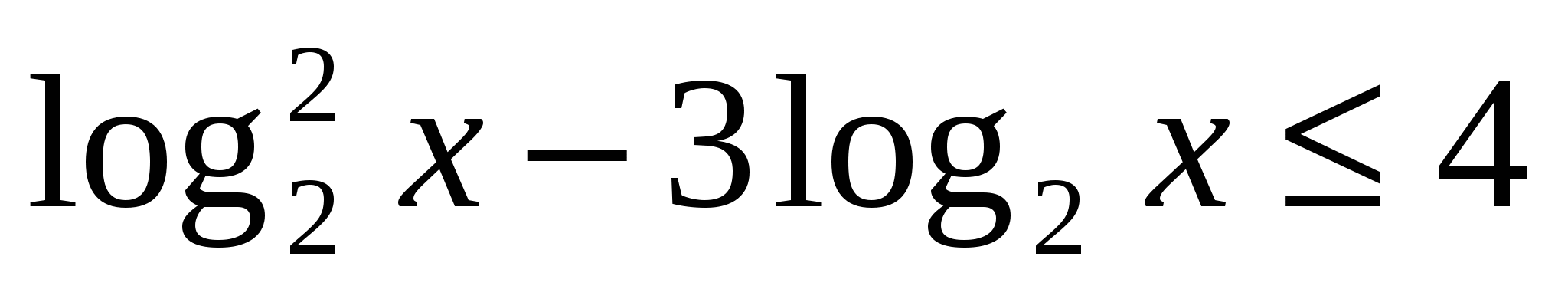
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
Тригонометрические формулы
Вариант № 1 Вариант № 2
1) Вычислить: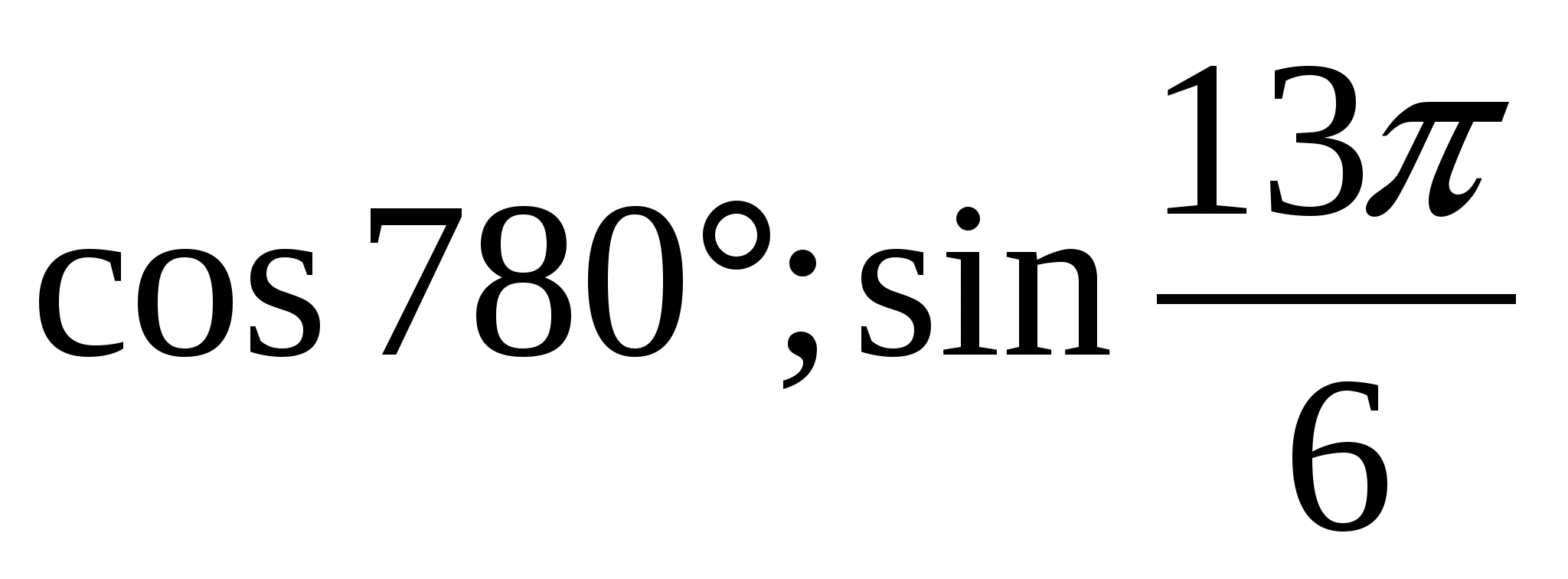 
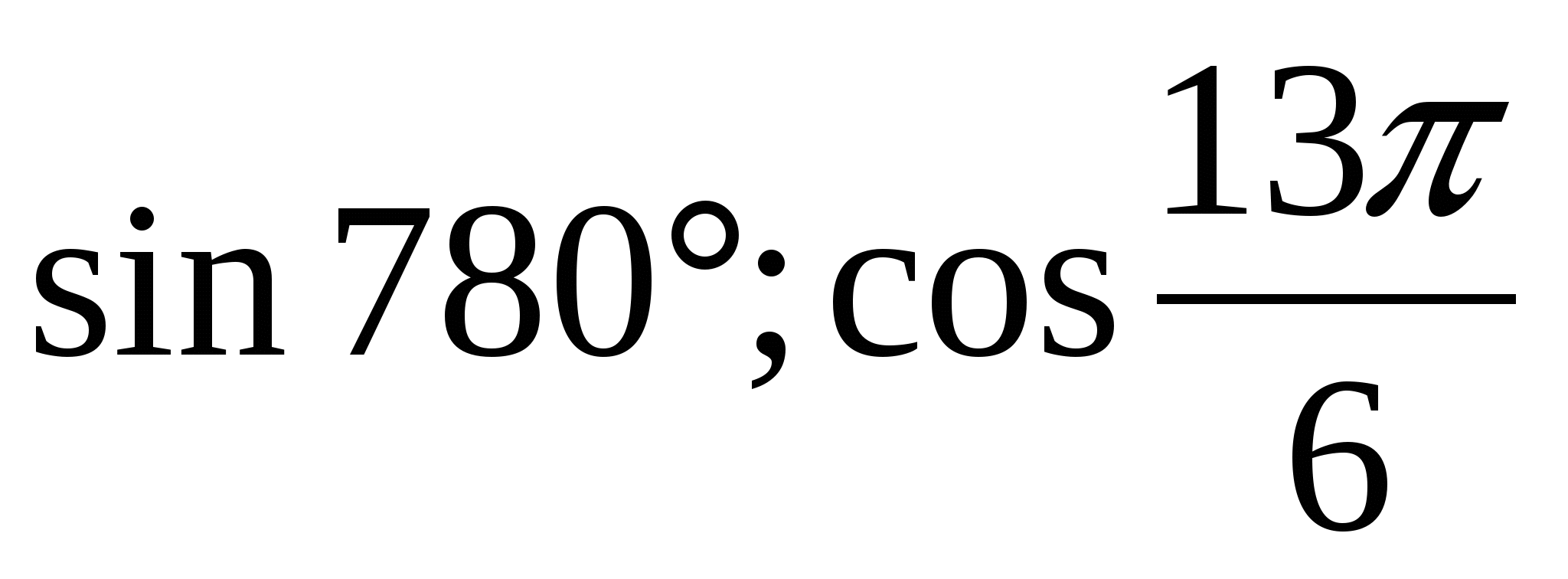
2) Найти: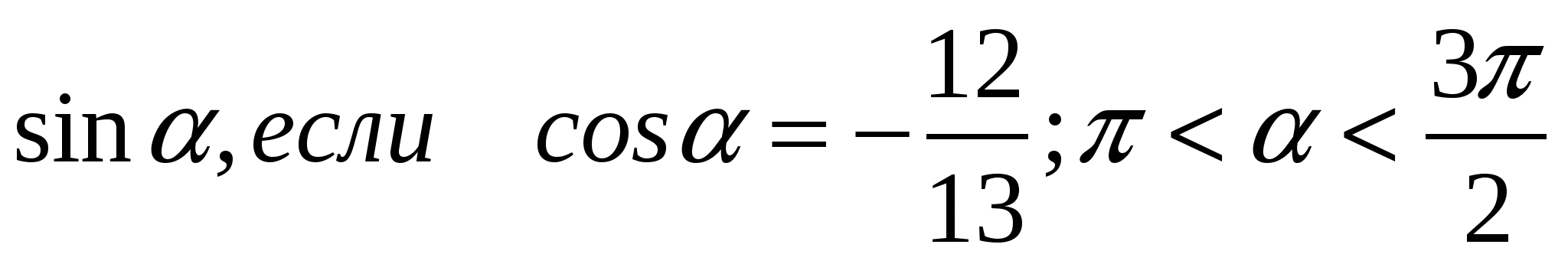 
; 
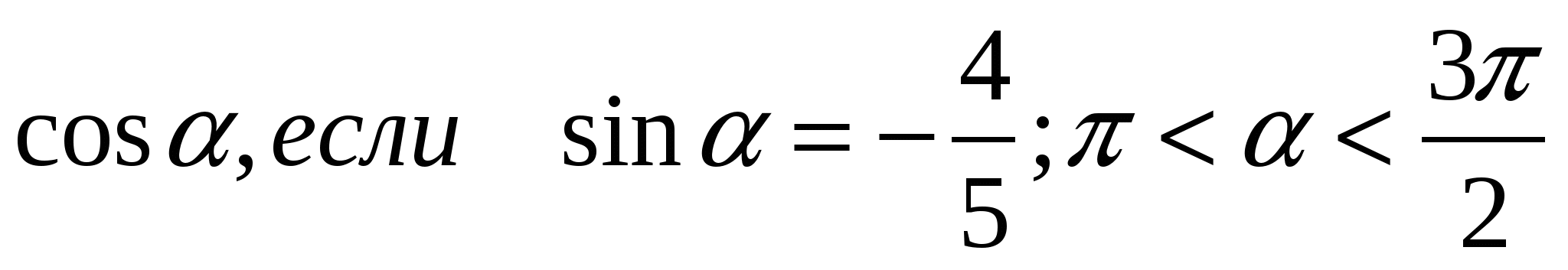
3) Упростить: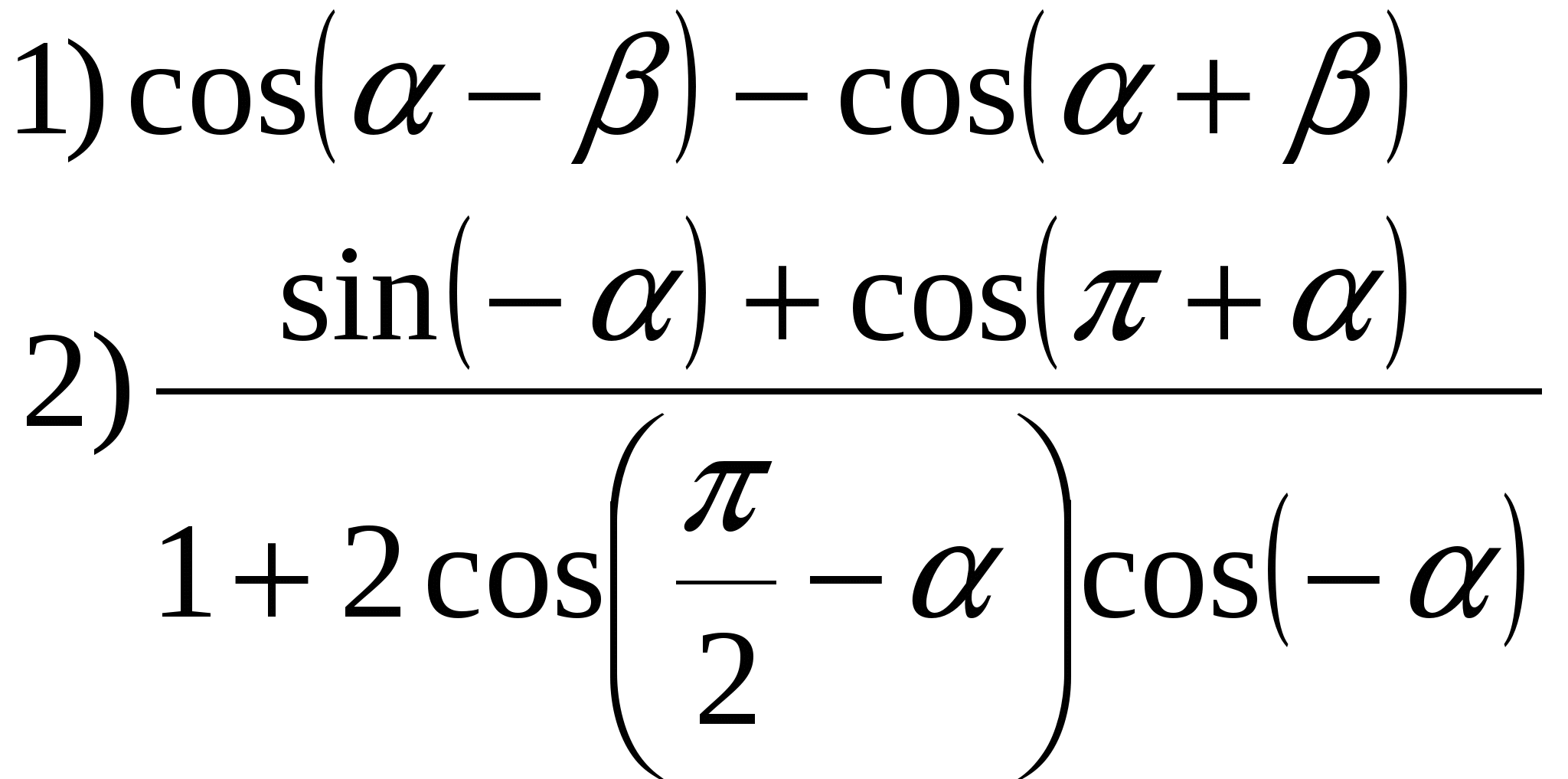 
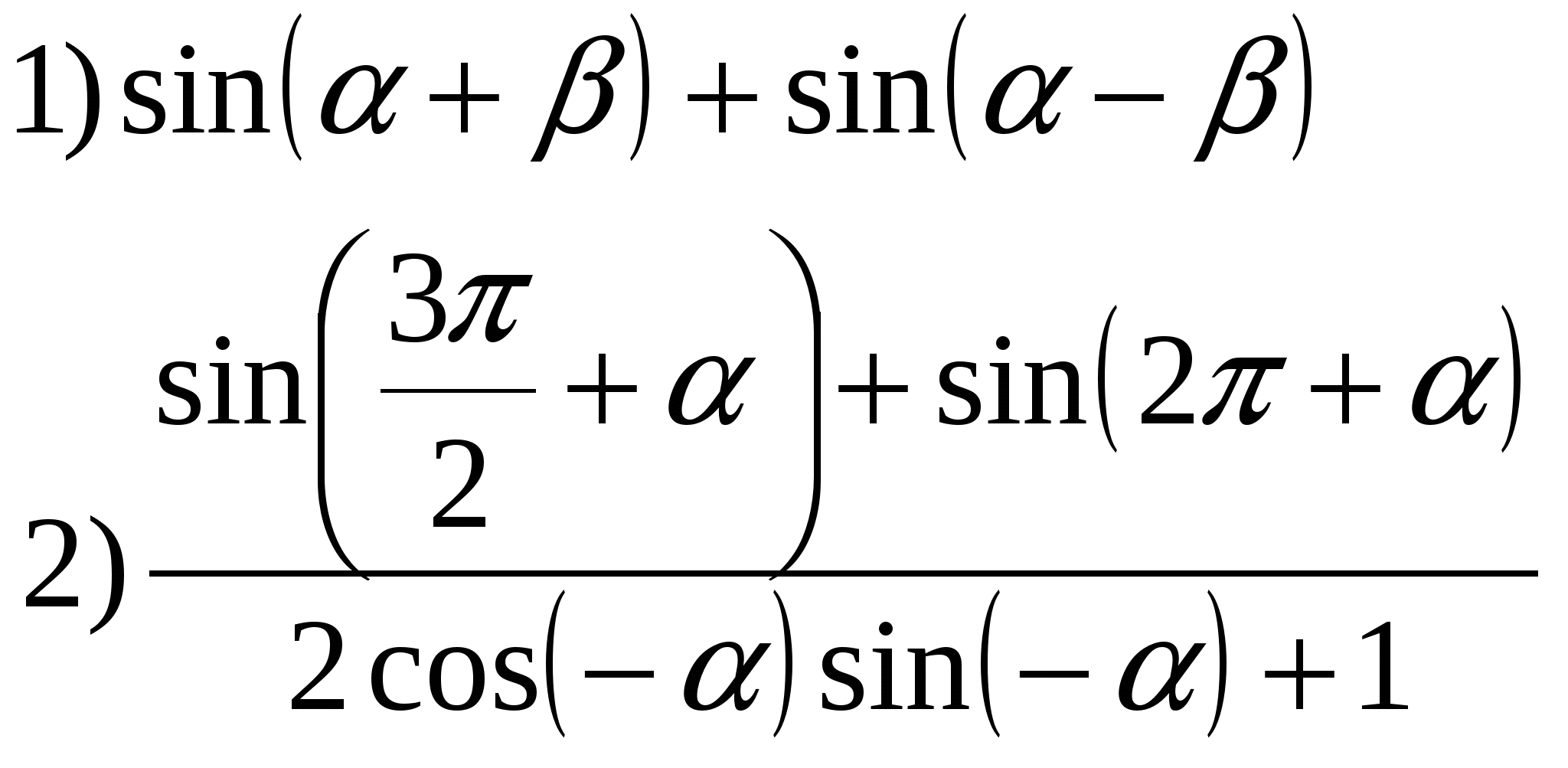
4*) Решить уравнение: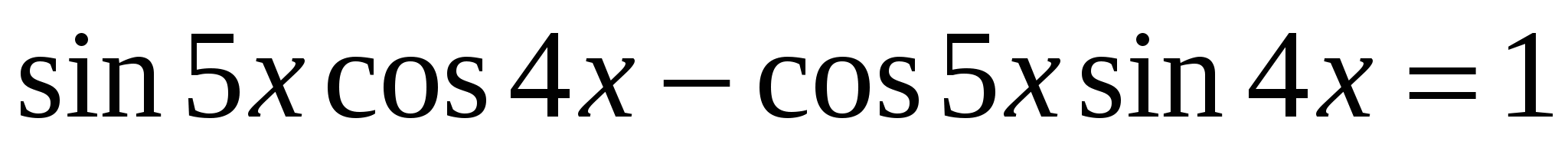 
; 
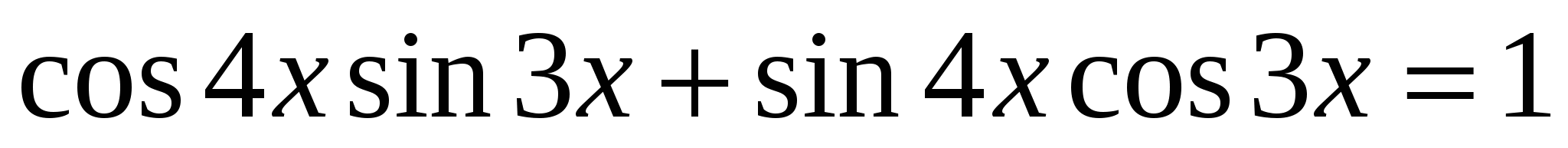
5*) Доказать: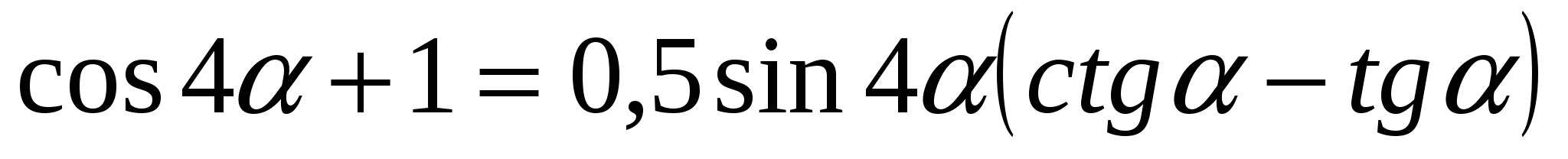 
; 
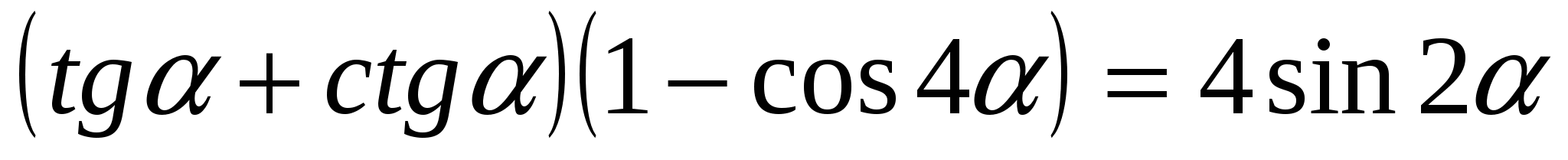
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
Тригонометрические уравнения
Вариант № 1 Вариант № 2
1) Решить уравнения: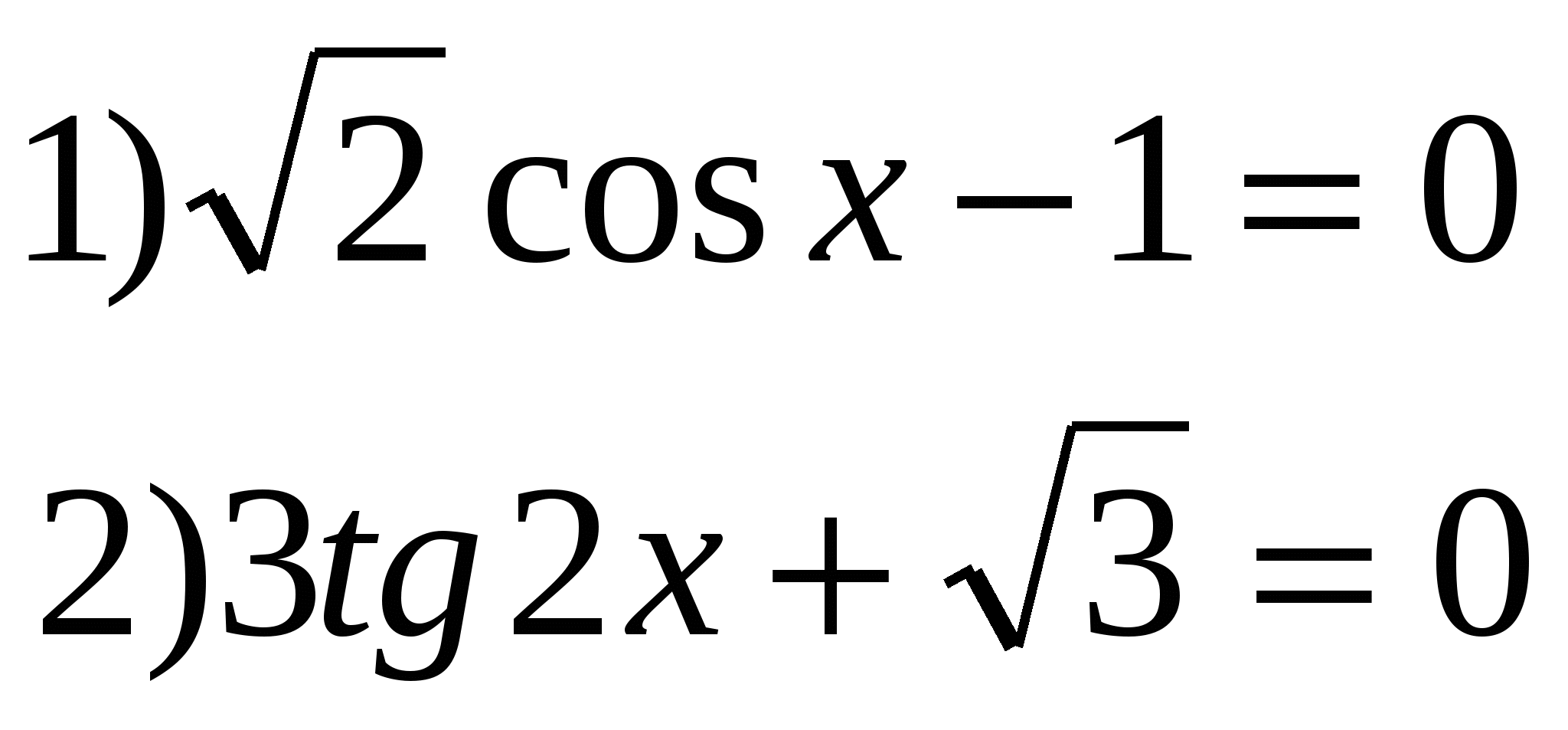 
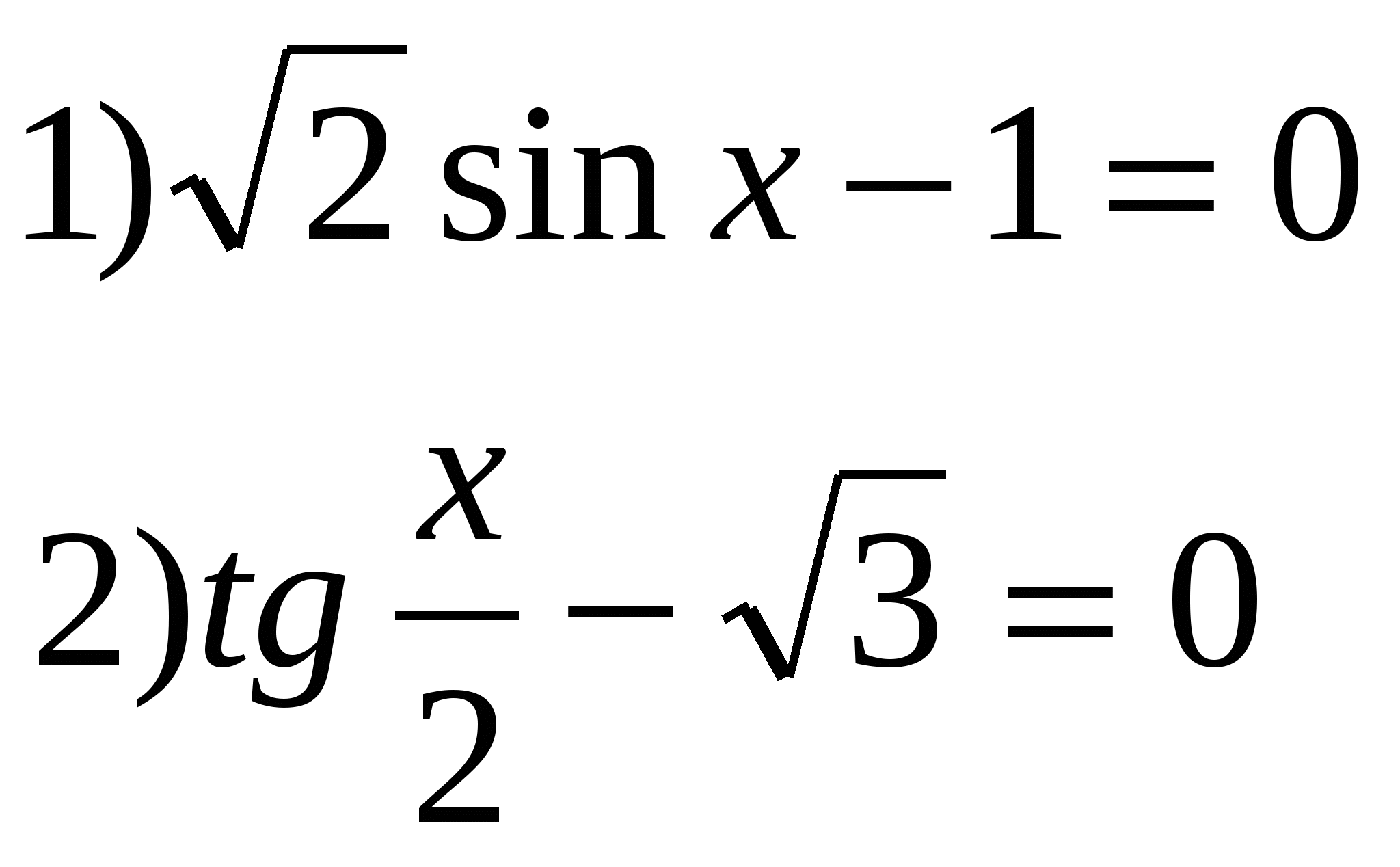
2) Найти корни уравнения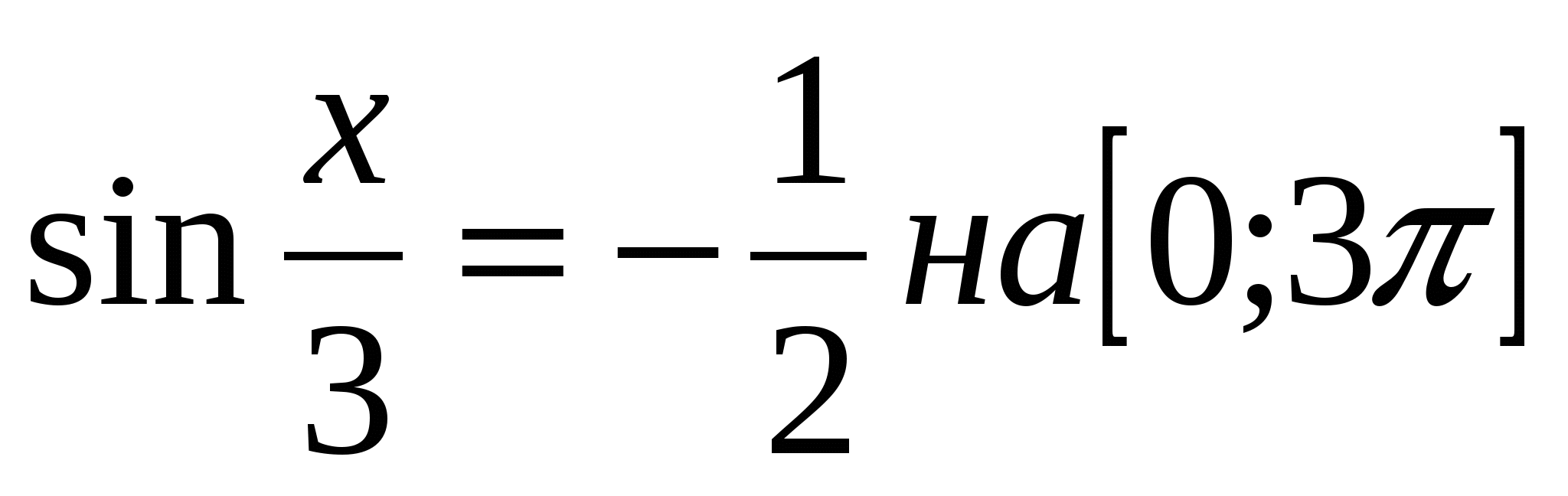 
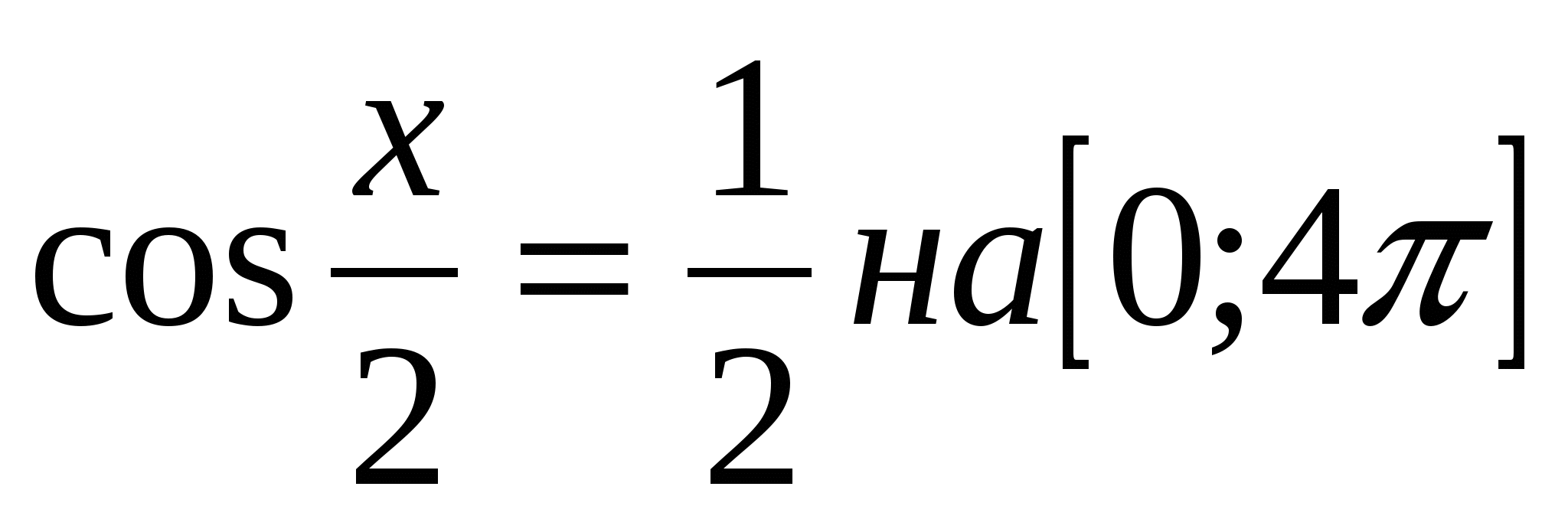
3Решить уравнения: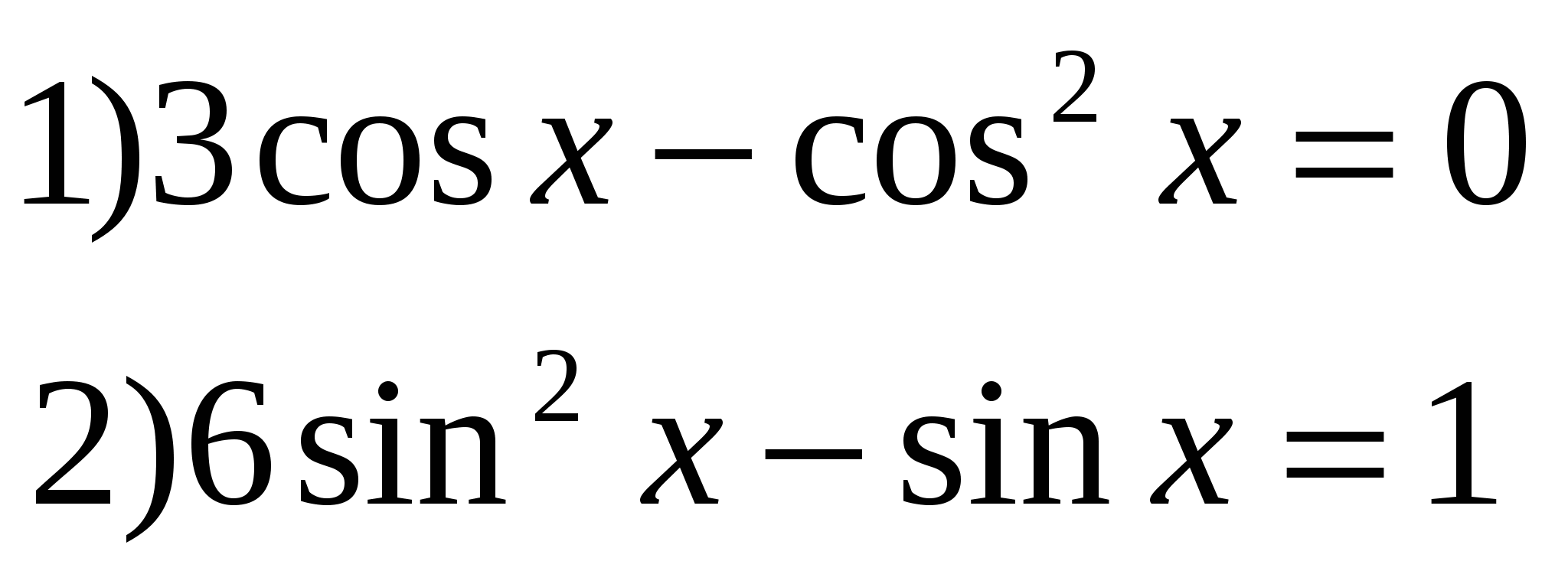 
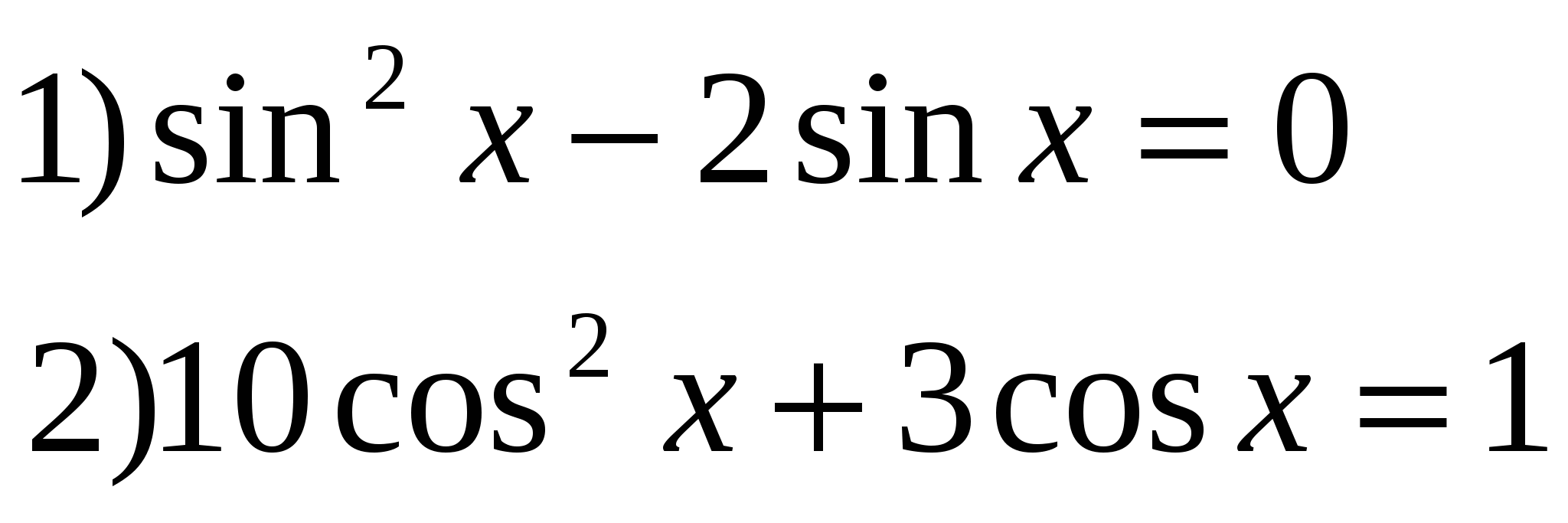
4*) Решить ур-ия: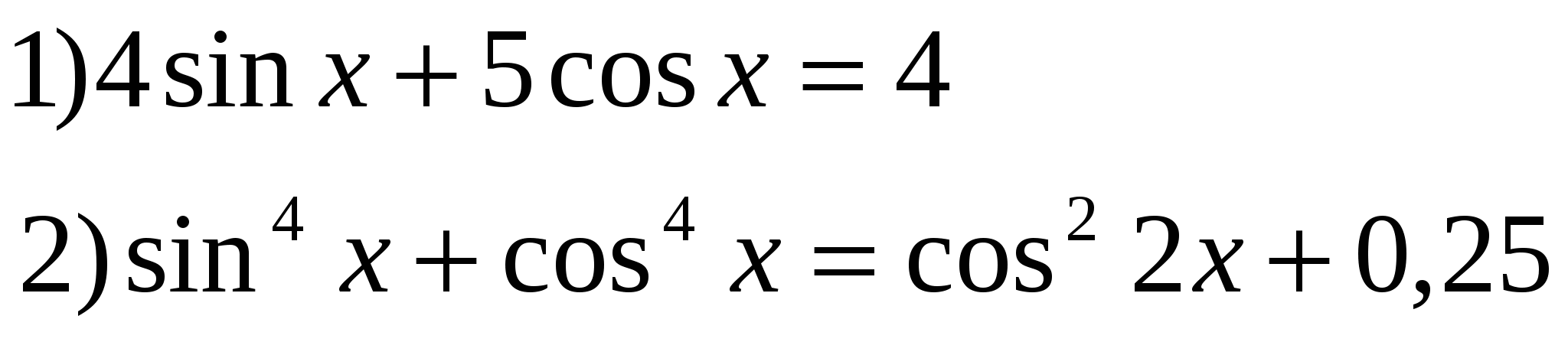 
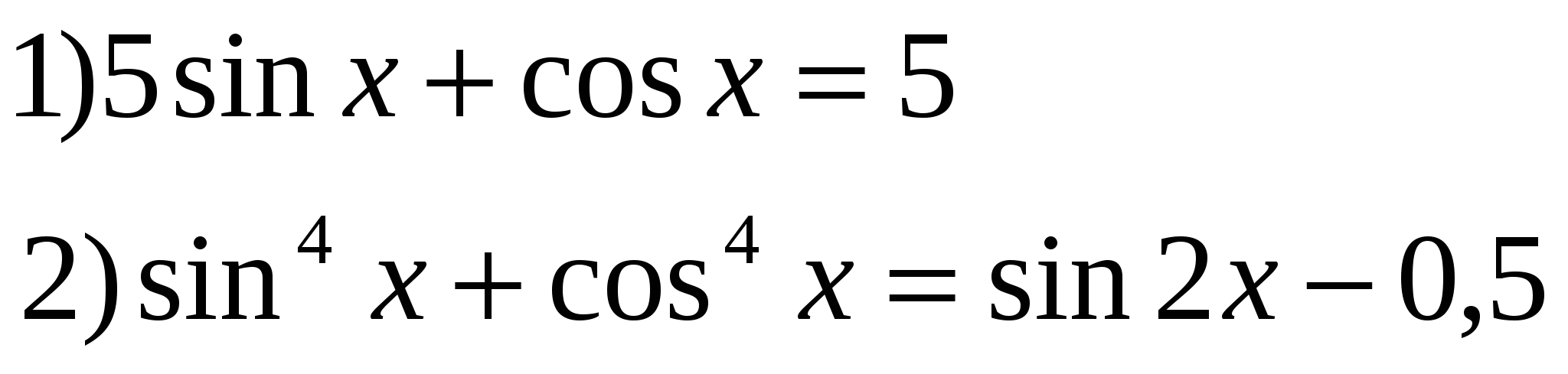
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
Тригонометрические функции
Вариант № 1 Вариант № 2
1) Найти область определения и множество значений функции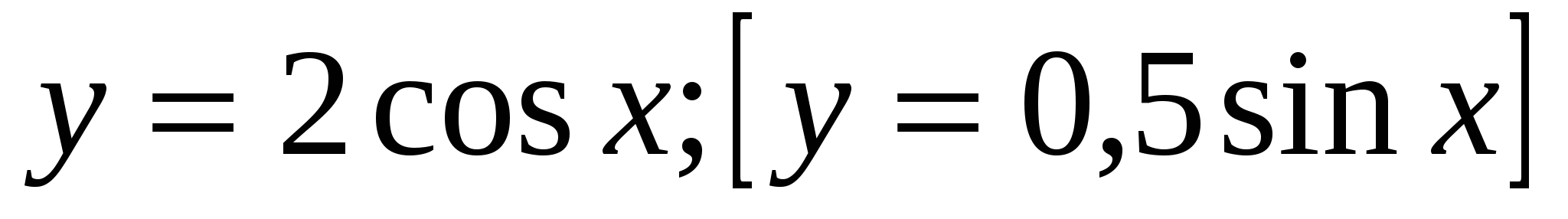 
2) Выяснить, является функция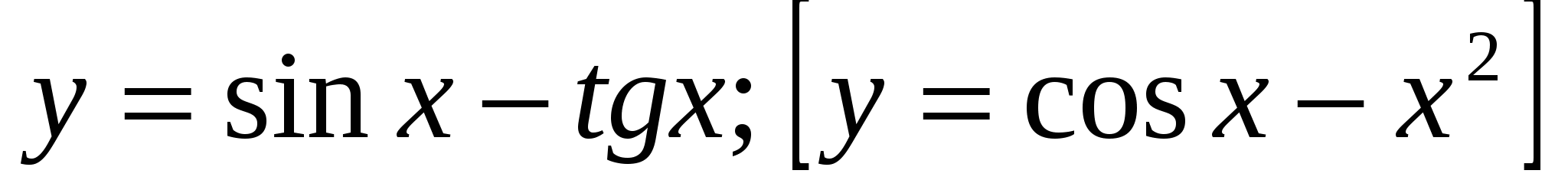 
чётной или нечётной.
3) Изобразить схематически график функции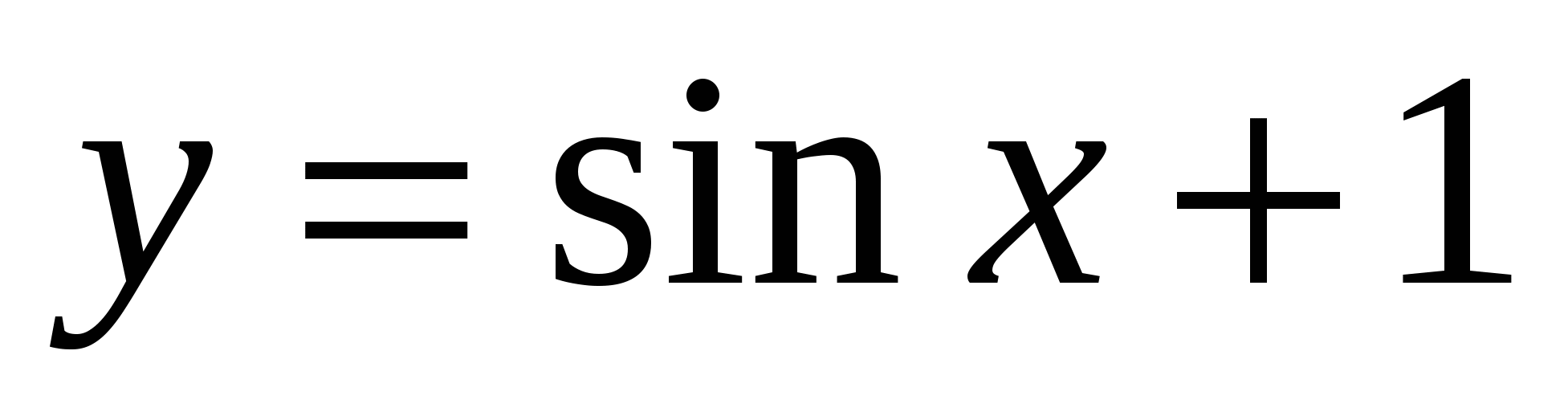 
; 
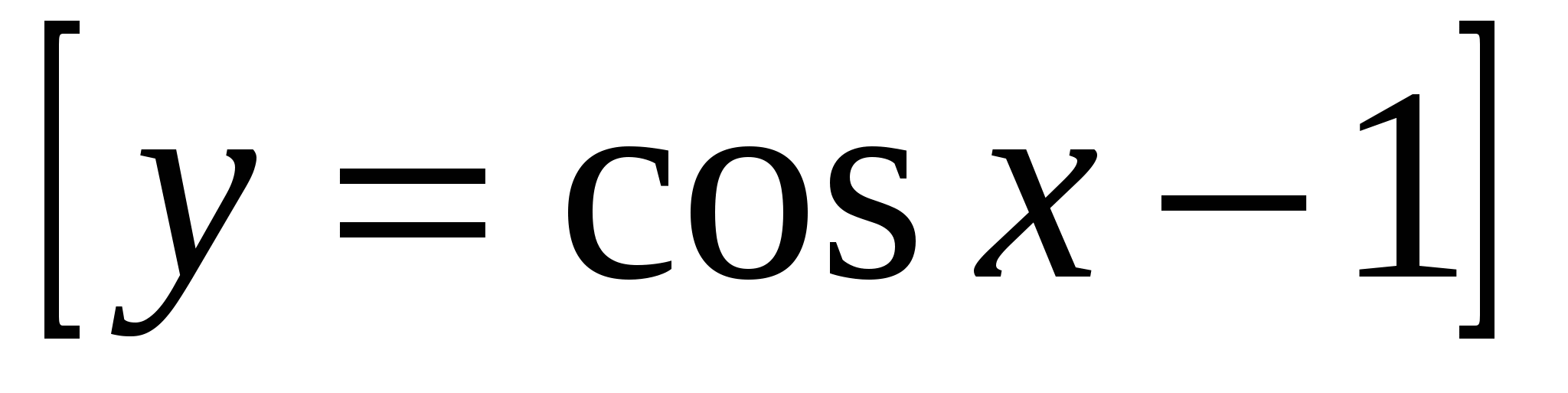на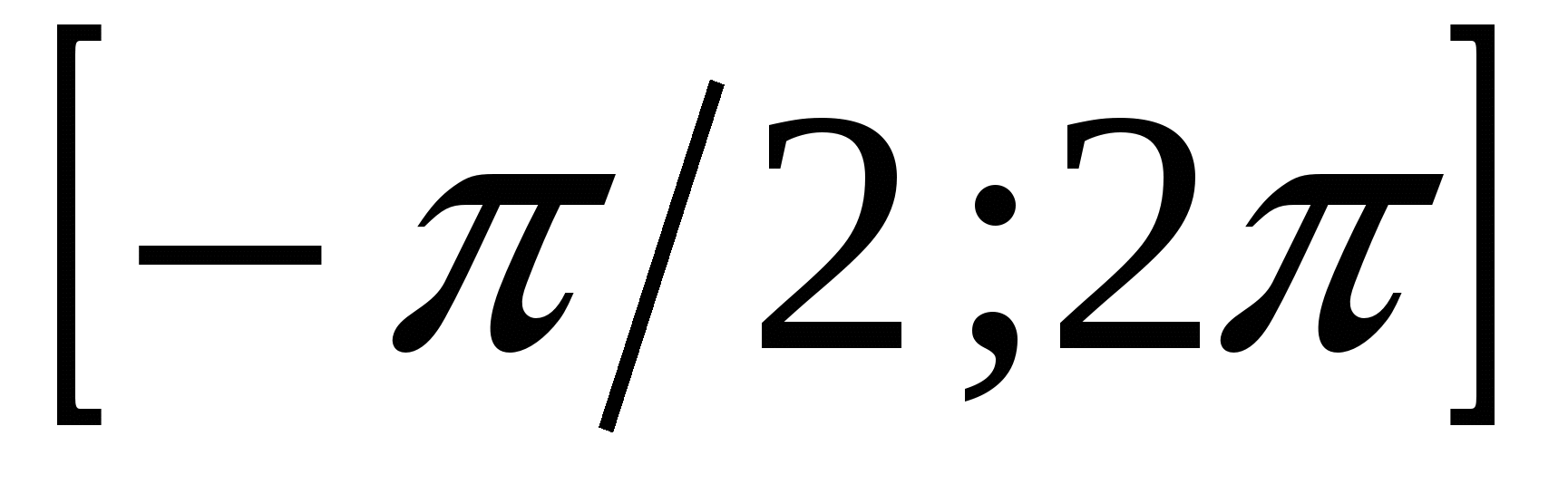 
4*) Найти наибольшее и наименьшее значения функции: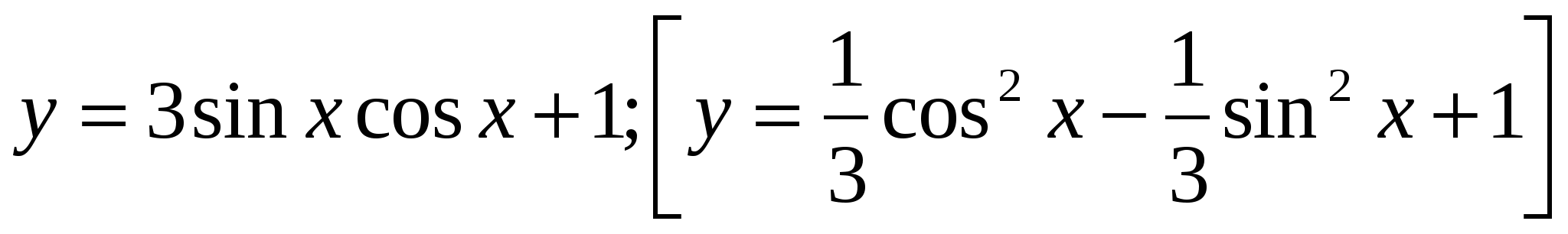 
5*) Построить график функции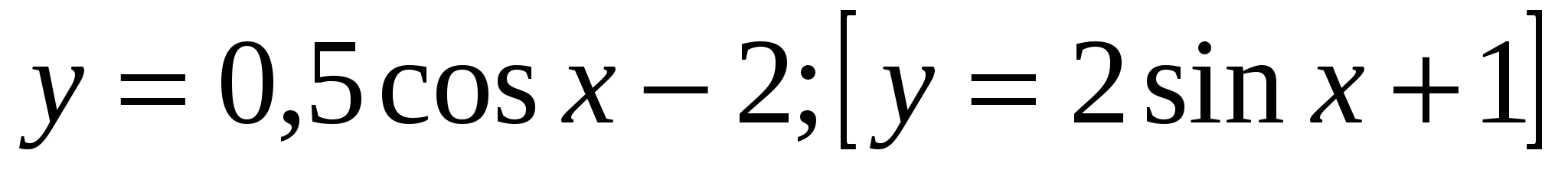 
. При каких значениях х функция возрастает [убывает]?
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
Производная
1) Найти производные функций: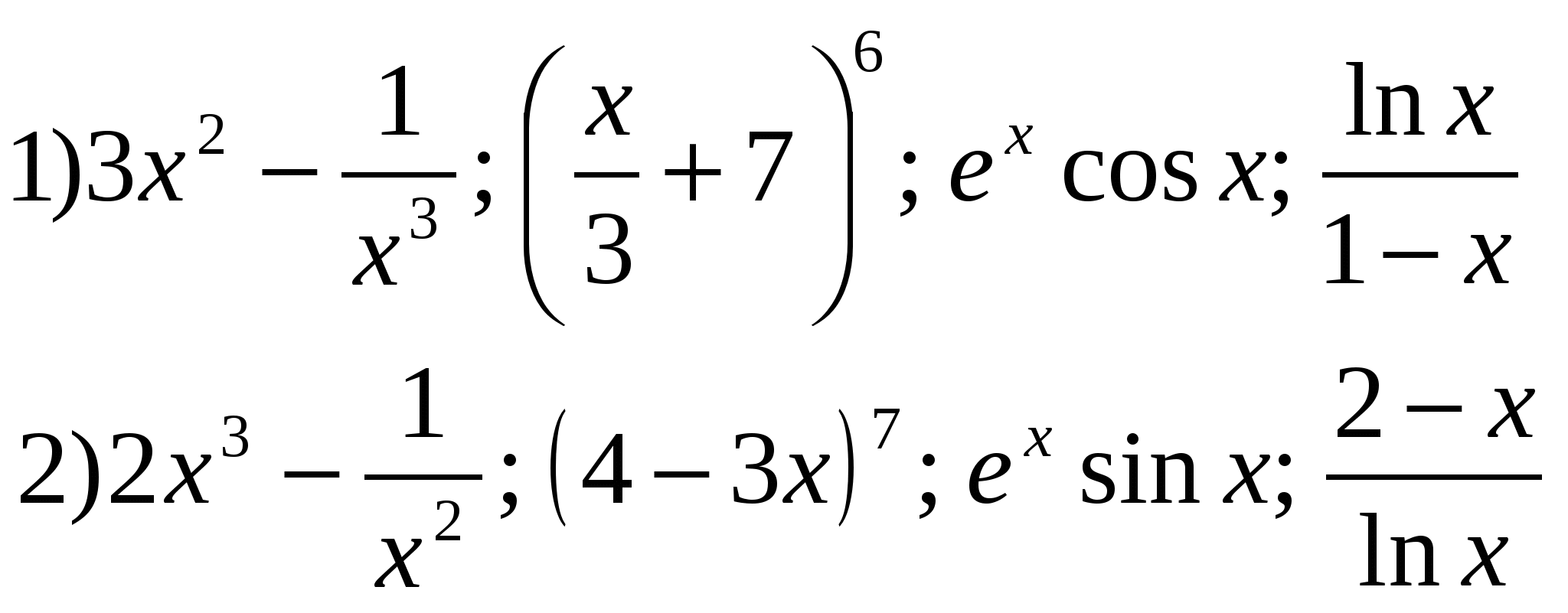 
2) Найти значение производной функции f (х) в точке хо, если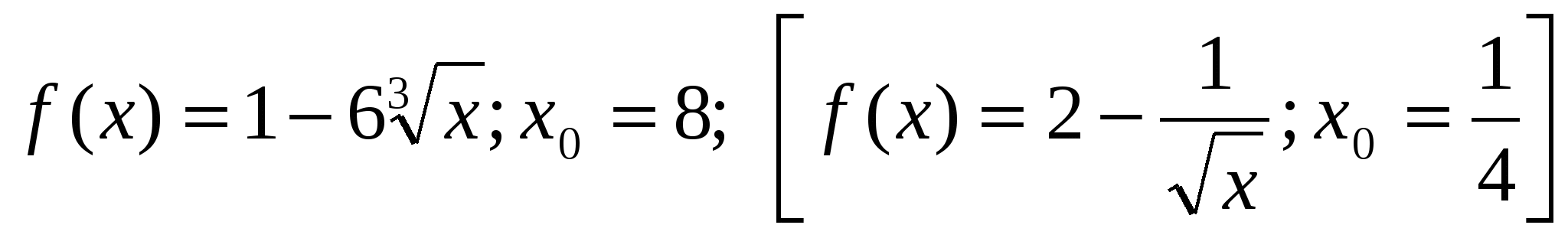 
3) Написать уравнение касательной к графику функции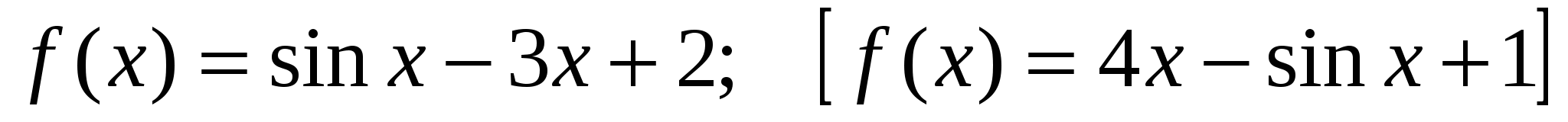 
в точке с абсциссой хо= 0
4*) Найти значения х , при которых значения производной функции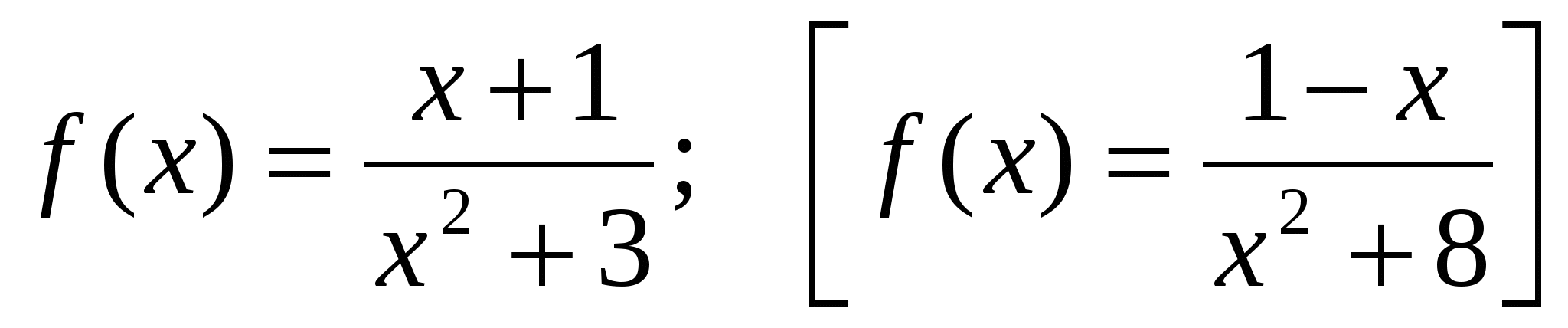 
положительны [отрицательны].
5*) Найти точки графика функции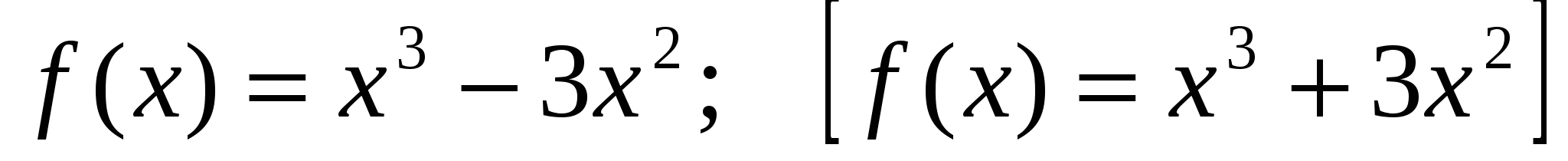 
, в которых касательная к нему параллельна оси абсцисс.
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
Производная
1) Найти экстремумы функции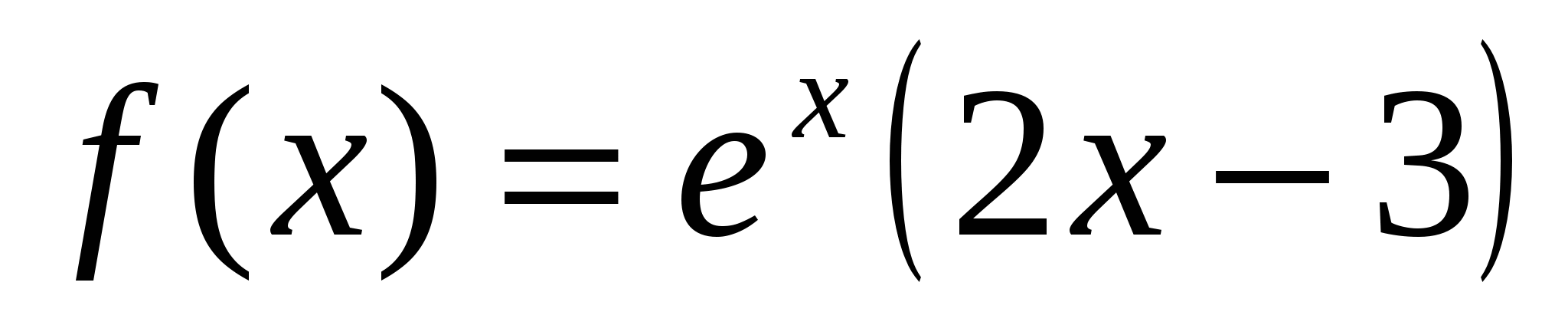 
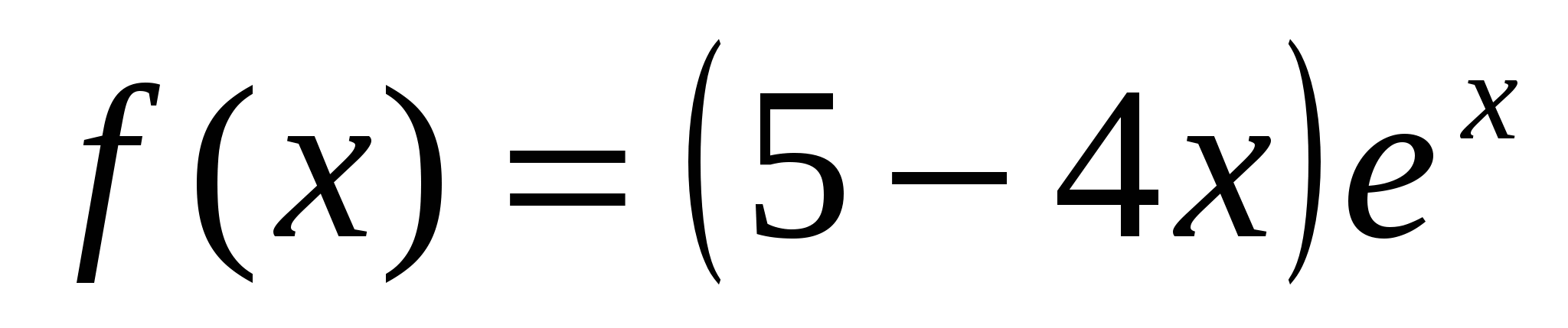
2) Найти интервалы возрастания и убывания функции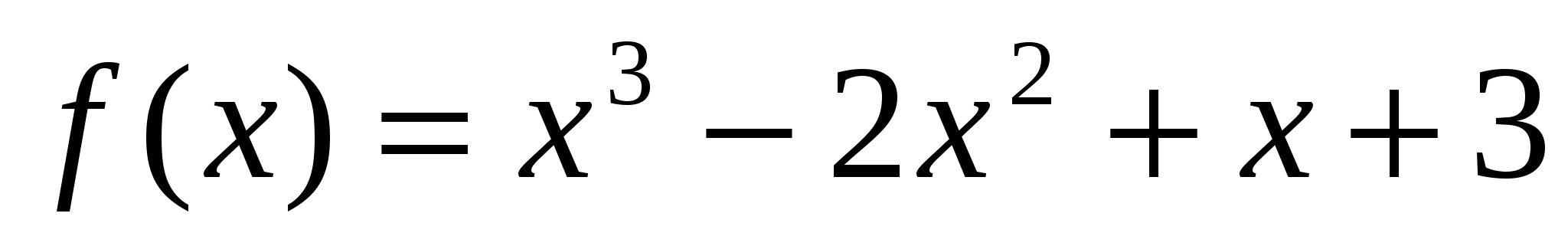 
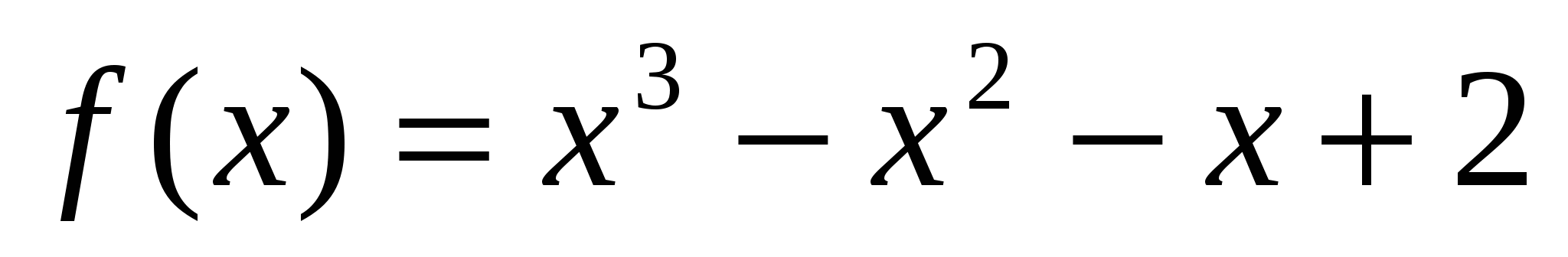
3) Построить график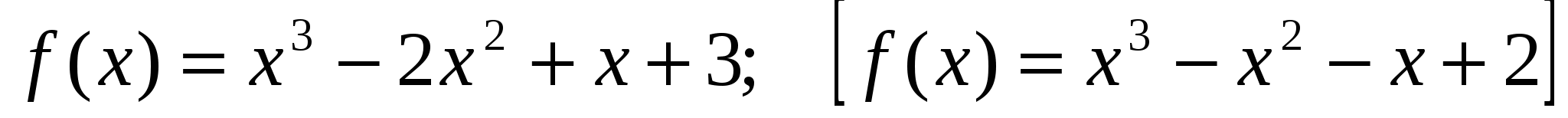 
на [-1; 2]
4*) Найти наименьшее и наибольшее значения функции 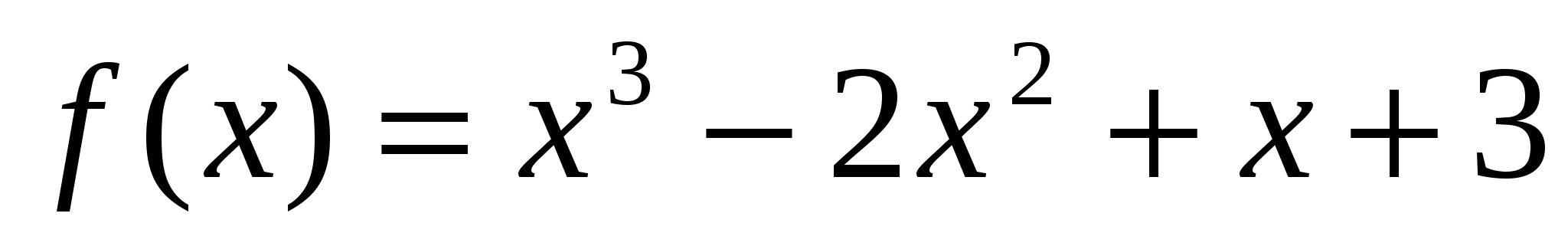на [0; 1,5] 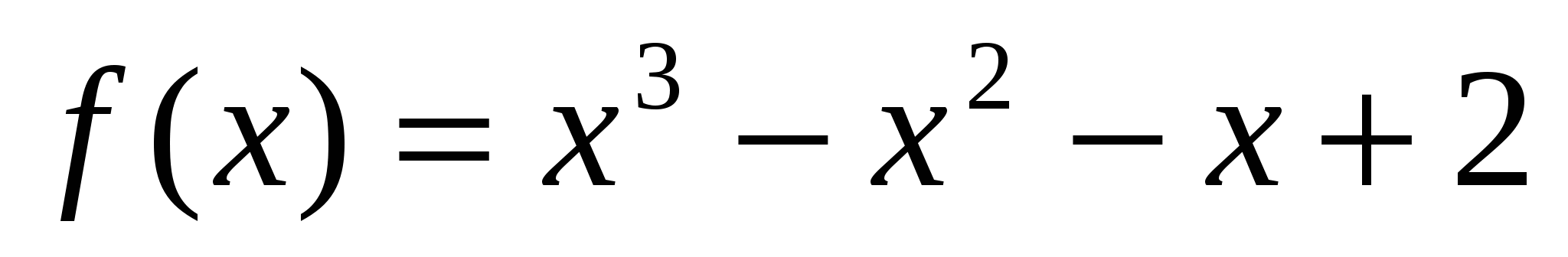на [-1; 1,5]
5*)1) Среди прямоугольников, сумма длин двух сторон у которых равна 20, найти прямоугольник наибольшей площади.
2) Найти ромб с наибольшей площадью, если известно, что сумма длин его диагоналей равна 10.
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
Первообразная
1) Доказать, что функция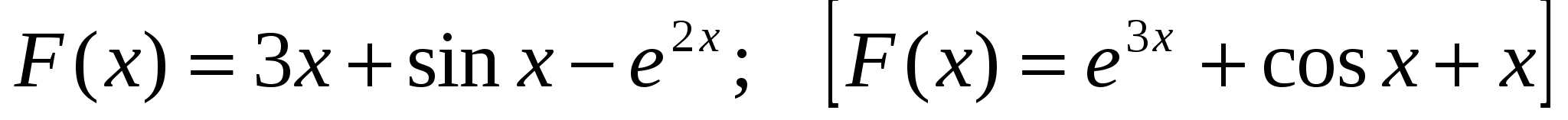 
является первообразной функции 
.
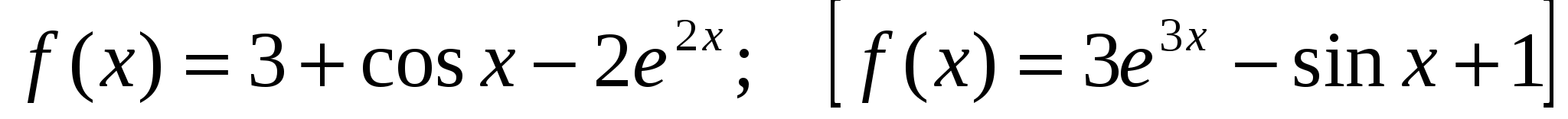2) Найти первообразную F(x) функции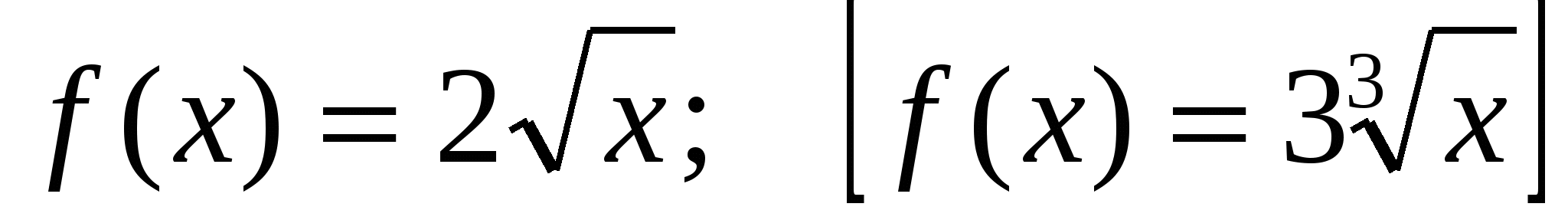 
, график которой проходит через точку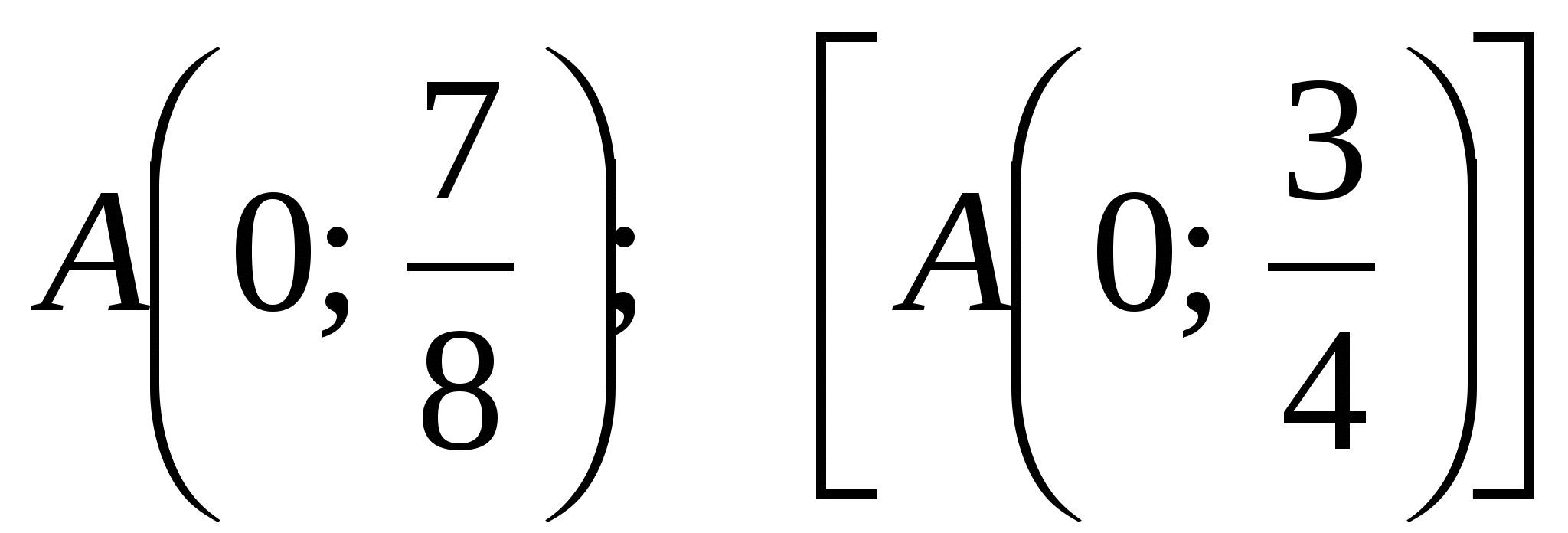 
3) Вычислить площадь фигуры, ограниченной линиями 1)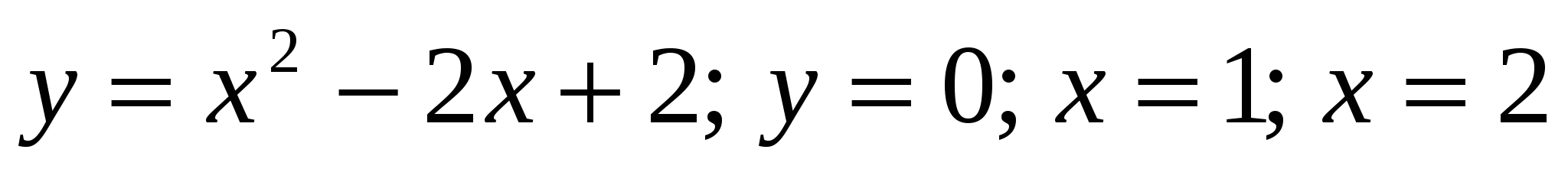
1)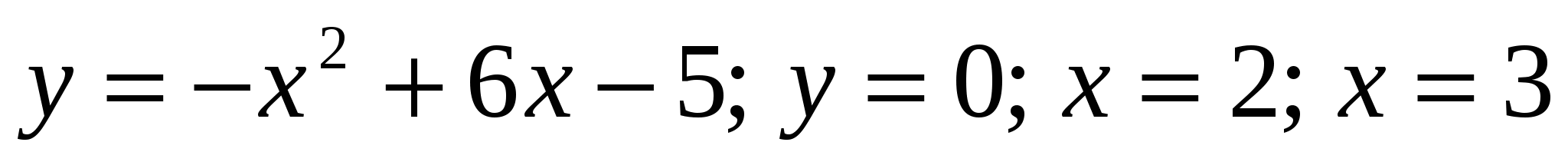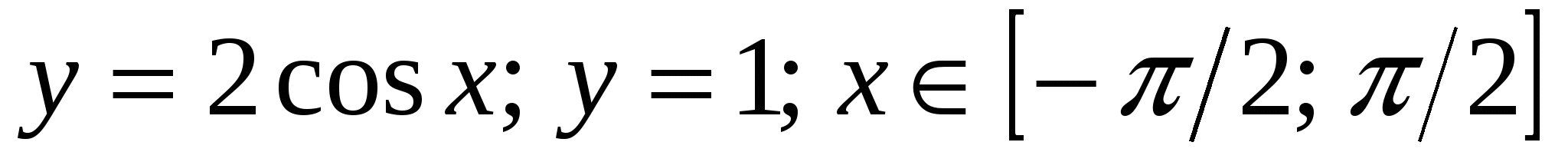
2*)
2*)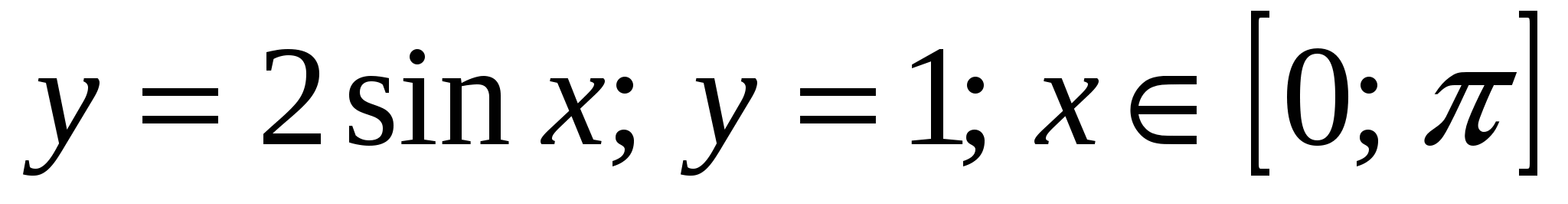
4*) Найти корни первообразной для функции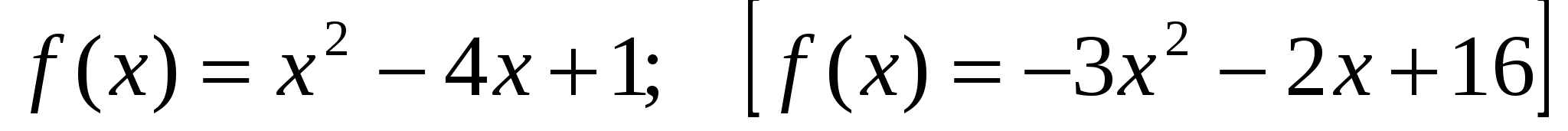 
, если один из них равен 2 [-1].
infourok.ru
