dx;
(2x3+3x2-36x+15)dx;
( x+
)dx;
( x-
)dx;
(
)dx;
dx;
dx;
dx;
;
;
;
.
Министерство образования Ульяновской области
Областное государственное бюджетное образовательное
учреждение среднего профессионального образования
«Ульяновский электромеханический колледж»
Утверждаю
заместитель директора по учебной работе ____________
« ______»________20_____г
Математика
Диагностические материалы контрольной работы
по теме «Интеграл и его приложения»
для всех специальностей первого курса
Одобрено на заседании предметно – цикловой комиссии
математических и естественно - научных дисциплин
протокол № от «___» ____20__ г.
Председатель ________
Разработал
Преподаватель
________Э.С.Статива
Ульяновск
1 Пояснительная записка
Контроль является одной из составляющих учебного процесса, и от его правильной организации на всех этапах обучения в конечном итоге зависит качество знаний студентов.
Контроль выполняет три функции:
- управляет процессом усвоения знаний, дает возможность увидеть ошибки, оценить результаты обучения, осуществить коррекцию знаний, умений и навыков;
- выполняет познавательную мотивацию и стимулирует творческую деятельность;
- является средством обучения и развития.
Структура каждого варианта заданий по форме приближена к структуре действующих форм итоговой проверки математической подготовки учащихся.
Каждый вариант состоит из двух частей и содержит 9 заданий.
Часть 1 состоит из 6 заданий. Часть 2 состоит из 3 более сложных заданий. При выполнении заданий надо записать полное решение и полный ответ.
Курс – для студентов первого курса всех специальностей
Форма проведения - контрольная работа
Время выполнения: 45 минут
Оценивание заданий: Часть 1. 1задание – 4 б
2 задание – 2 б
3 задание – 2 б
4 задание – 1 б
5 задание – 2 б
6 задание – 2 б
Часть 2. 7 задание – 3 б
8 задание – 3 б
9 задание – 3 б
Примечание: 1.Разрешается пользоваться справочниками и таблицами
Разрешается пользоваться МК
Отметка ставится только на основании правильных ответов; за ошибочные ответы баллы не снимаются
2 Критерии оценки
«5» - 20-21 балл
«4» – 13-19 баллов
«3» – 10-12 баллов
«2» -набрано менее 12 баллов.
Контрольная работа по математике
по теме «Интеграл и его приложения»
для студентов первого курса всех специальностей
Каждый вариант состоит из двух частей и содержит 9 заданий.
Часть 1 состоит из 6 заданий. Часть 2 состоит из 3 более сложных заданий. При выполнении заданий надо записать полное решение и полный ответ.
Вариант- 1.
Часть 1.
1. Указать первообразную для функции
Известно, что Найдите: 2
3. Вычислить интегралы:
а) б)
4. Вычислить площадь фигуры, изображенной на рисунке
5.Скорость точки движущейся прямолинейно, задана уравнением
. Вычислить ее путь за 5 сек от начала движения.
6.Вычислить (предварительно сделав рисунок) площадь фигуры, ограниченной линиями:
у = х2+1, у=0, х=0, х=2.
Часть 2.
7. Вычислить интеграл
8.Вычислить площадь фигуры, ограниченной линиями
у = -1
9. Вычислить объем тела, образованного вращением вокруг оси Ох
заштрихованной фигуры
Время выполнения: 45 минут
Оценивание заданий: Часть 1. 1задание – 1 б
2 задание – 1 б
3 задание – 2 б
4 задание – 2 б
5 задание – 2 б
6 задание – 2 б
Часть 2. 7 задание – 3 б
8 задание – 3 б
9 задание – 3 б
Примечание: 1.Разрешается пользоваться справочниками и таблицами
Разрешается пользоваться МК
Отметка ставится только на основании правильных ответов; за ошибочные ответы баллы не снимаются
2 Критерии оценки
«5» - 18-19 балл
«4» – 11-17 баллов
«3» – 8-10 баллов
«2» -набрано менее 8 баллов.
Контрольная работа по математике
по теме «Интеграл и его приложения»
для студентов первого курса всех специальностей
Каждый вариант состоит из двух частей и содержит 9 заданий.
Часть 1 состоит из 6 заданий. Часть 2 состоит из 3 более сложных заданий. При выполнении заданий надо записать полное решение и полный ответ.
Вариант- 2.
Часть 1.
1.Указать первообразную для функции
2.Известно, что Найдите:
3. Вычислить интегралы:
а) б)
4. Вычислить площадь фигуры, изображенной на рисунке
5.Скорость точки движущейся прямолинейно, задана уравнением
. Вычислить ее путь за 2 сек от начала движения.
6.Вычислить (предварительно сделав рисунок) площадь фигуры, ограниченной линиями: у = 4- х2 , у=0
Часть 2.
7. Вычислить интеграл
8.Вычислить площадь фигуры, ограниченной линиями
у =
9. Вычислить объем тела, образованного вращением вокруг оси Ох
заштрихованной фигуры
Время выполнения: 45 минут
Оценивание заданий: Часть 1. 1задание – 1 б
2 задание – 1 б
3 задание – 2 б
4 задание – 2 б
5 задание – 2 б
6 задание – 2 б
Часть 2. 7 задание – 3 б
8 задание – 3 б
9 задание – 3 б
Примечание: 1.Разрешается пользоваться справочниками и таблицами
Разрешается пользоваться МК
Отметка ставится только на основании правильных ответов; за ошибочные ответы баллы не снимаются
2 Критерии оценки
«5» - 18-19 балл
«4» – 11-17 баллов
«3» – 8-10 баллов
«2» -набрано менее 8 баллов.
Контрольная работа по математике
по теме «Интеграл и его приложения»
для студентов первого курса всех специальностей
Каждый вариант состоит из двух частей и содержит 9 заданий.
Часть 1 состоит из 6 заданий. Часть 2 состоит из 3 более сложных заданий. При выполнении заданий надо записать полное решение и полный ответ.
Вариант- 3.
Часть 1.
1.Указать первообразную для функции
2.Известно, что Найдите:
3. Вычислить интегралы:
а) б)
4. Вычислить площадь фигуры, изображенной на рисунке
5.Скорость точки движущейся прямолинейно, задана уравнением
. Вычислить ее путь за 3 сек от начала движения.
6.Вычислить (предварительно сделав рисунок) площадь фигуры, ограниченной линиями:
у = х2+2, у=0, х=-1, х=1.
Часть 2.
7. Вычислить интеграл
8.Вычислить площадь фигуры, ограниченной линиями
у =
9. Вычислить объем тела, образованного вращением вокруг оси Ох
заштрихованной фигуры
Время выполнения: 45 минут
Оценивание заданий: Часть 1. 1задание – 1 б
2 задание – 1 б
3 задание – 2 б
4 задание – 2 б
5 задание – 2 б
6 задание – 2 б
Часть 2. 7 задание – 3 б
8 задание – 3 б
9 задание – 3 б
Примечание: 1.Разрешается пользоваться справочниками и таблицами
Разрешается пользоваться МК
Отметка ставится только на основании правильных ответов; за ошибочные ответы баллы не снимаются
2 Критерии оценки
«5» - 18-19 балл
«4» – 11-17 баллов
«3» – 8-10 баллов
«2» -набрано менее 8 баллов.
Контрольная работа по математике
по теме «Интеграл и его приложения»
для студентов первого курса всех специальностей
Каждый вариант состоит из двух частей и содержит 9 заданий.
Часть 1 состоит из 6 заданий. Часть 2 состоит из 3 более сложных заданий. При выполнении заданий надо записать полное решение и полный ответ.
Вариант- 4.
Часть 1.
1.Указать первообразную для функции
2.Известно, что Найдите:
3. Вычислить интегралы:
а) б)
4. Вычислить площадь фигуры, изображенной на рисунке
5.Скорость точки движущейся прямолинейно, задана уравнением
. Вычислить ее путь за 1 сек от начала движения.
6.Вычислить (предварительно сделав рисунок) площадь фигуры, ограниченной линиями:
у = 1- х2, у=0
Часть 2.
7. Вычислить интеграл
8.Вычислить площадь фигуры, ограниченной линиями
у =
9. Вычислить объем тела, образованного вращением вокруг оси Ох
заштрихованной фигуры
Время выполнения: 45 минут
Оценивание заданий: Часть 1. 1задание – 1 б
2 задание – 1 б
3 задание – 2 б
4 задание – 2 б
5 задание – 2 б
6 задание – 2 б
Часть 2. 7 задание – 3 б
8 задание – 3 б
9 задание – 3 б
Примечание: 1.Разрешается пользоваться справочниками и таблицами
Разрешается пользоваться МК
Отметка ставится только на основании правильных ответов; за ошибочные ответы баллы не снимаются
2 Критерии оценки
«5» - 18-19 балл
«4» – 11-17 баллов
«3» – 8-10 баллов
«2» -набрано менее 8 баллов.
infourok.ru
Контрольная работа
Найдите интегралы, используя свойства интегралов и таблицу интегралов:
dx;
(2x3+3x2-36x+15)dx;
( x+)dx;
( x-)dx;
()dx;
dx;
dx;
dx;
;
;
;
.
Найдите интегралы методом введения новой переменной:
;
;
;
;
;
.
Найдите интегралы методом интегрирования по частям:
Сделайте чертёж и вычислите площадь фигуры, ограниченной данными линиями:
y=x3-1, y=0, x=0.
y=x2-3x-4 и осью Ох.
y=x3, y=x2, x=-1, x=0.
y=x2, y=x+2.
y=x2+2, y=2x+2.
Сделайте чертёж и вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной данными линиями:
y=x3, y=0, x=0, x=2.
xy=1, x=2, x=3, y=0.
y=x2, y=0, x-3=0, x=0.
Задачи:
Скорость прямолинейного движения тела задана уравнением V(t)=9t2-20t (V- в м/с). Вычислите его путь, пройденный за четвертую секунду.
Скорость прямолинейно движущегося тела равна V(t)=4t-t2 (V- в м/с). Вычислите путь, пройденный телом от начала движения до остановки.
Вычислите работу, которую нужно совершить при растяжении пружины на 8 см., если сила 3 Н растягивает пружину на 1 см.
При сжатии пружины на 4 см необходимо совершить работу 9,81 Дж. Какую работу надо произвести для сжатия пружины на 10 см.
multiurok.ru
КР+ДР+MAPLE (2) 18 КАНТ-2007
ОТЧЕТНОСТИ ЗА ВТОРОЙ СЕМЕСТР
(инструкция по выполнению)
ФИТ , группы АП-21 и АП-22
1. Найти общее решение уравнения с разделяющимися переменными (преподавателям – о стационарном решении даже не упоминать!)
.
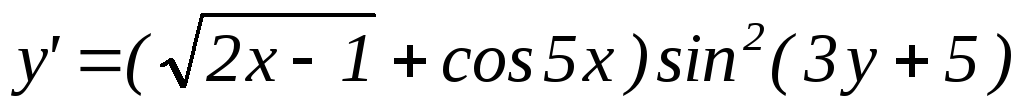а) Заменяем y’ на dy/dx. Получаем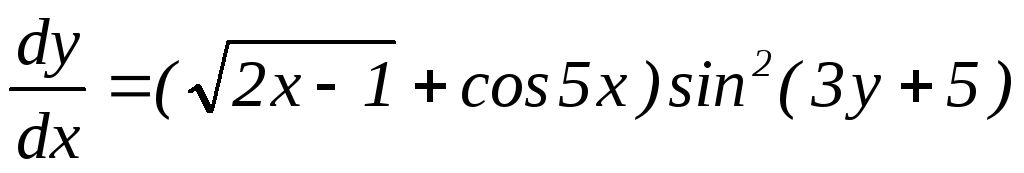 
.
б) Разделяем переменные (игреки – налево, иксы – направо) по правилу: «множители переносятся наискосок». Получаем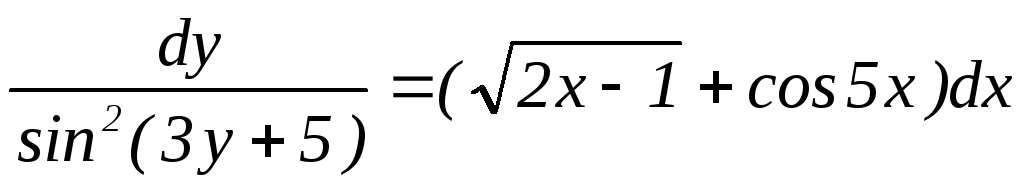 
.
в) Интегрируем полученное равенство. Получаем ответ
.
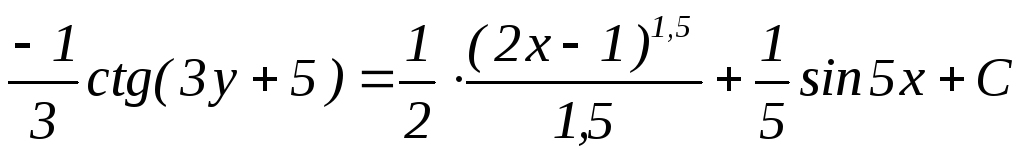Примечание. В этом примере используется правило линейной подстановки:
Если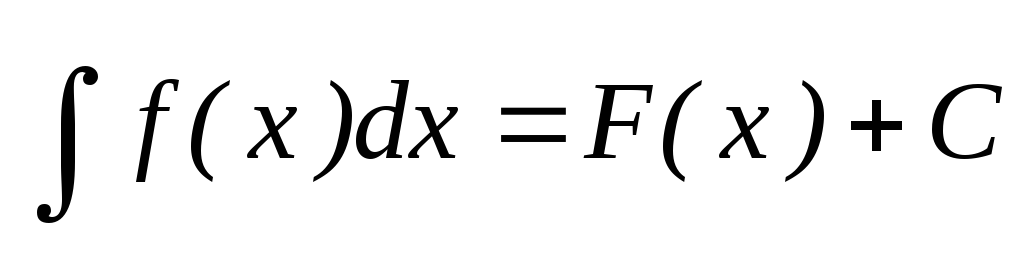 
, то
. Множитель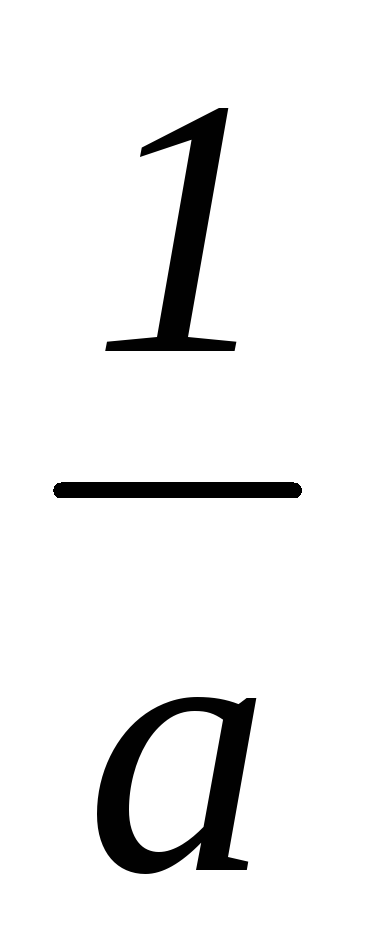
называется поправкой интегрирования.
2. Во втором примере применяют метод подведения под знак дифференциала. Используется одна из формул:
xdx=(1/2)d(x2), exdx=d(ex), (1/x)dx=d(lnx), sinxdx= – d(cosx), cosxdx=d(sinx) .
Пример.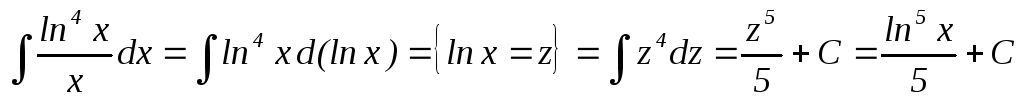 
.
3. В 3-м примере производят замену переменной по правилу: а) При наличии квадратного трехчлена ax2+bx+c делают замену x=t–b/(2a) , б) При наличии корня из линейной функции этот корень принимают за t и находят x(t).
Далее по функции x(t) находим dx=x’(t)dt и всё это подставляем в подынтегральное выражение. Проинтегрировав полученное выражение, следует сделать обратную замену, т.е. вернуться к старой переменной х.
Пример.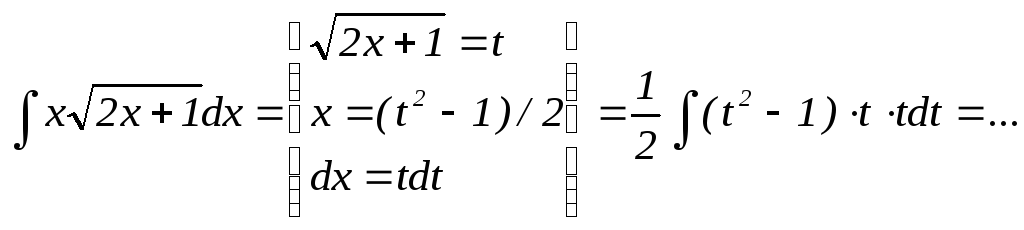 
4. В 4-м примере следует произвести интегрирование по частям. Для этого подынтегральное выражение разбиваем на два множителя u и dv. При помощи дифференцирования находим du , а при помощи интегрирования находим v. Затем применяем формулу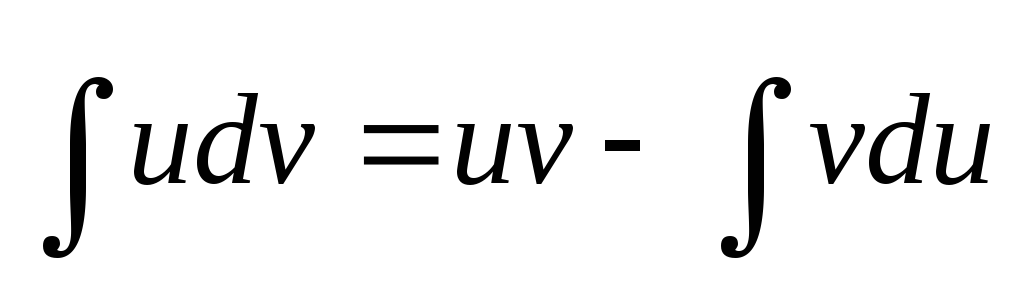 
. Указание. Заи принимаем множитель при Sin(.. ) , Cos(.. ) , e(.. ) . При наличии lnx за и принимаем этот логарифм.
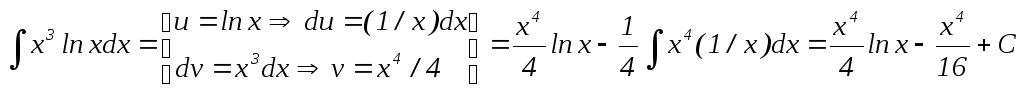
5. В последнем примере нужно проинтегрировать рациональную дробь. Если эта дробь неправильная, то при помощи деления «уголком» её превращают в сумму: многочлена и правильной дроби (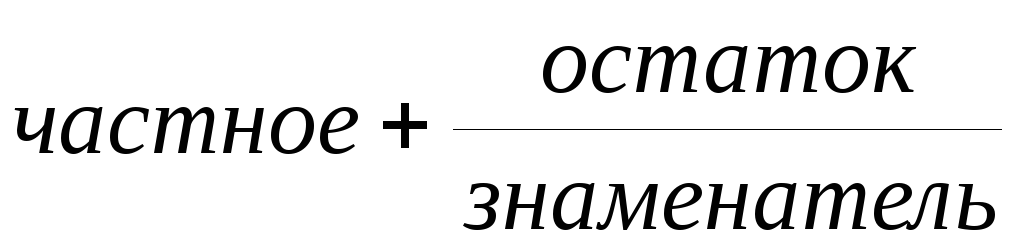
). Для интегрирования правильной дроби с простыми корнями в знаменателе следует разложить знаменатель на линейные множители и найти асимптотики правильной дроби в особых точках (метод «затыкания» и подстановки). Правильная дробь будет равна сумме этих асимптотик. Интеграл от каждой из асимптотик – это натуральный логарифм.
НА
1. Вычисление несобственного интеграла 1 рода по определению.
а) Бесконечный предел заменяем параметром А.
б) Вычисляем получившийся определенный интеграл.
в) Находим предел от полученного выражения при А .
Если этот предел существует и не равен бесконечности, то говорят, что интеграл сходится, и его значение равно значению этого предела. Если же предел не существует либо равен бесконечности, то говорят, что интеграл расходится. При вычислении предела следует использовать соотношения:
(+)= , (–)=0 , ехр(+)= , ехр(–)=0 , ln()= , arctg(+)=/2 .
Пример.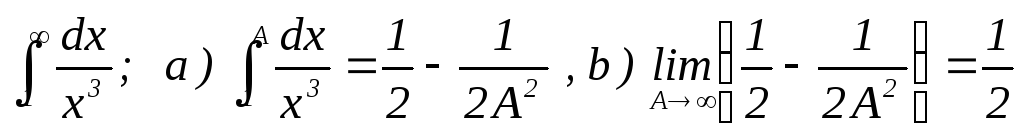 
. Вывод: Несобственный интеграл сходится и равен ½ .
2. Применение предельной теоремы сравнения. Подынтегральную функцию заменяем функцией, эквивалентной данной функции при х . Для этого используем соотношения эквивалентности, формулы Маклорена для функций ex , sinx , cosx , ln(1+x) ,(1+x)n , а также правило сохранения главных слагаемых. Получившийся упрощенный несобственный интеграл исследуем на сходимость по определению. Делаем вывод о сходимости исходного интеграла.
Пример.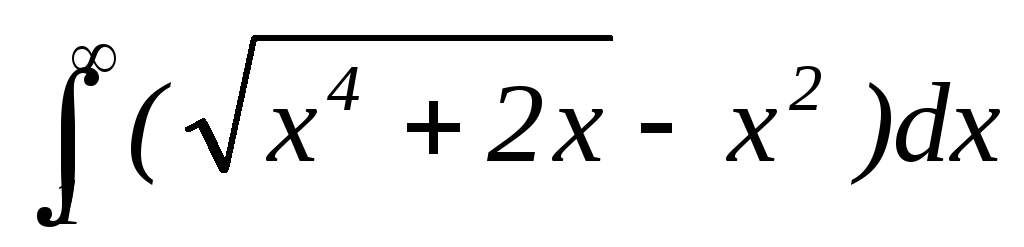 
. Рассмотрим подынтегральную функцию и используем соотношение эквивалентности
.
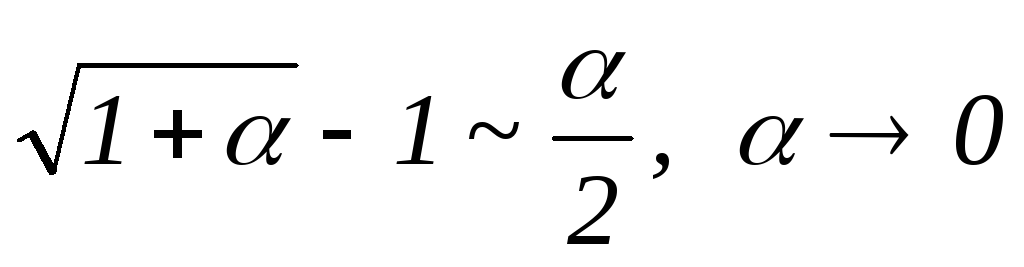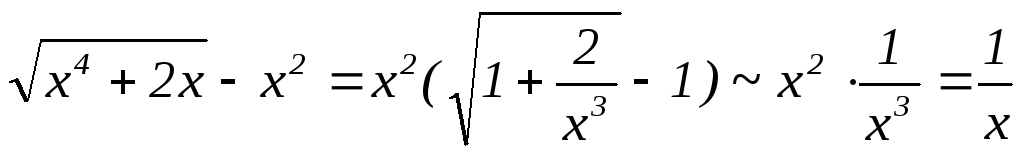. Интеграл 
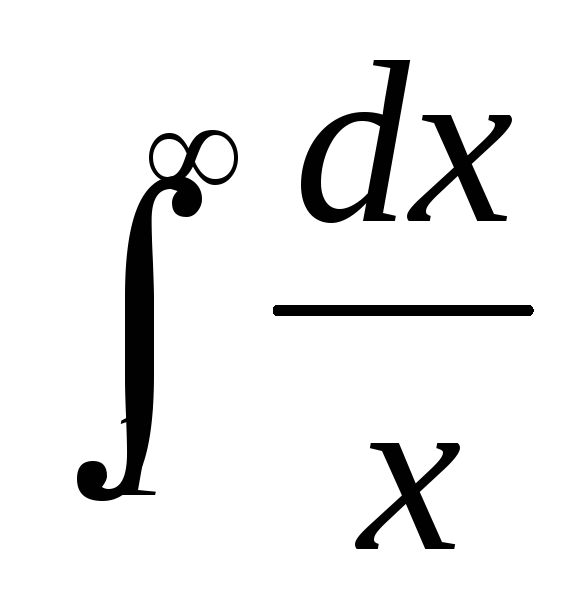расходится по определению. Следовательно, исходный интеграл также расходится по предельной теореме сравнения..
studfiles.net
