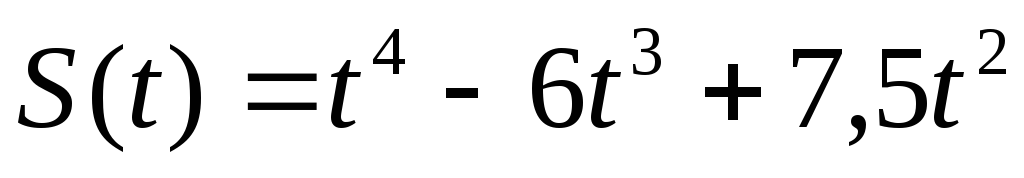 , Т=3.
, Т=3.171 – 180. Закон движения точки на прямой задан функцией S(t). Найти скорость V(t) и ускорение a(t) и их наибольшие абсолютные значения на отрезке [ 0 ; T ].
171. 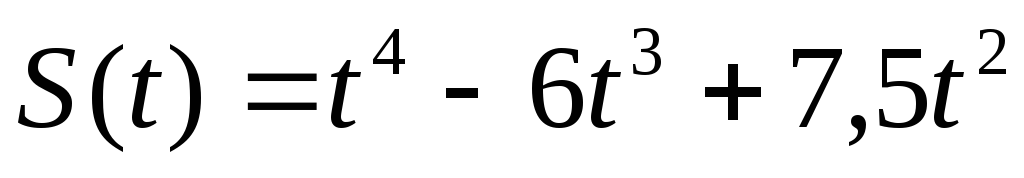 , Т=3.
, Т=3.
173.  , Т=1.
, Т=1.
175. 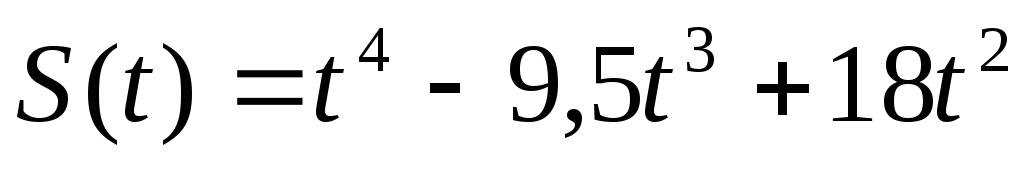 , Т=5.
, Т=5.
177. 
 , Т=3.
, Т=3.
179. 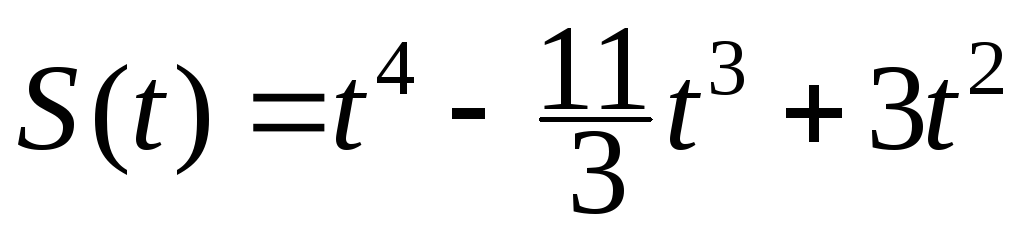 , Т=2.
, Т=2.
172. 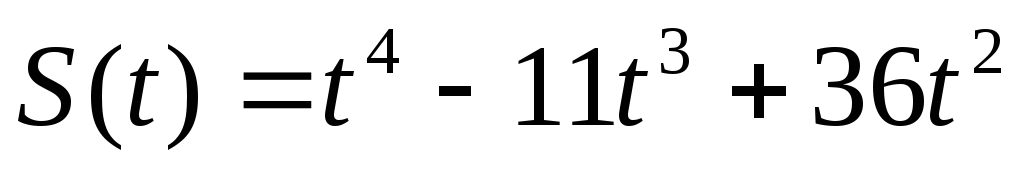 , Т=3.
, Т=3.
174. 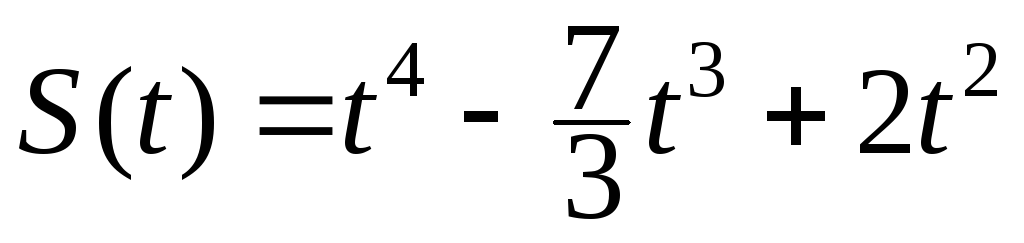 , Т=1.
, Т=1.
176. 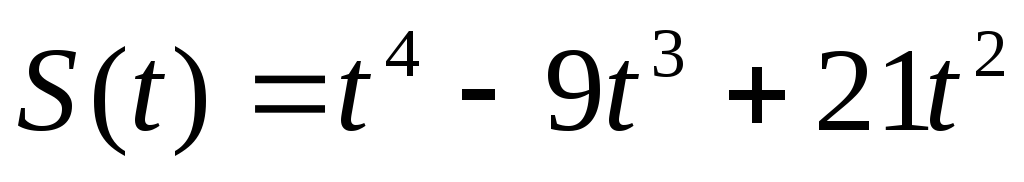 , Т=4.
, Т=4.
178. 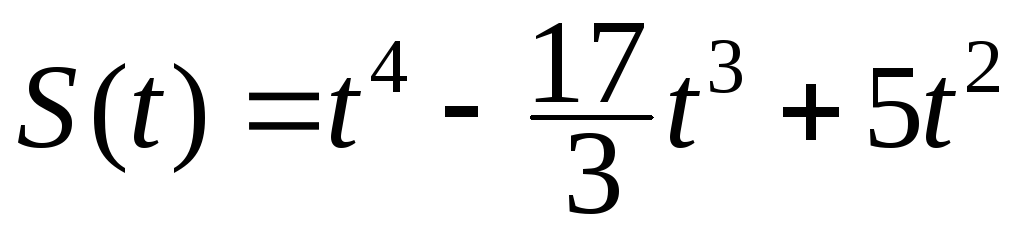 , Т=3.
, Т=3.
180. 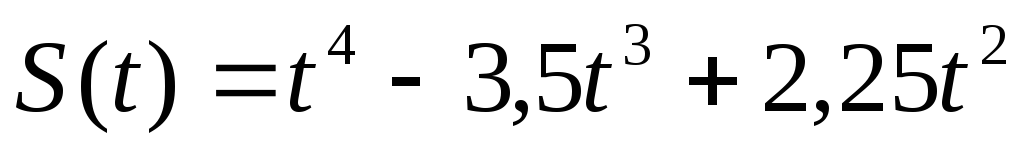 , Т=2.
, Т=2.
181 – 190. Найти неопределённые интегралы.
181. а) 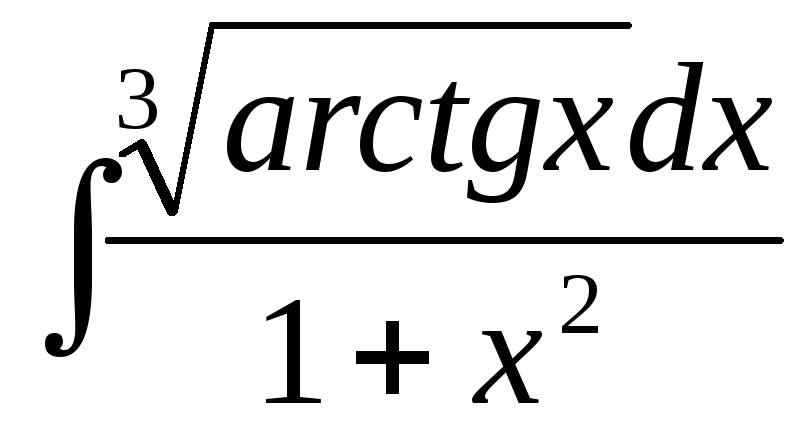 ,
,
в) 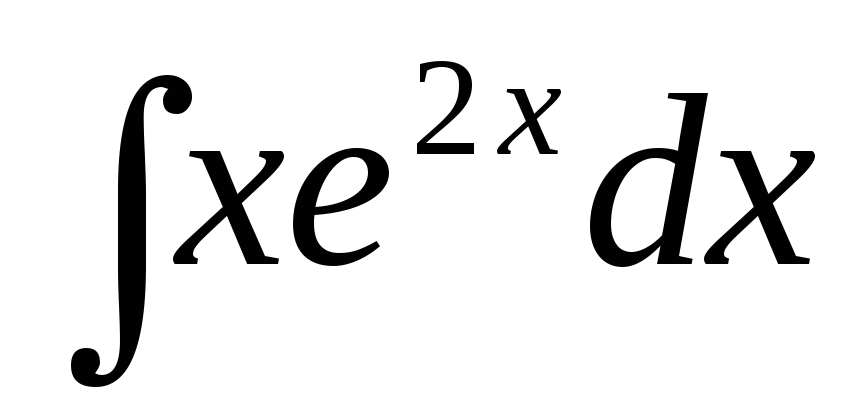 ,
,
д)  ,
,
б) 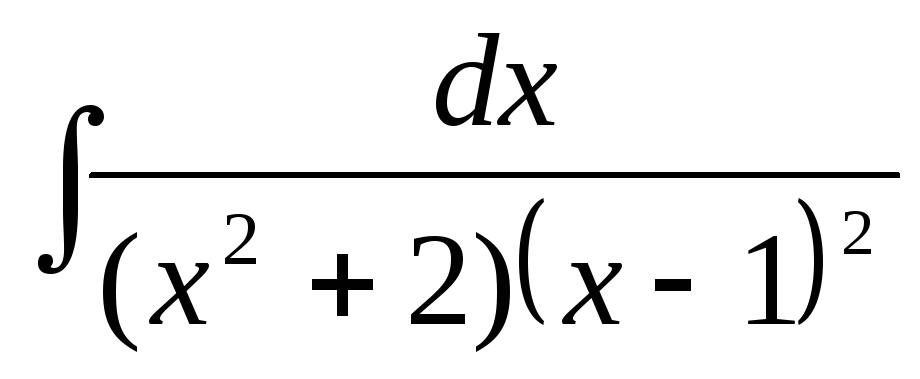 ,
,
г) 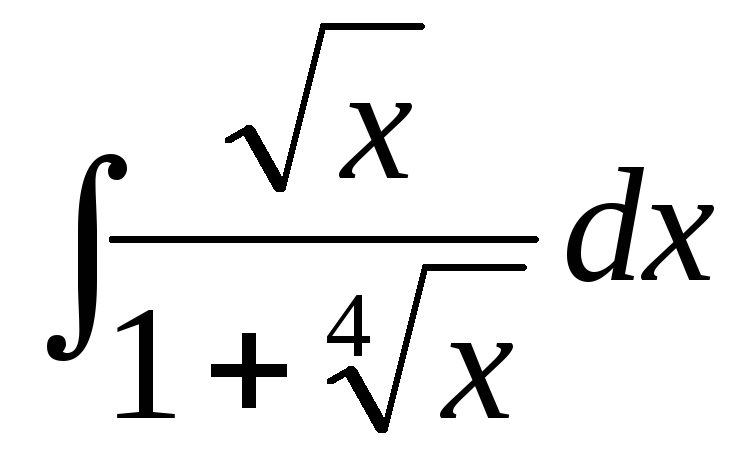 ,
,
е) 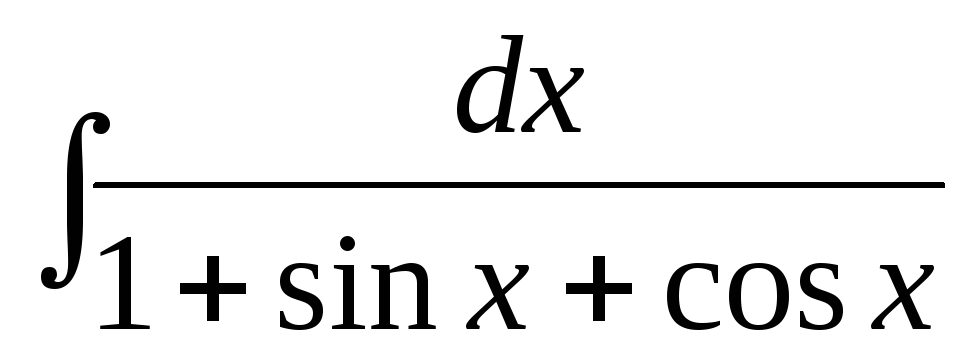 .
.
182. а) 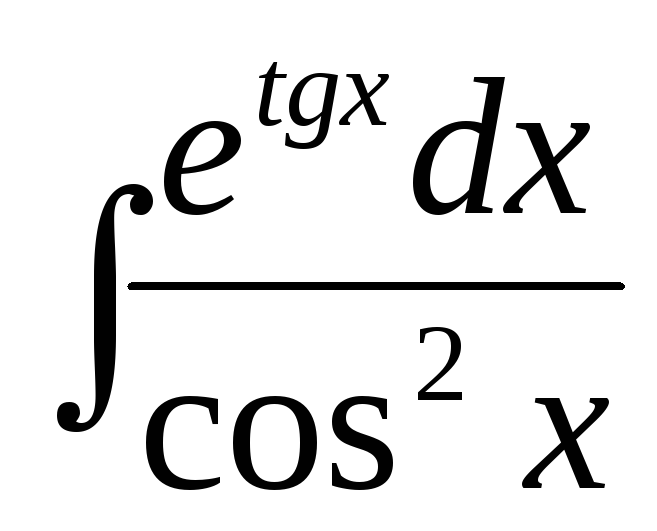 ,
,
в) 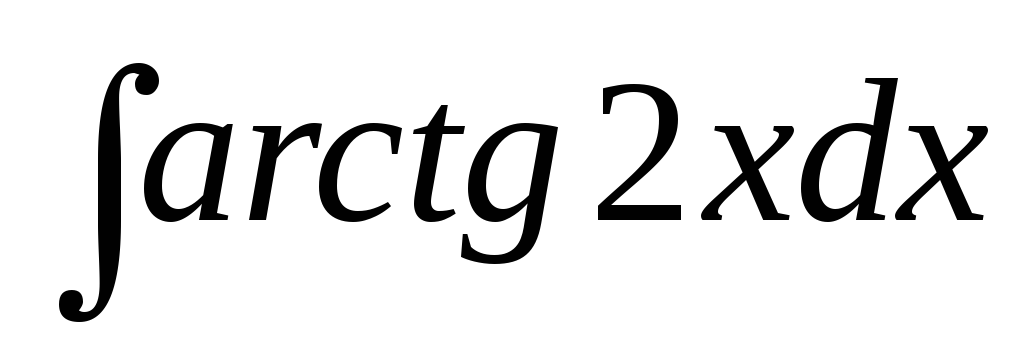 ,
,
д) 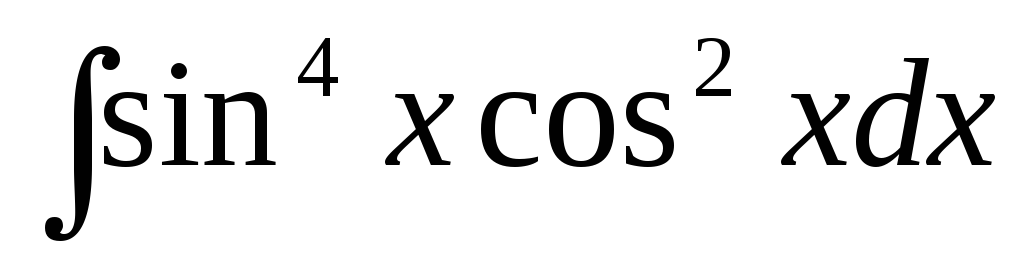 ,
,
б) 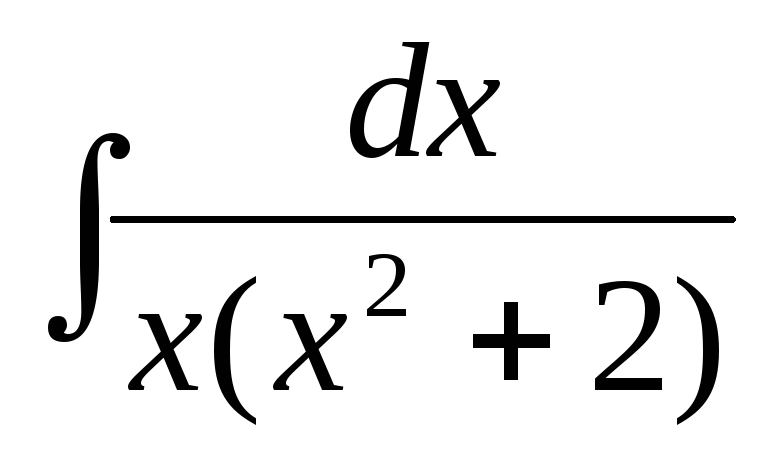 ,
,
г) 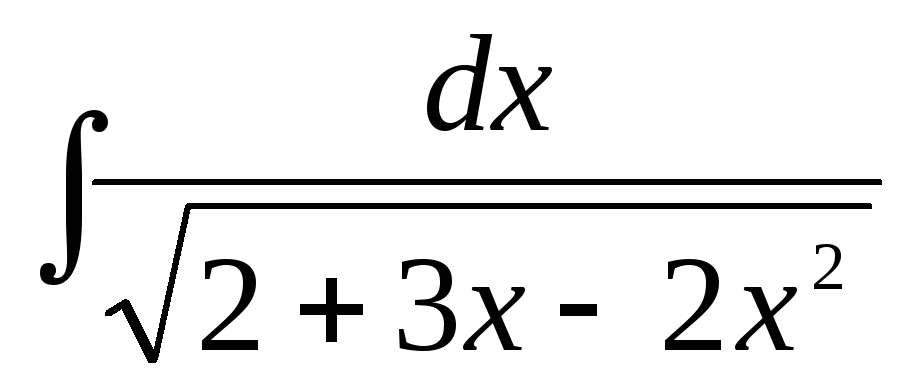 ,
,
е) 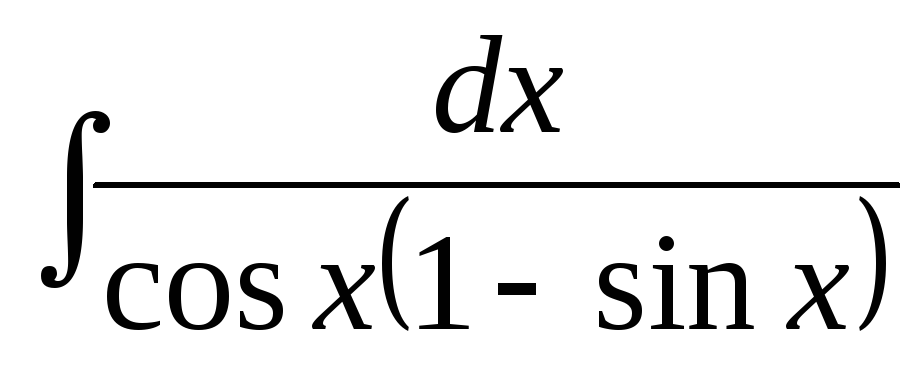 .
.
183. а) 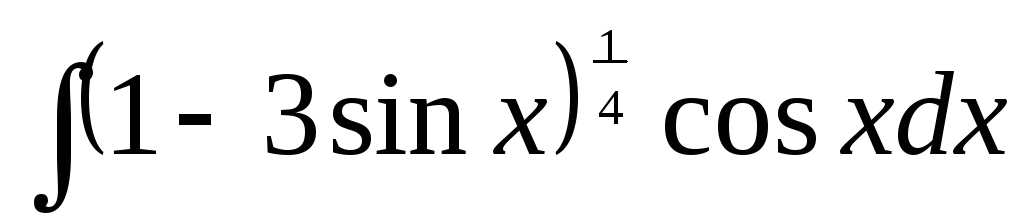 ,
,
в) 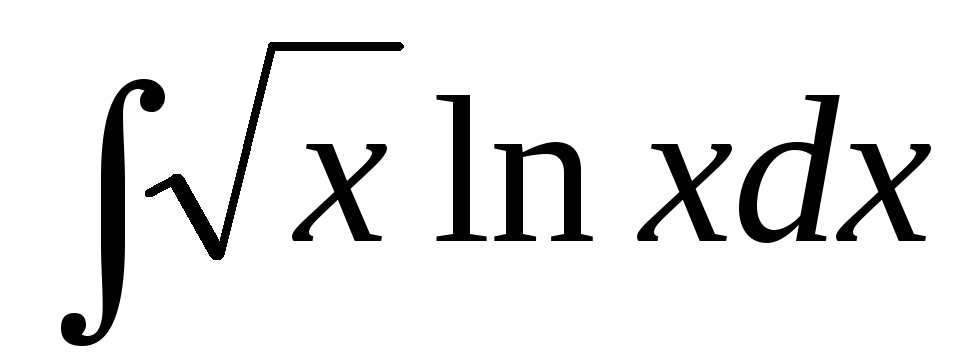 ,
,
д) 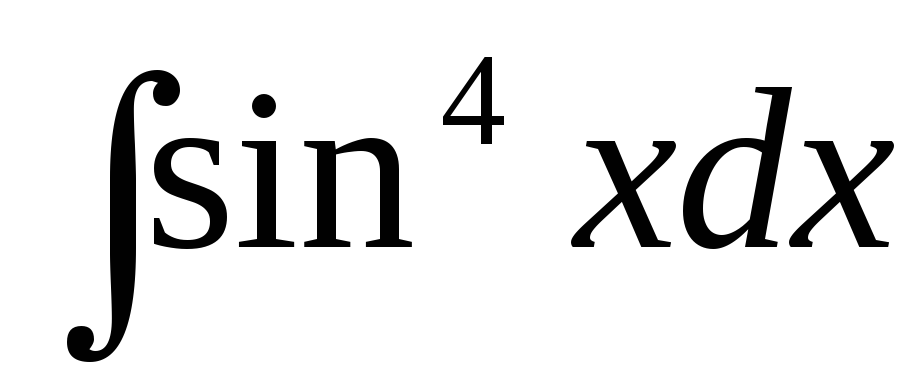 ,
,
б) 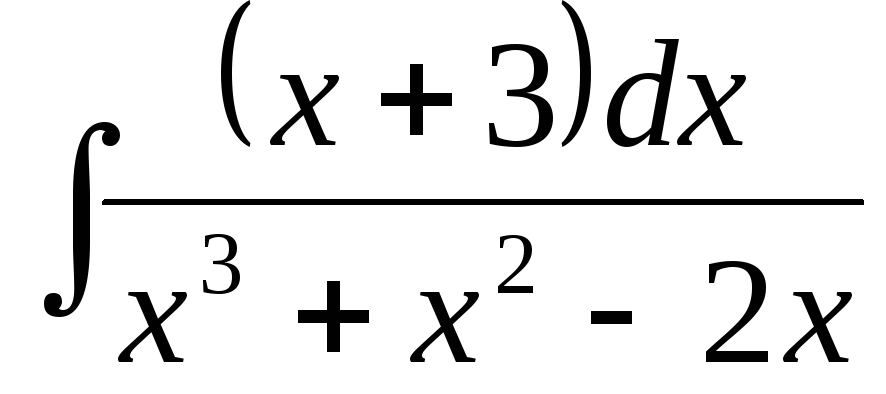 ,
,
г)  ,
,
е) 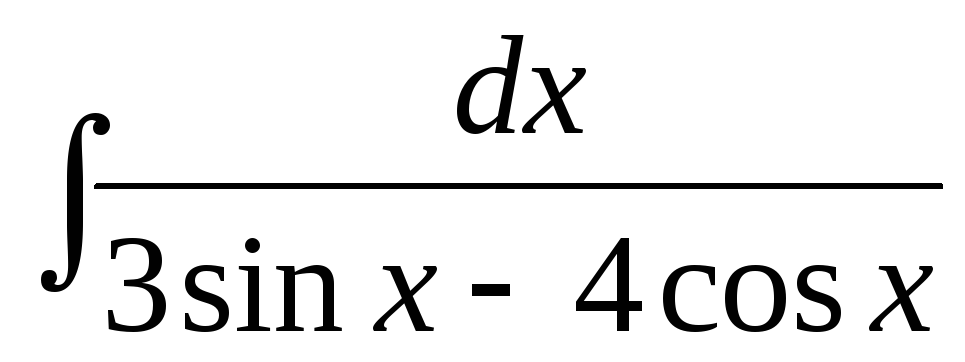 .
.
184. а) 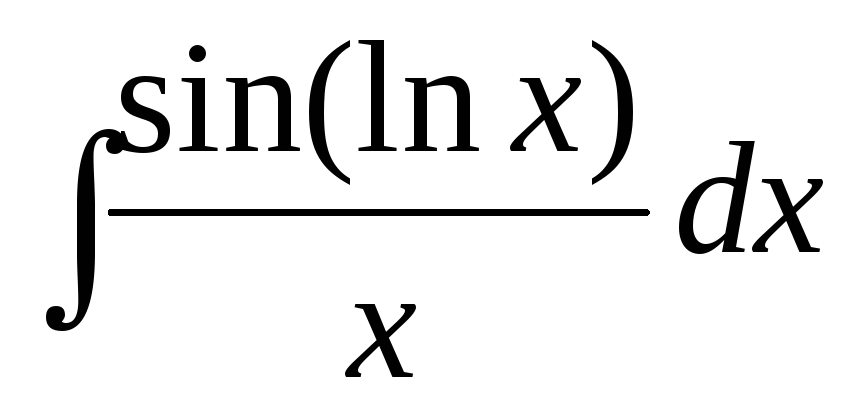 ,
,
в) 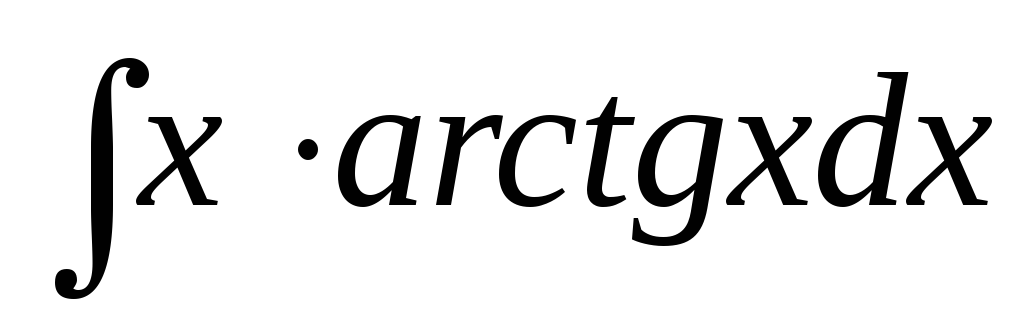 ,
,
д) 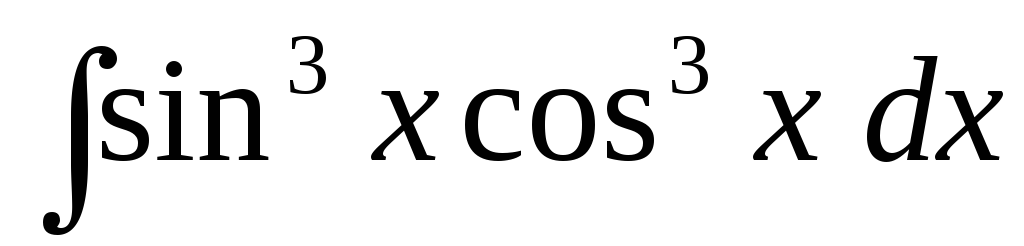 ,
,
б) 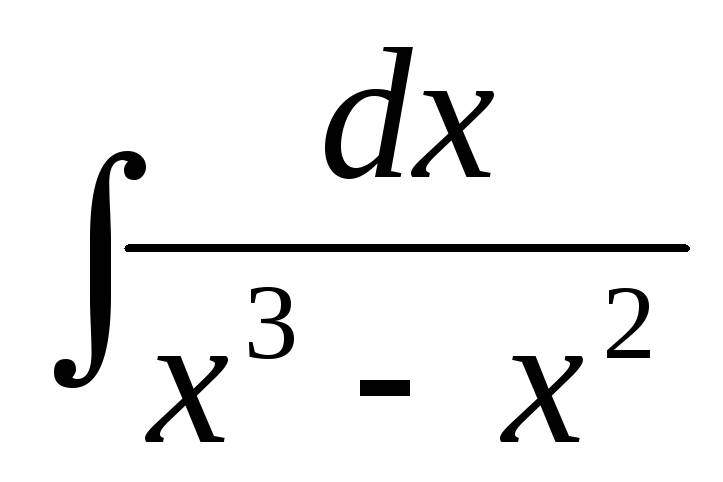 ,
,
г) 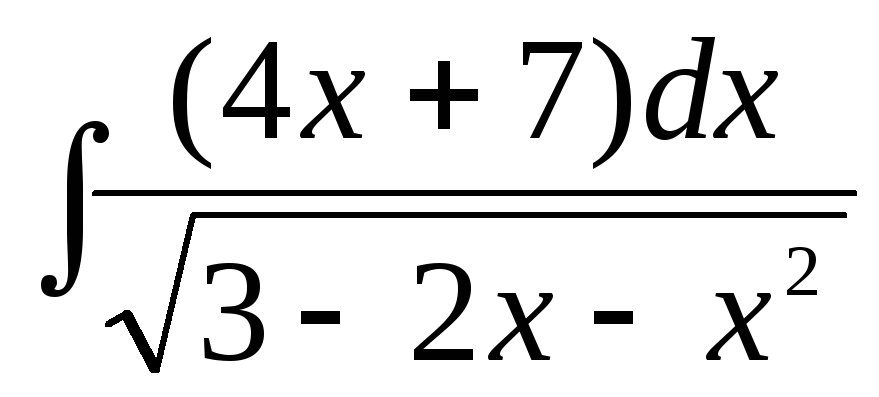 ,
,
е) 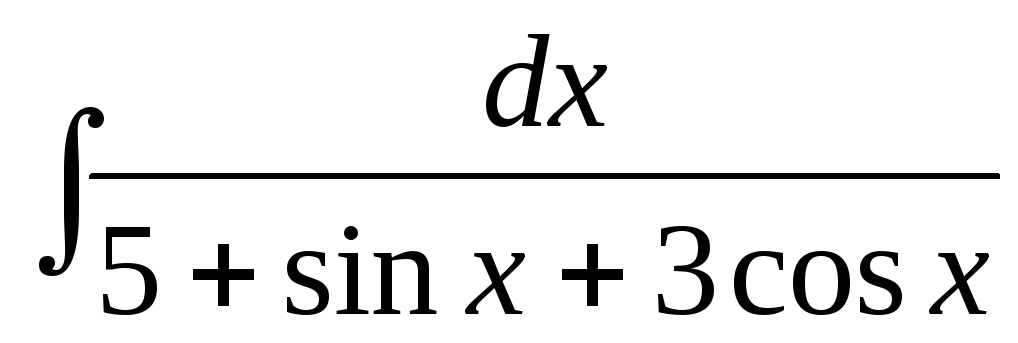 .
.
185. а) 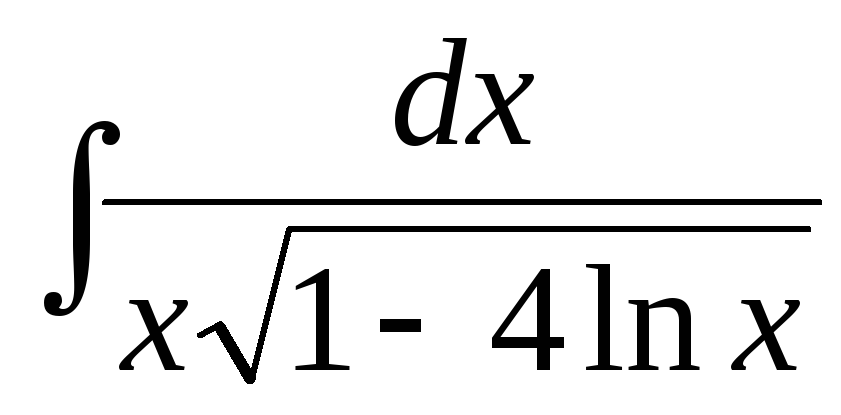 ,
,
в) 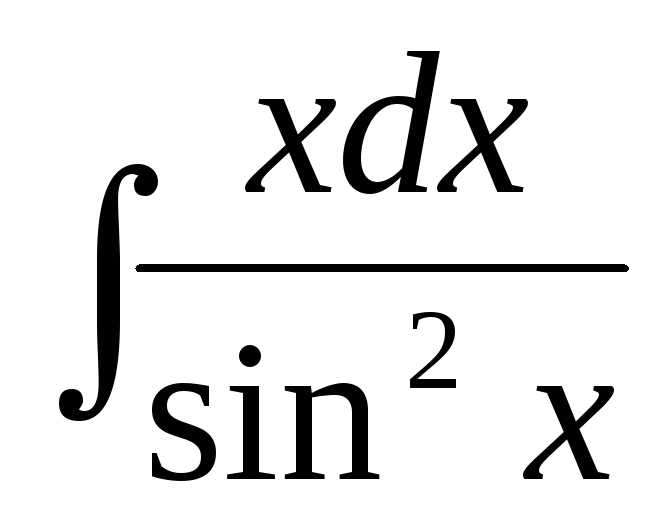 ,
,
д)  ,
,
б) 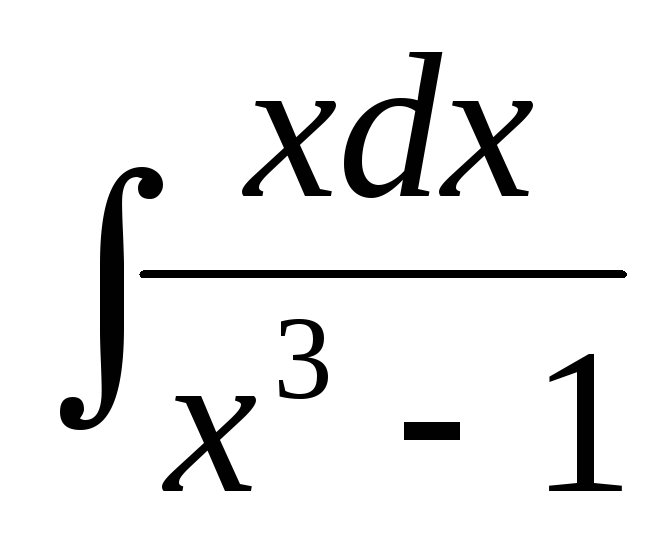 ,
,
г) 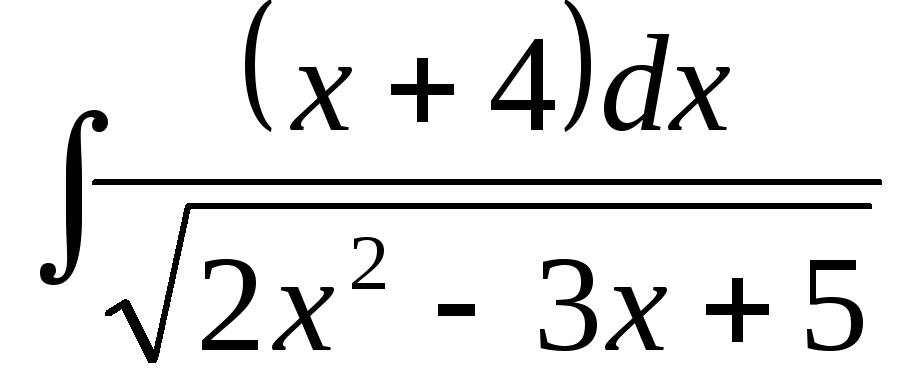 ,
,
е) 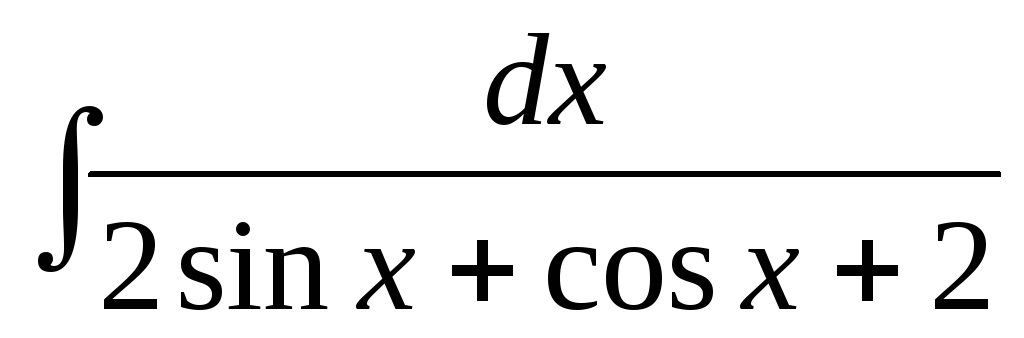 .
.
186. а) 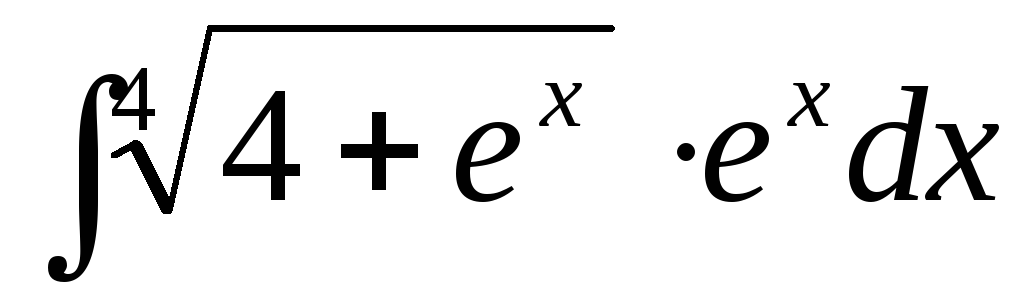 ,
,
в)  ,
,
д) 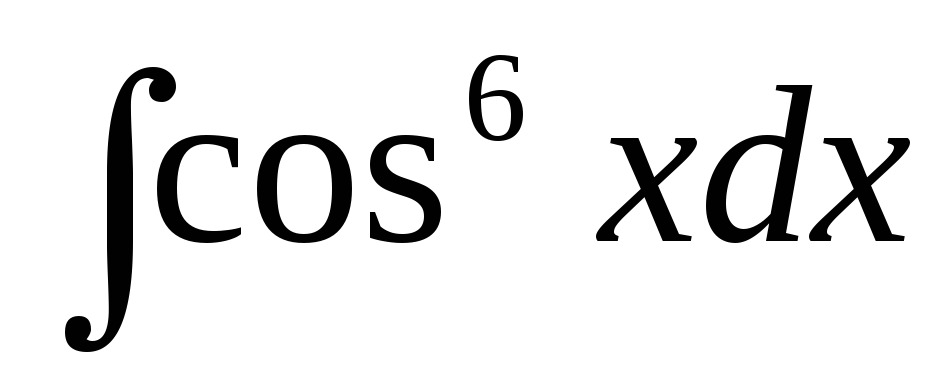 ,
,
б) 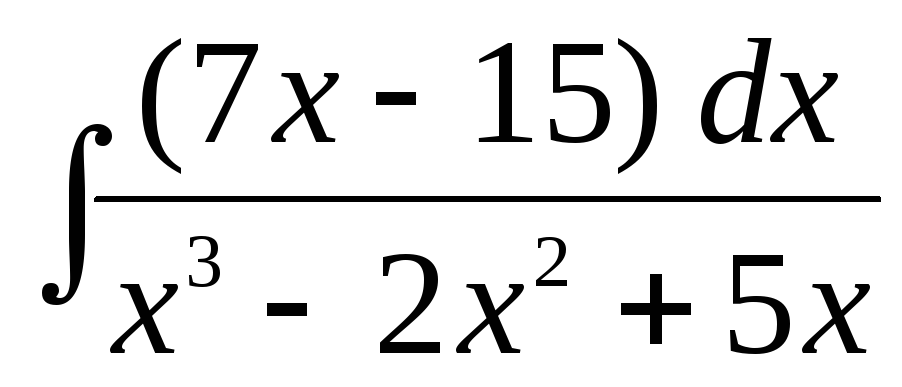 ,
,
г) 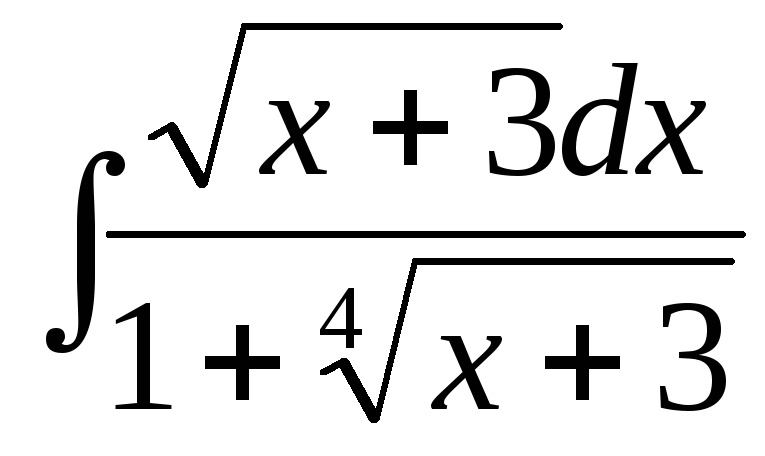 ,
,
е)  .
.
187. а) 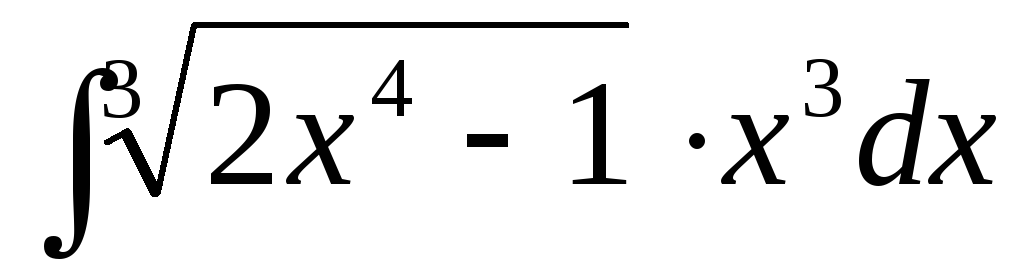 ,
,
в)  ,
,
д) 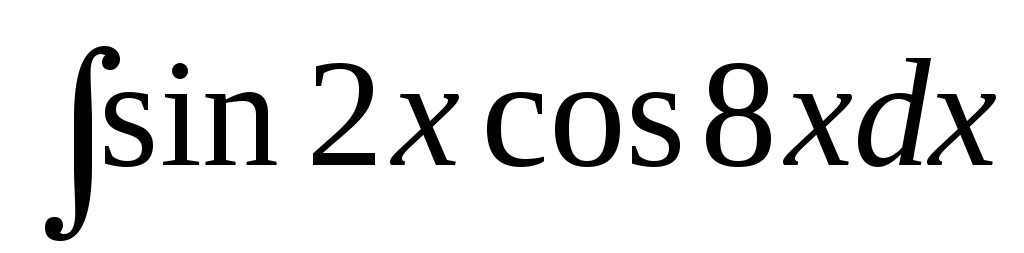 ,
,
б) 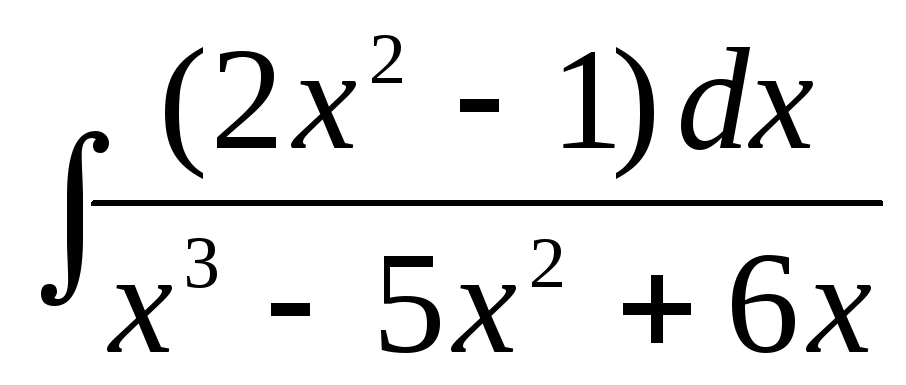 ,
,
г) 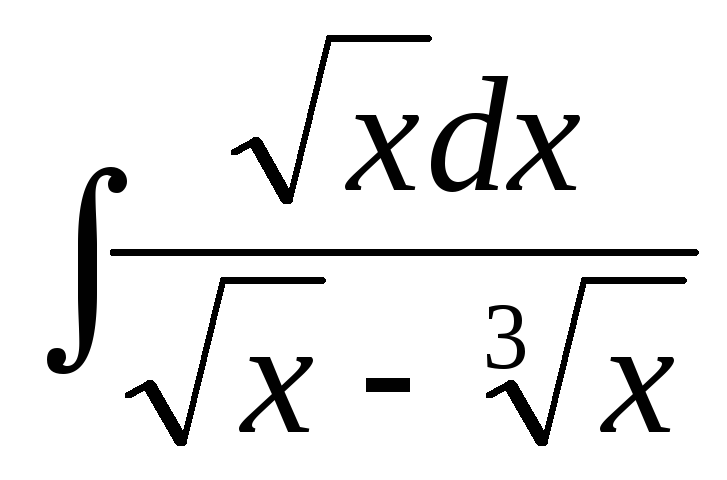 ,
,
е) 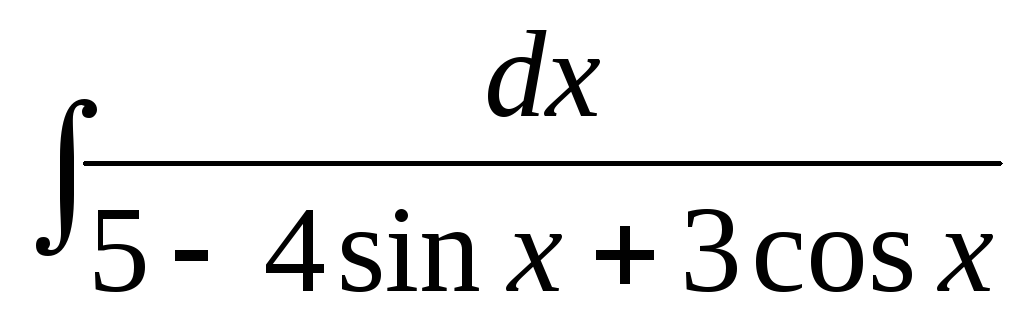 .
.
188. а) 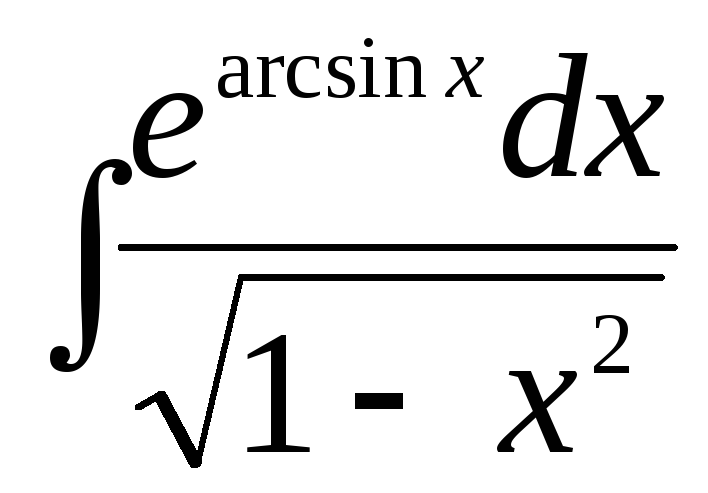 ,
,
в) 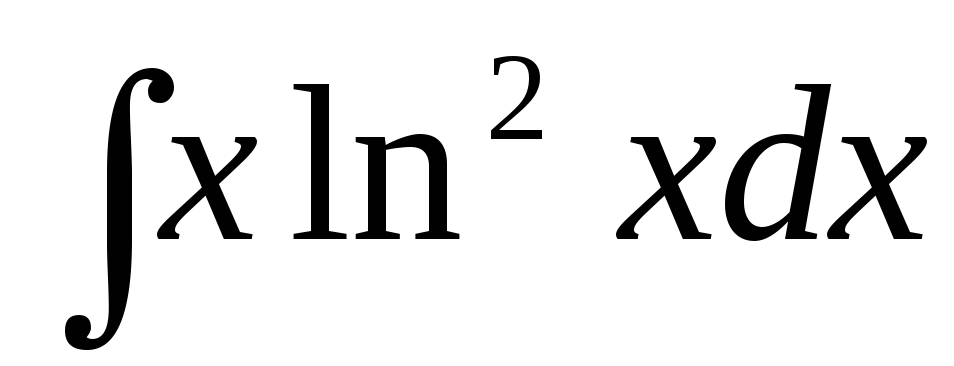 ,
,
д) 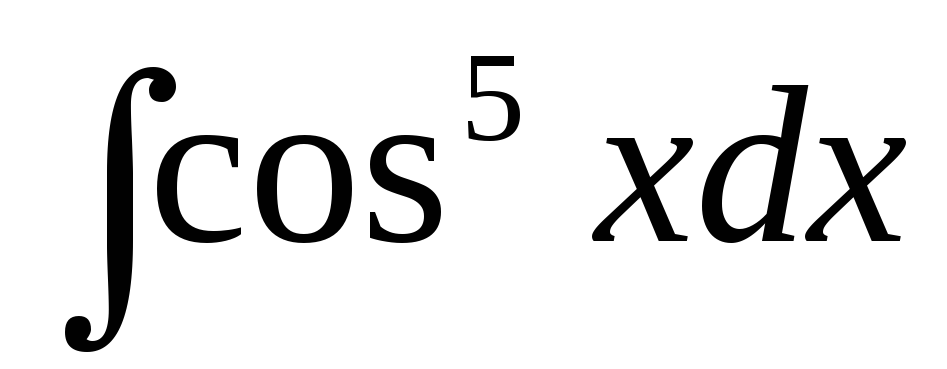 ,
,
б) 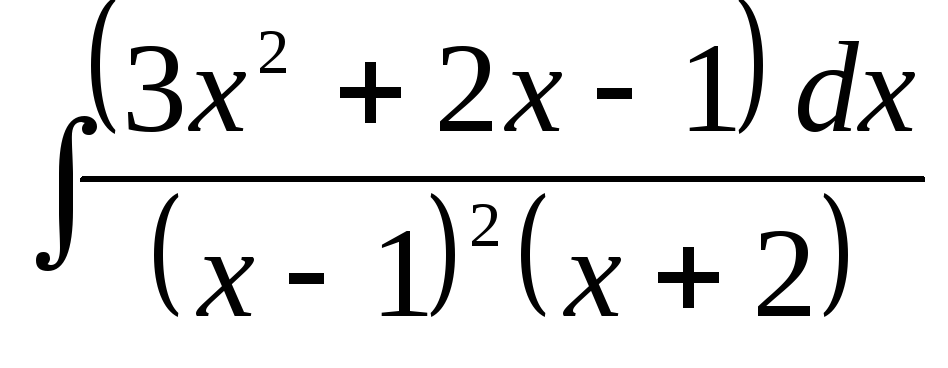 ,
,
г) 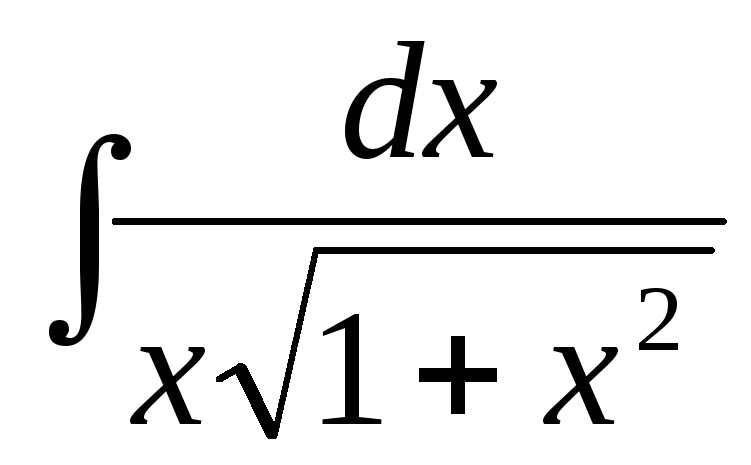 ,
,
е) 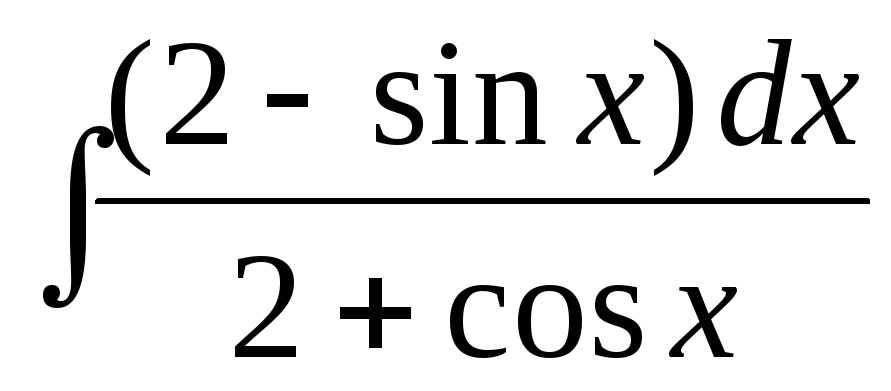 .
.
189. а)  ,
,
в) 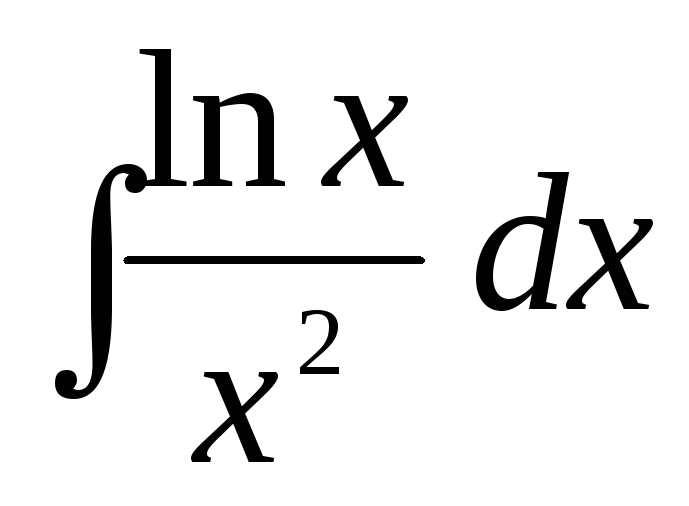 ,
,
б) 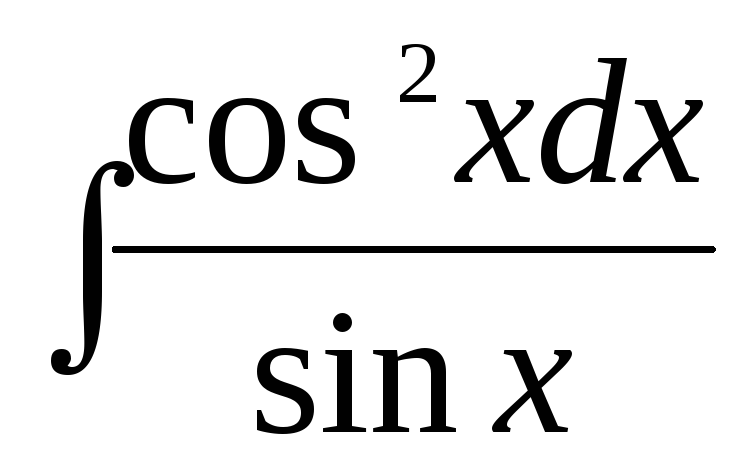 ,
,
г) 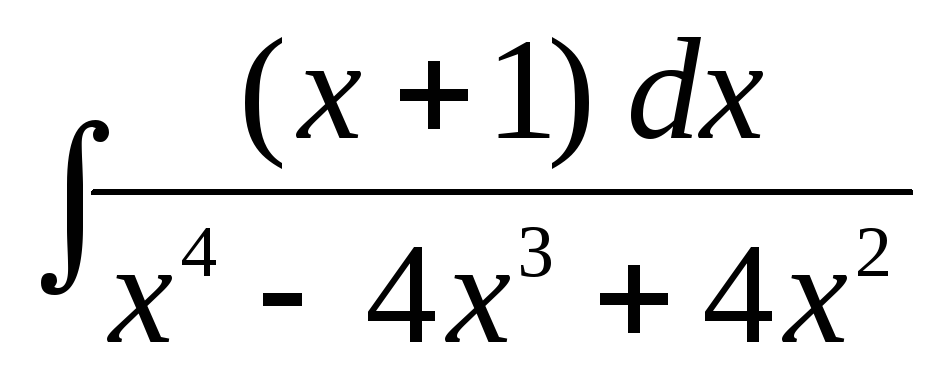 ,
,
д) 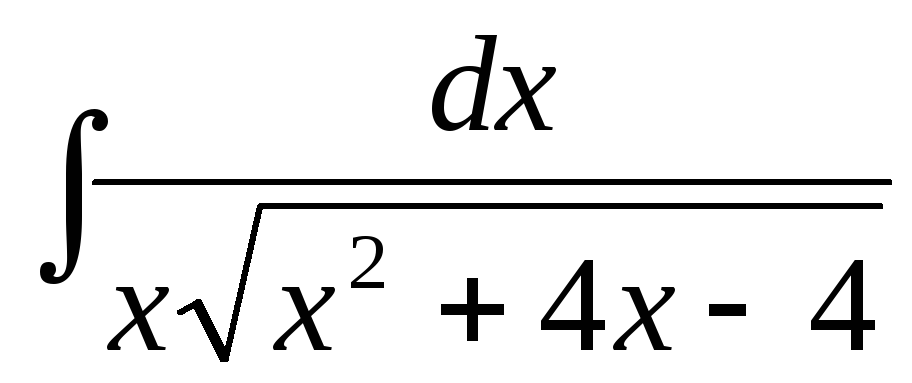 ,
,
е) 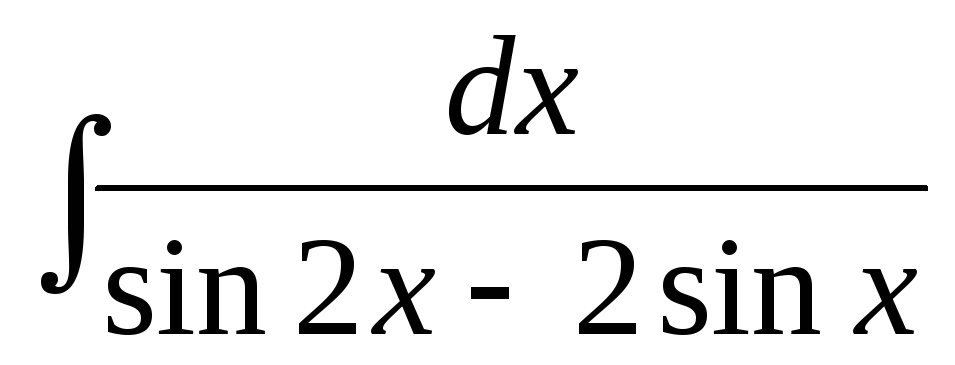 .
.
190. а) 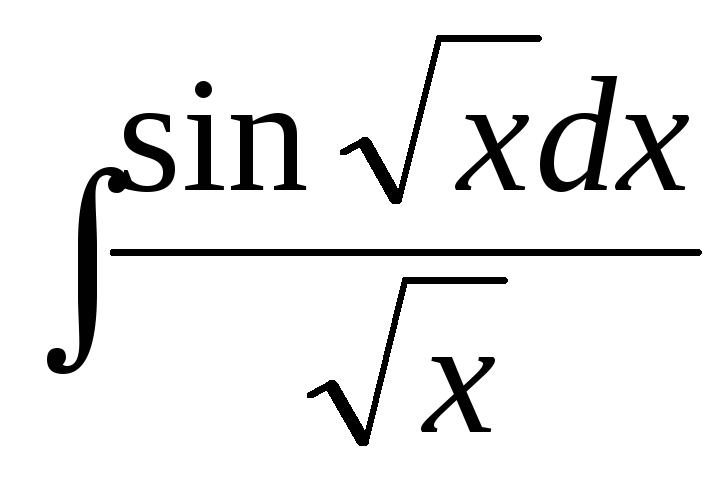 ,
,
в) 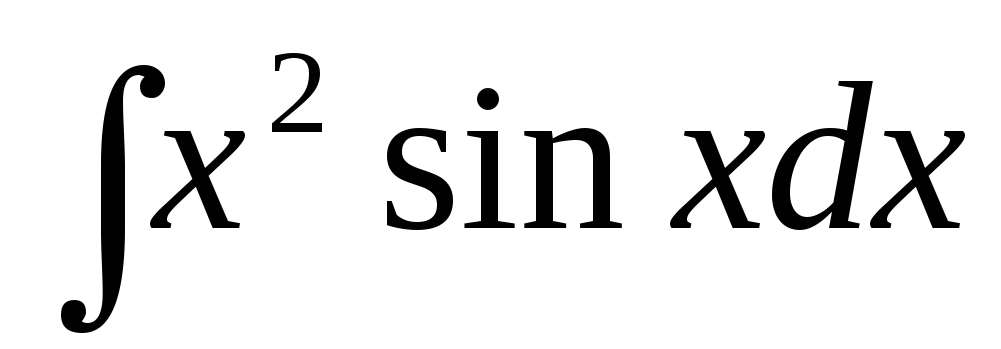 ,
,
д) 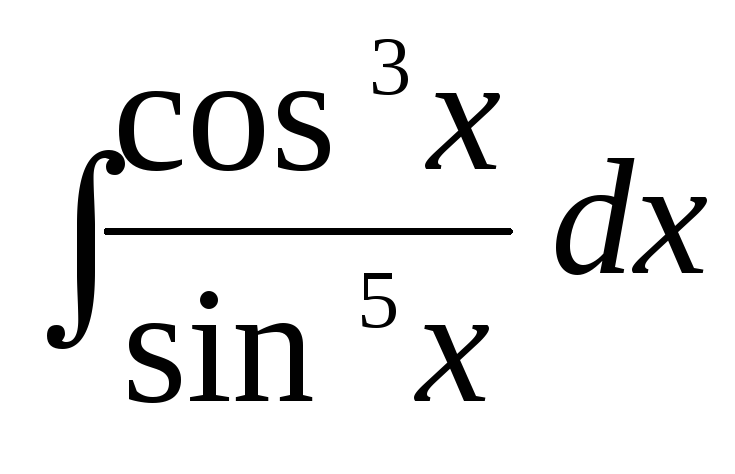 ,
,
б) 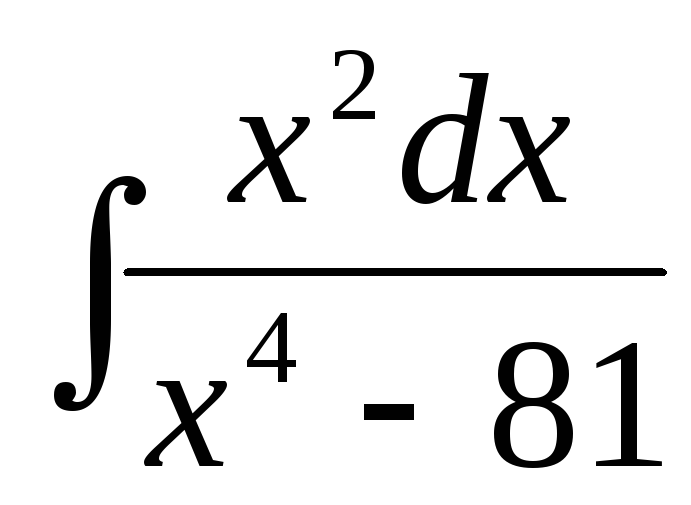 ,
,
г) 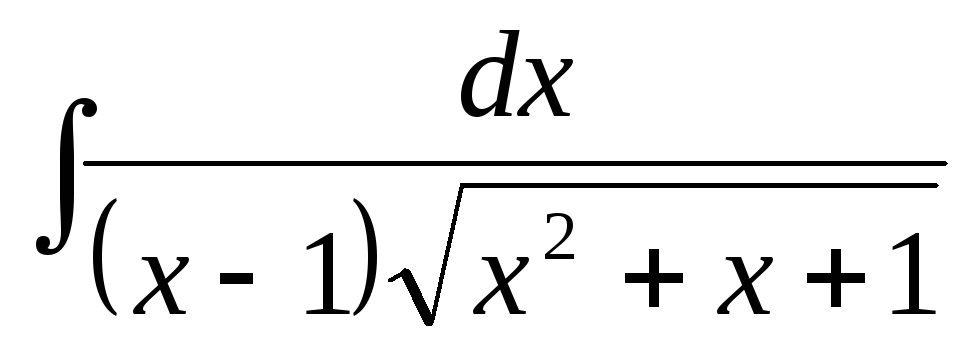 ,
,
е) 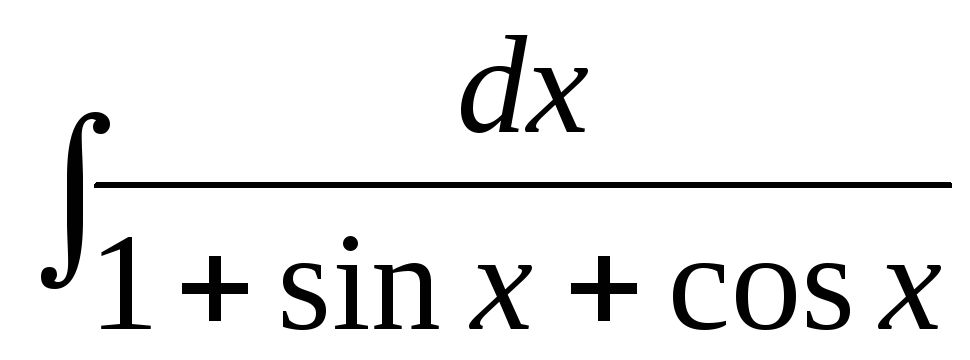 .
.
191 – 200. Вычислить определённый интеграл.
191. 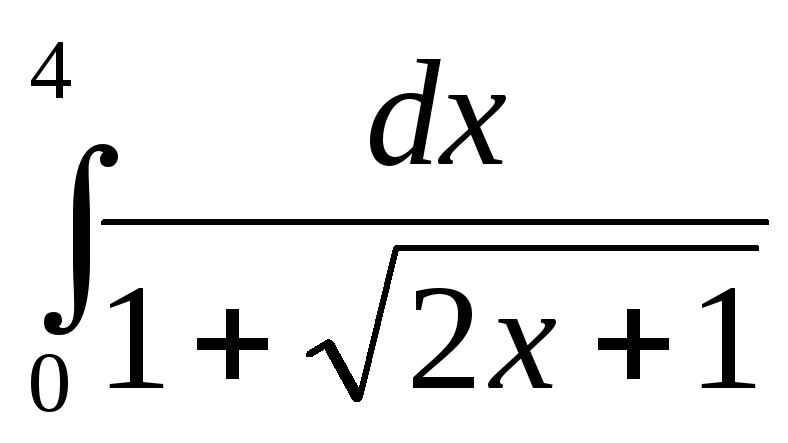 .
.
193. 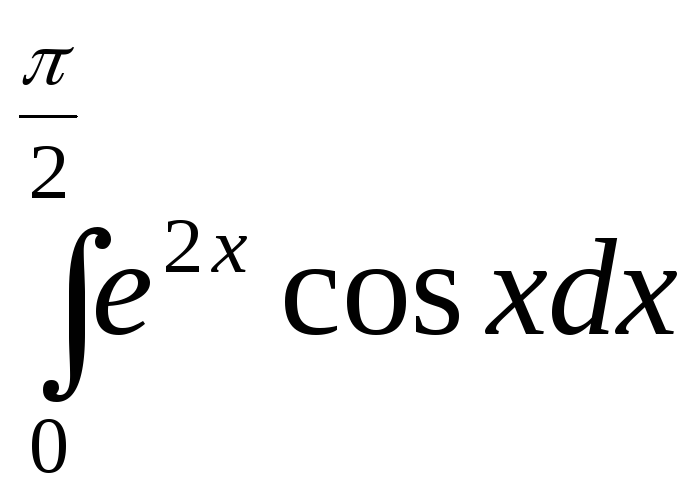 .
.
195. 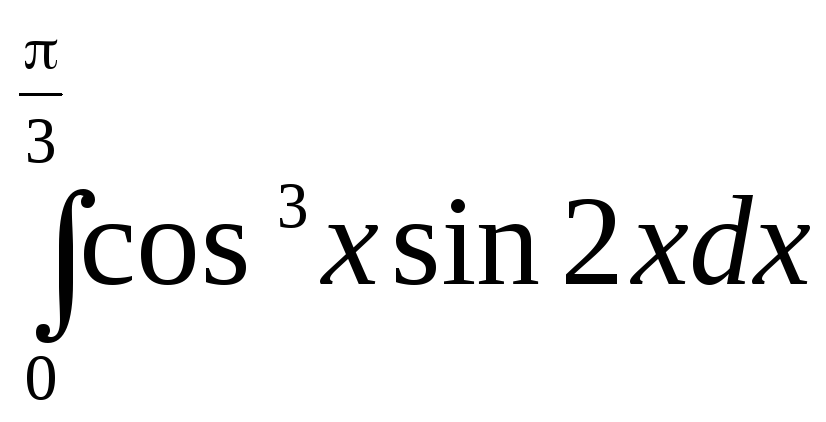 .
.
197.  .
.
199. 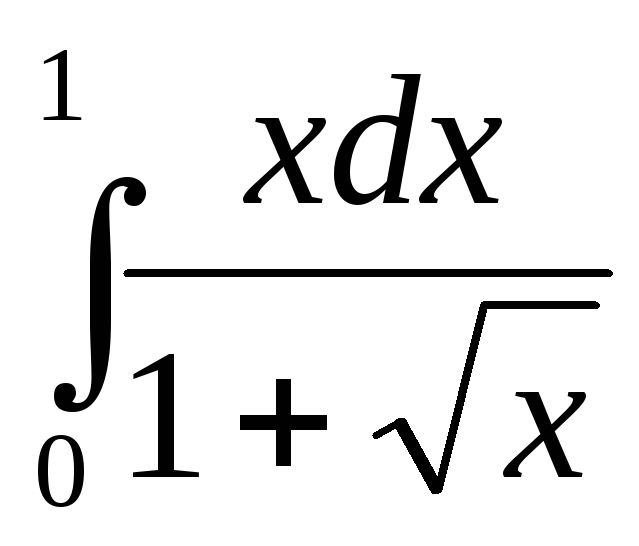 .
.
192. 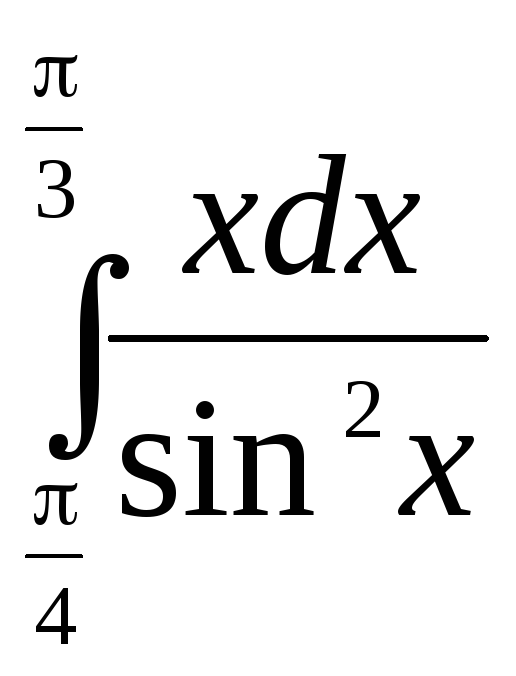 .
.
194. 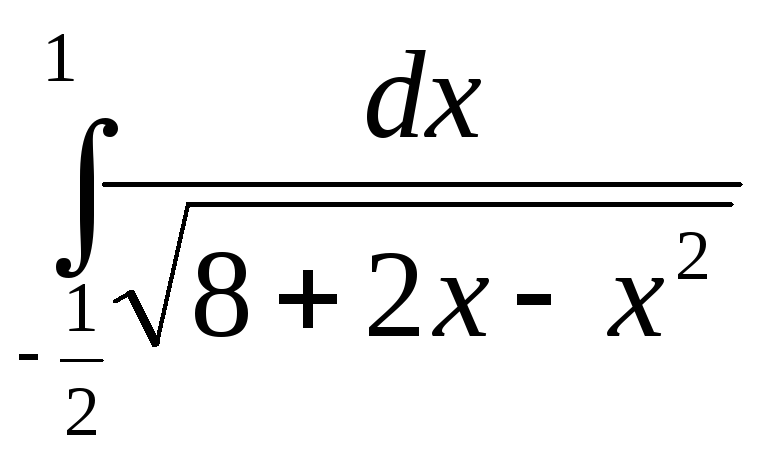 .
.
196. 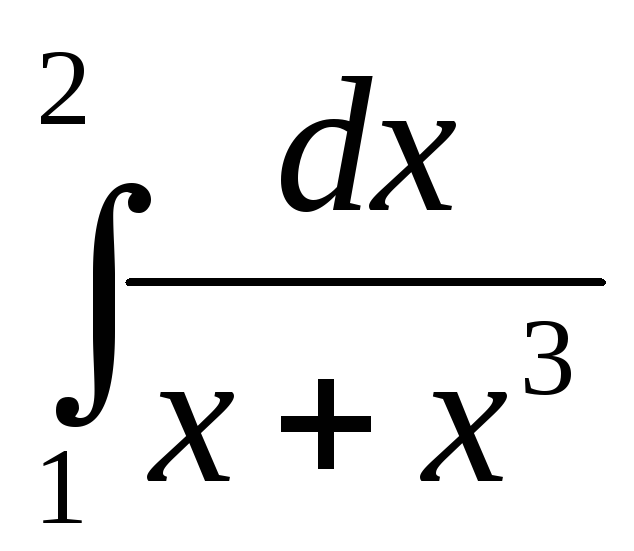 .
.
198. 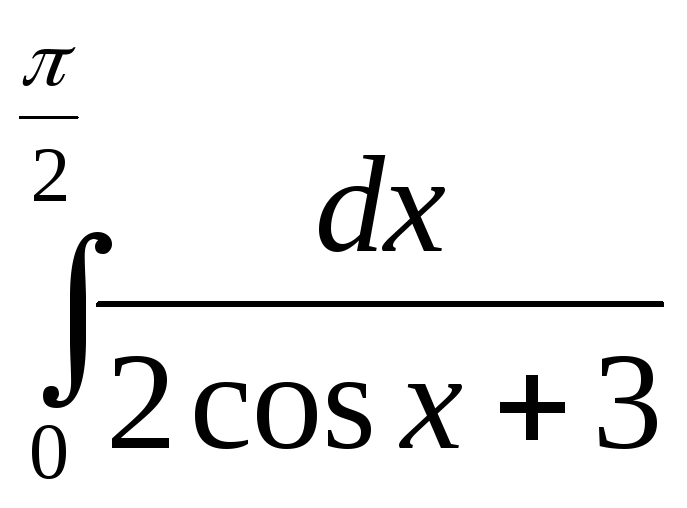 .
.
200. 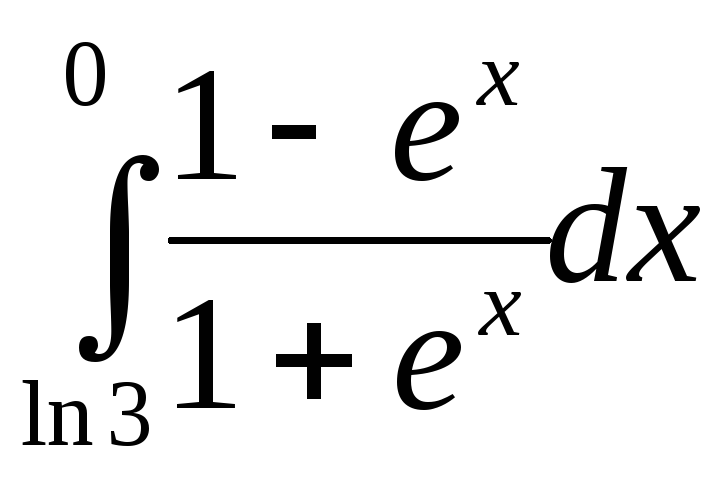 .
.
201 – 210.
Вычислить площадь фигуры, ограниченной параболой 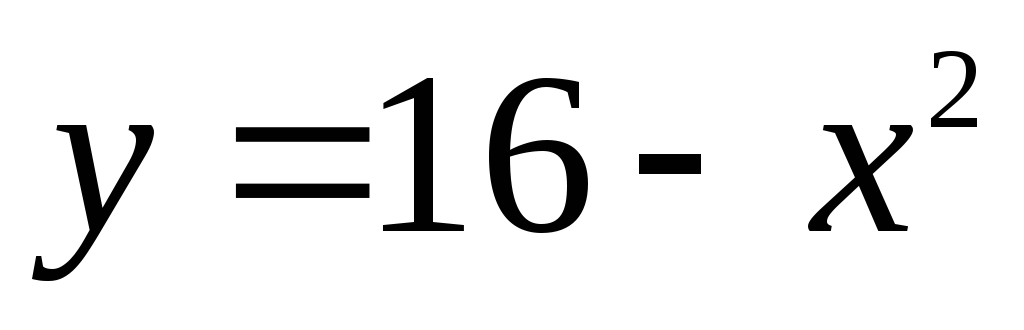 и полукубической параболой
и полукубической параболой .
.
Вычислить площадь фигуры, ограниченной кардиоидой 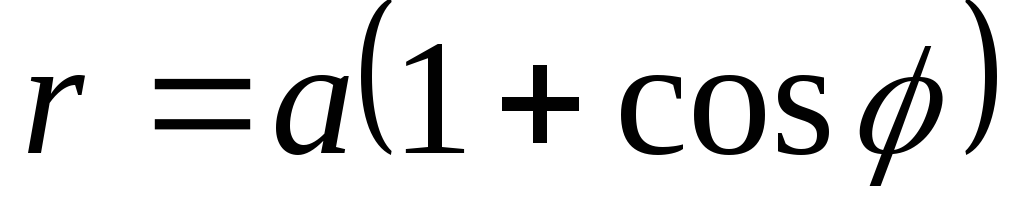 .
.
Вычислить площадь фигуры, ограниченной трёхлепестковой розой 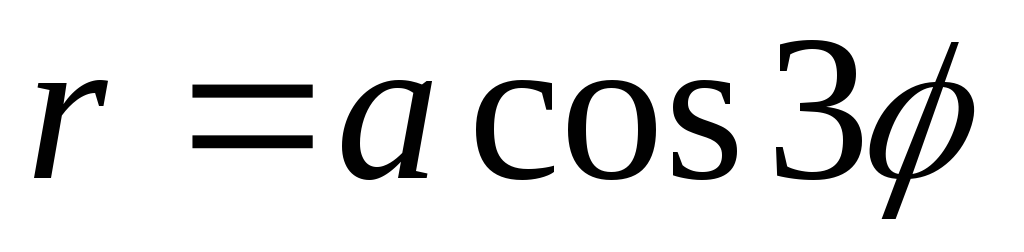
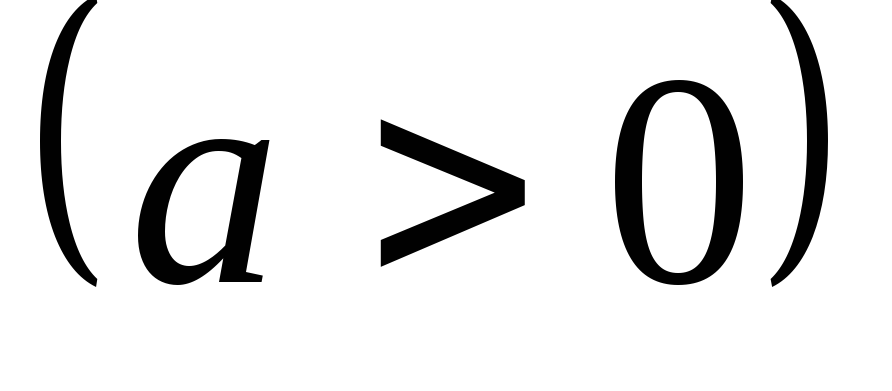 .
.
Вычислить площадь фигуры, ограниченной одной аркой циклоиды 
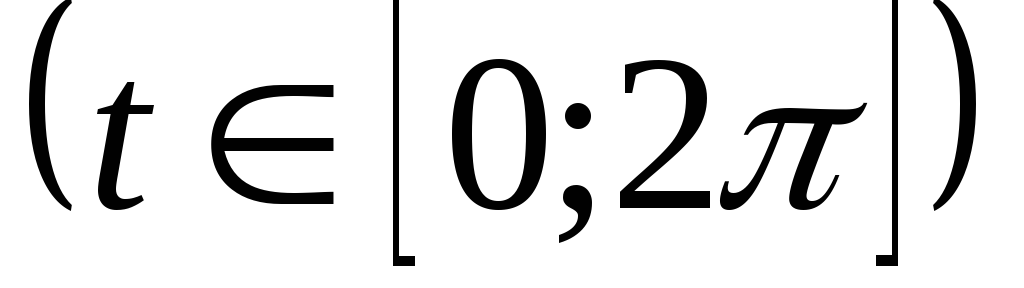 и осьюОх.
и осьюОх.
Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 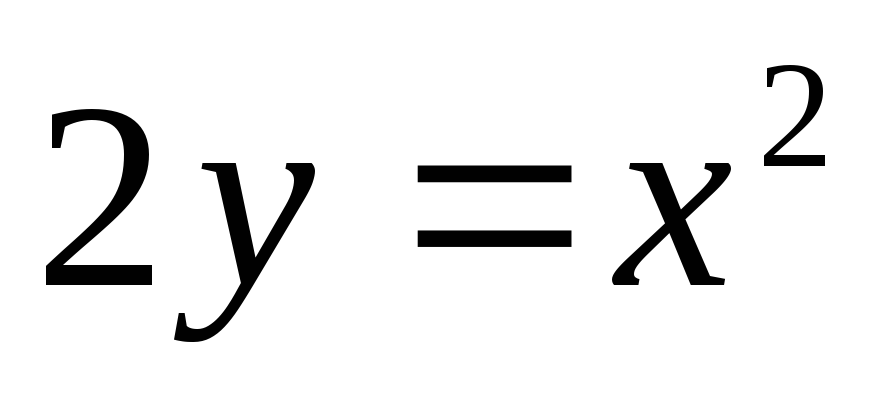 ,
, .
.
Вычислить объём тела, образованного вращением вокруг оси Оy астроиды 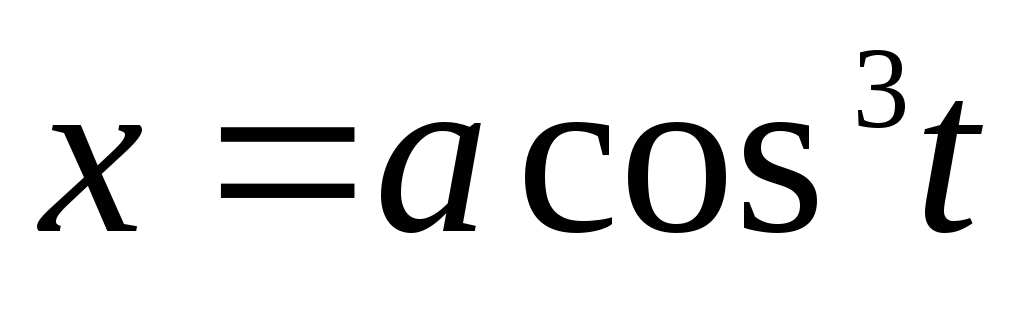 ,
,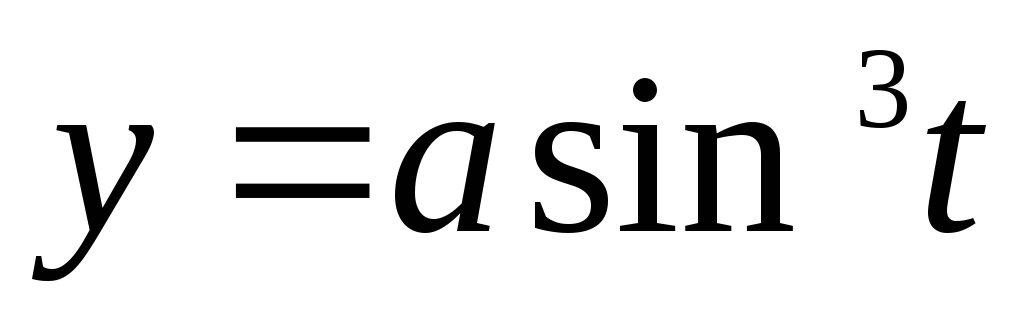 .
.
Вычислить длину дуги кривой 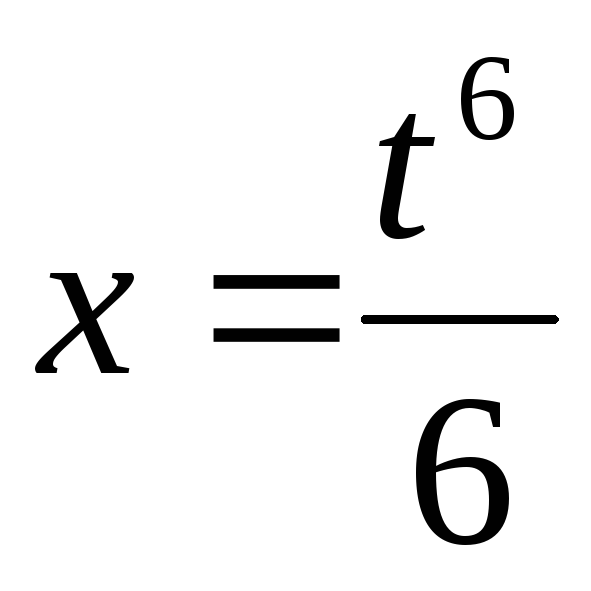 ,
,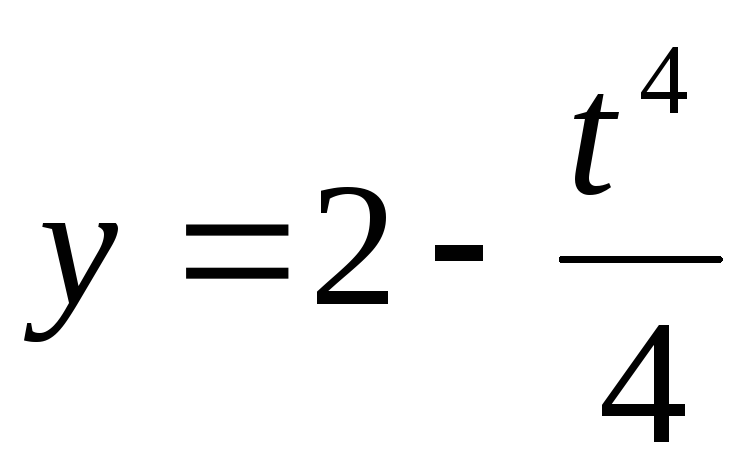 между точками её пересечения с осями координат.
между точками её пересечения с осями координат.
Вычислить длину дуги одной арки циклоиды 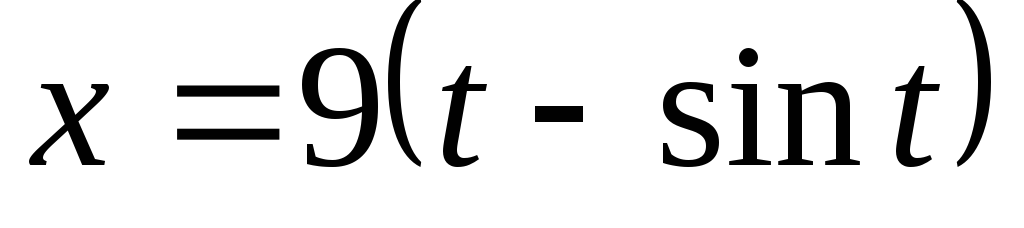 ,
, .
.
Вычислить длину дуги полукубической параболы 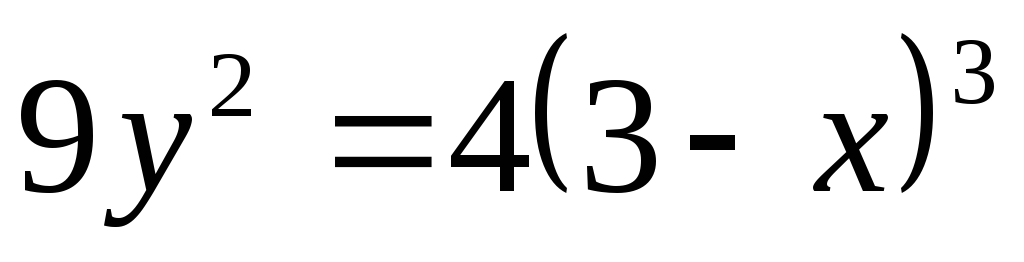 между точками пересечения с осьюОу.
между точками пересечения с осьюОу.
Вычислить длину кардиоиды  ,
,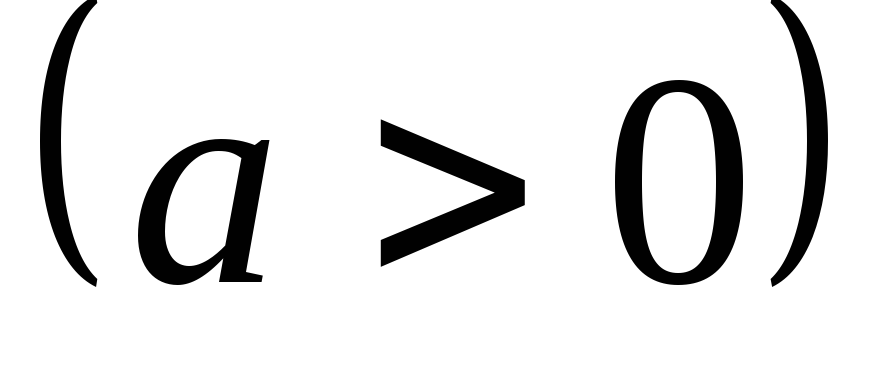 .
.
211 – 220. Вычислить несобственный интеграл или доказать его расходимость.
211. 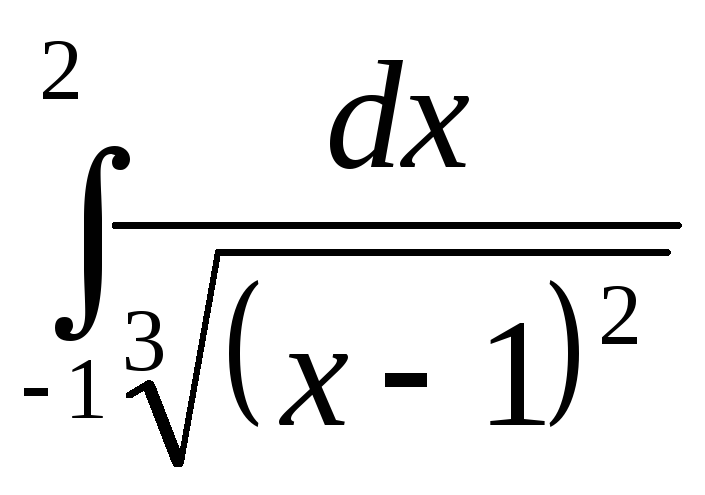 .
.
213. 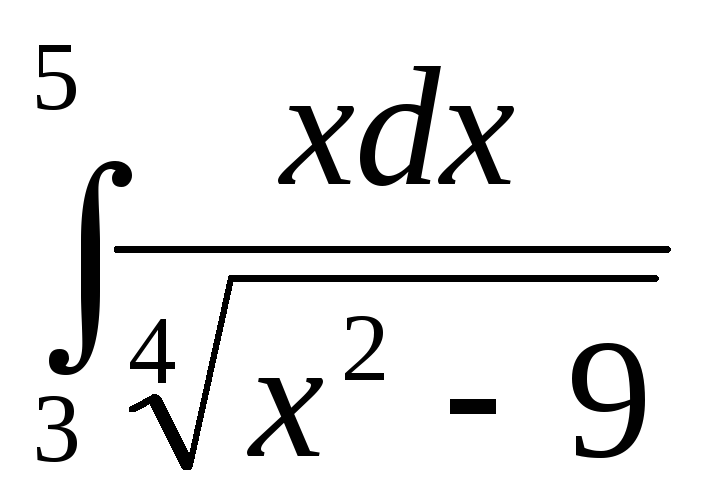 .
.
215. 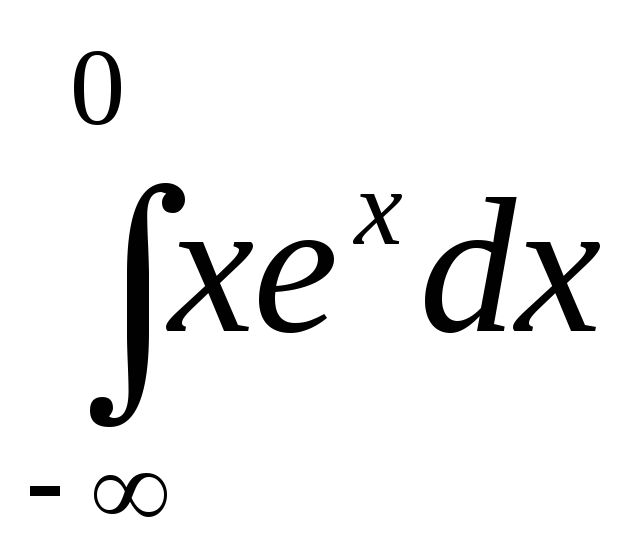 .
.
217.  .
.
219. 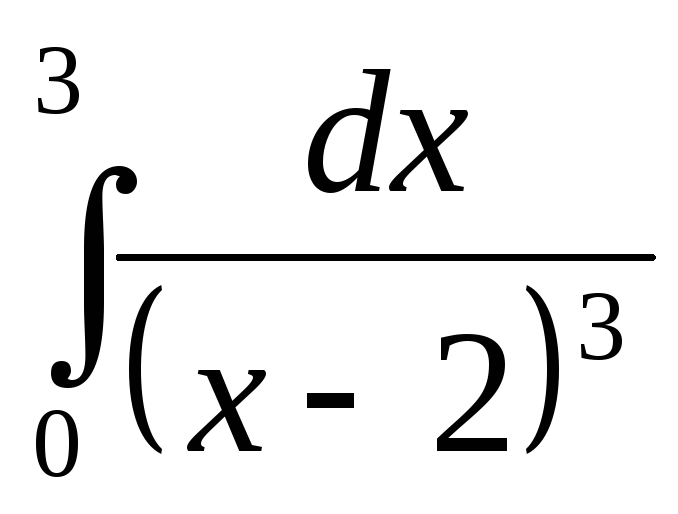 .
.
212. 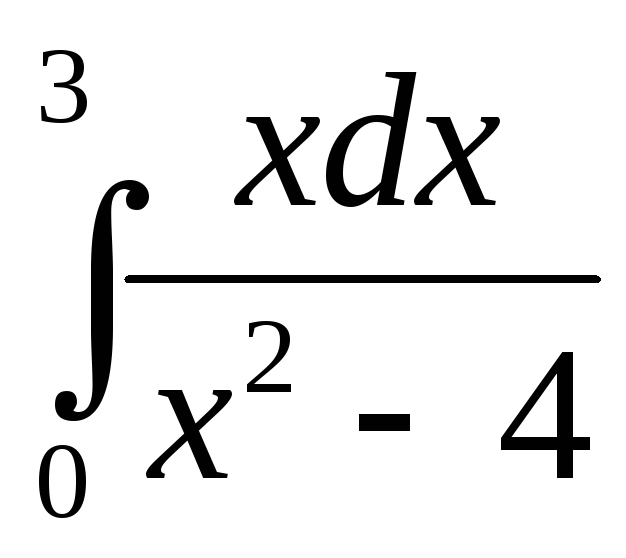 .
.
214. 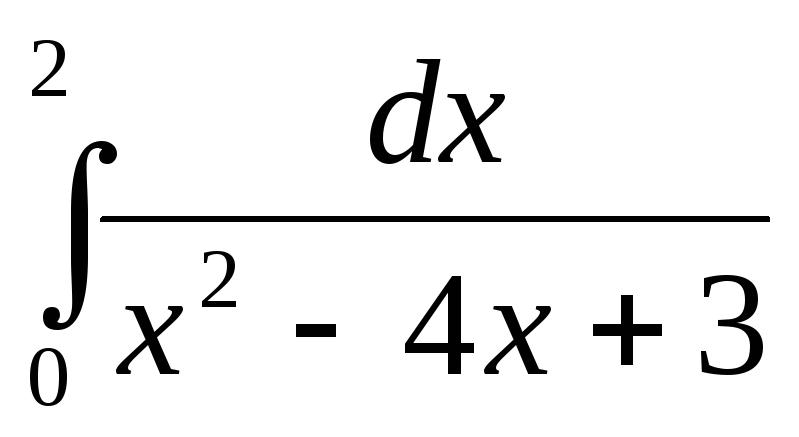 .
.
216. 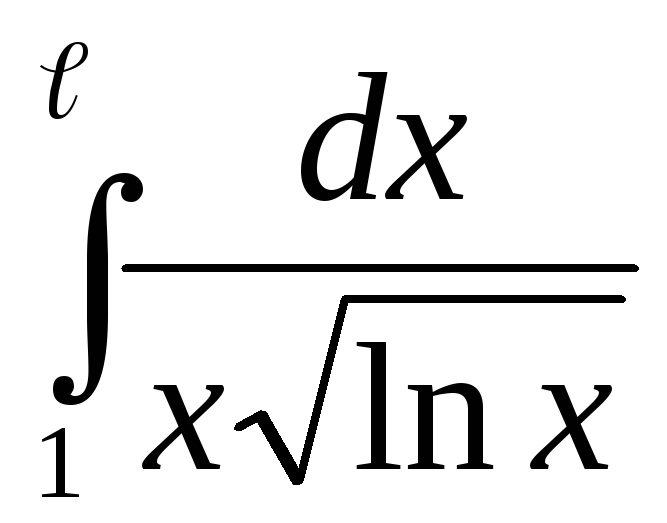 .
.
218. 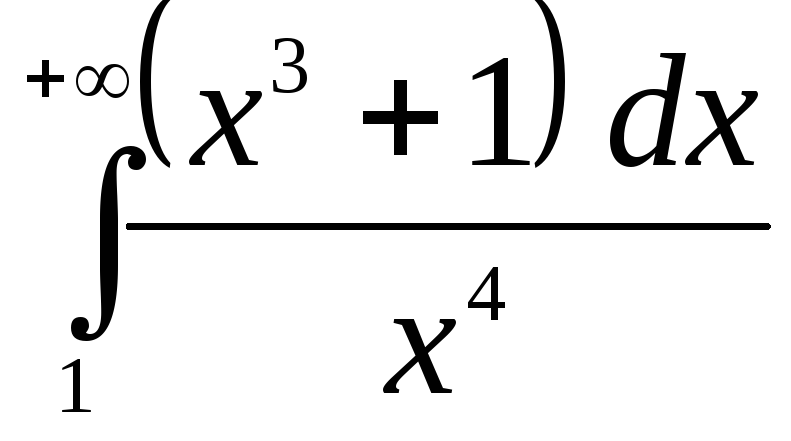 .
.
220. 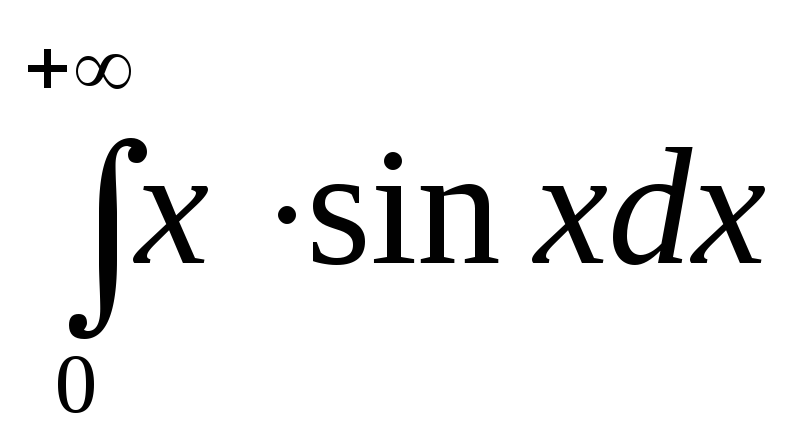 .
.
Запишем формулы для вычисления определителей второго и третьего порядка:
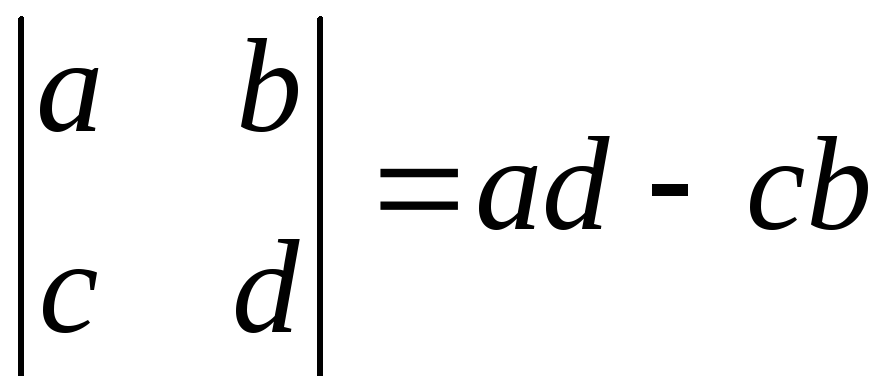 ,
,
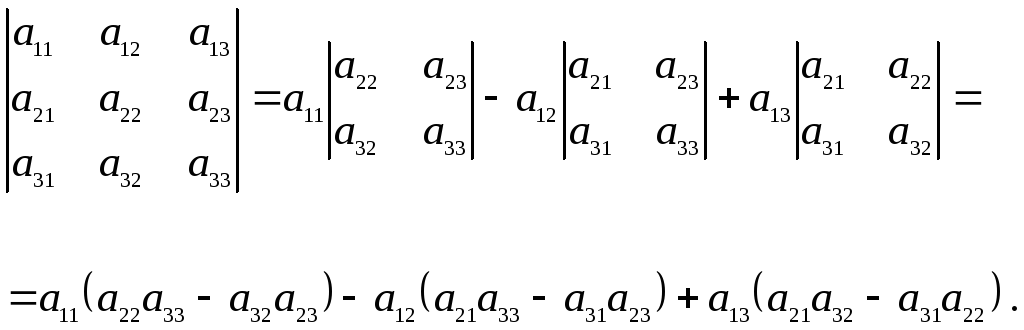
Примеры. 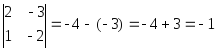 .
.
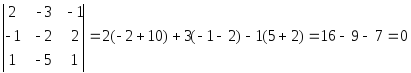 .
.
1) Если 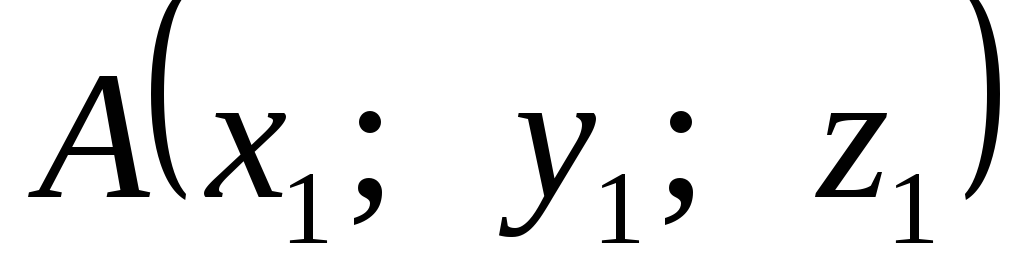 ,
,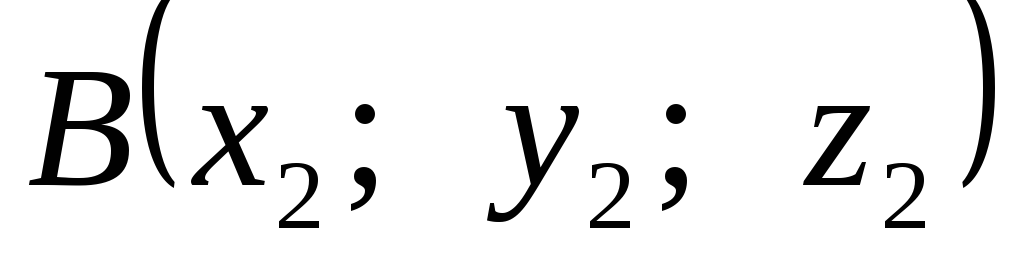 , то
, то
 .
.
2) Если 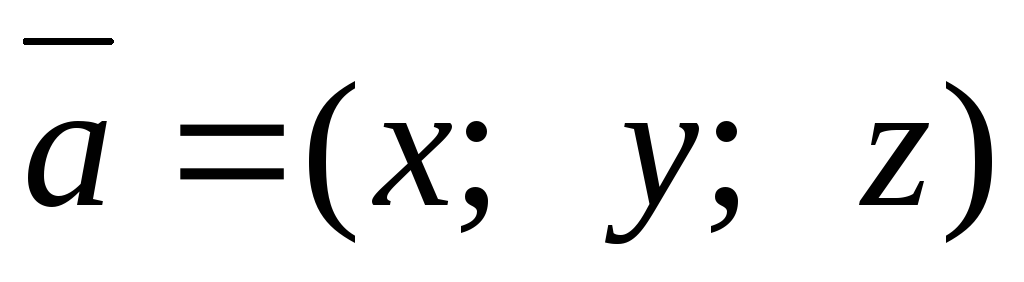 , то
, то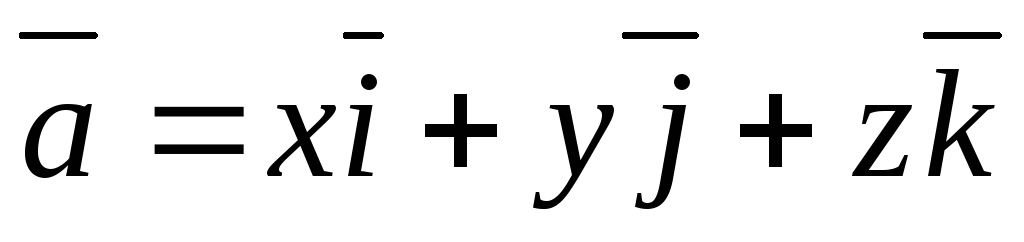 и
и
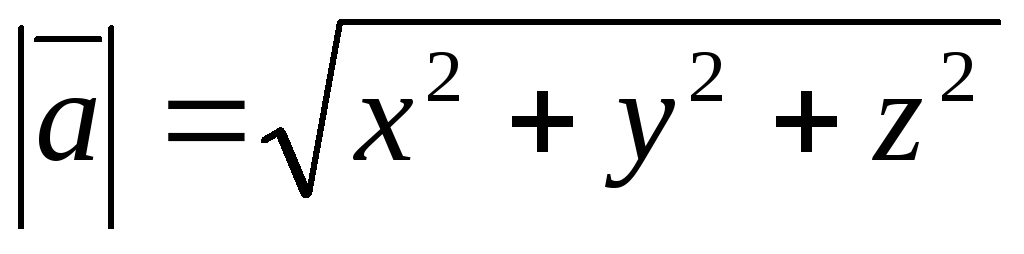 .
.
3) Скалярным произведением векторов  и
и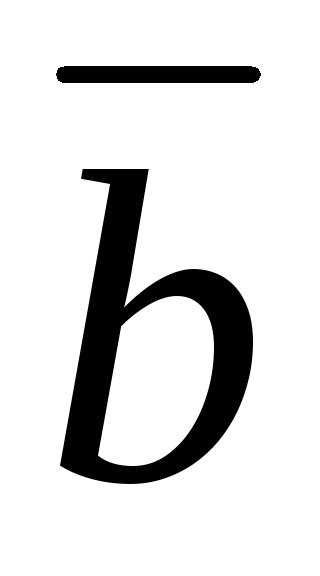 называется число
называется число , равное произведению модулей этих векторов и косинуса угла
, равное произведению модулей этих векторов и косинуса угла между этими векторами:
между этими векторами:
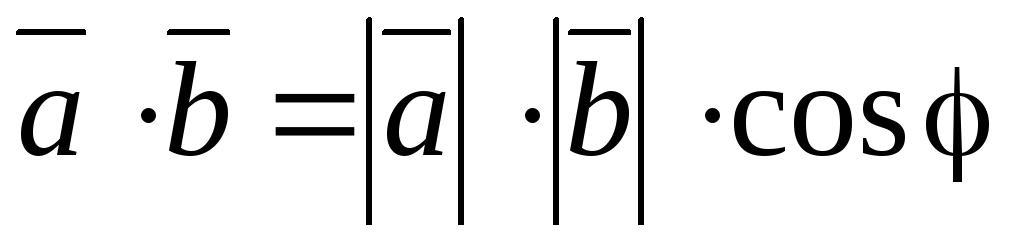 .
.
Если известны координаты векторов

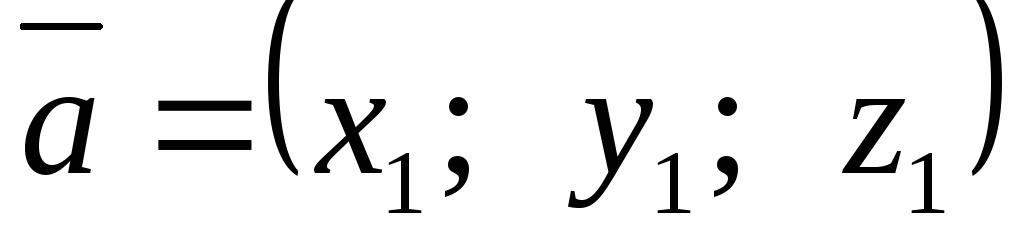 ,
, 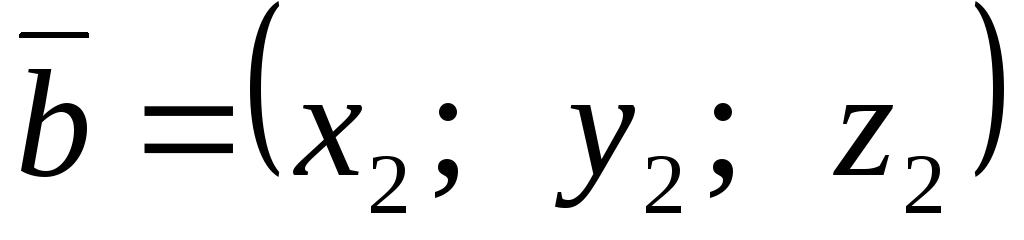 ,
,
то
 ,
,
угол  между векторами определяется формулой
между векторами определяется формулой

 .
.
4) Векторным произведением векторов  и
и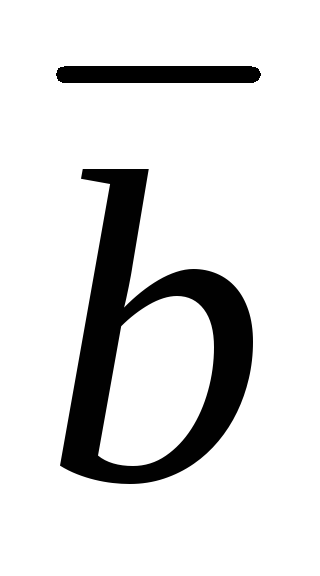 называется вектор
называется вектор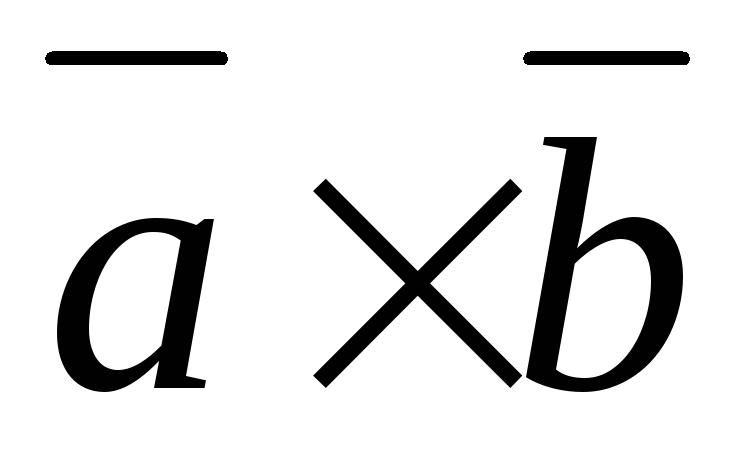 , перпендикулярный векторам
, перпендикулярный векторам и
и , модуль которого равен площади параллелограмма, построенного на векторах
, модуль которого равен площади параллелограмма, построенного на векторах и
и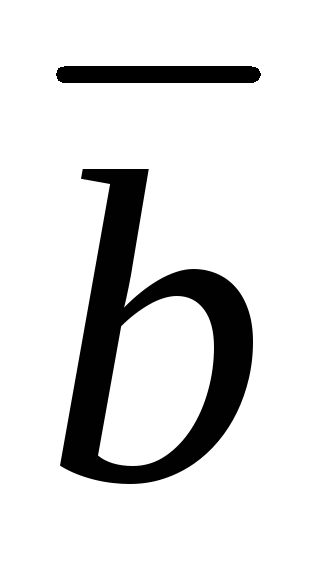 , и направленный так, что из его конца кратчайший поворот от вектора
, и направленный так, что из его конца кратчайший поворот от вектора к вектору
к вектору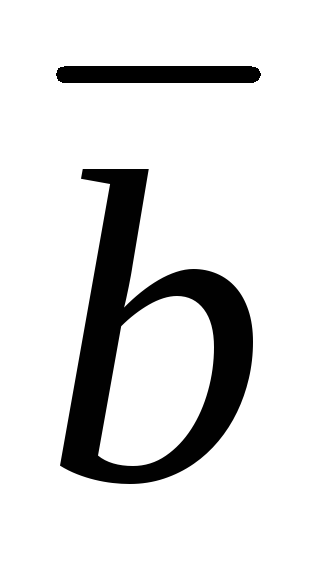 наблюдается происходящим против часовой стрелки.
наблюдается происходящим против часовой стрелки.

Рис. 1
Если известны координаты векторов  и
и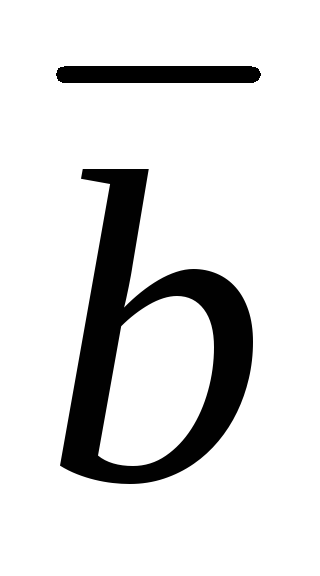

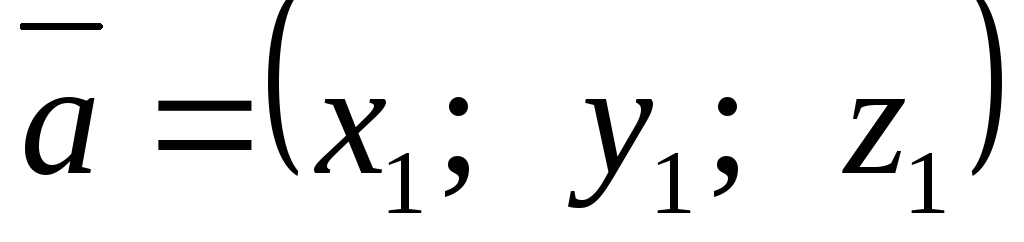 ,
, 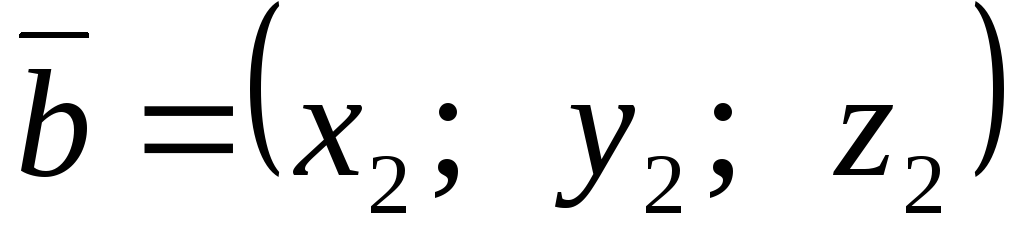 ,
,
то векторное произведение выражается через определитель третьего порядка:
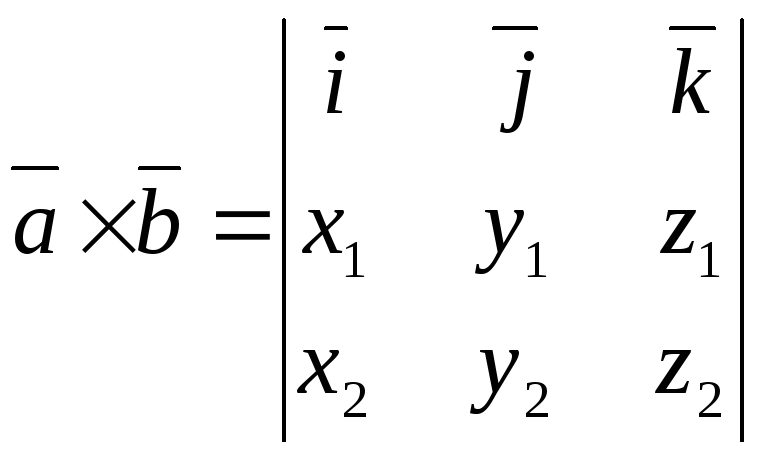 .
.
Площади параллелограмма и треугольника, построенных на векторах  и
и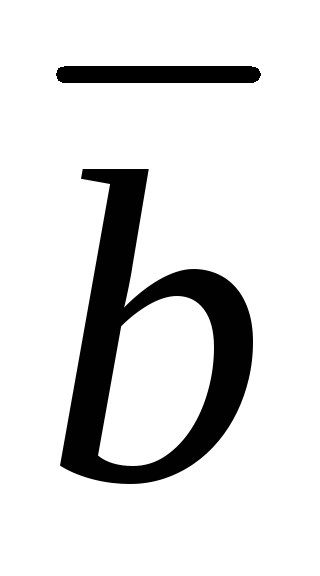 :
:
 ,
, 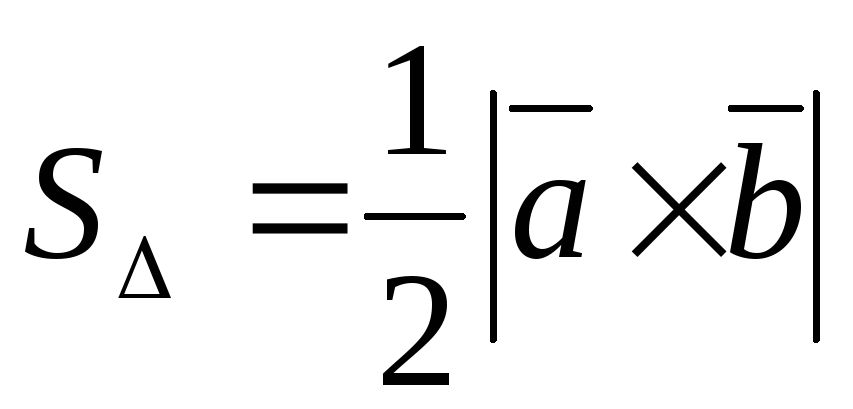 .
.
5) Смешанным произведением векторов  ,
,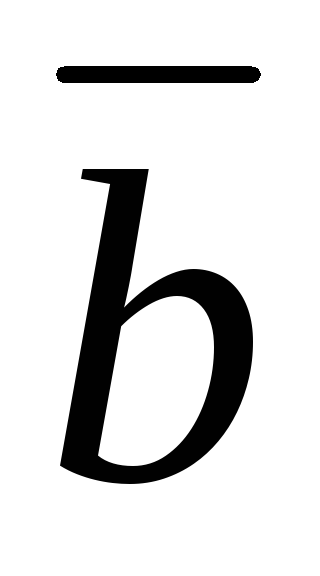 ,
, называется число
называется число
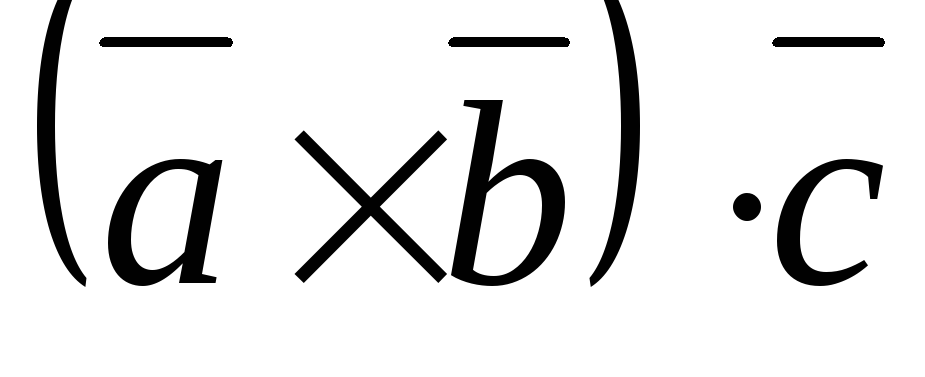 .
.
Если известны координаты векторов

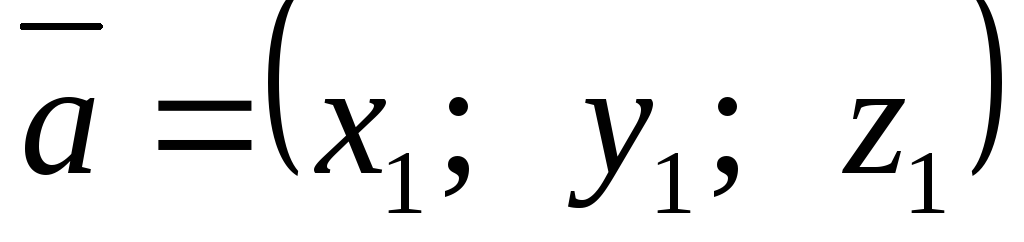 ,
, 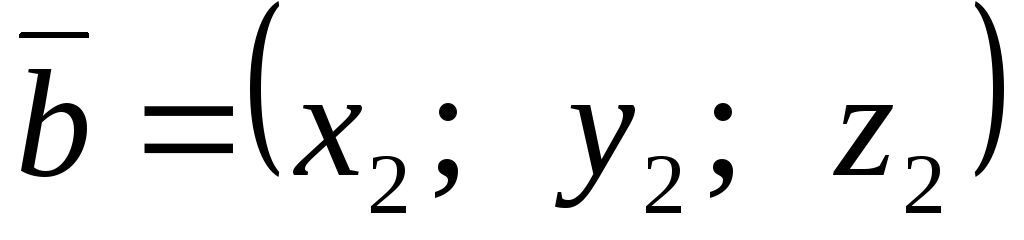 ,
,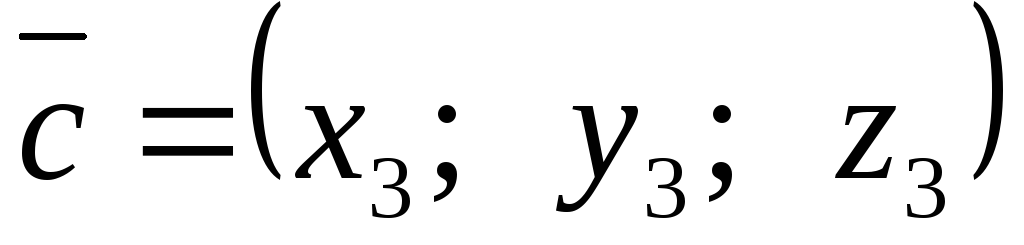 ,
,
то 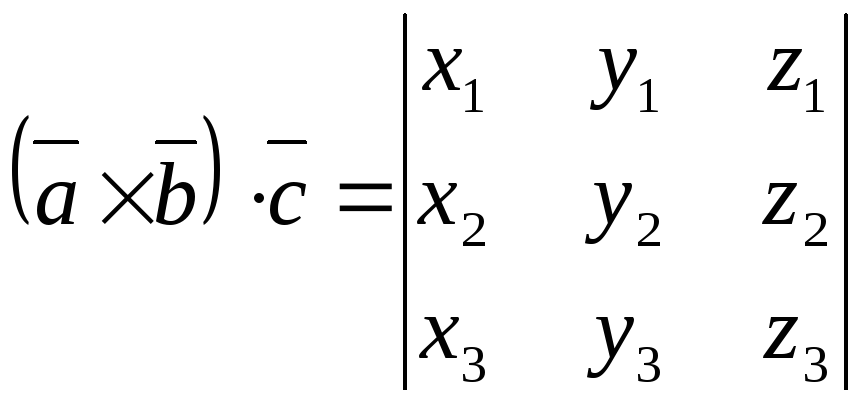 .
.
Смешанное произведение, взятое по абсолютной величине, равно объему параллелепипеда, построенного на векторах  ,
,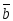 ,
,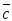 . Объем пирамиды, построенной на этих векторах, составляет шестую часть объема параллелепипеда.
. Объем пирамиды, построенной на этих векторах, составляет шестую часть объема параллелепипеда.
studfiles.net
Контрольная работа по теме «Интеграл».
Цели урока: проконтролировать знания учащихся.
Ход урока.
1. Организационный момент.
2. Контрольная работа.
Вариант 1.
1) Докажите, что функция 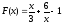 есть первообразная для функции
есть первообразная для функции  на промежутке
на промежутке 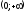 .
.
2) Известно, что функция 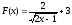 есть первообразная для функции f(x) на промежутке
есть первообразная для функции f(x) на промежутке  . Найти f(x).
. Найти f(x).
3) Для функции  найдите:
найдите:
а) общий вид первообразных;
б) первообразную график, которой проходит через точку 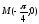 .
.
4) Вычислите площадь фигуры, ограниченной линиями 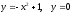 .
.
5) Найдите все первообразные функции  , графики которых имеют ровно две общие точки с графиком функции
, графики которых имеют ровно две общие точки с графиком функции  .
.
Вариант 2.
1) Докажите, что функция 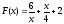 есть первообразная для функции
есть первообразная для функции 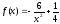 на промежутке
на промежутке  .
.
2) Известно, что функция 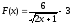 есть первообразная для функции f(x) на промежутке
есть первообразная для функции f(x) на промежутке  . Найти f(x).
. Найти f(x).
3) Для функции  найдите:
найдите:
а) общий вид первообразных;
б) первообразную график, которой проходит через точку 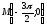 .
.
4) Вычислите площадь фигуры, ограниченной линиями 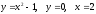 .
.
5) Найдите все первообразные функции  , графики которых имеют ровно две общие точки с графиком функции
, графики которых имеют ровно две общие точки с графиком функции  .
.
РЕШЕНИЕ:
Вариант 1.
1)  , то есть
, то есть  . Значит,
. Значит,  - первообразная для функции
- первообразная для функции  .
.
2) 
3) 
а) 
б) 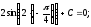
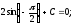
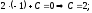
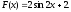
4)


Ответ:  .
.
5) Общий вид первообразных 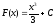 . Задача сводится к нахождению параметра С, когда уравнение
. Задача сводится к нахождению параметра С, когда уравнение 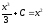 имеет два корня.
имеет два корня. 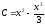
Рассмотрим функции 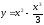 и
и  .
.
1) 
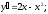

Критические точки: 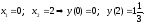
Определим знаки производной.

 - точка максимума.
- точка максимума.
 - точка минимума.
- точка минимума.
2)  - прямая параллельная оси ОХ, проходящая через точку
- прямая параллельная оси ОХ, проходящая через точку  .
.
Изобразим схематично графики функций в одной координатной плоскости.
Наглядно видно, что графики имеют две общие точки, если  и
и 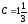 . Значит, графики первообразных
. Значит, графики первообразных  и
и  имеют ровно две общие точки с графиком функции
имеют ровно две общие точки с графиком функции  .
.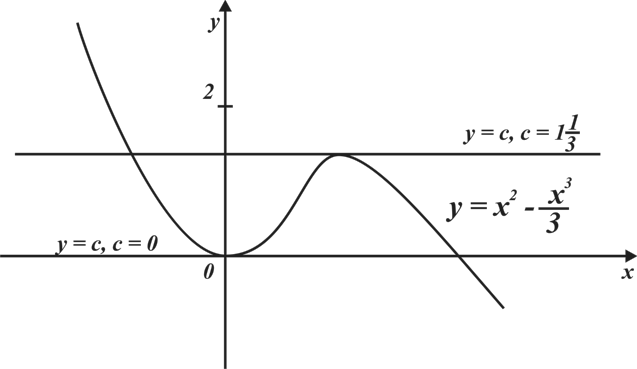
Ответ:  и
и  .
.
Вариант 2.
1)  , то есть
, то есть  . Значит,
. Значит,  - первообразная для функции
- первообразная для функции  .
.
2) 
3) 
а) 
б) 

4)
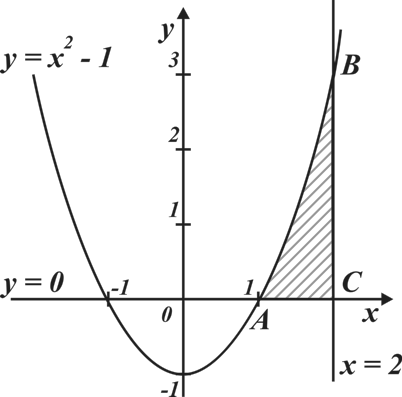
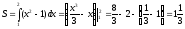
Ответ:  .
.
5) Общий вид первообразных  . Задача сводится к нахождению параметра С, когда уравнение
. Задача сводится к нахождению параметра С, когда уравнение 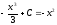 имеет два корня.
имеет два корня. 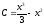
Рассмотрим функции 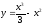 и
и  .
.
1) 
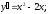

Критические точки: 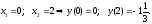
Определим знаки производной.
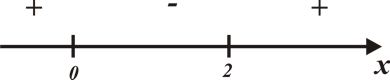
 - точка минимума.
- точка минимума.
 - точка максимума.
- точка максимума.
2)  - прямая параллельная оси ОХ, проходящая через точку
- прямая параллельная оси ОХ, проходящая через точку  .
.
Изобразим схематично графики функций в одной координатной плоскости.

Наглядно видно, что графики имеют две общие точки, если  и
и 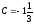 . Значит, графики первообразных
. Значит, графики первообразных  и
и  имеют ровно две общие точки с графиком функции
имеют ровно две общие точки с графиком функции  .
.
Ответ:  и
и  .
.
3. Итоги урока.
4. Домашнее задание.
Решить следующие задачи: стр. 205 №5(2).
xn--j1ahfl.xn--p1ai
![( ) ( ) ( ) ( ) ( ) ( ) () ( ) ( ) x [ ; ] ( ) ( ) ( ) ( ) ( ) ( ) () ( ) ( ) x [ ; ]](/800/600/http/docplayer.ru/thumbs/50/26554450.jpg) 8 Барроу Исаак (Brrow Is) -77 английский математик, филолог, богослов. Профессор Кембриджского университета. Автор труда лекции по оптике и геометрии (9-7). Из теоремы следует, что определенный интеграл
8 Барроу Исаак (Brrow Is) -77 английский математик, филолог, богослов. Профессор Кембриджского университета. Автор труда лекции по оптике и геометрии (9-7). Из теоремы следует, что определенный интеграл
 Глава Неопределенный интеграл Непосредственное интегрирование Функцию F() называют первообразной для функции f(), если выполняется равенство F'() f() Совокупность всех первообразных данной функции f()
Глава Неопределенный интеграл Непосредственное интегрирование Функцию F() называют первообразной для функции f(), если выполняется равенство F'() f() Совокупность всех первообразных данной функции f()
 Лекция..9. Несобственные интегралы Аннотация: Рассматриваются несобственные интегралы первого и второго рода. Вводится понятие главного значения несобственного интеграла. Определенный интеграл был введен
Лекция..9. Несобственные интегралы Аннотация: Рассматриваются несобственные интегралы первого и второго рода. Вводится понятие главного значения несобственного интеграла. Определенный интеграл был введен
 Металлургический факультет Кафедра высшей математики РЯДЫ Методические указания Новокузнецк 5 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
Металлургический факультет Кафедра высшей математики РЯДЫ Методические указания Новокузнецк 5 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
 17 Т е м а 4 Неопределенный интеграл Интегральное исчисление является составной частью математического анализа, и применяется при решении множества задач из области физики, химии, биологии, а именно в
17 Т е м а 4 Неопределенный интеграл Интегральное исчисление является составной частью математического анализа, и применяется при решении множества задач из области физики, химии, биологии, а именно в
 Министерство образования Российской Федерации «МАТИ» - Российский государственный технологический университет им КЭЦиолковского Кафедра «Высшая математика» НЕОПРЕДЕЛЕННЫЙ И ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Варианты
Министерство образования Российской Федерации «МАТИ» - Российский государственный технологический университет им КЭЦиолковского Кафедра «Высшая математика» НЕОПРЕДЕЛЕННЫЙ И ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Варианты
 ~ ~ Неопределенный и определенный интегралы Понятие первообразной и неопределѐнного интеграла. Определение: Функция F называется первообразной по отношению к функции f, если эти функции связаны следующим
~ ~ Неопределенный и определенный интегралы Понятие первообразной и неопределѐнного интеграла. Определение: Функция F называется первообразной по отношению к функции f, если эти функции связаны следующим
 82 4. Раздел 4. Функциональные и степенные ряды 4.2. Занятие 3 4.2. Занятие 3 4.2.. Разложение функции в ряд Тейлора ОПРЕДЕЛЕНИЕ 4.2.. Пусть функция y = f(x) бесконечно дифференцируема в некоторой окрестности
82 4. Раздел 4. Функциональные и степенные ряды 4.2. Занятие 3 4.2. Занятие 3 4.2.. Разложение функции в ряд Тейлора ОПРЕДЕЛЕНИЕ 4.2.. Пусть функция y = f(x) бесконечно дифференцируема в некоторой окрестности
 Математический анализ Раздел: Неопределенный интеграл Тема: Интегрирование рациональных дробей Лектор Пахомова Е.Г. 0 г. 5. Интегрирование рациональных дробей ОПРЕДЕЛЕНИЕ. Рациональной дробью называется
Математический анализ Раздел: Неопределенный интеграл Тема: Интегрирование рациональных дробей Лектор Пахомова Е.Г. 0 г. 5. Интегрирование рациональных дробей ОПРЕДЕЛЕНИЕ. Рациональной дробью называется
 ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Задачи, приводящие к понятию определённого интеграла J n d lm n m Δõ ξ Δ Геометрический смысл определённого интеграла площадь криволинейной трапеции Физический смысл определённого
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Задачи, приводящие к понятию определённого интеграла J n d lm n m Δõ ξ Δ Геометрический смысл определённого интеграла площадь криволинейной трапеции Физический смысл определённого
 Простейшие неопределенные интегралы Примеры решения задач Следующие интегралы сводятся к табличным путем тождественного преобразования подынтегрального выражения. 1. dx = dx = 2x 2/3 /3 + 2x 1/2 + C. >2.
Простейшие неопределенные интегралы Примеры решения задач Следующие интегралы сводятся к табличным путем тождественного преобразования подынтегрального выражения. 1. dx = dx = 2x 2/3 /3 + 2x 1/2 + C. >2.
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ТОЛЬЯТТИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра «Высшая математика и математическое моделирование» Ахметжанова ГВ, Бабенко НГ, Иванов ОИ ВЫСШАЯ МАТЕМАТИКА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ТОЛЬЯТТИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра «Высшая математика и математическое моделирование» Ахметжанова ГВ, Бабенко НГ, Иванов ОИ ВЫСШАЯ МАТЕМАТИКА
 58 Определенный интеграл Пусть на промежутке [] задана функция () Будем считать функцию непрерывной, хотя это не обязательно Выберем на промежутке [] произвольные числа,, 3,, n-, удовлетворяющие условию:
58 Определенный интеграл Пусть на промежутке [] задана функция () Будем считать функцию непрерывной, хотя это не обязательно Выберем на промежутке [] произвольные числа,, 3,, n-, удовлетворяющие условию:
 Лекция 7 Комплексные числа их изображение на плоскости Алгебраические операции над комплексными числами Комплексное сопряжение Модуль и аргумент комплексного числа Алгебраическая и тригонометрическая формы
Лекция 7 Комплексные числа их изображение на плоскости Алгебраические операции над комплексными числами Комплексное сопряжение Модуль и аргумент комплексного числа Алгебраическая и тригонометрическая формы
 Методы интегрирования Методы интегрирования. Интегралы, содержащие квадратный трехчлен в знаменателе. Понятия о рациональных функциях и их свойствах. Интегрирование простейших рациональных дробей. Теорема
Методы интегрирования Методы интегрирования. Интегралы, содержащие квадратный трехчлен в знаменателе. Понятия о рациональных функциях и их свойствах. Интегрирование простейших рациональных дробей. Теорема
 7 Занятие Несобственные интегралы. Несобственные интегралы первого и второго рода Понятие определенного интеграла f() от ограниченной функции по конечному отрезку [; b] распространяют на случаи, когда
7 Занятие Несобственные интегралы. Несобственные интегралы первого и второго рода Понятие определенного интеграла f() от ограниченной функции по конечному отрезку [; b] распространяют на случаи, когда
 1 Интегралы Определенные и Неопределенные Опр. Интеграл функции это естественный аналог суммы последовательности. Опр. Интегрирование процесс нахождения интеграла. Зам. Интегрирование это операция обратная
1 Интегралы Определенные и Неопределенные Опр. Интеграл функции это естественный аналог суммы последовательности. Опр. Интегрирование процесс нахождения интеграла. Зам. Интегрирование это операция обратная
 Гл Степенные ряды a a a Ряд вида a a a a a () называется степенным, где,,,, a, постоянные, называемые коэффициентами ряда Иногда рассматривают степенной ряд более общего вида: a a( a) a( a) a( a) (), где
Гл Степенные ряды a a a Ряд вида a a a a a () называется степенным, где,,,, a, постоянные, называемые коэффициентами ряда Иногда рассматривают степенной ряд более общего вида: a a( a) a( a) a( a) (), где
 НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ. Первообразная и неопределённый интеграл Основная задача дифференциального исчисления состоит в нахождении производной (или дифференциала) данной функции. Интегральное исчисление
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ. Первообразная и неопределённый интеграл Основная задача дифференциального исчисления состоит в нахождении производной (или дифференциала) данной функции. Интегральное исчисление
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УО «Белорусский государственный экономический университет» ТИ Гавриш, ЛНГайшун Р Я Д Ы Учебно-методическое пособие для студентов -го курса дневной и заочной
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УО «Белорусский государственный экономический университет» ТИ Гавриш, ЛНГайшун Р Я Д Ы Учебно-методическое пособие для студентов -го курса дневной и заочной
 Первообразная и неопределенный интеграл Основные понятия и формулы 1. Определение первообразной и неопределенного интеграла. Определение. Функция F(x) называется первообразной для функции f(x) на промежутке
Первообразная и неопределенный интеграл Основные понятия и формулы 1. Определение первообразной и неопределенного интеграла. Определение. Функция F(x) называется первообразной для функции f(x) на промежутке
 Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Уральский государственный университет путей сообщения» Кафедра «Высшая и прикладная математика» И
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Уральский государственный университет путей сообщения» Кафедра «Высшая и прикладная математика» И
 Математический анализ Определённый интеграл Краткий конспект лекций Составитель В.А.Чуриков Кандидат физ.-мат. наук, доцент кафедры Высшей математики Томского политехнического университета. Национальный
Математический анализ Определённый интеграл Краткий конспект лекций Составитель В.А.Чуриков Кандидат физ.-мат. наук, доцент кафедры Высшей математики Томского политехнического университета. Национальный
 Функциональные ряды Лекции 7-8 1 Область сходимости 1 Ряд вида u ( ) u ( ) u ( ) u ( ), 1 2 u ( ) где функции определены на некотором промежутке, называется функциональным рядом. Множество всех точек,
Функциональные ряды Лекции 7-8 1 Область сходимости 1 Ряд вида u ( ) u ( ) u ( ) u ( ), 1 2 u ( ) где функции определены на некотором промежутке, называется функциональным рядом. Множество всех точек,
 Федеральное агентство по образованию Федеральное государственное образовательное учреждение высшего профессионального образования Государственный технологический университет «Московский институт стали
Федеральное агентство по образованию Федеральное государственное образовательное учреждение высшего профессионального образования Государственный технологический университет «Московский институт стали
 Математический анализ Краткий конспект лекций Составитель В.А.Чуриков Кандидат физ.-мат. наук, доцент кафедры Высшей математики Томского политехнического университета. http://www.tpu.ru/ Национальный исследовательский
Математический анализ Краткий конспект лекций Составитель В.А.Чуриков Кандидат физ.-мат. наук, доцент кафедры Высшей математики Томского политехнического университета. http://www.tpu.ru/ Национальный исследовательский
 Неопределенный интеграл. Первообразная и неопределенный интеграл. Как по данной функции fх найти такую функцию Fх, производная которой равна данной функции. Опр. Функция Fх называется первообразной от
Неопределенный интеграл. Первообразная и неопределенный интеграл. Как по данной функции fх найти такую функцию Fх, производная которой равна данной функции. Опр. Функция Fх называется первообразной от
 Ряды Числовые ряды Общие понятия Опр Если каждому натуральному числу ставится в соответствие по определенному закону некоторое число, то множество занумерованных чисел, называется числовой последовательностью,
Ряды Числовые ряды Общие понятия Опр Если каждому натуральному числу ставится в соответствие по определенному закону некоторое число, то множество занумерованных чисел, называется числовой последовательностью,
 Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ Р Е
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ Р Е
 Математический анализ Раздел: Определенный интеграл Тема: Несобственные интегралы Лектор Рожкова С.В. 23 г. 5. Несобственные интегралы Для существования необходимы условия: [;] конечен, 2 f ограничена
Математический анализ Раздел: Определенный интеграл Тема: Несобственные интегралы Лектор Рожкова С.В. 23 г. 5. Несобственные интегралы Для существования необходимы условия: [;] конечен, 2 f ограничена
 3724 РЯДЫ КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ 1 РАБОЧАЯ ПРОГРАММА РАЗДЕЛОВ «РЯДЫ КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ» 11 Числовые ряды Понятие числового ряда Свойства числовых рядов Необходимый признак сходимости
3724 РЯДЫ КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ 1 РАБОЧАЯ ПРОГРАММА РАЗДЕЛОВ «РЯДЫ КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ» 11 Числовые ряды Понятие числового ряда Свойства числовых рядов Необходимый признак сходимости
docplayer.ru

Учебно – справочное пособие по курсу «ВЫСШАЯ МАТЕМАТИКА»
для студентов всех специальностей заочной формы обучения
Новоуральск 2007
УДК 519 О − 66
ББК 22.171
МиМ − 2.3. − __________ −07
Интегрирование.
Учебно – справочное пособие по курсу «ВЫСШАЯ МАТЕМАТИКА» для студентов всех специальностей заочной формы обучения
Новоуральск, изд. НГТИ. − 32 с.
Автор: старший преподаватель кафедры высшей математики НГТИ
Орлов Юрий Владимирович.
Пособие содержит 10 задач контрольной работы по теме «Интегралы и их применение» и справочник по данной теме.
Пособие обсуждено на заседании кафедры высшей математики НГТИ и рекомендовано к использованию в учебном процессе студентами всех специальностей заочной формы обучения.
“ ____ ” ______________ 200 ___ г.
Зав. кафедрой к.ф.м.н. ___________________ А.П. Золотарёв
Согласовано:
Председатель методической комиссии:
Профессор, д.т.н _____________ А.Е. Беляев
Содержание
| Введение ……………………………………….. | 4 | |
| 1 Контрольное задание: | ||
| Задача №1 …………………………………...... | 5 | |
| Задача №2 ….………………………………..... | 7 | |
| Задача №3 …………………………………...... | 9 | |
| Задача №4 …………………………………...... | 10 | |
| Задача №5 …………………………………...... | 11 | |
| Задача №6 ….………………………………..... | 13 | |
| Задача №7 …………………………………...... | 15 | |
| Задача №8 …………………………………...... | 16 | |
| Задача №9 …………………………………...... | 19 | |
| Задача №10 .………………………………..... | 20 | |
| 2 Справочник………..……………….................. | 21 | |
| Рекомендуемая литература …..…………… | 31 |
Введение
Данное пособие является сборником заданий второй контрольной работы (по теме «Интегралы и их применение») во втором семестре изучения курса «Высшая математика». Задания составлены для студентов заочной формы обучения, но могут выдаваться студентам и дневной и вечерней форм обучения. Первая контрольная работа в данном семестре выполняется по теме «Пределы, непрерывность и дифференцирование функции одной переменной».
Каждый студент при решении данной контрольной работы должен выполнить десять задач, которые заключаются в нахождении неопределенных, вычислении определенных интегралов либо в их применении. В соответствии с порядковым номером студента в списке группы в очередном задании выполняется соответствующий номер и решение всех задач оформляется в соответствии со стандартом НГТИ оформления текстовой документации.
Для удобства освоения данной темы пособие содержит справочник с таблицей интегралов и основными методами интегрирования. Более подробное изложение таких методов интегрирования можно изучить в литературе, список которой приведён в конце пособия.
1 Контрольное задание
Задача №1 Найти неопределенный интеграл, выполнив необходимые замены


Задача №2 Вычислить определенный интеграл, выполнив необходимые замены


Задача №3 Найти неопределенный интеграл, выполнив интегрирование по частям

Задача №4 Вычислить определенный интеграл, выполнив интегрирование по частям


Задача №5 Найти неопределенный интеграл, разложив функцию на сумму элементарных дробей


Задача №6 Найти определенный интеграл от тригонометрических функций


Задача №7 Вычислить площадь фигуры, ограниченной линиями в декартовой системе координат



Задача №8 Вычислить площадь фигуры, ограниченной линиями в декартовой системе координат



Задача №9 Вычислить площадь фигуры, ограниченной линиями в полярной системе координат

Задача №10 Вычислить объём тела, образованного вращением фигуры, ограниченной графиком функции. В вариантах 1 – 16 ось вращения ОХ, а в вариантах 17 – 32 ось вращения ОY.

Справочник
| Функция
| Первообразная
| Функция
| Первообразная
|
|
|
| 1 | х |
|
|
| ||
|
|
| ||
|
|
| ||
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б)  ;
;

а)  неправильная дробь,
неправильная дробь,
выделение целой части и правильной дроби:

 ,
,
 ;
;
б)  ,
,
 ,
,

 ,
, 
 ,
,
 ;
;
 ,
,
 ,
,
 ,
,
число коэффициентов каждый раз равно порядку многочлена в исходном знаменателе;
1)  ;
;
2)  ;
;
3)  ;
;

5) Интеграл вида  при
при находится по формуле
находится по формуле
 ;
;
Пусть  -рациональное выражение от
-рациональное выражение от .
.
Тогда
а)  находится с помощью универсальной подстановки
находится с помощью универсальной подстановки
 ,
,
получим интеграл от дробно-рациональной функции;
б)  или при чётности подынтегральной функции относительно синуса и косинуса находится с помощью подстановки
или при чётности подынтегральной функции относительно синуса и косинуса находится с помощью подстановки
 ;
;
в) 
в.1)  – любое
– любое замена
замена ;
;
в.2)  – любое
– любое замена
замена ;
;
в.3)  -нечётное положительное,
-нечётное положительное, – любое
– любое замена
замена

 -нечётное положительное,
-нечётное положительное,  – любое
– любое замена
замена

в.5)  – чётные положительные числа, тогда каждую степень
– чётные положительные числа, тогда каждую степень
понижают вдвое по формулам

г) При интегрировании произведения тригонометрических функций используются формулы
 ,
,
 ,
,
 ;
;
а) Площадь криволинейной трапеции, ограниченной осью ОХ, прямыми  слева,
слева, справа, и графиком функции
справа, и графиком функции при условии
при условии
 ;
;
Если  , то
, то ;
;
б) Площадь между графиком  и осью ОY
и осью ОY

в) Если фигура ограничена в декартовых координатах графиком функции  снизу, графиком
снизу, графиком сверху, вертикальными прямыми
сверху, вертикальными прямыми слева и
слева и справа, то
справа, то ;
;
при  и осями декартовой системы координат:
и осями декартовой системы координат:
г.1) С осью ОХ  ;
;
г.2) С осью ОY  ;
;


При а=1


 -угол поворота от полярной оси (оси ОХ) против часовой стрелки,
-угол поворота от полярной оси (оси ОХ) против часовой стрелки,  -расстояние до полюса (начала координат).
-расстояние до полюса (начала координат).
r
M


Полярная ось



Полюс





Если фигура ограничена исходящими из полюса лучами  ,
,
 и линией
и линией  , то площадь такого криволинейного сектора
, то площадь такого криволинейного сектора  ;
;
Если фигура ограничена исходящими из полюса лучами  ,
,
 и линиями
и линиями  ближе к полюсу,
ближе к полюсу, дальше от полюса, то площадь такой фигуры
дальше от полюса, то площадь такой фигуры  ;
;
а) Если для любой проекции  тела на ось ОХ известна площадь поперечного сечения
тела на ось ОХ известна площадь поперечного сечения такого тела,
такого тела,
то его объём тела  ;
;
б) Если в плоскости ХОY задана линия  и при
и при она вращается вокруг оси ОХ, то объём тела вращения
она вращается вокруг оси ОХ, то объём тела вращения
 ;
;
Если в плоскости ХОY задана линия  и при
и при она вращается вокруг оси ОY, то объём тела вращения
она вращается вокруг оси ОY, то объём тела вращения
 .
.
Рекомендуемая литература
1) Шнейдер В.Е., Слуцкий А.И., Шумов А.С.
Краткий курс высшей математики (в двух томах).
Т.1. – М.: Высшая школа, 1978.-530 с.;
2) Пискунов Н.С. Дифференциальное и интегральное исчисление
для ВТУЗов. Т.1. – М.: Наука, 1978 – 560с.;
3) Бугров Н.С., Никольский С.М.
Высшая математика. Дифференциальное и интегральное
исчисление. – М.: Наука, 1981.-432 с.;
4) Данко П.Е., Попов А.Г., Кожевникова Т.Я.
Высшая математика в примерах и задачах (в двух частях).
Ч.1. – М.: Высшая школа, 1986 – 304, 416 с.;
5) Задачи и упражнения по математическому анализу для ВТУЗов.
под ред. Демидовича Б.П. – М.: Наука, 1972.- 632 с.;
Шипачев В.С. Высшая математика: Учебное пособие для ВУЗов.
studfiles.net

Учебно – справочное пособие по курсу «ВЫСШАЯ МАТЕМАТИКА»
для студентов всех специальностей заочной формы обучения
Новоуральск 2007
УДК 519 О − 66
ББК 22.171
МиМ − 2.3. − __________ −07
Интегрирование.
Учебно – справочное пособие по курсу «ВЫСШАЯ МАТЕМАТИКА» для студентов всех специальностей заочной формы обучения
Новоуральск, изд. НГТИ. − 32 с.
Автор: старший преподаватель кафедры высшей математики НГТИ
Орлов Юрий Владимирович.
Пособие содержит 10 задач контрольной работы по теме «Интегралы и их применение» и справочник по данной теме.
Пособие обсуждено на заседании кафедры высшей математики НГТИ и рекомендовано к использованию в учебном процессе студентами всех специальностей заочной формы обучения.
“ ____ ” ______________ 200 ___ г.
Зав. кафедрой к.ф.м.н. ___________________ А.П. Золотарёв
Согласовано:
Председатель методической комиссии:
Профессор, д.т.н _____________ А.Е. Беляев
Содержание
| Введение ……………………………………….. | 4 | |
| 1 Контрольное задание: | ||
| Задача №1 …………………………………...... | 5 | |
| Задача №2 ….………………………………..... | 7 | |
| Задача №3 …………………………………...... | 9 | |
| Задача №4 …………………………………...... | 10 | |
| Задача №5 …………………………………...... | 11 | |
| Задача №6 ….………………………………..... | 13 | |
| Задача №7 …………………………………...... | 15 | |
| Задача №8 …………………………………...... | 16 | |
| Задача №9 …………………………………...... | 19 | |
| Задача №10 .………………………………..... | 20 | |
| 2 Справочник………..……………….................. | 21 | |
| Рекомендуемая литература …..…………… | 31 |
Введение
Данное пособие является сборником заданий второй контрольной работы (по теме «Интегралы и их применение») во втором семестре изучения курса «Высшая математика». Задания составлены для студентов заочной формы обучения, но могут выдаваться студентам и дневной и вечерней форм обучения. Первая контрольная работа в данном семестре выполняется по теме «Пределы, непрерывность и дифференцирование функции одной переменной».
Каждый студент при решении данной контрольной работы должен выполнить десять задач, которые заключаются в нахождении неопределенных, вычислении определенных интегралов либо в их применении. В соответствии с порядковым номером студента в списке группы в очередном задании выполняется соответствующий номер и решение всех задач оформляется в соответствии со стандартом НГТИ оформления текстовой документации.
Для удобства освоения данной темы пособие содержит справочник с таблицей интегралов и основными методами интегрирования. Более подробное изложение таких методов интегрирования можно изучить в литературе, список которой приведён в конце пособия.
1 Контрольное задание
Задача №1 Найти неопределенный интеграл, выполнив необходимые замены


Задача №2 Вычислить определенный интеграл, выполнив необходимые замены


Задача №3 Найти неопределенный интеграл, выполнив интегрирование по частям

Задача №4 Вычислить определенный интеграл, выполнив интегрирование по частям


Задача №5 Найти неопределенный интеграл, разложив функцию на сумму элементарных дробей


Задача №6 Найти определенный интеграл от тригонометрических функций


Задача №7 Вычислить площадь фигуры, ограниченной линиями в декартовой системе координат



Задача №8 Вычислить площадь фигуры, ограниченной линиями в декартовой системе координат



Задача №9 Вычислить площадь фигуры, ограниченной линиями в полярной системе координат

Задача №10 Вычислить объём тела, образованного вращением фигуры, ограниченной графиком функции. В вариантах 1 – 16 ось вращения ОХ, а в вариантах 17 – 32 ось вращения ОY.

Справочник
| Функция
| Первообразная
| Функция
| Первообразная
|
|
|
| 1 | х |
|
|
| ||
|
|
| ||
|
|
| ||
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б)  ;
;

а)  неправильная дробь,
неправильная дробь,
выделение целой части и правильной дроби:

 ,
,
 ;
;
б)  ,
,
 ,
,

 ,
, 
 ,
,
 ;
;
 ,
,
 ,
,
 ,
,
число коэффициентов каждый раз равно порядку многочлена в исходном знаменателе;
1)  ;
;
2)  ;
;
3)  ;
;

5) Интеграл вида  при
при находится по формуле
находится по формуле
 ;
;
Пусть  -рациональное выражение от
-рациональное выражение от .
.
Тогда
а)  находится с помощью универсальной подстановки
находится с помощью универсальной подстановки
 ,
,
получим интеграл от дробно-рациональной функции;
б)  или при чётности подынтегральной функции относительно синуса и косинуса находится с помощью подстановки
или при чётности подынтегральной функции относительно синуса и косинуса находится с помощью подстановки
 ;
;
в) 
в.1)  – любое
– любое замена
замена ;
;
в.2)  – любое
– любое замена
замена ;
;
в.3)  -нечётное положительное,
-нечётное положительное, – любое
– любое замена
замена

 -нечётное положительное,
-нечётное положительное,  – любое
– любое замена
замена

в.5)  – чётные положительные числа, тогда каждую степень
– чётные положительные числа, тогда каждую степень
понижают вдвое по формулам

г) При интегрировании произведения тригонометрических функций используются формулы
 ,
,
 ,
,
 ;
;
а) Площадь криволинейной трапеции, ограниченной осью ОХ, прямыми  слева,
слева, справа, и графиком функции
справа, и графиком функции при условии
при условии
 ;
;
Если  , то
, то ;
;
б) Площадь между графиком  и осью ОY
и осью ОY

в) Если фигура ограничена в декартовых координатах графиком функции  снизу, графиком
снизу, графиком сверху, вертикальными прямыми
сверху, вертикальными прямыми слева и
слева и справа, то
справа, то ;
;
при  и осями декартовой системы координат:
и осями декартовой системы координат:
г.1) С осью ОХ  ;
;
г.2) С осью ОY  ;
;


При а=1


 -угол поворота от полярной оси (оси ОХ) против часовой стрелки,
-угол поворота от полярной оси (оси ОХ) против часовой стрелки,  -расстояние до полюса (начала координат).
-расстояние до полюса (начала координат).
r
M


Полярная ось



Полюс





Если фигура ограничена исходящими из полюса лучами  ,
,
 и линией
и линией  , то площадь такого криволинейного сектора
, то площадь такого криволинейного сектора  ;
;
Если фигура ограничена исходящими из полюса лучами  ,
,
 и линиями
и линиями  ближе к полюсу,
ближе к полюсу, дальше от полюса, то площадь такой фигуры
дальше от полюса, то площадь такой фигуры  ;
;
а) Если для любой проекции  тела на ось ОХ известна площадь поперечного сечения
тела на ось ОХ известна площадь поперечного сечения такого тела,
такого тела,
то его объём тела  ;
;
б) Если в плоскости ХОY задана линия  и при
и при она вращается вокруг оси ОХ, то объём тела вращения
она вращается вокруг оси ОХ, то объём тела вращения
 ;
;
Если в плоскости ХОY задана линия  и при
и при она вращается вокруг оси ОY, то объём тела вращения
она вращается вокруг оси ОY, то объём тела вращения
 .
.
Рекомендуемая литература
1) Шнейдер В.Е., Слуцкий А.И., Шумов А.С.
Краткий курс высшей математики (в двух томах).
Т.1. – М.: Высшая школа, 1978.-530 с.;
2) Пискунов Н.С. Дифференциальное и интегральное исчисление
для ВТУЗов. Т.1. – М.: Наука, 1978 – 560с.;
3) Бугров Н.С., Никольский С.М.
Высшая математика. Дифференциальное и интегральное
исчисление. – М.: Наука, 1981.-432 с.;
4) Данко П.Е., Попов А.Г., Кожевникова Т.Я.
Высшая математика в примерах и задачах (в двух частях).
Ч.1. – М.: Высшая школа, 1986 – 304, 416 с.;
5) Задачи и упражнения по математическому анализу для ВТУЗов.
под ред. Демидовича Б.П. – М.: Наука, 1972.- 632 с.;
Шипачев В.С. Высшая математика: Учебное пособие для ВУЗов.
studfiles.net
Контрольная работа
по теме: «Интегральное исчисление»
Вариант №1
1. Вычислите неопределенные интегралы:
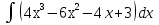
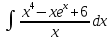
2. Вычислите определенные интегралы:
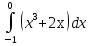
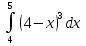
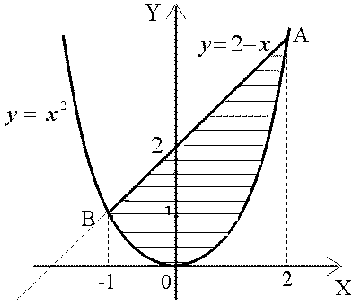
3. Найдите площадь фигуры, ограниченной линиями 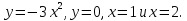
4. Вычислите площадь фигуры, ограниченной линиями.
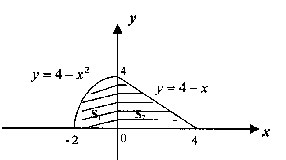
Контрольная работа
по теме: «Интегральное исчисление»
Вариант №2
Вычислите неопределенные интегралы:
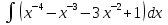
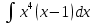
2. Вычислите определенные интегралы:
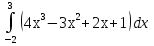
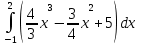
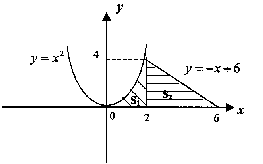 3. Найдите площадь фигуры, ограниченной линиями
3. Найдите площадь фигуры, ограниченной линиями 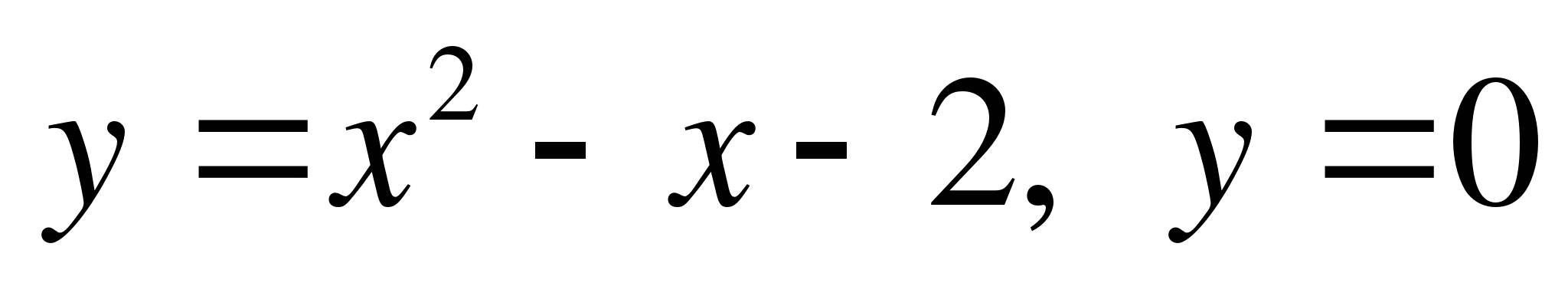
4. Вычислите площадь фигуры, ограниченной линиями
Контрольная работа по теме: «Интегральное исчисление»Вариант №3
1. Вычислите неопределенные интегралы:
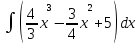
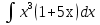
2. Вычислите определенные интегралы:
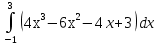
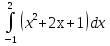
3. Найдите площадь фигуры, ограниченной линиями 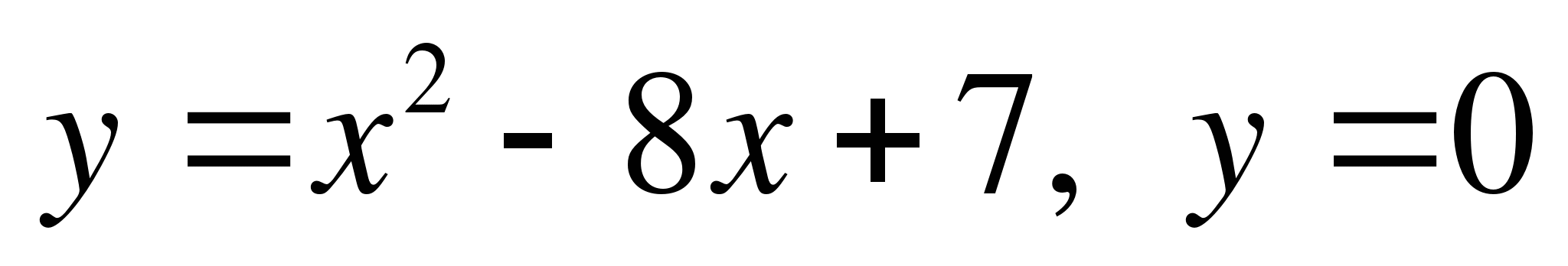
4. Вычислите площадь фигуры, ограниченной линиями.
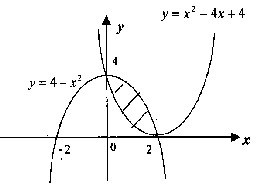
Контрольная работа по теме: «Интегральное исчисление»
Вариант №4
1. Вычислите неопределенные интегралы:
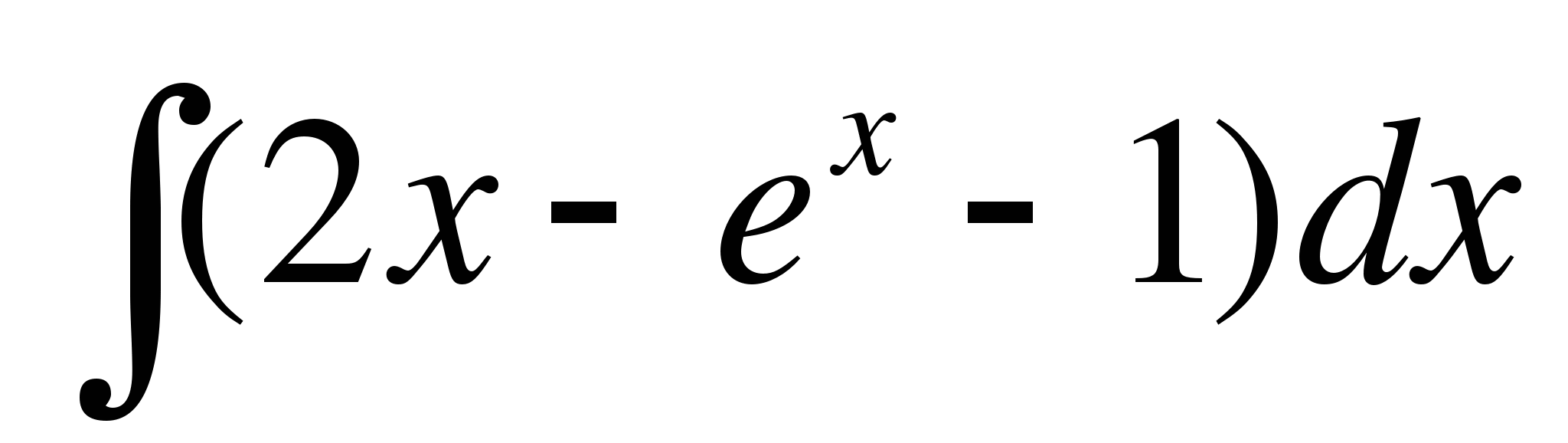
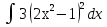
2. Вычислите определенные интегралы:
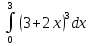
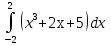
3. Найдите площадь фигуры, ограниченной линиями 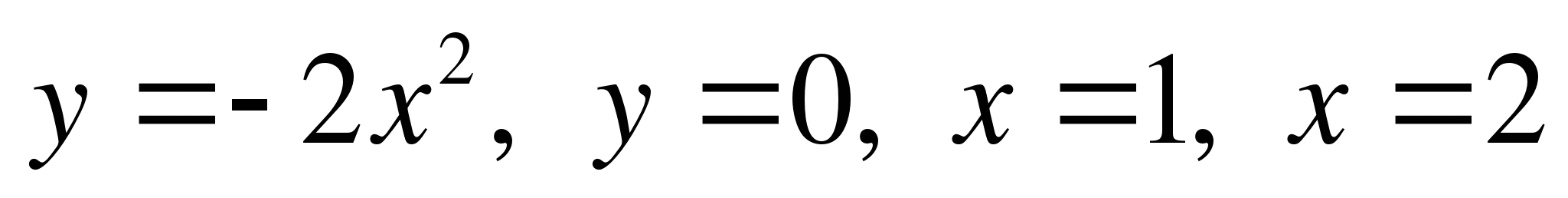
4. Вычислите площадь фигуры, ограниченной линиями.
infourok.ru
Первообразная. Неопределенный интеграл и его свойства. Таблица основных формул интегрирования. Непосредственное интегрирование. Интегрирование по частям и подстановкой. Интегрирование рациональных функций. Интегрирование выражений, содержащих тригонометрические функции. Интегрирование некоторых иррациональных функций.
Определение и геометрический смысл определенного интеграла. Основные свойства определенного интеграла. Производная интеграла по верхнему пределу. Формула Ньютона-Лейбница. Замена переменной в определенном интеграле. Интегрирование по частям. Геометрические приложения определенного интеграла: вычисление площади плоской фигуры, площади криволинейного сектора, объем тела вращения и длины дуги плоской кривой. Несобственные интегралы.
1 – 10. Даны векторы  ,
,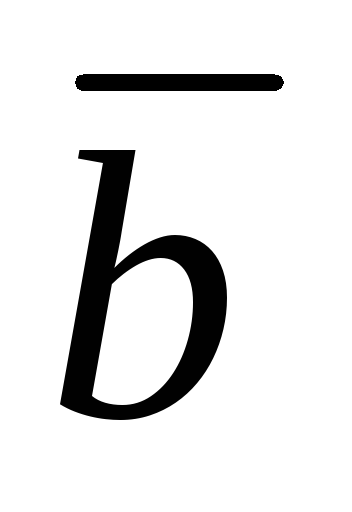 и
и . Найдите :
. Найдите :
а) скалярное произведение векторов 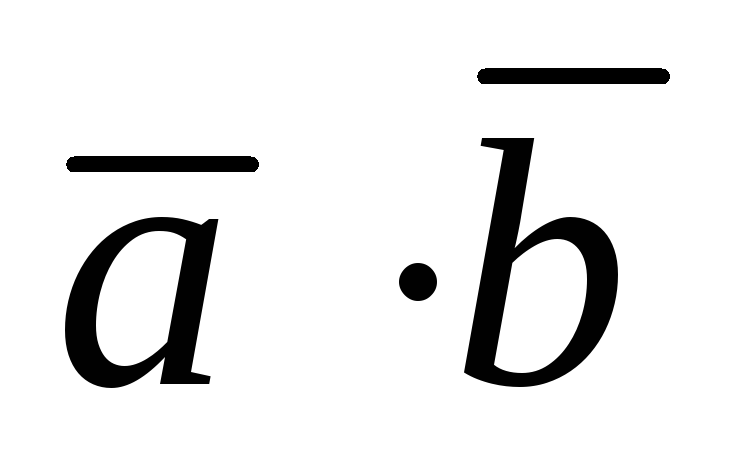 ;
;
б) векторное произведение векторов 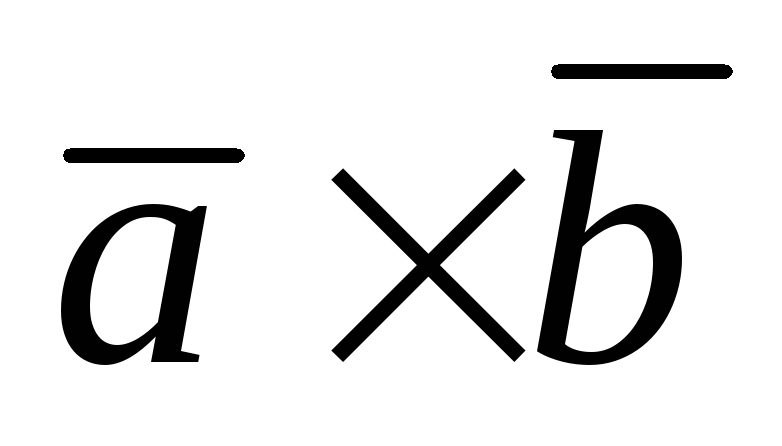 ;
;
в) смешанное произведение векторов 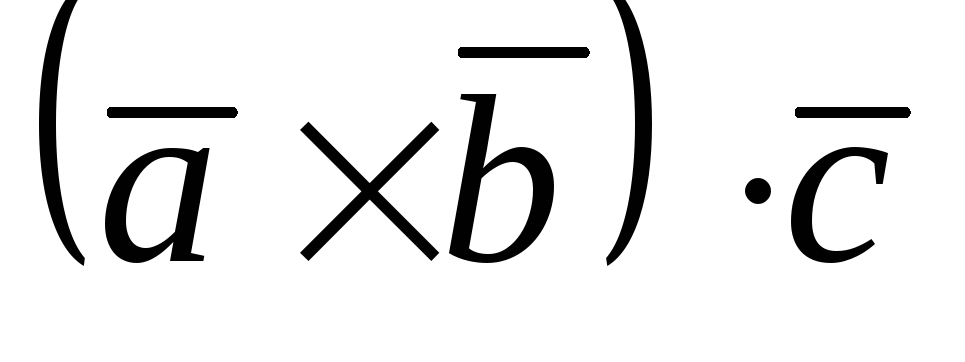 ;
;
г) проекцию вектора  на вектор
на вектор ;
;
д) площадь треугольника, построенного на векторах  ,
, ;
;
е) объем пирамиды, построенной на векторах  ,
, ,
, .
.
1.  ,А(1; 2;1),В(1; 0; 1),
,А(1; 2;1),В(1; 0; 1),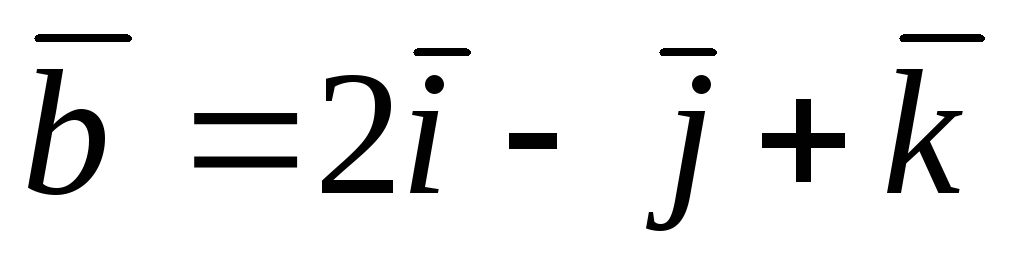 ,
,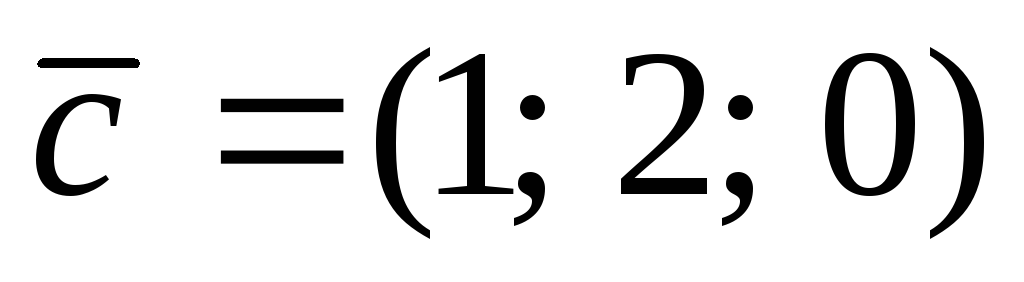 .
.
2. 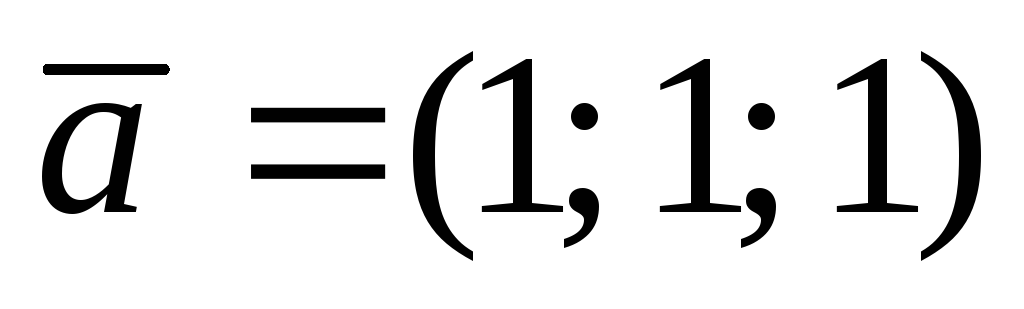 ,
, 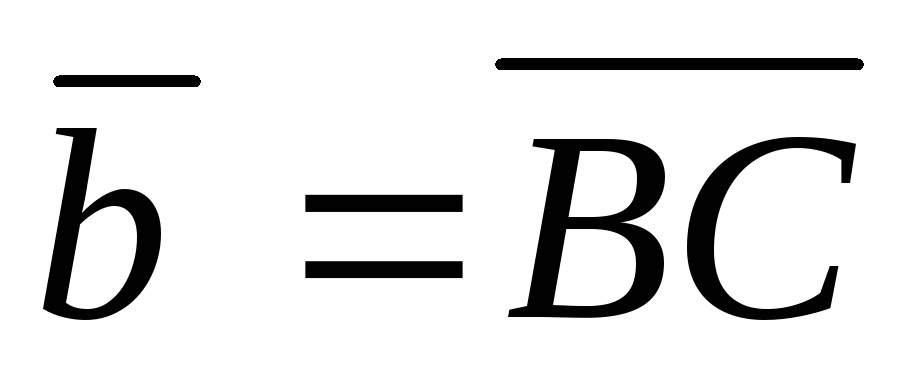 ,В(0; 1; 2),С(2;1; 0),
,В(0; 1; 2),С(2;1; 0),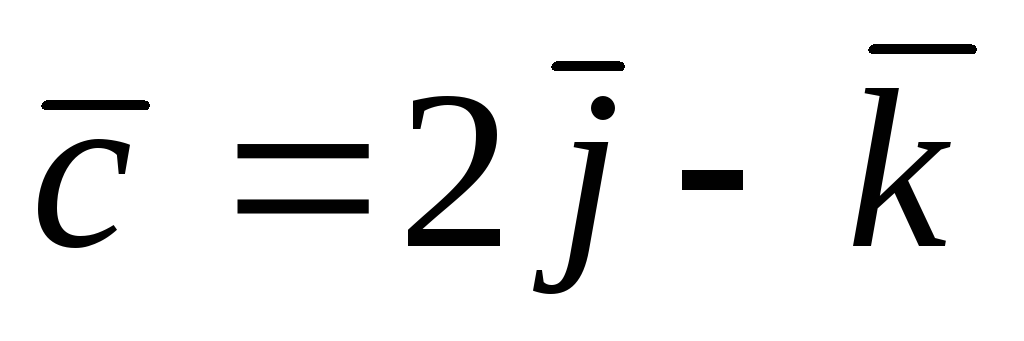 .
.
3. 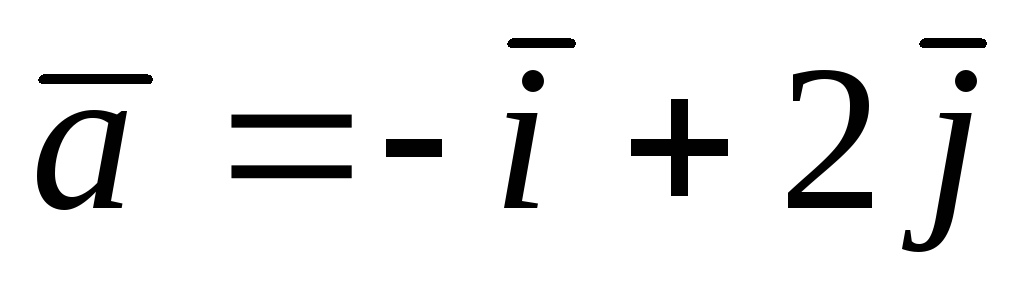 ,
,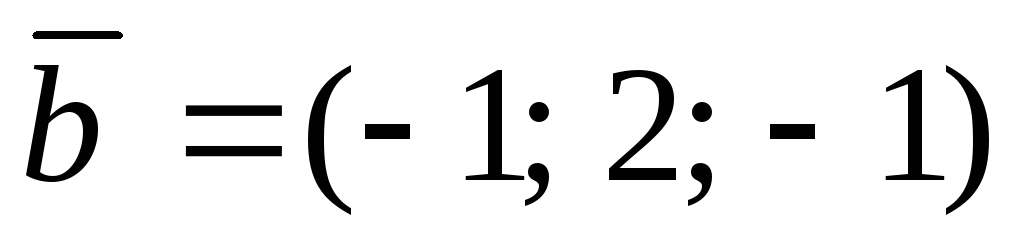 ,
, ,С(0; 2;1), D(1;2;1).
,С(0; 2;1), D(1;2;1).
4. 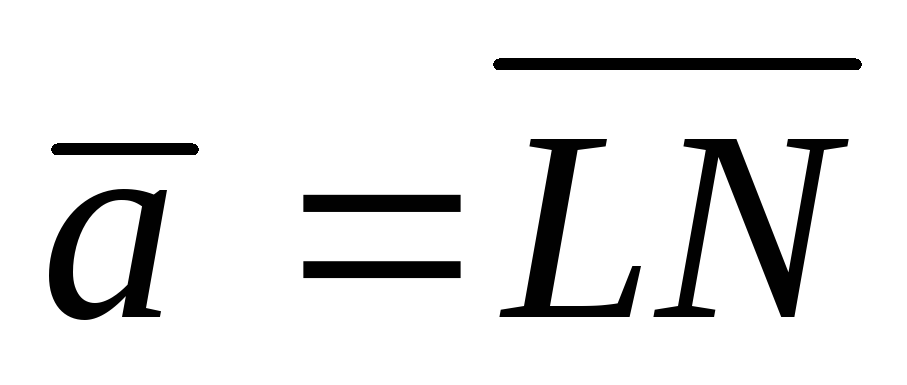 , L(1; 2; 3), N(1; 2; 0),
, L(1; 2; 3), N(1; 2; 0), 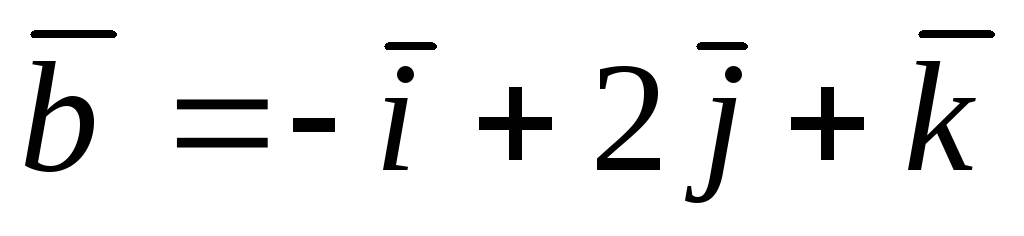 ,
,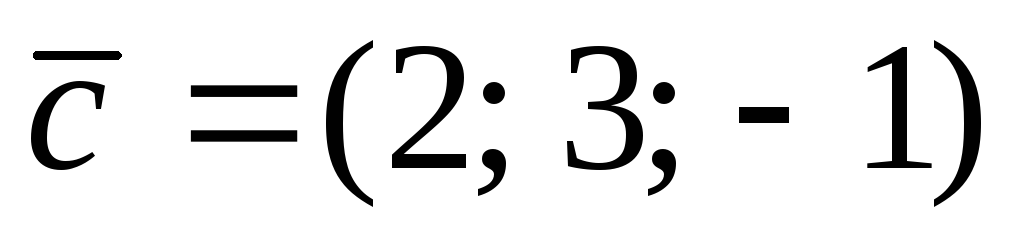 .
.
5. 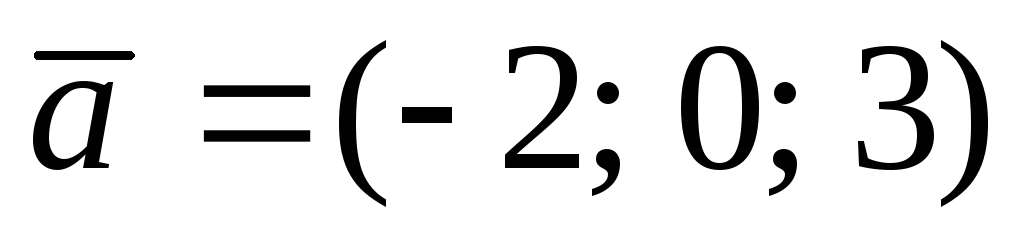 ,
,  ,
, 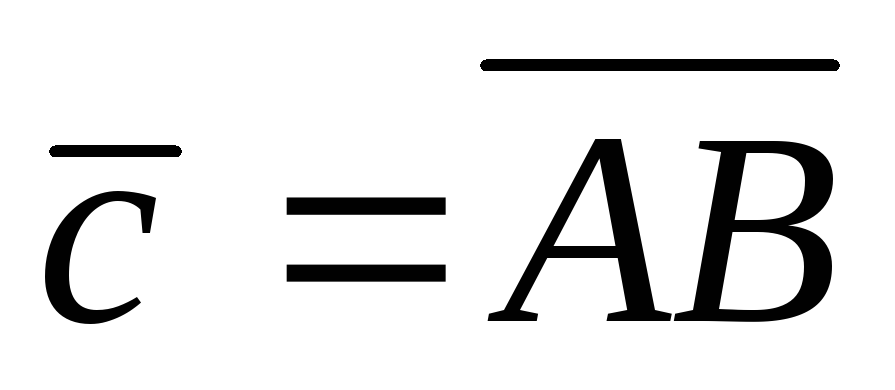 ,A(0;2; 1), B(1; 2;1).
,A(0;2; 1), B(1; 2;1).
6. 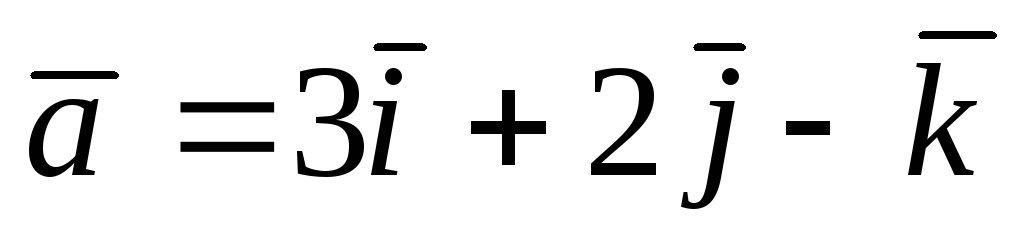 ,
,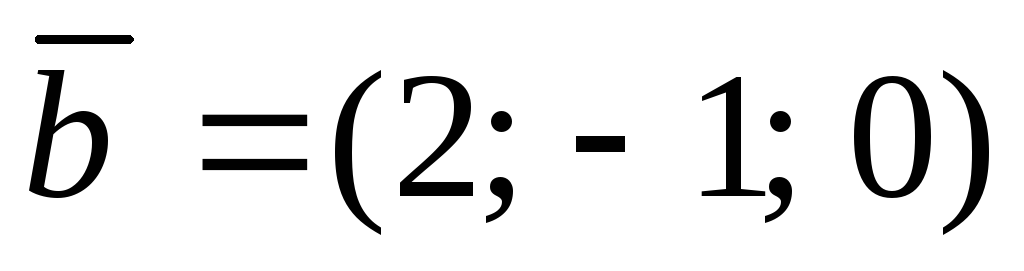 ,
, 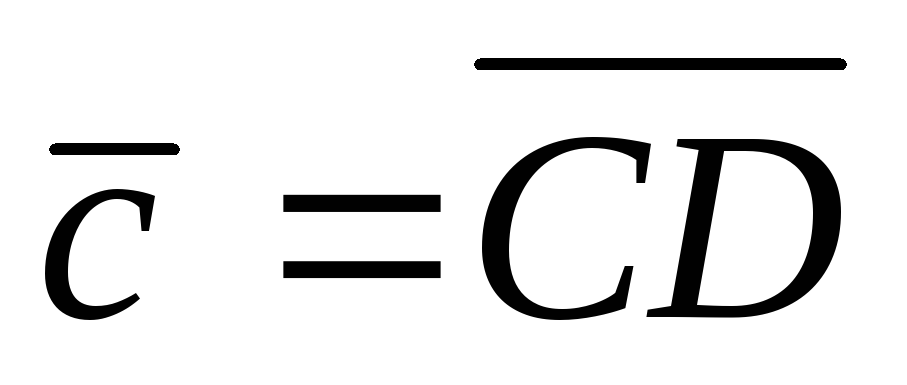 , C(0; 2; 3), D(2; 1; 1).
, C(0; 2; 3), D(2; 1; 1).
7. 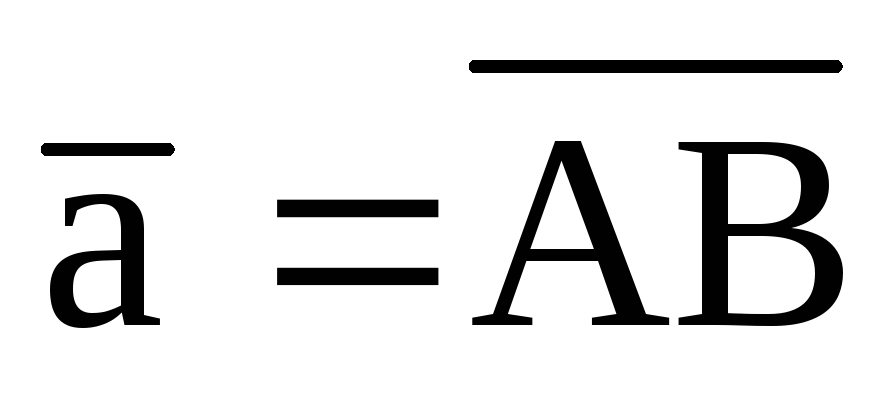 , A(2; 2; 2), B(1; 0; 1),
, A(2; 2; 2), B(1; 0; 1), 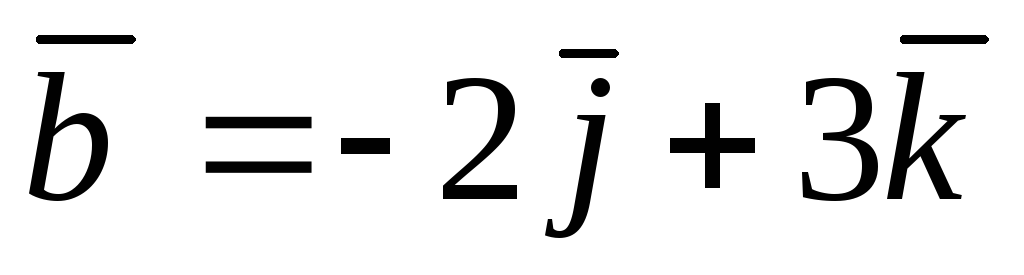 ,
,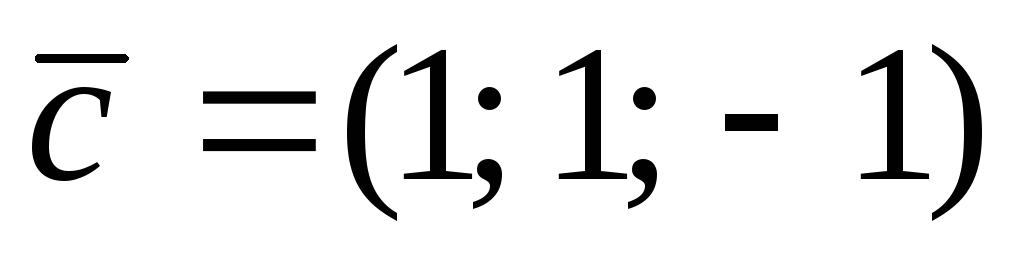 .
.
8. 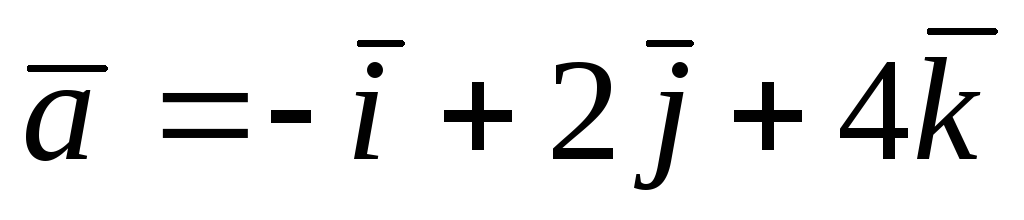 ,
, 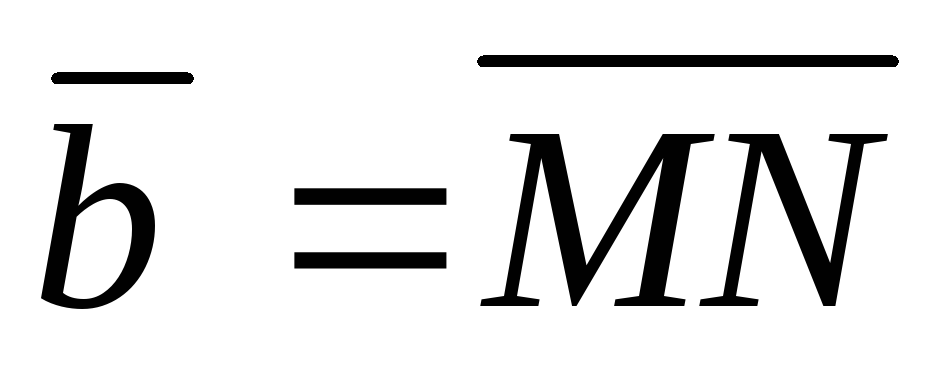 , M(3; 1; 2), N(0; 1; 2),
, M(3; 1; 2), N(0; 1; 2), 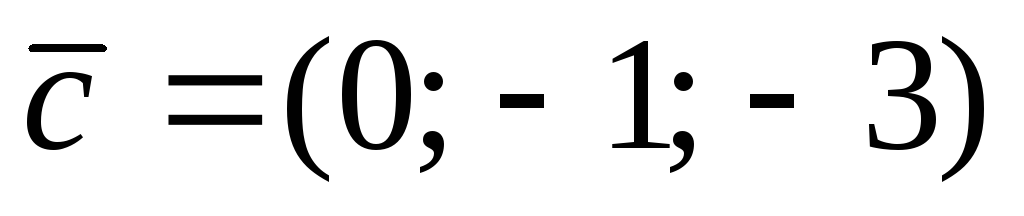 .
.
9. 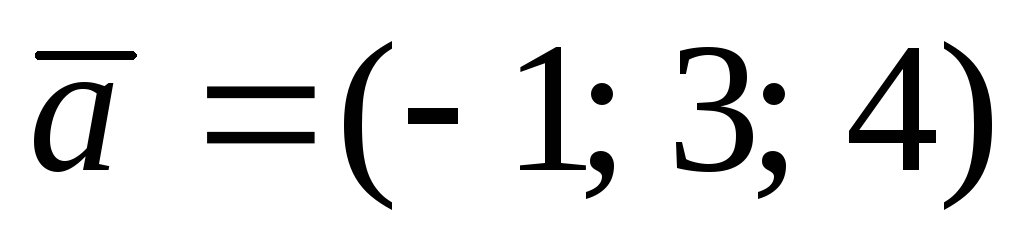 ,
, 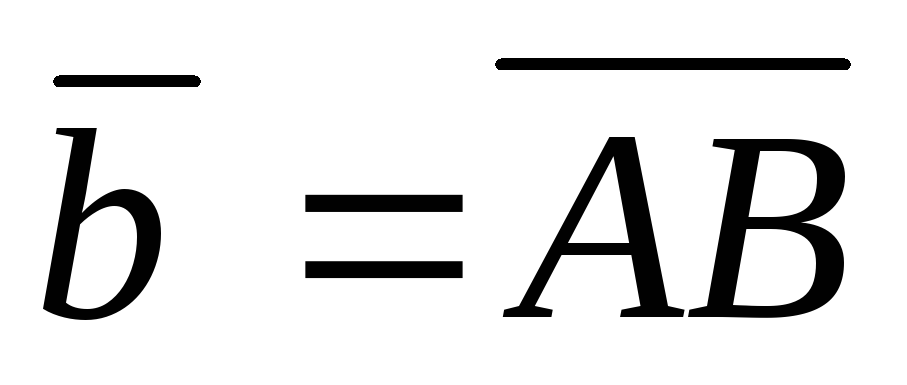 , A(2; 1; 3), B(1; 0; 3),
, A(2; 1; 3), B(1; 0; 3), 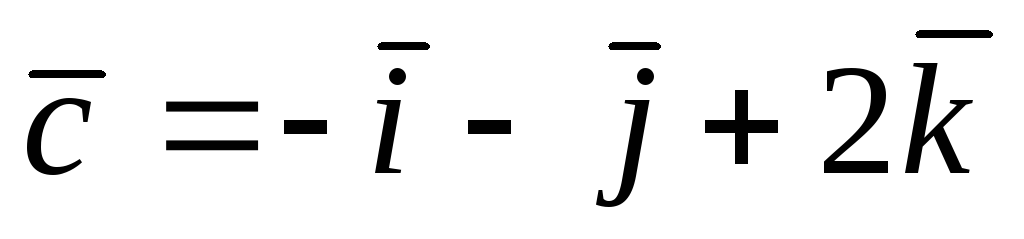 .
.
10. 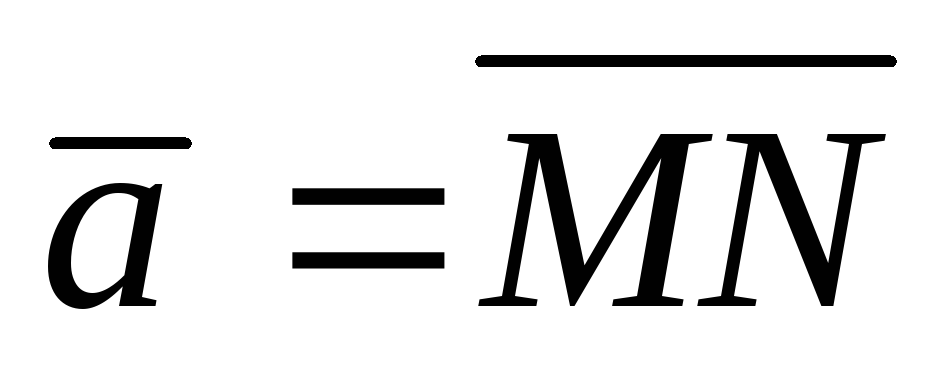 , M(2; 3; 4), N(0; 2; 3),
, M(2; 3; 4), N(0; 2; 3), 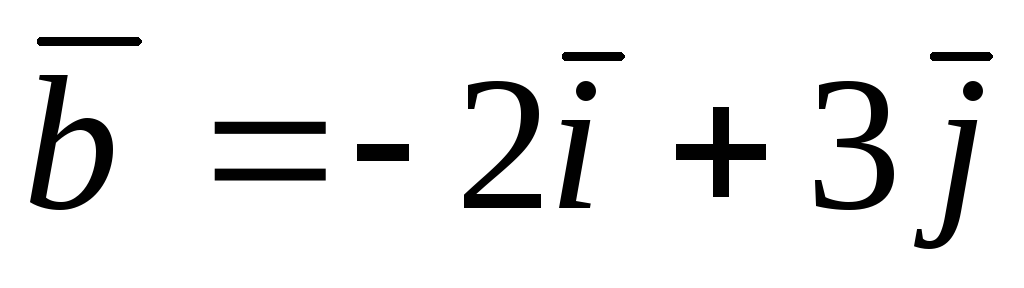 ,
,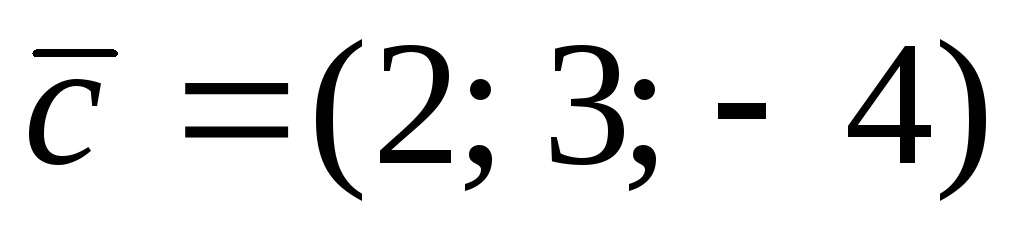 .
.
11 – 20. Заданы координаты вершин пирамиды ABCD.
1. Составьте:
а) уравнение плоскости, проходящей через точки А, В, С;
б) уравнение прямой, проходящей через точки А, В;
в) уравнение прямой, проходящей через точку D, перпендикулярно плоскости (АВС).
2. Найдите:
а) длину ребра АВ;
б) угол между ребрами АВ и АD;
в) угол между ребром AD и гранью ABC.
11. A(3; 5; 4), B(8; 7; 4), C(5; 10; 4), D(4; 7; 8).
12. A(2; 0; 0), B(1; 0; 1), C(0; 1; 0), D(1; 1; 1).
13. A(7; 7; 3), B(6; 5; 8), C(3; 5; 8), D(8; 4; 1).
14. A(0; 1; 0), B(1; 0; 0), C(1; 1; 1), D(2; 2; 1).
15. A(10; 6; 6), B(2; 8; 2), C(6; 8; 9), D(7; 10; 3).
16. A(4; 2; 5), B(0; 7; 2), C(0; 2; 7), D(1; 5; 0).
17. A(4; 4; 10), B(4; 10; 2), C(2; 8; 4), D(9; 6; 4).
18. A(1; 1; 0), B(0; 1; 2), C(1; 0; 1), D(1; 2; 1).
19. A(1; 2; 1), B(1; 1; 2), C(0; 2; 1), D(2; 1; 2).
20. A(1; 8; 2), B(5; 2; 6), C(5; 7; 4), D(4; 10; 9).
21 – 30. Задачи по аналитической геометрии на плоскости.
Точка С(1; 3) – вершина прямого угла равнобедренного прямоугольного треугольника, гипотенуза которого задана уравнением 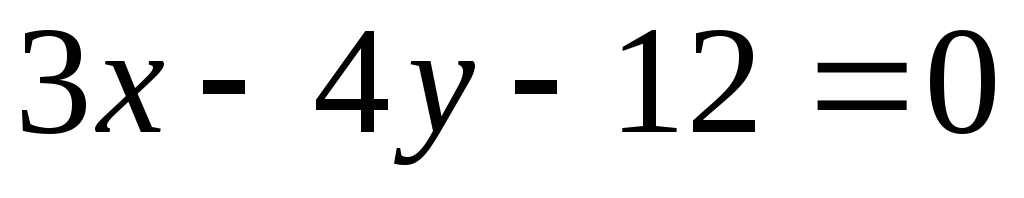 . Найдите уравнения катетов этого треугольника.
. Найдите уравнения катетов этого треугольника.
Заданы уравнение стороны прямоугольника 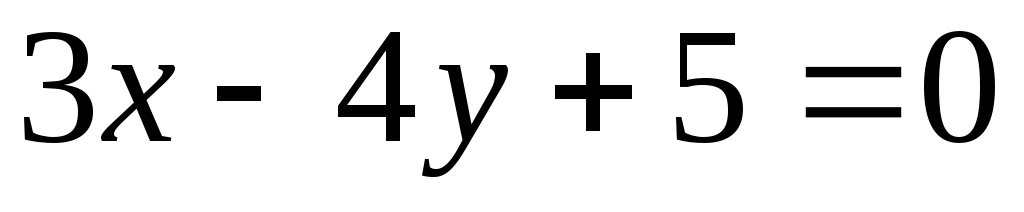 и две его вершины А(1;3) и С(1; 2). Найдите уравнения остальных сторон прямоугольника.
и две его вершины А(1;3) и С(1; 2). Найдите уравнения остальных сторон прямоугольника.
Заданы А(1; 3) вершина треугольника АВС и уравнения двух медиан 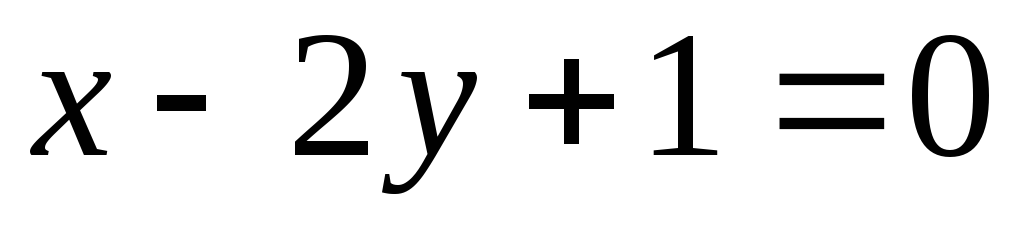 и
и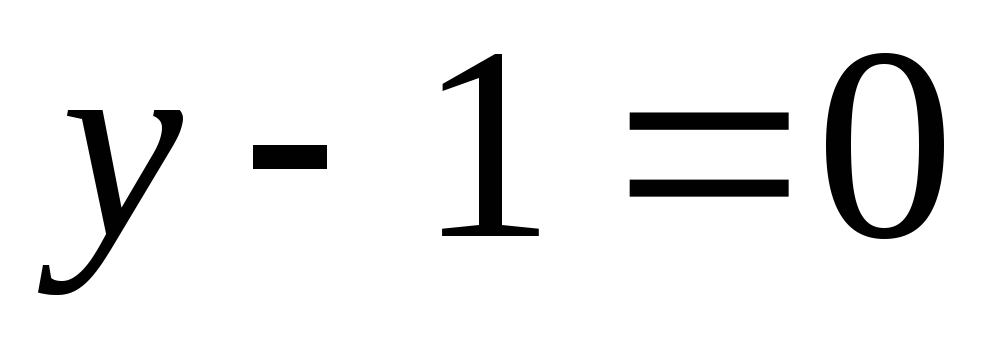 . Найдите уравнения сторон треугольника.
. Найдите уравнения сторон треугольника.
Составьте уравнения прямых, проходящих через точку М(2; 3) и образующих угол 45° с прямой 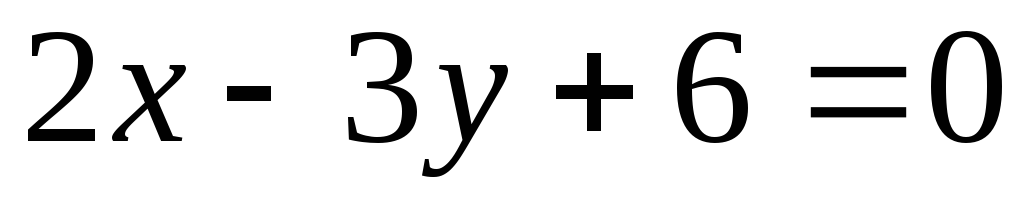 .
.
Точки А(3; 2), В(4; 1), С(1; 3) – вершины трапеции ABCD (AD||BC). Диагонали трапеции взаимно перпендикулярны. Найдите координаты вершины D этой трапеции.
Точки А(3; 4), В(1; 2), С(2; 1) – вершины треугольника. Найдите уравнение медианы, проведенной из вершины А, и уравнение средней линии, параллельной стороне ВС.
Заданы уравнения двух сторон параллелограмма 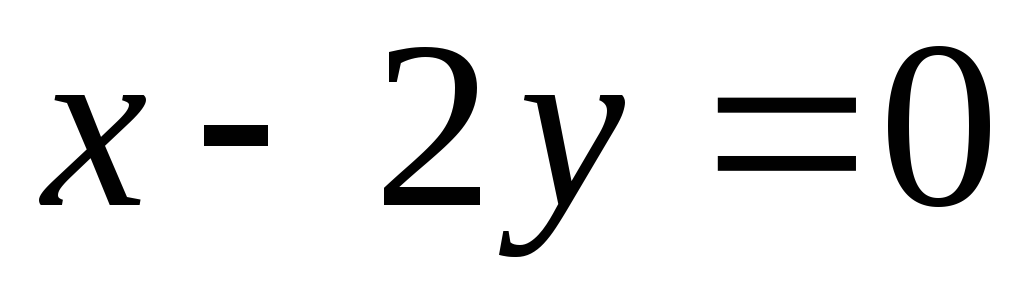 ,
,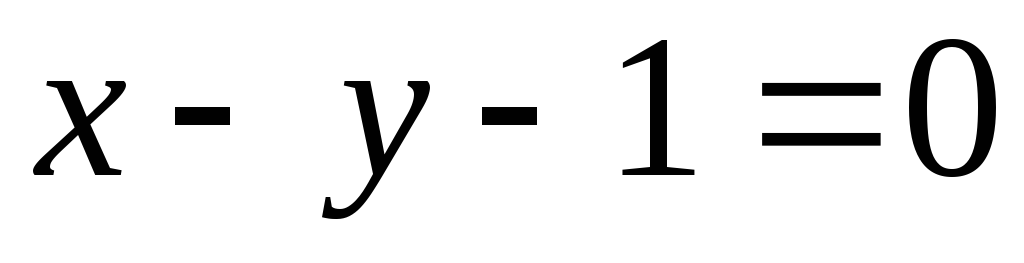 и точка пересечения диагоналей А(3;1). Найдите уравнения двух других сторон.
и точка пересечения диагоналей А(3;1). Найдите уравнения двух других сторон.
Найдите координаты центра и радиус окружности, проходящей через точки А(1; 5), B(4; 0), C(4; 4).
В треугольнике АВС заданы уравнения стороны АВ 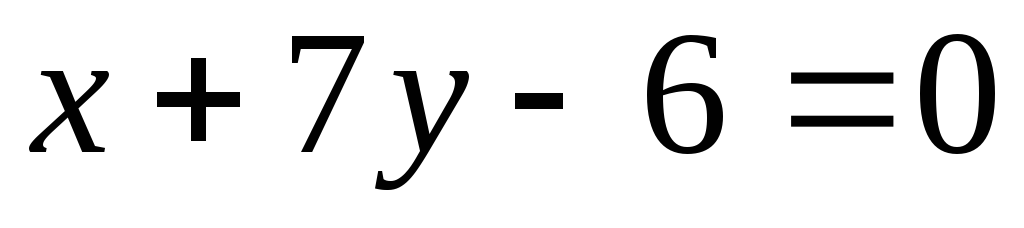 и биссектрисAD
и биссектрисAD  и ВЕ
и ВЕ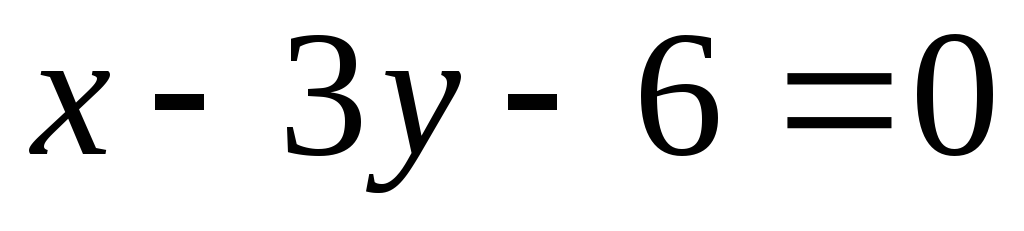 . Найдите координаты вершин.
. Найдите координаты вершин.
Найдите координаты точки А, симметричной точке В(3; 1) относительно прямой  .
.
31 – 40. Постройте кривые второго порядка:
31. а) 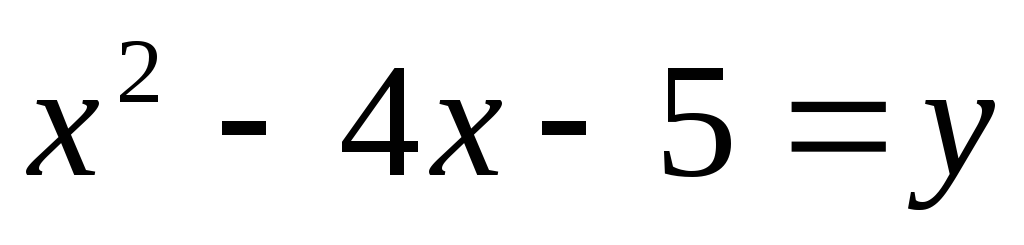 ,
,
32. а) 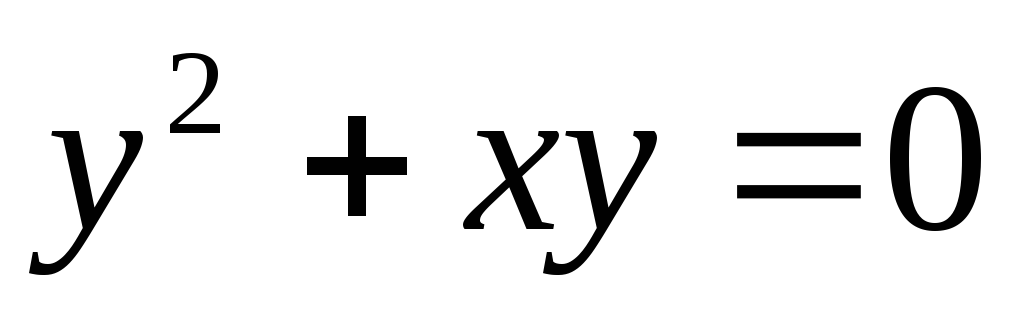 ,
,
33. а) 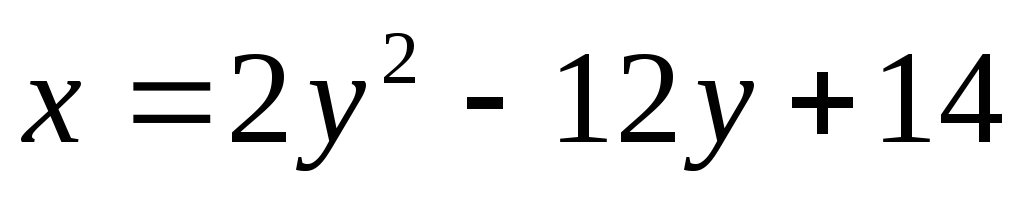 ,
,
34. а) 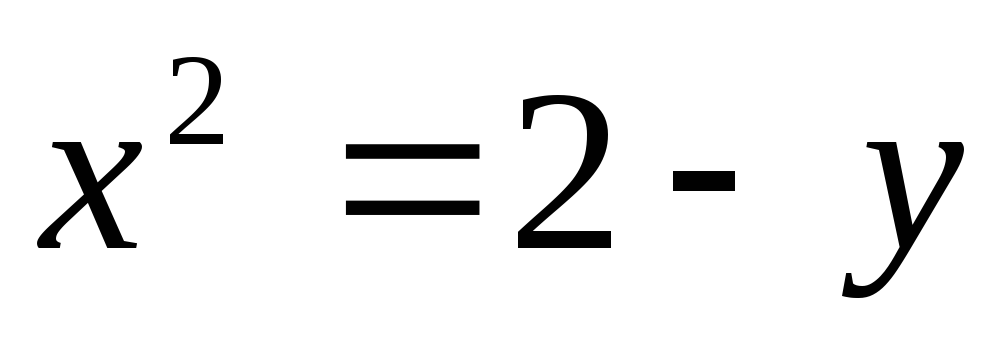 ,
,
35. а) 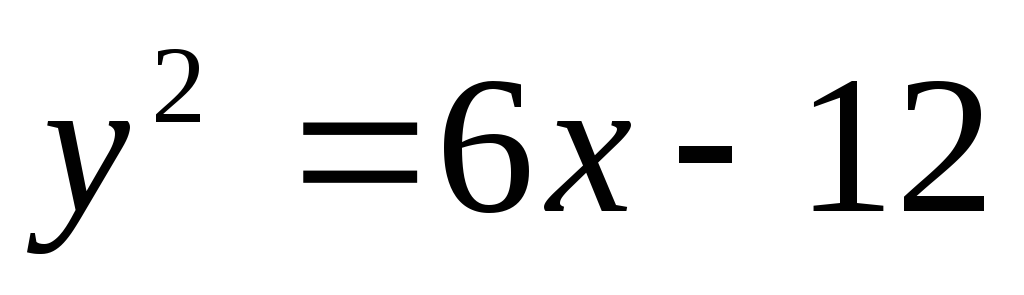 ,
,
36. а) 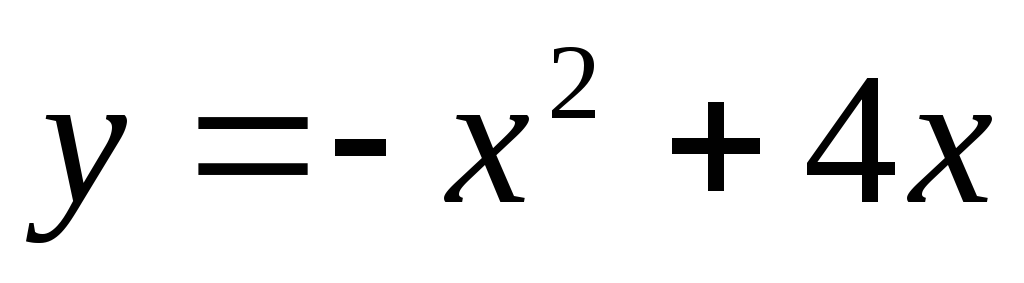 ,
,
б) 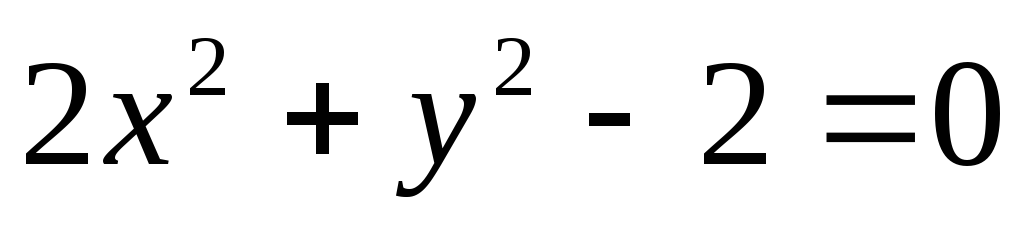 .
.
б)  .
.
б)  .
.
б)  .
.
б) 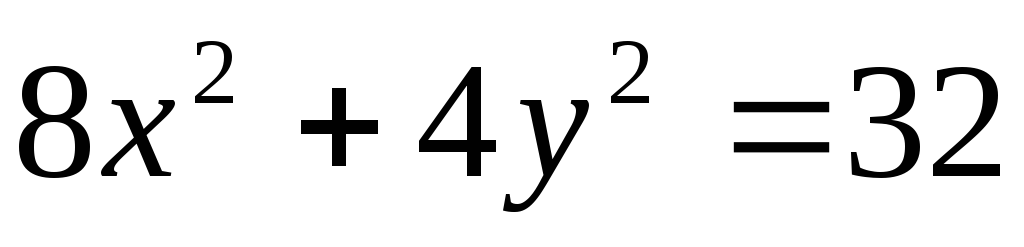 .
.
б) 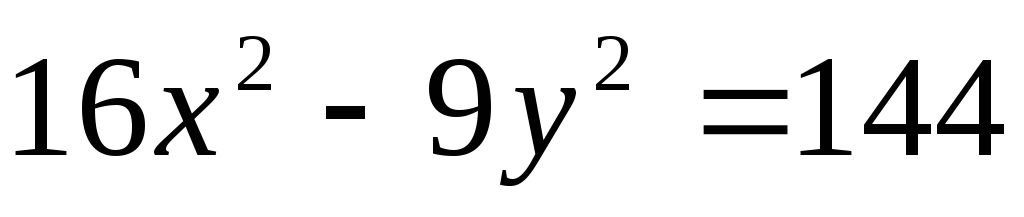 .
.
37. а) 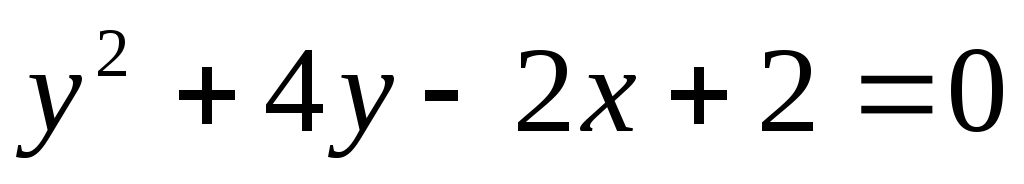 ,
,
38. а) 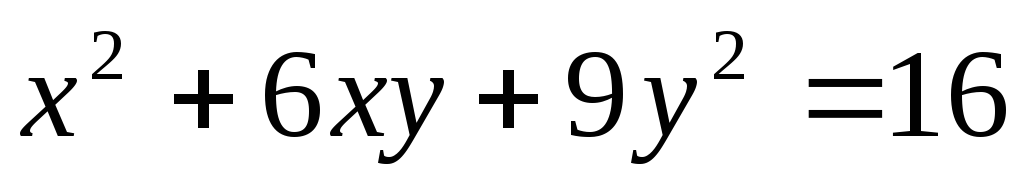 ,
,
39. а) 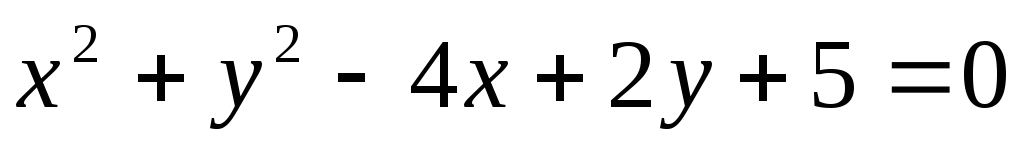 ,
,
40. а) 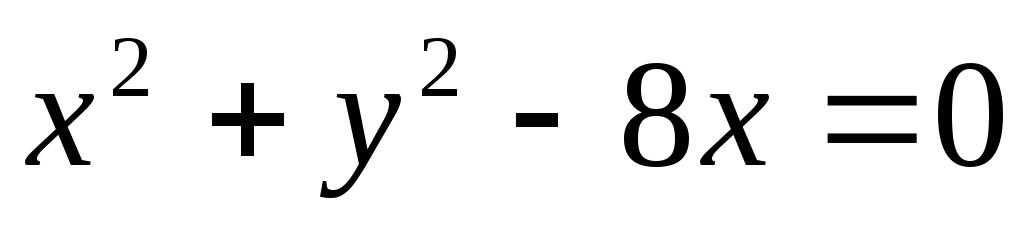 ,
,
б) 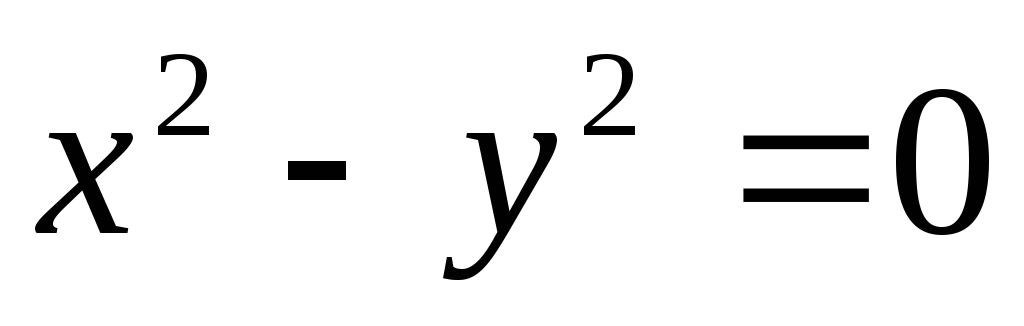 .
.
б) 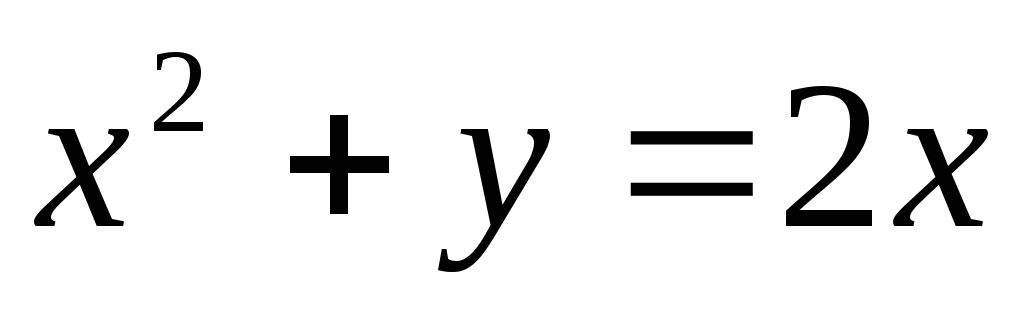 .
.
б) 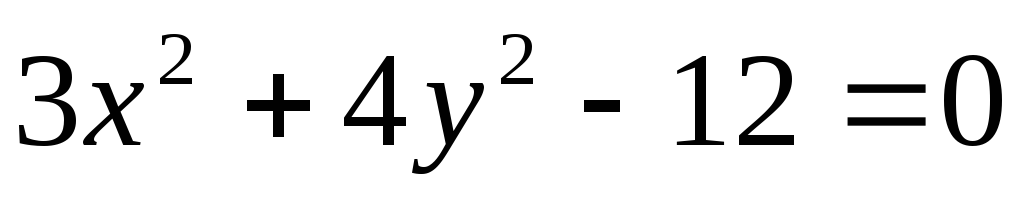 .
.
б) 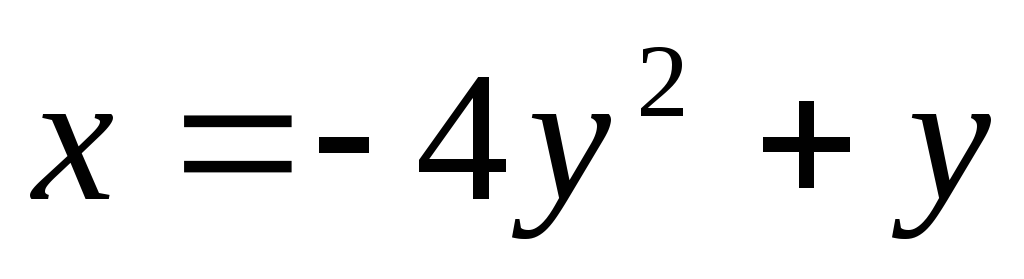 .
.
41 – 50. Постройте линию по уравнению в полярных координатах, задавая угол φ от 0 до 2π с шагом 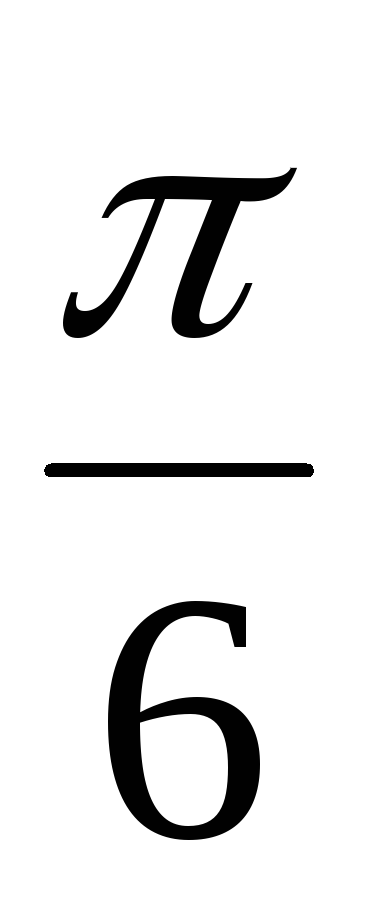 . Запишите уравнение кривой в декартовой прямоугольной системе координат и определите вид кривой.
. Запишите уравнение кривой в декартовой прямоугольной системе координат и определите вид кривой.
41. 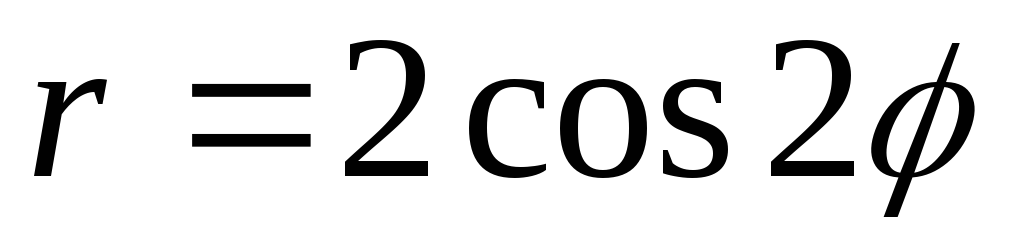 .
.
43. 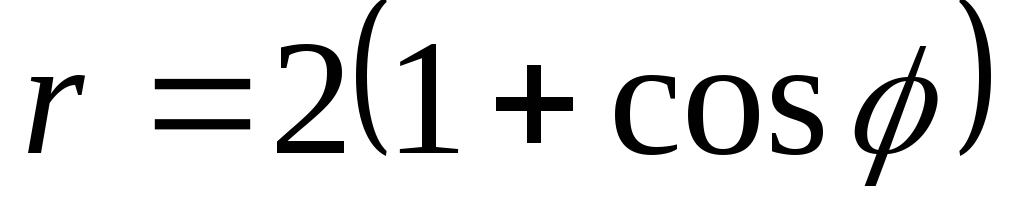 .
.
45.  .
.
47.  .
.
49. 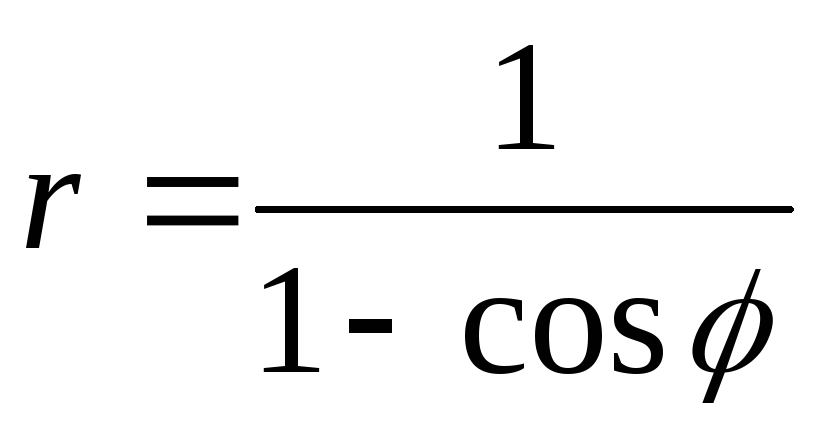 .
.
42. 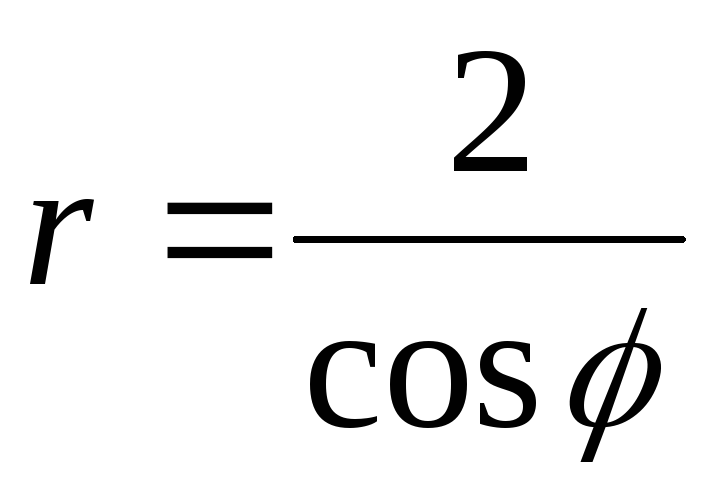 .
.
44. 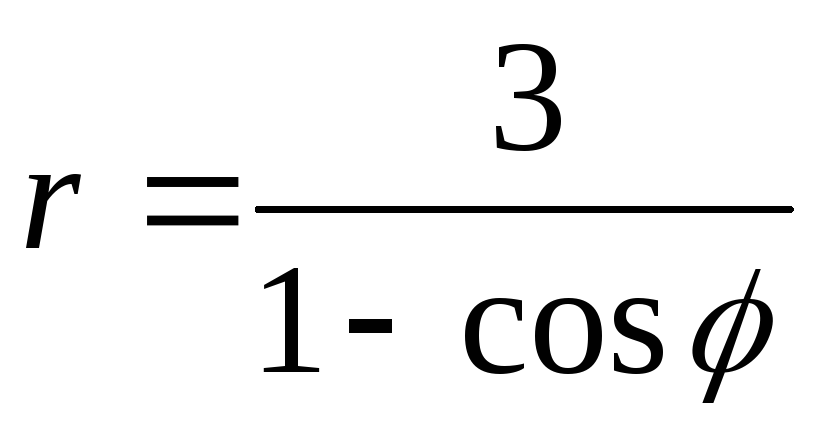 .
.
46. 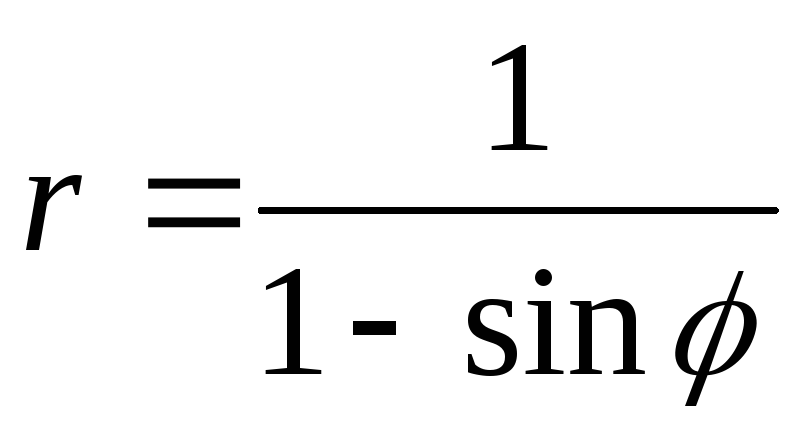 .
.
48. 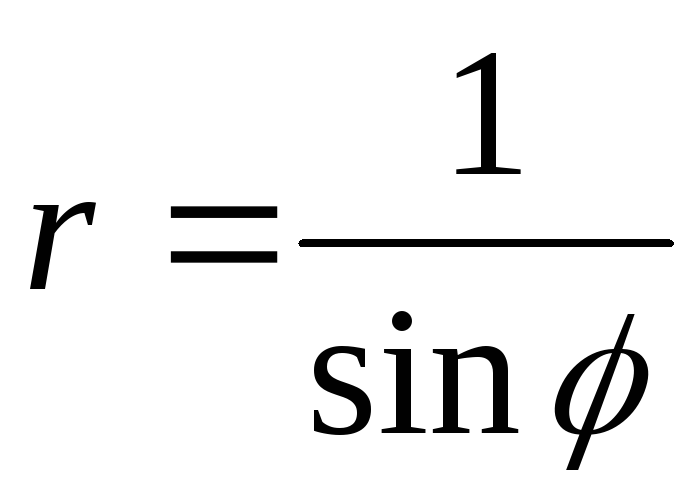 .
.
50. 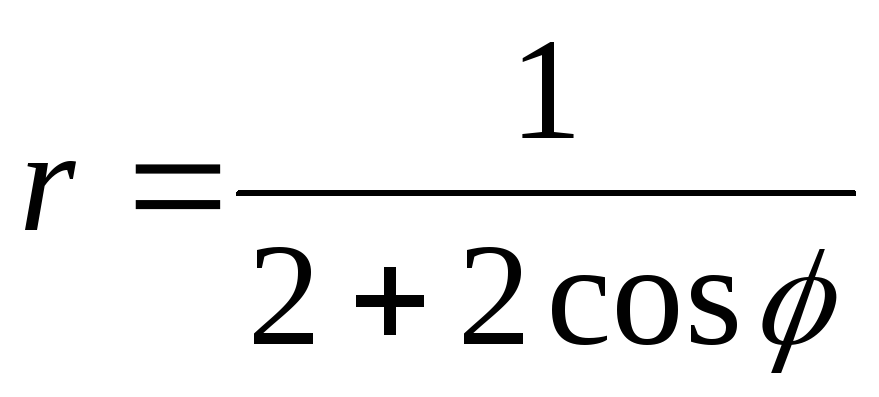 .
.
51 – 60. Задано комплексное число z.
a) Запишите число z в алгебраической, тригонометрической и показательной формах.
б) Найдите все корни уравнения 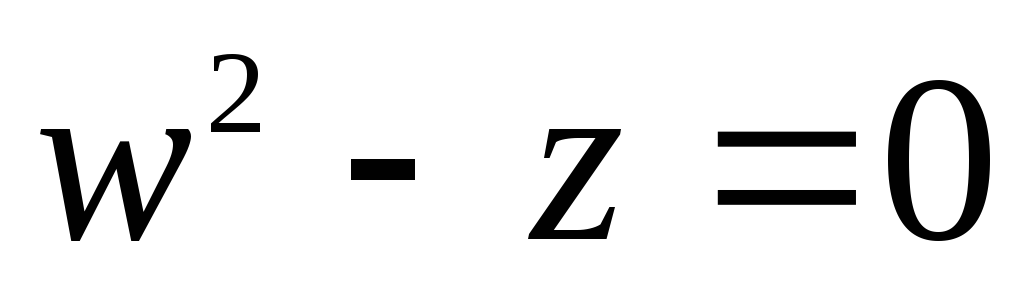 .
.
51. 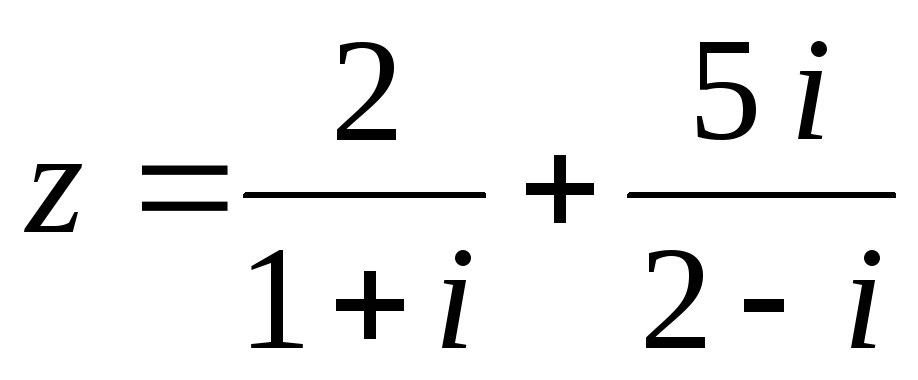 .
.
53.  .
.
55. 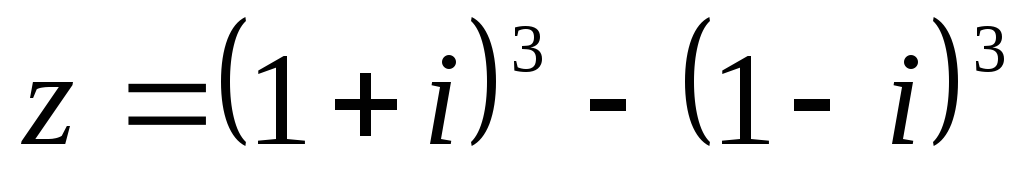 .
.
57. 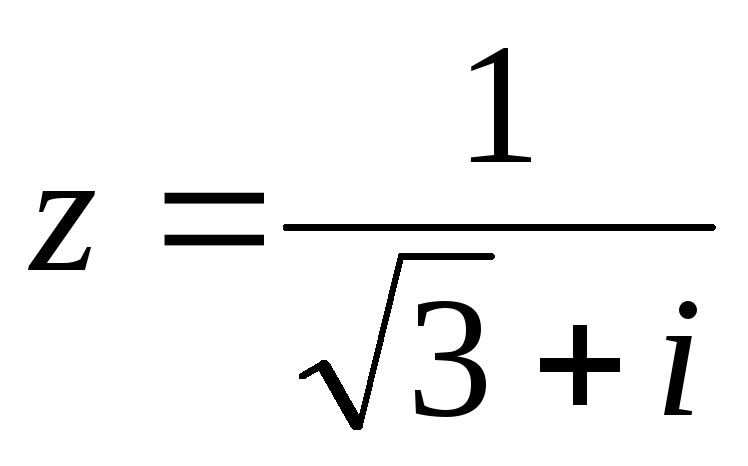 .
.
59. 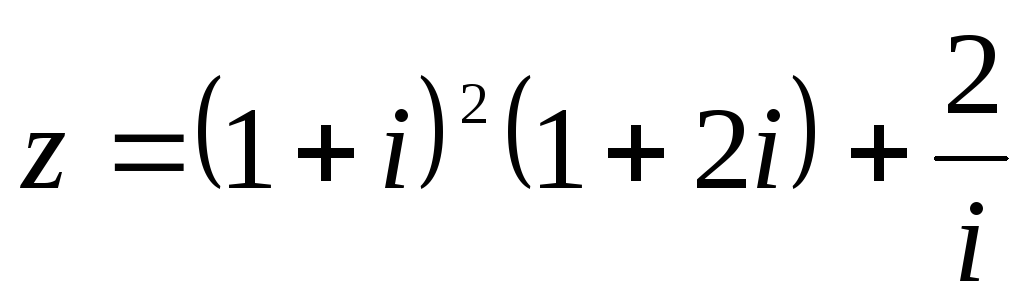 .
.
52. 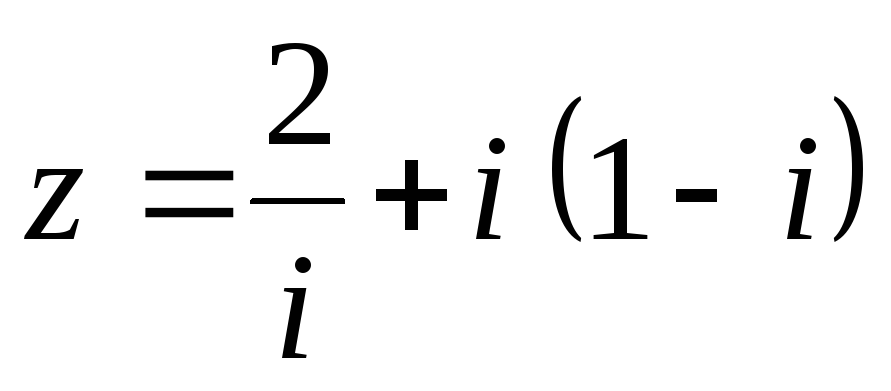 .
.
54.  .
.
56. 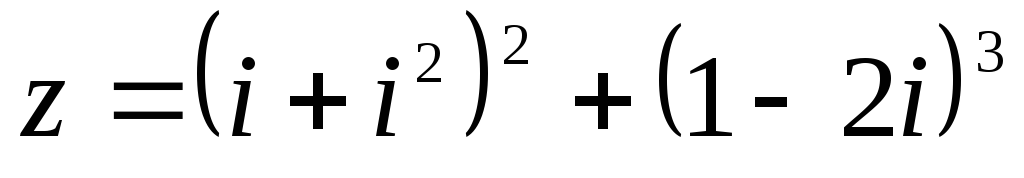 .
.
58. 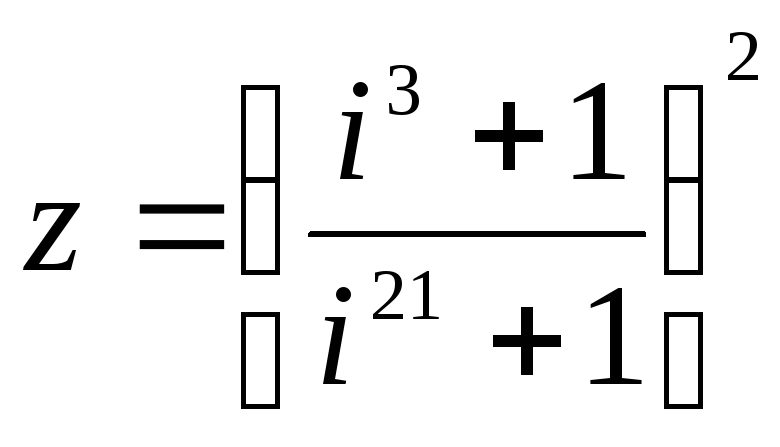 .
.
60. 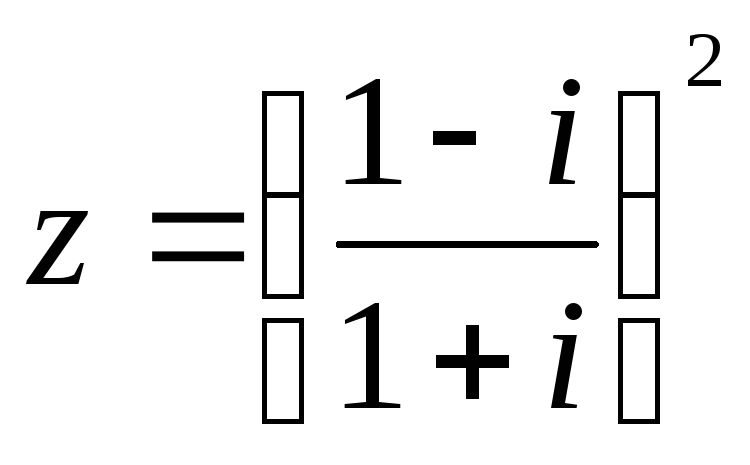 .
.
Контрольная работа № 2
Элементы линейной алгебры.
Введение в математический анализ
61 – 70. Решите систему линейных уравнений:
методом Гаусса,
б) средствами матричного исчисления,
в) по формулам Крамера.
61. 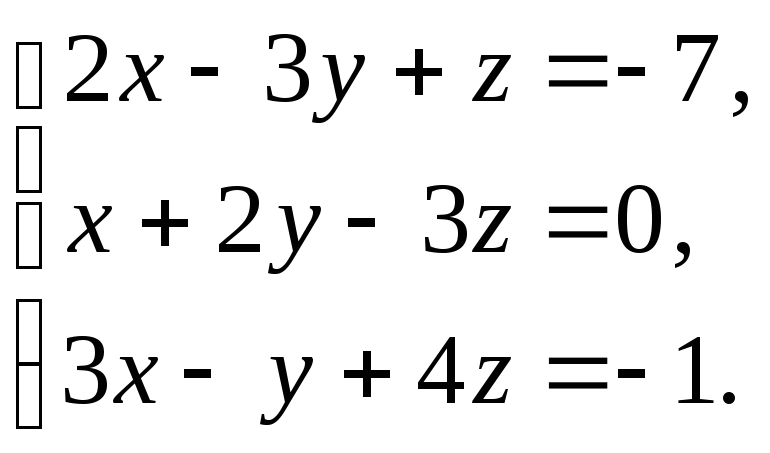 62.
62. 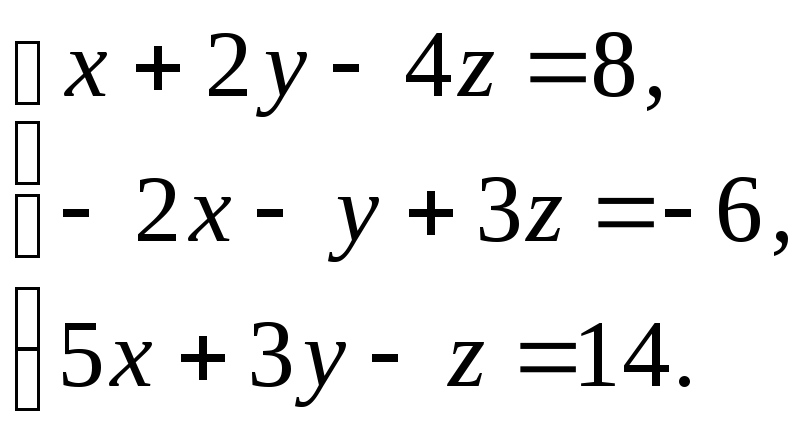
63. 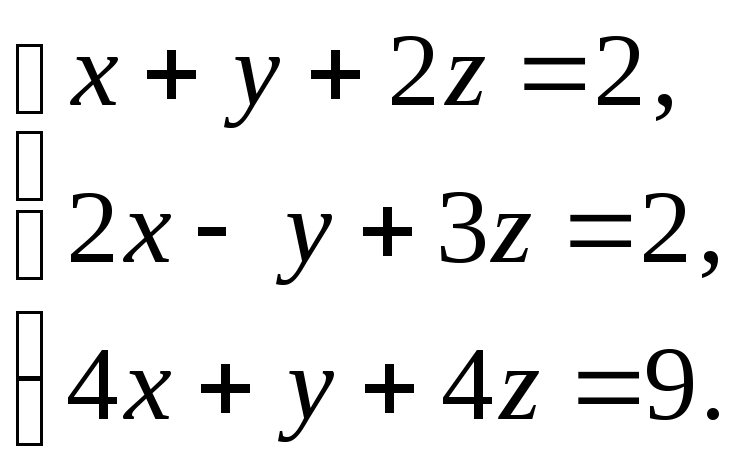 64.
64. 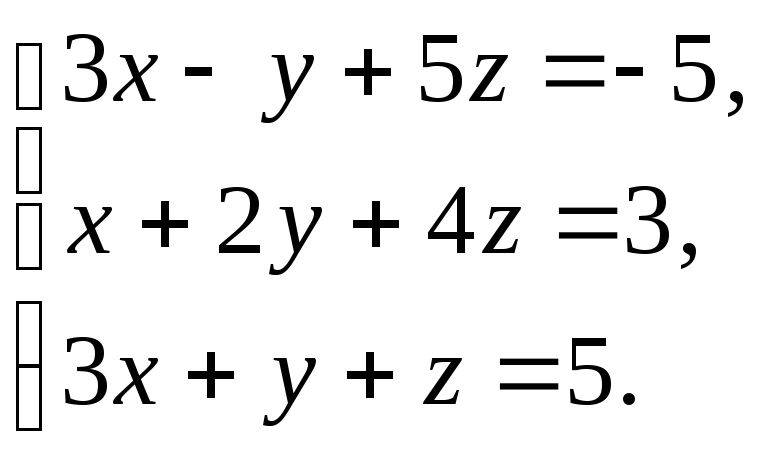
65. 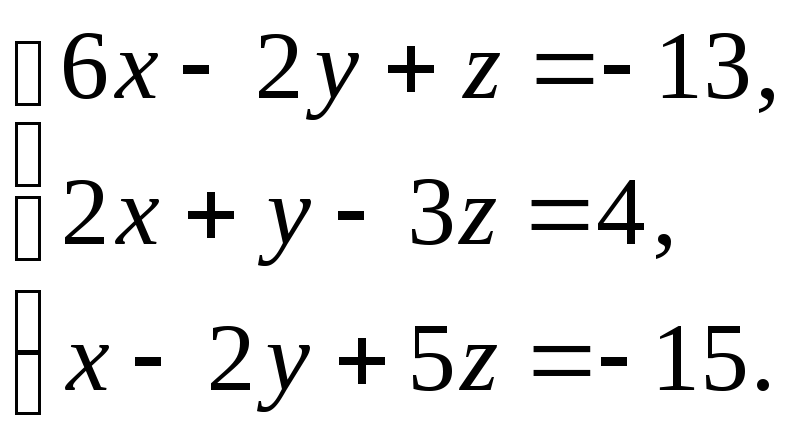 66.
66. 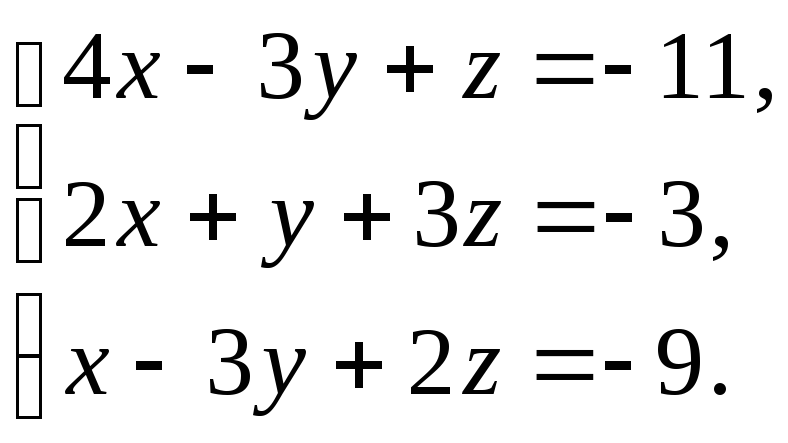
67. 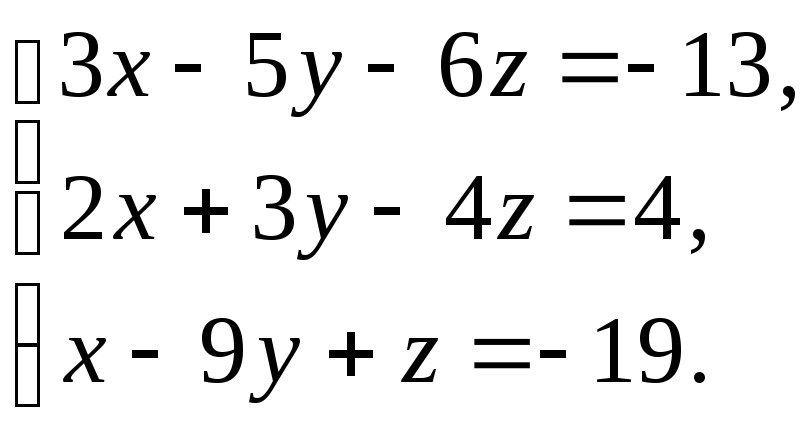 68.
68. 
69.  70.
70. 
71 – 80. Найдите собственные значения и собственные векторы линейного преобразования, заданного матрицей A.
71. А=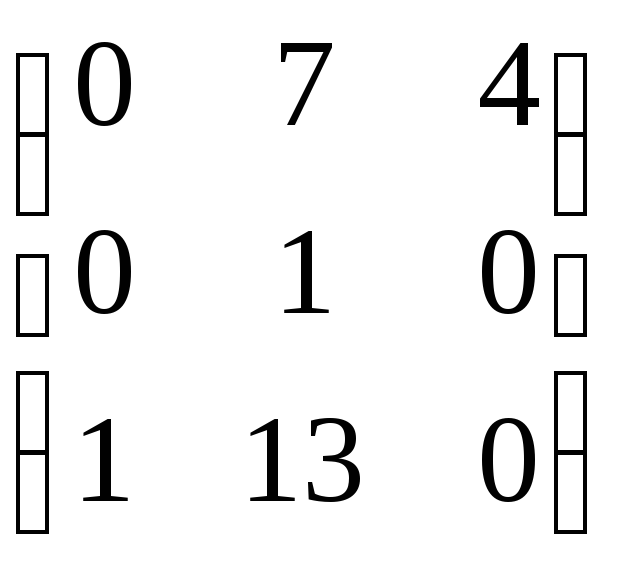 . 72. A=
. 72. A= .
.
73. A=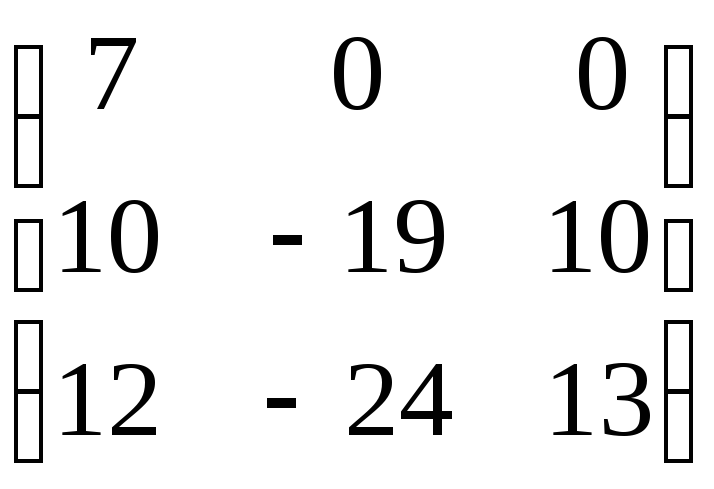 . 74. A=
. 74. A=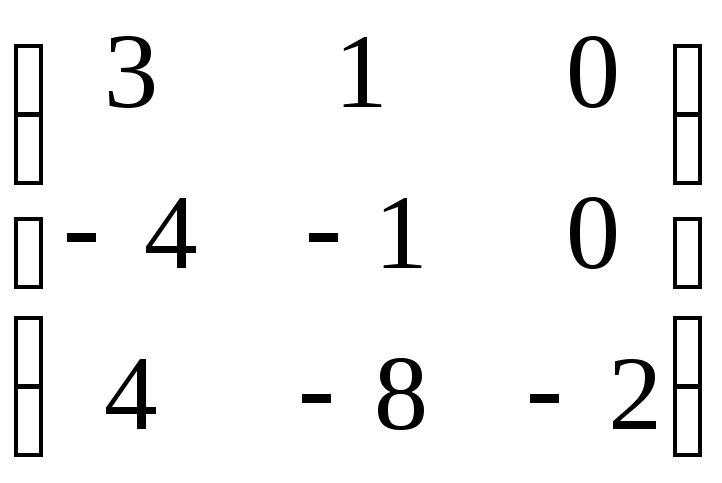 .
.
75. A=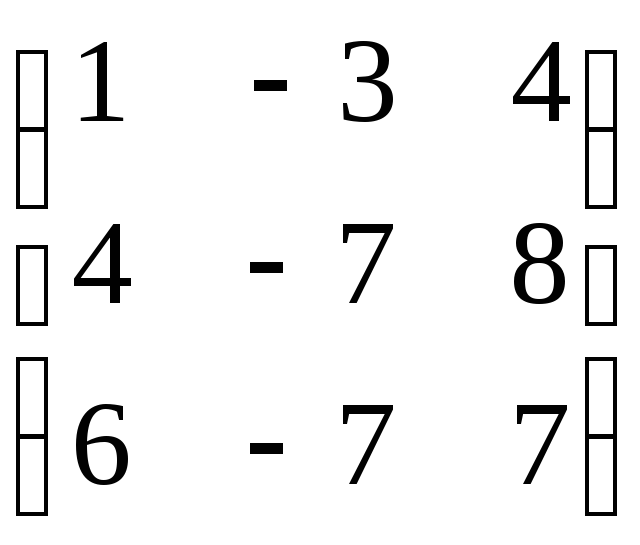 . 76. A=
. 76. A=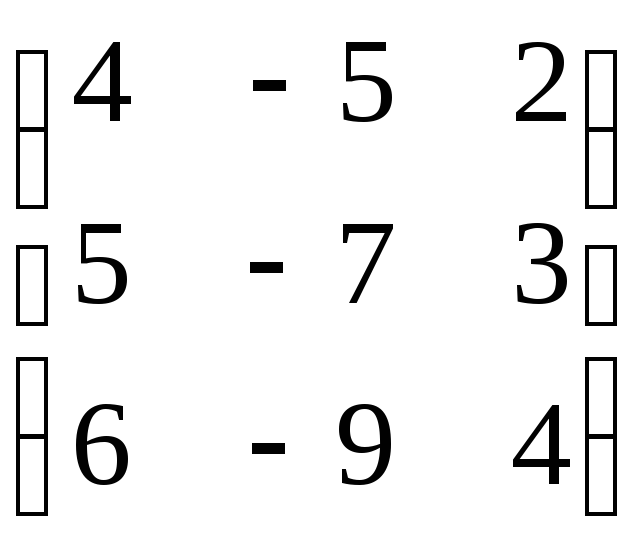 .
.
77. A= . 78. A=
. 78. A= .
.
79. A=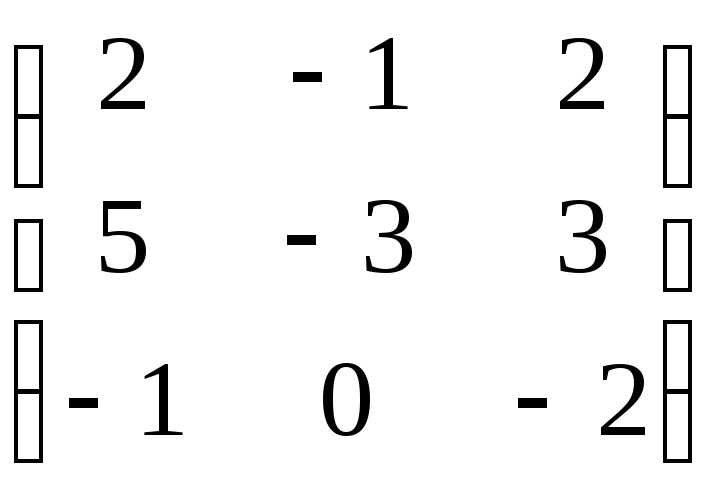 . 80. A=
. 80. A= .
.
81 – 90. Построить графики функций 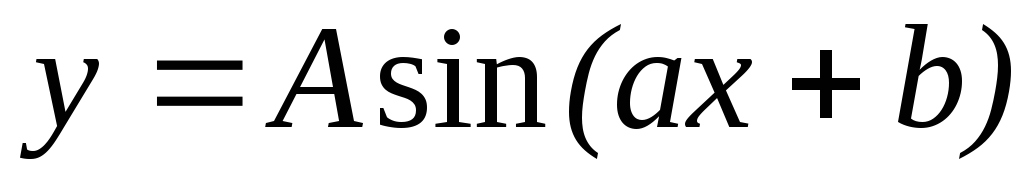 ,
, преобразованием графиков функций
преобразованием графиков функций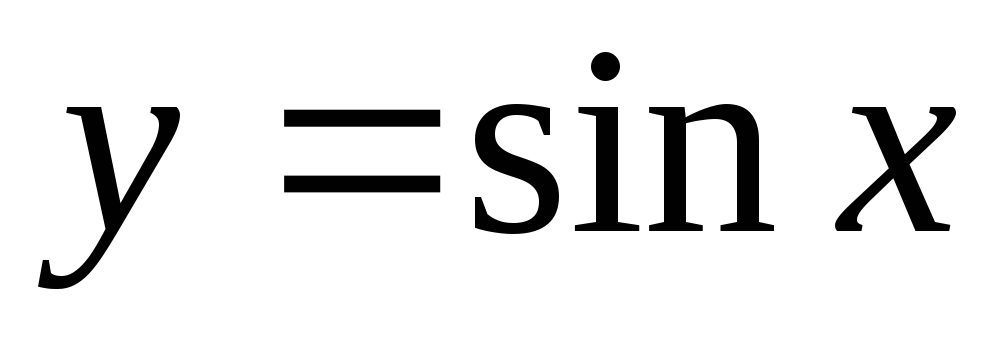 ,
,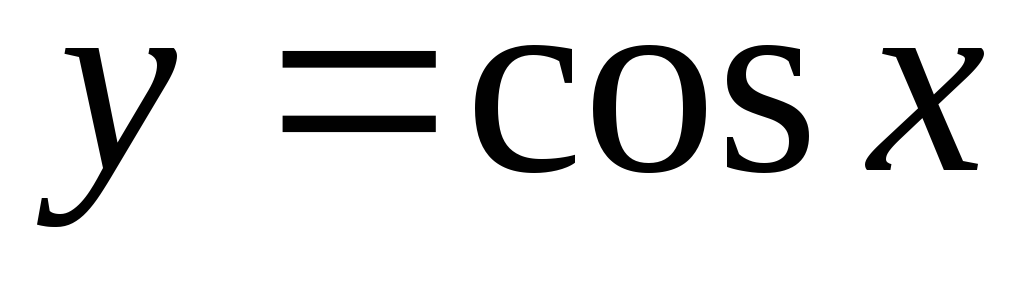 .
.
81. 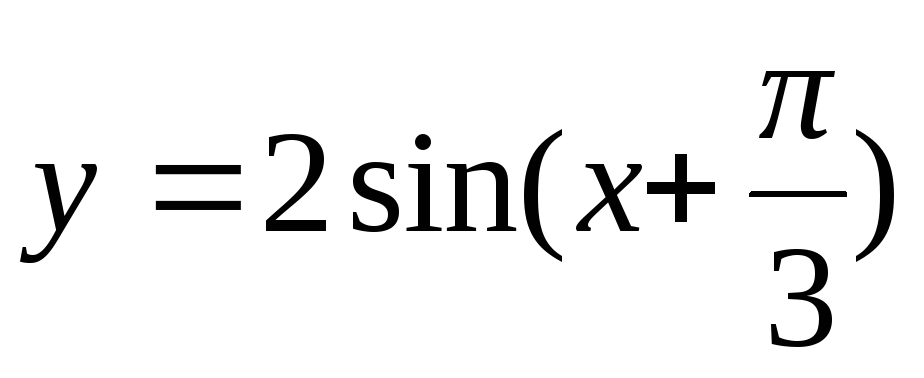 . 82.
. 82. 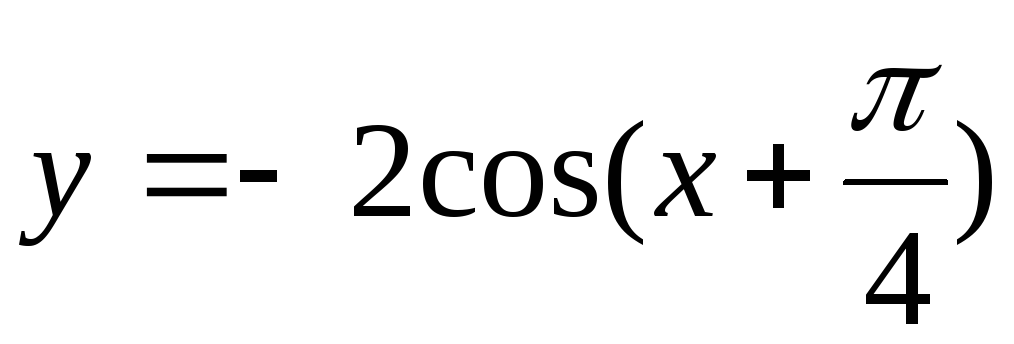 .
.
83. 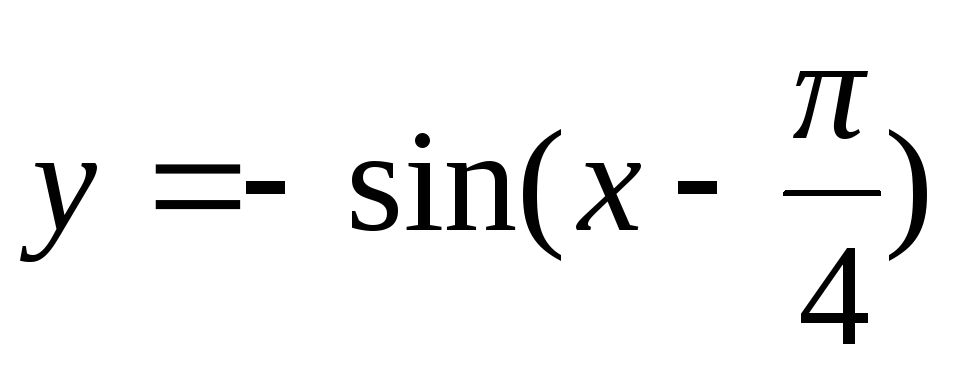 . 84.
. 84. 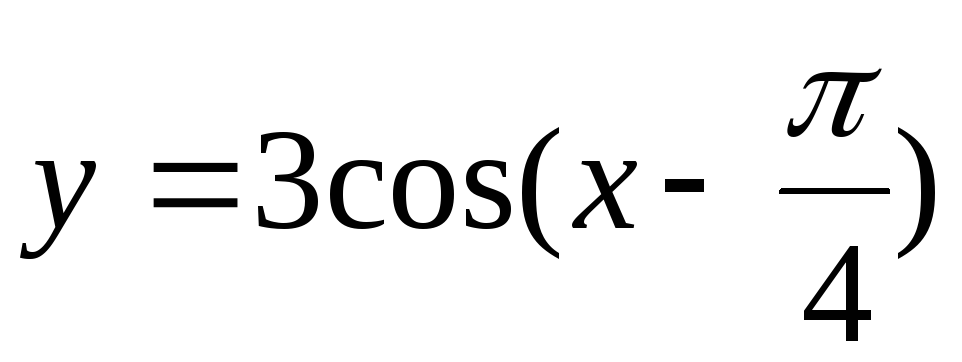 .
.
85. 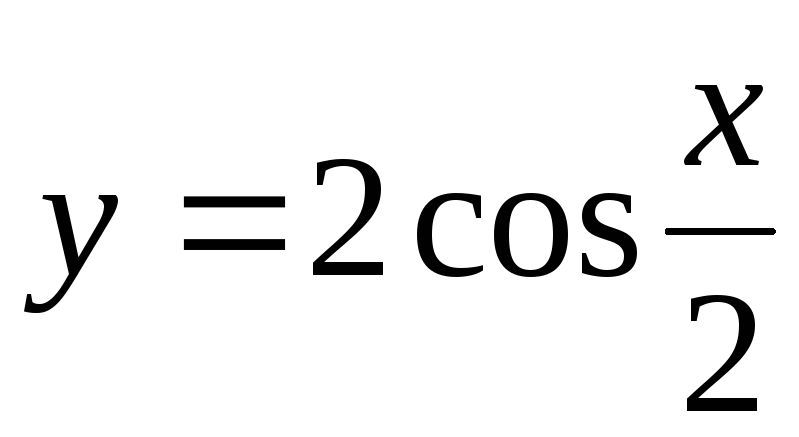 . 86.
. 86. 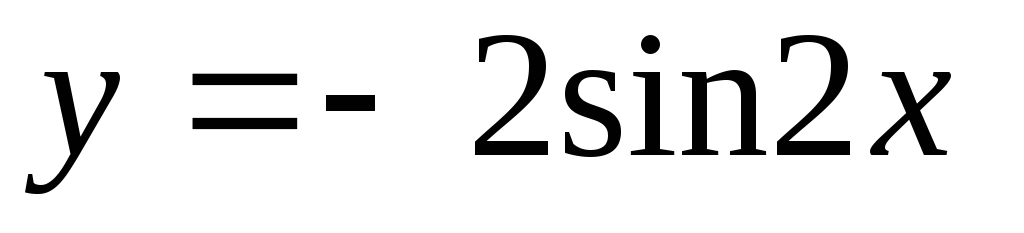 .
.
87. 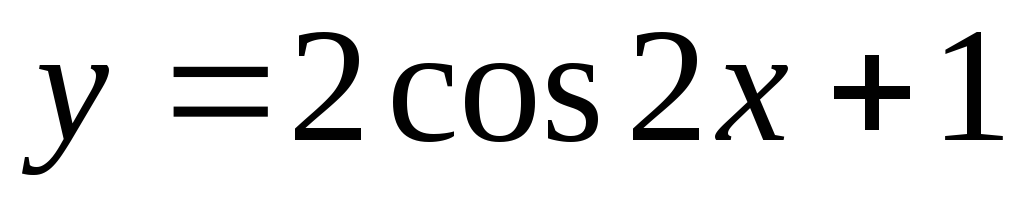 . 88.
. 88. 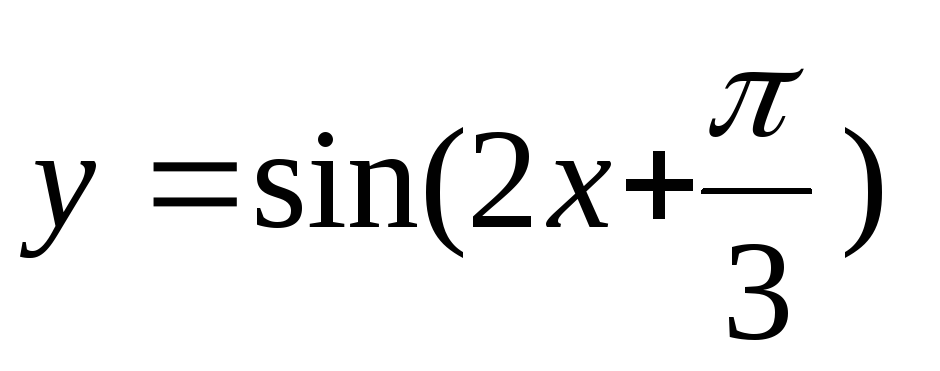 .
.
89. 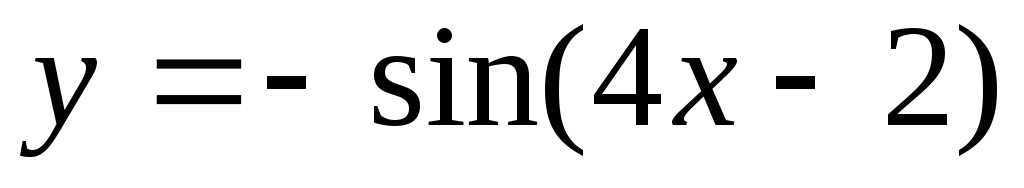 . 90.
. 90. 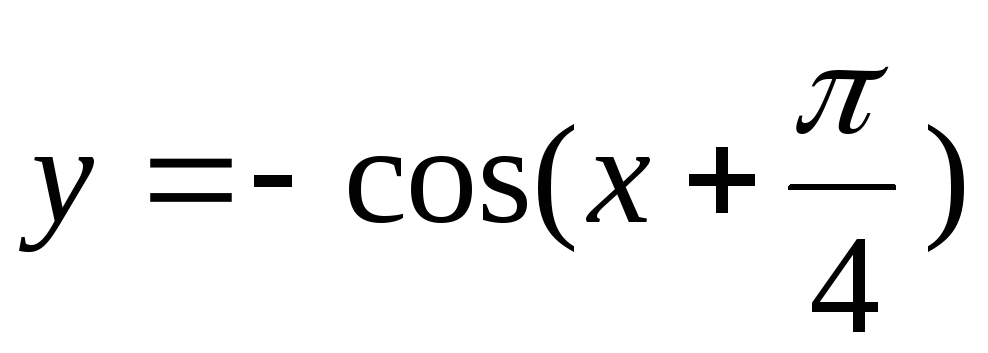 .
.
91 – 100. Найдите пределы функций, не пользуясь правилом Лопиталя.
91. a) 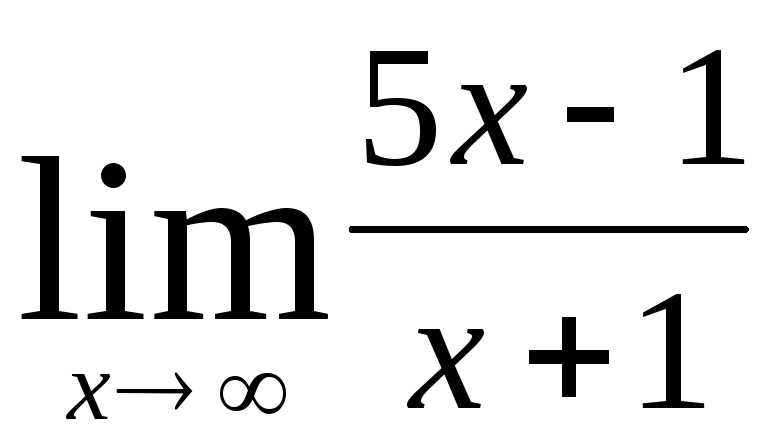 ,
,  ,
,
в) 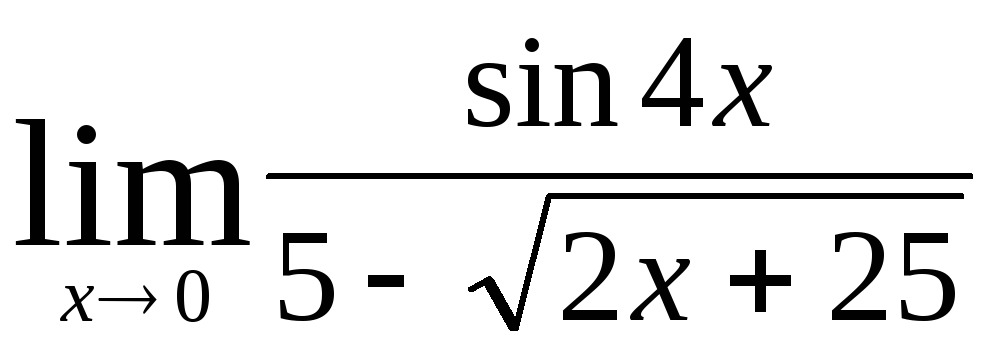 ,
, 
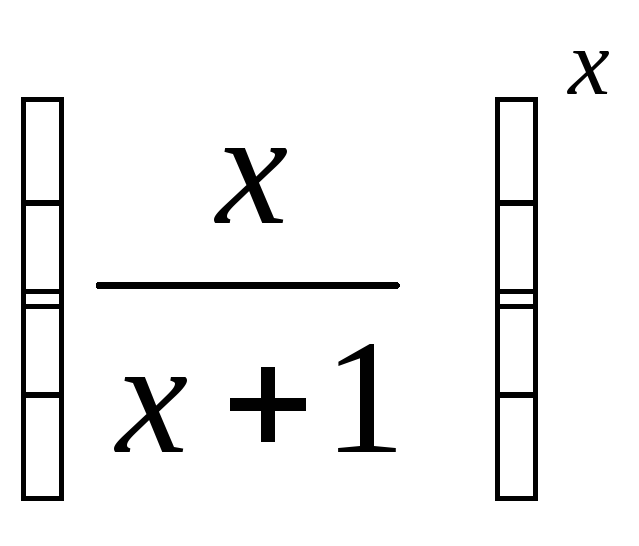 .
.
92. a)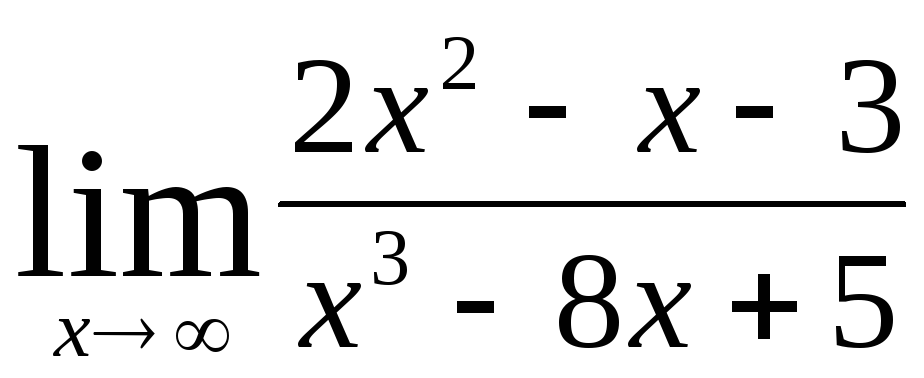 ,
, 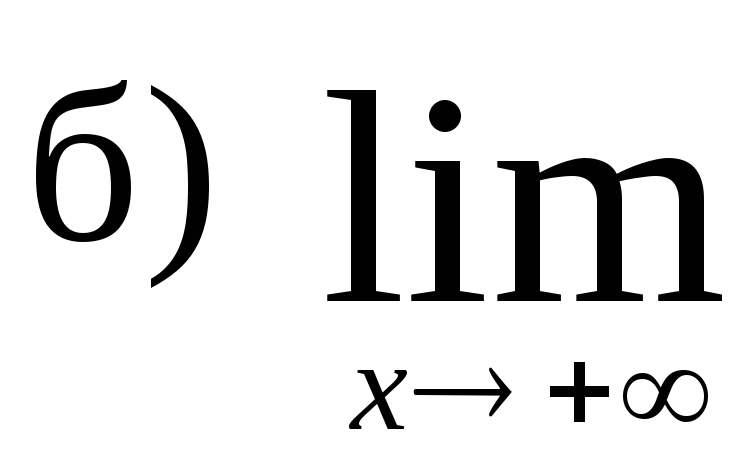
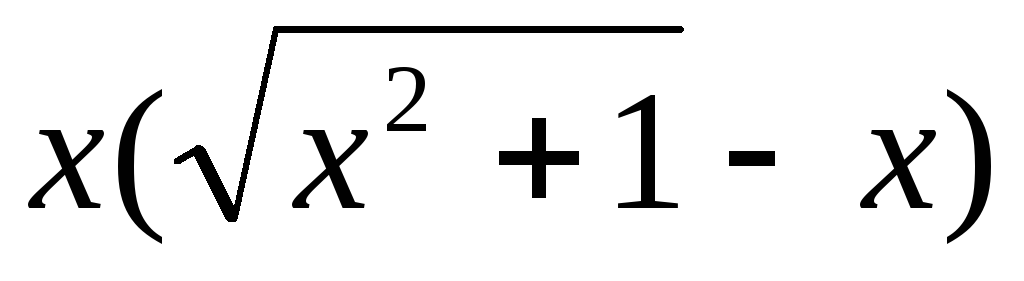 ,
,

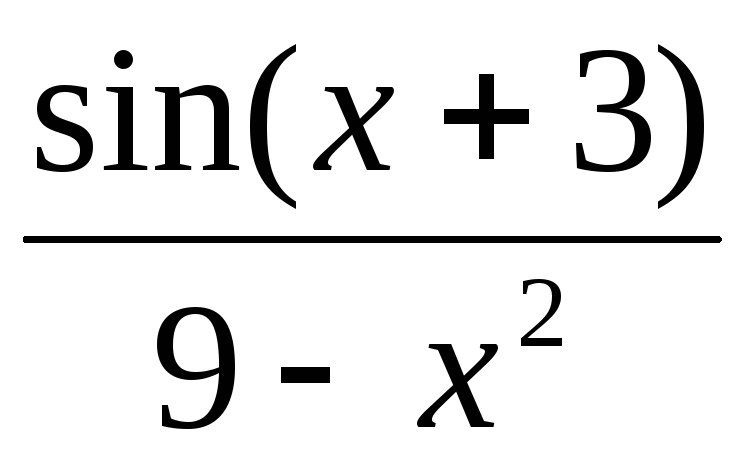 ,
, 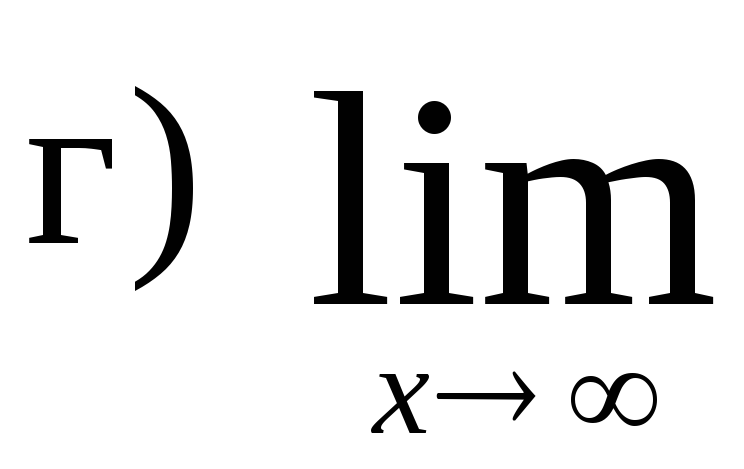
 .
.
93. 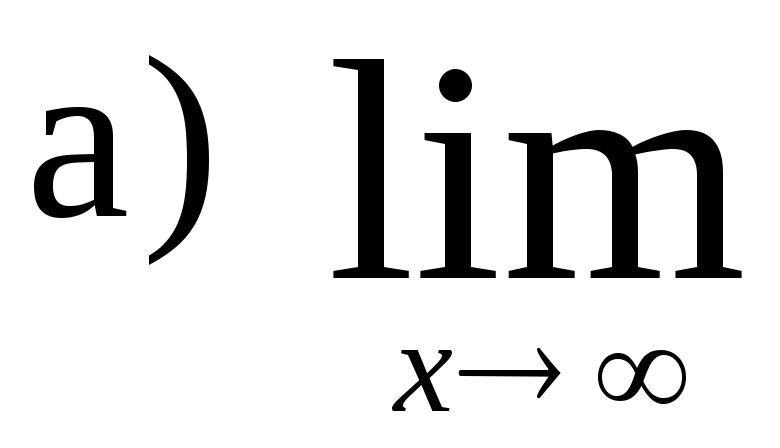
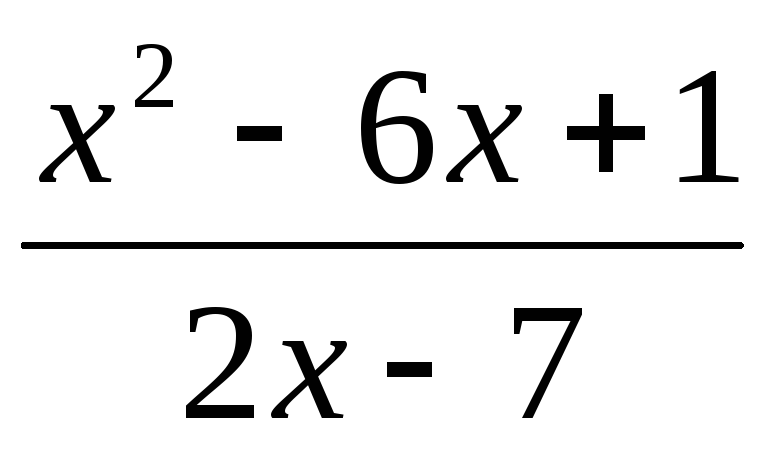 ,
, 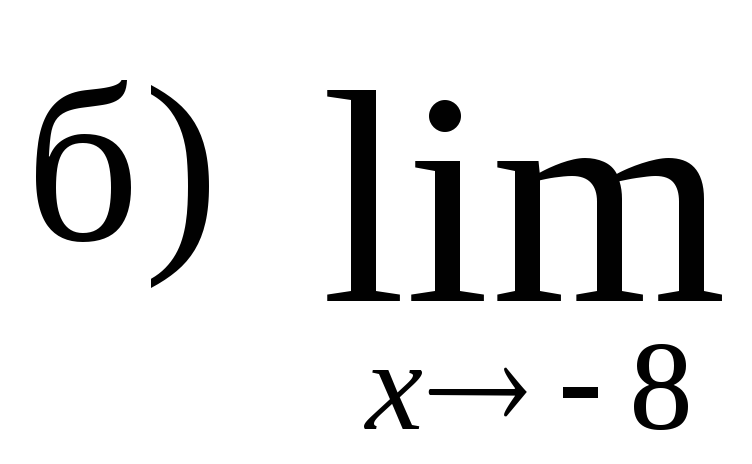
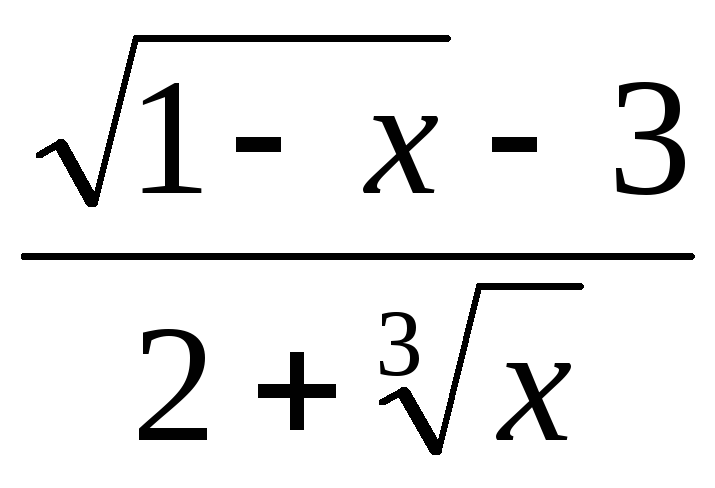 ,
,
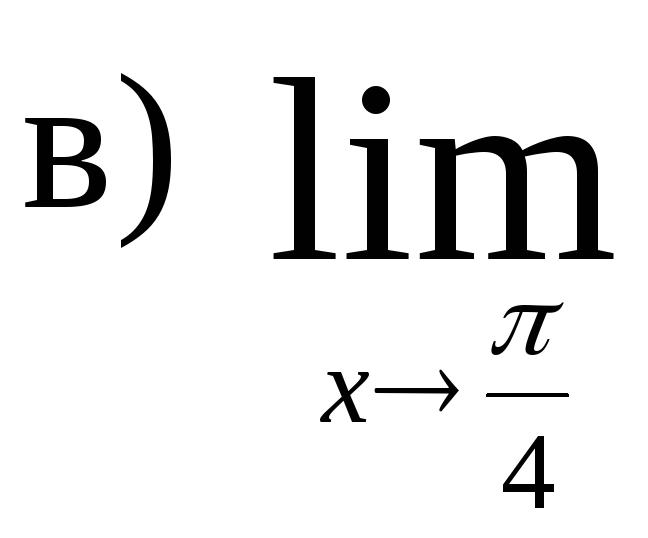
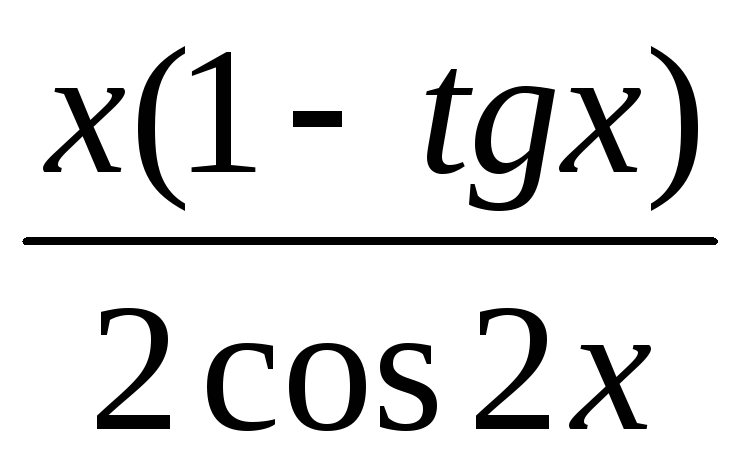 ,
, 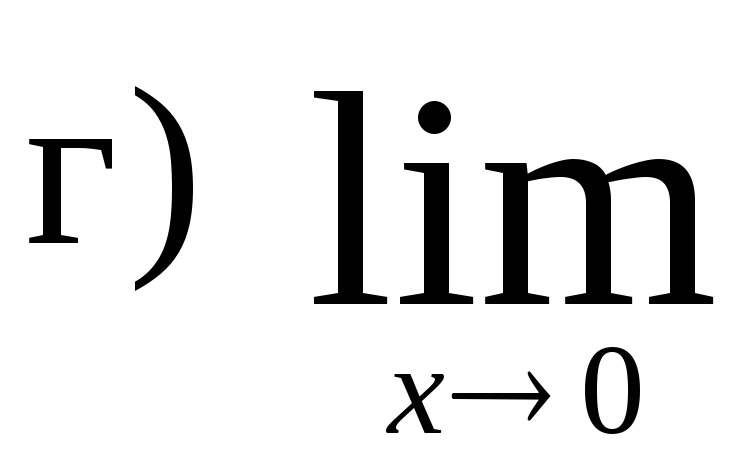
 .
.
94. 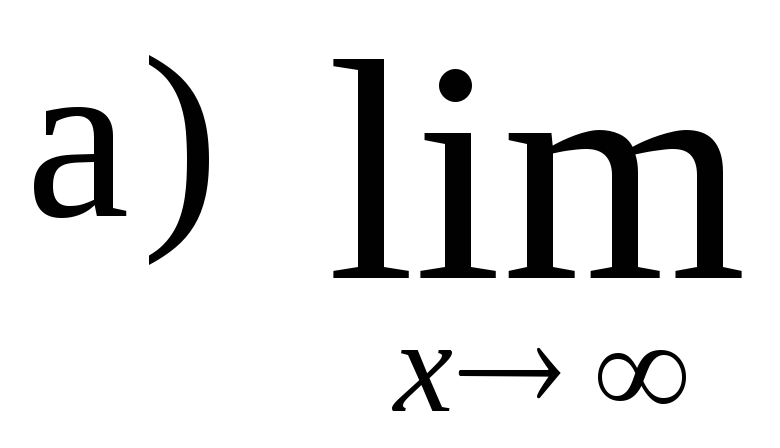
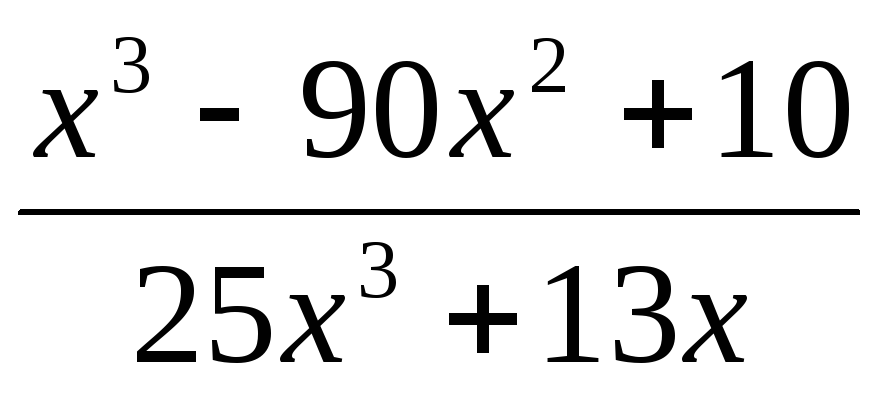 ,
, 
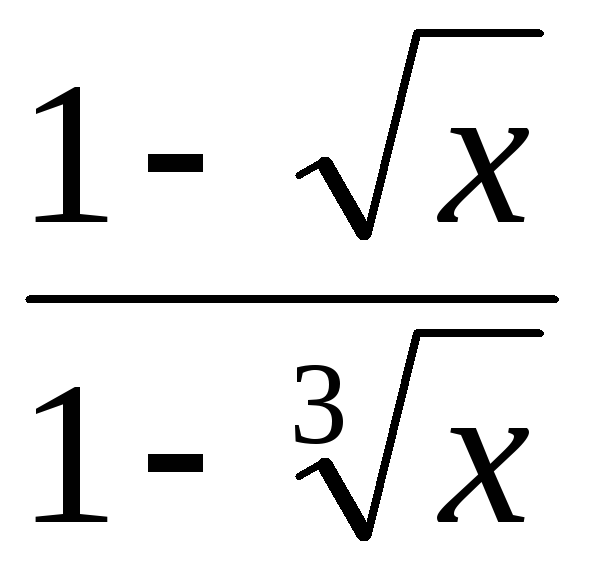 ,
,
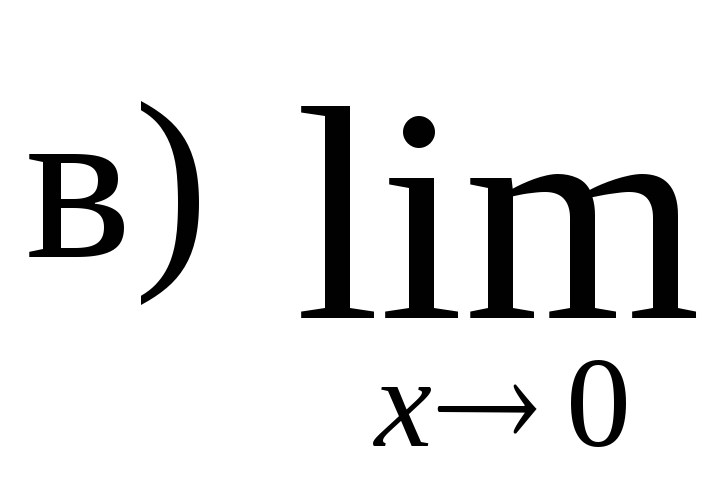
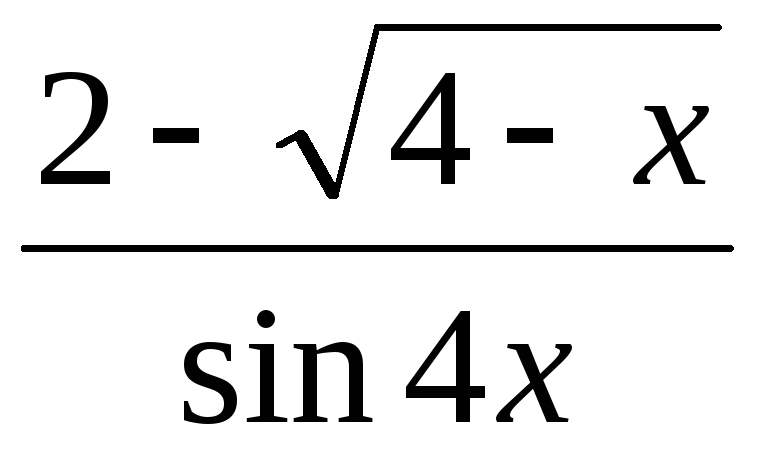 ,
, 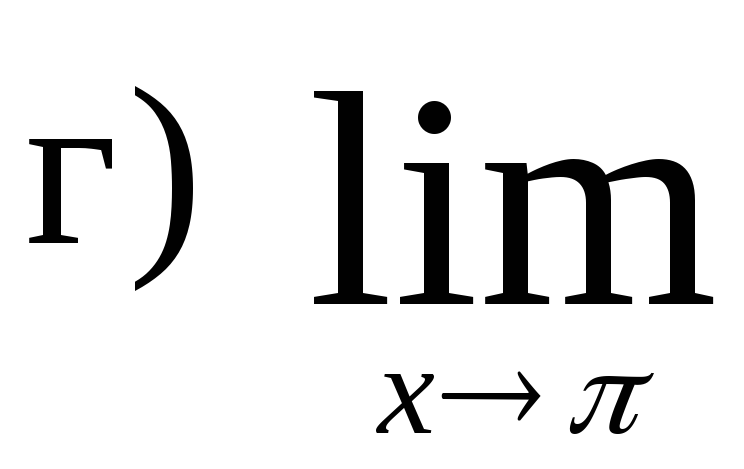
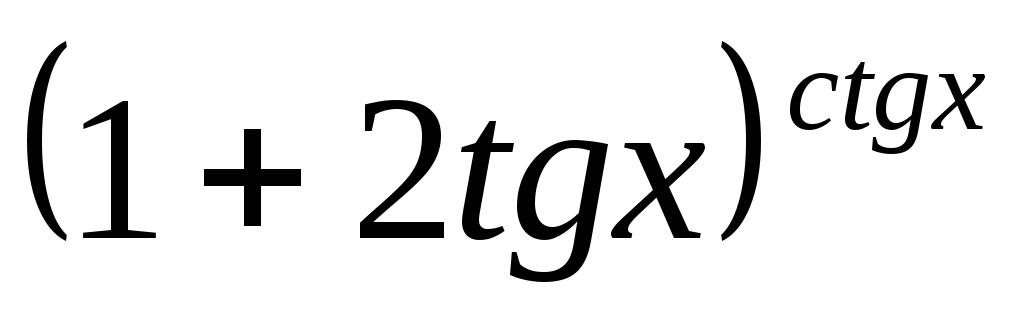 .
.
95. 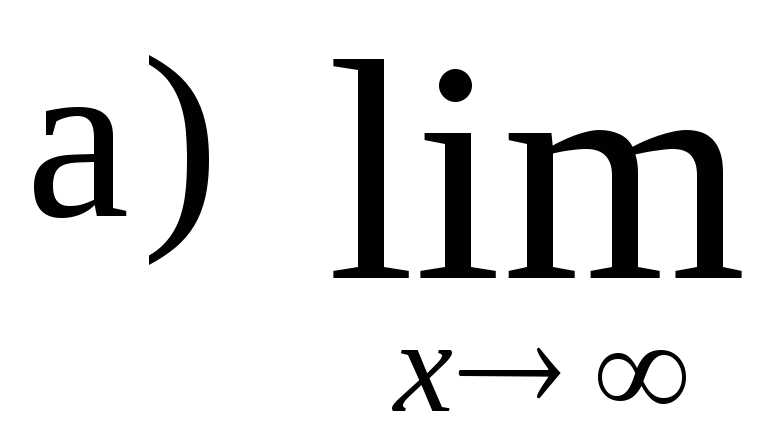
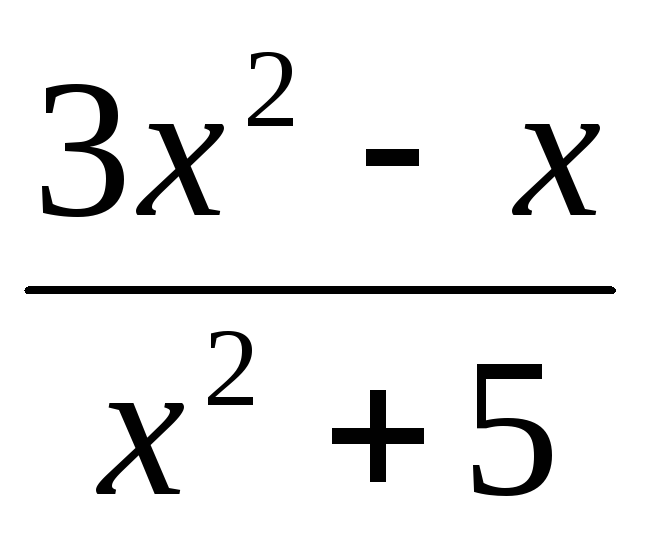 ,
, 
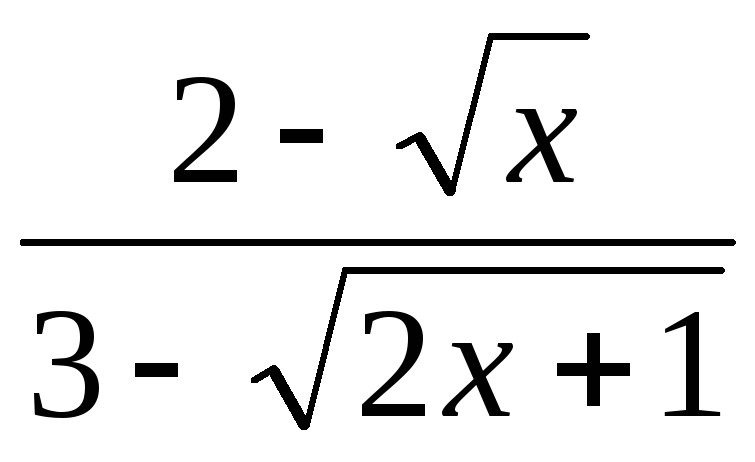 ,
,
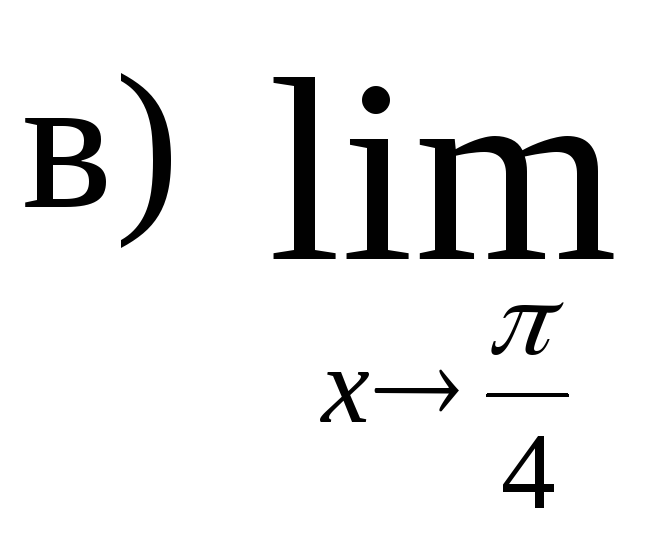
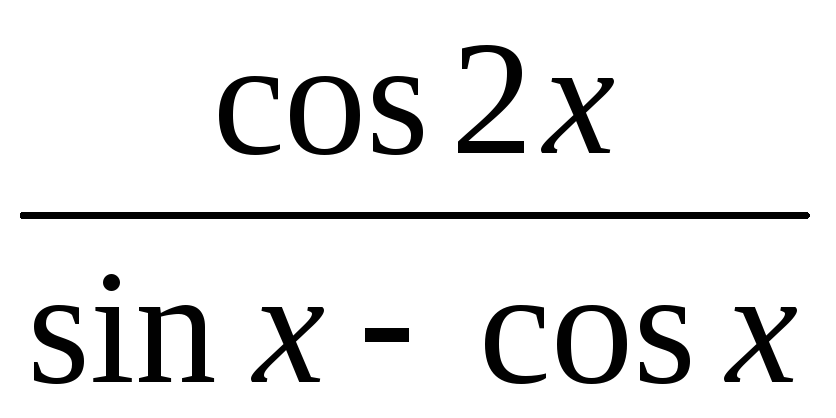 ,
, 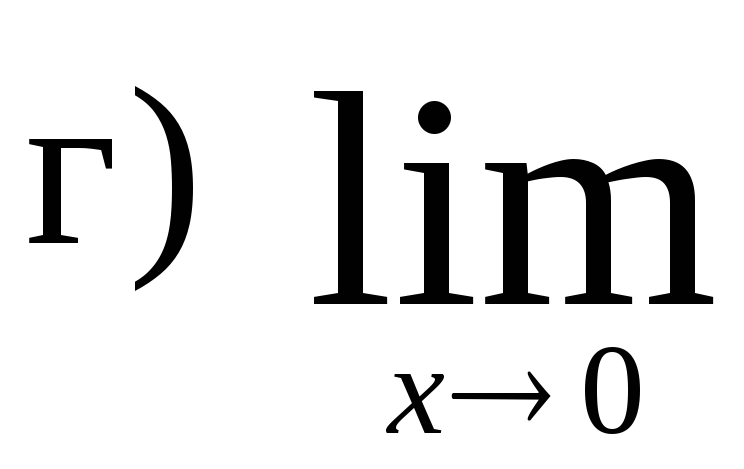
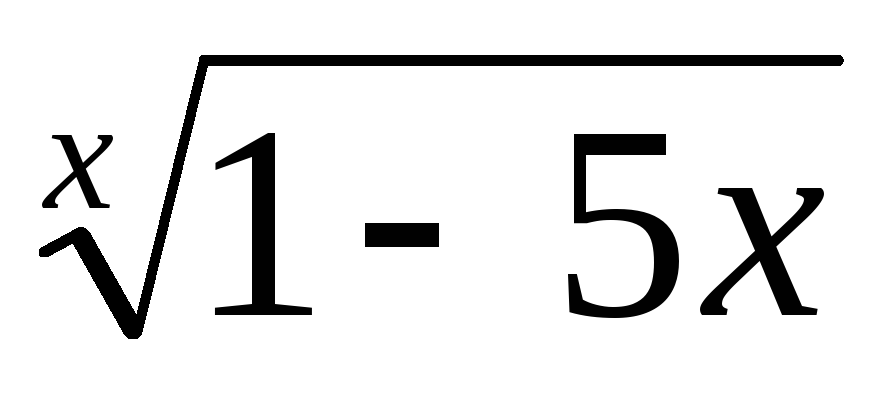 .
.
96. 
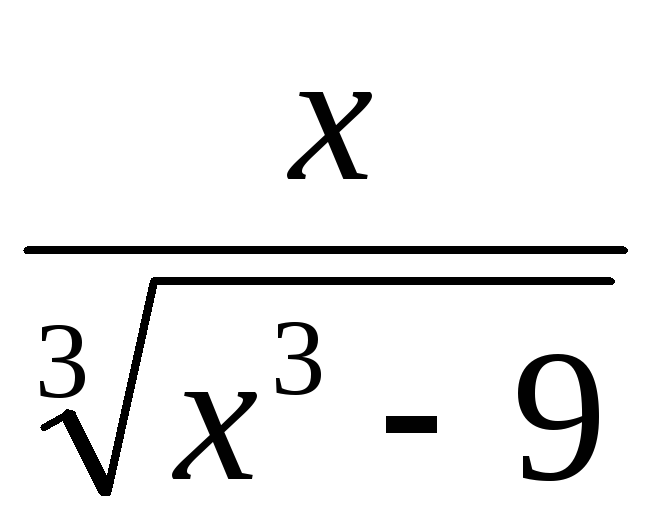 ,
, 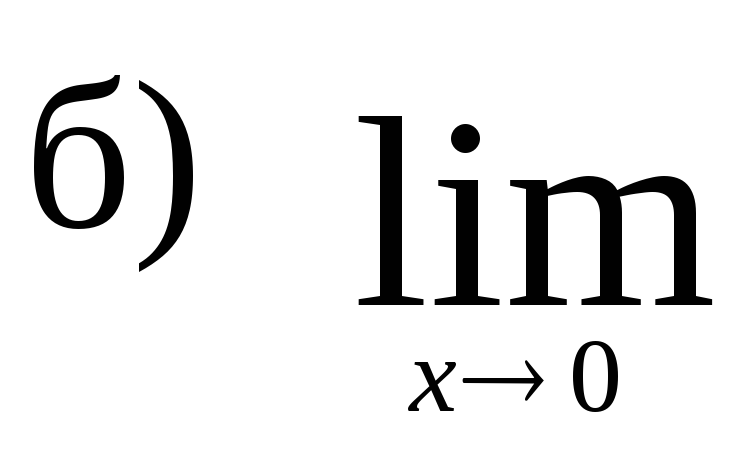
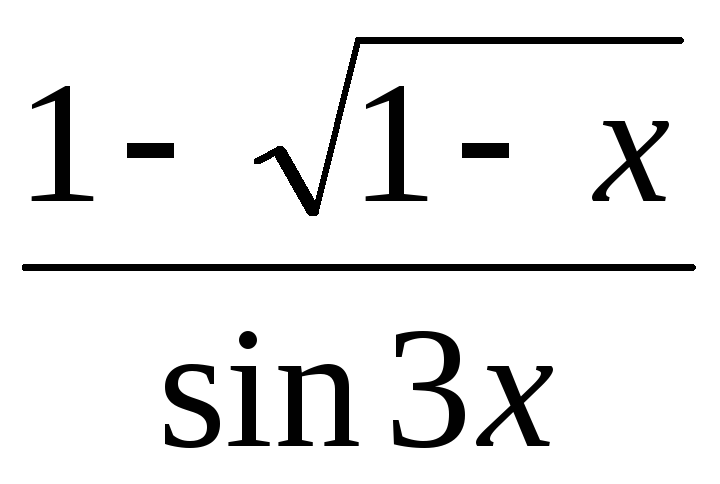 ,
,
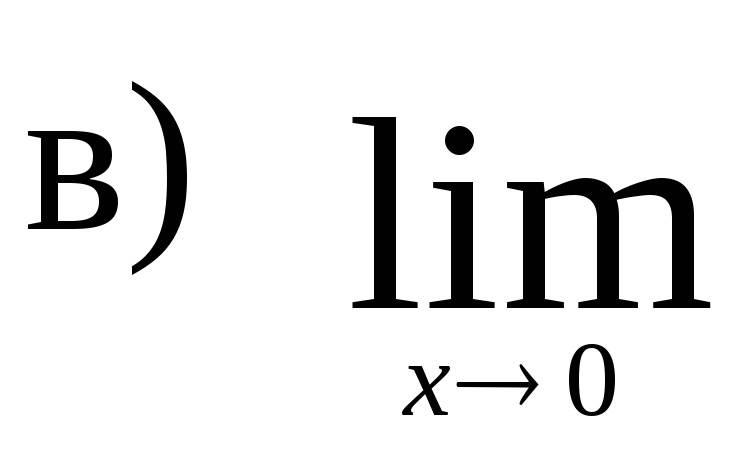
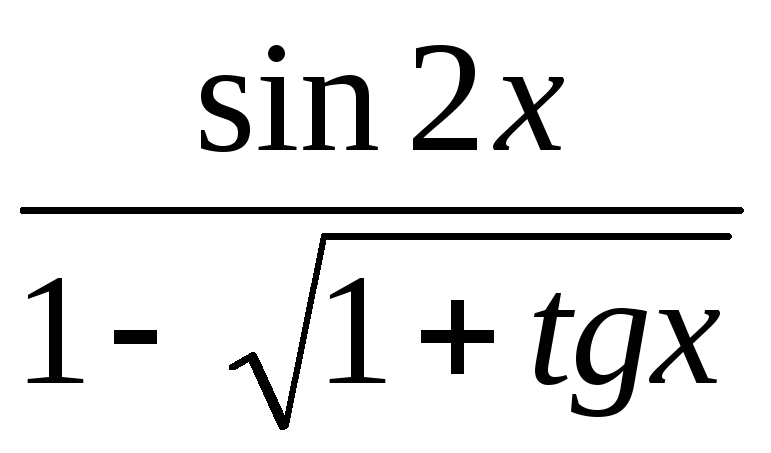 ,
, 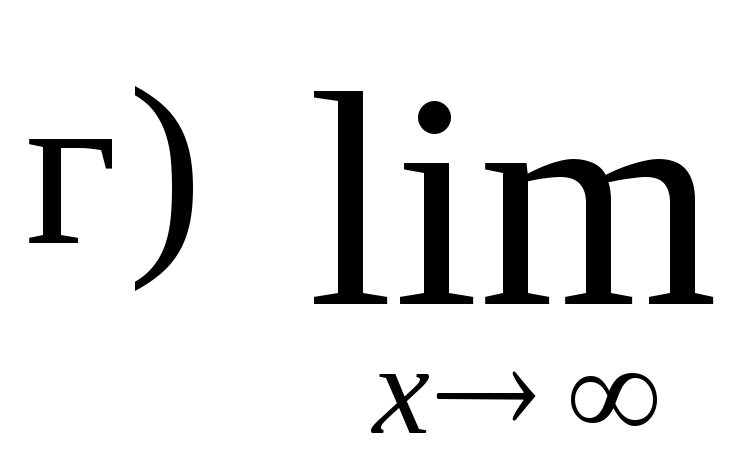
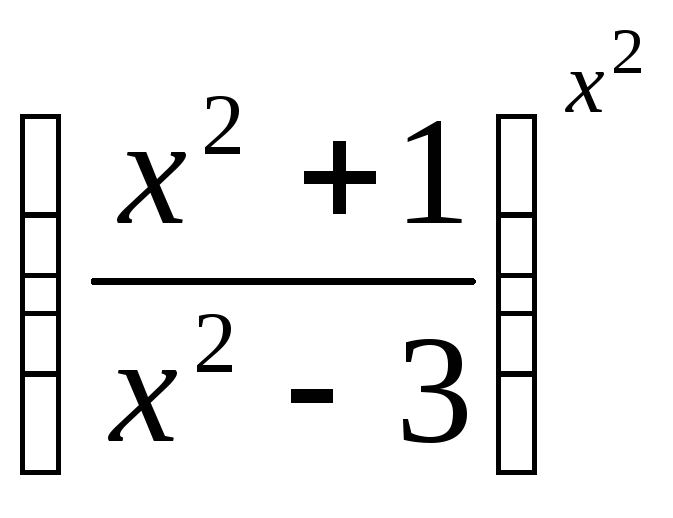 .
.
97. 
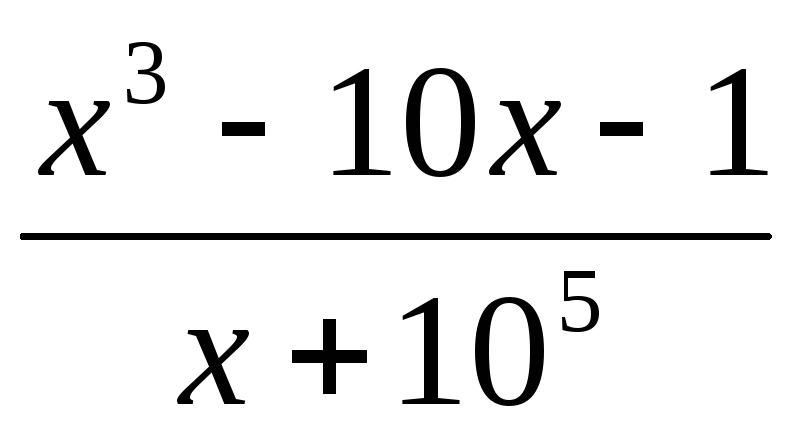 ,
, 
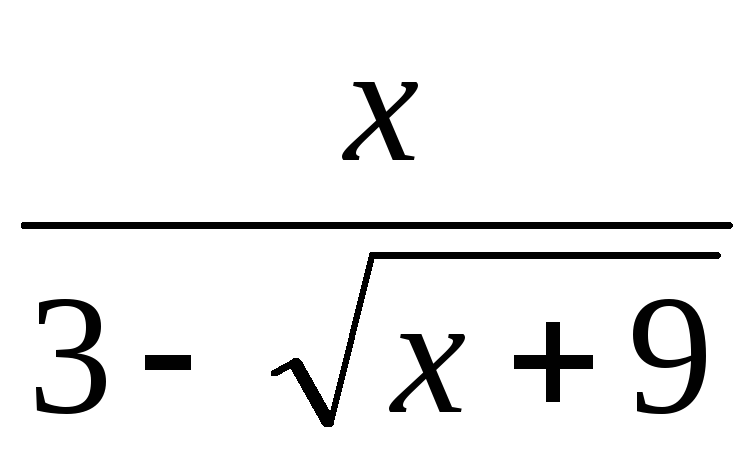 ,
,
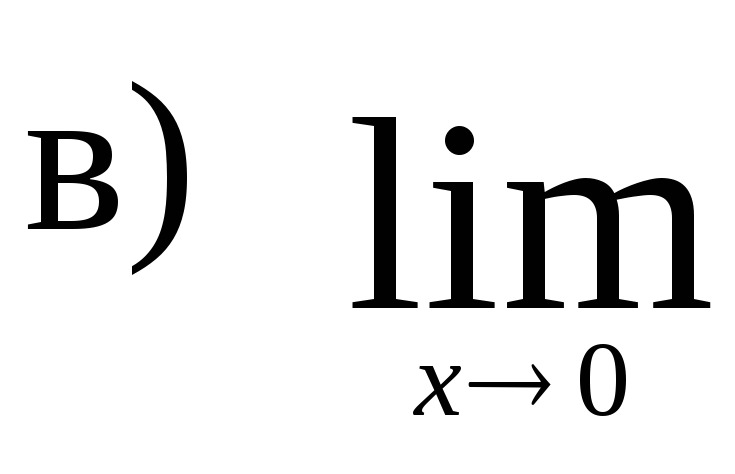
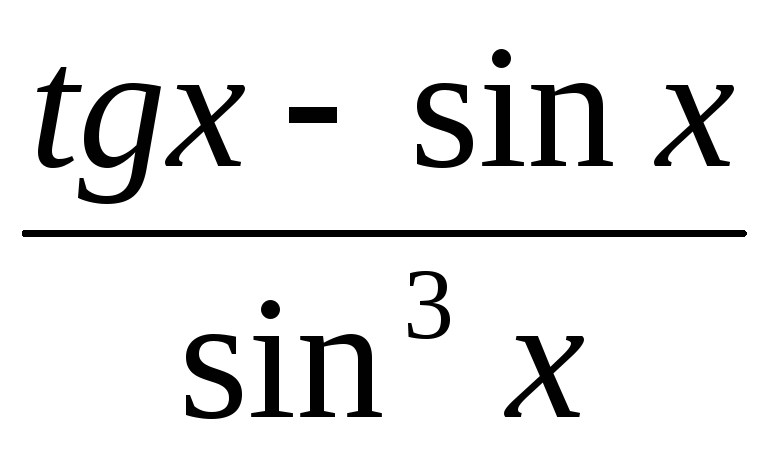 ,
, 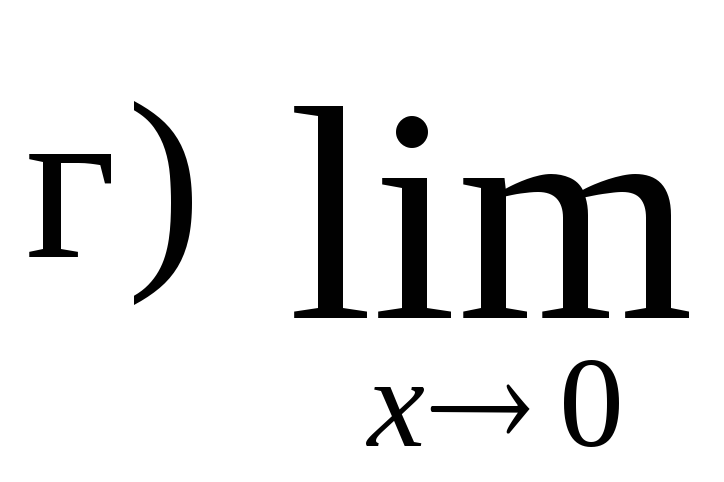
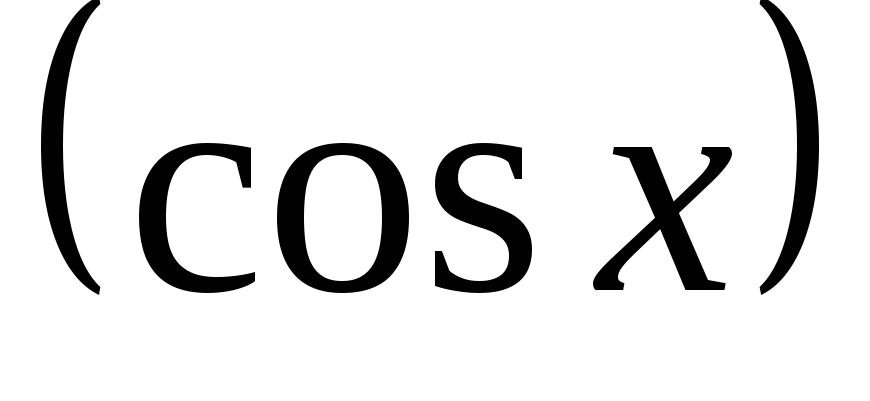
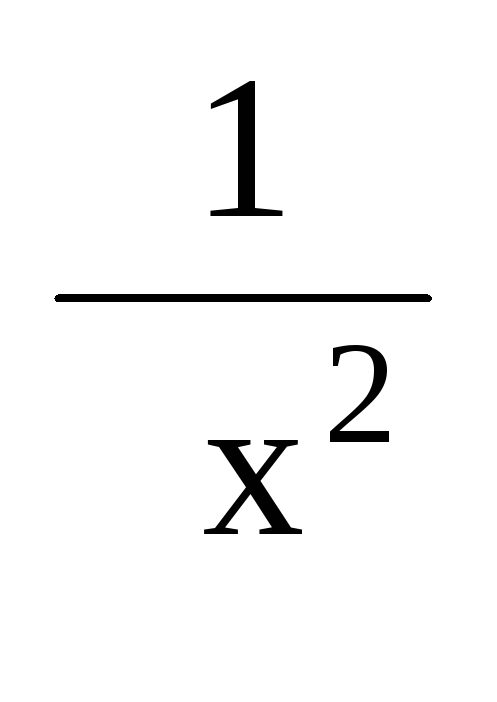 .
.
98. a) 
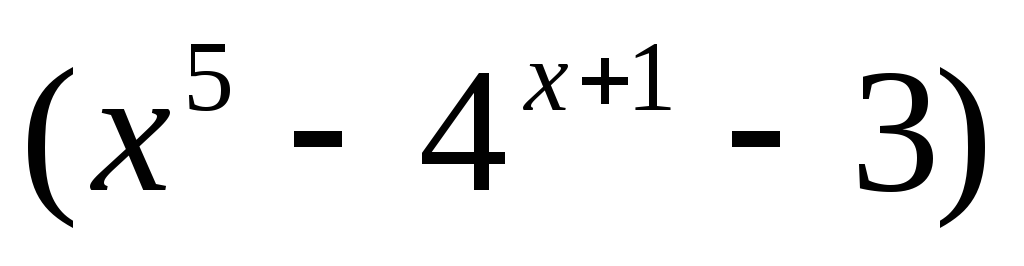 ,
,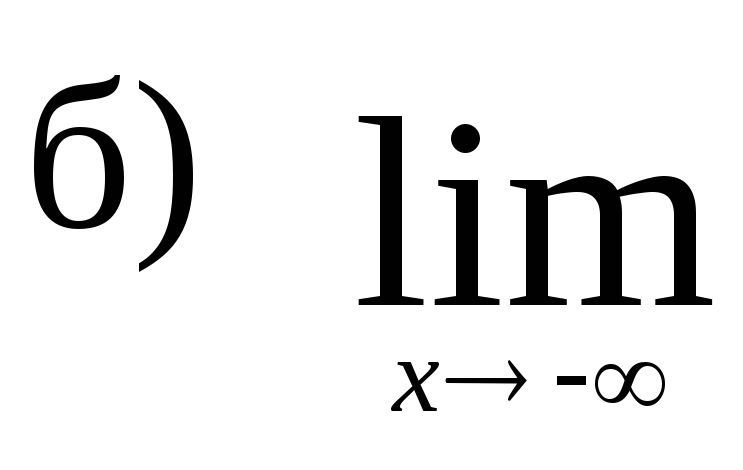

в) 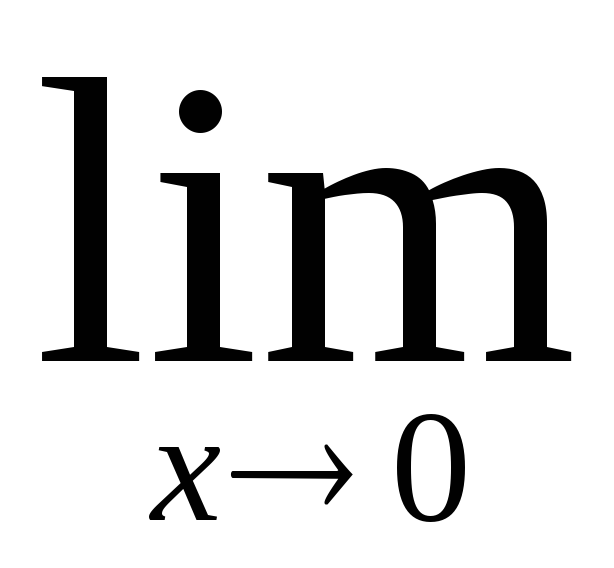
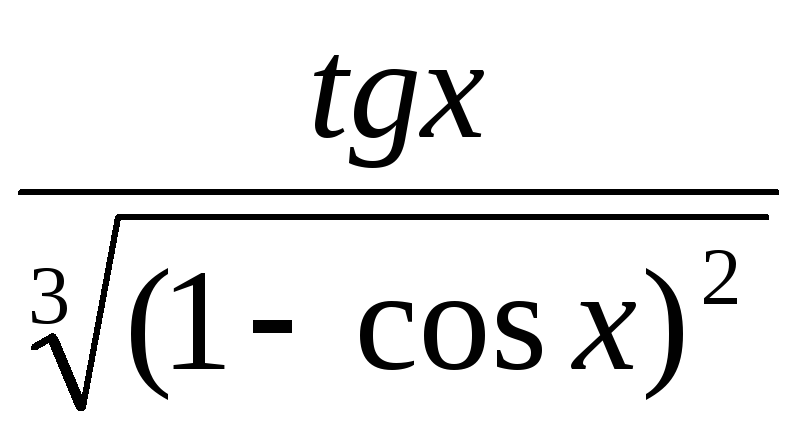 ,
,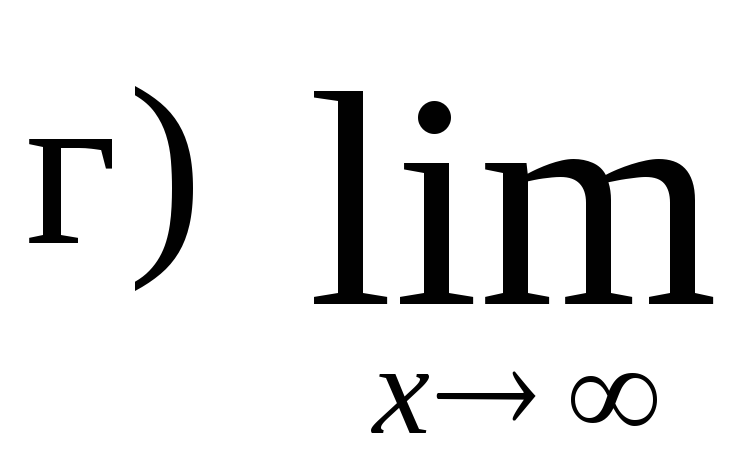
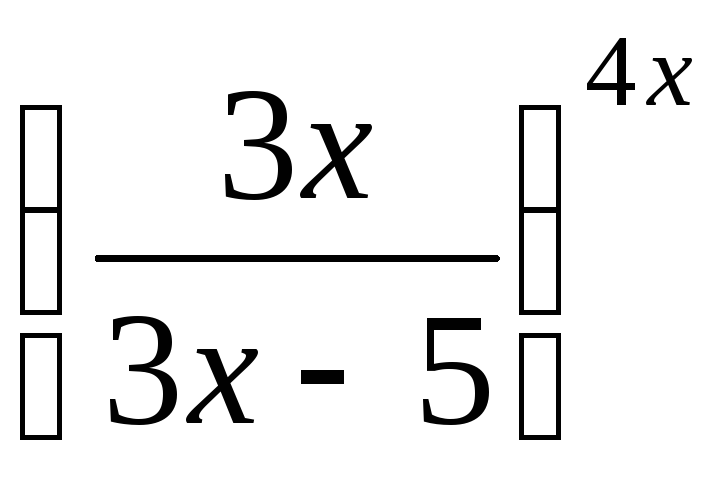 .
.
99. 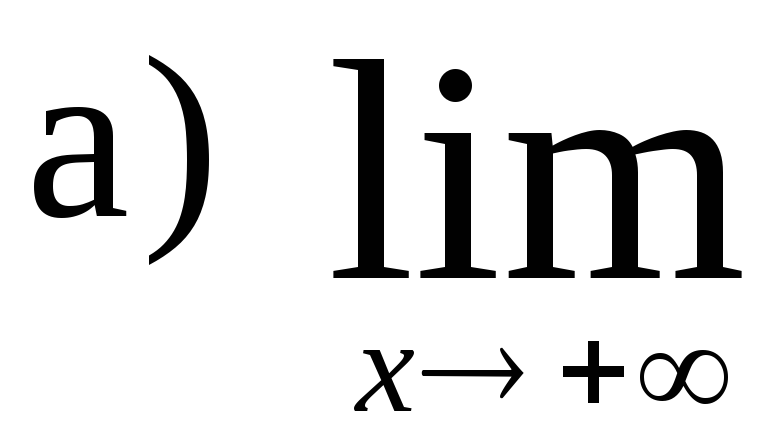
 ,
, 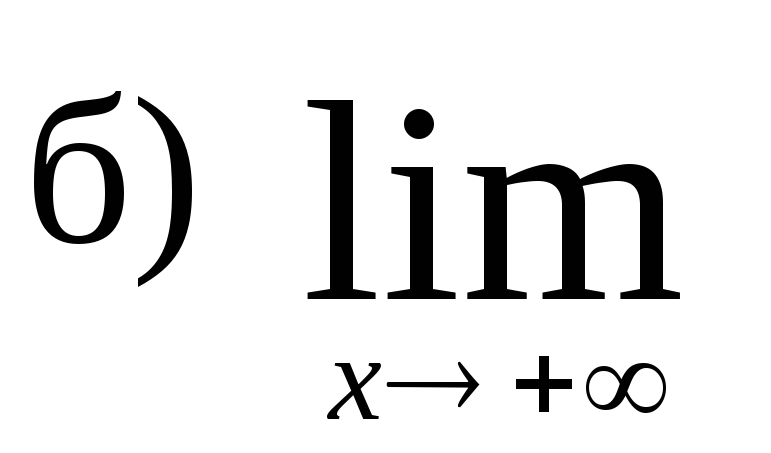
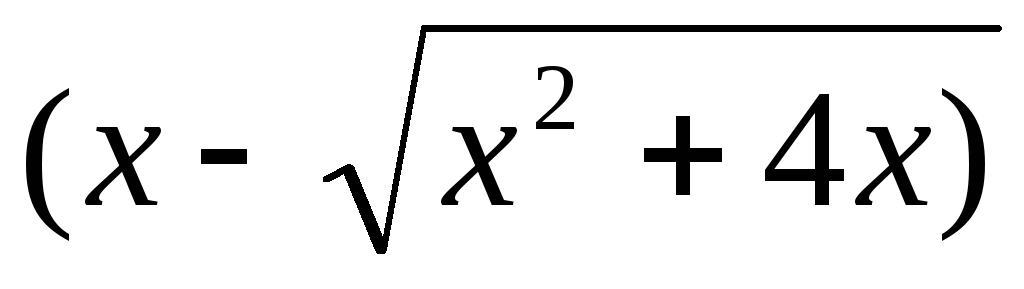 ,
,
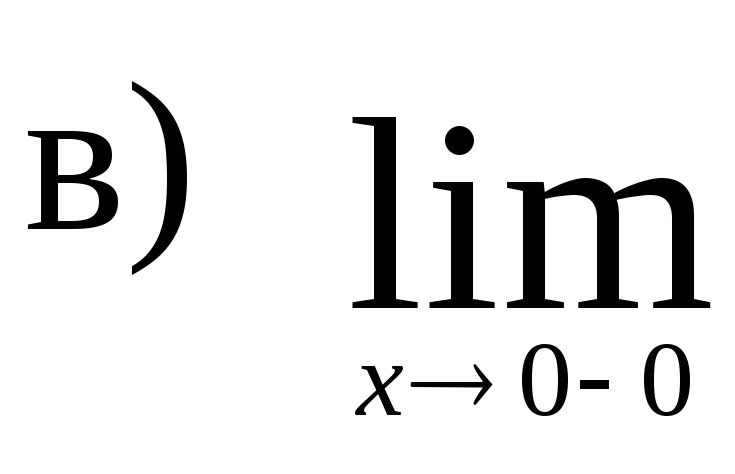
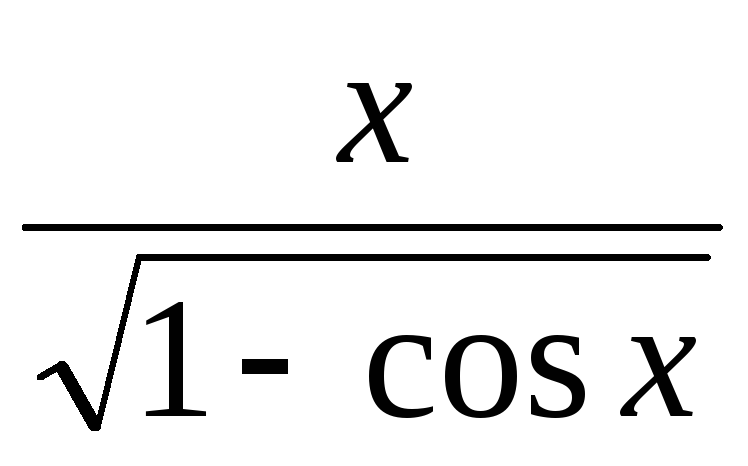 ,
, 
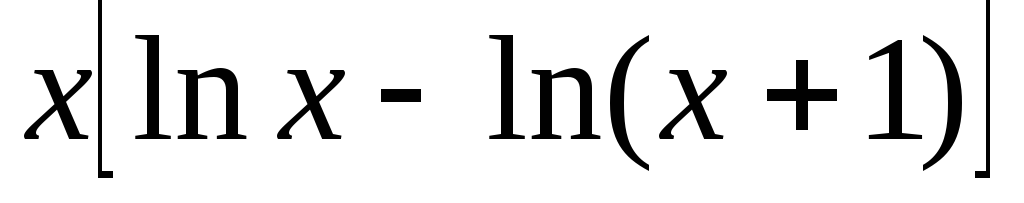 .
.
100. 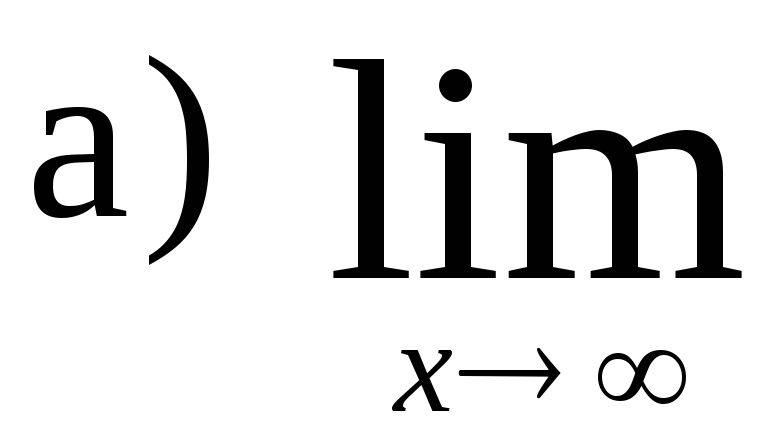
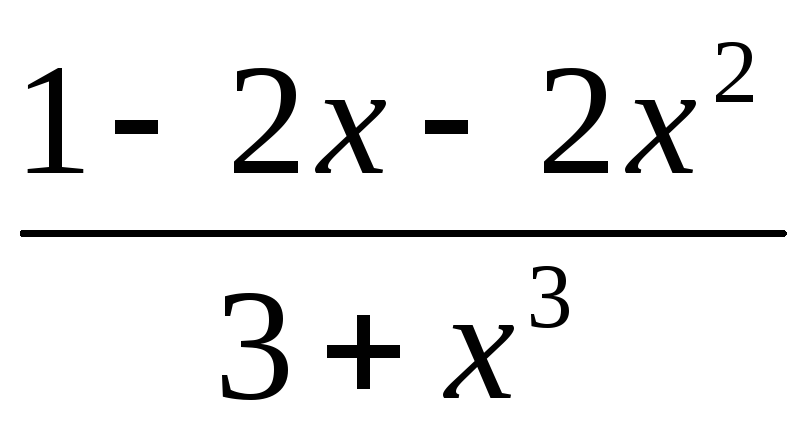 ,
, 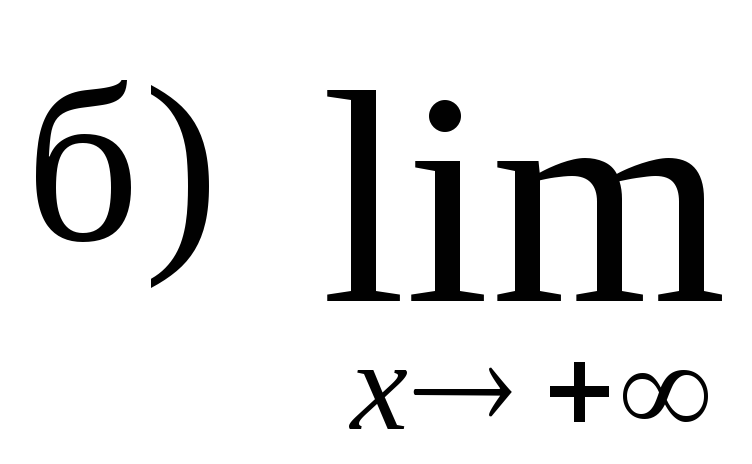
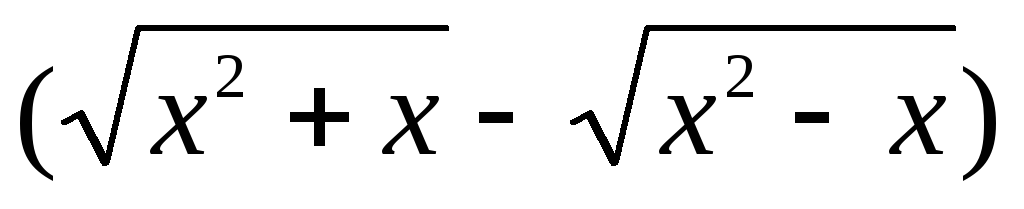 ,
,
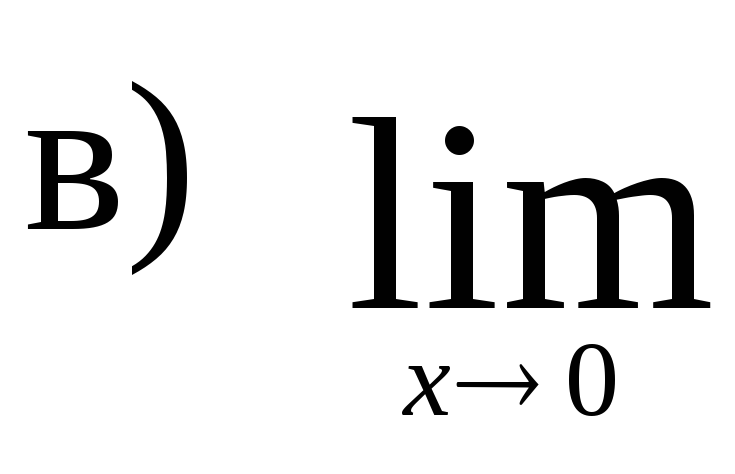
 ,
, 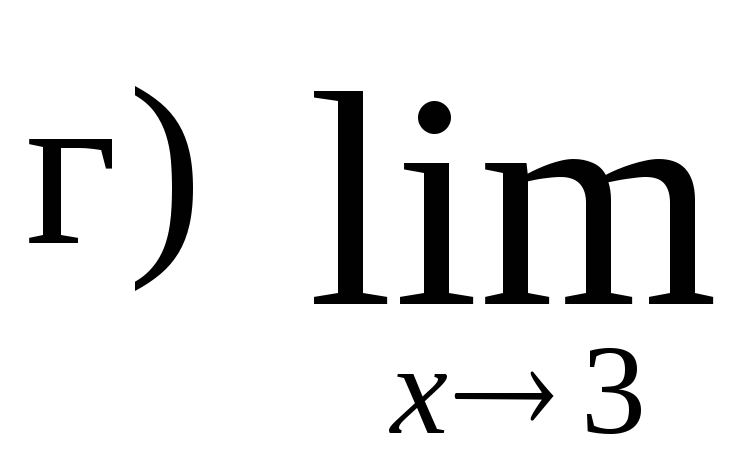
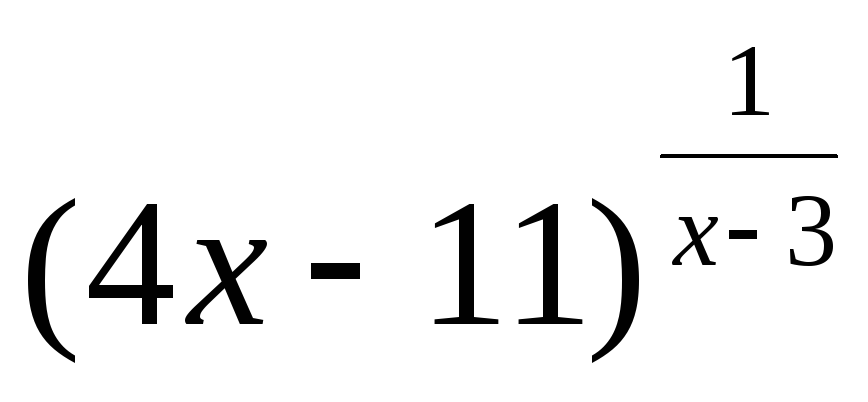 .
.
101 − 110. Найдите пределы функций при x→ + ∞ и при x→ − ∞ , односторонние пределы в точках разрыва и постройте график функции.

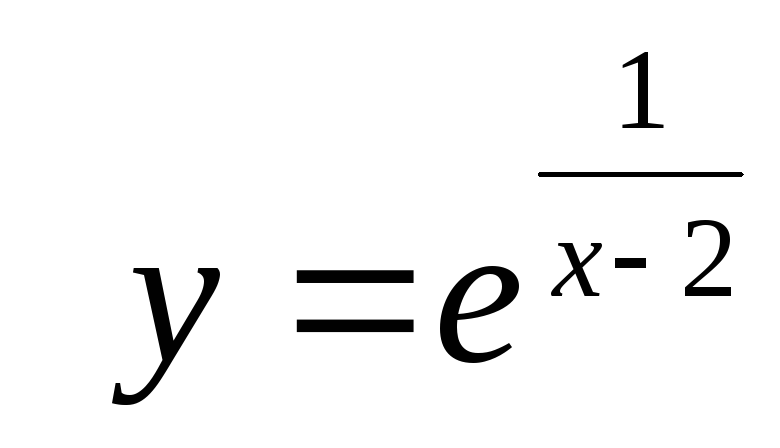 .
. 
 .
.
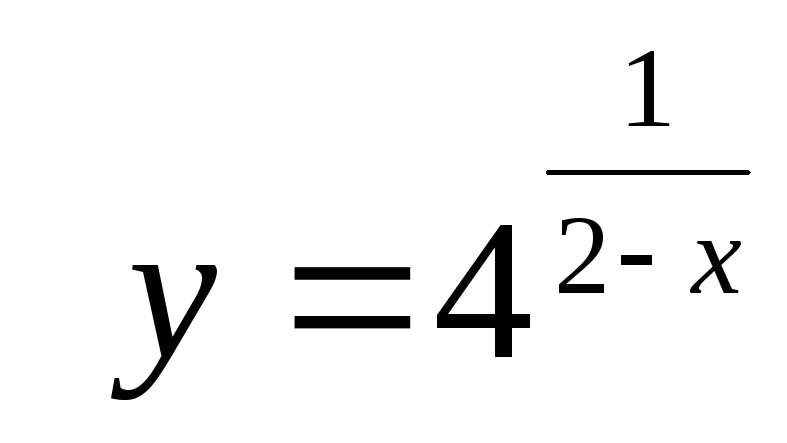 .
. 
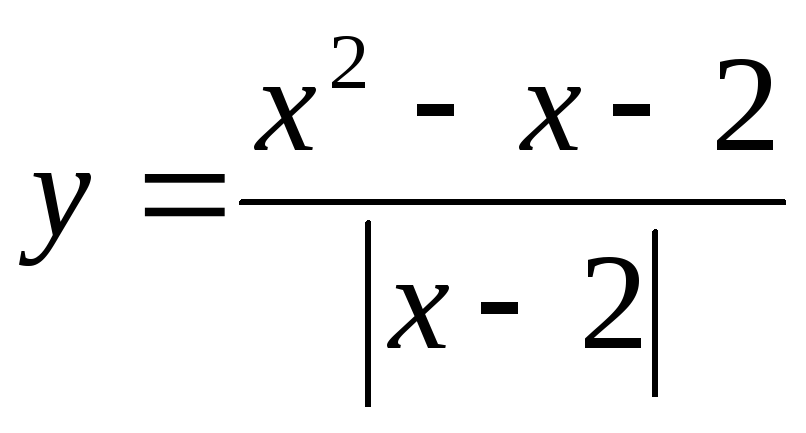 .
.
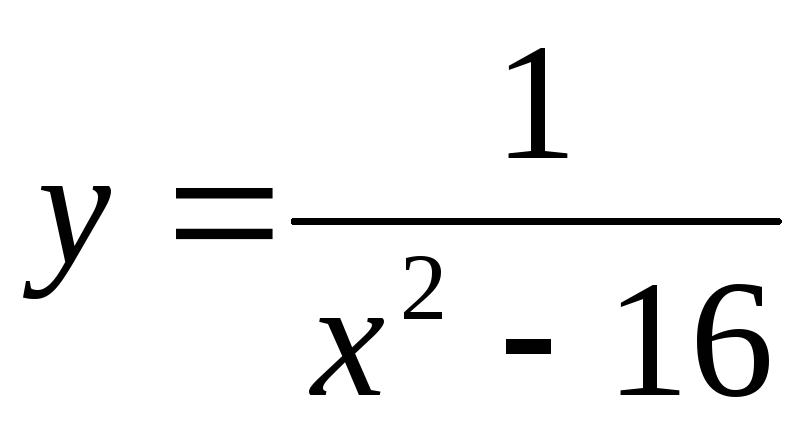 .
. 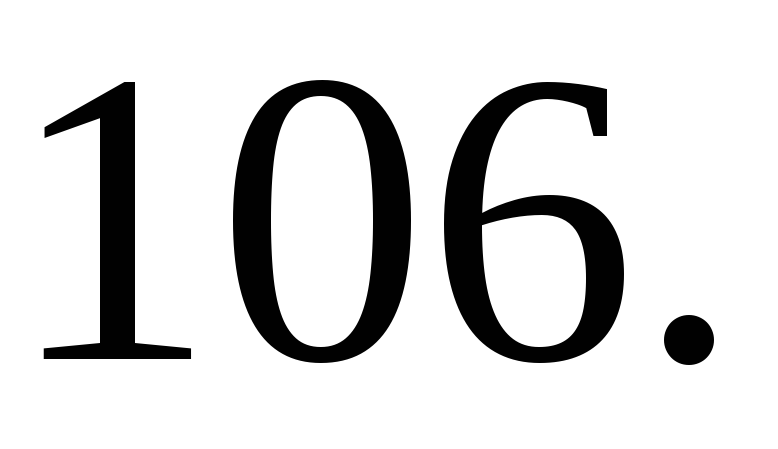
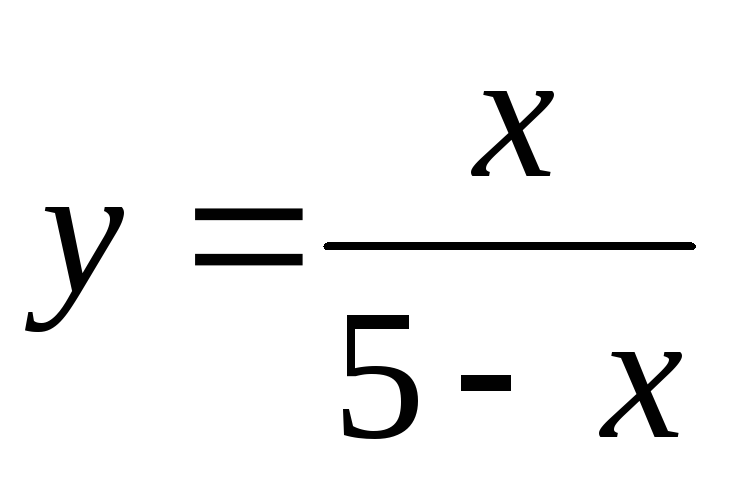 .
.

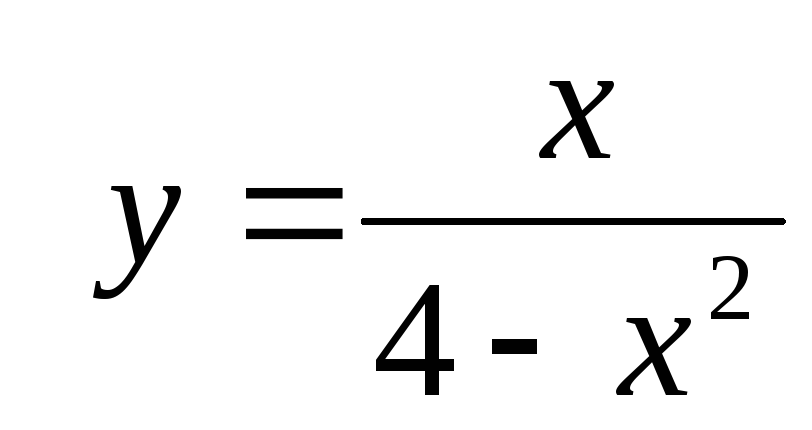 .
. 
 .
.
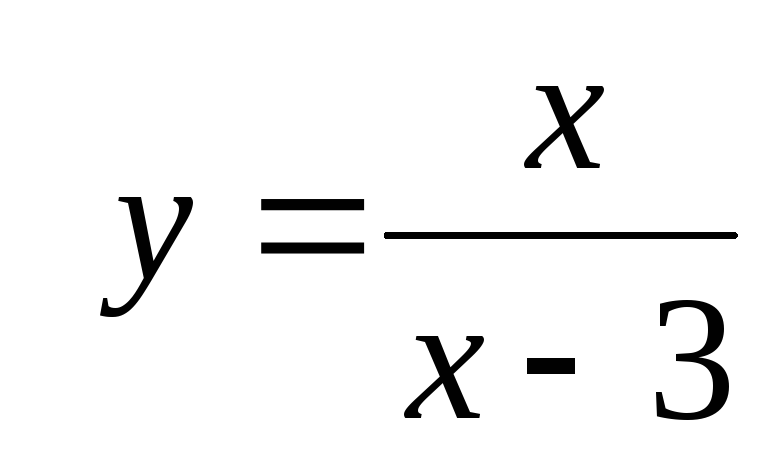 .
. 
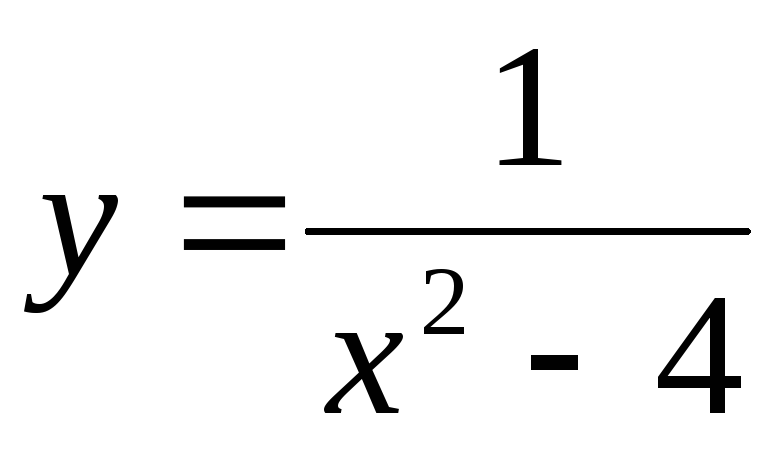 .
.
111 − 120. Постройте график функции y=f(x). Укажите точки разрыва функции, если они существуют.
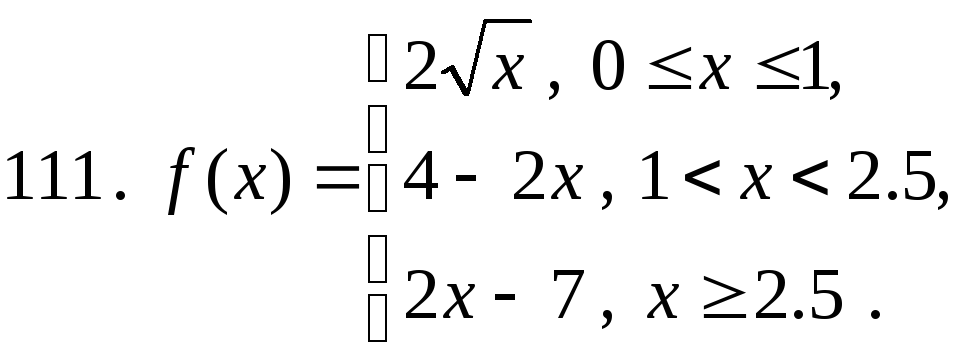


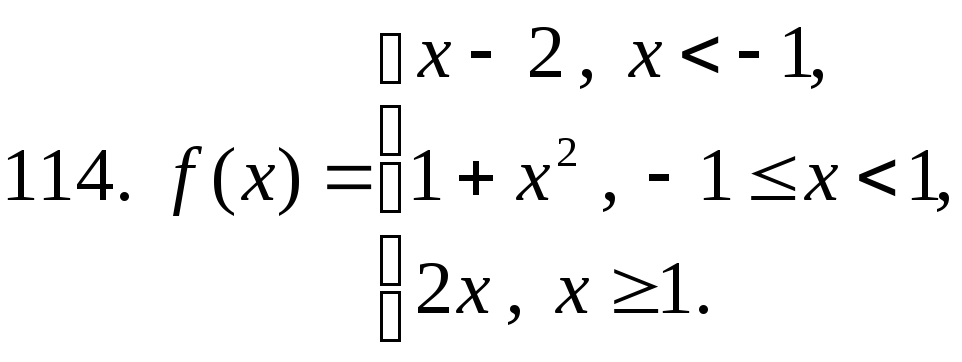
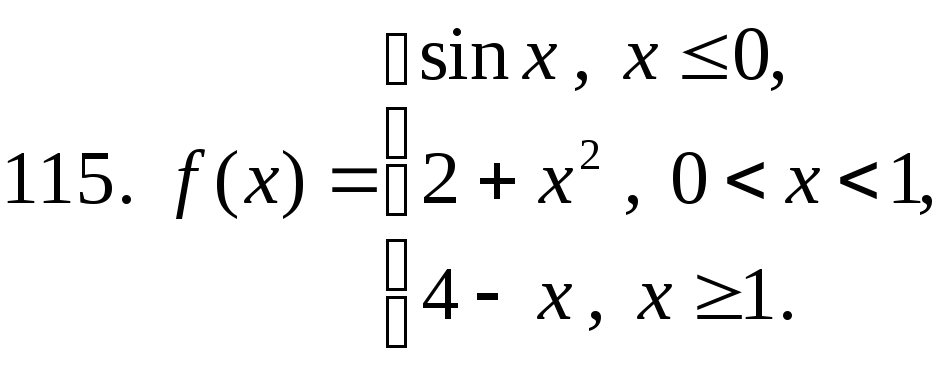
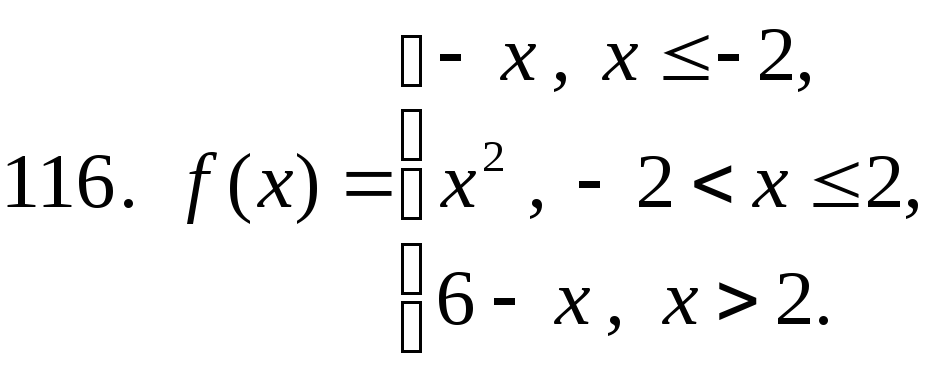
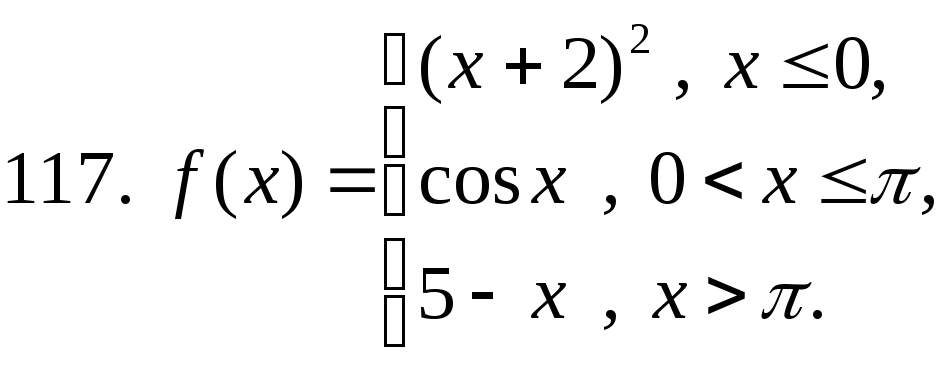
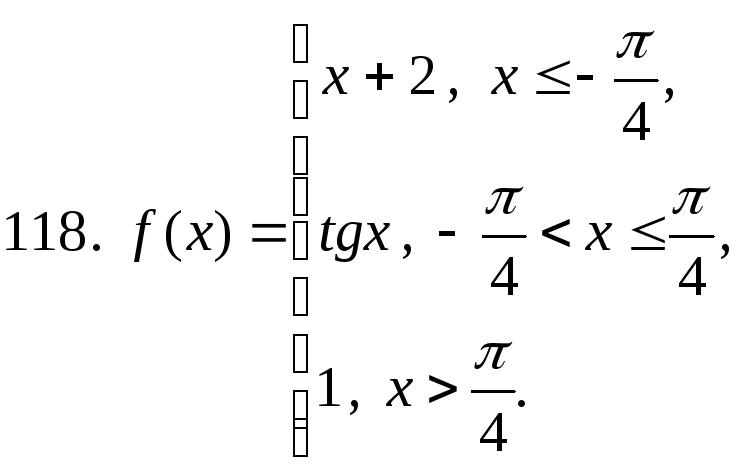
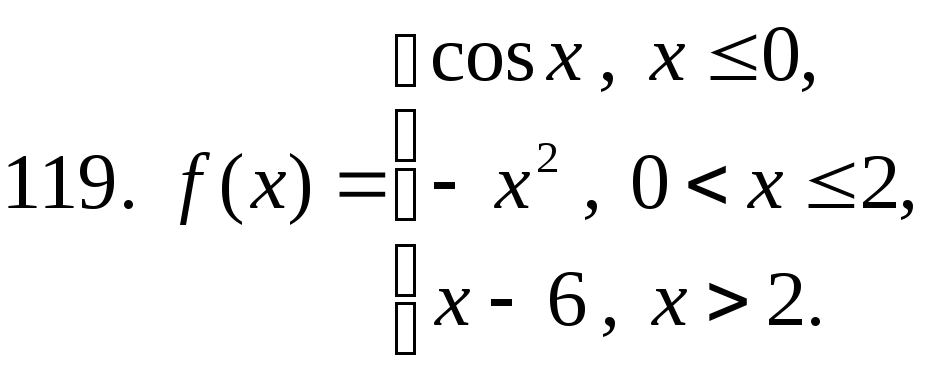

studfiles.net