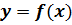 . Определить вид разрывов и изобразить график функции в окрестности этих точек.
. Определить вид разрывов и изобразить график функции в окрестности этих точек.I. Найти пределы функции.
II. Найти точки разрыва функции 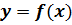 . Определить вид разрывов и изобразить график функции в окрестности этих точек.
. Определить вид разрывов и изобразить график функции в окрестности этих точек.
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ №3
«Производная и ее приложение к исследованию функции»
Вариант 0
I. Найти 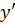 следующих функций:
следующих функций:
II. Найти 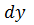 , если
, если 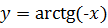 .
.
III. Найти 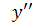 , если
, если 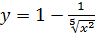
IV. Найти 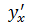 , если
, если 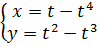
V. Исследовать и построить график функции
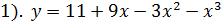 ;
;
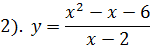
VI. Найти наибольшее и наименьшее значение функции
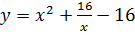 на отрезке
на отрезке 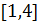 .
.
VII. Составить уравнения касательных к линии 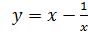 в точках её пересечения с осью абсцисс.
в точках её пересечения с осью абсцисс.
I. Решение.
1. 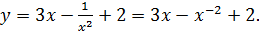
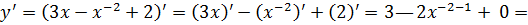
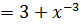 .
.
2. 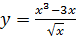
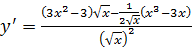
3. 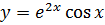
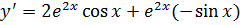 .
.
4. 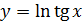
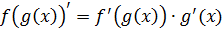 – производная сложной функции
– производная сложной функции
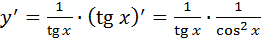
5. 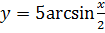
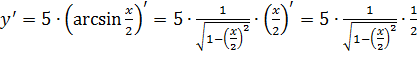
6. 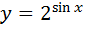 (обратить внимание
(обратить внимание 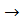 это показательная функция)
это показательная функция)
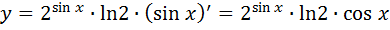
7. 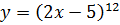
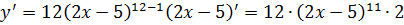
II. Найти 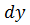 , если
, если 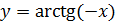
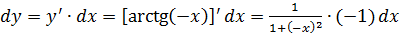
III. Найти 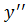 , если
, если 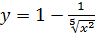
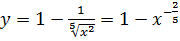
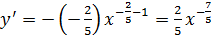
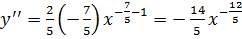
IV. Найти 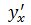 , если
, если 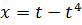 ;
; 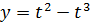
| Известно, | 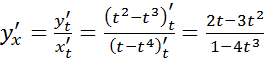 |
V. Исследовать и построить график функции
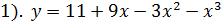
1. Функция определена всюду, т.е. область определения (-∞;+∞)
2. Функция общего вида
3. Вертикальные асимптоты. Т.к. нет особенностей в области определения, то функция вертикальных асимптот не имеет.
4. Асимптоты 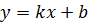 . Т.к. функция представляет собой многочлен, то ни наклонных, ни горизонтальных асимптот нет
. Т.к. функция представляет собой многочлен, то ни наклонных, ни горизонтальных асимптот нет
5. Интервалы монотонности и точки экстремумов.
а). Найдем производную:
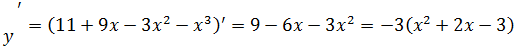
в).
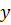 убывает на
убывает на 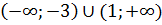 ;
;
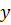 возрастает на
возрастает на 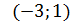 .
.
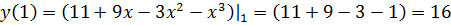 максимум;
максимум;
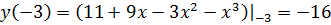 мининум.
мининум.
6. Интервалы выпуклости вогнутости, точки перегиба.
а). Найдем 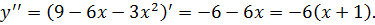
б). Найдем критические точки 2-го рода:
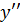 |
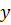 |
в).
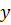 вогнута на
вогнута на 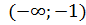 ;
;
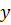 выпукла на
выпукла на 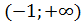 .
.
В точке 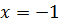 имеется перегиб
имеется перегиб
7. Точки пересечения с осью 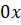 найти не можем (сложно)
найти не можем (сложно)
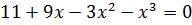 .
.
Точка пересечения с осью 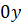 :
:
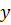 |
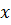 |
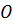 |
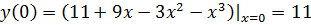 .
.
Из графика видно, что функция 3 раза пересекает ось Х.
2). 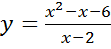
1. Функция определена всюду, кроме точки 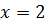 , так как знаменатель дроби не должен обращаться в нуль. Имеем область определения функции
, так как знаменатель дроби не должен обращаться в нуль. Имеем область определения функции 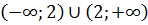 .
.
2. Функция общего вида.
3. Функция непрерывна на своей области определения. Исследуем функцию в точке 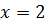 .
.
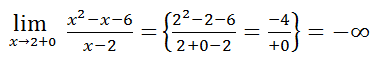
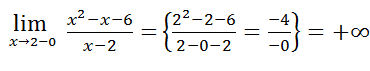
Эти пределы различны и бесконечны, т.е. в точке 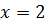 функция имеет разрыв второго рода.
функция имеет разрыв второго рода.
4. Так как функция имеет в точке 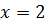 бесконечный разрыв, то прямая
бесконечный разрыв, то прямая 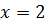 будет для графика этой функции вертикальной асимптотой. Наклонная асимптота имеет уравнение
будет для графика этой функции вертикальной асимптотой. Наклонная асимптота имеет уравнение 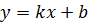 , коэффициенты которого определяются по формулам
, коэффициенты которого определяются по формулам
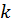
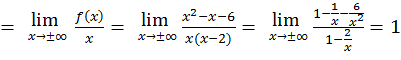
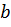
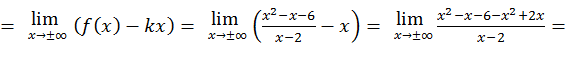
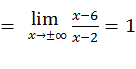
График имеет асимптоту 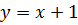 .
.
5. Найдем производную функции:
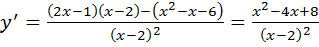
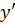 |
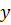 |
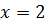 . Выясним, при каких значениях
. Выясним, при каких значениях 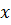 производная равна нулю. Решим уравнение
производная равна нулю. Решим уравнение 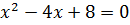 . Вычисляя дискриминант, получаем
. Вычисляя дискриминант, получаем 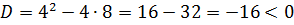 , поэтому корней у этого уравнения нет
, поэтому корней у этого уравнения нет
Производная всюду положительна, экстремумов у графика функции нет, функция возрастает на интервалах 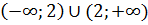 .
.
1. Найдем вторую производную функции:
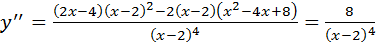
Вторая производная нигде не обращается в нуль, поэтому функция не имеет точек перегиба.
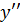 |
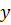 |
При 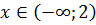 выполнено неравенство
выполнено неравенство 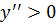 , поэтому на интервале
, поэтому на интервале 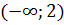 график функции является вогнутым. При
график функции является вогнутым. При 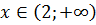 выполняется неравенство
выполняется неравенство 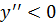 , поэтому на интервале
, поэтому на интервале 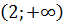 график функции является выпуклым.
график функции является выпуклым.
7. Найдем точки пересечения графика функции с осями координат. Имеем 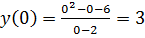 , поэтому с осью
, поэтому с осью 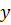 функция пересекается в точке
функция пересекается в точке 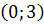 . Далее,
. Далее, 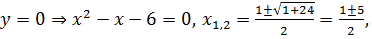
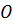 |
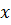 |
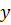 |
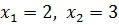 , поэтому с осью
, поэтому с осью 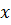 функция пересекается в точках
функция пересекается в точках 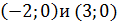
VI. 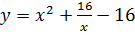 на
на 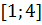 .
.
1. Найдем 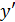
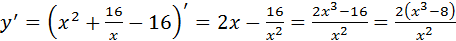
2. Найдем критические точки
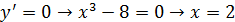
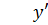 не существует
не существует 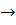
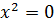 , но в этой точке не существует сама
, но в этой точке не существует сама
функция, поэтому ее рассматривать не нужно.
3. Посмотрим, все ли критические точки лежат в рассматриваемом интервале:
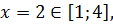 значит, она нам нужна.
значит, она нам нужна.
4. Найдем значение в оставшейся критической точке 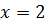 и на концах интервала
и на концах интервала 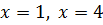
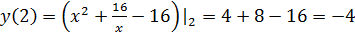
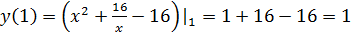
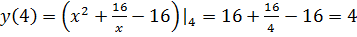
5. Из получившихся значений выбираем самое большое и самое маленькое
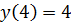 – наибольшее значение
– наибольшее значение 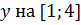 ;
;
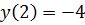 – наименьшее значение
– наименьшее значение 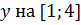 .
.
VII. 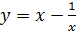
1. Найдем точки пересечения 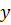 с осью
с осью 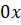
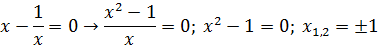
2. Т.к. уравнение касательной в точке 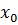 имеет вид:
имеет вид:
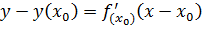 ,
,
то вычислим 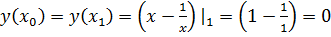 ;
;
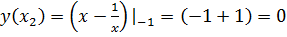 ;
;
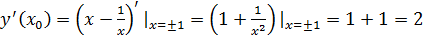 .
.
Имеем две касательные с уравнениям
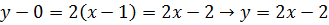 ;
;
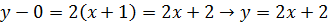 .
.
studopedya.ru
1.Определите: а) субъект, предикат, связку в суждении;
б) качество и количество суждения.
Проблема взаимоотношения религии и морали занимала умы мыслителей с глубокой древности.
2.Определите вид умозаключения.
Многие животные обладают сознанием. Следовательно, некоторые животные не имеют сознания.
3.Определите логическую ошибку в рассуждении.
Все люди пьют воду. Все люди смертны. Следовательно, вода является причиной смерти людей.
4.Какое из умозаключений является логически правильным.
а) Аристотель – философ. Тимирязев – не Аристотель. Следовательно, Тимирязев – не философ.
б) Студенты – люди. Люди – разумны. Следовательно, некоторые разумные существа – студенты.
в) Студенты – люди. Студенты – учащиеся. Следовательно, все учащиеся – люди.
г) Все студенты – учащиеся. Некоторые музыканты – учащиеся. Следовательно, некоторые музыканты – студенты.
5.Напишите формулу сложного суждения.
В коллективе возникает хороший психологический климат тогда и только тогда, когда будут четко определены задачи, ответственность и компетенция каждого сотрудника.
1.Определите логические отношения между понятиями и выразите их с помощью кругов Эйлера в одной схеме:
Пистолет, оружие, огнестрельное оружие, танк.
2. Установите логическую правильность определения понятия, если оно неверное, укажите ошибку.
Мода – это то, что выходит из моды (Коко Шанель).
3.Установите вид умозаключения, проверьте его правильность.
Некоторые студенты нашего института изучают астрологию, следовательно, некоторые студенты нашего института не изучают астрологию.
4.Какой из силлогизмов является логически правильным?
а) Все студенты – учащиеся. Некоторые артисты – учащиеся. Следовательно, некоторые артисты – студенты.
б) Студенты – люди. Студенты – учащиеся. Следовательно, все учащиеся – люди.
в) Инженеры – люди. Люди – разумны. Следовательно, некоторые разумные существа – инженеры.
г) Футболисты – спортсмены. Хоккеисты – спортсмены. Следовательно, футболисты и хоккеисты – спортсмены.
5. Напишите формулу сложного суждения.
Если эта фигура – ромб, то ее диагонали перпендикулярны, а стороны равны.
1.Определите логические отношения между понятиями и выразите их с помощью кругов Эйлера в одной схеме:
Юриспруденция. Физика. Математика. Наука. Ядерная физика.
2.Какие понятия находятся в отношении подчинения?
а) Философия, юриспруденция.
б) Логика, этика.
в) Уголовное право, криминалистика.
г) Философия, логика.
д) Логика, ораторское искусство.
3.Определите: а) субъект, предикат, связку в суждении;
б) качество и количество суждения.
Русский судебник XVI века предписывал смертную казнь за 12 видов преступлений.
4.Какое из умозаключений является логически правильным.
а) Шахматисты – люди. Студенты – люди. Следовательно, некоторые студенты – шахматисты.
б) Шахматисты – спортсмены. Шахматисты – не боксеры. Следовательно, некоторые спортсмены – не боксеры.
в) Бокс - спорт. Шахматы – не бокс. Следовательно, шахматы – не спорт.
г) Шахматисты – спортсмены. Спортсмены участвуют в соревнованиях. Следовательно, некоторые участники соревнований – шахматисты.
5.Определите логическую ошибку, ставшую причиной непонимания, в диалоге.
Ученик: отец мне сказал, что мы происходим от обезьяны. – Помолчите, останавливает его учитель. История вашей семьи меня не интересует.
studfiles.net
Домашнее контрольное задание № 2
«Основы химической термодинамики и кинетики»
Вариант 1
1. Для реакции: 2h3S(г) +3O2(г) =2h3O(ж) + 2 SO2(г)
а) Рассчитайте изменение стандартной энтальпии и стандартной энтропии реакции, используя данные из таблицы
| ΔH0обр кДж/моль | ΔS0обр Дж/(моль K) | ΔG0обр кДж/моль | С, Моль/л | |
| h3S(г) | -20,17 | 205,6 | -33,01 | 0,1 |
| h3O(ж) | -285,84 | 70,08 | -237,2 | 0,1 |
| SO2(г) | -296,9 | 248,1 | -300,4 | 0,01 |
| NO(г) | 90,37 | 210,62 | 86,71 | 0,01 |
| NO2(г) | 33,5 | 240,45 | 51,8 | 0,05 |
| O2(г) | 205,04 | 0,03 |
б) Покажите, какой из факторов процесса – энтальпийный или энтропийный – способствует самопроизвольному протеканию процесса в прямом направлении;
в) Определите, в каком направлении при 250С будет протекать реакция;
г) Рассчитайте температуру, при которой равновероятны оба направления реакции. При каких температурах, выше или ниже рассчитанной, более вероятно протекание указанной реакции в прямом направлении;
2. Для обратимой реакции, протекающей в газовой фазе: 2NO(г) + O2(г) ↔ 2NO2(г)
a) Рассчитайте стандартное изменение энергии Гиббса для T1=298 К и для Т2 = 1000K,
б) Рассчитайте значения константы равновесия при концентрациях веществ, указанных в таблице;
3. Для реакции: Ch3OHCh3C1 + KOH → Ch3OHCh3OH + KC1
а) По значениям констант скоростей реакции k1 = 1,13.10-2 л/(моль.c) и k2 = 8,72.10-2л/(моль.c) при двух температурах (Т1 = 298 K и Т2 = 303 К) определите значение температурного коэффициента реакции.
б) Рассчитайте константу скорости при температуре 318 K.
в) Во сколько раз изменится скорость вашей реакции при повышении температуры от Т1 до Т3?.
г) Определите количество вещества, израсходованное за время - 18 мин при 318 K , если начальные концентрации исходных веществ равны С0 =1 моль/л.
Домашнее контрольное задание № 2
«Основы химической термодинамики и кинетики»
Вариант 2
1. Для реакции: CO2(г)+С(к) = 2СО(г)
а) Рассчитайте изменение стандартной энтальпии и стандартной энтропии реакции; используя данные из таблицы
| ΔH0обр кДж/моль | ΔS0обр Дж/(моль K) | ΔG0обр кДж/моль | С Моль/л | |
| CO2(г) | -393,51 | 213,68 | -394,38 | |
| H 2 | 130,58 | 0,1 | ||
| С(к) | 5,74 | 0,2 | ||
| СО(г) | -110,5 | 197,54 | -137,14 | 0,3 |
| Сh4OH(г) | -238,6 | 126,8 | -166,23 | 0,2 |
б) Покажите, какой из факторов процесса – энтальпийный или энтропийный – способствует самопроизвольному протеканию процесса в прямом направлении;
в) Определите, в каком направлении при 250С будет протекать реакция;
г) Рассчитайте температуру, при которой равновероятны оба направления реакции. При каких температурах, выше или ниже рассчитанной, более вероятно протекание указанной реакции в прямом направлении;
2. Для обратимой реакции, протекающей в газовой фазе: 2 H 2+ СО↔Сh4OH
Рассчитайте стандартное изменение энергии Гиббса для T1=298 К и для Т2 =503К,
б) Рассчитайте значения константы равновесия при концентрациях веществ, указанных в таблице;
3. Для реакции: Ch4C6h5N2Cl + h3O→ Ch4C6h5OH + N2 + HCl
а) По значениям констант скоростей реакции k1 = 9.10-3 мин-1и k2 = 13.10-3 мин-1 при двух температурах (Т1 =298 K и Т2=303 K) определите значение температурного коэффициента.
б) Рассчитайте константу скорости при температуре T3 =308 K.
в) Во сколько раз изменится скорость вашей реакции при повышении температуры от Т1 до Т3?.
г) Определите количество вещества, израсходованное за время τ =10 мин, при Т3 ,если начальные концентрации исходных веществ равны С0 = 0,1 моль/л
Домашнее контрольное задание № 2
«Основы химической термодинамики и кинетики»
Вариант 3
1. Для реакции: N2(г)+3H 2(г) =2Nh4(г)
а) Рассчитайте изменение стандартной энтальпии и стандартной энтропии реакции; используя данные из таблицы
| ΔH0обр кДж/моль | ΔS0обр Дж/(моль K) | ΔG0обр кДж/моль | С Моль/л | |
| N2(г) | 191,5 | 0,2 | ||
| H 2(г) | 130,58 | 0,1 | ||
| Nh4 | -46,19 | 192,5 | -16,66 | 0,1 |
| F2(г) | 27,15 | 0,3 | ||
| 2HF(г) | -268,61 | 173,51 | -270,7 | 0,4 |
б) Покажите, какой из факторов процесса – энтальпийный или энтропийный – способствует самопроизвольному протеканию процесса в прямом направлении;
в) Определите в каком направлении при 250С будет протекать реакция;
г) Рассчитайте температуру, при которой равновероятны оба направления реакции. При каких температурах, выше или ниже рассчитанной, более вероятно протекание указанной реакции в прямом направлении;
2. Для обратимой реакции, протекающей в газовой фазе: F2(г) + h3(г) ↔2HF(г)
Рассчитайте стандартное изменение энергии Гиббса для T1=298 К и Т2 = 600K
б) Рассчитайте значения константы равновесия при концентрациях веществ, указанных в таблице;
3. Для реакции: 2NaBO3 + 2h3O→2Nah3BO3 + O2
а) По значениям констант скоростей реакции k1=2,2.10-3 мин-1 и k2=4,1.10-3 мин-1 при двух температурах (Т1 =303 K и Т2=308 K) определите значение температурного коэффициента.
б) Рассчитайте константу скорости при температуре T3 328 K.
в) Во сколько раз изменится скорость вашей реакции при повышении температуры от Т1 до Т3?.
г) Определите количество вещества, израсходованное за время - τ =60 мин при Т3, если начальные концентрации исходных веществ равны С0=0,05 моль/л
Домашнее контрольное задание № 2
«Основы химической термодинамики и кинетики»
Вариант 4
1. Для реакции: Cl2(г) + 2HI(г) = I2(г) + 2HCl(г)
а) Рассчитайте изменение стандартной энтальпии и стандартной энтропии реакции; используя данные из таблицы
| ΔH0обр кДж/моль | ΔS0обр Дж/(моль K) | ΔG0обр кДж/моль | С Моль/л | |
| Cl2(г) | 222,96 | 0,01 | ||
| 2HI(г) | 25,94 | 206,3 | 1,3 | 0,01 |
| I2(г) | 62,24 | 260,58 | 19,4 | 0,02 |
| HCl(г) | -166,9 | 56,5 | -131,2 | 0,3 |
| C2h5 | 52,27 | 219,4 | 68,11 | 0,1 |
| h3O(г) | -241,82 | 188,7 | -228,61 | 0,2 |
| C2H5OH(г) | -235,3 | 278,0 | -167,4 | 0,5 |
б) Покажите, какой из факторов процесса – энтальпийный или энтропийный – способствует самопроизвольному протеканию процесса в прямом направлении;
в) Определите в каком направлении при 250С будет протекать реакция;
г) Рассчитайте температуру, при которой равновероятны оба направления реакции. При каких температурах, выше или ниже рассчитанной, более вероятно протекание указанной реакции в прямом направлении;
2. Для обратимой реакции, протекающей в газовой фазе: C2h5 + h3O ↔ C2H5OH
Рассчитайте стандартное изменение энергии Гиббса для T1=298 К и для Т2 500K;, а также значения констант равновесия при этих температурах;
б) Рассчитайте значения константы равновесия при концентрациях веществ, указанных в таблице;
3. Для реакции: C6H5Ch4Br + C2H5OH → C6H5Ch3OC2H5 + HBr
а) По значениям констант скоростей реакции k1=1,44 л/(моль.мин) и k2 k2=2,01 л/(моль.мин) при двух температурах (Т1 298 K и Т2==318 K) определите значение температурного коэффициента.
б) Рассчитайте константу скорости при температуре T3 = 338 K.
в) Во сколько раз изменится скорость вашей реакции при повышении температуры от Т1 до Т3?.
г) Определите количество вещества, израсходованное за время – τ= 90 мин при Т3, если начальные концентрации исходных веществ равны С0=2,6 моль
Домашнее контрольное задание № 2
«Основы химической термодинамики и кинетики»
Вариант 5
1. Для реакции: CaO(к) + h3O(ж) = Ca(OH)2(к)
а) Рассчитайте изменение стандартной энтальпии и стандартной энтропии реакции; используя данные из таблицы
| ΔH0обр кДж/моль | ΔS0обр Дж/(моль K) | ΔG0обр кДж/моль | С Моль/л | |
| CaO(к) | -635,5 | 39,7 | -605,2 | |
| h3O(ж) | -285,84 | 70,08 | -237,2 | |
| Ca(OH)2(к) | -986,2 | 83,4 | -898,5 | |
| CO2(г) | -393,51 | -394,38 | -394,38 | |
| H 2(г) | 130,58 | |||
| Ch5 (г) | -74,85 | 186,19 | -50,79 | |
| h3O (г) | -241,82 | 188,7 | -228,61 |
б) Покажите, какой из факторов процесса – энтальпийный или энтропийный – способствует самопроизвольному протеканию процесса в прямом направлении;
в) Определите в каком направлении при 250С будет протекать реакция;
г) Рассчитайте температуру, при которой равновероятны оба направления реакции. При каких температурах, выше или ниже рассчитанной, более вероятно протекание указанной реакции в прямом направлении;
2. Для обратимой реакции, протекающей в газовой фазе: CO2(г) +4H 2(г) ↔Ch5 (г) +2 h3O (г)
Рассчитайте стандартное изменение энергии Гиббса для T1=298 К и для Т2 1000K,
б) Рассчитайте значения константы равновесия при концентрациях веществ, указанных в таблице;
3. Для реакции: C2H5ONa + Ch4I → С2Н5ОСН3 + NaI
а) По значениям констант скоростей реакции k1=0,0425 л/(моль.мин) и k2=3,255 л/(моль.мин ) при двух температурах (Т1 =327 K и Т2=335 K) определите значение температурного коэффициента.
б) Рассчитайте константу скорости при температуре T3 =398 K.
в) Во сколько раз изменится скорость вашей реакции при повышении температуры от Т1 до Т3?.
г) Определите количество вещества, израсходованное за время – τ= 77 мин при Т3, если начальные концентрации исходных веществ равны С0=1,9 моль/л
megalektsii.ru

Домашняя контрольная работа по высшей математике Ваш вариант соответствуют номеру в текущем списке группы у старост: 1 – 1,5,9,…, 2 – 2,6,10,…,… В этом файле содержатся функции и условия, соответствующие каждому варианту. Требуемые точки и векторы отмечаются на картинках, которые прилагаются к каждому варианту. Результаты или вручаются лично учебному ассистенту Катюхиной Ольге или складываются у куратора 2 курса Анатолию Ивановичу Саломатину комн. 726 до 19.12.13. Содержание работы 1. Найти вершины параллелограмма, ограниченного прямыми, заданными уравнениями gi(x,y) = 0 (i = 1,…,4), и обозначить их буквами на картинке. Укажите систему неравенств, задающих полученную область. 2. Найти критические точки функции f(x,y), обозначить буквами, указать на картинке или зафиксировать их отсутствие на картинке (необходимые условия) 3. Исследовать все найденные точки на локальный экстремум (составив матрицу Гессе H и проверив знак 2-го дифференциала при помощи критерия Сильвестра ((достаточные условия))). 4. Найти точки, подозрительные на условный локальный экстремум (необходимые условия) на каждой из четырех линий, заданных условиями gi(x,y) = 0 (i = 1,…,4), обозначить буквами, указать на картинке или зафиксировать их отсутствие на картинке 5. Исследовать все найденные точки на условный локальный экстремум при помощи «окаймленного гессиана» (достаточные условия) 6. Найти градиент функции f(x,y). 7. Найти и построить (укоротив) эти градиенты в вершинах параллелограмма и в точках условного экстремума 8. Найти векторы градиентов к gi(x,y) – левым частям условий gi(x,y)=0 и построить в тех же точках нормали к линиям условий 9. Указать на картинке острый угол градиента функции f(x,y) с линиями условий в тех же точках, кроме точек условного экстремума. 10. Указать стрелками направление роста функции f(x,y) вдоль линий условия на каждой стороне параллелограмма и на их продолжении рядом с вершинами. 11. Проверить, что результаты пп 10 и 5 согласуются 12. Найти значения функции f(x,y) в точках пп 3, 5 (входящих в параллелограмм) и п. 1. 13. Найти точки с наибольшим и наименьшим значениями функции f(x,y) на параллелограмме и сами эти значения. 14. Проверить, что результаты пп 13, 10 и 3 согласуются 15. Исследовать на локальный экстремум функцию u(x,y,z)=f(x,y)+h(z). Найти критические точки, записать матрицу Гессе в них, определить: являются ли эти точки локальными экстремумами. Указания. Если масштабы на осях разные, то углы могут быть немного изменены. В частности, угол между нормалью к прямой и самой прямой может отклоняться от прямого. Если между двумя смежными вершинами параллелограмма оказались две точки условного экстремума, то для выполнения п.10 на стороне параллелограмма между этими точками, надо выполнить п.9 для произвольной точки между этими точками. Вариант 1. Исследовать функцию двух переменных f(x,y) = 12y - y3 –15x - 9x2- x3 В области, ограниченной прямыми: x+3y+1.5=0 x+3y+12=0 2x-y-5=0 2x-y+9=0 В пункте 15 рассмотреть функцию h(z)=z3-7.5z2+18z+1 2 1 0 1 2 3 4 5 6 4 2 0 2 Вариант 2. Исследовать функцию двух переменных f(x,y) = x3 + 3 x2-24 x + 6 y -2 y3 В области, ограниченной прямыми: x+3y-3=0 x+3y+4=0 2x-y-6=0 2x-y+1=0 В пункте 15 рассмотреть функцию h(z)=z3-4.5z2+6z+1 1 .5 1 .0 0 .5 0 .0 0 .5 1 .0 1 .5 2 .0 1 0 1 2 3 Вариант 3. Исследовать функцию двух переменных f(x,y) = y3+3y2-24y-24x+9x2-x3 В области, ограниченной прямыми: x+3y-12=0 x+3y-2=0 2x-y-9=0 2x-y+1=0 В пункте 15 рассмотреть функцию h(z)=2z3+3z2-12z-21 4 3 2 1 0 1 0 2 4 6 8 Вариант 4. Исследовать функцию двух переменных f4(x,y) = 12y - y3 - 12x - x3 В области, ограниченной прямыми: x+3y-12=0 x+3y-2.5=0 2x-y-11=0 2x-y-1=0 В пункте 15 рассмотреть функцию h(z)=z3+3z2-9z+1 4 3 2 1 0 1 2 0 1 2 3 4 5 6 7
www.studocu.com

Домашняя контрольная работа по высшей математике Ваш вариант соответствуют номеру в текущем списке группы у старост: 1 – 1,5,9,…, 2 – 2,6,10,…,… В этом файле содержатся функции и условия, соответствующие каждому варианту. Требуемые точки и векторы отмечаются на картинках, которые прилагаются к каждому варианту. Результаты или вручаются лично учебному ассистенту Катюхиной Ольге или складываются у куратора 2 курса Анатолию Ивановичу Саломатину комн. 726 до 19.12.13. Содержание работы 1. Найти вершины параллелограмма, ограниченного прямыми, заданными уравнениями gi(x,y) = 0 (i = 1,…,4), и обозначить их буквами на картинке. Укажите систему неравенств, задающих полученную область. 2. Найти критические точки функции f(x,y), обозначить буквами, указать на картинке или зафиксировать их отсутствие на картинке (необходимые условия) 3. Исследовать все найденные точки на локальный экстремум (составив матрицу Гессе H и проверив знак 2-го дифференциала при помощи критерия Сильвестра ((достаточные условия))). 4. Найти точки, подозрительные на условный локальный экстремум (необходимые условия) на каждой из четырех линий, заданных условиями gi(x,y) = 0 (i = 1,…,4), обозначить буквами, указать на картинке или зафиксировать их отсутствие на картинке 5. Исследовать все найденные точки на условный локальный экстремум при помощи «окаймленного гессиана» (достаточные условия) 6. Найти градиент функции f(x,y). 7. Найти и построить (укоротив) эти градиенты в вершинах параллелограмма и в точках условного экстремума 8. Найти векторы градиентов к gi(x,y) – левым частям условий gi(x,y)=0 и построить в тех же точках нормали к линиям условий 9. Указать на картинке острый угол градиента функции f(x,y) с линиями условий в тех же точках, кроме точек условного экстремума. 10. Указать стрелками направление роста функции f(x,y) вдоль линий условия на каждой стороне параллелограмма и на их продолжении рядом с вершинами. 11. Проверить, что результаты пп 10 и 5 согласуются 12. Найти значения функции f(x,y) в точках пп 3, 5 (входящих в параллелограмм) и п. 1. 13. Найти точки с наибольшим и наименьшим значениями функции f(x,y) на параллелограмме и сами эти значения. 14. Проверить, что результаты пп 13, 10 и 3 согласуются 15. Исследовать на локальный экстремум функцию u(x,y,z)=f(x,y)+h(z). Найти критические точки, записать матрицу Гессе в них, определить: являются ли эти точки локальными экстремумами. Указания. Если масштабы на осях разные, то углы могут быть немного изменены. В частности, угол между нормалью к прямой и самой прямой может отклоняться от прямого. Если между двумя смежными вершинами параллелограмма оказались две точки условного экстремума, то для выполнения п.10 на стороне параллелограмма между этими точками, надо выполнить п.9 для произвольной точки между этими точками. Вариант 1. Исследовать функцию двух переменных f(x,y) = 12y - y3 –15x - 9x2- x3 В области, ограниченной прямыми: x+3y+1.5=0 x+3y+12=0 2x-y-5=0 2x-y+9=0 В пункте 15 рассмотреть функцию h(z)=z3-7.5z2+18z+1 2 1 0 1 2 3 4 5 6 4 2 0 2 Вариант 2. Исследовать функцию двух переменных f(x,y) = x3 + 3 x2-24 x + 6 y -2 y3 В области, ограниченной прямыми: x+3y-3=0 x+3y+4=0 2x-y-6=0 2x-y+1=0 В пункте 15 рассмотреть функцию h(z)=z3-4.5z2+6z+1 1 .5 1 .0 0 .5 0 .0 0 .5 1 .0 1 .5 2 .0 1 0 1 2 3 Вариант 3. Исследовать функцию двух переменных f(x,y) = y3+3y2-24y-24x+9x2-x3 В области, ограниченной прямыми: x+3y-12=0 x+3y-2=0 2x-y-9=0 2x-y+1=0 В пункте 15 рассмотреть функцию h(z)=2z3+3z2-12z-21 4 3 2 1 0 1 0 2 4 6 8 Вариант 4. Исследовать функцию двух переменных f4(x,y) = 12y - y3 - 12x - x3 В области, ограниченной прямыми: x+3y-12=0 x+3y-2.5=0 2x-y-11=0 2x-y-1=0 В пункте 15 рассмотреть функцию h(z)=z3+3z2-9z+1 4 3 2 1 0 1 2 0 1 2 3 4 5 6 7
www.studocu.com

Домашняя контрольная работа по высшей математике Ваш вариант соответствуют номеру в текущем списке группы у старост: 1 – 1,5,9,…, 2 – 2,6,10,…,… В этом файле содержатся функции и условия, соответствующие каждому варианту. Требуемые точки и векторы отмечаются на картинках, которые прилагаются к каждому варианту. Результаты или вручаются лично учебному ассистенту Катюхиной Ольге или складываются у куратора 2 курса Анатолию Ивановичу Саломатину комн. 726 до 19.12.13. Содержание работы 1. Найти вершины параллелограмма, ограниченного прямыми, заданными уравнениями gi(x,y) = 0 (i = 1,…,4), и обозначить их буквами на картинке. Укажите систему неравенств, задающих полученную область. 2. Найти критические точки функции f(x,y), обозначить буквами, указать на картинке или зафиксировать их отсутствие на картинке (необходимые условия) 3. Исследовать все найденные точки на локальный экстремум (составив матрицу Гессе H и проверив знак 2-го дифференциала при помощи критерия Сильвестра ((достаточные условия))). 4. Найти точки, подозрительные на условный локальный экстремум (необходимые условия) на каждой из четырех линий, заданных условиями gi(x,y) = 0 (i = 1,…,4), обозначить буквами, указать на картинке или зафиксировать их отсутствие на картинке 5. Исследовать все найденные точки на условный локальный экстремум при помощи «окаймленного гессиана» (достаточные условия) 6. Найти градиент функции f(x,y). 7. Найти и построить (укоротив) эти градиенты в вершинах параллелограмма и в точках условного экстремума 8. Найти векторы градиентов к gi(x,y) – левым частям условий gi(x,y)=0 и построить в тех же точках нормали к линиям условий 9. Указать на картинке острый угол градиента функции f(x,y) с линиями условий в тех же точках, кроме точек условного экстремума. 10. Указать стрелками направление роста функции f(x,y) вдоль линий условия на каждой стороне параллелограмма и на их продолжении рядом с вершинами. 11. Проверить, что результаты пп 10 и 5 согласуются 12. Найти значения функции f(x,y) в точках пп 3, 5 (входящих в параллелограмм) и п. 1. 13. Найти точки с наибольшим и наименьшим значениями функции f(x,y) на параллелограмме и сами эти значения. 14. Проверить, что результаты пп 13, 10 и 3 согласуются 15. Исследовать на локальный экстремум функцию u(x,y,z)=f(x,y)+h(z). Найти критические точки, записать матрицу Гессе в них, определить: являются ли эти точки локальными экстремумами. Указания. Если масштабы на осях разные, то углы могут быть немного изменены. В частности, угол между нормалью к прямой и самой прямой может отклоняться от прямого. Если между двумя смежными вершинами параллелограмма оказались две точки условного экстремума, то для выполнения п.10 на стороне параллелограмма между этими точками, надо выполнить п.9 для произвольной точки между этими точками. Вариант 1. Исследовать функцию двух переменных f(x,y) = 12y - y3 –15x - 9x2- x3 В области, ограниченной прямыми: x+3y+1.5=0 x+3y+12=0 2x-y-5=0 2x-y+9=0 В пункте 15 рассмотреть функцию h(z)=z3-7.5z2+18z+1 2 1 0 1 2 3 4 5 6 4 2 0 2 Вариант 2. Исследовать функцию двух переменных f(x,y) = x3 + 3 x2-24 x + 6 y -2 y3 В области, ограниченной прямыми: x+3y-3=0 x+3y+4=0 2x-y-6=0 2x-y+1=0 В пункте 15 рассмотреть функцию h(z)=z3-4.5z2+6z+1 1 .5 1 .0 0 .5 0 .0 0 .5 1 .0 1 .5 2 .0 1 0 1 2 3 Вариант 3. Исследовать функцию двух переменных f(x,y) = y3+3y2-24y-24x+9x2-x3 В области, ограниченной прямыми: x+3y-12=0 x+3y-2=0 2x-y-9=0 2x-y+1=0 В пункте 15 рассмотреть функцию h(z)=2z3+3z2-12z-21 4 3 2 1 0 1 0 2 4 6 8 Вариант 4. Исследовать функцию двух переменных f4(x,y) = 12y - y3 - 12x - x3 В области, ограниченной прямыми: x+3y-12=0 x+3y-2.5=0 2x-y-11=0 2x-y-1=0 В пункте 15 рассмотреть функцию h(z)=z3+3z2-9z+1 4 3 2 1 0 1 2 0 1 2 3 4 5 6 7
www.studocu.com

Домашняя контрольная работа по высшей математике Ваш вариант соответствуют номеру в текущем списке группы у старост: 1 – 1,5,9,…, 2 – 2,6,10,…,… В этом файле содержатся функции и условия, соответствующие каждому варианту. Требуемые точки и векторы отмечаются на картинках, которые прилагаются к каждому варианту. Результаты или вручаются лично учебному ассистенту Катюхиной Ольге или складываются у куратора 2 курса Анатолию Ивановичу Саломатину комн. 726 до 19.12.13. Содержание работы 1. Найти вершины параллелограмма, ограниченного прямыми, заданными уравнениями gi(x,y) = 0 (i = 1,…,4), и обозначить их буквами на картинке. Укажите систему неравенств, задающих полученную область. 2. Найти критические точки функции f(x,y), обозначить буквами, указать на картинке или зафиксировать их отсутствие на картинке (необходимые условия) 3. Исследовать все найденные точки на локальный экстремум (составив матрицу Гессе H и проверив знак 2-го дифференциала при помощи критерия Сильвестра ((достаточные условия))). 4. Найти точки, подозрительные на условный локальный экстремум (необходимые условия) на каждой из четырех линий, заданных условиями gi(x,y) = 0 (i = 1,…,4), обозначить буквами, указать на картинке или зафиксировать их отсутствие на картинке 5. Исследовать все найденные точки на условный локальный экстремум при помощи «окаймленного гессиана» (достаточные условия) 6. Найти градиент функции f(x,y). 7. Найти и построить (укоротив) эти градиенты в вершинах параллелограмма и в точках условного экстремума 8. Найти векторы градиентов к gi(x,y) – левым частям условий gi(x,y)=0 и построить в тех же точках нормали к линиям условий 9. Указать на картинке острый угол градиента функции f(x,y) с линиями условий в тех же точках, кроме точек условного экстремума. 10. Указать стрелками направление роста функции f(x,y) вдоль линий условия на каждой стороне параллелограмма и на их продолжении рядом с вершинами. 11. Проверить, что результаты пп 10 и 5 согласуются 12. Найти значения функции f(x,y) в точках пп 3, 5 (входящих в параллелограмм) и п. 1. 13. Найти точки с наибольшим и наименьшим значениями функции f(x,y) на параллелограмме и сами эти значения. 14. Проверить, что результаты пп 13, 10 и 3 согласуются 15. Исследовать на локальный экстремум функцию u(x,y,z)=f(x,y)+h(z). Найти критические точки, записать матрицу Гессе в них, определить: являются ли эти точки локальными экстремумами. Указания. Если масштабы на осях разные, то углы могут быть немного изменены. В частности, угол между нормалью к прямой и самой прямой может отклоняться от прямого. Если между двумя смежными вершинами параллелограмма оказались две точки условного экстремума, то для выполнения п.10 на стороне параллелограмма между этими точками, надо выполнить п.9 для произвольной точки между этими точками. Вариант 1. Исследовать функцию двух переменных f(x,y) = 12y - y3 –15x - 9x2- x3 В области, ограниченной прямыми: x+3y+1.5=0 x+3y+12=0 2x-y-5=0 2x-y+9=0 В пункте 15 рассмотреть функцию h(z)=z3-7.5z2+18z+1 2 1 0 1 2 3 4 5 6 4 2 0 2 Вариант 2. Исследовать функцию двух переменных f(x,y) = x3 + 3 x2-24 x + 6 y -2 y3 В области, ограниченной прямыми: x+3y-3=0 x+3y+4=0 2x-y-6=0 2x-y+1=0 В пункте 15 рассмотреть функцию h(z)=z3-4.5z2+6z+1 1 .5 1 .0 0 .5 0 .0 0 .5 1 .0 1 .5 2 .0 1 0 1 2 3 Вариант 3. Исследовать функцию двух переменных f(x,y) = y3+3y2-24y-24x+9x2-x3 В области, ограниченной прямыми: x+3y-12=0 x+3y-2=0 2x-y-9=0 2x-y+1=0 В пункте 15 рассмотреть функцию h(z)=2z3+3z2-12z-21 4 3 2 1 0 1 0 2 4 6 8 Вариант 4. Исследовать функцию двух переменных f4(x,y) = 12y - y3 - 12x - x3 В области, ограниченной прямыми: x+3y-12=0 x+3y-2.5=0 2x-y-11=0 2x-y-1=0 В пункте 15 рассмотреть функцию h(z)=z3+3z2-9z+1 4 3 2 1 0 1 2 0 1 2 3 4 5 6 7
www.studocu.com