Контрольные работы по геометрии с ответами к учебнику Атанасяна Л.С. за 1, 2, 3, 4 четверти. Геометрия контрольная
Контрольные работы по геометрии для 7 класса (УМК Л.С. Атанасян и др.)
Контрольная работа № 1 (7 класс)
по теме «Начальные геометрические сведения» (глава I, п.п. 1-13)
Три точки В, С, и D лежат на одной прямой а. Известно, что ВD = 17 см, DC = 25 см. Какой может быть длина отрезка ВС?
Сумма вертикальных углов MOE и DOC, образованных при пересечении прямых МС и DЕ, равна 204°. Найдите угол МОD.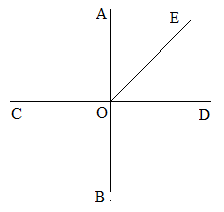
С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла. Укажите равные углы.
4* На рисунке прямая АВ перпендикулярна к прямой СD,
луч ОЕ биссектриса угла АОD. Найдите угол СОЕ.
_____________________________________________________________________________
Контрольная работа № 1 (7 класс)
по теме «Начальные геометрические сведения» (глава I, п.п. 1-13)
Вариант 2
Три точки М, N, и K лежат на одной прямой а. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние МK?
Сумма вертикальных углов АОВ и COD, образованных при пересечении прямых АD и ВС, равна 108°. Найдите угол ВОD.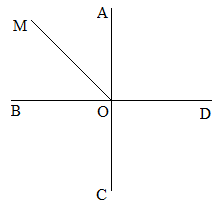
С помощью транспортира начертите угол, равный 132°, и проведите биссектрису смежного с ним угла. Укажите равные углы.
4* На рисунке прямая АС перпендикулярна к прямой ВD,
луч ОМ биссектриса угла АОВ. Найдите угол СОМ.
Контрольная работа № 2 (7 класс)
по теме «Треугольники. Задачи на построение» (глава II, п.п. 14-23)
Отрезки АВ и СD пересекаются в точке О, являющейся серединой каждого из них. Докажите, что: а) треугольники АОD и ВОС равны; б) 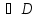 AО =
AО =  СВО.
СВО.
Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что  ADB =
ADB =  ADC. Докажите, что АВ = АС.
ADC. Докажите, что АВ = АС.
Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС.
4* Как с помощью циркуля и линейки построить угол в 11°15′?
_____________________________________________________________________________
Контрольная работа № 2 (7 класс)
по теме «Треугольники. Задачи на построение» (глава II, п.п. 14-23)
Вариант 2
Отрезки МЕ и РК пересекаются в точке D, являющейся серединой каждого из них. Докажите, что: а) треугольники РDЕ и КDМ равны; б)  PED =
PED = KMD.
KMD.
На сторонах угла D отмечены точки М и К так, что DM = DK. Точка Р лежит внутри угла D и РК = РМ. Докажите, что луч DР – биссектриса угла MDK.
Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту АН из вершины угла А.
4* Как с помощью циркуля и линейки построить угол в 67°30′?
Контрольная работа № 3 (7 класс)
по теме «Параллельные прямые» (глава III, п.п. 24-29)
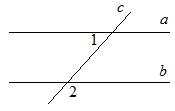
На рисунке прямые a и b параллельны,  1 = 55°. Найдите
1 = 55°. Найдите  2.
2.
Отрезки АС и BD пересекаются в их общей середине точке О. Докажите, что прямые АВ и CD параллельны.
Отрезок DM – биссектриса треугольника CDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если  СDЕ =68°.
СDЕ =68°.
4*. В треугольнике АВС  А =67°,
А =67°,  С =35°, BD – биссектриса угла АВС. Через вершину В
С =35°, BD – биссектриса угла АВС. Через вершину В
проведена прямая MN  AC. Найдите угол MBD. (Указание. Для каждого из возможных случаев сделайте чертеж.)
AC. Найдите угол MBD. (Указание. Для каждого из возможных случаев сделайте чертеж.)
____________________________________________________________________________
Контрольная работа № 3 (7 класс)
по теме «Параллельные прямые» (глава III, п.п. 24-29)
Вариант 2
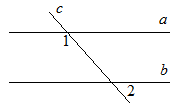
На рисунке прямые a и b параллельны,  1 = 115°. Найдите
1 = 115°. Найдите  2.
2.
Отрезки АD и BC пересекаются в их общей середине точке М. Докажите, что прямые АС и ВD параллельны.
Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне AB и пересекающая сторону AC в точке F. Найдите углы треугольника ADF, если  BAC =72°.
BAC =72°.
4*. В треугольнике CDE  С =59°,
С =59°,  Е =37°, DК – биссектриса угла CDE. Через вершину D
Е =37°, DК – биссектриса угла CDE. Через вершину D
проведена прямая AB  CE. Найдите угол ADK. (Указание. Для каждого из возможных случаев сделайте чертеж.)
CE. Найдите угол ADK. (Указание. Для каждого из возможных случаев сделайте чертеж.)
Контрольная работа № 4 (7 класс)
по теме «Сумма углов треугольника. Соотношения между сторонами и углами треугольника» (глава IV, п.п. 30-33)
В треугольнике АВС АВ > ВС > АС. Найдите  А,
А,  В,
В,  С, если известно, что один из углов треугольника равен 120°, а другой 40°.
С, если известно, что один из углов треугольника равен 120°, а другой 40°.
В треугольнике CDE точка М лежит на стороне СЕ, причем  CMD острый. Докажите, что DE > DM.
CMD острый. Докажите, что DE > DM.
Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
4*. На сторонах угла А, равного 45°, отмечены точки В и С, а во внутренней области угла –
точка D так, что  ABD = 95°,
ABD = 95°,  ACD = 90°. Найдите угол BDC.
ACD = 90°. Найдите угол BDC.
____________________________________________________________________________
Контрольная работа № 4 (7 класс)
по теме «Сумма углов треугольника. Соотношения между сторонами и углами треугольника» (глава IV, п.п. 30-33)
Вариант 2
В треугольнике АВС АВ < ВС < АС. Найдите  А,
А,  В,
В,  С, если известно, что один из углов треугольника прямой, а другой равен 30°.
С, если известно, что один из углов треугольника прямой, а другой равен 30°.
В треугольнике MNP точка K лежит на стороне MN, причем  NKP острый. Докажите, что KP < MP.
NKP острый. Докажите, что KP < MP.
Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
4*. На сторонах угла А, равного 125°, отмечены точки В и С, а внутри угла – точка D так,
что  ABD = 65°,
ABD = 65°,  ACD = 40°. Найдите угол BDC.
ACD = 40°. Найдите угол BDC.
Контрольная работа № 5 (7 класс)
по теме «Прямоугольный треугольник. Построение треугольника по трем элементам» (глава IV, п.п. 34-38)
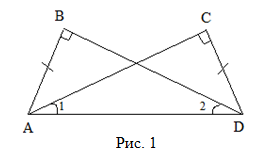
Дано: 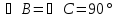 , AB = CD (Рис. 1).
, AB = CD (Рис. 1).
Доказать: 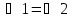 .
.
В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОК = 9 см. Найдите расстояние ОН от точки О до прямой MN.
Постройте прямоугольный треугольник по гипотенузе и острому углу.
4*. С помощью циркуля и линейки постройте угол, равный 105°.
____________________________________________________________________________
Контрольная работа № 5 (7 класс)
по теме «Прямоугольный треугольник. Построение треугольника по трем элементам» (глава IV, п.п. 34-38)
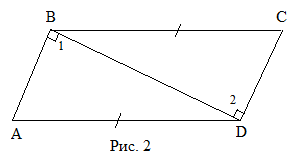
Дано: 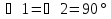 , AD = BC (Рис. 2).
, AD = BC (Рис. 2).
Доказать: AB = DC.
В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние FH от точки F до прямой DE.
Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.
4*. С помощью циркуля и линейки постройте угол, равный 165°.
infourok.ru
Геометрия в 7 классе, контрольные работы по Атанасяну за 1, 2, 3, 4 четверти
Контрольные на темы: "Начальные геометрические сведения", "Треугольник и окружность", "Параллельные прямые", "Треугольник. Соотношение между углами и сторонами"
Контрольная работа №1 на тему: "Прямая на плоскости. Углы"
Вариант I. 1. Начертите прямую АВ и отметьте точки: а) точку С, лежащую на луче ВА; б) точку D, не лежащую на прямой АВ; в) точку Е, не лежащую на прямой АВ, и проведите через эту точку прямую,+ пересекающую АВ.2. Решите задачу.а) Один из углов, образованных при пересечении двух прямых, равен 1230. Найдите остальные углы.б) Один из смежных углов в пять раз больше другого. Найдите эти углы.
3. На отрезке СD последовательно отмечены точки M и N. Найдите длину отрезка: а) MN, если CD=6 см, CN=4 см, CM=2 см.б) CN, если CM=3 см, MD=7 см, ND=1 см.
4. Биссектриса угла и прямая, пересекающая стороны угла, образуют угол α. Найдите исходный угол, если известно, что данная прямая перпендикулярна к одной из сторон.
5. Угол COD=1240, луч ОЕ является биссектрисой угла COD, а луч OF делит один из получившихся углов в отношении 3:1. Найдите получившиеся углы.
Вариант II.1. Начертите прямую АВ и отметьте точки:а) точку С, лежащую на отрезке АВ.б) точку F, не лежащую на прямой АВ.в) точку Е, не лежащую на прямой АВ, и проведите через эту точку прямую, пересекающую АВ.
2. Решите задачу.а) Один из углов, образованных при пересечении двух прямых, равен 1440. Найдите остальные углы.б) Один из смежных углов в 9 раз меньше другого. Найдите эти углы.
3. На отрезке СD последовательно отмечены точки M и N. Найдите длину отрезка:а) MN, если CD=8 см, CN=5 см, CM=1 см.б) CN, если CM=4 см, MD=9 см, ND=2 см.
4. Прямая перпендикулярна к одной из сторон угла и образует угол α с прямой проведенной из вершины угла. Найдите исходный угол.
5. Угол COD=1440, луч ОЕ и OF делят этот угол на три равных. В угле ЕOF проведена биссектриса OM. Найдите углы COM, MOD, EOM, MOF, COF.
Ответы на контрольную работу №1 на тему: "Прямая на плоскости. Углы"
Контрольная работа №2 на тему: "Треугольники"
Вариант I. 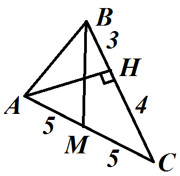 1. Используя рисунок выберите верный ответ: a) АH – медиана. б) BM – медиана. в) AH – высота. г) BM – биссектриса. д) $\bigtriangleup ABC$ – равнобедренный.
1. Используя рисунок выберите верный ответ: a) АH – медиана. б) BM – медиана. в) AH – высота. г) BM – биссектриса. д) $\bigtriangleup ABC$ – равнобедренный. 2. Периметр $\bigtriangleup ABC$ равен 12 см, сторона АС=5см, ВС=4см. Известно, что АВ=СD, ∠DCA=30°, ∠BAH=150°. а) Докажите, что $\bigtriangleup ABC=\bigtriangleup DCA$. б) Найдите длины сторон $\bigtriangleup DCA$.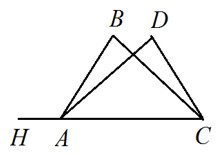 3. В $\bigtriangleup ABC$ AB=AC, AH – биссектриса, ∠ABC=57°. Найдите углы $\bigtriangleup ABC$.
3. В $\bigtriangleup ABC$ AB=AC, AH – биссектриса, ∠ABC=57°. Найдите углы $\bigtriangleup ABC$.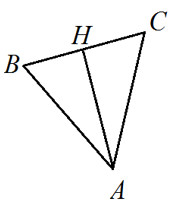 4. В окружности с центром в точке О проведены хорды АС и ВЕ, так что ∠AOB=∠COE.Докажите: а) АС=ВЕ; б) АЕ – диаметр окружности.
4. В окружности с центром в точке О проведены хорды АС и ВЕ, так что ∠AOB=∠COE.Докажите: а) АС=ВЕ; б) АЕ – диаметр окружности.
5. $\bigtriangleup ABC$ равнобедренный (ВС=АС). Точка D взята внутри треугольника так, что ВD=AD, ∠ADB=120°, ∠A=60°. Найдите ∠BDC и ∠DAC.
Вариант II. 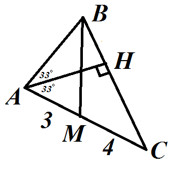 1. Используя рисунок выберите верный ответ:а) АH – биссектриса.б) BM – медиана.в) AH – высота.г) BM – биссектриса.д) $\bigtriangleup ABC$ – остроугольный.
1. Используя рисунок выберите верный ответ:а) АH – биссектриса.б) BM – медиана.в) AH – высота.г) BM – биссектриса.д) $\bigtriangleup ABC$ – остроугольный.
2. Периметр $\bigtriangleup ABC$ равен 18 см, сторона АС=6см, ВС=5см. Известно, что АВ=СD, ∠DCA=60°, ∠BAH=120°. а) Докажите, что $\bigtriangleup АВС$=$\bigtriangleup DCA$. б) Найдите длины сторон $\bigtriangleup DCA$.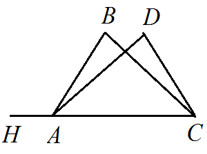 3. В $\bigtriangleup ABC$ AB=AC, AH – высота, ∠ABC=38°. Найдите углы $\bigtriangleup ABC$.
3. В $\bigtriangleup ABC$ AB=AC, AH – высота, ∠ABC=38°. Найдите углы $\bigtriangleup ABC$.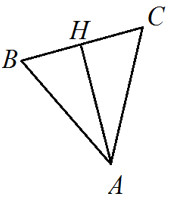 4. В окружности с центром в точке О проведены хорды АF и ВM так, что ∠AOF=∠BOM.Докажите: а) АB=FM; б) АM – диаметр окружности.
4. В окружности с центром в точке О проведены хорды АF и ВM так, что ∠AOF=∠BOM.Докажите: а) АB=FM; б) АM – диаметр окружности.
5. $\bigtriangleup ABC$ равнобедренный (ВС=АС). Точка D взята внутри треугольника, так что ВD=AD, ∠ADB=120°,; ∠A=60°. Найдите ∠BDC и ∠DAC.
Ответы на контрольную работу №2 на тему: "Треугольники"
Контрольная работа №3 на тему: "Параллельные прямые"
Вариант I. 1. Используя рисунок, докажите, что a||b и c||d.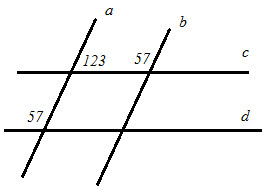
2. На рисунке ∠1=126°, а||b. Найдите ∠2, ∠3,∠4.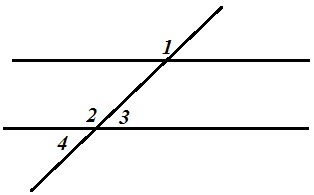
3. Прямые АВ и СD пересекаются в точке О. Докажите, что если AD||BC и OD=CO, то $\bigtriangleup AOD= \bigtriangleup COB$.
4. $\bigtriangleup ABC$ равнобедренный, МР||BC, MP||KH, ∠B=70°, AM:MB=1:2, MK:KB=1:3, AB=6 см. Найдите: ∠A, ∠AKH, ∠KHA, HC.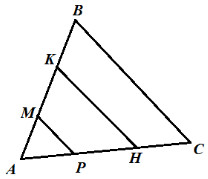
5. $\bigtriangleup ABC$ равнобедренный (AB=АС), AH – высота, ∠C=52° ∠MBA=76°. Докажите, что MB||AC.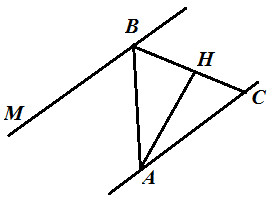
Вариант II. 1. Используя рисунок, докажите, что a||b и c||d.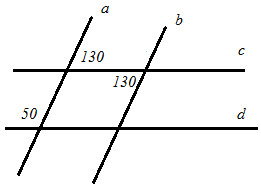
2. На рисунке ∠1=132°, а||b. Найдите ∠2, ∠3,∠4.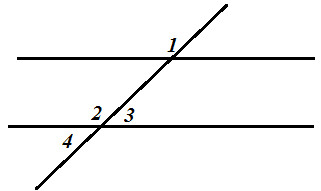
3. Прямые АВ и СD пересекаются в точке О. Докажите, что если AC||BD и AO=OB, то $\bigtriangleup AOC= \bigtriangleup ODB$.
4. $\bigtriangleup ABC$ равнобедренный, МР||BC, MP||KH, ∠B=80°, AM:MB=1:3, MK:KB=1:5, AB=8см. Найдите: ∠A, ∠AKH, ∠KHA, HC.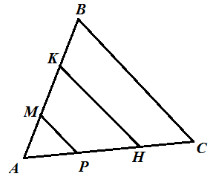
5. Дан $\bigtriangleup ABC$, AH – высота, ∠B=38° ∠MBA=104°. Докажите, что MB||AC.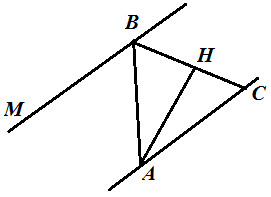
Ответы на контрольную работу №3 на тему: "Параллельные прямые"
Контрольная работа №4 на тему: "Соотношения между углами и сторонами треугольника"
Вариант I. 1. Используя рисунок, выберите верные утверждения: а) $\bigtriangleup ABC$ – равнобедренный; б) $\bigtriangleup ABC$ – тупоугольный; в) ∠C=80° г) ∠2 – внешний для $\bigtriangleup ABC$. 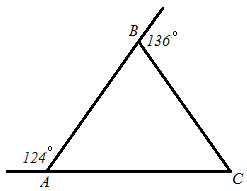
2. В равнобедренном $\bigtriangleup ABC$ с основанием АС, АН – высота, ∠B=45°. Найдите все возможные внутренние углы $\bigtriangleup ABC$.
3. В $\bigtriangleup ABC$ ∠B больше ∠A на 30°, а ∠C в $1\frac{1}{3} $раза больше ∠А. Найдите углы $\bigtriangleup ABC$.
4. Используя данные рисунка, найдите АВ.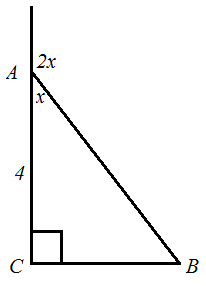
5. В равностороннем $\bigtriangleup ABC$ проведена высота АН. На стороне АВ отмечена точка М. Через эту точку проведен перпендикуляр к стороне АС, который пересекает ее в точке N. АН и MN пересекаются в точке О. Найдите углы четырехугольника MBHO.
Вариант II. 1. Используя рисунок, выберите верные утверждения:а) BC=AC;б) $\bigtriangleup ABC$ – прямоугольный;в) ∠A=67°г) внешний угол к ∠A=153°.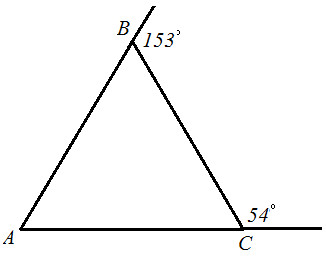
2. В равнобедренном $\bigtriangleup ABC$ с основанием АС, АН – высота, ∠B=50°. Найдите все возможные внутренние углы $\bigtriangleup ABC$.
3. В $\bigtriangleup ABC$ ∠B больше ∠A на 12°, а ∠C в 2 раза больше ∠А. Найдите углы $\bigtriangleup ABC$.
4. Используя данные рисунка, найдите BC.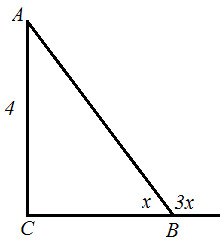
5. В равностороннем $\bigtriangleup ABC$ проведена высота АН. На стороне АВ отмечена точка М. Через эту точку проведена прямая, пересекающая сторону АС в точке N. АН и MN пересекаются в точке О. ∠MNA=60°. Найдите углы четырехугольника MBHO.
Ответы на контрольную работу №4 на тему: "Соотношения между углами и сторонами треугольника"
Контрольная работа №5 (итоговая)
Вариант I. 1. Используя рисунок, найдите равнобедренные треугольники: 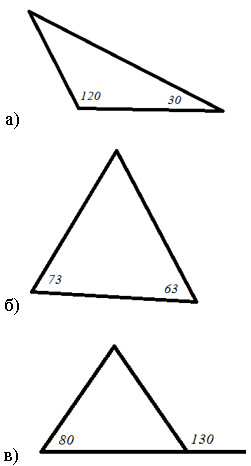
2. В равностороннем $\bigtriangleup ABC$ на биссектрисе ВН взята точка О так, что ON⊥BC; OM⊥AB (N∈BC, M∈AB). Докажите, что $\bigtriangleup AOM= \bigtriangleup NOC$. Найдите углы этих треугольников.
3. В окружности с центром в точке О хорды АВ и СD пересекаются в точке N. ∠CNB=150°; CD⊥OB; CO⊥AB. Найдите ∠COB.
4. В $\bigtriangleup ABC$ AB=BC, на сторонах AB и АC отмечены точки К и Е так, что КЕ||ВС, KH – биссектриса ∠BKE; ∠BKH=32°. Найдите углы $\bigtriangleup ABC$.
5. Докажите, что если два отрезка равны и точкой пересечения делятся в одинаковом отношении, то отрезки, соединяющие концы данных отрезков, параллельны.
Вариант II. 1. Используя рисунок, найдите равнобедренные треугольники: 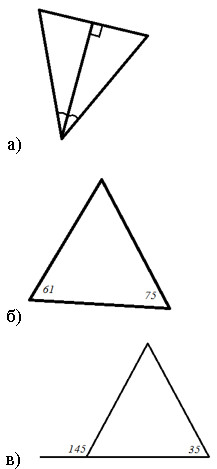
2. В равностороннем $\bigtriangleup ABC$ на высоте ВН взята точка О так, что ON⊥BC; OM⊥AB (N∈BC, M∈AB). Докажите, что $\bigtriangleup MOB= \bigtriangleup NOB$. Найдите углы $\bigtriangleup ABC$.
3. В окружности с центром в точке О хорды АВ и СD пересекаются в точке N. ∠AND=120°; CD⊥OB; CO⊥AB. Найдите ∠COB.
4. В $\bigtriangleup ABC$ AB=BC, на сторонах AB и АC отмечены точки M и N так, что MN||ВС, NH – биссектриса ∠MNC; ∠HNC=53°. Найдите углы $\bigtriangleup ABC$.
5. Докажите, что если два отрезка пересекаются в середине, то отрезки, соединяющие концы данных отрезков, параллельны.
Ответы на контрольную работу №5 (итоговая)
Ответы на контрольную работу №1 на тему: "Прямая на плоскости. Углы"Вариант I.2. a) 1230, 570, 570; б) 300 и 1500.3. а) 2 см б) 9см.4. 180-2α.5. COE=62, MOF=15.5, FOD=46.5.
Вариант II.2. a) 1440, 360, 360; б) 180 и 1620.3. а) 4 см б) 11 см.4. 2α-180.5. COM=72, MOD=72, EOM=24, MOF=24, COF=96.
Ответы на контрольную работу №2 на тему: "Треугольники"Вариант I.1. б, в. 2. DC=3; AC=5; AD=4.3. ∠B=57°; ∠C=57°; ∠A=66°. 5. ∠BDC=120°; ∠DAC=30°.
Вариант II.1. a, в, д. 2. DC=7; AC=6; AD=5.3. ∠B=38°; ∠C=38°; ∠A=104°. 5. ∠BDC=105°;∠DAC=45°.
Ответы на контрольную работу №3 на тему: "Параллельные прямые"Вариант I.2. ∠2=126°; ∠3= 54°;∠4=54°.4. ∠A=40°; ∠AKH=70°; ∠KHA=70°; HC=3.
Вариант II.2. ∠2=132°; ∠3=48°;∠4=48°.4. ∠A=20°; ∠AKH=80°; ∠KHA=80°; HC=5.
Ответы на контрольную работу №4 на тему: "Соотношения между углами и сторонами треугольника"Вариант I.1. 3 и 4.2. 67,5°; 22,5°; 45°; 90°; 90°; 45°. 3. 45°; 75°; 60°.4. AB=8.5. 150°; 60°; 90°; 60°.
Вариант II.1. 1 и 3.2. 40°; 25°; 65°; 90°; 90°; 50°. 3. 42°; 84°; 54°.4. BC=8.5. 120°; 60°; 90°; 60°.
Ответы на контрольную работу №5 (итоговая)Вариант I.1. а, в. 2. 60°; 30°; 90°.3. 30°.4. 32°; 32°; 116°.
Вариант II.1. а, в. 2. 30°; 30°; 120°.3. 60°.4. 32°; 74°; 74°.
mathematics-tests.com
Контрольные работы по геометрии 7 класс
Контрольная работа №2 М7кл l Вариант 1. На рисунке отрезки АВ и СD имеют общую середину. Докажите, что треугольники АОС и ВОD равны. 2. Даны прямая и отрезок. Постройте точку, такую, чтобы перпендикуляр, опущенный из этой точки на  прямую, равнялся данному отрезку. прямую, равнялся данному отрезку. 3. В треугольнике АВС АВ равно ВС. На медиане ВЕ отмечена точка М, а на сторонах АВ и ВС – точки Р и К соответственно. (Точки Р, М и К не лежат на одной прямой). Известно, что ВМР = ВМК. Докажите, что: а) углы ВРМ и ВКМ равны; б) прямые РК и ВМ взаимно перпендикулярны. 4* Дан угол в 54о. Можно ли с помощью циркуля и линейки построить угол в 18о? | Контрольная работа №2 М7кл ll Вариант 1. На рисунке луч ВD является биссектрисой угла АВС, а луч DВ является биссектрисой угла АDС. Докажите, что треугольники АВD и СВD равны.  2. Дан отрезок. Постройте две какие либо взаимно 2. Дан отрезок. Постройте две какие либо взаимно перпендикулярные прямые и на одной из них от точки пересечения отложите отрезок, равный данному. 3. Внутри треугольника АВС взята точка О, причём ВОС = ВОА, АО = ОС. а) Докажите, что углы ВАС и ВСА равны. б) Докажите, что прямая ВО проходит через середину отрезка АС. 4* Как с помощью циркуля и линейки построить угол 11о15’? | Контрольная работа №2 М7кл l Вариант 1. На рисунке отрезки АВ и СD имеют общую середину. Докажите, что треугольники АОС и ВОD равны. 2. Даны прямая и отрезок. Постройте точку, такую,  чтобы перпендикуляр, опущенный из этой точки на чтобы перпендикуляр, опущенный из этой точки на прямую, равнялся данному отрезку. 3. В треугольнике АВС АВ равно ВС. На медиане ВЕ отмечена точка М, а на сторонах АВ и ВС – точки Р и К соответственно. (Точки Р, М и К не лежат на одной прямой). Известно, что ВМР = ВМК. Докажите, что: а) углы ВРМ и ВКМ равны; б) прямые РК и ВМ взаимно перпендикулярны. 4* Дан угол в 54о. Можно ли с помощью циркуля и линейки построить угол в 18о? | Контрольная работа №2 М7кл ll Вариант 1. На рисунке луч ВD является биссектрисой угла АВС, а луч DВ является биссектрисой угла АDС. Докажите, что треугольники АВD и СВD равны.  2. Дан отрезок. Постройте две какие либо взаимно 2. Дан отрезок. Постройте две какие либо взаимно перпендикулярные прямые и на одной из них от точки пересечения отложите отрезок, равный данному. 3. Внутри треугольника АВС взята точка О, причём ВОС = ВОА, АО = ОС. а) Докажите, что углы ВАС и ВСА равны. б) Докажите, что прямая ВО проходит через середину отрезка АС. 4* Как с помощью циркуля и линейки построить угол 11о15’? | Контрольная работа №2 М7кл lll Вариант 
1. На рисунке отрезок АВ равен отрезку СD, а отрезок ВС равен отрезку АD. Докажите, что треугольники АВD и СВD равны. 2. Даны неразвёрнутый угол и отрезок. Постройте точку, удалённую от вершины угла на расстояние, равное половине данного отрезка. 3. На высоте равнобедренного треугольника АСВ, проведённой к основа- нию АС, взята точка Р, а на сторонах АВ и ВС – точки М и К соответственно. (Точки М,Р и К не лежат на одной прямой). Известно, что ВМ = ВК. а) Докажите, что углы ВМР и ВКР равны. б) Докажите, что углы КМР и РКМ равны. 4* Дан угол в 34о Можно ли с помощью циркуля и линейки построить угол в 12о? | Контрольная работа №2 М7кл  lV Вариант lV Вариант 1. На рисунке отрезки АВ и СD являются диаметрами окружности. Докажите, что треугольники АОD и ВОС равны. 2. Даны неразвёрнутый угол и отрезок. Постройте какой либо угол, равный данному, и на его стороне построй- те точку, удалённую от вершины угла на расстояние, равное половине данного отрезка. 3. На сторонах АВ, ВС, АС равнобедренного треугольника АВС с основа- нием АС отмечены точки М, К и Р соответственно так, что АМР = РКС и АМ = КС. а) Докажите, что МР = РК. б) Докажите, что прямые МК и ВР взаимно перпендикулярны. 4*Как с помощью циркуля и линейки построить угол в 67о30’? | Контрольная работа №2 М7кл lll Вариант 
1. На рисунке отрезок АВ равен отрезку СD, а отрезок ВС равен отрезку АD. Докажите, что треугольники АВD и СВD равны. 2. Даны неразвёрнутый угол и отрезок. Постройте точку, удалённую от вершины угла на расстояние, равное половине данного отрезка. 3. На высоте равнобедренного треугольника АСВ, проведённой к основа- нию АС, взята точка Р, а на сторонах АВ и ВС – точки М и К соответственно. (Точки М,Р и К не лежат на одной прямой). Известно, что ВМ = ВК. а) Докажите, что углы ВМР и ВКР равны. б) Докажите, что углы КМР и РКМ равны. 4* Дан угол в 34о Можно ли с помощью циркуля и линейки построить угол в 12о? | Контрольная работа №2 М7кл  lV Вариант lV Вариант 1. На рисунке отрезки АВ и СD являются диаметрами окружности. Докажите, что треугольники АОD и ВОС равны. 2. Даны неразвёрнутый угол и отрезок. Постройте какой либо угол, равный данному, и на его стороне построй- те точку, удалённую от вершины угла на расстояние, равное половине данного отрезка. 3. На сторонах АВ, ВС, АС равнобедренного треугольника АВС с основа- нием АС отмечены точки М, К и Р соответственно так, что АМР = РКС и АМ = КС. а) Докажите, что МР = РК. б) Докажите, что прямые МК и ВР взаимно перпендикулярны. 4*Как с помощью циркуля и линейки построить угол в 67о30’? | compedu.ru
Контрольные работы. Геометрия - 10. Атанасян Л.С.
Контрольная работа по геометрии
«Планиметрия»
1 вариант
-
Докажите, что если трапеция вписана в окружность, то она равнобедренная.
-
На окружности радиуса R последовательно отмечены точки A, B,C, D так, что величины дуг АВ и ВС равны 50˚ и 80˚, диагонали четырехугольника ABCD равны между собой. Найти длину наибольшей стороны четырехугольника.
-
Отрезок СН – высота прямоугольного треугольника АВС (). HL =3HK, где HL и HK – биссектрисы треугольников ВСН и АСН соответственно, АВ = . Найти площадь треугольника АВС.
Контрольная работа по геометрии
«Планиметрия»
2 вариант
-
Через точку пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны ВC и АD в точках N и Н соответственно. Докажите, что BN = DН.
-
На окружности радиуса R последовательно отмечены точки K, M, N, Q так, что величины дуг КМ и MN равны 40˚ и 100˚, хорды KN и MQ пересекаются под углом 70˚. Найти длину наибольшей стороны четырехугольника.
-
В прямоугольном треугольнике АВС () проведена высота СН. Отрезки АМ и СР – медианы треугольников АСН и НСВ, причем 3АМ = 4СР. Найти радиус окружности, описанной около треугольника АВС, если его площадь равна 96.
……………………………………………………………………………………………………
Контрольная работа по геометрии №1
«Взаимное расположение прямых в пространстве»
1 вариант
-
Прямая а параллельна плоскости , прямая в лежит в плоскости . Определите, могут ли прямые а и в:
а) быть параллельными;
б) пересекаться;
в) быть скрещивающимися.
-
Прямая МА проходит через вершину квадрата ABCD и не лежит в плоскости квадрата.
а) Докажите, что МА и ВС – скрещивающиеся прямые.
б) Найдите угол между прямыми МА и ВС, если ∠МАD = 45˚.
-
Плоскость проходит через середины боковых сторон АВ и СD трапеции ABCD – точки M и N.
а) Докажите, что AD║.
б) Найдите ВС, если AD = 10 см, MN = 8 см.
-
(Дополнительно) Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник – ромб.
Контрольная работа по геометрии №1
«Взаимное расположение прямых в пространстве»
2 вариант
-
Прямая а параллельна плоскости , прямая в пересекает плоскость . Определите, могут ли прямые а и в:
а) быть параллельными;
б) пересекаться;
в) быть скрещивающимися.
-
Прямая CD проходит через вершину треугольника ABC и не лежит в плоскости АВС. Е и F – середины отрезков АВ и ВС
а) Докажите, что СD и EF – скрещивающиеся прямые.
б) Найдите угол между прямыми СD и EF, если ∠DСА= 60˚.
-
Плоскость проходит через основание АD трапеции ABCD. M и N – середины боковых сторон трапеции
а) Докажите, что MN║.
б) Найдите AD, если ВС = 4 см, MN = 6 см.
-
(Дополнительно) Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник – ромб.
…………………………………………………………………………………………………………..
Контрольная работа по геометрии №1.2 Г - 10
«Параллельность плоскостей»
infourok.ru
Контрольные работы по геометрии(7класс)
Контрольная работа №1 Начальные геометрические сведения
Контрольная работа №1 Начальные геометрические сведения
Вариант I
1. Три точки В, С и D лежат на одной прямой. Известно, что ВD = 17 см, DС = 25 см. Какой может быть длина отрезка ВС?
2. Сумма вертикальных углов МОЕ и DОС, образованных при пересечении прямых МС и DЕ, равна 204о. Найдите угол МОD.
3. С помощью транспортира начертите угол, равный 78о, и проведите биссектрису смежного с ним угла.
Вариант II
1. Три точки M, N, K лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Какой может быть длина отрезка MK?
2. Сумма вертикальных углов AOB и COD, образованных при пересечении прямых AD и BC, равна 108о. Найдите угол BОD.
3. С помощью транспортира начертите угол, равный 132о, и проведите биссектрису одного из смежных с ним углов.
Контрольная работа №2 Треугольники
Контрольная работа №2 Треугольники
Вариант I

 1. На рисунке отрезки АВ и СD имеют общую середину О. Докажите, что
1. На рисунке отрезки АВ и СD имеют общую середину О. Докажите, что  .
.
2. Луч АD – биссектриса угла А. на сторонах угла А отмечены точки В и С так, что  . Докажите, что АВ = АС.
. Докажите, что АВ = АС.
3. Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС
Вариант II
1 . На рисунке отрезки МЕ и РК точкой D делятся пополам . Докажите, что
. На рисунке отрезки МЕ и РК точкой D делятся пополам . Докажите, что  .
.

2. На сторонах угла D отмечены точки М и К так, что DМ = DК. Точка Р лежит внутри угла D, и РК = РМ. Докажите, что луч DР – биссектриса угла МDК.
3. Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А
Контрольная работа №3 Параллельные прямые
Контрольная работа №3 Параллельные прямые
Вариант I
1. Отрезки EF и PQ пересекаются в их середине М. Докажите, что РЕ║QF.
2. Отрезок DM – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DMN, если 
Вариант II
1. Отрезки MN и EF пересекаются в их середине Р. Докажите, что ЕN║МF.
2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если  .
.
Контрольная работа №4 Соотношения между сторонами и углами треугольника.
Контрольная работа №4 Соотношения между сторонами и углами треугольника.
Вариант I
1 . На рисунке
. На рисунке  ,
,  , АC = 12 см. Найдите сторону АВ треугольника АВС.
, АC = 12 см. Найдите сторону АВ треугольника АВС.
2. В треугольнике СDЕ точка М лежит на стороне СЕ, причем угол СМD острый. Докажите, что DЕ > DМ.
3. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
Вариант II
1 . На рисунке
. На рисунке  ,
,  , BC = 9 см. Найдите сторону АC треугольника АВС.
, BC = 9 см. Найдите сторону АC треугольника АВС.
2 В треугольнике MNP точка K лежит на стороне MN, причем угол NKP острый. Докажите, что KP < МP.
3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
Контрольная работа №5 Прямоугольные треугольники
Контрольная работа №5 Прямоугольные треугольники.
Вариант I
1. В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОК = 9 см. Найдите расстояние от точки О до прямой МN.
2. Постройте прямоугольный треугольник по гипотенузе и острому углу.
3. С помощью циркуля и линейки постройте угол, равный 150о.
Вариант II
1. В прямоугольном треугольнике DCE c прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние от точки F до прямой DE.
2. Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.
3. С помощью циркуля и линейки постройте угол, равный 105о.
Итоговая контрольная работа
Итоговая контрольная работа
Вариант I
1.В равнобедренном треугольнике АВС с основанием АС на медиане ВД отмечена точка К, а на сторонах АВ и ВС – точки М и N соответственно. Известно, что ВКМ = ВКN, ВМК=110о. а) Найдите угол ВNК; б) Докажите, что прямые МN и ВК взаимно перпендикулярны.
2. На сторонах АВ, ВС и СА треугольника АВС отмечены точки D, E и F соответственно. Известно, что угол АВС=61о, угол CEF =60о, угол ADF=61о. а) найдите угол DEF; б) Докажите, то прямые АВ и EF пересекаются.
3. В прямоугольном треугольнике АВС катет АВ=3см, а угол С=15о . На катете АС отмечена точка так, что угол CBD= 15о. а) Найдите длину отрезка BD; б) Докажите, что ВС< 12 см.
Вариант II
1.В треугольнике АВС угол А=55о.Внутри треугольника отмечена точка О так, что углы АОВ=СОВ и АО=ОС. а) Найдите угол АСВ; б) Докажите, что прямая ВО является серединным перпендикуляром к стороне АС.
2.На прямой последовательно отложены отрезки АВ, ВС, СD.Точки E и F расположены по разные стороны от этой прямой, причём угол ABE=140о , угол ACF=40о, угол FBD=49о, угол ACE=48о. Докажите, что: а)прямые BE и CFпараллельны; б) прямые BF и CEпересекаются.
3. В треугольнике АВС угол В=90о, угол С=60о, ВС=2см. На стороне ВС=2см. На стороне АС отмечена точка D так, что угол ABD=30о. а) Найдите длину отрезка AD; б) Докажите, что периметр треугольника АВС меньше 10 см.
www.metod-kopilka.ru
Контрольные работы по геометрии с ответами к учебнику Атанасяна Л.С. за 1, 2, 3, 4 четверти
Контрольные на темы: "Аксиомы стереометрии. Взаимное расположение прямой и плоскости", "Перпендикулярность прямых и плоскостей", "Многогранники" и др.
Контрольная работа №1
Аксиомы стереометрии. Взаимное расположение прямой и плоскостиВариант I
Часть А
1) Прямые a и b скрещивающиеся. Прямая с параллельна прямой b. Могут ли прямые а и с пересекаться?
2) Плоскость α проходит через верхнее основание трапеции АВСD. Докажите, что любая прямая, лежащая в плоскости α и параллельная прямой ВС, параллельна прямой АD. Точки М и N - середины боковых сторон. Найдите АD, если BC=8, MN=12.
3) Прямая FА проходит через вершину параллелограмма АВСD и не лежит в плоскости параллелограмма.а) Докажите, что FA и CD скрещивающиеся.б) Чему равен угол между прямыми FA и CD, если угол FAB равен 30 градусов?
Часть Б
1) Прямая а параллельна плоскости α, прямая b также параллельна плоскости α. Могут ли а и b:а) Быть параллельными?б) Пересекаться?в) Быть скрещивающимися прямыми?
2) Точка М лежит вне плоскости параллелограмма АВСD.а) Докажите, что средние линии треугольников MAD и MBC параллельны.б) Найдите эти средние линии, если боковая сторона параллелограмма равна 5, а его высота равная 4 и делит сторону, к которой проведена, пополам.
3) Через вершину С квадрата АВСD, проходит прямая СК, не лежащая в плоскости квадрата.а) Докажите, что СК и АD скрещивающиеся.б) Чему равен угол между СК и АD. Угол СВК равен 45 градусов, угол СКВ равен 75 градусов?
Часть В
1) Две плоскости пересекаются по прямой L. Прямые L и A скрещивающиеся, прямые L и В параллельны. Могут ли прямые А и В:а) Лежать в одной из плоскостей?б) Лежать в разных плоскостях?в) Пересекать эти плоскости?В случае утвердительного ответа укажите взаимное расположение прямых L и A.
2) Плоскость α пересекает стороны АВ и ВС треугольника АВС в точках М и N соответственно. BN:NC=5:8. MB:AB=5:13.а) Докажите, что АС || α.б) Найдите MN, если АС=26.
3) Точки А, В, С и D не лежат в одной плоскости. Найдите угол между прямыми АС и BD, если АС=16, ВD=20. Расстояние между серединами AD и ВС равно 6.
Вариант II
Часть А
1) Прямые a и b параллельны. Прямая с скрещивающиеся с прямой b. Могут ли прямые b и с быть параллельны?
2) Плоскость α проходит через нижнее основание трапеции АВСD, докажите что любая прямая лежащая в плоскости α и параллельная прямой ВС, параллельна прямой АD. Точки М и N - это середины боковых сторон. Найдите ВС, если AD=24, MN=18.
3) Прямая GА проходит через вершину трапеции АВСD и не лежит в ее плоскости.а) Докажите, что GА и ВC скрещивающиеся.б) Чему равен угол между прямыми GА и ВC, если угол GAD равен 70 градусов?
Часть Б
1) Прямая а пересекает плоскость α, прямая b также пересекает плоскости α. Могут ли а и b:а) Быть параллельными?б) Пересекаться?в) Быть скрещивающимися прямыми?
2) Треугольник АВС и трапеция KMNP имеют общую среднюю линию EF, MN||EF, EF||BC.а) Докажите, что ВС|| KP.б) Найдите KP и MN, если ВС=24. КР:MN = 8:3.
3) Точка F лежит вне плоскости трапеции ABCD.а) Докажите, что AF и BC скрещивающиеся.б) Чему равен угол между AF и BC, если угол AFD равен 70 градусов, угол FDA равен 40 градусов?
Часть В
1) Две плоскости пересекаются по прямой L. Прямые L и A скрещивающиеся, прямые L и В скрещивающиеся. Могут ли прямые А и В:а) Лежать в одной из плоскостей?б) Лежать в разных плоскостях?в) Пересекать эти плоскости?В случае утвердительного ответа укажите взаимное расположение прямых L и A.
2) Плоскость α проходит через сторону АВ треугольника АВС. Прямая пересекает стороны ВС и АС в точках M и N соответственно. МС:ВC=6:13 NC:AN=6:7.а) Докажите, что MN || α.б) Найдите MN, если АС=39.
3) Точки А, В, С и D не лежат в одной плоскости. Найдите угол между прямыми АС и BD, если АС=10, ВD=10. Расстояние между серединами AD и ВС равно 5.
Ответы на контрольную работу №1
Контрольная работа №2
Перпендикулярность прямых и плоскостейВариант I
Часть А
1) Отрезок КС – перпендикуляр к плоскости треугольника АВС, КВ перпендикулярно АВ.а) Докажите, что треугольник АВС прямоугольный.б) Докажите перпендикулярность плоскостей КАС и АВС. в) Чему равен КВ, если АС=14, ВС=6. Угол КВС равен 45 градусам.
2) Основание АС равнобедренного треугольника лежит в плоскости α. Найдите расстояние от точки А до плоскости α, если АВ=5, $АС=2\sqrt{23}$, а двугранный угол между плоскостью треугольника и плоскостью α равен 60 градусам.
3) Из точки А к плоскости α проведены наклонные АВ и АС, образующие с плоскость угол 60 градусов. ВС=АС=6. Найдите АВ.
Часть Б
1) Отрезок КА – перпендикуляр к плоскости АВС. Точка М - середина ВС. КМ перпендикулярно ВС. АВ=ВСа) Докажите, что треугольник АВС - равносторонний.б) Докажите перпендикулярность плоскостей КВС и КАМ.в) Найдите площадь треугольника АВС, если ВК=8, $КА=\sqrt{39}$, ВС=6.
2) Точка S удалена от вершин правильного треугольника на $\sqrt{33\frac{3}{4}}$ см. Найдите двугранный угол SABC, если АВ=9.
3) Прямая АВ – ребро двугранного угла, равного 90 градусов. Прямые $АА_{1}$ и $ВВ_{1}$ принадлежат разным граням данного угла. $АА_{1}||ВВ_{1}$, $ВВ_{1}$ перпендикулярно АВ. Докажите, что прямые $АА_{1}$ и $ВВ_{1}$ скрещивающиеся. Найдите угол между этими прямыми.
Часть В
1) Точка О лежит на биссектрисе угла АВС, равного 60 градусов, отрезок DO перпендикулярен плоскости АВС. АВ=АС.а) Докажите, что точка D равноудалена от точек А и С.б) Докажите перпендикулярность плоскостей DAC и DOВ. в) Найдите DB, если АС=12 и DO=8.
2) Равнобедренные треугольники АВС и АДС имеют общее основание АС, двугранный угол ВАСД - прямой. Найдите двугранный угол ДСВА, если угол АСД равен 45 градусов, а угол САВ равен 60 градусов.
3) В кубе $АВСДА_{1}В_{1}С_{1}Д_{1}$ постройте и найдите линейный угол между плоскостями сечений $АВ_{1}С_{1}Д$ и $А_{1}Д_{1}СВ$.
Вариант II
Часть А
1) Отрезок КС – перпендикуляр к плоскости треугольника АВС, КВ перпендикулярно АВ.а) Докажите, что треугольник АВС - прямоугольный.б) Докажите перпендикулярность плоскостей КАС и АВС. в) Найдите КВ, если АС=16, ВС=8. Угол КВС равен 45 градусам.
2) Основание АС равнобедренного треугольника лежит в плоскости α. Найдите расстояние от точки А до плоскости α, если АВ=20, АС=25, а двугранный угол между плоскостью треугольника и плоскостью α равен 45 градусам.
3) Из точки А к плоскости α проведены наклонные АВ и АС и перпендикуляр АО. Наклонные образуют с этой плоскостью углы равные 60 градусам. Найдите ВС, если ВС=ВО, ОС=8.
Часть Б
1) Отрезок КА – перпендикуляр к плоскости прямоугольника АВСД. Точка О - пересечение АС и ВД. КО перпендикулярно ВД.а) Докажите, что АВСД - квадрат.б) Перпендикулярность плоскостей КВД и КОА.в) Найдите площадь прямоугольника АВСД, если КО=5, КА=3, угол ВКД равен 90 градусам.
2) Точка S удалена от вершин правильного треугольника на $\sqrt{48} см$. Найдите двугранный угол SABC, если АВ=12.
3) Прямая АВ – ребро двугранного угла, равного 45 градусам. Прямые $АА_{1}$ и $ВВ_{1}$ принадлежат разным граням данного угла. прямые $АА_{1}$ и $ВВ_{1}$ перпендикулярны прямой АВ. Каким может быть расположение прямых $АА_{1}$ и $ВВ_{1}$? Докажите свое утверждение.
Часть В
1) Отрезок ДО – перпендикуляр к плоскости угла АВС, равного 90 градусам. Точка О лежит внутри угла, а точка Д равноудалена от его сторон.а) Докажите, что прямая ВО делит угол АВС пополам.б) Докажите перпендикулярность плоскостей DAC и DOВ. в) Найдите DО, если АС=12 и DВ=16.
2) Равнобедренный треугольник АДС с углом Д равным 90 градусам, и равносторонний треугольник АВС имеют общее основание АС. Двугранный угол ВАСД - прямой. а) Найдите все углы между прямыми проведенными к вершинам треугольника АВС и этой плоскостью. б) Найдите углы треугольника образованного высотами треугольников АВС и АДС, опущенными к стороне АС.
3) В кубе $АВСДА_{1}В_{1}С_{1}Д_{1}$ постройте и найдите линейный угол между плоскостями сечений $С_{1}Д_{1}АВ$ и $ДСВ_{1}А_{1}$.
Ответы на контрольную работу №2
Контрольная работа №3
МногогранникиВариант I
Часть А
1) Основание прямой призмы – прямоугольный треугольник с гипотенузой 5см и катетом 4см. Найдите площадь боковой поверхности, если грань содержащая наименьший катет – квадрат.
2) Боковое ребро правильной четырехугольной пирамиды равно 8см, и образует угол 30 градусов с плоскостью основания.а) Найдите высоту пирамиды.б) Найдите площадь боковой поверхности.
3) Ребро правильного тетраэдра равно а. Постройте сечение плоскостью, проходящей через ребро АВ и делящее его в отношении 1:3, и проходящей параллельно ребру ВС. Найдите площадь сечения.
Часть Б
1) Основание прямого параллелепипеда – ромб с диагоналями 48 и 20 см. Большая диагональ параллелепипеда образует с плоскостью основания угол в 45 градусов. Найдите площадь полной поверхности.
2) Основание пирамиды - правильный треугольник с площадью равной $16\sqrt{3}$. Две боковые грани перпендикулярны плоскости основания, а третья наклонена к ней под углом 45 градусов. а) Найдите длину ребер пирамиды. б) Найдите площадь боковой поверхности.
3) Ребро куба $АВСДА_{1}В_{1}С_{1}Д_{1}$ равно а. Постройте сечение куба плоскостью, проходящей через прямую $АД_{1}$ и середину ВС. Найдите площадь сечения.
Часть В
1) Основание прямой призмы - прямоугольный треугольник с катетами 12 и 9 см. Найдите площадь боковой поверхности призмы, если ее наименьшее сечение, проходящее через боковое ребро - квадрат.
2) Основание пирамиды – ромб с меньшей диагональю d и тупым углом α. Все двугранные углы при основании пирамиды равны β. Найдите площадь боковой поверхности пирамиды.
3) Ребро куба $АВСДА_{1}В_{1}С_{1}Д_{1}$ равно а. Постройте сечения куба плоскостью, проходящей через середины ребер $АА_{1}$, АД, $А_{1}В_{1}$.
Вариант II
Часть А
1) Основание прямой призмы – прямоугольный треугольник с гипотенузой 5см и катетом 12см. Найдите площадь боковой поверхности, если грань содержащая больший катет – квадрат.
2) Высота правильной четырехугольной пирамиды равна 6 см, а боковое ребро образует угол 45 градусов с плоскостью основания.а) Найдите длину бокового ребра пирамиды. б) Найдите площадь боковой поверхности.
3) Ребро правильного тетраэдра равно а. Постройте сечение плоскостью, проходящей через ребро АС и делящее его в отношении 1:2, и проходящей параллельно ребру АВ. Найдите площадь сечения.
Часть Б
1) Основание прямого параллелепипеда – ромб с большей диагональю 30 см. Меньшая диагональ параллелепипеда образует с плоскостью основания угол в 45 градусов и равна $24\sqrt{2}$. Найдите площадь полной поверхности.
2) Основание пирамиды - равнобедренный прямоугольный треугольник с гипотенузой равной $6\sqrt{2}$. Две боковые грани, содержащие катеты, перпендикулярны плоскости основания, а третья наклонена к ней под углом 30 градусов. а) Найдите длину ребер пирамиды.б) Найдите площадь боковой поверхности.
3) Ребро куба $АВСДА_{1}В_{1}С_{1}Д_{1}$ равно а. Постройте сечение куба плоскостью, проходящей через точку В и середину ДА, параллельно $А_{1}Д$. Найдите площадь сечения.
Часть В
1) Основание прямой призмы - равнобедренный треугольник с боковой стороной 26 см и основанием 20 см. Найдите площадь боковой поверхности призмы, если ее наименьшее сечение, проходящее через боковое ребро - квадрат.
2) Основание пирамиды – ромб с боковой стороной равной а и острым углом α. Все двугранные углы при основании пирамиды равны β. Найдите площадь боковой поверхности пирамиды.
3) Ребро куба $АВСДА_{1}В_{1}С_{1}Д_{1}$ равно а. Постройте сечения куба плоскостью, проходящей через середины ребер АВ, $ДД_{1}$, $В_{1}С_{1}$.
Ответы на контрольную работу №3
Ответы на контрольную работу №1
Вариант IЧасть А1. Да, если лежат в одной плоскости.2. 16.3. 30 см.
Часть Б1. 2. 3.3. 60.
Часть В1. 2. 10.3. 90.
Вариант IIЧасть А1. Нет.2. 12.3. 70.
Часть Б1. 2. КР=32; MN=12.3. 70.
Часть В1. 2. 18.3. 60.
Ответы на контрольную работу №2
Вариант IЧасть А1. $\sqrt{116}$.2. 6.3. 6.
Часть Б1. 12.2. 45.3. 90.
Часть В1. 16.2. 60.3. 90.
Вариант IIЧасть А1. 4$\sqrt{10}$2. $7,5\sqrt{2}$.3. 8.
Часть Б1. 32.2. 60.
Часть В1. 8.2. а) 45, 45, 30; б) 30,60,90.3. 90.
Ответы на контрольную работу №3
Вариант IЧасть А1. 36.2. а) 4; б) $16\sqrt{15}$.3. $\frac{а^2\sqrt{3}}{64}$.
Часть Б1. 5952.2. a) $4\sqrt{3}$, $4\sqrt{7}$, $4\sqrt{7}$; б) $32\sqrt{3}+16\sqrt{6}$.3. $1,125а^2$.
Часть В1. 259,2.2. $\frac{d^2}{2}*tg(\frac{α}{2})*cos(β)$.3. $\frac{3а^2\sqrt{3}}{4}$.
Вариант IIЧасть А1. 360.2. а) $6\sqrt{2}$; б) $72\sqrt{3}$.3. $\frac{а^2\sqrt{3}}{36}$.
Часть Б1. $144\sqrt{41}+360$.2. а) 3, $3\sqrt{5}$, $3\sqrt{5}$; б) $18+18\sqrt{2}$.3. $\frac{9а^2}{8}$.
Часть В1. 1104.2. $\frac{a^2 sin(α)}{cos(β)}$.3. $\frac{3а^2\sqrt{3}}{4}$.
mathematics-tests.com
Контрольные работы по геометрии для 7 класса
Контрольные работы по геометрии для 7 класса.
К учебнику «Геометрия 7-9», автор Атанасян Л.С, Бутузов В.Ф,Кодомцев С.Б. и др.Москва, Просвещение, 2010г .
Составитель: Котова Лилия Анатольевна.
МБОУ СОШ №1 г. Сальск.
Контрольная работа №1.
Вариант 1.
1)Три точки В,С и Д лежат на одной прямой. Известно, что ВД=17см,ДС=25см.Какой может быть длина отрезка ВС?
2)Сумма вертикальных углов МОЕ и ДОС, образованных при пересечении прямых МС и ДЕ, равна 204°.Найдите угол МОД.
3)С помощью транспортира начертите угол, равный 78° ,и проведите биссектрису смежного с ним угла.
Контрольная работа №1.
Вариант 2.
1)Три точки М,N и К лежат на одной прямой. Известно, что MN=15см,NК=18см.Каким может быть расстояние МК?
2)Сумма вертикальных углов АОВ и СОД, образованных при пересечении прямых АД и ВС, равна 108°. Найдите угол ВОД.
3) С помощью транспортира начертите угол, равный 132°, и проведите биссектрису одного из смежных с ним углов. Контрольная работа №2.
Вариант 1.
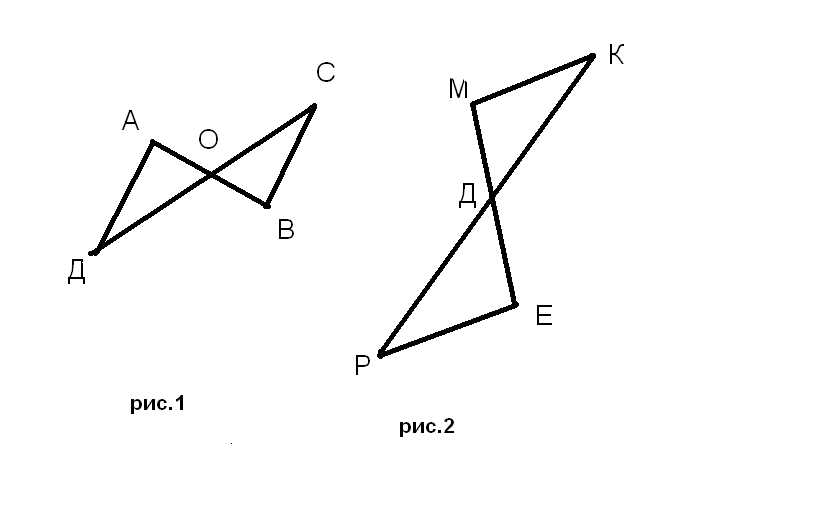
1)На рис.1 отрезки АВ и СД имеют общую середину О.Докажите, что
2)Луч АД - биссектриса угла А.На сторонах угла А отмечены точки В и С так, что
3)Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС.
Вариант 2.
1)На рис. 2 отрезки МЕ и РК точкой Д делятся пополам. Докажите, что
2)На сторонах угла Д отмечены точки М и К так, что ДМ=ДК. Точка Р лежит внутри угла Д и РК=РМ. Докажите, что луч ДР- биссектриса угла МДК.
3) Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А.
Контрольная работа №3.
Вариант 1.
1)Отрезки ЕF и РД пересекаются в их середине М.Докажите, что РЕ II ДF.
2)Отрезок ДМ- биссектриса треугольника СДЕ. Через точку М проведена прямая, параллельная стороне СД и пересекающая сторону ДЕ в точке N.Найдите углы треугольника ДМN, если
Контрольная работа №3.
Вариант 2.
Отрезки MN и EF пересекаются в их середине Р. Докажите, что EN II MF.
Отрезок АД-биссектриса треугольника АВС. Через точку Д проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F.Найдите углы треугольника АДF, если
Контрольная работа №4.
Вариант 1.
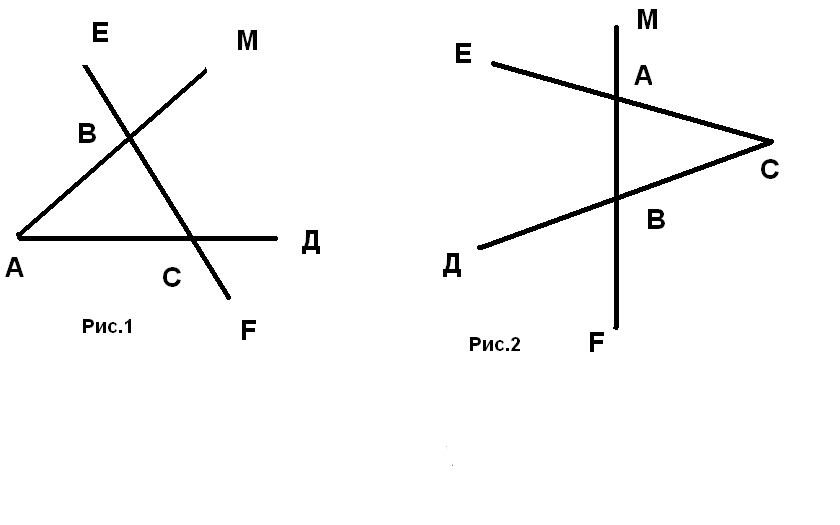
1)На рис.1 угол АВЕ равен 104°, угол ДСF равен 76°,АС=12 см.Найдите сторону АВ треугольника АВС.
2)В треугольнике СДЕ точка М лежит на стороне СЕ, причём угол СМД острый. Докажите, что ДЕ> ДМ.
3)Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
Вариант 2.
1)На рис.2 угол ВАЕ равен 112 °, угол ДВF равен 68° , ВС=9см.Найдите сторону АС треугольника АВС.
2)В треугольнике MNP точка К лежит на стороне МN, причём угол NКР острый. Докажите, что КР
3)Одна из сторон равнобедренного тупоугольного треугольника на 17см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77см.
Контрольная работа №5.
Вариант 1.
1)В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NК в точке О, причём ОК=9см.Найдите расстояние от точки О до прямой МN.
2)Постойте прямоугольный треугольник по гипотенузе и острому углу.
Дополнительное задание.
С помощью циркуля и линейки постройте угол равный 150°.
Контрольная работа №5.
Вариант 2.
1)В прямоугольном треугольнике ДСЕ с прямым углом С проведена биссектриса ЕF, причём FC=13cм.Найдите расстояние от точки F до прямой ДЕ.
2) Постойте прямоугольный треугольник по катету и прилежащему к нему острому углу.
Дополнительное задание.
С помощью циркуля и линейки постройте угол равный 105°.
doc4web.ru


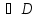 AО =
AО =  СВО.
СВО.
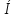 AC. Найдите угол MBD. (Указание. Для каждого из возможных случаев сделайте чертеж.)
AC. Найдите угол MBD. (Указание. Для каждого из возможных случаев сделайте чертеж.)

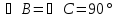 , AB = CD (Рис. 1).
, AB = CD (Рис. 1).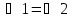 .
.
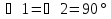 , AD = BC (Рис. 2).
, AD = BC (Рис. 2).  1. Используя рисунок выберите верный ответ: a) АH – медиана. б) BM – медиана. в) AH – высота. г) BM – биссектриса. д) $\bigtriangleup ABC$ – равнобедренный.
1. Используя рисунок выберите верный ответ: a) АH – медиана. б) BM – медиана. в) AH – высота. г) BM – биссектриса. д) $\bigtriangleup ABC$ – равнобедренный.  3. В $\bigtriangleup ABC$ AB=AC, AH – биссектриса, ∠ABC=57°. Найдите углы $\bigtriangleup ABC$.
3. В $\bigtriangleup ABC$ AB=AC, AH – биссектриса, ∠ABC=57°. Найдите углы $\bigtriangleup ABC$. 4. В окружности с центром в точке О проведены хорды АС и ВЕ, так что ∠AOB=∠COE.Докажите: а) АС=ВЕ; б) АЕ – диаметр окружности.
4. В окружности с центром в точке О проведены хорды АС и ВЕ, так что ∠AOB=∠COE.Докажите: а) АС=ВЕ; б) АЕ – диаметр окружности.  1. Используя рисунок выберите верный ответ:а) АH – биссектриса.б) BM – медиана.в) AH – высота.г) BM – биссектриса.д) $\bigtriangleup ABC$ – остроугольный.
1. Используя рисунок выберите верный ответ:а) АH – биссектриса.б) BM – медиана.в) AH – высота.г) BM – биссектриса.д) $\bigtriangleup ABC$ – остроугольный.  3. В $\bigtriangleup ABC$ AB=AC, AH – высота, ∠ABC=38°. Найдите углы $\bigtriangleup ABC$.
3. В $\bigtriangleup ABC$ AB=AC, AH – высота, ∠ABC=38°. Найдите углы $\bigtriangleup ABC$. 4. В окружности с центром в точке О проведены хорды АF и ВM так, что ∠AOF=∠BOM.Докажите: а) АB=FM; б) АM – диаметр окружности.
4. В окружности с центром в точке О проведены хорды АF и ВM так, что ∠AOF=∠BOM.Докажите: а) АB=FM; б) АM – диаметр окружности. 




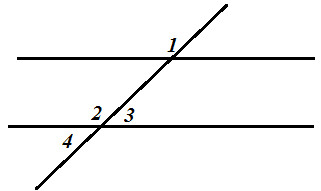





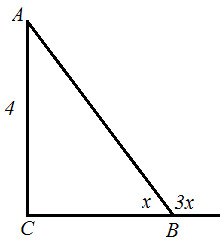


 прямую, равнялся данному отрезку.
прямую, равнялся данному отрезку.  2. Дан отрезок. Постройте две какие либо взаимно
2. Дан отрезок. Постройте две какие либо взаимно 
 lV Вариант
lV Вариант 
 1. На рисунке отрезки АВ и СD имеют общую середину О. Докажите, что
1. На рисунке отрезки АВ и СD имеют общую середину О. Докажите, что  .
. . Докажите, что АВ = АС.
. Докажите, что АВ = АС. . На рисунке отрезки МЕ и РК точкой D делятся пополам . Докажите, что
. На рисунке отрезки МЕ и РК точкой D делятся пополам . Докажите, что  .
.

 .
. . На рисунке
. На рисунке  ,
,  , АC = 12 см. Найдите сторону АВ треугольника АВС.
, АC = 12 см. Найдите сторону АВ треугольника АВС. . На рисунке
. На рисунке  ,
,  , BC = 9 см. Найдите сторону АC треугольника АВС.
, BC = 9 см. Найдите сторону АC треугольника АВС.






