Контрольные работы по геометрии 8 класс к учебнику Атанасяна Л.С. Геометрия 8 класс контрольная
Сборник контрольных работ по геометрии, (8 класс)
СБОРНИК
КОНТРОЛЬНЫХ РАБОР ПО ГЕОМЕТРИИ
8 класс
Пояснительная записка
Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний. Тематические контрольные работы включают критерии оценивания, позволяющие отследить уровень усвоения учащимися стандартов данной темы. Содержательная матрица дает возможность учителю провести качественный анализ контрольной работы и спланировать коррекционную работу индивидуально для каждого ученика.
Предложение содержательной матрицы и критериев оценивания дает возможность учащимся планировать свою учебную деятельность для достижения более качественных результатов и впоследствии ее коррекцию.
.
Контрольная работа №1 8 класс.
Тема: «Четырехугольники».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач свойства параллелограмма, ромба,
прямоугольника, квадрата;
- умение оформлять рисунки по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1.Стороны параллелограмма 3 см и 5 см. Найдите периметр параллелограмма. 2. Один из углов ромба равен 48 . Найти все углы ромба. . Найти все углы ромба. 3. Биссектриса угла прямоугольника делит его большую сторону на две части, каждая из которых равна 8 см. Найдите периметр прямоугольника. 4. Периметр ромба равен 80 см, один из углов равен 60 . Найдите длину диагонали, противолежащей этому углу. . Найдите длину диагонали, противолежащей этому углу. 5.Докажите, что если диагонали ромба равны, то он является ромбом. |
| II вариант. |
| 1. Стороны параллелограмма 4 см и 7 см. Найдите периметр параллелограмма. 2. Один из углов параллелограмма равен 48 . Найти все углы параллелограмма . . Найти все углы параллелограмма . 3.Биссектриса угла прямоугольника делит его большую сторону пополам, меньшая сторона равна 7 см. Найдите периметр прямоугольника. 4.Один из углов ромба равен 120 , а диагональ, исходящая из вершины этого угла равна 12см. Найдите периметр ромба. , а диагональ, исходящая из вершины этого угла равна 12см. Найдите периметр ромба. 5.Докажите, что если диагонали прямоугольника перпендикулярны, то он является квадратом. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Параллелограмм. Признаки и свойства. | №1, | | | 20 % |
| Ромб. Признаки и свойства. | №2 | №4 | | 40% |
| Прямоугольник. Признаки и свойства. | | №3 | | 20% |
| Квадрат. Признаки и свойства. | | | №5 | 20 % |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Параллелограмм. Признаки и свойства. | Знание свойств параллелограмма. | 1 балл | 3 балла |
| Знание формулы периметра. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 2 | Ромб. Признаки и свойства. | Знание свойств ромба. | 1 балл | 3 балла |
| Знание свойств углов в ромбе. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 3 | Прямоугольник. Признаки и свойства. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Определение биссектрисы. | 1 балл |
| Знание свойств углов, полученных при пересечении параллельных прямых секущей. | 1 балл |
| Знание свойств равнобедренного треугольника | 1 балл |
| Оформление решения задачи. | 1 балл |
| 4 | Ромб. Признаки и свойства. | Выполнение чертежа по условию задачи | 1 балл | 5 баллов |
| Знание свойства ромба и диагоналей ромба. | 2 балла |
| Оформление решения задачи. | 2 балла |
| 5 | Квадрат. Признаки и свойства. | Знание видов треугольников и их свойства. | 1 балл | 5 баллов |
| Применение признаков и свойств квадрата. | 2 балла |
| Оформление решения задачи. | 2 балла |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №2 8 класс.
Тема: «Трапеция. Средняя линия».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач свойств средней линии;
- знание и умение применять при решении задач свойства трапеции;
- умение выполнять чертежи по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1.В трапеции АВСД с основаниями АД и ВС. Угол В равен 100 ,а угол С равен 110 ,а угол С равен 110 . Найдите остальные углы. . Найдите остальные углы. 2. Основания трапеции равны 4 см и 12 см. Найти среднюю линию трапеции. 3.Диагональ трапеции делит среднюю линию на отрезки 5см и 9 см. Найдите основания трапеции. 4. В треугольнике АВС АВ=10 см. Через точку К на стороне АВ проведена прямая КМ параллельно АС, АК=5 см. Доказать, что ВМ=МС. 5. Докажите, что если диагонали четырехугольника перпендикулярны, то середины его сторон являются вершинами прямоугольника. |
| II вариант. |
| 1. В трапеции АВСД с основаниями АД и ВС. Угол А равен 40 ,а угол С равен 110 ,а угол С равен 110 . Найдите остальные углы. . Найдите остальные углы. 2. Основания трапеции равны 7 см и 15 см. Найти среднюю линию трапеции. 3. Основания трапеции равны 8 см и 14 см. Найдите отрезки, на которые диагональ трапеции делит среднюю линию. 4. В треугольнике АВС ВС=8 см. Через точку Е на стороне ВС проведена прямая ДЕ параллельно АС, ЕС=4 см.. Доказать, что АД=ВД. 5. Докажите, что если диагонали четырехугольника равны, то середины его сторон являются вершинами ромба. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Трапеция. | №1, | | | 20 % |
| Средняя линия трапеции. | №2 | | | 20% |
| Средняя линия треугольника. | | №3 | №5 | 40% |
| Теорема Фалеса. | | №4 | | 20 % |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Трапеция. | Знание свойств трапеции. | 1 балл | 3 балла |
| Нахождение углов трапеции. | 1 балл |
| Запись ответа. | 1 балл |
| 2 | Средняя линия трапеции. | Знание формулы средней линии. | 1 балл | 3 балла |
| Вычисления. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 3 | Средняя линия треугольника. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Знание и применение свойств средней линии. | 2 балла |
| Оформление решения задачи. | 2 балла |
| 4 | Теорема Фалеса. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Знание и применение теоремы Фалеса. | 2 балла |
| Оформление решения задачи. | 2 балла |
| 5 | Свойство средней линии треугольника. | Выполнение чертежа по условию задачи. | 1 балл | 6 баллов |
| Свойство средней линии треугольника. | 1 балл |
| Логичность рассуждений. | 2 балла |
| Оформление решения задачи. | 2 балла |
Критерии оценивания:
1-11 баллов – «2»
12-14 баллов – «3»
15-19 баллов – «4»
20-22 балла – «5»
Контрольная работа №4 8 класс.
Тема: «Теорема Пифагора».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач теорему Пифагора
- знание и умение применять при решении задач определения синуса, косинуса острого угла прямоугольного треугольника;
- виды треугольников (равнобедренный, равносторонний) и их свойства;
- виды трапеций и их свойства;
- умение выполнять чертеж по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1.Катеты прямоугольного треугольника 6 см и 8 см. Найдите гипотенузу. 2. Гипотенуза прямоугольного треугольника равна 12 см, один из катетов 9 см. Найдите синус противолежащего угла. 3. Периметр равностороннего треугольника равен 12 см.Найдите высоту треугольника. 4. Найдите катеты равнобедренного прямоугольного треугольника, гипотенуза которого равна 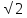 см. см. 5. Основание прямоугольной трапеции равны 2 см и 10 см, а боковые стороны относятся как 3:5. Найдите периметр трапеции. |
| II вариант. |
| 1. Гипотенуза прямоугольного треугольника равна 15 см, один из катетов 9 см. Найдите второй катет. 2. Гипотенуза прямоугольного треугольника равна 10 см, один из катетов 8 см. Найдите косинус прилежащего угла. 3. Периметр ромба равен 20см. Одна из диагоналей равна 8см. Найдите вторую диагональ ромба. 4. Найдите сторону квадрата, диагональ которого равна  см. см. 5. Основания равнобокой трапеции равны 8 см и 16 см, а боковая сторона относится к высоте как 5:3. Найдите периметр трапеции. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Теорема Пифагора. | №1, | №3 №4 | №5 | 80 % |
| Синус, косинус острого угла прямоугольного треугольника. | №2 | | | 20% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Теорема Пифагора. | Знание теоремы Пифагора. | 1 балл | 4 балла |
| Умение применять теорему Пифагора. | 1 балл |
| Вычисление. | 1 балл |
| Запись ответа. | 1 балл |
| 2 | Синус, косинус острого угла прямоугольного треугольника. | Выполнение чертежа по условию задачи. | 1 балл | 3 балла |
| Знание определения синуса (ко-синуса) острого угла прямоуголь-ного треугольника. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 3 | Теорема Пифагора. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Определение ромба (равностороннего треугольника). | 1 балл |
| Нахождение стороны. | 1 балл |
| Применение теоремы Пифагора. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 4 | Теорема Пифагора. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Определение квадрата (равнобедренного треугольника). | 1 балл |
| Составление уравнения. | 1 балл |
| Вычисления. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 5 | Теорема Пифагора. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Выход на прямоугольный треугольник. | 1 балл |
| Составление уравнения. | 1 балл |
| Вычисления. | 1 балл |
| Нахождение периметра. | 1 балл |
Критерии оценивания:
1-11 баллов – «2»
12-14 баллов – «3»
15-19 баллов – «4»
20-22 балла – «5»
Контрольная работа №4 8 класс.
Тема: «Соотношение между сторонами и углами в прямоугольном треугольнике».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач соотношения между сторонами и углами в прямоугольном треугольнике;
- умение оформлять рисунки по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1.В треугольнике АВС  С=90 С=90 , А=30 , А=30 , АВ=8 см. Найдите ВС. , АВ=8 см. Найдите ВС. 2. В треугольнике АВС  В=90 В=90 , ВС= , ВС=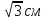 , АС=2 см. Найдите , АС=2 см. Найдите С. С. 3. Из точки, не лежащей на данной прямой, проведены перпендикуляр и наклонная к прямой. Длина перпендикуляра 24 см, а наклонная длиной 25 см. Найдите периметр, образованного треугольника. 4. В прямоугольном треугольнике гипотенуза равна 4 см, один из катетов равен 4 см. Найдите второй катет и острые углы. см, один из катетов равен 4 см. Найдите второй катет и острые углы. 5.Диагональ прямоугольной трапеции равна 4 см и делит трапецию на два равнобедренных прямоугольных треугольников. Найдите стороны и острый угол трапеции. см и делит трапецию на два равнобедренных прямоугольных треугольников. Найдите стороны и острый угол трапеции. |
| II вариант. |
| 1. В треугольнике  С=90 С=90 , В=45 , В=45 , АВ=8 см. Найдите АС. , АВ=8 см. Найдите АС. 2. В треугольнике АВС  В=90 В=90 , ВС= , ВС= , АС=2 см. Найдите , АС=2 см. Найдите С. С. 3. Из точки, не лежащей на данной прямой, проведены перпендикуляр и наклонная к прямой. Длина наклонной 26 см. Проекция наклонной на данную прямую равна 10 см. Найдите периметр, образованного треугольника. 4. В прямоугольном треугольнике гипотенуза равна 2 см, один из катетов равен  см. Найдите второй катет и острые углы. см. Найдите второй катет и острые углы. 5. Высоты равнобокой делят ее на квадрат и два равнобедренных треугольника. Боковая сторона трапеции 4 см. Найдите основания трапеции и тупой угол. см. Найдите основания трапеции и тупой угол. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Соотношения между сторонами и углами в прямоугольном треугольнике. | №1, №2 | №4 | №5 | 80 % |
| Перпендикуляр и наклонная. | | №3 | | 20% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Соотношения между сторонами и углами в прямоугольном треугольнике. | Знание определения синуса (косинуса) острого угла прямоугольного треугольника. | 1 балл | 4 балла |
| Умение применять. | 1 балл |
| Вычисление. | 1 балл |
| Запись ответа. | 1 балл |
| 2 | Синус, косинус острого угла прямоугольного треугольника. | Знание определения синуса (косинуса) острого угла прямоугольного треугольника. | 1 балл | 3 балла |
| Умение находить угол. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 3 | Перпендикуляр и наклонная. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Определения наклонной, перпендикуляра, проекции. | 1 балл |
| Применение теоремы Пифагора. | 1 балл |
| Вычисления. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 4 | Решение прямоугольного треугольника. | Определение неизвестных элементов. | 1 балл | 5 баллов |
| Нахождение катета. | 1 балл |
| Вычисления. | 2 балла |
| Оформление решения задачи. | 1 балл |
| 5 | Соотношения между сторонами и углами в прямоугольном треугольнике. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Выход на прямоугольный треугольник. | 1 балл |
| Нахождение стороны. | 1 балл |
| Нахождение угла. | 1 балл |
| Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-11 баллов – «2»
12-14 баллов – «3»
15-19 баллов – «4»
20-22 балла – «5»
Контрольная работа №5 8 класс.
Тема: «Площади фигур».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач формулы площадей треугольника, параллелограмма, ромба, прямоугольника, квадрата, трапеции;
- умение оформлять рисунки по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1.Сторона параллелограмма равна 6 см, а высота, проведенная к этой стороне равна 5см. Найдите площадь параллелограмма 2. Найдите высоту ромба, если его площадь равна 26 см2 , а сторона 6,5 см. 3.Разность оснований трапеции равна 6 см, а высота трапеции равна 8 см . Найдите основания трапеции, если ее площадь равна 56 см2 . 4. Найдите сторону треугольника, если высота, опущенная на эту сторону, в 2 раза меньше нее, а площадь треугольника равна 64 см2. 5.Периметр параллелограмма равен 32 см. Найдите площадь параллелограмма, если один из углов на 60° больше прямого, а одна из сторон равна 6 см. |
| II вариант. |
| 1. Стороны параллелограмма равны 8 см и 5 см, а угол между ними равен 30° . Найдите площадь параллелограмма 2. Найдите сторону ромба, если его площадь равна 12 см2 , а высота 2,4 см. 3. Высота трапеции равна 7 см, а одно из оснований в 5 раз больше другого. Найдите основания трапеции, если ее площадь равна 84 см2 . 4. Найдите высоту треугольника, если она в 4 раза больше стороны к которой проведена, а площадь треугольника равна 72 см2. 5. Периметр параллелограмма равен 36 см. Найдите площадь параллелограмма, если один из углов на 60° меньше прямого, а высота равна 6 см. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Площадь параллелограмма | №1 | | №5 | 40% |
| Площадь ромба | №2 | | | 20% |
| Площадь трапеции | | №3 | | 20% |
| Площадь треугольника | | №4 | | 20% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Площадь параллелограмма. | Знание формул. | 1 балл | 3 балла |
| Вычисления. | 1 балл |
| Запись ответа. | 1 балл |
| 2 | Площадь ромба. | Выполнение чертежа по условию задачи. | 1 балл | 4 балла |
| Знание формулы площади ромба. | 1 балл |
| Умение выразить неизвестный элемент. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 3 | Площадь трапеции. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Знание формулы площади трапеции. | 1 балл |
| Составление уравнения. | 1 балл |
| Вычисления. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 4 | Площадь треугольника. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Знание формулы площади треугольника. | 1 балл |
| Составление уравнения. | 1 балл |
| Вычисления. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 5 | Площадь параллелограмма. | Нахождение угла. | 1 балл | 5 баллов |
| Нахождение стороны. | 1 балл |
| Вычисления. | 1 балл |
| Нахождение площади. | 1 балл |
| Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-11 баллов – «2»
12-14 баллов – «3»
15-19 баллов – «4»
20-22 балла – «5»
xn--j1ahfl.xn--p1ai
Контрольные работы по геометрии 8 класс к учебнику Атанасяна Л.С.
| Контрольная работа № 1. Г-8. Вариант-1 № 1. Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360. Найдите угол AOD. № 2. Найдите углы прямоугольной трапеции, если один из его углов равен 200. № 3. Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма. № 4. В равнобедренной трапеции сумма углов при большем основании равна 960. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, АМ = 4 см. Найдите длину диагонали АD. | Контрольная работа № 1. Г-8. Вариант-2. № 1. Диагонали прямоугольника MNKP пересекаются в точке О, ∟MОN=640. Найдите угол OMP. № 2. Найдите углы равнобедренной трапеции, если один из его углов на 300 больше другого. № 3. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см. Найдите стороны параллелограмма. № 4. В прямоугольной трапеции разность углов при одной из боковых сторон равна 480. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, длина диагонали АС равна 6 см. Найдите AМ, если точка М лежит на продолжении стороны AD. |
| Контрольная работа № 1. Г-8. Вариант-3. № 1. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма. № 2. Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4: 5. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна одной из его сторон. № 4. В трапеции ABCD диагональ BD перпендикулярна боковой стороне AB, ∟ADB = ∟BDC = 300. Найдите длину АD, если периметр трапеции равен 60 см. № 5*. В параллелограмме ABCD биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М2, М 1М2 = 8см. Найдите AD. | Контрольная работа № 1. Г – 8. Вариант – 4. 1. Периметр параллелограмма 60 см. Одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма. № 2. Угол между диагоналями прямоугольника равен 800. Найдите угол между диагональю и меньшей стороной прямоугольника. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна половине неперпендикулярной к ней стороны параллелограмма. № 4. В трапеции ABCD диагональ AС перпендикулярна боковой стороне CD и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, ∟D = 600. № 5*. В параллелограмме ABCD AD = 6 см. Биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М 2. Найдите М1М2. |
| | |
| Контрольная работа № 2. Г-8 Вариант-1. № 1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. № 2. Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь этого треугольника. № 3. Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см. № 4*. В прямоугольной трапеции АВСК большая боковая сторона равна 3√2 см, угол К равен 450, а высота СН делит основание АК пополам. Найдите площадь трапеции. | Контрольная работа № 2. Г-8 Вариант-2. № 1. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника. № 2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь этого треугольника. № 3. Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр. № 4*. В прямоугольной трапеции АВСD большая боковая сторона равна 8 см, угол А равен 600, а высота ВН делит основание АD пополам. Найдите площадь трапеции. |
| Контрольная работа № 2. Г-8 Вариант-3. № 1. Смежные стороны параллелограмма равны 52 см и 30 см, а острый угол равен 300. Найдите площадь параллелограмма. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если А= 24 см, ВС = 16 см, ∟А= 45, ∟D=90 0. № 3. Дан треугольник АВС. На стороне АС отмечена точка К так, что АК = 6 см, КС = 9 см. Найдите площади треугольников АВК и СВК, если АВ = 13 см, ВС = 14 см. № 4*. Высота равностороннего треугольника равна 6 см. Найдите сумму расстояний от произвольной точки, взятой внутри этого треугольника, до его сторон. | Контрольная работа № 2. Г-8 Вариант-4. № 1.Высота ВК, проведенная к стороне АD параллелограмма АВСD, делит эту сторону на два отрезка АК = 7 см, КD = 15 см. Найдите площадь параллелограмма, если ∟А =450. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если ВС = 13 см, АD = 27 см, СD = 10см, ∟D = 300. № 3. Дан треугольник МКР. На стороне МК отмечена точка Т так, что МТ= 5 см, КТ = 10 см. Найдите площади треугольников МРТ и КРТ, если МР = 12 см, КР = 9 см. № 4*. В равностороннем треугольнике большая сторона составляет 75% суммы двух других. Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см. |
| | |
| Контрольная работа № 3. Г-8. Вариант-1. B № 1. Рисунок 1 Дано: ∟А = ∟В, СО = 4, DО = 6, АО = 5. С Найти: а) ОВ; б) АС : ВD; в) SAOC : SBOD. А О D № 2. В треугольнике АВС АВ = 4 см, ВС= 7 см, АС = 6 см, а в треугольнике МNК МК = 8 см, МN =12 см, КN = 14 см. Найдите углы треугольника МNК, если ∟А = 80, ∟В = 600. № 3. Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК ║АС, ВМ : АМ = 1: 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, А = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника АОD равна 45 см2. | Контрольная работа №3. Г-8. Вариант-2. N  № 1. Рисунок 1. P № 1. Рисунок 1. P
![]() Дано: РЕ ║NК, МР = 8, МN = 12, МЕ = 6. Дано: РЕ ║NК, МР = 8, МN = 12, МЕ = 6.
Найти: а) МК; б) РЕ : NК; в) SМЕР : SMKN. M E K № 2. В ∆АВС АВ = 12 см, ВС = 18 см, ∟В = 700,а в ∆ МNК MN = 6 cм, NК = 9 см, ∟N= 700. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, ∟К = 600. № 3. Отрезки АВ и СD пересекаются в точке О так, что ∟АСО = =∟ВDО, АО : ОВ = 2 : 3. Найдите периметр треугольника АСО, если периметр треугольника ВОD равен 21 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, SAOD= 32 см2, S BOC = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см. |
| Контрольная работа № 3. Г-8. Вариант-3. № 1. Рисунок 1. D B    Дано: АО = 6,8 см, СО = 8,4 см, Дано: АО = 6,8 см, СО = 8,4 см,
ОВ = 5,1 см, ОD = 6,3 см. O Доказать: АС ║ВD.  Найти: а) DВ : АС; б) РАОС : РDBO ; Найти: а) DВ : АС; б) РАОС : РDBO ;
в) SDBO: SAOC A C № 2. Диагонали ромба АВСD пересекаются в точке О, ВD = 16 см. На стороне АВ взята точка К так, что ОК ┴ АВ и ОК = 4√3 см. Найдите сторону ромба и второю диагональ. № 3. В выпуклом четырехугольнике АВСD АВ = 9 см, ВС = 8 см, СD = 16 см, АD = 6 см, ВD = 12 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике МNК с основанием МК, равным 10 см, МN= NК = 20 см. На стороне NК лежит точка А так, что АК : АN= 1 : 3. Найдите АМ. | Контрольная работа № 3. Г-8. Вариант-4.  № 1. Рисунок 1. B № 1. Рисунок 1. B
Дано: ВD = 3,1 см, ВЕ = 4,2 см, ВА = 9,3 см, ВС = 12,6 см. D E  Доказать: DЕ ║АС. Доказать: DЕ ║АС.
![]() Найти: а) DЕ : АС; б) РABC : РDBE ; Найти: а) DЕ : АС; б) РABC : РDBE ;
в) SDBE : SABC. A C № 2. Диагонали ромба АВСD пересекаются в точке О. На стороне АВ взята точка К так, что ОК ┴ АВ, АК = 2 см, ВК = 8 см. Найдите диагонали ромба. № 3. АВСD – выпуклый четырёхугольник, АВ = 6 см, ВС = 9 см, СD = 10 см, DА = 25 см, АС = 15 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике АВС АВ = ВС = 40 см, АС = 20 см. На стороне ВС отмечена точка Н так, что ВН : НС = 3 : 1. Найдите АН. |
| Контрольная работа № 4. Г-8. Вариант-1. № 1. Средние линии треугольника относятся как 2: 2: 4, а периметр треугольника равен 45 см. Найдите стороны треугольника. № 2. Медианы треугольника АВС пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС пересекающая стороны АВ и ВС в точках Е и F соответственно. Найдите ЕF, если сторона АС равна 15 см. № 3. В прямоугольном треугольнике АВС (∟С= 900) АС = 5 см, ВС = 5√3 см. Найдите угол В и гипотенузу АВ. № 4. В треугольнике АВС ∟А =α, ∟С =β, сторона ВС = 7 см, ВН-высота. Найдите АН. № 5. В трапеции АВСD продолжения боковых сторон пересекаются в точке К, причем точка В-середина отрезка АК. Найдите сумму оснований трапеции, если АD = 12 см. | Контрольная работа №4. Г-8. Вариант-2. № 1. Средние линии треугольника относятся как 4: 5: 6, а периметр треугольника, образованного средними линиями, равен 30 см. Найдите средние линии треугольника. № 2. Медианы треугольника MNK пересекаются в точке О. Через точку О проведена прямая, параллельная стороне MK пересекающая стороны MN и NK в точках A и B соответственно. Найдите MK, если длина отрезка АB равна 12 см. №3. В прямоугольном треугольнике РКТ (∟Т= 900), РТ = 7√3 см, КТ= 7 см. Найдите угол К и гипотенузу КР. № 4. В треугольнике АВС ∟А =α, ∟С =β , высота ВН равна 4 см. Найдите АС. № 5. В трапеции MNKP продолжения боковых сторон пересекаются в точке E, причем EK=KP. Найдите разность оснований трапеции, если NK = 7 см. |
| Контрольная работа № 4. Г-8. Вариант-3. № 1. На стороне ВС треугольника АВС выбрана точка D так, что ВD: DС = 3:2, точка К – середина отрезка АВ, точка F–середина отрезка АD, КF =6 см, ∟АDС=1000. Найдите ВС и ∟АFК. № 2. В прямоугольном треугольнике АВС ∟С= 900, АС = 4 см, СВ = 4√3 см, СМ –медиана. Найдите угол ВСМ. № 3. В равнобедренной трапеции основания равны 8 см и 12 см, меньший угол равен α . Найдите периметр и площадь трапеции. № 4.В равнобедренном треугольнике АВС с основанием АС медианы пересекаются в точке О. Найдите площадь треугольника АВС, если ОА =13 см, ОВ = 10 см. № 5. В трапеции АВС (ВС ║АD) АВ ┴ ВD, ВD =2√5 , AD =2√10, СЕ – высота треугольника ВСD, а tg∟ECD= 3. Найдите ВЕ. | Контрольная работа № 4. Г-8. Вариант-4. № 1. На стороне АМ треугольника АВМ отмечена точка Н так, что АН: НЬ = 4:7; точка С – середина стороны АВ, точка О –середина стороны отрезка ВН, АМ = 22 см, ∟ВОС = 1050. Найдите СО и угол ВНМ. № 2. В прямоугольном треугольнике MNK ∟K= 90, KM = 6см, NК =6√3 см, КD- медиана. Найдите угол КDN. № 3. В равнобедренной трапеции боковая сторона равна 6 см, меньшее основание 10 см, а меньший угол α . Найдите площадь трапеции. № 4. В прямоугольном треугольнике АВС (∟С =900) медианы пересекаются в точке О, ОВ = 10 см, ВС = 12 см. Найдите гипотенузу треугольника. № 5. В трапеции АВСD ∟А =90, АС= 6√2, ВС=6, DЕ –высота треугольника АСD, tg∟ACD= 2. Найдите СЕ. |
| Контрольная работа № 5. Г-8. Вариант-1. № 1. АВ и АС- отрезки касательных, проведенных к окружности радиуса 9 см. Найдите длины отрезков АС и АО, если АВ = 12 см. № 2. Рисунок 1. Дано: ᵕАВ : ᵕВС = 11 : 12.  Найдите ∟ВСА, ∟ВАС. Найдите ∟ВСА, ∟ВАС.
  ![]() B A B A
![]()

130O C № 3. Хорды MN и PK пересекаются точке E так, что ME =12 см, NE =3 см, PE=KE. Найдите PK. № 4.Окружность с центром в точке О радиусом 16 см описана около треугольника ABC так, что ∟OAB=300, ∟OCB=450. Найдите стороны AB и BC треугольника. | Контрольная работа № 5. Г-8. Вариант-2. № 1. MN и MK-отрезки касательных, проведенных к окружности радиуса 5 см. Найдите MN и MK, если МО= 13 см. № 2. Рисунок 1. Дано: ᵕАВ : ᵕАС = 5 : 3.  Найдите ∟ВОС, ∟АВС. Найдите ∟ВОС, ∟АВС.
 A B A B
  ![]()
 ![]() 60O 60O
C O № 3. Хорды АВ и СD пересекаются точке F так, что АF =4 см, ВF =16 см, СF=DF. Найдите CD. № 4.Окружность с центром в точке О радиусом 12 см описана около треугольника MNK так, что ∟MON=1200, ∟NOK=900. Найдите стороны MN и NK треугольника. |
| Контрольная работа № 5. Г-8. Вариант-3. № 1. В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 3 см,4 см,5 см. Определите вид треугольника № 2. Точки А и В делят окружность с центром О на дуги АВМ и АСВ так, что дуга АСВ на 600 меньше дуги АМВ. АМ- диаметр окружности. Найдите углы АМВ, АВМ, АСВ. № 3. Хорды АВ и СD пересекаются в точке Е так, что АЕ=3 см, ВЕ=36 см, СЕ: DЕ =3:4. Найдите СD и наименьшее значение радиуса этой окружности. № 4. В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведенная к основанию 8 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника. | Контрольная работа № 5. Г-8. Вариант-4. № 1. В прямоугольный треугольник вписана окружность радиусом 2 см так, что один из получившихся отрезков касательных равен 4 см. Найдите стороны треугольника, если его периметр равен 24 см. № 2.Точки Е и Н делят окружность с центром О на дуги ЕАН и ЕКН так, что дуга ЕКН на 900 меньше дуги ЕАН, ЕА- диаметр окружности. Найдите углы ЕКА, ЕАН, ЕКН. № 3. Хорды МN и РК пересекаются в точке А так, что МА= 3 см, NА= 16 см, РА: КА= 1: 3. Найдите РК и наименьшее значение радиуса этой окружности. № 4. В равнобедренном треугольнике основание равно 10 см, а высота, Проведенная к ней, 12 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника. |
Ответы.
| | | № 1 | № 2 | № 3 | № 4 | № 5 |
| Контрольная работа № 1. | Вариант-1 | ∟АОD=72 | 900 , 900, 1600, 200 | 5см, 10см, 5см, 10см | 480, 480, 1320, 1320 | DВ=6см |
| Вариант-2 | ∟ОМР=32 | 750, 1050, 1050, 750 | 5см, 15см, 5см, 15см | 660, 1140, 900, 900 | АМ=3см |
| Вариант-3 | 10см, 15см, 10см, 15см | 800 | 450, 1350 450,1350 | AD=24см | AD=8см |
| Вариант-4 | 18см, 12см, 18см, 12см | 500 | 300, 300, 1500, 1500 | АВ= 7см | М1 М2 =6см |
| Контрольная работа № 2. | Вариант-1 | 24см2 | 10см, 24см2 | Р=4√41см, S= 40cм2 | S АВСК= 13,5см2 | - |
| Вариант-2 | 24см2 | 5см, 30см2 | Р=4√61см, S= 60cм2 | S АВСD= 24√3см2 | - |
| Вариант-3 | 780cм2 | SABCD = 160cм2 | SABK =33,6см2, SCBK =50,4см2 | 6см | - |
| Вариант-4 | 154см2 | SABCD = 100cм2 | SKPT=36см2, SMPT =18см2 | 3см | - |
| Контрольная работа № 3. | Вариант-1 | а) 7,5; б)  ; ; в)  | 800, 600,400 | 5см | S = 5см2 | - |
| Вариант-2 | а) 9; б)  ; ; в)  | AC=14см, ∟С=600 | 14см | 5см2 | - |
| Вариант-3 | а) ; б) ; б)  ; в) ; в)  | АВ=6см; АС= 16√3 | - | 10см | - |
| Вариант-4 | а)  ; б) 3; в) ; б) 3; в)  | АС=4√5; ВD=8√5 | - | 20см | |
| Контрольная работа № 5. | Вариант-1 | 15см | ∟ВСА=550, ∟ВАС=600 | РЕ=6см, РК= 12см | АВ=16√3см, ВС= 16√2см | - |
| Вариант-2 | 12см | ∟ВОС=1200, ∟АВС=450 | СF=8см, СD=16см | МN=12√3см; NК=12√2см | - |
| Вариант-3 | 6см, 8см, 10 см | ∟АМВ=600, ∟АВМ=900, ∟ АСВ=1050 | СD=21см, 19,5см | 3см, 6,25см | |
| Вариант-4 | 6см, 8см, 10см | ∟ЕКА=90, ∟ЕАН=670 30١, ∟ЕКН=1120 30١ | РК=16см, 9,5см | 3см, 7см | |
kopilkaurokov.ru
Контрольные работы по геометрии 8 класс к учебнику Атанасяна Л.С.
|                       Контрольная работа № 1. Г-8. Контрольная работа № 1. Г-8.
Вариант-1 № 1. Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360. Найдите угол AOD. № 2. Найдите углы прямоугольной трапеции, если один из его углов равен 200. № 3. Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма. № 4. В равнобедренной трапеции сумма углов при большем основании равна 960. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, АМ = 4 см. Найдите длину диагонали АD. | Контрольная работа № 1. Г-8. Вариант-2. № 1. Диагонали прямоугольника MNKP пересекаются в точке О, ∟MОN=640. Найдите угол OMP. № 2. Найдите углы равнобедренной трапеции, если один из его углов на 300 больше другого. № 3. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см. Найдите стороны параллелограмма. № 4. В прямоугольной трапеции разность углов при одной из боковых сторон равна 480. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, длина диагонали АС равна 6 см. Найдите AМ, если точка М лежит на продолжении стороны AD. |
| Контрольная работа № 1. Г-8. Вариант-3. № 1. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма. № 2. Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4: 5. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна одной из его сторон. № 4. В трапеции ABCD диагональ BD перпендикулярна боковой стороне AB, ∟ADB = ∟BDC = 300. Найдите длину АD, если периметр трапеции равен 60 см. № 5*. В параллелограмме ABCD биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М2, М 1М2 = 8см. Найдите AD. | Контрольная работа № 1. Г – 8. Вариант – 4. 1. Периметр параллелограмма 60 см. Одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма. № 2. Угол между диагоналями прямоугольника равен 800. Найдите угол между диагональю и меньшей стороной прямоугольника. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна половине неперпендикулярной к ней стороны параллелограмма. № 4. В трапеции ABCD диагональ AС перпендикулярна боковой стороне CD и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, ∟D = 600. № 5*. В параллелограмме ABCD AD = 6 см. Биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М 2. Найдите М1М2. |
| | |
| Контрольная работа № 2. Г-8 Вариант-1. № 1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. № 2. Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь этого треугольника. № 3. Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см. № 4*. В прямоугольной трапеции АВСК большая боковая сторона равна 3√2 см, угол К равен 450, а высота СН делит основание АК пополам. Найдите площадь трапеции. | Контрольная работа № 2. Г-8 Вариант-2. № 1. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника. № 2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь этого треугольника. № 3. Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр. № 4*. В прямоугольной трапеции АВСD большая боковая сторона равна 8 см, угол А равен 600, а высота ВН делит основание АD пополам. Найдите площадь трапеции. |
| Контрольная работа № 2. Г-8 Вариант-3. № 1. Смежные стороны параллелограмма равны 52 см и 30 см, а острый угол равен 300. Найдите площадь параллелограмма. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если А= 24 см, ВС = 16 см, ∟А= 45, ∟D=90 0. № 3. Дан треугольник АВС. На стороне АС отмечена точка К так, что АК = 6 см, КС = 9 см. Найдите площади треугольников АВК и СВК, если АВ = 13 см, ВС = 14 см. № 4*. Высота равностороннего треугольника равна 6 см. Найдите сумму расстояний от произвольной точки, взятой внутри этого треугольника, до его сторон. | Контрольная работа № 2. Г-8 Вариант-4. № 1.Высота ВК, проведенная к стороне АD параллелограмма АВСD, делит эту сторону на два отрезка АК = 7 см, КD = 15 см. Найдите площадь параллелограмма, если ∟А =450. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если ВС = 13 см, АD = 27 см, СD = 10см, ∟D = 300. № 3. Дан треугольник МКР. На стороне МК отмечена точка Т так, что МТ= 5 см, КТ = 10 см. Найдите площади треугольников МРТ и КРТ, если МР = 12 см, КР = 9 см. № 4*. В равностороннем треугольнике большая сторона составляет 75% суммы двух других. Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см. |
| | |
| Контрольная работа № 3. Г-8. Вариант-1. B № 1. Рисунок 1 Дано: ∟А = ∟В, СО = 4, DО = 6, АО = 5. С Найти: а) ОВ; б) АС : ВD; в) SAOC : SBOD. А О D № 2. В треугольнике АВС АВ = 4 см, ВС= 7 см, АС = 6 см, а в треугольнике МNК МК = 8 см, МN =12 см, КN = 14 см. Найдите углы треугольника МNК, если ∟А = 80, ∟В = 600. № 3. Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК ║АС, ВМ : АМ = 1: 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, А = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника АОD равна 45 см2. | Контрольная работа №3. Г-8. Вариант-2. N № 1. Рисунок 1. P Дано: РЕ ║NК, МР = 8, МN = 12, МЕ = 6. Найти: а) МК; б) РЕ : NК; в) SМЕР : SMKN. M E K № 2. В ∆АВС АВ = 12 см, ВС = 18 см, ∟В = 700,а в ∆ МNК MN = 6 cм, NК = 9 см, ∟N= 700. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, ∟К = 600. № 3. Отрезки АВ и СD пересекаются в точке О так, что ∟АСО = =∟ВDО, АО : ОВ = 2 : 3. Найдите периметр треугольника АСО, если периметр треугольника ВОD равен 21 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, SAOD= 32 см2, S BOC = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см. |
| Контрольная работа № 3. Г-8. Вариант-3. № 1. Рисунок 1. D B Дано: АО = 6,8 см, СО = 8,4 см, ОВ = 5,1 см, ОD = 6,3 см. O Доказать: АС ║ВD. Найти: а) DВ : АС; б) РАОС : РDBO ; в) SDBO : SAOC A C № 2. Диагонали ромба АВСD пересекаются в точке О, ВD = 16 см. На стороне АВ взята точка К так, что ОК ┴ АВ и ОК = 4√3 см. Найдите сторону ромба и второю диагональ. № 3. В выпуклом четырехугольнике АВСD АВ = 9 см, ВС = 8 см, СD = 16 см, АD = 6 см, ВD = 12 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике МNК с основанием МК, равным 10 см, МN= NК = 20 см. На стороне NК лежит точка А так, что АК : АN= 1 : 3. Найдите АМ. | Контрольная работа № 3. Г-8. Вариант-4. № 1. Рисунок 1. B Дано: ВD = 3,1 см, ВЕ = 4,2 см, ВА = 9,3 см, ВС = 12,6 см. D E Доказать: DЕ ║АС. Найти: а) DЕ : АС; б) РABC : РDBE ; в) SDBE : SABC. A C № 2. Диагонали ромба АВСD пересекаются в точке О. На стороне АВ взята точка К так, что ОК ┴ АВ, АК = 2 см, ВК = 8 см. Найдите диагонали ромба. № 3. АВСD – выпуклый четырёхугольник, АВ = 6 см, ВС = 9 см, СD = 10 см, DА = 25 см, АС = 15 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике АВС АВ = ВС = 40 см, АС = 20 см. На стороне ВС отмечена точка Н так, что ВН : НС = 3 : 1. Найдите АН. |
Контрольная работа № 4. Г-8.
Вариант-1.
№ 1. Средние линии треугольника относятся как 2: 2: 4, а периметр треугольника равен 45 см. Найдите стороны треугольника.
№ 2. Медианы треугольника АВС пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС пересекающая стороны АВ и ВС в точках Е и F соответственно. Найдите ЕF, если сторона АС равна 15 см.
№ 3. В прямоугольном треугольнике АВС (∟С= 900) АС = 5 см,
ВС = 5√3 см. Найдите угол В и гипотенузу АВ.
№ 4. В треугольнике АВС ∟А =α, ∟С =β, сторона ВС = 7 см, ВН-высота. Найдите АН.
№ 5. В трапеции АВСD продолжения боковых сторон пересекаются в точке К, причем точка В-середина отрезка АК. Найдите сумму оснований трапеции, если АD = 12 см.
Контрольная работа №4. Г-8.
Вариант-2.
№ 1. Средние линии треугольника относятся как 4: 5: 6, а периметр треугольника, образованного средними линиями, равен 30 см. Найдите средние линии треугольника.
№ 2. Медианы треугольника MNK пересекаются в точке О. Через точку О проведена прямая, параллельная стороне MK пересекающая стороны MN и NK в точках A и B соответственно. Найдите MK, если длина отрезка АB равна 12 см.
№3. В прямоугольном треугольнике РКТ (∟Т= 900), РТ = 7√3 см,
КТ= 7 см. Найдите угол К и гипотенузу КР.
№ 4. В треугольнике АВС ∟А =α, ∟С =β , высота ВН равна 4 см. Найдите АС.
№ 5. В трапеции MNKP продолжения боковых сторон пересекаются в точке E, причем EK=KP. Найдите разность оснований трапеции, если
NK = 7 см.
Контрольная работа № 4. Г-8.
Вариант-3.
№ 1. На стороне ВС треугольника АВС выбрана точка D так, что
ВD: DС = 3:2, точка К – середина отрезка АВ, точка F–середина
отрезка АD, КF =6 см, ∟АDС=1000. Найдите ВС и ∟АFК.
№ 2. В прямоугольном треугольнике АВС ∟С= 900, АС = 4 см,
СВ = 4√3 см, СМ –медиана. Найдите угол ВСМ.
№ 3. В равнобедренной трапеции основания равны 8 см и 12 см, меньший угол равен α . Найдите периметр и площадь трапеции.
№ 4.В равнобедренном треугольнике АВС с основанием АС медианы пересекаются в точке О. Найдите площадь треугольника АВС, если ОА =13 см, ОВ = 10 см.
№ 5. В трапеции АВС (ВС ║АD) АВ ┴ ВD, ВD =2√5 , AD =2√10,
СЕ – высота треугольника ВСD, а tg∟ECD= 3. Найдите ВЕ.
Контрольная работа № 4. Г-8.
Вариант-4.
№ 1. На стороне АМ треугольника АВМ отмечена точка Н так, что
АН: НЬ = 4:7; точка С – середина стороны АВ, точка О –середина стороны отрезка ВН, АМ = 22 см, ∟ВОС = 1050. Найдите СО и
угол ВНМ.
№ 2. В прямоугольном треугольнике MNK ∟K= 90, KM = 6см,
NК =6√3 см, КD- медиана. Найдите угол КDN.
№ 3. В равнобедренной трапеции боковая сторона равна 6 см, меньшее основание 10 см, а меньший угол α . Найдите площадь трапеции.
№ 4. В прямоугольном треугольнике АВС (∟С =900) медианы пересекаются в точке О, ОВ = 10 см, ВС = 12 см. Найдите гипотенузу треугольника.
№ 5. В трапеции АВСD ∟А =90, АС= 6√2, ВС=6, DЕ –высота треугольника АСD, tg∟ACD= 2. Найдите СЕ.
Контрольная работа № 5. Г-8.
Вариант-1.
№ 1. АВ и АС- отрезки касательных, проведенных к окружности радиуса 9 см. Найдите длины отрезков АС и АО, если АВ = 12 см.
№ 2. Рисунок 1. Дано: ᵕАВ : ᵕВС = 11 : 12.
Найдите ∟ВСА, ∟ВАС.
B A
130O
C
№ 3. Хорды MN и PK пересекаются точке E так, что ME =12 см,
NE =3 см, PE=KE. Найдите PK.
№ 4.Окружность с центром в точке О радиусом 16 см описана около треугольника ABC так, что ∟OAB=300, ∟OCB=450. Найдите стороны AB и BC треугольника.
Контрольная работа № 5. Г-8.
Вариант-2.
№ 1. MN и MK-отрезки касательных, проведенных к окружности радиуса 5 см. Найдите MN и MK, если МО= 13 см.
№ 2. Рисунок 1. Дано: ᵕАВ : ᵕАС = 5 : 3.
Найдите ∟ВОС, ∟АВС.
A B
60O
C O
№ 3. Хорды АВ и СD пересекаются точке F так, что АF =4 см,
ВF =16 см, СF=DF. Найдите CD.
№ 4.Окружность с центром в точке О радиусом 12 см описана около треугольника MNK так, что ∟MON=1200, ∟NOK=900. Найдите стороны MN и NK треугольника.
Контрольная работа № 5. Г-8.
Вариант-3.
№ 1. В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 3 см,4 см,5 см. Определите вид треугольника
№ 2. Точки А и В делят окружность с центром О на дуги АВМ и
АСВ так, что дуга АСВ на 600 меньше дуги АМВ. АМ- диаметр окружности. Найдите углы АМВ, АВМ, АСВ.
№ 3. Хорды АВ и СD пересекаются в точке Е так, что АЕ=3 см, ВЕ=36 см, СЕ: DЕ =3:4. Найдите СD и наименьшее значение радиуса этой окружности.
№ 4. В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведенная к основанию 8 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника.
Контрольная работа № 5. Г-8.
Вариант-4.
№ 1. В прямоугольный треугольник вписана окружность радиусом 2 см так, что один из получившихся отрезков касательных равен 4 см. Найдите стороны треугольника, если его периметр равен 24 см.
№ 2.Точки Е и Н делят окружность с центром О на дуги ЕАН и ЕКН так, что дуга ЕКН на 900 меньше дуги ЕАН, ЕА- диаметр окружности. Найдите углы ЕКА, ЕАН, ЕКН.
№ 3. Хорды МN и РК пересекаются в точке А так, что МА= 3 см,
NА= 16 см, РА: КА= 1: 3. Найдите РК и наименьшее значение радиуса этой окружности.
№ 4. В равнобедренном треугольнике основание равно 10 см, а высота,
Проведенная к ней, 12 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника.
Ответы.
№ 1
№ 2
№ 3
№ 4
№ 5
Контрольная работа № 1.
Вариант-1
∟АОD=72
900 , 900,
1600, 200
5см, 10см,
5см, 10см
480, 480,
1320, 1320
DВ=6см
Вариант-2
∟ОМР=32
750, 1050,
1050, 750
5см, 15см,
5см, 15см
660, 1140,
900, 900
АМ=3см
Вариант-3
10см, 15см,
10см, 15см
800
450, 1350
450,1350
AD=24см
AD=8см
Вариант-4
18см, 12см,
18см, 12см
500
300, 300,
1500, 1500
АВ= 7см
М1 М2 =6см
Контрольная работа № 2.
Вариант-1
24см2
10см, 24см2
Р=4√41см, S= 40cм2
S АВСК= 13,5см2
-
Вариант-2
24см2
5см, 30см2
Р=4√61см, S= 60cм2
S АВСD= 24√3см2
-
Вариант-3
780cм2
SABCD = 160cм2
SABK =33,6см2,
SCBK =50,4см2
6см
-
Вариант-4
154см2
SABCD = 100cм2
SKPT=36см2,
SMPT =18см2
3см
-
Контрольная работа № 3.
Вариант-1
а) 7,5; б) 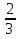 ;
;
в) 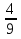
800, 600,400
5см
S = 5см2
-
Вариант-2
а) 9; б) 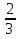 ;
;
в) 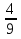
AC=14см,
∟С=600
14см
5см2
-
Вариант-3
а)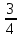 ; б)
; б) 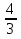 ; в)
; в) 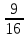
АВ=6см; АС= 16√3
-
10см
-
Вариант-4
а) 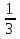 ; б) 3; в)
; б) 3; в) 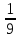
АС=4√5; ВD=8√5
-
20см
Контрольная работа № 5.
Вариант-1
15см
∟ВСА=550,
∟ВАС=600
РЕ=6см, РК= 12см
АВ=16√3см,
ВС= 16√2см
-
Вариант-2
12см
∟ВОС=1200,
∟АВС=450
СF=8см, СD=16см
МN=12√3см;
NК=12√2см
-
Вариант-3
6см, 8см, 10 см
∟АМВ=600, ∟АВМ=900, ∟ АСВ=1050
СD=21см, 19,5см
3см, 6,25см
Вариант-4
6см, 8см, 10см
∟ЕКА=90, ∟ЕАН=670 30١, ∟ЕКН=1120 30١
РК=16см, 9,5см
3см, 7см
infourok.ru
Геометрия 8 класс. Контрольная работа № 2
Контрольная работа № 2
Вариант 1
-
Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.
-
Катеты прямоугольного треугольника равны 6 и 8 см. найдите гипотенузу и площадь треугольника.
-
Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см.
4*. В прямоугольной трапеции АВСК большая боковая сторона равна см, угол К равен 45, а высота СН делит основание АК пополам. Найдите площадь трапеции.
Контрольная работа № 2
Вариант 1
-
Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.
-
Катеты прямоугольного треугольника равны 6 и 8 см. найдите гипотенузу и площадь треугольника.
-
Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см.
4*. В прямоугольной трапеции АВСК большая боковая сторона равна см, угол К равен 45, а высота СН делит основание АК пополам. Найдите площадь трапеции.
Контрольная работа № 2
Вариант 1
-
Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.
-
Катеты прямоугольного треугольника равны 6 и 8 см. найдите гипотенузу и площадь треугольника.
-
Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см.
4*. В прямоугольной трапеции АВСК большая боковая сторона равна см, угол К равен 45, а высота СН делит основание АК пополам. Найдите площадь трапеции.
Контрольная работа № 2
Вариант 1
-
Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.
-
Катеты прямоугольного треугольника равны 6 и 8 см. найдите гипотенузу и площадь треугольника.
-
Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см.
4*. В прямоугольной трапеции АВСК большая боковая сторона равна см, угол К равен 45, а высота СН делит основание АК пополам. Найдите площадь трапеции.
Контрольная работа № 2
Вариант 1
-
Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.
-
Катеты прямоугольного треугольника равны 6 и 8 см. найдите гипотенузу и площадь треугольника.
-
Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см.
4*. В прямоугольной трапеции АВСК большая боковая сторона равна см, угол К равен 45, а высота СН делит основание АК пополам. Найдите площадь трапеции.
Контрольная работа № 2
Вариант 2
-
Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника.
-
Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. найдите второй катет и площадь треугольника.
-
Диагонали ромба равны 10 и 12 см. найдите его площадь и периметр.
4*. В прямоугольной трапеции АВСD большая боковая сторона равна 8 см, угол А равен 60, а высота ВН делит основание пополам. Найдите площадь трапеции.
Контрольная работа № 2
Вариант 2
-
Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника.
-
Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. найдите второй катет и площадь треугольника.
-
Диагонали ромба равны 10 и 12 см. найдите его площадь и периметр.
infourok.ru
Контрольные работы по геометрии 8 класс
Контрольные работы по геометрии
8 класс
Контрольная работа № 1 по теме «Четырехугольники»

Контрольная работа № 1 по теме «Четырехугольники»

Контрольная работа № 1 по теме «Четырехугольники»

Контрольная работа № 1 по теме «Четырехугольники»

Контрольная работа № 2 по теме «Площадь»




Контрольная работа № 3 по теме «Признаки подобия треугольников»
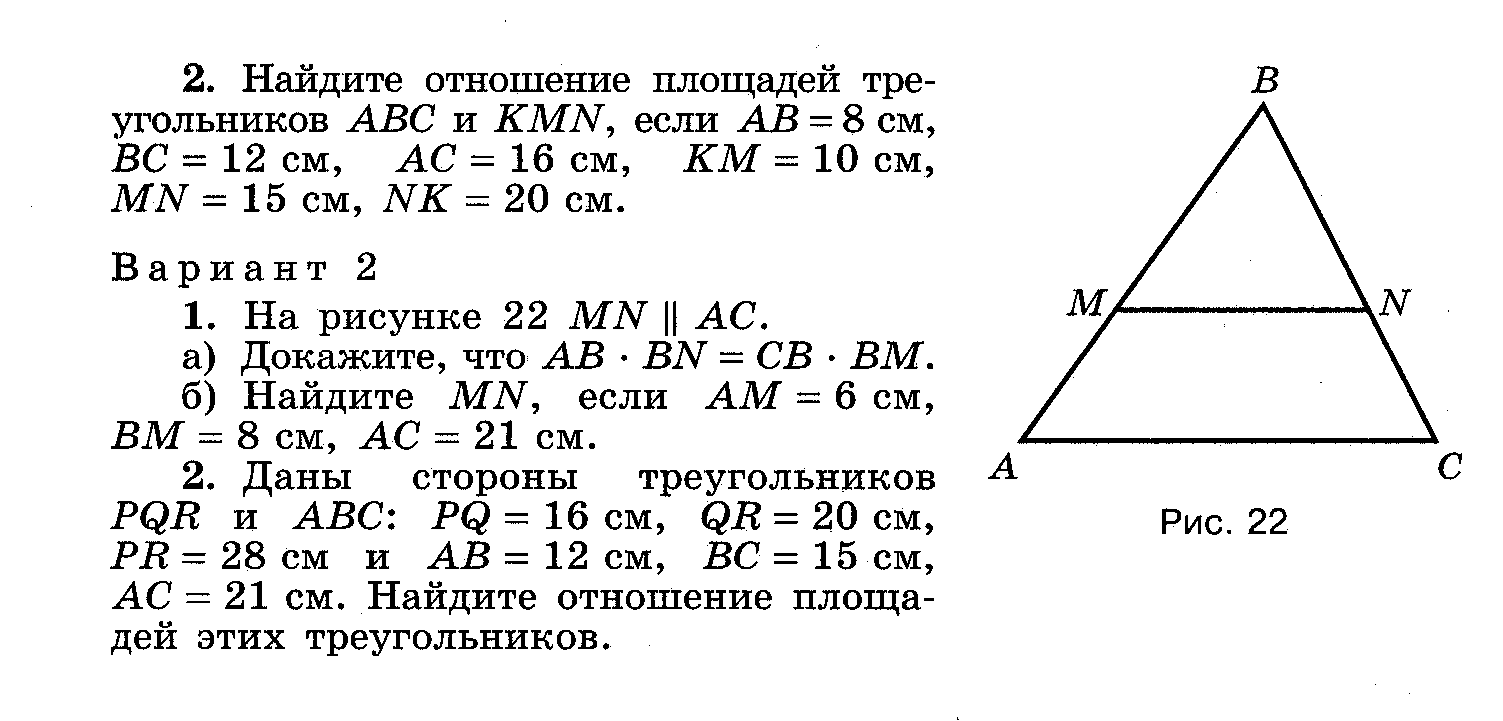






Контрольная работа № 4 по теме «Применение теории подобия треугольников, соотношение между сторонами и углами прямоугольного треугольника»




Контрольная работа № 5 по теме «Окружность»



infourok.ru
Контрольные работы по геометрии для 8 класса с ответами
Контрольная работа №1
Вариант I
Часть А
Запишите номера верных ответов к заданию 1.1. На рисунке ABCD – трапеция, AB||OD, AO||CD, AD=OD, AD≠AO.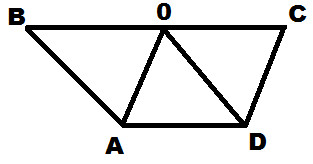 а) ABOD – параллелограмм.б) ABOD – ромб.в) AOCD – ромб.г) ∠COD=∠AODд) ∠AOD=∠BOA
а) ABOD – параллелограмм.б) ABOD – ромб.в) AOCD – ромб.г) ∠COD=∠AODд) ∠AOD=∠BOA
Часть В
Запишите ответы к заданиям 2 и 3.2. Диагонали прямоугольника ABCD пересекаются в точке O. Найдите периметр треугольника AOB, если AB=4, AD=3, BD=5.
3. Одна из сторон параллелограмма в 4 раза меньше другой стороны. Найдите длину большей стороны, если периметр параллелограмма равен 50 см.
Часть С
Запишите обоснование к заданиям 4-6.4. На рисунке ABCD – ромб, ∠BAD=150°. Найдите углы треугольника АОВ.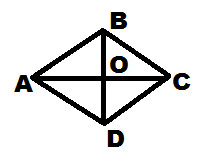 5. Начертите прямоугольный треугольник ABC, на стороне BC отметьте точку N, не являющейся ее серединой. Постройте фигуру, симметричную треугольнику ABC относительно точки N.
5. Начертите прямоугольный треугольник ABC, на стороне BC отметьте точку N, не являющейся ее серединой. Постройте фигуру, симметричную треугольнику ABC относительно точки N.
6. В параллелограмме ABCD, биссектриса угла D пересекает сторону AB в точке M, AM=15, MB=3. Найдите периметр параллелограмма.
Вариант II
Часть А
Запишите номера верных ответов к заданию 1.1. На рисунке ABCD – трапеция, AB||OD, AO||CD, AD=CD, AD≠BA.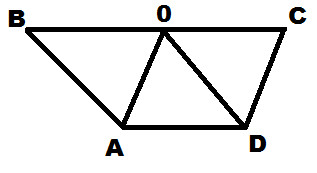 а) AOCD – параллелограмм.б) AOCD – ромб.в) ABOD – ромб.г) ∠COD=∠AODд) ∠AOD=∠BOA
а) AOCD – параллелограмм.б) AOCD – ромб.в) ABOD – ромб.г) ∠COD=∠AODд) ∠AOD=∠BOA
Часть В
Запишите ответы к заданиям 2 и 3.2. Диагонали прямоугольника ABCD пересекаются в точке O. Найдите периметр треугольника AOB, если AB=8, AD=6, BD=10.
3. Одна из сторон параллелограмма в 6 раза меньше другой стороны. Найдите длину большей стороны, если периметр параллелограмма равен 56 см.
Часть С
Запишите обоснование к заданиям 4-6.4. На рисунке ABCD – ромб, ∠ABC=40°. Найдите углы треугольника BOC.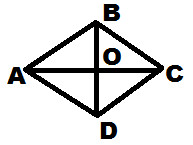 5. Начертите ромб ABCD. Постройте фигуру, симметричную ему относительно прямой BD.
5. Начертите ромб ABCD. Постройте фигуру, симметричную ему относительно прямой BD.
6. В параллелограмме ABCD, биссектриса угла С пересекает сторону AD в точке N, AN=6, ND=10. Найдите периметр параллелограмма.
Контрольная работа №2
Вариант I
Часть А
Запишите номера верных ответов к заданию 1.1. Используя данные рисунка, найдите площадь треугольника.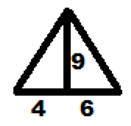 а) 45; б) 216; в) 50; г) 72.
а) 45; б) 216; в) 50; г) 72.
Часть В
Запишите ответ к заданию 2.2. Стороны прямоугольника 15 и 20. Чему равна диагональ прямоугольника?
Часть С
Запишите обоснование к заданиям 3-5.3. Высота равнобедренного треугольника, проведенная к основанию, равна 8 см, основание равно 12 см. Найдите боковую сторону.
4. Найдите площадь равнобедренной трапеции, если ее основания равны 4 и 10 см, а боковая сторона - 5 см.
5. На рисунке ABCD – прямоугольник. DH⊥AC. Сторона CD в три раза меньше диагонали AC. Найдите DH, если AD=16.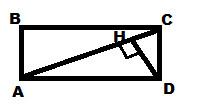
Вариант II
Часть А
Запишите номера верных ответов к заданию 1.1. Используя данные рисунка, найдите площадь треугольника.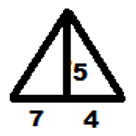 а) 27,5; б) 28; в) 27; г) 30.
а) 27,5; б) 28; в) 27; г) 30.
Часть В
Запишите ответ к заданию 2.2. Одна из сторон прямоугольника равна 12. Диагональ - 20. Найдите другую сторону.
Часть С
Запишите обоснование к заданиям 3-5.3. Найдите сторону ромба, если его диагонали равны 24 и 32 см.
4. Найдите площадь равнобедренной трапеции, если одно из оснований равно 6 см, боковая сторона - 15 см, высота - 9 см.
5. На рисунке ABCD – прямоугольник. ВH⊥AC. Сторона CD в четыре раза меньше стороны AD. Найдите DH, если AC=34.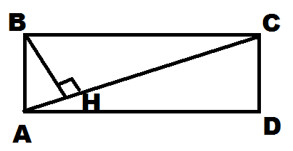
Контрольная работа №3
Вариант I
Часть А
Запишите номера верных ответов к заданиям 1 и 2.1. В прямоугольнике ABCD ∠BDC=α, диагональ равна 15. Найдите AD.а) 15sin(α), б) 15cos(α), в) 15tg(α), г) 15ctg(α).
2. В треугольнике ABC угол C прямой, AB=20, BC=16. Найдите длину средней линии MP, MϵAB, PϵBC.а) 7 см, б) 8 см, в) 6 см, г) 5 см.
Часть В
Запишите ответ к заданиям 3 и 4.3. Найдите длину основания АD, изображенной на рисунке трапеции ABCD, если BC=7, BO=3, OD=6.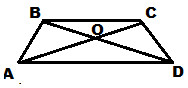 4. В равнобедренном треугольнике, основание равно 14, угол между боковыми сторонами равен 60°. Найдите длину высоты, проведенной к основанию.
4. В равнобедренном треугольнике, основание равно 14, угол между боковыми сторонами равен 60°. Найдите длину высоты, проведенной к основанию.
Часть С
Запишите обоснование к заданиям 5-6.5. На рисунке CM и BH высоты треугольника ABC. Докажите, что треугольники ACM и ABH подобны.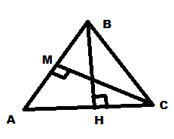 6. В треугольнике ABC прямая, параллельная стороне AB пересекает высоту CH в точке М, и сторону АС в точке К. Найдите cos(A), если AH=8, MK=4, AK=6.
6. В треугольнике ABC прямая, параллельная стороне AB пересекает высоту CH в точке М, и сторону АС в точке К. Найдите cos(A), если AH=8, MK=4, AK=6.
Вариант II
Часть А
Запишите номера верных ответов к заданиям 1 и 2.1. В прямоугольнике ABCD ∠ABD=β, диагональ равна 13. Найдите CD.а) 13sin(β), б) 13cos(β), в) 13tg(β), г) 13ctg(β).
2. В треугольнике ABC угол C - прямой, AС=8, BC=15. Найдите длину средней линии MP, MϵAС, PϵBC.а) 8,5; б) 9; в) 8; г) 9,5.
Часть В
Запишите ответ к заданиям 3 и 4.3. Найдите длину основания BC, изображенной на рисунке трапеции ABCD, если AD=15, BO=2, OD=6. 4. В равнобедренном треугольнике, основание равно 16, угол между основанием и боковой стороной 60°. Найдите длину высоты, проведенной к основанию.
4. В равнобедренном треугольнике, основание равно 16, угол между основанием и боковой стороной 60°. Найдите длину высоты, проведенной к основанию.
Часть С
Запишите обоснование к заданиям 5-6.5. На рисунке AM и CH высоты треугольника ABC. Докажите, что треугольники BHC и AMB подобны.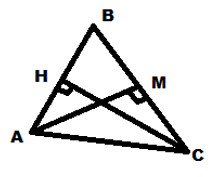 6. Треугольник ABC прямоугольный. Из точки H, лежащей на гипотенузе AB, опущен перпендикуляр к BC, он пересекает ее в точке М. Найдите cos(A), если AH=5, HM=6, AC=9.
6. Треугольник ABC прямоугольный. Из точки H, лежащей на гипотенузе AB, опущен перпендикуляр к BC, он пересекает ее в точке М. Найдите cos(A), если AH=5, HM=6, AC=9.
Контрольная работа №4
Вариант I
Часть А
Запишите номера верных ответов к заданиям 1 и 2.1. К окружности с центром точке О проведены касательные АВ и АС (В и С точки касания). Найдите ∠ВАС, если ∠АОВ=50°.
а) 60°, б) 80°, в) 75°, г) 95°.
2. На рисунке ∠CDA=65°, ∠АОВ=30°. Найдите ∠DAB.
а) 80°, б) 95°, в) 85°, г) 100°.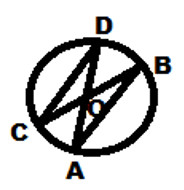 Часть В
Часть В
Запишите ответ к заданиям 3 и 4.3. Прямоугольный треугольник с катетами 8 и 15 вписан в окружность. Найдите радиус.
4. Две хорды одной окружности пересекаются в точке, делящей одну хорду на отрезки 3 и 25, а другую – на отрезки, один из которых в 3 раза больше другого. Найдите длину второй хорды.
Часть С
Запишите обоснование к заданиям 5-6.5. На рисунке АС - диаметр окружности, ВH⊥AC. Найдите длину хорды ВС, если АН=8см,НС=2см.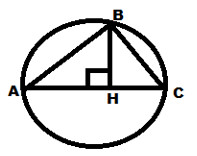 6. Треугольнике ABC - равнобедренный с основанием АС. Его периметр равен 40 см, АС=16см. Найдите длину отрезка ВМ (М – точка касания вписанной окружности со стороной ВС).
6. Треугольнике ABC - равнобедренный с основанием АС. Его периметр равен 40 см, АС=16см. Найдите длину отрезка ВМ (М – точка касания вписанной окружности со стороной ВС).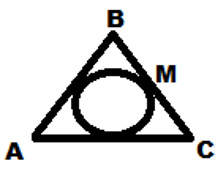
Вариант II
Часть А
Запишите номера верных ответов к заданиям 1 и 2.1. К окружности с центром точке О проведены касательные АВ и АС (В и С точки касания). Найдите ∠АОС, если ∠ВАС=82°.
а) 50°, б) 49°, в) 45°, г) 38°.
2. На рисунке ∠DOC=43°, ∠А=70°. Найдите ∠ABD.
а) 67°, б) 70°, в) 75°, г) 65°.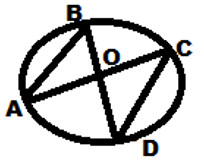 Часть В
Часть В
Запишите ответ к заданиям 3 и 4.3. В окружности с радиусом равным 8,5 см проведены диаметры АС и хорда АК=8см. Найдите длину хорды СК.
4. Хорды АВ и СD пересекаются в точке Е. Найдите длину отрезка АЕ, если он в 4 раза меньше отрезка ЕВ. Известно, что СЕ=8см, DE=18см.
Часть С
Запишите обоснование к заданиям 5-6.5. Найдите периметр треугольника АВС, изображенного на рисунке, если О – центр вписанной окружности, АМ=11см, МС=4см, АВ=16см.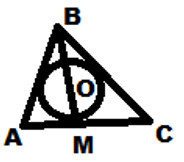 6. Треугольнике EFG - равнобедренный, с основанием EG. Его периметр равен 44 см, FG=14см. Найдите длину отрезка FМ (М – точка касания вписанной окружности со стороной ВС).
6. Треугольнике EFG - равнобедренный, с основанием EG. Его периметр равен 44 см, FG=14см. Найдите длину отрезка FМ (М – точка касания вписанной окружности со стороной ВС).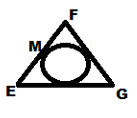
Контрольная работа №5
Вариант I
Часть А
Запишите номера верных ответов к заданиям 1-3.1. На каждом из приведенных ниже рисунков изображен параллелограмм, обладающий теми или иными свойствами. Используя данные, приведенные на рисунках укажите номера тех рисунков, на которых изображен ромб. 2. Используя данные рисунка, найдите площадь равнобедренной трапеции.
2. Используя данные рисунка, найдите площадь равнобедренной трапеции.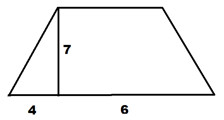 а) 42, б) 44, в) 38, г) 40.
а) 42, б) 44, в) 38, г) 40.
3. Найдите боковую сторону равнобедренного треугольника, если его основание равно 22, а угол при основании равен 60°.а) 12, б) 24, в) 22, г) 20.
Часть В
Запишите ответ к заданиям 4 и 5.4. В окружности с центром в точке О и радиусом равным 3 см, проведена касательная ВС (В - точка касания). Найдите длину отрезка ВС, если ОС=5.
5. На рисунке Р и Н середины сторон, ВК – высота треугольника. Найдите площадь треугольника, если РН=13см, ВК=8см.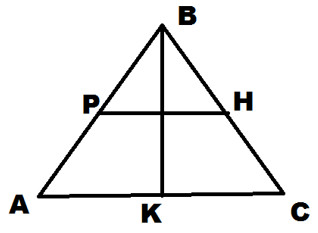 Часть С
Часть С
Запишите обоснование к заданиям 6-7.6. В треугольнике АВС на стороне АВ отмечена точка М, на стороне АС точка N, причем, ВС||MN. Найдите длину стороны ВС, если сторона АС=10см, NC=4см, MN=8см. 7. В ромбе ABCD диагональ АС пересекает высоту DM, проведенную к стороне ВС, в точке Р. Найдите длины отрезков DP и PM, если сторона ромба равна 17 см, а высота равна 8 см. Вариант II
Часть А
Запишите номера верных ответов к заданиям 1-3.1. На каждом из приведенных ниже рисунков изображен параллелограмм, обладающий теми или иными свойствами. Используя данные, приведенные на рисунках укажите номера тех рисунков, на которых изображен ромб.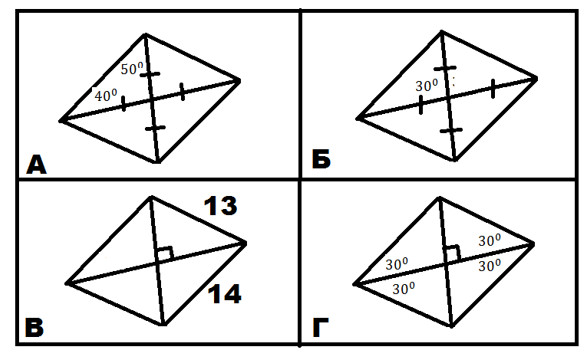 2. Используя данные рисунка, найдите площадь равнобедренной трапеции.
2. Используя данные рисунка, найдите площадь равнобедренной трапеции.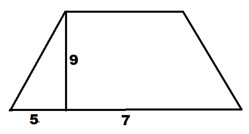 а) 35, б) 63, в) 90, г) 81.
а) 35, б) 63, в) 90, г) 81.
3. Найдите боковую сторону равнобедренного треугольника, если его высота равна 8, а угол при основании равен 30°.а) 16, б) 18, в) 63√, г) 14.
Часть В
Запишите ответ к заданиям 4 и 5.4. В окружности с центром в точке О и радиусом равным 8 см, проведена касательная ВС (В - точка касания). Найдите длину отрезка OС, если BС=15.
5. На рисунке Р и Н середины сторон, ВК – высота треугольника. Найдите площадь треугольника, если РН=18см, ВК=17см.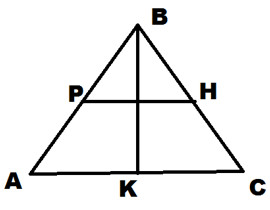 Часть С
Часть С
Запишите обоснование к заданиям 6-7.6. В треугольнике АВС на стороне АВ отмечена точка М, на стороне АС точка N, причем, ВС||MN. Найдите длину стороны ВС, если сторона АВ=12см, МВ=7см, MN=3см.
7. В квадрате ABCD диагональ АС пересекает отрезок ВM (МϵAD) в точке Р. Найдите длины отрезков ВР и РМ, если сторона квадрата равна 12 см, а отрезок АМ=5см.
Ответы на контрольную работу №1 для 8 класса
Вариант I1. а,б,д.2. 9.3. 20 см.4. ∠BAO=75°, ∠AOB=90°, ∠ABO=15°.5. Построение.6. 66.
Вариант II1. а,б,г.2. 18.3. 24 см.4. ∠BCO=70°, ∠BOC=90°, ∠CBO=20°.5. Построение.6. 52.
Ответы на контрольную работу №2 для 8 класса
Вариант I1. а.2. 25.3. 10 см.4. 28.5. 163.Вариант II1. а.2. 16.3. 20 см.4. 162.5. 8 см.
Ответы на контрольную работу №3 для 8 класса
Вариант I1. а.2. в.3. 14.4. 73√.6. 23.
Вариант II1. б.2. а.3. 5.4. 83√.6. 35.
Ответы на контрольную работу №4 для 8 класса
Вариант I1. б.2. в.3. 8,5.4. 5.5. 20−−√.6. 4.
Вариант II1. б.2. а.3. 15.4. 6.5. 40.6. 6.
Ответы на контрольную работу №5 для 8 класса
Вариант I1. а.2. а.3. в.4. 4.5. 104.6. 1313.7. РМ=3,75см, DP=4,25см.
Вариант IIа 1. а,г.2. б.3. а.4. 17.5. 306.6. 7,2.7. ВР=9317см. PМ=31417см.
infourok.ru
Контрольные работы по геометрии 8 класс
КОНТРОЛЬНЫЕ РАБОТЫ
Геометрия 8 класс
КОНТРОЛЬНАЯ РАБОТА №1
Вариант 1
▲1.
ABCD – ромб.
Вычислите градусные меры углов ромба.
2. Периметр параллелограмма равен 30см. Одна из его сторон больше другой на 3см.
Вычислите длины сторон параллелограмма.
■ 3. На диагонали МТ прямоугольника КМРТ отложены равные отрезки МА и ТВ. Докажите, что:
а) треугольники КМА и РТВ равны;
б) четырехугольник КАРВ является параллелограммом.
КОНТРОЛЬНАЯ РАБОТА №1
Вариант 2
▲1.
MNPQ – ромб.
Вычислите градусные меры углов треугольника MNP.
2. Периметр прямоугольника равен 36см. Одна из его сторон на 8см меньше другой. Вычислите длины сторон прямоугольника.
■ 3. Биссектрисы углов А и С параллелограмма ABCD пересекают его стороны BC и AD соответственно в точках E и F.
а) Докажите, что треугольники АВЕ и CDF равны;
б) Найдите длину отрезка EF, если AF=FD и периметр параллелограмма равен 48см.
КОНТРОЛЬНАЯ РАБОТА №2
Вариант 1
▲1.
Дано: NE║PF.
Вычислите длину отрезка МЕ.
2. Диагонали параллелограмма равны 8см и 10см. Середины его сторон последовательно соединены отрезками.
а) Вычислите периметр образовавшегося четырехугольника.
■ б) Определите вид образовавшегося четырехугольника. (Ответ поясните.)
3. Средняя линия равнобокой трапеции делится ее диагоналями на отрезки, длины которых равны 7см, 4см и 7см. Диагональ трапеции делит ее острый угол пополам. Вычислите:
а) длины оснований трапеции;
■ б) периметр трапеции.
КОНТРОЛЬНАЯ РАБОТА №2
Вариант 2
▲1.
Дано: МР║NT.
Вычислите длину отрезка KM.
2. Диагональ прямоугольника равна 26см. Середины его сторон последовательно соединены отрезками.
а) Вычислите периметр образовавшегося четырехугольника.
■ б) Определите вид образовавшегося четырехугольника. (Ответ поясните.)
3. Через вершину тупого угла С трапеции ABCD проведена прямая, параллельная боковой стороне АВ. Эта прямая пересекает большое основание AD в точке К. Периметр трапеции равен 37см, DK=6см, АК=9см. Вычислите:
а) длину средней линии трапеции;
■ б) периметр треугольника KCD.
КОНТРОЛЬНАЯ РАБОТА №3
Вариант 1
▲1.
Чему равны и ?
2. Вычислите длину диагонали прямоугольника, одна сторона которого равна 8 дм, а периметр – 46дм.
■ 3. Боковая сторона равнобокой трапеции равна 10см, большее ее основание - 17см, высота – 8см. Вычислите:
а) длину проекции боковой стороны трапеции на большее ее основание;
б) периметр трапеции.
КОНТРОЛЬНАЯ РАБОТА №3
Вариант 2
▲1.
Чему равны и ?
2. Диагонали ромба равны 12см и 16см. Вычислите периметр ромба.
■ 3. Боковые стороны прямоугольной трапеции равны 15дм и 9дм, меньшее основание – 28дм. Вычислите:
а) длину проекции боковой стороны трапеции на большее ее основание;
б) длину большей диагонали трапеции.
КОНТРОЛЬНАЯ РАБОТА №4
Вариант 1
▲1.
Дано: . Вычислите длину гипотенузы АВ.
2. Сторона AD прямоугольника ABCD равна 15м. Угол CADравен .
Вычислите расстояние от вершины D по диагонали AC.
■ 3. Диагональ МТ ромба КМРТ равна 2m, острый угол МКТ равен 2а. Найдите:
а) периметр ромба;
б) расстояние между серединами сторон КМ и МР.
КОНТРОЛЬНАЯ РАБОТА №4
Вариант 2
▲1.
Дано: . Вычислите длину катета АС.
2. Проекция стороны ВС прямоугольника ABCD на диагональ BD равна 20см. Угол CBD равен . Вычислите расстояние от вершины С до диагонали BD.
■ 3. Угол при вершине равнобедренного треугольника KMP (KM=MP) равен 2а. Основание треугольника равно m. Найдите:
а) периметр треугольника;
б) расстояние от середины основания треугольника до боковой стороны.
КОНТРОЛЬНАЯ РАБОТА №5
Вариант 1
▲1. Дан отрезок КМ; К(-2; 4), М(6; -2).
а) Вычислите длину отрезка КМ.
б) Постройте отрезок , симметричный отрезку КМ относительно оси ординат. Определите вид четырехугольника
в) Чему равны длины диагонали и средней линии четырехугольника ?
г) Запишите уравнение окружности с центром в начале координат, проходящей через точку К.
■2. Точки А(4; -1), В(2; -4), С(0; -1) являются вершинами параллелограмма ABCD.
а) Найдите координаты вершины D.
б) Докажите, что четырехугольник ABCD является ромбом.
в) Напишите уравнения прямых, на которых лежат диагонали четырехугольника ABCD.
КОНТРОЛЬНАЯ РАБОТА №5
Вариант 2
▲1. Дан отрезок AB; A(-4; -3), B(2; 5).
а) Вычислите длину отрезка AB.
б) Постройте отрезок , симметричный отрезку AB относительно оси абсцисс. Определите вид четырехугольника
в) Чему равны длины диагонали и средней линии четырехугольника ?
г) Запишите уравнение окружности с центром в начале координат, проходящей через точку А.
■2. Точки К(3; -3), М(-5; 1), Р(-3; 5) являются вершинами параллелограмма КМРТ.
а) Найдите координаты вершины Т.
б) Докажите, что четырехугольник КМРТ является прямоугольником.
в) Напишите уравнение прямой, на которой лежит диагональ МТ.
КОНТРОЛЬНАЯ РАБОТА №6
Вариант 1
▲1.
Дано: ABCD – параллелограмм. Вычислите его площадь.
2. Длина гипотенузы равнобедренного прямоугольного треугольника равна см. Вычислите площадь этого треугольника.
■ 3. Острый угол А прямоугольной трапеции ABCDравен . Сумма длин ее боковых сторон - см. Меньшее основание ВС равно 8см. Вычислите:
а) площадь трапеции;
б) расстояние от вершины В до диагонали.
КОНТРОЛЬНАЯ РАБОТА №6
Вариант 2
▲1.
Вычислите площадь треугольника КМР.
2. Острый угол ромба равен . Длина большей его диагонали - см.
Вычислите площадь ромба.
■ 3. Основания ADи ВС равнобокой трапеции ABCD соответственно 10см и 6см. Диагональ АС равна 10см. Вычислите:
а) площадь трапеции;
б) расстояние от вершины В до диагонали АС.
infourok.ru
 . Найти все углы ромба.
. Найти все углы ромба. . Найдите длину диагонали, противолежащей этому углу.
. Найдите длину диагонали, противолежащей этому углу. . Найти все углы параллелограмма .
. Найти все углы параллелограмма . , а диагональ, исходящая из вершины этого угла равна 12см. Найдите периметр ромба.
, а диагональ, исходящая из вершины этого угла равна 12см. Найдите периметр ромба. см.
см. см.
см. С=90
С=90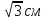 , АС=2 см. Найдите
, АС=2 см. Найдите см, один из катетов равен 4 см. Найдите второй катет и острые углы.
см, один из катетов равен 4 см. Найдите второй катет и острые углы. , АС=2 см. Найдите
, АС=2 см. Найдите
 № 1. Рисунок 1. P
№ 1. Рисунок 1. P

 Дано: АО = 6,8 см, СО = 8,4 см,
Дано: АО = 6,8 см, СО = 8,4 см,  № 1. Рисунок 1. B
№ 1. Рисунок 1. B Доказать: DЕ ║АС.
Доказать: DЕ ║АС. Найдите ∟ВСА, ∟ВАС.
Найдите ∟ВСА, ∟ВАС.


 A B
A B


 ;
;
 ; б)
; б)  ; в)
; в) 
 ; б) 3; в)
; б) 3; в) 










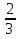 ;
;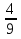
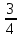 ; б)
; б) 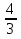 ; в)
; в) 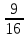
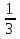 ; б) 3; в)
; б) 3; в) 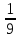





 а) ABOD – параллелограмм.б) ABOD – ромб.в) AOCD – ромб.г) ∠COD=∠AODд) ∠AOD=∠BOA
а) ABOD – параллелограмм.б) ABOD – ромб.в) AOCD – ромб.г) ∠COD=∠AODд) ∠AOD=∠BOA 5. Начертите прямоугольный треугольник ABC, на стороне BC отметьте точку N, не являющейся ее серединой. Постройте фигуру, симметричную треугольнику ABC относительно точки N.
5. Начертите прямоугольный треугольник ABC, на стороне BC отметьте точку N, не являющейся ее серединой. Постройте фигуру, симметричную треугольнику ABC относительно точки N. а) AOCD – параллелограмм.б) AOCD – ромб.в) ABOD – ромб.г) ∠COD=∠AODд) ∠AOD=∠BOA
а) AOCD – параллелограмм.б) AOCD – ромб.в) ABOD – ромб.г) ∠COD=∠AODд) ∠AOD=∠BOA 5. Начертите ромб ABCD. Постройте фигуру, симметричную ему относительно прямой BD.
5. Начертите ромб ABCD. Постройте фигуру, симметричную ему относительно прямой BD. а) 45; б) 216; в) 50; г) 72.
а) 45; б) 216; в) 50; г) 72.
 а) 27,5; б) 28; в) 27; г) 30.
а) 27,5; б) 28; в) 27; г) 30.
 4. В равнобедренном треугольнике, основание равно 14, угол между боковыми сторонами равен 60°. Найдите длину высоты, проведенной к основанию.
4. В равнобедренном треугольнике, основание равно 14, угол между боковыми сторонами равен 60°. Найдите длину высоты, проведенной к основанию. 6. В треугольнике ABC прямая, параллельная стороне AB пересекает высоту CH в точке М, и сторону АС в точке К. Найдите cos(A), если AH=8, MK=4, AK=6.
6. В треугольнике ABC прямая, параллельная стороне AB пересекает высоту CH в точке М, и сторону АС в точке К. Найдите cos(A), если AH=8, MK=4, AK=6. 6. Треугольник ABC прямоугольный. Из точки H, лежащей на гипотенузе AB, опущен перпендикуляр к BC, он пересекает ее в точке М. Найдите cos(A), если AH=5, HM=6, AC=9.
6. Треугольник ABC прямоугольный. Из точки H, лежащей на гипотенузе AB, опущен перпендикуляр к BC, он пересекает ее в точке М. Найдите cos(A), если AH=5, HM=6, AC=9. Часть В
Часть В 6. Треугольнике ABC - равнобедренный с основанием АС. Его периметр равен 40 см, АС=16см. Найдите длину отрезка ВМ (М – точка касания вписанной окружности со стороной ВС).
6. Треугольнике ABC - равнобедренный с основанием АС. Его периметр равен 40 см, АС=16см. Найдите длину отрезка ВМ (М – точка касания вписанной окружности со стороной ВС).
 Часть В
Часть В 6. Треугольнике EFG - равнобедренный, с основанием EG. Его периметр равен 44 см, FG=14см. Найдите длину отрезка FМ (М – точка касания вписанной окружности со стороной ВС).
6. Треугольнике EFG - равнобедренный, с основанием EG. Его периметр равен 44 см, FG=14см. Найдите длину отрезка FМ (М – точка касания вписанной окружности со стороной ВС).
 2. Используя данные рисунка, найдите площадь равнобедренной трапеции.
2. Используя данные рисунка, найдите площадь равнобедренной трапеции. а) 42, б) 44, в) 38, г) 40.
а) 42, б) 44, в) 38, г) 40. Часть С
Часть С 2. Используя данные рисунка, найдите площадь равнобедренной трапеции.
2. Используя данные рисунка, найдите площадь равнобедренной трапеции. а) 35, б) 63, в) 90, г) 81.
а) 35, б) 63, в) 90, г) 81. Часть С
Часть С





