
При описании результатов эмпирического исследования обычно приводится большое количество фактического и цифрового материала. Наглядность ему придает использование таблиц и схем.
Таблицы представляют собой упорядоченные по горизонтали и вертикали наборы количественных и качественных данных.
Таблицу следует располагать в работе непосредственно после текста, в котором она упоминается впервые, или на следующей странице. Таблицы слева, справа, сверху и снизу ограничиваются линиями. Таблицы нумеруются арабскими цифрами. Номер следует размещать в правом верхнем углу после слова «Таблица» (например, Таблица 1). Допускается нумерация таблиц как сквозная — по всей работе, так и в пределах раздела. Если в работе одна таблица, ее не нумеруют.
В таблицах рекомендуется использовать вертикальные линии для более четкого разделения столбцов или делать промежутки между столбцами не менее 4 мм. Горизонтальные линии следует использовать только для выделения главных разделов таблицы. Однако, когда колонки таблицы содержат цифры, чтение затрудняется; тогда можно использовать разделяющие линии (Куликов, 2001, с, 116).
Таблица должна иметь номер и заголовок. Номер ставится сразу после слова «Таблица». Заголовок помещается ниже слова «Таблица». Слово «Таблица» и заголовок начинаются с прописной (большой) бук вы, точка в конце заголовка не ставится. Кавычки для выделения слова «Таблица» или названия таблицы не используются.
Графы строк и столбцов таблицы также должны иметь заголовки, начинающиеся с прописных (больших) букв, подзаголовки — со строчных, если последние подчиняются заголовку. Заголовки граф указываются в единственном числе. Графу «№ п/п» (номер по порядку) в таблицу включать не следует. Если заголовки граф очень длинные, то они могут быть заменены краткими условными сокращениями или цифрами, пояснения которых должны быть помещены в текст заглавия всей таблицы.
Таблица
Распределение общей дисперсии (в %) каузальной атрибуции в зависимости ОТ трех критериальных параметров (по данным Л. МакАртура)
(Хекхауэен X. Мотивация и деятельность. 2-е изд., перераб. СПб.: Питер-Пресс; М.: Смысл, 2003. С. 642)
| Параметры | Каузальная атрибуция | Средняя доля дисперсии | |||
| объекту | обстоятельствам | субъекту | субъекту или объекту | ||
| Специфичность | 12 | 8 | 22 | 0 | 10 |
| Согласованность | 5 | 0 | 6 | 1 | 3 |
| Стабильность | 6 | 41 | 16 | 16 | 20 |
Стандартный вид таблиц для представления первичных результатов: по строкам — испытуемые, по столбцам — значения измеренных параметров. В таблицах целесообразно размещать сводные итоги статистической обработки, а также другие типы систематизированных данных.
Таблицу следует размещать так, чтобы читать ее можно было без поворота работы. Если такое размещение невозможно, таблицу располагают так, чтобы ее можно было читать, поворачивая работу по часовой стрелке.
При переносе таблицы на другую страницу ее заголовки следует повторить и над ней размещают слова «Продолжение таблицы», с указанием ее номера. Если заголовки таблицы велики, допускается их не повторять: в этом случае следует пронумеровать графы и повторить их нумерацию на следующей странице. Основой заголовок таблицы не повторяют.
Если цифровые или иные данные в какой-либо строке таблицы отсутствуют, то ставится прочерк. Если все показатели, приведенные в таблице, выражены в одной единице измерения, то ее обозначение указывается в пояснительном тексте заголовка таблицы. Если все показатели, приведенные в какой-либо графе, выражены в одних и тех же единицах измерения, то ее обозначение помещается в скобках после заголовка графы. Заменять кавычками повторяющиеся в таблице элементы — цифры, знаки и др. — не допускается. При наличии в тексте небольшого по объему цифрового материала его нецелесообразно оформлять в таблицу, а следует давать в виде текста, располагая цифровые данные в колонки. Нет необходимости в тексте повторять все коэффициенты и числовые критерии, представленные в таблице. Выделите в тексте, комментирующем таблицу, наиболее важные показатели, на которые должен обратить внимание читатель, подтверждающие вашу гипотезу и выводы.
Выделите курсивом соответствующие статистические символы, например, t, p, F и т.п.).
Для представления эмпирических данных полезно использовать такие графические формы, как диаграммы, гистограммы, полигоны распределения, а также различные графики. Их следует располагать в работе непосредственно после текста, в котором они упоминаются впервые, или на следующей странице, если в указанном месте они не помещаются.
Зависимости изучаемых параметров наглядно могут отражать графики.
График представляет собой линию, которая изображает зависимость между переменными. На осях откладываются значения изучаемых количественных показателей. При использовании двумерного графика по оси абсцисс обычно размещают независимую переменную, по оси ординат — зависимую переменную.
Л.В. Куликов дает следующие рекомендации по построению диаграмм и графиков.
1. График и текст должны взаимно дополнять друг друга.
График должен быть понятен «сам по себе» и включать все необходимые обозначения.
На одном графике не разрешается изображать больше четырех кривых.
Линии на графике должны отражать значимость параметрах важнейшие необходимо обозначать цифрами.
Надписи на осях следует располагать внизу и слева.
Точки на разных линиях принято обозначать кружками, квадратами и треугольниками (Куликов, 2001, с. 116).

Рис. 1. График. Возрастная динамика изменения значимости протестной мотивации употребления водки и других крепких спиртных напитков («Употребляю, потому что мне запрещают») среди юно шей и девушек (%)
(Собкин B.C., Адамчук Д. В. Особенности употребления алкоголя и подростковой среде // Вестник практической психологии образования. 2006. № 1 (6))
Диаграммы используются главным образом для изображения соотношения между величинами.
Это способ графического изображения величин при помощи фигур (секторов, столбцов и т.п.), площади которых пропорциональны величинам. Совмещенные диаграммы позволяют в одном поле объединить две диаграммы, имеющие одинаковые отметки на оси абсцисс, но разный размах варьирования значений признаков, величина которых отображается на оси ординат. Секторная диаграмма — диаграмма, и которой числа (обычно проценты) изображены в виде круговых секторов.

Рис. 2. Диаграмма. Отношение выпускников к ЕГЭ (в целом по республике)
( Мартынова Т.Ф., Павлова Л.Е. Социологический опрос выпускников в контексте организации эксперимента по введению ЕГЭ в Республике Саха (Якутия) // Психология образования: региональный опыт. Материалы Второй национальной научно-практической конфедерации. М., 2005)
Разновидностью диаграмм является гистограмма. Гистограмма — это столбчатая диаграмма, состоящая из вертикальных прямоугольников, расположенных основаниями на одной прямой (например, оси абсцисс).
Гистограммы часто используются для графического представления плотности распределения (частотного распределения), при котором число случаев в классе изображается в виде вертикальных полос (столбиков, полос). По оси абсцисс откладывают значения наблюдаемой величины, а по оси ординат — ее частоты (отношение числа наблюдений, попавших в данный промежуток, к числу всех наблюдений) в каждом из промежутков, деленные на длину промежутков. В результате получается ступенчатая линия (Куликов, 2001, с. 114).

Рис. 3. Гистограмма. Возрастная динамика юношей и девушек, употребляющих алкоголь на территории школы (% от числа учащихся, употребляющих спиртные напитки)
(Собкин B.C., Адамчук Д.В. Особенности употребления алкоголя в подростковой среде // Вестник практической психологии образования. 2006. № 1 (6))
Аналог диаграммы — полигон. Этот графический способ отображения данных преимущественно используется для изображения дискретных рядов.
Диаграммы и профили представляют результаты диагностики с использованием многопараметрических (многокомпонентных) тестов или тестовых наборов. Они позволяют в наглядной форме показать индивидуальные и усредненные оценки по тестам или по факторам.
Для отображения корреляционных связей между параметрами можно использовать схему, которая называется корреляционной плеядой. Параметры изображаются кружками, внутри них проставляются номера признаков или сокращенно записывается название признаков (параметра). Если записываются номера, то они должны быть рас шифрованы в подписях к рисунку Линии, соединяющие кружки, кодируют характер корреляционных связей. Например, положительные связи (положительной направленности) могут быть изображены сплошными линиями, отрицательные — прерывистыми, связи достоверные на уровне 5% — одной линией, а достоверные на уровне 1% - двумя линиями. Использованные обозначения должны быть объяснены в тексте под рисунком. Признаки лучше распределять группами, объединяющими их по какому-либо критерию. В центре корреляционной плеяды обычно размещают либо наиболее важный параметр

либо тот, у которого наибольшее число значимых коэффициентов корреляции.
Большую наглядность представлению результатов корреляционного анализа придают корреляционные кольца и корреляционные ряды. Подробнее со способами графического представления данных эмпирического исследования можно познакомиться в книге Л.В. Куликова
Все иллюстрации, графики, диаграммы в работе обозначаются как рисунки: «Рис. 1», «Рис. 2» и т.д. Они должны иметь названия, которые помещаются под ними после слов «Рис. 1» (или 2, 3 и т.п.). Их необходимо нумеровать арабскими цифрами порядковой нумерацией в пределах всей работы. При необходимости после заголовка помещается текст, поясняющий содержание и обозначения рисунка.
На все таблицы, диаграммы, схемы, иллюстрации должны быть даны ссылки в тексте. Недооценка словесного описания каждой таблицы, диаграммы, графика считается методической ошибкой. Неверно полагать, что в таблице, на диаграмме «и так все видно». Должны быть названы все сходства и различия, их оценки по величине, даны ссылки на статистическую значимость различий, отмечен размах варьирования показателей, названы наибольшие и наименьшие позиции. Детальное описание данных помогает анализу и обобщению результатов, придает доказательность выводам.
При ссылках на таблицы, следует писать: «в соответствии с данными в таблице 5»; или «как видно из таблицы 5»; или «результаты, при веденные в таблице 5, показывают, что...»; или давать ссылку в скобках: (таблица 5).
При ссылках на рисунки пишется: «как видно на рис. 3»; «как представлено на рис. 6»; или «из рис. 3 видно, что...»; или дается ссылка в скобках (рис. 3) и т.п. Если далее по тексту необходимо повторно обратиться к рисунку, то ссылка к нему делается следующим образом: (см. рис. 6) или (см. рис. 6 на с. 24).
При ссылках на формулы обычно пишется: «...по формуле 3». При ссылках на приложение пишется, например: «данные, полученные и результате первичной обработки, приведены в приложении 1», или: «программа развивающих занятий, использованная в нашей работе, приводится в приложении 2».
При использовании числительных нужно обратить внимание на правильное их написание. Однозначные количественные числительные (от нуля до девяти) пишутся словами, если при них нет единиц измерения. Например: «в двух случаях из восьми» (неправильно -2 случаях из 8»). Многозначные количественные числительные пишутся цифрами. Например: «67 испытуемых» (неправильно — «шестьдесят семь испытуемых»). Числа с сокращенным обозначением единиц измерения пишутся цифрами. При этом после сокращенных единиц измерения (миллиметр — мм) точки не ставятся. Количественные числительные при записи арабскими цифрами не имеют падежных окончаний, если сопровождаются существительными. Например, правильно написать «в 30 случаях из 100» (неправильно 30-ти случаях из 100»).
Однозначные и многозначные порядковые числительные часто пишутся словами: «девяносто пятый». Если порядковые числительные записываются арабскими цифрами и склоняются в тексте, для этого существуют определенные правила. Падежные окончания числительных, оканчивающиеся на две гласные, «й» или согласную, состоит из одной буквы. Например, «шестая» — «6-я», а не «6-ая». Падежные окончания числительных, оканчивающихся на гласную, состоят из двух букв. Например, «эксперимент первого типа» — «эксперимент 1-го типа» (а не «1-ого типа» или «1-о типа»).
Представляйте описание качественных показателей и данных в логичной и упорядоченной последовательности, которая сделает их ясными для читателя. В ряде исследований (или на отдельных его этапах) количественные показатели не используются. В этом случае исследователь сообщает об основных тенденциях и темах, которые выявляются при субъективном или объективном анализе полученных качественных данных (продуктов деятельности, описаний, интроспективных отчетов, стенографии интервью). Подзаголовки в анализе таких результатов делают более структурированными для читателя.
studfiles.net
Сказуемое этой таблицы не только характеризует распределение студентов по каждому из двух выделенных признаков, но и позволяет изучить состав каждой группы, выделенной по одному признаку — полу, по другому признаку — возрасту студента, т.е. имеет место комбинирование двух признаков.
Следовательно, таблицы со сложной разработкой показателей сказуемого обеспечивают более широкие возможности для анализа изучаемых показателей и взаимосвязей между ними. Простую и сложную разработку показателей сказуемого может иметь таблица любого вида: простая, групповая, комбинационная.
В зависимости от этапа статистического исследования таблицы делятся на:
Итак, мы рассмотрели табличный метод отображения исследуемых цифровых данных, широко используемый в ходе проведения анализа экономических явлений, статистических данных и хозяйственной деятельности организаций.
Графический метод –метод условных изображений при помощи геометрических знаков, точек, линий, фигур, и других символов.
Существует множество видов графических изображений (рис.1). Их классификация основана на ряде признаков: а) способ построения графического образа; б) геометрические знаки, изображающие статистические показатели; в) задачи, решаемые с помощью графического изображения.
Классификация статистических графиков по форме графического образа.
По способу построения статистические графики делятся на диаграммы, взаимосвязанные графики и статистические карты.
Диаграммы -наиболее распространенный способ графических изображений. Это графики количественных отношений. Виды и способы их построения разнообразны.
Линейная диаграмма
Линейные диаграммы для характеристики динамики применяют в следующих случаях:
На одном линейном графике можно построить несколько кривых, (рис.2), которые позволят сравнить динамику различных показателей или одного и того же показателя в разных регионах, отраслях и др.
Для построения этого графика воспользуемся данными о динамике производства овощей и картофеля в России.
Производство овощей в России, млн.
Динамика производства картофеля и овощей в России в 2006-2011 гг.
Радиальная диаграмма
Одним из видов линейных диаграмм являются радиальные диаграммы. Они строятся в полярной системе координат с целью отражения процессов, ритмически повторяющихся во времени. Радиальные диаграммы можно разделить на два вида: замкнутые и спиральные.
В замкнутых радиальных диаграммах в качестве базы отсчета берется центр круга (рис. 3). Вычерчивается круг радиусом, приравненным среднемесячному показателю изучаемого явления, который делится затем на двенадцать равных секторов. Каждый радиус изображает месяц, причем расположение их аналогично циферблату часов. На каждом радиусе делается отметка согласно масштабу, выбранному исходя из данных по каждому месяцу. Если данные превышают среднегодовой уровень, то отметка делается на продолжении радиуса вне окружности. Затем отметки всех месяцев соединяются отрезками.
Рассмотрим пример построения замкнутой радиальной диаграммы по месячным данным отправления грузов железнодорожным транспортом общего пользования в России в 1997 г.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
68,9 | 67,6 | 776,3 | 70,7 | 71,3 | 74,2 | 76,3 | 75,7 | 79,3 | 74,9 | 74,0 | 74,2 |
Отправление грузов железнодорожным транспортом общего пользования
Столбиковая диаграмма
Среди плоскостных диаграмм наибольшее распространение получили столбиковые, полосовые или ленточные, треугольные, квадратные, круговые, секторные, фигурные.
Столбиковые диаграммы изображаются в виде прямоугольников (столбиков), вытянутых по вертикали, высота которых соответствует значению показателя
Знаки Варзара
Более редкими, но не менее важными являются прямоугольные диаграммы, так называемые знаки Варзара.
Знаки Варзара применяются для графического сравнения трех разноименных мультипликативно связанных показателей, т.е. таких, один из которых представляет собой произведение двух других, являющихся сомножителями.
Используя свойство прямоугольника, производный показатель, который является произведением двух других показателей-сомножителей, изображают его площадью; при этом основание прямоугольника пропорционально величине одного из показателей-сомножителей, а высота - второму показателю-сомножителю.
Основание прямоугольника служит, как правило, для изображения объемных показателей (численности населения, выработанной энергии, объема вредных выбросов тепловых электростанций и т. д.), а его высота - для изображения качественных показателей (плотности населения, доли выработки электроэнергии определенным видом электростанций, процентного содержания вредных веществ и т. п.). При сравнении показателей, которые принадлежат к разным статистическим единицам - объектам или территориям, прямоугольники располагаются на горизонтальной базовой линии, или рядом друг с другом, или один на одном так, чтобы совмещались их нижние левые углы.
На графике показан общий объем производства электроэнергии, доля в ней атомной энергетики и объем производства электроэнергии атомными энергоблоками Украины, Германии, Франции в 1999 г.
Связь названных показателей имеет следующий вид: если за основание прямоугольника принять общую выработку электроэнергии млрд кВт-ч, а за его высоту- % выработки АЭС от общего производства электроэнергии в стране, то площадь прямоугольника будет отображать общую выработку электроэнергии на АЭС, млрд кВт-ч. Для построения прямоугольников по соответствующим показателям каждой страны установим масштаб для их основания 1 см = 200 млрд кВт-ч, а для их высоты - 1 см = 20 %. В соответствии с выбранным масштабом прямоугольник, который отображает общий объем производства электроэнергии АЭС Украины, млрд. кВт-ч, имеет основание и высоту, равные соответственно 0,77 и 2,17 см.
Знаки Варзара
Прямоугольники, изображенные на рис., имеют разные площади. Они наглядно показывают, что в Германии и Франции в 1999 г. почти при равном объеме выработки электроэнергии доля АЭС в Германии в 2,5 раза меньше, чем во Франции. При сравнении Украины и Германии видно, что доля АЭС в Украине превышает аналогичный показатель Германии в 1,5 раза, в то время как общее производство электроэнергии в Украине в 3,5 раза меньше, чем в Германии
Отметим, что недостатком знаков Варзара является то, что при незначительных отличиях показателей очень трудно оценить на глаз соотношения площадей прямоугольников, поэтому в таких случаях их использование становится нецелесообразным и малоэффективным.
Статистические карты представляют собой вид графических изображений статистических данных на схематичной географической карте, характеризующих уровень или степень распространения того или иного явления на определенной территории.
Средствами изображения территориального размещения являются штриховка, фоновая раскраска или геометрические фигуры. Различают картограммы и картодиаграммы.
Картограмма - это схематическая географическая карта, на которой штриховкой различной густоты, точками или окраской различной степени насыщенности показывается сравнительная интенсивность какого-либо показателя в пределах каждой единицы нанесенного на карту территориального деления (например, плотность населения по областям или республикам, распределение районов по урожайности зерновых культур и т.п.). Картограммы делятся на фоновые и точечные.
Картограмма фоновая - вид картограммы, на которой штриховкой различной густоты или окраской различной степени насыщенности показывают интенсивность какого-либо показателя в пределах территориальной единицы.
Картограмма точечная - вид картограммы, где уровень какого-либо явления изображается с помощью точек. Точка изображает одну единицу совокупности или некоторое их количество, чтобы
показать на географической карте плотность или частоту появления определенного признака.
Вторую большую группу статистических карт составляют картодиаграммы, представляющие собой сочетание диаграмм с географической картой. В качестве изобразительных знаков в картодиаграммах используются диаграммные фигуры (столбики, квадраты, круги, фигуры, полосы), которые размещаются на контуре географической карты. Картодиаграммы дают возможность географически отразить более сложные статистико-географические построения, чем картограммы.
Пример картограммы:
Картограмма плотности населения восьми районов области
Пример картодиаграммы:
В качестве примера картодиаграммы возьмем изображение валового сбора зерна Центрального района России.
Изолинии (от греч. 1зоз - равный, одинаковый, подобный)-это линии равного значения какой-либо величины в ее распространении на поверхности, в частности на географической карте или графике. Изолиния отражает непрерывное изменение исследуемой величины в зависимости от двух других переменных и применяется при картографировании природных и социально-экономических явлений. Изолинии используются для получения количественных характеристик исследуемых величин и для анализа корреляционных связей между ними
.Валовой сбор зерна Центрального района России (данные условные)
3. Выводы
Наиболее удобная и рациональная форма представления количественных данных — таблица. Статистическая таблица должна быть построена по определенным правилам. Она состоит из подлежащего (объект изучения) и сказуемого (цифровая характеристика объекта).
Вид таблицы определяется по подлежащему — по тому, как представлен объект изучения:
В работе мы также рассмотрели общие сведения о графическом методе как особой знаковой системе, выяснили значение графического метода в анализе и обобщения данных, элементов статистического графика, а также классифицировали графики по форме графического изображения и по способу построения и задачам изображения.
myunivercity.ru
Результаты сводок и группировок заносятся в статистические таблицы, являющиеся средством наглядного выражения результатов исследования.
Статистическая таблицапредставляет собой
. Основу статистической таблицы составляет графленная сетка, вертикальные столбцы которой называются графами, а горизонтальные – строками. Если__строки и графы имеют название, то это будет макет таблицы.
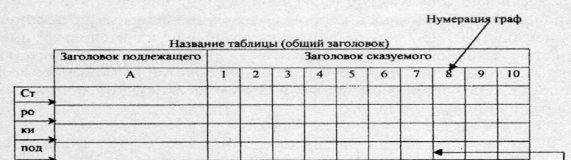

В таблице различают: заголовок, подлежащее и сказуемое.
Заголовок таблицы
Подлежащим таблицы является
Сказуемым являются–
Обычно подлежащее располагается слева в виде названий строк, а сказуемое – сверху в виде названий граф.
По содержанию подлежащего все статистические таблицы можно разделить на следующие группы:
• Простыетаблицы, в подлежащем которых отсутствуют группировки. Они содержат обобщающие показатели, относящиеся к перечню единиц совокупности (перечневые таблицы), к перечню хронологических дат (хронологические таблицы) или к перечню территорий (территориальные таблицы).
• Групповыетаблицы, в подлежащем которых изучаемый объект разделен на группы по определенному признаку. При этом каждая группа может быть охарактеризована рядом показателей.
• Комбинационныетаблицы, в подлежащем которых дана группировка единиц совокупности по двум и более признакам, взятым в комбинации.
Сказуемого таблицы может быть простым или сложным.
Простоесказуемое предусматривает параллельное расположение показателей, (графы 1,2 в макете таблицы) а сложное– комбинированное (графы 3, 4, 5).
При построении статистических таблиц необходимо соблюдать определенные правила по их оформлению:
1. Таблица должна быть компактной, легко обозримой. Ее не следует загружать излишними подробностями, затрудняющими анализ.
2. Заголовок таблицы должен ясно и кратко выражать ее содержание.
Заголовки строк подлежащего и граф сказуемого также должны быть сформулированы точно и кратко.
3. В таблице желательно давать нумерацию граф. Это облегчает пользование таблицей, показывает способ расчета чисел в графах. Графы, содержащие подлежащее, обозначаются заглавными буквами алфавита; графы, содержащие сказуемое, нумеруются арабскими числами. Не допускается в заголовках подлежащего и сказуемого сокращение слов.
4. Если единицы измерения различны, то они указываются в названиях строк и граф.
5.Приводимые в подлежащем и сказуемом признаки должны располагаться в логическом порядке с учетом необходимости их совместного рассмотрения. Информация размещается от частного к общему, т. е. сначала показывают слагаемые, а в конце подводят итоги.
6. Если в таблице приводятся не все данные, а только наиболее значимые из них то сначала показывают итог, а затем выделяют наиболее важные части с помощью оборотов «в том числе», «из них».
7. Следует различать «Итого» и «Всего». «Итого» является итогом для определенной части совокупности, а «Всего» - итог для всей совокупности.
8. При оформлении таблицы применяются следующие обозначения:
- прочерк (-) –когда явление отсутствует;
- символ «×» -если явление не имеет осмысленного содержания;
- многоточие (…) – если отсутствуют сведения (или делается запись «нет сведений»).
- если сведения имеются, но числовое их значение меньше принятой в таблице точности, оно выражается дробным числом 0,0.
9. Округление чисел, приводимых в таблице, должно проводится с одинаковой степенью точности.
10. Если одна величина превосходит другую многократно, то полученные относительные показатели лучше выражать не в процентах, а в количестве раз.
Соблюдение приведенных правил построения и оформления статистических таблиц делает их основным средством представления, обработки и обобщения статистической информации.
Основные виды графиков.
Иногда статистические таблицы дополняются графиками, когда ставится цель подчеркнуть какую-то особенность данных, провести их сравнение. Графики являются самой эффективной формой представления данных с точки зрения их восприятия. Часто графики используются и вне связи с таблицей. С помощью графиков достигается наглядность характеристики структуры, динамики, взаимосвязи явлений, их сравнения.
Статистические графики представляют собой условные изображения числовых величин и их соотношений посредством линий, геометрических фигур, рисунков или географических карт-схем.
По способу построения графики делятся на диаграммы, картограммы и картодиаграммы.
Наиболее распространенным способом графического изображения данных являются диаграммы. Они бывают разных видов: линейные, радиальные, точечные, плоскостные, объемные, фигурные. Вид диаграмм зависит от вида представляемых данных (одна переменная или один показатель, несколько переменных или показателей, количественные или неколичественные) и задачи построения графика.
В любом случае график обязательно сопровождается заголовком -над или под полем графика. В заголовке указывается, какой показатель изображен, в каких единицах измерения, по какой территории и за какое время он определен.
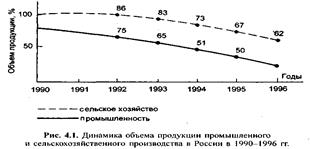
Линейные графикииспользуются для представления количественных переменных: характеристики вариации их значений, динамики, взаимосвязи между переменными. Например, на рис. 4.1 представлена динамика объема продукции промышленного и сельскохозяйственного производства в России в 1990-1996 гг
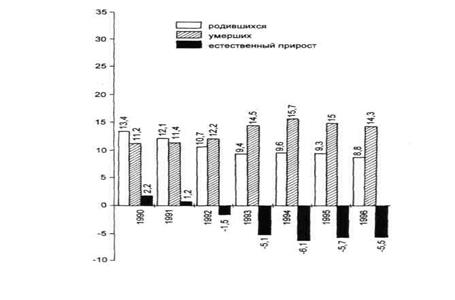 |
Среди плоскостных диаграммпо частоте использования выделяются столбиковые диаграммы, на которых показатель представляется в виде столбика, высота которого соответствует значению показателя. Пример столбиковой диаграммы представлен на рис. 4.4. Часто на столбиковой диаграмме показываются относительные величины: при сравнении показателей по группам, по разным совокупностям, одна из которых может быть принята за 100%.
| Рис.4.4. Общие показатели рождаемости, смертности и естественного прироста населения России |
Пропорциональность площади той или иной геометрической фигуры величине показателя лежит в основе других видов плоскостных диаграмм: треугольных, квадратных, прямоугольных.
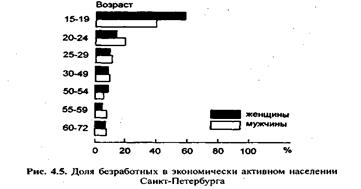
Ленточная диаграммапредставляет показатели в виде горизонтально вытянутых прямоугольников. Как столбиковые, так и ленточные диаграммы можно применять не только для сравнения самих величин, но и для сравнения их частей (рис. 4.5).
Из плоскостных диаграмм часто используется секторная диаграмма. Она применяется для иллюстрации структуры изучаемой совокупности. Вся совокупность принимается за 100%, ей соот ветствует общая площадь круга, площади секторов соответствуют частям совокупности (рис. 4.8).

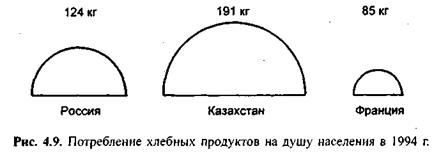
Фигурные (или картинные) диаграммы усиливают наглядность изображения, так как включают рисунок изображаемого показателя. Размер рисунка соответствует размеру показателя (рис. 4.9).
Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений. Они показывают размещение изучаемого явления, его интенсивность на определенной территории - в республике, области, экономическом или административном районе и т. д.
На картограммераспределение изучаемого признака по территории изображается условными знаками (точками, штриховкой, цветом и т. д.), соответствующими определенным интервалам значений величины этого признака. Эти знаки покрывают контур каждого района. Картограмма применяется в тех случаях, когда возникает необходимость показать территориальное распределение какого-нибудь одного статистического признака между отдельными районами для выявления закономерностей этого распределения.
 |
Картограммы бывают фоновые и точечные. На фоновых картограммах распределение изучаемого явления на территории изображается различными раскрасками территориальных единиц с разной густотой цвета. Часто вместо раскраски применяется штриховка различной интенсивности. Такие картограммы обычно используются для изображения уровня относительных и средних величин по территориям. Например, имеются данные об урожайности зерновых по 10 районам области: урожайность до 20 ц/га имеют три смежных района, 20-30 ц/га - четыре смежных района, свыше 30 ц/га -три смежных района. Соответствующая фоновая картограмма представлена на рис. 4.10. Чем более интенсивно явление, тем гуще штриховка (точки) или темнее окраска. Такая картограмма наглядно показывает географию урожайности зерновых культур по районам. Чем больше групп, тем точнее изображение, но большое число групп создает пестроту и снижает наглядность. Поэтому практически лучше всего применять не более четырех-пяти тонов или градаций плотности штриховки.
На точечной картограмме символами графического изображения статистических данных являются точки, размещенные в пределах определенных территориальных границ. Точечная картограмма применяется для размещения абсолютных величин. Каждой точке, нанесенной на картограмму, придается числовое значение, что позволяет использовать ее для прямого счета. Например, имеются четыре района с добычей угля в 200, 500, 1000 и 1400 тыс. т в год. Для составления картограммы примем точку за 100 тыс. т и нанесем на контур каждого района соответствующее количество точек (рис. 4.11).
 |
Картодиаграмма - это сочетание диаграммы с географической картой. В качестве изобразительных знаков в картодиаграммах используются те или иные фигуры, которые размещаются на контуре географической карты. Картодиаграммы дают возможность графически отразить более сложные статистико-географические соотношения, чем картограммы. Так, при помощи картодиаграммы можно выразить пространственную специфику в структурах изучаемых статистических совокупностей, особенности каждого района как единого целого и т. д. Например, структурная или секторная картодиаграмма, характеризующая порайонные различия в структуре посевных площадей. В качестве диаграммных знаков в картодиаграмме часто используют различные геометрические фигуры, особенно круги, которые наиболее просты и удобны для выражения сравниваемых количественных показателей на карте.
Кроме рассмотренных видов диаграмм, картограмм и картодиаграмм на практике встречаются и другие, более сложные графические изображения статистических данных.
Лекция 5. Средние величины.
1. Сущность и значение средних величин.
2. Степенные средние.
2.1Средняя арифметическая.
2.2 Средняя гармоническая.
2.3 Средняя геометрическая.
2.4 Средняя квадратическая.
1. Сущность и значение средних величин.
Средние показатели являются наиболее распространённой формой статистических показателей, используемых в социально-экономических исследованиях.
Средним называется
. Он выражает величину признака, отнесённую к единице совокупности. Особенности среднихпоказателей заключаются в том, что они, во-первых, отражают то общее, что присуще всем единицам совокупности; во-вторых, в них взаимопогашаются те отклонения значений признака, которые возникают под воздействием случайных факторов. Это означает, что средний показатель отражает типичный уровень признака, формирующийся под воздействием основных доминирующих неслучайных факторов. Применение средних величин позволяет охарактеризовать определенный признак совокупности одним числом, несмотря на то, что у разных единиц совокупности значения признака отличны друг от друга. В социально-экономическом анализе используются два класса средних величин:
- степенные средние;
- структурные средние.
Главное значение средних величин состоит в их обобщающей функции, т. е. замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений.
Если средняя величина обобщает качественно однородные значения признака, то она является типической характеристикой признака в данной совокупности.
Степенные средние.
К степенным средним относятся несколько видов средних, построенных по одному общему принципу:
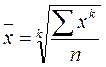
где i x - варианта,
n - объем статистической совокупности,
k - показатель степени.
Показатель степени k может принимать любые значения, но на практике обычно используются несколько его значений: при k = 1 получают среднюю арифметическую; k = -1 – среднюю гармоническую; k = 0 – среднюю геометрическую; k =2 – среднюю квадратическую.
 Степенные средние в зависимости от формы представления исходных данных могут быть простыми и взвешенными.
Степенные средние в зависимости от формы представления исходных данных могут быть простыми и взвешенными.
| Значение k | Виды средних | Простая средняя, рассчитывается по первичным стат. данным | Взвешенная средняя, рассчитывается по сгруппированным стат.данным |
| K= - 1 | Средняя гармоническая | ||
| K = 0 | Средняя геометрическая | ||
| K = 1 | Средняя арифметическая | ||
| K= 2 | Средняя квадратическая |
Мажорантное свойство средних величин:
 Хга<Xге<Ха<Хкв
Хга<Xге<Ха<Хкв
Средняя арифметическая.
Средняя арифметическая является наиболее распространенным видом степенных средних, используется в случаях, когда объём усредняемого признака является аддитивной величиной, т.е. образуется как сумма его значений по всем единицам статистической совокупности.
При этом если индивидуальные значения признака у статистических единиц заменить средней арифметической, то суммарный объем признака по совокупности в целом сохраняется неизменным. Это означает, что средняя арифметическая есть среднее слагаемое.
v Средняя арифметическая простая используется при работе с несгруппированными данными.
Например, при сборке урожая рабочие собрали следующее количество яблок:
| Рабочий | |||||
| Количество собранных яблок, кг. |
Требуется определить среднюю выработку бригады.
Для ее нахождения используется формула средней арифметической простой:
Средняя арифметическая простая рассчитывается как:
v Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным или вариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднюю сгруппированных величин.
Пример. Рассичать среднюю стоимость товара, поступившего на предприятии ЧП «Опт-торг» за июль 2008 г.
| № п/п | Дата | Стоимость/единица, руб | Кол-во поступивших, шт | Стоимость, руб |
| 08.07.08 | 18,50 | 9250,00 | ||
| 12.07.08 | 18,20 | 10920,00 | ||
| 19.07.08 | 18,60 | 7440,00 | ||
| 25.07.08 | 18,40 | 18400,00 | ||
| Итого: | 46010,00 |
Средняя гармоническая.
Средняя гармоническаяимеет более сложную конструкцию, чем средняя арифметическая. Используется в тех случаях, когда статистическая информация не содержит частот по отдельным значениям признака, а представлена произведением значения признака на частоту.
v Если исходные данные несгруппированны,то применяется средняя гармоническая простая:
К ней прибегают в случаях определения, например, средних затрат труда, материалов и т. д. на единицу продукции по нескольким предприятиям.
Пример использования средней гармонической простой:
Например, автомобиль с грузом от предприятия до склада ехал со скоростью 40 км/ч, а обратно порожняком - со скоростью 60 км/ч.
Средняя геометрическая.
Средняя геометрическаяприменяется в тех случаях, когда общий объем усредняемого признака является мультипликативной величиной, т.е. определяется не суммированием, а умножением индивидуальных значений признака.
Форма средней геометрической взвешенной в практических расчётах не применяется.
В социально-экономических исследованиях средняя геометрическая применяется в анализе рядов динамики при определении среднего коэффициента роста, когда задана последовательность относительных величин динамики.
Рассмотрим пример:
В результате инфляции за первый год цена товара возросла в 2 раза по сравнению к предыдущему году, а за второй ещё в 1,5 раза по сравнению к предыдущему. Необходимо определить средний коэффициент роста цены.
Средняя геометрическая используется также для определения равноудаленной величины от максимального и минимального значения признака.
Средняя квадратическая.
Средняя квадратическая используется в тех случаях, когда при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин.
Главная сфера её использования – измерение степени колеблемости индивидуальных значений признака относительно средней арифметической (среднее квадратическое отклонение). Кроме этого, средняя квадратическая применяется в тех случаях, когда необходимо вычислить средний величину признака, выраженного в квадратных или кубических единицах измерения (при вычислении средней величины квадратных участков, средних диаметров труб, стволов и т. д.).
Пример. Какую среднюю поставить студенту, получившего на сессии оценки 2 и 5. Каков его средний балл?
По средней гармонической:
По средней геометрической:
Если судить по средней арифметической, то средний балл равен:
А по средней квадратической:
infopedia.su
ВУЗ, город:
Москва
Предмет: Статистика
Реферат по теме:
Страниц: 14
Автор: Юлия
2010 год
Введение.…...3
1. Статистические таблицы…...4
2. Статистические графики…...8
Заключение...…...13
Список литературы…14
Статистические данные обязательно должны быть представлены так, чтобы удобно было ими пользоваться. Существует три основных формы представления статистических данных: текстовая — включение данных в текст; табличная — представление данных в таблицах; графическая — выражение данных в виде графиков.
Статистические таблицы являются средством наглядного выражения результатов исследования.
Использование графиков для изложения статистических показателей позволяет придать последним наглядность и выразительность, облегчить их восприятие, а во многих случаях помогает уяснить сущность изучаемого явления, его закономерности и особенности, увидеть тенденции его развития, взаимосвязь характеризующих его показателей.
Цель исследования — изучить сущность статистических таблиц и графиков.
Задачи работы:
— рассмотреть статистические таблицы;
— изучить статистические графики;
На основе изученной литературы можно сделать вывод, что данная тема является широко обсуждаемой такими авторами как А.В. Аксяновой, К.В. Балдиным, А.М. Годиным, И.И. Елисеевой, Т.М. Сизовой и др.
Структура данной работы состоит из введения, двух глав, заключения, списка литературы.
1. Аксянова А.В. Теория и практика статистики: [учеб. пособие для вузов, обучающихся по специальности «Статистика», а также др. экон. специальностям] /А. В. Аксянова, Н. Н. Валеев, Ас. М. Гумеров. — М.: КолосС, 2008. — 282 с.
2. Балдин К.В. Общая теория статистики: учеб. пособие /К. В. Балдин, А. В. Рукосуев. — М.: Дашков и К°, 2008. — 311с.
3. Годин А.М Статистика: учебник : [по направлению подгот. и специальности «Статистика» и др. экон. специальностям и направлениям] /А. М. Годин. — М.: Дашков и К°, 2008. — 457 с.
4. Едронова В.Н. Общая теория статистики: Учебник : [Для вузов по экон. специальностям и направлениям] /В.Н. Едронова, М.В. Едронова. — М.: Юристъ, 2001. — 511 с.
5. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. И.И. Елисеевой. — 5-е изд., перераб. и доп. — М.: Финансы и статистика, 2004. — 656 с.
6. Руденко В.И. Статистика: пособие студентам для подготовки к экзаменам /В. И. Руденко. — М.: Дашков и К°, 2008. — 186 с.
7. Сизова Т.М. Статистика: Учебное пособие. — СПб.: СПб ГУИТМО, 2005. — 80 с.
8. Статистика: учебник: [для студентов, обучающихся по специальностям «Финансы и кредит», «Бухгалт. учет, анализ и аудит», «Мировая экономика», «Налоги и налогообложение» /А. И. Демина, О. П. Мамченко, Ю. И. Растова]; Федер.
агентство по образованию, Алт. гос. ун-т. — Барнаул: Изд-во АГУ, 2009. — 360 с..
9. Теория статистики: Учебник : [Для экон. специальностей вузов /Г.Л. Громыко, А.Н. Воробьев, С.Е. Казаринова и др.]; Под ред. Г.Л. Громыко . — М.: ИНФРА-М, 2005. — 475 с.
10. Теория статистики: [Учебник для вузов] /Под ред. Р. А. Шмойловой. — М.: Финансы и статистика, 2004. — 576 с.


Статистические таблицы и графики
2013
ISBN 5215021937,9785215021934
Пособие привьет студентам навыки грамотного построения статистических таблиц и графиков

Статистика
Издательский дом "Питер" , 2013
ISBN 5498074409,9785498074405
Данная книга написана на основе специальных методических разработок авторов и призвана дать читателю...

General Theory of Statistics
Fultus Corporation , 2006
ISBN 1596820861,9781596820869
The present book (russian edition) is a statistical course for undergraduate students in all fields of...

Статистика
ISBN 576543584X,9785765435847

Статистика
ОЛМА Медиа Групп
ISBN 5765422284,9785765422281

Жáклады статистики
1961
ISBN
Экспозиция представляет собой научные документы, результаты исследований и таблиц, приборы, инструменты, рисунки и другие произведения искусства, связанные с сексом. Музей Wellcome Collection в центре Лондона проводит выставку с интригующим названием «Обнажи свое сознание» от Института сексологии. «Институт сексологии» - это крупнейший проект для выставок, который накопил в себе все возможные... далее

Защитник ЦСКА Василий Березуцкий считает, что не стоит выделять в составе «Ромы» только одного Франческо Тотти. Встреча пятого тура группового этапа Лиги чемпионов ЦСКА – «Рома» состоится 25 ноября в Химках. - Неприятно проигрывать в чемпионате три матча подряд, но это другой турнир, другие эмоции. О нашей игре в обороне можно в первую очередь судить по нашим результатам в Лиге чемпионов. В... далее

" - такими призывами украшено в эти дни здание музея Wellcome Collection в центре Лондона. И если сам по себе это лозунг при всей его заманчивости остается не до конца проясненным, тут же еще одна надпись – "Институт сексологии". Нет, не эротики, не порнографии – хотя попадается среди экспонатов выставки и то, и другое, – а именно секса. Масса научных документов, результатов исследований и... далее

"СЭ" представляет 10 статистических фактов о матче 14-го тура чемпионата России, в котором встретятся соседи по турнирной таблице, входящие на данный момент в тройку лидеров первенства. "Краснодар" после 13 туров премьер-лиги-2014/15 имеет в активе 24 очка. Это повторение рекордного в истории клуба графика прошлого сезона, однако тогда краснодарцы шли на 4-м месте, но при этом опережали... далее
nadfl.ru