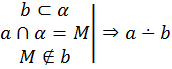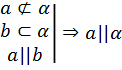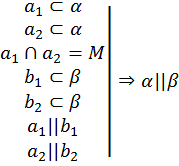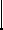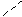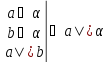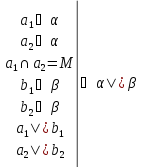|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
§ 2. Взаимное расположение прямых и плоскостей в пространстве. Взаимное расположение прямой и плоскости в пространстве реферат
§ 2. Взаимное расположение прямых и плоскостей в пространстве.
. Основные аксиомы стереометрии и следствия из них.
Как и планиметрия, стереометрия изучается в том же структурном плане: формулируются аксиомы (утверждения, принимаемые без доказательства ввиду их очевидности), теоремы (утверждения, которые доказываются с опорой на аксиомы, определения и ранее изученные теоремы) и определения.
Сформулируем три аксиомы, выражающие основные свойства плоскостей в пространстве.
Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2. Если две точки прямой принадлежат плоскости, то и вся прямая лежит в этой плоскости.
Аксиома 3. Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (т.е. плоскости имеют общую прямую, на которой лежат все общие точки этих плоскостей).
Следствием этих аксиом являются следующие теоремы (доказательства этих теорем и всех последующих опускаем):
Теорема 1. Через прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.
Теорема 2. Через две пересекающиеся прямые можно провести плоскость, и притом только одну.
Теорема 3. Через две параллельные прямые можно провести единственную плоскость.
. Взаимное расположение прямых.
Возможны три случая: две прямые параллельны, пересекаются или скрещиваются.
| Определение. Две прямые называются пересекающимися, если они имеют одну общую точку. Обозначение: a ∩ b = M |
α a
b M |
| Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. Обозначение: a || b |
a
α b |
| Определение. Две прямые, не лежащие в одной плоскости, называются скрещивающимися. Обозначение: a ∸ b |
a
b
M 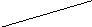
α |
| Теорема 4 (признак скрещивающихся прямых): Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются. | |
| Пример: Две прямые, содержащие ребра AA1 и CD куба ABCDA1B1C1D1 являются скрещивающимися. |
С1 В1 
D1 А1
В С 
D
А |
. Взаимное расположение прямой и плоскости.
Возможны три случая: прямая лежит в плоскости; прямая пересекает плоскость; прямая и плоскость параллельны.
| Определение. Прямая, все точки которой принадлежат плоскости, называется прямой, лежащей в плоскости. Обозначение: a α |
a α
|
| Определение. Прямая и плоскость называются пересекающимися, если у них есть одна общая точка. Обозначение: a ∩ β = M |
a 
β
M |
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Обозначение: a || a ∩ β =
| Теорема 5 (признак параллельности прямой и плоскости): Если прямая, не лежащая в плоскости, параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна данной плоскости.
|
a b α |
V. Взаимное расположение плоскостей.
Возможны два случая: две плоскости пересекаются или параллельны.
Определение. Две плоскости называются параллельными, если они не имеют общих точек
| Теорема 6 (признак параллельности плоскостей): Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то эти плоскости параллельны.
|
a1
a2
α M
b1 b2 β | ||
| Определение. Две плоскости называются пересекающимися, если они имеют общую прямую. В этом случае они не имеют других общих точек вне этой прямой. α ∩ β = a |
β α a | ||
| Вопросы и задачи | |||
Дан куб ABCDA1B1C1D1. Точка М – середина ребра B1C1, N – середина C1D1, K – середина DC, О – точка пересечения диагоналей основания ABCD. Укажите взаимное расположение между следующими прямыми:
а) АA1 иCС1; б) A1C1 и B1D1; в) A1C1и C1D1;
г) A1М и CC1; д) A1D и DC1; е) A1C1 и BD;
ё) A1C и АС; ж) A1B и D1С; з) A1C и ВB1;
и) A1D и АВ ; й) A1М и ВС; к) A1М и ВК ;
л) C1К и B1N; м) C1О и AB1; н) A1О и B1D.
Дан тетраэдр ABCD. Точка К – середина ребра AD, L – середина DB, М – середина АС, N – середина ВС. Определите взаимное расположение прямых и плоскостей.
а) DB и AMN; б) MN и ABC; в) КС и DMN;
г) MN и ABD; д) KL и DMN; е) LN и KML;
ё) CL и ADN; ж) LN и DMK.
Дан куб ABCDA1B1C1D1. Точка К – середина ребра AD, L – середина СC1, М – середина A1B1, N – середина B1C1, Т – середина DC, О – точка пересечения диагоналей четырёхугольника ABCD. Укажите взаимное расположение плоскостей:
а) A1B1C1 и ADC; б) MTK и BB1D; в) MNK и MNT;
г) D1KT и BMN; д) MNK и TLN; е) B1КТ и DMN;
ё) A1DC1 и АB1C; ж) A1C1С и MKT.
Отметьте верные утверждения
а) через точку, не принадлежащую данной прямой, можно провести только одну прямую, параллельную этой прямой.
б) через точку, не принадлежащую данной прямой, можно провести только одну прямую, перпендикулярную этой прямой.
в) прямые, перпендикулярные одной и той же прямой, параллельны.
г) прямая, пересекающая одну из двух данных параллельных прямых, пересекает и другую.
В параллелепипеде ABCDA1B1C1D1укажите параллельные прямые, на которых лежат его рёбра.
В тетраэдре DABC укажите все пары скрещивающихся прямых, на которых лежат его рёбра.
В пространстве даны три попарно пересекающиеся прямые. Изобразите возможные случаи их взаимного расположения.
Прямая с пересекает, по крайней мере, одну из двух пересекающихся прямых а, b. Как могут располагаться относительно друг друга эти три прямые? Сделайте рисунки.
Даны две параллельные прямые а и b. Как может быть расположена по отношению к ним третья прямая c? Сделайте рисунки.
Даны две скрещивающиеся прямые а и b. Как может быть расположена по отношению к ним третья прямая c? Сделайте рисунки.
Отметьте верные утверждения:
а) прямая, параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости.
б) существует единственная прямая, параллельная данной плоскости и проходящая через точку, не принадлежащую этой плоскости.
в) существует бесконечное множество прямых, параллельных данной плоскости и проходящих через точку, не принадлежащую этой плоскости.
г) через одну из двух параллельных прямых можно провести бесконечное множество плоскостей, параллельных другой прямой.
д) существует единственная плоскость, параллельная данной прямой и проходящая через точку, не принадлежащую этой прямой.
е) существует бесконечное множество плоскостей, параллельных данной прямой и проходящих через точку, не принадлежащую этой прямой.
Используя признак параллельности прямой и плоскости, укажите несколько пар параллельных прямой и плоскости в четырёхугольной призме ABCDA1B1C1D1.
Докажите, что в кубе ABCDA1B1C1D1 прямая AB1 параллельна плоскости грани DD1CC1.
Прямые а и b скрещиваются. Можно ли провести через одну из них плоскость, параллельную другой? Обоснуйте свой ответ.
Отметьте верные утверждения
а) через точку, не принадлежащую данной плоскости, проходит единственная плоскость, параллельная данной.
б) если прямая, лежащая в одной плоскости, параллельна прямой, лежащей в другой плоскости, то эти плоскости параллельны.
в) если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то эти плоскости параллельны.
г) если одна из двух данных плоскостей параллельна двум пересекающимся прямым, лежащим в другой плоскости, то эти плоскости параллельны.
д) если плоскость пересекает две данные плоскости по параллельным прямым, то эти плоскости параллельны.
е) если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
ж) если две плоскости параллельны одной и той же прямой, то они параллельны.
Используя признак параллельности плоскостей, укажите параллельные плоскости в прямоугольном параллелепипеде ABCDA1B1C1D1.
PABC – правильный тетраэдр, точка М – центр грани АВС, К – середина ребра АВ. Постройте сечения тетраэдра плоскостями:
а) APM; б) KPM.
Постройте общий отрезок этих сечений.
Постройте сечение тетраэдра плоскостью, проходящей через:
а) две вершины и точку на ребре, не содержащем эти вершины;
б) вершину и две точки на рёбрах, не проходящих через эту вершину;
в) три точки на трёх рёбрах, выходящих из одной вершины;
г) середины трёх рёбер, не выходящих из одной вершины.
В четырёхугольной пирамиде все рёбра равны. Докажите, что её сечение, проходящее через вершину пирамиды и диагональ основания, является прямоугольным треугольником.
Постройте сечение куба плоскостью, проходящей через точку на боковом ребре и две точки на рёбрах основания, не смежных с этим боковым ребром.
Постройте сечение куба плоскостью, проходящей через две точки на скрещивающихся рёбрах верхнего и нижнего оснований и точку на ребре:
а) пересекающимся с ними;
б) пересекающимся только с одним из этих рёбер.
Постройте сечение четырёхугольной пирамиды плоскостью, проходящей через три точки на боковых рёбрах.
В каждом из нижеследующих заданий найдите площадь построенного сечения, учитывая, что все рёбра всех данных многогранников равны 1.
Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через:
а) середины рёбер АА1, ВВ1, В1С1;
б) середины рёбер ВВ1, DD1 и вершину А;
в) середину ребра C1D1 и вершины А, С;
г) середины рёбер АА1, СС1 и точку М на ребре АВ такую, что АМ = 0,75.
Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через:
а) середины рёбер ВВ1, СС1, А1В1;
б) середины рёбер АА1, СС1 и вершину В;
в) середину ребра СC1 и вершины А1, В;
г) середины рёбер АА1, СС1 и точку М на ребре ВВ1 такую, что ВМ = 0,25.
Постройте сечение правильной треугольной пирамиды DABC плоскостью, проходящей через:
а) середины рёбер АВ, ВС и СD;
б) середины рёбер AD, BD и ВС.
Постройте сечение правильной четырёхугольной пирамиды MABCD плоскостью, проходящей через:
а) середину ребра МА и вершины В и С;
б) середину ребра МС и вершины А и В;
в) середины рёбер AD, ВC и MD.
Постройте сечение правильной треугольной призмы ABCA1B1C1 плоскостью, проходящей через:
а) середины рёбер АВ, ВС и А1В1;
б) середину ребра АС и вершины А1 и В1;
в) середины рёбер АА1, ВВ1 и А1С1;
г) середину ребра АС и вершины В и В1;
д) середину ребра А1С1 и вершины А и В.
Постройте сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 плоскостью, проходящей через:
а) вершины А, D и С1;
б) вершины А, С и D1;
в) вершины А, В и D1;
г) вершины B, D и Е1;
д) вершины С, F и E1.
studfiles.net
§ 2. Взаимное расположение прямых и плоскостей в пространстве.
. Основные аксиомы стереометрии и следствия из них.
Как и планиметрия, стереометрия изучается в том же структурном плане: формулируются аксиомы (утверждения, принимаемые без доказательства ввиду их очевидности), теоремы (утверждения, которые доказываются с опорой на аксиомы, определения и ранее изученные теоремы) и определения.
Сформулируем три аксиомы, выражающие основные свойства плоскостей в пространстве.
Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2. Если две точки прямой принадлежат плоскости, то и вся прямая лежит в этой плоскости.
Аксиома 3. Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (т.е. плоскости имеют общую прямую, на которой лежат все общие точки этих плоскостей).
Следствием этих аксиом являются следующие теоремы (доказательства этих теорем и всех последующих опускаем):
Теорема 1. Через прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.
Теорема 2. Через две пересекающиеся прямые можно провести плоскость, и притом только одну.
Теорема 3. Через две параллельные прямые можно провести единственную плоскость.
. Взаимное расположение прямых.
Возможны три случая: две прямые параллельны, пересекаются или скрещиваются.
| Определение. Две прямые называются пересекающимися, если они имеют одну общую точку. Обозначение: a ∩ b = M |
α a
b M |
| Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. Обозначение: a || b |
a α b |
| Определение. Две прямые, не лежащие в одной плоскости, называются скрещивающимися. Обозначение: a ∸ b |
a
b M  α |
| Теорема 4 (признак скрещивающихся прямых): Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются. | |
| Пример: Две прямые, содержащие ребра AA1 и CD куба ABCDA1B1C1D1 являются скрещивающимися. |
С1 В1  D1 А1 В С 
D А |
. Взаимное расположение прямой и плоскости.
Возможны три случая: прямая лежит в плоскости; прямая пересекает плоскость; прямая и плоскость параллельны.
| Определение. Прямая, все точки которой принадлежат плоскости, называется прямой, лежащей в плоскости. Обозначение: a α |
a α
|
| Определение. Прямая и плоскость называются пересекающимися, если у них есть одна общая точка. Обозначение: a ∩ β = M | a 
β
M |
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Обозначение: a || a ∩ β =
| Теорема 5 (признак параллельности прямой и плоскости): Если прямая, не лежащая в плоскости, параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна данной плоскости.
|
a b α |
V. Взаимное расположение плоскостей.
Возможны два случая: две плоскости пересекаются или параллельны.
Определение. Две плоскости называются параллельными, если они не имеют общих точек
| Теорема 6 (признак параллельности плоскостей): Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то эти плоскости параллельны.
| a1
a2
α M
b1 b2 β | |
| Определение. Две плоскости называются пересекающимися, если они имеют общую прямую. В этом случае они не имеют других общих точек вне этой прямой. α ∩ β = a |
β α a | |
|
Вопросы и задачи | ||
Дан куб ABCDA1B1C1D1. Точка М – середина ребра B1C1, N – середина C1D1, K – середина DC, О – точка пересечения диагоналей основания ABCD. Укажите взаимное расположение между следующими прямыми:
а) АA1 иCС1; б) A1C1 и B1D1; в) A1C1и C1D1;
г) A1М и CC1; д) A1D и DC1; е) A1C1 и BD;
ё) A1C и АС; ж) A1B и D1С; з) A1C и ВB1;
и) A1D и АВ ; й) A1М и ВС; к) A1М и ВК ;
л) C1К и B1N; м) C1О и AB1; н) A1О и B1D.
Дан тетраэдр ABCD. Точка К – середина ребра AD, L – середина DB, М – середина АС, N – середина ВС. Определите взаимное расположение прямых и плоскостей.
а) DB и AMN; б) MN и ABC; в) КС и DMN;
г) MN и ABD; д) KL и DMN; е) LN и KML;
ё) CL и ADN; ж) LN и DMK.
Дан куб ABCDA1B1C1D1. Точка К – середина ребра AD, L – середина СC1, М – середина A1B1, N – середина B1C1, Т – середина DC, О – точка пересечения диагоналей четырёхугольника ABCD. Укажите взаимное расположение плоскостей:
а) A1B1C1 и ADC; б) MTK и BB1D; в) MNK и MNT;
г) D1KT и BMN; д) MNK и TLN; е) B1КТ и DMN;
ё) A1DC1 и АB1C; ж) A1C1С и MKT.
Отметьте верные утверждения
а) через точку, не принадлежащую данной прямой, можно провести только одну прямую, параллельную этой прямой.
б) через точку, не принадлежащую данной прямой, можно провести только одну прямую, перпендикулярную этой прямой.
в) прямые, перпендикулярные одной и той же прямой, параллельны.
г) прямая, пересекающая одну из двух данных параллельных прямых, пересекает и другую.
В параллелепипеде ABCDA1B1C1D1укажите параллельные прямые, на которых лежат его рёбра.
В тетраэдре DABC укажите все пары скрещивающихся прямых, на которых лежат его рёбра.
В пространстве даны три попарно пересекающиеся прямые. Изобразите возможные случаи их взаимного расположения.
Прямая с пересекает, по крайней мере, одну из двух пересекающихся прямых а, b. Как могут располагаться относительно друг друга эти три прямые? Сделайте рисунки.
Даны две параллельные прямые а и b. Как может быть расположена по отношению к ним третья прямая c? Сделайте рисунки.
Даны две скрещивающиеся прямые а и b. Как может быть расположена по отношению к ним третья прямая c? Сделайте рисунки.
Отметьте верные утверждения:
а) прямая, параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости.
б) существует единственная прямая, параллельная данной плоскости и проходящая через точку, не принадлежащую этой плоскости.
в) существует бесконечное множество прямых, параллельных данной плоскости и проходящих через точку, не принадлежащую этой плоскости.
г) через одну из двух параллельных прямых можно провести бесконечное множество плоскостей, параллельных другой прямой.
д) существует единственная плоскость, параллельная данной прямой и проходящая через точку, не принадлежащую этой прямой.
е) существует бесконечное множество плоскостей, параллельных данной прямой и проходящих через точку, не принадлежащую этой прямой.
Используя признак параллельности прямой и плоскости, укажите несколько пар параллельных прямой и плоскости в четырёхугольной призме ABCDA1B1C1D1.
Докажите, что в кубе ABCDA1B1C1D1 прямая AB1 параллельна плоскости грани DD1CC1.
Прямые а и b скрещиваются. Можно ли провести через одну из них плоскость, параллельную другой? Обоснуйте свой ответ.
Отметьте верные утверждения
а) через точку, не принадлежащую данной плоскости, проходит единственная плоскость, параллельная данной.
б) если прямая, лежащая в одной плоскости, параллельна прямой, лежащей в другой плоскости, то эти плоскости параллельны.
в) если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то эти плоскости параллельны.
г) если одна из двух данных плоскостей параллельна двум пересекающимся прямым, лежащим в другой плоскости, то эти плоскости параллельны.
д) если плоскость пересекает две данные плоскости по параллельным прямым, то эти плоскости параллельны.
е) если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
ж) если две плоскости параллельны одной и той же прямой, то они параллельны.
Используя признак параллельности плоскостей, укажите параллельные плоскости в прямоугольном параллелепипеде ABCDA1B1C1D1.
PABC – правильный тетраэдр, точка М – центр грани АВС, К – середина ребра АВ. Постройте сечения тетраэдра плоскостями:
а) APM; б) KPM.
Постройте общий отрезок этих сечений.
Постройте сечение тетраэдра плоскостью, проходящей через:
а) две вершины и точку на ребре, не содержащем эти вершины;
б) вершину и две точки на рёбрах, не проходящих через эту вершину;
в) три точки на трёх рёбрах, выходящих из одной вершины;
г) середины трёх рёбер, не выходящих из одной вершины.
В четырёхугольной пирамиде все рёбра равны. Докажите, что её сечение, проходящее через вершину пирамиды и диагональ основания, является прямоугольным треугольником.
Постройте сечение куба плоскостью, проходящей через точку на боковом ребре и две точки на рёбрах основания, не смежных с этим боковым ребром.
Постройте сечение куба плоскостью, проходящей через две точки на скрещивающихся рёбрах верхнего и нижнего оснований и точку на ребре:
а) пересекающимся с ними;
б) пересекающимся только с одним из этих рёбер.
Постройте сечение четырёхугольной пирамиды плоскостью, проходящей через три точки на боковых рёбрах.
В каждом из нижеследующих заданий найдите площадь построенного сечения, учитывая, что все рёбра всех данных многогранников равны 1.
Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через:
а) середины рёбер АА1, ВВ1, В1С1;
б) середины рёбер ВВ1, DD1 и вершину А;
в) середину ребра C1D1 и вершины А, С;
г) середины рёбер АА1, СС1 и точку М на ребре АВ такую, что АМ = 0,75.
Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через:
а) середины рёбер ВВ1, СС1, А1В1;
б) середины рёбер АА1, СС1 и вершину В;
в) середину ребра СC1 и вершины А1, В;
г) середины рёбер АА1, СС1 и точку М на ребре ВВ1 такую, что ВМ = 0,25.
Постройте сечение правильной треугольной пирамиды DABC плоскостью, проходящей через:
а) середины рёбер АВ, ВС и СD;
б) середины рёбер AD, BD и ВС.
Постройте сечение правильной четырёхугольной пирамиды MABCD плоскостью, проходящей через:
а) середину ребра МА и вершины В и С;
б) середину ребра МС и вершины А и В;
в) середины рёбер AD, ВC и MD.
Постройте сечение правильной треугольной призмы ABCA1B1C1 плоскостью, проходящей через:
а) середины рёбер АВ, ВС и А1В1;
б) середину ребра АС и вершины А1 и В1;
в) середины рёбер АА1, ВВ1 и А1С1;
г) середину ребра АС и вершины В и В1;
д) середину ребра А1С1 и вершины А и В.
Постройте сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 плоскостью, проходящей через:
а) вершины А, D и С1;
б) вершины А, С и D1;
в) вершины А, В и D1;
г) вершины B, D и Е1;
д) вершины С, F и E1.
studfiles.net
Реферат Прямая
скачатьРеферат на тему:
План:
- Введение
- 1 Свойства прямой в евклидовой геометрии
- 2 Уравнения прямой на плоскости
- 2.1 Общее уравнение прямой
- 2.2 Уравнение прямой с угловым коэффициентом
- 2.3 Уравнение прямой в отрезках
- 2.4 Нормальное уравнение прямой
- 2.5 Уравнение прямой, проходящей через две заданные несовпадающие точки
- 2.6 Векторно-параметрическое уравнение прямой
- 2.7 Параметрические уравнения прямой
- 2.8 Каноническое уравнение прямой
- 2.9 Уравнение прямой в полярных координатах
- 2.10 Тангенциальное уравнение прямой
- 3 Уравнения прямой в пространстве
- 4 Взаимное расположение точек и прямых на плоскости
- 5 Взаимное расположение нескольких прямых на плоскости
Введение
Изображение прямых в прямоугольной системе координат.
Прямая — одно из основных понятий геометрии.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.
1. Свойства прямой в евклидовой геометрии
- Через любые две несовпадающие точки можно провести единственную прямую.
- Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными.
- В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
- прямые пересекаются;
- прямые параллельны;
- прямые скрещиваются.
- Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
2. Уравнения прямой на плоскости
2.1. Общее уравнение прямой
Общее уравнение прямой линии на плоскости в декартовых координатах:
где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.
При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде :
2.2. Уравнение прямой с угловым коэффициентом
Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось Oy в точке и образующая угол
с положительным направлением оси Ox:
Коэффициент k называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси Oy.
2.3. Уравнение прямой в отрезках
Прямая линия, пересекающая ось Ox в точке и ось Oy в точке
:
В этом виде невозможно представить прямую, проходящую через начало координат.
2.4. Нормальное уравнение прямой
где p — длина перпендикуляра, опущенного на прямую из начала координат, а θ — угол (измеренный в положительном направлении) между положительным направлением оси Ox и направлением этого перпендикуляра. Если p = 0, то прямая проходит через начало координат, а угол задаёт угол наклона прямой.
Вывод нормального уравнения прямой
Если прямая задана общим уравнением Ax + By + C = 0, то отрезки a и b, отсекаемые ею на осях, угловой коэффициент k, расстояние прямой от начала координат p, cosθ и sinθ выражаются через коэффициенты A, B и C следующим образом:
Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие p > 0. В этом случае cosθ и sinθ являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если C = 0, то прямая проходит через начало координат и выбор положительного направления произволен.
2.5. Уравнение прямой, проходящей через две заданные несовпадающие точки
Уравнение прямой, проходящей через две заданные несовпадающие точки и
или
или в общем виде
2.6. Векторно-параметрическое уравнение прямой
Векторно-параметрическое уравнение прямой задается вектором конец которого лежит на прямой и направляющим вектором прямой
. Параметр t пробегает все действительные значения.
2.7. Параметрические уравнения прямой
Параметрические уравнения прямой могут быть записаны в виде:
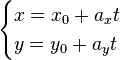
где t — производный параметр, ax, ay — координаты x и y направляющего вектора прямой, при этом
Смысл параметра t аналогичен параметру в векторно-параметрическом уравнении.
2.8. Каноническое уравнение прямой
Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
где — координаты
и
направляющего вектора прямой,
и
координаты точки, принадлежащей прямой.
2.9. Уравнение прямой в полярных координатах
Уравнение прямой в полярных координатах ρ и :
или
2.10. Тангенциальное уравнение прямой
Тангенциальное уравнение прямой на плоскости:
ξx + ηy = 1.Числа ξ и η называются её тангенциальными, линейными или плюккеровыми координатами.
3. Уравнения прямой в пространстве
Векторное параметрическое уравнение прямой в пространстве:
где — радиус-вектор некоторой фиксированной точки M0, лежащей на прямой,
— ненулевой вектор, коллинеарный этой прямой,
— радиус-вектор произвольной точки прямой.
Параметрическое уравнение прямой в пространстве:
где — координаты некоторой фиксированной точки M0, лежащей на прямой;
— координаты вектора, коллинеарного этой прямой.
Каноническое уравнение прямой в пространстве:
где — координаты некоторой фиксированной точки M0, лежащей на прямой;
— координаты вектора, коллинеарного этой прямой.
Общее векторное уравнение прямой в пространстве:
Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:то уравнение прямой можно задать системой этих уравнений:
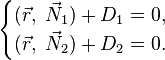
4. Взаимное расположение точек и прямых на плоскости
Три точки ,
и
лежат на одной прямой тогда и только тогда, когда выполняется условие
Отклонение точки от прямой Ax + By + C = 0 может быть найдено по формуле
где знак перед радикалом противоположен знаку C. Отклонение по модулю равно расстоянию между точкой и прямой; оно положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону.
В пространстве расстояние от точки до прямой, заданной параметрическим уравнением
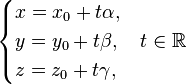
можно найти как минимальное расстояние от заданной точки до произвольной точки прямой. Коэффициент t этой точки может быть найден по формуле
5. Взаимное расположение нескольких прямых на плоскости
Две прямые, заданные уравнениями
или
пересекаются в точке
Угол γ12 между пересекающимися прямыми определяется формулой
При этом под γ12 понимается угол, на который надо повернуть первую прямую (заданную параметрами A1, B1, C1, k1 и b1) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.
Эти прямые параллельны, если A1B2 − A2B1 = 0 или k1 = k2, и перпендикулярны, если A1A2 + B1B2 = 0 или .
Любую прямую, параллельную A1x + B1y + C1 = 0, можно выразить уравнением A1x + B1y + C = 0. При этом расстояние между ними будет равно
Если знак перед радикалом противоположен C1, то δ будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.
Для того, чтобы три прямые
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
Если и
, то прямые
и
перпендикулярны.
wreferat.baza-referat.ru
6. Взаимное расположение прямых в пространстве
Пусть заданы две прямые
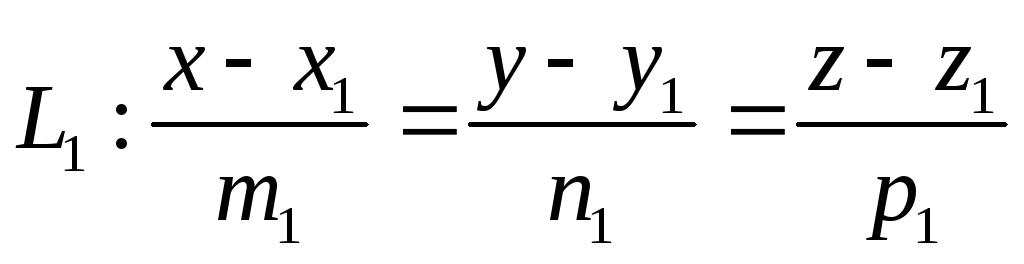 ,
,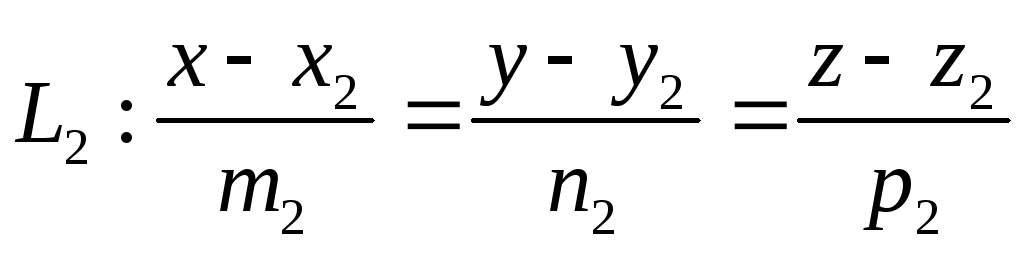 .
.
Прямая 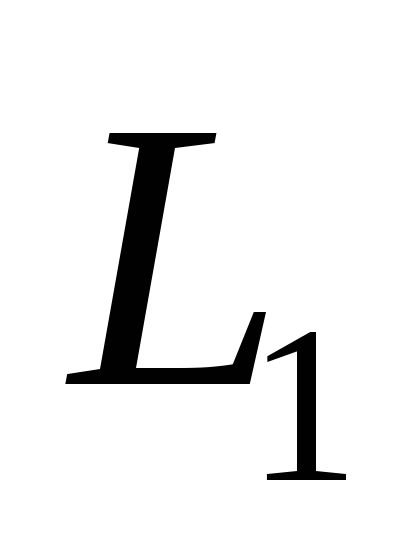 проходит через точку
проходит через точку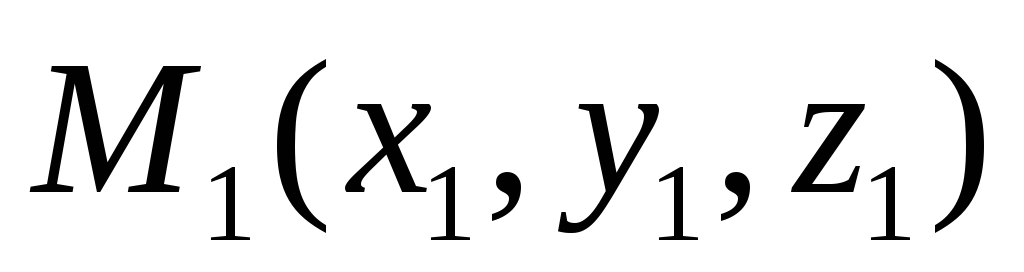 и имеет направляющий вектор
и имеет направляющий вектор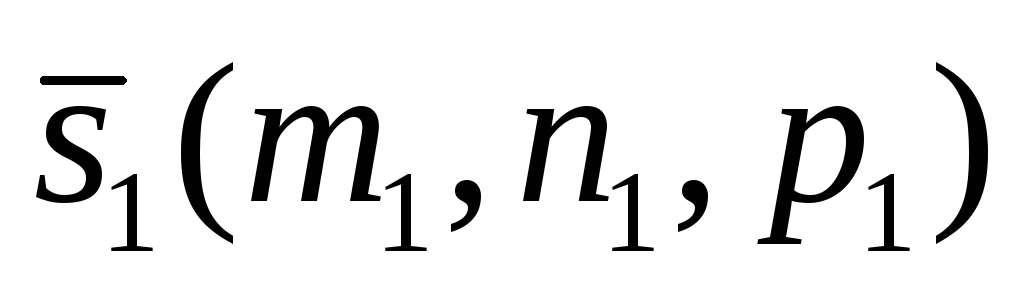 , прямая
, прямая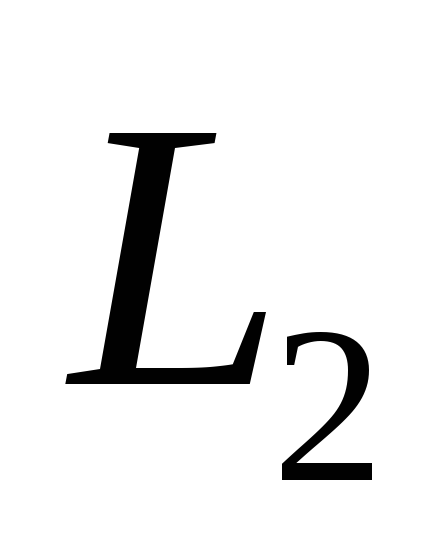 проходит через точку
проходит через точку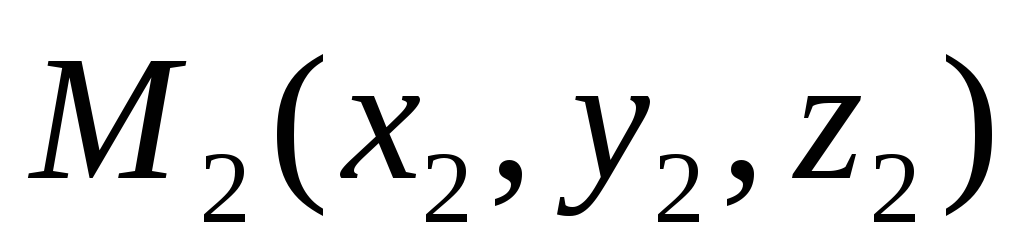 и имеет направляющий вектор
и имеет направляющий вектор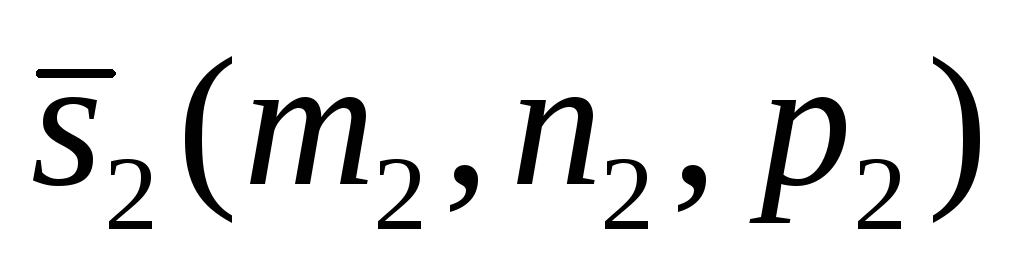 .
.
Определение. Углом между двумя прямыми в пространстве называется любой из двух углов, образованных прямыми, проведенными через произвольную точку пространства параллельно данным.
Возможны следующие случаи расположения прямых.
1). Прямые параллельны 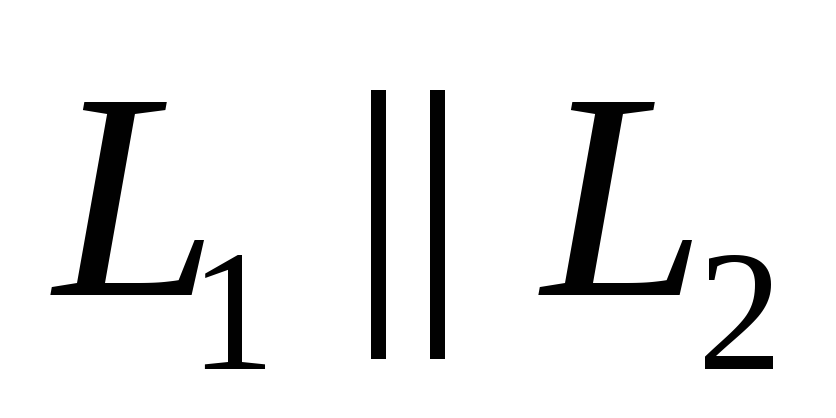 , тогда направляющие векторы этих прямых коллинеарны
, тогда направляющие векторы этих прямых коллинеарны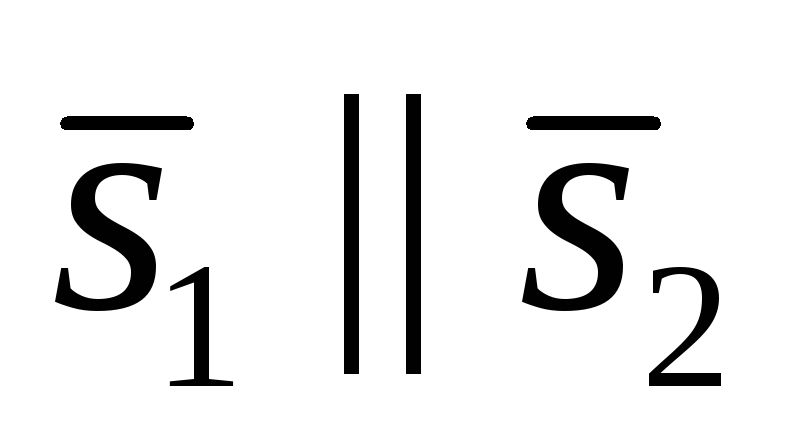 , следовательно, координаты направляющих векторов пропорциональны
, следовательно, координаты направляющих векторов пропорциональны
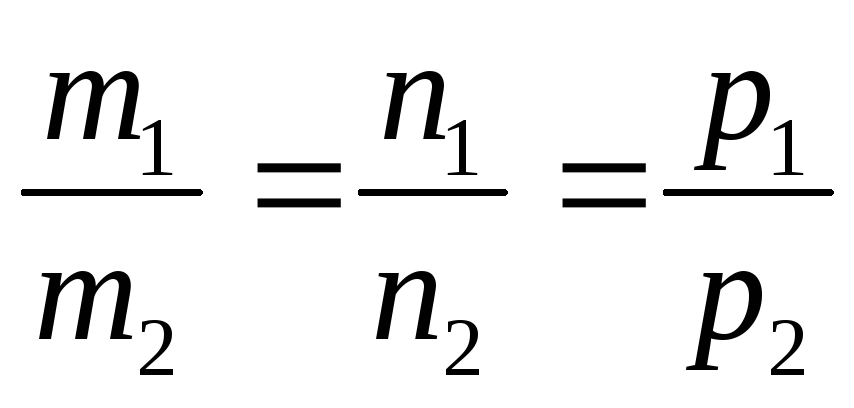 .
.
это условие параллельности прямых. В этом случае можно найти расстояние между параллельными прямыми, для этого надо воспользоваться формулой расстояния от точки до прямой в пространстве, получаем
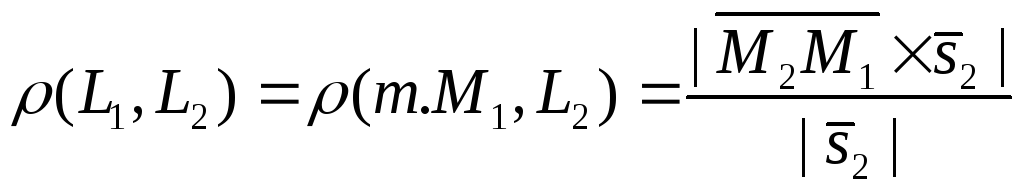 ,
,
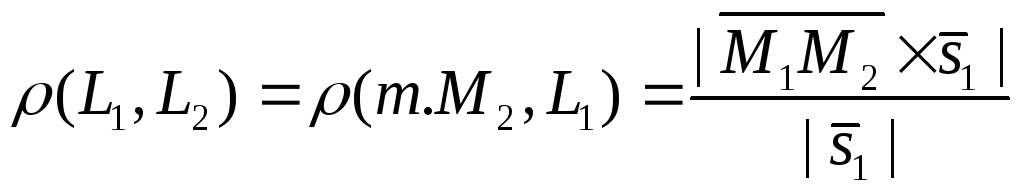 Если прямые параллельны и т.
Если прямые параллельны и т.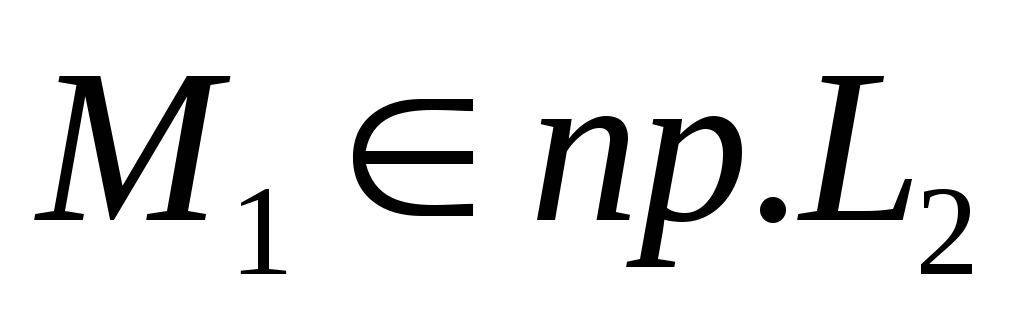 , прямые совпадают
, прямые совпадают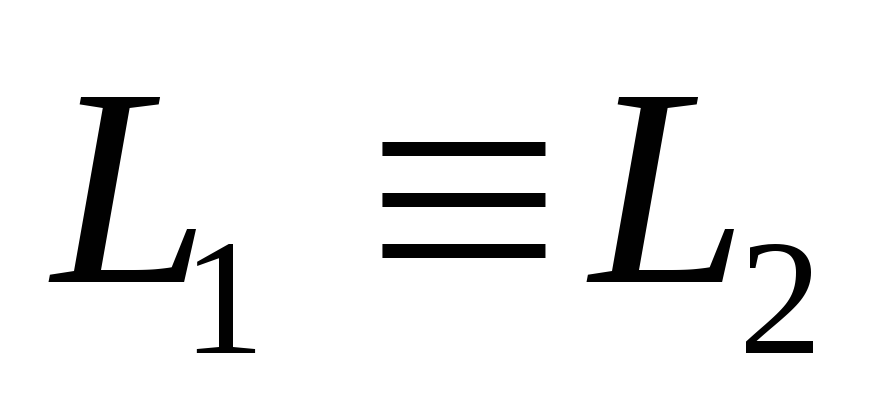 .
.
2). Прямые пересекаются 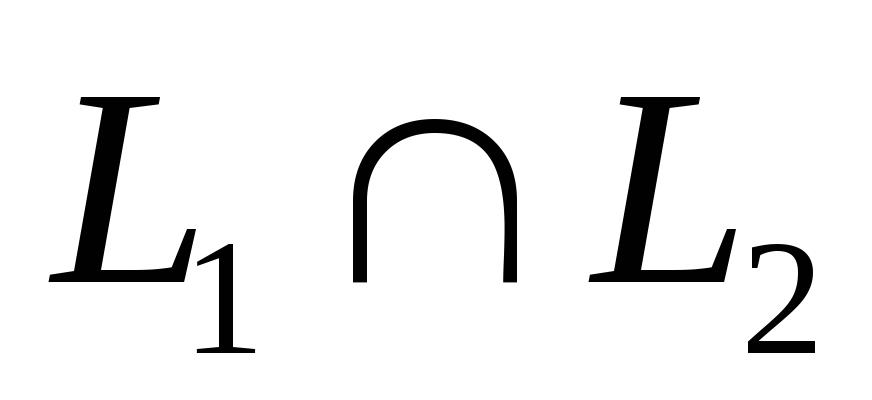 , в этом случае можно найти косинус угла между ними
, в этом случае можно найти косинус угла между ними
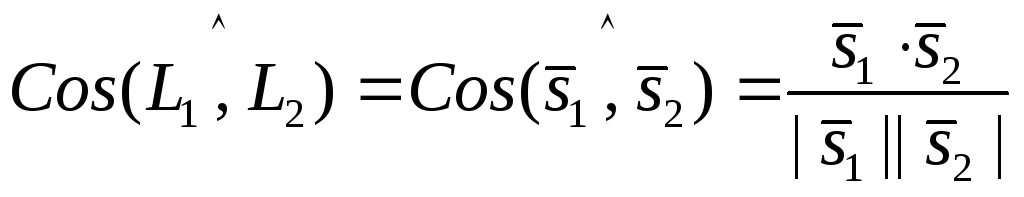 3). Прямые перпендикулярны
3). Прямые перпендикулярны 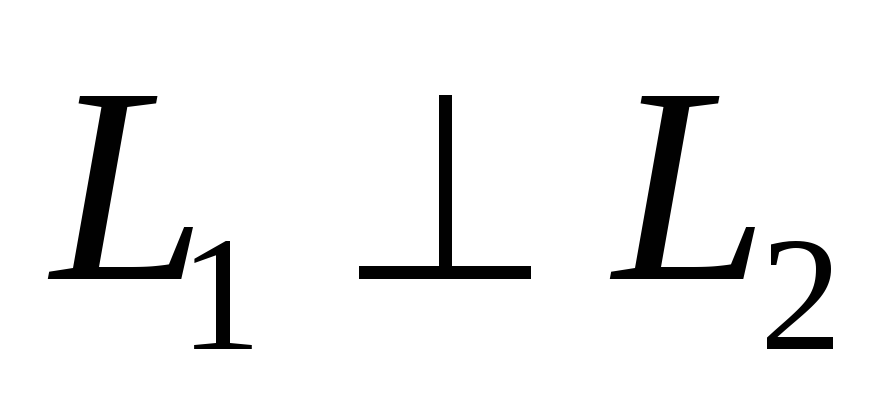 , тогда направляющие векторы этих прямых тоже перпендикулярны
, тогда направляющие векторы этих прямых тоже перпендикулярны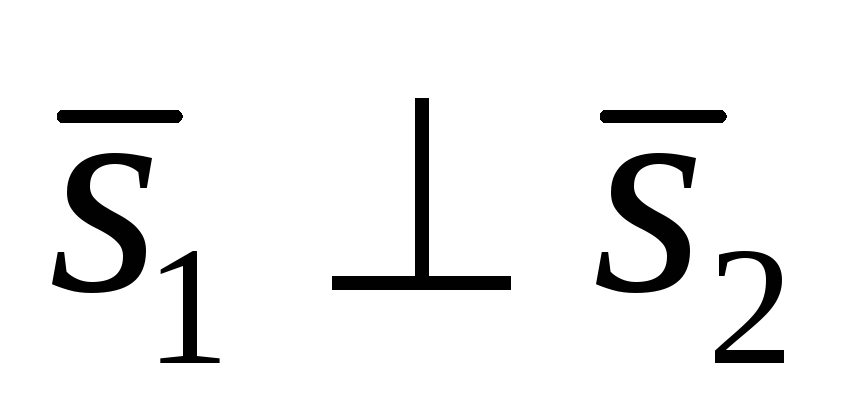 , следовательно, их скалярное произведение равно нулю
, следовательно, их скалярное произведение равно нулю
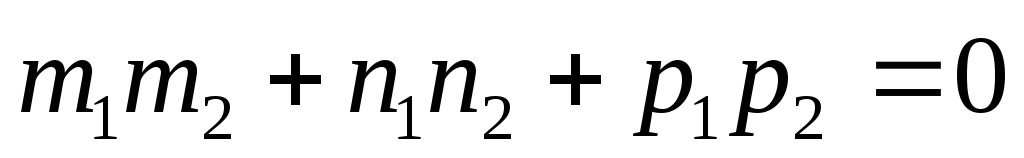 это условие перпендикулярности прямых в пространстве.
это условие перпендикулярности прямых в пространстве.
7. Взаимное расположение прямой и плоскости в пространстве. Общие точки прямой и плоскости
Пусть даны прямая и плоскость
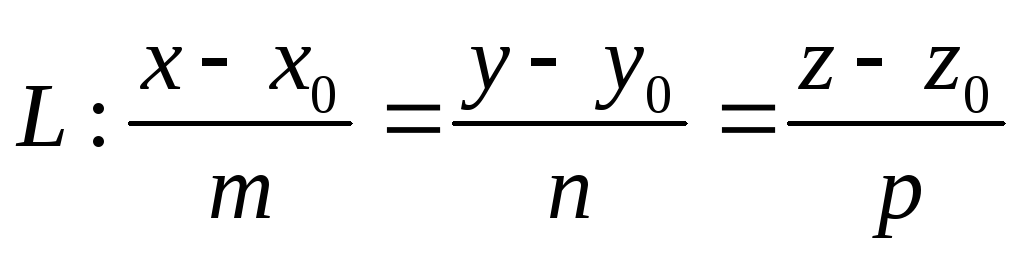 ,
, 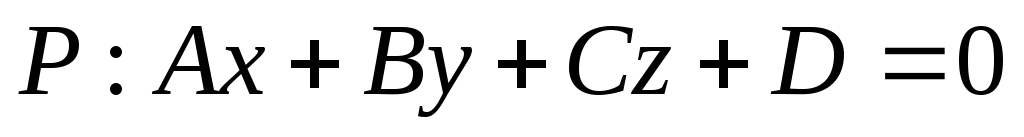 .
.
Прямая проходит через точку 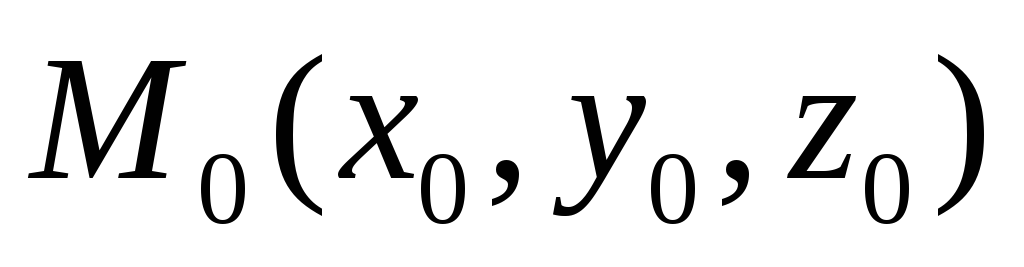 , ее направляющий вектор
, ее направляющий вектор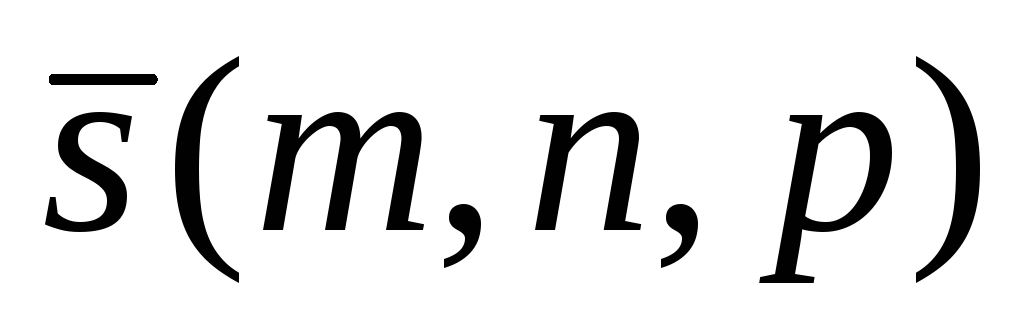 , вектор нормали плоскости
, вектор нормали плоскости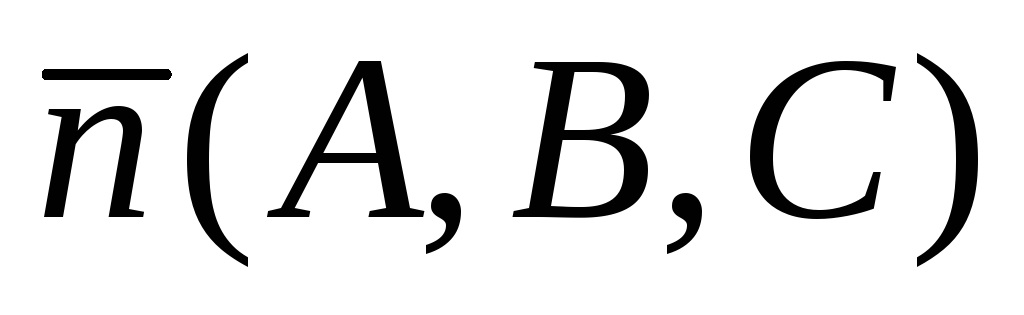 .
.
Определение 2.24. Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость.
Для взаимного расположения прямой и плоскости возможны следующие случаи.
1). Прямая и плоскость параллельны 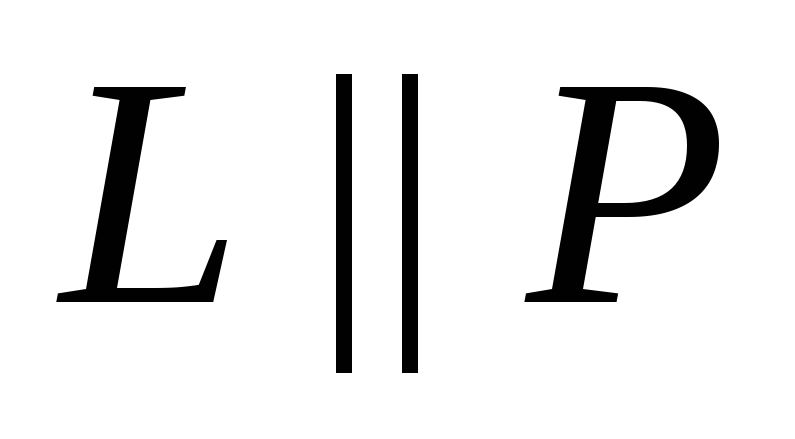 , тогда направляющий вектор прямой будет перпендикулярен вектору нормали плоскости
, тогда направляющий вектор прямой будет перпендикулярен вектору нормали плоскости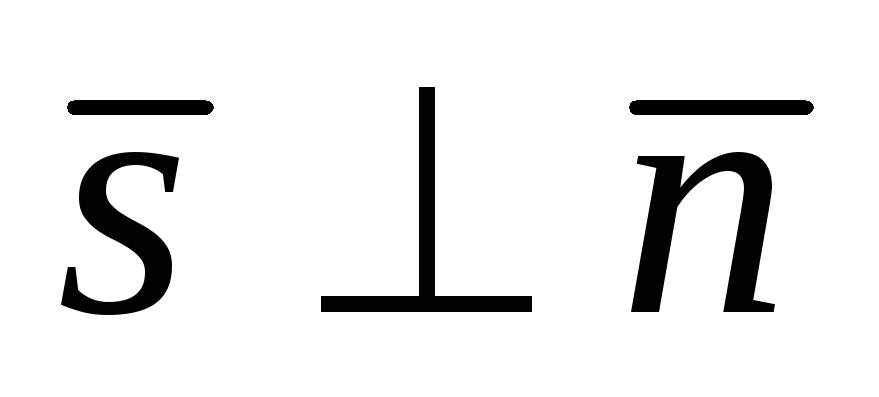 , значит их скалярное произведение равно нулю
, значит их скалярное произведение равно нулю
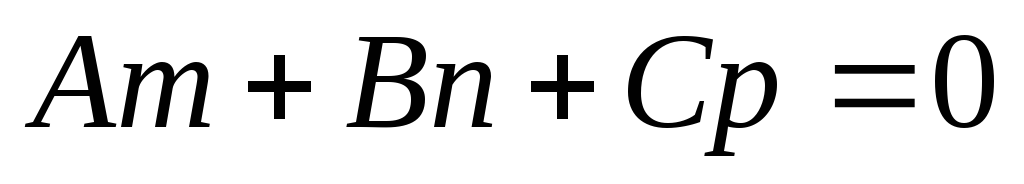 .
.
Это условие параллельности прямой и плоскости.
В этом случае можно найти расстояние между прямой и плоскостью, для этого надо воспользоваться формулой расстояния от точки до плоскости
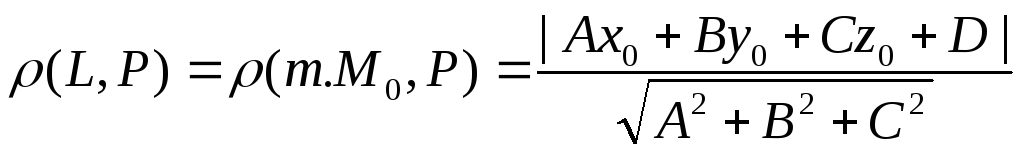 .
.
2). Если прямая и плоскость параллельны и точка 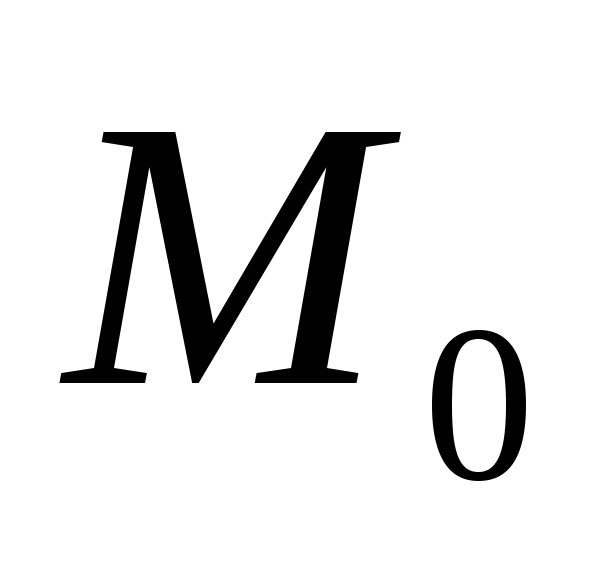 прямой принадлежит плоскости, то прямая лежит в плоскости, то есть должны выполняться следующие условия
прямой принадлежит плоскости, то прямая лежит в плоскости, то есть должны выполняться следующие условия
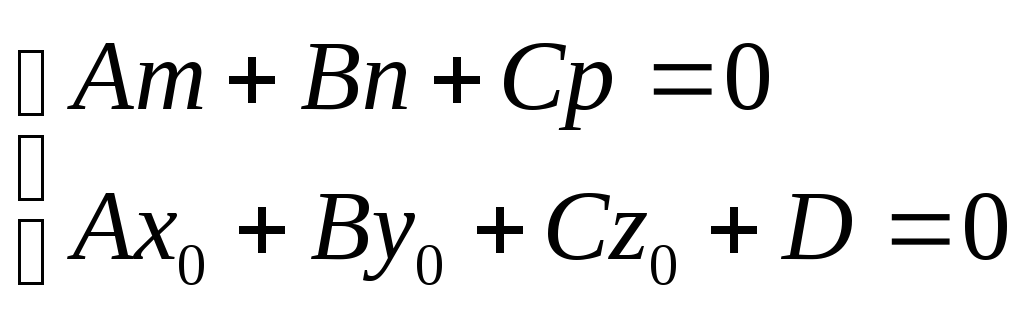
Это условия принадлежности прямой плоскости (прямая лежит в плоскости).
3). Прямая и плоскость перпендикулярны 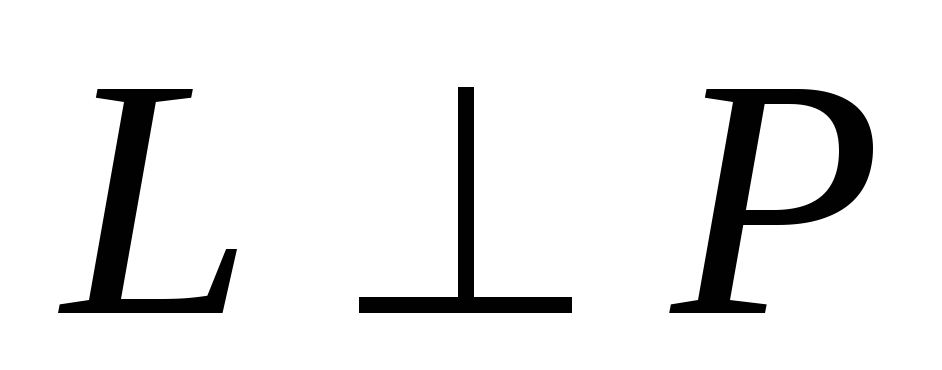 , тогда направляющий вектор прямой будет параллелен вектору нормали плоскости
, тогда направляющий вектор прямой будет параллелен вектору нормали плоскости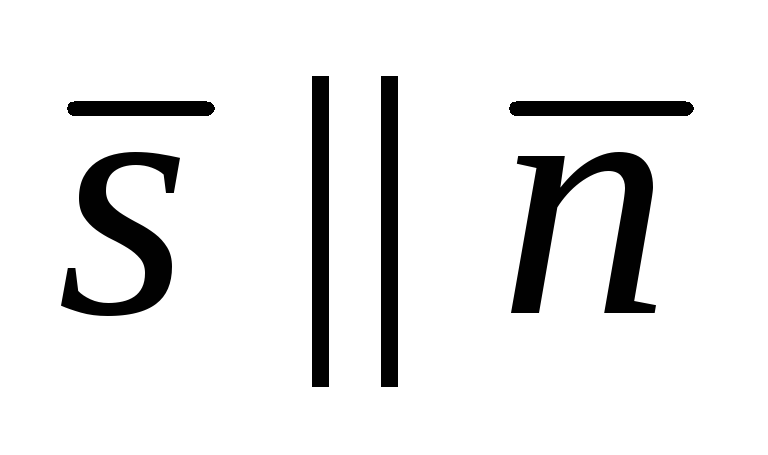 и их координаты пропорциональны
и их координаты пропорциональны
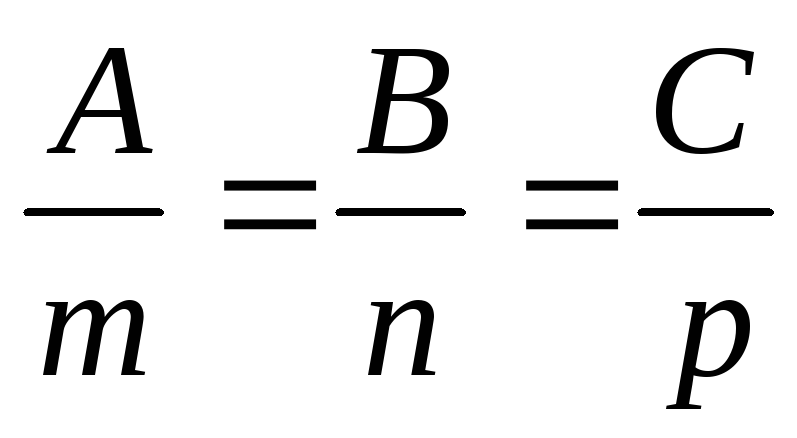 .
.
Это условие перпендикулярности прямой и плоскости.
4). Прямая и плоскость пересекаются 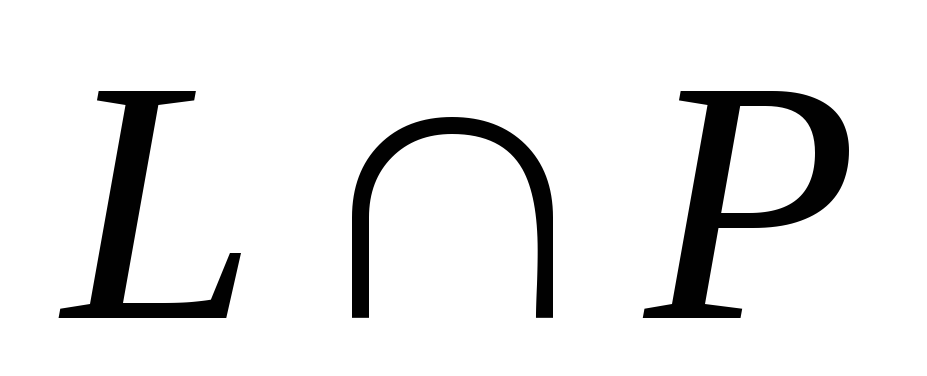 .
.
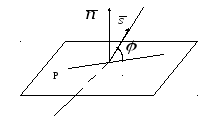
Пусть угол 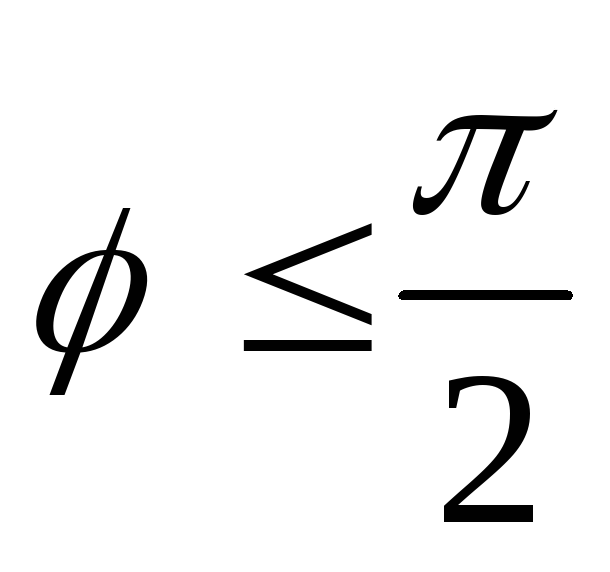 , тогда
, тогда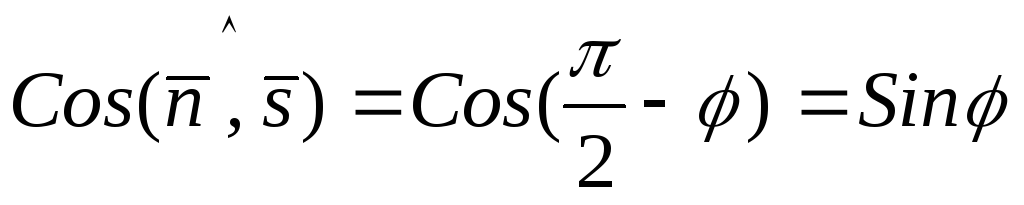 , следовательно,
, следовательно,
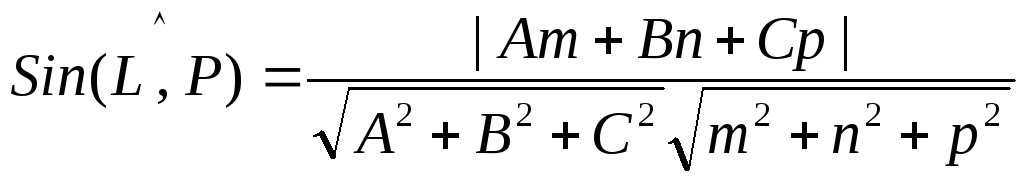 .
.
Общие точки прямой и плоскости
Пусть даны прямая и плоскость
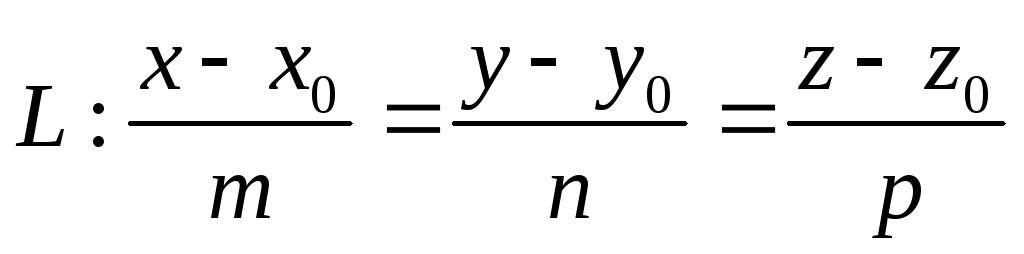 ,
, 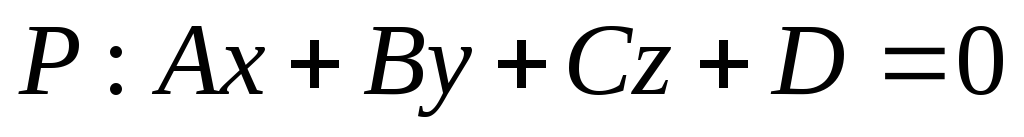 .
.
1). Если 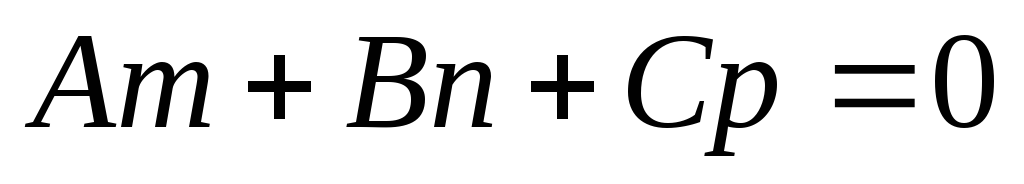 , а
, а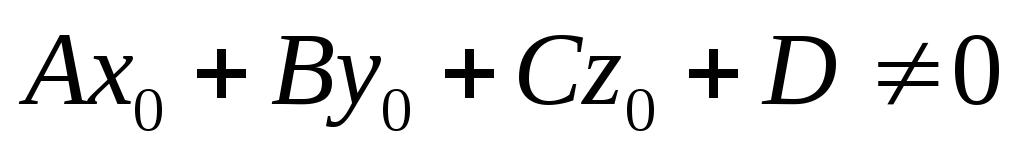 , то прямая и плоскость параллельны, значит, общих точек они не имеют.
, то прямая и плоскость параллельны, значит, общих точек они не имеют.
2). Если 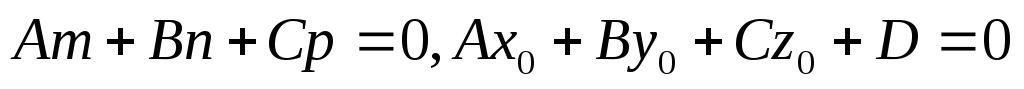 , то прямая лежит в плоскости, значит, все точки прямой лежат в плоскости.
, то прямая лежит в плоскости, значит, все точки прямой лежат в плоскости.
3). Если 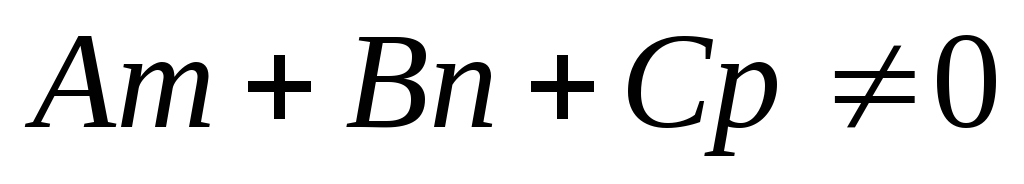 , прямая и плоскость пересекаются, чтобы найти точку пересечения прямой и плоскости, надо перейти к параметрическим уравнениям прямой и, подставив эти соотношения в уравнение плоскости, получить значение параметра
, прямая и плоскость пересекаются, чтобы найти точку пересечения прямой и плоскости, надо перейти к параметрическим уравнениям прямой и, подставив эти соотношения в уравнение плоскости, получить значение параметра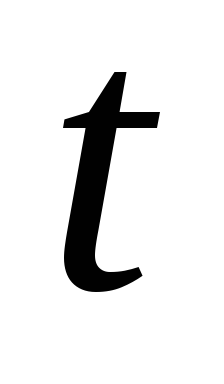 , соответствующего точке пересечения прямой и плоскости.
, соответствующего точке пересечения прямой и плоскости.
Пример. Найти точку пересечения прямой 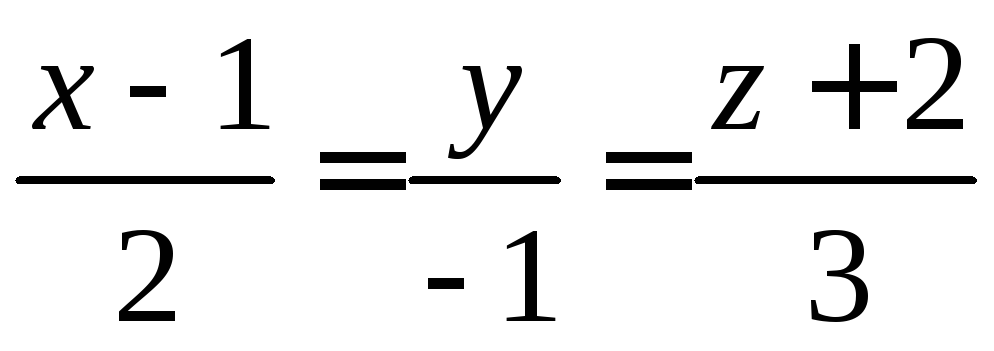 и плоскости
и плоскости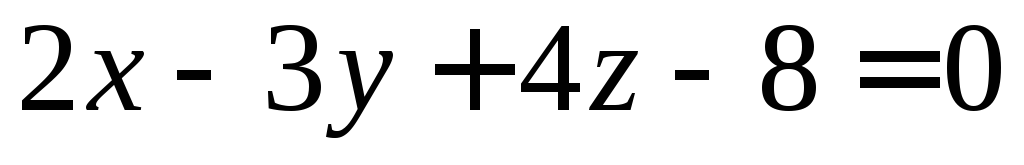 .
.
Решение. Перейдем к параметрическим уравнениям прямой
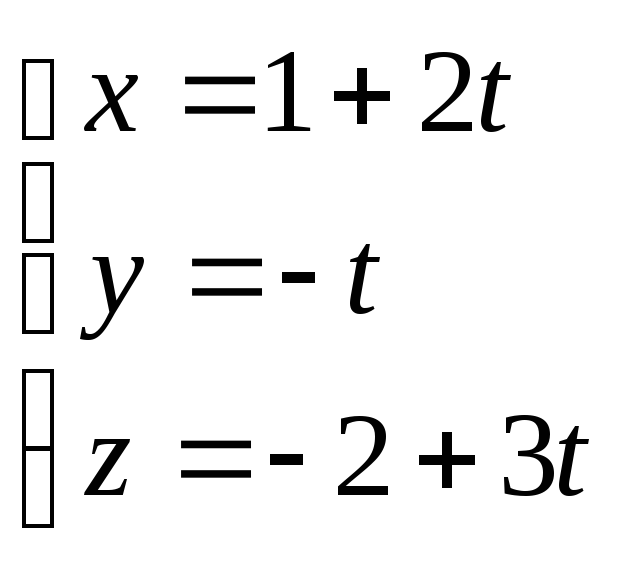
подставляем эти соотношения в уравнение плоскости, получим
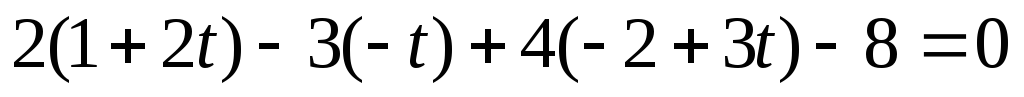 ,
,
отсюда находим 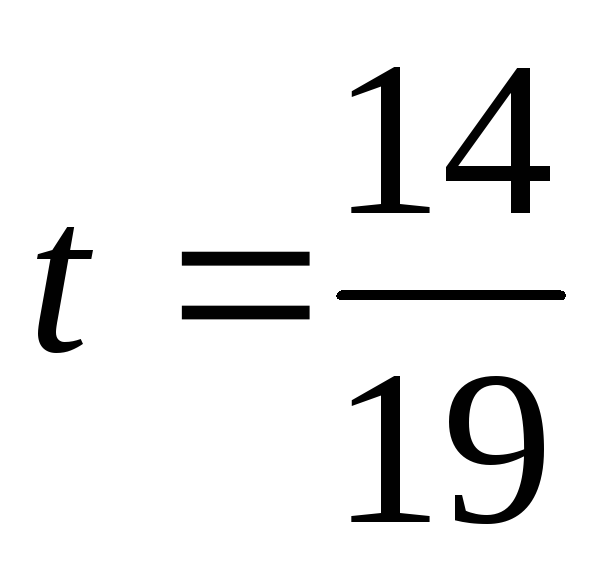 , тогда координаты точки пересечения
, тогда координаты точки пересечения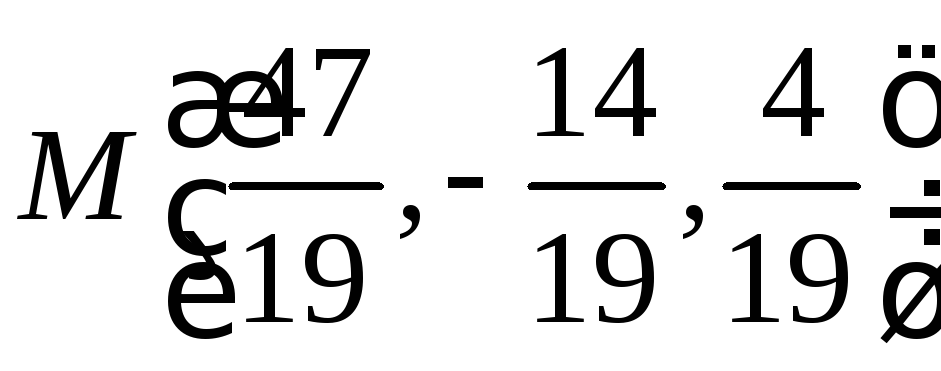 .
.
studfiles.net
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|