
В предыдущих параграфах мы говорили о логических операциях ограничения, обобщения, определения и деления понятий. Теперь рассмотрим еще две логические операции – сложение и умножение понятий.
Сложение понятий – это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник и спортсмен образуется новое понятие, в объем которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой, на схеме Эйлера изображается штриховкой:

Умножение понятий – это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий. Например, при умножении понятий школьник и спортсмен образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами, и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением, на схеме Эйлера изображается штриховкой (так же, как и результат сложения):

Выше были приведены примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения (школьник и спортсмен). В других случаях отношений между понятиями (о которых речь шла в § 1.3) результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. В приводимой ниже таблице штриховкой показаны результаты сложения и умножения понятий во всех видах отношений между ними.

Как видим, результаты сложения и умножения понятий полностью совпадают только в случае равнозначности между ними, частично совпадают в пересечении и подчинении и совершенно не совпадают в соподчинении, противоположности и противоречии (в этих трех случаях результатом умножения является нулевое или пустое понятие). В отношении подчинения результатом сложения является родовое понятие, а умножения – видовое.
Как правило, в естественном языке (то есть том, на котором мы общаемся) результат сложения понятий выражается союзом или, а умножения – союзом и. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является или школьником, или спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является и школьником, и спортсменом одновременно.
Относительно употребления союзов или и и в естественном языке в качестве выражения результатов логических операций сложения и умножения понятий удачный пример приводит В.И. Свинцов в уже упоминавшемся нами учебнике по логике (Свинцов В.И. Логика. Элементарный курс для гуманитарных специальностей. – М.: Скорина, 1998. – С. 60 – 61), отрывок из которого приводится ниже. «Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: «Безбилетный проезд и бесплатный провоз багажа наказывается штрафом»? Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билета, в другое – не оплатившие провоз багажа. Если союз «и» рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза «или» здесь следует признать предпочтительным».
Однако следует отметить, что и в данном случае могут возникнуть недоразумения. Дело в том, что разделительный союз или может употребляться в нестрогом (неисключающем) значении и в строгом (исключающем). Например, в высказывании: Можно изучать английский язык или немецкий союз или употребляется в нестрогом значении, так как можно изучать и тот, и другой язык одновременно, одно другое не исключает. В данном случае разделительный союз или очень близок к соединительному союзу и. С другой стороны, в высказывании: Он родился в 1987 году или в 1989 году союз или употребляется в строгом значении, так как если он родился в 1987 году, то – никак не в 1989 году, и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза или мы еще будем говорить в § 2.6, посвященном видам сложных суждений.) Если в рассмотренное выше правило пользования городским транспортом поставить союз или вместо союза и, как предлагает В.И. Свинцов, то получится следующее: «Безбилетный проезд или бесплатный провоз багажа наказываются штрафом». В данном случае союз или, являясь показателем логического сложения, должен восприниматься в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации. В силу всего сказанного надо отметить, что употребление союза или всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется.
studfiles.net

ТОП 10:
В предыдущих параграфах мы говорили о логических операциях ограничения, обобщения, определения и деления понятий. Теперь рассмотрим еще две логические операции – сложение и умножение понятий.
Сложение понятий– это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник и спортсмен образуется новое понятие, в объем которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой,на схеме Эйлера изображается штриховкой:

Умножение понятий– это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий. Например, при умножении понятий школьник и спортсмен образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами, и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением,на схеме Эйлера изображается штриховкой (так же, как и результат сложения):
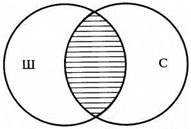
Выше были приведены примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения (школьник и спортсмен). В других случаях отношений между понятиями (о которых речь шла в § 1.3) результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. В приводимой ниже таблице штриховкой показаны результаты сложения и умножения понятий во всех видах отношений между ними.
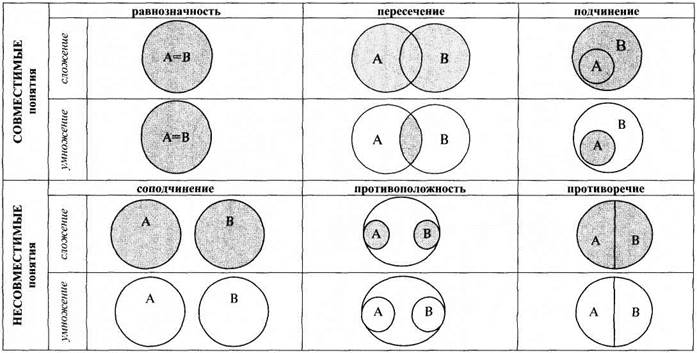
Как видим, результаты сложения и умножения понятий полностью совпадают только в случае равнозначности между ними, частично совпадают в пересечении и подчинении и совершенно не совпадают в соподчинении, противоположности и противоречии (в этих трех случаях результатом умножения является нулевое или пустое понятие). В отношении подчинения результатом сложения является родовое понятие, а умножения – видовое.
Как правило, в естественном языке (то есть том, на котором мы общаемся) результат сложения понятий выражается союзом или, а умножения – союзом и. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является или школьником, или спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является и школьником, и спортсменом одновременно.
Относительно употребления союзов или и и в естественном языке в качестве выражения результатов логических операций сложения и умножения понятий удачный пример приводит В.И. Свинцов в уже упоминавшемся нами учебнике по логике (Свинцов В.И. Логика. Элементарный курс для гуманитарных специальностей. – М.: Скорина, 1998. – С. 60 – 61), отрывок из которого приводится ниже. «Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: «Безбилетный проезд и бесплатный провоз багажа наказывается штрафом»? Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билета, в другое – не оплатившие провоз багажа. Если союз «и» рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза «или» здесь следует признать предпочтительным».
Однако следует отметить, что и в данном случае могут возникнуть недоразумения. Дело в том, что разделительный союз или может употребляться в нестрогом (неисключающем) значении и в строгом (исключающем). Например, в высказывании: Можно изучать английский язык или немецкий союз или употребляется в нестрогом значении, так как можно изучать и тот, и другой язык одновременно, одно другое не исключает. В данном случае разделительный союз или очень близок к соединительному союзу и. С другой стороны, в высказывании: Он родился в 1987 году или в 1989 году союз или употребляется в строгом значении, так как если он родился в 1987 году, то – никак не в 1989 году, и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза или мы еще будем говорить в § 2.6, посвященном видам сложных суждений.) Если в рассмотренное выше правило пользования городским транспортом поставить союз или вместо союза и, как предлагает В.И. Свинцов, то получится следующее: «Безбилетный проезд или бесплатный провоз багажа наказываются штрафом». В данном случае союз или, являясь показателем логического сложения, должен восприниматься в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации. В силу всего сказанного надо отметить, что употребление союза или всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется.
Глава 2. СУЖДЕНИЕ
infopedia.su
Московский государственный гуманитарный университет
Им. М.А. Шолохова
Реферат
по дисциплине «Логика»
на тему: «Операции с понятием»
Выполнил: студентка заочного отделения
Факультета психологии
Курс 3/3
Елисеева И.В.
Проверила: старший преподаватель
Воронина А.В.
Москва-Ступино
2008г.
СОДЕРЖАНИЕ
1. Введение. Характеристика понятия и операции над понятиями.
2. Операция с понятием — сложение.
3. Операция с понятием – умножение.
4. Операция с понятием — вычитание.
5. Операция с понятием — деление.
6. Отношения между понятиями.
7. Заключение
8. Литература
Введение
Разнообразие окружающего нас реального мира обусловлено существованием множества отдельных материальных предметов, обладающих различными свойствами и находящихся между собой в определенных связях. Познание природы этих предметов, выявление их сущности и оперирование ими в реальной жизни требует идеальных средств, которые заменяли бы эти предметы объективного мира и служили инструментом развития человеческого знания и наук. Одним из таких средств являются понятия.
Понятия не существуют в объективном мире. Они возникают в нашем сознании и заменяют предметы, процессы действительности логическими образами, делая естественный язык общения и языки наук информационно более емкими, насыщенными, давая возможность зафиксировать и передать знания с помощью наименьшего количества знаковых средств.
Характеристика понятия и операции над понятием.
Понятие – форма мышления, отражающая предметы в их общих существенных признаках.
Операции над понятиями – логические действия, вследствие которых создаются новые понятия.
К операциям с понятиями относят:
сложение, вычитание, умножение, деление.
Чтобы осмысленно оперировать понятиями, правильно их использовать в решении теоретических и практических задач необходимо уметь выявлять две основные логические характеристики: объем и содержание понятия.
Объем понятия – это совокупность(класс) предметов, которые мыслятся в данном понятии.
Содержание понятия – совокупность признаков предмета(предметов), мыслимых в данном понятии.
Характеристика видов понятия:
1. по объему: единичные, общие, нулевые, исчислимые, неисчислимые, регистрирующие, нерегистрирующие.
2. по содержанию: конкретные, абстрактные, относительные, безотносительные, положительные, отрицательные, собирательные, несобирательные
В зависимости от того, как соотносятся объемы понятий их делят на две группы:
1. совместимые – понятия, объемы которых совпадают полностью или частично.
2. несовместимые – понятия, объемы которых не совпадают ни в одном элементе, но они могут быть включены частично или полностью в объем общего для них понятия.
Операция с понятием — сложение.
Сложение — простейшая логическая операция с понятием, которая представляет собой объединение объемов двух или более понятий, даже если эти понятия и не пересекаются, не совпадают между собой по объему.
Например: Объединив понятие «школьник» и понятие «студент», мы получим область, отражающую признаки, присущие тому и другому понятию в рамках общего для них родового понятия «учащийся».рис №1
Например: Пусть «+» обозначает операцию сложения понятий.
1. «А» и «В» — равнозначные понятия.
Тогда А+В=А=В, т.е. результат сложения таких понятий равен любому из них. Как частный случай имеем: А+А=А
«Сиеста»+«полуденный отдых»=«сиеста»=«полуденный отдых»
«Сиеста»+ «сиеста»= «сиеста»
Таким образом, сложение двух равнозначных понятий не приводит к удвоенной сумме, как это имеет место при сложении натуральных чисел т.е не обладает свойством итерации(прибавления).
Операция с понятием — умножение.
Умножение, состоит в отыскании области, которая обладает одновременно свойствами как одного, так и другого понятия т.е пересечение.
Например: Умножение понятий «студент» и «спортсмена» дает область студентов, являющихся в то же время спортсменами, и наоборот. Рис №2
Например: Пусть «х» обозначает операцию умножения понятий.
1. «А» и «В» — равнозначные понятия.
Тогда АхВ=А=В, как и при сложении.
«Любовь»х «наслаждение вещью и соединение с нею»= «любовь»=«наслаждение вещью и соединение с нею» (согласно Б.Спинозе)
2. «А» и «В» — пересекающиеся понятия. Тогда АхВ=(А и В одновременно)
«Счастье» х «неожиданность»= «неожиданное счастье»
3. «А»- родовое, «В»- видовое понятие. Тогда АхВ=В
«Любовь» х «сильное чувство»= «любовь»
4. «А» и «В» – противоречащие понятия. Тогда АхВ=О, где символ О означает понятие с пустым (недопустимым) объемом.
«Синий» х «несиний» = О, так как невозможно существование цвета, который был бы синим и несиним одновременно.
5. «А» и «В» – противоположные понятия. Тогда АхВ=О, как и в предыдущем случае. «Любовь» х «ненависть» = О
6. «А» и «В» – соподчиненные понятия. Тогда АхВ=О, как и в предыдущем случае. «Любовь» х «безразличие» = О
7. «А» и «В» – частично совместимые понятия. Тогда АхВ=понятие, представляющее отрицание как А, так и В (нейтральная точка на шкале отношений между А и В)
«Неумные» х «неглупые» = «люди среднего ума»
8. «А» и «В» – противоречащие и противоположные понятия одновременно.
Тогда АхВ=И, как и при сложении подобных понятий.
«Мужчина» х «женщина» = «человек»
Операция с понятием – вычитание.
Вычитание объема одного понятия из другого даст в зависимости от видов рассматриваемых понятий усеченную область объема.
Вычитание возможно только между совместимыми, а точнее не пересекающимися и подчиненными понятиями.
Или: Вычитанием (разностью) понятия В из понятия А называется их преобразование в понятие, объем которого состоит из элементов объема А, противоречащих понятию В т.е. обладающих свойством- В
Например: Пусть «/» обозначает операцию вычитания понятия.
1. «А» и «В» — равнозначные понятия.
Тогда А/В=А=О В качестве частного случая имеем А/А=О
«Зависть» / « печаль по поводу счастья друзей» = «печаль по поводу счастья друзей» / «печаль» =О (согласно Сократу)
«Печаль»/ «печаль»= О
2. «А» и «В» — пересекающиеся понятия.
Тогда А/В=(А и –В), В/А=(В и –А)
«Справедливость» / «недействие»= «справедливое действие»,
«недействие» / «справедливость» = «несправедливое действие»
3.. «А»- родовое, «В»- видовое понятие. Тогда А/В=(А и –В), В/А=О
«Чувство»/ «ненависть» = «все чувства, не являющиеся ненавистью».
Этот случай вычитания тождествен конструированию дополнения понятия В до универсума И=А. «Ненависть» / «чувство»=О
4.«А» и «В» – противоречащие понятия. Тогда А/В=А, В/А=В
«Храбрость» / «нехрабрость»= «храбрость»,
«нехрабрость» / «храбрость»= «нехрабрость»
5.. «А» и «В» – противоположные понятия. Тогда А/В=А, В/А=В как и в предыдущем случае.
«Любовь» / «ненависть» = «любовь»,
«Ненависть» / « любовь»= «ненависть»
6… «А» и «В» – соподчиненные понятия. Тогда А/В=А, В/А=В как и в предыдущем случае.
«Любовь» / «безразличие» = «любовь»,
«Безразличие»/ « любовь»= «безразличие»
7. «А» и «В» – частично совместимые понятия. Тогда А/В=-В, В/А=-А
«Неумные люди»/ «неглупые люди» = «глупые люди»,
«Неглупые люди»/ «неумные люди» = «умные люди»
8. «А» и «В» – противоречащие и противоположные понятия одновременно. Тогда А/В=А, В/А=В
«Муж»/ «жена»= «муж»,
«жена»/ «муж»= «жена»
Операция с понятием — деление.
Деление – логическая операция, раскрывающая объем понятия, это распределение объема исходного понятия на виды, группы, классы, части по единому для них признаку(основанию деления).
В делении различают делимое понятие, основание(признак) деления и члены деления.
Основанием деления должен быть общий для всех членов деления признак; видоизменение этого признака как раз и отличает один член деления от другого. Наличие основания деления отличает эту операцию от простого расчленения предмета на части.
В зависимости от основания деления различают три вида данной логической операции:
1. Деление по видоизменению признака
Деление понятия в логике это такое раскрытие его объема, где каждый член деления как составная часть объема понятия сохраняет свойства делимого, т.е. целого, в то время как расчленение предмета дает такие части, которые не обладают свойствами целого( расчленяемого, делимого).
Например: 1. копейка, гривенник или полтинник в отдельности не составляют рубля, а разделенное по объему понятие «рубль» дает в результате такие группы, как «бумажный» или «металлический рубль», которые полностью сохраняют свойства делимого понятия, его содержательные признаки.
2. Минута не составляет часа, она лишь шестидесятая часть его, поэтому понятие «час» не делится по объему на «минуты», не включает в свой объем понятие «минута».
Понятие «час» может быть распределено по объему на «час академический», «час астрономический», «час учебный» и пр.
Тут все члены деления сохранили свойства делимого, а вот части этого предмета – «минута», «секунда» и пр., каждая в отдельности, естественно, часом не являются.
2. Дихотомическое деление
Дихотомия или дихотомическое деление – это деление любой предметной области, любого объема (класса) всего лишь на два члена деления
Главным законом структуры этой логической операции является требование – деление должно быть соразмерным.
Это значит, что объем делимого понятия должен быть равен сумме объемов всех членов деления.
Выполнение этого требования на практике не так просто, как может показаться, и предполагает основное знание того предмета, той предметной области, которую отражает делимое понятие.
Таким образом, делению поддаются общие понятия; единичные понятия, объемы которых индивидуальны, делению не подлежат.
Например: мир природы можно делить на органический и неорганический. Общий объем этих двух понятий соответствует объему делимого понятия, так что дихотомия никогда не нарушает главного закона этой операции: она всегда соразмерна.
3.Классификация.
Классификация — особый вид деления, это сложная по своей структуре операция, вид научного исследования, как довольно проблематичная задача по систематизации, упорядочения предметной области.
Классическим вариантом классификации по существенному признаку, классификации, отражающей закономерные связи в определенной предметной области, является система химических элементов Д.И. Менделеева.
Зачастую, классификации выступают завершающим моментом научного исследования различных предметных областей – это и классификация растительных и животных видов, химических элементов, наук и тд.
Отношения между понятиями:
Отрицание, обобщение, ограничение, определение.
Отрицание
Отрицание – осуществляется простым прибавлением к любому исходному понятию отрицательной частицы «не».
Производится неограниченное число раз с одним и тем же понятием.
Например: Отрицание отрицательного понятия «не-студент» даст в итоге понятие «не-не-студент», являющееся по существу положительным понятием «студент»
Обобщение
Обобщение рассматривается в логике и как метод, и как операция с понятием. Как операция с понятием «обобщение» заключается в увеличении объема исходного понятия- это переход от понятия с меньшим объемом к понятию с большим объемом за счет, естественно, уменьшения содержания исходного понятия.
Например: Переход от понятия «студент» к более общему понятию «учащийся» или «человек» совершается путем отбрасывания одного или нескольких содержательных признаков исходного понятия. Таким образом, увеличение объема понятия, т.е. обобщение, в то же время есть и уменьшение содержания.
Пределом обобщения выступают категории, как наиболее широкие по объему понятия.
Категории – это высший род, и с какого бы понятия мы не начали обобщение, конечным результатом его будет та или иная категория.
Например: обобщение понятия «студент», мы получим после понятия «человек» понятие «примат», «млекопитающее», «позвоночное», «животное», «живой организм», и наконец, «материя».
Дальше обобщить невозможно.
Ограничение
Ограничение – переход от понятия с большим объемом к понятию с меньшим объемом.
Ограничение совершается прибавлением к содержанию исходного понятия одного или нескольких новых признаков.
Например: Если к содержанию понятия «студент» прибавим признак, как обучение в университете, то получим понятие «студент университета», продолжая эту операцию, можно получить понятие «студент СПбГУ» и так вплоть до понятия о конкретном, отдельном студенте.
Таким образом, пределом ограничения выступает единичное понятие, ограничить которое невозможно
Определение.
Определение понятия, есть вид логической операции отношений между понятиями, раскрывающие содержание понятия, т.е. перечисление тех существенных и отличительных признаков того или иного предмета, которые отражаются мыслью о нем.
Как логическая операция, определение состоит из двух элементов: определяемого понятия(dfd) и определяющих понятий(dfn).
Формула закона выглядит так: Dfd=dfn.Это закон структуры данной операции, т.е. определение не должно заключать в себе круга т.е. определяемое понятие нельзя определять через само себя.
Например: человек есть разумное существо, потому что он мыслит.
Определение понятия подразделяется на:
1. явное определение
Явные определения, перечисляя существенные и отличительные признаки определяемого, раскрывая его сущность, подразделяются на виды: определение через род и видовое отличие(дефиниция), генетическое определение номинальное.
Дефиниция, т.е. определение через род и видовое отличие самим своим названием выделяет два этапа в своей структуре: первый- подведение определяемого понятия под ближайшее к нему родовое; второй этап – перечисление тех существенно-отличительных признаков, которые составляют специфику содержания определяемого понятия.
Например: определяемое понятие «логика» подводится под ближайшее родовое «философская наука» и далее перечисляются его отличительные, т.е. видовые признаки.
Генетическое определение указывает способ формирования, образования определяемого предмета.
Например: в геометрии: окружность определяется как замкнутая кривая на плоскости, образованная движением точки В отрезка АВ вокруг точки А.
Т.е. замкнутая кривая выступает родовым понятием по отношению к определяемому, а описание способа формирования есть не что иное, как перечисление отличительных признаков определяемого предмета.
Номинальное определение- определение направлено лишь на раскрытие смысла, назначения слова, или знака не касаясь признаков определяемого.
Например: « лавсан»- это слово, образованное сокращением названия «лаборатория высокомолекулярных соединений»
2.неявное определение
К неявным определениям относится большая группа приемов, сходных с определением: указание, описание, сравнение, характеристика, операциональное определение, контекстуальное определение.
Указание – словесное сопровождение явления, вещи на которую указывают пальцем(«остенсивное определение»).
Описание – подробная словесная характеристика предмета, который наблюдается непосредственно, или словесное художественное изображение картины для представления ее другим.
Например: описание Днепра у Гоголя
Сравнение – (различие, метафора), прием, используемый при сопоставлении двух или нескольких понятий.
Например: совесть- это внутренний суд, дети – цветы жизни.
Характеристика – подробное описание предмета с выделением отличительного, существенного признака в предмете, явления.
Операциональное определение – определение действием, экспериментом, заключающееся в выполнении правил, приемов определенной последовательности.
Например: кислота определяется, как вещество, которое окрашивает лакмусовую бумагу в красный цвет.
Контекстуальное определение – определение через текст, в котором определяемое явно не называется, а характеризуется, описывается косвенно.
Например: «близкие родственники» это «родители, дети, братья, сестры »
Правила:
1.Определение должно быть ясным, четким, свободным от двусмысленности, определение должно быть лаконичным.
2. Определение, по возможности, не должно быть отрицательным, ибо отрицание не раскрывает сущности, не перечисляет признаки предмета, отражаемого понятием: эвкалипт-дерево, которого нет Старом Петергофе.
Заключение
Таким образом, понятие и операции с ним, является одной из основных форм абстрактного мышления. Оно не только способно замещать или представлять предметы, но и позволяет анализировать их, отвлекаясь от несущественного, случайного, что дает возможность глубже проникать в действительность, отображать ее с большей полнотой.
Литература
1. Кобзарь В.И. Основы логических знаний: Учебное пособие.-СПбИВЭСЭП; О-во «Знание». 1999.172с.
2. Светлов В.А. Практическая логика. – С-Петербург: Изд-во РХГИ, 1995. -472с
www.ronl.ru
1.13. Как складываются и умножаются понятия?
Помимо ограничения, обобщения, определения и деления понятий существуют еще две логические операции – сложение и умножение понятий.
Сложение понятий – это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник и спортсмен образуется новое понятие, в объем которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой, на схеме Эйлера изображается штриховкой:

Умножение понятий – это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий. Например, при умножении понятий школьник и спортсмен образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением, на схеме Эйлера изображается штриховкой (так же, как и результат сложения):

Мы привели примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения (школьник и спортсмен). В других случаях отношений между понятиями результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. Читатель без труда сможет определить их для всех случаев отношений между понятиями с помощью круговых схем. Так, если два понятия находятся в отношении подчинения, например, карась и рыба, то результатом их сложения является родовое понятие рыба (т. е. логической суммой понятий карась и рыба будет множество всех рыб):

Результатом умножения понятий карась и рыба, находящихся в отношении родовидового подчинения, будет видовое понятие карась (т. е. логическим произведением понятий карась и рыба является множество всех карасей):

Так же, если два понятия находятся в отношении соподчинения, например, береза и сосна, то результат их сложения – это два объема данных понятий (т. е. логической суммой понятий береза и сосна будет как множество всех берез, так и множество всех сосен):

Результатом умножения соподчиненных понятий береза и сосна является нулевое понятие (т. е. логическое произведение понятий береза и сосна представляет собой пустое множество – не существует ни одной березы, которая могла бы быть сосной и наоборот):

Точно так же устанавливаются результаты сложения и умножения объемов двух понятий, которые находятся в отношениях равнозначности, противоположности и противоречия (см. 1.5.). Так, например, нетрудно догадаться, что если два понятия находятся в отношении равнозначности, то результат их сложения будет полностью совпадать с результатом их умножения (логическая сумма равнозначных понятий равна их логическому произведению). Так же понятно, что результатом умножения противоположных и противоречащих понятий является нулевое понятие и т. п.
Как правило, в естественном языке (т. е. том, на котором мы общаемся) результат сложения понятий выражается союзом или, а умножения – союзом и. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является или школьником, или спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является и школьником, и спортсменом одновременно.
Относительно употребления союзов или и и в естественном языке в качестве выражения результатов логических операций сложения и умножения понятий удачный пример приводит в своем учебнике по логике известный отечественный автор В. И. Свинцов (Логика. Элементарный курс для гуманитарных специальностей. М.: Скорина, 1998. С. 60–61), отрывок из которого приводится ниже. «Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: «Безбилетный проезд и бесплатный провоз багажа наказывается штрафом»? Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билета, в другое – не оплатившие провоз багажа. Если союз «и» рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза «или» здесь следует признать предпочтительным».
Здесь следует отметить неоднозначность разделительного союза или, который может употребляться в нестрогом (неисключающем) значении и в строгом (исключающем). Например, в высказывании: Можно изучать английский язык или немецкий союз или употребляется в нестрогом значении, т. к. можно изучать и тот, и другой язык одновременно, одно другое не исключает. В данном случае разделительный союз или очень близок к соединительному союзу и. С другой стороны, в высказывании: Он родился в 1987 году или в 1989 году союз или употребляется в строгом значении, т. к. если он родился в 1987 году, то – никак не в 1989 году и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза или мы еще будем говорить далее). Если в рассмотренное выше правило пользования городским транспортом поставить союз или вместо союза и, как предлагает В. И. Свинцов, то получится следующее: «Безбилетный проезд или бесплатный провоз багажа наказываются штрафом». В данном случае союз или, являющийся показателем логического сложения, надо воспринимать в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации.
В силу всего сказанного надо отметить, что употребление союза или всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется. Понятно, что без этого комментария вполне возможны разночтения, которые нередко приводят к различным и существенным недоразумениям.
Поделитесь на страничкеСледующая глава >
fil.wikireading.ru
Московский государственный гуманитарный университет
Им. М.А. Шолохова
Реферат
по дисциплине «Логика»
на тему: «Операции с понятием»
Выполнил: студентка заочного отделения
Факультета психологии
Курс 3/3
Елисеева И.В.
Проверила: старший преподаватель
Воронина А.В.
Москва-Ступино
2008г.
СОДЕРЖАНИЕ
1. Введение. Характеристика понятия и операции над понятиями.
2. Операция с понятием - сложение.
3. Операция с понятием – умножение.
4. Операция с понятием - вычитание.
5. Операция с понятием - деление.
6. Отношения между понятиями.
7. Заключение
8. Литература
Введение
Разнообразие окружающего нас реального мира обусловлено существованием множества отдельных материальных предметов, обладающих различными свойствами и находящихся между собой в определенных связях. Познание природы этих предметов, выявление их сущности и оперирование ими в реальной жизни требует идеальных средств, которые заменяли бы эти предметы объективного мира и служили инструментом развития человеческого знания и наук. Одним из таких средств являются понятия.
Понятия не существуют в объективном мире. Они возникают в нашем сознании и заменяют предметы, процессы действительности логическими образами, делая естественный язык общения и языки наук информационно более емкими, насыщенными, давая возможность зафиксировать и передать знания с помощью наименьшего количества знаковых средств.
Характеристика понятия и операции над понятием.
Понятие – форма мышления, отражающая предметы в их общих существенных признаках.
Операции над понятиями – логические действия, вследствие которых создаются новые понятия.
К операциям с понятиями относят:
сложение, вычитание, умножение, деление.
Чтобы осмысленно оперировать понятиями, правильно их использовать в решении теоретических и практических задач необходимо уметь выявлять две основные логические характеристики: объем и содержание понятия.
Объем понятия – это совокупность(класс) предметов, которые мыслятся в данном понятии.
Содержание понятия – совокупность признаков предмета(предметов) , мыслимых в данном понятии.
Характеристика видов понятия:
1. по объему: единичные, общие, нулевые, исчислимые, неисчислимые, регистрирующие, нерегистрирующие.
2. по содержанию: конкретные, абстрактные, относительные, безотносительные, положительные, отрицательные, собирательные, несобирательные
В зависимости от того, как соотносятся объемы понятий их делят на две группы :
1. совместимые – понятия, объемы которых совпадают полностью или частично.
2. несовместимые – понятия, объемы которых не совпадают ни в одном элементе, но они могут быть включены частично или полностью в объем общего для них понятия.
Операция с понятием - сложение.
Сложение - простейшая логическая операция с понятием, которая представляет собой объединение объемов двух или более понятий, даже если эти понятия и не пересекаются, не совпадают между собой по объему.
Например: Объединив понятие «школьник» и понятие «студент», мы получим область, отражающую признаки, присущие тому и другому понятию в рамках общего для них родового понятия «учащийся».рис №1

Например: Пусть «+» обозначает операцию сложения понятий.
1. «А» и «В» - равнозначные понятия.
Тогда А+В=А=В, т.е. результат сложения таких понятий равен любому из них. Как частный случай имеем: А+А=А
«Сиеста»+«полуденный отдых»=«сиеста»=«полуденный отдых»
«Сиеста»+ «сиеста»= «сиеста»
Таким образом, сложение двух равнозначных понятий не приводит к удвоенной сумме, как это имеет место при сложении натуральных чисел т.е не обладает свойством итерации(прибавления).
Операция с понятием - умножение.
Умножение, состоит в отыскании области, которая обладает одновременно свойствами как одного, так и другого понятия т.е пересечение.

Например: Умножение понятий «студент» и «спортсмена» дает область студентов, являющихся в то же время спортсменами, и наоборот. Рис №2
Например: Пусть «х» обозначает операцию умножения понятий.
1. «А» и «В» - равнозначные понятия.
Тогда АхВ=А=В, как и при сложении.
«Любовь»х «наслаждение вещью и соединение с нею»= «любовь»=«наслаждение вещью и соединение с нею» (согласно Б.Спинозе)
2. «А» и «В» - пересекающиеся понятия. Тогда АхВ=(А и В одновременно)
«Счастье» х «неожиданность»= «неожиданное счастье»
3. «А»- родовое, «В»- видовое понятие. Тогда АхВ=В
«Любовь» х «сильное чувство»= «любовь»
4. «А» и «В» – противоречащие понятия. Тогда АхВ=О, где символ О означает понятие с пустым (недопустимым) объемом.
«Синий» х «несиний» = О , так как невозможно существование цвета, который был бы синим и несиним одновременно.
5. «А» и «В» – противоположные понятия. Тогда АхВ=О, как и в предыдущем случае. «Любовь» х «ненависть» = О
6. «А» и «В» – соподчиненные понятия. Тогда АхВ=О, как и в предыдущем случае. «Любовь» х «безразличие» = О
7. «А» и «В» – частично совместимые понятия. Тогда АхВ=понятие, представляющее отрицание как А, так и В (нейтральная точка на шкале отношений между А и В)
«Неумные» х «неглупые» = «люди среднего ума»
8. «А» и «В» – противоречащие и противоположные понятия одновременно.
Тогда АхВ=И, как и при сложении подобных понятий.
«Мужчина» х «женщина» = «человек»
Операция с понятием – вычитание.
Вычитание объема одного понятия из другого даст в зависимости от видов рассматриваемых понятий усеченную область объема.
Вычитание возможно только между совместимыми, а точнее не пересекающимися и подчиненными понятиями.
Или: Вычитанием (разностью) понятия В из понятия А называется их преобразование в понятие, объем которого состоит из элементов объема А, противоречащих понятию В т.е. обладающих свойством- В
Например: Пусть «/» обозначает операцию вычитания понятия.
1. «А» и «В» - равнозначные понятия.
Тогда А/В=А=О В качестве частного случая имеем А/А=О
«Зависть» / « печаль по поводу счастья друзей» = «печаль по поводу счастья друзей» / «печаль» =О (согласно Сократу)
«Печаль»/ «печаль»= О
2. «А» и «В» - пересекающиеся понятия.
Тогда А/В=(А и –В), В/А=(В и –А)
«Справедливость» / «недействие»= «справедливое действие»,
«недействие» / «справедливость» = «несправедливое действие»
3. . «А»- родовое, «В»- видовое понятие. Тогда А/В=(А и –В), В/А=О
«Чувство»/ «ненависть» = «все чувства, не являющиеся ненавистью».
Этот случай вычитания тождествен конструированию дополнения понятия В до универсума И=А. «Ненависть» / «чувство»=О
4.«А» и «В» – противоречащие понятия. Тогда А/В=А, В/А=В
«Храбрость» / «нехрабрость»= «храбрость»,
«нехрабрость» / «храбрость»= «нехрабрость»
5. . «А» и «В» – противоположные понятия. Тогда А/В=А, В/А=В как и в предыдущем случае.
«Любовь» / «ненависть» = «любовь»,
«Ненависть» / « любовь»= «ненависть»
6.. «А» и «В» – соподчиненные понятия. Тогда А/В=А, В/А=В как и в предыдущем случае.
«Любовь» / «безразличие» = «любовь»,
«Безразличие»/ « любовь»= «безразличие»
7. «А» и «В» – частично совместимые понятия. Тогда А/В=-В,В/А=-А
«Неумные люди»/ «неглупые люди» = «глупые люди»,
«Неглупые люди»/ «неумные люди» = «умные люди»
8. «А» и «В» – противоречащие и противоположные понятия одновременно. Тогда А/В=А, В/А=В
«Муж»/ «жена»= «муж»,
«жена»/ «муж»= «жена»
Операция с понятием - деление.
Деление – логическая операция, раскрывающая объем понятия, это распределение объема исходного понятия на виды, группы, классы, части по единому для них признаку(основанию деления).
В делении различают делимое понятие, основание(признак) деления и члены деления.
Основанием деления должен быть общий для всех членов деления признак; видоизменение этого признака как раз и отличает один член деления от другого. Наличие основания деления отличает эту операцию от простого расчленения предмета на части.
В зависимости от основания деления различают три вида данной логической операции:
1. Деление по видоизменению признака
Деление понятия в логике это такое раскрытие его объема, где каждый член деления как составная часть объема понятия сохраняет свойства делимого, т.е. целого, в то время как расчленение предмета дает такие части, которые не обладают свойствами целого( расчленяемого, делимого).
Например: 1. копейка, гривенник или полтинник в отдельности не составляют рубля, а разделенное по объему понятие «рубль» дает в результате такие группы, как «бумажный» или «металлический рубль», которые полностью сохраняют свойства делимого понятия, его содержательные признаки.
2. Минута не составляет часа, она лишь шестидесятая часть его, поэтому понятие «час» не делится по объему на «минуты» , не включает в свой объем понятие «минута».
Понятие «час» может быть распределено по объему на «час академический», «час астрономический», «час учебный» и пр.
Тут все члены деления сохранили свойства делимого, а вот части этого предмета – «минута», «секунда» и пр., каждая в отдельности, естественно , часом не являются.
2. Дихотомическое деление
Дихотомия или дихотомическое деление – это деление любой предметной области, любого объема (класса) всего лишь на два члена деления
Главным законом структуры этой логической операции является требование – деление должно быть соразмерным.
Это значит, что объем делимого понятия должен быть равен сумме объемов всех членов деления.
mirznanii.com
СОДЕРЖАНИЕ 1. Введение. Характеристика понятия и операции над понятиями. 2. Операция с понятием - сложение. 3. Операция с понятием – умножение. 4. Операция с понятием - вычитание. 5. Операция с понятием - деление. 6. Отношения между понятиями. 7. Заключение 8. Литература
Введение Разнообразие окружающего нас реального мира обусловлено существованием множества отдельных материальных предметов, обладающих различными свойствами и находящихся между собой в определенных связях. Познание природы этих предметов, выявление их сущности и оперирование ими в реальной жизни требует идеальных средств, которые заменяли бы эти предметы объективного мира и служили инструментом развития человеческого знания и наук. Одним из таких средств являются понятия. Понятия не существуют в объективном мире. Они возникают в нашем сознании и заменяют предметы, процессы действительности логическими образами, делая естественный язык общения и языки наук информационно более емкими, насыщенными, давая возможность зафиксировать и передать знания с помощью наименьшего количества знаковых средств.
Характеристика понятия и операции над понятием. Понятие – форма мышления, отражающая предметы в их общих существенных признаках. Операции над понятиями – логические действия, вследствие которых создаются новые понятия. К операциям с понятиями относят: сложение, вычитание, умножение, деление. Чтобы осмысленно оперировать понятиями, правильно их использовать в решении теоретических и практических задач необходимо уметь выявлять две основные логические характеристики: объем и содержание понятия. Объем понятия – это совокупность(класс) предметов, которые мыслятся в данном понятии. Содержание понятия – совокупность признаков предмета(предметов) , мыслимых в данном понятии. Характеристика видов понятия: 1. по объему: единичные, общие, нулевые, исчислимые, неисчислимые, регистрирующие, нерегистрирующие. 2. по содержанию: конкретные, абстрактные, относительные, безотносительные, положительные, отрицательные, собирательные, несобирательные В зависимости от того, как соотносятся объемы понятий их делят на две группы : 1. совместимые – понятия, объемы которых совпадают полностью или частично. 2. несовместимые – понятия, объемы которых не совпадают ни в одном элементе, но они могут быть включены частично или полностью в объем общего для них понятия.
Операция с понятием - сложение. Сложение - простейшая логическая операция с понятием, которая представляет собой объединение объемов двух или более понятий, даже если эти понятия и не пересекаются, не совпадают между собой по объему. Например: Объединив понятие «школьник» и понятие «студент», мы получим область, отражающую признаки, присущие тому и другому понятию в рамках общего для них родового понятия «учащийся».рис №1 Например: Пусть «+» обозначает операцию сложения понятий. 1. «А» и «В» - равнозначные понятия. Тогда А+В=А=В, т.е. результат сложения таких понятий равен любому из них. Как частный случай имеем: А+А=А «Сиеста»+«полуденный отдых»=«сиеста»=«полуденный отдых» «Сиеста»+ «сиеста»= «сиеста» Таким образом, сложение двух равнозначных понятий не приводит к удвоенной сумме, как это имеет место при сложении натуральных чисел т.е не обладает свойством итерации(прибавления).
Операция с понятием - умножение. Умножение, состоит в отыскании области, которая обладает одновременно свойствами как одного, так и другого понятия т.е пересечение. Например: Умножение понятий «студент» и «спортсмена» дает область студентов, являющихся в то же время спортсменами, и наоборот. Рис №2 Например: Пусть «х» обозначает операцию умножения понятий. 1. «А» и «В» - равнозначные понятия. Тогда АхВ=А=В, как и при сложении. «Любовь»х «наслаждение вещью и соединение с нею»= «любовь»=«наслаждение вещью и соединение с нею» (согласно Б.Спинозе) 2. «А» и «В» - пересекающиеся понятия. Тогда АхВ=(А и В одновременно) «Счастье» х «неожиданность»= «неожиданное счастье» 3. «А»- родовое, «В»- видовое понятие. Тогда АхВ=В «Любовь» х «сильное чувство»= «любовь» 4. «А» и «В» – противоречащие понятия. Тогда АхВ=О, где символ О означает понятие с пустым (недопустимым) объемом. «Синий» х «несиний» = О , так как невозможно существование цвета, который был бы синим и несиним одновременно. 5. «А» и «В» – противоположные понятия. Тогда АхВ=О, как и в предыдущем случае. «Любовь» х «ненависть» = О 6. «А» и «В» – соподчиненные понятия. Тогда АхВ=О, как и в предыдущем случае. «Любовь» х «безразличие» = О 7. «А» и «В» – частично совместимые понятия. Тогда АхВ=понятие, представляющее отрицание как А, так и В (нейтральная точка на шкале отношений между А и В) «Неумные» х «неглупые» = «люди среднего ума» 8. «А» и «В» – противоречащие и противоположные понятия одновременно. Тогда АхВ=И, как и при сложении подобных понятий. «Мужчина» х «женщина» = «человек» Операция с понятием – вычитание. Вычитание объема одного понятия из другого даст в зависимости от видов рассматриваемых понятий усеченную область объема. Вычитание возможно только между совместимыми, а точнее не пересекающимися и подчиненными понятиями. Или: Вычитанием (разностью) понятия В из понятия А называется их преобразование в понятие, объем которого состоит из элементов объема А, противоречащих понятию В т.е. обладающих свойством- В Например: Пусть «/» обозначает операцию вычитания понятия. 1. «А» и «В» - равнозначные понятия. Тогда А/В=А=О В качестве частного случая имеем А/А=О «Зависть» / « печаль по поводу счастья друзей» = «печаль по поводу счастья друзей» / «печаль» =О (согласно Сократу) «Печаль»/ «печаль»= О 2. «А» и «В» - пересекающиеся понятия. Тогда А/В=(А и –В), В/А=(В и –А) «Справедливость» / «недействие»= «справедливое действие», «недействие» / «справедливость» = «несправедливое действие» 3. . «А»- родовое, «В»- видовое понятие. Тогда А/В=(А и –В), В/А=О «Чувство»/ «ненависть» = «все чувства, не являющиеся ненавистью». Этот случай вычитания тождествен конструированию дополнения понятия В до универсума И=А. «Ненависть» / «чувство»=О 4.«А» и «В» – противоречащие понятия. Тогда А/В=А, В/А=В «Храбрость» / «нехрабрость»= «храбрость», «нехрабрость» / «храбрость»= «нехрабрость» 5. . «А» и «В» – противоположные понятия. Тогда А/В=А, В/А=В как и в предыдущем случае. «Любовь» / «ненависть» = «любовь», «Ненависть» / « любовь»= «ненависть» 6.. «А» и «В» – соподчиненные понятия. Тогда А/В=А, В/А=В как и в предыдущем случае. «Любовь» / «безразличие» = «любовь», «Безразличие»/ « любовь»= «безразличие» 7. «А» и «В» – частично совместимые понятия. Тогда А/В=-В,В/А=-А «Неумные люди»/ «неглупые люди» = «глупые люди», «Неглупые люди»/ «неумные люди» = «умные люди» 8. «А» и «В» – противоречащие и противоположные понятия одновременно. Тогда А/В=А, В/А=В «Муж»/ «жена»= «муж», «жена»/ «муж»= «жена» Операция с понятием - деление. Деление – логическая операция, раскрывающая объем понятия, это распределение объема исходного понятия на виды, группы, классы, части по единому для них признаку(основанию деления). В делении различают делимое понятие, основание(признак) деления и члены деления. Основанием деления должен быть общий для всех членов деления признак; видоизменение этого признака как раз и отличает один член деления от другого. Наличие основания деления отличает эту операцию от простого расчленения предмета на части. В зависимости от основания деления различают три вида данной логической операции: 1. Деление по видоизменению признака Деление понятия в логике это такое раскрытие его объема, где каждый член деления как составная часть объема понятия сохраняет свойства делимого, т.е. целого, в то время как расчленение предмета дает такие части, которые не обладают свойствами целого( расчленяемого, делимого). Например: 1. копейка, гривенник или полтинник в отдельности не составляют рубля, а разделенное по объему понятие «рубль» дает в результате такие группы, как «бумажный» или «металлический рубль», которые полностью сохраняют свойства делимого понятия, его содержательные признаки. 2. Минута не составляет часа, она лишь шестидесятая часть его, поэтому понятие «час» не делится по объему на «минуты» , не включает в свой объем понятие «минута». Понятие «час» может быть распределено по объему на «час академический», «час астрономический», «час учебный» и пр. Тут все члены деления сохранили свойства делимого, а вот части этого предмета – «минута», «секунда» и пр., каждая в отдельности, естественно , часом не являются. 2. Дихотомическое деление Дихотомия или дихотомическое деление – это деление любой предметной области, любого объема (класса) всего лишь на два члена деления Главным законом структуры этой логической операции является требование – деление должно быть соразмерным. Это значит, что объем делимого понятия должен быть равен сумме объемов всех членов деления. Выполнение этого требования на практике не так просто, как может показаться, и предполагает основное знание того предмета, той предметной области, которую отражает делимое понятие. Таким образом, делению поддаются общие понятия ; единичные понятия, объемы которых индивидуальны, делению не подлежат. Например: мир природы можно делить на органический и неорганический. Общий объем этих двух понятий соответствует объему делимого понятия, так что дихотомия никогда не нарушает главного закона этой операции: она всегда соразмерна. 3.Классификация. Классификация - особый вид деления, это сложная по своей структуре операция, вид научного исследования, как довольно проблематичная задача по систематизации, упорядочения предметной области. Классическим вариантом классификации по существенному признаку, классификации, отражающей закономерные связи в определенной предметной области, является система химических элементов Д.И. Менделеева. Зачастую, классификации выступают завершающим моментом научного исследования различных предметных областей – это и классификация растительных и животных видов, химических элементов, наук и тд.
Отношения между понятиями: Отрицание, обобщение, ограничение, определение. Отрицание Отрицание – осуществляется простым прибавлением к любому исходному понятию отрицательной частицы «не». Производится неограниченное число раз с одним и тем же понятием. Например: Отрицание отрицательного понятия «не-студент» даст в итоге понятие «не-не-студент», являющееся по существу положительным понятием «студент» Обобщение Обобщение рассматривается в логике и как метод, и как операция с понятием. Как операция с понятием «обобщение» заключается в увеличении объема исходного понятия- это переход от понятия с меньшим объемом к понятию с большим объемом за счет, естественно, уменьшения содержания исходного понятия. Например: Переход от понятия «студент» к более общему понятию «учащийся» или «человек» совершается путем отбрасывания одного или нескольких содержательных признаков исходного понятия. Таким образом , увеличение объема понятия, т.е. обобщение, в то же время есть и уменьшение содержания. Пределом обобщения выступают категории, как наиболее широкие по объему понятия. Категории – это высший род, и с какого бы понятия мы не начали обобщение, конечным результатом его будет та или иная категория. Например: обобщение понятия «студент», мы получим после понятия «человек» понятие «примат», «млекопитающее», «позвоночное», «животное», «живой организм», и наконец, «материя». Дальше обобщить невозможно. Ограничение Ограничение – переход от понятия с большим объемом к понятию с меньшим объемом. Ограничение совершается прибавлением к содержанию исходного понятия одного или нескольких новых признаков. Например: Если к содержанию понятия «студент» прибавим признак , как обучение в университете, то получим понятие «студент университета», продолжая эту операцию, можно получить понятие «студент СПбГУ» и так вплоть до понятия о конкретном, отдельном студенте. Таким образом, пределом ограничения выступает единичное понятие, ограничить которое невозможно Определение. Определение понятия, есть вид логической операции отношений между понятиями, раскрывающие содержание понятия, т.е. перечисление тех существенных и отличительных признаков того или иного предмета, которые отражаются мыслью о нем. Как логическая операция , определение состоит из двух элементов: определяемого понятия(dfd) и определяющих понятий(dfn). Формула закона выглядит так : Dfd=dfn .Это закон структуры данной операции, т.е. определение не должно заключать в себе круга т.е. определяемое понятие нельзя определять через само себя. Например: человек есть разумное существо, потому что он мыслит. Определение понятия подразделяется на: 1. явное определение Явные определения, перечисляя существенные и отличительные признаки определяемого , раскрывая его сущность, подразделяются на виды: определение через род и видовое отличие(дефиниция), генетическое определение номинальное. Дефиниция, т.е. определение через род и видовое отличие самим своим названием выделяет два этапа в своей структуре: первый- подведение определяемого понятия под ближайшее к нему родовое; второй этап – перечисление тех существенно-отличительных признаков, которые составляют специфику содержания определяемого понятия. Например: определяемое понятие «логика» подводится под ближайшее родовое «философская наука» и далее перечисляются его отличительные, т.е. видовые признаки. Генетическое определение указывает способ формирования, образования определяемого предмета. Например: в геометрии: окружность определяется как замкнутая кривая на плоскости, образованная движением точки В отрезка АВ вокруг точки А. Т.е. замкнутая кривая выступает родовым понятием по отношению к определяемому, а описание способа формирования есть не что иное, как перечисление отличительных признаков определяемого предмета. Номинальное определение- определение направлено лишь на раскрытие смысла, назначения слова, или знака не касаясь признаков определяемого. Например: « лавсан»- это слово, образованное сокращением названия «лаборатория высокомолекулярных соединений» 2.неявное определение К неявным определениям относится большая группа приемов, сходных с определением: указание, описание, сравнение, характеристика, операциональное определение, контекстуальное определение. Указание – словесное сопровождение явления, вещи на которую указывают пальцем(«остенсивное определение»). Описание – подробная словесная характеристика предмета, который наблюдается непосредственно, или словесное художественное изображение картины для представления ее другим. Например: описание Днепра у Гоголя Сравнение – (различие, метафора), прием, используемый при сопоставлении двух или нескольких понятий. Например: совесть- это внутренний суд , дети – цветы жизни. Характеристика – подробное описание предмета с выделением отличительного, существенного признака в предмете, явления. Операциональное определение – определение действием, экспериментом, заключающееся в выполнении правил, приемов определенной последовательности. Например: кислота определяется, как вещество, которое окрашивает лакмусовую бумагу в красный цвет. Контекстуальное определение – определение через текст, в котором определяемое явно не называется, а характеризуется, описывается косвенно. Например: «близкие родственники» это «родители, дети, братья, сестры » Правила: 1.Определение должно быть ясным, четким, свободным от двусмысленности, определение должно быть лаконичным. 2. Определение, по возможности , не должно быть отрицательным, ибо отрицание не раскрывает сущности , не перечисляет признаки предмета, отражаемого понятием: эвкалипт-дерево, которого нет Старом Петергофе.
Заключение Таким образом, понятие и операции с ним, является одной из основных форм абстрактного мышления. Оно не только способно замещать или представлять предметы, но и позволяет анализировать их, отвлекаясь от несущественного, случайного, что дает возможность глубже проникать в действительность, отображать ее с большей полнотой.
Литература 1. Кобзарь В.И. Основы логических знаний: Учебное пособие.-СПбИВЭСЭП; О-во «Знание». 1999.172с. 2. Светлов В.А. Практическая логика. – С-Петербург: Изд-во РХГИ, 1995. -472с
www.coolreferat.com
Московский государственный гуманитарный университет
Им. М.А. Шолохова
Реферат
по дисциплине «Логика»
на тему: «Операции с понятием»
Выполнил: студентка заочного отделения
Факультета психологии
Курс 3/3
Елисеева И.В.
Проверила: старший преподаватель
Воронина А.В.
Москва-Ступино
2008г.
СОДЕРЖАНИЕ
1. Введение. Характеристика понятия и операции над понятиями.
2. Операция с понятием - сложение.
3. Операция с понятием – умножение.
4. Операция с понятием - вычитание.
5. Операция с понятием - деление.
6. Отношения между понятиями.
7. Заключение
8. Литература
Введение
Разнообразие окружающего нас реального мира обусловлено существованием множества отдельных материальных предметов, обладающих различными свойствами и находящихся между собой в определенных связях. Познание природы этих предметов, выявление их сущности и оперирование ими в реальной жизни требует идеальных средств, которые заменяли бы эти предметы объективного мира и служили инструментом развития человеческого знания и наук. Одним из таких средств являются понятия.
Понятия не существуют в объективном мире. Они возникают в нашем сознании и заменяют предметы, процессы действительности логическими образами, делая естественный язык общения и языки наук информационно более емкими, насыщенными, давая возможность зафиксировать и передать знания с помощью наименьшего количества знаковых средств.
Характеристика понятия и операции над понятием.
Понятие – форма мышления, отражающая предметы в их общих существенных признаках.
Операции над понятиями – логические действия, вследствие которых создаются новые понятия.
К операциям с понятиями относят:
сложение, вычитание, умножение, деление.
Чтобы осмысленно оперировать понятиями, правильно их использовать в решении теоретических и практических задач необходимо уметь выявлять две основные логические характеристики: объем и содержание понятия.
Объем понятия – это совокупность(класс) предметов, которые мыслятся в данном понятии.
Содержание понятия – совокупность признаков предмета(предметов) , мыслимых в данном понятии.
Характеристика видов понятия:
1. по объему: единичные, общие, нулевые, исчислимые, неисчислимые, регистрирующие, нерегистрирующие.
2. по содержанию: конкретные, абстрактные, относительные, безотносительные, положительные, отрицательные, собирательные, несобирательные
В зависимости от того, как соотносятся объемы понятий их делят на две группы :
1. совместимые – понятия, объемы которых совпадают полностью или частично.
2. несовместимые – понятия, объемы которых не совпадают ни в одном элементе, но они могут быть включены частично или полностью в объем общего для них понятия.
Операция с понятием - сложение.
Сложение - простейшая логическая операция с понятием, которая представляет собой объединение объемов двух или более понятий, даже если эти понятия и не пересекаются, не совпадают между собой по объему.
Например: Объединив понятие «школьник» и понятие «студент», мы получим область, отражающую признаки, присущие тому и другому понятию в рамках общего для них родового понятия «учащийся».рис №1
Например: Пусть «+» обозначает операцию сложения понятий.
1. «А» и «В» - равнозначные понятия.
Тогда А+В=А=В, т.е. результат сложения таких понятий равен любому из них. Как частный случай имеем: А+А=А
«Сиеста»+«полуденный отдых»=«сиеста»=«полуденный отдых»
«Сиеста»+ «сиеста»= «сиеста»
Таким образом, сложение двух равнозначных понятий не приводит к удвоенной сумме, как это имеет место при сложении натуральных чисел т.е не обладает свойством итерации(прибавления).
Операция с понятием - умножение.
Умножение, состоит в отыскании области, которая обладает одновременно свойствами как одного, так и другого понятия т.е пересечение.
Например: Умножение понятий «студент» и «спортсмена» дает область студентов, являющихся в то же время спортсменами, и наоборот. Рис №2
Например: Пусть «х» обозначает операцию умножения понятий.
1. «А» и «В» - равнозначные понятия.
Тогда АхВ=А=В, как и при сложении.
«Любовь»х «наслаждение вещью и соединение с нею»= «любовь»=«наслаждение вещью и соединение с нею» (согласно Б.Спинозе)
2. «А» и «В» - пересекающиеся понятия. Тогда АхВ=(А и В одновременно)
«Счастье» х «неожиданность»= «неожиданное счастье»
3. «А»- родовое, «В»- видовое понятие. Тогда АхВ=В
«Любовь» х «сильное чувство»= «любовь»
4. «А» и «В» – противоречащие понятия. Тогда АхВ=О, где символ О означает понятие с пустым (недопустимым) объемом.
«Синий» х «несиний» = О , так как невозможно существование цвета, который был бы синим и несиним одновременно.
5. «А» и «В» – противоположные понятия. Тогда АхВ=О, как и в предыдущем случае. «Любовь» х «ненависть» = О
6. «А» и «В» – соподчиненные понятия. Тогда АхВ=О, как и в предыдущем случае. «Любовь» х «безразличие» = О
7. «А» и «В» – частично совместимые понятия. Тогда АхВ=понятие, представляющее отрицание как А, так и В (нейтральная точка на шкале отношений между А и В)
«Неумные» х «неглупые» = «люди среднего ума»
8. «А» и «В» – противоречащие и противоположные понятия одновременно.
Тогда АхВ=И, как и при сложении подобных понятий.
«Мужчина» х «женщина» = «человек»
Операция с понятием – вычитание.
Вычитание объема одного понятия из другого даст в зависимости от видов рассматриваемых понятий усеченную область объема.
Вычитание возможно только между совместимыми, а точнее не пересекающимися и подчиненными понятиями.
Или: Вычитанием (разностью) понятия В из понятия А называется их преобразование в понятие, объем которого состоит из элементов объема А, противоречащих понятию В т.е. обладающих свойством- В
Например: Пусть «/» обозначает операцию вычитания понятия.
1. «А» и «В» - равнозначные понятия.
Тогда А/В=А=О В качестве частного случая имеем А/А=О
«Зависть» / « печаль по поводу счастья друзей» = «печаль по поводу счастья друзей» / «печаль» =О (согласно Сократу)
«Печаль»/ «печаль»= О
2. «А» и «В» - пересекающиеся понятия.
Тогда А/В=(А и –В), В/А=(В и –А)
«Справедливость» / «недействие»= «справедливое действие»,
«недействие» / «справедливость» = «несправедливое действие»
3. . «А»- родовое, «В»- видовое понятие. Тогда А/В=(А и –В), В/А=О
«Чувство»/ «ненависть» = «все чувства, не являющиеся ненавистью».
Этот случай вычитания тождествен конструированию дополнения понятия В до универсума И=А. «Ненависть» / «чувство»=О
4.«А» и «В» – противоречащие понятия. Тогда А/В=А, В/А=В
«Храбрость» / «нехрабрость»= «храбрость»,
«нехрабрость» / «храбрость»= «нехрабрость»
5. . «А» и «В» – противоположные понятия. Тогда А/В=А, В/А=В как и в предыдущем случае.
«Любовь» / «ненависть» = «любовь»,
«Ненависть» / « любовь»= «ненависть»
6.. «А» и «В» – соподчиненные понятия. Тогда А/В=А, В/А=В как и в предыдущем случае.
«Любовь» / «безразличие» = «любовь»,
«Безразличие»/ « любовь»= «безразличие»
7. «А» и «В» – частично совместимые понятия. Тогда А/В=-В,В/А=-А
«Неумные люди»/ «неглупые люди» = «глупые люди»,
«Неглупые люди»/ «неумные люди» = «умные люди»
8. «А» и «В» – противоречащие и противоположные понятия одновременно. Тогда А/В=А, В/А=В
«Муж»/ «жена»= «муж»,
«жена»/ «муж»= «жена»
Операция с понятием - деление.
Деление – логическая операция, раскрывающая объем понятия, это распределение объема исходного понятия на виды, группы, классы, части по единому для них признаку(основанию деления).
В делении различают делимое понятие, основание(признак) деления и члены деления.
Основанием деления должен быть общий для всех членов деления признак; видоизменение этого признака как раз и отличает один член деления от другого. Наличие основания деления отличает эту операцию от простого расчленения предмета на части.
В зависимости от основания деления различают три вида данной логической операции:
1. Деление по видоизменению признака
Деление понятия в логике это такое раскрытие его объема, где каждый член деления как составная часть объема понятия сохраняет свойства делимого, т.е. целого,
в то время как расчленение предмета дает такие части, которые не обладают свойствами целого( расчленяемого, делимого).Например: 1. копейка, гривенник или полтинник в отдельности не составляют рубля, а разделенное по объему понятие «рубль» дает в результате такие группы, как «бумажный» или «металлический рубль», которые полностью сохраняют свойства делимого понятия, его содержательные признаки.
2. Минута не составляет часа, она лишь шестидесятая часть его, поэтому понятие «час» не делится по объему на «минуты» , не включает в свой объем понятие «минута».
Понятие «час» может быть распределено по объему на «час академический», «час астрономический», «час учебный» и пр.
Тут все члены деления сохранили свойства делимого, а вот части этого предмета – «минута», «секунда» и пр., каждая в отдельности, естественно , часом не являются.
2. Дихотомическое деление
Дихотомия или дихотомическое деление – это деление любой предметной области, любого объема (класса) всего лишь на два члена деления
Главным законом структуры этой логической операции является требование – деление должно быть соразмерным.
Это значит, что объем делимого понятия должен быть равен сумме объемов всех членов деления.
Выполнение этого требования на практике не так просто, как может показаться, и предполагает основное знание того предмета, той предметной области, которую отражает делимое понятие.
Таким образом, делению поддаются общие понятия ; единичные понятия, объемы которых индивидуальны, делению не подлежат.
Например: мир природы можно делить на органический и неорганический. Общий объем этих двух понятий соответствует объему делимого понятия, так что дихотомия никогда не нарушает главного закона этой операции: она всегда соразмерна.
3.Классификация.
Классификация - особый вид деления, это сложная по своей структуре операция, вид научного исследования, как довольно проблематичная задача по систематизации, упорядочения предметной области.
Классическим вариантом классификации по существенному признаку, классификации, отражающей закономерные связи в определенной предметной области, является система химических элементов Д.И. Менделеева.
Зачастую, классификации выступают завершающим моментом научного исследования различных предметных областей – это и классификация растительных и животных видов, химических элементов, наук и тд.
Отношения между понятиями:
Отрицание, обобщение, ограничение, определение.
Отрицание
Отрицание – осуществляется простым прибавлением к любому исходному понятию отрицательной частицы «не».
Производится неограниченное число раз с одним и тем же понятием.
Например: Отрицание отрицательного понятия «не-студент» даст в итоге понятие «не-не-студент», являющееся по существу положительным понятием «студент»
Обобщение
Обобщение рассматривается в логике и как метод, и как операция с понятием. Как операция с понятием «обобщение» заключается в увеличении объема исходного понятия- это переход от понятия с меньшим объемом к понятию с большим объемом за счет, естественно, уменьшения содержания исходного понятия.
Например: Переход от понятия «студент» к более общему понятию «учащийся» или «человек» совершается путем отбрасывания одного или нескольких содержательных признаков исходного понятия. Таким образом , увеличение объема понятия, т.е. обобщение, в то же время есть и уменьшение содержания.
Пределом обобщения выступают категории, как наиболее широкие по объему понятия.
Категории – это высший род, и с какого бы понятия мы не начали обобщение, конечным результатом его будет та или иная категория.
Например: обобщение понятия «студент», мы получим после понятия «человек» понятие «примат», «млекопитающее», «позвоночное», «животное», «живой организм», и наконец, «материя».
Дальше обобщить невозможно.
Ограничение
Ограничение – переход от понятия с большим объемом к понятию с меньшим объемом.
Ограничение совершается прибавлением к содержанию исходного понятия одного или нескольких новых признаков.
Например: Если к содержанию понятия «студент» прибавим признак , как обучение в университете, то получим понятие «студент университета», продолжая эту операцию, можно получить понятие «студент СПбГУ» и так вплоть до понятия о конкретном, отдельном студенте.
Таким образом, пределом ограничения выступает единичное понятие, ограничить которое невозможно
Определение.
Определение понятия, есть вид логической операции отношений между понятиями, раскрывающие содержание понятия, т.е. перечисление тех существенных и отличительных признаков того или иного предмета, которые отражаются мыслью о нем.
Как логическая операция , определение состоит из двух элементов: определяемого понятия(dfd) и определяющих понятий(dfn).
Формула закона выглядит так : Dfd=dfn .Это закон структуры данной операции, т.е. определение не должно заключать в себе круга т.е. определяемое понятие нельзя определять через само себя.
Например: человек есть разумное существо, потому что он мыслит.
Определение понятия подразделяется на:
1. явное определение
Явные определения, перечисляя существенные и отличительные признаки определяемого , раскрывая его сущность, подразделяются на виды: определение через род и видовое отличие(дефиниция), генетическое определение номинальное.
Дефиниция, т.е. определение через род и видовое отличие самим своим названием выделяет два этапа в своей структуре: первый- подведение определяемого понятия под ближайшее к нему родовое; второй этап – перечисление тех существенно-отличительных признаков, которые составляют специфику содержания определяемого понятия.
Например: определяемое понятие «логика» подводится под ближайшее родовое «философская наука» и далее перечисляются его отличительные, т.е. видовые признаки.
Генетическое определение указывает способ формирования, образования определяемого предмета.
Например: в геометрии: окружность определяется как замкнутая кривая на плоскости, образованная движением точки В отрезка АВ вокруг точки А.
Т.е. замкнутая кривая выступает родовым понятием по отношению к определяемому, а описание способа формирования есть не что иное, как перечисление отличительных признаков определяемого предмета.
Номинальное определение- определение направлено лишь на раскрытие смысла, назначения слова, или знака не касаясь признаков определяемого.
Например: « лавсан»- это слово, образованное сокращением названия «лаборатория высокомолекулярных соединений»
2.неявное определение
К неявным определениям относится большая группа приемов, сходных с определением: указание, описание, сравнение, характеристика, операциональное определение, контекстуальное определение.
Указание – словесное сопровождение явления, вещи на которую указывают пальцем(«остенсивное определение»).
Описание – подробная словесная характеристика предмета, который наблюдается непосредственно, или словесное художественное изображение картины для представления ее другим.
Например: описание Днепра у Гоголя
Сравнение – (различие, метафора), прием, используемый при сопоставлении двух или нескольких понятий.
Например: совесть- это внутренний суд , дети – цветы жизни.
Характеристика – подробное описание предмета с выделением отличительного, существенного признака в предмете, явления.
Операциональное определение – определение действием, экспериментом, заключающееся в выполнении правил, приемов определенной последовательности.
Например: кислота определяется, как вещество, которое окрашивает лакмусовую бумагу в красный цвет.
Контекстуальное определение – определение через текст, в котором определяемое явно не называется, а характеризуется, описывается косвенно.
Например: «близкие родственники» это «родители, дети, братья, сестры »
Правила:
1.Определение должно быть ясным, четким, свободным от двусмысленности, определение должно быть лаконичным.
2. Определение, по возможности , не должно быть отрицательным, ибо отрицание не раскрывает сущности , не перечисляет признаки предмета, отражаемого понятием: эвкалипт-дерево, которого нет Старом Петергофе.
Заключение
Таким образом, понятие и операции с ним, является одной из основных форм абстрактного мышления. Оно не только способно замещать или представлять предметы, но и позволяет анализировать их, отвлекаясь от несущественного, случайного, что дает возможность глубже проникать в действительность, отображать ее с большей полнотой.
Литература
1. Кобзарь В.И. Основы логических знаний: Учебное пособие.-СПбИВЭСЭП; О-во «Знание». 1999.172с.
2. Светлов В.А. Практическая логика. – С-Петербург: Изд-во РХГИ, 1995. -472с
www.litsoch.ru