Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

$p\cdot V_M= R\cdot T,$

где

$\,p$ — давление,
$\,V_M$ — молярный объём,
$\,R$ — универсальная газовая постоянная
$\,T$ — абсолютная температура,К

Так как $V_M=\frac{V}{\nu}$ , где $\,\nu$ — количество вещества, а $\,\nu=\frac{m}{M}$ , где $\,m$ — масса, $\,M$ — молярная масса, уравнение состояния можно записать:

$p\cdot V=\frac{m}{M}R\cdot T.$

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

$\frac{p\cdot V}{T}=\nu\cdot R,$ $\frac{p\cdot V}{T}=\mathrm{const}.$

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

$T=\mathrm{const}\Rightarrow p\cdot V=\mathrm{const}$ — закон Бойля — Мариотта. $p=\mathrm{const}\Rightarrow\frac{V}{T}=\mathrm{const}$ — Закон Гей-Люссака. $V=\mathrm{const}\Rightarrow\frac{p}{T}=\mathrm{const}$ — закон Шарля (второй закон Гей-Люссака, 1808 г.)

С точки зрения химика этот закон может звучать несколько иначе: Объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:

$\,\mathrm{H}_2+\mathrm{Cl}_2=2\mathrm{HCl}.$

1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:

$\,\mathrm{N}_2+3\mathrm{H}_2=2\mathrm{NH}_3.$ $T=\mathrm{const}\Rightarrow p\cdot V=\mathrm{const}$ — закон Бойля — Мариотта.

Закон Бойля — Мариотта назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.

В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме

$p=(\gamma-1)\rho\varepsilon,$

где $\,\gamma$ — показатель адиабаты, $\,\varepsilon$ — внутренняя энергия единицы массы вещества.

Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. И это обстоятельство может быть прояснено на основании молекулярных представлений.

С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.

С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение $\,P\cdot V$ немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведение $\,P\cdot V$ увеличивается.

Литература

Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высш. шк., 2009. — 527 с. — ISBN 978-5-06-006161-1

wreferat.baza-referat.ru

Уравнение Клапейрона — Менделеева | Бесплатные курсовые, рефераты и дипломные работы

Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р, объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде дается выражением

f (p, V, T) = 0 ,

где каждая из переменных является функцией двух других.

Французский физик и инженер Б. Клапейрон (1799—1864) вывел уравнение состояния идеального газа, объединив законы Бойля — Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V1, имеет давление p1 и находится при температуре Т1. Эта же масса газа в другом произвольном состоянии характеризуется параметрами p2, V2, Т2 (рис.63). Переход из состояния 1 в состояние 2 осуществляется в … виде двух процессов:

1) изотермического (изотерма 1 — 1/),

2) изохорного (изохора 1/ — 2).

В соответствии с законами Бойля — Мариотта (41.1) и Гей-Люссака (41.5) запишем:

(42.1)

(42.2)

Исключив из уравнений (42.1) и (42.2) , получим

Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа

. (42.3)

Выражение (42.3) является уравнением Клапейрона, в котором В — газовая постоянная, различная для разных газов.

Русский ученый Д. И. Менделеев (1834—1907) объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (42.3) к одному молю, использовав молярный объем Vm . Согласно закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем Vm, поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной. Уравнению

(42.4)

удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона — Менделеева.

Числовое значение молярной газовой постоянной определим из формулы (42.4), полагая, что моль газа находится при нормальных условиях ( = 1,013×105 Па, = 273,15 K, = 22,41×10-3 м3/моль): R = 8,31 Дж/(моль×К).

От уравнения (42.4) для моля газа можно перейти к уравнению Клапейрона — Менделеева для произвольной массы газа. Если при некоторых заданных давлении и температуре один моль газа занимает молярный объем Vm, то при тех же условиях масса m газа займет объем V = (m/M) Vm, где М — молярная масса (масса одного моля вещества). Единица молярной массы — килограмм на моль (кг/моль). Уравнение Клапейрона — Менделеева для массы m газа

(42.5)

где = m/M — количество вещества.

Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана: = 1,38×10-23 Дж/К.

Исходя из этого, уравнение состояния (42.4) запишем в виде

где — концентрация молекул (число молекул в единице объема). Таким образом, из уравнения

(42.6)

следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м3 газа при нормальных условиях, называется числом Лошмидта (И. Лошмидт (1821—1895) — австрийский химик и физик): 2,68×1025 м-3.

refac.ru

Реферат Уравнение Клапейрона

скачать

Реферат на тему:

Уравнение состояния Thermodynamics navigation image.svg

Статья является частью серии «Термодинамика». Разделы термодинамики

Уравнение состояния идеального газа

Уравнение Ван-дер-Ваальса

Уравнение Дитеричи

Уравнение состояния Редлиха — Квонга

Уравнение состояния Барнера — Адлера

Уравнение состояния Суги — Лю

Уравнение состояния Бенедикта — Вебба — Рубина

Уравнение состояния Ли — Эрбара — Эдмистера

Начала термодинамики

Уравнение состояния

Термодинамические величины

Термодинамические потенциалы

Термодинамические циклы

Фазовые переходы

править

См. также «Физический портал»

$p\cdot V_M= R\cdot T,$

где

$\,p$ — давление,
$\,V_M$ — молярный объём,
$\,R$ — универсальная газовая постоянная
$\,T$ — абсолютная температура,К

$p\cdot V=\frac{m}{M}R\cdot T.$

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

$\frac{p\cdot V}{T}=\nu\cdot R,$ $\frac{p\cdot V}{T}=\mathrm{const}.$

$\,\mathrm{H}_2+\mathrm{Cl}_2=2\mathrm{HCl}.$

1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:

$\,\mathrm{N}_2+3\mathrm{H}_2=2\mathrm{NH}_3.$ $T=\mathrm{const}\Rightarrow p\cdot V=\mathrm{const}$ — закон Бойля — Мариотта.

В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме

$p=(\gamma-1)\rho\varepsilon,$

где $\,\gamma$ — показатель адиабаты, $\,\varepsilon$ — внутренняя энергия единицы массы вещества.

Литература

Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высш. шк., 2009. — 527 с. — ISBN 978-5-06-006161-1

wreferat.baza-referat.ru

Реферат Уравнение Клапейрона Менделеева

скачать

Реферат на тему:

Уравнение состояния Thermodynamics navigation image.svg

Статья является частью серии «Термодинамика». Разделы термодинамики

Уравнение состояния идеального газа

Уравнение Ван-дер-Ваальса

Уравнение Дитеричи

Уравнение состояния Редлиха — Квонга

Уравнение состояния Барнера — Адлера

Уравнение состояния Суги — Лю

Уравнение состояния Бенедикта — Вебба — Рубина

Уравнение состояния Ли — Эрбара — Эдмистера

Начала термодинамики

Уравнение состояния

Термодинамические величины

Термодинамические потенциалы

Термодинамические циклы

Фазовые переходы

править

См. также «Физический портал»

$p\cdot V_M= R\cdot T,$

где

$\,p$ — давление,
$\,V_M$ — молярный объём,
$\,R$ — универсальная газовая постоянная
$\,T$ — абсолютная температура,К

$p\cdot V=\frac{m}{M}R\cdot T.$

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

$\frac{p\cdot V}{T}=\nu\cdot R,$ $\frac{p\cdot V}{T}=\mathrm{const}.$

$\,\mathrm{H}_2+\mathrm{Cl}_2=2\mathrm{HCl}.$

1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:

$\,\mathrm{N}_2+3\mathrm{H}_2=2\mathrm{NH}_3.$ $T=\mathrm{const}\Rightarrow p\cdot V=\mathrm{const}$ — закон Бойля — Мариотта.

В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме

$p=(\gamma-1)\rho\varepsilon,$

где $\,\gamma$ — показатель адиабаты, $\,\varepsilon$ — внутренняя энергия единицы массы вещества.

Литература

Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высш. шк., 2009. — 527 с. — ISBN 978-5-06-006161-1

www.wreferat.baza-referat.ru

Уравнение Клапейрона — Менделеева

Количество просмотров публикации Уравнение Клапейрона — Менделеева - 326

Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р, объёмом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния, ĸᴏᴛᴏᴩᴏᴇ в общем виде дается выражением

f (p, V, T) = 0 ,

где каждая из переменных является функцией двух других.

Французский физик и инженер Б. Клапейрон (1799—1864) вывел уравнение состояния идеального газа, объединив законы Бойля — Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объём V1, имеет давление p1 и находится при температуре Т1. Эта же масса газа в другом произвольном состоянии характеризуется параметрами p2, V2, Т2 (рис.63). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов:

1) изотермического (изотерма 1 — 1/),

2) изохорного (изохора 1/ — 2).

В соответствии с законами Бойля — Мариотта (41.1) и Гей-Люссака (41.5) запишем:

(42.1)

(42.2)

Исключив из уравнений (42.1) и (42.2) , получим

Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа

. (42.3)

Выражение (42.3) является уравнением Клапейрона, в котором В — газовая постоянная, различная для разных газов.

Русский ученый Д. И. Менделеев (1834—1907) объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (42.3) к одному молю, использовав молярный объём Vm . На основании закона Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объём Vm, в связи с этим постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и принято называть молярной газовой постоянной. Уравнению

(42.4)

От уравнения (42.4) для моля газа можно перейти к уравнению Клапейрона — Менделеева для произвольной массы газа. В случае если при некоторых заданных давлении и температуре один моль газа занимает молярный объём Vm, то при тех же условиях масса m газа займет объём V = (m/M) Vm, где М — молярная масса (масса одного моля вещества). Единица молярной массы — килограмм на моль (кг/моль). Уравнение Клапейрона — Менделеева для массы m газа

(42.5)

где = m/M — количество вещества.

Исходя из этого, уравнение состояния (42.4) запишем в виде

где — концентрация молекул (число молекул в единице объёма). Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, из уравнения

(42.6)

следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объёма одинаковое число молекул. Число молекул, содержащихся в 1 м3 газа при нормальных условиях, принято называть числом Лошмидта (И. Лошмидт (1821—1895) — австрийский химик и физик): 2,68×1025 м-3.

referatwork.ru

Уравнение состояния идеального газа Менделеева-Клапейрона с выводом

Уравнение состояния идеального газа показывает корреляцию его основных макропараметров, а именно: объема V, давления P, а также температуры T.

Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)

P – давление [Па]

V- объем [м3]

ν - количество вещества [моль]

R – универсальная газовая постоянная, 8,31 [Дж/(моль · К)]

T – температура [K]

Данную формулу также называют уравнением Менделеева-Клапейрона для идеального газа в честь двух ученых впервые получившего (Бенуа Клапейрон (1799 – 1864)) и применившего (Дмитрий Иванович Менделеев (1834 – 1907)) его.

Вывод уравнения Менделеева-Клапейрона

Давление идеального газа зависит от концентрации частиц и температуры тела:

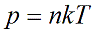
Давление идеального газа

n - концентрация частиц [м-3]

k – константа Больцмана k = 1,38 · 10-23 [Дж/К]

Т – абсолютная температура, в кельвинах [К]

Возьмем основное уравнение МКТ, выведенное через кинетическую энергию:

Основное уравнение МКТ через кинетическую энергию

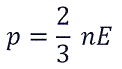
Подставим nkT вместо давления и выразим кинетическую энергию:

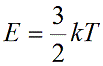
Кинетическая энергия через концентрацию частиц и температуру

Концентрация частиц газа n равна:

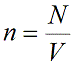
Концентрация частиц газа

N – число молекул газа в емкости объемом V [м3]. N также можно представить как произведение количества вещества ν и числа Авогадро NA:

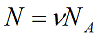
Число молекул газа

Подставим эти величины в уравнение давления идеального газа (p=nkT):

Вывод уравнения

Произведение числа Авогадро NA и константы Больцмана k дает универсальную газовую постоянную R, которая равна 8,31 [Дж/(моль · К)]. Используя это, упростим уравнение давления и получим искомое уравнение состояния идеального газа:

Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)

Учитывая, что количество вещества ν также можно определить, если известны масса вещества m и его молярная масса M:

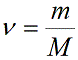
Количество вещества

можно привести уравнение к следующему виду:

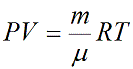
PV=m/v*RT

Частными случаями уравнения являются газовые законы, описывающие изопроцессы в идеальных газах, т.е. процессы, при которых один из макропараметров (T, P, V) в закрытой изолированной системе постоянный. Всего этих частных случаев 3.

Закон Бойля-Мариотта - изотермический процесс

Проходит при постоянной температуре: T= const.

P·V = const, то есть для конкретного вещества произведение давления на объем остается постоянным:

P1·V1 = P2·V2.

Закон Гей-Люссака - изобарный процесс

Проходит при постоянном давлении: P = const.

V/T = const, то есть для конкретного вещества отношение объема и температуры остается постоянным:

V1/T1 = V2/T2.

Закон Шарля - изобарный процесс

Проходит при постоянном объеме: V = const.

P/T = const, то есть для конкретного вещества отношение давления и температуры остается постоянным:

P1/T1 = P2/T2.

Понравилась статья, расскажите о ней друзьям:

Скорее всего, Вам будет интересно:

people-ask.ru

1.2. Уравнение Клапейрона-Менделеева

Как уже указывалось, состояние некоторой массы определяется тремя термодинамическими параметрами: давлением р , объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния.

Французский физик Б.Клапейрон вывел уравнение состояния идеального газа, объединив законы Бойля-Мариотта и Гей-Люссака.

Рис. 49

Пусть некоторая масса газа занимает объем V1, имеет давление p1 и находится при температуре T1. Эта же масса газа в другом произвольном состоянии характеризуется параметрами р2, V2, T2 (рис. 49).

Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов:

1) изотермического (изотерма 1-1),

2) изохорного (изохора 1-2).

В соответствии с законами Бойля-Мариотта (1.1) и Гей-Люссака (1.4) запишем:

(1.5)

. (1.6)

Исключив из уравнений (1.5) и (1.6) p1' , получим

Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа величина остается постоянной, т.е.

. (1.7) Выражение (1.7) является уравнением Клапейрона, в котором В - газовая постоянная, различная для разных газов.

Русский ученый Д.И.Менделеев объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (1.7) к одному молю, использовав молярный объем Vm. Согласно закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем Vm, поэтому постоянная В будет одинакова для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной. Уравнению

PVm=RT (1.8)

удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Менделеева-Клапейрона.

Числовое значение молярной газовой постоянной определим из формулы (1.8), полагая, что моль газа находится при нормальных условиях (р0=1,013105 Па, Т0=273,15 К, Vm=22,4110-3 м3 /моль): R=8,31 Дж/(моль К).

От уравнения (1.8) для моля газа можно перейти к уравнению Клапейрона-Менделеева для произвольной массы газа. Если при некотором заданном давлении и температуре один моль газа занимает объем Vm, то при тех же условиях масса m газа займет объем , где М - молярная масса (масса одного моля вещества). Единица молярной массы - килограмм на моль (кг/моль). Уравнение Клапейрона-Менделеева для массы m газа

, (1.9)

где - количество вещества.

Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана:

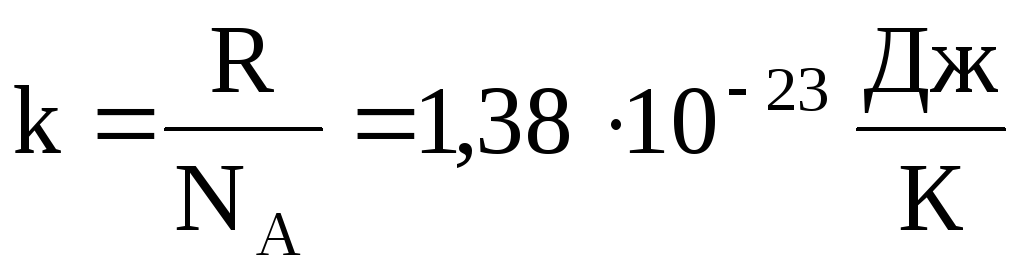Исходя из этого, уравнение состояния (1.8) запишем в виде

где - концентрация молекул (число молекул в единице объема). Таким образом, из уравнения

р=nkT (1.10) следует, что давление идеального газа при данной температуре прямо пропор-ционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м3 газа при нормальных условиях, называется числом Лошмидта:

studfiles.net

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..