Пространственной системой сходящихся сил называется система сил, линии действия которых не лежат в одной плоскости, но пересекаются в одной точке. Равнодействующая такой системы сил изображается диагональю прямоугольного параллелепипеда, построенного на этих силах как на сторонах (рис.11).
Рис.11
| |
Условие равновесия пространственной системы сходящихся сил: алгебраическая сумма проекций всех сил на три взаимно перпендикулярные оси координат должны быть равны нулю, т.е.
Для того чтобы найти момент силы 
относительно оси z, надо спроектировать силу на плоскость Н перпендикулярную оси z (рис. 12), затем найти момент проекции Fнотносительно точки О, которая является точкой пересечения плоскости Н сосью z. Момент проекции Fни будет являться моментом силы относительно оси z:
|
Рис.12
 |
Моменты сил, перпендикулярных или параллельных оси z, будут равны нулю (рис. 13).
Рис.13
Пространственной системой произвольно расположенных силназывается система сил, линии действия которых не лежат в одной плоскости и не пересекаются в одной точке. Равнодействующая такой системы сил также равна геометрической сумме этих сил, но изображается диагональю сложных объемных фигур (тетраэдр, октаэдр и т.д.).
Условие равновесия пространственной системы произвольно расположенных сил:алгебраическая сумма проекций всех сил на три взаимно перпендикулярные оси координат должна быть равна нулю и алгебраическая сумма моментов всех сил относительно тех же осей координат должна быть равна нулю, т.е.
Трение
Трениемназывается сопротивление движению тела. Сила, с которой тело сопротивляется движению, называется силой трения.
Сила трения всегда направлена в сторону, противоположную движению. Сила трения зависит от материала трущихся тел, чистоты обработки и наличия смазки и не зависит от величины трущихся поверхностей.
Трение бывает: сухое, полужидкостное, жидкостное.
Различают трение покоя, движения, скольжения и качения. Сила трения покоя больше, чем сила трения движения.
Сила трения равна произведению силы нормального давления на коэффициент трения скольжения (рис. 14):
Fтр=Rnƒ,
где Rn = mg cos a — сила нормального давления;
ƒ - коэффициент трения скольжения.
|
Рис.14
Коэффициентом трения скольженияназывается отношение силы трения к силе нормального давления:
ƒ= 
Материалы, обладающие очень малым трением, называются антифрикционными (баббит, бронза, графит).Применяются для изготовления подшипников и др.
Материалы, обладающие большим трением, называются фрикционными (специальные пластмассы с применением асбеста и меди). Применяются для накладок тормозных колодок, для накладок дисков сцепления.
При смазке поверхности скольжения тело начинает двигаться с меньшим трением.
Разложим силу тяжести G на составляющие G’и G" (рис.15)
 |
Рис.15
G' = Gcosa=Rn;
G" = Gsinα = FTp.
Коэффициент трения скольжения
Трение качениявызвано деформацией поверхности качения. Поверхность, по которой катится каток, деформируется на величину δ (рис. 16). Деформируется и само катящееся тело (например, колесо автомобиля).
|
Рис.16
Составим уравнение равновесия:
где h — расстояние от поверхности до линии действия силы;
k — коэффициент трения качения. Он равен отрезку ОС(см. рис16)
Так как
Fдв = Fтр,
то
Fтр=Rп k/h
Если h = d,
Fтр=Rп k/d
если h = г,
Fтр=Rп k/d
Frp = Rk/r =2Rk/d.
megaobuchalka.ru
Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил.
Пространственная система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке.
Теорема: пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.
Пусть дана пространственная система n сходящихся сил (F1, F2, F3,....Fn). На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основании аксиомы параллелограмма последовательно сложим все силы и получим их равнодействующую:
FΣ = F1 + F2 + F3 + ....+ Fn, или FΣ = ΣFi.
Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей пространственной системы сходящихся сил неприемлемы, а применяется только аналитический способ (метод проекций).
Проекция силы на ось в пространстве находится по проецирующим перпендикулярам, и может быть определена при помощи тригонометрических функций. При определении проекций сил пространственной системы потребуется система координат с осями X, Y, Z, поскольку силы системы не располагаются в одной плоскости.
Правило знаков для проекций будет таким же, как и для плоской системы сил – совпадающие по направлению с координатной осью силы считаются положительными, в противном случае – отрицательными. Если вектор силы параллелен какой-либо оси координат, то он проецируется на эту ось в натуральную величину, если же вектор перпендикулярен оси, его проекция на эту ось будет равна нулю.
***
Пусть дана сила F (см. рисунок 1). 
Возьмем систему координат так, чтобы начало координат совпадало с началом вектора силы F (т. е. с точкой приложения силы). Из конца этого вектора опустим перпендикуляр на плоскость xy и разложим силу F на составляющие Fxy и Fz, а составляющую Fxy – на составляющие Fx и Fy. Тогда:
F = Fx + Fy + Fz.
Достроим полученное изображение до параллелепипеда, у которого составляющие Fx, Fy и Fz являются ребрами, а сила F – диагональю.
Из изложенного можно сделать вывод: равнодействующая трех взаимно-перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах.
Из рисунка видно, что в случаях разложения силы F по трем взаимно-перпендикулярным направлениям x, y, z составляющие Fx, Fy и Fz равны по модулю проекциям силы F на эти оси.
Зная проекции силы на три взаимно-перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:
модуль силы: F = √(Fx2 + Fy2 + Fz2) (здесь и далее √ - знак корня);
направляющие косинусы: cos(F,x) = Fx/F; cos(F,y) = Fy/F; cos(F,z) = Fz/F.
***
Рассмотренный выше способ разложения силы F на три составляющие по направлению координатных осей x, y, z можно применить для каждой из сходящихся сил пространственной системы. Тогда вместо данной системы n сходящихся сил мы получим эквивалентную ей систему 3n сил, из которых n сил действуют по оси x, n сил – по оси y, и n сил – по оси z. Равнодействующая проекций сил системы на ось x равна их геометрической сумме, то же самое можно сказать и о равнодействующих проекций сил на оси y и z. Таким образом, систему 3n сил можно заменить эквивалентной ей системой трех сил, каждая из которых представляет собой равнодействующую проекций сил данной системы на ту или иную ось координат.
Проекции силы на три взаимно-перпендикулярные оси и составляющие силы, направленные по этим осям, равны по модулю, следовательно, проекции равнодействующей равны:
FΣx = ΣX; FΣy = ΣY; FΣz = ΣZ.
Очевидно, что равнодействующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах, и по известным проекциям равнодействующей можно определить модуль и направление самой равнодействующей.
***
Известно, что пространственная система сходящихся сил эквивалентна равнодействующей. Если такая система сил находится в равновесии, т. е. эквивалентна нулю, то можно сделать вывод, что равнодействующая этой системы равна нулю, а следовательно, и проекции равнодействующей тоже равны нулю, причем эти проекции равны сумме проекций составляющих. Отсюда вытекают условия равновесия пространственной системы сходящихся сил:
ΣX = 0; ΣY = 0; ΣZ = 0.
Эти условия формируются следующим образом: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую их трех координатных осей равнялась нулю.
***
Рассмотрим колесо червячной передачи, укрепленное на валу, вращающемся в подшипниках (см. рисунок 2). Червяк передает червячному колесу силу F, не лежащую в плоскости, перпендикулярной оси.
Разложим силу F на три взаимно-перпендикулярные составляющие F1, F2 и F3. Составляющую F1 назовем окружной силой, составляющую F2 – осевой силой, а составляющую F3 – радиальной силой. Из рисунка видно, что составляющая F1 вызывает вращательное действие, которое измеряется произведением силы F1 на радиус колеса r; составляющая F2 стремится сдвинуть червячное колесо вдоль оси, а составляющая F3 стремится изогнуть ось колеса. Очевидно, что вращающее действие сил F2 и F3 относительно оси колеса равно нулю. Таким образом, если нужно найти момент силы относительно оси, то следует принимать в расчет только составляющую F1, лежащую в плоскости, перпендикулярной оси, и не пересекающую ось (иначе ее момент будет равен нулю).
Ранее было отмечено, что проекция вектора силы на ось есть скалярная алгебраическая величина. В отличие от проекции на ось проекция силы на плоскость есть величина векторная, так как эта проекция характеризуется не только числовым значением, но и положением на плоскости, т. е. направлением. Поэтому моменту силы относительно оси можно дать такое определение: моментом силы относительно оси называется величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
Это определение поясняет рисунок 3. Момент силы относительно оси условимся записывать следующим образом:
Mz(F) = Fна.
Условимся считать момент силы положительным, если смотреть с положительного конца оси и сила стремится вызвать вращение против часовой стрелки, если же сила стремится вызвать вращение по часовой стрелке, ее момент считаем отрицательным.
Момент силы относительно оси не меняется при перемещении силы вдоль оси ее действия.
Момент силы будет равен нулю в двух случаях (не считая случаев, когда сила равна нулю или направлена вдоль оси):***
Пространственная система сил, в которой линии действия составляющих сил расположены произвольно, т. е. линии их действия могут не пересекаться и находиться в разных плоскостях, называется произвольно расположенной системой сил.
Для равновесия пространственной системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трех осей координат была равна нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из этих осей была равна нулю.
Строгое обоснование приведенного выше условия равновесия пространственной системы произвольно расположенных сил требует знания некоторых вопросов, не предусмотренных программами учреждений среднего профессионального образования, поэтому условие равновесия такой системы здесь приводится без доказательства.
Математически условие равновесия пространственной системы произвольно расположенных сил можно записать в виде уравнений:
Свободное тело в пространстве имеет шесть степеней свободы, а именно: возможность перемещаться в направлениях трех взаимно-перпендикулярных осей координат и возможность вращаться вокруг этих осей. Таким образом, шести степеням свободы тела в пространстве соответствуют шесть условий равновесия. Если система сил, приложенных к свободному телу, удовлетворяет всем шести условиям равновесия, то возможность трех перемещений и трех вращений тела под действием сил системы исключена, поэтому тело будет находится в равновесии.
Очевидно, что все выведенные ранее условия равновесия для различных систем сил являются частными случаями условия равновесия пространственной системы произвольно расположенных сил.
Так как условия равновесия пространственной системы сил справедливы для любых прямоугольных осей координат, то при решении данной задачи систему координат можно изменять, т. е. часть уравнений равновесия составить для одних осей координат, а часть – для измененных. В некоторых случаях этот прием упрощает решение задач.
***
Теорема: момент равнодействующей относительно оси равен алгебраической сумме моментов, составляющих сил относительно этой же оси.
Пусть даны пространственная система n произвольно расположенных сил, приложенных к телу, и равнодействующая этой системы сил FΣ (см. рисунок 4):
(F1, F2, F3,....Fn) ≡ FΣ.
Приложим к телу другую систему сил, равнодействующая которой F’Σ по модулю равна FΣ и направлена по той же линии действия, но в противоположную сторону, т. е. является уравновешивающей данной системы сил. Тогда можно записать:
(F1, F2, F3,....Fn, F’Σ) ≡ 0 , или (FΣ, F’Σ) ≡ 0.
Так как обе записанные выше системы сил эквивалентны нулю, т. е. уравновешены, то к ним можно применить любое условие равновесия, например
ΣMx(Fi) = 0.
Запишем это условие для обеих систем:
Mx(F1) = Mx(F2) + Mx(F2) + .... + Mx(Fn) + Mx(F’Σ) = 0; MΣ(FΣ) + Mx(F’Σ) = 0.
Так как правые части этих равенств равны, то будут равны и левые :
Mx(F1) = Mx(F2) + Mx(F3) + .... +Mx(Fn) + Mx(F’Σ) = Mx(FΣ) + Mx(F’Σ).
Сократив общее слагаемое Mx(F’Σ), получим:
Mx(F1) = Mx(F2) + Mx(F3) + .... +Mx(Fn) = Mx(FΣ) или ΣMx(Fi) + Mx(FΣ).
Теорема доказана.
***
Трение - сущность явления, законы и зависимости
k-a-t.ru
Произвольная пространственная система сил. - раздел Механика, Раздел Теоретическая механика
3.2.1. Момент силы относительно точки. Момент силы относительно оси. Теория пар в пространстве.
В случае плоской системы сил момент силы относительно точки определён как алгебраическая величина: 
. При пространственном расположении сил этого определения не достаточно, так как плоскости, проходящие через линии действия сил и точку, относительно которой определяется момент, различны. Поэтому момент 
силы P относительно точки О в пространстве определяют как векторное произведение 
, где 
- вектор радиус проведенный из точки О в точку приложения силы.
Таким образом вектор 
направлен перпендикулярно плоскости, содержащий линию действия силы и точку О, так что сила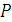 
с конца его вектора видно направление против часовой стрелки.
Рис. 1.40
Модуль вектора 
равен:
Моментом силы относительно оси называется скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.
Рис. 1.41
Если сила 
с конца оси z видно направление вокруг точки О против часовой стрелки то момент положительный.
Итак, момент силы относительно точки – вектор, а момент силы относительно оси – скалярная величина.
При вычислении моментов относительно оси надо иметь следующие частные случаи:
1. Если сила параллельна оси, то её момент относительно оси равен нулю 
.
2. Если линия действия силы пересекает ось, то её момент относительно оси равен нулю 
.
3. Если сила перпендикулярна оси, то её момент относительно оси равен произведению модуля силы на расстояние между силой и осью.
Получим аналитическое выражение для моментов силы относительно осей координат.
Рис. 1.42
Спроецируем силу 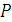на плоскость 
и разложим полученную проекцию на составляющие 
и 
; численно эти составляющие будут, очевидно, равны проекциям силы 
на оси 
. Тогда
Последнее равенство вытекает из теоремы Вариньона. Но как видно из чертежа, 
следовательно 
. Аналогично вычисляются моменты относительно других осей.
В результате получим:
3.2.2. Зависимость между моментом силы относительно центра и относительно оси.
Рис. 1.43
Пусть на тело действует приложенная в точке 
сила . Проведём ось 
и возьмем на ней произвольную точку 
. момент силы относительно центра будет изображаться вектором 
, перпендикулярным плоскости 
, причём по модулю
.
Проведём теперь через любую точку 
плоскость , перпендикулярную оси ; проецируя силу на эту плоскость, найдём:
Но треугольник 
представляет собой проекцию треугольника на плоскость . Угол между плоскостями треугольников равен 
.
Тогда 
.
Умножим обе части уравнения на 2, находим
Так как произведение 
даёт проекцию 
или 
.
Момент силы относительно оси равен проекции на эту ось вектора, изображающего момент данной силы относительно центра, лежащего на этой оси. Или проекция вектора момента силы относительно центра на ось, проходящую через центр, равен моменту силы относительно этой оси.
3.3.3. Главные векторы сил и моментов.
Главным вектором системы сил называется геометрическая сумма сил системы.
Рассмотрим систему сил, как угодно ориентированных в пространстве. Вычислим моменты этих сил относительно точки 
.
Векторы 
все приложены в точке. Построим многоугольник векторов моментов. Замыкающая сторона этого многоугольника – главный момент относительно неподвижного центра
Рис. 1.44 
Таким образом, главным моментом пространственной системы сил относительно центра называется геометрическая сумма моментов сил системы относительно того же центра.
Главным моментом пространственной системы сил относительно неподвижной оси называется алгебраическая сумма моментов сил системы той же оси.
3.2.4. Приведение пространственной системы сил к заданному центру.
Приведение силы к заданному центру (метод Пуансо).
Рис. 1.45
Приведём силу к центру . В точке приложим систему сил 
, причём
Силы 
образуют пару, момент которой 
.
При приведении сил к заданному центру получаем в этом центре силу, геометрически равную заданной, и пару, момент которой равен моменту силы относительно центра приведения.
Теорема
При приведении пространственной системы сил к центру всегда получим силу, называемую главным вектором сил, приложенную в центре приведения и пару сил, момент которой равен главному моменту системы сил относительно центра приведения.
Доказательство:
Пусть имеем систему сил, как угодно ориентированных в пространстве (ограничимся тремя силами). Каждую силу приводим к центру на основании метода Пуансо. В точке получим систему сходящихся сил 
. Геометрическая сумма этих сил – есть главный вектор: 
.
Векторы моментов
Рис. 1.46 так же образуют систему, сходящихся
векторов. Их геометрическая сумма – есть
главный момент системы сил
относительно центра 
.
3.2.5. Вычисление главного вектора и главного момента пространственной системы сил.
Главный вектор:
.
Спроектируем обе части этого векторного соотношения на оси 
.
Тогда модуль 
равен:
Направление определяется направлением косинусов:
Рис. 1.47 
Главный момент
Спроектируем данное векторное соотношение на оси 
:
Модуль главного момента равен
Направление определяем направлением косинусов:
3.2.6. Условия и уравнения равновесия пространственной системы сил.
Теорема
Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент равнялись нулю.
Доказательство:
Достаточность.
При 
, система сходящихся сил, приложенных в центре приведения эквивалентна нулю, а при 
- система пар сил эквивалентна нулю. Следовательно, исходная система сил эквивалентна нулю.
Необходимость. Пусть данная система сил эквивалентна нулю. Тогда необходимо, чтобы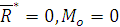 
.
Если какое-либо из этих условий не выполняется, то система сил приводится либо , либо к паре, момент которой 
и следовательно, не является уравновешенной, что противоречит исходной предпосылке.
Уравнения равновесия:
В случае произвольной пространственной системы сил задача является статически определенной, если число алгебраических неизвестных не более шести.
Аксиомы статики. Данные аксиомы сформулированы на основе наблюдения и изучения окружающих нас явлений реального м
Система сходящихся сил 2.1.1 Равновесие твёрдого тела, к которому приложена система сходящихся сил. Сходящимися называются сил
Произвольная плоская система сил 2.2.1 Равновесие твёрдого тела при наличии плоской системы сил. Случай параллельных сил. Равнодейст
Системы сходящихся сил. Равнодействующую пространственной системы сил можн
ЦЕНТР ТЯЖЕСТИ. Сила тяжести – равнодействующая сил притяжения к Земле, она распределена по всему объёму тела. Сил
КИНЕМАТИКА. 1. ВВЕДЕНИЕ Кинематикой называется раздел механики, в котором изучается движ
Поступательное движение тела. Поступательным движением твердого тела называется
Вращательное движение твердого тела. Вращательным называется такое движение твердого тела, при котором точки тела движутся в плоскостях, перпен
Уравнения равномерного вращения тела Вращение тела с постоянной угловой скоростью называется равномерным
Уравнения равнопеременного вращения тела Вращение тела, при котором угловое ускорение постоянно, называется равнопеременным вращением. Если ве
Сложение скоростей. Рассмотрим точку М, совершающую сложное движение. Пусть эта точка, двигаясь вдоль своей относительной трае
Сложение ускорений. Теорема Кориолиса. Найдем зависимость между абсолютным , относительным
Мгновенный центр скоростей (МЦС) МЦС называется точка плоской фигуры, скорость которой в данный момент времени равна нулю. Теорема.
Определение скорости точки плоской фигуры с помощью МЦС Выберем за полюс точку Р. Тогда скорость произвольной точки А
Ускорения точек при плоском движении. Покажем, что ускорение любой точки М тела при плоском или параллельном движении (так же как и скорость) с
Мгновенный центр ускорений (МЦУ) МЦУ называется точка плоской фигуры, ускорение которой равно нулю. Если в данный момент времени за
Частные случаи определения МЦУ. 1. Известна точка, ускорение которой равно нулю. Эта
Основные способы вычисления углового ускорения при плоском движении. 1. Если известен закон изменения угла поворота или угловой скорости от времени, то углово
Сложение поступательных движений. Пусть твердое тело движется поступательно со
Сложение вращений вокруг двух параллельных осей. Рассмотрим случай, когда относи
Пара вращений. Рассмотрим частный случай, когда вращения вокруг параллельных осей направлены в разные стороны, но по моду
Сложение вращений вокруг пересекающихся осей. Рассмотрим случай сложения вращения вокр
Сложение поступательного и вращательного движений. 6.5.1. Скорость поступательного движения перпендикулярно к оси вращения (
Законы динамики. В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений.
Задачи динамики для свободной и несвободной материальной точки. Для свободной материальной точки задачами динамики являются: 1. Зная закон движения, определить действ
Прямолинейное движение точки. Из кинематики известно, что при прямолинейном движении скорость и ускорение точки все время направлены вдо
Криволинейное движение точки. Рассмотрим свободную материальную точку,
Количество движения и кинетическая энергия точки. Это основные динамические характеристики движения. Количеством движения точки называется векторная велич
Импульс силы. Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени, вводим понятия об
Теорема об изменении количества движения точки. Так как масса точки постоянна, а ее ускорение , то ур
Работа силы. Мощность. Для характеристики действия, оказываемое силой на
Теорема об изменении кинетической энергии точки. Рассмотрим точку массой m, перемещающуюся под действием приложенных к ней сил из положения М0,
Теорема об изменении момента количества движения (теорема моментов). Иногда при изучении движения точки вместо изменения самого вектора (m
Прямолинейные колебания точки 4.1. Свободные колебания без учёта сил сопротивления. Рассмотрим точку М, движущуюся под де
Свободные колебания при сопротивлении, пропорциональном скорости (затухающие колебания) Рассмотрим, как влияет на свободные колебания сопротивления среды, считая, что сила сопротивления пропорци
Вынужденные колебания. Резонанс. Рассмотрим случай колебаний, когда на точку, кроме восстанавливающей силы F, действует ещё периодически
Механическая система. Механической системой материальных точек или тел называется такая их совокупность, в которой поло
Масса системы. Центр масс. Движение системы, кроме действующих сил, зависит от ее суммарной массы и распределения м
Дифференциальные уравнения движения системы. Рассмотрим систему, состоящую из «n» материальных точек. Выделим какую-нибудь точку системы с м
Теорема о движении центра масс. Сложим почленно левые и правые части уравнения (3).
Закон сохранения движения центра масс. Из теоремы о движении центра масс можно получить важные следствия. 1). Пусть сумма внешних сил, действую
Количество движения системы. Количеством движения системы будем называть векторную величину
Теорема об изменении количества движения. Рассмотрим систему, состоящую из «n» материальных точек, составим для этой системы дифференциальные уравне
Закон сохранения количества движения. Из теоремы об изменении количества движения системы можно получить важные следствия. 1). Пусть сумма вс
Момент инерции тела относительно оси. Положение центра масс характеризует распределение масс системы не полностью.
Главный момент количества движения системы. Главным моментом количества движения (или кинематическим моментом) системы относительно данного центра
Теорема об изменении главного момента количества движения системы (теорема моментов). Теорема моментов, доказанная для одной материальной точки, будет справедлива для каждой из точек системы. С
Закон сохранения главного момента количества движения. Из теоремы моментов можно получить следующие важные следствия. 1). Пусть сумма моментов относительно ц
Кинетическая энергия системы. Кинетической энергией системы называется скалярная величина Т, равная арифметической сумме кинетических
Некоторые случаи вычисления работы. Рассмотрим следующие случаи. 1). Работа сил тяжести, действующих на систему. Работа силы тяжести, д
Теорема об изменении кинетической энергии системы. Показанная в п. 3.5. теорема справедлива для любой точки системы. Следовательно, если рассмотреть какую-нибуд
Потенциальное силовое поле и силовая функция. Работа на перемещениесилы F приложенной в точке
Потенциальная энергия Для потенциальных сил можно вывести понятие о потенциальной энергии, как о величине, «характеризу
Закон сохранения механической энергии Допустим, что все действующие на систему внешние и внутренние силы потенциальны. Тогда для каждой из т
allrefers.ru
Пространственная система сил - раздел Образование, Аксиомы статики
Если система сил находится в равновесии, то в равновесии находится и эквивалентная ей система, состоящая из главного вектора и главного момента пары. Чтобы такая система сил была эквивалентна нулю, необходимо и достаточно, чтобы выполнялось условие:
( где О – произвольная точка)
Эти условия являются векторными условиями равновесия для любой системы сил. В аналитической форме это эквивалентно условиям: Rx=Ry=Rz=0; Mx=My=Mz=0,
то есть в самом общем случае имеем шесть скалярных уравнений равновесия (уравнений статики).
Система параллельных сил (рис. 15)
Пусть Fi параллельно оси Oz, тогда
Mz тождественно равно нулю и
.
Таким образом, имеем три уравнения равновесия
Рис.15
Плоская система сил(рис. 16)
После отбрасывания тождеств:
,
имеем три уравнения равновесия:
Рис.16
Для плоской системы параллельных сил (Рис. 17) имеем лишь два уравнения равновесия:
Рис.17
Различные формы условий равновесия плоской системы сил:
1. Ранее приведенная система
2. Эквивалентная ей система уравнений равновесия для любых трех точек, не лежащих на одной прямой.
3. Также эквивалентная первой система
для любых точек А и В, если ось X не перпендикулярна отрезку АВ.
Для плоской системы параллельных сил имеем аналогичную систему уравнений равновесия 
для любых точек А и В.
Аксиомы статики 1. Аксиома о равновесии системы двух сил. Для равновесия системы двух сил, приложенных
Аксиома связей. Абсолютно твёрдое тело имеет в трёхмерном пространстве шесть степеней свободы, в двумерном – три степени с
Теоремы статики 1.Теорема о переносе силы вдоль линии действия. Действие силы на твердое тело не измен
Система сходящихся сил Системой сходящихся сил (или пучком сил) называют такую
Условия равновесия системы сходящихся сил Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы силовой
Алгебраический момент силы относительно точки. Используется при рассмотрении плоской системы сил. Алгебраическим моментом силы относительно точки назыв
Момент силы относительно оси. Моментом силы относительно оси называют алгебраический момент
В декартовых координатах Положение точки М0 определяем радиус-вектором
В естественной системе координат Определим орт , он направлен по касательной к траектори
Скорость и ускорение точки в полярных координатах Положение точки на плоскости известно, если заданы радиус-вектор
Координатах Положение точки М в пространстве определяют заданием трех ее цилиндрических координ
Сложное движение точки Рассмотрим движение точки М по траектории в пространстве (рис. 21). Будем рассматривать параметры ее движ
Поступательное движение твердого тела Поступательным движением твердого тела называется такое его движение, при котором л
Вращение твердого тела вокруг неподвижной оси Вращательным движением твердого тела вокруг непод
Плоское движение твердого тела Плоским движением твердого тела называюттакое его движение, при котором каждая его
Мгновенный центр скоростей Выбираем точку А за полюс – начало отсчета подвижной системы координат, движущейся только поступательно, о
Способы нахождения мгновенного центра скоростей. Мгновенный центр скоростей можно найти либо из механических усло
Мгновенный центр ускорений За переносное движение тела примем поступательное движе
Законы динамики. (Законы Ньютона) 1. Каждое тело пребывает в состоянии покоя или равномерного прямолинейного движения до тех пор, по
Аксиома о суперпозиции сил При одновременном действии на материальную точку нескольких сил ускорение точки относительно ИСО от дейст
Дифференциальные уравнения движения материальной точки. Две основные задачи динамики точки − равнодейству
Криволинейное движение Дифференциальное уравнение прямолинейного движения точки вдоль
Простейшие свойства внутренних сил системы Механической системой называется любая совокупность материальных точек. Внеш
Дифференциальные уравнения движения системы Если к каждой точке системы приложить равнодействующую силу внеш
Количество движения точки и системы Количеством движения материальной точки
Теорема об изменении количества движения системы Для каждой точки системы, находящейся под действием внеш
Законы сохранения количества движения Эти законы представляют собой частные случаи теоремы об изменении количества движения системы.
Работа силы. Элементарная работа силы равна скалярному произведению сил
Работа силы тяжести В принятой системе координат (рис. 41 ): Px=0, Py=
Вычисление кинетической энергии системы Разложим движение механической системы на переносное поступательное вместе с центром масс и относительн
Теорема об изменении кинетической энергии точки Умножим скалярно обе части второго закона Ньютона на dr
Теорема об изменении кинетической энергии системы точек Для каждой точки системы имеем: Здесь
Потенциальное силовое поле и потенциальная энергия Силовым полем называют часть пространства, в каждой точке которого на мате
Закон сохранения механической энергии Для материальной точки ранее имели: Если материальная точка
Структура механизмов Существуют общие закономерности в структуре (строении) самых различных механизмов, связывающие чи
Принцип образования механизмов. Группа Ассура Простую и вместе с тем рациональную классификацию механизмов, тесно связанную с их образованием, с
Структурный анализ плоских рычажных механизмов Под структурным анализом понимают определение количества звеньев и кинематических пар, классифик
Задачи и методы Рычажные механизмы используются в качестве передаточных механизмов, воспроизводящих заданную функциона
Графоаналитический метод На практике широко применяют метод планов скоростей и ускорений. Метод основан на графическом реш
Силы, действующие в машинах Развитое машинное устройство, состоящее из двигателя, передаточных механизмов и рабочей машины и,
Силовой расчет Силовой расчет начинается с последней, т.е. наиболее удаленной от ведущего звена группы Ассура, и кончается
Вопросы для самопроверки. 1. Назовите виды трения. Их принципиальные отличия. 2. Напишите формулу Амонтона – Кулона для опре
Задачи и методы сопротивления материалов В процессе эксплуатации машин и механизмов всякий элемент конструкции в результате действия на не
И свойств материалов Для оценки прочности реальной конструкции следует правильно подобрать адекватную ей модель, и
Виды деформаций Проведение расчётов на прочность в сопротивлении материалов связано с необходимостью установления зависи
Понятие о деформациях В сопротивлении материалов, в отличие от теоретической механик
Понятие о напряжениях Для оценки уровня внутренних сил в какой-либо точке D
О физической взаимосвязи напряжений и деформаций Связь между перемещениями и деформациями впервые была сформулирована Робертом Гуком в конце XV
Вопросы для самопроверки 1. В чём отличие реального объекта от расчётной схемы? 2. Назовите основные формы моделей физичес
Определение продольной силы Растяжением (сжатием) называется такой вид деформации стержня, при котором в поперечных сече
Определение напряжения Если на поверхности призматического стержня нанести сетку линий, параллельных и перпендикулярных оси стер
Определение деформаций. Закон Гука Анализ деформации стержня при растяжении (рис. 7) показывает, что весь стержень удлинится на ∆
Испытание материалов на растяжение и сжатие Основные механические характеристики материалов получают в результате специальных лабораторных
Коэффициент запаса, допускаемое напряжение Расчёт на прочность и жёсткость осуществляется двумя методами: методом допускаемых напряжений,
Вопросы для самоконтроля 1. Как вычисляются значения продольной силы в поперечных сечениях стержня? 2. Что предста
Статические моменты площади
Моменты инерции сечения Осевыми моментами инерции сечения (рис. 3.1) относительно осей x, y называются интегралы вида:
Моменты сопротивления сечений При прочностном расчёте балок используются и такие характеристики сечения, как моменты сопр
Геометрические характеристики некоторых сечений Рассмотрим геометрические характеристики наиболее часто встречающихся форм сечений элементов ко
Вопросы для самопроверки 1. Что называется статическим моментом сечения относительно оси? Единица измерения. 2. Чему равен
Внутренние силовые факторы при изгибе На первом этапе анализа основная цель заключается в определении и построении эпюр (графиков) в
Теорема Д. И. Журавского Правильность построения эпюр поперечной силы и изгибающего момента можно проверить при помощи д
Нормальные напряжения при изгибе Для вывода основных расчётных формул рассмотрим частный случай плоского изгиба балки – состояние
Уравнение упругой линии балки Изогнутая ось, представляющая собой геометрическое мес
Вопросы для самопроверки 1.В чём отличие между изгибом прямым и косым, чистым и поперечным? 2. Какие внутренние силы возни
Кручение Кручением называется такой вид деформации стержня (вала), при котором в поперечных сечениях во
Вопросы для самопроверки 1. Что называется сдвигом? 2. Что называется абсолютным и относительным сдвигом? 3. Как фо
В двух направлениях Рассмотрим общий случай плоского (двухосного) напряжённого сос
Положения Пусть у некоторой выбранной точки D тела наблюдается плоское напряжённое состояние (рис. 33а,б
Теории прочности При центральном растяжении (сжатии) в нормальных сечениях стержня возникают одни нормальные напряжения
Вопросы для самопроверки 1. Что называют напряжённым состоянием в точке? 2. Какие виды напряжённого состояния могу
Работоспособности Машины, механизмы, приборы, аппараты и т. д. изготовляют из деталей. Деталью называют элемент ко
Проектирование Проектирование предшествует конструированию и представляет собой поиск научно обоснованных, техничес
Разработки конструкторской документации Конструированием создаётся конкретная однозначная конструкция изделия. Конструирование опирается н
Система автоматизированного производства Усложнение конструкций изделий с целью повышения механизации и автоматизации, выполняемых ими работ, увел
Взаимозаменяемость и стандартизация Взаимозаменяемостью называется такой принцип конструирования и производства деталей, который обеспеч
Изготовления деталей Размеры детали определяются расчётом на прочность, жёсткость или устанавливаются конструктивно, исходя из
Вопросы для самопроверки 1. Опишите типичный цикл жизни нового изделия. 2. Назовите основные элементы конструкций.
СОЕДИНЕНИЯ ДЕТАЛЕЙ МАШИН Под соединением понимают жёсткое скрепление отдельных деталей механизма или машины. Оно осуще
Сварные соединения Соединение частей в одно целое при сварке получается за счёт местного нагрева соединяемых частей
Резьбовые соединения Резьбовыми называются соединения, осуществляемые с помощью деталей, снабжённых резьбой: вин
Вопросы для самопроверки 1. Назовите виды соединения деталей. 2. С какой целью применяют различные соединения, и ка
Применяемые материалы. Валы и оси вращаются в опорах, в качестве которых служат подшипники качения и скольжения. Опорные части вал
Подбор подшипников качения Основным видом повреждения считают выкрашивание дорожек качения и тел качения подшипников под де
Определение коэффициентов X и Y Если приложить к подшипнику, имеющему нулевой радиальный зазор, радиальную силу Fr, то под
Вопросы для самоконтроля 1. Валы и оси. Назначение и классификация. 2. Конструктивные элементы валов и осей, применяемые ма
Подбор муфт Муфты выбирают в зависимости от диаметров соединяемых валов и передаваемого крутящего момента МК
Муфты постоянного сцепления Муфты постоянного сцепления служат для постоянного соединения в
Муфты сцепные управляемые Управляемые муфты делятся на муфты синхронные и фрикционны
Муфты сцепные самоуправляющиеся Самоуправляющиеся муфты служат для соединения или разъединения ведомого вала с ведущим при оп
Вопросы для самопроверки 1. Муфты, их назначение и классификация. 2. По каким параметрам подбирают муфты? 3. Какие м
Основные параметры витых пружин.
Определение диаметра проволоки пружины При работе цилиндрической винтовой пружины в осевых сечениях витков возникают напряжения кручени
Требования, предъявляемые к зубчатым зацеплениям Зацепление, применяющееся в зубчатых передачах, должно обеспечить: 1. Постоянство передаточно
Основной закон зацепления Как было сказано, важнейшим требованием, предъявляемым к передачам, является постоянство передаточного от
Уравнения эвольвенты Эвольвентой (от лат. evolvens (evolventis) – разворачивающий) или развёрткой окружности назы
Эвольвентное зацепление Пусть вращательное движения передаётся при помощи двух звеньев, профили которых выполнены по кривым Э1
Прямозубых передач За базу для определения элементов и размеров зубьев колёс принимаетс
Коэффициент торцового перекрытия Коэффициент торцового перекрытия учитывает непрерывно
Вопросы для самопроверки 1. Для чего применяют передаточные механизмы? Виды передаточных механизмов, их основные внешние характери
Библиографический список 1. Тарг, С.М. Краткий курс теоретической механики; М.: Высшая школа, 1995, − 416 с. 2. Теория меха
allrefers.ru
Пространственная сходящаяся система сил - Лекция, раздел Механика, Теоретическая механика
Пространственная сходящаяся система сил — система сил, не лежащих в одной плоскости, линии действия которых пересекаются в одной точке.
Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольник (рис. 7.3),
FΣ = F1+ F2 + F3 +……+ Fn
Доказано, что равнодействующая системы сходящихся сил приложена в точке пересечения линий действия сил системы.
Модуль равнодействующей пространственной системы сходящихся сил можно определить аналитически, использовав метод проекций.
Совмещаем начало координат с точкой пересечения линий действия сил системы. Проецируем все силы на оси координат и суммируем соответствующие проекции
(рис. 7.4). Получим проекции равнодействующей на оси координат:
FΣx = Σ Fkx ; FΣy = Σ Fky ; FΣz = Σ Fkz
Модуль равнодействующей системы сходящихся сил определим по формул
Задачи теоретической механики Теоретическая механика — наука о механическом движении материальных твердых тел и их взаимодействии.
Третья аксиома Не нарушая механического состояния тела, можно добавить или убрать уравновешенную систему сил (принцип отб
Следствие из второй и третьей аксиом Силу, действующую на твердое тело, можно перемещать вдоль линии ее действия (рис. 1.6).
Связи и реакции связей Все законы и теоремы статики справедливы для свободного твердого тела. Все тела делятся на свободные и
Жесткий стержень На схемах стержни изображают толсто сплошной линией (рис. 1.9).
Неподвижный шарнир Точка крепления перемещаться не может. Стержень может свободно поворачиваться вокруг оси шарнира. Реа
Плоская система сходящихся сил Система сил, линии действия которых пересекаются в одной точке, называется сходящейся (рис. 2.1).
Равнодействующая сходящихся сил Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника си
Условие равновесия плоской системы сходящихся сил При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом пос
Решение задач на равновесие геометрическим способом Геометрическим способом удобно пользоваться, если в системе три силы. При решении задач на равновесие тело
Решение 1. Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-
Проекция силы на ось Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на о
Сил аналитическим способом Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равноде
Сходящихся сил в аналитической форме Исходя из того, что равнодействующая равна нулю, получим:
Пара сил, момент пары сил Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны.
Момент силы относительно точки. Сила, не проходящая через точку крепления тела, вызывает вращение тела относительно точки, поэтом
Теорема Пуансо о параллельном переносе сил Силу можно перенести параллельно линии ее действия, при этом нужно добавить пару сил с моментом, рав
Расположенных сил Линии действия произвольной системы сил не пересекаются в одной точке, поэтому для оценки состояния тела т
Влияние точки приведения Точка приведения выбрана произвольно. При изменении положения точки приведения величина главного вектор
Плоской системы сил 1. При равновесии главный вектор системы равен нулю . Аналитическое определение главного вектора приво
Виды нагрузок По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузк
Момент силы относительно оси Момент силы относительно оси равен моменту проекции силы на плоскость, перпендикулярную оси, относительно
Вектор в пространстве В пространстве вектор силы проецируется на три взаимно перпендикулярные оси координат. Проекции вектора
Приведение произвольной пространственной системы сил к центру О Дана пространственная система сил (рис. 7.5а). Приведем ее к центру О. Силы необходимо параллельно пе
Центр тяжести однородных плоских тел (плоских фигур) Очень часто приходится определять центр тяжести различных плоских тел и геом
Определение координат центра тяжести плоских фигур Примечание. Центр тяжести симметричной фигуры находится на оси симметрии. Центр тяжести стержня наход
Кинематика точки Иметь представление о пространстве, времени, траектории, пути, скорости и ускорении .Знать способы задани
Пройденный путь Путь измеряется вдоль траектории в направлении движения. Обозначение — S, единицы измерения — метры.
Скорость движения Векторная величина, характеризующая в данный момент быстроту и направление движения по траектории, назыв
Ускорение точки Векторная величина, характеризующая быстроту изменения скорости по величине и направлению, называется у
Равномерное движение Равномерное движение — это движение с постоянной скоростью: v = const. Для прямолинейного ра
Равнопеременное движение Равнопеременное движение — это движение с постоянным касательным ускорением: at =
Поступательное движение Поступательным называют такое движение твердого тела, при котором всякая прямая линия на теле при движ
Вращательное движение При вращательном движении все точки тела описывают окружности вокруг общей неподвижной оси. Неподви
Частные случаи вращательного движения Равномерное вращение (угловая скорость постоянна): ω =const Уравнение (закон) равн
Скорости и ускорения точек вращающегося тела Тело вращается вокруг точки О. Определим параметры движения точки A , расположенной на расстоя
Решение 1. Участок 1 — неравномерное ускоренное движение, ω = φ’ ; ε = ω’ 2. Участок 2 — скорость посто
Основные определения Сложным движением считают движение, которое можно разложить на несколько простых. Простыми движениям
Плоскопараллельное движение твердого тела Плоскопараллельным, или плоским, называется такое движение твердого тела, при котором все точки тел
Поступательное и вращательное Плоскопараллельное движение раскладывают на два движения: поступательное вместе с некоторым полюсом и
Центра скоростей Скорость любой точки тела можно определять с помощью мгновенного центра скоростей. При этом сложно
Аксиомы динамики Законы динамики обобщают результаты многочисленных опытов и наблюдений. Законы динамики, которые принято
Понятие о трении. Виды трения Трение — сопротивление, возникающее при движении одного шероховатого тела по поверхности другого. При
Трение качения Сопротивление при качении связано с взаимной деформацией грунта и колеса и значительно меньше трения скол
Свободная и несвободная точки Материальная точка, движение которой в пространстве не ограничено какими-нибудь связями, называется сво
Сила инерции Инертность — способность сохранять свое состояние неизменным, это внутреннее свойство всех материал
Решение Активные силы: движущая сила, сила трения, сила тяжести. Реакция в опоре R. Прикладываем силу инерции в обра
Работа равнодействующей силы Под действием системы сил точка массой т перемещается из положения М1 в положение M 2 (рис
Мощность Для характеристики работоспособности и быстроты совершения работы введено понятие мощности. Мощнос
Мощность при вращении Рис. 16.2 Тело движется по дуге радиуса из точки М1 в точку М2 М1М2 = φr
Коэффициент полезного действия Каждая машина и механизм, совершая работу, тратит часть энергии на преодоление вредных сопротивлений.
Теорема об изменении количества движения Количеством движения материальной точки называется векторная величина, равная произведению массы точ
Теорема об изменении кинетической энергии Энергией называется способность тела совершать механическую работу. Существуют две формы механи
Основы динамики системы материальных точек Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической с
Основное уравнение динамики вращающегося тела Пусть твердое тело под действием внешних сил вращае
Напряжения Метод сечений позволяет определить величину внутреннего силового фактора в сечении, но не дает возмож
Внутренние силовые факторы, напряжения. Построение эпюр Иметь представление о продольных силах, о нормальных напряжениях в поперечных сечениях. Знать п
Продольных сил Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис.
Геометрические характеристики плоских сечений Иметь представление о физическом смысле и порядке определения осевых, центробежных и полярных моментов
Статический момент площади сечения Рассмотрим произвольное сечение (рис. 25.1). Если разбить сечение на бесконечно малые площадки dA и ум
Центробежный момент инерции Центробежным моментом инерции сечения называется взятая ковсей площади сумма произведений элементарн
Осевые моменты инерции Осевым моментом инерции сечения относительно некоторой реи, лежащей в этой же плоскости, называется вз
Полярный момент инерции сечения Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятая по всей площ
Моменты инерции простейших сечений Осевые моменты инерции прямоугольника (рис. 25.2)
Полярный момент инерции круга Для круга вначале вычисляют полярный момент инерции, затем — осевые. Представим круг в виде совокупности
Деформации при кручении Кручение круглого бруса происходит при нагружении его парами сил с моментами в плоскостях, перпендикуляр
Гипотезы при кручении 1. Выполняется гипотеза плоских сечений: поперечное сечение бруса, плоское и перпен- дикулярное продол
Внутренние силовые факторы при кручении Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутрен
Эпюры крутящих моментов Крутящие моменты могут меняться вдоль оси бруса. После определения величин моментов по сечениям строим гра
Напряжения при кручении Проводим на поверхности бруса сетку из продольных и поперечных линий и рассмотрим рисунок, образовавши
Максимальные напряжения при кручении Из формулы для определения напряжений и эпюры распределения касательных напряжений при кручении видно, ч
Виды расчетов на прочность Существует два вида расчета на прочность 1. Проектировочный расчет — определяется диамет
Расчет на жесткость При расчете на жесткость определяется деформация и сравнивается с допускаемой. Рассмотрим деформацию кру
Основные определения Изгибом называется такой вид нагружения, при котором в поперечном сечении бруса возникает внутренний
Внутренние силовые факторы при изгибе Пример 1.Рассмотрим балку, на которую действует пара сил с моментом т и внешняя сила F (рис. 29
Изгибающих моментов Поперечная сила в сечении считается положительн
Дифференциальные зависимости при прямом поперечном изгибе Построение эпюр поперечных сил и изгибающих моментов существенно упрощается при использовании дифференц
Методом сечения Полученное выражение можно обобщить Поперечная сила в рассматриваемом сечении равна алгебраической сумме всех сил, действующих на балку до рас
Напряжения Рассмотрим изгиб балки, защемленной справа и нагруженной сосредоточенной силой F (рис. 33.1).
Напряженное состояние в точке Напряженное состояние в точке характеризуется нормальными и касательными напряжениями, возникающими на
Понятие о сложном деформированном состоянии Совокупность деформаций, возникающих по различным направлениям и в различных плоскостях, проходящих чере
Расчет круглого бруса на изгиб с кручением В случае расчета круглого бруса при действии изгиба и кручения (рис. 34.3) необходимо учитывать нормальные и
Понятие об устойчивом и неустойчивом равновесии Относительно короткие и массивные стержни рассчитывают на сжатие, т.к. они выходят из строя в результате ра
Расчет на устойчивость Расчет на устойчивость заключается в определении допускаемой сжимающей силы и в сравнении с ней силы дейс
Расчет по формуле Эйлера Задачу определения критической силы математически решил Л. Эйлер в 1744 г. Для шарнирно закрепленн
Критические напряжения. Критическое напряжение — напряжение сжатия, соответствующее критической силе. Напряжение от сжи
Пределы применимости формулы Эйлера Формула Эйлера выполняется только в пределах упругих деформаций. Таким образом, критическое напряж
allrefers.ru
ВВЕДЕНИЕ
Для усвоения курса «Теоретическая механика. Статика и кинематика» необходимо изучить теорию, получить навыки в решении задач и выполнить индивидуальную курсовую работу.
Настоящее учебное пособие включает два раздела: статику и кинематику, по которым приводятся программа изучения и задания для курсовой работы.
Задание выполняется в отдельной тетради или на листах писчей бумаги формата А4, которые затем брошюруются. Решение каждой задачи должно сопровождаться чертежом, который выполняется согласно условиям конкретного варианта задания. Чертеж должен быть аккуратным и наглядным и выполнен с учетом применяемого масштаба. На рисунках должны быть показаны все заданные величины (размеры, векторы сил, скоростей, ускорений и т. п.) и координатные оси. Кроме того необходимо иметь в виду, что все линии на рисунках и в условиях, параллельные строкам, считаются горизонтальными, а перпендикулярные строкам - вертикальными.
Решение задач необходимо сопровождать краткими пояснениями (какие формулы или теоремы применяются, откуда получаются те или иные результаты и т. п.) и подробно излагать весь ход расчетов. На каждой странице оставлять поля для замечаний преподавателя.
Программа курса «Теоретическая механика»
Введение
Механическое движение как одна из форм движения материи. Предмет механики. Теоретическая механика и ее место среди естественных и технических наук. Механика как теоретическая база ряда областей современной техники. Объективный характер законов механики. Основные исторические этапы развития механики. Связь механики с общественным производством.
Статика твердого тела
Предмет статики
Основные понятия статики: абсолютно твердое тело, сила, эквивалентная система сил, равнодействующая, уравновешенная система сил, силы внешние и внутренние. Аксиомы статики. Связи и реакции связей. Основные виды связей: гладкая плоскость (поверхность и опора), гибкая нить, цилиндрический шарнир (подшипник), сферический шарнир (подпятник), невесомый (идеальный) стержень; реакции этих связей.
Система сходящихся сил
Геометрический и аналитический способы сложения сил. Сходящиеся силы. Равнодействующая сходящихся сил. Геометрическое условие равновесия сходящихся сил. Аналитические условия равновесия пространственной и плоской систем сходящихся сил. Теорема о равновесии трех непараллельных сил.
Теория пар сил
Момент силы относительно точки (центра) как вектор. Алгебраическое значение момента силы относительно точки. Пара сил и ее алгебраическое значение. Момент пары сил как вектор. Теоремы об эквивалентности пар. Сложение пар в плоскости и произвольно расположенных в пространстве. Условия равновесия системы пар.
Плоская система сил
Теорема о параллельном переносе силы. Основная теорема статики о приведении плоской системы сил к данному центру. Главный вектор и главный момент системы сил и их вычисление. Частные случаи приведения: приведение к паре сил, к равнодействующей и случай равновесия. Аналитические условия равновесия плоской системы сил. Три вида условий равновесия: а) равенство нулю сумм проекций сил на две координатные оси и суммы их моментов относительно любого центра; б) равенство нулю сумм моментов сил относительно двух центров и суммы их проекций на одну ось; в) равенство нулю сумм моментов сил относительно трех центров. Условия равновесия системы параллельных сил. Теорема Вариньона о моменте равнодействующей.
Сосредоточенные и распределенные силы. Силы, распределенные по отрезку прямой, и их равнодействующая. Реакция жесткой заделки. Равновесие системы тел. Статически определимые и статически неопределимые системы. Равновесие при наличии сил трения. Коэффициент трения. Предельная сила трения. Угол и конус трения. Условие самоторможения. Трение качения, коэффициент трения качения и момент трения качения.
Пространственная система сил
Момент силы относительно оси и его вычисление. Зависимость между моментом силы относительно центра и относительно оси, проходящей через этот центр. Аналитические формулы для вычисления моментов силы относительно трех координатных осей. Приведение пространственной системы сил к данному центру. Вычисление главного вектора и главного момента пространственной системы сил. Аналитические условия равновесия произвольной пространственной системы сил.
Центр тяжести
Центр параллельных сил. Формулы для определения координат центра параллельных сил. Центр тяжести твердого тела; формулы для определения его координат. Центры тяжести объема, площади и линии. Способы определения положения центров тяжести тел. Центры тяжести дуги окружности, треугольника и кругового сектора.
Кинематика
Кинематика точки
Предмет кинематики. Пространство и время в классической механике. Относительность механического движения. Системы отсчета. Задачи кинематики.
Векторный способ задания движения точки. Траектория точки. Скорость точки как производная ее радиуса-вектора по времени. Ускорение точки как производная от ее вектора скорости по времени.
Координатный способ задания движения точки в прямоугольных декартовых координатах. Определение траектории точки. Определение скорости и ускорения точки по их проекциям на координатные оси.
Естественный способ задания движения точки. Естественный трехгранник и его оси. Алгебраическая величина скорости точки. Определение ускорения точки по его проекциям на оси естественного трехгранника; касательное и нормальное ускорения точки. Выражение касательного ускорения точки через проекции скорости и ускорения на координатные оси.
studopedya.ru
7.1. Статические инварианты. Динамический винт
Ранее было установлено, что главный вектор системы сил, как угодно расположенных в пространстве,
(7.1) не изменяется при перемене центра приведения. Главный же момент при этом не изменяется и для нового центра приведения определяется формулой
, (7.2) где 
и 
– главные моменты относительно центров приведения О и 
. Второе слагаемое в правой части формулы (7.2) представляет собой момент главного вектора, приложенного в центре приведения О, относительно нового центра приведения .
Умножим скалярно обе части равенства (7.2) на вектор 
:
.
…
Так как вектор 
перпендикулярен вектору 
, то их скалярное произведение равно нулю. Следовательно,
, (7.3) т.е. скалярное произведение главного вектора на главный момент не зависит от центра приведения.
Таким образом, при перемене центра приведения не изменяются главный вектор и скалярное произведение главного вектора на главный момент. Говорят, что эти величины инвариантны относительно выбора центра приведения.
Первым статическим инвариантом называется главный вектор . В более узком смысле этого слова под первым инвариантом понимают квадрат модуля главного вектора
. (7.4)
Вторым статическим инвариантом называется скалярное произведение главного вектора на главный момент:
. (7.5)
Из второго инварианта вытекает простое геометрическое следствие. Действительно, запишем равенство (7.3) в следующем виде:
.
Если 
, то
.
Каждое из этих произведений представляет собой проекцию главного момента на направление главного вектора. Следовательно, при перемене центра приведения проекция главного момента на направление главного вектора не изменяется. Заметим, что при это следствие можно принять за определение второго инварианта.
Так как проекция главного момента на направление главного вектора не изменяется при перемене центра приведения, то можно утверждать, что для центра приведения, в котором главный вектор и главный момент направлены по одной прямой, модуль главного момента будет минимальным. В этом случае модуль главного момента равен его проекции на направление главного вектора.
Очевидно, что проекция 
главного момента на направление главного вектора определяется равенством
,
или, принимая во внимание значения первого и второго инвариантов,
. (7.6)
Совокупность силы и пары сил с моментом, коллинеарным силе, называется динамическим винтом или динамой. Так как плоскость действия пары перпендикулярна моменту пары, то динамический винт представляет собой совокупность силы и пары сил, действующей в плоскости, перпендикулярной силе. Различают правый и левый динамические винты. На рис. показан правый динамический винт, составленный из силы , равной главному вектору системы, и пары сил с моментом , равным главному моменту; на рис. показан левый винт, составленный из тех же элементов.
Может возникнуть вопрос, в каких случаях данную систему сил можно привести к динаме? На этот вопрос отвечает следующая теорема:
Если второй статический инвариант не равен нулю, то систему сил можно привести к динаме. На этот вопрос отвечает следующая теорема:
Если второй статический инвариант не равен нулю, то систему можно привести к динаме.
Пусть в произвольной точке О система приведена к силе, равной главному вектору , и паре сил с моментом, равным главному моменту . Так как по условию теоремы 
, то оба вектора, и , не 
равны нулю и они не перпендикулярны между собой. Разложим главный момент на две составляющие: одну 
направим по главному вектору и другую 
направим перпендикулярно главному вектору. Составляющая представляет собой момент пары сил, расположенной в плоскости, перпендикулярной вектору . Выберем силы 
и 
, составляющие эту 
пару, равными по модулю главному вектору и приложим силу к центру приведения. Система сил ( , ), как эквивалентная нулю, может быть отброшена. Так как момент – вектор свободный, то его можно перенести из точки О в точку 
. Таким образом, заданная система сил приведена в точке к силе 
и паре сил с моментом , расположенной в плоскости, перпендикулярной силе, т.е. мы получили динамический винт.
Из формулы (7.6) видно, что положительному второму инварианту 
отвечает правый динамический винт, а отрицательному второму инварианту 
– левый динамический винт.
Точка не единственная, где система сил приводится к динаме. В самом деле, силу можно переносить вдоль линии ее действия, момент же пары сил есть вектор свободный, следовательно, система сил может быть приведена к динаме во всех точках прямой, проходящей через точку и являющейся линией действия силы . Эта прямая называется центральной осью системы сил. Найдем теперь уравнение центральной оси.
Пусть – точка центральной оси. Тогда для этой точки главный вектор и главный момент должны быть коллинеарны друг другу. На основании формулы (7.2) главный момент для точки можно записать в виде
.
Условие коллинеарности главного вектора и главного момента для точки записывается следующим образом:
,
где 
– параметр винта, имеющий размерность длины.
Таким образом,
. (7.7)
Пусть 
и 
– соответственно проекции главного вектора и главного момента на оси х, у и z; тогда
Пусть координаты какой-либо точки центральной оси будут х, у, z, следовательно,
Подставляя соответствующие выражения в соотношение (7.7), получим
Приравнивая коэффициенты при единичных векторах 
, 
и 
, имеем
,
,
.
Следовательно,
(7.8) Это и есть искомые уравнения центральной оси.
refac.ru
