
Понятие “представление в ЭВМ” означает описание в терминах используемой системы программирования структуры данных, применяемой для хранения информации об объекте и алгоритмов, реализующих присущие данному объекту операций. Таким образом, применительно к множествам определение представления в ЭВМ подразумевает описание способа хранения информации о принадлежности элементов множеству и описание алгоритмов для вычисления объединения, пересечения и других теоретико-множественных операций. Будем предполагать, что в используемой системе программирования доступны такие структуры данных, как массивы, записи и указатели.
1. Операции с подмножествами заданного универсума.Пусть универсумU– конечный, и число его элементовnне превосходит разрядности ЭВМ. Занумеруем эти элементы:U= {u1,u2,…,un}. Тогда любое подмножество АUпредставляется машинным кодом С, в котором

В этом случае код пересечения произвольных множеств А и В получается, как поразрядное логическое произведение (в Паскале – операция and) кода множества А и кода множества В. Код объединения равен логической сумме (or), код дополнения – инверсии (not). При использовании в качестве носителей кодов 32-разрядных ячеек (в Паскале – данные типаLongint) можно успешно работать с унивесумом, содержащим до 32 элементов.
2. Представление упорядоченными списками.Если универсум велик, или бесконечен, а рассматриваемые его подмножества не очень велики, то множества удобнее представлять списками элементов. Элемент представляется записью с двумя полями: информационным и указателем на следующий элемент. Весь список представляется указателем на первый элемент, а набор списков – массивом указателей на первые элементы наборов. Описание алгоритмов, реализующих основные теоретико-множественные операции см.[Новиков, 1.4.4 – 1.4.7].
3. Специальные представления. В некоторых языках программирования предусмотрены данные, аналогичные множествам (в Паскале – типSet), а также соответствующие операции с ними. Однако, такие операции работают весьма медленно и при больших множествах подобный подход неэффективен.
Пусть Х – некоторое числовое множество. Говорят, что на множестве Х определена функция f, если каждому числу xХ ставится в соответствие определенное число y = f(x). Множество Х – область определения функции, а множество Y = {f(x) | xX} – область значений функции. Если в качестве множеств Х и Y рассматривать множества произвольной природы, а не только числовые, мы приходим к понятию отображения.
Def. Пусть X и Y – два произвольных множества. Говорят, что на X определено отображение f, принимающее значения из Y (f : X Y), если каждому элементу x из X ставится в соответствие единственный элемент y = f(x) из Y.
Множество элементов xX, для которых определено отображение f, называется областью определения f и обозначается f.
Если имеется какой-либо элемент хX, то соответствующий ему элемент yY будем называть образом x. Пусть A – некоторое подмножество множества X (AX), образ множества A определяется как множество образов элементов множества A и обозначается f(A), т.е. f(A) = {f(x) | xA}. Образ области определения называется областью значений отображения f и обозначается f (т.е. f= f(f) = f(X)).
Если задать yY, то множество соответствующих ему x, т.е. таких, что y = f(x), будем называть прообразом y и обозначать f –1(y), f –1(y) = {xX | y = f(x)}. В общем случае обратное отображение f –1 неоднозначно. Пусть B – некоторое подмножество множества Y (BY), прообраз множества B определяется как множество прообразов элементов множества B и обозначается f–1(B), т.е. f –1(B) = { xA | f(x) = y, y B}.
Отображение i : X X такое, что i(x) = x для любого xX называется тождественным отображением.
Пусть f : X Y и g : Y Z. Отображение h : X Z, такое, что каждому элементу xX ставится в соответствие единственный элемент h(x) = g(f(x)), называется композицией (или суперпозицией) отображений f и g и обозначается g о f.
Отображение f : X Y называется сюръекцией X на Y, если множество образов всех элементов из X совпадают с множеством Y. Это обозначается как f(X) = Y. Другое эквивалентное определение сюръекции – это отображение, при котором каждый элемент из Y имеет прообраз в множестве X.
Если для любых x1, x2X таких, что x1 x2, получается, что f(x1) f(x2), т.е. разным элементам соответствуют различные образы, то это отображение f называется инъекцией.
Отображение f, которое является одновременно сюръекцией и инъекцией, называется биекцией, или взаимно однозначным отображением.
Если между А и В установлено биективное отображение, то говорят, что множества А и В эквивалентны. Эквивалентность множеств обозначается A ~ B.
Легко видеть, что эквивалентность множеств обладает свойством транзитивности, т.е. если A ~ B и B ~ C, то A ~ C. Признаки эквивалентности множеств дают следующие
Теоремы Кантора-Бернштейна
1. Если A B C, причем A ~ C, то A ~ B.
2. Если A эквивалентно подмножеству множества B, а B эквивалентно подмножеству множества A, то A ~ B.
(Без доказательства).
Основные свойства отображений можно сформулировать в виде следующих теорем.
Теорема 1.1. f –1(A B) = f –1(A) f –1(B) – прообраз объединения двух множеств равен объединению их прообразов.
Доказательство. Пусть xf –1 (A) f –1 (B). Тогда или xf –1(A) или хf –1(B). В первом случае y = f(x)А, во втором yВ. В любом случае yА В, поэтому xf –1 (A B).
Докажем обратное включение. Пусть xf –1 (A B), тогда y = f(x) A B. Значит или yА, или yВ. Если yА, то f –1 (y) f –1 (A). Так как xf –1(y), то отсюда следует, что xf –1 (A). Если же yВ, то f –1 (y) f –1(B), что влечет xf –1 (В). В любом случае xf –1 (A) f –1 (B). Поэтому, если xf –1 (A B), то xf –1 (A) f –1 (B), что и требовалось доказать.
Теорема 1.2. f –1 (A B) = f –1 (A) f –1 (B) – прообраз пересечения двух множеств равен пересечению их прообразов.
Доказательство. Пусть xf –1 (A B), тогда y = f(x)A B. Значит, yА и yВ. Если yА, то f –1 (y) f –1 (A), а если yВ, то f –1 (y) f –1 (B). Эти включения должны выполняться одновременно, следовательно, f –1 (y) f –1 (A) f –1 (B), а значит, хf –1 (A) f –1 (B). Таким образом, f –1 (A B) f –1 (A) f –1 (B).
Докажем обратное включение. Пусть xf –1(A) f –1(B), тогда x f –1(A) и xf –1(B). Если xf –1(A), то y = f(x)A. Если же xf –1(B), то y = f(x)B. Так как yA и yB, то yAB и поэтому f –1(y) f –1(A B). Значит, хf –1(A B) и отсюда следует, что f –1(A) f –1(B) f –1(A B).
Эти два включения означают, что f –1(AB) = f –1(A)f -1(B), что и требовалось доказать.
Теорема 1.3. f (A B) = f (A) f (B) – образ объединения двух множеств равен объединению их образов.
Доказательство. Пусть yf(A B), тогда для любого x из множества f –1(y) выполняется принадлежность хA B. Поэтому xA или xB. В первом случае y = f(x)f(A), во втором – y = f(x)f(B). Так как yf(A) или yf(B), то yf(A) f(B) и, следовательно, f(A B) f(A) f(B).
Докажем обратное включение. Пусть yf(A) f(B), тогда yf(A) и f –1(y) A или yf(B) и f –1(y) B. Соответственно получаем, что xA или xB, т.е. xA B и тогда y = f(x)f(A B). Доказано включение f(A) f(B) f(A B). Следовательно, f(A B) = f(A) f(B). что и требовалось доказать.
Замечание. Образ пересечения двух множеств не обязательно совпадает с пересечением их образов. Рассмотрим пример.
Пусть A и B – множества точек на плоскости:
A = { (x, y) | 0 x 1, y = 2 },
B = { (x, y) | 0 x 1, y = 1 }.
С помощью проектирования точек на ось ОХ построим отображение А и В на множество С = { (x, y) | 0 x 1, y = 0 }. Так как f(A) = C, f(B) = C, то f(A) f(B) = C. Но множества A и B не пересекаются и f(A B) = f() = , т.е. мы показали, что f(A B) f(A) f(B).
Теоремы 1, 2, 3 остаются в силе при любом конечном и бесконечном числе множеств. Например, теорема 1.1 примет вид:
 . (1)
. (1)
где A1, A2, . . . – некоторая система множеств.
Докажем (1) с помощью метода математической индукции.
1. При n = 2 равенство f –1(A1 A2) = f –1(A1) f –1(A2) справедливо согласно теореме 1.1.
2. Предположим, что равенство верно при любом n k.
3. Докажем, что равенство верно при n = k+1. Обозначим B =  .
.
Тогда f –1 ) = f –1 (B Ak+1) = f –1 (B) f –1 (Ak+1),
) = f –1 (B Ak+1) = f –1 (B) f –1 (Ak+1),
так как для двух множеств В и Ak+1 теорема верна. Но по предположению индукции для k множеств теорема также верна, поэтому
f –1 (B)= .
.
Отсюда следует требуемое равенство.
studfiles.net
Стар
План реферата.
Оглавление
Понятия множества и элемента множества относятся к понятиям, не определимым явно, как, например, точка и прямая. Слова «совокупность», «семейство», «система», «набор» и т.п. – синонимы слова «множество». Это связано с тем, что некоторые понятия в математике должны быть исходными, служить теми «кирпичиками», из которых складывается общая теория. Мы определяем только, как соотносятся эти исходные понятия, не говоря о природе рассматриваемых объектов. Человеческое мышление устроено так, что мир представляется состоящим из отдельных «объектов». Философам давно ясно, что мир – единое неразрывное целое, и выделение в нем объектов – это не более чем произвольный акт нашего мышления, позволяющий сформировать доступную для рационального анализа картину мира. Но как бы то ни было, выделение объектов и из совокупностей – единственный (или даже единственно возможный) способ организации нашего мышления, поэтому неудивительно, что он лежит в основе главного инструмента описания точного знания – математики.
Можно сказать, что множество- это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличны друг от друга. Примерами множеств могут быть: множество людей, животных, растений на нашей планете, а также множество N натуральных чисел: 1,2,3,4…, множество Р простых чисел:2,3,5,7,11…, множество Z целых чисел:…, -2,-1,0,1,2,…, множество R вещественных чисел и т.д. Множество, не содержащее элементов, называется пустым. Обозначение Пустое множество является подмножеством любого множества. Мощность пустого множества равна нулю. Понятие пустого множества (подобно понятию «нуль») возникает из потребности, чтобы результат всякой операции над множествами был также множеством.
Обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества U, которое называется универсальным множеством ( или универсумом).
Если объект х является элементом множества M, то говорят, что х принадлежит М. Обозначение : В противном случае говорят, что х не принадлежит М. Обозначение: Элементы множества сами могут являться множествами. Например, множество групп студентов состоит из элементов (групп), которые, в свою очередь, состоят из студентов.
Рисунок 1 Множества.
Рассмотрим все на примере:
Пусть даны два множества А и В, тогда
Следующее понятие - подмножество в теории множеств. Множество С является подмножеством множества В ( в случае, если каждый элемент множества С является также и элементом множества В. Например, множество всех четных чисел является подмножеством множества всех целых чисел. Если С является подмножеством В, то В называется надмножеством.
Мощность множества – это обобщение понятия количества ( числа элементов множества ), которое имеет смысл для всех множеств, включая бесконечные.
Существует большие, есть меньшие бесконечные множества, среди них счётное множество является самым маленьким.
В теории множеств счётное множество есть бесконечное множества, элементы которого возможно занумеровать натуральными числами. Более формально: множество Х является счётным, если существует биекция , где N обозначает множество всех натуральных чисел. Значит , счётное множество – это множество, равномощное множеству натуральных чисел.
Счётное множество является «наименьшим» бесконечным множеством, т.е. в любом бесконечном множестве найдётся счётное подмножество.
Свойства счетного множества:
Несчётное множество – такое бесконечное множество, которое не является счётным. Таким образом, любое множество является либо конечным, либо счётным, либо несчётным. Множество рациональных чисел и множество алгебраических чисел счётны, однако множество вещественных чисел континуально и, следовательно, несчётно. Два множества называются равномощными, если между ними существует биекция. Существование биекции между множествами есть отношение эквивалентности, а мощность множества – это соответствующий ему класс эквивалентности.
В результате операций из исходных множеств получаются новые.
1 свойство – Сравнение множеств.множество элемент аксиоматический принность
Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент B:
.
Если и , то A называется собственным подмножеством В. Заметим, что . По определению .
Два множества называются равными, если они являются подмножествами друг друга:
Теорема о сравнении множеств. Для любых множеств A и B существует одна и только одна из следующих возможностей: |A| = |B|, |A| < |B|, |A| > |B|.
1 операция – объединение.
2 операция – пересечение.
3 операция – разность.
4 операция – симметрическая разность
5 операция – дополнение.
Операция дополнения подразумевает некоторый универсум (множество U, которое содержит A):
Для лучшего понимания смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.
Объединением двух множеств A È B (рис. 2.2.1) – называется третье множество, каждый элемент которого принадлежит хотя бы одному из множеств A и B
Пересечением множеств А∩В (рис 2.2.2), является множество, состоящее из всех тех элементов, которые принадлежат одновременно всем данным множествам.
Разностью множеств A \ B = A – B – называется такое множество, каждый элемент которого принадлежит множеству A, но не принадлежит множеству B.
Симметрическая разность A D B
Дополнение к множеству A называется множество всех элементов, не входящих в множество A
Пусть задан универсум U. Тогда
Пусть задан универсум U. Тогда для всех A,B,C Ì U выполняются следующие свойства (табл. 2.3.1):
Свойства операций над множествами
Для объединения ( È ) | Для пересечения ( Ç ) |
Идемпотентность | |
A È A = A | A Ç A =A |
Коммутативность | |
A È B = B È A | A Ç B = B Ç A |
Ассоциативность | |
A È (B È C) = (A È B) È C | A Ç (B Ç C) = (A Ç B) Ç C |
Дистрибутивность | |
A È (B Ç C) = (A È B) Ç (A È C) | A Ç (B È C) = (A Ç B) È (A Ç C) |
Поглощение | |
(A Ç B) È A = A | (A È B) Ç A = A |
Свойства нуля | |
A È Æ = A | A Ç Æ = Æ |
Свойства единицы | |
A È U = U | A Ç U = U |
Инволютивность | |
= A | |
Законы де Моргана | |
Свойства дополнения | |
Выражение для разности | |
Выражение для симметрической разности | |
В справедливости перечисленных свойств можно убедиться различными способами. Например, нарисовать диаграммы Эйлера для левой и правой частей равенства и убедиться, что они совпадают, или же провести формальное рассуждение для каждого равенства.
Рассмотрим для примера первое равенство: A È A = А. Возьмем произвольный элемент х, принадлежащий левой части равенства, х Î A È A. По определению операции объединения È имеем хÎ A È хÎ A. В любом случае хÎ A. Взяв произвольный элемент из множества в левой части равенства, обнаружили, что он принадлежит множеству в правой части. Отсюда по определению включения множеств получаем, что A È A Ì А. Пусть теперь хÎ A. Тогда, очевидно, верно хÎ A È хÎ A. Отсюда по определению операции объединения имеем х Î A È A. Таким образом, А Ì A È A. Следовательно, по определению равенства множеств, A È A = А. Аналогичные рассуждения нетрудно провести и для остальных равенств.
Термин «представление» (еще употребляют термин «реализация») применительно к программированию означает следующее. Задать представление какого-либо объекта (в данном случае множества) — значит описать в терминах используемой системы программирования структуру данных, используемую для хранения информации о представляемом объекте, и алгоритмы над выбранными структурами данных, которые реализуют присущие данному объекту операции. В данной работе предполагается, что в используемой системе программирования доступны такие общеупотребительные структуры данных, как массивы, структуры (или записи) и указатели. Таким образом, применительно к множествам определение представления подразумевает описание способа хранения информации о принадлежности элементов множеству и описание алгоритмов для вычисления объединения, пересечения и других введенных операций.
Следует подчеркнуть, что, как правило, один и тот же объект может быть представлен многими разными способами, причем нельзя указать способ, который является наилучшим для всех возможных случаев. В одних случаях выгодно использовать одно представление, а в других — другое. Выбор представления зависит от целого ряда факторов: особенностей представляемого объекта, состава и относительной частоты использования операций в конкретной задаче и т. д. Умение выбрать наиболее подходящее для данного случая представление является основой искусства практического программирования. Хороший программист отличается тем, что он знает много разных способов представления и умело выбирает наиболее подходящий.
Реферат выполнялся по теме: «Теория множеств». Здесь рассмотрены вопросы:
На основании найденной информации (учебная литература), можно выделить основные пункты, которые наиболее полно и точно дают представление о теории множеств. При выполнении работы были приведены примеры множеств, а также и те примеры, которые приводят к противоречиям при различном способе их задания.
После проделанной работы можно сделать следующий вывод:
Понятия «множества» и «элементы множеств» составляет основной словарь математической логики. Именно эти понятия закладывают основу, которая необходима для дальнейших построений.
yaneuch.ru
написании пособия использована следующая литература:
1. Ф.А. Новиков, Дискретная математика для программистов, Питер, 2000
2. С.В. Яблонский, Введение в дискретную математику, Наука, 1986
3. М. Свами, К. Тхуласираман, Графы,сети,алгоритмы, Мир, 1984 4. А. Я. Савельев, Основы информатики, Издательство МГТУ им. Н.Э.Баумана, 2001
Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличимы друг от друга.
Например, множество S страниц этого пособия, множество N натуральных чисел, множество R вещественных чисел, множество A различных символов на этой странице.
Если объект x является элементом множества M, то говорят, что х принадлежит М. Обозначение x∈ M , в противном случае x∉ M .
Множества, как объекты, могут быть элементами других множеств. Множество, не содержащее элементов, называется пустым. Обозначение ∅. Обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества U ( своего для каждого случая), которое называется универсумом.
Задать множество можно различными способами :
перечислением элементов M := {a1,a2,K,ak }; характеристическим предикатом M := {x | P( )x }; порождающей процедурой M := {x | x := f }.
1) M1 := {1,2,3,4,5,6,7,8,9};
2) M2 := {n | n∈ N & n <10};
3) M3 := {n | FOR n =1 TO 9 : PRINT n : NEXT n}.
Перечислением можно задавать только конечные множества.
Множество А называют подмножеством множества В, если каждый элемент множества А принадлежит множеству В. Обозначение A ⊂ B . Надо заметить, что ∅ есть подмножество любого множества. Из определения также следует, что любое множество является своим подмножеством.
 Мощность множества М обозначается как M . Для конечных множеств мощность – это количество
элементов.
Мощность множества М обозначается как M . Для конечных множеств мощность – это количество
элементов.
Обычно рассматриваются следующие операции над множествами: объединение
A∪ B := {x | x∈ A∨ x∈ B} ,где значком ∨ обозначено «или»; пересечение
A∩ B := {x | x∈ A& x∈ B} , где значком & обозначено «и»; разность
AΔB := {x | (x∈ A& x∉ B) ∨ (x∈ B & x∉ A)}; дополнение

A := {x | x∉ A}, операция подразумевает некоторый универсум
A3 = { }1,5 .
Пусть A = {1,2,3}, B = {3,4,5}, U = {1,2,3,4,5,6}. Тогда

A∪ B = {1,2,3,4,5}, A∩ B = {3}, A \ B = {1,2}, AΔB = {1,2,4,5}, A = {4,5,6}. На рисунке 1.1 приведены диаграммы Эйлера, иллюстрирующие операции над множествами. Множества изображены прямоугольниками, а результат операции выделен штриховкой.
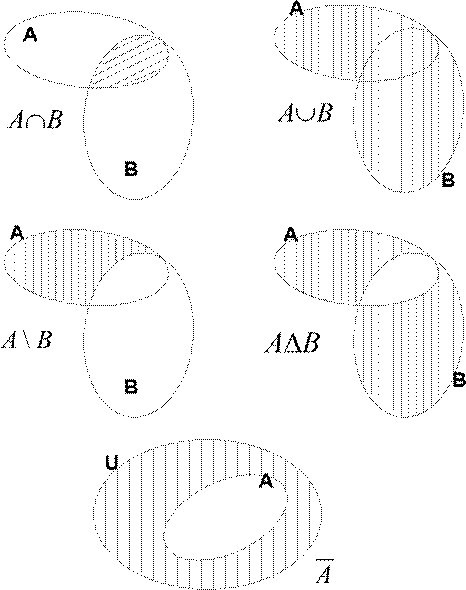
Рисунок 1.1

 Если мощность конечного
множества M , то мощность
множества всех его подмножеств 2
M .
Если мощность конечного
множества M , то мощность
множества всех его подмножеств 2
M .
Теорема позволяет подсчитать количество всех подмножеств конечного множества.
 У
множества M{1,2,3} восемь
подмножеств, то есть 2 M
=
23.
У
множества M{1,2,3} восемь
подмножеств, то есть 2 M
=
23.
A1 = {1,2,3}, A2 = { }1,2 , A3 = {1,3}, A4 = {2,3}, A5 = {1}, A6 = { }2 , A7 = { }3 , A8 = ∅.
Пусть универсум U – конечный, и число элементов в нем не превосходит разрядности ЭВМ:U<n. Элементы универсума нумеруются: U = {u1,u2,u3,K,un}.
Подмножество А универсума U представляется кодом (машинным словом или битовой шкалой), в котором каждый разряд:
⎧1,если ui ∈ A, ci = ⎨
⎩0,если ui ∉ A.
Код пересечения множеств А и В есть поразрядное логическое произведение кода множества А и кода множества В. Код объединения множеств А и В есть поразрядная логическая сумма кода множества А и кода множества В. Код дополнения множества А есть инверсия кода множества А. В большинстве ЭВМ для этих операций есть соответствующие машинные команды.
Для восьми подмножеств множества M{1,2,3}
A1 = {1,2,3}, A2 = { }1,2 , A3 = { }1,3 , A4 = {2,3}, A5 = {1}, A6 = {2}, A7 = {3}, A8 = ∅ можно составить трехразрядные двоичные коды : для А1 код – 111 для А2 код – 110 для А3 код – 101 для А4 код – 011 для А5 код – 100 для А6 код – 010 для А7 код – 001 для А8 код – 000

A1 ∩ A4 = {}1 = A5. Код для А1 –1 1 1
Код для А4 – 0 1 1
___________________
Код пересечения - 0 1 1
____________________
Код дополнения - 1 0 0 ,что является кодом для А5 .
Пусть А и В – два множества. Декартовым произведением двух множеств
A×B называется множество упорядоченных пар, в котором первый элемент каждой пары принадлежит А, а второй принадлежит В:
A× B = {(a,b)| a∈ A∧ b∈ B}
Степенью множества А называют его декартово произведение самого на себя.
A2 = A× A.
Точка плоскости может быть задана упорядоченной парой координат, то есть двумя точками на координатных осях, изображающих множества рациональных чисел R. Таким образом, R2 = R× R.
 Теорема
A×
B =
A ×
B .
Теорема
A×
B =
A ×
B .
 Пусть A = {1,2,6} и B = {3,4}. A = 3, B =
2
Пусть A = {1,2,6} и B = {3,4}. A = 3, B =
2
 Декартово произведение
A×
B =
{(1,3),(1,4),(2,3),(2,4),(6,3),(6,4)}, A× B = 6 .
Декартово произведение
A×
B =
{(1,3),(1,4),(2,3),(2,4),(6,3),(6,4)}, A× B = 6 .
 Декартов квадрат B× B = {(3,3),(3,4),(4,3),(4,4)}, B× B = 4 .
Декартов квадрат B× B = {(3,3),(3,4),(4,3),(4,4)}, B× B = 4 .
Отношением R на множествах А и В называется подмножество их декартова произведения: R ⊂ A× B .
На множествах чисел хорошо известны отношения =,≤,<,>,≥,≠ . Например, отношение « больше » будет состоять из таких пар чисел
vunivere.ru
Федеральное агентство по образованию
Федеральное государственное общеобразовательное учреждение
высшего профессионального образования
Чувашский государственный университет им. И.Н. Ульянова
Алатырский филиал
Факультет управления и экономики
Кафедра высшей математики и информационных технологий
Курсовая работа
по дисциплине: Дискретная математика для программистов
на тему: Графы и их представление на ЭВМ
Содержание
Введение
1. Определение графов
1.1 Основное определение
1.2 Смежность
1.3 Другие определения
2. Способы задания графов
2.1 Изображение графа
2.2 Способы численного представления графов
2.3 Представление ориентированных граф
3. Виды графов и операции над ними
3.1 Элементы графов
3.2 Изоморфизм графов
3.3 Тривиальные и полные графы
3.4 Двудольные графы
3.5 Направленные орграфы и сети
3.6 Операции над графами
4. Представление графов в ЭВМ
4.1 Требования к представлению графов
4.2 реализация алгоритмов поиска в глубину и ширину в программной среде Turbo Pascal
Заключение
Список использованной литературы
Введение
Среди дисциплин и методов дискретной математики теория графов и особенно алгоритмы на графах находят наиболее широкое применение в программировании. Между понятием графа и понятием отношения, имеется глубокая связь в сущности это равнообъемные понятия. Возникает естественный вопрос, почему же тогда графам оказывается столь явное предпочтение? Дело в том, что теория графов предоставляет очень удобный язык для описания программных (да и многих других) моделей. Этот тезис можно пояснить следующей аналогией. Понятие отношения также можно полностью выразить через понятие множества. Однако независимое определение понятия отношения удобнее введение специальных терминов и обозначений упрощает изложение теории и делает ее более понятной. То же относится и к теории графов. Стройная система специальных терминов и обозначений теории графов позволяют просто и доступно описывать сложные и тонкие вещи. Особенно важно наличие наглядной графической интерпретации понятия графа. Самоназвание граф подразумевает наличие графической интерпретации. Картинки позволяют сразу усмотреть суть дела на интуитивном уровне, дополняя и украшая утомительные рациональные текстовые доказательства и сложные формулы.
Графы представляют собой наиболее абстрактную структуру, с которой приходится сталкиваться в теории ЭВМ (computerscience). Графы используются для описания алгоритмов автоматического проектирования, в диаграммах машины конечных состояний, при решении задач маршрутизации потоков и т.д. Любая система, предполагающая наличие дискретных состояний или наличие узлов и переходов между ними может быть описана графом.
Как это ни удивительно, но для понятия граф нет общепризнанного едино го определения. Разные авторы, особенно применительно к разным приложениям, называют графом очень похожие, но все-таки различные объекты. Здесь используется терминология, которая была выбрана из соображений максимального упрощения определений и доказательств.
Теория графов многократно переоткрывалась разными авторами при решении различных прикладных задач.
Например, Задача о Кенигсбергских мостах. Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку Эта задача была решена Эйлером в 1736 году. Задача о трех домах и трех колодцах. Имеется три дома и три колодца. Про вести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались. Эта задача была решена Куратовским в 1930 году. Задача о четырех красках. Любую карту на плоскости раскрасить четырьмя красками так, чтобы никакие две соседние области не были закрашены одним цветом.
1. Определения графов
1.1 Основное определение
Графом G(V, Е) называется совокупность двух множеств непустого множества V (множества вершин) и множества Е неупорядоченных пар различных элемен тов множества V (Е множество ребер).
G ( V , E ) = V, E, V , E VV, E = E-
Соединения между узлами графа называются ребрами. Если узлы графа не нумерованы, то ребра являются неориентированными. У графа с нумерованными узлами ребра ориентированы. Ребрам могут быть присвоены определенные веса или метки. На рис. 1.1А и 1.1Б приведены примеры обычного и ориентированного графа.
Число вершин графа A обозначим р, а число ребер q:
p : = p ( A ) : = V , q : = = q ( A ) : = E ;
Более простое определение графа - совокупность точек и линий, в которой каждая линия соединяет две точки. Для ориентированного графа E Vx - конечный набор ориентированных ребер. Ребром может быть прямая или кривая линия. Ребра не могут иметь общих точек кроме вершин (узлов) графа. Замкнутая кривая в E может иметь только одну точку из множества V, а каждая незамкнутая кривая в E имеет ровно две точки множества V. Если V и E конечные множества, то и граф им соответствующий называется конечным. Граф называется вырожденным, если он не имеет ребер. Параллельными ребрами графа называются такие, которые имеют общие узлы начала и конца.
1.2 Смежность
Если ребро соединят две вершины, то говорят, что оно им инцидентно;
www.studsell.com