 то всё доказано. Если
то всё доказано. Если  то по свойству 2,
то по свойству 2,  по свойствам взаимно простых чисел
по свойствам взаимно простых чисел  ▲.
▲.Если  то всё доказано. Если
то всё доказано. Если  то по свойству 2,
то по свойству 2,  по свойствам взаимно простых чисел
по свойствам взаимно простых чисел  ▲.
▲.
Замечание: использовано следующее свойство взаимно простых чисел:

Доказательство: 
 ▲.
▲.
Следствие: Если произведение нескольких чисел делится на простое число р, то хотя бы один из сомножителей делится на это число р. (доказательство методом математической индукции по числу п сомножителей).
Теорема 1. (ОСНОВНАЯ ТЕОРЕМА АРИФМЕТИКИ). Всякое натуральное число, большее 1, может быть представлено в виде произведения простых сомножителей и два таких разложения могут отличаться только порядком следования сомножителей.
Доказательство: 1. Возможность указанного представления. Применим метод математической индукции.
1) Для числа 2 утверждение теоремы тривиально.
2) Допустим, что теорема верна для всех натуральных чисел, меньших п.
3) Докажем теорему для числа п. Если п — простое число, то всё доказано.
Если п — составное число, то  Тогда в силу индуктивного предположения
Тогда в силу индуктивного предположения  допускают разложение на простые множители:
допускают разложение на простые множители: 

Тогда  и возможность разложения числа п доказана.
и возможность разложения числа п доказана.
2. Однозначность разложения. Для доказательства однозначности разложения с точностью до порядка следования сомножителей также применим метод математической индукции.
1) Для числа 2 утверждение справедливо, т. к. 2 – простое число.
2) Допустим, что утверждение верно для всех натуральных чисел, меньших п.
3) Докажем утверждение для числа п. Допустим, что п двумя способами разложено в произведение простых сомножителей:  и
и  , где
, где  простые числа
простые числа  .
.
Тогда 
 один из сомножителей произведения
один из сомножителей произведения  делится на
делится на  .
.

Тогда  Но число
Но число  Тогда по индуктивному предположению для т утверждение справедливо, т. е. два разложения числа т могут отличаться только порядком следования сомножителей. Следовательно,
Тогда по индуктивному предположению для т утверждение справедливо, т. е. два разложения числа т могут отличаться только порядком следования сомножителей. Следовательно,  простые числа
простые числа  только порядком следования. Значит утверждение верно и для числа п.
только порядком следования. Значит утверждение верно и для числа п.
Итак, по методу математической индукции утверждение верно для любого натурального числа, большего 1. ▲.
Замечание: Среди сомножителей в разложении  могут быть равные. Их произведение принято записывать в виде степеней. Пусть
могут быть равные. Их произведение принято записывать в виде степеней. Пусть  различные простые сомножители числа п и число
различные простые сомножители числа п и число  входит в разложение числа п
входит в разложение числа п  раз
раз  , тогда число п можно записать в виде:
, тогда число п можно записать в виде:  . Такое разложение называется каноническим разложением числа п.
. Такое разложение называется каноническим разложением числа п.
Пример: Найдем каноническое разложение числа 1176.
 Значит
Значит 
Применения основной теоремы арифметики
Если у нас есть канонические разложения двух натуральных чисел, то мы можем считать, что эти разложения состоят из одинаковых простых сомножителей, добавляя сомножители вида  .
.
Например, 
 Считают, что
Считают, что 

Теорема 2. Пусть  канонические разложения натуральных чисел п и т. Тогда
канонические разложения натуральных чисел п и т. Тогда  где
где 
 где
где 
Примеры: 1. 

2. Пусть  . Найдем их канонические разложения:
. Найдем их канонические разложения:



matematiku5.ru
Федеральное агентство по образованию Российской Федерации
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИМЕНИ Н.Г.ЧЕРНЫШЕВСКОГО
Кафедра компьютерной алгебры и теории чисел
Основная теорема алгебры
Курсовая работа
студента 1 курса 121 группы механико-математического факультета
Батура Ирина Сергеевна
Научный руководитель Е.В. КОРОБЧЕНКО, ассистент
Зав. кафедрой В.Н.КУЗНЕЦОВ, д.т.н., профессор
САРАТОВ
2009 год
СОДЕРЖАНИЕ
1. Введение
2. Основные определения, используемые в курсовой работе
3. Элементы теории пределов для комплексных чисел
4. Доказательство основной теоремы
5. Список используемой литературы
1. ВВЕДЕНИЕ
Данная работа посвящена Основной теореме Алгебры, изучению существования корней в поле . Как предположение эта теорема впервые встречается у немецкого математика Питера Роуте(1617г.). Д’Аламбер первым в 1746г. опубликовал доказательство этой теоремы. Его доказательство основывалось на лемме. Доказательство это было бы совершенно строгим, если бы Д’Аламбер мог доказать, что-то на комплексной плоскости значение модуля многочлена достигает наименьшего значения. Во второй половине 18 века появляются доказательства Эйлера, Лапласа, Лагранжа и других. Во всех этих доказательствах предполагается заранее, что какие-то "идеальные" корни многочлена существуют, а затем доказывается, что, по крайней мере, один из них является комплексным числом. Со времен доказательства теоремы в алгебре было открыто очень много нового, поэтому сегодня "основной" эту теорему назвать уже нельзя: это название теперь является историческим.
. Как предположение эта теорема впервые встречается у немецкого математика Питера Роуте(1617г.). Д’Аламбер первым в 1746г. опубликовал доказательство этой теоремы. Его доказательство основывалось на лемме. Доказательство это было бы совершенно строгим, если бы Д’Аламбер мог доказать, что-то на комплексной плоскости значение модуля многочлена достигает наименьшего значения. Во второй половине 18 века появляются доказательства Эйлера, Лапласа, Лагранжа и других. Во всех этих доказательствах предполагается заранее, что какие-то "идеальные" корни многочлена существуют, а затем доказывается, что, по крайней мере, один из них является комплексным числом. Со времен доказательства теоремы в алгебре было открыто очень много нового, поэтому сегодня "основной" эту теорему назвать уже нельзя: это название теперь является историческим.
Целью моей работы является выявления, что поле комплексных чисел алгебраически замкнуто. Для доказательства Основной теоремы Алгебры я использовала ряд лемм: лемма Даламбера и лемма о достижении точной нижней грани значений.
комплексных чисел алгебраически замкнуто. Для доказательства Основной теоремы Алгебры я использовала ряд лемм: лемма Даламбера и лемма о достижении точной нижней грани значений.
При написании работы мною была использована следующая литература: Д.К.Фадеев "Лекции по алгебре", Л.Д.Кудрявцев "Курс математического анализа". А.Г.Курош "Курс высшей алгебры".
2. Основные определения, используемые в курсовой работе
Множества, удовлетворяющие требованиям:1-операция сложения,2-операция умножения,3-связь операций сложения и умножения, и содержащие хотя бы один элемент, отличный от нуля, называется полями.
Множество комплексных чисел можно определить как множество упорядоченных пар
можно определить как множество упорядоченных пар действительных чисел,
действительных чисел, ,
,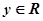 , в котором введены операции сложения и умножения согласно следующему определению:
, в котором введены операции сложения и умножения согласно следующему определению:


В результате этого определения множество указанных пар превращается в поле, т.е. удовлетворяет условиям 1,2,3. Полученное таким образом поле, называется полем комплексных чисел.
Последовательность комплексных чисел - это функция, определенная на множестве натуральных чисел и имеющая своими значениями комплексные числа.
Последовательность называется подпоследовательностью
называется подпоследовательностью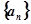 , если для любого k существует такое натуральное
, если для любого k существует такое натуральное , что
, что =
= , причем
, причем Б
Б тогда и только тогда, когда
тогда и только тогда, когда .
.
Комплексное число– расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма
. Любое комплексное число может быть представлено как формальная сумма , где x и y— вещественные числа, i— мнимая единица, то есть число, удовлетворяющее уравнению
, где x и y— вещественные числа, i— мнимая единица, то есть число, удовлетворяющее уравнению .
.
Вещественное число (действительное число)– любое положительное число, отрицательное число или нуль.
Функция– 1) Зависимая переменная величина; 2) Соответствие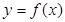 между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует определенное значение величины y (зависимой переменной или функции в значении 1).
между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует определенное значение величины y (зависимой переменной или функции в значении 1).
Теорема Больцано-Вейерштрасса: из любой ограниченной последовательности можно извлечь сходящуюся подпоследовательность.
Последовательность называется ограниченной на множестве Е, если существует такая постоянная М>0, что для всех и всех
и всех выполняется неравенства
выполняется неравенства
Последовательность сходится к функции f равномерно на множестве Е, если для любого существует такой номер
существует такой номер , что если
, что если , то для всех
, то для всех выполняется неравенство
выполняется неравенство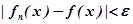 . Последовательность называется равномерно сходящейся на множестве Е, если существует функция f, к которой она равномерно сходится на Е.
. Последовательность называется равномерно сходящейся на множестве Е, если существует функция f, к которой она равномерно сходится на Е.
3. Элементы теории пределов для комплексных чисел
В моей работе полиномы рассматриваются только над полями и
и как функции от комплексной или вещественной переменной, так что моя работа является скорее главой математического анализа, а не алгебры, хотя теорема о существовании корня у любого отличного от константы полинома с комплексными коэффициентами (т.е. установление алгебраической замкнутости поля
как функции от комплексной или вещественной переменной, так что моя работа является скорее главой математического анализа, а не алгебры, хотя теорема о существовании корня у любого отличного от константы полинома с комплексными коэффициентами (т.е. установление алгебраической замкнутости поля ) носит название основной теоремы алгебры.
) носит название основной теоремы алгебры.
Определение: Пусть задана последовательность комплексных чисел . Число
. Число называется ее пределом, если для любого действительного числа
называется ее пределом, если для любого действительного числа существует такой номер
существует такой номер , что при
, что при выполняется неравенство
выполняется неравенство . В этом случае пишут lim
. В этом случае пишут lim , а=lim
, а=lim , b=lim
, b=lim . Предельное соотношение lim
. Предельное соотношение lim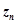 =c равносильно соотношению
=c равносильно соотношению , ибо
, ибо
max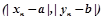





Последовательность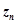 такая, что
такая, что
 R, при некотором R, называется ограниченной.
R, при некотором R, называется ограниченной.
Для вещественных переменных известная теорема Больцано-Вейерштрасса: из любой ограниченной последовательности можно извлечь сходящуюся подпоследовательность. То же самое верно и для последовательностей, составленных из комплексных чисел.
Действительно, пусть ограниченная последовательность, т.е.
ограниченная последовательность, т.е. , тогда
, тогда , так что
, так что есть ограниченная последовательность вещественных чисел. Из нее можно выбрать сходящуюся подпоследовательность
есть ограниченная последовательность вещественных чисел. Из нее можно выбрать сходящуюся подпоследовательность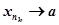 . Рассмотрим соответствующую подпоследовательность мнимых частей
. Рассмотрим соответствующую подпоследовательность мнимых частей . Она ограничена, и из нее можно извлечь сходящуюся подпоследовательность
. Она ограничена, и из нее можно извлечь сходящуюся подпоследовательность .
.
Соответствующая подпоследовательность комплексных чисел имеет сходящиеся последовательности вещественных и мнимых частей и, следовательно, сходятся, и ее предел равен .
.
4. Доказательство основной теоремы
Прежде чем приступить к формальному доказательству, наметим его идею. Пусть -полином, рассматриваемый как функция от комплексной переменной
-полином, рассматриваемый как функция от комплексной переменной .Представим себе "график" функции
.Представим себе "график" функции , считая , что значения
, считая , что значения изображаются на горизонтальной плоскости, перпендикулярной к плоскости чертежа, а значения
изображаются на горизонтальной плоскости, перпендикулярной к плоскости чертежа, а значения откладываются вверх в направлении оси
откладываются вверх в направлении оси . Мы установим, что
. Мы установим, что являются непрерывными функциями от
являются непрерывными функциями от на всей плоскости комплексной переменной. Функция
на всей плоскости комплексной переменной. Функция от комплексной переменной
от комплексной переменной называется непрерывной в точке
называется непрерывной в точке , если достаточно близким к
, если достаточно близким к значениями
значениями соответствует сколь угодно близкие к
соответствует сколь угодно близкие к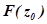 значения
значения .В более точных терминах - для любого
.В более точных терминах - для любого найдется такое
найдется такое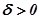 , что
, что , как только
, как только .
.
Непрерывность дает основания представлять себе график
дает основания представлять себе график в виде непрерывной поверхности, накрывающей плоскость
в виде непрерывной поверхности, накрывающей плоскость , и местами доходящей до этой плоскости. Собственно говоря, нам и нужно доказать, что существует такое значение
, и местами доходящей до этой плоскости. Собственно говоря, нам и нужно доказать, что существует такое значение , в котором
, в котором , и, тем самым,
, и, тем самым, , т.е. что поверхность
, т.е. что поверхность доходит до плоскости
доходит до плоскости в точке
в точке . Мы докажем, что если дана точка на поверхности
. Мы докажем, что если дана точка на поверхности ,которая расположена выше плоскости
,которая расположена выше плоскости , то в ее окрестности найдется точка поверхности расположенная ниже данной точки. Тогда останется только доказать, что на поверхности
, то в ее окрестности найдется точка поверхности расположенная ниже данной точки. Тогда останется только доказать, что на поверхности существует самая низкая точка, скажем, при
существует самая низкая точка, скажем, при . Она не может находиться выше плоскости
. Она не может находиться выше плоскости , ибо тогда она была бы самой низкой точкой. Следовательно,
, ибо тогда она была бы самой низкой точкой. Следовательно, и , следовательно
и , следовательно , т.е.
, т.е. корень полинома
корень полинома .
.
Теперь приступим к доказательству основной теоремы, разбив это доказательство на цепочку лемм.
Лемма 1. Дан полином c нулевым свободным членом.
c нулевым свободным членом.
Тогда для любого найдется такое
найдется такое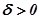 , что
, что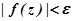 , как только
, как только .
.
Доказательство: Пусть . Тогда
. Тогда

Положим
 Если
Если
то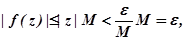
что и требовалось доказать.
Лемма 2. Полином есть непрерывная функция во всех точках плоскости комплексной переменной.
Доказательство: Пусть дан полином и точка
и точка .Расположим полином по степеням
.Расположим полином по степеням
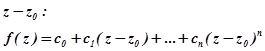 ,
,
Тогда так что
так что

Правая часть есть полином от с нулевым свободным членом.
с нулевым свободным членом.
По лемме 1 для любого найдется такое
найдется такое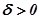 , что
, что как только
как только что и требовалось доказать.
что и требовалось доказать.
Лемма 3. Модуль полинома есть непрерывная функция.
Доказательство: Из неравенства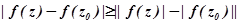 следует, что для данного
следует, что для данного то
то , которое "обслуживает"
, которое "обслуживает" , подходит и для
, подходит и для . Действительно, при
. Действительно, при имеем
имеем

Лемма 4. (о возрастании модуля полинома). Если -полином, отличный от константы, то для любого М>0 существует такое R>0, что
-полином, отличный от константы, то для любого М>0 существует такое R>0, что M,как только
M,как только .
.
Это означает, что любая горизонтальная плоскость отрезает от поверхности
отрезает от поверхности конечный кусок, накрывающий часть круга |z|≤R.
конечный кусок, накрывающий часть круга |z|≤R.
Доказательство: Пусть

где полином от
полином от c нулевым свободным членом.
c нулевым свободным членом.
В силу леммы 1 для найдется такое
найдется такое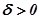 , что при
, что при , будет
, будет . Модуль
. Модуль может быть сделан сколь угодно большим, именно, при
может быть сделан сколь угодно большим, именно, при будет
будет . Возьмем
. Возьмем
 Тогда при
Тогда при будет
будет
 и
и так что
так что
Лемма 5. Точная нижняя грань значений достигается, т.е. существует такое
достигается, т.е. существует такое , что
, что при всех
при всех .
.
Доказательство: Обозначим точную нижнюю грань через
через . Возьмем последовательностью
. Возьмем последовательностью
 стремящихся к
стремящихся к сверху. Каждая из этих чисел не является нижней гранью значений
сверху. Каждая из этих чисел не является нижней гранью значений , ибо
, ибо -точная нижняя грань. Поэтому найдутся
-точная нижняя грань. Поэтому найдутся такие, что
такие, что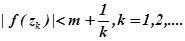 . Воспользуемся теперь леммой о возрастании модуля. Для
. Воспользуемся теперь леммой о возрастании модуля. Для найдем такое
найдем такое , что при
, что при будет
будет Отсюда следует, что
Отсюда следует, что при все
при все . Последовательностью
. Последовательностью оказалась ограниченной, и из нее можно извлечь сходящуюся подпоследовательность
оказалась ограниченной, и из нее можно извлечь сходящуюся подпоследовательность . Пусть ее предел равен
. Пусть ее предел равен . Тогда
. Тогда в силу непрерывности
в силу непрерывности . Кроме того,
. Кроме того, . Поэтому
. Поэтому Итак
Итак , что и требовалось доказать.
, что и требовалось доказать.
Лемма 6. (Лемма Даламбера). Пусть полином отличный от константы, и пусть
полином отличный от константы, и пусть . Тогда найдется такая точка
. Тогда найдется такая точка , что
, что

Геометрический смысл этой леммы: если на поверхности дана точка, находящаяся выше плоскости
дана точка, находящаяся выше плоскости , то на ней найдется другая точка, расположенная ниже первой.
, то на ней найдется другая точка, расположенная ниже первой.
Доказательство: Расположим полином по степеням
по степеням

Тогда Идея доказательства состоит в том, чтобы за счет первого отличного от нуля слагаемого "откусить кусочек" от
Идея доказательства состоит в том, чтобы за счет первого отличного от нуля слагаемого "откусить кусочек" от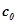 , а влияние дальнейших слагаемых сделать незначительным. Пусть
, а влияние дальнейших слагаемых сделать незначительным. Пусть – первое отличное от нуля слагаемое после
– первое отличное от нуля слагаемое после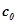 , так что
, так что (если k>1). Такое слагаемое имеется, так как
(если k>1). Такое слагаемое имеется, так как не константа. Тогда
не константа. Тогда

 +
+
+ (
( +…+
+…+ ))=
))=
=c0(1+ +
+
 ).
).
Здесь
 =
=

есть полином от с нулевым свободным членом. По лемме 1 для
с нулевым свободным членом. По лемме 1 для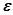 =
= найдется такое
найдется такое ,что |
,что | |<
|< , как только |
, как только | |<
|< . Положим
. Положим =
= (
( ) и
) и
 . Тогда
. Тогда
 .
.
Выберем так, что
так, что . Для этого нужно взять
. Для этого нужно взять . Далее, положим
. Далее, положим , т.е. возьмем
, т.е. возьмем . При таком выборе будет
. При таком выборе будет . Теперь положим
. Теперь положим
 при
при и
и . Тогда
. Тогда и
и
| |=
|=
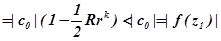 .
.
Лемма доказана.
Заметим, что с тем же успехом мы могли бы взять при
при так что при k>1 (т.е. в случае, когда
так что при k>1 (т.е. в случае, когда -корень кратности
-корень кратности полинома
полинома )имеется k направлений спуска по поверхности
)имеется k направлений спуска по поверхности
 . Они разделяются
. Они разделяются направлениями подъема при
направлениями подъема при
Действительно, в этих направлениях
 и
и
Так что если есть корень производной кратности
есть корень производной кратности , то поверхность
, то поверхность в окрестности точки
в окрестности точки "гофрирована" так, что на ней имеется
"гофрирована" так, что на ней имеется "долин" cпуска, раздельных
"долин" cпуска, раздельных "хребтами" подъема.
"хребтами" подъема.
Теорема: Полином с комплексными коэффициентами, отличный от постоянной, имеет по меньше мере один комплексный корень (т.е. поле , комплексных чисел алгебраически замкнуто).
, комплексных чисел алгебраически замкнуто).
Доказательство: Пусть - данный полином, отличный от константы. Пусть, далее,
- данный полином, отличный от константы. Пусть, далее, и
и - точка, в которой
- точка, в которой ; Она существует по лемме 5. Тогда
; Она существует по лемме 5. Тогда ибо иначе, согласно лемме 6, нашлась бы такая точка
ибо иначе, согласно лемме 6, нашлась бы такая точка что
что невозможно.
невозможно.
СПИСОК ЛИТЕРАТУРЫ
Д.К.Фадеев Лекции по алгебре. - СПб.: Изд-во "Лань", 2007. - 416с.
Л.Д.Кудрявцев Курс математического анализа. – М.: Изд-во "Высш. Школа", 1981г. – 687с.
А.Г.Курош Курс высшей алгебры. – М.: Изд-во "Наука", 1971 г. – 431с.
superbotanik.net
Ее обычно формулируют так:
всякое натуральное число, отличное от 1, единственным образом представляется в виде произведения простых чисел
или так:
всякое натуральное число единственным образом представляется в виде произведения степеней разных простых чисел
 последнее разложение часто называют каноническим, хотя и не всегда, требуя при этом, чтобы простые множители входили в это разложение в порядке возрастания.
последнее разложение часто называют каноническим, хотя и не всегда, требуя при этом, чтобы простые множители входили в это разложение в порядке возрастания.
При этом всегда подразумевается, что порядок этих множителей является несущественным, так что два таких представления, отличающиеся только порядком множителей, считаются совпадающими: например, 12=2x2x3=2x3x2=3x2x2 это одно и то же разложение числа 12, и именно такое понимание позволяет говорить о единственности разложения числа на простые множители. Еще одна тонкость в формулировке основной теоремы, быть может, не слишком заметная, но существенная для ее правильного понимания, рассматривается в статье «Крайние случаи в математике».
Основная теорема арифметики в школьном курсе не доказывается, т.е. принимается без доказательства, но ее можно неограниченно использовать. Более того, разрешается считать очевидными некоторые ее следствия, которые при этом также разрешается не доказывать. Так, очевидным можно считать часто используемое утверждение:
Если произведение двух целых чисел делится на простое число р, то хотя бы одно из этих чисел делится на р.
Это утверждение — одношаговое следствие основной теоремы арифметики: если произведение ab делится на с, то в его каноническом разложении есть множитель р, а попал он в это произведение либо от а, либо от b, а стало быть, р содержится в разложении на простые одного из чисел а и b — оно и делится на р.
После этого рассуждения легко понять, почему для числа р, не являющегося простым, аналогичное утверждение неверно: если р составное, то у него по крайней мере есть два простых множителя, один из которых может входить только в разложение а, а другой — только в разложение b. Соответствующий простейший пример очевиден: р=6, а=2, b=3.
А почему верно утверждение «Если а2 делится на b2, то а делится на b»? Сразу доказать его вряд ли возможно: совсем не ясно, как из равенства а2=kb2 получить равенство вида а=nb. Сделать это позволяет именно основная теорема: все простые множители в канонические разложения чисел а2 и b2 входят с четными показателями, поэтому при а2=kb2 все простые множители в каноническое разложение k также входят с четными показателями и, следовательно, k является точным квадратом: k=n2, а из равенства а2=n2b2 сразу же получаем а=nb, т.е. а делится на b.
Из основной теоремы арифметики следует совершенно необходимое для решения задач утверждение:
если натуральное число а делится на натуральные числа b и с, и числа b и с взаимно просты, то а делится на произведение bс.
В самом деле, в разложении числа а на простые множители имеются все простые множители, входящие в разложение числа b, причем с не меньшими, чем в b, показателями степени, и то же самое касается числа с. Но поскольку числа b и с взаимно просты, т.е. не имеют общих множителей, то в разложении числа а автоматически появляются все множители произведения bс в соответствующих степенях, так что а делится на bс, что и требовалось доказать.
Очень важно помнить, что это утверждение перестает быть истинным, если не предполагать, что b и с взаимно просты: например, 18 делится на 6 и на 9, но не делится на 6×9=54. Можно привести и еще более простой хотя и несколько «вырожденный» пример: 2 делится на 2, но 2 не делится на 2×2=4.
Из основной теоремы арифметики также следует критерий делимости одного числа на другое, основанный на знании канонических разложений этих чисел:
Число а делится на число b тогда и только тогда, когда все простые множители, входящие в разложение числа b, входят и в разложение числа а, причем с показателем степени, не меньшим чем в b.
Например, 23x52x7x114 делится на 23x5x114, но не делится ни на 23x52x114x13, ни на 24x5x7x114.
Из этого критерия, или необходимого и достаточного условия делимости, вытекает формула для числа делителей натурального числа. Именно, если $a={p_{1}}^{\alpha_{1}}{p_{2}}^{\alpha_{2}}…{p_{k}}^{\alpha_{k}}$, то число делителей а равно $(\alpha+1)(\alpha_{2}+1)…(\alpha_{k}+1)$.
В самом деле, чтобы число b было делителем числа a, надо, чтобы оно имело те же простые множители, но с показателями, не большими чем в а. Но тогда первый показатель можно выбрать любым от 0 до $\alpha_{1}$ т.е. числом способов $\alpha_{1}+1$, и точно так же второй показатель можно выбрать числом способов $\alpha_{2}+1$ и т.д., а всего для выбора делителя b имеется именно $(\alpha+1)(\alpha_{2}+1)…(\alpha_{k}+1)$ способов, что и требовалось доказать.
Материалы по теме:
Поделиться с друзьями:
 Загрузка...
Загрузка... matemonline.com
Название это несколько устарело, но сама теорема об однозначном разложении на простые множители не устарела. Теорема эта несколько суховата и аккуратно ее сформулировать не так-то просто. Но на ней, как на фундаменте держится вся арифметика, и все приложения теории чисел. Эта же теорема имеет место и для кольца многочленов над полем, а более широко для всех евклидовых колец. Для них мы ее и докажем.
Однозначность далеко не всегда имеет место. Например, игрушку Лего как не разбирай, простейшие детали окажутся одни и те же. А вот огурец можно разрезать вдоль, а можно и поперек.
Что понимать под однозначностью разложения на простые множители. Например, число 10 можно записать разными способами в виде произведения
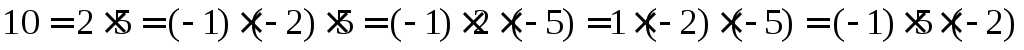 .
.
Можно предложить и другие. Однако, различия в этих представлениях не очень существенные. Минус единица и единица, это единственные обратимые элементы в кольце целых чисел (на обратимые элементы делятся любые элементы), а числа 2 и -2, 5 и -5 – ассоциированные, т.е. отличаются друг от друга на обратимые. То, что 2 и 5 в разных записях числа 10 переставлены местами тоже не существенно, поскольку имеем место коммутативность умножения. Все эти наблюдения подсказывают определение.
Определение. Два разложения элемента “a” коммутативного кольца К на простые множители

называются ассоциированными, если  - обратимые элементы,n=m, простые элементы pi и qj, возможно после перестановки, попарно ассоциированы, т.е. p1 ассоциирован с q1, p2 ассоциирован с q2 и т.д.
- обратимые элементы,n=m, простые элементы pi и qj, возможно после перестановки, попарно ассоциированы, т.е. p1 ассоциирован с q1, p2 ассоциирован с q2 и т.д.
В кольце многочленов простые элементы обычно называют неприводимыми многочленами. Так сложилось исторически, поскольку в прежние времена, разложение многочленов на множители называлось приведением к простому виду. Поэтому, если разложить не удавалось, то и называли неприводимым. Это примерно то же самое, почему у моряков не повар, а кок. Поскольку говорить, что неприводимые элемент кольца многочленов – это простой элемент кольца многочленов, излишний педантизм, то приведем и явное определение.
Определение. Многочлен называется неприводимым, если он не раскладывается в произведение многочленов меньшей степени.
Поиск простых элементов, в том числе и простых чисел и неприводимых многочленов, весьма нетривиальная задача, над которой в мире работают тысячи специалистов и миллионы микропроцессоров. Нам нужно доказать, что в кольце целых чисел Z и кольце P[x] многочленов над полем имеет место однозначное разложение на простые множители. Кстати, на этом факте держится вся криптография с открытым ключом, в том числе и знаменитый RSA.
Как обычно, сделаем это сразу для всех евклидовых колец.
Определение. Говорят, что кольца К является кольцом с однозначным разложением на простые множители, если в нем любой элемент имеет хотя бы одно разложение на простые множители и любые два такие разложения ассоциированы.
Кратко такие кольца называются факториальными. Но можно это слово и не запоминать. Некоторые племена Африки не знают слова зонтик, они просто говорят: “Домик, который белый человек носит в руках и раскрывает над головой, когда идет дождь.”
Фраза в определении факториального кольца о том, что каждый элемент должен иметь хотя бы одно разложение, не ритуальная. Не факт, что такие разложения есть вообще, а про то, чего нет можно доказать все что угодно. Например, я утверждаю, что все алмазы, хранящиеся у меня в доме, имеют вес больше 10 кг. (50 тыс. карат). Что бы меня опровергнуть требуется найти хотя бы один алмаз, который бы весил меньше 10 кг. Такого алмаза найти невозможно потому, что алмазов у меня нет вообще!
Теорема.
В евклидовом кольце любой элемент имеет разложение на простые множители.
Доказательство.
Идея доказательства очень проста. Поскольку каждый элемент евклидова кольца имеет степень, а степень сомножителя не больше чем степень произведения, то мы не сможем бесконечно раскладывать на множители. Неразложимые множители и будут простыми элементами. Теперь реализуем эту идею аккуратно. Запустим индукцию по степени  элемента “a”. База индукции – неразложимые элементы (независимо от их степени, так что, фактически, имеет место двойная индукция).
элемента “a”. База индукции – неразложимые элементы (независимо от их степени, так что, фактически, имеет место двойная индукция).
Шаг индукции. Пусть  , тогда, по предположению индукции сомножителиb и c имеют разложение на простые множители, а значит, разложим и исходный элемент “a”.
, тогда, по предположению индукции сомножителиb и c имеют разложение на простые множители, а значит, разложим и исходный элемент “a”.
Самый трудный случай. Пусть  , т.е. один из сомножителей не уменьшил свою степень, это допускается определением степени. Тогда применим деление с остатком, «непокорный» элемент “b” поделим на элемент a:
, т.е. один из сомножителей не уменьшил свою степень, это допускается определением степени. Тогда применим деление с остатком, «непокорный» элемент “b” поделим на элемент a: 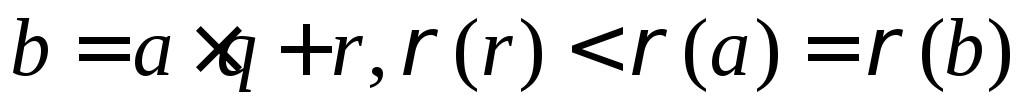 .
.
Следовательно, 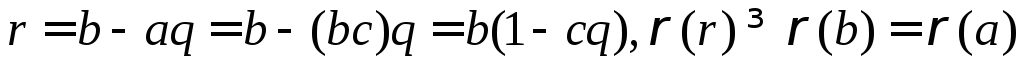 . Чтобы не возникло противоречия
. Чтобы не возникло противоречия 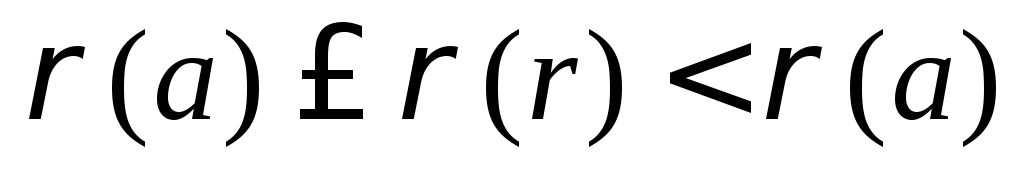 , остается согласиться, что 1–cq=0, т.е. cq=1. Значит элементы a и b ассоциированы, т.е., “а” – и принадлежит базе индукции.
, остается согласиться, что 1–cq=0, т.е. cq=1. Значит элементы a и b ассоциированы, т.е., “а” – и принадлежит базе индукции.
□
Для кольца с разложением на простые множители есть простой критерий, когда оно является факториальным. Доказательство критерия можно посмотреть, например, в учебнике А.И. Кострикина Введение в алгебру.
Теорема. (Критерий факториальности)
Если кольцо имеет разложение на простые множители, то оно факториально тогда и только тогда, когда для любого простого элемента p из того, что p\(ab) следует, что p\a или p\b.
Критерий кажется очевидным и даже несколько наивным. Однако, если Петю (p) смогли поднять вдвоем Антон (a) и Борис (b) не обязательно, что это они смогут сделать по отдельности.
Теорема (факториальность евклидовых колец).
Любое евклидово кольцо, в частности кольцо целых чисел и кольцо многочленов над полем, являются кольцам с однозначным разложением на простые множители.
Доказательство.
Применим критерий факториальности. Пусть простой элемент p делит произведение ab, но не делит элемент a. Так как элемент p простой, то НОД(p,a) = 1 и, значит, в силу алгоритма Эвклида найдутся элементы  такие, что ua+vp=1. Умножая это равенство почленно на элемент b, получаем uab+vpb=b. Так как оба слагаемых в левой части равенства делятся на элемент p, то и правая часть делится на p. Значит p\b. Если элемент p не делит b, то аналогично получим, что p\a.
такие, что ua+vp=1. Умножая это равенство почленно на элемент b, получаем uab+vpb=b. Так как оба слагаемых в левой части равенства делятся на элемент p, то и правая часть делится на p. Значит p\b. Если элемент p не делит b, то аналогично получим, что p\a.
□
Следствие. В евклидовом кольце число простых элементов бесконечно. В частности, бесконечно число простых чисел и неприводимых многочленов.
Идея использовать метод Евклида для получения новых простых чисел не безнадежна, но мало эффективна. Начнем с первых трех простых чисел 2, 3, 5. Далее получаем  , имея четыре числа 2, 3, 5, 31 получим
, имея четыре числа 2, 3, 5, 31 получим . Вновь появляющиеся числа не только не обязаны быть простыми, но даже и не обязательно дают простые множители, превосходящие предыдущие.
. Вновь появляющиеся числа не только не обязаны быть простыми, но даже и не обязательно дают простые множители, превосходящие предыдущие.
studfiles.net