Реферат: Иррациональные уравнения. Иррациональные числа реферат

Реферат Иррациональные числа

скачать

Реферат на тему:

План:

1 История
- 1.1 Средние века
- 1.2 Наше время
2 Свойства
3 Теоремы
- 3.1 Корень из 2 — иррациональное число
- 3.2 log23 — иррациональное число
- 3.3 e — иррациональное число
4 Другие иррациональные числа

Введение

Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть которое не может быть представленным в виде дроби $\frac{m}{n}$ , где m — целое число, n — натуральное число. О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа $\sqrt 2$ .

Множество иррациональных чисел обычно обозначается заглавной латинской буквой «и» в полужирном начертании без заливки — $\mathbb I$ . Таким образом: $\mathbb I =\R\backslash \Q$ , т.е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.

1. История

Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. — ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены.

Первое доказательство существования иррациональных чисел обычно приписывается Гиппасу из Метапонта (ок. 500 гг. до н. э.), пифагорейцу, который нашёл это доказательство, изучая длины сторон пентаграммы. Во времена пифагорейцев считалось, что существует единая единица длины, достаточно малая и неделимая, которая целое число раз входит в любой отрезок. Однако Гиппас обосновал, что не существует единой единицы длины, поскольку предположение о её существовании приводит к противоречию. Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число должно быть одновременно и четным, и нечетным. Доказательство выглядело следующим образом:

Отношение длины гипотенузы к длине катета равнобедренного прямоугольного треугольника может быть выражено как a:b, где a и b выбраны наименьшими из возможных.
По теореме Пифагора: a² = 2b².
Так как a² четное, a должно быть четным (так как квадрат нечетного числа был бы нечетным).
Поскольку a:b несократима, b обязано быть нечетным.
Так как a четное, обозначим a = 2y.
Тогда a² = 4y² = 2b².
b² = 2y², следовательно b² четное, тогда и b четно.
Однако было доказано, что b нечетное. Противоречие.

Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.

Феодор Киренский доказал иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17. По поводу того, каким могло быть это доказательство, историками математики было высказано несколько различных предположений. Согласно наиболее правдоподобному предположению Жана Итара (1961), оно было основано на пифагорейской теории чётных и нечётных чисел, в том числе — на теореме о том, что нечётное квадратное число за вычетом единицы делится на восемь треугольных чисел.

Позже Евдокс Книдский (410 или 408 г. до н. э. — 355 или 347 г. до н. э.) развил теорию пропорций, которая принимала во внимание как рациональные, так и иррациональные отношения. Это послужило основанием для понимания фундаментальной сути иррациональных чисел. Величина стала считаться не числом, но обозначением сущностей, таких как отрезки прямых, углы, площади, объёмы, промежутки времени — сущностей, которые могут меняться непрерывно (в современном понимании этого слова). Величины были противопоставлены числам, которые могут меняться лишь «прыжками» от одного числа к соседнему, например, с 4 на 5. Числа составляются из наименьшей неделимой величины, в то время как величины можно уменьшать бесконечно.

Поскольку никакое количественное значение не сопоставлялось величине, Евдокс смог охватить и соизмеримые, и несоизмеримые величины при определении дроби как отношения двух величин, и пропорции как равенства двух дробей. Убрав из уравнений количественные значения (числа), он избежал ловушки, состоящей в необходимости назвать иррациональную величину числом. Теория Евдокса позволила греческим математикам совершить невероятный прогресс в геометрии, предоставив им необходимое логическое обоснование для работы с несоизмеримыми величинами. «Книга 10 Элементов» Евклида посвящена классификации иррациональных величин.

1.1. Средние века

Средние века ознаменовались принятием таких понятий как ноль, отрицательные числа, целые и дробные числа, сперва индийскими, затем китайскими математиками. Позже присоединились арабские математики, которые первыми стали считать отрицательные числа алгебраическими объектами (наряду и на равных правах с положительными числами), что позволило развить дисциплину, ныне называемую алгеброй.

Арабские математики соединили древнегреческие понятия «числа» и «величины» в единую, более общую идею вещественных чисел. Они критически относились к представлениям Евклида об отношениях, в противовес ей они развили теорию отношений произвольных величин и расширили понятие числа до отношений непрерывных величин. В своих комментариях на Книгу 10 Элементов Евклида, персидский математик Аль Махани (ок 800 гг. н. э.) исследовал и классифицировал квадратичные иррациональные числа (числа вида) и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами. Он легко оперировал этими объектами, но рассуждал как об обособленных объектах, например:

Рациональной [величиной] является, например, 10, 12, 3%, 6% и так далее, поскольку эти величины произнесены и выражены количественно. Что не рационально, то иррационально, и невозможно произнести или представить соответствующую величину количественно. Например, квадратные корни чисел таких так 10, 15, 20 — не являющихся квадратами.

В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни — иррациональными. Он также ввел арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин:

результат сложения иррациональной величины и рациональной, результат вычитания рациональной величины из иррациональной, результат вычитания иррациональной величины из рациональной.

Египетский математик Абу Камил (ок. 850 г. н. э. — ок. 930 г. н. э.) был первым, кто счел приемлемым признать иррациональные числа решением квадратных уравнений или коэффициентами в уравнениях — в основном, в виде квадратных или кубических корней, а также корней четвёртой степени. В X веке иракский математик Аль Хашими вывел общие доказательства (а не наглядные геометрические демонстрации) иррациональности произведения, частного и результатов иных математических преобразований над иррациональными и рациональными числами. Ал Хазин (900 г. н. э. — 971 г. н. э.) приводит следующее определение рациональной и иррациональной величины:

Пусть единична величина содержится в данной величине один или несколько раз, тогда эта [данная] величина соответствует целому числу… Каждая величина, которая составляет половину, или треть, или четверть единичной величины, или, сравненная с единичной величиной составляет три пятых от нее, это рациональная величина. И в целом, всякая величина, которая относится к единичной как одно число к другому, является рациональной. Если же величина не может быть представлена как несколько или часть (l/n), или несколько частей (m/n) единичной длины, она иррациональная, то есть невыразимая иначе как с помощью корней.

Многие из этих идей были позже переняты европейскими математиками после перевода на латынь арабских текстов в XII веке. Аль Хассар, арабский математик из Магриба, специализировавшийся на исламских законах о наследстве, в XII веке ввел современную символьную математическую нотацию для дробей, разделив числитель и знаменатель горизонтальной чертой. Та же нотация появилась затем в работах Фибоначчи в XIII веке. В течение XIV—XVI вв. Мадхава из Сангамаграмы и представители Керальской школы астрономии и математики исследовали бесконечные ряды, сходящиеся к некоторым иррациональным числам, например, к π, а также показали иррациональность некоторых тригонометрических функций. Джестадева привел эти результаты в книге Йуктибхаза.

1.2. Наше время

В XVII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667—1754) и Леонард Эйлер (1707—1783). Когда теория комплексных чисел в XIX веке стала замкнутой и чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные (доказав при этом существование трансцендентных чисел), тем самым переосмыслив работы Евклида по классификации иррациональных чисел. По этой теме в 1872 были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ начал рассмотрения, схожие с Гейне, именно 1872 год принято считать годом рождения теории. Вейерштрасс, Кантор и Гейне обосновывали свои теории при помощи бесконечных рядов, в то время как Дедекинд работал с (ныне так называемым) Дедекиндовым сечением множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.

Цепные дроби, тесно связанные с иррациональными числами (цепная дробь, представляющая данное число, бесконечна тогда и только тогда, когда число является иррациональным), были впервые исследованы Катальди в 1613 году, затем снова привлекли к себе внимание в работах Эйлера, а в начале XIX века — в работах Лагранжа. Дирихле также внёс значительный вклад в развитие теории цепных дробей.

В 1761 году Ламберт показал, что π не может быть рационально, а также что en иррационально при любом ненулевом рациональном n. Хотя доказательство Ламберта можно назвать незавершённым, принято считать его достаточно строгим, особенно учитывая время его написания. Лежандр в 1794 году, после введения функции Бесселя-Клиффорда, показал, что π² иррационально, откуда иррациональность π следует тривиально (рациональное число в квадрате дало бы рациональное). Существование трансцендентных чисел было доказано Лиувиллем в 1844—1851 годах. Позже Георг Кантор (1873) показал их существование, используя другой метод, и обосновал, что любой интервал вещественного ряда содержит бесконечно много трансцендентных чисел. Шарль Эрмит доказал в 1873 году, что e трансцендентно, а Фердинанд и Линдеманн в 1882 года, основываясь на этом результате, показали трансцендентность π. Доказательство Линдеманна было затем упрощено Вейерштрассом в 1885 году, ещё более упрощено Давидом Гильбертом в 1893 году и, наконец, доведено до почти элементарного Адольфом Гурвицем и Паулем Горданом.

2. Свойства

Всякое вещественное число может быть записано в виде бесконечной десятичной дроби, при этом иррациональные числа и только они записываются непериодическими бесконечными десятичными дробями.
Иррациональные числа определяют Дедекиндовы сечения в множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.
Каждое трансцендентное число является иррациональным.
Каждое иррациональное число является либо алгебраическим, либо трансцендентным.
Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя числами имеется иррациональное число.
Множество иррациональных чисел несчётно, является множеством второй категории.[1]

3. Теоремы

3.1. Корень из 2 — иррациональное число

Допустим противное: $\sqrt{2}$ рационален, то есть представляется в виде несократимой дроби $\frac{m}{n}$ , где m и n — целые числа. Возведём предполагаемое равенство в квадрат:

$\sqrt{2} = \frac{m}{n} \Rightarrow 2 = \frac{m^2}{n^2} \Rightarrow m^2 = 2n^2$ .

Отсюда следует, что m2 чётно, значит, чётно и m. Пускай m = 2r, где r целое. Тогда

$(2r)^2=2n^2 \Rightarrow n^2=2r^2$

Следовательно, n2 чётно, значит, чётно и n. Мы получили, что m и n чётны, что противоречит несократимости дроби $\frac{m}{n}$ . Значит, исходное предположение было неверным, и $\sqrt{2}$ — иррациональное число.

3.2. log23 — иррациональное число

Допустим противное: log23 рационален, то есть представляется в виде дроби $\frac{m}{n}$ , где m и n — целые числа. Поскольку log23 > 0, m и n могут быть выбраны положительными. Тогда

$\log_2 3 = \frac{m}{n} \Rightarrow m = n \log_2 3 \Rightarrow 2^m = 2^{n \log_2 3} = \left (2^{\log_2 3}\right )^n = 3^n$

Но 2m чётно, а 3n нечётно. Получаем противоречие.

3.3. e — иррациональное число

См. раздел «Доказательство иррациональности» в статье «e».

4. Другие иррациональные числа

Иррациональными являются:

$\sqrt{n}$ для любого натурального n, не являющегося точным квадратом
ex для любого рационального $x\ne 0$
lnx для любого положительного рационального $x\ne 1$
π, а также πn для любого натурального n

wreferat.baza-referat.ru

Реферат Иррациональное число

скачать

Реферат на тему:

План:

1 История
- 1.1 Средние века
- 1.2 Наше время
2 Свойства
3 Теоремы
- 3.1 Корень из 2 — иррациональное число
- 3.2 log23 — иррациональное число
- 3.3 e — иррациональное число
4 Другие иррациональные числа

Введение

1. История

Отношение длины гипотенузы к длине катета равнобедренного прямоугольного треугольника может быть выражено как a:b, где a и b выбраны наименьшими из возможных.
По теореме Пифагора: a² = 2b².
Так как a² четное, a должно быть четным (так как квадрат нечетного числа был бы нечетным).
Поскольку a:b несократима, b обязано быть нечетным.
Так как a четное, обозначим a = 2y.
Тогда a² = 4y² = 2b².
b² = 2y², следовательно b² четное, тогда и b четно.
Однако было доказано, что b нечетное. Противоречие.

1.1. Средние века

1.2. Наше время

2. Свойства

Всякое вещественное число может быть записано в виде бесконечной десятичной дроби, при этом иррациональные числа и только они записываются непериодическими бесконечными десятичными дробями.
Иррациональные числа определяют Дедекиндовы сечения в множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.
Каждое трансцендентное число является иррациональным.
Каждое иррациональное число является либо алгебраическим, либо трансцендентным.
Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя числами имеется иррациональное число.
Множество иррациональных чисел несчётно, является множеством второй категории.[1]

3. Теоремы

3.1. Корень из 2 — иррациональное число

$\sqrt{2} = \frac{m}{n} \Rightarrow 2 = \frac{m^2}{n^2} \Rightarrow m^2 = 2n^2$ .

Отсюда следует, что m2 чётно, значит, чётно и m. Пускай m = 2r, где r целое. Тогда

$(2r)^2=2n^2 \Rightarrow n^2=2r^2$

3.2. log23 — иррациональное число

$\log_2 3 = \frac{m}{n} \Rightarrow m = n \log_2 3 \Rightarrow 2^m = 2^{n \log_2 3} = \left (2^{\log_2 3}\right )^n = 3^n$

Но 2m чётно, а 3n нечётно. Получаем противоречие.

3.3. e — иррациональное число

См. раздел «Доказательство иррациональности» в статье «e».

4. Другие иррациональные числа

Иррациональными являются:

$\sqrt{n}$ для любого натурального n, не являющегося точным квадратом
ex для любого рационального $x\ne 0$
lnx для любого положительного рационального $x\ne 1$
π, а также πn для любого натурального n

wreferat.baza-referat.ru

Реферат : Иррациональные уравнения (работа 1)

Иррациональные уравнения

ВВЕДЕНИЕ

В школьном курсе алгебры рассматриваются различные виды уравнений – линейные, квадратные, биквадратные, кубические, рациональные, с параметрами, иррациональные и другие. Данная курсовая работа посвящена иррациональным уравнениям, методам их решения. Кроме того, в работе введены понятия уравнений следствий и равносильных уравнений, а также приведены примеры задач, математическими моделями которых служат иррациональные уравнения. В данной работе содержится небольшая историческая справка, посвященная введению иррациональных чисел.

1. ИЗ ИСТОРИИ

Термин «рациональное» (число) происходит от латиноамериканского слова ratio – отношение, которое является переводом греческого слова “логос”в отличие от рациональных чисел, числа, выражающие отношение несоизмеримых величин, были названы еще в древности иррациональными, т.е. нерациональными (по-гречески “алогос”) правда, первоначально термины “рациональный” и “иррациональный” относились не к числам, а к соизмеримым и соответственно не соизмеримым величинам, которые пифагорейцы называли выразимыми и невыразимыми, Теодор Киренский же симметричными и ассимметричными. В V-VI вв. римские авторы Капелла и Кассиодор переводили эти термины на латынь словами rationalis и irrationalis. Термин «соизмеримый» (commensurabilis) ввел в первой половине VI в. другой римский автор- Боэций.

Древнегреческие математики классической эпохи пользовались только рациональными числами (вернее целыми, дробными и положительными). В своих «Началах» Евклид излагает учение об иррациональностях чисто геометрически.

Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных величин, которые, однако, длительное время не признавали за числа. Греки называли иррациональную величину, например, корень из квадратного числа, «алогос» – невыразимое словами, а позже европейские переводчики с арабского на латынь перевели это слово латинским словом surdus – глухой. В Европе термин surdus- глухой впервые появился в середине XII в. у Герарда Кремонского, известного переводчика математических прозведений с арабского на латынь, затем у итальянского математика Леонардо Фабоначчи и других европейских математиков, вплоть до XVIII в. Правда уже в XVI в. Отдельные ученые, в первую очередь итальянский математик Рафаэль Бомбелли и нидерландский математик Симон Стевин считали понятие иррационального числа равноправным с понятием рационального числа. Стевин писал: «Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной закономерностью.»

Еще до Бомбелли и Стевина многие ученые стран Среднего Востока в своих трудах употребляли иррациональные числа как полноправные объекты алгебры. Более того, комментируя «Начала» Евклида и исследуя общую теорию отношения Евдокса, Омар Хайям уже в начале XII в. теоретически расширяет понятие числа до положительного действительного числа. В том же направлении много было сделано крупнейшим математиком XIII в. ат-Туси.

Математики и астрономы Ближнего и Среднего Востока вслед за астрономами древнего Вавилона и эллинистической эпохи широко пользовались шестидесятеричными дробями, арифметические действия с которыми они называли «арифметикой астрономов». По аналогии с шестидесятеричными дробями самаркандский ученый XV в. ал-Каши в работе «Ключ арифметики» ввел десятичные дроби которыми он пользовался для повышения точности извлечения корней. Независимо от него по такому же пути шел открывший в 1585 г. десятичные дроби в Европе Симон Стевин, который в своих «приложениях к алгебре» (1594 г.) показал, что десятичные дроби можно использовать для бесконечно близкого приближения к действительному числу. Таким образом, уже в XVI в. зародилась идея о том, что естественным аппаратом для введения и обоснования понятия иррационального числа являются десятичные дроби. Появление «Геометрии» Декарта облегчило понимание связи между измерением любых отрезков (и геометрических величин вообще) и необходимости расширения понятия рационального числа. На числовой оси иррациональные числа, как и рациональные, изображаются точками. Это геометрическое толкование позволило лучше понять природу иррациональных чисел и способствовало их признанию.

В современных учебных руководствах основа определения иррационального числа опирается на идеи ал-Каши, Стевина и Декарта об измерении отрезков и о неограниченном приближении к искомому числу с помощью бесконечных десятичных дробей. Однако обоснованием свойств действительных чисел и полная теория их была разработана лишь в XIX в.

2. ОПРЕДЕЛЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ

Равносильные уравнения. Следствия уравнений.

При решении уравнений выполняются различные тождественные преобразования над выражениями, входящими в уравнение. При этом исходное уравнение изменяется другими, имеющими те же корни. Такие уравнения называются равносильными.

Определение: Уравнение f(x)=g(x) равносильно уравнению f1(x)=g1(x), если каждый корень первого уравнения является корнем второго и обратно, каждый корень второго уравнения является корнем первого, т.е. их решения совпадают.

Например, уравнения 3x-6=0; 2х–1=3 равносильны, т.к. каждое из уравнений имеет один корень х=2.

Любые два уравнения, имеющие пустое множество корней, считают равносильными.

Тот факт, что уравнения f(x)=g(x) и f1(x)=g1(x) равносильны, обозначают так:

f(x)=g(x) f1(x)=g1(x)

В процессе решения уравнений важно знать, при каких преобразованиях данное уравнение переходит в равносильное ему уравнение.

Теорема 1: Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив его знак, то получим уравнение, равносильное данному.

Доказательство: Докажем, что уравнение f(x) = g(x)+q(x) (1) равносильно уравнению

f(x) – q(x) = g(x) (2)

Пусть х=а – корень уравнения. Значит имеет место числовое равенство f(a)=g(a)+q(a) . Но тогда по свойству действительных чисел будет выполняться и числовое равенство f(a)-q(a)=g(a) показывающее, что а – корень уравнения (2). Аналогично доказывается, что каждый корень уравнения (2) является и корнем уравнения (1).

Что и требовалось доказатью.

Теорема 2: Если обе части уравнения умножить или разделить на отличное от нуля число, то получим уравнение, равносильное данному.

Доказательство: докажем, что уравнение 6х–3=0 равносильно уравнению 2х–1=0

решим уравнение 6х–3=0 и уравнение 2х–1=0

6х=3 2х=1

х=0,5 х=0,5

так как корни уравнений равны, то уравнения равносильны.

Что и требовалось доказать.

Рассмотрим уравнение

ОДЗ этого уравнения {х ≠ 1, х ≠ -3}

Мы знаем, что дробь равна нулю в том случае, когда ее числитель равен нулю, т.е. х²+х–2=0, а знаменатель не равен 0. Решая уравнение х²+х–2=0, находим корни х1=1, х2 = –2 . Но число 1 не входит в ОДЗ данного уравнения и значит, исходное уравнение имеет один корень х=-2.

В этом случае говорят, что уравнение х²+х–2=0, есть следствие уравнения

пусть даны два уравнения:

f1 (x) = g1 (x) (3)

f2 (x) = g2 (x) (4)

Если каждый корень уравнения (3) является корнем уравнения (4), то уравнение (4) называют следствием уравнения (3).

Этот факт записывают так:

В том случае, когда уравнение (3) - есть также следствие уравнения (4), эти уравнения равносильны.

Два уравнения равносильны в том, и только в том случае, когда каждое из них является следствием другого.

В приведенном выше примере уравнение – следствие х²+х–2=0, имеет два корня x1=1 и х2 =-2, а исходное уравнение имеет один корень х=-2. В этом случае корень х=1 называют посторонним для исходного уравнения

В общем случае корни уравнения-следствия, не являющиеся корнями исходного уравнения, называют посторонними.

Итак, если при решении уравнения происходит переход к уравнению – следствию, то могли появиться посторонние корни. В этом случае все корни уравнения-следствия нужно проверить, подставляя их в исходное уравнение. В некоторых случаях выявление посторонних корней облегчается знанием ОДЗ исходного уравнения – корни, не принадлежащие ОДЗ, можно сразу отбросить. Так, в приведенном примере посторонний корень х=1 не входит в ОДЗ уравнения и потому отброшен.

Иногда посторонние корни могут появиться и при тождественных преобразованиях, если они приводят к изменению ОДЗ уравнения. Например, после приведения подобных членов в левой части уравнения

ОДЗ которого {х -2},

получим уравнение следствие х²-4=0 имеющее два корня х1 = 2, х2 = -2 корень х2 = -2 – посторонний, так как не входит в ОДЗ исходного уравнения.

В тех случаях, когда в результате преобразований произошел переход от исходного уравнения к уравнению, не являющемуся его следствием, возможна потеря корней.

Например, уравнение (х+1)(х+3)= х+1 (5)

Имеет два корня. Действительно, перенося все члены уравнения в левую часть и вынося х+1 за скобки, получим (х+1)(х+2)=0, откуда находим х1=-1, х2=-2 .

Если же обе части уравнения (5) разделить («сократить») на х+1, то получим уравнение х+3=1, имеющее один корень х=-2. В результате такого преобразования корень х=-1 потерян. Поэтому делить обе части уравнения на выражение, содержащее переменную, можно лишь в том случае, когда это выражение отлично от нуля.

Для того, чтобы в процессе решения уравнения избежать потери корней, необходимо следить за тем, чтобы переход осуществлялся либо к равносильным уравнениям, либо к уравнениям-следствиям.

2.2. Определение иррациональных уравнений.

Иррациональными называются уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень.

Например:

3. МЕТОДЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ.

3.1. Решение иррациональных уравнений методом возведения обеих частей уравнения в одну и ту же степень.

Пример №1

Решить уравнение

Возведем обе части уравнения (1) в квадрат:

далее последовательно имеем:

5х – 16 = х² - 4х + 4

х² - 4х + 4 – 5х + 16 = 0

х² - 9х + 20 = 0

Проверка: Подставив х=5 в уравнение (1), получим – верное равенство. Подставив х= 4 в уравнение (1), получим – верное равенство. Значит оба найденных

значения – корни уравнения.

Ответ: 4; 5.

Пример №2

Решить уравнение:

(2)

Решение:

Преобразуем уравнение к виду:

и применим метод возведения в квадрат:

далее последовательно получаем.

Разделим обе части последнего уравнения почленно на 2:

еще раз применим метод возведения в квадрат:

далее находим:

9(х+2)=4–4х+х²

9х+18–4+4х-х²=0

-х²+13х+14=0

х²-13х–14=0

х1+х2 =13 х1 =19

х1 х2 = -14 х2 = -1

по теореме, обратной теореме Виета, х1=14, х2 = -1

корни уравнения х²-13х–14 =0

Проверка: подставив значение х=-14 в уравнение (2), получим–

- не верное равенство. Поэтому х = -14 – не корень уравнения (2).

Подставив значение x=-1 в уравнение (2), получим-

- верное равенство. Поэтому x=-1- корень уравнения (2).

Ответ: -1

3.2 Метод введения новых переменных.

Решить уравнение

Решение:

Конечно, можно решить это уравнение методом возведения обеих частей уравнения в одну и ту же степень. Но можно решить и другим способом – методом введения новых переменных.

Введем новую переменную Тогда получим 2y²+y–3=0 – квадратное уравнение относительно переменной y. Найдем его корни:

Т.к. , то – не корень уравнения, т.к. не

может быть отрицательным числом . А - верное равенство, значит x=1- корень уравнения.

Ответ: 1.

Искусственные приёмы решения иррациональных уравнений.

Решить уравнение:

(1)

Решение:

Умножим обе части заданного уравнения на выражение

сопряжённое выражению

Так как

То уравнение (1) примет вид:

Или

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом известен. Тогда x1=0.Остаётся решить уравнение:

(2)

Сложив уравнения (1) и (2), придём к уравнению

(3)

Решая уравнение (3) методом возведения в квадрат, получим:

Проверка:

x1=0, x2=4, x3= -4 подставим в уравнение

- не верное равенство, значит x1=0- не корень уравнения.

- верное равенство, значит x2=4- корень уравнения.

- не верное равенство, значит x3= -4- не корень уравнения.

Ответ: 4.

ЗАКЛЮЧЕНИЕ

Итак, уравнения, которые содержат переменную под знаком корня, называются иррациональными. Иррациональные уравнения решаются в основном возведением обеих частей уравнения в квадрат (или n-ую степень) или введением новой переменной. Кроме того, пользуются и искусственными приемами решения иррациональных уравнений.

Список литературы

1) А.Г.Мордкович. Алгебра 8 класс. Учебник для общеобразовательных учреждений - Москва: Издательство «Мнемозина», 1999.

2) М.Я.Выгодский. Справочник по элементарной математике - Москва: Издательство «Наука», 1986.

3) А.П.Савин. Энциклопедический словарь юного математика – Москва: Издательство «Педагогика», 1989.

4) А.И.Макушевич. Детская энциклопедия – Москва: Издательство «Педагогика», 1972.

5) Н.Я.Виленкин. Алгебра для 9 класс. Учебное пособие для учащихся школ и классов с углубленным изучением изучением математики – Москва: Издательство «Просвещение», 1998.

Для подготовки данной работы были использованы материалы с сайта http://www.ed.vseved.ru/

topref.ru

Реферат Иррациональность

скачать

Реферат на тему:

План:

1 История
- 1.1 Средние века
- 1.2 Наше время
2 Свойства
3 Теоремы
- 3.1 Корень из 2 — иррациональное число
- 3.2 log23 — иррациональное число
- 3.3 e — иррациональное число
4 Другие иррациональные числа

Введение

1. История

Отношение длины гипотенузы к длине катета равнобедренного прямоугольного треугольника может быть выражено как a:b, где a и b выбраны наименьшими из возможных.
По теореме Пифагора: a² = 2b².
Так как a² четное, a должно быть четным (так как квадрат нечетного числа был бы нечетным).
Поскольку a:b несократима, b обязано быть нечетным.
Так как a четное, обозначим a = 2y.
Тогда a² = 4y² = 2b².
b² = 2y², следовательно b² четное, тогда и b четно.
Однако было доказано, что b нечетное. Противоречие.

1.1. Средние века

1.2. Наше время

2. Свойства

Всякое вещественное число может быть записано в виде бесконечной десятичной дроби, при этом иррациональные числа и только они записываются непериодическими бесконечными десятичными дробями.
Иррациональные числа определяют Дедекиндовы сечения в множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.
Каждое трансцендентное число является иррациональным.
Каждое иррациональное число является либо алгебраическим, либо трансцендентным.
Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя числами имеется иррациональное число.
Множество иррациональных чисел несчётно, является множеством второй категории.[1]

3. Теоремы

3.1. Корень из 2 — иррациональное число

$\sqrt{2} = \frac{m}{n} \Rightarrow 2 = \frac{m^2}{n^2} \Rightarrow m^2 = 2n^2$ .

Отсюда следует, что m2 чётно, значит, чётно и m. Пускай m = 2r, где r целое. Тогда

$(2r)^2=2n^2 \Rightarrow n^2=2r^2$

3.2. log23 — иррациональное число

$\log_2 3 = \frac{m}{n} \Rightarrow m = n \log_2 3 \Rightarrow 2^m = 2^{n \log_2 3} = \left (2^{\log_2 3}\right )^n = 3^n$

Но 2m чётно, а 3n нечётно. Получаем противоречие.

3.3. e — иррациональное число

См. раздел «Доказательство иррациональности» в статье «e».

4. Другие иррациональные числа

Иррациональными являются:

$\sqrt{n}$ для любого натурального n, не являющегося точным квадратом
ex для любого рационального $x\ne 0$
lnx для любого положительного рационального $x\ne 1$
π, а также πn для любого натурального n

wreferat.baza-referat.ru

Иррациональные числа | Учеба-Легко.РФ - крупнейший портал по учебе

Мы уже неоднократно отмечали, что не все числа, с которыми приходится встречаться в реальной жизни, являются рациональными. Так, не является рациональным числом длина гипотенузы прямоугольного треугольника с катетами 1 см и 2 см: в самом деле, длина с гипотенузы этого треугольника и длины катетов связаны, по теореме Пифагора, соотношением с2 = I2 + 22. Значит, с = 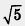см, а 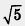- не рациональное число. Корни уравнения х2 = 7 также не являются рациональными числами — это числа 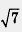и -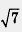 . Что же это за числа, которые не являются рациональными? Прежде всего заметим, что в математике не принято говорить «нерациональное число», обычно используют термин иррациональное число. Термины «рациональное число», «иррациональное число» происходят от латинского слова ratio — «разум» (буквальный перевод: «рациональное число — разумное число», «иррациональное число — неразумное число»; впрочем, так говорят и в реальной жизни: «он поступил рационально» — это значит, что он поступил разумно; «так действовать нерационально» — это значит, что так действовать неразумно).

Рассмотрим уже известное нам иррациональное число 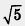. В § 15 мы отмечали, что оно заключено между числами 2 и 3; если точнее, то между числами 2,2 и 2,3; если еще точнее, — то между числами 2,23 и 2,24. Можно продолжить уточнения оценок числа 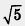и определить границы для третьего десятичного знака после запятой. Имеем 2,2362 = 4,999696, что меньше 5; 2,2372 = = 5,004167, что больше 5.

Итак, 2,236 < 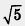< 2,237. Точно так же можно определить границы для четвертого знака после запятой, для пятого знака и т. д. Ясно, что выполняется приближенное равенство

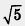
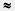2,236. Если же считать, что для числа 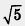выписаны все последующие десятичные знаки, то можно воспользоваться записью 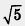= 2,236... . Это — бесконечная десятичная дробь. В предыдущем параграфе мы уже встречались с бесконечными десятичными дробями, но все они были периодическими и выражали рациональные числа. Иррациональное число 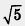выражается бесконечной десятичной непериодической дробью.

Вообще, иррациональным числом называют бесконечную десятичную непериодическую дробь. Такие числа встречаются не только при извлечении квадратного корня, но и во многих других случаях, в чем вы не раз убедитесь в старших классах.

Пока приведем только один пример. Если длину любой окружности разделить на ее диаметр, то в частном получится иррациональное число 3,141592... . Этот факт установил еще в III веке до н. э. греческий математик и философ Архимед. Для указанного числа в математике введено специальное обозначение % (буква греческого алфавита «пи»).

Любая арифметическая операция над рациональными числами приводит в результате к рациональному числу. Это и понятно, ведь сумма (разность, произведение, частное) обыкновенных дробей есть обыкновенная дробь (все логично, ведь рациональные числа — «разумные» числа). А как обстоит дело с иррациональными числами? Оказывается, ничего определенного сказать нельзя (что тоже логично, ведь иррациональные числа — «неразумные» числа). Смотрите: 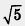— иррациональное число, 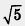. 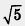=5 — рациональное число, т. е. произведение двух иррациональных чисел оказалось рациональным числом; 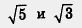— иррациональные числа, и их произведение, т. е. 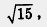— тоже иррациональное число. То же относится к сложению, вычитанию, делению иррациональных чисел: в ответе может получиться как рациональное, так и иррациональное число.

А что получится, если в операции участвуют одно рациональное число и одно иррациональное число, какое «пересилит»? Оказывается, «пересилит» иррациональное число. Рассмотрим такой пример: дано рациональное число 3 и иррациональное число ;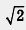

составим их сумму 3 + 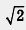• Предположим, что это — рациональное число r, т. е. 3 + 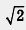= г. Тогда 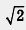= г - 3, а r - 3 — рациональное число (как разность двух рациональных чисел). Получается, что 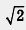— рациональное число, а это неверно, ведь мы знаем, что это число — иррациональное. Получили противоречие, значит, сделанное нами предположение неверно, т. е. 3 + 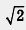— иррациональное число. Аналогично можно доказать, что 3- 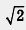— иррациональное число.

Замечание. Обратите внимание, что в проведенном рассуждении мы снова использовали метод доказательства от противного, о котором в первый раз говорили выше, в § 15.

Итак, можно сделать следующие выводы: • Любая арифметическая операция над рациональными числами (кроме деления на 0) приводит в результате к рациональному числу. • Арифметическая операция над иррациональными числами может привести в результате как к рациональному, так и к иррациональному числу. • Если в арифметической операции участвуют рациональное и иррациональное числа, то в результате получится иррациональное число (кроме умножения и деления на 0).

Поскольку операция извлечения квадратного корня из положительного числа часто приводит к иррациональным числам, условились алгебраическое выражение, в котором присутствует операция извлечения квадратного корня, называть иррациональным выражением.

Кстати, и термин «освобождение от иррациональности в знаменателе», который мы использовали в § 18, объясняется теми же причинами.

uclg.ru