|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
3 Модели кровообращения. Физические основы клинического метода измерения давления крови. Физические основы клинического метода измерения давления крови реферат
Лабораторная работа № 1.9 физические основы измерения артериального давления крови. Знакомство с аппаратом для измерения давления крови
83
Мотивационная характеристика темы. Одним из важных параметров гемодинамики - раздела биомеханики, изучающего движение крови, является артериальное давление. В связи с чем методы его измерения являются актуальными для медицинского работника
Цель лабораторной работы.
Изучить физические основы клинического метода измерения давления крови. Познакомиться с аппаратом для измерения давления крови - ИАД-1. Научиться косвенно измерять систолическое и диастолическое артериальное давление крови по методу Короткова.
| Знать | Уметь |
| 1.Чем определяется давление в текущей жидкости ? 2.Формулировку и запись уравнения Бернули и его следствий. 3.Как определяются статическое, гидростатическое и динамическое давления. 4.Какое давление определяется в методе Короткова. | 1.Пользоваться аппаратом для измерения артериального давления крови ИАД-1. 2.Объяснить физический смысл шумов Короткова. 3.Объяснить физический смысл систолического и диастолического давлений. |
Литература:
1.А.Н.Ремизов. Медицинская и биологическая физика. М., 1999, Гл. 11.
1.А.Н.Ремизов. Медицинская и биологическая физика. М., 1987, Гл.11.
2.А.Н.Ремизов. Курс физики, электроники и кибернетики. М., 1982, Гл.8.
Контрольные вопросы для определения исходного уровня знаний
Как объясняется явление внутреннего трения (вязкость) жидкости? Ньютоновские и неньютоновские жидкости.
От чего зависит характер течения жидкости? Число Рейнольдса.
Запишите и проанализируйте уравнение Бернули.
Как распределяется давление при течении реальной жидкости по трубам постоянного, переменного сечения и разветвленным?
Проанализируйте механические и электрические модели кровообращения, в чем их особенности? Ударный объем крови.
Объясните физические основы клинического метода измерения давления крови.
Краткая теория
Уравнение Бернулли. Давление в потоке жидкости. В стационарном потоке идеальной несжимаемой жидкости вырежем отсек тонкой трубки тока (рис.1) между сечениями S1 и S2 . Во входном сечении S1 давление p1, скорость u1 и высота сечения над произвольным уровнем h2; в выходном сечении S2 соответственно p2, u2, h3. За промежуток времени Dt масса входящей в отсек жидкости равна массе жидкости, выходящей из отсека.
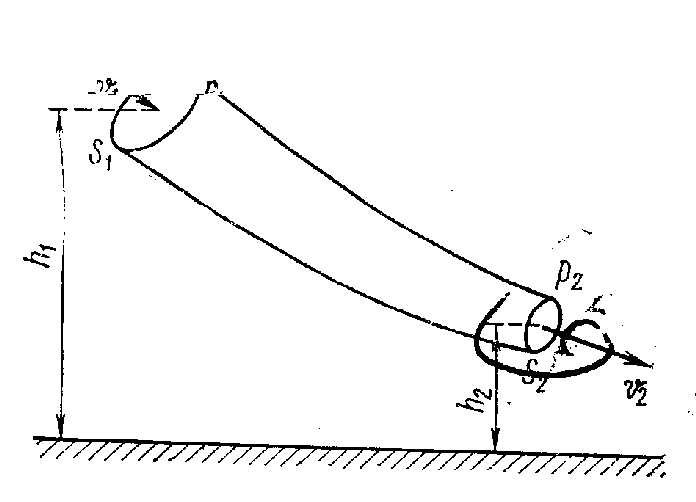
Рис.1 К выводу уравнения Бернулли
Масса жидкости, протекающей за время Dt через сечение S1, имеет кинетическую энергию, равную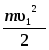 и обладает потенциальной энергией mgh2. В результате действия сил давления на сечения S1 и S2 со стороны слоев жидкости, находящихся слева от S1 и справа от S2, производится работа
и обладает потенциальной энергией mgh2. В результате действия сил давления на сечения S1 и S2 со стороны слоев жидкости, находящихся слева от S1 и справа от S2, производится работаA = p1S1l1 - p2S2l2
где путь l1 за время Dt равен l1= u Dt, а путь l2= u2Dt. Следовательно, работа А, совершаемая потоком, равна
Dt, а путь l2= u2Dt. Следовательно, работа А, совершаемая потоком, равна
A = p1S1u1Dt - p2S2u2Dt
Полная энергия потока, протекающего за время Dt через входное сечение S1, будет 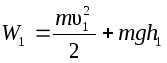 ,
,
а через сечение S2 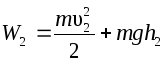
Между сечениями S1 и S2 аккумуляции энергии нет. Изменение полной энергии жидкости равно работе, совершенной внешними силами, т.е.
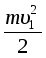 + mgh2-
+ mgh2- 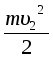 - mgh3= p2S2u2Dt - p1S1u1Dt (1)
- mgh3= p2S2u2Dt - p1S1u1Dt (1)
Согласно уравнению неразрывности объемы, входящие в S1 за время Dt и выходящие через S2, одинаковы, поэтому можно записать
S1u1Dt = S2u2Dt = V
Разделив левую и правую части уравнения (1) на V и используя формулу плотности
r = 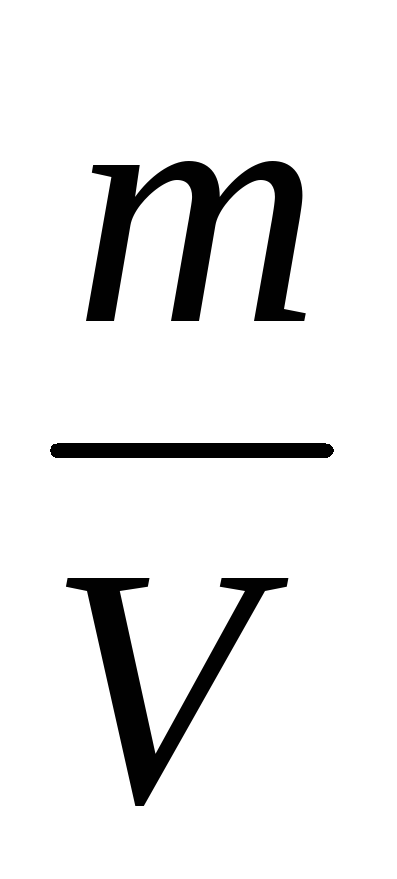
получаем уравнение Бернулли для двух различных сечений трубки тока
r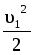 + rgh2 + p1= r
+ rgh2 + p1= r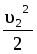 +rgh3+ p2 (2)
+rgh3+ p2 (2)
Если весь поток разбить на тонкие трубки тока, то для каждого сечения будет справедлива такая запись уравнения Бернулли:
r 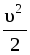 +rgh + p = const, (3)
+rgh + p = const, (3)
где слагаемое р называется статическим давлением; член, содержащий скорость и имеющий размерность давления, т.е. r 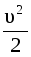 , называется динамическим давлением.
, называется динамическим давлением.
Это уравнение лежит в основе решения многих задач гидродинамики. Оно применимо для таких маловязких жидкостей, как вода, и во многих случаях для воздуха.
В качестве следствий из уравнения Бернулли рассмотрим два случая: горизонтальное течение жидкости и истечение жидкости из отверстия.
1. При горизонтальном течении жидкости (например, в горизонтальной трубе) h = const, поэтому в уравнении (3) выпадают члены, содержащие h, и оно принимает вид:
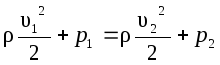 , (4)
, (4)
т.е. при горизонтальном течении жидкости сумма динамического и статистического давлений не меняется при отсутствии трения.
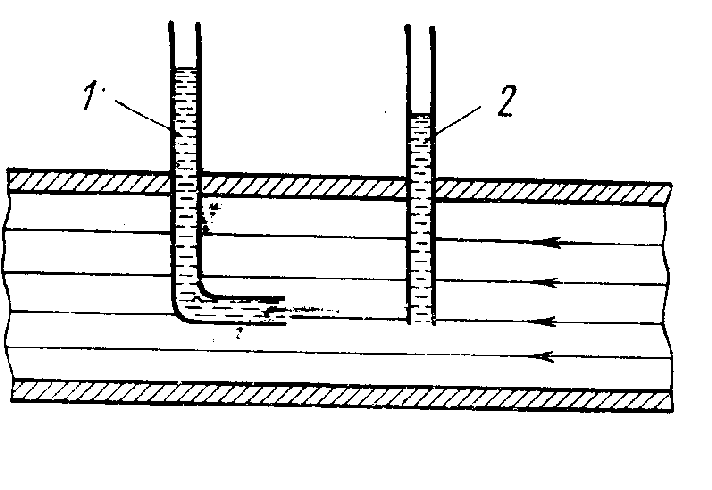
Рис.2. Манометры
Статистическое давление измеряется с помощью манометра, нижний срез которого параллелен направлению потока (рис.2). Если же измерительная трубка имеет изгиб и отверстие трубки направлено навстречу потоку, то частицы жидкости, входя в отверстие, будут тормозиться, т.е. возникает сила торможения, и трубка покажет большое давление. Манометр называется трубкой Пито, он измеряет полное давление - сумму статистического и динамического (скоростного) давлений. Разность уровней в трубках 2 и 1 определяет динамическое давление. На этом основано изменение скорости потока или скорости тел, движущихся в жидкостях или газе, например, скорости макетов самолетов в аэродинамических трубах. 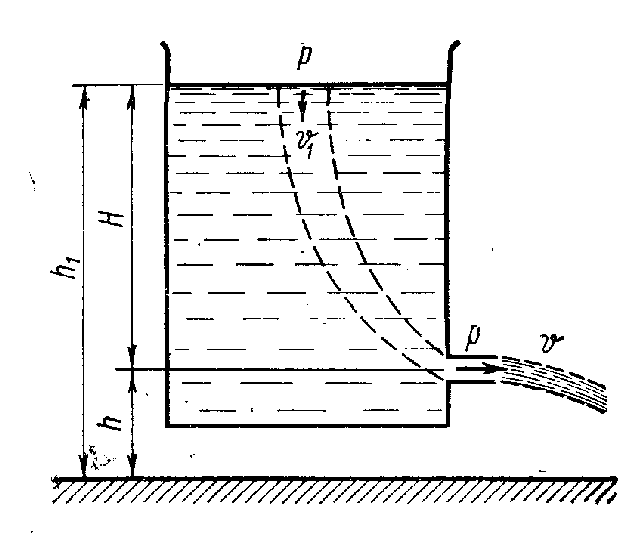 2. При истечении жидкости из отверстия (рис.3) будем считать, что внешнее давление р (например, атмосферное) неизменно и выходное отверстие по сечению мало в сравнении с площадью поверхности жидкости в сосуде.
2. При истечении жидкости из отверстия (рис.3) будем считать, что внешнее давление р (например, атмосферное) неизменно и выходное отверстие по сечению мало в сравнении с площадью поверхности жидкости в сосуде.
Рис.3. Истечение жидкости из отверстия
Скорости v частиц жидкости в сечении выходного отверстия считаем одинаковыми. Одинаковыми будут и скорости движения частиц поверхности, так как поверхность остается горизонтальной. Напишем уравнение Бернулли для любой трубки тока, одно сечение которой лежит на выходном отверстии, другое на поверхности жидкости в сосуде: 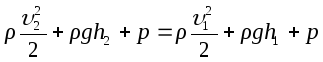
или перепишем его в виде
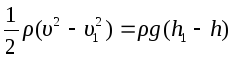
Так как h2- h = H и скорость u >> u , то членом u
, то членом u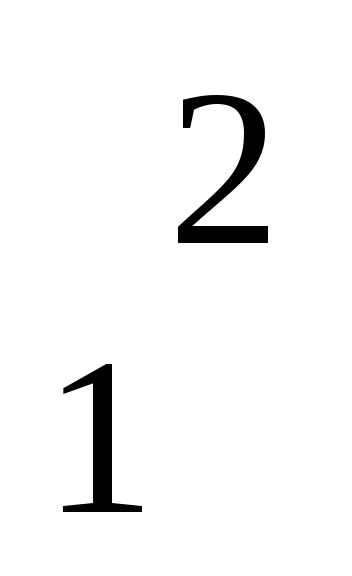 можно пренебречь, и мы получим
можно пренебречь, и мы получим
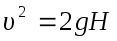
откуда
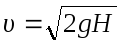 (5)
(5)
Следовательно, скорость истечения будет такой же, как и в том случае, если бы частицы жидкости падали свободно с высоты Н.
Формула (5) справедлива как для боковых, так и для донных отверстий и не зависит от угла наклона выходного отверстия.
Физические основы клинического метода измерения давления крови. Физический параметр - давление крови - играет большую роль в диагностике многих заболеваний.
Систолическое и диастолическое давления в какой-либо артерии могут быть измерены непосредственно с помощью иглы, соединенной с манометром. Однако, в медицине широко используется бескровный метод, предложенный Н.С. Коротковым. Рассмотрим физические основы этого метода на примере измерения давления в плечевой артерии.
Вокруг руки между плечом и локтем накладывают манжету. Сечения манжеты М, части руки Р, плечевой кости П и плечевой артерии А показаны на рис.4а -- 6а. При накачивании воздуха через шланг В в манжету рука сжимается. Затем через этот же шланг воздух выпускают и с помощью манометра Б измеряют давление воздуха в манжете. На поз. Б тех же рисунков изображены продольные сечения плечевой артерии, соответствующие каждому случаю. Сначала избыточное над артериальным давление воздуха в манжете равно нулю (рис.4), манжета не сжимает руку и артерию. По мере накачивания воздуха в манжету последняя сдавливает плечевую артерию и прекращает ток крови (рис.5). Если мускулатура расслаблена, то давление воздуха внутри манжеты, состоящей из эластичных стенок, приблизительно равно давлению в мягких тканях, соприкасающихся с манжетой. В этом заключается основная физическая идея бескровного метода измерения давления.
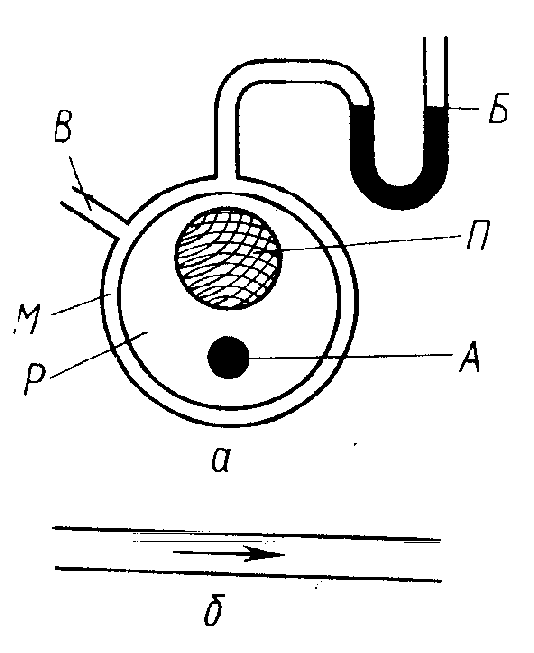
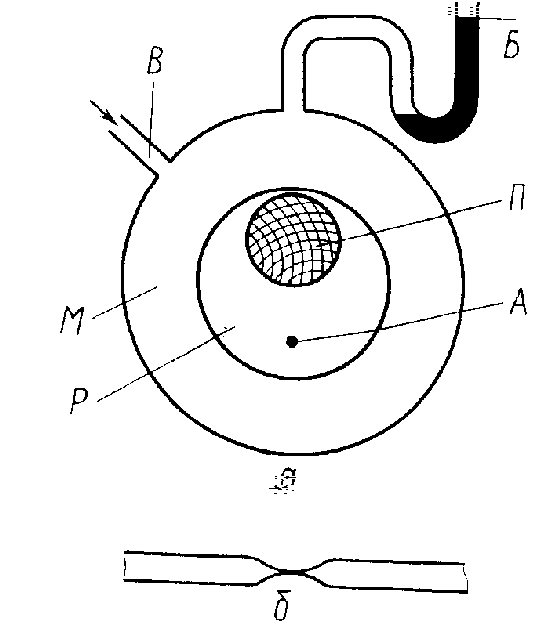
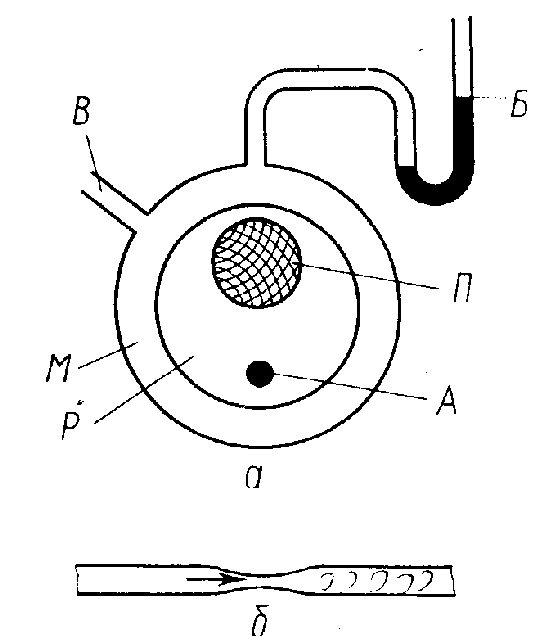
Рис.4 - 6. Физические основы метода Н.С.Короткова
Выпуская воздух, уменьшают давление в манжете и мягких тканях, с которыми она соприкасается. Когда давление станет равным систолическому, кровь будет способна пробиться через сдавленную артерию - возникает турбулентное течение (рис. 6).Характерные тоны и шумы, сопровождающие этот процесс, прослушивает врач при измерении давления, располагая фонендоскоп на артерии ниже манжеты, Продолжая уменьшать давление в манжете, можно восстановить ламинарное течение крови, что заметно по резкому ослаблению прослушиваемых тонов. Давление в манжете, соответствующее восстановлению ламинарного течения в артерии , регистрируют как диастолическое.
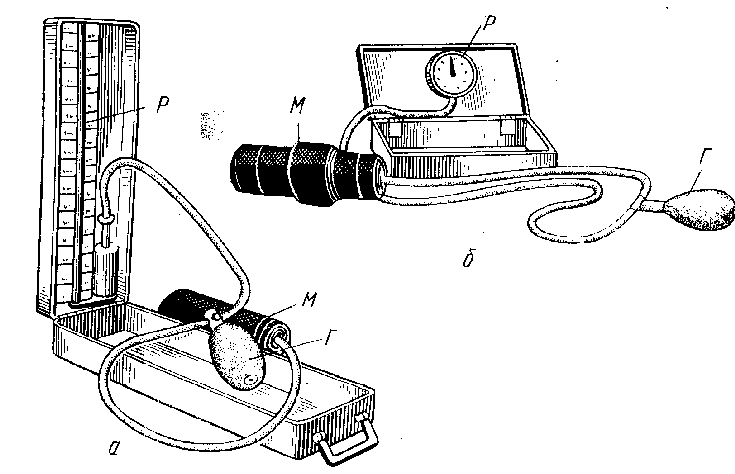
Рис.7. Аппараты для измерения артериального давления
Для измерения артериального давления применяют приборы, показанные на рис.7: а - сфигмоманометр с ртутным манометром, б - сфигмотонометр с металлическим мембранным манометром; здесь - М - манжета, Г - груша для накачивания воздуха, Р - манометр.Аппарат для измерения артериального давления ИАД-1. Измеритель артериального давления ИАД-1 ( далее измеритель) является электронным прибором, предназначенным для косвенного измерения систолического (верхнего) и диастолического (нижнего) артериального давления крови по методу Короткова.
При использовании данного измерителя для измерения артериального давления крови отпадает необходимость применения стетофонендоскопа.
Высокочувствительный датчик, встроенный в манжету, позволяет производить измерения артериального давления крови, не оголяя плеча, т.е. через рубашку или другую легкую одежду.
Основные технические характеристики:
Пределы измерения , мм.рт.ст. от 20 до 300
Предел допускаемой основной погрешности м.рт.ст. +4
3. Температура окружающей среды, при которой измеритель сохраняет правильность показаний, оС от + 10 до + 35
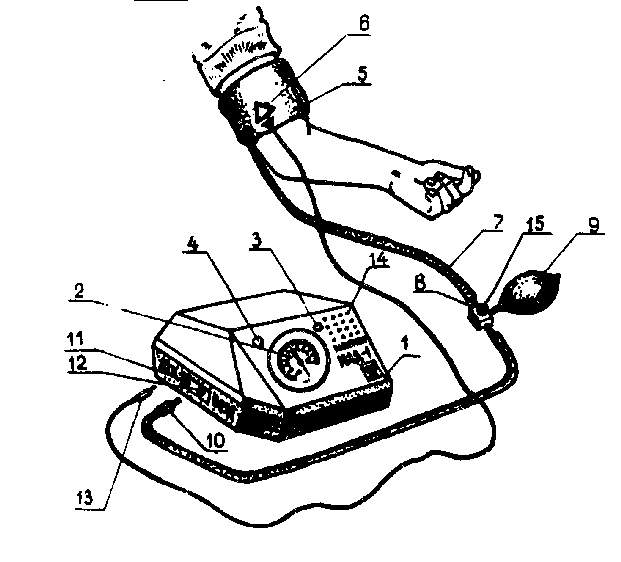 Устройство измерителя. Внешний вид измерителя изображен на Рис. 8. Измерительный блок 1 имеет встроенный манометр 2, световой индикатор 3 разряда батарей, световой индикатор 4 регистрации тонов Короткова, гнездо 11 для подключения датчика - «ДТК», гнездо 12 для подключения манжеты - «Воздух», перфорацию 14 на лицевой панели для выхода звукового сигнала..
Устройство измерителя. Внешний вид измерителя изображен на Рис. 8. Измерительный блок 1 имеет встроенный манометр 2, световой индикатор 3 разряда батарей, световой индикатор 4 регистрации тонов Короткова, гнездо 11 для подключения датчика - «ДТК», гнездо 12 для подключения манжеты - «Воздух», перфорацию 14 на лицевой панели для выхода звукового сигнала..
Рис.8
1 - измерительный блок; 2 - манометр; 3 - световой индикатор разряда батарей; 4 - световой индикатор регистрации тонов Короткова; 5 - компрессионная манжета; 6 - метка расположения датчика ДТК-1М; 7 - резиновая трубка; 8- тройник пневматического нагнетателя; 9 - пневматический нагнетатель; 10 - конусная муфта; 11 - гнездо подключения конусной муфты; 13 - штекер датчика; 14 - перфорация; 15 - вентиль тройника . (Рис.8.) 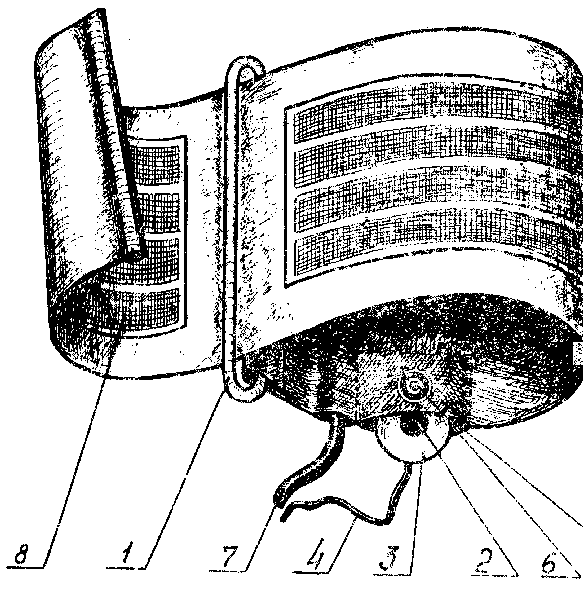 Компрессионная манжета 5 представляет собой резиновый мешок, помещенный в чехол. От нее6 отходит резиновая трубка 7 и шнур датчика. Шнур датчика заканчивается штекером 13. Через тройник 8 пневматического нагнетателя 9 резиновая трубка при помощи конусной муфты 10 подключается к измерительному блоку. Тройник пневматического нагнетателя снабжен вентилем, с помощью которого осуществляется плавное или ускоренное снабжение давления в манжете.
Компрессионная манжета 5 представляет собой резиновый мешок, помещенный в чехол. От нее6 отходит резиновая трубка 7 и шнур датчика. Шнур датчика заканчивается штекером 13. Через тройник 8 пневматического нагнетателя 9 резиновая трубка при помощи конусной муфты 10 подключается к измерительному блоку. Тройник пневматического нагнетателя снабжен вентилем, с помощью которого осуществляется плавное или ускоренное снабжение давления в манжете.
Рис.9 1 - металлическая скоба; 2 - пилот датчика; 3 - датчик ДТК - 1М; 4 - шнур датчика; 5 - карман для установки датчика; 6 - метка расположения датчика ДТК - 1М; 7 - резиновая трубка; 8 - текстильная застежка.
На Рис.9 показано, как устанавливается датчик 3 в карман % манжеты. На месте расположения датчика нанесена специальная метка 6 Пилот 2 датчика должен быть обращен к поверхности манжеты, которая прикладывается к плечу. На чехле манжеты имеется текстильная застежка 8, состоящая из петельной или крючковой ленты, с помощью которой осуществляется фиксация манжеты на плече (Рис.10).
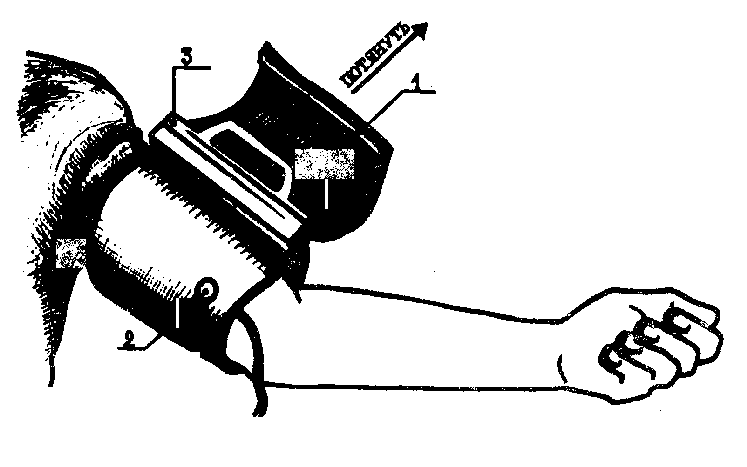
Датчик устанавливается пилотом к поверхности манжеты, которая прикладывается к плечу.
Рис.10
Принцип работы измерителя. Принцип работы измерителя заключается в выделении и преобразовании тонов Короткова в звуковую и световую индикации с одновременным визуальным наблюдением за величиной артериального давления крови на стрелочном манометре.По окончании измерения для быстрого стравливания воздуха нужно разъединить конусную муфту 10 от гнезда 12 при давлении в системе не более 100 мм.рт.ст.
studfiles.net
3 Модели кровообращения. Физические основы клинического метода измерения давления крови
3.1 Модели кровообращения
Гемодинамикой называют область биомеханики, в которой исследуются движения крови по сосудистой системе. Физической основой гемодинамики является гидродинамика.
Известно, что течение крови зависит как от свойств крови, так и от свойств кровеносных сосудов. Для анализа работы кровеносной системы были предложены различные модели: более простая модель, разработанная О. Франком; более сложная — модель Ростона. Хотя модель, предложенная О. Франком более проста, но она позволяет установить связь между ударным объёмом крови (объём крови, вырабатываемый за одну секунду), гидравлическом сопротивлением периферической части системы кровообращения Х0 и изменением давления в артериях. Модель представлена на рисунке 3.1.
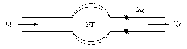
Рис 3.1
Рисунок 3.1 - Модель течения крови Франка
Артериальная часть системы моделируется упругим резервуаром (УР).
Так как кровь находиться в упругом резервуаре, то её объем в любой момент времени зависит от давления по следующему соотношению:
V = V0 + KP, (3.1)
где К – коэффициент пропорциональности, устанавливающий связь между давлением и объёмом;
V0 – объём резервуара при отсутствии давления (Р = 0).
Продифференцировав (3.1), получим:
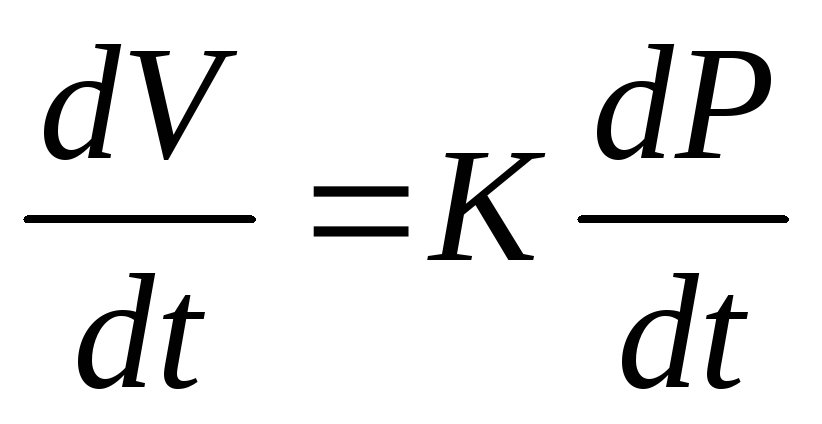 (3.2)
(3.2)
В УР (артерии) поступает кровь от сердца. При этом объёмная скорость кровотока = Q. От УР кровь оттекает с объёмной скоростью кровотока Q в периферическую систему. В предположении, что гидравлическое сопротивление периферической системы постоянно, то это моделируется „жёсткой“ (на рисунке 3.1) трубкой на выходе УР. Поэтому можно составить очевидное уравнение:
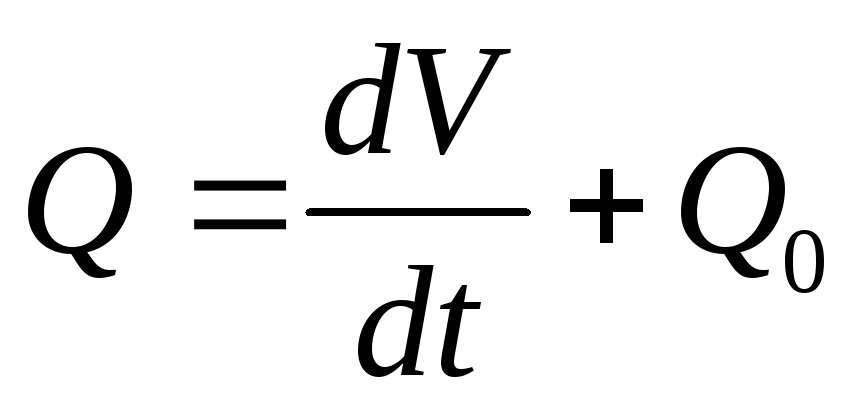 , (3.3)
, (3.3)
показывающее, что объёмная скорость кровотока из сердца равна скорости возрастания объёма УР и скорости оттока крови из УР (Q0).
На основании формулы Пуазейля можно записать для периферической части системы Х0 значение Q0.
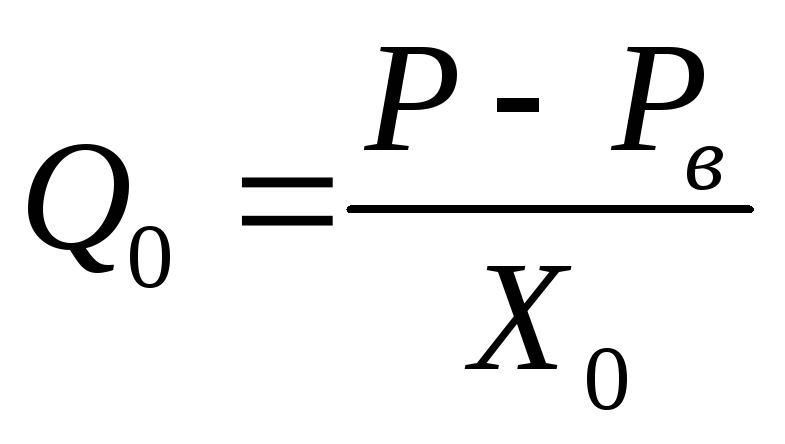 (3.4)
(3.4)
где Р – давление в УР
Рв – венозное давление, которое может быть принято 0, тогда (3.4) можно записать:
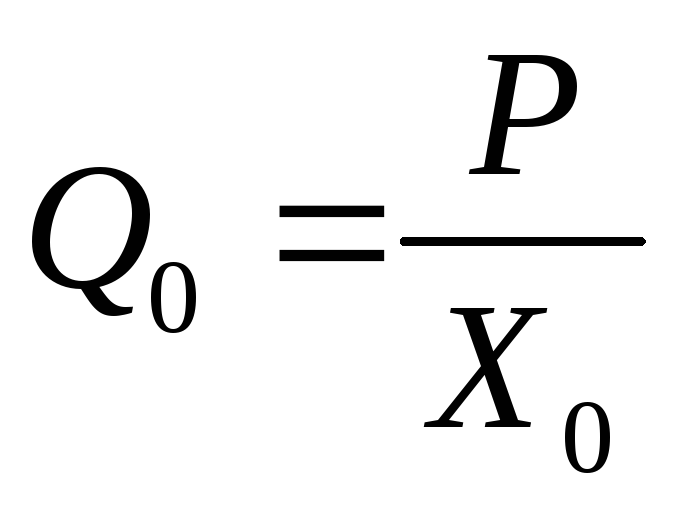 (3.5)
(3.5)
Далее, подставив (3.2) и (3.5) в (3.3), получим:
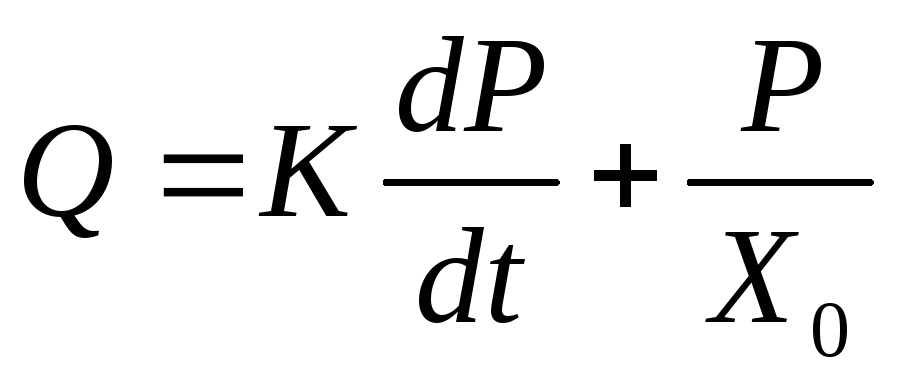 (3.6)
(3.6)
или
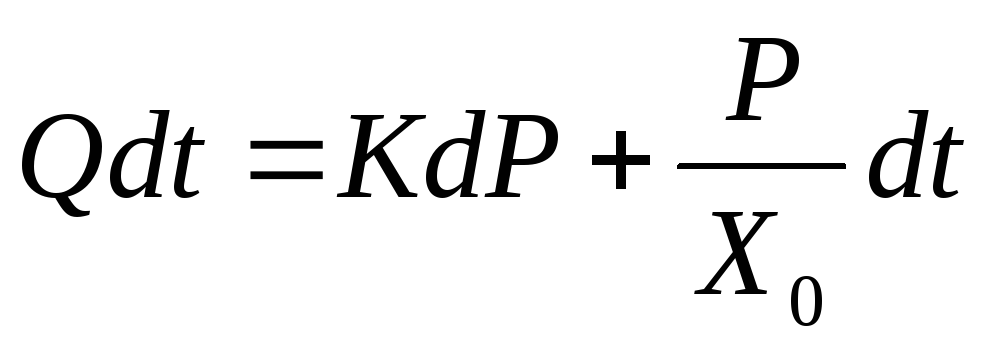 (3.6)
(3.6)
Проинтегрируем (3.6). Пределы интегрирования соответствуют периоду пульса (периоду сокращения сердца – время между зубцами R–R кардиограммы) от 0 до Тп. Этим временным пределам соответствуют одинаковые давления, т. е. минимальное
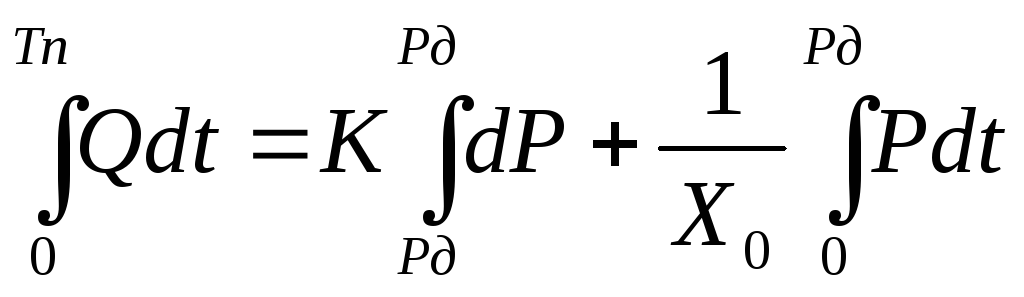 (3.7)
(3.7)
И
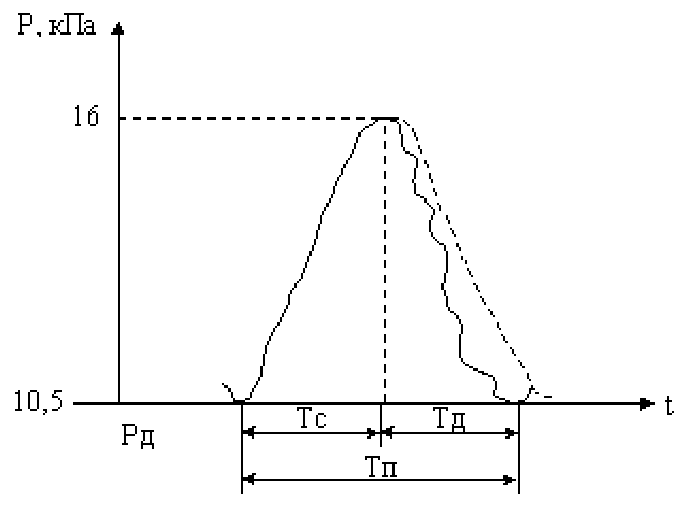
Рисунок 3.2 - Экспериментальная кривая зависимости давления крови от времени
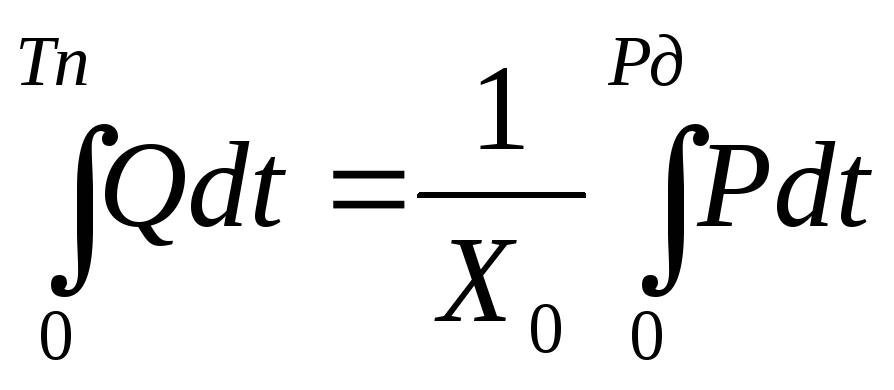 (3.8)
(3.8)
Экспериментальная кривая приведена на рисунке 3.2 (сплошная линия).
На рисунке показан период пульса Тп, длительность систолы Тс (верхнее давление 120 мм. рт. ст.) и Тд диастолы (нижнее давление 90 мм. рт. ст.). Интеграл в левой части (3.8) соответствует объёму крови, выталкиваемой из сердца за одно сокращение (ударный объём), который может быть найден экспериментально. Интеграл в правой части равен площади между кривой и осью времени (его тоже можно найти). Используя выражение (3.8), можно найти гидравлическое сопротивление периферической части системы кровообращения.
Во время систолы происходит расширение УР (штриховая линия рис. 3.2), во время диастолы – отток крови в периферии (Q0 = 0). Для этого периода из (3.6) получим:
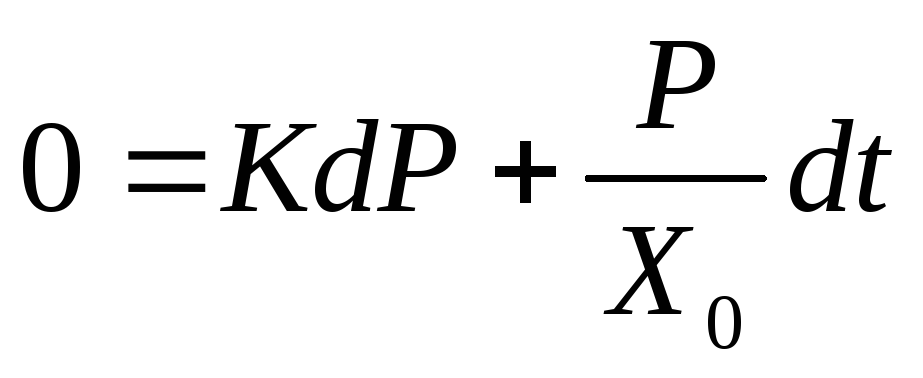 или
или 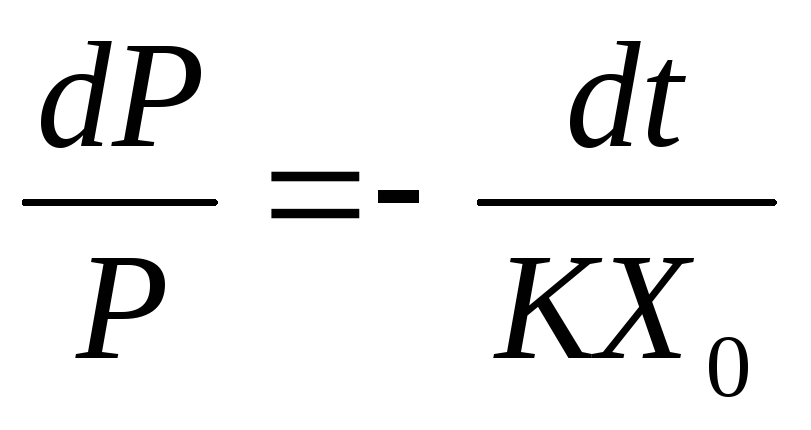 (3.9)
(3.9)
Проинтегрировав (3.9), получим зависимость давления в УР от времени. (это штриховая кривая на рис. 3.2). Аналогично можно определить зависимость объёмной скорости оттока крови во времени:
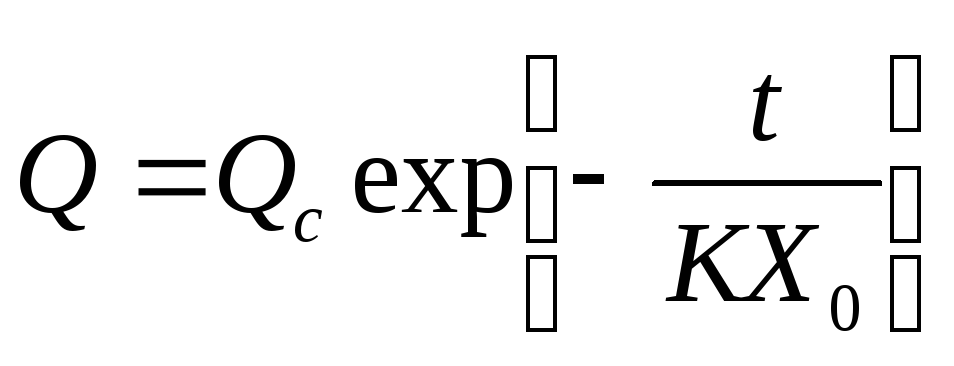
где 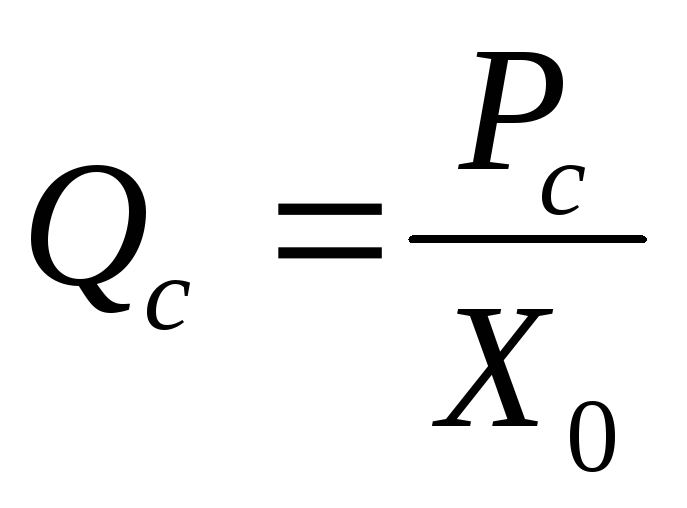 – объёмная скорость кровотока из упругого резервуара в конце систолы (начале диастолы).
– объёмная скорость кровотока из упругого резервуара в конце систолы (начале диастолы).
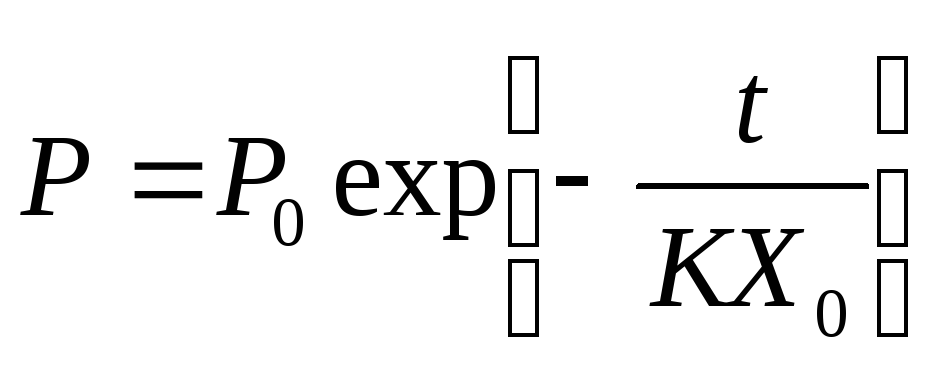 (3.10)
(3.10)
Примечание: При решении задач необходимо правильно учитывать размерность. Если речь идёт об объёмном кровотоке, то размерность равна 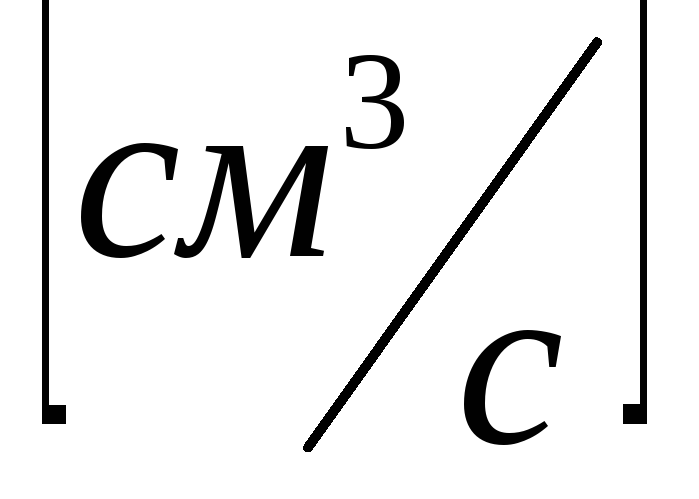 . Поэтому необходимо правильно предоставлять формулу Пуазелья. Формула Пуазелья для труб переменного сечения (а в реальной модели кровотока они изменяются, т. к. УР эластичен), то формула (3.4) примет вид:
. Поэтому необходимо правильно предоставлять формулу Пуазелья. Формула Пуазелья для труб переменного сечения (а в реальной модели кровотока они изменяются, т. к. УР эластичен), то формула (3.4) примет вид:
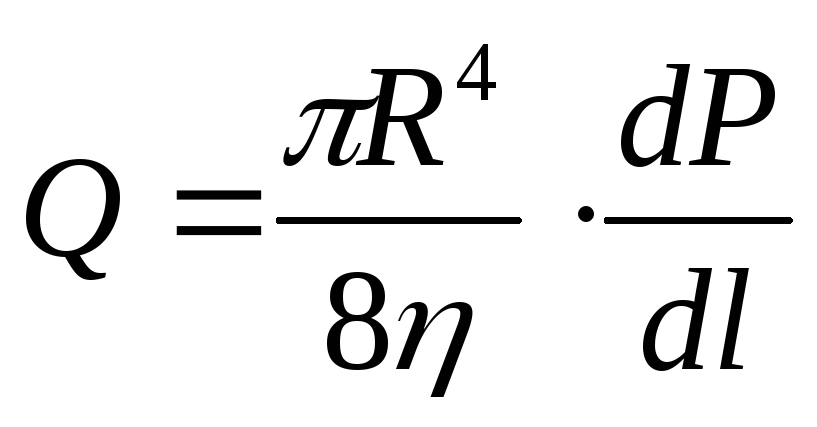 (3.11)
(3.11)
где R – радиус сосуда; η – коэффициент пропорциональности (коэффициент вязкости), размерность которого 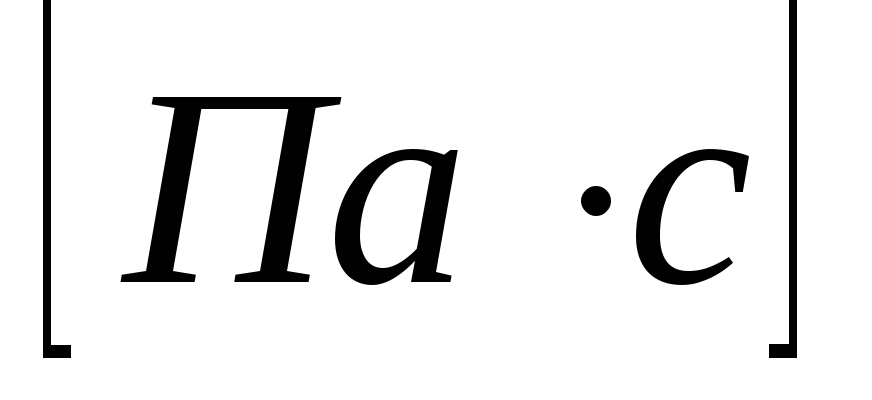 ;
;
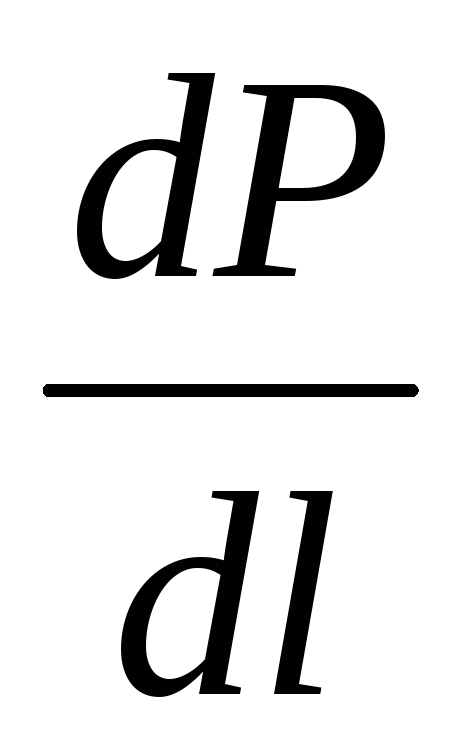 –изменение давления по длине сосуда
–изменение давления по длине сосуда 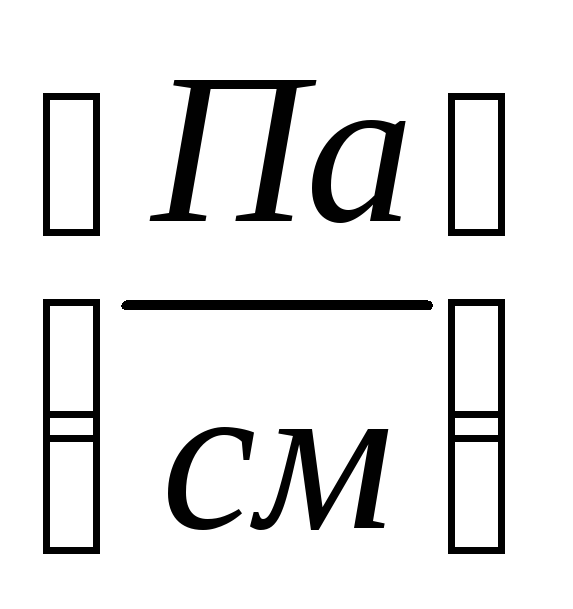 .
.
Величина Х в выражении (3.4) несёт смысл гидравлического сопротивления для „жёсткого“ сосуда и описывается выражением:
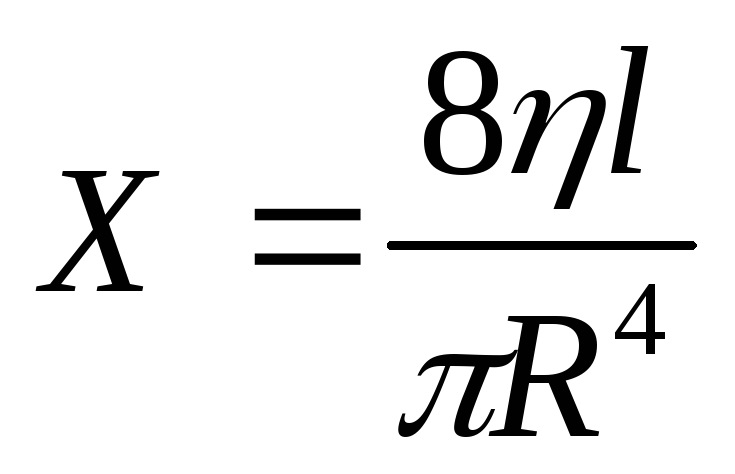 (3.12)
(3.12)
Задачи и упражнения.
Определить объёмную скорость кровотока Q0, если коэффициент вязкости равен: 11; 14; 17
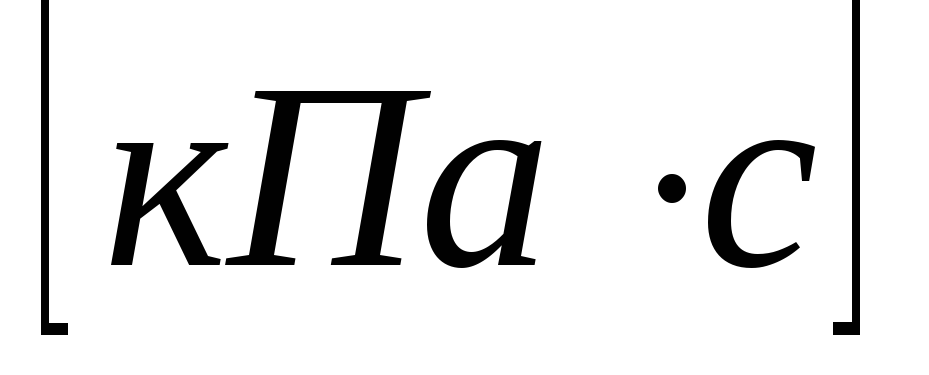 . Радиус сосуда 0,5 см. Изменение давления по длине сосуда 1
. Радиус сосуда 0,5 см. Изменение давления по длине сосуда 1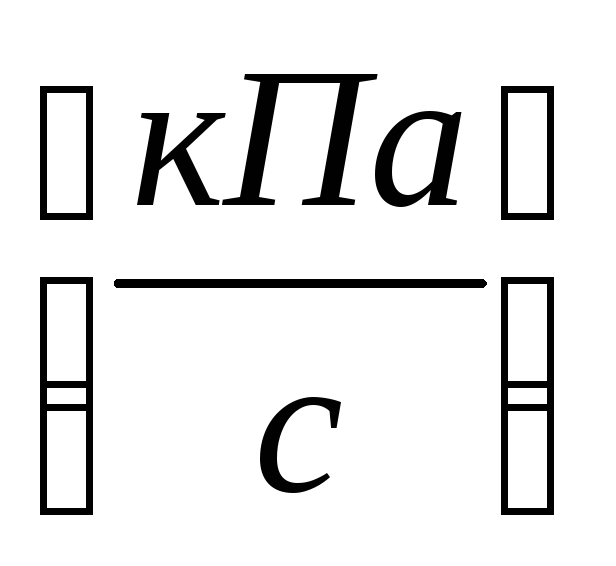 .
.Для расчётных значений определить объёмную скорость кровотока Q из сердца, если скорость изменения объёма в секунду потока крови
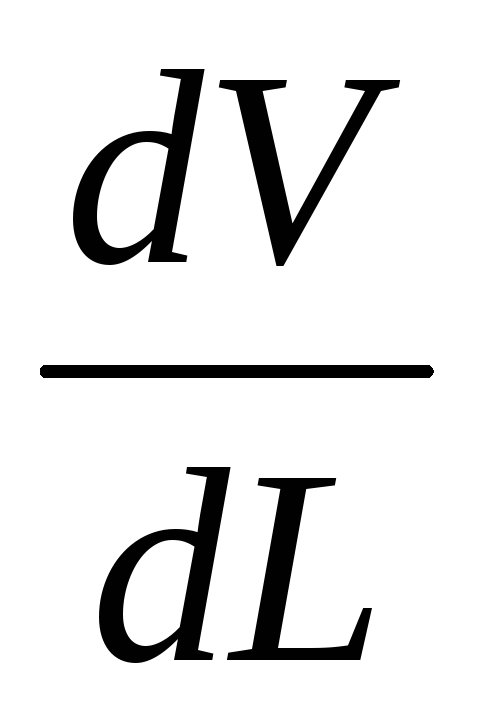 из сердца составляет
из сердца составляет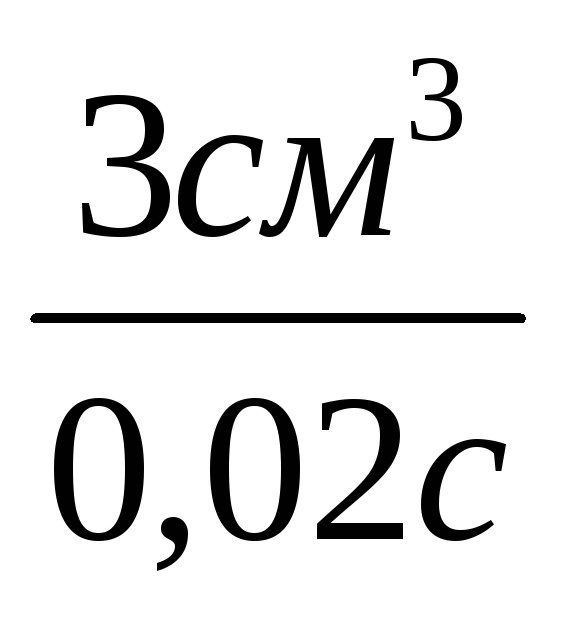 .
.Определить характер изменения давления в УР после систолы от времени для данных в п. 1. Учесть при этом длину участка сосуда l = 20 см, а коэффициент пропорциональность между давлением и объёмом принять К = 1.
Определить объёмную скорость оттока крови из УР от времени для данных п. 3.
Привести и объяснить на основании механической модели электрическую модель, пользуясь методом электромеханических аналогий.
studfiles.net
§ 9.3. Работа и мощность сердца. Аппарат искусственного кровообращения
Работа, совершаемая сердцем, затрачивается на преодоление сил давления и сообщение крови кинетической энергии.
Р ассчитаем работу, совершаемую при однократном сокращении левого желудочка. Изобразим Vy — ударный объем крови — в виде цилиндра (рис. 9.9). Можно считать, что сердце продавливает этот объем по аорте сечением S на расстояние I при среднем давлении р. Совершаемая при этом работа
ассчитаем работу, совершаемую при однократном сокращении левого желудочка. Изобразим Vy — ударный объем крови — в виде цилиндра (рис. 9.9). Можно считать, что сердце продавливает этот объем по аорте сечением S на расстояние I при среднем давлении р. Совершаемая при этом работа
Н а сообщение кинетической энергии этому объему крови затрачена работа
а сообщение кинетической энергии этому объему крови затрачена работа
г де р — плотность крови,v — скорость крови в аорте. Таким образом, работа левого желудочка сердца при сокращении равна
де р — плотность крови,v — скорость крови в аорте. Таким образом, работа левого желудочка сердца при сокращении равна
Т ак как работа правого желудочка принимается равной 0,2 от работы левого, то работа всего сердца при однократном сокращении
ак как работа правого желудочка принимается равной 0,2 от работы левого, то работа всего сердца при однократном сокращении
Ф ормула (9.17) справедлива как для покоя, так и для активного состояния организма. Эти состояния отличаются разной скоростью кровотока.
ормула (9.17) справедлива как для покоя, так и для активного состояния организма. Эти состояния отличаются разной скоростью кровотока.
П одставив в формулу (9.17) значения р = 13 кПа, Vy = 60 мл = 6 • Ю-5 м3,р = 1,05 • 103 кг/м3, v = 0,5 м/с, получим работу разового сокращения сердца в состоянии покоя: А1 ≈ 1 Дж. Считая, что в среднем сердце совершает одно сокращение в секунду, найдем работу сердца за сутки: Ас = 86 400 Дж. При активной мышечной деятельности работа сердца может возрасти в несколько раз.
одставив в формулу (9.17) значения р = 13 кПа, Vy = 60 мл = 6 • Ю-5 м3,р = 1,05 • 103 кг/м3, v = 0,5 м/с, получим работу разового сокращения сердца в состоянии покоя: А1 ≈ 1 Дж. Считая, что в среднем сердце совершает одно сокращение в секунду, найдем работу сердца за сутки: Ас = 86 400 Дж. При активной мышечной деятельности работа сердца может возрасти в несколько раз.
Если учесть, что продолжительность систолы около t ≈ 0,3 с, то средняя мощность сердца за время одного сокращения (W) = = A1/t = 3,3 Вт.
При операциях на сердце, которые требуют временного выключения его из системы кровообращения, пользуются специальными аппаратами искусственного кровообращения (рис. 9.10). По существу, этот аппарат является сочетанием искусственного сердца (насосная система) с искусственными легкими (оксигенатор — система, обеспечивающая насыщение крови кислородом).
§ 9.4. Физические основы клинического метода измерения давления крови
Ф изический параметр — давление крови — играет большуюроль в диагностике многих заболеваний. Систолическое и диастолическое давления в какой-либо артерии могут быть измерены непосредственно с помощью иглы, соединенной с манометром. Однако в медицине широко используется бескровный метод, предложенный Н. С. Коротковым. Рассмотрим физические основы этого метода на примере измерения давления крови в плечевой артерии. Вокруг руки между плечом и локтем накладывают манжету. Сечения манжеты М, части руки Р, плечевой кости П и плечевой артерии А показаны на рис. 9.11, а — 9.13, о. При накачивании воздуха через шланг В в манжету рука сжимается. Затем через этот же шланг воздух выпускают и с помощью манометра Б измеряют давление воздуха в манжете. На позиции б тех же рисунков изображены продольные сечения плечевой артерии, соответствующие каждому случаю. Сначала избыточное над атмосферным давление воздуха в манжете равно нулю (рис. 9.11), манжета не сжимает руку и артерию. По мере накачивания воздуха в манжету последняя сдавливает плечевую артерию и прекращает ток крови (рис. 9.12). Если мускулатура расслаблена, то давление воздуха внутри манжеты, состоящей из эластичных стенок, приблизительно равно давлению в мягких тканях, соприкасающихся с манжетой. В этом заключается основная физическая идея бескровного метода измерения давления.
изический параметр — давление крови — играет большуюроль в диагностике многих заболеваний. Систолическое и диастолическое давления в какой-либо артерии могут быть измерены непосредственно с помощью иглы, соединенной с манометром. Однако в медицине широко используется бескровный метод, предложенный Н. С. Коротковым. Рассмотрим физические основы этого метода на примере измерения давления крови в плечевой артерии. Вокруг руки между плечом и локтем накладывают манжету. Сечения манжеты М, части руки Р, плечевой кости П и плечевой артерии А показаны на рис. 9.11, а — 9.13, о. При накачивании воздуха через шланг В в манжету рука сжимается. Затем через этот же шланг воздух выпускают и с помощью манометра Б измеряют давление воздуха в манжете. На позиции б тех же рисунков изображены продольные сечения плечевой артерии, соответствующие каждому случаю. Сначала избыточное над атмосферным давление воздуха в манжете равно нулю (рис. 9.11), манжета не сжимает руку и артерию. По мере накачивания воздуха в манжету последняя сдавливает плечевую артерию и прекращает ток крови (рис. 9.12). Если мускулатура расслаблена, то давление воздуха внутри манжеты, состоящей из эластичных стенок, приблизительно равно давлению в мягких тканях, соприкасающихся с манжетой. В этом заключается основная физическая идея бескровного метода измерения давления.
Выпуская воздух, уменьшают давление в манжете и в мягких тканях, с которыми она соприкасается. Когда давление станет равным систолическому, кровь будет способна пробиться через сдавленную артерию — возникает турбулентное течение (рис. 9.13).
Характерные тоны и шумы, сопровождающие этот процесс, прослушивает врач при измерении давления, располагая фонендоскоп на артерии дистальнее манжеты (т. е. на большем расстоянии от сердца). Продолжая уменьшать давление в манжете, можно восстановить ламинарное течение крови, что заметно по резкому ослаблению прослушиваемых тонов. Давление в манжете, соответствующее восстановлению ламинарного течения в артерии, регистрируют как диастолическое.
Для измерения артериального давления применяют приборы, показанные на рис. 9.14: а — сфигмоманометр с ртутным мано-

метром, б — сфигмотонометр с металлическим мембранным манометром; здесь М — манжета, Г — груша для накачивания воздуха, Р — манометр. Такой же принцип работы имеют автоматические и полуавтоматические приборы, которые сейчас получают широкое распространение.
studfiles.net
Физические основы клинического метода измерения давления крови.
Энергетика  Физические основы клинического метода измерения давления крови.
Физические основы клинического метода измерения давления крови.
просмотров - 255
Ламинарное и турбулентное течение.
Г.
Семестр
Курс
Медицинская физика
ЯГМА
Лечебный факультет
«Гемодинамика»
Составил: Дигурова И.И.
Гемодинамика- раздел биомеханики, в котором изучается движение крови по сосудам. Физическая основа гемодинамики – гидродинамика.
Ламинарным принято называть течение, при котором слои жидкости текут не перемешиваясь, скользят друг относительно друга. При этом течении скорость различных частиц жидкости, попадающих поочерёдно в какую-либо точку пространства, одинакова. Такое движение возможно при малых скоростях, в трубах без резких изгибов, с одинаковым давлением по сечению. Ламинарным является течение крови по артерии в норме.
Турбулентным (вихревым) принято называть течение, при котором скорость движения частиц жидкости меняется. Частицы приходят в колебательное движение, приводящее к возникновению звука. Элементы жидкости совершают движения по сложным траекториям, что приводит к перемешиванию слоёв и образованию завихрений. Турбулентное течение связано с дополнительной затратой энергии. При течении жидкости, часть энергии расходуется на беспорядочное движение, направление которого отличается от основного направления потока. В случае с кровью это ведёт к дополнительной работе сердца. Шум, возникающий при турбулентном течении крови, используется для диагностики. Он прослушивается на плечевой артерии, при измерении артериального давления крови. В норме является турбулентное течение крови в аорте.
В медицине широко используется метод измерения давления крови, предложенный в 1905 году Коротковым. Суть метода состоит по сути в том, что измеряется давление, ĸᴏᴛᴏᴩᴏᴇ нужно приложить снаружи, чтобы сжать артерию для прекращения тока крови в ней.
а) Давление воздуха в манжетке избыточное над атмосферным и равно нулю. Манжеты не сжимают руку и артерию.
б) По мере накачивания воздуха в манжетку, она сдавливает плечевую артерию, и ток крови прекращается. При этом давление воздуха внутри манжетки равно давлению в мягких тканях, соприкасающихся с манжеткой.
в) Выпуская воздух, давление в манжетке и мягких тканях уменьшается. Когда давление на артерии становится равным систолическому, кровь начинает проталкиваться через сдавленную артерию. Создаётся турбулентный поток, сопровождающийся звуками. При дальнейшем уменьшении давления, просвет увеличивается до нормального. Течение крови становится ламинарным, звуки прекращаются. Показания манометра в момент исчезновения шумов соответствуют
диасталическому давлению.
Число Рейнольдса.
Характер течения жидкости течения по трубе зависит от скорости её течения, размеров трубы, природы жидкости. Экспериментально установлено, что турбулентность возникает, если определённые комбинации величин, характеризующих движение, превосходят некоторые критические значения. Эта безразмерная комбинация принято называть числомРейнольдса. ( Re)
Re= -Плотность жидкости
-Скорость течения
-Диаметр трубы
-Коэффициент абсолютной вязкости
В случае если Re превышает критическое значение, то движение турбулентное, а если меньше критического, то ламинарное. Для крови критическое значение около 1000
При течении воды по гладкой цилиндрической трубе критическое значение числа Re равно 2300. В случае если Re больше критического значения, то движение турбулентное, а если меньше, то ламинарное. В случае если Re равно критическому значению, то режим является переходным. При моделировании кровеносной системы крайне важно, чтобы модель имела такое же Re , что и объект. Иначе между ними не будет соответствия. Re определяет сопротивление, ĸᴏᴛᴏᴩᴏᴇ оказывает жидкая среда, перемещающихся в ней частицам. При ламинарном течении это сопротивление возрастает линейно с увеличением скорости, а при турбулентном прямо пропорционально квадрату скорости.
Кровь как физическая система. Её реологические особенности.
Кровь - жидкая тканевая среда. Она является суспензией, состоящей из дисперсной среды плазмы и дисперсной фазы форменных элементов. Их процентное содержание принято называть гематокритом. (Ht) Ht=45%-50%/. Коэффициент относительной вязкости крови равен 2,5-3,5. Реологически кровь – неньютоновская жидкость псевдопластического типа. Неньютоновские свойства крови связаны с наличием форменных элементов. Эти свойства проявляются при течении крови по сосудам малого диаметра, при небольших скоростях. Предел текучести 2-5мПа. С увеличением гематокрита линейно возрастает. Re=970+ 80.
Течение крови подчиняется закону Гагена-Пуазейля только при малой разности давления на концах сосуда.
Физическая модель сердечно-сосудистой системы (ссс) и её характеристика.
Ссс состоит из активной части – сердца и условно пассивной - сосудов. Основной функцией сердца является создание разности давления на входе и на выходе сосудов.
Ссс имеет следующие особенности:
1) Является замкнутой системой.
2) Разветвляется с последующим и параллельным соединением сосудов.
3) Уменьшение давления идет от центра к периферии.
4) Согласно уравнению неразрывности струи, скорость течения больше там, где площадь сечения меньше.
Наименьшее сечение имеет капилляр, и там же наблюдается наименьшая скорость течения крови. Но это не противоречит уравнению, т. к. общее сечение капилляров превосходит сечение аорты.
Гидравлическое сопротивление.
Гидравлическое сопротивление возникает в результате трения условных частиц о стенки сосуда и друг о друга. Проведём аналогию между движением крови и движением заряда по проводнику.
| Движение жидкости | Движение заряда |
Т.о. гидравлическое сопротивление прямо пропорционально вязкости жидкости и длине сосуда, и обратно пропорциональна площади сечения.
Аналогия между последовательным и параллельным соединением сосудов и параллельным и последовательным соединением проводников.
Понятие о критическом давлении замачивания и формуле Лапласа.
Минимальное давление крови в сосуде, при котором его просвет остаётся открытым, принято называть критическим.
PR=N [N] = Па м = Н/м
P-критическое давление замыкания
R-радиус сосуда
N-величина напряжения стенок сосуда
Движение жидкости по трубам с эластичными стенками.
Течение крови зависит как от её свойств, так и от свойств кровеносных сосудов.
Движение жидкости по трубам происходит под действием эластичного насоса (груши). В жёсткой трубе течение жидкости прерывистое, а в эластичной нет. Эластичность трубки сглаживает пульсацию давления, возникающего от насоса. При повышении давления эластичная трубка расширяется. Кинетическая энергия движения жидкости частично переходит в потенциальную энергию деформации. В момент прекращения работы насоса, эластичная трубка сжимается, изменение энергии идёт в обратном направлении, и жидкость продвигается по трубке. Возникшая деформация распространяется в виде пульсовой волны. Аналогичное явление происходит в артерии. При сокращении сердечной мышцы, кровь выбрасывается из сердца в аорту, затем в артерию. Вследствие эластичности стенок, крупные артерии принимают крови больше, чем её оттекает к периферии. Во время систолы давление равно 16 кПа. Во время диастолы (10,6 кПа) расширяются артерии, спадают их эластические свойства, сглаживаются перепады давления, способствуя непрерывному току и экономичному расходу энергии при движении крови.
Читайте также
Ламинарное и турбулентное течение. Число Рейнольдса. Течение жидкости при котором отдельные ее слои движутся параллельно друг другу без завихрений называют ламинарным. Турбулентным называют такое течение, при котором скорость частиц в каждом месте беспрерывно и... [читать подробенее]
Ламинарное и турбулентное течение. Число Рейнольдса. Течение жидкости при котором отдельные ее слои движутся параллельно друг другу без завихрений называют ламинарным. Турбулентным называют такое течение, при котором скорость частиц в каждом месте беспрерывно и... [читать подробенее]
Ламинарное и турбулентное течение. Г. Семестр Курс Медицинская физика ЯГМА Лечебный факультет«Гемодинамика» Составил: Дигурова И.И. Гемодинамика- раздел биомеханики, в котором изучается движение крови по сосудам. Физическая основа... [читать подробенее]
oplib.ru
3.2 Физические основы клинического метода измерения давления крови
Рассмотрим неинвазивный (безкровный, т. е. без вмешательство непосредственно в сосуд, по которому протекает кровь) метод. К такому методу относятся наиболее используемый в наше время метод Короткова Н. С. Физические основы этого метода. Вокруг руки между плечом и локтём накладывают манжету. При накачевании воздуха в манжету рука сжимается до тех пор, пока перестаёт проходить кровь через артерию. Если мускулатура расслаблена, то давление воздуха внутри манжеты, состоящей из эластичных стенок, приблизительно равно давлению в мягких тканях, соприкасающихся с манжетой.
При выпускании воздуха из манжеты изменяется давление в манжете и в мягких тканях, с которыми она соприкасается. Когда давление станет равным систолическому (верхнему), кровь начинает пробиваться через сдавленную артерию – возникает турбулентное движение. Характерные шумы и тоны, сопровождающие этот процесс прослушивает врач или сам пациент с помощью фонендоскопа, мембрана которого располагается на артерии. Продолжая уменьшать давление в манжете, можно восстановить ламинарное течение крови, что заметно по резкому ослаблению прослушиваемых тонов. Давление, соответствующее восстановлению ламинарного течения крови, регистрирует как диастолическое (нижнее). В среднем нормой считается 120 на 90 мм рт. ст. или 16 и 11 кПа.
На практических занятиях студентами используется 3 типа приборов: прибор, (полуавтоматический), входящий в комплект малого диагностического комплекса КТД–8; свигмотонометр с металлическим мембранным манометром и автоматический цифровой, позволяющий накапливать данные в процессе нескольких измерений. Студенты во время практических занятий проверяют давление друг другу в начале обычным свигмонометром, затем полуавтоматическим и автоматическим. Это позволяет освоить сам процесс измерения и определить допустимые отклонения используемых приборов.
4 Физические основы электрокардиографии (экг)
Живые ткани являются источником электрических потенциалов (биопотенциалов)
Регистрация биопотенциалов тканей и органов получила название электрографии. При исследовании различных органов этот термин конкретизируется:
электрокардиография (ЭКГ) — регистрация биопотенциалов в сердечной мышце при её возбуждении;
электромиография (ЭМГ) — метод регистрации биологической активности мышц;
электроэнцефолография (ЭЭГ) — метод регистрации биологической активности мозга и других.
В большинстве случаев биопотенциалы снимаются не непосредственно с органа, а с других соседних тканей. Конкретные физические аспекты можно сделать на примере электрокардиографии (ЭКГ). Одной из основных задач теоретической ЭКГ является вычисление трансменбранного потенциала клеток сердечных мышц по потенциалам, измеренным вне сердца. Теоретически такую задачу решить сложно, т. к. одно и тоже „внешнее“ проявление биопотенциалов сердца будет при разном „внутреннем“ их распределении.
Физический (биофизический) подход к выяснению связи между биопотенциалами сердца их внешнем проявлением заключается в моделировании источников этих потенциалов.
Всё сердце в электрическом отношении представляется как некоторый электрический генератор. Моделировать электрическую деятельность сердца вполне доступно, если использовать дипольный электрический генератор.
Дипольное представление о сердце лежит в основе теории Эйнтховена. Согласно ей сердце есть диполь с дипольным моментом (произведение заряда на плечо диполя) Р3с, который поворачивается, изменяет своё положение и точку приложения за время сердечного цикла.
Для человека с весом 71,5 кг, с весом сердца 300 г максимальный дипольный момент составляет 2,32 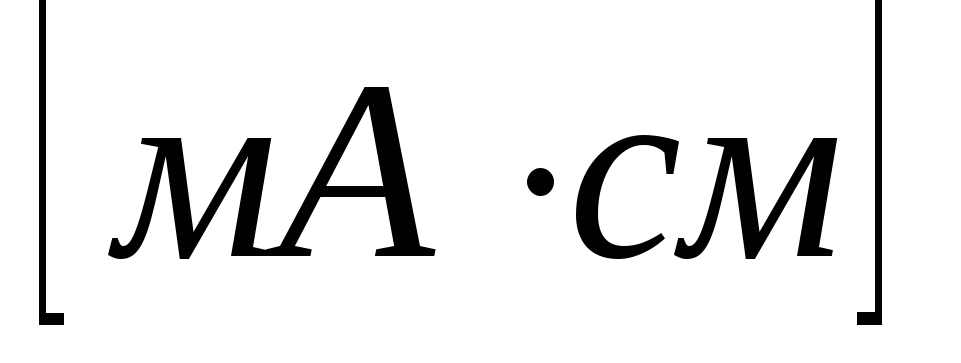 .
.
Э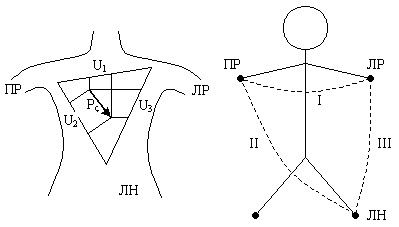 йнтховен предложил снимать разности биопотенциалов сердца между вершинами равностороннего треугольника, которые расположены в (ПР) и левой руки (ЛР) и левой ноге (ЛН).
йнтховен предложил снимать разности биопотенциалов сердца между вершинами равностороннего треугольника, которые расположены в (ПР) и левой руки (ЛР) и левой ноге (ЛН).
а) б)
Рисунок 4.1а,б - Отведение разности потенциалов по Эйнтховену
По терминологии физиологов, разность биопотенциалов, регистрируется между двумя точками тела, называемыми отведениями. Первое отведение I (правая рука – левая рука), II отведение (правая рука – левая нога) и III (левая рука – левая нога). Соответствующие разности потенциалов U1, U2 и U3.
Наиболее полную информацию о работе сердца несёт кардиограмма при расположении электродов в близи сердца с отведения по Нээбу. Вершины этого треугольника расположены у второго ребра правой части груди, у вершины сердца и на левой задней подмышечной линии на уровне пятого межреберья.
Задачи и упражнения
Исследование проводится с использованием малого диагностического комплекса КТД-8. В задачу входит настройка электронной части аппаратуры и непосредственным снятием ЭКГ с одновременной записью на лену (отведение по Эйнховену) при отведениях по Нээбу используется диагностический комплекс, разработанный фирмой СЭМ (прибор ДК-01-запись кардиограммы по Холтеру)
Комплекс позволяет записывать ЭКГ в течение суток. Пациент при этом находится при обычном рабочем режиме. после окончания записи данные анализируются на компьютере по специальной составленной программе.
Студенты осваивают на практических занятиях эту аппаратуру и снимают с желающих ЭКГ.
studfiles.net
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|


