Лекция: Арифметические и логические основы работы компьютера. Арифметические и логические основы работы компьютера реферат

Лекция: Арифметические и логические основы работы компьютера

Пользователю наиболее удобна десятичная система счисления. Поэтому многие цифровые устройства, работая с двоичными числами, осуществляют приём и выдачу пользователю десятичных чисел. При этом применяется двоично-десятичный код. Двоично-десятичный код образуется заменой каждой десятичной цифры числа четырёхразрядным двоичным представлением этой цифры в двоичном коде (см. таблицу 1). Например, число 15 представляется как 00010101 BCD (Binary Coded Decimal). При этом в каждом байте располагаются две десятичные цифры. Заметим, что двоично-десятичный код при таком преобразовании не является двоичным числом, эквивалентным десятичному числу. ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ Алгебра логики (булева алгебра) – это раздел математики, возникший в XIX веке благодаря усилиям английского математика Дж. Буля. Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем. Законы и аппарат алгебры логики стал использоваться при проектировании различных частей компьютеров (память, процессор). Хотя это не единственная сфера применения данной науки. Что же собой представляет алгебра логики? Во-первых, она изучает методы установления истинности или ложности сложных логических высказываний с помощью алгебраических методов. Во-вторых, булева алгебра делает это таким образом, что сложное логическое высказывание описывается функцией, результатом вычисления которой может быть либо истина, либо ложь (1, либо 0). При этом аргументы функции (простые высказывания) также могут иметь только два значения: 0, либо 1. Что такое простое логическое высказывание? Это фразы типа «два больше одного», «5.8 является целым числом». В первом случае мы имеем истину, а во втором ложь. Алгебра логики не касается сути этих высказываний. Если кто-то решит, что высказывание «Земля квадратная» истинно, то алгебра логики это примет как факт. Дело в том, что булева алгебра занимается вычислениями результата сложных логических высказываний на основе заранее известных значений простых высказываний. ЛОГИЧЕСКИЕ ОПЕРАЦИИ. ДИЗЪЮНКЦИЯ, КОНЪЮНКЦИЯ И ОТРИЦАНИЕ Так как же связываются между собой простые логические высказывания, образуя сложные? В естественном языке мы используем различные союзы и другие части речи. Например, «и», «или», «либо», «не», «если», «то», «тогда». Пример сложных высказываний: «у него есть знания и навыки», «она приедет во вторник, либо в среду», «я буду играть тогда, когда сделаю уроки», «5 не равно 6». Как мы решаем, что нам сказали правду или нет? Как-то логически, даже где-то неосознанно, исходя из предыдущего жизненного опыта, мы понимает, что правда при союзе «и» наступает в случае правдивости обоих простых высказываний. Стоит одному стать ложью и все сложное высказывание будет лживо. А вот, при связке «либо» должно быть правдой только одно простое высказывание, и тогда все выражение станет истинным. Булева алгебра переложила этот жизненный опыт на аппарат математики, формализовала его, ввела жесткие правила получения однозначного результата. Союзы стали называться здесь логическими операторами. Алгебра логики предусматривает множество логических операций. Однако три из них заслуживают особого внимания, т.к. с их помощью можно описать все остальные, и, следовательно, использовать меньше разнообразных устройств при конструировании схем. Такими операциями являются конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ). Часто конъюнкцию обозначают &, дизъюнкцию - ||, а отрицание - чертой над переменной, обозначающей высказывание. Название логической операции Логическая связка Инверсия «не»; «неверно, что» Конъюнкция «и»; «а»; «но»; «хотя» Дизъюнкция «или» Конъюнкция Рассмотрим два высказывания: A = «Основоположником алгебры логики является Джордж Буль», B = «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике». Очевидно, новое высказывание «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике» истинно только в том случае, когда одновременно истинны оба исходных высказывания. Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Конъюнкцию также называют логическим умножением. При конъюнкции истина сложного выражения возникает лишь в случае истинности всех простых выражений, из которых состоит сложное. Во всех остальных случаях сложное выражение будет ложно. Для записи конъюнкции используются следующие знаки: И,ˆ,⋅,&. Например: A И B, AˆB, A⋅B, A&B. Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности: A B A B 1 1 1 1 0 0 0 1 0 0 0 0 В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы A и B), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: 00, 01, 10, 11. В последнем столбце записан результат выполнения логической операции для соответствующих операндов. Дизъюнкция Рассмотрим два высказывания: A = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу», B = «Лейбниц является основоположником бинарной арифметики». Очевидно, новое высказывание «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания. Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны. Дизъюнкцию также называют логическим сложением. При дизъюнкции истина сложного выражения наступает при истинности хотя бы одного входящего в него простого выражения или двух сразу. Бывает, что сложное выражение состоит более, чем из двух простых. В этом случае достаточно, чтобы одно простое было истинным и тогда все высказывание будет истинным. Для записи дизъюнкции используются следующие знаки: ИЛИ; V;|;+. Например: A ИЛИ B; A∨B; A|B; A+B. Дизъюнкция определяется следующей таблицей истинности: A B A B 0 0 0 0 1 1 1 0 1 1 1 1 Инверсия Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.  Инверсию также называют логическим отрицанием. Отрицание – это унарная операция, т.к выполняется по отношению к одному простому выражению или по отношению к результату сложного. В результате отрицания получается новое высказывание, противоположное исходному. Для записи инверсии используются следующие знаки: НЕ;¬;−Например: НЕ А; ¬А; А−. Инверсия определяется следующей таблицей истинности: A A0 0 0 1 1 0 1 1 Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, что «У меня дома нет компьютера». Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке: «Я знаю китайский язык». Отрицанием высказывания «Все юноши 8-х классов – отличники» является высказывание «Неверно, что все юноши 8-х классов – отличники», другими словами, «Не все юноши 8-х классов – отличники». Таким образом, при построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что ...», либо отрицание строится к сказуемому, тогда к соответствующему глаголу добавляется частица «не». Любое сложное высказывание можно записать и виде логического выражения – выражения, содержащего логические переменные, знаки логических операций и скобки. Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция. Изменить порядок выполнения операций можно с помощью расстановки скобок. Логические операции при выполнении имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция. Таблицы истинности Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний. Простые высказывания обозначаются переменными (например, A и B).

ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА В ЭВМ используются различные устройства, работу которых прекрасно описывает алгебра логики. К таким устройствам относятся группы переключателей, триггеры, сумматоры. Кроме того, связь между булевой алгеброй и компьютерами лежит и в используемой в ЭВМ системе счисления. Как известно она двоичная. Поэтому в устройствах компьютера можно хранить и преобразовывать как числа, так и значения логических переменных. Переключательные схемы В ЭВМ применяются электрические схемы, состоящие из множества переключателей. Переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае – ток проходит, во втором – нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах. Вентили, триггеры и сумматоры Вентиль представляет собой логический элемент, который принимает одни двоичные значения и выдает другие в зависимости от своей реализации. Так, например, есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание.Триггеры и сумматоры – это относительно сложные устройства, состоящие из более простых элементов – вентилей. Триггер способен хранить один двоичный разряд, за счет того, что может находиться в двух устойчивых состояниях. В основном триггеры используется в регистрах процессора. Сумматоры широко используются в арифметико-логических устройствах (АЛУ) процессора и выполняют суммирование двоичных разрядов. Логические элементы. Вентили В основе построения компьютеров, а точнее аппаратного обеспечения, лежат так называемые вентили. Они представляют собой достаточно простые элементы, которые можно комбинировать между собой, создавая тем самым различные схемы. Одни схемы подходят для осуществления арифметических операций, а на основе других строят различную память ЭВМ. Вентель - это устройство, которое выдает результат булевой операции от введенных в него данных (сигналов). Простейший вентиль представляет собой транзисторный инвертор, который преобразует низкое напряжение в высокое или наоборот (высокое в низкое). Это можно представить как преобразование логического нуля в логическую единицу или наоборот. Т.е. получаем вентиль НЕ. Соединив пару транзисторов различным способом, получают вентили ИЛИ-НЕ и И-НЕ. Эти вентили принимают уже не один, а два и более входных сигнала. Выходной сигнал всегда один и зависит (выдает высокое или низкое напряжение) от входных сигналов. В случае вентиля ИЛИ-НЕ получить высокое напряжение (логическую единицу) можно только при условии низкого напряжении на всех входах. В случае вентиля И-НЕ все наоборот: логическая единица получается, если все входные сигналы будут нулевыми. Как видно, это обратно таким привычным логическим операциям как И и ИЛИ. Однако обычно используются вентили И-НЕ и ИЛИ-НЕ, т.к. их реализация проще: И-НЕ и ИЛИ-НЕ реализуются двумя транзисторами, тогда как логические И и ИЛИ тремя. Выходной сигнал вентиля можно выражать как функцию от входных. Транзистору требуется очень мало времени для переключения из одного состояния в другое (время переключения оценивается в наносекундах). И в этом одно из существенных преимуществ схем, построенных на их основе.

Сумматор и полусумматор Арифметико-логическое устройство процессора (АЛУ) обязательно содержит в своем составе такие элементы как сумматоры. Эти схемы позволяют складывать двоичные числа. Как происходит сложение? Допустим, требуется сложить двоичные числа 1001 и 0011. Сначала складываем младшие разряды (последние цифры): 1+1=10. Т.е. в младшем разряде будет 0, а единица – это перенос в старший разряд. Далее: 0 + 1 + 1(от переноса) = 10, т.е. в данном разряде снова запишется 0, а единица уйдет в старший разряд. На третьем шаге: 0 + 0 + 1(от переноса) = 1. В итоге сумма равна 1100. Полусумматор Теперь не будем обращать внимание на перенос из предыдущего разряда и рассмотрим только, как формируется сумма текущего разряда. Если были даны две единицы или два нуля, то сумма текущего разряда равна 0. Если одно из двух слагаемых равно единице, то сумма равна единицы. Получить такие результаты можно при использовании вентиля ИСКЛЮЧАЮЩЕГО ИЛИ. Перенос единицы в следующий разряд происходит, если два слагаемых равны единице. И это реализуемо вентилем И. Тогда сложение в пределах одного разряда (без учета возможной пришедшей единицы из младшего разряда) можно реализовать изображенной ниже схемой, которая называется полусумматором. У полусумматора два входа (для слагаемых) и два выхода (для суммы и переноса). На схеме изображен полусумматор, состоящий из вентилей ИСКЛЮЧАЮЩЕЕ ИЛИ и И.

Сумматор В отличие от полусумматора сумматор учитывает перенос из предыдущего разряда, поэтому имеет не два, а три входа. Чтобы учесть перенос приходится схему усложнять. По-сути она получается, состоящей из двух полусумматоров.

Рассмотрим один из случаев. Требуется сложить 0 и 1, а также 1 из переноса. Сначала определяем сумму текущего разряда. Судя по левой схеме ИСКЛЮЧАЮЩЕЕ ИЛИ, куда входят a и b, на выходе получаем единицу. В следующее ИСКЛЮЧАЮЩЕЕ ИЛИ уже входят две единицы. Следовательно, сумма будет равна 0. Теперь смотрим, что происходит с переносом. В один вентиль И входят 0 и 1 (a и b). Получаем 0. Во второй вентиль (правее) заходят две единицы, что дает 1. Проход через вентиль ИЛИ нуля от первого И и единицы от второго И дает нам 1. Проверим работу схемы простым сложением 0 + 1 + 1 = 10. Т.е. 0 остается в текущем разряде, и единица переходит в старший. Следовательно, логическая схема работает верно. Работу данной схемы при всех возможных входных значениях можно описать следующей таблицей истинности.

Триггер как элемент памяти. Схема RS-триггера Память (устройство, предназначенное для хранения данных и команд) является важной частью компьютера. Можно сказать, что она его и определяет: если вычислительное устройство не имеет памяти, то оно уже не компьютер. Элементарной единицей компьютерной памяти является бит. Поэтому требуется устройство, способное находиться в двух состояниях, т.е. хранить единицу или ноль. Также это устройство должно уметь быстро переключаться из одного состояния в другое под внешним воздействием, что дает возможность изменять информацию. Ну и наконец, устройство должно позволять определять его состояние, т.е. предоставлять во вне информацию о своем состоянии. Устройством, способным запоминать, хранить и позволяющим считывать информацию, является триггер. Он был изобретен в начале XX века Бонч-Бруевичем. Разнообразие триггеров весьма велико. Наиболее простой из них так называемый RS-триггер, который собирается из двух вентилей. Обычно используют вентили ИЛИ-НЕ или И-НЕ. RS-триггер на вентилях ИЛИ-НЕ RS-триггер «запоминает», на какой его вход подавался сигнал, соответствующий единице, в последний раз. Если сигнал был подан на S-вход, то триггер на выходе постоянно «сообщает», что хранит единицу. Если сигнал, соответствующий единице, подан на R-вход, то триггер на выходе имеет 0. Не смотря на то, что триггер имеет два выхода, имеется в виду выход Q. (Q с чертой всегда имеет противоположное Q значение.) Другими словами, вход S (set) отвечает за установку триггера в 1, а вход R (reset) – за установку триггера в 0. Установка производится сигналом, с высоким напряжением (соответствует единице). Просто все зависит от того, на какой вход он подается. Большую часть времени на входы подается сигнал равный 0 (низкое напряжение). При этом триггер сохраняет свое прежнее состояние. Возможны следующие ситуации: Q = 1, сигнал подан на S, следовательно, Q не меняется. Q = 0, сигнал подан на S, следовательно, Q = 1. Q = 1, сигнал подан на R, следовательно, Q = 0. Q = 0, сигнал подан на R, следовательно, Q не меняется. Ситуация, при которой на оба входа подаются единичные сигналы, недопустима. Как триггер сохраняет состояние? Допустим, триггер выдает на выходе Q логический 0. Тогда судя по схеме, этот 0 возвращается также и в верхний вентиль, где инвертируется (получается 1) и уже в этом виде передается нижнему вентилю. Тот в свою очередь снова инвертирует сигнал (получается 0), который и имеется на выходе Q. Состояние триггера сохраняется, он хранит 0. Теперь, допустим, был подан единичный сигнал на вход S. Теперь в верхний вентиль входят два сигнала: 1 от S и 0 от Q. Поскольку вентиль вида ИЛИ-НЕ, то на выходе из него получается 0. Ноль идет на нижний вентиль, там инвертируется (получается 1). Сигнал на выходе Q становится соответствующим 1.

educontest.net

Практическая работа №10 Арифметические и логические основы работы компьютера. Принцип обработки информации компьютером

Практическая работа №10

Тема: «Арифметические и логические основы работы компьютера. Принцип обработки информации компьютером».

Цели занятия:

- сформировать представление о принципах обработки информации компьютером;

- познакомить с логическими операциями и технической реализацией алгебры логики;

- дать представление о том, как в компьютере при помощи логических элементов выполняются арифметические и логические операции.

Теоретические сведения к работе

Принципы обработки информации компьютером

Между алгеброй логикой и двоичным кодированием существует следующая связь: основной системой счисления в компьютере является двоичная, а которой используются цифры 0 и 1, а значений логический переменных тоже два: «0» и «1» («ложь» и «истина».)

Вывод:

• одни и те же устройства компьютера могут применяться для обработки и хранения, как числовой информации, представленной в двоичной системе счисления, так и логических переменных;

• на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число основных узла компьютера.

В процессе обработки двоичной информации процессор выполняет арифметические и логические операции.

В основе логики работы компьютера, как правило, лежит преобразование сложных логических выражений. Для объяснения этого понятия нам понадобится ввести ряд операций алгебры логики (логических операций). Рассмотрим 3 основных логических операций.

Логическая операция КОНЪЮНКЦИЯ определяет соединение двух логических выражений (высказываний) с помощью союза И. Обозначается символами &(энд) and или ^.

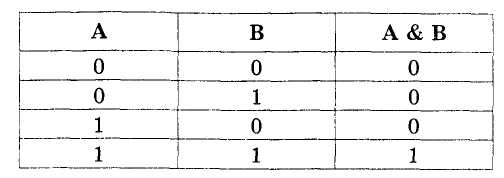В соответствии с таблицей истинности можно дать следующее определение: конъюнкция - логическая операция, ставящая в соответствие двум простым логическим выражениям новое — сложное логическое выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных (простых) логических выражения.

Техническая реализация И

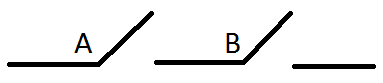
Логическая операция ДИЗЪЮНКЦИЯ определяет логическое соединение двух логических выражений (высказываний) с помощью союза ИЛИ. Эта операция называется также еще логическим, сложением и обозначается значком v.

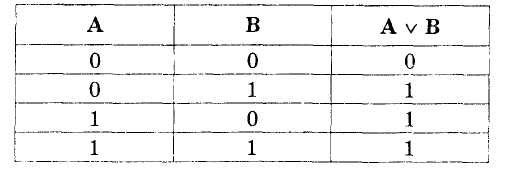
В соответствии с таблицей истинности можно дать определение: дизъюнкцией - логическая операция, ставящая в соответствие двум простым логическим выражениям новое — сложное логическое выражение, которое будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) логических выражений.

Техническая реализация ИЛИ

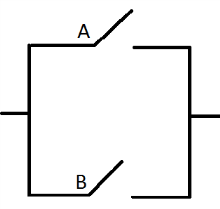
Логическая операция ОТРИЦАНИЕ (ИНВЕРСИЯ), определя­ется над одним аргументом (простым или сложным логическим вы­ражением) следующим образом: если исходное выражение истинно, то результат его отрицания будет ложным, и наоборот, если исходное выражение ложно, то его отрицание будет истинным. Данная опера­ция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО. Операция ОТРИЦАНИЕ обозначается символом -, а ее результат определяется следующей таб­лицей истинности:

infourok.ru

РАЗДЕЛ 1. АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА — КиберПедия

Сложение, вычитание, умножение.

10) Особенности представления чисел в ЭВМ: прямой, обратный, дополнительный коды.

· прямого кода. Прямой код двоичного числа совпадает по изображению с записью самого числа.

· обратного кода. Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.

· дополнительного кода. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.

Тема 2. ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ

11) Основные логические операции: конъюнкция, дизъюнкция, инверсия:

Алгебра логика строится на основе следующих аксиом:

1) Переменная может принимать только одно из возможных значений:

x = 0, если x < >1,

x = 1, если x < >0.

2) Инверсия

3) Дизъюнкция

4) Конъюнкция

5) Во избежании побочных записей вводится преоритетность выполнения операций

Инверсия(-)

Конъюнкция(&)

Дизъюнкция (v)

Равенство(=)

РАЗДЕЛ 5. КОМПЬЮТЕРНЫЕ СЕТИ

Тема 14. КЛАССИФИКАЦИЯ СЕТЕЙ. СТРУКТУРА И ПРИНЦИПЫ РАБОТЫ ЛОКАЛЬНЫХ И ГЛОБАЛЬНЫХ СЕТЕ

46. Понятие компьютерной сети

Компьютерная сеть – это система распределенной обработки информации, состоящая как минимум из двух компьютеров, взаимодействующих между собой с помощью специальных средств связи.

47. Виды сетей: локальные, глобальные.

· К локальным сетям (Local Area Network, LAN) обычно относят сети, компьютеры которых сосредоточены на относительно небольших территориях (как правило, в радиусе до 1-2 км). Классическим примером локальных сетей является сеть одного предприятия, расположенного в одном или нескольких стоящих рядом зданиях. Небольшой размер локальных сетей позволяет использовать для их построения достаточно дорогие и высококачественные технологии, что обеспечивает высокую скорость обмена информацией между компьютерами.

· Глобальные сети (Wide Area Network, WAN) – это сети, предназначенные для объединения отдельных компьютеров и локальных сетей, расположенных на значительном удалении (сотни и тысячи километров) друг от друга. Поскольку организация специализированных высококачественных каналов связи большой протяженности является достаточно дорогой, то в глобальных сетях нередко используются уже существующие и изначально не предназначенные для построения компьютерных сетей линии (например, телефонные или телеграфные). В связи с этим скорость передачи данных в таких сетях существенно ниже, чем в локальных.

48. Локальная сеть и ее основные компоненты

Аппаратное обеспечение:

- Кабели

- Серверы

- Сетевые интерфейсные платы (NIC, Network Interface Card)

- Концентраторы

- Коммутаторы

- Маршрутизаторы (территориально-распределенные сети)

- Серверы удаленного доступа (территориально-распределенные сети)

- Модемы (территориально-распределенные сети)

Программное обеспечение:

- Сетевую операционную систему

- Сетевое ПО управления

49. Адресация компьютера в сети

Каждый компьютер в компьютерной сети имеет имя. Для этого служит так

называемая IP (Internet Рго1осо1)-адресация.

IP-адрес - это уникальный номер компьютера в сети. IP-адрес определяет местонахождение узла в сети подобно тому, как адрес дома указывает его расположение в городе. IP-адрес может быть «статический - неизменный» или «динамический - выдается сервером». Каждый IP-адрес состоит из двух частей - идентификатора сети и идентификатора узла. Первый определяет физическую сеть. Он одинаков для всех узлов в одной сети и уникален для каждой из сетей, включенных в объединенную сеть. Идентификатор узла соответствует конкретной рабочей станции, серверу, маршрутизатору или другому TCP/IP-узлу в данной сети. Он должен иметь уникальное значение в данной сети. Каждый узел TCP/IP однозначно определяется по своему логическому IP-адресу. Такой уникальный адрес необходим всем сетевым компонентам, взаимодействующим по TCP/IP.

50. Понятие протокола передачи информации

Протокол — это набор правил и соглашений, используемых при передаче данных.

Протоколы передачи данных — это набор соглашений, который определяет обмен данных между различными программами. Протоколы задают способы передачи сообщений и обработки ошибок в сети, а также позволяют разрабатывать стандарты, не привязанные к конкретной аппаратной платформе.

51. Многоуровневая модель OSI

Сетевая модель OSI(базовая эталонная модель взаимодействия открытых систем) - сетевая модель стека сетевых протоколов OSI/ISO.

Начинается OSI с 7-го уровня, на котором пользовательские приложения обращаются к сети, заканчивается 1-м уровнем, на котором определены стандарты, предъявляемые независимыми производителями к средам передачи данных.

Любой протокол модели OSI должен взаимодействовать либо с протоколами своего уровня, либо с протоколами на единицу выше и/или ниже своего уровня. Взаимодействия с протоколами своего уровня называются горизонтальными, а с уровнями на единицу выше или ниже — вертикальными. Любой протокол модели OSI может выполнять только функции своего уровня и не может выполнять функции

Модель TCP/IP описывает функциональность протоколов, составляющих набор протоколов TCP/IP. Эти протоколы, которые выполняются как на отправляющем, так и на принимающим хостах, взаимодействуют для обеспечения доставки сообщений от одного конца к другому по сети.

- TCP (Transmission Control Protocol) – протокол управления передачи данных, сокет с виртуальным каналом.

- UDP (Users Datagram Protocol) – сокет дейтаграмм.

- IP (Internet Protocol) – маршрутизируемый протокол сетевого уровня стека TCP/IP.

- Разбиение сегментов информации на отдельные пакеты, которые могут перемещаться по сети по альтернативным маршрутам.

- RIP (Routing Information Protocol) - один из самых простых протоколов маршрутизации. Применяется в небольших компьютерных сетях, позволяет маршрутизаторам динамически обновлять маршрутную информацию (направление и дальность в хопах), получая ее от соседних маршрутизаторов.

- ICMP (Internet Control Messages Protocol- протокол межсетевых управляющих сообщений)- сетевой протокол, входящий в стек протоколов TCP/IP. Используется для передачи сообщения об ошибках и других исключительных ситуациях, возникших при передаче данных. Один из важнейших служебных протоколов Интернета. Как правило, используется самой операционной системой (ядром) или служебными программами.

52. Базовые технологии (архитектуры) локальных сетей: Ethernet; Token Ring; Arcnet; FDDI.

Шина (Bus)

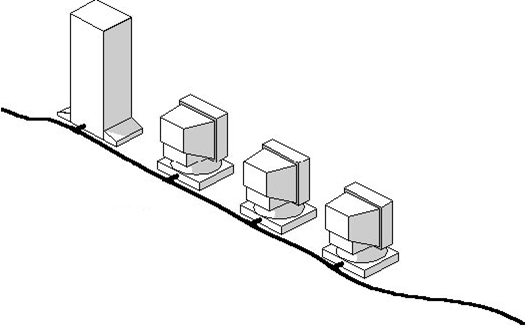
Используется один кабель, именуемый магистралью или сегментом, к которому подключены все компьютеры сети. Данные передаются всем компьютерам сети, однако информацию принимает только один компьютер, чей адрес соответствует адресу получателя, присутствующему среди передаваемых данных. В каждый момент времени передачу может вести только один компьютер.

Шина – пассивная топология. Компьютеры не перемещают данные от отправителя к получателю. Если один компьютер выходит из строя, это не скажется на работе сети. В активных топологиях компьютеры регенерируют сигналы и передают их дальше по сети.

Звезда (Star)

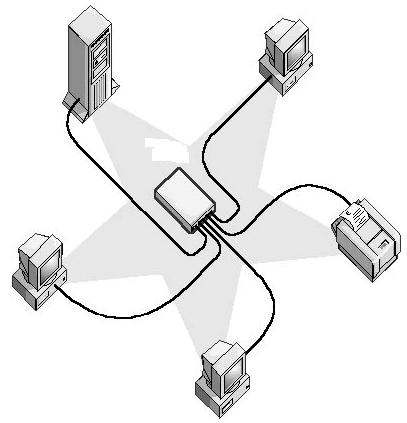
Все компьютеры с помощью сегментов кабеля подключаются к центральному устройству. При выходе из строя одного компьютера или одного сегмента кабеля, только этот компьютер не работает в сети. Если центральный компонент выходит из строя, не работает вся сеть.

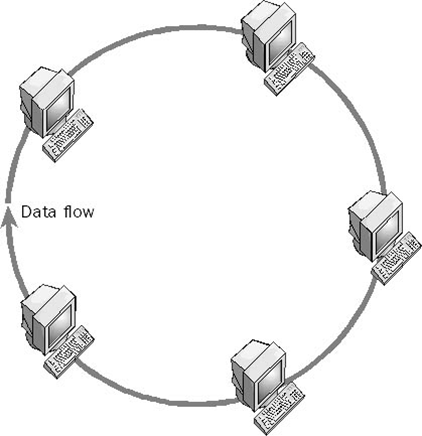
Кольцо (Ring)

Линейный алгаритм

Команда алгаритма выполняется последовательно от ночала до конца в том порядке в котором они записаны

Разветвляющийся алгоритм

В зависимости от поставленного условия выборочно выполняется одна или другая последовательность команды

В простей­шем случае, это ответ на вопрос «Да» или «Нет». Во всех языках программирования эта возможность реализована при помощи оператора ветвления If...[Else]...EndIf.

Циклический алгоритм

В алгоритме есть последовательность команд которая выполняется несколько раз. Число повторений может быть задано заранее иди может зависеть от конкретно поставленного условия

Циклический алгоритм может иметь несколько вариантов.

«Для» (For) служит для проведения определенного количества итераций (повторов).

«Пока» (While|Until) выполняется до тех пор, пока соблюдается определенное условие.

«Неопределенный цикл» (Do) выполняется бесконечно или пока внутри его тела не выполнится команда принудительного завершения цикла. Чаще всего задается с условием.

В некоторых языках программирования могут использоваться специализированные циклы: для обхода всех элементов набора объектов (For Each) или для просмотра всех записей в таблице базы данных (Scan).

Во всех случаях построения циклического алгоритма нужно внимательно следить за тем, чтобы при его выполнении происходило корректное завершение. Одна из наиболее распространенных ошибок – создание бесконечного цикла, который не завершается никогда.

Алгоритмы решения типовых задач.

РАЗДЕЛ 1. АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА

Тема 1. ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ, ЕДИНИЦЫ ИЗМЕРЕНИЯ ИНФОРМАЦИИ. СИСТЕМЫ СЧИСЛЕНИЯ

1) Единица измерения информации:

Количество информации- это мера уменьшения неопределенности - это самое распространенное и разумное определение величины.

Обычно=почти всегда, дела обстоят так:

• 1 бит– такое кол-во информации, которое содержит сообщение, уменьшающее неопределенность знаний в два раза. БИТ- это наименьшая единица измерения информации
• 1байт = 8 бит - (есть 6 и 32 битовый байты тоже)
• 1Кб (килобайт) = 210 байт = 1024 байт = 8192 бит ( не обязательно так, приставка "кило" иногда может обозначать и 103)
• 1Мб (мегабайт) = 210 Кб = 1024 Кб = 8 388 608 бит ( не обязательно так, приставка "кило" иногда может обозначать и 106)
• 1Гб (гигабайт)= 210 Мб = 1024 Мб = 8 589 934 592 бит ( не обязательно так, приставка "кило" иногда может обозначать и 109)

2) Кодирование текстовой информации:

Windows-1251 – введена компанией Microsoft; с учетом широкого распространения операционных систем (ОС) и других программных продуктов этой компании в Российской Федерации она нашла широкое распространение;

КОИ-8 (Код Обмена Информацией, восьмизначный) – другая популярная кодировка российского алфавита, распространенная в компьютерных сетях на территории Российской Федерации и в российском секторе Интернет;

ISO (International Standard Organization – Международный институт стандартизации) – международный стандарт кодирования символов русского языка. На практике эта кодировка используется редко.

Система 16-разрядного кодирования символов называется универсальной – UNICODE. Шестнадцать разрядов позволяет обеспечить уникальные коды для 65 536 символов, что вполне достаточно для размещения в одной таблице символов большинства языков. (используется на данный момент)

3) Кодирование графики:

o Например, чтобы записать на запоминающем устройстве векторное изображение круга, компьютеру достаточно в двоичный код закодировать тип объекта (окружность), координаты его центра на холсте, длину радиуса, толщину и цвет линии, цвет заливки.

o В растровой системе пришлось бы кодировать цвет каждого пикселя. И если размер изображения большой, для его хранения понадобилось бы значительно больше места на запоминающем устройстве.

4) Кодирование звука:

Программное обеспечение компьютера в настоящее время позволяет непрерывный звуковой сигнал преобразовывать в последовательность электрических импульсов, которые можно представить в двоичной форме. В процессе кодирования непрерывного звукового сигнала производится его временная дискретизация.

Декодирование — процесс восстановления изначальной формы представления информации, т. е. обратный процесс кодирования, при котором закодированное сообщение переводится на язык, понятный получателю.

5) Основные понятия системы счисления, алфавит и основные системы:

Система счисления – это способ записи чисел c помощью чисел.

Совокупность всех символов, при помощи которых можно записать любое число в заданной системе счисления называется алфавитом системы счисления.

Символы алфавита системы счисления называются цифрами системы счисления.

Системы счисления делятся на:

- непозиционные системы счисления;

- позиционные системы счисления.

6) Позиционная система счисления:

Позиционными называются системы счисления, в которых значение цифры зависит от ее места (позиции) в записи числа.

7) Непозиционная система счисления:

Непозиционными называются системы счисления, в которых значение цифры не зависит от ее места (позиции) в записи числа. (Римская (II, V, XII)).

8) Правила перевода из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную и наоборот:

· Из десятичной в двоичную:

Делим число на 2 до того, пока частное от деления не будет 1. И записываем наоборот (101000)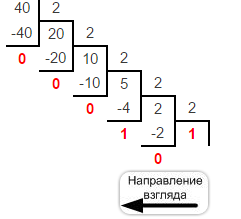

· Из десятичной в восьмеричную:

Делим число на 8 до того, пока частное от деления не будет 1 или меньше 8. И записываем наоборот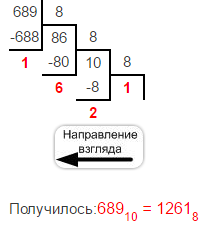

· Из десятичной в восьмеричную:

Делим число на 16 до того, пока частное от деления не будет 1 или меньше 16. И записываем наоборот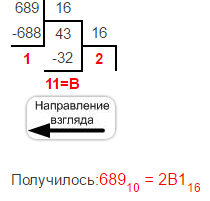

ТЕПЕРЬ НАОБОРОТ!!:

· Из восьмеричной в двоичную:

· Из восьмеричной в десятичную:

9) Основные арифметические действия в двоичной, восьмеричной, шестнадцатеричной системах счисления.

cyberpedia.su

Арифметические основы работы ЭВМ

НОУ « ВОЛГОГРАДСКИЙ ИНСТИТУТ БИЗНЕСА»

кафедра математики и естественных наук

КОНТРОЛЬНАЯ РАБОТА ПО ИНФОРМАТИКЕ

ТЕМА:

АРИФМЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ ЭВМ

Выполнил: студент группы 1- МТ71з

ШАЛИМОВ АЛЕКСЕЙ ЭДУАРДОВИЧ

«10 » мая 2008 года.

Проверил:

МАКАРОВА МАРИЯ АЛЕКСАНДРОВНА

ВОЛГОГРАД 2008

СОДЕРЖАНИЕ

Введение

1. Представление информации в компьютере

2. Системы счисления

3. Перевод числа из одной системы счисление в другую

4. Арифметические операции в позиционных системах счисления

Заключение

Список литературы

Введение

Качественно новое обслуживание информационных процессов, пронизывающих различные сферы человеческой деятельности тесным образом связано с использованием современной электронно-вычислительной техники.

Термин компьютер, так прочно вошедший в русский язык, в переводе означает «вычислитель», т.е. устройство для осуществления вычислений.

Потребность в автоматизации вычислений или, как сейчас говорят — обработки данных, возникла давно. Уже более полутора тысяч лет назад для облегчения вычислений стали использовать счеты.

Но только в 1642 году Блез Паскаль изобрел устройство для механического сложения чисел, а в 1673 году Г. В. Лейбниц сконструировал арифмометр, позволявший механическим способом выполнять четыре арифметических действия, И хотя, начиная с XIX века, арифмометры получили широкое распространение, у них был один существенный недостаток: расчеты производились очень медленно. Причина проста — выбор выполняемых действий и запись результатов при осуществлении расчетов производилась человеком, скорость работы которого весьма ограничена.

Для устранения этого недостатка английский математик Ч. Бэббидж попытался построить универсальное вычислительное устройство, выполняющее вычисления без участия человека. Для этого оно должно было уметь исполнять программы, вводимые с помощью перфокарт (прямоугольных пластин из плотной бумаги с информацией, наносимой при помощи отверстий). Бэббидж не смог довести до конца работу по созданию своей Аналитической машины: ее устройство оказалось слишком сложным для технического оснащения промышленности первой половины XIX века. Однако идеи, заложенные в основу этого устройства, позволили американцу Г. Эйкену в 1943 году построить на одном из предприятий фирмы IBM машину, функционирующую на электромеханических роле и получившую название «Марк-1».

К этому времени потребность в автоматизации обработки данных (в первую очередь, для военных нужд — баллистики, криптографии и т.д.) стала настолько ощутимой, что над созданием подобных машин одновременно работало несколько групп исследователей в разных странах мира. Начиная с 1943 года, группа специалистов под руководством Д. Мочли и П. Экерта в США занималась конструированием более современной вычислительной машины на основе электронных ламп, которая могла бы хранить выполняемую программу в своей памяти. Для ускорения работы в 1945 году к этому проекту был привлечен знаменитый математик Джон фон Нейман. В результате его участия был подготовлен доклад, содержавший целый ряд принципов, на основе которых и должна была функционировать разрабатываемая машина.

Первый компьютер, в котором в полной мере реализовались принципы фон Неймана был построен в 1949 году английским исследователем М. Уилксом. С той поры прошло более 50 лет, и тем не менее, большинство современных компьютеров в той или ином степени соответствуют принципам, изложенным фон Нейманом.

В своей работе Д. Фон Нейман описал, как должен быть устроен компьютер для того, чтобы он был универсальным и эффективным устройством обработки информации (рис.1). В состав такого компьютера должны входить:

♦ арифметико-логическое устройство, выполняющее арифметические и логические операции;

• устройство управления, организующее процесс выполнения программ и синхронизирующее работу остальных устройств компьютера;

• запоминающее устройство (память), предназначенное для хранения выполняемых программ и обрабатываемых данных;

• внешние устройства, предназначенные для ввода и вывода информации.

1 Представление информации в компьютере

Компьютер может обрабатывать только информацию, представленную в числовой форме. Вся остальная информация (например, звук, видео, графические изображения и т.д.) перед обработкой на компьютере должна быть преобразована в числовую форму. Так, чтобы привести к цифровому виду (оцифровать) музыкальный звук, можно через небольшие промежутки времени измерять интенсивность звука на определенных частотах, представляя результаты каждого измерения в числовой форме. Затем, с помощью специальной компьютерной программы осуществляются необходимые преобразования полученных данных: наложение звуков от различных источников друг на друга (эффект оркестра), изменение тональности отдельных звуков и т.п. После чего, окончательный результат преобразуется обратно в звуковую форму.

2. Системы счисления

Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр).

Двоичная система счисления. В этой системе всего две цифры - 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т.д. Самая правая цифра числа показывает число единиц, следующая цифра - число двоек, следующая - число четверок и т.д. Двоичная система счисления позволяет закодировать любое натуральное число - представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически.

Десятичная система счисления. Пришла в Европу из Индии, где она появилась не позднее VI века н.э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени: 10, 100, 1000 и т.д. Самая правая цифра числа показывает число единиц, вторая справа - число десятков, следующая - число сотен и т.д.

Восьмеричная система счисления. В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает - как и в десятичном числе - просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем 64 и т.д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.

Шестнадцатеричная система счисления. Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означат просто единицу. Та же цифра 1 в следующем - 16 (десятичное), в следующем - 256 (десятичное) и т.д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогочно тому, как это делается для восьмеричной системы.

Существуют позиционные и непозиционные системы счисления. В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.

Сама же запись числа 757,7 означает сокращенную запись выражения

700 + 50 + 7 + 0,7 = 7 * 102 + 5 * 101 + 7 * 100 + 7 * 10-1 = 757,7.

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения

an-1 qn-1 + an-2 qn-2+ ... + a1 q1 + a0 q0 + a-1 q-1 + ... + a-m q-m,

где ai – цифры системы счисления; n и m – число целых и дробных разрядов, соответственно.

В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.

В любой системе счисления для представления чисел выбираются некоторые символы (слова или знаки), называемые базисными числами, а все остальные числа получаются в результате каких-либо операций из базисных чисел данной системы счисления.

Системы счисления различаются выбором базисных чисел и правилами образования из них остальных чисел.

Единицей информации в компьютере является один бит (bit), т.е. двоичный разряд, который может принимать значение 0 или 1. Бит — это фундаментальная единица, определяющая количество информации, подвергаемое обработке или переносимое из одного места в другое. Поскольку биты записываются нулями и единицами, их последовательные совокупности позволяют кодировать двоичные числа (binary numbers) — значение в двоичной системе счисления.

В более привычной для человека десятичной системе счисления (по основанию 10) для представления чисел используется десять символов: 0, 1, 2, 3, 4,5,6,7,8и 9. Чтобы составить число, значение которого в десятичной системе счисления больше 9 (например, 27), комбинируют две цифры: при этом позиции символов имеют определенный смысл. Прогрессия значений, связанная с позицией цифры, возрастает, как показано на рис. 2., пропорционально степени основания.

Рис. 2. Пример представления числа в десятичной системе счисления

Десятичное число, состоящее хотя бы из двух цифр, является суммой различных степеней основания, умноженных на соответствующую цифру. Так, число 10 представляет собой сумму из одного десятка (101) и нуля единиц (100), а число 423 — сумму из четырех сотен (102), двух десятков (101) и трех единиц (100).

Рассмотренный метод представления чисел достаточно универсален и используется в других системах счисления, в которых основание отлично от десяти. Например, в системе с основанием 8 задействовано восемь символов: 0, 1, 2, 3, 4, 5, 6 и 7, а значимость каждой позиции возрастает пропорционально степени числа 8, как показано на рис.3.

Рис. 3. Пример предоставления числа в восьмеричной системе счисления.

Как уже отмечалось, компьютер способен обрабатывать информацию в двоичной системе счисления. В ней используются только два символа 0 и 1, а смещение символа на одну позицию влево увеличивает значение числа пропорционально степени основания 2. На рис. 4 показано восьмибитовое (1 байт) представление числа 58 в двоичной системе счисления.

Рис. 4. Пример представления числа в двоичной системе счисления.

3. Перевод числа из одной системы счисление в другую

Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления. Эта система имеет ряд преимуществ перед другими системами:

• для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

• представление информации посредством только двух состояний надежно и помехоустойчиво;

• возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

• двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел. Являясь удобной для компьютеров, для человека двоичная система неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

То есть, чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Как перевести целое число из десятичной системы в любую другую позиционную систему счисления?

При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.

Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ: 7510 = 1 001 0112 = 1138 = 4B16.

Как пеpевести пpавильную десятичную дpобь в любую другую позиционную систему счисления?

Пpи переводе правильной десятичной дpоби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывается как последовательность полученных целых частей произведения. Умножение производится до тех поp, пока дробная часть произведения не станет равной нулю. Это значит, что сделан точный пеpевод. В противном случае перевод осуществляется до заданной точности. Достаточно того количества цифp в pезультате, котоpое поместится в ячейку.

Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ: 0,3510 = 0,010112 = 0,2638 = 0,5916 .

Как перевести число из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную?

При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

4. Арифметические операции в позиционных системах счисления

Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления.

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.

Пример: Сложим числа 15 и 6 в шестнадцатеричной системе счисления: F16 + 61615 + 6 = 2110 = 101012 = 258;

Ответ: = 1516.

Проверка. Преобразуем полученные суммы к десятичному виду:

101012= 24 + 22 + 20 = 16+4+1=21,

258 = 2*81 + 5*80 = 16 + 5 = 21,

1516 = 1*161 + 5*160 = 16+5 = 21.

Вычитание

Пример: Вычтем единицу из чисел 102, 108 и 1016

Вычтем единицу из чисел 1002, 1008 и 10016.

Вычтем число 59,75 из числа 201,25.

Ответ: 201,2510 – 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816.

Проверка: Преобразуем полученные разности к десятичному виду:

10001101,12 = 27 + 23 + 22 + 20 + 2–1 = 141,5;

215,48 = 2*82 + 1*81 + 5*80 + 4*8–1 = 141,5;

8D,816 = 8*161 + D*160 + 8*16–1 = 141,5.

Умножение

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.

Пример: Перемножим числа 5 и 6.

Ответ: 5*6 = 3010 = 111102 = 368.

Проверка: Преобразуем полученные произведения к десятичному виду:

111102 = 24 + 23 + 22 + 21 = 30; 368 = 3•81 + 6•80 = 30.

Пример: Перемножим числа 115 и 51.

Ответ: 115*51 = 586510 = 10110111010012 = 133518.

Проверка: Преобразуем полученные произведения к десятичному виду:

10110111010012 = 212 + 210 + 29 + 27 + 26 + 25 + 23 + 20 = 5865;

133518 = 1*84 + 3*83 + 3*82 + 5*81 + 1*80 = 5865.

Деление

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.

Пример: Разделим число 30 на число 6.

Ответ: 30 : 6 = 510 = 1012 = 58.

Пример: Разделим число 5865 на число 115.

Восьмеричная: 133518 :1638

Ответ: 5865 : 115 = 5110 = 1100112 = 638.

Проверка: Преобразуем полученные частные к десятичному виду:

1100112 = 25 + 24 + 21 + 20 = 51; 638 = 6*81 + 3*80 = 51.

Заключение

В структуру автоматизированной информационной системы входят несколько подсистем. Одной из таких подсистем является математическое и программное обеспечение, то есть совокупность математических методов, моделей, алгоритмов и программ для реализации целей и задач информационной системы, а также нормального функционирования комплекса технических средств.

Фундаментом науки о вычислительных машинах является конструктивная математика, в основе которой лежит математическая логика и теория алгоритмов с их однозначностью в оценке суждений и процедур вывода. Для описания элементов и узлов ЭВМ с самого начала использовалась математическая логика, а для описания компьютерных программ - теория алгоритмов.

Математическая логика - это дисциплина, изучающая технику математических доказательств. Отличие математических суждений от обычных разговорных высказываний состоит в том, что математические суждения всегда предполагают однозначную интерпретацию, в то время как наши обычные высказывания зачастую допускают многозначную трактовку.

Работа ЭВМ как автоматических устройств основана исключительно на математически строгих правилах выполнения команд, программ и интерпретации данных. Тем самым работа компьютеров допускает строгую однозначную проверку правильности своей работы в плане заложенных в них процедур и алгоритмов обработки информации.

С появлением самых первых компьютерных программ, имитирующих интеллектуальную деятельность людей, возникло понятие «искусственный интеллект» и все компьютерные программы, демонстрирующие интеллектуальное поведение, основаны на использовании определенного математического аппарата, опирающегося на законы математической логики и соответственно, имеющего арифметические основы. Без понимания этих законов и основ невозможно понимание принципов работы вычислительных машин вообще и систем искусственного интеллекта в частности.

Список литературы

1. Громов Ю. Ю., О. Г. Иванова, А. В. Лагутин. Информатика: Учебное пособие. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2002.

2. Каймин В.А. Информатика: Учебник. - М.: ИНФРА-М, 2000.

3. Сергеева И.И., Мазулевская А.А., Тарасова Н.В. Информатика: учебник. – М.: ИД «Форум»: ИНФРА – М, 2007.

baza-referat.ru

Смотрите также

• 
  Единицы измерения реферат по геометрии 7 класс
• 
  Стрессы и способы выхода из них реферат
• 
  Сознание как высшая форма развития психики реферат
• 
  Реферат на тему общение 6 класс обществознание
• 
  Реферат на тему гласные и согласные звуки
• 
  Право на свободу и личную неприкосновенность реферат
• 
  Научная рациональность и проблема диалога культур реферат
• 
  Первая медицинская помощь при массовых поражениях реферат
• 
  Реферат по химии реакция горения на производстве
• 
  Реферат на тему как написать курсовую работу
• 
  Семья и семейные отношения 5 класс реферат