 ; б)
; б)  в)
в) 
УРОК № 58.
Дата проведения: по плану – 8а «____»______________ 201__ г., 8б «____»______________ 201__ г.,
фактически – 8а «____»________________ 201__ г. 8б «____»________________ 201__ г.
Причина корректировки ____________________________________________________________
| ТЕМА: | контрольная работа: «Рациональные уравнения» |
| ЦЕЛЬ УРОКА: | |
| ЗАДАЧИ УРОКА: | Образовательная:
Развивающая:
Воспитательная:
|
| ТИП УРОКА: | Урок проверки знаний. |
| СТРУКТУРА УРОКА |
|
| УЧЕБНЫЕ ПОСОБИЯ, ЛИТЕРАТУРА | Алгебра 8 класс. Учебник для 8 класса общеобразовательной школы, автор: А.Н. Шыныбеков, 4-е издательство Алматы: Атамұра, 2016 год. – 282 страницы. |
| ОБОРУДОВАНИЕ: | Мел, доска, карточки с контрольной рапботой. |
ХОД УРОКА
Организационный момент.
Приветствие:
- Здравствуйте! Садитесь.
Определение отсутствующих:
- Дежурный, скажите, пожалуйста, кто сегодня отсутствует на уроке?
Проверка готовности учащихся к уроку.
Проверка готовности классного помещения к уроку.
Учитель выделяет задачи, которые стоят перед учениками, и разбивает их на этапы урока
- Здравствуйте, ребята! Начинаем урок.
(контрольная работа: «Рациональные уравнения»). Открываем тетради, записываем число, тему контрольной работы и вариант.
Контрольная работ
УРОВЕНЬ А
В а р и а н т 1
1. Решите уравнение:
а)  ; б)
; б)  в)
в) 
2. Решить задачу
Из города в село, находящегося на расстоянии 120 км, выехали одновременно два автомобиля. Скорость одного была на 20 км/ч больше другого, и поэтому он пришел к месту назначения на 1 час раньше. Найдите скорость каждого автомобиля.
В а р и а н т 2
1. Решите уравнение:
а)  ; б)
; б)  б)
б)  .
.
2. Решить задачу:
Два автомобиля выезжают одновременно из одного города в другой. Скорость перового на 10 км/ч больше скорости другого, и поэтому первый автомобиль приезжает на место на 1 час раньше второго. Найдите скорость каждого автомобиля, зная, сто расстояние между ними городами равно 560 км.
УРОВЕНЬ В
В а р и а н т 3
1. Решите уравнение:
а)  ; б)
; б)  в)
в) 
2. Решить задачу:
Один из лыжников пришел расстояние в 20 км на 20 минут быстрее, чем другой. Найдите скорость каждого лыжника, зная, что один из них двигался со скоростью, на 2 км/ч больше, чем другой.
В а р и а н т 4
1. Решите уравнение:
а)  ; б)
; б)  в)
в) 
2. Решить задачу:
Чтобы ликвидировать опоздание на 1 час, поезд на перегоне в 720 км увеличил скорость, с которой шел по распиванию, на 10 км/ч. Какова скорость поезда по расписанию?
III. Рефлексия.
В о п р о с ы у ч а щ и м с я (работа в парах):
– Какие еще вопросы есть?
– Что осталось непонятным?
– Как решаются биквадратные уравнения?
– Как решаются дробно-рациональные уравнения?
– Как решаются текстовые задачи?
– Как проводится интерпретация полученных решений? – В каких случаях полученные корни уравнения могут не удовлетворять условию задачи?
IV. Домашнее задание: ________________________________________________________
Итог урока.
kopilkaurokov.ru
Контрольная работа №4
Квадратные уравнения
(по алгебре)
Вариант первый
1.Найдите решение уравнения




2. Решить уравнения




3. Найдите корни биквадратного уравнения
 -
-
49


4. Найдите меньшее из двух чисел, сумма которых равна 22, а сумма их квадратов-250.
5. Найдите наименьший корень уравнения

Контрольная работа №4
Квадратные уравнения
(по алгебре)
Вариант второй
1.Найдите решение уравнения




2. Решить уравнения




3. Найдите корни биквадратного уравнения




4. Найдите большее из двух чисел, если их разность равна 4, а разность квадратов-104.
5.Найдите наибольший корень уравнения

kopilkaurokov.ru
Контрольная работа по теме «Показательные уравнения и неравенства»
Вариант 1
Контрольная работа по теме «Показательные уравнения и неравенства»
Вариант 2
Решите уравнение:
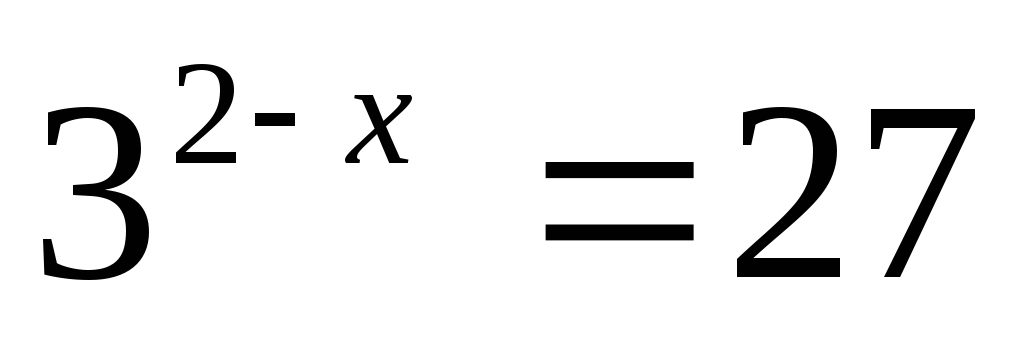
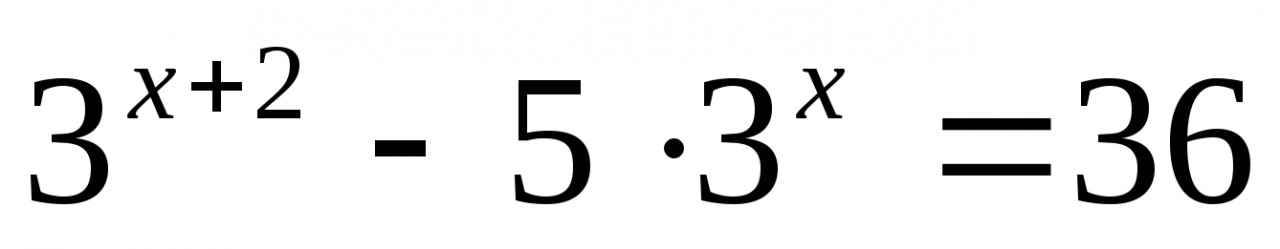
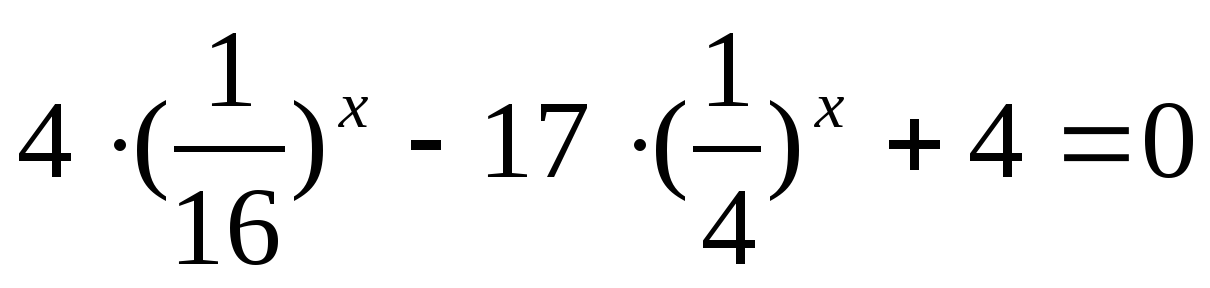
Решите неравенство:
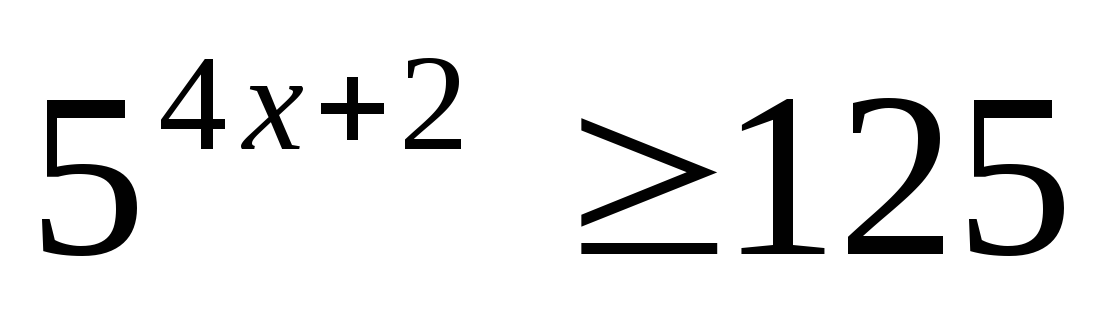
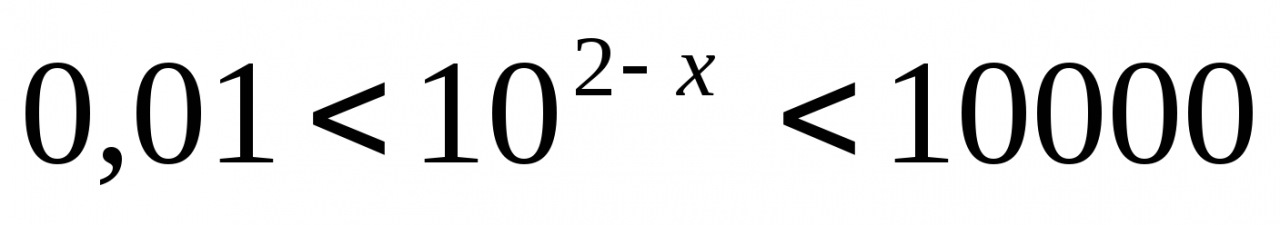
Решите систему уравнений:

Решите уравнение:
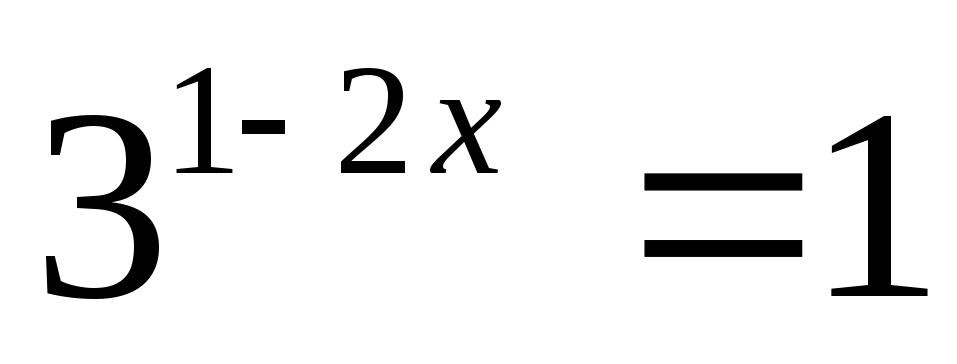
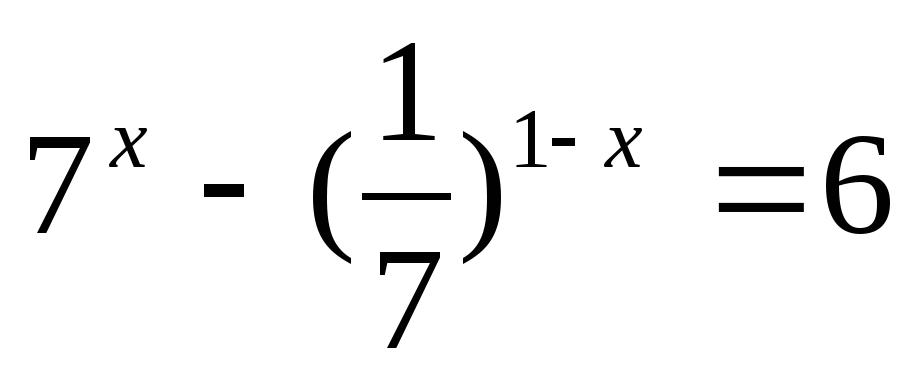
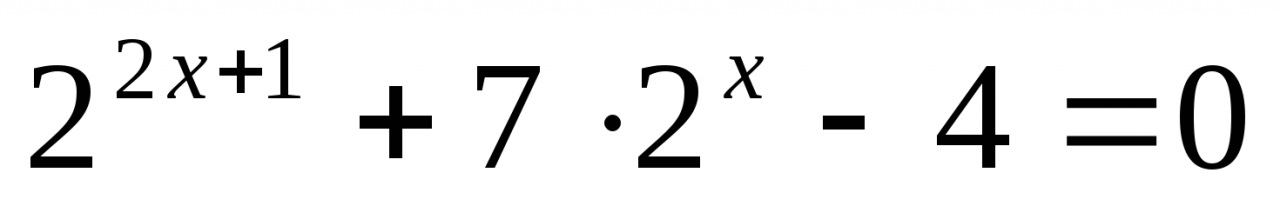
Решите неравенство:
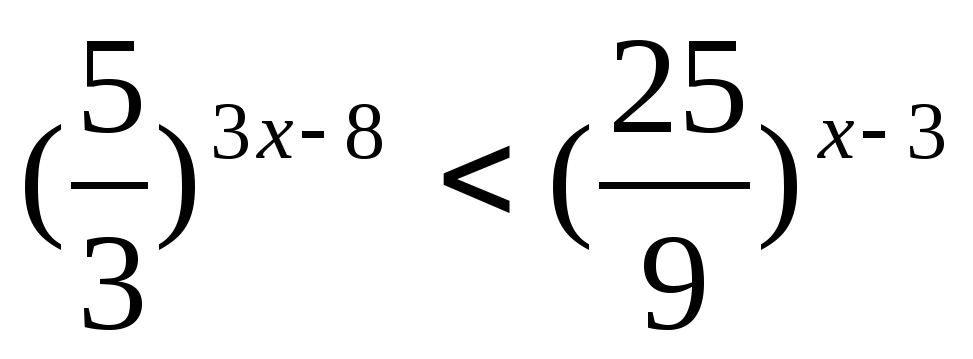
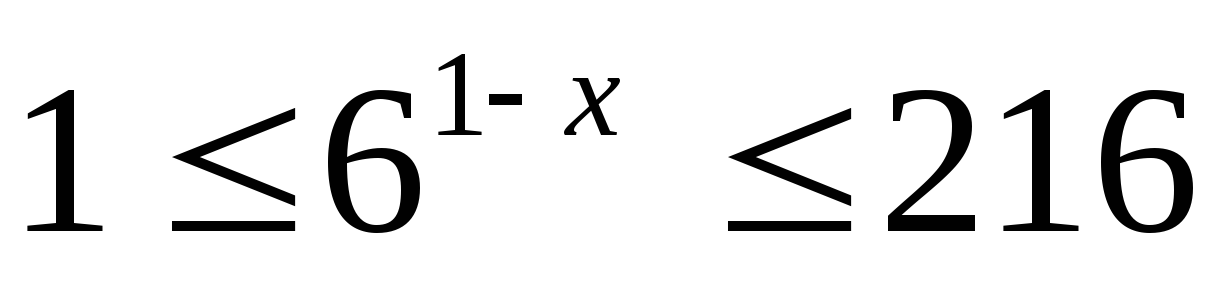
Решите систему уравнений:
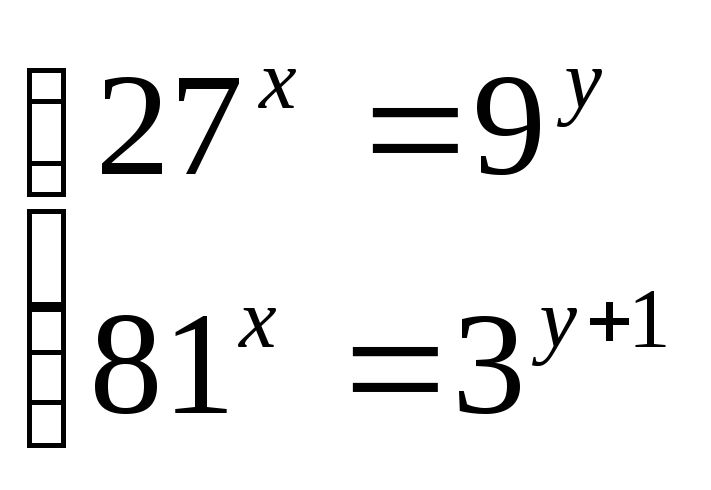
Контрольная работа по теме «Показательные уравнения и неравенства»
Вариант 3
Контрольная работа по теме «Показательные уравнения и неравенства»
Вариант 4
Решите уравнение:
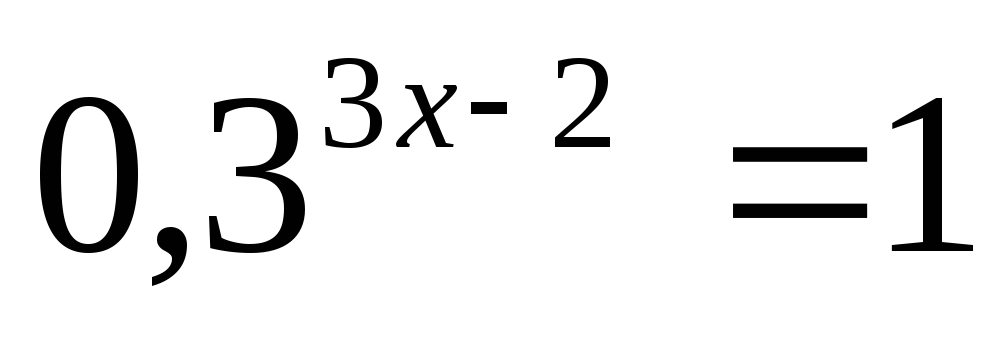
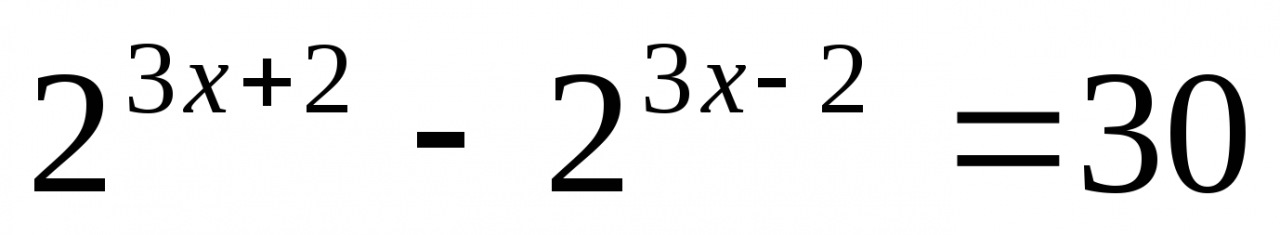
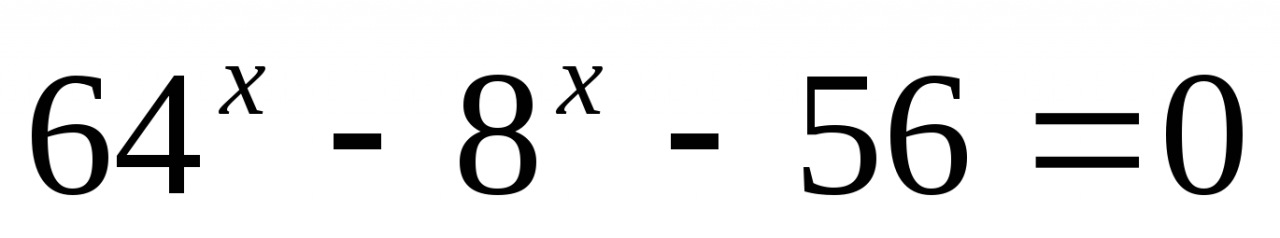
Решите неравенство:
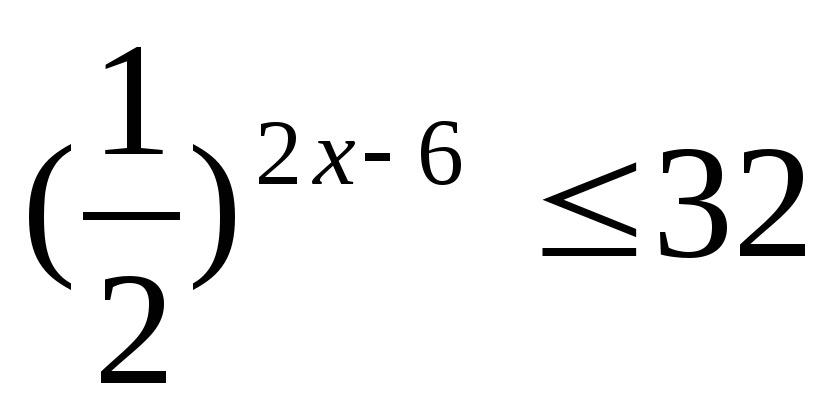
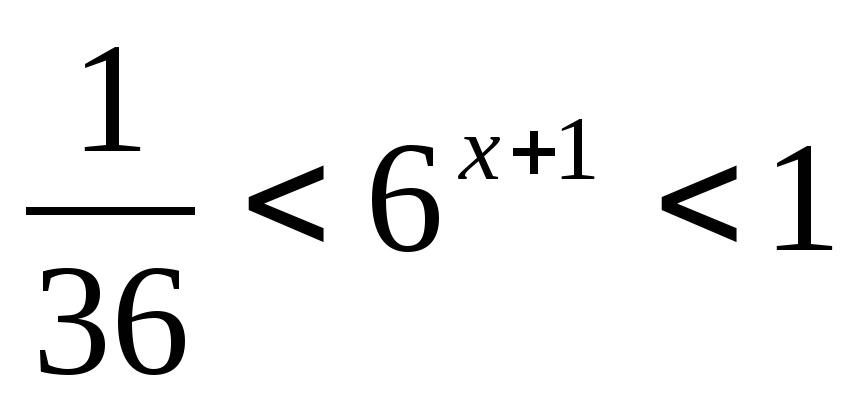
Решите систему уравнений:

Решите уравнение:
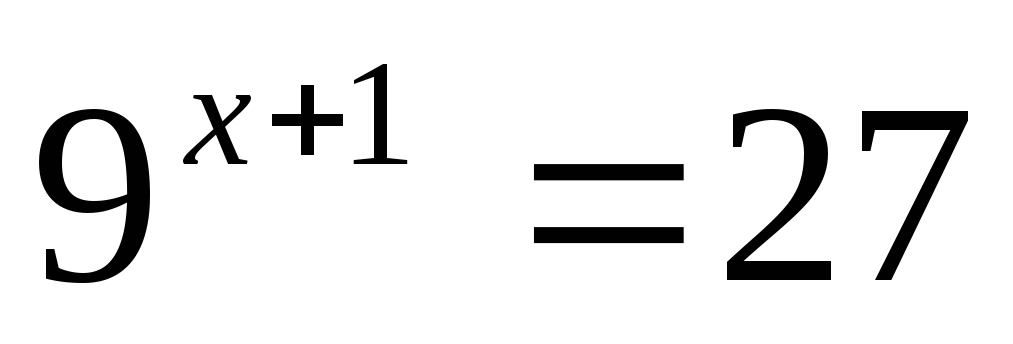
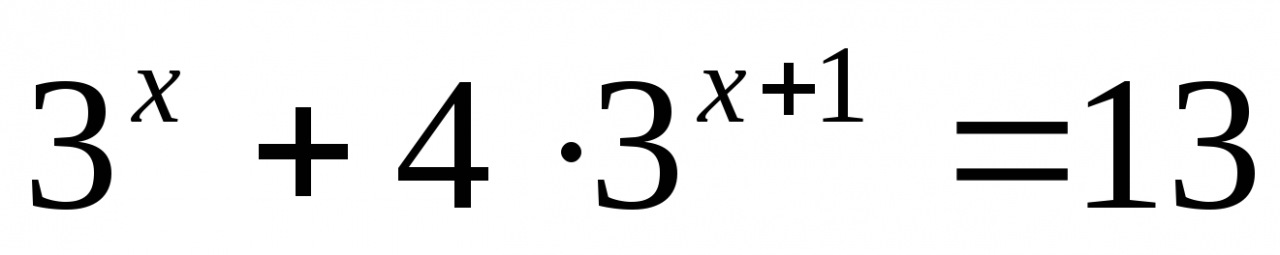
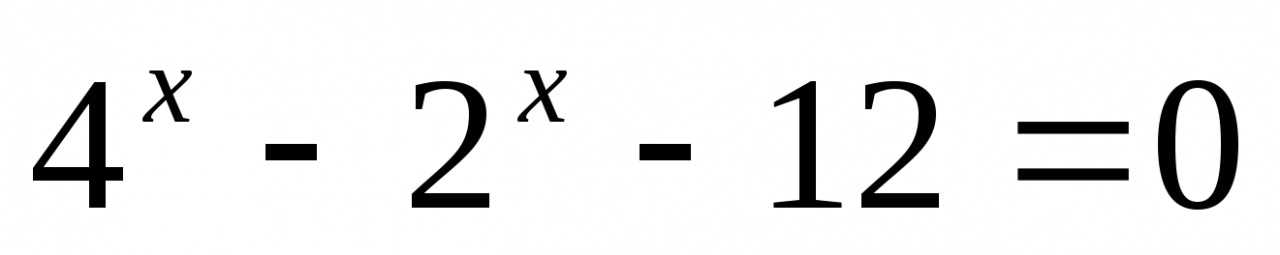
Решите неравенство:
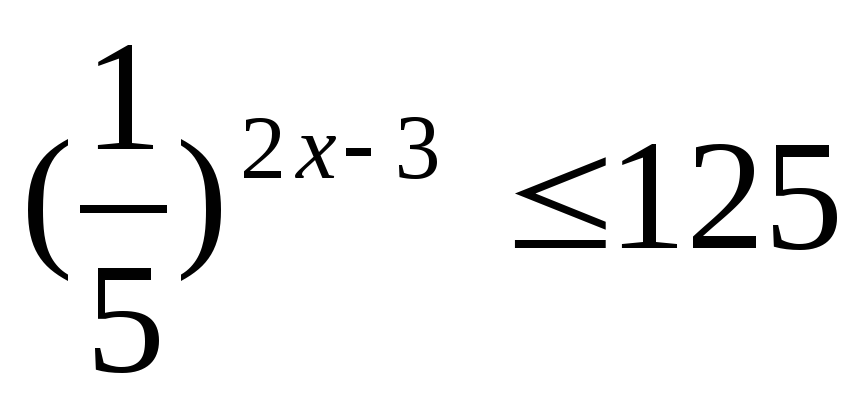
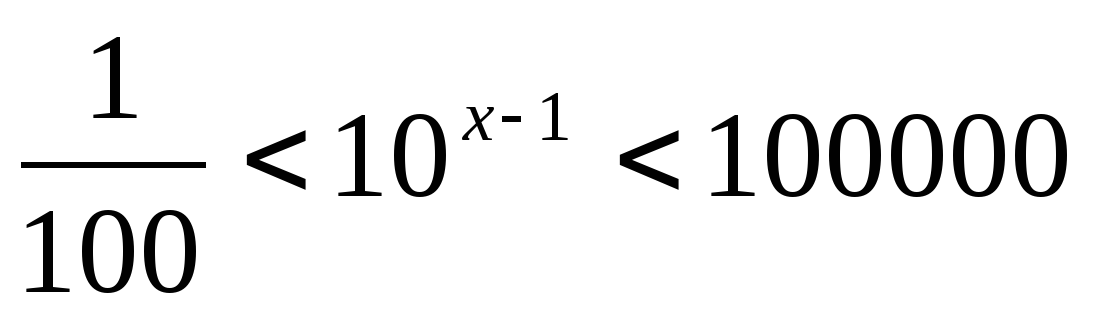
Решите систему уравнений:
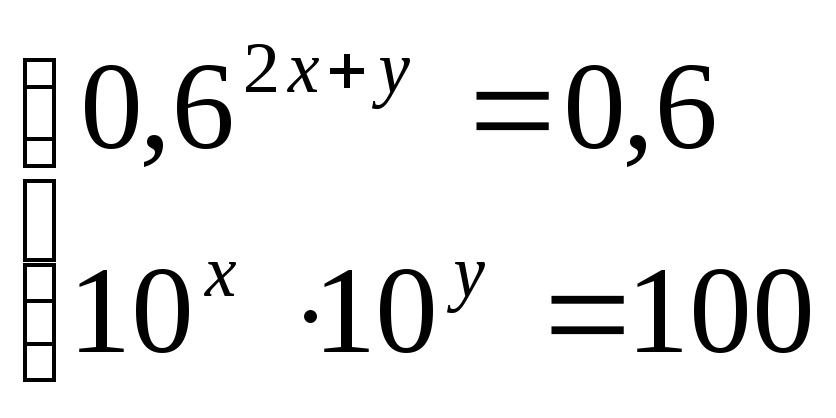
Контрольная работа по теме «Показательные уравнения и неравенства»
Вариант 5
Контрольная работа по теме «Показательные уравнения и неравенства»
Вариант 6
Решите уравнение:
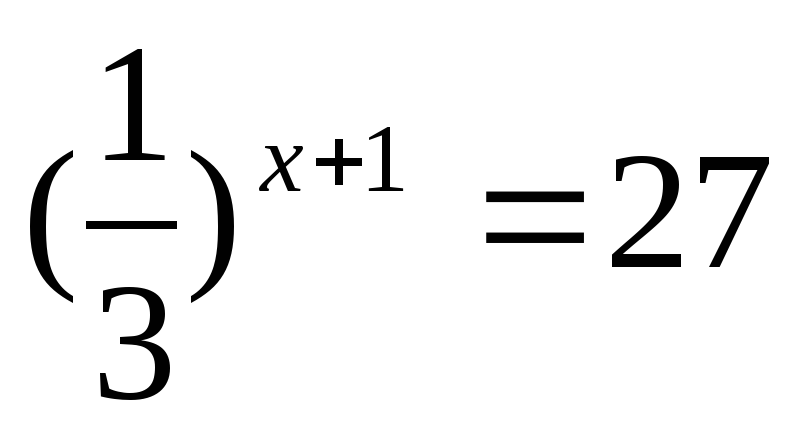
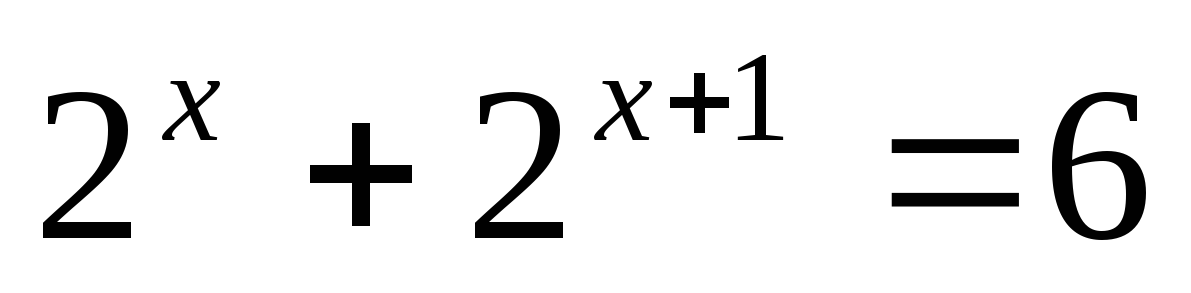
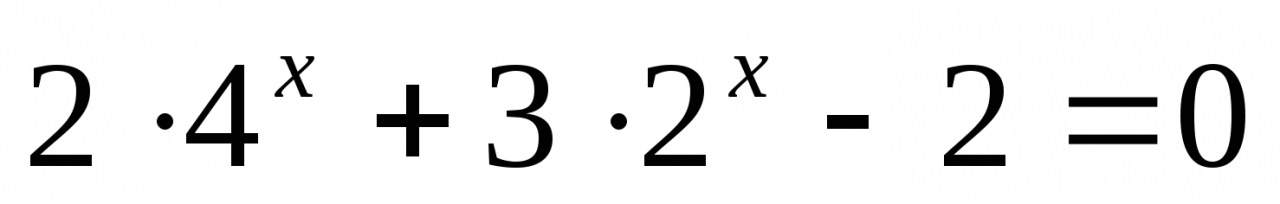
Решите неравенство:
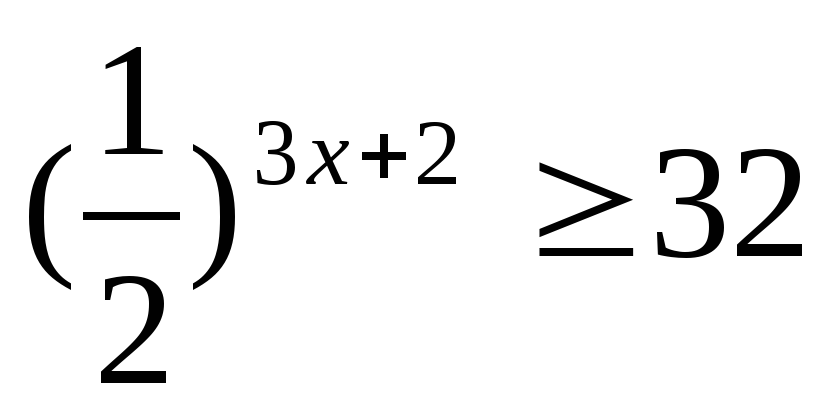
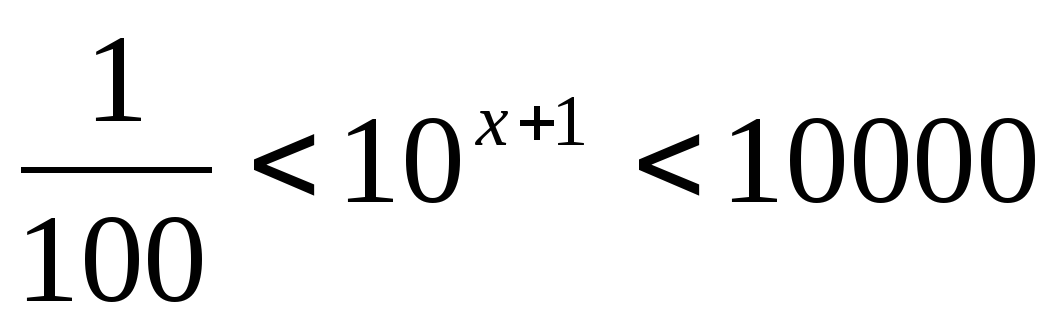
Решите систему уравнений:
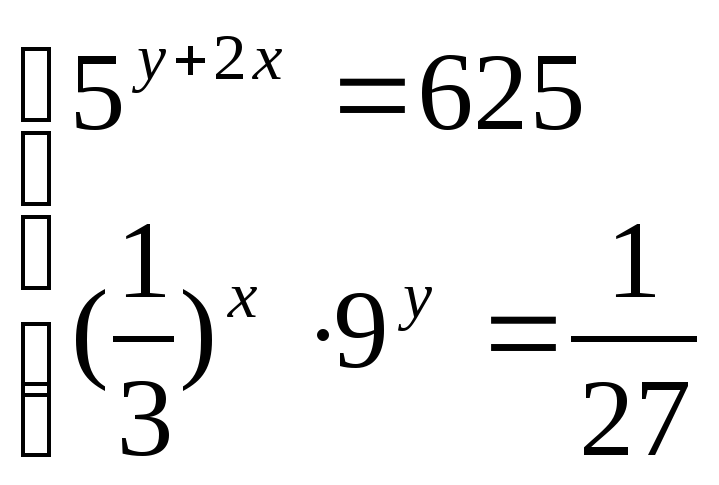
Решите уравнение:



Решите неравенство:

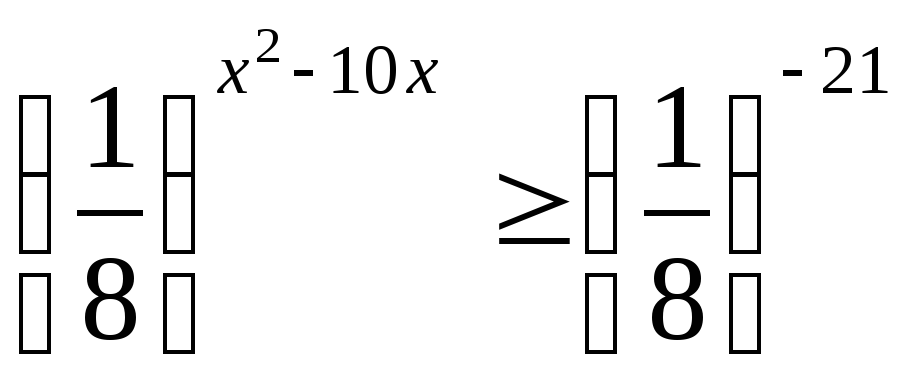
Решите систему уравнений:

Контрольная работа по теме «Показательные уравнения и неравенства»
Вариант 7
Контрольная работа по теме «Показательные уравнения и неравенства»
Вариант 8
Решите уравнение:



Решите неравенство:

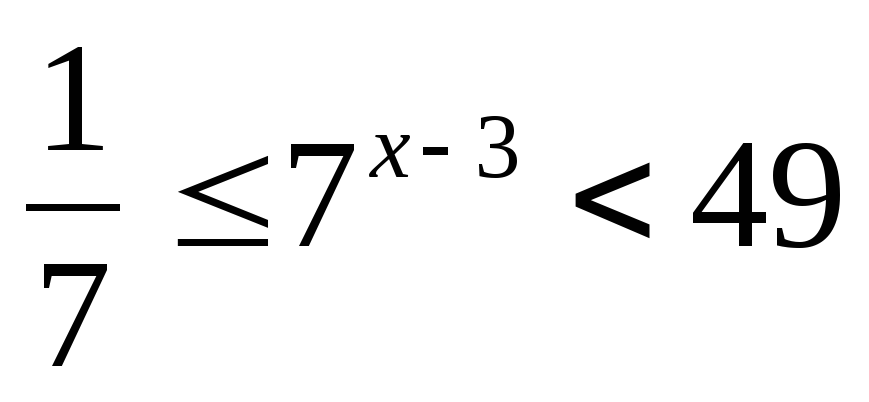
Решите систему уравнений:

Решите уравнение:
Решите неравенство:
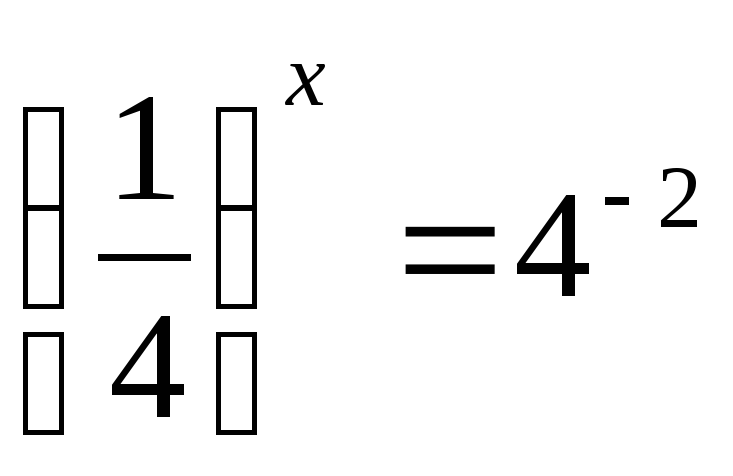
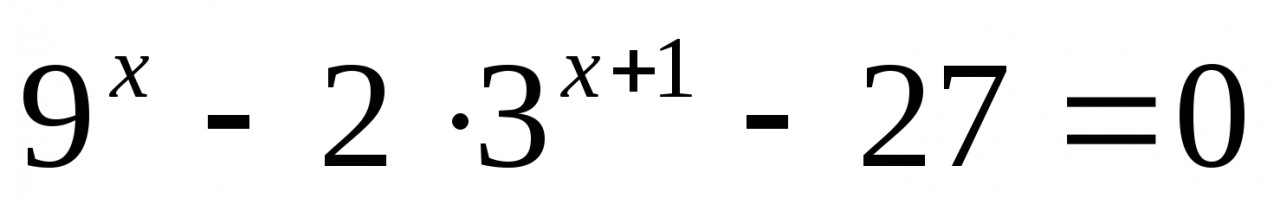
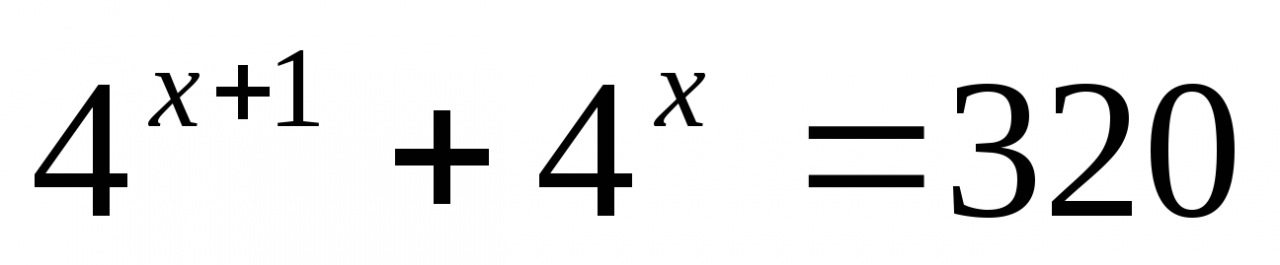
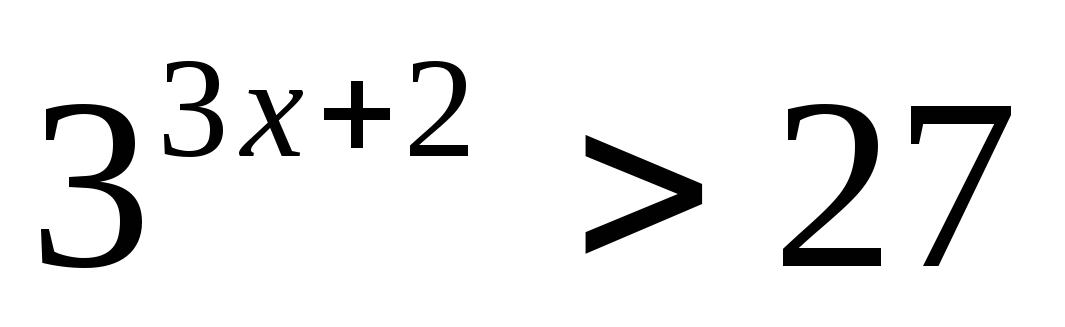
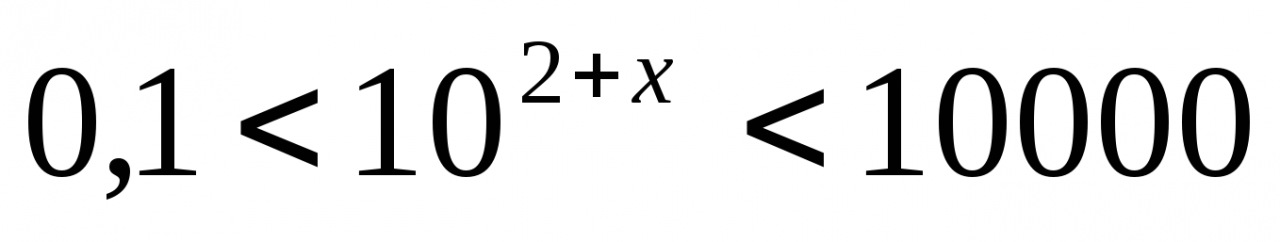
Решите систему уравнений:
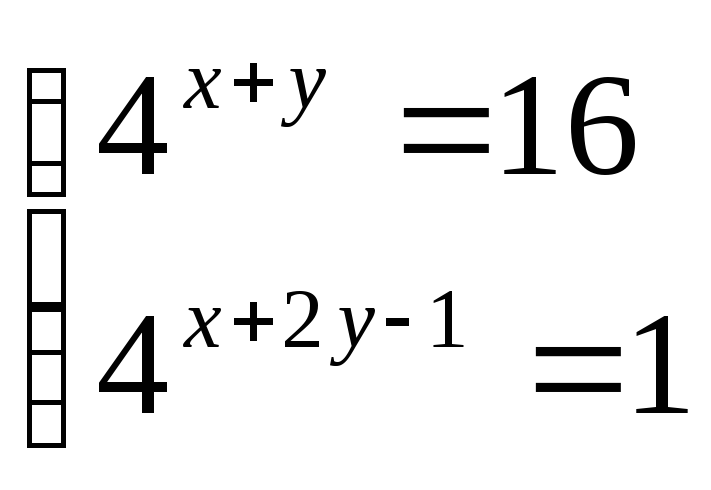
xn--j1ahfl.xn--p1ai

Возвратные, обобщенные возвратные и симметрические уравнения:
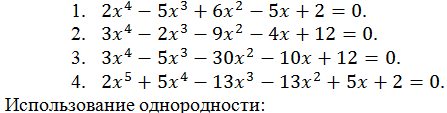
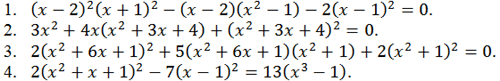
Самостоятельная работа.
Вариант 1.
Решите уравнения
Методом группировки x3 – 7x2 – 21x + 27 = 0
Используя Горнера 4x3 + x2 – 5 = 0
Методом замены переменной x4 + 2x3 – 9x2 – 6x + 9 =0
Методом замены переменной x(x – 1)(x – 2)(x – 3) = 8
Методом замены переменной (2x – 1)2(x + 2)2 – (2x – 1)(x2 – 4) – 2(x – 2)2 = 0
Найдите все значения b , при которых один из корней уравнения x3 + 3x2 – bx – 8 = 0 равен. Для каждого из найденных значений b определите остальные корни уравнения.
Самостоятельная работа.
Вариант 2.
Решите уравнения.
Методом группировки 3x3 – 5x2 + 15x – 81 = 0
Используя схему Горнера 2x3 – 3x2 – 4x + 1 = 0
Методом замены переменной x4 + 3x3 – 8x2 – 12x + 16 = 0
Методом замены переменной x(x + 2)(x + 3)(x + 5) = -5
Методом замены переменной (2x + 1)4 – (2x2 + 5x + 2)2 – 12(x + 2)4 = 0
Найдите все значения b, при которых один из корней уравнения равен -2. Для каждого из найденных значений b определите остальные корни уравнения.
Самостоятельная работа.
Вариант 2.
Решите уравнения.
Методом группировки 3x3 – 5x2 + 15x – 81 = 0
Используя схему Горнера 2x3 – 3x2 – 4x + 1 = 0
Методом замены переменной x4 + 3x3 – 8x2 – 12x + 16 = 0
Методом замены переменной x(x + 2)(x + 3)(x + 5) = -5
Методом замены переменной (2x + 1)4 – (2x2 + 5x + 2)2 – 12(x + 2)4 = 0
Найдите все значения b, при которых один из корней уравнения равен -2. Для каждого из найденных значений b определите остальные корни уравнения.
Контрольная работа 2 10 класс
Вариант 1.
Решите уравнения
1)Методом группировки x3 – 7x2 – 21x + 27 = 0
2)Используя схему Горнера 4x3 + x2 – 5 = 0
3)Симметрическое x4 + 2x3 – 6x2 + 2x + 1 =0
4)Методом замены переменной x(x – 1)(x – 2)(x – 3) = 8 5)Однородное 2(x – 1)2 – 5(x – 1)(x – 2) + 2(x – 2)2 = 0
6)Решите систему уравнений
Х2-3ху+2у2=0
Х2+у2= 20
Решить неравенство
(х+8) (х – 5)(х – 3)2
Х+2
Вариант 2.
Решите уравнения.
Методом группировки 3x3 – 5x2 + 15x – 81 = 0
Используя схему Горнера 2x3 – 3x2 – 4x + 1 = 0
Симметрическое x4 - 4x3 +6x2 – 4x + 1 = 0
Методом замены переменной x(x + 2)(x + 3)(x + 5) = -5
Однородное (2x + 1)4 – ((2x + 1)(x + 2))2 – 12(x + 2)4 = 0
Решить систему уравнений
2х2 – 3ху+ у2 =0
У 2– х2 =12
7 Решить неравенство
(6-х)2(х+4)
Х+1
Контрольная работа 2 10 класс
Вариант 1.
Решите уравнения
1)Методом группировки x3 – 7x2 – 21x + 27 = 0
2)Используя схему Горнера 4x3 + x2 – 5 = 0
3)Симметрическое x4 + 2x3 – 6x2 + 2x + 1 =0
4)Методом замены переменной x(x – 1)(x – 2)(x – 3) = 8 5)Однородное 2(x – 1)2 – 5(x – 1)(x – 2) + 2(x – 2)2 = 0
6)Решите систему уравнений
Х2-3ху+2у2=0
Х2+у2= 20
Решить неравенство
(х+8) (х – 5)(х – 3)2
Х+2
Вариант 2.
Решите уравнения.
Методом группировки 3x3 – 5x2 + 15x – 81 = 0
Используя схему Горнера 2x3 – 3x2 – 4x + 1 = 0
Симметрическое x4 - 4x3 +6x2 – 4x + 1 = 0
Методом замены переменной x(x + 2)(x + 3)(x + 5) = -5
Однородное (2x + 1)4 – ((2x + 1)(x + 2))2 – 12(x + 2)4 = 0
Решить систему уравнений
2х2 – 3ху+ у2 =0
У 2– х2 =12
7 Решить неравенство
(6-х)2(х+4)
Х+1
infourok.ru