Сборник контрольных работ по геометрии, (7класс). Сборник контрольных
Сборник контрольных работ по геометрии, (7класс)
СБОРНИК
КОНТРОЛЬНЫХ РАБОР ПО ГЕОМЕТРИИ
7 класс
Пояснительная записка
Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний. Тематические контрольные работы включают критерии оценивания, позволяющие отследить уровень усвоения учащимися стандартов данной темы. Содержательная матрица дает возможность учителю провести качественный анализ контрольной работы и спланировать коррекционную работу индивидуально для каждого ученика.
Предложение содержательной матрицы и критериев оценивания дает возможность учащимся планировать свою учебную деятельность для достижения более качественных результатов и впоследствии ее коррекцию.
.
Контрольная работа №1 7 класс.
Тема: «Начальные геометрические сведения».
Цель: проверить уровень усвоения госстандарта по теме «Начальные геометрические сведения»:
- знание определения геометрических фигур;
-знание определение вертикальных и смежных углов и их свойств, определение биссектрисы угла;
- умение оформлять решение задачи.
| I вариант. |
| 1. Три точки В, С и К лежат на одной прямой. Известно, что ВК = 17 см, КС = 25 см. Какой может быть длина отрезка ВС? 2.Угол DCB равен 1480, CK – биссектриса этого угла. Найдите угол ВСК. 3.Сумма вертикальных углов МОЕ, РОК, образованных при пересечении прямых МК и РЕ равна 198о. Найдите угол МОР. 4.С помощью транспортира начертите угол, равный 56о и проведите биссектрису смежного с ним угла. 5.Из точки В проведены три луча: ВМ, ВN, ВК. Найдите угол NBK, если  MBN= 84о, MBN= 84о,  МВК = 22о. МВК = 22о.
|
| II вариант. |
| 1.Три точки М, N и К лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние МК? 2.Угол DCL равен 126о, СМ – биссектриса этого угла. Найдите угол МСL. 3.Сумма вертикальных углов АОВ и СОК, образованных при пересечении прямых АК и ВС равна 108о. Найдите угол ВОК. 4.С помощью транспортира начертите угол, равный 132о и проведите биссектрису смежного с ним угла. 5.Из точки М проведены три луча: МО, МN, МК. Чему равен угол NMK, если  OMN = 78о, OMN = 78о,  ОМК = 30о. ОМК = 30о.
|
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Расположение точек на прямой. | №1 | | | 20% |
| Градусная мера угла. Биссектриса угла. | №2 | | | 20% |
| Вертикальные и смежные углы. | | №3 | | 20% |
| Построение угла заданной градусной меры. | | №4 | | 20% |
| Угол, его градусная мера. | | | №5 | 20% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Взаимное распо-ложение точек на прямой. Нахожде-ние длины отрезка. | Построение чертежа | 1 балл | 3 балла |
| Аксиома расположения точки на прямой | 1 балл |
| Понятие длины отрезка | 1 балл |
| 2 | Задача на нахожде-ние градусной меры угла. | Знание понятия угол, биссектрисы угла | 1 балл | 3 балла |
| Свойство биссектрисы угла | 1 балл |
| Построение чертежа | 1 балл |
| 3 | Задача на нахожде-ние величины уг-лов, образованных при пересечении двух прямых. | Понятие смежных углов и вертикальных углов | 1 балл | 5 баллов |
| Знание свойств смежных углов и вертикальных углов | 1 балл |
| Применение свойств смежных углов и вертикальных углов | 2 балла |
| Запись ответа | 1 балл |
| 4 | Задача на построе-ние угла, заданной градусной меры. | Понятие угла | 1 балл | 5 баллов |
| Понятие смежного угла | 1 балл |
| Построение угла заданной градус-ной меры с помощью транспортира | 1 балл |
| Нахождение градусной меры смежного угла и его построение | 1 балл |
| Построение биссектрисы угла | 1 балл |
| 5 | Задача на нахож-дение градусной меры угла. | Построение чертежа | 1 балл | 5 баллов |
| Обоснование построения | 1 балл |
| Применение аксиомы об измерении углов | 1 балл |
| Выбор рационального пути решения | 1 балл |
| Запись ответа | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 балов – «4»
20-21 балл – «5»
Контрольная работа №2 7 класс.
Тема: «Признаки равенства треугольников».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач признаков равенства тругольников;
- умение оформлять решение задачи.
| I вариант. |
| 1.Стороны треугольника равны 7,5 см, 6 см, 4,5 см . Вычислите периметр треугольника. 2.Каждый из отрезков АВ и CD на рисунке точкой О делится пополам. Докажите, треугольники DAO и CBO равны.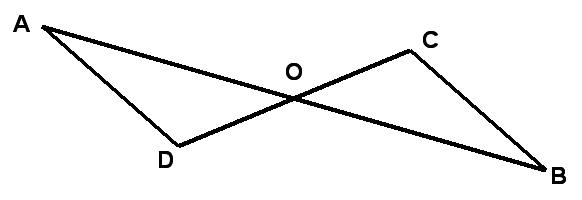 3.Внешние углы в двух вершинах треугольника равны 110о и 160о. Найдите каждый угол треугольника. 4.Луч АК – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что  АКВ = АКВ =  АКС. Докажите, что АВ = АС. АКС. Докажите, что АВ = АС. 5.На сторонах угла D отмечены точки М и К так, что DМ = DК. Точка Р лежит внутри угла D и РК = РМ . Докажите, что луч DР – биссектриса угла МDК . |
| II вариант. |
| 1.Стороны треугольника равны 5,5 см, 8 см, 12,5 см. Вычислите периметр треугольника. 2.Каждый из отрезков АВ и CD на рисунке точкой О делится пополам. Докажите, что треугольники СAO и DBO равны. 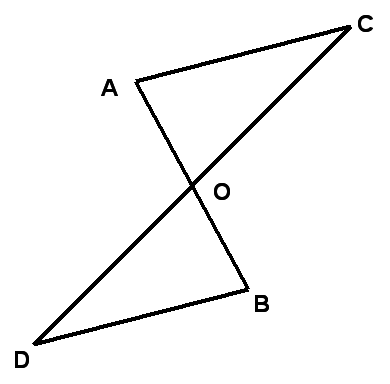
3.Внешние углы в двух вершинах треугольника равны 120о и 150о. Найдите третий внешний угол треугольника. 4.Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что  АDВ = АDВ =  АDС . Докажите, что АВ = АС . АDС . Докажите, что АВ = АС . 5.На сторонах угла А отмечены точки М и К так, что АМ = АК. Известно, что точка Р лежит внутри угла А и РК = РМ. Докажите, что АВ = АС. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Треугольники. Равенство треугольников. | №1,№2 | | | 40% |
| Внешний угол треугольника. | | №3, №4 | | 40% |
| Признаки равенства треугольников. | | | №5 | 20 % |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Задача на нахож-дение периметра треугольника. | Понятие периметр треугольника | 1 балл | 2 балла |
| Знание и применение формулы периметра треугольника | 1 балл |
| 2 | Задача на доказа-тельство равенства двух элементов, входящих в треугольники. | Знание понятия угол, биссектрисы угла | 1 балл | 3 балла |
| Построение чертежа | 1 балл |
| Знание 1 признака равенства треугольников | 1 балл |
| 3 | Задача на нахождение внешнего угла треугольника. | Понятие внешнего угла треугольника | 1 балл | 5 баллов |
| Знание свойства внешнего угла треугольника | 1 балл |
| Знание свойства углов треугольника | 1 балл |
| Применение свойств углов треугольника | 1 балл |
| Построение чертежа | 1 балл |
| 4 | Задача на доказательство равенства двух сторон. | Построение чертежа | 2 балла | 6 баллов |
| Понятие угла и его биссектрисы | 1 балл |
| Знание и применение 2 признака равенства треугольников | 2 балла |
| Доказательство равенства сторон | 1 балл |
| 5 | Задача на доказательство. | Построение чертежа | 1 балл | 7баллов |
| Знание и применение 3 признака равенства треугольников | 2 балла |
| Понятие угла и его биссектрисы | 1 балл |
| Умение делать выводы на основании доказанного | 1 балл |
| Выбор рационального пути решения | 1 балл |
| Запись решения | 1 балл |
Критерии оценивания:
1-11 баллов – «2»
12-18 баллов – «3»
19-21 балл – «4»
22-24 балла – «5»
Контрольная работа №3 7 класс.
Тема: «Признаки равенства прямоугольных треугольников».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач свойств внешнего угла треугольника,свойства медианы и биссектрисы равнобедренного треугольника;
- знания и умения применять при решении задач свойства катета, противолежащего углу в 30о;
-знание и применение признака равенства прямоугольных треугольников
- умение оформлять решение задачи.
| I вариант. |
| 1.Угол при вершине равнобедренного треугольника равен 75о. Найдите угол при основании. 2.В равнобедренном треугольнике боковая сторона 2 раза больше основания. Найдите стороны треугольника, если периметр равен 15 см. 3.Дан прямоугольный треугольник XYZ, где YZ гипотенуза. Внешний угол при вершине Z равен 120°, сторона XY равна 7 см. Чему равна длина гипотенузы? 4.В равнобедренном треугольнике KLM, на основании KM указана точка P. От этой точки проведены перпендикуляры к двум боковым сторонам, соответственно PA и PB. Докажите, что LP - биссектриса треугольника KLM, если КА=МВ. 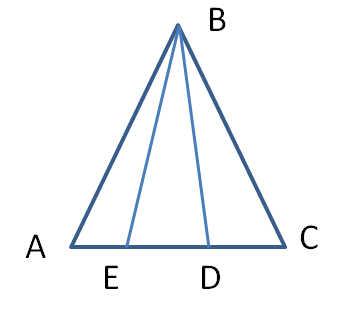 5.Дан равнобедренный треугольник ABC. Известно, что угол ABE равен углу CBD.Докажите, что треугольник DBE является равнобедренным треугольником. Найдите угол AEB, если известно, что угол BDE равен 65°. |
| II вариант. |
| 1.Угол при основании равнобедренного треугольника равен 55о. Найдите угол при вершине. 2.В равнобедренном треугольнике основание 3 раза меньше боковой стороны. Найдите стороны треугольника, если периметр равен 21 см. 3.Дан прямоугольный треугольник CDE, где DE гипотенуза. Внешний угол при вершине E равен 120°, сторона CD равна 5 см. Чему равна длина гипотенузы? 4.В равнобедренном треугольнике CDE, на основании CE указана точка N. От этой точки проведены перпендикуляры к двум боковым сторонам 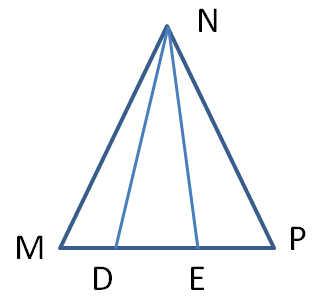 NA и NB соответственно. Докажите, что DN – медиана треугольника CDE, если DA=DB. 5. Дан равнобедренный треугольник MNP. Известно, что угол MND равен углу ENP. Докажите, что треугольник DNE является равнобедренным треугольником. Найдите угол MDN, если известно, что угол MEN равен 70°. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Треугольники. Равенство треугольников. | №1,№2 | | | 40 % |
| Равнобедренный треугольник. Его элементы. Признаки равенства треугольников. | | №3, №4 | №5 | 60 % |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Задача на нахождение углов равнобедренного треугольника. | 1.Знание элементов равнобедренного треугольника. | 1 балл | 3 балла |
| 2.Знание и применение свойства углов при основании равнобедренного треугольника. | 2 балла |
| 2 | Задача на нахождение сторон равнобедренного треугольника. | 1.Знание элементов равнобедренного треугольника. | 1 балл | 5 баллов |
| 2.Знание формулы периметра равнобедренного треугольника. | 1 балл |
| 3.Составление уравнения. | 1 балл |
| 4.Решение уравнения. | 1 балл |
| 5.Запись ответа. | 1 балл |
| 3 | Задача на нахождение элементов прямоугольного треугольника. | 1.Понятие внешнего угла треугольника. | 1 балл | 5 баллов |
| 2.Знание и применение свойств внешнего угла треугольника. | 1 балл |
| 3.Знание и применение свойства острых углов прямоугольного треугольника. | 1 балл |
| 4.Знание и применение свойства катета, противолежащего углу в 30о | 1 балл |
| 5.Построение чертежа. | 1 балл |
| 4 | Задача на доказательство равенства двух сторон. | 1.Построение чертежа. | 2 балла | 6 баллов |
| 2.Понятие перпендикуляра к прямой. | 1 балл |
| 3.Знание и применение признака равенства прямоугольных треугольников. | 1 балл |
| 4.Доказательство равенства сторон треугольника. | 1 балл |
| 5.Знание и применение свойства медианы и биссектрисы равнобедренного треугольника. | 1 балл |
| 5 | Задача на доказательство. | 1.Построение чертежа. | 1 балл | 7 баллов |
| 2.Знание и применение признаков равенства треугольников. | 2 балла |
| 3.Знание и применение свойства внешнего угла треугольника. | 1 балл |
| 4.Знание и применение свойства углов при основании равнобедренного треугольника. | 1 балл |
| 5.Выбор рационального пути решения. | 1 балл |
| 6.Запись решения. | 1 балл |
Критерии оценивания:
1-12 баллов – «2»
13-18 баллов – «3»
19-24 балла – «4»
25-26 баллов – «5»
Контрольная работа №4 7 класс.
Тема: «Признаки параллельности прямых. Сумма углов треугольника».
Цель: проверить уровень усвоения ГОСО:
- знание признаков и свойств параллельности прямых;
- знание теоремы о сумме углов треугольника;
- знание свойств равнобедренного треугольника
| I вариант. |
| 1.Параллельные прямые а и в пересечены 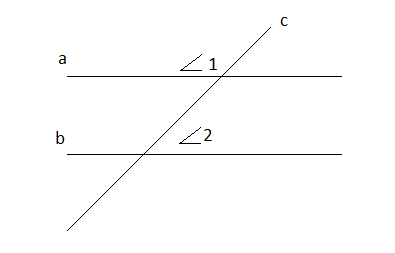 прямой с. Угол ے1=1220. Найдите ے 2. 2. В равнобедренном треугольнике МNK , с основанием МК, внешний угол при вершине N равен 1700. Вычислите углы при основании. 3. В равнобедренном треугольнике боковая сторона в два раза больше основания, а периметр равен 20 см. Найти стороны треугольника. 4. В равнобедренном треугольнике АВС с основанием АС = 14см, отрезок ВД- медиана, а ے АВД = 370 . Найди СД, и ے АВС. 5.Прямые ВС и АД параллельны, ВС=АД. 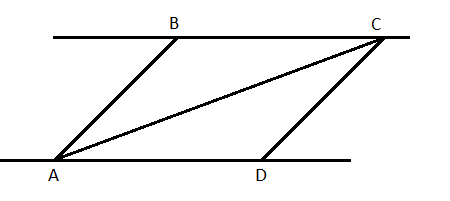 Докажите, что ▲АВС= ▲СДА. |
| II вариант. |
| 1.Параллельные прямые а и в пересечены 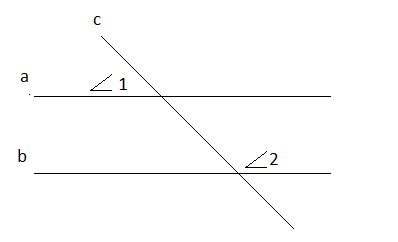 прямой с. Угол ے1= 780 . Найдите ے2. 2.В равнобедренном треугольнике АВС с основанием АС, внешний угол при вершине С равен 1300. Вычислите углы при основании. 3.В равнобедренном треугольнике основание в три раза меньше боковой стороны, а периметр равен 28 см. Найти стороны треугольника. 4. В равнобедренном треугольнике АВС с основанием АС, проведена высота ВД. Отрезок ДС = 6см, а ے ДСВ = 380 Найди АС и ے АВД. 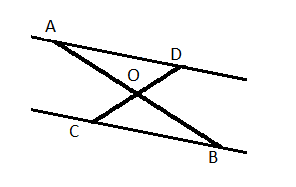 5. Отрезки АВ и СД пересекаются в точке О, причем АО= ВО, СО=ОД. Докажите, что прямая ВС параллельна прямой АД. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Углы, образованные при пересечении двух прямых секущей. | №1, | | | 20 % |
| Нахождение неизвестных элементов в равнобедренном треугольнике. | №2 | №3, №4 | | 60% |
| Решение задачи на доказательство параллельности прямых. | | | №5 | 20 % |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Нахождение углов, образованных при пересечении двух прямых секущей. | Знание теоремы о вертикальных углах. | 1 балл | 4 балла |
| Знание свойства параллельных прямых. | 1 балл |
| Применение свойства параллельных прямых | 2 балла |
| 2 | Нахождение углов равнобедренного треугольника. | Знание определения внешнего угла треугольника | 1 балл | 4 балла |
| Знание свойств углов при основании в равнобедренном треугольнике. | 1 балл |
| Применение теоремы о внешнем угле треугольника | 2 балла |
| 3 | Нахождение сторон равнобедренного треугольника. | Знание определения равнобед-ренного треугольника | 1 балл | 5 баллов |
| Умение составлять уравнение | 2 балла |
| Умение решать уравнение | 2 балла |
| 4 | Нахождение неизвестных элементов в равнобедренном треугольнике. | Знание определения биссектрисы треугольника | 1 балл | 5 баллов |
| Знание свойства биссектрисы равнобедренного треугольника, проведенной к основанию | 2 балла |
| Применение свойства биссект-рисы при решении задачи | 2 балла |
| 5 | Решение задачи на доказательство параллельности прямых. | Знание признаков равенства треугольников | 1 балл | 5 баллов |
| Применение признаков равенства треугольников. | 2 балла |
| Применение признаков параллельности прямых. | 2 балла |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-20 баллов – «4»
21-22 балла – «5»
Контрольная работа №5 7 класс.
Тема: «Окружность. Геометрические построения».
Цель: проверить уровень усвоения ГОСО:
- окружность и ее элементы;
- центральные углы;
- взаимное расположение двух окружностей;
- взаимное расположение прямой и окружности.
| I вариант. |
| 1.Окружности с радиусами 8см и 12 см касаются внешним образом. Найти расстояние между их центрами. 2.Найдите градусную меру дуги, если окружность разделена на 15 равных частей. 3.АВ и СД – диаметры окружности с центром в точке О. Докажите, что хорды АС и ВД равны и параллельны. 4.АС-касательная, а АВ- хорда окружности с центром в точке О, угол ВАС равен 75 градусов. Чему равен угол АОВ? 5.АВ – диаметр окружности с центром в точке О, ВС - хорда. Известно, что угол АОС в 2 раза больше, чем угол СОВ. Найдите углы АОС и СОВ. |
| II вариант. |
| 1.Окружности с радиусами 8см и 12 см касаются внутренним образом. Найти расстояние между их центрами. 2.Найдите градусную меру дуги, если окружность разделена на 12 равных частей 3.АК и СР – диаметры окружности с центром в точке О. Докажите, что хорды АР и КС равны и параллельны. 4.АС-касательная, а АВ- хорда окружности с центром в точке О, угол АОВ равен 70 градусов. Чему равен угол ВАС? 5.АВ – диаметр окружности с центром в точке О, ВС - хорда. Известно, что угол АОС в 3 раза меньше, чем угол СОВ. Найдите углы АОС и СОВ. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Нахождение расстояния между центрами окружностей при внешнем и внутреннем касании | №1 | | | 20 % |
| Нахождение градусной меры дуги окружности | №2 | | | 20% |
| Доказательство равенства хорд и их параллельности | | №3 | | 20% |
| Решение задачи на нахождение неизвестного угла. | | №4 | | 20 % |
| Решение задачи на нахождение центральных углов окружности. | | | №5 | 20 % |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Нахождение расс-тояния между цент-рами окружностей при внешнем и внутреннем касании. | Умение выполнять чертеж по условию задачи. | 1 балл | 3 балла |
| Применение знаний о видах каса-ния при нахождении расстояния между центрами окружностей. | 2 балла |
| 2 | Нахождение градусной меры дуги окружности. | Знание градусной меры полного круга. | 1 балл | 4 балла |
| Знание определения дуги окружности. | 1 балл |
| Умение находить градусную меру дуги. | 2 балла |
| 3 | Доказательство равенства хорд и их параллельности. | Знание признаков равенства треугольников. | 1 балл | 5 баллов |
| Умение выполнять чертеж по условию задачи. | 2 балла |
| Применение признаков параллельности прямых. | 2 балла |
| 4 | Решение задачи на нахождение углов. | Знание определения касательной к окружности. | 1 балл | 5 баллов |
| Умение выполнять чертеж по условию задачи. | 2 балла |
| Применение свойства касательной. | 2 балла |
| 5 | Решение задачи на нахождение центральных углов окружности. | Знание определения центрального угла. | 1 балл | 5 баллов |
| Умение выполнять чертеж по условию задачи. | 1 балл |
| Умение составлять и решать уравнение. | 3 балла |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-20 баллов – «4»
21-22 балла – «5»
Контрольная работа №6 7 класс.
Тема: «Решение задач на построение».
Цель: проверить уровень усвоения ГОСО по следующим темам:
- задачи на построение;
-этапы решения задач на построение.
| I вариант. |
| 1.Разделите отрезок на две равные части. 2.Начертите произвольный угол. Постройте его биссектрису. 3.Начертите треугольник МРК с тупым углом Р. Постройте высоту КА. 4.Постройте треугольник по трем сторонам: а=5см,в=4см,с=3см. 5.Через точку, лежащую внутри данного угла, проведите прямую, отсекающую равные отрезки на сторонах угла. |
| II вариант. |
| 1.Дан отрезок АВ. Постройте окружность, для которой отрезок АВ является диаметром. 2.Начертите произвольный треугольник АВС. Постройте биссектрису АМ. 3.Начертите прямоугольный треугольник АВС с прямым углом С. Постройте высоту СК. 4.Постройте равнобедренный треугольник по основанию и углу при основании. 5.Докажите, что прямая, перпендикулярная биссектрисе угла, отсекает равные отрезки на его сторонах. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Деление отрезка на равные части | №1 | | | 20 % |
| Построение биссектрисы угла | №2 | | | 20% |
| Построение перпендикуляра к отрезку | | №3 | | 20% |
| Построение треугольника | | №4 | | 20 % |
| Решение задачи на применение геометрического места точек | | | №5 | 20 % |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Деление отрезка на равные части. | Знание алгоритма построения середины отрезка. | 1 балл | 4 балла |
| Применение алгоритма при решении задачи. | 1 балла |
| Описание этапов построения. | 2 балла |
| 2 | Построение биссектрисы угла. | Знание алгоритма построения биссектрисы угла. | 1 балл | 4 балла |
| Применение алгоритма при построении биссектрисы. | 1 балл |
| Описание этапов построения. | 2 балла |
| 3 | Построение перпендикуляра к отрезку. | Знание алгоритма построения перпендикуляра к отрезку. | 1 балл | 4 балла |
| Применение алгоритма при построении перпендикуляра. | 1 балл |
| Описание этапов построения. | 2 балла |
| 4 | Построение треугольника. | Знание свойств равнобедренного треугольника. | 1 балл | 5 баллов |
| Применение свойств при выполнении построений. | 2 балла |
| Описание этапов построения. | 2 балла |
| 5 | Решение задачи на применение геометрического места точек. | Умение выполнять чертеж. | 2 балла | 5 баллов |
| Применение знаний геометриче-ского места точек к решению задачи. | 3 балла |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-20 баллов – «4»
21-22 балла – «5»
xn--j1ahfl.xn--p1ai
Методичка к защитам по химии

Московский государственный технический университет имени Н.Э. Баумана
Сборник контрольных вопросов и задач для защиты лабораторных работ
по курсу химии
Издательство МГТУ им. Н.Э. Баумана
Московский государственный технический университет имени Н.Э. Баумана
Cборник контрольных вопросов и задач для защиты лабораторных работ
по курсу химии
Методические указания
Под редакцией А.М. Голубева
Москва Издательство МГТУ им. Н.Э. Баумана
2009
УДК 541 ББК24
С23
Рецензент Б.Е. Винтайкин
Сборник контрольных вопросов и задач для защи- С23 ты лабораторных работ по курсу химии: методические
указания / С.Л. Березина, А.М. Голубев, Е.Е. Гончаренко и др. – М. : Изд-воМГТУ им. Н.Э. Баумана, 2009. – 84 с.
Приведены типовые задачи и контрольные вопросы по ос- новным разделам теоретического курса и лабораторным рабо- там практикума по химии.
Предназначены для студентов I курса всех специальностей МГТУ им. Н.Э. Баумана, изучающих химические дисциплины.
УДК 541 ББК24
© МГТУ им. Н.Э. Баумана, 2009
2
ВВЕДЕНИЕ
Курс химии в техническом университете включает теорию (лекционный материал), практику решения задач(семинарские занятия) и лабораторные работы. При выполнении лабораторного практикума студенты знакомятся с оборудованием, приборами и установками, осваивают основные методы проведения экспери- ментов, изучают химические свойства веществ, убеждаются в со- ответствии теории и практики химической науки.
Каждая лабораторная работа выполняется практически, сту- дент оформляет индивидуальный отчет по ней и на заключитель- ной стадии защищает работу. Как правило, защита заключается в решениидвух-трехтиповых задач по теме, изученной в практи- куме.
Создание сборника является попыткой унификации вопросов и задач для защиты лабораторных работ по курсу химии и имеет це- лью обеспечение единства требований преподавателей к студентам.
В сборник входят типовые вопросы и задачи по основным те- мам курса химии, отраженным в действующем лабораторном практикуме или планируемым к введению в него. Порядок изло- жения задач соответствует последовательности лабораторных ра- бот в учебном плане.
3

ОСНОВНЫЕ КЛАССЫ ХИМИЧЕСКИХ СОЕДИНЕНИЙ
В задачах 1–20 из приведенного списка выпишите формулы химических соединений, относящихся к сильным кислотам, сла- бым кислотам, основаниям(без амфотерных), амфотерным гидро- ксидам, основным, кислотным и амфотерным оксидам, средним, кислым и основным солям.
| № | Список формул химических соединений |
| п/п |
| |
| | |
| 1 | Nah3PO4, KOH, SO3, HCl, Al(OH)Cl2, MgO, CaCl2, Ch4COOH, |
| | CaCO3, h3SO4, Al(OH)3 |
| 2 | Zn(OH)Cl, Li2O, MgCl2, Na2HPO4, NaOH, P2O5, h3SO3, Zn(OH)2, |
| | HNO3, h3S, CaCO3 |
| 3 | HCl, Al(OH)Cl2, KHSO4, Ba(OH)2, CO2, CaO, Ch4COOH, MgCO3, |
| | h3SO4, Fe(OH)3, BaCl2 |
| 4 | KOH, HCOOH, LiHSO3, P2O5, HBr, Mg(OH)Cl, CaF2, Ca(HCO3)2, |
| | h3S, Cr(OH)3, BaO |
| 5 | Ch4COOH, Sn(OH)Cl, SrO, Al(OH)3, Ch4COONa, FeSO4, h3SO4, |
| | Csh3PO4, RbOH, SiO2, HI |
| 6 | SO2, HCN, Sn(OH)2, HCl, Ch4COOH, CaCO3, Cu(OH)Cl, Na2O, |
| | MgCl2, BaHPO4, KOH |
| 7 | HCl, Nah3PO4, NaOH, SO3, Cr(OH)Cl2, MgO, Ca(NO3)2, Ch4COOH, |
| | BaCO3, h3SO4, Al(OH)3 |
| 8 | P2O5, Zn(OH)Cl, Li2O, MgCl2, Na2HPO4, NaOH, h3SO3, Zn(OH)2, |
| | HNO3, h3S, CaCO3 |
| 9 | CO2, HCl, Al(OH)Cl2, KHSO4, KOH, CaO, Ch4COOH, MgCO3, h3SO4, |
| | Fe(OH)3, BaCl2 |
| 10 | HI, Ba(OH)2, HCOOH, LiHSO3, P2O5, Mg(OH)Br, CaF2, Ca(HCO3)2, |
| | h3S, Nh5OH, K2O |
| 11 | Ch4COOH, Sn(OH)Cl, SrO, Al(OH)3, CaBr2, FeSO4, h3SO4, Csh3PO4, |
| | RbOH, SiO2, HI |
| 4 | |

Окончание
№
Список формул химических соединений
п/п
12NO2, HCN, Pb(OH)2, HNO3, Ch4COOH, CaCO3, Cu(OH)Cl, Li2O, MgCl2, BaHPO4, KOH
13Nah3PO4, NaOH, SO3, HCl, Cr(OH)Cl2, MgO, CaCl2, Ch4COOH, Na2CO3, h3SO4, Al(OH)3
14Zn(OH)Cl2, Li2O, Fe2(SO4)3, Na2HPO4, NaOH, P2O5, h3SO3, Nh5OH, HNO3, h3S, K2SO4
15h3SO4, Al(OH)Cl2, KHSO4, KOH, CO2, Na2O, Ch4COOH, MgCO3, h3SO4, Fe(OH)3, BaCl2
16Ca(OH)2, HCOOH, LiHSO3, P2O5, h3SO4, Mg(OH)Br, ZnSO4, Ca(HCO3)2, h3S, Cr(OH)3, Al2O3
17Ch4COOH, Fe(OH)Cl2, SrO, Al(OH)3, AlCl3, FeSO4, HNO3, Csh3PO4, RbOH, SiO2, Cr2O3
18SO2, HCN, Sn(OH)2, HCl, h3S, CaCO3, Cu(OH)Cl, Li2O, FeCl2, BaHPO4, KOH
19Nah3PO4, KOH, SO3, Al2O3, Cr(OH)Cl2, MgO, CaCl2, Ch4COOH, Cu(NO3)2, h3SO4, Al(OH)3
20Zn(OH)Cl, Li2O, MgCl2, Na2HPO4, Nh5OH,СО2, h3CO3, NaOH, HNO3, h3S, Al2(SO4)3
Взадачах 21–40, используя приведенные выше соединения и воду, напишите уравнения реакций получения представителей ос- новных классов химических соединений в молекулярной, ионно- молекулярной и краткойионно-молекулярнойформах.
№ | Список продуктов реакций и номер задачи со списком |
п/п | исходных соединений |
| |
21 | Кислота, амфотерный гидроксид, средняя соль(задача1) |
22 | Амфотерный оксид, кислая соль, основание(задача2) |
| |
23 | Основная соль, средняя соль, кислота(задача3) |
24 | Кислая соль, кислота, основание(задача4) |
25 | Кислота, амфотерный гидроксид, средняя соль(задача5) |
| |
26 | Амфотерный оксид, кислая соль, основание(задача6) |
27 | Основная соль, средняя соль, кислота(задача7) |
5

| Окончание |
| |
№ | Список продуктов реакций и номер задачи со списком |
п/п | исходных соединений |
| |
28 | Основание, кислая соль, кислота(задача8) |
| |
29 | Кислота, амфотерный гидроксид, средняя соль(задача9) |
| |
30 | Основной оксид, кислая соль, основание(задача10) |
31 | Основная соль, средняя соль, основание(задача11) |
| |
32 | Основная соль, кислота, основание(задача12) |
| |
33 | Амфотерный гидроксид, кислота, средняя соль(задача13) |
34 | Средняя соль, кислая соль, основание(задача14) |
| |
35 | Основная соль, амфотерный гидроксид, кислота(задача15) |
| |
36 | Кислая соль, кислота, основание(задача16) |
37 | Кислота, амфотерный гидроксид, средняя соль(задача17) |
| |
38 | Средняя соль, основной оксид, основание(задача18) |
| |
39 | Основная соль, основание, кислота(задача19) |
40 | Кислота, кислая соль, основание(задача20) |
| |
ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ МАССЫ ЭКВИВАЛЕНТОВ МЕТАЛЛА
В задачах 1–14 определите молярные массы эквивалентов за- данных химических соединений и ионов. Дайте определение поня- тиям эквивалент и молярная масса эквивалентов вещества(ее раз- мерность), закона эквивалентов в современной трактовке, приве- дите его математическое выражение.
| № | Кислота | Гидроксид | Соль | Оксид | Ион |
| п/п | металла | металла |
| | | |
1 | h4AsO4 | Zn(OH)2 | Fe2(SO4)3 | Ag2O | PO3− |
| | | | | 4 |
| | | | | |
2 | h3SO4 | La(OH)3 | Cu(NO3)2 | CrO3 | NH+ |
| | | | | 4 |
| | | | | |
3 | Ch4COOH | Mn(OH)2 | (Nh5)2SO4 | Co2O3 | CrO2− |
| | | | | 4 |
| | | | | |
4 | h3TeO4 | Fe(OH)3 | KClO4 | Cu2O | Fe3+ |
6
| | | | | Окончание |
| | | | | | | |
№ | Кислота | Гидроксид | Соль | Оксид | | Ион |
п/п | металла | металла | |
| | | | |
| | | | | | |
5 | HCN | Ni(OH)2 | Cr2(SO4)3 | CdO | | CO2− |
| | | | | | | 3 |
| | | | | | |
6 | h4PO4 | Mn(OH)2 | Ca3(PO4)2 | Fe2O3 | | MnO2− |
| | | | | | | 4 |
| | | | | | |
7 | HMnO4 | Ti(OH)4 | Zn(NO3)2 | WO3 | | ClO3− |
| | | | | | |
8 | h3SiO3 | Ba(OH)2 | K2Cr2O7 | FeO | | SO2− |
| | | | | | | 3 |
| | | | | | |
9 | h5P2O7 | Al(OH)3 | LiClO4 | Cr2O3 | | AsO3− |
| | | | | | | 3 |
| | | | | | | |
10 | h3Cr2O7 | Ca(OH)2 | Na2SO3 | Na2O | | B | O2− |
| | | | | | 4 | 7 |
| | | | | | |
11 | HClO3 | NaOH | NiCl2 | ZnO | | SiO4− |
| | | | | | | 4 |
| | | | | | |
12 | h3MnO4 | Fe(OH)2 | K2MnO4 | Al2O3 | | SO2− |
| | | | | | | 3 |
| | | | | | |
13 | h3SeO3 | Co(OH)3 | Ch4COONa | MnO2 | | SeO2− |
| | | | | | | 3 |
| | | | | | |
14 | h5SiO4 | Cr(OH)3 | MgSO4 | MgO | | P O4− |
| | | | | | 2 | 7 |
| | | | | | | |
В задачах 15–19 рассчитайте молярные массы эквивалентов серы, если известны химические формулы соединений, получен- ных в результате взаимодействия ее с другими веществами.
| № | Соединение | Продукт реакции |
| п/п |
| | |
| | | |
| 15 | с водородом | h3S |
| | | |
| 16 | с кислородом | SO2 |
| | | |
| 17 | с кислородом | SO3 |
| | | |
| 18 | с цинком | ZnS |
| | | |
| 19 | с углеродом | CS2 |
| | | |
В задачах 20–22 рассчитайте молярные массы эквивалентов(г/моль) в реакциях обмена(а и б), в реакции а гидроксида метал- ла, в реакции б кислоты.
7

№
Реакция
п/п
20
а) 2Zn(OH)2 + h3SO4 = Zn2(OH)2SO4 + 2h3O
б) h3SO4 + 2NaOH = Na2SO4 + 2h3O
21
а) Al(OH)3 + 2HCl = Al(OH)Cl2 + 2h3Oб) h4PO4 + 2KOH =K2HPO4 + 2h3O
22
а) Al(OH)3 + HCl = Al(OH)2Cl + h3O
б) h4PO4 + NaOH = Nah3PO4 + h3O
В задачах 23–36 определите числа эквивалентностиz, факто- ры эквивалентностиf и молярные массы эквивалентов окислителя и восстановителя(г/моль) в следующих уравнениях окислительно- восстановительных реакций, протекающих в водном растворе. (Расчет вести на одну формульную единицу: атом, молекула, ион.)
| № | Ионные уравнения реакций |
| п/п |
| |
| 23 | 3Cu + 2NO3– + 8 H+ = 3Cu2+ + 2 NO + 4h3O |
| 24 | MnO4– + 8H+ + 2I– = I2 + Mn2+ + 4h3O |
| 25 | MnO4– + 6H+ + NO2– = Mn2+ + NO3– + 3h3O |
| 26 | Al + Cr2O72– + 14H+ = Al3++ 2Cr3++ 7h3O |
| 27 | I– + IO3– + 6H+ = I2 + 3h3O |
| 28 | SnO22– + Bi3+ + 2OH– = Bi + SnO32– + h3O |
| 29 | Cr2O72– + 6I– + 14H+ = 3I2 + 2Cr3+ + 7h3O |
| 30 | 2MnO4– + 16H+ + 10Fe2+ = 10Fe3+ + 2Mn2+ + 8h3O |
| 31 | Cr2O72– + 3h3S + 8H+ = 2Cr3+ + 3S + 7h3O |
| 32 | Cr2O72– + 3SO32– + 8H+ = 2Cr3+ + 3SO42– + 4h3O |
| 33 | Zn + 4H+ + SO42– = Zn2+ + SO2 + 2h3O |
| 34 | Mn2+ + 6OH– + h3O2 = MnO(OH)2 + O2 + 3h3O |
| 35 | Fe + 2H+ = Fe2+ + h3 |
| 36 | h3S + 2NO3– + 2H+ = S + 2NO2 + 2h3O |
В задачах 37–44 рассчитайте массу, молярную массу эквива- лентов, количество вещества эквивалентов вступившего в реакцию окислителя по известному количеству вещества эквивалентов вступившего в реакцию восстановителяn (моль). Используйте при решении задач закон эквивалентов.
8
| № | Уравнение реакции | n |
| п/п |
| | |
| | | |
| 37 | K2Cr2O7 + 7h3SO4 + 2Al = Al2(SO4)3 + Cr2(SO4)3 + K2SO4 + 7h3O | 0,05 |
| 38 | 2KMnO4 + 4h3SO4 + 2KI =2K2SO4 + 2MnSO4 + I2 + 4h3O | 0,075 |
| 39 | Fe + h3SO4 = FeSO4 + h3 | 0,25 |
| 40 | 2KMnO4 + 4KOH + Na2SO3 = Na2SO4 + 2K2MnO4 + h3O | 0,04 |
| 41 | 2KI + Cl2 =I2 + 2KCl | 0,02 |
| 42 | K2Cr2O7 + 6KI + 7h3SO4 = 3I2 + Cr2(SO4)3 + K2SO4 + 7h3O | 0,025 |
| 43 | Zn + 2h3SO4 = ZnSO4 + SO2 + 2h3O | 0,25 |
| 44 | 2KMnO4 + 6HCl + 5KNO2 = 2KCl + 2MnCl2 + 5 KNO3 + 3h3O | 5,0 |
В задачах 45–52 рассчитайте массы вступивших в реакцию металлов с заданными значениямиMэкв (г/моль), если при реакции металлов с кислотой выделяется известный объем водородаV (л), измеренный при н. у.
№ | MЭКВ | Vh3 | № | MЭКВ | Vh3 |
п/п | | | п/п | | |
45 | 32,70 | 0,560 | 49 | 68,67 | 0,333 |
| | | | | |
46 | 12,15 | 0,280 | 50 | 4,51 | 0,432 |
| | | | | |
47 | 27,93 | 0,210 | 51 | 56,21 | 0,230 |
| | | | | |
48 | 29,35 | 0,053 | 52 | 29,47 | 0,152 |
| | | | | |
В задачах 53–62 вычислите молярные массы эквивалентов ме- таллов и их оксидов(г/моль), если известно, что при восстановле- нии водородом данной массы оксида металлаm1 образовалась из- вестная масса водыm2, молярная масса эквивалентов которой рав- на9 г/моль. Укажите металл.
| № | m1,г | m2,г | № | m1,г | m2,г |
| п/п | п/п |
| | | | |
| | | | | | |
| 53 | 13,57 | 3,0 | 58 | 14,37 | 3,6 |
| | | | | | |
| 54 | 7,98 | 2,0 | 59 | 19,89 | 4,5 |
| | | | | | |
| 55 | 6,85 | 1,55 | 60 | 25,76 | 6,0 |
| | | | | | |
| 56 | 20,35 | 4,5 | 61 | 36,18 | 8,0 |
| | | | | | |
| 57 | 33,48 | 2,7 | 62 | 62,00 | 5,0 |
| | | | | | |
9
studfiles.net
Сборник контрольных работ по курсу общей химии
Казанский государственный технический университет им. А.Н. Туполева
Учебное пособие
H (реакции) =
=Hf (продуктов) – Hf (реагентов)
Казань – 2011
Печатается по рекомендации УМЦ КГТУ им.А.Н. Туполева
Рецензенты:
Будников Г.К. – докт. хим. наук, проф. Казанского Федерального университета
Евгеньев М.И. – докт. хим. наук, проф. Казанского государственного технологического университета
Авторы: А.Н.Глебов, А.Р.Буданов, И.Г.Григорьева, О.В.Лавриненко,
С.А. Мальцева, А.И.Шамкаева, Д.В.Фролов, Е.П.Чеклаукова
Сборник контрольных работ по курсу общей химии: Учебное пособие / Под ред. проф. А.Н. Глебова. 4-е изд. Казань: Изд-во «Экоцентр», 2011. 32 стр.
Учебное пособие предназначено для студентов технического университета, изучающих общую химию по дневной, вечерней и заочной формам обучения. Пособие составлено в соответствии с учебным планом, программой курса общей химии. «Сборник контрольных работ» способствует более полному освоению изучаемого материала и развитию навыков самостоятельной работы студентов. В пособии приведены контрольные задания по основным темам курса общей химии, необходимые расчетные формулы, даны решения типовых задач.
Издательство «Экоцентр», 2011 г.
Содержание
| 1. Основные классы неорганических соединений | 4 |
| 2. Основные законы химии | 6 |
| 3. Строение атома и химическая связь | 9 |
| 4. Химическая термодинамика | 11 |
| 5. Химическая кинетика и равновесие | 14 |
| 6. Растворы | 17 |
| 7. Теория электролитической диссоциации | 20 |
| 8. Окислительно-восстановительные реакции | 22 |
| 9. Электрохимические процессы и системы | 25 |
| 10. Примеры решения типовых задач | 28 |
| Литература | 30 |
1. Основные классы неорганических соединений
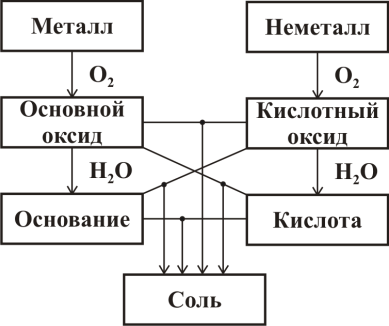
Взаимосвязь между основными классами неорганических веществ (оксиды, кислоты, основания, соли) можно упрощенно представить в виде схемы:
Химические свойства основных классов неорганических соединений:
| | Металл | Основной оксид | Основание | Соль |
| Неметалл | Fe + S = FeS | — | — | 2NaBr + Cl2 = 2NaCl + Br2 |
| Кислотный оксид | — | CaO + CO2 = CaCO3 | 2NaOH + CO2 = Na2CO3 + h3O | — |
| Кислота | Fe + 2HCl = FeCl2 + h3 | CaO + h3SO4 = CaSO4 + h3O | NaOH + HCl = NaCl + h3O | BaCl2 + h3SO4 = BaSO4↓ + 2HCl |
| Соль | Zn + CuSO4= Cu + ZnSO4 | — | CuSO4 + 2NaOH = Cu(OH)2↓ + Na2SO4 | AgNO3 + NaCl = AgCl↓ + NaNO3 |
1.1. Назовите вещество и укажите класс химических соединений:
Fe(OH)2Cl
K2CrO4
Mg(ClO3)2
NaHS
Al(OH)3
Nah3PO4
Nh5OH
Na2Cr2O7
Ba(HSO3)2
Na2SO3
Ba(OH)2
HClO4
(CuOH)2CO3
Ba2P2O7
HMnO4
Al(OH)SO4
Ca(ClO)2
Ca(h3PO4)2
Al(NO3)3
K2ZnO2
studfiles.net
Сборник контрольных работ по алгебре и началам анализа за курс средней школы
СБОРНИК
контрольных работ по алгебре и началам анализа
за курс средней школы
Пояснительная записка:
Сборник содержит 20 вариантов итоговых контрольных работ по алгебре и началам анализа за курс средней школы. Может быть использован учителями математики при подготовке выпускников к итоговой аттестации.
1 вариант
1.Упростите: 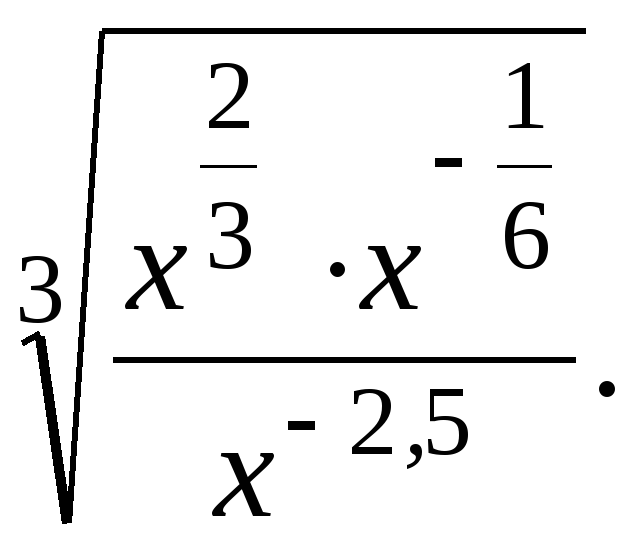
2. Найдите промежутки возрастания и убывания функции
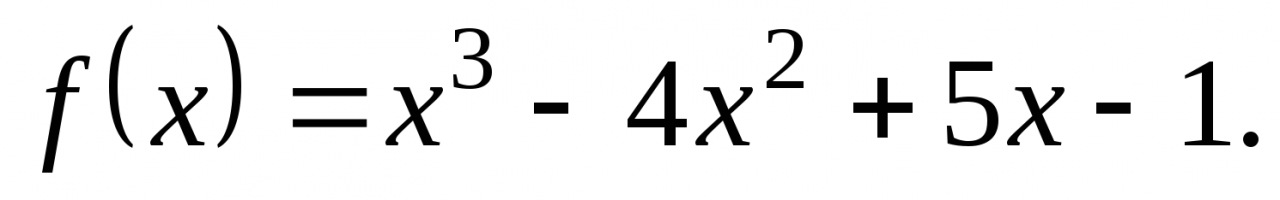
3. Решите систему неравенств 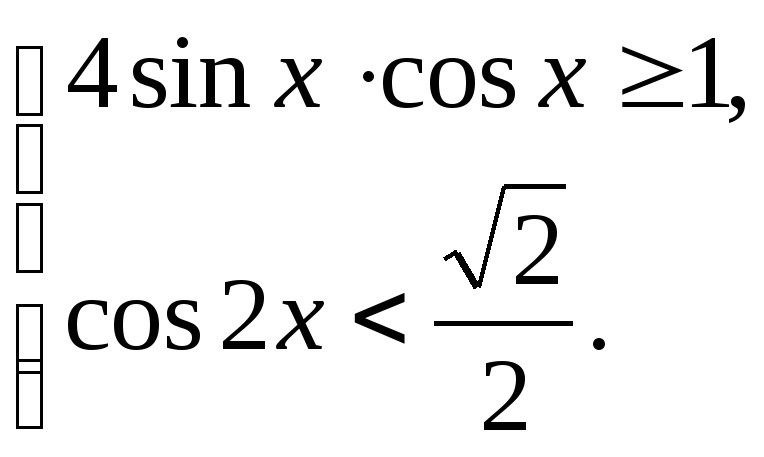
4. Решите уравнение 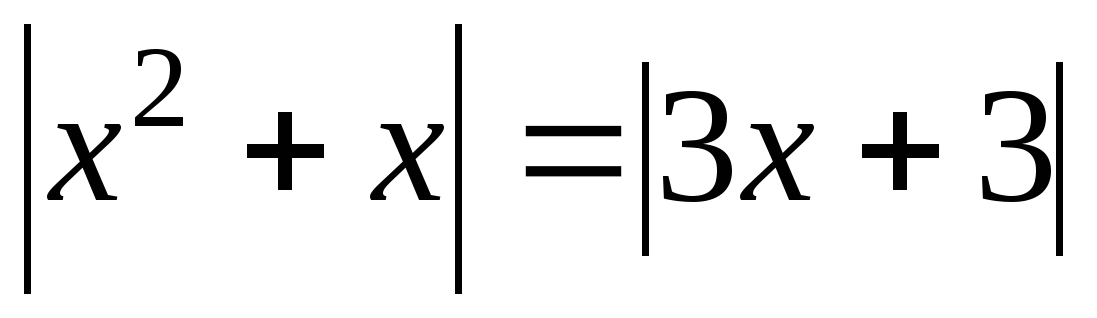 .
.
5. Найдите значение выражения 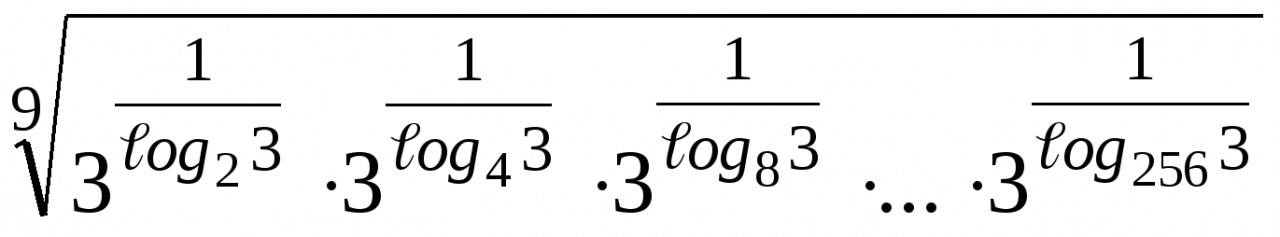 .
.
6. К графику функции 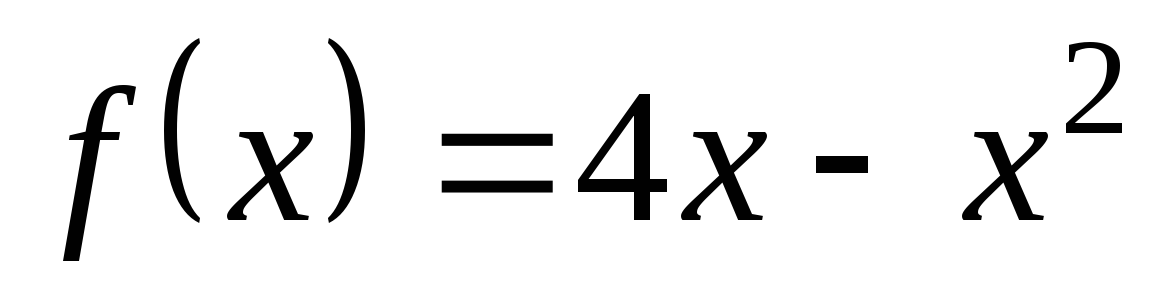 проведены касательные в точках с абсциссами х1=1 и х2=4. Найдите площадь треугольника, образованного этими касательными и осью Ох.
проведены касательные в точках с абсциссами х1=1 и х2=4. Найдите площадь треугольника, образованного этими касательными и осью Ох.
2 вариант
1. Упростите: 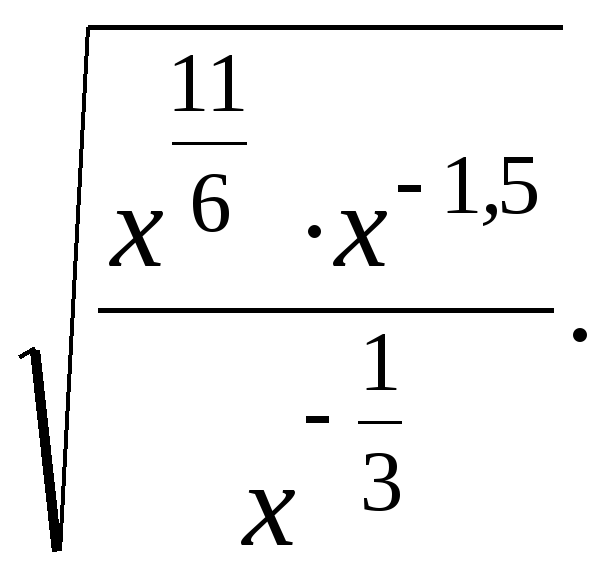
2. Найдите промежутки возрастания и убывания функции
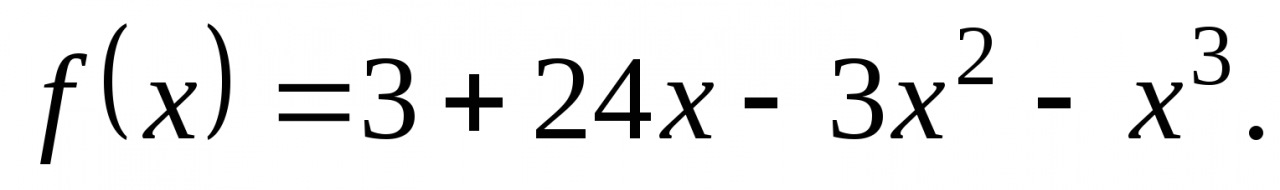
3. Решите систему неравенств 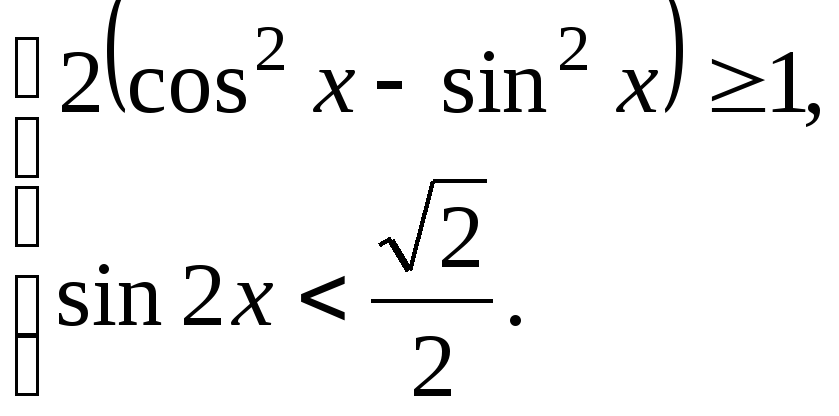
4. Решите уравнение 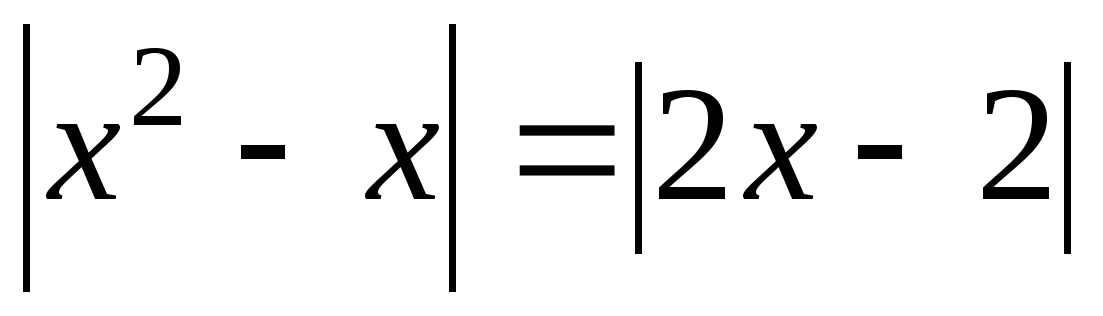 .
.
5. Найдите значение выражения 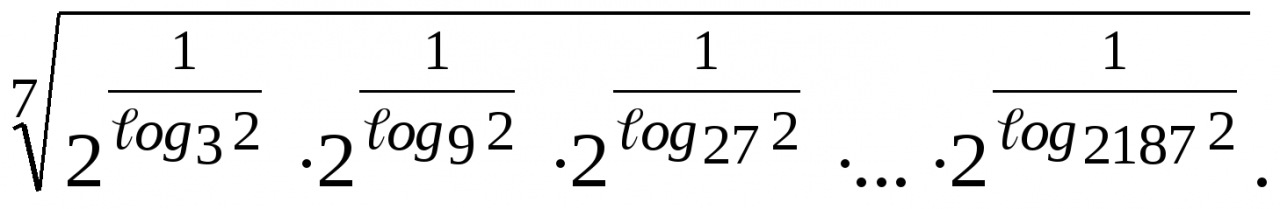
6. К графику функции 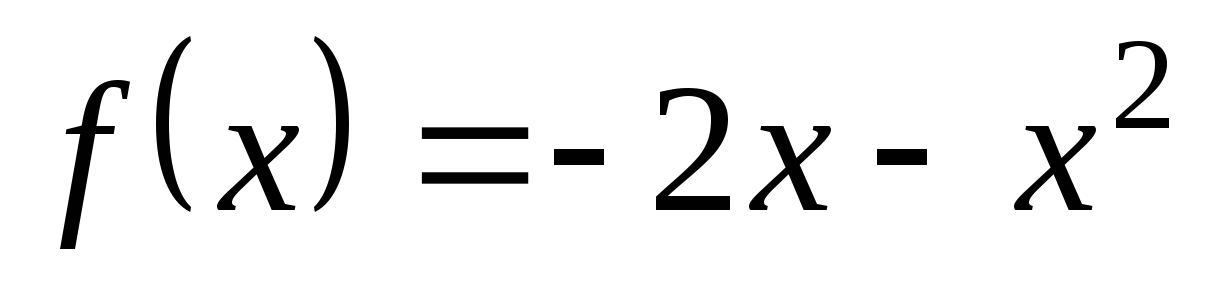 проведены касательные в точках с абсциссами х1=−2 и х2=1. Найдите площадь треугольника, образованного этими касательными и осью Ох.
проведены касательные в точках с абсциссами х1=−2 и х2=1. Найдите площадь треугольника, образованного этими касательными и осью Ох.
3 вариант
1. Вычислите 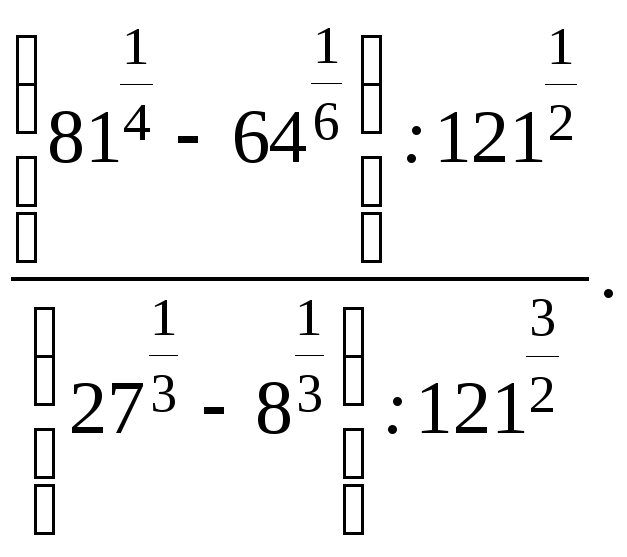
2. Решите уравнение 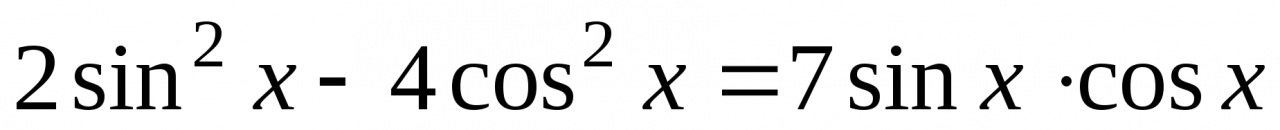 .
.
3. Число 9 разложите на два слагаемых так, чтобы их произведение было наибольшим.
4. Решите систему неравенств 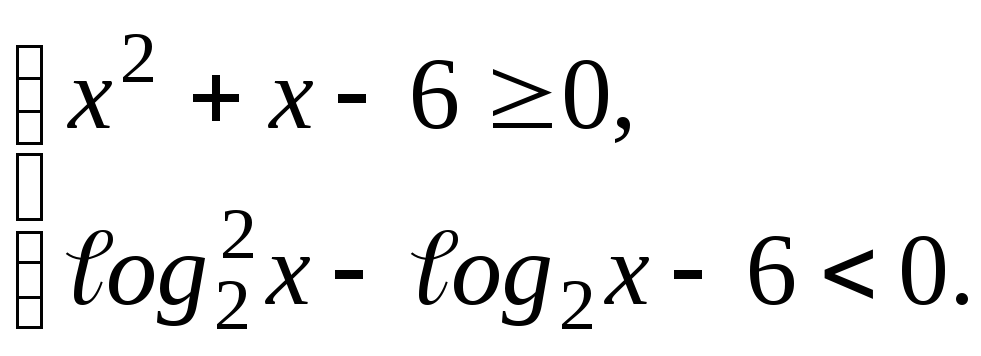
5. Найдите значение выражения 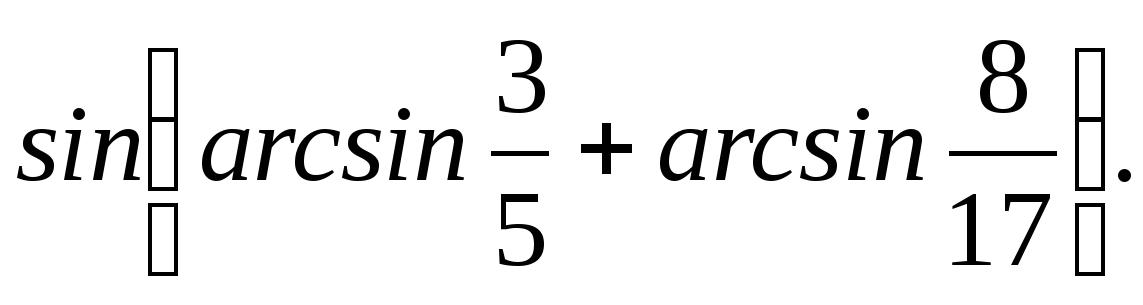
6. Постройте график функции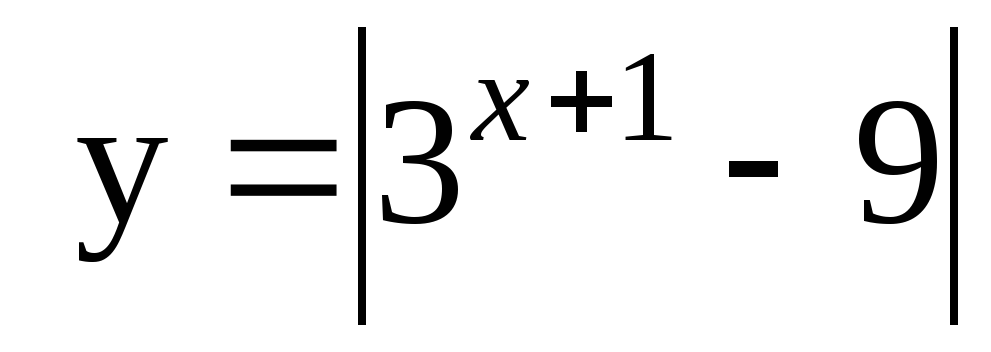 .
.
4 вариант
1. Вычислите 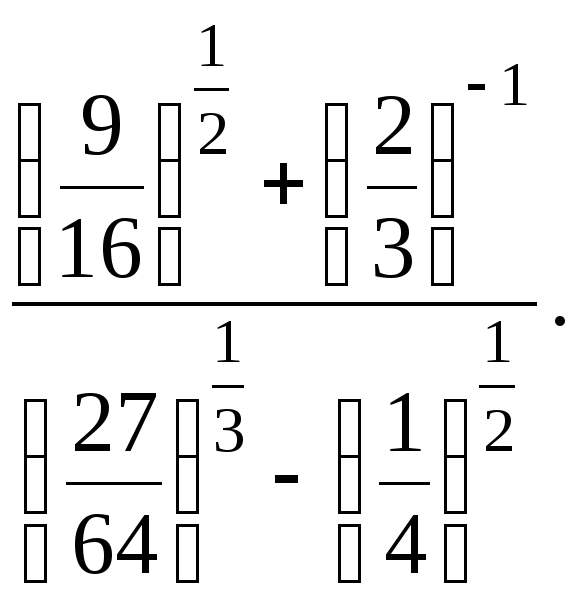
2. Решите уравнение 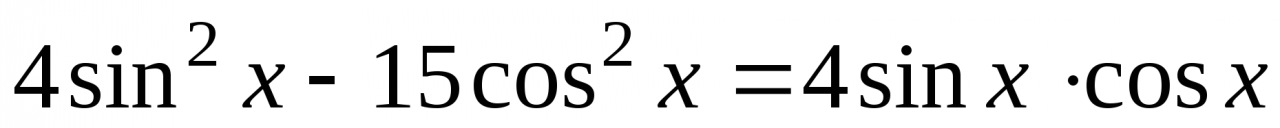 .
.
3. Число 12 разложите на два слагаемых так, чтобы сумма их квадратов была наименьшей.
4. Решите систему неравенств 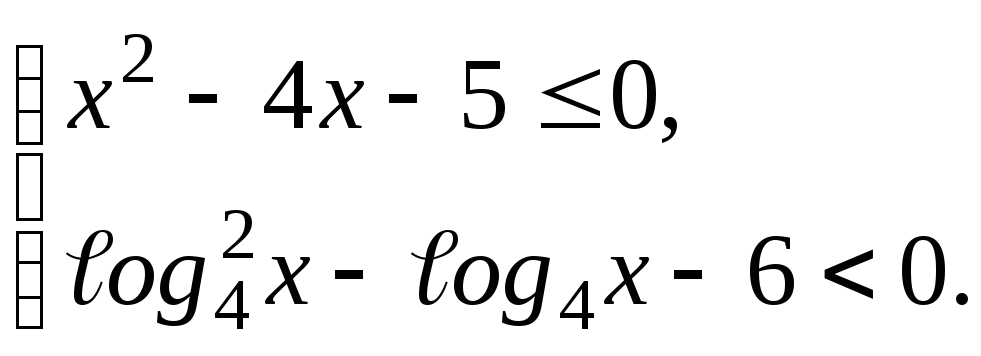
5. Найдите значение выражения 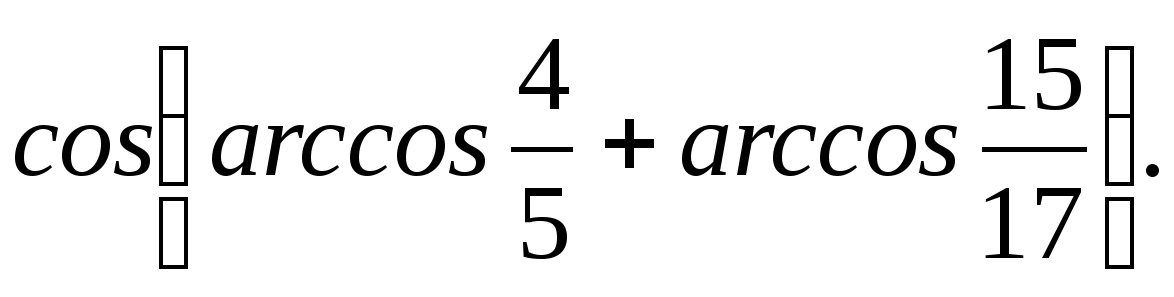
6. Постройте график функции 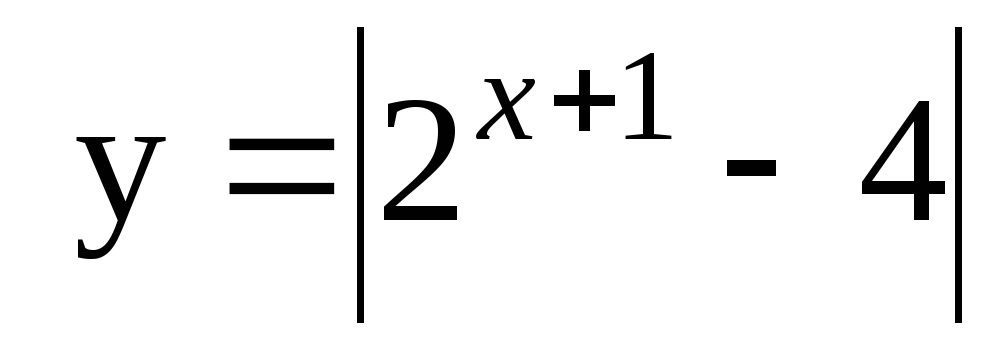 .
.
5 вариант
1. Найдите значение выражения 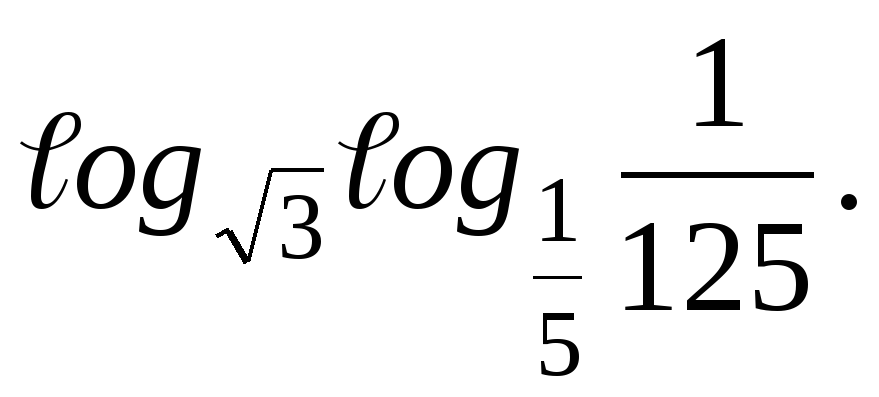
2. Упростите выражение 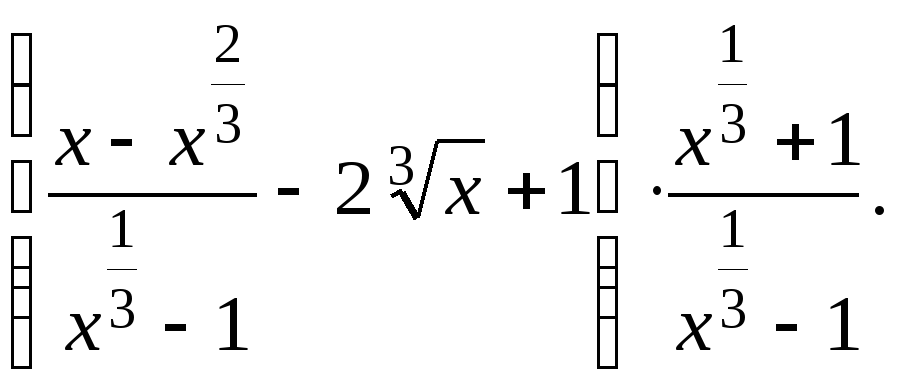
3. Найдите промежутки возрастания и убывания функции 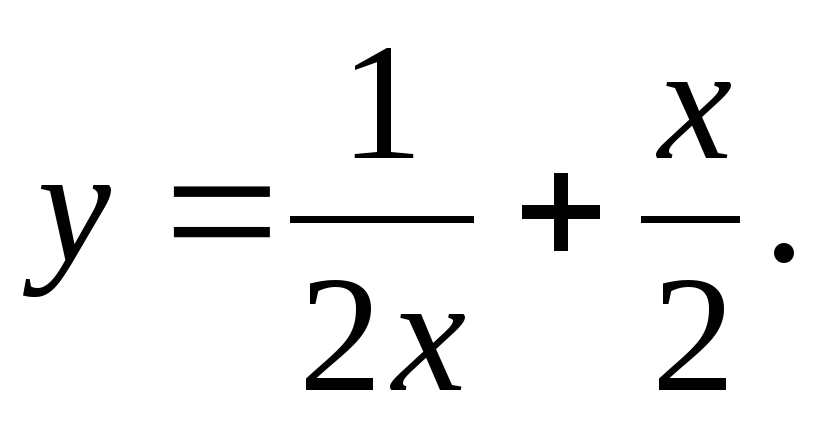
4. Решите неравенство 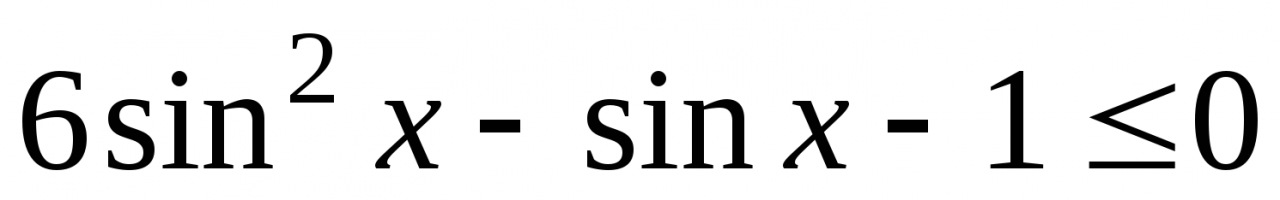 .
.
5. Решите систему уравнений 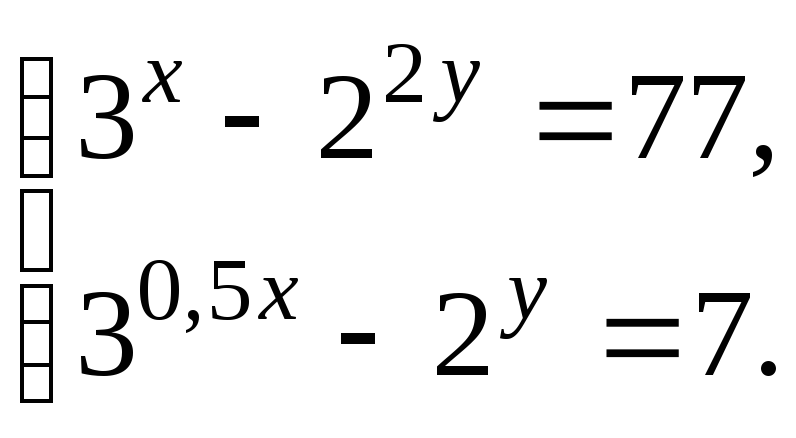
6. Найдите площадь плоской фигуры, ограниченной графиками функций 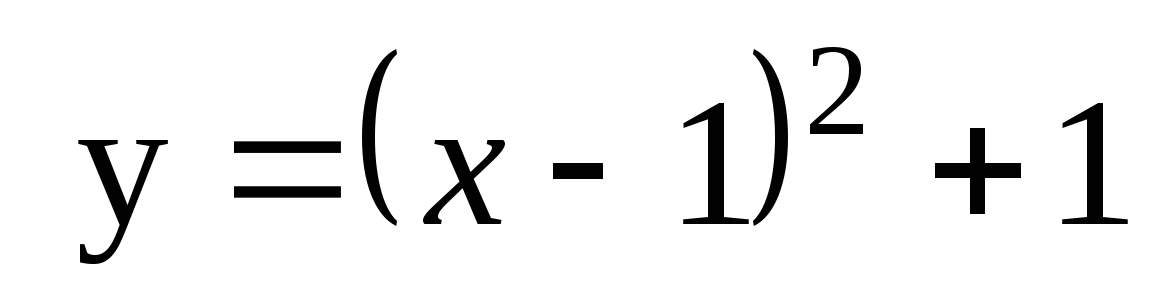 и
и 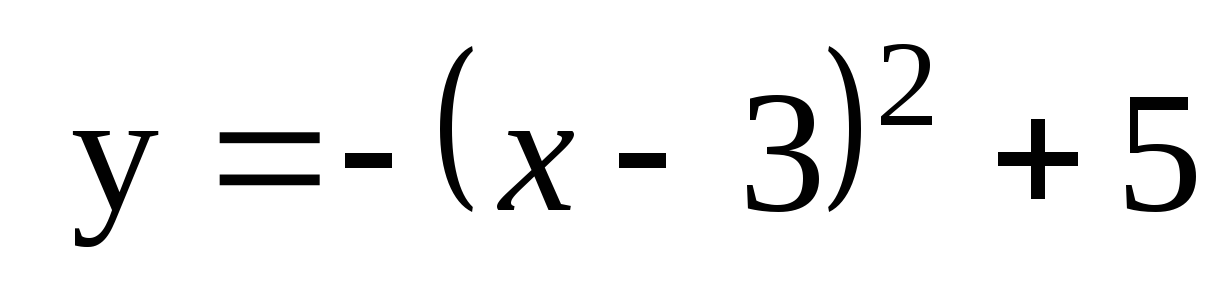 .
.
6 вариант
1. Найдите значение выражения 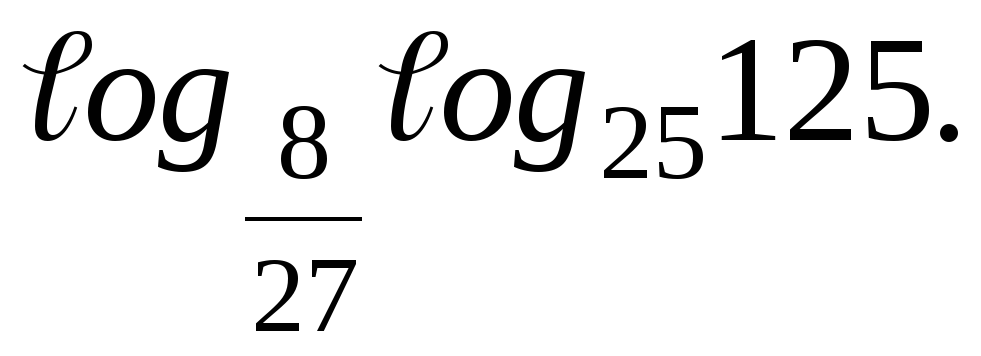
2. Упростите выражение 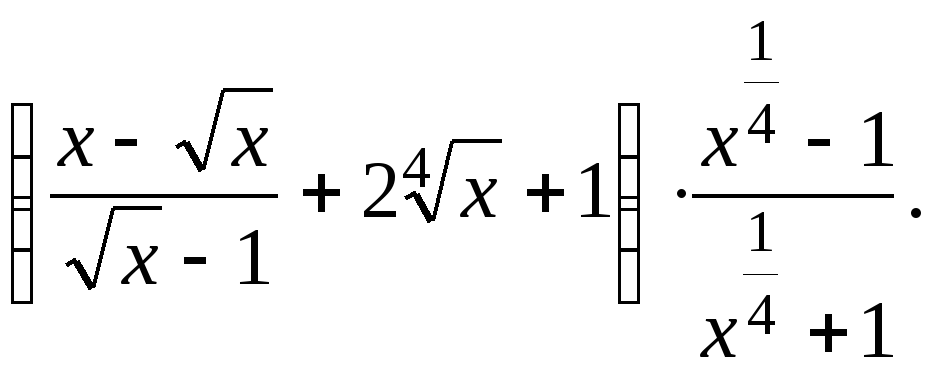
3. Найдите промежутки возрастания и убывания функции 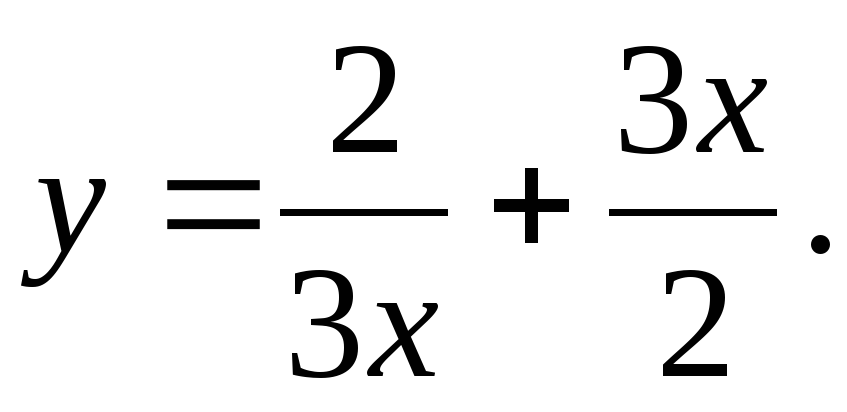
4. Решите неравенство 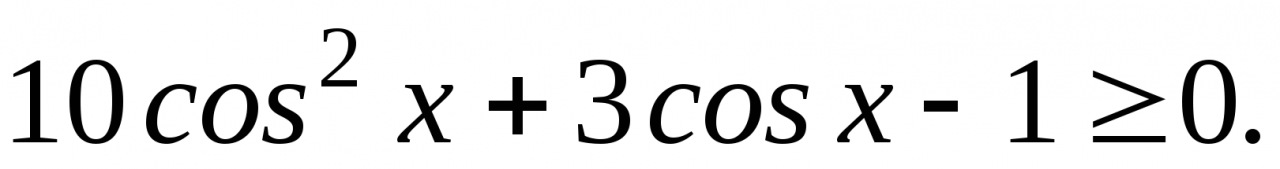
5. Решите систему уравнений 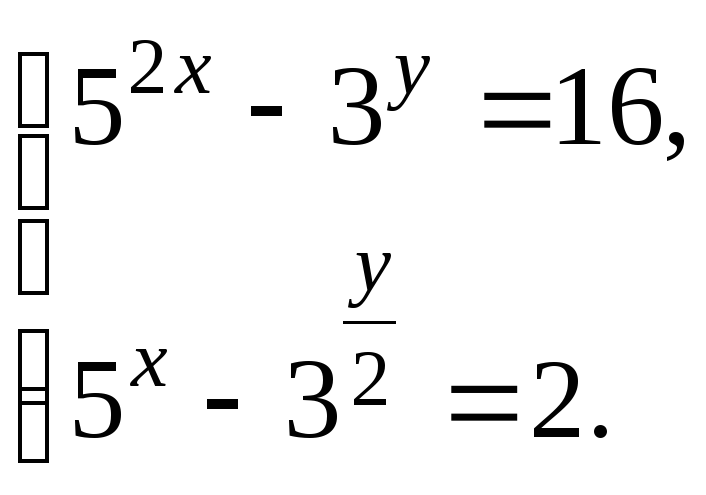
6. Найдите площадь плоской фигуры, ограниченной графиками функций. 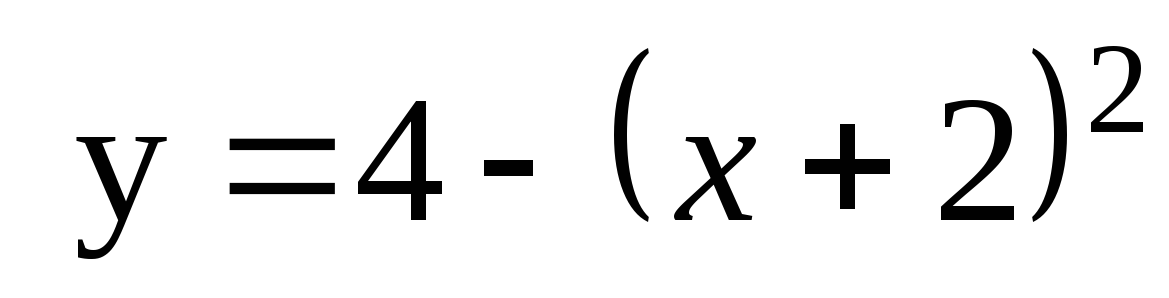 и
и 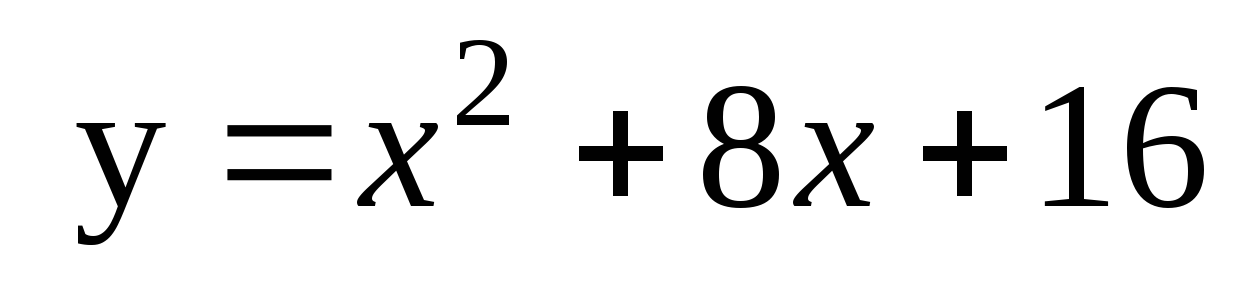 .
.
7 вариант
1. Вычислите 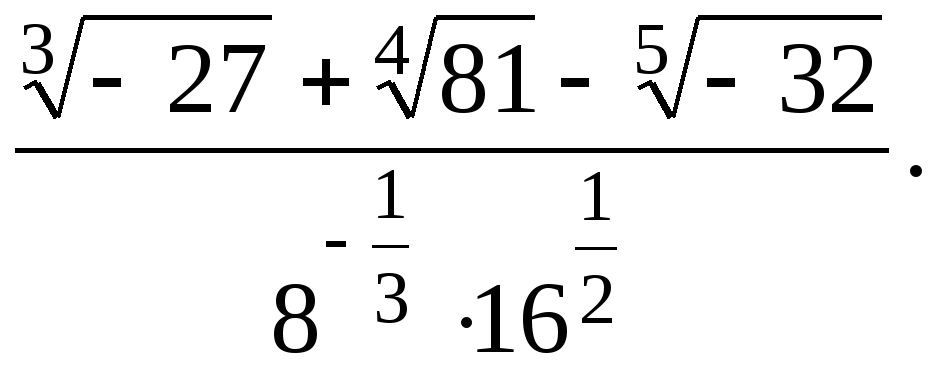
2. Упростите выражение 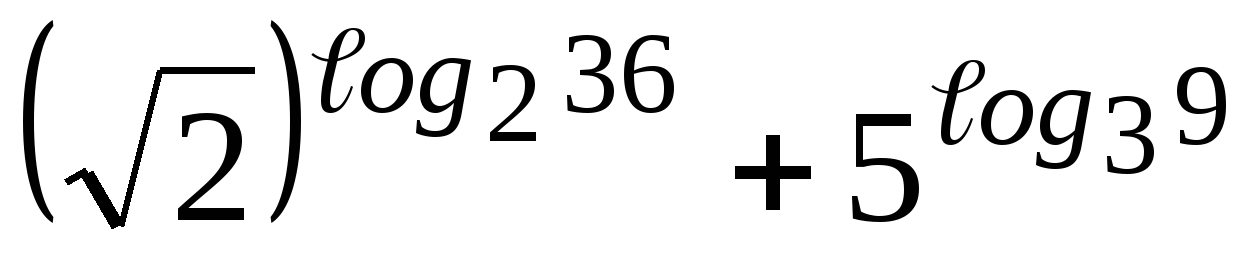 .
.
3. Решите уравнение 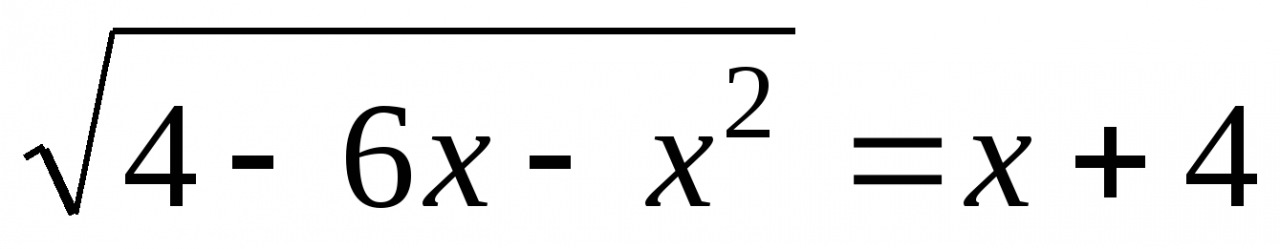 .
.
4. Решите систему неравенств 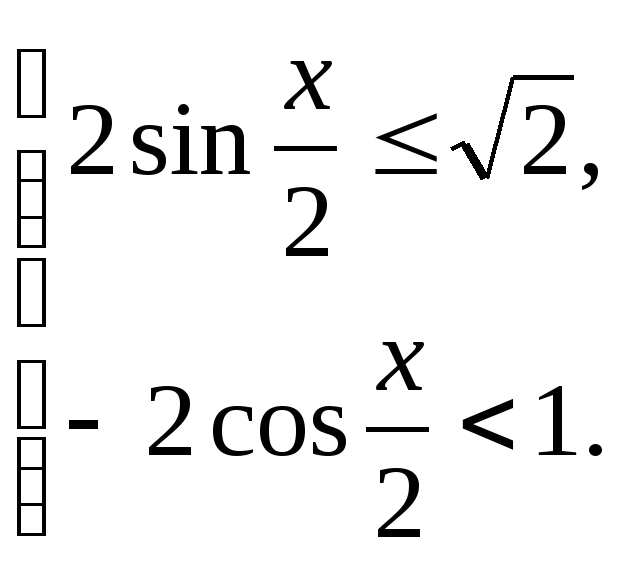
5. Точка движется прямолинейно по закону 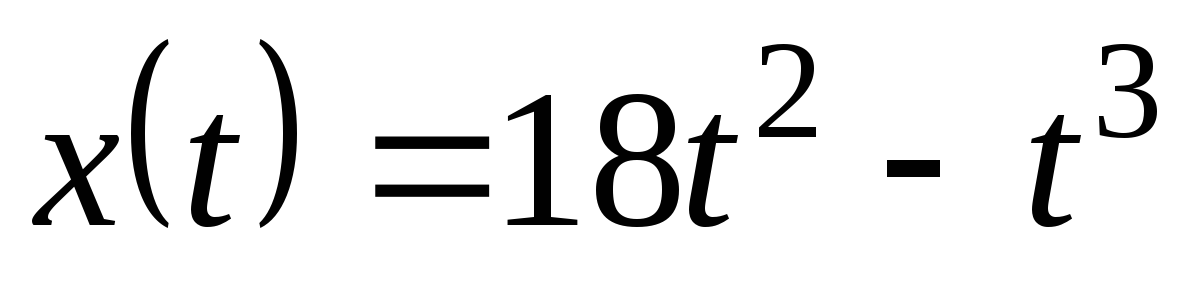 (х-в метрах, t-в cекундах). Найдите время, при котором скорость принимает наибольшее значение на промежутке времени
(х-в метрах, t-в cекундах). Найдите время, при котором скорость принимает наибольшее значение на промежутке времени 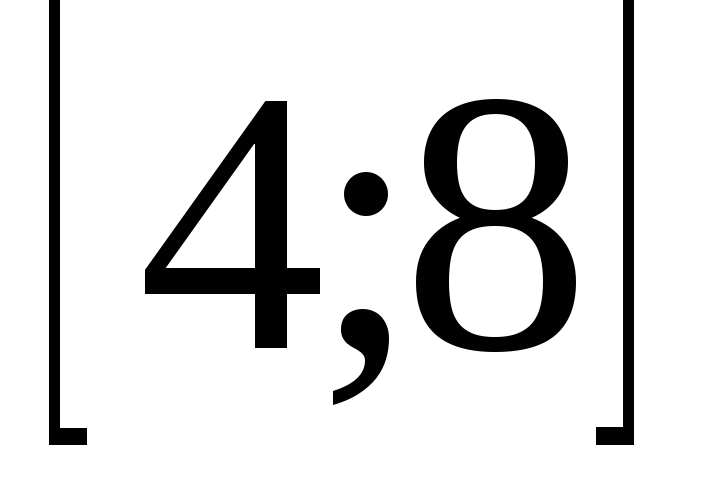 .
.
6. Найдите площадь плоской фигуры, ограниченной графиком функции 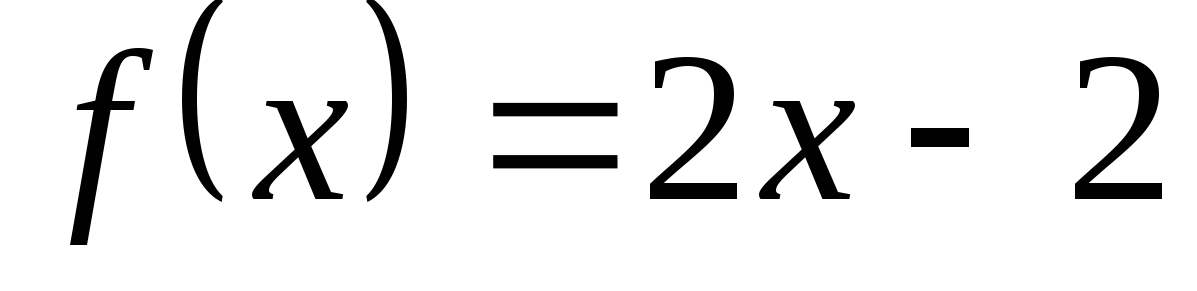 и графиком первообразной этой функции, для которой выполняется условие F(0)=1 .
и графиком первообразной этой функции, для которой выполняется условие F(0)=1 .
8 вариант
1. Вычислите 
2. Упростите выражение 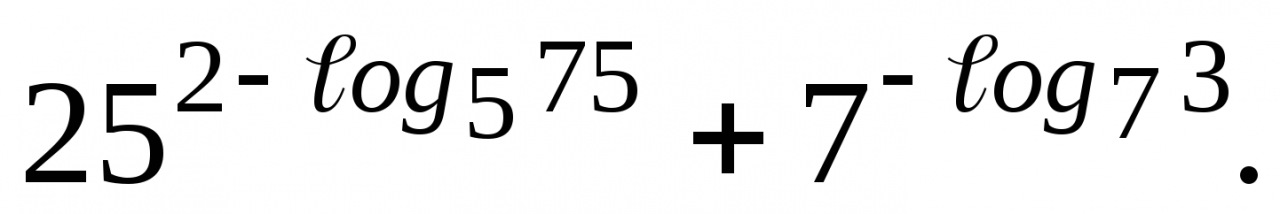
3. Решите уравнение 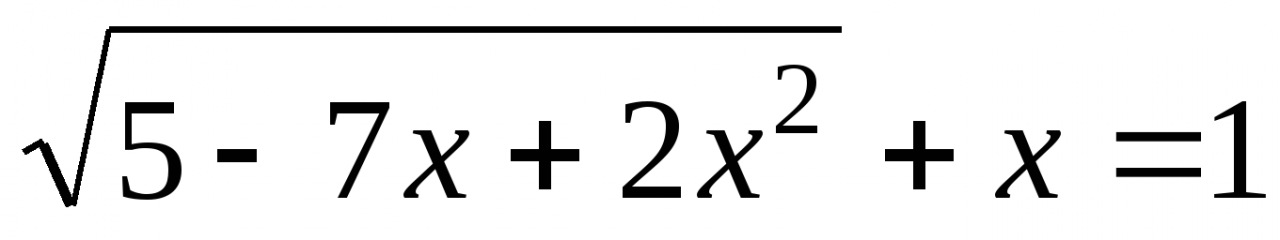 .
.
4. Решите систему неравенств 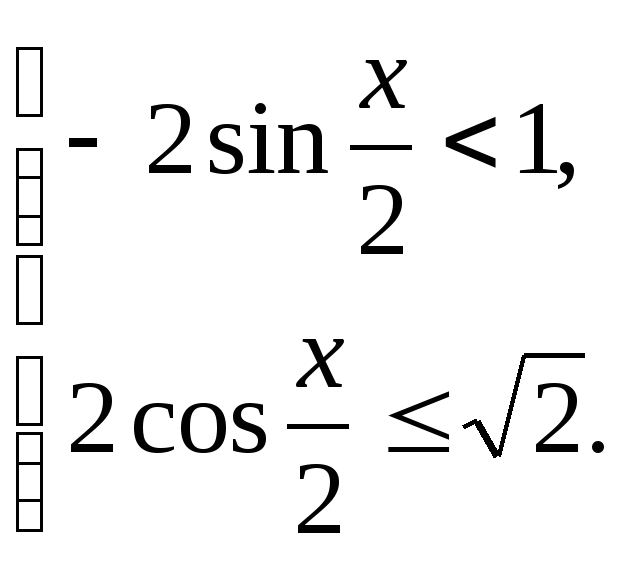
5. Точка движется прямолинейно по закону 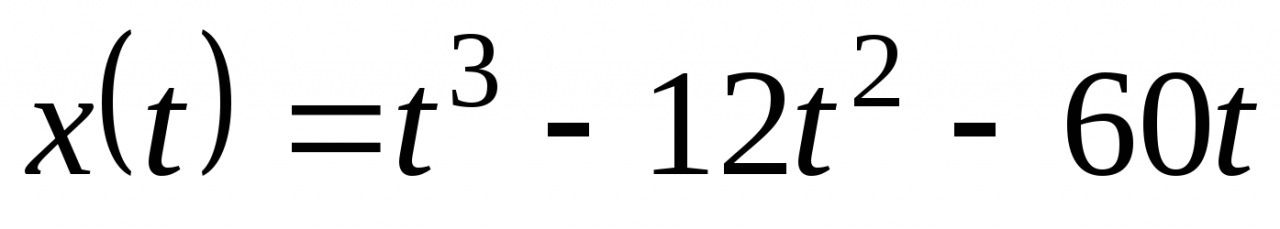 (х-в метрах, t- в cекундах). Найдите время, при котором скорость принимает наименьшее значение на промежутке времени
(х-в метрах, t- в cекундах). Найдите время, при котором скорость принимает наименьшее значение на промежутке времени 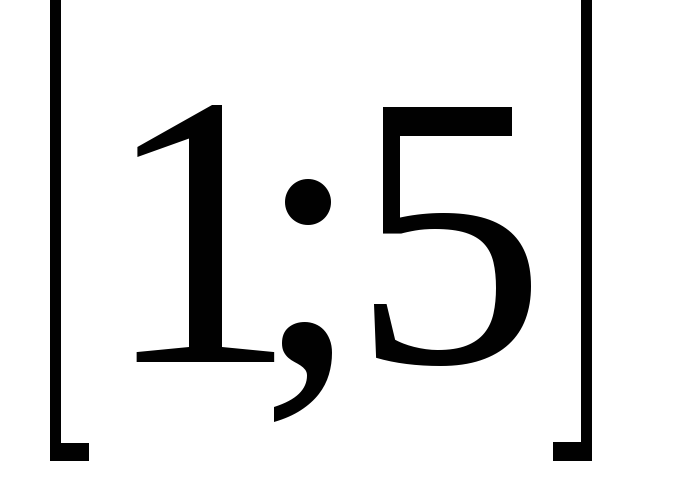 .
.
6. Функция F(х) является первообразной для функции 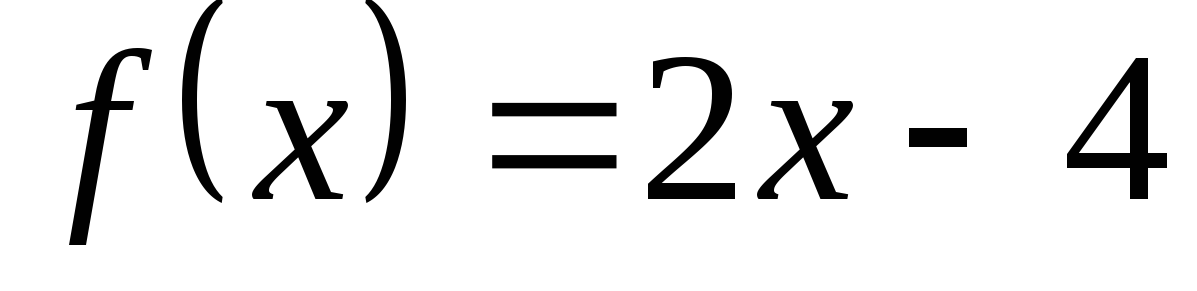 .
.
Зная, что F(0)= −4 , найдите площадь плоской фигуры, ограниченной графиками функций F(x) и f(x) .
9 вариант
1. Вычислите 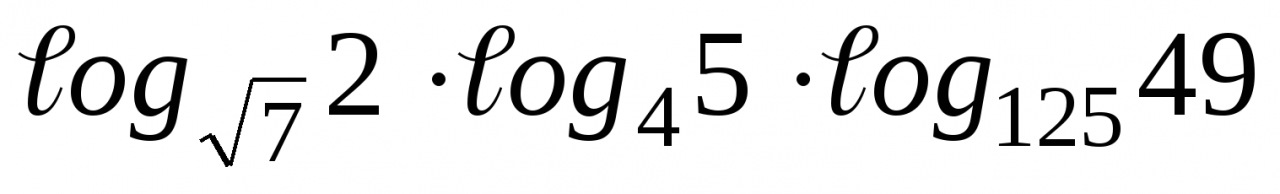 .
.
2. Найдите значение выражения 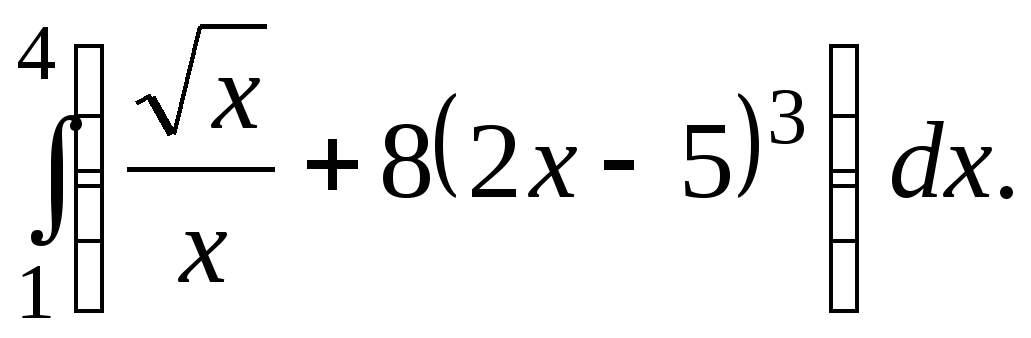
3. Решите неравенство 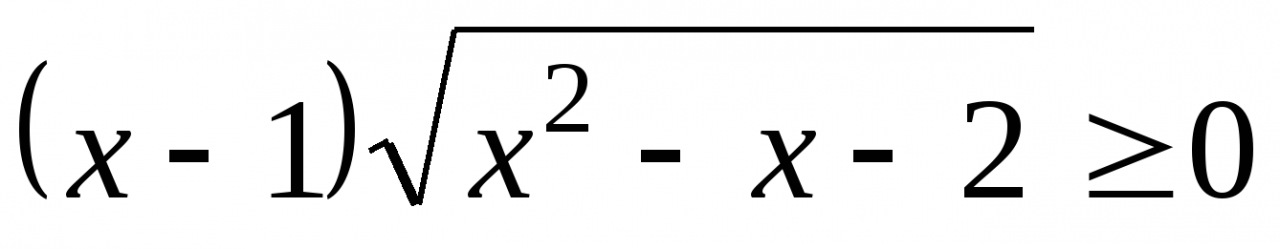 .
.
4. Решите систему уравнений 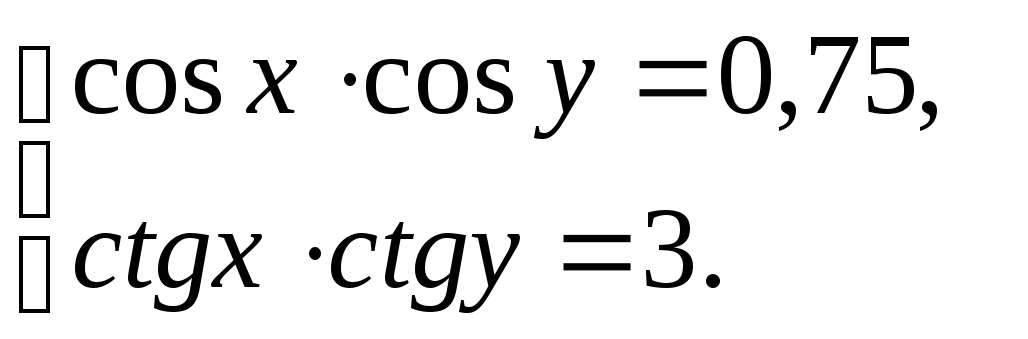
5. Материальная точка движется по закону 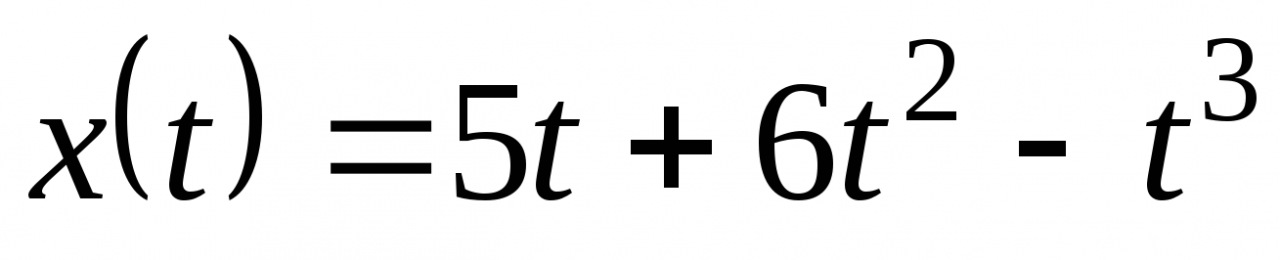 (х- в метрах,t-в секундах). Найдите скорость точки, в момент времени когда ускорение равен нулю.
(х- в метрах,t-в секундах). Найдите скорость точки, в момент времени когда ускорение равен нулю.
6. Исследуйте функцию и постройте ее график 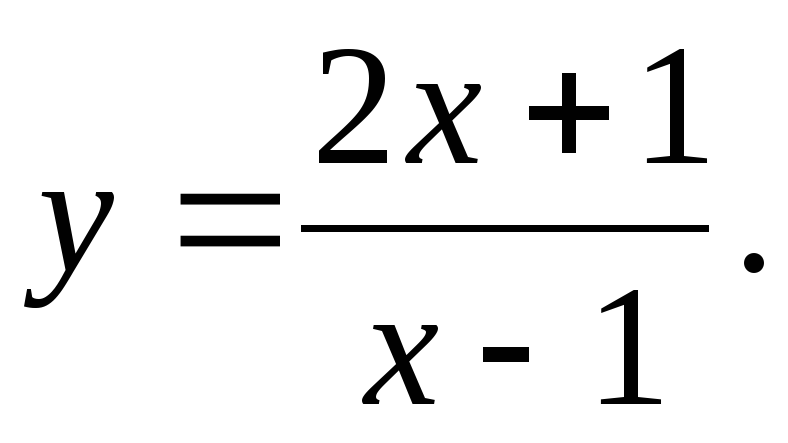
10 вариант
1. Вычислите 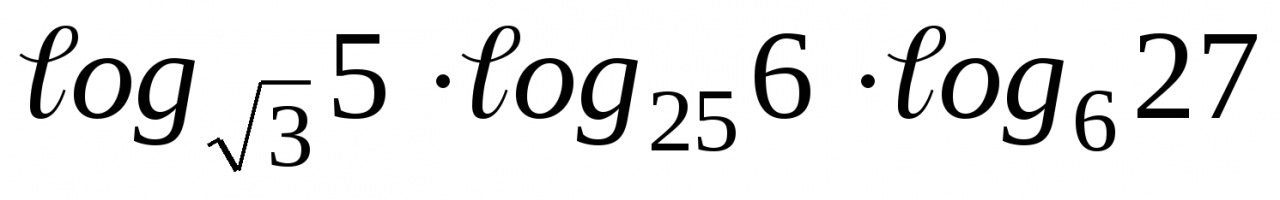 .
.
2. Найдите значение выражения 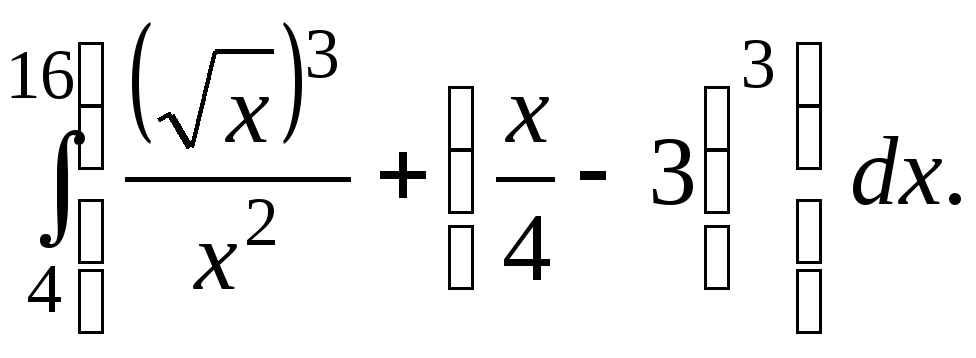
3. Решите неравенство 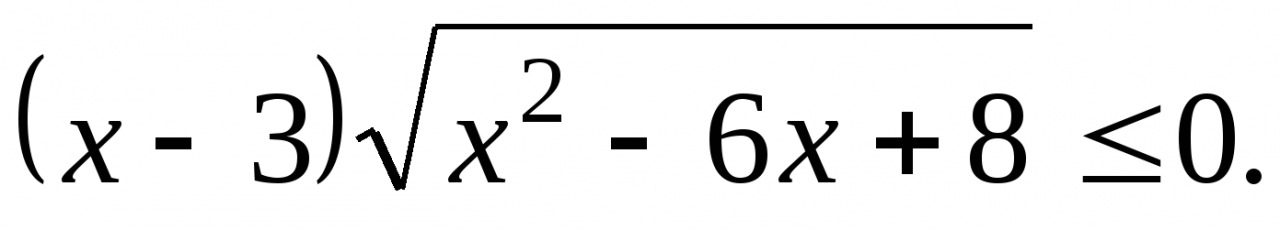
4. Решите систему уравнений 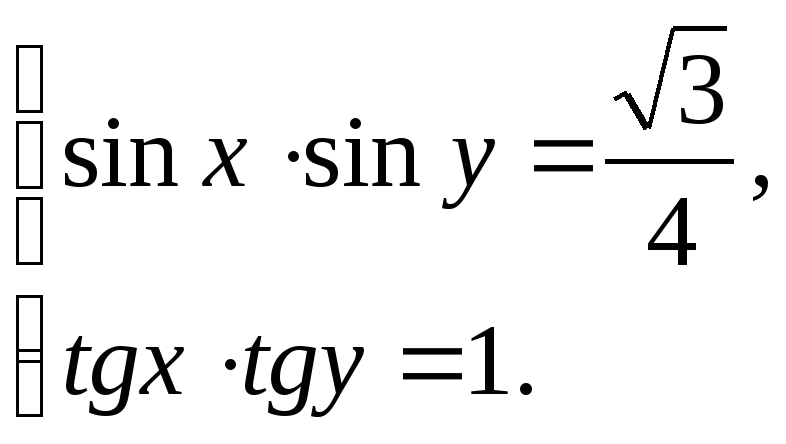
5. Материальная точка движется по закону 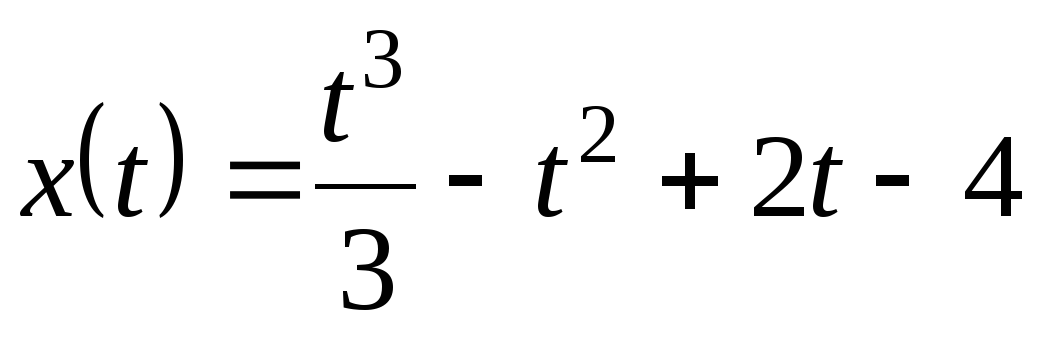 (х-в метрах, t-в секундах). Найдите ускорение точки в момент времени, когда скорость равен 1 м/с.
(х-в метрах, t-в секундах). Найдите ускорение точки в момент времени, когда скорость равен 1 м/с.
6. Исследуйте функцию и постройте ее график 
11 вариант
1. Решите неравенство 
2. Найдите область определения функции  .
.
3. Упростите выражение 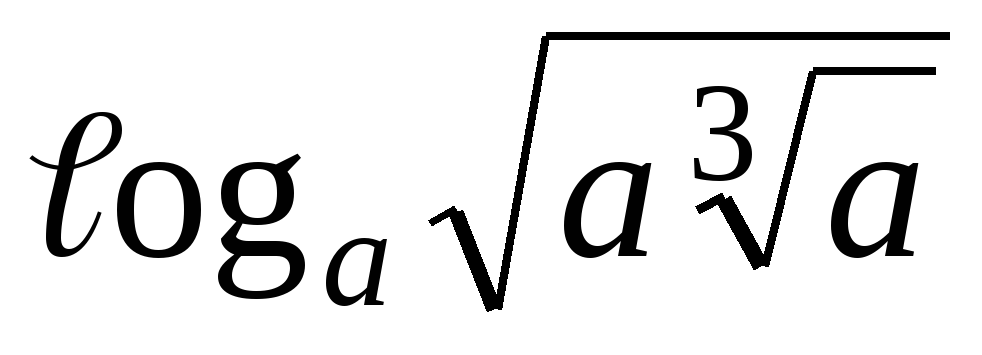 .
.
4. Вычислите 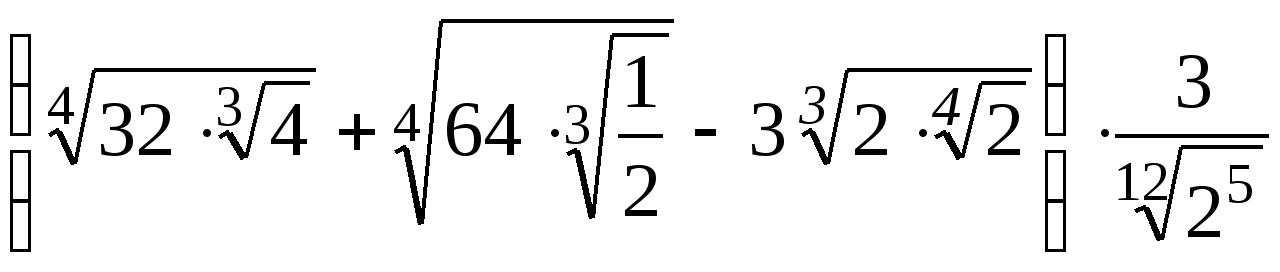 .
.
5. Решите систему уравнений 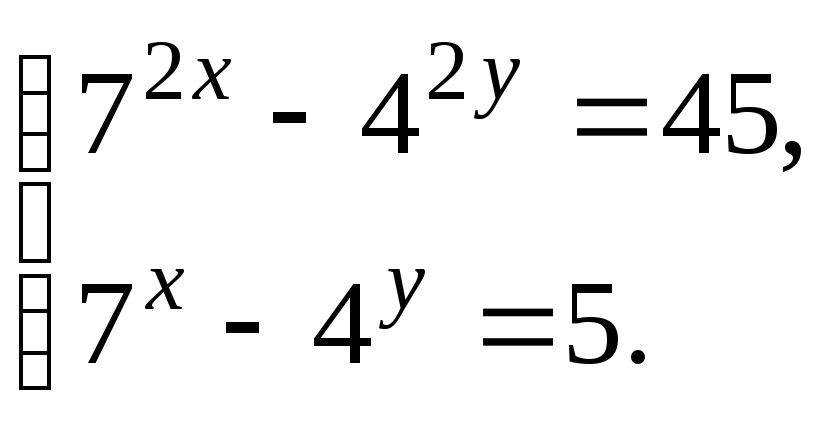
6. Найдите площадь плоской фигуры, ограниченной графиком функции 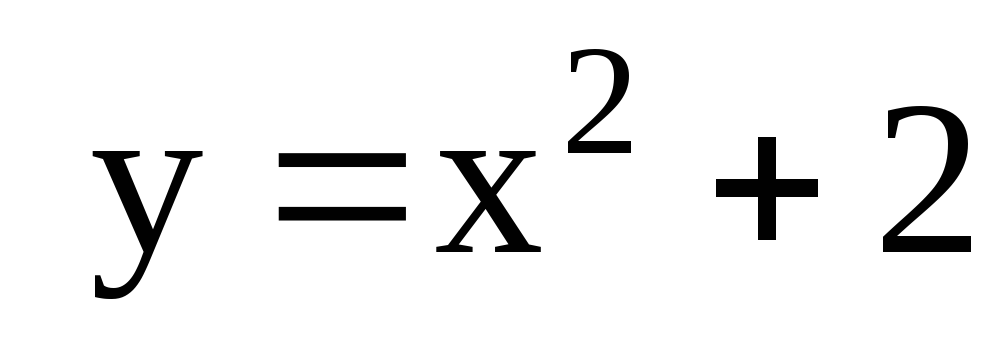 и касательными к графику проведенными в точке (2;2).
и касательными к графику проведенными в точке (2;2).
12 вариант
1. Решите неравенство 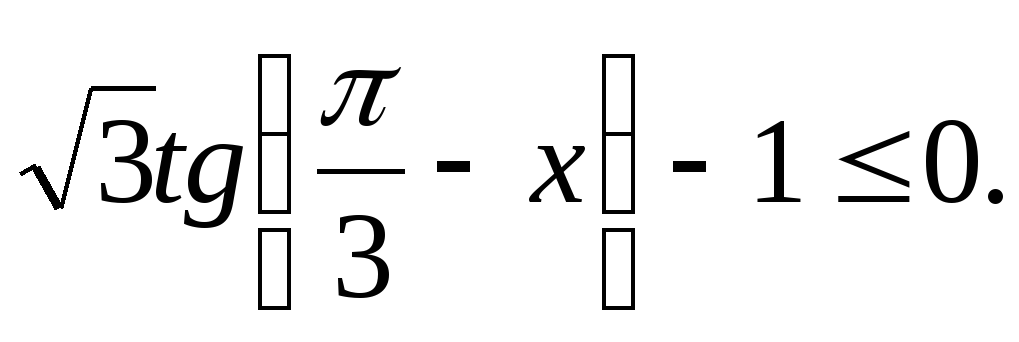
2. Найдите область определения функции 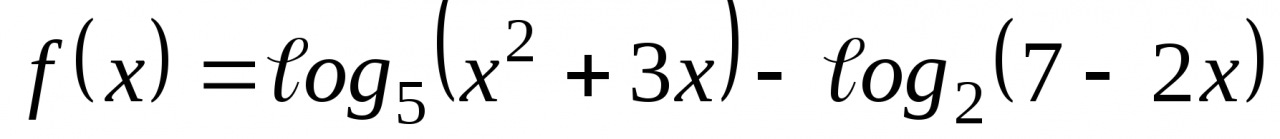 .
.
3. Упростите выражение  .
.
4. Вычислите 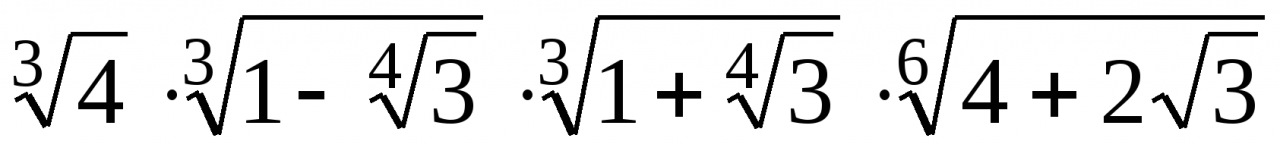 .
.
5. Решите систему уравнений 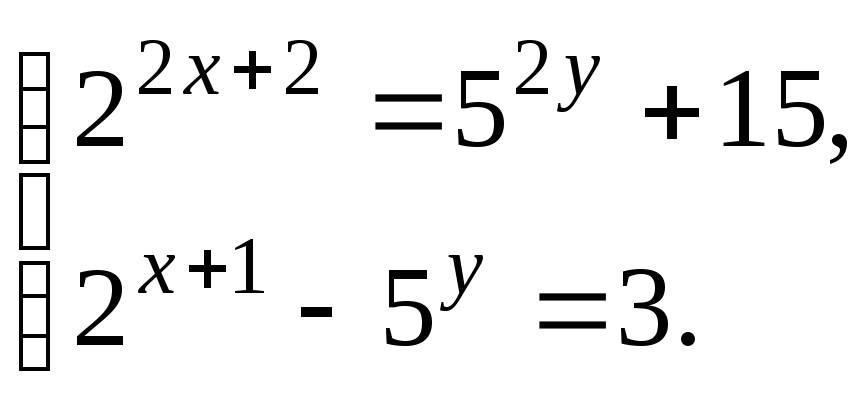
6. Найдите площадь плоской фигуры, ограниченной графиком функции 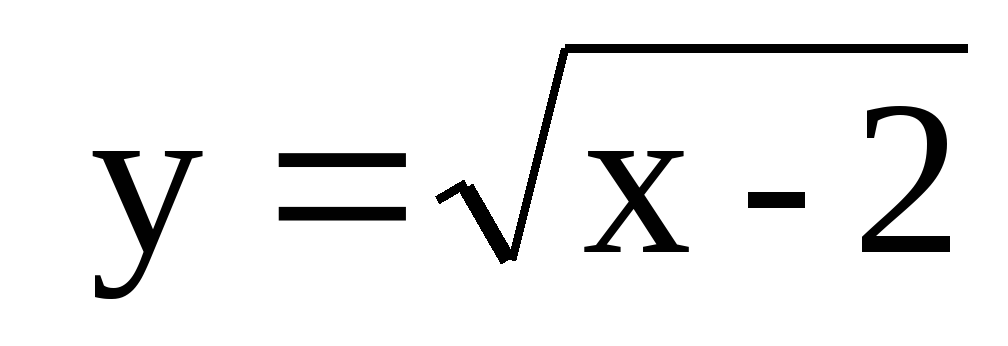 и касательными к графику проведенными в точке (2;1).
и касательными к графику проведенными в точке (2;1).
13 вариант
1. Вычислите 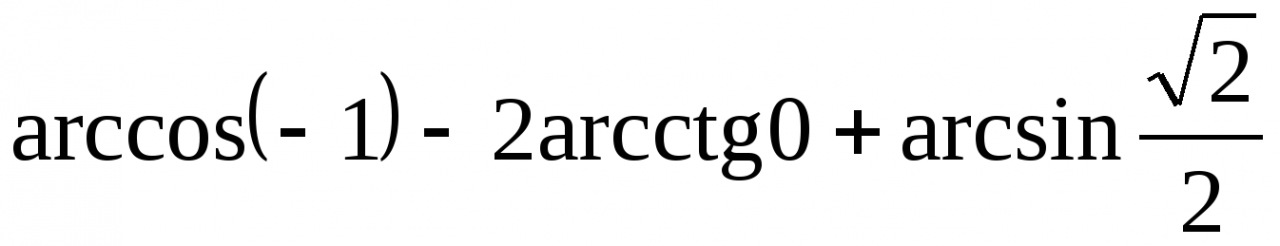 .
.
2. Если 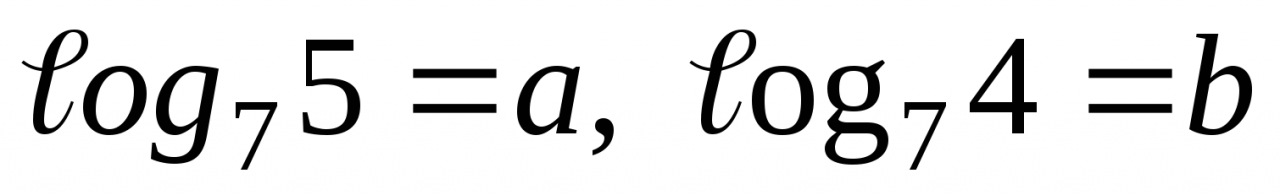 , то выразите
, то выразите 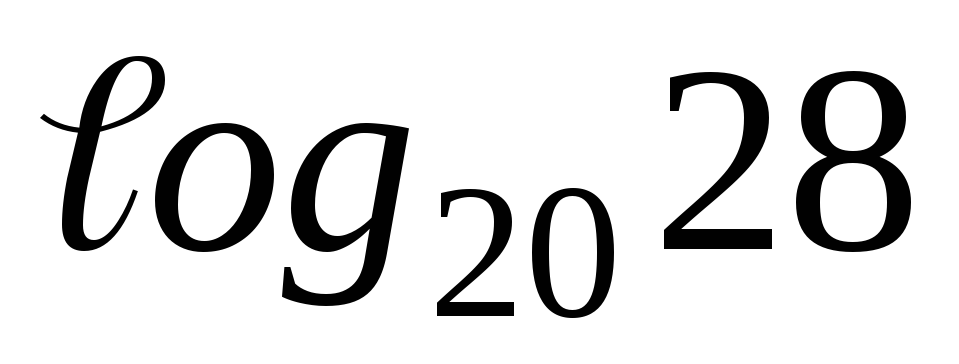 через
через  и
и 
3. Решите уравнение 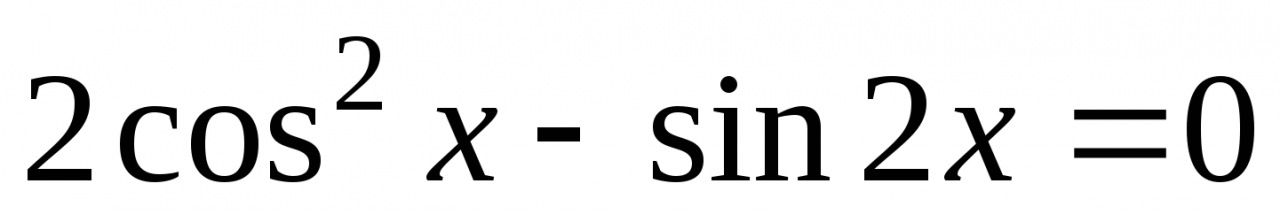 .
.
4. Решите систему неравенств 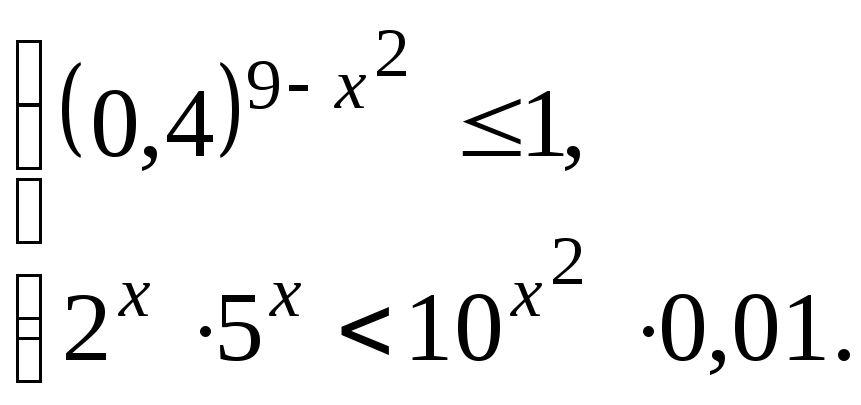
5. Периметр прямоугольника 120 м. Найдите стороны прямоугольника наибольшей площади.
6. Исследуйте и постройте график функции 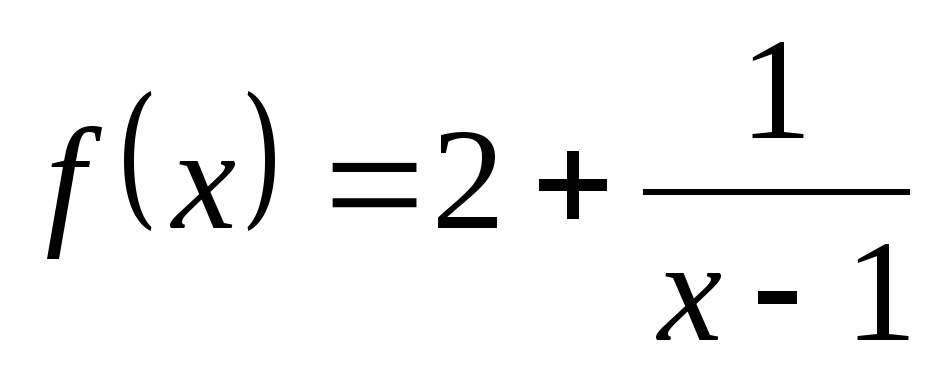 .
.
14 вариант
1. Вычислите 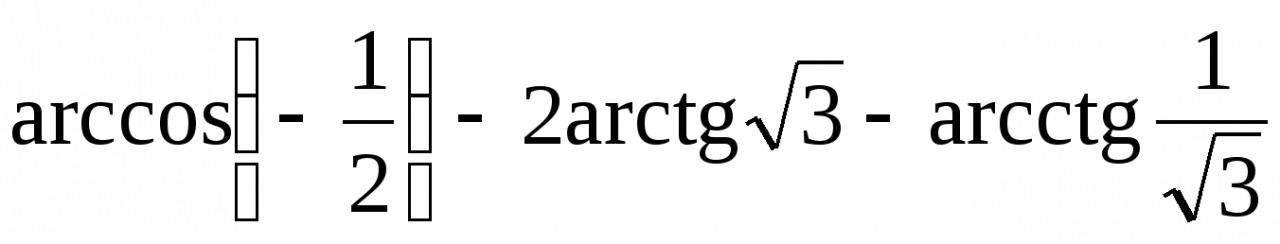 .
.
2. Если 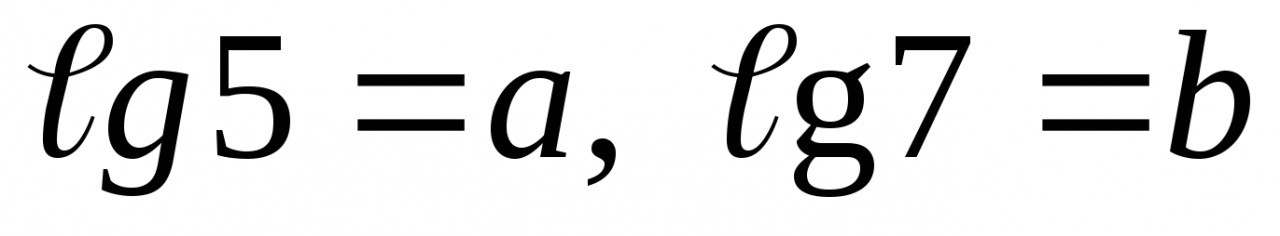 , то выразите
, то выразите 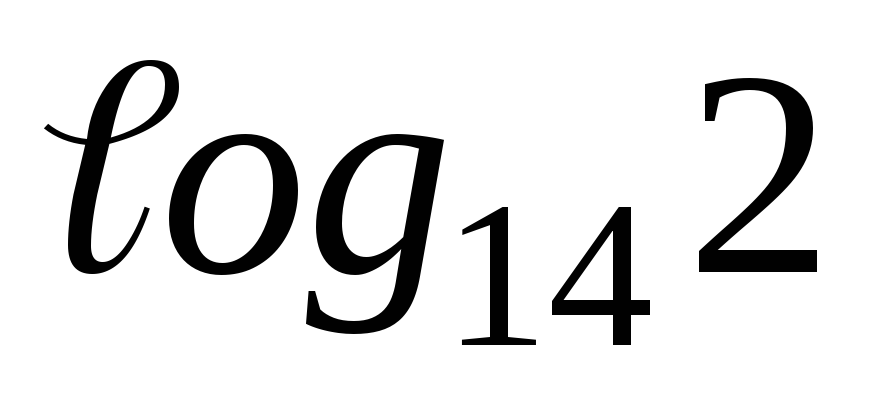 через
через  и
и 
3. Решите уравнение 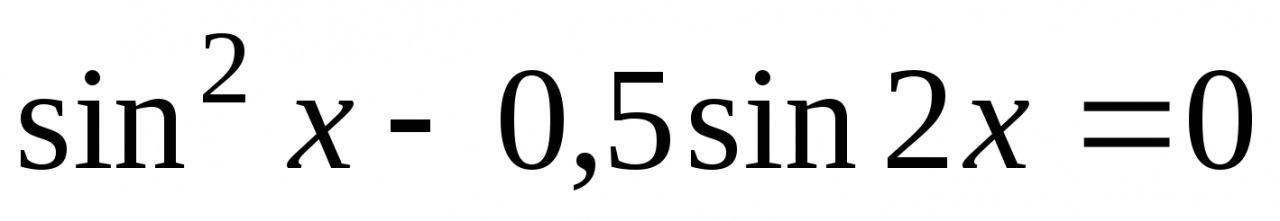 .
.
4. Решите систему неравенств 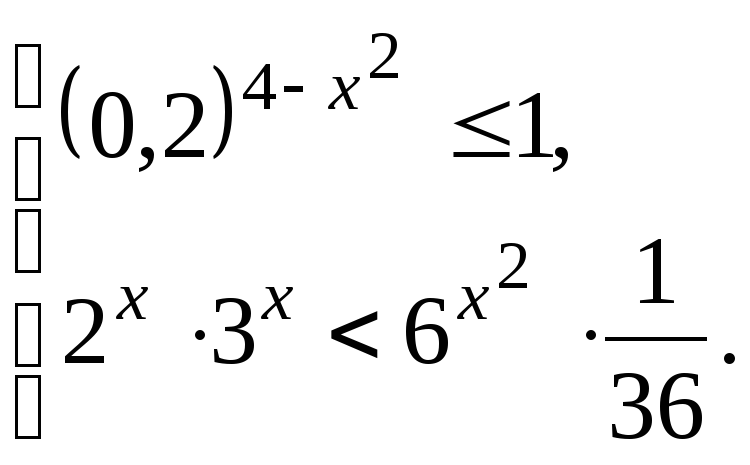
5. Участок в форме прямоугольника площадью 4 га огорожен забором. Найдите стороны участка имеющего наименьший периметр.
6. Исследуйте и постройте график функции. 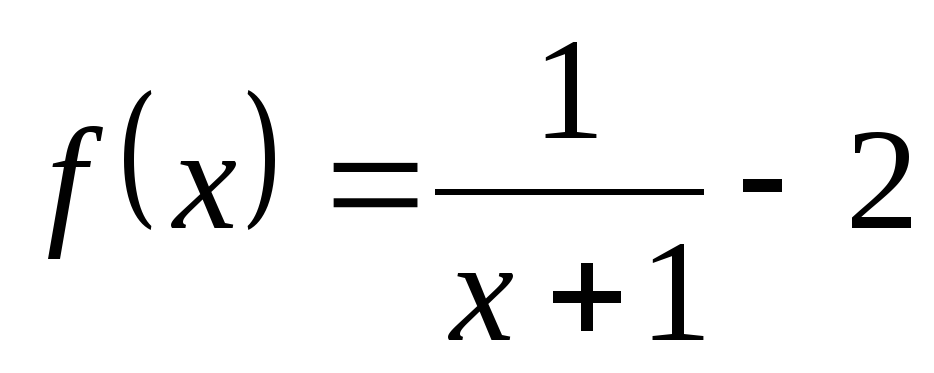
15 вариант
1. Вычислите 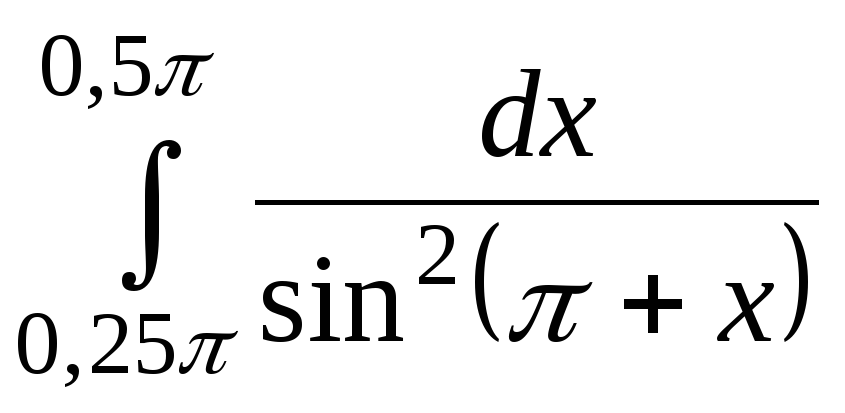 .
.
2. Найдите промежутки возрастания и убывания функции
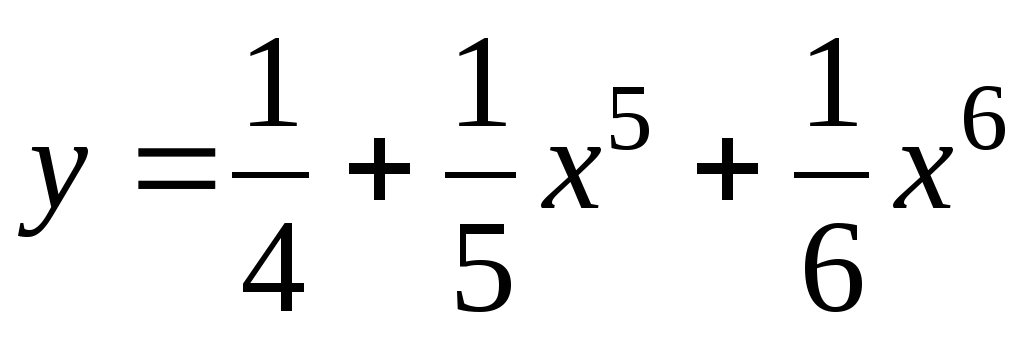 .
.
3. Найдите значение выражения 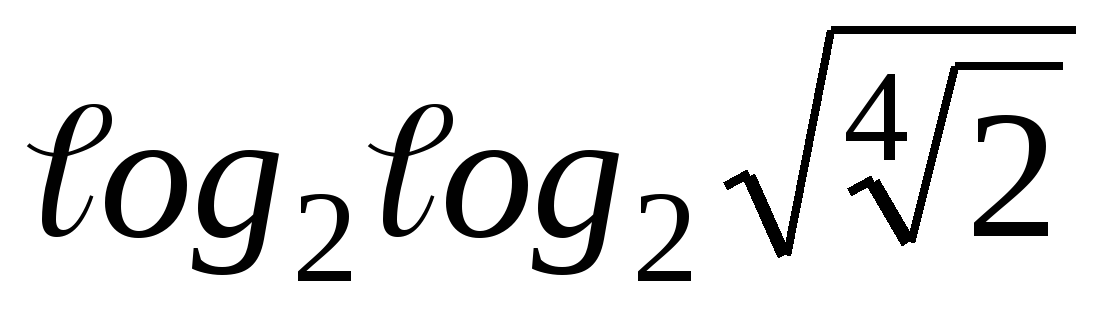 .
.
4. Решите уравнение 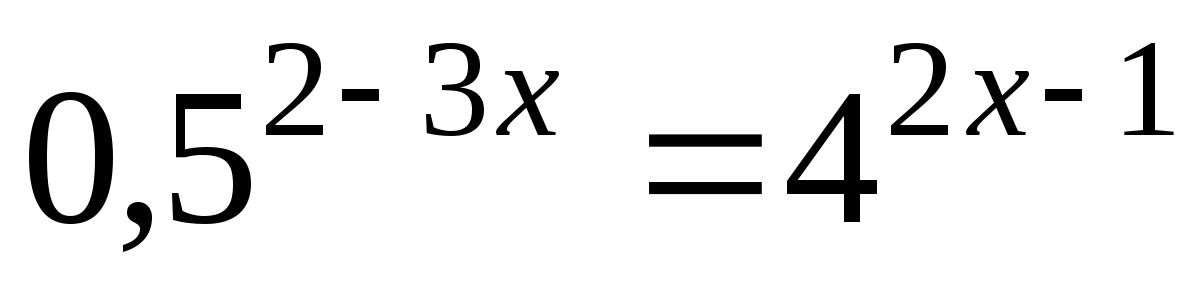 .
.
5. Решите систему неравенств 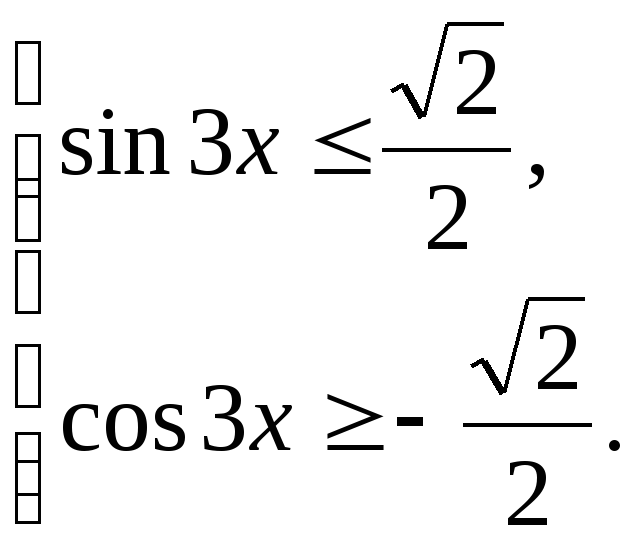
6. Найдите площадь плоской фигуры, ограниченной линиями 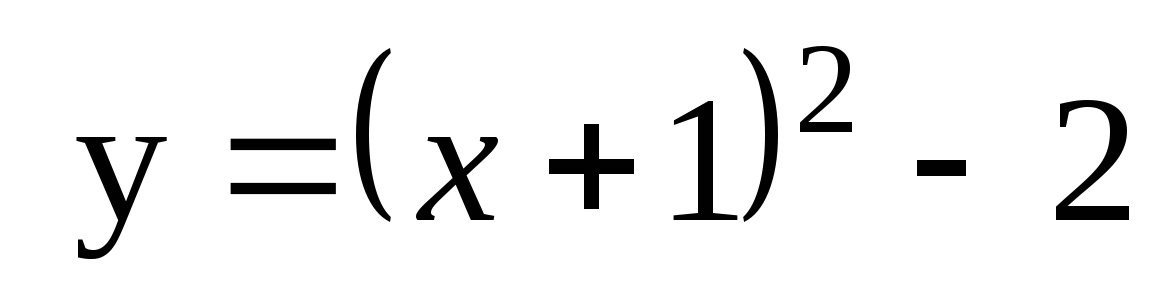 и
и 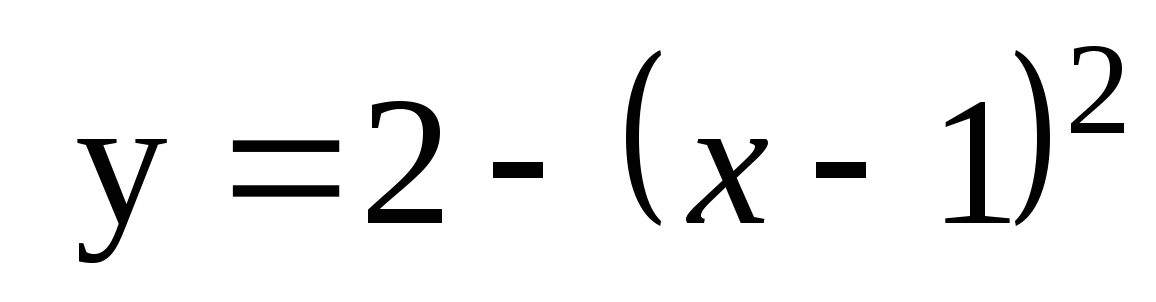 .
.
16 вариант
1. Вычислите 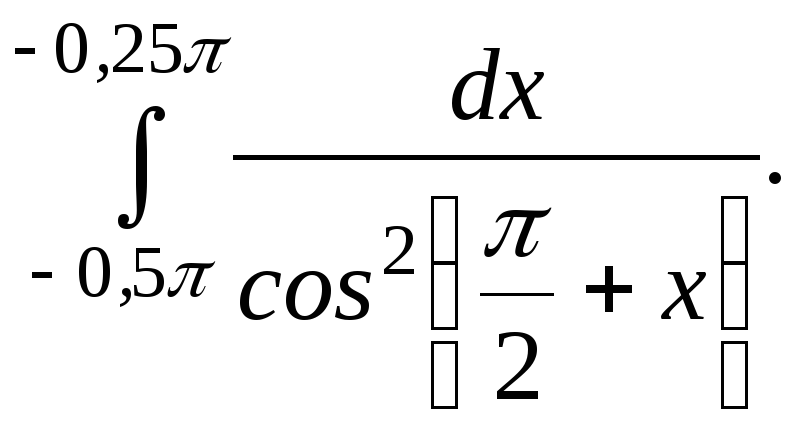
2. Найдите координаты точки экстремума функции
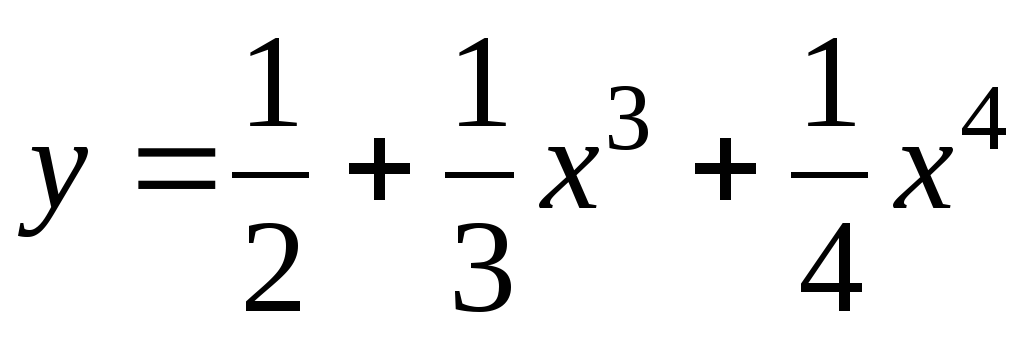 .
.
3. Найдите значение выражения. 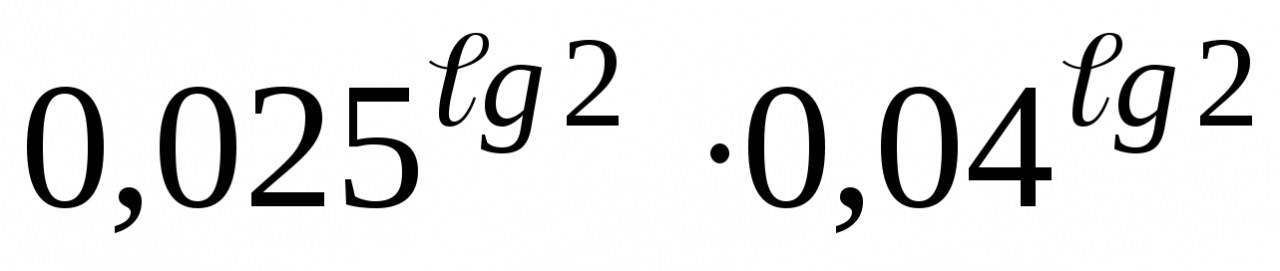 .
.
4. Решите уравнение 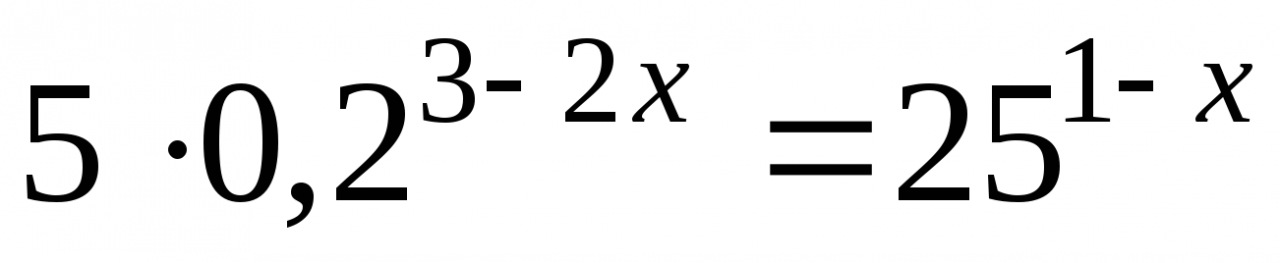 .
.
5. Решите систему неравенств 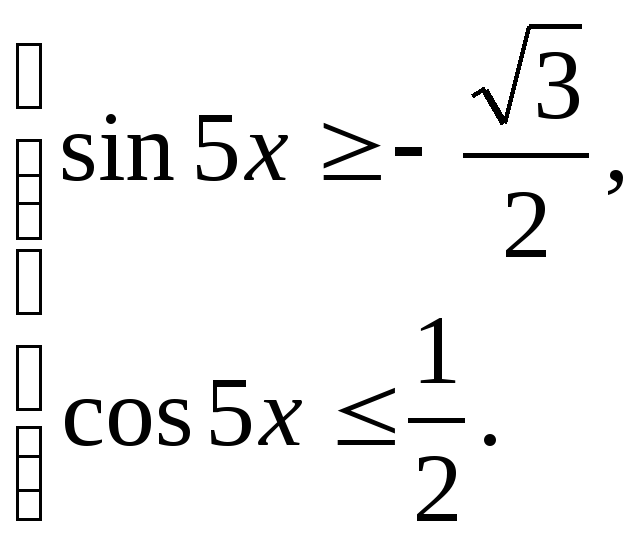
6. Найдите площадь плоской фигуры, ограниченной линиями
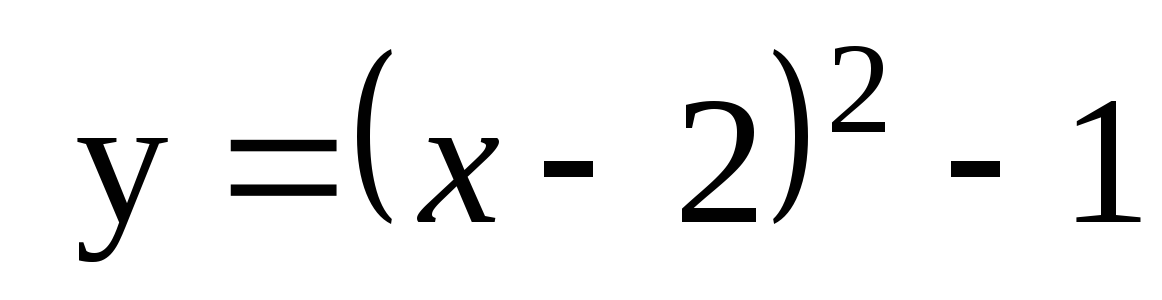 и
и 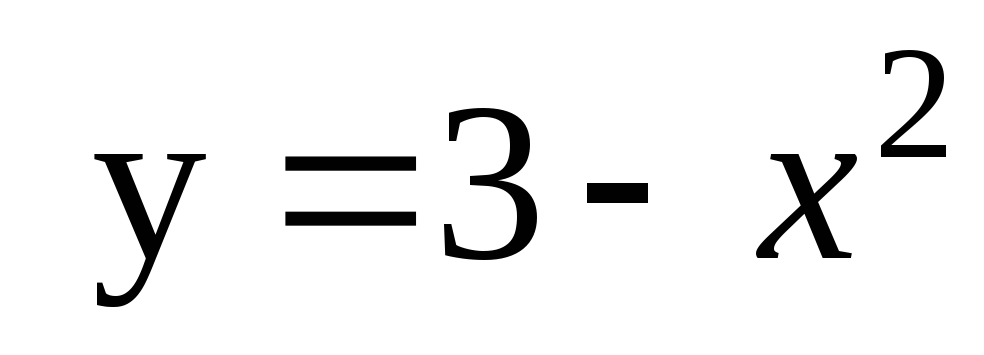 .
.
17 вариант
1. Найдите значение выражения 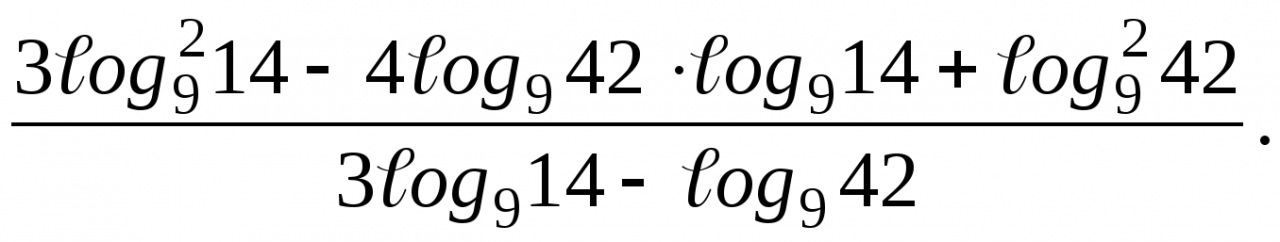
2. Упростите выражение 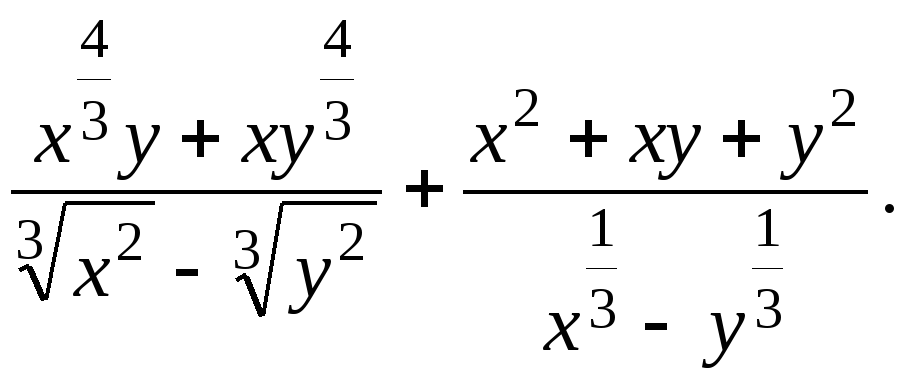
3. Решите неравенство 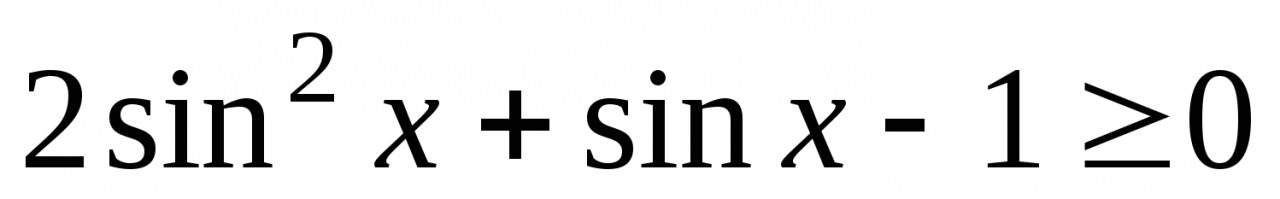 .
.
4. Найдите площадь плоской фигуры, ограниченной линиями
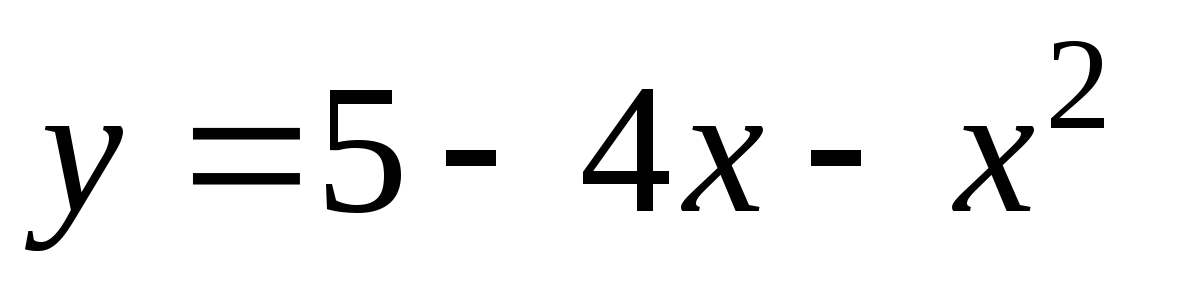 и y=0 .
и y=0 .
5. Решите систему уравнений 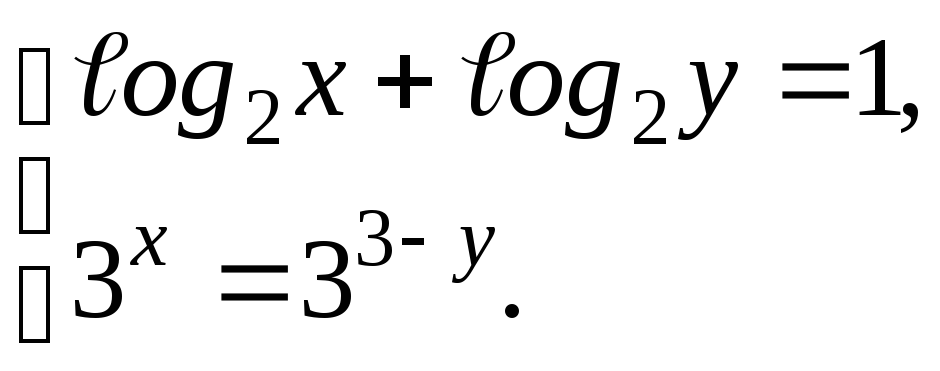
6. Разложите число 18 на три слагаемых так, чтобы одно из слагаемых было в 3 раза больше второго и их произведение было наибольшим.
18 вариант
1. Найдите значение выражения 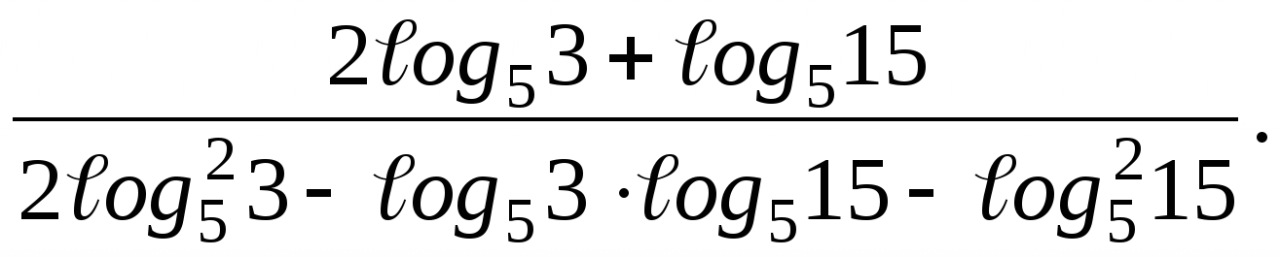
2. Упростите выражение 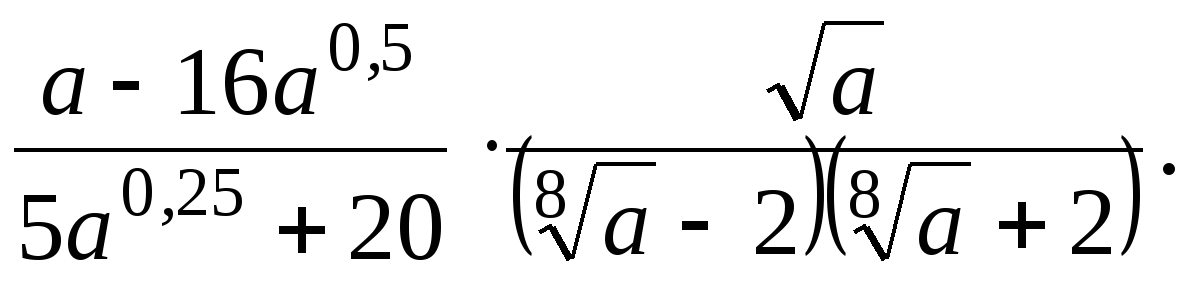
3. Решите неравенство 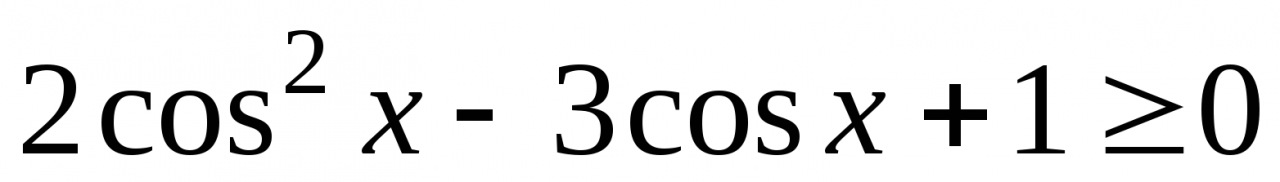 .
.
4. Найдите площадь плоской фигуры, ограниченной линиями
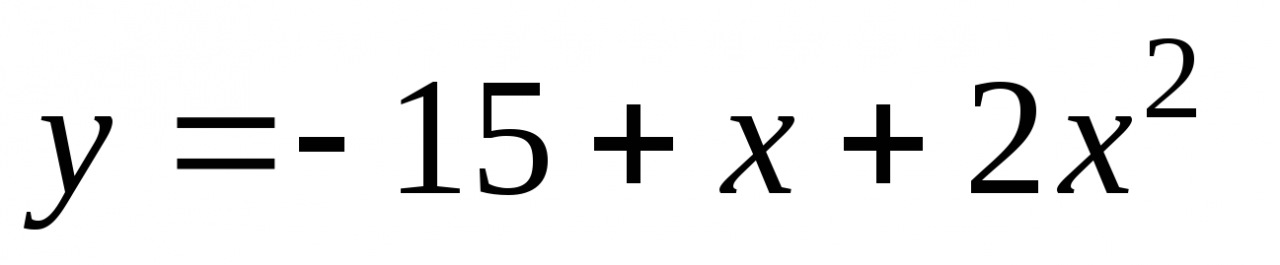 и y=0 .
и y=0 .
5. Решите систему уравнений 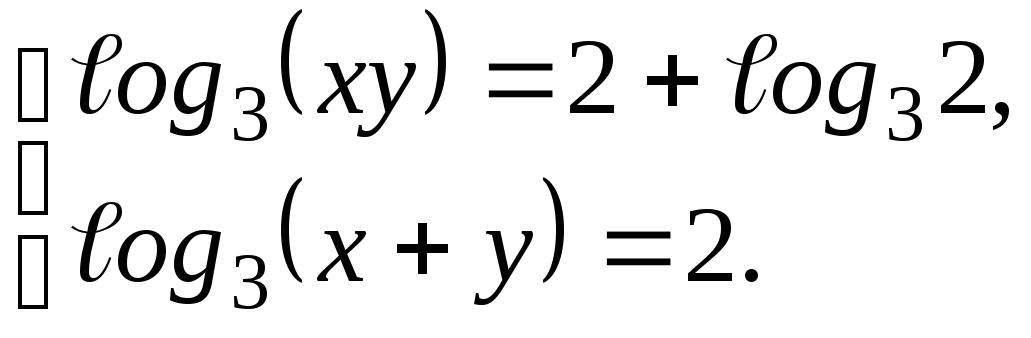
6. Разложите число 18 на три слагаемых так, чтобы одно из слагаемых было в 2 раза больше второго и их произведение было наибольшим.
19 вариант
1. Найдите значение выражения 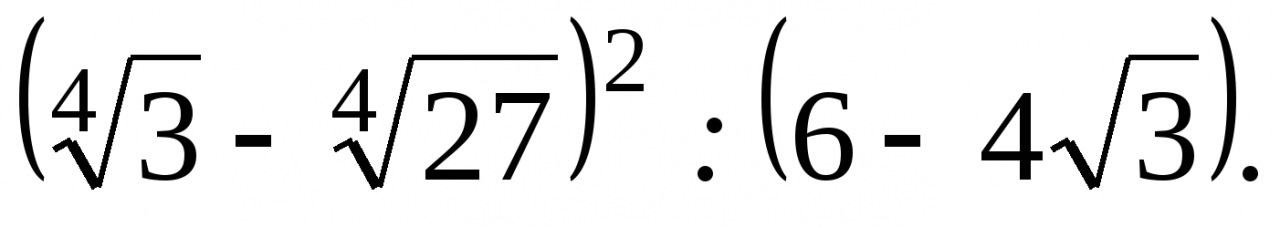
2. Упростите выражение 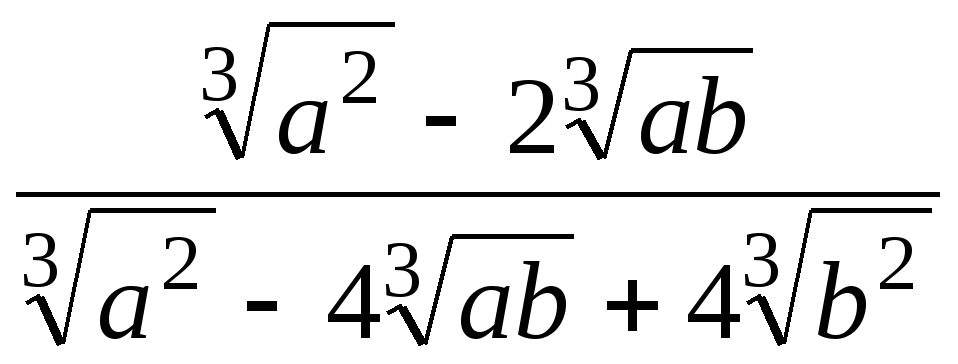 .
.
3. Решите уравнение 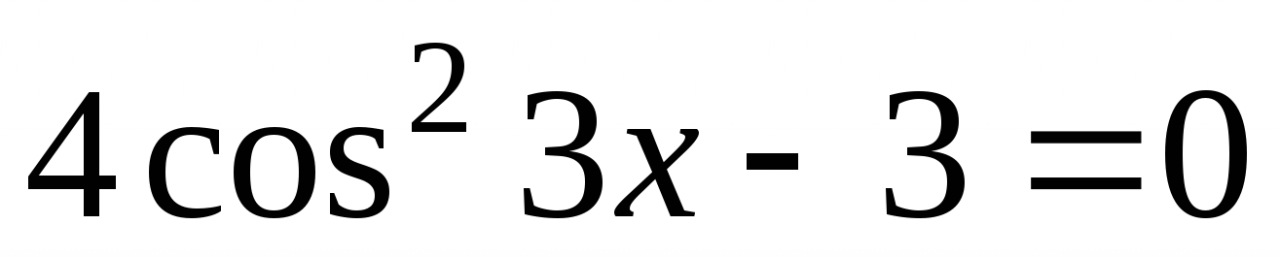 .
.
4. Решите систему неравенств 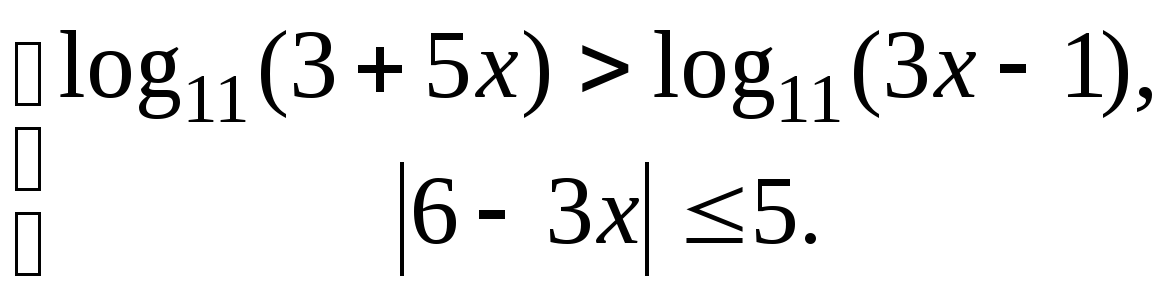
5. Найдите наибольшее и наименьшее значение функции 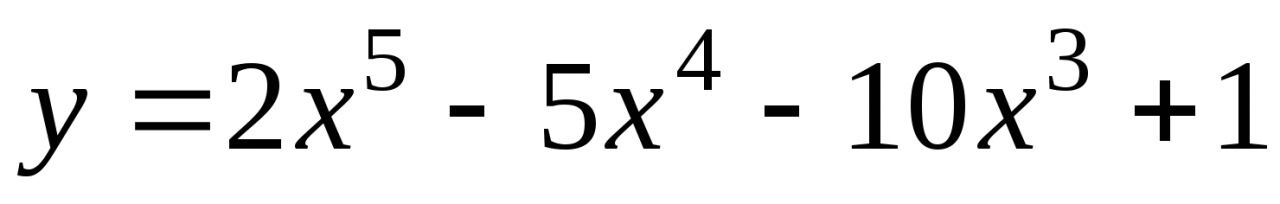 на отрезке [-1;2] .
на отрезке [-1;2] .
6. Найдите площадь плоской фигуры, ограниченной линиями
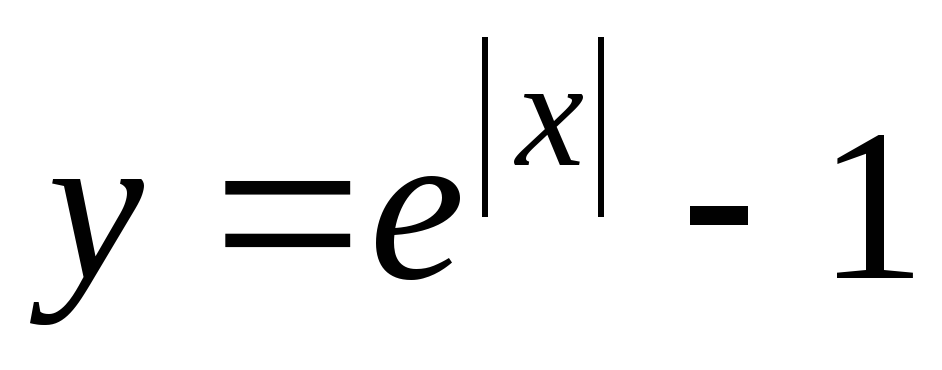 , y = e – 1.
, y = e – 1.
20 вариант
1. Найдите значение выражения 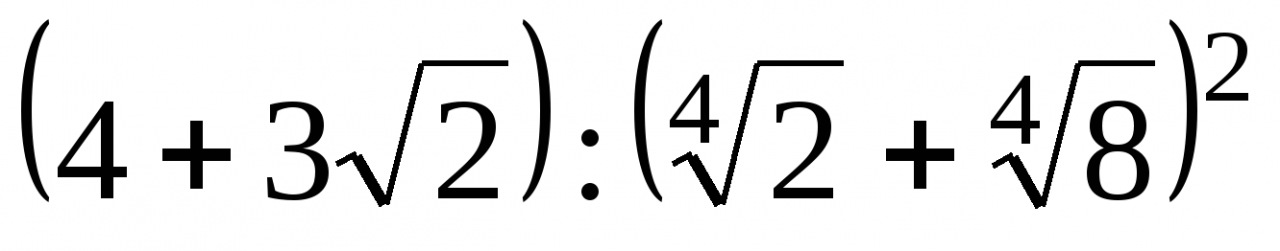 .
.
2. Упростите выражение 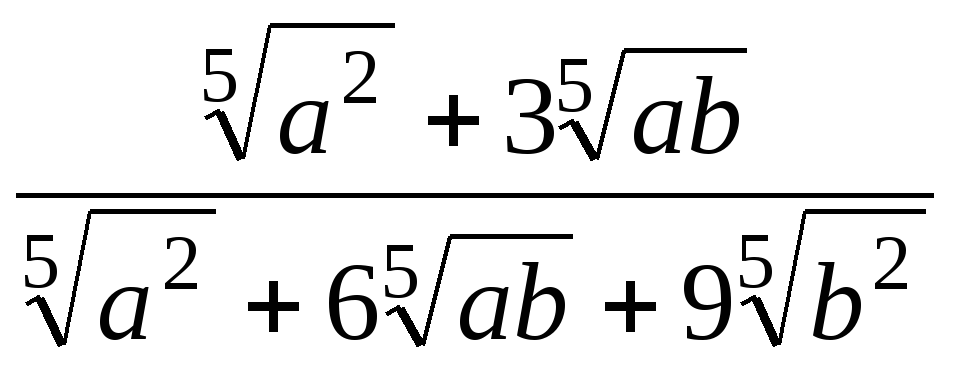 .
.
3. Решите уравнение 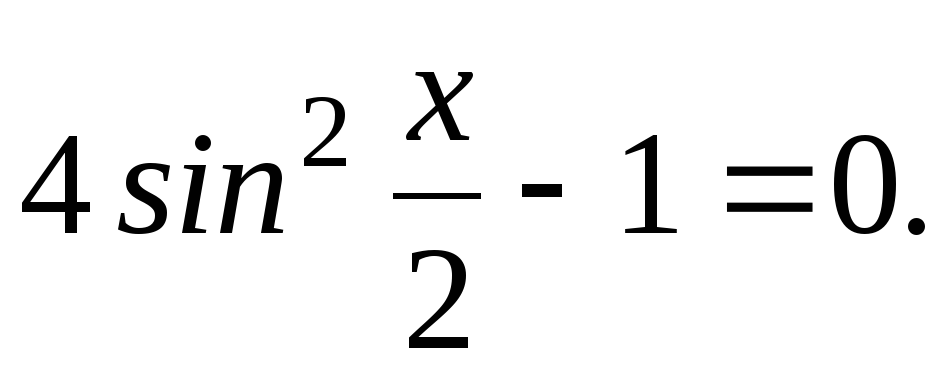
4. Решите систему неравенств 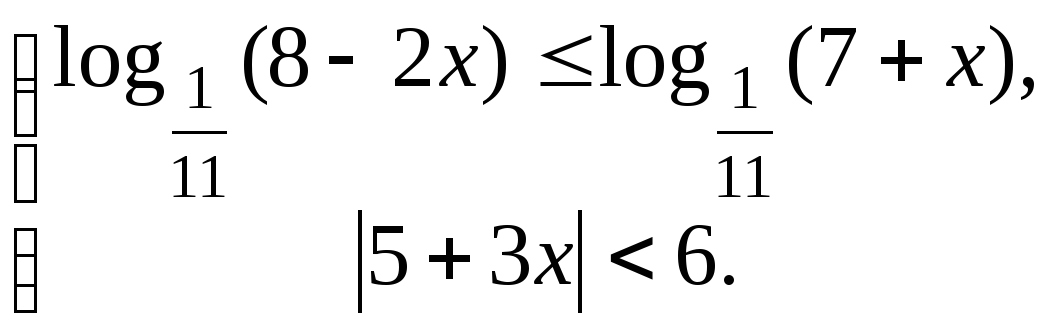
5. Найдите наибольшее и наименьшее значение функции 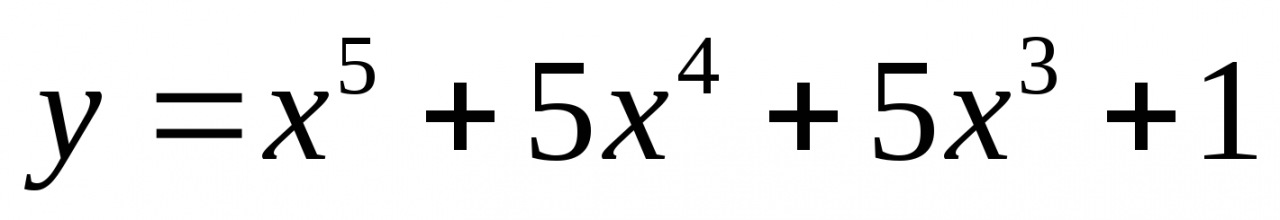 на отрезке [-2;1]
на отрезке [-2;1]
6. Найдите площадь плоской фигуры, ограниченной линиями 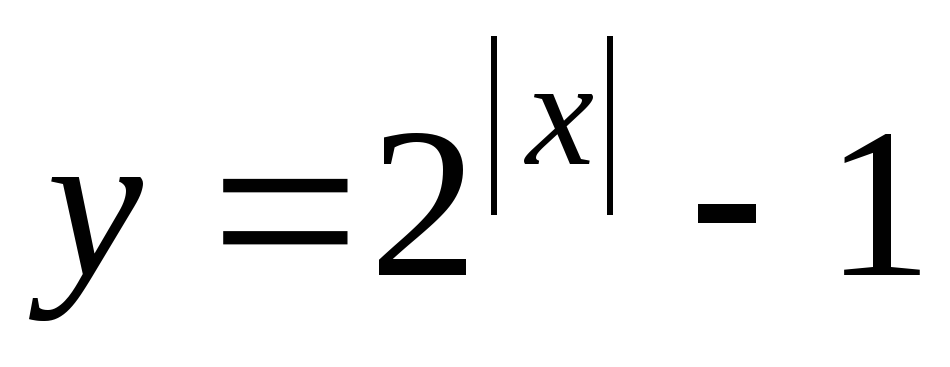 , y = 3.
, y = 3.
xn--j1ahfl.xn--p1ai
Сборник контрольных работ по алгебре, (10 класс)
Контрольная работа № 1
по теме «Функции и их свойства»
Цель: проверить уровень усвоение ГОСО
- умение находить значение функции в точке;
- умение находить область определения функции;
- умения строить эскиз графика функции и находить по эскизу промежутки
возрастания и убывания , экстремумы функции, точки пересечения с осями
координат;
- знания свойств четных и нечетных функций.
1. Вычислите:
y = f(x) является нечетной y = f(x) является четной
2 f(-4) + f(3) f(-3) + 2 f(1)
eсли f(4)=1, f(-3)=2 eсли f(3)=4, f(-1)=2
2. Найдите значение функции в точке X0.
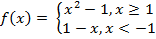
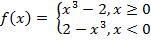
X0 = -2 и X0 = 4 X0 = -3 и X0 = 1
3. Постройте эскиз функции и найдите координаты точек его пересечения с осями координат.
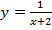
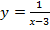
4. Найдите область определения функции
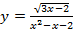
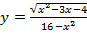
5. Найдите промежутки возрастания и убывания и экстремумы функции.
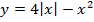
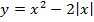
Критерии оценки.
0-10 баллов – «2»
11-14баллов – «3»
15-19 баллов – «4»
20-21 баллов – «5»
Распределение заданий по содержанию и видам деятельности.
| Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция знаний | Процентное Соотношение в тексте |
| Четные и нечетные функции. | №1 | | | 20% |
| Значения функции в точке | №2 | | | 20% |
| График функции и ее свойства | | №3,4 | №5 | 40% |
| Процентное Соотношение в тексте | 40% | 40% | 20% | 100% |
Критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
| 1 | Свойства четных и нечетных функций. | Знания свойств четных и нечетных функций | 2 | 3 |
| Запись ответа | 1 |
| 2 | Значение функции в точке | Правильно подставил | 2 | 3 |
| Вычисления | 1 |
| 3 | График функции и ее свойства | Построение эскиза графика | 2 | 5 |
| Пересечение с осью абсцисс | 1 |
| Пересечение с осью ординат | 2 |
| Запись ответа | 1 |
| 4 | Область определения функции | Составление условий для нахождения области определения | 2 | 5 |
| Решение неравенства | 1 |
| Запись ответа | 2 |
| 5 | Промежутки возрастания , убывания и экстремумы функции | Вершина параболы | 1 | 5 |
| Свойства модуля | 1 |
| Эскиз графика | 2 |
| Запись ответа | 1 |
Контрольная работа № 2
по теме «Тригонометрические функции»
Цель: проверить уровень усвоение ГОСО
- умение находить период тригонометрических функций;
- уменияупрощать тригонометрические выражения с помощью основных формул
тригонометрии;
- знание значений тригонометрических функций;
- умения строить графики тригонометрических функций;
- умения по графику определять свойства тригонометрических функций;
1. Найдите наименьший положительный период функции
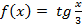
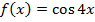
2. Вычислите значение выражения


3. Постройте график функции
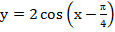
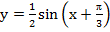
4. Не выполняя построений, найдите область определения и область значений функции.
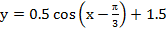
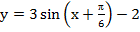
5. Вычислите:
cos(2 arcsin1\3) cos(2 arcsin1\5)
Критерии оценки.
0-10 баллов – «2»
11-14 баллов – «3»
15-19 баллов – «4»
20-21 баллов – «5»
Распределение заданий по содержанию и видам деятельности.
| Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция знаний | Процентное Соотношение в тексте |
| График и свойства тригонометрической функции | №1 | №3,4 | №5 | 80% |
| Преобразование тригонометрических выражений | №2 | | | 20% |
| Процентное Соотношение в тексте | 40% | 40% | 20% | 100% |
Критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
| 1 | Определение периода функции | Знание наименьшего периода тригонометрических функций | 1 | 3 |
| Нахождение периода по формуле | 1 |
| Запись ответа | 1 |
| 2 | Нахождение значения выражения, содержащего обратные тригонометрические функции | Определение обратных тригонометрических функций положительного аргумента | 1 | 3 |
| Определение обратных тригонометрических функций отрицательного аргумента | 1 |
| Вычисление значения выражения | 1 |
| 3 | График тригонометрической функции | Сдвиг по оси абсцисс | 1 | 5 |
| Растяжение по оси ординат | 1 |
| Аккуратность построения | 1 |
| Нули функции | 1 |
| Промежутки возрастания(убывания) | 1 |
| 4 | Область значений тригонометрических функций | Область определения | 1 | 5 |
| Область значений | 2 |
| Выбор ответа | 1 |
| Запись ответа | 1 |
| 5 | Свойства монотонности | Знание радианной меры | 1 | 5 |
| Промежутки монотонности | 3 |
| Запись ответа | 1 |
Контрольная работа № 3
по теме «Тригонометрические уравнения и неравенства»
Цель: проверить уровень усвоение ГОСО
- умение находить значение обратных тригонометрических функций;
- умение решать простейшие тригонометрические уравнения;
- умения решать однородные тригонометрические уравнения;
- умения преобразовывать уравнения с помощью основных формул тригонометрии.
- умения решать системы тригонометрических уравненийи неравенств;
1. Решите уравнение
а) 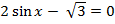 а)
а)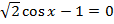
б)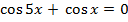 б)
б)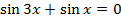
2. Решите уравнение
а) 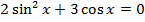 а)
а)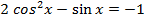
б) б)
б)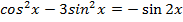
3. Решите неравенство
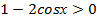
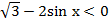
4. Решите систему уравнений
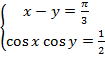
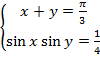
5. Решите систему неравенств

Критерии оценки.
0-12 баллов – «2»
13-16 баллов – «3»
17-21 баллов – «4»
22-23 баллов – «5»
Распределение заданий по содержанию и видам деятельности.
| Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция знаний | Процентное Соотношение в тексте |
| Тригонометрические уравнения | №1 | №2 | | 40% |
| Тригонометрические неравенства | №3 | | | 20% |
| Системы тригоно-метрических урав-нений и неравенств | | №4 | №5 | 40% |
| Процентное Соотношение в тексте | 40% | 40% | 20% | 100% |
Критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
| 1 | Решение тригонометрических уравнений | Решение простейших тригонометрических уравнений | 2 | 5 |
| Применение формул суммы тригонометрических функций | 1 |
| Решение однородных тригонометрических уравнений первой степени | 1 |
| Выбор ответа | 1 |
| 2 | Решение тригонометрических уравнений | Выбор способа решения тригонометрического уравнения | 3 | 5 |
| Решение квадратного уравнения | 1 |
| Вычисления и выбор ответа | 1 |
| Решение неравенств | 2 |
| Выбор ответа | 1 |
| Запись ответа | 1 |
| 3 | Решение тригонометрических неравенств | Преобразование неравенства | 1 | 3 |
| Решение неравенства | 1 |
| Выбор ответа | 1 |
| 4 | Решение системы тригонометрических уравнений | Применение метода подстановки | 1 | 5 |
| Применение формулы произведения тригонометрических функций | 1 |
| Решение тригонометрических уравнений | 2 |
| Запись ответа | 1 |
| 5 | Решениесистемы тригонометрических неравенств | Решение простейшего тригонометрического неравенства | 2 | 5 |
| Определение общего решения | 3 |
Контрольная работа № 4
по теме «Определение производной функции. Геометрический и физический смысл производной»
Цель: проверить уровень усвоения ГОСО
- знание формул и правил нахождения производных, уравнения касательной;
- умения применять таблицу и правила нахождения производных;
- умение составлять уравнение касательной к графику функции;
- умения находить производную в точке;
- умения составлять уравнения и неравенства с производной и решать их*
- умения применять производную при решении физических задач.
1. Найти производную функции:
а) 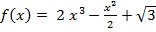 а)
а)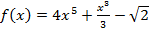 б)
б)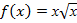 - 8х3 б) )
- 8х3 б) )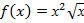 + 3х5
+ 3х5
2. Составьте уравнение касательной к графику функции f(x) в точке x0.
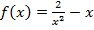 , x0=-1
, x0=-1 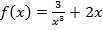 , x0 = 1
, x0 = 1
3. Решите уравнение:
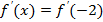
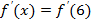
если 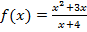 если
если 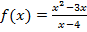
4. Составьте и решите неравенство 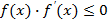
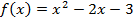
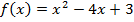
5.Материальная точка движется по закону
x(t)= 5t + 6t2 – t3 x(t) = 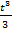 – t2 + 2t – 4
– t2 + 2t – 4
( х – метров, t – в секундах)
Определите
скорость точки в момент, когда ускорение точки в момент, когда
ее ускорение равно нулю. ее скорость равна 1м/с
Критерии оценки.
0-12 баллов – «2»
13-16 баллов – «3»
17-21 баллов – «4»
22-23 баллов – «5»
Распределение заданий по содержанию и видам деятельности.
| Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция знаний | Процентное Соотношение в тексте |
| Нахождение производной | №1 | №3,4 | | 60% |
| Геометрический смысл производной | №2 | | | 20% |
| Физический смысл производной | | | №5 | 20% |
| Процентное Соотношение в тексте | 40% | 40% | 20% | 100% |
Критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
| 1 | Нахождение производной | Знание таблицы производных | 1 | 3 |
| Производная произведения | 1 |
| Производная степенной функции | 1 |
| 2 | Составление уравнения касательной к графику функции | Знание уравнения касательной к графику функции | 1 | 5 |
| Нахождение производной | 1 |
| Нахождение значений функции и производной в точке | 1 |
| составление уравнения касательной к графику функции | 1 |
| Запись ответа | 1 |
| 3 | Составление и решение уравнения с производной. | Нахождение производной дроби | 1 | 5 |
| Нахождение производной в точке | 1 |
| Составление уравнения | 1 |
| Решение уравнения | 1 |
| Вычисления и запись ответа | 1 |
| 4 | Составление и решение неравенства с производной. | Нахождение производной | 1 | 5 |
| Составление неравенства | 1 |
| Решение неравенства | 2 |
| Запись ответа | 1 |
| 5 | Применение производной при решении физических задач | Нахождение скорости | 1 | 5 |
| Нахождение ускорения | 1 |
| Составление уравнения для нахождения времени | 2 |
| Нахождение конечного ответа | 1 |
Контрольная работа № 5
по теме «Производные сложных и тригонометрических функции»
Цель: проверить уровень усвоение ГОСО
- знание формул и правил нахождения производных тригономкерических функций,;
- умения находить производную сложной функции;
- умения составлять уравнения и неравенства с производной и решать их.
1. Найти производную функции:
б) ,
xn--j1ahfl.xn--p1ai
 MBN= 84о,
MBN= 84о,  МВК = 22о.
МВК = 22о. OMN = 78о,
OMN = 78о,  ОМК = 30о.
ОМК = 30о.

 АDВ =
АDВ = 












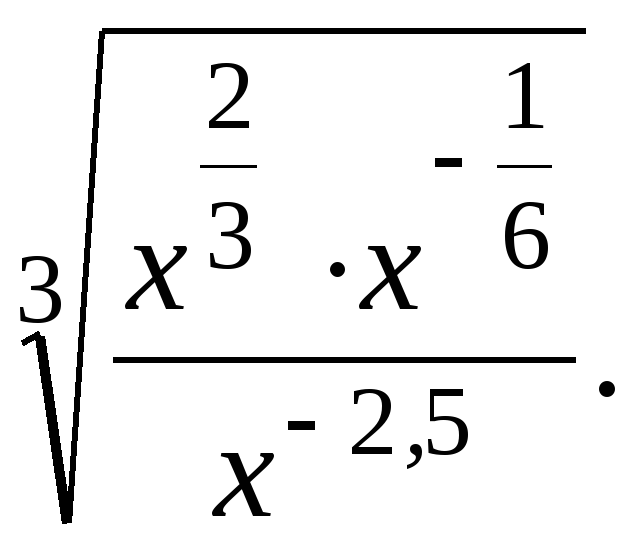
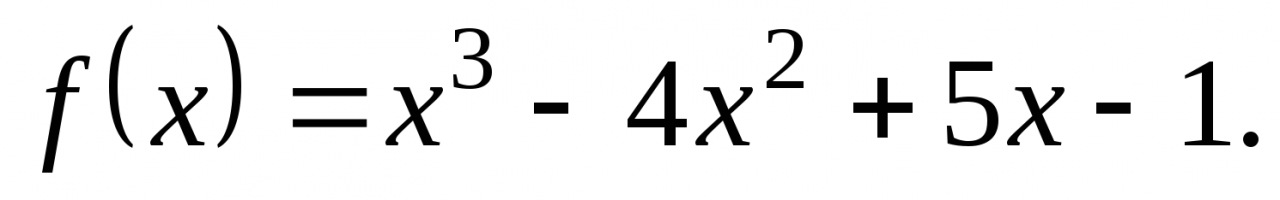
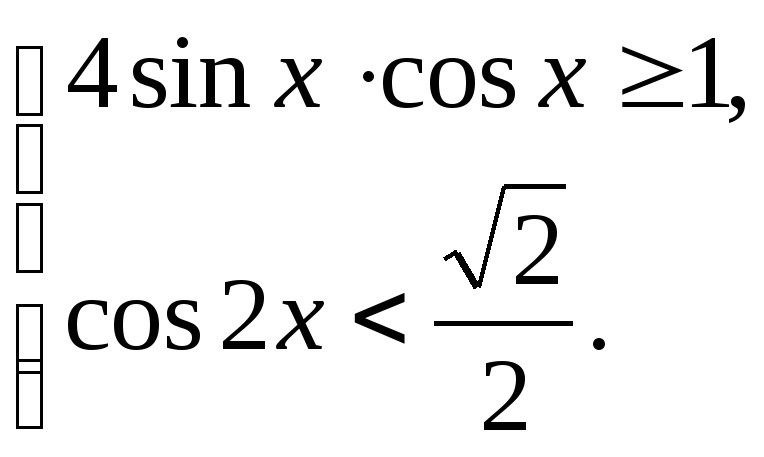
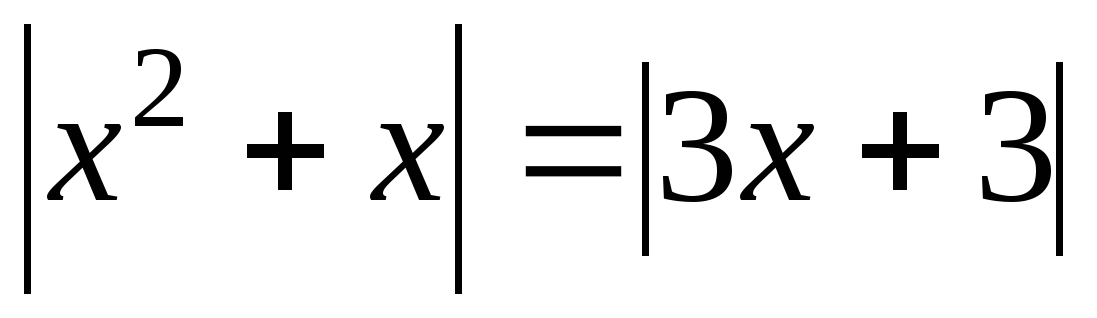 .
.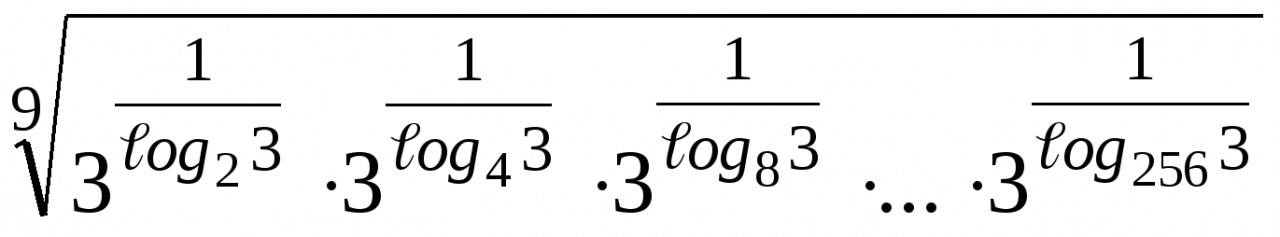 .
.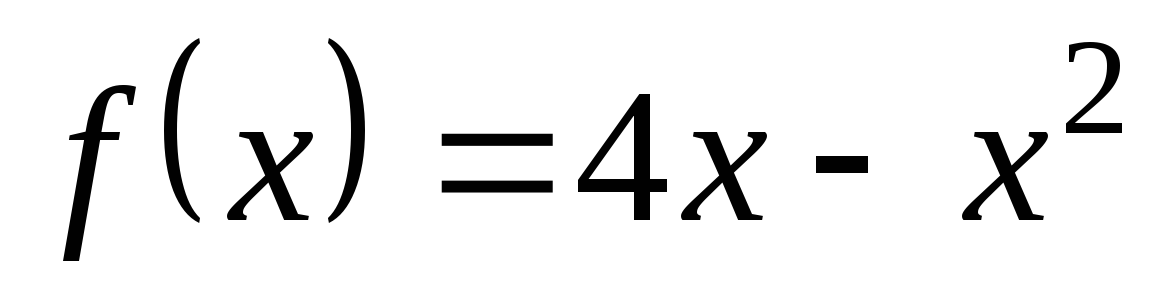 проведены касательные в точках с абсциссами х1=1 и х2=4. Найдите площадь треугольника, образованного этими касательными и осью Ох.
проведены касательные в точках с абсциссами х1=1 и х2=4. Найдите площадь треугольника, образованного этими касательными и осью Ох. 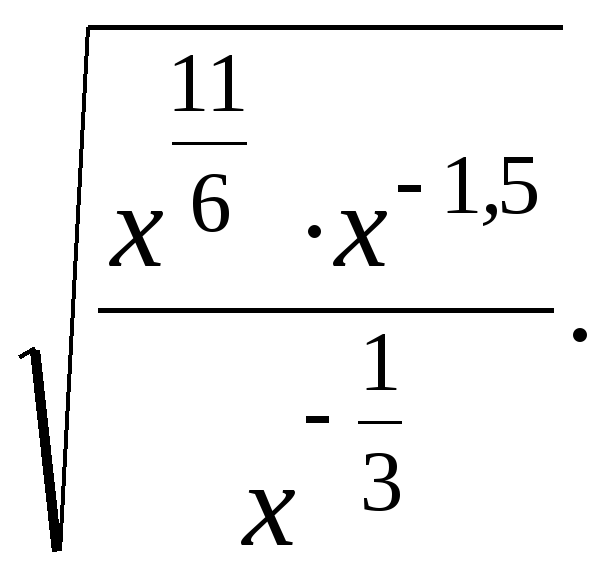
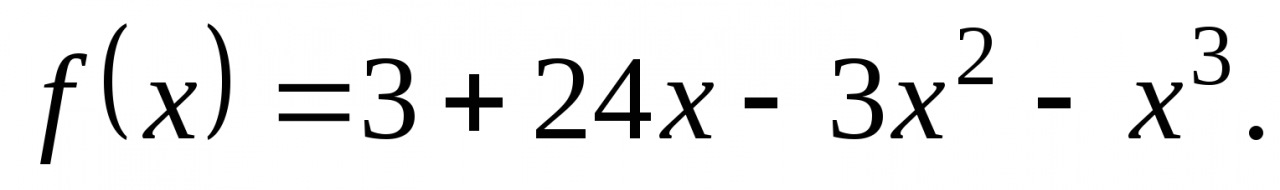
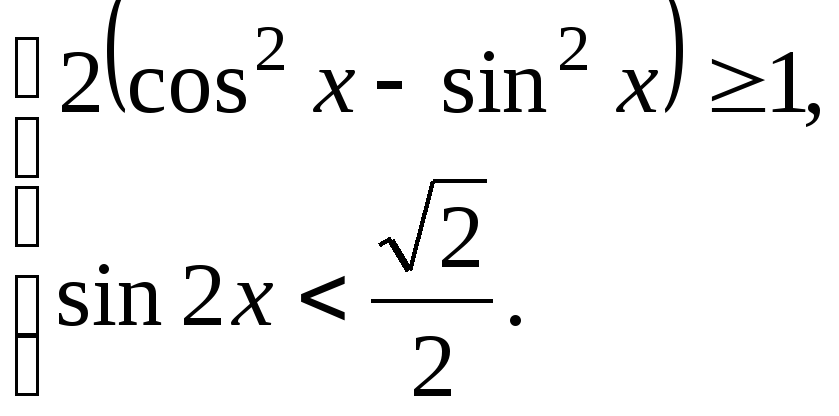
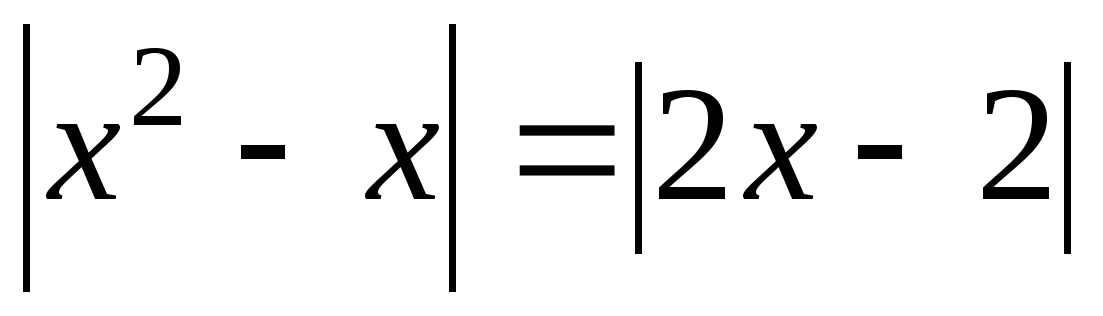 .
.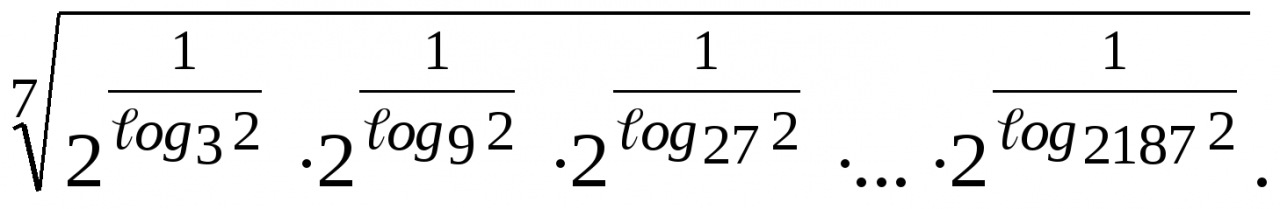
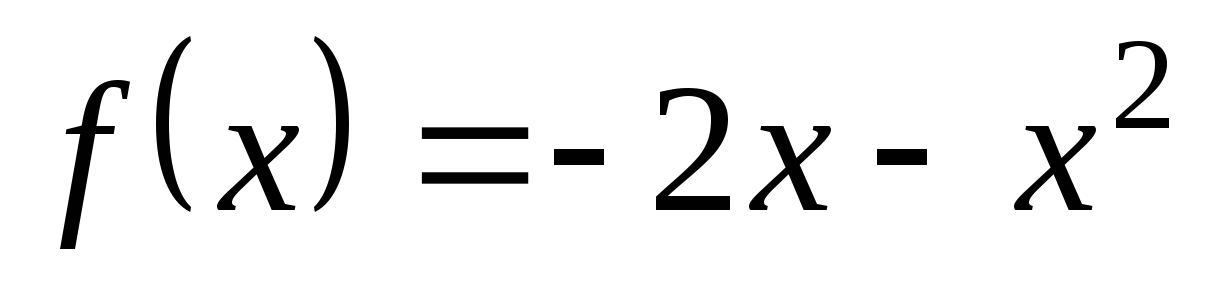 проведены касательные в точках с абсциссами х1=−2 и х2=1. Найдите площадь треугольника, образованного этими касательными и осью Ох.
проведены касательные в точках с абсциссами х1=−2 и х2=1. Найдите площадь треугольника, образованного этими касательными и осью Ох.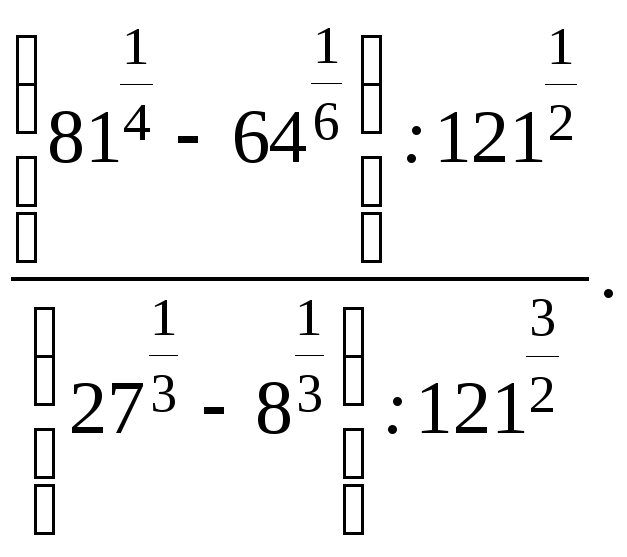
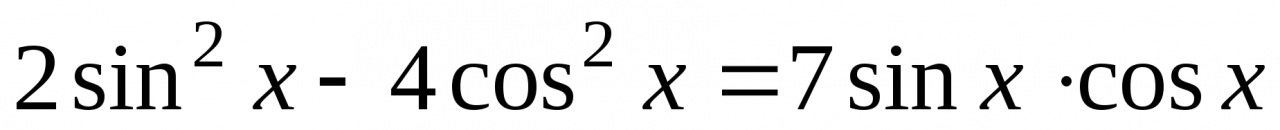 .
.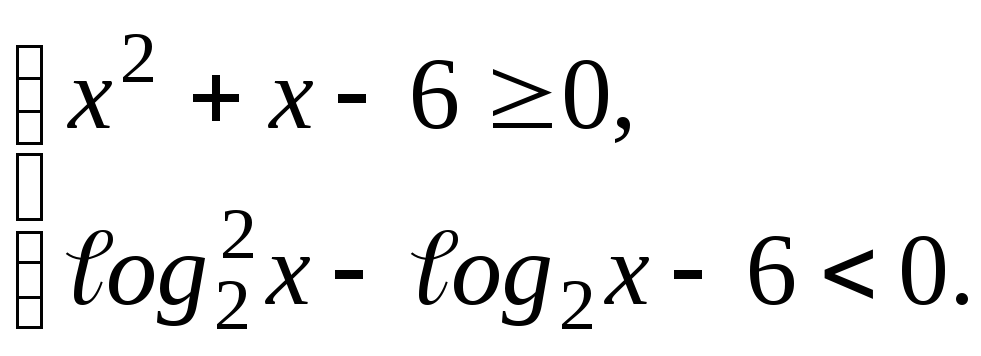
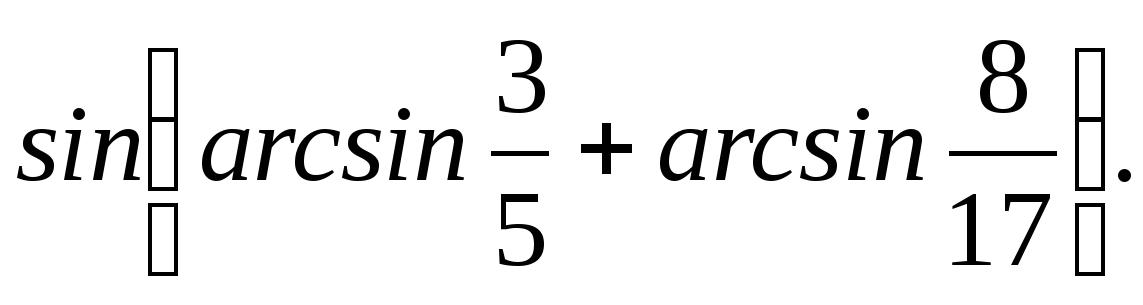
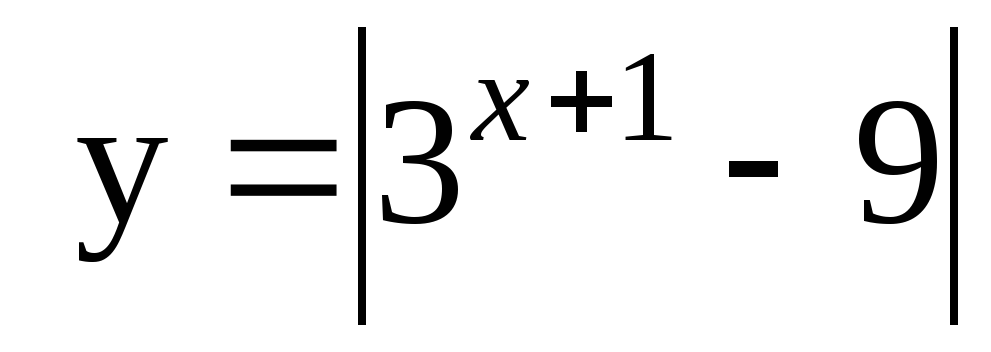 .
. 
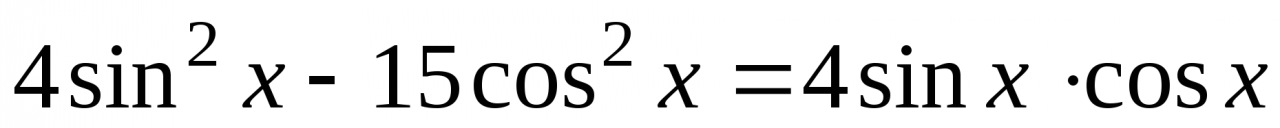 .
.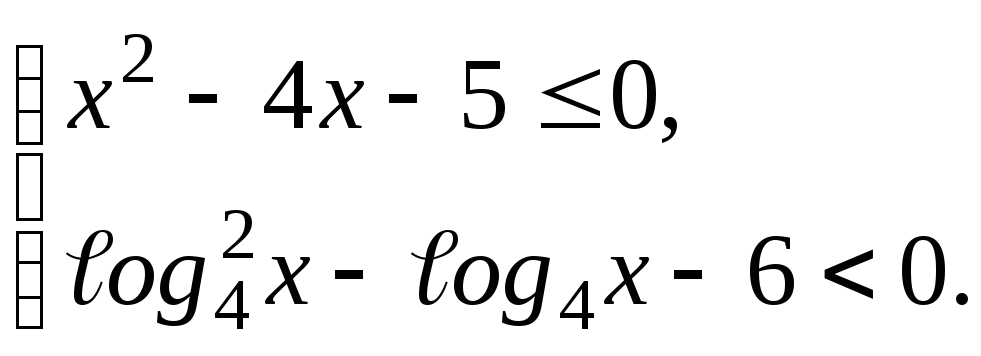
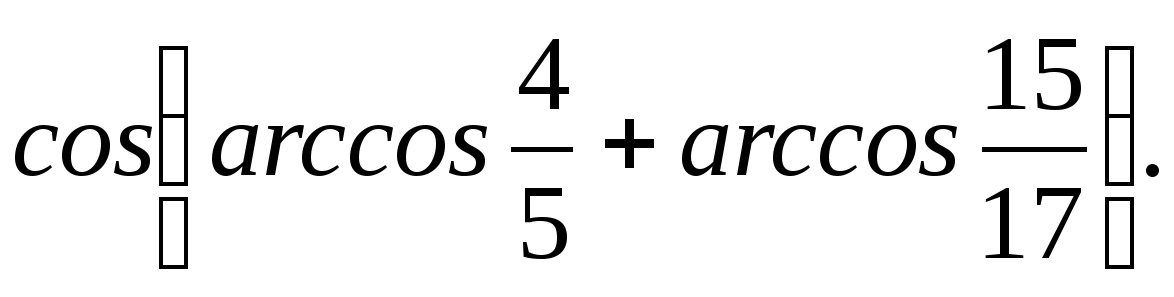
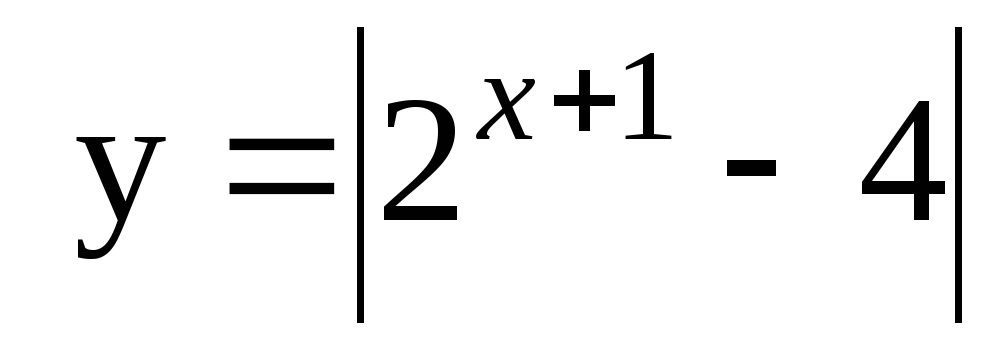 .
.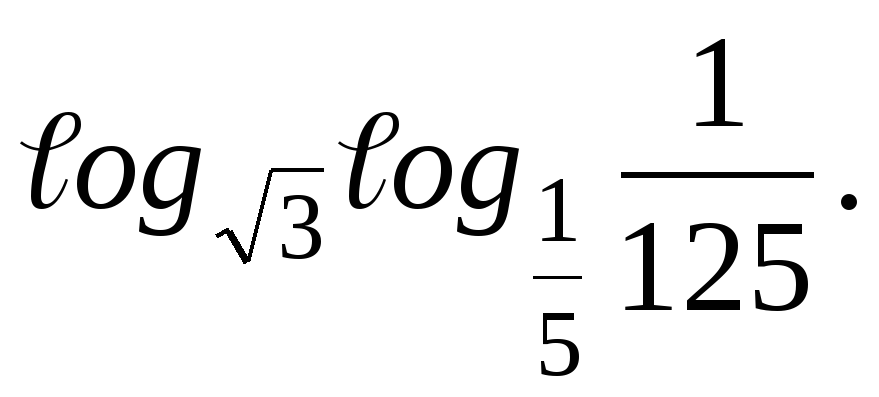
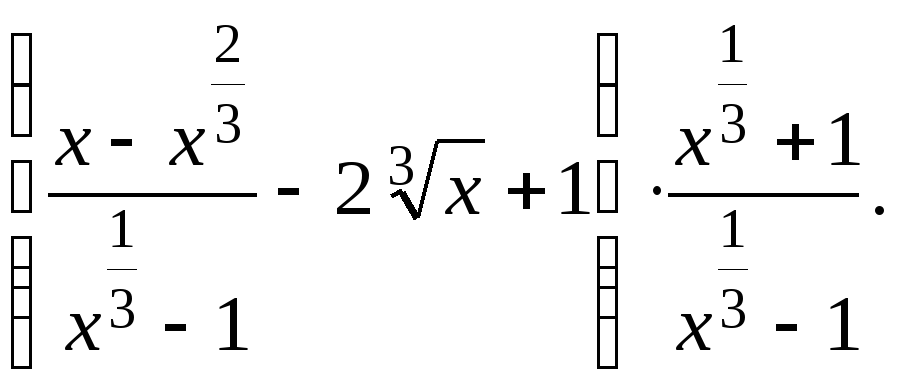
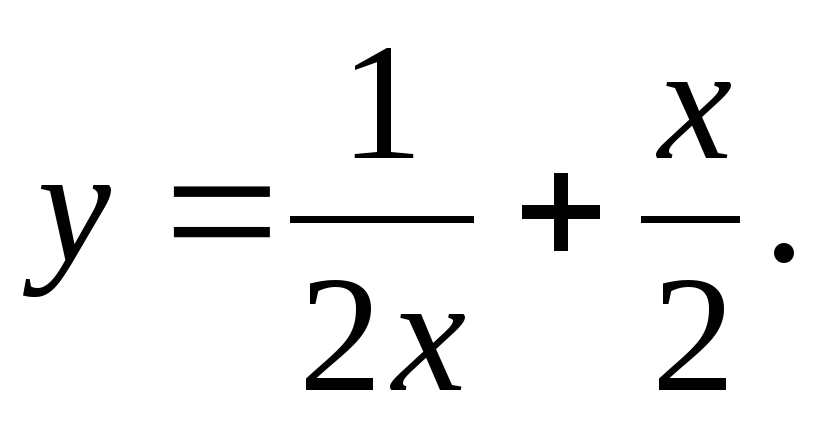
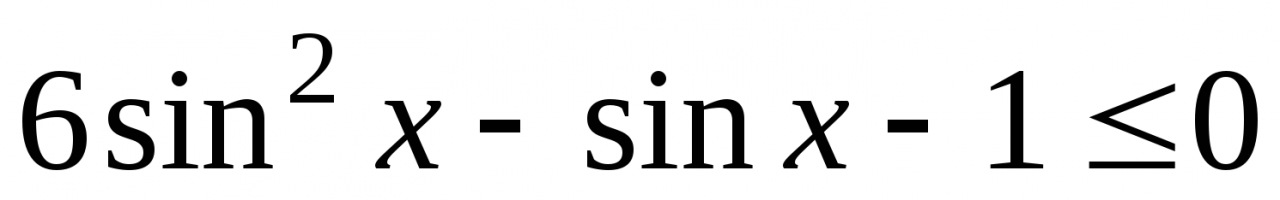 .
. 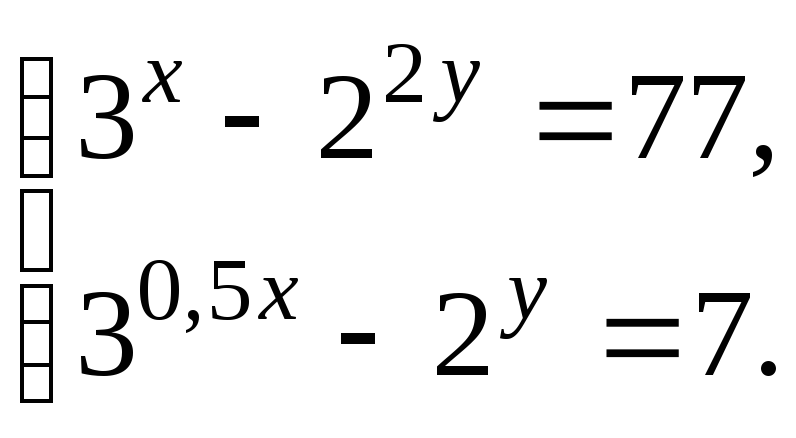
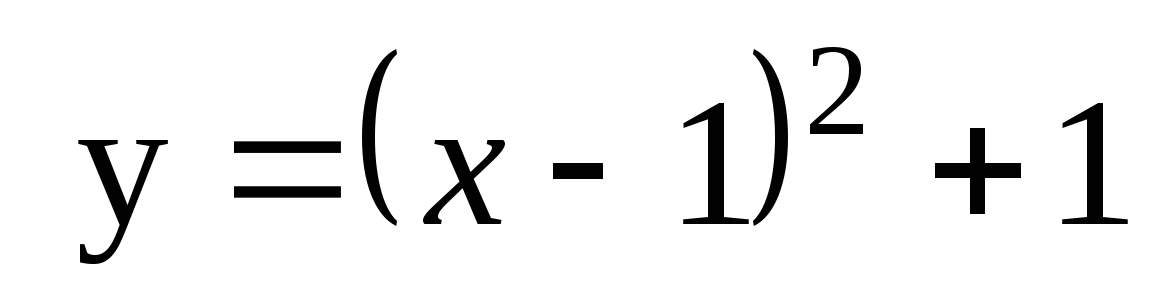 и
и 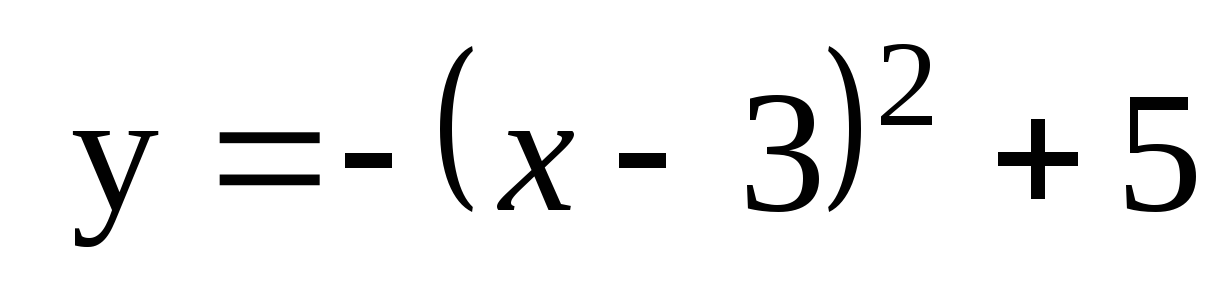 .
. 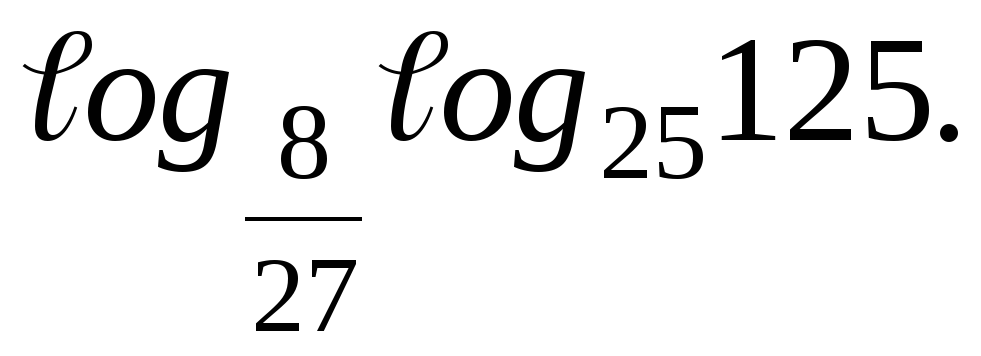
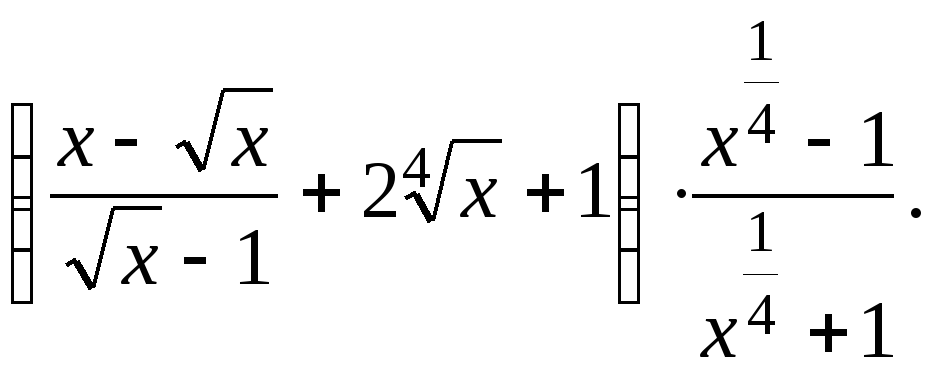
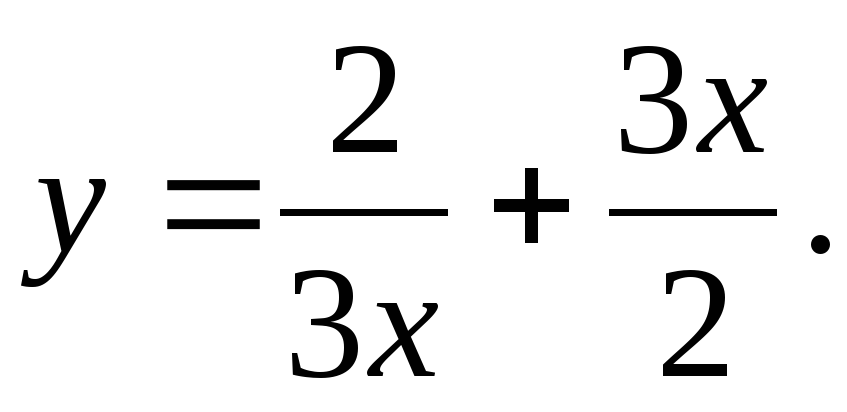
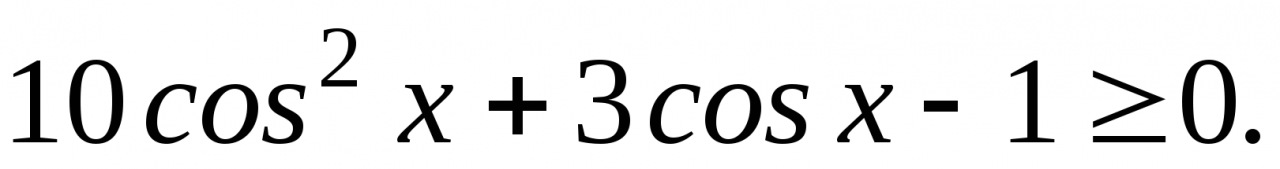
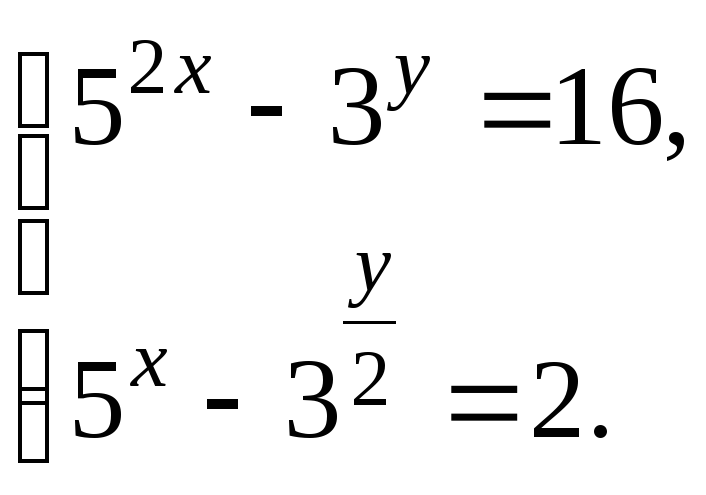
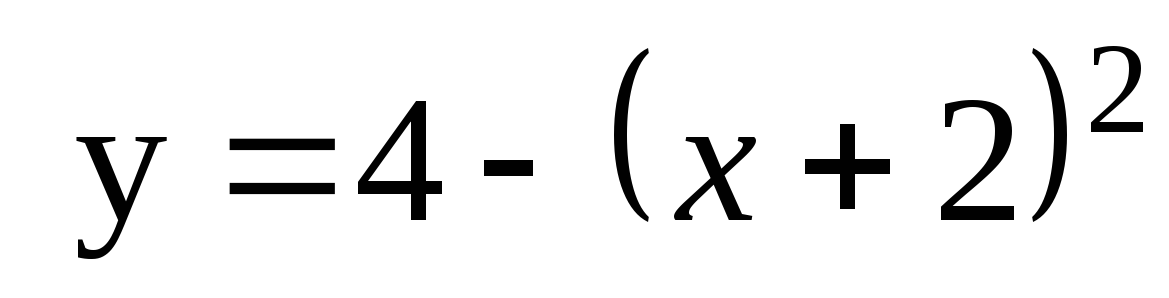 и
и 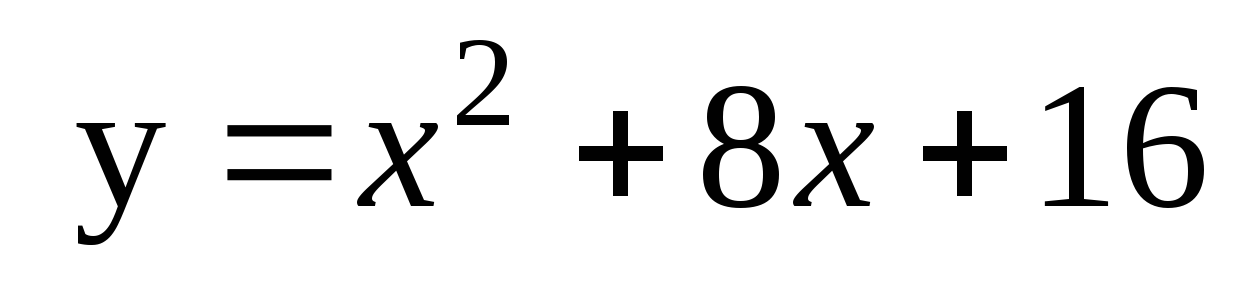 .
. 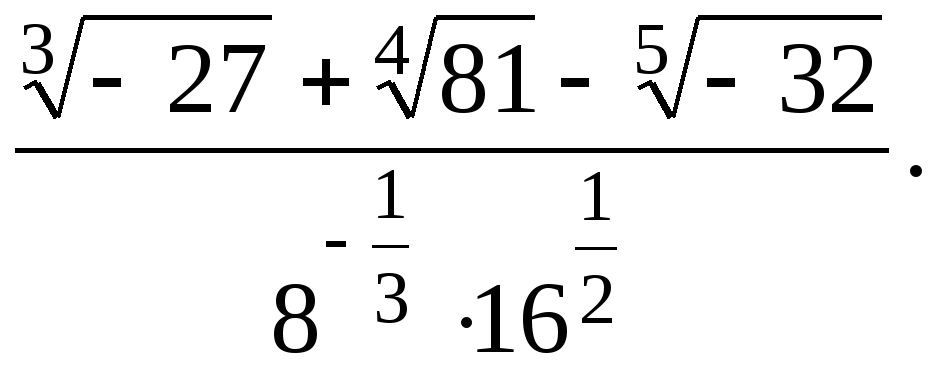
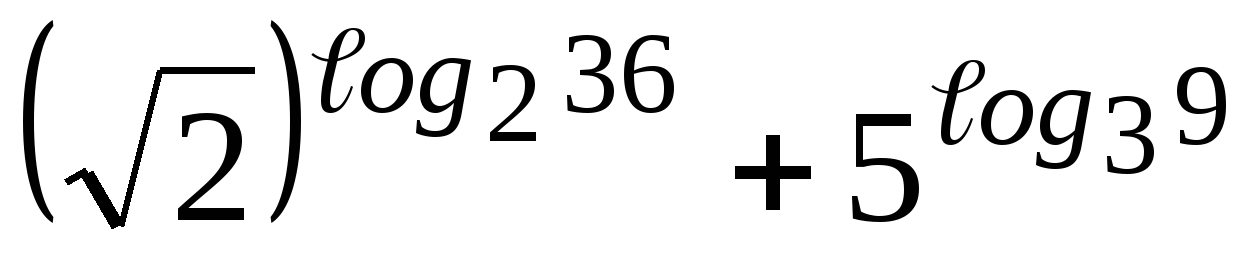 .
.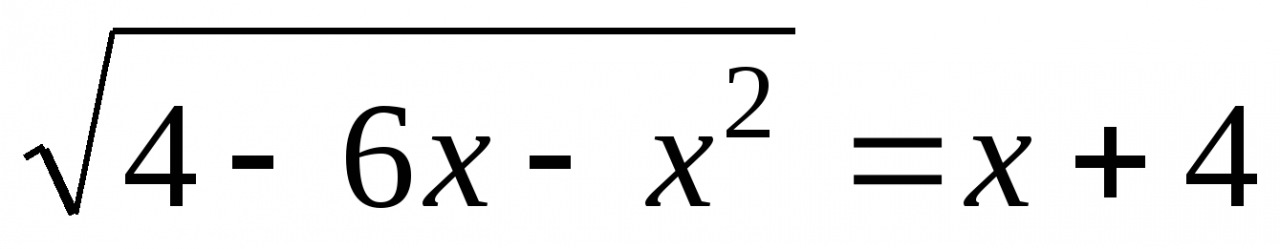 .
.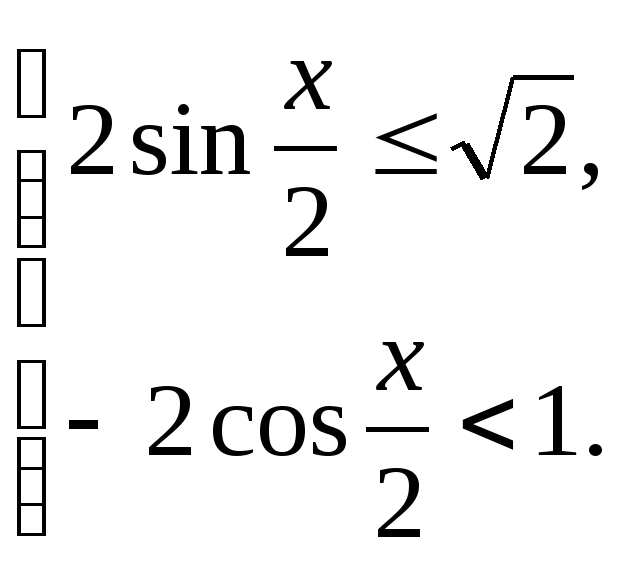
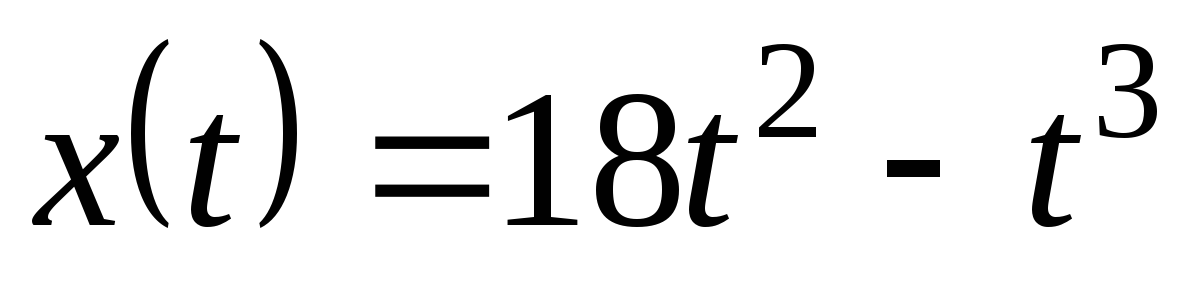 (х-в метрах, t-в cекундах). Найдите время, при котором скорость принимает наибольшее значение на промежутке времени
(х-в метрах, t-в cекундах). Найдите время, при котором скорость принимает наибольшее значение на промежутке времени 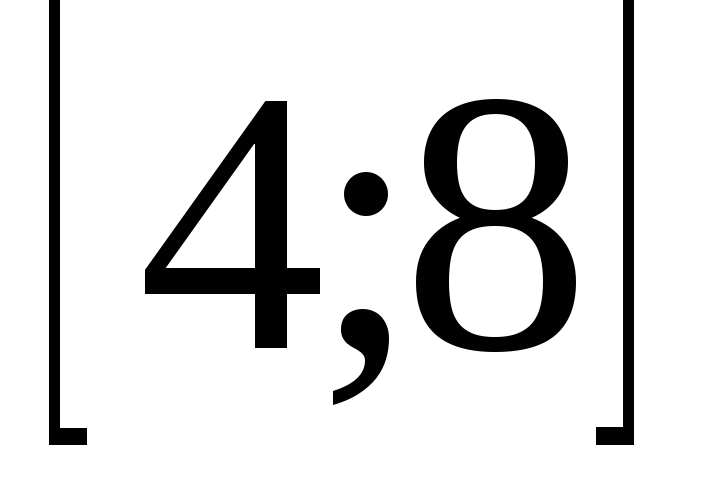 .
. 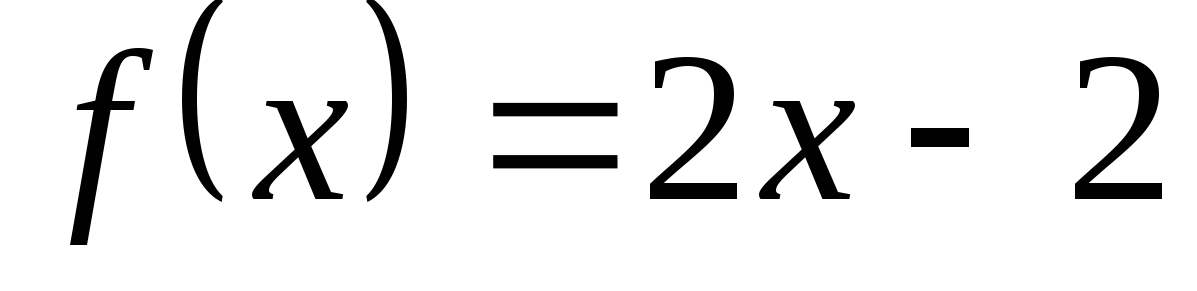 и графиком первообразной этой функции, для которой выполняется условие F(0)=1 .
и графиком первообразной этой функции, для которой выполняется условие F(0)=1 .
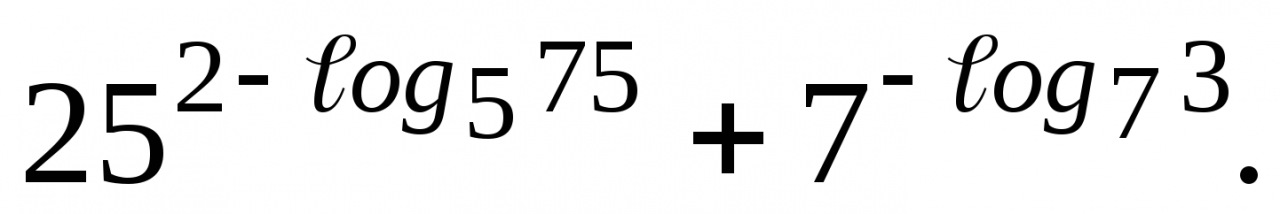
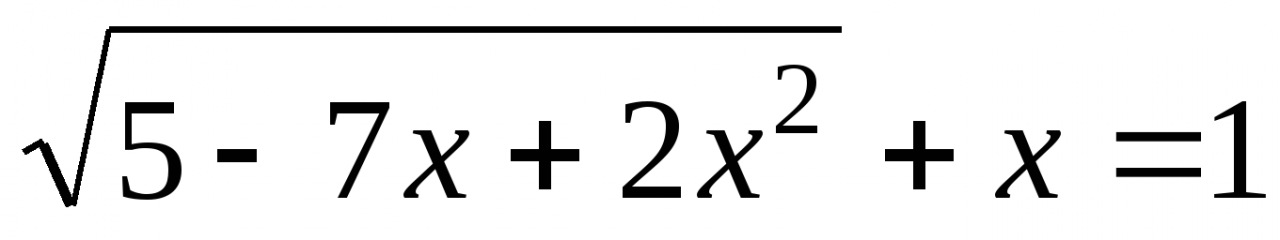 .
.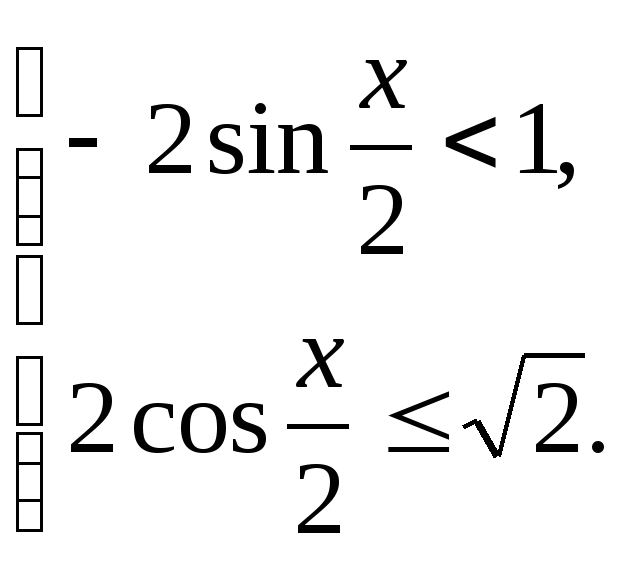
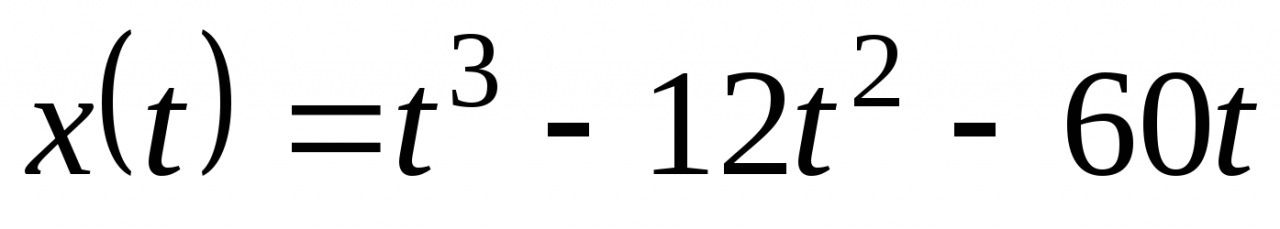 (х-в метрах, t- в cекундах). Найдите время, при котором скорость принимает наименьшее значение на промежутке времени
(х-в метрах, t- в cекундах). Найдите время, при котором скорость принимает наименьшее значение на промежутке времени 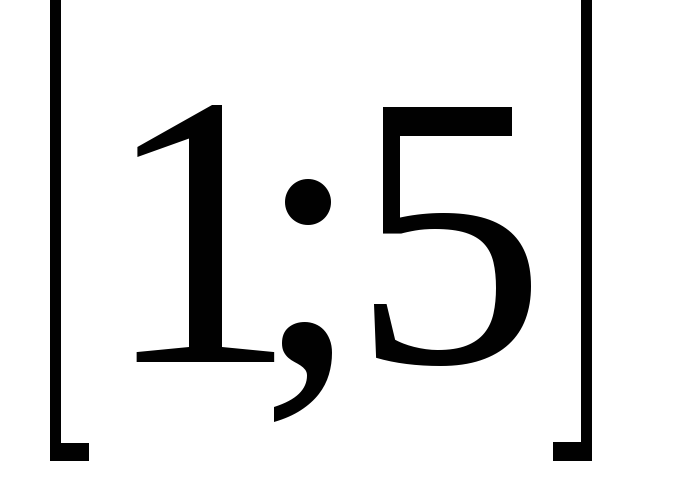 .
. 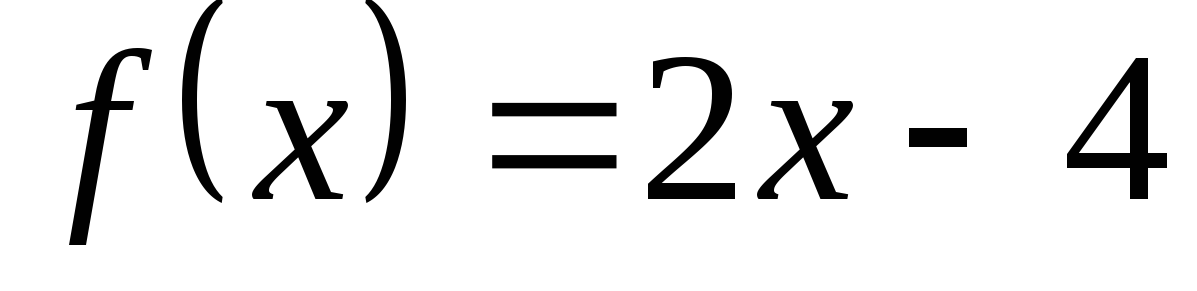 .
. 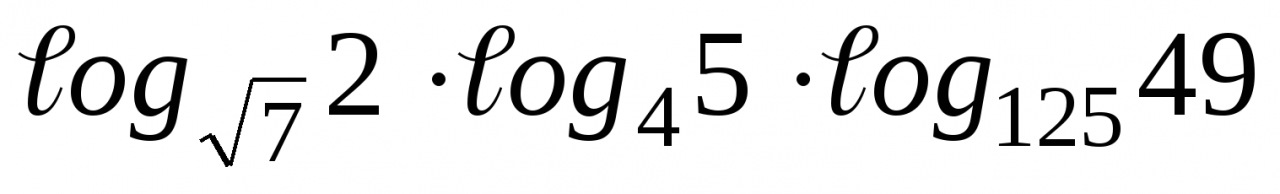 .
.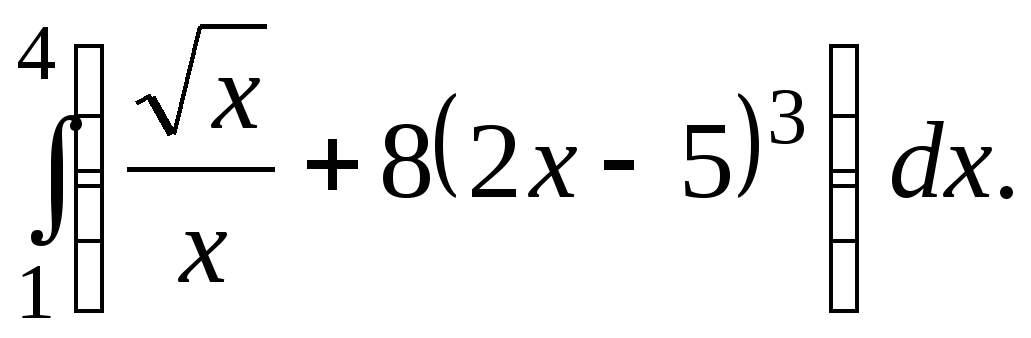
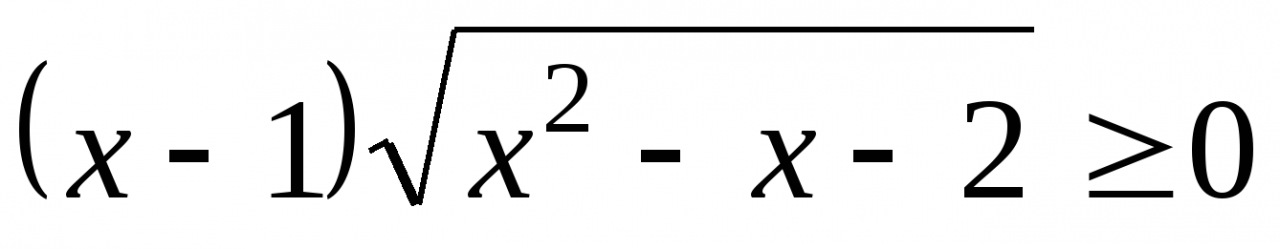 .
.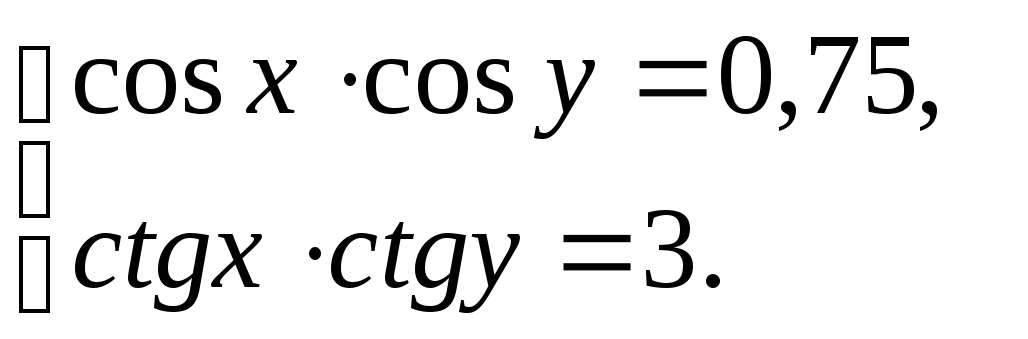
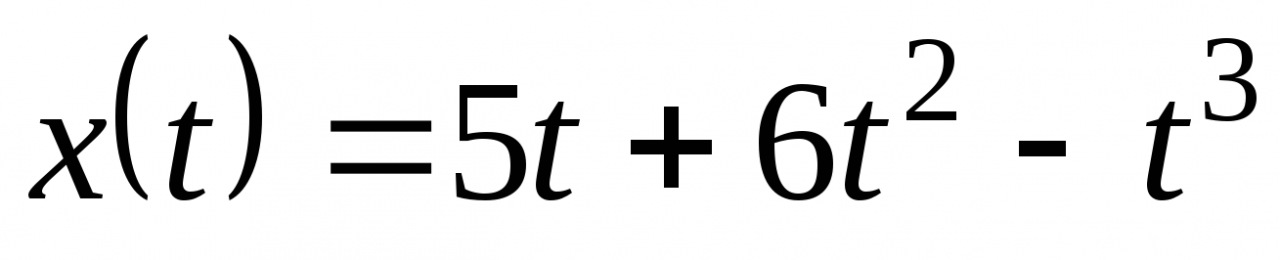 (х- в метрах,t-в секундах). Найдите скорость точки, в момент времени когда ускорение равен нулю.
(х- в метрах,t-в секундах). Найдите скорость точки, в момент времени когда ускорение равен нулю.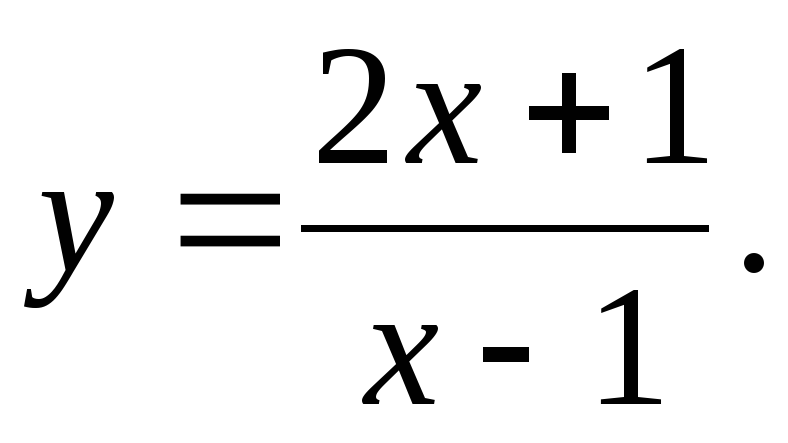
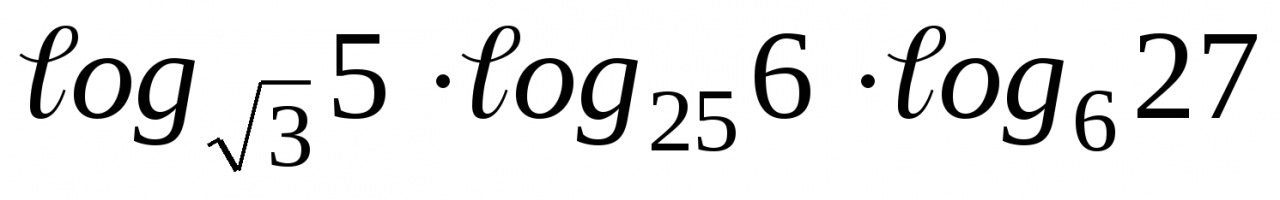 .
.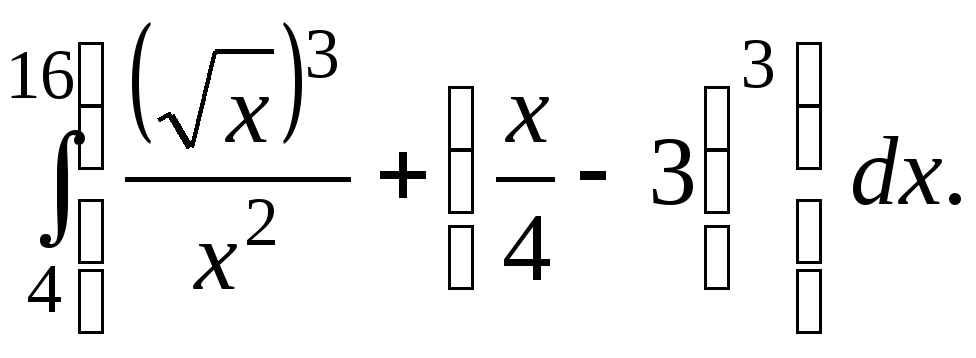
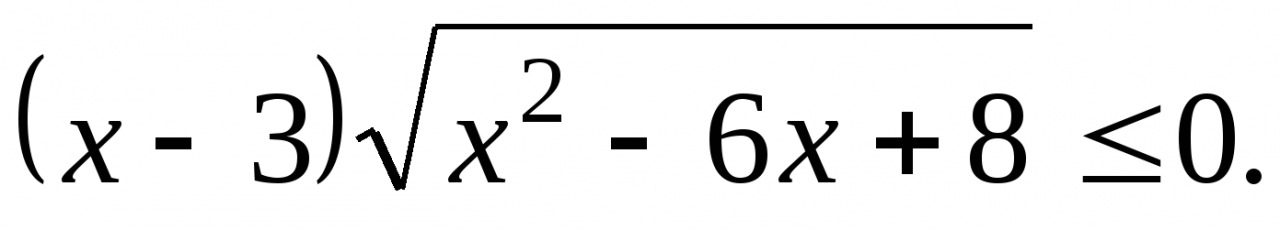
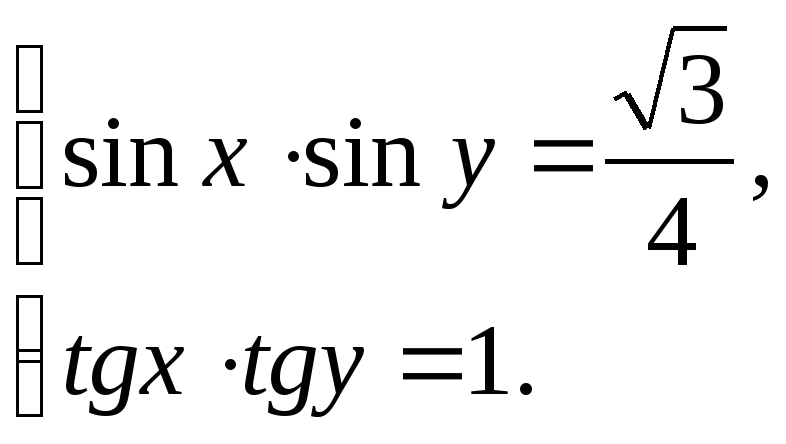
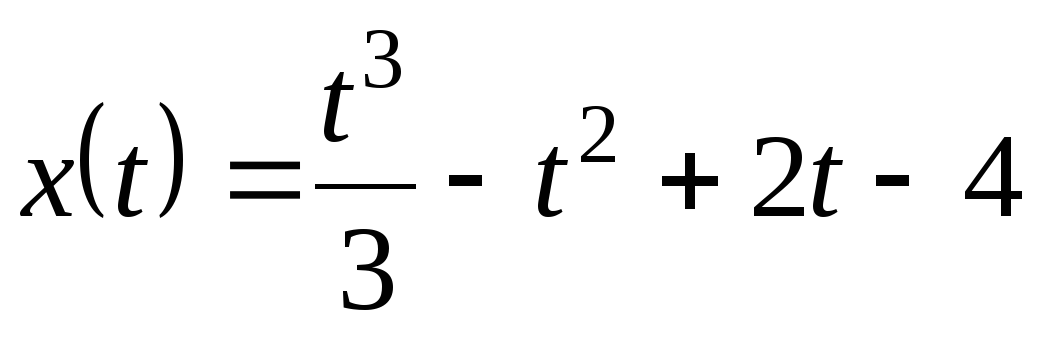 (х-в метрах, t-в секундах). Найдите ускорение точки в момент времени, когда скорость равен 1 м/с.
(х-в метрах, t-в секундах). Найдите ускорение точки в момент времени, когда скорость равен 1 м/с. 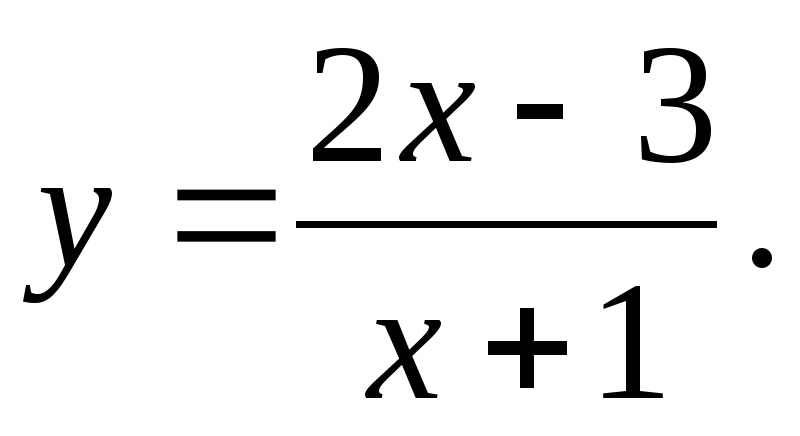
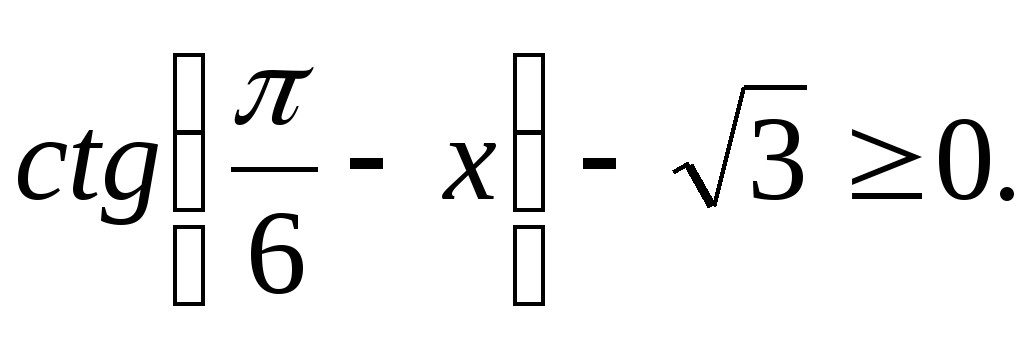
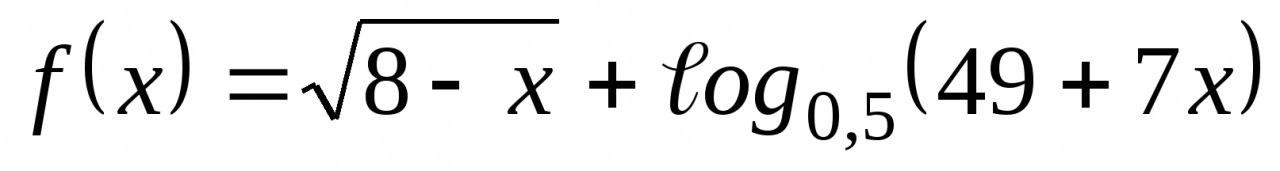 .
.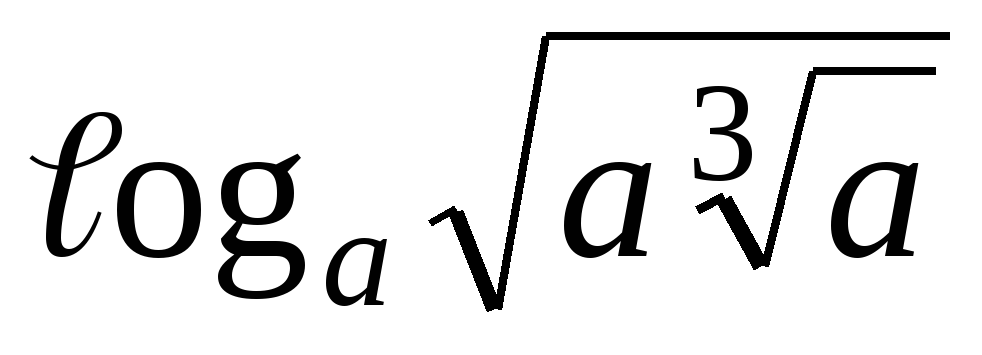 .
.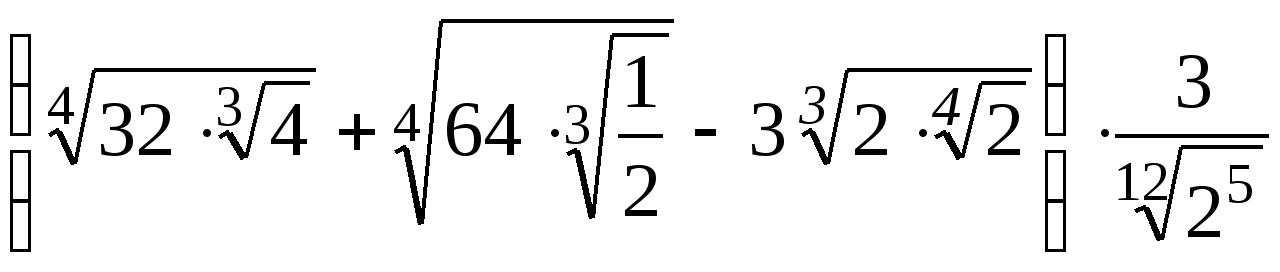 .
.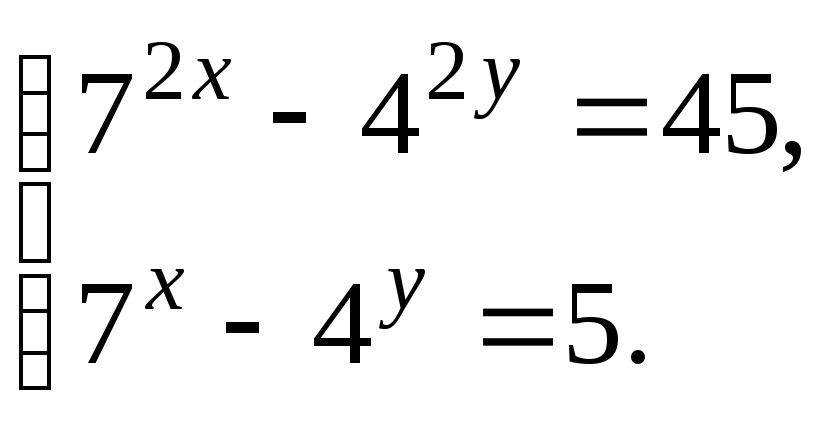
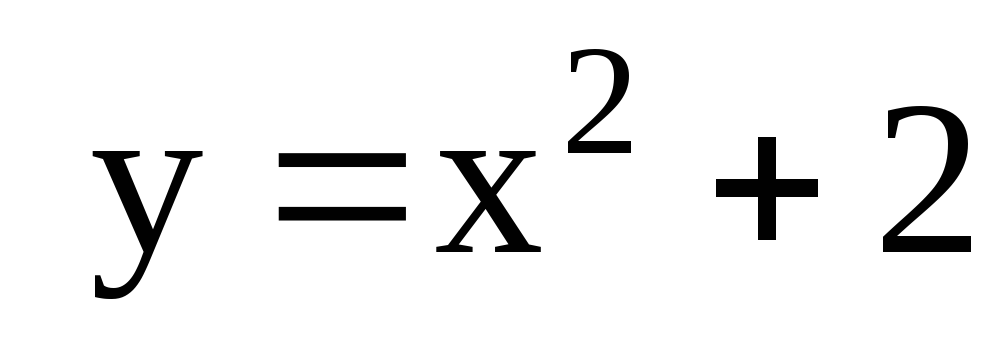 и касательными к графику проведенными в точке (2;2).
и касательными к графику проведенными в точке (2;2). 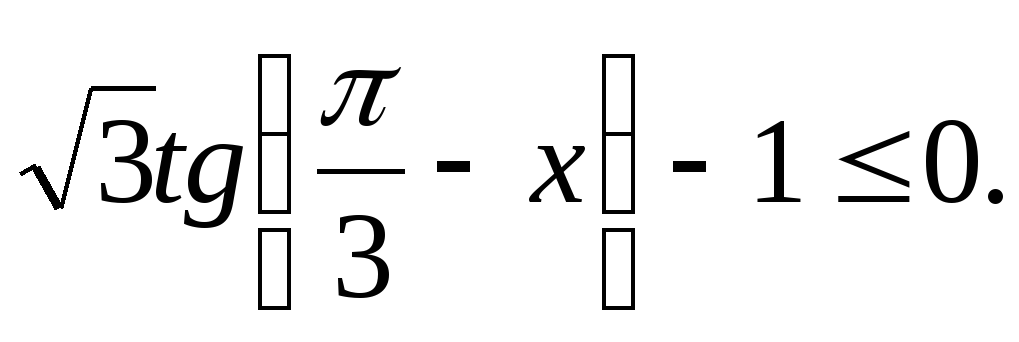
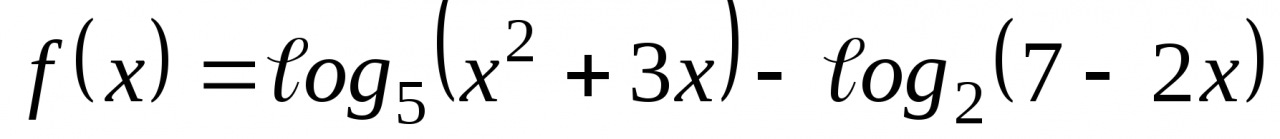 .
. .
.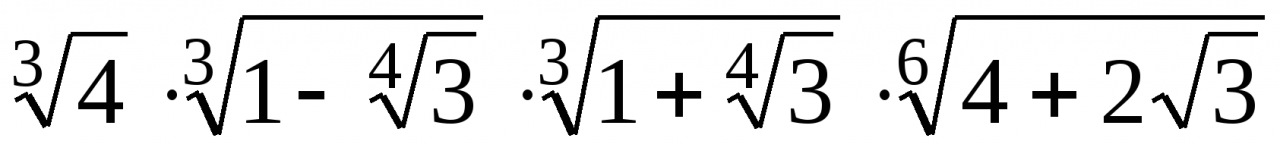 .
.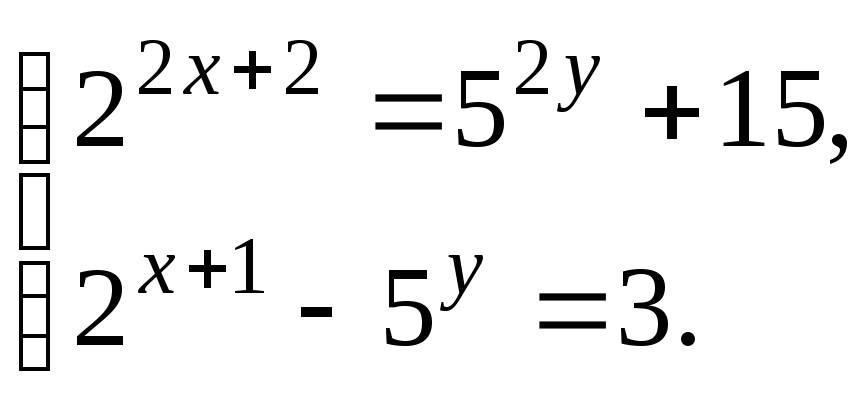
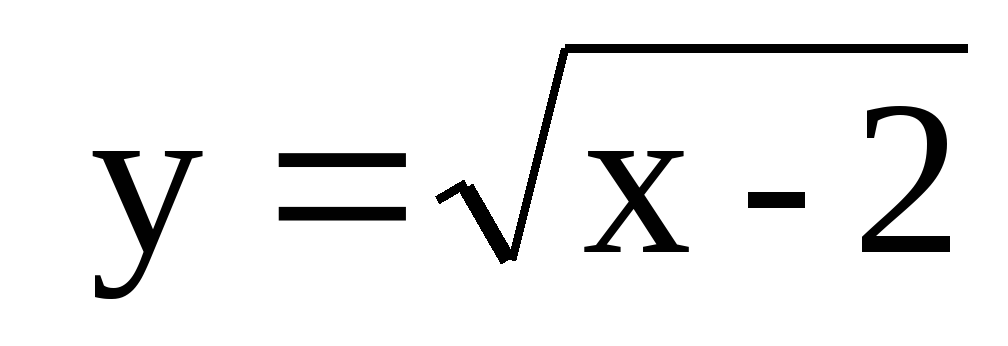 и касательными к графику проведенными в точке (2;1).
и касательными к графику проведенными в точке (2;1). 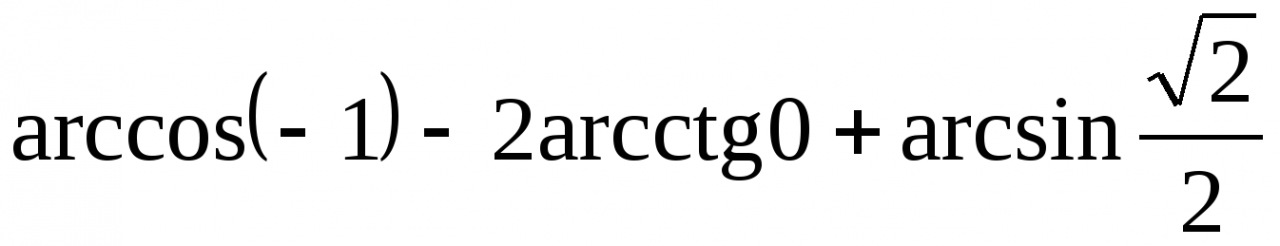 .
.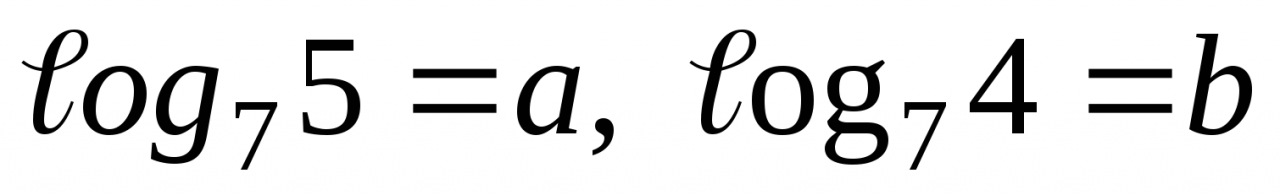 , то выразите
, то выразите 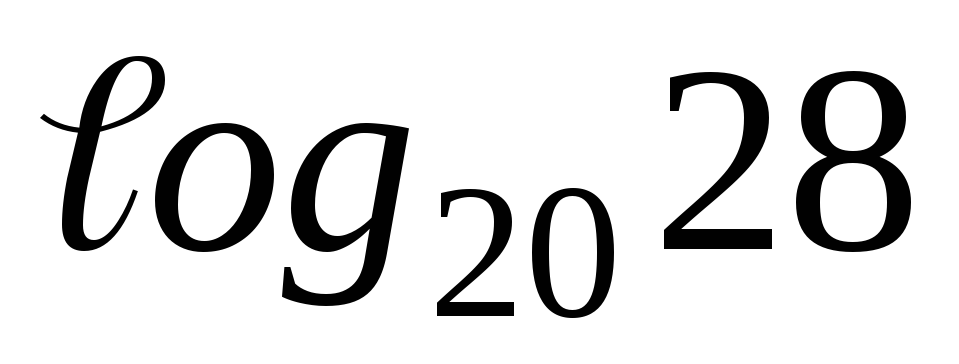 через
через  и
и 
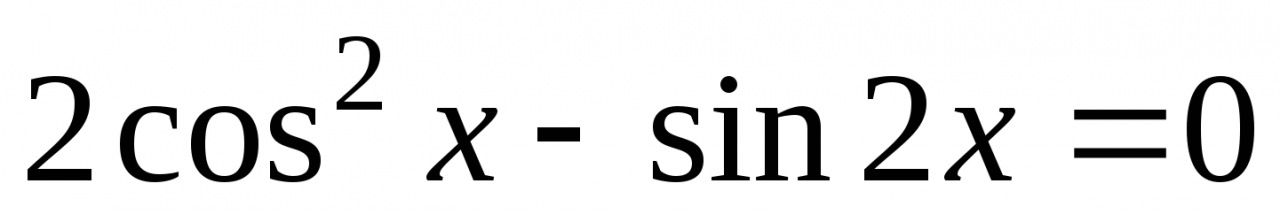 .
.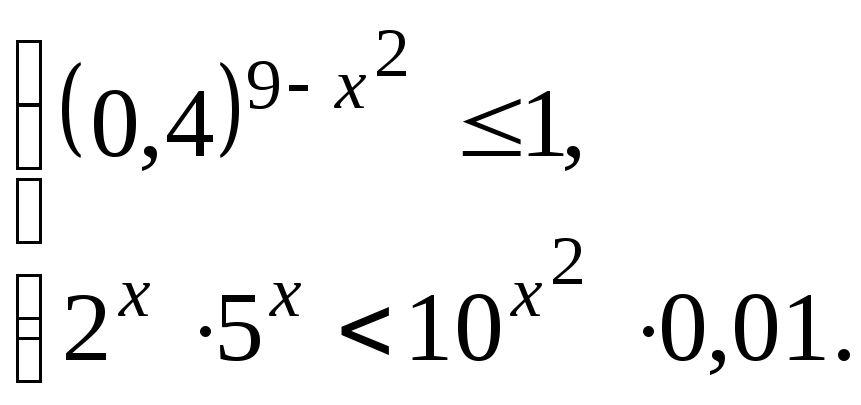
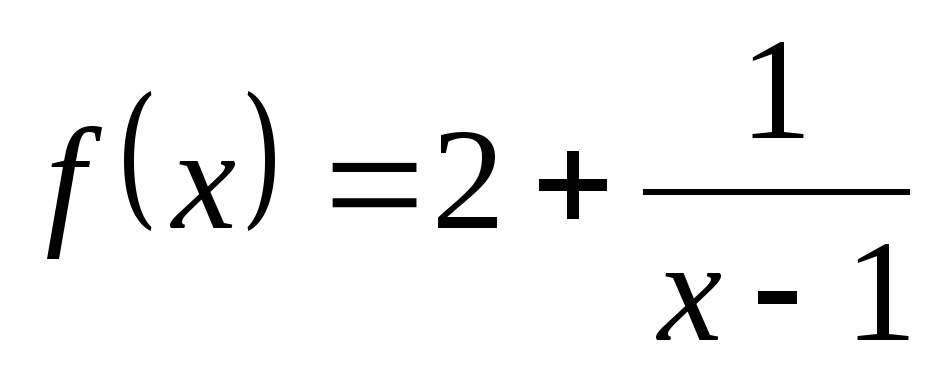 .
.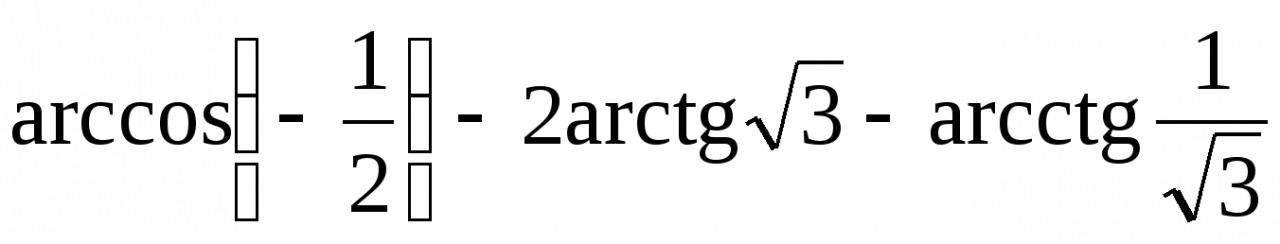 .
.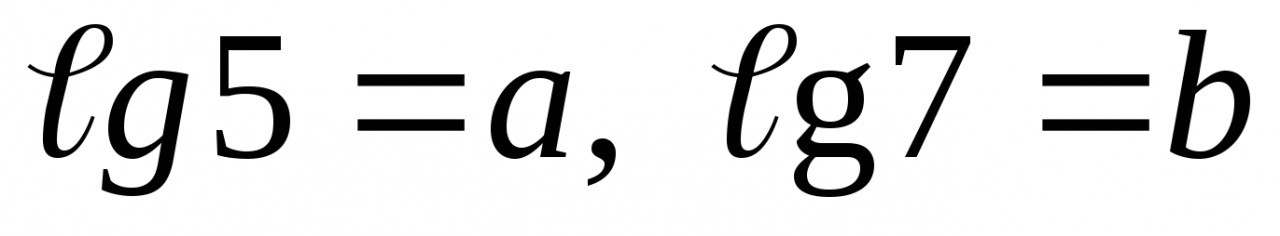 , то выразите
, то выразите 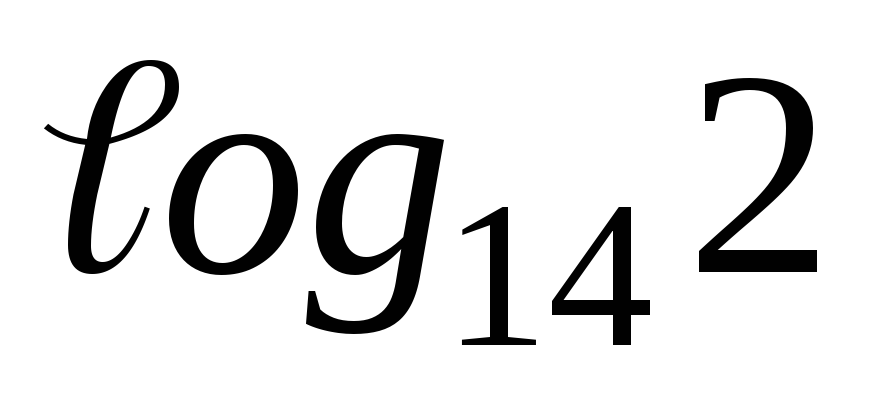 через
через 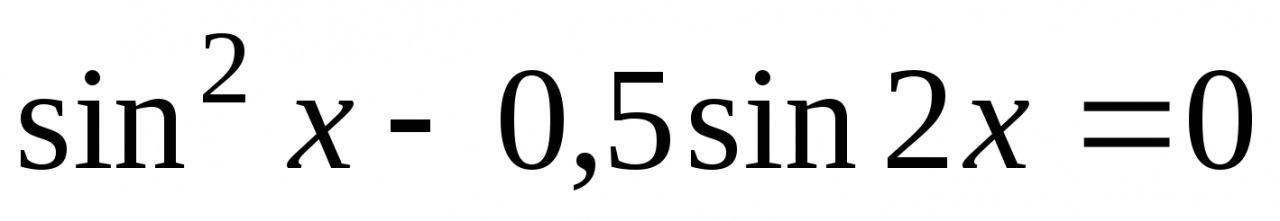 .
.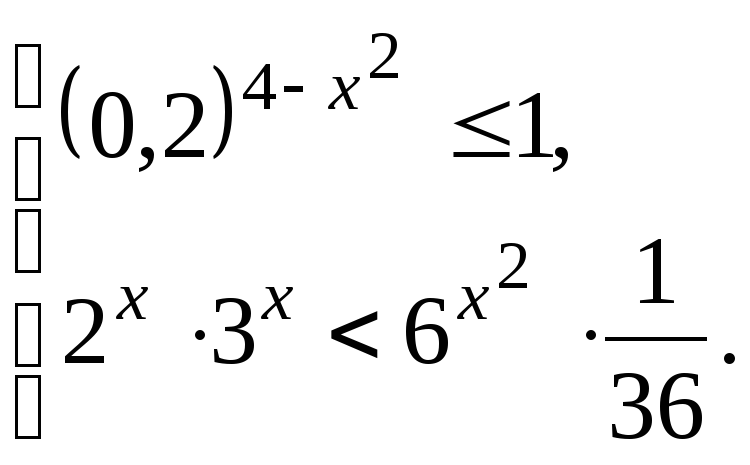
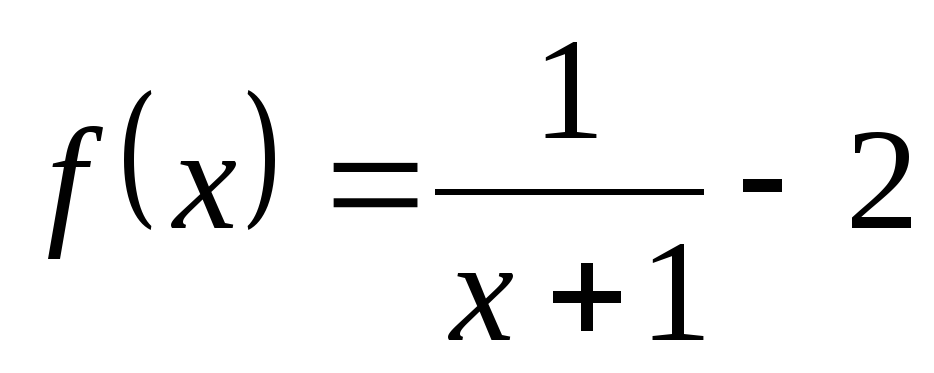
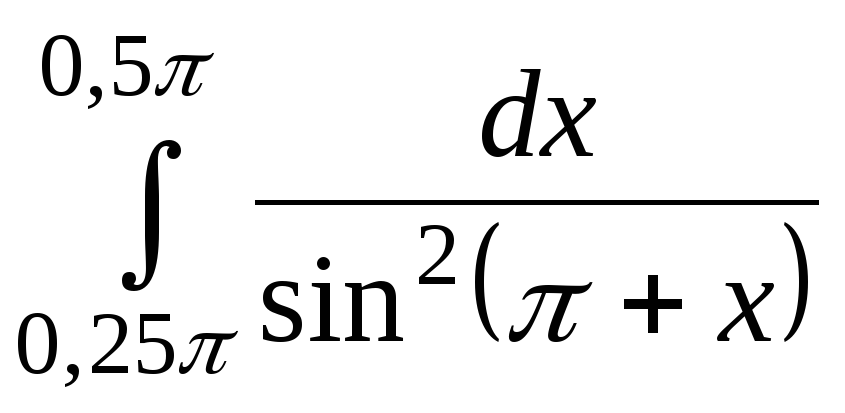 .
.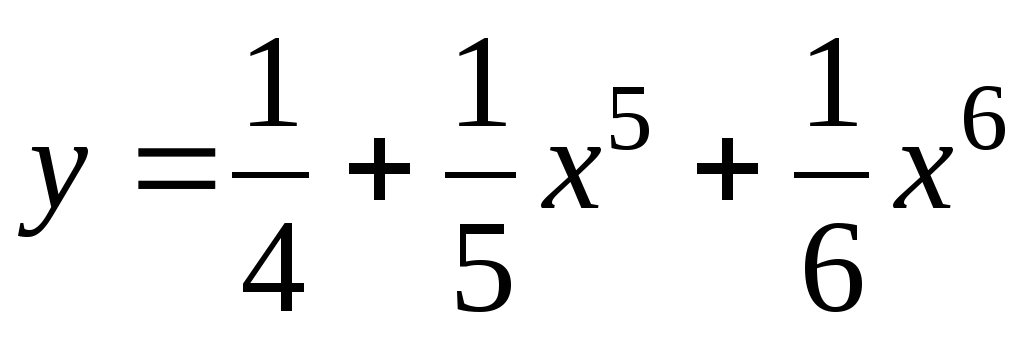 .
.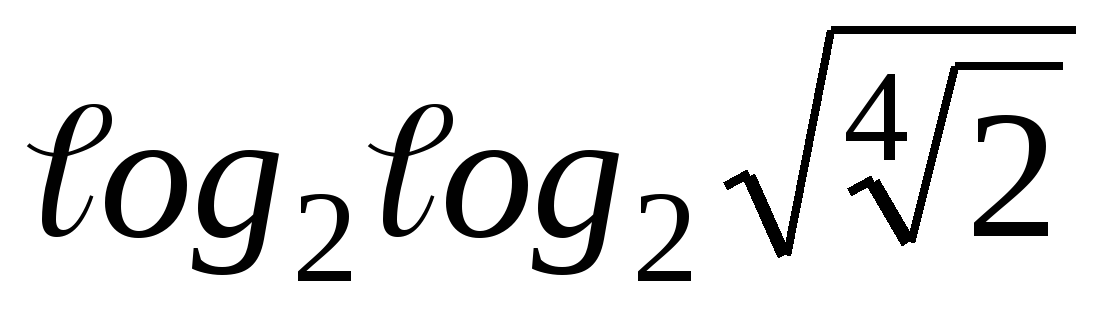 .
.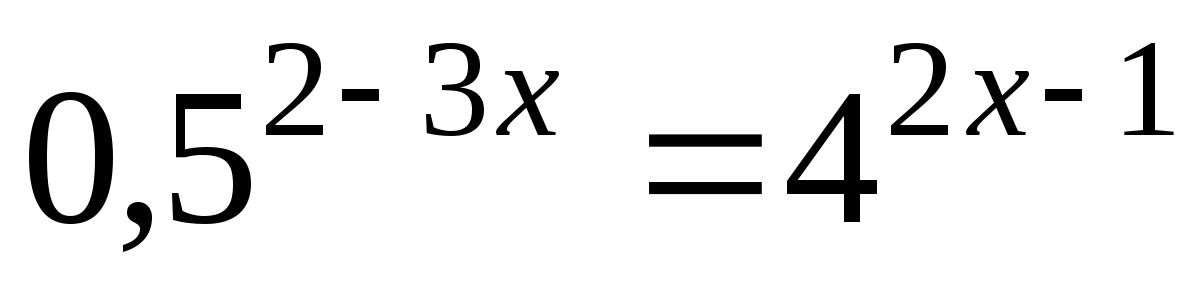 .
.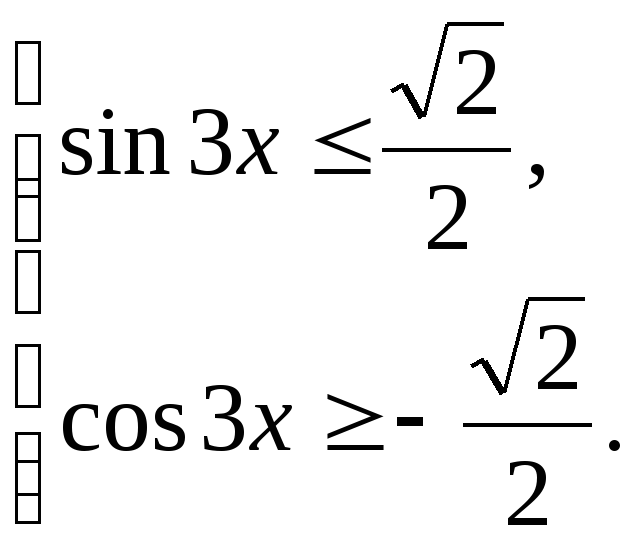
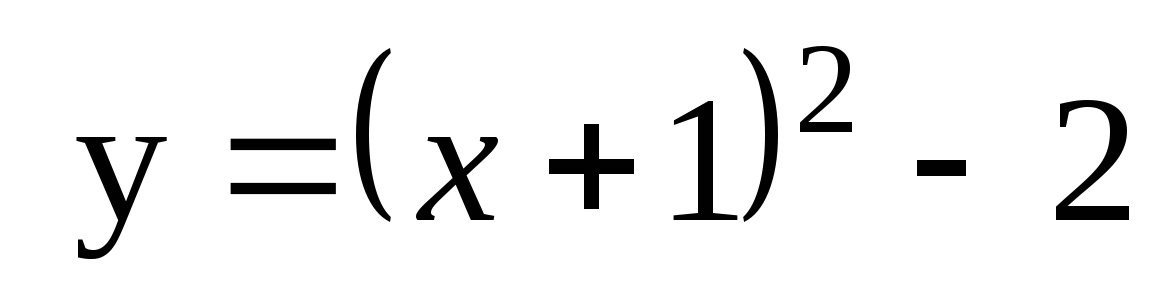 и
и 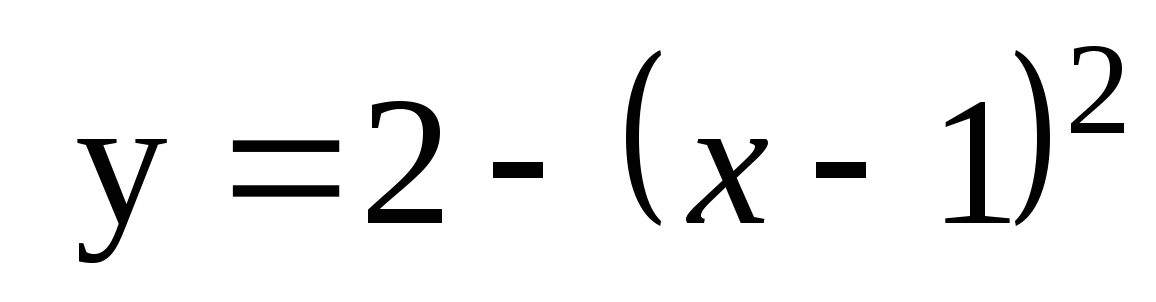 .
. 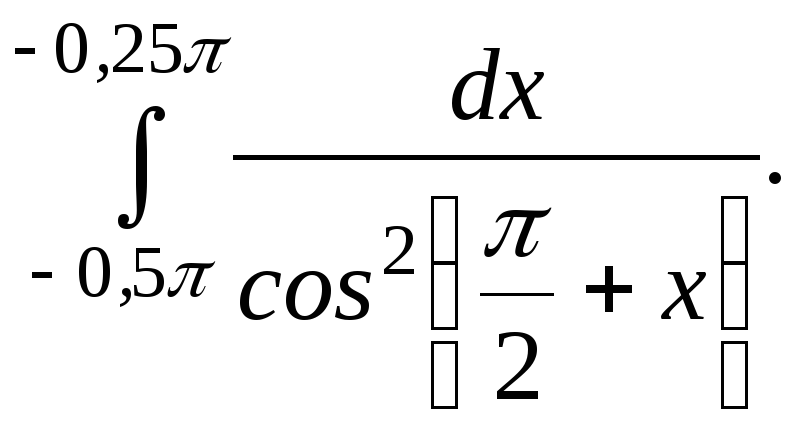
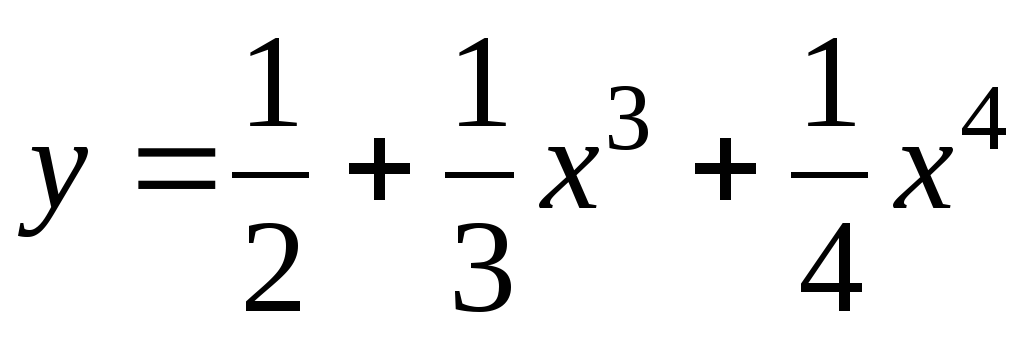 .
.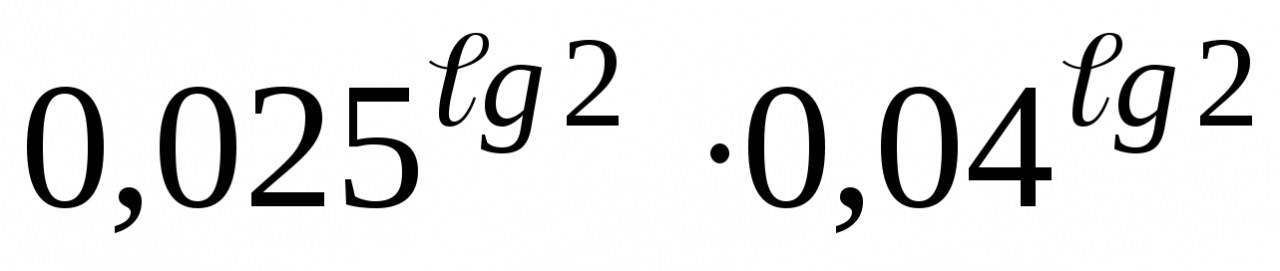 .
.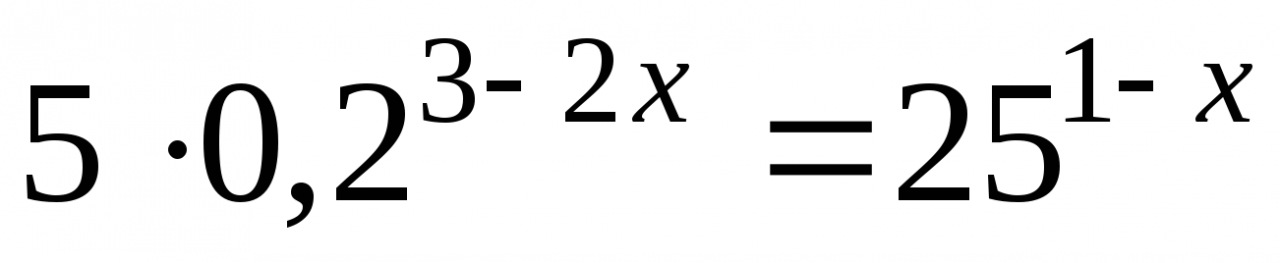 .
.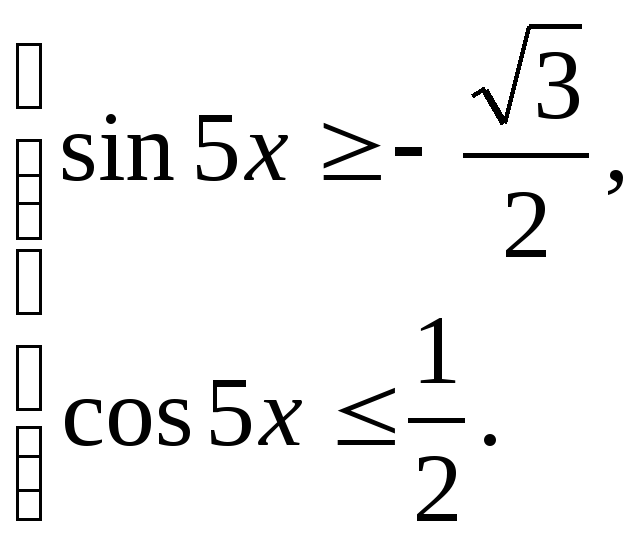
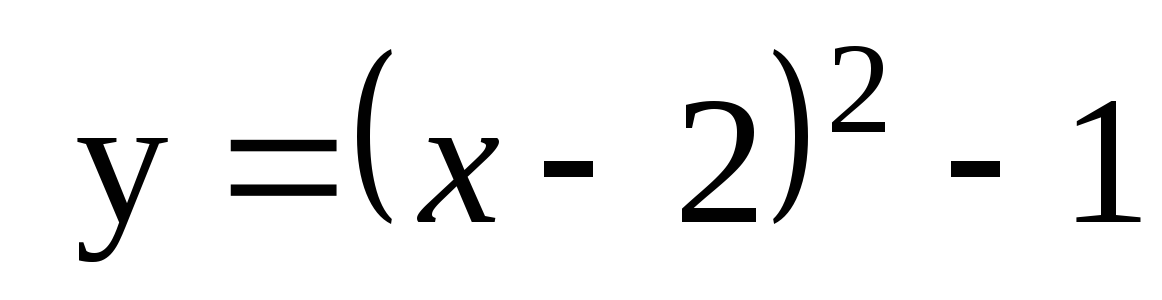 и
и 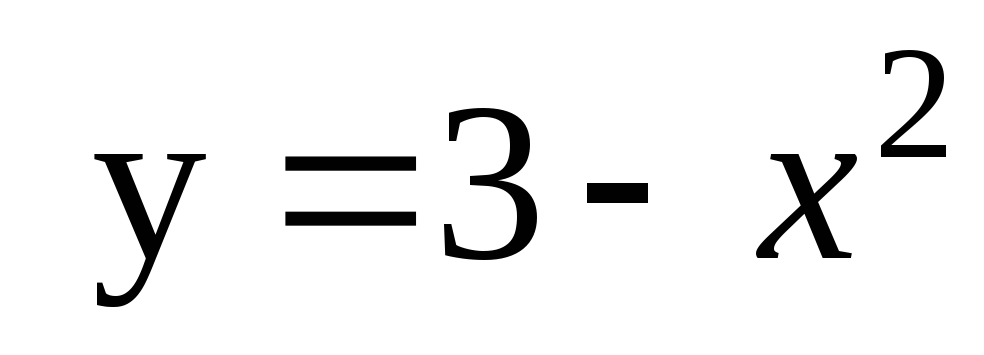 .
. 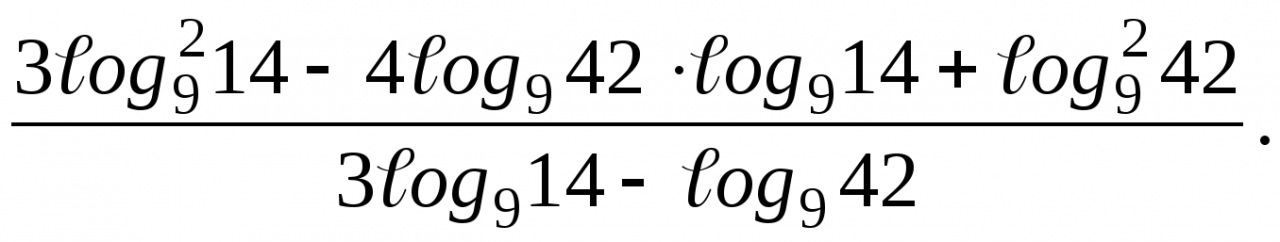
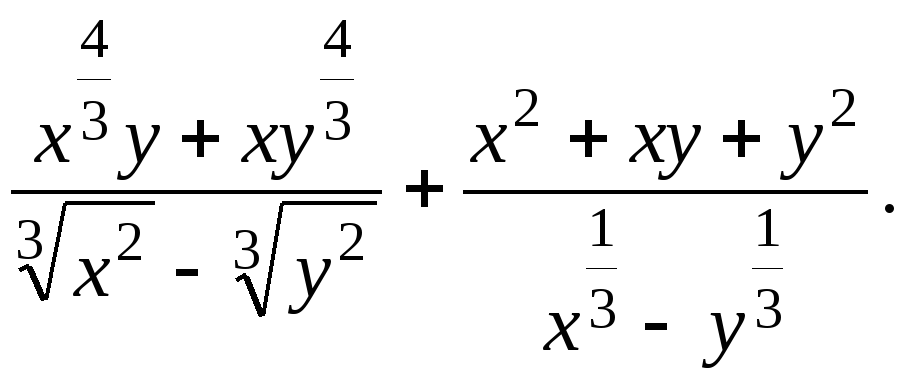
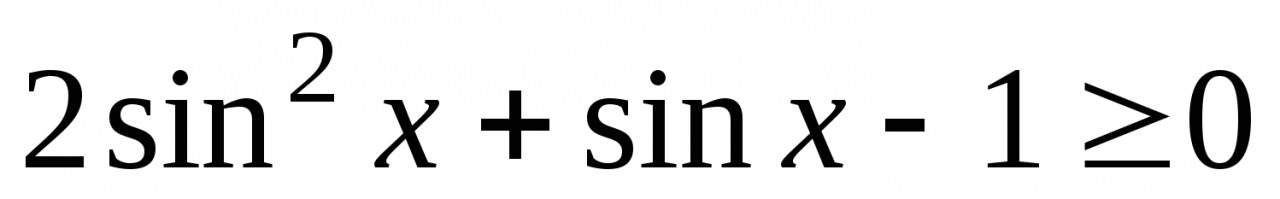 .
.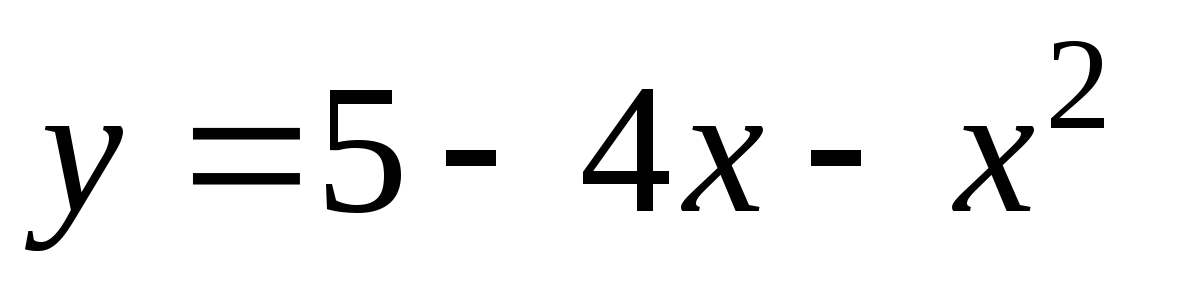 и y=0 .
и y=0 .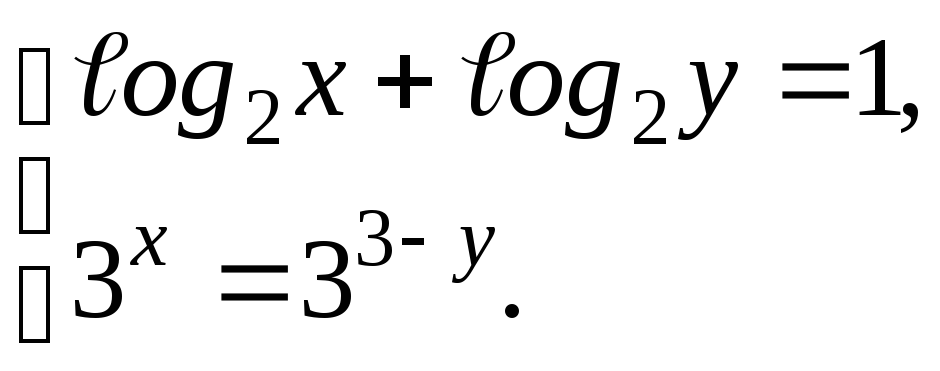
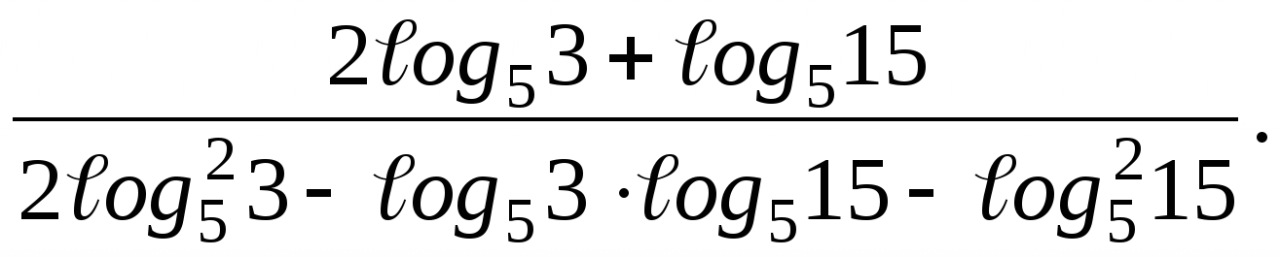
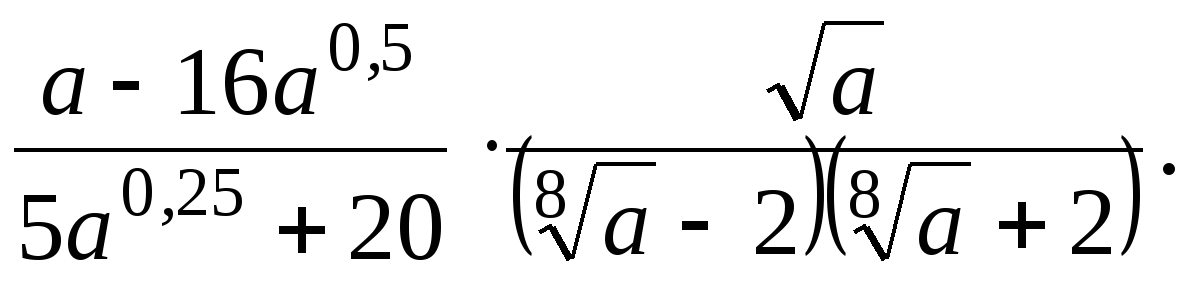
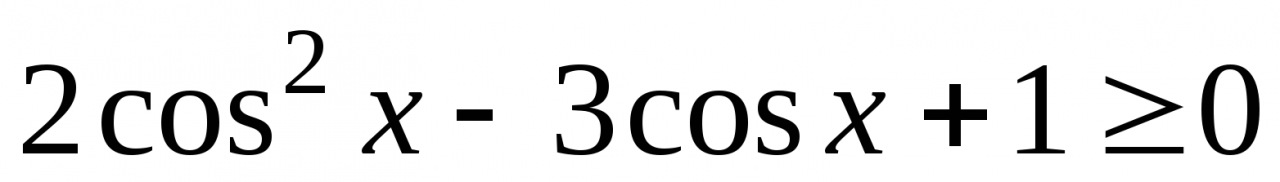 .
.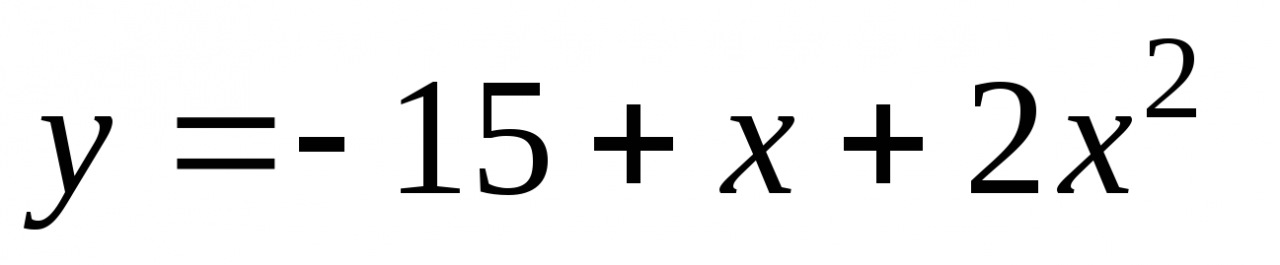 и y=0 .
и y=0 .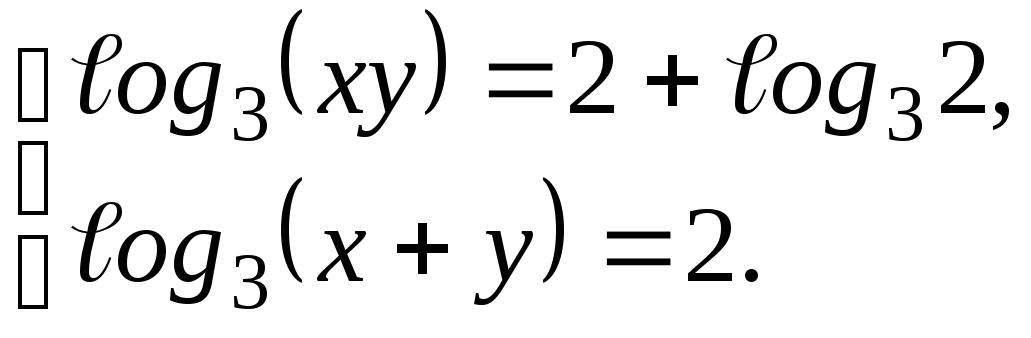
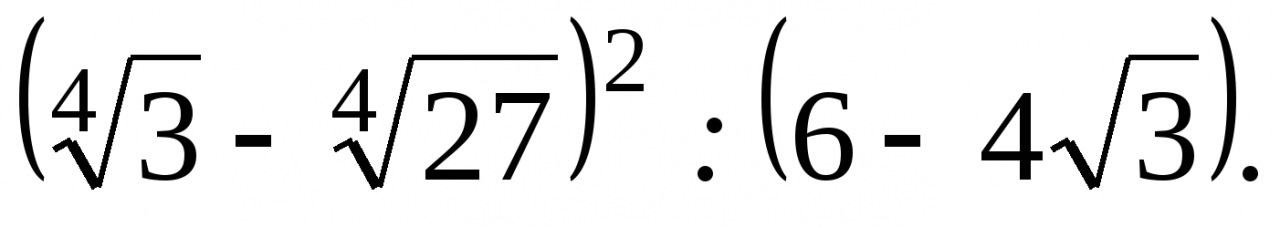
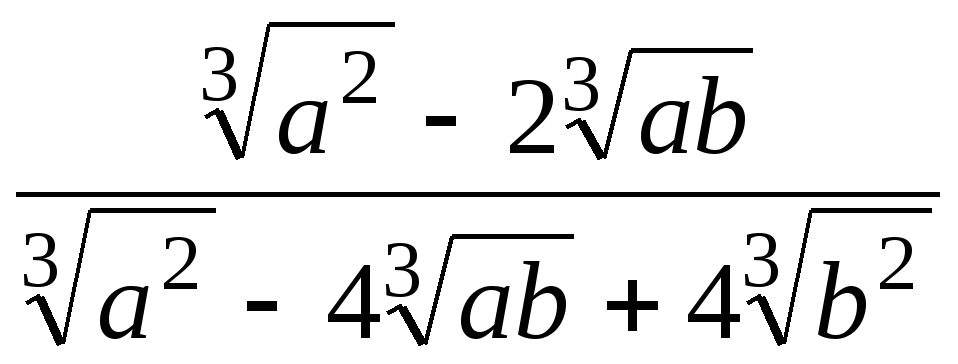 .
. 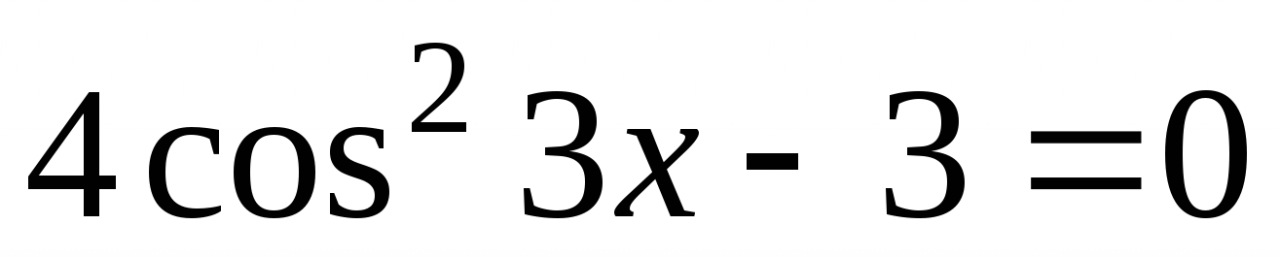 .
. 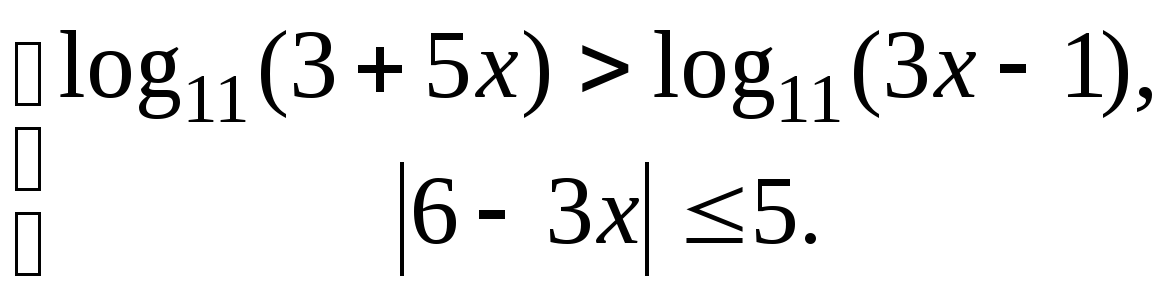
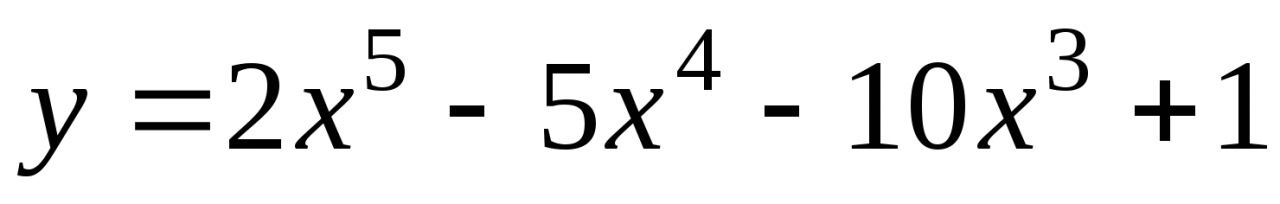 на отрезке [-1;2] .
на отрезке [-1;2] . 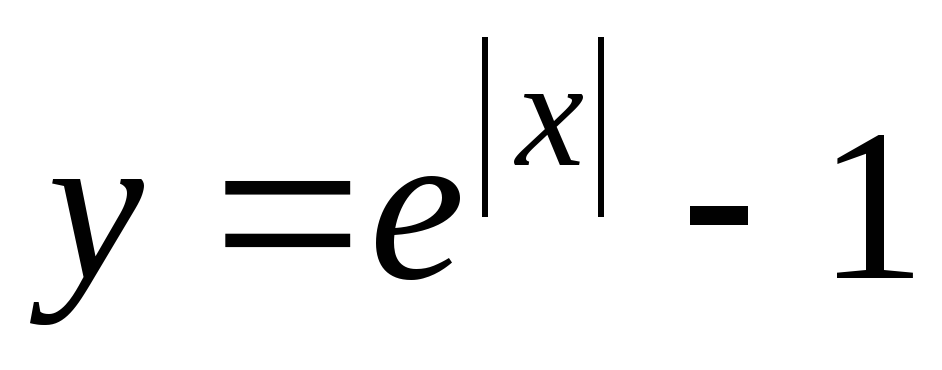 , y = e – 1.
, y = e – 1. 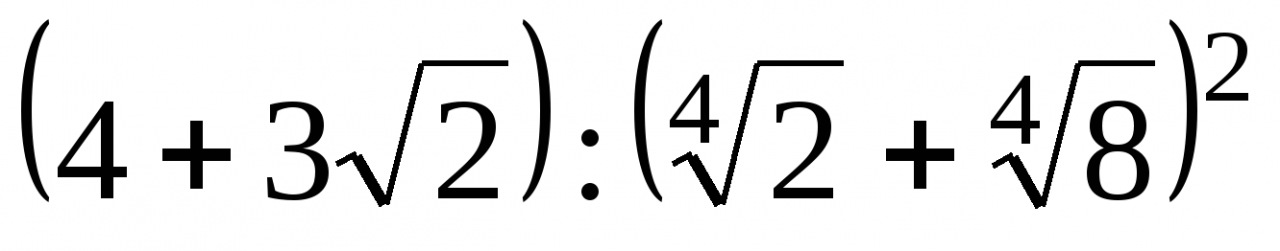 .
. 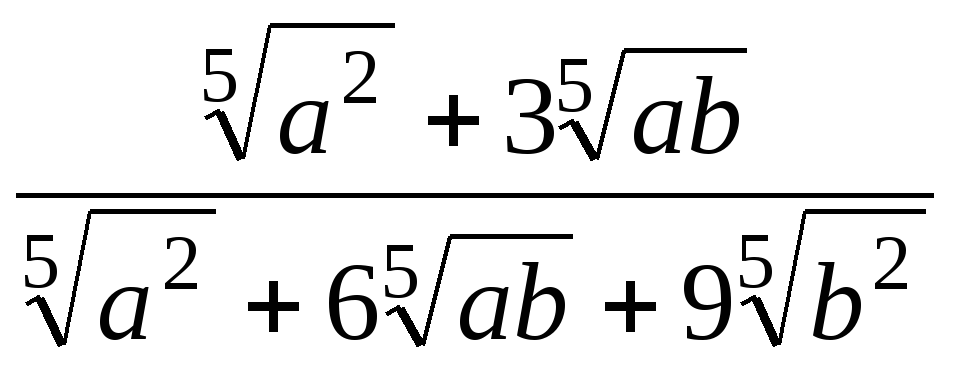 .
. 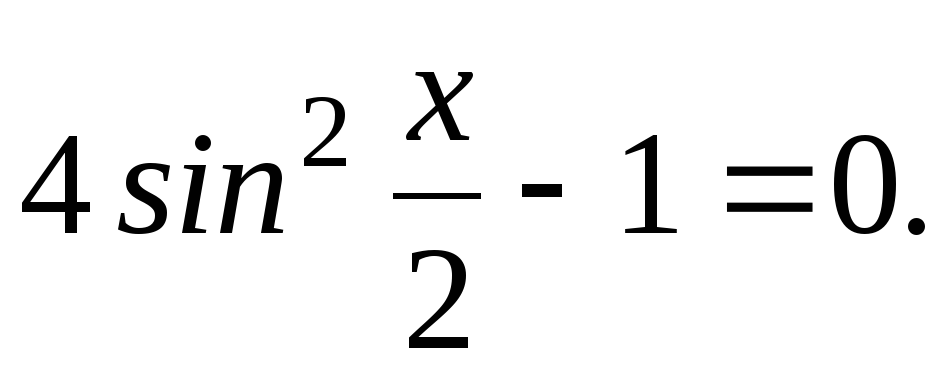
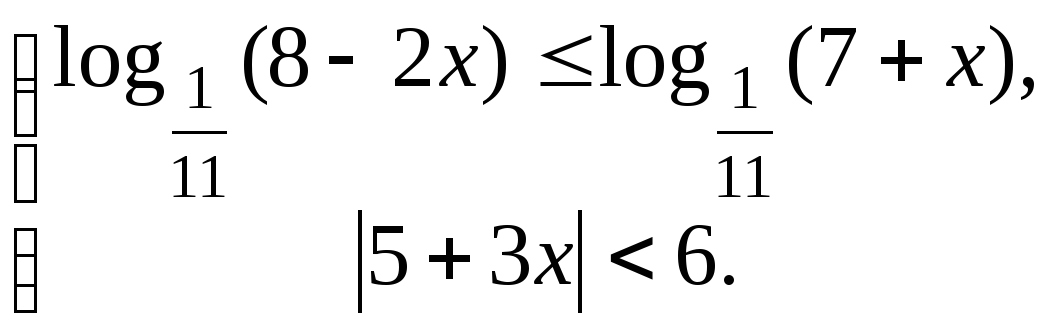
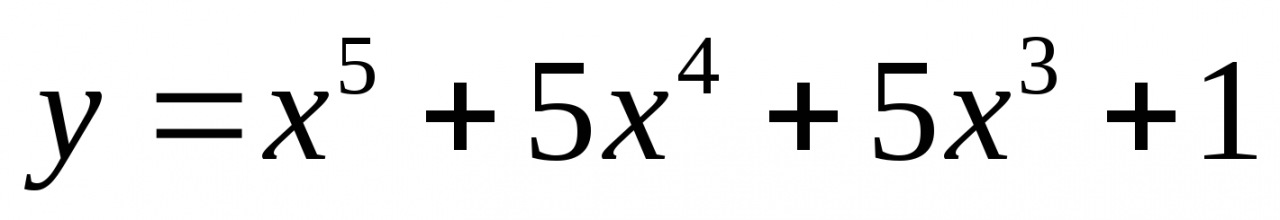 на отрезке [-2;1]
на отрезке [-2;1] 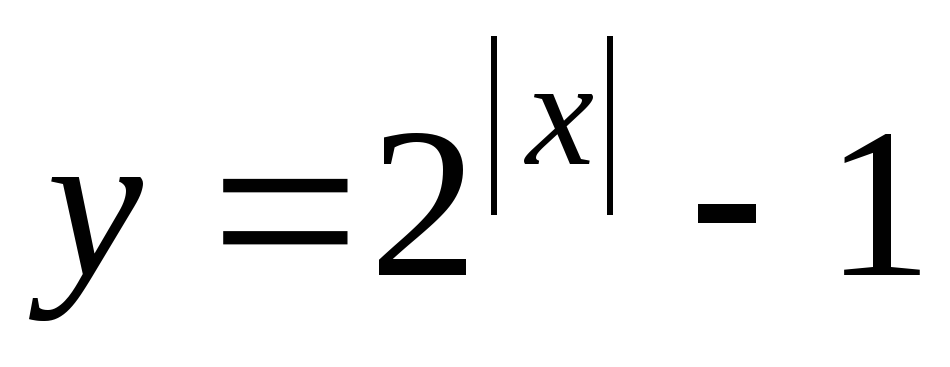 , y = 3.
, y = 3. 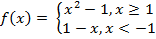
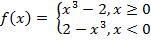
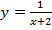
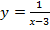
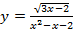
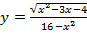
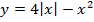
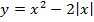
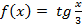
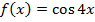

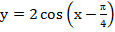
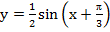
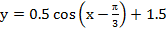
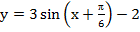
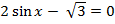 а)
а)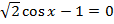
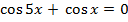 б)
б)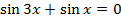
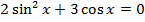 а)
а)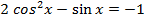
 б)
б)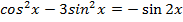
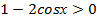
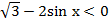
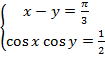
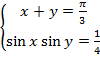

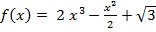 а)
а)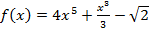 б)
б)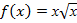 - 8х3 б) )
- 8х3 б) )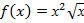 + 3х5
+ 3х5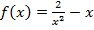 , x0=-1
, x0=-1 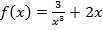 , x0 = 1
, x0 = 1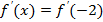
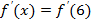
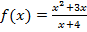 если
если 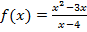
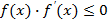
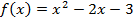
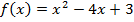
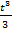 – t2 + 2t – 4
– t2 + 2t – 4








