Метод корреляционного анализа: пример. Корреляционный анализ - это... Корреляция контрольная
Метод корреляционного анализа: пример. Корреляционный анализ
В научных исследованиях часто возникает необходимость в нахождении связи между результативными и факторными переменными (урожайностью какой-либо культуры и количеством осадков, ростом и весом человека в однородных группах по полу и возрасту, частотой пульса и температурой тела и т.д.).
Вторые представляют собой признаки, способствующие изменению таковых, связанных с ними (первыми).
Понятие о корреляционном анализе
Существует множество определений термина. Исходя из вышеизложенного, можно сказать, что корреляционный анализ — это метод, применяющийся с целью проверки гипотезы о статистической значимости двух и более переменных, если исследователь их может измерять, но не изменять.
Есть и другие определения рассматриваемого понятия. Корреляционный анализ — это метод обработки статистических данных, заключающийся в изучении коэффициентов корреляции между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков, для установления между ними статистических взаимосвязей. Корреляционный анализ — это метод по изучению статистической зависимости между случайными величинами с необязательным наличием строгого функционального характера, при которой динамика одной случайной величины приводит к динамике математического ожидания другой.
Понятие о ложности корреляции
При проведении корреляционного анализа необходимо учитывать, что его можно провести по отношению к любой совокупности признаков, зачастую абсурдных по отношению друг к другу. Порой они не имеют никакой причинной связи друг с другом.
В этом случае говорят о ложной корреляции.
Задачи корреляционного анализа
Исходя из приведенных выше определений, можно сформулировать следующие задачи описываемого метода: получить информацию об одной из искомых переменных с помощью другой; определить тесноту связи между исследуемыми переменными.
Корреляционный анализ предполагает определение зависимости между изучаемыми признаками, в связи с чем задачи корреляционного анализа можно дополнить следующими:
- выявление факторов, оказывающих наибольшее влияние на результативный признак;
- выявление неизученных ранее причин связей;
- построение корреляционной модели с ее параметрическим анализом;
- исследование значимости параметров связи и их интервальная оценка.
Связь корреляционного анализа с регрессионным
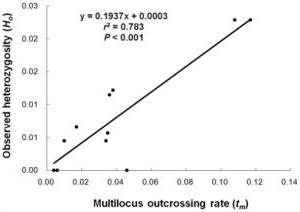 Метод корреляционного анализа часто не ограничивается нахождением тесноты связи между исследуемыми величинами. Иногда он дополняется составлением уравнений регрессии, которые получают с помощью одноименного анализа, и представляющих собой описание корреляционной зависимости между результирующим и факторным (факторными) признаком (признаками). Этот метод в совокупности с рассматриваемым анализом составляет метод корреляционно-регрессионного анализа.
Метод корреляционного анализа часто не ограничивается нахождением тесноты связи между исследуемыми величинами. Иногда он дополняется составлением уравнений регрессии, которые получают с помощью одноименного анализа, и представляющих собой описание корреляционной зависимости между результирующим и факторным (факторными) признаком (признаками). Этот метод в совокупности с рассматриваемым анализом составляет метод корреляционно-регрессионного анализа.
Условия использования метода
Результативные факторы зависят от одного до нескольких факторов. Метод корреляционного анализа может применяться в том случае, если имеется большое количество наблюдений о величине результативных и факторных показателей (факторов), при этом исследуемые факторы должны быть количественными и отражаться в конкретных источниках. Первое может определяться нормальным законом — в этом случае результатом корреляционного анализа выступают коэффициенты корреляции Пирсона, либо, в случае, если признаки не подчиняются этому закону, используется коэффициент ранговой корреляции Спирмена.
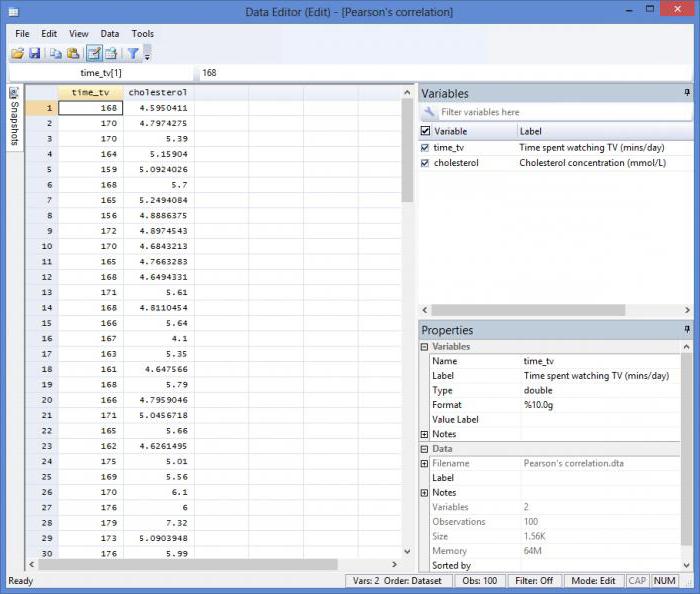
Правила отбора факторов корреляционного анализа
При применении данного метода необходимо определиться с факторами, оказывающими влияние на результативные показатели. Их отбирают с учетом того, что между показателями должны присутствовать причинно-следственные связи. В случае создания многофакторной корреляционной модели отбирают те из них, которые оказывают существенное влияние на результирующий показатель, при этом взаимозависимые факторы с коэффициентом парной корреляции более 0,85 в корреляционную модель предпочтительно не включать, как и такие, у которых связь с результативным параметром носит непрямолинейный или функциональный характер.
Отображение результатов
Результаты корреляционного анализа могут быть представлены в текстовом и графическом видах. В первом случае они представляются как коэффициент корреляции, во втором — в виде диаграммы разброса.
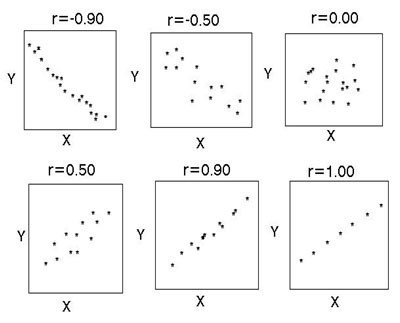
При отсутствии корреляции между параметрами точки на диаграмме расположены хаотично, средняя степень связи характеризуется большей степенью упорядоченности и характеризуется более-менее равномерной удаленностью нанесенных отметок от медианы. Сильная связь стремится к прямой и при r=1 точечный график представляет собой ровную линию. Обратная корреляция отличается направленностью графика из левого верхнего в нижний правый, прямая — из нижнего левого в верхний правый угол.
Трехмерное представление диаграммы разброса (рассеивания)
Помимо традиционного 2D-представления диаграммы разброса в настоящее время используется 3D-отображение графического представления корреляционного анализа.
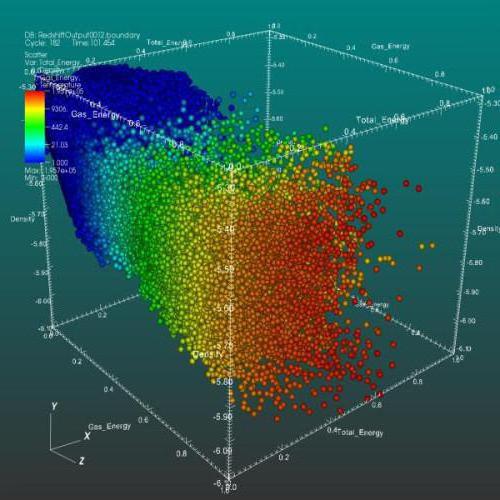
Также используется матрица диаграммы рассеивания, которая отображает все парные графики на одном рисунке в матричном формате. Для n переменных матрица содержит n строк и n столбцов. Диаграмма, расположенная на пересечении i-ой строки и j-ого столбца, представляет собой график переменных Xi по сравнению с Xj. Таким образом, каждая строка и столбец являются одним измерением, отдельная ячейка отображает диаграмму рассеивания двух измерений.
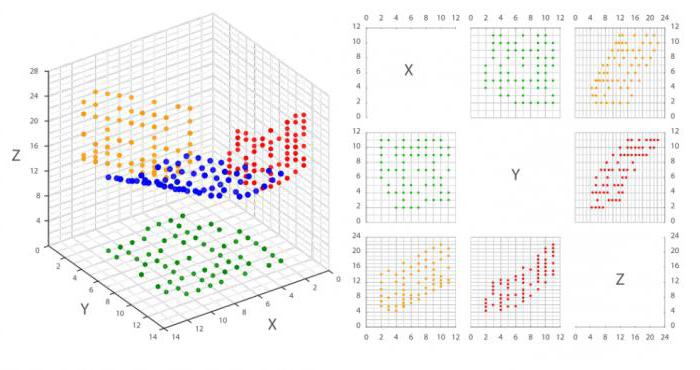
Оценка тесноты связи
Теснота корреляционной связи определяется по коэффициенту корреляции (r): сильная — r = ±0,7 до ±1, средняя — r = ±0,3 до ±0,699, слабая — r = 0 до ±0,299. Данная классификация не является строгой. На рисунке показана несколько иная схема.

Пример применения метода корреляционного анализа
В Великобритании было предпринято любопытное исследование. Оно посвящено связи курения с раком легких, и проводилось путем корреляционного анализа. Это наблюдение представлено ниже.
Исходные данные для корреляционного анализаПрофессиональная группа | курение | смертность |
Фермеры, лесники и рыбаки | 77 | 84 |
Шахтеры и работники карьеров | 137 | 116 |
Производители газа, кокса и химических веществ | 117 | 123 |
Изготовители стекла и керамики | 94 | 128 |
Работники печей, кузнечных, литейных и прокатных станов | 116 | 155 |
Работники электротехники и электроники | 102 | 101 |
Инженерные и смежные профессии | 111 | 118 |
Деревообрабатывающие производства | 93 | 113 |
Кожевенники | 88 | 104 |
Текстильные рабочие | 102 | 88 |
Изготовители рабочей одежды | 91 | 104 |
Работники пищевой, питьевой и табачной промышленности | 104 | 129 |
Производители бумаги и печати | 107 | 86 |
Производители других продуктов | 112 | 96 |
Строители | 113 | 144 |
Художники и декораторы | 110 | 139 |
Водители стационарных двигателей, кранов и т. д. | 125 | 113 |
Рабочие, не включенные в другие места | 133 | 146 |
Работники транспорта и связи | 115 | 128 |
Складские рабочие, кладовщики, упаковщики и работники разливочных машин | 105 | 115 |
Канцелярские работники | 87 | 79 |
Продавцы | 91 | 85 |
Работники службы спорта и отдыха | 100 | 120 |
Администраторы и менеджеры | 76 | 60 |
Профессионалы, технические работники и художники | 66 | 51 |
Начинаем корреляционный анализ. Решение лучше начинать для наглядности с графического метода, для чего построим диаграмму рассеивания (разброса).
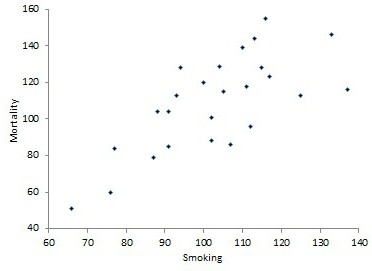
Она демонстрирует прямую связь. Однако на основании только графического метода сделать однозначный вывод сложно. Поэтому продолжим выполнять корреляционный анализ. Пример расчета коэффициента корреляции представлен ниже.
С помощью программных средств (на примере MS Excel будет описано далее) определяем коэффициент корреляции, который составляет 0,716, что означает сильную связь между исследуемыми параметрами. Определим статистическую достоверность полученного значения по соответствующей таблице, для чего нам нужно вычесть из 25 пар значений 2, в результате чего получим 23 и по этой строке в таблице найдем r критическое для p=0,01 (поскольку это медицинские данные, здесь используется более строгая зависимость, в остальных случаях достаточно p=0,05), которое составляет 0,51 для данного корреляционного анализа. Пример продемонстрировал, что r расчетное больше r критического, значение коэффициента корреляции считается статистически достоверным.
Использование ПО при проведении корреляционного анализа
Описываемый вид статистической обработки данных может осуществляться с помощью программного обеспечения, в частности, MS Excel. Корреляционный анализ в Excel предполагает вычисление следующих параметров с использованием функций:
1. Коэффициент корреляции определяется с помощью функции КОРРЕЛ [CORREL](массив1; массив2). Массив1,2 — ячейка интервала значений результативных и факторных переменных.
Линейный коэффициент корреляции также называется коэффициентом корреляции Пирсона, в связи с чем, начиная с Excel 2007, можно использовать функцию ПИРСОН (PEARSON) с теми же массивами.
Графическое отображение корреляционного анализа в Excel производится с помощью панели «Диаграммы» с выбором «Точечная диаграмма».
После указания исходных данных получаем график.
2. Оценка значимости коэффициента парной корреляции с использованием t-критерия Стьюдента. Рассчитанное значение t-критерия сравнивается с табличной (критической) величиной данного показателя из соответствующей таблицы значений рассматриваемого параметра с учетом заданного уровня значимости и числа степеней свободы. Эта оценка осуществляется с использованием функции СТЬЮДРАСПОБР (вероятность; степени_свободы).
3. Матрица коэффициентов парной корреляции. Анализ осуществляется с помощью средства «Анализ данных», в котором выбирается «Корреляция». Статистическую оценку коэффициентов парной корреляции осуществляют при сравнении его абсолютной величины с табличным (критическим) значением. При превышении расчетного коэффициента парной корреляции над таковым критическим можно говорить, с учетом заданной степени вероятности, что нулевая гипотеза о значимости линейной связи не отвергается.
В заключение
Использование в научных исследованиях метода корреляционного анализа позволяет определить связь между различными факторами и результативными показателями. При этом необходимо учитывать, что высокий коэффициент корреляции можно получить и из абсурдной пары или множества данных, в связи с чем данный вид анализа нужно осуществлять на достаточно большом массиве данных.
После получения расчетного значения r его желательно сравнить с r критическим для подтверждения статистической достоверности определенной величины. Корреляционный анализ может осуществляться вручную с использованием формул, либо с помощью программных средств, в частности MS Excel. Здесь же можно построить диаграмму разброса (рассеивания) с целью наглядного представления о связи между изучаемыми факторами корреляционного анализа и результативным признаком.
fb.ru
Корреляционный анализ
При изучении корреляций стараются установить, существует ли какая-то связь между двумя показателями в одной выборке (например, между ростом и весом детей или между уровнем IQ и школьной успеваемостью) либо между двумя различными выборками (например, при сравнении пар близнецов), и если эта связь существует, то сопровождается ли увеличение одного показателя возрастанием (положительная корреляция) или уменьшением (отрицательная корреляция) другого.
Иными словами, корреляционный анализ помогает установить, можно ли предсказывать возможные значения одного показателя, зная величину другого.
До сих пор при анализе результатов нашего опыта по изучению действия марихуаны мы сознательно игнорировали такой показатель, как время реакции. Между тем было бы интересно проверить, существует ли связь между эффективностью реакций и их быстротой. Это позволило бы, например, утверждать, что чем человек медлительнее, тем точнее и эффективнее будут его действия и наоборот.
С этой целью можно использовать два разных способа: параметрический метод расчета коэффициента Браве - Пирсона (r) и вычисление коэффициента корреляции рангов Спирмена (rs), который применяется к порядковым данным, т. е. является непараметрическим. Однако разберемся сначала в том, что такое коэффициент корреляции.
Коэффициент корреляции
Коэффициент корреляции - это величина, которая может варьировать в пределах от -1 до 1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной - минус 1. На графике этому соответствует прямая линия, проходящая через точки пересечения значений каждой пары данных:
Переменная
А
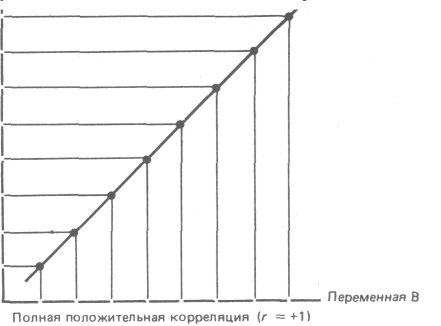
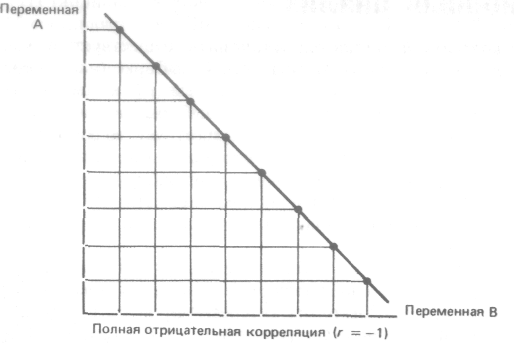
В случае же если эти точки не выстраиваются по прямой линии, а образуют «облако», коэффициент корреляции по абсолютной величине становится меньше единицы и по мере округления этого облака приближается к нулю:
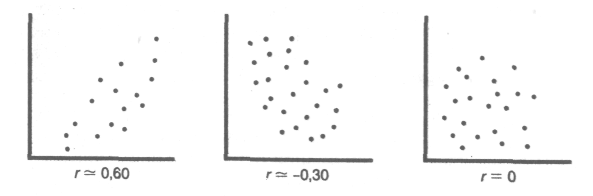
В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.
В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной. Однако для того, чтобы можно было делать выводы о связях между переменными, большое значение имеет объем выборки: чем выборка больше, тем достовернее величина полученного коэффициента корреляции. Существуют таблицы с критическими значениями коэффициента корреляции Браве-Пирсона и Спирмена для разного числа степеней свободы (оно равно числу пар за вычетом 2, т. е. n-2). Лишь в том случае, если коэффициенты корреляции больше этих критических значений, они могут считаться достоверными. Так, для того чтобы коэффициент корреляции 0,70 был достоверным, в анализ должно быть взято не меньше 8 пар данных ( = п - 2 = 6) при вычислении r (табл. В.4) и 7 пар данных ( = п - 2 = 5) при вычислении rs (табл. 5 в дополнении Б. 5).
Коэффициент Браве – Пирсона
Для вычисления этого коэффициента применяют следующую формулу (у разных авторов она может выглядеть по-разному):
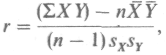
где XY - сумма произведений данных из каждой пары;
n - число пар;
- средняя для данных переменной X;
- средняя для данных переменной Y;
SХ - стандартное отклонение для распределения x;
sY - стандартное отклонение для распределения у.
Теперь мы можем использовать этот коэффициент для того, чтобы установить, существует ли связь между временем реакции испытуемых и эффективностью их действий. Возьмем, например, фоновый уровень контрольной группы.

n= 15 15,8 13,4 = 3175,8;
(n – 1)SxSy = 14 3,07 2,29 = 98,42;
r = 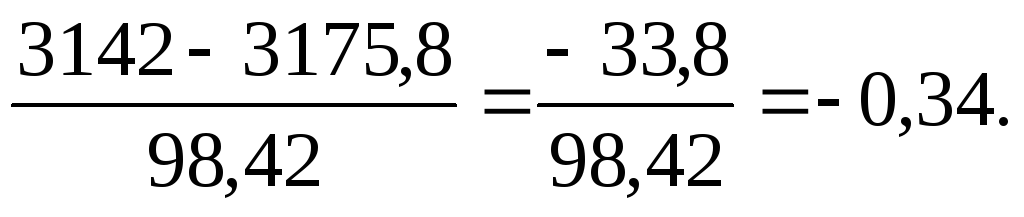
Отрицательное значение коэффициента корреляции может означать, что чем больше время реакции, тем ниже эффективность. Однако величина его слишком мала для того, чтобы можно было говорить о достоверной связи между этим двумя переменными.
Теперь попробуйте самостоятельно подсчитать коэффициент корреляции для экспериментальной группы после воздействия, зная, что ХУ= 2953:
nXY=………
(n - 1)SXSY =……
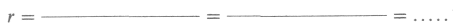
Какой вывод можно сделать из этих результатов? Если вы считаете, что между переменными есть связь, то какова она - прямая или обратная? Достоверна ли она [см. табл. 4 (в дополнении Б. 5) с критическими значениями r]?
Коэффициент корреляции рангов Спирмена rs
Этот коэффициент рассчитывать проще, однако результаты получаются менее точными, чем при использовании r. Это связано с тем, что при вычислении коэффициента Спирмена используют порядок следования данных, а не их количественные характеристики и интервалы между классами.
Дело в том, что при использовании коэффициента корреляции рангов Спирмена (rs) проверяют только, будет ли ранжирование данных для какой-либо выборки таким же, как и в ряду других данных для этой выборки, попарно связанных с первыми (например, будут ли одинаково «ранжироваться» студенты при прохождении ими как психологии, так и математики, или даже при двух разных преподавателях психологии?). Если коэффициент близок к + 1, то это означает, что оба ряда практически совпадают, а если этот коэффициент близок к - 1, можно говорить о полной обратной зависимости.
Коэффициент rs вычисляют по формуле
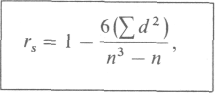
где d- разность между рангами сопряженных значений признаков (независимо от ее знака), а n-число пар.
Обычно этот непараметрический тест используется в тех случаях, когда нужно сделать какие-то выводы не столько об интервалах между данными, сколько об их рангах, а также тогда, когда кривые распределения слишком асимметричны и не позволяют использовать такие параметрические критерии, как коэффициент r (в этих случаях бывает необходимо превратить количественные данные в порядковые).
Поскольку именно так обстоит дело с распределением значений эффективности и времени реакции в экспериментальной группе после воздействия, можно повторить расчеты, которые вы уже проделали для этой группы, только теперь не для коэффициента r, а для показателя rs. Это позволит посмотреть, насколько различаются эти два показателя*.
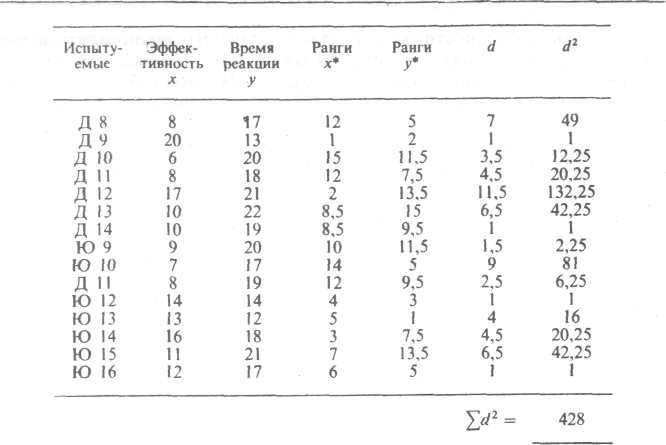
* Следует помнить, что
1) для числа попаданий 1-й ранг соответствует самой высокой, а 15-й-самой низкой результативности, тогда как для времени реакции 1-й ранг соответствует самому короткому времени, а 15-й-самому долгому;
2) данным ex aequo придается средний ранг.
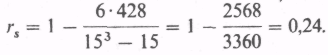
Таким образом, как и в случае коэффициента r, получен положительный, хотя и недостоверный, результат. Какой же из двух результатов правдоподобнее: r = -0,48 или rs = +0,24? Такой вопрос может встать лишь в том случае, если результаты достоверны.
Хотелось бы еще раз подчеркнуть, что сущность этих двух коэффициентов несколько различна. Отрицательный коэффициент r указывает на то, что эффективность чаще всего тем выше, чем время реакции меньше, тогда как при вычислении коэффициента rs требовалось проверить, всегда ли более быстрые испытуемые реагируют более точно, а более медленные - менее точно.
Поскольку в экспериментальной группе после воздействия был получен коэффициент rs, равный 0,24, подобная тенденция здесь, очевидно, не прослеживается. Попробуйте самостоятельно разобраться в данных для контрольной группы после воздействия, зная, что d2 = 122,5:
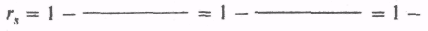 ; достоверно ли?
; достоверно ли?
Каков ваш вывод?………………………………… ……………………………………………………………
…………………………………………………………………………………………………………………….
Итак, мы рассмотрели различные параметрические и непараметрические статистические методы, используемые в психологии. Наш обзор был весьма поверхностным, и главная задача его заключалась в том, чтобы читатель понял, что статистика не так страшна, как кажется, и требует в основном здравого смысла. Напоминаем, что данные «опыта», с которыми мы здесь имели дело, - вымышленные и не могут служить основанием для каких-либо выводов. Впрочем, подобный эксперимент стоило бы действительно провести. Поскольку для этого опыта была выбрана сугубо классическая методика, такой же статистический анализ можно было бы использовать во множестве различных экспериментов. В любом случае нам кажется, что мы наметили какие-то главные направления, которые могут оказаться полезны тем, кто не знает, с чего начать статистический анализ полученных результатов.
Резюме
Существуют три главных раздела статистики: описательная статистика, индуктивная статистика и корреляционный анализ.
studfiles.net
Корреляция
Понятие корреляции
Все явления в мире взаимосвязаны. Это значит, что каждое событие оказывает влияние на все события, следующие за ним, а само происходит вследствие всех событий, случившихся до него.
До сих пор рассматривались основные статистические характеристики изолированно друг от друга, теперь будем изучать, как и в к5акой форме одно явление оказывает влияние на другое. Это является предметом корреляционно-регрессионного анализа.
Три основные задачи корреляционно-регрессионного анализа:
1. Определение факторов, которые оказывают определяющее воздействие на результативный признак.
2. Определение форм воздействия факторов и результата.
3. Определение степени влияния на результат учтенных и неучтенных факторов.
В статистике изучаются следующие виды связей:
1. Балансовая связь – характеризует зависимость между источниками формирования результатов и их использованием.
2. Компонентные связи – характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель, как множители.
Ipq=Ip*Iq
3. Факторные связи – характеризуются тем, что они появляются в согласованной вариации изучаемых показателей.
Одни выступают как факторные, другие как результативные.
При функциональной связи изменение результативного признака обусловлено всецело действием одного факторного признака х, т.е. одному факторному соответствует одно и только одно значение результативного признака y=f(x). Функциональная связь проявляется во всех случаях наблюдения и для каждой конкретной единицы изучаемой величины.
Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, в среднем при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная, при которой изменение среднего значения результатов признака обусловлено изменением факторных признаков. По степени тесноты связи различают количественные критерии оценки тесноты связи.
| Величина коэффициента корреляции | Характер связи |
| до |±0,3| | практически отсутствует |
| |±0,3|-|±0,5| | слабая |
| |±0,5|-|±0,7| | умеренная |
| |±0,7|-|±1,0| | сильная |
По направлению выделяют связь прямую, т.е. с увеличением или уменьшением значения факторного признака происходит увеличение или уменьшение результата.
Например, увеличение производительности труда способствует увеличению уровня рентабельности.
И обратную, когда значения результативного признака изменяются под воздействием факторного, но в противоположном направлении.
Например, с увеличением фондоотдачи снижается себестоимость единицы продукции.
По аналитическому выражению выделяют связи прямолинейные и нелинейные.
В статистике не всегда требуются количественные оценки, важно просто определить форму воздействия одних факторов на другие.
Для выявления наличия связи, и характера, и направления используются следующие методы:
- приведение параллельных данных
- аналитических группировок
- графический
- корреляции
1.Метод приведения параллельных данных - основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 5 | 6 | 9 | 10 | 14 | 17 | 15 | 20 | 23 |
Т.е. с увеличением x ↑ y, т.е. это может быть либо кривая, либо парабола 2 порядка.
2.Графически - взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а у – результативного.
При отсутствии тесных связей имеет место беспорядочное расположение точки на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.

Для социально-экономических явлений характерно, что наряду с существенными факторами, формирующими уровень результативного признака на него оказывают воздействие многие случайные факторы. Поэтому корреляционная связь отражается функцией у=ψ(х)+ε, где ε – влияние случайных факторов.
3.Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при котором изменение одной из случайных величин приводит к уменьшению математического ожидания другой. В статистике принято различать следующие варианты зависимостей:
1. Парная корреляция – связь между двумя признаками.
2. Частная корреляция – зависимость между результатом и одним факторным признаком при фиксированном значении других факторных признаков.
3. Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.
Корреляционный анализ имеет своей задачей кол-но определить тесноту связи между двумя признаками (при парной связи) и между результативными и множеством факторных признаков (при многофакторной связи).
Теснота связи количественно выражается величиной коэффициентов корреляции. Величина коэффициентов корреляции служит также оценкой соответствия уравнения регрессии выявленным причинно-следственным связям. Одновременно с корреляцией начала использоваться регрессия. Корреляция и регрессия тесно связаны между собой:
Первая оценивает силу статистической связи, вторая исследует ее форму. Та и другая служат для установления соотношения между явлениями.
Корреляционно-регрессионный анализ как общее понятие, включает в себя измерение тесноты направления связей и установления аналитического выражения (формы) связей (регрессионный анализ).
Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (результативный признак) обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Регрессия может быть однофакторной (парной).
 - линейная функция и многофакторной (множественной)
- линейная функция и многофакторной (множественной)

 +а2х2 - парабола
+а2х2 - парабола
 - гипербола нелинейная регрессия
- гипербола нелинейная регрессия
По направлению связи распределяют:
а) прямую регрессию (положительную)
б) обратную (отрицательную), т.е. с увеличением или уменьшением независимой величины зависимая соответственно уменьшается или увеличивается.
Прямая (положительная) регрессия

Обратная (отрицательная) регрессия

Методы корреляционно-регрессионного анализа связи показателей
Наиболее разработанная – метод парной корреляции, рассматривающая влияние вариации факторного признака (х) на результативный (у).
Для выявления связи применяются различные виды уравнения прямолинейной и криволинейной связей. Аналитическая связь между ними может быть описана следующими уравнениями:
Прямая 
Гипербола 
Парабола  +а2х2
+а2х2
Определить тип уравнения можно, исследуя зависимость графически. Однако есть более общее указание.
- если результативный и факторный признаки ↑ одинаково, примерно в арифметической прогрессии – прямая.
- при обратной – гиперболическая.
- если факторный признак увеличивается в арифметической, а результативный быстрее, то парабола или степенная.
Оценка параметров уравнений регрессии а0; а1; а2 осуществляется методом наименьших квадратов
при линейной зависимости

n – объем исследуемой совокупности.
 ; где а0 – усредненное влияние на результативный признак случайных факторов. а1 – коэффициент регрессии показывает насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
; где а0 – усредненное влияние на результативный признак случайных факторов. а1 – коэффициент регрессии показывает насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
Пример:
Имеются данные, характеризующие деловую активность ЗАО:
прибыль (тыс.р.) и затраты на 1 р. произведенной продукции (коп.)
| № | затраты на 1 р. произв. продукции (коп.) | прибыль (тыс.р.) | х2 | ху | 
|
| 1 | 77 | 1070 | 5929 | 82390 | 1016 |
| 2 | 77 | 1001 | 5929 | 77077 | 1016 |
| 3 | 81 | 789 | 5561 | 63909 | 853 |
| 4 | 82 | 779 | 6724 | 63878 | 812 |
| 5 | 89 | 606 | 7921 | 53934 | 527 |
| 6 | 96 | 221 | 9216 | 21216 | 242 |
| Итого: | 502 | 4466 | 42280 | 362404 | 4466 |

На практике часто исследования проводятся по большому числу наблюдений. В этом случае исходные данные представляют в сводной корреляционной таблице. При этом анализу подвергаются сгруппированные данные и по факторному х и по результативному у, т.е. уравнение парной регрессии целесообразно строить на основе сгруппированных данных.
Если значения х и у заданы в определенных интервалах (а-в), то для каждого интервала сначала определяют середину интервала (а+в)/2, а затем уже коррелируют значения х/ и у/ и строят уравнения регрессии между ними.
Корреляционная таблица дает общее представление о направлении связи. Если оба признака (х и у) располагаются в возрастающем порядке, а частоты (fxy) сосредоточены по диагонали сверху вниз направо.

прямая обратная
О тесноте связи между признаками х и у по корреляционной таблице можно судить по кучности расположения частот вокруг диагонали (поскольку заполненные клетки таблицы в стороне от нее).
Если клетки заполнены большими цифрами, то связь слабая. Чем ближе частоты (fxy) располагаются к одной из диагоналей, тем теснее связь. Если в расположении частот (fxy) нет системности, то можно судить об отсутствии связи.
Пример:
| величина капитала, тыс.р. у | величина работающих активов, тыс.р. х | Число банков fy | уfy | xyfy |
| | 14-70 | 70-126 | 126-182 | 182-238 |
| у/ср | х/ср | 42 | 98 | 154 | 210 |
| 145-2684 | 1714,5 | 4 | 6 | 2 | 3 | 15 | 25717,5 | 2904363 |
| 2684-4624 | 3654,0 | 1 | 3 | | | 4 | 14616 | 1227744 |
| 4624-6564 | 5594 | | 1 | 1 | | 2 | 11181 | 1409688 |
| 6564-8503 | 7533,5 | 1 | 1 | 2 | | 4 | 30134 | 3375008 |
| 8503-125842 | 67172,5 | 2 | | 1 | 2 | 5 | 335862,5 | 44199505 |
| Число предпр. fx | | 8 | 11 | 6 | 5 | 30 | 417518 | 53116308 |
| xfx | | 336 | 1078 | 924 | 1050 | 3388 | | |
| x2fx | | 14112 | 105644 | 142296 | 220500 | 482552 | | |
Если у нас наличие линейной связи:

где n=30 коммерческих банков.
fx и fy – число банков согласно распределению соответственно по факторному и результативному признакам.
yfy; xfx – значение результативного и факторного признаков по конкретной группе коммерческих банков.
Для 1 группы yfy= 1714,5*15=25717,5
xfx=42*8=336
хyfy=1714,5*4*42+1714,5*6*98+1714,5*2*154+1714,5*3*210=2904363
х2fx=42*42*8=14112

Статистические данные обладают ошибками упрощения, которые возникают как следствие:
1. Неполноты охвата единиц совокупности
2. Неполноты факторов, определяющих явление
3. Характера выбранного уравнения связи
Использование метода наименьших квадратов позволяет получить достоверные оценки при небольшом количестве наблюдений.
При изучении корреляционной связи показателей коммерческой деятельности в условиях наблюдения так называемого малого и среднего бизнеса, анализу подвергается сравнительно небольшие по составу единиц совокупности.
Коэффициент эластичности
Для оценки влияния факторного признака на результативный применяется коэффициент эластичности.
Он рассчитывается для каждой точки и в среднем по всей совокупности.
Коэффициент эластичности (Э)
Э= Коэффициент эластичности показывает, на сколько % изменяется результативный признак при изменении факторного признака на 1%.
Коэффициент эластичности показывает, на сколько % изменяется результативный признак при изменении факторного признака на 1%.
Если х=42, то при увеличении его на 1%, т.е. 42*(1+0,01)=42,42; С 42 до 42,42. Капитал. увеличится. Э=(59,7*42)/(7177,6+59,7*42)=2507,4/(7177,6+2507,4)=2507,4/9685=0,259
Это означает, что при увеличении фактического признака с 42 до 42,42 – результативный признак увеличится на 0,259%.
Измерение тесноты связи
Кроме состав. уравн. регрессии для коррелируемых переменных второй задачей является измерение тесноты связи между ними. Измерить ее означает определить насколько вариация результативного признака зависит от вариации факторного. Измерить тесноту зависимости между х и у можно при помощи:
1. Корреляционного отношения (η) (коэффициент корреляции по Персону)
2. Линейного коэффициента корреляции (r)
Первый применим ко всем зависимостям, второй только при линейной зависимости.
а) корреляционное отношение различается:
1. теоретическое
2. эмпирическое
Теоретическое представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения в ряду выравненных значений результативного признака ( ), рассчитанных по уравнению регресии, со средним квадратическим отклонением в ряду эмпирических значений результатов признака.
), рассчитанных по уравнению регресии, со средним квадратическим отклонением в ряду эмпирических значений результатов признака.
первое – δ, второе – σ.
Учитывая, что выравненные эмпирические совпадают, т.е.
 и средние значения признака у рядов одинаково (
и средние значения признака у рядов одинаково ( ), среднее квадратическое отклонение ряда выравненных значений результативного признака можно записать
), среднее квадратическое отклонение ряда выравненных значений результативного признака можно записать

Если дисперсию выравненного σ 2 обозначить через среднее квадратическое для эмпирического ряда результатов признака σ= σ 2=Dy, то корреляционное отношение можно записать
σ 2=Dy, то корреляционное отношение можно записать 
Возведя обе части в квадрат получим  ; это корреляционное отношение называется коэффициентом детерминации. σ2=Dy, характеризует вариацию в ряду (у) за счет всех факторов, включая и фактор (х), а δ2=
; это корреляционное отношение называется коэффициентом детерминации. σ2=Dy, характеризует вариацию в ряду (у) за счет всех факторов, включая и фактор (х), а δ2= характеризует вариацию результативного признака под влиянием фактора х. Если найдем отношение
характеризует вариацию результативного признака под влиянием фактора х. Если найдем отношение ,то получим малую долю, занимаемую дисперсией, определяемую влиянием факторного признака х. Т.е. в основе корреляционного отношения лежит правило сложения дисперсий
,то получим малую долю, занимаемую дисперсией, определяемую влиянием факторного признака х. Т.е. в основе корреляционного отношения лежит правило сложения дисперсий  .
.
При изучении корреляционных связей дисперсия в ряду  и является межгрупповой дисперсией δ2=
и является межгрупповой дисперсией δ2= ибо она отражает колеблемость групповых значений результативного признака (т.е. характерных для этой группы х) вокруг общей средней ряда, т.е. колеблемость за счет факторного признака.
ибо она отражает колеблемость групповых значений результативного признака (т.е. характерных для этой группы х) вокруг общей средней ряда, т.е. колеблемость за счет факторного признака.
Т.е. средняя из внутригрупповых дисперсий это и будет остаточная дисперсия, т.е. вариация в ряду у за счет всех остальных факторов, кроме х

Из правила сложения дисперсий

Корреляционное отношение, находится в пределах от 0 до 1.
1. Если результ. полностью зависит от фактора х

2. Фактор х не анализ. влияние на у

Т.е. чем ближе значение корреляционного отношения к 1, тем больше связь у и х. Чем ближе к 0, тем связь слабее. Обычно η меньше 0,3, зависимость маленькая; 0,3-0,6 – зависимость средняя, больше 0,6 – большая.
Пример.
| внесено удобр.,ц/га. х | урож.,ц/га у | 
|
| 1 | 6 | 6,2 |
| 2 | 9 | 8,5 |
| 3 | 10 | 10,4 |
| 4 | 12 | 11,9 |
| 5 | 13 | 13,0 |
| Итого:15 | 50 | 50 |
Зависимость параболическая.

5a0+15a1+55a2=50
15a0+55a1+225a2=167
55a0+225a1+979a2=649
a0=3,14
a1=2,98
a2=-0,241

Дисперсия ряда теоретическая. Значение результативного признака.
 Дисперсия ряда эмпирическая. Значение результативного признака.
Дисперсия ряда эмпирическая. Значение результативного признака.

Корреляционное отношение характеризует высокую степень тесноты зависимости изменения урожайности от количества внесенных удобрений.
От теоретического следует отличать эмпирическое корреляционное отношение, которое рассчитывается по данным групповых таблиц.

где  -дисперсия групповых средних результативного признака
-дисперсия групповых средних результативного признака
 -общая дисперсия результативного признака.
-общая дисперсия результативного признака.
Эмпирическое корреляционное отношение не требует знания и расчета уравнений регрессии, а основывается на сопоставлении межгрупповой и общей дисперсий результативного признака, рассчитанных по групповым таблицам.
Рассмотрим пример с корреляционной таблицей:
 На основе этого показателя можно сделать вывод о том, что вариация групповых средних несущественно зависит от вариации группировочного признака.
На основе этого показателя можно сделать вывод о том, что вариация групповых средних несущественно зависит от вариации группировочного признака.
Линейный коэффициент корреляции
В случае линейной зависимости между двумя коррелируемыми величинами тесноту связи измеряют линейным коэффициентом корреляции (r), который может быть рассчитан по нескольким формулам:
1.
где а1- коэффициент регрессии в управлении связи;
σх- среднее квадратическое отклонение факторного признака;
σу- среднее квадратическое отклонение результативного признака.
2. 
3. 
Рассчитаем линейный коэффициент корреляции по разным формулам:
| основные произв. фонды, млн.р. х | валовая продукция, млн.р. у | х2 | ху | 
|
| 1,2 | 2,8 | 1,44 | 3,36 | 1,5 |
| 1,6 | 4,0 | 2,56 | 6,4 | 2,4 |
| 2,5 | 3,8 | 6,25 | 9,5 | 4,3 |
| 3,8 | 6,5 | 14,44 | 24,7 | 7,0 |
| 4,3 | 8,0 | 18,49 | 34,4 | 8,1 |
| 5,5 | 10,1 | 30,25 | 55,55 | 10,6 |
| 6,0 | 9,5 | 36,0 | 57,0 | 11,7 |
| 8,0 | 12,5 | 64,0 | 100 | 15,6 |
| 9,1 | 18,3 | 82,81 | 166,53 | 18,3 |
| 10,0 | 24,5 | 100 | 245 | 20,2 |
| ∑х=52 | ∑у=100 | ∑х2=356,24 | ∑ху=702,44 | 100 |
studfiles.net
Значимость коэффициента корреляции, доверительный интервал
Проверка гипотезы для коэффициента корреляции
Вычисление уровня значимости коэффициента корреляции
Построение доверительного интервала для коэффициента корреляции
Проверка гипотезы для коэффициента корреляции
Пусть r обозначает выборочный коэффициент корреляции, полученный по извлеченным из двумерного нормального распределения пар наблюдений (x1, y1),…,(xn, yn).
Коэффициент корреляции  в популяции неизвестен, но может быть оценен по выборке с помощью выборочного коэффициента корреляции r:
в популяции неизвестен, но может быть оценен по выборке с помощью выборочного коэффициента корреляции r:
 (1)
(1)
где оценки среднего равны:
 .
.
Проверим значимость коэффициента корреляции.
Нулевая гипотеза состоит в том, что коэффициент корреляции равен нулю, альтернативная - не равен нулю:


Очевидно, достаточно большое по абсолютной величине значение величины r будет стремиться опровергнуть нулевую гипотезу.
Возникает вопрос.
Насколько большое должно быть абсолютное значение величины r?
Для того чтобы проверить гипотезу, мы должны знать распределение величины r.
Собственное распределение величины r довольно сложное, поэтому мы применим преобразование:
 (2)
(2)
Итак, выборочное распределение этой статистики есть распределение Стьюдента с n-2 степенями свободы.
При заданном уровне значимости (α) определяем критическое значение tкр.
Принимаем решение об отклонении или не отклонении нулевой гипотезы:
 - отклоняем H0
- отклоняем H0
 - не отклоняем H0
- не отклоняем H0
Вычисление уровня значимости коэффициента корреляции
Для определения фактического уровня значимости коэффициента корреляции запишем:

Где Т подчиняется распределению Стьюдента с n-2 степенями свободы, а значение величины t вычисляется в соответствии с формулой (2).
Вычисление уровня значимости эквивалентно определению площади под правым и левым хвостами функции, ограниченной значениями -t и t.

Построение доверительного интервала для коэффициента корреляции
Распределение выборочного коэффициента корреляции сложное, поэтому часто пользуются преобразованием Фишера для аппроксимации точного распределения коэффициента корреляции.
При больших значениях n распределение выборочного коэффициента корреляции r стремится к нормальному z.
Преобразование Фишера:

Для преобразованного z стандартная ошибка среднего равна 
Таким образом, двусторонний доверительный интервал для z будет определяться:
Нижняя граница: 
Верхняя граница: 
Для  и
и  получаем интервал
получаем интервал

Для построения доверительного интервала для коэффициента корреляции сделаем обратное преобразование, получим:

Связанные определения:Выборочный коэффициент корреляцииКорреляционный анализКорреляцияКоэффициент корреляцииНекоррелированный
В начало
Содержание портала
statistica.ru
 Метод корреляционного анализа часто не ограничивается нахождением тесноты связи между исследуемыми величинами. Иногда он дополняется составлением уравнений регрессии, которые получают с помощью одноименного анализа, и представляющих собой описание корреляционной зависимости между результирующим и факторным (факторными) признаком (признаками). Этот метод в совокупности с рассматриваемым анализом составляет метод корреляционно-регрессионного анализа.
Метод корреляционного анализа часто не ограничивается нахождением тесноты связи между исследуемыми величинами. Иногда он дополняется составлением уравнений регрессии, которые получают с помощью одноименного анализа, и представляющих собой описание корреляционной зависимости между результирующим и факторным (факторными) признаком (признаками). Этот метод в совокупности с рассматриваемым анализом составляет метод корреляционно-регрессионного анализа.








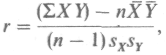

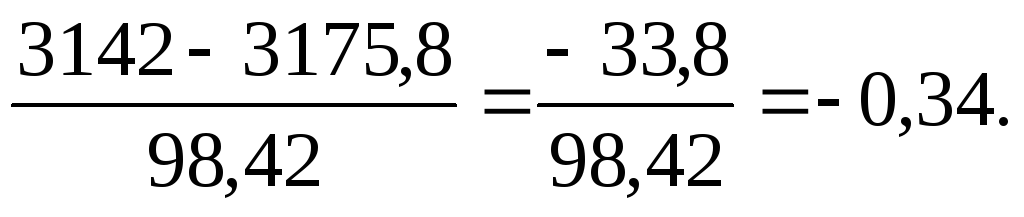
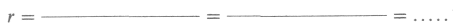
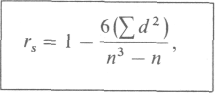

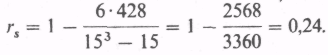
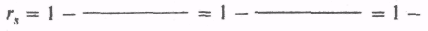 ; достоверно ли?
; достоверно ли? 
 - линейная функция и многофакторной (множественной)
- линейная функция и многофакторной (множественной)
 +а2х2 - парабола
+а2х2 - парабола - гипербола нелинейная регрессия
- гипербола нелинейная регрессия



 +а2х2
+а2х2
 ; где а0 – усредненное влияние на результативный признак случайных факторов. а1 – коэффициент регрессии показывает насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
; где а0 – усредненное влияние на результативный признак случайных факторов. а1 – коэффициент регрессии показывает насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.




 Коэффициент эластичности показывает, на сколько % изменяется результативный признак при изменении факторного признака на 1%.
Коэффициент эластичности показывает, на сколько % изменяется результативный признак при изменении факторного признака на 1%. ), рассчитанных по уравнению регресии, со средним квадратическим отклонением в ряду эмпирических значений результатов признака.
), рассчитанных по уравнению регресии, со средним квадратическим отклонением в ряду эмпирических значений результатов признака. и средние значения признака у рядов одинаково (
и средние значения признака у рядов одинаково ( ), среднее квадратическое отклонение ряда выравненных значений результативного признака можно записать
), среднее квадратическое отклонение ряда выравненных значений результативного признака можно записать
 σ 2=Dy, то корреляционное отношение можно записать
σ 2=Dy, то корреляционное отношение можно записать 
 ; это корреляционное отношение называется коэффициентом детерминации. σ2=Dy, характеризует вариацию в ряду (у) за счет всех факторов, включая и фактор (х), а δ2=
; это корреляционное отношение называется коэффициентом детерминации. σ2=Dy, характеризует вариацию в ряду (у) за счет всех факторов, включая и фактор (х), а δ2= характеризует вариацию результативного признака под влиянием фактора х. Если найдем отношение
характеризует вариацию результативного признака под влиянием фактора х. Если найдем отношение ,то получим малую долю, занимаемую дисперсией, определяемую влиянием факторного признака х. Т.е. в основе корреляционного отношения лежит правило сложения дисперсий
,то получим малую долю, занимаемую дисперсией, определяемую влиянием факторного признака х. Т.е. в основе корреляционного отношения лежит правило сложения дисперсий  .
. и является межгрупповой дисперсией δ2=
и является межгрупповой дисперсией δ2= ибо она отражает колеблемость групповых значений результативного признака (т.е. характерных для этой группы х) вокруг общей средней ряда, т.е. колеблемость за счет факторного признака.
ибо она отражает колеблемость групповых значений результативного признака (т.е. характерных для этой группы х) вокруг общей средней ряда, т.е. колеблемость за счет факторного признака.






 Дисперсия ряда эмпирическая. Значение результативного признака.
Дисперсия ряда эмпирическая. Значение результативного признака.

 -дисперсия групповых средних результативного признака
-дисперсия групповых средних результативного признака -общая дисперсия результативного признака.
-общая дисперсия результативного признака. На основе этого показателя можно сделать вывод о том, что вариация групповых средних несущественно зависит от вариации группировочного признака.
На основе этого показателя можно сделать вывод о том, что вариация групповых средних несущественно зависит от вариации группировочного признака.



 в популяции неизвестен, но может быть оценен по выборке с помощью выборочного коэффициента корреляции r:
в популяции неизвестен, но может быть оценен по выборке с помощью выборочного коэффициента корреляции r: .
.

 (2)
(2) - отклоняем H0
- отклоняем H0 - не отклоняем H0
- не отклоняем H0





 и
и 









