метод контрольных объёмов. Метод контрольных объемов

Теория метода контрольных объемов (1D)

Поскольку в статье [2] о реализации метода контрольных объемов теоретическая часть приведена только в виде ссылки на книгу [1], здесь будет перевод небольшого отрывка из этой самой книги. Теория метода контрольных объемов формулируется для некоторого абстрактного свойства $\phi$ (вместо температуры ).

Теория метода контрольных объемов (перевод)

Начало перевода ([1] стр. 115-118).

Раздел 4.1 — Введение

Сущность уравнений переноса, описывающих поток жидкости и перенос тепла была рассмотрена вместе с формальным описанием интегрирования по контрольным объемам в Главе 2. Здесь мы разработаем численный метод, базирующийся на таком интегрировании, который называется методом конечных объемов или методом контрольных объемов. В качестве примера возьмем самый простой процесс переноса: диффузия в установившемся состоянии. Уравнение установившегося процесса диффузии может быть выведено из общей формы уравнения переноса (2.39) для свойства $\phi$ :

$\frac{\partial (\rho\phi)}{\partial t} + \mathbf{div}(\rho\phi u) = \mathbf{div}(\Gamma\: \mathbf{grad} \phi)+S_{\phi}$ (2.39)

Для этого необходимо опустить нестационарный и конвективный члены уравнения. При этом (2.39) сведется к виду:

$\mathbf{div}\left(\Gamma\:\mathbf{grad}\:\phi\right)+S_{\phi}=0$ (4.1)

Интегрирование по контрольному объему представляет собой ключевой шаг метода контрольных объемов, отличающий этот метод от других техник вычислительной гидродинамики. В нашем случае интегрирование по контрольному объему (CV) принимает такую форму:

$\int_{CV}\mathbf{div}\left(\Gamma\:\mathbf{grad}\:\phi\right) dV + \int_{CV}S_{\phi}dV = 0$

или

$\int_{A}n\cdot \left(\Gamma\:\mathbf{grad}\:\phi\right)dA + \int_{CV}S_{\phi}dV=0$ (4.2)

Работая с одномерным стационарным уравнением диффузии далее, мы применим технику аппроксимации и получим так называемые дискретные уравнения (систему линейных уравнений). Метод может быть расширен на двух и трехмерные задачи установившейся диффузии. Решение практических задач приводится далее (с Главы 4.3), в ходе рассмотрения нескольких примеров. Точность будет оцениваться по данным аналитических решений.

4.2 Метод контрольных объемов для одномерной установившейся диффузии

Рассмотрим установившийся процесс диффузии некоторого свойства $\phi$ в одномерной области, показанной на рис. 4.1:

Рис 4.1: Теория метода контрольных объемов — обозначения.

Кружочки с синей обводкой — это узлы. Вертикальные черточки — это границы ячеек (контрольных объемов). W — узел на западе (West), то есть слева от рассматриваемого узла P. Малое w — это западная граница ячейки. Точка E (East) находится на востоке от P. Малое e — это восточная граница ячейки. $\delta x_{PE}$ , $\delta x_{WP}$ — это расстояния между узлами слева и справа. Размер контрольного объема равен расстоянию от границы w до границы e: $\Delta x= \delta x_{we}$ (на рисунке не показан).

Уравнение процесса (4.1) для одномерного случая имеет вид:

$\frac{\text{d}}{\text{d}x}\left(\Gamma\frac{\text{d}\phi}{\text{d}x}\right)+S=0$ (4.3)

Здесь $\Gamma$ — коэффициент диффузии, S — источник. Граничные значения $\phi$ в точках A и B считаются заданными. В качестве примера такого процесса можно привести одномерный установившийся процесс теплопередачи в стержне. Этот процесс рассмотрен детально в разделе 4.3.

Шаг 1 — Генерация сетки

Рассматриваемая область должна быть разбита на контрольные объемы. Для этого, распределим на прямой между A и B несколько узловых точек (узлов). Границы или грани контрольных объемов будем считать расположенными посередине, между смежными узлами. Таким образом, каждый узел оказывается окружен некоторым контрольным объемом, то есть ячейкой. Общепринятой практикой считается расположение контрольных объемов на границе расчетной области таким образом, чтобы их грани совпадали с границами расчетной области.

Стандартные обозначения для метода контрольных объемов показаны на рис. 4.1.

Шаг 2 — Дискретизация

Следующий ключевой шаг метода контрольных объемов — это интегрирование исходного дифференциального уравнения или уравнений по контрольному объему. Целью интегрирования является получение линейного (дискретного) уравнения для каждого узла P. Для контрольного объема, показанного на рис. 4.1, интегрирование по ячейке приводит к следующему:

$\int_{\Delta V}\frac{\text{d}}{\text{d}x}\left(\Gamma \frac{\text{d}\phi}{\text{d}x}\right)\text{d}V + \int_{\Delta V} S \text{d}V = \left(\Gamma A\frac{\text{d}\phi}{\text{d}x}\right)_{e} - \left(\Gamma A\frac{\text{d}\phi}{\text{d}x}\right)_{w} + \bar{S}\Delta V = 0$ (4.4)

Здесь — это площадь поперечного сечения границы контрольного объема, $\Delta V$ — объем ячейки и $\bar{S}$ — среднее значение источникового члена по ячейке, то есть по контрольному объему. Очень привлекательной особенностью метода контрольных объемов является то, что приведенное дискретное уравнение имеет наглядную физическую интерпретацию. Уравнение (4.4) означает, что диффузионный поток $\phi$ , покидающий восточную грань контрольного объема, за вычетом диффузионного потока, входящего в объем через западную грань, равен генерации $\phi$ в контрольном объеме. Таким образом, уравнение (4.4) представляет собой баланс $\phi$ в контрольном объеме.

Чтобы вывести применяемые на практике формы дискретных уравнений, необходимо определить коэффициент диффузии $\Gamma$ и градиент $\frac{\text{d}\phi}{\text{d}x}$ на гранях контрольного объема e и w. Следуя общепринятой практике, примем величину $\phi$ и значение $\Gamma$ заданными в узловых точках. Тогда, чтобы посчитать градиенты и потоки на гранях ячеек, возможно воспользоваться аппроксимацией этих свойств между узловыми точками. Самым очевидным развитием этого подхода является выбор линейной аппроксимации. Такая практика в сущности является применением формы центральной разности. На однородной сетке, при линейной интерполяции, для значений коэффициента $\Gamma$ на гранях имеем:

$\Gamma_{w}=\frac{\Gamma_{W}+\Gamma_{P}}{2}$ (4.5a)

$\Gamma_{e}=\frac{\Gamma_{P}+\Gamma_{E}}{2}$ (4.5b)

Для диффузионного потока:

$\left(\Gamma A\frac{\text{d}\phi}{\text{d}x}\right)_{e}=\Gamma_{e} A_{e}\left( \frac{\phi_{E}-\phi_{P}}{\delta x_{PE}}\right)$ (4.6)

$\left(\Gamma A\frac{\text{d}\phi}{\text{d}x}\right)_{w}=\Gamma_{w} A_{w}\left( \frac{\phi_{P}-\phi_{W}}{\delta x_{WP}}\right)$ (4.7)

Как это будет показано далее, источниковый член может быть функцией зависимой переменной ( $\phi$ ). В таких случаях метод контрольных объемов аппроксимирует S линейным законом:

$\bar{S}\Delta V=S_{u}+S_{p}\phi_{P}$ (4.8)

Подстановка (4.6), (4.7) и (4.8) в (4.4) дает:

$\Gamma_{e} A_{e}\left( \frac{\phi_{E}-\phi_{P}}{\delta x_{PE}}\right) - \Gamma_{w} A_{w}\left( \frac{\phi_{P}-\phi_{W}}{\delta x_{WP}}\right) + (S_{u}+S_{p}\phi_{P})=0$ (4.9)

Если разложить скобки на слагаемые и затем сгруппировать по $\phi$ , то (4.9) можно переписать в следующем виде:

$\left(\frac{\Gamma_{e}}{\delta x_{PE}}A_{e} + \frac{\Gamma_{w}}{\delta x_{WP}}A_{w} - S_{p}\right)\phi_{P} = \left(\frac{\Gamma_{w}}{\delta x_{WP}}A_{w}\right) \phi_{W} + \left(\frac{\Gamma_{e}}{\delta x_{PE}}A_{e}\right) \phi_{E} + S_{u}$ (4.10)

Обозначим коэффициенты при $\phi_{P}$ , $\phi_{W}$ и $\phi_{E}$ , как $a_{P}$ , $a_{W}$ и $a_{E}$ . Тогда (4.10) можно переписать так:

$a_{P} \phi_{P} = a_{W} \phi_{W} + a_{E} \phi_{E} + S_{u}$ (4.11)

Здесь $a_{W}=\frac{\Gamma_{w}}{\delta x_{WP}} A_{w}$ , $a_{E}=\frac{\Gamma_{e}}{\delta x_{PE}} A_{e}$ , $a_{P} = a_{W}+a_{E}-S_{p}$ .

Величины $S_{u}$ и $S_{p}$ могут быть получены из модели источника (4.8). Уравнения (4.11) и (4.8) являются дискретной формой уравнения (4.1). Этот тип дискретного уравнения является основным для дальнейших рассуждений.

Шаг 3 — решение системы уравнений

Дискретные уравнения по форме 4.11 должны быть построены для каждой узловой точки, только тогда можно будет решить задачу. Для контрольных объемов, прилегающих к границе области решения задачи, уравнение 4.11 изменяется так, чтобы оно содержало граничные условия. Результирующая система линейных алгебраических уравнений затем решается для того чтобы получить значения свойства $\phi$ в узловых точках. Годится любая техника решения системы в матричном виде. В Главе 7 мы рассмотрим матричные методы решения, разработанные специально для задач вычислительной гидродинамики. Техника обработки различных типов граничных условий детально разобрана в Главе 9.

Конец перевода.

Теория метода контрольных объемов — заключительные замечания

Здесь не даны принципы учета граничных условий. Работа с граничными условиями показана в реализации примера, данного в разделе 4.3 [3]. Уравнение (4.11) строится в указанном виде только для внутренних контрольных объемов. У граничной ячейки нет одной из соседних узловых точек: либо западной, либо восточной, вместо неё только граница самого контрольного объема с заданным ГУ. Для граничных ячеек (4.11) видоизменяется с целью учета граничных условий, поэтому в реализации все уравнения для граничных ячеек строятся отдельно от уравнений внутренних ячеек. Принцип тот же, но коэффициенты $a_{W}$ , $a_{E}$ , $a_{P}$ вычисляются по формулам для граничных ячеек.

Литература

[1] H.K. Versteeg, W Malalasekera — An Introduction to Computational Fluid Dynamics. The Finite Volume Method (2nd ed)

[2] Реализация 1D.

[3] Пример и учет ГУ 1D (продолжение).

xn--h1acbaaqgcqcheicn.xn--p1ai

4.3 Метод конечных объемов

Использование метода конечных (контрольных) объемов продемонстрируем на примере двумерного стационарного уравнения теплопроводности:

(31)

где α – коэффициент теплопроводности, S – скорость выделения теплоты в единице объема.

Решение задачи начнем с построения разностной сетки и разбиения расчетной области на непересекающиеся ячейки (объемы), каждая из которых содержит лишь один узел сетки (рис. 13). Проинтегрируем уравнение (31) по объему ячейки А:

(31а)

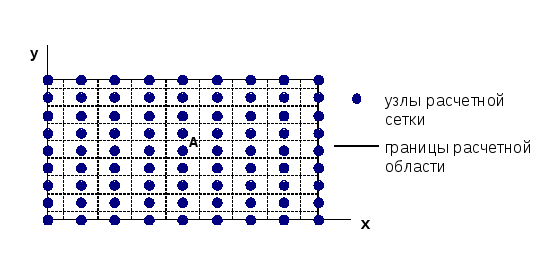
Рис. 13. Расчетная сетка, используемая для решения уравнения (31)

методом конечных объемов

Используя теорему о среднем можно записать

(32)

где Δх, Δу – длины граней ячейки, xW – абсцисса левой ("западной") границы ячейки А, xЕ – абсцисса правой ("восточной") границы, уN – ордината верхней ("северной") границы, уS – ордината нижней ("южной") границы, S* – средняя по ячейке скорость тепловыделения. Индекс у производных (*), в левой части (32), указывает на то, что их следует рассматривать как средние значения, определенные таким образом, чтобы правильно представить тепловые потоки на каждой из границ. С учетом данного обстоятельства, дискретный аналог (32) может быть получен без затруднений [Патанкар].

Таким образом, уравнение (32) описывает баланс тепла (закон сохранения энергии) в пределах ячейки А. При условии правильного описания тепловых потоков между ячейками, система, составленная из уравнений вида (32), примененных к каждому контрольному объему, будет верно описывать баланс тепла во всей расчетной области.

В завершение параграфа следует отметить, что в частных случаях расчетные формулы, полученные описанными выше способами, могут совпадать, а наиболее существенные отличия проявляются при использовании криволинейных неортогональных расчетных сеток.

5. Свойства дискретных схем

5.1 Точность

Точность характеризует приемлемость численной схемы для её практического использования. Оценка точности дискретной схемы представляется весьма сложной задачей, поскольку оказывается практически невозможно отделить ошибки, возникшие вследствие свойств схемы, от ошибок, возникших вследствие прочих факторов (таких как ошибки округления, неточность задания граничных и начальных условий и др.).

Когда говорят о точности дискретной схемы, обычно имеют в виду погрешность аппроксимации производных27. В частности, если погрешность аппроксимации сопоставима со второй степенью шага расчетной сетки, то говорят, что дискретная схема имеет второй порядок точности. Более подробно этот вопрос рассматривался в § 3.

5.2 Согласованность

Дискретная схема называется согласованной с исходным дифференциальным уравнением, если при измельчении расчетной сетки погрешность аппроксимации (см. § 3) стремится к нулю,

Известны расчетные схемы, у которых для достижения согласованности необходимо выполнение дополнительных условий, [Андерсон и К]. Поскольку проверка согласованности расчетных схем является задачей разработчиков (а не пользователей) программного обеспечения более подробно этот вопрос здесь обсуждаться не будет.

studfiles.net

Метод конечных объёмов Википедия

Неформальное

Выбирается некоторая замкнутая область течения жидкости или газа, для которой производится поиск полей макроскопических величин (например, скорости, давления), описывающих состояние среды во времени и удовлетворяющих определенным законам, сформулированным математически. Наиболее используемыми являются законы сохранения в Эйлеровых переменных.

Для любой величины ϕ{\displaystyle \phi }, в каждой точке O(x,y,z,t){\displaystyle O(x,y,z,t)} пространства, окруженной некоторым замкнутым конечным объемом, в момент времени t{\displaystyle t} существует следующая зависимость: общее количество величины ϕ{\displaystyle \phi } в объеме может изменяться за счет следующих факторов:

транспорт количества этой величины через поверхность, ограничивающую контрольный объем — поток;
генерация (уничтожение) некоторого количества величины ϕ{\displaystyle \phi } внутри контрольного объема — источники (стоки).

Другими словами, при формулировке МКО используется физическая интерпретация исследуемой величины. Например, при решении задач переноса тепла используется закон сохранения тепла в каждом контрольном объеме.

Математическое

∂φ∂t+∇⋅(Uφ)−∇⋅(Dφ∇φ)+φ=Sφ{\displaystyle {\frac {\partial \varphi }{\partial t}}+\nabla \cdot ({\mathbf {U} }\varphi )-\nabla \cdot (D_{\varphi }\nabla \varphi )+\varphi =S_{\varphi }}

где:

∂φ∂t{\displaystyle {\frac {\partial \varphi }{\partial t}}} — изменение некоторой физической величины φ{\displaystyle \varphi }
φ{\displaystyle \varphi } — реактивное слагаемое в абстрактном законе сохранения физической величины φ{\displaystyle \varphi }

∇⋅(Uφ){\displaystyle \nabla \cdot (\mathbf {U} \varphi )} — конвективное слагаемое в абстрактном законе сохранения физической величины φ{\displaystyle \varphi }

∇⋅(Dφ∇φ){\displaystyle \nabla \cdot (D_{\varphi }\nabla \varphi )} — диффузное слагаемое в абстрактном законе сохранения физической величины φ{\displaystyle \varphi }

Sφ{\displaystyle S_{\varphi }} — источниковое слагаемое в абстрактном законе сохранения физической величины φ{\displaystyle \varphi }

ruwikiorg.ru

метод контрольных объёмов - это... Что такое метод контрольных объёмов?

метод контрольных объёмов

Makarov: control volume method

Универсальный русско-английский словарь. Академик.ру. 2011.

метод контрольных карт
метод контрольных показателей

Смотреть что такое "метод контрольных объёмов" в других словарях:

НОРМАТИВНО-РЕСУРСНЫЙ МЕТОД ПЛАНИРОВАНИЯ — совокупность способов и приёмов увязки в планах развития с. х. предприятий, р нов, областей, республик заданий по реализации продукции с имеющимися и выделяемыми ресурсами. В соответствии с пост. ЦК КПСС и Сов. Мин. СССР от 20 марта 1986 “О… … Сельско-хозяйственный энциклопедический словарь
нормативно-ресурсный метод планирования — нормативно ресурсный метод планирования, совокупность способов и приёмов увязки в планах развития сельскохозяйственных предприятий, районов, областей, республик заданий по реализации продукции с имеющимися и выделяемыми ресурсами. В соответствии… … Сельское хозяйство. Большой энциклопедический словарь
Компьютерное моделирование — краш теста методом конечных элементов. Компьютерная модель (англ. computer model), или численная мод … Википедия
Численное моделирование — Компьютерное моделирование является одним из эффективных методов изучения сложных систем. Компьютерные модели проще и удобнее исследовать в силу их возможности проводить т.н. вычислительные эксперименты, в тех случаях когда реальные эксперименты… … Википедия
Российская Советская Федеративная Социалистическая Республика — РСФСР. I. Общие сведения РСФСР образована 25 октября (7 ноября) 1917. Граничит на С. З. с Норвегией и Финляндией, на З. с Польшей, на Ю. В. с Китаем, МНР и КНДР, а также с союзными республиками, входящими в состав СССР: на З. с… … Большая советская энциклопедия
Украинская Советская Социалистическая Республика — УССР (Украïнська Радянська Социалicтична Республika), Украина (Украïна). I. Общие сведения УССР образована 25 декабря 1917. С созданием Союза ССР 30 декабря 1922 вошла в его состав как союзная республика. Расположена на… … Большая советская энциклопедия
Заработная плата — (Wages) Важнейшее средство повышения заинтересованности работников Участие трудящихся в доле вновь созданных материальных и духовных благ Содержание Содержание. > заработная плата – это важнейшее средство повышения заинтересованности… … Энциклопедия инвестора
СССР. Технические науки — Авиационная наука и техника В дореволюционной России был построен ряд самолётов оригинальной конструкции. Свои самолёты создали (1909 1914) Я. М. Гаккель, Д. П. Григорович, В. А. Слесарев и др. Был построен 4 моторный самолёт… … Большая советская энциклопедия
Государственная программа — (Government program) Государственная программа это инструмент государственного регулирования экономики, обеспечивающий достижение перспективных целей Понятие государственной программы, виды государственных федеральных и муниципальных программ,… … Энциклопедия инвестора
Союз Советских Социалистических Республик — Cоветский Cоюз занимает почти 1/6 часть обитаемой суши 22 403,2 тыс. км2. Pасположен в Eвропе (ок. 1/4 терр. страны Eвропейская часть CCCP) и Aзии (св. 3/4 Aзиатская часть CCCP). Hac. 281,7 млн. чел. (на 1 янв. 1987). Cтолица Mосква. CCCP … Геологическая энциклопедия
ЗАОЧНОЕ ОБУЧЕНИЕ — форма организации уч. процесса для лиц, сочетающих получение образования с проф. трудовой деятельностью; часть системы непрерывного образования. Предполагает самостоят. прохождение учащимися отд. разделов уч. курсов в соответствии со специально… … Российская педагогическая энциклопедия

universal_ru_en.academic.ru

Метод конечных объёмов — википедия орг

Описание

Неформальное

Для любой величины ϕ{\displaystyle \phi } , в каждой точке O(x,y,z,t){\displaystyle O(x,y,z,t)} пространства, окруженной некоторым замкнутым конечным объемом, в момент времени t{\displaystyle t} существует следующая зависимость: общее количество величины ϕ{\displaystyle \phi } в объеме может изменяться за счет следующих факторов:

транспорт количества этой величины через поверхность, ограничивающую контрольный объем — поток;
генерация (уничтожение) некоторого количества величины ϕ{\displaystyle \phi } внутри контрольного объема — источники (стоки).

Математическое

∂φ∂t+∇⋅(Uφ)−∇⋅(Dφ∇φ)+φ=Sφ{\displaystyle {\frac {\partial \varphi }{\partial t}}+\nabla \cdot ({\mathbf {U}}\varphi )-\nabla \cdot (D_{\varphi }\nabla \varphi )+\varphi =S_{\varphi }}

где:

∂φ∂t{\displaystyle {\frac {\partial \varphi }{\partial t}}} — изменение некоторой физической величины φ{\displaystyle \varphi }
φ{\displaystyle \varphi } — реактивное слагаемое в абстрактном законе сохранения физической величины φ{\displaystyle \varphi }

∇⋅(Uφ){\displaystyle \nabla \cdot (\mathbf {U} \varphi )} — конвективное слагаемое в абстрактном законе сохранения физической величины φ{\displaystyle \varphi }

∇⋅(Dφ∇φ){\displaystyle \nabla \cdot (D_{\varphi }\nabla \varphi )} — диффузное слагаемое в абстрактном законе сохранения физической величины φ{\displaystyle \varphi }

Sφ{\displaystyle S_{\varphi }} — источниковое слагаемое в абстрактном законе сохранения физической величины φ{\displaystyle \varphi }

Применение

Этот метод применяется, в частности, при моделировании задач гидрогазодинамики в свободном пакете OpenFOAM.

Модификации

Примечания

Литература

Патанкар С. В. Численное решение задач теплопроводности и конвективного теплообмена при течении в каналах = Computation of conduction and Duct Flow Heat Transfer: Пер. с англ. — М.: Издательство МЭИ, 2003. — 312 с.

См. также

www-wikipediya.ru

метод контрольных объёмов. Метод контрольных объемов

Теория метода контрольных объемов (1D)

Теория метода контрольных объемов (перевод)

Раздел 4.1 — Введение

4.2 Метод контрольных объемов для одномерной установившейся диффузии

Шаг 1 — Генерация сетки

Шаг 2 — Дискретизация

Шаг 3 — решение системы уравнений

Теория метода контрольных объемов — заключительные замечания

Литература

4.3 Метод конечных объемов

5. Свойства дискретных схем

5.1 Точность

5.2 Согласованность

Метод конечных объёмов Википедия

Неформальное

Математическое

метод контрольных объёмов - это... Что такое метод контрольных объёмов?

Смотреть что такое "метод контрольных объёмов" в других словарях:

Метод конечных объёмов — википедия орг

Описание

Неформальное

Математическое

Применение

Модификации

Примечания

Литература

См. также

Смотрите также