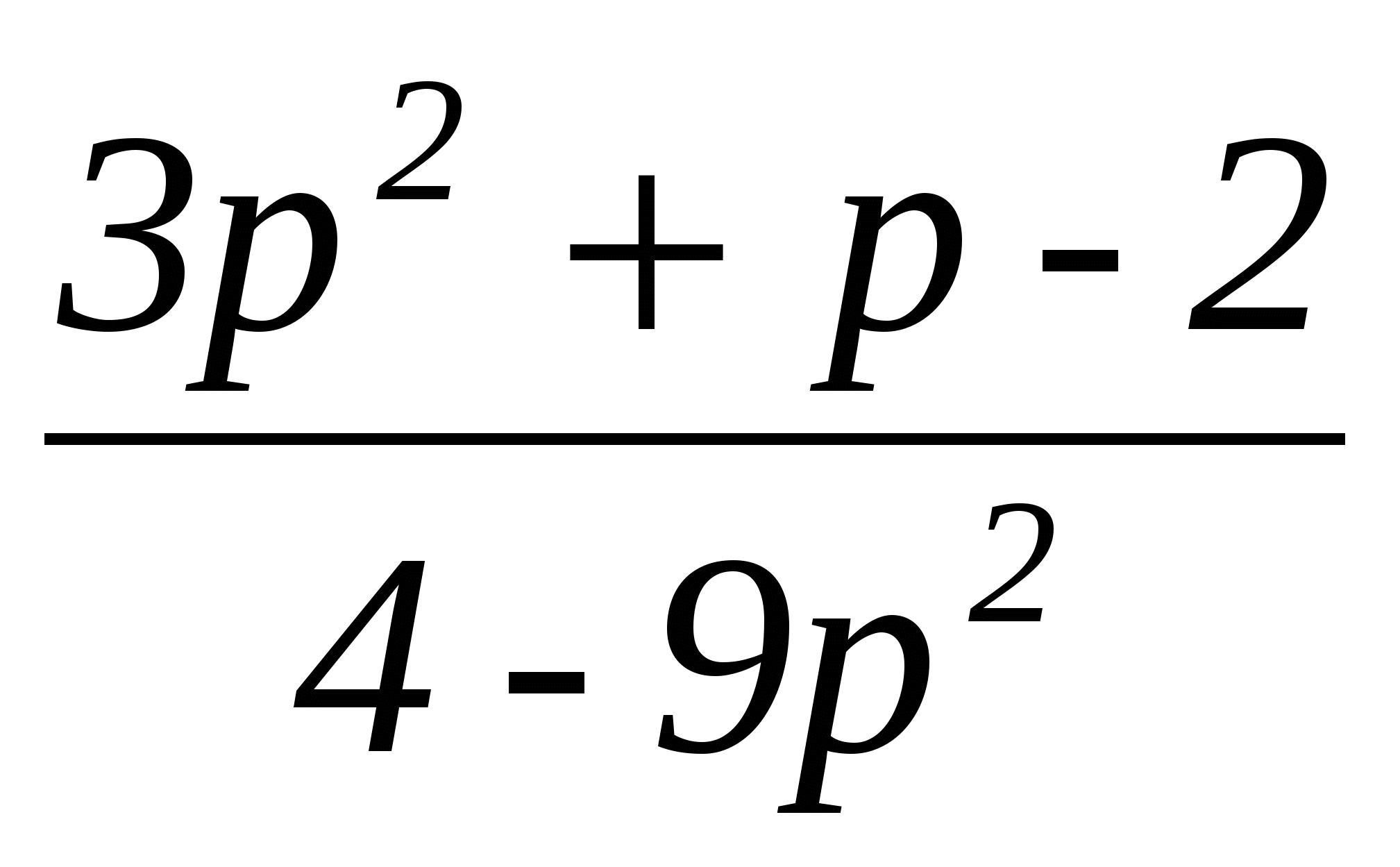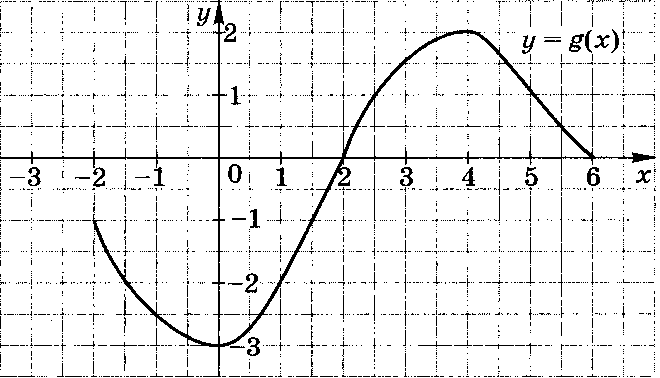
.
Контрольная работа №1 по алгебре в 9 классе
по теме «Функции и их свойства, квадратный трехчлен»
Вариант 1
• 1. Дана функция f (х) = 17х - 51. При каких значениях аргумента f (х) =0, f (х) < 0, f (х) > 0? Является ли эта функция возрастающей или убывающей?
• 2. Разложите на множители квадратный трехчлен: а) х2 -14х +45; б) 3у2 +7у-6.
• 3. Сократите дробь .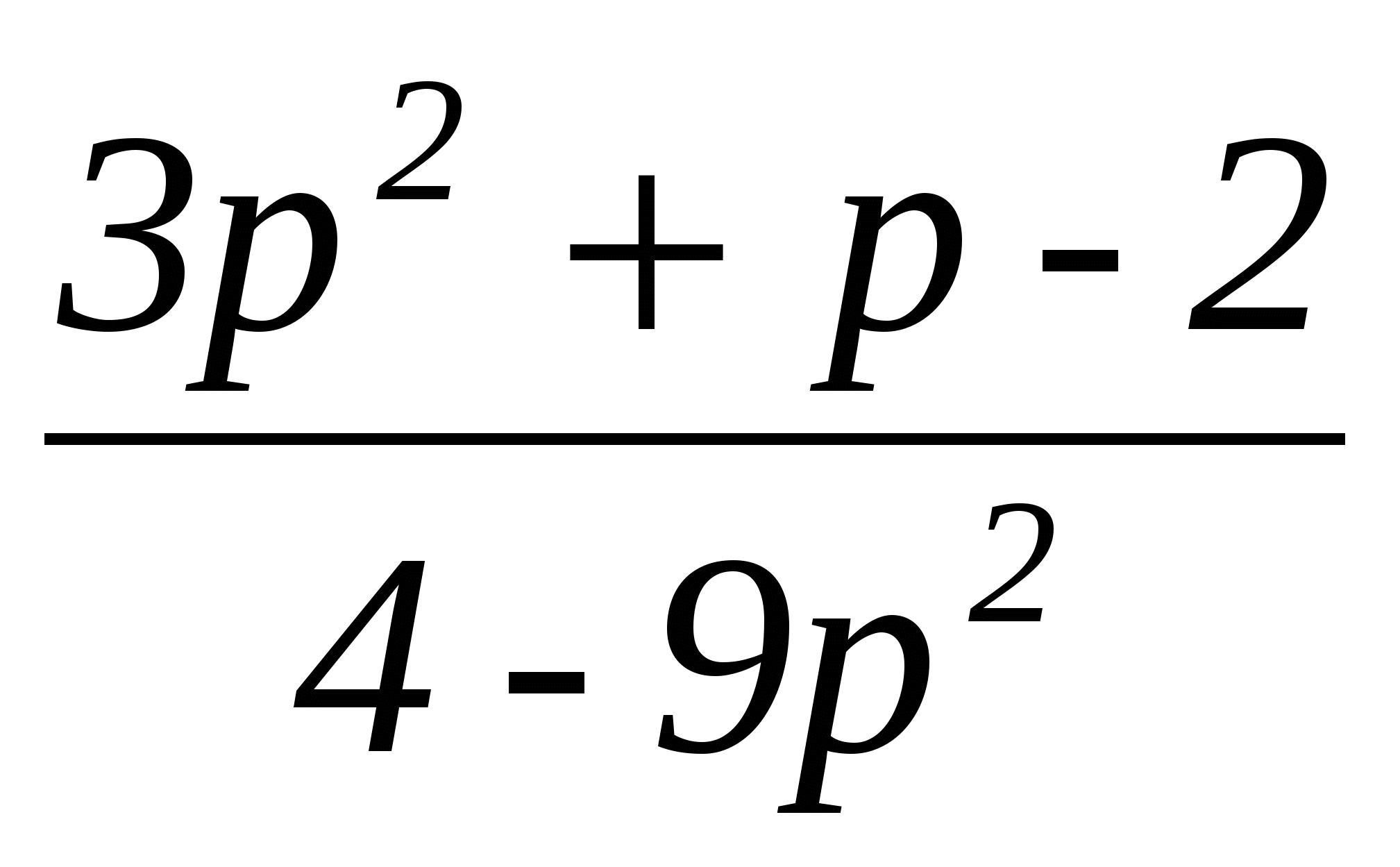
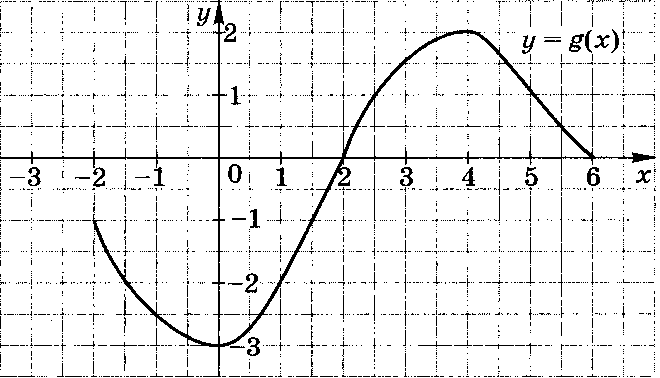
4
Рис. 1
. Область определения функции g (рис. 1) отрезок [-2; 6]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.
5. Сумма положительных чисел а и b равна 50. При каких значениях а и b их произведение будет наибольшим?
Вариант 2
• 1. Дана функция g(х) = -13х + 65. При каких значениях аргумента g(х) = 0, g (х) < 0, g (х) > 0? Является ли эта функция возрастающей или убывающей?
• 2. Разложите на множители квадратный трехчлен: а) х2-10х+21; б) 5у2+9у-2.
• 3. Сократите дробь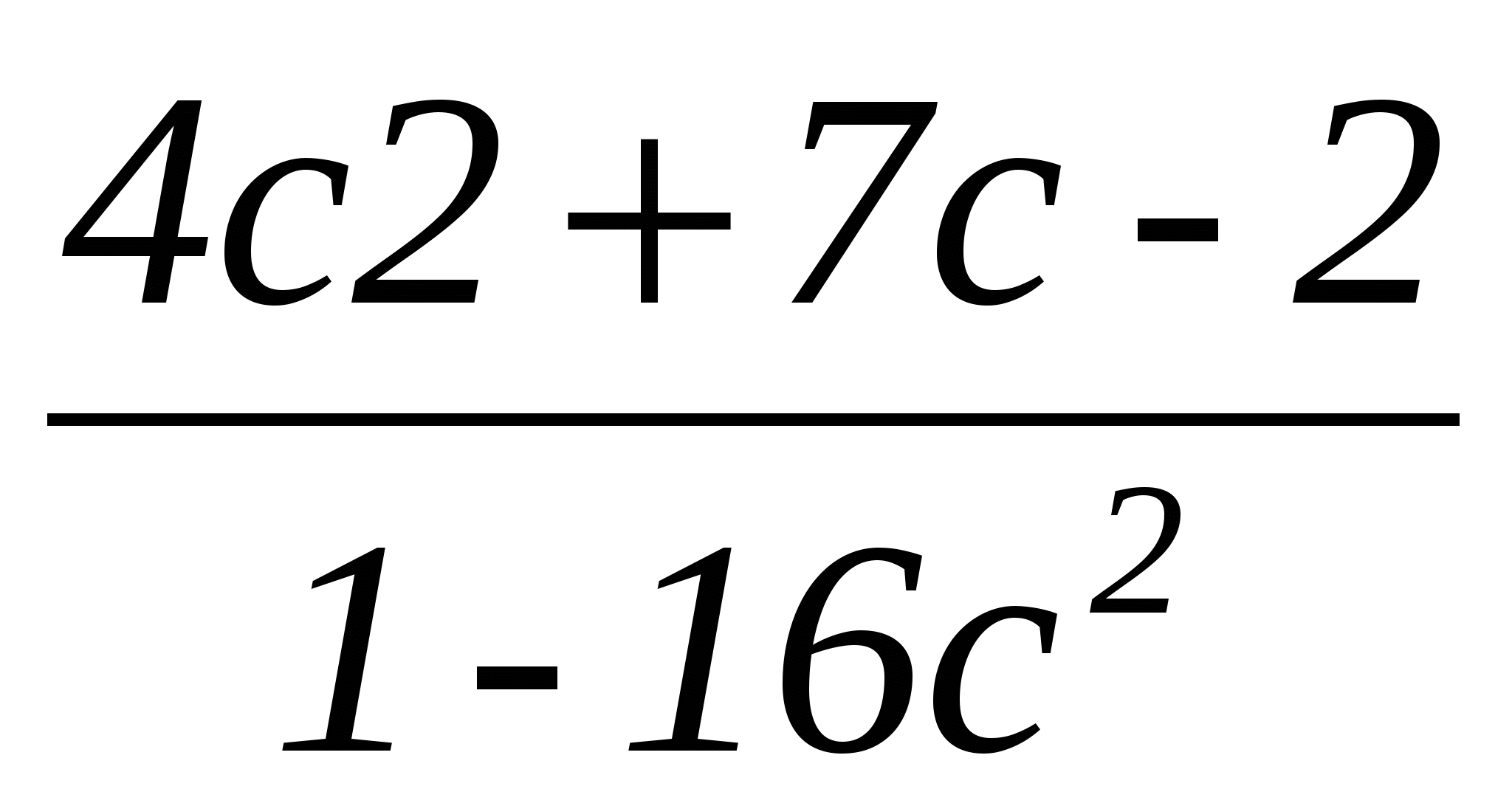 
.
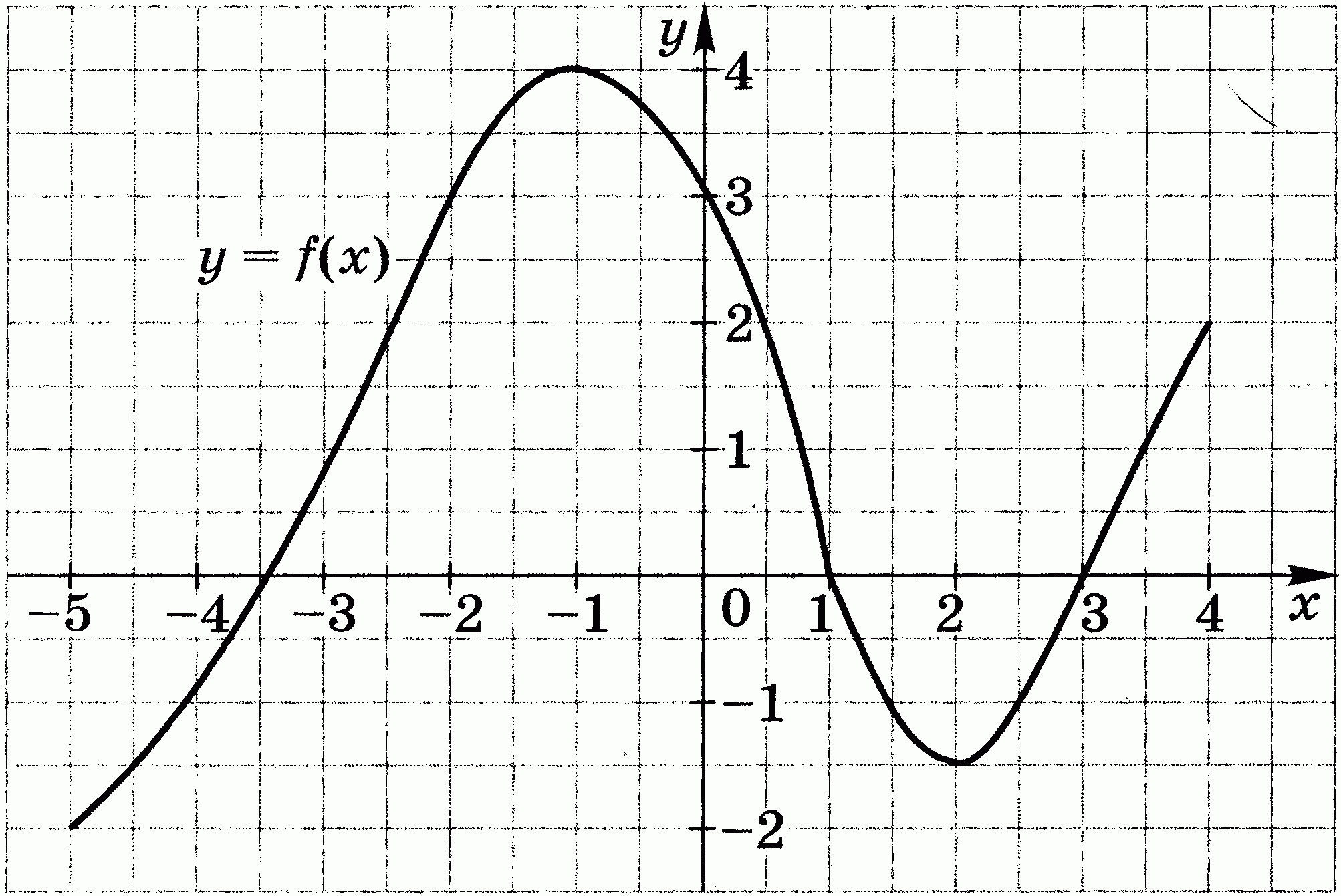
4. Область определения функции f (рис. 2) отрезок [-5; 4]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.
5
Рис. 2
. Сумма положительных чисел с и d равна 70. При каких значениях с и d их произведение будет наибольшим?
Контрольная работа №2 по алгебре в 9 классе
по теме «Квадратичная функция и ее график»
Вариант 1
• 1. Постройте график функции у = х2 - 6х + 5. Найдите с помощью графика:
а) значение у при х = 0,5; б) значения х, при которых у = -1;
в) нули функции; промежутки, в которых у > 0 и в которых у < 0;
г) промежуток, на котором функция возрастает.
• 2. Найдите наименьшее значение функции у = х2 - 8х + 7.
3. Не выполняя построения, определите, пересекаются ли парабола у =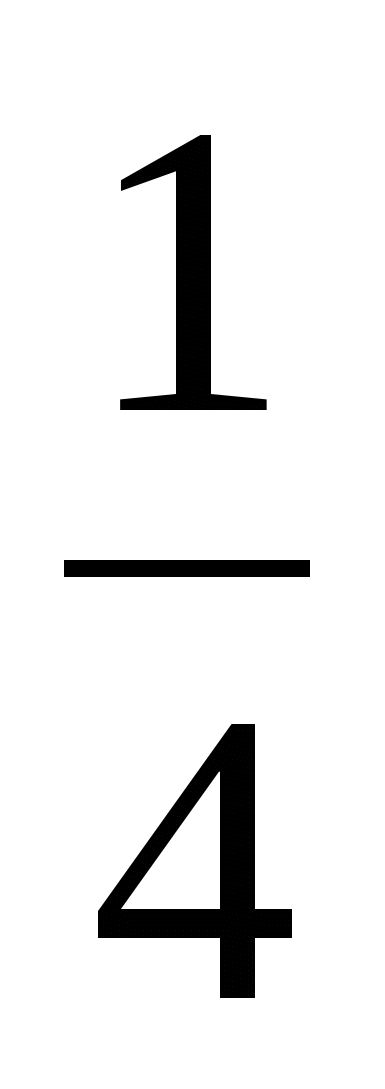
х2 и прямая у = 5х -16. Если точки пересечения существуют, то найдите их координаты.
4. Найдите значение выражения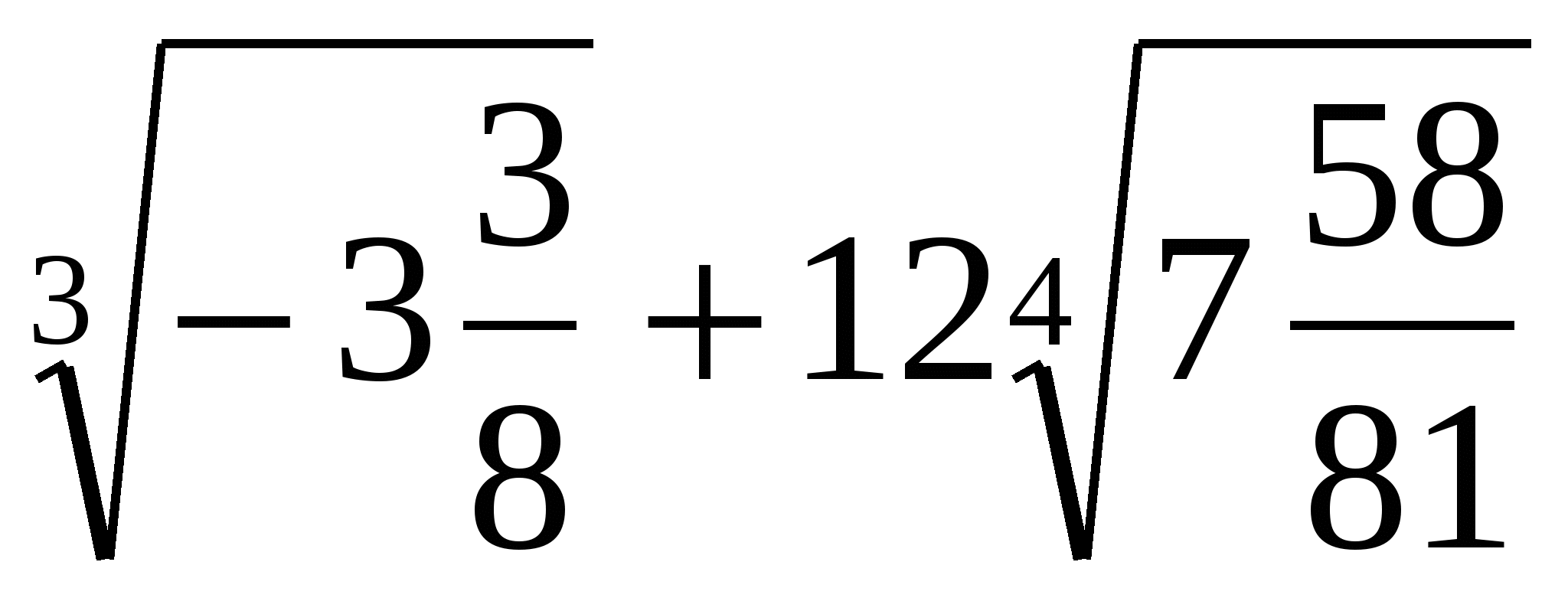 
.
Вариант 2
• 1. Постройте график функции у = х2 - 8х + 13. Найдите с помощью графика:
а) значение у при х = 1,5; б) значения х, при которых у = 2;
в) нули функции; промежутки, в которых у > 0 и в которых y < 0;
г) промежуток, в котором функция убывает.
• 2. Найдите наибольшее значение функции у = -х2 + 6х – 4.
3. Не выполняя построения, определите, пересекаются ли парабола у =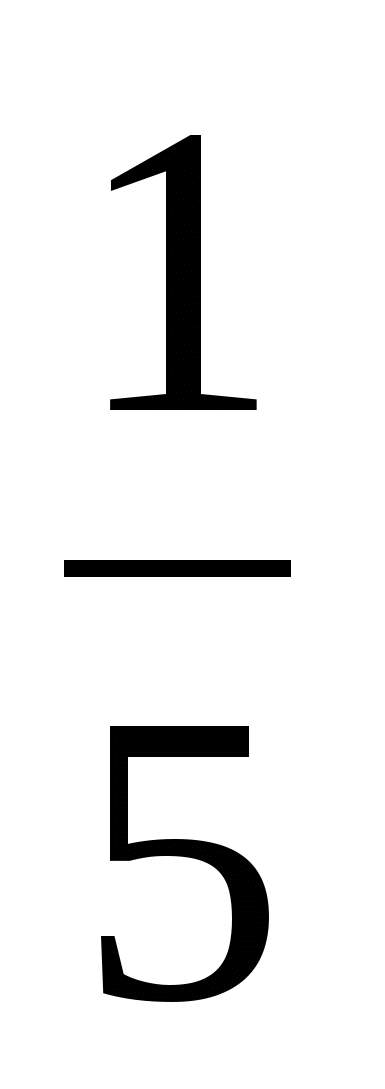
х2 и прямая у =20-3х. Если точки пересечения существуют, то найдите их координаты.
4. Найдите значение выражения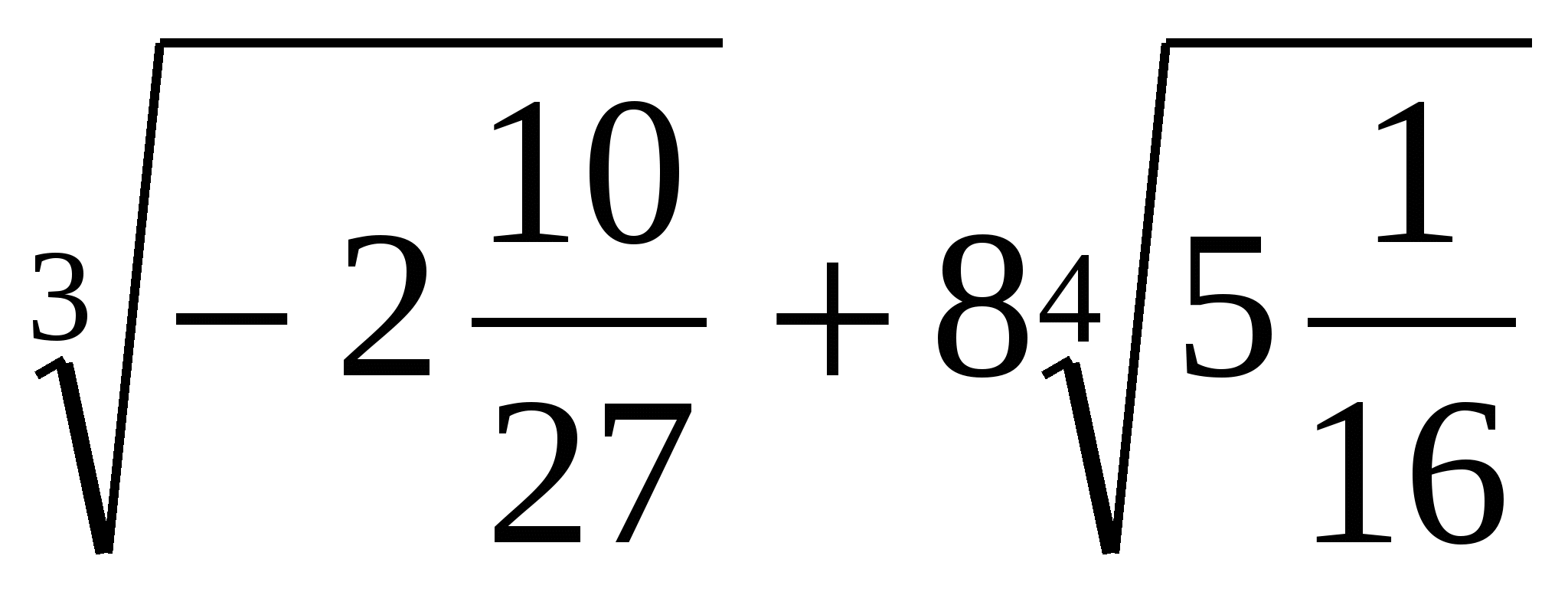 
.
Контрольная работа по алгебре в 9 классе
по теме «Уравнения и неравенства с одной переменной»
Вариант 1
• 1. Решите уравнение: а) х3 - 81х = 0; б)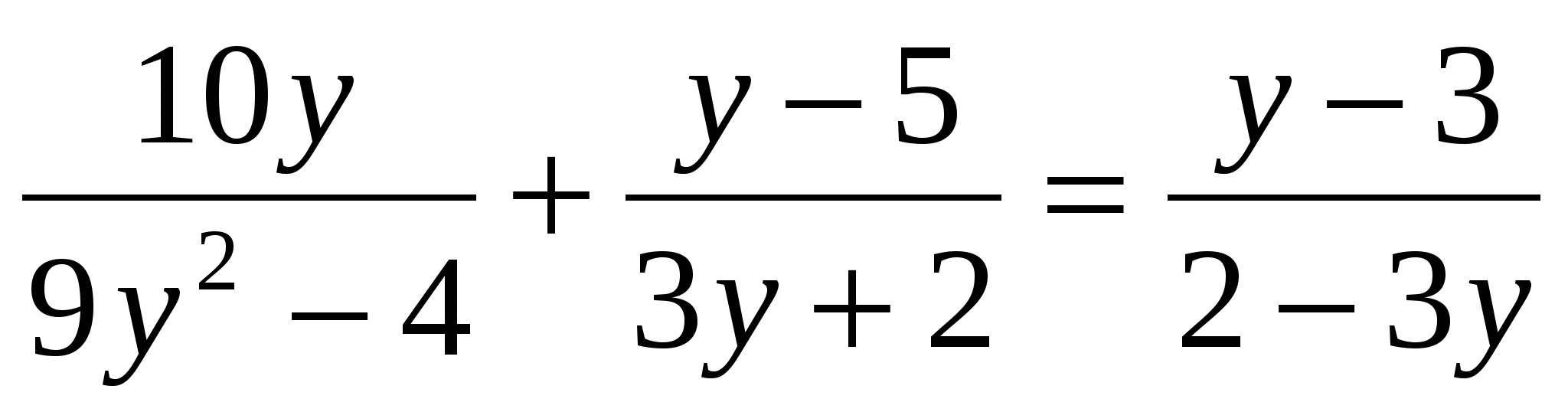 
.
• 2. Решите неравенство: а) 2х2 - 13х + 6 < 0; б) х2 > 9.
• 3. Решите неравенство методом интервалов:
а) (х + 8) (х - 4) (х - 7) > 0; б)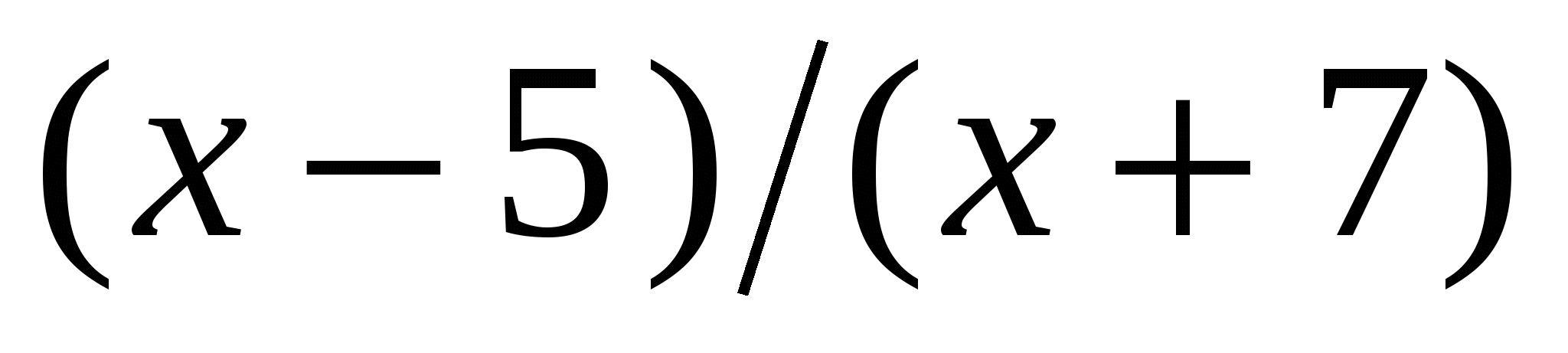
< 0.
• 4. Решите биквадратное уравнение х4 - 19х2 + 48 = 0
5. При каких значениях т уравнение 3х2 + тх + 3 = 0 имеет два корня?
6. Найдите область определения функции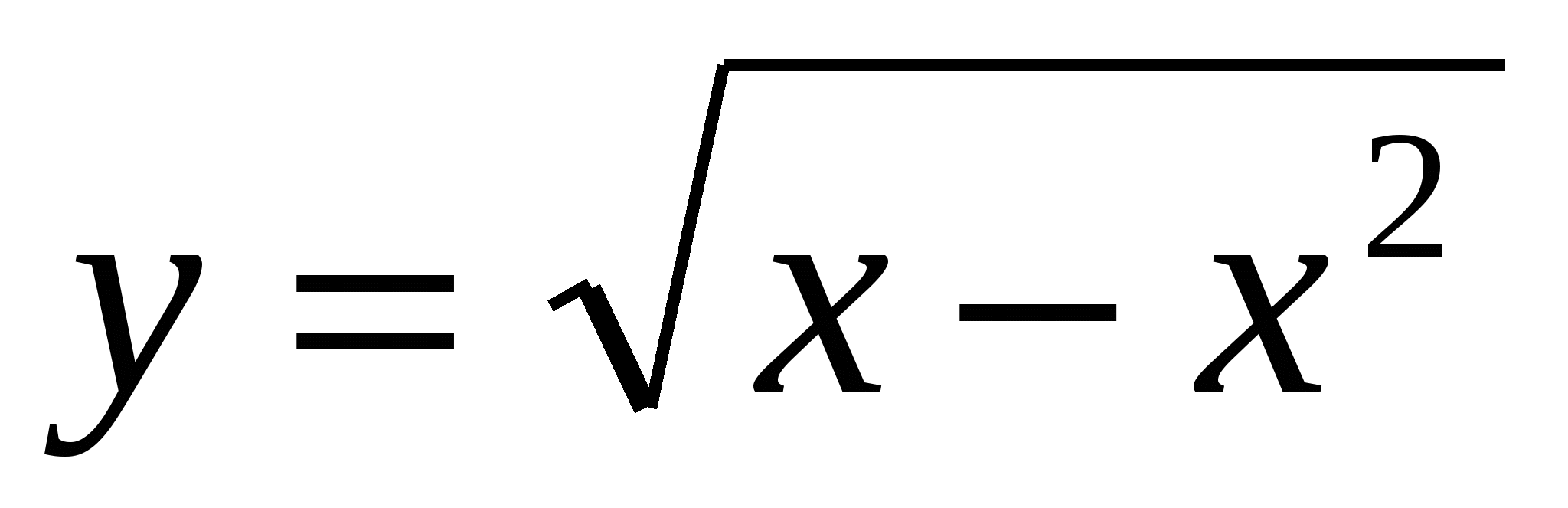 
.
Вариант 2
• 1. Решите уравнение: а) x3 - 25x = 0; б)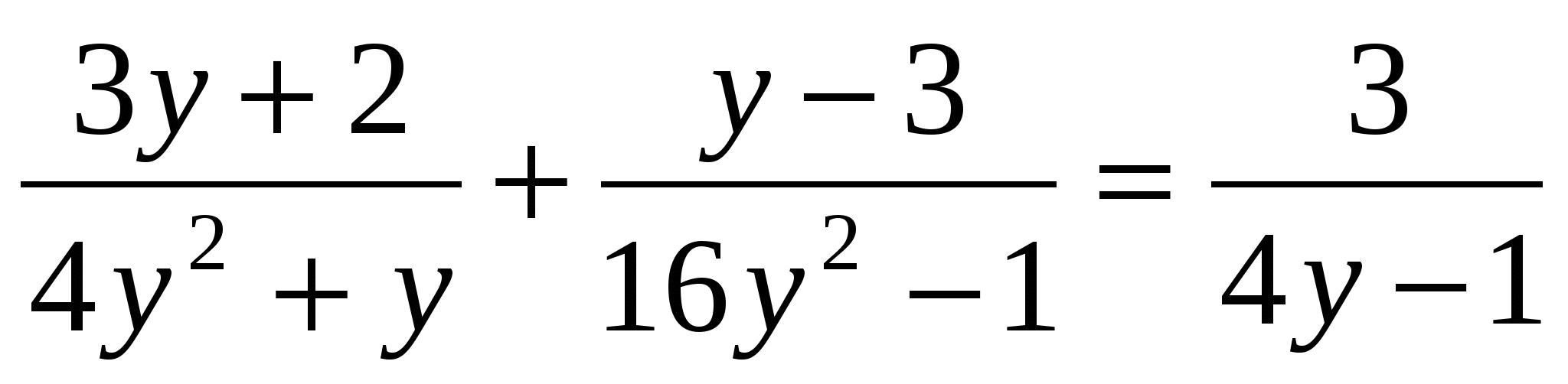 
.
• 2. Решите неравенство: а) 2х2 - х - 15 > 0; б) х2 < 16.
• 3. Решите неравенство методом интервалов:
а) (х + 11) (х + 2) (х - 9) < 0; б)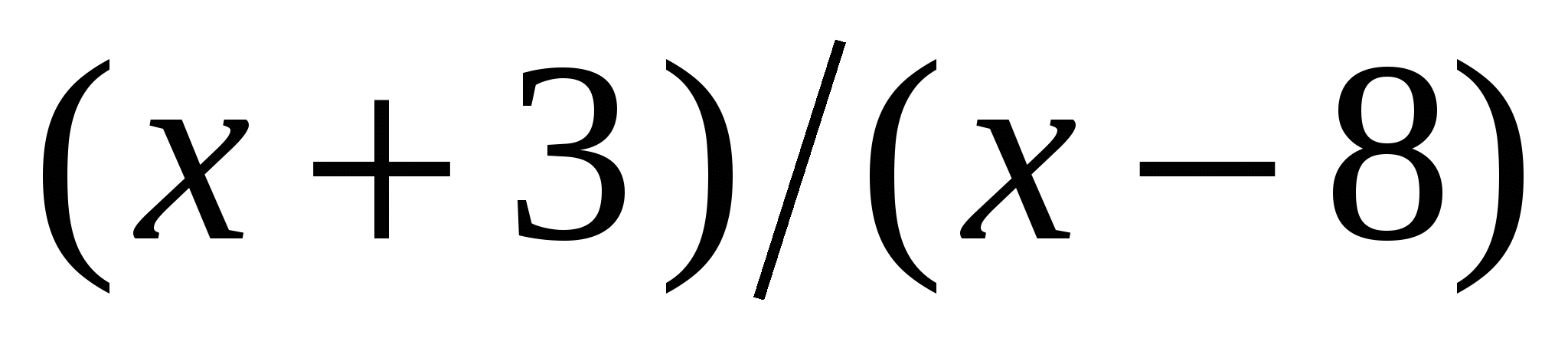 
> 0.
• 4. Решите биквадратное уравнение х4 - 4х2 - 45 = 0.
5. При каких значениях п уравнение 2х2 + пх + 8 = 0 не имеет корней?
infourok.ru
1. Разложите на множители квадратный трехчлен:
а) у2+3у-40; б) 9х2-2х-11.
2. Изобразите схематически график функции:
а) у=-3х2; б) у=2х2-3.
3. Постройте график функции у=х2-5х+6. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному 1,5;
б) значение аргумента, при которых значение функции равно 5;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
4. Пересекаются ли прямая у=2х-1 и парабола у=х2+3?
Вариант 21. Разложите на множители квадратный трехчлен:
а) а2+а-42; б) 6х2+х-22.
2. Изобразите схематически график функции:
а) у=3х2; б) у=-2(х+1)2.
3. Постройте график функции у=х2-х-2. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному -1,5;
б) значение аргумента, при которых значение функции равно 3;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
4. Пересекаются ли прямая у=5х-2 и парабола у=х2+4?
Вариант 11. Разложите на множители квадратный трехчлен:
а) у2+3у-40; б) 9х2-2х-11.
2. Изобразите схематически график функции:
а) у=-3х2; б) у=2х2-3.
3. Постройте график функции у=х2-5х+6. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному 1,5;
б) значение аргумента, при которых значение функции равно 5;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
4. Пересекаются ли прямая у=2х-1 и парабола у=х2+3?
Вариант 21. Разложите на множители квадратный трехчлен:
а) а2+а-42; б) 6х2+х-22.
2. Изобразите схематически график функции:
а) у=3х2; б) у=-2(х+1)2.
3. Постройте график функции у=х2-х-2. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному -1,5;
б) значение аргумента, при которых значение функции равно 3;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
4. Пересекаются ли прямая у=5х-2 и парабола у=х2+4?
Вариант 11. Разложите на множители квадратный трехчлен:
а) у2+3у-40; б) 9х2-2х-11.
2. Изобразите схематически график функции:
а) у=-3х2; б) у=2х2-3.
3. Постройте график функции у=х2-5х+6. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному 1,5;
б) значение аргумента, при которых значение функции равно 5;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
4. Пересекаются ли прямая у=2х-1 и парабола у=х2+3?
Вариант 21. Разложите на множители квадратный трехчлен:
а) а2+а-42; б) 6х2+х-22.
2. Изобразите схематически график функции:
а) у=3х2; б) у=-2(х+1)2.
3. Постройте график функции у=х2-х-2. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному -1,5;
б) значение аргумента, при которых значение функции равно 3;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
4. Пересекаются ли прямая у=5х-2 и парабола у=х2+4?
Вариант 11. Разложите на множители квадратный трехчлен:
а) у2+3у-40; б) 9х2-2х-11.
2. Изобразите схематически график функции:
а) у=-3х2; б) у=2х2-3.
3. Постройте график функции у=х2-5х+6. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному 1,5;
б) значение аргумента, при которых значение функции равно 5;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
4. Пересекаются ли прямая у=2х-1 и парабола у=х2+3?
Вариант 21. Разложите на множители квадратный трехчлен:
а) а2+а-42; б) 6х2+х-22.
2. Изобразите схематически график функции:
а) у=3х2; б) у=-2(х+1)2.
3. Постройте график функции у=х2-х-2. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному -1,5;
б) значение аргумента, при которых значение функции равно 3;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
4. Пересекаются ли прямая у=5х-2 и парабола у=х2+4?
multiurok.ru
Контрольная работа 8 класс
«Квадратичная функция»
Вариант 1
Сократите дробь:
.
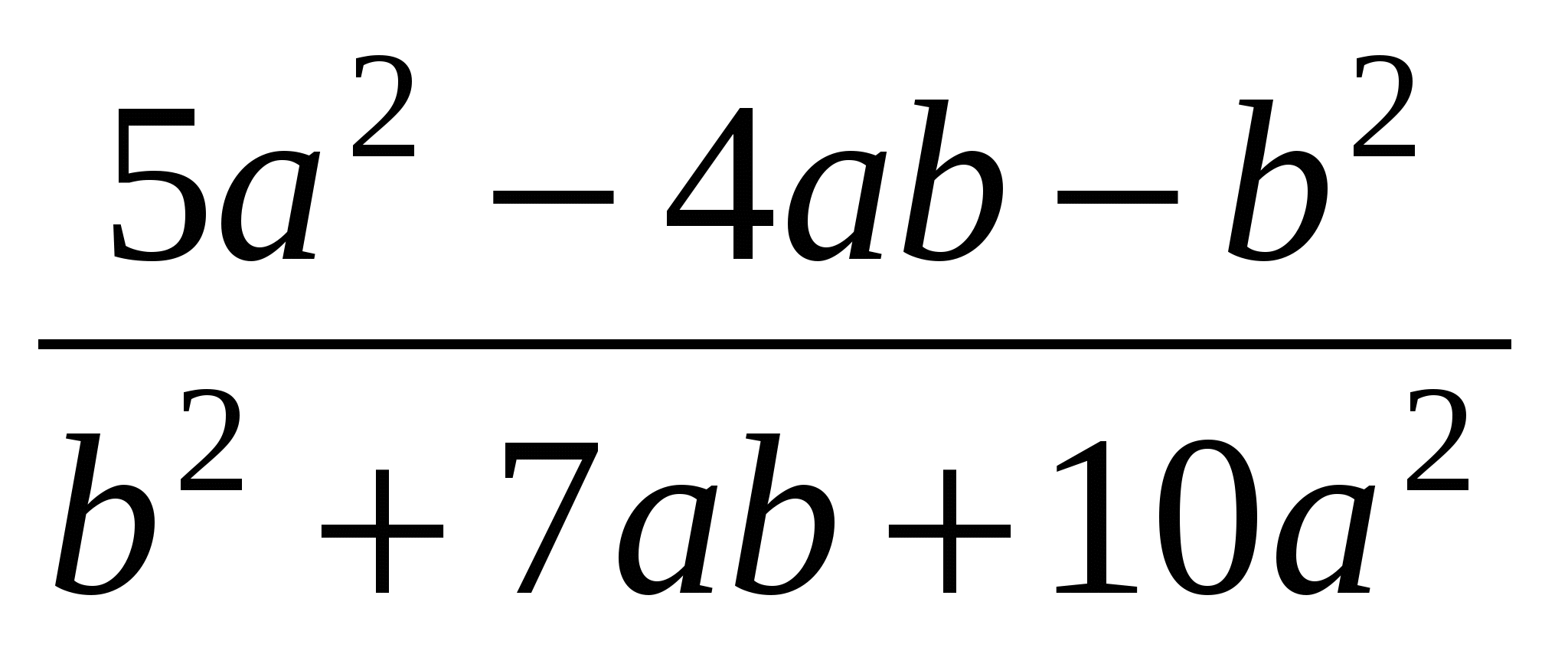Постройте график функции
.
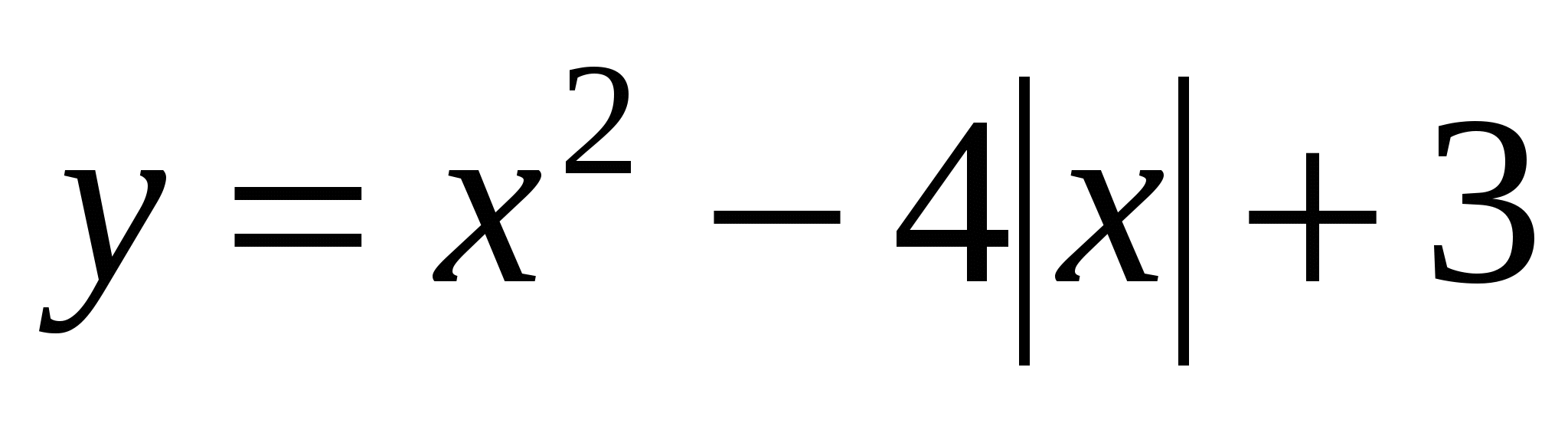Пользуясь графиком, найдите промежутки монотонности данной функции.
Задайте аналитически уравнение прямой, проходящей через точки пересечения графиков функци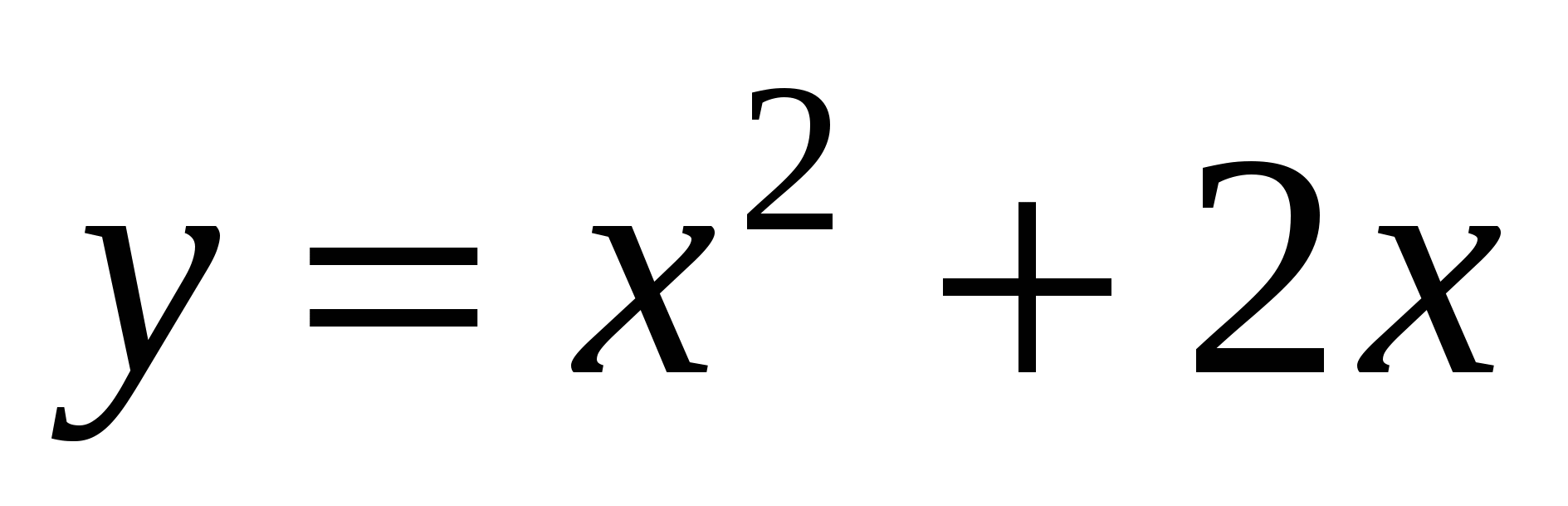й
и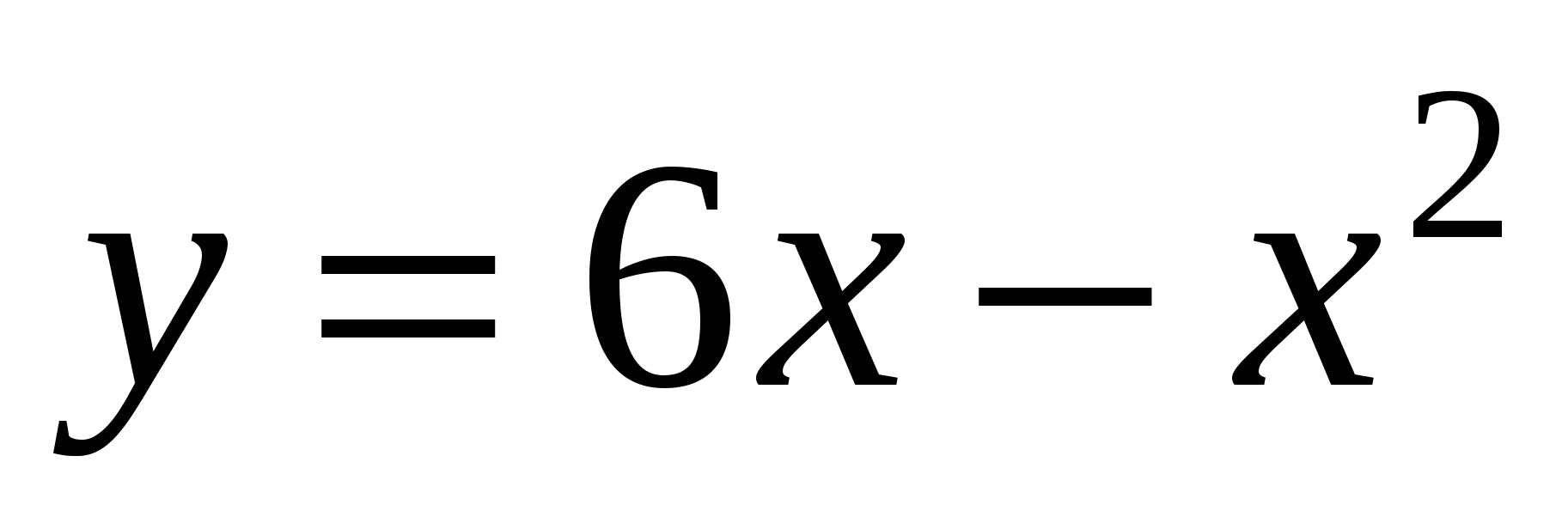 
.
Найдите такую квадратичную функцию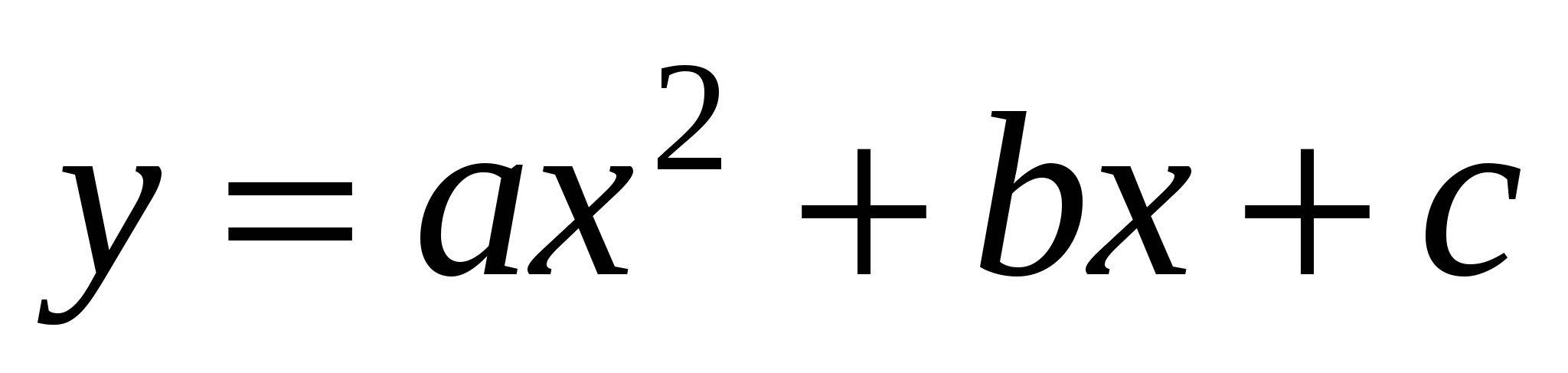 
, чтобы ее график пересекал ось абсцисс в точках (-3; 0) и (1; 0), а ось ординат в точке (0; -9).
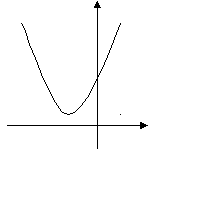
Пользуясь графиком функции 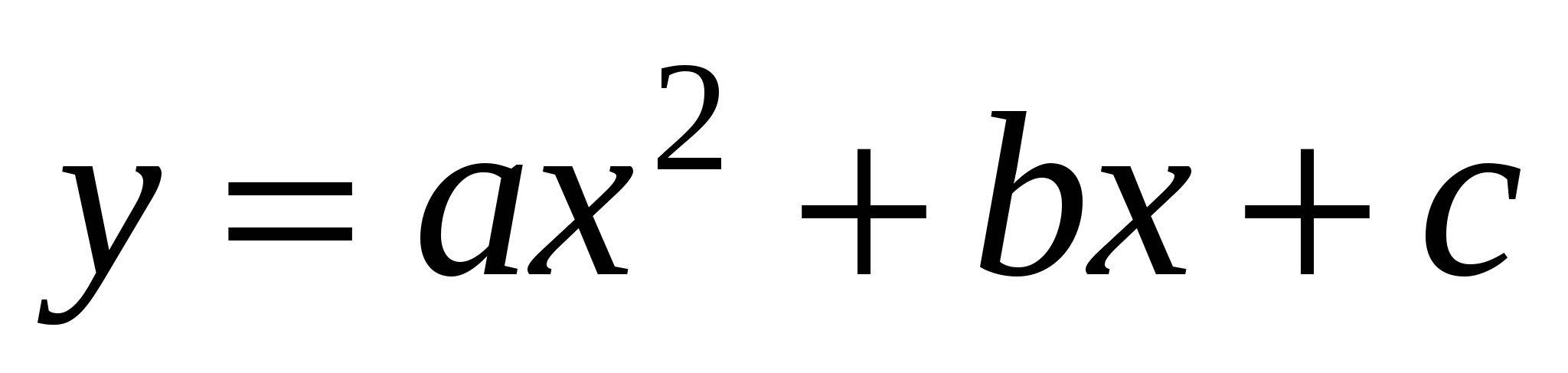, изображенным на рисунке, определите знаки a, b, c и дискриминанта квадратного трехчлена 
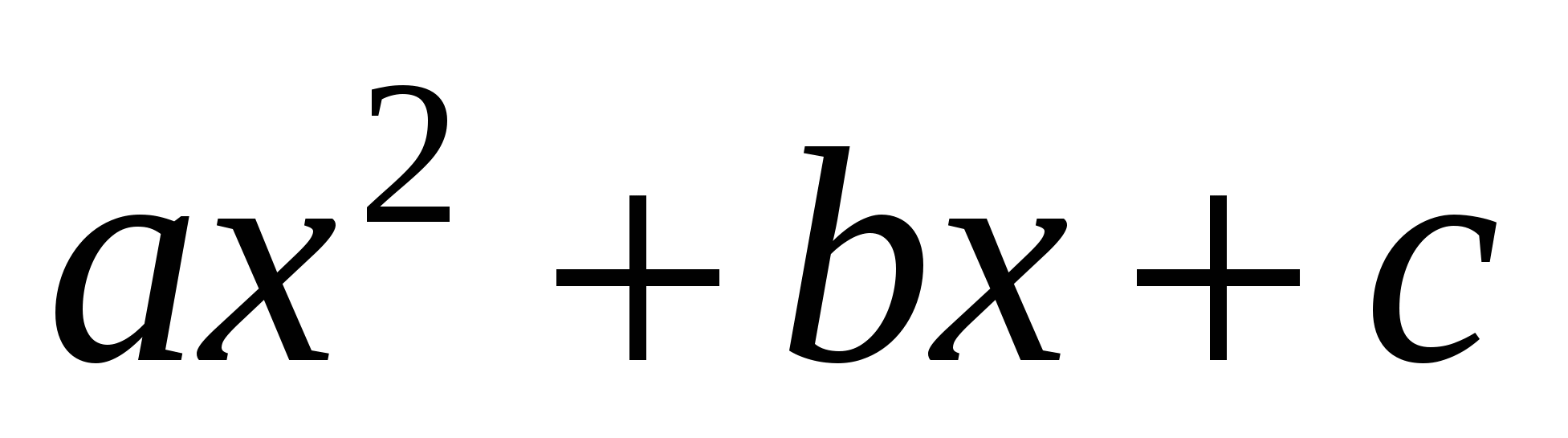. Ответ объясните.
_________________________________________________________
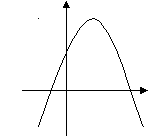
Дана квадратичная функция 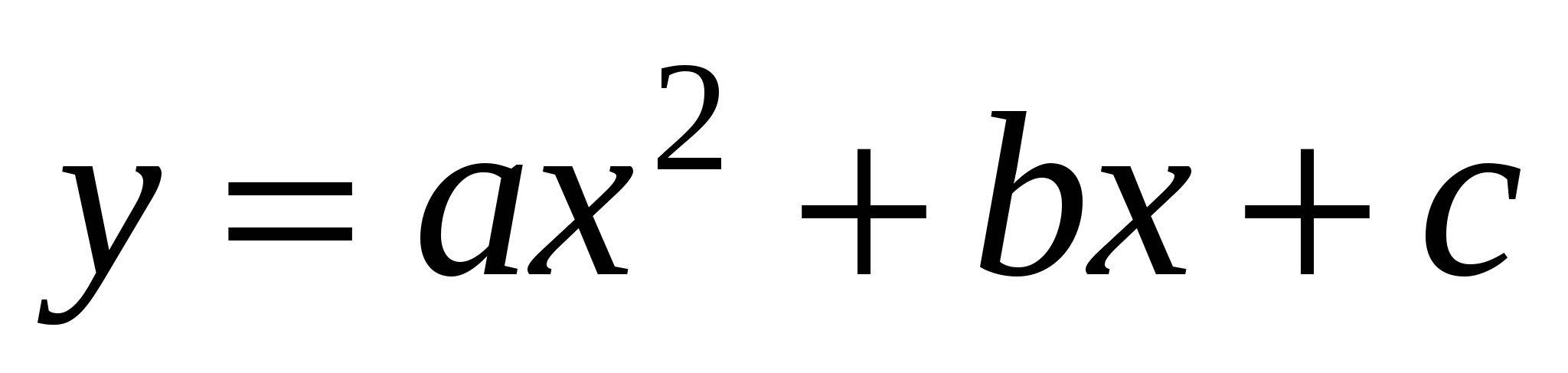такая, что y(-2) < 0, y(3) < 0, y(1) > 0. Сравните с нулем:
а) а; б)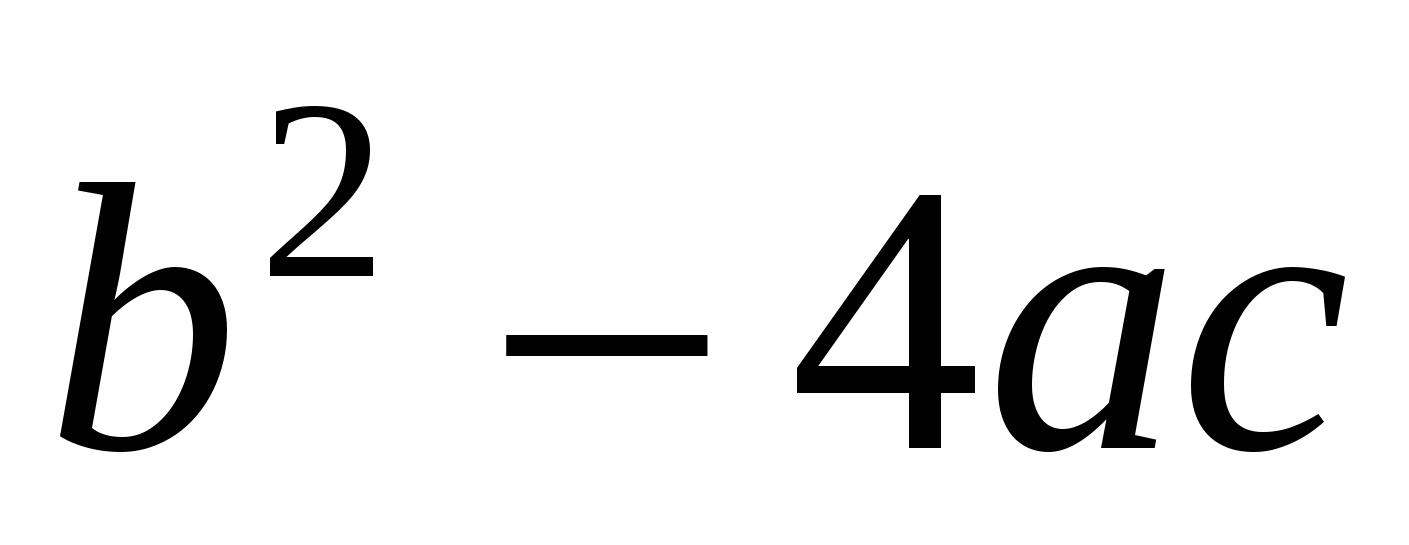 
; в) y(-4) y(6).
Контрольная работа 8 класс
«Квадратичная функция»
Вариант 2
Сократите дробь:
.
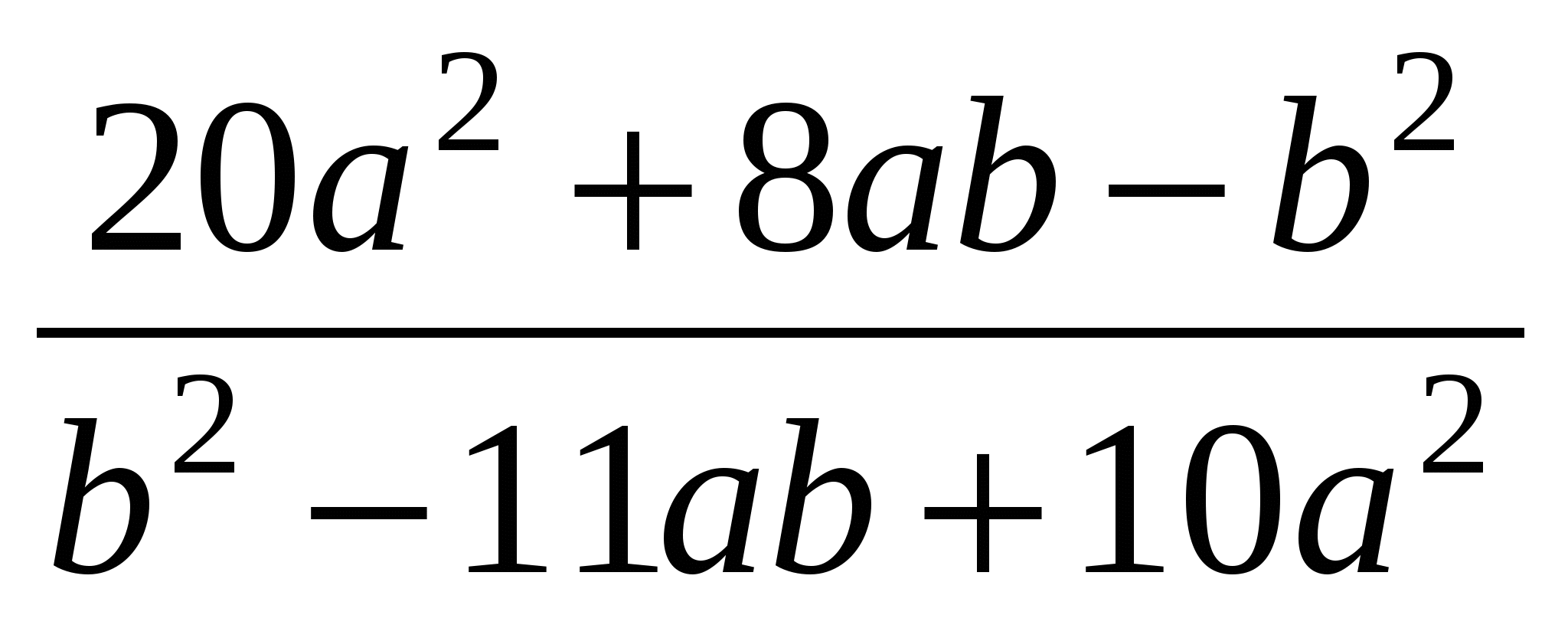Постройте график функции
.
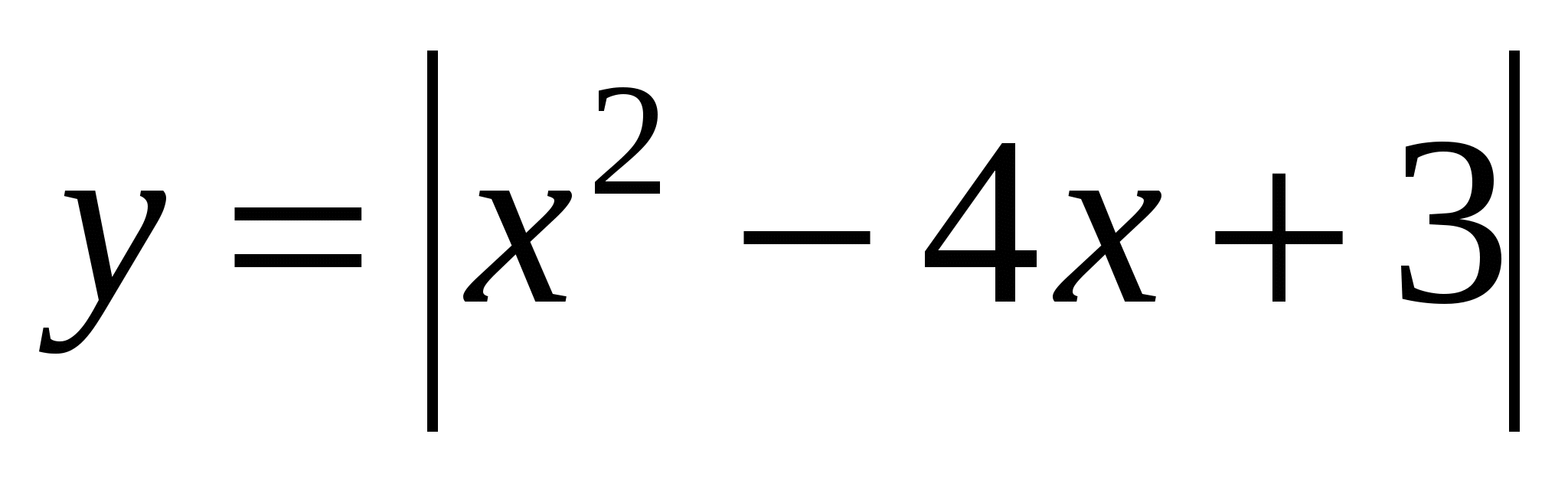Пользуясь графиком, найдите промежутки монотонности данной функции.
Задайте аналитически уравнение прямой, проходящей через точки пересечения графиков функци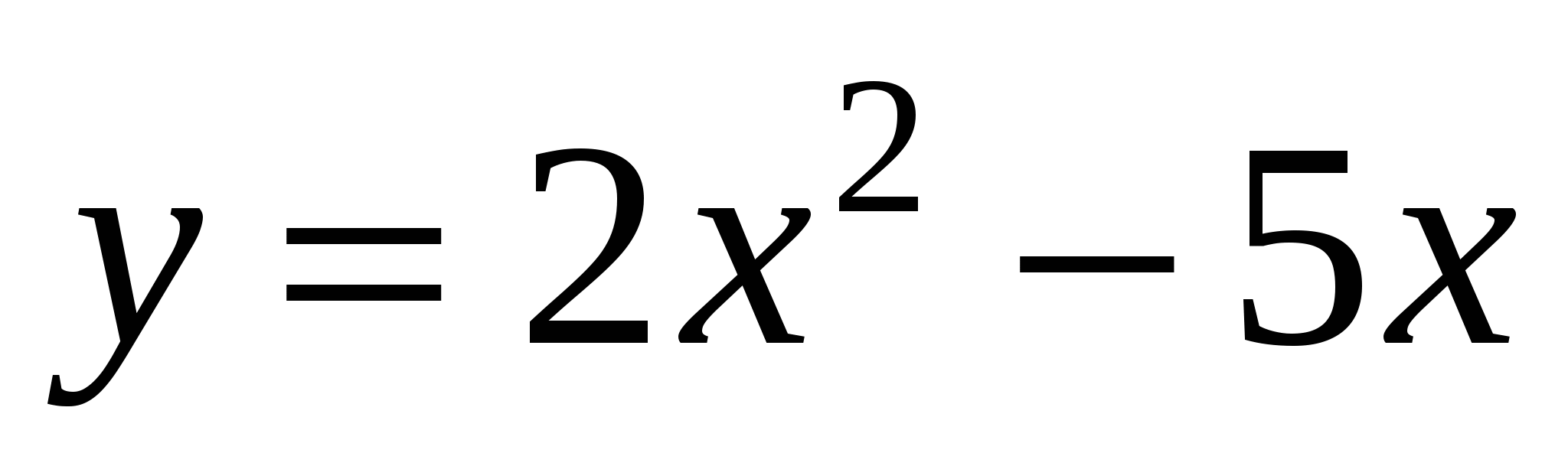й
и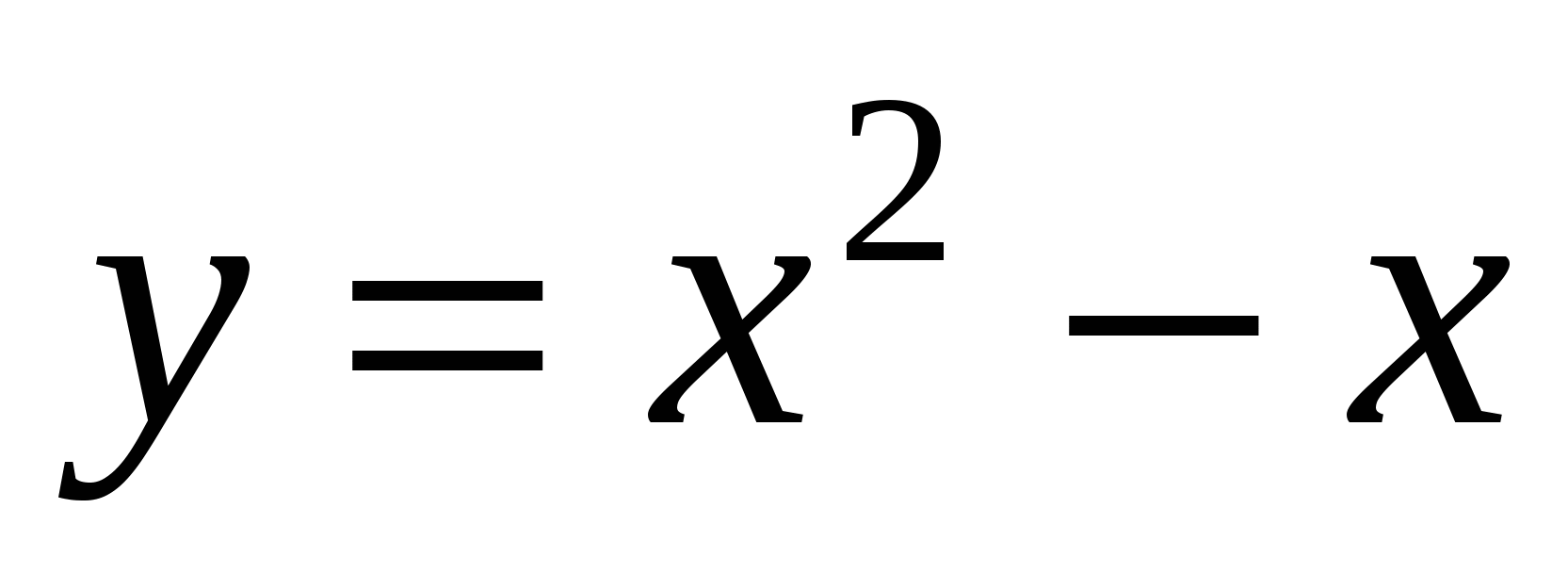 
.
Найдите такую квадратичную функцию 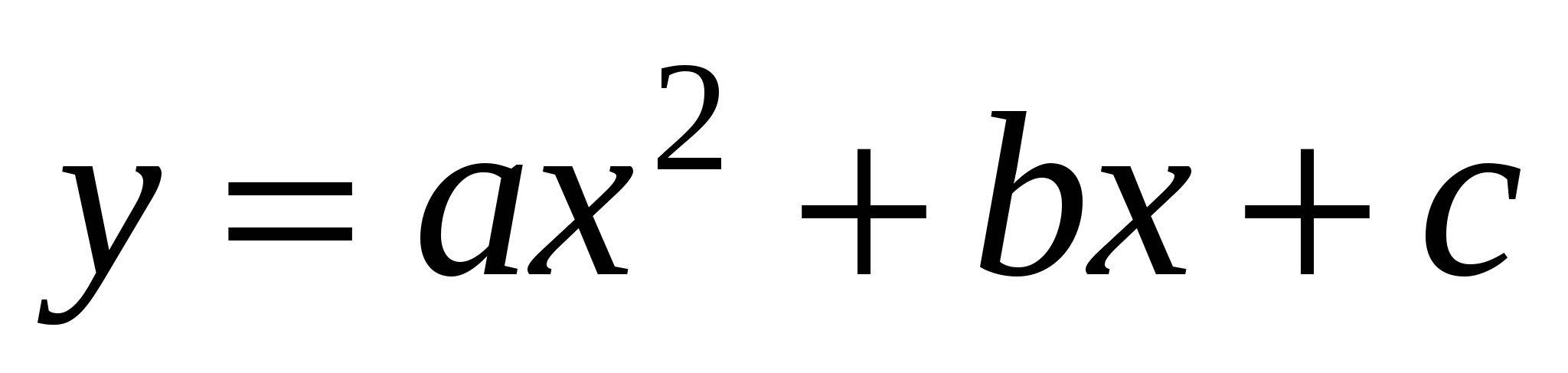, чтобы ее график пересекал ось абсцисс в точках (2; 0) и (-5; 0), а ось ординат в точке (0; 20).
Пользуясь графиком функции 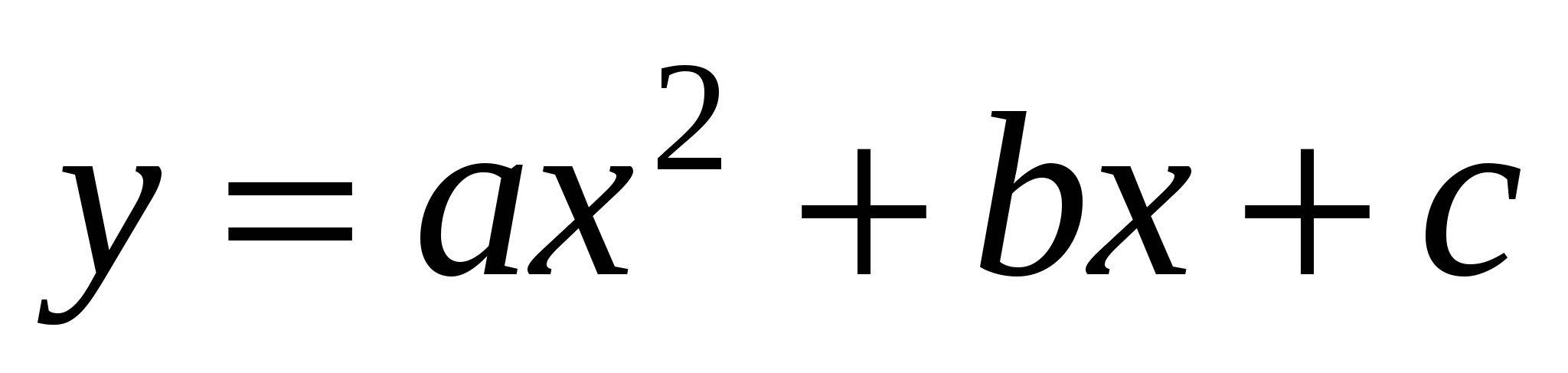, изображенным на рисунке, определите знаки a, b, c и дискриминанта квадратного трехчлена 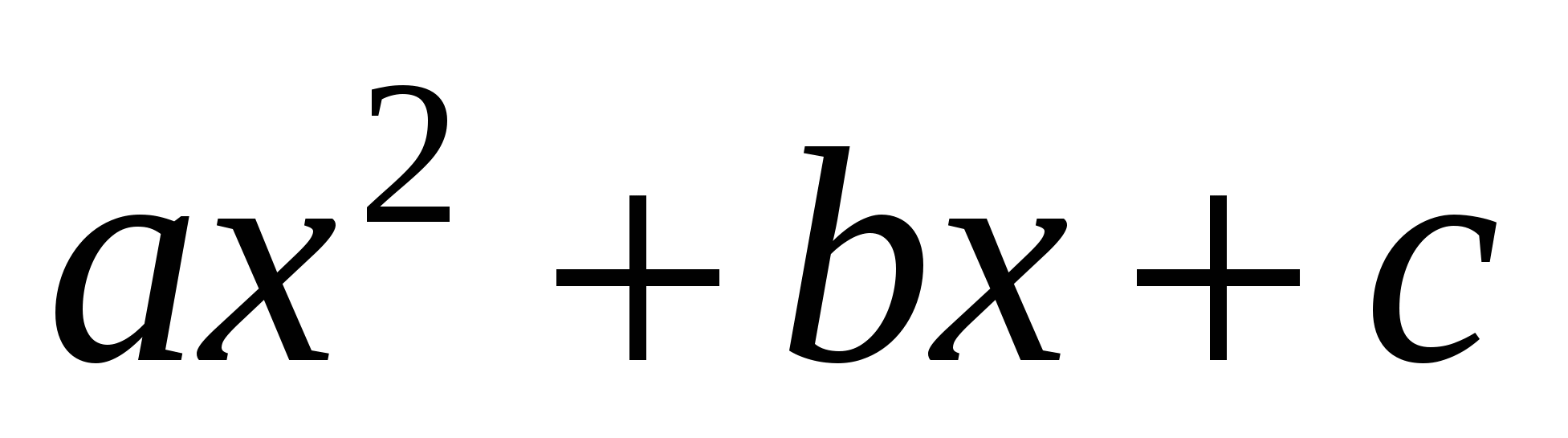. Ответ объясните.
________________________________________________________
Дана квадратичная функция 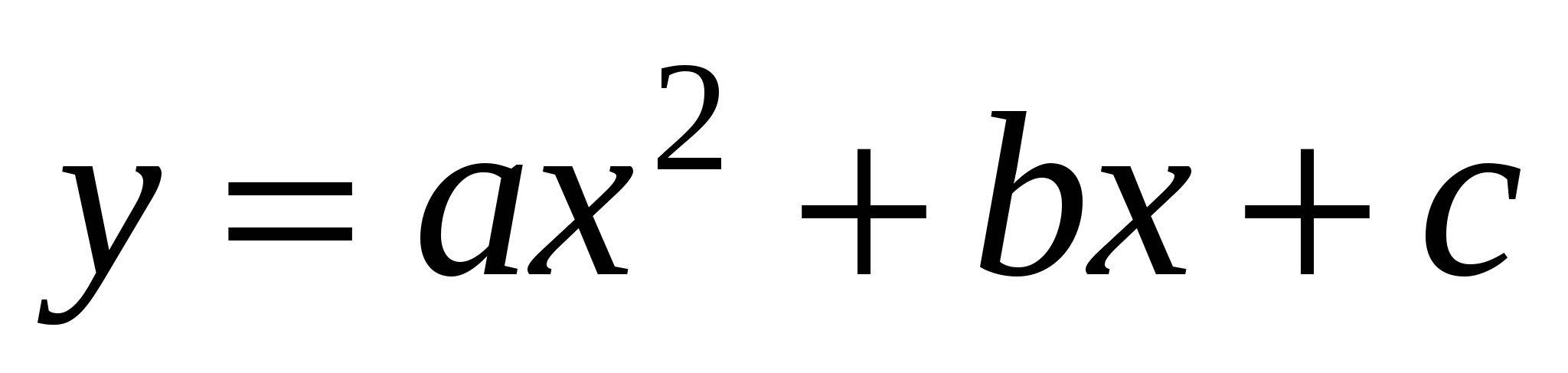такая, что y(-2) > 0, y(3) < 0, y(7) > 0. Сравните с нулем:
а) а; б) 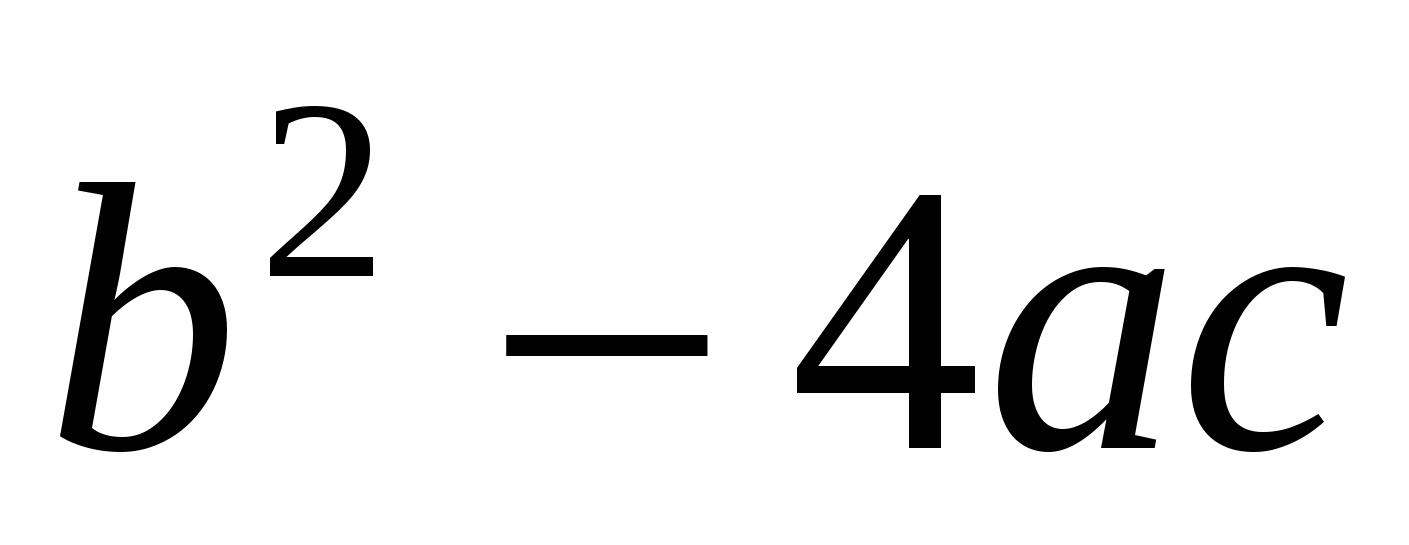; в) y(-5) + y(8).
infourok.ru
регулятивные: построить график функции (для построения графика необходимо применить определённый алгоритм)
Содержание контрольно-оценочного материала
Контрольная работа №5 «Линейная и квадратичная функции»
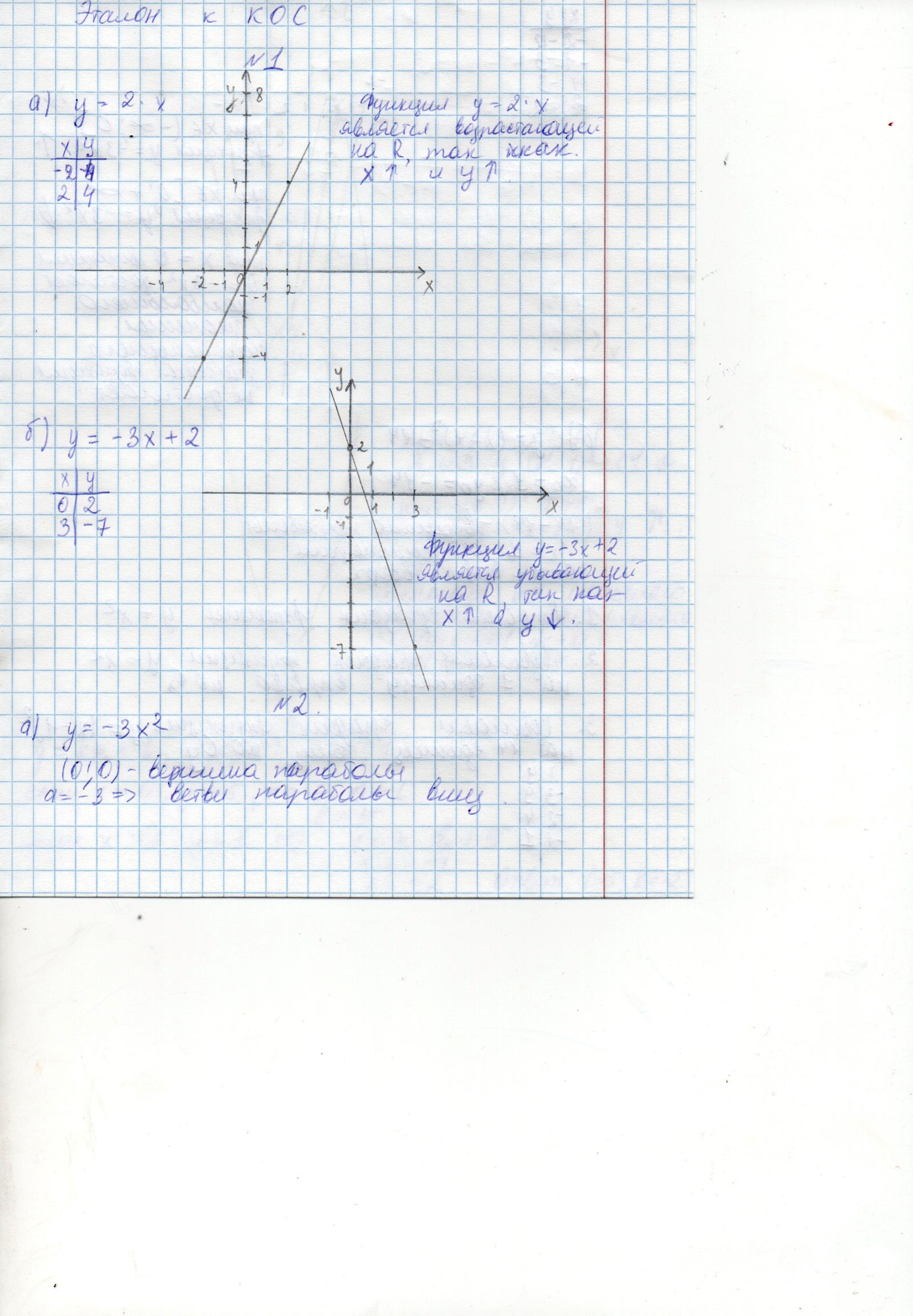
Постройте график функции: а) у= 2х б) у= -3х+2. Является ли функция возрастающей (убывающей) на множестве действительных чисел?
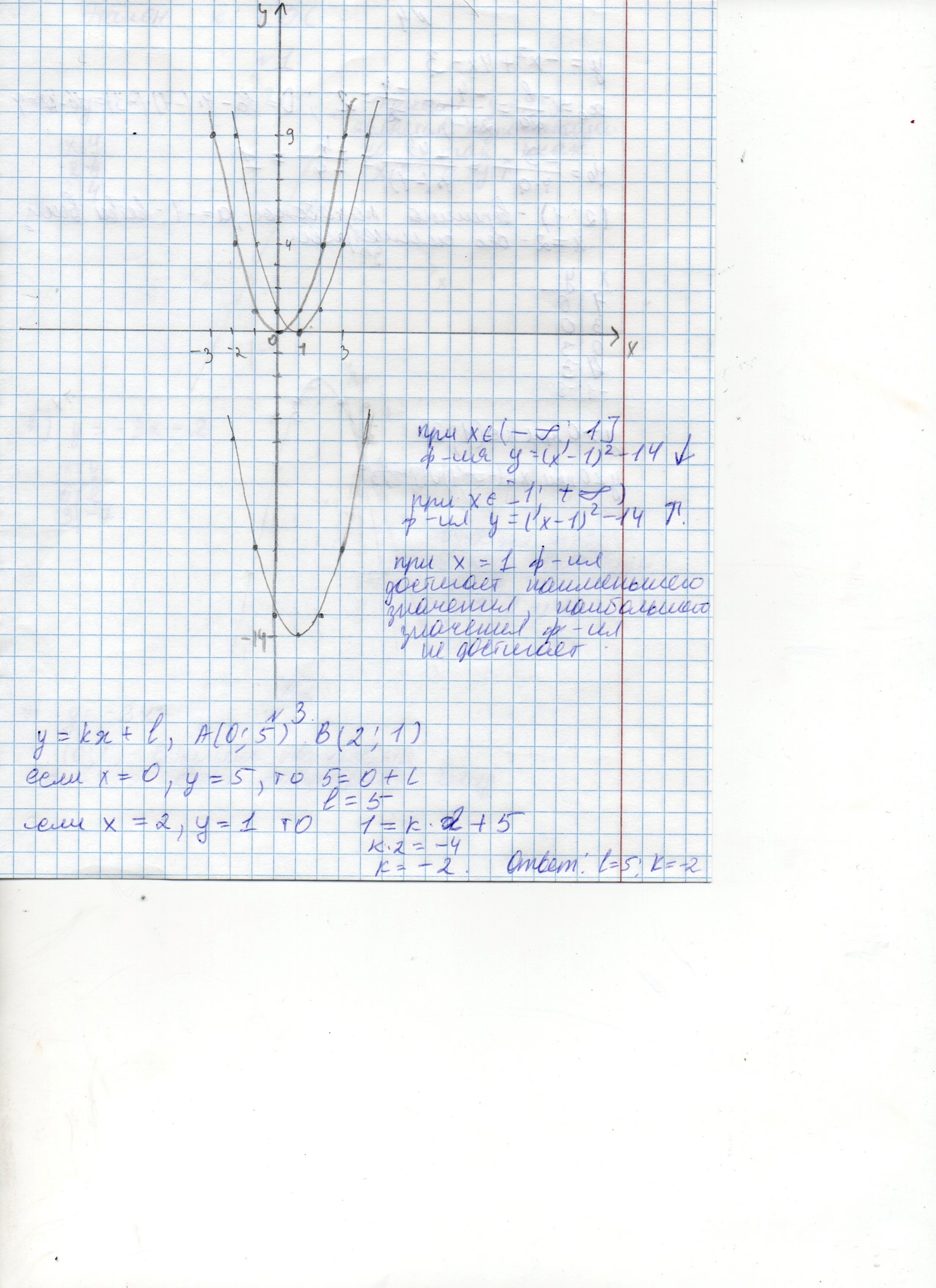
Постройте график функции: а) у= -3х2б) у=(х-1)2-14. Найдите промежутки возрастания (убывания) функции. Укажите значение х, при котором функция достигает наибольшего (наименьшего) значения.
График функции у=kx+l проходит через точки А(0;5) и В(2;1). Найдите k и l.
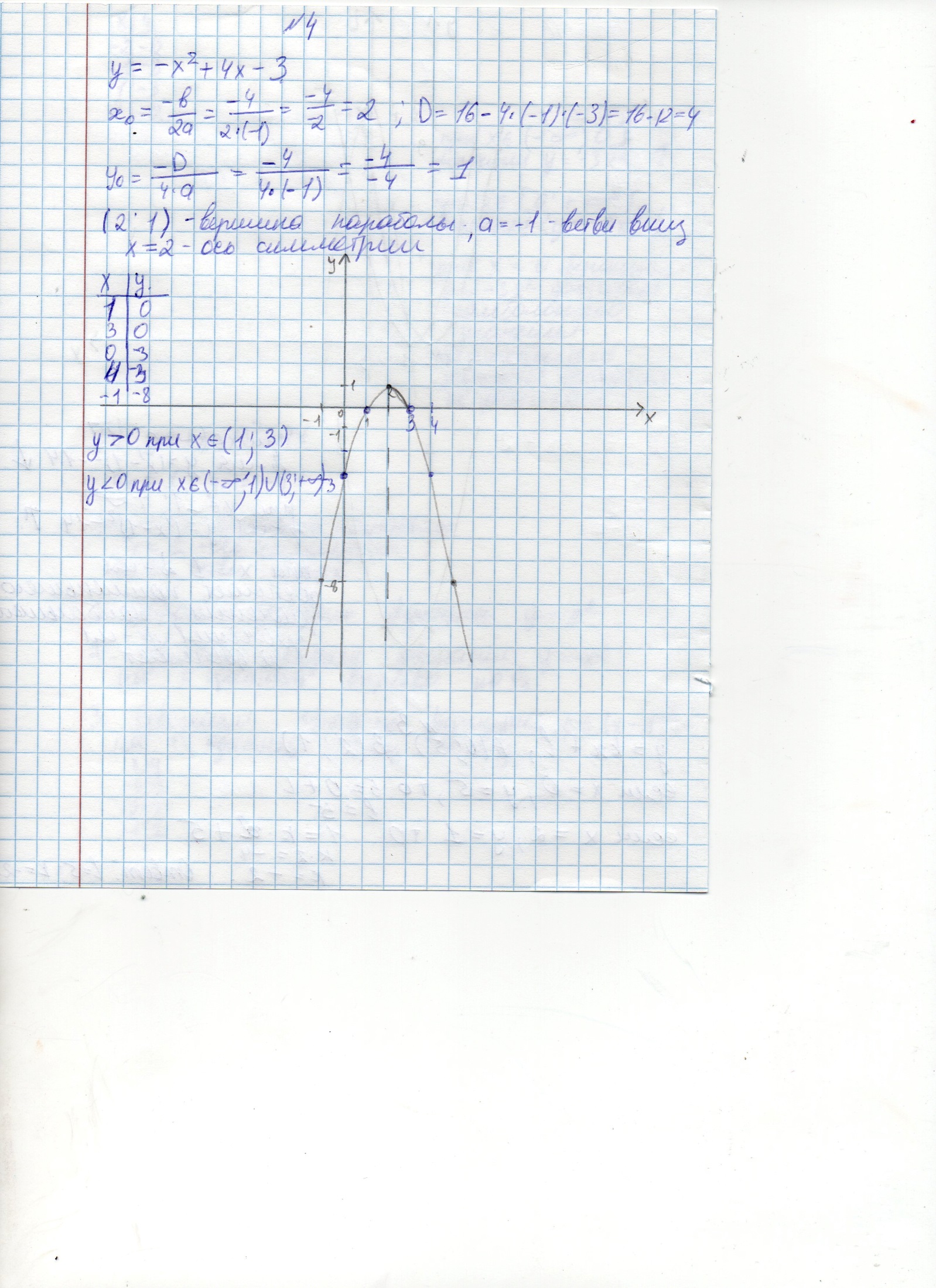
Постройте график функции у=-х2+4х-3. Определите по графику, на каком числовом промежутке функция принимает положительные значения.
Инструкция к выполнению контрольной работы №5 «Линейная и квадратичная функции»
Дорогие, ребята! Перед Вами текст контрольной работы №5 «Линейная и квадратичная функции». Контрольная работа состоит из четырёх заданий, на выполнение которых отводится 45 минут. Задания можно выполнять в любом порядке. Текст задания переписывать не надо, необходимо только указать его номер. Построение графиков функций выполнять строго с использованием чертёжных инструментов (карандаш, линейка).
Начать советуем с того задания, которое вызывает у Вас меньше всего затруднения, затем переходите к другим.
Желаем Успеха!
Поэлементный анализ выполнения работы
1Вычислить координаты точек, построить график функции, определить является ли функция возрастающей (убывающей)
1 балл
6 баллов
№2 А
Б
Вычислить координаты точек, построить график функции, используя график определить промежутки возрастания (убывания) функции, указать значение х, при котором функция достигает наибольшего (наименьшего) значения.
1 балл
13 баллов
Построить график функции у=х2, составить алгоритм построения графика функции
у=(х-1)2-14, построить график функции у=(х-1)2-14, используя график определить промежутки возрастания (убывания) функции, указать значение х, при котором функция достигает наибольшего (наименьшего) значения.
1 балл
№3
Подставить в функцию у=kx+l координаты точки А вычислить l, подставить в функцию у=kx+l координаты точки В и значение l, вычислить к.
1 балл
4 балла
№4
Вычислить координаты вершины параболы, определить ось симметрии и направление ветвей параболы, вычислить координаты точек, построить график функции.
Вычислить координаты точек пересечения графика с Ох (вычислить дискриминант, найти корни, записать и отметить координаты точек пересечения графика с Ох), записать по графику промежутки на которых функция принимает положительные значения.
1 балл
8 баллов
Итого:
31 балл
Критерии оценивания учебных достижений
31 балл17- 21 балл - отметка «3»
22-28 баллов - отметка «4»
29-31 балл – отметка «5»
Меньше 17 баллов – отметка «2»
Эталон выполнения КОС
infourok.ru
