Это один из стандартов, введенных IBM, в соответствии с которым информация в банках памяти хранится фрагментами по девять битов, причем восемь из них (составляющих один байт) предназначены собственно для данных, а девятый является битом четности (parity). Использование девятого бита позволяет схемам управления памятью на аппаратном уровне контролировать целостность каждого байта данных. Если обнаруживается ошибка, работа компьютера останавливается и на экран выводится сообщение о неисправности. Если вы работаете на компьютере под управлением Windows или OS/2, то при возникновении ошибки контроля четности сообщение, возможно, не появится, а просто произойдет блокировка системы.
Во всех процессорах, начиная с 386, схема контроля четности встроена в саму микросхему, поэтому никакие дополнительные микросхемы на системную плату устанавливать не нужно. В большинстве системных плат предусмотрена возможность отключения схем контроля четности для того, чтобы на них можно было устанавливать модули памяти без бита четности. К сожалению, некоторые системы вообще не поддерживают контроль четности. Данный факт ставит под сомнение четкую работу системы с критическими приложениями, требующими контроля четности.
При разработке схемы контроля четности IBM установила, что значение бита четности задается таким, чтобы количество единиц во всех девяти разрядах (восемь разрядов данных и разряд четности) было нечетным. Другими словами, когда байт (8 бит) данных заносится в память, специальная схема контроля четности (микросхема, установленная на системной плате или на плате памяти) подсчитывает количество единиц в байте. Если оно четное, на выходе микросхемы формируется сигнал логической единицы, который сохраняется в соответствующем разряде памяти как девятый бит (бит четности). Количество единиц во всех девяти разрядах при этом становится нечетным. Если же количество единиц в восьми разрядах исходных данных нечетное, то бит четности равен 0 и сумма двоичных цифр в девяти разрядах также остается нечетной.
Рассмотрим конкретный пример (имейте в виду, что разряды в байте нумеруются начиная с нуля).
Разряд данных: 0 1 2 3 4 5 6 7 Бит четности
Значение бита: 1 0 1 1 0 0 1 1 0
В данном случае общее число единичных битов данных нечетное (5), поэтому бит четности должен быть равен нулю, чтобы количество единиц во всех девяти разрядах было нечетным.
Рассмотрим еще один пример.
Разряд данных: 0 1 2 3 4 5 6 7 Бит четности
Значение бита: 0 0 1 1 0 0 1 1 1
В этом примере общее число единичных битов данных четное (4), поэтому бит четности должен быть равен единице, чтобы количество единиц во всех девяти разрядах, как и в предыдущем примере, было нечетным.
При считывании из памяти та же самая микросхема проверяет информацию на четность. Если в 9-разрядном байте число единиц четное и бит четности также равен единице, значит, при считывании или записи данных произошла ошибка. Определить, в каком разряде она произошла, невозможно (нельзя даже выяснить количество испорченных разрядов). Более того, если сбой произошел в трех разрядах (в нечетном их количестве), то ошибка будет зафиксирована; однако при двух ошибочных разрядах (или четном их количестве) сбой не регистрируется. Сообщения об ошибках четности имеют следующий вид:
В компьютере IBM PC: PARITY СНЕСК х
В компьютере IBM XT: PARITY СНЕСК х yyyyy (z)
В компьютере IBM PC и последних моделях XT: PARITY СНЕСК х yyyyy
Здесь x может принимать значения 1 (ошибка произошла на системной плате) или 2 (ошибка произошла в разъеме расширения). Символы yyyyy это шестнадцатеричное число от 00000 до FFFFF, указывающее адрес байта, в котором произошла ошибка. Символ z может принимать значение S (ошибка четности в системном блоке) или e (ошибка четности в корпусе-расширителе). (IBM разработала корпуса-расширители для компьютеров PC и XT, чтобы увеличить количество разъемов расширения.)
При обнаружении ошибки схема контроля четности на системной плате формирует немаскируемое прерывание (Non-maskable Interrupt NMI), по которому основная работа прекращается и инициируется специальная процедура, записанная в BIOS. В результате ее выполнения экран очищается и в левом верхнем углу выводится сообщение об ошибке. Текст сообщения зависит от типа компьютера. В некоторых старых компьютерах IBM при выполнении указанной процедуры приостанавливается работа процессора, компьютер блокируется и пользователю приходится перезапускать его с помощью кнопки сброса или выключать и через некоторое время вновь включать питание. При этом, естественно, теряется вся несохраненная информация. (Немаскируемое прерывание это системное предупреждение, которое программы не могут проигнорировать.)
В большинстве компьютеров в случае ошибки четности процессор не зависает и пользователю предоставляется возможность либо перезагрузить компьютер, либо продолжить работу как будто ничего не случилось. В подобных системах сообщение об ошибке может выглядеть иначе, чем в компьютерах IBM, хотя общий его смысл, конечно, остается прежним.
studfiles.net
Материал из Википедии — свободной энциклопедии
Бит чётности (англ. Parity bit) — контрольный бит в вычислительной технике и сетях передачи данных, служащий для проверки общей чётности двоичного числа (чётности количества единичных битов в числе).
В последовательной передаче данных часто используется формат 7 бит данных, бит чётности, один или два стоповых бита. Такой формат аккуратно размещает все 7-битные ASCII символы в удобный 8-битный байт. Также допустимы другие форматы: 8 бит данных и бит чётности.
В последовательных коммуникациях чётность обычно контролируется оборудованием интерфейса (например UART). Признак ошибки становится доступен процессору (и ОС) через статусный регистр оборудования. Восстановление ошибок обычно производится повторной передачей данных, подробности которого обрабатываются программным обеспечением (например, функциями ввода-вывода операционной системы)
Контроль некой двоичной последовательности (например, машинного слова) с помощью бита чётности также называют контролем по паритету. Контроль по паритету представляет собой наиболее простой и наименее мощный метод контроля данных. С его помощью можно обнаружить только одиночные ошибки в проверяемых данных. Двойная ошибка будет неверно принята за корректные данные. Поэтому контроль по паритету применяется к небольшим порциям данных, как правило к каждому байту, что даёт коэффициент избыточности для этого метода 1/8. Метод редко применяется в компьютерных сетях из-за невысоких диагностических способностей. Существует модификация этого метода — вертикальный и горизонтальный контроль по паритету. Отличие состоит в том, что исходные данные рассматриваются в виде матрицы, строки которой составляют байты данных. Контрольный разряд подсчитывается отдельно для каждой строки и для каждого столбца матрицы. Этот метод обнаруживает значительную часть двойных ошибок, однако обладает большей избыточностью. Он сейчас также почти не применяется при передаче информации по сети.
Контроль по чётности фактически является специальным случаем проверки избыточности циклической суммы с полиномом x+1.
Бит чётности или контрольный разряд формируется при выполнении операции «Исключающее-ИЛИ» последовательно (1 бит с 2, результат с 3, результат с 4 и т.д.).
Рассмотрим схему, использующую девятибитные кодовые слова, состоящие из восьми бит данных, за которыми следует бит чётности.
Пустой или несуществующий поток битов также имеет ноль единичных битов, поэтому бит чётности будет '0'.
o-ili-v.ru
Материал из Википедии — свободной энциклопедии
Бит чётности (англ. Parity bit) — контрольный бит в вычислительной технике и сетях передачи данных, служащий для проверки общей чётности двоичного числа (чётности количества единичных битов в числе).
В последовательной передаче данных часто используется формат 7 бит данных, бит чётности, один или два стоповых бита. Такой формат аккуратно размещает все 7-битные ASCII символы в удобный 8-битный байт. Также допустимы другие форматы: 8 бит данных и бит чётности.
В последовательных коммуникациях чётность обычно контролируется оборудованием интерфейса (например UART). Признак ошибки становится доступен процессору (и ОС) через статусный регистр оборудования. Восстановление ошибок обычно производится повторной передачей данных, подробности которого обрабатываются программным обеспечением (например, функциями ввода-вывода операционной системы)
Контроль некой двоичной последовательности (например, машинного слова) с помощью бита чётности также называют контролем по паритету. Контроль по паритету представляет собой наиболее простой и наименее мощный метод контроля данных. С его помощью можно обнаружить только одиночные ошибки в проверяемых данных. Двойная ошибка будет неверно принята за корректные данные. Поэтому контроль по паритету применяется к небольшим порциям данных, как правило к каждому байту, что даёт коэффициент избыточности для этого метода 1/8. Метод редко применяется в компьютерных сетях из-за невысоких диагностических способностей. Существует модификация этого метода — вертикальный и горизонтальный контроль по паритету. Отличие состоит в том, что исходные данные рассматриваются в виде матрицы, строки которой составляют байты данных. Контрольный разряд подсчитывается отдельно для каждой строки и для каждого столбца матрицы. Этот метод обнаруживает значительную часть двойных ошибок, однако обладает большей избыточностью. Он сейчас также почти не применяется при передаче информации по сети.
Контроль по чётности фактически является специальным случаем проверки избыточности циклической суммы с полиномом x+1.
Бит чётности или контрольный разряд формируется при выполнении операции «Исключающее-ИЛИ» последовательно (1 бит с 2, результат с 3, результат с 4 и т.д.).
Рассмотрим схему, использующую девятибитные кодовые слова, состоящие из восьми бит данных, за которыми следует бит чётности.
Пустой или несуществующий поток битов также имеет ноль единичных битов, поэтому бит чётности будет '0'.
wiki-org.ru
11.2. Контроль по четности / нечетности, контроль Хэмминга.
Контроль на чётность (нечётность) заключается в следующем: к передаваемым байтам данных (8 бит) добавляется 1 контрольный бит. Контрольный бит вычисляется по следующему правилу: если в информационном байте число единиц четное, то контрольный бит равен 1. При этом общее число единиц передаваемой информации должно быть нечетным. Данный способ контроля не позволяет обнаружить ошибки четной кратности (т.е. ошибки одновременно в двух, четырех и т.д. битах) и поэтому используется при невысоких требованиях к достоверности принимаемых данных (или при малой вероятности ошибок в линии передачи).
Хэммингом предложен способ добавления контрольных разрядов, при котором путем определенных проверок на четность достаточно просто находится в принятом слове ошибочный разряд. Рассмотрим этот способ.
Первый, второй, четвертый, восьмой и т. д. разряды (т. е. разряды с номерами, выражаемыми числами вида 2k) используются в качестве контрольных. Последующее изложение будем вести на примере так называемого 7/4 кода Хэмминга (общее число разрядов в словах равно 7, из них 4 разряда — информационные, 3 разряда — контрольные). Пусть а4, а3, а2, a1 — цифры информационных разрядов слова; k3, k2, k1 — цифры контрольных разрядов:
номера разрядов 7 6 5 4 3 2 1
цифры разрядов а4 а3 а2 k3 a1 k2 k1
Запишем представления номеров разрядов:
десятичное представление 7 6 5 4 3 2 1
двоичное представление 111 110 101 100 011 010 001
Значения цифр k3, k2, k1 контрольных разрядов находятся по следующему правилу.
Цифра контрольного разряда k1 должна обеспечивать четность числа единиц в разрядах, номера которых в двоичном представлении содержат единицу в первом разряде (это условие выполняется для первого, третьего, пятого и седьмого разрядов слова). Учитывая, какая информация хранится в указанных разрядах, получим условие k1(+)a1(+)а2(+)a4 = 0.
Цифра контрольного разряда k2 должна обеспечивать четность числа единиц в разрядах, двоичные номера которых имеют единицы во втором разряде (это условие выполняется для второго, третьего, шестого и седьмого разрядов слова). Следовательно, k2(+)al(+)a3(+)a4 = 0.
Цифра контрольного разряда k3 обеспечивает четность единиц в разрядах, двоичные номера которых имеют единицу в третьем разряде (это условие выполняется, для четвертого, пятого, шестого и седьмого разрядов слова). Отсюда k3(+)а2(+)а3(+)a4 = 0.
Прибавляя к обеим частям приведенных равенств соответственно k1, k2, k3 и учитывая, что k1(+)k1 = 0; k2(+)k 2= 0; k3(+)k3 = 0, условиям для цифр контрольных разрядов можно придать следующую форму:
k1 = a1(+)a2(+)a4; k2 = a1(+)a3(+)a4; k3 = а2(+)а3(+)а4.
Пусть информационная часть слова равна
1 0 1 0
а4 а3 а2 а1
Пользуясь приведенными выше выражениями, находим значения контрольных разрядов:
k1 = 0(+)1(+)1 = 0; k2 = 0(+)0(+)1 = 1; k3 = 1(+)0(+)1 = 0.
Следовательно, в данном примере слово имеет вид 1010010.
Принятое слово проверяется на выполнение условий, которым подчиняются контрольные разряды. Результат проверки каждого из условий определяет соответствующий разряд двоичного числа, называемого синдромом.
Пусть, например, вместо правильного значения слова 1010010 принято слово с ошибкой в пятом разряде, т. е. 1000010.
Результат проверки первого условия для принятого слова
k1(+)a1(+)а2 (+)a4 = 0(+)0(+)0(+)1= 1.
Нарушена четность, в первый разряд синдрома записывается 1. Результат проверки второго условия
k2(+)al(+)a3(+)a4 = 1(+)0(+)0(+)1= 0.
Четность не нарушена, во второй разряд синдрома записывается 0. Результат проверки третьего условия
k3(+)а2(+)а3(+)a4 = 0(+)0(+)0(+)1= 1.
Четность нарушена, в третий разряд синдрома записывается 1. Итак, получен синдром 1012 = 510, который указывает номер разряда, содержащего ошибку (ошибка в пятом разряде принятого слова).
Нетрудно убедиться в том, что синдром действительно должен указывать номер искаженного разряда. В рассмотренном примере получение единицы в результате первой проверки свидетельствует о том, что ошибка находится в одном из разрядов, двоичный номер которого должен содержать 1 в первом разряде. Последующие две проверки показали, что двоичный номер искаженного разряда содержит во втором разряде 0 и в третьем разряде 1. Следовательно, образуется двоичный номер искаженного разряда.
Определим необходимое число контрольных разрядов k.
Число проверок на четность равно числу контрольных разрядов, а так как в результате каждой проверки формируется цифра одного из разрядов синдрома, то число разрядов синдрома оказывается равным числу контрольных разрядов k. Такой k -разрядный синдром должен иметь п (n=m+k — общее число разрядов в слове) возможных комбинаций для указания номера каждого из п пораженных ошибкой разрядов и нулевую комбинацию, указывающую на отсутствие ошибок. Таким образом, должно выполняться условие 2k≥n+1 или 2k≥m+n+1, из которого число контрольных разрядов равно минимальному k, удовлетворяющему неравенству.
volkov-iy.narod.ru
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 июня 2016; проверки требует 1 правка.
 Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 июня 2016; проверки требует 1 правка.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 июня 2016; проверки требует 1 правка. Бит чётности (англ. Parity bit) — контрольный бит в вычислительной технике и сетях передачи данных, служащий для проверки общей чётности двоичного числа (чётности количества единичных битов в числе).
В последовательной передаче данных часто используется формат 7 бит данных, бит чётности, один или два стоповых бита. Такой формат аккуратно размещает все 7-битные ASCII символы в удобный 8-битный байт. Также допустимы другие форматы: 8 бит данных и бит чётности.
В последовательных коммуникациях чётность обычно контролируется оборудованием интерфейса (например UART). Признак ошибки становится доступен процессору (и ОС) через статусный регистр оборудования. Восстановление ошибок обычно производится повторной передачей данных, подробности которого обрабатываются программным обеспечением (например, функциями ввода-вывода операционной системы)
Контроль некой двоичной последовательности (например, машинного слова) с помощью бита чётности также называют контролем по паритету. Контроль по паритету представляет собой наиболее простой и наименее мощный метод контроля данных. С его помощью можно обнаружить только одиночные ошибки в проверяемых данных. Двойная ошибка будет неверно принята за корректные данные. Поэтому контроль по паритету применяется к небольшим порциям данных, как правило к каждому байту, что даёт коэффициент избыточности для этого метода 1/8. Метод редко применяется в компьютерных сетях из-за невысоких диагностических способностей. Существует модификация этого метода — вертикальный и горизонтальный контроль по паритету. Отличие состоит в том, что исходные данные рассматриваются в виде матрицы, строки которой составляют байты данных. Контрольный разряд подсчитывается отдельно для каждой строки и для каждого столбца матрицы. Этот метод обнаруживает значительную часть двойных ошибок, однако обладает большей избыточностью. Он сейчас также почти не применяется при передаче информации по сети.
Контроль по чётности фактически является специальным случаем проверки избыточности циклической суммы с полиномом x+1.
Бит чётности или контрольный разряд формируется при выполнении операции «Исключающее-ИЛИ» последовательно (1 бит с 2, результат с 3, результат с 4 и т.д.).
Рассмотрим схему, использующую девятибитные кодовые слова, состоящие из восьми бит данных, за которыми следует бит чётности.
Пустой или несуществующий поток битов также имеет ноль единичных битов, поэтому бит чётности будет '0'.
encyclopaedia.bid
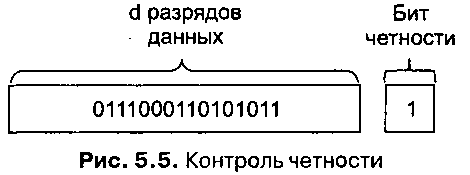
Возможно, простейшая форма обнаружения ошибок заключается в использовании одного бита четности. Предположим, что на рис. 5.4 передаваемые данные D имеют длину d разрядов. При проверке на четность отправитель просто добавляет к данным один бит, значение которого вычисляется как сумма всех d разрядов данных по модулю 2. В этом случае количество единиц в получающемся в результате числе всегда будет четным. Применяются также схемы, в которых контрольный бит инвертируется, в результате чего количество единиц в получающемся в результате числе всегда будет нечетным. На рис. 5.5 изображена схема проверки на четность, а единственный бит четности хранится в отдельном поле.

Действия, выполняемые получателем при использовании такой схемы, также очень просты. Получатель должен всего лишь сосчитать количество единиц в полученных d + 1 разрядах. Если при проверке на четность получатель обнаруживает, что в принятых им данных нечетное количество единичных разрядов, он понимает, что произошла ошибка, по меньшей мере, в одном разряде. В общем случае это означает, что в полученных данных инвертировано нечетное количество разрядов (произошла ошибка нечетной кратности).
Что произойдет, если в полученном пакете данных произойдет четное количество однобитовых ошибок? В этом случае получатель не сможет обнаружить ошибку. Если вероятность ошибки в одном разряде мала и можно предположить, что ошибки в отдельных разрядах возникают независимо друг от друга, тогда вероятность нескольких ошибок в одном пакете крайне мала. В таком случае единственного бита четности может быть достаточно. Однако практические наблюдения показали, что в действительности ошибки не являются независимыми, а часто группируются в пакеты ошибок. В случае пакетных ошибок вероятность того, что получатель не обнаружит ошибку в пакете, может приблизиться к величине 50 %. Очевидно, в такой ситуации требуется более надежная схема обнаружения ошибок! Но прежде чем перейти к изучению схем обнаружения ошибок, применяемых на практике, рассмотрим простую схему, которая обобщает предыдущую схему одноразрядного контроля четности и помогает понять принцип работы методов исправления ошибок.
На рис. 5.6 показано двухмерное обобщение одноразрядной схемы проверки на четность. В данной схеме d разрядов пакета данных разделяются на г строк и j столбцов, образуя прямоугольную матрицу. Значение четности вычисляется для каждой строки и каждого столбца. Получающиеся в результате i +j +1 битов четности образуют разряды обнаружения ошибок кадра канального уровня.

Предположим теперь, что в исходном блоке данных из d разрядов происходит однократная ошибка. В такой двухмерной схеме контроля четности об ошибке будут одновременно сигнализировать контрольные разряды строки и столбца. Таким образом, получатель сможет не только обнаружить сам факт ошибки, но и по номерам строки и столбца найти поврежденный бит данных и исправить его! На рисунке показан пример, в котором поврежден бит в позиции (2, 2) — он изменил свое значение с 1 на 0. Такую одиночную ошибку получатель может не только обнаружить, но и исправить. Хотя нас, в первую очередь, интересует обнаружение и исправление ошибок в исходных d разрядах, данная схема позволяет также обнаруживать и исправлять одиночные ошибки в самих битах четности. Кроме того, данная двухмерная схема контроля четности позволяет обнаруживать (но не исправлять!) любые комбинации из двух одиночных ошибок (то есть двойные ошибки) в пакете.
Способность приемника обнаруживать и исправлять ошибки иногда называют прямым исправлением ошибок (Forward Error Correction, FEC). Подобные приемы широко применяются в устройствах хранения и воспроизведения звука, например на лазерных компакт-дисках. В сетях методы обнаружения и исправления ошибок могут использоваться сами по себе, а также в сочетании с автоматическими запросами на повторную передачу, которые мы рассматривали в главе 3. Методы обнаружения и исправления ошибок очень полезны, так как позволяют снизить необходимое количество повторных передач. Кроме того (что, возможно, даже важнее), эти методы позволяют получателю немедленно исправлять ошибки. Таким образом, получатель данных может не ждать, пока отправитель получит его сообщение об ошибке и вышлет пакет еще раз, что может быть существенным преимуществом в сетевых приложениях реального времени.
Мой блог находят по следующим фразам
www.conlex.kz