Контрольная работа №3 (1 курс 2 семестр) «Ряды» Тематический план. Контрольная работа ряды
Проверочная работа по математике. Ряды. Сходимость числовых рядов. 2 курс
Контрольная работа. Ряды. Сходимость числовых рядов.
| Вариант 1 | Вариант 2 |
| Найдите первые четыре члена ряда по заданному общему члену:
А)  б) б)  | Найдите первые четыре члена ряда по заданному общему члену:
А)  б) б)  |
| Найдите формулу общего члена ряда:
А)  б) б)  | Найдите формулу общего члена ряда:
А) б) б)  |
| Исследовать ряд на сходимость, используя признак сравнения или предел общего члена:

| Исследовать ряд на сходимость, используя признак сравнения или предел общего члена:

|
| Используя признак Даламбера, исследовать ряд на сходимость:
a)  б)   | Используя признак Даламбера, исследовать ряд на сходимость:
a)  б)   |
| Исследовать ряд на сходимость:
а)   Б)   | Исследовать ряд на сходимость:
а)   Б)   |
xn--j1ahfl.xn--p1ai
Контрольная работа №3 (1 курс 2 семестр) «Ряды» Тематический план.
Числовой ряд и его сходимость.
Необходимое условие сходимости числового ряда.
Геометрический ряд. Гармонический ряд.
Ряды с положительными членами. Сравнение рядов.
Призрак Даламбера. Корневой признак Коши.
Интегральный признак сходимости ряда.
Признак Лейбница сходимости знакочередующегося ряда.
Ряды с членами любого знака. Абсолютная сходимость.
Свойства абсолютно сходящихся рядов.
Функциональный ряд. Область сходимости.
Степенной ряд. Теорема Абеля, радиус сходимости.
Интегрирование и дифференцирование степенных рядов.
Ряд Тейлора. Коэффициенты ряда Тейлора.
Разложение показательной и тригонометрических функций в ряд Тейлора. Формула Эйлера для показательной функции от мнимого аргумента.
Биномиальный ряд. Разложение логарифма в степенной ряд.
Тригонометрический ряд. Ряд Фурье. Коэффициенты ряда Фурье.
Неполные ряды Фурье. Свойства неполного ряда Фурье
Ряд Фурье в комплексной форме.
Преобразование Фурье. Понятие об интегральных преобразованиях.
Задания к контрольной работе №3.
Задачи 310-319.Исследовать сходимость числового ряда.
310. a)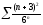 b)
b)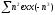
311. a) 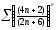 b)
b)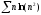
312. a) 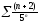 b)
b)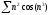
313. a) 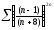 b)
b)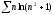
314. a) 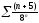 b)
b)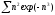
315. a) 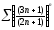 b)
b)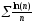
316. a) 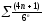 b)
b)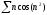
317. a) 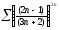 b)
b)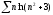
318. a) 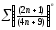 b)
b)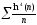
319. a) 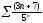 b)
b)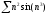
Задачи 320-329. Найти интервал сходимости степенного ряда.
320. a) 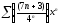 b)
b)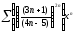
321. a) 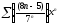 b)
b)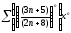
322. a) 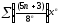 b)
b)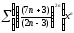
323. a) 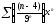 b)
b)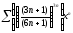
324. a) 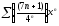 b)
b)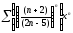
325. a) 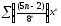 b)
b)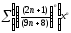
326. a) 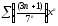 b)
b)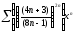
327. a) 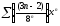 b)
b)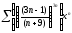
328. a) 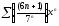 b)
b)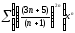
329. a) 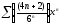 b)
b)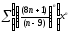
Задачи 330-339.Вычислить приближенное значение функцииf(х) в заданной точке, разложив ее в степенной ряд с точностью до четырех значимых слагаемых. Указать точность оценки.
330. 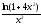
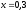 331.
331.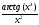
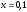
332. 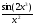
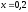 333.
333.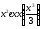
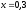
334. 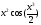
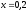 335.
335.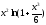
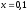
336. 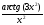
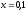 337.
337.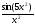
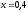
338. 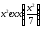
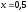 339.
339.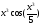
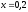
Задачи 340-349. Вычислить приближенное значение определенного интеграла 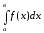 разложив подинтегральную функцию в степенной ряд с точностью до четырех значимых слагаемых и затем проинтегрировав его.
разложив подинтегральную функцию в степенной ряд с точностью до четырех значимых слагаемых и затем проинтегрировав его.
340. 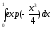 341.
341.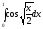
342. 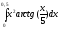 343.
343.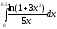
344. 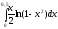 345.
345.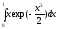
346. 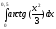 347.
347.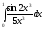
348. 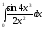 349.
349.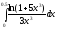
Задачи 350-359.Разложить данную функцию(х) в ряд Фурье в интервале
(а; в):
350. (х) = 2х + 1 в интервале (-1,1)
351. (х) = х + 4 в интервале (-2,2)
352. (х) = х - 1 в интервале (0,2)
353. (х) = 3 + х в интервале (-2,2)
354. (х) = -4 - 5х в интервале (-1,1)
355. (х) = 1 - 2х в интервале (-2,2)
356. (х) = х + 6 в интервале (-2,2)
357. (х) = х - 3 в интервале (0,2)
358. (х) = 3 - 4х в интервале (-2,2)
359. (х) = 2х + 3 в интервале (-2,2)
Контрольная работа №5 (2 курс 1 семестр) «Дифференциальные уравнения» Тематический план
Дифференциальное уравнение и его порядок. Задача Коши. Общее и частное решение, общий и частный интеграл.
Дифференциальные уравнения с разделяющимися переменными.
Однородные дифференциальные уравнения первого порядка.
Линейные дифференциальные уравнения первого порядка.
Интегрирование некоторых дифференциальных уравнений второго порядка путем понижения порядка уравнения.
Структура общего решения линейного дифференциального уравнения второго порядка без правой части.
Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами и без правой части. Характеристическое уравнение.
Структура общего решения линейного дифференциального уравнения с правой частью.
Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами и с правой частью специального вида.
Отыскание частного решения линейного дифференциального уравнения с постоянными коэффициентами и с правой частью специального вида.
Преобразование Лапласа.
Свойства преобразования Лапласа.
Изображения простейших оригиналов.
Основные теоремы операционного исчисления.
Изображение производных.
Теорема разложения в операционном исчислении.
Интегрирование дифференциальных уравнений операторным методом.
studfiles.net
Контрольная работа по теме: «Ряды»
ТестКонтрольная работа
по теме: «Ряды»Задача 1. Исследовать на сходимость числовой ряд  с помощью теорем сравнения.
с помощью теорем сравнения.
Решение.
Пусть  . Оценим
. Оценим  .
.
Так как  , то
, то  .
.
Увеличим числитель  - в результате дробь увеличится, затем уменьшим знаменатель - в результате дробь увеличится.
- в результате дробь увеличится, затем уменьшим знаменатель - в результате дробь увеличится.
 .
.
Ряд  сходится (ряд Дирихле, S = 2 >1). Следовательно, сходится ряд
сходится (ряд Дирихле, S = 2 >1). Следовательно, сходится ряд  .
.
Задача 2. Исследовать на сходимость числовой ряд  с помощью признака Даламбера.
с помощью признака Даламбера.
Решение.

 (гармонический ряд, S = 1).
(гармонический ряд, S = 1).
Следовательно, ряд  расходится.Задача 3. Исследовать на сходимость числовой ряд
расходится.Задача 3. Исследовать на сходимость числовой ряд  с помощью признака Коши.
с помощью признака Коши.
Решение.


Ряд  расходится.
расходится.
Задача 4. Найти сумму ряда  с точностью
с точностью  .
.
Решение.

Ряд  является знакочередующимся.
является знакочередующимся.
Так как  , то последовательность
, то последовательность  убывающая.
убывающая.
Следовательно, ряд  - ряд типа Лейбница.
- ряд типа Лейбница.
При этом  . По теореме Лейбница ряд
. По теореме Лейбница ряд  сходится.
сходится.
Сумма ряда  . Подберем такое n, при котором
. Подберем такое n, при котором  . Достаточно найти такое n, при котором
. Достаточно найти такое n, при котором  . Тогда
. Тогда  .
.


 Задача 5. Исследовать на сходимость числовой ряд с произвольными членами (в случае сходимости указать тип: абсолютная или условная):
Задача 5. Исследовать на сходимость числовой ряд с произвольными членами (в случае сходимости указать тип: абсолютная или условная):
а) 
б) 
Решение.
а) 

Значит, ряд  сходится абсолютно.б)
сходится абсолютно.б) 

По необходимому признаку сходимости ряд  расходится.
расходится.
Задача 6. Найти область сходимости степенного ряда  и исследовать его на сходимость на границе области.
и исследовать его на сходимость на границе области.
Решение.
 .
.
 .
.
Ряд  сходится на интервале
сходится на интервале  и расходится на интервалах
и расходится на интервалах  .
.
Исследуем поведение ряда  на границах интервала сходимости.
на границах интервала сходимости.
При  данный ряд принимает вид
данный ряд принимает вид

 , следовательно в точке
, следовательно в точке ряд ни сходится ни расходится.
ряд ни сходится ни расходится.
При  данный ряд принимает вид
данный ряд принимает вид
 , следовательно в точке
, следовательно в точке  ряд ни сходится ни расходится.
ряд ни сходится ни расходится.
Задача 7. Вычислить интеграл  с точностью
с точностью  .
.
Решение.
Разложим подынтегральную функцию в ряд Маклорена. Для этого используем формулу:

Преобразуем функцию  .
.

Здесь  .
.

Сходящийся степенной ряд можно почленно интегрировать, поэтому

Этот ряд знакочередующийся. Проверим, является ли он рядом типа Лейбница.
Проверим выполнение условия 

Последовательность  сходится. Значит, ряд является рядом типа Лейбница. Он сходится, так как
сходится. Значит, ряд является рядом типа Лейбница. Он сходится, так как
 .
.
Значит, сумма ряда  , если
, если  .
.
При 

При  .
.
При  .
.
При 

При 

При 



 .
.
Ответ:  .
.
shkolnie.ru
б)
б)
б)
б)
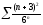 b)
b)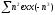
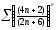 b)
b)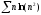
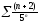 b)
b)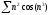
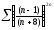 b)
b)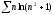
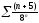 b)
b)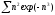
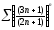 b)
b)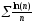
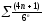 b)
b)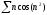
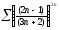 b)
b)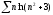
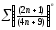 b)
b)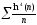
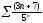 b)
b)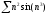
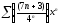 b)
b)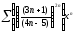
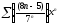 b)
b)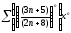
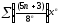 b)
b)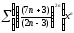
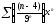 b)
b)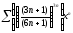
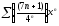 b)
b)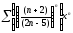
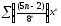 b)
b)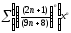
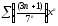 b)
b)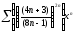
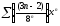 b)
b)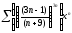
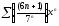 b)
b)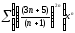
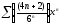 b)
b)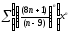
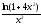
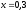 331.
331.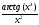
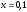
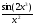
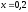 333.
333.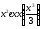
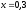
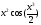
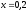 335.
335.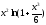
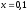
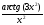
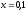 337.
337.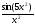
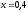
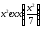
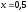 339.
339.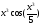
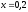
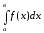 разложив подинтегральную функцию в степенной ряд с точностью до четырех значимых слагаемых и затем проинтегрировав его.
разложив подинтегральную функцию в степенной ряд с точностью до четырех значимых слагаемых и затем проинтегрировав его.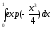 341.
341.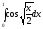
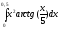 343.
343.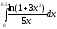
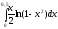 345.
345.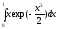
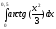 347.
347.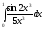
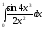 349.
349.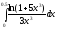
 с помощью теорем сравнения.
с помощью теорем сравнения. . Оценим
. Оценим  .
. , то
, то  .
. .
. сходится (ряд Дирихле, S = 2 >1). Следовательно, сходится ряд
сходится (ряд Дирихле, S = 2 >1). Следовательно, сходится ряд  с помощью признака Даламбера.
с помощью признака Даламбера.
 (гармонический ряд, S = 1).
(гармонический ряд, S = 1). с помощью признака Коши.
с помощью признака Коши.

 с точностью
с точностью  .
.
 является знакочередующимся.
является знакочередующимся. , то последовательность
, то последовательность  убывающая.
убывающая. . По теореме Лейбница ряд
. По теореме Лейбница ряд  . Подберем такое n, при котором
. Подберем такое n, при котором  . Достаточно найти такое n, при котором
. Достаточно найти такое n, при котором  . Тогда
. Тогда  .
.

 Задача 5. Исследовать на сходимость числовой ряд с произвольными членами (в случае сходимости указать тип: абсолютная или условная):
Задача 5. Исследовать на сходимость числовой ряд с произвольными членами (в случае сходимости указать тип: абсолютная или условная):



 и исследовать его на сходимость на границе области.
и исследовать его на сходимость на границе области. .
. .
. и расходится на интервалах
и расходится на интервалах  .
. данный ряд принимает вид
данный ряд принимает вид
 , следовательно в точке
, следовательно в точке данный ряд принимает вид
данный ряд принимает вид , следовательно в точке
, следовательно в точке  с точностью
с точностью  .
.
 .
.
 .
.



 сходится. Значит, ряд является рядом типа Лейбница. Он сходится, так как
сходится. Значит, ряд является рядом типа Лейбница. Он сходится, так как .
. , если
, если  .
.

 .
. .
.







 .
. .
.







