3 78* 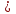 3 784; 2) 5 8*5
3 784; 2) 5 8*5 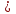 5 872.
5 872.
Контрольные работы по математике 5 класс
УМК Мерзляк А.Г., Полонский В.Б., Якир М.С.
Контрольная работа № 1
Натуральные числа
Вариант 1
Запишите цифрами число:
шестьдесят пять миллиардов сто двадцать три миллиона девятьсот сорок одна тысяча восемьсот тридцать семь;
восемьсот два миллиона пятьдесят четыре тысячи одиннадцать:
тридцать три миллиарда девять миллионов один.
Сравните числа: 1) 5 678 и 5 489; 2) 14 092 и 14 605.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 5, 7, 9.
Начертите отрезок FK, длина которого равна 5 см 6 мм, отметьте на нём точку C. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка К принадлежит отрезку МЕ, МК = 19 см, отрезок КЕ на 17 см больше отрезка МК. Найдите длину отрезка МЕ.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
3 78* 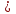 3 784; 2) 5 8*5
3 784; 2) 5 8*5 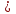 5 872.
5 872.
На отрезке CD длиной 40 см отметили точки P и Q так, что CP = 28 см, QD =26 см. Чему равна длина отрезка PQ?
Сравните: 1) 3 км и 2 974 м; 2) 912 кг и 8 ц.
Вариант 2
Запишите цифрами число:
семьдесят шесть миллиардов двести сорок два миллиона семьсот восемьдесят три тысячи сто девяносто пять;
четыреста три миллиона тридцать восемь тысяч сорок девять;
сорок восемь миллиардов семь миллионов два.
Сравните числа: 1) 6 894 и 6 983; 2) 12 471 и 12 324.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 3, 4, 6, 8.
Начертите отрезок АВ, длина которого равна 4 см 8 мм, отметьте на нём точку D. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка T принадлежит отрезку МN, МT = 19 см, отрезок TN на 18 см меньше отрезка МT. Найдите длину отрезка МN.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
2 *14 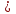 2 316; 2) 4 78*
2 316; 2) 4 78* 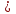 4 785.
4 785.
На отрезке SK длиной 30 см отметили точки A и B так, что SA = 14 см, BK =19 см. Чему равна длина отрезка AB?
Сравните: 1) 3 986 г и 4 кг; 2) 586 см и 6 м.
Вариант 3
Запишите цифрами число:
сорок семь миллиардов двести девяносто три миллиона восемьсот пятьдесят шесть тысяч сто двадцать четыре;
триста семь миллионов семьдесят восемь тысяч двадцать три;
восемьдесят пять миллиардов шесть миллионов пять.
Сравните числа: 1) 7 356 и 7 421; 2) 17 534 и 17 435.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 4, 6, 9.
Начертите отрезок MN, длина которого равна 6 см 4 мм, отметьте на нём точку A. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка E принадлежит отрезку CK, CE = 15 см, отрезок EK на 24 см больше отрезка CE. Найдите длину отрезка CK.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
3 344 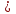 3 34*; 2) 2 724
3 34*; 2) 2 724 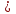 * 619.
* 619.
На отрезке AC длиной 60 см отметили точки E и F так, что AE = 32 см, FC =34 см. Чему равна длина отрезка EF?
Сравните: 1) 6 т и 5 934кг; 2) 4 м и 512 см.
Вариант 4
Запишите цифрами число:
восемьдесят шесть миллиардов пятьсот сорок один миллион триста семьдесят две тысячи триста сорок два;
шестьсот пять миллионов восемьдесят три тысячи десять;
сорок четыре миллиарда девять миллионов три.
Сравните числа: 1) 9 561 и 9 516; 2) 18 249 и 18 394.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 5, 8, 10.
Начертите отрезок АВ, длина которого равна 7 см 8 мм, отметьте на нём точку D. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка A принадлежит отрезку BM, BA = 25 см, отрезок AM на 9 см меньше отрезка BA. Найдите длину отрезка BM.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
5 64* 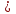 5 646; 2) 1 4*2
5 646; 2) 1 4*2 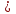 1 431.
1 431.
На отрезке OP длиной 50 см отметили точки M и N так, что OM = 24 см, NP =38 см. Чему равна длина отрезка M N?
Сравните: 1) 8 км и 7 962 м; 2) 60 см и 602 мм.
Контрольная работа № 2
Сложение и вычитание натуральных чисел. Числовые и буквенные выражения. Формулы.
Вариант 1
Вычислите: 1) 15 327+ 496 383; 2) 38 020 405 – 9 497 653.
На одной стоянке было 143 автомобиля, что на 17 автомобилей больше, чем на второй. Сколько автомобилей было на обеих стоянках?
Выполните сложение, выбирая удобный порядок вычислений:
(325 + 791) + 675; 2) 428 + 856 + 572 + 244.
Проверьте, верно ли неравенство:
1 674 – (736 + 328) 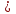 2 000 – (1 835 – 459).
2 000 – (1 835 – 459).
Найдите значение по формуле = 4 – 16 при = 8.
Упростите выражение 126 + + 474 и найдите его значение при = 278.
Вычислите:
4 м 73 см + 3 м 47 см; 2) 12 ч 16 мин – 7 ч 32 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(713 + 529) – 413; 2) 624 – (137 + 224).
Вариант 2
Вычислите: 1) 17 824+ 128 356; 2) 42 060 503 – 7 456 182.
На одной улице 152 дома, что на 18 домов меньше, чем на другой. Сколько всего домов на обеих улицах?
Выполните сложение, выбирая удобный порядок вычислений:
(624 + 571) + 376; 2) 212 + 497 + 788 + 803.
Проверьте, верно ли неравенство:
1 826 – (923 + 249) 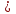 3 000 – (2 542 – 207).
3 000 – (2 542 – 207).
Найдите значение по формуле = 40 – 7 при = 4.
Упростите выражение 235 + y + 465 и найдите его значение при y = 153.
Вычислите:
6 м 23 см + 5 м 87 см; 2) 14 ч 17 мин – 5 ч 23 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(837 + 641) – 537; 2) 923 – (215 + 623).
Вариант 3
Вычислите: 1) 26 832 + 573 468; 2) 54 073 507 – 6 829 412.
В одном классе 37 учащихся, что на 9 человек больше, чем во втором. Сколько всего учащихся в обоих классах?
Выполните сложение, выбирая удобный порядок вычислений:
(736 + 821) + 264; 2) 573 + 381 + 919 + 627.
Проверьте, верно ли неравенство:
2 491 – (543 + 1 689) 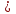 1 000 – (931 – 186).
1 000 – (931 – 186).
Найдите значение по формуле = 3 + 18 при = 5.
Упростите выражение 433 + + 267 и найдите его значение при = 249.
Вычислите:
7 м 23 см + 4 м 81 см; 2) 6 ч 38 мин – 4 ч 43 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(674 + 245) – 374; 2) 586 – (217 + 186).
Вариант 4
Вычислите: 1) 19 829 + 123 471; 2) 61 030 504 – 8 695 371.
На одной книжной полке стоят 23 книги, что на 5 книг меньше, чем на другой. Сколько всего книг стоит на обеих полках?
Выполните сложение, выбирая удобный порядок вычислений:
(349 + 856) + 651; 2) 166 + 452 + 834 + 748.
Проверьте, верно ли неравенство:
1 583 – (742 + 554) 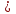 1 000 – (883 – 72).
1 000 – (883 – 72).
Найдите значение по формуле = 16 + 8 при = 7.
Упростите выражение 561 + + 139 и найдите его значение при = 165.
Вычислите:
9 м 41 см + 4 м 72 см; 2) 18 ч 18 мин – 5 ч 24 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(563 + 721) – 363; 2) 982 – (316 + 582).
Контрольная работа № 3
Уравнение. Угол. Многоугольники.
Вариант 1
Постройте угол МКА, величина которого равна 74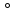 . Проведите произвольно луч КС между сторонами угла МКА. Запишите образовавшиеся углы и измерьте их величины.
. Проведите произвольно луч КС между сторонами угла МКА. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) +37 = 81 2) 150 – = 98.
Одна из сторон треугольника равна 24 см, вторая – в 4 раза короче первой, а третья – на 16 см длиннее второй. Вычислите периметр треугольника.
Решите уравнение: 1) (34 + ) – 83 = 42 2) 45 – ( – 16) = 28.
Из вершины развёрнутого угла АВС (см рис.) проведены два луча ВD и ВЕ так, что ∠АВЕ = 154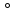 , ∠DВС = 128
, ∠DВС = 128 . Вычислите градусную меру угла DВЕ.
. Вычислите градусную меру угла DВЕ.
Какое число надо подставить вместо , чтобы корнем уравнения
52 – ( – ) = 24 было число 40?
Вариант 2
Постройте угол ABC, величина которого равна 168 . Проведите произвольно луч BM между сторонами угла ABC. Запишите образовавшиеся углы и измерьте их величины.
. Проведите произвольно луч BM между сторонами угла ABC. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) 21 + = 58 2) – 135 = 76.
Одна из сторон треугольника равна 32 см, вторая – в 2 раза короче первой, а третья – на 6 см короче первой. Вычислите периметр треугольника.
Решите уравнение: 1) (96 – ) – 15 = 64 2) 31 – ( + 11) = 18.
Из вершины прямого угла MNK (см рис.) проведены два луча ND и NE так, что ∠MND = 73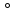 , ∠KNF = 48
, ∠KNF = 48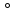 . Вычислите градусную меру угла DNF.
. Вычислите градусную меру угла DNF.
Какое число надо подставить вместо , чтобы корнем уравнения
64 – ( – ) = 17 было число 16?
Вариант 3
Постройте угол FDK, величина которого равна 56 . Проведите произвольно луч DT между сторонами угла FDK. Запишите образовавшиеся углы и измерьте их величины.
. Проведите произвольно луч DT между сторонами угла FDK. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) + 42 = 94 2) 284 – = 121.
Одна из сторон треугольника равна 12 см, вторая – в 3 раза длиннее первой, а третья – на 8 см короче второй. Вычислите периметр треугольника.
Решите уравнение: 1) (41 + ) – 12 = 83 2) 62 – ( – 17) = 31.
Из вершины развёрнутого угла FAN (см рис.) проведены два луча AK и AP так, что ∠NAP = 110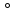 , ∠FAK = 132
, ∠FAK = 132 . Вычислите градусную меру угла PAK.
. Вычислите градусную меру угла PAK.
Какое число надо подставить вместо , чтобы корнем уравнения
(69 – ) – = 23 было число 12?
Вариант 4
Постройте угол NMC, величина которого равна 58 . Проведите произвольно луч MB между сторонами угла NMC. Запишите образовавшиеся углы и измерьте их величины.
. Проведите произвольно луч MB между сторонами угла NMC. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) + 53 = 97 2) 142 – = 76.
Одна из сторон треугольника равна 30 см, вторая – в 5 раза короче первой, а третья – на 22 см длиннее второй. Вычислите периметр треугольника.
Решите уравнение: 1) (58 + ) – 23 = 96 2) 54 – ( – 19) = 35.
Из вершины прямого угла DMK (см рис.) проведены два луча MB и MC так, что ∠DMB = 51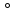 , ∠KMC = 65
, ∠KMC = 65 . Вычислите градусную меру угла BMC.
. Вычислите градусную меру угла BMC.
Какое число надо подставить вместо , чтобы корнем уравнения
( – ) – 14 = 56 было число 5?
 Контрольная работа № 4
Контрольная работа № 4
Умножение и деление натуральных чисел. Свойства умножения.
Вариант 1
Вычислите:
36 ∙ 2 418; 3) 1 456 : 28;
175 ∙ 204; 4) 177 000 : 120.
Найдите значение выражения: (326 ∙ 48 – 9 587) : 29.
Решите уравнение:
∙ 14 = 364; 2) 324 : = 9; 3) 19 - 12 = 126.
Найдите значение выражения наиболее удобным способом:
25 ∙ 79 ∙ 4; 2) 43 ∙ 89 + 89 ∙ 57.
Купили 7 кг конфет и 9 кг печенья, заплатив за всю покупку 1 200 р. Сколько стоит 1 кг печенья, если 1 кг конфет стоит 120 р?
С одной станции одновременно в одном направлении отправились два поезда. Один из поездов двигался со скоростью 56 км/ч, а второй – 64 км/ч. Какое расстояние будет между поездами через 6 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 19 до 35 включительно?
Вариант 2
Вычислите:
24 ∙ 1 246; 3) 1 856 : 32;
235 ∙ 108; 4) 175 700 : 140.
Найдите значение выражения: (625 ∙ 25 – 8 114) : 37.
Решите уравнение:
∙ 28 = 336; 2) 312 : = 8; 3) 16 - 11 = 225.
Найдите значение выражения наиболее удобным способом:
2 ∙ 83 ∙ 50; 2) 54 ∙ 73 + 73 ∙ 46.
Для проведения ремонта электрической проводки купили 16 одинаковых мотков алюминиевого и 11 одинаковых мотков медного провода. Общая длина купленного провода составляла 650 м. Сколько метров алюминиевого провода было в мотке, если медного провода в одном мотке было 30 м?
Из одного города одновременно в одном направлении выехали два автомобиля. Один из них двигался со скоростью 74 км/ч, а второй – 68 км/ч. Какое расстояние будет между автомобилями через 4 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 23 до 42 включительно?
Вариант 3
Вычислите:
32 ∙ 1 368; 3) 1 664 : 26;
145 ∙ 306; 4) 216 800 : 160.
Найдите значение выражения: (546 ∙ 31 – 8 154) : 43.
Решите уравнение:
∙ 22 = 396; 2) 318 : = 6; 3) 19 - 7 = 144.
Найдите значение выражения наиболее удобным способом:
5 ∙ 97 ∙ 20; 2) 68 ∙ 78 - 78 ∙ 58.
В автомобиль погрузили 5 одинаковых мешков сахара и 3 одинаковых мешка муки. Оказалось, что общая масса груза равна 370 кг. Какова масса одного мешка муки, если масса одного мешка сахара равна 50 кг?
Из одного села одновременно в одном направлении отправились пешеход и велосипедист. Пешеход двигался со скоростью 3 км/ч, а велосипедист – 12 км/ч. Какое расстояние будет между ними через 3 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 34 до 53 включительно?
Вариант 4
Вычислите:
28 ∙ 2 346; 3) 1 768 : 34;
185 ∙ 302; 4) 220 500 : 180.
Найдите значение выражения: (224 ∙ 46 – 3 232) : 34.
Решите уравнение:
∙ 16 = 384; 2) 371 : = 7; 3) 22 - 14 = 112.
Найдите значение выражения наиболее удобным способом:
2 ∙ 87 ∙ 50; 2) 167 ∙ 92 - 92 ∙ 67.
В школьную столовую завезли 8 одинаковых ящиков яблок и 6 одинаковых ящиков апельсинов. Сколько килограммов апельсинов было в одном ящике, если всего было 114 кг яблок и апельсинов, а яблок в каждом ящике было 9 кг?
От одной пристани одновременно в одном направлении отплыли лодка и катер. Лодка плыла со скоростью 14 км/ч, а катер – 21 км/ч. Какое расстояние будет между ними через 5 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 41 до 64 включительно?
Контрольная работа № 5
Деление с остатком. Площадь прямоугольника. Прямоугольный параллелепипед и его объем. Комбинаторные задачи.
Вариант 1
Выполните деление с остатком: 478 : 15.
Найдите площадь прямоугольника, одна сторона которого равна 14 см, а вторая сторона в 3 раза больше первой.
Вычислите объем и площадь поверхности куба с ребром 3 см.
Длина прямоугольного параллелепипеда равна 18 см, ширина – в 2 раза меньше длины, а высота – на 11 см больше ширины. Вычислите объем параллелепипеда.
Чему равно делимое, если делитель равен 11, неполное частное – 7, а остаток – 6?
Поле прямоугольной формы имеет площадь 6 га. Ширина поля 150 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 5, 6 и 0 (цифры не могут повторяться).
Сумма длин всех рёбер прямоугольного параллелепипеда равна 116 см, а два его измерения – 12 см и 11 см. Найдите третье измерение параллелепипеда.
Вариант 2
Выполните деление с остатком: 376 : 18.
Найдите площадь прямоугольника, одна сторона которого равна 21 см, а вторая сторона в 3 раза меньше первой.
Вычислите объем и площадь поверхности куба с ребром 4 дм.
Ширина прямоугольного параллелепипеда равна 6 см, длина – в 5 раз больше ширины, а высота – на 5 см меньше длины. Вычислите объем параллелепипеда.
Чему равно делимое, если делитель равен 17, неполное частное – 5, а остаток – 12?
Поле прямоугольной формы имеет площадь 3 га, его длина – 200 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 0, 9 и 4 (цифры не могут повторяться).
Сумма длин всех рёбер прямоугольного параллелепипеда равна 80 см, а два его измерения – 10 см и 4 см. Найдите третье измерение параллелепипеда.
Вариант 3
Выполните деление с остатком: 516 : 19.
Найдите площадь прямоугольника, одна сторона которого равна 17 см, а вторая сторона в 2 раза больше первой.
Вычислите объем и площадь поверхности куба с ребром 5 дм.
Высота прямоугольного параллелепипеда равна 20 см, длина – на 4 см больше высоты, а ширина – в 2 раза меньше длины. Вычислите объем параллелепипеда.
Чему равно делимое, если делитель равен 14, неполное частное – 8, а остаток – 9?
Поле прямоугольной формы имеет площадь 7 га, его длина – 350 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 1, 2 и 0 (цифры не могут повторяться).
Сумма длин всех рёбер прямоугольного параллелепипеда равна 100 дм, а два его измерения – 8 дм и 13 дм. Найдите третье измерение параллелепипеда.
Вариант 4
Выполните деление с остатком: 610 : 17.
Найдите площадь прямоугольника, одна сторона которого равна 45 см, а вторая сторона в 5 раз меньше первой.
Вычислите объем и площадь поверхности куба с ребром 2 см.
Длина прямоугольного параллелепипеда равна 20 см, высота – в 4 раза меньше длины, а ширина – на 7 см больше высоты. Вычислите объем параллелепипеда.
Чему равно делимое, если делитель равен 15, неполное частное – 6, а остаток – 14?
Поле прямоугольной формы имеет площадь 4 га, его ширина – 50 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 7, 0 и 8 (цифры не могут повторяться).
Сумма длин всех рёбер прямоугольного параллелепипеда равна 72 см, а два его измерения – 6 см и 8 см. Найдите третье измерение параллелепипеда.
Контрольная работа № 6
Обыкновенные дроби
Вариант 1
Сравните числа:
 и
и  ; 2)
; 2) 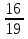 и 1; 3)
и 1; 3) 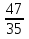 и 1.
и 1.
Выполните действия:
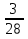 +
+ 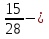
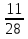 ; 3)
; 3) 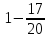 ;
;
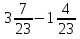 + 5
+ 5 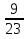 ; 4)
; 4) 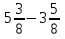 .
.
В саду растёт 72 дерева, из них 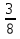 составляют яблони. Сколько яблонь растёт в саду?
составляют яблони. Сколько яблонь растёт в саду?
Кирилл прочёл 56 страниц, что составило 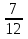 книги. Сколько страниц было в книге?
книги. Сколько страниц было в книге?
Преобразуйте в смешанное число дробь:
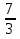 ; 2)
; 2) 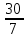 .
.
Найдите все натуральные значения , при которых верно неравенство 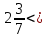
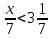 .
.
Каково наибольшее натуральное значение n, при котором верно неравенство n 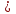
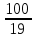 ?
?
Найдите все натуральные значения , при которых одновременно выполняются условия: дробь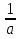 правильная, а дробь
правильная, а дробь 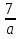 неправильная.
неправильная.
Вариант 2
Сравните числа:
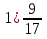 и
и 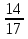 ; 2)
; 2) 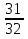 и 1; 3)
и 1; 3) 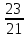 и 1.
и 1.
Выполните действия:
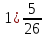 +
+ 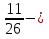
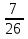 ; 3)
; 3) 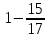 ;
;
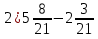 + 1
+ 1 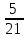 ; 4)
; 4) 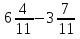 .
.
В гараже стоят 63 машины, из них 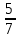 составляют легковые. Сколько легковых машин стоит в гараже?
составляют легковые. Сколько легковых машин стоит в гараже?
В классе 12 учеников изучают французский язык, что составляет 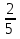 всех учеников класса. Сколько учеников в классе?
всех учеников класса. Сколько учеников в классе?
Преобразуйте в смешанное число дробь:
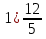 ; 2)
; 2) 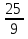 .
.
Найдите все натуральные значения , при которых верно неравенство 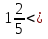
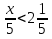 .
.
Каково наименьшее натуральное значение n, при котором верно неравенство n 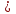
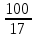 ?
?
Найдите все натуральные значения , при которых одновременно выполняются условия: дробь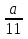 правильная, а дробь
правильная, а дробь 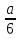 неправильная.
неправильная.
Вариант 3
Сравните числа:
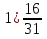 и
и 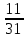 ; 2)
; 2) 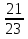 и 1; 3)
и 1; 3) 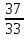 и 1.
и 1.
Выполните действия:
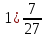 +
+ 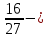
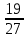 ; 3)
; 3) 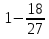 ;
;
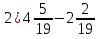 + 7
+ 7 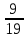 ; 4)
; 4) 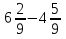 .
.
В классе 36 учеников, из них 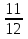 занимаются спортом. Сколько учеников занимаются спортом?
занимаются спортом. Сколько учеников занимаются спортом?
Ваня собрал 16 вёдер картофеля, что составляет 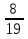 всего урожая. Сколько вёдер картофеля составляет урожай?
всего урожая. Сколько вёдер картофеля составляет урожай?
Преобразуйте в смешанное число дробь:
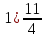 ; 2)
; 2) 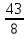 .
.
Найдите все натуральные значения , при которых верно неравенство 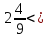
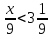 .
.
Каково наибольшее натуральное значение n, при котором верно неравенство n 
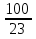 ?
?
Найдите все натуральные значения , при которых обе дроби 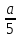 и
и 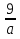 одновременно будут неправильными.
одновременно будут неправильными.
Вариант 4
Сравните числа:
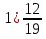 и
и 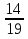 ; 2)
; 2) 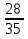 и 1; 3)
и 1; 3) 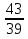 и 1.
и 1.
Выполните действия:
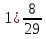 +
+ 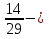
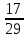 ; 3)
; 3) 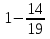 ;
;
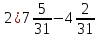 + 2
+ 2 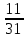 ; 4)
; 4) 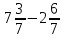 .
.
В пятых классах 64 ученика, из них 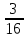 составляют отличники. Сколько отличников в пятых классах?
составляют отличники. Сколько отличников в пятых классах?
Мама приготовила вареники с творогом, а Коля съел 9 штук, что составляет 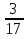 всех вареников. Сколько вареников приготовила мама?
всех вареников. Сколько вареников приготовила мама?
Преобразуйте в смешанное число дробь:
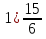 ; 2)
; 2) 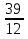 .
.
Найдите все натуральные значения , при которых верно неравенство 2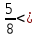
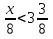 .
.
Каково наименьшее натуральное значение n, при котором верно неравенство n 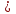
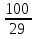 ?
?
Найдите все натуральные значения , при которых одновременно выполняются условия: дробь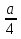 будет неправильная, а дробь
будет неправильная, а дробь 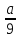 правильная.
правильная.
Контрольная работа № 7
Понятие о десятичной дроби. Сравнение, округление, сложение и вычитание десятичных дробей.
Вариант 1
Сравните: 1) 14,396 и 14,4; 2) 0,657 и 0, 6565.
Округлите: 1) 16,76 до десятых; 2) 0,4864 до тысячных.
Выполните действия: 1) 3,87 + 32,496; 2) 23,7 – 16,48; 3) 20 – 12,345.
Скорость катера по течению реки равна 24,2 км/ч, а собственная скорость катера – 22,8 км/ч. Найдите скорость катера против течения реки.
Вычислите, записав данные величины в килограммах:
3,4 кг + 839 г; 2) 2 кг 30 г – 1956 г.
Одна сторона треугольника равна 5,6 см, что на 1,4 см больше второй стороны и на 0,7 см меньше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 5,74 и меньше 5,76.
Найдите значение выражения, выбирая удобный порядок вычислений:
(8,63 + 3,298) – 5,63; 2) 0,927 – (0,327 + 0,429).
Вариант 2
Сравните: 1) 17,497 и 17,5; 2) 0,346 и 0, 3458.
Округлите: 1) 12,88 до десятых; 2) 0,3823 до сотых.
Выполните действия: 1) 5,62 + 43,299; 2) 25,6 – 14,52; 3) 30 – 14,265.
Скорость катера против течения реки равна 18,6 км/ч, а собственная скорость
катера – 19,8 км/ч. Найдите скорость катера по течению реки.
Вычислите, записав данные величины в метрах:
8,3 м + 784 см; 2) 5 м 4 см – 385 см.
Одна сторона треугольника равна 4,5 см, что на 3,3 см меньше второй стороны и на 0,6 см больше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 3,82 и меньше 3,84.
Найдите значение выражения, выбирая удобный порядок вычислений:
(5,94 + 2,383) – 3,94; 2) 0,852 – (0,452 + 0,214).
Вариант 3
Сравните: 1) 12,598 и 12,6; 2) 0,257 и 0, 2569.
Округлите: 1) 17,56 до десятых; 2) 0,5864 до тысячных.
Выполните действия: 1) 4,36 + 27,647; 2) 32,4 – 17,23; 3) 50 – 22,475.
Скорость катера по течению реки равна 19,6 км/ч, а собственная скорость катера – 18,3 км/ч. Найдите скорость катера против течения реки.
Вычислите, записав данные величины в центнерах:
6,7 ц + 584 кг; 2) 6 ц 2 кг – 487 кг.
Одна сторона треугольника равна 3,7 см, что на 0,9 см больше второй стороны и на 1,2 см меньше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 7,87 и меньше 7,89.
Найдите значение выражения, выбирая удобный порядок вычислений:
(6,73 + 4,594) – 2,73; 2) 0,791 – (0,291 + 0,196).
Вариант 4
Сравните: 1) 16,692 и 16,7; 2) 0,745 и 0, 7438.
Округлите: 1) 24,87 до десятых; 2) 0,8653 до тысячных.
Выполните действия: 1) 6,72 + 54,436; 2) 27,6 – 15,72; 3) 40 – 11,825.
Скорость катера против течения реки равна 17,8 км/ч, а собственная скорость
катера – 19,4 км/ч. Найдите скорость катера по течению реки.
Вычислите, записав данные величины в метрах:
2,8 м + 524 см; 2) 4 м 6 см – 257 см.
Одна сторона треугольника равна 5,1 см, что на 2,1 см меньше второй стороны и на 0,7 см больше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 1,34 и меньше 1,36.
Найдите значение выражения, выбирая удобный порядок вычислений:
(7,86 + 4,183) – 2,86; 2) 0,614 – (0,314 + 0,207).
Контрольная работа № 8
Умножение и деление десятичных дробей
Вариант 1
Вычислите:
0,024 ∙ 4,5; 3) 2,86 : 100; 5) 0,48 : 0,8;
29,41 ∙ 1 000; 4) 4 : 16; 6) 9,1 : 0,07.
Найдите значение выражения: (4 – 2,6) ∙ 4,3 + 1,08 : 1,2.
Решите уравнение: 2,4 ( + 0,98) = 4,08.
Моторная лодка плыла 1,4 ч по течению реки и 2,2 ч против течения. Какой путь преодолела лодка за всё время движения, если скорость течения равна 1,7 км/ч, а собственная скорость лодки – 19,8 км/ч?
Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она увеличится на 14,31. Найдите эту дробь.
Вариант 2
Вычислите:
0,036 ∙ 3,5; 3) 3,68 : 100; 5) 0,56 : 0,7;
37,53 ∙ 1 000; 4) 5 : 25; 6) 5,2 : 0,04.
Найдите значение выражения: (5 – 2,8) ∙ 2,4 + 1,12 : 1,6.
Решите уравнение: 0,084 : (6,2 – ) = 1,2.
Катер плыл 1,6 ч против течения реки и 2,4 ч по течению. На сколько больше проплыл катер, двигаясь по течению реки, чем против течения, если скорость течения реки равна 2,1 км/ч, а собственная скорость катера – 28,2 км/ч?
Если в некоторой десятичной дроби перенести запятую влево через одну цифру, то она уменьшится на 23,76. Найдите эту дробь.
Вариант 3
Вычислите:
0,064 ∙ 6,5; 3) 4,37 : 100; 5) 0,63 : 0,9;
46,52 ∙ 1 000; 4) 6 : 15; 6) 7,2 : 0,03.
Найдите значение выражения: (6 – 3,4) ∙ 1,7 + 1,44 : 1,6.
Решите уравнение: 1,6 ( + 0,78) = 4,64.
Теплоход плыл 1,8 ч против течения реки и 2,6 ч по течению. Какой путь преодолел теплоход за всё время движения, если скорость течения равна 2,5 км/ч, а собственная скорость теплохода – 35,5 км/ч?
Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она увеличится на 15,93. Найдите эту дробь.
Вариант 4
Вычислите:
0,096 ∙ 5,5; 3) 7,89 : 100; 5) 0,76 : 0,4;
78,53 ∙ 100; 4) 6 : 24; 6) 8,4 : 0,06.
Найдите значение выражения: (7 – 3,6) ∙ 2,8 + 1,32 : 2,2.
Решите уравнение: 0,144 : (3,4 – ) = 2,4.
Моторная лодка плыла 3,6 ч против течения реки и 1,8 ч по течению. На сколько километров больше проплыла лодка, двигаясь против течения , чем по течению, если скорость течения реки равна 1,2 км/ч, а собственная скорость лодки – 22,4 км/ч?
Если в некоторой десятичной дроби перенести запятую влево через одну цифру, то она уменьшится на 29,52. Найдите эту дробь.
Контрольная работа № 9
Среднее арифметическое. Проценты.
Вариант 1
Найдите среднее арифметическое чисел: 32,6; 38,5; 34; 35,3.
Площадь поля равна 300 га. Рожью засеяли 18 % поля. Сколько гектаров поля засеяли рожью?
Петя купил книгу за 90 р., что составляет 30 % всех денег, которые у него были. Сколько денег было у Пети?
Лодка плыла 2 ч со скоростью 12,3 км/ч и 4 ч со скоростью 13,2 км/ч. Найдите среднюю скорость лодки на всём пути.
Турист прошёл за три дня 48 км. В первый день он прошёл 35 % всего маршрута. Путь пройденный в первый день, составляет 80 % расстояния , пройденного во второй день. Сколько километров прошёл турист в третий день?
В первый день Петя прочитал 40 % всей книги, во второй – 60 % остального, а в третий - оставшиеся 144 страницы. Сколько всего страниц в книге?
Вариант 2
Найдите среднее арифметическое чисел: 26,3; 20,2; 24,7; 18.
В школе 800 учащихся. Сколько пятиклассников в этой школе, если известно, что их количество составляет 12 % количества всех учащихся?
Насос перекачал в бассейн 42 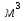 воды, что составляет 60 % объёма бассейна. Найдите объём бассейна.
воды, что составляет 60 % объёма бассейна. Найдите объём бассейна.
Автомобиль ехал 3 ч со скоростью 62,6 км/ч и 2 ч со скоростью 65 км/ч. Найдите среднюю скорость автомобиля на всём пути.
Токарь за три дня изготовил 80 деталей. В первый день он выполнил 30 % всей работы. Известно, что количество деталей, изготовленных в первый день, составляет 60 % количества деталей , изготовленных во второй день. Сколько деталей изготовил токарь в третий день?
В первый день тракторная бригада вспахала 30 % площади всего поля, во второй – 75% остального, а в третий - оставшиеся 14 га. Найдите площадь поля.
Вариант 3
Найдите среднее арифметическое чисел: 26,4; 42,6; 31,8; 15.
В магазин завезли 600 кг овощей. Картофель составляет 24% всех завезённых овощей. Сколько килограммов картофеля завезли в магазин?
За первый день турист прошёл расстояние 18 км, что составляет 40 % всего пути, который он должен преодолеть. Найдите длину пути, который должен пройти турист.
Катер плыл 1,5 ч со скоростью 34 км/ч и 2,5 ч со скоростью 30 км/ч. Найдите среднюю скорость катера на всём пути.
За три дня оператор набрал на компьютере 60 страниц. В первый день было выполнено 35 % всей работы. Объём работы, выполненной в первый день, составляет 70 % работы, выполненной во второй день. Сколько страниц было набрано в третий день?
За первый час было продано 84 % всего мороженого, за второй – 78 % остального, а за третий – оставшиеся 44 порции. Сколько порций мороженого было продано за три часа?
Вариант 4
Найдите среднее арифметическое чисел: 43,6; 21,8; 32,4; 11.
Площадь парка равна 40 га. Площадь озера составляет 15 % площади парка. Найдите площадь озера.
За первый час движения автомобиль преодолел расстояние 72 км, что составляет 24 % длины всего пути, который ему надо проехать. Найдите общий путь, который преодолел автомобиль.
Черепаха ползла 2 ч со скоростью 15,3 м/ч и 3 ч со скоростью 12, 4 м/ч. Найдите среднюю скорость черепахи на всём пути.
Три насоса наполнили водой бассейн объёмом 320 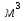 . Первый насос заполнил бассейн на 30 %, что составляет 80 % объёма воды, которую перекачал второй насос. Найдите объём воды, которую перекачал третий насос.
. Первый насос заполнил бассейн на 30 %, что составляет 80 % объёма воды, которую перекачал второй насос. Найдите объём воды, которую перекачал третий насос.
В первый день турист прошёл 20% всего пути, во второй – 60 % остального, а в третий – оставшиеся 24 км. Найдите длину пути, который прошёл турист за три дня.
Контрольная работа № 10
Обобщение и систематизация знаний учащихся
за курс математики 5 класса
Вариант 1
Найдите значение выражения: (4,1 – 0,66 : 1,2) ∙ 0,6.
Миша шёл из одного села в другое 0,7 ч по полю и 0,9 ч через лес, пройдя всего 5,31 км. С какой скоростью шёл Миша через лес, если по полю он двигался со скоростью 4,5 км/ч?
Решите уравнение: 9,2 – 6,8 + 0,64 = 1
Ширина прямоугольного параллелепипеда равна 4 см, что составляет 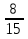 его длины, а высота составляет 40 % длины. Вычислите объем параллелепипеда.
его длины, а высота составляет 40 % длины. Вычислите объем параллелепипеда.
Выполните действия: 20 : (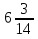 +
+ 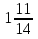 ) – (
) – (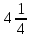 –
– 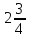 ) : 5.
) : 5.
Среднее арифметическое четырёх чисел равно 1,4, а среднее арифметическое трёх других чисел – 1,75. Найдите среднее арифметическое этих семи чисел.
Вариант 2
Найдите значение выражения: (0,49 : 1,4 – 0,325) ∙ 0,8.
Катер плыл 0,4 ч по течению реки и 0,6 ч против течения, преодолев всего 16,8 км. С какой скоростью плыл катер по течению, если против течения он плыл со скоростью 16 км/ч?
Решите уравнение: 7,2 – 5,4 + 0,55 = 1
Ширина прямоугольного параллелепипеда равна 3,6 см, что составляет 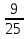 его длины, а высота составляет 42 % длины. Вычислите объем параллелепипеда.
его длины, а высота составляет 42 % длины. Вычислите объем параллелепипеда.
Выполните действия: 30 : (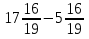 ) + (
) + (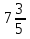 –
– 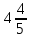 ) : 7.
) : 7.
Среднее арифметическое трёх чисел равно 2,5, а среднее арифметическое двух других чисел – 1,7. Найдите среднее арифметическое этих пяти чисел.
Вариант 3
Найдите значение выражения: (5,25 – 0,63 : 1,4) ∙ 0,4.
Пётр шёл из села к озеру 0,7 ч по одной дороге, а возвратился по другой дороге за 0,8 ч, пройдя всего 6,44 км. С какой скоростью шёл Пётр к озеру, если возвращался он со скоростью 3,5 км/ч?
Решите уравнение: 7,8 – 4,6 + 0,8 = 12.
Ширина прямоугольного параллелепипеда равна 4,8 см, что составляет 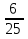 его длины, а высота составляет 45 % длины. Вычислите объем параллелепипеда.
его длины, а высота составляет 45 % длины. Вычислите объем параллелепипеда.
Выполните действия: 10 : (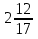 +
+ 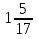 ) – (
) – (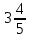 + 1
+ 1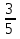 ) : 6.
) : 6.
Среднее арифметическое пяти чисел равно 2,3, а среднее арифметическое трёх других чисел – 1,9. Найдите среднее арифметическое этих восьми чисел.
Вариант 4
Найдите значение выражения: (4,4 – 0,63 :1,8) ∙ 0,8.
Автомобиль ехал 0,9 ч по асфальтированной дороге и 0,6 ч по грунтовой, проехав всего 93,6 км. С какой скоростью двигался автомобиль по асфальтированной дороге, если по грунтовой он ехал со скоростью 48 км/ч?
Решите уравнение: 3,23 + 0,97 + 0,74 = 2.
Ширина прямоугольного параллелепипеда равна 3,2 см, что составляет 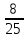 его длины, а высота составляет 54 % длины. Вычислите объем параллелепипеда.
его длины, а высота составляет 54 % длины. Вычислите объем параллелепипеда.
Выполните действия: 50 : (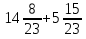 ) – (
) – ( –
–  ) : 9.
) : 9.
Среднее арифметическое шести чисел равно 2,8, а среднее арифметическое четырёх других чисел – 1,3. Найдите среднее арифметическое этих десяти чисел.
infourok.ru
Контрольно-измерительные материалы
по предмету «Математика» в 6 классе,
учебник Математика. 6 класс. Мерзляк А.Г., Полонский В.Б., Якир М.С.
Контрольная работа №1
Делимость натуральных чисел
Вариант 1
1. Из чисел 387, 756, 829, 2 148 выпишите те, которые делятся нацело
1) на 2; 2) на 9.
2. Разложите число 756 на простые множители.
3. Найдите наибольший общий делитель чисел
1) 24 и 54; 2)72 и 254.
4. Найдите наименьшее общее кратное чисел
1) 16 и 32; 2) 15 и 8; 3) 16 и 12.
5. Докажите, что числа 272 и 1365 – взаимно простые.
6. Вместо звездочки в записи 152* поставьте цифру так, чтобы полученное число было кратно 3 (рассмотрите все возможные случаи).
7. Петя расставил книги поровну на 12 полках, а потом переставил их, тоже поровну, на 8 полок. Сколько книг было у Пети, если известно, что их было больше 100, но меньше 140?
Вариант 2
1. Из чисел 405, 972, 865, 2394 выпишите те, которые делятся нацело
1) на 5; 2) на 9.
2. Разложите число 1176 на простые множители.
3. Найдите наибольший общий делитель чисел
1) 27 и 36; 2)168 и 252.
4. Найдите наименьшее общее кратное чисел
1) 11 и 33; 2) 9 и 10; 3) 18 и 12.
5. Докажите, что числа 297 и 304 – взаимно простые.
6. Вместо звездочки в записи 199* поставьте цифру так, чтобы полученное число было кратно 3 (рассмотрите все возможные случаи).
7. Собранный урожай яблок фермер может разложить поровну в корзину по 12 кг или в ящики по 15 кг. Сколько килограммов яблок собрал фермер, если известно, что их было больше 150 кг, но меньше 200 кг.
Контрольная работа №2
Сравнение, сложение и вычитание дробей
Вариант 1
1. Сократите дробь:
1) 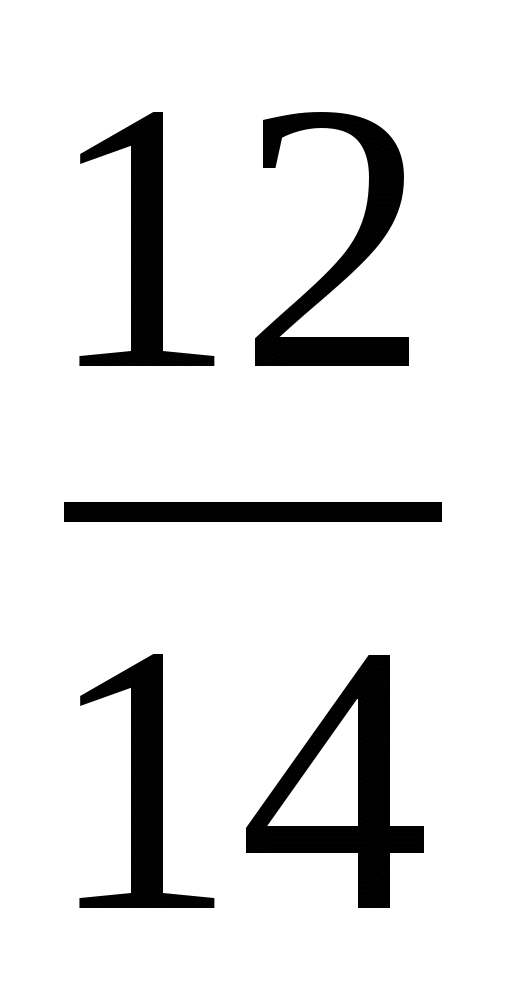 ; 2)
; 2) 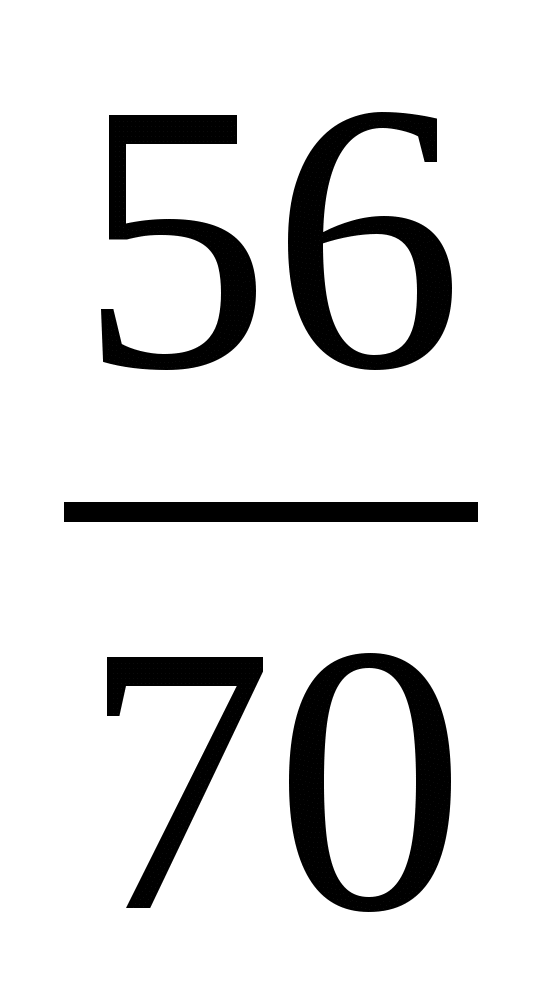 .
.
2. Сравните дроби:
1) 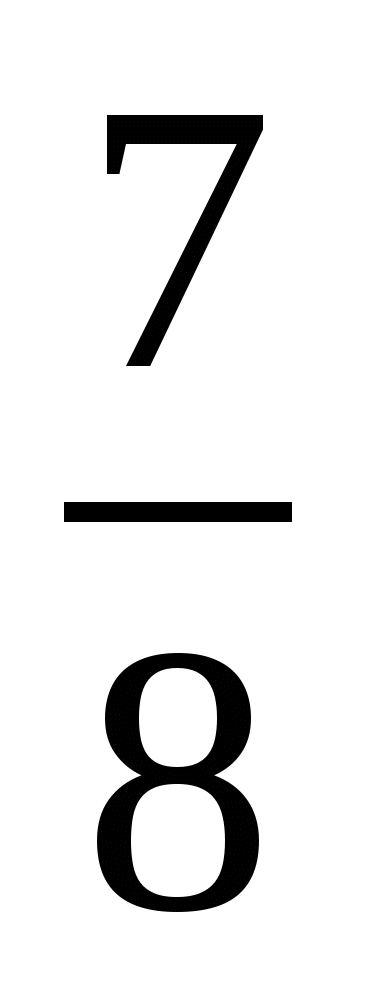 и
и  ; 2)
; 2)  и
и 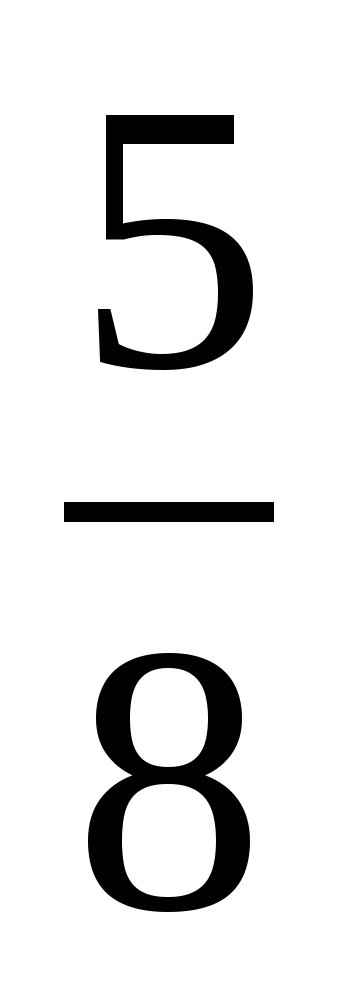 .
.
3. Вычислите:
1) 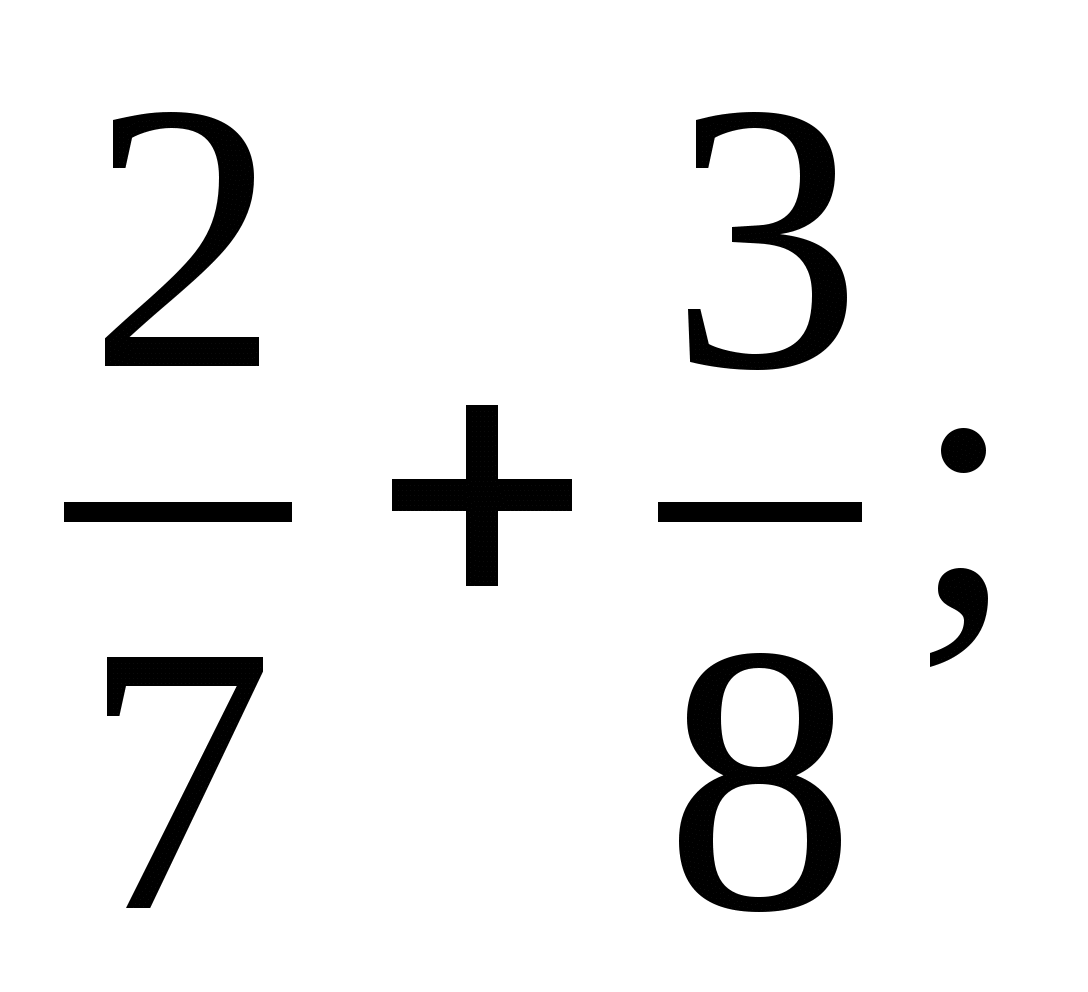 2)
2)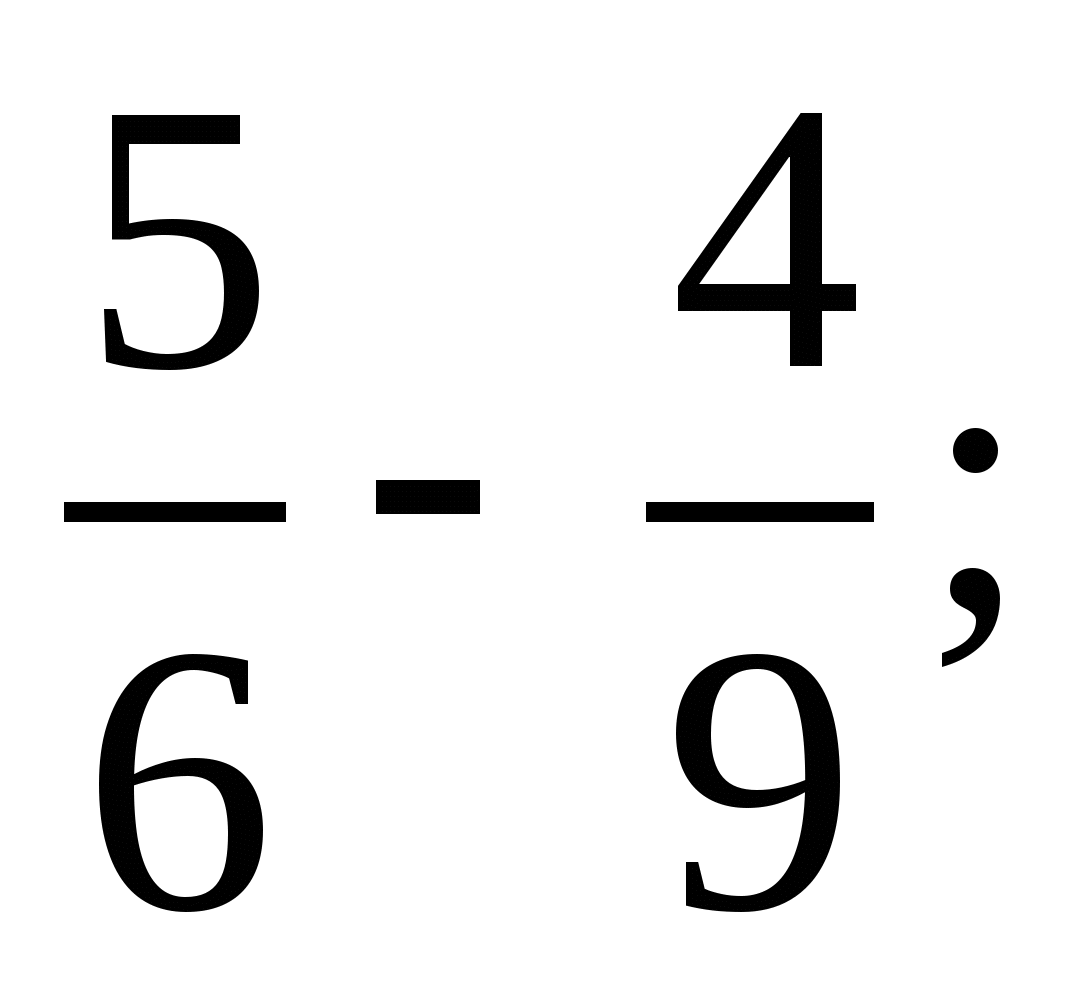 3)
3) 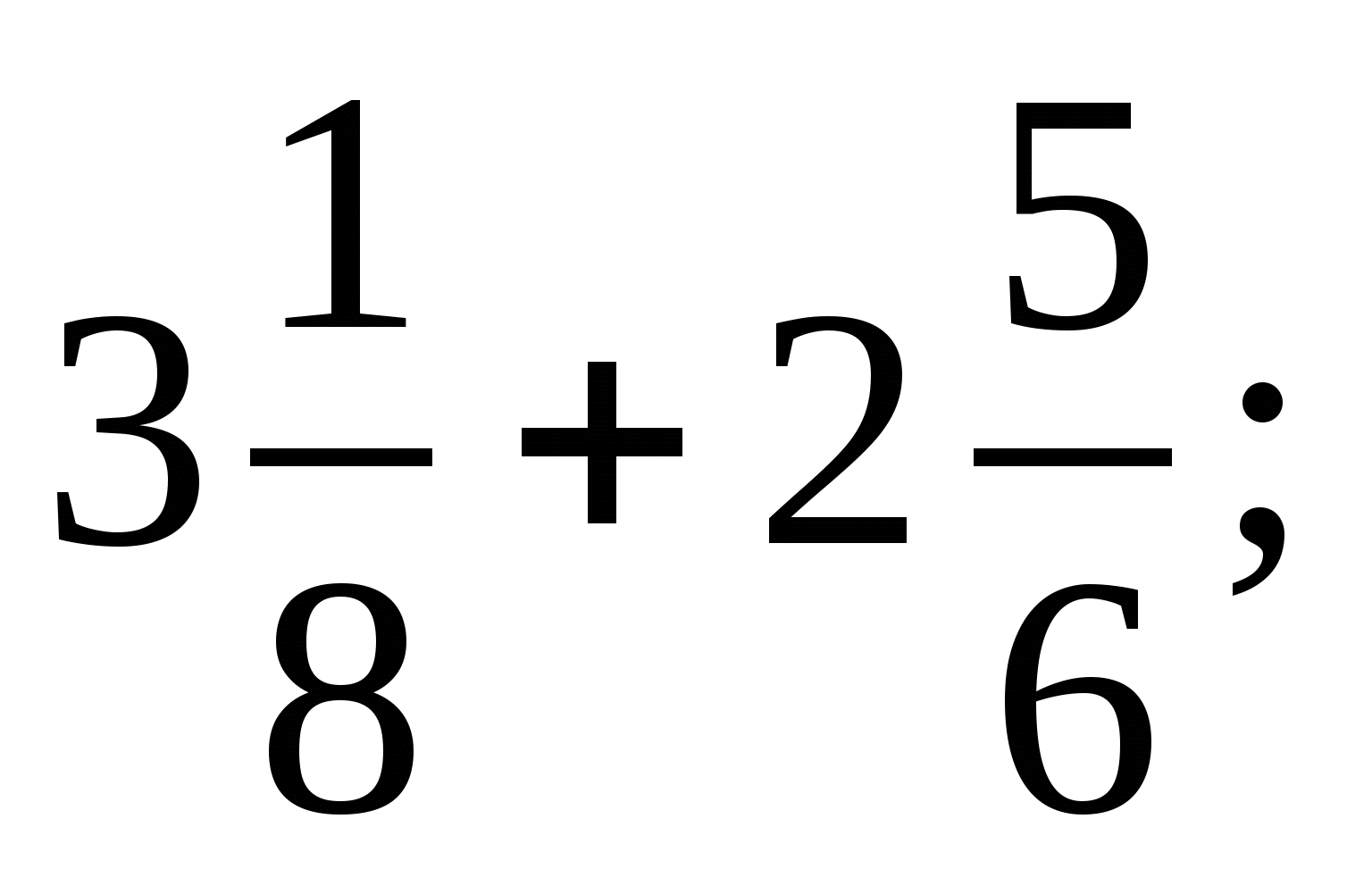 4)
4) 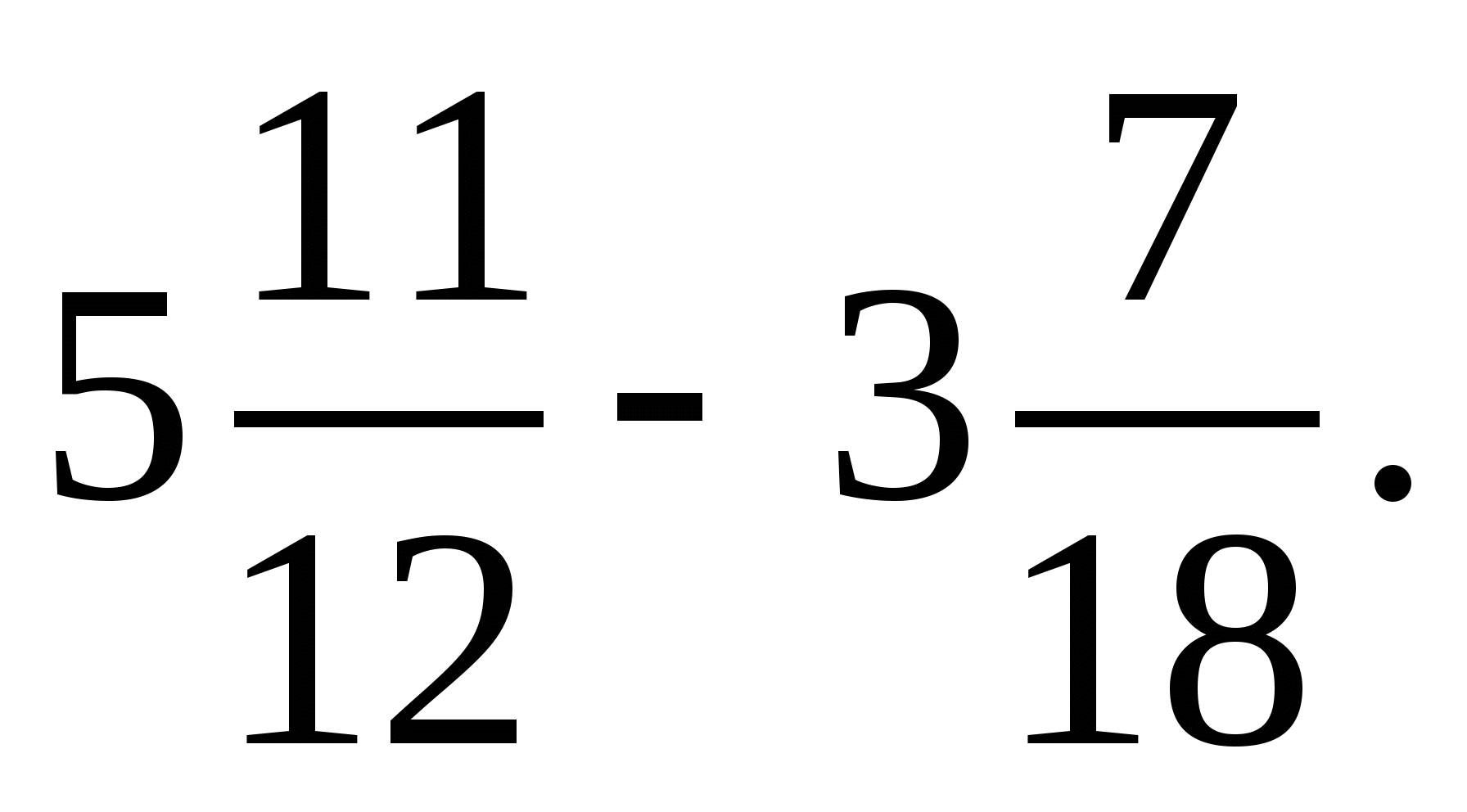
4. В первый день продали 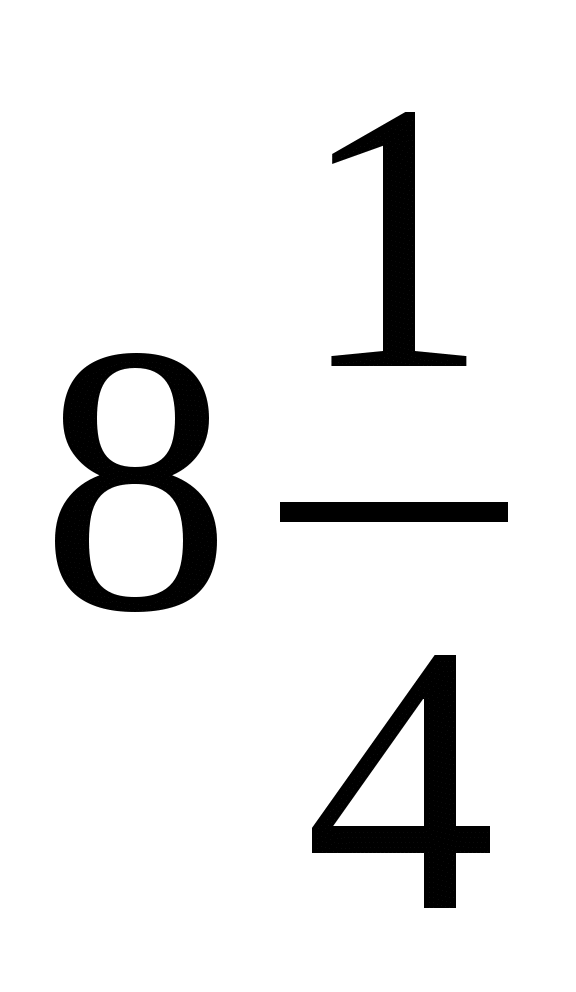 ц яблок, а во второй – на
ц яблок, а во второй – на 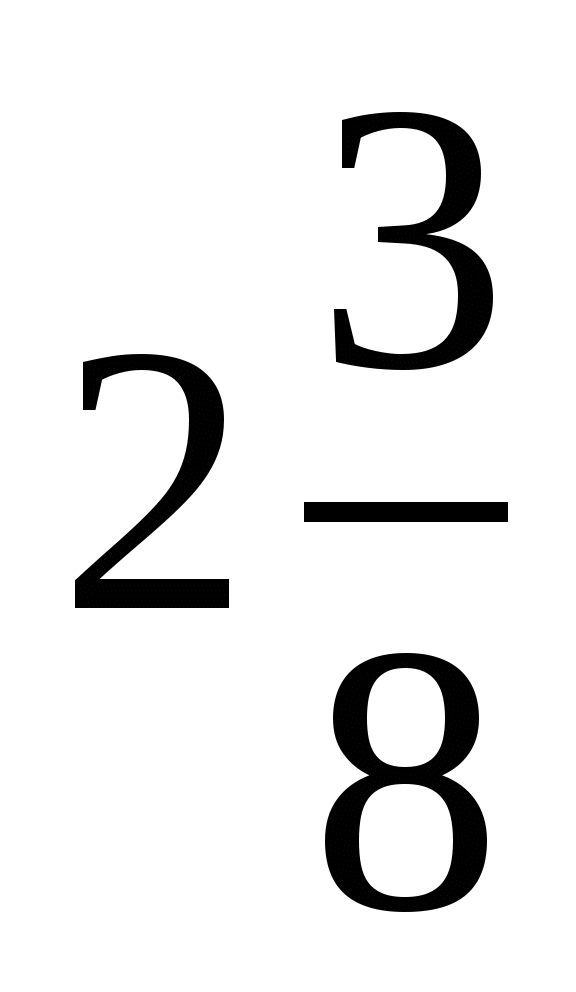 ц меньше. Сколько центнеров яблок продали за 2 дня?
ц меньше. Сколько центнеров яблок продали за 2 дня?
5. Решите уравнение:
1) 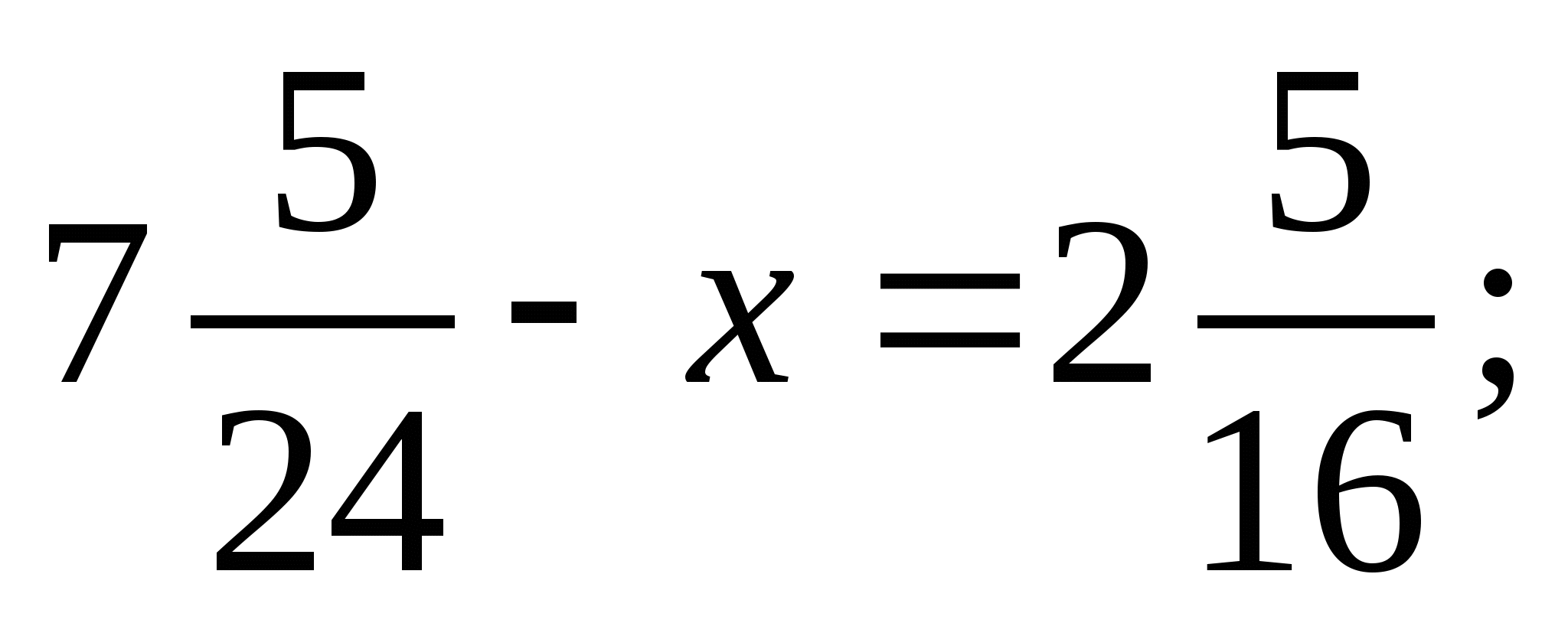 2)
2) 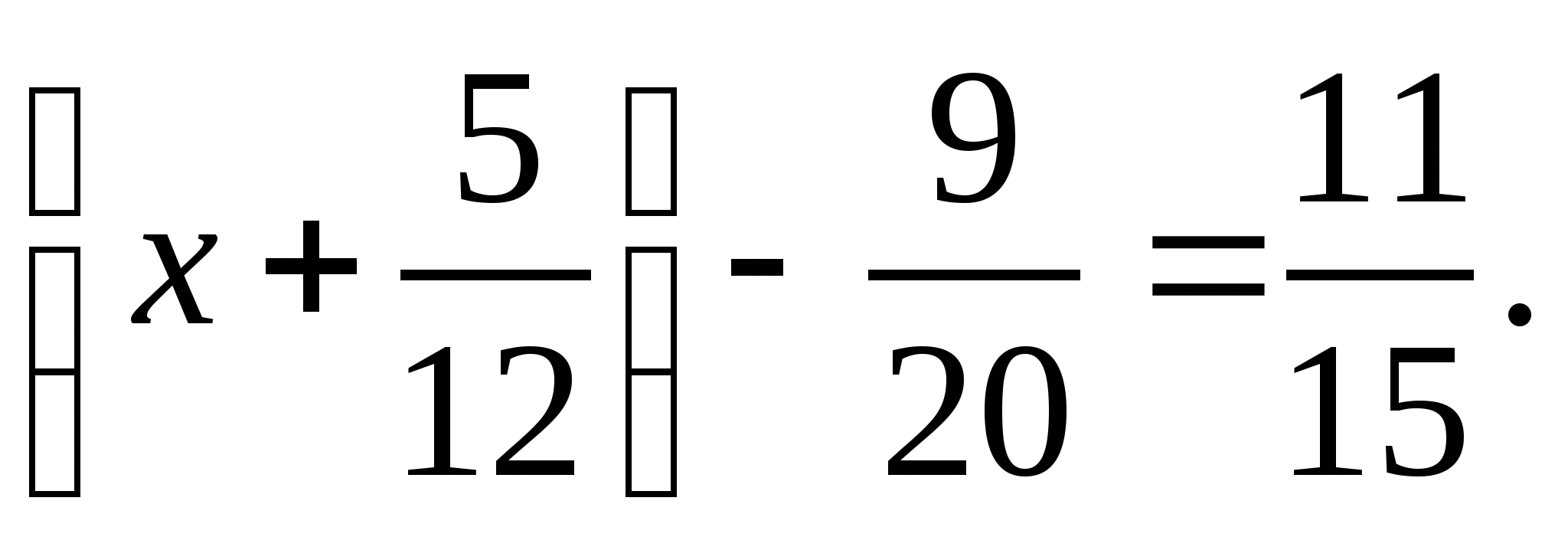
6. Миша потратил 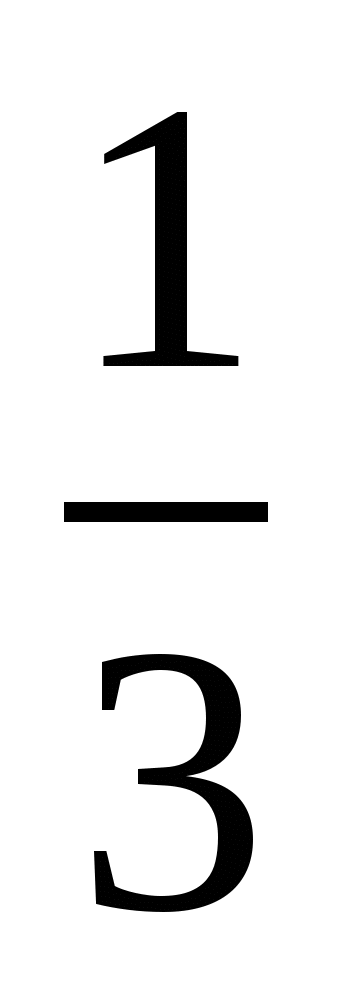 своих денег на покупку новой книги,
своих денег на покупку новой книги, 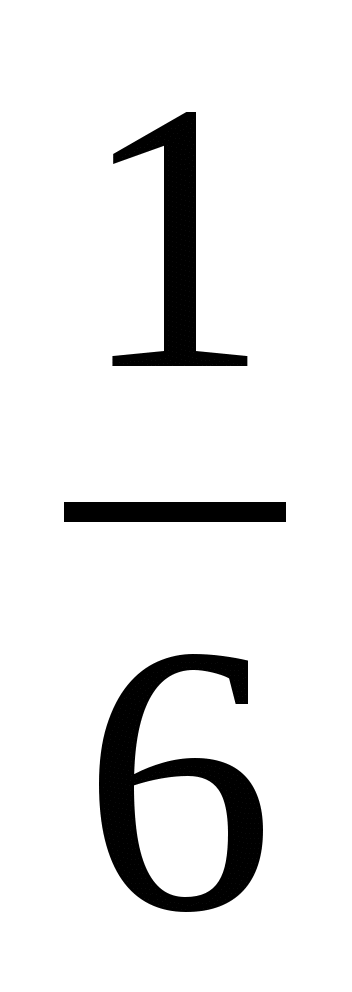 денег – на покупку тетрадей,
денег – на покупку тетрадей, 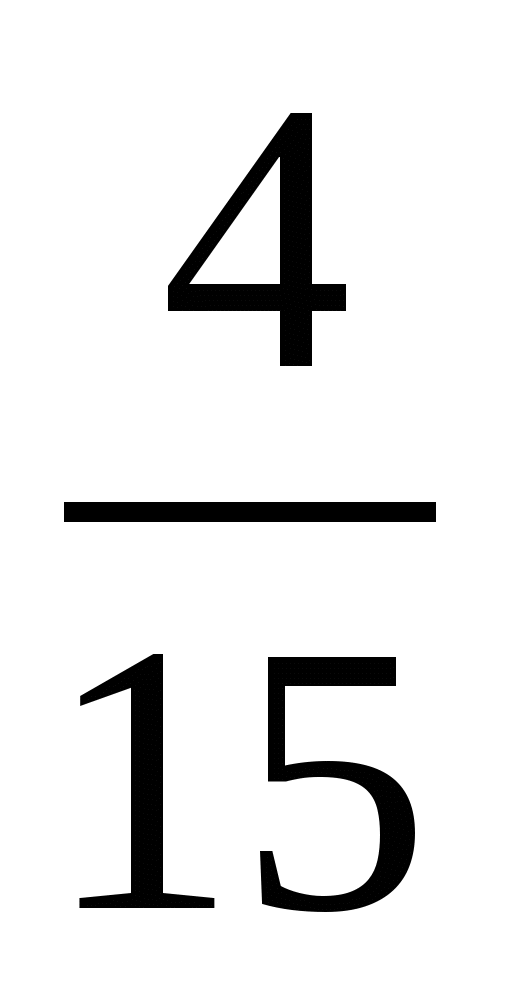 денег – на покупку карандашей, а остальные деньги - на покупку альбома. Какую часть своих денег Миша потратил на покупку альбома?
денег – на покупку карандашей, а остальные деньги - на покупку альбома. Какую часть своих денег Миша потратил на покупку альбома?
7. Найдите все натуральные значения 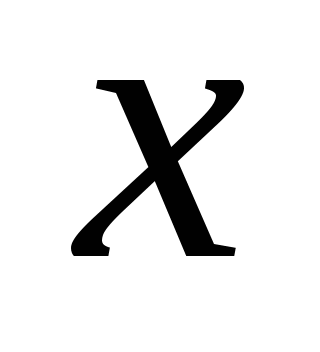 , при которых верно неравенство
, при которых верно неравенство 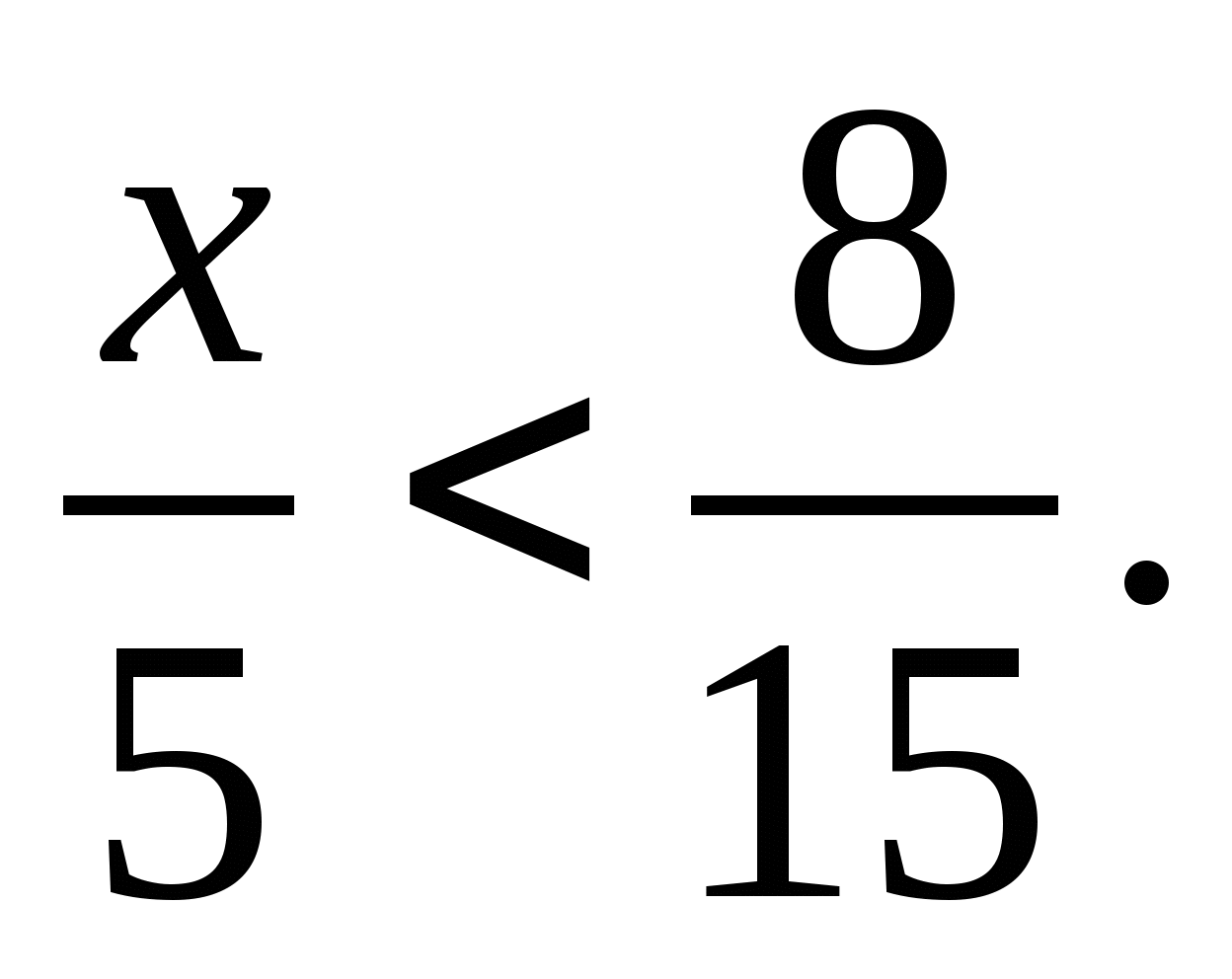
Вариант 2
1. Сократите дробь:
1) 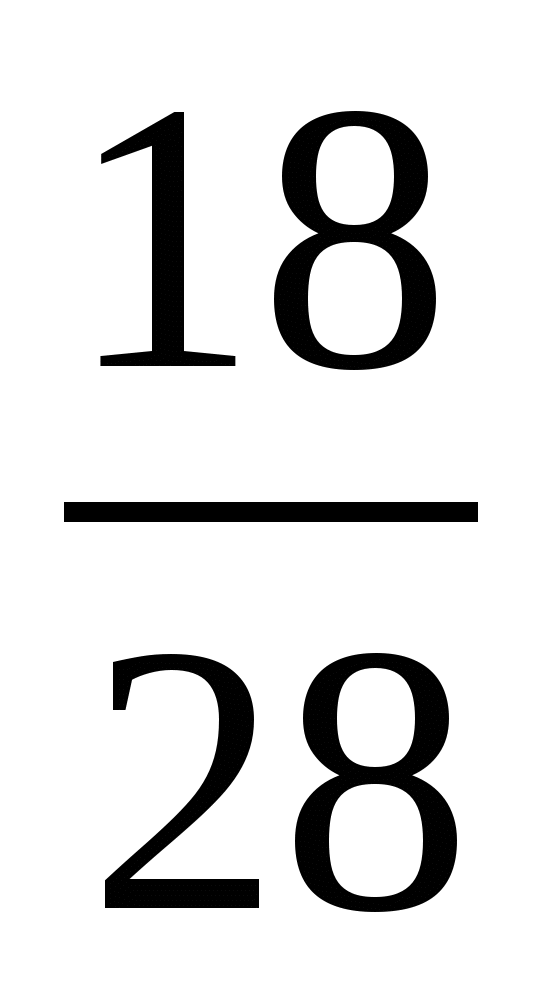 ; 2)
; 2) 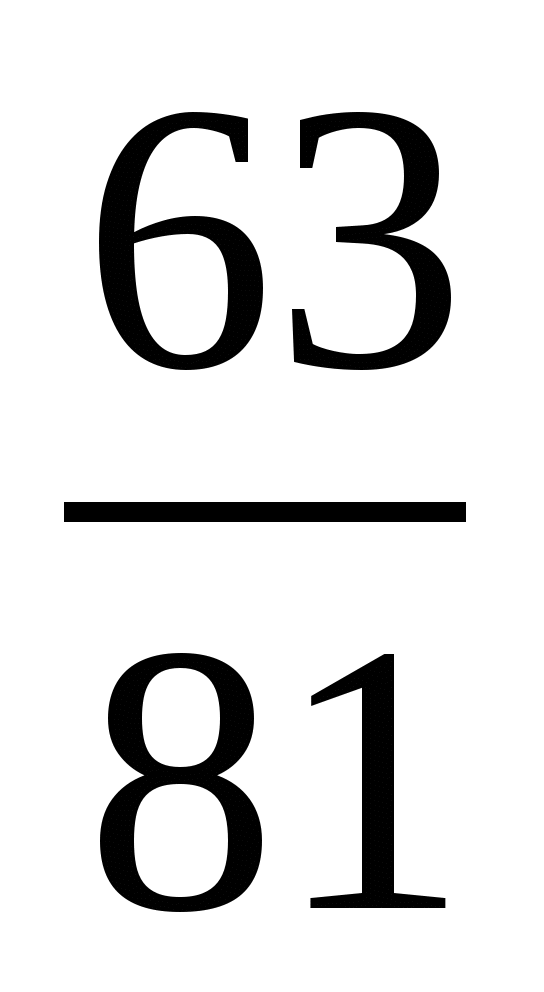 .
.
2. Сравните дроби:
1) 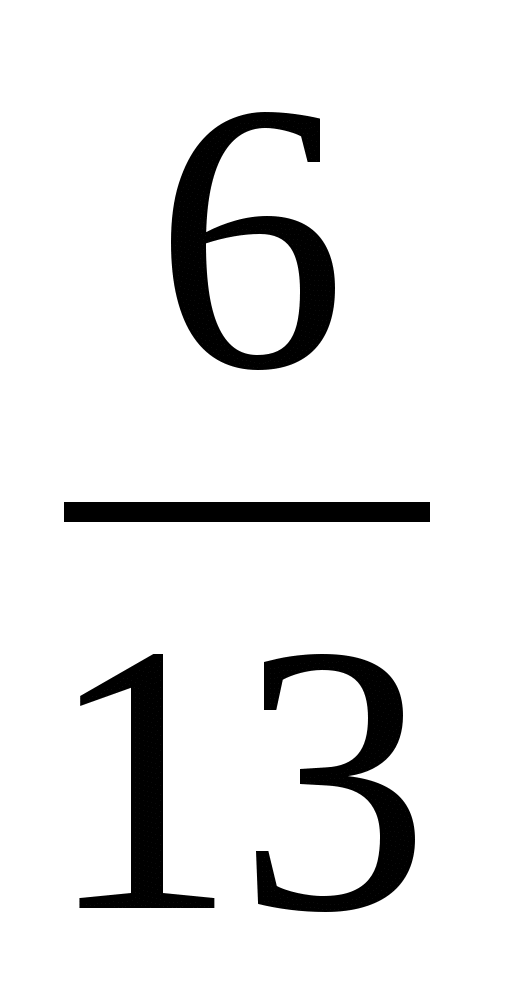 и
и 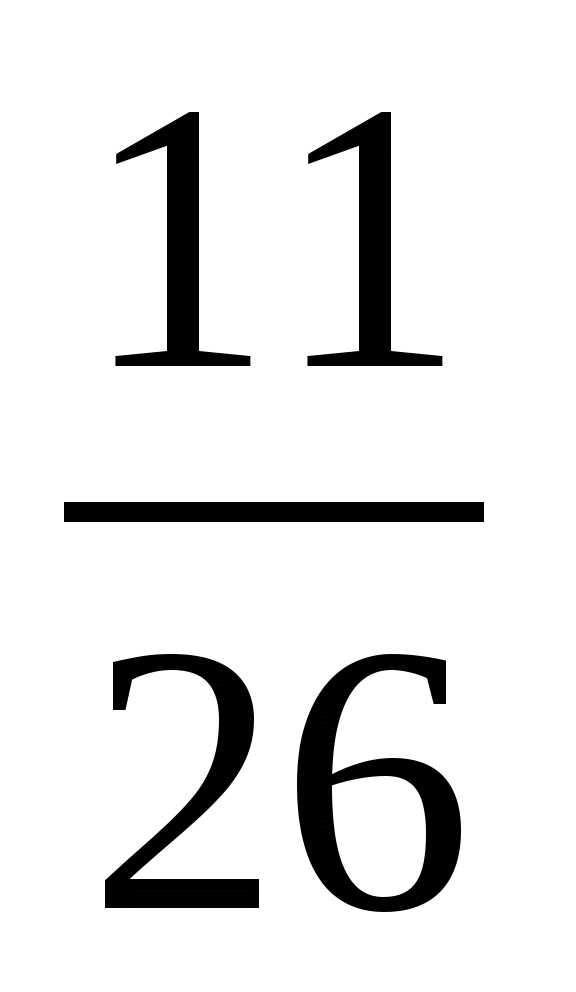 ; 2)
; 2) 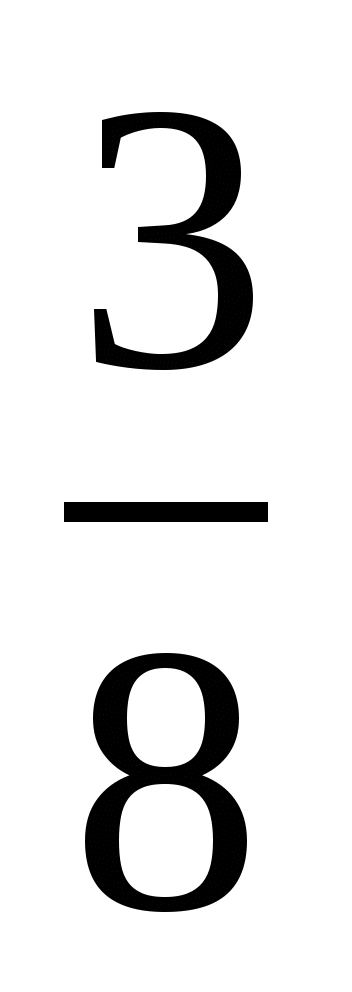 и
и 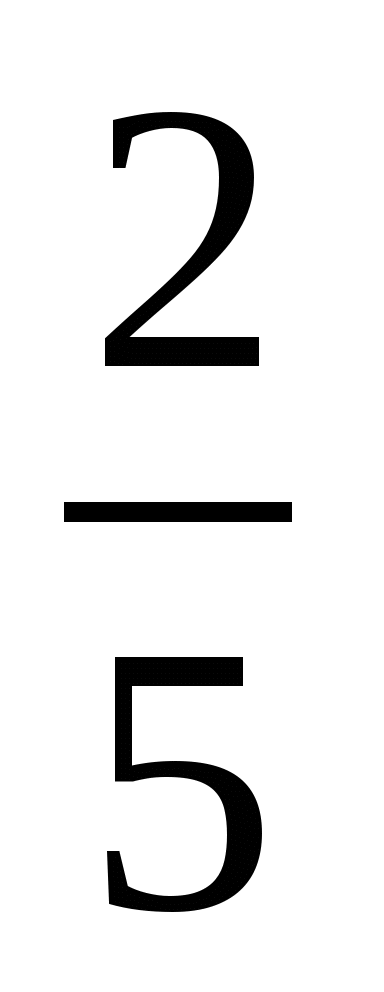 .
.
3. Вычислите:
1) 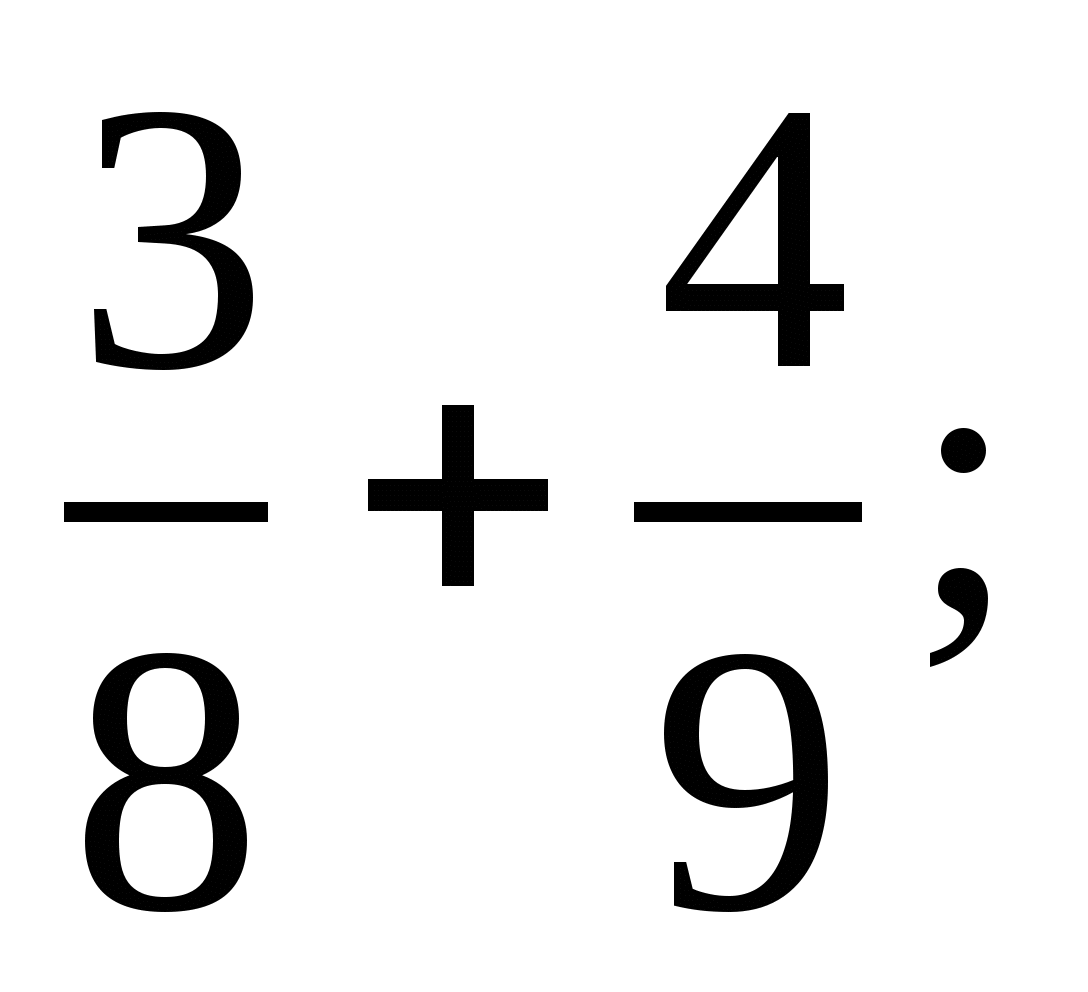 2)
2)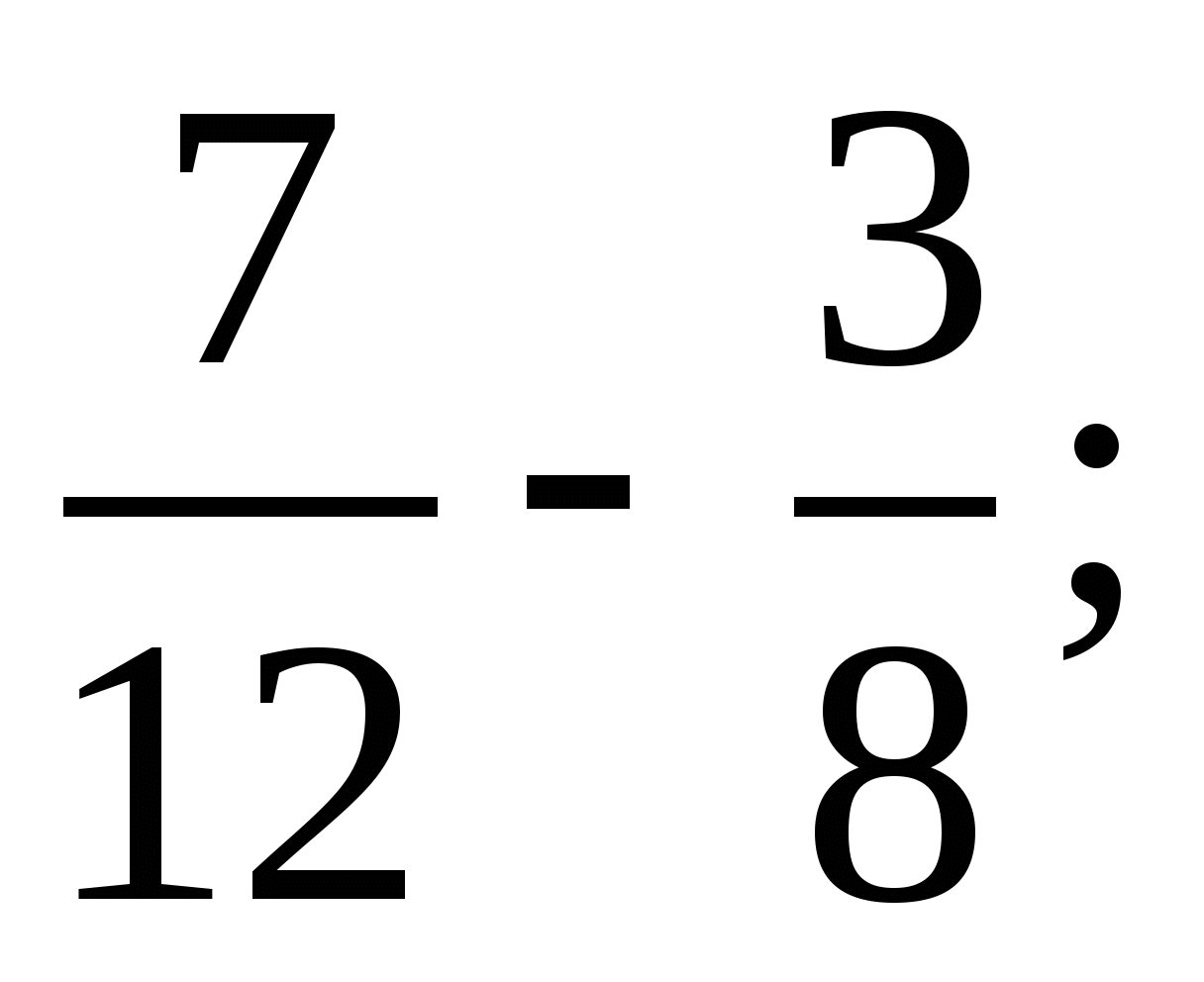 3)
3) 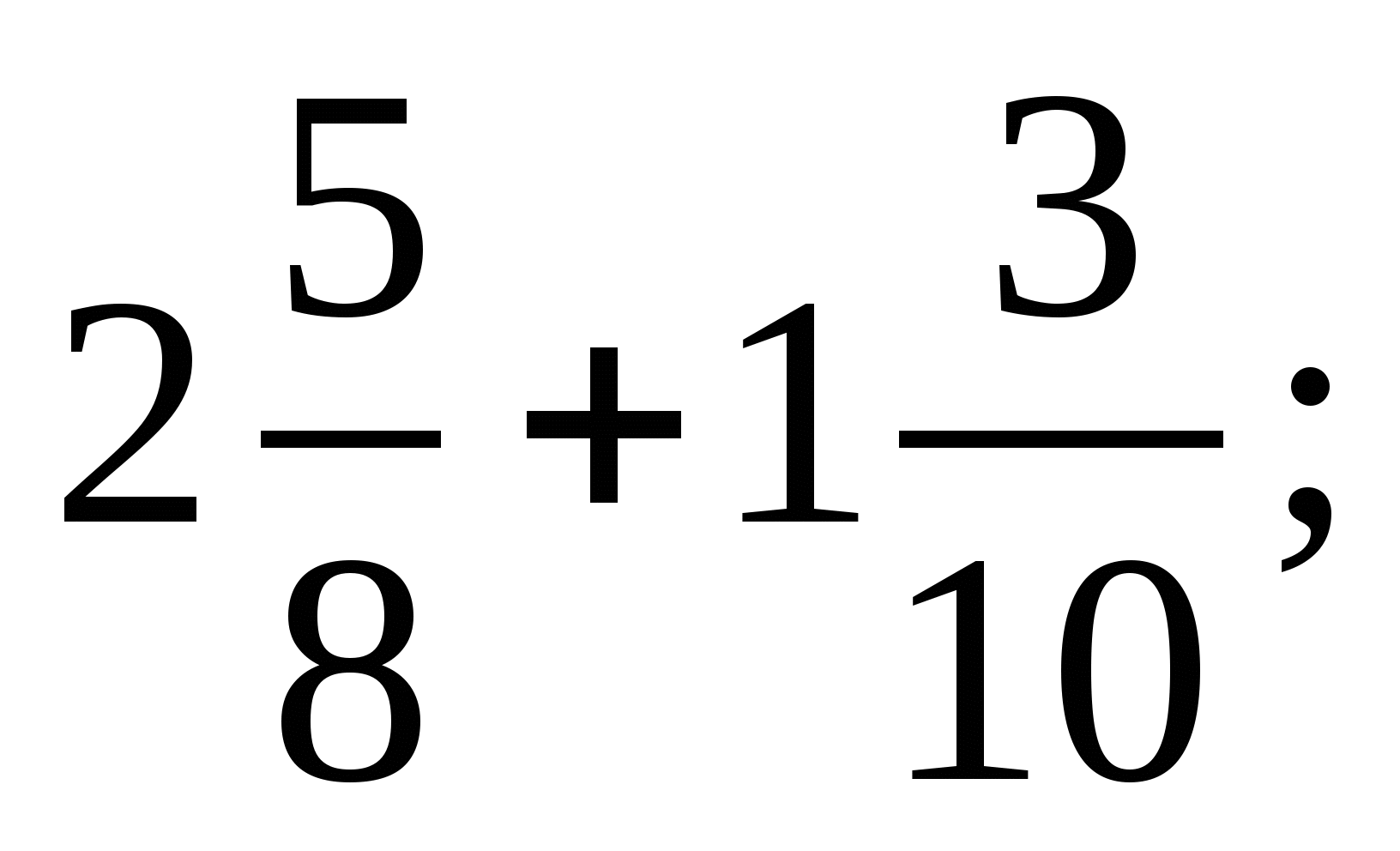 4)
4) 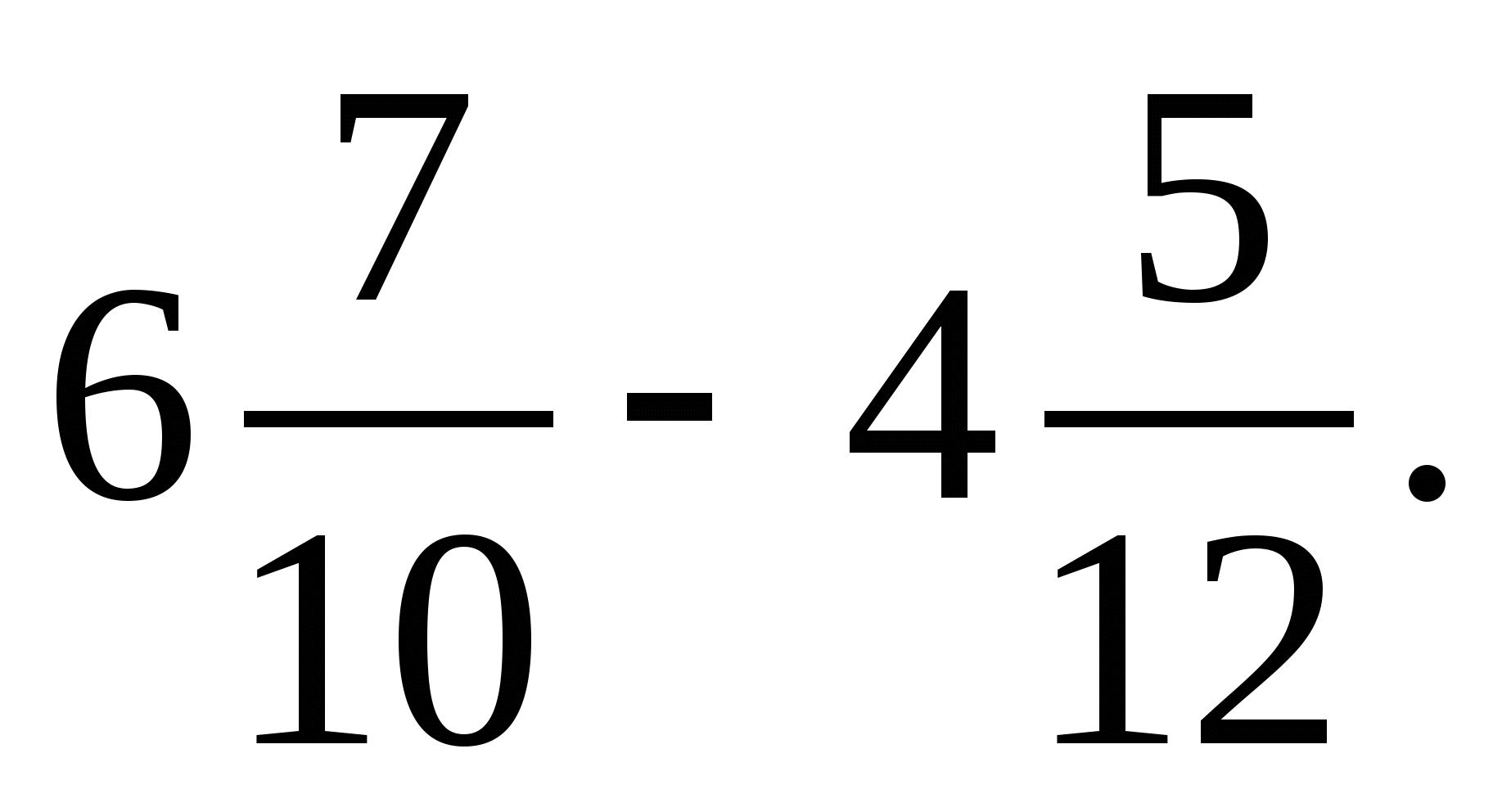
4. За первый час турист прошел 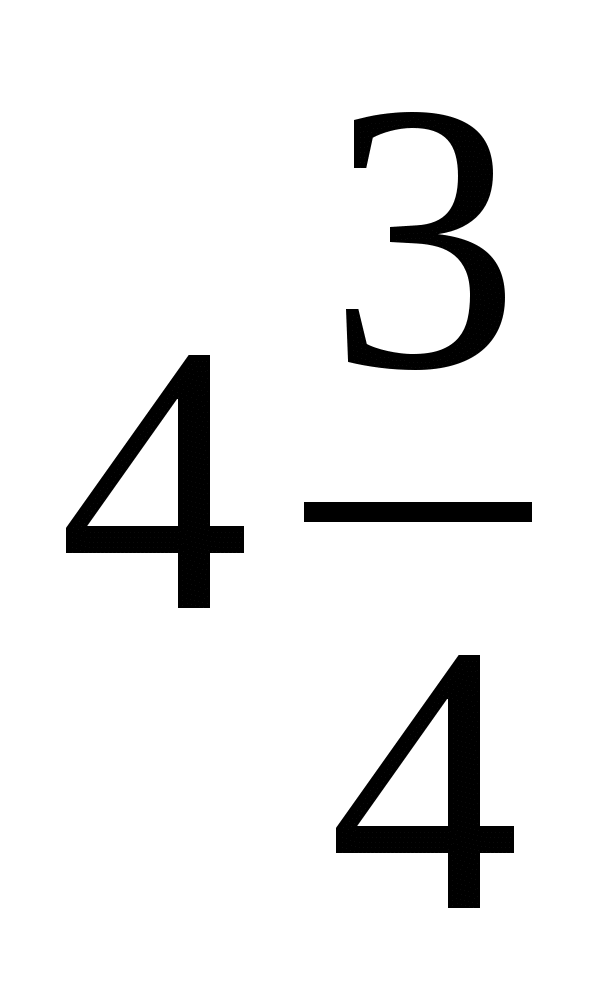 км, а за второй – на
км, а за второй – на 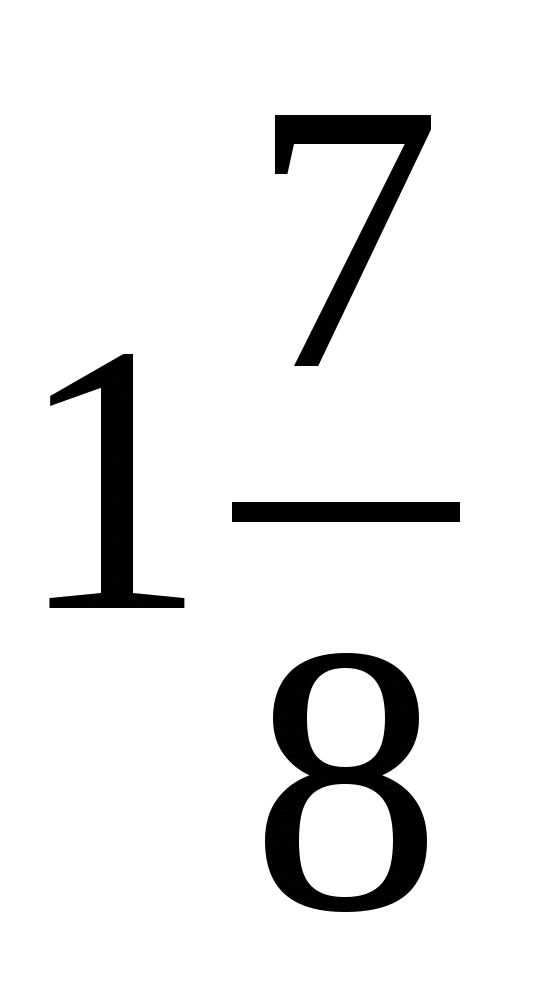 км меньше. Какой путь преодолел турист за 2 ч?
км меньше. Какой путь преодолел турист за 2 ч?
5. Решите уравнение:
1) 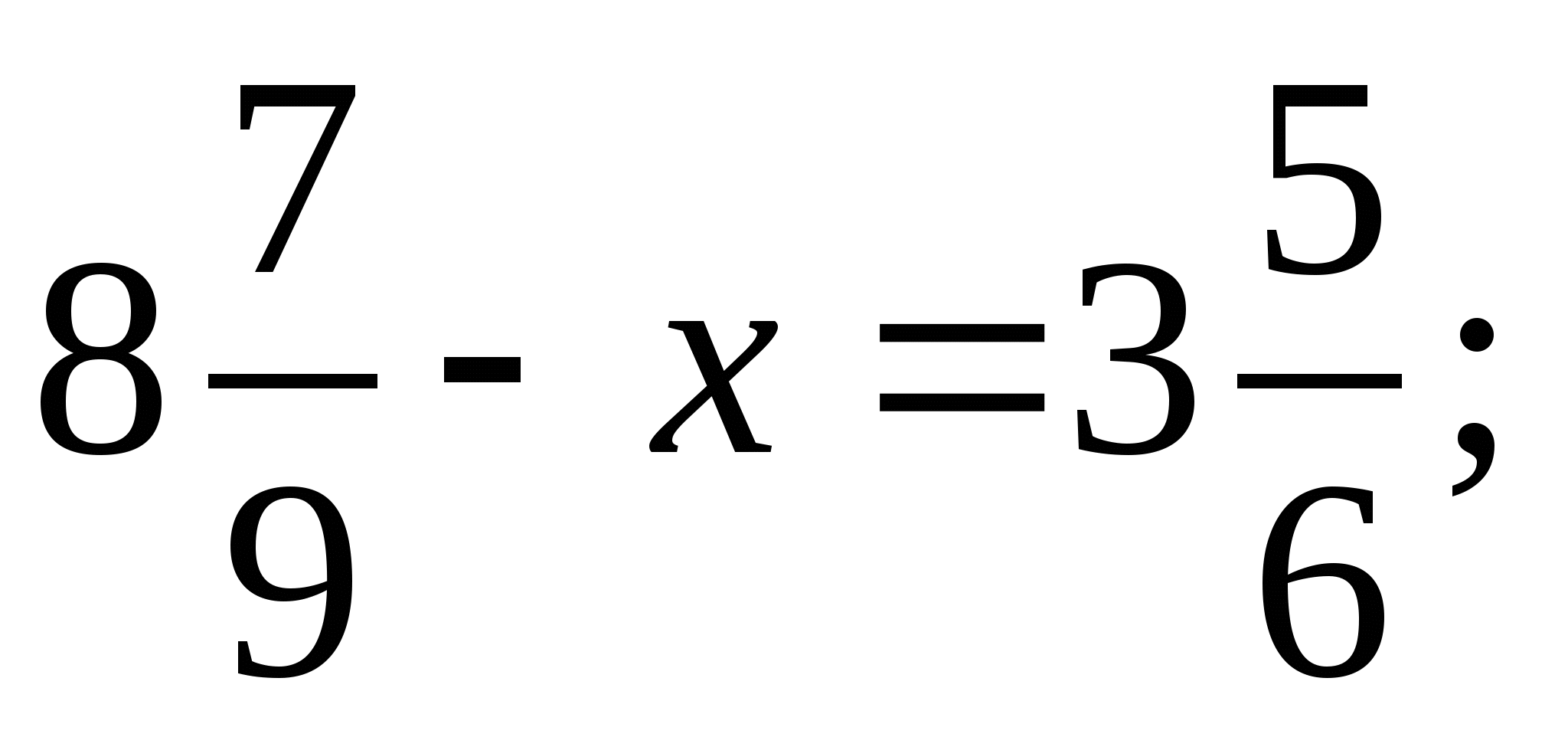 2)
2) 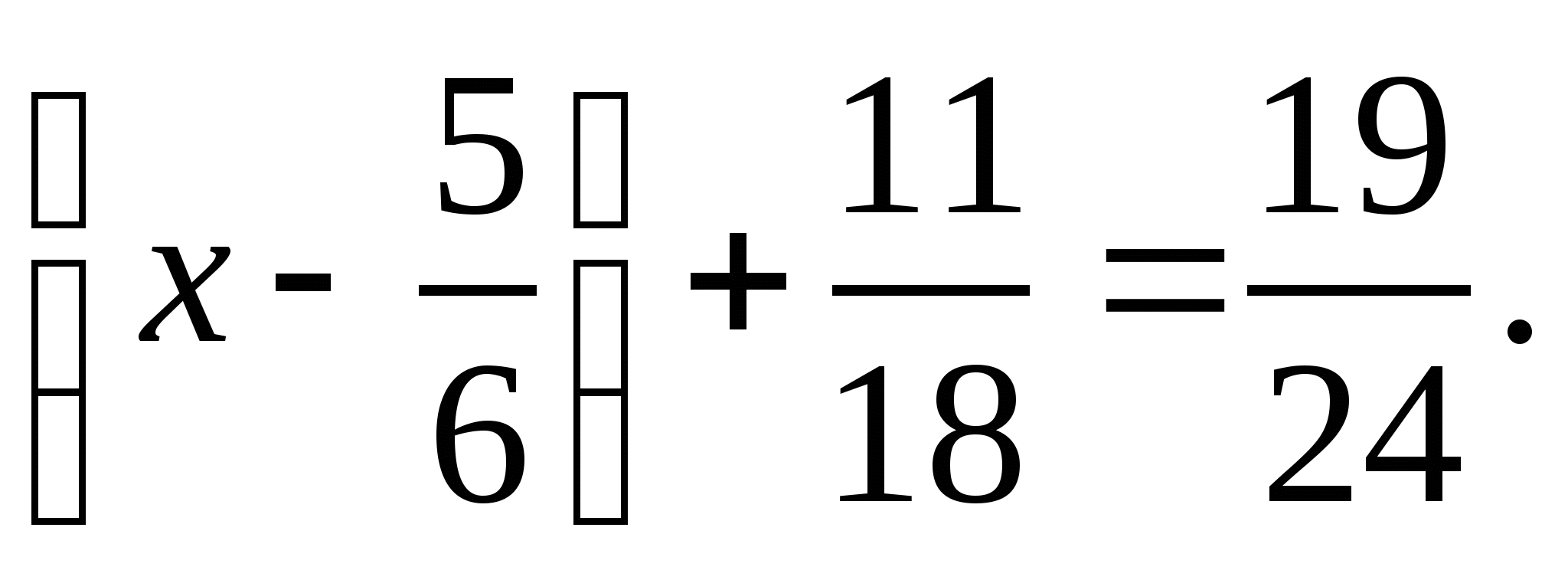
6. В магазин завезли фрукты. Яблоки составляли 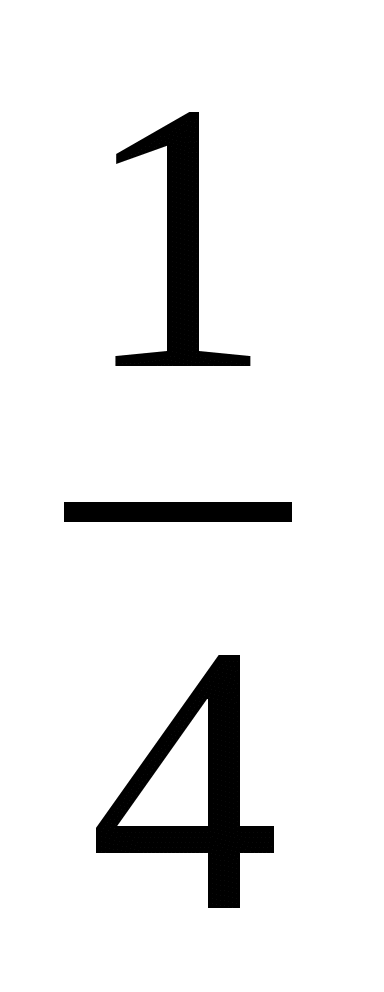 , сливы -
, сливы - 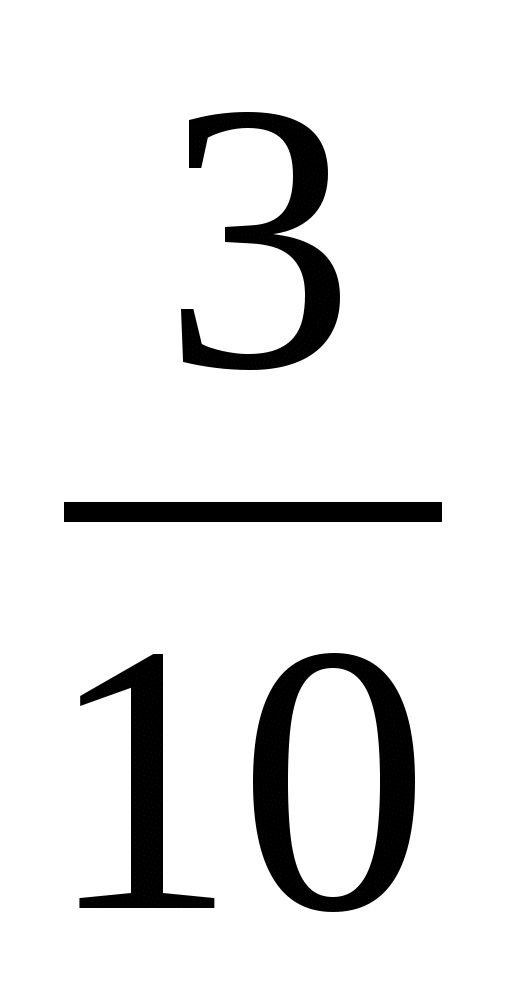 , а груши –
, а груши – 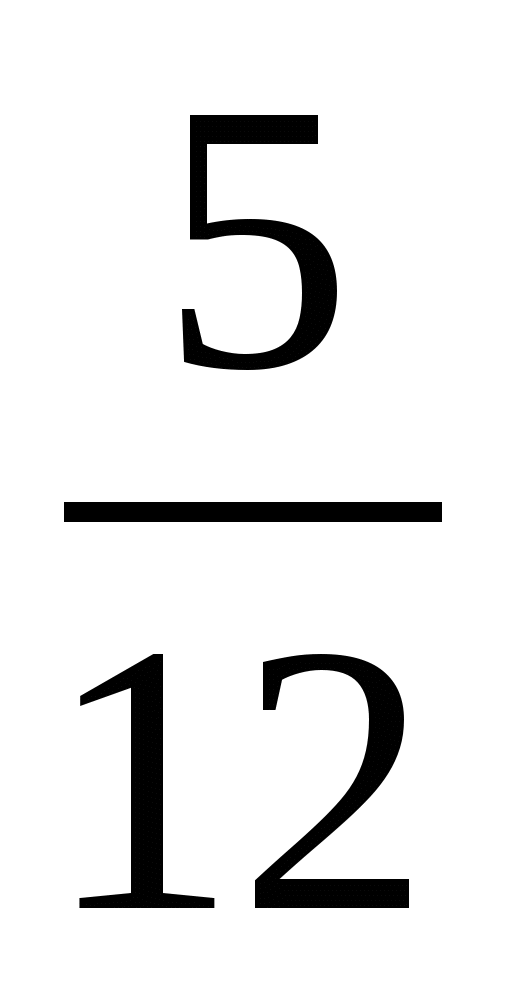 всех завезенных фруктов. Остальной завезенный товар составлял виноград. Какую часть всех фруктов составлял виноград?
всех завезенных фруктов. Остальной завезенный товар составлял виноград. Какую часть всех фруктов составлял виноград?
7. Найдите все натуральные значения 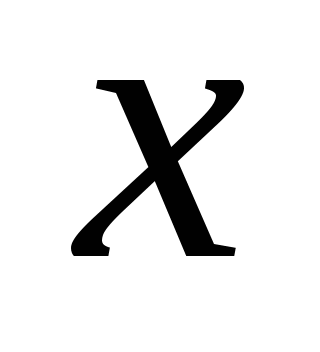 , при которых верно неравенство
, при которых верно неравенство 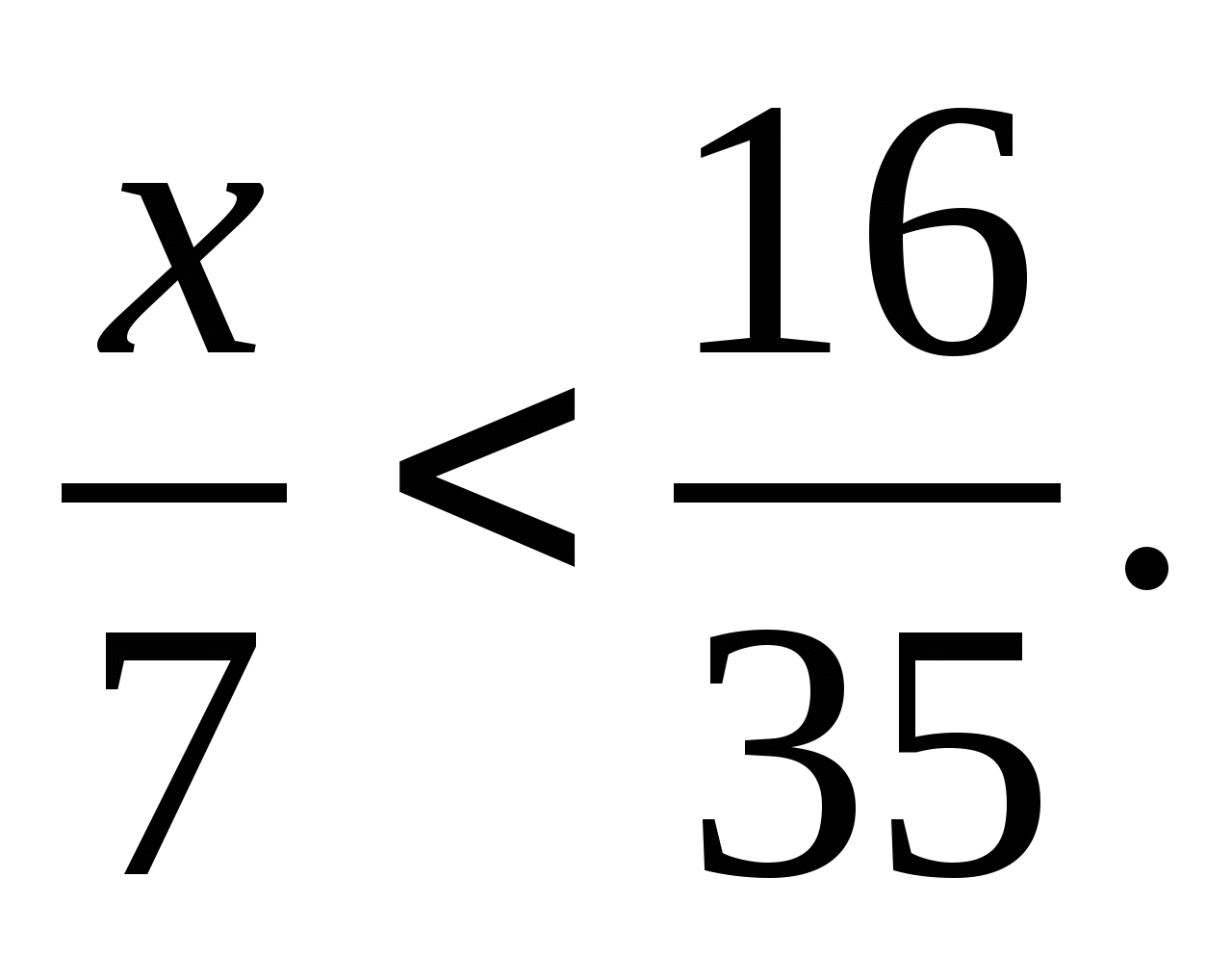
Контрольная работа №3
Умножение дробей
Вариант 1
1. Выполните умножение:
1) 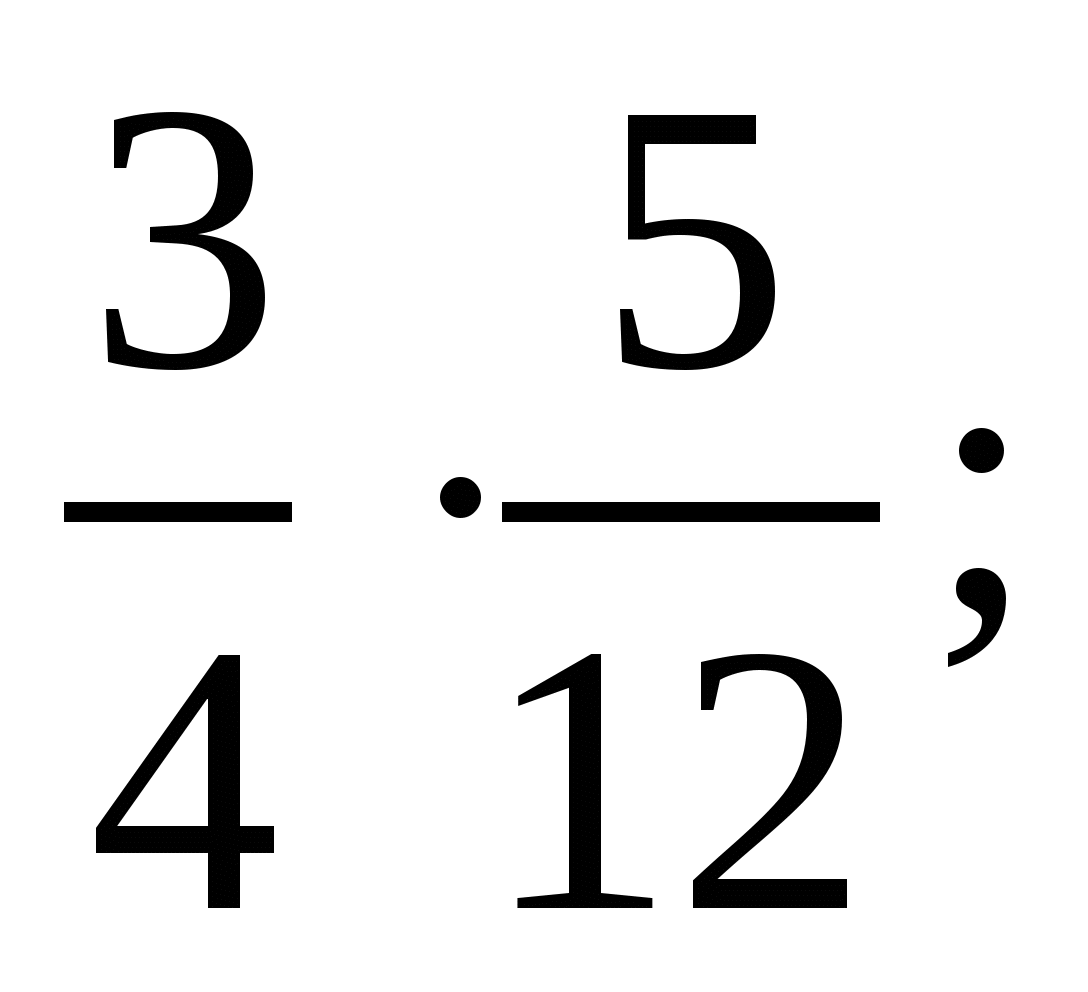 2)
2) 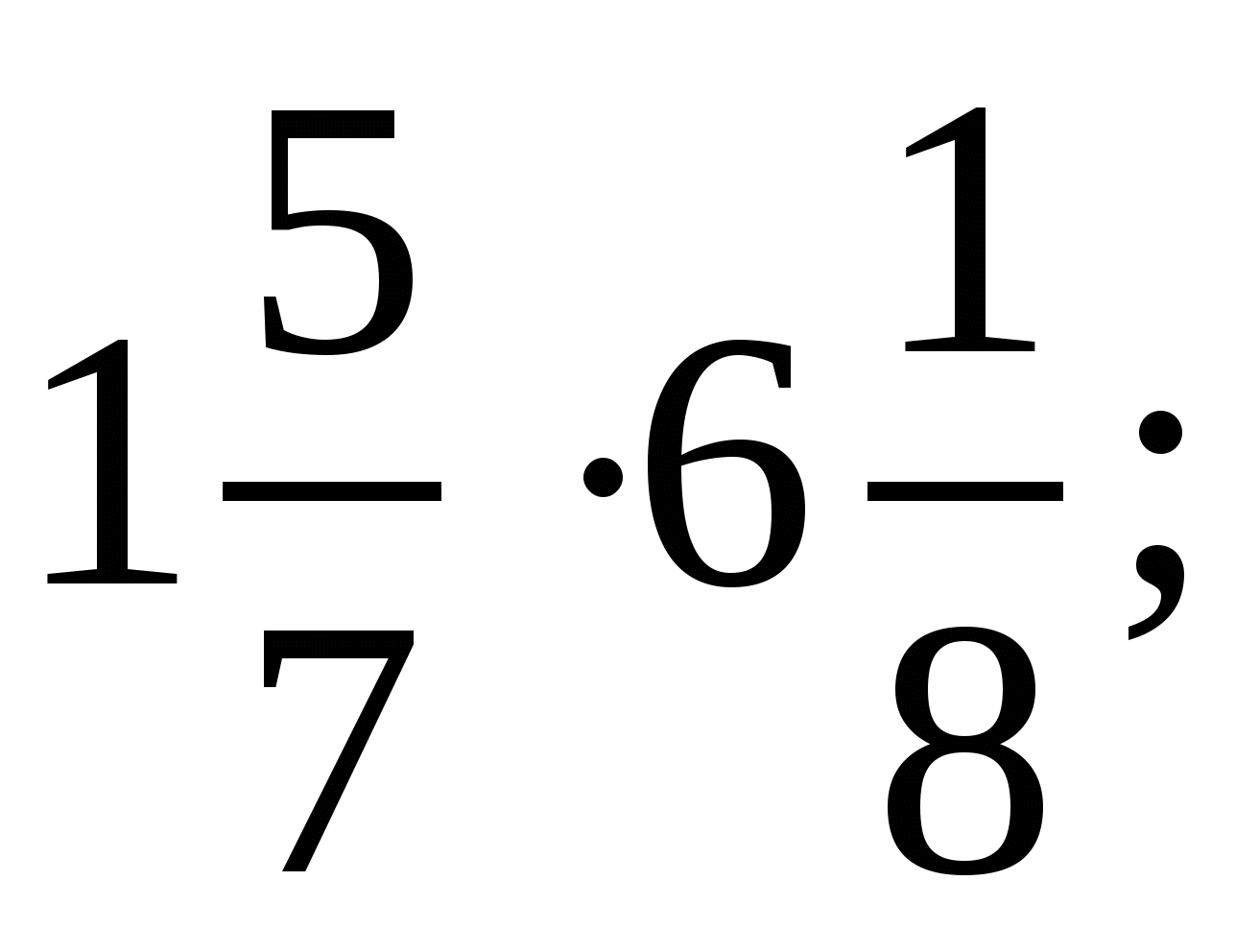 3)
3) 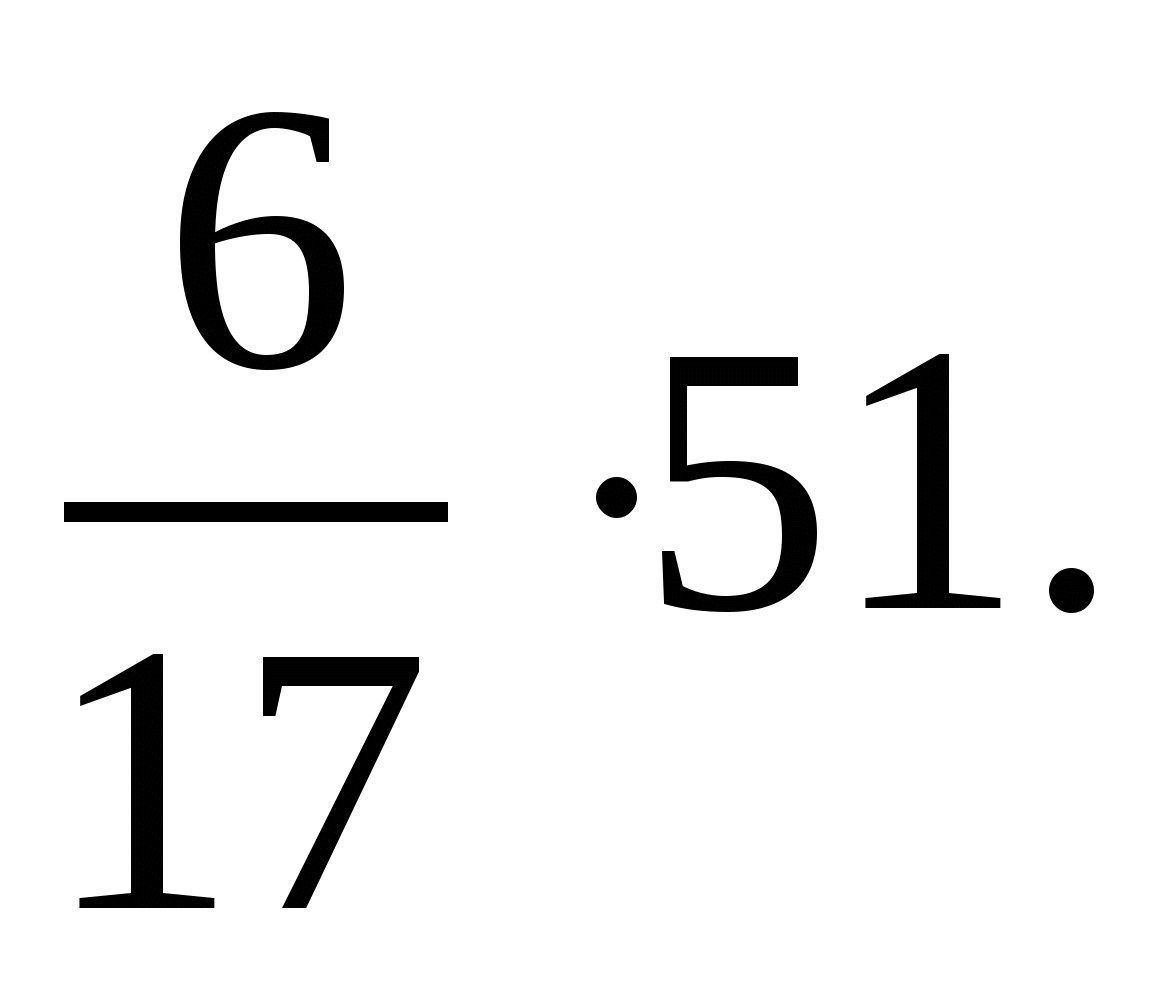
2. В магазин завезли 18 кг конфет, из них 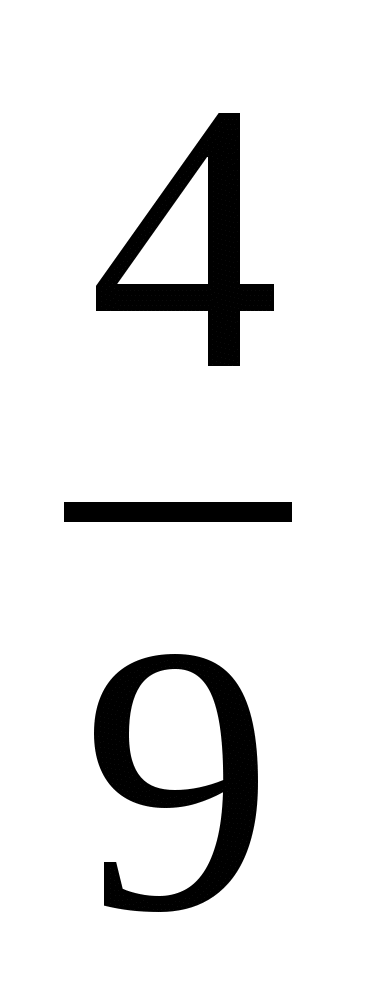 составляли шоколадные. Сколько килограммов шоколадных конфет завезли в магазин?
составляли шоколадные. Сколько килограммов шоколадных конфет завезли в магазин?
3. Найдите значение выражения: 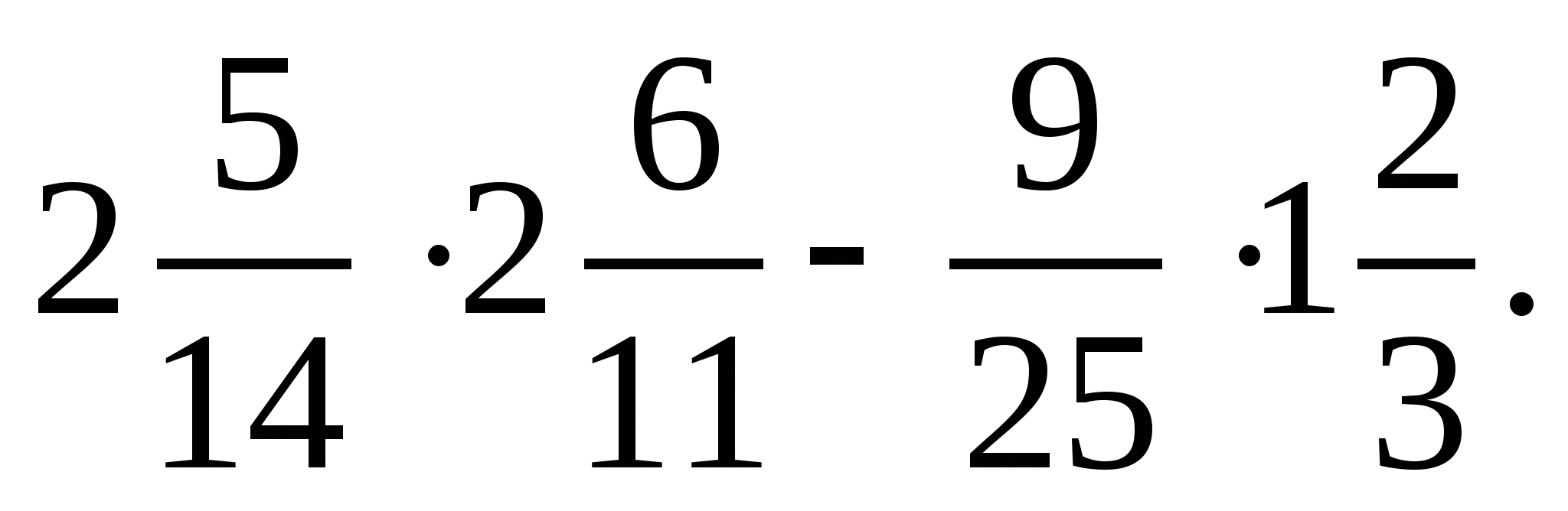
4. Ширина прямоугольного параллелепипеда равна 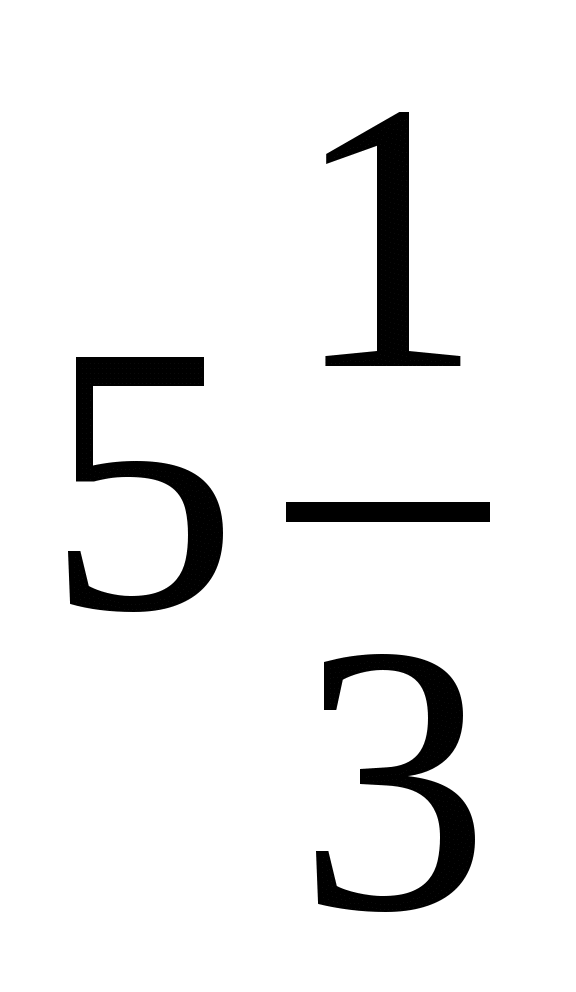 см, его длина в
см, его длина в 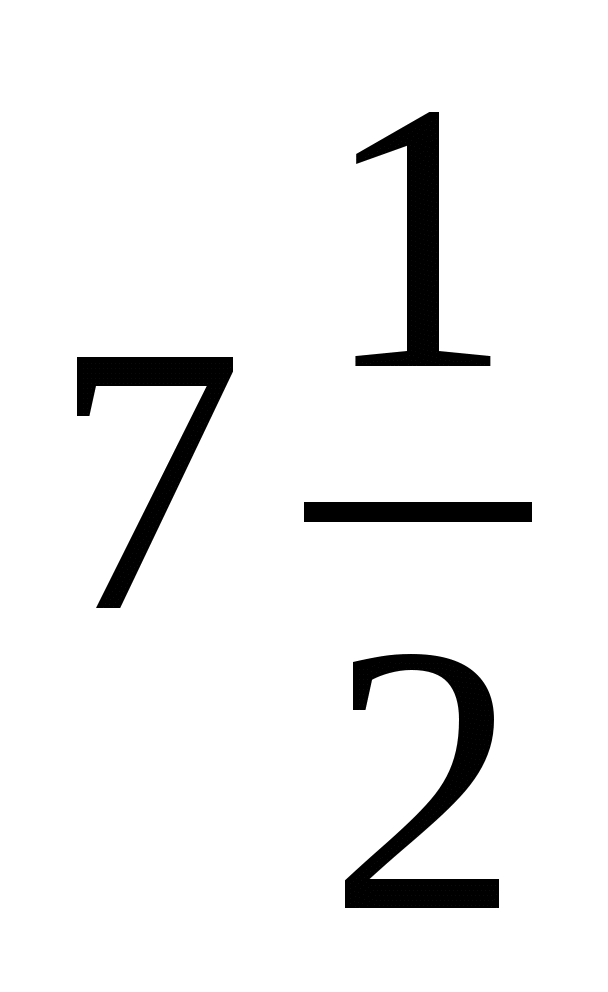 больше ширины, а высота составляет 30% длины. Вычислите объем параллелепипеда.
больше ширины, а высота составляет 30% длины. Вычислите объем параллелепипеда.
5. Вычислите значение выражения наиболее удобным способом:
infourok.ru
Контрольная работа № 1 «Делимость натуральных чисел»
Вариант 1
1. Из чисел 387, 756, 829, 2 148 выпишите те, которые делятся нацело:
1) на 2; 2) на 9.
2. Разложите число 756 на простые множители.
3. Найдите наибольший общий делитель чисел:
1) 24 и 54; 2) 72 и 264.
4. Найдите наименьшее общее кратное чисел:
1) 16 и 32; 2) 15 и 8; 3) 16 и 12.
5. Докажите, что числа 272 и 1 365 – взаимно простые.
6. Вместо звёздочки в записи 1 52* поставьте цифры так, чтобы полученное число было кратным 3 (рассмотрите все возможные случаи).
7. Петя расставил книги поровну на 12 полках, а потом переставил их, тоже поровну, на 8 полок. Сколько книг было у Пети, если известно, что их было больше 100, но меньше 140?
Контрольная работа № 1 «Делимость натуральных чисел»
Вариант 2
1. Из чисел 405, 972, 865, 2 394 выпишите те, которые делятся нацело:
1) на 5; 2) на 9.
2. Разложите число 1 176 на простые множители.
3. Найдите наибольший общий делитель чисел:
1) 27 и 36; 2) 168 и 252.
4. Найдите наименьшее общее кратное чисел:
1) 11 и 33; 2) 9 и 10; 3) 18 и 12.
5. Докажите, что числа 297 и 304 – взаимно простые.
6. Вместо звёздочки в записи 1 99* поставьте цифры так, чтобы полученное число было кратным 3 (рассмотрите все возможные случаи).
7. Собранный урожай яблок фермер может разложить поровну в корзины по 12 кг или в ящики по 15 кг. Сколько килограммов яблок собрал фермер, если известно, что их было больше 150 кг, но меньше 200 кг?
Вариант 1
1. Сократите дробь: 1) ; 2) .
2. Сравните дроби: 1) ; 2) .
3. Вычислите: 1) 2) 3) 4)
4. В первый день продали ц яблок, а во второй – на ц меньше. Сколько центнеров яблок продали за два дня?
5. Решите уравнение: 1) 2)
6. Миша потратил своих денег на покупку новой книги, денег – на покупку тетрадей, денег – на покупку карандашей, а остальные деньги – на покупку альбома. Какую часть своих денег потратил Миша на покупку альбома?
7. Найдите все натуральные значения х, при которых верно неравенство
Вариант 2
1. Сократите дробь: 1) ; 2) .
2. Сравните дроби: 1) ; 2) .
3. Вычислите: 1) 2) 3) 4)
4. За первый час турист прошёл км, а за второй – на км меньше. Какой путь преодолел турист за 2 ч?
5. Решите уравнение:
1) 2)
6. В магазин завезли фрукты. Яблоки составляли , сливы - , а груши - всех завезённых фруктов. Остальной завезённый товар составлял виноград. Какую часть всех фруктов составлял виноград?
7. Найдите все натуральные значения х, при которых верно неравенство
Контрольная работа № 3 по теме «Обыкновенные дроби»
Вариант 1
1. Выполните умножение: 1) 2) 3)
2. В магазин завезли 18 кг конфет, из них составляли шоколадные. Сколько килограммов шоколадных конфет завезли в магазин?
3. Найдите значение выражения: .
4. Ширина прямоугольного параллелепипеда равна см, его длина в раза больше ширины, а высота составляет 30% длины. Вычислите объём параллелепипеда.
5. Вычислите значение выражения наиболее удобным способом:
.
6. За первый день турист прошёл туристического маршрута, за второй - оставшейся части маршрута, а за третий – остальное. За какой день турист прошёл больше всего?
infourok.ru
5. Решите уравнение 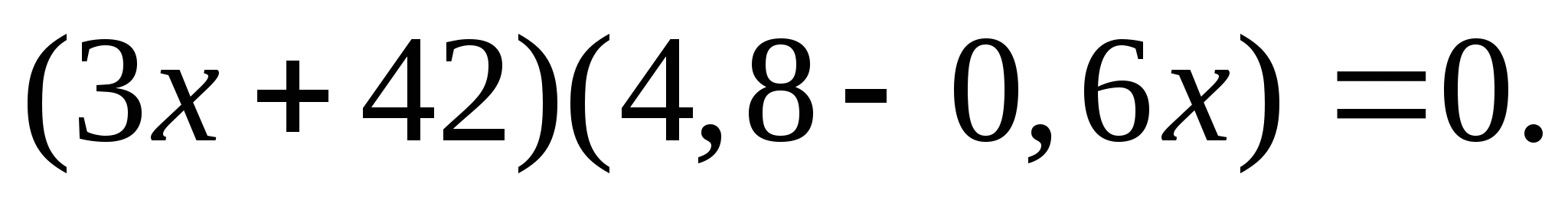
Контрольная работа № 11
Перпендикулярные и параллельные прямые.
Осевая и центральная симметрии. Координатная плоскость. Графики
Вариант 1
1.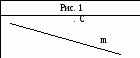 Перерисуйте в тетрадь рисунок 1. Проведите через точку С:
Перерисуйте в тетрадь рисунок 1. Проведите через точку С:
1) прямую а, параллельную прямой 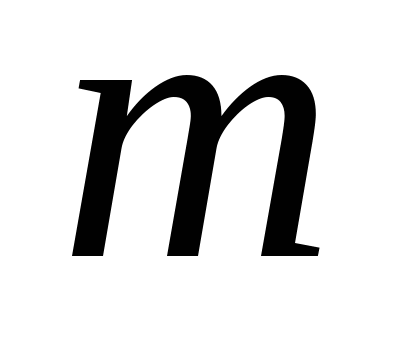 ;
;
2) прямую b, перпендикулярную прямой 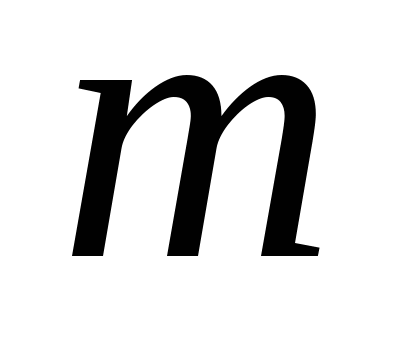 .
.
2. Начертите произвольный треугольник ABC.
Постройте фигуру, симметричную этому треугольнику относительно точки А.
3. Отметьте на координатной плоскости точки А(–1;4) и В(–4;–2). Проведите отрезок АВ.
1) Найдите координаты точки пересечения отрезка АВ с осью абсцисс.
2) Постройте отрезок, симметричный отрезку АВ относительно оси ординат, и найдите координаты концов полученного отрезка.
4.Начертите тупой угол BDK, отметьте на его стороне DK точку М. Проведите через точку М прямую, перпендикулярную прямой DK, и прямую, перпендикулярную прямой DB.
5. Турист вышел из базового лагеря и через некоторое время вернулся назад. На рисунке 2 изображен график движения туриста. 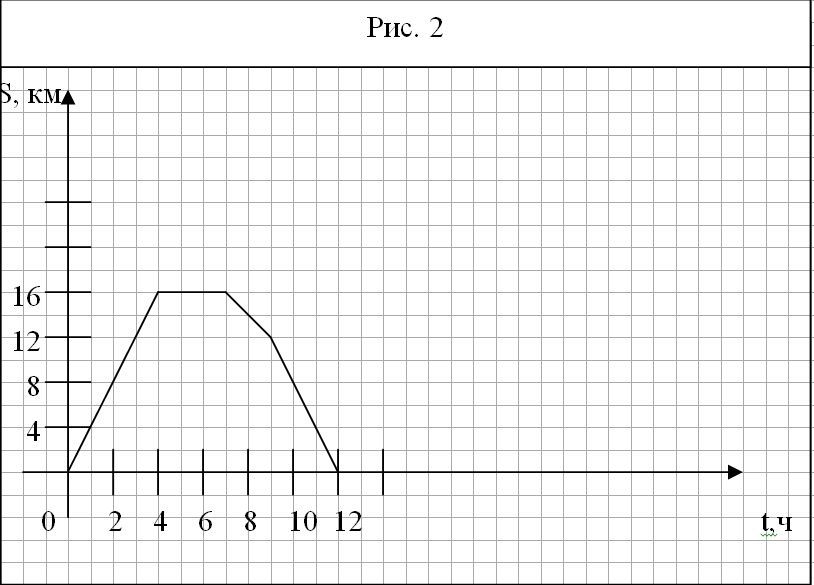
На каком расстоянии от лагеря был турист через 4 ч после начала движения?
Сколько времени турист затратил на остановку?
Через сколько часов после начала движения турист был на расстоянии 12 км от лагеря?
С какой скоростью турист шел до остановки?
6. Даны координаты трех вершин прямоугольника ABCD: А (–2;–3), В (–2;5) и С(4;5).
Начертите этот прямоугольник.
Найдите координаты вершины D.
Найдите координаты точки пересечения диагоналей прямоугольника.
Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
7. Изобразите на координатной плоскости все точки (х; y) такие, что x = 2, y – произвольное число.
Вариант 2
1.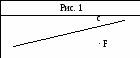 Перерисуйте в тетрадь рисунок 1. Проведите через точку F:
Перерисуйте в тетрадь рисунок 1. Проведите через точку F:
1) прямую а, параллельную прямой c;
2) прямую b, перпендикулярную прямой c.
2. Начертите произвольный треугольник DEF.
Постройте фигуру, симметричную этому треугольнику
относительно точки E.
3. Отметьте на координатной плоскости точки C (1;4) и D (–1;2). Проведите отрезок CD.
1) Найдите координаты точки пересечения отрезка CD с осью ординат.
2) Постройте отрезок, симметричный отрезку CD относительно оси абсцисс, и найдите координаты концов полученного отрезка.
4.Начертите тупой угол OCA, отметьте на его стороне CA точку P. Проведите через точку P прямую, перпендикулярную прямой CA, и прямую, перпендикулярную прямой CO.
5. Велосипедист выехал из дома и через некоторое время вернулся назад. На рисунке 2 изображен график движения велосипедиста. 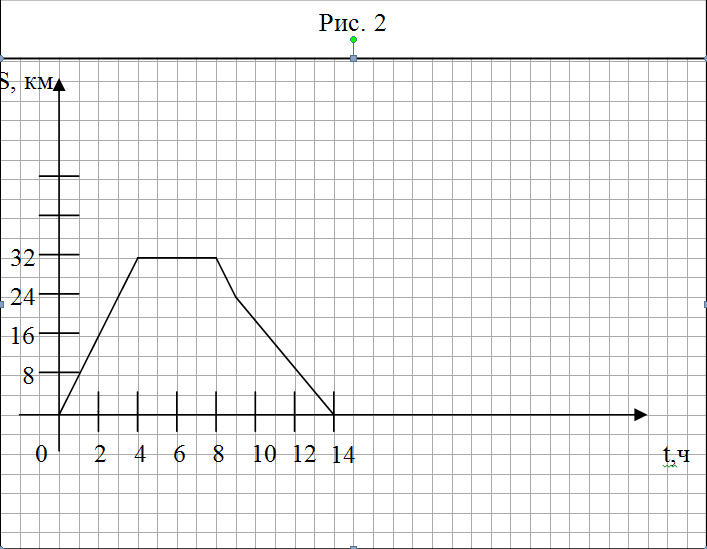
На каком расстоянии от дома был велосипедист через 4 ч после начала движения?
Сколько времени велосипедист затратил на остановку?
Через сколько часов после начала движения велосипедист был на расстоянии 24 км от дома?
С какой скоростью велосипедист ехал до остановки?
6. Даны координаты трех вершин прямоугольника ABCD: А (–1;–3), С(5; 1) и D (5; –3)
Начертите этот прямоугольник.
Найдите координаты вершины В.
Найдите координаты точки пересечения диагоналей прямоугольника.
Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
infourok.ru
Контрольные работы по алгебре 8 класс. УМК Мерзляк и др.
Составитель: Щёголева Л. Ф., учитель высшей категории.
Вариант 1. А8, к. р. №5
1.Решить неполное квадратное уравнение: а) 5х² - 125 = 0; б) 3х² + 4х = 0.
2.Решить уравнение: а) х² + 6х – 7 = 0; б) 3х² + 7х + 2 = 0; в) х² - 3х + 1 = 0; г) х² - х + 3 = 0.
3.Составить приведенное квадратное уравнение, сумма корней которого равна числу 6, а произведение – числу 4.
4.Решить задачу. Одна из сторон прямоугольника на 7 см больше другой. Найти стороны прямоугольника, если его площадь равна 44 см². (Площадь прямоугольника равна произведению его длины на ширину).
5.Число (- 6) является корнем уравнения 2х² + в х – 6 = 0. Найдите второй корень уравнения и значение в.
6.При каком значении а уравнение 2х² + 4х + а = 0 имеет единственный корень?
_______________________________________________________________________________________________
Вариант 2. А8, к. р. №5
1.Решить неполное квадратное уравнение: а) 3х² - 48 = 0; б) 4х² - 7х = 0.
2.Решить уравнение: а) х² + 8х – 9 = 0; б) 12х² - 5х - 2 = 0; в) х² - 6х - 3 = 0; г) х² - 3х + 11 = 0.
3.Составить приведенное квадратное уравнение, сумма корней которого равна числу 7, а произведение – числу (- 8).
4.Решить задачу. Одна из сторон прямоугольника на 5 см меньше другой. Найти стороны прямоугольника, если его площадь равна 84 см². (Площадь прямоугольника равна произведению его длины на ширину).
5.Число (- 2) является корнем уравнения 3х² + 4х + а = 0. Найдите второй корень уравнения и значение а.
6.При каком значении t уравнение t х² + 40х + 5 = 0 имеет единственный корень?
_______________________________________________________________________________________________
Вариант 3. А8, к. р. №5
1.Решить неполное квадратное уравнение: а) 4х² - 100 = 0; б) 7х² + 5х = 0.
2.Решить уравнение: а) х² - 6х – 16 = 0; б) 15х² - 4х - 3 = 0; в) х² - 7х + 4 = 0;
г) х² + 5 х + 9 = 0.
3.Составить приведенное квадратное уравнение, сумма корней которого равна числу 4, а произведение – числу (-3).
4.Решить задачу. Одна из сторон прямоугольника на 3 см больше другой. Найти стороны прямоугольника, если его площадь равна 88 см². (Площадь прямоугольника равна произведению его длины на ширину).
5.Число (- 3) является корнем уравнения 5х² + t х – 12 = 0. Найдите второй корень уравнения и значение t.
6.При каком значении а уравнение 3х² - 6х + а = 0 имеет единственный корень?
_______________________________________________________________________________________________
Вариант 4. А8, к. р. №5
1.Решить неполное квадратное уравнение: а) 2х² - 128 = 0; б) 8х² - 3х = 0.
2.Решить уравнение: а) х² - х – 20 = 0; б) 3х² - 2х – 8 = 0; в) х² + 6х – 2 = 0;
г) х² - 4х + 6 = 0.
3.Составить приведенное квадратное уравнение, сумма корней которого равна числу (-6), а произведение – числу 3.
4.Решить задачу. Одна из сторон прямоугольника на 6 см меньше другой. Найти стороны прямоугольника, если его площадь равна 72 см². (Площадь прямоугольника равна произведению его длины на ширину).
5.Число 5 является корнем уравнения 4х² + 6х + k = 0. Найдите второй корень уравнения и значение k.
6.При каком значении t уравнение t х² + 8х + 4 = 0 имеет единственный корень?
_________________________________________________________________________________________________
Вариант 31. А8, к. р. №5
1.Решить неполное квадратное уравнение: а) 64х² - 256 = 0; б) 7х² - 35х = 0.
2.Решить уравнение: а) х² - 8х + 7 = 0; б) 9х² + 5х – 26 = 0;
в) х² + 5х – 24 = 0; г) х² - 3х – 4 = 0.
3.Составить приведенное квадратное уравнение, сумма корней которого равна числу (- 10), а произведение – числу 13.
4.Решить задачу. Одна из сторон прямоугольника на 1 см меньше другой. Найти стороны прямоугольника, если его площадь равна 56 см². (Площадь прямоугольника равна произведению его длины на ширину).
5.В уравнении х² + р х – 4 = 0 один из его корней равен 4. Найдите другой корень и коэффициент р.
6.При каком значении t уравнение 6х² - t х + 15 = 0 имеет единственный корень?
_____________________________________________________________________________________________
Вариант 32. А8, к. р. №5
1.Решить неполное квадратное уравнение: а) 46х² - 414 = 0; б) 2х² - 10х = 0.
2.Решить уравнение: а) х² - 7х + 12 = 0; б) 2х² + 3х – 65 = 0;
в) х² + 8х + 12 = 0; г) х² - 6х + 13 = 0.
3.Составить приведенное квадратное уравнение, сумма корней которого равна числу (- 19), а произведение – числу 1.
4.Решить задачу. Одна из сторон прямоугольника на 13 см больше другой. Найти стороны прямоугольника, если его площадь равна 114 см². (Площадь прямоугольника равна произведению его длины на ширину).
5.В уравнении х² - р х +1 4 = 0 один из его корней равен ( - 7). Найдите другой корень и коэффициент р.
6.При каком значении t уравнение 9х² - t х + 5 = 0 имеет единственный корень?
Вариант 1 А8, к. р. №4
1.Найти значение выражения:
1) 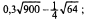 2)
2) 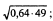 3)
3) 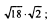 4)
4) 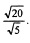
2.Упростить выражение:
1) 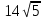 +
+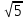 -
- 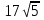 ; 2)
; 2)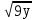 -
- 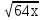 +
+ 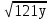 -
- 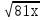 ;
;
3) 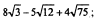 4)
4) 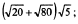 5)
5) 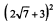
3.Сравнить числа: 1) 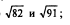 2)
2) 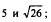 3)
3) 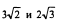 .
.
4.Освободитесь от иррациональности в знаменателе дроби:
1) 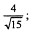 2)
2) 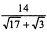 .
.
5. Постройте в одной системе координат графики функций у=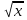 и у= - 0,5х +4 и укажите координаты точки их пересечения.
и у= - 0,5х +4 и укажите координаты точки их пересечения.
6.Решите уравнение:
1) х²= 81; 2)х² = - 36; 3)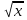 = 10; 4)
= 10; 4) 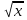 = - 15.
= - 15.
______________________________________________________________________________________________
Вариант 2 А8, к. р. №4
1.Найти значение выражения:
1) 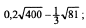 2)
2) 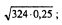 3)
3) 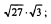 4)
4) 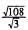 .
.
2.Упростить выражение:
1) 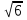 -
- 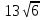 +
+ 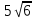 ; 2)
; 2) 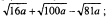 3)
3) 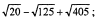
4) 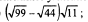 5)
5) 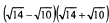 .
.
3.Сравнить числа: 1) 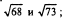 2)
2) 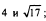 3)
3) 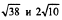 .
.
4.Освободитесь от иррациональности в знаменателе дроби:
1) 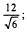 2)
2) 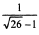 .
.
5. Решить графически уравнение: 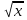 = х – 2.
= х – 2.
6. Не выполняя построения графика функции у = 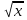 , укажите, через какие из данных точек проходит этот график: А(4; 2), В(16; -4), С(0,09; 0,3), D( - 100; 10), Е(12,25; 3,5).
, укажите, через какие из данных точек проходит этот график: А(4; 2), В(16; -4), С(0,09; 0,3), D( - 100; 10), Е(12,25; 3,5).
______________________________________________________________________________________________
Вариант 3 А8, к. р. №4
1.Найти значение выражения:
1) 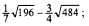 2)
2) 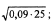 3)
3) 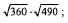 4)
4) 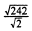 .
.
2.Упростить выражение:
1) 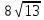 -
- 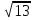 +
+ 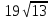 ; 2)
; 2)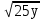 -
- 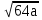 +
+ 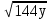 -
- 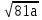 ;
;
3) 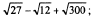 4)
4) 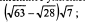 5)
5) 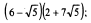
3.Сравнить числа: 1) 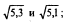 2)
2) 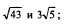 3)
3) 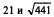 .
.
4.Освободитесь от иррациональности в знаменателе дроби:
1) 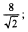 2)
2) 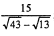 .
.
5. Постройте в одной системе координат графики функций у =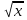
и у = 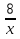 и укажите координаты точки их пересечения.
и укажите координаты точки их пересечения.
6. Вынесите множитель из-под знака корня:
1) 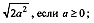 2)
2) 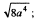 3)
3) 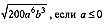 .
.
___________________________________________________________________________________________
infourok.ru
6. Цена товара снизилась со 180р. до 153 р. На сколько процентов снизилась цена товара?
7. Число а составляет 50 % от числа b. Сколько процентов число b составляет от числа а?
Контрольная работа № 6 по теме «Отношения и пропорции»
Вариант 1
1. Автомобиль проезжает некоторое расстояние за 1,8 ч. За какое время он проедет с той же скоростью расстояние в 4,5 раза больше?
2. За некоторую сумму денег можно купить 12 тонких тетрадей. Сколько можно купить за эту же сумму денег толстых тетрадей, которые в 3 раза дороже тонких?
3. Вычислите длину окружности, радиус которой равен 6,5 дм.
4. Найдите площадь круга, радиус которого равен 4 см.
5. Периметр треугольника равен 108 см, а длины его сторон относятся как 6:8:13. Найдите стороны треугольника.
6. С помощью циркуля и линейки постройте треугольник со сторонами 3 см, 5 см и 7 см.
7. В коробке лежат 6 красных и 8 белых шаров. Какова вероятность того, что выбранный наугад шар окажется: 1) красным; 2) жёлтым?
8. Заполните таблицу, если величина y прямо пропорциональна величине x.
x0,2
0,6
y
1,8
3,6
9. Заполните таблицу, если величина y обратно пропорциональна величине x.
x9
18
y
6
27
10. Представьте число 159 в виде суммы трёх слагаемых x, y, z таких, чтобы x:y=5:6, а y:z=9:10.
Вариант 2
1. Из некоторого количества свежих грибов получили 2,2 кг сухих грибов. Сколько сухих грибов можно получить, если свежих грибов взять в 3,2 раза больше?
2. За некоторую сумму денег можно купить 15 ручек. Сколько можно купить за эту же сумму денег карандашей, которые в 5 раз дешевле ручек?
3. Вычислите длину окружности, радиус которой равен 7,5 см.
4. Найдите площадь круга, радиус которого равен 8 дм.
5. Периметр треугольника равен 132 см, а длины его сторон относятся как 5:7:10. Найдите стороны треугольника.
6. С помощью циркуля и линейки постройте треугольник со сторонами 2 см, 5 см и 6 см.
7. В коробке лежат 6 белых и 9 синих шаров. Какова вероятность того, что выбранный наугад шар окажется: 1) белым; 2) белым или синим?
8. Заполните таблицу, если величина y прямо пропорциональна величине x.
x0,8
0,9
y
4
6
9. Заполните таблицу, если величина y обратно пропорциональна величине x.
x8
12
y
3
4
10. Представьте число 175 в виде суммы трёх слагаемых x, y, z таких, чтобы x:y=3:4, а y:z=6:7.
Контрольная работа № 7 по теме «Рациональные числа и действия над ними»
Вариант 1
1. Начертите координатную прямую и отметьте на ней точки A(3), B(4), C(4,5), D(-4,5). Какие из отмеченных точек имеют противоположные координаты?
2. Выберите среди чисел 4; -8; 0;-2,8; 6,8;10; -42; :
1) натуральные; 4) целые отрицательные;
2) целые; 5) дробные неотрицательные.
3) положительные;
3. Сравните числа: 1) -6,9 и 1,4; 2) -5,7 и -5,9.
4. Вычислите: 1) 2)
5. Найдите значение x, если: 1) –х = -12; 2) –(–х) = 1,6.
6. Решите уравнение: 1) 2)
7. Найдите наименьшее целое значение х, при котором верно неравенство
8. Какую цифру можно поставить вместо звёздочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи): -6,5*7>-6,526?
infourok.ru
4. Найдите процент содержания серебра в сплаве, если в 300 г сплава содержится 63 г серебра.
5. Решите уравнение 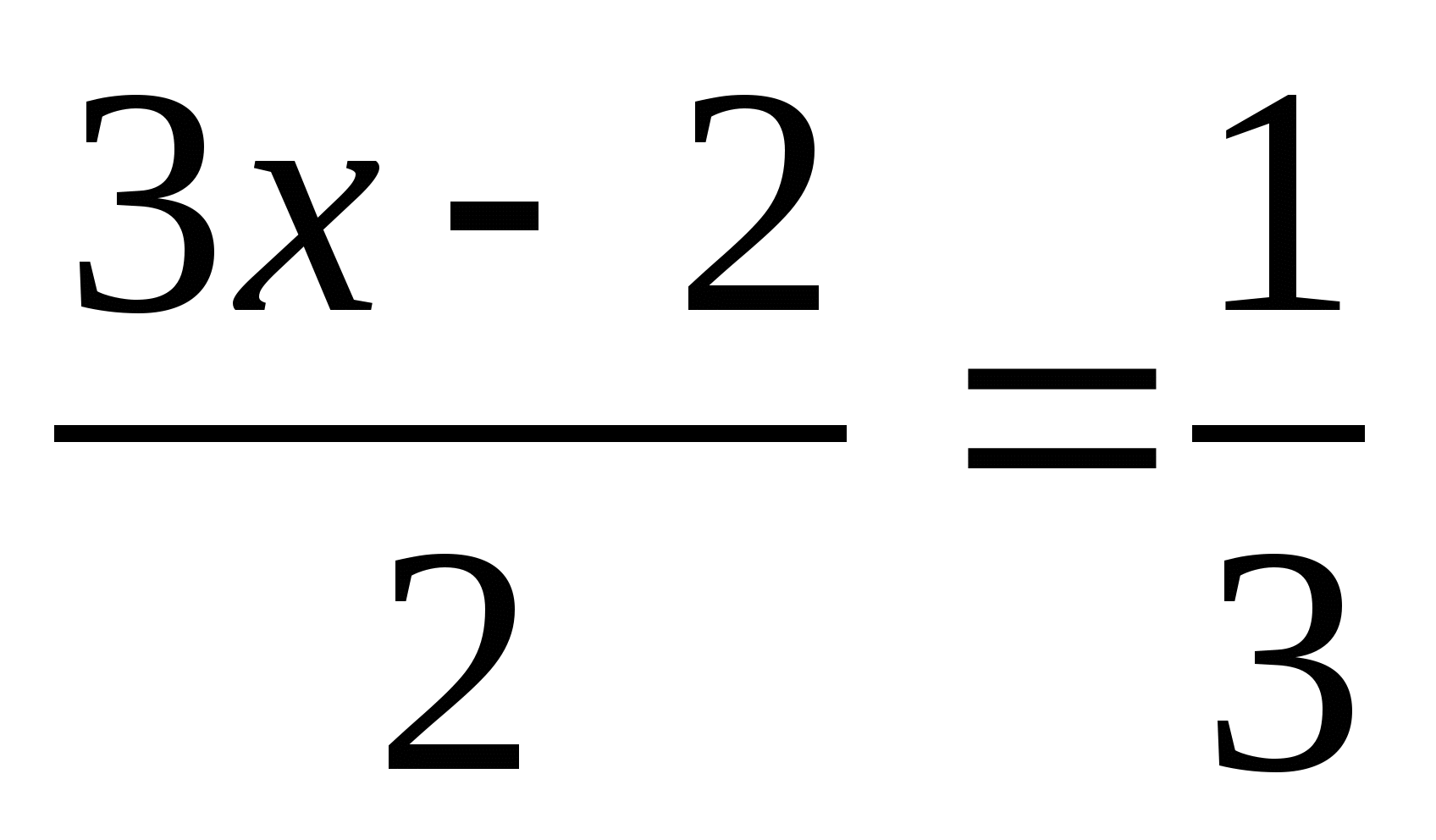 .
.
6. Цена товара снизилась с 180 р. до 153 р. На сколько процентов снизилась цена товара?
7. Число а составляет 50 % от числа 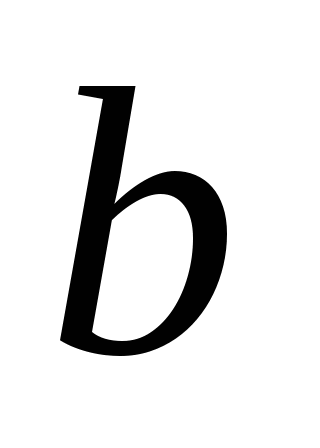 .Сколько процентов число
.Сколько процентов число 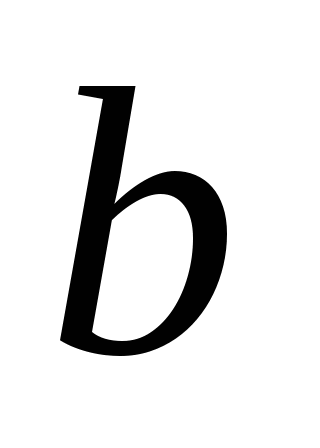 составляет от числа
составляет от числа  ?
?
Контрольная работа №6
Прямая и обратная пропорциональные зависимости.
Окружность и круг. Вероятность случайного события
Вариант 1
1. Автомобиль проезжает некоторое расстояние за 1,8 ч. За какое время он проедет с той же скоростью расстояние в 4,5 раза большее?
2. За некоторую сумму денег можно купить 12 тонких тетрадей. Сколько можно купить за эту же сумму денег толстых тетрадей, которые в 3 раза дороже тонких?
3. Вычислите длину окружности, радиус которой равен 6,5 дм.
4. Найдите площадь круга, радиус которого равен 4 см.
5. Периметр треугольника равен 108 см, а длины его сторон относятся как 6 : 8 : 13.Найдите стороны треугольника.
6. С помощью циркуля и линейки постройте треугольник со сторонами 3 см, 5 см и 7 см.
7. В коробке лежат 6 красных и 8 белых шаров. Какова вероятность того, что выбранный наугад шар окажется: 1) красным; 2) желтым?
8. Заполните таблицу, если величина 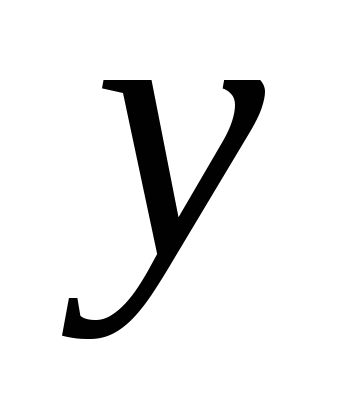 прямо пропорциональна величине
прямо пропорциональна величине 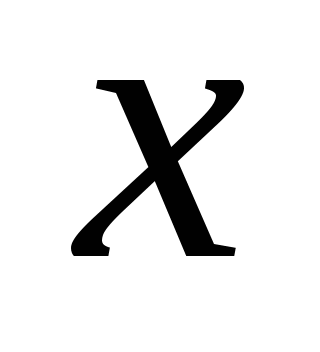 .
.
Вариант 2
1. Из некоторого количества свежих грибов получили 2,2 кг сухих грибов. Сколько сухих грибов можно получить, если свежих грибов взять в 3,2 раза больше?
2. За некоторую сумму денег можно купить 15ручек. Сколько можно купить за эту же сумму денег толстых карандашей, которые в 5 раз дешевле ручек?
3. Вычислите длину окружности, радиус которой равен 7,5 см.
4. Найдите площадь круга, радиус которого равен 8 дм.
5. Периметр треугольника равен 132 см, а длины его сторон относятся как 5 : 7 : 10. Найдите стороны треугольника.
6. С помощью циркуля и линейки постройте треугольник со сторонами 2 см, 5 см и 6 см.
7. В коробке лежат 6 белых и 9 синих шаров. Какова вероятность того, что выбранный наугад шар окажется: 1) белым; 2) белым или синим?
8. Заполните таблицу, если величина 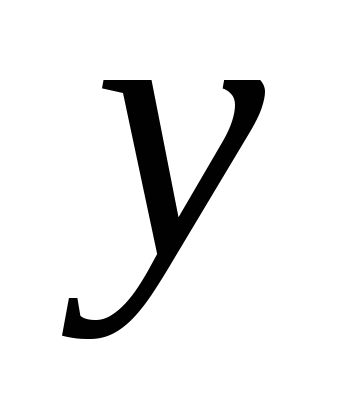 прямо пропорциональна величине
прямо пропорциональна величине 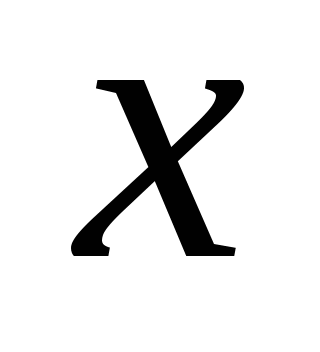 .
.
Контрольная работа №7
Рациональные числа. Сравнение рациональных чисел
Вариант 1
1.Начертите координатную прямую и отметьте на ней точки А (3), В (4), С (4,5), D (–4,5). Какие из отмеченных точек имеют противоположные координаты?
2. Выберите среди чисел 4; - 8 ; 0; 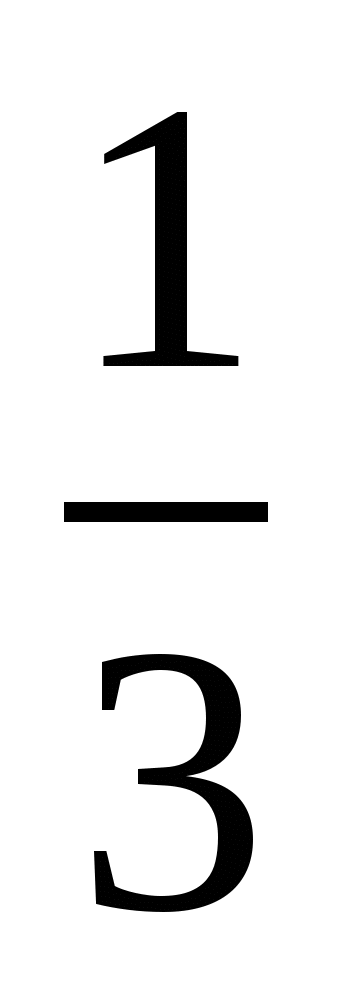 ; - 2,8; 6,8;
; - 2,8; 6,8; 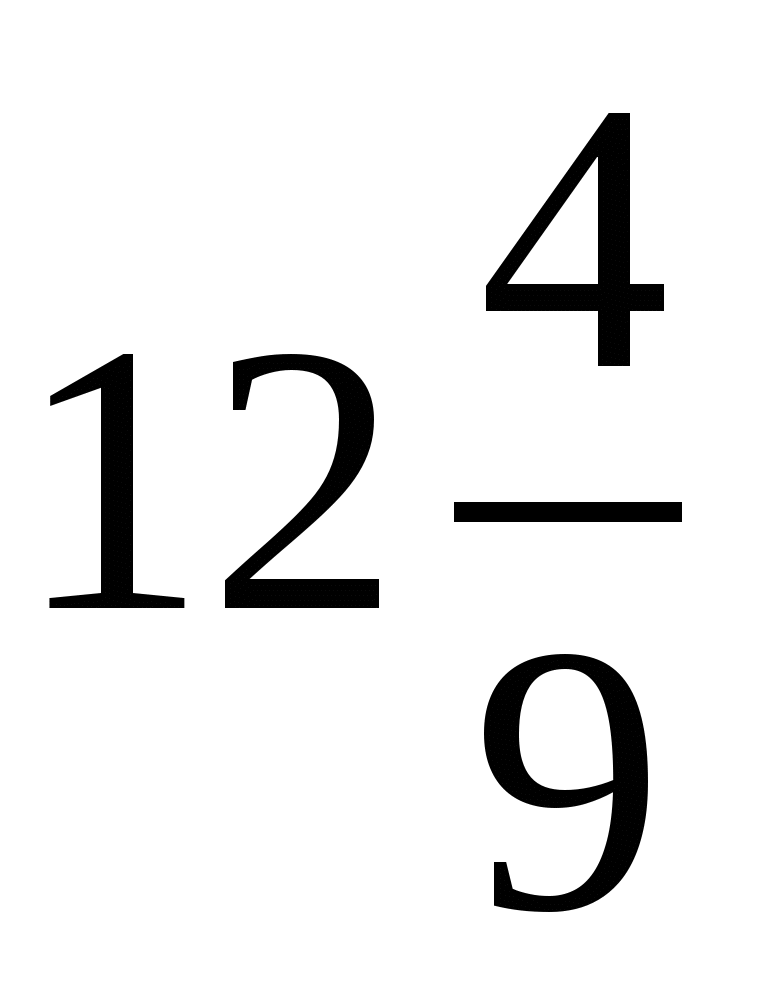 ; 10; - 42;
; 10; - 42; 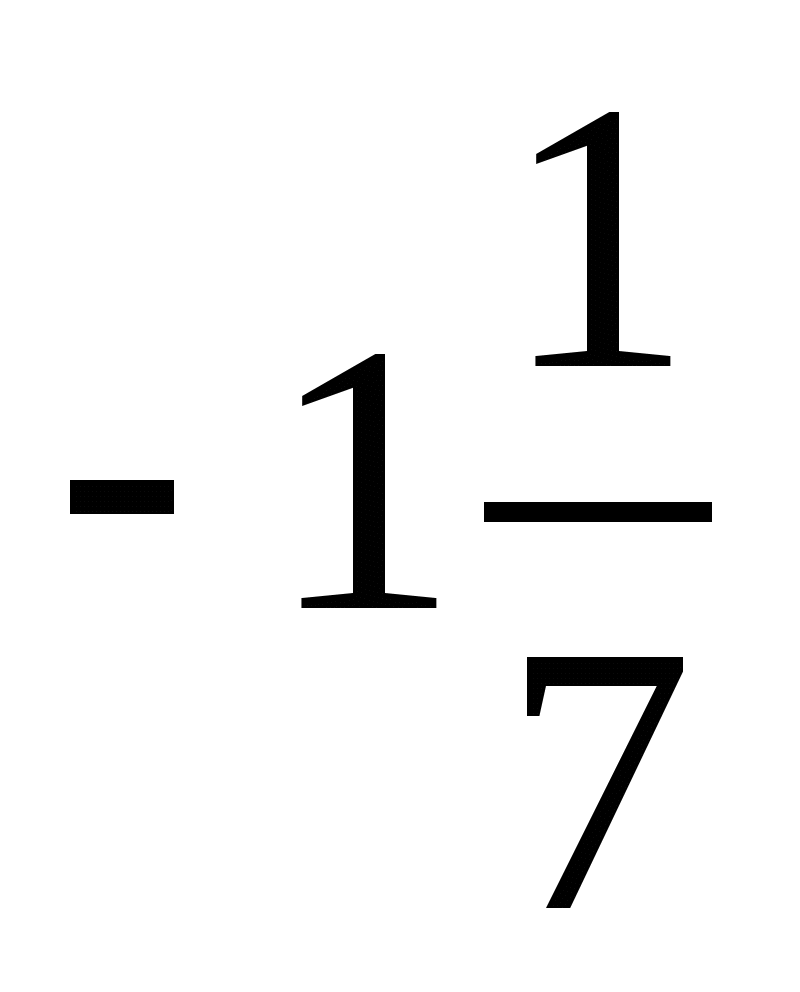 :
:
1) натуральные; 4) целые отрицательные;
2) целые; 5) дробные неотрицательные.
3) положительные;
3. Сравните числа: 1) – 6,9 и 1,4 ; 2) – 5,7 и – 5,9.
4. Вычислите : 1) 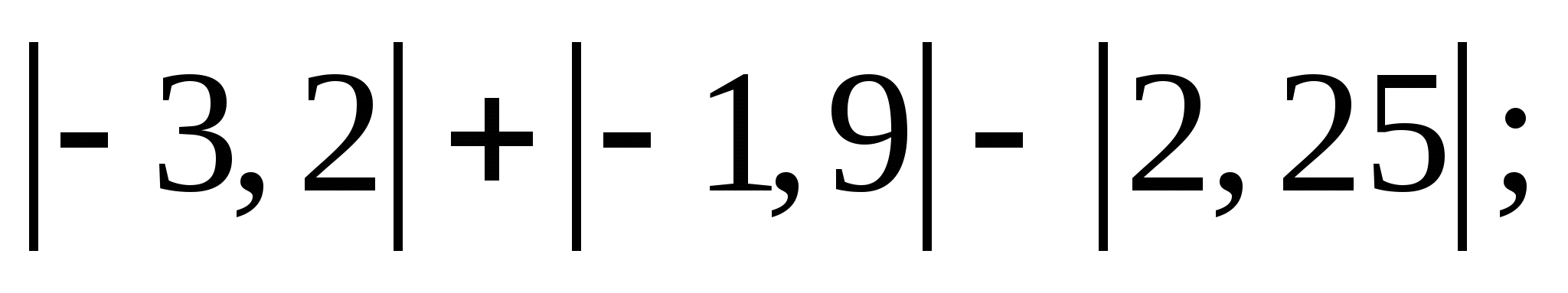 2)
2)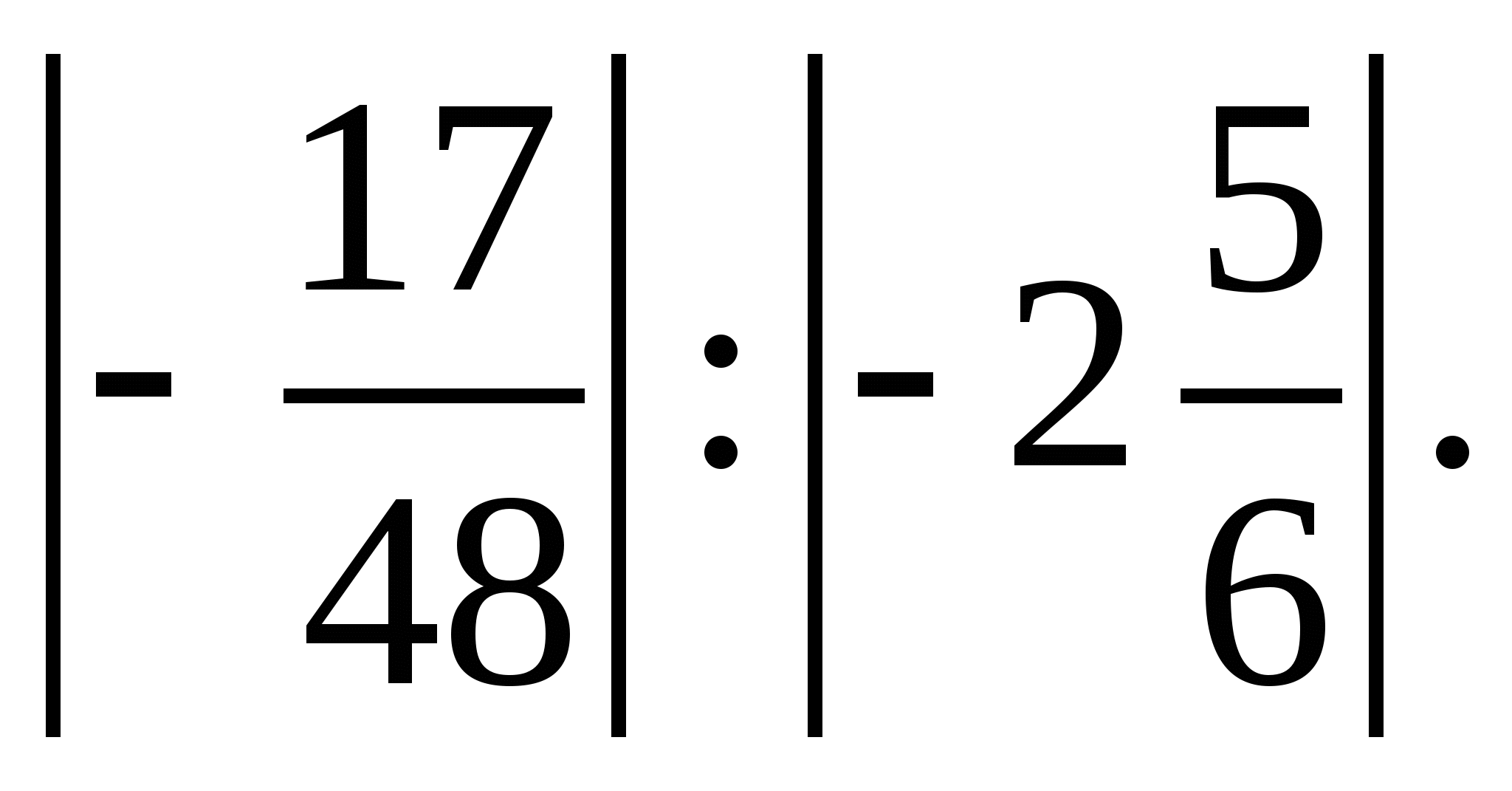
5.Найдите значение 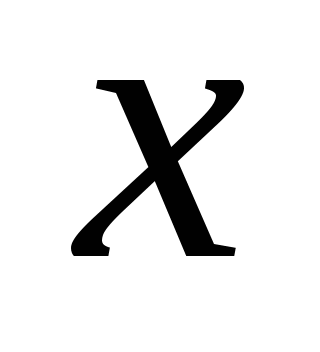 , если:
, если:
1) 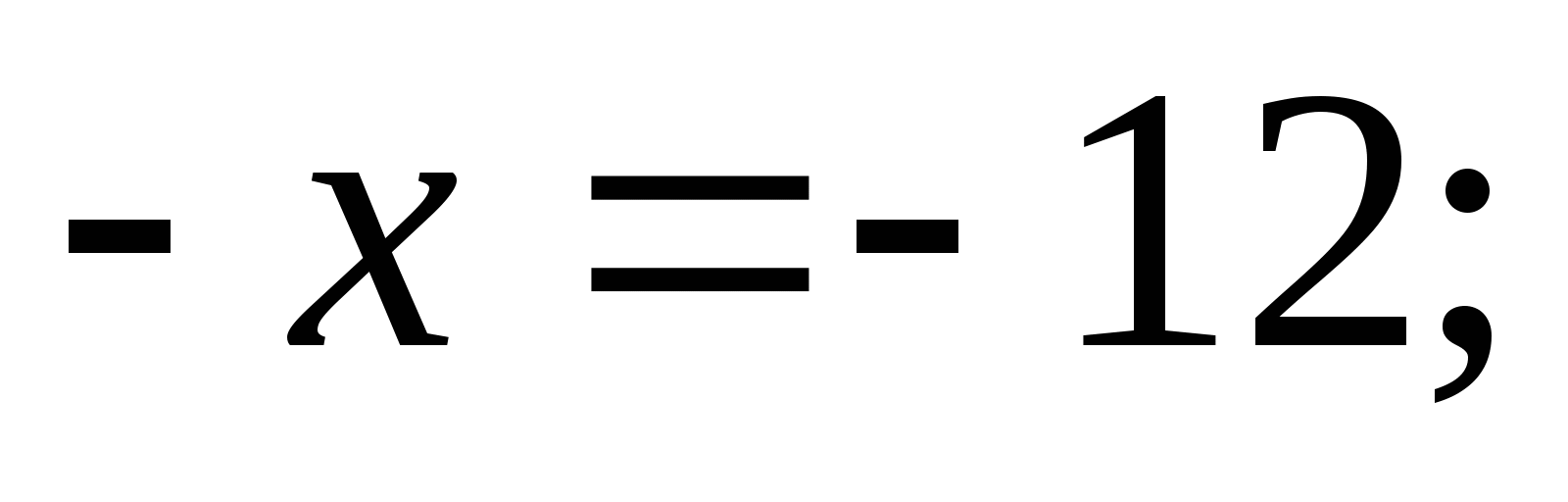 2)
2) 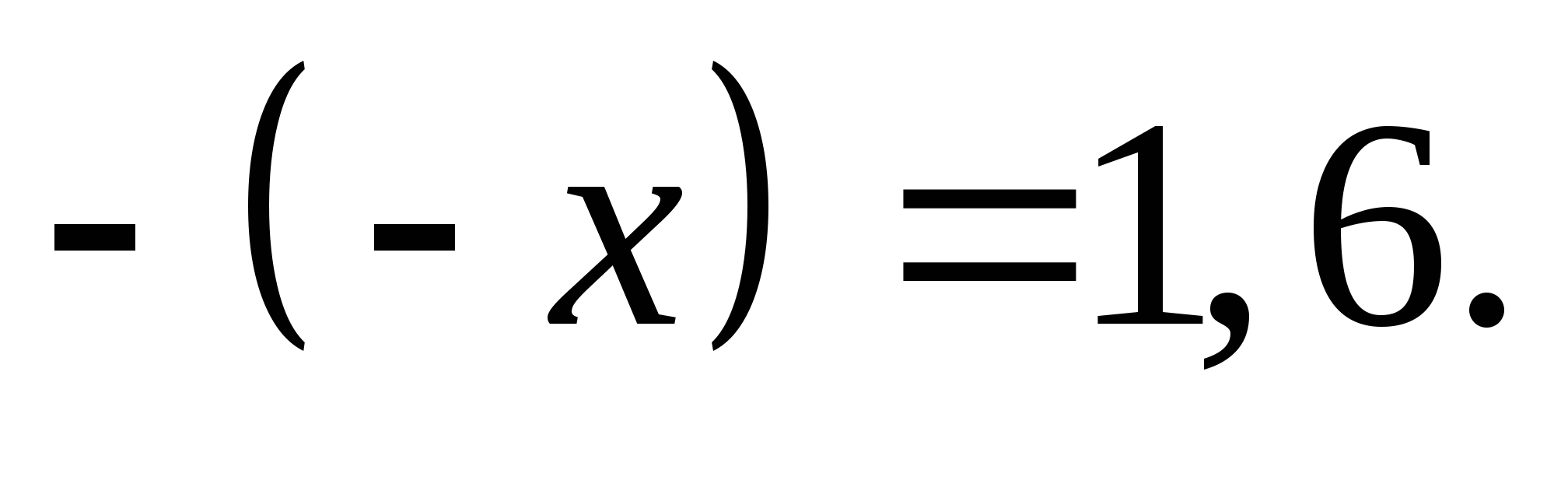
6. Решите уравнение: 1) 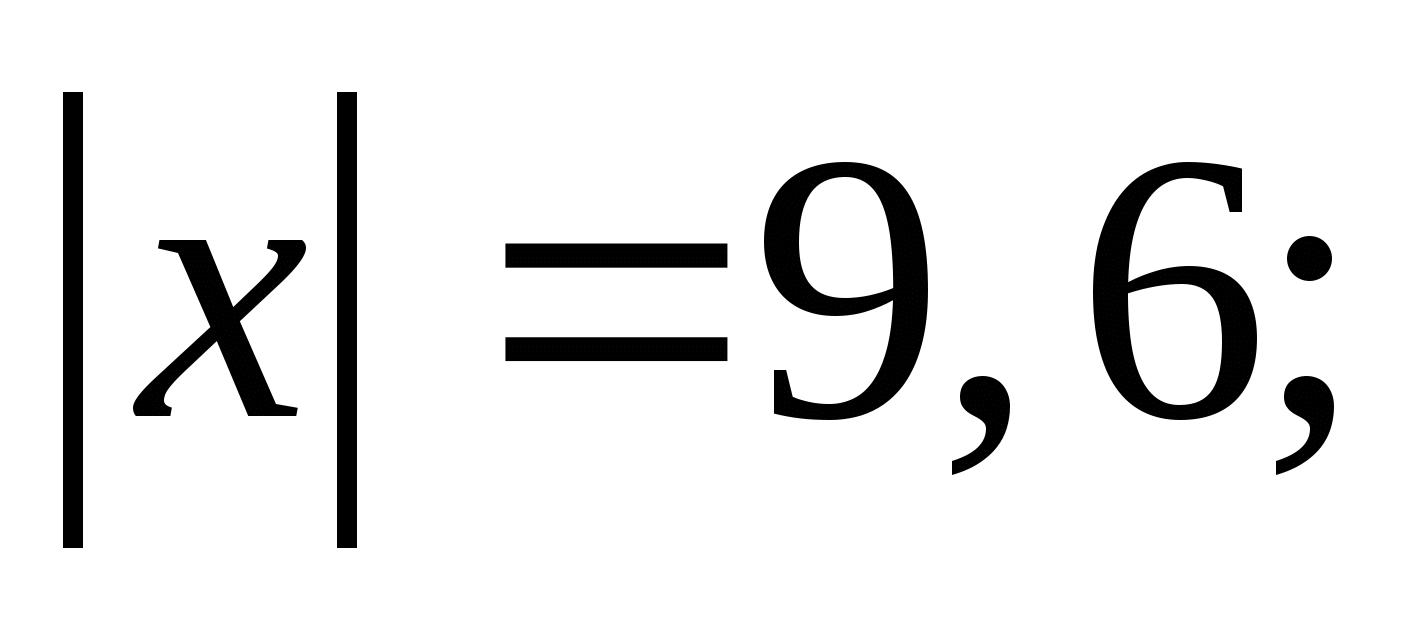 2)
2) 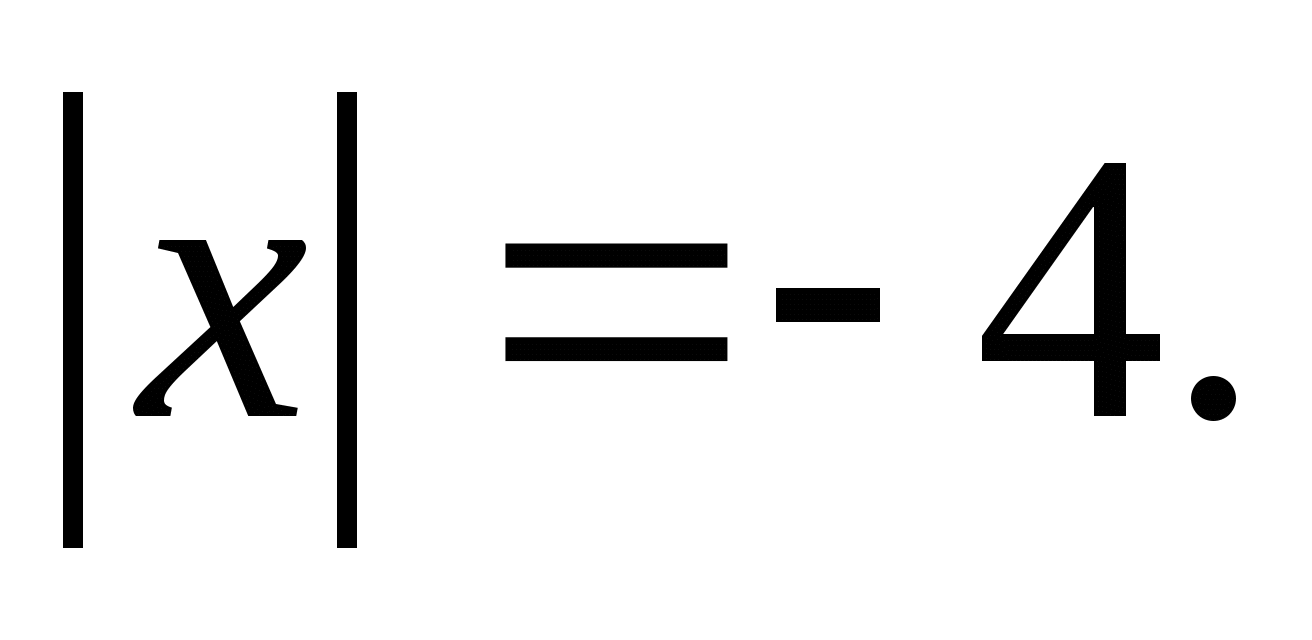
7. Найдите наименьшее целое значение 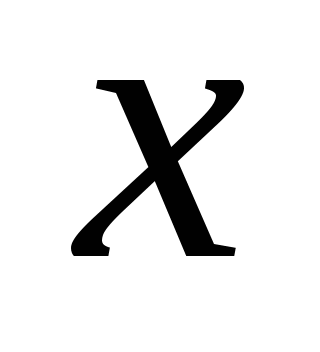 , при котором верно неравенство
, при котором верно неравенство 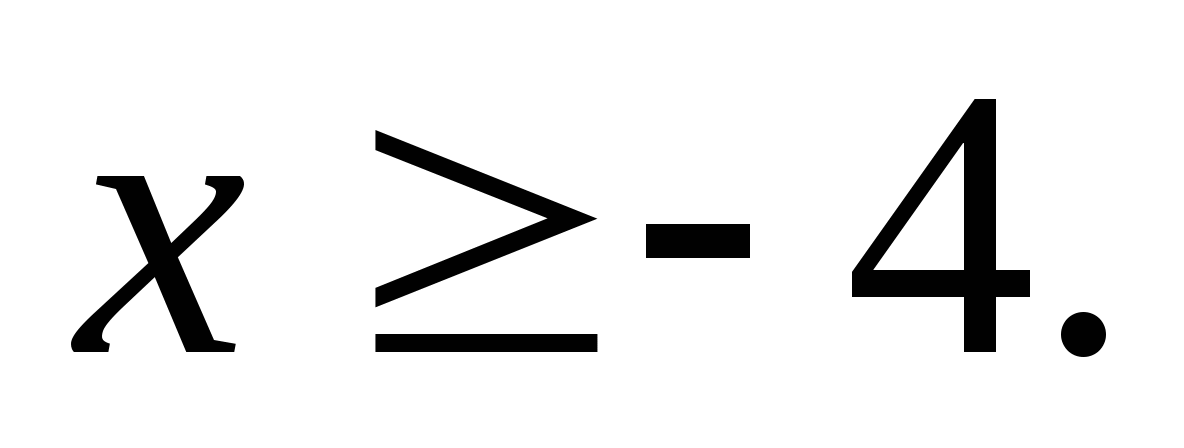
8. Какую цифру можно поставить вместо звездочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи): 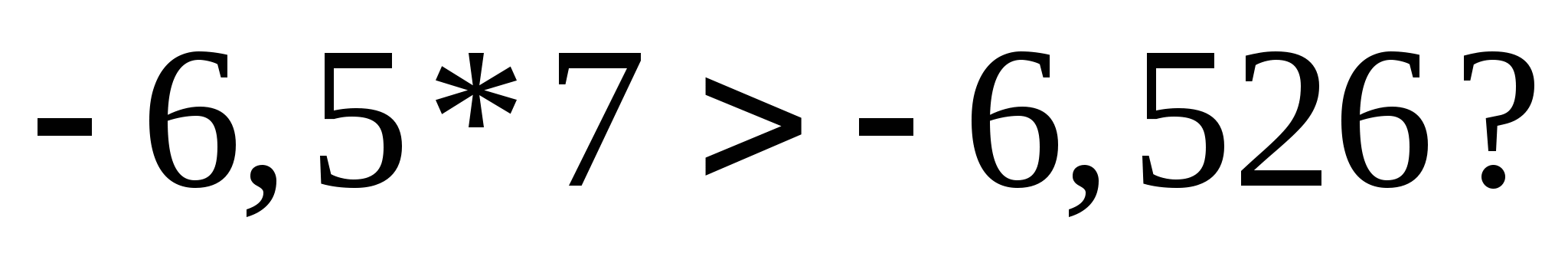
9. Найдите два числа, каждое из которых больше 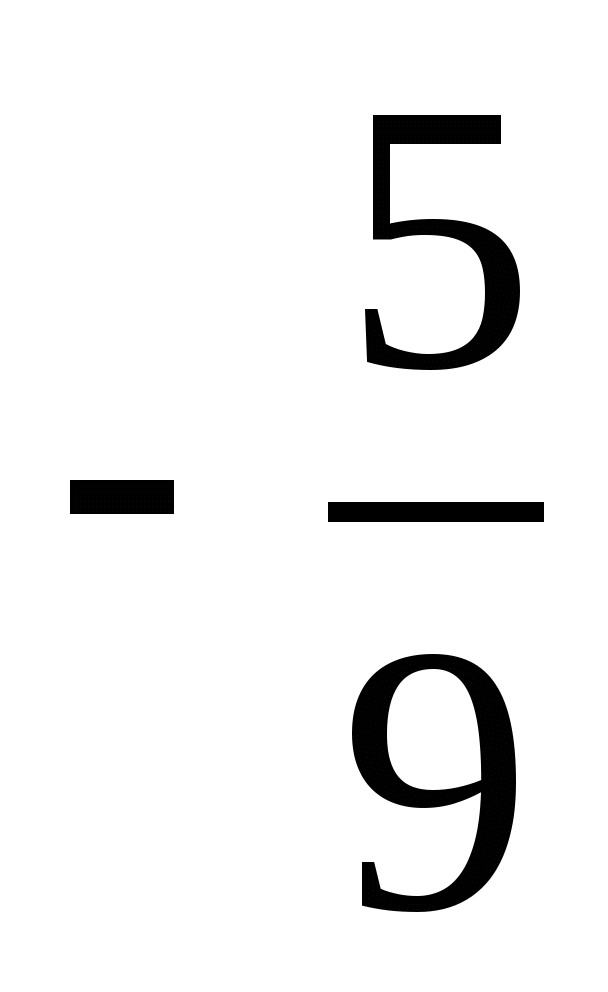 , но меньше
, но меньше 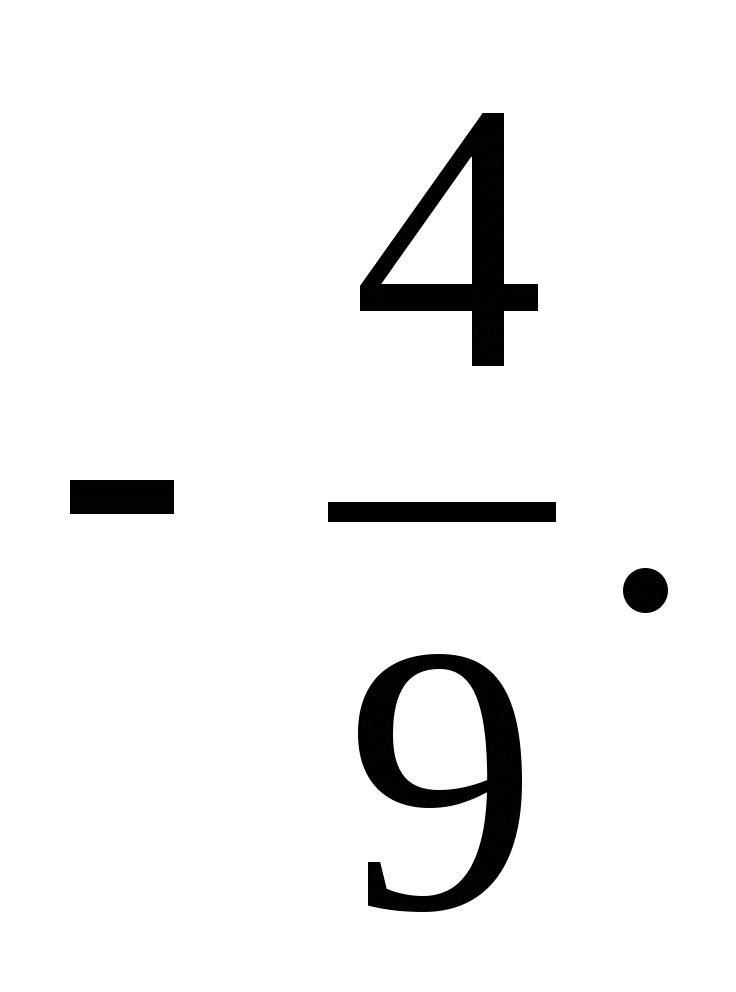
Вариант 2
1.Начертите координатную прямую и отметьте на ней точки М (2), К (–6), F (3,5), D (–3,5). Какие из отмеченных точек имеют противоположные координаты?
2. Выберите среди чисел 5; – 9 ; 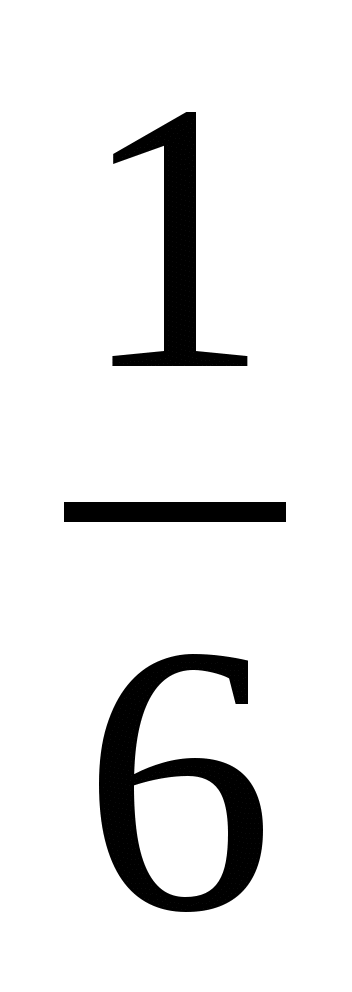 ; - 1,6; 8,1; 0;
; - 1,6; 8,1; 0; 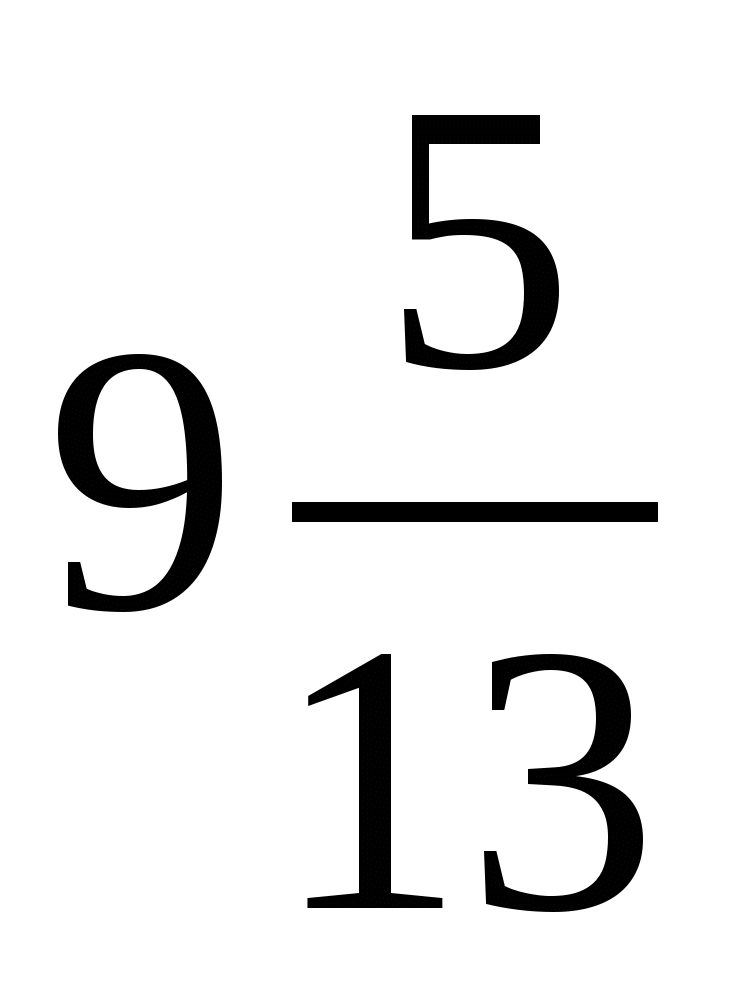 ; 18; –53;
; 18; –53; 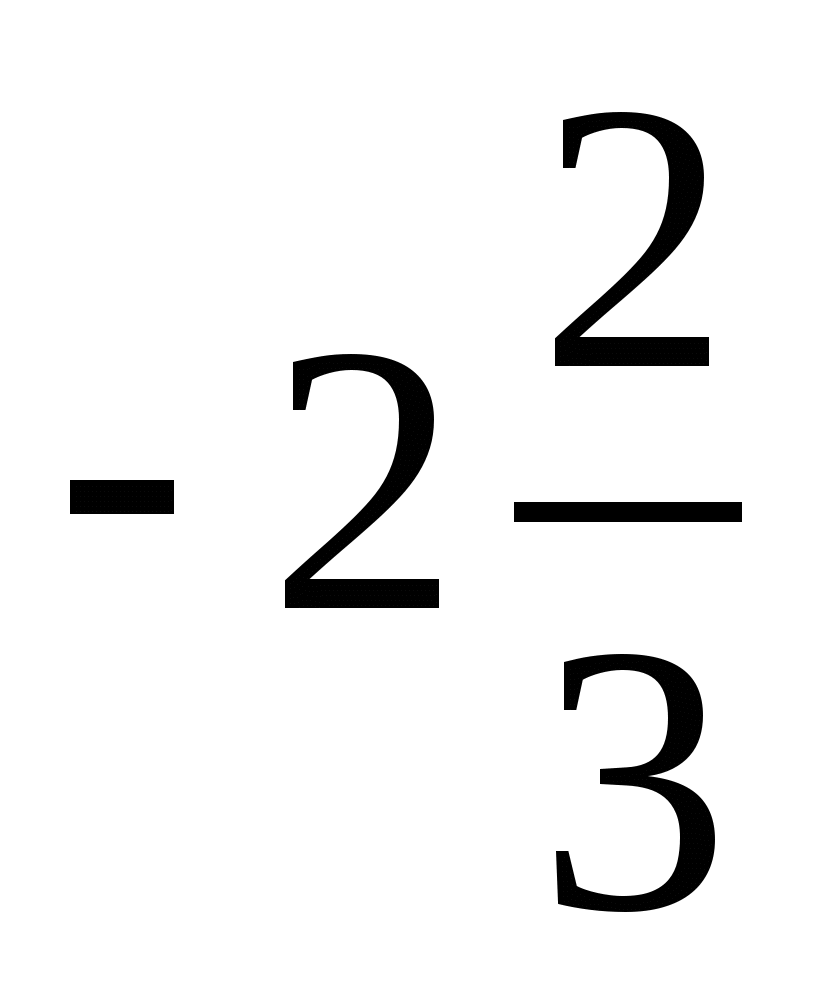 :
:
infourok.ru