

Рис.26
Задание№9
Комбинаторика.
Десятичное двоичное число, в котором нет рядом стоящих единиц, разделили на две равные части – левую и правую. Сколько существует 10-значных двоичных чисел, в каждом из которых слева единиц больше, чем справа?
Решение.
В левой части, может быть 0 единиц (т.е. ни одной), либо одна, либо две, либо три, либо четыре, либо пять. В соответствии с этим разобьём задачу на шесть более простых задач:
а) в левой части нет единиц. В этом случае нет ни одного десятизначного двоичного числа, удовлетворяющего условию задачи;
б) в левой части одна единица, тогда в правой части должны быть только нули. Всего существует 5 таких чисел:
00001 00000; 00010 00000; 00100 00000; 01000 00000; 10000 00000:
в) в левой части две единицы, тогда в правой может быть либо 0 единиц, либо одна единица. Две единицы в левой части дают  пятизначным числам. Одна единица в правой части может располагаться пятью способами. Тогда существует
пятизначным числам. Одна единица в правой части может располагаться пятью способами. Тогда существует  искомых чисел. Таким образом, всего существует 25+10=35 чисел, в каждом из которых слева две единицы, а справа нет единиц или одна единица;
искомых чисел. Таким образом, всего существует 25+10=35 чисел, в каждом из которых слева две единицы, а справа нет единиц или одна единица;
г) слева три единицы, тогда справа их может быть либо 0, либо 1, либо 2.Три единицы слева могут располагаться десятью способами. Если справа единиц нет, то получаем 10 искомых чисел. Если справа одна единица, то существует  искомых чисел. Если справа две единицы, то существует
искомых чисел. Если справа две единицы, то существует  искомых чисел. Таким образом, всего получаем: 10+100+50=160,
искомых чисел. Таким образом, всего получаем: 10+100+50=160,
т.е. существует 160 чисел, у которых слева три единицы, а справа 0, либо 1, либо 2 единицы;
д) слева четыре единицы. Справа может быть либо 0 единиц, либо 1, либо 2, либо 3. Четыре единицы слева дают пять вариантов их расположения. Если справа единиц нет, то получаем пять чисел из искомых. Если справа одна единица, то возможно 25 искомых чисел. Если справа две единицы, то существует  искомых чисел. Если справа три единицы, то возможно
искомых чисел. Если справа три единицы, то возможно  искомых чисел. Таким образом, всего получаем 25+50+50=125, т.е. существует 125 чисел, у которых слева четыре единицы, а справа 0, либо 1, либо 2, либо 3 единицы.
искомых чисел. Таким образом, всего получаем 25+50+50=125, т.е. существует 125 чисел, у которых слева четыре единицы, а справа 0, либо 1, либо 2, либо 3 единицы.
е) слева пять единиц . Справа может быть либо 0единиц, либо1, либо2, либо3, либо 4. Если справа единиц нет, то получаем одно число из искомых. Если справа одна единица, то возможно 5 искомых чисел. Если справа две единицы, то существует 10 искомых чисел. Если справа три единицы, то возможно 10 искомых чисел. Если справа четыре единицы, то возможно  искомых чисел. Сложим полученные результаты:
искомых чисел. Сложим полученные результаты:
1+5+10+10+5=31.
То есть всего существует 31 число, у которых слева пять единиц, а справа 0, либо 1, либо 2, либо 3, либо 4 единицы.
Сложим числа, полученные в результате решения всех шести задач:
0+5+35+160+125+31=356.
Ответ: 356 чисел.
Задание №10
Нахождение простых цепей в графе.
Найдите все простые цепи. Соединяющие вершины 3 и 6 графа: G={{1,2}, {1,3}, {1,5,}, {2,3}, {2,6}, {3,4}, {3,4}, {3,6}, {4,5}, {4,6}, {5,6}}.
Найдите все простые циклы, начинающиеся и оканчивающиеся в вершине 1.
Найдите все простые цепи, соединяющие вершины 1 и 6 графа, считая, что граф является ориентированным.
Решение.
На рис.27 представлен ориентированный граф.

Рис.27
а) На первом этапе найдём все варианты выхода из первой вершины, найдём все простые цепи, выходящие из вершины 3 и содержащие точно по одному ребру:
3-1, 3-2, 3-4, 3-6.
Одна простая цепь, соединяющая вершины 3 и 6 найдена (она подчёркнута).
На втором этапе найдём все простые цепи, содержащие точно по два ребра и выходящие из вершины 3. Для этого воспользуемся результатами предыдущего этапа:
3-1-2 3-2-6 3-4-1
3-1-4 3-2-1 3-4-5
3-1-5 3-4-6
Получены ещё две искомые цепи (они подчёркнуты).
На третьем этапе находим все простые цепи, ведущие из вершины 3 и содержащие точно по три ребра. Для этого воспользуемся результатами второго второго этапа:
3-1-2-6 3-2-1-4 3-4-1-2
3-1-4-5 3-2-1-5 3-4-1-5
3-1-4-6 3-4-5-1
3-4-5-6
На третьем этапе получено ещё три искомых цепи. Все они подчёркнуты.
В четвёртом этапе находим все простые цепи, ведущие из вершины 3 и содержащие точно по четыре ребра. Для этого воспользуемся результатами третьего этапа:
3-1-4-5-6 3-2-1-5-6 3-4-1-2-6
3-2-1-4-5 3-4-1-5-6
На четвёртом этапе получено ещё четыре искомых цепи. Все они подчёркнуты.
Пятый этап в случае данного графа является последним:
3-2-1-4-5-6
Таким образом, всего в графе, изображённом на рис.27, содержится 11 простых цепей, ведущих от вершины 3 к вершине 6. Среди них одна цепь состоит из одной дуги, две цепи состоят из двух дуг, три цепи из трёх дуг, четыре - из четырёх, и одна цепь содержит пять дуг.
б) Найдите все простые цепи. Соединяющие вершины 3 и 6 графа: G={{1,2}, {1,3}, {1,5,}, {2,3}, {2,6}, {3,4}, {3,4}, {3,6}, {4,5}, {4,6}, {5,6}}.
Найдите все простые циклы, начинающиеся и оканчивающиеся в вершине 1.
Найдите все простые цепи, соединяющие вершины 1 и 6 графа, считая, что граф является ориентированным.
Решение.
На первом этапе найдём все простые цепи, выходящие из вершины 1 и содержащие точно по одному ребру:
1-2, 1-3, 1-4, 1-5,
На втором этапе найдём все простые цепи, выходящие из вершины 1 и содержащие точно по два ребра:
1-2-1 1-3-1 1-4-1 1-5-1
1-2-3 1-3-2 1-4-3 1-5-4
1-2-6 1-3-4 1-4-5 1-5-6
1 -3-6 1-4-6
Найдено четыре простых цикла, правда, содержащих по два ребра (подчёркнуты).
Но формально и они удовлетворяют определению простого цикла: если в простой цепи при вершинном её представлении(т.е. в виде последовательности номеров вершин)первая и последняя вершины совпадают, то цепь называется простым циклом.
Третий этап:
1-2-3-1 1-3-2-1 1-4-3-1 1-5-4-1
1-2-3-4 1-3-2-6 1-4-3-2 1-5-4-3
1-2-3-6 1-3-4-1 1-4-3-6 1-5-4-6
1-2-6-3 1-3-4-5 1-4-5-1 1-5-6-2
1-2-6-4 1-3-4-6 1-4-5-6 1-5-6-3
1-2-6-5 1-3-6-2 1-4-6-2 1-5-6-4
1-3-6-4 1-4-6-3
1-3-6-5 1-4-6-5
На третьем этапе получено шесть искомых простых циклов, содержащих по три ребра.
Четвёртый этап, найдём все простые цепи, содержащие точно четыре ребра:
1-2-3-4-1 1-3-2-6-4 1-4-3-2-1 1-5-4-3-1
1-2-3-4-5 1-3-2-6-5 1-4-3-2-6 1-5-4-3-2
1-2-3-4-6 1-3-4-5-1 1-4-3-6-2 1-5-4-3-6
1-2-3-6-4 1-4-3-6-5 1-5-4-6-2
1-2-3-6-5 1-3-4-5-6 1-4-5-6-2 1-5-4-6-3
1-2-6-3-1 1-3-4-6-2 1-4-5-6-3 1-5-6-2-1
1-2-6-3-4 1-3-4-6-5 1-4-6-2-1 1-5-6-2-3
1-2-6-4-1 1-3-6-2-1 1-4-6-2-3 1-5-6-3-1
1-2-6-4-3 1-3-6-4-1 1-4-6-3-1 1-5-6-3-2
1-2-6-4-5 1-3-6-4-5 1-4-6-3-2 1-5-6-3-4
1-2-6-5-1 1-3-6-5-1 1-4-6-5-1 1-5-6-4-1
1-2-6-5-4 1-5-6-4-3
Четвёртый этап даёт 16 новых простых циклов.
Пятый этап:
1-2-3-4-5-1 1-3-2-6-4-1 1-4-3-2-6-5 1-5-4-3-2-1
1-2-3-4-5-6 1-3-2-6-4-5 1-4-3-6-2-1 1-5-4-3-2-6
1-2-3-4-6-5 1-3-2-6-5-1 1-4-3-6-5-1 1-5-4-3-6-2
1-2-3-6-4-1 1-3-2-6-5-1 1-4-5-6-2-1 1-5-4-6-2-1
1-2-3-6-4-5 1-3-2-6-5-4 1-4-5-6-2-3 1-5-4-6-2-3
1-2-3-6-5-1 1-3-4-5-6-2 1-4-5-6-3-1 1-5-4-6-3-1
1-2-3-6-5-4 1-3-4-6-2-1 1-4-5-6-3-2 1-5-4-6-3-2
1-2-6-4-3-1 1-3-4-6-5-1 1-4-6-2-3-1 1-5-6-2-3-1
1-2-6-4-5-1 1-3-6-4-5-1 1-4-6-3-2-1 1-5-6-2-3-4
1-2-6-5-4-1 1-5-6-3-2-1
1-2-6-5-4-3 1-5-6-3-4-1
1-5-6-4-3-1
1-5-6-4-3-2
На пятом этапе получается 25 новых простых циклов.
Заключительный шестой этап:
1-2-3-4-6-5-1 1-3-2-6-4-5-1 1-4-3-2-6-5-1 1-5-4-3-2-6-1
1-2-3-6-4-5-1 1-3-2-6-5-4-1 1-4-5-6-2-3-1 1-5-4-3-6-2-1
1-2-3-6-5-4-1 1-3-4-5-6-2-1 1-4-5-6-3-2-1 1-5-4-6-2-3-1
1-2-6-5-4-3-1 1-5-4-6-3-2-1
1-5-6-2-3-4-1
1-5-6-4-3-2-1
В шестом этапе получаем ещё 16 простых циклов.
Таким образом, всего в графе, приведённом на рис. 27, существует 67 простых циклов , начинающихся и оканчивающихся в вершине 1. Из них 4 цикла содержат по два ребра, 6 циклов содержат по три ребра, 16 циклов содержат по четыре ребра, 25 циклов содержат по пять рёбер, И 16 – по шесть рёбер.
в) Найдите все простые цепи. Соединяющие вершины 3 и 6 графа: G={{1,2}, {1,3}, {1,5,}, {2,3}, {2,6}, {3,4}, {3,4}, {3,6}, {4,5}, {4,6}, {5,6}}.
Найдите все простые циклы, начинающиеся и оканчивающиеся в вершине 1.
Найдите все простые цепи, соединяющие вершины 1 и 6 графа, считая, что граф является ориентированным.
Решение
На рис.28 представлен ориентированный граф.

Рис.28
На первом этапе. Из вершины 1 выходит четыре дуги:
1-2 1-3 1-4 1-5
Второй этап. Находим все простые цепи, выходящие вершины 1 и состоящие из двух дуг:
1-2-3 1-3-4 1-4-5 1-5-6
1-2-6 1-3-6 1-4-6
Получены четыре искомые цепи (они подчёркнуты).
Третий этап:
1-2-3-4 1-3-4-5 1-4-5-6
1-2-3-6 1-3-4-6
Получены три искомые цепи (подчёркнуты).
Четвёртый этап:
1-2-3-4-5 1-3-4-5-6
1-2-3-4-6
Получено две искомые цепи (подчёркнуты).
На пятом (заключительном) этапе получаем только одну простую цепь. Она проходит через все вершины данного ориентированного графа:
1-2-3-4-5-6
Таким образом, всего в ориентированном графе, изображённом на рис. 28, содержится 10 простых цепей, ведущих от вершины 1вершине 6. Среди них четыре цепи состоит из двух дуг, три цепи состоят из трёх дуг, две – из четырёх, и одна цепь из пяти дуг.
studfiles.net
Отзывы и предложения направлять по адресу:
432067, г. Ульяновск, проспект Созидателей, 13
телефон (8-422) 20-56-71, 20-09-20
факс: 54-54-66
E-mail: [email protected]
ВВЕДЕНИЕ 5
КОНТРОЛЬНЫЕ РАБОТЫ 6
КР № 1 Множества и отображения 6
КР № 2 Формулы логики и булевы функции 10
КР № 3 Комбинаторные конфигурации 14
КР № 4 Предикаты. Бинарные отношения 17
КР № 5 Основы теории графов 20
ИСТОЧНИКИ ЛИТЕРАТУРЫ 27
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Основная цель создания контрольно – оценочных средств по рубежному контролю заключается в определении качества знаний и умений студентов по окончании каждого раздела учебной дисциплины (контрольные работы по разделам), их соответствие требованиям ФГОС СПО.
Согласно требованиям к результатам освоения учебной дисциплины «Дискретная математика» обучающийся:
ДОЛЖЕН УМЕТЬ:
применять методы дискретной математики;
выполнять операции над множествами, применять аппарат теории множеств для решения задач;
выполнять операции над отображениями и подстановками;
строить таблицы истинности для формул логики;
представлять булевы функции в виде формул заданного типа;
определять полноту множества функций
определять вид комбинаторных объектов;
генерировать основные комбинаторные объекты;
выполнять операции над предикатами;
выполнять операции в алгебре вычетов;
применять простейшие криптографические шифры для шифрования текстов;
выполнять доказательство методом математической индукции;
исследовать бинарные отношения на заданные свойства;
представлять графы в памяти ЭВМ;
находить характеристики графов;
применять алгебру высказываний к синтезу и анализу схем дискретного действия;
ДОЛЖЕН ЗНАТЬ:
основные понятия теории множеств, теоретико-множественные операции и их связь с логическими операциями;
элементы теории отображений и алгебры подстановок;
логические операции, формулы логики, законы алгебры логики;
основные классы функций, полноту множеств функций, теорему Поста;
логику предикатов, бинарные отношения и их виды;
основы алгебры вычетов и их приложение к простейшим криптографическим шифрам;
метод математической индукции;
алгоритмическое перечисление основных комбинаторных объектов;
основы теории графов;
Задания рубежного контроля (контрольных работ) выполняются в любой последовательности в течение 45 минут, из которых 5 минут отводится на вводное инструктирование по порядку оформления, правилам выполнения заданий и 40 минут отводится для ответов на задания выполняемого варианта. Баллы, полученные за выполненные задания, суммируются и выставляется отметка.
Результаты рубежного контроля (контрольных работ) используются для оценки достижений обучающихся.
УЧЕБНАЯ ДИСЦИПЛИНА «ДИСКРЕТНАЯ МАТЕМАТИКА»
Специальность 09.02.05
Базовая подготовка
КОНТРОЛЬНАЯ РАБОТА № 1
МНОЖЕСТВА И ОТОБРАЖЕНИЯ
Цель: Проверка и закрепление знаний и умений по применению операций над множествами и построению диаграмм Эйлера-Венна; Проверить и закрепить знания и навыки по решению уравнений с подстановками, по решению задач шифрования простейшими криптографическими шифрами; проверка и закрепление знаний и умений работы с простейшими криптографическими шифрами.
Проверяемые умения и знания:
| 1 | ИЗОБРАЖЕНИЕ МНОЖЕСТВА НА ДИАГРАММЕ ЭЙЛЕРА-ВЕННА Изображение на диаграмме Эйлера – Венна заданного множества, выполняя построение по действиям, отмечая на каждом шаге полученное множество с помощью штриховки определенного вида. |
| 2 | ДЕЙСТВИЯ НАД МНОЖЕСТВАМИ Перечисление всех элементов множества, которое является декартовым произведением или декартовой степенью двух или трех указанных множеств. |
| 3 | РЕШЕНИЕ УРАВНЕНИЙ С ПОДСТАНОВКАМИ Решение уравнений с подстановками вида axb = c, где a, b, c – заданные подстановки, x – искомая подстановка. |
| 4 | ПРОСТЕЙШИЕ КРИПТОГРАФИЧЕСКИЕ ШИФРЫ Шифрование сообщений с помощью перестановочного шифра или шифра замены. |
«4» 3,8 – 4,7
«3» 2,8 – 3,7
«2» 1,8 – 2,7
«1» 0 – 1,7
ПРИМЕЧАНИЕ: 1. Не разрешается пользоваться справочниками, таблицами, выходить из аудитории.
2. Отметка ставится только на основании правильных решений.
УЧЕБНАЯ ДИСЦИПЛИНА «ДИСКРЕТНАЯ МАТЕМАТИКА»
Специальность 09.02.05
Базовая подготовка
КОНТРОЛЬНАЯ РАБОТА № 1
МНОЖЕСТВА И ОТОБРАЖЕНИЯ
ВАРИАНТ № 1.
1. Изобразить на диаграмме Эйлера – Венна множество A (B (A C))
2. Перечислить все элементы множества АВ, если А={1,4,-5} B={7,9,-1}
3. Решить уравнение с подстановками вида axb=c, где a, b, c – заданные подстановки:
a =  b =
b =  c =
c = 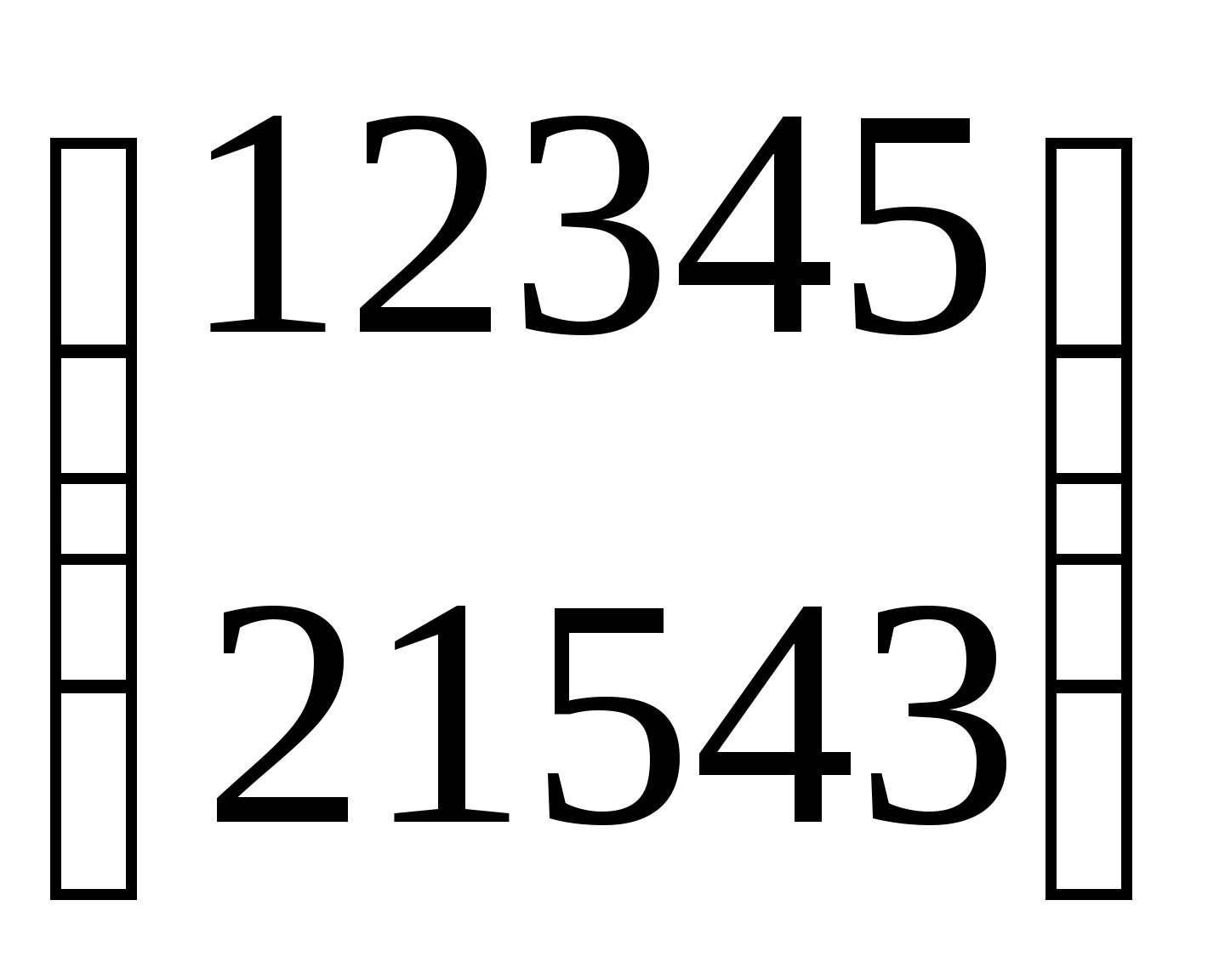
4. Зашифровать сообщение «Контрольная работа» с помощью перестановочного шифра с ключом a=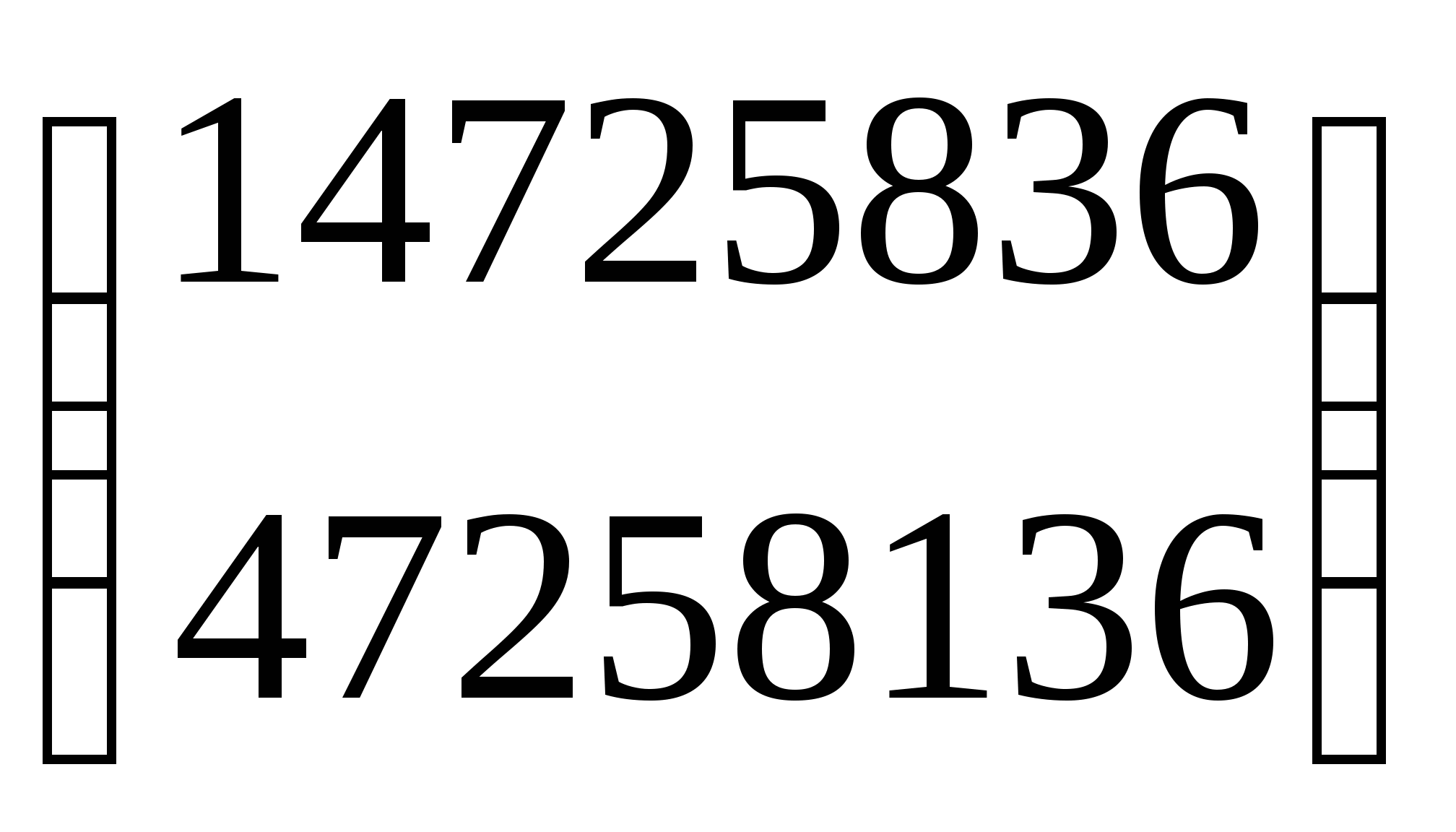
ВАРИАНТ № 2.
1. Изобразить на диаграмме Эйлера – Венна множество (A \ B)\C)
2. Перечислить все элементы множества ВA, если А={1,4,-5} B={7,9,-1}
3. Решить уравнение с подстановками вида ахв=с, где а, в, с – заданные подстановки:
a = 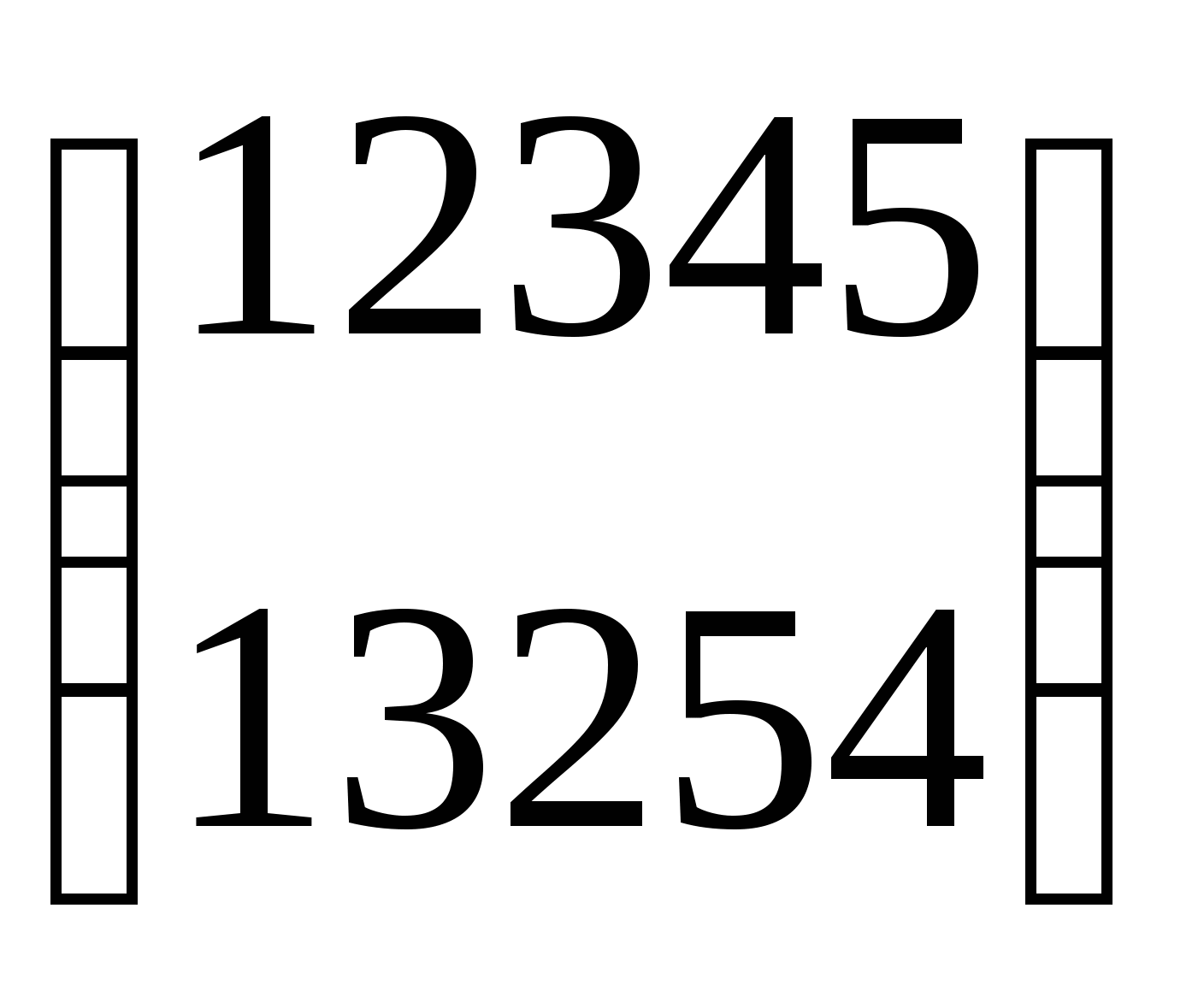 b =
b =  c =
c = 
4. Зашифровать сообщение «Контрольная работа» с помощью шифра замены с ключом 3
ВАРИАНТ № 3.
1. Изобразить на диаграмме Эйлера – Венна множество (A \ B) (A \ C)
2. Перечислить все элементы множества АВC, если А={1,4,-5} B={7,9,-1} C={0,2}
3. Решить уравнение с подстановками вида ахв=с, где а, в, с – заданные подстановки:
a =  b =
b = 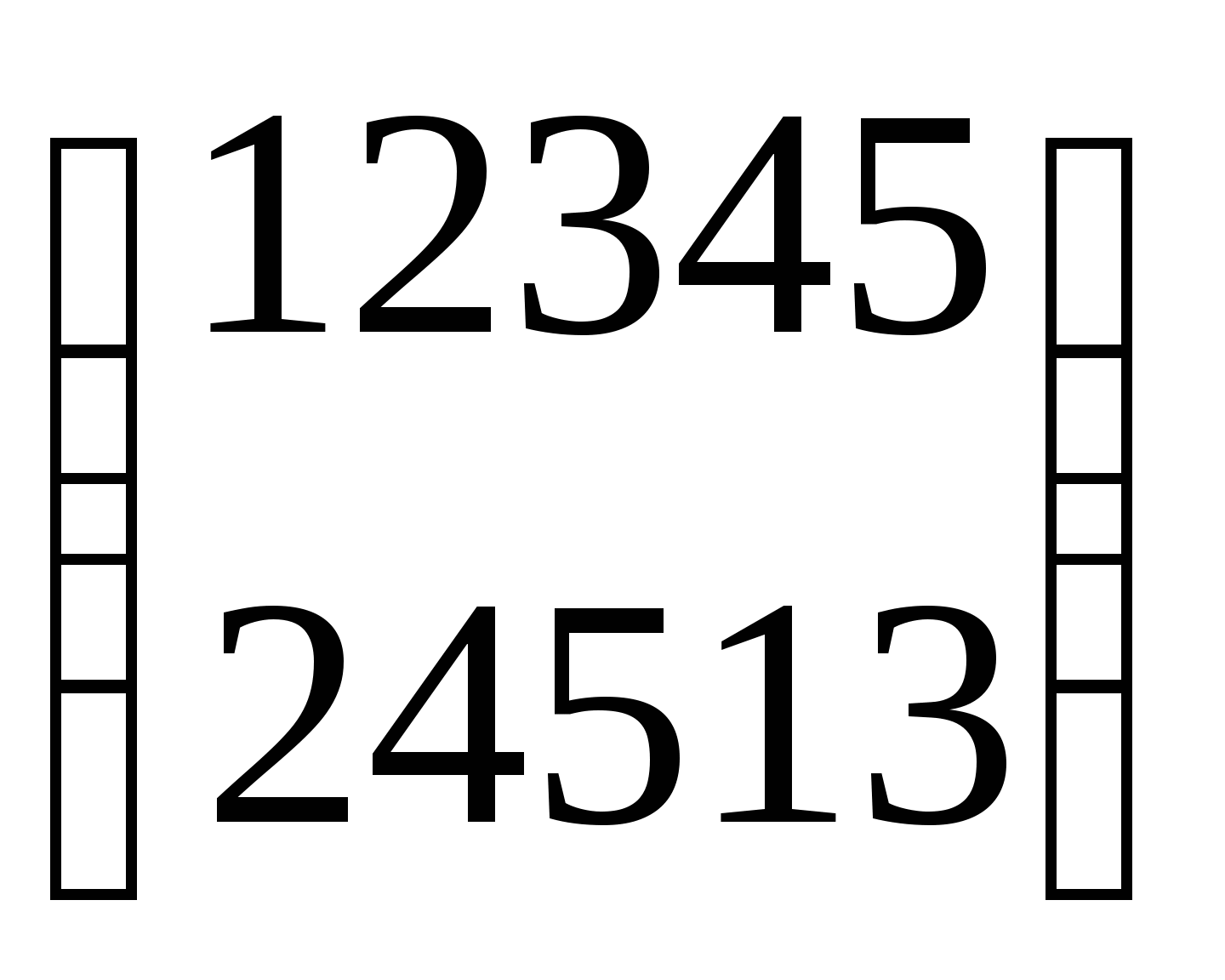 c =
c = 
4. Зашифровать сообщение «Контрольная работа» с помощью перестановочного шифра с ключом a=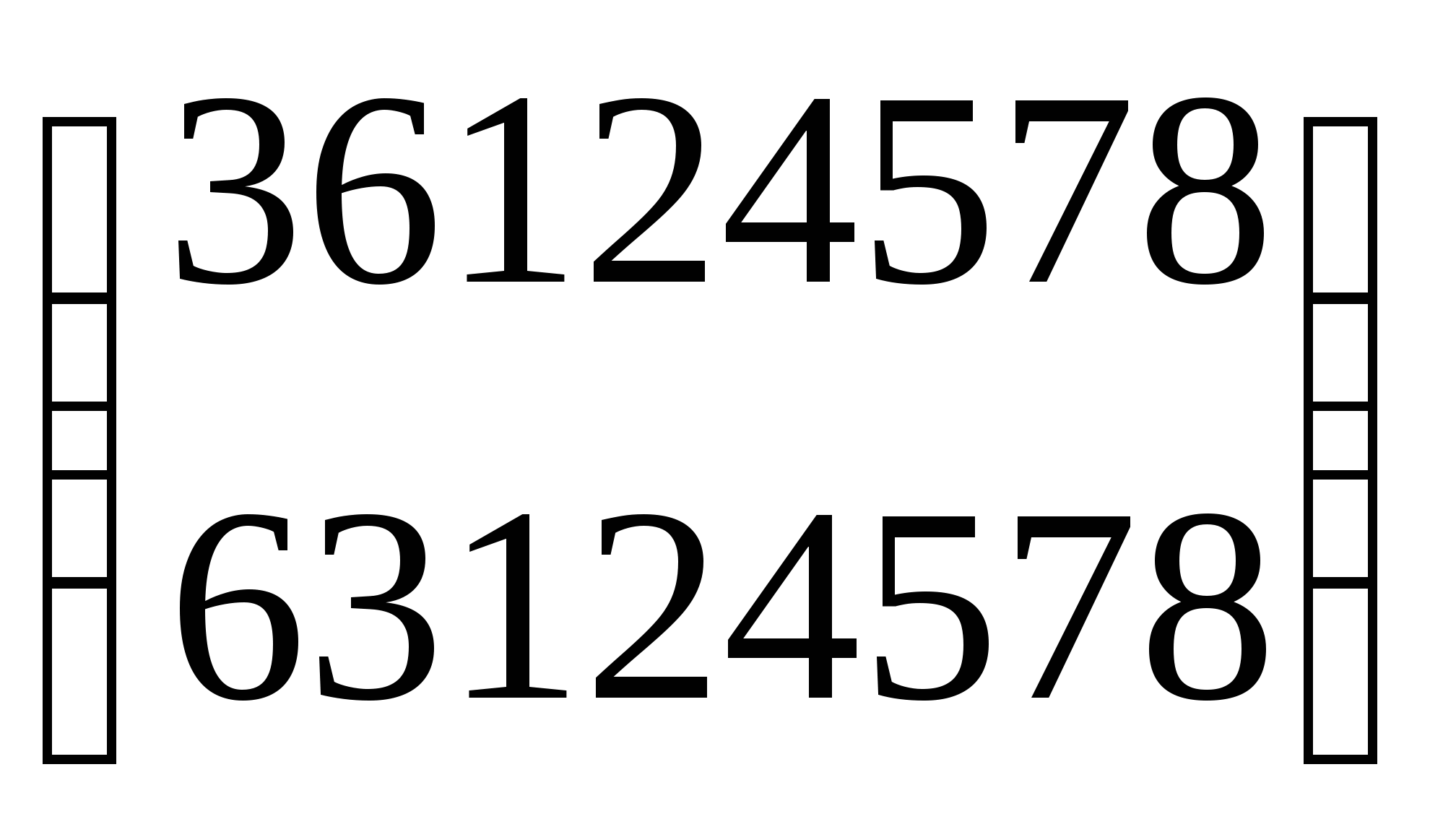
ВАРИАНТ № 4.
1. Изобразить на диаграмме Эйлера – Венна множество (A \ C) \ B
2. Перечислить все элементы множества CВA, если А={1,4,-5} B={7,9,-1} C={0,2}
3. Решить уравнение с подстановками вида ахв=с, где а, в, с – заданные подстановки.
a =  b =
b =  c =
c = 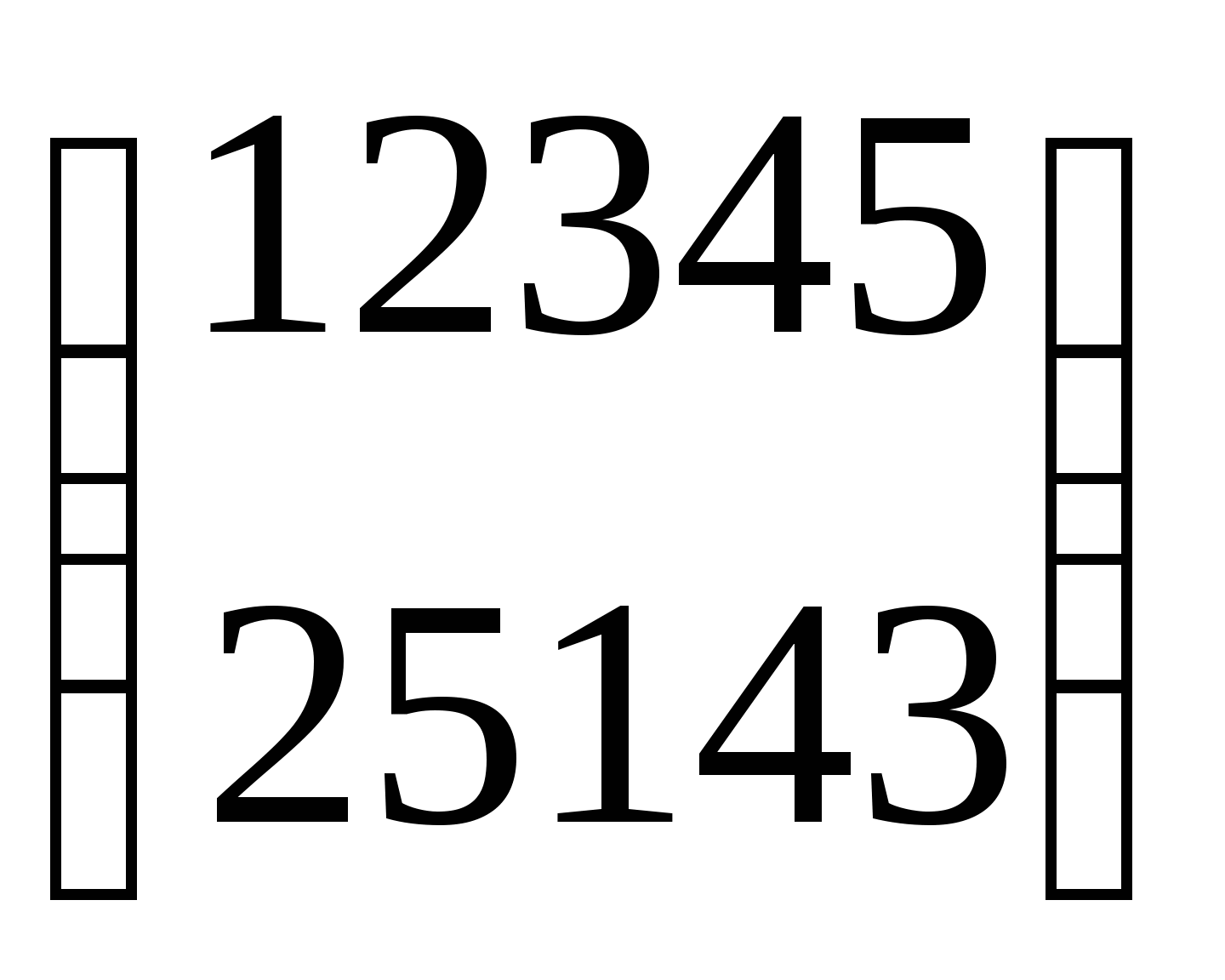
4. Зашифровать сообщение «Контрольная работа» с помощью шифра замены с ключом 4
ВАРИАНТ № 5.
1. Изобразить на диаграмме Эйлера – Венна множество A (B C)
2. Перечислить все элементы множества CВA, если А={1,-5} B={7,6,9} C={0,2}
3. Решить уравнение с подстановками вида ахв=с, где а, в, с – заданные подстановки:
a =  b =
b =  c =
c = 
4. Зашифровать сообщение «Контрольная работа» с помощью перестановочного шифра с ключом a=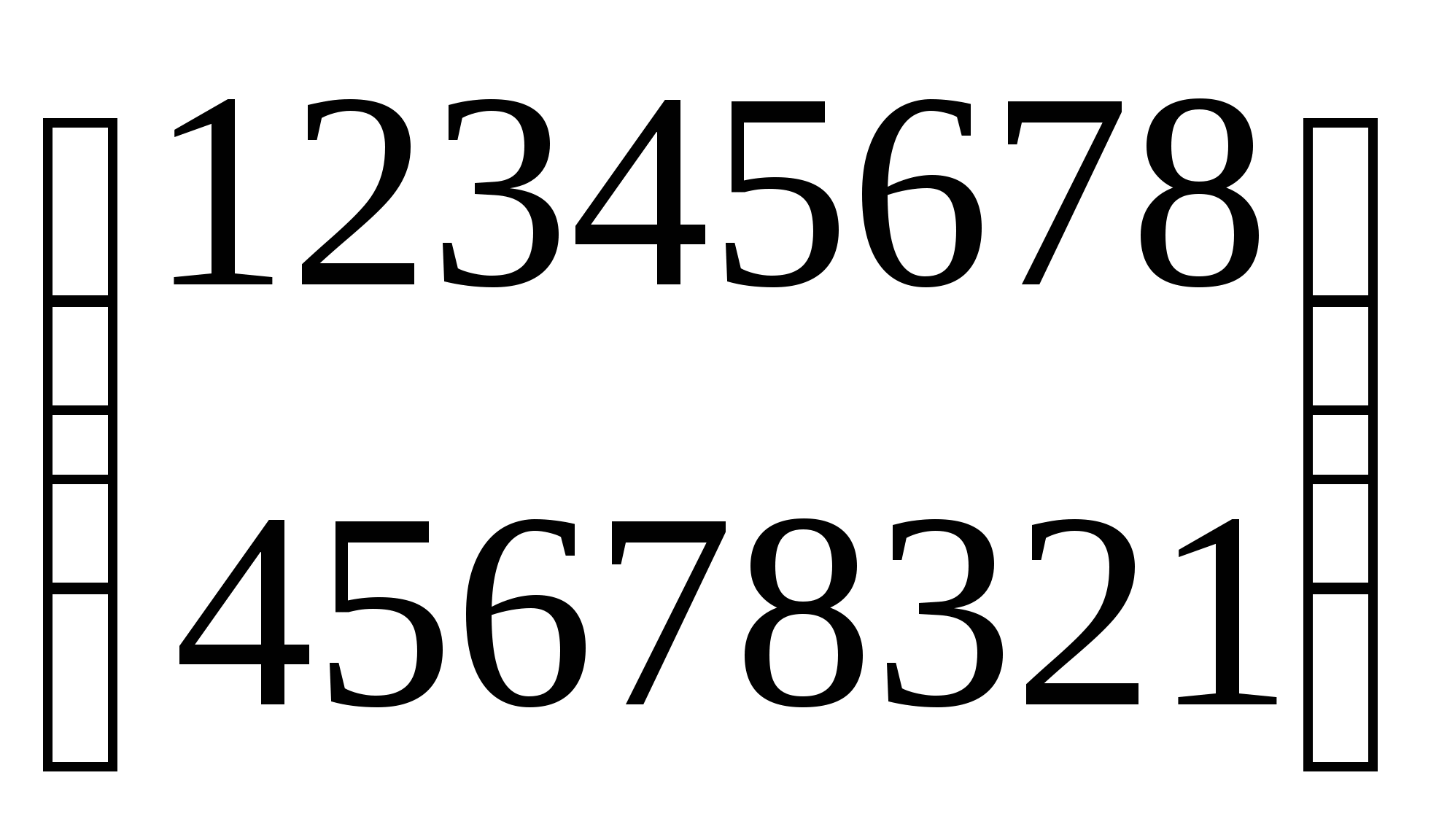
ВАРИАНТ № 6.
1. Изобразить на диаграмме Эйлера – Венна множество A \ (A B)
2. Перечислить все элементы множества АВC, если А={1,4} B={9,-1} C={0,2}
3. Решить уравнение с подстановками вида ахв=с, где а, в, с – заданные подстановки:
a =  b =
b =  c =
c = 
4. Зашифровать сообщение «Контрольная работа» с помощью шифра замены с ключом 5.
УЧЕБНАЯ ДИСЦИПЛИНА «ДИСКРЕТНАЯ МАТЕМАТИКА»
Специальность 09.02.05
Базовая подготовка
КОНТРОЛЬНАЯ РАБОТА № 2
ФОРМУЛЫ ЛОГИКИ И БУЛЕВЫ ФУНКЦИИ
Цель: Проверка и закрепление знаний и умений: - по представлению сложных высказываний через простые с помощью формул логики; - по построению таблиц истинности, построению СДНФ; - по нахождению минимальной ДНФ; - по определению полноты системы булевых функций.
Проверяемые умения и знания:
| 1 | ФОРМУЛЫ ЛОГИКИ Выделение элементарных высказываний в составном высказывании, обозначение их буквами, подчеркивание логических связок, запись составного высказывания в виде формулы. |
| 2 | ПОСТРОЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ И СДНФ Построение таблицы истинности и совершенной дизъюнктивной нормальной формы (СДНФ) по заданной функции трёх переменных f(x1,x2,x3) |
| 3 | НАХОЖДЕНИЕ МИНИМАЛЬНОЙ ДНФ Нахождение минимальной ДНФ для функции трёх переменных f(x1,x2,x3). |
| 4 | ПОЛНОТА СИСТЕМЫ ФУНКЦИЙ Определение полноты системы функций разными методами. |
«4» 3,8 – 4,7
«3» 2,8 – 3,7
«2» 1,8 – 2,7
«1» 0 – 1,7
ПРИМЕЧАНИЕ: 1. Не разрешается пользоваться справочниками, таблицами, выходить из аудитории.
2. Отметка ставится только на основании правильных решений.
УЧЕБНАЯ ДИСЦИПЛИНА «ДИСКРЕТНАЯ МАТЕМАТИКА»
Специальность 09.02.05
Базовая подготовка
КОНТРОЛЬНАЯ РАБОТА № 2
ФОРМУЛЫ ЛОГИКИ И БУЛЕВЫ ФУНКЦИИ
ВАРИАНТ № 1.
1. В составном высказывании выделить элементарные составляющие, обозначить их буквами, подчеркнуть логические связки и записать в виде формулы:
"если a>0 или b>0, то ab>0"
2. Задана функция от трёх переменных f(x1,x2,x3). По заданной функции построить таблицу истинности, совершенную дизъюнктивную нормальную форму (СДНФ):
f(x1,x2,x3)=(x1(x2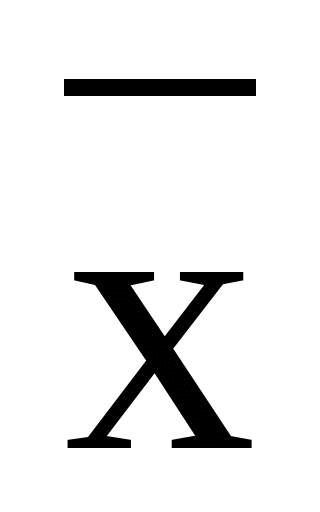 3)) (x2x3)
3)) (x2x3)
4. Найти минимальную ДНФ для функции трёх переменных f(x1,x2,x3).
3. Определить, является ли полной система функций. Указать, какой метод для этого применялся: {x y}
ВАРИАНТ № 2.
1. В составном высказывании выделить элементарные составляющие, обозначить их буквами, подчеркнуть логические связки и записать в виде формулы:
"данное число делится на 2 и делится на 3 или не делится на 6"
2. Задана функция от трёх переменных f(x1,x2,x3). По заданной функции построить таблицу истинности, совершенную дизъюнктивную нормальную форму (СДНФ):
f(x1,x2,x3)=(x1 (x2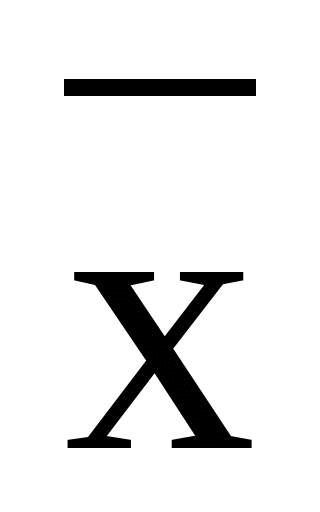 3)) (x2x3)
3)) (x2x3)
3. Найти минимальную ДНФ для функции трёх переменных f(x1,x2,x3).
4. Определить, является ли полной система функций. Указать, какой метод для этого применялся: {xy}
ВАРИАНТ № 3.
1. В составном высказывании выделить элементарные составляющие, обозначить их буквами, подчеркнуть логические связки и записать в виде формулы:
"если ab0 или a0, то b0"
2. Задана функция от трёх переменных f(x1,x2,x3). По заданной функции построить таблицу истинности, совершенную дизъюнктивную нормальную форму (СДНФ):
f(x1,x2,x3)=(x1 (x2x3)) (x2x3)
3. Найти минимальную ДНФ для функции трёх переменных f(x1,x2,x3).
4. Определить, является ли полной система функций. Указать, какой метод для этого применялся: {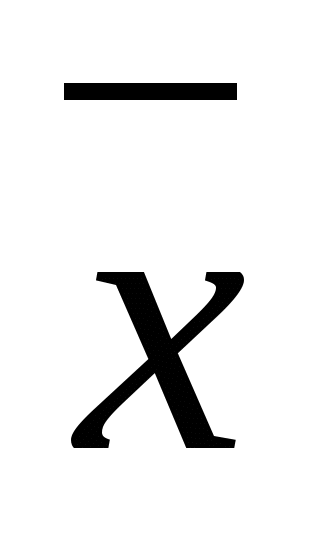 , xy, xy}
, xy, xy}
ВАРИАНТ № 4.
1. В составном высказывании выделить элементарные составляющие, обозначить их буквами, подчеркнуть логические связки и записать в виде формулы.
"Если я поеду на автобусе, то опоздаю на работу, или я воспользуюсь такси"
2. Задана функция от трёх переменных f(x1,x2,x3). По заданной функции построить таблицу истинности, совершенную дизъюнктивную нормальную форму (СДНФ):
f(x1,x2,x3)=(x2 (x1x3)) (x1x2)
3. Найти минимальную ДНФ для функции трёх переменных f(x1,x2,x3).
4. Определить, является ли полной система функций. Указать, какой метод для этого применялся: {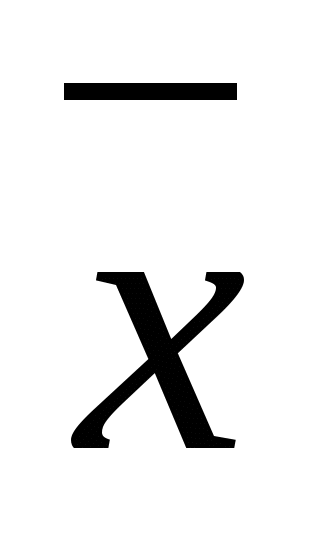 , xy}
, xy}
ВАРИАНТ № 5.
1. В составном высказывании выделить элементарные составляющие, обозначить их буквами, подчеркнуть логические связки и записать в виде формулы:
" если ab=0 или a=0, то b=0"
2. Задана функция от трёх переменных f(x1,x2,x3). По заданной функции построить таблицу истинности, совершенную дизъюнктивную нормальную форму (СДНФ):
f(x1,x2,x3)=(x2 (x1x3)) (x1x2)
3. Найти минимальную ДНФ для функции трёх переменных f(x1,x2,x3).
4. Определить, является ли полной система функций. Указать, какой метод для этого применялся: {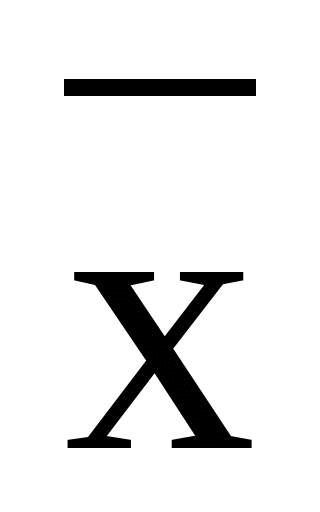 , xy }
, xy }
ВАРИАНТ № 6.
1. В составном высказывании выделить элементарные составляющие, обозначить их буквами, подчеркнуть логические связки и записать в виде формулы.
"Давление падает и система не работает"
2. Задана функция от трёх переменных f(x1,x2,x3). По заданной функции построить таблицу истинности, совершенную дизъюнктивную нормальную форму (СДНФ):
f(x1,x2,x3)=(x2 (x1x3)) (x1x2)
3. Найти минимальную ДНФ для функции трёх переменных f(x1,x2,x3).
4. Определить, является ли полной система функций. Указать, какой метод для этого применялся: {0,1, xy, xy}
УЧЕБНАЯ ДИСЦИПЛИНА «ДИСКРЕТНАЯ МАТЕМАТИКА»
Специальность 09.02.05
Базовая подготовка
КОНТРОЛЬНАЯ РАБОТА № 3
КОМБИНАТОРНЫЕ КОНФИГУРАЦИИ
Цель: Проверить и закрепить знания и навыки по решению комбинаторных задач, проверить и закрепить знания и навыки по созданию генераторов комбинаторных объектов.
Решение задач, содержащих комбинаторные объекты без повторений.
2
КОМБИНАТОРНЫЕ ОБЪЕКТЫ С ПОВТОРЕНИЯМИ
Решение задач, содержащих комбинаторные объекты с повторениями.
3
ГЕНЕРАТОР КОМБИНАТОРНЫХ ОБЪЕКТОВ
Выписывание результатов работы генератора сочетаний или генератора перестановок (без повторения).
«4» 3,8 – 4,7
«3» 2,8 – 3,7
«2» 1,8 – 2,7
«1» 0 – 1,7
ПРИМЕЧАНИЕ: 1. Не разрешается пользоваться справочниками, таблицами, выходить из аудитории.
2. Отметка ставится только на основании правильных решений.
УЧЕБНАЯ ДИСЦИПЛИНА «ДИСКРЕТНАЯ МАТЕМАТИКА»
Специальность 09.02.05
Базовая подготовка
КОНТРОЛЬНАЯ РАБОТА № 3
КОМБИНАТОРНЫЕ КОНФИГУРАЦИИ
ВАРИАНТ № 1.
Сколько имеется четырехзначных чисел, у которых каждая следующая цифра меньше предыдущей?
Сколько всего существует различных показаний n приборов по m показателям?
Выписать результаты работы генератора перестановок для n=3.
ВАРИАНТ № 2.
На собрании должны выступить четыре человека А, В, С, D. Сколькими способами их можно разместить в списке ораторов, если В не может выступить до того момента, пока не выступит А?
Сколько всего существует различных восьмизначных двоичных чисел?
Выписать результаты работы генератора сочетаний для n=5, k=3.
ВАРИАНТ № 3.
В некоторых видах спортивных соревнований исходом является определение участников, занявших 1-е, 2-е и 3-е места. Сколько всего возможно различных исходов, если в соревнованиях участвуют 80 человек.
Сколько всего существует перестановок из слова "Windows"?
Выписать результаты работы генератора перестановок для n=4.
ВАРИАНТ № 4.
Сколько имеется пятизначных чисел, у которых каждая следующая цифра больше предыдущей?
В магазине 5 сортов тульских пряников. Купить нужно 20 штук любых сортов или одного сорта. Сколько всего существует различных вариантов покупки?
Выписать результаты работы генератора сочетаний для n=5, k=2.
ВАРИАНТ № 5.
На собрании должны выступить пять человек А,В,С,D,E. Сколькими способами их можно разместить в списке ораторов, если D не может выступить до того момента, пока не выступит B?
Сколькими способами можно рассадить n вновь прибывших гостей среди m гостей, уже сидящих за круглым столом?
Выписать результаты работы генератора сочетаний для n=5, k=4.
ВАРИАНТ № 6.
В некоторых видах спортивных соревнований исходом является определение участников, занявших 1-е, 2-е и 3-е места. Сколько всего возможно различных исходов, если в соревнованиях участвуют 8 человек.
Трое детей собрали в саду 63 яблока и распределили их между собой. Сколькими способами можно было распределить яблоки между детьми?
Выписать результаты работы генератора сочетаний для n=6, k=4.
УЧЕБНАЯ ДИСЦИПЛИНА «ДИСКРЕТНАЯ МАТЕМАТИКА»
Специальность 09.02.05
Базовая подготовка
КОНТРОЛЬНАЯ РАБОТА № 4
ПРЕДИКАТЫ. БИНАРНЫЕ ОТНОШЕНИЯ. ВЫЧЕТЫ
Цель: Проверка и закрепление знаний и умений по построению таблиц истинности для предикатов, по определению области истинности предикатов, по нахождению значений выражений с кванторными операциями, по представлению бинарных отношений различными способами, по определению свойств бинарных отношений, по определению отношений эквивалентности, проверить умение решать уравнения в классах вычетов.
Проверяемые умения и знания:
| 1 | ПРЕДИКАТЫ Определение области истинности и построение таблицы значений предиката. |
| 2 | КВАНТОРНЫЕ ОПЕРАЦИИ Решение задач с кванторами всеобщности и кванторами существования. |
| 3 | БИНАРНЫЕ ОТНОШЕНИЯ Задание бинарного отношения, определение свойств бинарного отношения. |
| 4 | ВЫЧЕТЫ ПО МОДУЛЮ m Решение уравнений в алгебре вычетов; определение разрешимости уравнений в алгебре вычетов по модулю m |
«4» 3,8 – 4,7
«3» 2,8 – 3,7
«2» 1,8 – 2,7
«1» 0 – 1,7
ПРИМЕЧАНИЕ: 1. Не разрешается пользоваться справочниками, таблицами, выходить из аудитории.
2. Отметка ставится только на основании правильных решений.
УЧЕБНАЯ ДИСЦИПЛИНА «ДИСКРЕТНАЯ МАТЕМАТИКА»
Специальность 09.02.05
Базовая подготовка
КОНТРОЛЬНАЯ РАБОТА № 4
ПРЕДИКАТЫ. БИНАРНЫЕ ОТНОШЕНИЯ. ВЫЧЕТЫ
ВАРИАНТ № 1.
Построить таблицу значений предиката R(x,y)="животное x входит в класс y" xM1={кошка, лягушка, муха, слон, собака, комар} yM2={земноводные, насекомые, млекопитающие} и определить область истинности.
Пусть дан предикат P(x)="x делится на 3 без остатка" xN=множество натуральных чисел. Определить значение выражения xP(x) и значение выражения xP(x). Объяснить.
Задать бинарное отношение "быть строго меньше" с помощью матрицы, если М={1,2,3,4,5,6,7} и определить свойства бинарного отношения.
Решить уравнение в алгебре вычетов по модулю 7: 36х+8=16.
ВАРИАНТ № 2.
Построить таблицу значений предиката R(x,y,z)="x+yz" x,y,zM={1,2} и определить область истинности.
Пусть дан предикат P(x)="x делится на 3 без остатка" x{3,6,9,27}. Определить значение выражения xP(x). Объяснить.
Задать бинарное отношение "быть делителем" с помощью фактор-множества, если М={1,2,3,4,5,6,7} и определить его свойства.
Решить уравнение в алгебре вычетов по модулю 5: 4х+3=15.
ВАРИАНТ № 3.
Определить область истинности предиката P(x)="предмет x является цветком" xM M={роза, ваза, стол, ромашка, герань} и построить таблицу значений этого предиката.
Пусть даны предикаты P(x)="x четное число", Q(x)="x нечетное число" xN=множество натуральных чисел. Определить значение выражения x(P(x)Q(x)). Объяснить.
Задать бинарное отношение "иметь общий делитель отличный от единицы" перечнем дуг на множестве М={1,2,3,4,5,6,7} и определить его свойства.
Решить уравнение в алгебре вычетов по модулю 3: 2х+8=13.
ВАРИАНТ № 4.
Определить область истинности предиката P(x,y)="x=y" x,yM M={1,2,3} и построить таблицу значений этого предиката.
Пусть даны предикаты P(x)="x четное число", Q(x)="x делится на 4 без остатка"; xN=множество натуральных чисел. Определить значение выражения x(Q(x) P(x)). Объяснить.
Задать с помощью графа бинарное отношение "иметь один и тот же остаток от деления на 3" на множестве М={1,2,3,4,5,6,7} и определить его свойства.
Решить уравнение в алгебре вычетов по модулю 2: 5х+10=13.
ВАРИАНТ № 5.
Определить область истинности предиката P(x,y)="город x является столицей y" xM1={Ульяновск, Самара, Москва, Киев} yМ2={Россия, Беларусь, Украина, Германия} и построить таблицу значений этого предиката.
Пусть даны предикаты P(x)="x четное число", Q(x)="x нечетное"; xN=множество натуральных чисел. Определить значение выражения x(Q(x) P(x)). Объяснить.
Задать с помощью матрицы бинарное отношение "быть не меньше" на множестве М={1,2,3,4,5,6,7} и определить его свойства.
Решить уравнение в алгебре вычетов по модулю 11: 10х+8=22.
ВАРИАНТ № 6.
Определить область истинности предиката R(x,y)="x является валютой страны y" xM1={рубль, доллар, фунт стерлингов} yM2={США, Россия, Украина, Беларусь} и построить таблицу значений этого предиката.
Пусть дан предикат P(x)="x четное число", xМ={1,2,3,4,5,6,7}. Определить значение выражения x P(x). Объяснить.
Определить свойства бинарного отношения "быть делителем", определенного на множестве М, где М={1,2,3,4,5,6,7} и задать его перечнем дуг.
Решить уравнение в алгебре вычетов по модулю 13: 27х+15=44.
УЧЕБНАЯ ДИСЦИПЛИНА «ДИСКРЕТНАЯ МАТЕМАТИКА»
Специальность 09.02.05
Базовая подготовка
КОНТРОЛЬНАЯ РАБОТА № 5
ОСНОВЫ ТЕОРИИ ГРАФОВ
Цель: Проверка знаний основных определений по основам теории графов и умений по построению графов различных типов.
Проверяемые умения и знания:
Тестирование по определениям темы.
2
ЭЙЛЕРОВЫ ГРАФЫ
Выполнение заданий на построение эйлеровых графов.
3
ГАМИЛЬТОНОВЫ ГРАФЫ
Выполнение заданий на построение гамильтоновых графов.
4
ЦИКЛИЧЕСКИ СВЯЗНЫЕ ГРАФЫ
Выполнение заданий на построение циклически связных графов.
«4» 3,8 – 4,7
«3» 2,8 – 3,7
«2» 1,8 – 2,7
«1» 0 – 1,7
ПРИМЕЧАНИЕ: 1. Не разрешается пользоваться справочниками, таблицами, выходить из аудитории.
Отметка ставится только на основании правильных решений.
УЧЕБНАЯ ДИСЦИПЛИНА «ДИСКРЕТНАЯ МАТЕМАТИКА»
Специальность 09.02.05
Базовая подготовка
КОНТРОЛЬНАЯ РАБОТА № 5
ОСНОВЫ ТЕОРИИ ГРАФОВ
ВАРИАНТ № 1
1. Совокупность множеств V (точек) и Е (линий), между которыми определено отношение инцидентности, причем каждый элемент е из Е инцидентен ровно двум элементам v1 и v2 из множества V, называется . ..
неориентированным графом 3) мультиграфом
ориентированным графом 4) пустым графом
2. Граф, содержащий кратные ребра, называется . ..
гамильтонов
циклически связный
мультиграф
эйлеров
3. Граф, у которого множество вершин - пусто, называется . . .
неориентированным графом
ориентированным графом
пустым графом
мультиграфом
4. Конечная или бесконечная последовательность ребер, такая что каждые два соседних ребра имеют общую инцидентную вершину, причем каждое ребро встречается не более одного раза, называется ...
маршрутом 3) простой цепью
цепью 4) циклом
5. Конечная или бесконечная последовательность ребер, такая что каждые два соседних ребра имеют общую инцидентную вершину, причем каждое ребро встречается не более одного раза, любая вершина графа инцидентна не более чем двум его ребрам, а начальная вершина совпадает с конечной вершиной, называется .
маршрутом 3) циклом
цепью 4) простым циклом
6. Граф, который можно изобразить одним росчерком пера, причем процесс такого изображения начинается и заканчивается в одной точке, называется .. .
гамильтоновым
циклически связным
мультиграфом
эйлеровым
7. Нарисовать 2 эйлеровых графа (не менее 8 вершин).
8. Нарисовать 2 гамильтоновых графа (не менее 10 вершин), указать простой цикл, проходящий через все вершины графа, другим цветом или более жирно.
9. Нарисовать 2 циклически связных графа (не менее 8 вершин).
ВАРИАНТ № 2
1. Ребро S и вершина V(U) называются ..., если ребро S соединяет вершины V и U
смежными
инцидентами
связными
ориентированными
2. Последовательность ребер такая, что каждые два соседних ребра имеют общую инцидентную вершину, причем начальная вершина и конечная совпадают, называется ..
маршрутом
циклическим маршрутом
циклом
простым циклом
3. Совокупность множеств V (точек) и Е (линий), между которыми определено отношение инцидентности, причем каждый элемент е из Е инцидентен ровно двум элементам v1 и v2 из множества V, называется ...
мультиграфом
ориентированным графом
неориентированным графом
пустым графом
4. Граф, содержащий кратные ребра, называется ...
циклически связный
гамильтонов
эйлеров
мультиграф
5. Граф, содержащий простой цикл, проходящий через все вершины графа, называется ...
циклически связный
гамильтонов
эйлеров
мультиграф
6. Граф, содержащий направленные ребра, называется ...
неориентированным графом
ориентированным графом
мультиграфом
пустым графом
7. Нарисовать 2 эйлеровых графа (не менее 8 вершин).
8. Нарисовать 2 гамильтоновых графа (не менее 10 вершин), указать простой цикл, проходящий через все вершины графа, другим цветом или более жирно.
9. Нарисовать 2 циклически связных графа (не менее 8 вершин).
ВАРИАНТ № 3
1. Последовательность ребер такая, что каждые два соседних ребра имеют общую инцидентную вершину, причем начальная вершина и конечная совпадают, называется .. .
маршрутом
циклическим маршрутом
циклом
простым циклом
2. Граф, содержащий кратные ребра, называется . ..
мультиграф
гамильтонов
циклически связный
эйлеров
3. Ребро, соединяющее вершину саму с собой, называется ...
дуга
петля
цикл
простой цикл
4. Конечная или бесконечная последовательность ребер, такая, что каждые два соседних ребра имеют общую инцидентную вершину, причем каждое ребро встречаетсяне более одного раза, называется ...
маршрутом
цепью
простой цепью
циклом
5. Граф называется .. ., если через любые две вершины рассматриваемого графа может проходить простой цикл
гамильтоновым
эйлеровым
циклически связным
ориентированным
6. Граф, содержащий простой цикл, проходящий через все вершины графа, называется . . .
циклически связным
мультиграфом
гамильтоновым
эйлеровым
7. Нарисовать 2 эйлеровых графа (не менее 8 вершин).
Нарисовать 2 гамильтоновых графа (не менее 10 вершин), указать простой цикл, проходящий через все вершины графа, другим цветом или более жирно.
Нарисовать 2 циклически связных графа (не менее 8 вершин).
ВАРИАНТ № 4
1. Совокупность множеств V (точек) и Е (линий), между которыми определено отношение инцидентности, причем каждый элемент е из Е инцидентен ровно двум элементам V1 и V2 из множества V, называется ...
ориентированным графом
неориентированным графом
мультиграфом
пустым графом
2. Граф, содержащий кратные ребра, называется ...
гамильтонов
мультиграф
эйлеров
циклически связный
3. Конечная или бесконечная последовательность ребер, такая, что каждые два соседних ребра имеют общую инцидентную вершину, причем каждое ребро встречается не более одного раза, называется ...
маршрутом 3) циклом
простой цепью 4) цепью
4. Граф, который можно изобразить одним росчерком пера, причем процесс такого изображения начинается и заканчивается в одной точке, называется ...
гамильтоновым
эйлеровым
циклически связным
мультиграфом
5. Граф, содержащий простой цикл, проходящий через все вершины графа, называется...
циклически связный
эйлеров
мультиграф
гамильтонов
6. Конечная или бесконечная последовательность ребер, такая, что каждые два соседних ребра имеют общую инцидентную вершину, причем каждое ребро встречается не более одного раза, любая вершина графа инцидентна не более чем двум его ребрам, называется ...
цепью
простой цепью
циклом
простым циклом
7. Нарисовать 2 эйлеровых графа (не менее 8 вершин).
8. Нарисовать 2 гамильтоновых графа (не менее 10 вершин), указать простой цикл, проходящий через все вершины графа, другим цветом или более жирно.
Нарисовать 2 циклически связных графа (не менее 8 вершин).
ИСТОЧНИКИ ЛИТЕРАТУРЫ
Асеев Г. Г. Дискретная математика / Г. Г. Асеев, О. М. Абрамов, Д. Э. Ситников. – Ростов н/Д: «Феникс», Харьков: «Торсинг», 2003.
Введение в криптографию / под общ. ред. В. В. Ященко – СПб.: Питер, 2001.
Гончарова Г. А. Элементы дискретной математики: учеб. пособие / Г. А. Гончарова, А. А. Мочалин – М.: ФОРУМ: ИНФРА-М, 2004. (Серия «Профессиональное образование)
Горбатов В. А. "Основы дискретной математики" / В. А. Горбатов. – М.: Высшая школа, 1986.
Иванов Б. Н. «Дискретная математика» (Алгоритмы и программы) / Б. Н. Иванов. – М. Лаборатория Базовых Знаний, 2002.
Камышова Г. А. Дискретная математика. Конспект лекций : учеб. пособие / Г. А. Камышова. – 2003.
Кузнецов О. П. Дискретная математика для инженера / О. П. Кузнецов, Г. М. Адельсон-Вельский. – И. : Энергоиздат, 1988.
Москинова Г. И. Дискретная математика. Математика для менеджера в примерах и упражнениях: учеб. пособие / Г. И. Москинова. – М.: Логос, 2002.
Новиков Ф. А. Дискретная математика для программистов / Ф. А. Новиков. -СПб.: Питер, 2001.
Сигорский В. П. Математический аппарат инженера / В. П. Сигорский. - Киев: Техника, 1975.
infourok.ru
Учреждение образования
ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ
по дисциплине
для студентов уровня ВО заочной формы обучения
специальности 1-45 01 03 «Сети телекоммуникаций»
МИНСК 2009
Составитель: Петрович А.В.
Рецензент: Колодная Е.М.
Издание утверждено на заседании кафедры М и Ф
12.04.2009г., протокол № 8
Зав. кафедрой Гладков Л.Л.
ВВЕДЕНИЕ
В соответствии с учебным планом студенты третьего курса ВГКС специальности 1-45 01 03 – Сети телекоммуникаций в шестом семестре выполняют контрольную работу по дискретной математике.
Для того, чтобы успешно ее выполнить, необходимо изучить сначала теоретический материал по одному из учебников, указанных в списке литературы, и конспекту обзорных лекций. При этом следует ориентироваться на рабочую программу, приведенную ниже. Затем внимательно разберите решения примеров из данной методической разработки и выполните задания для самопроверки.
При оформлении контрольной работы для замечаний преподавателя оставляются поля. Перед решением задачи полностью записывается ее условие. Решение следует сопровождать короткими пояснениями с указанием использованных формул и теорем. Рисунки должны быть выполнены аккуратно. В конце работы ставится дата ее завершения, приводится список проработанной литературы. Работа подписывается.
Выбор варианта контрольной работы определяется двумя последними цифрами номера зачетной книжки. Получив проверенную работу, студент обязан выполнить указания, сделанные рецензентом. Если работа не зачтена, следует сделать работу над ошибками в той же тетради и представить работу на повторную рецензию.
К сдаче экзамена или зачета допускаются студенты, имеющие на руках зачтенные контрольные работы.
Таблица 1
| № варианта | №№ задач | ||||||
| 1 | 1 | 11 | 21 | 31 | 41 | 51 | 61 |
| 2 | 2 | 12 | 22 | 32 | 42 | 52 | 62 |
| 3 | 3 | 13 | 23 | 33 | 43 | 53 | 63 |
| 4 | 4 | 14 | 24 | 34 | 44 | 54 | 64 |
| 5 | 5 | 15 | 25 | 35 | 45 | 55 | 65 |
| 6 | 6 | 16 | 26 | 36 | 46 | 56 | 66 |
| 7 | 7 | 17 | 27 | 37 | 47 | 57 | 67 |
| 8 | 8 | 18 | 28 | 38 | 48 | 58 | 68 |
| 9 | 9 | 19 | 29 | 39 | 49 | 59 | 69 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 11 | 1 | 12 | 23 | 34 | 45 | 56 | 67 |
| 12 | 2 | 13 | 24 | 35 | 46 | 57 | 68 |
| 13 | 3 | 14 | 25 | 36 | 47 | 58 | 69 |
| 14 | 4 | 15 | 26 | 37 | 48 | 59 | 70 |
| 15 | 5 | 16 | 27 | 38 | 49 | 60 | 61 |
| 16 | 6 | 17 | 28 | 39 | 50 | 51 | 62 |
| 17 | 7 | 18 | 29 | 40 | 41 | 52 | 63 |
| 18 | 8 | 19 | 30 | 31 | 42 | 53 | 64 |
| 19 | 9 | 20 | 21 | 32 | 43 | 54 | 65 |
| 20 | 10 | 11 | 22 | 33 | 44 | 55 | 66 |
| 21 | 10 | 19 | 28 | 37 | 46 | 55 | 64 |
| 22 | 9 | 18 | 27 | 36 | 45 | 54 | 63 |
| 23 | 8 | 17 | 26 | 35 | 44 | 53 | 62 |
| 24 | 7 | 16 | 25 | 34 | 43 | 52 | 61 |
| 25 | 6 | 15 | 24 | 33 | 42 | 51 | 70 |
| 26 | 5 | 14 | 23 | 32 | 41 | 60 | 69 |
| 27 | 4 | 13 | 22 | 31 | 50 | 59 | 68 |
| 28 | 3 | 12 | 21 | 40 | 49 | 58 | 67 |
| 29 | 2 | 11 | 30 | 39 | 48 | 57 | 66 |
| 30 | 1 | 20 | 29 | 38 | 47 | 56 | 65 |
РАБОЧАЯ ПРОГРАММА
studfiles.net
Контрольная работа № 1
1. Даны множества A И B. Изобразить и записать с указанием характеристического свойства результат каждой операции:
А) AÈB ; б) AÇB; в) A \ B; г) B \ A; д)  ; е)
; е)  ; ж) A´ B; з) B´ A.
; ж) A´ B; з) B´ A.
A = {X| xÎR, X > 2}, B = {X| xÎR,-5 £ X £ 8}
Решение:
Изобразим на числовой прямой множества А и В:

Тогда
А) AÈB= ;

Б) AÇB= ;

В) A \ B= ;
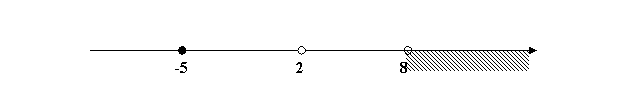
Г) B \ A= ;

Д)  = ;
= ;

Е)  = ;
= ;
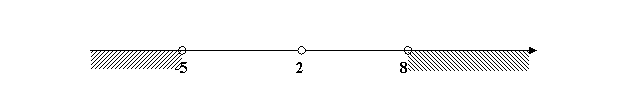
Ж) A´ B= ;

З) B´ A= .

2. На диаграммах Эйлера-Венна изобразить результат операций, предварительно указав порядок действий в формуле.

Решение:
Порядок действий:
1. 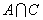
2. 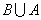
3. 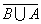
4. 
Изобразим на диаграмме Эйлера–Венна:
1.
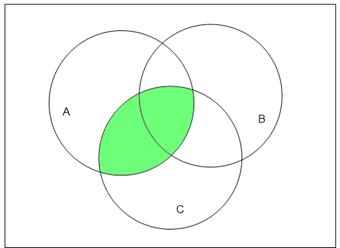
2.
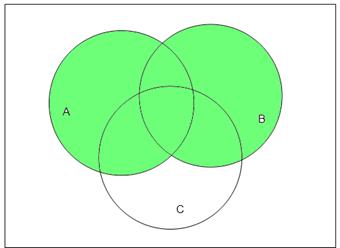
3.
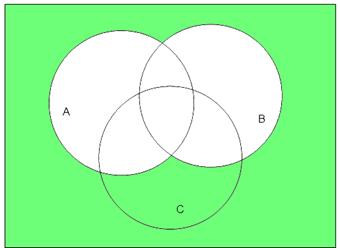
4.
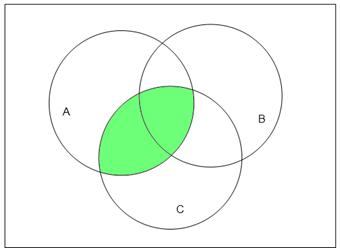
3. Упростить выражения, используя законы алгебры множеств
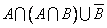
Решение:
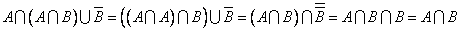 .
.
4. На множестве M Бинарное отношение RÍ M´M Задано характеристическим свойством. Представить отношение R Другими возможными способами. Выяснить какими свойствами оно обладает.
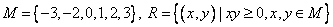
Решение:
Составим таблицу произведений элементов множества М, выделив те пары, которые удовлетворяют характеристическому свойству:
| -3 | -2 | 0 | 1 | 2 | 3 | |
| -3 | 9 | 6 | 0 | -3 | -6 | -9 |
| -2 | 6 | 4 | 0 | -2 | -4 | -6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | -3 | -2 | 0 | 1 | 2 | 3 |
| 2 | -6 | -4 | 0 | 2 | 4 | 6 |
| 3 | -9 | -6 | 0 | 3 | 6 | 9 |
Тогда выпишем в явном виде отношение:
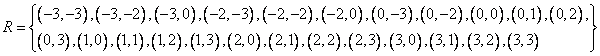
Изобразим графически отношение:
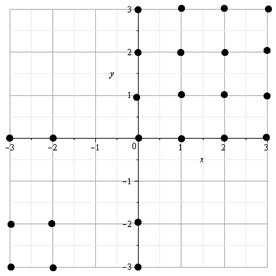
Свойства отношения:
1) Рефлексивность: так как 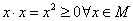 , то данное отношение рефлексивно.
, то данное отношение рефлексивно.
2) Так как 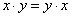 , то отношение будет симметричным.
, то отношение будет симметричным.
3) Тогда отношение не будет антирефлексивным и антисимметричным.
4) Транзитивность выполняется: 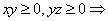 при положительном значении хотя бы одной переменной и две другие также будут положительны; при отрицательном значении одной переменной остальные также будут отрицательны. Тогда произведение любой их пары будет положительно.
при положительном значении хотя бы одной переменной и две другие также будут положительны; при отрицательном значении одной переменной остальные также будут отрицательны. Тогда произведение любой их пары будет положительно.
5. Докажите тождество:
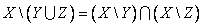
Доказательство:

6. Определите свойства отношений:
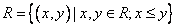 .
.
Решение:
1) Рефлексивность: так как 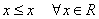 , то данное отношение рефлексивно.
, то данное отношение рефлексивно.
2) Так как из неравенства  не следует неравенство
не следует неравенство  , то отношение не будет симметричным.
, то отношение не будет симметричным.
3) Так как неравенства  и
и  могут одновременно выполняться лишь при условии
могут одновременно выполняться лишь при условии 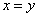 , то отношение антисимметричное.
, то отношение антисимметричное.
4) Транзитивность выполняется: 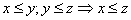 .
.
7. Для отношения, заданного матрицей, определить является ли оно отношением эквивалентности
| R | A | B | C | D | E | F |
| A | 1 | 0 | 0 | 0 | 1 | 0 |
| B | 0 | 1 | 1 | 0 | 0 | 0 |
| C | 0 | 1 | 1 | 0 | 0 | 0 |
| D | 0 | 0 | 0 | 1 | 0 | 1 |
| E | 1 | 0 | 0 | 0 | 1 | 0 |
| F | 0 | 0 | 0 | 1 | 0 | 1 |
Решение:
Отношение является отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Так как в матрице отношения по главной диагонали стоят все 1, то рефлексивность выполняется.
Так как матрица является симметричной, то отношение также является симметричным.
Исследуем на транзитивность:

Тогда транзитивность выполняется.
Следовательно, данное отношение является отношением эквивалентности.
| Следующая > |
matica.org.ua
1.5
Используя диаграммы Эйлера-Венна, решить задачу.
На кафедре иностранных языков работают 20 преподавателей, из них 12 преподают английский язык, 11 – немецкий, 9-французский; 5 преподавателей преподают английский и немецкий языки, 4 - английский и французский, 3 –немецкий и французский. Сколько преподавателей преподают все три языка? Только два языка?
Решение:
В качестве универсального выберем множество всех преподавателей. Число его элементов равно 20. Пусть А - множество преподавателей английского языка, В - немецкого, С - французского. Число элементов множества А обозначим n(A). Оно равно 12, т.е. n(A)=12. Аналогично, n(В)=11, n(С)=9. По условию задачи n(А∩В)=5, n(А∩С)=4 и n(В∩С)=3. Обратимся к диаграмме (рис. 1).

Рис. 1. Диаграмма Эйлера-Венна
Область 1 есть множество преподавателей, которые преподают все 3 языка, т.е. множество А∩В∩С.
Пусть область 5 – преподаватели, преподающие только английский язык, обозначим как a; область 6 – только немецкий язык, обозначим b; область 7 – только французский язык, обозначим c. Пусть x – преподаватели, преподающие все 3 языка. Тогда можно простроить систему уравнений:


n(А∩В∩С) = x = 0;
n(А∩В) + n(А∩С) + n(В∩С) – 3n(А∩В∩С) = 5+4+3 – 3*0 = 12;
Ответ: 0;12.
2.5
Получить СДНФ, СКНФ, используя таблицу истинности. Построить ДНФ, КНФ, упростив выражение.

| P | Q | S |
| P | Q P | | P Q |
|
| X |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
СДНФ = 
СКНФ = 









3.5
Упростить схему

Построим выражение по схеме:

Упростим:




| x | y | z | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Построим СКНФ:












Результаты упрощений равны, что и требовалось доказать.
Упрощённая схема:


y


4.5
Выяснить, каким из пяти замкнутых классов  принадлежит функция, заданная своим характеристическим множеством
принадлежит функция, заданная своим характеристическим множеством (или представленная в табличной форме). Построить полином Жегалкина.
(или представленная в табличной форме). Построить полином Жегалкина.

Построим таблицу истинности:
| x1 x2 x3 | f |
| 0 0 0 | 1 |
| 0 0 1 | 1 |
| 0 1 0 | 0 |
| 0 1 1 | 1 |
| 1 0 0 | 1 |
| 1 0 1 | 0 |
| 1 1 0 | 1 |
| 1 1 1 | 1 |
 , т.к. на противоположных наборах аргументов функция даёт равные значения
, т.к. на противоположных наборах аргументов функция даёт равные значения
f(0,0,0) = f(1,1,1)
 , т.к. f(0,0,0)
, т.к. f(0,0,0)  0
0
 , т.к. f(1,1,1)
, т.к. f(1,1,1)  1
1
 , т.к. f(1,0,1) > f(1,0,0)
, т.к. f(1,0,1) > f(1,0,0)
Построим полином Жегалкина:
Строим СДНФ

Заменяем все v на  , все
, все  на
на










 , т.к. полученный полином Жегалкина – не линейный.
, т.к. полученный полином Жегалкина – не линейный.
5.5
Найти методом Квайна-МакКласски минимальную ДНФ функции, заданной своим характеристическим множеством М1 ={0000, 0001, 1100, 1001, 1110, 1101, 1111}

| x1 | x1 | x1 | x1 | M | |||
| 0 | 0 | 0 | 0 | 1 | |||
| 0 | 0 | 0 | 1 | 0 | |||
| 0 | 0 | 1 | 0 | 0 | |||
| 0 | 0 | 1 | 1 | 0 | |||
| 0 | 1 | 0 | 0 | 0 | |||
| 0 | 1 | 0 | 1 | 1 | |||
| 0 | 1 | 1 | 0 | 0 | |||
| 0 | 1 | 1 | 1 | 0 | |||
| 1 | 0 | 0 | 0 | 1 | |||
| 1 | 0 | 0 | 1 | 1 | |||
| 1 | 0 | 1 | 0 | 0 | |||
| 1 | 0 | 1 | 1 | 1 | |||
| 1 | 1 | 0 | 0 | 0 | |||
| 1 | 1 | 0 | 1 | 1 | |||
| 1 | 1 | 1 | 0 | 1 | |||
| 1 | 1 | 1 | 1 | 1 | |||
| 0 | 0000 | *000 | |
| 1 | 1000 | -001 | |
| 2 | 1010 1001 | 11-0* 110-* 1-01 | 1**1 |
| 3 | 1011 1101 1110 | 111-* 11-1* | |
| 4 | 1111 |
Наборы не участвующие в склейке: *000, 100*, *101, 1**1, 111*
| 0000 | 1001 | 1000 | 0101 | 1101 | 1011 | 1111 | 1110 | |||
| p1 | *000 | 1 | 1 | |||||||
| p2 | 100* | 1 | 1 | |||||||
| р3 | *101 | 1 | 1 | |||||||
| р4 | 1**1 | 1 | 1 | 1 | 1 | |||||
| Р5 | 111* | 1 | 1 | |||||||
| vpi | p1 | p2v p4 | P1 v p2 | p3 | p3 v p4 | p4 | p4 v p5 | p5 | ||
ДНФmin = p1 v p3 v p4 v p5
ДНФmin = 
6.5
| x1 | x2 | x3 | x4 | x5 | x6 | |
| x1 | 0 | 1 | 0 | 1 | 1 | 0 |
| x2 | 1 | 0 | 1 | 0 | 1 | 0 |
| x3 | 0 | 1 | 0 | 1 | 1 | 1 |
| x4 | 1 | 0 | 1 | 0 | 1 | 1 |
| x5 | 1 | 1 | 1 | 1 | 0 | 1 |
| x6 | 0 | 0 | 1 | 1 | 1 | 0 |
Согласно отношениям смежности, изобразим граф G:

n-r+f = 2
f = 2-n+r = 2-6+11 = 7
Толщина графа равна 1, т.к. граф планарный.
Плотность графа это количество вершин в максимальной клике. Задача о поиске клики заданного размера NP-полна. Т.к. наш граф небольшого размера - воспользуемся полным перебором для поиска максимальной клики.
Найденная максимальная клика содержит вершины x6, x5, x4, x3.
Число независимости графа это число вершин в его наибольшем независимом множестве.
Проход алгоритма №1
| x1 | x2 | x3 | x4 | x5 | x6 | |
| x1 | 0 | 1 | 0 | 1 | 1 | 0 |
| x2 | 1 | 0 | 1 | 0 | 1 | 0 |
| x3 | 0 | 1 | 0 | 1 | 1 | 1 |
| x4 | 1 | 0 | 1 | 0 | 1 | 1 |
| x5 | 1 | 1 | 1 | 1 | 0 | 1 |
| x6 | 0 | 0 | 1 | 1 | 1 | 0 |
В искомое множество добавлена вершина: x1.
Проход алгоритма №2
В искомое множество добавлена вершина: x3.
Наибольшее независимое множество содержит вершины: x1, x3. А значит число независимости α0(G) = 2.
Мощность наименьшего вершинного покрытия называется числом вершинного покрытия графа.
Построим матрицу инцидентности графа G:
| x1x2 | x1x4 | x1x5 | x2x3 | x2x5 | x3x4 | x3x5 | x3x6 | x4x5 | x4x6 | x5x6 | |
| x1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| x2 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| x3 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| x4 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| x5 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| x6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
Проход алгоритма №1
В искомое множество добавлена вершина x1
| x2x3 | x2x5 | x3x4 | x3x5 | x3x6 | x4x5 | x4x6 | x5x6 | |
| x2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| x3 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| x4 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| x5 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| x6 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
Проход алгоритма №2
В искомое множество добавлена вершина x3
| x2x5 | x4x5 | x4x6 | x5x6 | |
| x2 | 1 | 0 | 0 | 0 |
| x4 | 0 | 1 | 1 | 0 |
| x5 | 1 | 1 | 0 | 1 |
| x6 | 0 | 0 | 1 | 1 |
studfiles.net
Учреждение образования
ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ
по дисциплине
для студентов уровня ВО заочной формы обучения
специальности 1-45 01 03 «Сети телекоммуникаций»
МИНСК 2009
Составитель: Петрович А.В.
Рецензент: Колодная Е.М.
Издание утверждено на заседании кафедры М и Ф
12.04.2009г., протокол № 8
Зав. кафедрой Гладков Л.Л.
ВВЕДЕНИЕ
В соответствии с учебным планом студенты третьего курса ВГКС специальности 1-45 01 03 – Сети телекоммуникаций в шестом семестре выполняют контрольную работу по дискретной математике.
Для того, чтобы успешно ее выполнить, необходимо изучить сначала теоретический материал по одному из учебников, указанных в списке литературы, и конспекту обзорных лекций. При этом следует ориентироваться на рабочую программу, приведенную ниже. Затем внимательно разберите решения примеров из данной методической разработки и выполните задания для самопроверки.
При оформлении контрольной работы для замечаний преподавателя оставляются поля. Перед решением задачи полностью записывается ее условие. Решение следует сопровождать короткими пояснениями с указанием использованных формул и теорем. Рисунки должны быть выполнены аккуратно. В конце работы ставится дата ее завершения, приводится список проработанной литературы. Работа подписывается.
Выбор варианта контрольной работы определяется двумя последними цифрами номера зачетной книжки. Получив проверенную работу, студент обязан выполнить указания, сделанные рецензентом. Если работа не зачтена, следует сделать работу над ошибками в той же тетради и представить работу на повторную рецензию.
К сдаче экзамена или зачета допускаются студенты, имеющие на руках зачтенные контрольные работы.
Таблица 1
| № варианта | №№ задач | ||||||
| 1 | 1 | 11 | 21 | 31 | 41 | 51 | 61 |
| 2 | 2 | 12 | 22 | 32 | 42 | 52 | 62 |
| 3 | 3 | 13 | 23 | 33 | 43 | 53 | 63 |
| 4 | 4 | 14 | 24 | 34 | 44 | 54 | 64 |
| 5 | 5 | 15 | 25 | 35 | 45 | 55 | 65 |
| 6 | 6 | 16 | 26 | 36 | 46 | 56 | 66 |
| 7 | 7 | 17 | 27 | 37 | 47 | 57 | 67 |
| 8 | 8 | 18 | 28 | 38 | 48 | 58 | 68 |
| 9 | 9 | 19 | 29 | 39 | 49 | 59 | 69 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 11 | 1 | 12 | 23 | 34 | 45 | 56 | 67 |
| 12 | 2 | 13 | 24 | 35 | 46 | 57 | 68 |
| 13 | 3 | 14 | 25 | 36 | 47 | 58 | 69 |
| 14 | 4 | 15 | 26 | 37 | 48 | 59 | 70 |
| 15 | 5 | 16 | 27 | 38 | 49 | 60 | 61 |
| 16 | 6 | 17 | 28 | 39 | 50 | 51 | 62 |
| 17 | 7 | 18 | 29 | 40 | 41 | 52 | 63 |
| 18 | 8 | 19 | 30 | 31 | 42 | 53 | 64 |
| 19 | 9 | 20 | 21 | 32 | 43 | 54 | 65 |
| 20 | 10 | 11 | 22 | 33 | 44 | 55 | 66 |
| 21 | 10 | 19 | 28 | 37 | 46 | 55 | 64 |
| 22 | 9 | 18 | 27 | 36 | 45 | 54 | 63 |
| 23 | 8 | 17 | 26 | 35 | 44 | 53 | 62 |
| 24 | 7 | 16 | 25 | 34 | 43 | 52 | 61 |
| 25 | 6 | 15 | 24 | 33 | 42 | 51 | 70 |
| 26 | 5 | 14 | 23 | 32 | 41 | 60 | 69 |
| 27 | 4 | 13 | 22 | 31 | 50 | 59 | 68 |
| 28 | 3 | 12 | 21 | 40 | 49 | 58 | 67 |
| 29 | 2 | 11 | 30 | 39 | 48 | 57 | 66 |
| 30 | 1 | 20 | 29 | 38 | 47 | 56 | 65 |
РАБОЧАЯ ПРОГРАММА
studfiles.net
ВАРИАНТ № 1
Даны множества
А = {1, 2, 3, 4, 5 ,6} В ={4, 7 ,8}
С = {3, 4, 5, 8} D ={2, 5, 8}
J = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Из каких элементов состоит множество
Составить таблицу истинности формулы логики высказываний
Составить таблицу истинности булевой функции
Упростить булеву функцию
Составить СДНФ функции, заданной таблицей истинности
y
z
F(x,y,z)
0
0
0
1
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
1
Упростить релейно-контактную схему.
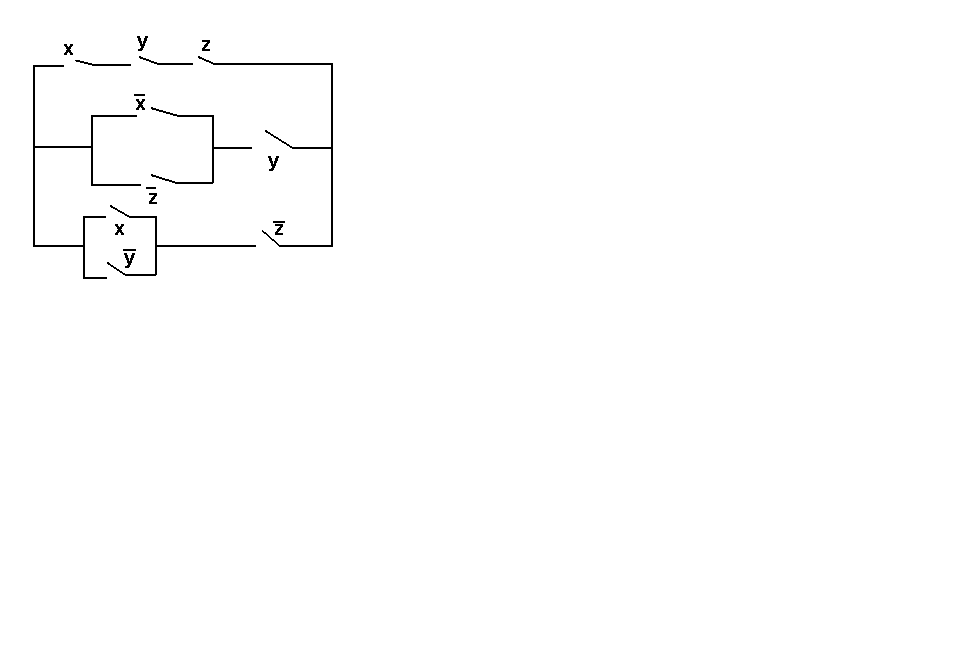
ВАРИАНТ № 2
Даны множества
А = {a, b, c, i} В = {a, d, f, g, i, o}
С = {g, t, o, d} D = {f, i, o, g}
J = {a, b, c, d, f, g, i, o, t}
Из каких элементов состоит множество
Составить таблицу истинности формулы высказываний
3. Составить таблицу истинности булевой функции
Упростить булеву функцию
Составить СКНФ функции, заданной таблицей истинности
y
z
F(x,y,z)
0
0
0
1
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
0
Упростить релейно-контактную схему.
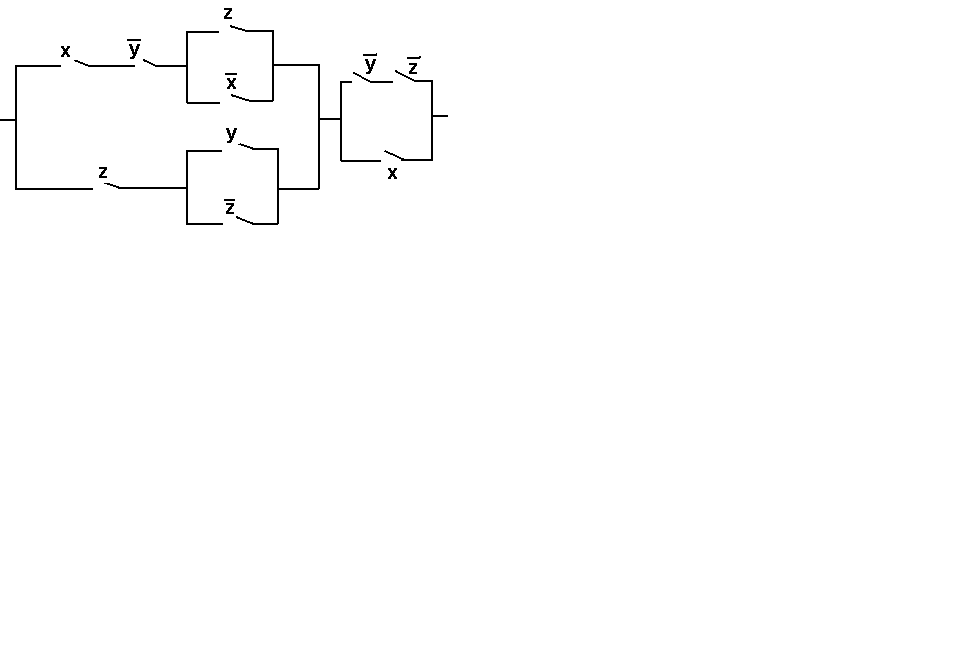
ВАРИАНТ № 3
Даны множества
А = {1, 2, 3, 4, 5 ,6} В ={4, 7 ,8}
С = {3, 4, 5, 8} D ={2, 5, 8}
J = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Из каких элементов состоит множество
Составить таблицу истинности формулы высказываний
Составить таблицу истинности булевой функции
Упростить булеву функцию
Составить СДНФ функции, заданной таблицей истинности
xy
z
F(x,y,z)
0
0
0
1
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
0
1
0
1
1
0
1
1
1
1
1
Упростить релейно-контактную схему.
ВАРИАНТ № 4
Даны множества
А = {a, b, c, i} В = {a, d, f, g, i, o}
С = {g, t, o, d} D = {f, i, o, g}
J = {a, b, c, d, i, f, g, o, t}
Из каких элементов состоит множество
Составить таблицу истинности формулы высказываний
3. Упростить булеву функцию
Упростить булеву функцию
Составить СКНФ функции, заданной таблицей истинности
y
z
F(x,y,z)
0
0
0
1
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
0
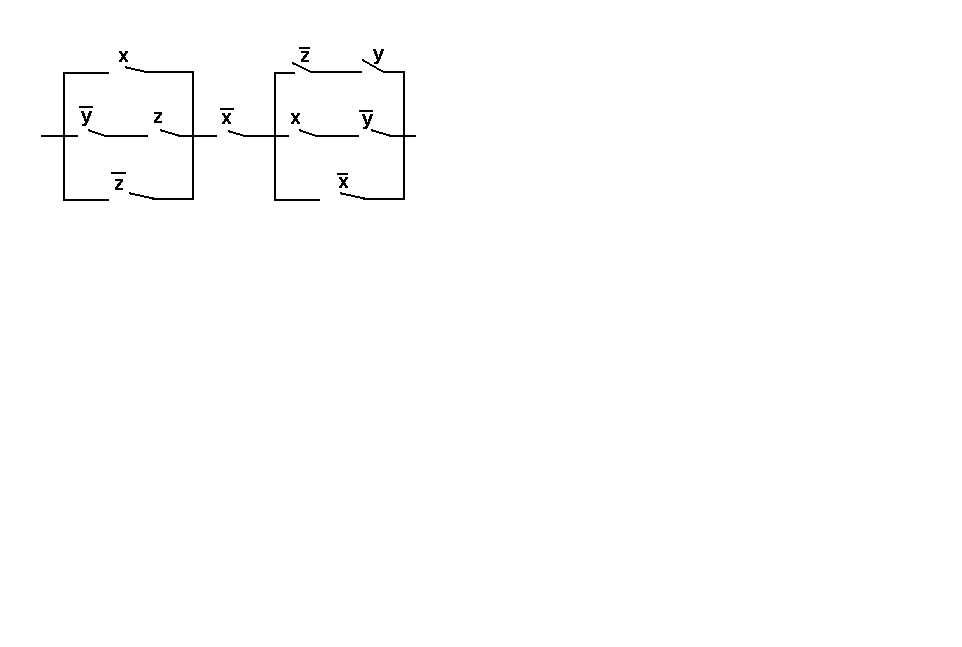
Упростить релейно-контактную схему.
ВАРИАНТ № 5
Даны множества
А = {x, y, z, w, v, r} В = {w, r, t, s}
С = {t, s, v, x, q} D = {y, z, w}
J = {x, y, z, v, w, r, s, t, q}
Из каких элементов состоит множество
2. Составить таблицу истинности формулы высказываний
Составить таблицу истинности булевой функции
Упростить булеву функцию
Составить СДНФ функции, заданной таблицей истинности
xy
z
F(x,y,z)
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
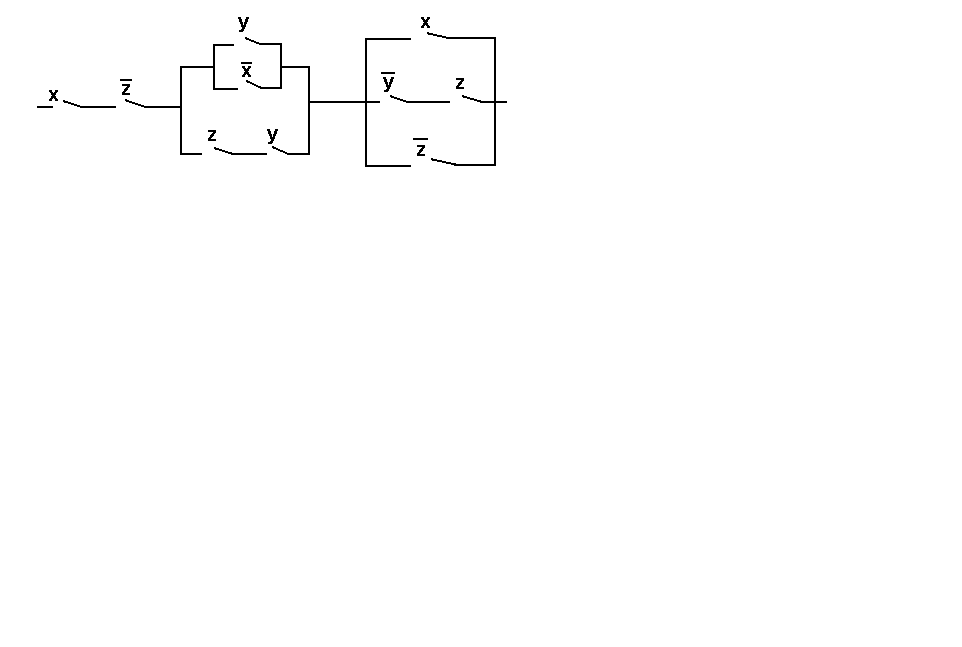
Упростить релейно-контактную схему.
ВАРИАНТ № 6
Даны множества
А = {3, 5, 6, 7, 10} В = {3, 5, 6, 8}
С = {4, 5, 6, 8, 11} D = {4, 9, 10}
J = {3, 4, 5, 6, 7, 8, 9, 10, 11}
Из каких элементов состоит множество
Составить таблицу истинности формулы высказываний
3. Упростить булеву функцию
Упростить булеву функцию
Составить СКНФ функции, заданной таблицей истинности
xy
z
F(x,y,z)
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
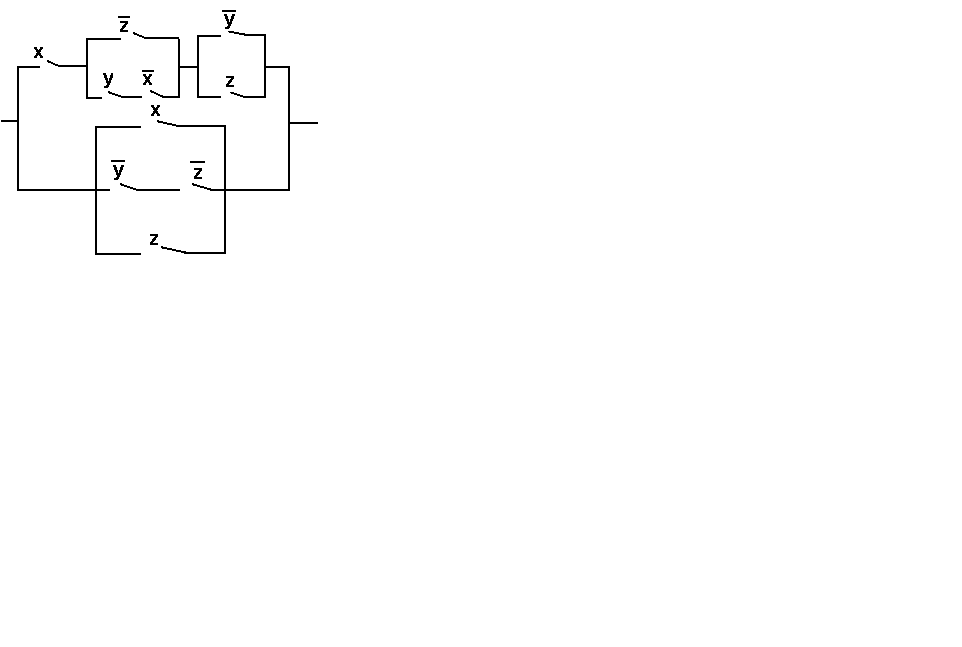
Упростить релейно-контактную схему.
ВАРИАНТ № 7
Даны множества
А = {x, y, z, w, v, r} В = {w, r, t, s}
С = {t, s, v, x, q} D = {y, z, w}
J = {x, y, z, v, w, r, s, t, q}
Из каких элементов состоит множество
2. Составить таблицу истинности формулы высказываний
Составить таблицу истинности булевой функции
Упростить булеву функцию
Составить СДНФ функции, заданной таблицей истинности
ab
c
F(a,b,c)
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
0
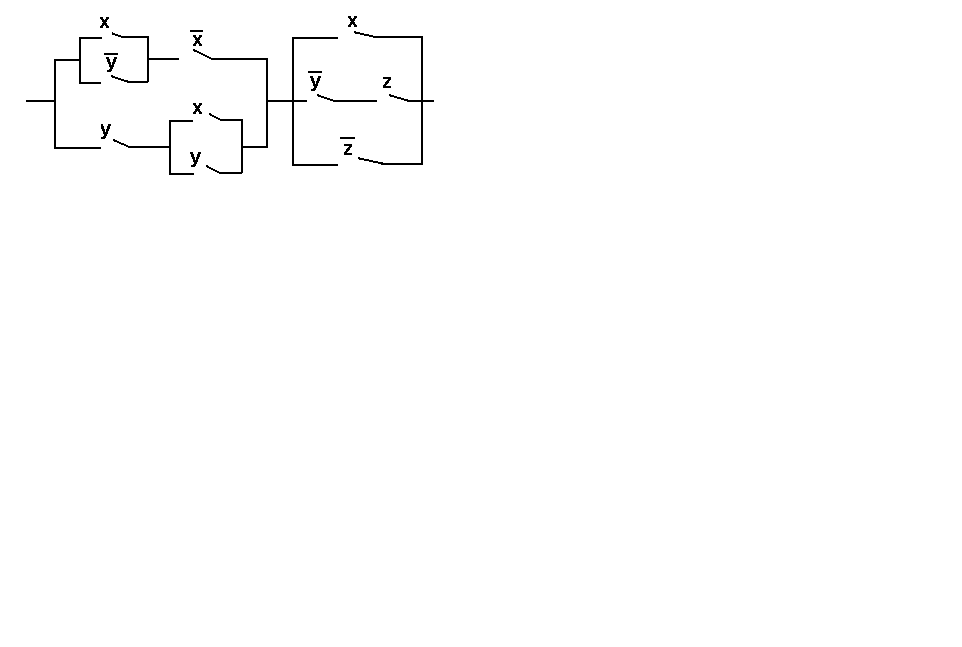
Упростить релейно-контактную схему.
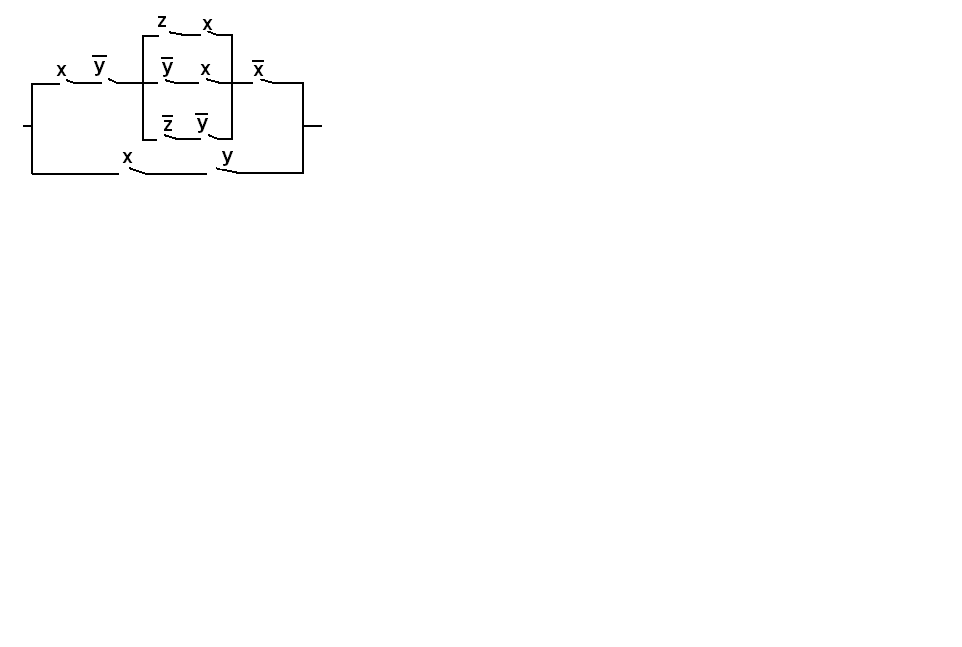
ВАРИАНТ № 8
Даны множества
А = {3, 5, 6, 7, 10} В = {3, 5, 6, 8}
С = {4, 5, 6, 8, 11} D = {4, 9, 10}
J = {3, 4, 5, 6, 7, 8, 9, 10, 11}
Из каких элементов состоит множество
Составить таблицу истинности формулы высказываний
3. Упростить булеву функцию
Упростить булеву функцию
Составить СКНФ функции, заданной таблицей истинности
xy
z
F(x,y,z)
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
0
Упростить релейно-контактную схему.
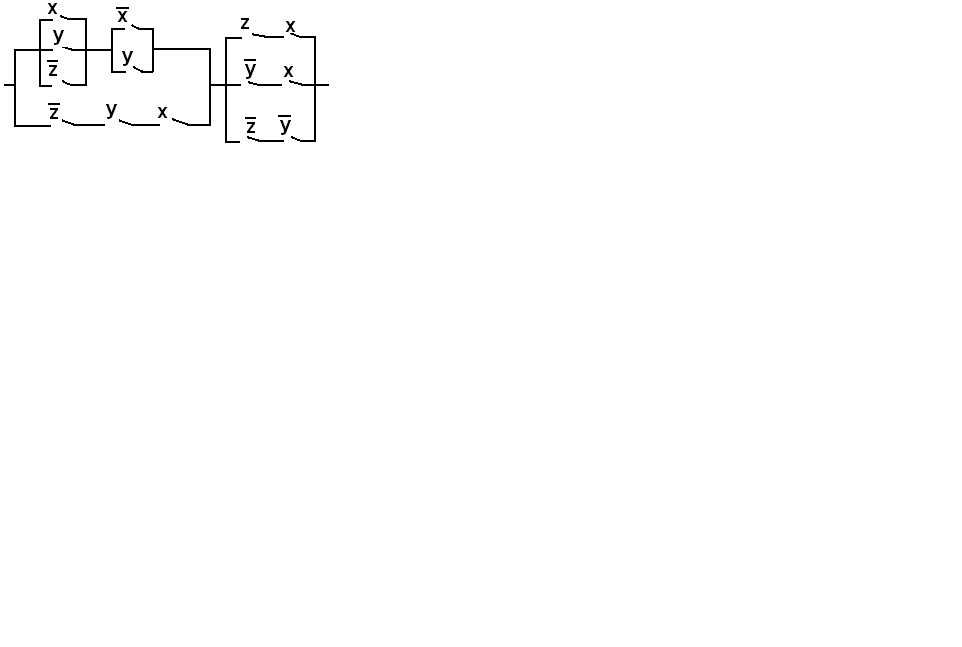
ВАРИАНТ № 9
Даны множества
А = {1, 2, 3, 4, 5 ,6} В ={4, 7 ,8}
С = {3, 4, 5, 8} D ={2, 5, 8}
J = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Из каких элементов состоит множество
2. Составить таблицу истинности формулы высказываний
Составить таблицу истинности булевой функции
Упростить булеву функцию
Составить СДНФ функции, заданной таблицей истинности
xy
z
F(x,y,z)
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
Упростить релейно-контактную схему.
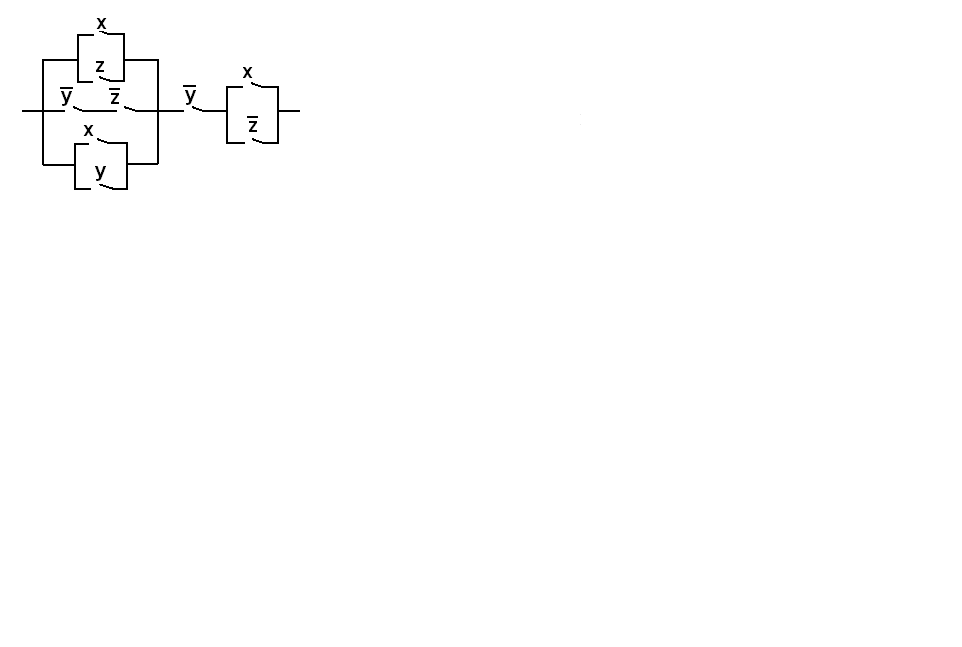
ВАРИАНТ № 10
Даны множества
А = {a, b, c, i} В = {a, d, f, g, i, o}
С = {g, t, o, d} D = {f, i, o, g}
J = {a, b, c, d, i, f, g, o, t}
Из каких элементов состоит множество
Составить таблицу истинности формулы высказываний
3. Упростить булеву функцию
Упростить булеву функцию
Составить СКНФ функции, заданной таблицей истинности
xy
z
F(x,y,z)
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
Упростить релейно-контактную схему.
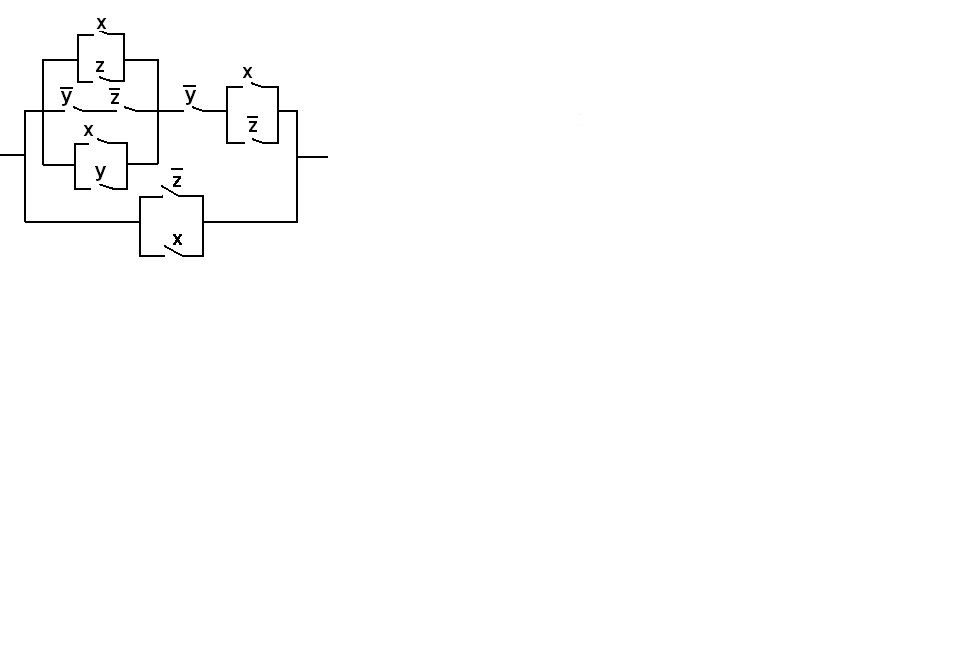
ВАРИАНТ № 11
Даны множества
А = {1, 2, 3, 4, 5 ,6} В ={4, 7 ,8}
С = {3, 4, 5, 8} D ={2, 5, 8}
J = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Из каких элементов состоит множество
2. Составить таблицу истинности формулы высказываний
Составить таблицу истинности булевой функции
Упростить булеву функцию
Составить СДНФ функции, заданной таблицей истинности
xy
z
F(x,y,z)
0
0
0
1
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
1
Упростить релейно-контактную схему.
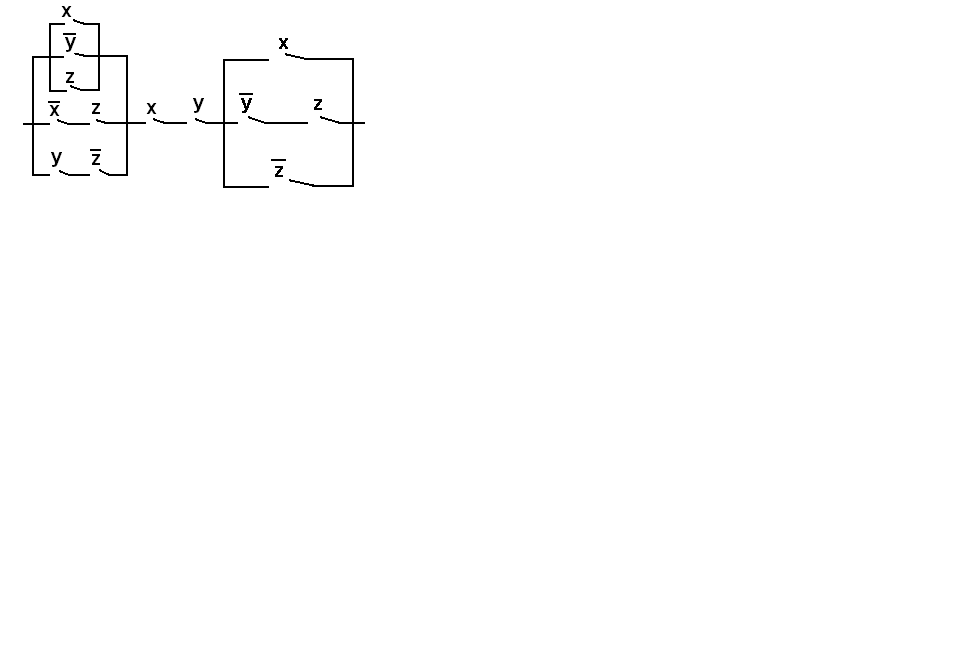
ВАРИАНТ № 12
Даны множества
А = {x, y, z, q} В = {x, p, r, t, q, m}
С = {t, n, m, p} D = {r, q, m, n}
J = {x, y, z, p, q, r, t, m, n}
Из каких элементов состоит множество
Составить таблицу истинности формулы высказываний
3. Упростить булеву функцию
Упростить булеву функцию
Составить СКНФ функции, заданной таблицей истинности
xy
z
F(x,y,z)
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
Упростить релейно-контактную схему.
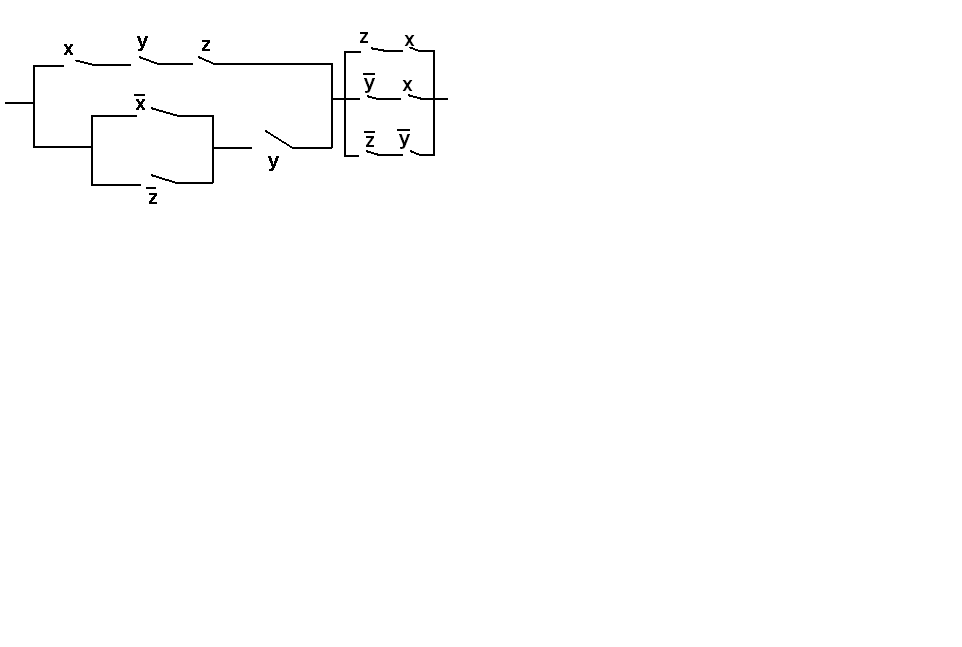
ВАРИАНТ № 13
Даны множества
А = {1, 2, 3, 5, 4, 6} В = {5, 6, 8, 7}
С = {8, 7, 4, 1, 9} D = {2, 3, 5}
J = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Из каких элементов состоит множество
2. Составить таблицу истинности формулы высказываний
Составить таблицу истинности булевой функции
Упростить булеву функцию
Составить СДНФ функции, заданной таблицей истинности
xy
z
F(x,y,z)
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
0
1
1
1
1
Упростить релейно-контактную схему.
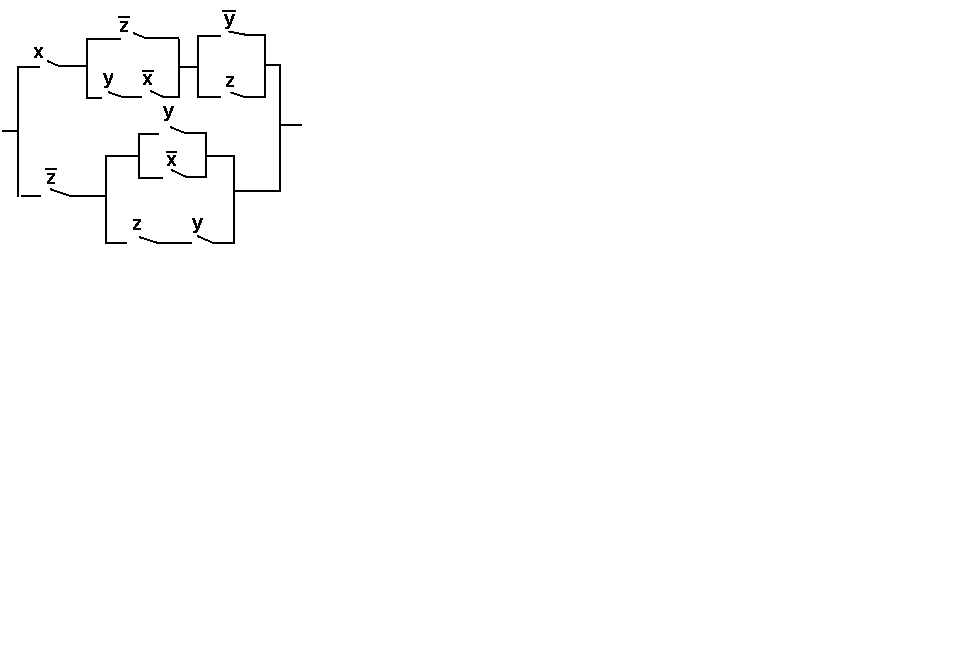
ВАРИАНТ № 14
Даны множества
А = {1, 2, 3, 4, 5 ,6} В ={4, 7 ,8}
С = {3, 4, 5, 8} D ={2, 5, 8}
J = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Из каких элементов состоит множество
Составить таблицу истинности формулы высказываний
3. Упростить булеву функцию
Упростить булеву функцию
Составить СКНФ функции, заданной таблицей истинности
xy
z
F(x,y,z)
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
0
1
1
1
0
Упростить релейно-контактную схему.
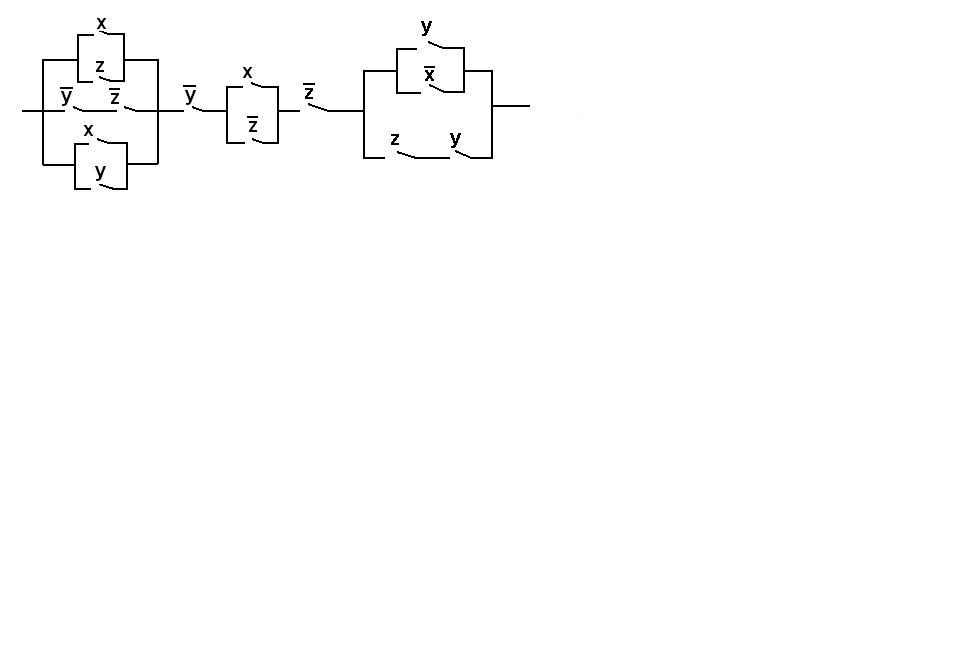
ВАРИАНТ № 15
Даны множества
А = {3, 5, 6, 7, 10} В = {3, 5, 6, 8}
С = {4, 5, 6, 8, 11} D = {4, 9, 10}
J = {3, 4, 5, 6, 7, 8, 9, 10, 11}
Из каких элементов состоит множество
Составить таблицу истинности формулы высказываний
3. Упростить булеву функцию
Упростить булеву функцию
Составить СКНФ функции, заданной таблицей истинности
xy
z
F(x,y,z)
0
0
0
1
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
0
Упростить релейно-контактную схему.

infourok.ru