 .
.А – 8 Контрольная работа "Числовые неравенства и их свойства".
1 вариант.
1 Зная, что а-b˃0, сравните выражения, вместо знака * вставить знаки ˃, ˂ или =.
а) а * b; б) b * а; в) 7а * 7b; г) -3а * -3b; д)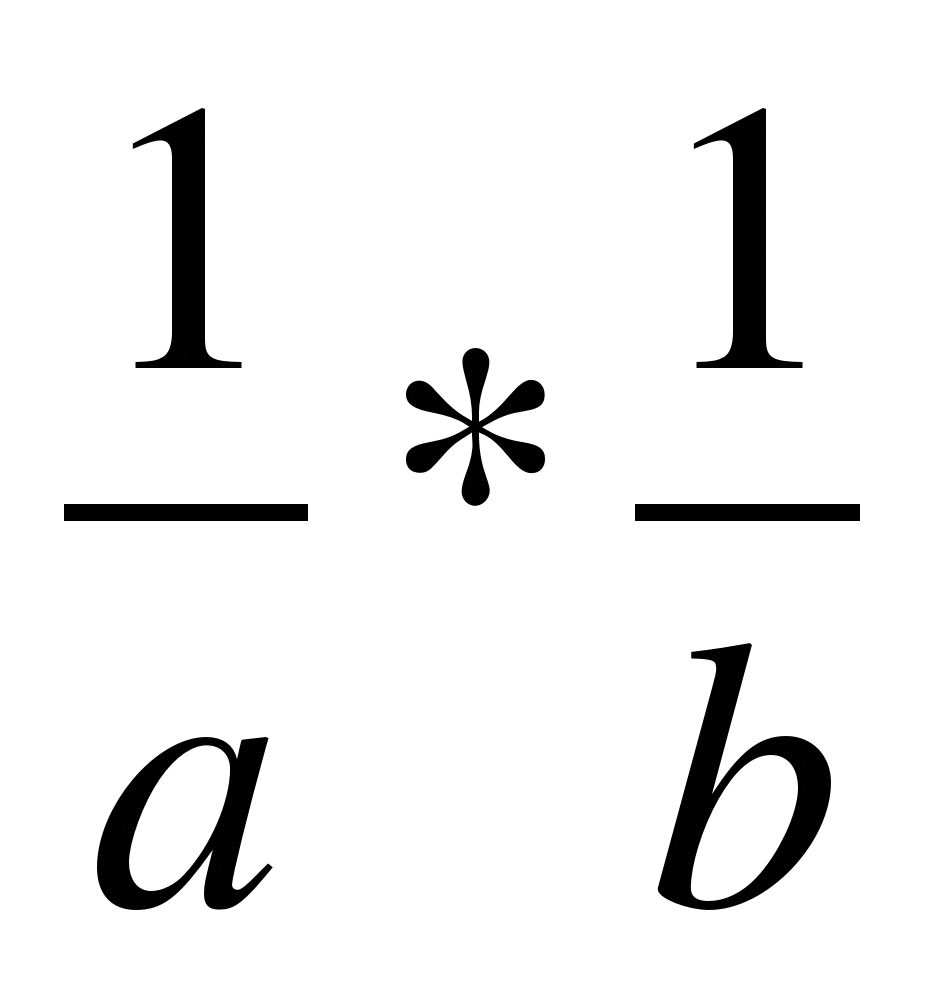 .
.
2 Доказать неравенство: а) 9х2+1 > 6х; б) (а + 3)(а +5) < (а + 4)2.
3 Зная, что 4 ˂ а ˂ 5 и 10 ˂ b ˂ 12. Оценить значения выражений:
а) ab; б) a - b; в) b / a; г) -3a + b
4 Разместить на числовой прямой точки, имеющие координаты а, в, с, к; если известно, что а ˂ с, с ˃ в; в ˃ а; к ˃ с. Сравнить а и к.
5 Оцените периметр равнобедренного треугольника с основанием а см и боковой стороной в см, если 10 ˂ а ˂ 13 и 11 ˂ b ˂ 16.
А – 8 Контрольная работа "Числовые неравенства и их свойства".
2 вариант
1 Зная что m-n˂0, сравните выражения, вместо знака * вставить знаки ˃, ˂ или =
а) m * n; б) n * m; в) 7m * 7n; г) -3m *-3 n; д)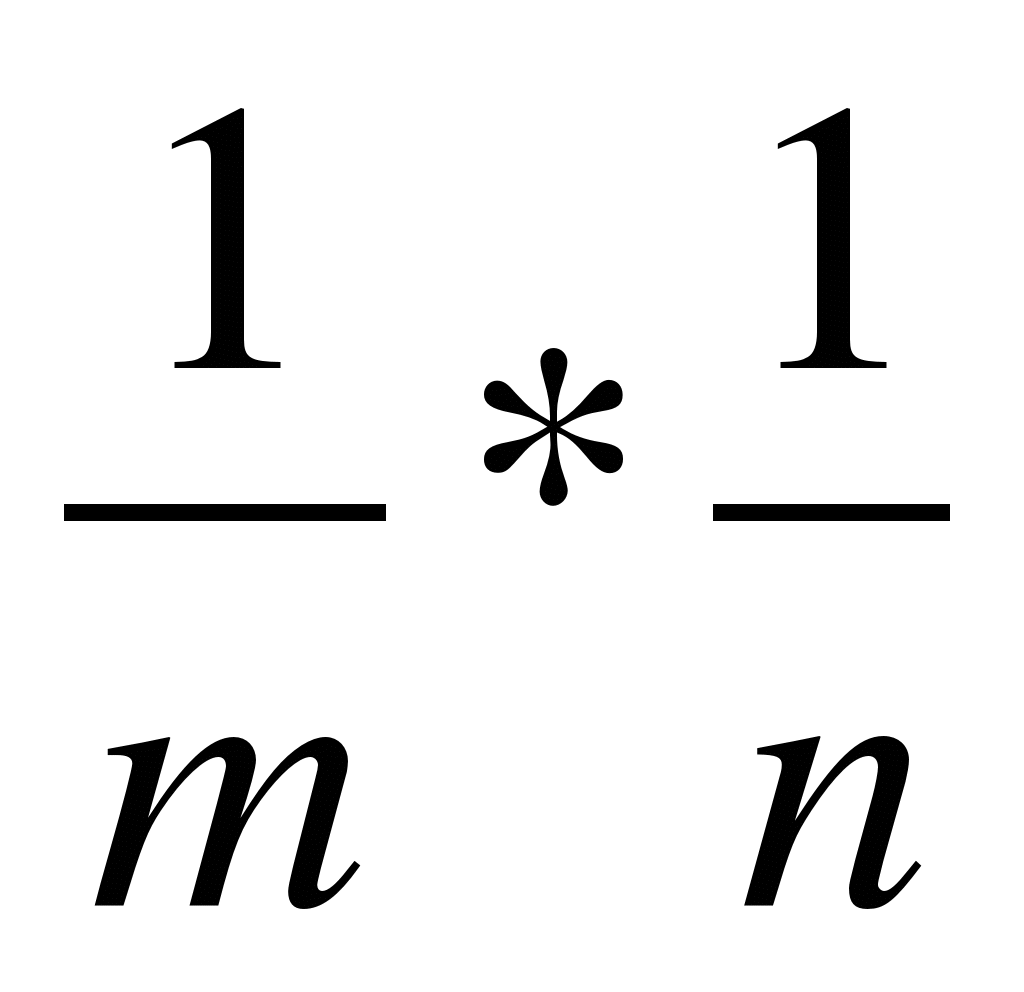 .
.
2. Доказать неравенство: а)16х + 1 ˃ 8х; b) (b – 2)(b – 4) < (b – 3)2.
3. Зная, что 4 ˂ m ˂ 9 и 18 ˂ n ˂ 24. Оценить значения выражений:
а) mn; б) m - n; в) n / m; г) 3m - n
4. Разместить на числовой прямой точки, имеющие координаты х, y, z, q; если известно, что x ˂ z, z ˃ y; y ˃ x; q ˃ z. Сравнить x и q.
5. Дан треугольник с углами α, β и γ. Известно, что 34о˂ α ˂ 45о, 52о˂ β ˂ 73о. Оцените угол γ.
А – 8 Контрольная работа "Числовые неравенства и их свойства".
1 вариант.
1 Зная, что а-b˃0, сравните выражения, вместо знака * вставить знаки ˃, ˂ или =.
а) а * b; б) b * а; в) 7а * 7b; г) -3а * -3b; д)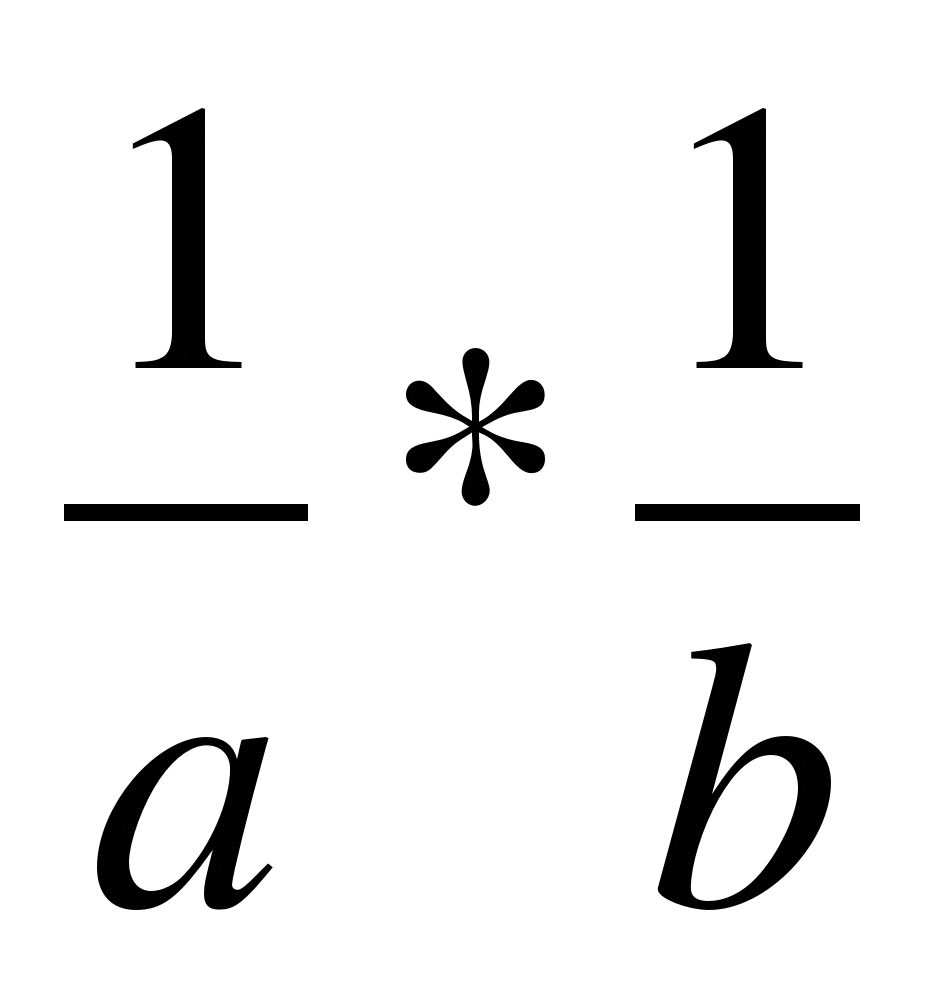 .
.
2 Доказать неравенство: а) 9х2+1 > 6х; б) (а + 3)(а +5) < (а + 4)2.
3 Зная, что 4 ˂ а ˂ 5 и 10 ˂ b ˂ 12. Оценить значения выражений:
а) ab; б) a - b; в) b / a; г) -3a + b
4 Разместить на числовой прямой точки, имеющие координаты а, в, с, к; если известно, что а ˂ с, с ˃ в; в ˃ а; к ˃ с. Сравнить а и к.
5 Оцените периметр равнобедренного треугольника с основанием а см и боковой стороной в см, если 10 ˂ а ˂ 13 и 11 ˂ b ˂ 16.
А – 8 Контрольная работа "Числовые неравенства и их свойства".
2 вариант
1 Зная что m-n˂0, сравните выражения, вместо знака * вставить знаки ˃, ˂ или =
а) m * n; б) n * m; в) 7m * 7n; г) -3m *-3 n; д)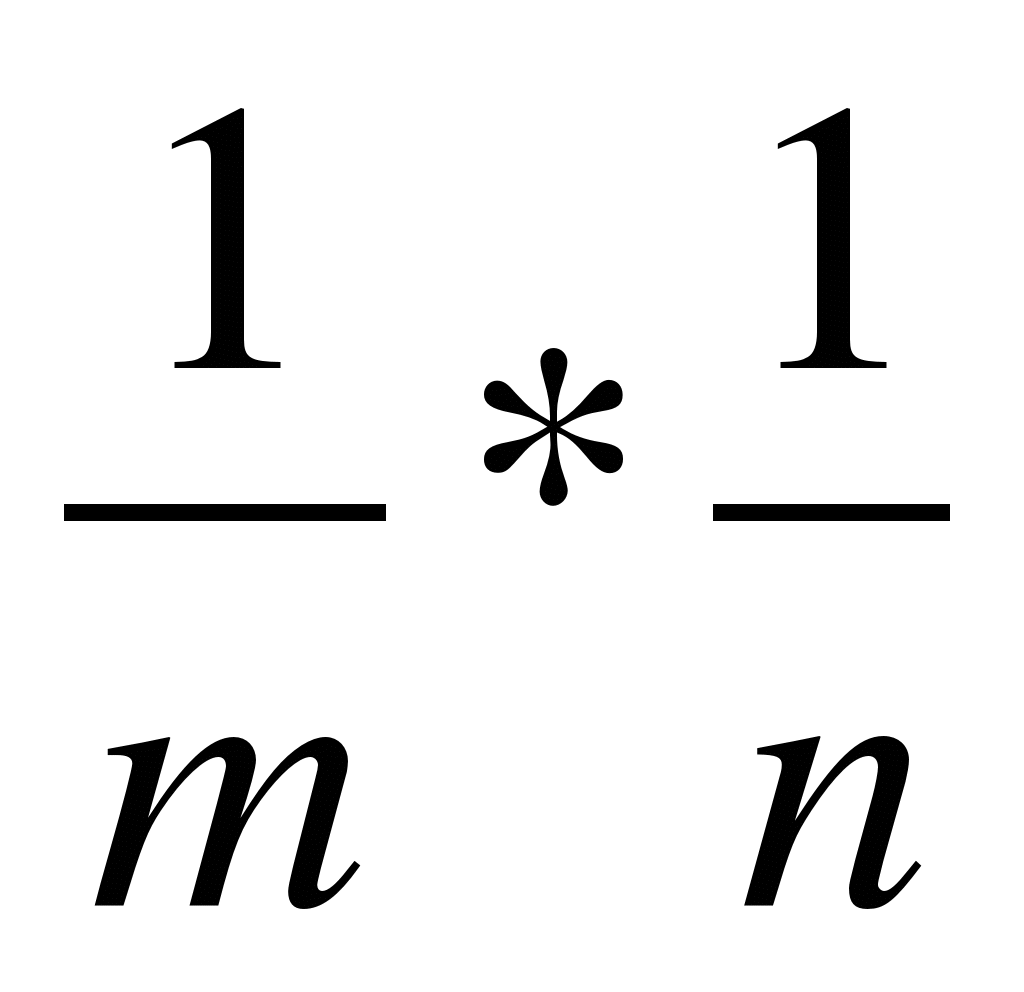 .
.
2. Доказать неравенство: а)16х + 1 ˃ 8х; b) (b – 2)(b – 4) < (b – 3)2.
3. Зная, что 4 ˂ m ˂ 9 и 18 ˂ n ˂ 24. Оценить значения выражений:
а) mn; б) m - n; в) n / m; г) 3m - n
4. Разместить на числовой прямой точки, имеющие координаты х, y, z, q; если известно, что x ˂ z, z ˃ y; y ˃ x; q ˃ z. Сравнить x и q.
5. Дан треугольник с углами α, β и γ. Известно, что 34о˂ α ˂ 45о, 52о˂ β ˂ 73о. Оцените угол γ.
А – 8 Контрольная работа "Числовые неравенства и их свойства".
1 вариант.
1 Зная, что а-b˃0, сравните выражения, вместо знака * вставить знаки ˃, ˂ или =.
а) а * b; б) b * а; в) 7а * 7b; г) -3а * -3b; д)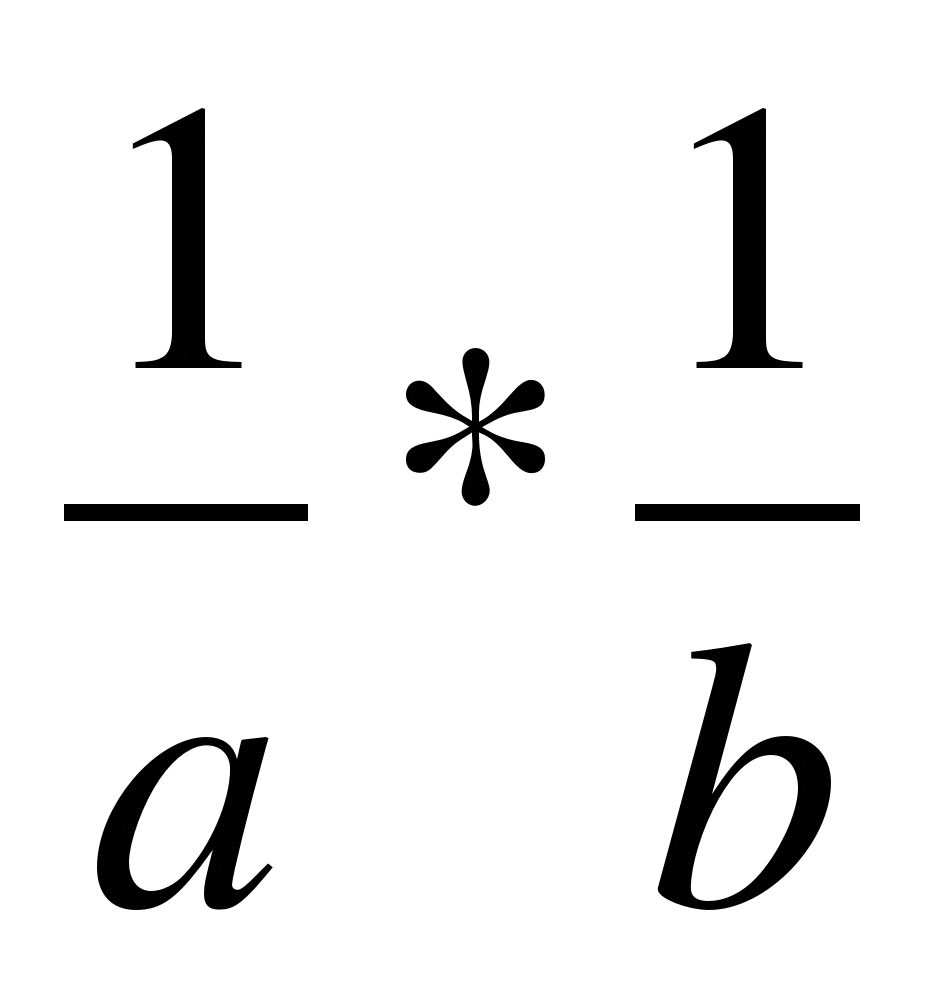 .
.
2 Доказать неравенство: а) 9х2+1 > 6х; б) (а + 3)(а +5) < (а + 4)2.
3 Зная, что 4 ˂ а ˂ 5 и 10 ˂ b ˂ 12. Оценить значения выражений:
а) ab; б) a - b; в) b / a; г) -3a + b
4 Разместить на числовой прямой точки, имеющие координаты а, в, с, к; если известно, что а ˂ с, с ˃ в; в ˃ а; к ˃ с. Сравнить а и к.
infourok.ru
Проверочный тест по теме
"Числовые неравенства" (8 класс)
I вариант:
Обязательная часть.
А1. Какие из неравенств верны?
Варианты ответов:
1) 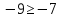
2) 2 ≥ -2
3) 6, 129 > 6,131
6, 129 > 6,131
4) 4 ∙ 103 > 4 ∙ 102
Ответ: ___
А2. Каким из данных чисел может выражаться разность х – у, если у > х?
Варианты ответов:
1) 0
2) 2,5
3) -3
4) -2,5
Ответ: ___
А3. Известно, что х > у. Расположите в порядке убывания числа: х +1; у -7; х + 10;
у – 15.
Варианты ответов:
1) у – 15; у -7; х +1; х + 10.
2) х + 10; х +1; у -7; у – 15.
3) у -7; х +1; х + 10; у – 15.
4) у -7; у – 15; х +1; х + 10.
Ответ: ___
А4. Выберите верное утверждение относительно чисел a и b, расположенных на числовой прямой.
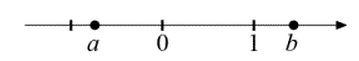
Варианты ответов:
1) 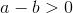
2) 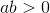
3) 
4) 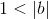
Ответ: ___
А5. Укажите решение неравенства -3 -3х > 7х – 9.
Варианты ответов:
1) (0,6; +∞)
2) (-∞; 1,2)
3) (1,2; +∞)
4) (-∞; 0,6)
Ответ: ___
Дополнительная часть.
В1. Решите неравенство 2(4х – 7) < -3 – 2х.
Решение:
______________________________________________________________________________________________________________________________________________________
_______________________________________________________________________
Ответ: ________
В2. В Докажите, что при любом значении х верно неравенство 4х2 + 1 ≥ 4х.
Решение:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ:_________
II вариант:
Обязательная часть.
А1. Какие из неравенств НЕверны?
Варианты ответов:
1) 
2) 2 ≤ -2
3) 6, 129 > 6,131
6, 129 > 6,131
4) 4 ∙ 103 > 4 ∙ 102
Ответ: ___
А2. Какое из неравенств является верным при любых значениях х и у, если х >-у?
Варианты ответов:
1) у – х > -1
2) у + х <1
3) 
4) х – у > 1
Ответ: ___
А3. Известно, что х > у. Расположите в порядке возрастания числа: х +1; у -7; х + 10;
у – 15.
Варианты ответов:
1) у – 15; у -7; х +1; х + 10.
2) х + 10; х +1; у -7; у – 15.
3) у -7; х +1; х + 10; у – 15.
4) у -7; у – 15; х +1; х + 10.
Ответ: ___
А4. На координатной прямой отмечено число  .
.
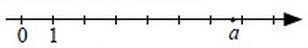
Какое из утверждений относительно этого числа является верным?
Варианты ответов:
1) 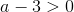 2)
2) 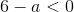
3) 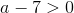 4)
4) 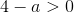
Ответ: ___
А5. Укажите решение неравенства 9х + 8 < 8х – 8.
Варианты ответов:
1) (-16; +∞)
2) (-∞; 0)
3) (0; +∞)
4) (-∞; -16)
Ответ: ___
Дополнительная часть.
В1. Решите неравенство -2(х – 1) < -7 + 4х.
Решение:
______________________________________________________________________________________________________________________________________________________
_______________________________________________________________________
Ответ: ________
В2. В Докажите, что при любом значении х верно неравенство 9х2 - 15 > (3х -4)(3х +4).
Решение:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ:_________
xn--j1ahfl.xn--p1ai
Самостоятельная работа «Числовые неравенства.
Свойства числовых неравенств»
1 вариант
1. Определить положительное или отрицательное
число а, если:
а) 56а < 0 б) – 3,5а > 0
2. Сравните числа a и b, если:
а) a – b >0 б) a – b < -3
в) a – b >5 г) a – b = 0
3. Даны выражения 7c(c + 3) и 3c(c - 5). Сравните их
значения при c = - 4 ( >, < или =).
4. Известно, что a < b. Сравнить:
а) a – 3 и b – 3; б) 3,4 + a и 3,4 + b;
в) и ; г) и .
5. Доказать, что, если 4а – 5b > 2a – 3b, то a > b
6. Доказать, что, если (a + 1)² < a(a + 3) , то a > 1
Самостоятельная работа «Числовые неравенства.
Свойства числовых неравенств»
2 вариант
1. Определить положительное или отрицательное
число b, если:
а) -2.8b < 0 б) 85b > 0
2. Сравните числа a и b, если:
а) a – b >6 б) a – b < 0
в) a – b < -1 г) a – b = 0
3. Даны выражения 5c(c + 2) и 4c(c - 4).. Сравните их
значения при c = - 3 ( >, < или =).
4. Известно, что a < b. Сравнить:
а) a – 2,1 и b – 2,1; б) 4 + a и 4 + b;
в) и ; г) и .
5. Доказать, что, если 6х + 5у < 3x + 8y, то x < y
6. Доказать, что, если (x - 2)² > x(x – 3) , то х < 4
Самостоятельная работа «Числовые неравенства.
Свойства числовых неравенств»
3 вариант
1. Определить положительное или отрицательное
число c, если:
а) 9,1c < 0 б) -5c > 0
2. Сравните числа a и b, если:
а) a – b >3 б) a – b < -8
в) a – b > 200 г) a – b = 0
3. Даны выражения 6c(c + 4) и 2c(c – 2). Сравните их
значения при c = - 3 ( >, < или =).
4. Известно, что a < b. Сравнить:
а) и ; б) и ;
в) a – 3,2 и b – 3,2; г) 5 + a и 5 + b.
5. Доказать, что, если 5m – 8n < 3n – 6m, то m < n
6. Доказать, что, если m(m + 5) > (m + 3)² , то m < -9
Самостоятельная работа «Числовые неравенства.
Свойства числовых неравенств»
4 вариант
1. Определить положительное или отрицательное
число m, если:
а) -92m < 0 б) 6,7m > 0
2. Сравните числа a и b, если:
а) a – b >30 б) a – b < -2
в) a – b > 0 г) a – b = 0
3. Даны выражения 2c(c – 3) и 8c(c + 2). Сравните их
значения при c = - 1 ( >, < или =).
4. Известно, что a < b. Сравнить:
а) и ; б) и ;
в) 7,1 + a и 7,1 + b; г) a – 5 и b – 5.
5. Доказать, что, если 3х – 5m > 2m – 4x, то x > m
6. Доказать, что, если n(n – 3) > (1 - n)² , то n < -1
Самостоятельная работа «Числовые неравенства.
Свойства числовых неравенств»
1 вариант
1. Определить положительное или отрицательное
число а, если:
а) 56а < 0 б) – 3,5а > 0
2. Сравните числа a и b, если:
а) a – b >0 б) a – b < -3
в) a – b >5 г) a – b = 0
3. Даны выражения 7c(c + 3) и 3c(c - 5). Сравните их
значения при c = - 4 ( >, < или =).
4. Известно, что a < b. Сравнить:
а) a – 3 и b – 3; б) 3,4 + a и 3,4 + b;
в) и ; г) и .
5. Доказать, что, если 4а – 5b > 2a – 3b, то a > b
6. Доказать, что, если (a + 1)² < a(a + 3) , то a > 1
Самостоятельная работа «Числовые неравенства.
Свойства числовых неравенств»
2 вариант
1. Определить положительное или отрицательное
число b, если:
а) -2.8b < 0 б) 85b > 0
2. Сравните числа a и b, если:
а) a – b >6 б) a – b < 0
в) a – b < -1 г) a – b = 0
3. Даны выражения 5c(c + 2) и 4c(c - 4).. Сравните их
значения при c = - 3 ( >, < или =).
4. Известно, что a < b. Сравнить:
а) a – 2,1 и b – 2,1; б) 4 + a и 4 + b;
в) и ; г) и .
5. Доказать, что, если 6х + 5у < 3x + 8y, то x < y
6. Доказать, что, если (x - 2)² > x(x – 3) , то x < 4
uchitelya.com
weburok.com