для 10 класса
Шамсутдинов М.Р.
(по учебнику Л.С. Атанасяна)
Контрольная работа №1.
I вариант.
№1. Основание АD трапеции ABCD лежит в плоскости  . Через точки В и С проведены параллельные прямые, пересекающие плоскость
. Через точки В и С проведены параллельные прямые, пересекающие плоскость 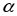 в точках E и F соответственно.
в точках E и F соответственно.
а) Каково взаимное положение прямых EF и AB?
б) Чему равен угол между прямыми EF и AB, если 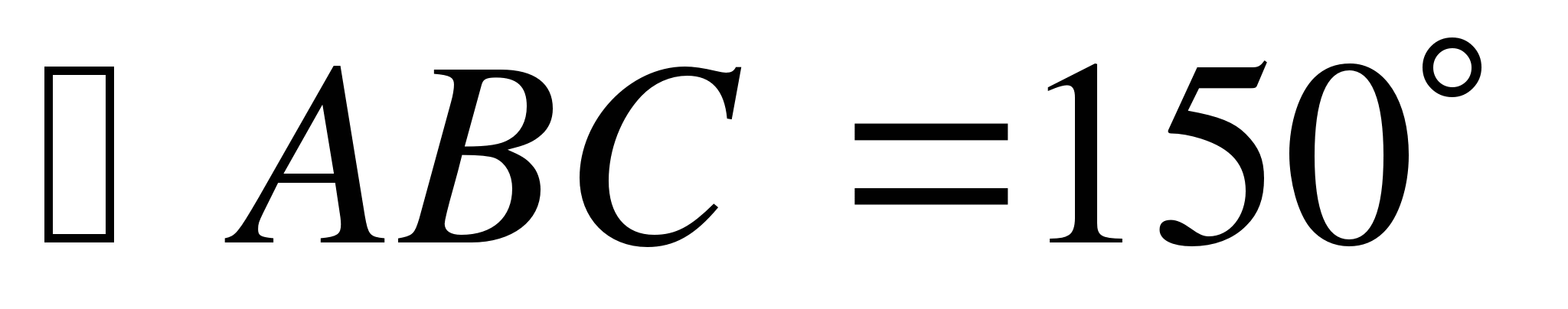 ? Поясните ответ.
? Поясните ответ.
№2. Дан пространственный четырехугольник ABCD, в котором диагонали AC и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник есть ромб.
II вариант.
№1. Треугольники ABC и ADC лежат в разных плоскостях и имеют общую сторону AC. Точка P – середина стороны AD, а K – середина стороны DC.
а) Каково взаимное положение прямых PK и AB?
б) Чему равен угол между прямыми PK и AB, если 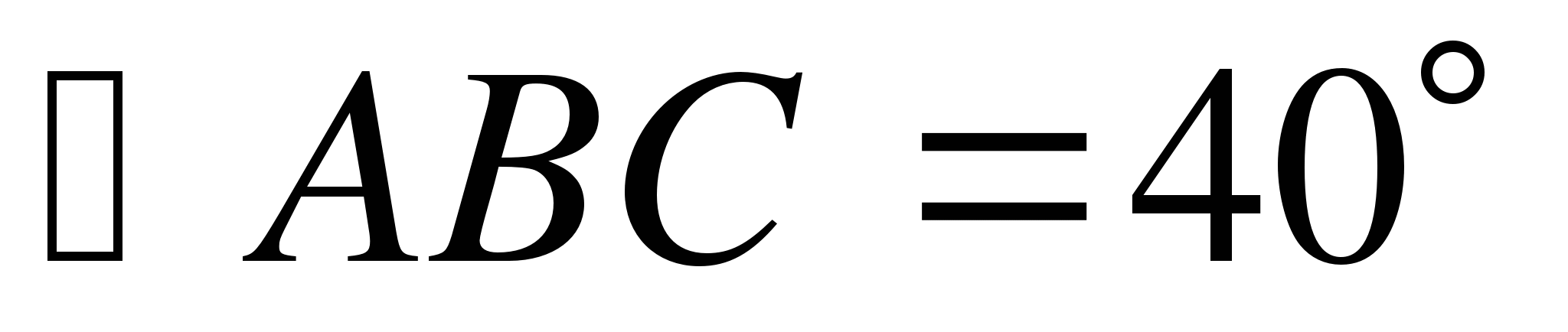 и
и 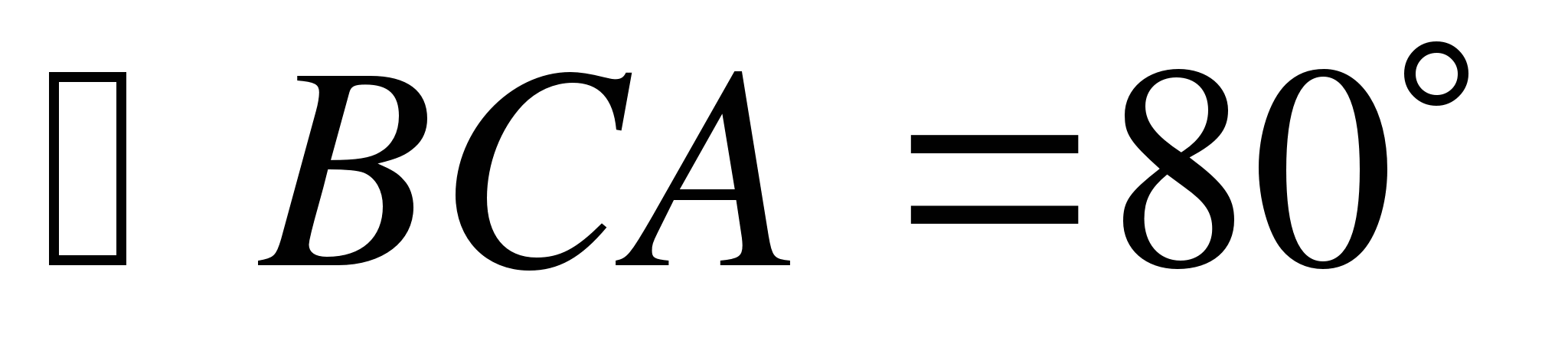 ? Поясните ответ.
? Поясните ответ.
№2. Дан пространственный четырехугольник ABCD, в котором M и N – середины сторон AB и BC соответственно.
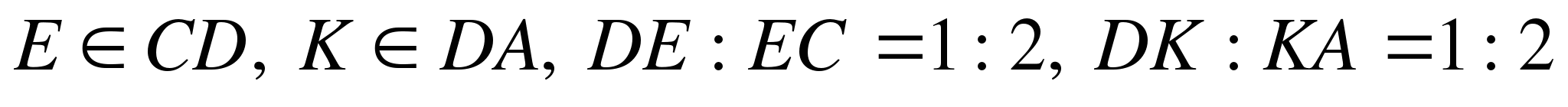 .
.
а) Выполните рисунок к задаче.
б) Докажите, что четырехугольник MNEK есть трапеция.
Контрольная работа №2.
I вариант.
№1. Прямые а и b лежат в параллельных плоскостях  и
и 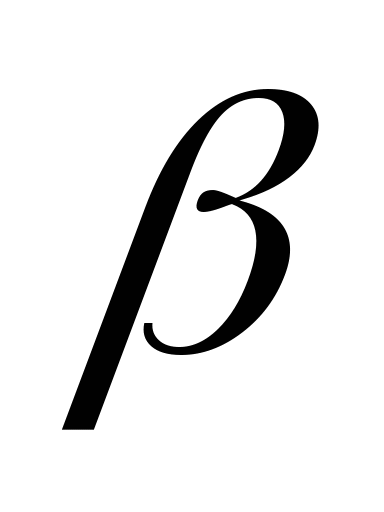 . Могут ли эти прямые быть:
. Могут ли эти прямые быть:
а) параллельными; б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
№2. Через точку О, лежащую между параллельными плоскостями 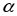 и
и 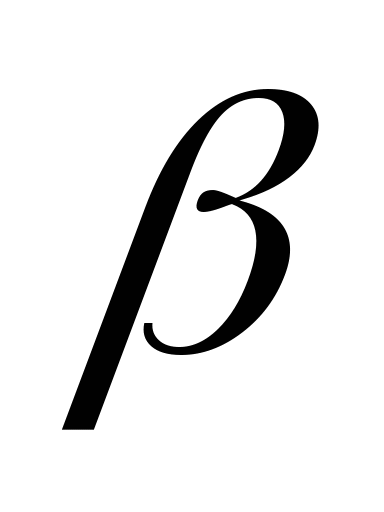 , проведены прямые l и m. Прямая l пересекает плоскости
, проведены прямые l и m. Прямая l пересекает плоскости 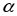 и
и 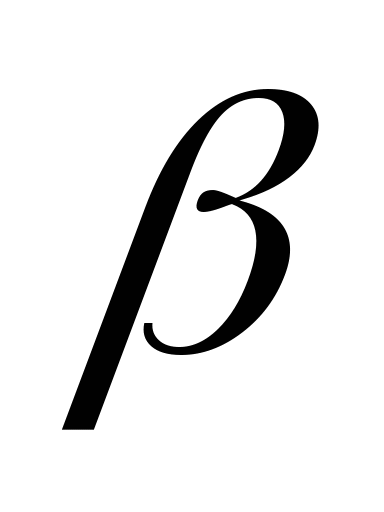 в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если
в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если 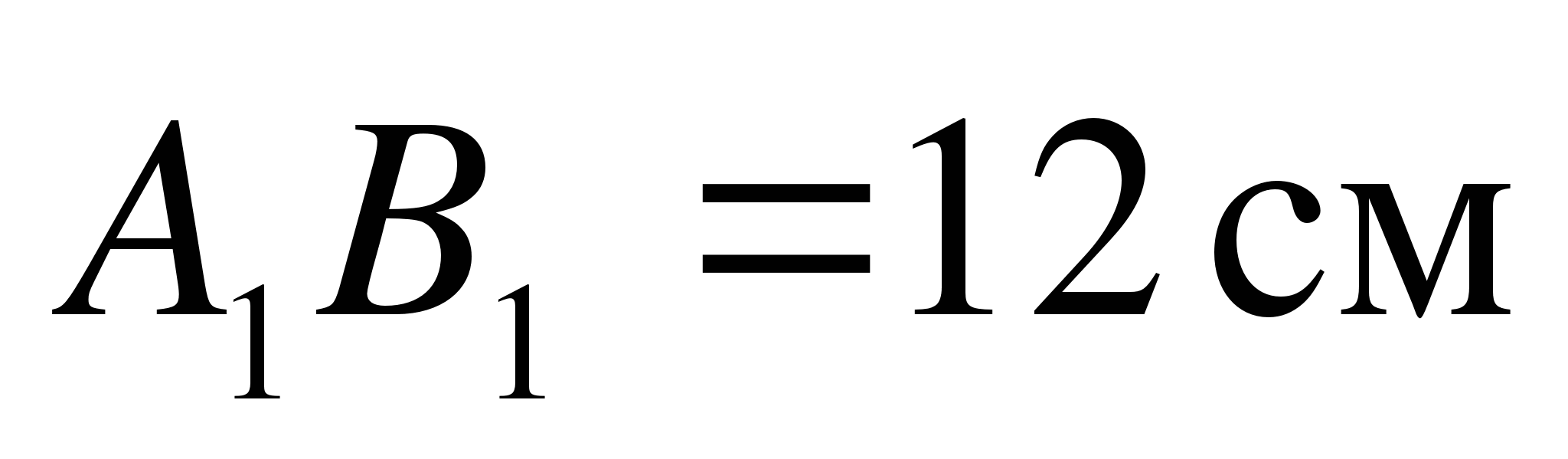 ,
, 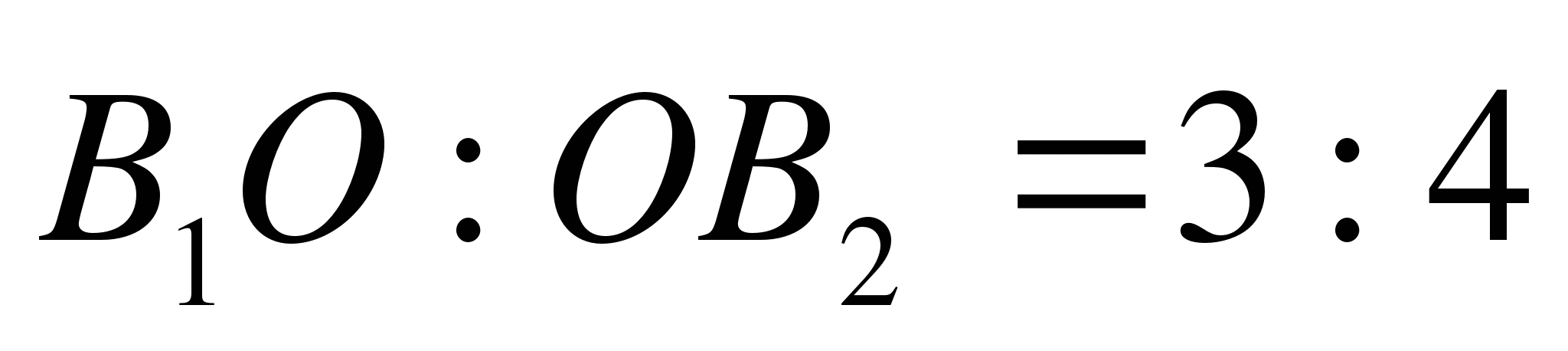 .
.
№3. Изобразите параллелепипед 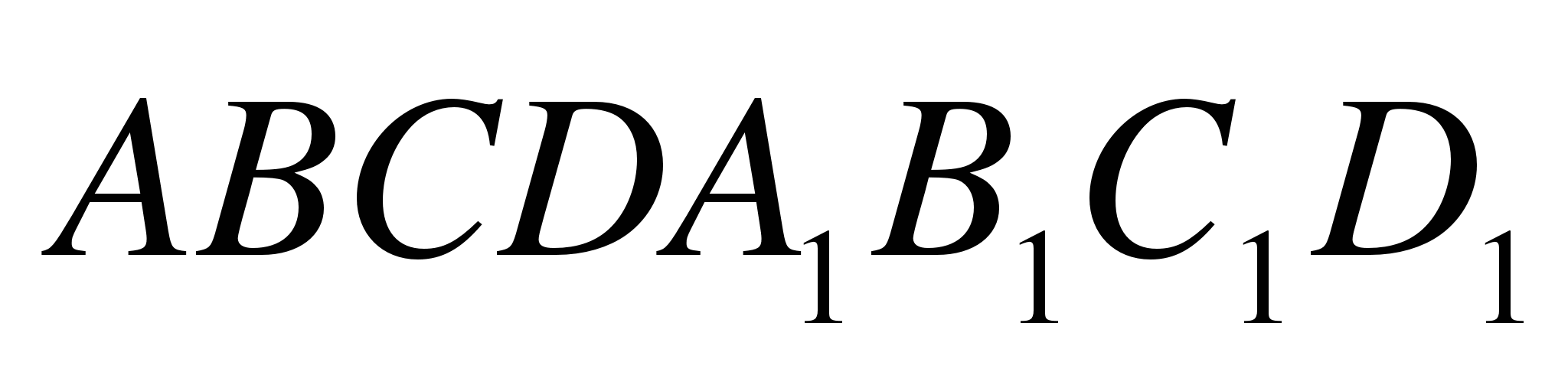 и постройте его сечение плоскостью, проходящей через точки М, N и К, являющиеся серединами ребер АВ, ВС и DD1.
и постройте его сечение плоскостью, проходящей через точки М, N и К, являющиеся серединами ребер АВ, ВС и DD1.
II вариант.
№1. Прямые а и b лежат в пересекающих плоскостях 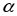 и
и 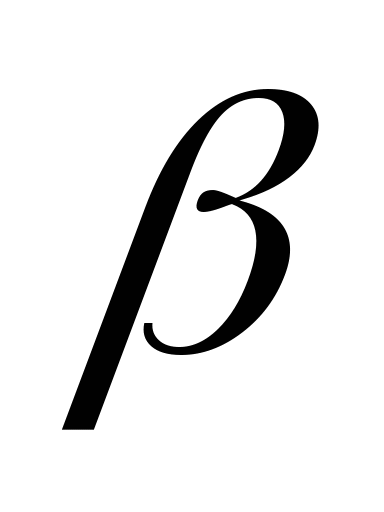 . Могут ли эти прямые быть:
. Могут ли эти прямые быть:
а) параллельными; б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
№2. Через точку О, не лежащую между параллельными плоскостями 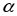 и
и 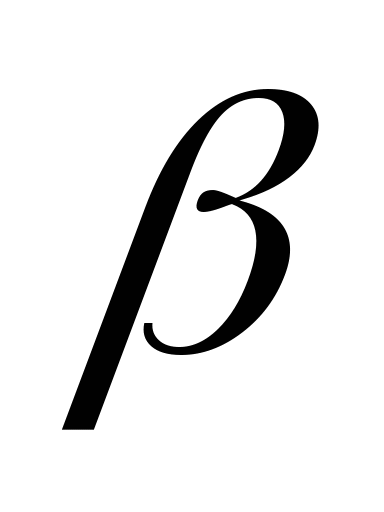 , проведены прямые l и m. Прямая l пересекает плоскости
, проведены прямые l и m. Прямая l пересекает плоскости 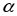 и
и 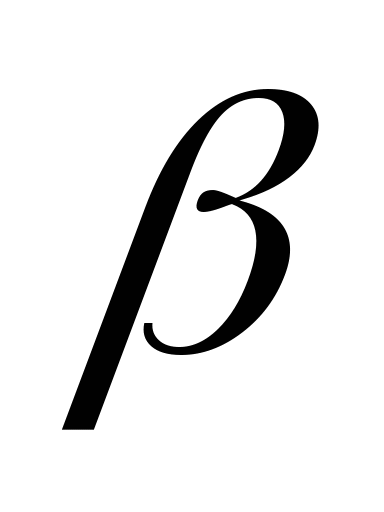 в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если
в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если 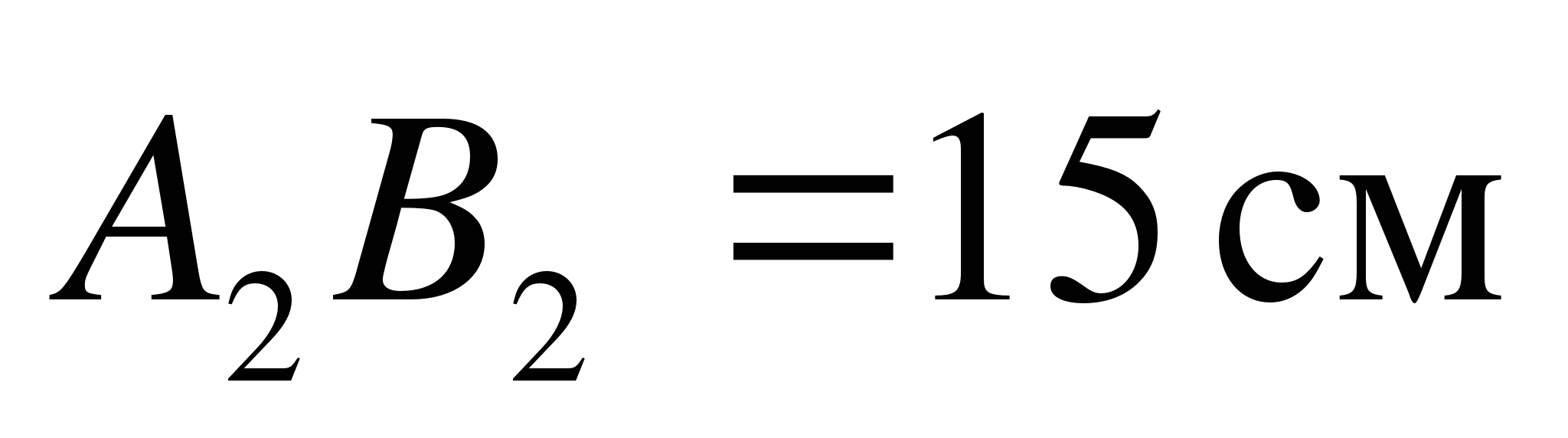 ,
, 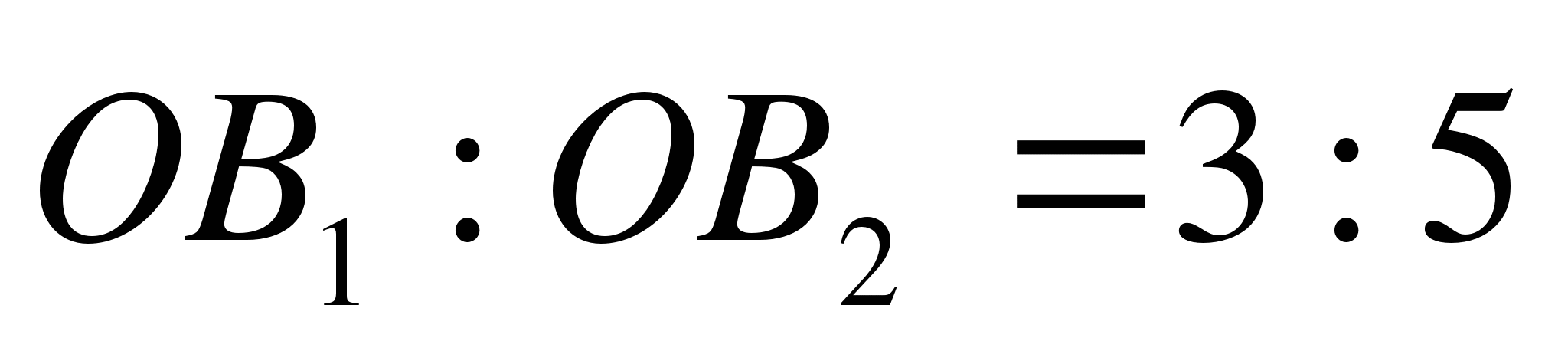 .
.
№3. Изобразите тетраэдр 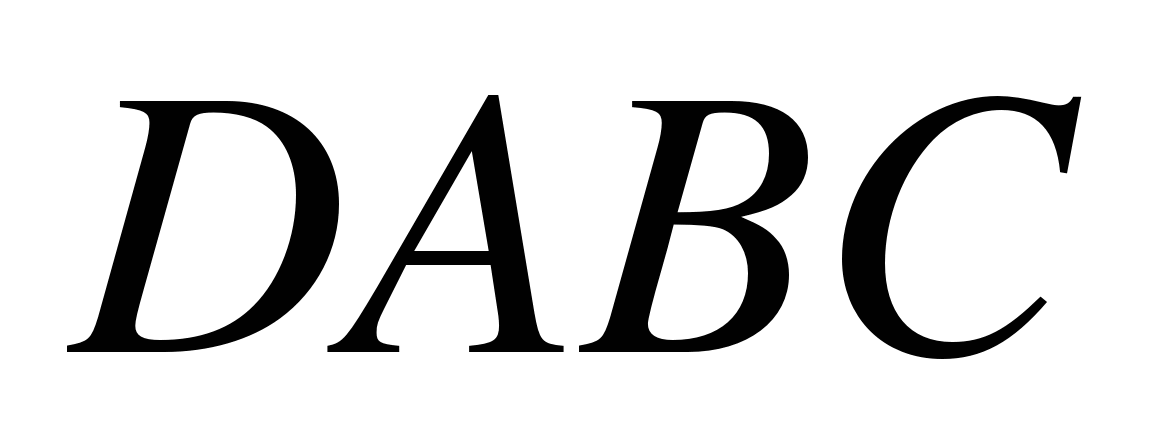 и постройте его сечение плоскостью, проходящей через точки М и N, являющиеся серединами ребер DC и ВС и точку K, такую, что
и постройте его сечение плоскостью, проходящей через точки М и N, являющиеся серединами ребер DC и ВС и точку K, такую, что 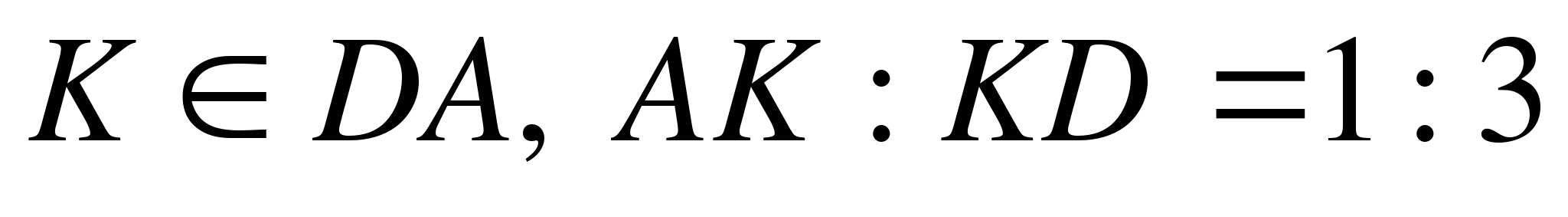 .
.
Контрольная работа №3.
I вариант.
№1. Диагональ куба равна 6 см. Найдите:
а) ребро куба;
б) косинус угла между диагоналями куба и плоскостью одной из его граней.
№2. Сторона AB ромба ABCD равна a, один из углов равен 60°. Через сторону AB проведена плоскость 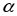 на расстоянии 0,5a, от точки D.
на расстоянии 0,5a, от точки D.
а) Найдите расстояние от точки С до плоскости 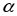 .
.
б) Покажите на рисунке линейный угол двугранного угла DABM, 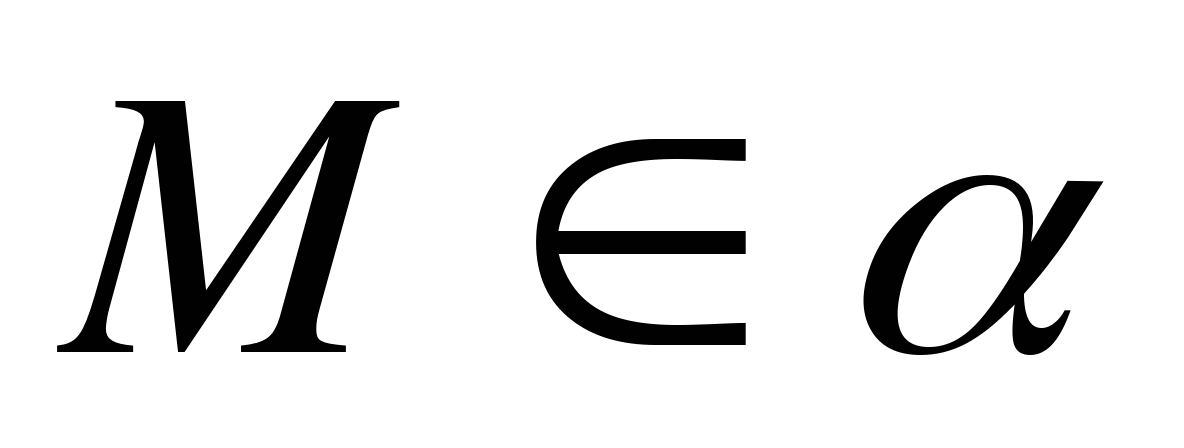 .
.
в) найдите синус угла между плоскостью ромба и плоскостью 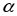 .
.
II вариант.
№1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 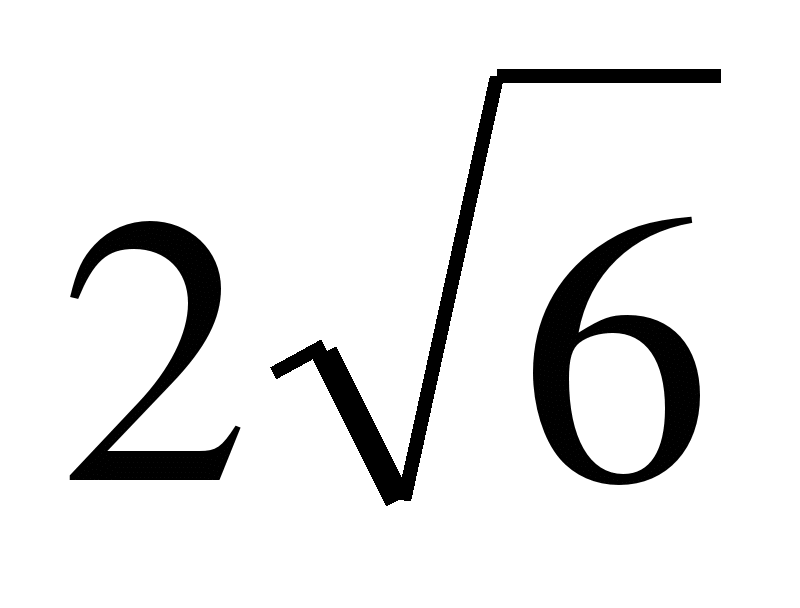 см, а его измерения относятся как 1:12 Найдите:
см, а его измерения относятся как 1:12 Найдите:
а) измерения параллелепипеда;
б) синус угла между диагональю параллелепипеда и плоскостью его основания.
№2. Сторона квадрата ABCD равна a. Через сторону AD проведена плоскость 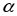 на расстоянии 0,5a, от точки B.
на расстоянии 0,5a, от точки B.
infourok.ru
Контрольная работа №3.1 (1уровень сложности)
«Многогранники»
2 вариант
Основание прямой призмы – прямоугольный треугольник с гипотенузой 13 см и катетом 12 см. Найдите площадь боковой поверхности призмы, если ее наименьшая боковая грань – квадрат.
Высота правильной четырехугольной пирамиды равна см, а боковое ребро наклонено к плоскости основания под углом 60º.
а) Найдите боковое ребро пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
Ребро правильного тетраэдра DABC равно а. Постройте сечение тетраэдра, проходящее через середины ребер DA и АВ параллельно ребру ВС, и найдите площадь этого сечения.
……………………………………………………………………………………………………
Контрольная работа №3.1 (2уровень сложности)
«Многогранники»
1 вариант
Основание прямого параллелепипеда – ромб с диагоналями 10 см и 24 см. Меньшая диагональ параллелепипеда образует с плоскостью основания угол 45º. Найдите площадь полной поверхности параллелепипеда.
Основание пирамиды – правильный треугольник с площадью см2. Две боковые грани пирамиды перпендикулярны к плоскости основания, а третья – наклонена к ней под углом 30º.
а) Найдите длины боковых ребер пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
Ребро куба АВСDA1B1C1D1 равно а. Постройте сечение куба, проходящее через прямую В1С и середину ребра АD, и найдите площадь этого сечения.
Контрольная работа №3.1 (2уровень сложности)
«Многогранники»
2 вариант
Основание прямого параллелепипеда – ромб с меньшей диагональю 12 см. Большая диагональ параллелепипеда равна см и образует с боковым ребром угол 45º. Найдите площадь полной поверхности параллелепипеда.
Основание пирамиды – равнобедренный прямоугольный треугольник с гипотенузой см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 45º.
а) Найдите длины боковых ребер пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
Ребро куба АВСDA1B1C1D1 равно а. Постройте сечение куба, проходящее через точку С и середину ребра AD параллельно прямой DA1, и найдите площадь этого сечения.
……………………………………………………………………………………………………
Контрольная работа по геометрии №3
«Призма. Пирамида»
1 вариант
Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм АВСD со сторонами 6 дм и 12 дм и углом, равным 60˚. Диагональ В1D призмы образует с плоскостью основания угол в 30˚. Найти площадь боковой поверхности призмы.
Сторона основания правильной треугольной пирамиды равна 3 см, а угол между боковой гранью и основанием пирамиды равен 45˚. Найти площадь полной поверхности пирамиды.
Контрольная работа по геометрии №3
«Призма. Пирамида»
2 вариант
Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм АВСD со сторонами 4 см и см и углом, равным 30˚. Диагональ АС1 призмы образует с плоскостью основания угол в 60˚. Найти площадь боковой поверхности призмы.
Высота основания правильной треугольной пирамиды равна 3 см, а угол между боковой гранью и основанием пирамиды равен 45˚. Найти площадь полной поверхности пирамиды.
…………………………………………………………………………………………………
infourok.ru
Контрольная работа № 1
Тема: «Параллельность прямых, прямой и плоскости»
1 вариант
1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.
а) Каково взаимное положение прямых ЕF и АВ?
б) Чему равен угол между прямыми ЕF и АВ, если  АВС = 150°? Поясните.
АВС = 150°? Поясните.
2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник есть ромб.
2 вариант
1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC.
а) Каково взаимное положение прямых РK и АВ?
б) Чему равен угол между прямыми РK и АВ, если  АВС = 40° и
АВС = 40° и  ВСА = 80°? Поясните.
ВСА = 80°? Поясните.
2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е  CD, K
CD, K  DA, DE : EC = 1 : 2, DK : KA = 1 : 2.
DA, DE : EC = 1 : 2, DK : KA = 1 : 2.
а) Выполните рисунок к задаче.
б) Докажите, что четырехугольник MNEK есть трапеция.
Контрольная работа № 2
Тема: «Параллельность плоскостей. Тетраэдр и параллелепипед.»
1 вариант
1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:
а) параллельными;
б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.
3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1.
2 вариант
1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:
а) параллельными;
б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5.
3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K  DA, АK : KD = 1 : 3.
DA, АK : KD = 1 : 3.
Контрольная работа № 3
Тема: «перпендикулярность в пространстве»
1 вариант
1. Диагональ куба равна 6 см. Найдите:
а) ребро куба;
б) косинус угла между диагональю куба и плоскостью одной из его граней.
2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии  от точки D.
от точки D.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла DABM,М  α.
α.
в) найдите синус угла между плоскостью ромба и плоскостью α
2 вариант
1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2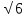 см, а его измерения
см, а его измерения
относятся как 1 : 1 : 2. Найдите:
а) измерения параллелепипеда;
б) синус угла между диагональю параллелепипеда и плоскостью его основания.
2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии  от точки В.
от точки В.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла BADM,М  α.
α.
в) Найдите синус угла между плоскостью квадрата и плоскостью α.
Контрольная работа № 4
Тема: «Многогранники»
1 вариант
1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.
2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:
а) высоту ромба;
б) высоту параллелепипеда;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда
2 вариант
1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны a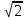
и 2a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а) меньшую высоту параллелограмма;
б) угол между плоскостью АВС1 и плоскостью основания;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
КОНТРОЛЬНАЯ РАБОТА № 5
ТЕМА: «ВЕКТОРЫ В ПРОСТРАНСТВЕ»
Вариант 1
1. Изобразите параллелепипед ABCDA1B1C1D1. Постройте на рисунке векторы, равные:
1) 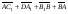 ; 2)
; 2) 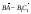 .
.
2. ABCDA1B1C1D1 – параллелепипед, отрезки АC и BD пересекаются в точке М. Разложите вектор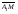 по векторам
по векторам 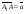 ,
, 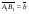 ,
, 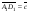 .
.
3. В тетраэдре DABC точка М – точка пересечения медиан грани DBC, Е – середина АС. Разложите вектор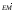 по векторам
по векторам  ,
, 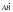 и
и 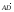 .
.
4. DABC – тетраэдр, О – точка пересечения медиан АВС, точка F лежит на AD, причем AF : FD = 3 : 1. Разложите вектор 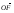 по векторам
по векторам 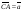 ,
, 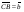 ,
, 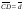 .
.
Вариант 2
1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный:
1) 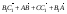 ; 2)
; 2) 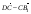 .
.
2. В параллелепипеде ABCDA1B1C1D1 диагонали грани АВCD пересекаются в точке О. Разложите вектор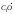 по векторам,
по векторам, 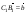 ,
, 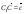 ,
, 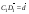 .
.
3. DABC – тетраэдр, точка Е – середина ребра АD, а точка М – точка пересечения медиан грани BDC. Разложите вектор 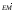 по векторам
по векторам 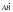 ,
,  и
и 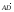 .
.
4. Дан тетраэдр DABC. Медианы грани АВС пересекаются в точке М, 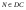 , причем DN : NC = 5 : 1. Разложите вектор
, причем DN : NC = 5 : 1. Разложите вектор 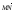 по векторам
по векторам 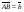 ,
, 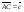 ,
, 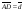 .
.
infourok.ru
Контрольная работа №1 (1 четверть). "Начальные геометрические сведения"
Вариант I
1. На отрезке KN отмечены две точки L и M. Найдите длину отрезка LM, если известно, что KN= 12 см, MN = 3,5 см, KL = 4,6 см. Укажите, какая точка лежит на отрезке KM?
2. На заданном рисунке OM биссектриса угла NOL.- Найдите угол KON, если угол NOM равен 60°.- Постройте угол KOP, который будет вертикальный LOM. Рассчитаете его градусную меру.- Сколько градусов будет в угле LOP?
3. Угол COD равен 135°. Лучами OE и OF, угол разделёна на 3 равных угла. Сколько прямых углов получилось?
Вариант II
1. На отрезке KM отмечены две точки L и N. Найдите длину отрезка LN, если известно, что KM= 8,6 см, NM = 1,5 см, KL = 2,6 см. Укажите, какая точка лежит на отрезке KN?
2. На заданном рисунке OB биссектриса угла AOC.- Найдите угол DOA, если угол AOB равен 70°.- Постройте угол DOE, который будет вертикальный COB. Рассчитаете его градусную меру.- Сколько градусов будет в угле DOE?
3. Угол EOF равен 120°. Лучами OA и OB, угол разделён на 4 равных угла. Сколько углов по 60° получилось?
Вариант III
1. На отрезке LK отмечены две точки N и M. Найдите длину отрезка NM, если известно, что LK= 13,8 см, LN = 4,5 см, MK = 1,6 см. Укажите, какая точка лежит на отрезке NK?
2. На заданном рисунке OG биссектриса угла FOH.- Найдите угол EOF, если угол FOG равен 30°.- Постройте угол EOI, который будет вертикальный GOH. Рассчитаете его градусную меру.- Сколько градусов будет в угле EOI?
3. Угол BOD равен 140°. Лучами OA, OC и OE угол разделён на 4 равных угла. Сколько углов по 70° получилось?
Контрольная работа №2 (2 четверть). "Треугольник и окружность"
Вариант I
1. Задан равнобедренный треугольник ABC. Известно, что угол ABE равен углу CBD.Докажите, что треугольник DBE является равнобедренным треугольником. Найдите угол AEB, если известно, что угол BDE равен 65°.
2. Задан отрезок AB равный 4 см и прямой угол. Постройте на биссектрисе угла точку, где расстояние от вершины угла до точки равно длине отрезка.
3. Задана окружность с центром О и с хордой CD. Радиус OE проведен перпендикулярно хорде CD. Докажите, что хорды CE и DE равны.
Вариант II
1. Задан равнобедренный треугольник MNP. Известно, что угол MND равен углу ENP.Докажите, что треугольник DNE является равнобедренным треугольником. Найдите угол MDN, если известно, что угол MEN равен 70°.
2. Задан отрезок AB равный 3 см и острый угол. Постройте на биссектрисе угла точку, где расстояние от вершины угла до точки равно удвоенной длине отрезка.
3. Задана окружность с центром О и с хордой EF. Радиус OD проведен перпендикулярно хорде EF. Докажите, что хорды DE и DF равны.
Вариант III
1. Задан равнобедренный треугольник XYZ. Известно, что угол XYD равен углу ZYE.Докажите, что треугольник DYE является равнобедренным треугольником. Найдите угол XDY, если известно, что угол XEY равен 50°.
2. Задан отрезок AB равный 4 см и угол равный 50°. Постройте на биссектрисе угла точку, где расстояние от вершины угла до точки равно половине длине отрезка.
3. Задана окружность с центром О и с хордой LM. Радиус OK проведен перпендикулярно хорде LM. Докажите, что хорды LK и MK равны.
Контрольная работа №3 (3 четверть). "Параллельные прямые"
Вариант I
1. На данном рисунке угол 1 равен 120°, угол 2 равен 110°, угол 3 равен 65#176;. Найдите, чему равен угол 4 и сколько ещё таких углов есть на рисунке?
2. Задан острый угол. На одной из сторон отмечены 2 точки K и L. ОТ этих точек проведены перпендикулярные прямые к другой стороне угла, соответственно KM и LN. Докажите, что эти прямые параллельны друг другу. Чему равен угол KLN, если угол MKL равен 120°?
3. Задан треугольник XYZ. На его двух сторонах XY и YZ, указаны точки A и B соответственно. Докажите, что если угол YAB равен углу YXZ, то угол ABY равен углу XZY.
Вариант II
1. На данном рисунке угол 1 равен 65°, угол 2 равен 105°, угол 3 равен 65°. Найдите, чему равен угол 4 и сколько ещё таких углов есть на рисунке?
2. Задан острый угол. На одной из сторон отмечены 2 точки С и D. От этих точек проведены перпендикулярные прямые к другой стороне угла, соответственно CE и DF. Докажите, что эти прямые параллельны друг другу. Чему равен угол CDF, если угол ECD равен 135°?
3. Задан треугольник MNL. На его двух сторонах MN и NL, указаны точки A и B соответственно. Докажите, что если угол NAB равен углу NML, то угол ABN равен углу MNL.
Вариант III
1. На данном рисунке угол 1 равен 80°, угол 2 равен 110°, угол 3 равен 80°. Найдите, чему равен угол 4 и сколько ещё таких углов есть на рисунке?
2. Задан острый угол. На одной из сторон отмечены 2 точки E и F. ОТ этих точек проведены перпендикулярные прямые к другой стороне угла, соответственно EG и FI. Докажите, что эти прямые параллельны друг другу. Чему равен угол EFI, если угол GEF равен 105°?
3. Задан треугольник DEF. На его двух сторонах DE и EF, указаны точки A и B соответственно. Докажите, что если угол EAB равен углу EDF, то угол ABE равен углу DFE.
Контрольная работа №4 (4 четверть). "Треугольник. Соотношение между углами и сторонами"
Вариант I
1. Задан треугольник DEF. Угол D меньше угла F на 40°, а угол E меньше угла В в 3 раза. Найдите все углы треугольника. Какая сторона больше DE или EF?
2. Задан прямоугольный треугольник XYZ, где YZ гипотенуза. Внешний угол при вершине Z равен 120°, сторона XY равна 7 см. Чему равна длина гипотенузы?
3. В равнобедренном треугольнике KLM, на основании KM указана точка P. От этой точки проведены перпендикуляры к двум боковым сторонам, соответственно PA и PB. Докажите, что эти отрезки PA и PB равны друг другу.
Вариант II
1. Задан треугольник KLM. Угол K меньше угла L в 2 раза, а угол М больше угла L на 30°. Найдите все углы треугольника. Какая сторона больше KL или LM?
2. Задан прямоугольный треугольник CDE, где DE гипотенуза. Внешний угол при вершине E равен 120°, сторона CD равна 5 см. Чему равна длина гипотенузы?
3. В равнобедренном треугольнике CDE, на основании CE указана точка N. От этой точки проведены перпендикуляры к двум боковым сторонам, соответственно NA и NB. Докажите, что эти отрезки NA и NB равны друг другу.
Вариант III
1. Задан треугольник ABC. Угол A меньше угла B в 3 раза, а угол B больше угла C на 70°. Найдите все углы треугольника. Какая сторона больше AB или BC?
2. Задан прямоугольный треугольник EFD, где FD гипотенуза. Внешний угол при вершине D равен 150°, сторона AB равна 10 см. Чему равна длина гипотенузы?
3. В равнобедренном треугольнике XYZ, на основании XZ указана точка М. От этой точки проведены перпендикуляры к двум боковым сторонам, соответственно MA и MB. Докажите, что эти отрезки MA и MB равны друг другу.
infourok.ru
Г- 9 Итоговая контрольная работа
Вариант 1
1. В треугольнике АВС точка D – середина стороны АВ, точка М – точка пересечения медиан.
а) Выразите вектор  через векторы
через векторы 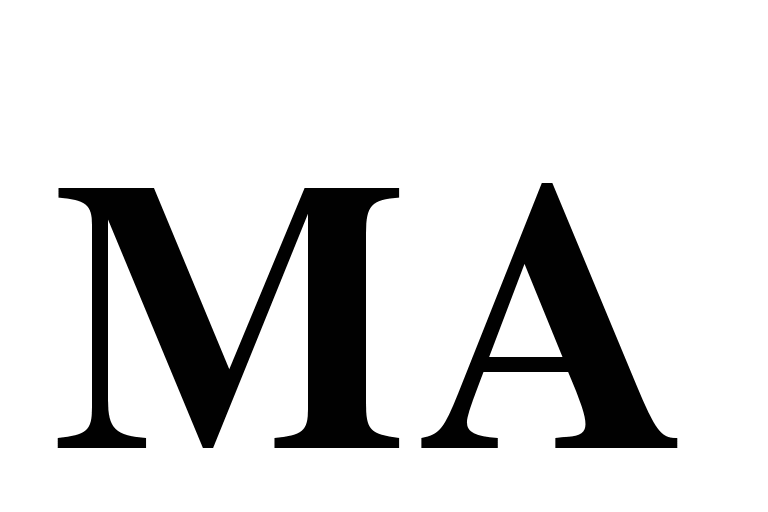 и
и 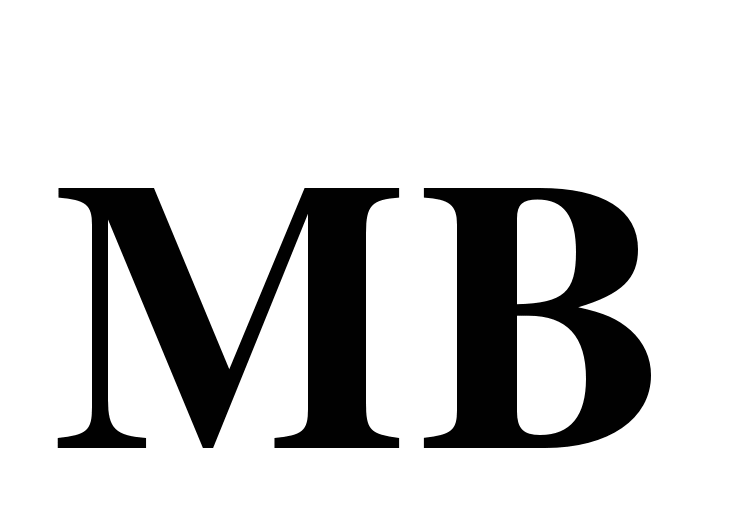 и вектор
и вектор 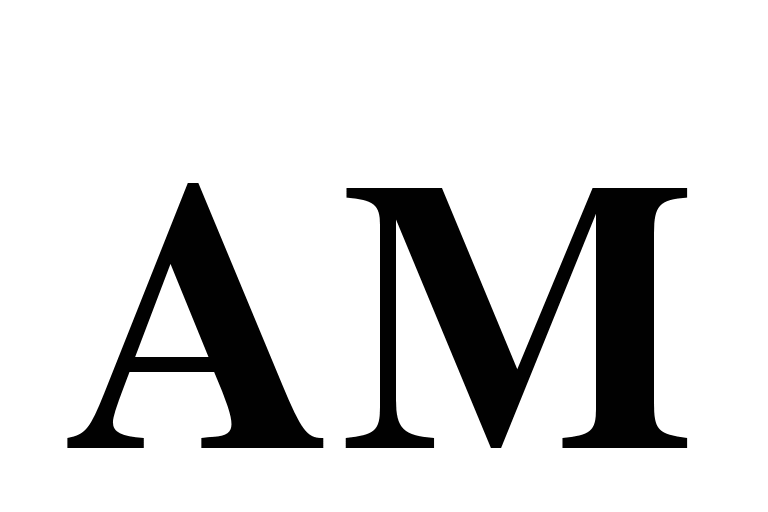 через векторы
через векторы 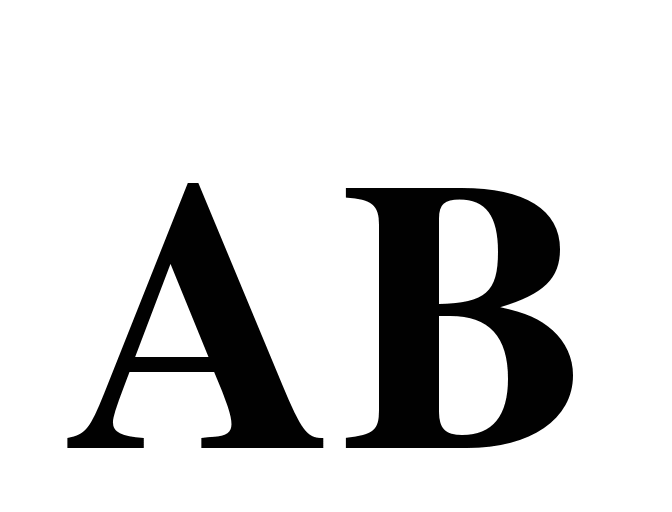 и
и 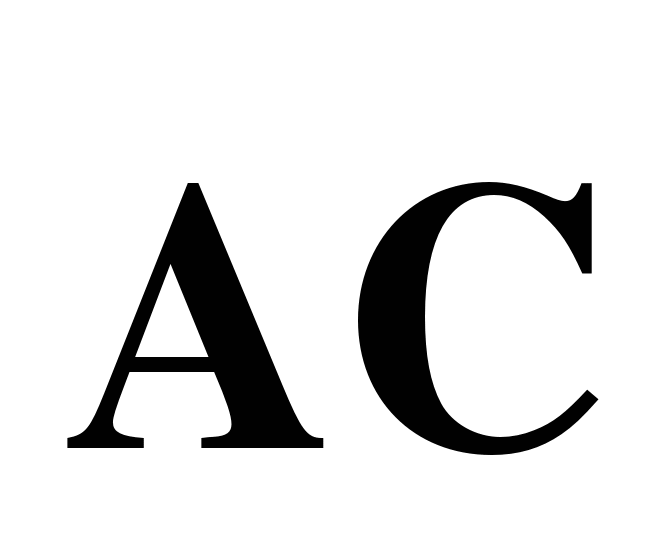 .
.
б) Найдите скалярное произведение 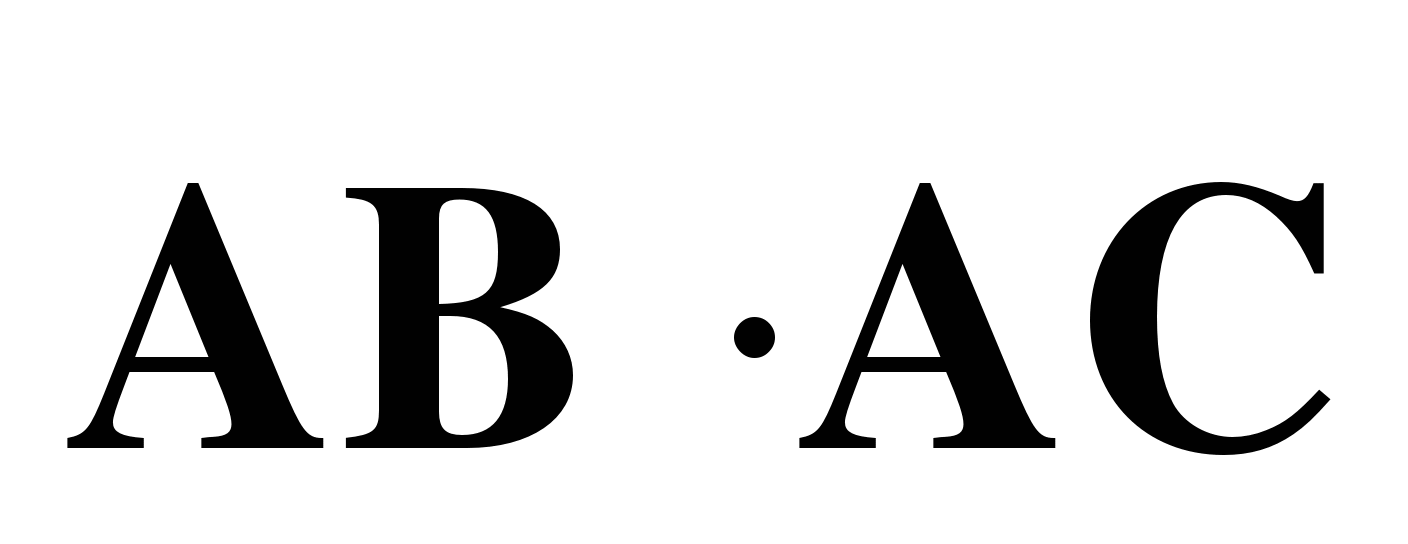 , если
, если 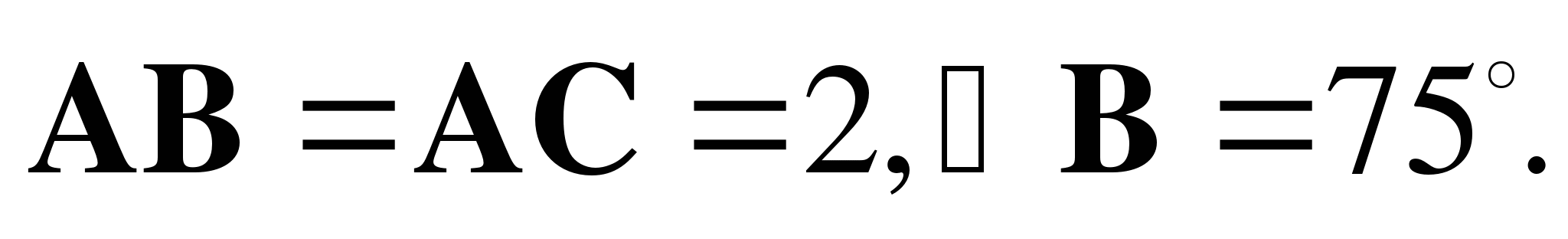
2. Даны точки А(1; 1), В(4; 5), С(-3; 4).
а) Докажите, что треугольник АВС равнобедренный и прямоугольный.
б) Найдите длину медианы СМ.
3. В треугольнике АВС 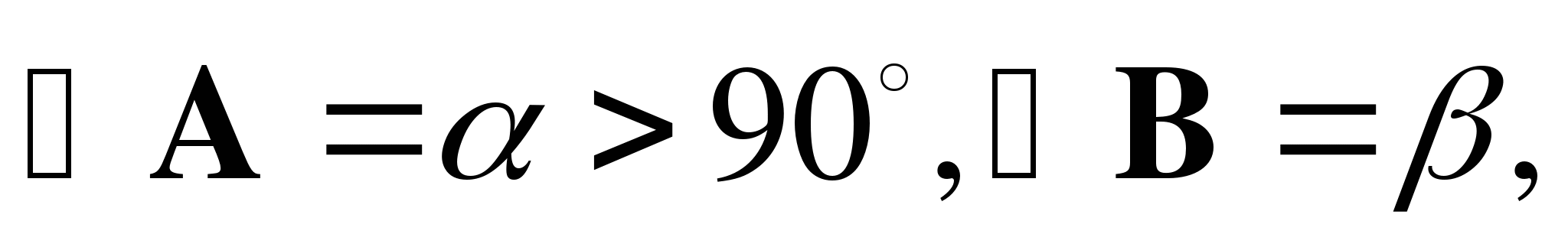 высота ВD равна h.
высота ВD равна h.
а) Найдите сторону АС и радиус R описанной окружности.
б) Вычислите значение R, если 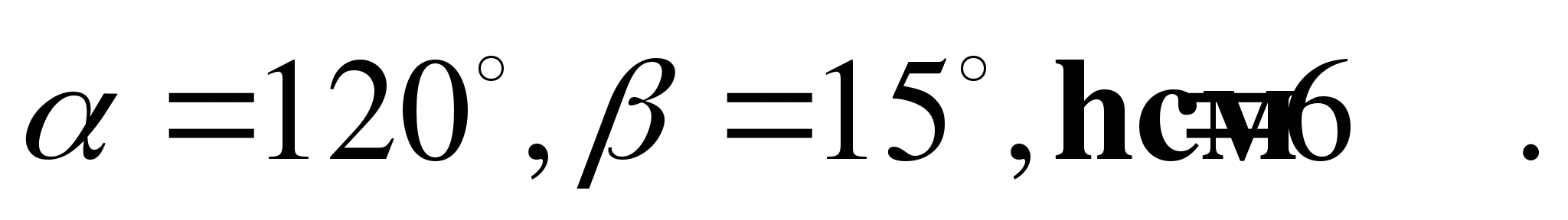
4. Хорда окружности равна а и стягивает дугу в 120о. Найдите: а) длину дуги; б) площадь сектора, ограниченного этой дугой и двумя радиусами.
Итоговая контрольная работа
Вариант 2
1. В параллелограмме АВСD диагонали пересекаются в точке О.
а) Выразите вектор 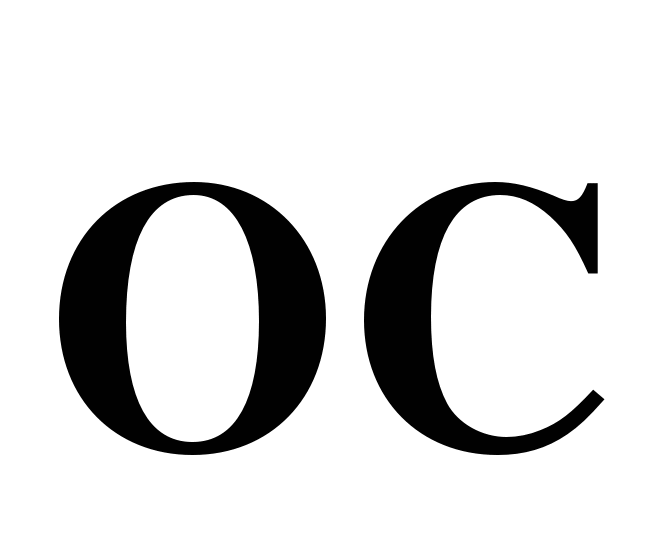 через векторы
через векторы 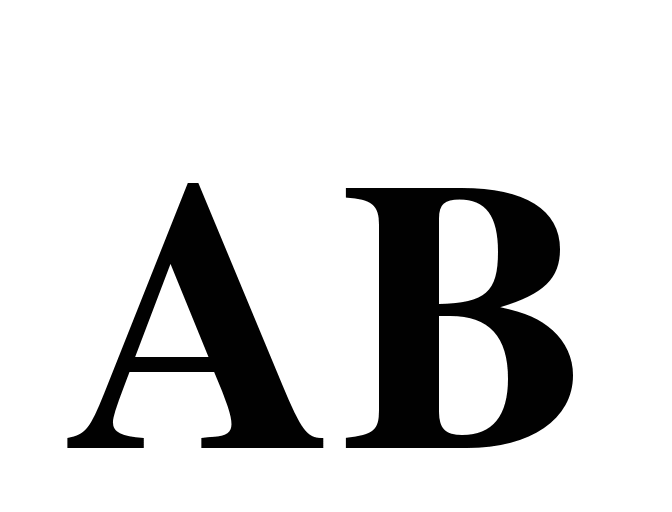 и
и 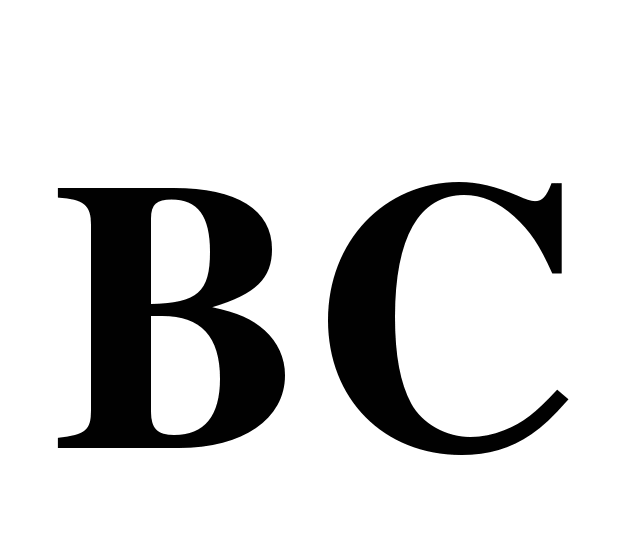 и вектор
и вектор 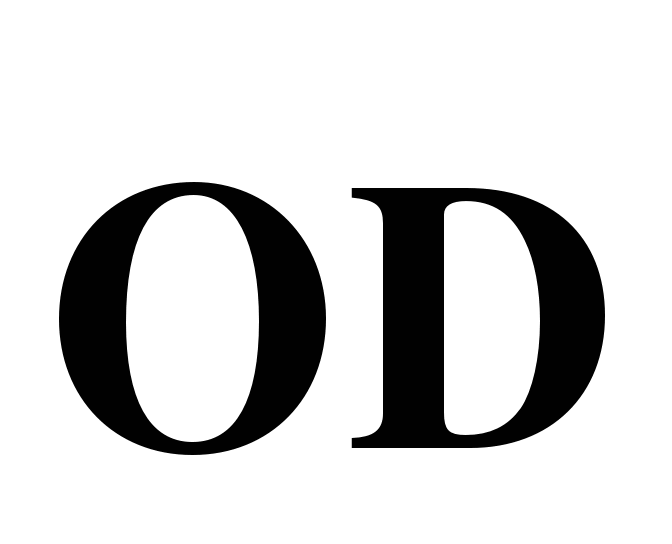 через векторы
через векторы 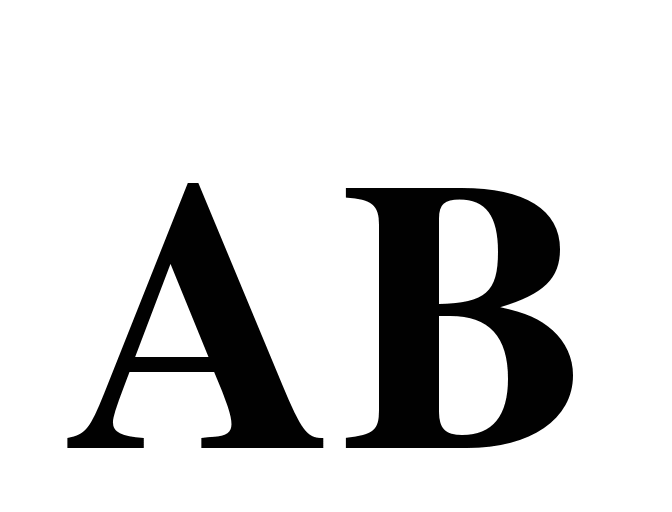 и
и  .
.
б) Найдите скалярное произведение 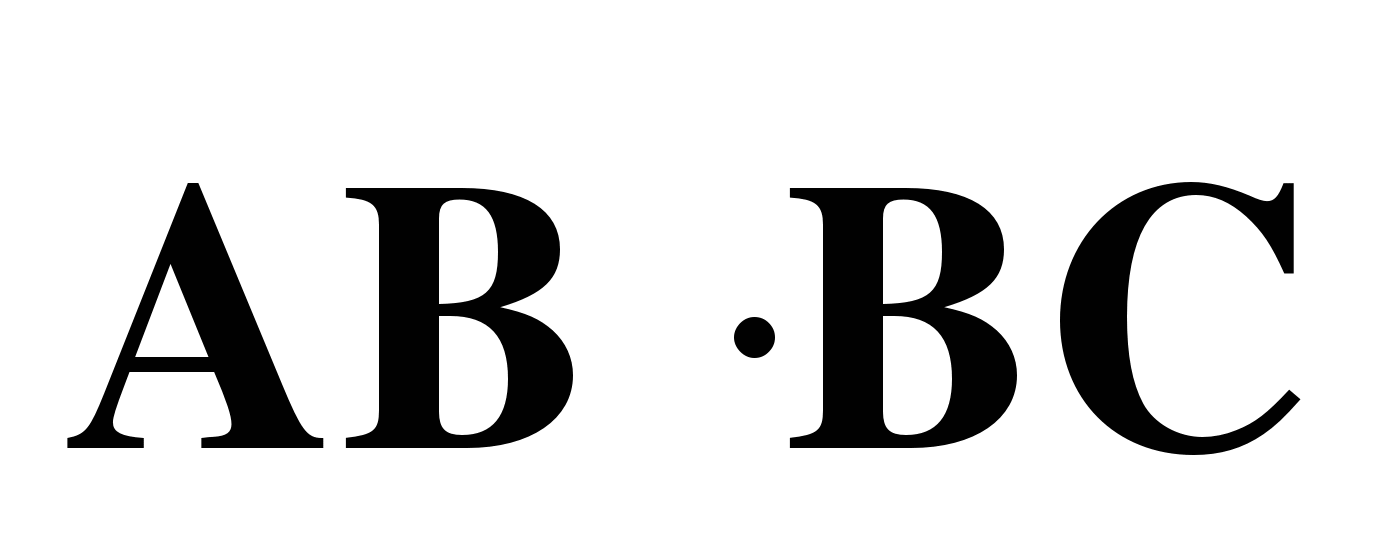 , если
, если 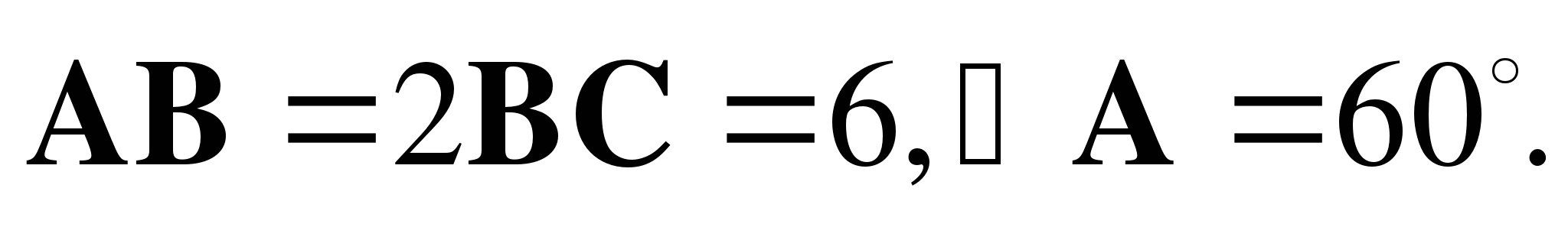
2. Даны точки К(0; 1), М(-3; -3), N(1; -6).
а) Докажите, что треугольник KMN равнобедренный и прямоугольный.
б) Найдите длину медианы NL.
3. В треугольнике АВС 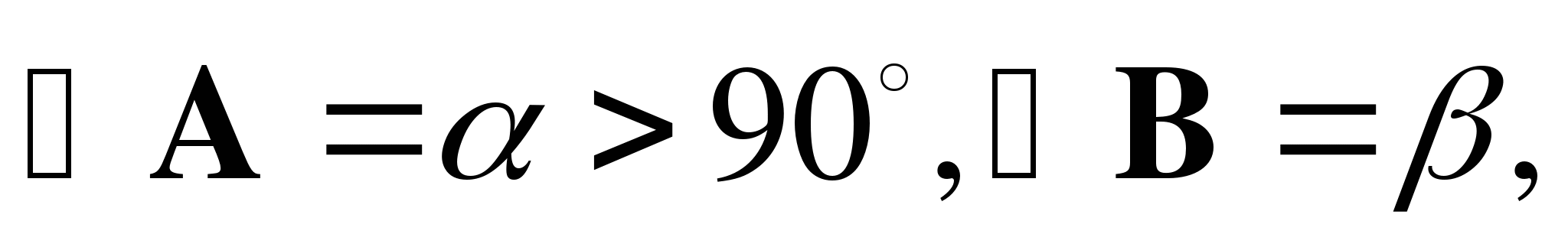 высота ВD равна h.
высота ВD равна h.
а) Найдите сторону АD и радиус R описанной окружности.
б) Вычислите значение R, если 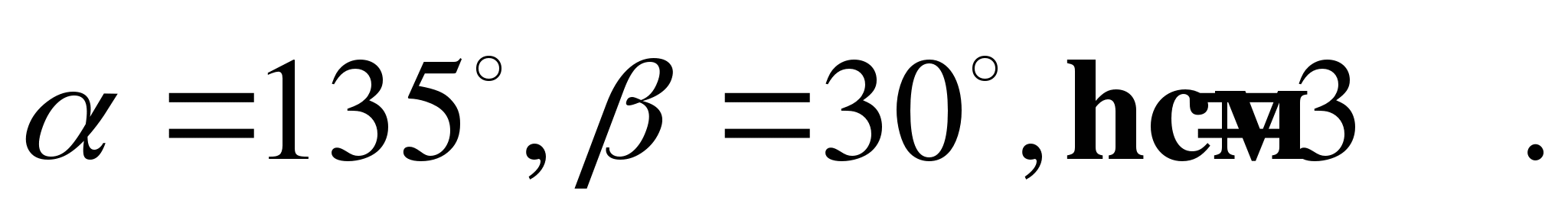
4. Хорда окружности равна а и стягивает дугу в 60о. Найдите: а) длину дуги; б) площадь сектора, ограниченного этой дугой и двумя радиусами.
infourok.ru