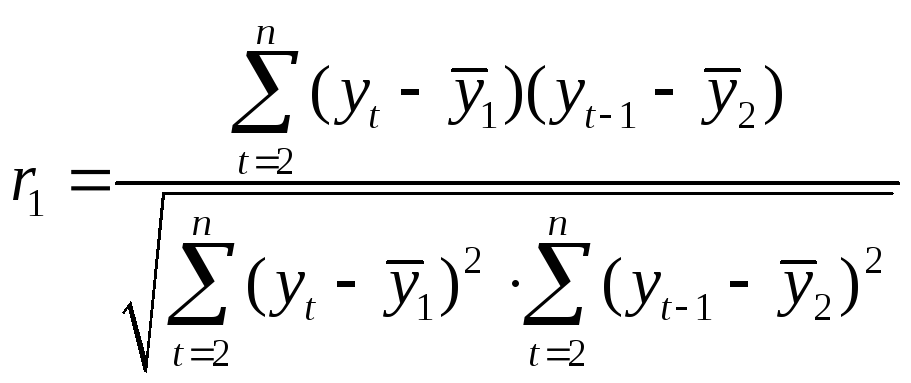 , (4.1)
, (4.1)ЗАДАЧА
Пользуясь исходными данными, приведенными в таблице (вариант выбирается по последней цифре в зачетной книжке):
Построить поле корреляции
Определить уравнение линейной регрессии
Оценить уравнение линейной регрессии в целом и каждого его параметра (критерий Фишера, Стьюдента)
Определить ошибку аппроксимации
Сделать прогноз при изменении фактора Х на 15%.
| ВАРИАНТ 1 | ВАРИАНТ 2 | ВАРИАНТ 3 | |||||||||
| Х | У | Х | У | Х | У | ||||||
| 1 | 25 | 2 | 1 | 42 | 16 | 1 | 59 | 25 | |||
| 2 | 29 | 5 | 2 | 46 | 17 | 2 | 61 | 27 | |||
| 3 | 31 | 8 | 3 | 49 | 19 | 3 | 64 | 29 | |||
| 4 | 35 | 10 | 4 | 52 | 21 | 4 | 68 | 31 | |||
| 5 | 39 | 12 | 5 | 56 | 23 | 5 | 72 | 35 | |||
| 6 | 40 | 14 | 6 | 59 | 25 | 6 | 76 | 38 | |||
| 7 | 42 | 16 | 7 | 61 | 27 | 7 | 79 | 39 | |||
| 8 | 46 | 17 | 8 | 64 | 29 | 8 | 81 | 42 | |||
| 9 | 49 | 19 | 9 | 68 | 31 | 9 | 89 | 44 | |||
| 10 | 52 | 21 | 10 | 72 | 35 | 10 | 25 | 2 | |||
| ВАРИАНТ 4 | ВАРИАНТ 5 | ВАРИАНТ 6 | |||||||||
| Х | У | Х | У | Х | У | ||||||
| 1 | 76 | 38 | 1 | 76 | 38 | 1 | 42 | 16 | |||
| 2 | 79 | 39 | 2 | 79 | 39 | 2 | 46 | 17 | |||
| 3 | 81 | 42 | 3 | 81 | 42 | 3 | 49 | 19 | |||
| 4 | 89 | 44 | 4 | 89 | 44 | 4 | 52 | 21 | |||
| 5 | 25 | 2 | 5 | 25 | 2 | 5 | 56 | 23 | |||
| 6 | 29 | 5 | 6 | 29 | 5 | 6 | 59 | 25 | |||
| 7 | 31 | 8 | 7 | 31 | 8 | 7 | 61 | 27 | |||
| 8 | 35 | 10 | 8 | 35 | 10 | 8 | 64 | 29 | |||
| 9 | 39 | 12 | 9 | 39 | 12 | 9 | 68 | 31 | |||
| 10 | 40 | 14 | 10 | 40 | 14 | 10 | 72 | 35 | |||
| ВАРИАНТ 7 | ВАРИАНТ 8 | ВАРИАНТ 9 | |||||||||
| Х | У | Х | У | Х | У | ||||||
| 1 | 35 | 10 | 1 | 49 | 19 | 1 | 59 | 25 | |||
| 2 | 39 | 12 | 2 | 52 | 21 | 2 | 61 | 27 | |||
| 3 | 40 | 14 | 3 | 56 | 23 | 3 | 64 | 29 | |||
| 4 | 42 | 16 | 4 | 59 | 25 | 4 | 68 | 31 | |||
| 5 | 46 | 17 | 5 | 61 | 27 | 5 | 71 | 35 | |||
| 6 | 49 | 19 | 6 | 64 | 29 | 6 | 76 | 38 | |||
| 7 | 52 | 21 | 7 | 68 | 31 | 7 | 79 | 39 | |||
| 8 | 56 | 23 | 8 | 72 | 35 | 8 | 81 | 42 | |||
| 9 | 59 | 25 | 9 | 76 | 38 | 9 | 89 | 44 | |||
| 10 | 61 | 27 | 10 | 79 | 39 | 10 | 25 | 2 | |||
| ВАРИАНТ 10 | |||||||||||
| Х | У | ||||||||||
| 1 | 53 | 24 | |||||||||
| 2 | 61 | 27 | |||||||||
| 3 | 64 | 29 | |||||||||
| 4 | 68 | 31 | |||||||||
| 5 | 71 | 35 | |||||||||
| 6 | 76 | 38 | |||||||||
| 7 | 79 | 39 | |||||||||
| 8 | 81 | 42 | |||||||||
| 9 | 89 | 44 | |||||||||
| 10 | 25 | 2 | |||||||||
Теоретические вопросы к контрольной работе:
| Вариант 1
|
| Вариант 2
|
| Вариант 3
|
| Вариант 4
|
| Вариант 5
|
| Вариант 6
|
| Вариант 7
|
| Вариант 8
|
| Вариант 9
|
| Вариант 10
|
studfiles.net
10
Имеются поквартальные условные данные об объемах потребления электроэнергии жителями региона.
Таблица 4.1
| Номер квартала | Потребление электроэнергии жителями региона, млн. кВтч | Номер квартала | Товарооборот % к предыдущему периоду |
| 1 | 6,0 | 9 | 8,0 |
| 2 | 4,4 | 10 | 5,6 |
| 3 | 5,0 | 11 | 6,4 |
| 4 | 9,0 | 12 | 11,0 |
| 5 | 7,2 | 13 | 9,0 |
| 6 | 4,8 | 14 | 6,6 |
| 7 | 6,0 | 15 | 7,0 |
| 8 | 10,0 | 16 | 10,8 |
Задания:
1. Постройте автокорреляционную функцию временного ряда. Охарактеризуйте структуру этого ряда.
2. Рассчитайте сезонную компоненты временного ряда и постройте его аддитивную и мультипликативную модели.
3. Рассчитайте трендовую компоненту временного ряда. Постройте графики построенных рядов.
4. Оцените качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.
Решение
1. При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называютавтокорреляцией уровней ряда.Количественно ее можно измерить с помощью коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутых на несколько шагов во времени. Число уровней, по которым рассчитывается коэффициент автокорреляции, называетсялагом. Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называетсяавтокорреляционной функциейвременного ряда. Анализ автокорреляционной функции позволяет выявить структуру временного ряда.
Для расчета коэффициентов автокорреляции исходного временного ряда составим таблицу (табл. 4.2):
Таблица 4.2
| t | yt | yt-1 | yt-2 | yt-3 | yt-4 | yt-5 | yt-6 |
| 1 | 6,0 | – | – | – | – | – | – |
| 2 | 4,4 | 6,0 | – | – | – | – | – |
| 3 | 5,0 | 4,4 | 6,0 | – | – | – | – |
| 4 | 9,0 | 5,0 | 4,4 | 6,0 | – | – | – |
| 5 | 7,2 | 9,0 | 5,0 | 4,4 | 6,0 | – | – |
| 6 | 4,8 | 7,2 | 9,0 | 5,0 | 4,4 | 6,0 | – |
| 7 | 6,0 | 4,8 | 7,2 | 9,0 | 5,0 | 4,4 | 6,0 |
| 8 | 10,0 | 6,0 | 4,8 | 7,2 | 9,0 | 5,0 | 4,4 |
| 9 | 8,0 | 10,0 | 6,0 | 4,8 | 7,2 | 9,0 | 5,0 |
| 10 | 5,6 | 8,0 | 10,0 | 6,0 | 4,8 | 7,2 | 9,0 |
| 11 | 6,4 | 5,6 | 8,0 | 10,0 | 6,0 | 4,8 | 7,2 |
| 12 | 11,0 | 6,4 | 5,6 | 8,0 | 10,0 | 6,0 | 4,8 |
| 13 | 9,0 | 11,0 | 6,4 | 5,6 | 8,0 | 10,0 | 6,0 |
| 14 | 6,6 | 9,0 | 11,0 | 6,4 | 5,6 | 8,0 | 10,0 |
| 15 | 7,0 | 6,6 | 9,0 | 11,0 | 6,4 | 5,6 | 8,0 |
| 16 | 10,8 | 7,0 | 6,6 | 9,0 | 11,0 | 6,4 | 5,6 |
Определим коэффициент корреляции между рядами ytиyt-1, т.е. коэффициент автокорреляции 1-го порядка
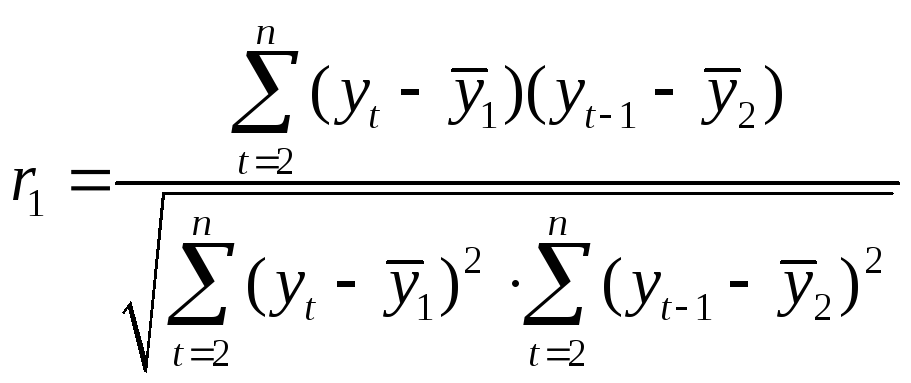 , (4.1)
, (4.1)
где
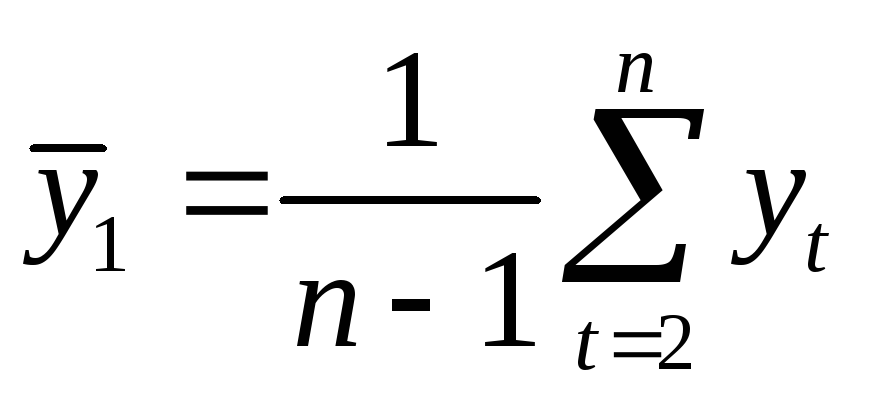 ,
, 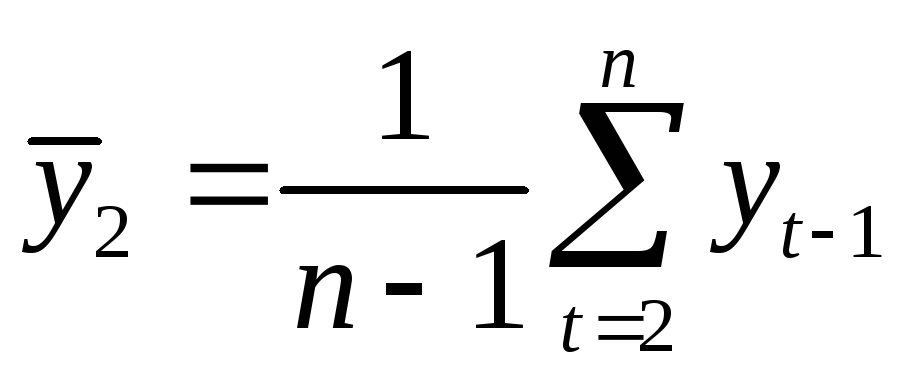 .
.
Отметим, что расчет коэффициента автокорреляции производится по 15, а не по 16 парам наблюдений.
Составим таблицу для расчета коэффициента автокорреляции 1-го порядка (таб. 4.3):
Таблица 4.3
| t | yt | yt-1 |
|
|
|
|
|
| 1 | 6,0 | – | – | – | – | – | – |
| 2 | 4,4 | 6,0 | -2,987 | -1,067 | 3,186 | 8,920 | 1,138 |
| 3 | 5,0 | 4,4 | -2,387 | -2,667 | 6,364 | 5,696 | 7,111 |
| 4 | 9,0 | 5,0 | 1,613 | -2,067 | -3,334 | 2,603 | 4,271 |
| 5 | 7,2 | 9,0 | -0,187 | 1,933 | -0,361 | 0,035 | 3,738 |
| 6 | 4,8 | 7,2 | -2,587 | 0,133 | -0,345 | 6,691 | 0,018 |
| 7 | 6,0 | 4,8 | -1,387 | -2,267 | 3,143 | 1,923 | 5,138 |
| 8 | 10,0 | 6,0 | 2,613 | -1,067 | -2,788 | 6,830 | 1,138 |
| 9 | 8,0 | 10,0 | 0,613 | 2,933 | 1,799 | 0,376 | 8,604 |
| 10 | 5,6 | 8,0 | -1,787 | 0,933 | -1,668 | 3,192 | 0,871 |
| 11 | 6,4 | 5,6 | -0,987 | -1,467 | 1,447 | 0,974 | 2,151 |
| 12 | 11,0 | 6,4 | 3,613 | -0,667 | -2,409 | 13,056 | 0,444 |
| 13 | 9,0 | 11,0 | 1,613 | 3,933 | 6,346 | 2,603 | 15,471 |
| 14 | 6,6 | 9,0 | -0,787 | 1,933 | -1,521 | 0,619 | 3,738 |
| 15 | 7,0 | 6,6 | -0,387 | -0,467 | 0,180 | 0,150 | 0,218 |
| 16 | 10,8 | 7,0 | 3,413 | -0,067 | -0,228 | 11,651 | 0,004 |
| 110,8 | 106 | 9,813 | 65,317 | 54,053 |
По данным таблицы находим
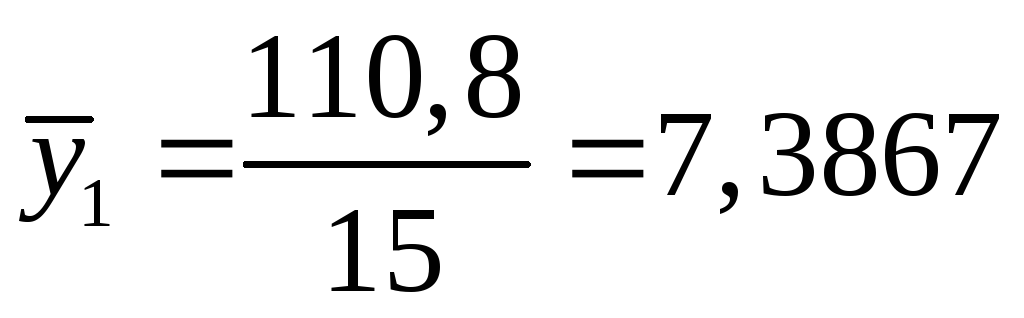 ,
, 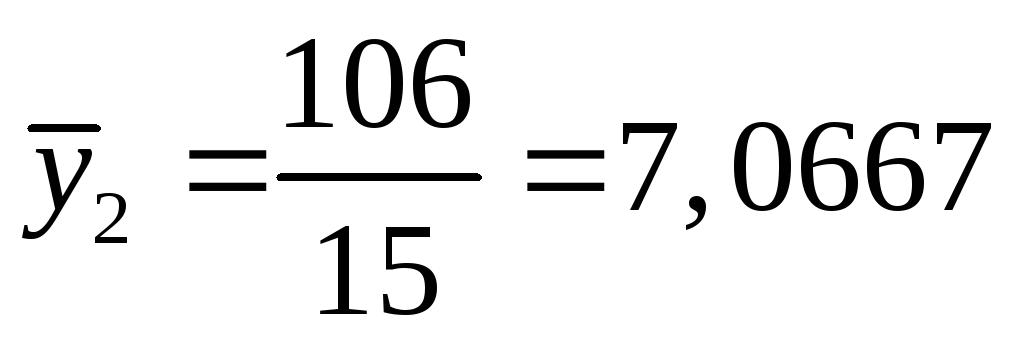 .
.
Используя формулу (3.1), находим
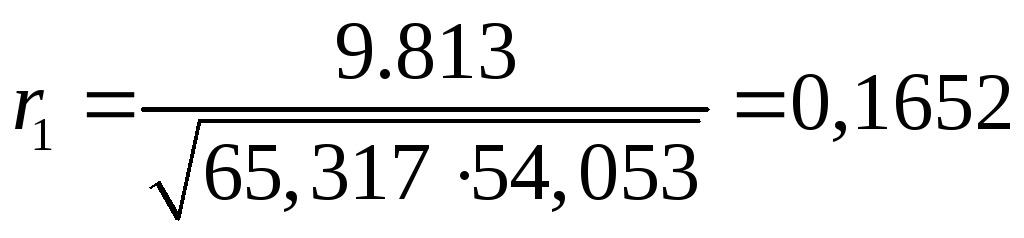 .
.
Определим теперь коэффициент автокорреляции 2-го порядка, коэффициент корреляции между рядами ytиyt-2, т.е.
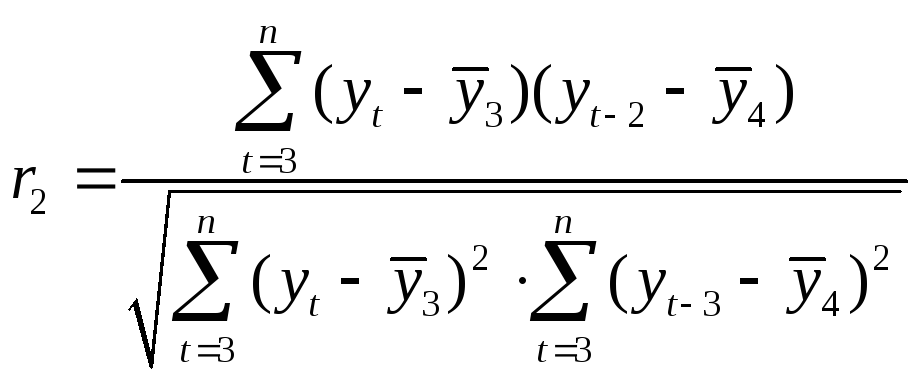 , (4.2)
, (4.2)
где
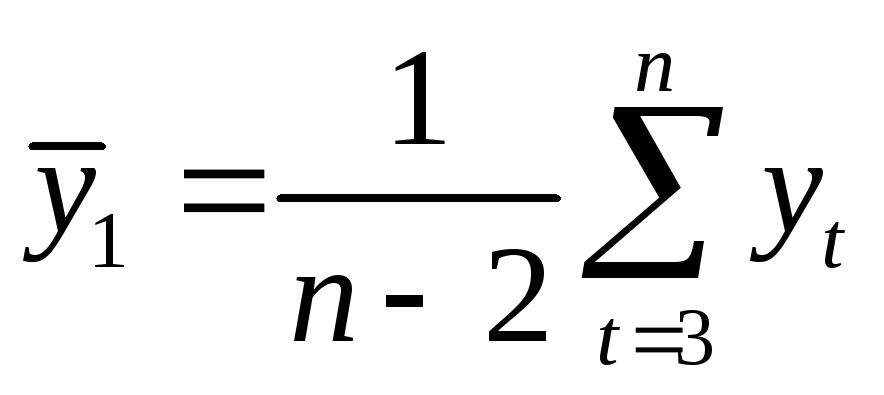 ,
, 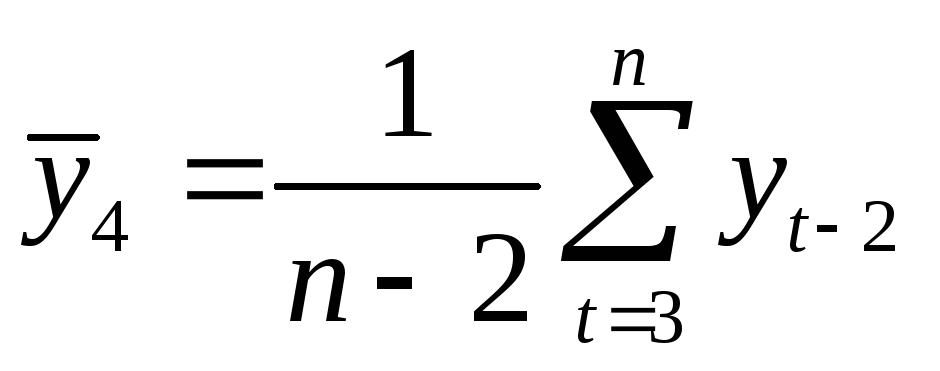 .
.
Отметим, что расчет коэффициента автокорреляции 2-го порядка уже будет производится по 14 парам наблюдений.
Составим таблицу для расчета коэффициента автокорреляции 2-го порядка (таб. 4.3):
Таблица 4.4
| t | yt | yt-2 |
|
|
|
|
|
| 1 | 6,0 | – | – | – | – | – | – |
| 2 | 4,4 | – | – | – | – | – | – |
| 3 | 5,0 | 6,0 | -2,600 | -1,071 | 2,786 | 6,760 | 1,148 |
| 4 | 9,0 | 4,4 | 1,400 | -2,671 | -3,740 | 1,960 | 7,137 |
| 5 | 7,2 | 5,0 | -0,400 | -2,071 | 0,829 | 0,160 | 4,291 |
| 6 | 4,8 | 9,0 | -2,800 | 1,929 | -5,400 | 7,840 | 3,719 |
| 7 | 6,0 | 7,2 | -1,600 | 0,129 | -0,206 | 2,560 | 0,017 |
| 8 | 10,0 | 4,8 | 2,400 | -2,271 | -5,451 | 5,760 | 5,159 |
| 9 | 8,0 | 6,0 | 0,400 | -1,071 | -0,429 | 0,160 | 1,148 |
| 10 | 5,6 | 10,0 | -2,000 | 2,929 | -5,857 | 4,000 | 8,577 |
| 11 | 6,4 | 8,0 | -1,200 | 0,929 | -1,114 | 1,440 | 0,862 |
| 12 | 11,0 | 5,6 | 3,400 | -1,471 | -5,003 | 11,560 | 2,165 |
| 13 | 9,0 | 6,4 | 1,400 | -0,671 | -0,940 | 1,960 | 0,451 |
| 14 | 6,6 | 11,0 | -1,000 | 3,929 | -3,929 | 1,000 | 15,434 |
| 15 | 7,0 | 9,0 | -0,600 | 1,929 | -1,157 | 0,360 | 3,719 |
| 16 | 10,8 | 6,6 | 3,200 | -0,471 | -1,509 | 10,240 | 0,222 |
| 106,4 | 99 | -31,120 | 55,760 | 54,049 |
По данным таблицы находим
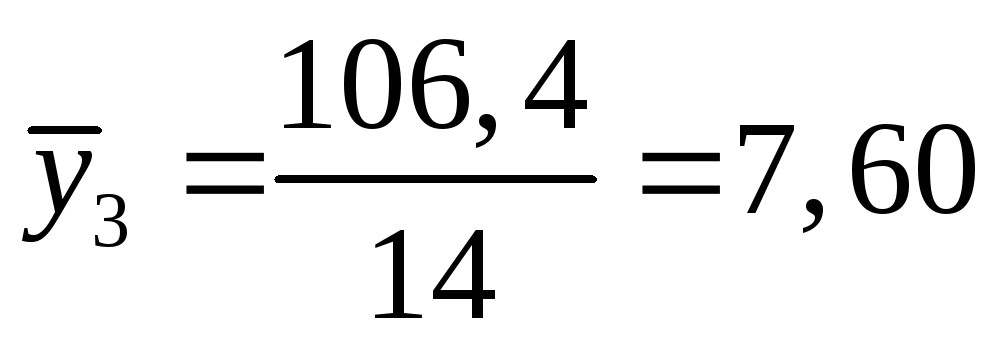 ,
, 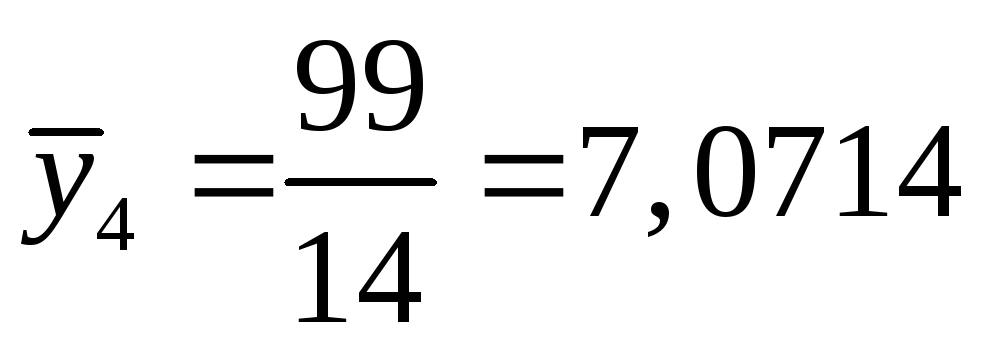 .
.
Используя формулу (3.2), находим
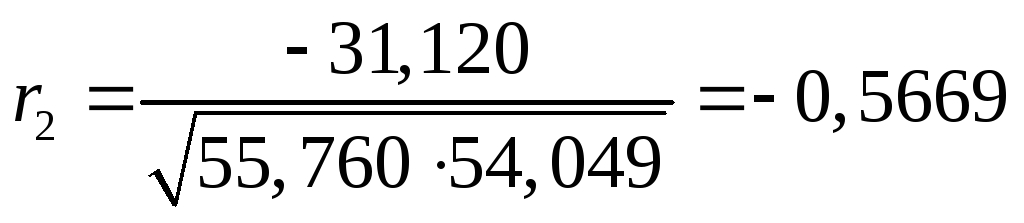 .
.
Аналогичным образом рассчитываем коэффициенты автокорреляции 3-го и более высоких порядков. (Заметим, что в программе Exelкоэффициенты корреляции рассчитываются при помощи функции КОРРЕЛ). В результате получим автокорреляционную функцию исходного временного ряда. Ее значения и коррелограмма приведены в таб. 3.5.
Таблица 4.5
| Лаг | Коэффициент автокорреляции уровней временного ряда | Коррелограмма |
| 1 | 0,1651548 | |
| 2 | -0,5668734 | |
| 3 | 0,1135581 | |
| 4 | 0,9830252 | |
| 5 | 0,1187113 | |
| 6 | -0,7220463 | |
| 7 | -0,0033676 | |
| 8 | 0,9738481 |
Анализ значений автокорреляционной функции позволяет сделать вывод о наличии в изучаемом временном ряде, во-первых, линейной тенденции,во-вторых, сезонных колебаний периодичностью в четыре квартала. Данный вывод подтверждается и графическим анализом структуры ряда (см. рис. 4.1).
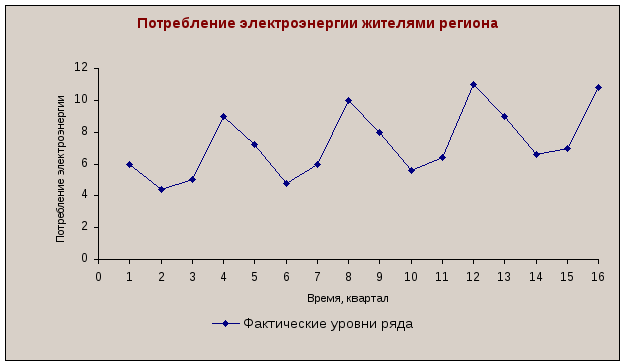
Рис. 4.1
studfiles.net
| № зачетной книжки: | 87453 |
| № варианта: | 23 |
| Форма обучения: | заочная |
| Специальность: | Финансы и кредит |
| Курс: | 3 |
| Группа: | ЭиП-302 |
| Выполнил: | Погрев С.П. |
| Номера задач по варианту: Зачтено: | 1 | 2 | 3 | 4 |
Челябинск 2005
ПРОГРАММА КУРСА ЭКОНОМЕТРИКА
| № | Содержание лекций | Содержание практических занятий |
| 1 | Введение в корреляционно-регрессионный анализ Соотношения между экономиче-скими переменными. Регрессионные модели как инструмент анализа и про-гнозирования экономических явлений. | |
| 2 | Линейная модель множественной регрессии Определения. Метод наименьших квадратов (МНК). Свойства оценок МНК. Показатели качества регрессии. Линейные регрессионные модели с гетероскедастичными и автокоррели-рованными остатками. Статистика Дарбина-Уотсона. Прогнозирование. | [5]: №22-29, стр. 90-105 |
| 3 | Нелинейные модели регрессии и их линеаризация Мультипликативные модели регресс-сии и их линеаризация. Гиперболическая регрессия. Полиномиальная и кусочно-полиномиальная регрессия. Степенная и показательная регрессии. | [5]: №17-25, стр. 36-47 |
| 4 | Временные ряды. Характеристики временных рядов. Выявление тренда в динамических рядах экономических показателей. Линейные и нелинейные тренды.. | [5]: № 1-23, стр. 163-177 |
| 5 | Системы эконометрических уравнений Система линейных одновременных уравнений. Косвенный, двухшаговый и трехшаговый метод наименьших квадратов |
КРАТКИЙ КУРС ЛЕКЦИЙ
Одна из наиболее общих задач в экономических исследованиях состоит в оценивании степени зависимости изучаемой величины Y от одной или нескольких случайных (или неслучайных) величин X, называемых факторами. Зависимость может быть функциональной, статистической, либо отсутствовать вовсе.
Строгая функциональная зависимость между экономическими показателями (наличие всегда выполняющегося равенства Y=f(X)) реализуется редко, так как они подвержены влиянию случайных факторов. При статистической зависимости изменение одной из величин влечет изменение распределения другой (в частности, среднего значения; в этом случае статистическую зависимость называют корреляционной).
Причем, всегда есть несколько величин, которые определяют главные тенденции изменения рассматриваемой величины, и в экономической теории и практике ограничиваются тем или иным кругом таких величин (объясняющих переменных). Однако всегда существует и воздействие большого числа других, менее важных или трудно идентифицируемых факторов, приводящее к отклонению значений объясняемой (зависимой) переменной от конкретной формулы ее связи с объясняющими переменными, сколь бы точной эта формула ни была. Нахождение, оценка и анализ таких связей, идентификация объясняющих переменных, построение формул зависимости и оценка их параметров и составляют предмет корреляционно-регрессионного анализа, при этом корреляционный анализ занимается исследованием взаимозависимости случайных величин, тогда как регрессионный анализ на базе выборочных данных исследует зависимость случайной величины от ряда неслучайных и случайных величин.
Примерами корреляционно, но не функционально, связанных величин являются объемы производства и себестоимость продукции, объемы продаж и прибыль, урожай зерна и количество внесенных удобрений. Действительно, в последнем примере с одинаковых по площади участков земли при равных количествах внесенных удобрений снимают различный урожай, т.е. отсутствует функциональная связь. Это объясняется влиянием случайных факторов (осадки, температура, качество семян и др.). Вместе с тем, как показывает опыт, средний урожай меняется с изменением количества удобрений, т.е. прослеживается корреляционная зависимость.
Рассмотрим сначала однофакторную регрессионную модель.
В этом случае имеется n пар наблюдений (xi,yi), i=1,2,…,n, над некоторыми случайными величинами Х={xi} и Y={yi}. Эти наблюдения можно представить точками на плоскости с координатами (xi,yi), получая так называемую диаграмму рассеяния. Задача построения регрессионной модели заключается в том, что необходимо подобрать некоторую кривую (график соответствующей функции) таким образом, чтобы она располагалась как можно “ближе” к этим точкам. Такого рода кривую называют эмпирической или аппроксимирующей кривой. Весьма часто тип эмпирической кривой определяется экспериментальными или теоретическими соображениями (исходя из законов экономической теории), в противном случае выбор кривой осуществить довольно трудно. Иногда точки на диаграмме рассеяния располагаются таким образом, что не наблюдается никакого их группирования, и, соответственно, нет никаких оснований предполагать наличие в наблюдениях какой-либо взаимозависимости.
Таким образом, результатом исследования статистической взаимозависимости на основе выборочных данных является построение уравнений регрессии вида y=f(x).
studfiles.net