Проектная работа на тему "Старинные математические задачи" (7 класс). Старинные задачи и способы их решения реферат
Решение старинных задач различными способами
Слайд 1
Работу выполнили Ильин Дмитрий и Яшин Кирилл, ученики 8-ого класса Руководитель: Жилова З.Г., учитель математикиСлайд 2
Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, и на занятии математического кружка, и в журнале или книжке. А меня очень заинтересовали старинные задачи, с которыми мы столкнулись на уроке математики. И я решил узнать о них больше. Старинные задачи пришли к нам из глубины веков, от наших предков. Разные народы нашей планеты придумывали их, оттачивали условия и логику заданий. Они неизбежно остроумны и занимательны, в них собраны замечательные находки многих поколений. Введение
Слайд 3
Старинные задачи позволяют не только развить смекалку и сообразительность, но и почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество, и я специально отобрал лучшие из них.
Слайд 4
Еще в древние века математика занимала основное место в умах ученых и благодаря сохранившимся рукописям у нас есть возможность проследить за развитием математической мысли и возможность прорешать старинные задачи и сравнить их решение с современным решением. Цель исследования: выявление роли и места старинных задач в современном мире, рассмотрение различных способов решения старинных задач. Задачи исследования: исследовать решение старинных задач методом перебора; методом подбора; методом предположения, алгебраическим способом; наглядно-геометрическим способом исследовать старинный способ решения задач на сплавы и смеси.
Слайд 5
Диофант Его называют отцом алгебры Диофант умел решать очень сложные уравнения, он применял для этого буквенные обозначения и другие приемы. Биографические данные зашифрованы в виде математической задачи, начертанной на его гробнице .
Слайд 6
Задача № 1 Жизнь Диофанта . По преданию, на могильном камне имелась такая надпись: «Путник! Под этим камнем покоится прах Диофанта, умершего в глубокой старости. Шестую часть своей долгой жизни он был ребёнком, двенадцатую- юношей, седьмую- провёл неженатым. Через 5 лет после женитьбы у него родился сын, который прожил вдвое меньше отца. Через четыре года после смерти сына уснул вечным сном и сам Диофант, оплакиваемый своими близкими. Скажи, если умеешь считать, сколько прожил Диофант?»
Слайд 12
Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты. При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости. Концентрацией вещества называется отношение массы этого вещества к массе всей смеси (раствора, сплава). Концентрация вещества, выраженная в процентах, называется процентным отношением вещества в смеси (растворе, сплаве). Существует старинный способ решения задач на смеси и сплавы. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Л.Ф.Магницкого.
Слайд 13
Лео́нтий Фили́ппович Магни́цкий (9(19)июня 1669- 19(30)октября 1739) Магницкий Л.Ф. (при рождении Телятин)- русский математик, педагог; преподаватель математики в Школе математических и навигацких наук в Москве (с 1701 по 1739), автор первой в России учебной энциклопедии по математике (в 1703г. «Арифметика»), которая более ста лет являлась основным учебным пособием по математике в России.
Слайд 14
Задача 1 . Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. В каком соотношении их необходимо взять? Параметры конечного продукта Параметры исходных продуктов Доли исходных продуктов в конечном продукте 30% 5% 40% 40-30 30-5 1-ый продукт 2-ой продукт 10 частей 25 частей Соотношение первого и второго растворов – 10:25 или 2:5.
Слайд 15
Задача 1а. Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. Сколько грамм каждой кислоты необходимо смешать, чтобы получить 140 г 30%- ого раствора? Решение: Сколько всего частей? 2 + 5 = 7(ч) Сколько грамм приходится на одну часть? 140 : 7 = 20(г) Сколько грамм 5%-го раствора взять? 2 · 20 = 40(г) Сколько грамм 40%-го раствора взять? 5 · 20 = 100(г) Ответ: для получения 140г 30%-ного раствора нужно взять 5%-ного раствора 40г, а 40%-ного - 100 г.
Слайд 16
Заключение Математика в настоящее время все шире проникает в повседневную жизнь, все более внедряется в традиционно далекие от нее области. Компьютеризация общества, внедрение современных информационных технологий требует математической грамотности человека почти на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой. Решение задач различными способами способствует углублению знаний, логического мышления, расширяет кругозор. «Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели». (А. Маркушевич) .
Слайд 17
Ознакомление с историческими фактами позволяет лучше понять роль математики в современном обществе, углубляют понимание изучаемого раздела программы. В результате изученной темы было выяснено, что существует множество методов различных старинных задач. Естественно, все их виды рассмотреть невозможно. Также мы научились правильно анализировать задачи и решать их разными методами (путём составления уравнений, т.е методом ложного положения, методом полного перебора вариантов и т.д) и разными способами: алгебраическим и арифметическим (старинным). Арифметические способы решения текстовых задач имеют больший развивающий потенциал, чем универсальный алгебраический способ решения. В наше время предпочтение отдаётся алгебраическому способу.
nsportal.ru
Старинные задачи и способы их решения


Введение
Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, и на занятии математического кружка, и в журнале или книжке. А меня очень заинтересовали старинные задачи, с которыми мы столкнулись на уроке математики. И я решил узнать о них больше. Старинные задачи пришли к нам из глубины веков, от наших предков. Разные народы нашей планеты придумывали их, оттачивали условия и логику заданий. Они неизбежно остроумны и занимательны, в них собраны замечательные находки многих поколений.

Старинные задачи позволяют не только развить смекалку и сообразительность, но и почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество, и я специально отобрал лучшие из них.

Еще в древние века математика занимала основное место в умах ученых и благодаря сохранившимся рукописям у нас есть возможность проследить за развитием математической мысли и возможность прорешать старинные задачи и сравнить их решение с современным решением.
Цель исследования: выявление роли и места старинных задач в современном мире, рассмотрение различных способов решения старинных задач.
Задачи исследования:
- исследовать решение старинных задач методом перебора; методом подбора; методом предположения, алгебраическим способом; наглядно-геометрическим способом
- исследовать старинный способ решения задач на сплавы и смеси.

Диофант
Его называют
отцом алгебры
Диофант умел решать
очень сложные уравнения,
он применял для этого
буквенные обозначения
и другие приемы.
Биографические данные
зашифрованы в виде
математической задачи,
начертанной на его гробнице .

Задача № 1
Жизнь Диофанта . По преданию, на могильном камне имелась такая надпись:
«Путник! Под этим камнем покоится прах Диофанта, умершего в глубокой старости. Шестую часть своей долгой жизни он был ребёнком, двенадцатую- юношей, седьмую- провёл неженатым. Через 5 лет после женитьбы у него родился сын, который прожил вдвое меньше отца. Через четыре года после смерти сына уснул вечным сном и сам Диофант, оплакиваемый своими близкими. Скажи, если умеешь считать, сколько прожил Диофант?»






Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты. При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости. Концентрацией вещества называется отношение массы этого вещества к массе всей смеси (раствора, сплава). Концентрация вещества, выраженная в процентах, называется процентным отношением вещества в смеси (растворе, сплаве). Существует старинный способ решения задач на смеси и сплавы. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Л.Ф.Магницкого.
После определения числового выражения - переход на следующий слайд (верхняя кнопка)
Попадая повторно на этот слайд повторяем определение буквенных выражений. Далее: Чтобы получить второе определение – нажмите на «Знайку». После определения буквенных выражений нажмите на вторую кнопу и Вы перейдете к практическому заданию.

Лео́нтий Фили́ппович Магни́цкий (9(19)июня 1669- 19(30)октября 1739)
Магницкий Л.Ф. (при рождении Телятин)-
русский математик, педагог;
преподаватель математики в Школе
математических и навигацких наук
в Москве (с 1701 по 1739),
автор первой в России учебной
энциклопедии по математике
(в 1703г. «Арифметика»), которая
более ста лет являлась основным
учебным пособием по математике
в России.

40-30
30-5
Задача 1 . Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. В каком соотношении их необходимо взять?
Параметры конечного продукта
Параметры исходных продуктов
Доли исходных продуктов в конечном продукте
5%
1-ый продукт
10 частей
30%
25 частей
40%
2-ой продукт
Соотношение первого и второго растворов – 10:25 или 2:5.

Задача 1а. Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. Сколько грамм каждой кислоты необходимо смешать, чтобы получить 140 г 30%- ого раствора?
Решение:
2 + 5 = 7(ч)
- Сколько грамм приходится на одну часть?
140 : 7 = 20(г)
- Сколько грамм 5%-го раствора взять?
2 · 20 = 40(г)
- Сколько грамм 40%-го раствора взять?
5 · 20 = 100(г)
Ответ: для получения 140г 30%-ного раствора нужно
взять 5%-ного раствора 40г, а 40%-ного - 100 г.

Заключение
Математика в настоящее время все шире проникает в повседневную жизнь, все более внедряется в традиционно далекие от нее области. Компьютеризация общества, внедрение современных информационных технологий требует математической грамотности человека почти на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой.
Решение задач различными способами способствует углублению знаний, логического мышления, расширяет кругозор.
«Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели». (А. Маркушевич)
.

Ознакомление с историческими фактами позволяет лучше понять роль математики в современном обществе, углубляют понимание изучаемого раздела программы.
В результате изученной темы было выяснено, что существует множество методов различных старинных задач. Естественно, все их виды рассмотреть невозможно. Также мы научились правильно анализировать задачи и решать их разными методами (путём составления уравнений, т.е методом ложного положения, методом полного перебора вариантов и т.д) и разными способами: алгебраическим и арифметическим (старинным). Арифметические способы решения текстовых задач имеют больший развивающий потенциал, чем универсальный алгебраический способ решения. В наше время предпочтение отдаётся алгебраическому способу.
videouroki.net
Реферат по теме "Старинные занимательные задачи"
Муниципальное образовательное учреждение –
Средняя общеобразовательная школа №3 «Пеликан»
«Старинные
занимательные
задачи»
Выполнила:
Кенжебулатова Н., ученица 6 А кл.
Руководитель: Грибкова О.В.
Бердск
2008
Содержание
-
Введение ………………………………………. 2
2. О математических знаниях на Руси …………… 4
3. Старинные занимательные задачи …………… 8
4 Старинные меры длины…………………………...13
5. Леонтий Филиппович Магницкий………………..14
6. Леонард Эйлер…………………………………….16
7. Заключение………………………………………….18
8. Список литературы …………………….…………..19
Введение
В русской математической литературе, в учебниках всегда уделялось большое внимание занимательным задачам, так как считалось, что элемент занимательности облегчает обучение. К занимательным задачам относят задачи с интересным содержанием или интересным способам решения, математические игры, задачи, касающиеся интересных свойств чисел и геометрических тел
Цель:
-
Рассмотреть старинные занимательные задачи из русских учебников математики, опубликованных в России до 1800 года, в частности, из знаменитой «Арифметики» Л.Ф. Магницкого.
Задачи:
Примечание. Старинные занимательные задачи можно использовать на уроках, факультативах, в математических кружках. Элемент занимательности облегчит обучение, зарядка для ума украсит досуг.
О математических знаниях на Руси
Из первых известных письменных источников известно, что математические знания на Руси были распространены уже в Х-Х1 веках. Они были связаны с практическими нуждами людей: летоисчислением, вычислением поголовья и стоимости стада, определением прибыли от сбора урожая и т. д.
В 16 - 17 веках в России начинает появляться и распространяться рукописная математическая литература. В настоящее время известно значительное количество математических рукописей того времени. В основном они предназначались для купцов, торговцев, чиновников, ремесленников, землемеров и носили практический характер. Материал их распределялся по «статьям», содержащим указания, как надо поступать при решении тех или иных задач. Правила пояснялись разнообразными примерами и задачами. Некоторые из этих задач интересны либо своей формулировкой, либо своим решением. Многие из них перешли в учебники по арифметике и алгебре XVIII века, некоторые сохранились и до нашего времени.
Перестройка государственной, общественной и культурной жизни страны, начатая Петром I, подняла и вопросы образования. Требовались специалисты для создания регулярной армии, для постройки торгового и военного флота, для развития промышленности и т.д. Для подготовки таких кадров, распространения в стране математических знаний нужны были учебники. В 1703 году такой учебник был издан типографским способом необычайно большим по тем временам тиражом - в количестве 2400 экземпляров. Назывался он «Арифметика, сиречь наука числительная...». Автором его был выдающийся педагог-математик - Леонтий Филиппович Магницкий (краткие биографические сведения о нём содержатся в приложении). Взяв за основу, имевшуюся рукописную математическую литературу, Магницкий создал книгу, которая на протяжении 50 лет была основным учебником по математике для почти всех учебных заведений России. Она сыграла большую роль в распространении математических знаний, в подготовке кадров для государственных учреждений страны.
infourok.ru
«Старинные задачи через века и страны»
скачать Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №3 г.Ртищево Саратовская область».
Боброва Наталья Сергеевна, учитель математики
РАЙОННАЯ НАУЧНО- ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ
«Надежда губернии»
СЕКЦИЯ «Математика»
«Старинные задачи через века и страны» Автор: Балберова Анастасия
Учащаяся 7 класса,
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №3 г.Ртищево»
Руководитель: Боброва Наталья Сергеевна,
учитель математики
г. Ртищево, 2012 г.
Содержание - Введение.…………………………………….……………………………….……3
- Способы решения текстовых задач
1. Правило ложного положения……………………………………………...…4 2. Метод перебора…………………………………………………………….….6
3. Старинный способ решения задач на сплавы и смеси……………………...7
- Заключение………………………………………………………………..………9
- Список используемой литературы …………………………………………....10
Введение
Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, и на занятии математического кружка, и в журнале или книжке. А меня очень заинтересовали старинные задачи, с которыми мы столкнулись на уроке математики. И я решили узнать о них больше. Старинные задачи пришли к нам из глубины веков, от наших предков. Разные народы нашей планеты придумывали их, оттачивали условия и логику заданий. Они неизбежно остроумны и занимательны, в них собраны замечательные находки многих поколений.
Старинные задачи позволяют не только развить смекалку и сообразительность, но и окунуться в атмосферу патриархальности, почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество, и я специально отобрала лучшие из них.
Еще в древние века математика занимала основное место в умах ученых и благодаря сохранившимся рукописям у нас есть возможность проследить за развитием математической мысли и возможность прорешать старинные задачи и сравнить их решение с современным решением.
Цель исследования: выявление роли и места старинных задач в современном мире, рассмотрение различных способов решения старинных задач.
Задачи исследования:
- исследовать решение старинных задач методом перебора;
- исследовать метод решения старинных задач «правило ложного положения»
- исследовать старинный способ решения задач на сплавы и смеси.
Способы решения текстовых задач Недостаточно лишь понять задачу, необходимо желание решить ее.
Без сильного желания решить трудную задачу невозможно,
Но при наличии такового – возможно. Где есть желание, найдется путь!
Пойя Д.
- Правило ложного положения.
Самой глубокой древности и до XIX в руководствах по арифметике занимал очень видное место так называемый метод ложного положения или метод предположений. Долгое время этот метод заменял применение уравнений первой степени при решении задач, приводимых к этим уравнениям. Сущность метода «ложного положения» в том, что неизвестной величине дают произвольное значение, пользуясь которым вычисляют значение одной из данных величин, устанавливают ошибку. Так как в задачах, решаемых этим способом, данная величина, значение которой определяется через значение неизвестной, есть линейная функция неизвестной, то приращение этой величины пропорционально приращению неизвестной. Пользуясь этим, исправляют значение неизвестной. Способ ложного положения - древний способ, применявшийся при решении задач, приводящихся к уравнениям первой степени, еще египтянами в древности. Этот способ рассматривался и в старинном русском учебнике Л.Ф. Магницкого под названием «Фальшивое правило». Этот способ полезно знать, он дает возможность решить арифметически многие задачи.
Задача 1: Летела стая гусей, а навстречу ей один гусь. «Здравствуйте, 100 гусей»,- говорит он, а вожак стаи отвечает: «Нас не 100 гусей. Если бы нас было столько, сколько теперь, да ещё столько, да ещё пол столько, да ещё четверть столько, да ещё ты, гусь, то нас было бы ровно 100гусей».
Сегодня бы школьник прочтя такую задачу, сразу же составит уравнение  и, если хорошо умеет справляться с дробями, найдет из него, что х=36. Но в Древнем Египте про то, что неизвестные числа можно обозначать буквами, а потом работать с ними как известными величинами, и не подозревали. С дробями у них тоже были сложности. Однако, египтяне придумали метод решения задач, который назвали «методом кучи» (по-египетски – «аха»).
и, если хорошо умеет справляться с дробями, найдет из него, что х=36. Но в Древнем Египте про то, что неизвестные числа можно обозначать буквами, а потом работать с ними как известными величинами, и не подозревали. С дробями у них тоже были сложности. Однако, египтяне придумали метод решения задач, который назвали «методом кучи» (по-египетски – «аха»).
Прочтя задачу про гусей, египетский писец Ахмес сказал бы: «считай с четырех». Это значило: «Считай, что в стае было четыре гуся». Тогда простой подсчет показывает , что столько, да еще столько, да еще полстолька, да еще четверть столько дают 4+4+2+1, то есть 11 гусей, а нужно получить не 11, а 99 гусей (100–1). Так как 99:11=9, то надо взятое вначале число 4 умножить на 9. Тогда получится правильный ответ 36.
Поскольку вначале делается предположение, что число гусей равнялось четырем, этот способ называют теперь «Правилом ложного положения»
Приведем решение задачи способом ложного положения, или «фальшивым правилом». Из книги Магницкого:
Задача 2: Спросил некто учителя: «Сколько у тебя в классе учеников, так как хочу отдать к тебе в учение своего сына». Учитель ответил: «Если придет еще столько же учеников сколько имею, и полстолька и четвертая часть и твой сын, тогда будет у меня учеников 100». Спрашивается, сколько было у учителя учеников?
Магницкий дает такой способ решения.
1). Делаем первое предположение: учеников было 24.
Тогда по смыслу задачи к этому числу надо прибавить «столько, полстолька, четверть столька и 1», то есть имели бы:
24+24+12+6+1=67, то есть на 100—67=33 меньше (чем требовалось по условию задачи), в этом случае число 33 называем «первым отклонением».
2. Делаем второе предположение: учеников было 32, тогда имели бы:
32+32+16+8+1=89, то есть на 100—89=11 меньше это «второе отклонение».
На случай, если при обоих предположениях получилось меньше, дается правило: помножить первое предположение на второе отклонение, а второе предположение на первое отклонение, отнять от большего произведения меньшее и разность разделить на разность отклонений:  .
.
Учеников было 36.
Таким же правилом надо руководствоваться, если при обоих предположениях получилось больше, чем полагается по условию. Например:
Первое предположение: 52, тогда имеем 52+52+26+13+1=144.
Получили на 144–100=44 больше (первое отклонение).
Второе предположение: 40, имеем: 40+40+20+10+1=111.
Получили на 111–100=11 больше (второе отклонение).
 .
.
Если при одном предположении получим больше, а при другом меньше, чем требуется по условию задачи, то нужно при указанных выше вычислениях брать не разности, а суммы.
При помощи самых начальных сведений алгебры эти правила легко обосновываются.
- Метод перебора
Как Вы уже знаете, существуют задачи, для которых доказано отсутствие общего алгоритма решения (например, задача о разрешимости Диофантова множества). В то же время, можно сказать, что, если бы мы обладали бесконечным запасом времени и соответствующими ресурсами, то мы могли бы найти решение любой задачи. Здесь имеется в виду не конструирование нового знания на основании имеющегося (вывод новых теорем из аксиом и уже выведенных теорем), а, прежде всего, "тупой" перебор вариантов. Еще в XVII столетии великий Лейбниц пытался раскрыть тайну "Всеобщего Искусства Изобретения". Он утверждал, что одной из двух частей этого искусства является комбинаторика - перебор постепенно усложняющихся комбинаций исходных данных. Второй частью является эвристика - свойство догадки человека. И сейчас вторая часть Искусства Изобретения все еще остается нераскрытой. На языке нашего времени эта часть - модель мышления человека, включающая в себя процессы генерации эвристик (догадок, изобретений, открытий).
Однако прежде чем перейти к рассмотрению улучшенных переборных алгоритмов (улучшенных потому, что для простого перебора у нас в запасе нет вечности), я бы отметила еще один универсальный метод ускорения перебора - быстрое отсечение ложных (или вероятно ложных, что и используется большинством алгоритмов) ветвей перебора.
Задача 2: В клетке находятся кролики и фазаны. Всего 6 голов и 20 ног. Сколько кроликов и сколько фазанов было в клетке?
- Если бы был 1 кролик, а фазанов – 5, то ног у них было бы 14 и т. д.
Решение лучше оформить в виде таблицы:
| Количество | Всего |
| кроликов | фазанов | голов | ног |
| 1 | 5 | 6 | 14 |
| 2 | 4 | 6 | 16 |
| 3 | 3 | 6 | 18 |
| 4 | 2 | 6 | 20 |
| 5 | 1 | 6 | 22 |
Ответ: 4 кролика и 2 фазана. - Старинный способ решения задач на сплавы и смеси
Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты. При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости. Концентрацией вещества называется отношение массы этого вещества к массе всей смеси (раствора, сплава). Концентрация вещества, выраженная в процентах, называется процентным отношением вещества в смеси (растворе, сплаве). Существует старинный способ решения задач на смеси и сплавы. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Л.Ф.Магницкого. Задача 4. При смешивании 5%-ного раствора кислоты с 40%-ным раствором кислоты получили 140г 30%-ного раствора. Сколько граммов каждого раствора было для этого взято?
1 способ решения:
Друг под другом пишутся содержания кислот имеющихся растворов, слева от них и примерно посередине - содержание кислоты в растворе, который должен получиться после смешивания. Соединив написанные числа черточками, получим такую схему:

Рассмотрим пары 30 и 5; 30 и 40.В каждой паре из большего числа вычтем меньшее, и результат запишем в конце соответствующей черточки. Получится такая схема:

- 25 +10 = 35 (частей всего)
- 140 : 35 = 4 ( г) - приходится на 1 часть
- 4*25 = 100 (г) – 40%-ного раствора
- 10 * 4 = 40 (г) – 30% - ного раствора
5% - ного раствора следует взять 10 частей, а 40%-ного - 25 частей (140 : 35 = 4 г приходится на одну часть), т. е. для получения 140 г 30%-ного раствора нужно взять 5%-ного раствора 40 граммов, а 40%-ного - 100 граммов.
Ответ: 40 г, 100 г.
Заключение
Математика в настоящее время все шире проникает в повседневную жизнь, все более внедряется в традиционно далекие от нее области. Компьютеризация общества, внедрение современных информационных технологий требует математической грамотности человека почти на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой.
Решение задач различными способами способствует углублению знаний, логического мышления, расширяет кругозор.
«Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели». (А. Маркушевич)
Ознакомление с историческими фактами позволяет лучше понять роль математики в современном обществе, углубляют понимание изучаемого раздела программы.
В результате изученной темы было выяснено, что существует множество методов различных старинных задач. Естественно, все их виды рассмотреть невозможно. Также мы научились правильно анализировать задачи и решать их разными методами (путём составления уравнений, т.е методом ложного положения, методом полного перебора вариантов и т.д) и разными способами: алгебраическим и арифметическим (старинным). Арифметические способы решения текстовых задач имеют больший развивающий потенциал, чем универсальный алгебраический способ решения. В наше время предпочтение отдаётся алгебраическому способу.
Список используемой литературы
- Бартенев Ф. А «Нестандартные задачи по алгебре» Москва «Просвещение» 1976 г
- Глейзер Г. И. История математики в школе. М., Просвещение, 1982.
- Денисов А.П. Леонтий Филиппович Магницкий. М., «Просвещение», 1967.
- Депман И. Я., Виленкин Н. Я. «За страницами учебника математики» Издательство «Просвещение» 1989 г.
- Журнал «Математика в школе» «Учимся решать задачи». №36. 2004г.
- Журнал «Математика в школе». «Задачи на смеси и сплавы». №17. №11 2004г
- Журнал «Математика» № 47-97. Приложение к газете «Первое сентября»
- Чистяков В. Д. Старинные задачи по элементарной математике. Мн., «Вышэйш. школа», 1978.
- Ресурсы сети Интернет
скачать nenuda.ru
Проектная работа на тему "Старинные математические задачи" (7 класс)

Проектная работа
Старинные математические задачи
Выполнили учащиеся 7 класса
Руководитель: Заугарова В.А.
Цели и задачи проекта.
1. Развитие творческого потенциала учащихся.
2. Развитие информационной культуры.
3. Формирование самостоятельности в сфере исследовательской деятельности.
4. Формирование умения решать старинные задачи разных стран.
5. Закрепление знаний по математике.
6. Повышение интереса к математике.
Содержание проекта
Задачи Древнего Египта.
Задачи Вавилона.
Задачи Древнего Китая.
Задачи Древней Индии.
Задачи Древней Руси.
Пояснительная записка
Выбор темы данного проекта обьясняется тем, что учащиеся имеют большой интерес к задачам древности, способам их решения. Позволяет показать связь истории и математики. Работа носит обучающий, практический характер.
Задачи Древнего Египта

Наиболее древние письменные математические тексты датируются примерно началом II тыс. до н. э. математические документы сохранились только в Египте, Вавилоне, Китае и Индии.
Около пяти тысяч лет назад при фараоне Джосере был признан богом мудрости великий врачеватель, государственный деятель и первый известный нам по имени математик Имхотен.
Математические правила, нужные для земледелия, астрономии и строительных работ, древние египтяне записывали на стенах храмов или на папирусах.
Еще IX тыс. лет назад они решали практические задачи по арифметике, алгебре и геометрии.
Задача 1.
У семи лиц по семи кошек, каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа из этого ряда и их сумма?
Задача 2.
Найти приближенное значение для числа π, приняв площадь круга равной площади квадрата со стороной  диаметра круга.
диаметра круга.
Задачи Вавилона
 В древнем Вавилоне математика зародилась задолго до нашей эры. Вавилонские памятники в виде глиняных плиток (всего около 50000, причем из них примерно лишь 150 с текстами математичес- ких задач и 200 с числовыми таблицами) с клинописными надписями хранятся в различных музеях мира. В этих текстах мы находим достаточно удобные способы решения ряда практических задач, связанных с землемерием, торговлей и строительством.
В древнем Вавилоне математика зародилась задолго до нашей эры. Вавилонские памятники в виде глиняных плиток (всего около 50000, причем из них примерно лишь 150 с текстами математичес- ких задач и 200 с числовыми таблицами) с клинописными надписями хранятся в различных музеях мира. В этих текстах мы находим достаточно удобные способы решения ряда практических задач, связанных с землемерием, торговлей и строительством.
Вавилоняне были основоположниками астрономии, создали шестидесятеричную систему счисления, решали уравнения второй степени, некоторые виды уравнений третей степени.
Задача 3. О глиняной табличке.
Площадь А, состоящая из суммы площадей двух квадратов, составляет 1000. Сторона одного из квадратов составляет уменьшенные на две трети стороны другого квадрата. Каковы стороны квадратов?

Задача 4
Разделить прямой угол на три равные части.
Задачи Древней Греции

Если от математики Древнего Востока до нас дошли отдельные задачи с решениями и таблицами, то в Древней Греции рождается наука математика, основанная на строгих доказательствах. Этот важнейший скачок в истории относится к VI-V вв. до н. э.
Задача 5. «Суд Париса»
Один из древнейших мифов содержит сказание троянского царевича Париса…Однажды на свадьбе богиня раздора Эрида подбросила собравшимся гостям яблоко с надписью «прекраснейшая». Из-за этого яблока возник спор между богиней мудрости и справедливой войны Афиной, богиней любви и красоты Афродитой и сестрой и супругой Зевса Герой. Они обратились к царю и отцу богов и людей Зевсу, чтобы он решил, кому должно достаться яблоко. Зевс отправил богинь на гору к Парису, который пас там там свои стада. Парис должен был решить, какая из богинь самая прекрасная. Каждая из богинь старалась склонить юношу на свою сторону: Афина предлагала ему мудрость и военную славу, Афродита- красивейшую женщину на земле в жены. Гера- власть и богатство. Как Парис определил р из богинь, можно узнать, решив старинную задачу.
Богини Гера, Афродита и Афина пришли к юному Парису, чтобы тот решил, кто из них прекраснее. Представ перед Парисом, богини высказали следующие утверждения.
Афродита. Я самая прекрасная. (1) Афина. Афродита не самая прекрасная (2) Гера. Я самая прекрасная. (3) Афина. Афродита не самая прекрасная. (4) Парис, прилегший отдохнуть на обочине дороги, не счел нужным даже снять платок, которым прикрыл глаза от яркого солнца. Но богини были настойчивы, и ему нужно было решить, какая из них самая прекрасная. Парис предложил, что все утверждения прекраснейшей из богинь истинны, а утверждения двух остальных богинь ложны. Мог ли Парис вынести решение, кто прекраснее из богинь?
Задача 6. Задача Дидоны.
В древнем мифе рассказывается, что Тирский царь Пигмалион убил Сихея, мужа своей сестры Дидоны, чтобы овладеть его богатством. Дидона, покинув Финикию, после многих приключений оказалась в Северной Африке. Король нумидийцев Ярт обещал подарить Дидоне участок земли на берегу моря «не больше, чем можно окружить воловьей шкурой». Хитрая Дидона разрезала воловью шкуру на тонкие полоски, связала из них очень длинную веревку и отмерила большой участок земли, на котором основала город Карфаген. Участок какой формы окружила Дидона веревкой данной длины, чтобы получить наибольшую площадь?
Задача 7. О школе Пифагора.
Пифагор Самосский (ок. 570- ок.500 г. до н. э.)- древнегреческий математик и филосов. Основал пифагорейский союз (школу). Пифагорейцы занимались астрономией, геометрией, гармонией (теорией музыки) и арифметикой (теорией чисел). В школе возникло представление о шарообразности Земли.
Тиран острова Самос Поликрат однажды спросил на пиру у Пифагора, сколько у того учеников. Охотно скажу тебе, о Поликрат,- отвечал Пифагор. Половина моих учеников изучает прекрасную математику, четверть исследует тайны вечной природы, седьмая часть молча упражняет силу духа, храня в сердце учение. Добавь еще к ним трех юношей, из которых Теон превосходит прочих своими способностями. Сколько учеников веду я к рождению вечной истины?
Задача 8.
Всякое нечетное число, кроме единицы, есть разность двух квадратов.
Задача 9.
Три грации имели по одинаковому числу плодов и встретили девять муз. Каждая из граций отдала каждой из муз по одинаковому числу плодов. После этого у каждой из муз и каждой из граций стало по одинаковому числу плодов. Сколько плодов было у каждой из граций до встречи с музами?
Задача 10.
Мул и осел под вьюком по дороге с мешками шагали. Жалобно охал осел, непосильною ношей придавлен. Это подметивший мул обратился к сопутчику с речью: «Что ж , старина, ты заныл и рыдаешь, будто девчонка? Нес бы вдвойне я, чем ты, если б отдал одну ты мне меру, Если ж бы ты у меня лишь одну взял, то мы бы сравнялись» Сколько нес каждый из них, о геометр, поведай нам это.
Задача 11. Герона Александрийского.
Из под земли бьют четыре источника. Первый заполняет бассейн за один день,- второй- за два дня, третий- за четыре дня. Сколько времени наполнят бассейн все четыре источника вместе?
Задача 12. Древнеримская задача (II в.)
Некто, умирая, завещал: « Если у моей жены родится сын, то пусть ему будет дано 2:3 имения, а жене – остальная часть. Если, же родится дочь, то ей  , а жене
, а жене  ». Родилась двойня - сын и дочь. Как разделить имение?
». Родилась двойня - сын и дочь. Как разделить имение?

Задачи Древнего Китая

Возникновение китайской цивилизации на берегах реки Хуанхе относиться к началу II тыс. до н. э. Сохранились обозначения цифр на гадальных костях животных XIII в. до н. э. Среди важнейших достижений китайской математики отметим: введение отрицательных чисел, десятичных дробей, методов решения систем линейных уравнений, уравнений высоких степеней. В Китайских рукописях содержатся наиболее ранние сведения о магических (волшебных) квадратах (V в. до н.э.).
Задача 13.
Заполнить натуральными числами от 1 до 9 квадратную таблицу размером 3X3 так, чтобы суммы чисел по всем строкам, столбцам и диагоналям были равны одному и тому же числу 15.
Задача 14. Имеются вещи, число их неизвестно. Если считать их тройками, то остаток 2; если считать их пятерками, то остаток 3; если считать их семерками, то остаток 2. Спрашивается, сколько вещей.
Задачи Древней Индии

Задача 15.
Повар готовит различные блюда с шестью вкусовыми оттенками: острым, горьким, вяжущим, кислым, соленым, сладким. Друг, скажи каково число их разновидностей?
Задача 16.
Прекрасная дева с блестящими очами, скажи мне величину такого числа, которое, будучи умножено на 3, затем увеличено на 3:4 этого произведения, разделено на 7, уменьшено на 1:3 частного, умножено само на себя, уменьшено на 52, после извлечения квадратного корня, прибавления 8 и деления на 10, дает число 2.
Задачи Древней Руси

Задача 17.
Три торговца, не желая отбивать друг у друга покупателей, решили продавать свои апельсины по одинаковой цене. У одного торговца было 50 апельсинов, у другого 30, у третьего только 10. Торговцы условились, что цену можно изменить, лишь бы продажа одновременно производилась у всех трех торговцев по одной и той же цене. Когда весь товар был распродан, то оказалось, что каждый из торговцев выручил за свои апельсины одинаковую сумму, а именно 50 копеек. Как и по какой цене они должны были продать апельсины?
Задача 18.
Сельский виноторговец призвал трех своих сыновей и велел поделить им поровну между собой 7 полных бочонков с вином, 7 таких же бочонков, наполненных вином поровну, и 7 таких же бочонков, но пустых. Как сыновья могут поделить вино и бочонки, чтобы каждому досталось и одинаковое количество вина, и одинаковое число бочонков, если переливать вино из одного бочонка в другой нельзя?
Задача 19.
На скотном дворе гуляли гуси и поросята. Хозяин двора и его сын вышли на двор, посмотрели на живность и пошли в поле. По дороге сын и спрашивает: «Папа, сколько у нас на скотном дворе гусей и сколько поросят?» - «А вот угадай-ка сам. Если считать по головам, то на дворе 25 голов, а если по ногам, то 70 ног». Сколько было гусей и сколько поросят?
Задача 20.
Хозяйка в продолжение поста накопила два горшка масла: один в 8 фунтов, другой в 3 фунта, а третий горшок в 5 фунтов остался у нее
пустым. Перед праздником хозяйке понадобилось одолжить 6 фунтов масла соседке. Как она это сделала, если меркой могли служить только те же три горшка?
Задача 21.
Дед, отец и сын встретили во время прогулки знакомого, который спросил, сколько каждому из них лет. «Нам 131 год и 10 месяцев», - ответил за всех дед и важно зашагал вперед. Тогда их знакомый, продолжая интересоваться их возрастом, спросил отца: «Ну скажите же, сколько вам лет?»- «Мне вместе с сыном 57 лет и 2 месяца,- ответил отец,- а сын на 19 лет и 10 месяцев моложе меня». Так знакомому и не пришлось узнать, сколько лет каждому из них. Сколько лет деду, отцу и сыну?
Решения задач
1. 7; 49; 343; 2401; 16807; 19607.
2.По условию задачи 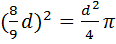
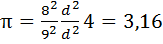 .
.
3. 30 и 10.
4. Пусть требуется разделить прямой угол ABC на три равные части. Для этого древние вавилоняне на отрезке AD стороны BA строили равносторонний треугольник BED. Тогда угол CBE будет составлять одну треть данного прямого угла. Остается только разделить пополам угол DBE, и задача будет решена.
С


A
D
E

В
5. Пусть Парис предложил, что Афина изрекла истину. Тогда она прекраснейшая из богинь, и по предложению утверждение (4) ложно. Мы приходим к противоречию, т.к. Гера не может быть прекраснейшей из богинь, коль скоро прекраснейшая из богинь Афина. Таким образом, исходное предложение ложно. Если Парис предложит, что истину изрекла Гера, то она прекраснейшая из богинь, и по предложению (2) ложно. Мы снова приходим к противоречию, т. к. Афродита не может быть прекраснейшей из богинь, коль скоро прекраснейшая из богинь Гера. И это исходное предложение ложно. Если Парис наконец предложит, что Афродита изрекла истину, то Афродита прекраснейшая из богинь. Отрицания утверждений (2), (3), (5) истинны и показывают, что Афродита – прекраснейшая из богинь.
6. Среди всех плоских фигур данного периметра максимальную площадь имеет круг. Это замечательное свойство круга было известно в Древней Греции. Поэтому Дидона окружила имевшейся веревкой участок земли в форме полукруга с центром на берегу моря.
7. Среди 28 учеников школы Пифагора математикой занимались 14, музыкой – 7, пребывали в молчании – 4 и было еще 3 женщины.
8. 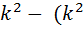 - 1) = 2k – 1 – нечетное число.
- 1) = 2k – 1 – нечетное число.
9. Пусть у каждой из грации было по x плодов и они отдали каждой из муз по y плодов. Тогда по условию задачи должно быть x – y = 3y или x = 12y, т. е. у каждой грации до встречи с музами число плодов было кратно 12.
10 . Если x – груз мула, то (x-1) – груз осла, увеличенный на единицу, а следовательно, первоначальный груз осла был (x-2). С другой стороны x+1 в два раза больше, чем груз осла, уменьшенный на 1, т. е. x-3. Таким образом, x+1 = 2(x – 3) x=7 – груз мула, x-2=5 –груз осла.
11. 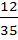 дня.
дня.
12. Имение следует разделить между сыном женой и дочерью пропорционально числам 4:2:1.
13. 4 9 2
3 5 7
8 1 6
14. 23 + 105t.
15. 23 разновидности.
16. Применив метод инверсии (правило обращения), получим;
1) 2 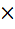 10 = 20; 2) 20 - 8 = 12 3)
10 = 20; 2) 20 - 8 = 12 3) 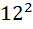 = 144;
= 144;
4) 144 + 52 = 196; 5) 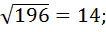 6) 14
6) 14 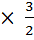 = 21;
= 21;
7) 21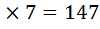 ; 8) 147
; 8) 147 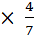 = 84; 9) 84 : 3 = 28.
= 84; 9) 84 : 3 = 28.
17. Сначала торговцы решили продавать свои апельсины по 5 копеек за каждые 7 штук. Первый торговец продал 7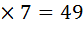 апельсинов и выручил 35 копеек. Второй торговец продал 7
апельсинов и выручил 35 копеек. Второй торговец продал 7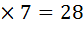 апельсинов и выручил 20 копеек. Третий торговец продал 7
апельсинов и выручил 20 копеек. Третий торговец продал 7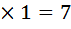 апельсинов и выручил 5 копеек. После этого у первого торговца остался 1 апельсин, у второго – 2 апельсина, у третьего – 3 апельсина. Оставшиеся апельсины торговцы решили продать по 15 копеек за штуку. Первый торговец выручил 15 копеек, а всего 15 + 35 = 50 копеек. Второй торговец выручил 30 копеек, а всего 20 +30 = 50 копеек. Третий торговец выручил 45 копеек, а всего 45 + 5 = 50 копеек.
апельсинов и выручил 5 копеек. После этого у первого торговца остался 1 апельсин, у второго – 2 апельсина, у третьего – 3 апельсина. Оставшиеся апельсины торговцы решили продать по 15 копеек за штуку. Первый торговец выручил 15 копеек, а всего 15 + 35 = 50 копеек. Второй торговец выручил 30 копеек, а всего 20 +30 = 50 копеек. Третий торговец выручил 45 копеек, а всего 45 + 5 = 50 копеек.
18. Каждый из сыновей должен получить по 7 бочонков. Все же вино можно представить себе так: 7 полных бочонков равны 14 полным наполовину бочонкам, плюс 7 полных наполовину бочонков, т.е. всего 21 полный наполовину бочонок. Следовательно, каждый из сыновей должен получить по 7 полных наполовину бочонков вина. Это можно сделать следующим образом:
Полных Полных Пустых
бочонков наполовину бочонков
бочонков
1 сын 2 3 2
2 сын 2 3 2
3 сын 3 1 3
19. Так как голов 25, всех гусей и поросят 25 штук. Если бы на дворе гулял только одни гуси, то у них было бы 50 ног. На самом деле ног у всех обитателей скотного двора 70. Следовательно, «лишние» 20 ног принадлежат гулявшим на дворе поросятам, у каждого из которых на 2 ноги больше, чем у гуся. Значит, поросят было 20 : 2 = 10, а гусей 25 – 10 =15.
20. В 5-фунтовый горшок хозяйка доложила масла из 8-фунтового горшка, в котором осталось такое количество масла, которое требовалось.
21.Деду-74 года и 8 месяцев, отцу-38 лет и 6 месяцев, сыну-18 лет и 8 месяцев.
infourok.ru
Старинные русские задачи по математике


Введение
Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, и на занятии математического кружка, и в журнале или книжке. А меня очень заинтересовали старинные задачи, с которыми мы столкнулись на уроке математики. И я решил узнать о них больше. Старинные задачи пришли к нам из глубины веков, от наших предков. Разные народы нашей планеты придумывали их, оттачивали условия и логику заданий. Они неизбежно остроумны и занимательны, в них собраны замечательные находки многих поколений.

Старинные задачи позволяют не только развить смекалку и сообразительность, но и почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество, и я специально отобрал лучшие из них.

Еще в древние века математика занимала основное место в умах ученых и благодаря сохранившимся рукописям у нас есть возможность проследить за развитием математической мысли и возможность прорешать старинные задачи и сравнить их решение с современным решением.
Цель исследования: выявление роли и места старинных задач в современном мире, рассмотрение различных способов решения старинных задач.
Задачи исследования:
- исследовать решение старинных задач методом перебора; методом подбора; методом предположения, алгебраическим способом; наглядно-геометрическим способом
- исследовать старинный способ решения задач на сплавы и смеси.

Диофант
Его называют
отцом алгебры
Диофант умел решать
очень сложные уравнения,
он применял для этого
буквенные обозначения
и другие приемы.
Биографические данные
зашифрованы в виде
математической задачи,
начертанной на его гробнице .

Задача № 1
Жизнь Диофанта . По преданию, на могильном камне имелась такая надпись:
«Путник! Под этим камнем покоится прах Диофанта, умершего в глубокой старости. Шестую часть своей долгой жизни он был ребёнком, двенадцатую- юношей, седьмую- провёл неженатым. Через 5 лет после женитьбы у него родился сын, который прожил вдвое меньше отца. Через четыре года после смерти сына уснул вечным сном и сам Диофант, оплакиваемый своими близкими. Скажи, если умеешь считать, сколько прожил Диофант?»





Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты. При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости. Концентрацией вещества называется отношение массы этого вещества к массе всей смеси (раствора, сплава). Концентрация вещества, выраженная в процентах, называется процентным отношением вещества в смеси (растворе, сплаве). Существует старинный способ решения задач на смеси и сплавы. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Л.Ф.Магницкого.
После определения числового выражения - переход на следующий слайд (верхняя кнопка)
Попадая повторно на этот слайд повторяем определение буквенных выражений. Далее: Чтобы получить второе определение – нажмите на «Знайку». После определения буквенных выражений нажмите на вторую кнопу и Вы перейдете к практическому заданию.

Лео́нтий Фили́ппович Магни́цкий (9(19)июня 1669- 19(30)октября 1739)
Магницкий Л.Ф. (при рождении Телятин)-
русский математик, педагог;
преподаватель математики в Школе
математических и навигацких наук
в Москве (с 1701 по 1739),
автор первой в России учебной
энциклопедии по математике
(в 1703г. «Арифметика»), которая
более ста лет являлась основным
учебным пособием по математике
в России.

40-30
30-5
Задача 1 . Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. В каком соотношении их необходимо взять?
Параметры исходных продуктов
Доли исходных продуктов в конечном продукте
Параметры конечного продукта
5%
1-ый продукт
10 частей
30%
25 частей
40%
2-ой продукт
Соотношение первого и второго растворов – 10:25 или 2:5.

Задача 1а. Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. Сколько грамм каждой кислоты необходимо смешать, чтобы получить 140 г 30%- ого раствора?
Решение:
2 + 5 = 7(ч)
- Сколько грамм приходится на одну часть?
140 : 7 = 20(г)
- Сколько грамм 5%-го раствора взять?
2 · 20 = 40(г)
- Сколько грамм 40%-го раствора взять?
5 · 20 = 100(г)
Ответ: для получения 140г 30%-ного раствора нужно
взять 5%-ного раствора 40г, а 40%-ного - 100 г.

Заключение
Математика в настоящее время все шире проникает в повседневную жизнь, все более внедряется в традиционно далекие от нее области. Компьютеризация общества, внедрение современных информационных технологий требует математической грамотности человека почти на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой.
Решение задач различными способами способствует углублению знаний, логического мышления, расширяет кругозор.
«Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели». (А. Маркушевич)
.

Ознакомление с историческими фактами позволяет лучше понять роль математики в современном обществе, углубляют понимание изучаемого раздела программы.
В результате изученной темы было выяснено, что существует множество методов различных старинных задач. Естественно, все их виды рассмотреть невозможно. Также мы научились правильно анализировать задачи и решать их разными методами (путём составления уравнений, т.е методом ложного положения, методом полного перебора вариантов и т.д) и разными способами: алгебраическим и арифметическим (старинным). Арифметические способы решения текстовых задач имеют больший развивающий потенциал, чем универсальный алгебраический способ решения. В наше время предпочтение отдаётся алгебраическому способу.
kopilkaurokov.ru
Проектная работа на тему 'Старинные математические задачи' (7 класс)

Проектная работа
Старинные математические задачи
Выполнили учащиеся 7 класса
Руководитель: Заугарова В.А.
Цели и задачи проекта.
1. Развитие творческого потенциала учащихся.
2. Развитие информационной культуры.
3. Формирование самостоятельности в сфере исследовательской деятельности.
4. Формирование умения решать старинные задачи разных стран.
5. Закрепление знаний по математике.
6. Повышение интереса к математике.
Содержание проекта
-
Задачи Древнего Египта.
-
Задачи Вавилона.
-
Задачи Древнего Китая.
-
Задачи Древней Индии.
-
Задачи Древней Руси.
Пояснительная записка
Выбор темы данного проекта обьясняется тем, что учащиеся имеют большой интерес к задачам древности, способам их решения. Позволяет показать связь истории и математики. Работа носит обучающий, практический характер.
Задачи Древнего Египта

Наиболее древние письменные математические тексты датируются примерно началом II тыс. до н. э. математические документы сохранились только в Египте, Вавилоне, Китае и Индии.
Около пяти тысяч лет назад при фараоне Джосере был признан богом мудрости великий врачеватель, государственный деятель и первый известный нам по имени математик Имхотен.
Математические правила, нужные для земледелия, астрономии и строительных работ, древние египтяне записывали на стенах храмов или на папирусах.
Еще IX тыс. лет назад они решали практические задачи по арифметике, алгебре и геометрии.
Задача 1.
У семи лиц по семи кошек, каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа из этого ряда и их сумма?
Задача 2.
Найти приближенное значение для числа π, приняв площадь круга равной площади квадрата со стороной  диаметра круга.
диаметра круга.
Задачи Вавилона
 В древнем Вавилоне математика зародилась задолго до нашей эры. Вавилонские памятники в виде глиняных плиток (всего около 50000, причем из них примерно лишь 150 с текстами математичес- ких задач и 200 с числовыми таблицами) с клинописными надписями хранятся в различных музеях мира. В этих текстах мы находим достаточно удобные способы решения ряда практических задач, связанных с землемерием, торговлей и строительством.
В древнем Вавилоне математика зародилась задолго до нашей эры. Вавилонские памятники в виде глиняных плиток (всего около 50000, причем из них примерно лишь 150 с текстами математичес- ких задач и 200 с числовыми таблицами) с клинописными надписями хранятся в различных музеях мира. В этих текстах мы находим достаточно удобные способы решения ряда практических задач, связанных с землемерием, торговлей и строительством.
Вавилоняне были основоположниками астрономии, создали шестидесятеричную систему счисления, решали уравнения второй степени, некоторые виды уравнений третей степени.
Задача 3. О глиняной табличке.
Площадь А, состоящая из суммы площадей двух квадратов, составляет 1000. Сторона одного из квадратов составляет уменьшенные на две трети стороны другого квадрата. Каковы стороны квадратов?

Задача 4
Разделить прямой угол на три равные части.
Задачи Древней Греции

Если от математики Древнего Востока до нас дошли отдельные задачи с решениями и таблицами, то в Древней Греции рождается наука математика, основанная на строгих доказательствах. Этот важнейший скачок в истории относится к VI-V вв. до н. э.
Задача 5. «Суд Париса»
Один из древнейших мифов содержит сказание троянского царевича Париса…Однажды на свадьбе богиня раздора Эрида подбросила собравшимся гостям яблоко с надписью «прекраснейшая». Из-за этого яблока возник спор между богиней мудрости и справедливой войны Афиной, богиней любви и красоты Афродитой и сестрой и супругой Зевса Герой. Они обратились к царю и отцу богов и людей Зевсу, чтобы он решил, кому должно достаться яблоко. Зевс отправил богинь на гору к Парису, который пас там там свои стада. Парис должен был решить, какая из богинь самая прекрасная. Каждая из богинь старалась склонить юношу на свою сторону: Афина предлагала ему мудрость и военную славу, Афродита- красивейшую женщину на земле в жены. Гера- власть и богатство. Как Парис определил р из богинь, можно узнать, решив старинную задачу.
Богини Гера, Афродита и Афина пришли к юному Парису, чтобы тот решил, кто из них прекраснее. Представ перед Парисом, богини высказали следующие утверждения.
Афродита. Я самая прекрасная. (1) Афина. Афродита не самая прекрасная (2) Гера. Я самая прекрасная. (3) Афина. Афродита не самая прекрасная. (4) Парис, прилегший отдохнуть на обочине дороги, не счел нужным даже снять платок, которым прикрыл глаза от яркого солнца. Но богини были настойчивы, и ему нужно было решить, какая из них самая прекрасная. Парис предложил, что все утверждения прекраснейшей из богинь истинны, а утверждения двух остальных богинь ложны. Мог ли Парис вынести решение, кто прекраснее из богинь?
Задача 6. Задача Дидоны.
В древнем мифе рассказывается, что Тирский царь Пигмалион убил Сихея, мужа своей сестры Дидоны, чтобы овладеть его богатством. Дидона, покинув Финикию, после многих приключений оказалась в Северной Африке. Король нумидийцев Ярт обещал подарить Дидоне участок земли на берегу моря «не больше, чем можно окружить воловьей шкурой». Хитрая Дидона разрезала воловью шкуру на тонкие полоски, связала из них очень длинную веревку и отмерила большой участок земли, на котором основала город Карфаген. Участок какой формы окружила Дидона веревкой данной длины, чтобы получить наибольшую площадь?
Задача 7. О школе Пифагора.
Пифагор Самосский (ок. 570- ок.500 г. до н. э.)- древнегреческий математик и филосов. Основал пифагорейский союз (школу). Пифагорейцы занимались астрономией, геометрией, гармонией (теорией музыки) и арифметикой (теорией чисел). В школе возникло представление о шарообразности Земли.
Тиран острова Самос Поликрат однажды спросил на пиру у Пифагора, сколько у того учеников. Охотно скажу тебе, о Поликрат,- отвечал Пифагор. Половина моих учеников изучает прекрасную математику, четверть исследует тайны вечной природы, седьмая часть молча упражняет силу духа, храня в сердце учение. Добавь еще к ним трех юношей, из которых Теон превосходит прочих своими способностями. Сколько учеников веду я к рождению вечной истины?
Задача 8.
Всякое нечетное число, кроме единицы, есть разность двух квадратов.
Задача 9.
Три грации имели по одинаковому числу плодов и встретили девять муз. Каждая из граций отдала каждой из муз по одинаковому числу плодов. После этого у каждой из муз и каждой из граций стало по одинаковому числу плодов. Сколько плодов было у каждой из граций до встречи с музами?
Задача 10.
Мул и осел под вьюком по дороге с мешками шагали. Жалобно охал осел, непосильною ношей придавлен. Это подметивший мул обратился к сопутчику с речью: «Что ж , старина, ты заныл и рыдаешь, будто девчонка? Нес бы вдвойне я, чем ты, если б отдал одну ты мне меру, Если ж бы ты у меня лишь одну взял, то мы бы сравнялись» Сколько нес каждый из них, о геометр, поведай нам это.
Задача 11. Герона Александрийского.
Из под земли бьют четыре источника. Первый заполняет бассейн за один день,- второй- за два дня, третий- за четыре дня. Сколько времени наполнят бассейн все четыре источника вместе?
Задача 12. Древнеримская задача (II в.)
Некто, умирая, завещал: « Если у моей жены родится сын, то пусть ему будет дано 2:3 имения, а жене - остальная часть. Если, же родится дочь, то ей  , а жене
, а жене  ». Родилась двойня - сын и дочь. Как разделить имение?
». Родилась двойня - сын и дочь. Как разделить имение?

Задачи Древнего Китая

Возникновение китайской цивилизации на берегах реки Хуанхе относиться к началу II тыс. до н. э. Сохранились обозначения цифр на гадальных костях животных XIII в. до н. э. Среди важнейших достижений китайской математики отметим: введение отрицательных чисел, десятичных дробей, методов решения систем линейных уравнений, уравнений высоких степеней. В Китайских рукописях содержатся наиболее ранние сведения о магических (волшебных) квадратах (V в. до н.э.).
Задача 13.
Заполнить натуральными числами от 1 до 9 квадратную таблицу размером 3X3 так, чтобы суммы чисел по всем строкам, столбцам и диагоналям были равны одному и тому же числу 15.
Задача 14. Имеются вещи, число их неизвестно. Если считать их тройками, то остаток 2; если считать их пятерками, то остаток 3; если считать их семерками, то остаток 2. Спрашивается, сколько вещей.
Задачи Древней Индии

Задача 15.
Повар готовит различные блюда с шестью вкусовыми оттенками: острым, горьким, вяжущим, кислым, соленым, сладким. Друг, скажи каково число их разновидностей?
Задача 16.
Прекрасная дева с блестящими очами, скажи мне величину такого числа, которое, будучи умножено на 3, затем увеличено на 3:4 этого произведения, разделено на 7, уменьшено на 1:3 частного, умножено само на себя, уменьшено на 52, после извлечения квадратного корня, прибавления 8 и деления на 10, дает число 2.
Задачи Древней Руси

Задача 17.
Три торговца, не желая отбивать друг у друга покупателей, решили продавать свои апельсины по одинаковой цене. У одного торговца было 50 апельсинов, у другого 30, у третьего только 10. Торговцы условились, что цену можно изменить, лишь бы продажа одновременно производилась у всех трех торговцев по одной и той же цене. Когда весь товар был распродан, то оказалось, что каждый из торговцев выручил за свои апельсины одинаковую сумму, а именно 50 копеек. Как и по какой цене они должны были продать апельсины?
Задача 18.
Сельский виноторговец призвал трех своих сыновей и велел поделить им поровну между собой 7 полных бочонков с вином, 7 таких же бочонков, наполненных вином поровну, и 7 таких же бочонков, но пустых. Как сыновья могут поделить вино и бочонки, чтобы каждому досталось и одинаковое количество вина, и одинаковое число бочонков, если переливать вино из одного бочонка в другой нельзя?
Задача 19.
На скотном дворе гуляли гуси и поросята. Хозяин двора и его сын вышли на двор, посмотрели на живность и пошли в поле. По дороге сын и спрашивает: «Папа, сколько у нас на скотном дворе гусей и сколько поросят?» - «А вот угадай-ка сам. Если считать по головам, то на дворе 25 голов, а если по ногам, то 70 ног». Сколько было гусей и сколько поросят?
Задача 20.
Хозяйка в продолжение поста накопила два горшка масла: один в 8 фунтов, другой в 3 фунта, а третий горшок в 5 фунтов остался у нее
пустым. Перед праздником хозяйке понадобилось одолжить 6 фунтов масла соседке. Как она это сделала, если меркой могли служить только те же три горшка?
Задача 21.
Дед, отец и сын встретили во время прогулки знакомого, который спросил, сколько каждому из них лет. «Нам 131 год и 10 месяцев», - ответил за всех дед и важно зашагал вперед. Тогда их знакомый, продолжая интересоваться их возрастом, спросил отца: «Ну скажите же, сколько вам лет?»- «Мне вместе с сыном 57 лет и 2 месяца,- ответил отец,- а сын на 19 лет и 10 месяцев моложе меня». Так знакомому и не пришлось узнать, сколько лет каждому из них. Сколько лет деду, отцу и сыну?
Решения задач
1. 7; 49; 343; 2401; 16807; 19607.
2.По условию задачи 
 .
.
3. 30 и 10.
4. Пусть требуется разделить прямой угол ABC на три равные части. Для этого древние вавилоняне на отрезке AD стороны BA строили равносторонний треугольник BED. Тогда угол CBE будет составлять одну треть данного прямого угла. Остается только разделить пополам угол DBE, и задача будет решена.
С


A
D
E
В
5. Пусть Парис предложил, что Афина изрекла истину. Тогда она прекраснейшая из богинь, и по предложению утверждение (4) ложно. Мы приходим к противоречию, т.к. Гера не может быть прекраснейшей из богинь, коль скоро прекраснейшая из богинь Афина. Таким образом, исходное предложение ложно. Если Парис предложит, что истину изрекла Гера, то она прекраснейшая из богинь, и по предложению (2) ложно. Мы снова приходим к противоречию, т. к. Афродита не может быть прекраснейшей из богинь, коль скоро прекраснейшая из богинь Гера. И это исходное предложение ложно. Если Парис наконец предложит, что Афродита изрекла истину, то Афродита прекраснейшая из богинь. Отрицания утверждений (2), (3), (5) истинны и показывают, что Афродита - прекраснейшая из богинь.
6. Среди всех плоских фигур данного периметра максимальную площадь имеет круг. Это замечательное свойство круга было известно в Древней Греции. Поэтому Дидона окружила имевшейся веревкой участок земли в форме полукруга с центром на берегу моря.
7. Среди 28 учеников школы Пифагора математикой занимались 14, музыкой - 7, пребывали в молчании - 4 и было еще 3 женщины.
8.  - 1) = 2k - 1 - нечетное число.
- 1) = 2k - 1 - нечетное число.
9. Пусть у каждой из грации было по x плодов и они отдали каждой из муз по y плодов. Тогда по условию задачи должно быть x - y = 3y или x = 12y, т. е. у каждой грации до встречи с музами число плодов было кратно 12.
10 . Если x - груз мула, то (x-1) - груз осла, увеличенный на единицу, а следовательно, первоначальный груз осла был (x-2). С другой стороны x+1 в два раза больше, чем груз осла, уменьшенный на 1, т. е. x-3. Таким образом, x+1 = 2(x - 3) x=7 - груз мула, x-2=5 -груз осла.
11.  дня.
дня.
12. Имение следует разделить между сыном женой и дочерью пропорционально числам 4:2:1.
13. 4 9 2
3 5 7
8 1 6
14. 23 + 105t.
15. 23 разновидности.
16. Применив метод инверсии (правило обращения), получим;
1) 2  10 = 20; 2) 20 - 8 = 12 3)
10 = 20; 2) 20 - 8 = 12 3)  = 144;
= 144;
4) 144 + 52 = 196; 5)  6) 14
6) 14  = 21;
= 21;
7) 21 ; 8) 147
; 8) 147  = 84; 9) 84 : 3 = 28.
= 84; 9) 84 : 3 = 28.
17. Сначала торговцы решили продавать свои апельсины по 5 копеек за каждые 7 штук. Первый торговец продал 7 апельсинов и выручил 35 копеек. Второй торговец продал 7
апельсинов и выручил 35 копеек. Второй торговец продал 7 апельсинов и выручил 20 копеек. Третий торговец продал 7
апельсинов и выручил 20 копеек. Третий торговец продал 7 апельсинов и выручил 5 копеек. После этого у первого торговца остался 1 апельсин, у второго - 2 апельсина, у третьего - 3 апельсина. Оставшиеся апельсины торговцы решили продать по 15 копеек за штуку. Первый торговец выручил 15 копеек, а всего 15 + 35 = 50 копеек. Второй торговец выручил 30 копеек, а всего 20 +30 = 50 копеек. Третий торговец выручил 45 копеек, а всего 45 + 5 = 50 копеек.
апельсинов и выручил 5 копеек. После этого у первого торговца остался 1 апельсин, у второго - 2 апельсина, у третьего - 3 апельсина. Оставшиеся апельсины торговцы решили продать по 15 копеек за штуку. Первый торговец выручил 15 копеек, а всего 15 + 35 = 50 копеек. Второй торговец выручил 30 копеек, а всего 20 +30 = 50 копеек. Третий торговец выручил 45 копеек, а всего 45 + 5 = 50 копеек.
18. Каждый из сыновей должен получить по 7 бочонков. Все же вино можно представить себе так: 7 полных бочонков равны 14 полным наполовину бочонкам, плюс 7 полных наполовину бочонков, т.е. всего 21 полный наполовину бочонок. Следовательно, каждый из сыновей должен получить по 7 полных наполовину бочонков вина. Это можно сделать следующим образом:
Полных Полных Пустых
бочонков наполовину бочонков
бочонков
1 сын 2 3 2
2 сын 2 3 2
3 сын 3 1 3
19. Так как голов 25, всех гусей и поросят 25 штук. Если бы на дворе гулял только одни гуси, то у них было бы 50 ног. На самом деле ног у всех обитателей скотного двора 70. Следовательно, «лишние» 20 ног принадлежат гулявшим на дворе поросятам, у каждого из которых на 2 ноги больше, чем у гуся. Значит, поросят было 20 : 2 = 10, а гусей 25 - 10 =15.
20. В 5-фунтовый горшок хозяйка доложила масла из 8-фунтового горшка, в котором осталось такое количество масла, которое требовалось.
21.Деду-74 года и 8 месяцев, отцу-38 лет и 6 месяцев, сыну-18 лет и 8 месяцев.
botana.cc
 и, если хорошо умеет справляться с дробями, найдет из него, что х=36. Но в Древнем Египте про то, что неизвестные числа можно обозначать буквами, а потом работать с ними как известными величинами, и не подозревали. С дробями у них тоже были сложности. Однако, египтяне придумали метод решения задач, который назвали «методом кучи» (по-египетски – «аха»).
и, если хорошо умеет справляться с дробями, найдет из него, что х=36. Но в Древнем Египте про то, что неизвестные числа можно обозначать буквами, а потом работать с ними как известными величинами, и не подозревали. С дробями у них тоже были сложности. Однако, египтяне придумали метод решения задач, который назвали «методом кучи» (по-египетски – «аха»).
















 .
. .
. 



 диаметра круга.
диаметра круга. В древнем Вавилоне математика зародилась задолго до нашей эры. Вавилонские памятники в виде глиняных плиток (всего около 50000, причем из них примерно лишь 150 с текстами математичес- ких задач и 200 с числовыми таблицами) с клинописными надписями хранятся в различных музеях мира. В этих текстах мы находим достаточно удобные способы решения ряда практических задач, связанных с землемерием, торговлей и строительством.
В древнем Вавилоне математика зародилась задолго до нашей эры. Вавилонские памятники в виде глиняных плиток (всего около 50000, причем из них примерно лишь 150 с текстами математичес- ких задач и 200 с числовыми таблицами) с клинописными надписями хранятся в различных музеях мира. В этих текстах мы находим достаточно удобные способы решения ряда практических задач, связанных с землемерием, торговлей и строительством.

 , а жене
, а жене  ». Родилась двойня - сын и дочь. Как разделить имение?
». Родилась двойня - сын и дочь. Как разделить имение?



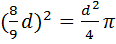
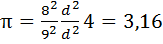 .
.


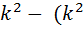 - 1) = 2k – 1 – нечетное число.
- 1) = 2k – 1 – нечетное число.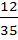 дня.
дня.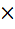 10 = 20; 2) 20 - 8 = 12 3)
10 = 20; 2) 20 - 8 = 12 3) 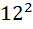 = 144;
= 144;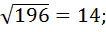 6) 14
6) 14 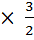 = 21;
= 21;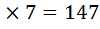 ; 8) 147
; 8) 147 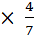 = 84; 9) 84 : 3 = 28.
= 84; 9) 84 : 3 = 28.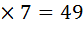 апельсинов и выручил 35 копеек. Второй торговец продал 7
апельсинов и выручил 35 копеек. Второй торговец продал 7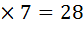 апельсинов и выручил 20 копеек. Третий торговец продал 7
апельсинов и выручил 20 копеек. Третий торговец продал 7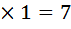 апельсинов и выручил 5 копеек. После этого у первого торговца остался 1 апельсин, у второго – 2 апельсина, у третьего – 3 апельсина. Оставшиеся апельсины торговцы решили продать по 15 копеек за штуку. Первый торговец выручил 15 копеек, а всего 15 + 35 = 50 копеек. Второй торговец выручил 30 копеек, а всего 20 +30 = 50 копеек. Третий торговец выручил 45 копеек, а всего 45 + 5 = 50 копеек.
апельсинов и выручил 5 копеек. После этого у первого торговца остался 1 апельсин, у второго – 2 апельсина, у третьего – 3 апельсина. Оставшиеся апельсины торговцы решили продать по 15 копеек за штуку. Первый торговец выручил 15 копеек, а всего 15 + 35 = 50 копеек. Второй торговец выручил 30 копеек, а всего 20 +30 = 50 копеек. Третий торговец выручил 45 копеек, а всего 45 + 5 = 50 копеек.

















 диаметра круга.
диаметра круга.  В древнем Вавилоне математика зародилась задолго до нашей эры. Вавилонские памятники в виде глиняных плиток (всего около 50000, причем из них примерно лишь 150 с текстами математичес- ких задач и 200 с числовыми таблицами) с клинописными надписями хранятся в различных музеях мира. В этих текстах мы находим достаточно удобные способы решения ряда практических задач, связанных с землемерием, торговлей и строительством.
В древнем Вавилоне математика зародилась задолго до нашей эры. Вавилонские памятники в виде глиняных плиток (всего около 50000, причем из них примерно лишь 150 с текстами математичес- ких задач и 200 с числовыми таблицами) с клинописными надписями хранятся в различных музеях мира. В этих текстах мы находим достаточно удобные способы решения ряда практических задач, связанных с землемерием, торговлей и строительством. 

 , а жене
, а жене  ». Родилась двойня - сын и дочь. Как разделить имение?
». Родилась двойня - сын и дочь. Как разделить имение? 




 .
. 


 - 1) = 2k - 1 - нечетное число.
- 1) = 2k - 1 - нечетное число.  дня.
дня.  10 = 20; 2) 20 - 8 = 12 3)
10 = 20; 2) 20 - 8 = 12 3)  = 144;
= 144;  6) 14
6) 14  = 21;
= 21;  ; 8) 147
; 8) 147  = 84; 9) 84 : 3 = 28.
= 84; 9) 84 : 3 = 28.  апельсинов и выручил 35 копеек. Второй торговец продал 7
апельсинов и выручил 35 копеек. Второй торговец продал 7 апельсинов и выручил 20 копеек. Третий торговец продал 7
апельсинов и выручил 20 копеек. Третий торговец продал 7 апельсинов и выручил 5 копеек. После этого у первого торговца остался 1 апельсин, у второго - 2 апельсина, у третьего - 3 апельсина. Оставшиеся апельсины торговцы решили продать по 15 копеек за штуку. Первый торговец выручил 15 копеек, а всего 15 + 35 = 50 копеек. Второй торговец выручил 30 копеек, а всего 20 +30 = 50 копеек. Третий торговец выручил 45 копеек, а всего 45 + 5 = 50 копеек.
апельсинов и выручил 5 копеек. После этого у первого торговца остался 1 апельсин, у второго - 2 апельсина, у третьего - 3 апельсина. Оставшиеся апельсины торговцы решили продать по 15 копеек за штуку. Первый торговец выручил 15 копеек, а всего 15 + 35 = 50 копеек. Второй торговец выручил 30 копеек, а всего 20 +30 = 50 копеек. Третий торговец выручил 45 копеек, а всего 45 + 5 = 50 копеек. 