
Содержание.Введение……………………………………………………………………………………….с.5.
1. Теоретическая часть.
Глава 1. Простой симплекс-метод.
1.1 Обоснование и описание вычислительной процедуры. Приведение задачи линейного программирования к стандартной форме……………………………с.7
1.2 Симплексный метод решения задач……………………………………..…...с.8.
1.3 Алгоритм симплекс-метода…………………………………………………с.10.
1.4 Решение задачи оптимизации. Построение аналитической модели……...с.12.
1.5 Приведение задачи к стандартной форме. Определение начального допустимого решения…………………………….……………………………...с.14.
Глава 2. Двухэтапный метод.
2.1 Искусственное начальное решение…………………………………………с.16.
2.2 Алгоритм двухэтапного метода……………………………………………..с.19.
Глава 3. Особые случаи симплекс-метода……………………………………………...23.
3.1 Вырожденность……………………………………………………………....с.24.
3.2 Альтернативные оптимальные решения…………………………………....с.27.
3.3 Неограниченные решения…………………………………………………...с.30.
3.4 Отсутствие допустимых решений…………………………………………..с.32.
2. Практическая часть.
2.1 Постановка задачи…………..……………………………………………………..с.34.
2.2 Решение…..…………………………………………………………………………с.36.
Заключение…………………………………………………………………………………...с.39.
Литература…………………………………………………………………………………....с.40.Введение.
Целью данной курсовой работы является решение конкретной задачи линейного программирования. Во всех таких задачах требуется найти максимум или минимум линейной функции при условии, что её переменные принимают неотрицательные значения и удовлетворяют некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные уравнения, так и линейные неравенства. Каждая из этих задач является частным случаем общей задачи линейного программирования.
Для решения задач линейного программирования созданы специальные методы. Изучению одного из них, а именно симплекс-методу, посвящена эта курсовая работа.
В настоящее время оптимизация находит применение в науке, технике и в любой другой области человеческой деятельности.
Оптимизация – целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно.
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:
· количество продукции - расход сырья
· количество продукции - качество продукции
Выбор компромиcного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого. Приведем примеры.
Типичный пример неправильной постановки задачи оптимизации:
«Получить максимальную производительность при минимальной себестоимости».
Ошибка заключается в том, что ставится задача поиска оптимальности 2-х величин, противоречащих друг другу по своей сути.
Правильная постановка задачи могла быть следующая:
а) получить максимальную производительность при заданной себестоимости;
б) получить минимальную себестоимость при заданной производительности;
В первом случае критерий оптимизации - производительность а во втором - себестоимость.
2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта.
3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
4. Учёт ограничений.1. Теоретическая часть.Глава 1. Простой симплекс-метод.1.1 Обоснование и описание вычислительной процедуры. Приведение задачи линейного программирования к стандартной форме.
Любая задача линейного программирования приводится к стандартной (канонической) форме основной задачи линейного программирования, которая формулируется следующим образом: найти неотрицательные значения переменных X1 , X2 , Xn , удовлетворяющих ограничениям в виде равенств:
A11X1 + A12X2 + … + A1nXn = B1;
A21X1 + A22X2 + … + A2nXn = B2;
……………………………………
Am1X1 + Am2X2 + … + AmnXn = Bm;
Xj ≥ 0, j=1,…,n
и обращающих в максимум линейную функцию этих переменных:
E = C1X1 + C2X2 + … + CnXn Þ max
При этом также требуется, чтобы правые части равенств были неотрицательны, т.е. должны соблюдаться условия:
Bj ≥ 0, j=1,…,n
Приведение к стандартной форме необходимо, так как большинство методов решения задач линейного программирования разработано именно для стандартной формы. Для приведения к стандартной форме задачи линейного программирования может потребоваться выполнить следующие действия:
- перейти от минимизации целевой функции к ее максимизации;
- изменить знаки правых частей ограничений;
- перейти от ограничений-неравенств к равенствам;
- избавиться от переменных, не имеющих ограничений на знак.
Для решения нашей задачи воспользуемся симплекс-методом, так как этот метод предназначен для решения задач линейного программирования любой размерности.
1.2 Симплексный метод решения задач.
Симплексный метод задач линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план, и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план. Рассмотрим задачу, для которой этот план можно непосредственно записать.
Пусть дана функция, для которой необходимо найти наибольшее или наименьшее значение, если значения всех неизвестных неотрицательные.
ѓ = C0 + C1x1 + C2x2 +...+ Cnxn
и система m линейных уравнений с n неизвестными. Это называется системой ограничений:
a11x1 + a12x2 +...+ a1nxn = b1
a21x1 + a12x2 +...+ a2nxn = b2
...
am1x1 +am2x12 +...+ amnxn = bm
Целевую функцию представим в виде:
ѓ - C1x1-C2x2 -...-Cnxn = C0
Составим симплекс-таблицу. В дальнейшем будем считать, что ранг матрицы системы ограничений равен r.В системе ограничений выбран базис (основные неизвестные)x1,x2,...xn и коэффициенты в правой части не отрицательны.
В этом случае система ограничений будет иметь вид:
x1 +...+ a1,r+1xr+1 +...+ a1nxn = b1
x2 + a2,r+1xr+1 +...+ a2nxn = b2
...
xr+ ar,r+1xr+1 +...+ arnxn = br
Тогда целевая функция имеет вид:
ѓ + Cr+1xr+1 + Cr+2xr+2 -...- Cnxn = C0
Нахождение оптимального плана симплексным методом включает следующие этапы:
1. Находят опорный план.
2. Составляют симплекс-таблицу. В общем виде:
| Базисные неизвестные | Свободные члены | x1 | x2 | xr | xr+1 | xj | xn |
| x1 x2 xi xr | b1 b2 bi br | 1 0 0 0 | 0 1 0 0 | 0 0 0 1 | a1,r+1 a2,r+1 ai,r+1 ar,r+1 | a1j a2j aij arj | a1n a2n ain arn |
| ѓ | C0 | 0 | 0 | 0 | Cr+2 | Cj | Cn |
3. В нижней строчке симплекс-таблицы необходимо отыскать отрицательные числа (не считая коэффициент Со). Если таких чисел нет, то данное базисное решение является оптимальным.
4. Пусть элемент Сj<0,тогда в j-ом столбце необходимо найти положительный элемент. Если все коэффициенты этого столбца отрицательные, то решения не существует.
5. Если положительный коэффициент в j-ом столбце один, то выбранную строку с номером i надо поделить все коэффициенты на число aij.Результат деления записываем в новую симплекс-таблицу. Если же положительных коэффициентов несколько, необходимо составить отношение bi/aij и из полученных значений выбрать наименьшее, соответствующее i-ой строке.
6. В новой симплекс-таблице в столбце базисных неизвестных вместо xi пишется xj. Продолжается заполняться таблица. В столбце с номером j необходимо получить нули(включая строку с целевой функцией). Для этого надо умножить i-ую записанную строку на нужное число и сложить с остальными строками.
В результате осуществился переход к новому базису, при этом значение целевой функции увеличилось.
1.3 Алгоритм симплекс-метода.
Пусть система приведена к каноническому виду.
X1+ q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
X2+q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
X3+q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
………………………………………………………
Xm+ qm,m+1 Xm+1 + …. + qm,m+n Xm+n =hm
В ней m базисных переменных, k свободных переменных. m+k=n - всего переменных.
Fmin= C1X1+ C2X2+ C3X3+....+ CnXn
Для дальнейших рассуждений вычислений будем пользоваться первой симплекс таблицей (таблица1).
Таблица 1.Симплекс таблица
| C | Б | H | C1 | C2 | … | Cm | Cm+1 | … | Cm+k |
| X1 | X2 | … | Xm | Xm+1 | … | Xm+k | |||
| C1 C2 C3 : : Cm | X1 X2 X3 : : Xm | h2 h3 h4 : : Hm | 1 0 0 : : 0 | 0 1 0 : : 0 | : : : : : : | 0 0 0 : : 0 | q1,m+1 q2,m+1 q3,m+1 : : qm,m+1 | : : : : : : | q1,m+k q2,m+k q3,m+k : : qm,m+k |
| F0 | F1 | F2 | … | Cm | Cm+1 | … | Cm+k |
Первый столбец - коэффициенты в целевой функции при базисных переменных.
Второй столбец - базисные переменные.
Третий столбец - свободные члены (hi00).
Самая верхняя строка - коэффициенты при целевой функции.
Вторая верхняя строка - сами переменные, входящие в целевую функцию и в систему ограничений.
Основное поле симплекс метода - система коэффициентов из уравнения.
Последняя строка - служит для того, чтобы ответить на вопрос: «оптимален план или нет».
Индексная строка позволяет нам судить об оптимальности плана:
При отыскании Fmin в индексной строке должны быть отрицательные и нулевые оценки.
При отыскании Fmax в индексной строке должны быть нулевые и положительные оценки.
Переход ко второй итерации:
Для этого отыскиваем ключевой (главный) столбец и ключевую (главную) строку.
Ключевым столбцом является тот в котором находится наибольший положительный элемент индексной строки при отыскании Fmin или наименьший отрицательный элемент при отыскании Fmax.
Ключевой строкой называется та, в которой содержится наименьшее положительное частное от деления элементов столбца H на соответствующие элементы ключевого столбца.
На пересечении строки и столбца находится разрешающий элемент.
На этом этапе осуществляется к переходу к последующим итерациям.
Переход к итерациям:
Выводится базис ключевой строки, уступая место переменной из ключевого столбца со своим коэффициентом.
Заполняется строка вновь введенного базиса путем деления соответствующих элементов выделенной строки предыдущей итерации на разрешающий элемент.
Если в главной строке содержится нулевой элемент, то столбец, в котором находиться этот элемент переноситься в последующую итерацию без изменения.
Если в главном столбце имеется нулевой элемент, то строка, в которой он находиться переноситься без изменения в последующую итерацию.
Остальные элементы переносятся по формуле:
1.4 Решение задачи оптимизации. Построение аналитической модели.
В цехе имеется токарный станок и станок-автомат. Цех выпускает детали 1,2 и 3 в комплекте: на каждую деталь 1 – по 2 детали 2 и 3. Часовая производительность станков по каждой из деталей приведена в таблице:
Таблица 1. Часовая производительность станков
| Станки | Детали | ||
| 1 | 2 | 3 | |
| 1. Токарный | 5 | 5 | 10 |
| 2. Автомат | 15 | 15 | 10 |
Составить программу работы станков, при которой в течение смены (8 часов) будет выпускаться максимальное количество комплектов деталей.
Составим аналитическую модель задачи. Для этого сначала введем переменные, которые требуется определить:
X1 – время, которое работал токарный станок над деталями типа 1 в течение рабочей смены;
X2 – время, которое работал токарный станок над деталями типа 2 в течение рабочей смены;
X3 – время, которое работал токарный станок над деталями типа 3 в течение рабочей смены;
X4 – время, которое работал станок-автомат над деталями типа 1 в течение рабочей смены;
X5 – время, которое работал станок-автомат над деталями типа 2 в течение рабочей смены;
X6 – время, которое работал станок-автомат над деталями типа 3 в течение рабочей смены.
Система ограничений состоит из двух групп. Первая группа устанавливает, что каждый из станков может работать не более 8 часов в смену.
Ограничение времени работы токарного станка:
X1 + X2 + X3 £ 8;
Ограничение времени работы станка-автомата:
X4 + X5 + X6 £ 8.
Вторая группа ограничений направлена на выполнение требования о комплектации деталей: на каждую деталь 1 должно приходиться по 2 детали 2 и 3. Но перед тем, как вводить это ограничение, определим, сколько деталей каждого типа у нас будет производиться за смену:
5X1 + 15X4 - будет произведено за смену деталей типа 1;
5X2 + 15X5 - будет произведено за смену деталей типа 2;
10X3 + 10X6 - будет произведено за смену деталей типа 3.
Теперь введем сами ограничения:
2(5X1 + 15X4) = 5X2 + 15X5;
2(5X1 + 15X4) = 10X3 + 10X6.
Очевидно, что все переменные в задаче неотрицательные (объем продукции не может быть отрицательным):
X1 , X2 , X3 , X4 , X5 , X6 ≥ 0.
Целевая функция в нашей задаче должна выражать количество комплектов деталей, выпускаемых за смену, поэтому сложим все выпускаемые детали и поделим на 5 (в комплект, как уже упоминалось, входят 1 деталь типа 1 и по 2 детали типа 2 и 3):
E= (5X1 + 15X4 + 5X2 + 15X5 + 10X3 + 10X6)/5 Þ max
или, если упростить это выражение, то получим:
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þ max
Целевую функцию надо максимизировать.
Таким образом, формальная постановка задачи оптимизации имеет следующий вид:
X1 + X2 + X3 £ 8;
X4 + X5 + X6 £ 8;
2(5X1 + 15X4) = 5X2 + 15X5;
2(5X1 + 15X4) = 10X1 + 10X6;
X1 , X2 , X3 , X4 , X5 , X6 ≥ 0.
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þ max1.5 Приведение задачи к стандартной форме. Определение начального допустимого решения.
Для приведения данной задачи к стандартной форме необходимо лишь перейти от ограничений – неравенств к равенствам. Для этого введем дополнительные балансовые неотрицательные переменные. Также для упрощения дальнейших вычислений разделим обе части ограничений на комплектацию деталей на 5:
X1 + X2 + X3 + X7 = 8;
X4 + X5 + X6 + X8 = 8;
2X1 – X2 + 6X4 – 3X5 = 0;
2X1 – 2X3 + 6X4 – 2X6 =0;
X1 , X2 , X3 , X4 , X5 , X6 , X7 , X8 ≥ 0.
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þ max
где Х7 , Х8 – остаточные переменные.
Итак, нашу исходную задачу мы привели к стандартной форме основной задачи линейного программирования.
Для задачи, представленной в стандартной форме, количество переменных обычно больше, чем количество ограничений. Поэтому для нахождения начального решения задачи требуется выразить m переменных (т.е. количество переменных, равное количеству уравнений) через остальные n-m переменных, принять эти n-m переменных равными нулю и, таким образом, найти значения m переменных (в заданной задаче m=4 и n=8). Переменные, значения которых принимаются равными нулю, называются небазисными, а остальные m переменных - базисными. Значения базисных переменных неотрицательны (некоторые из них могут оказаться равными нулю). Количество базисных переменных всегда равно количеству ограничений. Найденное таким образом решение называется начальным допустимым базисным решением. Оно соответствует всем ограничениям.
Начальное решение проще всего найти в случае, когда в каждом ограничении есть переменная, которая входит в него с коэффициентом 1 и при этом отсутствует в других ограничениях. Такие переменные принимаются в качестве базисных (они образуют начальный базис задачи). Остальные (небазисные) переменные принимаются равными нулю. Таким образом, базисные переменные принимают значения, равные правым частям ограничений.
Итак, для нахождения начального допустимого решения необходимо, чтобы в каждое из уравнений входила переменная с коэффициентом 1 и не входила в другие уравнения (базисная переменная). В нашем случае мы имеем только 2 базисные переменные (X7 и X8) , не хватает еще двух базисных переменных. Их можно создать с помощью специального способа, который называется построением искусственного базиса.
Методы искусственного базиса предназначены для построения начального базиса (т.е. для получения начального решения) в случаях, когда его построение непосредственно на основе стандартной формы невозможно. При использовании искусственного базиса начальное решение оказывается недопустимым; от него по определенным алгоритмам выполняется переход к начальному допустимому решению.
Для того, чтобы построить искусственный базис, необходимо в каждое уравнение стандартной формы, не содержащее базисных переменных (т.е. полученное из ограничения-равенства или "не меньше"), добавить по одной искусственной переменной. В нашем случае это:
2X1 – X2 + 6X4 – 3X5 + Х9 = 0;
2X1 – 2X3 + 6X4 – 2X6 + Х10 =0.
где Х9 и Х10 – искусственные переменные, не имеющие никакого физического смысла, причем Х9, Х10 ≥0.
После построения искусственного базиса, придав нулевые значения всем переменным, кроме базисных, получим начальный базис: Х7, Х8, Х9, Х10 . Всего в базисе имеется четыре переменные и их значения равны правым частям ограничений, т.е.:
Х7 = 8; Х8 = 8; Х9 = 0; Х10 = 0.
Теперь необходимо решить эту задачу, т.е. найти оптимальное допустимое решение. Для этого воспользуемся двухэтапным симплекс-методом.Глава 2. Двухэтапный метод.2.1 Искусственное начальное решение.В простом симплексе при начальном допустимом базисном решении гарантировалось, что все последующие базисные решения, получаемые при выполнении симплекс-метода, также будут допустимыми. В задачах линейного программирования, где все ограничения являются неравенствами типа «<=» (с неотрицательной правой частью), дополнительные (остаточные) переменные позволяют сформировать начальное допустимое базисное решение в задачах ЛП, где есть ограничения в виде равенств или неравенств типа «>=» ?
Наиболее общим способом построения начального допустимого базисного решения задачи ЛП является использование искусственных переменных. Эти переменные в первой итерации играют роль дополнительных остаточных переменных, но на последующих итерациях от них освобождаются. Разработано два тесно связанных между собой метода нахождения начального решения, которые используют искусственные переменные: М-метод и двухэтапный метод.
Для объяснения двухэтапного метода объясним сначала концепцию М-метода.Пусть задача ЛП записана в стандартной форме. Для любого равенства I, в котором не содержится дополнительная остаточная переменная, введём искусственную переменную Ri, которая далее войдёт в начальное базисное решение. Но поскольку эта переменная искусственна (другими словами, не имеет никакого «физического смысла» в данной задаче), необходимо сделать так, чтобы на последующих итерациях она обратилась в нуль. Для этого в выражение целевой функции вводят штраф.
Переменная Ri, с помощью достаточно большого положительного числа М, штрафуется путём ввода в целевую функцию выражения – MRi в случае максимизации целевой функции и выражения +MRi – в случае минимизации. Вследствие этого штрафа естественно предположить, что процесс оптимизации симплекс-метода приведёт к нулевому значению переменной Ri. Следующий пример проясняет детали этого метода.
Пример 3.4-1Минимизировать z = 4x1 + x2при выполнении условий 3x1 + x2 = 3,4x1 + 3x2 >= 6,
x1 + 2x2 <= 4,
x1, x2 >= 0.Стандартная форма этой задачи получается в результате добавления дополнительной (избыточной) переменной x3 во второе неравенство и дополнительной (остаточной) переменной x4 в третье неравенство. Эта задача в стандартной форме будет записана следующим образом.Минимизировать z = 4x1 + x2при выполнении условий3x1 + x2 = 3,
4x1 + 3x2 – x3 = 6,
x1 + 2x2 + x4 = 4,
x1, x2, x3, x4 >= 0.
В полученной задаче первое и второе уравнения не имеют дополнительных (остаточных) переменных, которые можно ввести в базисное решение. Поэтому введём в эти уравнения искусственные переменные R1 и R2, а в целевую функцию добавим штраф MR1 + MR2. В результате получим следующую задачу ЛП.Минимизировать z = 4x1 + x2 + MR1 + MR2при выполнении условий 3x1 + x2 + R1 = 3,
4x1 + 3x2 – x3 + R2 = 6,
x1 + 2x2 + x4 = 4,
x1, x2, x3, x4, R1, R2 >= 0.В этой модифицированной задаче переменные R1, R2 и x4 можно использовать в качестве начального допустимого базисного решения.При использовании М-метода следует обратить внимание на следующие два обстоятельства.1. Использование штрафа М может и не привести к исключению искусственной переменной в конечной симплекс-итерации. Если исходная задача линейного программирования не имеет допустимого решения (например, система ограничений несовместна), тогда в конечной симплекс-итерации, по крайней мере, одна искусственная переменная будет иметь положительное значение. Это «индикатор» того, что задача не имеет допустимого решения.
2. Теоретически применение М-метода требует, чтобы М → ∞. Однако с точки зрения компьютерных вычислений величина М должна быть конечной и, вместе с тем, достаточно большой. Как понимать термин «достаточно большая» – это открытый вопрос. Величина М должна быть настолько большой, чтобы выполнить роль «штрафа», но не слишком большой, чтобы не уменьшить точность вычислений. На практике вы должны помнить о возможных ошибках машинного округления при выполнении выполнений, в которых совместно участвуют как большие, так и малые числа.Правильный выбор значения М зависит от данных исходной задачи. Бездумное следование теоретическому требованию, что М должно быть «очень большим», может привести к значительным ошибкам округления. Именно поэтому М-метод никогда не применяется в коммерческих программах, реализующих симплекс-метод. Вместо него используется двухэтапный метод, который будет описан в следующем разделе.2.2 Алгоритм двухэтапного метода.Пример 2.2-2 демонстрирует проблемы, которые могут возникнуть при М-методе вследствие ошибок округления. Двухэтапный метод полностью лишён тех недостатков, которые присущи М-методу. Как следует из названия этого метода, процесс решения задачи ЛП разбивается на два этапа. На первом этапе ведётся поиск начального допустимого базисного решения. Если такое решение найдено, то на втором этапе решается исходная задача.Этап 1. Задача ЛП записывается в стандартной форме, а в ограничения добавляются необходимые искусственные переменные (как и в М-методе) для получения начального базисного решения. Решается задача ЛП минимизации суммы искусственных переменных с исходными ограничениями. Если минимальное значение этой новой целевой функции больше нуля, значит, исходная задача не имеет допустимого решения, и процесс вычислений заканчивается. (Напомним, что положительные значения искусственных переменных указывают на то, что исходная система ограничений несовместна.) Если новая целевая функция равна нулю, переходим ко второму этапу.
Этап 2. Оптимальное базисное решение, полученное на первом этапе, используется как начальное допустимое базисное решение исходной задачи.Пример 2.2-3К задаче из примера 2.2-3 применим двухэтапный метод.Этап 1Минимизировать r = R1 + R2С ограничениями 3x1 + x2 + R1 = 3,
4x1 + 3x2 – x3 + R2 = 6,
x1 + 2x2 + x4 = 4,
x1, x2, x3, x4, R1, R2, >= 0.Соответствующая таблица имеет следующий вид.
| Базис | x1 | x2 | x3 | R1 | R2 | x4 | Решение |
| r | 0 | 0 | 0 | -1 | -1 | 0 | 0 |
| R1 | 3 | 1 | 0 | 1 | 0 | 0 | 3 |
| R2 | 4 | 3 | -1 | 0 | 1 | 0 | 6 |
| x4 | 1 | 2 | 0 | 0 | 0 | 1 | 4 |
Как и в М-методе, сначала вычисляется новая r-строка.Старая r-строка: (0 0 0 -1 -1 0 | 0)
+ 1 * R1-строка: (3 1 0 1 0 0 | 3)
+ 1 * R2-строка: (4 3 -1 0 1 0 | 6)
= Новая r-строка: (7 4 -1 0 0 0 | 9)Новая строкаr + 7x1 + 4x2 – x3 + 0R1 + 0R2 + 0x4 = 9используется для решения первого этапа, что приведёт к следующему оптимальному решению (проверьте!).
| Базис | x1 | x2 | x3 | R1 | R2 | x4 | Решение |
| r | 0 | 0 | 0 | -1 | -1 | 0 | 0 |
| x1 | 1 | 0 | 1/5 | 3/5 | -1/5 | 0 | 3/5 |
| x2 | 0 | 1 | -3/5 | -4/5 | 3/5 | 0 | 6/5 |
| x4 | 0 | 0 | 1 | 1 | -1 | 1 | 1 |
x2 + 3/5 x3 = 6/5,
x3 + x4 = 1,
x1, x2, x3, x4 >= 0.Обратите внимание, что после первого этапа исходная задача претерпела некоторые изменения, которые учитывают полученное базисное решение. Этой трансформированной задаче соответствует следующая таблица:
| Базис | x1 | x2 | x3 | x4 | Решение |
| z | -4 | -1 | 0 | 0 | 0 |
| x1 | 1 | 0 | 1/5 | 0 | 3/5 |
| x2 | 0 | 1 | -3/5 | 0 | 6/5 |
| x4 | 0 | 0 | 1 | 1 | 1 |
Поскольку базисные переменные x1 и x2 имеют ненулевые коэффициенты в z-строке, эту строку следует преобразовать.Старая z-строка: (-4 -1 0 0 | 0)
+ 4 * x1-строка: (4 0 4/5 0 | 12/5)
+ 1 * x2-строка: (0 1 -3/5 0 | 6/5)
= Новая z-строка: (0 0 1/5 0 | 18/5)Начальная таблица второго этапа примет следующий вид:
| Базис | x1 | x2 | x3 | x4 | Решение |
| z | 0 | 0 | 1/5 | 0 | 18/5 |
| x1 | 1 | 0 | 1/5 | 0 | 3/5 |
| x2 | 0 | 1 | -3/5 | 0 | 6/5 |
| x4 | 0 | 0 | 1 | 1 | 1 |
Так как решается задача минимизации, следует ввести переменную x3 в базис. Применение алгоритма симплекс-метода уже на следующей итерации приведёт к оптимальному решению (проверьте!).Удаление искусственных переменных в конце первого этапа имеет смысл только тогда, когда все они являются небазисными (как в примере 2.2-4). Однако возможна ситуация, когда в конце первого этапа искусственные переменные останутся в базисе, но будут иметь нулевые значения. В этом случае такие переменные при необходимости будут формировать часть начального базисного решения для второго этапа. При этом необходимо так изменить вычисления, выполняемые на втором этапе, чтобы искусственные переменные никогда не смогли принять положительные значения ни в каких итерациях симплекс-метода.
Существует простое правило, которое гарантирует, что нулевая базисная искусственная переменная на втором этапе никогда не станет положительной. Если в ведущем столбце коэффициент, соответствующий нулевой базисной искусственной переменной, положителен, тогда ведущий элемент определяется автоматически (поскольку ему соответствует минимальное отношение, равное нулю) и искусственная переменная на следующей итерации становится небазисной. Если ведущий элемент равен нулю, следующая итерация оставляет искусственную переменную нулевой. И наконец, рассмотрим отрицательный ведущий элемент. В этом случае минимальное отношение не ассоциируется с базисной (нулевой) искусственной переменной. Если минимальное отношение будет положительным, то на следующей итерации искусственная переменная примет положительное значение (обоснуйте это утверждение). Чтобы исключить эту возможность, мы принуждаем искусственную переменную всегда оставаться в базисном решении. Поскольку искусственная переменная равна нулю, её удаление из базисного решения не влияет на то, будет ли допустимым решение из оставшихся в базисе переменных. (Было бы полезно для читателя рассмотреть все описанные случаи с помощью симплекс-таблиц.)
Итак, правило для второго этапа заключается в том, чтобы искусственные переменные оставлять в базисе всегда, когда коэффициент в ведущем столбце положительный или отрицательный. Фактически это правило применяется в конце первого этапа, когда удаляем нулевые искусственные переменные из базисного решения, перед тем как приступить ко второму этапу.Глава 3. Особые случаи симплекс-метода.В этом разделе рассмотрим четыре особых случая, встречающихся при использовании симплекс-метода.1. Вырожденность.
2. Альтернативные оптимальные решения.
3. Неограниченные решения.
4. Отсутствие допустимых решений.При изучении этих случаев основное внимание мы уделим (1) теоретическому обоснованию причин, приводящих к таким ситуациям, и (2) их практическим интерпретациям применительно к реальным задачам.3.1 Вырожденность.В ходе выполнения симплекс-метода проверка условия допустимости может привести к неоднозначному выбору исключаемой переменной. В этом случае на следующей итерации одна или более базисных переменных примут нулевое значение. Тогда новое решение будет вырожденным.
В вырожденном решении нет никакой опасности, за исключением небольших теоретических неудобств, которые мы далее кратко обсудим. С практической точки зрения вырожденность объясняется тем, что в исходной задаче присутствует, по крайней мере, одно избыточное ограничение. Для того чтобы лучше понять практические и теоретические аспекты явления вырожденности, рассмотрим численный пример. Графическая интерпретация задачи поможет наглядно разобраться в этом явлении.Пример 3.1-1. (Вырожденное оптимальное решение)Рассмотрим следующую задачу ЛП.Максимизировать z = 3x1 + 9x2При выполнении условий
X1 + 4x2 <= 8,
X1 + 2x2 <= 4,
X1, x2 >= 0.
| Итерация | Базис | x1 | x2 | x3 | x4 | Решение |
| Начальная | z | -3 | -9 | 0 | 0 | 0 |
| Вводится x3 | x3 | 1 | 4 | 1 | 0 | 8 |
| Исключается x3 | x4 | 1 | 2 | 0 | 1 | 4 |
| Первая | z | -3/4 | 0 | 9/4 | 0 | 18 |
| Вводится x1 | x2 | 1/4 | 1 | 1/4 | 0 | 2 |
| Исключается x4 | x4 | 1/2 | 0 | -1/2 | 1 | 0 |
| Вторая | z | 0 | 0 | 3/2 | 3/2 | 18 |
| Оптимум | x2 | 0 | 1 | 1/2 | -1/2 | 2 |
| x1 | 1 | 0 | -1 | 2 | 0 |
Что же практически приводит к вырожденности решения? Рассмотрим рис. 3.4, графически представляющий решение этой задачи. Точка оптимума x1 = 0, x2 = 2 является пересечением трёх прямых. Поскольку данная задача двухмерна, эта точка переопределена (на плоскости для определения точки достаточно двух прямых), и, следовательно, одно из ограничений избыточно. На практике информация о том, что некоторые ресурсы недефицитны, может быть полезной при интерпретации результатов решения задачи. Эти сведения также могут помочь выявить неточности и ошибки в постановке исходной задачи. К сожалению, не существует способов определить избыточное ограничение непосредственно из данных симплекс-таблиц.Рис. 3.1С вычислительной и теоретической точек зрения вырожденность может привести к двум последствиям. Во-первых, в процессе вычислений может возникнуть зацикливание. Если в приведённой выше таблице сравнить первую и вторую итерации, то можно заметить, что значение целевой функции не изменилось (z = 18). Поэтому может возникнуть ситуация, когда при реализации симплекс-метода некоторая последовательность будет повторяться, не изменяя значения целевой функции и не приводя к завершению вычислительного процесса. Существуют методы, предотвращающие зацикливание, однако они значительно замедляют процесс вычислений. Поэтому в большинстве программ, реализующих симплекс-метод, отсутствуют специальные средства защиты от зацикливания, тем более, что вероятность зацикливания очень мала.
Во-вторых, последствие вырожденности решения можно обнаружить, сравнивая первую и вторую итерации в приведённой выше таблице. Хотя в этих итерациях состав базисных и небазисных переменных различен, значения всех переменных и значение целевой функции не изменяются:x1 = 0, x2 = 2, x3 = 0, x4 = 0, z = 18.Можно ли, несмотря на то что оптимальное решение не достигнуто, остановить вычисления на первой итерации (когда впервые обнаруживается вырожденность)? Ответ отрицательный, так как решение может быть только временно.3.2. Альтернативные оптимальные решения.Когда прямая (если рассматривается двухмерная задача ЛП, в общем случае – гиперплоскость), представляющая целевую функцию, параллельна прямой (гиперплоскости), соответствующей связывающему неравенству (которое в точке оптимума выполняется как точное равенство), целевая функция принимает одно и то же оптимальное значение на некотором множестве точек границы области допустимых решений. Эти решения называются альтернативными оптимальными решениями. Следующий пример показывает, что таких решений (если они существуют) бесконечное множество. Этот пример также проиллюстрирует практическую значимость альтернативных практических решений.Пример 3.2-1 (Бесконечное множество решений)
Рассмотрим следующую задачу ЛП.
Максимизировать z = 2x1 + 4x2
при ограничениях
x1 + 2x2 <= 5,
x1 + x2 <= 4,
x1, x2 >= 0.На рис. 3.2 показано множество альтернативных оптимальных решений, которые являются следствием того, что прямая, представляющая целевую функцию, параллельна прямой, соответствующей связывающему ограничению. Каждая точка отрезка BC соответствует оптимальному решению со значением целевой функции z = 10.
Рис. 3.2Последовательные итерации выполнения симплекс-метода представлены в следующей таблице.
| Итерация | Базис | x1 | x2 | x3 | x4 | Решение |
| Начальная | z | -2 | -4 | 0 | 0 | 0 |
| Вводится x2 | x3 | 1 | 2 | 1 | 0 | 5 |
| Исключается x3 | x4 | 1 | 1 | 0 | 1 | 4 |
| Первая | z | 0 | 0 | 2 | 0 | 10 |
| Вводится x1 | x2 | 1/2 | 1 | 1/2 | 0 | 5/2 |
| Исключается x4 | x4 | 1/2 | 0 | -1/2 | 1 | 3/2 |
| Вторая | z | 0 | 0 | 2 | 0 | 10 |
| (Альтернативный | x2 | 0 | 1 | 1 | -1 | 1 |
| оптимум) | x1 | 1 | 0 | -1 | 2 | 3 |
На первой итерации получаем оптимальное решение x1 = 5/2 и z = 10, которое соответствует точке B на рис. 3.2. Как узнать из симплекс-таблицы, что существует альтернативное оптимальное решение? Посмотрите на коэффициенты небазисных переменных в z-строке первой итерации. Коэффициент небазисной переменной x1 равен нулю, это означает, что данную переменную можно ввести в базис без изменения значения целевой функции, но значение самой переменной x1 изменится. Введение переменной x1 в базисное решение выполнено на второй итерации, при этом из базиса исключена переменная x4. Получено новое решение x1 = 3, x2 = 1, z = 10, которое соответствует точке C на рис. 3.2.
Симплекс-метод может определить только две угловые точки B и C. Математически мы можем найти все точки (x1’,x2’) отрезка BC как взвешенное среднее (с неотрицательными весами) точек B и C. Полагая 0 <= α <= 1 и
B: x1 = 0, x2 = 5/2,
C: x1 = 3, x2 = 1,
координаты любой точки отрезка BC можно записать следующим образом:
x1’ = α * 0 + (1 - α) * 3 = 3 – 3 α,
x2’ = α * 5/2 + (1 - α) * 1 = 1 – 3/2 α,При α = 0 (x1’,x2’) = (3, 1), что соответствует точке C. При α = 1 получаем (x1’,x2’) = (0, 5/2) – это точка B. Если значение α лежит строго между 0 и 1, получаем внутренние точки отрезка BC.На практике альтернативные оптимальные решения весьма полезны, поскольку позволяют сделать выбор среди множества решений без ухудшения значения целевой функции. Например, в рассмотренной выше задаче переменная x2, принимает нулевое значение в точке B, тогда как в других альтернативных оптимальных решениях её значение положительно. Если интерпретировать задачу как задачу организации производства двух видов товара (которые соответствуют переменным x1 и x2), то, с учётом конкуренции на рынке, более рационально производить оба вида товара, а не один. В этом случае решение, соответствующее точке C, предпочтительнее.3.3 Неограниченные решения.В некоторых задачах ЛП значения переменных могут неограниченно возрастать без нарушения ограничений. Это говорит о том, что пространство допустимых решений не ограничено, по крайней мере, по одному направлению. В результате этого целевая функция может возрастать (задача максимизации) или убывать (задача минимизации) неограниченно.
Неограниченность решения задачи свидетельствует только об одном: модель разработана не достаточно корректно. Типичные ошибки, приводящие к построению таких моделей, заключается в том, что не учитываются ограничения, не являющиеся избыточными, и не точно оцениваются параметры (коэффициенты) ограничений.
В следующем примере показано, как на основе данных, приведённых в симплекс-таблице, можно определить, когда не ограничено пространство решений и значения целевой функции.Пример 3.3–1. (Неограниченная целевая функция)Рассмотрим задачуМаксимизировать z = 2x1 + x2при выполнении условий x1 – x2 <= 10,
2x1 <= 40,
x1, x2 >= 0.Симплекс-таблица начальной итерации этой задачи имеет следующий вид.
| Базис | x1 | x2 | x3 | x4 | Решение |
| z | -2 | -1 | 0 | 0 | 0 |
| x3 | 1 | -1 | 1 | 0 | 10 |
| x4 | 2 | 0 | 0 | 1 | 40 |
Из этой таблицы видно, что в качестве вводимой переменной можно взять как x1, так и x2. Поскольку переменная x1 имеет максимальный (по абсолютной величине) отрицательный коэффициент в z-строке, именно её следует ввести в базисное решение. Однако заметим, что во всех ограничениях коэффициенты, стоящие перед переменной x2, отрицательны или равны нулю. Это означает, что значение переменной x2 может возрастать до бесконечности, и при этом не нарушается ни одно ограничение. Поскольку увеличение на 1 значения переменной x2 приводит к увеличению на 1 значения целевой функции, значит, неограниченное увеличение значения переменной x2 ведёт к неограниченному увеличению значения целевой функции. Эта ситуация проиллюстрирована на рис. 3.3. На этом рисунке видно, что пространство допустимых решений не ограничено в направлении оси x2 и значение целевой функции может быть каким угодно большим.
Рис. 3.3Правило выявления неограниченности решения следующее. Если на какой-либо симплекс-итерации коэффициенты в ограничениях для какой-нибудь небазисной переменной будут неположительными, значит, пространство решений не ограничено в направлении возрастания этой переменной. Кроме того, если коэффициент этой переменной в z-строке отрицателен, когда рассматривается задача максимизации, или положителен в задаче минимизации, целевая функция также не ограничена.3.4 Отсутствие допустимых решений.Если ограничения задачи ЛП несовместны (т.е. они не могут выполняться одновременно), то задача не имеет допустимых решений. Такая ситуация не может возникнуть, если все неравенства, составляющие систему ограничений, имеют тип «<=» с неотрицательными правыми частями, так как в этом случае дополнительные переменные могут составить допустимое решение. Для других типов ограничений мы используем искусственные переменные. И хотя в оптимальном решении все искусственные переменные в силу штрафов равны нулю, такой исход возможен только тогда, когда задача имеет непустое пространство допустимых решений. В противном случае, в оптимальном решении будет присутствовать хотя бы одна положительная искусственная переменная.
С практической точки зрения отсутствие допустимых решений свидетельствует о том, что задача плохо сформулирована.Пример 3.4-1. (Отсутствие допустимых решений)Рассмотрим следующую задачу.Максимизировать z = 3x1 + 2x2при выполнении условий 2x1 + x2 <= 2,
3x1 + 4x3 >= 12,
x1, x2 >= 0.Результат применения симплекс-метода представлен в следующей таблице.
| Итерация | Базис | x1 | x2 | x4 | x3 | R | Решение |
| Начальная | z | -3 -3M | -2 -4M | M | 0 | 0 | -12M |
| Вводится | x3 | 2 | 1 | 0 | 1 | 0 | 2 |
| Исключается | R | 3 | 4 | -1 | 0 | 1 | 12 |
| Первая | z | 1 + 5M | 0 | M | 2 + 4M | 0 | 4 – 4M |
| (псевдооптимум) | x2 | 2 | 1 | 0 | 1 | 0 | 2 |
| R | -5 | 0 | 1 | -4 | 1 | 4 |
Данные из этой таблицы показывают, что в точке оптимума искусственная переменная R имеет положительное значение (= 4), что свидетельствует об отсутствии допустимого решения. На рис. 3.4 графически представлена ситуация данной задачи. Алгоритмы симплекс-метода, допуская положительные значения искусственной переменной, по существу, превращает неравенство 3x1 + 4x3 >= 12 в 3x1 + 4x3 <= 12. (Объясните, почему так происходит.) В результате получаем то, что можно назвать псевдооптимальным решением.
Рис. 3.42. Практическая часть.Постановка задачи.Решить задачи:
при ограничениях:4x1 + 2x2 + 2x3 + x4 <= 35;
x1 + x2 + 2x3 + 3x4 <= 30;
3x1 + x2 + 2x3 + x4 <= 40;
xj >= 0, j = 1, 2, 3, 4.
при ограничениях:x1 – 4x2 – 4 <= 0;
3x1 – x2 >= 0;
x1 + x2 – 4 >= 0;
x1 >= 0, x2 >= 0.Решение.1. F = 14x1 + 10x2 + 14x3 + 14x4 → max
при ограничениях:
4x1 + 2x2 + 2x3 + x4 <= 35;
x1 + x2 + 2x3 + 3x4 <= 30;
3x1 + x2 + 2x3 + x4 <= 40;
xj >= 0, j = 1, 2, 3, 4.Переведём систему в канонический вид для решения симплексным методом.
4x1 + 2x2 + 2x3 + x4 + x5 = 35;
x1 + x2 + 2x3 + 3x4 + x6 = 30;
3x1 + x2 + 2x3 + x4 + x7 = 40;
xj >= 0, j = 1, 2, 3, 4, 5, 6, 7.14x1 + 10x2 + 14x3 + 14x4 + 0x5 + 0x6 + 0x7 → max
Ответ: max z = 225 при x2 = 5, x3 = 12,5, x7 = 10, x1 = x4 = x5 = x6 = 0.Двухэтапный метод.2. F = x1 + x2 → max
x1 – 4x2 – 4 <= 0;
3x1 – x2 >= 0;
x1 + x2 – 4 >= 0;
x1, x2 >= 0.Переведём в канонический вид и добавим искусственные переменные.
f = x1 + x2 + 0x3 + 0x4 + 0x5 – Mx0 – Mx7 → max.
x1 – 4x2 – 4 + x3 = 0;
3x1 – x2 – x4 + x6 = 0;
x1 + x2 – 4 – x5 + x7 = 0;
x1, x2, x3, x4, x5, x6, x7 >= 0;Этап 1.
Z = x6 + x7 → min
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Решение |
| x3 | 1 | -4 | 1 | 0 | 0 | 0 | 0 | 4 |
| x6 | 3 | -1 | 0 | -1 | 0 | 1 | 0 | 0 |
| x7 | 1 | 1 | 0 | 0 | -1 | 0 | 1 | 4 |
| z - c | 0 | 0 | 0 | 0 | 0 | -1 | -1 | 0 |
+
1 * x6: 3 -1 0 -1 0 1 0 0
+
1 * x7: 1 1 0 0 -1 0 1 4
= (z - c): 4 0 0 -1 -1 0 0 4
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Решение | Отношение |
| x3 | 1 | -4 | 1 | 0 | 0 | 0 | 0 | 4 | 4 |
| x6 | 3 | -1 | 0 | -1 | 0 | 1 | 0 | 0 | 0 ← |
| x7 | 1 | 1 | 0 | 0 | -1 | 0 | 1 | 4 | 4 |
| (z - c)’ | 4 | 0 | 0 | -1 | -1 | 0 | 0 | 4 |
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Решение | Отношение |
| x3 | 0 | -3 и 2/3 | 1 | 1/3 | 0 | -1/3 | 0 | 4 | |
| x1 | 1 | -1/3 | 0 | -1/3 | 0 | 1/3 | 0 | 0 | |
| x2 | 0 | 1 и 1/3 | 0 | 1/3 | 1 | -1/3 | 1 | 4 | 3 ← |
| (z - c)’ | 0 | 4/3 | 0 | 1/3 | -1 | -4/3 | 0 | 4 |
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Решение | Отношение |
| x3 | 0 | 0 | 1 | 5/4 | 11/4 | -5/4 | 11/4 | 4 | |
| x1 | 1 | 0 | 0 | -1/4 | 1/4 | 1/4 | 1/4 | 0 | |
| x2 | 0 | 1 | 0 | 1/4 | 3/4 | -1/4 | 3/4 | 4 | |
| (z - c)’ | 0 | 0 | 0 | 0 | -2 | -5/3 | -1 | 4 |
Так как достигнуто min (z - c)’ = 0, то получено допустимое базисное решение для второго этапа: x1 = 1, x2 = 3, x3 = 15. Искусственные переменные могут быть исключены.Этап 2.
Перепишем исходную задачу с учётом полученного базисного решения:
f = x1 + x2 + 0x3 + 0x4 + 0x9 → maxx3 + 5/4 x4 + 11/4 x5 = 15;
x1 – 1/4 x4 + 1/4 x5 = 1;
x2 + 1/4 x4 + 3/4 x5 = 3;
x1, x2, x3, x4, x5 >= 0.
| Базис | x1 | x2 | x3 | x4 | x5 | Решение |
| x1 | 1 | 0 | 0 | 1/4 | 1/4 | 1 |
| x2 | 0 | 1 | 0 | 1/4 | 3/4 | 3 |
| x3 | 0 | 0 | 1 | 5/4 | 11/4 | 15 |
| (f - c) | 1 | -1 | 0 | 0 | 0 | 0 |
+
1 * x1: 1 0 0 -1/4 1/4 1
+
1 * x2: 0 1 0 1/4 3/4 3
= (f-c)’: 0 0 0 0 1 4Исходное решение является оптимальным.Ответ: max (f) = 4 при x1 = 1, x2 = 3, x3 = 15, x4 = 0, x5 = 0.
Так как небазисные переменные равны нулю, задача имет множество альтернативных оптимальных решений, находящихся н отрезке AB (x1+ x2 = 4).Заключение.Симлекс-метод – это характерный пример итерационных вычислений. используемых при решении большинства оптимизационных задач.
В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.
Из теоретических положений, лежащих в основе симплекс-метода, следует, что оптимальное решение задачи линейного программирования соответствует крайней точке пространства допустимых решений задачи. В свою очередь, крайние точки пространства допустимых решений полностью определяются базисными решениями задачи ЛП, представленной в стандартной форме. Для компьютерной реализации симплекс-метода разработан способ использования искусственных переменных, что позволяет найти начальное базисное решение задачи. В этой главе также рассмотрены теоретические и практические аспекты особых случаев реализации симплекс-метода: вырожденность, альтернативные оптимальные решения, неограниченность и отсутствие допустимых решений.Литература.1. Ашманов С.А. Линейное программирование. – М.: Наука, 1981.
2. Гасс С. Линейное программирование. – М.: Физматгиз, 1961.
3. Гольштейн Е.Г., Юдин Д.Б. Линейное программирование: Теория, методы и приложения. – М.: Наука, 1969.
4. Таха, Хэмди, А. Введение в исследование операций. 6-е издание. : Пер. с англ. — М.: Издательский дом "Вильяме", 2001. — 912 с. : ил. — Парал. тит. англ.
5. Н.Ш. Кремер, Б А Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. Исследование операций в экономике: Учеб. пособие для И87 вузов —М: ЮНИТИ, 2002.— 407 с.

bukvasha.ru
Содержание.
Введение……………………………………………………………………………………….с.5.
1. Теоретическая часть.
Глава 1. Простой симплекс-метод.
1.1 Обоснование и описание вычислительной процедуры. Приведение задачи линейного программирования к стандартной форме……………………………с.7
1.2 Симплексный метод решения задач……………………………………..…… с.8.
1.3 Алгоритм симплекс-метода…………………………………………………с.10.
1.4 Решение задачи оптимизации. Построение аналитической модели……… с.12.
1.5 Приведение задачи к стандартной форме. Определение начального допустимого решения…………………………….……………………………… с.14.
Глава 2. Двухэтапный метод.
2.1 Искусственное начальное решение…………………………………………с.16.
2.2 Алгоритм двухэтапного метода……………………………………………… с.19.
Глава 3. Особые случаи симплекс-метода……………………………………………...23.
3.1 Вырожденность……………………………………………………………… с.24.
3.2 Альтернативные оптимальные решения…………………………………… с.27.
3.3 Неограниченные решения…………………………………………………… с.30.
3.4 Отсутствие допустимых решений…………………………………………… с.32.
2. Практическая часть.
2.1 Постановка задачи…………..……………………………………………………… с.34.
2.2 Решение…..…………………………………………………………………………с.36.
Заключение…………………………………………………………………………………… с.39.
Литература…………………………………………………………………………………… с.40.
Введение.
Целью данной курсовой работы является решение конкретной задачи линейного программирования. Во всех таких задачах требуется найти максимум или минимум линейной функции при условии, что её переменные принимают неотрицательные значения и удовлетворяют некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные уравнения, так и линейные неравенства. Каждая из этих задач является частным случаем общей задачи линейного программирования.
Для решения задач линейного программирования созданы специальные методы. Изучению одного из них, а именно симплекс-методу, посвящена эта курсовая работа.
В настоящее время оптимизация находит применение в науке, технике и в любой другой области человеческой деятельности.
Оптимизация – целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев — невозможно.
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:
· количество продукции — расход сырья
· количество продукции — качество продукции
Выбор компромиcного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого. Приведем примеры.
Типичный пример неправильной постановки задачи оптимизации:
«Получить максимальную производительность при минимальной себестоимости».
Ошибка заключается в том, что ставится задача поиска оптимальности 2-х величин, противоречащих друг другу по своей сути.
Правильная постановка задачи могла быть следующая:
а) получить максимальную производительность при заданной себестоимости;
б) получить минимальную себестоимость при заданной производительности;
В первом случае критерий оптимизации — производительность а во втором — себестоимость.
2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта.
3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
4. Учёт ограничений.
1. Теоретическая часть.
Глава 1. Простой симплекс-метод.
1.1 Обоснование и описание вычислительной процедуры.Приведение задачи линейного программирования к стандартной форме.
Любая задача линейного программирования приводится к стандартной (канонической) форме основной задачи линейного программирования, которая формулируется следующим образом: найти неотрицательные значения переменных X1, X2, Xn, удовлетворяющих ограничениям в виде равенств:
A11X1 + A12X2 + … + A1nXn = B1;
A21X1 + A22X2 + … + A2nXn = B2;
……………………………………
Am1X1 + Am2X2 + … + AmnXn = Bm;
Xj ≥ 0, j=1,…,n
и обращающих в максимум линейную функцию этих переменных:
E = C1X1 + C2X2 + … + CnXn Þ max
При этом также требуется, чтобы правые части равенств были неотрицательны, т.е. должны соблюдаться условия:
Bj ≥ 0, j=1,…,n
Приведение к стандартной форме необходимо, так как большинство методов решения задач линейного программирования разработано именно для стандартной формы. Для приведения к стандартной форме задачи линейного программирования может потребоваться выполнить следующие действия:
— перейти от минимизации целевой функции к ее максимизации;
— изменить знаки правых частей ограничений;
— перейти от ограничений-неравенств к равенствам;
— избавиться от переменных, не имеющих ограничений на знак.
Для решения нашей задачи воспользуемся симплекс-методом, так как этот метод предназначен для решения задач линейного программирования любой размерности.
1.2 Симплексный метод решения задач.
Симплексный метод задач линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план, и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план. Рассмотрим задачу, для которой этот план можно непосредственно записать.
Пусть дана функция, для которой необходимо найти наибольшее или наименьшее значение, если значения всех неизвестных неотрицательные.
ѓ = C0 + C1x1 + C2x2 +...+ Cnxn
и система m линейных уравнений с n неизвестными. Это называется системой ограничений:
a11x1 + a12x2 +...+ a1nxn = b1
a21x1 + a12x2 +...+ a2nxn = b2
...
am1x1 +am2x12 +...+ amnxn = bm
Целевую функцию представим в виде:
ѓ — C1x1-C2x2 -...-Cnxn = C0
Составим симплекс-таблицу. В дальнейшем будем считать, что ранг матрицы системы ограничений равен r.В системе ограничений выбран базис (основные неизвестные)x1,x2,...xn и коэффициенты в правой части не отрицательны.
В этом случае система ограничений будет иметь вид:
x1 +...+ a1,r+1xr+1 +...+ a1nxn = b1
x2 + a2,r+1xr+1 +...+ a2nxn = b2
...
xr+ ar,r+1xr+1 +...+ arnxn = br
Тогда целевая функция имеет вид:
ѓ + Cr+1xr+1 + Cr+2xr+2 -...- Cnxn = C0
Нахождение оптимального плана симплексным методом включает следующие этапы:
1. Находят опорный план.
2. Составляют симплекс-таблицу. В общем виде:
| Базисные неизвестные | Свободные члены | x1 | x2 | xr | xr+1 | xj | xn |
x1 x2 xi xr | b1 b2 bi br | 1 | 1 | 1 | a1,r+1 a2,r+1 ai,r+1 ar,r+1 | a1j a2j aij arj | a1n a2n ain arn |
| ѓ | C0 | Cr+2 | Cj | Cn |
3. В нижней строчке симплекс-таблицы необходимо отыскать отрицательные числа (не считая коэффициент Со). Если таких чисел нет, то данное базисное решение является оптимальным.
4. Пусть элемент Сj<0, тогда в j-ом столбце необходимо найти положительный элемент. Если все коэффициенты этого столбца отрицательные, то решения не существует.
5. Если положительный коэффициент в j-ом столбце один, то выбранную строку с номером i надо поделить все коэффициенты на число aij.Результат деления записываем в новую симплекс-таблицу. Если же положительных коэффициентов несколько, необходимо составить отношение bi/aij и из полученных значений выбрать наименьшее, соответствующее i-ой строке.
6. В новой симплекс-таблице в столбце базисных неизвестных вместо xi пишется xj. Продолжается заполняться таблица. В столбце с номером j необходимо получить нули(включая строку с целевой функцией). Для этого надо умножить i-ую записанную строку на нужное число и сложить с остальными строками.
В результате осуществился переход к новому базису, при этом значение целевой функции увеличилось.
1.3 Алгоритм симплекс-метода.
Пусть система приведена к каноническому виду.
X1+ q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
X2+q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
X3+q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
………………………………………………………
Xm+ qm,m+1 Xm+1 + …. + qm,m+n Xm+n =hm
В ней m базисных переменных, k свободных переменных. m+k=n — всего переменных.
Fmin= C1X1+ C2X2+ C3X3+....+ CnXn
Для дальнейших рассуждений вычислений будем пользоваться первой симплекс таблицей (таблица1).
Таблица 1.Симплекс таблица
| C | Б | H | C1 | C2 | … | Cm | Cm+1 | … | Cm+k |
| X1 | X2 | … | Xm | Xm+1 | … | Xm+k | |||
C1 C2 C3 : : Cm | X1 X2 X3 : : Xm | h2 h3 h4 : : Hm | 1 : : | 1 : : | : : : : : : | : : | q1,m+1 q2,m+1 q3,m+1 : : qm,m+1 | : : : : : : | q1,m+k q2,m+k q3,m+k : : qm,m+k |
| F0 | F1 | F2 | … | Cm | Cm+1 | … | Cm+k |
Первый столбец — коэффициенты в целевой функции при базисных переменных.
Второй столбец — базисные переменные.
Третий столбец — свободные члены (hi00).
Самая верхняя строка — коэффициенты при целевой функции.
Вторая верхняя строка — сами переменные, входящие в целевую функцию и в систему ограничений.
Основное поле симплекс метода — система коэффициентов из уравнения.
Последняя строка — служит для того, чтобы ответить на вопрос: «оптимален план или нет».
Индексная строка позволяет нам судить об оптимальности плана:
При отыскании Fmin в индексной строке должны быть отрицательные и нулевые оценки.
При отыскании Fmax в индексной строке должны быть нулевые и положительные оценки.
Переход ко второй итерации:
Для этого отыскиваем ключевой (главный) столбец и ключевую (главную) строку.
Ключевым столбцом является тот в котором находится наибольший положительный элемент индексной строки при отыскании Fmin или наименьший отрицательный элемент при отыскании Fmax.
Ключевой строкой называется та, в которой содержится наименьшее положительное частное от деления элементов столбца H на соответствующие элементы ключевого столбца.
На пересечении строки и столбца находится разрешающий элемент.
На этом этапе осуществляется к переходу к последующим итерациям.
Переход к итерациям:
Выводится базис ключевой строки, уступая место переменной из ключевого столбца со своим коэффициентом.
Заполняется строка вновь введенного базиса путем деления соответствующих элементов выделенной строки предыдущей итерации на разрешающий элемент.
Если в главной строке содержится нулевой элемент, то столбец, в котором находиться этот элемент переноситься в последующую итерацию без изменения.
Если в главном столбце имеется нулевой элемент, то строка, в которой он находиться переноситься без изменения в последующую итерацию.
Остальные элементы переносятся по формуле:
1.4 Решение задачи оптимизации. Построение аналитической модели.
В цехе имеется токарный станок и станок-автомат. Цех выпускает детали 1,2 и 3 в комплекте: на каждую деталь 1 – по 2 детали 2 и 3. Часовая производительность станков по каждой из деталей приведена в таблице:
Таблица 1. Часовая производительность станков
| Станки | Детали | ||
| 1 | 2 | 3 | |
| 1.Токарный | 5 | 5 | 10 |
| 2. Автомат | 15 | 15 | 10 |
Составить программу работы станков, при которой в течение смены (8 часов) будет выпускаться максимальное количество комплектов деталей.
Составим аналитическую модель задачи. Для этого сначала введем переменные, которые требуется определить:
X1 – время, которое работал токарный станок над деталями типа 1 в течение рабочей смены;
X2 – время, которое работал токарный станок над деталями типа 2 в течение рабочей смены;
X3 – время, которое работал токарный станок над деталями типа 3 в течение рабочей смены;
X4 – время, которое работал станок-автомат над деталями типа 1 в течение рабочей смены;
X5 – время, которое работал станок-автомат над деталями типа 2 в течение рабочей смены;
X6 – время, которое работал станок-автомат над деталями типа 3 в течение рабочей смены.
Система ограничений состоит из двух групп. Первая группа устанавливает, что каждый из станков может работать не более 8 часов в смену.
Ограничение времени работы токарного станка:
X1 + X2 + X3 £ 8;
Ограничение времени работы станка-автомата:
X4 + X5 + X6 £ 8.
Вторая группа ограничений направлена на выполнение требования о комплектации деталей: на каждую деталь 1 должно приходиться по 2 детали 2 и 3. Но перед тем, как вводить это ограничение, определим, сколько деталей каждого типа у нас будет производиться за смену:
5X1 + 15X4 — будет произведено за смену деталей типа 1;
5X2 + 15X5 — будет произведено за смену деталей типа 2;
10X3 + 10X6 — будет произведено за смену деталей типа 3.
Теперь введем сами ограничения:
2(5X1 + 15X4) = 5X2 + 15X5;
2(5X1 + 15X4) = 10X3 + 10X6.
Очевидно, что все переменные в задаче неотрицательные (объем продукции не может быть отрицательным):
X1, X2, X3, X4, X5, X6 ≥ 0.
Целевая функция в нашей задаче должна выражать количество комплектов деталей, выпускаемых за смену, поэтому сложим все выпускаемые детали и поделим на 5 (в комплект, как уже упоминалось, входят 1 деталь типа 1 и по 2 детали типа 2 и 3):
E= (5X1 + 15X4 + 5X2 + 15X5 + 10X3 + 10X6)/5 Þ max
или, если упростить это выражение, то получим:
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þmax
Целевую функцию надо максимизировать.
Таким образом, формальная постановка задачи оптимизации имеет следующий вид:
X1 + X2 + X3 £ 8;
X4 + X5 + X6 £ 8;
2(5X1 + 15X4) = 5X2 + 15X5;
2(5X1 + 15X4) = 10X1 + 10X6;
X1, X2, X3, X4, X5, X6 ≥ 0.
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þmax
1.5 Приведение задачи к стандартной форме. Определение начального допустимого решения.
Для приведения данной задачи к стандартной форме необходимо лишь перейти от ограничений – неравенств к равенствам. Для этого введем дополнительные балансовые неотрицательные переменные. Также для упрощения дальнейших вычислений разделим обе части ограничений на комплектацию деталей на 5:
X1 + X2 + X3 + X7 = 8;
X4 + X5 + X6 + X8 = 8;
2X1 – X2 + 6X4 – 3X5 = 0;
2X1 – 2X3 + 6X4 – 2X6 =0;
X1, X2, X3, X4, X5, X6, X7, X8 ≥ 0.
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þmax
где Х7, Х8 – остаточные переменные.
Итак, нашу исходную задачу мы привели к стандартной форме основной задачи линейного программирования.
Для задачи, представленной в стандартной форме, количество переменных обычно больше, чем количество ограничений. Поэтому для нахождения начального решения задачи требуется выразить m переменных (т.е. количество переменных, равное количеству уравнений) через остальные n-m переменных, принять эти n-m переменных равными нулю и, таким образом, найти значения m переменных (в заданной задаче m=4 и n=8). Переменные, значения которых принимаются равными нулю, называются небазисными, а остальные m переменных — базисными. Значения базисных переменных неотрицательны (некоторые из них могут оказаться равными нулю). Количество базисных переменных всегда равно количеству ограничений. Найденное таким образом решение называется начальным допустимым базисным решением. Оно соответствует всем ограничениям.
Начальное решение проще всего найти в случае, когда в каждом ограничении есть переменная, которая входит в него с коэффициентом 1 и при этом отсутствует в других ограничениях. Такие переменные принимаются в качестве базисных (они образуют начальный базис задачи). Остальные (небазисные) переменные принимаются равными нулю. Таким образом, базисные переменные принимают значения, равные правым частям ограничений.
Итак, для нахождения начального допустимого решения необходимо, чтобы в каждое из уравнений входила переменная с коэффициентом 1 и не входила в другие уравнения (базисная переменная). В нашем случае мы имеем только 2 базисные переменные (X7 и X8), не хватает еще двух базисных переменных. Их можно создать с помощью специального способа, который называется построением искусственного базиса.
Методы искусственного базиса предназначены для построения начального базиса (т.е. для получения начального решения) в случаях, когда его построение непосредственно на основе стандартной формы невозможно. При использовании искусственного базиса начальное решение оказывается недопустимым; от него по определенным алгоритмам выполняется переход к начальному допустимому решению.
Для того, чтобы построить искусственный базис, необходимо в каждое уравнение стандартной формы, не содержащее базисных переменных (т.е. полученное из ограничения-равенства или «не меньше»), добавить по одной искусственной переменной. В нашем случае это:
2X1 – X2 + 6X4 – 3X5 + Х9 = 0;
2X1 – 2X3 + 6X4 – 2X6 + Х10 =0.
где Х9 и Х10 – искусственные переменные, не имеющие никакого физического смысла, причем Х9, Х10 ≥0.
После построения искусственного базиса, придав нулевые значения всем переменным, кроме базисных, получим начальный базис: Х7, Х8, Х9, Х10. Всего в базисе имеется четыре переменные и их значения равны правым частям ограничений, т.е.:
Х7 = 8; Х8 = 8; Х9 = 0; Х10 = 0.
Теперь необходимо решить эту задачу, т.е. найти оптимальное допустимое решение. Для этого воспользуемся двухэтапным симплекс-методом.
Глава 2. Двухэтапный метод.
2.1 Искусственное начальное решение.
В простом симплексе при начальном допустимом базисном решении гарантировалось, что все последующие базисные решения, получаемые при выполнении симплекс-метода, также будут допустимыми. В задачах линейного программирования, где все ограничения являются неравенствами типа «<=» (с неотрицательной правой частью), дополнительные (остаточные) переменные позволяют сформировать начальное допустимое базисное решение в задачах ЛП, где есть ограничения в виде равенств или неравенств типа «>=» ?
Наиболее общим способом построения начального допустимого базисного решения задачи ЛП является использование искусственных переменных. Эти переменные в первой итерации играют роль дополнительных остаточных переменных, но на последующих итерациях от них освобождаются. Разработано два тесно связанных между собой метода нахождения начального решения, которые используют искусственные переменные: М-метод и двухэтапный метод.
Для объяснения двухэтапного метода объясним сначала концепцию М-метода.
Пусть задача ЛП записана в стандартной форме. Для любого равенства I, в котором не содержится дополнительная остаточная переменная, введём искусственную переменную Ri, которая далее войдёт в начальное базисное решение. Но поскольку эта переменная искусственна (другими словами, не имеет никакого «физического смысла» в данной задаче), необходимо сделать так, чтобы на последующих итерациях она обратилась в нуль. Для этого в выражение целевой функции вводят штраф.
Переменная Ri, с помощью достаточно большого положительного числа М, штрафуется путём ввода в целевую функцию выражения – MRi в случае максимизации целевой функции и выражения +MRi – в случае минимизации. Вследствие этого штрафа естественно предположить, что процесс оптимизации симплекс-метода приведёт к нулевому значению переменной Ri. Следующий пример проясняет детали этого метода.
Пример 3.4-1
Минимизировать z = 4x1 + x2
при выполнении условий
3x1 + x2 = 3,
4x1 + 3x2 >= 6,
x1 + 2x2 <= 4,
x1, x2 >= 0.
Стандартная форма этой задачи получается в результате добавления дополнительной (избыточной) переменной x3 во второе неравенство и дополнительной (остаточной) переменной x4 в третье неравенство. Эта задача в стандартной форме будет записана следующим образом.
Минимизировать z = 4x1 + x2
при выполнении условий
3x1 + x2 = 3,
4x1 + 3x2 – x3 = 6,
x1 + 2x2 + x4 = 4,
x1, x2, x3, x4 >= 0.
В полученной задаче первое и второе уравнения не имеют дополнительных (остаточных) переменных, которые можно ввести в базисное решение. Поэтому введём в эти уравнения искусственные переменные R1 и R2, а в целевую функцию добавим штраф MR1 + MR2. В результате получим следующую задачу ЛП.
Минимизировать z = 4x1 + x2 + MR1 + MR2
при выполнении условий
3x1 + x2 + R1 = 3,
4x1 + 3x2 – x3 + R2 = 6,
x1 + 2x2 + x4 = 4,
x1, x2, x3, x4, R1, R2 >= 0.
В этой модифицированной задаче переменные R1, R2 и x4 можно использовать в качестве начального допустимого базисного решения.
При использовании М-метода следует обратить внимание на следующие два обстоятельства.
1. Использование штрафа М может и не привести к исключению искусственной переменной в конечной симплекс-итерации. Если исходная задача линейного программирования не имеет допустимого решения (например, система ограничений несовместна), тогда в конечной симплекс-итерации, по крайней мере, одна искусственная переменная будет иметь положительное значение. Это «индикатор» того, что задача не имеет допустимого решения.
2. Теоретически применение М-метода требует, чтобы М → ∞. Однако с точки зрения компьютерных вычислений величина М должна быть конечной и, вместе с тем, достаточно большой. Как понимать термин «достаточно большая» – это открытый вопрос. Величина М должна быть настолько большой, чтобы выполнить роль «штрафа», но не слишком большой, чтобы не уменьшить точность вычислений. На практике вы должны помнить о возможных ошибках машинного округления при выполнении выполнений, в которых совместно участвуют как большие, так и малые числа.
Правильный выбор значения М зависит от данных исходной задачи. Бездумное следование теоретическому требованию, что М должно быть «очень большим», может привести к значительным ошибкам округления. Именно поэтому М-метод никогда не применяется в коммерческих программах, реализующих симплекс-метод. Вместо него используется двухэтапный метод, который будет описан в следующем разделе.
2.2 Алгоритм двухэтапного метода.
Пример 2.2-2 демонстрирует проблемы, которые могут возникнуть при М-методе вследствие ошибок округления. Двухэтапный метод полностью лишён тех недостатков, которые присущи М-методу. Как следует из названия этого метода, процесс решения задачи ЛП разбивается на два этапа. На первом этапе ведётся поиск начального допустимого базисного решения. Если такое решение найдено, то на втором этапе решается исходная задача.
Этап 1. Задача ЛП записывается в стандартной форме, а в ограничения добавляются необходимые искусственные переменные (как и в М-методе) для получения начального базисного решения. Решается задача ЛП минимизации суммы искусственных переменных с исходными ограничениями. Если минимальное значение этой новой целевой функции больше нуля, значит, исходная задача не имеет допустимого решения, и процесс вычислений заканчивается. (Напомним, что положительные значения искусственных переменных указывают на то, что исходная система ограничений несовместна.) Если новая целевая функция равна нулю, переходим ко второму этапу.
Этап 2. Оптимальное базисное решение, полученное на первом этапе, используется как начальное допустимое базисное решение исходной задачи.
Пример 2.2-3
К задаче из примера 2.2-3 применим двухэтапный метод.
Этап 1
Минимизировать r = R1 + R2
С ограничениями
3x1 + x2 + R1 = 3,
4x1 + 3x2 – x3 + R2 = 6,
x1 + 2x2 + x4 = 4,
x1, x2, x3, x4, R1, R2, >= 0.
Соответствующая таблица имеет следующий вид.
| Базис | x1 | x2 | x3 | R1 | R2 | x4 | Решение |
| r | -1 | -1 | |||||
| R1 | 3 | 1 | 1 | 3 | |||
| R2 | 4 | 3 | -1 | 1 | 6 | ||
| x4 | 1 | 2 | 1 | 4 |
Как и в М-методе, сначала вычисляется новая r-строка.
Старая r-строка: (0 0 0 -1 -1 0 | 0)
+ 1 * R1-строка: (3 1 0 1 0 0 | 3)
+ 1 * R2-строка: (4 3 -1 0 1 0 | 6)
= Новая r-строка: (7 4 -1 0 0 0 | 9)
Новая строка
r + 7x1 + 4x2 – x3 + 0R1 + 0R2 + 0x4 = 9
используется для решения первого этапа, что приведёт к следующему оптимальному решению (проверьте!).
| Базис | x1 | x2 | x3 | R1 | R2 | x4 | Решение |
| r | -1 | -1 | |||||
| x1 | 1 | 1/5 | 3/5 | -1/5 | 3/5 | ||
| x2 | 1 | -3/5 | -4/5 | 3/5 | 6/5 | ||
| x4 | 1 | 1 | -1 | 1 | 1 |
Поскольку достигнут минимум r = 0, значит, на первом этапе получено допустимое базисное решение x1 = 3/5, x2 = 6/5 и x4 = 1. Искусственные переменные полностью выполнили свою «миссию», поэтому из последней таблицы можно удалить их столбцы. Переходим ко второму этапу.
Этап 2
После удаления искусственных переменных исходная задача будет записана следующим образом.
Минимизировать z = 4x1 + x2
с ограничениями
x1 + 1/5 x3 = 3/5,
x2 + 3/5 x3 = 6/5,
x3 + x4 = 1,
x1, x2, x3, x4 >= 0.
Обратите внимание, что после первого этапа исходная задача претерпела некоторые изменения, которые учитывают полученное базисное решение. Этой трансформированной задаче соответствует следующая таблица:
| Базис | x1 | x2 | x3 | x4 | Решение |
| z | -4 | -1 | |||
| x1 | 1 | 1/5 | 3/5 | ||
| x2 | 1 | -3/5 | 6/5 | ||
| x4 | 1 | 1 | 1 |
Поскольку базисные переменные x1 и x2 имеют ненулевые коэффициенты в z-строке, эту строку следует преобразовать.
Старая z-строка: (-4 -1 0 0 | 0)
+ 4 * x1-строка: (4 0 4/5 0 | 12/5)
+ 1 * x2-строка: (0 1 -3/5 0 | 6/5)
= Новая z-строка: (0 0 1/5 0 | 18/5)
Начальная таблица второго этапа примет следующий вид:
| Базис | x1 | x2 | x3 | x4 | Решение |
| z | 1/5 | 18/5 | |||
| x1 | 1 | 1/5 | 3/5 | ||
| x2 | 1 | -3/5 | 6/5 | ||
| x4 | 1 | 1 | 1 |
Так как решается задача минимизации, следует ввести переменную x3 в базис. Применение алгоритма симплекс-метода уже на следующей итерации приведёт к оптимальному решению (проверьте!).
Удаление искусственных переменных в конце первого этапа имеет смысл только тогда, когда все они являются небазисными (как в примере 2.2-4). Однако возможна ситуация, когда в конце первого этапа искусственные переменные останутся в базисе, но будут иметь нулевые значения. В этом случае такие переменные при необходимости будут формировать часть начального базисного решения для второго этапа. При этом необходимо так изменить вычисления, выполняемые на втором этапе, чтобы искусственные переменные никогда не смогли принять положительные значения ни в каких итерациях симплекс-метода.
Существует простое правило, которое гарантирует, что нулевая базисная искусственная переменная на втором этапе никогда не станет положительной. Если в ведущем столбце коэффициент, соответствующий нулевой базисной искусственной переменной, положителен, тогда ведущий элемент определяется автоматически (поскольку ему соответствует минимальное отношение, равное нулю) и искусственная переменная на следующей итерации становится небазисной. Если ведущий элемент равен нулю, следующая итерация оставляет искусственную переменную нулевой. И наконец, рассмотрим отрицательный ведущий элемент. В этом случае минимальное отношение не ассоциируется с базисной (нулевой) искусственной переменной. Если минимальное отношение будет положительным, то на следующей итерации искусственная переменная примет положительное значение (обоснуйте это утверждение). Чтобы исключить эту возможность, мы принуждаем искусственную переменную всегда оставаться в базисном решении. Поскольку искусственная переменная равна нулю, её удаление из базисного решения не влияет на то, будет ли допустимым решение из оставшихся в базисе переменных. (Было бы полезно для читателя рассмотреть все описанные случаи с помощью симплекс-таблиц.)
Итак, правило для второго этапа заключается в том, чтобы искусственные переменные оставлять в базисе всегда, когда коэффициент в ведущем столбце положительный или отрицательный. Фактически это правило применяется в конце первого этапа, когда удаляем нулевые искусственные переменные из базисного решения, перед тем как приступить ко второму этапу.
Глава 3. Особые случаи симплекс-метода.
В этом разделе рассмотрим четыре особых случая, встречающихся при использовании симплекс-метода.
1. Вырожденность.
2. Альтернативные оптимальные решения.
3. Неограниченные решения.
4. Отсутствие допустимых решений.
При изучении этих случаев основное внимание мы уделим (1) теоретическому обоснованию причин, приводящих к таким ситуациям, и (2) их практическим интерпретациям применительно к реальным задачам.
3.1 Вырожденность.
В ходе выполнения симплекс-метода проверка условия допустимости может привести к неоднозначному выбору исключаемой переменной. В этом случае на следующей итерации одна или более базисных переменных примут нулевое значение. Тогда новое решение будет вырожденным .
В вырожденном решении нет никакой опасности, за исключением небольших теоретических неудобств, которые мы далее кратко обсудим. С практической точки зрения вырожденность объясняется тем, что в исходной задаче присутствует, по крайней мере, одно избыточное ограничение. Для того чтобы лучше понять практические и теоретические аспекты явления вырожденности, рассмотрим численный пример. Графическая интерпретация задачи поможет наглядно разобраться в этом явлении.
Пример 3.1-1. (Вырожденное оптимальное решение)
Рассмотрим следующую задачу ЛП.
Максимизировать z = 3x1 + 9x2
При выполнении условий
X1 + 4x2 <= 8,
X1 + 2x2 <= 4,
X1, x2 >= 0.
| Итерация | Базис | x1 | x2 | x3 | x4 | Решение |
| Начальная | z | -3 | -9 | |||
| Вводится x3 | x3 | 1 | 4 | 1 | 8 | |
| Исключается x3 | x4 | 1 | 2 | 1 | 4 | |
| Первая | z | -3/4 | 9/4 | 18 | ||
| Вводится x1 | x2 | 1/4 | 1 | 1/4 | 2 | |
| Исключается x4 | x4 | 1/2 | -1/2 | 1 | ||
| Вторая | z | 3/2 | 3/2 | 18 | ||
| Оптимум | x2 | 1 | 1/2 | -1/2 | 2 | |
| x1 | 1 | -1 | 2 |
На начальной итерации в качестве исключаемой можно выбрать как переменную x3, так и x4. Если оставить в базисе переменную x4, на следующей итерации она примет значение 0 (как показано в таблице), т.е. получим вырожденное базисное решение. Оптимальное решение получается на следующей итерации.
Что же практически приводит к вырожденности решения? Рассмотрим рис. 3.4, графически представляющий решение этой задачи. Точка оптимума x1 = 0, x2 = 2 является пересечением трёх прямых. Поскольку данная задача двухмерна, эта точка переопределена (на плоскости для определения точки достаточно двух прямых), и, следовательно, одно из ограничений избыточно. На практике информация о том, что некоторые ресурсы недефицитны, может быть полезной при интерпретации результатов решения задачи. Эти сведения также могут помочь выявить неточности и ошибки в постановке исходной задачи. К сожалению, не существует способов определить избыточное ограничение непосредственно из данных симплекс-таблиц.
Рис. 3.1
С вычислительной и теоретической точек зрения вырожденность может привести к двум последствиям. Во-первых, в процессе вычислений может возникнуть зацикливание. Если в приведённой выше таблице сравнить первую и вторую итерации, то можно заметить, что значение целевой функции не изменилось (z = 18). Поэтому может возникнуть ситуация, когда при реализации симплекс-метода некоторая последовательность будет повторяться, не изменяя значения целевой функции и не приводя к завершению вычислительного процесса. Существуют методы, предотвращающие зацикливание, однако они значительно замедляют процесс вычислений. Поэтому в большинстве программ, реализующих симплекс-метод, отсутствуют специальные средства защиты от зацикливания, тем более, что вероятность зацикливания очень мала.
Во-вторых, последствие вырожденности решения можно обнаружить, сравнивая первую и вторую итерации в приведённой выше таблице. Хотя в этих итерациях состав базисных и небазисных переменных различен, значения всех переменных и значение целевой функции не изменяются:
x1 = 0, x2 = 2, x3 = 0, x4 = 0, z = 18.
Можно ли, несмотря на то что оптимальное решение не достигнуто, остановить вычисления на первой итерации (когда впервые обнаруживается вырожденность)? Ответ отрицательный, так как решение может быть только временно .
3.2. Альтернативные оптимальные решения.
Когда прямая (если рассматривается двухмерная задача ЛП, в общем случае – гиперплоскость), представляющая целевую функцию, параллельна прямой (гиперплоскости), соответствующей связывающему неравенству (которое в точке оптимума выполняется как точное равенство), целевая функция принимает одно и то же оптимальное значение на некотором множестве точек границы области допустимых решений. Эти решения называются альтернативными оптимальными решениями. Следующий пример показывает, что таких решений (если они существуют) бесконечное множество. Этот пример также проиллюстрирует практическую значимость альтернативных практических решений.
Пример 3.2-1 (Бесконечное множество решений)
Рассмотрим следующую задачу ЛП.
Максимизировать z = 2x1 + 4x2
при ограничениях
x1 + 2x2 <= 5,
x1 + x2 <= 4,
x1, x2 >= 0.
На рис. 3.2 показано множество альтернативных оптимальных решений, которые являются следствием того, что прямая, представляющая целевую функцию, параллельна прямой, соответствующей связывающему ограничению. Каждая точка отрезка BC соответствует оптимальному решению со значением целевой функции z = 10.
Рис. 3.2
Последовательные итерации выполнения симплекс-метода представлены в следующей таблице.
| Итерация | Базис | x1 | x2 | x3 | x4 | Решение |
| Начальная | z | -2 | -4 | |||
| Вводится x2 | x3 | 1 | 2 | 1 | 5 | |
| Исключается x3 | x4 | 1 | 1 | 1 | 4 | |
| Первая | z | 2 | 10 | |||
| Вводится x1 | x2 | 1/2 | 1 | 1/2 | 5/2 | |
| Исключается x4 | x4 | 1/2 | -1/2 | 1 | 3/2 | |
| Вторая | z | 2 | 10 | |||
| (Альтернативный | x2 | 1 | 1 | -1 | 1 | |
| оптимум) | x1 | 1 | -1 | 2 | 3 |
На первой итерации получаем оптимальное решение x1 = 5/2 и z = 10, которое соответствует точке B на рис. 3.2. Как узнать из симплекс-таблицы, что существует альтернативное оптимальное решение? Посмотрите на коэффициенты небазисных переменных в z-строке первой итерации. Коэффициент небазисной переменной x1 равен нулю, это означает, что данную переменную можно ввести в базис без изменения значения целевой функции, но значение самой переменной x1 изменится. Введение переменной x1 в базисное решение выполнено на второй итерации, при этом из базиса исключена переменная x4. Получено новое решение x1 = 3, x2 = 1, z = 10, которое соответствует точке Cна рис. 3.2.
Симплекс-метод может определить только две угловые точки Bи C. Математически мы можем найти все точки (x1’,x2’) отрезка BCкак взвешенное среднее (с неотрицательными весами) точек B и C. Полагая 0 <= α <= 1 и
B: x1 = 0, x2 = 5/2,
C: x1 = 3, x2 = 1,
координаты любой точки отрезка BC можно записать следующим образом:
x1’ = α * 0 + (1 — α) * 3 = 3 – 3 α,
x2’ = α * 5/2 + (1 — α) * 1 = 1 – 3/2 α,
При α = 0 (x1’,x2’) = (3, 1), что соответствует точке C. При α = 1 получаем (x1’,x2’) = (0, 5/2) – это точка B. Если значение α лежит строго между 0 и 1, получаем внутренние точки отрезка BC.
На практике альтернативные оптимальные решения весьма полезны, поскольку позволяют сделать выбор среди множества решений без ухудшения значения целевой функции. Например, в рассмотренной выше задаче переменная x2, принимает нулевое значение в точке B, тогда как в других альтернативных оптимальных решениях её значение положительно. Если интерпретировать задачу как задачу организации производства двух видов товара (которые соответствуют переменным x1 и x2), то, с учётом конкуренции на рынке, более рационально производить оба вида товара, а не один. В этом случае решение, соответствующее точке C, предпочтительнее.
3.3 Неограниченные решения.
В некоторых задачах ЛП значения переменных могут неограниченно возрастать без нарушения ограничений. Это говорит о том, что пространство допустимых решений не ограничено, по крайней мере, по одному направлению. В результате этого целевая функция может возрастать (задача максимизации) или убывать (задача минимизации) неограниченно.
Неограниченность решения задачи свидетельствует только об одном: модель разработана не достаточно корректно. Типичные ошибки, приводящие к построению таких моделей, заключается в том, что не учитываются ограничения, не являющиеся избыточными, и не точно оцениваются параметры (коэффициенты) ограничений.
В следующем примере показано, как на основе данных, приведённых в симплекс-таблице, можно определить, когда не ограничено пространство решений и значения целевой функции.
Пример 3.3–1. (Неограниченная целевая функция)
Рассмотрим задачу
Максимизировать z = 2x1 + x2
при выполнении условий
x1 – x2 <= 10,
2x1 <= 40,
x1, x2 >= 0.
Симплекс-таблица начальной итерации этой задачи имеет следующий вид.
| Базис | x1 | x2 | x3 | x4 | Решение |
| z | -2 | -1 | |||
| x3 | 1 | -1 | 1 | 10 | |
| x4 | 2 | 1 | 40 |
Из этой таблицы видно, что в качестве вводимой переменной можно взять как x1, так и x2. Поскольку переменная x1 имеет максимальный (по абсолютной величине) отрицательный коэффициент в z-строке, именно её следует ввести в базисное решение. Однако заметим, что во всех ограничениях коэффициенты, стоящие перед переменной x2, отрицательны или равны нулю. Это означает, что значение переменной x2 может возрастать до бесконечности, и при этом не нарушается ни одно ограничение. Поскольку увеличение на 1 значения переменной x2 приводит к увеличению на 1 значения целевой функции, значит, неограниченное увеличение значения переменной x2 ведёт к неограниченному увеличению значения целевой функции. Эта ситуация проиллюстрирована на рис. 3.3. На этом рисунке видно, что пространство допустимых решений не ограничено в направлении оси x2 и значение целевой функции может быть каким угодно большим.
Рис. 3.3
Правило выявления неограниченности решения следующее. Если на какой-либо симплекс-итерации коэффициенты в ограничениях для какой-нибудь небазисной переменной будут неположительными, значит, пространство решений не ограничено в направлении возрастания этой переменной. Кроме того, если коэффициент этой переменной в z-строке отрицателен, когда рассматривается задача максимизации, или положителен в задаче минимизации, целевая функция также не ограничена.
3.4 Отсутствие допустимых решений.
Если ограничения задачи ЛП несовместны (т.е. они не могут выполняться одновременно), то задача не имеет допустимых решений. Такая ситуация не может возникнуть, если все неравенства, составляющие систему ограничений, имеют тип «<=» с неотрицательными правыми частями, так как в этом случае дополнительные переменные могут составить допустимое решение. Для других типов ограничений мы используем искусственные переменные. И хотя в оптимальном решении все искусственные переменные в силу штрафов равны нулю, такой исход возможен только тогда, когда задача имеет непустое пространство допустимых решений. В противном случае, в оптимальном решении будет присутствовать хотя бы одна положительная искусственная переменная.
С практической точки зрения отсутствие допустимых решений свидетельствует о том, что задача плохо сформулирована.
Пример 3.4-1. (Отсутствие допустимых решений)
Рассмотрим следующую задачу.
Максимизировать z = 3x1 + 2x2
при выполнении условий
2x1 + x2 <= 2,
3x1 + 4x3 >= 12,
x1, x2 >= 0.
Результат применения симплекс-метода представлен в следующей таблице.
| Итерация | Базис | x1 | x2 | x4 | x3 | R | Решение |
| Начальная | z | -3 -3M | -2 -4M | M | -12M | ||
| Вводится | x3 | 2 | 1 | 1 | 2 | ||
| Исключается | R | 3 | 4 | -1 | 1 | 12 | |
| Первая | z | 1 + 5M | M | 2 + 4M | 4 – 4M | ||
| (псевдооптимум) | x2 | 2 | 1 | 1 | 2 | ||
| R | -5 | 1 | -4 | 1 | 4 |
Данные из этой таблицы показывают, что в точке оптимума искусственная переменная Rимеет положительное значение (= 4), что свидетельствует об отсутствии допустимого решения. На рис. 3.4 графически представлена ситуация данной задачи. Алгоритмы симплекс-метода, допуская положительные значения искусственной переменной, по существу, превращает неравенство 3x1 + 4x3 >= 12 в 3x1 + 4x3 <= 12. (Объясните, почему так происходит.) В результате получаем то, что можно назвать псевдооптимальным решением .
Рис. 3.4
2. Практическая часть.
Постановка задачи.
Решить задачи:
при ограничениях:
4x1 + 2x2 + 2x3 + x4 <= 35;
x1 + x2 + 2x3 + 3x4 <= 30;
3x1 + x2 + 2x3 + x4 <= 40;
xj >= 0, j = 1, 2, 3, 4.
при ограничениях:
x1 – 4x2 – 4 <= 0;
3x1 – x2 >= 0;
x1 + x2 – 4 >= 0;
x1 >= 0, x2 >= 0.
Решение.
1. F = 14x1 + 10x2 + 14x3 + 14x4→ max
при ограничениях:
4x1 + 2x2 + 2x3 + x4 <= 35;
x1 + x2 + 2x3 + 3x4 <= 30;
3x1 + x2 + 2x3 + x4 <= 40;
xj >= 0, j = 1, 2, 3, 4.
Переведём систему в канонический вид для решения симплексным методом.
4x1 + 2x2 + 2x3 + x4 + x5 = 35;
x1 + x2 + 2x3 + 3x4 + x6 = 30;
3x1 + x2 + 2x3 + x4 + x7= 40;
xj >= 0, j = 1, 2, 3, 4, 5, 6, 7.
14x1 + 10x2 + 14x3 + 14x4 + 0x5 + 0x6 + 0x7 → max
Ответ: maxz= 225 при x2 = 5, x3 = 12,5, x7 = 10, x1 = x4 = x5 = x6 = 0.
Двухэтапный метод.
2. F = x1 + x2→ max
при ограничениях:
x1 – 4x2 – 4 <= 0;
3x1 – x2 >= 0;
x1 + x2 – 4 >= 0;
x1, x2 >= 0.
Переведём в канонический вид и добавим искусственные переменные.
f = x1 + x2 + 0x3 + 0x4 + 0x5 – Mx0 – Mx7 → max.
x1 – 4x2 – 4 + x3 = 0;
3x1 – x2 – x4 + x6 = 0;
x1 + x2 – 4 – x5 + x7 = 0;
x1, x2, x3, x4, x5, x6, x7 >= 0;
Этап 1.
Z = x6 + x7 → min
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Решение |
| x3 | 1 | -4 | 1 | 4 | ||||
| x6 | 3 | -1 | -1 | 1 | ||||
| x7 | 1 | 1 | -1 | 1 | 4 | |||
| z — c | -1 | -1 |
Так как базисные переменные x6 и x7 имеют ненулевые коэффициенты в (z — c) – строке, эту строку следует преобразовать:
(z- c): 0 0 0 0 0 -1 -1 0
+
1 * x6: 3 -1 0 -1 0 1 0 0
+
1 * x7: 1 1 0 0 -1 0 1 4
= (z- c): 4 0 0 -1 -1 0 0 4
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Решение | Отношение |
| x3 | 1 | -4 | 1 | 4 | 4 | ||||
| x6 | 3 | -1 | -1 | 1 | 0 ← | ||||
| x7 | 1 | 1 | -1 | 1 | 4 | 4 | |||
| (z — c)’ | 4 | -1 | -1 | 4 |
↑
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Решение | Отношение |
| x3 | -3 и 2/3 | 1 | 1/3 | -1/3 | 4 | ||||
| x1 | 1 | -1/3 | -1/3 | 1/3 | |||||
| x2 | 1 и 1/3 | 1/3 | 1 | -1/3 | 1 | 4 | 3 ← | ||
| (z — c)’ | 4/3 | 1/3 | -1 | -4/3 | 4 |
↑
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Решение | Отношение |
| x3 | 1 | 5/4 | 11/4 | -5/4 | 11/4 | 4 | |||
| x1 | 1 | -1/4 | 1/4 | 1/4 | 1/4 | ||||
| x2 | 1 | 1/4 | 3/4 | -1/4 | 3/4 | 4 | |||
| (z — c)’ | -2 | -5/3 | -1 | 4 |
Так как достигнуто min (z — c)’ = 0, то получено допустимое базисное решение для второго этапа: x1 = 1, x2 = 3, x3 = 15. Искусственные переменные могут быть исключены.
Этап 2.
Перепишем исходную задачу с учётом полученного базисного решения:
f = x1 + x2 + 0x3 + 0x4 + 0x9→ max
x3 + 5/4 x4 + 11/4 x5 = 15;
x1 – 1/4 x4 + 1/4 x5 = 1;
x2 + 1/4 x4 + 3/4 x5 = 3;
x1, x2, x3, x4, x5 >= 0.
| Базис | x1 | x2 | x3 | x4 | x5 | Решение |
| x1 | 1 | 1/4 | 1/4 | 1 | ||
| x2 | 1 | 1/4 | 3/4 | 3 | ||
| x3 | 1 | 5/4 | 11/4 | 15 | ||
| (f — c) | 1 | -1 |
Согласуем значения в строке (f — c) с остальной частью таблицы:
(f — c): -1 -1 0 0 0 0
+
1 * x1: 1 0 0 -1/4 1/4 1
+
1 * x2: 0 1 0 1/4 3/4 3
= (f-c)’: 0 0 0 0 1 4
Исходное решение является оптимальным.
Ответ: max (f) = 4 при x1 = 1, x2 = 3, x3 = 15, x4 = 0, x5 = 0.
Так как небазисные переменные равны нулю, задача имет множество альтернативных оптимальных решений, находящихся н отрезке AB (x1+ x2 = 4).
Заключение.
Симлекс-метод – это характерный пример итерационных вычислений. используемых при решении большинства оптимизационных задач.
В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.
Из теоретических положений, лежащих в основе симплекс-метода, следует, что оптимальное решение задачи линейного программирования соответствует крайней точке пространства допустимых решений задачи. В свою очередь, крайние точки пространства допустимых решений полностью определяются базисными решениями задачи ЛП, представленной в стандартной форме. Для компьютерной реализации симплекс-метода разработан способ использования искусственных переменных, что позволяет найти начальное базисное решение задачи. В этой главе также рассмотрены теоретические и практические аспекты особых случаев реализации симплекс-метода: вырожденность, альтернативные оптимальные решения, неограниченность и отсутствие допустимых решений.
Литература.
1. Ашманов С.А. Линейное программирование. – М.: Наука, 1981.
2. Гасс С. Линейное программирование. – М.: Физматгиз, 1961.
3. Гольштейн Е.Г., Юдин Д.Б. Линейное программирование: Теория, методы и приложения. – М.: Наука, 1969.
4. Таха, Хэмди, А. Введение в исследование операций. 6-е издание.: Пер. с англ. — М.: Издательский дом «Вильяме», 2001. — 912 с.: ил. — Парал. тит. англ.
5. Н.Ш. Кремер, Б А Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. Исследование операций в экономике: Учеб. пособие для И87 вузов —М: ЮНИТИ, 2002.— 407 с.
www.ronl.ru
Министерство образования и науки Украины
Донбасская государственная машиностроительная академия
Факультет автоматизации машиностроения и информационных технологий
Кафедра интеллектуальных систем принятия решений
подисциплине «МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ»
на тему
« Симплексный метод решения ЗЛП»
Выполнила
подпись Германенко М.А.
подпись Протыняк С. И.
подпись Сташкевич И. И.
реферат
Курсовая работа по дисциплине «Математические методы исследования операций» на тему: «Симплексный метод решения ЗЛП» студентки группы ИС 09–1 Германенко М.А. содержит 53 страницы машинописного текста, 4 рисунка, 4 таблицы, 19 страниц приложения.
Данная работа имеет своей целью систематизацию и закрепление полученных знаний и практических умений, углубление теоретических знаний в соответствии с заданной темой, формирование умения применять теоретические знания при решении поставленных задач
В результате выполнения курсовой работы студент должен знать методы решения задач, уметь работать с научной литературой, строить математическую модель, использовать стандартный программный продукт при решении задач, осуществлять программную реализацию заданного метода решения задачи.
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ, ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ, ОПТИМИЗАЦИОННЫЕ ЗАДАЧИ, ЭМЕРДЖЕНТНОСТЬ, СИМПЛЕКС-МЕТОД, ПРЯМАЯ ЗАДАЧА, ДВОЙСТВЕННАЯ ЗАДАЧА, УСЛОВИЕ НЕОТРИЦАТЕЛЬНОСТИ, ЦЕЛЕВАЯ ФУНКЦИЯ, БАЗИСНОЕ РЕШЕНИЕ, ПРОГРАММНЫЙ ПРОДУКТ.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ…………………………………………………………………4
І Основные теоретические положения симплексного метода решения ЗЛП…………………………………………………….…6
1.1 Теория линейного программирования……………………………...6
1.2 Общий вид задач линейного программирования………………….8
1.3 Методы решения задач линейного программирования…………..10
1.4 Общая характеристика симплекс-метода……………………………12
ІІ РЕШЕНИЕ ЗЛП СИМПЛЕКСНЫМ МЕТОДОМ………………..…..14
2.1 Примеры использования симплекс-метода в экономике…………14
2.2 Алгоритм решения ЗЛП симплексным методом……………………15
2.3 Решение задачи линейного программирования симплекс-
методом…………………………………………………………………...17
2.4 Двойственная задача………………………………………………....23
ІІІ КОМПЬЮТЕРНАЯ РЕАЛИЗАЦИЯ СИМПЛЕКС-МЕТОДА ПРИ РЕШЕНИИ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ……….....28
3.1 Описание программного продукта……………………………...…28
3.2 Тестирование программного продукта………………….…………30
ВЫВОДЫ………………………………………………………………….32
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ………………………….34
ПРИЛОЖЕНИЕ А………………………………………………………...35
ВВЕДЕНИЕ
Проникновение математики в экономическую науку связано с преодолением значительных трудностей. В этом отчасти была «повинна» математика, развивающаяся на протяжении нескольких веков в основном в связи с потребностями физики и техники. Но главные причины лежат все же в природе экономических процессов, в специфике экономической науки.
Большинство объектов, изучаемых экономической наукой, может быть охарактеризовано кибернетическим понятием – сложная система.
Наиболее распространено понимание системы как совокупности элементов, находящихся во взаимодействии и образующих некоторую целостность, единство. Важным качеством любой системы является эмерджентность– наличие таких свойств, которые не присущи ни одному из элементов, входящих в систему. Поэтому при изучении систем недостаточно пользоваться методом их расчленения на элементы с последующим изучением этих элементов в отдельности. Одна из трудностей экономических исследований – в том, что почти не существует экономических объектов, которые можно было бы рассматривать как отдельные (внесистемные) элементы.
Сложность системы определяется количеством входящих в нее элементов, связями между этими элементами, а также взаимоотношениями между системой и средой. Экономика страны обладает всеми признаками очень сложной системы. Она объединяет огромное число элементов, отличается многообразием внутренних связей и связей с другими системами (природная среда, экономика других стран и т.д.). В народном хозяйстве взаимодействуют природные, технологические, социальные процессы, объективные и субъективные факторы.
Сложность экономики иногда рассматривалась как обоснование невозможности ее моделирования, изучения средствами математики. Но такая точка зрения в принципе неверна. Моделировать можно объект любой природы и любой сложности. И как раз сложные объекты представляют наибольший интерес для моделирования; именно здесь моделирование может дать результаты, которые нельзя получить другими способами исследования.
Потенциальная возможность математического моделирования любых экономических объектов и процессов не означает, разумеется, ее успешной осуществимости при данном уровне экономических и математических знаний, имеющейся конкретной информации и вычислительной технике. И хотя нельзя указать абсолютные границы математической формализации экономических проблем, всегда будут существовать еще неформализованные проблемы, а также ситуации, где математическое моделирование недостаточно эффективно.
І Основные теоретические положения симплексного метода решения ЗЛП
1.1 Теория линейного программирования
Как известно, в практике хозяйственной деятельности выбор между различными вариантами (планами, решениями) предполагает поиск наилучшего. Когда хозяйка отправляется на рынок для закупки мяса, а проектировщик стремится найти оптимальный способ размещения станков, они занимаются поисками вариантов, требующих минимума затрат или максимума результата с учетом определенных ограничений (денег, ресурсов, времени).
Решить подобную задачу бывает непросто, особенно при наличии большого числа вариантов. Время и затраты при выборе оптимума не всегда оправданны: издержки поиска и перебора вариантов могут превысить достигнутый выигрыш.Как показывает практика, опыт и интуиция оказываются недостаточными для обоснования оптимального решения.Более надежный и эффективный способ — использование математических (количественных) подходов и расчетов. Однако математические подходы и обоснования длительное время игнорировались теоретиками, делавшими “погоду” в экономической науке. Многие важные работы были заморожены, публикации экономистов-математиков тормозились и ограничивались. И все же в тот период математические изыскания продолжались, даже в условиях гонения на математиков были достигнуты блестящие результаты.Одним из наиболее значительных и ярких достижений в области экономико-математических исследований было открытие Леонидом Витальевичем Канторовичем (1912—1986) Метода линейного программирования.
Линейное программирование — решение линейных уравнений (уравнений первой степени) посредством составления программ и применения различных методов их последовательного решения, существенно облегчающих расчеты и достижение искомых результатов.
Условия задачи на оптимум и цель, которая должна быть достигнута, могут быть выражены с помощью системы линейных уравнений. Поскольку уравнений меньше, чем неизвестных, задача обычно имеет не одно, а множество решений. Найти же нужно одно, согласно терминологии математиков, экстремальное решение.В задаче по оптимизации выпуска фанеры Канторович представил переменную, которую следовало максимизировать в виде суммы стоимостей продукции, производимой всеми станками. Ограничители были представлены в форме уравнений, устанавливающих соотношения между всеми затрачиваемыми в производстве факторами (древесиной, клеем, электроэнергией, рабочим временем) и количеством выпускаемой продукции (фанеры) на каждом из станков. Для показателей факторов производства были введены коэффициенты, названные разрешающими множителями, или мультипликаторами. С их помощью разрешается поставленная задача. Если известны значения разрешающих множителей, то искомые величины, в частности, оптимальный объем выпускаемой продукции, могут быть сравнительно легко найдены.
.Для любой задачи линейного программирования существует сопряженная ей, или двойственная, задача. Если прямая задача заключается в минимизации целевой функции, то двойственная — в максимизации.Двойственные оценки дают принципиальную возможность соизмерять не только ценовые, затратные показатели, но и полезности. При этом двойственные, взаимосвязанные оценки соответствуют конкретным условиям. Если изменяются условия, то изменяются и оценки. В известной мере поиск оптимума — это определение общественно необходимых затрат, учитывающих, с одной стороны, трудовые, стоимостные затраты, а с другой стороны, общественные потребности, полезности продукта для потребителей.
1.2 Общий вид задач линейного программирования
В общем случае задача линейного программирования может быть записана в таком виде(формула 1.1)
Z(X)=c1 x1 +c2 x2 +…+cn xn → max(min), (1.1)
a11 x1 +a12 x2 +…+a1n xn =b1 ,
…………………………
ai1 x1 +ai2 x2 +…+ain xn =bi ,
a(i+1)1 x1 +a(i+1)2 x2 +…+a(i+1)n xn ≤bi+1 (1.2)
………………………..
am1 x1 +am2 x2 +…+amn xn ≤bm
xj ≥0, j=1,2,…,t; t≤n. (1.3)
Данная запись означает следующее: найти экстремум целевой функции (1.1) и соответствующие ему переменные X=(X1, X2 ,...,Xn ) при условии, что эти переменные удовлетворяют системе ограничений (1.2) и условиям неотрицательности (1.3).
Допустимым решением (планом) задачи линейного программирования называется любой n-мерный вектор X=(X1, X2 ,...,Xn ), удовлетворяющий системе ограничений и условиям неотрицательности.
Множество допустимых решений (планов) задачи образует область допустимых решений(ОДР).
Оптимальным решением(планом) задачи линейного программирования называется такое допустимое решение (план) задачи, при котором целевая функция достигает экстремума.
Каноническая форма задачи линейного программирования.
В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися.
В том случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической.
Она может быть представлена в координатной, векторной и матричной записи.
Каноническая задача линейного программирования в координатной записи имеет вид (формула 1.4):
Z(X)=c1 x1 +c2 x2 +…+cn xn → max (1.4)
a11 x1 +a12 x2 +…+a1n xn ≤b1 ,
a21 x1 +a22 x2 +…+a2n xn ≤b2
… … … … … … … …
am1 x1 +am2 x2 +…+amn xn ≤bm
xj ≥0, j=1,2,…,n.
Каноническая задача линейного программирования в матричной записи имеет вид (формулы 1.5, 1.6):
Z(X)=CX → max(min), (1.5)
AX=A0, Y≥θ,
A=, X=, A0=(1.6)
Здесь:
— А — матрица коэффициентов системы уравнений
— Х — матрица-столбец переменных задачи
— Ао — матрица-столбец правых частей системы ограничений
Приведение общей задачи линейного программирования к канонической форме.
В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако при составлении моделей экономических задач ограничения в основном формируются в виде системы неравенств, поэтому необходимо уметь переходить от системы неравенств к системе уравнений.
Возьмем линейное неравенство a1 x1 +a2 x2 +...+an xn ≤b и прибавим.
Это может быть сделано следующим образом: к его левой части некоторую величину xn+1, такую, что неравенство превратилось в равенство a1 x1 +a2 x2 +...+an xn +xn+1 =b. При этом данная величина xn+1 является неотрицательной.
1.3 Методы решения задач линейного программирования
Методы решения задач линейного программирования относятся к вычислительной математике, а не к экономике. Однако экономисту полезно знать о свойствах интеллектуального инструмента, которым он пользуется.
С ростом мощности компьютеров необходимость применения изощренных методов снижается, поскольку во многих случаях время счета перестает быть лимитирующим фактором, поскольку весьма мало (доли секунд). Поэтому мы разберем лишь три метода.
Простой перебор. Возьмем некоторый многомерный параллелепипед, в котором лежит многогранник, задаваемый ограничениями. Как его построить? Например, если имеется ограничение типа 2Х1 + 5Х2 ≤ 10, то, очевидно, 0 ≤ Х1 ≤ 10/2 = 5 и 0 ≤ Х2 ≤ 10/2 = 5. Аналогичным образом от линейных ограничений общего вида можно перейти к ограничениям на отдельные переменные. Остается взять максимальные границы по каждой переменной. Если многогранник, задаваемый ограничениями, неограничен, как было в задаче о диете, можно похожим, но несколько более сложным образом выделить его «обращенную» к началу координат часть, содержащую решение, и заключить ее в многомерный параллелепипед.
Проведем перебор точек параллелепипеда с шагом 1/10n последовательно при n=2,3,…, вычисляя значения целевой функции и проверяя наличие ограничений. Из всех точек, удовлетворяющих ограничениям, возьмем ту, в которой целевая функция максимальна. Решение найдено! (Более строго выражаясь, найдено с точностью до 1/10n ).
Направленный перебор.Начнем с точки, удовлетворяющей ограничениям (ее можно найти простым перебором). Будем последовательно (или случайно — т.н. метод случайного поиска) менять ее координаты на определенную величину ∆, каждый раз в точку с более высоким значением целевой функции. Если выйдем на плоскость ограничения, будем двигаться по ней (находя одну из координат по уравнению ограничения). Затем движение по ребру (когда два ограничения-неравенства переходят в равенства)… Остановка — в вершине линейного многогранника. Решение найдено! (Более строго выражаясь, найдено с точностью до ∆; если необходимо, в окрестности найденного решения проводим направленный перебор с шагом ∆/2, ∆/4 и т.д.)
Симплекс-метод. Этот один из первых специализированных методов оптимизации, нацеленный на решение задач линейного программирования, в то время как методы простого и направленного перебора могут быть применены для решения практически любой задачи оптимизации. Он был предложен американцем Г. Данцигом в 1951 г. Симплекс-метод состоит в продвижении по выпуклому многограннику ограничений от вершины к вершине, при котором на каждом шаге значение целевой функции улучшается до тех пор, пока не будет достигнут оптимум.
1.4 Общая характеристика симплекс-метода
Симплекс метод — это характерный пример итерационных вычислений, используемых при решении большинства оптимизационных задач. В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению (рис.1.1).
Рисунок 1.1 – Переход от одной вершины к другой
Симплекс-метод, известный также в нашей литературе под названием метода последовательного улучшения плана, впервые разработал Г.Данциг в 1947 г. Этот метод позволяет переходить от одного допустимого базисного решения к другому, причем так, что значения целевой функции непрерывно возрастают. В результате оптимальное решение находят за конечное число шагов.
Симплекс метод — универсальный метод для решения линейной системы уравнений или неравенств и линейного функционала.
Общая идея симплексного метода (метода последовательного улучшения плана) для решения ЗЛП (задачи линейного программирования) состоит:
— умение находить начальный опорный план;
— наличие признака оптимальности опорного плана;
-умение переходить к нехудшему опорному плану.
ІІ РЕШЕНИЕ ЗЛП СИМПЛЕКСНЫМ МЕТОДОМ
2.1 Примеры использования симплекс-метода в экономике
Задачи ЛП нашли широкое применение в экономике. Рассмотрим это на примерах.
Пример 1. Рассматривается работа промышленного предприятия под углом зрения его рентабельности, причём приводится ряд мер с целью повышения этой рентабельности. Показатель эффективности — прибыль ( или средняя прибыль ), приносимая предприятием за хозяйственный год.
Пример 2. Группа истребителей поднимается в воздух для перехвата одиночного самолёта противника. Цель операции — сбить самолёт. Показатель эффективности — вероятность поражения цели.
Пример 3. Ремонтная мастерская занимается обслуживанием машин; её рентабельность определяется количеством машин, обслуженных в течение дня. Показатель эффективности — среднее число машин, обслуженных за день.
Пример 4. Группа радиолокационных станций в определённом районе ведёт наблюдение за воздушным пространством. Задача группы — обнаружить любой самолёт, если он появится в районе. Показатель эффективности — вероятность обнаружения любого самолёта, появившегося в районе.
Пример 5. Предпринимается ряд мер по повышения надёжности электронной цифровой вычислительной техники. Цель операции — уменьшить частоту появления неисправностей ( «сбоев» ) ЭЦВТ, или, что равносильно, увеличить средний промежуток времени между сдоями ( «наработку на отказ» ). Показатель эффективности — среднее время безотказной работы ЭЦВТ.
Пример 6. Проводится борьба за экономию средств при производстве определённого вида товара. Показатель эффективности — количество сэкономленных средств.
С помощью анализа модели на чувствительность определить параметр, от которого результат зависит больше и решить, каким способом возможно увеличение эффективности и на сколько, а так же многое другое.
Программа использования симплекс-метода предусмотрена для решения систем линейных неравенств табличным методом, а так же для попытки оптимизации различных экономических, социальных и т. д. проблем.
Симплекс-метод может применяться на государственных и частных предприятиях для улучшения эффективности производства.
2.2 Алгоритм решения ЗЛП симплексным методом
Симплекс-метод подразумевает последовательный перебор всех вершин области допустимых значений с целью нахождения той вершины, где функция принимает экстремальное значение. На первом этапе находится какое-нибудь решение, которое улучшается на каждом последующем шаге. Такое решение называется базисным.
Первый шаг.В составленной таблице сначала необходимо просмотреть столбец со свободными членами. Если в нем имеются отрицательные элементы, то необходимо осуществить переход ко второму шагу, если же нет, то к пятому.
Второй шаг.На втором шаге необходимо определиться, какую переменную исключить из базиса, а какую включить, для того, что бы произвести перерасчет симплекс-таблицы. Для этого просматриваем столбец со свободными членами и находим в нем отрицательный элемент. Строка с отрицательным элементом будет называться ведущей. В ней находим максимальный по модулю отрицательный элемент, соответствующий ему столбец — ведомый. Если же среди свободных членов есть отрицательные значения, а в соответствующей строке нет, то такая таблица не будет иметь решений. Переменная в ведущей строке, находящаяся в столбце свободных членов исключается из базиса, а переменная, соответствующая ведущему столбцу включается в базис. В Таб.2.1 приведен пример симплекс-таблицы.
Таблица 2.1 –Пример симплекс-таблицы
| базисные переменные | Свободные члены в ограничениях | Небазисные переменные | |||||
| x1 | x2 | ... | xl | ... | xn | ||
| xn+1 | b1 | a11 | a12 | ... | a1l | ... | a1n |
| xn+2 | b2 | a21 | a22 | ... | a2l | ... | a2n |
| … | … | ... | ... | ... | ... | ... | ... |
| … | … | … | … | … | … | … | … |
| … | ... | ... | ... | ... | ... | ... | ... |
| xn+r | b2 | ar1 | ar2 | ... | arl | ... | arn |
| … | … | … | … | … | … | … | … |
| … | ... | ... | ... | ... | ... | ... | ... |
| … | … | … | … | … | … | … | … |
| xn+m | bm | am1 | am2 | ... | aml | ... | amn |
| F(x)max | F0 | -c1 | -c2 | ... | -c1 | ... | -cn |
Третий шаг. На третьем шаге пересчитываем всю симплекс-таблицу по специальным формулам.
Четвертый шаг.Если после перерасчета в столбце свободных членов остались отрицательные элементы, то переходим к первому шагу, если таких нет, то к пятому.
Пятый шаг.Если Вы дошли до пятого шага, значит нашли решение, которое допустимо. Однако, это не значит, что оно оптимально. Оптимальным оно будет только в том случае, если положительны все элементы в F-строке. Если же это не так, то необходимо улучшить решение, для чего находим для следующего перерасчета ведущие строку и столбец по следующему алгоритму. Первоначально, находим минимальное отрицательное число в строке F, исключая значение функции. Столбец с этим числом и будем ведущим. Для того, что бы найти ведущую строку, находим отношение соответствующего свободного члена и элемента из ведущего столбца, при условии, что они положительны. Минимальное отношение позволит определить ведущую строку. Вновь пересчитываем таблицу по формулам, т.е. переходим к шагу 3.
Шестой шаг.Если невозможно найти ведущую строку, так как нет положительных элементов в ведущем столбце, то функция в области допустимых решений задачи не ограничена сверху и Fmax ->∞. Если в строке F и в столбце свободных членов все элементы положительные, то найдено оптимальное решение.
2.3 Решение задачи линейного программирования симплекс-методом
Идея симплекс-метода относительно проста. Пусть в задаче линейного программирования имеется п переменных и т независимых линейных ограничений, заданных в форме уравнений. Мы знаем, что оптимальное решение (если оно существует) достигается в одной из опорных точек (вершин ОДР), где по крайней мере k = n — m из переменных равны нулю. Выберем какие-то к переменных в качестве свободных и выразим через них остальные т базисных переменных. Пусть, например, в качестве свободных выбраны первые k = n — m переменныхx1, x2 ,…,xk, а
остальные m выражены через них(формула 2.1):
xk+1 =αk+1.1 x1 +αk+1.2 x2 + +αk+1.k xk +βk+1 ;
xk+2 = αk+2.1 x1 +αk+2.2 x2 + +αk+2.k xk +βk+2 ;(2.1)
……………………………………
xn = αn1 x1 +αn2 x2 + +αnk xk +βn.
Предположим, что все свободные переменныеx1, x2 ,…,xk равны нулю.
При этом мы получим:
xk+1 =βk+1 ;
xk+2 =βk+2 ;
……… (2.2)
Xn =βn
Это решение может быть допустимым или недопустимым. Оно допустимо, если все свободные членыβk+1, βk+2 ,…,βn (2.2)неотрицательны. Предположим, что это условие выполнено. Тогда мы получили опорное решение. Но является ли оно оптимальным? Чтобы проверить это, выразим целевую функцию Z через свободные переменныеx1, x2 ,…,xk .
Z=γ0+γ1 x1 +γ2 x2 +…+γk xk (2.3)
Очевидно, что приx1 =x2 =…=xk =0, Z=γ0. Проверим, может ли быть улучшено решение, т. е. получено уменьшение функции Z c увеличением каких-нибудь из переменныхx1, x2 ,…, xk (2.2) (уменьшать их мы не можем, так как все они равны нулю, а отрицательные значения переменных недопустимы). Если все коэффициентыγ1 ,γ2 ,…,γk в (2.3) положительны, то увеличение каких-либо из переменныхx1 ,x2 ,…,xk (2.2) не может уменьшить Z; следовательно, найденное опорное решение является оптимальным. Если же среди коэффициентовγ1 ,γ2 ,…,γk есть отрицательные, то, увеличивая некоторые из переменныхx1 ,x2 ,…,xk (те, коэффициенты при которых отрицательны), мы можем улучшить решение.
Пусть, например, коэффициентγ1 в (2.3) отрицателен. Значит, есть смысл увеличитьx1, т. е. перейти от данного опорного решения к другому, где переменнаяx1 не равна нулю, а вместо нее равна нулю какая-то другая. Однако увеличиватьx1 следует с осторожностью, так чтобы не стали отрицательными другие переменныеxk+1, xk+2 ,…,xn выраженные через свободные переменные, в частности черезx1 формулами (2.2).
Например, если коэффициент приx1 в соответствующемxj уравнении (2.2) отрицателен, то увеличениеx1 может сделатьxj отрицательным. Наоборот, если среди уравнений (2.2) нет уравнения с отрицательным коэффициентом приx1 то величинуx1 можно увеличивать беспредельно, а, значит, линейная функция Z не ограничена снизу и оптимального решения ОЗ не существует.
Допустим, что это не так и что среди уравнений (2.2) есть такие, в которых коэффициент приx1 отрицателен. Для переменных, стоящих в левых частях этих уравнений, увеличениеx1 опасно — оно может сделать их отрицательными.
Возьмем одну из таких переменныхxl и посмотрим, до какой степени можно увеличитьx1, пока переменнаяxl не станет отрицательной. Выпишемl-eуравнение из системы (2.2):
xl =αl1 x1 +αl2 x2 +…+αlk xk +βl (2.4)
Здесь свободный членβl ≥0, а коэффициентαl1 отрицателен.
Легко понять, что если мы оставимx2 =x3 =…=xk =0, тоxk можно увеличивать только до значения, равного–βl /αl1, а при дальнейшем увеличенииx1 переменнаяx1 станет отрицательной.
Выберем ту из переменныхxk+1 ,xk+2 ,…,xn, которая раньше всех обратится в нуль при увеличении x1, т. е. ту, для которой величина–βl /αl1 наименьшая. Пусть это будетxr. Тогда имеет смысл разрешить систему уравнений (2.2) относительно других базисных переменных, исключаяиз числа свободных переменныхx1 и переводя вместо нее в группу свободных переменныхxr. Действительно, мы хотим перейти от опорного решения, задаваемого равенствамиx1 =x2 =…=xn =0 к опорному решению, в котором ужеx1 ≠0, аx2 =…=xk =xr =0. Первое опорное решение мы получили, положив равными нулю все прежние свободные переменныеx1 ,x2 ,…,xk второе мы получим, если обратим в нуль все новые свободные переменныеx2 ,x3 ,…,xk ,xr.
Базисными переменными при этом будутxl ,xk+1 ,xk+2 ,…,xr-1, xr-1 ,…,xr .
Предположим, что уравнения типа (2.2) для нового набора базисных и свободных переменных составлены. Тогда можно выразить через новые свободные переменные и линейную функцию Z.Если все коэффициенты при переменных в этой формуле положительны, то мы нашли оптимальное решение: оно получится, если все свободные переменные положить равными нулю. Если среди коэффициентов при переменных есть отрицательные, то процедура улучшения решения продолжается: система вновь разрешается относительно других базисных переменных, и так далее, пока не будет найдено оптимальное решение, обращающее функцию Z в минимум.
Пример 2. Пусть имеется задача линейного программирования с ограничениями-неравенствами:
-5x1 -x2 +2x3 ≤2;
-x1 +x3 +x4 ≤5; (2.5)
-3x1 +5x4 ≤7.
Требуется минимизировать линейную функцию
Z=5x1 -2x3
Приводя неравенства к стандартному виду (≥0) и вводя добавочные переменныеy1 ,y2 ,y3 переходим к условиям-равенствам:
y1 =5x1 +x2 -2x3 +2
y2 =x1 -x3 -x4 +5 (2.5)
y3 =3x1 -5x4 +7
Число переменных (n = 7) на 4 превышает число уравнений (т = 3). Значит, четыре переменные могут быть выбраны в качестве свободных.
Пусть в качестве свободных переменных выступаютx1 ,x2 ,x3 ,x4. Положим их равными нулю и получим опорное решение:
x1 =x2 =x3 =x4 =0;
y1 =2, y2 =5, y3 =7.
При этих значениях переменных Z= 0.
Это решение не оптимально, поскольку в линейной функции Z коэффициент приx3 отрицателен. Значит, увеличиваяx3 можно уменьшить Z.
Попробуем увеличиватьx3.Из выражений (2.5) видно, что вy1 и y2 переменнаяx3 входит с отрицательным коэффициентом, значит, при увеличенииx3 соответствующие переменные могут стать отрицательными.
Определим, какая из этих переменных (y1 илиy2 )раньше обратится в нуль при увеличенииx3 Очевидно, что этоy1 она станет равной нулю приx3 =1, а величинаy2 — только приx3 = 5.
Выбирается переменная у, и вводится в число свободных вместоx3 Чтобы разрешить систему (2.5) относительноx3, y2, y3 поступим следующим образом. Разрешим первое уравнение (2.5) относительно новой базисной переменнойx3 :
x3 =5/2*x1 +1/2*x2 -1/2*y1 +1
Это выражение подставляется вместоx3 во второе уравнение:
x3 =5/2*x1 +1/2*x2 -1/2y1 +1;
y2 =-3/2*x1 -1/2*x2 +1/2*y1 -x4 +4; (2.6)
y3 =3x1 -5x4 +7.
Что касается третьего уравнения, то оно, как не содержащееx3 не изменится. Система (2.2) приведена к виду со свободными переменнымиx1, x2, y1, x4 и базиснымиx3, y2, y3 .
Положим теперь свободные переменные равными нулю. Функция приобретает значение Z=-2, что меньше (лучше), чем прежнее значение Z= 0.
Это решение все еще не оптимально, так как коэффициент приx2 в выражении (2.7) отрицателен, и переменнаяx2 может быть увеличена. Это увеличение, как это видно из системы (2.6), может сделать отрицательнойy2 (в первое уравнениеx2 входит с положительным коэффициентом, а в третьем — отсутствует).
Поменяем местами переменныеx2 и y2 — первую исключим
из числа свободных, а вторую — включим. Для этого разрешим второе уравнение (2.6) относительноx2 и подставимx2 в первое уравнение. Получим следующий вид системы (2.5):
x3 =x1 -y2 -x4 +5
y2 =-3x1 -2y2 +y1 -2x4 +8 (2.7)
y3 =3x1 -5x4 +7
Выразим Z через новые свободные переменные:
Z=3x1 +2y2 -y1 +2x4 -8+y1 -2=3x1 +2y2 +2x4 -10 (2.8)
Полагаяx1 =y1 =y2 =x4 =0, получим Z = -10.
Это решение является оптимальным, так как коэффициенты при всех свободных переменных в выражении (2.8) неотрицательны. Итак, оптимальное решение ОЗ найдено (2.9):
x1* =0, x2* =8, x3* =5, x4* =0, y1* =0, y2* =0, y3* =7. (2.9)
При таких значениях переменных линейная функция Z принимает минимальное значение (2.10):
Zmin =-10 (2.10)
Заметим, что в рассмотренном примере нам не пришлось искать опорное решение: оно сразу же получилось, когда мы положили свободные переменные равными нулю. Это объясняется тем, что в уравнениях (2.5) все свободные члены были неотрицательны и, значит, первое же попавшееся решение оказалось опорным. Если это окажется не так, можно будет прийти к опорному решению с помощью такой же процедуры обмена местами некоторых базисных и свободных переменных, повторно решая уравнения до тех пор, пока свободные члены не станут неотрицательными
2.4 Двойственная задача
Использование идей двойственности в сочетании с общей идеей симплекс-метода позволило разработать еще один метод решения задач ЛП — двойственный симплекс-метод. Впервые этот метод был предложен Лемке в 1954г. Решение задачи ЛП двойственным симплекс-методом сводится к отысканию оптимального плана прямой задачи последовательным переходом от одного базиса к другому.
Задача ЛП в канонической форме имеет вид: максимизировать L(x) = сумма от j=1 до n (сjчj) при условиях: сумма от j=1 до n (аjXj)=bv, (v=1,2,....m) или сумма от j=1 до n (АjXj)=b, xj>=0, j=1,2,...n
Составим двойственную задачу по условиям прямой задачи и определим области допустимых решений ДП: Прямая задача Двойственная задача
maxZ=x1 -3x3 -3x4 -MR1 -MR2
y1: x1 +2x3 -2x4 +x5 =4
y2: 3x1 -4x3 +4x4 +R1 =11
y3: x1 +x3 -x4 -x6 +R2 =0
minW=4y1 +12y2
x1: y1 +3y2 +y3 ≥1
x3: 2y1 -4y2 +y3 ≥-3
-2y1 +4y2 -y3 ≤3(1)
X4: -2y1 +4y2 -y3 ≥3 (2)
X5: y1 ≥0
X6: -y3 ≥0 => y3 ≤0
R1: y2 ≥-M
R2: y3 ≥-M Итак, получено: y1 ≥0,y2 ≤≥0 ,y3 ≤0.
2. Приведём запись двойственной задачи к канонической форме. На основании полученных ОДР двойственных переменных введём необходимые подстановки:y2 =y4 -y5; y3 =-ỹ3; ỹ3 ,y4 ,y5 ≥0 Для удобства решения свернём ограничения (1) и (2) в одно со знаком равенства, а также введем в ограничения и целевую функцию избыточные, остаточные и искусственные переменные.
minW=4y1 +12y4 -12y5 +MR1 +MR2
y1 +3y4 -3y5 -ỹ3 -y6 +R1 =1 (3)
-2y1 +4y4 -4y5 +ỹ3 +R2 =3 (4)
3. Решим ДЗ симплекс методом: Из (3) выразим: R1 =1-y1 -3y4 +3y5 +ỹ3 +y6 Из (4) выразим:R2 =3+2y1 -4y4 +4y5 -ỹ3
W+y1 (-4-M)+y4 (-12+7M)+y5 (12-7M)-My6 =4M
Создаём симплекс-таблицы:
Таблица 2.2 – симплекс-таблица №1
| W | y1 | y4 | y5 | ỹ3 | y6 | R1 | R2 | ПЧ | |
| W | 1 | -4-M | 7M-12 | 12-7M | -M | 4M | |||
| R1 | 0 | 1 | 3 | -3 | -1 | -1 | 1 | 0 | 1 |
| R2 | 0 | -2 | 4 | -4 | 1 | 0 | 0 | 1 | 3 |
B-1 (0)=B(0)=
Таблица 2.3 – симплекс-таблица №2
| W | y1 | y4 | y5 | ỹ3 | y6 | R1 | R2 | ПЧ | |
| W | 1 | -10/3M | 7/3M-4 | 4/3M-4 | -7/3M+4 | 5/3M+4 | |||
| y4 | 0 | 1/3 | 1 | -1 | -1/3 | -1/3 | 1/3 | 0 | 1/3 |
| R2 | 0 | -10/3 | 0 | 0 | 7/3 | 4/3 | -4/3 | 1 | 5/3 |
B-1 (1)=B(1)=
Таблица 2.4 – симплекс-таблица №3
| W | y1 | y4 | ỹ5 | ỹ3 | y6 | R1 | R2 | ПЧ | |
| W | 1 | -40/7 | 0 | 0 | 0 | -12/7 | -7/3M+4 | -M+12/7 | 48/7 |
| y4 | 0 | -1/7 | 1 | -1 | 0 | -1/7 | 1/3 | 1/7 | 4/7 |
| ỹ3 | -10/7 | 1 | 4/7 | -4/3 | -3/7 | 5/7 |
Симплекс-таблица №3 – оптимальная, т. к. коэффициенты приНБП≥0 minW=48/7, maxZ=minW=48/7,
y1* =0, y2* =y4* -y5* =4/7, y3* =-5/7
Двухфазовый симплекс метод, иначе называют методом искусственного базиса:
Если в условии задачи линейного программирования не все ограничения представлены неравенствами типа «≤», то далеко не всегда нулевой вектор будет допустимым решением. Однако каждая итерация симплекс-метода является переходом от одной вершины к другой, и если неизвестно ни одной вершины, алгоритм вообще не может быть начат.
Процесс нахождения исходной вершины не сильно отличается от однофазного симплекс-метода, однако может в итоге оказаться сложнее, чем дальнейшая оптимизация. Из изложенного выше не прозвучало отчетливо почему если ограничения отличается от <= не всякий 0-вектор будет допустимым решением. В самом деле пусть i — уравнение имеет вид Ai1X1+...AinXn>=Bi но просто можно изменить знаки записав -Ai1X1-… AinXn<=-Bi и тем самым привести все неравенства к канонической форме. Это было бы нельзя сделать если бы на вектор B было наложено условие неотрицательностиBi>=0 Но в формулировке выше ограничения вектор B отсутствуют. (это очевидная неточность для теоретической статьи в энциклопедии, где все предпосылки должны формулироваться полно) Если бы все было так просто и легко, непонятно зачем изобретали двухфазный метод… Кроме того по этой же причине классический симплекс метод не годится для решения задачи Min F (точнее не годится в случае положительности всех коэфф целевой функции, т.к. тогда метод не сделает ни одной итерации).
ІІІ КОМПЬЮТЕРНАЯ РЕАЛИЗАЦИЯ СИМПЛЕКС-МЕТОДА ПРИ РЕШЕНИИ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
3.1 описание программного продукта
Методы линейного программирования оказались весьма эффективными для решения задач из различных областей человеческой деятельности. Исключительно важное значение приобретает использование таких методов и средств при решении задач оптимального проектирования, в которых необходимо учитывать огромное количество ограничивающих факторов, что связано с большим объемом вычислений. Разработанный программный комплекс позволяет решать следующие задачи:
• порождение начального базисного допустимого решения;
• поиск оптимального плана и экстремума нецелочисленной задачи линейного программирования;
• поиск оптимального плана и экстремума полностью целочисленной задачи линейного программирования;
• поиск оптимального плана и экстремума частично целочисленной задачи линейного программирования;
При проектировании был использован принцип модульного программирования, что упрощает отладку программы и позволяет расширять ее функциональные возможности. Алгоритмическая часть программы имеет модульно-иерархическую структуру, в которой каждый модуль является самостоятельной частью программы и взаимодействует с другими модулями в порядке, установленном разработчиками. Методы решения задач линейной оптимизации, реализованные в программно-алгоритмическом комплексе, основаны на построении симплекс-таблиц, поэтому в структуре программы все алгоритмические модули связаны с модулем, организующим решение задачи линейного программирования симплекс-методом. Входными данными для этого модуля является целевая функция с указанием типа экстремума (максимум или минимум) и ограничения, накладываемые на управляемые переменные. Ограничения задаются в виде уравнений или неравенств. Далее управление передается второму модулю, где формируется начальное допустимое базисное решение. Второй, третий и четвертый модули на каждой итерации реализуемого метода вызывают модуль построения симплекс-таблиц, которому они передают текущий результат. Связь между модулями организована через внешние структуры данных. Так, например, для задания линейного критерия оптимальности, вектора управляемых переменных, вектора ограничений и матрицы ограничений используются одномерные и двумерные статические массивы, а симплекс-таблица в памяти ЭВМ представлена как двумерный динамический массив, способный изменять свою размерность, удаляя или добавляя строки и столбцы к симплекс-таблице.
Рассмотрим особенность функционирования программного комплекса. Для организации диалога с пользователем применяется стандартный графический интерфейс Windows, построенный на основе библиотеки визуальных компонентов VCL (VisualComponentLibrary), поставляемой вместе с пакетом Delphi. При разработке программы использовалась MDI-технология (MultipleDocumentInterface – многодокументный пользовательский интерфейс), что позволяет пользователю работать сразу с несколькими задачами линейного программирования. В программе реализована активная форма диалога, позволяющая выбирать режимы: расчет, просмотр и редактирование информации, получение справки и т.д.
Главное меню содержит следующие пункты: файл, правка, вид, вычисления, окно, справка. Все пункты главного меню вызывают подменю. В начале работы программы некоторые пункты запрещены и становятся разрешенными только по мере выбора других пунктов меню (например, меню «Правка», «Вычисления» и т. д.).
В программе предусмотрена возможность настройки параметров задачи: максимизация или минимизация; выбор опции, позволяющей просматривать промежуточные результаты итераций; ограничения количества итераций; установка размерности задачи т.п.
3.2 Тестирование программного продукта
Рисунок 3.1 – Поиск максимизирующего прибыль плана производства
Рисунок 3.2 — Поиск максимизирующего прибыль плана производства
Рисунок 3.3 – Оптимальный план производства
ЗАКЛЮЧЕНИЕ
Описанная в курсовой работе задача линейного программирования и методы ее решения – только отдельный пример огромного множества задач линейного программирования.Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Линейное программирование представляет собой наиболее часто используемый метод оптимизации. Линейное программирование является одной из основных частей того раздела современной математики, который получил название математического программирования.Задачи линейного программирования решаются несколькими методами:1. графический метод;2. симплекс-метод;3. двойственный симплекс-метод.При построении симплексного метода предполагалось, что все опорные планы невырожденные, что обеспечивало получение оптимального плана за конечное количество шагов. В случае вырожденного плана вычисления производят аналогично, но в этом случае возможен возврат к старому базису, что приводи к так называемому зацикливанию.В основу модифицированного симплекс – метода положены такие особенности линейной алгебры, которые позволяют в ходе решения задачи работать с частью матрицы ограничений. Иногда метод называют методом обратной матрицы. В целом, метод отражает традиционные черты общего подхода к решению задач линейного программирования, включающего в себя канонизацию условий задачи, расчёт симплекс-разностей, проверку условий оптимальности.СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1 Акулич И.Л. Математическое программирование в примерах и задачах: учеб.пособие для ВУЗов / И. Л. Акулич. – М.: Высшая школа, 1986.
2 Гончаров Е. Н. Исследование операций. Примеры и задачи: учеб.пособие / Е. Н. Гончаров, А. И. Ерзин, В. В. Залюбовский. –Н.: Гос. ун-т. Новосибирск, 2005.
3 Павлова Т. Н. Линейное программирование: учеб.пособие / Т. Н. Павлова, О. А. Ракова. – Д.: 2002.
4 БерюховаТ.Н.Банк производственных задач в расчетах на ЭВМ: учебное пособие. – Тюмень.: ТюмИИ, 1992. – 124с. Карманов В.Г. Математическое программирование: учебное пособие для студентов вузов. – М.: Физматлит, 2001. – 264с.
5 Кузнецов А.В. Математическое программирование: учебное пособие для вузов. – М.: Высшая школа, 1976. – 352с.
6 Мочалов И.А. Нечеткое линейное программирование. // Промышленные АСУ и контроллеры. – 2006. — № 10. – с.26-29.
7 Пашутин С.Оптимизация издержек и технология формирования оптимального ассортимента. // Управление персоналом. – 2005. — №5. – с.20-24.
8 Жиглявский А.А., Жилинкас А.Г. Методы поиска глобального экстремума. — М.: Наука, Физматлит, 1991.
9 Карманов В.Г. Математическое программирование = Математическое программирование. — Изд-во физ.-мат. литературы, 2004.
10 Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
11 Сайт ru.wikipedia.org/wiki
12 Сайт revolution
13 Сайт fessagicadif.web44.net
www.ronl.ru
Содержание.
Введение……………………………………………………………………………………….с.5.
1. Теоретическая часть.
Глава 1. Простой симплекс-метод.
1.1 Обоснование и описание вычислительной процедуры. Приведение задачи линейного программирования к стандартной форме……………………………с.7
1.2 Симплексный метод решения задач……………………………………..…...с.8.
1.3 Алгоритм симплекс-метода…………………………………………………с.10.
1.4 Решение задачи оптимизации. Построение аналитической модели……...с.12.
1.5 Приведение задачи к стандартной форме. Определение начального допустимого решения…………………………….……………………………...с.14.
Глава 2. Двухэтапный метод.
2.1 Искусственное начальное решение…………………………………………с.16.
2.2 Алгоритм двухэтапного метода……………………………………………..с.19.
Глава 3. Особые случаи симплекс-метода……………………………………………...23.
3.1 Вырожденность……………………………………………………………....с.24.
3.2 Альтернативные оптимальные решения…………………………………....с.27.
3.3 Неограниченные решения…………………………………………………...с.30.
3.4 Отсутствие допустимых решений…………………………………………..с.32.
2. Практическая часть.
2.1 Постановка задачи…………..……………………………………………………..с.34.
2.2 Решение…..…………………………………………………………………………с.36.
Заключение…………………………………………………………………………………...с.39.
Литература…………………………………………………………………………………....с.40.
Введение.
Целью данной курсовой работы является решение конкретной задачи линейного программирования. Во всех таких задачах требуется найти максимум или минимум линейной функции при условии, что её переменные принимают неотрицательные значения и удовлетворяют некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные уравнения, так и линейные неравенства. Каждая из этих задач является частным случаем общей задачи линейного программирования.
Для решения задач линейного программирования созданы специальные методы. Изучению одного из них, а именно симплекс-методу, посвящена эта курсовая работа.
В настоящее время оптимизация находит применение в науке, технике и в любой другой области человеческой деятельности.
Оптимизация – целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно.
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:
· количество продукции - расход сырья
· количество продукции - качество продукции
Выбор компромиcного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого. Приведем примеры.
Типичный пример неправильной постановки задачи оптимизации:
«Получить максимальную производительность при минимальной себестоимости».
Ошибка заключается в том, что ставится задача поиска оптимальности 2-х величин, противоречащих друг другу по своей сути.
Правильная постановка задачи могла быть следующая:
а) получить максимальную производительность при заданной себестоимости;
б) получить минимальную себестоимость при заданной производительности;
В первом случае критерий оптимизации - производительность а во втором - себестоимость.
2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта.
3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
4. Учёт ограничений.
1. Теоретическая часть.
Глава 1. Простой симплекс-метод.
1.1 Обоснование и описание вычислительной процедуры. Приведение задачи линейного программирования к стандартной форме.
Любая задача линейного программирования приводится к стандартной (канонической) форме основной задачи линейного программирования, которая формулируется следующим образом: найти неотрицательные значения переменных X1 , X2 , Xn , удовлетворяющих ограничениям в виде равенств:
A11X1 + A12X2 + … + A1nXn = B1;
A21X1 + A22X2 + … + A2nXn = B2;
……………………………………
Am1X1 + Am2X2 + … + AmnXn = Bm;
Xj ≥ 0, j=1,…,n
и обращающих в максимум линейную функцию этих переменных:
E = C1X1 + C2X2 + … + CnXn Þ max
При этом также требуется, чтобы правые части равенств были неотрицательны, т.е. должны соблюдаться условия:
Bj ≥ 0, j=1,…,n
Приведение к стандартной форме необходимо, так как большинство методов решения задач линейного программирования разработано именно для стандартной формы. Для приведения к стандартной форме задачи линейного программирования может потребоваться выполнить следующие действия:
- перейти от минимизации целевой функции к ее максимизации;
- изменить знаки правых частей ограничений;
- перейти от ограничений-неравенств к равенствам;
- избавиться от переменных, не имеющих ограничений на знак.
Для решения нашей задачи воспользуемся симплекс-методом, так как этот метод предназначен для решения задач линейного программирования любой размерности.
1.2 Симплексный метод решения задач.
Симплексный метод задач линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план, и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план. Рассмотрим задачу, для которой этот план можно непосредственно записать.
Пусть дана функция, для которой необходимо найти наибольшее или наименьшее значение, если значения всех неизвестных неотрицательные.
ѓ = C0 + C1x1 + C2x2 +...+ Cnxn
и система m линейных уравнений с n неизвестными. Это называется системой ограничений:
 a11x1 + a12x2 +...+ a1nxn = b1
a11x1 + a12x2 +...+ a1nxn = b1
a21x1 + a12x2 +...+ a2nxn = b2
...
am1x1 +am2x12 +...+ amnxn = bm
Целевую функцию представим в виде:
ѓ - C1x1-C2x2 -...-Cnxn = C0
Составим симплекс-таблицу. В дальнейшем будем считать, что ранг матрицы системы ограничений равен r.В системе ограничений выбран базис (основные неизвестные)x1,x2,...xn и коэффициенты в правой части не отрицательны.
В этом случае система ограничений будет иметь вид:
 |
x1 +...+ a1,r+1xr+1 +...+ a1nxn = b1
x2 + a2,r+1xr+1 +...+ a2nxn = b2
...
xr+ ar,r+1xr+1 +...+ arnxn = br
Тогда целевая функция имеет вид:
ѓ + Cr+1xr+1 + Cr+2xr+2 -...- Cnxn = C0
Нахождение оптимального плана симплексным методом включает следующие этапы:
1. Находят опорный план.
2. Составляют симплекс-таблицу. В общем виде:
|
Базисные неизвестные |
Свободные члены |
x1 |
x2 |
xr |
xr+1 |
xj |
xn |
|
x1 x2 xi xr |
b1 b2 bi br |
1 0 0 0 |
0 1 0 0 |
0 0 0 1 |
a1,r+1 a2,r+1 ai,r+1 ar,r+1 |
a1j a2j aij arj |
a1n a2n ain arn |
|
ѓ |
C0 |
0 |
0 |
0 |
Cr+2 |
Cj |
Cn |
3. В нижней строчке симплекс-таблицы необходимо отыскать отрицательные числа (не считая коэффициент Со). Если таких чисел нет, то данное базисное решение является оптимальным.
4. Пусть элемент Сj<0,тогда в j-ом столбце необходимо найти положительный элемент. Если все коэффициенты этого столбца отрицательные, то решения не существует.
5. Если положительный коэффициент в j-ом столбце один, то выбранную строку с номером i надо поделить все коэффициенты на число aij.Результат деления записываем в новую симплекс-таблицу. Если же положительных коэффициентов несколько, необходимо составить отношение bi/aij и из полученных значений выбрать наименьшее, соответствующее i-ой строке.
6. В новой симплекс-таблице в столбце базисных неизвестных вместо xi пишется xj. Продолжается заполняться таблица. В столбце с номером j необходимо получить нули(включая строку с целевой функцией). Для этого надо умножить i-ую записанную строку на нужное число и сложить с остальными строками.
В результате осуществился переход к новому базису, при этом значение целевой функции увеличилось.
1.3 Алгоритм симплекс-метода.
 Пусть система приведена к каноническому виду.
Пусть система приведена к каноническому виду.
X1+ q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
X2+q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
X3+q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
………………………………………………………
Xm+ qm,m+1 Xm+1 + …. + qm,m+n Xm+n =hm
В ней m базисных переменных, k свободных переменных. m+k=n - всего переменных.
Fmin= C1X1+ C2X2+ C3X3+....+ CnXn
Для дальнейших рассуждений вычислений будем пользоваться первой симплекс таблицей (таблица1).
Таблица 1.Симплекс таблица
|
C |
Б |
H |
C1 |
C2 |
… |
Cm |
Cm+1 |
… |
Cm+k |
|
|
|
|
X1 |
X2 |
… |
Xm |
Xm+1 |
… |
Xm+k |
|
C1 C2 C3 : : Cm |
X1 X2 X3 : : Xm |
h2 h3 h4 : : Hm |
1 0 0 : : 0 |
0 1 0 : : 0 |
: : : : : : |
0 0 0 : : 0 |
q1,m+1 q2,m+1 q3,m+1 : : qm,m+1 |
: : : : : : |
q1,m+k q2,m+k q3,m+k : : qm,m+k |
|
|
|
F0 |
F1 |
F2 |
… |
Cm |
Cm+1 |
… |
Cm+k |
Первый столбец - коэффициенты в целевой функции при базисных переменных.
Второй столбец - базисные переменные.
Третий столбец - свободные члены (hi00).
Самая верхняя строка - коэффициенты при целевой функции.
Вторая верхняя строка - сами переменные, входящие в целевую функцию и в систему ограничений.
Основное поле симплекс метода - система коэффициентов из уравнения.
Последняя строка - служит для того, чтобы ответить на вопрос: «оптимален план или нет».
Индексная строка позволяет нам судить об оптимальности плана:
При отыскании Fmin в индексной строке должны быть отрицательные и нулевые оценки.
При отыскании Fmax в индексной строке должны быть нулевые и положительные оценки.
Переход ко второй итерации:
Для этого отыскиваем ключевой (главный) столбец и ключевую (главную) строку.
Ключевым столбцом является тот в котором находится наибольший положительный элемент индексной строки при отыскании Fmin или наименьший отрицательный элемент при отыскании Fmax.
Ключевой строкой называется та, в которой содержится наименьшее положительное частное от деления элементов столбца H на соответствующие элементы ключевого столбца.
На пересечении строки и столбца находится разрешающий элемент.
На этом этапе осуществляется к переходу к последующим итерациям.
Переход к итерациям:
Выводится базис ключевой строки, уступая место переменной из ключевого столбца со своим коэффициентом.
Заполняется строка вновь введенного базиса путем деления соответствующих элементов выделенной строки предыдущей итерации на разрешающий элемент.
Если в главной строке содержится нулевой элемент, то столбец, в котором находиться этот элемент переноситься в последующую итерацию без изменения.
Если в главном столбце имеется нулевой элемент, то строка, в которой он находиться переноситься без изменения в последующую итерацию.
Остальные элементы переносятся по формуле:

1.4 Решение задачи оптимизации. Построение аналитической модели.
В цехе имеется токарный станок и станок-автомат. Цех выпускает детали 1,2 и 3 в комплекте: на каждую деталь 1 – по 2 детали 2 и 3. Часовая производительность станков по каждой из деталей приведена в таблице:
Таблица 1. Часовая производительность станков
|
Станки |
Детали |
||
|
1 |
2 |
3 |
|
|
1. Токарный |
5 |
5 |
10 |
|
2. Автомат |
15 |
15 |
10 |
Составить программу работы станков, при которой в течение смены (8 часов) будет выпускаться максимальное количество комплектов деталей.
Составим аналитическую модель задачи. Для этого сначала введем переменные, которые требуется определить:
X1 – время, которое работал токарный станок над деталями типа 1 в течение рабочей смены;
X2 – время, которое работал токарный станок над деталями типа 2 в течение рабочей смены;
X3 – время, которое работал токарный станок над деталями типа 3 в течение рабочей смены;
X4 – время, которое работал станок-автомат над деталями типа 1 в течение рабочей смены;
X5 – время, которое работал станок-автомат над деталями типа 2 в течение рабочей смены;
X6 – время, которое работал станок-автомат над деталями типа 3 в течение рабочей смены.
Система ограничений состоит из двух групп. Первая группа устанавливает, что каждый из станков может работать не более 8 часов в смену.
Ограничение времени работы токарного станка:
X1 + X2 + X3 £ 8;
Ограничение времени работы станка-автомата:
X4 + X5 + X6 £ 8.
Вторая группа ограничений направлена на выполнение требования о комплектации деталей: на каждую деталь 1 должно приходиться по 2 детали 2 и 3. Но перед тем, как вводить это ограничение, определим, сколько деталей каждого типа у нас будет производиться за смену:
5X1 + 15X4 - будет произведено за смену деталей типа 1;
5X2 + 15X5 - будет произведено за смену деталей типа 2;
10X3 + 10X6 - будет произведено за смену деталей типа 3.
Теперь введем сами ограничения:
2(5X1 + 15X4) = 5X2 + 15X5;
2(5X1 + 15X4) = 10X3 + 10X6.
Очевидно, что все переменные в задаче неотрицательные (объем продукции не может быть отрицательным):
X1 , X2 , X3 , X4 , X5 , X6 ≥ 0.
Целевая функция в нашей задаче должна выражать количество комплектов деталей, выпускаемых за смену, поэтому сложим все выпускаемые детали и поделим на 5 (в комплект, как уже упоминалось, входят 1 деталь типа 1 и по 2 детали типа 2 и 3):
E= (5X1 + 15X4 + 5X2 + 15X5 + 10X3 + 10X6)/5 Þ max
или, если упростить это выражение, то получим:
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þ max
Целевую функцию надо максимизировать.
Таким образом, формальная постановка задачи оптимизации имеет следующий вид:
X1 + X2 + X3 £ 8;
X4 + X5 + X6 £ 8;
2(5X1 + 15X4) = 5X2 + 15X5;
2(5X1 + 15X4) = 10X1 + 10X6;
X1 , X2 , X3 , X4 , X5 , X6 ≥ 0.
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þ max
1.5 Приведение задачи к стандартной форме. Определение начального допустимого решения.
Для приведения данной задачи к стандартной форме необходимо лишь перейти от ограничений – неравенств к равенствам. Для этого введем дополнительные балансовые неотрицательные переменные. Также для упрощения дальнейших вычислений разделим обе части ограничений на комплектацию деталей на 5:
X1 + X2 + X3 + X7 = 8;
X4 + X5 + X6 + X8 = 8;
2X1 – X2 + 6X4 – 3X5 = 0;
2X1 – 2X3 + 6X4 – 2X6 =0;
X1 , X2 , X3 , X4 , X5 , X6 , X7 , X8 ≥ 0.
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þ max
где Х7 , Х8 – остаточные переменные.
Итак, нашу исходную задачу мы привели к стандартной форме основной задачи линейного программирования.
Для задачи, представленной в стандартной форме, количество переменных обычно больше, чем количество ограничений. Поэтому для нахождения начального решения задачи требуется выразить m переменных (т.е. количество переменных, равное количеству уравнений) через остальные n-m переменных, принять эти n-m переменных равными нулю и, таким образом, найти значения m переменных (в заданной задаче m=4 и n=8). Переменные, значения которых принимаются равными нулю, называются небазисными, а остальные m переменных - базисными. Значения базисных переменных неотрицательны (некоторые из них могут оказаться равными нулю). Количество базисных переменных всегда равно количеству ограничений. Найденное таким образом решение называется начальным допустимым базисным решением. Оно соответствует всем ограничениям.
Начальное решение проще всего найти в случае, когда в каждом ограничении есть переменная, которая входит в него с коэффициентом 1 и при этом отсутствует в других ограничениях. Такие переменные принимаются в качестве базисных (они образуют начальный базис задачи). Остальные (небазисные) переменные принимаются равными нулю. Таким образом, базисные переменные принимают значения, равные правым частям ограничений.
Итак, для нахождения начального допустимого решения необходимо, чтобы в каждое из уравнений входила переменная с коэффициентом 1 и не входила в другие уравнения (базисная переменная). В нашем случае мы имеем только 2 базисные переменные (X7 и X8) , не хватает еще двух базисных переменных. Их можно создать с помощью специального способа, который называется построением искусственного базиса.
Методы искусственного базиса предназначены для построения начального базиса (т.е. для получения начального решения) в случаях, когда его построение непосредственно на основе стандартной формы невозможно. При использовании искусственного базиса начальное решение оказывается недопустимым; от него по определенным алгоритмам выполняется переход к начальному допустимому решению.
Для того, чтобы построить искусственный базис, необходимо в каждое уравнение стандартной формы, не содержащее базисных переменных (т.е. полученное из ограничения-равенства или "не меньше"), добавить по одной искусственной переменной. В нашем случае это:
2X1 – X2 + 6X4 – 3X5 + Х9 = 0;
2X1 – 2X3 + 6X4 – 2X6 + Х10 =0.
где Х9 и Х10 – искусственные переменные, не имеющие никакого физического смысла, причем Х9, Х10 ≥0.
После построения искусственного базиса, придав нулевые значения всем переменным, кроме базисных, получим начальный базис: Х7, Х8, Х9, Х10 . Всего в базисе имеется четыре переменные и их значения равны правым частям ограничений, т.е.:
Х7 = 8; Х8 = 8; Х9 = 0; Х10 = 0.
Теперь необходимо решить эту задачу, т.е. найти оптимальное допустимое решение. Для этого воспользуемся двухэтапным симплекс-методом.
Глава 2. Двухэтапный метод.
2.1 Искусственное начальное решение.
В простом симплексе при начальном допустимом базисном решении гарантировалось, что все последующие базисные решения, получаемые при выполнении симплекс-метода, также будут допустимыми. В задачах линейного программирования, где все ограничения являются неравенствами типа «<=» (с неотрицательной правой частью), дополнительные (остаточные) переменные позволяют сформировать начальное допустимое базисное решение в задачах ЛП, где есть ограничения в виде равенств или неравенств типа «>=» ?
Наиболее общим способом построения начального допустимого базисного решения задачи ЛП является использование искусственных переменных. Эти переменные в первой итерации играют роль дополнительных остаточных переменных, но на последующих итерациях от них освобождаются. Разработано два тесно связанных между собой метода нахождения начального решения, которые используют искусственные переменные: М-метод и двухэтапный метод.
Для объяснения двухэтапного метода объясним сначала концепцию М-метода.
Пусть задача ЛП записана в стандартной форме. Для любого равенства I, в котором не содержится дополнительная остаточная переменная, введём искусственную переменную Ri, которая далее войдёт в начальное базисное решение. Но поскольку эта переменная искусственна (другими словами, не имеет никакого «физического смысла» в данной задаче), необходимо сделать так, чтобы на последующих итерациях она обратилась в нуль. Для этого в выражение целевой функции вводят штраф.
Переменная Ri, с помощью достаточно большого положительного числа М, штрафуется путём ввода в целевую функцию выражения – MRi в случае максимизации целевой функции и выражения +MRi – в случае минимизации. Вследствие этого штрафа естественно предположить, что процесс оптимизации симплекс-метода приведёт к нулевому значению переменной Ri. Следующий пример проясняет детали этого метода.
Пример 3.4-1
Минимизировать z = 4x1 + x2
при выполнении условий
3x1 + x2 = 3,
4x1 + 3x2 >= 6,
x1 + 2x2 <= 4,
x1, x2 >= 0.
Стандартная форма этой задачи получается в результате добавления дополнительной (избыточной) переменной x3 во второе неравенство и дополнительной (остаточной) переменной x4 в третье неравенство. Эта задача в стандартной форме будет записана следующим образом.
Минимизировать z = 4x1 + x2
при выполнении условий
3x1 + x2 = 3,
4x1 + 3x2 – x3 = 6,
x1 + 2x2 + x4 = 4,
x1, x2, x3, x4 >= 0.
В полученной задаче первое и второе уравнения не имеют дополнительных (остаточных) переменных, которые можно ввести в базисное решение. Поэтому введём в эти уравнения искусственные переменные R1 и R2, а в целевую функцию добавим штраф MR1 + MR2. В результате получим следующую задачу ЛП.
Минимизировать z = 4x1 + x2 + MR1 + MR2
при выполнении условий
3x1 + x2 + R1 = 3,
4x1 + 3x2 – x3 + R2 = 6,
x1 + 2x2 + x4 = 4,
x1, x2, x3, x4, R1, R2 >= 0.
В этой модифицированной задаче переменные R1, R2 и x4 можно использовать в качестве начального допустимого базисного решения.
При использовании М-метода следует обратить внимание на следующие два обстоятельства.
1. Использование штрафа М может и не привести к исключению искусственной переменной в конечной симплекс-итерации. Если исходная задача линейного программирования не имеет допустимого решения (например, система ограничений несовместна), тогда в конечной симплекс-итерации, по крайней мере, одна искусственная переменная будет иметь положительное значение. Это «индикатор» того, что задача не имеет допустимого решения.
2. Теоретически применение М-метода требует, чтобы М → ∞. Однако с точки зрения компьютерных вычислений величина М должна быть конечной и, вместе с тем, достаточно большой. Как понимать термин «достаточно большая» – это открытый вопрос. Величина М должна быть настолько большой, чтобы выполнить роль «штрафа», но не слишком большой, чтобы не уменьшить точность вычислений. На практике вы должны помнить о возможных ошибках машинного округления при выполнении выполнений, в которых совместно участвуют как большие, так и малые числа.
Правильный выбор значения М зависит от данных исходной задачи. Бездумное следование теоретическому требованию, что М должно быть «очень большим», может привести к значительным ошибкам округления. Именно поэтому М-метод никогда не применяется в коммерческих программах, реализующих симплекс-метод. Вместо него используется двухэтапный метод, который будет описан в следующем разделе.
2.2 Алгоритм двухэтапного метода.
Пример 2.2-2 демонстрирует проблемы, которые могут возникнуть при М-методе вследствие ошибок округления. Двухэтапный метод полностью лишён тех недостатков, которые присущи М-методу. Как следует из названия этого метода, процесс решения задачи ЛП разбивается на два этапа. На первом этапе ведётся поиск начального допустимого базисного решения. Если такое решение найдено, то на втором этапе решается исходная задача.
Этап 1. Задача ЛП записывается в стандартной форме, а в ограничения добавляются необходимые искусственные переменные (как и в М-методе) для получения начального базисного решения. Решается задача ЛП минимизации суммы искусственных переменных с исходными ограничениями. Если минимальное значение этой новой целевой функции больше нуля, значит, исходная задача не имеет допустимого решения, и процесс вычислений заканчивается. (Напомним, что положительные значения искусственных переменных указывают на то, что исходная система ограничений несовместна.) Если новая целевая функция равна нулю, переходим ко второму этапу.
Этап 2. Оптимальное базисное решение, полученное на первом этапе, используется как начальное допустимое базисное решение исходной задачи.
Пример 2.2-3
К задаче из примера 2.2-3 применим двухэтапный метод.
Этап 1
Минимизировать r = R1 + R2
С ограничениями
3x1 + x2 + R1 = 3,
4x1 + 3x2 – x3 + R2 = 6,
x1 + 2x2 + x4 = 4,
x1, x2, x3, x4, R1, R2, >= 0.
Соответствующая таблица имеет следующий вид.
|
Базис |
x1 |
x2 |
x3 |
R1 |
R2 |
x4 |
Решение |
|
r |
0 |
0 |
0 |
-1 |
-1 |
0 |
0 |
|
R1 |
3 |
1 |
0 |
1 |
0 |
0 |
3 |
|
R2 |
4 |
3 |
-1 |
0 |
1 |
0 |
6 |
|
x4 |
1 |
2 |
0 |
0 |
0 |
1 |
4 |
Как и в М-методе, сначала вычисляется новая r-строка.
Старая r-строка: (0 0 0 -1 -1 0 | 0)
+ 1 * R1-строка: (3 1 0 1 0 0 | 3)
+ 1 * R2-строка: (4 3 -1 0 1 0 | 6)
= Новая r-строка: (7 4 -1 0 0 0 | 9)
Новая строка
r + 7x1 + 4x2 – x3 + 0R1 + 0R2 + 0x4 = 9
используется для решения первого этапа, что приведёт к следующему оптимальному решению (проверьте!).
|
Базис |
x1 |
x2 |
x3 |
R1 |
R2 |
x4 |
Решение |
|
r |
0 |
0 |
0 |
-1 |
-1 |
0 |
0 |
|
x1 |
1 |
0 |
1/5 |
3/5 |
-1/5 |
0 |
3/5 |
|
x2 |
0 |
1 |
-3/5 |
-4/5 |
3/5 |
0 |
6/5 |
|
x4 |
0 |
0 |
1 |
1 |
-1 |
1 |
1 |
Поскольку достигнут минимум r = 0, значит, на первом этапе получено допустимое базисное решение x1 = 3/5, x2 = 6/5 и x4 = 1. Искусственные переменные полностью выполнили свою «миссию», поэтому из последней таблицы можно удалить их столбцы. Переходим ко второму этапу.
Этап 2
После удаления искусственных переменных исходная задача будет записана следующим образом.
Минимизировать z = 4x1 + x2
с ограничениями
x1 + 1/5 x3 = 3/5,
x2 + 3/5 x3 = 6/5,
x3 + x4 = 1,
x1, x2, x3, x4 >= 0.
Обратите внимание, что после первого этапа исходная задача претерпела некоторые изменения, которые учитывают полученное базисное решение. Этой трансформированной задаче соответствует следующая таблица:
|
Базис |
x1 |
x2 |
x3 |
x4 |
Решение |
|
z |
-4 |
-1 |
0 |
0 |
0 |
|
x1 |
1 |
0 |
1/5 |
0 |
3/5 |
|
x2 |
0 |
1 |
-3/5 |
0 |
6/5 |
|
x4 |
0 |
0 |
1 |
1 |
1 |
Поскольку базисные переменные x1 и x2 имеют ненулевые коэффициенты в z-строке, эту строку следует преобразовать.
Старая z-строка: (-4 -1 0 0 | 0)
+ 4 * x1-строка: (4 0 4/5 0 | 12/5)
+ 1 * x2-строка: (0 1 -3/5 0 | 6/5)
= Новая z-строка: (0 0 1/5 0 | 18/5)
Начальная таблица второго этапа примет следующий вид:
|
Базис |
x1 |
x2 |
x3 |
x4 |
Решение |
|
z |
0 |
0 |
1/5 |
0 |
18/5 |
|
x1 |
1 |
0 |
1/5 |
0 |
3/5 |
|
x2 |
0 |
1 |
-3/5 |
0 |
6/5 |
|
x4 |
0 |
0 |
1 |
1 |
1 |
Так как решается задача минимизации, следует ввести переменную x3 в базис. Применение алгоритма симплекс-метода уже на следующей итерации приведёт к оптимальному решению (проверьте!).
Удаление искусственных переменных в конце первого этапа имеет смысл только тогда, когда все они являются небазисными (как в примере 2.2-4). Однако возможна ситуация, когда в конце первого этапа искусственные переменные останутся в базисе, но будут иметь нулевые значения. В этом случае такие переменные при необходимости будут формировать часть начального базисного решения для второго этапа. При этом необходимо так изменить вычисления, выполняемые на втором этапе, чтобы искусственные переменные никогда не смогли принять положительные значения ни в каких итерациях симплекс-метода.
Существует простое правило, которое гарантирует, что нулевая базисная искусственная переменная на втором этапе никогда не станет положительной. Если в ведущем столбце коэффициент, соответствующий нулевой базисной искусственной переменной, положителен, тогда ведущий элемент определяется автоматически (поскольку ему соответствует минимальное отношение, равное нулю) и искусственная переменная на следующей итерации становится небазисной. Если ведущий элемент равен нулю, следующая итерация оставляет искусственную переменную нулевой. И наконец, рассмотрим отрицательный ведущий элемент. В этом случае минимальное отношение не ассоциируется с базисной (нулевой) искусственной переменной. Если минимальное отношение будет положительным, то на следующей итерации искусственная переменная примет положительное значение (обоснуйте это утверждение). Чтобы исключить эту возможность, мы принуждаем искусственную переменную всегда оставаться в базисном решении. Поскольку искусственная переменная равна нулю, её удаление из базисного решения не влияет на то, будет ли допустимым решение из оставшихся в базисе переменных. (Было бы полезно для читателя рассмотреть все описанные случаи с помощью симплекс-таблиц.)
Итак, правило для второго этапа заключается в том, чтобы искусственные переменные оставлять в базисе всегда, когда коэффициент в ведущем столбце положительный или отрицательный. Фактически это правило применяется в конце первого этапа, когда удаляем нулевые искусственные переменные из базисного решения, перед тем как приступить ко второму этапу.
Глава 3. Особые случаи симплекс-метода.
В этом разделе рассмотрим четыре особых случая, встречающихся при использовании симплекс-метода.
1. Вырожденность.
2. Альтернативные оптимальные решения.
3. Неограниченные решения.
4. Отсутствие допустимых решений.
При изучении этих случаев основное внимание мы уделим (1) теоретическому обоснованию причин, приводящих к таким ситуациям, и (2) их практическим интерпретациям применительно к реальным задачам.
3.1 Вырожденность.
В ходе выполнения симплекс-метода проверка условия допустимости может привести к неоднозначному выбору исключаемой переменной. В этом случае на следующей итерации одна или более базисных переменных примут нулевое значение. Тогда новое решение будет вырожденным.
В вырожденном решении нет никакой опасности, за исключением небольших теоретических неудобств, которые мы далее кратко обсудим. С практической точки зрения вырожденность объясняется тем, что в исходной задаче присутствует, по крайней мере, одно избыточное ограничение. Для того чтобы лучше понять практические и теоретические аспекты явления вырожденности, рассмотрим численный пример. Графическая интерпретация задачи поможет наглядно разобраться в этом явлении.
Пример 3.1-1. (Вырожденное оптимальное решение)
Рассмотрим следующую задачу ЛП.
Максимизировать z = 3x1 + 9x2
При выполнении условий
X1 + 4x2 <= 8,
X1 + 2x2 <= 4,
X1, x2 >= 0.
|
Итерация |
Базис |
x1 |
x2 |
x3 |
x4 |
Решение |
|
Начальная |
z |
-3 |
-9 |
0 |
0 |
0 |
|
Вводится x3 |
x3 |
1 |
4 |
1 |
0 |
8 |
|
Исключается x3 |
x4 |
1 |
2 |
0 |
1 |
4 |
|
Первая |
z |
-3/4 |
0 |
9/4 |
0 |
18 |
|
Вводится x1 |
x2 |
1/4 |
1 |
1/4 |
0 |
2 |
|
Исключается x4 |
x4 |
1/2 |
0 |
-1/2 |
1 |
0 |
|
Вторая |
z |
0 |
0 |
3/2 |
3/2 |
18 |
|
Оптимум |
x2 |
0 |
1 |
1/2 |
-1/2 |
2 |
|
|
x1 |
1 |
0 |
-1 |
2 |
0 |
На начальной итерации в качестве исключаемой можно выбрать как переменную x3, так и x4. Если оставить в базисе переменную x4, на следующей итерации она примет значение 0 (как показано в таблице), т.е. получим вырожденное базисное решение. Оптимальное решение получается на следующей итерации.
Что же практически приводит к вырожденности решения? Рассмотрим рис. 3.4, графически представляющий решение этой задачи. Точка оптимума x1 = 0, x2 = 2 является пересечением трёх прямых. Поскольку данная задача двухмерна, эта точка переопределена (на плоскости для определения точки достаточно двух прямых), и, следовательно, одно из ограничений избыточно. На практике информация о том, что некоторые ресурсы недефицитны, может быть полезной при интерпретации результатов решения задачи. Эти сведения также могут помочь выявить неточности и ошибки в постановке исходной задачи. К сожалению, не существует способов определить избыточное ограничение непосредственно из данных симплекс-таблиц.

Рис. 3.1
С вычислительной и теоретической точек зрения вырожденность может привести к двум последствиям. Во-первых, в процессе вычислений может возникнуть зацикливание. Если в приведённой выше таблице сравнить первую и вторую итерации, то можно заметить, что значение целевой функции не изменилось (z = 18). Поэтому может возникнуть ситуация, когда при реализации симплекс-метода некоторая последовательность будет повторяться, не изменяя значения целевой функции и не приводя к завершению вычислительного процесса. Существуют методы, предотвращающие зацикливание, однако они значительно замедляют процесс вычислений. Поэтому в большинстве программ, реализующих симплекс-метод, отсутствуют специальные средства защиты от зацикливания, тем более, что вероятность зацикливания очень мала.
Во-вторых, последствие вырожденности решения можно обнаружить, сравнивая первую и вторую итерации в приведённой выше таблице. Хотя в этих итерациях состав базисных и небазисных переменных различен, значения всех переменных и значение целевой функции не изменяются:
x1 = 0, x2 = 2, x3 = 0, x4 = 0, z = 18.
Можно ли, несмотря на то что оптимальное решение не достигнуто, остановить вычисления на первой итерации (когда впервые обнаруживается вырожденность)? Ответ отрицательный, так как решение может быть только временно.
3.2. Альтернативные оптимальные решения.
Когда прямая (если рассматривается двухмерная задача ЛП, в общем случае – гиперплоскость), представляющая целевую функцию, параллельна прямой (гиперплоскости), соответствующей связывающему неравенству (которое в точке оптимума выполняется как точное равенство), целевая функция принимает одно и то же оптимальное значение на некотором множестве точек границы области допустимых решений. Эти решения называются альтернативными оптимальными решениями. Следующий пример показывает, что таких решений (если они существуют) бесконечное множество. Этот пример также проиллюстрирует практическую значимость альтернативных практических решений.
Пример 3.2-1 (Бесконечное множество решений)
Рассмотрим следующую задачу ЛП.
Максимизировать z = 2x1 + 4x2
при ограничениях
x1 + 2x2 <= 5,
x1 + x2 <= 4,
x1, x2 >= 0.
На рис. 3.2 показано множество альтернативных оптимальных решений, которые являются следствием того, что прямая, представляющая целевую функцию, параллельна прямой, соответствующей связывающему ограничению. Каждая точка отрезка BC соответствует оптимальному решению со значением целевой функции z = 10.

Рис. 3.2
Последовательные итерации выполнения симплекс-метода представлены в следующей таблице.
|
Итерация |
Базис |
x1 |
x2 |
x3 |
x4 |
Решение |
|
Начальная |
z |
-2 |
-4 |
0 |
0 |
0 |
|
Вводится x2 |
x3 |
1 |
2 |
1 |
0 |
5 |
|
Исключается x3 |
x4 |
1 |
1 |
0 |
1 |
4 |
|
Первая |
z |
0 |
0 |
2 |
0 |
10 |
|
Вводится x1 |
x2 |
1/2 |
1 |
1/2 |
0 |
5/2 |
|
Исключается x4 |
x4 |
1/2 |
0 |
-1/2 |
1 |
3/2 |
|
Вторая |
z |
0 |
0 |
2 |
0 |
10 |
|
(Альтернативный |
x2 |
0 |
1 |
1 |
-1 |
1 |
|
оптимум) |
x1 |
1 |
0 |
-1 |
2 |
3 |
На первой итерации получаем оптимальное решение x1 = 5/2 и z = 10, которое соответствует точке B на рис. 3.2. Как узнать из симплекс-таблицы, что существует альтернативное оптимальное решение? Посмотрите на коэффициенты небазисных переменных в z-строке первой итерации. Коэффициент небазисной переменной x1 равен нулю, это означает, что данную переменную можно ввести в базис без изменения значения целевой функции, но значение самой переменной x1 изменится. Введение переменной x1 в базисное решение выполнено на второй итерации, при этом из базиса исключена переменная x4. Получено новое решение x1 = 3, x2 = 1, z = 10, которое соответствует точке C на рис. 3.2.
Симплекс-метод может определить только две угловые точки B и C. Математически мы можем найти все точки (x1’,x2’) отрезка BC как взвешенное среднее (с неотрицательными весами) точек B и C. Полагая 0 <= α <= 1 и
B: x1 = 0, x2 = 5/2,
C: x1 = 3, x2 = 1,
координаты любой точки отрезка BC можно записать следующим образом:
x1’ = α * 0 + (1 - α) * 3 = 3 – 3 α,
x2’ = α * 5/2 + (1 - α) * 1 = 1 – 3/2 α,
При α = 0 (x1’,x2’) = (3, 1), что соответствует точке C. При α = 1 получаем (x1’,x2’) = (0, 5/2) – это точка B. Если значение α лежит строго между 0 и 1, получаем внутренние точки отрезка BC.
На практике альтернативные оптимальные решения весьма полезны, поскольку позволяют сделать выбор среди множества решений без ухудшения значения целевой функции. Например, в рассмотренной выше задаче переменная x2, принимает нулевое значение в точке B, тогда как в других альтернативных оптимальных решениях её значение положительно. Если интерпретировать задачу как задачу организации производства двух видов товара (которые соответствуют переменным x1 и x2), то, с учётом конкуренции на рынке, более рационально производить оба вида товара, а не один. В этом случае решение, соответствующее точке C, предпочтительнее.
3.3 Неограниченные решения.
В некоторых задачах ЛП значения переменных могут неограниченно возрастать без нарушения ограничений. Это говорит о том, что пространство допустимых решений не ограничено, по крайней мере, по одному направлению. В результате этого целевая функция может возрастать (задача максимизации) или убывать (задача минимизации) неограниченно.
Неограниченность решения задачи свидетельствует только об одном: модель разработана не достаточно корректно. Типичные ошибки, приводящие к построению таких моделей, заключается в том, что не учитываются ограничения, не являющиеся избыточными, и не точно оцениваются параметры (коэффициенты) ограничений.
В следующем примере показано, как на основе данных, приведённых в симплекс-таблице, можно определить, когда не ограничено пространство решений и значения целевой функции.
Пример 3.3–1. (Неограниченная целевая функция)
Рассмотрим задачу
Максимизировать z = 2x1 + x2
при выполнении условий
x1 – x2 <= 10,
2x1 <= 40,
x1, x2 >= 0.
Симплекс-таблица начальной итерации этой задачи имеет следующий вид.
|
Базис |
x1 |
x2 |
x3 |
x4 |
Решение |
|
z |
-2 |
-1 |
0 |
0 |
0 |
|
x3 |
1 |
-1 |
1 |
0 |
10 |
|
x4 |
2 |
0 |
0 |
1 |
40 |
Из этой таблицы видно, что в качестве вводимой переменной можно взять как x1, так и x2. Поскольку переменная x1 имеет максимальный (по абсолютной величине) отрицательный коэффициент в z-строке, именно её следует ввести в базисное решение. Однако заметим, что во всех ограничениях коэффициенты, стоящие перед переменной x2, отрицательны или равны нулю. Это означает, что значение переменной x2 может возрастать до бесконечности, и при этом не нарушается ни одно ограничение. Поскольку увеличение на 1 значения переменной x2 приводит к увеличению на 1 значения целевой функции, значит, неограниченное увеличение значения переменной x2 ведёт к неограниченному увеличению значения целевой функции. Эта ситуация проиллюстрирована на рис. 3.3. На этом рисунке видно, что пространство допустимых решений не ограничено в направлении оси x2 и значение целевой функции может быть каким угодно большим.

Рис. 3.3
Правило выявления неограниченности решения следующее. Если на какой-либо симплекс-итерации коэффициенты в ограничениях для какой-нибудь небазисной переменной будут неположительными, значит, пространство решений не ограничено в направлении возрастания этой переменной. Кроме того, если коэффициент этой переменной в z-строке отрицателен, когда рассматривается задача максимизации, или положителен в задаче минимизации, целевая функция также не ограничена.
3.4 Отсутствие допустимых решений.
Если ограничения задачи ЛП несовместны (т.е. они не могут выполняться одновременно), то задача не имеет допустимых решений. Такая ситуация не может возникнуть, если все неравенства, составляющие систему ограничений, имеют тип «<=» с неотрицательными правыми частями, так как в этом случае дополнительные переменные могут составить допустимое решение. Для других типов ограничений мы используем искусственные переменные. И хотя в оптимальном решении все искусственные переменные в силу штрафов равны нулю, такой исход возможен только тогда, когда задача имеет непустое пространство допустимых решений. В противном случае, в оптимальном решении будет присутствовать хотя бы одна положительная искусственная переменная.
С практической точки зрения отсутствие допустимых решений свидетельствует о том, что задача плохо сформулирована.
Пример 3.4-1. (Отсутствие допустимых решений)
Рассмотрим следующую задачу.
Максимизировать z = 3x1 + 2x2
при выполнении условий
2x1 + x2 <= 2,
3x1 + 4x3 >= 12,
x1, x2 >= 0.
Результат применения симплекс-метода представлен в следующей таблице.
|
Итерация |
Базис |
x1 |
x2 |
x4 |
x3 |
R |
Решение |
|
Начальная |
z |
-3 -3M |
-2 -4M |
M |
0 |
0 |
-12M |
|
Вводится |
x3 |
2 |
1 |
0 |
1 |
0 |
2 |
|
Исключается |
R |
3 |
4 |
-1 |
0 |
1 |
12 |
|
Первая |
z |
1 + 5M |
0 |
M |
2 + 4M |
0 |
4 – 4M |
|
(псевдооптимум) |
x2 |
2 |
1 |
0 |
1 |
0 |
2 |
|
|
R |
-5 |
0 |
1 |
-4 |
1 |
4 |
Данные из этой таблицы показывают, что в точке оптимума искусственная переменная R имеет положительное значение (= 4), что свидетельствует об отсутствии допустимого решения. На рис. 3.4 графически представлена ситуация данной задачи. Алгоритмы симплекс-метода, допуская положительные значения искусственной переменной, по существу, превращает неравенство 3x1 + 4x3 >= 12 в 3x1 + 4x3 <= 12. (Объясните, почему так происходит.) В результате получаем то, что можно назвать псевдооптимальным решением.

Рис. 3.4
2. Практическая часть.
Постановка задачи.
Решить задачи:
при ограничениях:
 4x1 + 2x2 + 2x3 + x4 <= 35;
4x1 + 2x2 + 2x3 + x4 <= 35;
x1 + x2 + 2x3 + 3x4 <= 30;
3x1 + x2 + 2x3 + x4 <= 40;
xj >= 0, j = 1, 2, 3, 4.
при ограничениях:
 x1 – 4x2 – 4 <= 0;
x1 – 4x2 – 4 <= 0;
3x1 – x2 >= 0;
x1 + x2 – 4 >= 0;
x1 >= 0, x2 >= 0.
Решение.
1. F = 14x1 + 10x2 + 14x3 + 14x4 → max
при ограничениях:
 |
4x1 + 2x2 + 2x3 + x4 <= 35;
x1 + x2 + 2x3 + 3x4 <= 30;
3x1 + x2 + 2x3 + x4 <= 40;
xj >= 0, j = 1, 2, 3, 4.
Переведём систему в канонический вид для решения симплексным методом.
 4x1 + 2x2 + 2x3 + x4 + x5 = 35;
4x1 + 2x2 + 2x3 + x4 + x5 = 35;
x1 + x2 + 2x3 + 3x4 + x6 = 30;
3x1 + x2 + 2x3 + x4 + x7 = 40;
xj >= 0, j = 1, 2, 3, 4, 5, 6, 7.
14x1 + 10x2 + 14x3 + 14x4 + 0x5 + 0x6 + 0x7 → max

Ответ: max z = 225 при x2 = 5, x3 = 12,5, x7 = 10, x1 = x4 = x5 = x6 = 0.
Двухэтапный метод.
2. F = x1 + x2 → max
 при ограничениях:
при ограничениях:
x1 – 4x2 – 4 <= 0;
3x1 – x2 >= 0;
x1 + x2 – 4 >= 0;
x1, x2 >= 0.
Переведём в канонический вид и добавим искусственные переменные.
f = x1 + x2 + 0x3 + 0x4 + 0x5 – Mx0 – Mx7 → max.
 |
x1 – 4x2 – 4 + x3 = 0;
3x1 – x2 – x4 + x6 = 0;
x1 + x2 – 4 – x5 + x7 = 0;
x1, x2, x3, x4, x5, x6, x7 >= 0;
Этап 1.
Z = x6 + x7 → min
|
Базис |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
Решение |
|
x3 |
1 |
-4 |
1 |
0 |
0 |
0 |
0 |
4 |
|
x6 |
3 |
-1 |
0 |
-1 |
0 |
1 |
0 |
0 |
|
x7 |
1 |
1 |
0 |
0 |
-1 |
0 |
1 |
4 |
|
z - c |
0 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
Так как базисные переменные x6 и x7 имеют ненулевые коэффициенты в (z - c) – строке, эту строку следует преобразовать:
(z - c): 0 0 0 0 0 -1 -1 0
+
1 * x6: 3 -1 0 -1 0 1 0 0
+
1 * x7: 1 1 0 0 -1 0 1 4
= (z - c): 4 0 0 -1 -1 0 0 4
|
Базис |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
Решение |
Отношение |
|
x3 |
1 |
-4 |
1 |
0 |
0 |
0 |
0 |
4 |
4 |
|
x6 |
3 |
-1 |
0 |
-1 |
0 |
1 |
0 |
0 |
0 ← |
|
x7 |
1 |
1 |
0 |
0 |
-1 |
0 |
1 |
4 |
4 |
|
(z - c)’ |
4 |
0 |
0 |
-1 |
-1 |
0 |
0 |
4 |
|
↑
|
Базис |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
Решение |
Отношение |
|
x3 |
0 |
-3 и 2/3 |
1 |
1/3 |
0 |
-1/3 |
0 |
4 |
|
|
x1 |
1 |
-1/3 |
0 |
-1/3 |
0 |
1/3 |
0 |
0 |
|
|
x2 |
0 |
1 и 1/3 |
0 |
1/3 |
1 |
-1/3 |
1 |
4 |
3 ← |
|
(z - c)’ |
0 |
4/3 |
0 |
1/3 |
-1 |
-4/3 |
0 |
4 |
|
↑
|
Базис |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
Решение |
Отношение |
|
x3 |
0 |
0 |
1 |
5/4 |
11/4 |
-5/4 |
11/4 |
4 |
|
|
x1 |
1 |
0 |
0 |
-1/4 |
1/4 |
1/4 |
1/4 |
0 |
|
|
x2 |
0 |
1 |
0 |
1/4 |
3/4 |
-1/4 |
3/4 |
4 |
|
|
(z - c)’ |
0 |
0 |
0 |
0 |
-2 |
-5/3 |
-1 |
4 |
|
Так как достигнуто min (z - c)’ = 0, то получено допустимое базисное решение для второго этапа: x1 = 1, x2 = 3, x3 = 15. Искусственные переменные могут быть исключены.
Этап 2.
Перепишем исходную задачу с учётом полученного базисного решения:
f = x1 + x2 + 0x3 + 0x4 + 0x9 → max
 x3 + 5/4 x4 + 11/4 x5 = 15;
x3 + 5/4 x4 + 11/4 x5 = 15;
x1 – 1/4 x4 + 1/4 x5 = 1;
x2 + 1/4 x4 + 3/4 x5 = 3;
x1, x2, x3, x4, x5 >= 0.
|
Базис |
x1 |
x2 |
x3 |
x4 |
x5 |
Решение |
|
x1 |
1 |
0 |
0 |
1/4 |
1/4 |
1 |
|
x2 |
0 |
1 |
0 |
1/4 |
3/4 |
3 |
|
x3 |
0 |
0 |
1 |
5/4 |
11/4 |
15 |
|
(f - c) |
1 |
-1 |
0 |
0 |
0 |
0 |
Согласуем значения в строке (f - c) с остальной частью таблицы:
(f - c): -1 -1 0 0 0 0
+
1 * x1: 1 0 0 -1/4 1/4 1
+
1 * x2: 0 1 0 1/4 3/4 3
= (f-c)’: 0 0 0 0 1 4
Исходное решение является оптимальным.
Ответ: max (f) = 4 при x1 = 1, x2 = 3, x3 = 15, x4 = 0, x5 = 0.
Так как небазисные переменные равны нулю, задача имет множество альтернативных оптимальных решений, находящихся н отрезке AB (x1+ x2 = 4).

Заключение.
Симлекс-метод – это характерный пример итерационных вычислений. используемых при решении большинства оптимизационных задач.
В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.
Из теоретических положений, лежащих в основе симплекс-метода, следует, что оптимальное решение задачи линейного программирования соответствует крайней точке пространства допустимых решений задачи. В свою очередь, крайние точки пространства допустимых решений полностью определяются базисными решениями задачи ЛП, представленной в стандартной форме. Для компьютерной реализации симплекс-метода разработан способ использования искусственных переменных, что позволяет найти начальное базисное решение задачи. В этой главе также рассмотрены теоретические и практические аспекты особых случаев реализации симплекс-метода: вырожденность, альтернативные оптимальные решения, неограниченность и отсутствие допустимых решений.
Литература.
1. Ашманов С.А. Линейное программирование. – М.: Наука, 1981.
2. Гасс С. Линейное программирование. – М.: Физматгиз, 1961.
3. Гольштейн Е.Г., Юдин Д.Б. Линейное программирование: Теория, методы и приложения. – М.: Наука, 1969.
4. Таха, Хэмди, А. Введение в исследование операций. 6-е издание. : Пер. с англ. — М.: Издательский дом "Вильяме", 2001. — 912 с. : ил. — Парал. тит. англ.
5. Н.Ш. Кремер, Б А Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. Исследование операций в экономике: Учеб. пособие для И87 вузов —М: ЮНИТИ, 2002.— 407 с.
www.referatmix.ru
Содержание.
Введение……………………………………………………………………………………….с.5.
1. Теоретическая часть.
Глава 1. Простой симплекс-метод.
1.1 Обоснование и описание вычислительной процедуры. Приведение задачи линейного программирования к стандартной форме……………………………с.7
1.2 Симплексный метод решения задач……………………………………..…...с.8.
1.3 Алгоритм симплекс-метода…………………………………………………с.10.
1.4 Решение задачи оптимизации. Построение аналитической модели……...с.12.
1.5 Приведение задачи к стандартной форме. Определение начального допустимого решения…………………………….……………………………...с.14.
Глава 2. Двухэтапный метод.
2.1 Искусственное начальное решение…………………………………………с.16.
2.2 Алгоритм двухэтапного метода……………………………………………..с.19.
Глава 3. Особые случаи симплекс-метода……………………………………………...23.
3.1 Вырожденность……………………………………………………………....с.24.
3.2 Альтернативные оптимальные решения…………………………………....с.27.
3.3 Неограниченные решения…………………………………………………...с.30.
3.4 Отсутствие допустимых решений…………………………………………..с.32.
2. Практическая часть.
2.1 Постановка задачи…………..……………………………………………………..с.34.
2.2 Решение…..…………………………………………………………………………с.36.
Заключение…………………………………………………………………………………...с.39.
Литература…………………………………………………………………………………....с.40.
Введение.
Целью данной курсовой работы является решение конкретной задачи линейного программирования. Во всех таких задачах требуется найти максимум или минимум линейной функции при условии, что её переменные принимают неотрицательные значения и удовлетворяют некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные уравнения, так и линейные неравенства. Каждая из этих задач является частным случаем общей задачи линейного программирования.
Для решения задач линейного программирования созданы специальные методы. Изучению одного из них, а именно симплекс-методу, посвящена эта курсовая работа.
В настоящее время оптимизация находит применение в науке, технике и в любой другой области человеческой деятельности.
Оптимизация – целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно.
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:
· количество продукции - расход сырья
· количество продукции - качество продукции
Выбор компромиcного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого. Приведем примеры.
Типичный пример неправильной постановки задачи оптимизации:
«Получить максимальную производительность при минимальной себестоимости».
Ошибка заключается в том, что ставится задача поиска оптимальности 2-х величин, противоречащих друг другу по своей сути.
Правильная постановка задачи могла быть следующая:
а) получить максимальную производительность при заданной себестоимости;
б) получить минимальную себестоимость при заданной производительности;
В первом случае критерий оптимизации - производительность а во втором - себестоимость.
2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта.
3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
4. Учёт ограничений.
1. Теоретическая часть.
Глава 1. Простой симплекс-метод.
1.1 Обоснование и описание вычислительной процедуры.Приведение задачи линейного программирования к стандартной форме.
Любая задача линейного программирования приводится к стандартной (канонической) форме основной задачи линейного программирования, которая формулируется следующим образом: найти неотрицательные значения переменных X1 , X2 , Xn , удовлетворяющих ограничениям в виде равенств:
A11X1 + A12X2 + … + A1nXn = B1;
A21X1 + A22X2 + … + A2nXn = B2;
……………………………………
Am1X1 + Am2X2 + … + AmnXn = Bm;
Xj ≥ 0, j=1,…,n
и обращающих в максимум линейную функцию этих переменных:
E = C1X1 + C2X2 + … + CnXn Þ max
При этом также требуется, чтобы правые части равенств были неотрицательны, т.е. должны соблюдаться условия:
Bj ≥ 0, j=1,…,n
Приведение к стандартной форме необходимо, так как большинство методов решения задач линейного программирования разработано именно для стандартной формы. Для приведения к стандартной форме задачи линейного программирования может потребоваться выполнить следующие действия:
- перейти от минимизации целевой функции к ее максимизации;
- изменить знаки правых частей ограничений;
- перейти от ограничений-неравенств к равенствам;
- избавиться от переменных, не имеющих ограничений на знак.
Для решения нашей задачи воспользуемся симплекс-методом, так как этот метод предназначен для решения задач линейного программирования любой размерности.
1.2 Симплексный метод решения задач.
Симплексный метод задач линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план, и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план. Рассмотрим задачу, для которой этот план можно непосредственно записать.
Пусть дана функция, для которой необходимо найти наибольшее или наименьшее значение, если значения всех неизвестных неотрицательные.
ѓ = C0 + C1x1 + C2x2 +...+ Cnxn
и система m линейных уравнений с n неизвестными. Это называется системой ограничений:
 a11x1 + a12x2 +...+ a1nxn = b1
a11x1 + a12x2 +...+ a1nxn = b1
a21x1 + a12x2 +...+ a2nxn = b2
...
am1x1 +am2x12 +...+ amnxn = bm
Целевую функцию представим в виде:
ѓ - C1x1-C2x2 -...-Cnxn = C0
Составим симплекс-таблицу. В дальнейшем будем считать, что ранг матрицы системы ограничений равен r.В системе ограничений выбран базис (основные неизвестные)x1,x2,...xn и коэффициенты в правой части не отрицательны.
В этом случае система ограничений будет иметь вид:
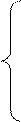 |
x1 +...+ a1,r+1xr+1 +...+ a1nxn = b1
x2 + a2,r+1xr+1 +...+ a2nxn = b2
...
xr+ ar,r+1xr+1 +...+ arnxn = br
Тогда целевая функция имеет вид:
ѓ + Cr+1xr+1 + Cr+2xr+2 -...- Cnxn = C0
Нахождение оптимального плана симплексным методом включает следующие этапы:
1. Находят опорный план.
2. Составляют симплекс-таблицу. В общем виде:
| Базисные неизвестные | Свободные члены | x1 | x2 | xr | xr+1 | xj | xn |
x1 x2 xi xr | b1 b2 bi br | 1 0 0 0 | 0 1 0 0 | 0 0 0 1 | a1,r+1 a2,r+1 ai,r+1 ar,r+1 | a1j a2j aij arj | a1n a2n ain arn |
| ѓ | C0 | 0 | 0 | 0 | Cr+2 | Cj | Cn |
3. В нижней строчке симплекс-таблицы необходимо отыскать отрицательные числа (не считая коэффициент Со). Если таких чисел нет, то данное базисное решение является оптимальным.
4. Пусть элемент Сj<0,тогда в j-ом столбце необходимо найти положительный элемент. Если все коэффициенты этого столбца отрицательные, то решения не существует.
5. Если положительный коэффициент в j-ом столбце один, то выбранную строку с номером i надо поделить все коэффициенты на число aij.Результат деления записываем в новую симплекс-таблицу. Если же положительных коэффициентов несколько, необходимо составить отношение bi/aij и из полученных значений выбрать наименьшее, соответствующее i-ой строке.
6. В новой симплекс-таблице в столбце базисных неизвестных вместо xi пишется xj. Продолжается заполняться таблица. В столбце с номером j необходимо получить нули(включая строку с целевой функцией). Для этого надо умножить i-ую записанную строку на нужное число и сложить с остальными строками.
В результате осуществился переход к новому базису, при этом значение целевой функции увеличилось.
1.3 Алгоритм симплекс-метода.
 Пусть система приведена к каноническому виду.
Пусть система приведена к каноническому виду.
X1+ q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
X2+q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
X3+q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
………………………………………………………
Xm+ qm,m+1 Xm+1 + …. + qm,m+n Xm+n =hm
В ней m базисных переменных, k свободных переменных. m+k=n - всего переменных.
Fmin= C1X1+ C2X2+ C3X3+....+ CnXn
Для дальнейших рассуждений вычислений будем пользоваться первой симплекс таблицей (таблица1).
Таблица 1.Симплекс таблица
| C | Б | H | C1 | C2 | … | Cm | Cm+1 | … | Cm+k |
| X1 | X2 | … | Xm | Xm+1 | … | Xm+k | |||
C1 C2 C3 : : Cm | X1 X2 X3 : : Xm | h2 h3 h4 : : Hm | 1 0 0 : : 0 | 0 1 0 : : 0 | : : : : : : | 0 0 0 : : 0 | q1,m+1 q2,m+1 q3,m+1 : : qm,m+1 | : : : : : : | q1,m+k q2,m+k q3,m+k : : qm,m+k |
| F0 | F1 | F2 | … | Cm | Cm+1 | … | Cm+k |
Первый столбец - коэффициенты в целевой функции при базисных переменных.
Второй столбец - базисные переменные.
Третий столбец - свободные члены (hi00).
Самая верхняя строка - коэффициенты при целевой функции.
Вторая верхняя строка - сами переменные, входящие в целевую функцию и в систему ограничений.
Основное поле симплекс метода - система коэффициентов из уравнения.
Последняя строка - служит для того, чтобы ответить на вопрос: «оптимален план или нет».
Индексная строка позволяет нам судить об оптимальности плана:
При отыскании Fmin в индексной строке должны быть отрицательные и нулевые оценки.
При отыскании Fmax в индексной строке должны быть нулевые и положительные оценки.
Переход ко второй итерации:
Для этого отыскиваем ключевой (главный) столбец и ключевую (главную) строку.
Ключевым столбцом является тот в котором находится наибольший положительный элемент индексной строки при отыскании Fmin или наименьший отрицательный элемент при отыскании Fmax.
Ключевой строкой называется та, в которой содержится наименьшее положительное частное от деления элементов столбца H на соответствующие элементы ключевого столбца.
На пересечении строки и столбца находится разрешающий элемент.
На этом этапе осуществляется к переходу к последующим итерациям.
Переход к итерациям:
Выводится базис ключевой строки, уступая место переменной из ключевого столбца со своим коэффициентом.
Заполняется строка вновь введенного базиса путем деления соответствующих элементов выделенной строки предыдущей итерации на разрешающий элемент.
Если в главной строке содержится нулевой элемент, то столбец, в котором находиться этот элемент переноситься в последующую итерацию без изменения.
Если в главном столбце имеется нулевой элемент, то строка, в которой он находиться переноситься без изменения в последующую итерацию.
Остальные элементы переносятся по формуле:

1.4 Решение задачи оптимизации. Построение аналитической модели.
В цехе имеется токарный станок и станок-автомат. Цех выпускает детали 1,2 и 3 в комплекте: на каждую деталь 1 – по 2 детали 2 и 3. Часовая производительность станков по каждой из деталей приведена в таблице:
Таблица 1. Часовая производительность станков
| Станки | Детали | ||
| 1 | 2 | 3 | |
| 1.Токарный | 5 | 5 | 10 |
| 2. Автомат | 15 | 15 | 10 |
Составить программу работы станков, при которой в течение смены (8 часов) будет выпускаться максимальное количество комплектов деталей.
Составим аналитическую модель задачи. Для этого сначала введем переменные, которые требуется определить:
X1 – время, которое работал токарный станок над деталями типа 1 в течение рабочей смены;
X2 – время, которое работал токарный станок над деталями типа 2 в течение рабочей смены;
X3 – время, которое работал токарный станок над деталями типа 3 в течение рабочей смены;
X4 – время, которое работал станок-автомат над деталями типа 1 в течение рабочей смены;
X5 – время, которое работал станок-автомат над деталями типа 2 в течение рабочей смены;
X6 – время, которое работал станок-автомат над деталями типа 3 в течение рабочей смены.
Система ограничений состоит из двух групп. Первая группа устанавливает, что каждый из станков может работать не более 8 часов в смену.
Ограничение времени работы токарного станка:
X1 + X2 + X3 £ 8;
Ограничение времени работы станка-автомата:
X4 + X5 + X6 £ 8.
Вторая группа ограничений направлена на выполнение требования о комплектации деталей: на каждую деталь 1 должно приходиться по 2 детали 2 и 3. Но перед тем, как вводить это ограничение, определим, сколько деталей каждого типа у нас будет производиться за смену:
5X1 + 15X4 - будет произведено за смену деталей типа 1;
5X2 + 15X5 - будет произведено за смену деталей типа 2;
10X3 + 10X6 - будет произведено за смену деталей типа 3.
Теперь введем сами ограничения:
2(5X1 + 15X4) = 5X2 + 15X5;
2(5X1 + 15X4) = 10X3 + 10X6.
Очевидно, что все переменные в задаче неотрицательные (объем продукции не может быть отрицательным):
X1 , X2 , X3 , X4 , X5 , X6 ≥ 0.
Целевая функция в нашей задаче должна выражать количество комплектов деталей, выпускаемых за смену, поэтому сложим все выпускаемые детали и поделим на 5 (в комплект, как уже упоминалось, входят 1 деталь типа 1 и по 2 детали типа 2 и 3):
E= (5X1 + 15X4 + 5X2 + 15X5 + 10X3 + 10X6)/5 Þ max
или, если упростить это выражение, то получим:
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þmax
Целевую функцию надо максимизировать.
Таким образом, формальная постановка задачи оптимизации имеет следующий вид:
X1 + X2 + X3 £ 8;
X4 + X5 + X6 £ 8;
2(5X1 + 15X4) = 5X2 + 15X5;
2(5X1 + 15X4) = 10X1 + 10X6;
X1 , X2 , X3 , X4 , X5 , X6 ≥ 0.
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þmax
1.5 Приведение задачи к стандартной форме. Определение начального допустимого решения.
Для приведения данной задачи к стандартной форме необходимо лишь перейти от ограничений – неравенств к равенствам. Для этого введем дополнительные балансовые неотрицательные переменные. Также для упрощения дальнейших вычислений разделим обе части ограничений на комплектацию деталей на 5:
X1 + X2 + X3 + X7 = 8;
X4 + X5 + X6 + X8 = 8;
2X1 – X2 + 6X4 – 3X5 = 0;
2X1 – 2X3 + 6X4 – 2X6 =0;
X1 , X2 , X3 , X4 , X5 , X6 , X7 , X8 ≥ 0.
E= X1 + X2 + 2X3 + 3X4 + 3X5 + 2X6 Þmax
где Х7 , Х8 – остаточные переменные.
Итак, нашу исходную задачу мы привели к стандартной форме основной задачи линейного программирования.
Для задачи, представленной в стандартной форме, количество переменных обычно больше, чем количество ограничений. Поэтому для нахождения начального решения задачи требуется выразить m переменных (т.е. количество переменных, равное количеству уравнений) через остальные n-m переменных, принять эти n-m переменных равными нулю и, таким образом, найти значения m переменных (в заданной задаче m=4 и n=8). Переменные, значения которых принимаются равными нулю, называются небазисными, а остальные m переменных - базисными. Значения базисных переменных неотрицательны (некоторые из них могут оказаться равными нулю). Количество базисных переменных всегда равно количеству ограничений. Найденное таким образом решение называется начальным допустимым базисным решением. Оно соответствует всем ограничениям.
Начальное решение проще всего найти в случае, когда в каждом ограничении есть переменная, которая входит в него с коэффициентом 1 и при этом отсутствует в других ограничениях. Такие переменные принимаются в качестве базисных (они образуют начальный базис задачи). Остальные (небазисные) переменные принимаются равными нулю. Таким образом, базисные переменные принимают значения, равные правым частям ограничений.
Итак, для нахождения начального допустимого решения необходимо, чтобы в каждое из уравнений входила переменная с коэффициентом 1 и не входила в другие уравнения (базисная переменная). В нашем случае мы имеем только 2 базисные переменные (X7 и X8) , не хватает еще двух базисных переменных. Их можно создать с помощью специального способа, который называется построением искусственного базиса.
Методы искусственного базиса предназначены для построения начального базиса (т.е. для получения начального решения) в случаях, когда его построение непосредственно на основе стандартной формы невозможно. При использовании искусственного базиса начальное решение оказывается недопустимым; от него по определенным алгоритмам выполняется переход к начальному допустимому решению.
Для того, чтобы построить искусственный базис, необходимо в каждое уравнение стандартной формы, не содержащее базисных переменных (т.е. полученное из ограничения-равенства или "не меньше"), добавить по одной искусственной переменной. В нашем случае это:
2X1 – X2 + 6X4 – 3X5 + Х9 = 0;
2X1 – 2X3 + 6X4 – 2X6 + Х10 =0.
где Х9 и Х10 – искусственные переменные, не имеющие никакого физического смысла, причем Х9, Х10 ≥0.
После построения искусственного базиса, придав нулевые значения всем переменным, кроме базисных, получим начальный базис: Х7, Х8, Х9, Х10 . Всего в базисе имеется четыре переменные и их значения равны правым частям ограничений, т.е.:
Х7 = 8; Х8 = 8; Х9 = 0; Х10 = 0.
Теперь необходимо решить эту задачу, т.е. найти оптимальное допустимое решение. Для этого воспользуемся двухэтапным симплекс-методом.
Глава 2. Двухэтапный метод.
2.1 Искусственное начальное решение.
В простом симплексе при начальном допустимом базисном решении гарантировалось, что все последующие базисные решения, получаемые при выполнении симплекс-метода, также будут допустимыми. В задачах линейного программирования, где все ограничения являются неравенствами типа «<=» (с неотрицательной правой частью), дополнительные (остаточные) переменные позволяют сформировать начальное допустимое базисное решение в задачах ЛП, где есть ограничения в виде равенств или неравенств типа «>=» ?
Наиболее общим способом построения начального допустимого базисного решения задачи ЛП является использование искусственных переменных. Эти переменные в первой итерации играют роль дополнительных остаточных переменных, но на последующих итерациях от них освобождаются. Разработано два тесно связанных между собой метода нахождения начального решения, которые используют искусственные переменные: М-метод и двухэтапный метод.
Для объяснения двухэтапного метода объясним сначала концепцию М-метода.
Пусть задача ЛП записана в стандартной форме. Для любого равенства I, в котором не содержится дополнительная остаточная переменная, введём искусственную переменную Ri, которая далее войдёт в начальное базисное решение. Но поскольку эта переменная искусственна (другими словами, не имеет никакого «физического смысла» в данной задаче), необходимо сделать так, чтобы на последующих итерациях она обратилась в нуль. Для этого в выражение целевой функции вводят штраф.
Переменная Ri, с помощью достаточно большого положительного числа М, штрафуется путём ввода в целевую функцию выражения – MRi в случае максимизации целевой функции и выражения +MRi – в случае минимизации. Вследствие этого штрафа естественно предположить, что процесс оптимизации симплекс-метода приведёт к нулевому значению переменной Ri. Следующий пример проясняет детали этого метода.
Пример 3.4-1
Минимизировать z = 4x1 + x2
при выполнении условий
3x1 + x2 = 3,
4x1 + 3x2 >= 6,
x1 + 2x2 <= 4,
x1, x2 >= 0.
Стандартная форма этой задачи получается в результате добавления дополнительной (избыточной) переменной x3 во второе неравенство и дополнительной (остаточной) переменной x4 в третье неравенство. Эта задача в стандартной форме будет записана следующим образом.
Минимизировать z = 4x1 + x2
при выполнении условий
3x1 + x2 = 3,
4x1 + 3x2 – x3 = 6,
x1 + 2x2 + x4 = 4,
x1, x2, x3, x4 >= 0.
В полученной задаче первое и второе уравнения не имеют дополнительных (остаточных) переменных, которые можно ввести в базисное решение. Поэтому введём в эти уравнения искусственные переменные R1 и R2, а в целевую функцию добавим штраф MR1 + MR2. В результате получим следующую задачу ЛП.
Минимизировать z = 4x1 + x2 + MR1 + MR2
при выполнении условий
3x1 + x2 + R1 = 3,
4x1 + 3x2 – x3 + R2 = 6,
x1 + 2x2 + x4 = 4,
x1, x2, x3, x4, R1, R2 >= 0.
В этой модифицированной задаче переменные R1, R2 и x4 можно использовать в качестве начального допустимого базисного решения.
При использовании М-метода следует обратить внимание на следующие два обстоятельства.
1. Использование штрафа М может и не привести к исключению искусственной переменной в конечной симплекс-итерации. Если исходная задача линейного программирования не имеет допустимого решения (например, система ограничений несовместна), тогда в конечной симплекс-итерации, по крайней мере, одна искусственная переменная будет иметь положительное значение. Это «индикатор» того, что задача не имеет допустимого решения.
2. Теоретически применение М-метода требует, чтобы М → ∞. Однако с точки зрения компьютерных вычислений величина М должна быть конечной и, вместе с тем,достаточно большой. Как понимать термин «достаточно большая» – это открытый вопрос. Величина М должна быть настолько большой, чтобы выполнить роль «штрафа», но не слишком большой, чтобы не уменьшить точность вычислений. На практике вы должны помнить о возможных ошибках машинного округления при выполнении выполнений, в которых совместно участвуют как большие, так и малые числа.
Правильный выбор значения М зависит от данных исходной задачи. Бездумное следование теоретическому требованию, что М должно быть «очень большим», может привести к значительным ошибкам округления. Именно поэтому М-метод никогда не применяется в коммерческих программах, реализующих симплекс-метод. Вместо него используется двухэтапный метод, который будет описан в следующем разделе.
2.2 Алгоритм двухэтапного метода.
Пример 2.2-2 демонстрирует проблемы, которые могут возникнуть при М-методе вследствие ошибок округления. Двухэтапный метод полностью лишён тех недостатков, которые присущи М-методу. Как следует из названия этого метода, процесс решения задачи ЛП разбивается на два этапа. На первом этапе ведётся поиск начального допустимого базисного решения. Если такое решение найдено, то на втором этапе решается исходная задача.
Этап 1.Задача ЛП записывается в стандартной форме, а в ограничения добавляются необходимые искусственные переменные (как и в М-методе) для получения начального базисного решения. Решается задача ЛПминимизациисуммы искусственных переменных с исходными ограничениями. Если минимальное значение этой новой целевой функции больше нуля, значит, исходная задача не имеет допустимого решения, и процесс вычислений заканчивается. (Напомним, что положительные значения искусственных переменных указывают на то, что исходная система ограничений несовместна.) Если новая целевая функция равна нулю, переходим ко второму этапу.
Этап 2.Оптимальное базисное решение, полученное на первом этапе, используется как начальное допустимое базисное решениеисходнойзадачи.
Пример 2.2-3
К задаче из примера 2.2-3 применим двухэтапный метод.
Этап 1
Минимизировать r = R1 + R2
С ограничениями
3x1 + x2 + R1 = 3,
4x1 + 3x2 – x3 + R2 = 6,
x1 + 2x2 + x4 = 4,
x1, x2, x3, x4, R1, R2, >= 0.
Соответствующая таблица имеет следующий вид.
| Базис | x1 | x2 | x3 | R1 | R2 | x4 | Решение |
| r | 0 | 0 | 0 | -1 | -1 | 0 | 0 |
| R1 | 3 | 1 | 0 | 1 | 0 | 0 | 3 |
| R2 | 4 | 3 | -1 | 0 | 1 | 0 | 6 |
| x4 | 1 | 2 | 0 | 0 | 0 | 1 | 4 |
Как и в М-методе, сначала вычисляется новая r-строка.
Старая r-строка: (0 0 0 -1 -1 0 | 0)
+ 1 * R1-строка: (3 1 0 1 0 0 | 3)
+ 1 * R2-строка: (4 3 -1 0 1 0 | 6)
= Новая r-строка: (7 4 -1 0 0 0 | 9)
Новая строка
r + 7x1 + 4x2 – x3 + 0R1 + 0R2 + 0x4 = 9
используется для решения первого этапа, что приведёт к следующему оптимальному решению (проверьте!).
| Базис | x1 | x2 | x3 | R1 | R2 | x4 | Решение |
| r | 0 | 0 | 0 | -1 | -1 | 0 | 0 |
| x1 | 1 | 0 | 1/5 | 3/5 | -1/5 | 0 | 3/5 |
| x2 | 0 | 1 | -3/5 | -4/5 | 3/5 | 0 | 6/5 |
| x4 | 0 | 0 | 1 | 1 | -1 | 1 | 1 |
Поскольку достигнут минимум r = 0, значит, на первом этапе получено допустимое базисное решение x1 = 3/5, x2 = 6/5 и x4 = 1. Искусственные переменные полностью выполнили свою «миссию», поэтому из последней таблицы можно удалить их столбцы. Переходим ко второму этапу.
Этап 2
После удаления искусственных переменныхисходнаязадача будет записана следующим образом.
Минимизировать z = 4x1 + x2
с ограничениями
x1 + 1/5 x3 = 3/5,
x2 + 3/5 x3 = 6/5,
x3 + x4 = 1,
x1, x2, x3, x4 >= 0.
Обратите внимание, что после первого этапа исходная задача претерпела некоторые изменения, которые учитывают полученное базисное решение. Этой трансформированной задаче соответствует следующая таблица:
| Базис | x1 | x2 | x3 | x4 | Решение |
| z | -4 | -1 | 0 | 0 | 0 |
| x1 | 1 | 0 | 1/5 | 0 | 3/5 |
| x2 | 0 | 1 | -3/5 | 0 | 6/5 |
| x4 | 0 | 0 | 1 | 1 | 1 |
Поскольку базисные переменные x1 и x2 имеют ненулевые коэффициенты в z-строке, эту строку следует преобразовать.
Старая z-строка: (-4 -1 0 0 | 0)
+ 4 * x1-строка: (4 0 4/5 0 | 12/5)
+ 1 * x2-строка: (0 1 -3/5 0 | 6/5)
= Новая z-строка: (0 0 1/5 0 | 18/5)
Начальная таблица второго этапа примет следующий вид:
| Базис | x1 | x2 | x3 | x4 | Решение |
| z | 0 | 0 | 1/5 | 0 | 18/5 |
| x1 | 1 | 0 | 1/5 | 0 | 3/5 |
| x2 | 0 | 1 | -3/5 | 0 | 6/5 |
| x4 | 0 | 0 | 1 | 1 | 1 |
Так как решается задача минимизации, следует ввести переменную x3 в базис. Применение алгоритма симплекс-метода уже на следующей итерации приведёт к оптимальному решению (проверьте!).
Удаление искусственных переменных в конце первого этапа имеет смысл только тогда, когда все они являютсянебазисными(как в примере 2.2-4). Однако возможна ситуация, когда в конце первого этапа искусственные переменныеостанутся в базисе, но будут иметьнулевые значения. В этом случае такие переменные при необходимости будут формировать часть начального базисного решения для второго этапа. При этом необходимо так изменить вычисления, выполняемые на втором этапе, чтобы искусственные переменные никогда не смогли принять положительные значения ни в каких итерациях симплекс-метода.
Существует простое правило, которое гарантирует, чтонулеваябазисная искусственная переменная на втором этапе никогда не станет положительной. Если в ведущем столбце коэффициент, соответствующий нулевой базисной искусственной переменной, положителен, тогдаведущий элементопределяется автоматически (поскольку ему соответствует минимальное отношение, равное нулю) и искусственная переменная на следующей итерации становится небазисной. Если ведущий элемент равен нулю, следующая итерация оставляет искусственную переменную нулевой. И наконец, рассмотрим отрицательный ведущий элемент. В этом случае минимальное отношение не ассоциируется с базисной (нулевой) искусственной переменной. Если минимальное отношение будет положительным, то на следующей итерации искусственная переменная примет положительное значение (обоснуйте это утверждение). Чтобы исключить эту возможность, мыпринуждаемискусственную переменную всегда оставаться в базисном решении. Поскольку искусственная переменная равна нулю, её удаление из базисного решения не влияет на то, будет ли допустимым решение из оставшихся в базисе переменных. (Было бы полезно для читателя рассмотреть все описанные случаи с помощью симплекс-таблиц.)
Итак, правило для второго этапа заключается в том, чтобы искусственные переменные оставлять в базисе всегда, когда коэффициент в ведущем столбце положительный или отрицательный. Фактически это правило применяется в конце первого этапа, когда удаляем нулевые искусственные переменные из базисного решения, перед тем как приступить ко второму этапу.
Глава 3. Особые случаи симплекс-метода.
В этом разделе рассмотрим четыре особых случая, встречающихся при использовании симплекс-метода.
1. Вырожденность.
2. Альтернативные оптимальные решения.
3. Неограниченные решения.
4. Отсутствие допустимых решений.
При изучении этих случаев основное внимание мы уделим (1)теоретическомуобоснованию причин, приводящих к таким ситуациям, и (2) ихпрактическиминтерпретациям применительно к реальным задачам.
3.1 Вырожденность.
В ходе выполнения симплекс-метода проверка условия допустимости может привести к неоднозначному выбору исключаемой переменной. В этом случае на следующей итерации одна или болеебазисныхпеременных примут нулевое значение. Тогда новое решение будетвырожденным.
В вырожденном решении нет никакой опасности, за исключением небольших теоретических неудобств, которые мы далее кратко обсудим. С практической точки зрения вырожденность объясняется тем, что в исходной задаче присутствует, по крайней мере, одно избыточное ограничение. Для того чтобы лучше понять практические и теоретические аспекты явления вырожденности, рассмотрим численный пример. Графическая интерпретация задачи поможет наглядно разобраться в этом явлении.
Пример 3.1-1. (Вырожденное оптимальное решение)
Рассмотрим следующую задачу ЛП.
Максимизировать z = 3x1 + 9x2
При выполнении условий
X1 + 4x2 <= 8,
X1 + 2x2 <= 4,
X1, x2 >= 0.
| Итерация | Базис | x1 | x2 | x3 | x4 | Решение |
| Начальная | z | -3 | -9 | 0 | 0 | 0 |
| Вводится x3 | x3 | 1 | 4 | 1 | 0 | 8 |
| Исключается x3 | x4 | 1 | 2 | 0 | 1 | 4 |
| Первая | z | -3/4 | 0 | 9/4 | 0 | 18 |
| Вводится x1 | x2 | 1/4 | 1 | 1/4 | 0 | 2 |
| Исключается x4 | x4 | 1/2 | 0 | -1/2 | 1 | 0 |
| Вторая | z | 0 | 0 | 3/2 | 3/2 | 18 |
| Оптимум | x2 | 0 | 1 | 1/2 | -1/2 | 2 |
| x1 | 1 | 0 | -1 | 2 | 0 |
На начальной итерации в качестве исключаемой можно выбрать как переменную x3, так и x4. Если оставить в базисе переменную x4, на следующей итерации она примет значение 0 (как показано в таблице), т.е. получим вырожденное базисное решение. Оптимальное решение получается на следующей итерации.
Что же практически приводит к вырожденности решения? Рассмотрим рис. 3.4, графически представляющий решение этой задачи. Точка оптимума x1 = 0, x2 = 2 является пересечением трёх прямых. Поскольку данная задача двухмерна, эта точка переопределена (на плоскости для определения точки достаточно двух прямых), и, следовательно, одно из ограничений избыточно. На практике информация о том, что некоторые ресурсы недефицитны, может быть полезной при интерпретации результатов решения задачи. Эти сведения также могут помочь выявить неточности и ошибки в постановке исходной задачи. К сожалению, не существует способов определить избыточное ограничение непосредственно из данных симплекс-таблиц.

Рис. 3.1
С вычислительной и теоретической точек зрения вырожденность может привести к двум последствиям. Во-первых, в процессе вычислений может возникнуть зацикливание. Если в приведённой выше таблице сравнить первую и вторую итерации, то можно заметить, что значение целевой функции не изменилось (z = 18). Поэтому может возникнуть ситуация, когда при реализации симплекс-метода некоторая последовательность будет повторяться, не изменяя значения целевой функции и не приводя к завершению вычислительного процесса. Существуют методы, предотвращающие зацикливание, однако они значительно замедляют процесс вычислений. Поэтому в большинстве программ, реализующих симплекс-метод, отсутствуют специальные средства защиты от зацикливания, тем более, что вероятность зацикливания очень мала.
Во-вторых, последствие вырожденности решения можно обнаружить, сравнивая первую и вторую итерации в приведённой выше таблице. Хотя в этих итерациях состав базисных и небазисных переменных различен, значения всех переменных и значение целевой функции не изменяются:
x1 = 0, x2 = 2, x3 = 0, x4 = 0, z = 18.
Можно ли, несмотря на то что оптимальное решение не достигнуто, остановить вычисления на первой итерации (когда впервые обнаруживается вырожденность)? Ответ отрицательный, так как решение может быть тольковременно.
3.2. Альтернативные оптимальные решения.
Когда прямая (если рассматривается двухмерная задача ЛП, в общем случае – гиперплоскость), представляющая целевую функцию, параллельна прямой (гиперплоскости), соответствующейсвязывающемунеравенству (которое в точке оптимума выполняется как точное равенство), целевая функция принимаетодно и то же оптимальное значениена некотором множестве точек границы области допустимых решений. Эти решения называютсяальтернативными оптимальными решениями. Следующий пример показывает, что таких решений (если они существуют) бесконечное множество. Этот пример также проиллюстрирует практическую значимость альтернативных практических решений.
Пример 3.2-1 (Бесконечное множество решений)
Рассмотрим следующую задачу ЛП.
Максимизировать z = 2x1 + 4x2
при ограничениях
x1 + 2x2 <= 5,
x1 + x2 <= 4,
x1, x2 >= 0.
На рис. 3.2 показано множество альтернативных оптимальных решений, которые являются следствием того, что прямая, представляющая целевую функцию, параллельна прямой, соответствующей связывающему ограничению. Каждая точкаотрезкаBCсоответствует оптимальному решению со значением целевой функции z = 10.

Рис. 3.2
Последовательные итерации выполнения симплекс-метода представлены в следующей таблице.
| Итерация | Базис | x1 | x2 | x3 | x4 | Решение |
| Начальная | z | -2 | -4 | 0 | 0 | 0 |
| Вводится x2 | x3 | 1 | 2 | 1 | 0 | 5 |
| Исключается x3 | x4 | 1 | 1 | 0 | 1 | 4 |
| Первая | z | 0 | 0 | 2 | 0 | 10 |
| Вводится x1 | x2 | 1/2 | 1 | 1/2 | 0 | 5/2 |
| Исключается x4 | x4 | 1/2 | 0 | -1/2 | 1 | 3/2 |
| Вторая | z | 0 | 0 | 2 | 0 | 10 |
| (Альтернативный | x2 | 0 | 1 | 1 | -1 | 1 |
| оптимум) | x1 | 1 | 0 | -1 | 2 | 3 |
На первой итерации получаем оптимальное решение x1 = 5/2 и z = 10, которое соответствует точке B на рис. 3.2. Как узнать из симплекс-таблицы, что существует альтернативное оптимальное решение? Посмотрите на коэффициентынебазисныхпеременных в z-строке первой итерации. Коэффициент небазисной переменной x1 равен нулю, это означает, что данную переменную можно ввести в базис без изменения значения целевой функции, но значение самой переменной x1 изменится. Введение переменной x1 в базисное решение выполнено на второй итерации, при этом из базиса исключена переменная x4. Получено новое решение x1 = 3, x2 = 1, z = 10, которое соответствует точке Cна рис. 3.2.
Симплекс-метод может определить только две угловые точки Bи C. Математически мы можем найти все точки (x1’,x2’) отрезка BCкак взвешенное среднее (с неотрицательными весами) точек B и C. Полагая 0 <= α <= 1 и
B: x1 = 0, x2 = 5/2,
C: x1 = 3, x2 = 1,
координаты любой точки отрезка BC можно записать следующим образом:
x1’ = α * 0 + (1 - α) * 3 = 3 – 3 α,
x2’ = α * 5/2 + (1 - α) * 1 = 1 – 3/2 α,
При α = 0 (x1’,x2’) = (3, 1), что соответствует точке C. При α = 1 получаем (x1’,x2’) = (0, 5/2) – это точка B. Если значение α лежит строго между 0 и 1, получаем внутренние точки отрезка BC.
На практике альтернативные оптимальные решения весьма полезны, поскольку позволяют сделать выбор среди множества решений без ухудшения значения целевой функции. Например, в рассмотренной выше задаче переменная x2, принимает нулевое значение в точке B, тогда как в других альтернативных оптимальных решениях её значение положительно. Если интерпретировать задачу как задачу организации производства двух видов товара (которые соответствуют переменным x1 и x2), то, с учётом конкуренции на рынке, более рационально производить оба вида товара, а не один. В этом случае решение, соответствующее точке C, предпочтительнее.
3.3 Неограниченные решения.
В некоторых задачах ЛП значения переменных могут неограниченно возрастать без нарушения ограничений. Это говорит о том, что пространство допустимых решенийне ограничено, по крайней мере, по одному направлению. В результате этого целевая функция может возрастать (задача максимизации) или убывать (задача минимизации) неограниченно.
Неограниченность решения задачи свидетельствует только об одном: модель разработана не достаточно корректно. Типичные ошибки, приводящие к построению таких моделей, заключается в том, что не учитываются ограничения, не являющиеся избыточными, и не точно оцениваются параметры (коэффициенты) ограничений.
В следующем примере показано, как на основе данных, приведённых в симплекс-таблице, можно определить, когда не ограничено пространство решений и значения целевой функции.
Пример 3.3–1. (Неограниченная целевая функция)
Рассмотрим задачу
Максимизировать z = 2x1 + x2
при выполнении условий
x1 – x2 <= 10,
2x1 <= 40,
x1, x2 >= 0.
Симплекс-таблица начальной итерации этой задачи имеет следующий вид.
| Базис | x1 | x2 | x3 | x4 | Решение |
| z | -2 | -1 | 0 | 0 | 0 |
| x3 | 1 | -1 | 1 | 0 | 10 |
| x4 | 2 | 0 | 0 | 1 | 40 |
Из этой таблицы видно, что в качестве вводимой переменной можно взять как x1, так и x2. Поскольку переменная x1 имеет максимальный (по абсолютной величине) отрицательный коэффициент в z-строке, именно её следует ввести в базисное решение. Однако заметим, чтово всех ограниченияхкоэффициенты, стоящие перед переменной x2,отрицательныилиравны нулю. Это означает, что значение переменной x2 может возрастать до бесконечности, и при этом не нарушается ни одно ограничение. Поскольку увеличение на 1 значения переменной x2 приводит к увеличению на 1 значения целевой функции, значит, неограниченное увеличение значения переменной x2 ведёт к неограниченному увеличению значения целевой функции. Эта ситуация проиллюстрирована на рис. 3.3. На этом рисунке видно, что пространство допустимых решений не ограничено в направлении оси x2 и значение целевой функции может быть каким угодно большим.
Рис. 3.3
Правило выявления неограниченности решения следующее. Если на какой-либо симплекс-итерации коэффициенты в ограничениях для какой-нибудьнебазиснойпеременной будут неположительными, значит,пространство решенийне ограничено в направлении возрастания этой переменной. Кроме того, если коэффициент этой переменной в z-строке отрицателен, когда рассматривается задача максимизации, или положителен в задаче минимизации,целевая функциятакже не ограничена.
3.4 Отсутствие допустимых решений.
Если ограничения задачи ЛП несовместны (т.е. они не могут выполняться одновременно), то задача не имеет допустимых решений. Такая ситуация не может возникнуть, есливсенеравенства, составляющие систему ограничений, имеют тип «<=» с неотрицательными правыми частями, так как в этом случае дополнительные переменные могут составить допустимое решение. Для других типов ограничений мы используем искусственные переменные. И хотя в оптимальном решении все искусственные переменные в силу штрафов равны нулю, такой исход возможен только тогда, когда задача имеет непустое пространство допустимых решений. В противном случае, в оптимальном решении будет присутствовать хотя бы однаположительнаяискусственная переменная.
С практической точки зрения отсутствие допустимых решений свидетельствует о том, что задача плохо сформулирована.
Пример 3.4-1. (Отсутствие допустимых решений)
Рассмотрим следующую задачу.
Максимизировать z = 3x1 + 2x2
при выполнении условий
2x1 + x2 <= 2,
3x1 + 4x3 >= 12,
x1, x2 >= 0.
Результат применения симплекс-метода представлен в следующей таблице.
| Итерация | Базис | x1 | x2 | x4 | x3 | R | Решение |
| Начальная | z | -3 -3M | -2 -4M | M | 0 | 0 | -12M |
| Вводится | x3 | 2 | 1 | 0 | 1 | 0 | 2 |
| Исключается | R | 3 | 4 | -1 | 0 | 1 | 12 |
| Первая | z | 1 + 5M | 0 | M | 2 + 4M | 0 | 4 – 4M |
| (псевдооптимум) | x2 | 2 | 1 | 0 | 1 | 0 | 2 |
| R | -5 | 0 | 1 | -4 | 1 | 4 |
Данные из этой таблицы показывают, что в точке оптимума искусственная переменная Rимеет положительное значение (= 4), что свидетельствует об отсутствии допустимого решения. На рис. 3.4 графически представлена ситуация данной задачи. Алгоритмы симплекс-метода, допуская положительные значения искусственной переменной, по существу, превращает неравенство 3x1 + 4x3 >= 12 в 3x1 + 4x3 <= 12. (Объясните, почему так происходит.) В результате получаем то, что можно назватьпсевдооптимальным решением.

Рис. 3.4
2. Практическая часть.
Постановка задачи.
Решить задачи:
при ограничениях:
 4x1 + 2x2 + 2x3 + x4 <= 35;
4x1 + 2x2 + 2x3 + x4 <= 35;
x1 + x2 + 2x3 + 3x4 <= 30;
3x1 + x2 + 2x3 + x4 <= 40;
xj >= 0, j = 1, 2, 3, 4.
при ограничениях:
 x1 – 4x2 – 4 <= 0;
x1 – 4x2 – 4 <= 0;
3x1 – x2 >= 0;
x1 + x2 – 4 >= 0;
x1 >= 0, x2 >= 0.
Решение.
1. F = 14x1 + 10x2 + 14x3 + 14x4→ max
при ограничениях:
 |
4x1 + 2x2 + 2x3 + x4 <= 35;
x1 + x2 + 2x3 + 3x4 <= 30;
3x1 + x2 + 2x3 + x4 <= 40;
xj >= 0, j = 1, 2, 3, 4.
Переведём систему в канонический вид для решения симплексным методом.
 4x1 + 2x2 + 2x3 + x4 + x5 = 35;
4x1 + 2x2 + 2x3 + x4 + x5 = 35;
x1 + x2 + 2x3 + 3x4 + x6 = 30;
3x1 + x2 + 2x3 + x4 + x7= 40;
xj >= 0, j = 1, 2, 3, 4, 5, 6, 7.
14x1 + 10x2 + 14x3 + 14x4 + 0x5 + 0x6 + 0x7 → max

Ответ: maxz= 225 при x2 = 5, x3 = 12,5, x7 = 10, x1 = x4 = x5 = x6 = 0.
Двухэтапный метод.
2. F = x1 + x2→ max
 при ограничениях:
при ограничениях:
x1 – 4x2 – 4 <= 0;
3x1 – x2 >= 0;
x1 + x2 – 4 >= 0;
x1, x2 >= 0.
Переведём в канонический вид и добавим искусственные переменные.
f = x1 + x2 + 0x3 + 0x4 + 0x5 – Mx0 – Mx7 → max.
 |
x1 – 4x2 – 4 + x3 = 0;
3x1 – x2 – x4 + x6 = 0;
x1 + x2 – 4 – x5 + x7 = 0;
x1, x2, x3, x4, x5, x6, x7 >= 0;
Этап 1.
Z = x6 + x7 → min
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Решение |
| x3 | 1 | -4 | 1 | 0 | 0 | 0 | 0 | 4 |
| x6 | 3 | -1 | 0 | -1 | 0 | 1 | 0 | 0 |
| x7 | 1 | 1 | 0 | 0 | -1 | 0 | 1 | 4 |
| z - c | 0 | 0 | 0 | 0 | 0 | -1 | -1 | 0 |
Так как базисные переменные x6 и x7 имеют ненулевые коэффициенты в (z - c) – строке, эту строку следует преобразовать:
(z- c): 0 0 0 0 0 -1 -1 0
+
1 * x6: 3 -1 0 -1 0 1 0 0
+
1 * x7: 1 1 0 0 -1 0 1 4
= (z- c): 4 0 0 -1 -1 0 0 4
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Решение | Отношение |
| x3 | 1 | -4 | 1 | 0 | 0 | 0 | 0 | 4 | 4 |
| x6 | 3 | -1 | 0 | -1 | 0 | 1 | 0 | 0 | 0 ← |
| x7 | 1 | 1 | 0 | 0 | -1 | 0 | 1 | 4 | 4 |
| (z - c)’ | 4 | 0 | 0 | -1 | -1 | 0 | 0 | 4 |
↑
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Решение | Отношение |
| x3 | 0 | -3 и 2/3 | 1 | 1/3 | 0 | -1/3 | 0 | 4 | |
| x1 | 1 | -1/3 | 0 | -1/3 | 0 | 1/3 | 0 | 0 | |
| x2 | 0 | 1 и 1/3 | 0 | 1/3 | 1 | -1/3 | 1 | 4 | 3 ← |
| (z - c)’ | 0 | 4/3 | 0 | 1/3 | -1 | -4/3 | 0 | 4 |
↑
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Решение | Отношение |
| x3 | 0 | 0 | 1 | 5/4 | 11/4 | -5/4 | 11/4 | 4 | |
| x1 | 1 | 0 | 0 | -1/4 | 1/4 | 1/4 | 1/4 | 0 | |
| x2 | 0 | 1 | 0 | 1/4 | 3/4 | -1/4 | 3/4 | 4 | |
| (z - c)’ | 0 | 0 | 0 | 0 | -2 | -5/3 | -1 | 4 |
Так как достигнуто min (z - c)’ = 0, то получено допустимое базисное решение для второго этапа: x1 = 1, x2 = 3, x3 = 15. Искусственные переменные могут быть исключены.
Этап 2.
Перепишем исходную задачу с учётом полученного базисного решения:
f = x1 + x2 + 0x3 + 0x4 + 0x9→ max
 x3 + 5/4 x4 + 11/4 x5 = 15;
x3 + 5/4 x4 + 11/4 x5 = 15;
x1 – 1/4 x4 + 1/4 x5 = 1;
x2 + 1/4 x4 + 3/4 x5 = 3;
x1, x2, x3, x4, x5 >= 0.
| Базис | x1 | x2 | x3 | x4 | x5 | Решение |
| x1 | 1 | 0 | 0 | 1/4 | 1/4 | 1 |
| x2 | 0 | 1 | 0 | 1/4 | 3/4 | 3 |
| x3 | 0 | 0 | 1 | 5/4 | 11/4 | 15 |
| (f - c) | 1 | -1 | 0 | 0 | 0 | 0 |
Согласуем значения в строке (f - c) с остальной частью таблицы:
(f - c): -1 -1 0 0 0 0
+
1 * x1: 1 0 0 -1/4 1/4 1
+
1 * x2: 0 1 0 1/4 3/4 3
= (f-c)’: 0 0 0 0 1 4
Исходное решение является оптимальным.
Ответ: max (f) = 4 при x1 = 1, x2 = 3, x3 = 15, x4 = 0, x5 = 0.
Так как небазисные переменные равны нулю, задача имет множество альтернативных оптимальных решений, находящихся н отрезке AB (x1+ x2 = 4).

Заключение.
Симлекс-метод – это характерный пример итерационных вычислений. используемых при решении большинства оптимизационных задач.
В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.
Из теоретических положений, лежащих в основе симплекс-метода, следует, что оптимальное решение задачи линейного программирования соответствует крайней точке пространства допустимых решений задачи. В свою очередь, крайние точки пространства допустимых решений полностью определяются базисными решениями задачи ЛП, представленной в стандартной форме. Для компьютерной реализации симплекс-метода разработан способ использования искусственных переменных, что позволяет найти начальное базисное решение задачи. В этой главе также рассмотрены теоретические и практические аспекты особых случаев реализации симплекс-метода: вырожденность, альтернативные оптимальные решения, неограниченность и отсутствие допустимых решений.
Литература.
1. Ашманов С.А. Линейное программирование. – М.: Наука, 1981.
2. Гасс С. Линейное программирование. – М.: Физматгиз, 1961.
3. Гольштейн Е.Г., Юдин Д.Б. Линейное программирование: Теория, методы и приложения. – М.: Наука, 1969.
4. Таха, Хэмди, А. Введение в исследование операций. 6-е издание. : Пер. с англ. — М.: Издательский дом "Вильяме", 2001. — 912 с. : ил. — Парал. тит. англ.
5. Н.Ш. Кремер, Б А Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. Исследование операций в экономике: Учеб. пособие для И87 вузов —М: ЮНИТИ, 2002.— 407 с.
superbotanik.net