Доклад
по математике на тему:
«Треугольники в жизни человека»
Подготовила: ученица 8 «А» класса
Чичина Вера
Руководитель: учитель математики
Виноградова Светлана Анатольевна.
Саратов 2015
Оглавление
Введение.
Моя работа на тему «Треугольники в жизни человека» призвана доказать, что треугольник и математика с ним окружают нас везде и всегда. Стоит только внимательно присмотреться.
Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Эта фигура встречается везде, но не всегда её замечают.
Часто треугольники встречаются в символах: Треугольник - универсальная геометрическая фигура, чья символическая трактовка определяется типом, видом расположения или комбинацией треугольников. Наиболее отчетливой символикой обладает только один тип этой плоскостной фигуры - равносторонний треугольник. Его значения, связанные с целым рядом ассоциацией, напрямую зависят от того, куда направлена вершина треугольника. Равносторонний треугольник с вершиной, направленной вверх, олицетворяет божественное совершенство и гармонию, служит знаком солнца и огня, жизни и сердца, горы и духовного подъема. Треугольник, перевернутый вершиной вниз, является знаком Луны, воды и дождя. Два таких треугольника, соприкасающиеся вершинами, символизируют цикличность, растущую и убывающую Луну, начало и конец, жизнь и смерть. В точке их соприкосновения происходит коренная трансформация, одно явление переходит в противоположное. Наконец, два пересекающихся равносторонних треугольника, образующих гексаграмму (шестиконечную звезду, именуемую в оккультизме "щитом Давида" или "печатью Соломона"), знаменуют единство противоположностей. Символика равностороннего треугольника теснейшим образом связана с человеком.
Равносторонний треугольник символизирует «ЗАВЕРШЕНИЕ».
Треугольник в круге означает мир форм, заключенный в круге вечности.
В философии пифагорейцев геометрическая фигура с тремя углами была символом числа "3" и эмблемой мудрости, по праву принадлежащей богине Афине. Любопытное истолкование получили разные виды треугольников в учении Ксенократа из Калхидона (ок. 395 - 312 гг. до н. э.). Руководитель Афинской платоновской академии называл равносторонний треугольник "божественным", равнобедренный - "демоническим", а разносторонний - "человеческим". В первом из них, по мнению Ксенократа, воплотились божественная гармония и совершенство; во втором - скрытая ущербность при кажущейся правильности; что же до третьего, то его неправильная форма прозрачно намекает на несовершенство человека.
Два смыкающихся треугольника - союз противоположностей, которые становятся жидким огнем или огненной водой.
Существует магическое слово в виде треугольника «Абракадабра». Оно выписывалось столбиком на дощечке 11 раз, при этом последняя буква каждый раз отсекалась. Получался треугольник. Такое постепенное укорачивание этого слова должно было уничтожать силу злого духа, и больной, надевая амулет, должен был постепенно выздоравливать. 
Египетские пирамиды тоже в форме треугольника. Пирамида имеет квадрат в плане и треугольник в вертикальном сечении, квадрат соответствует кресту, образованному четырьмя кардинальными точками. 
Песочные часы часто появляются в изображении благочестивого, тихого образа жизни, для иллюстрации краткости человеческого бытия, как атрибут Отца-Времени и иногда Смерти. Они разделяют символизм двух треугольников, один из которых перевернут, что означает циклы созидания и разрушения
Треугольники многое значат. Например, равносторонний треугольник свидетельствует об упрямстве, несговорчивости и методичности 
Неравнобедренные треугольники - структурное подразделение некой организации. 
РОМБ - жестокая самодостаточность
В 1934 году шведским художником Оскаром Реутерсвардом была открыта невозможная фигура под названием «Треугольник Пенроуза». В 1980 году этот вариант невозможного треугольника был напечатан на шведских почтовых марках.
В Атлантическом океане есть район, в котором якобы происходят таинственные исчезновения морских и воздушных судов – бермудский треугольник. Район является очень сложным для навигации: здесь большое количество отмелей, часто зарождаются циклоны и штормы. Люди выдвигают различные гипотезы для их объяснения: от необычных погодных явлений до похищений инопланетянами или жителями Атлантиды. Сторонники теории упоминают об исчезновении примерно 100 крупных морских и воздушных судов за последние сто лет. Кроме исчезновений, сообщается об исправных судах, брошенных экипажем, и о других необычных явлениях, таких как мгновенные перемещения в пространстве, аномалии со временем и т. п. Лоуренс Куше и другие исследователи показали, что некоторые из этих случаев произошли за пределами Бермудского треугольника. О некоторых происшествиях вообще не удалось найти никакой информации в официальных источниках. 
Звезда Давида — древний символ, эмблема в форме шестиконечной звезды , в которой два одинаковых равносторонних треугольника наложены друг на друга, образуя структуру из шести одинаковых равносторонних треугольников, присоединённых к сторонам правильного шестиугольника. С XIX века Звезда Давида считается еврейским символом. Звезда Давида изображена на флаге Государства Израиль и является одним из основных его символов. Шестиконечные звёзды также встречаются в символике других государств и населённых пунктов.
"Глаз в треугольнике" (или «Всевидящее око», или «сияющая дельта») считается символом Бога. Происхождение свое он ведет с глубокой древности. Возможно, традиция изображать подобным образом божество берет свое начало еще в Древнем Египте. В этом государстве часто использовался религиозный знак "соколиное око Гора". В Древней Индии существовал похожий символ – "третий глаз Шивы".
Знаки дорожного движения тоже состоят из треугольников. 
Треугольники ЛЕГО – детская игрушка.
Прошло то военное время, когда умение складывать письма по-солдатски треугольником было актуальным. Даже дети дошкольного возраста, играя «в комиссаров и фашистов», складывали листы газетной бумаги наподобие такого письма и «отправляли» его на фронт отцам. В годы чеченских войн наши бойцы иногда вынужденно прибегали к тому же способу складывания писем солдатским треугольником. 
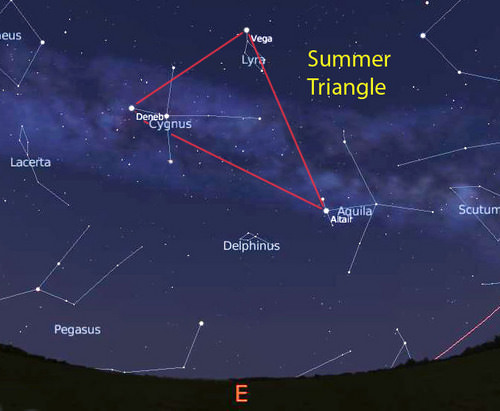
Треугольник — созвездие северного полушария неба.С одержит 25 звёзд, видимых невооружённым глазом.
Треугольник — ударный музыкальный инструмент в виде металлического прута (обычно из стали или алюминия), изогнутого в форме треугольника. Один из углов оставлен открытым (концы прута почти касаются).
Самолёт летит по небу,
Треугольное крыло, На моём велосипеде,Треугольное седло, Есть такой предмет - угольник, И всё это - ТРЕУГОЛЬНИК.
В старших классах каждый
школьник изучает треугольник.
Три каких-то уголка, А работы - на века.
infourok.ru
ЦЕЛИ:
1. Изучить понятие треугольника и его элементов в ходе практической работы;
2. Развитие логического мышления учащихся. Формирование устойчивого познавательного интереса к изучению геометрии.
3. Воспитание отношений взаимопомощи и сотрудничества между учащимися в процессе познавательной деятельности; развитие их самостоятельности и творчества.
ХОД УРОКА
1. Организационный момент.
2. Мотивация урока.
Кто из вас не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? (Он находится в Атлантическом океане между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида).
А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного.
Зовётся он треугольник,
И с ним хлопот не оберётся школьник!
^ 3. Актуализация опорных знаний.
Среди множества различных геометрических фигур на плоскости выделяется большое семейство МНОГОУГОЛЬНИКОВ.
Названия геометрических фигур имеют вполне определенный смысл. Присмотритесь внимательно к слову “многоугольник”, и скажите из каких частей оно состоит. Слово “многоугольник” указывает на то, что у всех фигур этого семейства “много углов”.
Подставьте в слово “многоугольник” вместо части “много” конкретное число, например 5. Вы получите ПЯТИУГОЛЬНИК. Или 6. Тогда – ШЕСТИУГОЛЬНИК. Заметьте, сколько углов, столько и сторон, поэтому эти фигуры вполне можно было бы назвать и многосторонниками.
На рисунке геометрические фигуры. Используя рисунок, назовите эти фигуры.
Каким наименьшим числом можно заменить “много” в многоугольнике? (Ответ: 3)
^ 4. Изучение нового материала.
Часто знает и дошкольник,
Что такое треугольник,
А уж вам-то, как не знать…
Но совсем другое дело —
Очень быстро и умело
Треугольники считать!
Например, в фигуре этой
Сколько разных? Рассмотри!
Все внимательно исследуй
И “по краю” и “внутри”.
Треугольник – простейшая фигура: три стороны, три вершины, три угла. Математики называют его двумерным “симплексом” - по латыни означает простейший. Именно в силу своей простоты треугольник явился основой многих измерений.
Через площадь треугольника выражается площадь любого многоугольника, достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты.
Еще 4000 лет назад в одном египетском папирусе говорилось о площади треугольника.
Через 2000 лет в Древней Греции очень активно велось изучение свойств треугольника. Пифагор открыл свою знаменитую формулу.
Особенно плодотворно свойства треугольника исследовались в XV-XVI веках. Большой вклад в эту теорию внес знаменитый математик Леонард Эйлер.
Император Франции Наполеон свободное время посвящал занятием математики и, в частности, изучению свойства треугольников.
ТРЕУГОЛЬНИК – геометрическая фигура, состоящая из трех точек (вершин) и трех попарно соединяющих их отрезков (стороны).
Задача
Земельный участок имеет треугольную форму. Сколько потребуется метров проволоки, чтобы обнести этот участок забором?
(Ответ: измерить стороны и сложить их длины.)
Как мы называем сумму длин всех сторон треугольника?
(Ответ: периметр.)
Р = АВ + ВС + СА (ед.)
Практическая работа.
Медиана.
Начертите треугольник АВС и найдите середину стороны ВС – точку М.
Что называется серединой отрезка? (Серединой отрезка называется точка отрезка, которая делит его пополам, то есть на два равных отрезка).
Запись на доске: АМ=МС.
Соедините точку М с вершиной В. Отрезок ВМ называется медианой треугольника.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Сколько вершин у треугольника? (3).
Сколько у него сторон? (3).
Сколько медиан можно провести в треугольнике?(3).
“Проведите” три медианы на моделях треугольников.
Какое свойство медиан вы заметили?
В любом треугольнике все медианы пересекаются в одной точке.
Эта точка называется центром тяжести треугольника.
Высота.
Запись на доске: ВН АС.
С помощью чертёжного угольника из вершины В треугольника АВС проведём перпендикуляр ВН к прямой АС. Он называется высотой треугольника.
Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону.
Сколько высот имеет треугольник? (3).
“Постройте” все три высоты на модели вашего треугольника. Обладают ли высоты аналогичным свойством, что и медианы? (Да). Высоты или их продолжения пересекаются в одной точке.
Биссектриса.
Вспомните определение биссектрисы угла.
Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
Запись на доске: АВК = СВК
Постройте биссектрису ВК угла В с помощью транспортира. Она пересечёт отрезок АС в точке К. Отрезок ВК называется биссектрисой угла В треугольника АВС.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину угла треугольника с точкой противоположной стороны треугольника.
Покажите все три биссектрисы на вашей модели треугольника.
Сформулируйте свойство биссектрис треугольника.
В любом треугольнике биссектрисы пересекаются в одной точке.
Классификация треугольников.
По величине углов
1). Остроугольные.
2). Прямоугольные.
3). Тупоугольные.
По длине сторон:
Разносторонние.
Равнобедренные.
Равносторонние.
“Перпендикуляр” - от латинского слова “PERPENDICULARIS” - “отвесный”. Термин был образован в средние века.
“Биссектриса” - от латинских слов (дважды, надвое) и “SECTRIX” - “секущая”.
“Медиана” - от латинского слова “MEDIANA” - “средняя” (линия).
^ 5. Закрепление нового материала.
Решить № 260, 261, 269(а).
6. Итоги урока. Рефлексия.
Что больше всего тебе запомнилось на уроке?
Что удивило?
Что понравились больше всего?
Каким ты хочешь увидеть следующий урок?
Домашнее задание: выучить п.9, вопросы с.77, решить № 263, 269(б), 262.
(творческое):
Сочинить рассказ, сказку или стихотворение о стране треугольников.
Составить картинку из различных видов треугольников.
Тема: Сумма углов треугольника. Внешний угол треугольника.
Цели урока:
Образовательные:
1) Практическим путем выяснить чему равна сумма углов треугольника, познакомиться с формулировкой теоремы о сумме углов треугольника, доказать теорему, доказать следствия из теоремы, научиться применять изученную теорему при решении задач;
Развивающие:
1) совершенствовать умения логически мыслить и выражать свои мысли вслух;
2) стимулировать познавательную деятельность учащихся постановкой проблемного задания, оценкой и поощрением;
Воспитательные:
1) воспитывать у учащихся стремление к совершенствованию своих знаний;
2) воспитывать интерес к предмету.
^ ХОД УРОКА
1. Организационный момент.
2. Мотивация урока.
3. Актуализация опорных знаний.
Вспомните, какая фигура называется треугольником.
Какими могут быть треугольники в зависимости от величины углов?
Какой треугольник называется прямоугольным?
Как называются стороны прямоугольного треугольника?
Какой треугольник называется тупоугольным?
Может ли в треугольнике быть два тупых угла? Объяснить ответ.
6. Параллельны ли прямые т и п?
Решить № 266, 268.
^ 4. Изучение нового материала.
Практическое задание.
Измерить с помощью транспортира углы треугольников (остальным учащимся модели треугольников заранее раздать) и найти их сумму.(каждый ученик говорит свой результат)
Что получилось? Сумма углов треугольника равна 180°?
Выскажите гипотезу. «Сумма углов любого треугольника равна 180°»
Гипотеза сформулирована. Чтобы она стала истиной – требуется доказать.
Итак, теорема
Формулировка: Сумма углов треугольника равна 180°
^ Дано:
Доказать:
Доказательство:
1)Проведём DE ׀׀ AC.
3)
4) ■
Впервые доказал теорему Пифагор, затем Евклид.
^ Закрепление теоремы в ходе устных упражнений по готовым чертежам.
Введение понятия внешнего угла треугольника.
Внешним углом треугольника называется угол, смежный с внутренним углом треугольника.
Свойство внешнего угла треугольника: внешний угол треугольника равен
сумме двух внутренних углов, не смежных с ним.
^ 5. Закрепление нового материала.
Решить № 296, 297 (а), 306 (а, в).
6. Физкультминутка.
Одолела вас дремота,
(Зеваем.)
Шевельнуться неохота?
Ну-ка, делайте со мною
Упражнение такое:
Вверх, вниз потянись,
(Руки вверх, потянулись.)
Окончательно проснись.
Руки вытянуть пошире.
(Руки в стороны.)
Раз, два, три, четыре.
Наклониться — три, четыре
(Наклоны туловища.)
И на месте поскакать.
(Прыжки на месте.)
На носок, потом на пятку.
Все мы делаем зарядку.
^ 7. Самостоятельная работа.
Тренировочный тест по готовым чертежам.
1.Найдите =…
2.Найдите =….., =….
3.Найдите =…, = .., =…
4.Найдите
^ 8. Итоги урока. Д/з.
Выучить п.10. Решить № 297 (б), 298, 300.ть п.рока. Д/з.абота.риала.
Вот и подошел к концу наш урок. Давайте подведем итоги.
Мы выучили - ….
Мы умеем - …
Сделаем выводы - ….
Тема: Равные треугольники.
Цели урока:
образовательная: дальнейшее изучение геометрических фигур, ввести понятие равенства геометрических фигур; умение правильно дать определение треугольника и определение равных треугольников;
развивающая: уметь сравнивать фигуру, находить равные элементы, анализировать и делать выводы;
воспитательная: содействовать воспитанию интереса к предмету, активности и самостоятельности обучающихся; воспитывать внимательность, уверенность в своих силах; умение работать над проблемой, преодолевать трудности.
^ ХОД УРОКА
1. Организационный момент.
2. Мотивация урока.
3. Актуализация опорных знаний.
Что называется треугольником?
Постройте треугольник АВС. Назовите:
Стороны, вершины, углы треугольника;
Сторону, противоположную углу АВС;
Углы, прилежащие к стороне АВ, АС;
Угол, противоположный стороне ВС;
Между какими сторонами заключены углы СВА, ВАС;
Найдите периметр треугольника, если АВ = 7 см, ВС = 5 см, АС = 8 см.
Решить № 297 (в), 299.
^ 4. Изучение нового материала.
-Как можно сравнить два прямоугольника? (Чтобы сравнить два прямоугольника, надо один прямоугольник наложить на другой, если из-за верхнего прямоугольника будет виден нижний, значит верхний прямоугольник меньше нижнего и наоборот. А если они совместятся, то данные прямоугольники равны.)
– Как сравнить два треугольника, изображенных на доске (внешне два треугольника должны быть почти равными)? (Скопировать один треугольник на прозрачный материал, например на кальку, и наложить на второй.)
– Какие две геометрические фигуры можно назвать равными? (Две геометрические фигуры называются равными, если при наложении они совмещаются)
Фигуры называются равными, если при наложении совпадают.
Справка из истории: Если мы обратимся к истории, то в самом первом учебнике по геометрии “Началах” Евклида можно найти следующее определение:
“…Совмещающиеся друг с другом равны между собой…”
Прошло столько лет, а определение практически не изменилось.
Эти определения о равенстве фигур можно отнести и к треугольникам, так как треугольник это фигура.
^ 5. Закрепление нового материала
Решить № 317, 318, 321 устно, 323, 331, 340.
6. Историческая пауза.
Треугольник - самая простая замкнутая прямолинейная фигура, одна из первых, свойства которой человек узнал еще в глубокой древности, так как эта фигура всегда имела широкое применение в практической жизни. В строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей. Изображение треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и в других древних документах.
В древней Греции учения о треугольниках развивалось в ионийской школе, основанной в VII веке до н.э. Фалесом, в школе Пифагора число три определялось через треугольник. Три - треугольник, образующий плоскость двух измерений, и возврат к определенности. Числа пифагорийцы изображали в виде точек, известны, так называемые, треугольные числа ( 1, 3, 6, 10...), которые образуют правильный треугольник. Учение о треугольниках было полностью изложено в первой книге “Начал” Евклида. Среди определений, которыми начинается эта книга, имеются и следующие: ”Из трехсторонних фигур равносторонний треугольник есть фигура, имеющая три равных стороны, равнобедренный же - имеющая только две равные стороны, разносторонний - имеющая три неравные стороны”. Понятие о треугольнике исторически развивалось, по-видимому, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники.
^ 7. Самостоятельная работа.
Решить № 338.
8. Итоги урока. Д/з.
Выучить п.11, вопросы с.89. Решить № 329. 332, 301.
Тема: Первый и второй признаки равенства треугольников
Цель:
Доказать первый и второй признаки равенства треугольников; обеспечить закрепление изучаемого материала, умений и навыков применения признаков равенства треугольников;
развивать логическое мышление, речь, память, реакцию, фантазию;
воспитывать общую культуру, активность, самостоятельность, умение общаться.
^ ХОД УРОКА
1. Организационный момент.
2. Мотивация урока.
Три пути ведут к знаниям: путь размышления - это путь самый благородный, путь
подражания - это путь самый легкий и путь опыта - это путь самый горький.
Какой путь выберите вы? 3. Актуализация опорных знаний.
Теоретический опрос по вопросам:
объясните, какая фигура называется треугольником;
начертите треугольник и покажите его стороны вершины и углы;
что такое периметр треугольника?
какие треугольники называются равными?
Назовите углы:
а) Углы ∆DEK, прилежащие к стороне ЕК;
б) углы ∆MNP, прилежащие к стороне MN.
Назовите угол:
а) ∆DEK, заключенный между сторонами DE и DК;
б) ∆MNP, заключенный между сторонами NP и РМ.
Между какими сторонами:
а) ∆DEK заключен угол К;
б) ∆MNP заключен угол N?
∆АВС= ∆КМР. Назовите равные стороны и равные углы этих треугольников.
^ 4. Изучение нового материала.
Какие треугольники равны?- Но всегда ли нам удаётся реально совместить треугольники? (Нет)
- Действительно, иногда совместить треугольники нет возможности. Что же делать? Достаточно сравнить лишь три элемента одного треугольника с тремя элементами другого треугольника. Вот тут нам на помощь придут признаки равенства треугольников, они нам расскажут, какие именно элементы нужно сравнивать. Что такое признак равенства треугольников и сколько существует признаков? Некоторые условия, при которых два данных треугольника оказываются равными, называются признаками равенства треугольников. Можно сказать, что признак – это примета, по которой можно узнать те или иные свойства фигур.
- Сегодня на уроке мы познакомимся с первым и вторым признаками равенства треугольников.
^ Первый признак равенства треугольников.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Дано: ∆ АВС, ∆ А1В1С1, АВ = А1В1,
АС = А1С1, А = А1.
Доказать: ∆ АВС = ∆ А1В1С1.
Доказательство:
- Вспомним определение равных треугольников.
[Два треугольника называются равными, если их можно совместить наложением.]
- Так и поступим: будем накладывать ∆ АВС на ∆ А1В1С1. Теперь нужно решить, с чего начать: Накладывать сразу весь треугольник или сначала одну сторону?
[Конечно, сначала одну сторону. Это легче.]
- И еще вопрос: сразу накладывать сторону или сначала вершину?
[Сначала вершину треугольника.]
- Обязательно обратите внимание, в ходе доказательства необходимо четко различать, какие элементы треугольника совпадают благодаря наложению
(мы их занумеруем), а какие – по условию теоремы. Будем накладывать ∆ АВС на ∆ А1В1С1 так, чтобы
1) точка А совместилась с точкой А1;
2) луч АС прошел по лучу А1С1.
Что можно сказать про точку С?
[Так как АС = А1С1, то точка С совпадает с точкой С1.]
- Правильно. Так как А = А1 по условию, то мы можем наложить
∆ АВС на ∆ А1В1С1 Так, чтобы: 3) луч АВ прошел по лучу А1В1.
Что происходит дальше?
[Так как АВ = А1В1, то точка В совпадет с точкой В1. И сторона ВС совпадет со стороной В1С1..]
- Почему? Точка В совпала сточкой В1, точка С совпала сточкой С1, а через две точки можно провести только одну прямую – есть такое утверждение. Треугольники АВС и А1В1С1 полностью совместились, значит они равны по определению равных треугольников. Теорема доказана.
^ Второй признак равенства треугольников.
Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим углам другого треугольника, то такие треугольники равны.
^ Доказательство рассмотреть дома самостоятельно.
Из 5 треугольников только 3 равных. Назовите их.
5. Физминутка
Почти 90% всей информации человек воспринимает глазами. Если устают глаза, снижается наше внимание и активность. Давайте перед следующей задачей дадим отдых глазам и себе.
Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, расслабив мышцы. Повторите 3-4 раза.
Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль. Повторите 3-4 раза.
Медленно наклоняйте голову: вперед – влево – вправо - назад. Повторите 3-4 раза.
Поморгайте несколько раз глазами, не напрягая мышц. Сделайте глубокий вздох и медленный выдох.
^ 6. Закрепление нового материала.
№1. Доказать: ∆ МЕF = ∆DЕС. №2. Доказать: В = D.
Решить № 363, 360.
^ 7. Итоги урока. Д/з.
- Что нового вы узнали сегодня на уроке? С чем познакомились? Сформулируйте первый и второй признаки равенства треугольников? Помогли ли они вам при решении задач?
Ребята, математика наука точная, поэтому все определения и теоремы воспроизводить своими словами нельзя? Послушайте одну старинную историю.
Это произошло в те времена, когда на улицах городов еще не было освещения. Как-то ночью мэр столкнулся с горожанином. Это было неприятно и больно. Тогда мэр отдал приказ, чтобы никто не выходил ночью на улицу без фонаря. Следующей ночью мэр опять столкнулся с тем же горожанином.
- Вы не читали моего приказа? — спросил мэр сердито.
- Читал, — ответил горожанин. — Вот мой фонарь.
- Но в фонаре у вас нет ничего.
- В приказе об этом не упоминалось.
Наутро появился новый приказ, обязывающий вставлять свечу в фонарь при выходе ночью на улицу. Вечером мэр опять налетел на того же горожанина,
- Где фонарь?! — закричал мэр.
- Вот он.
- Но в нем нет свечи!
- Нет, есть. Вот она.
- Но она не зажжена!
- В приказе ничего не сказано о том, что надо зажигать свечу.
И мэру пришлось издать еще один приказ, обязывающий граждан зажигать свечи в фонарях при выходе ночью на улицу.
Вот почему следует формулировки определений, аксиом и теорем учить наизусть. Если вы можете своими словами передать их точный смысл — пожалуйста! Если же нет, то, чтобы не уподобляться тому мэру, о котором только что услышали, следует учить наизусть.
Выучить п.12, решить № 355, 357, 364.
^ Тема: Первый и второй признаки равенства треугольников
Цель:
закрепить первый и второй признаки равенства треугольников; обеспечить закрепление умений и навыков применения признаков равенства треугольников;
развивать логическое мышление, речь, память, реакцию, фантазию;
воспитывать общую культуру, активность, самостоятельность, умение общаться.
^ ХОД УРОКА
1. Организационный момент.
2. Мотивация урока.
Можно сказать, что почти вся геометрия со времен “Начал” Евклида покоится на “трех китах” - трех признаках равенства треугольников. Лишь на рубеже ХIХ - ХХ в.в. математики научились строить геометрию на основе более фундаментального и общего, чем равенство треугольников, понятия геометрического преобразования.
За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о “геометрии треугольника” как о самостоятельном разделе элементарной геометрии.
И сегодня мы продолжить работать над закреплением первого и второго признаков равенства треугольников.
^ 3. Актуализация опорных знаний.
Решение задач (устно) по готовым чертежам на доске (используются цветные мелки для выделения одним цветом равных элементов).
Задание: Найдите пары равных треугольников (см. рис. 1-4) и докажите их равенство.
Тестовые задания № 1-10 с.102.
^ 4. Решение упражнений на первый и второй признаки равенства треугольников.
Решить № 1, 2, 4, 5, 6 с. 103.
5. Физкультминутка
Что такое физкультура?
Тренировка и игра.
Что такое физкультура?
Физ и куль и ту и ра!
Руки вверх, руки вниз – это физ.
Крутим шею, словно руль – это куль.
Ловко прыгай в высоту – это ту.
Бегай пол часа с утра – это Ра.
Занимаясь этим делом,
Станешь сильным, ловким, смелым.
Плюс – хорошая фигура.
Вот что значит физкультура!
На четыре - руки шире,
Пять – руками помахать.
Шесть – за парту тихо сесть.
^ 6. Самостоятельная работа.
Решить № 2, 3 (вариант 3). с.99.
7. Итоги урока. Д/з.
Решить вариант 1 (вариант 2) с.99.
Тема: Равнобедренный треугольник.
Цели урока:
Образовательные – знакомство со свойствами равнобедренного треугольника; выработка основных навыков;
Развивающие – развивать внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь;
Воспитательные – посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручку, самостоятельность.
^ ХОД УРОКА
1. Организационный момент.
2. Мотивация урока.
Треугольник - самая простая замкнутая прямолинейная фигура, одна из первых, свойства которой человек узнал еще в глубокой древности, так как эта фигура всегда имела широкое применение в практической жизни. В строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей. Изображение треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и в других древних документах.
И сегодня нам предстоит познакомиться с одним из его представителей.
^ 3. Актуализация опорных знаний.
1. Определение медианы, высоты и биссектрисы треугольника.
2. Что такое треугольник? Его элементы?
3. Какие виды треугольников вы знаете?
4. Как их различаются?
5. Дайте определение каждого треугольника?
( остроугольного, тупоугольного, прямоугольного,
равностороннего, равнобедренного, разностороннего)
Зовусь я – треугольник.
Со мной хлопот не оберётся школьник.
По всякому я называюсь.
Когда углы или стороны даны.
С одним тупым тупоуголен я.
Бывают острых два, а третий прям – прямоуголен я.
Бываю я равносторонним,
Когда все стороны равны.
Когда все разные даны, то я зовусь разносторонним.
И если, наконец, равны две стороны,
То я равнобедренным называюсь.
6. Чему равна сумма углов треугольника?
7. Какие углы называют внешними?
8. Чему равны внешние углы треугольника?
9.Сформулируйте 1 признак равенства треугольника.
10. Сформулируйте второй признак треугольника.
^ 4. Изучение нового материала.
Учитель демонстрирует рисунки с изображениями треугольников (плакаты):
Какой особенностью обладают эти треугольники? Учащиеся замечают равные стороны (или углы). Учитель дает определение равнобедренного треугольника, показывает его основание и боковые стороны.
^ Вопрос: дать определение равнобедренного треугольника.
Практическое задание: построить равнобедренный треугольник ABC (BC – основание) на
нелинованной бумаге (учитель выполняет построение на доске).
Провести биссектрису AD (с помощью транспортира).
^ Вопрос: какие еще равные элементы вы замечаете в этом треугольнике?
Формулируется теорема: В равнобедренном треугольнике углы при основании равны
(первое свойство равнобедренного треугольника).
Доказательство обсуждается по рисунку на доске.
^ Вопросы учителя: - Какие треугольники мы видим на рисунке?
- Какие равные элементы можно выделить в этих треугольниках?
- Что можно сказать об элементах равных треугольников?
Затем учитель предлагает учащимся записать доказательство в тетрадь.
В доказательстве этой теоремы скрыто еще одно свойство равнобедренного треугольника: мы доказали равенство треугольников ABD и ACD, но не назвали соответствующие равные элементы. Какие же элементы остались неназванными?
BD = DC и ﮮADB = ﮮ ADC.
Делаем вывод: AD – медиана и высота.
Учитель еще раз формулирует второе свойство равнобедренного треугольника и просит учащихся отметить, на какие слова в формулировке следует обратить внимание?
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой (биссектриса проводится к основанию, две другие биссектрисы таким свойством не обладают).
Треугольник, у которого все стороны равны, называется равносторонним.
Людей с давних времен волновал вопрос, подчиняются ли такие неуловимые вещи как красота и гармония, каким- либо математическим расчетам. Можно ли «проверить алгеброй гармонию?»- как сказал А.С.Пушкин.
Конечно, все законы красоты невозможно вместить в несколько формул, но, изучая математику, мы можем открыть некоторые слагаемые прекрасного.
Одним из символов прекрасного в геометрии, является равносторонний треугольник. У него все стороны и все углы равны, поэтому его еще и называют правильным треугольником.
Докажите, что у равностороннего треугольника все углы равны. ^ Работа в парах.
Равнобедренный треугольник в древности
Равнобедренный треугольник обладает рядом геометрических свойств, которые привлекали к себе внимание еще в древности. В задачах на треугольники, содержащихся в папирусе Ахмеса, на первый план выступают равнобедренный и прямоугольный треугольники. На практике часто применялось свойство медиан равнобедренного треугольника, являющейся одновременно и высотой и биссектрисой. То, что углы при основании равнобедренного треугольника равны, было известно еще древним вавилонянам 4000 лет назад. Сейчас это утверждение сформулировано в виде теоремы и изучается в школьном курсе геометрии в 7 классе.
^ 5. Закрепление нового материала.
Задачи на готовых чертежах (рисунки на плакатах)
а) б) в)
г) д)
Решить № 386, 388, 390 (1), 394 (1).
^ 6. Итоги урока. Рефлексия. Д/з.
Принцип «Микрофон». (Ученики по очереди дают аргументированный ответ на один из вопросов).
На уроке я работал активно / пассивно
Своей работой на уроке я доволен / не доволен
Урок для меня показался коротким / длинным
За урок я не устал / устал
Мое настроение стало лучше / стало хуже
Материал урока мне был полезен / бесполезен
интересен / скучен
Домашнее задание мне кажется легким / трудным
интересно / не интересно
Выучить п.13.
Вопросы с. 106.
Решить № 387. 389, 394 (2).
Тема: Третий признак равенства треугольников.
Цели урока:
Образовательные – доказать теорему о третьем признаке равенства двух треугольников. Показать применение признака при решении простейших задач на готовых чертежах. Развивающие – развивать внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь;
Воспитательные – посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручку, самостоятельность.
^ ХОД УРОКА
1. Организационный момент.
2. Мотивация урока.
Девизом нашего урока является высказывание: “Есть в математике нечто, вызывающее человеческий восторг”, так как на уроках геометрии очень важно уметь, смотреть и видеть, замечать и отмечать различные особенности геометрических фигур. Даю “установку”: Развивать и тренировать свое геометрическое зрение.
Кто ничего не замечает,
Тот ничего не изучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает.
^ 3. Актуализация опорных знаний.
Какой треугольник называется равнобедренным?
Какой треугольник называется равносторонним?
Является ли равносторонний треугольник равнобедренным?
Каким свойством обладают углы равнобедренного треугольника?
Каким свойством обладает биссектриса равнобедренного треугольника?
Любая ли биссектриса обладает этим свойством? Какая?
Любая ли биссектриса равностороннего треугольника обладает этим свойством?
Повторить I и II признаки равенства тре
www.ronl.ru
МОУ «БОЛЬШЕЕЛХОВСКАЯ СОШ»
(урок открытия новых знаний в 4 «А» классе)
Подготовила и провела
учитель начальных классов
Бухарова Н.А.
с. Б.Елховка
2011г.
Тема урока: Виды треугольников.
Цели урока:
Формировать представление о видах треугольников.
Развивать вычислительные навыки при решении задач и примеров.
Воспитывать умение вести себя у дороги.
Ход урока
I. Организационный момент, сообщение целей урока
Настроимся на урок
Мы находимся …
Сейчас мы будем…
Я радуюсь…
Мое внимание…
Моя память…
^ II. Устный счёт
Сегодня мы совершим путешествие по стране Геометрия. А о каких фигурах пойдет речь на уроке, вы узнаете, если правильно выполните задание.
1. На доске:
О
40·80:100
Е
200·7-300
Т
3·26-18
Н
649-40-19
У
250+700
Р
880:44·9
Г
4+96:2
И
482-60
Л
560:7·4
Ь
300·9-200
К
902-348
60
180
1100
950
52
32
320
2500
590
422
554
2. Жители страны Геометрия передвигаются на таких космических кораблях. Но один корабль затерялся и его нужно найти.
3. Задача
Скорость Мухтара 350 м/мин.
Скорость Фунтика 300м/мин
Какое расстояние пробежит каждая собака за 3 минуты?
Какая собака пробежит дальше и на сколько метров?
В стране Геометрии есть волшебник, который зашифровал все слайды. Нам придется находить шифр к некоторым этапам урока. А это не сложно. Главное хорошо подумать.
Итак, давайте отгадаем первый шифр.
Шифр найден и мы можем работать дальше.
Молодцы, итак, сегодня речь о треугольниках.
Ты на меня, ты на него,
На всех нас посмотри.
У нас всего, у нас всего,
У нас всего по три.
Три стороны и три угла
И столько же вершин.
И трижды трудные дела
Мы трижды совершим.
Все в нашем городе, друзья,
Дружнее — не сыскать.
Мы треугольников семья,
Нас каждый должен знать!
III. Работа по теме урока.
1. На слайде:
— Что общего у этих фигур? (Это треугольники, 3 стороны, 3 вершиныЗ угла)
А чем отличаются эти треугольники? (Углами)
У треугольника с каким номером есть прямой угол? (№ 1)
Как можно назвать такой треугольник? (Прямоугольный)
У треугольника с каким номером есть острые углы? (№3)
А как называется такой треугольник? (Остроугольный)
Под каким номером у треугольника есть тупой угол? (№3)
А этот треугольник как назовем? (Тупоугольный)
2. Прочитайте сведения в учебнике, с. 4
3. №8 (устно)
- А как могут называться треугольники в зависимости от сторон?
(равнобедренный, равносторонний, разносторонний)
4 .№ 15.
Разделите треугольники на данные группы по углам. Запишите номера.
Разделите треугольники на данные группы в зависимости от сторон. Запишите номера.
Прямоугольные:1,5
Остроугольные:3,4
Тупоугольные:2,6
Разносторонние:1,5
Равнобедренные:2,3,4,6
^ IV. Работа над задачей
В стране Геометрия живут не только треугольники, но другие геометрические фигуры: отрезки, лучи, прямые.
№10
Сейчас мы к задаче № 10 построим чертеж и решим ее.
Что нам известно в задаче? (Наносим на чертеж расстояние, скорость)
Весь ли путь прошел автобус? (Нет, осталось 85 км)
Что нужно узнать? (Время)
Как найти, какой путь он прошел? (325 — 85 = 240 км)
А как найти время, зная расстояние и скорость? (240: 60 = 4 ч)
^ V. Физкультминутка (зарядка для глаз)
VI. Работа над задачей
1.№ 18, стр. 5.
- Что известно в задаче?
Что нужно узнать, чтобы ответить на вопрос задачи? (Площадь каждой комнаты)
А как найти площадь прямоугольника? (Длину умножаем на ширину)
Что теперь нам нужно узнать? (Общую площадь)
Как узнать, сколько потребуется краски? (100·44=4400)
А можно ли решить эту задачу другим способом? Как?
-Я знаю, что вы любите работать в группе, давайте подберем шифр.
VII. Работа над пройденным материалом
1. Работа над вычислительными навыками № 20.
— Вспомним порядок действий. Какое действие выполняем первым? Какие потом?
Решаем 1 пример у доски. 2 и 3 – самостоятельно
После выполнения — проверка по слайду.
VIII. Групповая работа
Постройте с помощью семи палочек три равносторонних треугольника.
^ IX. Рассказ учителя про Бермудский треугольник
В Атлантическом океане есть место, по форме напоминающее эту фигуру. Это место, расположенное между Бермудскими островами, государством Пуэрто-Рико, полуостровом Флорида и называется “бермудским треугольником”. А ещё его называют “дьявольский треугольник”, “треугольник проклятых”. Загадочность его заключается в том, что в нём бесследно исчезают корабли и самолёты. Природа “бермудского треугольника” остаётся тайной и по сей день.
X. Итог урока.
—Какие треугольники называются равнобедренными, разносторонними?
—Какое задание вам понравилось выполнять? Какие задания вызывали затруднения?
—Вы хорошо поработали на уроке. Я должна задать вам на дом. Но для этого нам нужно подобрать шифр к окончанию урока. Расставьте ответы примеров в порядке возрастания, уберите повторяющиеся цифры и прочтите число. (762)
XI. Домашнее задание.
№ 17, пр. № 27
www.ronl.ru
«Средняя общеобразовательная школа № 2»
Треугольники
Работу выполнил:
Иванов Алексей
Ученик 9в класса
МОУ СОШ № 2
Руководитель: Кабакова С.В.
Алапаевск
2006 г.План
Стр.
Введение. 2. Сумма углов треугольника;
3. Площадь треугольника;
4. Виды треугольников;
5. Свойства равнобедренного треугольника;
6. Свойства прямоугольного треугольника;
7. Равные треугольники. Признаки равенства;
8. Признаки равенства прямоугольных треугольников;
9. Теорема Пифагора;
10. Медианы, биссектрисы, высоты треугольника;
11. Подобные треугольники. Признаки подобия;
12. Пропорциональные отрезки в прямоугольном треугольнике;
13. Средняя линия треугольника;
14. Описанный и вписанный треугольник;
15. Соотношение между сторонами и углами:
а) треугольника
б) прямоугольного треугольника
Введение
Простейший из многоугольников – треугольник – играет в геометрии особую роль. Без преувеличения можно сказать, что вся(или почти вся) геометрия со времен Начал Евклида покоится на “трёх китах” – трёх признаках равенства треугольников. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о “геометрии треугольника” как о самостоятельном разделе элементарной геометрии. Учитывая всю значимость треугольников для геометрии, я решил взять для написания реферата именно эту тему, при этом я поставил для себя следующие задачи:
При написании реферата я использовал учебное пособие – “Геометрия” 7-9 класс Л.С.Атанасян, материалы на электронном носителе, а также сборники задач – “Задачи повышенной трудности по геометрии 7-11класс” И.В.Парнасский, подготовительные курсы “Математика” Г.А.Гальперин, а также материал для подготовки учащихся к Единому государственному экзамену под редакцией Иванова О.А.
Надеюсь, что моя работа по изучению темы “Треугольники” не ограничится написанием реферата, я собираюсь продолжить работу и в старших классах, для более тщательной подготовки к сдаче выпускных экзаменов и поступлению в ВУЗ.
Треугольник – геометрическая фигура, состоящая из трёх отрезков, попарно соединяющих три точки не лежащие на одной прямой.
Отрезки – стороны треугольника, точки – вершины.
В
Обозначение – ∆АВС
Треугольник имеет:
1) Три стороны – АВ, ВС, АС.
2) Три вершины – А, В, С.
3) Три угла – 
А, В, С.
А СПериметром треугольника называется сумма длин трёх его сторон.
Сумма углов треугольника.
Сумма углов треугольника ровна 180°.
Дано:
∆АВС
Доказать: А+ В+ С = 180°
Доказательство:
1) Проведём через вершину В прямую ?, параллельную стороне АС.
2) Т.к. ? | | АС => 1 = 4 (как накрест лежащие углы)
3 = 5 (как накрест лежащие углы).
3
) 4+ 2+ 5 = 180° (как углы развёрнутого угла)
1 = 4 => 1+ 2+ 3 = 180° =>
3 = 5
=> А+ В+ С = 180°
Что и требовалось доказать.
Пример 1
Найдите угол С треугольника ∆АВС, если 
А=650, В=570
Решение:
1
) По теореме о сумме углов треугольника А+В+С=180°
А=650 =>С=180°-(650+570)=580
В=570
Ответ: С=580
Площадь треугольников.
I. Площадь треугольника ровна половине произведения его основания на высоту.
Дано:
∆АВС
ВК – высота
АС – основание
Доказать: S∆АВС =
АС · ВК
Доказательство:
1) Достроим ∆АВС до параллелограмма АВСD, так чтобы ВD||АС и СВ||АВ.
2) Т.к. АВСD – параллелограмм => АВ = CD
ВD = АС.
3
) SАВСD= АС · ВК
=> S∆АВС + S∆BDC= АС · ВК.
SАВСD= S∆АВС + S∆BDC
4) Рассмотрим ∆АВС и ∆ВDС.
ВС – общая сторона
АВ = CD => ∆АВС = ∆ВDС (по трём сторонам) => S∆АВС = S∆BDC
ВD = АС
5
) Т.к. S∆АВС + S∆BDC= АС · ВК
S∆АВС = S∆BDC => 2S∆АВС = АС · ВК => S∆АВС = АС · ВК
Что и требовалось доказать.II. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Д
ано:
∆АВС
ВС = а
АС = b
S – площадь треугольника
Доказать: S∆ABC = 
Доказательство:
1) Введём прямоугольную систему координат с началом в точке С, так чтобы точка В лежала на положительной полуоси Сх, а точка А имела положительную ординату, тогда точка С(0;0), В(а;0) т.к. ВС = а, А(b cosC; b sinC)
2
) S∆ABC = СВ ∙ АК
ВС = а => S∆ABC =
АК = b sinC
Что и требовалось доказать.
Теорема об отношении площадей треугольников, имеющих по равному углу.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Д
ано:
∆АВС
∆А1В1С1
А=А1
Доказать: 
Доказательство:
1) Наложим ∆АВС на ∆ А1В1С1 так, чтобы вершина А1 совместилась с вершиной А, а стороны А1В1 и А1С1 наложились соответственно на лучи АВ и АС
2) Рассмотрим ∆АВС и ∆АВ1С
СН – общая высота => 
3) Рассмотрим ∆АВ1С и ∆АВ1С1
В1Н1 – общая высота => 
4) . =>
Что и требовалось доказать.Пример 2
Пусть а – основание, н – высота, S – площадь треугольника. Найдите:
1) S, если а=7см, н=11см
2) н, если S=37,8см2, а=14см
Решение
1) S=∙а∙н
а=7см => S=∙7см∙11см=38,5см2
н=11см
2
) н=
S=37,8см2 => н=
=5,4см
а=14см
Ответ: 1) S=38,5см2
2) н=5,4см
Пример 3
Н
айдите площадь треугольника ∆АВС, если ВС=3см, АВ=18
cм,В=450
Дано:
∆АВСВС=3см
АВ=18см
В=450
Найти: S∆АВСРешение:
1
) S∆АВС=АВ∙ВС∙SinВ
ВС=3см
АВ=18см => S∆АВС=∙18см∙3см∙
=
=27см2
Sin450=
Ответ: S∆АВС=27см2Пример 4
Площадь треугольника ∆АВС равна 60см2. Найдите сторону АВ, если АС=15см,
А=300
Дано:
∆АВС
S∆АВС=60см2
АС=15см
А=300
Найти: АВ
Решение:1) S∆АВС=АВ∙АС∙SinА => АВ=
2
) АВ=
S∆АВС=60см2 => АВ=
АС=15см
А=300
Ответ: АВ=16см
Виды треугольников
По углам По сторонам Остроугольный Прямоугольный Равнобедренный Равносторонний
Тупоугольный
– остроугольный – все углы острые;
– тупоугольный – один угол тупой, два других острые;
– прямоугольный – один из углов прямой, два других острые;
– равнобедренный – две стороны равны;
– равносторонний – все стороны равны.
Свойства равнобедренного треугольника.Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
АВ = ВС => ∆АВС – равнобедренный
АВ, ВС – боковые стороны
АС – основание
I. В равнобедренном треугольнике углы при основании ровны.
Дано:
∆АВС – равнобедренный
АВ, ВС – боковые стороны
АС – основание
Доказать: А=С
Доказательство:
1) Т.к. ∆АВС – равнобедренный => АВ = ВС
2) Проведём ВD – биссектрису ∆АВС
3) Т.к. ВD – биссектрису ∆АВС =>
4) Рассмотрим ∆АВD и ∆DВС
1=2
АВ = ВС => ∆АВD = ∆DВС => А=С
ВD – общая
Что и требовалось доказать.
II. В равнобедренном треугольнике биссектриса, проведённая к основаниюявляется, является медианой и высотой.
Дано:
∆АВС – равнобедренный
АС – основание
ВD – биссектриса
Доказать: 1) BD – медиана (AD = DC)
2) BD – высота (BD
АС)
Доказательство:
1) Т.к. ∆АВС – равнобедренный => АВ = АС
2) Т.к. BD – биссектриса => 1=2
3) Рассмотрим ∆АВD и ∆DВС
1=2
АВ = ВС => ∆АВD = ∆DВС => 3=4;
ВD – общая AD = DC
4) Т.к. AD = DC => D – середина АС => BD – медиана
5) Т.к. 3=4
=> 3=4=900 => BDАС => BD – высота
3+4=1800 (смежн.) Что и требовалось доказать.
Следствия:1) Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.2) Медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.
Пример 5
В равнобедренном треугольнике ∆АВС с основанием АС проведена биссектриса ВD.
Доказать, что ВD – медиана и высота ∆АВС.
Д
ано:
∆АВС – равнобедренный
АС – основание
ВD – биссектриса
Доказать: 1) ВD – медиана
2) ВD – высота
Доказательство:
1) Т.к. ∆АВС – равнобедренный => АВ=ВС
2) Т.к. ВD – биссектриса => 1=2
3
) Рассмотрим ∆АВD и ∆DВС
1=2
АВ=ВС =>∆АВD=∆DВС =>3=4; AD=DC
ВD – оющая
4) Т.к. AD=DC => D – середина AC => BD – медиана
5) Т.к. 3=4
=>3=4=900 => ВD
AC=>BD – высота
3+4=1800(как смежные)
Что и требовалось доказать.
Пример 6
В равнобедренном треугольнике ∆DEK c основанием DK отрезок ЕF – биссектриса, DK =16см, DEF=430. Найдите KF, DEК, EFD.
Д
ано:
∆DEK – равнобедренный
EF – биссектриса
DK=16см
DEF=430
Найти: KF, DEК, EFD
Решение:
1
) Т.к. ∆DEK – равнобедренный => DE=EK
2) EF – биссектриса => DEF=FEK
DEF+FEK=DEК =>DEК=860
DEF=430
3
) Рассмотрим ∆ DEF и ∆ FEK
DE=EK
DEF=FEK => ∆DEF=∆FEK
E
F – общая
4) ∆DEF=∆FEK => DF=FK
DF+FK=DK => FK=8см
DK=16см
5
) ∆DEK – равнобедренный
=> EF –высота => EFDK=>EFD=900
EF – биссектриса
Ответ: DEК=860, FK=8см, EFD=900
Свойства прямоугольного треугольника.Треугольник, у которого один из углов прямой, называют прямоугольным треугольником.
∆АВС – прямоугольный
С = 900
АС, СВ – катеты
АВ – гипотенуза
Свойства:I. Сумма двух острых углов прямоугольного треугольника равна 900
Дано:
∆АВС – прямоугольный
В = 900
Доказать: А+С = 900
Д
оказательство:
1) А+В+С = 1800(По теореме о сумме углов ∆)
=> А+С = 1800 – 900 = 900
В = 900
Что и требовалось доказать.
II. Катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы.
Дано:
∆АВС – прямоугольный
В = 900
ВАС = 300
Доказать: ВС = 
АС
Доказательство:
1) Приложим к ∆АВС равный ему ∆АВD
2) Т.к. ∆АВС = ∆АВD (из построения) => АD = АС; С = D;
DВ = ВС; DAB = ВАС
3) Т.к. DAB = ВАС
=> DAB = 300
ВАС = 300
4
) Т.к. ∆АВС – прямоугольный
=> С = 900 – 300 = 600
ВАС = 300
5)Т.к. С = D
=> D = 600
С = 600
6) Т.к. DВ = ВС
=> DВ = ВС = DC
DВ + ВС = DC
7) DAC = DAB + BAC
=> DAC = 600
DAB = ВАС = 300
8) Т.к. С = 600
D = 600 => С =D =DAC => ∆DAC – равносторонний =>AD=AC=DC
DAC = 600
9
) Т.к. AC=DC
ВС = DC => ВС = АСЧто и требовалось доказать.
III. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 300.
Дано:
∆АВС – прямоугольный
В = 900
ВС = АС
Доказать: ВАС = 300
Доказательство:
1) Приложим к ∆АВС равный ему ∆АВD
2) Т.к. ∆АВС = ∆АВD (из построения) => АD = АС; С = D;
DВ = ВС; DAB = ВАС
3
) ВС = АС
ВD = АD =>AD = DC = AC =>∆DAC – равносторонний =>D=C=A=600
АD = АС
4
) ВАС = А
=> ВАС = 300
А = 600 Что и требовалось доказать.
Пример 7
Один из углов прямоугольного треугольника равен 600, а сумма гипотенузы и меньшего из катетов равна 26,4см. Найдите гипотенузу треугольника.
Дано:
∆АВС – прямоугольный
АС+ВС=26,4см
С=600
Найти: АСРешение:
1) ∆АВС – прямоугольный =>A+C=900
=> A=300
С=600
2) ∆АВС – прямоугольный
=> ВС=
A=300
3
) АС+ВС=26,4см
=> АС+=26,4см=>
=26,4см =>АС=17,6см
ВС=
Ответ: АС=17,6см
Равные треугольники.
Два треугольника ровны, если элементы одного треугольника (стороны и углы) соответственно ровны элементам другого. ∆
АВС = ∆А1В1С1
АВ = А1В1
ВС = В1С1
АС = А1С1
А=А1
В=В1
С=С1
Первый признак равенства треугольников.Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Дано:
∆АВС, ∆А1В1С1
АВ=А1В1
АС=А1С1
А=А1
Доказать: ∆АВС=∆А1В1С1Доказательство:
А=А1 (по условию) => вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1Пример 8
На рисунке ВD=АС, ОВ=ОС. Докажите, что треугольник ∆АОВ равен треугольнику ∆СОD
Дано:
ВD=АС
ОВ=ОС
Доказать: ∆АОВ=∆СОD
Доказательство:
1) ВD=АС
ВD=ВО+ОD => ВО+ОD= ОС+ОА
АС=ОС+ОА => OD=OA
ОВ=ОС
2) Рассмотрим ∆АОВ и ∆СОD
OD=OA
ОВ=ОС =>∆АОВ=∆СОD(по I признаку равенства треугольников)
(как вертикальные)
Что и требовалось доказать.
Второй признак равенства треугольников.Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Дано:
∆АВС, ∆А1В1С1
АВ=А1В1
А=А1
В=В1
Доказать: ∆АВС=∆А1В1С1Доказательство:
А=А1 (по условию) => сторона АС наложится на луч А1С1.В=В1 (по условию)=> сторона ВС наложится на луч В1С1.Пример 9
Н
а рисунке О – середина АВ, угол 1 равен углу 2. Доказать, что ∆СВО равен ∆AOD.
Дано:
О – середина АВ
Доказать: ∆СВО=∆AOD
Доказательство:
1) О – середина АВ => АО=ОВ
2) Рассмотрим ∆СВО и ∆AOD
АО=ОВ
=>∆СВО=∆AOD(по II признаку равенства треугольников)
(как вертикальные)
Что и требовалось доказать.Третий признак равенства треугольников.Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Дано:
∆АВС, ∆А1В1С1
АВ=А1В1
ВС=В1С1
АС=А1С1
Доказать: ∆АВС=∆А1В1С1
Доказательство:
1) Приложим ∆АВС к ∆ А1В1С1 так, чтобы вершина А совместилась с вершиной А1, вершина В – с В1, а вершина С и С1 оказались по разные стороны от прямой А1В1.
2) Т.к. АС=А1С1 (по условию) => А1С1С – равнобедренный => 1=2 (как углы при основании равнобедренного треугольника).
3) Т.к. ВС=В1С1 (по условию) => В1С1С – равнобедренный => 3=4 (как углы при основании равнобедренного треугольника).
4) Т.к. 1=2
=> А1СВ1=А1С1В1.
3=4
.к. ВС=В1С1А1СВ1=А1С1В1 Что и требовалось доказать.Пример 10
В равнобедренной трапеции АВСD проведены диагонали АС и ВD. Докажите, что ∆АВС равен ∆ВСD
Дано:
АВСD – равнобедренная тропеция
АС и ВD – диагонали трапеции
Доказать: ∆АВС=∆ВСD Доказательство:
1) Т.к. АВСD – равнобедренная тропеция => AB=CD; AC=BD
2) Рассмотрим ∆АВС и ∆ВСD
AB=CD
AC=BD => ∆АВС=∆ВСD(по III признаку равенства треугольников)
ВС – общая
Что и требовалось доказать.
Скачать файл (2012 kb.)gendocs.ru
Неравенство треугольника
Неравенство треугольника – один из важнейших геометрических фактов. Представляя собой одно из интуитивных свойств расстояния, оно нередко помогает в решении непростых геометрических и текстовых задач. С помощью неравенства треугольника представляется возможным отсеять часть из возможных вариантов расположения каких-либо элементов в громоздких геометрических задачах. Часто именно невыполнение строгого неравенства треугольника (а именно – достижение в нем равенства) дает основание утверждать о принадлежности трех точек одной прямой.
Таким образом, неравенство треугольника является одновременно интуитивно понятным, даже очевидным, но весьма часто становится мощным инструментом при решении серьезных математических задач.
^ Несколько слов о неравенствах
В математике неравенство есть утверждение об относительной величине или порядке двух рассматриваемых объектов или о том, что они просто не одинаковы. Классическое неравенство как объект исследования можно также рассматривать как частный случай отношения порядка.
Различают строгие и нестрогие неравенства. Или же, переходя на язык отношений, строгое неравенство можно считать отношением строгого порядка на множестве действительных чисел (то есть отношением, которое обладает свойствами антирефлексивности, антисимметричности и транзитивности). Если же речь идет о нестрогом неравенстве, то можно говорить о нем как об отношении нестрогого порядка на том же множестве (то есть рассматривать вместо антирефлексивности рефлексивность).
Напомним, что об отношениях как математическом объекте и их свойствах мы уже упоминали в Лекции 7 (были рассмотрены свойства отношения делимости). Более подробное их изучение нам предстоит в будущем, поскольку они довольно успешно систематизируют и обобщают ряд элементарных математических понятий. Теперь же мы приведем несколько примеров неравенств каждого из названных типов.
Строгими неравенствами называют такие неравенства:
a < b – означает, что a меньше b;
a > b – означает, что a больше b;
a ≠ b – означает, что a не равно b или же что a и b различны.
К нестрогим неравенствам относят следующие математические отношения:
a ≤ b – означает, что a меньше либо равно b или, что то же самое, a не больше (не превосходит, не превышает) b;
a ≥ b – означает, что a больше либо равно b или, что то же самое, a не меньше b.
Пока что мы не будем утруждать себя более глубоким исследованием неравенств. Сегодня нам вполне хватит уже устоявшихся представлений о неравенствах.
^ Неравенство треугольника
Теорема (неравенство треугольника):
Каждая сторона треугольника меньше суммы двух других его сторон.
Замечание. Иногда используют также и несколько другую формулировку этой теоремы, подключая попутно и случай вырожденного треугольника:
Длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон.
Заметим, что разница между двумя приведенными формулировками столь незначительна, что нет смысла рассматривать их отдельно. В дальнейшем при решении задач мы будем использовать как первую формулировку теоремы, так и вторую, не оговаривая это отдельно.
Неравенство треугольника возникло, судя по всему, тогда же, когда человек научился ходить и хоть как-то мыслить. Известно, что одну из первых его формализаций приводит Евклид в знаменитых «Началах». Там он доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного. Из нее выводится теорема о том, что против большей стороны треугольника лежит больший внутренний угол. Далее, методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. А из этой теоремы выводится неравенство треугольника. Вот такая вот непростая логическая цепочка для доказательства вполне очевидного, казалось бы, неравенства!
Рис. 1Доказательство теоремы. Рассмотрим треугольник ABC и покажем, что AB < AC + BC. При доказательстве воспользуемся одним из видов дополнительных построений – откладыванием равных отрезков (метод спрямления).
В треугольнике ABC (рис. 1) на продолжении стороны ^ BC отложим отрезок CD, равный AC. В равнобедренном треугольнике ACD . В треугольнике ABD угол ADB меньше угла BAD, значит, BD > AB, или BC + CD > AB. Но CD = AC, значит, AC + BC > AB.
Замечание. Обратите внимание, что, исходя из формулировки теоремы, следует записать сразу три неравенства:
AB < AC + BC;
AC < AB + BC;
BC < AB + AC.
Нередко, записав одно неравенство, о двух других почему-то забывают. Помните, что это может привести к довольно неприятным ошибкам.
Неравенство треугольника может служить одним из простых критериев принадлежности трех точек одной прямой. Три точки будут принадлежать одной прямой тогда и только тогда, когда в неравенстве треугольника достигается равенство. Естественно, равенство может достигаться лишь в одном из трех неравенств (см. замечание), поскольку одна из точек будет лежать четко между двумя другими.
Упражнение. Докажите, что в треугольнике каждая сторона больше разности двух других сторон.
Приведем в качестве примера использования неравенства треугольника несколько сравнительно несложных геометрических задач.
Задача 1. Докажите, что в произвольном четырехугольнике ABCD AB + CD < AC + BD.
Рис. 2Решение. Пусть O – точка пересечения диагоналей четырехугольника ABCD (рис. 2). По неравенству треугольника:
AO + OB > AB;
CO + OD > CD.
Рассмотрим сумму AC + BD:
AC + BD = (AO + OC) + (BO + OD) =
= (AO + BO) + (OC + OD) > AB + CD.
Задача 2. Докажите, что в треугольнике ABC выполнено неравенство (a, b, c – стороны треугольника ABC).
Решение. Воспользуемся следствием из неравенства треугольника (см. упражнение): (предполагаем, что ). Тогда, возведя в квадрат обе части неравенства, получим:
.
Аналогично:
;
.
Складывая все три неравенства, получим требуемое.
Упражнение. Докажите, что медиана AM в произвольном треугольнике ABC по длине меньше, чем .
Задача 3. На плоскости дан квадрат ABCD и точка O. Докажите, что расстояние от точки O до одной из вершин квадрата не превосходит суммы расстояний от O до трех других вершин квадрата.
Решение. Сложите неравенства треугольника AC + OC > OA и OB + OD > BD. Так как AC = BD, то, сокращая, получаем требуемое.
Задача 4. Найдите внутри выпуклого четырехугольника точку, такую, что сумма расстояний от нее до вершин минимальна.
Решение. Так как четырехугольник выпуклый, то его диагонали пересекаются в точке ^ O внутри него. Обозначим вершины четырехугольника через A, B, C и D (по часовой стрелке). Тогда сумма расстояний от O до вершин равна сумме длин диагоналей AC и BD. Но для любой другой точки P имеем, во-первых, что сумма расстояний от P до вершин не меньше AC + BD, а во-вторых, либо PA + PC > AC, либо PB + PD > BD. Значит, эта сумма равна AC + BD только если P совпадает с точкой O. Значит, точка O – искомая.
Неравенство треугольника успешно применяется и в довольно запутанных текстовых задачах. Что интересно, в таких задачах многое может зависеть от того, насколько удачно Вы построите геометрическую интерпретацию.
Задача 5. В некоторой стране расположены 4 города: A, B, C и D. Два самолета одновременно вылетели из города A. Маршрут первого самолета: A-B-D-C-A-D-B-C-A, а маршрут второго: A-B-C-D-A-B-C-D-A-B-C-D-A. Какой из самолетов раньше закончит свой маршрут, если их скорости одинаковы?
Не бойтесь экспериментировать! Если в задаче не задано конкретное расположение объектов, Вы вправе рисовать в своем решении всё, что не противоречит условию – оно ведь Ваше. В том числе, и города в Задаче 5 Вы можете расставить как угодно. Следует лишь помнить, что в некоторых задачах после разбора «нормального», общего случая, необходимо разобрать и некоторые «патологические», частные случаи. К примеру, в Задаче 5 может понадобиться рассмотрение случая, когда некоторые три города лежат на одной прямой – всё зависит от того, каково Ваше решение для общего случая.
Решение задачи 5. Запишем длины маршрутов каждого из самолетов в виде сумм расстояний между городами. Длина маршрута первого самолета будет равна
.
Второй же самолет пролетит расстояние
.
Рассмотрим разность между расстоянием, которое пролетел первый самолет, и расстоянием, которое преодолел второй.
.
Докажем, что независимо от расположения точек A, B, C, D на плоскости (городов A, B, C, D в стране) выражение будет неположительным.
Для этого следует рассмотреть два случая.
1. Предположим, что точки A, B, C, D создают на плоскости четырехугольник ABCD с диагоналями AC и BD. Тогда запишем последовательно неравенства треугольника для треугольников ABC, BCD, CDA и DAB (см. рис. 2):
AB + BC > AC;
BC + CD > BD;
CD + DA > CA;
DA + AB > DB.
Сложив все четыре неравенства, получим
;
;
.
2. Рассмотрим случай, когда точки A, B, C, D создают на плоскости четырехугольник ACBD с диагоналями AB и CD (нарисуйте себе соответствующий рисунок). Заметим, что неравенства треугольника выполняются для тех же треугольников, что и в первом случае.
Оказывается, что решение задачи останется тем же, несмотря на то, что расположение точек на плоскости существенно изменилось. Это можно считать еще одной характерной чертой многих решений задач, использующих неравенство треугольника.
Следовательно, первый самолет прилетит раньше, поскольку его маршрут короче маршрута второго.
Заметьте, что решение Задачи 5 требует небольшого анализа, что является непременным качеством всех олимпиадных задач. Будьте внимательны – Ваше решение задачи будет правильным лишь тогда, когда Вы рассмотрите все возможные случаи, подходящие под условие.
Следует также отметить, что зачастую на рисунке, изображающем условие задачи, не видно треугольника, применение неравенства треугольника для которого дало бы моментальное решение. В таком случае может помочь удачно подобранное геометрическое преобразование. Об этом мы поговорим несколько позже. Знакомство с неравенством треугольника на этом следует объявить законченным. Но новая встреча с ним уже не за горами.
7 класс Лекция 13. Неравенство треугольника
www.ronl.ru
Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Text /> Graphics Геометрия 7 класс Основные темы Graphics Вертикальные углы Вертикальные углы равны. Graphics Параллельные прямые определение Прямые называются параллельными, если -они лежат в одной плоскости -они не пересекаются Graphics Параллельные прямые Признаки Если две прямые с поперечиной образуют равные накрест лежащие углы, то прямые параллельны Graphics Параллельные прямые Признаки Если сумма внутренних односторонних углов равна 1800, то прямые параллельны Graphics Треугольники Треугольник и его элементы Медиана-отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Graphics Треугольники Треугольник и его элементы Биссектриса-отрезок биссектрисы угла треугольника от его вершины до противолежащей стороны. Graphics Треугольники Треугольник и его элементы Высота- перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону Graphics Треугольники Треугольник и его элементы Сумма углов треугольника равна 1800 Graphics Треугольники Треугольник и его элементы Угол, смежный с углом треугольника, называют внешним углом. . Graphics Треугольники Треугольник и его виды По углам: Graphics Graphics Треугольники Треугольник и его виды Graphics Треугольники Треугольник и его виды По сторонам Graphics Треугольники Признаки равенства Первый признак Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Graphics Треугольники Признаки равенства Второй признак Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Graphics Треугольники Признаки равенства Третий признак Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны. Graphics Равнобедренный треугольник Определение Треугольник называется равнобедренным, если у него две стороны равны. Graphics Равнобедренный треугольник Свойства В равнобедренном треугольнике углы при основании равны, а биссектриса, проведённая к основанию, является медианой и высотой. Graphics Равнобедренный треугольник Признаки Graphics Равносторонний треугольник Определение Треугольник называется равносторонним, если у него все стороны равны. Graphics Равносторонний треугольник Свойства В равностороннем треугольнике все углы равны. В равностороннем треугольнике каждая биссектриса является медианой и высотой. В равностороннем треугольнике все три медианы равны. Graphics Аксиомы Точки и прямые Какова бы не была прямая, существуют точки, принадлежащие этой прямой, и точки не принадлежащие ей. Graphics Равносторонний треугольник Признаки Если все углы в треугольнике равны, то он равносторонний. Graphics Прямоугольный треугольник Определение Треугольник называется прямоугольным, если один из его углов прямой. Graphics Прямоугольный треугольник Признаки Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого, то такие треугольники равны. Graphics Прямоугольный треугольник Признаки Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого, то такие треугольники равны. Graphics Прямоугольный треугольник Признаки Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого, то такие треугольники равны. Graphics Прямоугольный треугольник Признаки Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны. Graphics Прямоугольный треугольник Свойства Катет прямоугольного треугольника, лежащий против угла 300, равен половине гипотенузы. Graphics Прямоугольный треугольник Свойства В прямоугольном треугольнике сумма острых углов равна 900. Graphics Аксиомы точки и прямые Через любые две точки можно провести прямую, и притом только одну. Graphics Аксиомы точки и прямые Из трёх точек на прямой одна, и только одна, лежит между двумя другими. Graphics Аксиомы Отрезки и их длины Каждый отрезок имеет определённую длину. Graphics Аксиомы Отрезки и их длины Длина отрезка равна сумме длин частей, на которые он разбивается любой внутренней точкой. Graphics Аксиомы Углы и их меры Каждый угол имеет определённую градусную меру. Graphics Аксиомы Углы и их меры Мера угла равна сумме мер углов, на которые данный угол разбивается любым его внутренним лучом. Graphics Смежные углы Сумма мер смежных углов равна 1800
www.ronl.ru
Разработка внеклассного мероприятия по геометрии.
В стране треугольника.
Цели:
1)Повторить и обобщить с учащимися тему «Треугольники».
2)Вспомнить основные понятия, свойства, новые определения, которые они узнали в ходе изучения этой темы.
Задачи:
Научить детей общению.
Научить детей творчески мыслить.
Развивать речь учеников.
Воспитать вдумчивого, творчески мыслящего, заинтересованного в своем труде человека.
Заранее учащиеся получили задания:
1)Сочинить оду «Треугольнику».
2)Рисунок «В стране треугольника».
3)Определения в стихах.
4)Сказки, рассказы о треугольниках.
Оборудование: выставка рисунков, плакаты.
Ход урока
^ Звучит тихая музыка. Девочка читает оду, посвященную геометрии «О, геометрия».
О, геометрия, тебя все уважают
Такая углубленная наука,
В которой каждый понимает,
Что геометрия нужна.
Ведь ты построена логично,
В тебе так много аксиом.
Ты светишь в темноте знакомой нам луною,
Ты Зевс среди простых Богов.
Тебе я эту оду посвящаю, как
Благодарность за твой дар.
Простою с виду я наукой занимаюсь
И понимаю, что наука эта непроста,
Она так сложна и трудна.
Ведь даже маленькой деталью
Мы целый мир построить можем;
Не нужно нам бояться знаний
Ведь каждый что-то сделать должен.
Лишь вместе мы преодолеем
Все трудности преград судьбы;
Построим дом, построим терем
И в жизнь мы превратим мечты.
Ведущий. Итак, сегодня мы посвящаем наш урок геометрической фигуре, которая называется «Треугольник».
1)Что же называется треугольником?(10б.)
Каждый вопрос оценивается определенным количеством баллов по уровню сложности. При этом раздаются треугольники разного цвета: красный-30 баллов, синий-15 баллов, зеленый-10 баллов.
2)Какие треугольники называются равными?(15б.)
^ Далее звучит ода треугольнику.
О. треугольник, как ты прекрасен.
Как красив и богат,
Ибо ты имеешь три стороны.
Три угла, три вершины.
Ты один можешь быть:
И равнобедренным, и равносторонним,
И прямоугольным…
Ибо ты могуч…
…По тебе судят теоремы,
Тебе посвятили три признака равенства.
Ведь, чтобы доказать, что ты равен,
Нужно приложить силы.
Ибо даже медиана, проведенная
К основанию равнобедренного треугольника
Является высотой и биссектрисой.
И не каждый знает, что в треугольнике
Медианы, высоты, биссектрисы
Пересекаются в одной точке.
И что бы мы знали без Великого треугольника!
Ибо даже стол не может стоять на двух ножках.
^ Ода треугольнику в стихах.
Вы всем известны,
Без вас не обойтись нигде,
Вы так чудесны,
Вы так нужны везде.
Вы - Геометрические фигуры,
Треугольники мои.
«Треугольник, треугольник».
Самый лучший из фигур,
Ты родился из трех точек
И прекрасных трех прямых.
Но не думайте, ребята,
Треугольник не простой…
Он бывает и прямой,
Равнобедренный…любой!!!
Ведущий. А почему треугольник так важен для нас?
Ответ на стр.39. Сообщение о треугольнике – жесткая фигура.
Ведущий. Теперь мы с вами в Стране Треугольников. Что же она из себя представляет?
^ Учащиеся по готовым рисункам рассказывают необычные условия.
Далее продолжается опрос:
3)Что такое теорема и доказательство?(15б.)
Ведущий. В ходе изучения темы нам встретились новые понятия. Давайте вспомним где – какие?
^ Начинается аукцион, последний получит (30б.)
Каждое определение нам нужно запомнить. А нельзя ли их запомнить как шутку?
Зачитываются стихи – определения.
Медиана – она мышка Яна,
Зацепившись хвостом за вершину,
Спустилась к основанию
Прямо в середину!
Высота стоит столбом – вертикально.
Она измерит даже дом капитально.
Биссектриса - почему так назвали, не пойму…
Потому что, потому
Она ходит по углам
И делит угол пополам.
Биссектриса – это киска,
Которая ловит мышку по углам,
И делит угол пополам!
Медианка – хулиганка
Бросит вещи по углам и
Стороны делит пополам
В треугольнике она стоит
Прямо – как всегда.
Высота, высота!
С высоты глядит на нас:
«С медианой ты не путай,
Есть ведь разница у нас».
Медиана – как лиана,
Только разница одна –
Из вершины в середину
Не промахнется никогда.
^ Опрос продолжается…
4) Какой отрезок называется перпендикуляром, проведенным из данной точки к данной прямой?(15б.)
5) Какой отрезок называется медианой треугольника?(15б.)
6) Какой отрезок называется биссектрисой треугольника?(15б.)
7) Какой отрезок называется высотой треугольника?(15б.)
На доске рисунок треугольника. Каждый отвечающий строит медиану, высоту, биссектрису.
Ведущий. Переходим к самым важным вопросам – это три признака равенства треугольников. Прежде, чем перейти к доказательству теорем, прозвучит ода трем признакам!
^ Ода трем признакам равенства треугольников
О, треугольники, вы так прекрасны,
Три признака ваши для нас не сложны.
Вот первый из них:
Если две стороны и угол между ними
Одного треугольника равны
Двум сторонам и углу между ними другого треугольника,
То такие треугольники равны.
А теперь будьте умны…
Приставьте числительные одна и два
К словам «сторона» и «угла»
И пред ваши очи вмиг
Второй признак подбежит.
А у третьего признака нет углов,
А только три стороны равны.
Третий признак легче всех.
Ну, а вы, мной ободрены,
Додумайте его непременно.
Вы отроки – други, запомните ныне
Сии признаки равенства треугольников.
^ По рисункам доказываются признаки равенства треугольников. Количество балло
www.ronl.ru
