Парадоксы теории множеств и их философская интерпретация. Реферат парадоксы теории множеств

Парадоксы теории множеств и их философская интерпретация / Хабрахабр

Краткий синопсис

P.S. Весьма «сухой язык», но вполне читабельно после университетской программы. По большей части определения парадоксов брались из Википедии (упрощённая формулировка и готовая TeX-разметка).

Введение

Следует начать с определения.

Что есть множество? Вопрос достаточно простой, ответ на него вполне интуитивен. Множество это некий набор элементов, представляемый единым объектом. Кантор в своей работе Beiträge zur Begründung der transfiniten Mengenlehre даёт определение: под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M)[1]. Как видим, суть не изменилась, разница лишь в той части, которая зависит от мировоззрения определяющего. История же теории множеств как в логике так и в математике весьма противоречива. Фактически начало ей положил Кантор в XIX веке, далее Рассел и остальные продолжили работу.

Парадоксы (логики и теории множеств) — (греч. 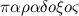— неожиданный) — формально-логические противоречия, которые возникают в содержательной множеств теории и формальной логике при сохранении логической правильности рассуждения. Парадоксы возникают тогда, когда два взаимоисключающих (противоречащих) суждения оказываются в равной мере доказуемыми. Парадоксы могут появиться как в пределах научной теории, так и в обычных рассуждениях (например, приводимая Расселом перифраза его парадокса о множестве всех нормальных множеств: «Деревенский парикмахер бреет всех тех и только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?»). Поскольку формально-логическое противоречие разрушает рассуждение как средство обнаружения и доказательства истины (в теории, в которой появляется парадокс, доказуемо любое, как истинное, так и ложное, предложение), возникает задача выявления источников подобных противоречий и нахождения способов их устранения. Проблема философского осмысления конкретных решений парадоксов — одна из важных методологических проблем формальной логики и логических оснований математики.

Целью данной работы является изучение парадоксов теории множеств как наследников античных антиномий и вполне логичных следствий перехода к новому уровню абстракции — бесконечности. Задача — рассмотреть основные парадоксы, их философскую интерпретацию.

Основные парадоксы теории множеств

Некторые из логических парадоксов были известны с античных времён, однако по причине того, что математическая теория ограничивалась одной лишь арифметикой и геометрией, соотнести их с теорией множеств было невозможно. В XIX веке ситуация изменилась коренным образом: Кантор в своих работах вышел на новый уровень абстракции. Он ввёл понятие бесконечности, создав тем самым новый раздел математики и позволив тем самым сравнивать различные бесконечности с помощью понятия «мощность множества» [2]. Однако тем самым он породил множество парадоксов. Самым первым является так называемый парадокс Бурали-Форти. В математической литературе встречаются различные формулировки, опирающиеся на разную терминологию и предполагаемый набор известных теорем. Вот одно из формальных определений.

Можно доказать, что если x — произвольное множество порядковых чисел, то множество-сумма 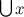есть порядковое число, большее или равное каждому из элементов x. Предположим теперь, что 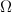— множество всех порядковых чисел. Тогда 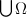— порядковое число, большее или равное любому из чисел в 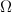. Но тогда и 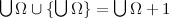— порядковое число, причём уже строго большее, а значит, и не равное любому из чисел в . Но это противоречит условию, по которому — множество всех порядковых чисел.

Сущность же парадокса в том, что при образовании множества всех порядковых чисел образуется новый порядковый тип, которого ещё не было среди «всех» трансфинитных порядковых чисел, существовавших до образования множества всех порядковых чисел. Этот парадокс был обнаружен самим Кантором, независимо открыт и опубликован итальянским математиком Бурали-Форти, ошибки же последнего были исправлены Расселом, после чего формулировка приобрела окончательный вид [2,3].

Среди всех попыток избежать подобных парадоксов и в какой-то мере попробовать их объяснить наибольшего внимания заслуживает идея уже упомянутого Рассела. Он предложил исключить из математики и логики импредикативные предложения, в которых определение элемента множества зависит от последнего, что и вызывает парадоксы. Правило звучит так: «никакое множество С не может содержать элементов m, определяемых лишь в терминах множества С, а так же элементов n, предполагающих в своём определении это множество» [4]. Подобное ограничение определения множества позволяет избежать парадоксов, но при этом значительно сужает область его применения в математике. Вдобавок этого недостаточно для объяснения их природы и причин появления, коренящихся в дихотомии мышления и языка, в особенностях формальной логики [4]. В какой-то мере в данном ограничении можно проследить аналогию с тем, что в более поздний период когнитивные психологи и лингвисты начали называть «категоризацией основного уровня»: определение сведено к наиболее легкой для понимания и изучения концепцией.

Далее Кантор в 1899 году открыл парадокс, названный его именем.

Предположим, что множество всех множеств 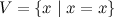существует. В этом случае справедливо 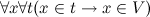, то есть всякое множество t является подмножеством V. Но из этого следует 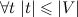— мощность любого множества не превосходит мощности V. Но в силу аксиомы множества всех подмножеств, для V, как и любого множества, существует множество всех подмножеств 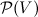, и по теореме Кантора 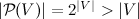, что противоречит предыдущему утверждению. Следовательно, V не может существовать, что вступает в противоречие с «наивной» гипотезой о том, что любое синтаксически корректное логическое условие определяет множество, то есть что 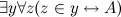для любой формулы A, не содержащей y свободно. Замечательное доказательство отсутствия подобных противоречий на основе аксиоматизированной теории множеств Цермело-Френкеля приводится у Поттера [3].

Оба вышеуказанных парадокса с логической точки зрения идентичны «Лжецу» либо «Брадобрею»: высказываемое суждение обращено не только на нечто объективное по отношению к нему, но и само на себя. Однако следует обращать внимание не только на логическую сторону, но и на понятие бесконечности, которое тут наличествует. В литературе ссылаются на работу Пуанкаре, в которой он пишет: «вера в существование актуальной бесконечности… делает необходимым эти непредикативные определения'' [2]. В целом же имеют место основные моменты [2]:

• в данных парадоксах нарушается правило чётко разделять „сферы“ предиката и субъекта; степень смешения близка к подмене одного понятия другим;
• обычно в логике предполагается, что в процессе рассуждения субъект и предикат сохраняют свой объём и содержание, в данном же случае происходит переход из одной категории в другую, что даёт в результате несоответствие;
• наличие слова „все“ имеет смысл для конечного числа элементов, в случае же бесконечного их количества возможно наличие такого, которое для определения себя потребует определение множества;
• нарушаются основные логические законы:
  • закон тождества нарушается тогда, когда обнаруживается нетождественность себе субъекта и предиката;
  • закон противоречия — когда с одинаковым правом выводятся два противоречащих друг другу суждения;
  • закон исключённого третьего — когда это третье приходится признавать, а не исключать, поскольку ни первое, ни второе не могут быть признаны одно без другого, т.к. они оказываются одинаково правомерными.

Парадокс Тристрама Шенди: В романе Стерна «Жизнь и мнения Тристрама Шенди, джентльмена» герой обнаруживает, что ему потребовался целый год, чтобы изложить события первого дня его жизни, и еще один год понадобился, чтобы описать второй день. В связи с этим герой сетует, что материал его биографии будет накапливаться быстрее, чем он сможет его обработать, и он никогда не сможет ее завершить. «Теперь я утверждаю, — возражает на это Рассел, — что если бы он жил вечно и его работа не стала бы ему в тягость, даже если бы его жизнь продолжала быть столь же богатой событиями, как вначале, то ни одна из частей его биографии не осталась бы ненаписанной». Действительно, события n-го дня Шенди мог бы описать за n-й год и, таким образом, в его автобиографии каждый день оказался бы запечатленным.

Иначе говоря, если бы жизнь длилась бесконечно, то она насчитывала бы столько же лет, сколько дней.

Рассел проводит аналогию между этим романом и Зеноном с его черепахой. По его мнению решение лежит в том, что целое эквивалентно его части в бесконечности. Т.е. к противоречию приводит только «аксиома здравого смысла» [2]. Однако же разрешение проблемы лежит в области чистой математики. Очевидно, что имеется два множества — года и дни, между элементами которых установлено взаимно-однозначное соответствие — биекция. Тогда при условии бесконечной жизни главного героя имеется два бесконечных равномощных множества, что, если рассматривать мощность как обобщение понятия количества элементов в множестве, разрешает парадокс.

Парадокс (теорема) Банаха-Тарского или парадокс удвоения шара — теорема в теории множеств, утверждающая, что трёхмерный шар равносоставлен двум своим копиям. Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число частей, передвинуть их, и составить из них второе. Более точно, два множества A и B являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств 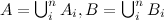так, что для каждого i подмножество 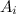конгруэнтно .

Если же пользоваться теоремой выбора, то определение звучит так[3]: Аксиома выбора подразумевает, что существует разбиение поверхности единичной сферы на конечное количество частей, которые преобразованиями трёхмерного Евклидова пространства, не меняющими форму этих составляющих, могут быть собраны в две сферы единичного радиуса.

Очевидно, что при требовании для данных частей быть измеримыми, данное постоение неосуществимо. Известный физик Ричард Фейнман в своей биографии рассказывал, как в своё время у него получилось победить в споре о разбиении апельсина на конечное количество частей и пересоставлении его [5].

В определённых моментах этот парадокс используется для опровержения аксиомы выбора, однако проблема в том, что то, что мы считаем элементарной геометрией, — несущественно. Те понятия, которые мы считаем интуитивными, должны быть расширены до уровня свойств трансцендентных функций [3].

Чтобы и дальше ослабить уверенность тех, кто считает аксиому выбора неверной, следует упомянуть теорему Мазуркевича и Серпинского, которая утверждает, что существует непустое подмножество Е Евклидовой плоскости, которое имеет два непересекающихся подмножества, каждое из которых может быть разбито на конечное количество частей, так что их можно перевести изометриями в покрытие множества Е. При этом доказательство не требует использования аксиомы выбора[3]. Дальнейшие же построения на основе аксиомы определённости дают разрешение парадокса Банаха-Тарского, но не представляют такого интереса [3].

• Парадокс Ришара: требуется назвать «наименьшее число, не названное в этой книге». Противоречие в том, что с одной стороны, это можно сделать, так как есть наименьшее число, названное в этой книге. Исходя из него, можно назвать и наименьшее неназванное. Но тут возникает проблема: континуум является несчётным, между двумя любыми числами можно вставить ещё бесконечное множество промежуточных чисел. С другой стороны, если бы мы могли назвать это число, оно автоматически бы перешло из класса неупомянутых в книге, в класс упомянутых [2].
• Парадокс Греллинга-Нильсона: слова либо знаки могут обозначать какое-либо свойство и при этом иметь его или нет. Самая тривиальная формулировка звучит так: является ли слово «гетерологичный» (что означает «неприменимый к самому себе»), гетерологичным?.. Весьма схож с парадоксом Рассела в связи с наличием диалектического противоречия: нарушается двойственность формы и содержания. В случае со словами, имеющими высокий уровень абстракции, невозможно решить, являются ли эти слова гетерологичными [2].
• Парадокс Сколема: используя теорему Гёделя о полноте и теорему Лёвенхейма-Сколема[3] получаем, что аксиоматическая теория множеств остаётся истинной и тогда, когда будет предполагаться (иметься) для её интерпретации только счётная совокупность множеств. В то же время аксиоматическая теория включает в себя уже упомянутую теорему Кантора, что приводит нас к несчётным бесконечным множествам. [2]

Разрешение парадоксов

Логицизм был попыткой свести всю известную математику к терминам арифметики, а потом термины арифметики свести к понятиям математической логики. Вплотную этим занялся Фреге, однако после окончания работы над трудом, он вынужден был указать о своей несостоятельности, после того, как Рассел указал на имеющиеся в теории противоречия. Тот же Рассел, как уже был упомянуто ранее, попытался исключить использование импредикативных определений с помощью «теории типов». Однако его понятия множества и бесконечности, а так же аксиома сводимости оказались нелогичными. Основной проблемой было то, что не учитывались качественные различия между формальной и математической логикой, а так же наличие лишних понятий, в том числе и интуитивного характера. В итоге теория логицизма не смогла устранить диалектических противоречий парадоксов, связанных с бесконечностью. Имели место лишь принципы и методы, которые позволяли избавиться хотя бы от непредикативных определений. В свох же рассуждениях Рассел был наследником Кантора [2]

В конце XIX — начале XX в. распространение формалистической точки зрения на математику было связано с развитием аксиоматического метода и той программой обоснования математики, которую выдвинул Д. Гильберт. На степень важности этого факта указывает то, что первой проблемой из двадцати трёх, которые он поставил перед математическим сообществом, была проблема бесконечности. Формализация была необходима для доказательства непротиворечивости классической математики, «исключив при этом из неё всю метафизику». Учитывая средства и методы, которыми пользовался Гильберт, его цель оказалась принципиально невыполнимой, но его программа имела огромное влияние на все последующее развитие оснований математики. Гильберт достаточно долго работал над этой проблемой, построив первоначально аксиоматику геометрии. Поскольку решение проблемы оказалось достаточно успешным, он решил применить аксиоматический метод к теории натуральных чисел. Вот что он писал в связи с этим: «Я преследую важную цель: именно я хотел бы разделаться с вопросами обоснования математики как таковыми, превратив каждое математическое высказывание в строго выводимую формулу.» От бесконечности при этом планировалось избавиться с помощью сведения её к некому конечному числу операций. Для этого он обращался к физике с её атомизмом, дабы показать всю несостоятельность бесконечных величин. Фактически Гильберт поставил вопрос о соотношении теории и объективной реальности.

Более или менее полное представление о финитных методах дает ученик Гильберта Ж. Эрбран. Под финитными рассуждениями он понимает такие рассуждения, которые удовлетворяют следующим условиям: логические парадоксы " — всегда рассматривается лишь конечное и определенное число предметов и функций;

— функции имеют точное определение, и это определение позволяет нам вычислить их значение;

— никогда не утверждается «Этот объект существует», если не известен способ его построения;

— никогда не рассматривается множество всех предметов X какой-либо бесконечной совокупности;

— если известно, что какое-либо рассуждение или теорема верны для всех этих X, то это означает, что это общее рассуждение можно повторить для каждого конкретного X, причем само это общее рассуждение следует рассматривать только как образец для проведения таких конкретных рассуждений."

Однако в момент последней публикации в этой области Гёдель уже получил свои результаты, в сущности опять обнаружил и утвердил наличие диалектики в процессе познания. По сути своей дальнейшее развитие математики продемонстрировало несостоятельность программы Гильберта.

Что же, собственно, доказал Гёдель? Можно выделить три основных результата:

1. Гёдель показал невозможность математического доказательства непротиворечивости любой системы, достаточно обширной, чтобы включать в себя всю арифметику, доказательства, которое не использовало бы каких-либо иных правил вывода, кроме тех, что имеются в самой данной системе. Такое доказательство, которое использует более мощное правило вывода, может оказаться полезным. Но если эти правила вывода сильнее логических средств арифметического исчисления, то уверенности в непротиворечивости используемых в доказательстве допущений не будет. Во всяком случае, если используемые методы не будут финитистскими, то программа Гильберта окажется невыполнимой. Гёдель как раз и показывает несостоятельность расчетов на нахождение финитистского доказательства непротиворечивости арифметики. 2. Гёдель указал на принципиальную ограниченность возможностей аксиоматического метода: система Principia Mathematica, как и всякая иная система, с помощью которой строится арифметика, существенно неполна, т. е. для любой непротиворечивой системы арифметических аксиом имеются истинные арифметические предложения, которые не выводятся из аксиом этой системы. 3. Теорема Гёделя показывает, что никакое расширение арифметической системы не может сделать ее полной, и даже если мы наполним ее бесконечным множеством аксиом, то в новой системе всегда найдутся истинные, но не выводимые средствами этой системы положения. Аксиоматический подход к арифметике натуральных чисел не в состоянии охватить всю область истинных арифметических суждений, и то, что мы понимаем под процессом математического доказательства, не сводится к использованию аксиоматического метода. После теоремы Гёделя стало бессмысленно рассчитывать, что понятию убедительного математического доказательства можно будет придать раз и навсегда очерченные формы. [2,4,6]

Последним в этой череде попыток объяснить теорию множеств был интуиционизм.

Он прошел ряд этапов в своей эволюции — полуинтуиционизм, собственно интуиционизм, ультраинтуиционизм. На разных этапах математиков волновали разные проблемы, но одной из основных проблем математики является проблема бесконечности. Математические понятия бесконечности, непрерывности служили предметом философского анализа с момента их появления (идеи атомистов, апории Зенона Элейского, инфинитезимальные методы в античности, исчисление бесконечно малых в Новое время и пр.). Наибольшие споры вызывало применение различных видов бесконечности (потенциальной, актуальной) как математических объектов и их интерпретация. Все эти проблемы, на наш взгляд, были порождены более глубокой проблемой — о роли субъекта в научном познании. Дело в том, что состояние кризиса в математике порождено эпистемологической неопределенностью соизмерения мира объекта (бесконечности) и мира субъекта. Математик как субъект имеет возможность выбора средств познания — или потенциальной, или актуальной бесконечности. Применение потенциальной бесконечности как становящейся, дает ему возможность осуществлять, конструировать бесконечное множество построений, которые можно надстраивать над конечными, не имея конечного шага, не завершая построение, оно только возможно. Применение актуальной бесконечности дает ему возможность работать с бесконечностью как с уже осуществимой, завершенной в своем построении, как актуально данной одновременно.

На этапе полуинтуиционизма проблема бесконечности еще не была самостоятельной, а была вплетена в проблему построения математических объектов и способов его обоснования. Полуинтуиционизм А. Пуанкаре и представителей парижской школы теории функций Бэра, Лебега и Бореля был направлен против принятия аксиомы свободного выбора, с помощью которой доказывается теорема Цермело, утверждавшая, что всякое множество можно сделать вполне упорядоченным, но без указания теоретического способа определения элементов любого подмножества искомого множества. Нет способа построения математического объекта, нет и самого математического объекта. Математики считали, что наличие или отсутствие теоретического способа построения последовательности объектов исследования может служить основой обоснования или опровержения этой аксиомы. В российском варианте полуинтуиционистская концепция в философских основаниях математики получила развитие в таком направлении, как эффективизм, развиваемый Н.Н. Лузиным. Эффективизм представляет собой оппозицию к основным абстракциям учения множества Кантора о бесконечном — актуальности, выбора, трансфинитной индукции и др.

Для эффективизма гносеологически более ценными абстракциями является абстракция потенциальной осуществимости, чем абстракция актуальной бесконечности. Благодаря этому становится возможным введение понятия о трансфинитных ординалах (бесконечных порядковых числах) на основе эффективного понятия о росте функций. Гносеологическая установка эффективизма для отображения непрерывного (континуума) опиралась на дискретные средства (арифметики) и созданную Н.Н.Лузиным дескриптивную теорию множеств (функций). Интуиционизм голландца Л. Э. Я. Брауэра, Г. Вейля, А. Гейтинга в качестве традиционного объекта исследования видит свободно становящиеся последовательности различных видов. На этом этапе, решая собственно математические проблемы, в том числе о перестройке всей математики на новой основе, интуиционисты подняли философский вопрос о роли математика как познающего субъекта. Каково его положение, где он более свободен и активен в выборе средств познания? Интуиционисты первыми (и на этапе полуинтуиционизма) стали критиковать концепцию актуальной бесконечности, канторовскую теорию множеств, усмотрев в ней ущемление возможностей субъекта влиять на процесс научного поиска решения конструктивной задачи. В случае использования потенциальной бесконечности субъект себя не обманывает, так как для него идея потенциальной бесконечности интуитивно значительно яснее, чем идея актуальной бесконечности. Для интуициониста объект считается существующим, если он дан непосредственно математику или известен метод его построения, конструирования. Субъект в любом случае может приступить к процессу достраивания ряда элементов своего множества. Непостроенный объект для интуиционистов не существует. В то же время субъект, работающий с актуальной бесконечностью, будет лишен этой возможности и будет чувствовать двойную уязвимость принятой позиции:

1) никогда нельзя осуществить это бесконечное построение; 2) он принимает решение оперировать с актуальной бесконечностью как с конечным объектом и в этом случае теряет свою специфику понятия бесконечности. Интуиционизм сознательно ограничивает возможности математика тем, что тот может осуществлять построение математических объектов исключительно посредством таких средств, которые хотя и получаемы с помощью абстрактных понятий, но эффективны, убедительны, доказуемы, функционально конструктивны именно практически и сами интуитивно ясны как конструкции, построения, надежность которых на практике не вызывает никаких сомнений. Интуиционизм, опираясь на понятие потенциальной бесконечности и конструктивные методы исследования, имеет дело с математикой становления, теория множеств относится к математике бытия.

Для интуициониста Брауэра как представителя математического эмпиризма логика вторична, он критикует ее и закон исключённого третьего.

В своих отчасти мистических работах он не отрицает наличие бесконечности, однако не допускает её актуализации, лишь потенциализацию. Главное для него — интерпретация и обоснование практически используемых логических средств и математических рассуждений. Принятое интуиционистами ограничение преодолевает неопределенность использования понятия бесконечности в математике и выражает стремление преодолеть кризис в основании математики.

Ультраинтуиционизм (А.Н. Колмогоров, А.А.Марков и др.) — последняя стадия развития интуиционизма, на которой модернизируются, существенно дополняются и преобразуются основные его идеи, не изменяя его сущности, но преодолевая недостатки и усиливая позитивные стороны, руководствуясь критериями математической строгости. Слабостью подхода интуиционистов было узкое понимание роли интуиции как единственного источника обоснования правильности и эффективности математических методов. Принимая «интуитивную ясность» в качестве критерия истинности в математике, интуиционисты методологически обедняли возможности математика как субъекта познания, сводили его деятельность лишь к мыслительным операциям на основе интуиции и не включали практику в процесс математического познания. Ультраинтуиционистская программа обоснования математики является российским приоритетом. Поэтому отечественные математики, преодолевая ограниченность интуиционизма, принимали действенной методологию материалистической диалектики, признающей человеческую практику источником формирования как математических понятий, так и математических методов (умозаключений, построений). Проблему существования математических объектов ультраинтуиционисты решали, опираясь уже не на неопределяемое субъективное понятие интуиции, а на математическую практику и конкретный механизм построения математического объекта — алгоритм, выражаемый вычислимой, рекурсивной функцией.

Ультраинтуиционизм усиливает достоинства интуиционизма, заключающиеся в возможности упорядочивания и обобщения приемов решения конструктивных проблем, употребляемых математиками любого направления. Поэтому интуиционизм последней стадии (ультраинтуиционизм) близок конструктивизму в математике. В гносеологическом аспекте основные идеи и принципы ультраинтуиционизма таковы: критика классической аксиоматики логики; использование и значительное усиление (по явному указанию А.А. Маркова) роли абстракции отождествления (мысленного отвлечения от несходных свойств предметов и одновременного вычленения общих свойств предметов) как способа построения и конструктивного понимания абстрактных понятий, математических суждений; доказательство непротиворечивости непротиворечивых теорий. В формальном аспекте применение абстракции отождествления оправдывается тремя ее свойствами (аксиомами) равенства — рефлексивности, транзитивности и симметрии.

Для решения основного противоречия в математике по проблеме бесконечности, породившего кризис ее оснований, на этапе ультраинтуиционизма в работах А.Н. Колмогорова были предложены пути выхода из кризиса посредством решения проблемы отношений между классической и интуиционистской логикой, классической и интуиционистской математикой. Интуиционизм Брауэра в целом отрицал логику, но так как любой математик не может обойтись без логики, в интуиционизме все-таки сохранилась практика логических рассуждений, допускались некоторые принципы классической логики, имеющей в качестве своей базы аксиоматику. С.К. Клини, Р. Весли даже отмечают, что интуиционистскую математику можно описать в виде некоторого исчисления, а исчисление является способом организации математического знания на основах логики, формализации и ее формы — алгоритмизации. Новый вариант соотношения логики и математики в рамках интуиционистских требований к интуитивной ясности суждений, особенно тех, которые включали отрицание, А.Н. Колмогоров предложил следующим образом: интуиционистскую логику, тесно связанную с интуиционистской математикой, он представил в форме аксиоматического импликативного минимального исчисления высказываний и предикатов. Тем самым ученый представил новую модель математического знания, преодолевающую ограниченность интуиционизма в признании лишь интуиции как средства познания и ограниченность логицизма, абсолютизирующего возможности логики в математике. Эта позиция позволила в математической форме продемонстрировать синтез интуитивного и логического как основы гибкой рациональности и ее конструктивной эффективности.

Выводы. Таким образом, эпистемологический аспект математического познания позволяет оценить революционные изменения на этапе кризиса оснований математики на рубеже XIX-XX вв. с новых позиций в понимании процесса познания, природы и роли субъекта в нем. Гносеологический субъект традиционной теории познания, соответствующий периоду господства теоретико-множественного подхода в математике, — это абстрактный, неполный, «частичный» субъект, представленный в субъектно-объектных отношениях, оторванный абстракциями, логикой, формализмом от действительности, рационально, теоретически познающий свой объект и понимаемый как зеркало, точно отражающее и копирующее действительность. По сути, субъект исключался из познания как реального процесса и результата взаимодействия с объектом. Выход интуиционизма на арену борьбы философских направлений в математике привел к новому пониманию математика как субъекта познания — человека познающего, философская абстракция которого должна быть выстроена как бы заново. Математик предстал как эмпирический субъект, понимаемый уже как целостный реальный человек, включающий все те свойства, от которых отвлекались в гносеологическом субъекте, — эмпирическую конкретность, изменчивость, историчность; это действующий и познающий в реальном познании, творческий, интуитивный, изобретательный субъект. Философия интуиционистской математики стала базой, фундаментом современной эпистемологической парадигмы, построенной на концепции гибкой рациональности, в которой человек — это цельный (целостный) субъект познания, обладающий новыми познавательными качествами, методами, процедурами; он синтезирует свою как абстрактно-гносеологическую и логико-методологическую природу и форму, так и одновременно получает экзистенциально-антропологическое и «историко-метафизическое» осмысление.

Важным моментом так же является интуиция в познании и, в частности, в образовании математических понятий. Опять же идёт борьба с философией, попытки исключить закон исключённого третьего, как не имеющий смысла в математике и пришедший в неё из философии. Однако же наличие излишнего акцента на интуицию и отстутствие чётких математических обоснований не позволили перевести математику на твёрдый фундамент. [2,4,7]

Однако после появления в 1930-х годах строгого понятия алгоритма эстафету от интуиционизма принял математический конструктивизм, представители которого внесли немалый вклад в современную теорию вычислимости. Кроме того, в 1970-е и 1980-е годы обнаружились существенные связи между некоторыми идеями интуиционистов (даже теми, которые раньше казались абсурдными) и математической теорией топосов. Математика, имеющаяся в некоторых топосах, весьма напоминает ту, которую пытались создать интуиционисты.

В качестве итога можно сделать утверждение: большинство из вышеуказанных парадоксов попросту не существуют в теории множеств с самопринадлежностью [8]. Является ли подобный подход окончательным — спорный вопрос, дальнейшие работы в этой области покажут.

Заключение

Закончен ли третий кризис математики (потому как он находился в причинно-следственной связи с парадоксами; теперь же парадоксы — неотъемлемая часть) — тут мнения расходятся, хотя формально известные парадоксы к 1907-му году были устранены. Впрочем, сейчас в математике имеются и другие обстоятельства, которые можно считать либо кризисными, либо предвещающими кризис (например), отсутствие строгого обснования у континуального интеграла).

Что же касается парадоксов, то весьма важную роль в математике сыграл известный парадокс лжеца, а так же целая серия парадоксов в так называемой наивной (предшествовавшей аксиоматической) теории множеств, вызвавших кризис оснований (один из таких парадоксов сыграл роковую роль в жизни Г. Фреге). Но, возможно, одним из самых недооценённых явлений в современной математике, которое вполне можно назвать и парадоксальным, и кризисным, является решение Полом Коэном в 1963 году первой проблемы Гильберта. Точнее, не сам факт решения, а характер этого решения [9].

Литература

1. Georg Cantor. Beiträge zur begründung der transfiniten mengenlehre. Mathematische Annalen, 46:481--512, 1895.
2. И.Н. Бурова. Парадоксы теории множеств и диалектика. Наука, 1976.
3. M.D. Potter. Set theory and its philosophy: a critical introduction. Oxford University Press, Incorporated, 2004.
4. Жуков Н.И. Философские основания математики. Мн.: Университетское, 1990.
5. Фейнман Р.Ф., С. Ильин. Вы, конечно, шутите, мистер Фейнман!: похождения удивительного человека, поведанные им Р. Лейтону. КоЛибри, 2008.
6. О. М. Мижевич. Два способа преодоления парадоксов в теории множеств Г. Кантора. Логико-философские штудии, (3):279--299, 2005.
7. С. И. Масалова. ФИЛОСОФИЯ ИНТУИЦИОНИСТСКОЙ МАТЕМАТИКИ. Вестник ДГТУ, (4), 2006.
8. Чечулин В.Л. Теория множеств с самопринадлежностью (основания и некоторые приложения). Перм. гос. ун-т. – Пермь, 2012.
9. С. Н. Тронин. Краткий конспект лекций по дисциплине ''Философия математики''. Казань, 2012.
10. Гришин В.Н., Бочвар Д.А. Исследования по теории множеств и неклассическим логикам. Наука, 1976.
11. Хофштадтер Д. Гедель, Эшер, Бах: эта бесконечная гирлянда. Бахрах-М, 2001.
12. Кабаков Ф.А., Мендельсон Э. Введение в математическую логику. Издательство «Наука», 1976.
13. Д.А. Бочвар. К вопросу о парадоксах математической логики и теории множеств. Математический сборник, 57(3):369--384, 1944.

habrahabr.ru

Парадоксы теории множеств, реферат — allRefers.ru

Парадоксы теории множеств - раздел Образование, Учебник ПО ЛОГИКЕ

В письме Готтлобу Фреге от 16 июня 1902 г. Бертран Рассел сообщил о том, что он обнаружил парадокс множества всех нормальных множеств (нормальным множеством называется множество, не содержащее себя в качестве элемента).

Примерами таких парадоксов являются «каталог всех нормальных каталогов», «мэр города», «генерал и брадобрей» и др.

Парадокс «мэр города» состоит в следующем: каждый мэр города живет или в своем городе, или вне его. Был издан приказ о выделении одного специального города, где бы жили только эти мэры, не живущие в своем городе. Где должен жить мэр этого специального города? Если он хочет жить в своем городе, то он не может этого сделать, так как там могут жить только мэры, не живущие в своем городе; если же он не хочет жить в своем городе, то, как и все мэры, не живущие в своих городах, он должен жить в отведенном городе, т. е. в своем. Итак, он не может жить ни в своем городе, ни вне его.

Парадокс «генерал и брадобрей» состоит в следующем: каждый солдат может сам себя брить или бриться у другого солдата. Генерал издал приказ о выделении одного специального солдата-брадобрея, у которого брились бы только те содаты, которые себя не бреют. У кого должен бриться этот специально выделен­ный солдат-брадобрей? Если он хочет сам себя брить, то он не может этого сделать, так как он может брить только тех солдат, которые себя не бреют; если же он не будет себя брить, то, как и все солдаты, не бреющие себя, он должен бриться только у одного специального солдата-брадобрея, т. е. у себя. Итак, он не может ни брить себя, ни не брить себя.

Этот парадокс аналогичен парадоксу «мэр города».

Рассмотрим парадокс Рассела о нормальных множествах в ви­де парадокса о «каталоге всех нормальных каталогов».

Парадокс этот получается так: каталоги подразделяются на два рода: 1) такие, которые в числе перечисленных каталогов не упоминают себя (нормальные), и 2) такие, которые сами входят в число перечисляемых каталогов (ненормальные).

Библиотекарю дается задание составить каталог всех нор­мальных и только нормальных каталогов. Должен ли он при составлении своего каталога упомянуть и составленный им? Если он упомянет его, то составленный им каталог окажется ненор­мальным, т. е. он не имел права упоминать его. Если же библио­текарь не упомянет его, то один из нормальных каталогов — тот, который он составил, — окажется не упомянутым, хотя он должен был упомянуть все нормальные каталоги. Итак, он не может ни упомянуть, ни не упомянуть составляемый им каталог. Как же тут быть? На этом же примере видно, как могут быть разрешены соответствующие парадоксы. В самом деле, естест­венно заметить, что понятие «нормальный каталог» не имеет фиксированного объема, пока не установлено, какие каталоги следует рассматривать: в какой, например, библиотеке и в какое время они находятся. Если будет дано задание составить каталог всех нормальных каталогов на 10 мая 1985 г., то объем понятия «каталог всех нормальных каталогов» будет фиксирован и при составлении своего каталога библиотекарь не должен будет упо­минать его же. Но если перед ним поставят снова аналогичное задание после того, как его прежний каталог уже будет составлен, то ему придется учесть и этот каталог. Так будет разрешен парадокс.

Таким образом, в логику входит категория времени, катего­рия изменения: приходится рассматривать изменяющиеся объ­емы понятий. А рассмотрение объема в процессе его измене­ния — это уже аспект диалектической логики. Трактовка парадо­ксов математической логики и теории множеств, связанных с на­рушением требований диалектической логики, принадлежит про­фессору С. А. Яновской.

Имеются и другие способы избежать противоречий такого рода.

Все темы данного раздела:

МЫШЛЕНИЕ КАК ПРЕДМЕТ ИЗУЧЕНИЯ ЛОГИКИ Познание как отражение действительности Познание есть диалектический процесс отражения мира в со­зн

Понятие логической формы Логической формой конкретной мысли является строение этой мысли, т. е. способ связи ее составных частей. В л

Теоретическое и практическое значение логики Можно логично рассуждать, правильно строить свои умозак­лючения, опровергать доводы противника и не зная п

ЛОГИКА И ЯЗЫК Предметом изучения логики являются формы и законы пра­вильного мышления. Мышление есть функция человеческ

Семантические категории Выражения (слова и словосочетания) естественного языка, имеющие какой-либо самостоятельный смысл, можно ра

ПОНЯТИЕ КАК ФОРМА МЫШЛЕНИЯ Понятие является одной из форм абстрактного мышления. Конкретные предметы и их свойства отражаются с помощ

ВИДЫ ПОНЯТИЙ   Понятия можно классифицировать по объему и по содержа­нию. По объему понятия делятся на единичные,

Конкретные и абстрактные понятия Конкретными называются понятия, в которых отражены од­ноэлементные или многоэлементные классы предме

Относительные и безотносительные понятия Относительные — такие понятия, в которых мыслятся пред­меты, существование одного из которых предпола

Положительные и отрицательные понятия Положительные понятия характеризуют в предмете наличие того или иного качества или отношения. Наприме

Собирательные и несобирательные понятия Собирательными называются понятия, в которых группа од­нородных предметов мыслится как единое целое (н

ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ   Предметы мира находятся друг с другом во взаимосвязи и взаимообусловленности. Поэтому и понятия, о

Типы несовместимости: соподчинение, противоположность, противоречие Соподчинение (координация) — это отношение между объема­ми двух или нескольких понятий, исключающих др

ОПРЕДЕЛЕНИЕ ПОНЯТИЙ   Определение (или дефиниция) понятия есть логическая опера­ция, которая раскрывает содержание

Реальные и номинальные определения Если определяется понятие, то определение будет реальным. Если определяется термин, обозначающий понят

Использование определений; понятий в процессе обучения Определение через род и видовое отличие и номинальное определение широко используются в процессе обучения

Правила явного определения. Ошибки, возможные в определении 1. Определение должно быть соразмерным, т. е. объем опре­деляющего понятия должен быть равен объему опре

Неявные определения Вотличие от явных определений, имеющих структуру в неявных опреде

Определение через аксиомы В современной математике и в математической логике широ­ко применяется так называемый аксиоматический ме

Приемы, сходные с определением понятий Всем понятиям определение дать невозможно (к тому же в этом нет необходимости), поэтому в науке и в процессе

Значение определений в науке и в рассуждении Кроме учета формально-логических требований при опреде­лении понятия надо учитывать и методологические т

Правила деления понятий Чтобы деление было правильным, необходимо соблюдать следующие правила. 1. Соразмерность деления: объ

Виды деления: по видообразующему признаку и дихотомическое деление При делении понятия по видообразующему признаку основа­нием деления является тот признак, по которому обр

ОГРАНИЧЕНИЕ И ОБОБЩЕНИЕ ПОНЯТИЙ   Предположим, мы знаем, что некто — ученый, и хотим уточ­нить наши знания о нем. Уточняем: это русски

ОБЩАЯ ХАРАКТЕРИСТИКА СУЖДЕНИЯ Суждение — форма мышления, в которой что-либо утверж­дается или отрицается о существовании предметов,

Суждение и предложение Понятия в языке выражаются одним словом или группой слов. Суждения выражаются повествовательными предложе

Виды простых суждений 1. Суждения свойства (атрибутивные). В суждениях этого вида утверждается или отрицается принадлежность

Распределенность терминов в категорических суждениях В суждениях термины S и Р могут быть либо распределены, либо не распределены. Термин считается распредел

СЛОЖНОЕ СУЖДЕНИЕ И ЕГО ВИДЫ   Сложные суждения образуются из простых суждений с помо­щью логических связок: конъюнкции, дизъюнк

Способы отрицания суждений Два суждения называются отрицающими или противоречащи­ми друг другу, если одно из них истинно, а др

Отрицание сложных суждений Чтобы получить отрицание сложных суждений, имеющих в своем составе лишь операции конъюнкции и дизъюнкции,

ВЫРАЖЕНИЕ ЛОГИЧЕСКИХ СВЯЗОК (ЛОГИЧЕСКИХ ПОСТОЯННЫХ) В ЕСТЕСТВЕННОМ ЯЗЫКЕ В мышлении мы оперируем не только простыми, но и слож­ными суждениями, образуемыми из простых посредством л

ОТНОШЕНИЯ МЕЖДУ СУЖДЕНИЯМИ ПО ЗНАЧЕНИЯМ ИСТИННОСТИ   Суждения, как и понятия, делятся на сравнимые (имеют об­щий субъект или предикат) и несравнимые. Сра

ДЕЛЕНИЕ СУЖДЕНИЙ ПО МОДАЛЬНОСТИ   В логике мы до сих пор рассматривали простые суждения, которые называются ассерторическими, а

ПОНЯТИЕ О ЛОГИЧЕСКОМ ЗАКОНЕ Фундамент материалистической диалектики — наиболее глу­бокого и всестороннего учения о развитии — соста

Закон тождества Закон тождества является одним из законов правильного мышления, соблюдение этого закона гарантирует опред

Закон непротиворечия Диалектика исходит из реального онтологического сущест­вования диалектических противоречий во всех пред

Закон исключенного третьего Для двузначной логики онтологическим аналогом этого закона является то, что в предмете указанный признак л

Закон достаточного основания Этот закон формулируется так: «Всякая истинная мысль должна быть достаточно обоснованной». Речь идет о

ИСПОЛЬЗОВАНИЕ ФОРМАЛЬНО-ЛОГИЧЕСКИХ ЗАКОНОВ В ОБУЧЕНИИ Формально-логические законы действуют во всяком мышле­нии, но в обучении особенно необходимо их сознатель

ОБЩЕЕ ПОНЯТИЕ ОБ УМОЗАКЛЮЧЕНИИ   Формами мышления являются понятия, суждения и умозак­лючения. Опосредованно, с помощью многообраз

Понятие логического следования Выведение следствий из данных посылок — широко распрост­раненная логическая операция. Как известно, услов

ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ Дедуктивные умозаключения— те умозаключения, у которых между посылками и заключением имеется от

Понятие правила вывода Умозаключение дает истинное заключение, если исходные посылки истинны и соблюдены правила вывода. Правила

Превращение Превращение — вид непосредственного умозаключения, при котором изменяется качество посылки без измен

Противопоставление предикату Это такое непосредственное умозаключение, при котором (в заключении) предикатом является субъект, субъекто

Фигуры категорического силлогизма Фигурами категорического силлогизма называются формы силлогизма, различаемые по положению среднего т

Модусы категорического силлогизма Модусами фигур категорического силлогизма называются разновидности силлогизма, отличающиеся друг от

I. Правила терминов 1. В каждом силлогизме должно быть только три термина (S, Р, М). Ошибка называется «учетверение терминов».

СОКРАЩЕННЫЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ (ЭНТИМЕМА)   Энтимемой, или сокращенным категорическим силлогизмом, называется силлогизм, в котором пропущ

СЛОЖНЫЕ И СЛОЖНОСОКРАЩЕННЫЕ СИЛЛОГИЗМЫ (ПОЛИСИЛЛОГИЗМЫ, СОРИТЫ, ЭПИХЕЙРЕМА)   Полисиллогизмом (сложным силлогизмом) называются два или несколько простых категорических си

Формализация эсихейрем с общими посылками Эпихейремой в традиционной логике называется такой слож­носокращенный силлогизм, обе посылки которог

УСЛОВНЫЕ УМОЗАКЛЮЧЕНИЯ   Чисто условным умозаключением называется такое опосред­ствованное умозаключение, в котором о

Условно-категорические умозаключения Условно-категорическое умозаключение — это такое дедук­тивное умозаключение, в котором одна из посыло

Простая конструктивная дилемма Это умозаключение состоит из двух посылок. В первой посыл­ке утверждается, что из двух различных оснований

Сложная конструктивная дилемма Это умозаключение строится из двух посылок. В первой посылке имеются два основания, из которых вытекают соо

Сложная деструктивная дилемма Дилемма такого вида содержит одну посылку, состоящую из двух условных суждений с разными основаниями и раз

Трилемма Трилеммы, так же как и дилеммы, могут быть конструктив­ными и деструктивными; каждая из этих форм в свою оче

Логическая природа индукции Дедуктивные умозаключения позволяют выводить из истин­ных посылок при соблюдении соответствующих правил

Математическая индукция Один из важнейших методов доказательства в математике основан на аксиоме (принципе) математической индукц

ВИДЫ НЕПОЛНОЙ ИНДУКЦИИ   Неполная индукция применяется в тех случаях, когда мы, во-первых, не можем рассмотреть все элементы

II вид. Индукция через анализ и отбор фактов В популярной индукции наблюдаемые объекты выбираются случайно, без всякой системы. В индукции через анализ

Понятие вероятности Различаются два вида понятия «вероятность» — объективная и субъективная вероятность. Объективная вероя

III вид. Научная индукция Научной индукцией называется такое умозаключение, в кото­ром на основании познания необходимых призна

Понятие причины и следствия Причина — явление или совокупность явлений, которые непо­средственно обусловливают, порождают другое

Методы установления причинной связи Причинная связь между явлениями определяется посредством ряда методов, описание и классификация которых в

ДЕДУКЦИЯ И ИНДУКЦИЯ В УЧЕБНОМ ПРОЦЕССЕ   Как в любом процессе мышления (научного или обыденного), так и в процессе обучения дедукция и индук

УМОЗАКЛЮЧЕНИЕ ПО АНАЛОГИИ И ЕГО ВИДЫ. ИСПОЛЬЗОВАНИЕ АНАЛОГИЙ В ПРОЦЕССЕ ОБУЧЕНИЯ   Термин «аналогия» означает сходство двух предметов22 (или двух групп предметов) в каких-либо

Строгая аналогия Характерным признаком, отличающим строгую аналогию от нестрогой и ложной, является наличие необходимой св

Нестрогая аналогия В отличие от строгой аналогии нестрогая аналогия дает не достоверное, а лишь вероятное заключение. Если лож

Ложная аналогия При нарушении указанных выше правил аналогия может дать ложное заключение, т. е. стать ложной. Вероятность з

Использование аналогий в процессе обучения Аналогии используются на уроках по всем школьным дисцип­линам. Мы приведем лишь некоторые примеры использ

ПОНЯТИЕ ДОКАЗАТЕЛЬСТВА Познание отдельных предметов, их свойств происходит по­средством форм чувственного познания (ощущений и в

ПРЯМОЕ И НЕПРЯМОЕ (КОСВЕННОЕ) ДОКАЗАТЕЛЬСТВО   Доказательства по форме делятся на прямые и непрямые (косвенные). Прямое доказательство идет от ра

ПОНЯТИЕ ОПРОВЕРЖЕНИЯ   Опровержение — логическая операция установления ложно­сти или необоснованности ранее выдвин

II. Критика аргументов Подвергаются критике аргументы, которые были выдвинуты оппонентом в обоснование его тезиса. Доказывается

III. Выявление несостоятельности демонстрации Этот способ опровержения состоит в том, что показываются ошибки в форме доказательства. Наиболее распростр

ЛОГИЧЕСКИЕ ОШИБКИ, ВСТРЕЧАЮЩИЕСЯ В ДОКАЗАТЕЛЬСТВЕ И ОПРОВЕРЖЕНИИ   Если будет нарушено хотя бы одно из перечисленных ниже правил, то могут произойти ошибки, относящи

Ошибки, совершаемые относительно доказываемого тезиса 1. «Подмена тезиса». Согласно правилам доказательного рассуждения, тезис должен быть ясно сформулирова

Ошибки в основаниях (аргументах) доказательства 1. Ложность оснований («Основное заблуждение»). В качестве аргументов берутся не истинные, а ложные сужд

Ошибки в форме доказательства 1. Мнимое следование. Если тезис не следует из приводимых в его подтверждение аргументов, то возникает о

ПОНЯТИЕ О СОФИЗМАХ И ЛОГИЧЕСКИХ ПАРАДОКСАХ   Непреднамеренная ошибка, допущенная человеком в мышле­нии, называется паралогизмом. Преднаме

Понятие о логических парадоксах Парадокс — это рассуждение, доказывающее как истинность, так и ложность некоторого суждения, иными сло

ДОКАЗАТЕЛЬСТВО И ДИСКУССИЯ   Роль доказательства в научном познании и дискуссиях сводит­ся к подбору достаточных оснований (ар

ГИПОТЕЗА КАК ФОРМА РАЗВИТИЯ ЗНАНИЙ   В науке, обыденном мышлении мы идем от незнания к зна­нию, от неполного знания к более полному; нам

Виды гипотез В зависимости от степени общности научные гипотезы можно разделить на общие, частные и единичные. Об

ПОСТРОЕНИЕ ГИПОТЕЗЫ И ЭТАПЫ ЕЕ РАЗВИТИЯ   Гипотезы строятся тогда, когда возникает потребность объяс­нить ряд новых фактов, которые не укла

СПОСОБЫ ПОДТВЕРЖДЕНИЯ ГИПОТЕЗ   1. Самый действенный способ подтверждения гипотезы — обнаружение предполагаемого объекта, явлени

ОПРОВЕРЖЕНИЕ ГИПОТЕЗ   Опровержение гипотез осуществляется путем опровержения (фальсификации) их следствий. При этом мож

ЛОГИЧЕСКАЯ СТРУКТУРА ВОПРОСА   Вопрос в познании играет особенно большую роль, так как все познание мира начинается с вопроса, с п

Виды вопросов Обычно различают два вида (типа) вопросов: I тип — уточняющие (определенные, прямые, или «ли» вопросы)

Предпосылки вопросов Предпосылкой, или базисом, вопроса является содержащееся в вопросе исходное знание, неполноту или неопреде

Правила постановки простых и сложных вопросов 1. Корректность постановки вопроса. Итак, вопросы должны быть правильно поставленными, корректными. Провока

Логическая структура и виды ответов 1. Ответы на простые вопросы. Ответ на простой вопрос первого вида (уточняющий, определенный, прямой, «ли

Постановка вопросов в процессе проблемного обучения Под проблемным обучением понимается такое изучение мате­риала, которое вызывает в сознании учащихся позна

В НАЧАЛЬНОЙ ШКОЛЕ   Большое значение в процессе обучения придавал логике чешс­кий педагог Я. А. Коменский. Он предлага

РАЗВИТИЕ ЛОГИЧЕСКОГО МЫШЛЕНИЯ МЛАДШИХ ШКОЛЬНИКОВ   В процессе обучения оперированию понятиями отводится ведущая роль. В третьем классе начальной шко

Развитое логического мышления на уроках математики Математика способствует развитию творческого мышления, заставляя учащихся искать решения нестандартных з

Развитие логического мышления на уроках истории В начальной школе при изучении материала по истории при­меняются различные приемы, способствующие развити

Логика в Древней Индии История логики Индии связана с развитием индийской фило­софии. Древнейший литературный памятник Индии — В

Логика в Древней Греции В Древней Греции логическую форму доказательства в виде цепи дедуктивных умозаключений мы встречаем в эле

Логика в средние века Средневековая логика (VI—XV вв.) изучена еще недостаточ­но. В средние века теоретический поиск в логике разве

РАЗВИТИЕ ЛОГИКИ В СВЯЗИ С ПРОБЛЕМОЙ ОБОСНОВАНИЯ МАТЕМАТИКИ   Немецкий математик и логик Готтлоб Фреге (1848—1925) предпринял попытку свести математику к логике. С

МНОГОЗНАЧНЫЕ ЛОГИКИ Если в двузначной логике высказывание бывает истинным или ложным, то в многозначных логиках число значений

Трехзначная система Рейтинга В двузначной логике из закона исключенного третьего выво­дятся: 1)2

Бесконечнозначная логика как обобщение многозначной системы Поста Исходя из системы Рщ Поста, мы (А. Г.) строим бесконечнозначную систему Gх0. Значениями

ИНТУИЦИОНИСТСКАЯ ЛОГИКА   Интуиционистская логика построена в связи с развитием ин­туиционистской математики. Интуиционис

КОНСТРУКТИВНЫЕ ЛОГИКИ   Конструктивная логика, отличная от логики классической, своим рождением обязана конструктивной м

Конструктивные исчисления высказываний В. И. Гливенко и А. Н. Колмогорова Первыми представителями конструктивной логики были на­ши отечественные математики — А. Н. Колмогоров (1903—

Конструктивная логика А. А. Маркова Проблема конструктивного понимания логических связок, в частности отрицания и импликации, требует примене

МОДАЛЬНЫЕ ЛОГИКИ   В классической двузначной логике рассматривались простые и сложные ассерторические суждения, т. е

ПОЛОЖИТЕЛЬНЫЕ ЛОГИКИ   Положительные логики — это логики, построенные без опе­рации отрицания. Их можно разделить на два

ПАРАНЕПРОТИВОРЕЧИВАЯ ЛОГИКА   Эта логика представляет одно из направлений современной неклассической математической логики. Об

allrefers.ru

Парадоксы теории множеств и их философская интерпретация / СоХабр

Краткий синопсис

P.S. Весьма «сухой язык», но вполне читабельно после университетской программы. По большей части определения парадоксов брались из Википедии (упрощённая формулировка и готовая TeX-разметка).

Введение

Следует начать с определения.

Что есть множество? Вопрос достаточно простой, ответ на него вполне интуитивен. Множество это некий набор элементов, представляемый единым объектом. Кантор в своей работе Beiträge zur Begründung der transfiniten Mengenlehre даёт определение: под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M)[1]. Как видим, суть не изменилась, разница лишь в той части, которая зависит от мировоззрения определяющего. История же теории множеств как в логике так и в математике весьма противоречива. Фактически начало ей положил Кантор в XIX веке, далее Рассел и остальные продолжили работу.

Парадоксы (логики и теории множеств) — (греч. — неожиданный) — формально-логические противоречия, которые возникают в содержательной множеств теории и формальной логике при сохранении логической правильности рассуждения. Парадоксы возникают тогда, когда два взаимоисключающих (противоречащих) суждения оказываются в равной мере доказуемыми. Парадоксы могут появиться как в пределах научной теории, так и в обычных рассуждениях (например, приводимая Расселом перифраза его парадокса о множестве всех нормальных множеств: «Деревенский парикмахер бреет всех тех и только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?»). Поскольку формально-логическое противоречие разрушает рассуждение как средство обнаружения и доказательства истины (в теории, в которой появляется парадокс, доказуемо любое, как истинное, так и ложное, предложение), возникает задача выявления источников подобных противоречий и нахождения способов их устранения. Проблема философского осмысления конкретных решений парадоксов — одна из важных методологических проблем формальной логики и логических оснований математики.

Целью данной работы является изучение парадоксов теории множеств как наследников античных антиномий и вполне логичных следствий перехода к новому уровню абстракции — бесконечности. Задача — рассмотреть основные парадоксы, их философскую интерпретацию.

Основные парадоксы теории множеств

Некторые из логических парадоксов были известны с античных времён, однако по причине того, что математическая теория ограничивалась одной лишь арифметикой и геометрией, соотнести их с теорией множеств было невозможно. В XIX веке ситуация изменилась коренным образом: Кантор в своих работах вышел на новый уровень абстракции. Он ввёл понятие бесконечности, создав тем самым новый раздел математики и позволив тем самым сравнивать различные бесконечности с помощью понятия «мощность множества» [2]. Однако тем самым он породил множество парадоксов. Самым первым является так называемый парадокс Бурали-Форти. В математической литературе встречаются различные формулировки, опирающиеся на разную терминологию и предполагаемый набор известных теорем. Вот одно из формальных определений.

Можно доказать, что если x — произвольное множество порядковых чисел, то множество-сумма есть порядковое число, большее или равное каждому из элементов x. Предположим теперь, что — множество всех порядковых чисел. Тогда — порядковое число, большее или равное любому из чисел в . Но тогда и — порядковое число, причём уже строго большее, а значит, и не равное любому из чисел в . Но это противоречит условию, по которому — множество всех порядковых чисел.

Сущность же парадокса в том, что при образовании множества всех порядковых чисел образуется новый порядковый тип, которого ещё не было среди «всех» трансфинитных порядковых чисел, существовавших до образования множества всех порядковых чисел. Этот парадокс был обнаружен самим Кантором, независимо открыт и опубликован итальянским математиком Бурали-Форти, ошибки же последнего были исправлены Расселом, после чего формулировка приобрела окончательный вид [2,3].

Среди всех попыток избежать подобных парадоксов и в какой-то мере попробовать их объяснить наибольшего внимания заслуживает идея уже упомянутого Рассела. Он предложил исключить из математики и логики импредикативные предложения, в которых определение элемента множества зависит от последнего, что и вызывает парадоксы. Правило звучит так: «никакое множество С не может содержать элементов m, определяемых лишь в терминах множества С, а так же элементов n, предполагающих в своём определении это множество» [4]. Подобное ограничение определения множества позволяет избежать парадоксов, но при этом значительно сужает область его применения в математике. Вдобавок этого недостаточно для объяснения их природы и причин появления, коренящихся в дихотомии мышления и языка, в особенностях формальной логики [4]. В какой-то мере в данном ограничении можно проследить аналогию с тем, что в более поздний период когнитивные психологи и лингвисты начали называть «категоризацией основного уровня»: определение сведено к наиболее легкой для понимания и изучения концепцией.

Далее Кантор в 1899 году открыл парадокс, названный его именем.

Предположим, что множество всех множеств существует. В этом случае справедливо , то есть всякое множество t является подмножеством V. Но из этого следует — мощность любого множества не превосходит мощности V. Но в силу аксиомы множества всех подмножеств, для V, как и любого множества, существует множество всех подмножеств , и по теореме Кантора , что противоречит предыдущему утверждению. Следовательно, V не может существовать, что вступает в противоречие с «наивной» гипотезой о том, что любое синтаксически корректное логическое условие определяет множество, то есть что для любой формулы A, не содержащей y свободно. Замечательное доказательство отсутствия подобных противоречий на основе аксиоматизированной теории множеств Цермело-Френкеля приводится у Поттера [3].

Оба вышеуказанных парадокса с логической точки зрения идентичны «Лжецу» либо «Брадобрею»: высказываемое суждение обращено не только на нечто объективное по отношению к нему, но и само на себя. Однако следует обращать внимание не только на логическую сторону, но и на понятие бесконечности, которое тут наличествует. В литературе ссылаются на работу Пуанкаре, в которой он пишет: «вера в существование актуальной бесконечности… делает необходимым эти непредикативные определения'' [2]. В целом же имеют место основные моменты [2]:

• в данных парадоксах нарушается правило чётко разделять „сферы“ предиката и субъекта; степень смешения близка к подмене одного понятия другим;
• обычно в логике предполагается, что в процессе рассуждения субъект и предикат сохраняют свой объём и содержание, в данном же случае происходит переход из одной категории в другую, что даёт в результате несоответствие;
• наличие слова „все“ имеет смысл для конечного числа элементов, в случае же бесконечного их количества возможно наличие такого, которое для определения себя потребует определение множества;
• нарушаются основные логические законы:
  • закон тождества нарушается тогда, когда обнаруживается нетождественность себе субъекта и предиката;
  • закон противоречия — когда с одинаковым правом выводятся два противоречащих друг другу суждения;
  • закон исключённого третьего — когда это третье приходится признавать, а не исключать, поскольку ни первое, ни второе не могут быть признаны одно без другого, т.к. они оказываются одинаково правомерными.

Парадокс Тристрама Шенди: В романе Стерна «Жизнь и мнения Тристрама Шенди, джентльмена» герой обнаруживает, что ему потребовался целый год, чтобы изложить события первого дня его жизни, и еще один год понадобился, чтобы описать второй день. В связи с этим герой сетует, что материал его биографии будет накапливаться быстрее, чем он сможет его обработать, и он никогда не сможет ее завершить. «Теперь я утверждаю, — возражает на это Рассел, — что если бы он жил вечно и его работа не стала бы ему в тягость, даже если бы его жизнь продолжала быть столь же богатой событиями, как вначале, то ни одна из частей его биографии не осталась бы ненаписанной». Действительно, события n-го дня Шенди мог бы описать за n-й год и, таким образом, в его автобиографии каждый день оказался бы запечатленным.

Иначе говоря, если бы жизнь длилась бесконечно, то она насчитывала бы столько же лет, сколько дней.

Рассел проводит аналогию между этим романом и Зеноном с его черепахой. По его мнению решение лежит в том, что целое эквивалентно его части в бесконечности. Т.е. к противоречию приводит только «аксиома здравого смысла» [2]. Однако же разрешение проблемы лежит в области чистой математики. Очевидно, что имеется два множества — года и дни, между элементами которых установлено взаимно-однозначное соответствие — биекция. Тогда при условии бесконечной жизни главного героя имеется два бесконечных равномощных множества, что, если рассматривать мощность как обобщение понятия количества элементов в множестве, разрешает парадокс.

Парадокс (теорема) Банаха-Тарского или парадокс удвоения шара — теорема в теории множеств, утверждающая, что трёхмерный шар равносоставлен двум своим копиям. Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число частей, передвинуть их, и составить из них второе. Более точно, два множества A и B являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств так, что для каждого i подмножество конгруэнтно .

Если же пользоваться теоремой выбора, то определение звучит так[3]: Аксиома выбора подразумевает, что существует разбиение поверхности единичной сферы на конечное количество частей, которые преобразованиями трёхмерного Евклидова пространства, не меняющими форму этих составляющих, могут быть собраны в две сферы единичного радиуса.

Очевидно, что при требовании для данных частей быть измеримыми, данное постоение неосуществимо. Известный физик Ричард Фейнман в своей биографии рассказывал, как в своё время у него получилось победить в споре о разбиении апельсина на конечное количество частей и пересоставлении его [5].

В определённых моментах этот парадокс используется для опровержения аксиомы выбора, однако проблема в том, что то, что мы считаем элементарной геометрией, — несущественно. Те понятия, которые мы считаем интуитивными, должны быть расширены до уровня свойств трансцендентных функций [3].

Чтобы и дальше ослабить уверенность тех, кто считает аксиому выбора неверной, следует упомянуть теорему Мазуркевича и Серпинского, которая утверждает, что существует непустое подмножество Е Евклидовой плоскости, которое имеет два непересекающихся подмножества, каждое из которых может быть разбито на конечное количество частей, так что их можно перевести изометриями в покрытие множества Е. При этом доказательство не требует использования аксиомы выбора[3]. Дальнейшие же построения на основе аксиомы определённости дают разрешение парадокса Банаха-Тарского, но не представляют такого интереса [3].

• Парадокс Ришара: требуется назвать «наименьшее число, не названное в этой книге». Противоречие в том, что с одной стороны, это можно сделать, так как есть наименьшее число, названное в этой книге. Исходя из него, можно назвать и наименьшее неназванное. Но тут возникает проблема: континуум является несчётным, между двумя любыми числами можно вставить ещё бесконечное множество промежуточных чисел. С другой стороны, если бы мы могли назвать это число, оно автоматически бы перешло из класса неупомянутых в книге, в класс упомянутых [2].
• Парадокс Греллинга-Нильсона: слова либо знаки могут обозначать какое-либо свойство и при этом иметь его или нет. Самая тривиальная формулировка звучит так: является ли слово «гетерологичный» (что означает «неприменимый к самому себе»), гетерологичным?.. Весьма схож с парадоксом Рассела в связи с наличием диалектического противоречия: нарушается двойственность формы и содержания. В случае со словами, имеющими высокий уровень абстракции, невозможно решить, являются ли эти слова гетерологичными [2].
• Парадокс Сколема: используя теорему Гёделя о полноте и теорему Лёвенхейма-Сколема[3] получаем, что аксиоматическая теория множеств остаётся истинной и тогда, когда будет предполагаться (иметься) для её интерпретации только счётная совокупность множеств. В то же время аксиоматическая теория включает в себя уже упомянутую теорему Кантора, что приводит нас к несчётным бесконечным множествам. [2]

Разрешение парадоксов

Логицизм был попыткой свести всю известную математику к терминам арифметики, а потом термины арифметики свести к понятиям математической логики. Вплотную этим занялся Фреге, однако после окончания работы над трудом, он вынужден был указать о своей несостоятельности, после того, как Рассел указал на имеющиеся в теории противоречия. Тот же Рассел, как уже был упомянуто ранее, попытался исключить использование импредикативных определений с помощью «теории типов». Однако его понятия множества и бесконечности, а так же аксиома сводимости оказались нелогичными. Основной проблемой было то, что не учитывались качественные различия между формальной и математической логикой, а так же наличие лишних понятий, в том числе и интуитивного характера. В итоге теория логицизма не смогла устранить диалектических противоречий парадоксов, связанных с бесконечностью. Имели место лишь принципы и методы, которые позволяли избавиться хотя бы от непредикативных определений. В свох же рассуждениях Рассел был наследником Кантора [2]

В конце XIX — начале XX в. распространение формалистической точки зрения на математику было связано с развитием аксиоматического метода и той программой обоснования математики, которую выдвинул Д. Гильберт. На степень важности этого факта указывает то, что первой проблемой из двадцати трёх, которые он поставил перед математическим сообществом, была проблема бесконечности. Формализация была необходима для доказательства непротиворечивости классической математики, «исключив при этом из неё всю метафизику». Учитывая средства и методы, которыми пользовался Гильберт, его цель оказалась принципиально невыполнимой, но его программа имела огромное влияние на все последующее развитие оснований математики. Гильберт достаточно долго работал над этой проблемой, построив первоначально аксиоматику геометрии. Поскольку решение проблемы оказалось достаточно успешным, он решил применить аксиоматический метод к теории натуральных чисел. Вот что он писал в связи с этим: «Я преследую важную цель: именно я хотел бы разделаться с вопросами обоснования математики как таковыми, превратив каждое математическое высказывание в строго выводимую формулу.» От бесконечности при этом планировалось избавиться с помощью сведения её к некому конечному числу операций. Для этого он обращался к физике с её атомизмом, дабы показать всю несостоятельность бесконечных величин. Фактически Гильберт поставил вопрос о соотношении теории и объективной реальности.

Более или менее полное представление о финитных методах дает ученик Гильберта Ж. Эрбран. Под финитными рассуждениями он понимает такие рассуждения, которые удовлетворяют следующим условиям: логические парадоксы " — всегда рассматривается лишь конечное и определенное число предметов и функций;

— функции имеют точное определение, и это определение позволяет нам вычислить их значение;

— никогда не утверждается «Этот объект существует», если не известен способ его построения;

— никогда не рассматривается множество всех предметов X какой-либо бесконечной совокупности;

— если известно, что какое-либо рассуждение или теорема верны для всех этих X, то это означает, что это общее рассуждение можно повторить для каждого конкретного X, причем само это общее рассуждение следует рассматривать только как образец для проведения таких конкретных рассуждений."

Однако в момент последней публикации в этой области Гёдель уже получил свои результаты, в сущности опять обнаружил и утвердил наличие диалектики в процессе познания. По сути своей дальнейшее развитие математики продемонстрировало несостоятельность программы Гильберта.

Что же, собственно, доказал Гёдель? Можно выделить три основных результата:

1. Гёдель показал невозможность математического доказательства непротиворечивости любой системы, достаточно обширной, чтобы включать в себя всю арифметику, доказательства, которое не использовало бы каких-либо иных правил вывода, кроме тех, что имеются в самой данной системе. Такое доказательство, которое использует более мощное правило вывода, может оказаться полезным. Но если эти правила вывода сильнее логических средств арифметического исчисления, то уверенности в непротиворечивости используемых в доказательстве допущений не будет. Во всяком случае, если используемые методы не будут финитистскими, то программа Гильберта окажется невыполнимой. Гёдель как раз и показывает несостоятельность расчетов на нахождение финитистского доказательства непротиворечивости арифметики. 2. Гёдель указал на принципиальную ограниченность возможностей аксиоматического метода: система Principia Mathematica, как и всякая иная система, с помощью которой строится арифметика, существенно неполна, т. е. для любой непротиворечивой системы арифметических аксиом имеются истинные арифметические предложения, которые не выводятся из аксиом этой системы. 3. Теорема Гёделя показывает, что никакое расширение арифметической системы не может сделать ее полной, и даже если мы наполним ее бесконечным множеством аксиом, то в новой системе всегда найдутся истинные, но не выводимые средствами этой системы положения. Аксиоматический подход к арифметике натуральных чисел не в состоянии охватить всю область истинных арифметических суждений, и то, что мы понимаем под процессом математического доказательства, не сводится к использованию аксиоматического метода. После теоремы Гёделя стало бессмысленно рассчитывать, что понятию убедительного математического доказательства можно будет придать раз и навсегда очерченные формы. [2,4,6]

Последним в этой череде попыток объяснить теорию множеств был интуиционизм.

Он прошел ряд этапов в своей эволюции — полуинтуиционизм, собственно интуиционизм, ультраинтуиционизм. На разных этапах математиков волновали разные проблемы, но одной из основных проблем математики является проблема бесконечности. Математические понятия бесконечности, непрерывности служили предметом философского анализа с момента их появления (идеи атомистов, апории Зенона Элейского, инфинитезимальные методы в античности, исчисление бесконечно малых в Новое время и пр.). Наибольшие споры вызывало применение различных видов бесконечности (потенциальной, актуальной) как математических объектов и их интерпретация. Все эти проблемы, на наш взгляд, были порождены более глубокой проблемой — о роли субъекта в научном познании. Дело в том, что состояние кризиса в математике порождено эпистемологической неопределенностью соизмерения мира объекта (бесконечности) и мира субъекта. Математик как субъект имеет возможность выбора средств познания — или потенциальной, или актуальной бесконечности. Применение потенциальной бесконечности как становящейся, дает ему возможность осуществлять, конструировать бесконечное множество построений, которые можно надстраивать над конечными, не имея конечного шага, не завершая построение, оно только возможно. Применение актуальной бесконечности дает ему возможность работать с бесконечностью как с уже осуществимой, завершенной в своем построении, как актуально данной одновременно.

На этапе полуинтуиционизма проблема бесконечности еще не была самостоятельной, а была вплетена в проблему построения математических объектов и способов его обоснования. Полуинтуиционизм А. Пуанкаре и представителей парижской школы теории функций Бэра, Лебега и Бореля был направлен против принятия аксиомы свободного выбора, с помощью которой доказывается теорема Цермело, утверждавшая, что всякое множество можно сделать вполне упорядоченным, но без указания теоретического способа определения элементов любого подмножества искомого множества. Нет способа построения математического объекта, нет и самого математического объекта. Математики считали, что наличие или отсутствие теоретического способа построения последовательности объектов исследования может служить основой обоснования или опровержения этой аксиомы. В российском варианте полуинтуиционистская концепция в философских основаниях математики получила развитие в таком направлении, как эффективизм, развиваемый Н.Н. Лузиным. Эффективизм представляет собой оппозицию к основным абстракциям учения множества Кантора о бесконечном — актуальности, выбора, трансфинитной индукции и др.

Для эффективизма гносеологически более ценными абстракциями является абстракция потенциальной осуществимости, чем абстракция актуальной бесконечности. Благодаря этому становится возможным введение понятия о трансфинитных ординалах (бесконечных порядковых числах) на основе эффективного понятия о росте функций. Гносеологическая установка эффективизма для отображения непрерывного (континуума) опиралась на дискретные средства (арифметики) и созданную Н.Н.Лузиным дескриптивную теорию множеств (функций). Интуиционизм голландца Л. Э. Я. Брауэра, Г. Вейля, А. Гейтинга в качестве традиционного объекта исследования видит свободно становящиеся последовательности различных видов. На этом этапе, решая собственно математические проблемы, в том числе о перестройке всей математики на новой основе, интуиционисты подняли философский вопрос о роли математика как познающего субъекта. Каково его положение, где он более свободен и активен в выборе средств познания? Интуиционисты первыми (и на этапе полуинтуиционизма) стали критиковать концепцию актуальной бесконечности, канторовскую теорию множеств, усмотрев в ней ущемление возможностей субъекта влиять на процесс научного поиска решения конструктивной задачи. В случае использования потенциальной бесконечности субъект себя не обманывает, так как для него идея потенциальной бесконечности интуитивно значительно яснее, чем идея актуальной бесконечности. Для интуициониста объект считается существующим, если он дан непосредственно математику или известен метод его построения, конструирования. Субъект в любом случае может приступить к процессу достраивания ряда элементов своего множества. Непостроенный объект для интуиционистов не существует. В то же время субъект, работающий с актуальной бесконечностью, будет лишен этой возможности и будет чувствовать двойную уязвимость принятой позиции:

1) никогда нельзя осуществить это бесконечное построение; 2) он принимает решение оперировать с актуальной бесконечностью как с конечным объектом и в этом случае теряет свою специфику понятия бесконечности. Интуиционизм сознательно ограничивает возможности математика тем, что тот может осуществлять построение математических объектов исключительно посредством таких средств, которые хотя и получаемы с помощью абстрактных понятий, но эффективны, убедительны, доказуемы, функционально конструктивны именно практически и сами интуитивно ясны как конструкции, построения, надежность которых на практике не вызывает никаких сомнений. Интуиционизм, опираясь на понятие потенциальной бесконечности и конструктивные методы исследования, имеет дело с математикой становления, теория множеств относится к математике бытия.

Для интуициониста Брауэра как представителя математического эмпиризма логика вторична, он критикует ее и закон исключённого третьего.

В своих отчасти мистических работах он не отрицает наличие бесконечности, однако не допускает её актуализации, лишь потенциализацию. Главное для него — интерпретация и обоснование практически используемых логических средств и математических рассуждений. Принятое интуиционистами ограничение преодолевает неопределенность использования понятия бесконечности в математике и выражает стремление преодолеть кризис в основании математики.

Ультраинтуиционизм (А.Н. Колмогоров, А.А.Марков и др.) — последняя стадия развития интуиционизма, на которой модернизируются, существенно дополняются и преобразуются основные его идеи, не изменяя его сущности, но преодолевая недостатки и усиливая позитивные стороны, руководствуясь критериями математической строгости. Слабостью подхода интуиционистов было узкое понимание роли интуиции как единственного источника обоснования правильности и эффективности математических методов. Принимая «интуитивную ясность» в качестве критерия истинности в математике, интуиционисты методологически обедняли возможности математика как субъекта познания, сводили его деятельность лишь к мыслительным операциям на основе интуиции и не включали практику в процесс математического познания. Ультраинтуиционистская программа обоснования математики является российским приоритетом. Поэтому отечественные математики, преодолевая ограниченность интуиционизма, принимали действенной методологию материалистической диалектики, признающей человеческую практику источником формирования как математических понятий, так и математических методов (умозаключений, построений). Проблему существования математических объектов ультраинтуиционисты решали, опираясь уже не на неопределяемое субъективное понятие интуиции, а на математическую практику и конкретный механизм построения математического объекта — алгоритм, выражаемый вычислимой, рекурсивной функцией.

Ультраинтуиционизм усиливает достоинства интуиционизма, заключающиеся в возможности упорядочивания и обобщения приемов решения конструктивных проблем, употребляемых математиками любого направления. Поэтому интуиционизм последней стадии (ультраинтуиционизм) близок конструктивизму в математике. В гносеологическом аспекте основные идеи и принципы ультраинтуиционизма таковы: критика классической аксиоматики логики; использование и значительное усиление (по явному указанию А.А. Маркова) роли абстракции отождествления (мысленного отвлечения от несходных свойств предметов и одновременного вычленения общих свойств предметов) как способа построения и конструктивного понимания абстрактных понятий, математических суждений; доказательство непротиворечивости непротиворечивых теорий. В формальном аспекте применение абстракции отождествления оправдывается тремя ее свойствами (аксиомами) равенства — рефлексивности, транзитивности и симметрии.

Для решения основного противоречия в математике по проблеме бесконечности, породившего кризис ее оснований, на этапе ультраинтуиционизма в работах А.Н. Колмогорова были предложены пути выхода из кризиса посредством решения проблемы отношений между классической и интуиционистской логикой, классической и интуиционистской математикой. Интуиционизм Брауэра в целом отрицал логику, но так как любой математик не может обойтись без логики, в интуиционизме все-таки сохранилась практика логических рассуждений, допускались некоторые принципы классической логики, имеющей в качестве своей базы аксиоматику. С.К. Клини, Р. Весли даже отмечают, что интуиционистскую математику можно описать в виде некоторого исчисления, а исчисление является способом организации математического знания на основах логики, формализации и ее формы — алгоритмизации. Новый вариант соотношения логики и математики в рамках интуиционистских требований к интуитивной ясности суждений, особенно тех, которые включали отрицание, А.Н. Колмогоров предложил следующим образом: интуиционистскую логику, тесно связанную с интуиционистской математикой, он представил в форме аксиоматического импликативного минимального исчисления высказываний и предикатов. Тем самым ученый представил новую модель математического знания, преодолевающую ограниченность интуиционизма в признании лишь интуиции как средства познания и ограниченность логицизма, абсолютизирующего возможности логики в математике. Эта позиция позволила в математической форме продемонстрировать синтез интуитивного и логического как основы гибкой рациональности и ее конструктивной эффективности.

Выводы. Таким образом, эпистемологический аспект математического познания позволяет оценить революционные изменения на этапе кризиса оснований математики на рубеже XIX-XX вв. с новых позиций в понимании процесса познания, природы и роли субъекта в нем. Гносеологический субъект традиционной теории познания, соответствующий периоду господства теоретико-множественного подхода в математике, — это абстрактный, неполный, «частичный» субъект, представленный в субъектно-объектных отношениях, оторванный абстракциями, логикой, формализмом от действительности, рационально, теоретически познающий свой объект и понимаемый как зеркало, точно отражающее и копирующее действительность. По сути, субъект исключался из познания как реального процесса и результата взаимодействия с объектом. Выход интуиционизма на арену борьбы философских направлений в математике привел к новому пониманию математика как субъекта познания — человека познающего, философская абстракция которого должна быть выстроена как бы заново. Математик предстал как эмпирический субъект, понимаемый уже как целостный реальный человек, включающий все те свойства, от которых отвлекались в гносеологическом субъекте, — эмпирическую конкретность, изменчивость, историчность; это действующий и познающий в реальном познании, творческий, интуитивный, изобретательный субъект. Философия интуиционистской математики стала базой, фундаментом современной эпистемологической парадигмы, построенной на концепции гибкой рациональности, в которой человек — это цельный (целостный) субъект познания, обладающий новыми познавательными качествами, методами, процедурами; он синтезирует свою как абстрактно-гносеологическую и логико-методологическую природу и форму, так и одновременно получает экзистенциально-антропологическое и «историко-метафизическое» осмысление.

Важным моментом так же является интуиция в познании и, в частности, в образовании математических понятий. Опять же идёт борьба с философией, попытки исключить закон исключённого третьего, как не имеющий смысла в математике и пришедший в неё из философии. Однако же наличие излишнего акцента на интуицию и отстутствие чётких математических обоснований не позволили перевести математику на твёрдый фундамент. [2,4,7]

Однако после появления в 1930-х годах строгого понятия алгоритма эстафету от интуиционизма принял математический конструктивизм, представители которого внесли немалый вклад в современную теорию вычислимости. Кроме того, в 1970-е и 1980-е годы обнаружились существенные связи между некоторыми идеями интуиционистов (даже теми, которые раньше казались абсурдными) и математической теорией топосов. Математика, имеющаяся в некоторых топосах, весьма напоминает ту, которую пытались создать интуиционисты.

В качестве итога можно сделать утверждение: большинство из вышеуказанных парадоксов попросту не существуют в теории множеств с самопринадлежностью [8]. Является ли подобный подход окончательным — спорный вопрос, дальнейшие работы в этой области покажут.

Заключение

Закончен ли третий кризис математики

sohabr.net

Парадоксы теории множеств и их философская интерпретация

Краткий синопсис

По образованию я физик-теоретик, однако имею неплохую математическую базу. В магистратуре одним из предметов была философия, необходимо было выбрать тему и сдать по ней работу. Поскольку большинство вариантов не единожды было обмусолено, то решил выбрать что-то более экзотическое. На новизну не претендую, просто получилось аккумулировать всю/почти всю доступную литературу по этой теме. Философы и математики могут кидаться в меня камнями, буду лишь благодарен за конструктивную критику.

P.S. Весьма «сухой язык», но вполне читабельно после университетской программы. По большей части определения парадоксов брались из Википедии (упрощённая формулировка и готовая TeX-разметка).

Введение

Как сама теория множеств, так и парадоксы, ей присущие, появились не так уж и давно, чуть более ста лет назад. Однако за этот период был пройден большой путь, теория множеств так или иначе фактически стала основой большинства разделов математики. Парадоксы же её, связанные с бесконечностью Кантора, были успешно объяснены буквально за половину столетия.

Следует начать с определения.

Что есть множество? Вопрос достаточно простой, ответ на него вполне интуитивен. Множество это некий набор элементов, представляемый единым объектом. Кантор в своей работе Beiträge zur Begründung der transfiniten Mengenlehre даёт определение: под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M)[1]. Как видим, суть не изменилась, разница лишь в той части, которая зависит от мировоззрения определяющего. История же теории множеств как в логике так и в математике весьма противоречива. Фактически начало ей положил Кантор в XIX веке, далее Рассел и остальные продолжили работу.

Парадоксы (логики и теории множеств) — (греч. — неожиданный) — формально-логические противоречия, которые возникают в содержательной множеств теории и формальной логике при сохранении логической правильности рассуждения. Парадоксы возникают тогда, когда два взаимоисключающих (противоречащих) суждения оказываются в равной мере доказуемыми. Парадоксы могут появиться как в пределах научной теории, так и в обычных рассуждениях (например, приводимая Расселом перифраза его парадокса о множестве всех нормальных множеств: «Деревенский парикмахер бреет всех тех и только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?»). Поскольку формально-логическое противоречие разрушает рассуждение как средство обнаружения и доказательства истины (в теории, в которой появляется парадокс, доказуемо любое, как истинное, так и ложное, предложение), возникает задача выявления источников подобных противоречий и нахождения способов их устранения. Проблема философского осмысления конкретных решений парадоксов — одна из важных методологических проблем формальной логики и логических оснований математики.

Целью данной работы является изучение парадоксов теории множеств как наследников античных антиномий и вполне логичных следствий перехода к новому уровню абстракции — бесконечности. Задача — рассмотреть основные парадоксы, их философскую интерпретацию.

Основные парадоксы теории множеств

Продолжим кратким экскурсом в историю.

Некторые из логических парадоксов были известны с античных времён, однако по причине того, что математическая теория ограничивалась одной лишь арифметикой и геометрией, соотнести их с теорией множеств было невозможно. В XIX веке ситуация изменилась коренным образом: Кантор в своих работах вышел на новый уровень абстракции. Он ввёл понятие бесконечности, создав тем самым новый раздел математики и позволив тем самым сравнивать различные бесконечности с помощью понятия «мощность множества» [2]. Однако тем самым он породил множество парадоксов. Самым первым является так называемый парадокс Бурали-Форти. В математической литературе встречаются различные формулировки, опирающиеся на разную терминологию и предполагаемый набор известных теорем. Вот одно из формальных определений.

Можно доказать, что если x — произвольное множество порядковых чисел, то множество-сумма есть порядковое число, большее или равное каждому из элементов x. Предположим теперь, что — множество всех порядковых чисел. Тогда — порядковое число, большее или равное любому из чисел в . Но тогда и 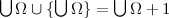— порядковое число, причём уже строго большее, а значит, и не равное любому из чисел в . Но это противоречит условию, по которому — множество всех порядковых чисел.

Сущность же парадокса в том, что при образовании множества всех порядковых чисел образуется новый порядковый тип, которого ещё не было среди «всех» трансфинитных порядковых чисел, существовавших до образования множества всех порядковых чисел. Этот парадокс был обнаружен самим Кантором, независимо открыт и опубликован итальянским математиком Бурали-Форти, ошибки же последнего были исправлены Расселом, после чего формулировка приобрела окончательный вид [2,3].

Среди всех попыток избежать подобных парадоксов и в какой-то мере попробовать их объяснить наибольшего внимания заслуживает идея уже упомянутого Рассела. Он предложил исключить из математики и логики импредикативные предложения, в которых определение элемента множества зависит от последнего, что и вызывает парадоксы. Правило звучит так: «никакое множество С не может содержать элементов m, определяемых лишь в терминах множества С, а так же элементов n, предполагающих в своём определении это множество» [4]. Подобное ограничение определения множества позволяет избежать парадоксов, но при этом значительно сужает область его применения в математике. Вдобавок этого недостаточно для объяснения их природы и причин появления, коренящихся в дихотомии мышления и языка, в особенностях формальной логики [4]. В какой-то мере в данном ограничении можно проследить аналогию с тем, что в более поздний период когнитивные психологи и лингвисты начали называть «категоризацией основного уровня»: определение сведено к наиболее легкой для понимания и изучения концепцией.

Далее Кантор в 1899 году открыл парадокс, названный его именем.

Предположим, что множество всех множеств существует. В этом случае справедливо 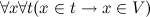, то есть всякое множество t является подмножеством V. Но из этого следует 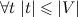— мощность любого множества не превосходит мощности V. Но в силу аксиомы множества всех подмножеств, для V, как и любого множества, существует множество всех подмножеств , и по теореме Кантора 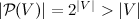, что противоречит предыдущему утверждению. Следовательно, V не может существовать, что вступает в противоречие с «наивной» гипотезой о том, что любое синтаксически корректное логическое условие определяет множество, то есть что 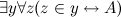для любой формулы A, не содержащей y свободно. Замечательное доказательство отсутствия подобных противоречий на основе аксиоматизированной теории множеств Цермело-Френкеля приводится у Поттера [3].

Оба вышеуказанных парадокса с логической точки зрения идентичны «Лжецу» либо «Брадобрею»: высказываемое суждение обращено не только на нечто объективное по отношению к нему, но и само на себя. Однако следует обращать внимание не только на логическую сторону, но и на понятие бесконечности, которое тут наличествует. В литературе ссылаются на работу Пуанкаре, в которой он пишет: «вера в существование актуальной бесконечности… делает необходимым эти непредикативные определения'' [2]. В целом же имеют место основные моменты [2]:

• в данных парадоксах нарушается правило чётко разделять „сферы“ предиката и субъекта; степень смешения близка к подмене одного понятия другим;
• обычно в логике предполагается, что в процессе рассуждения субъект и предикат сохраняют свой объём и содержание, в данном же случае происходитпереход из одной категории в другую, что даёт в результате несоответствие;
• наличие слова „все“ имеет смысл для конечного числа элементов, в случае же бесконечного их количества возможно наличие такого, которое для определения себя потребует определение множества;
• нарушаются основные логические законы:
  • закон тождества нарушается тогда, когда обнаруживается нетождественность себе субъекта и предиката;
  • закон противоречия — когда с одинаковым правом выводятся два противоречащих друг другу суждения;
  • закон исключённого третьего — когда это третье приходится признавать, а не исключать, поскольку ни первое, ни второе не могут быть признаны одно без другого, т.к. они оказываются одинаково правомерными.

Третий парадокс носит имя Рассела. Один из вариантов определения приведён далее.Пусть K — множество всех множеств, которые не содержат себя в качестве своего элемента.Содержит ли K само себя в качестве элемента? Если да, то, по определению K, оно не должно быть элементом K — противоречие.Если нет — то, по определению K, оно должно быть элементом K — вновь противоречие. Данное утверждение логически выводится из парадокса Кантора, что показывает их взаимосвязь. Однако философская сущность проявляется более чётко, поскольку „самодвижение'' понятий происходит прямо “на наших глазах» [2].

Парадокс Тристрама Шенди:В романе Стерна «Жизнь и мнения Тристрама Шенди, джентльмена» герой обнаруживает, что ему потребовался целый год, чтобы изложить события первого дня его жизни, и еще один год понадобился, чтобы описать второй день. В связи с этим герой сетует, что материал его биографии будет накапливаться быстрее, чем он сможет его обработать, и он никогда не сможет ее завершить. «Теперь я утверждаю, — возражает на это Рассел, — что если бы он жил вечно и его работа не стала бы ему в тягость, даже если бы его жизнь продолжала быть столь же богатой событиями, как вначале, то ни одна из частей его биографии не осталась бы ненаписанной».Действительно, события n-го дня Шенди мог бы описать за n-й год и, таким образом, в его автобиографии каждый день оказался бы запечатленным.

Иначе говоря, если бы жизнь длилась бесконечно, то она насчитывала бы столько же лет, сколько дней.

Рассел проводит аналогию между этим романом и Зеноном с его черепахой. По его мнению решение лежит в том, что целое эквивалентно его части в бесконечности. Т.е. к противоречию приводит только «аксиома здравого смысла» [2]. Однако же разрешение проблемы лежит в области чистой математики. Очевидно, что имеется два множества — года и дни, между элементами которых установлено взаимно-однозначное соответствие — биекция. Тогда при условии бесконечной жизни главного героя имеется два бесконечных равномощных множества, что, если рассматривать мощность как обобщение понятия количества элементов в множестве, разрешает парадокс.

Парадокс (теорема) Банаха-Тарского или парадокс удвоения шара — теорема в теории множеств, утверждающая, что трёхмерный шар равносоставлен двум своим копиям.Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число частей, передвинуть их, и составить из них второе. 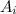Более точно, два множества A и B являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств так, что для каждого i подмножество конгруэнтно .

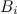Если же пользоваться теоремой выбора, то определение звучит так[3]:Аксиома выбора подразумевает, что существует разбиение поверхности единичной сферы на конечное количество частей, которые преобразованиями трёхмерного Евклидова пространства, не меняющими форму этих составляющих, могут быть собраны в две сферы единичного радиуса.

Очевидно, что при требовании для данных частей быть измеримыми, данное постоение неосуществимо. Известный физик Ричард Фейнман в своей биографии рассказывал, как в своё время у него получилось победить в споре о разбиении апельсина на конечное количество частей и пересоставлении его [5].

В определённых моментах этот парадокс используется для опровержения аксиомы выбора, однако проблема в том, что то, что мы считаем элементарной геометрией, — несущественно. Те понятия, которые мы считаем интуитивными, должны быть расширены до уровня свойств трансцендентных функций [3].

Чтобы и дальше ослабить уверенность тех, кто считает аксиому выбора неверной, следует упомянуть теорему Мазуркевича и Серпинского, которая утверждает, что существует непустое подмножество Е Евклидовой плоскости, которое имеет два непересекающихся подмножества, каждое из которых может быть разбито на конечное количество частей, так что их можно перевести изометриями в покрытие множества Е.При этом доказательство не требует использования аксиомы выбора[3].Дальнейшие же построения на основе аксиомы определённости дают разрешение парадокса Банаха-Тарского, но не представляют такого интереса [3].

• Парадокс Ришара: требуется назвать «наименьшее число, не названное в этой книге». Противоречие в том, что с одной стороны, это можно сделать, так как есть наименьшее число, названное в этой книге. Исходя из него, можно назвать и наименьшее неназванное. Но тут возникает проблема: континуум является несчётным, между двумя любыми числами можно вставить ещё бесконечное множество промежуточных чисел. С другой стороны, если бы мы могли назвать это число, оно автоматически бы перешло из класса неупомянутых в книге, в класс упомянутых [2].
• Парадокс Греллинга-Нильсона: слова либо знаки могут обозначать какое-либо свойство и при этом иметь его или нет. Самая тривиальная формулировка звучит так: является ли слово «гетерологичный» (что означает «неприменимый к самому себе»), гетерологичным?.. Весьма схож с парадоксом Рассела в связи с наличием диалектического противоречия: нарушается двойственность формы и содержания. В случае со словами, имеющими высокий уровень абстракции, невозможно решить, являются ли эти слова гетерологичными [2].
• Парадокс Сколема: используя теорему Гёделя о полноте и теорему Лёвенхейма-Сколема[3] получаем, что аксиоматическая теория множеств остаётся истинной и тогда, когда будет предполагаться (иметься) для её интерпретации только счётная совокупность множеств. В то же время аксиоматическая теория включает в себя уже упомянутую теорему Кантора, что приводит нас к несчётным бесконечным множествам. [2]

Разрешение парадоксов

Создание теории множеств породило то, что считают третьим кризисом математики, который до сих пор не был разрешён удовлитворительно для всех [4].Исторически сложилось, что первым подходом был теоретико-множественный. Он основывался на использовании актуальной бесконечности, когда считалось, что любая бесконечная последовательность является завершённой в бесконечности. Идея заключалась в том, что в теории множеств часто приходилось оперировать множествами, которые могли являться части других, более обширных множеств. Успешные действия в таком случае были возможны лишь в одном случае: данные множества (конечные и бесконечные) завершены. Определённый успех был очевиден: аксиоматическая теория множеств Цермело-Френкеля, целая школа математики Николя Бурбаки, которая существует уже больше половины столетия и до сих пор вызывает множество критики.

Логицизм был попыткой свести всю известную математику к терминам арифметики, а потом термины арифметики свести к понятиям математической логики. Вплотную этим занялся Фреге, однако после окончания работы над трудом, он вынужден был указать о своей несостоятельности, после того, как Рассел указал на имеющиеся в теории противоречия. Тот же Рассел, как уже был упомянуто ранее, попытался исключить использование импредикативных определений с помощью «теории типов». Однако его понятия множества и бесконечности, а так же аксиома сводимости оказались нелогичными. Основной проблемой было то, что не учитывались качественные различия между формальной и математической логикой, а так же наличие лишних понятий, в том числе и интуитивного характера.В итоге теория логицизма не смогла устранить диалектических противоречий парадоксов, связанных с бесконечностью. Имели место лишь принципы и методы, которые позволяли избавиться хотя бы от непредикативных определений. В свох же рассуждениях Рассел был наследником Кантора [2]

В конце XIX — начале XX в. распространение формалистической точки зрения на математику было связано с развитием аксиоматического метода и той программой обоснования математики, которую выдвинул Д. Гильберт. На степень важности этого факта указывает то, что первой проблемой из двадцати трёх, которые он поставил перед математическим сообществом, была проблема бесконечности. Формализация была необходима для доказательства непротиворечивости классической математики, «исключив при этом из неё всю метафизику». Учитывая средства и методы, которыми пользовался Гильберт, его цель оказалась принципиально невыполнимой, но его программа имела огромное влияние на все последующее развитие оснований математики. Гильберт достаточно долго работал над этой проблемой, построив первоначально аксиоматику геометрии. Поскольку решение проблемы оказалось достаточно успешным, он решил применить аксиоматический метод к теории натуральных чисел. Вот что он писал в связи с этим: «Я преследую важную цель: именно я хотел бы разделаться с вопросами обоснования математики как таковыми, превратив каждое математическое высказывание в строго выводимую формулу.» От бесконечности при этом планировалось избавиться с помощью сведения её к некому конечному числу операций. Для этого он обращался к физике с её атомизмом, дабы показать всю несостоятельность бесконечных величин. Фактически Гильберт поставил вопрос о соотношении теории и объективной реальности.

Более или менее полное представление о финитных методах дает ученик Гильберта Ж. Эрбран. Под финитными рассуждениями он понимает такие рассуждения, которые удовлетворяют следующим условиям: логические парадоксы " — всегда рассматривается лишь конечное и определенное число предметов и функций;

— функции имеют точное определение, и это определение позволяет нам вычислить их значение;

— никогда не утверждается «Этот объект существует», если не известен способ его построения;

— никогда не рассматривается множество всех предметов X какой-либо бесконечной совокупности;

— если известно, что какое-либо рассуждение или теорема верны для всех этих X, то это означает, что это общее рассуждение можно повторить для каждого конкретного X, причем само это общее рассуждение следует рассматривать только как образец для проведения таких конкретных рассуждений."

Однако в момент последней публикации в этой области Гёдель уже получил свои результаты, в сущности опять обнаружил и утвердил наличие диалектики в процессе познания. По сути своей дальнейшее развитие математики продемонстрировало несостоятельность программы Гильберта.

Что же, собственно, доказал Гёдель? Можно выделить три основных результата:

1. Гёдель показал невозможность математического доказательства непротиворечивости любой системы, достаточно обширной, чтобы включать в себя всю арифметику, доказательства, которое не использовало бы каких-либо иных правил вывода, кроме тех, что имеются в самой данной системе. Такое доказательство, которое использует более мощное правило вывода, может оказаться полезным. Но если эти правила вывода сильнее логических средств арифметического исчисления, то уверенности в непротиворечивости используемых в доказательстве допущений не будет. Во всяком случае, если используемые методы не будут финитистскими, то программа Гильберта окажется невыполнимой. Гёдель как раз и показывает несостоятельность расчетов на нахождение финитистского доказательства непротиворечивости арифметики.2. Гёдель указал на принципиальную ограниченность возможностей аксиоматического метода: система Principia Mathematica, как и всякая иная система, с помощью которой строится арифметика, существенно неполна, т. е. для любой непротиворечивой системы арифметических аксиом имеются истинные арифметические предложения, которые не выводятся из аксиом этой системы.3. Теорема Гёделя показывает, что никакое расширение арифметической системы не может сделать ее полной, и даже если мы наполним ее бесконечным множеством аксиом, то в новой системе всегда найдутся истинные, но не выводимые средствами этой системы положения. Аксиоматический подход к арифметике натуральных чисел не в состоянии охватить всю область истинных арифметических суждений, и то, что мы понимаем под процессом математического доказательства, не сводится к использованию аксиоматического метода. После теоремы Гёделя стало бессмысленно рассчитывать, что понятию убедительного математического доказательства можно будет придать раз и навсегда очерченные формы. [2,4,6]

Последним в этой череде попыток объяснить теорию множеств был интуиционизм.

Он прошел ряд этапов в своей эволюции — полуинтуиционизм, собственно интуиционизм, ультраинтуиционизм. На разных этапах математиков волновали разные проблемы, но одной из основных проблем математики является проблема бесконечности. Математические понятия бесконечности, непрерывности служили предметом философского анализа с момента их появления (идеи атомистов, апории Зенона Элейского, инфинитезимальные методы в античности, исчисление бесконечно малых в Новое время и пр.). Наибольшие споры вызывало применение различных видов бесконечности (потенциальной, актуальной) как математических объектов и их интерпретация. Все эти проблемы, на наш взгляд, были порождены более глубокой проблемой — о роли субъекта в научном познании. Дело в том, что состояние кризиса в математике порождено эпистемологической неопределенностью соизмерения мира объекта (бесконечности) и мира субъекта. Математик как субъект имеет возможность выбора средств познания — или потенциальной, или актуальной бесконечности. Применение потенциальной бесконечности как становящейся, дает ему возможность осуществлять, конструировать бесконечное множество построений, которые можно надстраивать над конечными, не имея конечного шага, не завершая построение, оно только возможно. Применение актуальной бесконечности дает ему возможность работать с бесконечностью как с уже осуществимой, завершенной в своем построении, как актуально данной одновременно.

На этапе полуинтуиционизма проблема бесконечности еще не была самостоятельной, а была вплетена в проблему построения математических объектов и способов его обоснования. Полуинтуиционизм А. Пуанкаре и представителей парижской школы теории функций Бэра, Лебега и Бореля был направлен против принятия аксиомы свободного выбора, с помощью которой доказывается теорема Цермело, утверждавшая, что всякое множество можно сделать вполне упорядоченным, но без указания теоретического способа определения элементов любого подмножества искомого множества. Нет способа построения математического объекта, нет и самого математического объекта. Математики считали, что наличие или отсутствие теоретического способа построения последовательности объектов исследования может служить основой обоснования или опровержения этой аксиомы. В российском варианте полуинтуиционистская концепция в философских основаниях математики получила развитие в таком направлении, как эффективизм, развиваемый Н.Н. Лузиным. Эффективизм представляет собой оппозицию к основным абстракциям учения множества Кантора о бесконечном — актуальности, выбора, трансфинитной индукции и др.

Для эффективизма гносеологически более ценными абстракциями является абстракция потенциальной осуществимости, чем абстракция актуальной бесконечности. Благодаря этому становится возможным введение понятия о трансфинитных ординалах (бесконечных порядковых числах) на основе эффективного понятия о росте функций. Гносеологическая установка эффективизма для отображения непрерывного (континуума) опиралась на дискретные средства (арифметики) и созданную Н.Н.Лузиным дескриптивную теорию множеств (функций). Интуиционизм голландца Л. Э. Я. Брауэра, Г. Вейля, А. Гейтинга в качестве традиционного объекта исследования видит свободно становящиеся последовательности различных видов. На этом этапе, решая собственно математические проблемы, в том числе о перестройке всей математики на новой основе, интуиционисты подняли философский вопрос о роли математика как познающего субъекта. Каково его положение, где он более свободен и активен в выборе средств познания? Интуиционисты первыми (и на этапе полуинтуиционизма) стали критиковать концепцию актуальной бесконечности, канторовскую теорию множеств, усмотрев в ней ущемление возможностей субъекта влиять на процесс научного поиска решения конструктивной задачи. В случае использования потенциальной бесконечности субъект себя не обманывает, так как для него идея потенциальной бесконечности интуитивно значительно яснее, чем идея актуальной бесконечности. Для интуициониста объект считается существующим, если он дан непосредственно математику или известен метод его построения, конструирования. Субъект в любом случае может приступить к процессу достраивания ряда элементов своего множества. Непостроенный объект для интуиционистов не существует. В то же время субъект, работающий с актуальной бесконечностью, будет лишен этой возможности и будет чувствовать двойную уязвимость принятой позиции:

1) никогда нельзя осуществить это бесконечное построение; 2) он принимает решение оперировать с актуальной бесконечностью как с конечным объектом и в этом случае теряет свою специфику понятия бесконечности. Интуиционизм сознательно ограничивает возможности математика тем, что тот может осуществлять построение математических объектов исключительно посредством таких средств, которые хотя и получаемы с помощью абстрактных понятий, но эффективны, убедительны, доказуемы, функционально конструктивны именно практически и сами интуитивно ясны как конструкции, построения, надежность которых на практике не вызывает никаких сомнений. Интуиционизм, опираясь на понятие потенциальной бесконечности и конструктивные методы исследования, имеет дело с математикой становления, теория множеств относится к математике бытия.

Для интуициониста Брауэра как представителя математического эмпиризма логика вторична, он критикует ее и закон исключённого третьего.

В своих отчасти мистических работах он не отрицает наличие бесконечности, однако не допускает её актуализации, лишь потенциализацию. Главное для него — интерпретация и обоснование практически используемых логических средств и математических рассуждений. Принятое интуиционистами ограничение преодолевает неопределенность использования понятия бесконечности в математике и выражает стремление преодолеть кризис в основании математики.

Ультраинтуиционизм (А.Н. Колмогоров, А.А.Марков и др.) — последняя стадия развития интуиционизма, на которой модернизируются, существенно дополняются и преобразуются основные его идеи, не изменяя его сущности, но преодолевая недостатки и усиливая позитивные стороны, руководствуясь критериями математической строгости. Слабостью подхода интуиционистов было узкое понимание роли интуиции как единственного источника обоснования правильности и эффективности математических методов. Принимая «интуитивную ясность» в качестве критерия истинности в математике, интуиционисты методологически обедняли возможности математика как субъекта познания, сводили его деятельность лишь к мыслительным операциям на основе интуиции и не включали практику в процесс математического познания. Ультраинтуиционистская программа обоснования математики является российским приоритетом. Поэтому отечественные математики, преодолевая ограниченность интуиционизма, принимали действенной методологию материалистической диалектики, признающей человеческую практику источником формирования как математических понятий, так и математических методов (умозаключений, построений). Проблему существования математических объектов ультраинтуиционисты решали, опираясь уже не на неопределяемое субъективное понятие интуиции, а на математическую практику и конкретный механизм построения математического объекта — алгоритм, выражаемый вычислимой, рекурсивной функцией.

Ультраинтуиционизм усиливает достоинства интуиционизма, заключающиеся в возможности упорядочивания и обобщения приемов решения конструктивных проблем, употребляемых математиками любого направления. Поэтому интуиционизм последней стадии (ультраинтуиционизм) близок конструктивизму в математике. В гносеологическом аспекте основные идеи и принципы ультраинтуиционизма таковы: критика классической аксиоматики логики; использование и значительное усиление (по явному указанию А.А. Маркова) роли абстракции отождествления (мысленного отвлечения от несходных свойств предметов и одновременного вычленения общих свойств предметов) как способа построения и конструктивного понимания абстрактных понятий, математических суждений; доказательство непротиворечивости непротиворечивых теорий. В формальном аспекте применение абстракции отождествления оправдывается тремя ее свойствами (аксиомами) равенства — рефлексивности, транзитивности и симметрии.

Для решения основного противоречия в математике по проблеме бесконечности, породившего кризис ее оснований, на этапе ультраинтуиционизма в работах А.Н. Колмогорова были предложены пути выхода из кризиса посредством решения проблемы отношений между классической и интуиционистской логикой, классической и интуиционистской математикой. Интуиционизм Брауэра в целом отрицал логику, но так как любой математик не может обойтись без логики, в интуиционизме все-таки сохранилась практика логических рассуждений, допускались некоторые принципы классической логики, имеющей в качестве своей базы аксиоматику. С.К. Клини, Р. Весли даже отмечают, что интуиционистскую математику можно описать в виде некоторого исчисления, а исчисление является способом организации математического знания на основах логики, формализации и ее формы — алгоритмизации. Новый вариант соотношения логики и математики в рамках интуиционистских требований к интуитивной ясности суждений, особенно тех, которые включали отрицание, А.Н. Колмогоров предложил следующим образом: интуиционистскую логику, тесно связанную с интуиционистской математикой, он представил в форме аксиоматического импликативного минимального исчисления высказываний и предикатов. Тем самым ученый представил новую модель математического знания, преодолевающую ограниченность интуиционизма в признании лишь интуиции как средства познания и ограниченность логицизма, абсолютизирующего возможности логики в математике. Эта позиция позволила в математической форме продемонстрировать синтез интуитивного и логического как основы гибкой рациональности и ее конструктивной эффективности.

Выводы. Таким образом, эпистемологический аспект математического познания позволяет оценить революционные изменения на этапе кризиса оснований математики на рубеже XIX-XX вв. с новых позиций в понимании процесса познания, природы и роли субъекта в нем. Гносеологический субъект традиционной теории познания, соответствующий периоду господства теоретико-множественного подхода в математике, — это абстрактный, неполный, «частичный» субъект, представленный в субъектно-объектных отношениях, оторванный абстракциями, логикой, формализмом от действительности, рационально, теоретически познающий свой объект и понимаемый как зеркало, точно отражающее и копирующее действительность. По сути, субъект исключался из познания как реального процесса и результата взаимодействия с объектом. Выход интуиционизма на арену борьбы философских направлений в математике привел к новому пониманию математика как субъекта познания — человека познающего, философская абстракция которого должна быть выстроена как бы заново. Математик предстал как эмпирический субъект, понимаемый уже как целостный реальный человек, включающий все те свойства, от которых отвлекались в гносеологическом субъекте, — эмпирическую конкретность, изменчивость, историчность; это действующий и познающий в реальном познании, творческий, интуитивный, изобретательный субъект. Философия интуиционистской математики стала базой, фундаментом современной эпистемологической парадигмы, построенной на концепции гибкой рациональности, в которой человек — это цельный (целостный) субъект познания, обладающий новыми познавательными качествами, методами, процедурами; он синтезирует свою как абстрактно-гносеологическую и логико-методологическую природу и форму, так и одновременно получает экзистенциально-антропологическое и «историко-метафизическое» осмысление.

Важным моментом так же является интуиция в познании и, в частности, в образовании математических понятий. Опять же идёт борьба с философией, попытки исключить закон исключённого третьего, как не имеющий смысла в математике и пришедший в неё из философии. Однако же наличие излишнего акцента на интуицию и отстутствие чётких математических обоснований не позволили перевести математику на твёрдый фундамент. [2,4,7]

Однако после появления в 1930-х годах строгого понятия алгоритма эстафету от интуиционизма принял математический конструктивизм, представители которого внесли немалый вклад в современную теорию вычислимости. Кроме того, в 1970-е и 1980-е годы обнаружились существенные связи между некоторыми идеями интуиционистов (даже теми, которые раньше казались абсурдными) и математической теорией топосов. Математика, имеющаяся в некоторых топосах, весьма напоминает ту, которую пытались создать интуиционисты.

В качестве итога можно сделать утверждение: большинство из вышеуказанных парадоксов попросту не существуют в теории множеств с самопринадлежностью [8]. Является ли подобный подход окончательным — спорный вопрос, дальнейшие работы в этой области покажут.

Заключение

Диалектико-материалистический анализ показывает, что парадоксы являются следствием дихотомии языка и мышления, выражением глубоких диалектических (теорема Гёделя позволила проявить диалектику в процессе познания) и гносеологических трудностей, связанных с понятиями предмета и предметной области в формальной логике, множества (класса) в логике и теории множеств, с употреблением принципа абстракции, позволяющего вводить в рассмотрение новые (абстрактные) объекты (бесконечность), со способами определения абстрактных объектов в науке и т. п. Поэтому не может быть дано универсального способа устранения всех парадоксов.

Закончен ли третий кризис математики (потому как он находился в причинно-следственной связи с парадоксами; теперь же парадоксы — неотъемлемая часть) — тут мнения расходятся, хотя формально известные парадоксы к 1907-му году были устранены. Впрочем, сейчас в математике имеются и другие обстоятельства, которые можно считать либо кризисными, либо предвещающими кризис (например), отсутствие строгого обснования у континуального интеграла).

Что же касается парадоксов, то весьма важную роль в математике сыграл известный парадокс лжеца, а так же целая серия парадоксов в так называемой наивной (предшествовавшей аксиоматической) теории множеств, вызвавших кризис оснований (один из таких парадоксов сыграл роковую роль в жизни Г. Фреге). Но, возможно, одним из самых недооценённых явлений в современной математике, которое вполне можно назвать и парадоксальным, и кризисным, является решение Полом Коэном в 1963 году первой проблемы Гильберта. Точнее, не сам факт решения, а характер этого решения [9].

Литература

1. Georg Cantor. Beiträge zur begründung der transfiniten mengenlehre. Mathematische Annalen, 46:481--512, 1895.
2. И.Н. Бурова. Парадоксы теории множеств и диалектика. Наука, 1976.
3. M.D. Potter. Set theory and its philosophy: a critical introduction. Oxford University Press, Incorporated, 2004.
4. Жуков Н.И. Философские основания математики. Мн.: Университетское, 1990.
5. Фейнман Р.Ф., С. Ильин. Вы, конечно, шутите, мистер Фейнман!: похождения удивительного человека, поведанные им Р. Лейтону. КоЛибри, 2008.
6. О. М. Мижевич. Два способа преодоления парадоксов в теории множеств Г. Кантора. Логико-философские штудии, (3):279--299, 2005.
7. С. И. Масалова. ФИЛОСОФИЯ ИНТУИЦИОНИСТСКОЙ МАТЕМАТИКИ. Вестник ДГТУ, (4), 2006.
8. Чечулин В.Л. Теория множеств с самопринадлежностью (основания и некоторые приложения). Перм. гос. ун-т. – Пермь, 2012.
9. С. Н. Тронин. Краткий конспект лекций по дисциплине ''Философия математики''. Казань, 2012.
10. Гришин В.Н., Бочвар Д.А. Исследования по теории множеств и неклассическим логикам. Наука, 1976.
11. Хофштадтер Д. Гедель, Эшер, Бах: эта бесконечная гирлянда. Бахрах-М, 2001.
12. Кабаков Ф.А., Мендельсон Э. Введение в математическую логику. Издательство «Наука», 1976.
13. Д.А. Бочвар. К вопросу о парадоксах математической логики и теории множеств. Математический сборник, 57(3):369--384, 1944.

Автор: Psychopompe

Источник

www.pvsm.ru

Парадоксы теории множеств. Инженерная эвристика

Парадоксы теории множеств

«Никто не может изгнать нас из рая, созданного нам Кантором!» — заявил Давид Гильберт по поводу теории множеств Георга Кантора. Таково было чувство восторга от новой «игрушки» у математиков того времени. В 1873 году Кантор ввел понятие множества. Первоначально новая теория помогла решить ряд проблем. Однако очень скоро в ней обнаружились противоречия.

Первое противоречие возникло благодаря введению и анализу самого большого множества из всех: множества всех множеств. Простейший вопрос «Существует ли множество всех множеств?» тут же приводит к парадоксу. Для этого надо напомнить, что в теории множеств разрешима процедура включения одного множества в состав другого или «взятие множества от множества». (Это вам ничего не напоминает? Правильно — вездесущую рекурсию!)

Можно включать какие угодно множества в состав одного — их объединяющего, до тех пор пока все множества не исчерпаются. Тогда мы получим сверхмножество, которое включает в себя все остальные множества. Все! Но не все! Само сверхмножество (множество всех множеств) оказалось не включённым! Ведь его вначале не было, а теперь оно появилось. Ну что же, включим теперь и его. Но тогда появляется новое сверхмножество, которого только что ещё не было. Тогда и его включим, и так до бесконечности! То есть множество всех множеств и существует, и не существует одновременно!

Причиной парадокса является возможность быть множеству элементом самого себя. Можно конечно ограничить эту возможность, но тогда исчезнут многие очень полезные возможности теории множеств. Лучше локализовать проблему, и для этого разделить все множества на два типа, те, которые содержат себя в качестве своего элемента, и те, которые не содержат..

В 1901 году Бертран Рассел в письме коллеге изложил мысль, которая в популярной форме известна как «Парадокс брадобрея»: «В одной военной части был брадобрей. Ему было разрешено под угрозой смертной казни брить только тех военнослужащих, которые не бреются сами. Но вот беда — сам брадобрей тоже был на службе. Мог ли он в таком случае побриться сам?»

Если он себя побреет, то окажется тем, кого ему брить категорически запрещено, а если не побреет, то окажется среди тех, кого брить ему можно!

Словом, в теории множеств выявилось много противоречий[92], а на их устранение потратили огромное количество усилий. Собственно, как и в случае с математическим анализом, который первоначально был противоречив и только трудами титанов — Коши, Вейерштрасс, Гейне — приведён в образцовое состояние. В условно образцовое. Ибо все противоречия математического анализа были упрятаны в его определения, совмещающие в себе невозможное. Достаточно вспомнить бесконечно малые и бесконечно большие величины, которые «куда-то стремятся, но никогда своего предела не достигают». При этом само стремление к пределу происходит вне времени, что невозможно само по себе — в природе такое не наблюдается.

ВОПРОС № 98

Сколько яблок на рисунке?[93]

Следующая глава >

tech.wikireading.ru

Смотрите также

• 
  Реферат закон сохранения импульса
• 
  История развития математики реферат
• 
  Реферат декоративно прикладное искусство
• 
  Реферат по обж землетрясения
• 
  Образование в великобритании реферат
• 
  О петре 1 реферат
• 
  Темы рефератов по физике
• 
  Беспроводные зарядные устройства реферат
• 
  Росписи пещеры альтамира реферат
• 
  Славянофилы западники евразийцы реферат
• 
  Сванте аррениус қазақша реферат